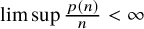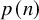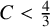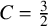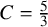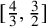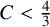1 Introduction
The main objects of study in symbolic dynamics are subshifts, which are dynamical systems defined by a finite alphabet
![]() $\mathcal {A}$
, a closed shift-invariant set of sequences
$\mathcal {A}$
, a closed shift-invariant set of sequences
![]() $X \subset \mathcal {A}^{\mathbb {Z}}$
and the left-shift map
$X \subset \mathcal {A}^{\mathbb {Z}}$
and the left-shift map
![]() $\sigma $
. We sometimes speak of subshifts as measure-theoretic dynamical systems by associating a measure
$\sigma $
. We sometimes speak of subshifts as measure-theoretic dynamical systems by associating a measure
![]() $\mu $
; in this case,
$\mu $
; in this case,
![]() $\mu $
is always assumed to be a Borel probability measure invariant under
$\mu $
is always assumed to be a Borel probability measure invariant under
![]() $\sigma $
. One of the most basic ways to measure the ‘size’ of a subshift X is the word complexity function
$\sigma $
. One of the most basic ways to measure the ‘size’ of a subshift X is the word complexity function
![]() $p(n)$
, which measures the number of finite words of length n which appear within points of X. In addition to being intimately connected with the fundamental notion of topological entropy (the entropy
$p(n)$
, which measures the number of finite words of length n which appear within points of X. In addition to being intimately connected with the fundamental notion of topological entropy (the entropy
![]() $h(X)$
is just the exponential growth rate of
$h(X)$
is just the exponential growth rate of
![]() $p(n)$
when
$p(n)$
when
![]() $p(n)$
grows exponentially), many recent works prove that slow growth of
$p(n)$
grows exponentially), many recent works prove that slow growth of
![]() $p(n)$
forces various strong structural properties of X.
$p(n)$
forces various strong structural properties of X.
The well-known Morse–Hedlund theorem [Reference Morse and HedlundMH38] implies that if X is infinite, then
![]() $p(n) \geq n+1$
for all n. There are subshifts which achieve this minimal value (i.e.,
$p(n) \geq n+1$
for all n. There are subshifts which achieve this minimal value (i.e.,
![]() $p(n) = n+1$
for all n), which are called Sturmian subshifts. We do not give a full treatment here, but briefly say that Sturmian subshifts are defined by symbolic codings of orbits for irrational circle rotations and in fact are measure-theoretically isomorphic to these rotations (associated with Lebesgue measure).
$p(n) = n+1$
for all n), which are called Sturmian subshifts. We do not give a full treatment here, but briefly say that Sturmian subshifts are defined by symbolic codings of orbits for irrational circle rotations and in fact are measure-theoretically isomorphic to these rotations (associated with Lebesgue measure).
Slightly above the minimum possible complexity is the property of linear complexity, meaning that
![]() $\limsup p(n)/n = C < \infty $
. This implies a great deal about X; a full list is beyond this work, but we list a few such results here. In the following, X is transitive when there exists
$\limsup p(n)/n = C < \infty $
. This implies a great deal about X; a full list is beyond this work, but we list a few such results here. In the following, X is transitive when there exists
![]() $x \in X$
whose orbit
$x \in X$
whose orbit
![]() $\{\sigma ^n x\}$
is dense in X and minimal when every
$\{\sigma ^n x\}$
is dense in X and minimal when every
![]() $x \in X$
has dense orbit.
$x \in X$
has dense orbit.
-
1. If X is transitive, then the number of ergodic measures on X is bounded from above by
 $\lfloor C \rfloor $
. If
$\lfloor C \rfloor $
. If
 $C < 3$
, then in fact there is only one
$C < 3$
, then in fact there is only one
 $\sigma $
-invariant measure on X, in which case X is said to be uniquely ergodic. ([Reference BoshernitzanBos92], [Reference Dykstra, Ormes and PavlovDOP22])
$\sigma $
-invariant measure on X, in which case X is said to be uniquely ergodic. ([Reference BoshernitzanBos92], [Reference Dykstra, Ormes and PavlovDOP22]) -
2. For all X, the number of nonatomic generic measures on X is bounded from above by
 $\lfloor C \rfloor $
([Reference Cyr and KraCK19])
$\lfloor C \rfloor $
([Reference Cyr and KraCK19]) -
3. If X is minimal, then the automorphism group of X is virtually
 $\mathbb {Z}$
(in particular, there are at most
$\mathbb {Z}$
(in particular, there are at most
 $\lfloor C \rfloor $
cosets once one mods out by the shift action) ([Reference Cyr and KraCK15], [Reference Donoso, Durand, Maass and PetiteDDMP16])
$\lfloor C \rfloor $
cosets once one mods out by the shift action) ([Reference Cyr and KraCK15], [Reference Donoso, Durand, Maass and PetiteDDMP16]) -
4. If X is minimal, then X has finite topological rank ([Reference Donoso, Durand, Maass and PetiteDDMP21])
-
5. X cannot have any nontrivial strongly mixing measure ([Reference FerencziFer96])
-
6. If X is transitive and
 $C < 1.5$
, then X is minimal ([Reference Ormes and PavlovOP19])
$C < 1.5$
, then X is minimal ([Reference Ormes and PavlovOP19])
(In fact, the weaker condition
![]() $\liminf p(n)/n < \infty $
is sufficient for some of the structure above, but as our results don’t involve this quantity, we don’t comment on it further here.) The final item above is one of surprisingly few results proved about subshifts with C close to
$\liminf p(n)/n < \infty $
is sufficient for some of the structure above, but as our results don’t involve this quantity, we don’t comment on it further here.) The final item above is one of surprisingly few results proved about subshifts with C close to
![]() $1$
, and understanding more about the structure of such shifts was a main motivation of this work. In a sense, we show that for C sufficiently close to
$1$
, and understanding more about the structure of such shifts was a main motivation of this work. In a sense, we show that for C sufficiently close to
![]() $1$
, a subshift must have structure more and more similar to the Sturmian subshifts, which achieve minimal possible complexity. Recall that Sturmian subshifts are measure-theoretically isomorphic to a (compact abelian) group rotation; this property is called discrete spectrum. In fact, this property is equivalent to
$1$
, a subshift must have structure more and more similar to the Sturmian subshifts, which achieve minimal possible complexity. Recall that Sturmian subshifts are measure-theoretically isomorphic to a (compact abelian) group rotation; this property is called discrete spectrum. In fact, this property is equivalent to
![]() $L^2(X)$
being spanned by the measurable eigenfunctions of
$L^2(X)$
being spanned by the measurable eigenfunctions of
![]() $\sigma $
(i.e., f for which
$\sigma $
(i.e., f for which
![]() $f(\sigma x) = \lambda f(x)$
for some
$f(\sigma x) = \lambda f(x)$
for some
![]() $\lambda $
). When X has no eigenfunctions at all, it is said to be weak mixing, which is in a sense an opposite property to discrete spectrum.
$\lambda $
). When X has no eigenfunctions at all, it is said to be weak mixing, which is in a sense an opposite property to discrete spectrum.
Ferenczi ([Reference FerencziFer96]) proved that the property of strong mixing (which means that
![]() $\mu (A \cap \sigma ^{-n} B) \rightarrow \mu (A) \mu (B)$
for all measurable
$\mu (A \cap \sigma ^{-n} B) \rightarrow \mu (A) \mu (B)$
for all measurable
![]() $A,B$
) cannot hold for any nontrivial measure on a linear complexity subshift. He also gave an example of X with a strongly mixing measure and
$A,B$
) cannot hold for any nontrivial measure on a linear complexity subshift. He also gave an example of X with a strongly mixing measure and
![]() $p(n)$
quadratic and asked whether this complexity was the lowest possible. This was proved not to be the case in [Reference CreutzCre22] and [Reference Creutz, Pavlov and RodockCPR23], which provided examples first on the order of
$p(n)$
quadratic and asked whether this complexity was the lowest possible. This was proved not to be the case in [Reference CreutzCre22] and [Reference Creutz, Pavlov and RodockCPR23], which provided examples first on the order of
![]() $n \log n$
and then below any possible superlinear growth rate, establishing linear complexity as the ‘threshold’ for existence of such a measure. In a different work, Ferenczi ([Reference FerencziFer95]) examined the same question for weakly mixing measures, where it is known that linear complexity can occur via the well-known Chacon subshift. He there gave an example of X with a nontrivial weakly mixing measure and
$n \log n$
and then below any possible superlinear growth rate, establishing linear complexity as the ‘threshold’ for existence of such a measure. In a different work, Ferenczi ([Reference FerencziFer95]) examined the same question for weakly mixing measures, where it is known that linear complexity can occur via the well-known Chacon subshift. He there gave an example of X with a nontrivial weakly mixing measure and
![]() $C = 5/3$
and again asked whether this was minimal. This was shown not to be the case in [Reference CreutzCre23], where examples were given of C arbitrarily close to (but above)
$C = 5/3$
and again asked whether this was minimal. This was shown not to be the case in [Reference CreutzCre23], where examples were given of C arbitrarily close to (but above)
![]() $3/2$
.
$3/2$
.
Our main results are the following.
Theorem 4.1 . If X is an infinite transitive subshift with
![]() $\limsup \frac {p(q)}{q} < \frac {4}{3}$
, then X is uniquely ergodic with unique measure which has discrete spectrum.
$\limsup \frac {p(q)}{q} < \frac {4}{3}$
, then X is uniquely ergodic with unique measure which has discrete spectrum.
Theorem 5.1 . There exists an infinite transitive subshift X which is uniquely ergodic, has unique measure which is weak mixing and for which
![]() $\limsup \frac {p(q)}{q} = \frac {3}{2}$
.
$\limsup \frac {p(q)}{q} = \frac {3}{2}$
.
In [Reference CreutzCre23], it was also suggested that perhaps a subshift X having a nontrivial weakly mixing measure forces
![]() $\limsup \frac {p(q)}{q}> \frac {3}{2}$
; Theorem 5.1 answers this negatively. In fact, the examples from Theorem 5.1 satisfy
$\limsup \frac {p(q)}{q}> \frac {3}{2}$
; Theorem 5.1 answers this negatively. In fact, the examples from Theorem 5.1 satisfy
![]() $\lim p(q) - 1.5q = -\infty $
, in contrast to Theorem C from [Reference CreutzCre23], which showed that for rank-one subshifts, even total ergodicity implies
$\lim p(q) - 1.5q = -\infty $
, in contrast to Theorem C from [Reference CreutzCre23], which showed that for rank-one subshifts, even total ergodicity implies
![]() $\limsup p(q) - 1.5q = \infty $
. The examples also satisfy
$\limsup p(q) - 1.5q = \infty $
. The examples also satisfy
![]() $\liminf \frac {p(q)}{q} = 1$
and for any
$\liminf \frac {p(q)}{q} = 1$
and for any
![]() $f(q) \to \infty $
, there exist examples such that
$f(q) \to \infty $
, there exist examples such that
![]() $p(q) < q + f(q)$
infinitely often.
$p(q) < q + f(q)$
infinitely often.
The proof of Theorem 4.1 depends on proving a substitutive structure for subshifts with
![]() $C < \frac {4}{3}$
. In fact, for any
$C < \frac {4}{3}$
. In fact, for any
![]() $C < 2$
, Corollary 5.28 from [Reference Pavlov and SchmeidingPS23] already implies that X can be generated by a sequence of substitutions
$C < 2$
, Corollary 5.28 from [Reference Pavlov and SchmeidingPS23] already implies that X can be generated by a sequence of substitutions
![]() $\tau _k$
on the alphabet
$\tau _k$
on the alphabet
![]() $\{0,1\}$
; this is known as having alphabet rank two. Similar results from [Reference Donoso, Durand, Maass and PetiteDDMP21] prove that even
$\{0,1\}$
; this is known as having alphabet rank two. Similar results from [Reference Donoso, Durand, Maass and PetiteDDMP21] prove that even
![]() $\liminf p(n)/n < \infty $
implies finite alphabet rank. However, in general it is not so easy to prove dynamical properties of a subshift purely from such a structure; the key of our arguments is that when C is closer to
$\liminf p(n)/n < \infty $
implies finite alphabet rank. However, in general it is not so easy to prove dynamical properties of a subshift purely from such a structure; the key of our arguments is that when C is closer to
![]() $1$
, these substitutions come from a very restricted class. We would like to note that subshifts with
$1$
, these substitutions come from a very restricted class. We would like to note that subshifts with
![]() $p(n) \leq 4n/3 + 1$
were also studied in [Reference AberkaneAbe01], where the author proved a substitutive structure and gave some interesting examples.
$p(n) \leq 4n/3 + 1$
were also studied in [Reference AberkaneAbe01], where the author proved a substitutive structure and gave some interesting examples.
Specifically, our Proposition 3.1 shows that any such subshift is induced by a sequence of substitutions of the form
![]() $\tau _{m_k,n_k}: 0 \mapsto 0^{m_k-1} 1, 1 \mapsto 0^{n_k-1} 1$
, where
$\tau _{m_k,n_k}: 0 \mapsto 0^{m_k-1} 1, 1 \mapsto 0^{n_k-1} 1$
, where
![]() $n \leq 2m$
for
$n \leq 2m$
for
![]() $m> 1$
and
$m> 1$
and
![]() $n \leq 3$
for
$n \leq 3$
for
![]() $m = 1$
. This is related to the well-known Pisot conjecture for subshifts, which states that a subshift generated by iterating a single substitution
$m = 1$
. This is related to the well-known Pisot conjecture for subshifts, which states that a subshift generated by iterating a single substitution
![]() $\tau $
should have discrete spectrum if the associated matrix (in which the
$\tau $
should have discrete spectrum if the associated matrix (in which the
![]() $(a,b)$
entry is the number of occurrences of b in
$(a,b)$
entry is the number of occurrences of b in
![]() $\tau (a)$
) has largest eigenvalue which is a Pisot number (i.e., a complex number with modulus greater than
$\tau (a)$
) has largest eigenvalue which is a Pisot number (i.e., a complex number with modulus greater than
![]() $1$
all of whose conjugates have modulus less than
$1$
all of whose conjugates have modulus less than
![]() $1$
).
$1$
).
The Pisot conjecture has been proved in some settings, including when
![]() $|\mathcal {A}| = 2$
([Reference Barge and DiamondBD02], [Reference Hollander and SolomyakHS03]) and whenever the so-called balanced pair algorithm terminates ([Reference Sirvent and SolomyakSS02]). Our proof of Theorem 4.1 is in fact based on this algorithm.
$|\mathcal {A}| = 2$
([Reference Barge and DiamondBD02], [Reference Hollander and SolomyakHS03]) and whenever the so-called balanced pair algorithm terminates ([Reference Sirvent and SolomyakSS02]). Our proof of Theorem 4.1 is in fact based on this algorithm.
In our case, the substitutive structure comes from a sequence of substitutions and not a single one; this is sometimes called the S-adic Pisot conjecture, based on the often-used term ‘S-adic’ (among other references, see [Reference Durand, Leroy and RichommeDLR13]) to refer to sequences obtained by a sequence of substitutions on a fixed alphabet. This is much more difficult. The strongest result is due to [Reference Berthé, Steiner and ThuswaldnerBST19], which is too long to state formally here but which proves discrete spectrum in a fairly general S-adic setting. They do require, however, that the sequence of substitutions
![]() $(\tau _n)$
be recurrent, meaning that for every k, there exists L so that
$(\tau _n)$
be recurrent, meaning that for every k, there exists L so that
![]() $\tau _i = \tau _{i+L}$
for
$\tau _i = \tau _{i+L}$
for
![]() $1 \leq i \leq k$
.
$1 \leq i \leq k$
.
We cannot enforce any such condition on our substitutions, as it’s quite possible to have low complexity for
![]() $\tau _{m_k, n_k}$
all distinct (for instance, consider Sturmian subshifts, which can be generated by an infinite sequence of distinct substitutions if the digits of its continued fraction expansion are distinct). Nevertheless, due to the extremely simple form of
$\tau _{m_k, n_k}$
all distinct (for instance, consider Sturmian subshifts, which can be generated by an infinite sequence of distinct substitutions if the digits of its continued fraction expansion are distinct). Nevertheless, due to the extremely simple form of
![]() $\tau _{m_k, n_k}$
(in which both
$\tau _{m_k, n_k}$
(in which both
![]() $0$
and
$0$
and
![]() $1$
are mapped to words of the form
$1$
are mapped to words of the form
![]() $0^i 1$
), we are able to prove discrete spectrum.
$0^i 1$
), we are able to prove discrete spectrum.
We note that indeed our substitutive structure is in some sense Pisot; the associated matrix for
![]() $\tau _{m,n}$
is
$\tau _{m,n}$
is
![]() $\left (\begin {smallmatrix}m-1 & 1\\ n-1 & 1 \end {smallmatrix}\right )$
, whose eigenvalues are
$\left (\begin {smallmatrix}m-1 & 1\\ n-1 & 1 \end {smallmatrix}\right )$
, whose eigenvalues are
![]() $\frac {\sqrt {m^2 + 4(n-m)}\pm m}{2}$
. This matrix is Pisot when
$\frac {\sqrt {m^2 + 4(n-m)}\pm m}{2}$
. This matrix is Pisot when
![]() $m < n \leq 2m$
. Our Proposition 3.1 implies
$m < n \leq 2m$
. Our Proposition 3.1 implies
![]() $m < n \leq 2m$
, with the possible exception
$m < n \leq 2m$
, with the possible exception
![]() $m = 1, n = 3$
. Though this substitution is not Pisot, Proposition 3.1 implies that when it occurs, the previous substitution has
$m = 1, n = 3$
. Though this substitution is not Pisot, Proposition 3.1 implies that when it occurs, the previous substitution has
![]() $n = m+1$
, and the composition of those substitutions has matrix
$n = m+1$
, and the composition of those substitutions has matrix
![]() $\left (\begin {smallmatrix}0 & 1\\ 2 & 1 \end {smallmatrix}\right ) \left (\begin {smallmatrix}m-1 & 1\\ m & 1 \end {smallmatrix}\right ) = \left (\begin {smallmatrix}m & 1\\ 3m-2 & 3 \end {smallmatrix}\right )$
, which is always Pisot.
$\left (\begin {smallmatrix}0 & 1\\ 2 & 1 \end {smallmatrix}\right ) \left (\begin {smallmatrix}m-1 & 1\\ m & 1 \end {smallmatrix}\right ) = \left (\begin {smallmatrix}m & 1\\ 3m-2 & 3 \end {smallmatrix}\right )$
, which is always Pisot.
One of course should not expect that simply assuming each
![]() $\tau _i$
to be Pisot should guarantee discrete spectrum; informally, if the second eigenvalues have moduli each less than
$\tau _i$
to be Pisot should guarantee discrete spectrum; informally, if the second eigenvalues have moduli each less than
![]() $1$
but which converge to
$1$
but which converge to
![]() $1$
quickly, then the ‘average behavior’ will be that of a non-Pisot number. This is essentially the construction of our example from Theorem 5.1, which not only does not have discrete spectrum but is weak mixing (i.e., has no eigenvalue at all).
$1$
quickly, then the ‘average behavior’ will be that of a non-Pisot number. This is essentially the construction of our example from Theorem 5.1, which not only does not have discrete spectrum but is weak mixing (i.e., has no eigenvalue at all).
2 Definitions and preliminaries
Let
![]() $\mathcal {A}$
be a finite subset of
$\mathcal {A}$
be a finite subset of
![]() $\mathbb {Z}$
; the full shift is the set
$\mathbb {Z}$
; the full shift is the set
![]() $\mathcal {A}^{\mathbb {Z}}$
associated with the product topology. We use
$\mathcal {A}^{\mathbb {Z}}$
associated with the product topology. We use
![]() $\sigma $
to denote the left shift homeomorphism on
$\sigma $
to denote the left shift homeomorphism on
![]() $\mathcal {A}^{\mathbb {Z}}$
. A subshift is a closed
$\mathcal {A}^{\mathbb {Z}}$
. A subshift is a closed
![]() $\sigma $
-invariant subset
$\sigma $
-invariant subset
![]() $X \subset \mathcal {A}^{\mathbb {Z}}$
. The orbit of
$X \subset \mathcal {A}^{\mathbb {Z}}$
. The orbit of
![]() $x \in X$
is the set
$x \in X$
is the set
![]() $\{\sigma ^n x\}_{n \in \mathbb {Z}}$
. A subshift X is transitive when it is the closure of the orbit of a single sequence x and minimal when it is the closure of the orbit of every
$\{\sigma ^n x\}_{n \in \mathbb {Z}}$
. A subshift X is transitive when it is the closure of the orbit of a single sequence x and minimal when it is the closure of the orbit of every
![]() $x \in X$
. For a minimal subshift X, in a slight abuse of notation, we sometimes refer to X as the orbit closure of a one-sided sequence
$x \in X$
. For a minimal subshift X, in a slight abuse of notation, we sometimes refer to X as the orbit closure of a one-sided sequence
![]() $y \in \mathcal {A}^{\mathbb {N}}$
; this simply means that X is the orbit closure of a two-sided sequence
$y \in \mathcal {A}^{\mathbb {N}}$
; this simply means that X is the orbit closure of a two-sided sequence
![]() $x \in X$
containing y.
$x \in X$
containing y.
A word is any element of
![]() $\mathcal {A}^n$
for some
$\mathcal {A}^n$
for some
![]() $n \in \mathbb {N}$
, referred to as its length and denoted by
$n \in \mathbb {N}$
, referred to as its length and denoted by
![]() $| w |$
. We denote
$| w |$
. We denote
![]() $\mathcal {A}^* = \bigcup _{n \geq 1} \mathcal {A}^n$
. We represent the concatenation of words
$\mathcal {A}^* = \bigcup _{n \geq 1} \mathcal {A}^n$
. We represent the concatenation of words
![]() $w_1, w_2, \ldots , w_n$
by
$w_1, w_2, \ldots , w_n$
by
![]() $w_1 w_2 \ldots w_n$
.
$w_1 w_2 \ldots w_n$
.
The language of a subshift X on
![]() $\mathcal {A}$
, denoted
$\mathcal {A}$
, denoted
![]() $L(X)$
, is the set of all finite words appearing as subwords of points in X. For any
$L(X)$
, is the set of all finite words appearing as subwords of points in X. For any
![]() $n \in \mathbb {N}$
, we denote
$n \in \mathbb {N}$
, we denote
![]() $L_n(X) = L(X) \cap \mathcal {A}^n$
, the set of n-letter words in
$L_n(X) = L(X) \cap \mathcal {A}^n$
, the set of n-letter words in
![]() $L(X)$
. For a subshift X, the word complexity function of X is defined by
$L(X)$
. For a subshift X, the word complexity function of X is defined by
![]() $p(n) := |L_{n}(X)|$
. For a subshift X and word
$p(n) := |L_{n}(X)|$
. For a subshift X and word
![]() $w \in L(X)$
we denote by
$w \in L(X)$
we denote by
![]() $[w]$
the clopen subset in X consisting of all
$[w]$
the clopen subset in X consisting of all
![]() $x \in X$
such that
$x \in X$
such that
![]() $x_{0}\ldots x_{|w|-1} = w$
.
$x_{0}\ldots x_{|w|-1} = w$
.
One way to generate subshifts is via substitutions. A substitution (sometimes called a morphism) is a map
![]() $\tau : \mathcal {A} \rightarrow \mathcal {B}^*$
for finite alphabets
$\tau : \mathcal {A} \rightarrow \mathcal {B}^*$
for finite alphabets
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
. An example is the well-known Thue–Morse substitution
$\mathcal {B}$
. An example is the well-known Thue–Morse substitution
![]() $\{ 0, 1 \} \to \{ 0, 1 \}^{*}$
given by
$\{ 0, 1 \} \to \{ 0, 1 \}^{*}$
given by
![]() $0 \mapsto 01$
and
$0 \mapsto 01$
and
![]() $1 \mapsto 10$
.
$1 \mapsto 10$
.
Substitutions can be composed when viewed as homomorphisms on the monoid of words under composition, that is, if
![]() $\tau : \mathcal {A} \rightarrow \mathcal {B}^*$
and
$\tau : \mathcal {A} \rightarrow \mathcal {B}^*$
and
![]() $\rho : \mathcal {B} \rightarrow \mathcal {C}^*$
, then
$\rho : \mathcal {B} \rightarrow \mathcal {C}^*$
, then
![]() $\rho \circ \tau : \mathcal {A} \rightarrow \mathcal {C}^*$
can be defined by
$\rho \circ \tau : \mathcal {A} \rightarrow \mathcal {C}^*$
can be defined by
![]() $(\rho \circ \tau )(a) = \rho (b_1) \rho (b_2) \ldots \rho (b_k)$
, where
$(\rho \circ \tau )(a) = \rho (b_1) \rho (b_2) \ldots \rho (b_k)$
, where
![]() $\tau (a) = b_1 \ldots b_k$
.
$\tau (a) = b_1 \ldots b_k$
.
When a sequence of substitutions
![]() $\tau _k: \mathcal {A} \rightarrow \mathcal {A}^*$
shares the same alphabet, and when there exists
$\tau _k: \mathcal {A} \rightarrow \mathcal {A}^*$
shares the same alphabet, and when there exists
![]() $a \in \mathcal {A}$
for which
$a \in \mathcal {A}$
for which
![]() $\tau _k(a)$
begins with a for all k, clearly
$\tau _k(a)$
begins with a for all k, clearly
![]() $(\tau _1 \circ \cdots \circ \tau _k)(a)$
is a prefix of
$(\tau _1 \circ \cdots \circ \tau _k)(a)$
is a prefix of
![]() $(\tau _1 \circ \cdots \circ \tau _{k+1})(a)$
for all k. In this situation, one may then speak of the (right-infinite) limit of
$(\tau _1 \circ \cdots \circ \tau _{k+1})(a)$
for all k. In this situation, one may then speak of the (right-infinite) limit of
![]() $(\tau _1 \circ \cdots \circ \tau _k)(a)$
. For example, if all
$(\tau _1 \circ \cdots \circ \tau _k)(a)$
. For example, if all
![]() $\tau _k$
are equal to the Thue–Morse substitution and
$\tau _k$
are equal to the Thue–Morse substitution and
![]() $a = 0$
, the limiting sequence is
$a = 0$
, the limiting sequence is
![]() $.0110100110010110 \ldots $
, and the orbit closure of this sequence is called the Thue–Morse substitution subshift.
$.0110100110010110 \ldots $
, and the orbit closure of this sequence is called the Thue–Morse substitution subshift.
For any subshift X, there is a convenient way to represent the n-language and possible transitions between words in points of X by a directed graph called the Rauzy graph.
Definition 2.1. For a subshift X and
![]() $n \in \mathbb {N}$
, the nth Rauzy graph of X is the directed graph
$n \in \mathbb {N}$
, the nth Rauzy graph of X is the directed graph
![]() $G_{X, n}$
with vertex set
$G_{X, n}$
with vertex set
![]() $L_{n}(X)$
, and directed edges from
$L_{n}(X)$
, and directed edges from
![]() $w_1 \ldots w_{n}$
to
$w_1 \ldots w_{n}$
to
![]() $w_2 \ldots w_{n+1}$
for all
$w_2 \ldots w_{n+1}$
for all
![]() $w_1 \ldots w_{n+1} \in L_{n+1}(X)$
.
$w_1 \ldots w_{n+1} \in L_{n+1}(X)$
.
Example 2.2. If X is the golden mean subshift consisting of bi-infinite sequences on
![]() $\{0,1\}$
without consecutive
$\{0,1\}$
without consecutive
![]() $1$
s and
$1$
s and
![]() $n = 3$
, then
$n = 3$
, then
![]() $G_{X, 3}$
is the following directed graph:
$G_{X, 3}$
is the following directed graph:

There is a natural association from bi-infinite paths on the Rauzy graph to sequences in
![]() $\mathcal {A}^{\mathbb {Z}}$
; a sequence of vertices
$\mathcal {A}^{\mathbb {Z}}$
; a sequence of vertices
![]() $(v_k)$
corresponds to the sequence
$(v_k)$
corresponds to the sequence
![]() $x \in A^{\mathbb {Z}}$
defined by
$x \in A^{\mathbb {Z}}$
defined by
![]() $x(k) \ldots x(k+n-1) = v_k$
for all k. The main usage of the Rauzy graph is that every point of X corresponds to a bi-infinite path in the Rauzy graph. However, the opposite is not necessarily true; if X has restrictions/forbidden words of length greater than
$x(k) \ldots x(k+n-1) = v_k$
for all k. The main usage of the Rauzy graph is that every point of X corresponds to a bi-infinite path in the Rauzy graph. However, the opposite is not necessarily true; if X has restrictions/forbidden words of length greater than
![]() $n+1$
, then there may be paths in the Rauzy graph whose associated sequences are not in X. However, when X has low word complexity function, the set of paths in the Rauzy graph is sufficiently restrictive to give us useful information about (but not necessarily a complete description of) X.
$n+1$
, then there may be paths in the Rauzy graph whose associated sequences are not in X. However, when X has low word complexity function, the set of paths in the Rauzy graph is sufficiently restrictive to give us useful information about (but not necessarily a complete description of) X.
We note that when X is transitive,
![]() $G_{X,n}$
is strongly connected for all n, that is, there is a path between any two vertices. Rauzy graphs are particularly useful for working with so-called left/right special words in
$G_{X,n}$
is strongly connected for all n, that is, there is a path between any two vertices. Rauzy graphs are particularly useful for working with so-called left/right special words in
![]() $L(X)$
.
$L(X)$
.
Definition 2.3. A word
![]() $w \in L(X)$
is left-special (resp. right-special) if there exist
$w \in L(X)$
is left-special (resp. right-special) if there exist
![]() $a \neq b \in \mathcal {A}$
so that
$a \neq b \in \mathcal {A}$
so that
![]() $aw, bw \in L(X)$
(resp.
$aw, bw \in L(X)$
(resp.
![]() $wa, wb \in L(X)$
). A word is bispecial if it is both left- and right-special.
$wa, wb \in L(X)$
). A word is bispecial if it is both left- and right-special.
For a given n, the left- and right-special words in
![]() $L_n(X)$
correspond to vertices of
$L_n(X)$
correspond to vertices of
![]() $G_{X,n}$
with multiple incoming/outgoing edges respectively. When
$G_{X,n}$
with multiple incoming/outgoing edges respectively. When
![]() $G_{X,n}$
has relatively few such vertices, large portions of bi-infinite paths are ‘forced’ in the sense that when such a path visits a vertex which is not right-special, there is only one choice for the following edge. Note that if X contains no right-special words of some length n, then any edge of
$G_{X,n}$
has relatively few such vertices, large portions of bi-infinite paths are ‘forced’ in the sense that when such a path visits a vertex which is not right-special, there is only one choice for the following edge. Note that if X contains no right-special words of some length n, then any edge of
![]() $G_{X,n}$
forces all subsequent edges, meaning that
$G_{X,n}$
forces all subsequent edges, meaning that
![]() $G_{X,n}$
has only finitely many bi-infinite paths and X is finite. Therefore, every infinite subshift X has right-special words of every length, and a similar argument shows that it has left-special words of every length as well.
$G_{X,n}$
has only finitely many bi-infinite paths and X is finite. Therefore, every infinite subshift X has right-special words of every length, and a similar argument shows that it has left-special words of every length as well.
A particularly simple case that we deal with repeatedly is when
![]() $p(n+1) - p(n) = 1$
; this means that
$p(n+1) - p(n) = 1$
; this means that
![]() $G_{X, n}$
has exactly one more edge than the number of vertices, which means that it has a single vertex r with two outgoing edges and a single vertex
$G_{X, n}$
has exactly one more edge than the number of vertices, which means that it has a single vertex r with two outgoing edges and a single vertex
![]() $\ell $
with two incoming edges (
$\ell $
with two incoming edges (
![]() $\ell $
and r may be the same vertex), which correspond to the unique right- and left-special words in
$\ell $
and r may be the same vertex), which correspond to the unique right- and left-special words in
![]() $L_n(X)$
. It’s not hard to show that when X is transitive and
$L_n(X)$
. It’s not hard to show that when X is transitive and
![]() $p(n+1) - p(n) = 1$
, the structure of the Rauzy graph
$p(n+1) - p(n) = 1$
, the structure of the Rauzy graph
![]() $G_{X, n}$
must be a (possibly empty) path from
$G_{X, n}$
must be a (possibly empty) path from
![]() $\ell $
to r and two edge-disjoint paths from r to
$\ell $
to r and two edge-disjoint paths from r to
![]() $\ell $
.
$\ell $
.
We will frequently make use of the following standard lemma, essentially contained in [Reference Morse and HedlundMH38], for estimating word complexity.
Lemma 2.4. Let X be a subshift on alphabet
![]() $\mathcal {A}$
, for all n let
$\mathcal {A}$
, for all n let
![]() $RS_n(X)$
denote the set of right-special words of length n in the language of X and for all right-special w, let
$RS_n(X)$
denote the set of right-special words of length n in the language of X and for all right-special w, let
![]() $F(w)$
denote the set of letters which can follow w, that is,
$F(w)$
denote the set of letters which can follow w, that is,
![]() $\{a \ : \ wa \in L(X)\}$
. Then, for all
$\{a \ : \ wa \in L(X)\}$
. Then, for all
![]() $q> r$
,
$q> r$
,
 $$\begin{align*}p(q) = p(r) + \sum_{i = r}^{q-1} \sum_{w \in RS_i(X)} (|F(w)| - 1). \end{align*}$$
$$\begin{align*}p(q) = p(r) + \sum_{i = r}^{q-1} \sum_{w \in RS_i(X)} (|F(w)| - 1). \end{align*}$$
Proof. Consider the map
![]() $f: L_{r+1}(X) \rightarrow L_r(X)$
obtained by removing the final letter, that is,
$f: L_{r+1}(X) \rightarrow L_r(X)$
obtained by removing the final letter, that is,
![]() $f(wa) = w$
. It’s clear that f is surjective and that
$f(wa) = w$
. It’s clear that f is surjective and that
![]() $|f^{-1}(w)| = 1$
for w which is not right-special and
$|f^{-1}(w)| = 1$
for w which is not right-special and
![]() $|f^{-1}(w)| = |F(w)|$
for
$|f^{-1}(w)| = |F(w)|$
for
![]() $w \in RS_r(X)$
. The result for
$w \in RS_r(X)$
. The result for
![]() $q = r+1$
follows immediately, and the general case follows by induction.
$q = r+1$
follows immediately, and the general case follows by induction.
The following corollary is immediate.
Corollary 2.5. If X is an infinite subshift and
![]() $T \subset \mathbb {N}$
denotes the set of lengths n for which
$T \subset \mathbb {N}$
denotes the set of lengths n for which
![]() $|RS_n(X)|> 1$
, then for all
$|RS_n(X)|> 1$
, then for all
![]() $q> r$
,
$q> r$
,
If
![]() $|RS_i(X)| \leq 2$
for all
$|RS_i(X)| \leq 2$
for all
![]() $m \leq i < n$
and
$m \leq i < n$
and
![]() $|F(w)| = 2$
for all right-special w with lengths in
$|F(w)| = 2$
for all right-special w with lengths in
![]() $[r,q)$
, then the inequality above is an equality.
$[r,q)$
, then the inequality above is an equality.
3 Structure of subshifts with 
As mentioned above, our results rely on a substitutive/S-adic structure for subshifts with sufficiently low complexity. The substitutions in question all have the same form. Namely, for all positive integers
![]() $m<n$
, define the substitution
$m<n$
, define the substitution
 $$\begin{align*}\tau_{m,n}: \begin{cases} 0 \mapsto 0^{m-1} 1\\ 1\mapsto 0^{n-1} 1. \end{cases} \end{align*}$$
$$\begin{align*}\tau_{m,n}: \begin{cases} 0 \mapsto 0^{m-1} 1\\ 1\mapsto 0^{n-1} 1. \end{cases} \end{align*}$$
When
![]() $m_1, \ldots , m_k$
and
$m_1, \ldots , m_k$
and
![]() $n_1, \ldots , n_k$
are understood, we use the shorthand notation
$n_1, \ldots , n_k$
are understood, we use the shorthand notation
Proposition 3.1. If X is an infinite transitive subshift with
![]() $\limsup \frac {p(q)}{q} < \frac {4}{3}$
, then there exists a substitution
$\limsup \frac {p(q)}{q} < \frac {4}{3}$
, then there exists a substitution
![]() $\pi : \{0,1\} \rightarrow \mathcal {A}^*$
, where
$\pi : \{0,1\} \rightarrow \mathcal {A}^*$
, where
![]() $\pi (0), \pi (1)$
begin with different letters and
$\pi (0), \pi (1)$
begin with different letters and
![]() $|\pi (0)| < |\pi (1)| < 2|\pi (0)|$
and sequences
$|\pi (0)| < |\pi (1)| < 2|\pi (0)|$
and sequences
![]() $(m_k), (n_k)$
satisfying
$(m_k), (n_k)$
satisfying
![]() $0 < m_k < n_k$
so that X is the orbit closure of
$0 < m_k < n_k$
so that X is the orbit closure of
In addition,
-
•
 $n_{k} \leq 2m_{k}$
whenever
$n_{k} \leq 2m_{k}$
whenever
 $m_{k}> 1$
;
$m_{k}> 1$
; -
•
 $n_{k} < 1.9m_{k}$
whenever
$n_{k} < 1.9m_{k}$
whenever
 $m_{k}> 4$
;
$m_{k}> 4$
; -
•
 $n_{k} \leq 3$
whenever
$n_{k} \leq 3$
whenever
 $m_{k} = 1$
;
$m_{k} = 1$
; -
• if
 $m_{k+1} = 1, n_{k+1} = 3$
then
$m_{k+1} = 1, n_{k+1} = 3$
then
 $n_{k} = m_{k} + 1$
; and
$n_{k} = m_{k} + 1$
; and -
• every right-special word of length at least
 $| s(\pi (0))^{m_{1}-1} |$
, where s is the maximal common suffix of
$| s(\pi (0))^{m_{1}-1} |$
, where s is the maximal common suffix of
 $(\pi (0))^{\infty }$
and
$(\pi (0))^{\infty }$
and
 $(\pi (0))^{\infty }\pi (1)$
, is a suffix of a concatenation of
$(\pi (0))^{\infty }\pi (1)$
, is a suffix of a concatenation of
 $\pi (0)$
and
$\pi (0)$
and
 $\pi (1)$
.
$\pi (1)$
.
Definition 3.2. A word v is a root of w if
![]() $| v | \leq | w |$
and w is a suffix of the left-infinite word
$| v | \leq | w |$
and w is a suffix of the left-infinite word
![]() $v^{\infty }$
. The minimal root of w is the shortest v which is a root of w.
$v^{\infty }$
. The minimal root of w is the shortest v which is a root of w.
Every word w has a unique minimal root since it is a root of itself (and all roots of w are suffixes of w).
Lemma 3.3 ([Reference CreutzCre22] Lemma 5.7).
If w and v are words with
![]() $| v | \leq | w |$
such that
$| v | \leq | w |$
such that
![]() $wv$
has w as a suffix, then v is a root of w.
$wv$
has w as a suffix, then v is a root of w.
Lemma 3.4 ([Reference CreutzCre22] Lemma 5.8).
If
![]() $uv = vu$
, then u and v are powers of the same word, that is, there exists a word
$uv = vu$
, then u and v are powers of the same word, that is, there exists a word
![]() $v_{0}$
and integers
$v_{0}$
and integers
![]() $t,s> 0$
such that
$t,s> 0$
such that
![]() $u = v_{0}^{t}$
and
$u = v_{0}^{t}$
and
![]() $v = v_{0}^{s}$
.
$v = v_{0}^{s}$
.
Lemma 3.5. Let u and v be words with
![]() $| v | < | u |$
. Let s be the maximal common suffix of
$| v | < | u |$
. Let s be the maximal common suffix of
![]() $v^{\infty }$
and
$v^{\infty }$
and
![]() $v^{\infty }u$
. If
$v^{\infty }u$
. If
![]() $| s | \geq | vu |$
, then u and v are powers of the same word.
$| s | \geq | vu |$
, then u and v are powers of the same word.
Proof. If
![]() $| s | \geq | vu |$
, then s has
$| s | \geq | vu |$
, then s has
![]() $vu$
as a suffix. Since v is a root of s, v is a root of u so
$vu$
as a suffix. Since v is a root of s, v is a root of u so
![]() $u = u^{\prime }v^{t}$
for some
$u = u^{\prime }v^{t}$
for some
![]() $t \geq 1$
and suffix
$t \geq 1$
and suffix
![]() $u^{\prime }$
of v. Then s has
$u^{\prime }$
of v. Then s has
![]() $u^{\prime }v^{t}v$
as a suffix since that is a suffix of
$u^{\prime }v^{t}v$
as a suffix since that is a suffix of
![]() $v^{\infty }$
and
$v^{\infty }$
and
![]() $| s | \geq | u^{\prime }v^{t}v |$
. Then
$| s | \geq | u^{\prime }v^{t}v |$
. Then
![]() $uv$
is a suffix of s so
$uv$
is a suffix of s so
![]() $uv = vu$
as they are both suffixes of s and have the same length so Lemma 3.4 gives the claim.
$uv = vu$
as they are both suffixes of s and have the same length so Lemma 3.4 gives the claim.
Lemma 3.6. Let v and u be words with
![]() $| v | < | u |$
which are not powers of the same word and where v is a suffix of u. Let s be the maximal common suffix of
$| v | < | u |$
which are not powers of the same word and where v is a suffix of u. Let s be the maximal common suffix of
![]() $v^{\infty }$
and
$v^{\infty }$
and
![]() $v^{\infty }u$
(which must be finite by Lemma 3.5). Then s is a suffix of any left-infinite concatenation of u and v.
$v^{\infty }u$
(which must be finite by Lemma 3.5). Then s is a suffix of any left-infinite concatenation of u and v.
Proof. By Lemma 3.5,
![]() $| s | < | vu |$
so we need only verify that s is a suffix of
$| s | < | vu |$
so we need only verify that s is a suffix of
![]() $uv^{q}$
for
$uv^{q}$
for
![]() $q \geq 1$
and of
$q \geq 1$
and of
![]() $uu$
. Since v is a suffix of u,
$uu$
. Since v is a suffix of u,
![]() $uu$
has
$uu$
has
![]() $vu$
as a suffix hence has s as a suffix. If
$vu$
as a suffix hence has s as a suffix. If
![]() $| s | \geq | u |$
, then v is a root of u so
$| s | \geq | u |$
, then v is a root of u so
![]() $u = u^{\prime }v^{t}$
and
$u = u^{\prime }v^{t}$
and
![]() $uv^{q} = u^{\prime }v^{t}v^{q}$
is a suffix of
$uv^{q} = u^{\prime }v^{t}v^{q}$
is a suffix of
![]() $v^{\infty }$
so s is a suffix of
$v^{\infty }$
so s is a suffix of
![]() $uv^{q}$
. If
$uv^{q}$
. If
![]() $| s | < | u |$
, then
$| s | < | u |$
, then
![]() $u = u_{0}s^{\prime }v^{t}$
for some (possibly empty) suffix
$u = u_{0}s^{\prime }v^{t}$
for some (possibly empty) suffix
![]() $s^{\prime }$
of v and
$s^{\prime }$
of v and
![]() $t \geq 1$
(as
$t \geq 1$
(as
![]() $s = s^{\prime }v^{t}$
has v as a root and
$s = s^{\prime }v^{t}$
has v as a root and
![]() $| s | \geq | v |$
as v is a suffix of u). Then
$| s | \geq | v |$
as v is a suffix of u). Then
![]() $uv^{q} = u_{0}s^{\prime }v^{t+q}$
has
$uv^{q} = u_{0}s^{\prime }v^{t+q}$
has
![]() $s = s^{\prime }v^{t}$
as a suffix.
$s = s^{\prime }v^{t}$
as a suffix.
Lemma 3.7. Let v and u be words and s be the maximal common suffix of
![]() $v^{\infty }$
and
$v^{\infty }$
and
![]() $v^{\infty }u$
. Let y and z be suffixes of some (possibly distinct) concatenations of u and v, both of length at least
$v^{\infty }u$
. Let y and z be suffixes of some (possibly distinct) concatenations of u and v, both of length at least
![]() $| s |$
. Then for any word w, the maximal common suffix of
$| s |$
. Then for any word w, the maximal common suffix of
![]() $yvw$
and
$yvw$
and
![]() $zuw$
is
$zuw$
is
![]() $sw$
.
$sw$
.
Proof. Since y is a suffix of a concatenation of u and v, so is
![]() $yv$
. Then
$yv$
. Then
![]() $yv$
has
$yv$
has
![]() $sv$
as a suffix by Lemma 3.6. Likewise,
$sv$
as a suffix by Lemma 3.6. Likewise,
![]() $zu$
has
$zu$
has
![]() $su$
as a suffix. As s is a suffix of
$su$
as a suffix. As s is a suffix of
![]() $v^{\infty }$
, then so is
$v^{\infty }$
, then so is
![]() $yv$
. Likewise,
$yv$
. Likewise,
![]() $zu$
is a suffix of
$zu$
is a suffix of
![]() $v^{\infty }u$
. Therefore, the maximal common suffix of
$v^{\infty }u$
. Therefore, the maximal common suffix of
![]() $yv$
and
$yv$
and
![]() $zu$
is s (as they are both at least as long as s).
$zu$
is s (as they are both at least as long as s).
Lemma 3.8. If
![]() $p(q + 1) - p(q) = 1$
, then there exists a bispecial word which has length in
$p(q + 1) - p(q) = 1$
, then there exists a bispecial word which has length in
![]() $[q, q+p(q)]$
, has exactly two successors and is the unique right-special word of its length and also the unique left-special word of its length.
$[q, q+p(q)]$
, has exactly two successors and is the unique right-special word of its length and also the unique left-special word of its length.
Proof. Let w be the unique right-special word of length q (which must have exactly two successors) and y be the unique left-special word, and write z for the label of the path from y to w in the Rauzy graph. Then
![]() $| z | \leq p(| w |)$
. The word
$| z | \leq p(| w |)$
. The word
![]() $yz$
is left-special and right-special and
$yz$
is left-special and right-special and
![]() $| yz | = | y | + | z | \leq q + p(q)$
.
$| yz | = | y | + | z | \leq q + p(q)$
.
If x is a word of the same length as
![]() $yz$
which is right-special, then x must have w as a suffix. Then
$yz$
which is right-special, then x must have w as a suffix. Then
![]() $x = x_{0}w$
and
$x = x_{0}w$
and
![]() $| x_{0} | = | z |$
. Since there is only one path in the Rauzy graph ending at w of length
$| x_{0} | = | z |$
. Since there is only one path in the Rauzy graph ending at w of length
![]() $| z |$
(due to y being the unique left-special word), we have that
$| z |$
(due to y being the unique left-special word), we have that
![]() $x = yz$
.
$x = yz$
.
Lemma 3.9. Let X be an infinite transitive subshift with
![]() $p(q) \leq \frac {4}{3}q$
for all sufficiently large q. Then there exist words a and b which begin with different letters with
$p(q) \leq \frac {4}{3}q$
for all sufficiently large q. Then there exist words a and b which begin with different letters with
![]() $| a | < | b | < 2| a |$
and
$| a | < | b | < 2| a |$
and
![]() $p(q) < \frac {4}{3}q$
for all
$p(q) < \frac {4}{3}q$
for all
![]() $q \geq | a |$
and where a is a root of b such that every
$q \geq | a |$
and where a is a root of b such that every
![]() $x \in X$
can be written in exactly one way as a concatenation of a and b. If we define s to be the maximal common suffix of
$x \in X$
can be written in exactly one way as a concatenation of a and b. If we define s to be the maximal common suffix of
![]() $a^{\infty }$
and
$a^{\infty }$
and
![]() $a^{\infty }b$
, there exists
$a^{\infty }b$
, there exists
![]() $t \geq 0$
so
$t \geq 0$
so
![]() $sa^{t}$
is the unique right-special and left-special word of its length.
$sa^{t}$
is the unique right-special and left-special word of its length.
Proof. There exist infinitely many q such that
![]() $p(q+1) - p(q) = 1$
by Corollary 2.5. By Lemma 3.8, there exists a bispecial word w with
$p(q+1) - p(q) = 1$
by Corollary 2.5. By Lemma 3.8, there exists a bispecial word w with
![]() $| w |$
arbitrarily large which is the unique left-special and right-special word of its length and which has exactly two successors. We may assume
$| w |$
arbitrarily large which is the unique left-special and right-special word of its length and which has exactly two successors. We may assume
![]() $p(q) \leq \frac {4}{3}q$
for all
$p(q) \leq \frac {4}{3}q$
for all
![]() $q \geq | w |$
. We note that by [Reference Ormes and PavlovOP19], X is infinite and minimal.
$q \geq | w |$
. We note that by [Reference Ormes and PavlovOP19], X is infinite and minimal.
Let u and v be the shortest two return words for w (meaning
![]() $wu$
and
$wu$
and
![]() $wv$
both have w as a suffix) which will be the labels of the two paths from w to itself in the Rauzy graph
$wv$
both have w as a suffix) which will be the labels of the two paths from w to itself in the Rauzy graph
![]() $G_{X,| w |}$
for words of length
$G_{X,| w |}$
for words of length
![]() $| w |$
, with v being the shorter of the two. All bi-infinite words in X can be written in exactly one way as a concatenation of v and u, as every such word must be the label of a path in the Rauzy graph (which visits the vertex w infinitely many times by minimality of X), and the only two such paths have labels v and u.
$| w |$
, with v being the shorter of the two. All bi-infinite words in X can be written in exactly one way as a concatenation of v and u, as every such word must be the label of a path in the Rauzy graph (which visits the vertex w infinitely many times by minimality of X), and the only two such paths have labels v and u.
Since
![]() $| u | + | v | \leq p(| w |) + 1 \leq \frac {4}{3}| w | + 1$
, we have
$| u | + | v | \leq p(| w |) + 1 \leq \frac {4}{3}| w | + 1$
, we have
![]() $2| v | \leq \frac {4}{3}| w | + 1$
so
$2| v | \leq \frac {4}{3}| w | + 1$
so
![]() $| v | \leq \frac {2}{3}| w | + \frac {1}{2}$
. This is less than
$| v | \leq \frac {2}{3}| w | + \frac {1}{2}$
. This is less than
![]() $| w |$
(since
$| w |$
(since
![]() $| w |> 1$
), and so v is a root of w by Lemma 3.3. Note that v cannot be a proper power of any word since if
$| w |> 1$
), and so v is a root of w by Lemma 3.3. Note that v cannot be a proper power of any word since if
![]() $v = v_{0}^{t}$
, then
$v = v_{0}^{t}$
, then
![]() $wv_{0}$
has w as a suffix so
$wv_{0}$
has w as a suffix so
![]() $v_{0}$
is a root of w making
$v_{0}$
is a root of w making
![]() $v_{0}$
a return word for w which is shorter than v.
$v_{0}$
a return word for w which is shorter than v.
Observe that if
![]() $| w | < 3 | v |$
, then
$| w | < 3 | v |$
, then
![]() $| u | \leq \frac {4}{3} | w | + 1 - | v | < \frac {4}{3}| w | - \frac {1}{3} | w | + 1$
so u is a suffix of w making v a root of u. We write
$| u | \leq \frac {4}{3} | w | + 1 - | v | < \frac {4}{3}| w | - \frac {1}{3} | w | + 1$
so u is a suffix of w making v a root of u. We write
![]() $u = u^{\star }v^{s}$
for some proper suffix
$u = u^{\star }v^{s}$
for some proper suffix
![]() $u^{\star }$
of v (which cannot be empty as u and v start with different letters) and define
$u^{\star }$
of v (which cannot be empty as u and v start with different letters) and define
![]() $a = v$
and
$a = v$
and
![]() $b = u^{\star }v$
. Then as before, every bi-infinite word in X can be written uniquely as a concatenation of
$b = u^{\star }v$
. Then as before, every bi-infinite word in X can be written uniquely as a concatenation of
![]() $v = a$
and
$v = a$
and
![]() $u = ba^{s-1}$
, hence the same is true of a and b (since
$u = ba^{s-1}$
, hence the same is true of a and b (since
![]() $a = v$
). Clearly, a is a root of b, and
$a = v$
). Clearly, a is a root of b, and
![]() $| a | < | b | < 2| a |$
as
$| a | < | b | < 2| a |$
as
![]() $0 < | u^{\star } | < | a |$
.
$0 < | u^{\star } | < | a |$
.
So assume from here on that
![]() $| w | \geq 3 | v |$
.
$| w | \geq 3 | v |$
.
Suppose now that for every suffix
![]() $w_{0}$
of w with
$w_{0}$
of w with
![]() $| v | \leq | w_{0} | < 2 | v |$
, we have
$| v | \leq | w_{0} | < 2 | v |$
, we have
![]() $p(| w_{0} |+1) - p(| w_{0} |) \geq 2$
. Then, by Corollary 2.5,
$p(| w_{0} |+1) - p(| w_{0} |) \geq 2$
. Then, by Corollary 2.5,
![]() $p(2| v |) = p(2 | v |) - p(| v |) + p(| v |) \geq 2(2 | v | - | v |) + | v | + 1 = 3| v | + 1$
so
$p(2| v |) = p(2 | v |) - p(| v |) + p(| v |) \geq 2(2 | v | - | v |) + | v | + 1 = 3| v | + 1$
so
![]() $\frac {p(2 | v |)}{2| v |}> \frac {3}{2}$
, contradicting our hypothesis.
$\frac {p(2 | v |)}{2| v |}> \frac {3}{2}$
, contradicting our hypothesis.
Therefore, there exists
![]() $w_{0}$
a suffix of w with
$w_{0}$
a suffix of w with
![]() $| v | \leq | w_{0} | < 2 | v |$
which is the unique right-special word of its length and it has exactly two successors.
$| v | \leq | w_{0} | < 2 | v |$
which is the unique right-special word of its length and it has exactly two successors.
Since
![]() $w_{0}$
is a suffix of w, v is a root of
$w_{0}$
is a suffix of w, v is a root of
![]() $w_{0}$
. As there must also be a unique left-special word of the same length as
$w_{0}$
. As there must also be a unique left-special word of the same length as
![]() $w_{0}$
,
$w_{0}$
,
![]() $w_{0}$
extends to a bispecial word
$w_{0}$
extends to a bispecial word
![]() $w_{00}$
which is the unique left-special and right-special word of its length and which has exactly two successors (Lemma 3.8). Now,
$w_{00}$
which is the unique left-special and right-special word of its length and which has exactly two successors (Lemma 3.8). Now,
![]() $| w_{00} | \leq | w_{0} | + | v |$
since the path from the left-special to the right-special vertex in the Rauzy graph for words of length
$| w_{00} | \leq | w_{0} | + | v |$
since the path from the left-special to the right-special vertex in the Rauzy graph for words of length
![]() $| w_{0} |$
must be no longer than v (as
$| w_{0} |$
must be no longer than v (as
![]() $w_{0}v$
must have
$w_{0}v$
must have
![]() $w_{0}$
as a suffix). Then
$w_{0}$
as a suffix). Then
![]() $| w_{00} | < 2 | v | + | v | = 3| v | \leq | w |$
so
$| w_{00} | < 2 | v | + | v | = 3| v | \leq | w |$
so
![]() $w_{00}$
is a proper suffix, and prefix, of w.
$w_{00}$
is a proper suffix, and prefix, of w.
Let
![]() $v_{0}$
and
$v_{0}$
and
![]() $u_{0}$
be the shortest return words for
$u_{0}$
be the shortest return words for
![]() $w_{00}$
with
$w_{00}$
with
![]() $v_{0}$
beginning with the same letter as v (and
$v_{0}$
beginning with the same letter as v (and
![]() $u_0$
beginning with a different letter). Then all bi-infinite words in X are concatenations of
$u_0$
beginning with a different letter). Then all bi-infinite words in X are concatenations of
![]() $u_{0}$
and
$u_{0}$
and
![]() $v_{0}$
. Since v is a return word for
$v_{0}$
. Since v is a return word for
![]() $w_{00}$
, v must be a concatenation of
$w_{00}$
, v must be a concatenation of
![]() $u_{0}$
and
$u_{0}$
and
![]() $v_{0}$
which means that
$v_{0}$
which means that
![]() $v_{0}$
must be a prefix of v by virtue of sharing a common first letter. Likewise,
$v_{0}$
must be a prefix of v by virtue of sharing a common first letter. Likewise,
![]() $u_{0}$
must be a prefix of u.
$u_{0}$
must be a prefix of u.
Since v is a suffix of w, then
![]() $vv_{0}$
has v as a suffix so
$vv_{0}$
has v as a suffix so
![]() $v_{0}$
is a root of v by Lemma 3.3. Write
$v_{0}$
is a root of v by Lemma 3.3. Write
![]() $v = v^{\prime }v_{0}^{t}$
for some
$v = v^{\prime }v_{0}^{t}$
for some
![]() $t \geq 1$
and
$t \geq 1$
and
![]() $v^{\prime }$
a proper suffix of
$v^{\prime }$
a proper suffix of
![]() $v_{0}$
. Then
$v_{0}$
. Then
![]() $v_{0} = v^{\prime \prime }v^{\prime }$
so v has
$v_{0} = v^{\prime \prime }v^{\prime }$
so v has
![]() $v^{\prime }v_{0} = v^{\prime }v^{\prime \prime }v^{\prime }$
as a prefix. But
$v^{\prime }v_{0} = v^{\prime }v^{\prime \prime }v^{\prime }$
as a prefix. But
![]() $v_{0}$
is also a prefix of v so both
$v_{0}$
is also a prefix of v so both
![]() $v^{\prime }v^{\prime \prime }$
and
$v^{\prime }v^{\prime \prime }$
and
![]() $v^{\prime \prime }v^{\prime }$
are prefixes of v. Therefore, they are equal so by Lemma 3.4 both are powers of the same word. But then v is a power of that word and it cannot be a proper power of any word so either
$v^{\prime \prime }v^{\prime }$
are prefixes of v. Therefore, they are equal so by Lemma 3.4 both are powers of the same word. But then v is a power of that word and it cannot be a proper power of any word so either
![]() $v^{\prime }$
or
$v^{\prime }$
or
![]() $v^{\prime \prime }$
is empty and so
$v^{\prime \prime }$
is empty and so
![]() $v_{0} = v$
.
$v_{0} = v$
.
If
![]() $| u_{0} | \leq | v |$
, then
$| u_{0} | \leq | v |$
, then
![]() $u_{0}$
is a root of
$u_{0}$
is a root of
![]() $w_{00}$
hence of v. Write
$w_{00}$
hence of v. Write
![]() $v = v^{\star }u_{0}^{s}$
for some proper suffix
$v = v^{\star }u_{0}^{s}$
for some proper suffix
![]() $v^{\star }$
of
$v^{\star }$
of
![]() $u_{0}$
(which cannot be empty as v begins with a different letter than u) and
$u_{0}$
(which cannot be empty as v begins with a different letter than u) and
![]() $s \geq 1$
. Taking
$s \geq 1$
. Taking
![]() $a = u_{0}$
and
$a = u_{0}$
and
![]() $b = v^{\star }u_{0}$
, then every bi-infinite word in X is a concatenation of
$b = v^{\star }u_{0}$
, then every bi-infinite word in X is a concatenation of
![]() $u_{0} = a$
and
$u_{0} = a$
and
![]() $v = ba^{s-1}$
. Clearly, a is a root of b and
$v = ba^{s-1}$
. Clearly, a is a root of b and
![]() $| a | < | b | < 2| a |$
.
$| a | < | b | < 2| a |$
.
So we are left with
![]() $| u_{0} |> | v |$
. Here,
$| u_{0} |> | v |$
. Here,
![]() $| u_{0} | \leq p(| w_{00} |) + 1 - | v | < \frac {4}{3}| w_{00} | + 1 - \frac {1}{3}| w_{00} |$
as
$| u_{0} | \leq p(| w_{00} |) + 1 - | v | < \frac {4}{3}| w_{00} | + 1 - \frac {1}{3}| w_{00} |$
as
![]() $| w_{00} | < 3| v |$
. Therefore,
$| w_{00} | < 3| v |$
. Therefore,
![]() $| u_{0} | \leq | w_{00} |$
. So
$| u_{0} | \leq | w_{00} |$
. So
![]() $u_{0}$
is a suffix of w hence v is a root of
$u_{0}$
is a suffix of w hence v is a root of
![]() $u_{0}$
. Writing
$u_{0}$
. Writing
![]() $u_{0} = u^{\star }v^{s}$
for some proper suffix
$u_{0} = u^{\star }v^{s}$
for some proper suffix
![]() $u^{\star }$
of v and
$u^{\star }$
of v and
![]() $s \geq 1$
then taking
$s \geq 1$
then taking
![]() $a = v$
and
$a = v$
and
![]() $b = u^{\star }v$
, just as before we have that every bi-infinite word in X is a unique concatenation of
$b = u^{\star }v$
, just as before we have that every bi-infinite word in X is a unique concatenation of
![]() $v = a$
and
$v = a$
and
![]() $u_{0} = ba^{s-1}$
, hence of a and b. As before, clearly a is a root of b and
$u_{0} = ba^{s-1}$
, hence of a and b. As before, clearly a is a root of b and
![]() $| a | < | b | < 2| a |$
.
$| a | < | b | < 2| a |$
.
In all cases, one of
![]() $a,b$
is a prefix of u and the other is a prefix of v. Since u and v begin with different letters, a and b begin with different letters. It remains to verify the claim about the maximal common suffix s and that a may be taken arbitrarily long.
$a,b$
is a prefix of u and the other is a prefix of v. Since u and v begin with different letters, a and b begin with different letters. It remains to verify the claim about the maximal common suffix s and that a may be taken arbitrarily long.
In the case when a is a root of w (and
![]() $w_{00}$
was not introduced), set
$w_{00}$
was not introduced), set
![]() $w_{00} = w$
and
$w_{00} = w$
and
![]() $t=0$
. Then in all cases, a is a root of
$t=0$
. Then in all cases, a is a root of
![]() $w_{00}$
as a is either v or
$w_{00}$
as a is either v or
![]() $u_{0}$
so
$u_{0}$
so
![]() $w_{00}$
is a suffix of
$w_{00}$
is a suffix of
![]() $a^{\infty }$
. In all cases,
$a^{\infty }$
. In all cases,
![]() $ba^{t}$
is the other return word for
$ba^{t}$
is the other return word for
![]() $w_{00}$
for some
$w_{00}$
for some
![]() $t \geq 0$
. Then
$t \geq 0$
. Then
![]() $w_{00}a^{\ell }ba^{t}$
has
$w_{00}a^{\ell }ba^{t}$
has
![]() $w_{00}$
as a suffix for all
$w_{00}$
as a suffix for all
![]() $\ell \geq 0$
so
$\ell \geq 0$
so
![]() $w_{00}$
is a suffix of
$w_{00}$
is a suffix of
![]() $a^{\infty }ba^{t}$
. Since
$a^{\infty }ba^{t}$
. Since
![]() $w_{00}$
is left-special and a and
$w_{00}$
is left-special and a and
![]() $ba^{t}$
are its two return words, the maximal common suffix of
$ba^{t}$
are its two return words, the maximal common suffix of
![]() $a^{\infty }$
and
$a^{\infty }$
and
![]() $a^{\infty }ba^{t}$
must be no longer than
$a^{\infty }ba^{t}$
must be no longer than
![]() $w_{00}$
. Therefore,
$w_{00}$
. Therefore,
![]() $w_{00} = sa^{t}$
, where s is the maximal common suffix of
$w_{00} = sa^{t}$
, where s is the maximal common suffix of
![]() $a^{\infty }$
and
$a^{\infty }$
and
![]() $a^{\infty }ba$
.
$a^{\infty }ba$
.
Let
![]() $\{ w_{\ell } \}$
be a sequence of such bispecial words with
$\{ w_{\ell } \}$
be a sequence of such bispecial words with
![]() $| w_{\ell } |$
increasing to
$| w_{\ell } |$
increasing to
![]() $\infty $
, and let
$\infty $
, and let
![]() $\{ a_{\ell } \}$
and
$\{ a_{\ell } \}$
and
![]() $\{ v_{\ell } \}$
be the corresponding a and v above. Since either
$\{ v_{\ell } \}$
be the corresponding a and v above. Since either
![]() $a = v$
or
$a = v$
or
![]() $a = u_{0}$
, and in both cases it is a root of
$a = u_{0}$
, and in both cases it is a root of
![]() $w_{00}$
,
$w_{00}$
,
![]() $a_{\ell }$
is a root of
$a_{\ell }$
is a root of
![]() $v_{\ell }$
.
$v_{\ell }$
.
Since
![]() $w_{\ell }$
is the unique right-special word of its length, it is a suffix of
$w_{\ell }$
is the unique right-special word of its length, it is a suffix of
![]() $w_{\ell +1}$
and therefore
$w_{\ell +1}$
and therefore
![]() $v_{\ell }$
is a suffix of
$v_{\ell }$
is a suffix of
![]() $v_{\ell +1}$
. If
$v_{\ell +1}$
. If
![]() $| v_{\ell } |$
were bounded, then there would exist L such that
$| v_{\ell } |$
were bounded, then there would exist L such that
![]() $v_{\ell } = v_{L}$
for
$v_{\ell } = v_{L}$
for
![]() $\ell \geq L$
but then
$\ell \geq L$
but then
![]() $v_{L}$
would be a root of
$v_{L}$
would be a root of
![]() $w_{\ell }$
for
$w_{\ell }$
for
![]() $\ell \geq L$
so
$\ell \geq L$
so
![]() $v_{L}^{\infty } \in X$
, a contradiction. So
$v_{L}^{\infty } \in X$
, a contradiction. So
![]() $| v_{\ell } | \to \infty $
. Likewise, since
$| v_{\ell } | \to \infty $
. Likewise, since
![]() $a_{\ell }$
is a root of
$a_{\ell }$
is a root of
![]() $v_{\ell }$
, if
$v_{\ell }$
, if
![]() $| a_{\ell } |$
were bounded, then for some L we would have
$| a_{\ell } |$
were bounded, then for some L we would have
![]() $a_{L}^{\infty } \in X$
. Therefore,
$a_{L}^{\infty } \in X$
. Therefore,
![]() $| a_{\ell } | \to \infty $
so we may take a and b such that for all
$| a_{\ell } | \to \infty $
so we may take a and b such that for all
![]() $q \geq | a |$
, we have
$q \geq | a |$
, we have
![]() $p(q) < \frac {4}{3}q$
.
$p(q) < \frac {4}{3}q$
.
The following lemma is our main tool to recursively demonstrate the structure from Proposition 3.1. The key is control over the lengths of the suffixes from Lemmas 3.5 and 3.6.
Lemma 3.10. Let X be an infinite transitive subshift with
![]() $\frac {p(q)}{q} < \frac {4}{3}$
for
$\frac {p(q)}{q} < \frac {4}{3}$
for
![]() $q> N$
. Let u and v be words with
$q> N$
. Let u and v be words with
![]() $N < | v | < | u |$
such that v is a suffix of u and v is not a prefix of u. Let s be the maximal common suffix of
$N < | v | < | u |$
such that v is a suffix of u and v is not a prefix of u. Let s be the maximal common suffix of
![]() $v^{\infty }$
and
$v^{\infty }$
and
![]() $v^{\infty }u$
, and let p be the maximal common prefix of u and v.
$v^{\infty }u$
, and let p be the maximal common prefix of u and v.
Assume that
![]() $| p | + | s | < | u | + | v |$
and
$| p | + | s | < | u | + | v |$
and
![]() $| p | + | s | < 3| v |$
and that every bi-infinite word in X can be written as a concatenation of u and v. Then there exist
$| p | + | s | < 3| v |$
and that every bi-infinite word in X can be written as a concatenation of u and v. Then there exist
![]() $0 < m < n$
such that every concatenation of u and v which represents a point in X has only
$0 < m < n$
such that every concatenation of u and v which represents a point in X has only
![]() $v^{m-1}$
and
$v^{m-1}$
and
![]() $v^{n-1}$
appearing between nearest occurrences of u and satisfying:
$v^{n-1}$
appearing between nearest occurrences of u and satisfying:
-
•
 $n \leq 2m$
whenever
$n \leq 2m$
whenever
 $m> 1$
;
$m> 1$
; -
•
 $n < 1.9m$
whenever
$n < 1.9m$
whenever
 $m> 4$
;
$m> 4$
; -
•
 $n \leq 3$
whenever
$n \leq 3$
whenever
 $m = 1$
$m = 1$
and the words
![]() $sv^{n-2}p$
and
$sv^{n-2}p$
and
![]() $sv^{m-1}uv^{m-1}p$
are right-special.
$sv^{m-1}uv^{m-1}p$
are right-special.
Proof. For brevity, whenever we refer to a ‘concatenation’ in the following, it is a concatenation of
![]() $u,v$
which represents a point of X or a subword of such a point. We again note that by [Reference Ormes and PavlovOP19], X is infinite and minimal, and so no concatenation can contain infinitely many consecutive v. Similarly, if there was only a single number of v which may occur between nearest occurrences of u, then X would be finite, contradicting our assumptions. So there are at least two different numbers of v which can occur between nearest occurrences of u.
$u,v$
which represents a point of X or a subword of such a point. We again note that by [Reference Ormes and PavlovOP19], X is infinite and minimal, and so no concatenation can contain infinitely many consecutive v. Similarly, if there was only a single number of v which may occur between nearest occurrences of u, then X would be finite, contradicting our assumptions. So there are at least two different numbers of v which can occur between nearest occurrences of u.
Suppose for a contradiction that
![]() $uv^{x}u$
and
$uv^{x}u$
and
![]() $uv^{y}u$
and
$uv^{y}u$
and
![]() $uv^{z}u$
all appear in some concatenations and that
$uv^{z}u$
all appear in some concatenations and that
![]() $x < y < z$
. We may assume that x is the minimal value such that
$x < y < z$
. We may assume that x is the minimal value such that
![]() $uv^{x}u$
appears in a concatenation. Since
$uv^{x}u$
appears in a concatenation. Since
![]() $uv^{x}u$
and
$uv^{x}u$
and
![]() $uv^{y}u$
are necessarily preceded by
$uv^{y}u$
are necessarily preceded by
![]() $v^{x}$
(due to x being minimal), then
$v^{x}$
(due to x being minimal), then
![]() $v^{x}uv^{x}u$
and
$v^{x}uv^{x}u$
and
![]() $v^{x}uv^{x}v$
both appear in concatenations (as
$v^{x}uv^{x}v$
both appear in concatenations (as
![]() $y> x$
). By Lemma 3.6 (as v is not a prefix of u, they cannot be powers of the same word), s is a suffix of every left-infinite concatenation. This means that
$y> x$
). By Lemma 3.6 (as v is not a prefix of u, they cannot be powers of the same word), s is a suffix of every left-infinite concatenation. This means that
![]() $v^x u v^x u$
and
$v^x u v^x u$
and
![]() $v^x u v^x v$
are both preceded by s in the bi-infinite concatenations they respectively appear in, and so
$v^x u v^x v$
are both preceded by s in the bi-infinite concatenations they respectively appear in, and so
![]() $sv^{x}uv^{x}$
can be followed by either u or v, meaning that
$sv^{x}uv^{x}$
can be followed by either u or v, meaning that
![]() $sv^{x}uv^{x}p$
is right-special (since the letters appearing after p in u and v are distinct by maximality of p).
$sv^{x}uv^{x}p$
is right-special (since the letters appearing after p in u and v are distinct by maximality of p).
Likewise,
![]() $v^{x}uv^{y}u$
and
$v^{x}uv^{y}u$
and
![]() $v^{x}uv^{y}v$
appear in some concatenations (due to
$v^{x}uv^{y}v$
appear in some concatenations (due to
![]() $z> y$
) so
$z> y$
) so
![]() $sv^{x}uv^{y}p$
is also right-special. By Lemma 3.7, the maximal common suffix of
$sv^{x}uv^{y}p$
is also right-special. By Lemma 3.7, the maximal common suffix of
![]() $sv^{x}uv^{x}p$
and
$sv^{x}uv^{x}p$
and
![]() $sv^{x}uv^{y}p$
is
$sv^{x}uv^{y}p$
is
![]() $sv^{x}p$
. Therefore, there are at least two right-special words of length
$sv^{x}p$
. Therefore, there are at least two right-special words of length
![]() $\ell $
for
$\ell $
for
![]() $| sv^{x}p | < \ell \leq | sv^{x}uv^{x}p |$
(namely, the unequal suffixes of
$| sv^{x}p | < \ell \leq | sv^{x}uv^{x}p |$
(namely, the unequal suffixes of
![]() $sv^{x}uv^{x}p$
and
$sv^{x}uv^{x}p$
and
![]() $sv^{x}uv^{y}p$
of length
$sv^{x}uv^{y}p$
of length
![]() $\ell $
). Then, since
$\ell $
). Then, since
![]() $| p | + | s | < | v | + | u | < 2| u |$
, by Corollary 2.5
$| p | + | s | < | v | + | u | < 2| u |$
, by Corollary 2.5
The final expression is increasing for
![]() $x \geq 0$
, hence is at least
$x \geq 0$
, hence is at least
![]() $\frac {4}{3}$
(its value at
$\frac {4}{3}$
(its value at
![]() $x = 0$
), contradicting our hypothesis that
$x = 0$
), contradicting our hypothesis that
![]() $p(q)/q < \frac {4}{3}$
for
$p(q)/q < \frac {4}{3}$
for
![]() $q> N$
. Therefore, such
$q> N$
. Therefore, such
![]() $x < y < z$
cannot exist so there are only two distinct values x and y. Writing
$x < y < z$
cannot exist so there are only two distinct values x and y. Writing
![]() $x = m - 1$
and
$x = m - 1$
and
![]() $y = n - 1$
then shows that
$y = n - 1$
then shows that
![]() $v^{m-1}$
and
$v^{m-1}$
and
![]() $v^{n-1}$
are the only words appearing between occurrences of u in a concatenation.
$v^{n-1}$
are the only words appearing between occurrences of u in a concatenation.
By similar reasoning as above, we observe that
![]() $sv^{m-1}uv^{m-1}p$
is right-special and that
$sv^{m-1}uv^{m-1}p$
is right-special and that
![]() $sv^{n-2}p$
is also right-special since
$sv^{n-2}p$
is also right-special since
![]() $sv^{n-1}u$
appears in a concatenation and it has
$sv^{n-1}u$
appears in a concatenation and it has
![]() $sv^{n-2}v$
as a prefix and
$sv^{n-2}v$
as a prefix and
![]() $sv^{n-2}u$
as a suffix. Again, by similar reasoning as above, their maximal common suffix is
$sv^{n-2}u$
as a suffix. Again, by similar reasoning as above, their maximal common suffix is
![]() $sv^{m-1}p$
.
$sv^{m-1}p$
.
Suppose
![]() $| sv^{m-1}uv^{m-1}p | \leq | sv^{n-2}p |$
. Then there are at least two right-special words of length
$| sv^{m-1}uv^{m-1}p | \leq | sv^{n-2}p |$
. Then there are at least two right-special words of length
![]() $\ell $
for
$\ell $
for
![]() $| sv^{m-1}p | < \ell \leq | sv^{m-1}uv^{m-1}p |$
so, by Corollary 2.5 and the fact that
$| sv^{m-1}p | < \ell \leq | sv^{m-1}uv^{m-1}p |$
so, by Corollary 2.5 and the fact that
![]() $| p | + | s | < | u | + | v | < 2| u |$
,
$| p | + | s | < | u | + | v | < 2| u |$
,
 $$\begin{align*}\frac{p(| sv^{m-1}uv^{m-1}p |)}{| sv^{m-1}uv^{m-1}p |} \geq 1 + \frac{(m-1)| v | + | u |}{| p | + | s | + 2(m-1)| v | + | u |}> 1 + \frac{(m-1)| v | + | u |}{2(m-1)| v | + 3| u |} \geq \frac{4}{3} \end{align*}$$
$$\begin{align*}\frac{p(| sv^{m-1}uv^{m-1}p |)}{| sv^{m-1}uv^{m-1}p |} \geq 1 + \frac{(m-1)| v | + | u |}{| p | + | s | + 2(m-1)| v | + | u |}> 1 + \frac{(m-1)| v | + | u |}{2(m-1)| v | + 3| u |} \geq \frac{4}{3} \end{align*}$$
which contradicts our hypothesis.
So instead
![]() $| sv^{n-2}p | < | sv^{m-1}uv^{m-1}p |$
. Then there are at least two right-special words of length
$| sv^{n-2}p | < | sv^{m-1}uv^{m-1}p |$
. Then there are at least two right-special words of length
![]() $\ell $
for
$\ell $
for
![]() $| sv^{m-1}p | < \ell \leq | sv^{n-2}p |$
so, by Corollary 2.5 and the fact that
$| sv^{m-1}p | < \ell \leq | sv^{n-2}p |$
so, by Corollary 2.5 and the fact that
![]() $| p | + | s | < 3| v |$
,
$| p | + | s | < 3| v |$
,
 $$\begin{align*}\frac{p(| sv^{n-2}p |)}{| sv^{n-2}p |} \geq 1 + \frac{(n - m - 1)| v |}{| p | + | s | + (n-2)| v |}> 1 + \frac{(n-m-1)| v |}{3| v | + (n-2)| v |} = 1 + \frac{n-m-1}{n+1}. \end{align*}$$
$$\begin{align*}\frac{p(| sv^{n-2}p |)}{| sv^{n-2}p |} \geq 1 + \frac{(n - m - 1)| v |}{| p | + | s | + (n-2)| v |}> 1 + \frac{(n-m-1)| v |}{3| v | + (n-2)| v |} = 1 + \frac{n-m-1}{n+1}. \end{align*}$$
Consider first when
![]() $m=1$
. If
$m=1$
. If
![]() $n \geq 4$
, then
$n \geq 4$
, then
![]() $\frac {n-m-1}{n+1} = \frac {n-2}{n+1} \geq \frac {2}{5}> \frac {1}{3}$
which contradicts our hypothesis.
$\frac {n-m-1}{n+1} = \frac {n-2}{n+1} \geq \frac {2}{5}> \frac {1}{3}$
which contradicts our hypothesis.
Now, consider when
![]() $m> 1$
. If
$m> 1$
. If
![]() $n \geq 2m + 1$
, then
$n \geq 2m + 1$
, then
![]() $\frac {n-m-1}{n+1} \geq \frac {2m+1 - m - 1}{2m+1+1} = \frac {m}{2m+2} \geq \frac {2}{2(2)+2} = \frac {1}{3}$
contradicting our hypothesis. So
$\frac {n-m-1}{n+1} \geq \frac {2m+1 - m - 1}{2m+1+1} = \frac {m}{2m+2} \geq \frac {2}{2(2)+2} = \frac {1}{3}$
contradicting our hypothesis. So
![]() $n \leq 2m$
when
$n \leq 2m$
when
![]() $m> 1$
.
$m> 1$
.
Finally, consider when
![]() $m \geq 5$
. Suppose
$m \geq 5$
. Suppose
![]() $n \geq 1.9m$
. Then
$n \geq 1.9m$
. Then
contradicting our hypothesis. So
![]() $n < 1.9m$
whenever
$n < 1.9m$
whenever
![]() $m> 4$
.
$m> 4$
.
Proof of Proposition 3.1.
We prove by induction that such sequences exist, using the notation
![]() $v_k := \pi (\rho _{k-1}(0))$
and
$v_k := \pi (\rho _{k-1}(0))$
and
![]() $u_k := \pi (\rho _{k-1}(1))$
.
$u_k := \pi (\rho _{k-1}(1))$
.
By [Reference Ormes and PavlovOP19], X is minimal. Write
![]() $s_k$
for the maximal common suffix of
$s_k$
for the maximal common suffix of
![]() $v_{k}^{\infty }$
and
$v_{k}^{\infty }$
and
![]() $v_{k}^{\infty }u_{k}$
and
$v_{k}^{\infty }u_{k}$
and
![]() $p_{k}$
for the maximal common prefix of
$p_{k}$
for the maximal common prefix of
![]() $v_{k}$
and
$v_{k}$
and
![]() $u_{k}$
.
$u_{k}$
.
Our inductive hypotheses are the following:
-
• all
 $x \in X$
can be written as concatenations of
$x \in X$
can be written as concatenations of
 $u_k$
and
$u_k$
and
 $v_k$
;
$v_k$
; -
•
 $v_k$
is a suffix of
$v_k$
is a suffix of
 $u_k$
and is not a prefix of
$u_k$
and is not a prefix of
 $u_k$
;
$u_k$
; -
•
 $| p_k | + | s_k | < \min (| v_k | + | u_k |, 3| v_k |)$
;
$| p_k | + | s_k | < \min (| v_k | + | u_k |, 3| v_k |)$
; -
•
 $v_{k} = (\pi \circ \tau _{m_{1},n_{1}} \circ \cdots \circ \tau _{m_{k-1},n_{k-1}})(0) = \pi (\rho _{k-1}(0))$
and
$v_{k} = (\pi \circ \tau _{m_{1},n_{1}} \circ \cdots \circ \tau _{m_{k-1},n_{k-1}})(0) = \pi (\rho _{k-1}(0))$
and
 $u_{k} = (\pi \circ \tau _{m_{1},n_{1}} \circ \cdots \circ \tau _{m_{k-1},n_{k-1}})(1) = \pi (\rho _{k-1}(1))$
.
$u_{k} = (\pi \circ \tau _{m_{1},n_{1}} \circ \cdots \circ \tau _{m_{k-1},n_{k-1}})(1) = \pi (\rho _{k-1}(1))$
.
Since
![]() $\limsup \frac {p(q)}{q} < \frac {4}{3}$
, eventually
$\limsup \frac {p(q)}{q} < \frac {4}{3}$
, eventually
![]() $p(q) < \frac {4}{3}q$
. Lemma 3.9 gives
$p(q) < \frac {4}{3}q$
. Lemma 3.9 gives
![]() $v_{1}$
and
$v_{1}$
and
![]() $u_{1}$
with
$u_{1}$
with
![]() $v_{1}$
a suffix of
$v_{1}$
a suffix of
![]() $u_{1}$
and
$u_{1}$
and
![]() $| v_1 | < | u_{1} | < 2| v_{1} |$
which start with different letters such that every infinite word is a concatenation of
$| v_1 | < | u_{1} | < 2| v_{1} |$
which start with different letters such that every infinite word is a concatenation of
![]() $u_{1}$
and
$u_{1}$
and
![]() $v_{1}$
. By Lemma 3.5,
$v_{1}$
. By Lemma 3.5,
![]() $| s_{1} | < | v_{1}u_{1} | < 3| v_{1} |$
. As
$| s_{1} | < | v_{1}u_{1} | < 3| v_{1} |$
. As
![]() $u_{1}$
and
$u_{1}$
and
![]() $v_{1}$
begin with different letters,
$v_{1}$
begin with different letters,
![]() $p_1$
is empty. Therefore, the base case is established by setting
$p_1$
is empty. Therefore, the base case is established by setting
![]() $\pi (0) = v_{1}$
and
$\pi (0) = v_{1}$
and
![]() $\pi (1) = u_{1}$
. Lemma 3.9 ensures that
$\pi (1) = u_{1}$
. Lemma 3.9 ensures that
![]() $p(q) < \frac {4}{3}q$
for all
$p(q) < \frac {4}{3}q$
for all
![]() $q \geq | \pi (0) |$
.
$q \geq | \pi (0) |$
.
Given
![]() $v_k$
and
$v_k$
and
![]() $u_k$
, by Lemma 3.10 there exist
$u_k$
, by Lemma 3.10 there exist
![]() $0 < m_k < n_k$
such that every infinite word is a concatenation of
$0 < m_k < n_k$
such that every infinite word is a concatenation of
![]() $v_{k+1} = v_{k}^{m_{k}-1}u_{k}$
and
$v_{k+1} = v_{k}^{m_{k}-1}u_{k}$
and
![]() $u_{k+1} = v_{k}^{n_{k}-1}u_{k}$
. Observe that
$u_{k+1} = v_{k}^{n_{k}-1}u_{k}$
. Observe that
 $u_{k+1} = v_{k}^{n_{k}-1}u_{k} = (\pi (\rho _{k-1}(0)))^{n_{k}-1} \pi (\rho _{k-1}(1)) = \pi (\rho _{k-1}(0^{n_k - 1} 1)) = \pi (\rho _{k-1}(\tau _{m_k,n_k}(1))) = \pi (\rho _k(1))$
and similarly
$u_{k+1} = v_{k}^{n_{k}-1}u_{k} = (\pi (\rho _{k-1}(0)))^{n_{k}-1} \pi (\rho _{k-1}(1)) = \pi (\rho _{k-1}(0^{n_k - 1} 1)) = \pi (\rho _{k-1}(\tau _{m_k,n_k}(1))) = \pi (\rho _k(1))$
and similarly
![]() $v_{k+1} = \pi (\rho _k(0))$
.
$v_{k+1} = \pi (\rho _k(0))$
.
Clearly,
![]() $v_{k+1}$
is a suffix of
$v_{k+1}$
is a suffix of
![]() $u_{k+1}$
. If
$u_{k+1}$
. If
![]() $v_{k+1}$
were a prefix of
$v_{k+1}$
were a prefix of
![]() $u_{k+1}$
, then
$u_{k+1}$
, then
![]() $u_{k}$
would be a prefix of
$u_{k}$
would be a prefix of
![]() $v_{k}^{n_{k}-m_{k}}u_{k}$
but that would make
$v_{k}^{n_{k}-m_{k}}u_{k}$
but that would make
![]() $v_{k}$
a prefix of
$v_{k}$
a prefix of
![]() $u_{k}$
. So
$u_{k}$
. So
![]() $v_{k+1}$
is not a prefix of
$v_{k+1}$
is not a prefix of
![]() $u_{k+1}$
, and
$u_{k+1}$
, and
![]() $p_{k+1} = v_{k}^{m_{k}-1}p_{k}$
.
$p_{k+1} = v_{k}^{m_{k}-1}p_{k}$
.
By definition,
![]() $s_{k+1}$
is the maximal common suffix of
$s_{k+1}$
is the maximal common suffix of
![]() $v_{k+1}^{\infty }$
and
$v_{k+1}^{\infty }$
and
![]() $v_{k+1}^{\infty } u_{k+1}$
. We can rewrite these as
$v_{k+1}^{\infty } u_{k+1}$
. We can rewrite these as
![]() $y = \ldots u_k v_k^{m_k - 1} u_k$
and
$y = \ldots u_k v_k^{m_k - 1} u_k$
and
![]() $z = \ldots v_k v_k^{m_k - 1} u_k$
. These share a suffix of
$z = \ldots v_k v_k^{m_k - 1} u_k$
. These share a suffix of
![]() $v_k^{m_k - 1} u_k$
, so we must just find the maximal common suffix of the portions with this removed, that is,
$v_k^{m_k - 1} u_k$
, so we must just find the maximal common suffix of the portions with this removed, that is,
![]() $y' = \ldots u_k$
, a concatenation ending with
$y' = \ldots u_k$
, a concatenation ending with
![]() $u_k$
, and
$u_k$
, and
![]() $z' = \ldots v_k$
, a concatenation ending with
$z' = \ldots v_k$
, a concatenation ending with
![]() $v_k$
. But
$v_k$
. But
![]() $y'$
then agrees with
$y'$
then agrees with
![]() $v_k^{\infty } u_k$
on a suffix of length
$v_k^{\infty } u_k$
on a suffix of length
![]() $|u_k| + |s_k|> |s_k|$
by Lemma 3.6 and
$|u_k| + |s_k|> |s_k|$
by Lemma 3.6 and
![]() $z'$
agrees with
$z'$
agrees with
![]() $v_k^{\infty }$
on a suffix of length
$v_k^{\infty }$
on a suffix of length
![]() $|v_k| + |s_k|> |s_k|$
by Lemma 3.6, meaning that
$|v_k| + |s_k|> |s_k|$
by Lemma 3.6, meaning that
![]() $y'$
and
$y'$
and
![]() $z'$
have maximal common suffix
$z'$
have maximal common suffix
![]() $s_k$
. Therefore,
$s_k$
. Therefore,
![]() $s_{k+1} = s_{k}v_{k}^{m_{k}-1}u_{k} = s_{k}v_{k+1}$
. Then,
$s_{k+1} = s_{k}v_{k}^{m_{k}-1}u_{k} = s_{k}v_{k+1}$
. Then,
and since
![]() $| v_{k+1} | + | v_k | \leq | u_{k+1} |$
and
$| v_{k+1} | + | v_k | \leq | u_{k+1} |$
and
![]() $| v_k | < | v_{k+1} |$
, the inductive hypotheses are verified.
$| v_k | < | v_{k+1} |$
, the inductive hypotheses are verified.
Lemma 3.10 gives that
![]() $n_k \leq 2m_k$
when
$n_k \leq 2m_k$
when
![]() $m_k> 1$
and
$m_k> 1$
and
![]() $n_k \leq 1.9m_k$
when
$n_k \leq 1.9m_k$
when
![]() $m_k> 4$
and that
$m_k> 4$
and that
![]() $n_k \leq 3$
when
$n_k \leq 3$
when
![]() $m_k = 1$
.
$m_k = 1$
.
Suppose that
![]() $m_{k} = 1$
and
$m_{k} = 1$
and
![]() $n_{k} = 3$
and
$n_{k} = 3$
and
![]() $n_{k-1} \geq m_{k-1} + 2$
. By Lemma 3.10, the words
$n_{k-1} \geq m_{k-1} + 2$
. By Lemma 3.10, the words
![]() $s_{k}v_{k}p_{k}$
and
$s_{k}v_{k}p_{k}$
and
![]() $s_{k-1}v_{k-1}^{n_{k-1}-2}p_{k}$
and
$s_{k-1}v_{k-1}^{n_{k-1}-2}p_{k}$
and
![]() $s_{k}u_{k}p_{k}$
are right-special. By Lemma 3.7, the maximal common suffix of
$s_{k}u_{k}p_{k}$
are right-special. By Lemma 3.7, the maximal common suffix of
![]() $s_{k}v_{k}p_{k}$
and
$s_{k}v_{k}p_{k}$
and
![]() $s_{k}u_{k}p_{k}$
is
$s_{k}u_{k}p_{k}$
is
![]() $s_{k}p_{k}$
. Using Lemma 3.6 and that
$s_{k}p_{k}$
. Using Lemma 3.6 and that
![]() $p_{k} = v_{k-1}^{m_{k-1}-1}p_{k-1}$
, both
$p_{k} = v_{k-1}^{m_{k-1}-1}p_{k-1}$
, both
![]() $s_{k}v_{k}p_{k}$
and
$s_{k}v_{k}p_{k}$
and
![]() $s_{k}u_{k}p_{k}$
have
$s_{k}u_{k}p_{k}$
have
![]() $s_{k-1}u_{k-1}v_{k-1}^{m_{k-1}-1}p_{k-1}$
as a suffix. By Lemma 3.7, the maximal common suffix of either of them and
$s_{k-1}u_{k-1}v_{k-1}^{m_{k-1}-1}p_{k-1}$
as a suffix. By Lemma 3.7, the maximal common suffix of either of them and
![]() $s_{k-1}v_{k-1}^{n_{k-1}-2}p_{k-1}$
is then
$s_{k-1}v_{k-1}^{n_{k-1}-2}p_{k-1}$
is then
![]() $s_{k-1}v_{k-1}^{m_{k-1}-1}p_{k-1}$
. Therefore, there are least
$s_{k-1}v_{k-1}^{m_{k-1}-1}p_{k-1}$
. Therefore, there are least
![]() $ | s_{k}v_{k}p_{k} | + | s_{k}v_{k}p_{k} | - | s_{k}p_{k} | + | s_{k-1}v_{k-1}^{n_{k-1}-1}p_{k-1} | - | s_{k-1}v_{k-1}^{m_{k-1}-1}p_{k-1} | $
right-special words of length at most
$ | s_{k}v_{k}p_{k} | + | s_{k}v_{k}p_{k} | - | s_{k}p_{k} | + | s_{k-1}v_{k-1}^{n_{k-1}-1}p_{k-1} | - | s_{k-1}v_{k-1}^{m_{k-1}-1}p_{k-1} | $
right-special words of length at most
![]() $| s_{k}v_{k}p_{k} |$
.
$| s_{k}v_{k}p_{k} |$
.
Since
![]() $p_{k} = v_{k-1}^{m_{k}-1}p_{k-1}$
,
$p_{k} = v_{k-1}^{m_{k}-1}p_{k-1}$
,
![]() $s_{k} = s_{k-1}v_{k}$
and
$s_{k} = s_{k-1}v_{k}$
and
![]() $| p_{k-1} | + | s_{k-1} | < 3| v_{k-1} |$
,
$| p_{k-1} | + | s_{k-1} | < 3| v_{k-1} |$
,
Therefore, since
![]() $n_{k-1} \geq m_{k-1} + 2$
,
$n_{k-1} \geq m_{k-1} + 2$
,
 $$ \begin{align*} \frac{p(| s_{k}v_{k}^{n_{k}-2}p_{k} |)}{| s_{k}v_{k}^{n_{k}-2}p_{k} |} &\geq 1 + \frac{| v_{k} | + (n_{k-1} - m_{k-1} - 1)| v_{k-1} |}{| v_{k} | + | p_{k} | + | s_{k} |}> 1 + \frac{| v_{k} | + | v_{k-1} |}{3| v_{k} | - | u_{k-1} | + 3| v_{k-1} |} > 1 + \frac{1}{3} \end{align*} $$
$$ \begin{align*} \frac{p(| s_{k}v_{k}^{n_{k}-2}p_{k} |)}{| s_{k}v_{k}^{n_{k}-2}p_{k} |} &\geq 1 + \frac{| v_{k} | + (n_{k-1} - m_{k-1} - 1)| v_{k-1} |}{| v_{k} | + | p_{k} | + | s_{k} |}> 1 + \frac{| v_{k} | + | v_{k-1} |}{3| v_{k} | - | u_{k-1} | + 3| v_{k-1} |} > 1 + \frac{1}{3} \end{align*} $$
contradicting our hypothesis. So if
![]() $m_{k}=1$
and
$m_{k}=1$
and
![]() $n_{k} = 3$
, then
$n_{k} = 3$
, then
![]() $n_{k-1} = m_{k-1} + 1$
.
$n_{k-1} = m_{k-1} + 1$
.
Since
![]() $s_{1}v_{1}^{t}$
is the unique right-special and unique left-special word of its length for some
$s_{1}v_{1}^{t}$
is the unique right-special and unique left-special word of its length for some
![]() $t \geq 0$
(Lemma 3.9) and
$t \geq 0$
(Lemma 3.9) and
![]() $u_{1}v_{1}^{t}$
and
$u_{1}v_{1}^{t}$
and
![]() $v_{1}$
are the two return words for
$v_{1}$
are the two return words for
![]() $s_{1}v_{1}^{t}$
, we have that
$s_{1}v_{1}^{t}$
, we have that
![]() $t \leq m_{1} - 1$
as
$t \leq m_{1} - 1$
as
![]() $u_{1}$
is always followed by
$u_{1}$
is always followed by
![]() $v_{1}^{t}$
. Since
$v_{1}^{t}$
. Since
![]() $s_{1}v_{1}^{t}$
is left-special,
$s_{1}v_{1}^{t}$
is left-special,
![]() $u_{1}v^{t}s_{1}v^{t}$
must appear meaning that
$u_{1}v^{t}s_{1}v^{t}$
must appear meaning that
![]() $t = m_{1} - 1$
. Therefore, any right-special word of length at least
$t = m_{1} - 1$
. Therefore, any right-special word of length at least
![]() $| s_{1}v_{1}^{m_{1}-1} |$
must have
$| s_{1}v_{1}^{m_{1}-1} |$
must have
![]() $s_{1}v_{1}^{m_{1}-1}$
as a suffix. As the return words for
$s_{1}v_{1}^{m_{1}-1}$
as a suffix. As the return words for
![]() $s_{1}v_{1}$
are
$s_{1}v_{1}$
are
![]() $v_{1}$
and
$v_{1}$
and
![]() $u_{1}v_{1}^{m_{1}-1}$
, then every right-special word of at least that length is a suffix of a concatenation of
$u_{1}v_{1}^{m_{1}-1}$
, then every right-special word of at least that length is a suffix of a concatenation of
![]() $u_{1}$
and
$u_{1}$
and
![]() $v_{1}$
.
$v_{1}$
.
Finally, since
![]() $v_k$
is in the language for all k, there exists a two-sided sequence containing
$v_k$
is in the language for all k, there exists a two-sided sequence containing
![]() $x^{(m_k), (n_k)} = \lim v_{k}$
. Then since X is minimal, X is the orbit closure of
$x^{(m_k), (n_k)} = \lim v_{k}$
. Then since X is minimal, X is the orbit closure of
![]() $x^{(m_k), (n_k)}$
.
$x^{(m_k), (n_k)}$
.
Remark 3.11. In future arguments, for any subshift X satisfying the structure of Proposition 3.1, we use the notation of the proof, that is,
![]() $u_k = \pi (\rho _{k-1}(1))$
,
$u_k = \pi (\rho _{k-1}(1))$
,
![]() $v_k = \pi (\rho _{k-1}(0))$
,
$v_k = \pi (\rho _{k-1}(0))$
,
![]() $p_k$
is the maximal prefix of
$p_k$
is the maximal prefix of
![]() $v_k$
and
$v_k$
and
![]() $u_k$
, and
$u_k$
, and
![]() $s_k$
is the maximal suffix of
$s_k$
is the maximal suffix of
![]() $v_k^{\infty }$
and
$v_k^{\infty }$
and
![]() $v_k^{\infty } u_k$
. In addition, as shown in the proof of Proposition 3.1, the sequence
$v_k^{\infty } u_k$
. In addition, as shown in the proof of Proposition 3.1, the sequence
![]() $(p_k)$
satisfies the recursion
$(p_k)$
satisfies the recursion
![]() $p_{k+1} = v_{k}^{m_{k}-1}p_{k} = v_k p_{k+1}$
, the sequence
$p_{k+1} = v_{k}^{m_{k}-1}p_{k} = v_k p_{k+1}$
, the sequence
![]() $(s_k)$
satisfies the recursion
$(s_k)$
satisfies the recursion
![]() $s_{k+1} = s_{k}v_{k+1}$
, and
$s_{k+1} = s_{k}v_{k+1}$
, and
![]() $|p_k| + |s_k| < \min (|u_k| + |v_k|, 3|v_k|)$
for all k.
$|p_k| + |s_k| < \min (|u_k| + |v_k|, 3|v_k|)$
for all k.
Remark 3.12. By induction on k, each substitution
![]() $\pi \circ \rho _k$
is uniquely decomposable, in the sense that each
$\pi \circ \rho _k$
is uniquely decomposable, in the sense that each
![]() $x \in X$
can be decomposed uniquely into words
$x \in X$
can be decomposed uniquely into words
![]() $(\pi \circ \rho _k)(a)$
for
$(\pi \circ \rho _k)(a)$
for
![]() $a \in \{0,1\}$
. For
$a \in \{0,1\}$
. For
![]() $k = 0$
, this follows from Lemma 2.9 since
$k = 0$
, this follows from Lemma 2.9 since
![]() $\pi (0) = v_1$
and
$\pi (0) = v_1$
and
![]() $\pi (1) = u_1$
were constructed using that lemma. If
$\pi (1) = u_1$
were constructed using that lemma. If
![]() $\pi \circ \rho _k$
is uniquely decomposable, then every x is representable uniquely as a concatenation of
$\pi \circ \rho _k$
is uniquely decomposable, then every x is representable uniquely as a concatenation of
![]() $(\pi \circ \rho _k)(0)$
and
$(\pi \circ \rho _k)(0)$
and
![]() $(\pi \circ \rho _k)(1)$
, and then the same must be true of
$(\pi \circ \rho _k)(1)$
, and then the same must be true of
![]() $(\pi \circ \rho _{k+1})(0) = (\pi \circ \rho _k)(0)^{m_{k+1} - 1} (\pi \circ \rho _k)(1)$
and
$(\pi \circ \rho _{k+1})(0) = (\pi \circ \rho _k)(0)^{m_{k+1} - 1} (\pi \circ \rho _k)(1)$
and
![]() $(\pi \circ \rho _{k+1})(1) = (\pi \circ \rho _k)(0)^{n_{k+1} - 1} (\pi \circ \rho _k)(1)$
(since each of these contains
$(\pi \circ \rho _{k+1})(1) = (\pi \circ \rho _k)(0)^{n_{k+1} - 1} (\pi \circ \rho _k)(1)$
(since each of these contains
![]() $(\pi \circ \rho _k)(1)$
exactly once).
$(\pi \circ \rho _k)(1)$
exactly once).
4 Subshifts with
 have discrete spectrum
have discrete spectrum
Theorem 4.1. If X is an infinite transitive subshift with
![]() $\limsup \frac {p(q)}{q} < \frac {4}{3}$
, then X is uniquely ergodic with unique measure which has discrete spectrum.
$\limsup \frac {p(q)}{q} < \frac {4}{3}$
, then X is uniquely ergodic with unique measure which has discrete spectrum.
Our proof relies on first proving exponential decay of some quantities, which will later be used to verify discrete spectrum via so-called mean almost periodicity.
Proposition 4.2. Let X be the orbit closure of
![]() $x^{(m_{k}),(n_{k})}$
, where
$x^{(m_{k}),(n_{k})}$
, where
![]() $(m_k), (n_k)$
satisfy the conclusions of Proposition 3.1. Then there exist
$(m_k), (n_k)$
satisfy the conclusions of Proposition 3.1. Then there exist
![]() $\epsilon _k$
which converge to
$\epsilon _k$
which converge to
![]() $0$
exponentially so that, for every k,
$0$
exponentially so that, for every k,
 $$\begin{align*}\frac{(n_{k+1}+1)| \pi(0) |\prod_{i=1}^k (n_i - m_i)}{| (\pi \circ \rho_{k+1})(0) |} < \epsilon_k. \end{align*}$$
$$\begin{align*}\frac{(n_{k+1}+1)| \pi(0) |\prod_{i=1}^k (n_i - m_i)}{| (\pi \circ \rho_{k+1})(0) |} < \epsilon_k. \end{align*}$$
Proof. We first set some preliminary notation. Define
![]() $a_{1} = 1$
and
$a_{1} = 1$
and
![]() $a_{k} = n_{k-1} - m_{k-1}$
and
$a_{k} = n_{k-1} - m_{k-1}$
and
![]() $b_{k} = m_{k}$
for
$b_{k} = m_{k}$
for
![]() $k> 0$
. Note that by Proposition 3.1, all
$k> 0$
. Note that by Proposition 3.1, all
![]() $b_k$
and
$b_k$
and
![]() $a_k$
are positive;
$a_k$
are positive;
![]() $a_{k+1} \leq b_k$
whenever
$a_{k+1} \leq b_k$
whenever
![]() $b_k> 1$
;
$b_k> 1$
;
![]() $a_{k+1} < 0.9b_{k}$
whenever
$a_{k+1} < 0.9b_{k}$
whenever
![]() $b_{k}> 4$
; and
$b_{k}> 4$
; and
![]() $a_{k+1} \leq 2$
whenever
$a_{k+1} \leq 2$
whenever
![]() $b_{k} = 1$
. We also define
$b_{k} = 1$
. We also define
![]() $d_{k} = | (\pi \circ \rho _k)(0) |$
and note that
$d_{k} = | (\pi \circ \rho _k)(0) |$
and note that
![]() $(d_k)$
satisfies the recursion
$(d_k)$
satisfies the recursion
where
![]() $d_{-1} = | \pi (1) | - | \pi (0) |$
and
$d_{-1} = | \pi (1) | - | \pi (0) |$
and
![]() $d_{0} = | \pi (0) |$
.
$d_{0} = | \pi (0) |$
.
For ease of notation, define
 $$\begin{align*}\beta_j = \frac{a_{j+1} d_{j-1}}{d_j} \end{align*}$$
$$\begin{align*}\beta_j = \frac{a_{j+1} d_{j-1}}{d_j} \end{align*}$$
and observe that, by equation (4.1),
 $$\begin{align*}\beta_{j+1} = \frac{a_{j+2}d_{j}}{d_{j+1}} = \frac{a_{j+2}}{b_{j+1} + a_{j+1}\frac{d_{j-1}}{d_{j}}} = \frac{a_{j+2}}{b_{j+1} + \beta_{j}}. \end{align*}$$
$$\begin{align*}\beta_{j+1} = \frac{a_{j+2}d_{j}}{d_{j+1}} = \frac{a_{j+2}}{b_{j+1} + a_{j+1}\frac{d_{j-1}}{d_{j}}} = \frac{a_{j+2}}{b_{j+1} + \beta_{j}}. \end{align*}$$
Note that
![]() $\beta _{0} = \frac {a_{1}d_{-1}}{d_{0}} = \frac {d_{-1}}{| \pi (0) |}$
. Then
$\beta _{0} = \frac {a_{1}d_{-1}}{d_{0}} = \frac {d_{-1}}{| \pi (0) |}$
. Then
 $$ \begin{align} \frac{| \pi(0) |a_{1}\cdots a_{k+1}}{d_{k}} = \frac{| \pi(0) |}{d_{-1}}\prod_{j=0}^{k} \frac{a_{j+1}d_{j-1}}{d_{j}} = \frac{| \pi(0) |}{d_{-1}}\beta_{0} \prod_{j=1}^{k} \beta_{j} = \prod_{j=1}^{k} \beta_{j}. \end{align} $$
$$ \begin{align} \frac{| \pi(0) |a_{1}\cdots a_{k+1}}{d_{k}} = \frac{| \pi(0) |}{d_{-1}}\prod_{j=0}^{k} \frac{a_{j+1}d_{j-1}}{d_{j}} = \frac{| \pi(0) |}{d_{-1}}\beta_{0} \prod_{j=1}^{k} \beta_{j} = \prod_{j=1}^{k} \beta_{j}. \end{align} $$
Claim.
![]() $0 < \beta _{j} < 2$
for all
$0 < \beta _{j} < 2$
for all
![]() $j \geq 0$
.
$j \geq 0$
.
Proof. Since
![]() $a_{j+1} \leq b_{j} + 1$
for all j,
$a_{j+1} \leq b_{j} + 1$
for all j,
![]() $\beta _{j} \leq \frac {b_{j}+1}{b_{j}+\beta } < 1 + \frac {1}{b_{j}} \leq 2$
.
$\beta _{j} \leq \frac {b_{j}+1}{b_{j}+\beta } < 1 + \frac {1}{b_{j}} \leq 2$
.
Claim. If
![]() $a_{j+1} \leq b_{j}$
, then
$a_{j+1} \leq b_{j}$
, then
![]() $\beta _{j} < 1$
.
$\beta _{j} < 1$
.
Proof. Since
![]() $\beta _{j-1}> 0$
,
$\beta _{j-1}> 0$
,
![]() $\beta _{j} = \frac {a_{j+1}}{b_{j} + \beta _{j-1}} < \frac {a_{j+1}}{b_{j}} \leq 1$
.
$\beta _{j} = \frac {a_{j+1}}{b_{j} + \beta _{j-1}} < \frac {a_{j+1}}{b_{j}} \leq 1$
.
Claim. If
![]() $a_{j+1} = b_{j} + 1$
, then at least one of
$a_{j+1} = b_{j} + 1$
, then at least one of
![]() $\beta _{j} < 1$
or
$\beta _{j} < 1$
or
![]() $\beta _{j}\beta _{j-1} \leq 1$
.
$\beta _{j}\beta _{j-1} \leq 1$
.
Proof. When
![]() $a_{j+1} = 2$
and
$a_{j+1} = 2$
and
![]() $b_{j} = 1$
, by Proposition 3.1,
$b_{j} = 1$
, by Proposition 3.1,
![]() $\tau _{1,3}$
cannot occur for consecutive values so we have
$\tau _{1,3}$
cannot occur for consecutive values so we have
![]() $a_{j} \leq b_{j}$
so
$a_{j} \leq b_{j}$
so
![]() $\beta _{j-1} \leq 1$
. Since
$\beta _{j-1} \leq 1$
. Since
![]() $\beta _{j} = \frac {2}{1 + \beta _{j-1}} \geq 1$
, we have
$\beta _{j} = \frac {2}{1 + \beta _{j-1}} \geq 1$
, we have
![]() $\beta _{j}\beta _{j-1} = 2 - \beta _{j} \leq 1$
.
$\beta _{j}\beta _{j-1} = 2 - \beta _{j} \leq 1$
.
This implies
![]() $\prod _{j=1}^{k} \beta _{j} \leq \beta _{1} \leq 2$
.
$\prod _{j=1}^{k} \beta _{j} \leq \beta _{1} \leq 2$
.
By the assumptions on
![]() $(m_k)$
and
$(m_k)$
and
![]() $(n_k)$
, we see that
$(n_k)$
, we see that
![]() $a_{k+1} \leq b_k$
when
$a_{k+1} \leq b_k$
when
![]() $b_k> 1$
and
$b_k> 1$
and
![]() $a_{k+1} \leq 2$
when
$a_{k+1} \leq 2$
when
![]() $b_{k}=1$
and
$b_{k}=1$
and
![]() $a_{k+1} < 0.9 b_k$
when
$a_{k+1} < 0.9 b_k$
when
![]() $b_k> 4$
. We now break into several cases.
$b_k> 4$
. We now break into several cases.
Case 1: If
![]() $b_{j}> 4$
, then
$b_{j}> 4$
, then
![]() $\beta _{j} < 0.9$
.
$\beta _{j} < 0.9$
.
Proof. If
![]() $b_{j}> 4$
, then, as
$b_{j}> 4$
, then, as
![]() $d_{j}> b_{j}d_{j-1}$
by equation (4.1),
$d_{j}> b_{j}d_{j-1}$
by equation (4.1),
![]() $\beta _{j} = \frac {a_{j+1}d_{j-1}}{d_{j}} < 0.9$
.
$\beta _{j} = \frac {a_{j+1}d_{j-1}}{d_{j}} < 0.9$
.
Case 2: If
![]() $a_{j+1} \leq b_{j} \leq 4$
and
$a_{j+1} \leq b_{j} \leq 4$
and
![]() $b_{j-1} \leq 4$
, then
$b_{j-1} \leq 4$
, then
![]() $\beta _{j} < 0.96$
.
$\beta _{j} < 0.96$
.
Proof. If
![]() $a_{j+1} \leq b_{j} \leq 4$
and
$a_{j+1} \leq b_{j} \leq 4$
and
![]() $b_{j-1} \leq 4$
, then by equation (4.1),
$b_{j-1} \leq 4$
, then by equation (4.1),
Then, again by equation (4.1), using that
![]() $a_{j+1} \leq b_{j}$
,
$a_{j+1} \leq b_{j}$
,
 $$\begin{align*}\frac{d_{j}}{d_{j-1}} = b_{j} + \frac{a_{j} d_{j-2}}{d_{j-1}}> b_{j} + \frac{1}{6} \geq a_{j+1} + \frac{1}{6}. \end{align*}$$
$$\begin{align*}\frac{d_{j}}{d_{j-1}} = b_{j} + \frac{a_{j} d_{j-2}}{d_{j-1}}> b_{j} + \frac{1}{6} \geq a_{j+1} + \frac{1}{6}. \end{align*}$$
Therefore, since
![]() $a_{j+1} \leq b_{j} \leq 4$
,
$a_{j+1} \leq b_{j} \leq 4$
,
 $$\begin{align*}\beta_{j} = \frac{a_{j+1} d_{j-1}}{d_{j}} < \frac{a_{j+1}}{a_{j+1} + (1/6)} = \left(1 + \frac{1}{6a_{j+1}}\right)^{-1} <\left(1 + \frac{1}{24}\right)^{-1} = 0.96. \end{align*}$$
$$\begin{align*}\beta_{j} = \frac{a_{j+1} d_{j-1}}{d_{j}} < \frac{a_{j+1}}{a_{j+1} + (1/6)} = \left(1 + \frac{1}{6a_{j+1}}\right)^{-1} <\left(1 + \frac{1}{24}\right)^{-1} = 0.96. \end{align*}$$
Case 3: If
![]() $a_{j+1} \leq b_{j} \leq 4$
and
$a_{j+1} \leq b_{j} \leq 4$
and
![]() $b_{j-1}> 4$
, then at least one of
$b_{j-1}> 4$
, then at least one of
![]() $\beta _{j} < 0.96$
or
$\beta _{j} < 0.96$
or
![]() $\beta _{j}\beta _{j-1} < 0.5$
holds.
$\beta _{j}\beta _{j-1} < 0.5$
holds.
Proof. Consider when
![]() $a_{j+1} \leq b_{j} \leq 4$
and
$a_{j+1} \leq b_{j} \leq 4$
and
![]() $b_{j-1}> 4$
so
$b_{j-1}> 4$
so
![]() $\beta _{j-1} < 0.96$
. Suppose
$\beta _{j-1} < 0.96$
. Suppose
![]() $\beta _{j}> \frac {8}{9}$
. Then
$\beta _{j}> \frac {8}{9}$
. Then
 $$\begin{align*}\frac{8}{9} < \frac{a_{j+1}}{b_{j} + \beta_{j-1}} \leq \frac{b_{j}}{b_{j} + \beta_{j-1}} \leq \frac{4}{4 + \beta_{j-1}}, \end{align*}$$
$$\begin{align*}\frac{8}{9} < \frac{a_{j+1}}{b_{j} + \beta_{j-1}} \leq \frac{b_{j}}{b_{j} + \beta_{j-1}} \leq \frac{4}{4 + \beta_{j-1}}, \end{align*}$$
so
![]() $8 + 2\beta _{j-1} < 9$
so
$8 + 2\beta _{j-1} < 9$
so
![]() $\beta _{j-1} < \frac {1}{2}$
. Then
$\beta _{j-1} < \frac {1}{2}$
. Then
![]() $\beta _{j}\beta _{j-1} < \beta _{j-1} < 0.5$
since
$\beta _{j}\beta _{j-1} < \beta _{j-1} < 0.5$
since
![]() $a_{j+1} \leq b_{j}$
implies
$a_{j+1} \leq b_{j}$
implies
![]() $\beta _{j} < 1$
. So at least one of
$\beta _{j} < 1$
. So at least one of
![]() $\beta _{j} \leq \frac {8}{9} < 0.96$
or
$\beta _{j} \leq \frac {8}{9} < 0.96$
or
![]() $\beta _{j}\beta _{j-1} < 0.5$
must hold.
$\beta _{j}\beta _{j-1} < 0.5$
must hold.
Any j where
![]() $a_{j+1} \leq b_j$
is covered by Case 1 if
$a_{j+1} \leq b_j$
is covered by Case 1 if
![]() $b_j> 4$
and Case 2 or 3 if
$b_j> 4$
and Case 2 or 3 if
![]() $b_j \leq 4$
. The only remaining case is then
$b_j \leq 4$
. The only remaining case is then
![]() $a_{j+1}> b_j$
, which happens only if
$a_{j+1}> b_j$
, which happens only if
![]() $a_{j+1} = 2$
and
$a_{j+1} = 2$
and
![]() $b_j = 1$
.
$b_j = 1$
.
Case 4: If
![]() $a_{j+1} = 2$
and
$a_{j+1} = 2$
and
![]() $b_{j} = 1$
, then at least one of
$b_{j} = 1$
, then at least one of
![]() $\beta _{j}\beta _{j-1} < \frac {48}{49}$
or
$\beta _{j}\beta _{j-1} < \frac {48}{49}$
or
![]() $\beta _{j}\beta _{j-1}\beta _{j-2} < 0.52$
holds.
$\beta _{j}\beta _{j-1}\beta _{j-2} < 0.52$
holds.
Proof. Consider any such j. By Proposition 3.1,
![]() $\tau _{1,3}$
cannot occur consecutively so
$\tau _{1,3}$
cannot occur consecutively so
![]() $a_j \leq b_{j-1}$
, and so
$a_j \leq b_{j-1}$
, and so
![]() $j-1$
is in one of Cases 1–3. If
$j-1$
is in one of Cases 1–3. If
![]() $\beta _{j-1} < 0.96$
, then
$\beta _{j-1} < 0.96$
, then
 $$\begin{align*}\beta_{j}\beta_{j-1} = \frac{a_{j+1}}{b_{j} + \beta_{j-1}}\beta_{j-1} = \frac{2\beta_{j-1}}{1 + \beta_{j}-1} = 1 + \frac{\beta_{j-1} - 1}{\beta_{j-1} + 1} < 1 + \frac{0.96 - 1}{0.96 + 1} = \frac{48}{49}. \end{align*}$$
$$\begin{align*}\beta_{j}\beta_{j-1} = \frac{a_{j+1}}{b_{j} + \beta_{j-1}}\beta_{j-1} = \frac{2\beta_{j-1}}{1 + \beta_{j}-1} = 1 + \frac{\beta_{j-1} - 1}{\beta_{j-1} + 1} < 1 + \frac{0.96 - 1}{0.96 + 1} = \frac{48}{49}. \end{align*}$$
If
![]() $\beta _{j-1} \geq 0.96$
, then
$\beta _{j-1} \geq 0.96$
, then
![]() $j-1$
must be in Case 3 and
$j-1$
must be in Case 3 and
![]() $\beta _{j-1}\beta _{j-2} < 0.5$
. Then
$\beta _{j-1}\beta _{j-2} < 0.5$
. Then
Claim. For all
![]() $k \geq 1$
,
$k \geq 1$
,
 $$\begin{align*}\prod_{j=1}^{k} \beta_{j} < 2 \Big{(}\frac{48}{49}\Big{)}^{k/2}. \end{align*}$$
$$\begin{align*}\prod_{j=1}^{k} \beta_{j} < 2 \Big{(}\frac{48}{49}\Big{)}^{k/2}. \end{align*}$$
Proof. All
![]() $j>2$
are in one of the cases above, and so at least one of the following hold:
$j>2$
are in one of the cases above, and so at least one of the following hold:
![]() $\beta _{j} < 0.96$
,
$\beta _{j} < 0.96$
,
![]() $\beta _{j}\beta _{j-1} < \frac {48}{49}$
, or
$\beta _{j}\beta _{j-1} < \frac {48}{49}$
, or
![]() $\beta _{j}\beta _{j-1}\beta _{j-2} < 0.52$
. For every k, we can group the product
$\beta _{j}\beta _{j-1}\beta _{j-2} < 0.52$
. For every k, we can group the product
![]() $\prod _{j=1}^{k} \beta _{j}$
into products of one, two or three consecutive terms bounded from above in this way, with the possible exception of
$\prod _{j=1}^{k} \beta _{j}$
into products of one, two or three consecutive terms bounded from above in this way, with the possible exception of
![]() $\beta _1$
or
$\beta _1$
or
![]() $\beta _1 \beta _2$
. As
$\beta _1 \beta _2$
. As
![]() $0.96 < \sqrt {\frac {48}{49}}$
and
$0.96 < \sqrt {\frac {48}{49}}$
and
![]() $0.52 < (\frac {48}{49})^{3/2}$
, and since
$0.52 < (\frac {48}{49})^{3/2}$
, and since
![]() $\beta _1 \beta _2 < 1$
whenever
$\beta _1 \beta _2 < 1$
whenever
![]() $\beta _1> 1$
, this yields
$\beta _1> 1$
, this yields
 $$\begin{align*}\prod_{j=1}^{k} \beta_{j} < \beta_{1} \Big{(}\frac{48}{49}\Big{)}^{k/2} < 2 \Big{(}\frac{48}{49}\Big{)}^{k/2}.\\[-40pt] \end{align*}$$
$$\begin{align*}\prod_{j=1}^{k} \beta_{j} < \beta_{1} \Big{(}\frac{48}{49}\Big{)}^{k/2} < 2 \Big{(}\frac{48}{49}\Big{)}^{k/2}.\\[-40pt] \end{align*}$$
Since
![]() $n_{k+1} \leq 2m_{k+1} + 1 = 2b_{k+1} + 1$
, we have
$n_{k+1} \leq 2m_{k+1} + 1 = 2b_{k+1} + 1$
, we have
![]() $\frac {(n_{k+1}+1)d_{k}}{d_{k+1}} \leq \frac {(2b_{k+1}+2)d_{k}}{b_{k+1}d_{k}} = 2 + \frac {2}{b_{k+1}} \leq 4$
, and so
$\frac {(n_{k+1}+1)d_{k}}{d_{k+1}} \leq \frac {(2b_{k+1}+2)d_{k}}{b_{k+1}d_{k}} = 2 + \frac {2}{b_{k+1}} \leq 4$
, and so
 $$\begin{align*}\frac{n_{k+1}| \pi(0) |\prod_{i=1}^k (n_i - m_i)}{d_{k+1}} = \frac{n_{k+1}d_{k}}{d_{k+1}}\frac{| \pi(0) |a_{1} \cdots a_{k+1}}{d_{k}} \leq 4 \prod_{j=1}^{k} \beta_{j} < 8\left(\frac{48}{49}\right)^{k/2}. \end{align*}$$
$$\begin{align*}\frac{n_{k+1}| \pi(0) |\prod_{i=1}^k (n_i - m_i)}{d_{k+1}} = \frac{n_{k+1}d_{k}}{d_{k+1}}\frac{| \pi(0) |a_{1} \cdots a_{k+1}}{d_{k}} \leq 4 \prod_{j=1}^{k} \beta_{j} < 8\left(\frac{48}{49}\right)^{k/2}. \end{align*}$$
Defining
![]() $\epsilon _{k} := 8(\frac {48}{49})^{k/2}$
completes the proof.
$\epsilon _{k} := 8(\frac {48}{49})^{k/2}$
completes the proof.
Proof of Theorem 4.1.
Our technique for verifying discrete spectrum of X is by using mean almost periodicity, which requires a definition. The upper density of
![]() $A \subset \mathbb {N}$
, denoted
$A \subset \mathbb {N}$
, denoted
![]() $\overline {d}(A)$
, is
$\overline {d}(A)$
, is
![]() $\limsup \frac {|A \cap \{1, \ldots , n\}|}{n}$
. It’s easy to check that upper density is subadditive, that is,
$\limsup \frac {|A \cap \{1, \ldots , n\}|}{n}$
. It’s easy to check that upper density is subadditive, that is,
![]() $\overline {d}(A \cup B) \leq \overline {d}(A) + \overline {d}(B)$
for every
$\overline {d}(A \cup B) \leq \overline {d}(A) + \overline {d}(B)$
for every
![]() $A, B$
.
$A, B$
.
A subshift X is mean almost periodic if for all
![]() $\epsilon> 0$
and all
$\epsilon> 0$
and all
![]() $x \in X$
, there exists a syndetic set S so that for all
$x \in X$
, there exists a syndetic set S so that for all
![]() $s \in S$
, x and
$s \in S$
, x and
![]() $\sigma ^s x$
differ on a set of locations with upper density less than
$\sigma ^s x$
differ on a set of locations with upper density less than
![]() $\epsilon $
. It is well-known that mean almost periodicity implies discrete spectrum; see, for instance, Theorem 2.8 of [Reference Lenz and StrungaruLS09].
$\epsilon $
. It is well-known that mean almost periodicity implies discrete spectrum; see, for instance, Theorem 2.8 of [Reference Lenz and StrungaruLS09].
Examples of aperiodic but mean almost periodic subshifts are given by the Sturmian subshifts and also so-called regular Toeplitz subshifts. Since our hypotheses are satisfied by Sturmian subshifts, their mean almost periodicity follows as a corollary of our proof.
By Proposition 3.1, X is the orbit closure of
for some
![]() $\pi : \{0,1\} \rightarrow \mathcal {A}^*$
where
$\pi : \{0,1\} \rightarrow \mathcal {A}^*$
where
![]() $\pi (0), \pi (1)$
begin with different letters and
$\pi (0), \pi (1)$
begin with different letters and
![]() $|\pi (0)| < |\pi (1)| < 2|\pi (0)|$
and some sequences
$|\pi (0)| < |\pi (1)| < 2|\pi (0)|$
and some sequences
![]() $(m_k), (n_k)$
satisfying
$(m_k), (n_k)$
satisfying
![]() $0 < m_k < n_k \leq 2m_k$
or
$0 < m_k < n_k \leq 2m_k$
or
![]() $(m_{k},n_{k}) = (1,3)$
.
$(m_{k},n_{k}) = (1,3)$
.
We again use the notations
![]() $a_{k+1} = n_k - m_k$
and
$a_{k+1} = n_k - m_k$
and
![]() $d_k = |(\pi \circ \rho _k)(0)|$
as in the proof of Proposition 4.2.
$d_k = |(\pi \circ \rho _k)(0)|$
as in the proof of Proposition 4.2.
For any
![]() $k> 0$
and
$k> 0$
and
![]() $p \in \mathbb {N}$
, define the words
$p \in \mathbb {N}$
, define the words
 $$ \begin{align*} y_{0,k,p} = ((\pi \circ \rho_k)(0))^p (\pi \circ \rho_k)(1), \ & z_{0,k,p} = (\pi \circ \rho_k)(1) ( (\pi \circ \rho_k)(0))^p, \\ y_{1,k,p} = ((\pi \circ \rho_k)(1))^p (\pi \circ \rho_k)(0), \ & z_{1,k,p} = (\pi \circ \rho_k)(0) ( (\pi \circ \rho_k)(1))^p.\ \end{align*} $$
$$ \begin{align*} y_{0,k,p} = ((\pi \circ \rho_k)(0))^p (\pi \circ \rho_k)(1), \ & z_{0,k,p} = (\pi \circ \rho_k)(1) ( (\pi \circ \rho_k)(0))^p, \\ y_{1,k,p} = ((\pi \circ \rho_k)(1))^p (\pi \circ \rho_k)(0), \ & z_{1,k,p} = (\pi \circ \rho_k)(0) ( (\pi \circ \rho_k)(1))^p.\ \end{align*} $$
We will prove the following by induction:
The base case
![]() $k = 0$
trivially holds since the lengths of
$k = 0$
trivially holds since the lengths of
![]() $y_{0,0,p}, z_{0,0,p}, y_{1,0,p}, z_{1,0,p}$
are less than
$y_{0,0,p}, z_{0,0,p}, y_{1,0,p}, z_{1,0,p}$
are less than
![]() $2p|\pi (1)|$
.
$2p|\pi (1)|$
.
Assume now that equation (4.3) holds for some
![]() $k-1$
(and all p).
$k-1$
(and all p).
Consider first the case when
![]() $n_{k} \leq 2m_{k}$
.
$n_{k} \leq 2m_{k}$
.
Then by definition of
![]() $\tau _{m_k, n_k}$
, if we write
$\tau _{m_k, n_k}$
, if we write
![]() $u = (\pi \circ \rho _{k-1})(1)$
,
$u = (\pi \circ \rho _{k-1})(1)$
,
![]() $v = (\pi \circ \rho _{k-1})(0)$
,
$v = (\pi \circ \rho _{k-1})(0)$
,
![]() $m = m_k$
, and
$m = m_k$
, and
![]() $n = n_k$
, then
$n = n_k$
, then
![]() $y_{0,k,p} = (v^{m-1} u)^p v^{n-1} u$
and
$y_{0,k,p} = (v^{m-1} u)^p v^{n-1} u$
and
![]() $z_{0,k,p} = v^{n-1} u (v^{m-1} u)^p$
.
$z_{0,k,p} = v^{n-1} u (v^{m-1} u)^p$
.
Since v is a suffix of u, write
![]() $u = u^{\prime }v$
. Then, using that
$u = u^{\prime }v$
. Then, using that
![]() $m < n \leq 2m$
,
$m < n \leq 2m$
,
 $$ \begin{align*} y_{0,k,p} &= (v^{m-1}u)^{p} v^{n-1}u = (v^{m-1}u^{\prime}v)^{p} v^{m-1}v^{n-m}u = v^{m-1}(u^{\prime}v^{m})^{p}v^{n-m}u \\ &= v^{m-1}(u^{\prime}v^{n-m}v^{2m-n})^{p}v^{n-m}u, \\ z_{0,k,p} &= v^{n-1}u(v^{m-1}u)^{p} = v^{m-1}v^{n-m}(u^{\prime}v^{m})^{p}u = v^{m-1}v^{n-m}(u^{\prime}v^{2m-n}v^{n-m})^{p}u \\ &= v^{m-1}(v^{n-m}u^{\prime}v^{2m-n})^{p}v^{n-m}u. \end{align*} $$
$$ \begin{align*} y_{0,k,p} &= (v^{m-1}u)^{p} v^{n-1}u = (v^{m-1}u^{\prime}v)^{p} v^{m-1}v^{n-m}u = v^{m-1}(u^{\prime}v^{m})^{p}v^{n-m}u \\ &= v^{m-1}(u^{\prime}v^{n-m}v^{2m-n})^{p}v^{n-m}u, \\ z_{0,k,p} &= v^{n-1}u(v^{m-1}u)^{p} = v^{m-1}v^{n-m}(u^{\prime}v^{m})^{p}u = v^{m-1}v^{n-m}(u^{\prime}v^{2m-n}v^{n-m})^{p}u \\ &= v^{m-1}(v^{n-m}u^{\prime}v^{2m-n})^{p}v^{n-m}u. \end{align*} $$
Since
![]() $| u^{\prime }v^{n-m} | = | v^{n-m}u^{\prime } |$
, this means
$| u^{\prime }v^{n-m} | = | v^{n-m}u^{\prime } |$
, this means
![]() $y_{0,k,p}$
and
$y_{0,k,p}$
and
![]() $z_{0,k,p}$
differ at a number of locations equal to p times the number of locations where
$z_{0,k,p}$
differ at a number of locations equal to p times the number of locations where
![]() $u^{\prime }v^{n-m}$
and
$u^{\prime }v^{n-m}$
and
![]() $v^{n-m}u^{\prime }$
differ. Clearly,
$v^{n-m}u^{\prime }$
differ. Clearly,
![]() $u^{\prime }v^{n-m}$
and
$u^{\prime }v^{n-m}$
and
![]() $v^{n-m}u^{\prime }$
differ on the same number of locations as
$v^{n-m}u^{\prime }$
differ on the same number of locations as
![]() $u^{\prime }v^{n-m}v = uv^{n-m}$
and
$u^{\prime }v^{n-m}v = uv^{n-m}$
and
![]() $v^{n-m}u^{\prime }v = v^{n-m}u$
differ. Since
$v^{n-m}u^{\prime }v = v^{n-m}u$
differ. Since
![]() $uv^{n-m} = z_{0,k-1,n-m}$
and
$uv^{n-m} = z_{0,k-1,n-m}$
and
![]() $v^{n-m}u = y_{0,k-1,n-m}$
, the inductive hypothesis gives that they differ on fewer than
$v^{n-m}u = y_{0,k-1,n-m}$
, the inductive hypothesis gives that they differ on fewer than
![]() $2|\pi (1)|(n-m)a_{1}\cdots a_{k}$
locations. Then
$2|\pi (1)|(n-m)a_{1}\cdots a_{k}$
locations. Then
![]() $y_{0,k,p}$
and
$y_{0,k,p}$
and
![]() $z_{0,k,p}$
differ on fewer than
$z_{0,k,p}$
differ on fewer than
![]() $2|\pi (1)|p(n-m)a_{1}\cdots a_{k}$
locations. Since
$2|\pi (1)|p(n-m)a_{1}\cdots a_{k}$
locations. Since
![]() $a_{k+1} = n - m$
, this proves the claim. Similarly,
$a_{k+1} = n - m$
, this proves the claim. Similarly,
 $$ \begin{align*} y_{1,k,p} &= (v^{n-1}u)^{p}v^{m-1}u = v^{n-1}(u^{\prime}v^{n})^{p-1}u^{\prime}v^{m}u \\ &= v^{m-1}v^{n-m}(u^{\prime}v^{m}v^{n-m})^{p-1}u^{\prime}v^{m}u = v^{m-1}(v^{n-m}u^{\prime}v^{m})^{p}u, \\ z_{1,k,p} &= v^{m-1}u(v^{n-1}u)^{p} = v^{m-1}(u^{\prime}v^{n})^{p}u = v^{m-1}(u^{\prime}v^{n-m}v^{m})^{p}u, \end{align*} $$
$$ \begin{align*} y_{1,k,p} &= (v^{n-1}u)^{p}v^{m-1}u = v^{n-1}(u^{\prime}v^{n})^{p-1}u^{\prime}v^{m}u \\ &= v^{m-1}v^{n-m}(u^{\prime}v^{m}v^{n-m})^{p-1}u^{\prime}v^{m}u = v^{m-1}(v^{n-m}u^{\prime}v^{m})^{p}u, \\ z_{1,k,p} &= v^{m-1}u(v^{n-1}u)^{p} = v^{m-1}(u^{\prime}v^{n})^{p}u = v^{m-1}(u^{\prime}v^{n-m}v^{m})^{p}u, \end{align*} $$
so
![]() $y_{1,k,p}$
and
$y_{1,k,p}$
and
![]() $z_{1,k,p}$
differ on fewer than
$z_{1,k,p}$
differ on fewer than
![]() $2|\pi (1)|pa_{1}\cdots a_{k+1}$
locations.
$2|\pi (1)|pa_{1}\cdots a_{k+1}$
locations.
Consider now the case when
![]() $n_{k} = 3$
and
$n_{k} = 3$
and
![]() $m_{k} = 1$
. Here,
$m_{k} = 1$
. Here,
By Proposition 3.1,
![]() $n_{k-1} = m_{k-1} + 1$
so we have
$n_{k-1} = m_{k-1} + 1$
so we have
![]() $(\pi \circ \rho _{k-1})(1) = (\pi \circ \rho _{k-2})(0) (\pi \circ \rho _{k-1})(0)$
.
$(\pi \circ \rho _{k-1})(1) = (\pi \circ \rho _{k-2})(0) (\pi \circ \rho _{k-1})(0)$
.
First, consider when
![]() $m_{k-1}> 1$
. Here,
$m_{k-1}> 1$
. Here,
![]() $(\pi \circ \rho _{k-2})(0)$
is a prefix of
$(\pi \circ \rho _{k-2})(0)$
is a prefix of
![]() $(\pi \circ \rho _{k-1})(0)$
so there are words
$(\pi \circ \rho _{k-1})(0)$
so there are words
![]() $g = (\pi \circ \rho _{k-2})(0)$
and h such that
$g = (\pi \circ \rho _{k-2})(0)$
and h such that
![]() $(\pi \circ \rho _{k-1})(0) = gh$
and
$(\pi \circ \rho _{k-1})(0) = gh$
and
![]() $(\pi \circ \rho _{k-1})(1) = ggh$
. Then
$(\pi \circ \rho _{k-1})(1) = ggh$
. Then
![]() $ (\pi \circ \rho _{k})(0) = ggh$
and
$ (\pi \circ \rho _{k})(0) = ggh$
and
![]() $(\pi \circ \rho _{k})(1) = (gh)^{2}ggh$
so
$(\pi \circ \rho _{k})(1) = (gh)^{2}ggh$
so
 $$ \begin{align*} y_{0,k,p} &= (ggh)^{p} (ghghggh) = ggh (ggh)^{p-1} ghghggh \\ z_{0,k,p} &= (ghghggh) (ggh)^{p} = ghg (hgg)^{p-1} hgghggh \end{align*} $$
$$ \begin{align*} y_{0,k,p} &= (ggh)^{p} (ghghggh) = ggh (ggh)^{p-1} ghghggh \\ z_{0,k,p} &= (ghghggh) (ggh)^{p} = ghg (hgg)^{p-1} hgghggh \end{align*} $$
which differ on two pairs of
![]() $gh$
and
$gh$
and
![]() $hg$
and on
$hg$
and on
![]() $p-1$
pairs of
$p-1$
pairs of
![]() $ggh$
and
$ggh$
and
![]() $hgg$
.
$hgg$
.
Our inductive hypothesis does apply directly to
![]() $gh$
and
$gh$
and
![]() $hg$
; however,
$hg$
; however,
![]() $gh$
and
$gh$
and
![]() $hg$
differ on the same number of letters as
$hg$
differ on the same number of letters as
![]() $ggh = (\pi \circ \rho _{k-2})(0) ((\pi \circ \rho _{k-2})(0))^{m_{k-1}-1} (\pi \circ \rho _{k-2})(1)$
and
$ggh = (\pi \circ \rho _{k-2})(0) ((\pi \circ \rho _{k-2})(0))^{m_{k-1}-1} (\pi \circ \rho _{k-2})(1)$
and
![]() $ghg = ((\pi \circ \rho _{k-2})(0))^{m_{k-1}-1} (\pi \circ \rho _{k-2})(1) (\pi \circ \rho _{k-2})(0)$
. Those words differ on the same number of letters as
$ghg = ((\pi \circ \rho _{k-2})(0))^{m_{k-1}-1} (\pi \circ \rho _{k-2})(1) (\pi \circ \rho _{k-2})(0)$
. Those words differ on the same number of letters as
![]() $(\pi \circ \rho _{k-2})(0)(\pi \circ \rho _{k-2})(1)$
and
$(\pi \circ \rho _{k-2})(0)(\pi \circ \rho _{k-2})(1)$
and
![]() $(\pi \circ \rho _{k-2})(1)(\pi \circ \rho _{k-2})(0)$
, and by hypothesis they differ on fewer than
$(\pi \circ \rho _{k-2})(1)(\pi \circ \rho _{k-2})(0)$
, and by hypothesis they differ on fewer than
![]() $2| \pi (1) |a_{1}\cdots a_{k-1}$
locations.
$2| \pi (1) |a_{1}\cdots a_{k-1}$
locations.
Similarly,
![]() $gggh = ((\pi \circ \rho _{k-2})(0))^{m_{k-1}+1}(\pi \circ \rho _{k-2})(1)$
and
$gggh = ((\pi \circ \rho _{k-2})(0))^{m_{k-1}+1}(\pi \circ \rho _{k-2})(1)$
and
![]() $ghgg = ((\pi \circ \rho _{k-2})(0))^{m_{k-1}-1}(\pi \circ \rho _{k-2})(1)((\pi \circ \rho _{k-2})(0))^{2}$
differ on the same number of letters as
$ghgg = ((\pi \circ \rho _{k-2})(0))^{m_{k-1}-1}(\pi \circ \rho _{k-2})(1)((\pi \circ \rho _{k-2})(0))^{2}$
differ on the same number of letters as
![]() $(\pi \circ \rho _{k-2})(1)((\pi \circ \rho _{k-2})(0))^{2}$
and
$(\pi \circ \rho _{k-2})(1)((\pi \circ \rho _{k-2})(0))^{2}$
and
![]() $((\pi \circ \rho _{k-2})(0))^{2}(\pi \circ \rho _{k-2})(1)$
which by hypothesis is fewer than
$((\pi \circ \rho _{k-2})(0))^{2}(\pi \circ \rho _{k-2})(1)$
which by hypothesis is fewer than
![]() $2| \pi (1) |2a_{1}\cdots a_{k-1}$
locations.
$2| \pi (1) |2a_{1}\cdots a_{k-1}$
locations.
Therefore,
![]() $y_{0,k,p}$
and
$y_{0,k,p}$
and
![]() $z_{0,k,p}$
differ on fewer than
$z_{0,k,p}$
differ on fewer than
![]() $2 \cdot 2| \pi (1) |a_{1}\cdots a_{k-1} + 2(p-1)2| \pi (1) |a_{1}\cdots a_{k-1}$
locations. Since
$2 \cdot 2| \pi (1) |a_{1}\cdots a_{k-1} + 2(p-1)2| \pi (1) |a_{1}\cdots a_{k-1}$
locations. Since
![]() $a_{k} = 1$
and
$a_{k} = 1$
and
![]() $a_{k+1} = 2$
, they differ on fewer than
$a_{k+1} = 2$
, they differ on fewer than
![]() $2| \pi (1) |p a_{1} \cdots a_{k+1}$
locations. Similarly,
$2| \pi (1) |p a_{1} \cdots a_{k+1}$
locations. Similarly,
 $$ \begin{align*} y_{1,k,p} &= (ghghggh)^{p}ggh = ghg(hgghghg)^{p-1} hgghggh \\ z_{1,k,p} &= ggh(ghghggh)^{p} = ggh (ghghggh)^{p-1} ghghggh \end{align*} $$
$$ \begin{align*} y_{1,k,p} &= (ghghggh)^{p}ggh = ghg(hgghghg)^{p-1} hgghggh \\ z_{1,k,p} &= ggh(ghghggh)^{p} = ggh (ghghggh)^{p-1} ghghggh \end{align*} $$
differ on two pairs of
![]() $gh$
and
$gh$
and
![]() $hg$
and on
$hg$
and on
![]() $p-1$
pairs of
$p-1$
pairs of
![]() $hgghghg$
and
$hgghghg$
and
![]() $ghghggh$
. As
$ghghggh$
. As
![]() $hgghghg$
and
$hgghghg$
and
![]() $ghghggh$
differ on two pairs of
$ghghggh$
differ on two pairs of
![]() $gh$
and
$gh$
and
![]() $hg$
, the total number of differences is
$hg$
, the total number of differences is
![]() $2p$
times the number of differences between
$2p$
times the number of differences between
![]() $gh$
and
$gh$
and
![]() $hg$
. Since
$hg$
. Since
![]() $gh$
and
$gh$
and
![]() $hg$
differ on fewer than
$hg$
differ on fewer than
![]() $2| \pi (1) | a_{1} \cdots a_{k-1}$
locations, and since
$2| \pi (1) | a_{1} \cdots a_{k-1}$
locations, and since
![]() $a_{k} = 1$
and
$a_{k} = 1$
and
![]() $a_{k+1} = 2$
,
$a_{k+1} = 2$
,
![]() $y_{1,k,p}$
and
$y_{1,k,p}$
and
![]() $z_{1,k,p}$
differ on fewer than
$z_{1,k,p}$
differ on fewer than
![]() $2| \pi (1) |p a_{1} \cdots a_{k+1}$
locations.
$2| \pi (1) |p a_{1} \cdots a_{k+1}$
locations.
Now, consider when
![]() $m_{k-1} = 1$
. Here,
$m_{k-1} = 1$
. Here,
![]() $(\pi \circ \rho _{k-1})(0) = (\pi \circ \rho _{k-2})(1)$
so
$(\pi \circ \rho _{k-1})(0) = (\pi \circ \rho _{k-2})(1)$
so
![]() $(\pi \circ \rho _{k-2})(0)$
is a suffix of
$(\pi \circ \rho _{k-2})(0)$
is a suffix of
![]() $(\pi \circ \rho _{k-1})(1)$
. So there are words
$(\pi \circ \rho _{k-1})(1)$
. So there are words
![]() $g = (\pi \circ \rho _{k-2})(0)$
and h such that
$g = (\pi \circ \rho _{k-2})(0)$
and h such that
![]() $(\pi \circ \rho _{k-1})(0) = hg$
. Then
$(\pi \circ \rho _{k-1})(0) = hg$
. Then
![]() $(\pi \circ \rho _{k})(0) = ghg$
and
$(\pi \circ \rho _{k})(0) = ghg$
and
![]() $(\pi \circ \rho _{k})(1) = (hg)^{2}ghg$
so
$(\pi \circ \rho _{k})(1) = (hg)^{2}ghg$
so
 $$ \begin{align*} y_{0,k,p} &= (ghg)^{p}hghgghg = gh(ggh)^{p-1}ghghgghg \\ z_{0,k,p} &= hghgghg(ghg)^{p} = hg(hgg)^{p-1}hgghgghg \end{align*} $$
$$ \begin{align*} y_{0,k,p} &= (ghg)^{p}hghgghg = gh(ggh)^{p-1}ghghgghg \\ z_{0,k,p} &= hghgghg(ghg)^{p} = hg(hgg)^{p-1}hgghgghg \end{align*} $$
which differ on two pairs of
![]() $gh$
and
$gh$
and
![]() $hg$
and on
$hg$
and on
![]() $p-1$
pairs of
$p-1$
pairs of
![]() $ggh$
and
$ggh$
and
![]() $hgg$
. Since
$hgg$
. Since
![]() $gghg = (\pi \circ \rho _{k-2})(0)^{2} (\pi \circ \rho _{k-1})(0) = (\pi \circ \rho _{k-2})(0)^{2} (\pi \circ \rho _{k-2})(1)$
and
$gghg = (\pi \circ \rho _{k-2})(0)^{2} (\pi \circ \rho _{k-1})(0) = (\pi \circ \rho _{k-2})(0)^{2} (\pi \circ \rho _{k-2})(1)$
and
![]() $hggg = (\pi \circ \rho _{k-2})(1) ((\pi \circ \rho _{k-2})(0))^{2}$
by hypothesis they differ on fewer than
$hggg = (\pi \circ \rho _{k-2})(1) ((\pi \circ \rho _{k-2})(0))^{2}$
by hypothesis they differ on fewer than
![]() $2| \pi (1) |2a_{1}\cdots a_{k-1}$
locations. Then, as above,
$2| \pi (1) |2a_{1}\cdots a_{k-1}$
locations. Then, as above,
![]() $y_{0,k,p}$
and
$y_{0,k,p}$
and
![]() $z_{0,k,p}$
differ on fewer than
$z_{0,k,p}$
differ on fewer than
![]() $2| \pi (1) |p a_{1} \cdots a_{k+1}$
locations. Similarly,
$2| \pi (1) |p a_{1} \cdots a_{k+1}$
locations. Similarly,
 $$ \begin{align*} y_{1,k,p} &= (hghgghg)^{p}ghg = hg (hgghghg)^{p-1} hgghgghg \\ z_{1,k,p} &= ghg(hghgghg)^{p} = gh(ghghggh)^{p-1} ghghgghg \end{align*} $$
$$ \begin{align*} y_{1,k,p} &= (hghgghg)^{p}ghg = hg (hgghghg)^{p-1} hgghgghg \\ z_{1,k,p} &= ghg(hghgghg)^{p} = gh(ghghggh)^{p-1} ghghgghg \end{align*} $$
differ on
![]() $2p$
pairs of
$2p$
pairs of
![]() $gh$
and
$gh$
and
![]() $hg$
so
$hg$
so
![]() $y_{1,k,p}$
and
$y_{1,k,p}$
and
![]() $z_{1,k,p}$
differ on fewer than
$z_{1,k,p}$
differ on fewer than
![]() $2| \pi (1) | p a_{1} \cdots a_{k+1}$
locations.
$2| \pi (1) | p a_{1} \cdots a_{k+1}$
locations.
We will now prove that X is mean almost periodic. Fix any k, and as before, define
![]() $u = (\pi \circ \rho _{k-1})(1)$
,
$u = (\pi \circ \rho _{k-1})(1)$
,
![]() $v = (\pi \circ \rho _{k-1})(0)$
,
$v = (\pi \circ \rho _{k-1})(0)$
,
![]() $m = m_k$
, and
$m = m_k$
, and
![]() $n = n_k$
. Choose any
$n = n_k$
. Choose any
![]() $y \in X$
; by minimality of X, y can be written as a bi-infinite concatenation of the words
$y \in X$
; by minimality of X, y can be written as a bi-infinite concatenation of the words
![]() $(\pi \circ \rho _k)(0) = v^{m-1} u$
and
$(\pi \circ \rho _k)(0) = v^{m-1} u$
and
![]() $(\pi \circ \rho _k)(1) = v^{n-1} u$
. We may assume without loss of generality that y contains
$(\pi \circ \rho _k)(1) = v^{n-1} u$
. We may assume without loss of generality that y contains
![]() $v^{m-1} u$
starting at the origin, since any syndetic set S as in the definition of mean almost periodicity for y also works for any shift of y. Since
$v^{m-1} u$
starting at the origin, since any syndetic set S as in the definition of mean almost periodicity for y also works for any shift of y. Since
![]() $d_{k} = |v^{m-1}u|$
, let us write
$d_{k} = |v^{m-1}u|$
, let us write
 $$ \begin{align*} y & = \ldots.v^{m-1} u v^{i_1 - 1} u v^{i_2 - 1} u \ldots\\ \sigma^{d_k} y & = \ldots.v^{i_1 - 1} u v^{i_2 - 1} u \ldots, \end{align*} $$
$$ \begin{align*} y & = \ldots.v^{m-1} u v^{i_1 - 1} u v^{i_2 - 1} u \ldots\\ \sigma^{d_k} y & = \ldots.v^{i_1 - 1} u v^{i_2 - 1} u \ldots, \end{align*} $$
where each
![]() $i_k$
is either m or n. We can rewrite as
$i_k$
is either m or n. We can rewrite as
 $$ \begin{align*} y & = \ldots.v^{m-1} (u v^{i_1 - m}) v^{m-1} (u v^{i_2 - m}) v^{m-1} \ldots\\ \sigma^{d_k} y & = \ldots.v^{m-1} (v^{i_1 - m} u) v^{m-1} (v^{i_2 - m} u) v^{m-1} \ldots \end{align*} $$
$$ \begin{align*} y & = \ldots.v^{m-1} (u v^{i_1 - m}) v^{m-1} (u v^{i_2 - m}) v^{m-1} \ldots\\ \sigma^{d_k} y & = \ldots.v^{m-1} (v^{i_1 - m} u) v^{m-1} (v^{i_2 - m} u) v^{m-1} \ldots \end{align*} $$
The words inside parentheses are unequal exactly when
![]() $i_j = n$
, in which case they are the pair
$i_j = n$
, in which case they are the pair
![]() $u v^{n-m}$
,
$u v^{n-m}$
,
![]() $v^{n-m} u$
. Since the lengths of
$v^{n-m} u$
. Since the lengths of
![]() $u v^{n-m}$
and
$u v^{n-m}$
and
![]() $v^{n-m} u$
are the same, this means that the only differences in y and
$v^{n-m} u$
are the same, this means that the only differences in y and
![]() $\sigma ^{d_k} y$
occur within pairs
$\sigma ^{d_k} y$
occur within pairs
![]() $u v^{n-m}$
,
$u v^{n-m}$
,
![]() $v^{n-m} u$
. By equation (4.3), the number of differences in any such pair is bounded from above by
$v^{n-m} u$
. By equation (4.3), the number of differences in any such pair is bounded from above by
![]() $2|\pi (1)| (n-m) a_1 \ldots a_k = 2|\pi (1)| a_1 \ldots a_{k+1}$
. When y is partitioned into its level-
$2|\pi (1)| (n-m) a_1 \ldots a_k = 2|\pi (1)| a_1 \ldots a_{k+1}$
. When y is partitioned into its level-
![]() $(k+1)$
words
$(k+1)$
words
![]() $(\pi \circ \rho _{k+1})(0)$
and
$(\pi \circ \rho _{k+1})(0)$
and
![]() $(\pi \circ \rho _{k+1})(1)$
(and
$(\pi \circ \rho _{k+1})(1)$
(and
![]() $\sigma ^{d_k}$
is partitioned at the same locations), each partitioned segment contains exactly one such pair
$\sigma ^{d_k}$
is partitioned at the same locations), each partitioned segment contains exactly one such pair
![]() $u v^{n-m}$
,
$u v^{n-m}$
,
![]() $v^{n-m} u$
. Since each such segment has length at least
$v^{n-m} u$
. Since each such segment has length at least
![]() $|(\pi \circ \rho _{k+1})(0)| = d_{k+1}$
,
$|(\pi \circ \rho _{k+1})(0)| = d_{k+1}$
,
For ease of notation, we define
![]() $D_q = \{t \ : \ y(t) \neq y(t+q)\}$
for every q; by the above,
$D_q = \{t \ : \ y(t) \neq y(t+q)\}$
for every q; by the above,
Now, fix any k and consider the set
 $$\begin{align*}S_k := \left\{\sum_{i = k}^{r} p_i d_i \ : \ r> k, 0 \leq p_i \leq n_{i+1}+1\right\}. \end{align*}$$
$$\begin{align*}S_k := \left\{\sum_{i = k}^{r} p_i d_i \ : \ r> k, 0 \leq p_i \leq n_{i+1}+1\right\}. \end{align*}$$
We claim that
![]() $S_k$
is syndetic. To see this, note that
$S_k$
is syndetic. To see this, note that
![]() $n_{i+1} d_i> d_{i+1}$
for all i since
$n_{i+1} d_i> d_{i+1}$
for all i since
![]() $d_{i+1} = m_{i+1}d_{i} + (n_{i} - m_{i})d_{i-1} \leq m_{i+1}d_{i} + (m_{i}+1)d_{i-1} < m_{i+1}d_{i} + d_{i} + d_{i-1} \leq (m_{i+1}+2)d_{i} \leq (n_{i+1}+1)d_{i}$
, and so a simple greedy algorithm shows that for all
$d_{i+1} = m_{i+1}d_{i} + (n_{i} - m_{i})d_{i-1} \leq m_{i+1}d_{i} + (m_{i}+1)d_{i-1} < m_{i+1}d_{i} + d_{i} + d_{i-1} \leq (m_{i+1}+2)d_{i} \leq (n_{i+1}+1)d_{i}$
, and so a simple greedy algorithm shows that for all
![]() $M \in \mathbb {N}$
, there exists
$M \in \mathbb {N}$
, there exists
![]() $s \in S_k$
with
$s \in S_k$
with
![]() $M \leq s < M + d_k$
.
$M \leq s < M + d_k$
.
Finally, choose any
![]() $s = \sum _{i = k}^{r} p_i d_i \in S_k$
. For any
$s = \sum _{i = k}^{r} p_i d_i \in S_k$
. For any
![]() $\ell _1, \ell _2 \in \mathbb {N}$
,
$\ell _1, \ell _2 \in \mathbb {N}$
,
![]() $D_{\ell _1 + \ell _2} \subset D_{\ell _1} \cup (D_{\ell _2} - \ell _1)$
since
$D_{\ell _1 + \ell _2} \subset D_{\ell _1} \cup (D_{\ell _2} - \ell _1)$
since
![]() $t \in D_{\ell _{1}+\ell _{2}}$
implies at least one of
$t \in D_{\ell _{1}+\ell _{2}}$
implies at least one of
![]() $y(t) \ne y(t+\ell _{1})$
or
$y(t) \ne y(t+\ell _{1})$
or
![]() $y(t+\ell _{1}) \ne y(t+\ell _{1}+\ell _{2})$
, and so
$y(t+\ell _{1}) \ne y(t+\ell _{1}+\ell _{2})$
, and so
![]() $\overline {d}(D_{\ell _1 + \ell _2}) \leq \overline {d}(D_{\ell _1}) + \overline {d}(D_{\ell _2})$
. Using this repeatedly implies
$\overline {d}(D_{\ell _1 + \ell _2}) \leq \overline {d}(D_{\ell _1}) + \overline {d}(D_{\ell _2})$
. Using this repeatedly implies
 $$\begin{align*}\overline{d}(D_s) = \overline{d}\left(D_{\sum_{i = k}^{r} p_i d_i}\right) \leq \sum_{i = k}^r p_i \overline{d}(D_{d_i}) \leq \sum_{i = k}^r \frac{2|\pi(1)| n_{i+1} a_1 \ldots a_{i+1}}{d_{i+1}}. \end{align*}$$
$$\begin{align*}\overline{d}(D_s) = \overline{d}\left(D_{\sum_{i = k}^{r} p_i d_i}\right) \leq \sum_{i = k}^r p_i \overline{d}(D_{d_i}) \leq \sum_{i = k}^r \frac{2|\pi(1)| n_{i+1} a_1 \ldots a_{i+1}}{d_{i+1}}. \end{align*}$$
Proposition 4.2 implies that
![]() $\frac {(n_{i+1}+1) | \pi (0) | a_{1}\cdots a_{i+1}}{d_{i+1}} < \epsilon _i$
for a sequence
$\frac {(n_{i+1}+1) | \pi (0) | a_{1}\cdots a_{i+1}}{d_{i+1}} < \epsilon _i$
for a sequence
![]() $\epsilon _i$
which is exponentially decaying. Then
$\epsilon _i$
which is exponentially decaying. Then
![]() $ \overline {d}(D_s) < \sum _{i=k}^r \frac {2| \pi (1) |}{| \pi (0) |} \epsilon _i $
. Since
$ \overline {d}(D_s) < \sum _{i=k}^r \frac {2| \pi (1) |}{| \pi (0) |} \epsilon _i $
. Since
![]() $(\epsilon _i)$
is summable, the right-hand side becomes arbitrarily small as
$(\epsilon _i)$
is summable, the right-hand side becomes arbitrarily small as
![]() $k \rightarrow \infty $
, and so X is mean almost periodic, and therefore has discrete spectrum.
$k \rightarrow \infty $
, and so X is mean almost periodic, and therefore has discrete spectrum.
Remark 4.3. We remark that in fact this proof yields an explicit formula for an eigenvalue of X. Namely, define a sequence
![]() $(c_k)$
by
$(c_k)$
by
![]() $c_{-1} = 1$
,
$c_{-1} = 1$
,
![]() $c_0 = 0$
and the same recursion
$c_0 = 0$
and the same recursion
![]() $c_{k+1} = b_{k+1} c_k + a_{k+1} c_{k-1}$
. Basic continued fraction theory implies that
$c_{k+1} = b_{k+1} c_k + a_{k+1} c_{k-1}$
. Basic continued fraction theory implies that
![]() $\frac {c_k}{d_k}$
approaches a limit
$\frac {c_k}{d_k}$
approaches a limit
![]() $\alpha $
, and that for all k,
$\alpha $
, and that for all k,
 $$\begin{align*}\left| \frac{c_k}{d_k} - \alpha \right| < \left| \frac{c_k}{d_k} - \frac{c_{k+1}}{d_{k+1}} \right| = \frac{|\pi(0)|a_1 \ldots a_{k+1}}{d_k d_{k+1}} = \frac{|\pi(0)| \prod_{i=1}^k (n_i - m_i)}{d_k d_{k+1}}. \end{align*}$$
$$\begin{align*}\left| \frac{c_k}{d_k} - \alpha \right| < \left| \frac{c_k}{d_k} - \frac{c_{k+1}}{d_{k+1}} \right| = \frac{|\pi(0)|a_1 \ldots a_{k+1}}{d_k d_{k+1}} = \frac{|\pi(0)| \prod_{i=1}^k (n_i - m_i)}{d_k d_{k+1}}. \end{align*}$$
Therefore, the distance from
![]() $d_k \alpha $
to the nearest integer is less than
$d_k \alpha $
to the nearest integer is less than
![]() $\frac {|\pi (0)| \prod _{i=1}^k (n_i - m_i)}{d_{k+1}}$
, which decays exponentially by Proposition 4.2. If we define
$\frac {|\pi (0)| \prod _{i=1}^k (n_i - m_i)}{d_{k+1}}$
, which decays exponentially by Proposition 4.2. If we define
![]() $\lambda = e^{2\pi i \alpha }$
, then
$\lambda = e^{2\pi i \alpha }$
, then
![]() $\lambda ^{d_k} = \lambda ^{|(\pi \circ \rho _k)(0)|}$
approaches
$\lambda ^{d_k} = \lambda ^{|(\pi \circ \rho _k)(0)|}$
approaches
![]() $1$
with exponential rate. By definition,
$1$
with exponential rate. By definition,
![]() $|(\pi \circ \rho _k)(1)| = d_k + (n_k - m_k) d_{k-1}$
. The distance from
$|(\pi \circ \rho _k)(1)| = d_k + (n_k - m_k) d_{k-1}$
. The distance from
![]() $(n_k - m_k) d_{k-1} \alpha $
to the nearest integer is less than
$(n_k - m_k) d_{k-1} \alpha $
to the nearest integer is less than
![]() $\frac {n_k |\pi (0)| \prod _{i=1}^{k-1} (n_i - m_i)}{d_k}$
, which again decays exponentially by Proposition 4.2. Therefore,
$\frac {n_k |\pi (0)| \prod _{i=1}^{k-1} (n_i - m_i)}{d_k}$
, which again decays exponentially by Proposition 4.2. Therefore,
![]() $\lambda ^{|(\pi \circ \rho _k)(1)|}$
approaches
$\lambda ^{|(\pi \circ \rho _k)(1)|}$
approaches
![]() $1$
with exponential rate as well.
$1$
with exponential rate as well.
From this, an essentially identical argument to that of Host from [Reference HostHos86] (see also pp. 170–171 from [Reference QueffélecQue10]) shows that
![]() $\lambda $
is an eigenvalue (in fact a continuous one). (His argument was for a single substitution
$\lambda $
is an eigenvalue (in fact a continuous one). (His argument was for a single substitution
![]() $\tau $
, but the construction can be done virtually without change with
$\tau $
, but the construction can be done virtually without change with
![]() $\tau ^k$
replaced by
$\tau ^k$
replaced by
![]() $\pi \circ \rho _k$
.)
$\pi \circ \rho _k$
.)
We can even represent
![]() $\alpha $
(and therefore
$\alpha $
(and therefore
![]() $\lambda $
) in terms of generalized continued fractions. If we defined an alternate sequence
$\lambda $
) in terms of generalized continued fractions. If we defined an alternate sequence
![]() $(e_k)$
by the same recursion with
$(e_k)$
by the same recursion with
![]() $e_{-1} = 0$
and
$e_{-1} = 0$
and
![]() $e_0 = 1$
, then
$e_0 = 1$
, then
![]() $\frac {c_k}{e_k}$
is just the kth convergent to the generalized continued fraction
$\frac {c_k}{e_k}$
is just the kth convergent to the generalized continued fraction
 $$\begin{align*}\beta = \cfrac{a_1}{b_1+\cfrac{a_2}{b_2+\cfrac{a_3}{b_3+\ddots}}} = \cfrac{1}{m_1+\cfrac{n_1-m_1}{m_2+\cfrac{n_2-m_2}{m_3+\ddots}}}. \end{align*}$$
$$\begin{align*}\beta = \cfrac{a_1}{b_1+\cfrac{a_2}{b_2+\cfrac{a_3}{b_3+\ddots}}} = \cfrac{1}{m_1+\cfrac{n_1-m_1}{m_2+\cfrac{n_2-m_2}{m_3+\ddots}}}. \end{align*}$$
In particular,
![]() $\frac {c_k}{e_k} \rightarrow \beta $
. Since
$\frac {c_k}{e_k} \rightarrow \beta $
. Since
![]() $c_{-1}=1, c_{0}=0, e_{-1}=0, e_{1}=1$
and
$c_{-1}=1, c_{0}=0, e_{-1}=0, e_{1}=1$
and
![]() $c_{k}$
,
$c_{k}$
,
![]() $d_{k}$
and
$d_{k}$
and
![]() $e_{k}$
are all defined by the same (linear) recursion,
$e_{k}$
are all defined by the same (linear) recursion,
![]() $d_{k} = d_{-1}c_{k} + d_{0}e_{k}$
for all k. Then, as
$d_{k} = d_{-1}c_{k} + d_{0}e_{k}$
for all k. Then, as
![]() $d_{-1} = | \pi (1) | - | \pi (0) |$
and
$d_{-1} = | \pi (1) | - | \pi (0) |$
and
![]() $d_{0} = | \pi (0) |$
,
$d_{0} = | \pi (0) |$
,
Therefore, the eigenvalue
![]() $\lambda $
can be written as
$\lambda $
can be written as
![]() $\exp \left (2\pi i \left (\frac {\beta }{|\pi (1)| \beta + |\pi (0)|(1-\beta )}\right )\right )$
.
$\exp \left (2\pi i \left (\frac {\beta }{|\pi (1)| \beta + |\pi (0)|(1-\beta )}\right )\right )$
.
5 A weak mixing subshift with

Theorem 5.1. There exists an infinite transitive subshift X which is uniquely ergodic, has unique measure which is weak mixing and for which
![]() $\limsup \frac {p(q)}{q} = \frac {3}{2}$
.
$\limsup \frac {p(q)}{q} = \frac {3}{2}$
.
The complexity estimates in Theorem 5.1 will follow from a general formula for word complexity of subshifts with the structure from Proposition 3.1, which may be of independent interest.
Proposition 5.2. Let X be the orbit closure of
![]() $x^{(m_{k}),(n_{k})}$
for
$x^{(m_{k}),(n_{k})}$
for
![]() $\pi $
and
$\pi $
and
![]() $(\tau _{m_{k},n_{k}})$
satisfying the conclusions of Proposition 3.1. Then there exists a constant K such that for
$(\tau _{m_{k},n_{k}})$
satisfying the conclusions of Proposition 3.1. Then there exists a constant K such that for
![]() $k \geq 2$
,
$k \geq 2$
,
 $$ \begin{align*}p(q) &= \left\{ \begin{array}{ll} q + \sum_{j=2}^{k} (n_{j} - m_{j} - 1)| v_{j} | + K & \text{if}~| s_{k}v_{k}^{n_{k}-2}p_{k} | \leq q \leq | s_{k+1}v_{k+1}^{m_{k+1}-1}p_{k+1} | \\2q - | s_{k}v_{k}^{m_{k}-1}p_{k} | + \sum_{j=2}^{k-1} (n_{j} - m_{j} - 1)| v_{j} | + K & \text{if}~| s_{k}v_{k}^{m_{k}-1}p_{k} | \leq q \leq | s_{k}v_{k}^{n_{k}-2}p_{k} |. \end{array} \right. \end{align*} $$
$$ \begin{align*}p(q) &= \left\{ \begin{array}{ll} q + \sum_{j=2}^{k} (n_{j} - m_{j} - 1)| v_{j} | + K & \text{if}~| s_{k}v_{k}^{n_{k}-2}p_{k} | \leq q \leq | s_{k+1}v_{k+1}^{m_{k+1}-1}p_{k+1} | \\2q - | s_{k}v_{k}^{m_{k}-1}p_{k} | + \sum_{j=2}^{k-1} (n_{j} - m_{j} - 1)| v_{j} | + K & \text{if}~| s_{k}v_{k}^{m_{k}-1}p_{k} | \leq q \leq | s_{k}v_{k}^{n_{k}-2}p_{k} |. \end{array} \right. \end{align*} $$
Proof. We claim first that the words
![]() $p_{\infty } := \lim s_{k}p_{k} = \lim s_{1}v_{2} \cdots v_{k} v_{k}^{m_{k}-1}v_{k-1}^{m_{k-1}-1} \cdots v_{1}^{m_{1}-1}$
and
$p_{\infty } := \lim s_{k}p_{k} = \lim s_{1}v_{2} \cdots v_{k} v_{k}^{m_{k}-1}v_{k-1}^{m_{k-1}-1} \cdots v_{1}^{m_{1}-1}$
and
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
for
$s_{k}v_{k}^{n_{k}-2}p_{k}$
for
![]() $k> 0$
are right-special.
$k> 0$
are right-special.
Since
![]() $v_{k+1} = v_{k}^{m_{k}-1}u_{k}$
and
$v_{k+1} = v_{k}^{m_{k}-1}u_{k}$
and
![]() $u_{k+1} = v_{k}^{n_{k}-1}u_{k}$
,
$u_{k+1} = v_{k}^{n_{k}-1}u_{k}$
,
![]() $p_{k+1} = v_{k}^{m_{k}-1}p_{k}$
. By induction, then
$p_{k+1} = v_{k}^{m_{k}-1}p_{k}$
. By induction, then
![]() $p_{k+1} = v_{k}^{m_{k}-1}\cdots v_{1}^{m_{1}-1}$
as
$p_{k+1} = v_{k}^{m_{k}-1}\cdots v_{1}^{m_{1}-1}$
as
![]() $p_{1}$
is empty. By Lemma 3.6,
$p_{1}$
is empty. By Lemma 3.6,
![]() $s_{k}p_{k}$
is a suffix of
$s_{k}p_{k}$
is a suffix of
![]() $s_{k+1}p_{k+1} = s_{k}v_{k}^{m_{k}-1}u_{k}v_{k}^{m_{k}-1}p_{k}$
. As
$s_{k+1}p_{k+1} = s_{k}v_{k}^{m_{k}-1}u_{k}v_{k}^{m_{k}-1}p_{k}$
. As
![]() $| s_{k+1} |> | s_{k} |$
, this shows
$| s_{k+1} |> | s_{k} |$
, this shows
![]() $p_{\infty }$
exists and is left-infinite.
$p_{\infty }$
exists and is left-infinite.
By definition of
![]() $p_{k}$
as the maximal common prefix,
$p_{k}$
as the maximal common prefix,
![]() $p_{k}\pi (0)$
and
$p_{k}\pi (0)$
and
![]() $p_{k}\pi (1)$
are both in the language since each of
$p_{k}\pi (1)$
are both in the language since each of
![]() $u_{k}$
and
$u_{k}$
and
![]() $v_{k}$
must have one of them as a prefix and they cannot have the same one. So
$v_{k}$
must have one of them as a prefix and they cannot have the same one. So
![]() $p_{k}$
is right-special for each k (as
$p_{k}$
is right-special for each k (as
![]() $\pi (0)$
and
$\pi (0)$
and
![]() $\pi (1)$
begin with different letters) hence
$\pi (1)$
begin with different letters) hence
![]() $p_{\infty }$
is right-special. That
$p_{\infty }$
is right-special. That
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
is right-special follows from Lemma 3.10.
$s_{k}v_{k}^{n_{k}-2}p_{k}$
is right-special follows from Lemma 3.10.
Next, we claim that every right-special word is a suffix of
![]() $p_{\infty }$
or of
$p_{\infty }$
or of
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
for some
$s_{k}v_{k}^{n_{k}-2}p_{k}$
for some
![]() $k> 0$
.
$k> 0$
.
Since every right-special word of length at least
![]() $| s_{1}v_{1}^{m_{1}-1} |$
is a suffix of a concatenation of
$| s_{1}v_{1}^{m_{1}-1} |$
is a suffix of a concatenation of
![]() $u_{1}$
and
$u_{1}$
and
![]() $v_{1}$
, any right-special word with
$v_{1}$
, any right-special word with
![]() $s_{2}p_{2} = s_{1}v_{1}^{m_{1}-1}u_{1}v_{1}^{m_{1}-1}$
as a suffix is of the form
$s_{2}p_{2} = s_{1}v_{1}^{m_{1}-1}u_{1}v_{1}^{m_{1}-1}$
as a suffix is of the form
![]() $xu_{1}v_{1}^{m_{1}-1}$
, where x is a suffix of a concatenation of
$xu_{1}v_{1}^{m_{1}-1}$
, where x is a suffix of a concatenation of
![]() $u_{1}$
and
$u_{1}$
and
![]() $v_{1}$
. If x were not a suffix of a concatenation of
$v_{1}$
. If x were not a suffix of a concatenation of
![]() $v_{2}$
and
$v_{2}$
and
![]() $u_{2}$
, then
$u_{2}$
, then
![]() $u_{1}v_{1}^{r}u_{1}$
for
$u_{1}v_{1}^{r}u_{1}$
for
![]() $r \ne m_{1}-1, n_{1}-1$
must appear somewhere in x but this is impossible by definition of
$r \ne m_{1}-1, n_{1}-1$
must appear somewhere in x but this is impossible by definition of
![]() $\tau _{m_1, n_1}$
. So every right-special word with
$\tau _{m_1, n_1}$
. So every right-special word with
![]() $s_{2}p_{2}$
as a suffix is of the form
$s_{2}p_{2}$
as a suffix is of the form
![]() $xp_{2}$
, where x is a suffix of a concatenation of
$xp_{2}$
, where x is a suffix of a concatenation of
![]() $v_{2}$
and
$v_{2}$
and
![]() $u_{2}$
.
$u_{2}$
.
Assume that any word with
![]() $s_{k}p_{k}$
as a suffix is necessarily of the form
$s_{k}p_{k}$
as a suffix is necessarily of the form
![]() $xp_{k}$
, where x is a concatenation of
$xp_{k}$
, where x is a concatenation of
![]() $u_{k}$
and
$u_{k}$
and
![]() $v_{k}$
. Let w be a word which has
$v_{k}$
. Let w be a word which has
![]() $s_{k+1}p_{k+1}$
as a suffix. Since
$s_{k+1}p_{k+1}$
as a suffix. Since
![]() $s_{k+1}p_{k+1} = s_{k}v_{k+1}v_{k}^{m_{k}-1}p_{k}$
which has
$s_{k+1}p_{k+1} = s_{k}v_{k+1}v_{k}^{m_{k}-1}p_{k}$
which has
![]() $s_{k}p_{k}$
as a suffix,
$s_{k}p_{k}$
as a suffix,
![]() $w = xv_{k+1}v_{k}^{m_{k}-1}p_{k}$
, where x is a suffix of a concatenation of
$w = xv_{k+1}v_{k}^{m_{k}-1}p_{k}$
, where x is a suffix of a concatenation of
![]() $u_{k}$
and
$u_{k}$
and
![]() $v_{k}$
. If x were not a suffix of a concatenation of
$v_{k}$
. If x were not a suffix of a concatenation of
![]() $u_{k+1}$
and
$u_{k+1}$
and
![]() $v_{k+1}$
, then somewhere in
$v_{k+1}$
, then somewhere in
![]() $xv_{k+}$
there must appear
$xv_{k+}$
there must appear
![]() $u_{k}v_{k}^{r}u_{k}$
for
$u_{k}v_{k}^{r}u_{k}$
for
![]() $r \ne n_{k}-1, m_{k}-1$
or
$r \ne n_{k}-1, m_{k}-1$
or
![]() $v_{k}^{t}$
for
$v_{k}^{t}$
for
![]() $t> n_{k}-1$
. But this is impossible by definition of
$t> n_{k}-1$
. But this is impossible by definition of
![]() $\tau _{m_k, n_k}$
. By induction, then for all k, any word with suffix
$\tau _{m_k, n_k}$
. By induction, then for all k, any word with suffix
![]() $s_{k}p_{k}$
is of the form
$s_{k}p_{k}$
is of the form
![]() $xp_{k}$
, where x is a suffix of a concatenation of
$xp_{k}$
, where x is a suffix of a concatenation of
![]() $u_{k}$
and
$u_{k}$
and
![]() $v_{k}$
.
$v_{k}$
.
Since
![]() $v_{k}$
is a suffix of
$v_{k}$
is a suffix of
![]() $u_{k}$
for
$u_{k}$
for
![]() $k> 1$
, write
$k> 1$
, write
![]() $u_{k} = u_{k}^{\prime }v_{k}^{\ell _{k}}$
for
$u_{k} = u_{k}^{\prime }v_{k}^{\ell _{k}}$
for
![]() $\ell _{k} \geq 1$
maximal. Note that
$\ell _{k} \geq 1$
maximal. Note that
![]() $s_{k}$
has
$s_{k}$
has
![]() $v_{k}^{\ell _{k}}$
as a suffix.
$v_{k}^{\ell _{k}}$
as a suffix.
Let w be a right-special word with
![]() $| w | \geq | s_{1}p_{1} |$
. Take
$| w | \geq | s_{1}p_{1} |$
. Take
![]() $k \geq 1$
maximal so that w has
$k \geq 1$
maximal so that w has
![]() $s_{k}p_{k}$
as a suffix. By the above,
$s_{k}p_{k}$
as a suffix. By the above,
![]() $w = xp_{k}$
is where x is a suffix of a concatenation of
$w = xp_{k}$
is where x is a suffix of a concatenation of
![]() $u_{k}$
and
$u_{k}$
and
![]() $v_{k}$
in any left-infinite word. Choose
$v_{k}$
in any left-infinite word. Choose
![]() $t \geq 0$
maximal so that
$t \geq 0$
maximal so that
![]() $v_{k}^{t}p_{k}$
is a suffix of w.
$v_{k}^{t}p_{k}$
is a suffix of w.
Suppose w is not a suffix of
![]() $s_{k}v_{k}^{t-\ell _{k}}p_{k}$
. Then
$s_{k}v_{k}^{t-\ell _{k}}p_{k}$
. Then
![]() $u_{k}v_{k}^{t-\ell _{k}}p_{k}$
must be right-special since all letters to the left of
$u_{k}v_{k}^{t-\ell _{k}}p_{k}$
must be right-special since all letters to the left of
![]() $s_{k}$
are forced to come from
$s_{k}$
are forced to come from
![]() $u_{k}$
by maximality of
$u_{k}$
by maximality of
![]() $\ell _{k}$
. As the
$\ell _{k}$
. As the
![]() $p_{k}$
must appear as a prefix of both
$p_{k}$
must appear as a prefix of both
![]() $v_{k}$
and
$v_{k}$
and
![]() $u_{k}$
, then
$u_{k}$
, then
![]() $u_{k}v_{k}^{t-\ell _{k}}u_{k}$
and
$u_{k}v_{k}^{t-\ell _{k}}u_{k}$
and
![]() $u_{k}v_{k}^{t-\ell _{k}}v_{k}$
are in the language so
$u_{k}v_{k}^{t-\ell _{k}}v_{k}$
are in the language so
![]() $t - \ell _{k} = m_{k} - 1$
. But then w has
$t - \ell _{k} = m_{k} - 1$
. But then w has
![]() $v_{k}^{m_{k}-1}p_{k} = p_{k+1}$
as a suffix, contradicting the maximality of k.
$v_{k}^{m_{k}-1}p_{k} = p_{k+1}$
as a suffix, contradicting the maximality of k.
So w is a suffix of
![]() $s_{k}v_{k}^{t - \ell _{k}}p_{k}$
. Suppose
$s_{k}v_{k}^{t - \ell _{k}}p_{k}$
. Suppose
![]() $t - \ell _{k} \geq n_{k} - 1$
. Then w has
$t - \ell _{k} \geq n_{k} - 1$
. Then w has
![]() $v_{k}^{n_{k}-1+\ell _{k}}p_{k}$
as a suffix. As w is right-special, this requires
$v_{k}^{n_{k}-1+\ell _{k}}p_{k}$
as a suffix. As w is right-special, this requires
![]() $v_{k}^{n_{k}-1+\ell _{k}}v_{k}$
be in the language. But that is only possible if
$v_{k}^{n_{k}-1+\ell _{k}}v_{k}$
be in the language. But that is only possible if
![]() $u_{k}$
has
$u_{k}$
has
![]() $v_{k}^{\ell _{k}+1}$
as a suffix, contradicting the maximality of
$v_{k}^{\ell _{k}+1}$
as a suffix, contradicting the maximality of
![]() $\ell _{k}$
.
$\ell _{k}$
.
So
![]() $t - \ell _{k} \leq n_{k} - 2$
. Then w, being a suffix of
$t - \ell _{k} \leq n_{k} - 2$
. Then w, being a suffix of
![]() $s_{k}v_{k}^{t-\ell _{k}}p_{k}$
, is a suffix of
$s_{k}v_{k}^{t-\ell _{k}}p_{k}$
, is a suffix of
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
.
$s_{k}v_{k}^{n_{k}-2}p_{k}$
.
Finally, we establish the complexity function is as claimed. Since
![]() $p_{\infty }$
has
$p_{\infty }$
has
![]() $s_{k+1}p_{k+1} = s_{k}v_{k+1}v_{k}^{m_{k}-1}p_{k}$
as a suffix, by Lemma 3.6, it has
$s_{k+1}p_{k+1} = s_{k}v_{k+1}v_{k}^{m_{k}-1}p_{k}$
as a suffix, by Lemma 3.6, it has
![]() $s_{k}u_{k}v_{k}^{m_{k}-1}p_{k}$
as a suffix. By Lemma 3.7, the maximal common suffix of
$s_{k}u_{k}v_{k}^{m_{k}-1}p_{k}$
as a suffix. By Lemma 3.7, the maximal common suffix of
![]() $p_{\infty }$
and
$p_{\infty }$
and
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
is then
$s_{k}v_{k}^{n_{k}-2}p_{k}$
is then
![]() $s_{k}v_{k}^{m_{k}-1}p_{k}$
. Likewise the maximal common suffix of
$s_{k}v_{k}^{m_{k}-1}p_{k}$
. Likewise the maximal common suffix of
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
and
$s_{k}v_{k}^{n_{k}-2}p_{k}$
and
![]() $s_{k^{\prime }}v_{k^{\prime }}^{n_{k^{\prime }}-2}p_{k^{\prime }}$
for
$s_{k^{\prime }}v_{k^{\prime }}^{n_{k^{\prime }}-2}p_{k^{\prime }}$
for
![]() $k^{\prime }> k$
is
$k^{\prime }> k$
is
![]() $s_{k}v_{k}^{m_{k}-1}p_{k}$
as
$s_{k}v_{k}^{m_{k}-1}p_{k}$
as
![]() $v_{k+1}$
has
$v_{k+1}$
has
![]() $u_{k}$
as a suffix. Therefore, each
$u_{k}$
as a suffix. Therefore, each
![]() $s_{k}v_{k}^{n_{k}-2}p_{k}$
provides
$s_{k}v_{k}^{n_{k}-2}p_{k}$
provides
![]() $(n_{k}-2 - (m_{k}-1))| v_{k} |$
right-special words (with lengths in
$(n_{k}-2 - (m_{k}-1))| v_{k} |$
right-special words (with lengths in
![]() $(| s_k v_k^{m_k-1} p_k |, | s_{k}v_{k}^{n_{k}-2}p_{k} |]$
) which are not suffixes of
$(| s_k v_k^{m_k-1} p_k |, | s_{k}v_{k}^{n_{k}-2}p_{k} |]$
) which are not suffixes of
![]() $p_{\infty }$
. Set
$p_{\infty }$
. Set
![]() $K = p(| s_{2}p_{2} |) - | s_{2}p_{2} |$
and the claim follows.
$K = p(| s_{2}p_{2} |) - | s_{2}p_{2} |$
and the claim follows.
Proof of Theorem 5.1.
Define any increasing
![]() $(n_k)$
,
$(n_k)$
,
![]() $(m_k)$
so that
$(m_k)$
so that
![]() $n_k = 2m_k$
for all k,
$n_k = 2m_k$
for all k,
![]() $m_1 = 1$
, and the sum
$m_1 = 1$
, and the sum
![]() $\sum _k (n_k)^{-1} < \infty $
. Then define
$\sum _k (n_k)^{-1} < \infty $
. Then define
![]() $\pi $
to be the identity, define
$\pi $
to be the identity, define
![]() $\tau _{m_k, n_k}$
,
$\tau _{m_k, n_k}$
,
![]() $\rho _k, a_k, b_k, c_k, d_k$
as in the proof of Proposition 4.2, and note that
$\rho _k, a_k, b_k, c_k, d_k$
as in the proof of Proposition 4.2, and note that
![]() $a_{k+1} = n_k - m_k = m_k = b_k$
for all k and
$a_{k+1} = n_k - m_k = m_k = b_k$
for all k and
![]() $\sum _k (b_k)^{-1} < \infty $
. Just as before,
$\sum _k (b_k)^{-1} < \infty $
. Just as before,
![]() $d_k = |\rho _k(0)|$
for all k, and we wish to impose the additional condition that
$d_k = |\rho _k(0)|$
for all k, and we wish to impose the additional condition that
![]() $d_k$
is prime for every
$d_k$
is prime for every
![]() $k>1$
. This is easily achieved via induction. First,
$k>1$
. This is easily achieved via induction. First,
![]() $d_0 = d_1 = 1$
, so
$d_0 = d_1 = 1$
, so
![]() $d_2 = b_2 d_1 + a_2 d_0 = m_2 + 1$
, which can clearly be chosen prime. Then, assume that
$d_2 = b_2 d_1 + a_2 d_0 = m_2 + 1$
, which can clearly be chosen prime. Then, assume that
![]() $d_k$
is prime, and recall that
$d_k$
is prime, and recall that
![]() $d_{k+1} = b_{k+1}d_k+a_{k+1}d_{k-1}$
. Both
$d_{k+1} = b_{k+1}d_k+a_{k+1}d_{k-1}$
. Both
![]() $a_{k+1} = b_k$
and
$a_{k+1} = b_k$
and
![]() $d_{k-1}$
are positive and less than the prime
$d_{k-1}$
are positive and less than the prime
![]() $d_k$
(since
$d_k$
(since
![]() $d_k = b_k d_{k-1} + a_k d_{k-2}$
and
$d_k = b_k d_{k-1} + a_k d_{k-2}$
and
![]() $d_{k-2}$
is positive for
$d_{k-2}$
is positive for
![]() $k> 1$
), meaning that
$k> 1$
), meaning that
![]() $d_k$
and
$d_k$
and
![]() $a_{k+1}d_{k-1}$
are positive and coprime. Then by Dirichlet’s theorem, there exist infinitely many choices of
$a_{k+1}d_{k-1}$
are positive and coprime. Then by Dirichlet’s theorem, there exist infinitely many choices of
![]() $b_{k+1}$
so that
$b_{k+1}$
so that
![]() $d_{k+1}$
is prime. As long as the sequence
$d_{k+1}$
is prime. As long as the sequence
![]() $(b_k)$
is chosen large enough at each step, we will maintain the condition
$(b_k)$
is chosen large enough at each step, we will maintain the condition
![]() $\sum _k (b_k)^{-1} < \infty $
.
$\sum _k (b_k)^{-1} < \infty $
.
Let X be the orbit closure of
![]() $x^{(m_{k}),(n_{k})}$
. X is minimal by construction, so by [Reference BoshernitzanBos92], X is uniquely ergodic with unique measure
$x^{(m_{k}),(n_{k})}$
. X is minimal by construction, so by [Reference BoshernitzanBos92], X is uniquely ergodic with unique measure
![]() $\mu $
.
$\mu $
.
Suppose for a contradiction that X is not weak mixing, and so there is an eigenvalue
![]() $\lambda \neq 1$
with measurable eigenfunction f. Our method is again based on the Host’s arguments from [Reference HostHos86], where he showed that the existence of an eigenfunction can be used to obtain Diophantine conditions involving the lengths of substitution words, which can be viewed as heights of Rokhlin towers.
$\lambda \neq 1$
with measurable eigenfunction f. Our method is again based on the Host’s arguments from [Reference HostHos86], where he showed that the existence of an eigenfunction can be used to obtain Diophantine conditions involving the lengths of substitution words, which can be viewed as heights of Rokhlin towers.
One can define Rokhlin towers by
![]() $B_k = [\rho _k(0)]$
,
$B_k = [\rho _k(0)]$
,
![]() $h_k = |\rho _k(0)|$
and
$h_k = |\rho _k(0)|$
and
![]() $T_k = \bigcup _{j = 0}^{h_k - 1} \sigma ^j B_k$
; since
$T_k = \bigcup _{j = 0}^{h_k - 1} \sigma ^j B_k$
; since
![]() $m_k, n_k \rightarrow \infty $
,
$m_k, n_k \rightarrow \infty $
,
![]() $\mu (T_k) \rightarrow 1$
. By Remark 3.12, X is uniquely decomposable so the levels of the towers are disjoint. Then, for each k, define
$\mu (T_k) \rightarrow 1$
. By Remark 3.12, X is uniquely decomposable so the levels of the towers are disjoint. Then, for each k, define

that is,
![]() $f_{k}(x) = (\mu (B_k))^{-1}(\int _{\sigma ^j B_k} f \ d\mu )$
for
$f_{k}(x) = (\mu (B_k))^{-1}(\int _{\sigma ^j B_k} f \ d\mu )$
for
![]() $x \in \sigma ^j B_{k}$
and
$x \in \sigma ^j B_{k}$
and
![]() $f_{k}(x) = 0$
for
$f_{k}(x) = 0$
for
![]() $x \notin T_k$
.
$x \notin T_k$
.
By the Lebesgue differentiation theorem, as
![]() $\mu (T_k) \to 1$
and
$\mu (T_k) \to 1$
and
![]() $\mu (\sigma ^{j}B_{k}) \to 0$
,
$\mu (\sigma ^{j}B_{k}) \to 0$
,
![]() $f_{k}$
converge almost everywhere to f.
$f_{k}$
converge almost everywhere to f.
Observe that
![]() $\sigma ^{d_{k}} = \sigma ^{|\rho _{k}(0)|}$
takes every occurrence of
$\sigma ^{d_{k}} = \sigma ^{|\rho _{k}(0)|}$
takes every occurrence of
![]() $\rho _{k}(0)$
to an occurrence of
$\rho _{k}(0)$
to an occurrence of
![]() $\rho _{k}(0)$
except for those which are immediately prior to an occurrence of
$\rho _{k}(0)$
except for those which are immediately prior to an occurrence of
![]() $\rho _{k}(1)$
in some
$\rho _{k}(1)$
in some
![]() $\rho _{k+1}(0)$
or
$\rho _{k+1}(0)$
or
![]() $\rho _{k+1}(1)$
. Then for all
$\rho _{k+1}(1)$
. Then for all
![]() $t> 0$
,
$t> 0$
,
![]() $\sigma ^{d_{k+t}}$
takes all occurrences of
$\sigma ^{d_{k+t}}$
takes all occurrences of
![]() $\rho _{k}(0)$
appearing in a
$\rho _{k}(0)$
appearing in a
![]() $\rho _{k+t}(0)$
to an occurrence of
$\rho _{k+t}(0)$
to an occurrence of
![]() $\rho _{k}(0)$
except possibly for those appearing in a
$\rho _{k}(0)$
except possibly for those appearing in a
![]() $\rho _{k+t}(0)$
immediately prior to a
$\rho _{k+t}(0)$
immediately prior to a
![]() $\rho _{k+t}(1)$
.
$\rho _{k+t}(1)$
.
Let
![]() $\{ i_{k} \}$
be any sequence such that
$\{ i_{k} \}$
be any sequence such that
![]() $0 < i_{k} < 0.5(m_{k+1}-1)$
. Then as above, for all
$0 < i_{k} < 0.5(m_{k+1}-1)$
. Then as above, for all
![]() $t> 0$
,
$t> 0$
,
![]() $\sigma ^{i_{k+t}d_{k+t}}$
takes all occurrences of
$\sigma ^{i_{k+t}d_{k+t}}$
takes all occurrences of
![]() $\rho _{k}(0)$
in a
$\rho _{k}(0)$
in a
![]() $\rho _{k+t}(0)$
to an occurrence of
$\rho _{k+t}(0)$
to an occurrence of
![]() $\rho _{k}(0)$
except possibly for those appearing in a
$\rho _{k}(0)$
except possibly for those appearing in a
![]() $\rho _{k+t}(0)$
less than
$\rho _{k+t}(0)$
less than
![]() $i_{k+t}$
occurrences before a
$i_{k+t}$
occurrences before a
![]() $\rho _{k+t}(1)$
in some
$\rho _{k+t}(1)$
in some
![]() $\rho _{k+t+1}(0)$
or
$\rho _{k+t+1}(0)$
or
![]() $\rho _{k+t+1}(1)$
. We also note that since
$\rho _{k+t+1}(1)$
. We also note that since
![]() $n_{k+t+1} = 2m_{k+t+1}$
, at least one-third of the
$n_{k+t+1} = 2m_{k+t+1}$
, at least one-third of the
![]() $\rho _k(0)$
appearing in any
$\rho _k(0)$
appearing in any
![]() $x \in X$
are part of some
$x \in X$
are part of some
![]() $\rho _{k+t}(0)$
. Therefore,
$\rho _{k+t}(0)$
. Therefore,
 $$\begin{align*}\mu(\sigma^{i_{k+t}d_{k+t}}[\rho_{k}(0)] \cap [\rho_{k}(0)]) \geq \frac{m_{k+t}-1-i_{k+t}}{m_{k+t}-1} \left( \frac{1}{3} \mu([\rho_{k}(0)])\right) \end{align*}$$
$$\begin{align*}\mu(\sigma^{i_{k+t}d_{k+t}}[\rho_{k}(0)] \cap [\rho_{k}(0)]) \geq \frac{m_{k+t}-1-i_{k+t}}{m_{k+t}-1} \left( \frac{1}{3} \mu([\rho_{k}(0)])\right) \end{align*}$$
so, since
![]() $i_{k+t} < 0.5(m_{k+t}-1)$
,
$i_{k+t} < 0.5(m_{k+t}-1)$
,
Then
![]() $f_{k}(\sigma ^{i_{k+t}d_{k+t}}x) = f_k(x)$
for a set of measure at least
$f_{k}(\sigma ^{i_{k+t}d_{k+t}}x) = f_k(x)$
for a set of measure at least
![]() $\frac {1}{6}\mu (T_{k})$
. Since
$\frac {1}{6}\mu (T_{k})$
. Since
![]() $f_{k} \to f$
almost everywhere and
$f_{k} \to f$
almost everywhere and
![]() $\mu (T_{k}) \to 1$
, there is then a positive measure set such that for any sufficiently small
$\mu (T_{k}) \to 1$
, there is then a positive measure set such that for any sufficiently small
![]() $\epsilon> 0$
and almost every x in the set, there exists k so that for all t,
$\epsilon> 0$
and almost every x in the set, there exists k so that for all t,
![]() $|f(\sigma ^{i_{k+t}d_{k+t}}x) - f(x)| < \epsilon $
. Therefore,
$|f(\sigma ^{i_{k+t}d_{k+t}}x) - f(x)| < \epsilon $
. Therefore,
![]() $\lambda ^{i_{k}d_{k}} \to 1$
.
$\lambda ^{i_{k}d_{k}} \to 1$
.
We will prove that this is impossible. Define
![]() $r \in (0,1)$
by
$r \in (0,1)$
by
![]() $\lambda = e^{2\pi i r}$
; then
$\lambda = e^{2\pi i r}$
; then
![]() $\langle i_k d_k r \rangle \rightarrow 0$
whenever
$\langle i_k d_k r \rangle \rightarrow 0$
whenever
![]() $0 < i_k < 0.5(m_{k+1} - 1)$
, which implies that for large enough k (say
$0 < i_k < 0.5(m_{k+1} - 1)$
, which implies that for large enough k (say
![]() $k \geq k_0$
),
$k \geq k_0$
),
![]() $\langle d_k r \rangle < 0.05(m_{k+1} - 1)^{-1}$
. Clearly, r cannot be rational since all
$\langle d_k r \rangle < 0.05(m_{k+1} - 1)^{-1}$
. Clearly, r cannot be rational since all
![]() $d_k$
are
$d_k$
are
![]() $1$
or prime. Since
$1$
or prime. Since
![]() $5n_{k+1} = 10m_{k+1} < 20(m_{k+1}-1)$
, for
$5n_{k+1} = 10m_{k+1} < 20(m_{k+1}-1)$
, for
![]() $k \geq k_0$
,
$k \geq k_0$
,
![]() $\langle d_k r \rangle < 0.2(n_{k+1})^{-1}$
. This implies that for all
$\langle d_k r \rangle < 0.2(n_{k+1})^{-1}$
. This implies that for all
![]() $k \geq k_0$
, there exists
$k \geq k_0$
, there exists
![]() $c^{\prime }_k \in \mathbb {Z}$
so that
$c^{\prime }_k \in \mathbb {Z}$
so that
![]() $\left |r - \frac {c^{\prime }_k}{d_k} \right | < 0.2(d_k n_{k+1})^{-1} < 0.2(d_{k+1})^{-1}$
. (Recall that
$\left |r - \frac {c^{\prime }_k}{d_k} \right | < 0.2(d_k n_{k+1})^{-1} < 0.2(d_{k+1})^{-1}$
. (Recall that
![]() $d_{k+1} = b_{k+1} d_k + a_{k+1} d_{k-1} < 2b_{k+1} d_k = n_{k+1} d_k$
.) We will prove the following: for all
$d_{k+1} = b_{k+1} d_k + a_{k+1} d_{k-1} < 2b_{k+1} d_k = n_{k+1} d_k$
.) We will prove the following: for all
![]() $k> k_0$
,
$k> k_0$
,
Assume that
![]() $k> k_0$
, and denote the right-hand side of equation (5.1) by
$k> k_0$
, and denote the right-hand side of equation (5.1) by
![]() $c^{\prime \prime }_{k+1}$
. Then,
$c^{\prime \prime }_{k+1}$
. Then,
 $$ \begin{align} \left|r - \frac{c^{\prime}_k}{d_k} \right| < 0.2(d_{k+1})^{-1} \textrm{ and } \left|r - \frac{c^{\prime}_{k-1}}{d_{k-1}} \right| < 0.2(d_k)^{-1}, \end{align} $$
$$ \begin{align} \left|r - \frac{c^{\prime}_k}{d_k} \right| < 0.2(d_{k+1})^{-1} \textrm{ and } \left|r - \frac{c^{\prime}_{k-1}}{d_{k-1}} \right| < 0.2(d_k)^{-1}, \end{align} $$
and so
 $$ \begin{align} \left|d_{k+1} r - c^{\prime}_k \frac{d_{k+1}}{d_k} \right| < 0.2. \end{align} $$
$$ \begin{align} \left|d_{k+1} r - c^{\prime}_k \frac{d_{k+1}}{d_k} \right| < 0.2. \end{align} $$
We can simplify
 $$ \begin{align} \left|c^{\prime}_k \frac{d_{k+1}}{d_k} - c^{\prime\prime}_{k+1}\right| = \left|c^{\prime}_k\left(b_{k+1} + \frac{a_{k+1} d_{k-1}}{d_k}\right) - b_{k+1} c^{\prime}_k - a_{k+1} c^{\prime}_{k-1}\right| = \left| c^{\prime}_k a_{k+1} \frac{d_{k-1}}{d_k} - a_{k+1} c^{\prime}_{k-1} \right|. \end{align} $$
$$ \begin{align} \left|c^{\prime}_k \frac{d_{k+1}}{d_k} - c^{\prime\prime}_{k+1}\right| = \left|c^{\prime}_k\left(b_{k+1} + \frac{a_{k+1} d_{k-1}}{d_k}\right) - b_{k+1} c^{\prime}_k - a_{k+1} c^{\prime}_{k-1}\right| = \left| c^{\prime}_k a_{k+1} \frac{d_{k-1}}{d_k} - a_{k+1} c^{\prime}_{k-1} \right|. \end{align} $$
By the second inequality in equation (5.2),
Similarly, by the first inequality in equation (5.2),
 $$ \begin{align} \left|a_{k+1} d_{k-1} r - c^{\prime}_k a_{k+1} \frac{d_{k-1}}{d_k}\right| < \frac{0.2a_{k+1} d_{k-1}}{d_{k+1}} = \frac{0.2b_k d_{k-1}}{d_{k+1}} < 0.2. \end{align} $$
$$ \begin{align} \left|a_{k+1} d_{k-1} r - c^{\prime}_k a_{k+1} \frac{d_{k-1}}{d_k}\right| < \frac{0.2a_{k+1} d_{k-1}}{d_{k+1}} = \frac{0.2b_k d_{k-1}}{d_{k+1}} < 0.2. \end{align} $$
Therefore, by the triangle inequality and equations 5.4–5.6,
 $$\begin{align*}\left|c^{\prime}_k \frac{d_{k+1}}{d_k} - c^{\prime\prime}_{k+1}\right| < 0.4. \end{align*}$$
$$\begin{align*}\left|c^{\prime}_k \frac{d_{k+1}}{d_k} - c^{\prime\prime}_{k+1}\right| < 0.4. \end{align*}$$
Combining with equation (5.3) via the triangle inequality yields
Recall that by definition,
 $$ \begin{align} \left|r - \frac{c^{\prime}_{k+1}}{d_{k+1}}\right| < 0.2 (d_{k+2})^{-1}, \textrm{ and so } \left|d_{k+1} r - c^{\prime}_{k+1}\right| < 0.2 \frac{d_{k+1}}{d_{k+2}} < 0.2. \end{align} $$
$$ \begin{align} \left|r - \frac{c^{\prime}_{k+1}}{d_{k+1}}\right| < 0.2 (d_{k+2})^{-1}, \textrm{ and so } \left|d_{k+1} r - c^{\prime}_{k+1}\right| < 0.2 \frac{d_{k+1}}{d_{k+2}} < 0.2. \end{align} $$
Finally, equations (5.7) and (5.8) imply that
![]() $c^{\prime }_{k+1} = c^{\prime \prime }_{k+1}$
(since they are both integers), completing the proof that equation (5.1) holds for
$c^{\prime }_{k+1} = c^{\prime \prime }_{k+1}$
(since they are both integers), completing the proof that equation (5.1) holds for
![]() $k> k_0$
.
$k> k_0$
.
Since r is irrational and
![]() $\frac {c^{\prime }_k}{d_k} \rightarrow r$
, we may also assume without loss of generality (by increasing
$\frac {c^{\prime }_k}{d_k} \rightarrow r$
, we may also assume without loss of generality (by increasing
![]() $k_0$
) that
$k_0$
) that
![]() $\frac {c^{\prime }_{k_0}}{d_{k_0}} \neq \frac {c^{\prime }_{1+k_0}}{d_{1+k_0}}$
. Then, it is easily proved by induction that for all
$\frac {c^{\prime }_{k_0}}{d_{k_0}} \neq \frac {c^{\prime }_{1+k_0}}{d_{1+k_0}}$
. Then, it is easily proved by induction that for all
![]() $k> k_0$
,
$k> k_0$
,
 $$\begin{align*}\left| \frac{c^{\prime}_k}{d_k} - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right| = |c^{\prime}_{1+k_0} d_{k_0} - c^{\prime}_{k_0} d_{1+k_0}| \frac{a_{1+k_0} \ldots a_{k+1}}{d_k d_{k+1}}. \end{align*}$$
$$\begin{align*}\left| \frac{c^{\prime}_k}{d_k} - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right| = |c^{\prime}_{1+k_0} d_{k_0} - c^{\prime}_{k_0} d_{1+k_0}| \frac{a_{1+k_0} \ldots a_{k+1}}{d_k d_{k+1}}. \end{align*}$$
We abbreviate
![]() $Q = |c^{\prime }_{1+k_0} d_{k_0} - c^{\prime }_{k_0} d_{1+k_0}|$
and note that
$Q = |c^{\prime }_{1+k_0} d_{k_0} - c^{\prime }_{k_0} d_{1+k_0}|$
and note that
![]() $Q \neq 0$
by the assumption that
$Q \neq 0$
by the assumption that
![]() $\frac {c^{\prime }_{k_0}}{d_{k_0}} \neq \frac {c_{1+k_0}}{d_{1+k_0}}$
. We can now bound the distance from above using that
$\frac {c^{\prime }_{k_0}}{d_{k_0}} \neq \frac {c_{1+k_0}}{d_{1+k_0}}$
. We can now bound the distance from above using that
![]() $a_{j+1}d_{j-1} \leq d_{j}$
:
$a_{j+1}d_{j-1} \leq d_{j}$
:
 $$ \begin{align} \left| \frac{c^{\prime}_k}{d_k} - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right| = \frac{Q a_{1+k_0} \ldots a_{k+1}}{d_k d_{k+1}} = \frac{Q}{d_{k_0 - 1} d_{k+1}} \prod_{j=k_0}^{k} \frac{a_{j+1} d_{j-1}}{d_j}> \frac{Q}{d_{k_0 - 1} d_{k+1}} \prod_{j=k_0}^{\infty} \frac{a_{j+1} d_{j-1}}{d_j}. \end{align} $$
$$ \begin{align} \left| \frac{c^{\prime}_k}{d_k} - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right| = \frac{Q a_{1+k_0} \ldots a_{k+1}}{d_k d_{k+1}} = \frac{Q}{d_{k_0 - 1} d_{k+1}} \prod_{j=k_0}^{k} \frac{a_{j+1} d_{j-1}}{d_j}> \frac{Q}{d_{k_0 - 1} d_{k+1}} \prod_{j=k_0}^{\infty} \frac{a_{j+1} d_{j-1}}{d_j}. \end{align} $$
Note that
 $$\begin{align*}\frac{d_j}{a_{j+1} d_{j-1}} = \frac{b_j}{a_{j+1}} + \frac{a_j d_{j-2}}{a_{j+1} d_{j-1}} \leq \frac{b_j}{a_{j+1}} + \frac{b_{j-1} d_{j-2}}{a_{j+1} d_{j-1}} < \frac{b_j + 1}{a_{j+1}} < \frac{b_j}{a_{j+1} - 1} = \frac{b_{j}}{b_{j} - 1} = \left(1 - b_j^{-1}\right)^{-1}. \end{align*}$$
$$\begin{align*}\frac{d_j}{a_{j+1} d_{j-1}} = \frac{b_j}{a_{j+1}} + \frac{a_j d_{j-2}}{a_{j+1} d_{j-1}} \leq \frac{b_j}{a_{j+1}} + \frac{b_{j-1} d_{j-2}}{a_{j+1} d_{j-1}} < \frac{b_j + 1}{a_{j+1}} < \frac{b_j}{a_{j+1} - 1} = \frac{b_{j}}{b_{j} - 1} = \left(1 - b_j^{-1}\right)^{-1}. \end{align*}$$
Therefore, the product
![]() $\prod _{j=k_0}^{\infty } \frac {a_{j+1} d_{j-1}}{d_j}$
is greater than
$\prod _{j=k_0}^{\infty } \frac {a_{j+1} d_{j-1}}{d_j}$
is greater than
![]() $\prod _{j=k_0}^{\infty } \left (1 - \frac {1}{b_j}\right )$
, which converges to a positive limit L by the assumption that
$\prod _{j=k_0}^{\infty } \left (1 - \frac {1}{b_j}\right )$
, which converges to a positive limit L by the assumption that
![]() $\sum b_k^{-1}<\infty $
. Combining with equation (5.9) yields that there exists a positive constant
$\sum b_k^{-1}<\infty $
. Combining with equation (5.9) yields that there exists a positive constant
![]() $K = \frac {Q L}{d_{k_0 - 1}}$
so that for all
$K = \frac {Q L}{d_{k_0 - 1}}$
so that for all
![]() $k> k_0$
,
$k> k_0$
,
 $$ \begin{align} \left| \frac{c^{\prime}_k}{d_k} - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right|> \frac{K}{d_{k+1}}. \end{align} $$
$$ \begin{align} \left| \frac{c^{\prime}_k}{d_k} - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right|> \frac{K}{d_{k+1}}. \end{align} $$
However, recall that
![]() $|r - \frac {c_{k}^\prime }{d_{k}}| < 0.2(d_{k}n_{k+1})^{-1}$
meaning
$|r - \frac {c_{k}^\prime }{d_{k}}| < 0.2(d_{k}n_{k+1})^{-1}$
meaning
![]() $|r d_{k+1} n_{k+1} - c_{k}^{\prime }n_{k+1}| < 0.2$
so
$|r d_{k+1} n_{k+1} - c_{k}^{\prime }n_{k+1}| < 0.2$
so
![]() $c_{k}^{\prime }n_{k+1}$
is the closest integer to
$c_{k}^{\prime }n_{k+1}$
is the closest integer to
![]() $r d_{k+1} n_{k+1}$
. Since
$r d_{k+1} n_{k+1}$
. Since
![]() $\langle 0.25n_{k+1}d_{k}r \rangle \to 0$
, this implies there exists
$\langle 0.25n_{k+1}d_{k}r \rangle \to 0$
, this implies there exists
![]() $k_{1}> k_{0}$
such that
$k_{1}> k_{0}$
such that
![]() $|r d_{k+1} n_{k+1} - c_{k}^{\prime } n_{k+1}| < 0.5K$
. Then
$|r d_{k+1} n_{k+1} - c_{k}^{\prime } n_{k+1}| < 0.5K$
. Then
![]() $|r - \frac {c_{k}^{\prime }}{d_{k}}| < 0.5K (n_{k+1}d_{k})^{-1}$
. Since
$|r - \frac {c_{k}^{\prime }}{d_{k}}| < 0.5K (n_{k+1}d_{k})^{-1}$
. Since
![]() $d_{k+1} < n_{k+1}d_{k}$
, then
$d_{k+1} < n_{k+1}d_{k}$
, then
![]() $|r - \frac {c_{k}^{\prime }}{d_{k}}| < 0.5K (d_{k+1})^{-1}$
. Then for
$|r - \frac {c_{k}^{\prime }}{d_{k}}| < 0.5K (d_{k+1})^{-1}$
. Then for
![]() $k> k_1$
,
$k> k_1$
,
 $$\begin{align*}\left| r - \frac{c^{\prime}_k}{d_k} \right| < 0.5K(d_{k+1})^{-1} \textrm{ and } \left| r - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right| < 0.5K(d_{k+2})^{-1} < 0.5K(d_{k+1})^{-1}, \end{align*}$$
$$\begin{align*}\left| r - \frac{c^{\prime}_k}{d_k} \right| < 0.5K(d_{k+1})^{-1} \textrm{ and } \left| r - \frac{c^{\prime}_{k+1}}{d_{k+1}} \right| < 0.5K(d_{k+2})^{-1} < 0.5K(d_{k+1})^{-1}, \end{align*}$$
which contradicts equation (5.10) by the triangle inequality. Therefore, our original assumption is false and X is weak mixing.
It remains only to show that the complexity function satisfies the claimed bounds. Since
![]() $| p_1 | = 0$
and by Remark 3.11,
$| p_1 | = 0$
and by Remark 3.11,
![]() $p_{k+1} = v_{k}^{m_{k}-1}p_{k}$
, we have
$p_{k+1} = v_{k}^{m_{k}-1}p_{k}$
, we have
![]() $| p_{k} | = \sum _{j=1}^{k-1} (m_{j}-1)| v_{j} |$
and therefore, since
$| p_{k} | = \sum _{j=1}^{k-1} (m_{j}-1)| v_{j} |$
and therefore, since
![]() $n_{j} - m_{j} = m_{j}$
,
$n_{j} - m_{j} = m_{j}$
,
 $$\begin{align*}\sum_{j=1}^{k}(n_{j} - m_{j} - 1)| v_{j} | = \sum_{j=1}^{k}(m_{j}-1)| v_{j} | = (m_{k}-1)| v_{k} | + | p_{k} |. \end{align*}$$
$$\begin{align*}\sum_{j=1}^{k}(n_{j} - m_{j} - 1)| v_{j} | = \sum_{j=1}^{k}(m_{j}-1)| v_{j} | = (m_{k}-1)| v_{k} | + | p_{k} |. \end{align*}$$
By Proposition 5.2, then
Since
![]() $| p_{k} | + | s_{k} | < 3| v_{k} |$
and
$| p_{k} | + | s_{k} | < 3| v_{k} |$
and
![]() $m_{k} \to \infty $
,
$m_{k} \to \infty $
,
![]() $\lim \frac {p(| s_{k}v_{k}^{2m_{k}-2}p_{k} |)}{| s_{k}v_{k}^{2m_{k}-2}p_{k} |} = 1.5$
. Proposition 5.2 implies that the limsup of
$\lim \frac {p(| s_{k}v_{k}^{2m_{k}-2}p_{k} |)}{| s_{k}v_{k}^{2m_{k}-2}p_{k} |} = 1.5$
. Proposition 5.2 implies that the limsup of
![]() $\frac {p(q)}{q}$
is achieved along some subsequence of
$\frac {p(q)}{q}$
is achieved along some subsequence of
![]() $| s_{k}v_{k}^{n_{k}-2}p_{k} |$
, so
$| s_{k}v_{k}^{n_{k}-2}p_{k} |$
, so
![]() $\limsup \frac {p(q)}{q} = 1.5$
.
$\limsup \frac {p(q)}{q} = 1.5$
.
Remark 5.3. The examples in Theorem 5.1 also satisfy
![]() $p(q) - 1.5q \to -\infty $
and
$p(q) - 1.5q \to -\infty $
and
![]() $\liminf \frac {p(q)}{q} = 1$
. For any
$\liminf \frac {p(q)}{q} = 1$
. For any
![]() $f(q) \to \infty $
, such a subshift exists which also satisfies
$f(q) \to \infty $
, such a subshift exists which also satisfies
![]() $p(q) < q + f(q)$
infinitely often.
$p(q) < q + f(q)$
infinitely often.
Proof. By Remark 3.11,
![]() $s_{k+1} = s_{k}v_{k+1}$
, so we have
$s_{k+1} = s_{k}v_{k+1}$
, so we have
![]() $| s_{k} | - | p_{k} | \leq | s_{k} | - | v_{k} | = | s_{k-1} | \to \infty $
so
$| s_{k} | - | p_{k} | \leq | s_{k} | - | v_{k} | = | s_{k-1} | \to \infty $
so
![]() $p(q) - 1.5q \to -\infty $
. By Proposition 5.2,
$p(q) - 1.5q \to -\infty $
. By Proposition 5.2,
 $$\begin{align*}p(| v_{k}^{m_{k}-1}p_{k} |) = | v_{k}^{m_{k}-1}p_{k} | + \sum_{j=1}^{k-1} (n_{j} - m_{j} - 1)| v_{j} | +K = | v_{k}^{m_{k}-1}p_{k} | + | p_{k} | + K \end{align*}$$
$$\begin{align*}p(| v_{k}^{m_{k}-1}p_{k} |) = | v_{k}^{m_{k}-1}p_{k} | + \sum_{j=1}^{k-1} (n_{j} - m_{j} - 1)| v_{j} | +K = | v_{k}^{m_{k}-1}p_{k} | + | p_{k} | + K \end{align*}$$
and
![]() $| p_{k} | < 3| v_{k} |$
so since
$| p_{k} | < 3| v_{k} |$
so since
![]() $m_{k} \to \infty $
,
$m_{k} \to \infty $
,
![]() $\liminf \frac {p(q)}{q} = 1$
. Now, let
$\liminf \frac {p(q)}{q} = 1$
. Now, let
![]() $f(q) \to \infty $
be arbitrary. For all k, if
$f(q) \to \infty $
be arbitrary. For all k, if
![]() $v_{k}$
and
$v_{k}$
and
![]() $p_{k}$
are given, we can choose
$p_{k}$
are given, we can choose
![]() $b_{k} = m_k$
large enough so that
$b_{k} = m_k$
large enough so that
![]() $f((m_{k}-1)| v_{k} |+| p_k |)> | p_{k} | + K$
, which implies that
$f((m_{k}-1)| v_{k} |+| p_k |)> | p_{k} | + K$
, which implies that
![]() $p(| v_{k}^{m_{k}-1}p_{k} |) < | v_{k}^{m_{k}-1}p_{k} | + f(| v_{k}^{m_{k}-1}p_{k} |)$
.
$p(| v_{k}^{m_{k}-1}p_{k} |) < | v_{k}^{m_{k}-1}p_{k} | + f(| v_{k}^{m_{k}-1}p_{k} |)$
.
Acknowledgments
The authors would like to thank the anonymous referees for their extremely careful and useful reports.
Competing interest
The authors have no competing interest to declare.
Funding statement
The second author gratefully acknowledges the support of a Simons Foundation Collaboration Grant.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.