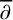1 Introduction
In this paper, we calculate the long-time asymptotics of solutions to the defocussing modified KdV equation (MKdV):
There is a vast body of literature regarding the MKdV equation, in particular with the local and global well-posedness of the Cauchy problem. For a summary of known results, we refer the reader to Linares-Ponce [Reference Linares and Ponce35]. Without trying to be exhaustive, we mention the works by Kato [Reference Kato28], Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29], Colliander-Keel-Staffilani-Takaoka-Tao [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32]. In particular, we know that the MKdV for both the focussing and defocussing cases on the line is locally well-posed (compare Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29]) and globally well-posed, (compare Colliander-Keel-Staffilani-Takaoka-Tao [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32]), in
![]() $H^{s}\left (\mathbb {R}\right )$
for
$H^{s}\left (\mathbb {R}\right )$
for
![]() $s\ge \frac {1}{4}$
. These results are complemented by several ill-posedness results (compare Christ-Colliander-Tao [Reference Christ, Colliander and Tao5] and references therein), which establish that
$s\ge \frac {1}{4}$
. These results are complemented by several ill-posedness results (compare Christ-Colliander-Tao [Reference Christ, Colliander and Tao5] and references therein), which establish that
![]() $H^{\frac {1}{4}}(\mathbb {R})$
is optimal if one requires that solutions depend uniformly continuously on the initial data. Since the completion of the first version of the current paper, there has been significant progress regarding the global well-posedness of integrable PDEs on the real line, in particular for the KdV, mKdV and NLS equations; see Killip-Visan [Reference Killip and Visan34], Harrop-Griffiths-Killip-Visan [Reference Harrop-Griffiths, Killip and Visan22]. In [Reference Harrop-Griffiths, Killip and Visan22], for the mKdV equation, global well-posedness is obtained in
$H^{\frac {1}{4}}(\mathbb {R})$
is optimal if one requires that solutions depend uniformly continuously on the initial data. Since the completion of the first version of the current paper, there has been significant progress regarding the global well-posedness of integrable PDEs on the real line, in particular for the KdV, mKdV and NLS equations; see Killip-Visan [Reference Killip and Visan34], Harrop-Griffiths-Killip-Visan [Reference Harrop-Griffiths, Killip and Visan22]. In [Reference Harrop-Griffiths, Killip and Visan22], for the mKdV equation, global well-posedness is obtained in
![]() $H^\tau (\mathbb {R})$
for
$H^\tau (\mathbb {R})$
for
![]() $\tau>-\frac {1}{2}$
. It is also known that instantaneous norm inflation happens in
$\tau>-\frac {1}{2}$
. It is also known that instantaneous norm inflation happens in
![]() $H^\tau (\mathbb {R})$
for
$H^\tau (\mathbb {R})$
for
![]() $\tau =-\frac {1}{2}$
. We again refer to [Reference Harrop-Griffiths, Killip and Visan22] for details.
$\tau =-\frac {1}{2}$
. We again refer to [Reference Harrop-Griffiths, Killip and Visan22] for details.
Besides well-posedness, another fundamental question for dispersive PDEs is long-time asymptotics. Using the complete integrability of the MKdV equation, Deift and Zhou, in their seminal work [Reference Deift and Zhou11], developed the celebrated nonlinear steepest descent method for oscillatory Riemann-Hilbert problems. In the same paper, the authors give explicit asymptotic formulae and error terms for Schwartz class initial data. Since then, analysis of the long-time behaviour of integrable systems has been extensively treated by many authors. The nonlinear steepest descent method provides a systematic way to reduce the original RHP to a canonical model RHP whose solution is calculated in terms of special functions. This reduction is done through a sequence of transformations whose effects do not change the long-time behaviour of the recovered solution at leading order. In this way, one obtains the asymptotic behaviour of the solution in terms of the spectral data (and thus in terms of the initial conditions).
A natural question to ask is whether it is possible to study the asymptotic behaviour of the MKdV equation without relying on the completely integrable structure. A proof of global existence and a (partial) derivation of the asymptotic behaviour for small localised solutions were later given by Hayashi and Naumkin in [Reference Hayashi and Naumkin23, Reference Hayashi and Naumkin24] using the method of factorisation of operators. Recently, Germain-Pusateri-Rousset [Reference Germain, Pusateri and Rousset17] used the idea of space-time resonance to study the long-time asymptotics of small data and the soliton stability problem. Also, a precise derivation of asymptotics and a proof of asymptotic completeness were given by Harrop-Griffiths [Reference Harrop-Griffiths21] using wave packets analysis. Overall, although PDE techniques do not rely on complete integrability, to our best knowledge, certain smallness assumptions on the initial data are required.
In the present paper, we use the inverse scattering transform/nonlinear steepest descent to study the long-time asymptotics of the solution to the MKdV equation without a smallness assumption on the initial data. We give a full description of the long-time behaviour of solutions in the weighted Sobolev space
![]() $H^{2,1}$
, which is necessary to construct the solution via inverse scattering and extend these results to other Sobolev spaces, including
$H^{2,1}$
, which is necessary to construct the solution via inverse scattering and extend these results to other Sobolev spaces, including
![]() $H^{1,1}$
,
$H^{1,1}$
,
![]() $H^{\frac {1}{4},1}$
and
$H^{\frac {1}{4},1}$
and
![]() $L^{2,1}$
, via a global approximation argument.
$L^{2,1}$
, via a global approximation argument.
In Deift-Zhou [Reference Deift and Zhou11], a key step in the nonlinear steepest descent method consists of deforming the contour associated to the RHP in such a way that the phase function with oscillatory dependence on parameters becomes exponential decay. In general, the entries of the jump matrix are not analytic, so direct analytic extension off the real axis is not possible. Instead, they must be approximated by rational functions, and this results in some error terms in the recovered solution. Therefore, in the context of nonlinear steepest descent, most results are carried out under the assumption that the initial data belong to the Schwartz space.
In [Reference Zhou45], Xin Zhou developed a rigorous analysis of the direct and inverse scattering transform of the AKNS system for a class of initial conditions
![]() $u_0(x)=u(x,t=0)$
belonging to the space
$u_0(x)=u(x,t=0)$
belonging to the space
![]() $H^{i,j}(\mathbb {R})$
. Here,
$H^{i,j}(\mathbb {R})$
. Here,
![]() $H^{i,j}(\mathbb {R})$
denotes the completion of
$H^{i,j}(\mathbb {R})$
denotes the completion of
![]() $C_0^\infty (\mathbb {R})$
in the norm
$C_0^\infty (\mathbb {R})$
in the norm
Recently, much effort has been devoted to relaxing the regularities of the initial data. In particular, among the most celebrated results concerning nonlinear Schrödinger equations, we point out the work of Deift-Zhou [Reference Deift and Zhou14], where they provide the asymptotics for the NLS in the weighted space
![]() $L^{2,1}$
. This topology is more or less optimal from the views of PDE and inverse scattering transformations. The global
$L^{2,1}$
. This topology is more or less optimal from the views of PDE and inverse scattering transformations. The global
![]() $L^{2}$
existence of the cubic NLS can be carried out by the
$L^{2}$
existence of the cubic NLS can be carried out by the
![]() $L_{t}^{4}L_{x}^{\infty }$
Strichartz estimate and conservation of the
$L_{t}^{4}L_{x}^{\infty }$
Strichartz estimate and conservation of the
![]() $L^{2}$
norm. But in order to obtain the precise asymptotics, one needs to “pay the price of weights”: that is, work with the weighted space
$L^{2}$
norm. But in order to obtain the precise asymptotics, one needs to “pay the price of weights”: that is, work with the weighted space
![]() $L^{2,1}$
.
$L^{2,1}$
.
Dieng and McLaughlin, in [Reference Dieng and McLaughlin15] (see also an extended version, [Reference Dieng, McLaughlin and Miller16]), developed a variant of the Deift-Zhou method. In their approach, rational approximation of the reflection coefficient is replaced by some nonanalytic extension of the jump matrices off the real axis, which leads to a
![]() $\bar {\partial }$
-problem to be solved in some regions of the complex plane. The new
$\bar {\partial }$
-problem to be solved in some regions of the complex plane. The new
![]() $\bar {\partial }$
-problem can be reduced to an integral equation and is solvable through Neumann series. These ideas were originally implemented by Miller and McLaughlin [Reference McLaughlin and Miller37] to study the asymptotics of orthogonal polynomials. This method has shown its robustness in its application to other integrable models. Notably, for focussing NLS and derivative NLS, they were successfully applied to address the soliton resolution in [Reference Borghese, Jenkins and McLaughlin4] and [Reference Jenkins, Liu, Perry and Sulem26], respectively. In this paper, we incorporate this approach into the framework of [Reference Deift and Zhou11] to calculate the long-time behaviour of the defocussing MKdV equation in weighted Sobolev spaces. The soliton resolution of the focussing MKdV equation is addressed in a subsequent article [Reference Chen and Liu7].
$\bar {\partial }$
-problem can be reduced to an integral equation and is solvable through Neumann series. These ideas were originally implemented by Miller and McLaughlin [Reference McLaughlin and Miller37] to study the asymptotics of orthogonal polynomials. This method has shown its robustness in its application to other integrable models. Notably, for focussing NLS and derivative NLS, they were successfully applied to address the soliton resolution in [Reference Borghese, Jenkins and McLaughlin4] and [Reference Jenkins, Liu, Perry and Sulem26], respectively. In this paper, we incorporate this approach into the framework of [Reference Deift and Zhou11] to calculate the long-time behaviour of the defocussing MKdV equation in weighted Sobolev spaces. The soliton resolution of the focussing MKdV equation is addressed in a subsequent article [Reference Chen and Liu7].
1.1 Direct and inverse scattering formalism
To describe our approach, we recall that equation (1.1) generates an iso-spectral flow for the problem
where
 $$ \begin{align*}\sigma_3 = \left( \begin{array}{cc} {1} & 0 \\ 0 & {-1} \end{array} \right) , \,\,\, U(x) = \left( \begin{array}{cc} 0 & {iu(x)} \\ {\overline{iu(x)}} & 0 \end{array} \right) .\end{align*} $$
$$ \begin{align*}\sigma_3 = \left( \begin{array}{cc} {1} & 0 \\ 0 & {-1} \end{array} \right) , \,\,\, U(x) = \left( \begin{array}{cc} 0 & {iu(x)} \\ {\overline{iu(x)}} & 0 \end{array} \right) .\end{align*} $$
This is a standard AKNS system. If
![]() $u \in L^1(\mathbb {R}) $
, equation (1.3) admits bounded solutions for
$u \in L^1(\mathbb {R}) $
, equation (1.3) admits bounded solutions for
![]() $z \in \mathbb {R}$
. There exist unique solutions
$z \in \mathbb {R}$
. There exist unique solutions
![]() $\Psi ^\pm $
of equation (1.3) obeying the following space asymptotic conditions:
$\Psi ^\pm $
of equation (1.3) obeying the following space asymptotic conditions:
 $$ \begin{align*}\lim_{x \rightarrow \pm \infty} \Psi^\pm(x,z) e^{-ix z \sigma_3} = \left( \begin{array}{cc} {1} & 0 \\ 0 & {1} \end{array} \right) ;\end{align*} $$
$$ \begin{align*}\lim_{x \rightarrow \pm \infty} \Psi^\pm(x,z) e^{-ix z \sigma_3} = \left( \begin{array}{cc} {1} & 0 \\ 0 & {1} \end{array} \right) ;\end{align*} $$
and there is a matrix
![]() $T(z)$
, the transition matrix, with
$T(z)$
, the transition matrix, with
![]() $\Psi ^+(x,z)=\Psi ^-(x,z) T(z)$
. The matrix
$\Psi ^+(x,z)=\Psi ^-(x,z) T(z)$
. The matrix
![]() $T(z)$
takes the form
$T(z)$
takes the form
 $$ \begin{align} T(z) = \left( \begin{array}{cc} {a(z)} & {\breve{b}(z)} \\ {b(z)} & {\breve{a}(z)} \end{array} \right), \end{align} $$
$$ \begin{align} T(z) = \left( \begin{array}{cc} {a(z)} & {\breve{b}(z)} \\ {b(z)} & {\breve{a}(z)} \end{array} \right), \end{align} $$
and the determinant relation gives
Combining this with the symmetry relations
we arrive at
and conclude that
![]() $a(z)$
is zero-free.
$a(z)$
is zero-free.
By the standard inverse scattering theory, we formulate the reflection coefficient:
The functions
![]() $r(z)$
is called the scattering data for the initial data
$r(z)$
is called the scattering data for the initial data
![]() $u_0$
satisfying the following symmetry relation:
$u_0$
satisfying the following symmetry relation:
We also have the following identity
We have the following proposition from [Reference Deift and Zhou14]:
Proposition 1.1. For
![]() $k, j$
integers with
$k, j$
integers with
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $j\geq 1$
, the direct scattering map
$j\geq 1$
, the direct scattering map
maps
![]() $H^{k,j}(\mathbb {R})$
onto
$H^{k,j}(\mathbb {R})$
onto
![]() $H^{j,k}_1=H^{j,k}(\mathbb {R})\cap \lbrace r: \left \Vert {r} \right \Vert {}_{L^\infty } <1\rbrace $
, where
$H^{j,k}_1=H^{j,k}(\mathbb {R})\cap \lbrace r: \left \Vert {r} \right \Vert {}_{L^\infty } <1\rbrace $
, where
![]() $H^{j,k}$
norm is defined in equation (1.2) and map
$H^{j,k}$
norm is defined in equation (1.2) and map
![]() $\mathcal {R}$
is Lipschitz continuous.
$\mathcal {R}$
is Lipschitz continuous.
Since we are dealing with the defocussing mKdV, only the reflection coefficient r is needed for the reconstruction of the solution. The long-time behaviour of the solution to the mKdV equation is obtained through a sequence of transformations of the following RHP:
Problem 1.2. Given
![]() $r \in H^{1,2}(\mathbb {R})$
for
$r \in H^{1,2}(\mathbb {R})$
for
![]() $z \in \mathbb {R}$
, find a
$z \in \mathbb {R}$
, find a
![]() $2\times 2$
matrix-valued function
$2\times 2$
matrix-valued function
![]() $m(z;x,t)$
on
$m(z;x,t)$
on
![]() $\mathbb {C} \setminus \mathbb {R}$
with the following properties:
$\mathbb {C} \setminus \mathbb {R}$
with the following properties:
-
(1)
 $m(z;x,t) \rightarrow I$
as
$m(z;x,t) \rightarrow I$
as
 $|z| \rightarrow \infty $
,
$|z| \rightarrow \infty $
, -
(2)
 $m(z;,x,t)$
is analytic for
$m(z;,x,t)$
is analytic for
 $z \in \mathbb {C} \setminus \mathbb {R}$
with continuous boundary values
$z \in \mathbb {C} \setminus \mathbb {R}$
with continuous boundary values  $$ \begin{align*}m_\pm(z;x,t) = \lim_{\varepsilon \downarrow 0} m(z\pm i\varepsilon;x,t),\end{align*} $$
$$ \begin{align*}m_\pm(z;x,t) = \lim_{\varepsilon \downarrow 0} m(z\pm i\varepsilon;x,t),\end{align*} $$
-
(3) The jump relation
 $m_+(z;x,t) = m_ -(z;x,t) e^{-i\theta \operatorname {\mathrm {ad}} \sigma _3} v(z)$
holds, where (1.8)and the real phase function
$m_+(z;x,t) = m_ -(z;x,t) e^{-i\theta \operatorname {\mathrm {ad}} \sigma _3} v(z)$
holds, where (1.8)and the real phase function $$ \begin{align} e^{-i\theta \operatorname{\mathrm{ad}} \sigma_3} v(z) = \left( \begin{array}{cc} {1-|r(z)|^2} & {-\overline{r(z)}e^{-2i\theta}} \\[10pt] {r(z)e^{2i\theta}} & {1} \end{array} \right), \end{align} $$
$$ \begin{align} e^{-i\theta \operatorname{\mathrm{ad}} \sigma_3} v(z) = \left( \begin{array}{cc} {1-|r(z)|^2} & {-\overline{r(z)}e^{-2i\theta}} \\[10pt] {r(z)e^{2i\theta}} & {1} \end{array} \right), \end{align} $$
 $\theta $
is given by (1.9)where
$\theta $
is given by (1.9)where $$ \begin{align} \theta(z;x,t) = 4tz^3+xz, \end{align} $$
(1.10)are the stationary points whenever
$$ \begin{align} \theta(z;x,t) = 4tz^3+xz, \end{align} $$
(1.10)are the stationary points whenever $$ \begin{align} \pm z_0=\pm \sqrt{ \dfrac{|x|}{12t}} \end{align} $$
$$ \begin{align} \pm z_0=\pm \sqrt{ \dfrac{|x|}{12t}} \end{align} $$
 $x<0$
.
$x<0$
.
Note that the jump matrix v admits the following factorisation on
![]() $\mathbb {R}$
:
$\mathbb {R}$
:
 $$ \begin{align*} e^{-i\theta \operatorname{\mathrm{ad}} \sigma_3} v(z) &= \left( \begin{array}{cc} {1} & {-\overline{r} e^{-2i\theta}} \\ {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\ {r e^{2i\theta}} & {1} \end{array} \right) \\ &=(1-w_\theta^-)^{-1}(1+ w_\theta^+). \end{align*} $$
$$ \begin{align*} e^{-i\theta \operatorname{\mathrm{ad}} \sigma_3} v(z) &= \left( \begin{array}{cc} {1} & {-\overline{r} e^{-2i\theta}} \\ {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\ {r e^{2i\theta}} & {1} \end{array} \right) \\ &=(1-w_\theta^-)^{-1}(1+ w_\theta^+). \end{align*} $$
We define
Then it is well known that the solvability of the RHP above is equivalent to the solvability of the following Beals-Coifman integral equation:
Here
![]() $C^\pm $
is the Cauchy projection
$C^\pm $
is the Cauchy projection
and
![]() $+(-)$
denotes taking the limit from the positive (negative) side of the oriented contour. From the solution of Problem 1.2, we recover
$+(-)$
denotes taking the limit from the positive (negative) side of the oriented contour. From the solution of Problem 1.2, we recover
 $$ \begin{align} &\qquad\qquad =\left[ \dfrac{-i}{\pi}\int_{\mathbb{R}} \mu (w_\theta^-+w_\theta^+) \right]_{12}, \end{align} $$
$$ \begin{align} &\qquad\qquad =\left[ \dfrac{-i}{\pi}\int_{\mathbb{R}} \mu (w_\theta^-+w_\theta^+) \right]_{12}, \end{align} $$
where the limit is taken in
![]() $\mathbb {C}\setminus \mathbb {R}$
along any direction not tangent to
$\mathbb {C}\setminus \mathbb {R}$
along any direction not tangent to
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
1.2 Main results
The central results of this paper are the following theorems that give the long-time behaviour of the solution
![]() $u(x,t)$
of equation (1.1) in different regions in the
$u(x,t)$
of equation (1.1) in different regions in the
![]() $(x,t)$
plane, respectively.
$(x,t)$
plane, respectively.
For
![]() $M>1$
and
$M>1$
and
![]() $z_0$
given by equation (1.10) and
$z_0$
given by equation (1.10) and
![]() $\tau $
a parameter given by equation (1.17), we define the regions as follows:
$\tau $
a parameter given by equation (1.17), we define the regions as follows:
-
○ Region I:
 $x<0$
,
$x<0$
,
 $M^{-1}<z_0=\sqrt { \frac {|x|}{12t}}<M,\,\tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\gg 1$
;
$M^{-1}<z_0=\sqrt { \frac {|x|}{12t}}<M,\,\tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\gg 1$
; -
○ Region II:
 $x<0$
,
$x<0$
,
 $M^{-1}\leq \tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2} $
;
$M^{-1}\leq \tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2} $
; -
○ Region III:
 $\tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\leq M$
;
$\tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\leq M$
; -
○ Region IV:
 $x>0$
,
$x>0$
,
 $z_0=\sqrt { \frac {|x|}{12t}}\leq M, \, \tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\geq M^{-1}$
;
$z_0=\sqrt { \frac {|x|}{12t}}\leq M, \, \tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\geq M^{-1}$
; -
○ Region V:
 $x>0$
,
$x>0$
,
 $ z_0=\sqrt { \frac {|x|}{12t}}> M^{-1}, \, \tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\gg 1$
.
$ z_0=\sqrt { \frac {|x|}{12t}}> M^{-1}, \, \tau =\left ( \frac {|x|}{12t^{1/3}}\right )^{3/2}\gg 1$
.
Theorem 1.3. Given initial data
![]() $u_0 \in H^{2,1}(\mathbb {R})$
, let u be the solution to the MKdV equation
$u_0 \in H^{2,1}(\mathbb {R})$
, let u be the solution to the MKdV equation
given by the reconstruction formula in equation (1.14). Let
![]() $z_0$
be given by equation (1.10), and define
$z_0$
be given by equation (1.10), and define
 $$ \begin{align} \tau=z_0^3 t=\left( \dfrac{|x|}{12t^{1/3}}\right)^{3/2} \end{align} $$
$$ \begin{align} \tau=z_0^3 t=\left( \dfrac{|x|}{12t^{1/3}}\right)^{3/2} \end{align} $$
and
where r is defined in equation (1.6). Then we have the following asymptotics:
-
(i) In Region
 $\text {I}$
, (1.19)where
$\text {I}$
, (1.19)where $$ \begin{align} u(x,t) &= \left( \dfrac{\kappa}{3tz_0}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right) + \mathcal{O}\left( (z_0 t)^{-\frac{3}{4}}\right) \\ \nonumber &= \left( \dfrac{\kappa}{3tz_0}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right) + \mathcal{O} \left( t^{-\frac{1}{2}}\left( \frac{|x|}{t^{\frac{1}{3}}} \right)^{-\frac{3}{8}} \right), \end{align} $$
$$ \begin{align} u(x,t) &= \left( \dfrac{\kappa}{3tz_0}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right) + \mathcal{O}\left( (z_0 t)^{-\frac{3}{4}}\right) \\ \nonumber &= \left( \dfrac{\kappa}{3tz_0}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right) + \mathcal{O} \left( t^{-\frac{1}{2}}\left( \frac{|x|}{t^{\frac{1}{3}}} \right)^{-\frac{3}{8}} \right), \end{align} $$
 $$ \begin{align*} \phi(z_0) &=\arg \Gamma(i\kappa)-\dfrac{\pi}{4}-\arg r(z_0) +\dfrac{1}{\pi}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z_0}. \end{align*} $$
$$ \begin{align*} \phi(z_0) &=\arg \Gamma(i\kappa)-\dfrac{\pi}{4}-\arg r(z_0) +\dfrac{1}{\pi}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z_0}. \end{align*} $$
-
(ii) In Region
 $\text {II}$
, (1.20)
$\text {II}$
, (1.20) $$ \begin{align} u(x,t)=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+ \mathcal{O} \left( t^{-\frac{1}{2}}\left( \frac{|x|}{t^{\frac{1}{3}}} \right)^{-\frac{3}{8}} \right). \end{align} $$
$$ \begin{align} u(x,t)=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+ \mathcal{O} \left( t^{-\frac{1}{2}}\left( \frac{|x|}{t^{\frac{1}{3}}} \right)^{-\frac{3}{8}} \right). \end{align} $$
-
(iii) In Region
 $\text {III}$
, (1.21)
$\text {III}$
, (1.21) $$ \begin{align} u(x,t)=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{ -\frac{1}{2} } \right). \end{align} $$
$$ \begin{align} u(x,t)=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{ -\frac{1}{2} } \right). \end{align} $$
-
(iv) In Region
 $\text {IV}$
, (1.22)
$\text {IV}$
, (1.22) $$ \begin{align} u(x,t)&=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( (t\tau)^{-\frac{1}{2}}\right)\\ \nonumber &=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{-\frac{1}{2}}\left( \frac{|x|}{t^{\frac{1}{3}}} \right)^{-\frac{3}{4}} \right). \end{align} $$
$$ \begin{align} u(x,t)&=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( (t\tau)^{-\frac{1}{2}}\right)\\ \nonumber &=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{-\frac{1}{2}}\left( \frac{|x|}{t^{\frac{1}{3}}} \right)^{-\frac{3}{4}} \right). \end{align} $$
-
(v) In Region
 $\text {V}$
, (1.23)
$\text {V}$
, (1.23) $$ \begin{align} u(x,t)=\mathcal{O} \left( t^{-1}\right). \end{align} $$
$$ \begin{align} u(x,t)=\mathcal{O} \left( t^{-1}\right). \end{align} $$
In the above asymptotics for Regions
![]() $\text {II}$
,
$\text {II}$
,
![]() $\text {III}$
,
$\text {III}$
,
![]() $\text {IV}$
, P is a solution of the Painlevé
$\text {IV}$
, P is a solution of the Painlevé
![]() $\text {II}$
equation
$\text {II}$
equation
determined by
![]() $r(0)$
. Note that given
$r(0)$
. Note that given
![]() $r(z)\in H^1(\mathbb {R})$
, r is defined pointwise and
$r(z)\in H^1(\mathbb {R})$
, r is defined pointwise and
![]() $r(0)$
makes sense. Also note that in all the asymptotics above, the implicit constants in the remainder terms depend only on
$r(0)$
makes sense. Also note that in all the asymptotics above, the implicit constants in the remainder terms depend only on
![]() $ \left \Vert {r} \right \Vert {}_{H^{1}(\mathbb {R})} $
. It is possible to combine Region II, Region III and Region IVFootnote
1
to conclude that in these regions,
$ \left \Vert {r} \right \Vert {}_{H^{1}(\mathbb {R})} $
. It is possible to combine Region II, Region III and Region IVFootnote
1
to conclude that in these regions,
 $$ \begin{align*} \left|u(x,t)-\frac{1}{(3t)^{\frac{1}{3}}}P\left(\frac{x}{(3t)^{\frac{1}{3}}}\right)\right|\lesssim t^{-\frac{1}{2}}\left (1+\left(\frac{|x|}{t^{\frac{1}{3}}}\right)^{-\frac{3}{8}}\right). \end{align*} $$
$$ \begin{align*} \left|u(x,t)-\frac{1}{(3t)^{\frac{1}{3}}}P\left(\frac{x}{(3t)^{\frac{1}{3}}}\right)\right|\lesssim t^{-\frac{1}{2}}\left (1+\left(\frac{|x|}{t^{\frac{1}{3}}}\right)^{-\frac{3}{8}}\right). \end{align*} $$
We give several remarks on the statements above.
Remark 1.4. First, we have the following comments on the various regions above:
-
(1) The three main regions of interest are Regions I, III and V. In the case of focussing mKdV, they are called the oscillatory region, self-similar region and soliton region, respectively. The remaining two regions, Region II and Region IV, can be regarded as transitions. They are treated separately because the asymptotics are calculated differently.
-
(2) Throughout the paper,
 $z_0$
is positive. The calculations for Region I involve the large parameter
$z_0$
is positive. The calculations for Region I involve the large parameter
 $\tau $
and
$\tau $
and
 $z_0$
is bounded below. In Regions II and III,
$z_0$
is bounded below. In Regions II and III,
 $z_0$
can decay to
$z_0$
can decay to
 $0$
as
$0$
as
 $t\to \infty $
while
$t\to \infty $
while
 $\tau $
is bounded above. The calculations instead depend on scaling out
$\tau $
is bounded above. The calculations instead depend on scaling out
 $z_0$
and
$z_0$
and
 $t^{-1/3}$
, respectively. Region V is the fast-decaying region.
$t^{-1/3}$
, respectively. Region V is the fast-decaying region. -
(3) To match the asymptotic formulas in the overlaps of the regions, we have the following statements:
-
○ The matching of asymptotic formulas in Region I and Region II is discussed in [Reference Deift and Zhou11, Section 6].
-
○ The matching of asymptotic formulas in Region II and Region III is given in remark 7.1. Moreover, the matching of asymptotic formulas in Region III and Region IV is explicit, depending on whether
 $\tau $
is bounded.
$\tau $
is bounded. -
○ The matching between Region IV and Region V can be read off from the fact that
 $\tau =\mathcal {O}(t)$
in Region V and the Painlevé asymptotics given in [Reference Deift and Zhou12, (1.18),(4.19)].
$\tau =\mathcal {O}(t)$
in Region V and the Painlevé asymptotics given in [Reference Deift and Zhou12, (1.18),(4.19)].
-
-
(4) Indeed, in [Reference Harrop-Griffiths21] and [Reference Germain, Pusateri and Rousset17], the asymptotics are stated in three regions. But we prefer to keep our five-region statements since the calculations in these regions differ. As discussed above, Region II and Region IV play the role of transition regions. We believe that these will give a refined picture of the full asymptotics.
Remark 1.5. In this paper, to derive asymptotics, our main focus is to establish estimates for the error terms that only depend on
![]() $ \left \Vert {r} \right \Vert {}_{H^{1}(\mathbb {R})}, $
which is equivalent to
$ \left \Vert {r} \right \Vert {}_{H^{1}(\mathbb {R})}, $
which is equivalent to
![]() $ \left \Vert {u_0} \right \Vert {}_{L^{2,1}(\mathbb {R})} $
by proposition 1.1. We claim that this dependence is uniform in each of the five regions defined in Figure 1.1. All leading-order terms from the asymptotic formulae in all regions are obtained from special functions, namely parabolic cylinder functions and Painlevé II. For brevity, we do not repeat lengthy identical steps. We refer to Deift-Zhou [Reference Deift and Zhou11] for full details.
$ \left \Vert {u_0} \right \Vert {}_{L^{2,1}(\mathbb {R})} $
by proposition 1.1. We claim that this dependence is uniform in each of the five regions defined in Figure 1.1. All leading-order terms from the asymptotic formulae in all regions are obtained from special functions, namely parabolic cylinder functions and Painlevé II. For brevity, we do not repeat lengthy identical steps. We refer to Deift-Zhou [Reference Deift and Zhou11] for full details.

Figure 1.1 Five regions.
Remark 1.6. From the view of the scattering theory, it is natural to ask if one can determine the initial data uniquely from the asymptotics of a solution. Here we point out that in our asymptotics formulae, the solution P to the Painlevé II equation only depends on
![]() $r\left (0\right )$
, the reflection coefficient evaluated at the origin. For an explicit relation between
$r\left (0\right )$
, the reflection coefficient evaluated at the origin. For an explicit relation between
![]() $r(0)$
and P the solution to Painlevé II; see [Reference Deift and Zhou11, p.358-p.359]. Therefore, if one only looks at the asymptotics in regions
$r(0)$
and P the solution to Painlevé II; see [Reference Deift and Zhou11, p.358-p.359]. Therefore, if one only looks at the asymptotics in regions
![]() $\text {II}, \text {III}, \text {IV}$
and
$\text {II}, \text {III}, \text {IV}$
and
![]() $\text {V}$
, these pieces of information are not sufficient to determine the initial data that produce this solution. To obtain the full information of the initial data, we have to go to Region
$\text {V}$
, these pieces of information are not sufficient to determine the initial data that produce this solution. To obtain the full information of the initial data, we have to go to Region
![]() $\text {I}$
, from which one can determine the phase and modulus of the reflection coefficient from the formulae given by the parabolic cylinder. For more details, see Deift-Zhou [Reference Deift and Zhou11]. In this defocussing case, Region
$\text {I}$
, from which one can determine the phase and modulus of the reflection coefficient from the formulae given by the parabolic cylinder. For more details, see Deift-Zhou [Reference Deift and Zhou11]. In this defocussing case, Region
![]() $\text {I}$
is the most physically interesting. But in the focussing problem, breathers can appear in other regions. For more details, see our subsequent article, [Reference Chen and Liu7].
$\text {I}$
is the most physically interesting. But in the focussing problem, breathers can appear in other regions. For more details, see our subsequent article, [Reference Chen and Liu7].
Remark 1.7. In [Reference Germain, Pusateri and Rousset17] and [Reference Harrop-Griffiths21], the long-time asymptotics of small solutions to the mKdV are established. Moreover, the decay of the spacial derivatives of the solutions is also obtained. In [Reference Harrop-Griffiths21], the
![]() $L^2$
estimates of error terms are estimated. In the theorem above, we only compute the asymptotics in the pointwise sense. In principle, with the analysis of the
$L^2$
estimates of error terms are estimated. In the theorem above, we only compute the asymptotics in the pointwise sense. In principle, with the analysis of the
![]() $L^2$
mapping properties of the
$L^2$
mapping properties of the
![]() $\overline {\partial }$
problem, we can also obtain the
$\overline {\partial }$
problem, we can also obtain the
![]() $L^2$
estimates for error terms, but we do not pursue it here since this will require a different argument. Taking
$L^2$
estimates for error terms, but we do not pursue it here since this will require a different argument. Taking
![]() $z_0=\sqrt {\frac {|x|}{12t}}$
in the leading-order terms in expressions from the theorem above, the resulting formulas are the same as the leading-order terms in [Reference Germain, Pusateri and Rousset17] and [Reference Harrop-Griffiths21]. Plugging
$z_0=\sqrt {\frac {|x|}{12t}}$
in the leading-order terms in expressions from the theorem above, the resulting formulas are the same as the leading-order terms in [Reference Germain, Pusateri and Rousset17] and [Reference Harrop-Griffiths21]. Plugging
![]() $z_0$
into the error terms above, we observe that actually, in the pointwise sense, the error terms are sharper than those in [Reference Germain, Pusateri and Rousset17] and [Reference Harrop-Griffiths21].
$z_0$
into the error terms above, we observe that actually, in the pointwise sense, the error terms are sharper than those in [Reference Germain, Pusateri and Rousset17] and [Reference Harrop-Griffiths21].
The paper ends with a section to extend the asymptotics from Theorem 1.3 to rougher solutions. With the uniform estimates on error terms, we apply approximation arguments to study solutions in various low-regularity spaces:
![]() $H^{1}$
,
$H^{1}$
,
![]() $H^{1/4}$
and
$H^{1/4}$
and
![]() $L^2$
with some weights. Using the local well-posedness in
$L^2$
with some weights. Using the local well-posedness in
![]() $H^{k}\left (\mathbb {R}\right )$
with
$H^{k}\left (\mathbb {R}\right )$
with
![]() $k\ge \frac {1}{4}$
obtained by Kenig-Ponce-Vega (see [Reference Kenig, Ponce and Vega29]); the growth estimates for the
$k\ge \frac {1}{4}$
obtained by Kenig-Ponce-Vega (see [Reference Kenig, Ponce and Vega29]); the growth estimates for the
![]() $H^{k}$
norm due to Colliander-Keel-Staffilani-Takaoka-Tao [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32]; and the recent advance on globally well-posedness by Harrop-Griffiths-Killip-Visan [Reference Harrop-Griffiths, Killip and Visan22] in
$H^{k}$
norm due to Colliander-Keel-Staffilani-Takaoka-Tao [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32]; and the recent advance on globally well-posedness by Harrop-Griffiths-Killip-Visan [Reference Harrop-Griffiths, Killip and Visan22] in
![]() $H^\tau (\mathbb {R})$
,
$H^\tau (\mathbb {R})$
,
![]() $\tau>-1/2$
, we employ a global approximation argument to extend our long-time asymptotics to
$\tau>-1/2$
, we employ a global approximation argument to extend our long-time asymptotics to
![]() $H^{k,1}$
with
$H^{k,1}$
with
![]() $k\geq 0$
. Then we can extend the results in the previous theorem and obtain the following:
$k\geq 0$
. Then we can extend the results in the previous theorem and obtain the following:
Theorem 1.8. For any initial data
![]() $u_{0}\in H^{k,1}\left (\mathbb {R}\right )$
with
$u_{0}\in H^{k,1}\left (\mathbb {R}\right )$
with
![]() $k\geq 0$
, the solutionFootnote
2
to the MKdV equation
$k\geq 0$
, the solutionFootnote
2
to the MKdV equation
has the same asymptotics as in our main Theorem 1.3.
We notice that one can trace all the details in our implementation of the nonlinear steepest descent and that it suffices to require the weights in x to be
![]() $\left \langle x\right \rangle ^{s}$
with
$\left \langle x\right \rangle ^{s}$
with
![]() $s>\frac {1}{2}$
since for the general case,
$s>\frac {1}{2}$
since for the general case,
![]() $s>\frac {1}{2}$
is sufficient for us to apply the Sobolev embedding and the estimate of modulus of continuity of the reflection coefficients in the Riemann-Hilbert problem. Therefore, we can conclude the following corollary:
$s>\frac {1}{2}$
is sufficient for us to apply the Sobolev embedding and the estimate of modulus of continuity of the reflection coefficients in the Riemann-Hilbert problem. Therefore, we can conclude the following corollary:
Corollary 1.9. For any initial data
![]() $u_{0}\in H^{k,s}\left (\mathbb {R}\right )$
with
$u_{0}\in H^{k,s}\left (\mathbb {R}\right )$
with
![]() $s>\frac {1}{2}$
and
$s>\frac {1}{2}$
and
![]() $k\geq 0$
, the solution to the MKdV equation (1.24) has the same leading-order terms as equations (1.19)–(1.22) (first term on the right-hand side of the equation) in main Theorem 1.3. And the error terms (big-O notation) can be found in Remark 7.2.
$k\geq 0$
, the solution to the MKdV equation (1.24) has the same leading-order terms as equations (1.19)–(1.22) (first term on the right-hand side of the equation) in main Theorem 1.3. And the error terms (big-O notation) can be found in Remark 7.2.
After establishing the computations for
![]() $s=1$
, to get the general results for
$s=1$
, to get the general results for
![]() $s>\frac {1}{2}$
, one just needs to use the standard analysis of Jost functions and mollifiers. Computations from
$s>\frac {1}{2}$
, one just needs to use the standard analysis of Jost functions and mollifiers. Computations from
![]() $s=1$
to general
$s=1$
to general
![]() $s>\frac {1}{2}$
are quite routine; see Cuccagna-Pelinovsky [Reference Cuccagna and Pelinovsky8] for computations for the cubic NLS. In particular, the direct scattering problem for the mKdV equation is the same as the NLS. Hereinafter, for the sake of simplicity, we just focus on the case where
$s>\frac {1}{2}$
are quite routine; see Cuccagna-Pelinovsky [Reference Cuccagna and Pelinovsky8] for computations for the cubic NLS. In particular, the direct scattering problem for the mKdV equation is the same as the NLS. Hereinafter, for the sake of simplicity, we just focus on the case where
![]() $s=1$
.
$s=1$
.
1.3 Notations
Let
![]() $\sigma _3$
be the third Pauli matrix
$\sigma _3$
be the third Pauli matrix
 $$ \begin{align*}\sigma_3= \left( \begin{array}{cc} {1} & {0} \\ {0} & {-1} \end{array} \right) \end{align*} $$
$$ \begin{align*}\sigma_3= \left( \begin{array}{cc} {1} & {0} \\ {0} & {-1} \end{array} \right) \end{align*} $$
and define the matrix operation
 $$ \begin{align*}e^{\operatorname{\mathrm{ad}}\sigma_3}A= \left( \begin{array}{cc} {a} & {e^{2} b} \\ {e^{-2}c} & {d} \end{array} \right). \end{align*} $$
$$ \begin{align*}e^{\operatorname{\mathrm{ad}}\sigma_3}A= \left( \begin{array}{cc} {a} & {e^{2} b} \\ {e^{-2}c} & {d} \end{array} \right). \end{align*} $$
We define Fourier transforms as
Using the Fourier transform, one can define the fractional weighted Sobolev spaces:
 $$ \begin{align} H^{k,s}\left(\mathbb{R}\right):=\left\{ h:\,\left\langle 1+\left|\xi\right|{}^{2}\right\rangle ^{\frac{k}{2}}\hat{h}\left(\xi\right)\in L^{2}\left(\mathbb{R}\right),\:\left\langle 1+x^{2}\right\rangle ^{\frac{s}{2}}h\in L^{2}\left(\mathbb{R}\right)\right\}. \end{align} $$
$$ \begin{align} H^{k,s}\left(\mathbb{R}\right):=\left\{ h:\,\left\langle 1+\left|\xi\right|{}^{2}\right\rangle ^{\frac{k}{2}}\hat{h}\left(\xi\right)\in L^{2}\left(\mathbb{R}\right),\:\left\langle 1+x^{2}\right\rangle ^{\frac{s}{2}}h\in L^{2}\left(\mathbb{R}\right)\right\}. \end{align} $$
As usual, ‘
![]() $A:=B$
’ or ‘
$A:=B$
’ or ‘
![]() $B=:A$
’ is the definition of A by means of the expression B. We use the notation
$B=:A$
’ is the definition of A by means of the expression B. We use the notation
![]() $\langle x\rangle =\left (1+|x|^{2}\right )^{\frac {1}{2}}$
. For positive quantities a and b, we write
$\langle x\rangle =\left (1+|x|^{2}\right )^{\frac {1}{2}}$
. For positive quantities a and b, we write
![]() $a\lesssim b$
for
$a\lesssim b$
for
![]() $a\leq Cb$
, where C is some prescribed constant. Also,
$a\leq Cb$
, where C is some prescribed constant. Also,
![]() $a\simeq b$
for
$a\simeq b$
for
![]() $a\lesssim b$
and
$a\lesssim b$
and
![]() $b\lesssim a$
. Throughout, we use
$b\lesssim a$
. Throughout, we use
![]() $u_{t}:=\frac {\partial }{\partial _{t}}u$
,
$u_{t}:=\frac {\partial }{\partial _{t}}u$
,
![]() $u_{x}:=\frac {\partial }{\partial x}u$
.
$u_{x}:=\frac {\partial }{\partial x}u$
.
1.4 Some discussion
To finish the introduction, we highlight certain features of this paper.
Firstly, compared with the analysis of the nonlinear Schrödinger equation in weighted Sobolev spaces [Reference Deift and Zhou14], the defocussing MKdV exhibits more complicated behaviour in terms of long-time asymptotics. This follows from the fact that the phase function for the nonlinear Schrödinger equation has a single stationary point, while the phase function for the MKdV equation has two stationary points. The MKdV equation has the oscillatory region (Region I), the self-similar region (Region II-IV) and the decaying region (Region V), each of which has different leading-order terms and error terms. These two stationary points, due to symmetry, will lead to a real-valued solution to the equation plus a higher-order correction term. More importantly, unlike the NLS equation, where we can build parametrices directly out of the parabolic cylinder functions, for the MKdV equation, extra terms have to be eliminated before arriving at the model problem. Thus, due to the complicated structure of the MKdV equation, we will explore some new applications of the
![]() $\bar {\partial }$
-steepest descent method. We instead conjugate the jump matrices by a diagonal matrix
$\bar {\partial }$
-steepest descent method. We instead conjugate the jump matrices by a diagonal matrix
![]() $\mathcal {P}$
(compare equation (4.2)). Meanwhile, in certain self-similar regions, the two stationary points will approach each other as
$\mathcal {P}$
(compare equation (4.2)). Meanwhile, in certain self-similar regions, the two stationary points will approach each other as
![]() $t\to \infty $
. In this case, the decay in time results from a scaling factor instead of oscillation. We believe these are new applications of the
$t\to \infty $
. In this case, the decay in time results from a scaling factor instead of oscillation. We believe these are new applications of the
![]() $\overline {\partial }$
nonlinear steepest descent method and can be used to treat other integrable models.
$\overline {\partial }$
nonlinear steepest descent method and can be used to treat other integrable models.
Secondly, we extend the asymptotics of the MKdV equation to solutions with initial data in lower regularity spaces using a global approximation via PDE techniques. In Deift-Zhou [Reference Deift and Zhou14], due to the
![]() $L_{t}^{4}L_{x}^{\infty }$
Strichartz estimates for the linear Schrödinger equation and the conservation of the
$L_{t}^{4}L_{x}^{\infty }$
Strichartz estimates for the linear Schrödinger equation and the conservation of the
![]() $L^{2}$
norm, the authors can globally approximate the solution to the nonlinear Schrödinger equation with data in
$L^{2}$
norm, the authors can globally approximate the solution to the nonlinear Schrödinger equation with data in
![]() $L^{2,1}$
using the Beals-Coifman representation of solutions directly. Unlike the Schrödinger equation, the smoothing estimates and Strichartz estimates for the Airy equation and the MKdV equation are much more involved. For example, one needs the
$L^{2,1}$
using the Beals-Coifman representation of solutions directly. Unlike the Schrödinger equation, the smoothing estimates and Strichartz estimates for the Airy equation and the MKdV equation are much more involved. For example, one needs the
![]() $L_{x}^{4}L_{t}^{\infty }$
estimate that acts like a maximal operator. To directly work on the solution to the MKdV equation via inverse scattering to establish the smoothing estimates and Strichartz estimates, one needs estimates for pseudo-differential operators with very rough symbols. To avoid these technicalities, we first identify the solution by inverse scattering with the solution given by the Duhamel formula, which we call a strong solution. The equivalence of these two types of solutions in
$L_{x}^{4}L_{t}^{\infty }$
estimate that acts like a maximal operator. To directly work on the solution to the MKdV equation via inverse scattering to establish the smoothing estimates and Strichartz estimates, one needs estimates for pseudo-differential operators with very rough symbols. To avoid these technicalities, we first identify the solution by inverse scattering with the solution given by the Duhamel formula, which we call a strong solution. The equivalence of these two types of solutions in
![]() $H^{2,1}\left (\mathbb {R}\right )$
is not transparent since there is not enough smoothness for taking derivatives. Relying on smoothing estimates and the bijectivity of the scattering and inverse scattering transforms by Zhou [Reference Zhou45], which plays the role of the Plancherel theorem in Fourier analysis, we show that these two types of solutions are the same at the level of
$H^{2,1}\left (\mathbb {R}\right )$
is not transparent since there is not enough smoothness for taking derivatives. Relying on smoothing estimates and the bijectivity of the scattering and inverse scattering transforms by Zhou [Reference Zhou45], which plays the role of the Plancherel theorem in Fourier analysis, we show that these two types of solutions are the same at the level of
![]() $H^{2,1}\left (\mathbb {R}\right )$
, which is necessary to construct the solutions by inverse scattering. Since the strong solutions by construction enjoy Strichartz estimates and smoothing estimates, by our identification, the solutions by inverse scattering also satisfy these estimates. Then we can use Strichartz estimates and smoothing estimates to pass limits of solutions by inverse scattering to obtain the asymptotics for rougher initial data in
$H^{2,1}\left (\mathbb {R}\right )$
, which is necessary to construct the solutions by inverse scattering. Since the strong solutions by construction enjoy Strichartz estimates and smoothing estimates, by our identification, the solutions by inverse scattering also satisfy these estimates. Then we can use Strichartz estimates and smoothing estimates to pass limits of solutions by inverse scattering to obtain the asymptotics for rougher initial data in
![]() $H^{1,1}\left (\mathbb {R}\right )$
and
$H^{1,1}\left (\mathbb {R}\right )$
and
![]() $H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
. To illustrate the importance of
$H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
. To illustrate the importance of
![]() $H^{1}\left (\mathbb {R}\right )$
and
$H^{1}\left (\mathbb {R}\right )$
and
![]() $H^{\frac {1}{4}}\left (\mathbb {R}\right )$
, we note that in
$H^{\frac {1}{4}}\left (\mathbb {R}\right )$
, we note that in
![]() $H^{1}\left (\mathbb {R}\right )$
, the MKdV equation has energy conservation. On the other hand,
$H^{1}\left (\mathbb {R}\right )$
, the MKdV equation has energy conservation. On the other hand,
![]() $H^{\frac {1}{4}}\left (\mathbb {R}\right )$
is the optimal space to use iterations to construct the solution to the MKdV equation. With the recent advances in global well-posedness of mKdV equations [Reference Harrop-Griffiths, Killip and Visan22], with appropriate notation of solutions, our results can be naturally extended to solutions with initial data in the weighted
$H^{\frac {1}{4}}\left (\mathbb {R}\right )$
is the optimal space to use iterations to construct the solution to the MKdV equation. With the recent advances in global well-posedness of mKdV equations [Reference Harrop-Griffiths, Killip and Visan22], with appropriate notation of solutions, our results can be naturally extended to solutions with initial data in the weighted
![]() $L^2(\mathbb {R)}$
space. For details of the proof, we refer the reader to Section 8.
$L^2(\mathbb {R)}$
space. For details of the proof, we refer the reader to Section 8.
Finally, we give a general description of the derivation of the long-time asymptotics and performing nonlinear steepest descent. The major part of this paper is devoted to the study of Region I, whose leading behaviour is given by parabolic cylinder functions.
The first step (Section 2), is to conjugate the matrix m with a scalar function
![]() $\delta (z)$
, which solves the scalar model RHP Problem 2.1. This conjugation leads to a new RHP, Problem 2.3. This is to prepare for the lower/upper factorisation of the jump matrix on the part of the real axis between two stationary points. This is needed in the contour deformation described in Section 3.
$\delta (z)$
, which solves the scalar model RHP Problem 2.1. This conjugation leads to a new RHP, Problem 2.3. This is to prepare for the lower/upper factorisation of the jump matrix on the part of the real axis between two stationary points. This is needed in the contour deformation described in Section 3.
The second step ( Section 3) is a deformation of the contour from
![]() $\mathbb {R}$
to a new contour
$\mathbb {R}$
to a new contour
![]() $\Sigma ^{(2)}$
(Figure 4.1). It is to guarantee that the phase factors in the jump matrix in equation (2.4) have the desired exponential decay in time along the deformed contours. Inevitably, this transformation results in certain nonanalyticity in sectors
$\Sigma ^{(2)}$
(Figure 4.1). It is to guarantee that the phase factors in the jump matrix in equation (2.4) have the desired exponential decay in time along the deformed contours. Inevitably, this transformation results in certain nonanalyticity in sectors
![]() $\Omega _1\cup \Omega _3 \cup \Omega _4 \cup \Omega _6\cup \Omega _7^\pm \cup \Omega _8^\pm $
, which leads to a mixed
$\Omega _1\cup \Omega _3 \cup \Omega _4 \cup \Omega _6\cup \Omega _7^\pm \cup \Omega _8^\pm $
, which leads to a mixed
![]() $\overline {\partial }$
–RHP-problem, Problem 3.3.
$\overline {\partial }$
–RHP-problem, Problem 3.3.
The third step is a ‘factorisation’ of
![]() $m^{(2)}$
in the form
$m^{(2)}$
in the form
![]() $m^{(2)} = m^{(3)} m^{\mathrm {LC}}$
, where
$m^{(2)} = m^{(3)} m^{\mathrm {LC}}$
, where
![]() $m^{\mathrm {LC}}$
is the solution of a localised RHP, Problem 4.1 and
$m^{\mathrm {LC}}$
is the solution of a localised RHP, Problem 4.1 and
![]() $m^{(3)}$
a solution of
$m^{(3)}$
a solution of
![]() $\bar \partial $
problem, Problem 5.1. The term ‘localised’ means the reflection coefficient
$\bar \partial $
problem, Problem 5.1. The term ‘localised’ means the reflection coefficient
![]() $r(z)$
is fixed at
$r(z)$
is fixed at
![]() $\pm z_0$
along the deformed contours. We then solve this localised RHP, whose solution is given by parabolic cylinder functions. Since we have to separate the contribution from two stationary points
$\pm z_0$
along the deformed contours. We then solve this localised RHP, whose solution is given by parabolic cylinder functions. Since we have to separate the contribution from two stationary points
![]() $\pm z_0$
, some error terms appear alongside, and their decay rates are estimated.
$\pm z_0$
, some error terms appear alongside, and their decay rates are estimated.
The fourth step (Section 5) is the solution of the
![]() $\overline {\partial }$
-problem by solving an integral equation. The integral operator has a small
$\overline {\partial }$
-problem by solving an integral equation. The integral operator has a small
![]() $L^\infty $
-norm at a large t, allowing the use of the Neumann series. The contribution of this
$L^\infty $
-norm at a large t, allowing the use of the Neumann series. The contribution of this
![]() $\overline {\partial }$
problem is another higher-order error term.
$\overline {\partial }$
problem is another higher-order error term.
The fifth step (Section 6) is to group together all the previous transformations to derive the long-time asymptotics of the solution of the MKdV equation in Region I, using the large-z behaviour of the RHP solutions. These five steps above are more or less standard, and during the proof we mainly follow the outline of [Reference Liu, Perry and Sulem36].
The sixth step is the study of Regions II–V. The leading-order term in these regions is given by a solution to the Painlevé II equation, and error estimates are obtained from scaling.
2 Conjugation
We introduce a new matrix-valued function
where
![]() $\delta (z)$
solves the scalar RHP Problem 2.1 below:
$\delta (z)$
solves the scalar RHP Problem 2.1 below:
Problem 2.1. Given
![]() $\pm z_0 \in \mathbb {R}$
and
$\pm z_0 \in \mathbb {R}$
and
![]() $r \in H^{1}(\mathbb {R})$
, find a scalar function
$r \in H^{1}(\mathbb {R})$
, find a scalar function
![]() $\delta (z) = \delta (z; z_0)$
, analytic for
$\delta (z) = \delta (z; z_0)$
, analytic for
![]() $z \in \mathbb {C} \setminus [-z_0, z_0]$
, with the following properties:
$z \in \mathbb {C} \setminus [-z_0, z_0]$
, with the following properties:
-
(1)
 $\delta (z) \rightarrow 1$
as
$\delta (z) \rightarrow 1$
as
 $z \rightarrow \infty $
,
$z \rightarrow \infty $
, -
(2)
 $\delta (z)$
has continuous boundary values
$\delta (z)$
has continuous boundary values
 $\delta _\pm (z) =\lim _{\varepsilon \downarrow 0} \delta (z \pm i\varepsilon )$
for
$\delta _\pm (z) =\lim _{\varepsilon \downarrow 0} \delta (z \pm i\varepsilon )$
for
 $z \in (-z_0, z_0)$
,
$z \in (-z_0, z_0)$
, -
(3)
 $\delta _\pm $
obey the jump relation
$\delta _\pm $
obey the jump relation  $$ \begin{align*}\delta_+(z) = \begin{cases} \delta_-(z) \left(1 - \left| r(z) \right|{}^2 \right), & z\in (-z_0, z_0)\\ \delta_-(z), & z \in \mathbb{R}\setminus (-z_0, z_0) \end{cases}. \end{align*} $$
$$ \begin{align*}\delta_+(z) = \begin{cases} \delta_-(z) \left(1 - \left| r(z) \right|{}^2 \right), & z\in (-z_0, z_0)\\ \delta_-(z), & z \in \mathbb{R}\setminus (-z_0, z_0) \end{cases}. \end{align*} $$
Lemma 2.2. Suppose
![]() $r \in H^{1}(\mathbb {R})$
and
$r \in H^{1}(\mathbb {R})$
and
![]() $\kappa (s)$
is given by equation (1.18). Then
$\kappa (s)$
is given by equation (1.18). Then
-
(i) Problem 2.1 has the unique solution
(2.2)where $$ \begin{align} \delta(z) = \left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa} e^{\chi(z)}, \end{align} $$
$$ \begin{align} \delta(z) = \left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa} e^{\chi(z)}, \end{align} $$
 $\kappa $
is given by equation (1.18) and (2.3)
$\kappa $
is given by equation (1.18) and (2.3) $$ \begin{align} \chi(z)=\dfrac{1}{2\pi i}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z}\qquad\qquad\quad \end{align} $$
Here we choose the branch of the logarithm with
$$ \begin{align} \chi(z)=\dfrac{1}{2\pi i}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z}\qquad\qquad\quad \end{align} $$
Here we choose the branch of the logarithm with $$ \begin{align*}\left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa}=\exp\left( i\kappa \left( \log\left\vert \dfrac{z-z_0}{z+z_0} \right\vert +i\arg(z-z_0)-i\arg(z+z_0) \right) \right).\end{align*} $$
$$ \begin{align*}\left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa}=\exp\left( i\kappa \left( \log\left\vert \dfrac{z-z_0}{z+z_0} \right\vert +i\arg(z-z_0)-i\arg(z+z_0) \right) \right).\end{align*} $$
 $-\pi < \arg (z) < \pi $
.
$-\pi < \arg (z) < \pi $
.
-
(ii)
 $$ \begin{align*} \delta(z) =(\overline{\delta(\overline{z})})^{-1}=\overline{\delta(-\overline{z})} \end{align*} $$
$$ \begin{align*} \delta(z) =(\overline{\delta(\overline{z})})^{-1}=\overline{\delta(-\overline{z})} \end{align*} $$
-
(iii) For
 $z\in \mathbb {R}$
,
$z\in \mathbb {R}$
,
 $|\delta _\pm (z)|<\infty $
; for
$|\delta _\pm (z)|<\infty $
; for
 $z\in \mathbb {C}\setminus \mathbb {R}$
,
$z\in \mathbb {C}\setminus \mathbb {R}$
,
 $|\delta ^{\pm 1}(z)|<\infty $
.
$|\delta ^{\pm 1}(z)|<\infty $
. -
(iv) Along any ray of the form
 $\pm z_0+ e^{i\phi }\mathbb {R}^+$
with
$\pm z_0+ e^{i\phi }\mathbb {R}^+$
with
 $0<\phi <\pi $
or
$0<\phi <\pi $
or
 $\pi < \phi < 2\pi $
, The implied constant depends on r through its
$\pi < \phi < 2\pi $
, The implied constant depends on r through its $$ \begin{align*} \left| \delta(z) - \left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa} e^{\chi(\pm z_0)} \right| \leq C_r |z \mp z_0|^{1/2}.\end{align*} $$
$$ \begin{align*} \left| \delta(z) - \left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa} e^{\chi(\pm z_0)} \right| \leq C_r |z \mp z_0|^{1/2}.\end{align*} $$
 $H^{1}(\mathbb {R})$
-norm and is independent of
$H^{1}(\mathbb {R})$
-norm and is independent of
 $\pm z_0\in \mathbb {R}$
.
$\pm z_0\in \mathbb {R}$
.
Proof. The proofs of (i)–(iii) can be found in [Reference Deift and Zhou11]. To establish (iv), we first note that
 $$ \begin{align*}\left\vert \left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa}\right\vert \leq e^{\pi \kappa}.\end{align*} $$
$$ \begin{align*}\left\vert \left( \dfrac{z-z_0}{z+z_0} \right)^{i\kappa}\right\vert \leq e^{\pi \kappa}.\end{align*} $$
To bound the difference
![]() $e^{\chi (z)}-e^{\chi (\pm z_0)}$
, notice that
$e^{\chi (z)}-e^{\chi (\pm z_0)}$
, notice that
 $$ \begin{align*} \left\vert e^{\chi(z)}-e^{\chi(\pm z_0)}\right\vert &\leq\left\vert e^{\chi(\pm z_0)}\right\vert \left\vert e^{\chi(z)-\chi(\pm z_0)}-1 \right\vert\\ &\lesssim \left\vert \int_0^1 \dfrac{d}{ds} e^{s( \chi(z)-\chi(\pm z_0) )ds } \right\vert\\ &\lesssim |z \mp z_0|^{1/2} \sup_{0\leq s\leq 1} \left\vert e^{s( \chi(z)-\chi(\pm z_0) )}\right\vert\\ &\lesssim |z \mp z_0|^{1/2}, \end{align*} $$
$$ \begin{align*} \left\vert e^{\chi(z)}-e^{\chi(\pm z_0)}\right\vert &\leq\left\vert e^{\chi(\pm z_0)}\right\vert \left\vert e^{\chi(z)-\chi(\pm z_0)}-1 \right\vert\\ &\lesssim \left\vert \int_0^1 \dfrac{d}{ds} e^{s( \chi(z)-\chi(\pm z_0) )ds } \right\vert\\ &\lesssim |z \mp z_0|^{1/2} \sup_{0\leq s\leq 1} \left\vert e^{s( \chi(z)-\chi(\pm z_0) )}\right\vert\\ &\lesssim |z \mp z_0|^{1/2}, \end{align*} $$
where the third inequality follows from [Reference Beals, Deift and Tomei3, Lemma 23].
It is straightforward to check that if
![]() $m(z;x,t)$
solves Problem 1.2, then the new matrix-valued function
$m(z;x,t)$
solves Problem 1.2, then the new matrix-valued function
![]() $m^{(1)}(z;x,t)=m(z;x,t)\delta (z)^{\sigma _3}$
is the solution to the following RHP.
$m^{(1)}(z;x,t)=m(z;x,t)\delta (z)^{\sigma _3}$
is the solution to the following RHP.
Problem 2.3. Given
![]() $r \in H^{1,0}(\mathbb {R})$
, find a matrix-valued function
$r \in H^{1,0}(\mathbb {R})$
, find a matrix-valued function
![]() $m^{(1)}(z;x,t)$
on
$m^{(1)}(z;x,t)$
on
![]() $\mathbb {C} \setminus \mathbb {R}$
with the following properties:
$\mathbb {C} \setminus \mathbb {R}$
with the following properties:
-
(1)
 $m^{(1)}(z;x,t) \rightarrow I$
as
$m^{(1)}(z;x,t) \rightarrow I$
as
 $|z| \rightarrow \infty $
.
$|z| \rightarrow \infty $
. -
(2)
 $m^{(1)}(z;x,t)$
is analytic for
$m^{(1)}(z;x,t)$
is analytic for
 $z \in \mathbb {C} \setminus \mathbb {R}$
with continuous boundary values
$z \in \mathbb {C} \setminus \mathbb {R}$
with continuous boundary values  $$ \begin{align*}m^{(1)}_\pm(z;x,t) = \lim_{\varepsilon \downarrow 0} m^{(1)}(z+i\varepsilon;x,t).\end{align*} $$
$$ \begin{align*}m^{(1)}_\pm(z;x,t) = \lim_{\varepsilon \downarrow 0} m^{(1)}(z+i\varepsilon;x,t).\end{align*} $$
-
(3) The jump relation
holds, where $$ \begin{align*}m^{(1)}_+(z;x,t)=m^{(1)}_-(z;x,t) e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{(1)}(z)\end{align*} $$
$$ \begin{align*}m^{(1)}_+(z;x,t)=m^{(1)}_-(z;x,t) e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{(1)}(z)\end{align*} $$
 $$ \begin{align*}v^{(1)}(z) = \delta_-(z)^{\sigma_3} v(z) \delta_+(z)^{-\sigma_3}.\end{align*} $$
$$ \begin{align*}v^{(1)}(z) = \delta_-(z)^{\sigma_3} v(z) \delta_+(z)^{-\sigma_3}.\end{align*} $$
The jump matrix
 $e^{-i\theta \operatorname {\mathrm {ad}}\sigma _3} v^{(1)} $
is factorised as (2.4)
$e^{-i\theta \operatorname {\mathrm {ad}}\sigma _3} v^{(1)} $
is factorised as (2.4) $$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{(1)}(z) = \begin{cases} \left( \begin{array}{cc} {1} & {0} \\[10pt] {\dfrac{\delta_-^{-2} r}{1-|r|^2} e^{2i\theta}} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {-\dfrac{\delta_+^2 \overline{r}}{1- |r|^2} e^{-2i\theta}} \\[10pt] {0} & {1} \end{array} \right) , & z \in (-z_0, z_0),\\ \\ \left( \begin{array}{cc} {1} & {-\overline{r} \delta^2 e^{-2i\theta}} \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r \delta^{-2} e^{2i\theta}} & {1} \end{array} \right) , & z \in(-\infty, -z_0)\cup (z_0,\infty). \end{cases} \end{align} $$
$$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{(1)}(z) = \begin{cases} \left( \begin{array}{cc} {1} & {0} \\[10pt] {\dfrac{\delta_-^{-2} r}{1-|r|^2} e^{2i\theta}} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {-\dfrac{\delta_+^2 \overline{r}}{1- |r|^2} e^{-2i\theta}} \\[10pt] {0} & {1} \end{array} \right) , & z \in (-z_0, z_0),\\ \\ \left( \begin{array}{cc} {1} & {-\overline{r} \delta^2 e^{-2i\theta}} \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r \delta^{-2} e^{2i\theta}} & {1} \end{array} \right) , & z \in(-\infty, -z_0)\cup (z_0,\infty). \end{cases} \end{align} $$
3 Contour deformation
We now perform contour deformation on Problem 2.3, following the standard procedure outlined in [Reference Liu, Perry and Sulem36, Section 4]. Since the phase function in equation (1.9) has two critical points at
![]() $\pm z_0$
, our new contour is chosen to be
$\pm z_0$
, our new contour is chosen to be
(shown in Figure 3.1) and consists of rays of the form
![]() $\pm z_0+ e^{i\phi }\mathbb {R}^+$
, where
$\pm z_0+ e^{i\phi }\mathbb {R}^+$
, where
![]() $\phi = \pi /4, 3\pi /4,5\pi /4, 7\pi /4$
.
$\phi = \pi /4, 3\pi /4,5\pi /4, 7\pi /4$
.

Figure 3.1 Deformation from
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\Sigma ^{(2)}$
.
$\Sigma ^{(2)}$
.
We now introduce another matrix-valued function
![]() $m^{(2)}$
:
$m^{(2)}$
:
Here
![]() $\mathcal {R}^{(2)}$
is chosen to remove the jump on the real axis and brings about new analytic jump matrices with the desired exponential decay along the contour
$\mathcal {R}^{(2)}$
is chosen to remove the jump on the real axis and brings about new analytic jump matrices with the desired exponential decay along the contour
![]() $\Sigma ^{(2)}$
. Straightforward computation gives
$\Sigma ^{(2)}$
. Straightforward computation gives
 $$ \begin{align*} m^{(2)}_+ &=m^{(1)}_+ \mathcal{R}^{(2)}_+ \\ &= m^{(1)}_- \left( e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3} v^{(1)} \right) \mathcal{R}^{(2)}_+ \\ &= m^{(2)}_- \left(\mathcal{R}^{(2)}_-\right)^{-1} \left( e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3} v^{(1)} \right) \mathcal{R}^{(2)}_+. \end{align*} $$
$$ \begin{align*} m^{(2)}_+ &=m^{(1)}_+ \mathcal{R}^{(2)}_+ \\ &= m^{(1)}_- \left( e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3} v^{(1)} \right) \mathcal{R}^{(2)}_+ \\ &= m^{(2)}_- \left(\mathcal{R}^{(2)}_-\right)^{-1} \left( e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3} v^{(1)} \right) \mathcal{R}^{(2)}_+. \end{align*} $$
We want to make sure the following condition is satisfied
where
![]() $\mathcal {R}_\pm ^{(2)}$
are the boundary values of
$\mathcal {R}_\pm ^{(2)}$
are the boundary values of
![]() $\mathcal {R}^{(2)}(z)$
as
$\mathcal {R}^{(2)}(z)$
as
![]() $\pm \operatorname {\mathrm {Im}}(z) \downarrow 0$
. In this case, the jump matrix associated to
$\pm \operatorname {\mathrm {Im}}(z) \downarrow 0$
. In this case, the jump matrix associated to
![]() $m^{(2)}_\pm $
will be the identity matrix on
$m^{(2)}_\pm $
will be the identity matrix on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
From the signature table [Reference Deift and Zhou11, Figure 0.1], we find that the function
![]() $e^{2i\theta }$
is exponentially decreasing on
$e^{2i\theta }$
is exponentially decreasing on
![]() $\Sigma _3, \Sigma _4$
,
$\Sigma _3, \Sigma _4$
,
![]() $\Sigma _5$
,
$\Sigma _5$
,
![]() $\Sigma _6$
and increasing on
$\Sigma _6$
and increasing on
![]() $\Sigma _1$
,
$\Sigma _1$
,
![]() $\Sigma _2$
,
$\Sigma _2$
,
![]() $\Sigma _7$
,
$\Sigma _7$
,
![]() $\Sigma _8$
away from the stationary point, while the reverse is true of
$\Sigma _8$
away from the stationary point, while the reverse is true of
![]() $e^{-2i\theta }$
. Letting
$e^{-2i\theta }$
. Letting
 $$ \begin{align} \eta(z; z_0) = \left( \dfrac{ z-z_0}{z+z_0} \right)^{i\kappa}, \end{align} $$
$$ \begin{align} \eta(z; z_0) = \left( \dfrac{ z-z_0}{z+z_0} \right)^{i\kappa}, \end{align} $$
we define
![]() $\mathcal {R}^{(2)}$
as follows (Figures 3.2–3.3): the functions
$\mathcal {R}^{(2)}$
as follows (Figures 3.2–3.3): the functions
![]() $R_1$
,
$R_1$
,
![]() $R_3$
,
$R_3$
,
![]() $R_4$
,
$R_4$
,
![]() $R_6$
,
$R_6$
,
![]() $R_7^+$
,
$R_7^+$
,
![]() $R_8^+$
,
$R_8^+$
,
![]() $R_7^-$
,
$R_7^-$
,
![]() $R_{8}^-$
satisfy
$R_{8}^-$
satisfy
 $$ \begin{align} R_1(z) &= \begin{cases} -{r(z)} \delta(z)^{-2} & z \in (z_0,\infty)\\[10pt] -{r(z_0 )} e^{-2\chi(z_0)} \eta(z; z_0)^{-2} & z \in \Sigma_1, \end{cases}\qquad \end{align} $$
$$ \begin{align} R_1(z) &= \begin{cases} -{r(z)} \delta(z)^{-2} & z \in (z_0,\infty)\\[10pt] -{r(z_0 )} e^{-2\chi(z_0)} \eta(z; z_0)^{-2} & z \in \Sigma_1, \end{cases}\qquad \end{align} $$
 $$ \begin{align} R_3(z) &= \begin{cases} -{r(z)} \delta(z)^{-2} & z \in (-\infty, -z_0)\\[10pt] -{r(-z_0 )} e^{-2\chi(-z_0)} \eta(z; z_0)^{-2} & z \in \Sigma_2, \end{cases} \end{align} $$
$$ \begin{align} R_3(z) &= \begin{cases} -{r(z)} \delta(z)^{-2} & z \in (-\infty, -z_0)\\[10pt] -{r(-z_0 )} e^{-2\chi(-z_0)} \eta(z; z_0)^{-2} & z \in \Sigma_2, \end{cases} \end{align} $$
 $$ \begin{align} R_4(z) &= \begin{cases} -\overline{r(z)} \delta(z)^{2} & z \in (-\infty, -z_0)\\[10pt] -\overline{r(-z_0)} e^{2\chi(-z_0)} \eta(z; z_0)^{2} & z \in \Sigma_3, \end{cases}\quad \end{align} $$
$$ \begin{align} R_4(z) &= \begin{cases} -\overline{r(z)} \delta(z)^{2} & z \in (-\infty, -z_0)\\[10pt] -\overline{r(-z_0)} e^{2\chi(-z_0)} \eta(z; z_0)^{2} & z \in \Sigma_3, \end{cases}\quad \end{align} $$

Figure 3.2 The matrix
![]() $\mathcal {R}^{(2)}$
for Region I, near
$\mathcal {R}^{(2)}$
for Region I, near
![]() $z_0$
.
$z_0$
.

Figure 3.3 The matrix
![]() $\mathcal {R}^{(2)}$
for Region I, near
$\mathcal {R}^{(2)}$
for Region I, near
![]() $-z_0$
.
$-z_0$
.
 $$ \begin{align} R_6(z) &= \begin{cases} -\overline{r(z)} \delta(z)^{2} & z \in (-\infty, -z_0)\\[10pt] -\overline{r(z_0)} e^{2\chi(z_0)} \eta(z; z_0)^{2} & z \in \Sigma_4, \end{cases}\qquad \end{align} $$
$$ \begin{align} R_6(z) &= \begin{cases} -\overline{r(z)} \delta(z)^{2} & z \in (-\infty, -z_0)\\[10pt] -\overline{r(z_0)} e^{2\chi(z_0)} \eta(z; z_0)^{2} & z \in \Sigma_4, \end{cases}\qquad \end{align} $$
 $$ \begin{align} R_7^+(z) &= \begin{cases} \dfrac{\delta_-^{-2}(z)r(z)}{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] \dfrac{e^{-2\chi(z_0)} \eta(z; z_0)^{-2} r(z_0)}{1-|r(z_0)|^2} \quad & z \in \Sigma_6, \end{cases}\qquad \end{align} $$
$$ \begin{align} R_7^+(z) &= \begin{cases} \dfrac{\delta_-^{-2}(z)r(z)}{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] \dfrac{e^{-2\chi(z_0)} \eta(z; z_0)^{-2} r(z_0)}{1-|r(z_0)|^2} \quad & z \in \Sigma_6, \end{cases}\qquad \end{align} $$
 $$ \begin{align} R_8^+(z) &= \begin{cases} \dfrac{\delta_+^{2}(z) \overline{r(z)} }{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] {\dfrac{e^{2\chi(z_0)} \eta(z; z_0)^{2} \overline{r(z_0)} }{1-|r(z_0)|^2}} & z \in \Sigma_8, \end{cases}\qquad \end{align} $$
$$ \begin{align} R_8^+(z) &= \begin{cases} \dfrac{\delta_+^{2}(z) \overline{r(z)} }{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] {\dfrac{e^{2\chi(z_0)} \eta(z; z_0)^{2} \overline{r(z_0)} }{1-|r(z_0)|^2}} & z \in \Sigma_8, \end{cases}\qquad \end{align} $$
 $$ \begin{align} R_7^-(z) &= \begin{cases} \dfrac{\delta_-^{-2}(z)r(z)}{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] \dfrac{e^{-2\chi(-z_0)} \eta(z; z_0)^{-2} r(-z_0)}{1-|r(-z_0)|^2} \quad & z \in \Sigma_5, \end{cases} \end{align} $$
$$ \begin{align} R_7^-(z) &= \begin{cases} \dfrac{\delta_-^{-2}(z)r(z)}{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] \dfrac{e^{-2\chi(-z_0)} \eta(z; z_0)^{-2} r(-z_0)}{1-|r(-z_0)|^2} \quad & z \in \Sigma_5, \end{cases} \end{align} $$
 $$ \begin{align} R_{8}^-(z) &= \begin{cases} \dfrac{\delta_+^{2}(z) \overline{r(z)} }{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] {\dfrac{e^{2\chi(-z_0)} \eta(z; z_0)^{2} \overline{r(-z_0)} }{1-|r(-z_0)|^2}} & z \in \Sigma_7. \end{cases} \end{align} $$
$$ \begin{align} R_{8}^-(z) &= \begin{cases} \dfrac{\delta_+^{2}(z) \overline{r(z)} }{1-|r(z)|^2} & z \in (-z_0, z_0)\\[10pt] {\dfrac{e^{2\chi(-z_0)} \eta(z; z_0)^{2} \overline{r(-z_0)} }{1-|r(-z_0)|^2}} & z \in \Sigma_7. \end{cases} \end{align} $$
Each
![]() $R_i(z)$
in
$R_i(z)$
in
![]() $\Omega _i$
is constructed in such a way that the jump matrices on the contour and
$\Omega _i$
is constructed in such a way that the jump matrices on the contour and
![]() $\overline {\partial } R_i(z)$
along with their relevant exponentials enjoys the property of exponential decay as
$\overline {\partial } R_i(z)$
along with their relevant exponentials enjoys the property of exponential decay as
![]() $t\to \infty $
. We formulate Problem 2.3 into a mixed RHP-
$t\to \infty $
. We formulate Problem 2.3 into a mixed RHP-
![]() $\overline {\partial }$
problem. In the following sections, we will separate this mixed problem into a localised RHP and a pure
$\overline {\partial }$
problem. In the following sections, we will separate this mixed problem into a localised RHP and a pure
![]() $\overline {\partial }$
problem whose long-time contribution to the asymptotics of
$\overline {\partial }$
problem whose long-time contribution to the asymptotics of
![]() $u(x,t)$
is of a higher order than the leading term.
$u(x,t)$
is of a higher order than the leading term.
The following lemma [Reference Dieng and McLaughlin15, Proposition 2.1] will be used in the error estimates of
![]() $\bar \partial $
-problem in Section 5.
$\bar \partial $
-problem in Section 5.
We first denote the entries that appear in equations (3.3)–(3.10) by
 $$ \begin{align*} p_1(z)=p_3(z) &= -r(z). & p_4(z)=p_6(z) &= - \overline{r(z)},&\\ p_{7^-}(z)=p_{7^+}(z) &= \dfrac{r(z)}{1-|r(z)|^2},& p_{8^-}(z)=p_{8^+}(z) &= \dfrac{ \overline{r(z)}}{1 -|r(z)|^2}. \end{align*} $$
$$ \begin{align*} p_1(z)=p_3(z) &= -r(z). & p_4(z)=p_6(z) &= - \overline{r(z)},&\\ p_{7^-}(z)=p_{7^+}(z) &= \dfrac{r(z)}{1-|r(z)|^2},& p_{8^-}(z)=p_{8^+}(z) &= \dfrac{ \overline{r(z)}}{1 -|r(z)|^2}. \end{align*} $$
Lemma 3.1. Suppose
![]() $r \in H^{1}(\mathbb {R})$
. There exist functions
$r \in H^{1}(\mathbb {R})$
. There exist functions
![]() $R_i$
on
$R_i$
on
![]() $\Omega _i$
,
$\Omega _i$
,
![]() $i=1,3,4,6,7^\pm ,8^\pm $
satisfying equations (3.3)–(3.10), so that
$i=1,3,4,6,7^\pm ,8^\pm $
satisfying equations (3.3)–(3.10), so that
where
![]() $\xi =\pm z_0$
and the implied constants are uniform for
$\xi =\pm z_0$
and the implied constants are uniform for
![]() $r $
in a bounded subset of
$r $
in a bounded subset of
![]() $H^{1}(\mathbb {R})$
.
$H^{1}(\mathbb {R})$
.
Proof. We only prove the lemma for
![]() $R_1$
. Define
$R_1$
. Define
![]() $f_1(z)$
on
$f_1(z)$
on
![]() $\Omega _1$
by
$\Omega _1$
by
and let
where
![]() $\phi = \arg (z-\xi )$
and
$\phi = \arg (z-\xi )$
and
![]() $\mathcal {K}$
is a smooth function on
$\mathcal {K}$
is a smooth function on
![]() $(0, \pi /4)$
with
$(0, \pi /4)$
with
 $$ \begin{align} \mathcal{K}(\phi)= \begin{cases} 1 & z\in [0, \pi/12], \\ 0 & z \in[\pi/6, \pi/4] \end{cases}. \end{align} $$
$$ \begin{align} \mathcal{K}(\phi)= \begin{cases} 1 & z\in [0, \pi/12], \\ 0 & z \in[\pi/6, \pi/4] \end{cases}. \end{align} $$
It is easy to see that
![]() $R_1$
as constructed has the boundary values in equation (3.3). Writing
$R_1$
as constructed has the boundary values in equation (3.3). Writing
![]() $z-z_0= \rho e^{i\phi }$
, we have
$z-z_0= \rho e^{i\phi }$
, we have
 $$ \begin{align*}\overline{\partial} = \frac{1}{2}\left( \frac{\partial}{\partial x} + i \frac{\partial}{\partial y} \right) = \frac{1}{2} e^{i\phi} \left( \frac{\partial}{\partial \rho} + \frac{i}{\rho} \frac{\partial}{\partial \phi} \right). \end{align*} $$
$$ \begin{align*}\overline{\partial} = \frac{1}{2}\left( \frac{\partial}{\partial x} + i \frac{\partial}{\partial y} \right) = \frac{1}{2} e^{i\phi} \left( \frac{\partial}{\partial \rho} + \frac{i}{\rho} \frac{\partial}{\partial \phi} \right). \end{align*} $$
We calculate
 $$ \begin{align*}\overline{\partial} R_1 (z) = \frac{1}{2} p_1'(\operatorname{\mathrm{Re}} z) \mathcal{K}(\phi) ~ \delta(z)^{-2} - \left[ p_1(\operatorname{\mathrm{Re}} z) - f_1(z) \right]\delta(z)^{-2} \frac{ie^{i\phi}}{|z-\xi|} \mathcal{K}'(\phi). \end{align*} $$
$$ \begin{align*}\overline{\partial} R_1 (z) = \frac{1}{2} p_1'(\operatorname{\mathrm{Re}} z) \mathcal{K}(\phi) ~ \delta(z)^{-2} - \left[ p_1(\operatorname{\mathrm{Re}} z) - f_1(z) \right]\delta(z)^{-2} \frac{ie^{i\phi}}{|z-\xi|} \mathcal{K}'(\phi). \end{align*} $$
It follows from Lemma 2.2 (iv) that
where the implied constants depend on
![]() $ \left \Vert {r} \right \Vert {}_{H^{1}} $
and the cutoff function
$ \left \Vert {r} \right \Vert {}_{H^{1}} $
and the cutoff function
![]() $\mathcal {K}$
. The estimates in the remaining sectors are identical.
$\mathcal {K}$
. The estimates in the remaining sectors are identical.
The unknown
![]() $m^{(2)}$
satisfies a mixed
$m^{(2)}$
satisfies a mixed
![]() $\overline {\partial }$
-RHP. We first identify the jumps of
$\overline {\partial }$
-RHP. We first identify the jumps of
![]() $m^{(2)}$
along the contour
$m^{(2)}$
along the contour
![]() $\Sigma ^{(2)}$
. Recall that
$\Sigma ^{(2)}$
. Recall that
![]() $m^{(1)}$
is analytic along the contour, and the jumps are determined entirely by
$m^{(1)}$
is analytic along the contour, and the jumps are determined entirely by
![]() $\mathcal {R}^{(2)}$
; see equations (3.3)–(3.10). Away from
$\mathcal {R}^{(2)}$
; see equations (3.3)–(3.10). Away from
![]() $\Sigma ^{(2)}$
, using the triangularity of
$\Sigma ^{(2)}$
, using the triangularity of
![]() $\mathcal {R}^{(2)}$
, we have that
$\mathcal {R}^{(2)}$
, we have that
Remark 3.2. Note that the interpolation defined through equation (3.11) introduces a new jump on
![]() $\Sigma ^{'(2)}_9$
of Figure 3.4 with a jump matrix given by
$\Sigma ^{'(2)}_9$
of Figure 3.4 with a jump matrix given by
 $$ \begin{align} v_9(z)=\begin{cases} I, & z\in \left(-iz_0 \tan(\pi/12), iz_0 \tan(\pi/12) \right)\\ \\ \left( \begin{array}{cc} {1} & { (R_7^--R_7^+)e^{-2i\theta} } \\ {0} & {1} \end{array} \right) , & z\in \left(iz_0 \tan(\pi/12), iz_0 \right) \\ \\ \left( \begin{array}{cc} {1} & {0} \\ { (R_8^--R_8^+)e^{2i\theta} } & {1} \end{array} \right) , & z\in \left(-iz_0 , -iz_0 \tan(\pi/12), \right). \end{cases} \end{align} $$
$$ \begin{align} v_9(z)=\begin{cases} I, & z\in \left(-iz_0 \tan(\pi/12), iz_0 \tan(\pi/12) \right)\\ \\ \left( \begin{array}{cc} {1} & { (R_7^--R_7^+)e^{-2i\theta} } \\ {0} & {1} \end{array} \right) , & z\in \left(iz_0 \tan(\pi/12), iz_0 \right) \\ \\ \left( \begin{array}{cc} {1} & {0} \\ { (R_8^--R_8^+)e^{2i\theta} } & {1} \end{array} \right) , & z\in \left(-iz_0 , -iz_0 \tan(\pi/12), \right). \end{cases} \end{align} $$
But
![]() $v_9$
is exponentially small due to the construction of
$v_9$
is exponentially small due to the construction of
![]() $\mathcal {K}(\phi )$
in equation (3.12).
$\mathcal {K}(\phi )$
in equation (3.12).

Figure 3.4
![]() $\Sigma ^{\prime (2)}$
.
$\Sigma ^{\prime (2)}$
.
Now we arrive at the following Riemann-Hilbert-
![]() $\overline {\partial }$
problem.
$\overline {\partial }$
problem.
Problem 3.3. Given
![]() $r \in H^{1}(\mathbb {R})$
, find a matrix-valued function
$r \in H^{1}(\mathbb {R})$
, find a matrix-valued function
![]() $m^{(2)}(z;x,t)$
on
$m^{(2)}(z;x,t)$
on
![]() $\mathbb {C} \setminus \Sigma ^{'(2)} $
with the following properties:
$\mathbb {C} \setminus \Sigma ^{'(2)} $
with the following properties:
-
(1)
 $m^{(2)}(z;x,t) \rightarrow I $
as
$m^{(2)}(z;x,t) \rightarrow I $
as
 $|z| \rightarrow \infty $
in
$|z| \rightarrow \infty $
in
 $\mathbb {C} \setminus \Sigma ^{'(2)}$
.
$\mathbb {C} \setminus \Sigma ^{'(2)}$
. -
(2)
 $m^{(2)}(z;x,t)$
is continuous for
$m^{(2)}(z;x,t)$
is continuous for
 $z \in \mathbb {C} \setminus \Sigma ^{'(2)}$
with continuous boundary values
$z \in \mathbb {C} \setminus \Sigma ^{'(2)}$
with continuous boundary values
 $m^{(2)}_\pm (z;x,t) $
(where
$m^{(2)}_\pm (z;x,t) $
(where
 $\pm $
is defined by the orientation in Figure 3.4).
$\pm $
is defined by the orientation in Figure 3.4). -
(3) The jump relation
 $m^{(2)}_+(z;x,t)=m^{(2)}_-(z;x,t) e^{-i\theta \operatorname {\mathrm {ad}}\sigma }v^{(2)}(z)$
holds, where
$m^{(2)}_+(z;x,t)=m^{(2)}_-(z;x,t) e^{-i\theta \operatorname {\mathrm {ad}}\sigma }v^{(2)}(z)$
holds, where
 $e^{-i\theta \operatorname {\mathrm {ad}}\sigma }v^{(2)}(z) $
is given in Figures 3.5–3.6 and equation (3.14).
$e^{-i\theta \operatorname {\mathrm {ad}}\sigma }v^{(2)}(z) $
is given in Figures 3.5–3.6 and equation (3.14).
Figure 3.5 Jump matrices
 $v^{(2)}$
for
$v^{(2)}$
for
 $m^{(2)}$
near
$m^{(2)}$
near
 $z_0$
.
$z_0$
.
Figure 3.6 Jump matrices
 $v^{(2)}$
for
$v^{(2)}$
for
 $m^{(2)}$
near
$m^{(2)}$
near
 $-z_0$
.
$-z_0$
. -
(4) The equation
holds in $$ \begin{align*} \overline{\partial} m^{(2)} = m^{(2)} \, \overline{\partial} \mathcal{R}^{(2)} \end{align*} $$
$$ \begin{align*} \overline{\partial} m^{(2)} = m^{(2)} \, \overline{\partial} \mathcal{R}^{(2)} \end{align*} $$
 $\mathbb {C} \setminus \Sigma ^{'(2)}$
, where
$\mathbb {C} \setminus \Sigma ^{'(2)}$
, where  $$ \begin{align*} \overline{\partial} \mathcal{R}^{(2)}= \left\{ \begin{array}{lllll} \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_1) e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_1 && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_7^+)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_7^+ \\ \\ \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_8^+)e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_8^+ && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_6)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_6 \\ \\ \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_3) e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_3 && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_4)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_4 \\ \\ \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_8^-)e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_8^- && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_7^-)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_7^- \\ \\ 0 &\hspace{-5pt} z\in \Omega_2\cup\Omega_5. \end{array} \right. \end{align*} $$
$$ \begin{align*} \overline{\partial} \mathcal{R}^{(2)}= \left\{ \begin{array}{lllll} \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_1) e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_1 && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_7^+)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_7^+ \\ \\ \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_8^+)e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_8^+ && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_6)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_6 \\ \\ \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_3) e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_3 && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_4)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_4 \\ \\ \left( \begin{array}{cc} {0} & {0} \\[6pt] {(\overline{\partial} R_8^-)e^{2i\theta}} & {0} \end{array} \right) , & z \in \Omega_8^- && \left( \begin{array}{cc} {0} & {(\overline{\partial} R_7^-)e^{-2i\theta}} \\[6pt] {0} & {0} \end{array} \right) , & z \in \Omega_7^- \\ \\ 0 &\hspace{-5pt} z\in \Omega_2\cup\Omega_5. \end{array} \right. \end{align*} $$
Figures 3.5 illustrates the jump matrices of RHP Problem 3.3.
4 The localised Riemann-Hilbert problem
We perform the following factorisation of
![]() $m^{(2)}$
:
$m^{(2)}$
:
Here we require that
![]() $m^{(3)} $
to be the solution of the pure
$m^{(3)} $
to be the solution of the pure
![]() $\overline {\partial }$
-problem; hence no jump and
$\overline {\partial }$
-problem; hence no jump and
![]() $ m^{\mathrm {LC}}$
solution of the localised RHP Problem 4.1 below with the jump matrix
$ m^{\mathrm {LC}}$
solution of the localised RHP Problem 4.1 below with the jump matrix
![]() $v^{\mathrm {LC}}=v^{(2)}$
. The current section focuses on
$v^{\mathrm {LC}}=v^{(2)}$
. The current section focuses on
![]() $ m^{\mathrm {LC}}$
.
$ m^{\mathrm {LC}}$
.
Problem 4.1. Find a
![]() $2\times 2$
matrix-valued function
$2\times 2$
matrix-valued function
![]() $m^{\mathrm {LC}}(z; x,t)$
, analytic on
$m^{\mathrm {LC}}(z; x,t)$
, analytic on
![]() $\mathbb {C} \setminus \Sigma ^{\prime (2)}$
(See Figure 3.4), with the following properties:
$\mathbb {C} \setminus \Sigma ^{\prime (2)}$
(See Figure 3.4), with the following properties:
-
(1)
 $m^{\mathrm {LC}}(z;x,t) \rightarrow I$
as
$m^{\mathrm {LC}}(z;x,t) \rightarrow I$
as
 $|z| \rightarrow \infty $
in
$|z| \rightarrow \infty $
in
 $\mathbb {C} \setminus \Sigma ^{\prime (2)}$
, where I is the
$\mathbb {C} \setminus \Sigma ^{\prime (2)}$
, where I is the
 $2\times 2$
identity matrix.
$2\times 2$
identity matrix. -
(2)
 $m^{\mathrm {LC}}(z; x,t)$
is analytic for
$m^{\mathrm {LC}}(z; x,t)$
is analytic for
 $z \in \mathbb {C} \setminus \Sigma ^{\prime (2)}$
with continuous boundary values
$z \in \mathbb {C} \setminus \Sigma ^{\prime (2)}$
with continuous boundary values
 $m^{\mathrm {LC}}_\pm $
on
$m^{\mathrm {LC}}_\pm $
on
 $\Sigma ^{\prime (2)}$
.
$\Sigma ^{\prime (2)}$
. -
(3) The jump relation
 $m^{\mathrm {LC}}_+(z;x,t) = m^{\mathrm {LC}}_-(z; x,t ) v^{\mathrm {LC}}(z)$
holds on
$m^{\mathrm {LC}}_+(z;x,t) = m^{\mathrm {LC}}_-(z; x,t ) v^{\mathrm {LC}}(z)$
holds on
 $\Sigma ^{\prime (2)}$
, where
$\Sigma ^{\prime (2)}$
, where  $$ \begin{align*} v^{\mathrm{LC}}(z) = v^{(2)}(z). \end{align*} $$
$$ \begin{align*} v^{\mathrm{LC}}(z) = v^{(2)}(z). \end{align*} $$
4.1 Construction of the parametrix
For some fixed
![]() $\rho>0$
, we define
$\rho>0$
, we define
 $$ \begin{align*} L_\rho &=\lbrace z: z=z_0+u e^{3i\pi/4}, \rho \leq u\leq \sqrt{2}z_0 \rbrace\\ &\cup \lbrace z: z=z_0+u e^{i\pi/4}, u \geq \rho \rbrace\\ & \cup \lbrace z: z=-z_0+u e^{i\pi/4}, \rho \leq u\leq \sqrt{2} z_0 \rbrace\\ & \cup \lbrace z: z=-z_0+u e^{3i\pi/4}, u \geq \rho \rbrace\\ \Sigma'&=\Sigma^{\prime (2)}\setminus (L_\rho \cup \overline{L_\rho}\cup \Sigma^{\prime (2)}_9). \end{align*} $$
$$ \begin{align*} L_\rho &=\lbrace z: z=z_0+u e^{3i\pi/4}, \rho \leq u\leq \sqrt{2}z_0 \rbrace\\ &\cup \lbrace z: z=z_0+u e^{i\pi/4}, u \geq \rho \rbrace\\ & \cup \lbrace z: z=-z_0+u e^{i\pi/4}, \rho \leq u\leq \sqrt{2} z_0 \rbrace\\ & \cup \lbrace z: z=-z_0+u e^{3i\pi/4}, u \geq \rho \rbrace\\ \Sigma'&=\Sigma^{\prime (2)}\setminus (L_\rho \cup \overline{L_\rho}\cup \Sigma^{\prime (2)}_9). \end{align*} $$
Problem 4.2. Find a matrix-valued function
![]() $m^{A'}(z;x,t)$
on
$m^{A'}(z;x,t)$
on
![]() $\mathbb {C} \setminus \Sigma _A'$
with the following properties:
$\mathbb {C} \setminus \Sigma _A'$
with the following properties:
-
(1)
 $m^{A'}(z;x,t) \rightarrow I$
as
$m^{A'}(z;x,t) \rightarrow I$
as
 $ z \rightarrow \infty $
.
$ z \rightarrow \infty $
.
Figure 4.1
 $\Sigma '=\Sigma ^{\prime }_{A}\cup \Sigma ^{\prime }_{B}$
.
$\Sigma '=\Sigma ^{\prime }_{A}\cup \Sigma ^{\prime }_{B}$
. -
(2)
 $m^{A' }(z;x,t)$
is analytic for
$m^{A' }(z;x,t)$
is analytic for
 $z \in \mathbb {C} \setminus \Sigma _A' $
with continuous boundary values
$z \in \mathbb {C} \setminus \Sigma _A' $
with continuous boundary values
 $m^{A'}_\pm (z;x,t)$
.
$m^{A'}_\pm (z;x,t)$
. -
(3) On
 $ \Sigma _A'$
, we have the jump conditions where
$ \Sigma _A'$
, we have the jump conditions where $$ \begin{align*}m^{A'}_+(z;x,t)=m^{A'}_-(z;x,t) e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{A'}(z),\end{align*} $$
$$ \begin{align*}m^{A'}_+(z;x,t)=m^{A'}_-(z;x,t) e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{A'}(z),\end{align*} $$
 $v^{A'}=v^{(2)}\restriction _{\Sigma _A' }$
.
$v^{A'}=v^{(2)}\restriction _{\Sigma _A' }$
.
Problem 4.3. Find a matrix-valued function
![]() $m^{B'}(z;x,t)$
on
$m^{B'}(z;x,t)$
on
![]() $\mathbb {C} \setminus \Sigma _B'$
with the following properties:
$\mathbb {C} \setminus \Sigma _B'$
with the following properties:
-
(1)
 $m^{B'}(z;x,t) \rightarrow I$
as
$m^{B'}(z;x,t) \rightarrow I$
as
 $ z \rightarrow \infty $
.
$ z \rightarrow \infty $
. -
(2)
 $m^{B'}(z;x,t)$
is analytic for
$m^{B'}(z;x,t)$
is analytic for
 $z \in \mathbb {C} \setminus \Sigma _B' $
with continuous boundary values
$z \in \mathbb {C} \setminus \Sigma _B' $
with continuous boundary values
 $m^{B'}_\pm (z;x,t)$
.
$m^{B'}_\pm (z;x,t)$
. -
(3) On
 $ \Sigma _B'$
, we have the jump conditions where
$ \Sigma _B'$
, we have the jump conditions where $$ \begin{align*}m^{B'}_+(z;x,t)=m^{B}_-(z;x,t) e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{B'}(z),\end{align*} $$
$$ \begin{align*}m^{B'}_+(z;x,t)=m^{B}_-(z;x,t) e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v^{B'}(z),\end{align*} $$
 $v^{B'}=v^{(2)}\restriction _{\Sigma _B' }$
.
$v^{B'}=v^{(2)}\restriction _{\Sigma _B' }$
.
To construct solutions to Problems 4.2–4.3, we need the following matrix-valued function:
 $$ \begin{align} \mathcal{P}=\begin{cases} \left( \begin{array}{cc} {\mathcal{P}_-} & {0 } \\ {0} & {\mathcal{P}_-^{-1}} \end{array} \right) , \quad &\left\vert z + z_0 \right\vert<\rho \\ \left( \begin{array}{cc} {\mathcal{P}_+} & {0 } \\ {0} & {\mathcal{P}_+^{-1}} \end{array} \right) , \quad & \left\vert z - z_0 \right\vert <\rho \\ \left( \begin{array}{cc} {1} & {0} \\ {0} & {1} \end{array} \right) , \quad & \left\vert z \pm z_0 \right\vert \geq \rho \end{cases} \end{align} $$
$$ \begin{align} \mathcal{P}=\begin{cases} \left( \begin{array}{cc} {\mathcal{P}_-} & {0 } \\ {0} & {\mathcal{P}_-^{-1}} \end{array} \right) , \quad &\left\vert z + z_0 \right\vert<\rho \\ \left( \begin{array}{cc} {\mathcal{P}_+} & {0 } \\ {0} & {\mathcal{P}_+^{-1}} \end{array} \right) , \quad & \left\vert z - z_0 \right\vert <\rho \\ \left( \begin{array}{cc} {1} & {0} \\ {0} & {1} \end{array} \right) , \quad & \left\vert z \pm z_0 \right\vert \geq \rho \end{cases} \end{align} $$
where
 $$ \begin{align*} \mathcal{P}_-&= (192 \tau)^{i \kappa / 2} e^{-8 i \tau} e^{\chi\left(-z_{0}\right)} \eta(z; -z_0)^{-1}(-\zeta_-)^{i\kappa} e^{i \zeta_-^{2} / 4}e^{i\theta} \\ \mathcal{P}_+&= (192 \tau)^{-i \kappa / 2} e^{8 i \tau} e^{\chi\left(z_{0}\right)} \eta(z; z_0)^{-1}\zeta_+^{i\kappa} e^{-i \zeta_+^{2} / 4}e^{i\theta} \end{align*} $$
$$ \begin{align*} \mathcal{P}_-&= (192 \tau)^{i \kappa / 2} e^{-8 i \tau} e^{\chi\left(-z_{0}\right)} \eta(z; -z_0)^{-1}(-\zeta_-)^{i\kappa} e^{i \zeta_-^{2} / 4}e^{i\theta} \\ \mathcal{P}_+&= (192 \tau)^{-i \kappa / 2} e^{8 i \tau} e^{\chi\left(z_{0}\right)} \eta(z; z_0)^{-1}\zeta_+^{i\kappa} e^{-i \zeta_+^{2} / 4}e^{i\theta} \end{align*} $$
with
![]() $\zeta _\mp =\sqrt {48 z_{0} t}\left (z \pm z_{0}\right )$
. Then we further set
$\zeta _\mp =\sqrt {48 z_{0} t}\left (z \pm z_{0}\right )$
. Then we further set
where
 $$ \begin{align} \tilde{m_p}\restriction \lbrace z: \left\vert z + z_0 \right\vert < \rho \rbrace &=m^{A'} \left( \begin{array}{cc} {\mathcal{P}_-} & {0 } \\ {0} & {\mathcal{P}_-^{-1}} \end{array} \right) := m^{A} , \end{align} $$
$$ \begin{align} \tilde{m_p}\restriction \lbrace z: \left\vert z + z_0 \right\vert < \rho \rbrace &=m^{A'} \left( \begin{array}{cc} {\mathcal{P}_-} & {0 } \\ {0} & {\mathcal{P}_-^{-1}} \end{array} \right) := m^{A} , \end{align} $$
 $$ \begin{align} \tilde{m_p}\restriction \lbrace z: \left\vert z - z_0 \right\vert < \rho \rbrace &=m^{B'} \left( \begin{array}{cc} {\mathcal{P}_+} & {0 } \\ {0} & {\mathcal{P}_+^{-1}} \end{array} \right) := m^{B}. \end{align} $$
$$ \begin{align} \tilde{m_p}\restriction \lbrace z: \left\vert z - z_0 \right\vert < \rho \rbrace &=m^{B'} \left( \begin{array}{cc} {\mathcal{P}_+} & {0 } \\ {0} & {\mathcal{P}_+^{-1}} \end{array} \right) := m^{B}. \end{align} $$
Set
 $$ \begin{align*} \delta^0_A(z) &= (192\tau)^{i\kappa/2} e^{-8i\tau} e^{\chi(-z_0)}\\ \delta^0_B(z) &= (192\tau)^{-i\kappa/2} e^{8i\tau} e^{\chi(z_0)}.\\ \end{align*} $$
$$ \begin{align*} \delta^0_A(z) &= (192\tau)^{i\kappa/2} e^{-8i\tau} e^{\chi(-z_0)}\\ \delta^0_B(z) &= (192\tau)^{-i\kappa/2} e^{8i\tau} e^{\chi(z_0)}.\\ \end{align*} $$
Let
![]() $\Sigma _A$
and
$\Sigma _A$
and
![]() $\Sigma _B$
denote the contours
$\Sigma _B$
denote the contours
with the same orientation as those of
![]() $\Sigma _{A'}$
and
$\Sigma _{A'}$
and
![]() $\Sigma _{B'}$
, respectively.
$\Sigma _{B'}$
, respectively.
![]() $m^A$
solves the following Riemann-Hilbert problem:
$m^A$
solves the following Riemann-Hilbert problem:
 $$ \begin{align} \left\{\begin{array}{ll}m_{+}^{A}(\zeta) & =m_{-}^{A}(\zeta) v^{B}(\zeta), \quad \zeta \in \Sigma_{A} \\\\ m^{A}(\zeta) & = I-\frac{m_{1}^{B}}{\zeta}+O\left(\zeta^{-2}\right), \quad \zeta \rightarrow \infty.\end{array} \right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll}m_{+}^{A}(\zeta) & =m_{-}^{A}(\zeta) v^{B}(\zeta), \quad \zeta \in \Sigma_{A} \\\\ m^{A}(\zeta) & = I-\frac{m_{1}^{B}}{\zeta}+O\left(\zeta^{-2}\right), \quad \zeta \rightarrow \infty.\end{array} \right. \end{align} $$
We have from the list of entries stated in equations (3.3), (3.5), (3.7) and (3.8) the rescaled jump matrices on
![]() $\Sigma _A$
:
$\Sigma _A$
:
 $$ \begin{align} v^{A}=\begin{cases} \left( \begin{array}{cc} {1} & {0} \\[10pt] {(\delta^0_A(z) )^{-2} r(z_0) (-\zeta_-)^{ 2i\kappa} e^{- i\zeta_-^2/2} } & {1} \end{array} \right) , \quad \zeta_- \in \Sigma_A^2 \\[18pt] \left( \begin{array}{cc} {1} & {0} \\[10pt] { \dfrac{ (\delta^0_A(z) )^{-2} r(z_0)}{1-|r(z_0)|^2} (-\zeta_-)^{ 2i\kappa} e^{- i\zeta_-^2/2} } & {1} \end{array} \right) , \quad \zeta_- \in \Sigma_A^4 \\[18pt] \left( \begin{array}{cc} {1} & {-(\delta^0_A(z) )^{2} \overline{ r(z_0)} (-\zeta_-)^{ -2i\kappa} e^{ i\zeta_-^2/2} } \\[10pt] {0} & {0} \end{array} \right) ,\quad \zeta_- \in \Sigma_A^3 \\[18pt] \left( \begin{array}{cc} {1} & {\dfrac{ (\delta^0_A(z) )^{2} \overline{r(z_0)}}{1-|r(z_0)|^2} (-\zeta_-)^{ -2i\kappa} e^{ i\zeta_-^2/2}} \\[10pt] {0} & {1} \end{array} \right) ,\quad \zeta_- \in \Sigma_A^1. \end{cases} \end{align} $$
$$ \begin{align} v^{A}=\begin{cases} \left( \begin{array}{cc} {1} & {0} \\[10pt] {(\delta^0_A(z) )^{-2} r(z_0) (-\zeta_-)^{ 2i\kappa} e^{- i\zeta_-^2/2} } & {1} \end{array} \right) , \quad \zeta_- \in \Sigma_A^2 \\[18pt] \left( \begin{array}{cc} {1} & {0} \\[10pt] { \dfrac{ (\delta^0_A(z) )^{-2} r(z_0)}{1-|r(z_0)|^2} (-\zeta_-)^{ 2i\kappa} e^{- i\zeta_-^2/2} } & {1} \end{array} \right) , \quad \zeta_- \in \Sigma_A^4 \\[18pt] \left( \begin{array}{cc} {1} & {-(\delta^0_A(z) )^{2} \overline{ r(z_0)} (-\zeta_-)^{ -2i\kappa} e^{ i\zeta_-^2/2} } \\[10pt] {0} & {0} \end{array} \right) ,\quad \zeta_- \in \Sigma_A^3 \\[18pt] \left( \begin{array}{cc} {1} & {\dfrac{ (\delta^0_A(z) )^{2} \overline{r(z_0)}}{1-|r(z_0)|^2} (-\zeta_-)^{ -2i\kappa} e^{ i\zeta_-^2/2}} \\[10pt] {0} & {1} \end{array} \right) ,\quad \zeta_- \in \Sigma_A^1. \end{cases} \end{align} $$
Similarly, we have from the rescaled jump matrices on
![]() $\Sigma _B$
:
$\Sigma _B$
:
 $$ \begin{align} v^{B}=\begin{cases} \left( \begin{array}{cc} {1} & {0} \\[10pt] {(\delta^0_B(z) )^{-2} r(z_0) \zeta_+^{- 2i\kappa} e^{ i \zeta_+^2/2} } & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^1 \\[18pt] \left( \begin{array}{cc} {1} & {0} \\[10pt] { \dfrac{ (\delta^0_B(z) )^{-2} r(z_0)}{1-|r(z_0)|^2} \zeta_+^{- 2i\kappa} e^{ i \zeta_+^2/2} } & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^3 \\[18pt] \left( \begin{array}{cc} {1} & {-(\delta^0_B(z) )^{2} \overline{ r(z_0)} \zeta_+^{2i\kappa} e^{- i \zeta_+^2/2} } \\[10pt] {0} & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^4 \\[18pt] \left( \begin{array}{cc} {1} & {\dfrac{ (\delta^0_B(z) )^{2} \overline{r(z_0)}}{1-|r(z_0)|^2} \zeta_+^{ 2i\kappa} e^{ -i \zeta_+^2/2} } \\[10pt] {0} & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^2. \end{cases} \end{align} $$
$$ \begin{align} v^{B}=\begin{cases} \left( \begin{array}{cc} {1} & {0} \\[10pt] {(\delta^0_B(z) )^{-2} r(z_0) \zeta_+^{- 2i\kappa} e^{ i \zeta_+^2/2} } & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^1 \\[18pt] \left( \begin{array}{cc} {1} & {0} \\[10pt] { \dfrac{ (\delta^0_B(z) )^{-2} r(z_0)}{1-|r(z_0)|^2} \zeta_+^{- 2i\kappa} e^{ i \zeta_+^2/2} } & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^3 \\[18pt] \left( \begin{array}{cc} {1} & {-(\delta^0_B(z) )^{2} \overline{ r(z_0)} \zeta_+^{2i\kappa} e^{- i \zeta_+^2/2} } \\[10pt] {0} & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^4 \\[18pt] \left( \begin{array}{cc} {1} & {\dfrac{ (\delta^0_B(z) )^{2} \overline{r(z_0)}}{1-|r(z_0)|^2} \zeta_+^{ 2i\kappa} e^{ -i \zeta_+^2/2} } \\[10pt] {0} & {1} \end{array} \right) , \quad \zeta_+ \in \Sigma_B^2. \end{cases} \end{align} $$
![]() $m^B$
solves the following Riemann-Hilbert problem:
$m^B$
solves the following Riemann-Hilbert problem:
 $$ \begin{align} \left\{\begin{array}{ll}m_{+}^{B}(\zeta) & =m_{-}^{B^{0}}(\zeta) v^{B}(\zeta), \quad \zeta \in \Sigma_{B} \\\\ m^{B}(\zeta) & = I-\frac{m_{1}^{B}}{\zeta}+O\left(\zeta^{-2}\right), \quad \zeta \rightarrow \infty.\end{array} \right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll}m_{+}^{B}(\zeta) & =m_{-}^{B^{0}}(\zeta) v^{B}(\zeta), \quad \zeta \in \Sigma_{B} \\\\ m^{B}(\zeta) & = I-\frac{m_{1}^{B}}{\zeta}+O\left(\zeta^{-2}\right), \quad \zeta \rightarrow \infty.\end{array} \right. \end{align} $$
The explicit form of
![]() $m^{B^0}_1$
is given as follows (see [Reference Deift and Zhou11, Section 4])
$m^{B^0}_1$
is given as follows (see [Reference Deift and Zhou11, Section 4])
 $$ \begin{align} m^{B}_1= \left( \begin{array}{cc} {0} & {-( \delta^0_B)^2 i\beta_{12}} \\ { ( \delta^0_B)^{-2} i\beta_{21}} & {0} \end{array} \right), \end{align} $$
$$ \begin{align} m^{B}_1= \left( \begin{array}{cc} {0} & {-( \delta^0_B)^2 i\beta_{12}} \\ { ( \delta^0_B)^{-2} i\beta_{21}} & {0} \end{array} \right), \end{align} $$
where
 $$ \begin{align*}\beta_{12}=\dfrac{\sqrt{2\pi } e^{i\pi/4} e^{-\pi \kappa } }{r(z_0) \Gamma(-i\kappa)}, \qquad \beta_{21}=\dfrac{-\sqrt{2\pi } e^{-i\pi/4} e^{-\pi \kappa } }{ \overline{ r(z_0) } \Gamma(i\kappa)}\end{align*} $$
$$ \begin{align*}\beta_{12}=\dfrac{\sqrt{2\pi } e^{i\pi/4} e^{-\pi \kappa } }{r(z_0) \Gamma(-i\kappa)}, \qquad \beta_{21}=\dfrac{-\sqrt{2\pi } e^{-i\pi/4} e^{-\pi \kappa } }{ \overline{ r(z_0) } \Gamma(i\kappa)}\end{align*} $$
and
![]() $\Gamma (z)$
is the Gamma function. Using the explicit form of
$\Gamma (z)$
is the Gamma function. Using the explicit form of
![]() $v^{B}$
given by equation (4.8), symmetry reduction given by equation (1.7) and their analogue for
$v^{B}$
given by equation (4.8), symmetry reduction given by equation (1.7) and their analogue for
![]() $v^{A}$
, we verify that
$v^{A}$
, we verify that
which in turn implies by uniqueness that
and from this, we deduce that
 $$ \begin{align} m^{A}_1 &=-\sigma_3 \overline{ m^{B}_1 } \sigma_3 \\ \nonumber &= \left( \begin{array}{cc} {0} & { ( \delta^0_A)^{-2} i \overline{\beta}_{12}} \\ {- ( \delta^0_A)^{-2} i \overline{\beta}_{21} } & {0} \end{array} \right). \end{align} $$
$$ \begin{align} m^{A}_1 &=-\sigma_3 \overline{ m^{B}_1 } \sigma_3 \\ \nonumber &= \left( \begin{array}{cc} {0} & { ( \delta^0_A)^{-2} i \overline{\beta}_{12}} \\ {- ( \delta^0_A)^{-2} i \overline{\beta}_{21} } & {0} \end{array} \right). \end{align} $$
Collecting all the computations above, we write down the asymptotic expansions of solutions to Problem 4.2 and Problem 4.3, respectively.

Figure 4.2
![]() $\Sigma _A,\Sigma _B$
.
$\Sigma _A,\Sigma _B$
.
Proposition 4.4. Recall that
![]() $\zeta _-=\sqrt {48z_0 t}(z + z_0) $
, the solution to RHP Problem 4.2
$\zeta _-=\sqrt {48z_0 t}(z + z_0) $
, the solution to RHP Problem 4.2
![]() $m^{A'}$
, admits the following expansion:
$m^{A'}$
, admits the following expansion:
 $$ \begin{align} m^{A'}(z(\zeta) ;x,t)=I +\dfrac{1}{\zeta_-} \left( \begin{array}{cc} {0} & {i ( \delta^0_A)^2 \overline{\beta}_{12}} \\ {-i ( \delta^0_A)^{-2}\overline{\beta}_{21} } & {0} \end{array} \right) +\mathcal{O}(t^{-1}). \end{align} $$
$$ \begin{align} m^{A'}(z(\zeta) ;x,t)=I +\dfrac{1}{\zeta_-} \left( \begin{array}{cc} {0} & {i ( \delta^0_A)^2 \overline{\beta}_{12}} \\ {-i ( \delta^0_A)^{-2}\overline{\beta}_{21} } & {0} \end{array} \right) +\mathcal{O}(t^{-1}). \end{align} $$
Similarly, for
![]() $\zeta _+=\sqrt {48z_0 t}(z - z_0) $
, the solution to RHP Problem 4.3
$\zeta _+=\sqrt {48z_0 t}(z - z_0) $
, the solution to RHP Problem 4.3
![]() $m^{B'}$
admits the following expansion:
$m^{B'}$
admits the following expansion:
 $$ \begin{align} m^{B'}(z(\zeta) ;x,t)=I +\dfrac{1}{\zeta_+} \left( \begin{array}{cc} {0} & {-i ( \delta^0_B)^2 {\beta}_{12}} \\ {i ( \delta^0_B)^{-2}{\beta}_{21} } & {0} \end{array} \right) +\mathcal{O}(t^{-1}). \end{align} $$
$$ \begin{align} m^{B'}(z(\zeta) ;x,t)=I +\dfrac{1}{\zeta_+} \left( \begin{array}{cc} {0} & {-i ( \delta^0_B)^2 {\beta}_{12}} \\ {i ( \delta^0_B)^{-2}{\beta}_{21} } & {0} \end{array} \right) +\mathcal{O}(t^{-1}). \end{align} $$
Now we construct
![]() $m^{\mathrm {LC}}$
needed in the factorisation of
$m^{\mathrm {LC}}$
needed in the factorisation of
![]() $m^{(2)}$
in equation (4.1). In Figure 4.3, we let
$m^{(2)}$
in equation (4.1). In Figure 4.3, we let
![]() $\rho $
be the radius of the circle
$\rho $
be the radius of the circle
![]() $C_A$
(
$C_A$
(
![]() $C_B$
) centred at
$C_B$
) centred at
![]() $z_0$
(
$z_0$
(
![]() $-z_0$
). We seek a solution of the form
$-z_0$
). We seek a solution of the form
 $$ \begin{align} m^{\mathrm{LC}}(z)=\begin{cases} E(z) \quad &\left\vert z\pm z_0 \right\vert>\rho \\ E(z) m^{A'}(z) \quad &\left\vert z + z_0 \right\vert\leq\rho \\ E(z) m^{B'}(z) \quad & \left\vert z - z_0 \right\vert\leq \rho \end{cases} \end{align} $$
$$ \begin{align} m^{\mathrm{LC}}(z)=\begin{cases} E(z) \quad &\left\vert z\pm z_0 \right\vert>\rho \\ E(z) m^{A'}(z) \quad &\left\vert z + z_0 \right\vert\leq\rho \\ E(z) m^{B'}(z) \quad & \left\vert z - z_0 \right\vert\leq \rho \end{cases} \end{align} $$

Figure 4.3
![]() $\Sigma _E$
.
$\Sigma _E$
.
Since
![]() $ m^{A'}$
and
$ m^{A'}$
and
![]() $ m^{B'}$
solve Problem 4.2 and Problem 4.3, respectively, we can construct the solution
$ m^{B'}$
solve Problem 4.2 and Problem 4.3, respectively, we can construct the solution
![]() $m^{\mathrm {LC}}(z)$
if we find
$m^{\mathrm {LC}}(z)$
if we find
![]() $E(z)$
. Indeed, E solves the following Riemann-Hilbert problem:
$E(z)$
. Indeed, E solves the following Riemann-Hilbert problem:
Problem 4.5. Find a matrix-valued function
![]() $E(z)$
on
$E(z)$
on
![]() $\mathbb {C} \setminus \Sigma _E$
with the following properties:
$\mathbb {C} \setminus \Sigma _E$
with the following properties:
-
(1)
 $E(z) \rightarrow I$
as
$E(z) \rightarrow I$
as
 $ z \rightarrow \infty $
.
$ z \rightarrow \infty $
. -
(2)
 $E(z) $
is analytic for
$E(z) $
is analytic for
 $z \in \mathbb {C} \setminus \left ( C_A\cup C_B \right )$
with continuous boundary values
$z \in \mathbb {C} \setminus \left ( C_A\cup C_B \right )$
with continuous boundary values
 $E_{\pm }(z)$
.
$E_{\pm }(z)$
. -
(3) On
 $ C_A\cup C_B $
, we have the following jump conditions where
$ C_A\cup C_B $
, we have the following jump conditions where $$ \begin{align*}E_{+}(z)=E_{-}(z) v^{ (E) }(z),\end{align*} $$
(4.17)
$$ \begin{align*}E_{+}(z)=E_{-}(z) v^{ (E) }(z),\end{align*} $$
(4.17) $$ \begin{align} v^{ (E) }(z)=\begin{cases} m^{A'}(z(\zeta) ), \quad &z\in C_A\\ m^{B'}(z(\zeta) ), \quad &z\in C_B\\ v^{(2)} , \quad &z\in \Sigma_E\setminus\left( C_A\cup C_B\right). \end{cases} \end{align} $$
$$ \begin{align} v^{ (E) }(z)=\begin{cases} m^{A'}(z(\zeta) ), \quad &z\in C_A\\ m^{B'}(z(\zeta) ), \quad &z\in C_B\\ v^{(2)} , \quad &z\in \Sigma_E\setminus\left( C_A\cup C_B\right). \end{cases} \end{align} $$
Proposition 4.6.
![]() $E(z)$
admits a classical solution: that is, the jump condition in equation (4.17) holds pointwise on the contour
$E(z)$
admits a classical solution: that is, the jump condition in equation (4.17) holds pointwise on the contour
![]() $\Sigma _E$
.
$\Sigma _E$
.
Proof. Here we invoke to the well-established existence and uniqueness theory from [Reference Zhou44] (see also chapter 2 [Reference Trogdon and Olver42]). First, it is easy to check that
where the
![]() $\dagger $
denotes the Hermitian conjugate of the given matrix. We then take care of the zero-sum condition at the self-intersecting points of
$\dagger $
denotes the Hermitian conjugate of the given matrix. We then take care of the zero-sum condition at the self-intersecting points of
![]() $\Sigma _E$
. Since the remaining cases follows from symmetry, we will only look
$\Sigma _E$
. Since the remaining cases follows from symmetry, we will only look
![]() $\Sigma ^{\prime (2)}_5 \cap \Sigma ^{\prime (2)}_6\cap \Sigma ^{\prime (2)}_{9} $
and
$\Sigma ^{\prime (2)}_5 \cap \Sigma ^{\prime (2)}_6\cap \Sigma ^{\prime (2)}_{9} $
and
![]() $\Sigma ^{\prime (2)}_6\cap C_A $
. The zero-sum condition holds at the first point by comparing equations (3.8) and (3.14). For
$\Sigma ^{\prime (2)}_6\cap C_A $
. The zero-sum condition holds at the first point by comparing equations (3.8) and (3.14). For
![]() $\Sigma ^{\prime (2)}_6\cap C_A $
, (after adding contour with identity jumps and reorientation; compare page 1058 [Reference Deift and Zhou14]), we explicitly compute
$\Sigma ^{\prime (2)}_6\cap C_A $
, (after adding contour with identity jumps and reorientation; compare page 1058 [Reference Deift and Zhou14]), we explicitly compute
 $$ \begin{align*} I & = m^{A'}(z(\zeta) ) \left[ v^{(2)} \right]^{-1} \left[ m^{A'}(z(\zeta) ) \right] ^{-1}\\ &= m^{A'}_+(z(\zeta) )\left( v^{(2)} \right)^{-1} \left( m^{A'}_-(z(\zeta))\right)^{-1}. \end{align*} $$
$$ \begin{align*} I & = m^{A'}(z(\zeta) ) \left[ v^{(2)} \right]^{-1} \left[ m^{A'}(z(\zeta) ) \right] ^{-1}\\ &= m^{A'}_+(z(\zeta) )\left( v^{(2)} \right)^{-1} \left( m^{A'}_-(z(\zeta))\right)^{-1}. \end{align*} $$
Since
![]() $v^{(2)}$
is smooth away from the intersections and zero-sum conditions have been verified, this completes the proof.
$v^{(2)}$
is smooth away from the intersections and zero-sum conditions have been verified, this completes the proof.
Setting
then by standard theory, we have the following singular integral equation
where the singular integral operator is defined by
We first deduce from equations (4.14)–(4.15) that
hence the operator norm of
![]() $C_{v^{(E)}} $
$C_{v^{(E)}} $
Then the resolvent operator
![]() $(1-C_{v^{(E)}})^{-1}$
can be obtained through Neumann series, and we obtain the unique solution to Problem 4.5
$(1-C_{v^{(E)}})^{-1}$
can be obtained through Neumann series, and we obtain the unique solution to Problem 4.5
 $$ \begin{align} E(z)=I+ \dfrac{1}{2\pi i}\int_{C_A\cup C_B} \dfrac{ (1+\eta(s))(v^{(E)}(s)-I ) }{s-z}ds, \end{align} $$
$$ \begin{align} E(z)=I+ \dfrac{1}{2\pi i}\int_{C_A\cup C_B} \dfrac{ (1+\eta(s))(v^{(E)}(s)-I ) }{s-z}ds, \end{align} $$
which admits the following asymptotic expansion in z:
 $$ \begin{align} E_2(z)=I+ \dfrac{E_{1}}{z} +\mathcal{O}\left( \dfrac{1}{z^2} \right). \end{align} $$
$$ \begin{align} E_2(z)=I+ \dfrac{E_{1}}{z} +\mathcal{O}\left( \dfrac{1}{z^2} \right). \end{align} $$
Using the bound on the operator norm in equation (4.19), we obtain
Given the form of
![]() $v^{(E)}$
in equation (4.17) and the asymptotic expansions in equations (4.14)–(4.15), an application of Cauchy’s integral formula leads to
$v^{(E)}$
in equation (4.17) and the asymptotic expansions in equations (4.14)–(4.15), an application of Cauchy’s integral formula leads to
 $$ \begin{align} E_{1}&=\dfrac{1}{\sqrt{48 z_0 t}} \left( \begin{array}{cc} {0} & {-i ( \delta^0_B)^2 {\beta}_{12}} \\ {i ( \delta^0_B)^{-2}{\beta}_{21} } & {0} \end{array} \right) + \dfrac{1}{\sqrt{48 z_0 t}} \left( \begin{array}{cc} {0} & { i ( \delta^0_A)^2 \overline{\beta}_{12} } \\ {-i ( \delta^0_A)^{-2}\overline{\beta}_{21} } & {0} \end{array} \right) + \mathcal{O}(t^{-1}). \end{align} $$
$$ \begin{align} E_{1}&=\dfrac{1}{\sqrt{48 z_0 t}} \left( \begin{array}{cc} {0} & {-i ( \delta^0_B)^2 {\beta}_{12}} \\ {i ( \delta^0_B)^{-2}{\beta}_{21} } & {0} \end{array} \right) + \dfrac{1}{\sqrt{48 z_0 t}} \left( \begin{array}{cc} {0} & { i ( \delta^0_A)^2 \overline{\beta}_{12} } \\ {-i ( \delta^0_A)^{-2}\overline{\beta}_{21} } & {0} \end{array} \right) + \mathcal{O}(t^{-1}). \end{align} $$
After possible reorientation of the contours, using the reconstruction formula given by equation (1.14), we expect that
 $$ \begin{align} u(x,t)&=\left( \dfrac{\kappa}{3z_0 t}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right) + O\left(\dfrac{c(z_0)}{\sqrt{z_0 t} \tau^{1/2}}\right) + \mathcal{E}_1, \end{align} $$
$$ \begin{align} u(x,t)&=\left( \dfrac{\kappa}{3z_0 t}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right) + O\left(\dfrac{c(z_0)}{\sqrt{z_0 t} \tau^{1/2}}\right) + \mathcal{E}_1, \end{align} $$
where
 $$ \begin{align*}\phi(z_0)=\arg \Gamma(i\kappa)-\dfrac{\pi}{4}-\arg r(z_0)+\dfrac{1}{\pi}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z_0}\end{align*} $$
$$ \begin{align*}\phi(z_0)=\arg \Gamma(i\kappa)-\dfrac{\pi}{4}-\arg r(z_0)+\dfrac{1}{\pi}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z_0}\end{align*} $$
and
![]() $\mathcal {E}_1$
is the error induced by a pure-
$\mathcal {E}_1$
is the error induced by a pure-
![]() $\overline {\partial }$
problem to be studied in the following section.
$\overline {\partial }$
problem to be studied in the following section.
5 The
 $\overline {\partial }$
-Problem
$\overline {\partial }$
-Problem
From equation (4.1), we have matrix-valued function
The goal of this section is to show that
![]() $m^{(3)}$
only results in an error term
$m^{(3)}$
only results in an error term
![]() $E_1$
with higher-order decay rate than the leading-order term of the asymptotic formula in equation (4.25).
$E_1$
with higher-order decay rate than the leading-order term of the asymptotic formula in equation (4.25).
Since
![]() $m^{\mathrm {LC}}(z; x, t)$
is analytic in
$m^{\mathrm {LC}}(z; x, t)$
is analytic in
![]() $\mathbb {C} \setminus \Sigma ^{'(2)}$
, we may compute
$\mathbb {C} \setminus \Sigma ^{'(2)}$
, we may compute
 $$ \begin{align*} \overline{\partial} m^{(3)}(z;x,t) &= \overline{\partial} m^{(2)}(z;x,t) m^{\mathrm{LC}}(z; x,t)^{-1}\\ &= m^{(2)}(z;x,t) \, \overline{\partial} \mathcal{R}^{(2)}(z) m^{\mathrm{LC}}(z; x,t)^{-1} &\mbox{(by equation (3.13))}\\ &= m^{(3)}(z;x,t) m^{\mathrm{LC}}(z; x, t) \, \overline{\partial} \mathcal{R}^{(2)}(z) m^{\mathrm{LC}}(z; x,t)^{-1} & \mbox{(by equation (5.1))}\\ &= m^{(3)}(z;x,t) W(z;x,t), \end{align*} $$
$$ \begin{align*} \overline{\partial} m^{(3)}(z;x,t) &= \overline{\partial} m^{(2)}(z;x,t) m^{\mathrm{LC}}(z; x,t)^{-1}\\ &= m^{(2)}(z;x,t) \, \overline{\partial} \mathcal{R}^{(2)}(z) m^{\mathrm{LC}}(z; x,t)^{-1} &\mbox{(by equation (3.13))}\\ &= m^{(3)}(z;x,t) m^{\mathrm{LC}}(z; x, t) \, \overline{\partial} \mathcal{R}^{(2)}(z) m^{\mathrm{LC}}(z; x,t)^{-1} & \mbox{(by equation (5.1))}\\ &= m^{(3)}(z;x,t) W(z;x,t), \end{align*} $$
where
We thus arrive at the following pure
![]() $\overline {\partial }$
-problem:
$\overline {\partial }$
-problem:
Problem 5.1. Give
![]() $r \in H^{1}(\mathbb {R})$
, find a continuous matrix-valued function
$r \in H^{1}(\mathbb {R})$
, find a continuous matrix-valued function
![]() $m^{(3)}(z;x,t)$
on
$m^{(3)}(z;x,t)$
on
![]() $\mathbb {C}$
with the following properties:
$\mathbb {C}$
with the following properties:
-
(1)
 $m^{(3)}(z;x,t) \rightarrow I$
as
$m^{(3)}(z;x,t) \rightarrow I$
as
 $|z| \rightarrow \infty $
,
$|z| \rightarrow \infty $
, -
(2)
 $\overline {\partial } m^{(3)}(z;x,t) = m^{(3)}(z;x,t) W(z;x,t)$
.
$\overline {\partial } m^{(3)}(z;x,t) = m^{(3)}(z;x,t) W(z;x,t)$
.
It is well understood (see for example [Reference Ablowitz and Fokas1, Chapter 7]) that the solution to this
![]() $\overline {\partial }$
problem is equivalent to the solution of a Fredholm-type integral equation involving the solid Cauchy transform
$\overline {\partial }$
problem is equivalent to the solution of a Fredholm-type integral equation involving the solid Cauchy transform
where d denotes Lebesgue measure on
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Lemma 5.2. A bounded and continuous matrix-valued function
![]() $m^{(3)}(z;x,t)$
solves Problem (5.1) if and only if
$m^{(3)}(z;x,t)$
solves Problem (5.1) if and only if
Using the integral equation formulation in equation (5.3), we will prove:
Proposition 5.3. Suppose that
![]() $r \in H^{1}(\mathbb {R})$
. Then for
$r \in H^{1}(\mathbb {R})$
. Then for
![]() $t\gg 1$
, there exists a unique solution
$t\gg 1$
, there exists a unique solution
![]() $m^{(3)}(z;x,t)$
for Problem 5.1 with the property that
$m^{(3)}(z;x,t)$
for Problem 5.1 with the property that
 $$ \begin{align} m^{(3)}(z;x,t) = I + \dfrac{1}{z} m^{(3)}_1(x,t) + o\left( \frac{1}{z} \right) \end{align} $$
$$ \begin{align} m^{(3)}(z;x,t) = I + \dfrac{1}{z} m^{(3)}_1(x,t) + o\left( \frac{1}{z} \right) \end{align} $$
for
![]() $z=i\sigma $
with
$z=i\sigma $
with
![]() $\sigma \rightarrow +\infty $
. Here,
$\sigma \rightarrow +\infty $
. Here,
where the implicit constant in equation (5.5) is uniform for r in a bounded subset of
![]() $H^{1}(\mathbb {R})$
.
$H^{1}(\mathbb {R})$
.
Proof. Given Lemmas 5.4–5.8, as in [Reference Liu, Perry and Sulem36], we first show that, for large t, the integral operator
![]() $K_W$
defined by
$K_W$
defined by
is bounded by
where the implied constants depend only on
![]() $ \left \Vert {r} \right \Vert {}_{H^{1}} $
. This is the goal of Lemma 5.6. It implies that
$ \left \Vert {r} \right \Vert {}_{H^{1}} $
. This is the goal of Lemma 5.6. It implies that
exists as an
![]() $L^\infty $
solution of equation (5.3).
$L^\infty $
solution of equation (5.3).
We then show in Lemma 5.7 that the solution
![]() $m^{(3)}(z;x,t)$
has a large-z asymptotic expansion of the form in equation (5.4) where
$m^{(3)}(z;x,t)$
has a large-z asymptotic expansion of the form in equation (5.4) where
![]() $z \rightarrow \infty $
along the positive imaginary axis. Note that, for such z, we can bound
$z \rightarrow \infty $
along the positive imaginary axis. Note that, for such z, we can bound
![]() $|z-\zeta |$
below by a constant times
$|z-\zeta |$
below by a constant times
![]() $|z|+|\zeta |$
. Finally, in Lemma 5.8, we prove the estimate in equation (5.5), where the constants are uniform in r belonging to a bounded subset of
$|z|+|\zeta |$
. Finally, in Lemma 5.8, we prove the estimate in equation (5.5), where the constants are uniform in r belonging to a bounded subset of
![]() $H^{1}(\mathbb {R})$
. The estimates given by equations (5.4), (5.5) and (5.6) result from the bounds obtained in the next four lemmas.
$H^{1}(\mathbb {R})$
. The estimates given by equations (5.4), (5.5) and (5.6) result from the bounds obtained in the next four lemmas.
Lemma 5.4. Set
![]() $\xi =\pm z_0$
and
$\xi =\pm z_0$
and
![]() $z=(u +\xi )+iv$
. We have
$z=(u +\xi )+iv$
. We have
Proof. We only show the inequalities above in
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _7^+$
. Recall that near
$\Omega _7^+$
. Recall that near
![]() $z_0$
$z_0$
In
![]() $\Omega _1$
, we use the facts that
$\Omega _1$
, we use the facts that
![]() $u\geq 0$
,
$u\geq 0$
,
![]() $v\geq 0$
and
$v\geq 0$
and
![]() $|u|\geq |v|$
to deduce
$|u|\geq |v|$
to deduce
 $$ \begin{align*} \mathrm{Re}(2i\theta) &=8it(3iu^2v-iv^3+6iuvz_0)\\ &=8t(-3u^2v+v^3-6uvz_0)\\ &\leq 8t(-3u^2v +u^2v-6uvz_0)\\ &\leq 8t (-2u^2v-6uvz_0)\\ &\leq -8|u| |v| z_0 t. \end{align*} $$
$$ \begin{align*} \mathrm{Re}(2i\theta) &=8it(3iu^2v-iv^3+6iuvz_0)\\ &=8t(-3u^2v+v^3-6uvz_0)\\ &\leq 8t(-3u^2v +u^2v-6uvz_0)\\ &\leq 8t (-2u^2v-6uvz_0)\\ &\leq -8|u| |v| z_0 t. \end{align*} $$
Similarly, in
![]() $\Omega _7^+$
, we have
$\Omega _7^+$
, we have
![]() $u\leq 0$
,
$u\leq 0$
,
![]() $v\geq 0$
and
$v\geq 0$
and
![]() $|u|\geq |v|$
, hence
$|u|\geq |v|$
, hence
 $$ \begin{align*} \mathrm{Re}(-2i\theta) &=-8it(3iu^2v-iv^3+6iuvz_0)\\ &=8t(3u^2v+6uvz_0)\\ &\leq 8t(-3u z_0v +6uvz_0)\\ &\leq -8|u| |v| z_0 t. \end{align*} $$
$$ \begin{align*} \mathrm{Re}(-2i\theta) &=-8it(3iu^2v-iv^3+6iuvz_0)\\ &=8t(3u^2v+6uvz_0)\\ &\leq 8t(-3u z_0v +6uvz_0)\\ &\leq -8|u| |v| z_0 t. \end{align*} $$
The estimate given by equation (5.8) then follows from Lemma 3.1. The quantities
![]() $p_i'(\operatorname {\mathrm {Re}} z)$
are all bounded uniformly for r in a bounded subset of
$p_i'(\operatorname {\mathrm {Re}} z)$
are all bounded uniformly for r in a bounded subset of
![]() $H^{1}(\mathbb {R})$
.
$H^{1}(\mathbb {R})$
.
Lemma 5.5. For the localised Riemann-Hilbert problem from Problem 4.1, we have
All implied constants are uniform for r in a bounded subset of
![]() $H^{1}(\mathbb {R})$
.
$H^{1}(\mathbb {R})$
.
The proof of this lemma is a consequence of the previous section.
Lemma 5.6. Suppose that
![]() $r\in H^{1}(\mathbb {R})$
. Then the estimate given by equation (5.6) holds, where the implied constants depend on
$r\in H^{1}(\mathbb {R})$
. Then the estimate given by equation (5.6) holds, where the implied constants depend on
![]() $ \left \Vert {r} \right \Vert {}_{H^{1}} $
.
$ \left \Vert {r} \right \Vert {}_{H^{1}} $
.
Proof. To prove equation (5.6), first note that
so that we need only estimate the right-hand integral. We will prove the estimate in the region
![]() $ z\in \Omega _1$
since estimates for the remaining regions are identical. From equation (5.2),
$ z\in \Omega _1$
since estimates for the remaining regions are identical. From equation (5.2),
Setting
![]() $z=\alpha +i\beta $
and
$z=\alpha +i\beta $
and
![]() $\zeta =(u+z_0)+iv$
, the region
$\zeta =(u+z_0)+iv$
, the region
![]() $\Omega _1$
corresponds to
$\Omega _1$
corresponds to
![]() $u\geq v \geq 0 $
. We then have from equations (5.8), (5.9) and (5.10) that
$u\geq v \geq 0 $
. We then have from equations (5.8), (5.9) and (5.10) that
where
 $$ \begin{align*} I_1 &= \int_0^\infty \int_v^\infty \frac{1}{|z-\zeta|} |p_1'(u)| e^{-tz_0uv} \, du \, dv \\[5pt] I_2 &= \int_0^\infty \int_v^\infty \frac{1}{|z-\zeta|} \left| u+iv \right|{}^{-1/2} e^{-t z_0 uv} \, du \, dv. \end{align*} $$
$$ \begin{align*} I_1 &= \int_0^\infty \int_v^\infty \frac{1}{|z-\zeta|} |p_1'(u)| e^{-tz_0uv} \, du \, dv \\[5pt] I_2 &= \int_0^\infty \int_v^\infty \frac{1}{|z-\zeta|} \left| u+iv \right|{}^{-1/2} e^{-t z_0 uv} \, du \, dv. \end{align*} $$
It now follows from [Reference Borghese, Jenkins and McLaughlin4, proof of Proposition D.1] that
It then follows that
which, together with similar estimates for the integrals over the remaining
![]() $\Omega _i$
s, proves equation (5.6).
$\Omega _i$
s, proves equation (5.6).
Lemma 5.7. For
![]() $z=i\sigma $
with
$z=i\sigma $
with
![]() $\sigma \rightarrow +\infty $
, the expansion in equation (5.4) holds with
$\sigma \rightarrow +\infty $
, the expansion in equation (5.4) holds with
Proof. We write equation (5.3) as
where
![]() $m^{(3)}_1$
is given by equation (5.12). If
$m^{(3)}_1$
is given by equation (5.12). If
![]() $z=i\sigma $
, it is easy to see that
$z=i\sigma $
, it is easy to see that
![]() $|\zeta |/|z-\zeta |$
is bounded above by a fixed constant independent of z, while
$|\zeta |/|z-\zeta |$
is bounded above by a fixed constant independent of z, while
![]() $|m^{(3)}(\zeta ;x,t)| \lesssim 1$
by the remarks following equation (5.7). If we can show that
$|m^{(3)}(\zeta ;x,t)| \lesssim 1$
by the remarks following equation (5.7). If we can show that
![]() $\int _{\mathbb {C}} |W(\zeta ;x,t)| \, d\zeta $
is finite, it will follow from the Dominated Convergence Theorem that
$\int _{\mathbb {C}} |W(\zeta ;x,t)| \, d\zeta $
is finite, it will follow from the Dominated Convergence Theorem that
which implies the required asymptotic estimate. We will estimate
![]() $\displaystyle {\int }_{\hspace {-1.25mm} \Omega _1} |W(\zeta )| \, dm(\zeta )$
since the other estimates are identical. One can write
$\displaystyle {\int }_{\hspace {-1.25mm} \Omega _1} |W(\zeta )| \, dm(\zeta )$
since the other estimates are identical. One can write
Using equations (5.8), (5.9) and (5.10), we may then estimate
where
 $$ \begin{align*} I_1 &= \int_0^\infty \, \int_v^\infty \left| p_1'(u+z_0) \right| e^{-tz_0uv} \, du \, dv\\ I_2 &= \int_0^\infty \int_v^\infty \left| u^2 + v^2 \right|{}^{-1/2} e^{-tz_0 uv} \, du \, dv. \\ \end{align*} $$
$$ \begin{align*} I_1 &= \int_0^\infty \, \int_v^\infty \left| p_1'(u+z_0) \right| e^{-tz_0uv} \, du \, dv\\ I_2 &= \int_0^\infty \int_v^\infty \left| u^2 + v^2 \right|{}^{-1/2} e^{-tz_0 uv} \, du \, dv. \\ \end{align*} $$
It now follows from [Reference Borghese, Jenkins and McLaughlin4, Proposition D.2] that
These estimates together show that
and that the implied constant depends only on
![]() $ \left \Vert {r} \right \Vert {}_{H^{1}} $
. In particular, the integral in equation (5.13) is bounded uniformly as
$ \left \Vert {r} \right \Vert {}_{H^{1}} $
. In particular, the integral in equation (5.13) is bounded uniformly as
![]() $t \rightarrow \infty $
.
$t \rightarrow \infty $
.
Lemma 5.8. The estimate in equation (5.5) holds with constants uniform in r in a bounded subset of
![]() $H^{1}(\mathbb {R})$
.
$H^{1}(\mathbb {R})$
.
Proof. From the representation formula given by equation (5.12), Lemma 5.6 and the remarks following, we have
In the proof of Lemma 5.7, we bounded this integral by
![]() $( z_0t)^{-3/4}$
modulo constants with the required uniformity.
$( z_0t)^{-3/4}$
modulo constants with the required uniformity.
6 Long-time asymptotics
We now put together our previous results and formulate the long-time asymptotics of
![]() $u(x,t)$
in Region I. Undoing all transformations we carried out previously, we get back m:
$u(x,t)$
in Region I. Undoing all transformations we carried out previously, we get back m:
By stand inverse scattering theory, the coefficient of
![]() $z^{-1}$
in the large-z expansion for
$z^{-1}$
in the large-z expansion for
![]() $m(z;x,t)$
will be the solution to the MKdV equation:
$m(z;x,t)$
will be the solution to the MKdV equation:
Lemma 6.1. For
![]() $z=i\sigma $
and
$z=i\sigma $
and
![]() $\sigma \rightarrow +\infty $
, the asymptotic relations
$\sigma \rightarrow +\infty $
, the asymptotic relations
 $$ \begin{align}\qquad m(z;x,t) &= I + \frac{1}{z} m_1(x,t) + o\left(\frac{1}{z}\right) \end{align} $$
$$ \begin{align}\qquad m(z;x,t) &= I + \frac{1}{z} m_1(x,t) + o\left(\frac{1}{z}\right) \end{align} $$
 $$ \begin{align} m^{\mathrm{LC}}(z;x,t) &= I + \frac{1}{z} m^{\mathrm{LC}}_1(x,t) + o\left(\frac{1}{z}\right) \end{align} $$
$$ \begin{align} m^{\mathrm{LC}}(z;x,t) &= I + \frac{1}{z} m^{\mathrm{LC}}_1(x,t) + o\left(\frac{1}{z}\right) \end{align} $$
hold. Moreover,
Proof. By Lemma 2.2(iii), the expansion
 $$ \begin{align} \delta(z)^{\sigma_3} = \left( \begin{array}{cc} {1} & {0} \\ {0} & {1} \end{array} \right) + \frac{1}{z} \left( \begin{array}{cc} {\delta_1} & {0} \\ {0} & {\delta_1^{-1}} \end{array} \right) + \mathcal{O}\left(z^{-2}\right) \end{align} $$
$$ \begin{align} \delta(z)^{\sigma_3} = \left( \begin{array}{cc} {1} & {0} \\ {0} & {1} \end{array} \right) + \frac{1}{z} \left( \begin{array}{cc} {\delta_1} & {0} \\ {0} & {\delta_1^{-1}} \end{array} \right) + \mathcal{O}\left(z^{-2}\right) \end{align} $$
holds, with the remainders in equation (6.5) uniform in r in a bounded subset of
![]() $H^{1}$
. Equation (6.2) follows from equations (6.1) and (6.3), the fact that
$H^{1}$
. Equation (6.2) follows from equations (6.1) and (6.3), the fact that
![]() $\mathcal {R}^{(2)} \equiv I$
in
$\mathcal {R}^{(2)} \equiv I$
in
![]() $\Omega _2$
and equation (6.5). Notice the fact that the diagonal matrix in equation (6.5) does not affect the
$\Omega _2$
and equation (6.5). Notice the fact that the diagonal matrix in equation (6.5) does not affect the
![]() $12$
-component of m. Hence, for
$12$
-component of m. Hence, for
![]() $z=i\sigma $
,
$z=i\sigma $
,
 $$ \begin{align*}\left(m(z;x,t)\right)_{12} = \frac{1}{z}\left(m^{(3)}_1(x,t)\right)_{12} + \frac{1}{z}\left(m^{\mathrm{LC}}_1(x,t)\right)_{12} + o\left(\frac{1}{z}\right), \end{align*} $$
$$ \begin{align*}\left(m(z;x,t)\right)_{12} = \frac{1}{z}\left(m^{(3)}_1(x,t)\right)_{12} + \frac{1}{z}\left(m^{\mathrm{LC}}_1(x,t)\right)_{12} + o\left(\frac{1}{z}\right), \end{align*} $$
and the result now follows from equation (5.5).
We arrive at the asymptotic formula in Region I:
Proposition 6.2. The function
takes the form
where
 $$ \begin{align*}u_{as}(x,t)=\left( \dfrac{\kappa}{3tz_0}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right),\end{align*} $$
$$ \begin{align*}u_{as}(x,t)=\left( \dfrac{\kappa}{3tz_0}\right)^{1/2}\cos \left(16tz_0^3-\kappa\log(192tz_0^3)+\phi(z_0) \right),\end{align*} $$
with
 $$ \begin{align*}\phi(z_0)=\arg \Gamma(i\kappa)-\dfrac{\pi}{4}-\arg r(z_0)+\dfrac{1}{\pi}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z_0}\end{align*} $$
$$ \begin{align*}\phi(z_0)=\arg \Gamma(i\kappa)-\dfrac{\pi}{4}-\arg r(z_0)+\dfrac{1}{\pi}\int_{-z_0}^{z_0}\log\left( \dfrac{1-|r(\zeta)|^2}{1-|r(z_0)|^2} \right)\dfrac{d\zeta}{\zeta-z_0}\end{align*} $$
obtained from equation (4.25).
See Section 4 in Deift-Zhou [Reference Deift and Zhou11] for full details on the derivation for the explicit formula of
![]() $u_{as}$
.
$u_{as}$
.
7 Regions II–V
We now turn to the study of Regions II–V. We first study Region III, then Region II and finally Region IV and Region V. Our starting point is RHP Problem 1.2, and the strategy of the proof is as follows:
-
1. We scale the RHP Problem 1.2 by a factor determined by the region.
-
2. We use
 $\overline {\partial }$
-steepest descent to study the scaled RHP and obtain both the leading term and the error term.
$\overline {\partial }$
-steepest descent to study the scaled RHP and obtain both the leading term and the error term. -
3. We multiply by the scaling factor to get the asymptotic formula for the original RHP Problem 1.2.
7.1 Region III
In this region,
![]() $\tau \leq M$
.
$\tau \leq M$
.
7.1.1
 $x<0$
$x<0$
We first notice that
so we do not need the lower/upper factorisation given by equation (2.4) for
![]() $|z|<z_0$
and are left with the following upper/lower factorisation:
$|z|<z_0$
and are left with the following upper/lower factorisation:
 $$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v(z) = \left( \begin{array}{cc} {1} & {-\overline{r(z)} e^{-2i\theta}} \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r(z) e^{2i\theta}} & {1} \end{array} \right) , \quad z \in\mathbb{R}. \end{align} $$
$$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3}v(z) = \left( \begin{array}{cc} {1} & {-\overline{r(z)} e^{-2i\theta}} \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r(z) e^{2i\theta}} & {1} \end{array} \right) , \quad z \in\mathbb{R}. \end{align} $$
Now we carry out the following scaling:
and equation (7.1) becomes
 $$ \begin{align} \left( \begin{array}{cc} {1} & {-\overline{r(\zeta t^{-1/3 } ) } e^{-2i\theta (\zeta t^{-1/3 } ) } } \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r(\zeta t^{-1/3 } ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {1} \end{array} \right) , \quad z \in\mathbb{R}, \end{align} $$
$$ \begin{align} \left( \begin{array}{cc} {1} & {-\overline{r(\zeta t^{-1/3 } ) } e^{-2i\theta (\zeta t^{-1/3 } ) } } \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r(\zeta t^{-1/3 } ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {1} \end{array} \right) , \quad z \in\mathbb{R}, \end{align} $$
where
Note that the stationary points become
![]() $\pm z_0 t^{1/3}$
.
$\pm z_0 t^{1/3}$
.

Figure 7.1
![]() $\Sigma -\text {Region-III}$
.
$\Sigma -\text {Region-III}$
.
We now study the scaled Riemann-Hilbert problem with the jump matrix given by equation (7.3). We will again perform contour deformation and write the solution as a product of the solution to a
![]() $\overline {\partial }$
-problem and a ‘localised’ Riemann-Hilbert problem.
$\overline {\partial }$
-problem and a ‘localised’ Riemann-Hilbert problem.
For brevity, we only discuss the
![]() $\overline {\partial }$
-problem in
$\overline {\partial }$
-problem in
![]() $\Omega _1$
. In
$\Omega _1$
. In
![]() $\Omega _1$
, we write
$\Omega _1$
, we write
Then
 $$ \begin{align*} \mathrm{Re} (2i\theta (\zeta t^{-1/3})) &=8\left( -3(u+z_0 t^{1/3})^2 v +v^3 +3\tau^{2/3}v\right)\qquad\qquad\qquad\qquad\qquad\\ & \leq 8 \left( -3u^2v -6 uv z_0 t^{1/3} +v^3 \right)\\ &\leq -16u^2 v \end{align*} $$
$$ \begin{align*} \mathrm{Re} (2i\theta (\zeta t^{-1/3})) &=8\left( -3(u+z_0 t^{1/3})^2 v +v^3 +3\tau^{2/3}v\right)\qquad\qquad\qquad\qquad\qquad\\ & \leq 8 \left( -3u^2v -6 uv z_0 t^{1/3} +v^3 \right)\\ &\leq -16u^2 v \end{align*} $$
 $$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta t^{-1/3} ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in (z_0t^{1/3},\infty)\\[10pt] \\ \left( \begin{array}{cc} {0} & {0} \\ {r( z_0 ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in \Sigma_1 \end{cases} \end{align*} $$
$$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta t^{-1/3} ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in (z_0t^{1/3},\infty)\\[10pt] \\ \left( \begin{array}{cc} {0} & {0} \\ {r( z_0 ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in \Sigma_1 \end{cases} \end{align*} $$
and the interpolation is given by
So we arrive at the
![]() $\overline {\partial }$
-derivative in
$\overline {\partial }$
-derivative in
![]() $\Omega _1$
in the
$\Omega _1$
in the
![]() $\zeta $
variable:
$\zeta $
variable:

Figure 7.2
![]() $\Sigma $
-Painlevé.
$\Sigma $
-Painlevé.
 $$ \begin{align} \overline{\partial} R_1 = \left( {t^{-1/3}} r'\left( u t^{-1/3} \right) \cos 2\phi- 2\dfrac{ r(ut^{-1/3} ) -r(z_0) }{ \left\vert \zeta-z_0 t^{1/3} \right\vert } e^{i\phi} \sin 2\phi \right) e^{2i\theta}, \end{align} $$
$$ \begin{align} \overline{\partial} R_1 = \left( {t^{-1/3}} r'\left( u t^{-1/3} \right) \cos 2\phi- 2\dfrac{ r(ut^{-1/3} ) -r(z_0) }{ \left\vert \zeta-z_0 t^{1/3} \right\vert } e^{i\phi} \sin 2\phi \right) e^{2i\theta}, \end{align} $$
 $$ \begin{align} \left| \overline{\partial} R_1 e^{\pm 2i\theta} \right| \lesssim\left( | t^{-1/3} r'\left( u t^{-1/3} \right) | +\dfrac{ \left\Vert {r'} \right\Vert{}_{L^2} }{ t^{1/3} |\zeta t^{-1/3}-z_0 |^{1/2} }\right) e^{-16u^2 v}.\qquad\qquad\qquad\quad \end{align} $$
$$ \begin{align} \left| \overline{\partial} R_1 e^{\pm 2i\theta} \right| \lesssim\left( | t^{-1/3} r'\left( u t^{-1/3} \right) | +\dfrac{ \left\Vert {r'} \right\Vert{}_{L^2} }{ t^{1/3} |\zeta t^{-1/3}-z_0 |^{1/2} }\right) e^{-16u^2 v}.\qquad\qquad\qquad\quad \end{align} $$
We will derive an exactly solvable model problem before dealing with the
![]() $\overline {\partial }-$
error estimates. We apply the fundamental theorem of calculus to get
$\overline {\partial }-$
error estimates. We apply the fundamental theorem of calculus to get
 $$ \begin{align*}r(\zeta t^{-1/3}) e^{2i\theta}-r(0)e^{2i\theta} \leq \left\vert \dfrac{\zeta}{t^{1/6}} e^{8i (\zeta^3-3 \tau^{2/3}\zeta)}\right\vert.\end{align*} $$
$$ \begin{align*}r(\zeta t^{-1/3}) e^{2i\theta}-r(0)e^{2i\theta} \leq \left\vert \dfrac{\zeta}{t^{1/6}} e^{8i (\zeta^3-3 \tau^{2/3}\zeta)}\right\vert.\end{align*} $$
Given the fact that
![]() $z_0 t^{1/3}=\tau ^{1/3}\leq (M)^{1/3}$
, we have that
$z_0 t^{1/3}=\tau ^{1/3}\leq (M)^{1/3}$
, we have that
 $$ \begin{align*}\left\Vert { \dfrac{\zeta}{t^{1/6}} e^{8i (\zeta^3-3 \tau^{2/3}\zeta)}} \right\Vert{}_{L^1\cap L^2\cap L^\infty} \lesssim t^{-1/6}.\end{align*} $$
$$ \begin{align*}\left\Vert { \dfrac{\zeta}{t^{1/6}} e^{8i (\zeta^3-3 \tau^{2/3}\zeta)}} \right\Vert{}_{L^1\cap L^2\cap L^\infty} \lesssim t^{-1/6}.\end{align*} $$
So we can reduce the problem to a problem on the contour given by Figure 7.1 with the following jump matrices:
 $$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3 } v^{(2)}(\zeta) &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {0} \\ {{r(0)}} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{III})}_1\cup \Sigma^{(\mathrm{III})}_2 \\ \nonumber &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {-\overline{r(0)}} \\ {0} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{III})}_3 \cup \Sigma^{(\mathrm{III})}_4\\ \nonumber &= e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } v(0), \quad \zeta\in [-z_0t^{1/3}, z_0t^{1/3}]. \end{align} $$
$$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3 } v^{(2)}(\zeta) &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {0} \\ {{r(0)}} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{III})}_1\cup \Sigma^{(\mathrm{III})}_2 \\ \nonumber &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {-\overline{r(0)}} \\ {0} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{III})}_3 \cup \Sigma^{(\mathrm{III})}_4\\ \nonumber &= e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } v(0), \quad \zeta\in [-z_0t^{1/3}, z_0t^{1/3}]. \end{align} $$
Following the same argument on page 357 of [Reference Deift and Zhou11], the RH problem is further reduced to one defined on the following contour as shown in Figure 7.2, which will be related to solve a Painlevé II equation:
 $$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3 } v^{(2)}(\zeta) &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {0} \\ {{r(0)}} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{P})}_1\cup \Sigma^{(\mathrm{P})}_2 \\ \nonumber &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {-\overline{r(0)}} \\ {0} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{P})}_3 \cup \Sigma^{(\mathrm{P})}_4, \end{align} $$
$$ \begin{align} e^{-i\theta\operatorname{\mathrm{ad}}\sigma_3 } v^{(2)}(\zeta) &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {0} \\ {{r(0)}} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{P})}_1\cup \Sigma^{(\mathrm{P})}_2 \\ \nonumber &=e^{-4i\left(\zeta^3+\left( x/(4 t^{1/3}) \right) \zeta \right) \operatorname{\mathrm{ad}}\sigma_3 } \left( \begin{array}{cc} {1} & {-\overline{r(0)}} \\ {0} & {1} \end{array} \right) , \quad \zeta\in \Sigma^{(\mathrm{P})}_3 \cup \Sigma^{(\mathrm{P})}_4, \end{align} $$
which is exactly solvable.
Let P be a solution of the Painlevé
![]() $\text {II}$
equation
$\text {II}$
equation
determined by
![]() $r(0)$
. Then the reduced factorisation problem above is related to the Painlevé II equation by an isomonodromy problem associated to the linear problem
$r(0)$
. Then the reduced factorisation problem above is related to the Painlevé II equation by an isomonodromy problem associated to the linear problem
 $$\begin{align*}\frac{d\psi}{dz}=\left(\begin{array}{cc} -4iz^{2}-is-2iP^{2} & 4Piz-2P'\\ -4Piz-2P' & 4iz^{2}+is+2iP^{2} \end{array}\right)\psi, \end{align*}$$
$$\begin{align*}\frac{d\psi}{dz}=\left(\begin{array}{cc} -4iz^{2}-is-2iP^{2} & 4Piz-2P'\\ -4Piz-2P' & 4iz^{2}+is+2iP^{2} \end{array}\right)\psi, \end{align*}$$
with
![]() $s=x/t^{1/3}$
and, as
$s=x/t^{1/3}$
and, as
![]() $\zeta \to \infty $
,
$\zeta \to \infty $
,
Here, over six sections (compare [Reference Deift and Zhou11, Figure 5.7]), one has the jump relations
where
![]() $S_{i}$
s are determined by three parameters
$S_{i}$
s are determined by three parameters
![]() $\left (\mathrm {p},\mathrm {q},\mathrm {r}\right )$
satisfying
$\left (\mathrm {p},\mathrm {q},\mathrm {r}\right )$
satisfying
In our setting, we have that
Then one can reconstruct P from
![]() $\psi $
([Reference Deift and Zhou11, (5.44)]):
$\psi $
([Reference Deift and Zhou11, (5.44)]):
Since this isomonodromy problem is standard, we refer to Deift-Zhou [Reference Deift and Zhou11, Sec.5] for full details.
We then proceed as in the previous section and study the integral equation related to the
![]() $\overline {\partial }$
problem. Setting
$\overline {\partial }$
problem. Setting
![]() $z=\alpha +i\beta $
and
$z=\alpha +i\beta $
and
![]() $\zeta =(u+z_0t^{1/3})+iv$
, the region
$\zeta =(u+z_0t^{1/3})+iv$
, the region
![]() $\Omega _1$
corresponds to
$\Omega _1$
corresponds to
![]() $u\geq v \geq 0 $
. We decompose the integral operator into three parts:
$u\geq v \geq 0 $
. We decompose the integral operator into three parts:
where
 $$ \begin{align*} I_1 &= \int_0^\infty \int_v^\infty \dfrac{1}{|z-\zeta|} \left\vert t^{-1/3} r'\left( u t^{-1/3} \right) \right\vert e^{-16u^2v} \, du \, dv \\[5pt] I_2 &= \int_0^\infty \int_v^\infty \frac{1}{|z-\zeta|} \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } e^{-16u^2v} \, du \, dv. \end{align*} $$
$$ \begin{align*} I_1 &= \int_0^\infty \int_v^\infty \dfrac{1}{|z-\zeta|} \left\vert t^{-1/3} r'\left( u t^{-1/3} \right) \right\vert e^{-16u^2v} \, du \, dv \\[5pt] I_2 &= \int_0^\infty \int_v^\infty \frac{1}{|z-\zeta|} \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } e^{-16u^2v} \, du \, dv. \end{align*} $$
We first note that
 $$ \begin{align*}\left( \int_{\mathbb{R}} \left\vert t^{-1/3} r'\left( u t^{-1/3} \right) \right\vert{}^2 du \right)^{1/2} = t^{-1/6} \left\Vert {r'} \right\Vert{}_{L^2}. \end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}} \left\vert t^{-1/3} r'\left( u t^{-1/3} \right) \right\vert{}^2 du \right)^{1/2} = t^{-1/6} \left\Vert {r'} \right\Vert{}_{L^2}. \end{align*} $$
Using this and the following estimate from [Reference Borghese, Jenkins and McLaughlin4, proof of Proposition D.1]
 $$ \begin{align} \left\Vert {\frac{1}{|z-\zeta|}} \right\Vert{}_{L^2(v,\infty)} \leq \frac{\pi^{1/2}}{|v-\beta|^{1/2}}. \end{align} $$
$$ \begin{align} \left\Vert {\frac{1}{|z-\zeta|}} \right\Vert{}_{L^2(v,\infty)} \leq \frac{\pi^{1/2}}{|v-\beta|^{1/2}}. \end{align} $$
and Cauchy-Schwarz’s inequality on the u-integration, we may bound
![]() $I_1$
by constants times
$I_1$
by constants times
 $$ \begin{align*}t^{-1/6} \left\Vert {r'} \right\Vert{}_{2} \int_0^\infty \frac{1}{|v-\beta|^{1/2}} e^{-v^3} \, dv \lesssim t^{-1/6}. \end{align*} $$
$$ \begin{align*}t^{-1/6} \left\Vert {r'} \right\Vert{}_{2} \int_0^\infty \frac{1}{|v-\beta|^{1/2}} e^{-v^3} \, dv \lesssim t^{-1/6}. \end{align*} $$
For
![]() $I_2$
, we estimate
$I_2$
, we estimate
 $$ \begin{align*} \left\Vert { \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } } \right\Vert{}_{ L^p (v, \infty) } &\leq \left( \int_v ^\infty t^{-p/3} \left( \dfrac{ 1 }{ (u t^{-1/3} )^2 + (v t^{-1/3})^2 } \right)^{p/4} du \right)^{1/p}\\ &=t^{-1/6} \left( \int_{v }^\infty \left( \dfrac{ 1 }{ u^2 + v^2 } \right)^{p/4} du \right)^{1/p}\\ &\leq c t^{-1/6}v^{1/p-1/2}. \end{align*} $$
$$ \begin{align*} \left\Vert { \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } } \right\Vert{}_{ L^p (v, \infty) } &\leq \left( \int_v ^\infty t^{-p/3} \left( \dfrac{ 1 }{ (u t^{-1/3} )^2 + (v t^{-1/3})^2 } \right)^{p/4} du \right)^{1/p}\\ &=t^{-1/6} \left( \int_{v }^\infty \left( \dfrac{ 1 }{ u^2 + v^2 } \right)^{p/4} du \right)^{1/p}\\ &\leq c t^{-1/6}v^{1/p-1/2}. \end{align*} $$
Now, by equation (7.8) and an application of the Hölder’s inequality with
![]() $P>2$
, we get
$P>2$
, we get
 $$ \begin{align*} |I_2| &\leq \int_0^\infty \left\Vert { \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } } \right\Vert{}_{ L^p (v, \infty) } \left\Vert { \dfrac{1}{|z-\zeta|}} \right\Vert{}_{L^q (v, \infty)} e^{-16v^3} dv\\ &\leq c \int_0^\infty t ^{-1/6 }v^{1/p-1/2} \left\vert v-\beta \right\vert{}^{1/q-1} e^{-16v^3} dv\\ &\leq c t ^{-1/6 }. \end{align*} $$
$$ \begin{align*} |I_2| &\leq \int_0^\infty \left\Vert { \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } } \right\Vert{}_{ L^p (v, \infty) } \left\Vert { \dfrac{1}{|z-\zeta|}} \right\Vert{}_{L^q (v, \infty)} e^{-16v^3} dv\\ &\leq c \int_0^\infty t ^{-1/6 }v^{1/p-1/2} \left\vert v-\beta \right\vert{}^{1/q-1} e^{-16v^3} dv\\ &\leq c t ^{-1/6 }. \end{align*} $$
This proves that
We now show that
Again, we decompose the integral above into two parts:
 $$ \begin{align*} I_1 &= \int_0^\infty \int_v^\infty \left\vert t^{-1/3} r'\left( u t^{-1/3} \right) \right\vert e^{-16u^2v} \, du \, dv \\[5pt] I_2 &= \int_0^\infty \int_v^\infty \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } e^{-16u^2v} \, du \, dv.\end{align*} $$
$$ \begin{align*} I_1 &= \int_0^\infty \int_v^\infty \left\vert t^{-1/3} r'\left( u t^{-1/3} \right) \right\vert e^{-16u^2v} \, du \, dv \\[5pt] I_2 &= \int_0^\infty \int_v^\infty \dfrac {1} { t^{1/3} \left| u t^{-1/3} +ivt^{-1/3} \right|{}^{1/2} } e^{-16u^2v} \, du \, dv.\end{align*} $$
By Cauchy-Schwarz’s inequality:
 $$ \begin{align*} I_1 &\leq \int_0^\infty t^{-1/6} \left\Vert {r'} \right\Vert{}_{2} \left( \int_v^\infty e^{-16u^2 v} du\right)^{1/2} dv\\[5pt] &\leq c t^{-1/6} \int_0^\infty \dfrac{e^{-16 v^3} }{\sqrt[4]{v}}dv\\[5pt] &\leq c t^{-1/6}. \end{align*} $$
$$ \begin{align*} I_1 &\leq \int_0^\infty t^{-1/6} \left\Vert {r'} \right\Vert{}_{2} \left( \int_v^\infty e^{-16u^2 v} du\right)^{1/2} dv\\[5pt] &\leq c t^{-1/6} \int_0^\infty \dfrac{e^{-16 v^3} }{\sqrt[4]{v}}dv\\[5pt] &\leq c t^{-1/6}. \end{align*} $$
By Hölder’s inequality:
 $$ \begin{align*} I_2 &\leq c t^{-1/6 } \int_0^\infty v^{1/p-1/2} \left( \int_v^\infty e^{-16qu^2 v} du \right)^{1/q} dv\\[5pt] &\leq c t^{-1/6 } \int_0^\infty v^{3/2p-1} e^{-16v^3}dv\\[5pt] &\leq c t^{-1/6 }. \end{align*} $$
$$ \begin{align*} I_2 &\leq c t^{-1/6 } \int_0^\infty v^{1/p-1/2} \left( \int_v^\infty e^{-16qu^2 v} du \right)^{1/q} dv\\[5pt] &\leq c t^{-1/6 } \int_0^\infty v^{3/2p-1} e^{-16v^3}dv\\[5pt] &\leq c t^{-1/6 }. \end{align*} $$
We now follow the argument of Section 6 and [Reference Deift and Zhou11, Section 5] to obtain the long-time asymptotic formula in Region III (
![]() $x<0$
):
$x<0$
):
 $$ \begin{align} u(x,t)&= \lim_{z\to \infty}-2z m_{12}(x, t; z)\\[5pt] \nonumber &= \lim_{\zeta\to \infty}-2 t^{-1/3}\zeta m_{12}(x, t; \zeta)\\[3pt] \nonumber &=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{ -1/2 } \right), \end{align} $$
$$ \begin{align} u(x,t)&= \lim_{z\to \infty}-2z m_{12}(x, t; z)\\[5pt] \nonumber &= \lim_{\zeta\to \infty}-2 t^{-1/3}\zeta m_{12}(x, t; \zeta)\\[3pt] \nonumber &=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{ -1/2 } \right), \end{align} $$
where P is a solution of the Painlevé II equation
determined by
![]() $r(0)$
.
$r(0)$
.
7.1.2
 $x>0$
$x>0$
In this case, we have the stationary points
 $$ \begin{align*}\pm iz_0=\pm i \sqrt{\dfrac{ |x| }{ 12 t }}\end{align*} $$
$$ \begin{align*}\pm iz_0=\pm i \sqrt{\dfrac{ |x| }{ 12 t }}\end{align*} $$
stay on the imaginary axis. Given the signature table of
![]() $\theta $
function (see [Reference Deift and Zhou11, Figure 5.9]), we again perform the scaling
$\theta $
function (see [Reference Deift and Zhou11, Figure 5.9]), we again perform the scaling
and contour deformation

We again only discuss the
![]() $\overline {\partial }$
-problem in
$\overline {\partial }$
-problem in
![]() $\Omega _1$
. In
$\Omega _1$
. In
![]() $\Omega _1$
, we write
$\Omega _1$
, we write
and then
 $$ \begin{align*} \mathrm{Re} (i\theta (\zeta t^{-1/3})) &=8\left( -3u^2 v +v^3 -xvt^{-1/3}\right) \\ & \leq 8 \left( -3u^2v +u^2v \right)\\ &\leq -16u^2 v. \end{align*} $$
$$ \begin{align*} \mathrm{Re} (i\theta (\zeta t^{-1/3})) &=8\left( -3u^2 v +v^3 -xvt^{-1/3}\right) \\ & \leq 8 \left( -3u^2v +u^2v \right)\\ &\leq -16u^2 v. \end{align*} $$
To apply the
![]() $\overline {\partial }$
method, we define
$\overline {\partial }$
method, we define
 $$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta t^{-1/3} ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in (0, \infty)\\[10pt] \\ \left( \begin{array}{cc} {0} & {0} \\ {r( 0 ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in \Sigma^{(\mathrm{III+})}_1 \end{cases} \end{align*} $$
$$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta t^{-1/3} ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in (0, \infty)\\[10pt] \\ \left( \begin{array}{cc} {0} & {0} \\ {r( 0 ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in \Sigma^{(\mathrm{III+})}_1 \end{cases} \end{align*} $$
and the interpolation is given by
We can now repeat the analysis in the case above for
![]() $x<0$
and obtain the same long-time asymptotics as equation (7.10).
$x<0$
and obtain the same long-time asymptotics as equation (7.10).
7.2 Region II
We follow the strategy of the previous subsection. We now scale
and the jump matrix becomes
 $$ \begin{align} \left( \begin{array}{cc} {1} & {-\overline{r(\zeta z_0 ) } e^{-2i\theta (\zeta z_0 ) } } \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r(\zeta z_0) e^{2i\theta (\zeta z_0 ) } } & {1} \end{array} \right) , \quad z \in\mathbb{R}, \end{align} $$
$$ \begin{align} \left( \begin{array}{cc} {1} & {-\overline{r(\zeta z_0 ) } e^{-2i\theta (\zeta z_0 ) } } \\[10pt] {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\[10pt] {r(\zeta z_0) e^{2i\theta (\zeta z_0 ) } } & {1} \end{array} \right) , \quad z \in\mathbb{R}, \end{align} $$
where

Figure 7.3
![]() $\Sigma -\text {Region-II}$
.
$\Sigma -\text {Region-II}$
.
For brevity, we again only discuss the
![]() $\overline {\partial }$
-problem in
$\overline {\partial }$
-problem in
![]() $\Omega _1$
of Figure 7.3. In
$\Omega _1$
of Figure 7.3. In
![]() $\Omega _1$
, we write
$\Omega _1$
, we write
then
 $$ \begin{align} \mathrm{Re} (2i\theta (\zeta z_0)) &=8\tau \left( -3(u+1)^2 v +v^3 +3v\right)\qquad\qquad\qquad\quad \\ \nonumber & \leq 8\tau \left( -3u^2v -6 uv +v^3 \right)\\ \nonumber &\leq -16 \tau u v \end{align} $$
$$ \begin{align} \mathrm{Re} (2i\theta (\zeta z_0)) &=8\tau \left( -3(u+1)^2 v +v^3 +3v\right)\qquad\qquad\qquad\quad \\ \nonumber & \leq 8\tau \left( -3u^2v -6 uv +v^3 \right)\\ \nonumber &\leq -16 \tau u v \end{align} $$
 $$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta z_0 ) e^{2i\theta (\zeta z_0 ) } } & {0} \end{array} \right) & z \in ( 1, \infty)\\[10pt] \\ \left( \begin{array}{cc} {0} & {0} \\ {r( z_0 ) e^{2i\theta (\zeta z_0 ) } } & {0} \end{array} \right) & z \in \Sigma^{(\mathrm{II})}_1 \end{cases} \end{align*} $$
$$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta z_0 ) e^{2i\theta (\zeta z_0 ) } } & {0} \end{array} \right) & z \in ( 1, \infty)\\[10pt] \\ \left( \begin{array}{cc} {0} & {0} \\ {r( z_0 ) e^{2i\theta (\zeta z_0 ) } } & {0} \end{array} \right) & z \in \Sigma^{(\mathrm{II})}_1 \end{cases} \end{align*} $$
and the interpolation is given by
So we arrive at the
![]() $\overline {\partial }$
-derivative in
$\overline {\partial }$
-derivative in
![]() $\Omega _1$
in the
$\Omega _1$
in the
![]() $\zeta $
variable:
$\zeta $
variable:
 $$ \begin{align} \overline{\partial} R_1 = \left( z_0 r'\left( u z_0\right) \cos 2\phi- 2\dfrac{ r(uz_0) -r(z_0) }{ \left\vert \zeta-1\right\vert } e^{i\phi} \sin 2\phi \right) e^{2i\theta } \end{align} $$
$$ \begin{align} \overline{\partial} R_1 = \left( z_0 r'\left( u z_0\right) \cos 2\phi- 2\dfrac{ r(uz_0) -r(z_0) }{ \left\vert \zeta-1\right\vert } e^{i\phi} \sin 2\phi \right) e^{2i\theta } \end{align} $$
 $$ \begin{align} \left| \overline{\partial} R_1 e^{\pm 2i\theta} \right| \lesssim\left( | z_0 r'\left( u z_0 \right) | +\dfrac{ z_0 \left\Vert {r'} \right\Vert{}_{L^2} }{ |\zeta z_0 -z_0 |^{1/2} }\right) e^{-16\tau u v}.\qquad\qquad\qquad \end{align} $$
$$ \begin{align} \left| \overline{\partial} R_1 e^{\pm 2i\theta} \right| \lesssim\left( | z_0 r'\left( u z_0 \right) | +\dfrac{ z_0 \left\Vert {r'} \right\Vert{}_{L^2} }{ |\zeta z_0 -z_0 |^{1/2} }\right) e^{-16\tau u v}.\qquad\qquad\qquad \end{align} $$
We now replace
![]() $t^{-1/3}$
and
$t^{-1/3}$
and
![]() $e^{-16u^2 v}$
in the previous subsection with
$e^{-16u^2 v}$
in the previous subsection with
![]() $z_0$
and
$z_0$
and
![]() $e^{-16\tau u v}$
, respectively, and conclude that
$e^{-16\tau u v}$
, respectively, and conclude that
and arrive at the following long-time asymptotics:
 $$ \begin{align} u(x,t) &=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( \tau^{-3/4} z_0^{ 3/2 } \right) \end{align} $$
$$ \begin{align} u(x,t) &=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( \tau^{-3/4} z_0^{ 3/2 } \right) \end{align} $$
 $$ \begin{align} & \kern28pt =\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( (z_0t) ^{-3/4} \right). \end{align} $$
$$ \begin{align} & \kern28pt =\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( (z_0t) ^{-3/4} \right). \end{align} $$
Remark 7.1. In the overlap between Regions II and III, we take
![]() $\text {Re} (2i\theta (\zeta z_0))<-16\tau u^2v$
in equation (7.12). The corresponding estimate in equation (7.15) becomes
$\text {Re} (2i\theta (\zeta z_0))<-16\tau u^2v$
in equation (7.12). The corresponding estimate in equation (7.15) becomes
and the resulting asymptotics in Region II is:
 $$ \begin{align} u(x,t) =\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{-1/2}\right), \end{align} $$
$$ \begin{align} u(x,t) =\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( t^{-1/2}\right), \end{align} $$
which matches up with equation (7.10).
7.3 Region IV

Figure 7.4
![]() $\Sigma -\text {Region-IV}$
.
$\Sigma -\text {Region-IV}$
.
In this region, we have
 $$ \begin{align*}\tau=\left( \dfrac{x}{12t^{1/3}} \right)^{3/2}>(M)^{-1}>0\end{align*} $$
$$ \begin{align*}\tau=\left( \dfrac{x}{12t^{1/3}} \right)^{3/2}>(M)^{-1}>0\end{align*} $$
and choose a constant
![]() $\eta $
such that
$\eta $
such that
![]() $0<\eta < (M)^{-1/3}$
. The contour deformation is given in Figure 7.4, and we carry out the same scaling
$0<\eta < (M)^{-1/3}$
. The contour deformation is given in Figure 7.4, and we carry out the same scaling
We extend r to Part (1) of
![]() $\Omega _2$
by setting
$\Omega _2$
by setting
![]() $r=r( \text {Re}\zeta t^{-1/3} )$
. Also in this region,
$r=r( \text {Re}\zeta t^{-1/3} )$
. Also in this region,
 $$ \begin{align*} \mathrm{Re} (2i\theta (\zeta t^{-1/3})) &=8\left( -3 u^2v +v^3 \right) -2 (x t^{-1/3})v\\ & = 8 \left( -3u^2v +v^3 \right)-24 \tau^{2/3}v\\ & =-24u^2 v-16\tau^{2/3} v. \end{align*} $$
$$ \begin{align*} \mathrm{Re} (2i\theta (\zeta t^{-1/3})) &=8\left( -3 u^2v +v^3 \right) -2 (x t^{-1/3})v\\ & = 8 \left( -3u^2v +v^3 \right)-24 \tau^{2/3}v\\ & =-24u^2 v-16\tau^{2/3} v. \end{align*} $$
We now integrate and find that
 $$ \begin{align} \int_{(1)} \left\vert t^{-1/3} r'(u t^{-1/3}) e^{2i\theta(\zeta t^{-1/3})} \right\vert d\zeta & =\int_0^\eta \int_{-\infty}^{\infty} \left\vert t^{-1/3} r'(u t^{-1/3}) e^{-24u^2v-16\tau^{2/3}v} \right\vert dudv\\ \nonumber & \lesssim t^{-1/6}\tau^{-1/2}. \end{align} $$
$$ \begin{align} \int_{(1)} \left\vert t^{-1/3} r'(u t^{-1/3}) e^{2i\theta(\zeta t^{-1/3})} \right\vert d\zeta & =\int_0^\eta \int_{-\infty}^{\infty} \left\vert t^{-1/3} r'(u t^{-1/3}) e^{-24u^2v-16\tau^{2/3}v} \right\vert dudv\\ \nonumber & \lesssim t^{-1/6}\tau^{-1/2}. \end{align} $$
In Part (2), we write
and then
 $$ \begin{align} \mathrm{Re} (2i\theta (\zeta t^{-1/3})) &=8\left( -3 u^2 (v+\eta) +(v+\eta)^3 \right) -2 (x t^{-1/3}) (v+\eta )\\ \nonumber & \leq 8 \left( -3u^2v -3u^2 \eta +v^3 +3 v^3\eta +3v\eta^2 +\eta^3 \right) -24\tau^{2/3}(v+\eta)\\ \nonumber &\leq -16(u^2 v+\tau^{2/3}\eta). \end{align} $$
$$ \begin{align} \mathrm{Re} (2i\theta (\zeta t^{-1/3})) &=8\left( -3 u^2 (v+\eta) +(v+\eta)^3 \right) -2 (x t^{-1/3}) (v+\eta )\\ \nonumber & \leq 8 \left( -3u^2v -3u^2 \eta +v^3 +3 v^3\eta +3v\eta^2 +\eta^3 \right) -24\tau^{2/3}(v+\eta)\\ \nonumber &\leq -16(u^2 v+\tau^{2/3}\eta). \end{align} $$
For the
![]() $\overline {\partial }$
problem, we set
$\overline {\partial }$
problem, we set
 $$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta t^{-1/3} ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in \mathbb{R}\\[15pt] \left( \begin{array}{cc} {0} & {0} \\ {r( 0 ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right)& z \in \Sigma^{(\mathrm{IV})}_1 \end{cases} \end{align*} $$
$$ \begin{align*} R_1 &= \begin{cases} \left( \begin{array}{cc} {0} & {0} \\ {r(\zeta t^{-1/3} ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right) & z \in \mathbb{R}\\[15pt] \left( \begin{array}{cc} {0} & {0} \\ {r( 0 ) e^{2i\theta (\zeta t^{-1/3 } ) } } & {0} \end{array} \right)& z \in \Sigma^{(\mathrm{IV})}_1 \end{cases} \end{align*} $$
and the interpolation is given by
So we arrive at the
![]() $\overline {\partial }$
-derivative in
$\overline {\partial }$
-derivative in
![]() $\Omega _1$
in the
$\Omega _1$
in the
![]() $\zeta $
variable:
$\zeta $
variable:
 $$ \begin{align} \overline{\partial} R_1 = \left( {t^{-1/3}} r'\left( u t^{-1/3} \right) \cos 2\phi- 2\dfrac{ r(ut^{-1/3} ) -r(0) }{ \left\vert \zeta-i\eta \right\vert } e^{i\phi} \sin 2\phi \right) e^{2i\theta}, \end{align} $$
$$ \begin{align} \overline{\partial} R_1 = \left( {t^{-1/3}} r'\left( u t^{-1/3} \right) \cos 2\phi- 2\dfrac{ r(ut^{-1/3} ) -r(0) }{ \left\vert \zeta-i\eta \right\vert } e^{i\phi} \sin 2\phi \right) e^{2i\theta}, \end{align} $$
 $$ \begin{align*} \left| \overline{\partial} R_1 e^{\pm 2i\theta} \right| &\lesssim\left( | t^{-1/3} r'\left( u t^{-1/3} \right) | +\dfrac{ \left\Vert {r'} \right\Vert{}_{L^2} }{ t^{1/3} |u t^{-1/3} +ivt^{-1/3} |^{1/2} }\right) e^{-16(u^2 v + \tau^{2/3}\eta)}. \end{align*} $$
$$ \begin{align*} \left| \overline{\partial} R_1 e^{\pm 2i\theta} \right| &\lesssim\left( | t^{-1/3} r'\left( u t^{-1/3} \right) | +\dfrac{ \left\Vert {r'} \right\Vert{}_{L^2} }{ t^{1/3} |u t^{-1/3} +ivt^{-1/3} |^{1/2} }\right) e^{-16(u^2 v + \tau^{2/3}\eta)}. \end{align*} $$
Following the same procedure, we show that
 $$ \begin{align} \int_{(2)} |W(\zeta)| \, d\zeta \lesssim t ^{-1/6 } e^{-16\tau^{2/3}\eta}, \end{align} $$
$$ \begin{align} \int_{(2)} |W(\zeta)| \, d\zeta \lesssim t ^{-1/6 } e^{-16\tau^{2/3}\eta}, \end{align} $$
which is the error term resulting from the
![]() $\overline {\partial }$
estimate. We can now combine equations (7.20) and (7.23) and follow the argument in Section 6 and [Reference Deift and Zhou11, Section 5] to obtain the long-time asymptotic formula in Region IV:
$\overline {\partial }$
estimate. We can now combine equations (7.20) and (7.23) and follow the argument in Section 6 and [Reference Deift and Zhou11, Section 5] to obtain the long-time asymptotic formula in Region IV:
 $$ \begin{align} u(x,t)=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( (t\tau)^{-1/2}+ \dfrac{e^{-16\tau^{2/3}\eta}} {t^{ 1/2 } }\right), \end{align} $$
$$ \begin{align} u(x,t)=\dfrac{1}{(3t)^{1/3}}P\left( \dfrac{x}{ (3t)^{1/3} } \right)+\mathcal{O} \left( (t\tau)^{-1/2}+ \dfrac{e^{-16\tau^{2/3}\eta}} {t^{ 1/2 } }\right), \end{align} $$
where P is a solution of the Painlevé II equation
determined by
![]() $r(0)$
.
$r(0)$
.
7.4 Region V

Figure 7.5
![]() $\Sigma -\text {Region-V}$
.
$\Sigma -\text {Region-V}$
.
Given
![]() $|z_0|>M^{-1}$
, let
$|z_0|>M^{-1}$
, let
![]() $h=1/(2M)$
, then we can directly read off that for
$h=1/(2M)$
, then we can directly read off that for
![]() $z=u+iv\in \Omega _1$
of Figure 7.5,
$z=u+iv\in \Omega _1$
of Figure 7.5,
So we simply factorise
 $$ \begin{align*} e^{-i\theta \operatorname{\mathrm{ad}} \sigma_3} v(z) = \left( \begin{array}{cc} {1} & {-\overline{r} e^{-2i\theta}} \\ {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\ {r e^{2i\theta}} & {1} \end{array} \right) \end{align*} $$
$$ \begin{align*} e^{-i\theta \operatorname{\mathrm{ad}} \sigma_3} v(z) = \left( \begin{array}{cc} {1} & {-\overline{r} e^{-2i\theta}} \\ {0} & {1} \end{array} \right) \left( \begin{array}{cc} {1} & {0} \\ {r e^{2i\theta}} & {1} \end{array} \right) \end{align*} $$
and deform
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\Sigma ^{(V)}_1$
and
$\Sigma ^{(V)}_1$
and
![]() $\Sigma ^{(V)}_2$
. We only study the case of
$\Sigma ^{(V)}_2$
. We only study the case of
![]() $\Omega _1$
. It is obvious that
$\Omega _1$
. It is obvious that
![]() $r(u)e^{2i\theta }$
decays exponentially on
$r(u)e^{2i\theta }$
decays exponentially on
![]() $\Sigma ^{(V)}_1$
, so we are only left with the error term
$\Sigma ^{(V)}_1$
, so we are only left with the error term
 $$ \begin{align*} \int_{\Omega_{2}}\left|r^{\prime}(u) e^{2 i \theta(z)}\right| d z &=\int_{0}^{\eta} \int_{-\infty}^{\infty}\left|r^{\prime}(u) e^{-\left(24 u^{2} v+2 c v\right) t}\right| d u d v \\ &\lesssim\int_{0}^{\infty} \frac{e^{-2 c v t}}{\sqrt[4]{v t}} d v \\ & \lesssim t^{-1} \end{align*} $$
$$ \begin{align*} \int_{\Omega_{2}}\left|r^{\prime}(u) e^{2 i \theta(z)}\right| d z &=\int_{0}^{\eta} \int_{-\infty}^{\infty}\left|r^{\prime}(u) e^{-\left(24 u^{2} v+2 c v\right) t}\right| d u d v \\ &\lesssim\int_{0}^{\infty} \frac{e^{-2 c v t}}{\sqrt[4]{v t}} d v \\ & \lesssim t^{-1} \end{align*} $$
and the analysis in
![]() $\Omega _2$
is identical. So we obtain in Region V
$\Omega _2$
is identical. So we obtain in Region V
Remark 7.2. If we instead let the initial condition
![]() $u_0\in H^{2,s}(\mathbb {R})$
, where
$u_0\in H^{2,s}(\mathbb {R})$
, where
![]() $s>1/2$
, then following a similar and simpler argument as in [Reference Chen, Liu and Lu9, section 3], we can deduce that the reflection coefficient
$s>1/2$
, then following a similar and simpler argument as in [Reference Chen, Liu and Lu9, section 3], we can deduce that the reflection coefficient
![]() $r\in H^{s'}(\mathbb {R})$
for any fixed
$r\in H^{s'}(\mathbb {R})$
for any fixed
![]() $1/2<s'<s$
for
$1/2<s'<s$
for
![]() $\frac {1}{2}<s<1$
and
$\frac {1}{2}<s<1$
and
![]() $s'=1$
for
$s'=1$
for
![]() $s=1$
. Then replacing
$s=1$
. Then replacing
![]() $r(z)$
by the convolution form as given in [Reference Chen, Liu and Lu9, (5.15)], we can deduce that the resulting error terms in equations (5.13), (7.10), (7.16), (7.24) and (7.28) become
$r(z)$
by the convolution form as given in [Reference Chen, Liu and Lu9, (5.15)], we can deduce that the resulting error terms in equations (5.13), (7.10), (7.16), (7.24) and (7.28) become
8 Global approximation of solutions
The goal of this section is to extend our long-time asymptotics given by Theorem 1.3 to the MKdV equation with rougher initial data. Three important spaces are
![]() $H^{1}$
,
$H^{1}$
,
![]() $H^{\frac {1}{4}}$
and
$H^{\frac {1}{4}}$
and
![]() $L^2$
. In
$L^2$
. In
![]() $H^{1}$
, the MKdV equation has certain conserved quantities (compare Subsection 8.2). For
$H^{1}$
, the MKdV equation has certain conserved quantities (compare Subsection 8.2). For
![]() $H^{\frac {1}{4}}$
, this space is the lowest regularity at which the solution can be constructed by iterations (compare Theorem 8.2 and Subsection 8.3). Finally, in
$H^{\frac {1}{4}}$
, this space is the lowest regularity at which the solution can be constructed by iterations (compare Theorem 8.2 and Subsection 8.3). Finally, in
![]() $L^2$
, the mKdV enjoys the conservation of mass. We will show that the long-time asymptotics remain valid in these spaces after we introduce decay at
$L^2$
, the mKdV enjoys the conservation of mass. We will show that the long-time asymptotics remain valid in these spaces after we introduce decay at
![]() $\pm \infty $
.
$\pm \infty $
.
We first sketch the local existence and uniqueness of the strong solution in
![]() $H^{s}$
for
$H^{s}$
for
![]() $s\ge \frac {1}{4}$
. We mainly follow Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29] and Linares-Ponce [Reference Linares and Ponce35].
$s\ge \frac {1}{4}$
. We mainly follow Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29] and Linares-Ponce [Reference Linares and Ponce35].
First, we define the solution operator to the linear Airy equation by
In other words, using the Fourier transform, one has
Definition 8.1. The strong solution is defined in the following integral sense: we say the function
![]() $u\left (x,t\right )$
is a strong solution in
$u\left (x,t\right )$
is a strong solution in
![]() $H^{s}\left (\mathbb {R}\right )$
to
$H^{s}\left (\mathbb {R}\right )$
to
if and only if
![]() $u\in C\left (I,H^{s}\left (\mathbb {R}\right )\right )$
satisfies
$u\in C\left (I,H^{s}\left (\mathbb {R}\right )\right )$
satisfies
 $$ \begin{align} u=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds. \end{align} $$
$$ \begin{align} u=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds. \end{align} $$
We also define
Then with the notations introduced above, we have the classical local well-posedness results due to Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29].
Theorem 8.2 (Kenig-Ponce-Vega).
Let
![]() $s\ge \frac {1}{4}$
. Then for any
$s\ge \frac {1}{4}$
. Then for any
![]() $u_{0}\in H^{s}\left (\mathbb {R}\right )$
, there is
$u_{0}\in H^{s}\left (\mathbb {R}\right )$
, there is
 $T=T\left (\left \Vert \mathcal {D}_{x}^{\frac {1}{4}}u_{0}\right \Vert _{L^{2}}\right )\sim \left \Vert \mathcal {D}_{x}^{\frac {1}{4}}u_{0}\right \Vert _{L^{2}}^{-4}$
such that there exists a unique strong solution
$T=T\left (\left \Vert \mathcal {D}_{x}^{\frac {1}{4}}u_{0}\right \Vert _{L^{2}}\right )\sim \left \Vert \mathcal {D}_{x}^{\frac {1}{4}}u_{0}\right \Vert _{L^{2}}^{-4}$
such that there exists a unique strong solution
![]() $u\left (t\right )$
to the initial value problem
$u\left (t\right )$
to the initial value problem
satisfying
 $$ \begin{align} \left\Vert \mathcal{D}_{x}^{s-\frac{1}{4}}\partial_{x}u\right\Vert _{L_{x}^{20}\left(\mathbb{R}:L_{t}^{\frac{5}{2}}\left[-T,T\right]\right)}<\infty, \end{align} $$
$$ \begin{align} \left\Vert \mathcal{D}_{x}^{s-\frac{1}{4}}\partial_{x}u\right\Vert _{L_{x}^{20}\left(\mathbb{R}:L_{t}^{\frac{5}{2}}\left[-T,T\right]\right)}<\infty, \end{align} $$
and
Moreover, there exists a neighbourhood
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $u_{0}$
in
$u_{0}$
in
![]() $H^{s}\left (\mathbb {R}\right )$
such that the solution map
$H^{s}\left (\mathbb {R}\right )$
such that the solution map
![]() $\tilde {u}_{0}\in \mathcal {N}\longmapsto \tilde {u}$
is smooth with respect to the norms given by equations (8.3)–(8.7).
$\tilde {u}_{0}\in \mathcal {N}\longmapsto \tilde {u}$
is smooth with respect to the norms given by equations (8.3)–(8.7).
Proof. Given T and
![]() $\mathcal {C}$
, define the spaces
$\mathcal {C}$
, define the spaces
and
where
 $$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T}^{s}} & =\left\Vert \mathcal{D}_{x}^{s}v\right\Vert _{L_{t}^{\infty}\left(\left[-T,T\right]:H^{s}\left(\mathbb{R}\right)\right)}+\left\Vert v\right\Vert _{L_{x}^{4}\left(\mathbb{R}:L_{t}^{\infty}\left[-T,T\right]\right)}\\ & \quad +\left\Vert \mathcal{D}_{x}^{s}v\right\Vert _{L_{x}^{5}\left(\mathbb{R}:L_{t}^{10}\left[-T,T\right]\right)}+\left\Vert \mathcal{D}_{x}^{s-\frac{1}{4}}\partial_{x}v\right\Vert _{L_{x}^{20}\left(\mathbb{R}:L_{t}^{\frac{5}{2}}\left[-T,T\right]\right)}+\left\Vert \mathcal{D}_{x}^{s}\partial_{x}v\right\Vert _{L_{x}^{\infty}\left(\mathbb{R}:L_{t}^{2}\left[-T,T\right]\right)}. \end{align*} $$
$$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T}^{s}} & =\left\Vert \mathcal{D}_{x}^{s}v\right\Vert _{L_{t}^{\infty}\left(\left[-T,T\right]:H^{s}\left(\mathbb{R}\right)\right)}+\left\Vert v\right\Vert _{L_{x}^{4}\left(\mathbb{R}:L_{t}^{\infty}\left[-T,T\right]\right)}\\ & \quad +\left\Vert \mathcal{D}_{x}^{s}v\right\Vert _{L_{x}^{5}\left(\mathbb{R}:L_{t}^{10}\left[-T,T\right]\right)}+\left\Vert \mathcal{D}_{x}^{s-\frac{1}{4}}\partial_{x}v\right\Vert _{L_{x}^{20}\left(\mathbb{R}:L_{t}^{\frac{5}{2}}\left[-T,T\right]\right)}+\left\Vert \mathcal{D}_{x}^{s}\partial_{x}v\right\Vert _{L_{x}^{\infty}\left(\mathbb{R}:L_{t}^{2}\left[-T,T\right]\right)}. \end{align*} $$
To obtain a strong solution to the initial-value problem, we need to find appropriate T and
![]() $\mathcal {C}$
such that the operator
$\mathcal {C}$
such that the operator
 $$\begin{align*}\mathcal{S}\left(v,u_{0}\right)=\mathcal{S}\left(v\right)=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6v^{2}\partial_{x}v\left(s\right)\right)\,ds \end{align*}$$
$$\begin{align*}\mathcal{S}\left(v,u_{0}\right)=\mathcal{S}\left(v\right)=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6v^{2}\partial_{x}v\left(s\right)\right)\,ds \end{align*}$$
is a contraction map on
![]() $\mathcal {X}_{T,\mathcal {C}}^{s}$
.
$\mathcal {X}_{T,\mathcal {C}}^{s}$
.
Using linear estimates for
![]() $W\left (t\right )$
and the Leibniz rule for fractional derivatives, one can show that
$W\left (t\right )$
and the Leibniz rule for fractional derivatives, one can show that
where c is from linear estimates independent of the initial data. We refer the reader to Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29] and Linares-Ponce [Reference Linares and Ponce35] for details. Then choosing
![]() $\mathcal {C}=2c\left \Vert u_{0}\right \Vert _{H^{s}}$
and T such that
$\mathcal {C}=2c\left \Vert u_{0}\right \Vert _{H^{s}}$
and T such that
![]() $c\mathcal {C}^{2}T^{\frac {1}{2}}<\frac {1}{4}$
, we obtain that
$c\mathcal {C}^{2}T^{\frac {1}{2}}<\frac {1}{4}$
, we obtain that
Similarly, one can also show
 $$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert \mathcal{S}\left(v_{1}\right)-\mathcal{S}\left(v_{2}\right) \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T}^{s}} & \leq cT^{\frac{1}{2}}\left({\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{1} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T}}^{2}+{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T}}^{2}\right){\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{1}-v_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T}^{s}}\\ & \leq2cT^{\frac{1}{2}}\mathcal{C}^{2}{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{1}-v_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T}^{s}}. \end{align*} $$
$$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert \mathcal{S}\left(v_{1}\right)-\mathcal{S}\left(v_{2}\right) \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T}^{s}} & \leq cT^{\frac{1}{2}}\left({\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{1} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T}}^{2}+{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T}}^{2}\right){\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{1}-v_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T}^{s}}\\ & \leq2cT^{\frac{1}{2}}\mathcal{C}^{2}{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert v_{1}-v_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T}^{s}}. \end{align*} $$
Therefore, with our choice of T and
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
![]() $\mathcal {S}\left (\cdot ,u_{0}\right )$
is a contraction on
$\mathcal {S}\left (\cdot ,u_{0}\right )$
is a contraction on
![]() $\mathcal {X}_{T,\mathcal {C}}^{s}$
. So there is a unique fixed point of this
$\mathcal {X}_{T,\mathcal {C}}^{s}$
. So there is a unique fixed point of this
![]() $\mathcal {S}\left (\cdot ,u_{0}\right )$
in
$\mathcal {S}\left (\cdot ,u_{0}\right )$
in
![]() $\mathcal {X}_{T,\mathcal {C}}^{s}$
. Hence we obtain the unique, strong solution:
$\mathcal {X}_{T,\mathcal {C}}^{s}$
. Hence we obtain the unique, strong solution:
 $$\begin{align*}u=\mathcal{S}\left(u\right)=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds. \end{align*}$$
$$\begin{align*}u=\mathcal{S}\left(u\right)=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds. \end{align*}$$
To check the dependence on the initial data, using arguments similar to those above, one can show that
 $$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert \mathcal{S}\left(u_{1},u_{1}\left(0\right)\right)-\mathcal{S}\left(u_{2},u_{2}\left(0\right)\right) \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T_{1}}^{s}} & \leq c\left\Vert u_{1}\left(0\right)-u_{2}\left(0\right)\right\Vert _{H^{s}}\\ & +cT_{1}^{\frac{1}{2}}\left({\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert u_{1} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T_{1}}^{s}}^{2}+{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert u_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T_{1}}^{s}}^{2}\right){\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert u_{1}-u_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T_{1}}^{s}}. \end{align*} $$
$$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert \mathcal{S}\left(u_{1},u_{1}\left(0\right)\right)-\mathcal{S}\left(u_{2},u_{2}\left(0\right)\right) \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T_{1}}^{s}} & \leq c\left\Vert u_{1}\left(0\right)-u_{2}\left(0\right)\right\Vert _{H^{s}}\\ & +cT_{1}^{\frac{1}{2}}\left({\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert u_{1} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T_{1}}^{s}}^{2}+{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert u_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} _{\mathcal{X}_{T_{1}}^{s}}^{2}\right){\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert u_{1}-u_{2} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{\mathcal{X}_{T_{1}}^{s}}. \end{align*} $$
This can be used to show that for
![]() $T_{1}\in \left (0,T\right )$
, the solution map from a neighbourhood
$T_{1}\in \left (0,T\right )$
, the solution map from a neighbourhood
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $u_{0}$
depending on
$u_{0}$
depending on
![]() $T_{1}$
to
$T_{1}$
to
![]() $\mathcal {X}_{T_{1},\mathcal {C}}^{s}$
is Lipschitz. Further work can be used to show the solution map is actually smooth. For more details, see Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29] and Linares-Ponce [Reference Linares and Ponce35].
$\mathcal {X}_{T_{1},\mathcal {C}}^{s}$
is Lipschitz. Further work can be used to show the solution map is actually smooth. For more details, see Kenig-Ponce-Vega [Reference Kenig, Ponce and Vega29] and Linares-Ponce [Reference Linares and Ponce35].
Finally, we notice that if
![]() $u_{0}$
is Schwartz, then the solution u to the initial-value problem is also smooth and hence a classical solution. The uniqueness of the classical solution is well-known. We refer the reader to Bona-Smith [Reference Bona and Smith2], Temam [Reference Temam41] and Saut-Temam [Reference Saut and Temam40] for the KdV problem and Saut [Reference Saut39] for more general KdV type equations including the MKdV equation.
$u_{0}$
is Schwartz, then the solution u to the initial-value problem is also smooth and hence a classical solution. The uniqueness of the classical solution is well-known. We refer the reader to Bona-Smith [Reference Bona and Smith2], Temam [Reference Temam41] and Saut-Temam [Reference Saut and Temam40] for the KdV problem and Saut [Reference Saut39] for more general KdV type equations including the MKdV equation.
8.1 Solutions of mKdV by inverse scattering and strong solutions
As before, given
![]() $u_{0}\in H^{2,1}\left (\mathbb {R}\right )$
, one can solve the MKdV equation using the inverse scattering transform.
$u_{0}\in H^{2,1}\left (\mathbb {R}\right )$
, one can solve the MKdV equation using the inverse scattering transform.
Recall from equation (1.15) that we have the solution to the MKdV equation in terms of the solution by inverse scattering:
 $$ \begin{align} u &= \left[ \dfrac{-i}{\pi} \int\mu\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12} \\ & = \left[ \dfrac{-i}{\pi} \int\left(\mu-I\right)\left(w_{\theta}^{+} +w_{\theta}^{-}\right) \right]_{12} + \left[ \dfrac{-i}{\pi} \int\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12},\nonumber \end{align} $$
$$ \begin{align} u &= \left[ \dfrac{-i}{\pi} \int\mu\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12} \\ & = \left[ \dfrac{-i}{\pi} \int\left(\mu-I\right)\left(w_{\theta}^{+} +w_{\theta}^{-}\right) \right]_{12} + \left[ \dfrac{-i}{\pi} \int\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12},\nonumber \end{align} $$
where
![]() $\mu $
is constructed using the reflection coefficients r. But as we discussed above, using PDE techniques, one can construct solutions with rougher data, at least locally. Motivated by Deift-Zhou [Reference Deift and Zhou14], we try to understand the relations between Beals-Coifman solutions and strong solutions. First, if
$\mu $
is constructed using the reflection coefficients r. But as we discussed above, using PDE techniques, one can construct solutions with rougher data, at least locally. Motivated by Deift-Zhou [Reference Deift and Zhou14], we try to understand the relations between Beals-Coifman solutions and strong solutions. First, if
![]() $u_{0}$
is Schwartz, one can also show that u is Schwartz (compareDeift-Zhou [Reference Deift and Zhou11]). So in this case, the strong solution is the same as the solution via inverse scattering. Our goal is to identify the solution by inverse scattering with the strong solution whenever the former makes sense. Starting from the local construction, we will try to extend these results globally later on.
$u_{0}$
is Schwartz, one can also show that u is Schwartz (compareDeift-Zhou [Reference Deift and Zhou11]). So in this case, the strong solution is the same as the solution via inverse scattering. Our goal is to identify the solution by inverse scattering with the strong solution whenever the former makes sense. Starting from the local construction, we will try to extend these results globally later on.
Firstly, we show that one can always take the limit of a sequence of smooth solutions to the MKdV equation in weighted
![]() $L^2$
spaces without regularity assumptions.
$L^2$
spaces without regularity assumptions.
Lemma 8.3. Suppose there is a sequence
![]() $\left \{ u_{0,k}\right \} $
of Schwartz functions, which is a Cauchy sequence in
$\left \{ u_{0,k}\right \} $
of Schwartz functions, which is a Cauchy sequence in
![]() $H^{j,1}\left (\mathbb {R}\right )$
and
$H^{j,1}\left (\mathbb {R}\right )$
and
![]() $u_{0,k}\rightarrow u_{0}$
in
$u_{0,k}\rightarrow u_{0}$
in
![]() $H^{j,1}\left (\mathbb {R}\right )$
with
$H^{j,1}\left (\mathbb {R}\right )$
with
![]() $j\geq 0$
. Then for fixed
$j\geq 0$
. Then for fixed
![]() $t>0$
, one can always conclude that the sequence of solution
$t>0$
, one can always conclude that the sequence of solution
![]() $\lbrace u_k \rbrace $
to the MKdV equation with initial data
$\lbrace u_k \rbrace $
to the MKdV equation with initial data
![]() $u_{0,k}$
obtained via inverse scattering in the sense of equation (8.10) has a
$u_{0,k}$
obtained via inverse scattering in the sense of equation (8.10) has a
![]() $L^\infty $
limit.
$L^\infty $
limit.
Proof. Since
![]() $u_{0,k}$
is Schwartz, from the inverse scattering transform, we can write down the Beals-Coifman solutions
$u_{0,k}$
is Schwartz, from the inverse scattering transform, we can write down the Beals-Coifman solutions
 $$ \begin{align} u_{k}= \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} \end{align} $$
$$ \begin{align} u_{k}= \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} \end{align} $$
with initial data
![]() $u_{0,k}$
. Using the mapping properties of the direct scattering due to Zhou [Reference Zhou45, Theorem 1.8] and Deift-Zhou [Reference Deift and Zhou14, Theorem 3.2], in terms of reflection coefficients, we have that
$u_{0,k}$
. Using the mapping properties of the direct scattering due to Zhou [Reference Zhou45, Theorem 1.8] and Deift-Zhou [Reference Deift and Zhou14, Theorem 3.2], in terms of reflection coefficients, we have that
and by the Lipschitz continuity of the map, we have
By the integral representation of
![]() $u_k$
given in equation (8.11), resolvent estimates in [Reference Zhou45] (see also [Reference Deift and Zhou14, (2.19) (2.21)]) and Lipschitz continuity of the direct and inverse scattering map, one also has
$u_k$
given in equation (8.11), resolvent estimates in [Reference Zhou45] (see also [Reference Deift and Zhou14, (2.19) (2.21)]) and Lipschitz continuity of the direct and inverse scattering map, one also has
Since
![]() $r_{k}$
converges to a function
$r_{k}$
converges to a function
![]() $r_{\infty }$
in
$r_{\infty }$
in
![]() $H^{1}\left (\mathbb {R}\right )$
, we claim that the corresponding solution by inverse scattering converges to a limit
$H^{1}\left (\mathbb {R}\right )$
, we claim that the corresponding solution by inverse scattering converges to a limit
in the sense of the
![]() $L^{\infty }$
norm. Indeed, we can write
$L^{\infty }$
norm. Indeed, we can write
 $$ \begin{align*} u_{k} & = \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12}\\ & = \left[ \dfrac{-i}{\pi} \int\left(\mu_{k}-I\right)\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} + \left[ \dfrac{-i}{\pi} \int\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} \\ & =\textrm{ I}_{k}+\textrm{ II}_{k}. \end{align*} $$
$$ \begin{align*} u_{k} & = \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12}\\ & = \left[ \dfrac{-i}{\pi} \int\left(\mu_{k}-I\right)\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} + \left[ \dfrac{-i}{\pi} \int\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} \\ & =\textrm{ I}_{k}+\textrm{ II}_{k}. \end{align*} $$
Then due to the resolvent estimate,
![]() $\left (\mu _{k}-I\right )$
is bounded in the
$\left (\mu _{k}-I\right )$
is bounded in the
![]() $L^{2}$
, and the
$L^{2}$
, and the
![]() $L^{2}$
estimate for
$L^{2}$
estimate for
![]() $w_{k,\theta }^{+}+w_{k,\theta }^{-}$
is straightforward, so
$w_{k,\theta }^{+}+w_{k,\theta }^{-}$
is straightforward, so
![]() $\textrm { I}_{k}$
makes sense pointwise. For
$\textrm { I}_{k}$
makes sense pointwise. For
![]() $\textrm { II}_{k}$
, one simply notices that
$\textrm { II}_{k}$
, one simply notices that
![]() $\int \left (w_{k,\theta }^{\pm }\right )$
is proportional to
$\int \left (w_{k,\theta }^{\pm }\right )$
is proportional to
![]() $W\left (t\right )\check {r}_{k}=e^{-t\partial _{xxx}}\check {r}_{k}$
, so by the standard stationary phase analysis, for
$W\left (t\right )\check {r}_{k}=e^{-t\partial _{xxx}}\check {r}_{k}$
, so by the standard stationary phase analysis, for
![]() $r_{k}\in H^{1}$
,
$r_{k}\in H^{1}$
,
![]() $\textrm { II}_{k}$
is a function in
$\textrm { II}_{k}$
is a function in
![]() $L^{\infty }\left (\mathbb {R}\right )$
for
$L^{\infty }\left (\mathbb {R}\right )$
for
![]() $t\geq 0$
with the standard pointwise decay estimates for the Airy equation (compare[Reference Germain, Pusateri and Rousset17, Lemma 2.1]).
$t\geq 0$
with the standard pointwise decay estimates for the Airy equation (compare[Reference Germain, Pusateri and Rousset17, Lemma 2.1]).
Hence for fixed
![]() $t\neq 0$
,
$t\neq 0$
,
as desired.
Remark 8.4. Note that a priori, when we pass the solutions by inverse scattering to the pointwise limit above, it is not clear what the limit means since the limit is rougher than the required regularity from the inverse scattering transform when
![]() $j<2$
.
$j<2$
.
In the following subsections, we use PDE techniques to conclude that indeed, the limit constructed by the lemma above is a solution to the MKdV equation as long as we have enough regularity to perform the Picard iteration. First, we illustrate that the solutions we analysed in earlier sections are strong solutions.
Corollary 8.5. Suppose
![]() $u_{0}\in H^{2,1}\left (\mathbb {R}\right )$
. Then the solution by inverse scattering and the strong solution are the same (up to a measure zero set):
$u_{0}\in H^{2,1}\left (\mathbb {R}\right )$
. Then the solution by inverse scattering and the strong solution are the same (up to a measure zero set):
 $$ \begin{align*} u & = \left[ \dfrac{-i}{\pi} \int\mu\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12} \\ & =W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*} $$
$$ \begin{align*} u & = \left[ \dfrac{-i}{\pi} \int\mu\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12} \\ & =W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*} $$
in
![]() $\left [-T,T\right ]$
, where T is given as in Theorem 8.2.
$\left [-T,T\right ]$
, where T is given as in Theorem 8.2.
Remark 8.6. At such a high level of regularity, by the uniqueness of weak solutions – see, for example, Ginibre-Tsutsumi [Reference Ginibre and Tsutsumi18] and Ginibre-Tsutsumi-Velo [Reference Ginibre, Tsutsumi and Velo19] – one might expect this identification. But here, we provide a direct approach in this specific situation.
Proof. Suppose
![]() $u_{0}\in H^{2,1}\left (\mathbb {R}\right )$
. We can find a sequence
$u_{0}\in H^{2,1}\left (\mathbb {R}\right )$
. We can find a sequence
![]() $\left \{ u_{0,k}\right \} $
of Schwartz functions such that it is a Cauchy sequence in
$\left \{ u_{0,k}\right \} $
of Schwartz functions such that it is a Cauchy sequence in
![]() $H^{2,1}\left (\mathbb {R}\right )$
and
$H^{2,1}\left (\mathbb {R}\right )$
and
![]() $u_{0,k}\rightarrow u_{0}$
in
$u_{0,k}\rightarrow u_{0}$
in
![]() $H^{2,1}\left (\mathbb {R}\right )$
.
$H^{2,1}\left (\mathbb {R}\right )$
.
We may assume that for all k, there is a uniform bound
Then applying Theorem 8.2, we can find a strong solution
![]() $u_{k}$
with initial data
$u_{k}$
with initial data
![]() $u_{0,k}$
in
$u_{0,k}$
in
![]() $\mathcal {X}_{T,\mathcal {C}}^{2}$
, where T and
$\mathcal {X}_{T,\mathcal {C}}^{2}$
, where T and
![]() $\mathcal {C}$
are chosen as in Theorem 8.2.
$\mathcal {C}$
are chosen as in Theorem 8.2.
By Theorem 8.2, we also have
So in
![]() $\mathcal {X}_{T,C}^{2}$
,
$\mathcal {X}_{T,C}^{2}$
,
![]() $u_{k}$
converges to a limit
$u_{k}$
converges to a limit
![]() $u_{\infty }$
, which is a strong solution. Using the notation from above, we have
$u_{\infty }$
, which is a strong solution. Using the notation from above, we have
From the inverse scattering transform, we also have solutions via inverse scattering
 $$\begin{align*}\tilde{u}_{k}= \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} \end{align*}$$
$$\begin{align*}\tilde{u}_{k}= \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k,\theta}^{+}+w_{k,\theta}^{-}\right) \right]_{12} \end{align*}$$
with initial data
![]() $u_{0,k}$
.
$u_{0,k}$
.
Since
![]() $u_{0,k}$
is Schwartz,
$u_{0,k}$
is Schwartz,
![]() $u_{k}$
and
$u_{k}$
and
![]() $\tilde {u}_{k}$
are also Schwartz. Therefore, we have
$\tilde {u}_{k}$
are also Schwartz. Therefore, we have
![]() $u_{k}=\tilde {u}_{k}.$
By Lemma 8.3, one can conclude that there exists
$u_{k}=\tilde {u}_{k}.$
By Lemma 8.3, one can conclude that there exists
![]() $\tilde {u}_{\infty }$
such that for
$\tilde {u}_{\infty }$
such that for
![]() $t\neq 0$
,
$t\neq 0$
,
By the convergence of the strong solutions, it follows that as
![]() $k\rightarrow \infty $
, we have
$k\rightarrow \infty $
, we have
In particular, as
![]() $k\rightarrow \infty $
, one has
$k\rightarrow \infty $
, one has
By construction, as
![]() $k\rightarrow \infty ,$
$k\rightarrow \infty ,$
Hence
up to a measure zero set.
Therefore, we can conclude that
 $$ \begin{align*} u & = \left[ \dfrac{-i}{\pi} \int\mu\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12} \\ & =W\left(t\right)u_{0}+ \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*} $$
$$ \begin{align*} u & = \left[ \dfrac{-i}{\pi} \int\mu\left(w_{\theta}^{+}+w_{\theta}^{-}\right) \right]_{12} \\ & =W\left(t\right)u_{0}+ \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*} $$
in
![]() $\left [-T,T\right ]$
.
$\left [-T,T\right ]$
.
Next, we will try to use this local identification to understand the limits of solutions via inverse scattering in various low-regularity spaces.
8.2 Approximation of solutions in
 $H^{1}\left (\mathbb {R}\right )$
$H^{1}\left (\mathbb {R}\right )$
First we consider
with initial data in
![]() $H^{1}\left (\mathbb {R}\right )$
.
$H^{1}\left (\mathbb {R}\right )$
.
The following three quantities are preserved by the solution flow:
Using the local existence results and the conservation laws above, we can extend a local solution to a global solution in
![]() $H^{1}\left (\mathbb {R}\right )$
.
$H^{1}\left (\mathbb {R}\right )$
.
More precisely, using the Sobolev embedding, one has
 $$ \begin{align*} E\left(u\right) & =\int_{-\infty}^{\infty}\left[\left(\partial_{x}u\right)^{2} + u^{4}\right]\,dx\\ & \geq\left\Vert \partial_{x}u\right\Vert _{L^{2}\left(\mathbb{R}\right)}^{2} +\left\Vert u\right\Vert _{L^{4}\left(\mathbb{R}\right)}^{4}\\ & \geq\left\Vert \partial_{x}u\right\Vert _{L^{2}\left(\mathbb{R}\right)}^{2} + c_{4}\left\Vert \partial_{x}u\right\Vert _{L^{2}\left(\mathbb{R}\right)}\left\Vert u\right\Vert _{L^{2}\left(\mathbb{R}\right)}^{3}. \end{align*} $$
$$ \begin{align*} E\left(u\right) & =\int_{-\infty}^{\infty}\left[\left(\partial_{x}u\right)^{2} + u^{4}\right]\,dx\\ & \geq\left\Vert \partial_{x}u\right\Vert _{L^{2}\left(\mathbb{R}\right)}^{2} +\left\Vert u\right\Vert _{L^{4}\left(\mathbb{R}\right)}^{4}\\ & \geq\left\Vert \partial_{x}u\right\Vert _{L^{2}\left(\mathbb{R}\right)}^{2} + c_{4}\left\Vert \partial_{x}u\right\Vert _{L^{2}\left(\mathbb{R}\right)}\left\Vert u\right\Vert _{L^{2}\left(\mathbb{R}\right)}^{3}. \end{align*} $$
From
![]() $I_{2}$
, we know the
$I_{2}$
, we know the
![]() $L^{2}\left (\mathbb {R}\right )$
norm is conserved.
$L^{2}\left (\mathbb {R}\right )$
norm is conserved.
If we denote
then one has
so
![]() $f\left (t\right )$
is bounded globally. In other words,
$f\left (t\right )$
is bounded globally. In other words,
Hence, with the conserved
![]() $L^{2}\left (\mathbb {R}\right )$
norm, we conclude that
$L^{2}\left (\mathbb {R}\right )$
norm, we conclude that
Theorem 8.7. For
![]() $u_{0}\in H^{1,1}\left (\mathbb {R}\right )$
, the strong solution given by the Duhamel formulation in equation (8.2) has the same asymptotics as in our main Theorem 1.3.
$u_{0}\in H^{1,1}\left (\mathbb {R}\right )$
, the strong solution given by the Duhamel formulation in equation (8.2) has the same asymptotics as in our main Theorem 1.3.
Proof. We perform a construction similar to the construction in the proof of Corollary 8.5. Let
![]() $\left \{ u_{0,k}\right \} \in H^{2,1}\left (\mathbb {R}\right )$
be a Cauchy sequence in
$\left \{ u_{0,k}\right \} \in H^{2,1}\left (\mathbb {R}\right )$
be a Cauchy sequence in
![]() $H^{1,1}\left (\mathbb {R}\right )$
such that
$H^{1,1}\left (\mathbb {R}\right )$
such that
in
![]() $H^{1,1}\left (\mathbb {R}\right )$
and
$H^{1,1}\left (\mathbb {R}\right )$
and
![]() $\sup _{k}\left \Vert u_{0,k}\right \Vert _{H^{1,1}\left (\mathbb {R}\right )}\leq C.$
$\sup _{k}\left \Vert u_{0,k}\right \Vert _{H^{1,1}\left (\mathbb {R}\right )}\leq C.$
Then we can use the inverse scattering transform to solve the initial-value problem in equation (8.1) and obtain solutions
![]() $u_{k}$
by inverse scattering
$u_{k}$
by inverse scattering
 $$ \begin{align} u_{k}= \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k, \theta}^{+}+w_{k, \theta}^{-}\right)\right]_{12} \end{align} $$
$$ \begin{align} u_{k}= \left[ \dfrac{-i}{\pi} \int\mu_{k}\left(w_{k, \theta}^{+}+w_{k, \theta}^{-}\right)\right]_{12} \end{align} $$
with initial data
![]() $u_{0,k}$
. By Lemma 8.3, one can conclude that there exists
$u_{0,k}$
. By Lemma 8.3, one can conclude that there exists
![]() $u_{\infty }$
such that for
$u_{\infty }$
such that for
![]() $t\neq 0$
,
$t\neq 0$
,
For
![]() $t=0$
, this convergence can be implied by Sobolev’s embedding.
$t=0$
, this convergence can be implied by Sobolev’s embedding.
However, by Corollary 8.5, we know
![]() $u_{k}$
is also a strong solution: that is,
$u_{k}$
is also a strong solution: that is,
 $$\begin{align*}u_{k}(t)=W\left(t\right)u_{0,k} +\int_{0}^{t}W\left(t-s\right)\left(6\left(u_{k}\right)^{2}\partial_{x}\left(u_{k}\right)\right)\,ds. \end{align*}$$
$$\begin{align*}u_{k}(t)=W\left(t\right)u_{0,k} +\int_{0}^{t}W\left(t-s\right)\left(6\left(u_{k}\right)^{2}\partial_{x}\left(u_{k}\right)\right)\,ds. \end{align*}$$
Then we can use T and
![]() $\mathcal {C}$
as in Theorem 8.2 to conclude that
$\mathcal {C}$
as in Theorem 8.2 to conclude that
where
![]() $\mathcal {X}_{T,\mathcal {C}}^{1}$
is given as equation (8.9).
$\mathcal {X}_{T,\mathcal {C}}^{1}$
is given as equation (8.9).
Hence
![]() $\left \{ u_{k}\right \} $
is also a Cauchy sequence in
$\left \{ u_{k}\right \} $
is also a Cauchy sequence in
![]() $\mathcal {X}_{T,\mathcal {C}}^{1}$
, which converges to u satisfying
$\mathcal {X}_{T,\mathcal {C}}^{1}$
, which converges to u satisfying
 $$\begin{align*}u(t)=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*}$$
$$\begin{align*}u(t)=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*}$$
by construction. So u is a strong solution.
By the definition of space
![]() $\mathcal {X}_{T,\mathcal {C}}^{1}$
equation (8.9), we have
$\mathcal {X}_{T,\mathcal {C}}^{1}$
equation (8.9), we have
Combining
we can conclude that
![]() $u(t)=u_{\infty }(t)$
pointwise (up to a measure zero set) for
$u(t)=u_{\infty }(t)$
pointwise (up to a measure zero set) for
![]() $t\in [-T,T]$
. Since the
$t\in [-T,T]$
. Since the
![]() $H^{1}$
norms of u are uniformly bounded as equation (8.12), we can repeat the above construct infinity many times to extend the interval
$H^{1}$
norms of u are uniformly bounded as equation (8.12), we can repeat the above construct infinity many times to extend the interval
![]() $\left [-T,T\right ]$
to
$\left [-T,T\right ]$
to
![]() $\mathbb {R}$
and conclude that for
$\mathbb {R}$
and conclude that for
![]() $t\in \mathbb {R}_{+}$
,
$t\in \mathbb {R}_{+}$
,
Since
![]() $u_{\infty }$
is the pointwise limit of solutions by inverse scattering, which have asymptotic behaviour in our main theorem obtained from the nonlinear steepest descent with uniform error terms estimates,
$u_{\infty }$
is the pointwise limit of solutions by inverse scattering, which have asymptotic behaviour in our main theorem obtained from the nonlinear steepest descent with uniform error terms estimates,
![]() $u_{\infty }$
also has the desired asymptotics. More precisely, we can write
$u_{\infty }$
also has the desired asymptotics. More precisely, we can write
where
![]() $L_{k}\left (x,t\right )$
gives the leading-order behaviour and
$L_{k}\left (x,t\right )$
gives the leading-order behaviour and
![]() $E_{k}\left (x,t\right )$
collects the error term. By the convergence of scattering data, we know
$E_{k}\left (x,t\right )$
collects the error term. By the convergence of scattering data, we know
pointwise. Hence for an arbitrary fixed t, as the pointwise limit of
![]() $u_{k}\left (t\right )$
, one can write
$u_{k}\left (t\right )$
, one can write
where the decay estimates for
![]() $E_{\infty }\left (x,t\right )$
is the same as
$E_{\infty }\left (x,t\right )$
is the same as
![]() $E_{k}\left (x,t\right )$
due to the uniform error estimates. Therefore u also has the asymptotic behaviour as claimed.
$E_{k}\left (x,t\right )$
due to the uniform error estimates. Therefore u also has the asymptotic behaviour as claimed.
Remark 8.8. Similar to the situation of the NLS in Deift-Zhou [Reference Deift and Zhou14], the solution u as the limit of the sequences of solutions by inverse scattering also enjoys the conservation law
since it is also a strong solution. It is not clear how to obtain this conservation law using the inverse scattering transform due to the low regularity.
8.3 Approximation of solutions in
 $H^{\frac {1}{4}}\left (\mathbb {R}\right )$
$H^{\frac {1}{4}}\left (\mathbb {R}\right )$
For the MKdV equation, as in Theorem 8.2, Kenig, Ponce and Vega obtained the lowest regularity for the local well-posedness in
![]() $H^{s}\left (\mathbb {R}\right )$
,
$H^{s}\left (\mathbb {R}\right )$
,
![]() $s\ge \frac {1}{4},$
in [Reference Kenig, Ponce and Vega29]. They also showed in [Reference Kenig, Ponce and Vega30] that when
$s\ge \frac {1}{4},$
in [Reference Kenig, Ponce and Vega29]. They also showed in [Reference Kenig, Ponce and Vega30] that when
![]() $s<\frac {1}{4}$
, the data-to-solution map fails to be uniformly continuous as a map from
$s<\frac {1}{4}$
, the data-to-solution map fails to be uniformly continuous as a map from
![]() $H^{s}$
to
$H^{s}$
to
![]() $C\left (\left [-T,T\right ]H^{s}\left (\mathbb {R}\right )\right )$
(see also Christ-Colliander-Tao [Reference Christ, Colliander and Tao5]). These imply that the space
$C\left (\left [-T,T\right ]H^{s}\left (\mathbb {R}\right )\right )$
(see also Christ-Colliander-Tao [Reference Christ, Colliander and Tao5]). These imply that the space
![]() $H^{\frac {1}{4}}\left (\mathbb {R}\right )$
has the lowest regularity at which the solution can be obtained by iteration. These local results form the basis for global well-posedness. For example, one can use energy conservation and
$H^{\frac {1}{4}}\left (\mathbb {R}\right )$
has the lowest regularity at which the solution can be obtained by iteration. These local results form the basis for global well-posedness. For example, one can use energy conservation and
![]() $L^{2}$
conservation to obtain global well-posedness. But in the space
$L^{2}$
conservation to obtain global well-posedness. But in the space
![]() $H^{\frac {1}{4}}$
, there are no conservation laws that allow us to do similar extensions. Then one needs to use the “I-method”, introduced by Colliander-Keel-Staffilani-Takaoka-Tao [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], which plays a great role in constructing global solutions. They obtained global well-posedness for KdV for
$H^{\frac {1}{4}}$
, there are no conservation laws that allow us to do similar extensions. Then one needs to use the “I-method”, introduced by Colliander-Keel-Staffilani-Takaoka-Tao [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], which plays a great role in constructing global solutions. They obtained global well-posedness for KdV for
![]() $s>-\frac {3}{4}$
and then used the Miura transform to obtain global well-posedness for the MKdV equation in
$s>-\frac {3}{4}$
and then used the Miura transform to obtain global well-posedness for the MKdV equation in
![]() $H^{s}\left (\mathbb {R}\right )$
for
$H^{s}\left (\mathbb {R}\right )$
for
![]() $s>\frac {1}{4}$
. In Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32], the authors use more delicate spaces to handle ‘logarithmic divergence’ and combine with the I-method to conclude the global well-posedness for KdV in
$s>\frac {1}{4}$
. In Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32], the authors use more delicate spaces to handle ‘logarithmic divergence’ and combine with the I-method to conclude the global well-posedness for KdV in
![]() $H^{-\frac {3}{4}}$
. Then, with the Miura transform given by [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], they also obtain global well-posedness for the MKdV equation in
$H^{-\frac {3}{4}}$
. Then, with the Miura transform given by [Reference Colliander, Keel, Staffilani, Takaoka and Tao6], they also obtain global well-posedness for the MKdV equation in
![]() $H^{\frac {1}{4}}$
. The most important ingredient shown in these papers for the MKdV equation is that for some
$H^{\frac {1}{4}}$
. The most important ingredient shown in these papers for the MKdV equation is that for some
![]() $\kappa>0$
, one has the following growth estimate:
$\kappa>0$
, one has the following growth estimate:
Theorem 8.9. For
![]() $u_{0}\in H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
, the strong solution given by the integral representation in equation (8.2) has the same asymptotics as in our main Theorem 1.3.
$u_{0}\in H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
, the strong solution given by the integral representation in equation (8.2) has the same asymptotics as in our main Theorem 1.3.
Proof. As in Theorem 8.7, we first show that locally the limit of solutions by inverse scattering is the strong solution in
![]() $H^{\frac {1}{4}}\left (\mathbb {R}\right )$
. The difference here is that we use the growth rate estimate to extend the identification globally.
$H^{\frac {1}{4}}\left (\mathbb {R}\right )$
. The difference here is that we use the growth rate estimate to extend the identification globally.
Let
![]() $\left \{ u_{0,k}\right \} \in H^{2,1}\left (\mathbb {R}\right )$
be a Cauchy sequence in
$\left \{ u_{0,k}\right \} \in H^{2,1}\left (\mathbb {R}\right )$
be a Cauchy sequence in
![]() $H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
such that
$H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
such that
in
![]() $H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
and
$H^{\frac {1}{4},1}\left (\mathbb {R}\right )$
and
![]() $\sup _{k}\left \Vert u_{0,k}\right \Vert _{H^{\frac {1}{4},1}\left (\mathbb {R}\right )}\leq C.$
$\sup _{k}\left \Vert u_{0,k}\right \Vert _{H^{\frac {1}{4},1}\left (\mathbb {R}\right )}\leq C.$
Using the inverse scattering transform to solve the initial-value problem in equation (8.1), we obtain a sequence of solutions
 $$ \begin{align} u_{k}= \left[ \dfrac{-i}{\pi} \int\mu\left(w_{k, \theta}^{+}+w_{k, \theta}^{-}\right) \right]_{12}. \end{align} $$
$$ \begin{align} u_{k}= \left[ \dfrac{-i}{\pi} \int\mu\left(w_{k, \theta}^{+}+w_{k, \theta}^{-}\right) \right]_{12}. \end{align} $$
By Lemma 8.3, one can conclude that there exists
![]() ${u}_{\infty }$
such that for
${u}_{\infty }$
such that for
![]() $t\neq 0$
,
$t\neq 0$
,
For
![]() $t=0$
, the pointwise convergence can be achieved by the standard
$t=0$
, the pointwise convergence can be achieved by the standard
![]() $L^p$
spaces argument up to a subsequence.
$L^p$
spaces argument up to a subsequence.
Moreover, by Corollary 8.5, we also know
![]() $u_{k}$
is also a strong solution: that is,
$u_{k}$
is also a strong solution: that is,
 $$\begin{align*}u_{k}=W\left(t\right)u_{0,k} + \int_{0}^{t}W\left(t-s\right)\left(6\left(u_{k}\right)^{2}\partial_{x}\left(u_{k}\right)\right)\,ds. \end{align*}$$
$$\begin{align*}u_{k}=W\left(t\right)u_{0,k} + \int_{0}^{t}W\left(t-s\right)\left(6\left(u_{k}\right)^{2}\partial_{x}\left(u_{k}\right)\right)\,ds. \end{align*}$$
Then we can use T and
![]() $\mathcal {C}$
as in Theorem 8.2 to conclude that
$\mathcal {C}$
as in Theorem 8.2 to conclude that
where
![]() $\mathcal {X}_{T,\mathcal {C}}^{\frac {1}{4}}$
is given as equation (8.9).
$\mathcal {X}_{T,\mathcal {C}}^{\frac {1}{4}}$
is given as equation (8.9).
Hence
![]() $\left \{ u_{k}\right \} $
is also a Cauchy sequence in
$\left \{ u_{k}\right \} $
is also a Cauchy sequence in
![]() $\mathcal {X}_{T,\mathcal {C}}^{\frac {1}{4}}$
, which converges to u satisfying
$\mathcal {X}_{T,\mathcal {C}}^{\frac {1}{4}}$
, which converges to u satisfying
 $$\begin{align*}u=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*}$$
$$\begin{align*}u=W\left(t\right)u_{0} + \int_{0}^{t}W\left(t-s\right)\left(6u^{2}\partial_{x}u\left(s\right)\right)\,ds \end{align*}$$
by construction.
By the definition of space
![]() $\mathcal {X}_{T,\mathcal {C}}^{\frac {1}{4}}$
equation (8.9), we have
$\mathcal {X}_{T,\mathcal {C}}^{\frac {1}{4}}$
equation (8.9), we have
And combining
we can conclude that
![]() $u=u_{\infty }$
pointwise in
$u=u_{\infty }$
pointwise in
![]() $\left [-T,T\right ]$
(up to a measure zero set).
$\left [-T,T\right ]$
(up to a measure zero set).
By global well-posedness, u exists in
![]() $H^{\frac {1}{4}}\left (\mathbb {R}\right )$
globally. By construction, one can also define
$H^{\frac {1}{4}}\left (\mathbb {R}\right )$
globally. By construction, one can also define
![]() $u_{\infty }\left (t\right )$
for all
$u_{\infty }\left (t\right )$
for all
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
By symmetry, we consider
![]() $t\ge 0$
. Suppose
$t\ge 0$
. Suppose
![]() $u_{\infty }\left (t\right )= u\left (t\right )$
does not hold for all
$u_{\infty }\left (t\right )= u\left (t\right )$
does not hold for all
![]() $t\ge 0$
. Let
$t\ge 0$
. Let
Clearly, by the above argument,
![]() $T<t_{\star }<\infty $
.
$T<t_{\star }<\infty $
.
By the growth rate estimate from Guo [Reference Guo20] and Kishimoto [Reference Kishimoto32], we have for
![]() $t\leq t_{\star }$
$t\leq t_{\star }$
Also by construction, for
![]() $t<t_{\star },$
$t<t_{\star },$
By Theorem 8.2, we can find
![]() $\mathcal {C}_{\star }$
and
$\mathcal {C}_{\star }$
and
![]() $T_{\star }$
depending on
$T_{\star }$
depending on
![]() $C\left (1+t_{\star }\right )^{\kappa }\left \Vert u_{0}\right \Vert _{H^{\frac {1}{4}}\left (\mathbb {R}\right )}<\infty $
to construct
$C\left (1+t_{\star }\right )^{\kappa }\left \Vert u_{0}\right \Vert _{H^{\frac {1}{4}}\left (\mathbb {R}\right )}<\infty $
to construct
![]() $\mathcal {X}_{T_{\star },\mathcal {C}_{\star }}^{\frac {1}{4}}$
. due to the explicit dependence of T on the size of the initial data in Theorem 8.2,
$\mathcal {X}_{T_{\star },\mathcal {C}_{\star }}^{\frac {1}{4}}$
. due to the explicit dependence of T on the size of the initial data in Theorem 8.2,
![]() $T_{\star }\geq \epsilon _{\star }>0$
.
$T_{\star }\geq \epsilon _{\star }>0$
.
By the definition of
![]() $t_{\star }$
, we have two situations: firstly,
$t_{\star }$
, we have two situations: firstly,
or for any
![]() $\eta>0$
, there exists
$\eta>0$
, there exists
![]() $t_{\star }<t_{\eta }<t_{\star }+\eta $
such that
$t_{\star }<t_{\eta }<t_{\star }+\eta $
such that
in particular, we can take
![]() $\eta <\frac {\epsilon _{\star }}{8}$
.
$\eta <\frac {\epsilon _{\star }}{8}$
.
Again, by construction, we have
Applying Theorem 8.2 and the first part of this proof using space
![]() $\mathcal {X}_{T_{\star },\mathcal {C}_{\star }}^{\frac {1}{4}}$
, we have
$\mathcal {X}_{T_{\star },\mathcal {C}_{\star }}^{\frac {1}{4}}$
, we have
for
![]() $s\in \left [0,\epsilon _{\star }\right ]\subset \left [0,T_{\star }\right ].$
In particular,
$s\in \left [0,\epsilon _{\star }\right ]\subset \left [0,T_{\star }\right ].$
In particular,
![]() $u_{\infty }\left (t_{\star }\right )=u\left (t_{\star }\right )$
and
$u_{\infty }\left (t_{\star }\right )=u\left (t_{\star }\right )$
and
![]() $u_{\infty }\left (t_{\star }+s\right )=u\left (t_{\star }+s\right )$
for
$u_{\infty }\left (t_{\star }+s\right )=u\left (t_{\star }+s\right )$
for
![]() $s\in \left [0,\frac {\epsilon _{\star }}{4}\right ].$
This is a contraction with either equation (8.15) or equation (8.16). So our assumption for the existence of
$s\in \left [0,\frac {\epsilon _{\star }}{4}\right ].$
This is a contraction with either equation (8.15) or equation (8.16). So our assumption for the existence of
![]() $t_{\star }$
fails.
$t_{\star }$
fails.
Thus we can conclude that
![]() $u_{\infty }\left (t\right )=u\left (t\right )$
for all
$u_{\infty }\left (t\right )=u\left (t\right )$
for all
![]() $t\ge 0$
. Then the asymptotic behaviour of u is obtained as in Theorem 8.7.
$t\ge 0$
. Then the asymptotic behaviour of u is obtained as in Theorem 8.7.
Remark 8.10. For an alternative approach using low-regularity conservation laws developed in Koch-Tataru [Reference Koch and Tataru33] and Killip-Visan-Zhang [Reference Killip, Vişan and Zhang31], see our work on the focusing MKdV in [Reference Chen and Liu7].
8.4 Approximation of solutions in
 $L^2(\mathbb {R})$
$L^2(\mathbb {R})$
As we introduced before, it is known from [Reference Christ, Colliander and Tao5] and [Reference Kenig, Ponce and Vega30] that
![]() $H^{\frac {1}{4}}$
is the optimal space to perform the Picard iteration to construction the strong solution in the sense of the Duhamel formula. With appropriation notations and topology, in the work by Harrop-Griffiths-Killip-Visan[Reference Harrop-Griffiths, Killip and Visan22], the well-posedness of the mKdV equation can be obtained in
$H^{\frac {1}{4}}$
is the optimal space to perform the Picard iteration to construction the strong solution in the sense of the Duhamel formula. With appropriation notations and topology, in the work by Harrop-Griffiths-Killip-Visan[Reference Harrop-Griffiths, Killip and Visan22], the well-posedness of the mKdV equation can be obtained in
![]() $H^{\tau }(\mathbb {R})$
with
$H^{\tau }(\mathbb {R})$
with
![]() $\tau>-\frac {1}{2}$
.:
$\tau>-\frac {1}{2}$
.:
Theorem 8.11 [Reference Harrop-Griffiths, Killip and Visan22].
Let
![]() $\tau>-\frac {1}{2}$
. Then the mKdV equation (1.1) is globally well-posed for all initial data in the sense that the solution map
$\tau>-\frac {1}{2}$
. Then the mKdV equation (1.1) is globally well-posed for all initial data in the sense that the solution map
![]() $\Phi $
extends uniquely from Schwartz spaces to a jointly continuous map
$\Phi $
extends uniquely from Schwartz spaces to a jointly continuous map
![]() $\Phi :\,\mathbb {R}\times H^{\tau }(\mathbb {R})\rightarrow H^{\tau }(\mathbb {R}).$
$\Phi :\,\mathbb {R}\times H^{\tau }(\mathbb {R})\rightarrow H^{\tau }(\mathbb {R}).$
The notation of the solution used above can be understood as the unique limit of Schwartz solutions. We also refer to Definition 1.1 in Kappeler-Topalov [Reference Kappeler and Topalov27] for the interpretation of this notation of solution. This notation is well-suited for our global approximation argument since the Schwartz solutions can be obtained via inverse scattering, and their asymptotics can be computed with uniform error estimates.
From the view of the standard analysis of Jost functions, it suffices to require the potential to be in
![]() $L^1$
, which contains
$L^1$
, which contains
![]() $L^{2,s}$
with
$L^{2,s}$
with
![]() $s>\frac {1}{2}$
. The well-posedness theory above can extend the asymptotics of solutions of the mKdV equations with initial data in
$s>\frac {1}{2}$
. The well-posedness theory above can extend the asymptotics of solutions of the mKdV equations with initial data in
![]() $L^{2,s}$
. Again, here we focus on
$L^{2,s}$
. Again, here we focus on
![]() $s=1$
.
$s=1$
.
Theorem 8.12. For
![]() $u_{0}\in L^{2,1}\left (\mathbb {R}\right )$
, the solution given by Theorem 8.11 has the same asymptotics as in Theorem 1.3.
$u_{0}\in L^{2,1}\left (\mathbb {R}\right )$
, the solution given by Theorem 8.11 has the same asymptotics as in Theorem 1.3.
Proof. For any
![]() $u_0\in L^{2,1}(\mathbb {R})$
, we pick a sequence of Schwartz functions
$u_0\in L^{2,1}(\mathbb {R})$
, we pick a sequence of Schwartz functions
![]() $\{u_{0,k}\}$
such that
$\{u_{0,k}\}$
such that
in
![]() $L^{2,1}\left (\mathbb {R}\right )$
and
$L^{2,1}\left (\mathbb {R}\right )$
and
![]() $\sup _{k}\left \Vert u_{0,k}\right \Vert _{L^{2,1}\left (\mathbb {R}\right )}\leq C.$
$\sup _{k}\left \Vert u_{0,k}\right \Vert _{L^{2,1}\left (\mathbb {R}\right )}\leq C.$
Let
![]() $u(x,t)$
be the solution to equation (1.1) in the sense of 8.11 with initial data
$u(x,t)$
be the solution to equation (1.1) in the sense of 8.11 with initial data
![]() $u_0$
and
$u_0$
and
![]() $\tau =0$
. Let
$\tau =0$
. Let
![]() $u_k(t)$
be the Schwartz solution to equation (1.1) with initial data
$u_k(t)$
be the Schwartz solution to equation (1.1) with initial data
![]() $u_{0,k}$
. By construction, we know that
$u_{0,k}$
. By construction, we know that
![]() $\forall t\in \mathbb {R}$
,
$\forall t\in \mathbb {R}$
,
![]() $u_k(t)\rightarrow u(t)$
in
$u_k(t)\rightarrow u(t)$
in
![]() $L^2(\mathbb {R})$
. Then we also know that up to a subsequence,
$L^2(\mathbb {R})$
. Then we also know that up to a subsequence,
![]() $u_k(t)\rightarrow u(t)$
almost everywhere.
$u_k(t)\rightarrow u(t)$
almost everywhere.
Now for each
![]() $u_k(t)$
, via the nonlinear steepest descent, we can write
$u_k(t)$
, via the nonlinear steepest descent, we can write
where
![]() $L_{k}\left (x,t\right )$
gives the leading-order behaviour and
$L_{k}\left (x,t\right )$
gives the leading-order behaviour and
![]() $E_{k}\left (x,t\right )$
collects the error term, which only depend the
$E_{k}\left (x,t\right )$
collects the error term, which only depend the
![]() $L^{2,1}(\mathbb {R})$
norm of
$L^{2,1}(\mathbb {R})$
norm of
![]() $u_{0,k}$
. From the convergence in equation (8.17), by direct scattering, one has the convergence of the reflection coefficients
$u_{0,k}$
. From the convergence in equation (8.17), by direct scattering, one has the convergence of the reflection coefficients
![]() $\lim _{k\rightarrow \infty } r_k=r$
in
$\lim _{k\rightarrow \infty } r_k=r$
in
![]() $H^1(\mathbb {R})$
. Then by the convergence of reflection coefficients, we know
$H^1(\mathbb {R})$
. Then by the convergence of reflection coefficients, we know
pointwise. Since the error term
![]() $E_k(x,t)$
is uniform in k, we can conclude that for an arbitrary fixed t, as the pointwise limit of
$E_k(x,t)$
is uniform in k, we can conclude that for an arbitrary fixed t, as the pointwise limit of
![]() $u_{k}\left (t\right )$
(up to measure zero set), one can write
$u_{k}\left (t\right )$
(up to measure zero set), one can write
where the decay estimate for
![]() $E_{\infty }\left (x,t\right )$
is the same as
$E_{\infty }\left (x,t\right )$
is the same as
![]() $E_{k}\left (x,t\right )$
due to the uniform error estimates. Therefore u also has the asymptotic behaviour as claimed.
$E_{k}\left (x,t\right )$
due to the uniform error estimates. Therefore u also has the asymptotic behaviour as claimed.
Acknowledgements
We would like to thank Professor Jean-Claude Saut for pointing out references [Reference Saut39], [Reference Saut and Temam40] and [Reference Temam41]. We are very grateful to the anonymous referees, whose detailed comments improved the presentation of the paper significantly.
Conflicts of Interest
None.
Financial support
J. Liu was supported by the research start-up fund (No.118900M030) from the University of the Chinese Academy of Sciences.