Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T11:46:49.307Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART II: COMPACTLY GENERATED SIMPLE GROUPS

Part of: Locally compact groups and their algebras Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  22 May 2017

PIERRE-EMMANUEL CAPRACE ,
COLIN D. REID  and
GEORGE A. WILLIS
PIERRE-EMMANUEL CAPRACE
Affiliation:
Université catholique de Louvain, IRMP, Chemin du Cyclotron 2, bte L7.01.02, 1348 Louvain-la-Neuve, Belgique; [email protected]
COLIN D. REID
Affiliation:
University of Newcastle, School of Mathematical and Physical Sciences, Callaghan, NSW 2308, Australia; [email protected], [email protected]
GEORGE A. WILLIS
Affiliation:
University of Newcastle, School of Mathematical and Physical Sciences, Callaghan, NSW 2308, Australia; [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

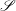We use the structure lattice, introduced in Part I, to undertake a systematic study of the class $\mathscr{S}$ consisting of compactly generated, topologically simple, totally disconnected locally compact groups that are nondiscrete. Given 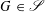$G\in \mathscr{S}$, we show that compact open subgroups of 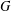$G$ involve finitely many isomorphism types of composition factors, and do not have any soluble normal subgroup other than the trivial one. By results of Part I, this implies that the centralizer lattice and local decomposition lattice of 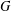$G$ are Boolean algebras. We show that the 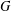$G$-action on the Stone space of those Boolean algebras is minimal, strongly proximal, and microsupported. Building upon those results, we obtain partial answers to the following key problems: Are all groups in $\mathscr{S}$ abstractly simple? Can a group in 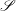$\mathscr{S}$ be amenable? Can a group in 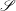$\mathscr{S}$ be such that the contraction groups of all of its elements are trivial?

MSC classification

Primary: 22D05: General properties and structure of locally compact groups
Secondary: 20E15: Chains and lattices of subgroups, subnormal subgroups 20E32: Simple groups
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e12
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Abels, H., ‘Kompakt definierbare topologische Gruppen’, Math. Ann. 197 (1972), 221–233.CrossRefGoogle Scholar
Abels, H., ‘Specker-Kompaktifizierungen von lokal kompakten topologischen Gruppen’, Math. Z. 135 (1974), 325–361.CrossRefGoogle Scholar
Arens, R., ‘Topologies for homeomorphism groups’, Amer. J. Math. 68 (1946), 593–610.CrossRefGoogle Scholar
Banks, C., Elder, M. and Willis, G. A., ‘Simple groups of automorphisms of trees determined by their actions on finite subtrees’, J. Group Theory 18(2) (2015), 235–261.CrossRefGoogle Scholar
Barnea, Y., Ershov, M. and Weigel, T., ‘Abstract commensurators of profinite groups’, Trans. Amer. Math. Soc. 363(10) (2011), 5381–5417.CrossRefGoogle Scholar
Baumgartner, U., Ramagge, J. and Rémy, B., ‘Contraction groups in complete Kac–Moody groups’, Groups Geom. Dyn. 2(3) (2008), 337–352.CrossRefGoogle Scholar
Baumgartner, U. and Willis, G. A., ‘Contraction groups and scales of automorphisms of totally disconnected locally compact groups’, Israel J. Math. 142 (2004), 221–248.CrossRefGoogle Scholar
Belyaev, V. V., ‘Locally finite groups with a finite nonseparable subgroup (Russian) Sibirsk’, Mat. Ž. 34(2) (1993), 23–41. 226, 233. Translation in Siberian Math. J. 34 (1993), no. 2, 218–232 (1994).Google Scholar
Bieri, R. and Strebel, R., On Groups of PL-Homeomorphisms of the Real Line, Mathematical Surveys and Monographs, 215 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Borel, A. and Tits, J., ‘Homomorphismes ‘abstraits’ de groupes algébriques simples’, Ann. of Math. 97 (1973), 499–571.CrossRefGoogle Scholar
Bourbaki, N., ‘Groupes et algèbres de Lie’, inChapitre II: Algèbres de Lie libres. Chapitre III: Groupes de Lie, Actualités Scientifiques et Industrielles, 1349 (Hermann, Paris, 1972), 320.Google Scholar
Bouziad, A. and Troallic, J.-P., ‘Some remarks about strong proximality of compact flows’, Colloq. Math. 115(2) (2009), 159–170.CrossRefGoogle Scholar
Bruhat, F. and Tits, J., ‘Groupes réductifs sur un corps local’, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–251.CrossRefGoogle Scholar
Burger, M. and Mozes, Sh., ‘Groups acting on trees: from local to global structure’, Publ. Math. Inst. Hautes Études Sci. 92 (2000), 113–150.CrossRefGoogle Scholar
Caprace, P.-E., ‘Automorphism groups of right-angled buildings: simplicity and local splittings’, Fund. Math. 224 (2014), 17–51.CrossRefGoogle Scholar
Caprace, P.-E. and De Medts, T., ‘Simple locally compact groups acting on trees and their germs of automorphisms’, Transform. Groups 16(2) (2011), 375–411.CrossRefGoogle Scholar
Caprace, P.-E. and De Medts, T., ‘Trees, contraction groups, and Moufang sets’, Duke Math. J. 162(13) (2013), 2413–2449.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N., ‘Decomposing locally compact groups into simple pieces’, Math. Proc. Cambridge Philos. Soc. 150(1) (2011), 97–128.CrossRefGoogle Scholar
Caprace, P.-E., Reid, C. D. and Willis, G. A., ‘Locally normal subgroups of simple locally compact groups’, C. R. Acad. Sci. Paris Ser. I 351(17–18) (2013), 657–661.CrossRefGoogle Scholar
Caprace, P.-E., Reid, C. D. and Willis, G. A., ‘Limits of contraction groups and the Tits core’, J. Lie Theory 24(4) (2014), 957–967.Google Scholar
Caprace, P.-E., Reid, C. D. and Willis, G. A., ‘Locally normal subgroups of totally disconnected groups; Part I: general theory’, Forum of Mathematics, Sigma 5 (2017), doi:10.1017/fms.2017.9.Google Scholar
Caprace, P.-E. and Stulemeijer, T., ‘Totally disconnected locally compact groups with a linear open subgroup’, Int. Math. Res. Not. IMRN 24 (2015), 13800–13829.CrossRefGoogle Scholar
Cluckers, R., Cornulier, Y., Louvet, N., Tessera, R. and Valette, A., ‘The Howe–Moore property for real and p-adic groups’, Math. Scand. 109(2) (2011), 201–224.CrossRefGoogle Scholar
Cornulier, Y. and de la Harpe, P., Metric Geometry of Locally Compact Groups, EMS Tracts in Mathematics, 25 (European Math. Soc., Zurich, 2016).CrossRefGoogle Scholar
De Medts, T., Silva, A. C. and Struyve, K., ‘Universal groups for right-angled buildings’, Preprint, 2016, arXiv:1603.04754.Google Scholar
Epstein, D. B. A., ‘The simplicity of certain groups of homeomorphisms’, Compos. Math. 22 (1970), 165–173.Google Scholar
Furstenberg, H., ‘Boundary theory and stochastic processes on homogeneous spaces’, inHarmonic Analysis on Homogeneous Spaces, Proc. Sympos. Pure Math., XXVI (Williams Coll., Williamstown, Mass., 1972) (Amer. Math. Soc., Providence, RI, 1973), 193–229.CrossRefGoogle Scholar
Garrido, A., ‘On the congruence subgroup problem for branch groups’, Israel J. Math. 216(1) (2016), 1–13.CrossRefGoogle Scholar
Glasner, S., ‘Topological dynamics and group theory’, Trans. Amer. Math. Soc. 187 (1974), 327–334.CrossRefGoogle Scholar
Gruenberg, K. W., ‘Residual properties of infinite soluble groups’, Proc. Lond. Math. Soc. 7(3) (1957), 29–62.CrossRefGoogle Scholar
Haglund, F. and Paulin, F., ‘Simplicité de groupes d’automorphismes d’espaces à courbure négative’, inThe Epstein Birthday Schrift, Geom. Topol. Monogr., 1 (Geom. Topol. Publ., Coventry, 1998), 181–248. (electronic).Google Scholar
Juschenko, K. and Monod, N., ‘Cantor systems, piecewise translations and simple amenable groups’, Ann. of Math. (2) 178(2) (2013), 775–787.CrossRefGoogle Scholar
Kakutani, S. and Kodaira, K., ‘Über das Haarsche Mass in der lokal bikompakten Gruppe’, Proc. Imp. Acad. Tokyo 20 (1944), 444–450.Google Scholar
Kapoudjian, C., ‘Simplicity of Neretin’s group of spheromorphisms’, Ann. Inst. Fourier (Grenoble) 49(4) (1999), 1225–1240.CrossRefGoogle Scholar
Kramer, L., ‘The topology of a semisimple Lie group is essentially unique’, Adv. Math. 228(5) (2011), 2623–2633.CrossRefGoogle Scholar
Lazarovich, N., ‘On regular CAT(0) cube complexes’, Preprint, 2014, arXiv:1411.0178.Google Scholar
Le Boudec, A., ‘Adrien Groups acting on trees with almost prescribed local action’, Comment. Math. Helv. 91(2) (2016), 253–293.CrossRefGoogle Scholar
Malcev, A., ‘On isomorphic matrix representations of infinite groups’, Mat. Sb. 8(50) (1940), 405–422 (Russian).Google Scholar
Margulis, G., Discrete Subgroups of Semi-Simple Lie Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 17 (Springer, Berlin, 1991).CrossRefGoogle Scholar
Marquis, T., ‘Abstract simplicity of locally compact Kac–Moody groups’, Compos. Math. 150(4) (2014), 713–728.CrossRefGoogle Scholar
Möller, R. and Vonk, J., ‘Normal subgroups of groups acting on trees and automorphism groups of graphs’, J. Group Theory 15(6) (2012), 831–850.CrossRefGoogle Scholar
Monod, N., Continuous Bounded Cohomology of Locally Compact Groups, Lecture Notes in Mathematics, 1758 (Springer, Berlin, 2001).CrossRefGoogle Scholar
Montgomery, D. and Zippin, L., Topological Transformation Groups, (Interscience Publishers, New York–London, 1955).Google Scholar
Nekrashevych, V., ‘Finitely presented groups associated with expanding maps’. Preprint, 2013, arXiv:1312.5654.Google Scholar
Nekrashevych, V., ‘Palindromic subshifts and simple periodic groups of intermediate growth’, Preprint, 2016, arXiv:1601.01033.Google Scholar
Neretin, Yu. A., ‘On combinatorial analogs of the group of diffeomorphisms of the circle’, Izv. Math. 41(2) (1993), 337–349 (Russian).CrossRefGoogle Scholar
Nikolov, N., ‘Algebraic properties of profinite groups’, Preprint, 2011, arXiv:1108.5130.Google Scholar
Nikolov, N. and Segal, D., ‘Generators and commutators in finite groups; abstract quotients of compact groups’, Invent. Math. 190(3) (2012), 513–602.CrossRefGoogle Scholar
Reid, C. D. and Wesolek, P., ‘Homomorphisms into totally disconnected, locally compact groups with dense image’, Preprint, 2015, arXiv:1509.00156v1.Google Scholar
Reid, C. D. and Wesolek, P., ‘The essentially chief series of a compactly generated locally compact group’, Preprint, 2015, arXiv:1509.06593v4.Google Scholar
Rémy, B., ‘Topological simplicity, commensurator superrigidity and non-linearities of Kac–Moody groups’, Geom. Funct. Anal. 14(4) (2004), 810–852. With an appendix by P. Bonvin.CrossRefGoogle Scholar
Rémy, B. and Ronan, M., ‘Topological groups of Kac–Moody type, right-angled twinnings and their lattices’, Comment. Math. Helv. 81(1) (2006), 191–219.CrossRefGoogle Scholar
Ribes, L. and Zalesskii, P., Profinite Groups, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 40 (Springer, Berlin, 2010).CrossRefGoogle Scholar
Riehm, C., ‘The congruence subgroup problem over local fields’, Amer. J. Math. 92 (1970), 771–778.CrossRefGoogle Scholar
Rosenlicht, M., ‘On a result of Baer’, Proc. Amer. Math. Soc. 13 (1962), 99–101.CrossRefGoogle Scholar
Rubin, M., ‘On the reconstruction of topological spaces from their groups of homeomorphisms’, Trans. Amer. Math. Soc. 312(2) (1989), 487–538.CrossRefGoogle Scholar
Schur, J., ‘Über die Darstellung der endlichen Gruppen durch gebrochen lineare Substitutionen’, J. Reine Angew. Math. 127 (1904), 20–50.Google Scholar
Shalom, Y. and Willis, G. A., ‘Commensurated subgroups of arithmetic groups, totally disconnected groups and adelic rigidity’, Geom. Funct. Anal. 23(5) (2013), 1631–1683.CrossRefGoogle Scholar
Smith, S. M., ‘A product for permutation groups and topological groups’, Preprint, 2015, arXiv:1407.5697v2.Google Scholar
Thomas, S. and Velickovic, B., ‘On the complexity of the isomorphism relation for finitely generated groups’, J. Algebra 217(1) (1999), 352–373.CrossRefGoogle Scholar
Tits, J., ‘Algebraic and abstract simple groups’, Ann. of Math. 80 (1964), 313–329.CrossRefGoogle Scholar
Tits, J., ‘Sur le groupe des automorphismes d’un arbre’, inEssays on Topology and Related Topics (Mémoires dédiés à Georges de Rham) (Springer, New York, 1970), 188–211.CrossRefGoogle Scholar
Tits, J., ‘Reductive groups over local fields’, inAutomorphic Forms, Representations and L-Functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proc. Sympos. Pure Math., XXXIII (Amer. Math. Soc., Providence, RI, 1979), 29–69.Google Scholar
Tits, J., ‘Uniqueness and presentation of Kac–Moody groups over fields’, J. Algebra 105(2) (1987), 542–573.CrossRefGoogle Scholar
Ušakov, V. I., ‘Topological FC -groups’, Sibirsk. Mat. Ž. 4 (1963), 1162–1174.Google Scholar
Wang, S. P., ‘Compactness properties of topological groups’, Trans. Amer. Math. Soc. 154 (1971), 301–314.CrossRefGoogle Scholar
Wesolek, P., ‘Elementary totally disconnected locally compact groups’, Proc. Lond. Math. Soc. 110(6) (2015), 1387–1434.CrossRefGoogle Scholar
Wesolek, P., ‘Commensurated subgroups in finitely generated branch groups’, J. Group Theory 20(2) (2017), 385–392.CrossRefGoogle Scholar
Willis, G. A., ‘The number of prime factors of the scale function on a compactly generated group is finite’, Bull. Lond. Math. Soc. 33(2) (2001), 168–174.CrossRefGoogle Scholar
Willis, G. A., ‘Compact open subgroups in simple totally disconnected groups’, J. Algebra 312(1) (2007), 405–417.CrossRefGoogle Scholar
Willis, G. A., ‘The nub of an automorphism of a totally disconnected, locally compact group’, Ergodic Theory Dynam. Systems 34(4) (2014), 1365–1394.CrossRefGoogle Scholar