Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T11:16:55.767Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART I: GENERAL THEORY

Part of: Locally compact groups and their algebras Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  22 May 2017

PIERRE-EMMANUEL CAPRACE ,
COLIN D. REID  and
GEORGE A. WILLIS
PIERRE-EMMANUEL CAPRACE
Affiliation:
Université catholique de Louvain, IRMP, Chemin du Cyclotron 2, bte L7.01.02, 1348 Louvain-la-Neuve, Belgique; [email protected]
COLIN D. REID
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia; [email protected], [email protected]
GEORGE A. WILLIS
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia; [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 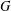$G$ be a totally disconnected, locally compact group. A closed subgroup of 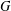$G$ is locally normal if its normalizer is open in 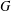$G$. We begin an investigation of the structure of the family of closed locally normal subgroups of 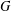$G$. Modulo commensurability, this family forms a modular lattice 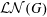${\mathcal{L}}{\mathcal{N}}(G)$, called the structure lattice of 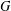$G$. We show that 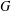$G$ admits a canonical maximal quotient 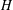$H$ for which the quasicentre and the abelian locally normal subgroups are trivial. In this situation 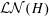${\mathcal{L}}{\mathcal{N}}(H)$ has a canonical subset called the centralizer lattice, forming a Boolean algebra whose elements correspond to centralizers of locally normal subgroups. If 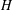$H$ is second-countable and acts faithfully on its centralizer lattice, we show that the topology of 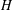$H$ is determined by its algebraic structure (and thus invariant by every abstract group automorphism), and also that the action on the Stone space of the centralizer lattice is universal for a class of actions on profinite spaces. Most of the material is developed in the more general framework of Hecke pairs.

MSC classification

Primary: 22D05: General properties and structure of locally compact groups
Secondary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e11
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Baer, R., ‘Finiteness properties of groups’, Duke Math. J. 15(4) (1948), 1021–1032.CrossRefGoogle Scholar
Barnea, Y., Ershov, M. and Weigel, T., ‘Abstract commensurators of profinite groups’, Trans. Amer. Math. Soc. 363(10) (2011), 5381–5417.Google Scholar
Bartholdi, L., Siegenthaler, O. and Zalesskii, P., ‘The congruence subgroup problem for branch groups’, Israel J. Math. 187(1) (2012), 419–450.CrossRefGoogle Scholar
Belyaev, V. V., ‘Locally finite groups with a finite nonseparable subgroup (Russian) Sibirsk’, Mat. Zh. 34(2) (1993), 23–41. 226, 233. Translation in Siberian Math. J. 34 (1993), no. 2, 218–232 (1994).Google Scholar
Bourbaki, N., ‘Groupes et algèbres de Lie’, inChapitre II: Algèbres de Lie libres. Chapitre III: Groupes de Lie, Actualités Scientifiques et Industrielles, 1349 (Hermann, Paris, 1972), 320.Google Scholar
Burger, M. and Mozes, Sh., ‘Groups acting on trees: from local to global structure’, Publ. Math. Inst. Hautes Études Sci. 92 (2000), 113–150.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N., ‘Decomposing locally compact groups into simple pieces’, Math. Proc. Cambridge Philos. Soc. 150(1) (2011), 97–128.CrossRefGoogle Scholar
Caprace, P.-E., Reid, C. D. and Willis, G. A., ‘Locally normal subgroups of totally disconnected groups. Part II: Compactly generated simple groups’, Forum of Mathematics, Sigma 5 (2017), doi:10.1017/fms.2017.8.Google Scholar
Caprace, P.-E. and Stulemeijer, T., ‘Totally disconnected locally compact groups with a linear open subgroup’, Int. Math. Res. Not. IMRN 2015(24) (2015), 13800–13829.CrossRefGoogle Scholar
Cluckers, R., Cornulier, Y., Louvet, N., Tessera, R. and Valette, A., ‘The Howe–Moore property for real and p-adic groups’, Math. Scand. 109(2) (2011), 201–224.Google Scholar
Dietzmann, A. P., ‘On the criteria of non-simplicity of groups’, C. R. (Dokl.) Acad. Sci. URSS n. Ser. 44 (1944), 89–91.Google Scholar
Hall, M. Jr, The Theory of Groups. Reprinting of the 1968 edition (Chelsea Publishing Co., New York, 1976).Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis (Berlin–Göttingen–Heidelberg, 1963).Google Scholar
Jacobson, N., Basic Algebra. I, Second edn (W. H. Freeman and Company, New York, 1985).Google Scholar
Kakutani, S. and Kodaira, K., ‘Über das Haarsche Mass in der lokal bikompakten Gruppe’, Proc. Imp. Acad. Tokyo 20 (1944), 444–450.Google Scholar
Kelley, J. L., General Topology, Reprint of the 1955 edition, Graduate Texts in Mathematics, 27 (Springer, New York–Berlin, 1975).Google Scholar
Kramer, L., ‘The topology of a semisimple Lie group is essentially unique’, Adv. Math. 228(5) (2011), 2623–2633.CrossRefGoogle Scholar
Kurosh, A. G., The Theory of Groups (ed. Hirsch, K. A.) (Chelsea Publishing Co., New York, 1960), (Translated from the Russian).Google Scholar
Möller, R. G. and Vonk, J., ‘Normal subgroups of groups acting on trees and automorphism groups of graphs’, J. Group Theory 15(6) (2012), 831–850.Google Scholar
Nekrashevych, V., ‘Free subgroups in groups acting on rooted trees’, Groups Geom. Dyn. 4(4) (2010), 847–862.Google Scholar
Reid, C. D. and Wesolek, P., ‘Homomorphisms into totally disconnected, locally compact groups with dense image’, Preprint, 2015, arXiv:1509.00156v1.Google Scholar
Reid, C. D., ‘The generalised fitting subgroup of a profinite group’, Commun. Algebra 41(1) (2013), 294–308.CrossRefGoogle Scholar
Schlichting, G., ‘Operationen mit periodischen Stabilisatoren’, Arch. Math. (Basel) 34(2) (1980), 97–99.CrossRefGoogle Scholar
Wesolek, P., ‘Elementary totally disconnected locally compact groups’, Proc. Lond. Math. Soc. (3) 110(6) (2015), 1387–1434.Google Scholar
Willis, G. A., ‘The structure of totally disconnected, locally compact groups’, Math. Ann. 300(2) (1994), 341–363.Google Scholar
Wilson, J. S., ‘On just infinite abstract and profinite groups’, inNew Horizons in Pro-p Groups (eds. du Sautoy, M., Segal, D. and Shalev, A.) Ch. 5, (Birkhäuser, Boston, 2000).Google Scholar