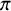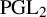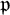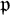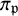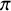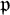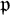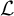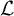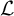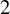Introduction
The purpose of this article is threefold: First, let
![]() $\pi $
be a cuspidal, cohomological automorphic representation of an inner form G of
$\pi $
be a cuspidal, cohomological automorphic representation of an inner form G of
![]() $\operatorname {{PGL}}_2$
over a number field F of arbitrary signature and
$\operatorname {{PGL}}_2$
over a number field F of arbitrary signature and
![]() $\mathfrak {p}$
be a prime of F such that G is split at
$\mathfrak {p}$
be a prime of F such that G is split at
![]() $\mathfrak {p}$
and the local component
$\mathfrak {p}$
and the local component
![]() $\pi _{\mathfrak {p}}$
of
$\pi _{\mathfrak {p}}$
of
![]() $\pi $
at
$\pi $
at
![]() $\mathfrak {p}$
is the Steinberg representation. We want to give a general construction of automorphic
$\mathfrak {p}$
is the Steinberg representation. We want to give a general construction of automorphic
![]() $\mathcal {L}$
-invariants (also known as Teitelbaum, Darmon or Orton
$\mathcal {L}$
-invariants (also known as Teitelbaum, Darmon or Orton
![]() $\mathcal {L}$
-invariants) for
$\mathcal {L}$
-invariants) for
![]() $\pi $
. For representations which are cohomological with respect to the trivial coefficient system, or in other words for forms of parallel weight
$\pi $
. For representations which are cohomological with respect to the trivial coefficient system, or in other words for forms of parallel weight
![]() $2$
, these
$2$
, these
![]() $\mathcal {L}$
-invariants have been defined in general (see, for example, [Reference Gehrmann23]) but for higher weights they have been defined only in certain situations:
$\mathcal {L}$
-invariants have been defined in general (see, for example, [Reference Gehrmann23]) but for higher weights they have been defined only in certain situations:
-
1. In case
 $F=\mathbb {Q}$
and G is compact at infinity by Teitelbaum in [Reference Teitelbaum41],
$F=\mathbb {Q}$
and G is compact at infinity by Teitelbaum in [Reference Teitelbaum41], -
2. In case
 $F=\mathbb {Q}$
and G is split by Orton in [Reference Orton33],
$F=\mathbb {Q}$
and G is split by Orton in [Reference Orton33], -
3. In case
 $F=\mathbb {Q}$
and G is split at infinity by Rotger and Seveso in [Reference Rotger and Seveso34],
$F=\mathbb {Q}$
and G is split at infinity by Rotger and Seveso in [Reference Rotger and Seveso34], -
4. In case F is imaginary quadratic and G is split by Barrera-Salazar and Williams in [Reference Barrera Salazar and Williams3] and
-
5. In case F is totally real and G is compact at infinity by Chida, Mok and Park in [Reference Chida, Mok and Park14].
An obstacle that might have prevented the construction in general is the following: Whereas in case of the trivial coefficient system the representation is always ordinary and therefore noncritical at
![]() $\mathfrak {p}$
, this is no longer true for higher weights. But note that for the cases 1–4 above the representation has still noncritical slope at
$\mathfrak {p}$
, this is no longer true for higher weights. But note that for the cases 1–4 above the representation has still noncritical slope at
![]() $\mathfrak {p}$
and, thus, is noncritical at
$\mathfrak {p}$
and, thus, is noncritical at
![]() $\mathfrak {p}$
(see the end of Section 2.4 for a detailed discussion on noncritical slopes). It seems to the authors of this paper that in [Reference Chida, Mok and Park14] it is implicitly assumed that the representation is noncritical at
$\mathfrak {p}$
(see the end of Section 2.4 for a detailed discussion on noncritical slopes). It seems to the authors of this paper that in [Reference Chida, Mok and Park14] it is implicitly assumed that the representation is noncritical at
![]() $\mathfrak {p}$
(see Remark 2.6 for more details). Our first main result (see Definition 3.2) is the construction of automorphic
$\mathfrak {p}$
(see Remark 2.6 for more details). Our first main result (see Definition 3.2) is the construction of automorphic
![]() $\mathcal {L}$
-invariants under the assumption that the representation
$\mathcal {L}$
-invariants under the assumption that the representation
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
. We point out that our construction of
$\mathfrak {p}$
. We point out that our construction of
![]() $\mathcal {L}$
-invariants is novel as it does not involve the Bruhat–Tits tree at any stage.
$\mathcal {L}$
-invariants is novel as it does not involve the Bruhat–Tits tree at any stage.
Our second goal is to bridge the gap between works using overconvergent cohomology à la Ash–Stevens, for example, [Reference Barrera Salazar and Williams3] and [Reference Barrera Salazar, Dimitrov and Jorza2], and Spieß’ more representation-theoretic approach (cf. [Reference Spieß39]). In particular, we show that the noncriticality condition for classes in overconvergent cohomology that is discussed in [Reference Barrera Salazar, Dimitrov and Jorza2] respectively [Reference Bergdall and Hansen5] is equivalent to a more representation-theoretic one: Assume for the moment that
![]() $\pi _{\mathfrak {p}}$
is not necessarily Steinberg but merely has an Iwahori-fixed vector. We explain that choosing a
$\pi _{\mathfrak {p}}$
is not necessarily Steinberg but merely has an Iwahori-fixed vector. We explain that choosing a
![]() $\mathfrak {p}$
-stabilization of
$\mathfrak {p}$
-stabilization of
![]() $\pi $
, that is, an Iwahori-fixed vector of
$\pi $
, that is, an Iwahori-fixed vector of
![]() $\pi _{\mathfrak {p}}$
, yields a cohomology class of a
$\pi _{\mathfrak {p}}$
, yields a cohomology class of a
![]() $\mathfrak {p}$
-arithmetic subgroup of
$\mathfrak {p}$
-arithmetic subgroup of
![]() $G(F)$
with values in the dual of a locally algebraic principal series representation of
$G(F)$
with values in the dual of a locally algebraic principal series representation of
![]() $G(F_{\mathfrak {p}})$
. Noncriticality is then equivalent to that this class can be lifted uniquely to a class in the cohomology with values in the continuous dual of the corresponding locally analytic principal series representation (see Proposition 2.13). The main tool to prove this equivalence is the resolution of locally analytic principal series representations by Kohlhaase and Schraen (see [Reference Kohlhaase and Schraen31]).
$G(F_{\mathfrak {p}})$
. Noncriticality is then equivalent to that this class can be lifted uniquely to a class in the cohomology with values in the continuous dual of the corresponding locally analytic principal series representation (see Proposition 2.13). The main tool to prove this equivalence is the resolution of locally analytic principal series representations by Kohlhaase and Schraen (see [Reference Kohlhaase and Schraen31]).
Finally, we show that, if the number field F is totally real the automorphic
![]() $\mathcal {L}$
-invariants attached to
$\mathcal {L}$
-invariants attached to
![]() $\pi $
agree with the derivatives of the
$\pi $
agree with the derivatives of the
![]() $U_{\mathfrak {p}}$
-eigenvalue of a p-adic family passing through
$U_{\mathfrak {p}}$
-eigenvalue of a p-adic family passing through
![]() $\pi $
(cf. Theorem 4.3). This equality is known in case
$\pi $
(cf. Theorem 4.3). This equality is known in case
![]() $F=\mathbb {Q}$
by the work of Bertolini–Darmon–Iovita (see [Reference Bertolini, Darmon and Iovita6]) and Seveso (see [Reference Seveso38]). For Hilbert modular forms of parallel weight
$F=\mathbb {Q}$
by the work of Bertolini–Darmon–Iovita (see [Reference Bertolini, Darmon and Iovita6]) and Seveso (see [Reference Seveso38]). For Hilbert modular forms of parallel weight
![]() $2$
the equality was recently proven by Rosso and the first named author (see [Reference Gehrmann and Rosso25]). As we do not work with general reductive groups as in loc.cit the arguments simplify substantially, making them more accessible to people who are only interested in Hilbert modular forms. Furthermore, it is known that the derivatives of the
$2$
the equality was recently proven by Rosso and the first named author (see [Reference Gehrmann and Rosso25]). As we do not work with general reductive groups as in loc.cit the arguments simplify substantially, making them more accessible to people who are only interested in Hilbert modular forms. Furthermore, it is known that the derivatives of the
![]() $U_{\mathfrak {p}}$
-eigenvalue agree with the Fontaine–Mazur
$U_{\mathfrak {p}}$
-eigenvalue agree with the Fontaine–Mazur
![]() $\mathcal {L}$
-invariant of the associated Galois representation, if that Galois representation is noncritical. Thus, we deduce the equality of automorphic and Fontaine–Mazur
$\mathcal {L}$
-invariant of the associated Galois representation, if that Galois representation is noncritical. Thus, we deduce the equality of automorphic and Fontaine–Mazur
![]() $\mathcal {L}$
-invariants (see [Reference Spieß40] for an independent proof of this equality in case of parallel weight
$\mathcal {L}$
-invariants (see [Reference Spieß40] for an independent proof of this equality in case of parallel weight
![]() $2$
). The equality of
$2$
). The equality of
![]() $\mathcal {L}$
-invariants in parallel weight
$\mathcal {L}$
-invariants in parallel weight
![]() $2$
is necessary for the construction of plectic Stark–Heegner points in recent work of Fornea and the first named author (cf. [Reference Fornea and Gehrmann20]). This article should be seen as a precursor for defining plectic Stark–Heegner cycles for arbitrary cohomological weights.
$2$
is necessary for the construction of plectic Stark–Heegner points in recent work of Fornea and the first named author (cf. [Reference Fornea and Gehrmann20]). This article should be seen as a precursor for defining plectic Stark–Heegner cycles for arbitrary cohomological weights.
Notations
All rings will be commutative and unital. The units of a ring R will be denoted by
![]() $R^\times .$
Given a prime ideal
$R^\times .$
Given a prime ideal
![]() $\mathfrak {m}$
of a ring R and an R-module M, we write
$\mathfrak {m}$
of a ring R and an R-module M, we write
![]() $M_{\mathfrak {m}}$
for the localization of M at
$M_{\mathfrak {m}}$
for the localization of M at
![]() $\mathfrak {m}$
. If R is a ring and G is a group, we denote the group algebra of G over R by
$\mathfrak {m}$
. If R is a ring and G is a group, we denote the group algebra of G over R by
![]() $R[G]$
. The trivial character of any group will be denoted by
$R[G]$
. The trivial character of any group will be denoted by ![]() . Given two sets X and Y, we will write
. Given two sets X and Y, we will write
![]() $\mathcal {F}(X,Y)$
for the set of all maps from X to Y. If X and Y are topological spaces, we write
$\mathcal {F}(X,Y)$
for the set of all maps from X to Y. If X and Y are topological spaces, we write
![]() $C(X,Y)\subseteq \mathcal {F}(X,Y)$
for the set of all continuous maps. If Y is a topological group, we denote by
$C(X,Y)\subseteq \mathcal {F}(X,Y)$
for the set of all continuous maps. If Y is a topological group, we denote by
![]() $C_c(X,Y)\subseteq C(X,Y)$
the subset of functions with compact support.
$C_c(X,Y)\subseteq C(X,Y)$
the subset of functions with compact support.
Setup
A number field. We fix an algebraic number field
![]() $F\subseteq \mathbb {C}$
with ring of integers
$F\subseteq \mathbb {C}$
with ring of integers
![]() $\mathcal {O}_F$
. We write
$\mathcal {O}_F$
. We write
![]() $S_\infty $
for the set of infinite places of F and
$S_\infty $
for the set of infinite places of F and
![]() $\Sigma $
for the set of all embeddings from F into the algebraic closure
$\Sigma $
for the set of all embeddings from F into the algebraic closure
![]() $\overline {\mathbb {Q}}$
of
$\overline {\mathbb {Q}}$
of
![]() $\mathbb {Q}$
in
$\mathbb {Q}$
in
![]() $\mathbb {C}$
. The action of complex conjugation on
$\mathbb {C}$
. The action of complex conjugation on
![]() $\Sigma $
will be denoted by c. We write
$\Sigma $
will be denoted by c. We write
![]() $\delta $
for the number of complex places of F. For any place
$\delta $
for the number of complex places of F. For any place
![]() $\mathfrak {q}$
of F, we will denote by
$\mathfrak {q}$
of F, we will denote by
![]() $F_{\mathfrak {q}}$
the completion of F at
$F_{\mathfrak {q}}$
the completion of F at
![]() $\mathfrak {q}$
. If
$\mathfrak {q}$
. If
![]() $\mathfrak {q}$
is a finite place, we let
$\mathfrak {q}$
is a finite place, we let
![]() $\mathcal {O}_{\mathfrak {q}}$
denote the valuation ring of
$\mathcal {O}_{\mathfrak {q}}$
denote the valuation ring of
![]() $F_{\mathfrak {q}}$
and
$F_{\mathfrak {q}}$
and
![]() $\operatorname {{ord}}_{\mathfrak {q}}$
the additive valuation such that
$\operatorname {{ord}}_{\mathfrak {q}}$
the additive valuation such that
![]() $\operatorname {{ord}}_{\mathfrak {q}}(\varpi )=1$
for any local uniformizer
$\operatorname {{ord}}_{\mathfrak {q}}(\varpi )=1$
for any local uniformizer
![]() $\varpi \in \mathcal {O}_{\mathfrak {q}}$
. We write
$\varpi \in \mathcal {O}_{\mathfrak {q}}$
. We write
![]() $\mathcal {N}(\mathfrak {q})$
for the cardinality of the residue field
$\mathcal {N}(\mathfrak {q})$
for the cardinality of the residue field
![]() $\mathcal {O}/\mathfrak {q}$
. We normalize the
$\mathcal {O}/\mathfrak {q}$
. We normalize the
![]() $\mathfrak {q}$
-adic absolute valuation
$\mathfrak {q}$
-adic absolute valuation
![]() $|\cdot |_{\mathfrak {q}}$
by
$|\cdot |_{\mathfrak {q}}$
by
![]() $|\varpi |_{\mathfrak {p}}=\mathcal {N}(\mathfrak {q})^{-1}.$
$|\varpi |_{\mathfrak {p}}=\mathcal {N}(\mathfrak {q})^{-1}.$
For a finite set S of places of F, we define the ‘S-truncated adeles’
![]() $\mathbb {A}^{S}$
as the restricted product of all completions
$\mathbb {A}^{S}$
as the restricted product of all completions
![]() $F_{v}$
with
$F_{v}$
with
![]() $v\notin S$
. In case S is the empty set, we drop the superscript S from the notation. We will often write
$v\notin S$
. In case S is the empty set, we drop the superscript S from the notation. We will often write
![]() $\mathbb {A}^{S,\infty }$
instead of
$\mathbb {A}^{S,\infty }$
instead of
![]() $\mathbb {A}^{S\cup S_\infty }$
. If H is an algebraic group over F, we will put
$\mathbb {A}^{S\cup S_\infty }$
. If H is an algebraic group over F, we will put
![]() $H_{\mathfrak {q}}=H(F_{\mathfrak {q}})$
for any place
$H_{\mathfrak {q}}=H(F_{\mathfrak {q}})$
for any place
![]() $\mathfrak {q}$
of F. If S is a finite set of places of F, we will write
$\mathfrak {q}$
of F. If S is a finite set of places of F, we will write
![]() $H_S=\prod _{\mathfrak {q}\in S} H_{\mathfrak {q}}$
. Further, we abbreviate
$H_S=\prod _{\mathfrak {q}\in S} H_{\mathfrak {q}}$
. Further, we abbreviate
![]() $H_\infty =H_{S_\infty }$
.
$H_\infty =H_{S_\infty }$
.
A quaternion algebra. We fix a quaternion algebra D over F. We denote by
![]() $\operatorname {{ram}}(D)$
the set of places of F at which D is ramified and put
$\operatorname {{ram}}(D)$
the set of places of F at which D is ramified and put
Let
![]() $D^\times $
be the group of units of D considered as an algebraic group over F. The centre
$D^\times $
be the group of units of D considered as an algebraic group over F. The centre
![]() $Z\subseteq D^\times $
is naturally isomorphic to the multiplicative group
$Z\subseteq D^\times $
is naturally isomorphic to the multiplicative group
![]() $\mathbb {G}_m$
. We put
$\mathbb {G}_m$
. We put
![]() $G=D^\times /Z.$
For any place
$G=D^\times /Z.$
For any place
![]() $\mathfrak {q}\notin \operatorname { {ram}}(D)$
, we fix an isomorphism
$\mathfrak {q}\notin \operatorname { {ram}}(D)$
, we fix an isomorphism
![]() $D_{\mathfrak {q}}\cong M_2(F_{\mathfrak {q}})$
that in turn induces an isomorphism
$D_{\mathfrak {q}}\cong M_2(F_{\mathfrak {q}})$
that in turn induces an isomorphism
![]() $G_{\mathfrak {q}}\cong \operatorname { {PGL}}_2(F_{\mathfrak {q}}).$
For any Archimedean place
$G_{\mathfrak {q}}\cong \operatorname { {PGL}}_2(F_{\mathfrak {q}}).$
For any Archimedean place
![]() $\mathfrak {q}\in \operatorname { {ram}}(D)$
, we fix an isomorphism of
$\mathfrak {q}\in \operatorname { {ram}}(D)$
, we fix an isomorphism of
![]() $D_{\mathfrak {q}}$
with the Hamilton quaternions, which yields an embedding
$D_{\mathfrak {q}}$
with the Hamilton quaternions, which yields an embedding
![]() $G_{\mathfrak {q}}\hookrightarrow \operatorname { {PGL}}_2(\mathbb {C})$
. In particular, we get an injection
$G_{\mathfrak {q}}\hookrightarrow \operatorname { {PGL}}_2(\mathbb {C})$
. In particular, we get an injection ![]() for every embedding
for every embedding
![]() $\sigma \in \Sigma $
with underlying place
$\sigma \in \Sigma $
with underlying place
![]() $\mathfrak {q}$
. We write
$\mathfrak {q}$
. We write
for the diagonal embedding.
Let
![]() $S_\infty (D)$
be the set of all Archimedean places of F at which D is split. We put
$S_\infty (D)$
be the set of all Archimedean places of F at which D is split. We put
Let
![]() $S_{\mathbb {R}}(D)\subseteq S_\infty (D)$
be the subset of real places. We denote by
$S_{\mathbb {R}}(D)\subseteq S_\infty (D)$
be the subset of real places. We denote by
![]() $G_\infty ^+$
the connected component of the identity of
$G_\infty ^+$
the connected component of the identity of
![]() $G_\infty $
. The group
$G_\infty $
. The group
![]() $\operatorname { {PGL}}_2(\mathbb {C})$
and the units of the Hamilton quaternions are connected, whereas
$\operatorname { {PGL}}_2(\mathbb {C})$
and the units of the Hamilton quaternions are connected, whereas
![]() $\operatorname { {PGL}}_2(\mathbb {R})$
has two connected components. Therefore, we can identify
$\operatorname { {PGL}}_2(\mathbb {R})$
has two connected components. Therefore, we can identify
If
![]() $A\subseteq G_\infty $
is a subgroup, we put
$A\subseteq G_\infty $
is a subgroup, we put
![]() $A^+=A\cap G_\infty ^+.$
$A^+=A\cap G_\infty ^+.$
An automorphic representation. Let
![]() $\pi ^\prime =\otimes _{\mathfrak {q}} \pi ^\prime _{\mathfrak {q}}$
be a cuspidal automorphic representation of
$\pi ^\prime =\otimes _{\mathfrak {q}} \pi ^\prime _{\mathfrak {q}}$
be a cuspidal automorphic representation of
![]() $\operatorname { {PGL}}_2(\mathbb {A})$
that is cohomological (see Section 1.1.2). If F is totally real, then such automorphic representations (up to twists by the norm character) are in one-to-one correspondence with cuspidal Hilbert modular newforms with even weights and trivial Nebentypus. We assume that the local component
$\operatorname { {PGL}}_2(\mathbb {A})$
that is cohomological (see Section 1.1.2). If F is totally real, then such automorphic representations (up to twists by the norm character) are in one-to-one correspondence with cuspidal Hilbert modular newforms with even weights and trivial Nebentypus. We assume that the local component
![]() $\pi ^\prime _{\mathfrak {q}}$
is either a twist of the Steinberg representation or supercuspidal for all primes
$\pi ^\prime _{\mathfrak {q}}$
is either a twist of the Steinberg representation or supercuspidal for all primes
![]() $\mathfrak {q}$
dividing
$\mathfrak {q}$
dividing
![]() $\operatorname { {disc}}(D)$
. Thus, there exists a Jacquet–Langlands transfer
$\operatorname { {disc}}(D)$
. Thus, there exists a Jacquet–Langlands transfer
![]() $\pi $
of
$\pi $
of
![]() $\pi '$
to
$\pi '$
to
![]() $G(\mathbb {A})$
, that is, an automorphic representation of
$G(\mathbb {A})$
, that is, an automorphic representation of
![]() $G(\mathbb {A})$
such that
$G(\mathbb {A})$
such that
![]() $\pi ^\prime _{\mathfrak {q}}\cong \pi _{\mathfrak {q}}$
for all places
$\pi ^\prime _{\mathfrak {q}}\cong \pi _{\mathfrak {q}}$
for all places
![]() $\mathfrak {q}\notin \operatorname { {ram}}(D).$
Moreover, the representation
$\mathfrak {q}\notin \operatorname { {ram}}(D).$
Moreover, the representation
![]() $\pi _{\mathfrak {q}}$
is one-dimensional for all
$\pi _{\mathfrak {q}}$
is one-dimensional for all
![]() $\mathfrak {q} \mid \operatorname { {disc}}(D)$
such that
$\mathfrak {q} \mid \operatorname { {disc}}(D)$
such that
![]() $\pi ^\prime _{\mathfrak {q}}$
is a twist of the Steinberg representation. We put
$\pi ^\prime _{\mathfrak {q}}$
is a twist of the Steinberg representation. We put
1. Cohomology of p-arithmetic groups
We recollect some basic facts about the cohomology of
![]() $\mathfrak {p}$
-arithmetic groups with values in duals of smooth representations.
$\mathfrak {p}$
-arithmetic groups with values in duals of smooth representations.
1.1. The Eichler–Shimura isomorphism
In this section, we recall how the representation
![]() $\pi $
contributes to the cohomology of the locally symmetric space attached to G.
$\pi $
contributes to the cohomology of the locally symmetric space attached to G.
1.1.1. Weights and coefficient modules
Let
![]() $k\geq 0$
be an even integer. For any ring R, we let
$k\geq 0$
be an even integer. For any ring R, we let
![]() $V_{k}(R)\subseteq R[X,Y]$
be the space of homogeneous polynomials of degree k with
$V_{k}(R)\subseteq R[X,Y]$
be the space of homogeneous polynomials of degree k with
![]() $\operatorname { {PGL}}_2(R)$
-action given by
$\operatorname { {PGL}}_2(R)$
-action given by
 $$\begin{align*}(g.f)(X,Y)=\operatorname{det}(g)^{-k/2}f(bY+dX, aY+cX)\ \text{for}\ g=\begin{pmatrix} a & b \\ c& d \end{pmatrix}\in \operatorname{{PGL}}_2(R). \end{align*}$$
$$\begin{align*}(g.f)(X,Y)=\operatorname{det}(g)^{-k/2}f(bY+dX, aY+cX)\ \text{for}\ g=\begin{pmatrix} a & b \\ c& d \end{pmatrix}\in \operatorname{{PGL}}_2(R). \end{align*}$$
We may attach to
![]() $f\in V_{k}(R)$
an R-valued function
$f\in V_{k}(R)$
an R-valued function
![]() $\psi _f$
on
$\psi _f$
on
![]() $\operatorname { {PGL}}_2(R)$
via
$\operatorname { {PGL}}_2(R)$
via
In case
 $b=\begin {pmatrix}b_1 & u\\ 0 & b_2 \end {pmatrix}$
is an upper triangular matrix, we have
$b=\begin {pmatrix}b_1 & u\\ 0 & b_2 \end {pmatrix}$
is an upper triangular matrix, we have
 $$ \begin{align} \nonumber \psi_f(bg)=(bg.f)(1,0) &=(b.(g.f))(1,0)\\ &= b_1^{-k/2} b_2^{k/2} \cdot (g.f)(1,0)\\ \nonumber &= b_1^{-k/2} b_2^{k/2} \cdot \psi_f(g) \end{align} $$
$$ \begin{align} \nonumber \psi_f(bg)=(bg.f)(1,0) &=(b.(g.f))(1,0)\\ &= b_1^{-k/2} b_2^{k/2} \cdot (g.f)(1,0)\\ \nonumber &= b_1^{-k/2} b_2^{k/2} \cdot \psi_f(g) \end{align} $$
for all
![]() $g\in \operatorname { {PGL}}_2(R)$
.
$g\in \operatorname { {PGL}}_2(R)$
.
Given a weight
![]() $\boldsymbol {k}=(k_\sigma )_{\sigma \in \Sigma }\in 2\mathbb {Z}_{\geq 0}[\Sigma ]$
we define the
$\boldsymbol {k}=(k_\sigma )_{\sigma \in \Sigma }\in 2\mathbb {Z}_{\geq 0}[\Sigma ]$
we define the
![]() $\operatorname { {PGL}}_2(R)^{\Sigma }$
-representation
$\operatorname { {PGL}}_2(R)^{\Sigma }$
-representation
and
![]() $V_{{\boldsymbol {k}}}(R)^\vee $
as the R-linear dual of
$V_{{\boldsymbol {k}}}(R)^\vee $
as the R-linear dual of
![]() $V_{{\boldsymbol {k}}}(R).$
One may view
$V_{{\boldsymbol {k}}}(R).$
One may view
![]() $V_{\boldsymbol {k}}(\mathbb {C})$
as a representation of
$V_{\boldsymbol {k}}(\mathbb {C})$
as a representation of
![]() $G(F)$
via the embedding j. In fact, there exists a number field
$G(F)$
via the embedding j. In fact, there exists a number field
![]() $E\subseteq \mathbb {C}$
such that every embedding
$E\subseteq \mathbb {C}$
such that every embedding
![]() $\sigma \colon F\hookrightarrow \mathbb {C}$
factors over E and such that
$\sigma \colon F\hookrightarrow \mathbb {C}$
factors over E and such that
![]() $G(F)$
acts on
$G(F)$
acts on
![]() $V_{\boldsymbol {k}}(E)\subseteq V_{\boldsymbol {k}}(\mathbb {C})$
. We fix E for the remainder of the article.
$V_{\boldsymbol {k}}(E)\subseteq V_{\boldsymbol {k}}(\mathbb {C})$
. We fix E for the remainder of the article.
1.1.2.
 $(\mathfrak {g},K_\infty ^+)$
-cohomology
$(\mathfrak {g},K_\infty ^+)$
-cohomology
Let
![]() $\mathfrak {g}$
denote the complexification of the Lie algebra of
$\mathfrak {g}$
denote the complexification of the Lie algebra of
![]() $G_\infty $
. We fix a maximal compact subgroup
$G_\infty $
. We fix a maximal compact subgroup
![]() $K_\infty $
of
$K_\infty $
of
![]() $G_\infty $
with connected component
$G_\infty $
with connected component
![]() $K_\infty ^+$
. Let us recall that
$K_\infty ^+$
. Let us recall that
![]() $\pi $
is cohomological if and only if there exists a weight
$\pi $
is cohomological if and only if there exists a weight
![]() $\boldsymbol {k}=(k_\sigma )_{\sigma \in \Sigma }$
such that
$\boldsymbol {k}=(k_\sigma )_{\sigma \in \Sigma }$
such that
See [Reference Borel and Wallach8] for the notion of
![]() $(\mathfrak {g},K_\infty ^+)$
-cohomology. The weight
$(\mathfrak {g},K_\infty ^+)$
-cohomology. The weight
![]() $\boldsymbol {k}$
is uniquely determined by
$\boldsymbol {k}$
is uniquely determined by
![]() $\pi _\infty $
, and we fix it from here on. By [Reference Harder28, 3.6.1], the equality
$\pi _\infty $
, and we fix it from here on. By [Reference Harder28, 3.6.1], the equality
holds for all
![]() $\sigma \in \Sigma $
. The group
$\sigma \in \Sigma $
. The group
![]() $\pi _0(G_\infty )\cong \pi _0(K_\infty )$
acts on
$\pi _0(G_\infty )\cong \pi _0(K_\infty )$
acts on
![]() $(\mathfrak {g},K_\infty ^+)$
-cohomology. For every character
$(\mathfrak {g},K_\infty ^+)$
-cohomology. For every character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
we have the following dimension formulas for the
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
we have the following dimension formulas for the
![]() $\epsilon $
-isotypic component:
$\epsilon $
-isotypic component:
 $$ \begin{align} \dim_{\mathbb{C}}\mathrm{{H}}^{i}(\mathfrak{g},K_\infty^+,\pi_\infty \otimes V_{\boldsymbol{k}}(\mathbb{C})^\vee)^\epsilon =\binom{\delta}{i-q}. \end{align} $$
$$ \begin{align} \dim_{\mathbb{C}}\mathrm{{H}}^{i}(\mathfrak{g},K_\infty^+,\pi_\infty \otimes V_{\boldsymbol{k}}(\mathbb{C})^\vee)^\epsilon =\binom{\delta}{i-q}. \end{align} $$
Via the Künneth theorem one may reduce the computation to that of the cohomology for each place
![]() $\mathfrak {q}\mid \infty $
separately. In case
$\mathfrak {q}\mid \infty $
separately. In case
![]() $G_{\mathfrak {q}}$
is split, the computation is spelled out in [Reference Harder28, Section 3.6.2]. The nonsplit case is trivial.
$G_{\mathfrak {q}}$
is split, the computation is spelled out in [Reference Harder28, Section 3.6.2]. The nonsplit case is trivial.
1.1.3. Local systems
Let us fix an open compact subgroup
![]() $K\subseteq G(\mathbb {A}^\infty )$
and consider the locally symmetric space
$K\subseteq G(\mathbb {A}^\infty )$
and consider the locally symmetric space
together with the projection map
Let
![]() $\{g_1,\ldots ,g_h\}$
be a set of representatives of the finite double coset
$\{g_1,\ldots ,g_h\}$
be a set of representatives of the finite double coset
and put
These are discrete subgroups of the real Lie group
![]() $G(F_\infty )^+$
. We may decompose
$G(F_\infty )^+$
. We may decompose
 $$ \begin{align} \mathcal{X}_K= \bigcup_{i=1}^{h} \Gamma^{g_i}\backslash G(F_\infty)^+/K_\infty^+. \end{align} $$
$$ \begin{align} \mathcal{X}_K= \bigcup_{i=1}^{h} \Gamma^{g_i}\backslash G(F_\infty)^+/K_\infty^+. \end{align} $$
If K is neat, then
![]() $\Gamma ^{g_i}$
is torsion free for every
$\Gamma ^{g_i}$
is torsion free for every
![]() $i=1,\ldots ,h$
and, thus, the topological space
$i=1,\ldots ,h$
and, thus, the topological space
![]() $\mathcal {X}_K$
carries the structure of a locally symmetric space.
$\mathcal {X}_K$
carries the structure of a locally symmetric space.
We fix a field
![]() $\Omega $
of characteristic zero. Given an
$\Omega $
of characteristic zero. Given an
![]() $\Omega [G(F)]$
-module N define the sheaf
$\Omega [G(F)]$
-module N define the sheaf
![]() $\underline {N}$
on
$\underline {N}$
on
![]() $\mathcal {X}_K$
by
$\mathcal {X}_K$
by
In case K is neat,
![]() $\underline {N}$
is a local system. In any case, the group of global sections of
$\underline {N}$
is a local system. In any case, the group of global sections of
![]() $\underline {N}$
is given by
$\underline {N}$
is given by
where
![]() $G(F)$
acts on
$G(F)$
acts on
![]() $\mathcal {F}(G(\mathbb {A})/G(F_\infty )^{+} K , N)$
via
$\mathcal {F}(G(\mathbb {A})/G(F_\infty )^{+} K , N)$
via
![]() $(\gamma .f)(g)=\gamma .f(\gamma ^{-1}g)$
. Right translation defines commuting actions of the component group
$(\gamma .f)(g)=\gamma .f(\gamma ^{-1}g)$
. Right translation defines commuting actions of the component group
![]() $\pi _0(G_\infty )$
and the Hecke algebra
$\pi _0(G_\infty )$
and the Hecke algebra
![]() $\mathbb {T}_K(\Omega ):=\Omega [K\backslash G(\mathbb {A}^\infty )/K]$
of level K on
$\mathbb {T}_K(\Omega ):=\Omega [K\backslash G(\mathbb {A}^\infty )/K]$
of level K on
![]() $\underline {N}$
-valued cohomology
$\underline {N}$
-valued cohomology
![]() $\mathrm{{H}}^\bullet (\mathcal {X}_K,\underline {N})$
.
$\mathrm{{H}}^\bullet (\mathcal {X}_K,\underline {N})$
.
We assume in the following that K is of the form
![]() $K=\prod _{\mathfrak {q}}K_{\mathfrak {q}}$
and that
$K=\prod _{\mathfrak {q}}K_{\mathfrak {q}}$
and that
Let S be a finite set of primes of F such that S contains every
![]() $\mathfrak {q}$
such that
$\mathfrak {q}$
such that
![]() $K_{\mathfrak {q}}$
is not maximal and put
$K_{\mathfrak {q}}$
is not maximal and put
![]() $K^S=\prod _{\mathfrak {q}\notin S}K_{\mathfrak {q}}$
. The Hecke algebra
$K^S=\prod _{\mathfrak {q}\notin S}K_{\mathfrak {q}}$
. The Hecke algebra
away from S is central in
![]() $\mathbb {T}_K(\Omega )$
. We will assume for the rest of this article that
$\mathbb {T}_K(\Omega )$
. We will assume for the rest of this article that
![]() $\pi ^\infty $
has a model over E, which we denote
$\pi ^\infty $
has a model over E, which we denote
![]() $\pi _E^\infty .$
We may always assume this by enlarging E slightly (see [Reference Januszewski29, Theorem C]). If
$\pi _E^\infty .$
We may always assume this by enlarging E slightly (see [Reference Januszewski29, Theorem C]). If
![]() $\Omega $
is an extension of E, we put
$\Omega $
is an extension of E, we put
![]() $\pi _\Omega ^\infty =\pi _E^\infty \otimes _E \Omega $
. The Hecke algebra
$\pi _\Omega ^\infty =\pi _E^\infty \otimes _E \Omega $
. The Hecke algebra
![]() $\mathbb {T}_{K^S}^S(\Omega )$
acts on
$\mathbb {T}_{K^S}^S(\Omega )$
acts on
![]() $\pi _\Omega ^\infty $
. For every
$\pi _\Omega ^\infty $
. For every
![]() $\mathfrak {q}\notin S$
, the subgroup
$\mathfrak {q}\notin S$
, the subgroup
![]() $K_{\mathfrak {q}}\subset G_{\mathfrak {q}}$
is a maximal open compact subgroup and, thus, by Casselman’s theorem on newforms (see [Reference Casselman13]) we have
$K_{\mathfrak {q}}\subset G_{\mathfrak {q}}$
is a maximal open compact subgroup and, thus, by Casselman’s theorem on newforms (see [Reference Casselman13]) we have
It follows that
![]() $\mathbb {T}_{K^S}^S(\Omega )$
acts on
$\mathbb {T}_{K^S}^S(\Omega )$
acts on
![]() $(\pi _\Omega ^\infty )^K$
via a character
$(\pi _\Omega ^\infty )^K$
via a character
Let
![]() $\mathfrak {m}_\pi ^S\subseteq \mathbb {T}_{K^S}^S(\Omega )$
be the kernel of
$\mathfrak {m}_\pi ^S\subseteq \mathbb {T}_{K^S}^S(\Omega )$
be the kernel of
![]() $\lambda _\pi ^S$
. It is a maximal ideal. Let M be a
$\lambda _\pi ^S$
. It is a maximal ideal. Let M be a
![]() $\mathbb {T}_K(\Omega )$
-module. Since
$\mathbb {T}_K(\Omega )$
-module. Since
![]() $\mathbb {T}_{K^S}^S(\Omega )\subseteq \mathbb {T}_K(\Omega )$
is a central subalgebra it follows that
$\mathbb {T}_{K^S}^S(\Omega )\subseteq \mathbb {T}_K(\Omega )$
is a central subalgebra it follows that
![]() $\mathbb {T}_K(\Omega )$
acts on the localization
$\mathbb {T}_K(\Omega )$
acts on the localization
![]() $M_{\mathfrak {m}_\pi ^S}$
.
$M_{\mathfrak {m}_\pi ^S}$
.
Theorem 1.1. Let
![]() $\Omega $
be any extension of E. For every character
$\Omega $
be any extension of E. For every character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
we have
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
we have
 $$\begin{align*}\dim_\Omega \operatorname{{Hom}}_{\mathbb{T}_K(\Omega)}((\pi_\Omega^\infty)^K, \mathrm{{H}}^i(\mathcal{X}_K,\underline{V_{\boldsymbol{k}}(\Omega)^\vee})^\epsilon) =\binom{\delta}{i-q}. \end{align*}$$
$$\begin{align*}\dim_\Omega \operatorname{{Hom}}_{\mathbb{T}_K(\Omega)}((\pi_\Omega^\infty)^K, \mathrm{{H}}^i(\mathcal{X}_K,\underline{V_{\boldsymbol{k}}(\Omega)^\vee})^\epsilon) =\binom{\delta}{i-q}. \end{align*}$$
Moreover, the localization
![]() $\mathrm{{H}}^i(\mathcal {X}_K,\underline {V_{\boldsymbol {k}}(\Omega )^\vee })_{\mathfrak {m}_\pi ^S}$
is equal to the sum of the images of all homomorphisms from
$\mathrm{{H}}^i(\mathcal {X}_K,\underline {V_{\boldsymbol {k}}(\Omega )^\vee })_{\mathfrak {m}_\pi ^S}$
is equal to the sum of the images of all homomorphisms from
![]() $(\pi _\Omega ^\infty )^K$
to
$(\pi _\Omega ^\infty )^K$
to
![]() $\mathrm{{H}}^i(\mathcal {X}_K,\underline {V_{\boldsymbol {k}}(\Omega )^\vee })$
.
$\mathrm{{H}}^i(\mathcal {X}_K,\underline {V_{\boldsymbol {k}}(\Omega )^\vee })$
.
Proof. The Borel–Serre compactification
![]() $\bar {\mathcal {X}}_K$
of
$\bar {\mathcal {X}}_K$
of
![]() $\mathcal {X}_K$
(see [Reference Borel and Serre7]) is homotopic to
$\mathcal {X}_K$
(see [Reference Borel and Serre7]) is homotopic to
![]() $\mathcal {X}_K$
and every local system – such as
$\mathcal {X}_K$
and every local system – such as
![]() $\underline {V_{\boldsymbol {k}}(\Omega )^\vee }$
– naturally extends to it. Moreover, it is homeomorphic to a compact manifold with boundary and, thus, has a finite triangulation. One deduces that the canonical map
$\underline {V_{\boldsymbol {k}}(\Omega )^\vee }$
– naturally extends to it. Moreover, it is homeomorphic to a compact manifold with boundary and, thus, has a finite triangulation. One deduces that the canonical map
is an isomorphism for every extension
![]() $\Omega $
of E. Thus, we may reduce to the case
$\Omega $
of E. Thus, we may reduce to the case
![]() $\Omega =\mathbb {C}$
. In that case, the first claim follows from standard arguments about cohomological representations and Equation (1.3) (see, for example, [Reference Harder28, Section II] for details in the case G is split).
$\Omega =\mathbb {C}$
. In that case, the first claim follows from standard arguments about cohomological representations and Equation (1.3) (see, for example, [Reference Harder28, Section II] for details in the case G is split).
The second claim follows from strong multiplicity one.
1.1.4. Cohomology of arithmetic groups
We are going to recast the above cohomology groups in terms of group cohomology. Let
![]() $K\subseteq G(\mathbb {A}^\infty )$
be an open compact subgroup and N an
$K\subseteq G(\mathbb {A}^\infty )$
be an open compact subgroup and N an
![]() $\Omega [G(F)]$
-module. The group
$\Omega [G(F)]$
-module. The group
![]() $G(F)$
acts on the space
$G(F)$
acts on the space
![]() $\mathcal {F}(G(\mathbb {A}^\infty )/K,N)$
via
$\mathcal {F}(G(\mathbb {A}^\infty )/K,N)$
via
![]() $(\gamma .f)(g)=\gamma .f(\gamma ^{-1}g)$
and the Hecke algebra
$(\gamma .f)(g)=\gamma .f(\gamma ^{-1}g)$
and the Hecke algebra
![]() $\mathbb {T}_K(\Omega )$
via right translation. Thus, we have commuting actions of the component group
$\mathbb {T}_K(\Omega )$
via right translation. Thus, we have commuting actions of the component group
![]() $\pi _0(G_\infty )$
and the Hecke algebra
$\pi _0(G_\infty )$
and the Hecke algebra
![]() $\mathbb {T}_K(\Omega )=\Omega [K\backslash G(\mathbb {A}^\infty )/K]$
on the spaces
$\mathbb {T}_K(\Omega )=\Omega [K\backslash G(\mathbb {A}^\infty )/K]$
on the spaces
Lemma 1.2. There are canonical isomorphisms
that are equivariant with respect to the actions of the component group and the Hecke algebra.
Proof. The proof is rather standard. For the sake of completeness, we give a sketch of it. Since the homomorphism
![]() $G(F)\to \pi _0(G(F_\infty ))$
is surjective, Frobenius reciprocity implies that
$G(F)\to \pi _0(G(F_\infty ))$
is surjective, Frobenius reciprocity implies that
 $$ \begin{align*} \mathrm{{H}}^0(X_K,N)&=\mathcal{F}(G(\mathbb{A}^\infty)/K,N)^{G(F)^{+}}\\ &=\mathcal{F}(G(\mathbb{A})/G(F_\infty)^+K,N)^{G(F)}\\ &=\Gamma(\mathcal{X}_K,\underline{N}). \end{align*} $$
$$ \begin{align*} \mathrm{{H}}^0(X_K,N)&=\mathcal{F}(G(\mathbb{A}^\infty)/K,N)^{G(F)^{+}}\\ &=\mathcal{F}(G(\mathbb{A})/G(F_\infty)^+K,N)^{G(F)}\\ &=\Gamma(\mathcal{X}_K,\underline{N}). \end{align*} $$
The assignment
![]() $N\mapsto \mathrm{{H}}^\bullet (X_K,N)$
defines an effaceable
$N\mapsto \mathrm{{H}}^\bullet (X_K,N)$
defines an effaceable
![]() $\delta $
-functor. Thus, by [Reference Grothendieck26, Proposition 2.2.1] it is enough to prove that the assignment
$\delta $
-functor. Thus, by [Reference Grothendieck26, Proposition 2.2.1] it is enough to prove that the assignment
![]() $N\mapsto \mathrm{{H}}^\bullet (\mathcal {X}_K,N)$
defines an effaceable
$N\mapsto \mathrm{{H}}^\bullet (\mathcal {X}_K,N)$
defines an effaceable
![]() $\delta $
-functor as well. It suffices to show that the functor
$\delta $
-functor as well. It suffices to show that the functor
![]() $N \mapsto \underline {N}$
from the category of
$N \mapsto \underline {N}$
from the category of
![]() $\Omega [G(F)]$
-modules to the category of sheaves on
$\Omega [G(F)]$
-modules to the category of sheaves on
![]() $\mathcal {X}_K$
sends injective
$\mathcal {X}_K$
sends injective
![]() $G(F)$
-modules to acyclic sheaves and is exact.
$G(F)$
-modules to acyclic sheaves and is exact.
Firstly, as every injective
![]() $G(F)$
-modules is a direct summand of a coinduced module, it is enough to check that sheaves associated to coinduced modules are acyclic. Let V be a
$G(F)$
-modules is a direct summand of a coinduced module, it is enough to check that sheaves associated to coinduced modules are acyclic. Let V be a
![]() $\Omega $
-vector space. Consider the coinduced
$\Omega $
-vector space. Consider the coinduced
![]() $G(F)$
-module
$G(F)$
-module
![]() $\operatorname { {Coind}}_{1}^{G(F)}V$
as well as the constant sheaf
$\operatorname { {Coind}}_{1}^{G(F)}V$
as well as the constant sheaf
![]() $\tilde {V}$
on
$\tilde {V}$
on
![]() $G(\mathbb {A}) / K K_\infty ^+$
. One readily computes that
$G(\mathbb {A}) / K K_\infty ^+$
. One readily computes that
Since the fibres of
![]() $p_K$
are discrete, the higher direct images
$p_K$
are discrete, the higher direct images
![]() $R^q(p_K)(\tilde {V})$
vanish and we get
$R^q(p_K)(\tilde {V})$
vanish and we get
Since
![]() $G(\mathbb {A}) / K K_\infty ^+$
is a disjoint union of contractible spaces, the claim follows.
$G(\mathbb {A}) / K K_\infty ^+$
is a disjoint union of contractible spaces, the claim follows.
Secondly, to prove exactness it is enough to check exactness at the level of stalks. Let x be a point of
![]() $\mathcal {X}_K$
and
$\mathcal {X}_K$
and
![]() $g_i \in G(F)^+$
such that x lives in the connected component corresponding to
$g_i \in G(F)^+$
such that x lives in the connected component corresponding to
![]() $g_i$
with respect to the decomposition (1.4). Consider a preimage
$g_i$
with respect to the decomposition (1.4). Consider a preimage
![]() $\tilde {x}\in G(F_\infty )^{+}/K_\infty ^+$
of x and denote by
$\tilde {x}\in G(F_\infty )^{+}/K_\infty ^+$
of x and denote by
![]() $\Gamma ^{g_i}_{\tilde {x}}\subseteq \Gamma ^{g_i}$
the stabilizer of
$\Gamma ^{g_i}_{\tilde {x}}\subseteq \Gamma ^{g_i}$
the stabilizer of
![]() $\tilde {x}$
in
$\tilde {x}$
in
![]() $\Gamma ^{g_i}$
. The stalk of
$\Gamma ^{g_i}$
. The stalk of
![]() $\underline {N}$
at x is given by
$\underline {N}$
at x is given by
Exactness follows since the group
![]() $\Gamma ^{g_i}_{\tilde {x}}$
is finite and, hence, taking invariance in characteristic zero is exact.
$\Gamma ^{g_i}_{\tilde {x}}$
is finite and, hence, taking invariance in characteristic zero is exact.
1.2. Cohomology of
 $\mathfrak {p}$
-arithmetic groups
$\mathfrak {p}$
-arithmetic groups
Let
![]() $\mathfrak {p}$
be a prime of F and
$\mathfrak {p}$
be a prime of F and
![]() $\Omega $
a field of characteristic zero. Given an open compact subgroup
$\Omega $
a field of characteristic zero. Given an open compact subgroup
![]() ${K^{\mathfrak {p}}\subseteq G(\mathbb {A}^{\mathfrak {p},\infty })}$
, an
${K^{\mathfrak {p}}\subseteq G(\mathbb {A}^{\mathfrak {p},\infty })}$
, an
![]() $\Omega [G_{\mathfrak {p}}]$
-module M and an
$\Omega [G_{\mathfrak {p}}]$
-module M and an
![]() $\Omega [G(F)]$
-module N, we let
$\Omega [G(F)]$
-module N, we let
![]() $G(F)$
act on the
$G(F)$
act on the
![]() $\Omega $
-vector space
$\Omega $
-vector space
![]() $\mathcal {F}(G(\mathbb {A}^{\mathfrak {p},\infty })/K^{\mathfrak {p}},\operatorname { {Hom}}_\Omega (M,N))$
via
$\mathcal {F}(G(\mathbb {A}^{\mathfrak {p},\infty })/K^{\mathfrak {p}},\operatorname { {Hom}}_\Omega (M,N))$
via
![]() $(\gamma .f)(g)(m)=\gamma .f(\gamma ^{-1}g)(\gamma ^{-1}(m))$
and put
$(\gamma .f)(g)(m)=\gamma .f(\gamma ^{-1}g)(\gamma ^{-1}(m))$
and put
These cohomology groups carry commuting actions of the component group
![]() $\pi _0(G_\infty )$
and the Hecke algebra
$\pi _0(G_\infty )$
and the Hecke algebra
In case
![]() $M=\Omega $
with the trivial
$M=\Omega $
with the trivial
![]() $G_{\mathfrak {p}}$
-action, we put
$G_{\mathfrak {p}}$
-action, we put
Suppose that
![]() $M=M_1\otimes _\Omega M_2$
with both
$M=M_1\otimes _\Omega M_2$
with both
![]() $M_1$
and
$M_1$
and
![]() $M_2$
being
$M_2$
being
![]() $\Omega [G_{\mathfrak {p}}]$
-modules. Then by definition, we have
$\Omega [G_{\mathfrak {p}}]$
-modules. Then by definition, we have
where
![]() $G(F)$
acts on
$G(F)$
acts on
![]() $M_2$
via the embedding
$M_2$
via the embedding
![]() $G(F)\hookrightarrow G_{\mathfrak {p}}.$
For later purposes, we also define the following continuous variant: Let A be an affinoid
$G(F)\hookrightarrow G_{\mathfrak {p}}.$
For later purposes, we also define the following continuous variant: Let A be an affinoid
![]() $\mathbb {Q}_p$
-algebra. Given a continuous A-module M with a continuous
$\mathbb {Q}_p$
-algebra. Given a continuous A-module M with a continuous
![]() $G_{\mathfrak {p}}$
-action and an
$G_{\mathfrak {p}}$
-action and an
![]() $A[G(F)]$
-module N that is finitely generated and free over A, we put
$A[G(F)]$
-module N that is finitely generated and free over A, we put
It also carries actions by the Hecke algebra
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(A):=A[K^{\mathfrak {p}}\backslash G(\mathbb {A}^{\mathfrak {p},\infty })/K^{\mathfrak {p}}]$
and the component group
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(A):=A[K^{\mathfrak {p}}\backslash G(\mathbb {A}^{\mathfrak {p},\infty })/K^{\mathfrak {p}}]$
and the component group
![]() $\pi _0(G_\infty )$
.
$\pi _0(G_\infty )$
.
Let us discuss an example of the above construction. First, we are going to recall the notion of compact induction: Let
![]() $K_{\mathfrak {p}}\subset G_{\mathfrak {p}}$
be an open compact subgroup and L a
$K_{\mathfrak {p}}\subset G_{\mathfrak {p}}$
be an open compact subgroup and L a
![]() $\Omega [K_{\mathfrak {p}}]$
-module. The compact induction
$\Omega [K_{\mathfrak {p}}]$
-module. The compact induction
![]() $\operatorname {{c-ind}}_{K_{\mathfrak {p}}}^{G_{\mathfrak {p}}}L$
of L to
$\operatorname {{c-ind}}_{K_{\mathfrak {p}}}^{G_{\mathfrak {p}}}L$
of L to
![]() $G_{\mathfrak {p}}$
is given by the set of functions
$G_{\mathfrak {p}}$
is given by the set of functions
![]() $f\colon G_{\mathfrak {p}}\to L$
that satisfy
$f\colon G_{\mathfrak {p}}\to L$
that satisfy
![]() $f(gk) = k^{-1}.f(g)$
for all
$f(gk) = k^{-1}.f(g)$
for all
![]() $g\in G_{\mathfrak {p}}$
,
$g\in G_{\mathfrak {p}}$
,
![]() $k\in K_{\mathfrak {p}}$
and have finite support modulo
$k\in K_{\mathfrak {p}}$
and have finite support modulo
![]() $K_{\mathfrak {p}}$
. The group
$K_{\mathfrak {p}}$
. The group
![]() $G_{\mathfrak {p}}$
acts on
$G_{\mathfrak {p}}$
acts on
![]() $\operatorname { {c-ind}}_{K_{\mathfrak {p}}}^{G_{\mathfrak {p}}}L$
via left translation. If L is a
$\operatorname { {c-ind}}_{K_{\mathfrak {p}}}^{G_{\mathfrak {p}}}L$
via left translation. If L is a
![]() $\Omega [G_{\mathfrak {p}}]$
-module, the map
$\Omega [G_{\mathfrak {p}}]$
-module, the map
is a
![]() $G_{\mathfrak {p}}$
-equivariant isomorphism. For any
$G_{\mathfrak {p}}$
-equivariant isomorphism. For any
![]() $\Omega [G(F)]$
-module N, the bilinear pairing
$\Omega [G(F)]$
-module N, the bilinear pairing
 $$\begin{align*}\mathcal{F}(G_{\mathfrak{p}}/K_{\mathfrak{p}}, N) \times \operatorname{{c-ind}}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}\Omega \longrightarrow N,\quad (f_1,f_2)\longmapsto \sum_{k\in G_{\mathfrak{p}}/K_{\mathfrak{p}}} f_1(g)\cdot f_2(g) \end{align*}$$
$$\begin{align*}\mathcal{F}(G_{\mathfrak{p}}/K_{\mathfrak{p}}, N) \times \operatorname{{c-ind}}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}\Omega \longrightarrow N,\quad (f_1,f_2)\longmapsto \sum_{k\in G_{\mathfrak{p}}/K_{\mathfrak{p}}} f_1(g)\cdot f_2(g) \end{align*}$$
induces an isomorphism
of
![]() $G(F)$
-modules. This in turn induces a canonical
$G(F)$
-modules. This in turn induces a canonical
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant isomorphism
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant isomorphism
for every
![]() $i\geq 0$
. More generally, by using Equation (1.5) we get canonical
$i\geq 0$
. More generally, by using Equation (1.5) we get canonical
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant isomorphisms
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant isomorphisms
Consider the projective limit
taken over all open compact subgroups
![]() $K_{\mathfrak {p}}\subseteq G_{\mathfrak {p}}.$
This space carries commuting actions of
$K_{\mathfrak {p}}\subseteq G_{\mathfrak {p}}.$
This space carries commuting actions of
![]() $\pi _0(G_\infty )$
,
$\pi _0(G_\infty )$
,
![]() $G_{\mathfrak {p}}$
and
$G_{\mathfrak {p}}$
and
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
. Since
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
. Since
![]() $\Omega $
has characteristic
$\Omega $
has characteristic
![]() $0$
, one deduces that the canonical map
$0$
, one deduces that the canonical map
is an isomorphism for all open compact subgroups
![]() $K_{\mathfrak {p}}\subseteq G_{\mathfrak {p}}$
. Thus,
$K_{\mathfrak {p}}\subseteq G_{\mathfrak {p}}$
. Thus,
![]() $\tilde {\mathrm{{H}}}^i(X_{K^{\mathfrak {p}}},N)$
is a smooth representation of
$\tilde {\mathrm{{H}}}^i(X_{K^{\mathfrak {p}}},N)$
is a smooth representation of
![]() $G_{\mathfrak {p}}$
. Moreover, it is admissible in case N is finite-dimensional. The goal of this section is to compare
$G_{\mathfrak {p}}$
. Moreover, it is admissible in case N is finite-dimensional. The goal of this section is to compare
![]() $\operatorname { {Hom}}_{\Omega [G_{\mathfrak {p}}]}(M,\tilde {\mathrm{{H}}}^i(X_{K^{\mathfrak {p}}},N))$
and
$\operatorname { {Hom}}_{\Omega [G_{\mathfrak {p}}]}(M,\tilde {\mathrm{{H}}}^i(X_{K^{\mathfrak {p}}},N))$
and
![]() $\mathrm{{H}}^i_{\Omega }(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},M,N)$
in certain situations.
$\mathrm{{H}}^i_{\Omega }(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},M,N)$
in certain situations.
Lemma 1.3. Let M be a smooth
![]() $\Omega [G_{\mathfrak {p}}]$
-representation of finite length. Then, there exists a resolution
$\Omega [G_{\mathfrak {p}}]$
-representation of finite length. Then, there exists a resolution
where
![]() $P_i$
,
$P_i$
,
![]() $i=0,1$
are finitely generated projective smooth representations.
$i=0,1$
are finitely generated projective smooth representations.
Proof. In case
![]() $\mathfrak {p}\in \operatorname { {ram}}(D)$
, the group
$\mathfrak {p}\in \operatorname { {ram}}(D)$
, the group
![]() $G_{\mathfrak {p}}$
is compact. Thus, the category of smooth representations of
$G_{\mathfrak {p}}$
is compact. Thus, the category of smooth representations of
![]() $G_{\mathfrak {p}}$
with
$G_{\mathfrak {p}}$
with
![]() $\Omega $
-coefficients is semisimple and M is projective itself. In case D is split at
$\Omega $
-coefficients is semisimple and M is projective itself. In case D is split at
![]() $\mathfrak {p}$
and therefore
$\mathfrak {p}$
and therefore
![]() $G_{\mathfrak {p}}\cong \operatorname { {PGL}}_2(F_{\mathfrak {p}})$
, this is a consequence of the main theorem of [Reference Schneider and Stuhler36].
$G_{\mathfrak {p}}\cong \operatorname { {PGL}}_2(F_{\mathfrak {p}})$
, this is a consequence of the main theorem of [Reference Schneider and Stuhler36].
Let
![]() $\pi ^{\mathfrak {p},\infty }$
be the restricted tensor product of all local components of
$\pi ^{\mathfrak {p},\infty }$
be the restricted tensor product of all local components of
![]() $\pi $
away from
$\pi $
away from
![]() $\mathfrak {p}$
and
$\mathfrak {p}$
and
![]() $\infty $
. This is a smooth irreducible representation of
$\infty $
. This is a smooth irreducible representation of
![]() $G(\mathbb {A}^{\mathfrak {p},\infty })$
. We fix models
$G(\mathbb {A}^{\mathfrak {p},\infty })$
. We fix models
![]() $\pi _E^{\mathfrak {p},\infty }$
, respectively
$\pi _E^{\mathfrak {p},\infty }$
, respectively
![]() $\pi _{\mathfrak {p},E}$
of
$\pi _{\mathfrak {p},E}$
of
![]() $\pi ^{\mathfrak {p},\infty }$
, respectively
$\pi ^{\mathfrak {p},\infty }$
, respectively
![]() $\pi _{\mathfrak {p}}$
over E and a
$\pi _{\mathfrak {p}}$
over E and a
![]() $G(\mathbb {A}^\infty )$
-equivariant isomorphism
$G(\mathbb {A}^\infty )$
-equivariant isomorphism
From now on,
![]() $\Omega $
will always be an extension of E and we put
$\Omega $
will always be an extension of E and we put
![]() $\pi _\Omega ^{\mathfrak {p},\infty }=\pi _E^{\mathfrak {p},\infty }\otimes _E \Omega $
as well as
$\pi _\Omega ^{\mathfrak {p},\infty }=\pi _E^{\mathfrak {p},\infty }\otimes _E \Omega $
as well as
![]() $\pi _{\mathfrak {p},\Omega }=\pi _{\mathfrak {p},E}\otimes _E \Omega $
. Further, we assume that
$\pi _{\mathfrak {p},\Omega }=\pi _{\mathfrak {p},E}\otimes _E \Omega $
. Further, we assume that
![]() $K^{\mathfrak {p}}$
is of the form
$K^{\mathfrak {p}}$
is of the form
![]() $K^{\mathfrak {p}}=\prod _{\mathfrak {q}\neq \mathfrak {p}} K_{\mathfrak {q}}$
and that
$K^{\mathfrak {p}}=\prod _{\mathfrak {q}\neq \mathfrak {p}} K_{\mathfrak {q}}$
and that
![]() $(\pi _\Omega ^{\mathfrak {p},\infty })^{K^{\mathfrak {p}}}\neq 0$
. We fix a finite set S of primes of F as before such that
$(\pi _\Omega ^{\mathfrak {p},\infty })^{K^{\mathfrak {p}}}\neq 0$
. We fix a finite set S of primes of F as before such that
![]() $\mathfrak {p}\in S$
. In particular, the Hecke algebra
$\mathfrak {p}\in S$
. In particular, the Hecke algebra
![]() $T^S_{K^S}(\Omega )$
is a central subalgebra of
$T^S_{K^S}(\Omega )$
is a central subalgebra of
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
.
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
.
Proposition 1.4. Let M be a smooth
![]() $\Omega [G_{\mathfrak {p}}]$
-representation of finite length. There are isomorphisms
$\Omega [G_{\mathfrak {p}}]$
-representation of finite length. There are isomorphisms
that are functorial in M and equivariant under the actions of
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
and
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
and
![]() $\pi _0(G_\infty )$
. Furthermore, we have
$\pi _0(G_\infty )$
. Furthermore, we have
for all
![]() $d \geq 0$
.
$d \geq 0$
.
Proof. If
![]() $M=P$
is projective, there are functorial isomorphisms
$M=P$
is projective, there are functorial isomorphisms
for all
![]() $d\geq 0$
by [Reference Gehrmann24, Lemma 3.5(b)]. In particular, we have
$d\geq 0$
by [Reference Gehrmann24, Lemma 3.5(b)]. In particular, we have
for all
![]() $d<q$
by Theorem 1.1. Thus, the short exact sequence
$d<q$
by Theorem 1.1. Thus, the short exact sequence
of Lemma 1.3 induces the exact sequence
and the first claim follows from the isomorphism (1.8) for
![]() $P=P_0, P_1$
.
$P=P_0, P_1$
.
Since
![]() $\tilde {\mathrm{{H}}}^d(X_{K^{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )$
is admissible, the isomorphism (1.8) implies that
$\tilde {\mathrm{{H}}}^d(X_{K^{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )$
is admissible, the isomorphism (1.8) implies that
in case P is finitely generated and projective. For M of finite length, consider again the long exact sequence induces by the short exact sequence of Lemma 1.3.
Remark 1.5. A typical projective smooth representation is the compact induction
![]() $\operatorname { {c-ind}}_{K_{\mathfrak {p}}}^{G_{\mathfrak {p}}}\Omega $
of the trivial representation from an open compact subgroup
$\operatorname { {c-ind}}_{K_{\mathfrak {p}}}^{G_{\mathfrak {p}}}\Omega $
of the trivial representation from an open compact subgroup
![]() $K_{\mathfrak {p}}\subseteq G_{\mathfrak {p}}$
. In that case, the result of [Reference Gehrmann24] used above simply follows from the composition of isomorphisms
$K_{\mathfrak {p}}\subseteq G_{\mathfrak {p}}$
. In that case, the result of [Reference Gehrmann24] used above simply follows from the composition of isomorphisms
 $$ \begin{align*} \mathrm{{H}}^d_{\Omega}(X^{\mathfrak{p}}_{K^{\mathfrak{p}}},\operatorname{{c-ind}}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}\Omega,N) \cong &\mathrm{{H}}^d_{\Omega}(X_{K^{\mathfrak{p}}\times K_{\mathfrak{p}}},N)\\ \cong &\tilde{\mathrm{{H}}}^d(X_{K^{\mathfrak{p}}},N)^{K_{\mathfrak{p}}}\\ \cong &\operatorname{{Hom}}_{\Omega[G_{\mathfrak{p}}]}(\operatorname{{c-ind}}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}\Omega,\tilde{\mathrm{{H}}}^d(X_{K^{\mathfrak{p}}},N)), \end{align*} $$
$$ \begin{align*} \mathrm{{H}}^d_{\Omega}(X^{\mathfrak{p}}_{K^{\mathfrak{p}}},\operatorname{{c-ind}}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}\Omega,N) \cong &\mathrm{{H}}^d_{\Omega}(X_{K^{\mathfrak{p}}\times K_{\mathfrak{p}}},N)\\ \cong &\tilde{\mathrm{{H}}}^d(X_{K^{\mathfrak{p}}},N)^{K_{\mathfrak{p}}}\\ \cong &\operatorname{{Hom}}_{\Omega[G_{\mathfrak{p}}]}(\operatorname{{c-ind}}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}\Omega,\tilde{\mathrm{{H}}}^d(X_{K^{\mathfrak{p}}},N)), \end{align*} $$
where the first isomorphism is a special case of Equation (1.7) and the third follows from Frobenius reciprocity.
Proposition 1.4 together with Theorem 1.1 implies the following:
Corollary 1.6. Let
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
be a character and M an irreducible smooth
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
be a character and M an irreducible smooth
![]() $\Omega [G_{\mathfrak {p}}]$
-representation. Then
$\Omega [G_{\mathfrak {p}}]$
-representation. Then
unless
![]() $M\cong \pi _{\mathfrak {p},\Omega }.$
Furthermore, there is an isomorphism
$M\cong \pi _{\mathfrak {p},\Omega }.$
Furthermore, there is an isomorphism
of
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-modules. In particular, it is an absolutely irreducible
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-modules. In particular, it is an absolutely irreducible
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-module.
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-module.
Remark 1.7. The corollary above was implicitly proven in [Reference Spieß39] under the assumption that the local representation
![]() $\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector by using an explicit resolution of
$\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector by using an explicit resolution of
![]() $\pi _{\mathfrak {p}}$
constructed via the Bruhat–Tits tree.
$\pi _{\mathfrak {p}}$
constructed via the Bruhat–Tits tree.
1.3. The Steinberg case
We now assume that D is split at
![]() $\mathfrak {p}$
. We define the
$\mathfrak {p}$
. We define the
![]() $\Omega $
-valued smooth Steinberg representation
$\Omega $
-valued smooth Steinberg representation
![]() $\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )$
of
$\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )$
of
![]() $G_{\mathfrak {p}}$
as the space of locally constant
$G_{\mathfrak {p}}$
as the space of locally constant
![]() $\Omega $
-valued functions on
$\Omega $
-valued functions on
![]() $\mathbb {P}^1(F_{\mathfrak {p}})$
modulo constant functions. The group
$\mathbb {P}^1(F_{\mathfrak {p}})$
modulo constant functions. The group
![]() $G_{\mathfrak {p}}\cong \operatorname { {PGL}}_2(F_{\mathfrak {p}})$
naturally acts on
$G_{\mathfrak {p}}\cong \operatorname { {PGL}}_2(F_{\mathfrak {p}})$
naturally acts on
![]() $\mathbb {P}^1(F_{\mathfrak {p}})$
and thus also on
$\mathbb {P}^1(F_{\mathfrak {p}})$
and thus also on
![]() $\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega ).$
We assume for the moment that
$\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega ).$
We assume for the moment that
![]() $\pi _{\mathfrak {p}}\cong \operatorname { {St}}_{\mathfrak {p}}^\infty (\mathbb {C}).$
Then, Corollary 1.6 implies that the
$\pi _{\mathfrak {p}}\cong \operatorname { {St}}_{\mathfrak {p}}^\infty (\mathbb {C}).$
Then, Corollary 1.6 implies that the
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-module
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-module
![]() $\mathrm{{H}}^q_{\Omega }(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega ),V_{\boldsymbol {k}}(\Omega )^\vee )^{\epsilon }_{\mathfrak {m}_\pi ^{S}}$
is irreducible.
$\mathrm{{H}}^q_{\Omega }(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega ),V_{\boldsymbol {k}}(\Omega )^\vee )^{\epsilon }_{\mathfrak {m}_\pi ^{S}}$
is irreducible.
Given smooth
![]() $\Omega $
-representations V and W of
$\Omega $
-representations V and W of
![]() $G_{\mathfrak {p}}$
, we denote by
$G_{\mathfrak {p}}$
, we denote by
![]() $\operatorname { {Ext}}^i_\infty (V,W)$
the Ext-groups in the category of smooth representations. It is well known that
$\operatorname { {Ext}}^i_\infty (V,W)$
the Ext-groups in the category of smooth representations. It is well known that
 $$ \begin{align} \dim_\Omega \operatorname{{Ext}}^i_\infty(\Omega,\operatorname{{St}}_{\mathfrak{p}}^\infty(\Omega))= \begin{cases} 1 & \text{if}\ i=1\\ 0 & \text{otherwise} \end{cases} \end{align} $$
$$ \begin{align} \dim_\Omega \operatorname{{Ext}}^i_\infty(\Omega,\operatorname{{St}}_{\mathfrak{p}}^\infty(\Omega))= \begin{cases} 1 & \text{if}\ i=1\\ 0 & \text{otherwise} \end{cases} \end{align} $$
and
 $$ \begin{align} \dim_\Omega \operatorname{{Ext}}^i_\infty(\operatorname{{St}}_{\mathfrak{p}}^\infty(\Omega),\operatorname{{St}}_{\mathfrak{p}}^\infty(\Omega))= \begin{cases} 1 & \text{if}\ i=0\\ 0 & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \dim_\Omega \operatorname{{Ext}}^i_\infty(\operatorname{{St}}_{\mathfrak{p}}^\infty(\Omega),\operatorname{{St}}_{\mathfrak{p}}^\infty(\Omega))= \begin{cases} 1 & \text{if}\ i=0\\ 0 & \text{otherwise}. \end{cases} \end{align} $$
The above calculations follow directly from the existence of the following two projective resolutions:
and
Here
![]() $K_{\mathfrak {p}}=\operatorname { {PGL}}_2(\mathcal {O}_{\mathfrak {p}})$
is a maximal compact subgroup,
$K_{\mathfrak {p}}=\operatorname { {PGL}}_2(\mathcal {O}_{\mathfrak {p}})$
is a maximal compact subgroup,
![]() $J_{\mathfrak {p}}\subset G_{\mathfrak {p}}$
is an open compact subgroup that contains an Iwahori subgroup as a normal subgroup and
$J_{\mathfrak {p}}\subset G_{\mathfrak {p}}$
is an open compact subgroup that contains an Iwahori subgroup as a normal subgroup and
![]() $\chi _{-}\colon J_{\mathfrak {p}}\to \{\pm 1\}$
is a nontrivial character that is trivial on the Iwahori subgroup. The exactness of the first sequence is just a reformulation of the contractibility of the Bruhat–Tits tree. The second follows from the fact that the cohomology with compact support of the Bruhat–Tits tree is the Steinberg representation (see, for example, [Reference Spieß39, equation (18)]). To keep with our promise not to use the Bruhat–Tits tree, let us mention that alternative calculations of these Ext-groups that do not invoke the Bruhat–Tits tree – and work for more general reductive groups – can be found in [Reference Orlik32] and [Reference Dat15].
$\chi _{-}\colon J_{\mathfrak {p}}\to \{\pm 1\}$
is a nontrivial character that is trivial on the Iwahori subgroup. The exactness of the first sequence is just a reformulation of the contractibility of the Bruhat–Tits tree. The second follows from the fact that the cohomology with compact support of the Bruhat–Tits tree is the Steinberg representation (see, for example, [Reference Spieß39, equation (18)]). To keep with our promise not to use the Bruhat–Tits tree, let us mention that alternative calculations of these Ext-groups that do not invoke the Bruhat–Tits tree – and work for more general reductive groups – can be found in [Reference Orlik32] and [Reference Dat15].
Let
![]() $\mathcal {E}^\infty $
be the unique (up to multiplication by a scalar) nontrivial extension of
$\mathcal {E}^\infty $
be the unique (up to multiplication by a scalar) nontrivial extension of
![]() $\Omega $
by
$\Omega $
by
![]() $\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )$
, that is, there exists a nonsplit exact sequence
$\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )$
, that is, there exists a nonsplit exact sequence
of
![]() $G_{\mathfrak {p}}$
-modules. The short exact sequence (1.11) induces the short exact sequence
$G_{\mathfrak {p}}$
-modules. The short exact sequence (1.11) induces the short exact sequence
which in turn induces the boundary map
in cohomology. Given a character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
, we write
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
, we write
for the induced map on the
![]() $\mathfrak{m}_\pi ^{S}$
-localization of the
$\mathfrak{m}_\pi ^{S}$
-localization of the
![]() $\epsilon $
-isotypic part. It is a homomorphism of
$\epsilon $
-isotypic part. It is a homomorphism of
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-modules.
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-modules.
The following generalization of [Reference Spieß39, Lemma 6.2 (b)] holds. Its proof is an adaption of that of [Reference Gehrmann24, Lemma 3.7].
Lemma 1.8. The map
is an isomorphism for every sign character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
and every
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
and every
![]() $d\geq 0$
.
$d\geq 0$
.
Proof. We have to show that
for all
![]() $d\geq 0$
. Let
$d\geq 0$
. Let
be a projective resolution of
![]() $\mathcal {E}^\infty $
as in Lemma 1.3. Again, by [Reference Gehrmann24, Lemma 3.5(b)] we have
$\mathcal {E}^\infty $
as in Lemma 1.3. Again, by [Reference Gehrmann24, Lemma 3.5(b)] we have
for all
![]() $d\geq 0$
and
$d\geq 0$
and
![]() $i=0,1$
. As a
$i=0,1$
. As a
![]() $G_{\mathfrak {p}}$
-module
$G_{\mathfrak {p}}$
-module
![]() $\tilde {\mathrm{{H}}}^d(X_{K^{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )^\epsilon _{\mathfrak {m}_\pi ^{S}}$
is isomorphic to some copies of
$\tilde {\mathrm{{H}}}^d(X_{K^{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )^\epsilon _{\mathfrak {m}_\pi ^{S}}$
is isomorphic to some copies of
![]() $\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )$
by our assumption and Theorem 1.1. Thus, analyzing the long exact sequence induced from Equation (1.13) it is enough to show that
$\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )$
by our assumption and Theorem 1.1. Thus, analyzing the long exact sequence induced from Equation (1.13) it is enough to show that
for all
![]() $d\geq 0$
. But this follows directly from applying
$d\geq 0$
. But this follows directly from applying
![]() $\operatorname { {Ext}}_{G_{\mathfrak {p}}}(\cdot ,\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega ) )$
to the short exact sequence (1.11) and the computations (1.9) and (1.10) of dimensions of smooth Ext-groups.
$\operatorname { {Ext}}_{G_{\mathfrak {p}}}(\cdot ,\operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega ) )$
to the short exact sequence (1.11) and the computations (1.9) and (1.10) of dimensions of smooth Ext-groups.
2. Stabilizations
We explain the connection between overconvergent cohomology and the cohomology of
![]() $\mathfrak {p}$
-arithmetic subgroups with values in duals of locally analytic principal series representations. We fix a prime
$\mathfrak {p}$
-arithmetic subgroups with values in duals of locally analytic principal series representations. We fix a prime
![]() $\mathfrak {p}$
of F, at which the quaternion algebra D is split, and an embedding
$\mathfrak {p}$
of F, at which the quaternion algebra D is split, and an embedding
where p denotes the rational prime underlying
![]() $\mathfrak {p}$
. We define
$\mathfrak {p}$
. We define
![]() $E_p$
to be the completion of E with respect to the topology induced by
$E_p$
to be the completion of E with respect to the topology induced by
![]() $\iota _p$
.
$\iota _p$
.
2.1. Smooth principal series
We will give a representation-theoretic description of
![]() $\mathfrak {p}$
-stabilizations as in [Reference Gehrmann21, Section 2.2]. Most of the basic results on smooth representations of
$\mathfrak {p}$
-stabilizations as in [Reference Gehrmann21, Section 2.2]. Most of the basic results on smooth representations of
![]() $\operatorname { {PGL}}_2$
over local fields that are used in this section can be found in [Reference Bump12, Section 4.5].
$\operatorname { {PGL}}_2$
over local fields that are used in this section can be found in [Reference Bump12, Section 4.5].
As mentioned before, we may identify
![]() $G_{\mathfrak {p}}$
with
$G_{\mathfrak {p}}$
with
![]() $\operatorname { {PGL}}_2(F_{\mathfrak {p}})$
. Let B be the standard Borel subgroup of
$\operatorname { {PGL}}_2(F_{\mathfrak {p}})$
. Let B be the standard Borel subgroup of
![]() $G_{\mathfrak {p}}$
of upper triangular matrices. Given a smooth
$G_{\mathfrak {p}}$
of upper triangular matrices. Given a smooth
![]() $\Omega $
-representation
$\Omega $
-representation
![]() $\tau $
of B its smooth parabolic induction is the space
$\tau $
of B its smooth parabolic induction is the space
The group
![]() $G_{\mathfrak {p}}$
acts on
$G_{\mathfrak {p}}$
acts on
![]() $i_B(\tau )$
via right translation. We identify the spaces of locally constant characters on B with those on
$i_B(\tau )$
via right translation. We identify the spaces of locally constant characters on B with those on
![]() $F_{\mathfrak {p}}^\times $
by mapping a locally constant character
$F_{\mathfrak {p}}^\times $
by mapping a locally constant character
![]() $\chi \colon F_{\mathfrak {p}}^\times \longrightarrow \Omega ^{\times }$
to the character
$\chi \colon F_{\mathfrak {p}}^\times \longrightarrow \Omega ^{\times }$
to the character
 $$ \begin{align} B \longrightarrow \Omega^{\times},\quad \begin{pmatrix}b_1 & u \\ 0 & b_2\end{pmatrix}\longmapsto \chi(b_1/b_2). \end{align} $$
$$ \begin{align} B \longrightarrow \Omega^{\times},\quad \begin{pmatrix}b_1 & u \\ 0 & b_2\end{pmatrix}\longmapsto \chi(b_1/b_2). \end{align} $$
Definition 2.1. A
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
of
$(\chi ,\vartheta )$
of
![]() $\pi _{\Omega }$
consists of a locally constant character
$\pi _{\Omega }$
consists of a locally constant character
![]() $\chi \colon F_{\mathfrak {p}}^\times \longrightarrow \Omega ^{\times }$
together with a nonzero
$\chi \colon F_{\mathfrak {p}}^\times \longrightarrow \Omega ^{\times }$
together with a nonzero
![]() $G_{\mathfrak {p}}$
-equivariant homomorphism
$G_{\mathfrak {p}}$
-equivariant homomorphism
Let
![]() $(\chi ,\vartheta )$
be a
$(\chi ,\vartheta )$
be a
![]() $\mathfrak {p}$
-stabilization of
$\mathfrak {p}$
-stabilization of
![]() $\pi _{\Omega }$
. Since
$\pi _{\Omega }$
. Since
![]() $\pi _{\mathfrak {p},\Omega }$
is irreducible,
$\pi _{\mathfrak {p},\Omega }$
is irreducible,
![]() $\vartheta $
is automatically surjective. Moreover,
$\vartheta $
is automatically surjective. Moreover,
![]() $(\chi ,\vartheta )$
induces a
$(\chi ,\vartheta )$
induces a
![]() $\mathfrak {p}$
-stabilization of
$\mathfrak {p}$
-stabilization of
![]() $\pi _{\Omega ^\prime }$
for every extension
$\pi _{\Omega ^\prime }$
for every extension
![]() $\Omega ^\prime $
of
$\Omega ^\prime $
of
![]() $\Omega $
. By the classification of smooth irreducible representations of
$\Omega $
. By the classification of smooth irreducible representations of
![]() $G_{\mathfrak {p}}$
, we know that
$G_{\mathfrak {p}}$
, we know that
![]() $\pi _{\mathfrak {p}}$
is either supercuspidal or a quotient of a smooth parabolic induction as above (with
$\pi _{\mathfrak {p}}$
is either supercuspidal or a quotient of a smooth parabolic induction as above (with
![]() $\Omega =\mathbb {C}$
). In the first case,
$\Omega =\mathbb {C}$
). In the first case,
![]() $\pi _{\Omega }$
admits no
$\pi _{\Omega }$
admits no
![]() $\mathfrak {p}$
-stabilization. In the later case, there always exists a finite extension
$\mathfrak {p}$
-stabilization. In the later case, there always exists a finite extension
![]() $\Omega ^\prime $
of
$\Omega ^\prime $
of
![]() $\Omega $
such that
$\Omega $
such that
![]() $\pi _{\Omega ^\prime }$
admits a
$\pi _{\Omega ^\prime }$
admits a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
. Furthermore, the map
$(\chi ,\vartheta )$
. Furthermore, the map
![]() $\vartheta $
is unique up to multiplication with a scalar. The character
$\vartheta $
is unique up to multiplication with a scalar. The character
![]() $\chi $
is in general not unique. Suppose
$\chi $
is in general not unique. Suppose
![]() $\pi _{\Omega ^\prime }$
admits a
$\pi _{\Omega ^\prime }$
admits a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
. If
$(\chi ,\vartheta )$
. If
![]() $\vartheta $
is an isomorphism, then
$\vartheta $
is an isomorphism, then ![]() and
and
![]() $\chi ^{2}\neq |\cdot |_{\mathfrak {p}}^2$
. Moreover,
$\chi ^{2}\neq |\cdot |_{\mathfrak {p}}^2$
. Moreover,
![]() $i_B(\chi )$
is isomorphic to
$i_B(\chi )$
is isomorphic to
![]() $i_B(\chi ^{-1}|\cdot |_{\mathfrak {p}})$
but to no other principal series. Thus, as long as
$i_B(\chi ^{-1}|\cdot |_{\mathfrak {p}})$
but to no other principal series. Thus, as long as
![]() $\chi ^{2}\neq |\cdot |_{\mathfrak {p}}$
there are two essentially different
$\chi ^{2}\neq |\cdot |_{\mathfrak {p}}$
there are two essentially different
![]() $\mathfrak {p}$
-stabilizations.
$\mathfrak {p}$
-stabilizations.
If
![]() $\vartheta $
is not an isomorphism, then
$\vartheta $
is not an isomorphism, then ![]() and the kernel of
and the kernel of
![]() $\vartheta $
is one-dimensional generated by the function
$\vartheta $
is one-dimensional generated by the function
![]() $g\mapsto \chi (\operatorname {det}(g)).$
Moreover, the sequence
$g\mapsto \chi (\operatorname {det}(g)).$
Moreover, the sequence
is nonsplit. We have
![]() $\pi _{\mathfrak {p},\Omega }\cong \operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )\otimes \chi $
in this case.
$\pi _{\mathfrak {p},\Omega }\cong \operatorname { {St}}_{\mathfrak {p}}^\infty (\Omega )\otimes \chi $
in this case.
From the discussion above and Proposition 1.4, we get the following:
Corollary 2.2. Suppose
![]() $\pi _{\Omega }$
admits a
$\pi _{\Omega }$
admits a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
. Then for every character
$(\chi ,\vartheta )$
. Then for every character
![]() ${\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}}$
, there is an isomorphism
${\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}}$
, there is an isomorphism
of
![]() $\mathbb {T}_{K^{\mathfrak {p}}}(\Omega )$
-modules. In particular, it is an absolutely irreducible
$\mathbb {T}_{K^{\mathfrak {p}}}(\Omega )$
-modules. In particular, it is an absolutely irreducible
![]() $\mathbb {T}_{K^{\mathfrak {p}}}(\Omega )$
-module.
$\mathbb {T}_{K^{\mathfrak {p}}}(\Omega )$
-module.
Remark 2.3. We will be mostly interested in the case that the representation
![]() $\pi _{\mathfrak {p}}$
admits an invariant vector under the Iwahori group
$\pi _{\mathfrak {p}}$
admits an invariant vector under the Iwahori group
It is well known that having an Iwahori-fixed vector is equivalent to having a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
with respect to an unramified character
$(\chi ,\vartheta )$
with respect to an unramified character
![]() $\chi $
, that is,
$\chi $
, that is,
![]() $\chi (\mathcal {O}_{\mathfrak {p}}^\times )=1$
.
$\chi (\mathcal {O}_{\mathfrak {p}}^\times )=1$
.
2.2. Noncritical
 $\mathfrak {p}$
-stabilizations
$\mathfrak {p}$
-stabilizations
Composing an embedding
![]() $\sigma \colon F\hookrightarrow E\subseteq \overline {\mathbb {Q}}$
with
$\sigma \colon F\hookrightarrow E\subseteq \overline {\mathbb {Q}}$
with
![]() $\iota _p$
induces a p-adic topology on F. We define
$\iota _p$
induces a p-adic topology on F. We define
![]() $\Sigma _{\mathfrak {p}}\subseteq \Sigma $
to be the set of all embeddings inducing the topology coming from our chosen prime
$\Sigma _{\mathfrak {p}}\subseteq \Sigma $
to be the set of all embeddings inducing the topology coming from our chosen prime
![]() $\mathfrak {p}$
and put
$\mathfrak {p}$
and put
![]() $\Sigma ^{\mathfrak {p}}=\Sigma \setminus \Sigma _{\mathfrak {p}}$
. We identify
$\Sigma ^{\mathfrak {p}}=\Sigma \setminus \Sigma _{\mathfrak {p}}$
. We identify
![]() $\Sigma _{\mathfrak {p}}\subseteq \Sigma $
with the set of embeddings
$\Sigma _{\mathfrak {p}}\subseteq \Sigma $
with the set of embeddings
![]() $F_{\mathfrak {p}}\hookrightarrow E_p$
.
$F_{\mathfrak {p}}\hookrightarrow E_p$
.
Suppose
![]() $\Omega $
is a finite extension of
$\Omega $
is a finite extension of
![]() $E_p$
, which we will do from now on. We may decompose
$E_p$
, which we will do from now on. We may decompose
with
 $$\begin{align*}V_{\boldsymbol{k}_{\mathfrak{p}}}(\Omega)= \bigotimes_{\sigma \in \Sigma_{\mathfrak{p}}} V_{k_\sigma}(\Omega) \qquad \text{and}\qquad V_{\boldsymbol{k}^{\mathfrak{p}}}(\Omega)=\bigotimes_{\sigma \in \Sigma^{\mathfrak{p}}} V_{k_\sigma}(\Omega). \end{align*}$$
$$\begin{align*}V_{\boldsymbol{k}_{\mathfrak{p}}}(\Omega)= \bigotimes_{\sigma \in \Sigma_{\mathfrak{p}}} V_{k_\sigma}(\Omega) \qquad \text{and}\qquad V_{\boldsymbol{k}^{\mathfrak{p}}}(\Omega)=\bigotimes_{\sigma \in \Sigma^{\mathfrak{p}}} V_{k_\sigma}(\Omega). \end{align*}$$
For each
![]() $\sigma \in \Sigma _{\mathfrak {p}}$
, the group
$\sigma \in \Sigma _{\mathfrak {p}}$
, the group
![]() $G_{\mathfrak {p}}$
acts on
$G_{\mathfrak {p}}$
acts on
![]() $V_{k_\sigma }$
via the embedding
$V_{k_\sigma }$
via the embedding
![]() $\sigma \colon F_{\mathfrak {p}}\hookrightarrow E_p\subseteq \Omega $
. Hence, the representation
$\sigma \colon F_{\mathfrak {p}}\hookrightarrow E_p\subseteq \Omega $
. Hence, the representation
![]() $V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
of
$V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
of
![]() $G(F)$
extends to an algebraic representation of the group
$G(F)$
extends to an algebraic representation of the group
![]() $G_{\mathfrak {p}}$
.
$G_{\mathfrak {p}}$
.
We will assume for the reminder of this section that
![]() $\pi _{\Omega }$
admits a
$\pi _{\Omega }$
admits a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
. We define the locally algebraic
$(\chi ,\vartheta )$
. We define the locally algebraic
![]() $G_{\mathfrak {p}}$
-representation
$G_{\mathfrak {p}}$
-representation
Then, by Equation (1.5), we have a canonical
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant isomorphism
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant isomorphism
Let A be an affinoid
![]() $\mathbb {Q}_p$
-algebra. As in §2.1, we identify locally
$\mathbb {Q}_p$
-algebra. As in §2.1, we identify locally
![]() $\mathbb {Q}_p$
-analytic characters from
$\mathbb {Q}_p$
-analytic characters from
![]() $F_{\mathfrak {p}}^\times $
to
$F_{\mathfrak {p}}^\times $
to
![]() $A^\times $
with those from B to
$A^\times $
with those from B to
![]() $A^\times $
. Given a locally analytic representation
$A^\times $
. Given a locally analytic representation
![]() $\tau $
of B, its locally analytic parabolic induction is given by
$\tau $
of B, its locally analytic parabolic induction is given by
The group
![]() $G_{\mathfrak {p}}$
acts on it via right translation. Suppose that
$G_{\mathfrak {p}}$
acts on it via right translation. Suppose that
![]() $A=\Omega $
and
$A=\Omega $
and
![]() $\tau $
is finite-dimensional. In that case, the locally analytic parabolic induction is a strongly admissible locally analytic representation of
$\tau $
is finite-dimensional. In that case, the locally analytic parabolic induction is a strongly admissible locally analytic representation of
![]() $G_{\mathfrak {p}}$
. The case of one-dimensional representations is [Reference Emerton19, Proposition 1.21]. The proof works verbatim for every finite-dimensional representation.
$G_{\mathfrak {p}}$
. The case of one-dimensional representations is [Reference Emerton19, Proposition 1.21]. The proof works verbatim for every finite-dimensional representation.
To any locally constant character
![]() $\chi \colon F_{\mathfrak {p}}^\times \to \Omega ^\times $
, we associate the locally analytic character
$\chi \colon F_{\mathfrak {p}}^\times \to \Omega ^\times $
, we associate the locally analytic character
![]() $\chi _{\boldsymbol {k}_{\mathfrak {p}}}$
by
$\chi _{\boldsymbol {k}_{\mathfrak {p}}}$
by
 $$\begin{align*}\chi_{\boldsymbol{k}_{\mathfrak{p}}}(x)=\chi(x)\prod_{\sigma\in \Sigma_{\mathfrak{p}}} \sigma(x)^{-k_\sigma/2}. \end{align*}$$
$$\begin{align*}\chi_{\boldsymbol{k}_{\mathfrak{p}}}(x)=\chi(x)\prod_{\sigma\in \Sigma_{\mathfrak{p}}} \sigma(x)^{-k_\sigma/2}. \end{align*}$$
We may identify
![]() $i_B(\chi _{\boldsymbol {k}_{\mathfrak {p}}})$
with a subspace of
$i_B(\chi _{\boldsymbol {k}_{\mathfrak {p}}})$
with a subspace of
![]() $\operatorname {\mathbb {I}}_B(\chi _{\boldsymbol {k}_{\mathfrak {p}}})$
as follows: Given an embedding
$\operatorname {\mathbb {I}}_B(\chi _{\boldsymbol {k}_{\mathfrak {p}}})$
as follows: Given an embedding
![]() $\sigma \in \Sigma _{\mathfrak {p}}$
and
$\sigma \in \Sigma _{\mathfrak {p}}$
and
![]() $f_{\sigma }\in V_{k_{\sigma }}(\Omega ),$
we consider the
$f_{\sigma }\in V_{k_{\sigma }}(\Omega ),$
we consider the
![]() $\Omega $
-valued function
$\Omega $
-valued function
![]() $\psi _{f_\sigma }$
on
$\psi _{f_\sigma }$
on
![]() $\operatorname { {PGL}}_2(\Omega )$
constructed in Section 1.1.1. The embedding
$\operatorname { {PGL}}_2(\Omega )$
constructed in Section 1.1.1. The embedding
![]() $\sigma \colon F_{\mathfrak {p}} \hookrightarrow E_p$
induces an embedding of
$\sigma \colon F_{\mathfrak {p}} \hookrightarrow E_p$
induces an embedding of
![]() $G_{\mathfrak {p}}$
into
$G_{\mathfrak {p}}$
into
![]() $\operatorname { {PGL}}_2(\Omega )$
. We denote the restriction of
$\operatorname { {PGL}}_2(\Omega )$
. We denote the restriction of
![]() $\psi _{f_\sigma }$
to
$\psi _{f_\sigma }$
to
![]() $G_{\mathfrak {p}}$
also by
$G_{\mathfrak {p}}$
also by
![]() $\psi _{f_\sigma }$
. It is clearly a
$\psi _{f_\sigma }$
. It is clearly a
![]() $\mathbb {Q}_p$
-analytic function. By Equation (1.1), the map
$\mathbb {Q}_p$
-analytic function. By Equation (1.1), the map
 $$ \begin{align*} \beta\colon i_B(\chi)\otimes \bigotimes_{\sigma\in\Sigma_{\mathfrak{p}}} V_{k_{\sigma}}(\Omega) &\longrightarrow \operatorname{\mathbb{I}}_B(\chi_{\boldsymbol{k}_{\mathfrak{p}}})\\ (f_{\infty}, (f_{\sigma})_{\sigma\in\Sigma_{\mathfrak{p}}}) &\longmapsto f_\infty\cdot \prod_{\sigma\in\Sigma_{\mathfrak{p}}} \psi_{f_\sigma} \end{align*} $$
$$ \begin{align*} \beta\colon i_B(\chi)\otimes \bigotimes_{\sigma\in\Sigma_{\mathfrak{p}}} V_{k_{\sigma}}(\Omega) &\longrightarrow \operatorname{\mathbb{I}}_B(\chi_{\boldsymbol{k}_{\mathfrak{p}}})\\ (f_{\infty}, (f_{\sigma})_{\sigma\in\Sigma_{\mathfrak{p}}}) &\longmapsto f_\infty\cdot \prod_{\sigma\in\Sigma_{\mathfrak{p}}} \psi_{f_\sigma} \end{align*} $$
is well defined.
Definition 2.4. A
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
of
$(\chi ,\vartheta )$
of
![]() $\pi _{\Omega }$
is called noncritical if the canonical map
$\pi _{\Omega }$
is called noncritical if the canonical map
is an isomorphism for all
![]() $d\geq 0$
.
$d\geq 0$
.
Note that the notion of noncriticality depends on the level
![]() $K^{\mathfrak {p}}$
away from
$K^{\mathfrak {p}}$
away from
![]() $\mathfrak {p}$
and the set S: If
$\mathfrak {p}$
and the set S: If
![]() $\beta ^\ast $
is an isomorphism for
$\beta ^\ast $
is an isomorphism for
![]() $K^{\mathfrak {p}}$
, it is clearly an isomorphism for every open compact subgroup containing
$K^{\mathfrak {p}}$
, it is clearly an isomorphism for every open compact subgroup containing
![]() $K^{\mathfrak {p}}$
. But on the other hand, while one can completely describe the right-hand side of Equation (2.2) when making
$K^{\mathfrak {p}}$
. But on the other hand, while one can completely describe the right-hand side of Equation (2.2) when making
![]() $K^{\mathfrak {p}}$
smaller, one a priori does not have any control over the left-hand side. Similarly, strong multiplicity one implies that the right-hand side does not change when enlarging S, while the left-hand side might get larger.
$K^{\mathfrak {p}}$
smaller, one a priori does not have any control over the left-hand side. Similarly, strong multiplicity one implies that the right-hand side does not change when enlarging S, while the left-hand side might get larger.
2.2.1. Locally algebraic and locally analytic Steinberg representation
Assume for the moment that
![]() $\pi _{\mathfrak {p}}$
is the Steinberg representation. As mentioned above there is a unique
$\pi _{\mathfrak {p}}$
is the Steinberg representation. As mentioned above there is a unique
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization ![]() which has a one-dimensional kernel. We say
which has a one-dimensional kernel. We say
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
if this unique
$\mathfrak {p}$
if this unique
![]() $\mathfrak {p}$
-stabilization is noncritical.
$\mathfrak {p}$
-stabilization is noncritical.
We define the locally algebraic Steinberg representation of weight
![]() $\boldsymbol {k}_{\mathfrak {p}}$
via
$\boldsymbol {k}_{\mathfrak {p}}$
via
Sending
![]() $(f_\sigma )_{\sigma \in \Sigma _{\mathfrak {p}}}\in V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
to
$(f_\sigma )_{\sigma \in \Sigma _{\mathfrak {p}}}\in V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
to
![]() $\prod _{\sigma \in \Sigma _{\mathfrak {p}}}\psi _{f_\sigma }$
, we can view
$\prod _{\sigma \in \Sigma _{\mathfrak {p}}}\psi _{f_\sigma }$
, we can view
![]() $V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
as a subspace of
$V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
as a subspace of ![]() . We define the locally analytic Steinberg representation of weight
. We define the locally analytic Steinberg representation of weight
![]() $\boldsymbol {k}_{\mathfrak {p}}$
as the quotient
$\boldsymbol {k}_{\mathfrak {p}}$
as the quotient
Thus, we have a natural embedding
Proposition 2.5. Suppose that
![]() $\pi _{\mathfrak {p}}\cong \operatorname { {St}}_{\mathfrak {p}}^\infty (\mathbb {C})$
and
$\pi _{\mathfrak {p}}\cong \operatorname { {St}}_{\mathfrak {p}}^\infty (\mathbb {C})$
and
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
. Then the canonical map
$\mathfrak {p}$
. Then the canonical map
is an isomorphism for all
![]() $d\geq 0$
.
$d\geq 0$
.
Proof. We have the short exact sequence
and the commutative diagram

where the vertical arrows on both sides are given by quotient out by
![]() $V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
. For all
$V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
. For all
![]() $d\geq 0$
, it induces the following commutative diagram in cohomology
$d\geq 0$
, it induces the following commutative diagram in cohomology

Since
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
, the lower horizontal map is an isomorphism and hence also the upper one.
$\mathfrak {p}$
, the lower horizontal map is an isomorphism and hence also the upper one.
Remark 2.6. On page 653 of [Reference Chida, Mok and Park14], it is claimed that a property closely related to noncriticality always holds if the quaternion algebra D is totally definite. It is alluded to an Amice–Vélu and Vishik-type argument. But to the knowledge of the authors of this article the most general results of that type are in [Reference Breuil11, Section 7], which essentially only cover the case of noncritical slope.
In the following, we are going to show that if the representation
![]() $\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector the above definition of noncriticality is equivalent to the one given in terms of overconvergent cohomology that is used, for example, in [Reference Barrera Salazar, Dimitrov and Jorza2] or [Reference Bergdall and Hansen5]. The classicality theorem for overconvergent cohomology will give a numerical criterion for the noncriticality of a
$\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector the above definition of noncriticality is equivalent to the one given in terms of overconvergent cohomology that is used, for example, in [Reference Barrera Salazar, Dimitrov and Jorza2] or [Reference Bergdall and Hansen5]. The classicality theorem for overconvergent cohomology will give a numerical criterion for the noncriticality of a
![]() $\mathfrak {p}$
-stabilization. In order to state this criterion, later we will need the following definition.
$\mathfrak {p}$
-stabilization. In order to state this criterion, later we will need the following definition.
Definition 2.7. Let
![]() $(\chi ,\vartheta )$
be a
$(\chi ,\vartheta )$
be a
![]() $\mathfrak {p}$
-stabilization of
$\mathfrak {p}$
-stabilization of
![]() $\pi _{\Omega }$
. The p-adic valuation of
$\pi _{\Omega }$
. The p-adic valuation of
![]() $\prod _{\sigma \in \Sigma _{\mathfrak {p}}}\sigma (\varpi _{\mathfrak {p}})^{\frac {k_\sigma }{2}}\chi (\varpi _{\mathfrak {p}})$
is called the slope of
$\prod _{\sigma \in \Sigma _{\mathfrak {p}}}\sigma (\varpi _{\mathfrak {p}})^{\frac {k_\sigma }{2}}\chi (\varpi _{\mathfrak {p}})$
is called the slope of
![]() $(\chi ,\vartheta ).$
We say that
$(\chi ,\vartheta ).$
We say that
![]() $(\chi ,\vartheta )$
has noncritical slope if its slope is less than
$(\chi ,\vartheta )$
has noncritical slope if its slope is less than
![]() $\frac {1}{e_{\mathfrak {p}}}\min _{\sigma \in \Sigma _{\mathfrak {p}}}(k_\sigma +1)$
, where
$\frac {1}{e_{\mathfrak {p}}}\min _{\sigma \in \Sigma _{\mathfrak {p}}}(k_\sigma +1)$
, where
![]() $e_\mathfrak{p}$
denotes the ramification index of
$e_\mathfrak{p}$
denotes the ramification index of
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
2.3. Overconvergent cohomology
We give a quick overview over the basics of overconvergent cohomology.
2.3.1. Locally analytic inductions
For
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $I_{\mathfrak {p}}^n$
be the subgroup
$I_{\mathfrak {p}}^n$
be the subgroup
 $$\begin{align*}I_{\mathfrak{p}}^n=\left\{g\in \operatorname{{PGL}}_2(\mathcal{O}_{\mathfrak{p}}) \mid g\equiv \begin{pmatrix} 1 & 0\\ 0 & 1\end{pmatrix} \bmod {\mathfrak{p}^n}\right\}, \end{align*}$$
$$\begin{align*}I_{\mathfrak{p}}^n=\left\{g\in \operatorname{{PGL}}_2(\mathcal{O}_{\mathfrak{p}}) \mid g\equiv \begin{pmatrix} 1 & 0\\ 0 & 1\end{pmatrix} \bmod {\mathfrak{p}^n}\right\}, \end{align*}$$
and set
![]() $I_{\mathfrak {p}}^0=I_{\mathfrak {p}}$
. Then,
$I_{\mathfrak {p}}^0=I_{\mathfrak {p}}$
. Then,
![]() $(I_{\mathfrak {p}}^n)_{n\geq 0}$
is a family of open normal subgroups of
$(I_{\mathfrak {p}}^n)_{n\geq 0}$
is a family of open normal subgroups of
![]() $I_{\mathfrak {p}}$
and it is a fundamental system of neighbourhoods of the identity. Let A be an affinoid
$I_{\mathfrak {p}}$
and it is a fundamental system of neighbourhoods of the identity. Let A be an affinoid
![]() $\mathbb {Q}_p$
-algebra and
$\mathbb {Q}_p$
-algebra and
![]() $\chi \colon B\cap I_{\mathfrak {p}}\rightarrow A^\times $
a locally analytic character. This means that there exists a minimal integer
$\chi \colon B\cap I_{\mathfrak {p}}\rightarrow A^\times $
a locally analytic character. This means that there exists a minimal integer
![]() $n_\chi \geq 1$
such that
$n_\chi \geq 1$
such that
![]() $\chi $
restricted to
$\chi $
restricted to
![]() $B\cap I_{\mathfrak {p}}^{n_\chi }$
is analytic. For any integer
$B\cap I_{\mathfrak {p}}^{n_\chi }$
is analytic. For any integer
![]() $n\geq n_\chi $
, define the
$n\geq n_\chi $
, define the
![]() $A[I_{\mathfrak {p}}]$
-module
$A[I_{\mathfrak {p}}]$
-module
![]() $\mathcal {A}_\chi ^n$
of functions
$\mathcal {A}_\chi ^n$
of functions
![]() $f\colon I_{\mathfrak {p}}\longrightarrow A$
such that
$f\colon I_{\mathfrak {p}}\longrightarrow A$
such that
-
○
 $f\ \text {is analytic on any coset of}\ I_{\mathfrak {p}}/I_{\mathfrak {p}}^n$
,
$f\ \text {is analytic on any coset of}\ I_{\mathfrak {p}}/I_{\mathfrak {p}}^n$
, -
○
 $f(bk)=\chi (b)f(k)\quad \forall b\in B\cap I_{\mathfrak {p}},\ k\in I_{\mathfrak {p}}$
$f(bk)=\chi (b)f(k)\quad \forall b\in B\cap I_{\mathfrak {p}},\ k\in I_{\mathfrak {p}}$
with the action of
![]() $I_{\mathfrak {p}}$
given by
$I_{\mathfrak {p}}$
given by
![]() $(h\cdot f)(k)=f(kh)$
, and put
$(h\cdot f)(k)=f(kh)$
, and put
 $$ \begin{align*}\mathcal{A}_\chi=\bigcup_{n\geq n_\chi}\mathcal{A}_\chi^n.\end{align*} $$
$$ \begin{align*}\mathcal{A}_\chi=\bigcup_{n\geq n_\chi}\mathcal{A}_\chi^n.\end{align*} $$
The
![]() $A[I_{\mathfrak {p}}]$
-module
$A[I_{\mathfrak {p}}]$
-module
![]() $\mathcal {A}_\chi $
is the locally analytic induction of
$\mathcal {A}_\chi $
is the locally analytic induction of
![]() $\chi $
to
$\chi $
to
![]() $I_{\mathfrak {p}}$
. In the special case that
$I_{\mathfrak {p}}$
. In the special case that
![]() $A=\Omega $
is a finite extension of
$A=\Omega $
is a finite extension of
![]() $E_p$
and
$E_p$
and ![]() , we put
, we put
The Iwahori decomposition gives an isomorphism
![]() $I_{\mathfrak {p}}\cong (I_{\mathfrak {p}}\cap \overline {\mathbf {N}})\times (I_{\mathfrak {p}}\cap B)$
, where
$I_{\mathfrak {p}}\cong (I_{\mathfrak {p}}\cap \overline {\mathbf {N}})\times (I_{\mathfrak {p}}\cap B)$
, where
![]() $\overline {\mathbf {N}}$
denotes the group of unipotent lower triangular matrices. Thus, restricting a function
$\overline {\mathbf {N}}$
denotes the group of unipotent lower triangular matrices. Thus, restricting a function
![]() $f\in \mathcal {A}_\chi $
to
$f\in \mathcal {A}_\chi $
to
![]() $I_{\mathfrak {p}}\cap \overline {\mathbf {N}}$
induces an isomorphism between
$I_{\mathfrak {p}}\cap \overline {\mathbf {N}}$
induces an isomorphism between
![]() $\mathcal {A}_\chi $
and the space
$\mathcal {A}_\chi $
and the space
![]() $\mathcal {A}(I_{\mathfrak {p}}\cap \overline {\mathbf {N}},A)$
of locally analytic A-valued functions on
$\mathcal {A}(I_{\mathfrak {p}}\cap \overline {\mathbf {N}},A)$
of locally analytic A-valued functions on
![]() $I_{\mathfrak {p}}\cap \overline {\mathbf {N}}$
. An analogous bijection holds between
$I_{\mathfrak {p}}\cap \overline {\mathbf {N}}$
. An analogous bijection holds between
![]() $\mathcal {A}_\chi ^n$
and
$\mathcal {A}_\chi ^n$
and
![]() $\mathcal {A}_n(I_{\mathfrak {p}}\cap \overline {\mathbf {N}},A)$
, the space of n-locally analytic functions on
$\mathcal {A}_n(I_{\mathfrak {p}}\cap \overline {\mathbf {N}},A)$
, the space of n-locally analytic functions on
![]() $I_{\mathfrak {p}}\cap \overline {\mathbf {N}}$
.
$I_{\mathfrak {p}}\cap \overline {\mathbf {N}}$
.
2.3.2. The
 $U_{\mathfrak {p}}$
operator
$U_{\mathfrak {p}}$
operator
Consider the compact induction
![]() $\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\mathcal {A}_{\chi }^n)$
. By Frobenius reciprocity, the ring
$\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\mathcal {A}_{\chi }^n)$
. By Frobenius reciprocity, the ring
![]() $\operatorname { {End}}_{A[G_{\mathfrak {p}}]}(\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\mathcal {A}_{\chi }^n))$
can be identified with the space of all functions
$\operatorname { {End}}_{A[G_{\mathfrak {p}}]}(\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\mathcal {A}_{\chi }^n))$
can be identified with the space of all functions
![]() $\Psi \colon G_{\mathfrak {p}}\longrightarrow \operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
such that
$\Psi \colon G_{\mathfrak {p}}\longrightarrow \operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
such that
-
○
 $\Psi $
is
$\Psi $
is
 $I_{\mathfrak {p}}$
-biequivariant, that is,
$I_{\mathfrak {p}}$
-biequivariant, that is,
 $\Psi (k_1 g k_2)=k_1\Psi (g) k_2$
in
$\Psi (k_1 g k_2)=k_1\Psi (g) k_2$
in
 $\operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
, for all
$\operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
, for all
 $k_1,k_2\in I_{\mathfrak {p}}$
,
$k_1,k_2\in I_{\mathfrak {p}}$
,
 $g\in G_{\mathfrak {p}}$
, and
$g\in G_{\mathfrak {p}}$
, and -
○ for any element
 $f\in \mathcal {A}_\chi ^n$
, the function
$f\in \mathcal {A}_\chi ^n$
, the function
 $G_{\mathfrak {p}}\to \mathcal {A}_\chi ^n$
,
$G_{\mathfrak {p}}\to \mathcal {A}_\chi ^n$
,
 $g\mapsto \Psi (g)(f)$
is compactly supported.
$g\mapsto \Psi (g)(f)$
is compactly supported.
Let
 $u_{\mathfrak {p}}:=\begin {pmatrix} \varpi _{\mathfrak {p}} & 0\\ 0 & 1 \end {pmatrix}$
. Consider the element
$u_{\mathfrak {p}}:=\begin {pmatrix} \varpi _{\mathfrak {p}} & 0\\ 0 & 1 \end {pmatrix}$
. Consider the element
![]() $\varphi _{u_{\mathfrak {p}}}\in \operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
defined by
$\varphi _{u_{\mathfrak {p}}}\in \operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
defined by
By [Reference Kohlhaase and Schraen31, Lemma 2.2], there exists a unique
![]() $I_{\mathfrak {p}}$
-biequivariant function
$I_{\mathfrak {p}}$
-biequivariant function
![]() $\Psi _{u_{\mathfrak {p}}}\colon G_{\mathfrak {p}}\to \operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
such that
$\Psi _{u_{\mathfrak {p}}}\colon G_{\mathfrak {p}}\to \operatorname { {End}}_A(\mathcal {A}_\chi ^n)$
such that
![]() $\text {supp}(\Psi _{u_{\mathfrak {p}}})=I_{\mathfrak {p}} u_{\mathfrak {p}}^{-1} I_{\mathfrak {p}}$
and
$\text {supp}(\Psi _{u_{\mathfrak {p}}})=I_{\mathfrak {p}} u_{\mathfrak {p}}^{-1} I_{\mathfrak {p}}$
and
![]() $\Psi _{u_{\mathfrak {p}}}(u_{\mathfrak {p}}^{-1})=\varphi _{u_{\mathfrak {p}}}$
. Abusing notation, we will simply denote by
$\Psi _{u_{\mathfrak {p}}}(u_{\mathfrak {p}}^{-1})=\varphi _{u_{\mathfrak {p}}}$
. Abusing notation, we will simply denote by
![]() $u_{\mathfrak {p}}$
the
$u_{\mathfrak {p}}$
the
![]() $G_{\mathfrak {p}}$
-equivariant endomorphism of
$G_{\mathfrak {p}}$
-equivariant endomorphism of
![]() $\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\mathcal {A}_\chi ^n)$
corresponding to
$\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\mathcal {A}_\chi ^n)$
corresponding to
![]() $\Psi _{u_{\mathfrak {p}}}$
.
$\Psi _{u_{\mathfrak {p}}}$
.
We define the module of distributions
![]() $\mathcal {D}_{\chi ,\boldsymbol {k}^{\mathfrak {p}}}^n:=\operatorname { {Hom}}_{A,\operatorname { {ct}}}(\mathcal {A}_\chi ^n, A)\otimes _\Omega V_{\boldsymbol {k}^{\mathfrak {p}}}(\Omega )^\vee $
with its natural
$\mathcal {D}_{\chi ,\boldsymbol {k}^{\mathfrak {p}}}^n:=\operatorname { {Hom}}_{A,\operatorname { {ct}}}(\mathcal {A}_\chi ^n, A)\otimes _\Omega V_{\boldsymbol {k}^{\mathfrak {p}}}(\Omega )^\vee $
with its natural
![]() $I_{\mathfrak {p}}$
-action. For
$I_{\mathfrak {p}}$
-action. For
![]() $d\geq 0$
, we set
$d\geq 0$
, we set
This notation is justified as follows: To any
![]() $I_{\mathfrak {p}}$
-module M, one can attach a sheaf on the locally symmetric space
$I_{\mathfrak {p}}$
-module M, one can attach a sheaf on the locally symmetric space
![]() $\mathcal {X}_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}}$
(see, for example, [Reference Salazar and Williams4, Definition 3.2 (ii)]). With similar arguments as in the proof of Lemma 1.2, one can show that the cohomology of the sheaf associated to
$\mathcal {X}_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}}$
(see, for example, [Reference Salazar and Williams4, Definition 3.2 (ii)]). With similar arguments as in the proof of Lemma 1.2, one can show that the cohomology of the sheaf associated to
![]() $\mathcal {D}_{\chi ,\boldsymbol {k}^{\mathfrak {p}}}^n$
is computed by the groups above.
$\mathcal {D}_{\chi ,\boldsymbol {k}^{\mathfrak {p}}}^n$
is computed by the groups above.
For now, we are mostly interested in the following special case:
![]() $A=\Omega $
is a finite extension of
$A=\Omega $
is a finite extension of
![]() $E_p$
and
$E_p$
and ![]() . In this situation, we abbreviate
. In this situation, we abbreviate
Later, we will also need the case that A is the coordinate ring of an affinoid subspace of the weight space (see Section 4.1).
Remark 2.8. In [Reference Barrera Salazar, Dimitrov and Jorza2], overconvergent cohomology groups are introduced depending on a subset of the set of all primes of F lying above p. The spaces defined above correspond to the subset consisting only of the prime
![]() $\mathfrak {p}$
.
$\mathfrak {p}$
.
The endomorphism
![]() $u_{\mathfrak {p}}$
induces an operator, that we denote by
$u_{\mathfrak {p}}$
induces an operator, that we denote by
![]() $U_{\mathfrak {p}}^{\circ }$
, on cohomology:
$U_{\mathfrak {p}}^{\circ }$
, on cohomology:
Similarly as before, we may identify
![]() $V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
with the space of (globally) algebraic vectors in
$V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
with the space of (globally) algebraic vectors in
![]() $\mathcal {A}_{\boldsymbol {k}_{\mathfrak {p}}}^n$
. It induces an embedding
$\mathcal {A}_{\boldsymbol {k}_{\mathfrak {p}}}^n$
. It induces an embedding
and the subspace
![]() $\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ))$
is clearly invariant under the action of
$\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ))$
is clearly invariant under the action of
![]() $u_{\mathfrak {p}}$
. Thus, by invoking Equation (1.7) we get a
$u_{\mathfrak {p}}$
. Thus, by invoking Equation (1.7) we get a
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant map
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-equivariant map
in cohomology. We denote the natural operator on the right-hand side induced by
![]() $u_{\mathfrak {p}}$
by
$u_{\mathfrak {p}}$
by
![]() $U_{\mathfrak {p}}$
. The map (2.3) intertwines the action of the Hecke operator
$U_{\mathfrak {p}}$
. The map (2.3) intertwines the action of the Hecke operator
![]() $U_{\mathfrak {p}}^{\circ }$
on
$U_{\mathfrak {p}}^{\circ }$
on
![]() $H^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\boldsymbol {k}}^n)$
with the action of
$H^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\boldsymbol {k}}^n)$
with the action of
![]() $\prod _{\sigma \in \Sigma _{\mathfrak {p}}}\sigma (\varpi _{\mathfrak {p}})^{\frac {k_\sigma }{2}} U_{\mathfrak {p}}$
on
$\prod _{\sigma \in \Sigma _{\mathfrak {p}}}\sigma (\varpi _{\mathfrak {p}})^{\frac {k_\sigma }{2}} U_{\mathfrak {p}}$
on
![]() $H_c^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )$
. This follows from a simple analysis of the change of action of
$H_c^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )$
. This follows from a simple analysis of the change of action of
![]() $u_{\mathfrak {p}}$
under the isomorphism
$u_{\mathfrak {p}}$
under the isomorphism
given by Equation (1.6). We define the Hecke operator
![]() $U_{\mathfrak {p}}^{\circ }$
on the right-hand side of Equation (2.3) by
$U_{\mathfrak {p}}^{\circ }$
on the right-hand side of Equation (2.3) by
 $$ \begin{align*}U_{\mathfrak{p}}^{\circ}=\prod_{\sigma\in\Sigma_{\mathfrak{p}}}\sigma(\varpi_{\mathfrak{p}})^{\frac{k_\sigma}{2}} U_{\mathfrak{p}},\end{align*} $$
$$ \begin{align*}U_{\mathfrak{p}}^{\circ}=\prod_{\sigma\in\Sigma_{\mathfrak{p}}}\sigma(\varpi_{\mathfrak{p}})^{\frac{k_\sigma}{2}} U_{\mathfrak{p}},\end{align*} $$
and similarly we define an action of
![]() $U_{\mathfrak {p}}$
on the left-hand side of Equation (2.3).
$U_{\mathfrak {p}}$
on the left-hand side of Equation (2.3).
2.3.3. Slope decompositions and classicality
We give a reminder on slope decompositions. As before, A denotes a affinoid
![]() $\mathbb {Q}_p$
-algebra. Let M be an A-module equipped with an A-linear endomorphism
$\mathbb {Q}_p$
-algebra. Let M be an A-module equipped with an A-linear endomorphism
![]() $u\colon M \to M$
. Fix a rational number
$u\colon M \to M$
. Fix a rational number
![]() $h\geq 0$
. A polynomial
$h\geq 0$
. A polynomial
![]() $Q\in A[x]$
is multiplicative of slope
$Q\in A[x]$
is multiplicative of slope
![]() $\leq h$
if
$\leq h$
if
-
○ the leading coefficient of Q is a unit in A and
-
○ every edge of the Newton polygon of Q has slope
 $\leq h$
.
$\leq h$
.
We put
![]() $Q^\ast (x)= x^{\deg Q} Q(1/x).$
An element
$Q^\ast (x)= x^{\deg Q} Q(1/x).$
An element
![]() $m\in M$
is said to be of slope
$m\in M$
is said to be of slope
![]() $\leq h$
if there is a multiplicative polynomial
$\leq h$
if there is a multiplicative polynomial
![]() $Q\in A[x]$
of slope
$Q\in A[x]$
of slope
![]() $\leq h$
such that
$\leq h$
such that
![]() $Q^{\ast }(u) m=0$
. Let
$Q^{\ast }(u) m=0$
. Let
![]() $M^{\leq h} \subseteq M$
be the submodule of elements of M of slope
$M^{\leq h} \subseteq M$
be the submodule of elements of M of slope
![]() $\leq h$
.
$\leq h$
.
Definition 2.9. A slope
![]() $\leq h$
decomposition of M is an
$\leq h$
decomposition of M is an
![]() $A[u]$
-module isomorphism
$A[u]$
-module isomorphism
such that
-
○
 $M^{\leq h}$
is a finitely generated A-module and
$M^{\leq h}$
is a finitely generated A-module and -
○
 $Q^\ast (u)$
acts invertibly on
$Q^\ast (u)$
acts invertibly on
 $M^{>h}$
for every multiplicative polynomial
$M^{>h}$
for every multiplicative polynomial
 $Q\in A[x]$
of slope
$Q\in A[x]$
of slope
 $\leq h$
.
$\leq h$
.
Note that if
![]() $A=\Omega $
is a finite extension of
$A=\Omega $
is a finite extension of
![]() $E_p$
and M is finite-dimensional, then a slope
$E_p$
and M is finite-dimensional, then a slope
![]() $\leq h$
decomposition always exists. If M admits a slope
$\leq h$
decomposition always exists. If M admits a slope
![]() $\leq h$
decomposition for all
$\leq h$
decomposition for all
![]() $h\geq 0$
, we put
$h\geq 0$
, we put
The most remarkable result about slope decomposition is the following theorem which was first proved by Ash and Stevens [Reference Ash and Stevens1] in special cases over
![]() $\mathbb {Q}$
and then generalized by Urban [Reference Urban42] and Hansen [Reference Hansen27] to more general settings. See also [Reference Salazar and Williams4] for a detailed treatment of the case of
$\mathbb {Q}$
and then generalized by Urban [Reference Urban42] and Hansen [Reference Hansen27] to more general settings. See also [Reference Salazar and Williams4] for a detailed treatment of the case of
![]() $\operatorname { {PGL}}_2$
over arbitrary number fields. In these results, one always considers all primes above
$\operatorname { {PGL}}_2$
over arbitrary number fields. In these results, one always considers all primes above
![]() $\mathfrak {p}$
simultaneously. The modifications necessary to allow subsets of all primes above
$\mathfrak {p}$
simultaneously. The modifications necessary to allow subsets of all primes above
![]() $\mathfrak {p}$
are explained in the proof of [Reference Barrera Salazar, Dimitrov and Jorza2, Theorem 2.7].
$\mathfrak {p}$
are explained in the proof of [Reference Barrera Salazar, Dimitrov and Jorza2, Theorem 2.7].
Theorem 2.10. For every
![]() $d\geq 0$
and every
$d\geq 0$
and every
![]() $h\geq 0$
the cohomology groups
$h\geq 0$
the cohomology groups
admit a slope
![]() $\leq h$
decomposition with respect to the Hecke operator
$\leq h$
decomposition with respect to the Hecke operator
![]() $U_{\mathfrak {p}}^{\circ }$
.
$U_{\mathfrak {p}}^{\circ }$
.
If
![]() $h<\frac {1}{e_{\mathfrak {p}}}\min _{\sigma \in \Sigma _{\mathfrak {p}}}(k_\sigma +1)$
, where
$h<\frac {1}{e_{\mathfrak {p}}}\min _{\sigma \in \Sigma _{\mathfrak {p}}}(k_\sigma +1)$
, where
![]() $e_{\mathfrak {p}}$
is the ramification index of
$e_{\mathfrak {p}}$
is the ramification index of
![]() $\mathfrak {p}$
, then for all
$\mathfrak {p}$
, then for all
![]() $d\geq 0$
the map (2.3) induces the following
$d\geq 0$
the map (2.3) induces the following
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}$
-equivariant isomorphism
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}$
-equivariant isomorphism
Here, the slope decomposition is taken with respect to
![]() $U_{\mathfrak {p}}^{\circ }$
on both sides.
$U_{\mathfrak {p}}^{\circ }$
on both sides.
2.4. Overconvergent cohomology and noncritical
 $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
Let A be an affinoid algebra and
![]() $\chi \colon F_{\mathfrak {p}}^\times \longrightarrow A^\times $
be a locally analytic character. Denote by
$\chi \colon F_{\mathfrak {p}}^\times \longrightarrow A^\times $
be a locally analytic character. Denote by
![]() $\chi _0$
its restriction to
$\chi _0$
its restriction to
![]() $\mathfrak {O}_{\mathfrak {p}}^{\times} $
. An element
$\mathfrak {O}_{\mathfrak {p}}^{\times} $
. An element
![]() $f\in \mathcal {A}_{\chi _0}^{n}$
can uniquely extended to a function on
$f\in \mathcal {A}_{\chi _0}^{n}$
can uniquely extended to a function on
![]() $B I_{\mathfrak {p}} \subset G_{\mathfrak {p}}$
by putting
$B I_{\mathfrak {p}} \subset G_{\mathfrak {p}}$
by putting
![]() $f(bk)=\chi (b)f(k).$
Since
$f(bk)=\chi (b)f(k).$
Since
![]() $B I_{\mathfrak {p}} \subset G_{\mathfrak {p}}$
is open, extension by zero yields an
$B I_{\mathfrak {p}} \subset G_{\mathfrak {p}}$
is open, extension by zero yields an
![]() $I_{\mathfrak {p}}$
-equivariant A-linear injection
$I_{\mathfrak {p}}$
-equivariant A-linear injection
By Frobenius reciprocity, it induces a unique
![]() $G_{\mathfrak {p}}$
-equivariant A-linear morphism
$G_{\mathfrak {p}}$
-equivariant A-linear morphism
The following theorem is due to Kohlhaase and Schraen.
Theorem 2.11. For every
![]() $n\geq n_{\chi _0}$
, the sequence
$n\geq n_{\chi _0}$
, the sequence
is exact.
Proof. See [Reference Kohlhaase and Schraen31, Proposition 2.4 and Theorem 2.5].
Let
![]() $\chi \colon F_{\mathfrak {p}}^\times \to \Omega ^\times $
be an unramified character. Similarly as above, the sequence
$\chi \colon F_{\mathfrak {p}}^\times \to \Omega ^\times $
be an unramified character. Similarly as above, the sequence
is exact. This can be deduced from Borel’s theorem that
![]() $\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\Omega )$
is a flat module over the Iwahori–Hecke algebra (see the end of [Reference Gehrmann and Rosso25, Section 3.1]). Tensoring the above exact sequence with
$\operatorname { {c-ind}}_{I_{\mathfrak {p}}}^{G_{\mathfrak {p}}}(\Omega )$
is a flat module over the Iwahori–Hecke algebra (see the end of [Reference Gehrmann and Rosso25, Section 3.1]). Tensoring the above exact sequence with
![]() $V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
and using Equation (1.6), we get a short exact sequence
$V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
and using Equation (1.6), we get a short exact sequence
Suppose that
![]() $\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector. Given a
$\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector. Given a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
of
$(\chi ,\vartheta )$
of
![]() $\pi _\Omega $
(with
$\pi _\Omega $
(with
![]() $\chi $
not necessarily unramified), we define
$\chi $
not necessarily unramified), we define
to be the maximal ideal generated by
![]() $\mathfrak {m}_{\pi }^S$
and
$\mathfrak {m}_{\pi }^S$
and
![]() $U_{\mathfrak {p}}-\chi (\varpi _{\mathfrak {p}}).$
In accordance with [Reference Barrera Salazar, Dimitrov and Jorza2, Definition 2.12] and [Reference Bergdall and Hansen5, Definition 1.5.1], we make the following definition:
$U_{\mathfrak {p}}-\chi (\varpi _{\mathfrak {p}}).$
In accordance with [Reference Barrera Salazar, Dimitrov and Jorza2, Definition 2.12] and [Reference Bergdall and Hansen5, Definition 1.5.1], we make the following definition:
Definition 2.12. The maximal ideal
![]() $\mathfrak {m}_{\pi ,(\chi ,\vartheta )}^S\subseteq \mathbb {T}_K^S(\Omega )[U_{\mathfrak {p}}]$
is noncritical if the map
$\mathfrak {m}_{\pi ,(\chi ,\vartheta )}^S\subseteq \mathbb {T}_K^S(\Omega )[U_{\mathfrak {p}}]$
is noncritical if the map
induced by Equation (2.3) is an isomorphism for all
![]() $d\geq 0$
.
$d\geq 0$
.
Proposition 2.13. Suppose that
![]() $\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector, and let
$\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector, and let
![]() $(\chi ,\vartheta )$
be a
$(\chi ,\vartheta )$
be a
![]() $\mathfrak {p}$
-stabilization of
$\mathfrak {p}$
-stabilization of
![]() $\pi _\Omega $
. Then the following are equivalent:
$\pi _\Omega $
. Then the following are equivalent:
-
(i)
 $(\chi ,\vartheta )$
is noncritical
$(\chi ,\vartheta )$
is noncritical -
(ii)
 $\mathfrak {m}_{\pi ,(\chi ,\vartheta )}^S$
is noncritical.
$\mathfrak {m}_{\pi ,(\chi ,\vartheta )}^S$
is noncritical.
Proof. Note that
![]() $\chi $
is an unramified character. Thus, the long exact sequences induced by Equations (2.5) and (2.6) yield the following diagram with exact columns:
$\chi $
is an unramified character. Thus, the long exact sequences induced by Equations (2.5) and (2.6) yield the following diagram with exact columns:

The existence of slope decompositions (see Theorem 2.10) implies that we may replace
![]() $\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\boldsymbol {k}}^n)_{\mathfrak {m}_{\pi }^S}$
by
$\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\boldsymbol {k}}^n)_{\mathfrak {m}_{\pi }^S}$
by
![]() $\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\boldsymbol {k}}^n)_{\mathfrak {m}_{\pi ,(\chi ,\vartheta )}^S}$
in the diagram above (and similarly for cohomology with coefficients in
$\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\boldsymbol {k}}^n)_{\mathfrak {m}_{\pi ,(\chi ,\vartheta )}^S}$
in the diagram above (and similarly for cohomology with coefficients in
![]() $V_{\boldsymbol {k}}(\Omega )$
): Indeed, the operator
$V_{\boldsymbol {k}}(\Omega )$
): Indeed, the operator
![]() $U_{\mathfrak {p}}^{\circ }-\chi _{\boldsymbol {k}_{\mathfrak {p}}}(\varpi _{\mathfrak {p}})$
is an isomorphism on the part of cohomology where the slope is bigger than h as long as h is large enough. On the other hand, the slope
$U_{\mathfrak {p}}^{\circ }-\chi _{\boldsymbol {k}_{\mathfrak {p}}}(\varpi _{\mathfrak {p}})$
is an isomorphism on the part of cohomology where the slope is bigger than h as long as h is large enough. On the other hand, the slope
![]() $\leq \hspace {-0.3em} h$
-part is finite-dimensional and localizing at the ideal generated by
$\leq \hspace {-0.3em} h$
-part is finite-dimensional and localizing at the ideal generated by
![]() $U_{\mathfrak {p}}^{\circ }-\chi _{\boldsymbol {k}_{\mathfrak {p}}}(\varpi _{\mathfrak {p}})$
is the same as taking the corresponding generalized eigenspace.
$U_{\mathfrak {p}}^{\circ }-\chi _{\boldsymbol {k}_{\mathfrak {p}}}(\varpi _{\mathfrak {p}})$
is the same as taking the corresponding generalized eigenspace.
The five lemma immediately gives the implication (ii)
![]() $\Rightarrow $
(i). The other direction is proven by induction on d: Let us assume that
$\Rightarrow $
(i). The other direction is proven by induction on d: Let us assume that
![]() $(\chi ,\vartheta )$
is noncritical and that
$(\chi ,\vartheta )$
is noncritical and that
is an isomorphism. Choose a positive integer N that is large enough. The assumptions above imply that the map
viewed as a homomorphism of finitely generated
![]() $\Omega [T]/T^N$
-modules by letting T act via
$\Omega [T]/T^N$
-modules by letting T act via
![]() $U_{\mathfrak {p}}^{\circ }-\chi _{\boldsymbol {k}_{\mathfrak {p}}}(\varpi _{\mathfrak {p}})$
fulfils the assumption of Lemma 2.14 below. In particular, it is an isomorphism.
$U_{\mathfrak {p}}^{\circ }-\chi _{\boldsymbol {k}_{\mathfrak {p}}}(\varpi _{\mathfrak {p}})$
fulfils the assumption of Lemma 2.14 below. In particular, it is an isomorphism.
Given a
![]() $\Omega [T]/T^N$
-module M put
$\Omega [T]/T^N$
-module M put
Lemma 2.14. Let
![]() $f\colon M_1 \to M_2$
be a homomorphism of finitely generated
$f\colon M_1 \to M_2$
be a homomorphism of finitely generated
![]() $\Omega [T]/T^N$
-modules. Assume that
$\Omega [T]/T^N$
-modules. Assume that
-
○ f induces an isomorphism from
 $M_1[T]$
to
$M_1[T]$
to
 $M_2[T]$
and
$M_2[T]$
and -
○ f induces an injection from
 $M_1/T M_1$
to
$M_1/T M_1$
to
 $M_2/T M_2$
.
$M_2/T M_2$
.
Then f is an isomorphism.
Proof. One immediately checks that f also induces an isomorphism from
![]() $M_1/T M_1$
to
$M_1/T M_1$
to
![]() $M_2/T M_2$
since
$M_2/T M_2$
since
![]() $\dim _\Omega M_i[T]=\dim _{\Omega } M_i/T M_i$
for
$\dim _\Omega M_i[T]=\dim _{\Omega } M_i/T M_i$
for
![]() $i=1,2$
. Surjectivity of f then follows from Nakayama’s lemma. It remains to prove injectivity: Let a be in the kernel of f. Assume that
$i=1,2$
. Surjectivity of f then follows from Nakayama’s lemma. It remains to prove injectivity: Let a be in the kernel of f. Assume that
![]() $a\neq 0$
. There exists a maximal integer
$a\neq 0$
. There exists a maximal integer
![]() $0\leq n\leq N$
such that
$0\leq n\leq N$
such that
![]() $T^n \cdot a\neq 0$
. By construction,
$T^n \cdot a\neq 0$
. By construction,
![]() $T^n \cdot a$
is an element of
$T^n \cdot a$
is an element of
![]() $M_1[T]\cap \ker (f)=\{0\}$
, which is a contradiction.
$M_1[T]\cap \ker (f)=\{0\}$
, which is a contradiction.
Applying the second part of Theorem 2.10 one deduces the following:
Corollary 2.15. Suppose that
![]() $\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector. If a
$\pi _{\mathfrak {p}}$
has an Iwahori-fixed vector. If a
![]() $\mathfrak {p}$
-stabilization
$\mathfrak {p}$
-stabilization
![]() $(\chi ,\vartheta )$
of
$(\chi ,\vartheta )$
of
![]() $\pi _\Omega $
has noncritical slope, then it is noncritical.
$\pi _\Omega $
has noncritical slope, then it is noncritical.
Suppose
![]() $\pi _{\mathfrak {p}}=\operatorname { {St}}_{\mathfrak {p}}^\infty (\mathbb {C}).$
Then the corollary above shows that
$\pi _{\mathfrak {p}}=\operatorname { {St}}_{\mathfrak {p}}^\infty (\mathbb {C}).$
Then the corollary above shows that
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
if
$\mathfrak {p}$
if
-
(i)
 $k_\sigma =0$
for all
$k_\sigma =0$
for all
 $\sigma \in \Sigma _{\mathfrak {p}}$
or
$\sigma \in \Sigma _{\mathfrak {p}}$
or -
(ii)
 $F_{\mathfrak {p}}=\mathbb {Q}_p$
or
$F_{\mathfrak {p}}=\mathbb {Q}_p$
or -
(iii)
 $[F_{\mathfrak {p}}:\mathbb {Q}_p]=2$
and
$[F_{\mathfrak {p}}:\mathbb {Q}_p]=2$
and
 $k_{\sigma _1}=k_{\sigma _2},$
where
$k_{\sigma _1}=k_{\sigma _2},$
where
 $\Sigma _{\mathfrak {p}}=\{\sigma _1,\sigma _2\}.$
$\Sigma _{\mathfrak {p}}=\{\sigma _1,\sigma _2\}.$
This always holds in case
![]() $F=\mathbb {Q}$
or F is imaginary quadratic by Equation (1.2).
$F=\mathbb {Q}$
or F is imaginary quadratic by Equation (1.2).
3. Automorphic L-invariants
The main aim of this section is to define automorphic
![]() $\mathcal {L}$
-invariants for the representation
$\mathcal {L}$
-invariants for the representation
![]() $\pi $
under the assumption that the local component of
$\pi $
under the assumption that the local component of
![]() $\pi $
at a prime
$\pi $
at a prime
![]() $\mathfrak {p}$
is Steinberg.
$\mathfrak {p}$
is Steinberg.
3.1. Extensions of locally analytic Steinberg representations
Let
![]() $\Omega $
be a finite extension of
$\Omega $
be a finite extension of
![]() $E_p$
. The following construction of extensions is due to Breuil (see [Reference Breuil9, Section 2.1]). Let
$E_p$
. The following construction of extensions is due to Breuil (see [Reference Breuil9, Section 2.1]). Let
![]() $\lambda \colon F_{\mathfrak {p}}^{\times }\to \Omega $
be a continuous homomorphism. Note that
$\lambda \colon F_{\mathfrak {p}}^{\times }\to \Omega $
be a continuous homomorphism. Note that
![]() $\lambda $
is automatically locally
$\lambda $
is automatically locally
![]() $\mathbb {Q}_p$
-analytic. We define
$\mathbb {Q}_p$
-analytic. We define
![]() $\tau _\lambda $
to be the two-dimensional
$\tau _\lambda $
to be the two-dimensional
![]() $\Omega $
-representation of B given by
$\Omega $
-representation of B given by
 $$ \begin{align*}\begin{pmatrix} a & u \\ 0 & d \end{pmatrix} \longmapsto \begin{pmatrix} 1 & \lambda(a/d) \\ 0 & 1 \end{pmatrix} \end{align*} $$
$$ \begin{align*}\begin{pmatrix} a & u \\ 0 & d \end{pmatrix} \longmapsto \begin{pmatrix} 1 & \lambda(a/d) \\ 0 & 1 \end{pmatrix} \end{align*} $$
and put ![]() . As the short exact sequence
. As the short exact sequence
is split in the category of topological vector spaces, the induced sequence of locally analytic representations
is exact (see, for example, Proposition 5.1 and Remark 5.4 of [Reference Kohlhaase30]). Pullback via ![]() and pushforward along
and pushforward along ![]() yields the exact sequence
yields the exact sequence
Let
![]() $W_1$
and
$W_1$
and
![]() $W_2$
be
$W_2$
be
![]() $\mathbb {Q}_p$
-analytic
$\mathbb {Q}_p$
-analytic
![]() $\Omega $
-representations of
$\Omega $
-representations of
![]() $G_{\mathfrak {p}}$
. We write
$G_{\mathfrak {p}}$
. We write
![]() $\operatorname { {Ext}}^{1}_{\operatorname {\mathrm {an}}}(W_1,W_2)$
for the space of locally
$\operatorname { {Ext}}^{1}_{\operatorname {\mathrm {an}}}(W_1,W_2)$
for the space of locally
![]() $\mathbb {Q}_p$
-analytic extensions of
$\mathbb {Q}_p$
-analytic extensions of
![]() $W_2$
by
$W_2$
by
![]() $W_1$
. The map
$W_1$
. The map
is an isomorphism. In the case
![]() $F_{\mathfrak {p}}=\mathbb {Q}_p,$
this is due to Breuil. In fact, an analogous statement is true for more general split reductive groups (see [Reference Ding18, Theorem 1] and [Reference Gehrmann24, Theorem 2.15]).
$F_{\mathfrak {p}}=\mathbb {Q}_p,$
this is due to Breuil. In fact, an analogous statement is true for more general split reductive groups (see [Reference Ding18, Theorem 1] and [Reference Gehrmann24, Theorem 2.15]).
Tensoring with
![]() $V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
yields a canonical homomorphism
$V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega )$
yields a canonical homomorphism
which is an isomorphism by [Reference Schraen37, Proposition 4.14]. Moreover, by [Reference Schraen37, Proposition 4.15] the canonical injection
is an isomorphism. Let
![]() $\mathcal {E}^\infty $
be the smooth extension of Equation (1.11). It follows that
$\mathcal {E}^\infty $
be the smooth extension of Equation (1.11). It follows that
is a generator of
![]() $ \operatorname { {Ext}}^{1}_{\operatorname { {an}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ),\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\infty }(\Omega ))$
. The following lemma compares this generator with Breuil’s extension associated to the p-adic valuation.
$ \operatorname { {Ext}}^{1}_{\operatorname { {an}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ),\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\infty }(\Omega ))$
. The following lemma compares this generator with Breuil’s extension associated to the p-adic valuation.
Lemma 3.1. The natural map
![]() $\operatorname { {Ext}}^{1}_{\operatorname { {an}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ),\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\infty }(\Omega ))\to \operatorname { {Ext}}^{1}_{\operatorname { {an}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ),\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\operatorname { {an}}}(\Omega ))$
is injective. It sends the generator
$\operatorname { {Ext}}^{1}_{\operatorname { {an}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ),\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\infty }(\Omega ))\to \operatorname { {Ext}}^{1}_{\operatorname { {an}}}(V_{\boldsymbol {k}_{\mathfrak {p}}}(\Omega ),\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\operatorname { {an}}}(\Omega ))$
is injective. It sends the generator
![]() $\mathcal {E}_{\boldsymbol {k}_{\mathfrak {p}}}^\infty $
to a multiple of
$\mathcal {E}_{\boldsymbol {k}_{\mathfrak {p}}}^\infty $
to a multiple of
![]() $\mathcal {E}_{\operatorname { {ord}}_{\mathfrak {p}},\boldsymbol {k}_{\mathfrak {p}}}$
.
$\mathcal {E}_{\operatorname { {ord}}_{\mathfrak {p}},\boldsymbol {k}_{\mathfrak {p}}}$
.
Proof. This is [Reference Schraen37, Corollary 4.16].
3.2. Definition of the L-invariant
We assume for the rest of this article that
![]() $\pi _{\mathfrak {p}}$
is the Steinberg representation.
$\pi _{\mathfrak {p}}$
is the Steinberg representation.
Let
![]() $\lambda \colon F_{\mathfrak {p}}^\times \to \Omega $
be a continuous character. The short exact sequence (3.1) induces the short exact sequence
$\lambda \colon F_{\mathfrak {p}}^\times \to \Omega $
be a continuous character. The short exact sequence (3.1) induces the short exact sequence
which in turn induces the boundary map
in cohomology. Given a character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\},$
we write
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\},$
we write
for the induced map, which is clearly a
![]() $\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-module homomorphism.
$\mathbb {T}^{\mathfrak {p}}_{K^{\mathfrak {p}}}(\Omega )$
-module homomorphism.
Definition 3.2. The automorphic
![]() $\mathcal {L}$
-invariant of
$\mathcal {L}$
-invariant of
![]() $\pi $
at
$\pi $
at
![]() $\mathfrak {p}$
with respect to the sign character
$\mathfrak {p}$
with respect to the sign character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
is the subspace
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
is the subspace
Proposition 3.3. Assume that
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
. Then for every sign character
$\mathfrak {p}$
. Then for every sign character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
the codimension of the
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
the codimension of the
![]() $\mathcal {L}$
-invariant
$\mathcal {L}$
-invariant
![]() $\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon \subseteq \operatorname { {Hom}}_{\operatorname {{ct}}}(F_{\mathfrak {p}}^\times ,\Omega )$
is equal to one. Moreover, it does not contain the space of locally constant homomorphisms.
$\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon \subseteq \operatorname { {Hom}}_{\operatorname {{ct}}}(F_{\mathfrak {p}}^\times ,\Omega )$
is equal to one. Moreover, it does not contain the space of locally constant homomorphisms.
Proof. By Equation (1.10), the
![]() $\Omega $
-vector space
$\Omega $
-vector space
![]() $\operatorname {{Hom}}_{\Omega [G_{\mathfrak {p}}]}(\operatorname {{St}}_{\mathfrak {p}}^\infty ,\operatorname {{St}}_{\mathfrak {p}}^\infty )$
is one-dimensional. Thus, combining Proposition 2.5 and Lemma 1.8 one deduces that the space of
$\operatorname {{Hom}}_{\Omega [G_{\mathfrak {p}}]}(\operatorname {{St}}_{\mathfrak {p}}^\infty ,\operatorname {{St}}_{\mathfrak {p}}^\infty )$
is one-dimensional. Thus, combining Proposition 2.5 and Lemma 1.8 one deduces that the space of
![]() $\mathbb {T}_{K^{\mathfrak {p}}}^{\mathfrak {p}}(\Omega )$
-linear homomorphisms between the two modules
$\mathbb {T}_{K^{\mathfrak {p}}}^{\mathfrak {p}}(\Omega )$
-linear homomorphisms between the two modules
![]() $\mathrm{{H}}^q_{\Omega ,\operatorname {{ct}}}(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\operatorname {{an}}}(\Omega ),V_{\boldsymbol {k}^{\mathfrak {p}}}(\Omega )^\vee )^\epsilon _{\mathfrak {m}_\pi ^{S}}$
and
$\mathrm{{H}}^q_{\Omega ,\operatorname {{ct}}}(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},\operatorname { {St}}_{\boldsymbol {k}_{\mathfrak {p}}}^{\operatorname {{an}}}(\Omega ),V_{\boldsymbol {k}^{\mathfrak {p}}}(\Omega )^\vee )^\epsilon _{\mathfrak {m}_\pi ^{S}}$
and
![]() $\mathrm{{H}}^{q+1}_{\Omega }(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )^\epsilon _{\mathfrak {m}_\pi ^{S}}$
is one-dimensional as well. One concludes that the codimension of the
$\mathrm{{H}}^{q+1}_{\Omega }(X^{\mathfrak {p}}_{K^{\mathfrak {p}}},V_{\boldsymbol {k}}(\Omega )^\vee )^\epsilon _{\mathfrak {m}_\pi ^{S}}$
is one-dimensional as well. One concludes that the codimension of the
![]() $\mathcal {L}$
-invariant is at most one.
$\mathcal {L}$
-invariant is at most one.
We now show that the codimension is exactly one by showing that there exists a nontrivial element in
![]() $\operatorname {{Hom}}_{\operatorname {{ct}}}(F_{\mathfrak {p}}^\times ,\Omega )$
which is not contained in
$\operatorname {{Hom}}_{\operatorname {{ct}}}(F_{\mathfrak {p}}^\times ,\Omega )$
which is not contained in
![]() $\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
. Consider the homomorphism
$\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
. Consider the homomorphism
![]() $c_{\operatorname {{ord}}_{\mathfrak {p}}}^\epsilon $
. By Lemma 3.1,
$c_{\operatorname {{ord}}_{\mathfrak {p}}}^\epsilon $
. By Lemma 3.1,
![]() $c_{\operatorname {{ord}}_{\mathfrak {p}}}^\epsilon =c_{\infty }^{q,\epsilon } \circ \kappa ^\ast $
up to a nonzero constant, where
$c_{\operatorname {{ord}}_{\mathfrak {p}}}^\epsilon =c_{\infty }^{q,\epsilon } \circ \kappa ^\ast $
up to a nonzero constant, where
![]() $c_{\infty }^{q,\epsilon }$
denotes the homomorphism constructed in Equation (1.12). By Lemma 1.8, the homomorphism
$c_{\infty }^{q,\epsilon }$
denotes the homomorphism constructed in Equation (1.12). By Lemma 1.8, the homomorphism
![]() $c_{\infty }^{q,\epsilon }$
is an isomorphism, while
$c_{\infty }^{q,\epsilon }$
is an isomorphism, while
![]() $\kappa ^\ast $
is an isomorphism by Proposition 2.5. Therefore,
$\kappa ^\ast $
is an isomorphism by Proposition 2.5. Therefore,
![]() $\operatorname { {ord}}_{\mathfrak {p}}\notin \mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
. The second statement follows observing that locally constant homomorphisms in
$\operatorname { {ord}}_{\mathfrak {p}}\notin \mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
. The second statement follows observing that locally constant homomorphisms in
![]() $\operatorname { {Hom}}_{\operatorname { {ct}}}(F_{\mathfrak {p}}^\times ,\Omega )$
are multiples of
$\operatorname { {Hom}}_{\operatorname { {ct}}}(F_{\mathfrak {p}}^\times ,\Omega )$
are multiples of
![]() $\operatorname { {ord}}_{\mathfrak {p}}$
.
$\operatorname { {ord}}_{\mathfrak {p}}$
.
Remark 3.4. As in [Reference Gehrmann22], one could also define automorphic
![]() $\mathcal {L}$
-invariants for higher degree cohomology groups, for which its
$\mathcal {L}$
-invariants for higher degree cohomology groups, for which its
![]() $\pi $
-isotypic component does not vanish. As these
$\pi $
-isotypic component does not vanish. As these
![]() $\mathcal {L}$
-invariants neither seem to show up in exceptional zero formulas nor are they used to define (plectic) Darmon cycles, we will not consider them here.
$\mathcal {L}$
-invariants neither seem to show up in exceptional zero formulas nor are they used to define (plectic) Darmon cycles, we will not consider them here.
4. P-adic families
For this section, we assume that F is totally real,
![]() $\pi _{\mathfrak {p}}$
is the Steinberg representation and
$\pi _{\mathfrak {p}}$
is the Steinberg representation and
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
. We give a formula for the automorphic
$\mathfrak {p}$
. We give a formula for the automorphic
![]() $\mathcal {L}$
-invariant in terms of derivatives of
$\mathcal {L}$
-invariant in terms of derivatives of
![]() $U_{\mathfrak {p}}$
-eigenvalues of p-adic families passing through
$U_{\mathfrak {p}}$
-eigenvalues of p-adic families passing through
![]() $\pi $
. Comparing with the corresponding formula for the Fontaine–Mazur
$\pi $
. Comparing with the corresponding formula for the Fontaine–Mazur
![]() $\mathcal {L}$
-invariant of the corresponding Galois representation we deduce that automorphic and Fontaine–Mazur
$\mathcal {L}$
-invariant of the corresponding Galois representation we deduce that automorphic and Fontaine–Mazur
![]() $\mathcal {L}$
-invariants agree.
$\mathcal {L}$
-invariants agree.
4.1. The weight space
Let
![]() $\Omega $
be a finite extension of
$\Omega $
be a finite extension of
![]() $E_p$
. Define the (partial) weight space
$E_p$
. Define the (partial) weight space
![]() $\mathcal {W}_{\mathfrak {p}}$
to be the rigid analytic space over
$\mathcal {W}_{\mathfrak {p}}$
to be the rigid analytic space over
![]() $\Omega $
associated to the completed group algebra
$\Omega $
associated to the completed group algebra ![]() . There is a universal character
. There is a universal character
Let
![]() $\mathcal {U}\subseteq \mathcal {W}_{\mathfrak {p}}$
be an affinoid and
$\mathcal {U}\subseteq \mathcal {W}_{\mathfrak {p}}$
be an affinoid and
![]() $\mathcal {O}(\mathcal {U})$
be the ring of its rigid analytic functions. We will denote by
$\mathcal {O}(\mathcal {U})$
be the ring of its rigid analytic functions. We will denote by
![]() $\kappa ^{\mathrm {un}}_{\mathcal {U}}\colon \mathcal {O}_{\mathfrak {p}}^\times \rightarrow \mathcal {O}(\mathcal {U})^\times $
the restriction of the universal character to
$\kappa ^{\mathrm {un}}_{\mathcal {U}}\colon \mathcal {O}_{\mathfrak {p}}^\times \rightarrow \mathcal {O}(\mathcal {U})^\times $
the restriction of the universal character to
![]() $\mathcal {U}$
. For an affinoid
$\mathcal {U}$
. For an affinoid
![]() $\mathcal {U}\subseteq \mathcal {W}_{\mathfrak {p}}$
and a locally analytic character
$\mathcal {U}\subseteq \mathcal {W}_{\mathfrak {p}}$
and a locally analytic character
![]() $\chi \colon B\cap I_{\mathfrak {p}}\rightarrow \mathcal {O}(\mathcal {U})^\times $
, recall from section 2.3 the
$\chi \colon B\cap I_{\mathfrak {p}}\rightarrow \mathcal {O}(\mathcal {U})^\times $
, recall from section 2.3 the
![]() $\mathcal {O}(\mathcal {U})[I_{\mathfrak {p}}]$
-module
$\mathcal {O}(\mathcal {U})[I_{\mathfrak {p}}]$
-module
![]() $\mathcal {A}_\chi ^n$
defined as the locally n-analytic induction of
$\mathcal {A}_\chi ^n$
defined as the locally n-analytic induction of
![]() $\chi $
to
$\chi $
to
![]() $I_{\mathfrak {p}}$
, and the cohomology groups
$I_{\mathfrak {p}}$
, and the cohomology groups
![]() $\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\chi ,\boldsymbol {k}^{\mathfrak {p}}}^n)$
. If
$\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\chi ,\boldsymbol {k}^{\mathfrak {p}}}^n)$
. If
![]() $\chi $
is the universal character
$\chi $
is the universal character
![]() $\kappa _{\mathcal {U}}^{\mathrm {un}}$
, we simply write
$\kappa _{\mathcal {U}}^{\mathrm {un}}$
, we simply write
![]() $\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\mathcal {U},\boldsymbol {k}^{\mathfrak {p}}}^n)$
in place of
$\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\mathcal {U},\boldsymbol {k}^{\mathfrak {p}}}^n)$
in place of
![]() $\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\kappa _{\mathcal {U}}^{\mathrm {un}},\boldsymbol {k}^{\mathfrak {p}}}^n)$
. If
$\mathrm{{H}}^d(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}_{\kappa _{\mathcal {U}}^{\mathrm {un}},\boldsymbol {k}^{\mathfrak {p}}}^n)$
. If
![]() $\mathcal{U}$
contains
$\mathcal{U}$
contains
![]() $\boldsymbol {k}_{\mathfrak{p}}$
, the evaluation
$\boldsymbol {k}_{\mathfrak{p}}$
, the evaluation
![]() $\mathcal {O}(\mathcal {U})\rightarrow \Omega $
at
$\mathcal {O}(\mathcal {U})\rightarrow \Omega $
at
![]() $\boldsymbol {k}_{\mathfrak {p}}$
induces the map
$\boldsymbol {k}_{\mathfrak {p}}$
induces the map
4.2. Étaleness at
 $\mathfrak {m}_\pi ^{S}$
$\mathfrak {m}_\pi ^{S}$
Let
![]() $\mathcal {U}$
be an admissible open affinoid in
$\mathcal {U}$
be an admissible open affinoid in
![]() $\mathcal {W}_{\mathfrak {p}}$
containing
$\mathcal {W}_{\mathfrak {p}}$
containing
![]() $\boldsymbol {k}_{\mathfrak {p}}$
, and let
$\boldsymbol {k}_{\mathfrak {p}}$
, and let
![]() $\mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak{p}}}$
be the rigid localization of
$\mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak{p}}}$
be the rigid localization of
![]() $\mathcal {O}(\mathcal {U})$
at
$\mathcal {O}(\mathcal {U})$
at
![]() $\boldsymbol {k}_{\mathfrak {p}}\in \mathcal {U}$
. It is the local ring defined as
$\boldsymbol {k}_{\mathfrak {p}}\in \mathcal {U}$
. It is the local ring defined as
where the limit is taken over all admissible open subaffinoids
![]() $\mathcal {U}'$
in
$\mathcal {U}'$
in
![]() $\mathcal {U}$
containing
$\mathcal {U}$
containing
![]() $\boldsymbol {k_{\mathfrak {p}}}$
. Thus, it contains the algebraic localization of
$\boldsymbol {k_{\mathfrak {p}}}$
. Thus, it contains the algebraic localization of
![]() $\mathcal {O}(\mathcal {U})$
at the maximal ideal
$\mathcal {O}(\mathcal {U})$
at the maximal ideal
![]() $\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
attached to
$\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
attached to
![]() $\boldsymbol {k}_{\mathfrak {p}}$
. By a slight abuse of notation, we write
$\boldsymbol {k}_{\mathfrak {p}}$
. By a slight abuse of notation, we write
![]() $\mathfrak {m}^S_\pi \subseteq \mathbb {T}_{K^S}^S(\mathcal {O}(\mathcal {U}))=\mathbb {T}_{K^S}^S(\Omega )\otimes _\Omega \mathcal {O}(\mathcal {U})$
for the ideal generated by
$\mathfrak {m}^S_\pi \subseteq \mathbb {T}_{K^S}^S(\mathcal {O}(\mathcal {U}))=\mathbb {T}_{K^S}^S(\Omega )\otimes _\Omega \mathcal {O}(\mathcal {U})$
for the ideal generated by
![]() $\mathfrak {m}^S_\pi \subseteq \mathbb {T}_{K^S}^S(\Omega )$
and
$\mathfrak {m}^S_\pi \subseteq \mathbb {T}_{K^S}^S(\Omega )$
and
![]() $\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}\subseteq \mathcal {O}(\mathcal {U})$
.
$\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}\subseteq \mathcal {O}(\mathcal {U})$
.
The assumption that
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
has strong implications on the existence of p-adic families interpolating the system of Hecke-eigenvalues attached to
$\mathfrak {p}$
has strong implications on the existence of p-adic families interpolating the system of Hecke-eigenvalues attached to
![]() $\pi $
.
$\pi $
.
Theorem 4.1. Let
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
be a character. Up to shrinking
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
be a character. Up to shrinking
![]() $\mathcal {U}$
to a small enough open affinoid containing
$\mathcal {U}$
to a small enough open affinoid containing
![]() $\boldsymbol {k}_{\mathfrak {p}}$
the following holds:
$\boldsymbol {k}_{\mathfrak {p}}$
the following holds:
for
![]() $d=q$
it is a free
$d=q$
it is a free
![]() $\mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak {p}}}$
-module of finite rank and the map of
$\mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak {p}}}$
-module of finite rank and the map of
![]() $\mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak {p}}}$
-modules obtained by localizing the composition of Equation (2.3) with the map (4.1) induces an isomorphism
$\mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak {p}}}$
-modules obtained by localizing the composition of Equation (2.3) with the map (4.1) induces an isomorphism
Moreover, the operator
![]() $U_{\mathfrak {p}}^\circ $
acts on it via a scalar
$U_{\mathfrak {p}}^\circ $
acts on it via a scalar
![]() $\alpha _{\mathfrak {p}}^{\epsilon }\in \mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak {p}}}^\times $
.
$\alpha _{\mathfrak {p}}^{\epsilon }\in \mathcal {O}(\mathcal {U})_{\boldsymbol {k}_{\mathfrak {p}}}^\times $
.
Proof. Since F is totally real, the constant
![]() $\delta $
is equal to
$\delta $
is equal to
![]() $0$
. Thus, Theorem 1.1 implies that
$0$
. Thus, Theorem 1.1 implies that
The first claims follow using the same arguments as in the proof of [Reference Barrera Salazar, Dimitrov and Jorza2, Theorem 2.14]. The statement about the operator
![]() $U_{\mathfrak {p}}^\circ $
can be deduced from the fact that
$U_{\mathfrak {p}}^\circ $
can be deduced from the fact that
is an absolutely irreducible
![]() $\mathbb {T}_{K^{\mathfrak {p}}}(\Omega )$
-module.
$\mathbb {T}_{K^{\mathfrak {p}}}(\Omega )$
-module.
Theorem 4.1 can be rephrased in more geometric terms: It implies that the map from a certain eigenvariety to weight space is étale at the point corresponding to
![]() $\pi $
.
$\pi $
.
4.3. Infinitesimal deformations and
 $\mathcal {L}$
-invariants
$\mathcal {L}$
-invariants
Let
![]() $\Omega [\varepsilon ]:=\Omega [X]/(X^2)$
be the
$\Omega [\varepsilon ]:=\Omega [X]/(X^2)$
be the
![]() $\Omega $
-algebra of dual numbers over
$\Omega $
-algebra of dual numbers over
![]() $\Omega $
and
$\Omega $
and
![]() $\pi \colon \Omega [\varepsilon ]\rightarrow \Omega $
be the natural surjection sending
$\pi \colon \Omega [\varepsilon ]\rightarrow \Omega $
be the natural surjection sending
![]() $\varepsilon $
to
$\varepsilon $
to
![]() $0$
. If
$0$
. If
![]() $X=\text {Spec }(A)$
is an affine
$X=\text {Spec }(A)$
is an affine
![]() $\Omega $
-scheme and
$\Omega $
-scheme and
![]() $x\colon A\rightarrow A/\mathfrak {m}_x=\Omega $
is a
$x\colon A\rightarrow A/\mathfrak {m}_x=\Omega $
is a
![]() $\Omega $
-valued point, then the space of morphisms
$\Omega $
-valued point, then the space of morphisms
![]() $\boldsymbol {v}_x \colon A\rightarrow \Omega [\varepsilon ]$
such that
$\boldsymbol {v}_x \colon A\rightarrow \Omega [\varepsilon ]$
such that
![]() $\pi \circ \boldsymbol {v}_x=x$
is identified with the tangent space of X at x.
$\pi \circ \boldsymbol {v}_x=x$
is identified with the tangent space of X at x.
Let
![]() $\mathcal {U}$
be an admissible open affinoid containing
$\mathcal {U}$
be an admissible open affinoid containing
![]() $\boldsymbol {k}_{\mathfrak {p}}$
and
$\boldsymbol {k}_{\mathfrak {p}}$
and
![]() $\chi \colon B\rightarrow \mathcal {O}(\mathcal {U})^\times $
a locally analytic character, that we identify with an element of
$\chi \colon B\rightarrow \mathcal {O}(\mathcal {U})^\times $
a locally analytic character, that we identify with an element of
![]() $\operatorname { {Hom}}(F_{\mathfrak {p}}^\times ,\mathcal {O}(\mathcal {U})^\times )$
as in section 2.1. Let
$\operatorname { {Hom}}(F_{\mathfrak {p}}^\times ,\mathcal {O}(\mathcal {U})^\times )$
as in section 2.1. Let
![]() $\boldsymbol {v}\colon \mathcal {O}(\mathcal {U})\rightarrow \Omega [\varepsilon ]$
be an element of the tangent space of
$\boldsymbol {v}\colon \mathcal {O}(\mathcal {U})\rightarrow \Omega [\varepsilon ]$
be an element of the tangent space of
![]() $\mathcal {U}$
at
$\mathcal {U}$
at
![]() $\boldsymbol {k}_{\mathfrak {p}}$
. Then the pullback
$\boldsymbol {k}_{\mathfrak {p}}$
. Then the pullback
![]() $\chi _{\boldsymbol {v}}=\boldsymbol {v}\circ \chi \in \operatorname { {Hom}}(F_{\mathfrak {p}}^\times , \Omega [\varepsilon ])$
of
$\chi _{\boldsymbol {v}}=\boldsymbol {v}\circ \chi \in \operatorname { {Hom}}(F_{\mathfrak {p}}^\times , \Omega [\varepsilon ])$
of
![]() $\chi $
along
$\chi $
along
![]() $\boldsymbol {v}$
can be written in a unique way as
$\boldsymbol {v}$
can be written in a unique way as
where
![]() $\overline {\chi }\colon F_{\mathfrak {p}}^\times \rightarrow (\mathcal {O}(\mathcal {U})/\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}})^\times =\Omega ^\times $
denotes the reduction of
$\overline {\chi }\colon F_{\mathfrak {p}}^\times \rightarrow (\mathcal {O}(\mathcal {U})/\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}})^\times =\Omega ^\times $
denotes the reduction of
![]() $\chi $
modulo
$\chi $
modulo
![]() $\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
and
$\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
and
![]() $\partial _{\boldsymbol {v}}(\chi )$
is a homomorphism from
$\partial _{\boldsymbol {v}}(\chi )$
is a homomorphism from
![]() $F_{\mathfrak {p}}^\times $
to
$F_{\mathfrak {p}}^\times $
to
![]() $\Omega $
.
$\Omega $
.
Now, assume that
![]() $\chi \colon B\rightarrow \mathcal {O}(\mathcal {U})^\times $
is a locally analytic character such that
$\chi \colon B\rightarrow \mathcal {O}(\mathcal {U})^\times $
is a locally analytic character such that ![]() . Then, for an element
. Then, for an element
![]() $\boldsymbol {v}$
in the tangent space of
$\boldsymbol {v}$
in the tangent space of
![]() $\mathcal {U}$
at
$\mathcal {U}$
at
![]() $\boldsymbol {k}_{\mathfrak {p}}$
we have
$\boldsymbol {k}_{\mathfrak {p}}$
we have ![]() . Consider the map induced in cohomology by the reduction of
. Consider the map induced in cohomology by the reduction of
![]() $\chi $
modulo
$\chi $
modulo
![]() $\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
:
$\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
:
Proposition 4.2. Let
![]() $\epsilon \colon \pi _{0}(G_\infty )\to \{\pm 1\}$
be a sign character. If
$\epsilon \colon \pi _{0}(G_\infty )\to \{\pm 1\}$
be a sign character. If
![]() $\operatorname { {red}}_{\chi }^{\epsilon }$
is surjective, then
$\operatorname { {red}}_{\chi }^{\epsilon }$
is surjective, then
![]() $\partial _{\boldsymbol {v}}(\chi )$
belongs to
$\partial _{\boldsymbol {v}}(\chi )$
belongs to
![]() $\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
for every element
$\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
for every element
![]() $\boldsymbol {v}$
of the tangent space of
$\boldsymbol {v}$
of the tangent space of
![]() $\mathcal {U}$
at
$\mathcal {U}$
at
![]() $\boldsymbol {k}$
.
$\boldsymbol {k}$
.
Proof. The locally analytic character
![]() $\chi _{\boldsymbol {v}}$
of B over
$\chi _{\boldsymbol {v}}$
of B over
![]() $\Omega [\varepsilon ]$
can be seen as a two-dimensional representation
$\Omega [\varepsilon ]$
can be seen as a two-dimensional representation
![]() $\tau _{\chi _{\boldsymbol {v}}}$
of B over
$\tau _{\chi _{\boldsymbol {v}}}$
of B over
![]() $\Omega $
. It is in fact the representation that we denoted by
$\Omega $
. It is in fact the representation that we denoted by
![]() $\tau _{\partial _{\boldsymbol {v}}(\chi ),\boldsymbol {k}_{\mathfrak {p}}}$
in Section 3.1. It follows from the discussion in Section 3.1 that there is a commutative diagram
$\tau _{\partial _{\boldsymbol {v}}(\chi ),\boldsymbol {k}_{\mathfrak {p}}}$
in Section 3.1. It follows from the discussion in Section 3.1 that there is a commutative diagram

where
![]() $\hat {c}_{\partial _{\boldsymbol {v}}(\chi )}^\epsilon $
and
$\hat {c}_{\partial _{\boldsymbol {v}}(\chi )}^\epsilon $
and
![]() $c_{\partial _{\boldsymbol {v}}(\chi )}^\epsilon $
are the boundary maps induced by the dual of the short exact sequences
$c_{\partial _{\boldsymbol {v}}(\chi )}^\epsilon $
are the boundary maps induced by the dual of the short exact sequences
and
respectively. It is sufficient to prove that
![]() $\hat {c}_{\partial _{\boldsymbol {v}}(\chi )}^\epsilon $
is the zero map, which would follow from the surjectivity of the homomorphism
$\hat {c}_{\partial _{\boldsymbol {v}}(\chi )}^\epsilon $
is the zero map, which would follow from the surjectivity of the homomorphism
induced by the dual of Equation (4.3). Our assumption on the surjectivity of
![]() $\operatorname { {red}}_{\chi }^{\epsilon }$
immediately implies that the map
$\operatorname { {red}}_{\chi }^{\epsilon }$
immediately implies that the map
is surjective. The surjectivity of Equation (4.4) now follows from [Reference Gehrmann and Rosso25, Lemma 2.1].
Recall that we denoted by
![]() $\alpha _{\mathfrak {p}}^{\epsilon }\in \mathcal {O}(\mathcal {U})^\times _{\boldsymbol {k}_{\mathfrak {p}}}$
the eigenvalue of the Hecke operator
$\alpha _{\mathfrak {p}}^{\epsilon }\in \mathcal {O}(\mathcal {U})^\times _{\boldsymbol {k}_{\mathfrak {p}}}$
the eigenvalue of the Hecke operator
![]() $U_{\mathfrak {p}}^\circ $
acting on
$U_{\mathfrak {p}}^\circ $
acting on
![]() $\mathrm{{H}}^q(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}^n_{\mathcal {U},\boldsymbol {k}_{\mathfrak {p}}})^\epsilon _{(\mathfrak {m}_\pi ^S,U_{\mathfrak {p}}-1)}$
. Up to shrinking
$\mathrm{{H}}^q(X_{K^{\mathfrak {p}}\times I_{\mathfrak {p}}},\mathcal {D}^n_{\mathcal {U},\boldsymbol {k}_{\mathfrak {p}}})^\epsilon _{(\mathfrak {m}_\pi ^S,U_{\mathfrak {p}}-1)}$
. Up to shrinking
![]() $\mathcal {U},$
we can assume that
$\mathcal {U},$
we can assume that
![]() $\alpha _{\mathfrak {p}}^{\epsilon }\in \mathcal {O}(\mathcal {U})^\times $
. Let
$\alpha _{\mathfrak {p}}^{\epsilon }\in \mathcal {O}(\mathcal {U})^\times $
. Let
![]() $\chi _{\alpha _{\mathfrak {p}}^{\epsilon }}\colon B\rightarrow \mathcal {O}(\mathcal {U})^\times $
be the character defined by
$\chi _{\alpha _{\mathfrak {p}}^{\epsilon }}\colon B\rightarrow \mathcal {O}(\mathcal {U})^\times $
be the character defined by
 $$ \begin{align*} \chi_{\alpha_{\mathfrak{p}}^{\epsilon}}\vert_{B\cap I_{\mathfrak{p}}} &= \kappa^{\mathrm{un}}_{\mathcal{U}}\\ \chi_{\alpha_{\mathfrak{p}}^{\epsilon}}(u_{\mathfrak{p}}) &= \alpha_{\mathfrak{p}}^{\epsilon}. \end{align*} $$
$$ \begin{align*} \chi_{\alpha_{\mathfrak{p}}^{\epsilon}}\vert_{B\cap I_{\mathfrak{p}}} &= \kappa^{\mathrm{un}}_{\mathcal{U}}\\ \chi_{\alpha_{\mathfrak{p}}^{\epsilon}}(u_{\mathfrak{p}}) &= \alpha_{\mathfrak{p}}^{\epsilon}. \end{align*} $$
Now, we are ready to prove the main result of this section.
Theorem 4.3. Let
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
be a sign character. For every element
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
be a sign character. For every element
![]() $\boldsymbol {v}$
of the tangent space of
$\boldsymbol {v}$
of the tangent space of
![]() $\mathcal {U}$
at
$\mathcal {U}$
at
![]() $\boldsymbol {k}_{\mathfrak {p}},$
we have
$\boldsymbol {k}_{\mathfrak {p}},$
we have
Proof. By Proposition 4.2, it is enough to prove that
![]() $\operatorname { {red}}_{\chi _{\alpha _{\mathfrak {p}}^{\epsilon }}}^{\epsilon }$
is surjective. By Theorem 2.11, with the same arguments as in the proof of Proposition 2.13, the map in cohomology
$\operatorname { {red}}_{\chi _{\alpha _{\mathfrak {p}}^{\epsilon }}}^{\epsilon }$
is surjective. By Theorem 2.11, with the same arguments as in the proof of Proposition 2.13, the map in cohomology
induced by Equation (2.5) is an isomorphism. By Theorem 4.1, the reduction modulo
![]() $\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
yields a surjective map
$\mathfrak {m}_{\boldsymbol {k}_{\mathfrak {p}}}$
yields a surjective map
Furthermore, one has the isomorphisms

where the first isomorphism can be deduced from the arguments in the proof of Proposition 2.13, and the second one follows from the noncriticality of
![]() $\pi $
at
$\pi $
at
![]() $\mathfrak {p}$
. Recollecting all the maps, one deduces the claim.
$\mathfrak {p}$
. Recollecting all the maps, one deduces the claim.
4.4. Relation with Galois representations
Let
![]() $\rho =\rho _\pi \colon \operatorname {{Gal}}(\overline {F}/F) \rightarrow \operatorname {{GL}}_2(\Omega )$
be the two-dimensional Galois representation attached to
$\rho =\rho _\pi \colon \operatorname {{Gal}}(\overline {F}/F) \rightarrow \operatorname {{GL}}_2(\Omega )$
be the two-dimensional Galois representation attached to
![]() $\pi $
, and let
$\pi $
, and let
![]() $\rho _{\mathfrak {p}}$
be its restriction to a decomposition group
$\rho _{\mathfrak {p}}$
be its restriction to a decomposition group
![]() $\operatorname {{Gal}}(\overline {F_{\mathfrak {p}}}/F_{\mathfrak {p}})$
at
$\operatorname {{Gal}}(\overline {F_{\mathfrak {p}}}/F_{\mathfrak {p}})$
at
![]() $\mathfrak {p}$
. As local-global compatibility is known in this case by Saito (cf. [Reference Saito35]), the representation
$\mathfrak {p}$
. As local-global compatibility is known in this case by Saito (cf. [Reference Saito35]), the representation
![]() $\rho _{\mathfrak {p}}$
is semistable, noncrystalline, that is:
$\rho _{\mathfrak {p}}$
is semistable, noncrystalline, that is:
is a free
![]() $\Omega \otimes _{\mathbb {Q}_p} F_{\mathfrak {p},0}$
-module (where
$\Omega \otimes _{\mathbb {Q}_p} F_{\mathfrak {p},0}$
-module (where
![]() $F_{\mathfrak {p},0}$
denotes the maximal unramified subfield of
$F_{\mathfrak {p},0}$
denotes the maximal unramified subfield of
![]() $F_{\mathfrak {p}}$
) and the nilpotent linear map
$F_{\mathfrak {p}}$
) and the nilpotent linear map
![]() $N_{\mathfrak {p}}$
inherited from the corresponding map on Fontaine’s semistable period ring
$N_{\mathfrak {p}}$
inherited from the corresponding map on Fontaine’s semistable period ring
![]() $B_{\mathrm {st}}$
is nonzero. Moreover, the kernel of
$B_{\mathrm {st}}$
is nonzero. Moreover, the kernel of
![]() $N_{\mathfrak {p}}$
is a free
$N_{\mathfrak {p}}$
is a free
![]() $\Omega \otimes _{\mathbb {Q}_p} F_{\mathfrak {p},0}$
-module of rank one. It follows that there exists a basis
$\Omega \otimes _{\mathbb {Q}_p} F_{\mathfrak {p},0}$
-module of rank one. It follows that there exists a basis
![]() $\{e_1,e_2\}$
of Frobenius eigenvectors such that
$\{e_1,e_2\}$
of Frobenius eigenvectors such that
![]() $e_1=N_{\mathfrak {p}}(e_2)$
. Furthermore, it is known that the zeroth step of the de Rham filtration
$e_1=N_{\mathfrak {p}}(e_2)$
. Furthermore, it is known that the zeroth step of the de Rham filtration
is a free
![]() $\Omega \otimes _{\mathbb {Q}_p}F_{\mathfrak {p}}$
-module of rank one. In particular there exist
$\Omega \otimes _{\mathbb {Q}_p}F_{\mathfrak {p}}$
-module of rank one. In particular there exist
![]() $a_1^{\rho _{\mathfrak {p}}},a_2^{\rho _{\mathfrak {p}}}\in \Omega \otimes _{\mathbb {Q}_p}F_{\mathfrak {p}}$
such that
$a_1^{\rho _{\mathfrak {p}}},a_2^{\rho _{\mathfrak {p}}}\in \Omega \otimes _{\mathbb {Q}_p}F_{\mathfrak {p}}$
such that
![]() $\mathrm {Fil}^0(\mathcal {D}_{\mathrm {st}}(\rho _{\mathfrak {p}}))$
is generated by
$\mathrm {Fil}^0(\mathcal {D}_{\mathrm {st}}(\rho _{\mathfrak {p}}))$
is generated by
![]() $a_1^{\rho _{\mathfrak {p}}}\cdot e_1 + a_2^{\rho _{\mathfrak {p}}} \cdot e_2$
.
$a_1^{\rho _{\mathfrak {p}}}\cdot e_1 + a_2^{\rho _{\mathfrak {p}}} \cdot e_2$
.
Definition 4.4. We call the local Galois representation
![]() $\rho _{\mathfrak {p}}$
noncritical if
$\rho _{\mathfrak {p}}$
noncritical if
![]() $a_2^{\rho _{\mathfrak {p}}}\in (\Omega \otimes _{\mathbb {Q}_p}F_{\mathfrak {p}})^\times $
.
$a_2^{\rho _{\mathfrak {p}}}\in (\Omega \otimes _{\mathbb {Q}_p}F_{\mathfrak {p}})^\times $
.
It is expected that every
![]() $\rho _{\mathfrak {p}}$
coming from a Hilbert modular form as above is noncritical. If
$\rho _{\mathfrak {p}}$
coming from a Hilbert modular form as above is noncritical. If
![]() $F_{\mathfrak {p}}=\mathbb {Q}_p$
or
$F_{\mathfrak {p}}=\mathbb {Q}_p$
or
![]() $k_\sigma =0$
for all
$k_\sigma =0$
for all
![]() $\sigma \in \Sigma _p$
, the fact that
$\sigma \in \Sigma _p$
, the fact that
![]() $\mathcal {D}_{\mathrm {st}}(\rho _{\mathfrak {p}})$
is weakly admissible implies that
$\mathcal {D}_{\mathrm {st}}(\rho _{\mathfrak {p}})$
is weakly admissible implies that
![]() $\rho _{\mathfrak {p}}$
is noncritical. It seems to the authors of this article that in [Reference Chida, Mok and Park14, Section 3.2] noncriticality of the Galois representation is assumed implicitly. Note that the main theorem of [Reference Xie43] states that a Galois representation as above is noncritical if
$\rho _{\mathfrak {p}}$
is noncritical. It seems to the authors of this article that in [Reference Chida, Mok and Park14, Section 3.2] noncriticality of the Galois representation is assumed implicitly. Note that the main theorem of [Reference Xie43] states that a Galois representation as above is noncritical if
![]() $\mathfrak {p}$
is the only prime of F above p. But similar as on page 653 of [Reference Chida, Mok and Park14] an Amice–Vélu and Vishik-type argument is used in the crucial Proposition 7.3 of loc.cit. and it is not clear to the authors of this article, whether such an argument is applicable here (see Remark 2.6 above).
$\mathfrak {p}$
is the only prime of F above p. But similar as on page 653 of [Reference Chida, Mok and Park14] an Amice–Vélu and Vishik-type argument is used in the crucial Proposition 7.3 of loc.cit. and it is not clear to the authors of this article, whether such an argument is applicable here (see Remark 2.6 above).
To any tuple
 $$ \begin{align*}a=(a_\sigma)\in \Omega\otimes_{\mathbb{Q}_p}F_{\mathfrak{p}} \cong \prod_{\sigma\in\Sigma_{\mathfrak{p}}} \Omega,\end{align*} $$
$$ \begin{align*}a=(a_\sigma)\in \Omega\otimes_{\mathbb{Q}_p}F_{\mathfrak{p}} \cong \prod_{\sigma\in\Sigma_{\mathfrak{p}}} \Omega,\end{align*} $$
we attach a codimension one subspace
![]() $\mathcal {L}^{a}\subseteq \operatorname { {Hom}}(F_{\mathfrak {p}}^\times ,\Omega )$
as follows: Define
$\mathcal {L}^{a}\subseteq \operatorname { {Hom}}(F_{\mathfrak {p}}^\times ,\Omega )$
as follows: Define
where
![]() $\log _p$
is the usual branch of the p-adic logarithm fulfilling
$\log _p$
is the usual branch of the p-adic logarithm fulfilling
![]() $\log _p(p)=0$
and put
$\log _p(p)=0$
and put
where
![]() $\operatorname {{ord}}_p$
denotes the p-adic valuation of
$\operatorname {{ord}}_p$
denotes the p-adic valuation of
![]() $F_{\mathfrak {p}}^\times $
fulfilling
$F_{\mathfrak {p}}^\times $
fulfilling
![]() $\operatorname {{ord}}_p(p)=1$
. Since the elements
$\operatorname {{ord}}_p(p)=1$
. Since the elements
![]() $\log _\sigma $
,
$\log _\sigma $
,
![]() $\sigma \in \Sigma _{\mathfrak {p}}$
, together with
$\sigma \in \Sigma _{\mathfrak {p}}$
, together with
![]() $\operatorname {{ord}}_p$
form a basis of
$\operatorname {{ord}}_p$
form a basis of
![]() $\operatorname {{Hom}}(F_{\mathfrak {p}}^\times ,\Omega )$
one deduces that
$\operatorname {{Hom}}(F_{\mathfrak {p}}^\times ,\Omega )$
one deduces that
![]() $\mathcal {L}^{a}\subseteq \operatorname {{Hom}}(F_{\mathfrak {p}}^\times ,\Omega )$
is a subspace of codimension one that does not contain the subspace of smooth homomorphisms.
$\mathcal {L}^{a}\subseteq \operatorname {{Hom}}(F_{\mathfrak {p}}^\times ,\Omega )$
is a subspace of codimension one that does not contain the subspace of smooth homomorphisms.
Definition 4.5. Suppose that
![]() $\rho _{\mathfrak {p}}$
is noncritical. The Fontaine–Mazur
$\rho _{\mathfrak {p}}$
is noncritical. The Fontaine–Mazur
![]() $\mathcal {L}$
-invariant of
$\mathcal {L}$
-invariant of
![]() $\rho _{\mathfrak {p}}$
is the codimension one subspace
$\rho _{\mathfrak {p}}$
is the codimension one subspace
Theorem 4.6. Suppose that
![]() $\pi $
is noncritical at
$\pi $
is noncritical at
![]() $\mathfrak {p}$
and that
$\mathfrak {p}$
and that
![]() $\rho _{\mathfrak {p}}$
is noncritical. Then the equality
$\rho _{\mathfrak {p}}$
is noncritical. Then the equality
holds for every sign character
![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
. In particular, the automorphic
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$
. In particular, the automorphic
![]() $\mathcal {L}$
-invariant
$\mathcal {L}$
-invariant
![]() $\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
does not depend on the sign character
$\mathcal {L}_{\mathfrak {p}}(\pi )^\epsilon $
does not depend on the sign character
![]() $\epsilon $
.
$\epsilon $
.
Proof. This follows directly by comparing Theorem 4.3 with the corresponding formula on the Galois side (cf. [Reference Zhang44, Theorem 1.1]) for the family of Galois representations attached to the family passing through
![]() $\pi $
. See [Reference Gehrmann and Rosso25, Theorem 4.1] for more details in case
$\pi $
. See [Reference Gehrmann and Rosso25, Theorem 4.1] for more details in case
![]() $k_\sigma =0$
for all
$k_\sigma =0$
for all
![]() $\sigma \in \Sigma _{\mathfrak {p}}$
.
$\sigma \in \Sigma _{\mathfrak {p}}$
.
In [Reference Ding16] respectively [Reference Ding17], Ding proves that in case D is split at exactly one Archimedean place the Fontaine–Mazur
![]() $\mathcal {L}$
-invariant can be detected by completed cohomology of the associated Shimura curve. Thus, by the theorem above the automorphic
$\mathcal {L}$
-invariant can be detected by completed cohomology of the associated Shimura curve. Thus, by the theorem above the automorphic
![]() $\mathcal {L}$
-invariant can also be detected by completed cohomology in that case. For the modular curve, Breuil gives a direct proof of this consequence in [Reference Breuil10]. It would be worthwhile to explore whether Breuil’s proof extends to our more general setup.
$\mathcal {L}$
-invariant can also be detected by completed cohomology in that case. For the modular curve, Breuil gives a direct proof of this consequence in [Reference Breuil10]. It would be worthwhile to explore whether Breuil’s proof extends to our more general setup.
Acknowledgements
We would like to thank Yiwen Ding for an enlightening correspondence about noncriticality of Galois representations. We thank Daniel Barrera Salazar and the anonymous referees for their comments and corrections, which greatly improved the paper.
Competing interest
The authors have no competing interest to declare.