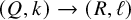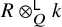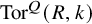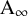1 Introduction
The phenomenon of Koszul duality has been observed in many forms across algebra, geometry and topology. It provides explicit computational tools for answering homological questions and opens up deep connections between a number of seemingly unrelated areas of mathematics. The goal of the present work is to develop a relative theory of Koszul duality in local commutative algebra and to give concrete applications for understanding infinite free resolutions.
For a finite homomorphism
![]() $\varphi \colon Q\to R$
of commutative noetherian local rings, the derived fiber
$\varphi \colon Q\to R$
of commutative noetherian local rings, the derived fiber
![]() $F=R\otimes ^{\mathsf {L}}_Qk$
, where k is the residue field of Q, is a differential graded k-algebra that encodes important ring theoretic properties of
$F=R\otimes ^{\mathsf {L}}_Qk$
, where k is the residue field of Q, is a differential graded k-algebra that encodes important ring theoretic properties of
![]() $\varphi $
. We define
$\varphi $
. We define
![]() $\varphi $
to be Koszul if F is formal (see 2.3) and if its homology
$\varphi $
to be Koszul if F is formal (see 2.3) and if its homology
![]() $\mathrm {H}(F)=\operatorname {Tor}^{Q}(R,k)$
is a Koszul k-algebra (see 2.1). This recovers the classical definition when the source is a field. Through the looking glass that connects local algebra with rational homotopy theory, the definition is directly analogous to Berglund’s notion of a Koszul space.
$\mathrm {H}(F)=\operatorname {Tor}^{Q}(R,k)$
is a Koszul k-algebra (see 2.1). This recovers the classical definition when the source is a field. Through the looking glass that connects local algebra with rational homotopy theory, the definition is directly analogous to Berglund’s notion of a Koszul space.
Flat local maps that have a Koszul fiber are natural examples of Koszul homomorphisms, but the non-flat case is significantly more interesting: all complete intersection and all Golod quotient homomorphisms are Koszul, and we give many other monomial and Gorenstein examples. In particular, there is no need for the homomorphism to be quadratic in any sense.
The definition also has structural consequences connecting the homological algebra over R and Q. Our main theorem provides an algorithmic way to transfer free resolutions over Q into free resolutions over R. To achieve this, we introduce a slightly stronger ‘strictly Koszul property (see 7.2) that is satisfied in our main examples. These ideas borrow from a long history, and we will discuss the context and technology behind the construction following this summary of our main results.
Theorem A. For any strictly Koszul local homomorphism
![]() $\varphi \colon Q \to R$
, there is a non-negatively graded, degreewise finite rank free Q-module C such that
$\varphi \colon Q \to R$
, there is a non-negatively graded, degreewise finite rank free Q-module C such that
-
(1) For each finitely generated R-module M with a minimal Q-free resolution
 $G\to M$
, there is a differential
$G\to M$
, there is a differential
 $\partial ^{\tau }$
on the graded R-module
$\partial ^{\tau }$
on the graded R-module
 $R \otimes C \otimes G$
such that the resulting ‘twisted tensor product’ complex is an R-free resolution of M. If R and M have finite projective dimension over Q, then both C and the twisted tensor product differential can be explicitly described in their entirety with a finite amount of data.
$R \otimes C \otimes G$
such that the resulting ‘twisted tensor product’ complex is an R-free resolution of M. If R and M have finite projective dimension over Q, then both C and the twisted tensor product differential can be explicitly described in their entirety with a finite amount of data. $$ \begin{align*} (R \otimes C\otimes G,\partial^\tau) \xrightarrow{\ \simeq\ } M \end{align*} $$
$$ \begin{align*} (R \otimes C\otimes G,\partial^\tau) \xrightarrow{\ \simeq\ } M \end{align*} $$
-
(2) Assume that
 $\varphi $
is small (a central case of interest is
$\varphi $
is small (a central case of interest is
 $(Q,\mathfrak {m}_Q)$
regular and
$(Q,\mathfrak {m}_Q)$
regular and
 $\ker (\varphi )\subseteq \mathfrak {m}^2_Q$
). The twisted tensor product complex is minimal for the residue field k of R. More generally, the resolution is minimal whenever M is inert with respect to
$\ker (\varphi )\subseteq \mathfrak {m}^2_Q$
). The twisted tensor product complex is minimal for the residue field k of R. More generally, the resolution is minimal whenever M is inert with respect to
 $\varphi $
, in the sense of Lescot. In particular,
$\varphi $
, in the sense of Lescot. In particular,  $$\begin{align*}\textstyle{\sum_i }\operatorname{\mathrm{rank}}_Q(C_i)t^i=\frac{ \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}. \end{align*}$$
$$\begin{align*}\textstyle{\sum_i }\operatorname{\mathrm{rank}}_Q(C_i)t^i=\frac{ \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}. \end{align*}$$
The following homomorphisms are strictly Koszul:
-
(a) Surjective complete intersection homomorphisms.
-
(b) Surjective Golod homomorphisms.
-
(c) Surjective Gorenstein homomorphisms of projective dimension three or less.
-
(d) Cohen presentations of compressed artinian Gorenstein rings having characteristic zero, odd embedding dimension, and socle degree not
 $3$
.
$3$
.
Part (1) of the Theorem, with an explicit description of the twisted tensor product differential, is Theorem 7.8, while part (2) is contained in Theorem 7.11. The examples (a)–(d), and several more, are introduced in Section 3 and treated again in Section 8, with a complete description of the corresponding C in each case.
Universal resolutions – that is, free resolutions over a ring that are defined in a uniform way for all finitely generated modules – have been of central interest in homological commutative algebra since at least the 1960s, often importing tools such as Massey operations and bar resolutions from algebraic topology.
Let
![]() $\varphi \colon Q \to R$
be a local homomorphism. Shamash constructed universal resolutions for R-modules when
$\varphi \colon Q \to R$
be a local homomorphism. Shamash constructed universal resolutions for R-modules when
![]() $\varphi $
is a hypersurface quotient [Reference ShamashSha69], and these were clarified and extended to complete intersection quotients by Eisenbud using the theory of higher homotopies [Reference EisenbudEis80]. Burke recognized in [Reference BurkeBur15] that the higher homotopies are a manifestation of certain
$\varphi $
is a hypersurface quotient [Reference ShamashSha69], and these were clarified and extended to complete intersection quotients by Eisenbud using the theory of higher homotopies [Reference EisenbudEis80]. Burke recognized in [Reference BurkeBur15] that the higher homotopies are a manifestation of certain
![]() $\mathrm {A}_{\infty }$
-structures (we will return to these later in the introduction). In the presence of a Q-free differential graded algebra resolution
$\mathrm {A}_{\infty }$
-structures (we will return to these later in the introduction). In the presence of a Q-free differential graded algebra resolution
![]() $A\to R$
, and a Q-free differential graded A-module resolution G of an R-module M, Iyengar constructed a bar resolution for M over R [Reference IyengarIye97]. By endowing A with an
$A\to R$
, and a Q-free differential graded A-module resolution G of an R-module M, Iyengar constructed a bar resolution for M over R [Reference IyengarIye97]. By endowing A with an
![]() $\mathrm {A}_{\infty }$
-algebra structure, and G with an
$\mathrm {A}_{\infty }$
-algebra structure, and G with an
![]() $\mathrm {A}_{\infty }$
-module structure over A, Burke constructed a bar resolution even when associative multiplicative resolutions do not exist [Reference BurkeBur15]. The resulting resolution is minimal when M is Golod with respect to
$\mathrm {A}_{\infty }$
-module structure over A, Burke constructed a bar resolution even when associative multiplicative resolutions do not exist [Reference BurkeBur15]. The resulting resolution is minimal when M is Golod with respect to
![]() $\varphi $
, and is otherwise typically far from minimal. Theorem A recovers both the resolutions of Shamash and Eisenbud, when
$\varphi $
, and is otherwise typically far from minimal. Theorem A recovers both the resolutions of Shamash and Eisenbud, when
![]() $\varphi $
is a complete intersection quotient, and the bar resolutions of Iyengar and Burke, when
$\varphi $
is a complete intersection quotient, and the bar resolutions of Iyengar and Burke, when
![]() $\varphi $
is a Golod quotient.
$\varphi $
is a Golod quotient.
In parallel, the universal resolutions introduced by Priddy over Koszul algebras [Reference PriddyPri70] have had far-reaching impact, not least as a computational tool. Our theory directly builds on and recovers his construction, while providing a common framework for the universal resolutions above.
The technical foundation for our universal resolutions is in Section 6. Here, we develop a general theory of twisted tensor products over a commutative ring Q. The data that goes into this construction is a curved differential graded coalgebra C over Q, a quasi-isomorphism
![]() ${\mathsf {\Omega }}{C}\to R$
from the cobar construction of C to R, and a differential graded module structure over
${\mathsf {\Omega }}{C}\to R$
from the cobar construction of C to R, and a differential graded module structure over
![]() ${\mathsf {\Omega }}{C}$
on G. These terms are defined in Section 4. From this, in Theorem 6.5, we construct a canonical resolution
${\mathsf {\Omega }}{C}$
on G. These terms are defined in Section 4. From this, in Theorem 6.5, we construct a canonical resolution
The key to proving Theorem A is to show that C can be defined in an explicit, canonical and minimal way when
![]() $\varphi $
is strictly Koszul. We will return to this at the end of the introduction, with more context in hand.
$\varphi $
is strictly Koszul. We will return to this at the end of the introduction, with more context in hand.
We turn our attention back to the Koszul homomorphisms. The first half of this work develops the theory of these maps; this part of the paper does not involve
![]() $\mathrm {A}_{\infty }$
-structures, using only ordinary differential graded algebras.
$\mathrm {A}_{\infty }$
-structures, using only ordinary differential graded algebras.
Similar Koszul-type conditions have been considered by other authors [Reference Croll, Dellaca, Gupta, Hoffmeier, Mukundan, Şega, Sosa, Thompson and TracyCDG+20, Reference Herzog and IyengarHI05, Reference Herzog, Reiner and WelkerHRW98, Reference MyersMye21], and we compare our definition with theirs in Remark 2.18. We motivate our condition as well by drawing connections with other areas, such as rational homotopy theory (Remarks 2.5 and 3.18) and toric topology (Remark 3.27).
We pay particular attention to the case that Q is regular. In this situation, the resolutions constructed in Theorem A essentially depend only on the ring R, and they are always finitely determined. When R is a local ring such that every Cohen presentation
![]() $\varphi \colon Q\to \widehat {R}$
is a Koszul homomorphism, we say that R is Cohen Koszul; see Section 2.8. These rings enjoy excellent homological properties while being surprisingly abundant; they behave in many ways like classical Koszul algebras despite not necessarily being quadratic.
$\varphi \colon Q\to \widehat {R}$
is a Koszul homomorphism, we say that R is Cohen Koszul; see Section 2.8. These rings enjoy excellent homological properties while being surprisingly abundant; they behave in many ways like classical Koszul algebras despite not necessarily being quadratic.
We show that Cohen Koszul local rings have rational Poincaré series that can be computed explicitly from their Koszul homology:
 $$\begin{align*}\operatorname{\mathrm{P}}^R_k(t)=\frac{(1+t)^e}{\sum_{i,w}(-1)^w \operatorname{\mathrm{rank}}_k (\mathrm{H}_{i}(K^R)_{(w)})t^{i+w}}\,; \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{P}}^R_k(t)=\frac{(1+t)^e}{\sum_{i,w}(-1)^w \operatorname{\mathrm{rank}}_k (\mathrm{H}_{i}(K^R)_{(w)})t^{i+w}}\,; \end{align*}$$
see Proposition 2.11, where the notation is explained.
Section 3 is devoted entirely to examples, and we prove that surjective complete intersection homomorphisms are Koszul (Example 3.2), along with surjective Golod homomorphisms (Example 3.5), and surjective Gorenstein homomorphisms of projective dimension three (Example 3.12). We exactly determine the local rings of codepth three or less that are Cohen Koszul in terms of the classification into the types described in [Reference Avramov, Kustin and MillerAKM88]; we find that in every type except one, the local ring is Cohen Koszul (Theorem 3.10). Graded local rings having an almost linear resolution in the sense of [Reference Dao and EisenbudDE22] are also Cohen Koszul (Remark 3.17). We treat monomial rings in Section 3.20, making connections with combinatorial commutative algebra and with the topology of moment angle complexes. Monomial rings are classically Koszul exactly when they are quadratic [Reference FröbergFrö75], while Cohen Koszul monomial rings need not be, and we produce many nontrivial examples in Proposition 3.22. We further give examples that illuminate how the Koszul condition relates with classical Koszulity, formality, being quadratic, and various other technical conditions.
One of our main examples is a class of rings that we call almost Golod Gorenstein, treated in Section 3.13. Within the class of Gorenstein local rings, these display extremal homological behavior analogous to Golod rings within the class of all local rings; cf. Proposition 3.19. In Theorem 3.16, we establish a characterization in terms of the derived fiber that is similar to Avramov’s characterization of Golod rings [Reference Avramov and RoosAvr86], and, under some additional technical assumptions, we deduce that almost Golod Gorenstein rings are Cohen Koszul.
In the second half of the paper, we study Koszul homomorphims from the perspective of
![]() $\mathrm {A}_{\infty }$
-structures on resolutions. An
$\mathrm {A}_{\infty }$
-structures on resolutions. An
![]() $\mathrm {A}_{\infty }$
-algebra is a complex A equipped with multilinear operations
$\mathrm {A}_{\infty }$
-algebra is a complex A equipped with multilinear operations
![]() $m_n\colon A^{\otimes n}\to A$
for
$m_n\colon A^{\otimes n}\to A$
for
![]() $n\geqslant 2$
that together satisfy certain associativity conditions generalizing the definition of a differential graded algebra (which one recovers by assuming
$n\geqslant 2$
that together satisfy certain associativity conditions generalizing the definition of a differential graded algebra (which one recovers by assuming
![]() $m_n=0$
for
$m_n=0$
for
![]() $n\geqslant 3$
). These objects were introduced by Stasheff to characterize loop spaces in algebraic topology [Reference StasheffSta63a].
$n\geqslant 3$
). These objects were introduced by Stasheff to characterize loop spaces in algebraic topology [Reference StasheffSta63a].
Koszulity is well known to be connected with formality (Remark 2.5), and in turn, it has been understood since [Reference KadeishviliKad82] that formality can be made visible through
![]() $\mathrm {A}_{\infty }$
-structures. In the present context, these structures are important because they carry the information necessary to construct the universal resolutions in Theorem A while being flexible enough that all resolutions can always be given
$\mathrm {A}_{\infty }$
-structures. In the present context, these structures are important because they carry the information necessary to construct the universal resolutions in Theorem A while being flexible enough that all resolutions can always be given
![]() $\mathrm {A}_{\infty }$
-structures.
$\mathrm {A}_{\infty }$
-structures.
An introduction to
![]() $\mathrm {A}_{\infty }$
-algebras and
$\mathrm {A}_{\infty }$
-algebras and
![]() $\mathrm {A}_{\infty }$
-modules over commutative rings is given in Section 4. In Section 5, we prove some quite general transfer results – in particular, constructing
$\mathrm {A}_{\infty }$
-modules over commutative rings is given in Section 4. In Section 5, we prove some quite general transfer results – in particular, constructing
![]() $\mathrm {A}_{\infty }$
-structures on minimal resolutions of local rings and modules. Burke was one of the first to develop and apply the theory of
$\mathrm {A}_{\infty }$
-structures on minimal resolutions of local rings and modules. Burke was one of the first to develop and apply the theory of
![]() $\mathrm {A}_{\infty }$
-algebras over a commutative ring (rather than over a field) [Reference BurkeBur15, Reference BurkeBur18], and our treatment owes a substantial intellectual debt to his work.
$\mathrm {A}_{\infty }$
-algebras over a commutative ring (rather than over a field) [Reference BurkeBur15, Reference BurkeBur18], and our treatment owes a substantial intellectual debt to his work.
We develop the theory of cyclic
![]() $\mathrm {A}_{\infty }$
-algebras over commutative rings in Section 5.6. These were introduced by Kontsevich as part of his homological mirror symmetry program [Reference KontsevichKon94]. These
$\mathrm {A}_{\infty }$
-algebras over commutative rings in Section 5.6. These were introduced by Kontsevich as part of his homological mirror symmetry program [Reference KontsevichKon94]. These
![]() $\mathrm {A}_{\infty }$
-algebras possess extra structure that takes advantage of the Poincaré duality on the minimal resolution of a Gorenstein ring, and we apply this theory to almost Golod Gorenstein rings.
$\mathrm {A}_{\infty }$
-algebras possess extra structure that takes advantage of the Poincaré duality on the minimal resolution of a Gorenstein ring, and we apply this theory to almost Golod Gorenstein rings.
With this perspective in hand, we return to Koszul homomorphisms in Section 7. The next result shows that, at the derived level, Koszul homomorphisms may be thought of as deformations of classical Koszul algebras. A more precise and more general statement is given in Theorem 7.1. We write ![]() for the tensor algebra
for the tensor algebra
![]() $\bigoplus _{n\geqslant 0}V^{\otimes _Q n}$
on a graded Q-module V.
$\bigoplus _{n\geqslant 0}V^{\otimes _Q n}$
on a graded Q-module V.
Theorem B. A surjective local homomorphism
![]() $\varphi \colon Q \to R$
is Koszul if and only if there is a positively graded, degreewise finite rank free Q-module V, a direct summand
$\varphi \colon Q \to R$
is Koszul if and only if there is a positively graded, degreewise finite rank free Q-module V, a direct summand
![]() $W\subseteq V \otimes _Q V$
, and an
$W\subseteq V \otimes _Q V$
, and an
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n\}$
on
$\{m_n\}$
on ![]() such that
such that
-
1. the induced quotient
 $A\to R$
is an
$A\to R$
is an
 $\mathrm {A}_{\infty }$
-algebra quasi-isomorphism,
$\mathrm {A}_{\infty }$
-algebra quasi-isomorphism, -
2. modulo the maximal ideal of Q, the
 $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
 $\{m_n\}$
on A agrees with the usual algebra structure on
$\{m_n\}$
on A agrees with the usual algebra structure on  ; that is, where
; that is, where $$ \begin{align*} m_2 \otimes_Q k=\mu \otimes_Q k \quad\text{and}\quad m_n\otimes_Q k = 0 \ \text{ for }\ n \neq 2, \end{align*} $$
$$ \begin{align*} m_2 \otimes_Q k=\mu \otimes_Q k \quad\text{and}\quad m_n\otimes_Q k = 0 \ \text{ for }\ n \neq 2, \end{align*} $$
 $\mu $
is the usual product on the quotient of a tensor algebra,
$\mu $
is the usual product on the quotient of a tensor algebra,
-
3. the k-algebra
 is Koszul with this algebra structure.
is Koszul with this algebra structure.
Coming full circle, we are now able to describe the coalgebra C that appears in Theorem A. Fixing a Koszul homomorphism
![]() $\varphi $
with V and W as in Theorem B, we define
$\varphi $
with V and W as in Theorem B, we define
This is modeled on the work of Priddy [Reference PriddyPri70]. By construction, the graded Q-dual
![]() $C^\vee $
is the quadratic dual
$C^\vee $
is the quadratic dual ![]() of the algebra
of the algebra ![]() . The strict Koszul condition introduced in Section 7.2 guarantees that the
. The strict Koszul condition introduced in Section 7.2 guarantees that the
![]() $\mathrm {A}_{\infty }$
-structure on A induces the structure of a curved differential graded coalgebra on C; see Definition 7.3. We think of C as Koszul dual to R relative to Q, as justified by Theorem 7.6.
$\mathrm {A}_{\infty }$
-structure on A induces the structure of a curved differential graded coalgebra on C; see Definition 7.3. We think of C as Koszul dual to R relative to Q, as justified by Theorem 7.6.
We conclude the paper with a reexamination of examples in Section 8. We start by showing that certain deformations of classical Koszul algebras yield strictly Koszul homomorphisms, and we obtain resolutions that directly deform the original resolutions of Priddy. We study surjective Golod homomorphisms in Example 8.2; in this case, ![]() is the bar construction of the
is the bar construction of the
![]() $\mathrm {A}_{\infty }$
-algebra A, and we recover the bar resolution of Iyengar and Burke. In Example 8.4, we show that surjective Gorenstein homomorphisms of projective dimension three are strictly Koszul, and we describe C as the dual of a noncommutative hypersurface. We show that surjective complete intersection homomorphisms are strictly Koszul in Section 8.7, and we show that C is the free divided power algebra on V; our twisted tensor products encode the theory of higher homotopies, and the resulting resolutions recover those of Shamash and Eisenbud. We end by treating almost Golod Gorenstein rings in Section 8.15; this requires a substantial amount of machinery, and the result is a large class of interesting Gorenstein rings over which we have explicit, small, universal resolutions.
$\mathrm {A}_{\infty }$
-algebra A, and we recover the bar resolution of Iyengar and Burke. In Example 8.4, we show that surjective Gorenstein homomorphisms of projective dimension three are strictly Koszul, and we describe C as the dual of a noncommutative hypersurface. We show that surjective complete intersection homomorphisms are strictly Koszul in Section 8.7, and we show that C is the free divided power algebra on V; our twisted tensor products encode the theory of higher homotopies, and the resulting resolutions recover those of Shamash and Eisenbud. We end by treating almost Golod Gorenstein rings in Section 8.15; this requires a substantial amount of machinery, and the result is a large class of interesting Gorenstein rings over which we have explicit, small, universal resolutions.
2 Koszul homomorphisms
In this section, we discuss the Koszul property in various settings, starting from the classical notion for an algebra over a field and leading up to a definition of a Koszul local homomorphism. Examples have been collected in the Section 3. While later sections exploit the machinery of
![]() $\mathrm {A}_{\infty }$
-algebras, this section requires only knowledge of differential graded (dg) algebras; a suitable reference for the latter is [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98].
$\mathrm {A}_{\infty }$
-algebras, this section requires only knowledge of differential graded (dg) algebras; a suitable reference for the latter is [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98].
We fix a field k and work with local rings having residue field k. We also consider modules with two
![]() $\mathbb {Z}$
-gradings, the weight grading and the homological grading. The weight grading is denoted
$\mathbb {Z}$
-gradings, the weight grading and the homological grading. The weight grading is denoted
![]() $M = M_{(\star )}$
and the corresponding shift
$M = M_{(\star )}$
and the corresponding shift
![]() $M(d)$
is given by
$M(d)$
is given by
![]() $M(d)_{(w)} = M_{(w+d)}$
. For the homological grading, we write
$M(d)_{(w)} = M_{(w+d)}$
. For the homological grading, we write
![]() $M = M_{\bullet }$
, and the suspension
$M = M_{\bullet }$
, and the suspension
![]() $\Sigma ^d M$
is given by
$\Sigma ^d M$
is given by
![]() $(\Sigma ^d M)_i = M_{i-d}$
. The homological degree of an element
$(\Sigma ^d M)_i = M_{i-d}$
. The homological degree of an element
![]() $m\in M$
is denoted
$m\in M$
is denoted
![]() $|m|$
. We assume that the two gradings are compatible in the sense that M is bigraded by its submodules
$|m|$
. We assume that the two gradings are compatible in the sense that M is bigraded by its submodules ![]() . If M is a complex, the differential
. If M is a complex, the differential
![]() $\partial ^M$
should preserve the weight grading and decrease the homological grading by one, and we equip
$\partial ^M$
should preserve the weight grading and decrease the homological grading by one, and we equip
![]() $\Sigma M$
with the differential
$\Sigma M$
with the differential ![]() .
.
Definition 2.1. An augmented k-algebra K is Koszul (over k) if it admits an algebra grading
![]() $K=\bigoplus _{w\geqslant 0} K_{(w)}$
, known as a weight grading, such that
$K=\bigoplus _{w\geqslant 0} K_{(w)}$
, known as a weight grading, such that
![]() $K_{(0)}=k$
and such that the minimal resolution of k is linear with respect to this grading.
$K_{(0)}=k$
and such that the minimal resolution of k is linear with respect to this grading.
Remark 2.2. Definition 2.1 is essentially the classical definition of a Koszul algebra due to Priddy [Reference PriddyPri70, Section 2] (see also [Reference LöfwallLöf86, Reference Fröberg, Dobbs, Fontana and KabbajFrö99]), except that we do not consider the weight grading to be part of the given data. We emphasize that the additional grading may be different to the given one; cf. Remark 3.3. By [Reference Beilinson, Ginzburg and SoergelBGS96, Secton 2.3], a Koszul algebra is quadratic with respect to this new grading – that is, generated as an associative k-algebra by elements of weight one, subject to relations of weight two. For example, if U is a graded vector space, then the trivial extension algebra
![]() $K=k \ltimes U$
is a graded augmented algebra, and the weight grading
$K=k \ltimes U$
is a graded augmented algebra, and the weight grading
![]() $K_{(0)}=k$
and
$K_{(0)}=k$
and
![]() $K_{(1)}=U$
makes K Koszul; see Example 3.4.
$K_{(1)}=U$
makes K Koszul; see Example 3.4.
Next, we define a Koszul property for dg algebras. This definition appears implicitly in the work of Berglund [Reference BerglundBer14], where it is applied to Sullivan models for topological spaces; it is not the same as the Koszul property introduced in [Reference He and WuHW08], which is too general for our purposes.
2.3. Let A and B be dg k-algebras. Recall that A is quasi-isomorphic to B, denoted
![]() $A \simeq B$
, if there exists a zig-zag of quasi-isomorphisms of dg k-algebras connecting A and B. A dg k-algebra K is called formal if it is quasi-isomorphic to
$A \simeq B$
, if there exists a zig-zag of quasi-isomorphisms of dg k-algebras connecting A and B. A dg k-algebra K is called formal if it is quasi-isomorphic to
![]() $\mathrm {H}(K)$
.
$\mathrm {H}(K)$
.
Definition 2.4. An augmented dg k-algebra K is Koszul if it is formal and
![]() $\mathrm {H}(K)$
is Koszul in the sense of Definition 2.1.
$\mathrm {H}(K)$
is Koszul in the sense of Definition 2.1.
Remark 2.5. It is well known that formality is closely related with the Koszul property. In fact, an augmented k-algebra K is Koszul in the sense of Definition 2.1 if and only if the dg k-algebra
![]() $\operatorname {\mathsf {R}Hom}_{K}(k,k)$
is formal; see [Reference Gugenheim and MayGM74] and also [Reference Keller, Happel and ZhangKel02, 2.2] and [Reference BerglundBer14, Theorem 2.9]. This condition is sometimes called coformality of K. From this perspective, a dg k-algebra K is Koszul in the sense of Definition 2.4 if and only if it is both formal and coformal.
$\operatorname {\mathsf {R}Hom}_{K}(k,k)$
is formal; see [Reference Gugenheim and MayGM74] and also [Reference Keller, Happel and ZhangKel02, 2.2] and [Reference BerglundBer14, Theorem 2.9]. This condition is sometimes called coformality of K. From this perspective, a dg k-algebra K is Koszul in the sense of Definition 2.4 if and only if it is both formal and coformal.
Before introducing the Koszul property for local homomorphisms, we need to recall the notion of the derived fiber. Let
![]() $\varphi \colon Q \to R$
be a local homomorphism of commutative noetherian local rings having maximal ideals
$\varphi \colon Q \to R$
be a local homomorphism of commutative noetherian local rings having maximal ideals
![]() $\mathfrak {m}_Q$
and
$\mathfrak {m}_Q$
and
![]() $\mathfrak {m}_R$
, respectively, and common residue field k.
$\mathfrak {m}_R$
, respectively, and common residue field k.
Let
![]() $A \to R$
be a dg algebra resolution of R over Q – that is, A is a dg algebra concentrated in non-negative degrees, such that A is degreewise a free Q-module, and
$A \to R$
be a dg algebra resolution of R over Q – that is, A is a dg algebra concentrated in non-negative degrees, such that A is degreewise a free Q-module, and
![]() $A\to R$
is a morphism of dg algebras inducing an isomorphism in homology. The derived fiber of
$A\to R$
is a morphism of dg algebras inducing an isomorphism in homology. The derived fiber of
![]() $\varphi $
is the dg k-algebra
$\varphi $
is the dg k-algebra
Up to a zig-zag of quasi-isomorphisms of dg k-algebras,
![]() $R \otimes ^{\mathsf {L}}_Q k$
is independent of the choice of A. For more information, see [Reference Avramov and RoosAvr86]. We remark that one can equally well use a different species of model for the resolution A, such as simplicial algebras or
$R \otimes ^{\mathsf {L}}_Q k$
is independent of the choice of A. For more information, see [Reference Avramov and RoosAvr86]. We remark that one can equally well use a different species of model for the resolution A, such as simplicial algebras or
![]() $\mathrm {A}_{\infty }$
-algebras, and obtain an equivalent definition of Koszul homomorphism. Indeed, we make use of
$\mathrm {A}_{\infty }$
-algebras, and obtain an equivalent definition of Koszul homomorphism. Indeed, we make use of
![]() $\mathrm {A}_{\infty }$
-models in Section 7.
$\mathrm {A}_{\infty }$
-models in Section 7.
Definition 2.6. Let
![]() $\varphi \colon Q \to R$
be a finite local homomorphism. We say that
$\varphi \colon Q \to R$
be a finite local homomorphism. We say that
![]() $\varphi $
is Koszul if
$\varphi $
is Koszul if
![]() $R \otimes ^{\mathsf {L}}_Q k$
is a Koszul dg k-algebra; that is,
$R \otimes ^{\mathsf {L}}_Q k$
is a Koszul dg k-algebra; that is,
![]() $R \otimes ^{\mathsf {L}}_Q k$
is formal and its homology
$R \otimes ^{\mathsf {L}}_Q k$
is formal and its homology
![]() $\operatorname {Tor}^{Q}(R,k)$
is Koszul in the sense of Definition 2.1.
$\operatorname {Tor}^{Q}(R,k)$
is Koszul in the sense of Definition 2.1.
According to Definition 2.1, when
![]() $\varphi $
is Koszul, the Tor algebra
$\varphi $
is Koszul, the Tor algebra
![]() $\operatorname {Tor}^{Q}(R,k)$
admits a quadratic presentation, albeit not necessarily generated by elements in homological degree one.
$\operatorname {Tor}^{Q}(R,k)$
admits a quadratic presentation, albeit not necessarily generated by elements in homological degree one.
Taking
![]() $Q=k$
to be a field, we recover the classical definition: The homomorphism
$Q=k$
to be a field, we recover the classical definition: The homomorphism
![]() $k\to R$
is Koszul if and only if R is a Koszul k-algebra; cf. Definition 2.1.
$k\to R$
is Koszul if and only if R is a Koszul k-algebra; cf. Definition 2.1.
The examples given in the next section show that Koszul homomorphisms are extremely common. In particular, this class includes all flat local homomorphisms whose fibers are (classically) Koszul; all complete intersection and all Golod homomorphisms; Cohen presentations of most local rings having codepth at most
![]() $3$
, and of generic Gorenstein rings.
$3$
, and of generic Gorenstein rings.
Remark 2.7. When the minimal Q-free resolution A of R admits a dg algebra structure, the derived fiber
![]() $R\otimes ^{\mathsf {L}}_Q k= A\otimes _Rk$
has zero differential and is automatically formal. This is the case for complete intersection homomorphisms (Example 3.2) and when
$R\otimes ^{\mathsf {L}}_Q k= A\otimes _Rk$
has zero differential and is automatically formal. This is the case for complete intersection homomorphisms (Example 3.2) and when
![]() $\operatorname {\mbox {proj dim}}_Q(R)\leqslant 3$
(Theorem 3.10). When
$\operatorname {\mbox {proj dim}}_Q(R)\leqslant 3$
(Theorem 3.10). When
![]() $\varphi $
is Golod, the minimal resolution typically does not support a dg algebra structure (cf. Remark 8.3), but nonetheless,
$\varphi $
is Golod, the minimal resolution typically does not support a dg algebra structure (cf. Remark 8.3), but nonetheless,
![]() $R\otimes ^{\mathsf {L}}_Q k$
is formal (Example 3.5). The monomial rings presented in Examples 3.6 and 3.24 yield non-Koszul homomorphisms; the corresponding minimal resolution does not admit a dg algebra structure in the former example (see [Reference AvramovAvr81, 2.2]), but it does in the latter example.
$R\otimes ^{\mathsf {L}}_Q k$
is formal (Example 3.5). The monomial rings presented in Examples 3.6 and 3.24 yield non-Koszul homomorphisms; the corresponding minimal resolution does not admit a dg algebra structure in the former example (see [Reference AvramovAvr81, 2.2]), but it does in the latter example.
2.8 Cohen Koszul local rings
Recall that every local ring R admits a Cohen presentation – that is, a surjection
![]() $\varphi \colon Q\to \widehat {R}$
from a regular local ring Q – and one may assume that
$\varphi \colon Q\to \widehat {R}$
from a regular local ring Q – and one may assume that
![]() $\varphi $
is minimal in the sense that
$\varphi $
is minimal in the sense that
![]() $\ker (\varphi ) \subseteq \mathfrak {m}_Q^2$
.
$\ker (\varphi ) \subseteq \mathfrak {m}_Q^2$
.
Definition 2.9. A local ring R is Cohen Koszul if every homomorphism
![]() $\varphi \colon Q\to \widehat {R}$
is Koszul, where Q is a regular local ring and
$\varphi \colon Q\to \widehat {R}$
is Koszul, where Q is a regular local ring and
![]() $\varphi $
is surjective with
$\varphi $
is surjective with
![]() $\ker (\varphi ) \subseteq \mathfrak {m}_Q^2$
. In other words, every minimal Cohen presentation of R is Koszul.
$\ker (\varphi ) \subseteq \mathfrak {m}_Q^2$
. In other words, every minimal Cohen presentation of R is Koszul.
Remark 2.10. For equicharacteristic rings, the minimal Cohen presentation
![]() $Q\to \widehat {R}$
is essentially unique. In this situation, if R is already a quotient of a regular local ring, then by Proposition 2.16, there is no need to complete R to determine whether R is Cohen Koszul.
$Q\to \widehat {R}$
is essentially unique. In this situation, if R is already a quotient of a regular local ring, then by Proposition 2.16, there is no need to complete R to determine whether R is Cohen Koszul.
If we assume that R contains its residue field k, then the Koszul complex
![]() $K^R$
on the maximal ideal of R is a dg k-algebra. It is well known that
$K^R$
on the maximal ideal of R is a dg k-algebra. It is well known that
as dg k-algebras; see, for example, [Reference Avramov, Buchweitz, Iyengar and MillerABIM10, Theorem 8.1]. Therefore, in this situation, we can say that R is Cohen Koszul exactly when
![]() $K^R$
is a Koszul dg k-algebra.
$K^R$
is a Koszul dg k-algebra.
If R does not contain its residue field, the fact that
![]() $K^R$
is not a dg k-algebra introduces subtleties. The distinction between formality of dg k-algebras and formality of dg rings means that it is not clear whether Definition 2.9 is independent of the choice of Cohen presentation. In all of our examples, however, the choice will be irrelevant.
$K^R$
is not a dg k-algebra introduces subtleties. The distinction between formality of dg k-algebras and formality of dg rings means that it is not clear whether Definition 2.9 is independent of the choice of Cohen presentation. In all of our examples, however, the choice will be irrelevant.
Complete intersection rings are Cohen Koszul by Example 3.2, Golod rings are Cohen Koszul by Example 3.5, and most rings of codepth
![]() $3$
are Cohen Koszul according to Theorem 3.10.
$3$
are Cohen Koszul according to Theorem 3.10.
Cohen Koszul local rings have rational Poincaré series. Recall that the Poincaré series of a finitely generated R-module M is
Proposition 2.11. Let R be a Cohen Koszul local ring with embedding dimension e and residue field k. Fix a weight grading making the Koszul homology
![]() $\mathrm {H}(K^R)$
a Koszul k-algebra. Then
$\mathrm {H}(K^R)$
a Koszul k-algebra. Then
 $$\begin{align*}\operatorname{\mathrm{P}}^R_k(t)=\frac{(1+t)^e}{\sum_{i,w}(-1)^w \operatorname{\mathrm{rank}}_k (\mathrm{H}_i(K^R)_{(w)})t^{i+w}}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{P}}^R_k(t)=\frac{(1+t)^e}{\sum_{i,w}(-1)^w \operatorname{\mathrm{rank}}_k (\mathrm{H}_i(K^R)_{(w)})t^{i+w}}. \end{align*}$$
Remark 2.12. We note that since
![]() $\mathrm {H}_*(K^R)$
is generated in weight
$\mathrm {H}_*(K^R)$
is generated in weight
![]() $1$
, the rank of
$1$
, the rank of
![]() $\mathrm {H}_i(K^R)_{(w)}$
is equal to the rank of
$\mathrm {H}_i(K^R)_{(w)}$
is equal to the rank of
![]() $[\mathrm {H}_{>0}(K^R)^{w}/\mathrm {H}_{>0}(K^R)^{w+1}]_i$
. Therefore, it is not necessary to choose a weight grading to calculate the Poincaré series above.
$[\mathrm {H}_{>0}(K^R)^{w}/\mathrm {H}_{>0}(K^R)^{w+1}]_i$
. Therefore, it is not necessary to choose a weight grading to calculate the Poincaré series above.
Proof. Let
![]() $T=\mathrm {H}(K^R)$
, bigraded by homological degree and by weight, and write
$T=\mathrm {H}(K^R)$
, bigraded by homological degree and by weight, and write
In
![]() $\operatorname {Tor}^{T}_{w}{(k,k)}_{i}$
, the index w is the usual homological grading of
$\operatorname {Tor}^{T}_{w}{(k,k)}_{i}$
, the index w is the usual homological grading of
![]() $\operatorname {Tor}$
, and i is the extra grading that comes from the homological grading on T. Since T is Koszul with respect to its weight grading, the usual computation of the Poincaré series of a Koszul algebra shows that
$\operatorname {Tor}$
, and i is the extra grading that comes from the homological grading on T. Since T is Koszul with respect to its weight grading, the usual computation of the Poincaré series of a Koszul algebra shows that
![]() $\mathrm {H}_T(s,t)\operatorname {\mathrm {P}}^T_k(-s,t)=1$
; see [Reference LöfwallLöf86].
$\mathrm {H}_T(s,t)\operatorname {\mathrm {P}}^T_k(-s,t)=1$
; see [Reference LöfwallLöf86].
Let
![]() $Q\to \widehat {R}$
be a minimal Cohen presentation. Formality of
$Q\to \widehat {R}$
be a minimal Cohen presentation. Formality of
![]() $\widehat {R}\otimes ^{\mathsf {L}}_Qk$
implies that the spectral sequence [Reference AvramovAvr81, 6.2.1] is degenerate, and so from [Reference AvramovAvr81, 6.2 (b’)], we obtain the first equality below, which yields the desired series
$\widehat {R}\otimes ^{\mathsf {L}}_Qk$
implies that the spectral sequence [Reference AvramovAvr81, 6.2.1] is degenerate, and so from [Reference AvramovAvr81, 6.2 (b’)], we obtain the first equality below, which yields the desired series
Proposition 2.11 recovers the known Poincaré series for complete intersection rings, Golod rings and almost Golod Gorenstein rings; see Section 3 for the latter.
There are a number of results that apply to certain subsets of Cohen Koszul rings, motivating the study of whether such a property holds for these rings in general. We highlight a couple instances below.
Remark 2.13. Recently, Brown–Dao–Sridhar have shown that over complete intersection and Golod rings, the ideals of minors of differentials in minimal free resolutions are eventually two-periodic [Reference Brown, Dao and SridharBDS23]. It would be worthwhile, and seems plausible (in light of the structural result in Theorem 7.8), to determine whether (strictly) Cohen Koszul rings satisfy this property more generally.
Remark 2.14. Lower bounds on the Loewy length of the homology module of perfect complexes are of interest in both algebra and topology; see, for example, [Reference Avramov, Buchweitz, Iyengar and MillerABIM10, Reference Allday and PuppeAP93, Reference CarlssonCar83, Reference Iyengar and WalkerIW18, Reference WalkerWal17]. For Cohen Koszul rings, one can establish such bounds.
Let R be a local ring with residue field k, and let
![]() $k[\chi _1,\ldots ,\chi _n]$
denote a maximal polynomial subalgebra of the graded k-algebra
$k[\chi _1,\ldots ,\chi _n]$
denote a maximal polynomial subalgebra of the graded k-algebra
![]() $\operatorname {Ext}_{R}(k,k)$
, generated by elements in even degree. For example, if R is complete intersection, then n is the codimension of R. If R is Cohen Koszul, then for any finite free R-complex F with
$\operatorname {Ext}_{R}(k,k)$
, generated by elements in even degree. For example, if R is complete intersection, then n is the codimension of R. If R is Cohen Koszul, then for any finite free R-complex F with
![]() $\mathrm {H}(F)\neq 0$
, one has the inequality
$\mathrm {H}(F)\neq 0$
, one has the inequality
One can use similar ideas to those in [Reference Avramov, Buchweitz, Iyengar and MillerABIM10], as well as [Reference Briggs, Grifo and PollitzBGP24], to establish this bound; here, however, formality of the derived fiber of a Cohen presentation of R is a main ingredient. Moreover, when R is complete intersection, it agrees with the common bounds from [Reference Avramov, Buchweitz, Iyengar and MillerABIM10, Reference Briggs, Grifo and PollitzBGP24].
2.15 Properties of Koszul homomorphisms
Before moving on to examples, we establish some basic change of rings properties for Koszul homomorphisms. First, we note that being Koszul is invariant under certain flat base changes and, in particular, under completion.
Proposition 2.16. Given a finite local homomorphism
![]() $\varphi \colon Q\to R$
and a flat local homomorphism
$\varphi \colon Q\to R$
and a flat local homomorphism
![]() $\psi \colon Q\to Q'$
inducing an isomorphism on residue fields,
$\psi \colon Q\to Q'$
inducing an isomorphism on residue fields,
![]() $\varphi $
is Koszul if and only if
$\varphi $
is Koszul if and only if
![]() $\varphi \otimes Q' \colon Q'\to R\otimes _Q Q'$
is Koszul.
$\varphi \otimes Q' \colon Q'\to R\otimes _Q Q'$
is Koszul.
Proof. The natural map
![]() $R\otimes ^{\mathsf {L}}_{Q} k\to (R\otimes _Q Q')\otimes ^{\mathsf {L}}_{Q'} k$
is a quasi-isomorphism of dg k-algebras. Indeed, if A is a dg algebra resolution of R over Q, then
$R\otimes ^{\mathsf {L}}_{Q} k\to (R\otimes _Q Q')\otimes ^{\mathsf {L}}_{Q'} k$
is a quasi-isomorphism of dg k-algebras. Indeed, if A is a dg algebra resolution of R over Q, then
![]() $A\otimes _QQ'$
is a dg algebra resolution of
$A\otimes _QQ'$
is a dg algebra resolution of
![]() $R\otimes _Q Q'$
over
$R\otimes _Q Q'$
over
![]() $Q'$
, and
$Q'$
, and
![]() $(A\otimes _QQ')\otimes _{Q'}k \cong A\otimes _Q k$
.
$(A\otimes _QQ')\otimes _{Q'}k \cong A\otimes _Q k$
.
The next proposition will often be useful in reducing the dimension of Q or R.
Proposition 2.17. Let
![]() $\varphi \colon Q\to R$
be a finite local homomorphism, and let
$\varphi \colon Q\to R$
be a finite local homomorphism, and let
![]() $x\in \mathfrak {m}_Q$
and
$x\in \mathfrak {m}_Q$
and
![]() $y\in \mathfrak {m}_R$
.
$y\in \mathfrak {m}_R$
.
-
(1) If x is regular on Q and y is regular on R, with
 $\varphi (x)=y$
, then
$\varphi (x)=y$
, then
 $\varphi $
is Koszul if and only if the map of quotients
$\varphi $
is Koszul if and only if the map of quotients
 $Q/(x)\to R/(y)$
is Koszul.
$Q/(x)\to R/(y)$
is Koszul. -
(2) If y is regular on R, then
 $\varphi $
is Koszul if and only if the composition
$\varphi $
is Koszul if and only if the composition
 $Q\to R/(y)$
is Koszul.
$Q\to R/(y)$
is Koszul. -
(3) If
 $\varphi (x)=0$
and x generates a free R-module summand of
$\varphi (x)=0$
and x generates a free R-module summand of
 $\ker (\varphi )/\ker (\varphi )^2$
, then
$\ker (\varphi )/\ker (\varphi )^2$
, then
 $\varphi $
is Koszul if and only if the induced map
$\varphi $
is Koszul if and only if the induced map
 $Q/(x)\to R$
is Koszul.
$Q/(x)\to R$
is Koszul.
Proof. For part (1), let
![]() $A\xrightarrow {\simeq } R$
be a dg algebra resolution of R over Q. The assumptions on x and y imply that
$A\xrightarrow {\simeq } R$
be a dg algebra resolution of R over Q. The assumptions on x and y imply that
![]() $A\otimes _Q Q/(x)$
is a dg algebra resolution of
$A\otimes _Q Q/(x)$
is a dg algebra resolution of
![]() $R/(y)$
over
$R/(y)$
over
![]() $Q/(x)$
. In particular, there are quasi-isomorphisms
$Q/(x)$
. In particular, there are quasi-isomorphisms
of dg k-algebras, and the claim follows.
For part (2), if A is is a dg algebra resolution of R over Q, as above, then there is an element
![]() $\tilde {y}\in \mathfrak {m}_QA_0$
mapping to
$\tilde {y}\in \mathfrak {m}_QA_0$
mapping to
![]() $y\in R$
. Taking an exterior variable e of degree
$y\in R$
. Taking an exterior variable e of degree
![]() $1$
, and setting
$1$
, and setting
![]() $\partial (e)=\tilde {y}$
, the extension
$\partial (e)=\tilde {y}$
, the extension
![]() $A\langle e\rangle $
is then a dg algebra resolution of
$A\langle e\rangle $
is then a dg algebra resolution of
![]() $R/(y)$
over Q; see [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, 6.1]. We see that
$R/(y)$
over Q; see [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, 6.1]. We see that
where
![]() $\Lambda _k(e)$
is the exterior algebra over k on the degree
$\Lambda _k(e)$
is the exterior algebra over k on the degree
![]() $1$
variable e. Hence, it remains to note that the tensor product of dg k-algebras is formal if and only if both of its factors are formal, and hence Koszul if and only if both of its factors are Koszul; see [Reference Fröberg, Dobbs, Fontana and KabbajFrö99, Theorem 2] for the latter.
$1$
variable e. Hence, it remains to note that the tensor product of dg k-algebras is formal if and only if both of its factors are formal, and hence Koszul if and only if both of its factors are Koszul; see [Reference Fröberg, Dobbs, Fontana and KabbajFrö99, Theorem 2] for the latter.
For part (3), we invoke [Reference IyengarIye01, Proposition 2.1] to obtain a dg algebra resolution A of R over Q and an isomorphism of dg k-algebras
![]() $A\otimes _Q k \cong W \otimes _k \Lambda _k(e)$
, where W is a dg subalgebra of
$A\otimes _Q k \cong W \otimes _k \Lambda _k(e)$
, where W is a dg subalgebra of
![]() $A\otimes _Q k$
and
$A\otimes _Q k$
and
![]() $\Lambda _k(e)$
is the exterior algebra on a generator of degree
$\Lambda _k(e)$
is the exterior algebra on a generator of degree
![]() $1$
(this result is based upon André’s theory of special cycles [Reference AndréAnd82]). Moreover, the proof in [Reference IyengarIye01] identifies the inclusion
$1$
(this result is based upon André’s theory of special cycles [Reference AndréAnd82]). Moreover, the proof in [Reference IyengarIye01] identifies the inclusion
![]() $\Lambda _k(e)\to A\otimes _Q k $
with the natural map
$\Lambda _k(e)\to A\otimes _Q k $
with the natural map
![]() $Q/(x)\otimes ^{\mathsf {L}}_Qk \to R\otimes ^{\mathsf {L}}_Qk$
. It follows that
$Q/(x)\otimes ^{\mathsf {L}}_Qk \to R\otimes ^{\mathsf {L}}_Qk$
. It follows that
As in part (2), we may deduce that
![]() $R\otimes ^{\mathsf {L}}_{Q/(x)}k$
is Koszul dg k-algebra if and only if
$R\otimes ^{\mathsf {L}}_{Q/(x)}k$
is Koszul dg k-algebra if and only if
![]() $R\otimes ^{\mathsf {L}}_{Q}k\simeq (R\otimes ^{\mathsf {L}}_{Q/(x)}k)\otimes _k \Lambda _k(e) $
is as well.
$R\otimes ^{\mathsf {L}}_{Q}k\simeq (R\otimes ^{\mathsf {L}}_{Q/(x)}k)\otimes _k \Lambda _k(e) $
is as well.
Remark 2.18. Many other Koszul-like properties have appeared in the literature. Within local commutative algebra, Herzog, Reiner and Welker introduced a notion of Koszul local ring in [Reference Herzog, Reiner and WelkerHRW98], and the same condition is investigated in [Reference Herzog and IyengarHI05]. The local ring ![]() is Koszul in the sense of these references, but it is not a Koszul k-algebra according to Definition 2.1, since it does not admit a quadratic presentation. However, the same ring
is Koszul in the sense of these references, but it is not a Koszul k-algebra according to Definition 2.1, since it does not admit a quadratic presentation. However, the same ring ![]() is Koszul as a
is Koszul as a ![]() -algebra by Example 3.1, and it is Koszul as a
-algebra by Example 3.1, and it is Koszul as a ![]() -algebra by Example 3.2 – in other words, it is Cohen Koszul.
-algebra by Example 3.2 – in other words, it is Cohen Koszul.
Myers studied a Koszulity condition in [Reference MyersMye21] that is closely related to ours. That work begins with a standard graded k-algebra R, and its Koszul homology
![]() $\mathrm {H}(K^R)$
is said to be strand Koszul if it is Koszul with respect to the induced weight grading by strands:
$\mathrm {H}(K^R)$
is said to be strand Koszul if it is Koszul with respect to the induced weight grading by strands:
![]() $\mathrm {H}(K^R)_{(w)}=\bigoplus _{i+j=w}\mathrm {H}_i(K^R)_j$
(the total of the homological and internal gradings). According to [Reference MyersMye21, Theorem B], the Koszul complex
$\mathrm {H}(K^R)_{(w)}=\bigoplus _{i+j=w}\mathrm {H}_i(K^R)_j$
(the total of the homological and internal gradings). According to [Reference MyersMye21, Theorem B], the Koszul complex
![]() $K^R$
is automatically quasi-formal; this is a weakening of formality defined in terms of the degeneration of a certain Eilenberg–Moore spectral on its second page; see [Reference MyersMye21, 2.3]. In contrast, R is Cohen Koszul if
$K^R$
is automatically quasi-formal; this is a weakening of formality defined in terms of the degeneration of a certain Eilenberg–Moore spectral on its second page; see [Reference MyersMye21, 2.3]. In contrast, R is Cohen Koszul if
![]() $K^R$
is formal and
$K^R$
is formal and
![]() $\mathrm {H}(K^R)$
is Koszul with respect to some weight grading. In the next section, we see that there are many natural examples for which
$\mathrm {H}(K^R)$
is Koszul with respect to some weight grading. In the next section, we see that there are many natural examples for which
![]() $\mathrm {H}(K^R)$
is Koszul with respect to a different grading than the strand grading.
$\mathrm {H}(K^R)$
is Koszul with respect to a different grading than the strand grading.
The authors of [Reference Croll, Dellaca, Gupta, Hoffmeier, Mukundan, Şega, Sosa, Thompson and TracyCDG+20] have also investigated how the Koszul condition on a local ring affects the algebra structure of the Koszul homology
![]() $\mathrm {H}(K^R)$
. While this is connected to the present work, we note that there are many examples of local k-algebras that are Cohen Koszul but not Koszul as k-algebras.
$\mathrm {H}(K^R)$
. While this is connected to the present work, we note that there are many examples of local k-algebras that are Cohen Koszul but not Koszul as k-algebras.
Remark 2.19. We end this section with remarks on the generality of Definition 2.6.
We have chosen to focus on the setting of finite Q-algebras because this is necessary to meaningfully talk about transferring homological information from Q to R. However, the notion of Koszul homomorphism can be extended fruitfully to all local homomorphisms, with some additional technicalities. In particular, to accommodate non-finite algebras, Definition 2.1 should be adapted to require that the completion of K at its augmentation ideal is isomorphic to
![]() $\prod _{w\geqslant 0} K_{(w)}$
, and that k admits a linear resolution over the corresponding graded ring
$\prod _{w\geqslant 0} K_{(w)}$
, and that k admits a linear resolution over the corresponding graded ring
![]() $\bigoplus _{w\geqslant 0} K_{(w)}$
.
$\bigoplus _{w\geqslant 0} K_{(w)}$
.
For Q non-local, one can say a Q-algebra R is Koszul at a prime
![]() $\mathfrak {p} \in \operatorname {Spec}(Q)$
if
$\mathfrak {p} \in \operatorname {Spec}(Q)$
if
![]() $\kappa (\mathfrak {p}) \otimes ^{\mathsf {L}}_Q R$
is a Koszul dg algebra over
$\kappa (\mathfrak {p}) \otimes ^{\mathsf {L}}_Q R$
is a Koszul dg algebra over
![]() $\kappa (\mathfrak {p})=Q_{\mathfrak {p}}/\mathfrak {p} Q_{\mathfrak {p}}$
. From this perspective, it is natural to replace R with a sheaf of algebras on some scheme; examples related to this have appeared in the literature, such as the sheaf of Clifford algebras constructed by Buchweitz in [Reference Buchweitz, Eisenbud and HerzogBEH87, Appendix].
$\kappa (\mathfrak {p})=Q_{\mathfrak {p}}/\mathfrak {p} Q_{\mathfrak {p}}$
. From this perspective, it is natural to replace R with a sheaf of algebras on some scheme; examples related to this have appeared in the literature, such as the sheaf of Clifford algebras constructed by Buchweitz in [Reference Buchweitz, Eisenbud and HerzogBEH87, Appendix].
In this work, we focus on applications to commutative algebra. The natural generalization to non-commutative algebras is interesting as well, using exactly the same definitions.
3 Examples of Koszul homomorphisms
This section contains examples (and counterexamples) demonstrating the ubiquity of the Koszul condition. The first class of examples generalizes the class of Koszul algebras over a field in a straightforward manner.
Example 3.1 (Flat homomorphisms with Koszul fiber).
A flat finite local homomorphism
![]() $\varphi \colon Q \to R$
is Koszul if and only if its fiber
$\varphi \colon Q \to R$
is Koszul if and only if its fiber
![]() $R \otimes _Q k$
is a Koszul k-algebra. Such examples are readily constructed by deforming presentations of known Koszul algebras. For example, the k-algebra
$R \otimes _Q k$
is a Koszul k-algebra. Such examples are readily constructed by deforming presentations of known Koszul algebras. For example, the k-algebra
![]() $k[x]/(x^2)$
is Koszul, and so the homomorphism
$k[x]/(x^2)$
is Koszul, and so the homomorphism
is Koszul for any
![]() $a,b\in \mathfrak {m}_Q$
.
$a,b\in \mathfrak {m}_Q$
.
We will see that the non-flat case is significantly more interesting, and crucially there is no need for the map
![]() $\varphi \colon Q \to R$
to be quadratic in any sense, as the following examples demonstrate. Nonetheless, later we return to the idea that Koszul homomorphisms look like deformations of classical Koszul presentations; cf. Theorem 7.1.
$\varphi \colon Q \to R$
to be quadratic in any sense, as the following examples demonstrate. Nonetheless, later we return to the idea that Koszul homomorphisms look like deformations of classical Koszul presentations; cf. Theorem 7.1.
Example 3.2 (Complete intersection homomorphisms).
Let
![]() $\varphi \colon Q\to R$
be a surjective, local, complete intersection homomorphism of codimension c. That is,
$\varphi \colon Q\to R$
be a surjective, local, complete intersection homomorphism of codimension c. That is,
![]() $\ker (\varphi )$
is generated by a Q-regular sequence
$\ker (\varphi )$
is generated by a Q-regular sequence ![]() . In this case, the Koszul complex
. In this case, the Koszul complex ![]() is a dg algebra resolution of R over Q. Then
is a dg algebra resolution of R over Q. Then
is the exterior algebra on a k-space of rank c in homological degree one, with zero differential. Thus, the derived fiber of
![]() $\varphi $
is clearly formal, and it is well known to be a Koszul k-algebra with its weight homological gradings coinciding; cf. [Reference PriddyPri70, Examples 2.2(2)]. In particular, a local complete intersection ring is Cohen Koszul.
$\varphi $
is clearly formal, and it is well known to be a Koszul k-algebra with its weight homological gradings coinciding; cf. [Reference PriddyPri70, Examples 2.2(2)]. In particular, a local complete intersection ring is Cohen Koszul.
Remark 3.3. For a Cohen Koszul ring R, the homological and weight grading on
![]() $\mathrm {H}(K^R)$
coincide if and only if R is complete intersection. Indeed, the reverse implication was indicated in Example 3.2, and the forward implication follows from a Theorem of Wiebe [Reference WiebeWie69]; see also [Reference Bruns and HerzogBH98, Theorem 2.3.15].
$\mathrm {H}(K^R)$
coincide if and only if R is complete intersection. Indeed, the reverse implication was indicated in Example 3.2, and the forward implication follows from a Theorem of Wiebe [Reference WiebeWie69]; see also [Reference Bruns and HerzogBH98, Theorem 2.3.15].
Example 3.4 (Trivial extension algebras).
Given a graded ring B and a graded B-module U, let
![]() $B\ltimes U$
denote the trivial extension of B by U. This is the graded module
$B\ltimes U$
denote the trivial extension of B by U. This is the graded module
![]() $B\oplus U$
with multiplication
$B\oplus U$
with multiplication
and zero differential. The main case of interest is that B is augmented to k, and U is a graded k-space thought of as a trivial B-module. If B is also a k-algebra, then B is a Koszul if and only if
![]() $B\ltimes U$
is by [Reference ChengChe17].
$B\ltimes U$
is by [Reference ChengChe17].
In particular, for any k-space U, the local k-algebra
![]() $k\ltimes U$
is Koszul. It is also Cohen Koszul, according to Example 3.5.
$k\ltimes U$
is Koszul. It is also Cohen Koszul, according to Example 3.5.
For a surjective local map
![]() $\varphi \colon Q\to R$
and R-module M, there is the following coefficientwise inequality of Poincaré series:
$\varphi \colon Q\to R$
and R-module M, there is the following coefficientwise inequality of Poincaré series:
 $$ \begin{align} \operatorname{\mathrm{P}}^R_M(t)\preccurlyeq \dfrac{\operatorname{\mathrm{P}}^Q_M(t)}{1-t(\operatorname{\mathrm{P}}^Q_R(t)-1)}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{P}}^R_M(t)\preccurlyeq \dfrac{\operatorname{\mathrm{P}}^Q_M(t)}{1-t(\operatorname{\mathrm{P}}^Q_R(t)-1)}. \end{align} $$
This fact is due to Serre; see, for example, [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, Proposition 3.3.2].
Example 3.5 (Golod homomorphisms).
Let
![]() $\varphi \colon Q \to R$
be a surjective, local, Golod homomorphism. That is, the Serre bound (3.4.1) is an equality for the residue field
$\varphi \colon Q \to R$
be a surjective, local, Golod homomorphism. That is, the Serre bound (3.4.1) is an equality for the residue field
![]() $M=k$
.
$M=k$
.
Avramov proved that a surjective, local homomorphism is Golod if and only if there is a quasi-isomorphism of dg algebras
where U is a positively graded vector space over k. This follows by applying [Reference Avramov and RoosAvr86, Theorem 2.3] to a (possibily non-minimal) dg k-algebra model for
![]() $R \otimes ^{\mathsf {L}}_Q k$
. The trivial extension algebra
$R \otimes ^{\mathsf {L}}_Q k$
. The trivial extension algebra
![]() $k\ltimes U$
is Koszul by [Reference Loday and ValletteLV12, Proposition 3.4.9] – see also Example 3.4 – and hence,
$k\ltimes U$
is Koszul by [Reference Loday and ValletteLV12, Proposition 3.4.9] – see also Example 3.4 – and hence,
![]() $\varphi $
is Koszul.
$\varphi $
is Koszul.
The examples above provide many instances of Cohen Koszul k-algebras appearing in local commutative algebra, and some of these examples are Koszul in the classical sense: for example, a local complete intersection k-algebra is Koszul if and only if it is quadratic; see [Reference Fröberg, Dobbs, Fontana and KabbajFrö99, 3.1]. We give a small example of a local k-algebra that is neither Koszul nor Cohen Koszul.
Example 3.6. Suppose ![]() . A computation shows
. A computation shows
![]() $\Lambda _k(e_1,e_2,e_3)/(e_1e_2e_3)$
is an algebra retract of
$\Lambda _k(e_1,e_2,e_3)/(e_1e_2e_3)$
is an algebra retract of
![]() $\mathrm {H}(K^R)$
; one could, for example, use Macaulay2 [Reference Grayson and StillmanGS] for this calculation. In particular,
$\mathrm {H}(K^R)$
; one could, for example, use Macaulay2 [Reference Grayson and StillmanGS] for this calculation. In particular,
![]() $\mathrm {H}(K^R)$
has a relation of weight
$\mathrm {H}(K^R)$
has a relation of weight
![]() $3$
in any weight grading, and so
$3$
in any weight grading, and so
![]() $\mathrm {H}(K^R)$
cannot be a Koszul k-algebra. Thus, R is not Cohen Koszul. Moreover, R is the completion of a quadratic algebra that is not Koszul in the classical sense. One can see this by computing the third differential in the minimal free resolution of k over R; alternatively, see [Reference Backelin and FröbergBF85].
$\mathrm {H}(K^R)$
cannot be a Koszul k-algebra. Thus, R is not Cohen Koszul. Moreover, R is the completion of a quadratic algebra that is not Koszul in the classical sense. One can see this by computing the third differential in the minimal free resolution of k over R; alternatively, see [Reference Backelin and FröbergBF85].
In Theorem 3.10, we see that this is part of an exceptional class of non-Cohen Koszul local rings among rings having embedding dimension at most three.
Example 3.7 (Short Gorenstein local rings).
A local ring R with maximal ideal
![]() $\mathfrak {m}_R$
is called short Gorenstein if it is Gorenstein and
$\mathfrak {m}_R$
is called short Gorenstein if it is Gorenstein and
![]() $\mathfrak {m}_R^3=0$
. Equivalently, these are the local rings having Hilbert series
$\mathfrak {m}_R^3=0$
. Equivalently, these are the local rings having Hilbert series
![]() $\mathrm {H}_R(t)=1+nt+t^2$
for some n. This is an important class of local rings that occurs frequently in what follows. If R is also a k-algebra, then R is Koszul by [Reference FröbergFrö82] or [Reference SchenzelSch80] (this follows as well from the slightly earlier computations in [Reference Levin and AvramovLA78]). Short Gorenstein rings are also Cohen Koszul by Example 3.15.
$\mathrm {H}_R(t)=1+nt+t^2$
for some n. This is an important class of local rings that occurs frequently in what follows. If R is also a k-algebra, then R is Koszul by [Reference FröbergFrö82] or [Reference SchenzelSch80] (this follows as well from the slightly earlier computations in [Reference Levin and AvramovLA78]). Short Gorenstein rings are also Cohen Koszul by Example 3.15.
3.8 Rings of small codepth
Recall that for a local ring R with maximal ideal
![]() $\mathfrak {m}_R$
and residue field k, its codepth is
$\mathfrak {m}_R$
and residue field k, its codepth is
This value is a measure of the singularity of R in the sense that
![]() $\operatorname {\mathrm {codepth}}(R)=0$
if and only if R is regular. The next result illustrates that a local ring of small codepth is almost always Cohen Koszul. First, we remind the reader of the structure theorem on Koszul homology for rings having codepth three.
$\operatorname {\mathrm {codepth}}(R)=0$
if and only if R is regular. The next result illustrates that a local ring of small codepth is almost always Cohen Koszul. First, we remind the reader of the structure theorem on Koszul homology for rings having codepth three.
3.9. Assume R has codepth three and fix a minimal Cohen presentation
![]() $\varphi \colon Q\to \widehat {R}$
. The minimal Q-free resolution A of
$\varphi \colon Q\to \widehat {R}$
. The minimal Q-free resolution A of
![]() $\widehat {R}$
supports a dg algebra structure; see, for example, [Reference Buchsbaum and EisenbudBE77]. Hence,
$\widehat {R}$
supports a dg algebra structure; see, for example, [Reference Buchsbaum and EisenbudBE77]. Hence,
![]() $\widehat {R}\otimes ^{\mathsf {L}}_Q k$
is formal, and the algebra structure of its homology
$\widehat {R}\otimes ^{\mathsf {L}}_Q k$
is formal, and the algebra structure of its homology
![]() $T=\operatorname {Tor}^{Q}({\widehat {R}},k)=\mathrm {H}(K^R)$
has been classified as follows.
$T=\operatorname {Tor}^{Q}({\widehat {R}},k)=\mathrm {H}(K^R)$
has been classified as follows.
Fix bases
![]() $\{e_1, \ldots , e_\ell \}$
,
$\{e_1, \ldots , e_\ell \}$
,
![]() $\{f_1, \ldots , f_m\}$
and
$\{f_1, \ldots , f_m\}$
and
![]() $\{g_1, \ldots , g_n\}$
for
$\{g_1, \ldots , g_n\}$
for
![]() $T_1$
,
$T_1$
,
![]() $T_2$
and
$T_2$
and
![]() $T_3$
, respectively. By [Reference Avramov, Kustin and MillerAKM88], there are non-negative integer parameters
$T_3$
, respectively. By [Reference Avramov, Kustin and MillerAKM88], there are non-negative integer parameters
![]() $p,q,r$
, satisfying
$p,q,r$
, satisfying
such that T is one of the graded-commutative algebras determined below, where products between the basis elements not listed are zero:
-
CI:
 $e_1e_2=f_3$
,
$e_1e_2=f_3$
,
 $e_1e_3=f_2$
,
$e_1e_3=f_2$
,
 $e_2e_3=f_1$
,
$e_2e_3=f_1$
,
 $e_if_i=g_1$
for
$e_if_i=g_1$
for
 $i=1,2,3.$
$i=1,2,3.$
-
TE:
 $e_1e_2=f_3$
,
$e_1e_2=f_3$
,
 $e_1e_3=f_2$
,
$e_1e_3=f_2$
,
 $e_2e_3=f_1$
.
$e_2e_3=f_1$
. -
B:
 $e_1e_2=f_3$
,
$e_1e_2=f_3$
,
 $e_1f_1=g_1$
,
$e_1f_1=g_1$
,
 $e_2f_2=g_1$
.
$e_2f_2=g_1$
. -
G
 $(r)$
:
$(r)$
:
 $e_if_i=g_1$
for
$e_if_i=g_1$
for
 $i=1,\ldots , r$
and
$i=1,\ldots , r$
and
 $r\ge 2$
$r\ge 2$
-
H
 $(p,q)$
:
$(p,q)$
:
 $e_{p+1}e_i=f_i$
for
$e_{p+1}e_i=f_i$
for
 $i=1,\ldots ,p$
, and
$i=1,\ldots ,p$
, and
 $e_{p+1}f_{p+i}=g_i$
for
$e_{p+1}f_{p+i}=g_i$
for
 $i=1,\ldots , q$
.
$i=1,\ldots , q$
.
In each case, let
![]() $T'$
denote the corresponding subalgebra on the basis elements appearing in the multiplication table above. If U is the k-space spanned by the basis of elements of T not recorded in the same multiplication table, then note that there is an isomorphism of graded k-algebras
$T'$
denote the corresponding subalgebra on the basis elements appearing in the multiplication table above. If U is the k-space spanned by the basis of elements of T not recorded in the same multiplication table, then note that there is an isomorphism of graded k-algebras
Finally, as a matter of terminology, we say a local ring R belongs to one of these classes if
![]() $T=\operatorname {Tor}^{Q}({\widehat {R}},k)$
has the corresponding algebra structure.
$T=\operatorname {Tor}^{Q}({\widehat {R}},k)$
has the corresponding algebra structure.
Theorem 3.10. A local ring of codepth two or less is Cohen Koszul. A local ring of codepth three is Cohen Koszul if and only if it belongs to
![]() $\mathbf {CI}$
,
$\mathbf {CI}$
,
![]() $\mathbf {B}$
,
$\mathbf {B}$
,
![]() $\mathbf {G}(r)$
or
$\mathbf {G}(r)$
or
![]() $\mathbf {H}(p,q)$
.
$\mathbf {H}(p,q)$
.
Proof. Let R be a local ring of codepth c with residue field k. Fix a minimal Cohen presentation
![]() $\varphi \colon Q\to \widehat {R}$
and set
$\varphi \colon Q\to \widehat {R}$
and set
![]() $T=\operatorname {Tor}^{Q}({\widehat {R}},k)$
.
$T=\operatorname {Tor}^{Q}({\widehat {R}},k)$
.
If
![]() $c\leqslant 2$
, then R must be complete intersection or Golod; that is,
$c\leqslant 2$
, then R must be complete intersection or Golod; that is,
![]() $\varphi $
is a complete intersection or Golod homomorphism. This follows from the Hilbert–Burch theorem (see [Reference BurchBur68], as well [Reference Bruns and HerzogBH98, Theorem 1.4.17]) combined with a result of [Reference LevinLev76, Theorem 2.3]; see also [Reference AvramovAvr99, Proposition 5.3.4]. Therefore, by Examples 3.2 and 3.5, R is Cohen Koszul in either case.
$\varphi $
is a complete intersection or Golod homomorphism. This follows from the Hilbert–Burch theorem (see [Reference BurchBur68], as well [Reference Bruns and HerzogBH98, Theorem 1.4.17]) combined with a result of [Reference LevinLev76, Theorem 2.3]; see also [Reference AvramovAvr99, Proposition 5.3.4]. Therefore, by Examples 3.2 and 3.5, R is Cohen Koszul in either case.
Now assume
![]() $c=3$
. The simplest case is when R belongs to CI, since in this case, R is complete intersection and so R is Cohen Koszul; cf. Example 3.2.
$c=3$
. The simplest case is when R belongs to CI, since in this case, R is complete intersection and so R is Cohen Koszul; cf. Example 3.2.
For the remainder of the proof, we adopt the notation from 3.9 and analyze the graded algebra structure of T. By Example 3.4 and (3.9.1), T is Koszul if and only if
![]() $T'$
is, and so we replace T by
$T'$
is, and so we replace T by
![]() $T'$
in what follows.
$T'$
in what follows.
If T is H
![]() $(p,q)$
, then it is the tensor product of a trivial extension algebra on
$(p,q)$
, then it is the tensor product of a trivial extension algebra on
![]() $e_1,\dots ,e_p,f_{p+1},\dots ,f_{p+q}$
and the exterior algebra on
$e_1,\dots ,e_p,f_{p+1},\dots ,f_{p+q}$
and the exterior algebra on
![]() $e_{p+1}$
, where each of these have weight 1. Hence, T is a tensor product of Koszul k-algebras and so it is Koszul.
$e_{p+1}$
, where each of these have weight 1. Hence, T is a tensor product of Koszul k-algebras and so it is Koszul.
If T is G
![]() $(r)$
, we give
$(r)$
, we give
![]() $\{e_i\}$
and
$\{e_i\}$
and
![]() $\{f_i\}$
weight one and
$\{f_i\}$
weight one and
![]() $g_1$
weight two. Then T is a short Gorenstein k-algebra and hence Koszul; see Example 3.7.
$g_1$
weight two. Then T is a short Gorenstein k-algebra and hence Koszul; see Example 3.7.
If T is B, then we give T weight grading
 $$\begin{align*}T_{(w)}=\begin{cases} k & w=0\\ k e_1 \oplus k e_2 \oplus k f_1 \oplus k f_2& w=1 \\ kf_3\oplus kg_1 & w=2 \\ 0 & w\geqslant 3. \end{cases} \end{align*}$$
$$\begin{align*}T_{(w)}=\begin{cases} k & w=0\\ k e_1 \oplus k e_2 \oplus k f_1 \oplus k f_2& w=1 \\ kf_3\oplus kg_1 & w=2 \\ 0 & w\geqslant 3. \end{cases} \end{align*}$$
As an algebra, T is the quotient of the exterior algebra
The graded k-algebra T is Koszul since its defining ideal has a quadratic Gröbner basis, and is therefore Koszul by [Reference McCullough and MereMM22].
Finally, if T is type TE, then T is not quadratic with respect to any weight grading. Indeed, the products in 3.9 force
![]() $e_1,e_2,e_3$
to all have weight one, as well as the minimal relation
$e_1,e_2,e_3$
to all have weight one, as well as the minimal relation
![]() $e_1e_2e_3=0$
. Hence, T is not Koszul.
$e_1e_2e_3=0$
. Hence, T is not Koszul.
Remark 3.11. Theorem 3.10 deals with the ‘absolute’ case. That is to say, when a local ring is Cohen Koszul. However, given a surjective map of local rings
![]() $\varphi \colon Q\to R$
, one has that this is always Koszul for
$\varphi \colon Q\to R$
, one has that this is always Koszul for
![]() $\operatorname {\mbox {proj dim}}_Q(R)\leqslant 2$
. Indeed, in this case,
$\operatorname {\mbox {proj dim}}_Q(R)\leqslant 2$
. Indeed, in this case,
![]() $\varphi $
is either a complete intersection homomorphism or a Golod homomorphism. For the case
$\varphi $
is either a complete intersection homomorphism or a Golod homomorphism. For the case
![]() $\operatorname {\mbox {proj dim}}_Q(R)=3$
, the structure theorem on
$\operatorname {\mbox {proj dim}}_Q(R)=3$
, the structure theorem on
![]() $T=\operatorname {Tor}^{Q}(R,k)$
discussed in 3.9 can be applied assuming that
$T=\operatorname {Tor}^{Q}(R,k)$
discussed in 3.9 can be applied assuming that
![]() $\ker (\varphi )$
is a perfect ideal. In this case,
$\ker (\varphi )$
is a perfect ideal. In this case,
![]() $\varphi $
is Koszul except in the case that T belongs to TE.
$\varphi $
is Koszul except in the case that T belongs to TE.
A surjective local homomorphism
![]() $\varphi \colon Q\to R$
of finite projective dimension is Gorenstein of projective dimension d if
$\varphi \colon Q\to R$
of finite projective dimension is Gorenstein of projective dimension d if
 $$ \begin{align} \mathrm{Ext}_Q^i(R,Q)=\begin{cases} R &i=d \\ 0 & i\neq d.\end{cases} \end{align} $$
$$ \begin{align} \mathrm{Ext}_Q^i(R,Q)=\begin{cases} R &i=d \\ 0 & i\neq d.\end{cases} \end{align} $$
For example, Gorenstein rings of codimension d are exactly those whose minimal Cohen presentations are Gorenstein of projective dimension d. If
![]() $d=3$
, then
$d=3$
, then
![]() $\operatorname {Tor}^{Q}(R,k)$
belongs to G
$\operatorname {Tor}^{Q}(R,k)$
belongs to G
![]() $(r)$
and the dg algebra structure on the minimal resolution of R over Q can be described explicitly; one can hence verify directly, as is done below, that such maps are Koszul.
$(r)$
and the dg algebra structure on the minimal resolution of R over Q can be described explicitly; one can hence verify directly, as is done below, that such maps are Koszul.
Example 3.12 (Gorenstein homomorphisms of projective dimension
 $3$
).
$3$
).
Assume that
![]() $\varphi $
is Gorenstein of projective dimension
$\varphi $
is Gorenstein of projective dimension
![]() $3$
. Buchsbaum and Eisenbud constructed the minimal free resolution of R over Q in [Reference Buchsbaum and EisenbudBE77, Theorem 2.1 & 4.1]:
$3$
. Buchsbaum and Eisenbud constructed the minimal free resolution of R over Q in [Reference Buchsbaum and EisenbudBE77, Theorem 2.1 & 4.1]:
where
![]() $r \geqslant 3$
is odd and the first and third differential of A depend on Pfaffians of submatrices of the alternating matrix
$r \geqslant 3$
is odd and the first and third differential of A depend on Pfaffians of submatrices of the alternating matrix
![]() $\psi $
. Furthermore, A is a graded-commutative dg algebra with the following multiplication: We fix bases
$\psi $
. Furthermore, A is a graded-commutative dg algebra with the following multiplication: We fix bases
![]() $\{e_i\}_{i=1}^r$
,
$\{e_i\}_{i=1}^r$
,
![]() $\{f_i\}_{i=1}^r,$
and
$\{f_i\}_{i=1}^r,$
and
![]() $\{g\}$
for
$\{g\}$
for
![]() $A_1$
,
$A_1$
,
![]() $A_2$
and
$A_2$
and
![]() $A_3$
, respectively. The multiplication is determined by
$A_3$
, respectively. The multiplication is determined by

where
![]() $\psi _{ij\ell }$
is the submatrix of
$\psi _{ij\ell }$
is the submatrix of
![]() $\psi $
obtained by deleting the ith, jth and
$\psi $
obtained by deleting the ith, jth and
![]() $\ell $
th row and column, and
$\ell $
th row and column, and
![]() $\delta _{ij}$
is the Kronecker delta function. The exact description is not important for the sequel; see [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, Example 2.1.3] for detail.
$\delta _{ij}$
is the Kronecker delta function. The exact description is not important for the sequel; see [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, Example 2.1.3] for detail.
When
![]() $r=3$
, it follows that A is a Koszul complex on three elements and so
$r=3$
, it follows that A is a Koszul complex on three elements and so
![]() $\varphi $
is a surjective complete intersection map; hence,
$\varphi $
is a surjective complete intersection map; hence,
![]() $\varphi $
is Koszul by Example 3.2.
$\varphi $
is Koszul by Example 3.2.
When
![]() $r \geqslant 5$
, we have that
$r \geqslant 5$
, we have that
![]() $\operatorname {pf}(\psi _{ij\ell }) \in \mathfrak {m}_Q$
for any i, j and
$\operatorname {pf}(\psi _{ij\ell }) \in \mathfrak {m}_Q$
for any i, j and
![]() $\ell $
. Hence, the only nonzero products in the graded algebra
$\ell $
. Hence, the only nonzero products in the graded algebra
![]() $A\otimes _Q k$
are
$A\otimes _Q k$
are
Giving
![]() $A\otimes _Q k$
the weight grading
$A\otimes _Q k$
the weight grading
 $$\begin{align*}(A\otimes_Q k)_{(w)}=\begin{cases} A_0\otimes_Qk & w=0\\ (A_1\otimes_Qk)\oplus (A_2 \otimes_Qk)& w=1\\ A_3\otimes_Qk & w=2\\ 0 & \text{else}, \end{cases} \end{align*}$$
$$\begin{align*}(A\otimes_Q k)_{(w)}=\begin{cases} A_0\otimes_Qk & w=0\\ (A_1\otimes_Qk)\oplus (A_2 \otimes_Qk)& w=1\\ A_3\otimes_Qk & w=2\\ 0 & \text{else}, \end{cases} \end{align*}$$
it belongs to G(r) in 3.9. The fact that
![]() $A\otimes _Q k$
is a Koszul k-algebra was established in the proof of Theorem 3.10. Thus,
$A\otimes _Q k$
is a Koszul k-algebra was established in the proof of Theorem 3.10. Thus,
![]() $\varphi $
is a Koszul homomorphism.
$\varphi $
is a Koszul homomorphism.
3.13 Almost Golod Gorenstein rings
We discuss here a large class of local Gorenstein rings displaying interesting homological behavior, that has been studied before in [Reference Rossi and ŞegaRŞ14, Section 6].
Definition 3.14. We say that an artinian local ring R is almost Golod if the socle quotient
![]() $R/\operatorname {\mathrm {soc}}(R)$
is Golod. A general local ring is almost Golod if it is Cohen–Macaulay and
$R/\operatorname {\mathrm {soc}}(R)$
is Golod. A general local ring is almost Golod if it is Cohen–Macaulay and ![]() is an almost Golod artinian ring, where
is an almost Golod artinian ring, where ![]() is a maximal regular sequence that is part of a minimal generating set for
is a maximal regular sequence that is part of a minimal generating set for
![]() $\mathfrak {m}_R$
.
$\mathfrak {m}_R$
.
Example 3.15 (Almost Golod Gorenstein rings).
Let R be an almost Golod local ring that is also Gorenstein of codepth d.
Fix a minimal Cohen presentation
![]() $\varphi \colon Q \to \widehat {R}$
and set
$\varphi \colon Q \to \widehat {R}$
and set
![]() $T= \operatorname {Tor}^{Q}({\widehat {R}},k)$
. Since Q is regular and R is Gorenstein, T is a Poincaré duality algebra by [Reference Avramov and GolodAG71]. That is to say, for each
$T= \operatorname {Tor}^{Q}({\widehat {R}},k)$
. Since Q is regular and R is Gorenstein, T is a Poincaré duality algebra by [Reference Avramov and GolodAG71]. That is to say, for each
![]() $0 \leqslant i \leqslant d$
, the multiplication maps
$0 \leqslant i \leqslant d$
, the multiplication maps
are perfect pairings. Furthermore, by [Reference Levin and AvramovLA78, Theorem 1], the quotient
![]() $T/T_d$
is a subalgebra of the trivial extension algebra
$T/T_d$
is a subalgebra of the trivial extension algebra
![]() $\operatorname {Tor}^{Q}(R/\operatorname {\mathrm {soc}}(R),k)$
, and hence is itself a trivial extension algebra. It follows that T is a short Gorenstein k-algebra. Moreover, prescribing T with the following weight grading
$\operatorname {Tor}^{Q}(R/\operatorname {\mathrm {soc}}(R),k)$
, and hence is itself a trivial extension algebra. It follows that T is a short Gorenstein k-algebra. Moreover, prescribing T with the following weight grading
makes T a Koszul k-algebra, with the multiplication of T being equivalent to a perfect pairing on
![]() $T_{(1)}$
; see the proof of Theorem 3.10.
$T_{(1)}$
; see the proof of Theorem 3.10.
We prove that these rings are Cohen Koszul under the assumption that R contains a field of characteristic zero and d is odd, by giving a characterization analogous to Avramov’s characterization of Golod rings [Reference Avramov and RoosAvr86]. We do not know whether the assumption on the characteristic or on d is necessary (but see Remark 5.10).
Theorem 3.16. Let R be a local with a minimal Cohen presentation
![]() $Q\to \widehat {R}$
. If there is a quasi-isomorphism of dg k-algebras
$Q\to \widehat {R}$
. If there is a quasi-isomorphism of dg k-algebras
![]() $\widehat {R}\otimes ^{\mathsf {L}}_Qk\simeq T$
, where T is a short Gorenstein graded k-algebra, then R is almost Golod Gorenstein. Assuming that R contains a field of characteristic zero, and that
$\widehat {R}\otimes ^{\mathsf {L}}_Qk\simeq T$
, where T is a short Gorenstein graded k-algebra, then R is almost Golod Gorenstein. Assuming that R contains a field of characteristic zero, and that
![]() $\operatorname {\mathrm {codepth}}(R)$
is odd, the converse holds as well. In particular, almost Golod Gorenstein rings (of characterstic zero and odd codepth) are Cohen Koszul.
$\operatorname {\mathrm {codepth}}(R)$
is odd, the converse holds as well. In particular, almost Golod Gorenstein rings (of characterstic zero and odd codepth) are Cohen Koszul.
Proof. If R is almost Golod Gorenstein, we have already seen that
![]() $T=\operatorname {Tor}^{Q}({\widehat {R}},k)$
is a short Gorenstein algebra, and in particular Koszul. The proof that
$T=\operatorname {Tor}^{Q}({\widehat {R}},k)$
is a short Gorenstein algebra, and in particular Koszul. The proof that
![]() $\widehat {R}\otimes ^{\mathsf {L}}_Q k$
is formal under the stated assumptions will be given in Theorem 5.7 and Lemma 8.17.
$\widehat {R}\otimes ^{\mathsf {L}}_Q k$
is formal under the stated assumptions will be given in Theorem 5.7 and Lemma 8.17.
Conversely, assume that
![]() $\widehat {R}\otimes ^{\mathsf {L}}_Qk$
is quasi-isomorphic to a short Gorenstein algebra T, and write e for the embedding dimension of R. By Proposition 2.11,
$\widehat {R}\otimes ^{\mathsf {L}}_Qk$
is quasi-isomorphic to a short Gorenstein algebra T, and write e for the embedding dimension of R. By Proposition 2.11,
and hence as a consequence of [Reference Rossi and ŞegaRŞ14, Proposition 6.2], R is almost Golod.
Remark 3.17. The prototypical example of an almost Golod Gorenstein ring is a short Gorenstein local ring R. In this case,
![]() $R/\operatorname {\mathrm {soc}}(R)=R/\mathfrak {m}_R^2$
is Golod by [Reference GolodGol78].
$R/\operatorname {\mathrm {soc}}(R)=R/\mathfrak {m}_R^2$
is Golod by [Reference GolodGol78].
Among the complete intersection local rings, the almost Golod Gorenstein rings are exactly those having codimension two or less; see Theorem 3.16. If R is a Gorenstein local ring of codimension
![]() $3$
that is not complete intersection, then R is almost Golod Gorenstein by Example 3.12 and Theorem 3.16.
$3$
that is not complete intersection, then R is almost Golod Gorenstein by Example 3.12 and Theorem 3.16.
By [Reference Rossi and ŞegaRŞ14, Proposition 6.3], every Gorenstein compressed local ring of socle degree at least
![]() $4$
is almost Golod Gorenstein. Moreover, for fixed emdedding dimension and socle degree, the generic Gorenstein local k-algebra is compressed by [Reference IarrobinoIar84, Theorem I]. Hence, the almost Golod Gorenstein condition is extremely common.
$4$
is almost Golod Gorenstein. Moreover, for fixed emdedding dimension and socle degree, the generic Gorenstein local k-algebra is compressed by [Reference IarrobinoIar84, Theorem I]. Hence, the almost Golod Gorenstein condition is extremely common.
Recall that if Q is a standard graded polynomial algebra, a homogeneous quotient
![]() $R=Q/I$
is said to have an almost linear resolution over Q if the ideal I is generated by forms of degree e, and for all
$R=Q/I$
is said to have an almost linear resolution over Q if the ideal I is generated by forms of degree e, and for all
![]() $0<i<\operatorname {\mbox {proj dim}}_Q(R)$
, we have
$0<i<\operatorname {\mbox {proj dim}}_Q(R)$
, we have
![]() $\operatorname {Tor}_i^Q{(R,k)}_j=0$
unless
$\operatorname {Tor}_i^Q{(R,k)}_j=0$
unless
![]() $j-i=e-1$
; confer [Reference Eisenbud, Huneke and UlrichEHU06]. Graded Gorenstein rings with almost linear resolutions are always almost Golod Gorenstein. This will be justified later in the paper, in Example 8.19, along with the fact that such algebras with
$j-i=e-1$
; confer [Reference Eisenbud, Huneke and UlrichEHU06]. Graded Gorenstein rings with almost linear resolutions are always almost Golod Gorenstein. This will be justified later in the paper, in Example 8.19, along with the fact that such algebras with
![]() $e \geqslant 3$
are also Cohen Koszul; this is done without the assumptions on characteristic and codepth in Theorem 3.16.
$e \geqslant 3$
are also Cohen Koszul; this is done without the assumptions on characteristic and codepth in Theorem 3.16.
Remark 3.18. In rational homotopy theory, Golod rings correspond to spaces that are (rationally) homotopy equivalent to a wedge of spheres, while Gorenstein rings are analogous to manifolds, or more generally Poincaré duality spaces; see the looking glass [Reference Avramov, Halperin and RoosAH86] for more information.
To be more precise, if M is a simply connected manifold and the punctured space
![]() $M\smallsetminus \{\mathrm {pt}\}$
is rationally homotopy equivalent to a wedge of spheres, then the cohomology ring
$M\smallsetminus \{\mathrm {pt}\}$
is rationally homotopy equivalent to a wedge of spheres, then the cohomology ring
![]() $\mathrm {H}^*(M;\mathbb {Q})$
is an almost Golod Gorenstein ring. In [Reference StasheffSta83], Stasheff proved such spaces are formal, and therefore, they are Koszul in the sense of Berglund [Reference BerglundBer14]. A well-studied class of manifolds satisfying this property are the highly connected manifolds – that is, those M with
$\mathrm {H}^*(M;\mathbb {Q})$
is an almost Golod Gorenstein ring. In [Reference StasheffSta83], Stasheff proved such spaces are formal, and therefore, they are Koszul in the sense of Berglund [Reference BerglundBer14]. A well-studied class of manifolds satisfying this property are the highly connected manifolds – that is, those M with
![]() $\mathrm {H}^i(M;\mathbb {Q})=0$
when
$\mathrm {H}^i(M;\mathbb {Q})=0$
when
![]() $0<i<\lfloor \dim (M)/2\rfloor $
.
$0<i<\lfloor \dim (M)/2\rfloor $
.
Since Gorenstein rings that are not regular or hypersurfaces are never Golod, the Serre bound (3.4.1) must be strict for such rings. However, a tighter bound can be established for Gorenstein local rings, as we show now. The case of equality below is equivalent (when
![]() $d=0$
) to the formula for
$d=0$
) to the formula for
![]() $\operatorname {\mathrm {P}}^R_k(t)$
given in [Reference Rossi and ŞegaRŞ14, Proposition 6.2], and our proof is essentially equivalent to that of loc. cit.
$\operatorname {\mathrm {P}}^R_k(t)$
given in [Reference Rossi and ŞegaRŞ14, Proposition 6.2], and our proof is essentially equivalent to that of loc. cit.
Proposition 3.19. Let R be a local ring having dimension d and embedding dimension e, with residue field k and Koszul complex
![]() $K^R$
. If R is Gorenstein but not regular or a hypersurface, then there is a coefficientwise inequality
$K^R$
. If R is Gorenstein but not regular or a hypersurface, then there is a coefficientwise inequality
 $$ \begin{align*} \frac{\operatorname{\mathrm{P}}^R_k(t)}{(1+t)^d-t^2 \operatorname{\mathrm{P}}^R_k(t)} \preccurlyeq \frac{(1+t)^{e-d}}{1 - t^2 (1+t)^{e-d} + t^{e-d+2}-\sum_{i=1}^{e-d-1} \operatorname{\mathrm{rank}}_k \mathrm{H}_i(K^R) t^{i+1}}, \end{align*} $$
$$ \begin{align*} \frac{\operatorname{\mathrm{P}}^R_k(t)}{(1+t)^d-t^2 \operatorname{\mathrm{P}}^R_k(t)} \preccurlyeq \frac{(1+t)^{e-d}}{1 - t^2 (1+t)^{e-d} + t^{e-d+2}-\sum_{i=1}^{e-d-1} \operatorname{\mathrm{rank}}_k \mathrm{H}_i(K^R) t^{i+1}}, \end{align*} $$
and equality holds if and only if R is almost Golod.
While the left-hand side is not equal to
![]() $\operatorname {\mathrm {P}}^R_k(t)$
, it increases monotonically with
$\operatorname {\mathrm {P}}^R_k(t)$
, it increases monotonically with
![]() $\operatorname {\mathrm {P}}^R_k(t)$
, and so it directly measures the growth of the resolution of k. Therefore, within the class of Gorenstein local rings, almost Golod rings display extremal behavior analogous to Golod rings.
$\operatorname {\mathrm {P}}^R_k(t)$
, and so it directly measures the growth of the resolution of k. Therefore, within the class of Gorenstein local rings, almost Golod rings display extremal behavior analogous to Golod rings.
Proof. As R is Gorenstein, prime avoidance yields a regular sequence ![]() that is part of a minimal generating set for
that is part of a minimal generating set for
![]() $\mathfrak {m}_R$
, so that
$\mathfrak {m}_R$
, so that ![]() is artinian Gorenstein and of embedding dimension
is artinian Gorenstein and of embedding dimension
![]() $e-d$
. By Nagata’s theorem [Reference NagataNag62, Section 27], we have
$e-d$
. By Nagata’s theorem [Reference NagataNag62, Section 27], we have
![]() $\operatorname {\mathrm {P}}^R_k(t)=\operatorname {\mathrm {P}}^{\bar {R}}_k(t)(1+t)^d$
, and so the first equality below holds:
$\operatorname {\mathrm {P}}^R_k(t)=\operatorname {\mathrm {P}}^{\bar {R}}_k(t)(1+t)^d$
, and so the first equality below holds:
 $$ \begin{align*} \frac{\operatorname{\mathrm{P}}^R_k(t)}{(1+t)^d-t^2 \operatorname{\mathrm{P}}^R_k(t)} &=\frac{\operatorname{\mathrm{P}}^{\bar{R}}_k(t)}{1-t^2 \operatorname{\mathrm{P}}^{\bar{R}}_k(t)}\\ &=\operatorname{\mathrm{P}}^{\bar{R}/\operatorname{\mathrm{soc}}(\bar{R})}_k(t) \\ &\preccurlyeq \frac{\operatorname{\mathrm{P}}^Q_k(t)}{1 - t (\operatorname{\mathrm{P}}^Q_{\bar{R}/\operatorname{\mathrm{soc}}(\bar{R})}(t) - 1)}\\ &= \frac{\operatorname{\mathrm{P}}^Q_{k}(t)}{1 - t (\operatorname{\mathrm{P}}^Q_{\bar{R}}(t) - t^{e-d} + t \operatorname{\mathrm{P}}^Q_{k}(t) - t^{e-d+1} - 1)}. \end{align*} $$
$$ \begin{align*} \frac{\operatorname{\mathrm{P}}^R_k(t)}{(1+t)^d-t^2 \operatorname{\mathrm{P}}^R_k(t)} &=\frac{\operatorname{\mathrm{P}}^{\bar{R}}_k(t)}{1-t^2 \operatorname{\mathrm{P}}^{\bar{R}}_k(t)}\\ &=\operatorname{\mathrm{P}}^{\bar{R}/\operatorname{\mathrm{soc}}(\bar{R})}_k(t) \\ &\preccurlyeq \frac{\operatorname{\mathrm{P}}^Q_k(t)}{1 - t (\operatorname{\mathrm{P}}^Q_{\bar{R}/\operatorname{\mathrm{soc}}(\bar{R})}(t) - 1)}\\ &= \frac{\operatorname{\mathrm{P}}^Q_{k}(t)}{1 - t (\operatorname{\mathrm{P}}^Q_{\bar{R}}(t) - t^{e-d} + t \operatorname{\mathrm{P}}^Q_{k}(t) - t^{e-d+1} - 1)}. \end{align*} $$
The second equality holds using [Reference Levin and AvramovLA78, Theorem 2], the coefficientwise inequality is the Serre bound (3.4.1) for
![]() $\bar {R}/\operatorname {\mathrm {soc}}(\bar {R})$
, and the last equality holds using [Reference Levin and AvramovLA78, Theorem 1]. Since
$\bar {R}/\operatorname {\mathrm {soc}}(\bar {R})$
, and the last equality holds using [Reference Levin and AvramovLA78, Theorem 1]. Since
![]() $\operatorname {\mathrm {P}}^Q_{k}(t)=(1+t)^{e-d}$
and
$\operatorname {\mathrm {P}}^Q_{k}(t)=(1+t)^{e-d}$
and
![]() $\operatorname {\mathrm {P}}^Q_{\bar {R}}(t)=\sum _{i=0}^{i=e-d}\operatorname {\mathrm {rank}}_k \mathrm {H}_i(K^R) t^{i}$
, we obtain the claimed inequality. It remains to note that R is almost Golod if and only if
$\operatorname {\mathrm {P}}^Q_{\bar {R}}(t)=\sum _{i=0}^{i=e-d}\operatorname {\mathrm {rank}}_k \mathrm {H}_i(K^R) t^{i}$
, we obtain the claimed inequality. It remains to note that R is almost Golod if and only if
![]() $\bar {R}/\operatorname {\mathrm {soc}}(\bar {R})$
is Golod, if and only if equality holds in the third line above.
$\bar {R}/\operatorname {\mathrm {soc}}(\bar {R})$
is Golod, if and only if equality holds in the third line above.
Later, in Section 8.15, we explicitly construct resolutions over almost Golod Gorenstein rings that achieve the bound of Proposition 3.19.
3.20 Monomial rings
In this subsection, we consider rings of the form
![]() $R=Q/I$
, where
$R=Q/I$
, where
![]() $Q=k[x_1,\ldots ,x_n]$
and I is generated by monomials
$Q=k[x_1,\ldots ,x_n]$
and I is generated by monomials
![]() $m_1,\ldots ,m_r$
. By Fröberg’s theorem [Reference FröbergFrö75], R is Koszul as a k-algebra if and only if each
$m_1,\ldots ,m_r$
. By Fröberg’s theorem [Reference FröbergFrö75], R is Koszul as a k-algebra if and only if each
![]() $m_i$
is quadratic. However, the condition that R is Cohen Koszul is more common and more subtle.
$m_i$
is quadratic. However, the condition that R is Cohen Koszul is more common and more subtle.
Example 3.21 (Almost linear monomial ring).
As discussed in Remark 3.17, graded Gorenstein rings having almost linear resolutions are Cohen Koszul. To give an explicit example, let I be the ideal in
![]() $Q=k[x_1,\ldots ,x_8]$
generated by
$Q=k[x_1,\ldots ,x_8]$
generated by
The Betti table of
![]() $R=Q/I$
is
$R=Q/I$
is
 $$\begin{align*}\begin{array}{c|c c c c c } & 0 & 1 & 2 & 3 & 4 \\ \hline \text{0} & 1 & \cdot & \cdot & \cdot & \cdot \\ \text{1} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \text{2} & \cdot & 16 & 30 & 16 & \cdot \\ \text{3} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \text{4} & \cdot & \cdot & \cdot & \cdot & 1 \mbox{.} \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c|c c c c c } & 0 & 1 & 2 & 3 & 4 \\ \hline \text{0} & 1 & \cdot & \cdot & \cdot & \cdot \\ \text{1} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \text{2} & \cdot & 16 & 30 & 16 & \cdot \\ \text{3} & \cdot & \cdot & \cdot & \cdot & \cdot \\ \text{4} & \cdot & \cdot & \cdot & \cdot & 1 \mbox{.} \end{array} \end{align*}$$
Of course, this example was found with the help of Macaulay2 [Reference Grayson and StillmanGS]; it is the Stanley–Reisner ring of a triangulation of the
![]() $3$
-sphere, taken from the enumeration compiled by Lutz [Reference LutzLut17].
$3$
-sphere, taken from the enumeration compiled by Lutz [Reference LutzLut17].
An exact combinatorial characterization of which monomial rings are Cohen Koszul would be very interesting; this seems possible but likely nontrivial. We describe a special case that produces a large number of explicit examples.
Let
![]() $Q=k[x_1,\ldots ,x_n]$
be a polynomial ring over a field k. A monomial ideal I is called dominant if it is generated by a set of monomials G such that for all
$Q=k[x_1,\ldots ,x_n]$
be a polynomial ring over a field k. A monomial ideal I is called dominant if it is generated by a set of monomials G such that for all
![]() $m\in G$
, there is a variable
$m\in G$
, there is a variable
![]() $x_i$
and an integer a such that
$x_i$
and an integer a such that
![]() $x_i^a$
divides m and
$x_i^a$
divides m and
![]() $x_i^a$
does not divide any monomial
$x_i^a$
does not divide any monomial
![]() $m'\in G\smallsetminus \{m\}$
; see [Reference AlesandroniAle17, Definition 4.1].
$m'\in G\smallsetminus \{m\}$
; see [Reference AlesandroniAle17, Definition 4.1].
Proposition 3.22. If
![]() $Q=k[x_1,\ldots ,x_n]$
is a polynomial ring over a field k and I is a dominant monomial ideal in Q, then
$Q=k[x_1,\ldots ,x_n]$
is a polynomial ring over a field k and I is a dominant monomial ideal in Q, then
![]() $R=Q/I$
is Cohen Koszul.
$R=Q/I$
is Cohen Koszul.
Proof. The Taylor resolution A of R over Q has a basis
![]() $\{e_I\}$
indexed by subsets
$\{e_I\}$
indexed by subsets
![]() $I\subseteq \{1,\ldots ,n\}$
, with
$I\subseteq \{1,\ldots ,n\}$
, with
![]() $e_I$
in homological degree
$e_I$
in homological degree
![]() $|I|$
, and the differential is defined by
$|I|$
, and the differential is defined by
where
![]() $m_I=\operatorname {lcm}\left \{m_i \,\middle |\, i\in I\right \}$
; see [Reference TaylorTay66] for details and signs. The hypothesis of the proposition exactly guarantees that the Taylor resolution is minimal by [Reference AlesandroniAle17, Theorem 4.4].
$m_I=\operatorname {lcm}\left \{m_i \,\middle |\, i\in I\right \}$
; see [Reference TaylorTay66] for details and signs. The hypothesis of the proposition exactly guarantees that the Taylor resolution is minimal by [Reference AlesandroniAle17, Theorem 4.4].
Gemeda [Reference GemedaGem76] proved that the Taylor resolution has a dg algebra structure with product
when
![]() $I\cap J=\varnothing $
, and with
$I\cap J=\varnothing $
, and with
![]() $e_Ie_J = 0$
otherwise. By Remark 2.7, it follows that
$e_Ie_J = 0$
otherwise. By Remark 2.7, it follows that
![]() $R\otimes ^{\mathsf {L}}_Qk=A\otimes _Qk$
is formal.
$R\otimes ^{\mathsf {L}}_Qk=A\otimes _Qk$
is formal.
It remains to show that
![]() $A\otimes _Qk$
is a Koszul k-algebra. Let M be the graph with vertices
$A\otimes _Qk$
is a Koszul k-algebra. Let M be the graph with vertices
![]() $\{1,\ldots , r\}$
and an edge connecting i and j if and only if
$\{1,\ldots , r\}$
and an edge connecting i and j if and only if
![]() $\gcd (m_i,m_j)\neq 1$
. From the description of A above, it follows that
$\gcd (m_i,m_j)\neq 1$
. From the description of A above, it follows that
where
![]() $k[e_I]$
is the free graded-commutative algebra on the indicated
$k[e_I]$
is the free graded-commutative algebra on the indicated
![]() $e_I$
; compare this with [Reference BerglundBer05, 6.2]. Assigning each
$e_I$
; compare this with [Reference BerglundBer05, 6.2]. Assigning each
![]() $e_I$
weight
$e_I$
weight
![]() $1$
, we are done because quadratic monomial quotients of free graded-commutative algebras are Koszul by Fröberg’s theorem [Reference FröbergFrö75] (such rings belong to class B in [Reference FröbergFrö75, Section 3], and Fröberg constructs linear resolutions of the residue field for all rings of class B).
$1$
, we are done because quadratic monomial quotients of free graded-commutative algebras are Koszul by Fröberg’s theorem [Reference FröbergFrö75] (such rings belong to class B in [Reference FröbergFrö75, Section 3], and Fröberg constructs linear resolutions of the residue field for all rings of class B).
Remark 3.23. One can readily exhibit monomial rings satisfying the hypothesis of the proposition, and not falling into the other classes described above. For example, ![]() .
.
The next examples are k-algebras that fail to be Cohen Koszul; the first is a Koszul k-algebra, and the second has
![]() $\mathrm {H}(K^R)$
a Koszul k-algebra. Both examples fail to be Cohen Koszul since in each case,
$\mathrm {H}(K^R)$
a Koszul k-algebra. Both examples fail to be Cohen Koszul since in each case,
![]() $K^R$
admits a nonzero triple Massey product, and hence is not formal; cf. [Reference MayMay69] for more details on Massey products.
$K^R$
admits a nonzero triple Massey product, and hence is not formal; cf. [Reference MayMay69] for more details on Massey products.
Example 3.24. The k-algebra ![]() is the completion of a Koszul k-algebra (in the classical sense) by [Reference FröbergFrö75, Corollary 1]. However, the map
is the completion of a Koszul k-algebra (in the classical sense) by [Reference FröbergFrö75, Corollary 1]. However, the map ![]() is not Koszul. Indeed, by [Reference AvramovAvr81, Example 5.1.4],
is not Koszul. Indeed, by [Reference AvramovAvr81, Example 5.1.4],
![]() $K^R$
has a nonzero triple Massey product, and so
$K^R$
has a nonzero triple Massey product, and so
![]() $K^R$
is not formal.
$K^R$
is not formal.
Example 3.25. Let ![]() and consider the quotient map
and consider the quotient map
In [Reference KatthänKat17, Theorem 3.1], it is shown that
![]() $\mathrm {H}(K^R)$
is a trivial extension that admits a nonzero triple Massey product; the latter is an obstruction to the formality of
$\mathrm {H}(K^R)$
is a trivial extension that admits a nonzero triple Massey product; the latter is an obstruction to the formality of
![]() $K^R$
, while the former justifies that
$K^R$
, while the former justifies that
![]() $\mathrm {H}(K^R)$
is a Koszul k-algebra.
$\mathrm {H}(K^R)$
is a Koszul k-algebra.
Remark 3.26. To any monomial ideal
![]() $I\subseteq Q$
, one may associate a square-free monomial ideal
$I\subseteq Q$
, one may associate a square-free monomial ideal
![]() $I^\circ $
in a larger polynomial ring
$I^\circ $
in a larger polynomial ring
![]() $Q^\circ $
, known as the polarization of I. Fröberg [Reference FröbergFrö82] proved that there is a regular sequence of linear forms
$Q^\circ $
, known as the polarization of I. Fröberg [Reference FröbergFrö82] proved that there is a regular sequence of linear forms
![]() $y_1,\ldots ,y_t$
in the quotient
$y_1,\ldots ,y_t$
in the quotient
![]() $R^\circ =Q^\circ /I^\circ $
such that
$R^\circ =Q^\circ /I^\circ $
such that
![]() $ R=R^\circ /(y_1,\ldots ,y_t)$
. From Proposition 2.17, it follows that R is Cohen Koszul if and only if
$ R=R^\circ /(y_1,\ldots ,y_t)$
. From Proposition 2.17, it follows that R is Cohen Koszul if and only if
![]() $R^\circ $
is Cohen Koszul.
$R^\circ $
is Cohen Koszul.
A simplicial complex
![]() $\Delta $
on
$\Delta $
on
![]() $[n]=\{1,\ldots ,n\}$
is a nonempty family of subsets of
$[n]=\{1,\ldots ,n\}$
is a nonempty family of subsets of
![]() $[n]$
, closed under taking subsets. The Stanley–Reisner ring associated to
$[n]$
, closed under taking subsets. The Stanley–Reisner ring associated to
![]() $\Delta $
, denoted
$\Delta $
, denoted
![]() $k[\Delta ]$
, is the quotient of
$k[\Delta ]$
, is the quotient of
![]() $k[x_1,\ldots ,x_n]$
by the ideal generated by monomials
$k[x_1,\ldots ,x_n]$
by the ideal generated by monomials
![]() $x_{i_1}\cdots x_{i_t}$
such that
$x_{i_1}\cdots x_{i_t}$
such that
![]() $\{i_1,\ldots ,i_t\}\notin \Delta $
. Every square free monomial ring is the Stanley–Reisner ring of some simplical complex, and so by Remark 3.26, we may restrict to such monomials rings.
$\{i_1,\ldots ,i_t\}\notin \Delta $
. Every square free monomial ring is the Stanley–Reisner ring of some simplical complex, and so by Remark 3.26, we may restrict to such monomials rings.
Remark 3.27. We make some remarks about the connections to toric topology; for precise definitions and background on this area, the reader may consult [Reference Buchstaber, Panov and Topology (Math.BP15].
To a simplical complex
![]() $\Delta $
on
$\Delta $
on
![]() $[n]$
, one also associates the moment angle complex
$[n]$
, one also associates the moment angle complex
![]() $\mathcal {Z}_\Delta $
, a finite CW-complex with an action of the torus
$\mathcal {Z}_\Delta $
, a finite CW-complex with an action of the torus
![]() $(S^1)^n$
. The homotopy quotient
$(S^1)^n$
. The homotopy quotient
![]() $\mathcal {DJ}_\Delta =\mathcal {Z}_\Delta /\!/(S^1)^n$
is known as the Davis–Januszkiewicz space of
$\mathcal {DJ}_\Delta =\mathcal {Z}_\Delta /\!/(S^1)^n$
is known as the Davis–Januszkiewicz space of
![]() $\Delta $
. By [Reference Davis and JanuszkiewiczDJ91, Theorem 4.8] and [Reference Notbohm and RayNR05, Theorem 4.8], the cochain algebra of this space is formal, and quasi-isomorphic to the Stanley–Reisner ring:
$\Delta $
. By [Reference Davis and JanuszkiewiczDJ91, Theorem 4.8] and [Reference Notbohm and RayNR05, Theorem 4.8], the cochain algebra of this space is formal, and quasi-isomorphic to the Stanley–Reisner ring:
where the variables
![]() $x_i$
are given cohomological degree
$x_i$
are given cohomological degree
![]() $2$
. From this, it follows that
$2$
. From this, it follows that
![]() $k[\Delta ]$
is a Koszul k-algebra if and only if
$k[\Delta ]$
is a Koszul k-algebra if and only if
![]() $\mathcal {DJ}_\Delta $
is a Koszul space in the sense of [Reference BerglundBer14]. As remarked in [Reference BerglundBer14, Example 5.8], this happens exactly when
$\mathcal {DJ}_\Delta $
is a Koszul space in the sense of [Reference BerglundBer14]. As remarked in [Reference BerglundBer14, Example 5.8], this happens exactly when
![]() $k[\Delta ]$
is a quadratic algebra, or equivalently if
$k[\Delta ]$
is a quadratic algebra, or equivalently if
![]() $\Delta $
is a flag complex – that is, the minimal faces not belonging to
$\Delta $
is a flag complex – that is, the minimal faces not belonging to
![]() $\Delta $
are all edges.
$\Delta $
are all edges.
The question of when
![]() $\mathcal {Z}_\Delta $
is a Koszul space seems to be more interesting. By [Reference Buchstaber, Panov and Topology (Math.BP15, Lemma 3.1], there is a quasi-isomorphism of dg k-algebras
$\mathcal {Z}_\Delta $
is a Koszul space seems to be more interesting. By [Reference Buchstaber, Panov and Topology (Math.BP15, Lemma 3.1], there is a quasi-isomorphism of dg k-algebras
Thus,
![]() $k[\Delta ]$
is Cohen Koszul if and only if
$k[\Delta ]$
is Cohen Koszul if and only if
![]() $\mathcal {Z}_\Delta $
is a Koszul space, since the latter means that
$\mathcal {Z}_\Delta $
is a Koszul space, since the latter means that
![]() $C^*(\mathcal {Z}_\Delta ;k)$
is formal with Koszul homology algebra. The related condition that
$C^*(\mathcal {Z}_\Delta ;k)$
is formal with Koszul homology algebra. The related condition that
![]() $\mathcal {Z}_\Delta $
is formal has been investigated in [Reference Denham and SuciuDS07, Reference LimonchenkoLim19].
$\mathcal {Z}_\Delta $
is formal has been investigated in [Reference Denham and SuciuDS07, Reference LimonchenkoLim19].
The almost Golod condition is also connected with the minimally non-Golod condition for simplicial complexes introduced in [Reference Berglund and JöllenbeckBJ07]. Indeed, the proof of [Reference AmelotteAme20, Theorem 1.1] shows that if
![]() $M=\mathcal {Z}_\Delta $
is a moment angle manifold, and if
$M=\mathcal {Z}_\Delta $
is a moment angle manifold, and if
![]() $M\smallsetminus \{\mathrm {pt}\}$
is rationally homotopy equivalent to a wedge of spheres, then
$M\smallsetminus \{\mathrm {pt}\}$
is rationally homotopy equivalent to a wedge of spheres, then
![]() $\Delta $
is minimally non-Golod (over
$\Delta $
is minimally non-Golod (over
![]() $\mathbb {Q}$
).
$\mathbb {Q}$
).
4 Background on
 $\mathrm {A}_{\infty }$
-algebras and coalgebras
$\mathrm {A}_{\infty }$
-algebras and coalgebras
Stasheff introduced
![]() $\mathrm {A}_{\infty }$
-algebras in topology to characterize loop spaces [Reference StasheffSta63a, Reference StasheffSta63b], and they have since proven a powerful tool in algebra as a flexible generalization of dg algebras; for an overview, see [Reference KellerKel01]. In our context, the minimal Q-free resolution of a finite Q-algebra R can be equipped with an
$\mathrm {A}_{\infty }$
-algebras in topology to characterize loop spaces [Reference StasheffSta63a, Reference StasheffSta63b], and they have since proven a powerful tool in algebra as a flexible generalization of dg algebras; for an overview, see [Reference KellerKel01]. In our context, the minimal Q-free resolution of a finite Q-algebra R can be equipped with an
![]() $\mathrm {A}_{\infty }$
-algebra structure (see Section 5), and this will be leveraged to characterize Koszul homomorphisms in terms of presentations similar to the quadratic presentations for classical Koszul algebras (see Section 7).
$\mathrm {A}_{\infty }$
-algebra structure (see Section 5), and this will be leveraged to characterize Koszul homomorphisms in terms of presentations similar to the quadratic presentations for classical Koszul algebras (see Section 7).
From now on, Q is always a local ring with maximal ideal
![]() $\mathfrak {m}_Q$
and residue field k, and unadorned tensor products and Hom sets are taken over Q.
$\mathfrak {m}_Q$
and residue field k, and unadorned tensor products and Hom sets are taken over Q.
4.1. An
![]() $\mathrm {A}_{\infty }$
-algebra is a graded Q-module A equipped with Q-linear maps
$\mathrm {A}_{\infty }$
-algebra is a graded Q-module A equipped with Q-linear maps
of degree
![]() $(n-2)$
satisfying the Stasheff identities
$(n-2)$
satisfying the Stasheff identities
 $$ \begin{align} \sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{r+st} m_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right) = 0. \end{align} $$
$$ \begin{align} \sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{r+st} m_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right) = 0. \end{align} $$
Taking
![]() $n=1$
, this says that
$n=1$
, this says that
![]() $m_1$
is a degree
$m_1$
is a degree
![]() $-1$
square zero endomorphism of A, so we can (and will) make A a complex with
$-1$
square zero endomorphism of A, so we can (and will) make A a complex with
![]() $\partial =m_1$
. Taking
$\partial =m_1$
. Taking
![]() $n=2$
yields a product satisfying the Leibniz rule
$n=2$
yields a product satisfying the Leibniz rule
![]() $\partial m_2=m_2(\partial \otimes \operatorname {\mathrm {id}}+\operatorname {\mathrm {id}}\otimes \partial )$
. The next Stasheff identity, for
$\partial m_2=m_2(\partial \otimes \operatorname {\mathrm {id}}+\operatorname {\mathrm {id}}\otimes \partial )$
. The next Stasheff identity, for
![]() $n=3$
, can be interpreted as saying that
$n=3$
, can be interpreted as saying that
![]() $m_2$
is associative up to a homotopy given by
$m_2$
is associative up to a homotopy given by
![]() $m_3$
; that is,
$m_3$
; that is,
If for some n the Stasheff identity (4.1.1) holds for every integer less than n, then the obstruction

is a chain map
![]() $A^{\otimes n}\to A$
; see [Reference Lefèvre-HasegawaLH03, Corollaire B.1.2].
$A^{\otimes n}\to A$
; see [Reference Lefèvre-HasegawaLH03, Corollaire B.1.2].
A morphism of
![]() $\mathrm {A}_{\infty }$
-algebras
$\mathrm {A}_{\infty }$
-algebras
![]() $\varphi \colon A \to B$
consists of Q-linear maps
$\varphi \colon A \to B$
consists of Q-linear maps
of degree
![]() $(n-1)$
satisfying
$(n-1)$
satisfying

where ![]() and
and ![]() , with
, with ![]() .
.
If for some n the Stasheff identity (4.1.3) holds for every integer less than n, then we define

Then the Stasheff identity (4.1.3) holds if and only if
A morphism
![]() $\varphi $
of
$\varphi $
of
![]() $\mathrm {A}_{\infty }$
-algebras is a quasi-isomorphism if the chain map
$\mathrm {A}_{\infty }$
-algebras is a quasi-isomorphism if the chain map
![]() $\varphi _1$
is a quasi-isomorphism of complexes. The morphism
$\varphi _1$
is a quasi-isomorphism of complexes. The morphism
![]() $\varphi $
is strict if
$\varphi $
is strict if
![]() $\varphi _n = 0$
for
$\varphi _n = 0$
for
![]() $n> 1$
. In this case, (4.1.3) simplifies to
$n> 1$
. In this case, (4.1.3) simplifies to
The composition of morphisms
![]() $\varphi \colon A \to B$
and
$\varphi \colon A \to B$
and
![]() $\psi \colon B \to C$
is defined by
$\psi \colon B \to C$
is defined by

4.2. An
![]() $\mathrm {A}_{\infty }$
-algebra A is strictly unital if there exists
$\mathrm {A}_{\infty }$
-algebra A is strictly unital if there exists
![]() $1_A \in A_0$
such that
$1_A \in A_0$
such that
 $$ \begin{align} \begin{gathered} m_2(1_A \otimes a) = a = m_2(a \otimes 1_A) \quad\text{for all } a \in A \quad\text{and} \\ m_n(a_1 \otimes \cdots \otimes a_{i-1} \otimes 1_A \otimes a_{i+1} \otimes \cdots \otimes a_n) = 0 \quad\text{for all } 1 \leqslant i \leqslant n \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} m_2(1_A \otimes a) = a = m_2(a \otimes 1_A) \quad\text{for all } a \in A \quad\text{and} \\ m_n(a_1 \otimes \cdots \otimes a_{i-1} \otimes 1_A \otimes a_{i+1} \otimes \cdots \otimes a_n) = 0 \quad\text{for all } 1 \leqslant i \leqslant n \end{gathered} \end{align} $$
for any
![]() $a_1, \ldots , a_n \in A$
and
$a_1, \ldots , a_n \in A$
and
![]() $n> 2$
. A morphism of strictly unital
$n> 2$
. A morphism of strictly unital
![]() $\mathrm {A}_{\infty }$
-algebras
$\mathrm {A}_{\infty }$
-algebras
![]() $\varphi \colon A \to B$
is a morphism of
$\varphi \colon A \to B$
is a morphism of
![]() $\mathrm {A}_{\infty }$
-algebras such that
$\mathrm {A}_{\infty }$
-algebras such that
 $$ \begin{align} \begin{gathered} \varphi_1(1_A) = 1_B \quad\text{and} \\ \varphi_n(a_1 \otimes \cdots \otimes a_{i-1} \otimes 1_A \otimes a_{i+1} \otimes \cdots \otimes a_n) = 0 \quad\text{for all } 1 \leqslant i \leqslant n \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} \varphi_1(1_A) = 1_B \quad\text{and} \\ \varphi_n(a_1 \otimes \cdots \otimes a_{i-1} \otimes 1_A \otimes a_{i+1} \otimes \cdots \otimes a_n) = 0 \quad\text{for all } 1 \leqslant i \leqslant n \end{gathered} \end{align} $$
for any
![]() $a_j \in A$
and
$a_j \in A$
and
![]() $n> 1$
.
$n> 1$
.
4.3. An
![]() $\mathrm {A}_{\infty }$
-algebra is connective if it is concentrated in non-negative degrees. If
$\mathrm {A}_{\infty }$
-algebra is connective if it is concentrated in non-negative degrees. If
![]() $A = Q \oplus \bar {A}$
is a graded module and
$A = Q \oplus \bar {A}$
is a graded module and
![]() $1_A$
a free generator of the direct summand Q, then A is an
$1_A$
a free generator of the direct summand Q, then A is an
![]() $\mathrm {A}_{\infty }$
-algebra with a split unit.
$\mathrm {A}_{\infty }$
-algebra with a split unit.
A split unital
![]() $\mathrm {A}_{\infty }$
-algebra structure on a graded module concentrated in non-negative degrees is equivalent to the existence of Q-linear maps
$\mathrm {A}_{\infty }$
-algebra structure on a graded module concentrated in non-negative degrees is equivalent to the existence of Q-linear maps
of degree
![]() $(n-2)$
and Q-linear maps
$(n-2)$
and Q-linear maps
of degrees
![]() $-1$
and
$-1$
and
![]() $0$
, respectively, such that for
$0$
, respectively, such that for
![]() $n \neq 2,3$
, the Stasheff identities (4.1.1) hold when replacing
$n \neq 2,3$
, the Stasheff identities (4.1.1) hold when replacing
![]() $m_i$
by
$m_i$
by
![]() $\bar {m}_i$
, and for
$\bar {m}_i$
, and for
![]() $n=2,3$
,
$n=2,3$
,
 $$ \begin{align*} \sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{r+st} \bar{m}_{r+1+t} (\operatorname{\mathrm{id}}^{\otimes r} \otimes \bar{m}_s \otimes \operatorname{\mathrm{id}}^{\otimes t}) + (h_{n-1} \otimes \operatorname{\mathrm{id}} - \operatorname{\mathrm{id}} \otimes h_{n-1}) = 0, \end{align*} $$
$$ \begin{align*} \sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{r+st} \bar{m}_{r+1+t} (\operatorname{\mathrm{id}}^{\otimes r} \otimes \bar{m}_s \otimes \operatorname{\mathrm{id}}^{\otimes t}) + (h_{n-1} \otimes \operatorname{\mathrm{id}} - \operatorname{\mathrm{id}} \otimes h_{n-1}) = 0, \end{align*} $$
and additionally,
 $$ \begin{align*} \begin{aligned} h_1 \bar{m}_1 &= 0 ,\quad h_1 \bar{m}_2 - h_2 (\bar{m}_1 \otimes \operatorname{\mathrm{id}} + \operatorname{\mathrm{id}} \otimes \bar{m}_1) = 0 \quad \text{and} \\& \qquad h_1 \bar{m}_3 + h_2 (\bar{m}_2 \otimes \operatorname{\mathrm{id}} - \operatorname{\mathrm{id}} \otimes \bar{m}_2) = 0\,; \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} h_1 \bar{m}_1 &= 0 ,\quad h_1 \bar{m}_2 - h_2 (\bar{m}_1 \otimes \operatorname{\mathrm{id}} + \operatorname{\mathrm{id}} \otimes \bar{m}_1) = 0 \quad \text{and} \\& \qquad h_1 \bar{m}_3 + h_2 (\bar{m}_2 \otimes \operatorname{\mathrm{id}} - \operatorname{\mathrm{id}} \otimes \bar{m}_2) = 0\,; \end{aligned} \end{align*} $$
the former replaces the second and third Stasheff identity and the latter supplements the first three Stasheff identities. In particular, for
![]() $n> 2$
, the maps
$n> 2$
, the maps
![]() $\bar {m}_n$
are the appropriate restrictions of
$\bar {m}_n$
are the appropriate restrictions of
![]() $m_n$
. For
$m_n$
. For
![]() $n=2$
, we obtain
$n=2$
, we obtain
![]() $m_2$
by
$m_2$
by
![]() $\bar {m}_2 + h_2$
and additionally enforcing (4.2.1). For
$\bar {m}_2 + h_2$
and additionally enforcing (4.2.1). For
![]() $n=1$
, we have
$n=1$
, we have
![]() $m_1 = \bar {m}_1 + h_1$
. This treatment is similar to [Reference BurkeBur15, Section 3] but is slightly more general since we allow
$m_1 = \bar {m}_1 + h_1$
. This treatment is similar to [Reference BurkeBur15, Section 3] but is slightly more general since we allow
![]() $\bar {A}_0\neq 0$
and hence need
$\bar {A}_0\neq 0$
and hence need
![]() $h_2$
as well as
$h_2$
as well as
![]() $h_1$
. If A were not connective, then we would also need maps
$h_1$
. If A were not connective, then we would also need maps
![]() $h_n$
for
$h_n$
for
![]() $n\geqslant 3$
. Taken together, the
$n\geqslant 3$
. Taken together, the
![]() $h_n$
will correspond to the curvature term on the bar construction of A; see 4.7.
$h_n$
will correspond to the curvature term on the bar construction of A; see 4.7.
Remark 4.4. Let A be a connective
![]() $\mathrm {A}_{\infty }$
-algebra with a split unit. Then the projection
$\mathrm {A}_{\infty }$
-algebra with a split unit. Then the projection
![]() $A \to Q$
onto the free summand containing the unit need not be a morphism of strictly unital
$A \to Q$
onto the free summand containing the unit need not be a morphism of strictly unital
![]() $\mathrm {A}_{\infty }$
-algebras. In fact, this happens if and only if
$\mathrm {A}_{\infty }$
-algebras. In fact, this happens if and only if
![]() $h_1 = 0$
and
$h_1 = 0$
and
![]() $h_2 = 0$
. Such
$h_2 = 0$
. Such
![]() $\mathrm {A}_{\infty }$
-algebras are called augmented.
$\mathrm {A}_{\infty }$
-algebras are called augmented.
4.5. Fix a graded coalgebra
![]() $(C,\Delta )$
. Recall C is counital if there exists a counit map
$(C,\Delta )$
. Recall C is counital if there exists a counit map
![]() $\varepsilon \colon C \to Q$
such that
$\varepsilon \colon C \to Q$
such that
We say C is a curved dg coalgebra if it is equipped with a coderivation
![]() $\partial $
of degree
$\partial $
of degree
![]() $-1$
and a curvature term
$-1$
and a curvature term
![]() $h \colon C \to Q$
of degree
$h \colon C \to Q$
of degree
![]() $-2$
such that
$-2$
such that
A curved dg coalgebra C is connected if it is non-negatively graded, counital and
![]() $C_0 = Q$
. In this setting, we write
$C_0 = Q$
. In this setting, we write
![]() $C = Q \oplus \bar {C}$
for
$C = Q \oplus \bar {C}$
for
![]() $\bar {C} = \ker (\varepsilon )$
and set
$\bar {C} = \ker (\varepsilon )$
and set

for the restrictions to
![]() $\bar {C}$
. These maps satisfy the same relations as
$\bar {C}$
. These maps satisfy the same relations as
![]() $\Delta $
,
$\Delta $
,
![]() $\partial $
and h.
$\partial $
and h.
4.6. The tensor algebra ![]() on a graded Q-module V has underlying graded module
on a graded Q-module V has underlying graded module ![]() , and the multiplication
, and the multiplication
The tensor algebra is bigraded by
![]() $\mathrm {T}^{a}_{(n)}(V)_i=(V^{\otimes n})_i$
.
$\mathrm {T}^{a}_{(n)}(V)_i=(V^{\otimes n})_i$
.
The tensor coalgebra
![]() $\mathrm {T}^{c}(V)$
on a graded Q-module V has underlying graded module
$\mathrm {T}^{c}(V)$
on a graded Q-module V has underlying graded module ![]() , and the comultiplication
, and the comultiplication

The tensor coalgebra is bigraded by
![]() $\mathrm {T}^{c}_{(n)}(V)_i=(V^{\otimes n})_i$
. The data of an
$\mathrm {T}^{c}_{(n)}(V)_i=(V^{\otimes n})_i$
. The data of an
![]() $\mathrm {A}_{\infty }$
-algebra can equivalently be encoded as a differential on a tensor coalgebra, as we see next.
$\mathrm {A}_{\infty }$
-algebra can equivalently be encoded as a differential on a tensor coalgebra, as we see next.
4.7. Let A be a split unital connective
![]() $\mathrm {A}_{\infty }$
-algebra. Then the tensor coalgebra
$\mathrm {A}_{\infty }$
-algebra. Then the tensor coalgebra ![]() has an induced curved dg coalgebra structure. The curvature term has components
has an induced curved dg coalgebra structure. The curvature term has components
and zero otherwise. The coderivation
![]() $\partial $
has components
$\partial $
has components
 $$ \begin{align*} (-1)^{\frac{k(k+1)}{2}} \sum_{\substack{i+j=n-k\\i,j \geqslant 0}} (\operatorname{\mathrm{id}}^{\otimes i} \otimes {\scriptstyle\mathsf{\Sigma}} \bar{m}_{k} ({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes k} \otimes \operatorname{\mathrm{id}}^{\otimes j}) \colon \mathrm{T}^{c}_{(n)}{(\Sigma \bar{A})} \to \mathrm{T}^{c}_{(n-k+1)}{(\Sigma \bar{A})} \end{align*} $$
$$ \begin{align*} (-1)^{\frac{k(k+1)}{2}} \sum_{\substack{i+j=n-k\\i,j \geqslant 0}} (\operatorname{\mathrm{id}}^{\otimes i} \otimes {\scriptstyle\mathsf{\Sigma}} \bar{m}_{k} ({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes k} \otimes \operatorname{\mathrm{id}}^{\otimes j}) \colon \mathrm{T}^{c}_{(n)}{(\Sigma \bar{A})} \to \mathrm{T}^{c}_{(n-k+1)}{(\Sigma \bar{A})} \end{align*} $$
for
![]() $k \geqslant 1$
, and zero otherwise. The map
$k \geqslant 1$
, and zero otherwise. The map
![]() $\partial $
is well defined since A is concentrated in non-negative homological degree. With this structure,
$\partial $
is well defined since A is concentrated in non-negative homological degree. With this structure, ![]() is a connected curved dg coalgebra, and we call
is a connected curved dg coalgebra, and we call
the bar construction of A. For
![]() $a_1, \ldots , a_n \in \bar {A}$
, we write
$a_1, \ldots , a_n \in \bar {A}$
, we write
For a split unital connective
![]() $\mathrm {A}_{\infty }$
-algebra, the canonical projection and inclusion induce a degree
$\mathrm {A}_{\infty }$
-algebra, the canonical projection and inclusion induce a degree
![]() $-1$
map of graded modules
$-1$
map of graded modules
Let C be a connected curved dg coalgebra. Then the algebra ![]() has an induced dg algebra structure. The differential
has an induced dg algebra structure. The differential
![]() $m_1$
has components
$m_1$
has components
 $$ \begin{align*} \begin{aligned} -\bar{h} {\scriptstyle\mathsf{\Sigma}} \colon \mathrm{T}^{a}_{(1)}&{(\Sigma^{-1} \bar{C})} \to \mathrm{ T}^{a}_{(0)}{(\Sigma^{-1} \bar{C})} ,\quad -{\scriptstyle\mathsf{\Sigma}}^{-1} \bar{\partial} {\scriptstyle\mathsf{\Sigma}} \colon \mathrm{T}^{a}_{(1)}{(\Sigma^{-1} \bar{C})} \to \mathrm{T}^{a}_{(1)}{(\Sigma^{-1} \bar{C})} \\& \qquad\text{and}\quad ({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes 2} \bar{\Delta} {\scriptstyle\mathsf{\Sigma}} \colon \mathrm{T}^{a}_{(1)}{(\Sigma^{-1} \bar{C})} \to \mathrm{ T}^{a}_{(2)}{(\Sigma^{-1} \bar{C})}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} -\bar{h} {\scriptstyle\mathsf{\Sigma}} \colon \mathrm{T}^{a}_{(1)}&{(\Sigma^{-1} \bar{C})} \to \mathrm{ T}^{a}_{(0)}{(\Sigma^{-1} \bar{C})} ,\quad -{\scriptstyle\mathsf{\Sigma}}^{-1} \bar{\partial} {\scriptstyle\mathsf{\Sigma}} \colon \mathrm{T}^{a}_{(1)}{(\Sigma^{-1} \bar{C})} \to \mathrm{T}^{a}_{(1)}{(\Sigma^{-1} \bar{C})} \\& \qquad\text{and}\quad ({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes 2} \bar{\Delta} {\scriptstyle\mathsf{\Sigma}} \colon \mathrm{T}^{a}_{(1)}{(\Sigma^{-1} \bar{C})} \to \mathrm{ T}^{a}_{(2)}{(\Sigma^{-1} \bar{C})}, \end{aligned} \end{align*} $$
and zero otherwise. With this structure, ![]() is a split unital connective dg algebra, and we call
is a split unital connective dg algebra, and we call
the cobar construction of C. For
![]() $c_1, \ldots , c_n \in \bar {C}$
, we write
$c_1, \ldots , c_n \in \bar {C}$
, we write
For a connected curved dg coalgebra, the canonical inclusion and projection maps induces a degree
![]() $-1$
map of graded modules
$-1$
map of graded modules
Remark 4.8. The bar and cobar constructions define an adjoint pair of functors when restricted to split unital connective dg algebras and connected curved dg coalgebras; see [Reference LyubashenkoLyu13, Section 3]. It remains an adjunction when restricted to augmented connective dg algebras and connected dg coalgebras.
4.9. A morphism
![]() $\varphi \colon (C,\Delta ,\varepsilon ,\partial ,h) \to (C',\Delta ',\varepsilon ',\partial ',h')$
of connected curved dg coalgebras consists of Q-linear maps
$\varphi \colon (C,\Delta ,\varepsilon ,\partial ,h) \to (C',\Delta ',\varepsilon ',\partial ',h')$
of connected curved dg coalgebras consists of Q-linear maps
of degree
![]() $-1$
and 0, respectively, satisfying
$-1$
and 0, respectively, satisfying
 $$ \begin{align*} \begin{aligned} &\varepsilon = \varepsilon ' \varphi_1 ,\quad h' \varphi_1 = h - \varphi_0 \partial + (\varphi_0 \otimes \varphi_0) \Delta , \\\partial' \varphi_1 = \varphi_1 \partial &+ (\varphi_0 \otimes \varphi_1 - \varphi_1 \otimes \varphi_0) \Delta \quad \text{and} \quad \Delta' \varphi_1 = (\varphi_1 \otimes \varphi_1) \Delta\,; \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\varepsilon = \varepsilon ' \varphi_1 ,\quad h' \varphi_1 = h - \varphi_0 \partial + (\varphi_0 \otimes \varphi_0) \Delta , \\\partial' \varphi_1 = \varphi_1 \partial &+ (\varphi_0 \otimes \varphi_1 - \varphi_1 \otimes \varphi_0) \Delta \quad \text{and} \quad \Delta' \varphi_1 = (\varphi_1 \otimes \varphi_1) \Delta\,; \end{aligned} \end{align*} $$
see [Reference PositselskiPos11, Chapter 4]. This induces a map of dg algebras
![]() $\mathsf {\Omega }{(\varphi )} \colon \mathsf {\Omega }{(C)} \to \mathsf {\Omega }{(C')}$
, and we say
$\mathsf {\Omega }{(\varphi )} \colon \mathsf {\Omega }{(C)} \to \mathsf {\Omega }{(C')}$
, and we say
![]() $\varphi $
is a weak equivalence if
$\varphi $
is a weak equivalence if
![]() $\mathsf {\Omega }{(\varphi )}$
is a quasi-isomorphism.
$\mathsf {\Omega }{(\varphi )}$
is a quasi-isomorphism.
4.10. Let A be an
![]() $\mathrm {A}_{\infty }$
-algebra. An
$\mathrm {A}_{\infty }$
-algebra. An
![]() $\mathrm {A}_{\infty }$
-module over A is a graded module M equipped with maps
$\mathrm {A}_{\infty }$
-module over A is a graded module M equipped with maps
of degree
![]() $(n-2)$
, satisfying
$(n-2)$
, satisfying
 $$ \begin{align*} \sum_{\substack{r+s+t=n\\r \geqslant 0, s,t \geqslant 1}} (-1)^{r+st} m^M_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right) + \sum_{\substack{r+s=n\\r \geqslant 0, s \geqslant 1}} (-1)^r m^M_{r+1} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s^M\right) = 0. \end{align*} $$
$$ \begin{align*} \sum_{\substack{r+s+t=n\\r \geqslant 0, s,t \geqslant 1}} (-1)^{r+st} m^M_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right) + \sum_{\substack{r+s=n\\r \geqslant 0, s \geqslant 1}} (-1)^r m^M_{r+1} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s^M\right) = 0. \end{align*} $$
If A is strictly unital, we say an
![]() $\mathrm {A}_{\infty }$
-module M over A is strictly unital if
$\mathrm {A}_{\infty }$
-module M over A is strictly unital if
 $$ \begin{align*} \begin{aligned} &m_2(1_A \otimes m) = m \quad\text{for all } m \in M \quad\text{and} \\m_n(a_1 \otimes \cdots \otimes a_{i-1} &\otimes 1_A \otimes a_{i+1} \otimes \cdots \otimes a_{n-1} \otimes m) = 0 \quad \text{for all } 1 \leqslant i \leqslant n-1 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &m_2(1_A \otimes m) = m \quad\text{for all } m \in M \quad\text{and} \\m_n(a_1 \otimes \cdots \otimes a_{i-1} &\otimes 1_A \otimes a_{i+1} \otimes \cdots \otimes a_{n-1} \otimes m) = 0 \quad \text{for all } 1 \leqslant i \leqslant n-1 \end{aligned} \end{align*} $$
for any
![]() $a_1, \ldots , a_{n-1} \in A$
and
$a_1, \ldots , a_{n-1} \in A$
and
![]() $m \in M$
with
$m \in M$
with
![]() $n \neq 2$
.
$n \neq 2$
.
If A is connective and has a split unit, then a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure over A on M is equivalent to the existence of maps
$\mathrm {A}_{\infty }$
-module structure over A on M is equivalent to the existence of maps
of degree
![]() $(n-2)$
such that for
$(n-2)$
such that for
![]() $n \neq 2,3$
, the Stasheff identities hold when replacing m by
$n \neq 2,3$
, the Stasheff identities hold when replacing m by
![]() $\bar {m}$
, and for
$\bar {m}$
, and for
![]() $n=2,3$
, there is an extra curvature term
$n=2,3$
, there is an extra curvature term
![]() $h_{n-1} \otimes \operatorname {\mathrm {id}}$
similar to 4.3.
$h_{n-1} \otimes \operatorname {\mathrm {id}}$
similar to 4.3.
4.11. Let A be a split unital connective
![]() $\mathrm {A}_{\infty }$
-algebra. The data of a strictly unital
$\mathrm {A}_{\infty }$
-algebra. The data of a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure over A is equivalent to that of a strictly unital dg module structure over
$\mathrm {A}_{\infty }$
-module structure over A is equivalent to that of a strictly unital dg module structure over
![]() $\mathsf {\Omega }{(\mathsf {B}{(A)})}$
. Explicitly, if
$\mathsf {\Omega }{(\mathsf {B}{(A)})}$
. Explicitly, if
![]() $\{\bar {m}^M_n\}$
is a strictly unital
$\{\bar {m}^M_n\}$
is a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure on a graded module M, then the dg module structure on M is given by the same differential
$\mathrm {A}_{\infty }$
-module structure on a graded module M, then the dg module structure on M is given by the same differential
![]() $m^M_1$
, and the multiplication
$m^M_1$
, and the multiplication
![]() $\mathsf {\Omega }{(\mathsf {B}{(A)})} \otimes M \to M$
induced by
$\mathsf {\Omega }{(\mathsf {B}{(A)})} \otimes M \to M$
induced by
Moreover, this construction is natural in A and M, and any quasi-isomorphism of
![]() $\mathrm {A}_{\infty }$
-modules over A yields a quasi-isomorphism of dg modules over
$\mathrm {A}_{\infty }$
-modules over A yields a quasi-isomorphism of dg modules over
![]() $\mathsf {\Omega }{(\mathsf {B}{(A)})}$
.
$\mathsf {\Omega }{(\mathsf {B}{(A)})}$
.
5 Transfer of
 $\mathrm {A}_{\infty }$
-algebra structures
$\mathrm {A}_{\infty }$
-algebra structures
In this section, as above, Q is a local ring with maximal ideal
![]() $\mathfrak {m}_Q$
and residue field k. Let R be an
$\mathfrak {m}_Q$
and residue field k. Let R be an
![]() $\mathrm {A}_{\infty }$
-algebra over Q, and let
$\mathrm {A}_{\infty }$
-algebra over Q, and let
![]() $A \to R$
be a quasi-isomorphism of complexes over Q. We would like to know whether the
$A \to R$
be a quasi-isomorphism of complexes over Q. We would like to know whether the
![]() $\mathrm {A}_{\infty }$
-algebra structure on R induces an
$\mathrm {A}_{\infty }$
-algebra structure on R induces an
![]() $\mathrm {A}_{\infty }$
-algebra structure on A. This is well understood in the case that Q is field, so that
$\mathrm {A}_{\infty }$
-algebra structure on A. This is well understood in the case that Q is field, so that
![]() $A \to R$
is a homotopy equivalence; the first result is due to Kadeishvili [Reference KadeishviliKad82] when
$A \to R$
is a homotopy equivalence; the first result is due to Kadeishvili [Reference KadeishviliKad82] when
![]() $A = \mathrm {H}(R)$
. For general homotopy equivalences, this was studied, for example, in [Reference Markl and ČadekMar06]. Burke has shown that if R is a quotient of Q and A is a Q-free resolution of R, then the product on R lifts to an
$A = \mathrm {H}(R)$
. For general homotopy equivalences, this was studied, for example, in [Reference Markl and ČadekMar06]. Burke has shown that if R is a quotient of Q and A is a Q-free resolution of R, then the product on R lifts to an
![]() $\mathrm {A}_{\infty }$
-structure on A [Reference BurkeBur18, Proposition 3.6]. We give a proof in a more general situation.
$\mathrm {A}_{\infty }$
-structure on A [Reference BurkeBur18, Proposition 3.6]. We give a proof in a more general situation.
Proposition 5.1. Let R be a strictly unital connective
![]() $\mathrm {A}_{\infty }$
-algebra and
$\mathrm {A}_{\infty }$
-algebra and
![]() $\varepsilon \colon A \to R$
a surjective quasi-isomorphism of complexes over Q, with A degree-wise free and concentrated in non-negative degrees. Then there exists an
$\varepsilon \colon A \to R$
a surjective quasi-isomorphism of complexes over Q, with A degree-wise free and concentrated in non-negative degrees. Then there exists an
![]() $\mathrm {A}_{\infty }$
-algebra structure with a split unit on A such that
$\mathrm {A}_{\infty }$
-algebra structure with a split unit on A such that
![]() $\varepsilon $
is a strict quasi-isomorphism of
$\varepsilon $
is a strict quasi-isomorphism of
![]() $\mathrm {A}_{\infty }$
-algebras.
$\mathrm {A}_{\infty }$
-algebras.
Proof. Since
![]() $\varepsilon $
is surjective, we may choose a splitting
$\varepsilon $
is surjective, we may choose a splitting
![]() $A = \bar {A} \oplus Q$
such that
$A = \bar {A} \oplus Q$
such that
![]() $\varepsilon $
maps the free generator of Q to the unit of R. We inductively construct higher multiplication maps
$\varepsilon $
maps the free generator of Q to the unit of R. We inductively construct higher multiplication maps
![]() $m_n$
on A satisfying the nth Stasheff identity. To begin with, we set
$m_n$
on A satisfying the nth Stasheff identity. To begin with, we set ![]() where
where
![]() $\partial $
is the differential of A.
$\partial $
is the differential of A.
For
![]() $n=2$
, we consider the commutative diagram
$n=2$
, we consider the commutative diagram

The morphism of complexes
![]() $m_2^A \colon A^{\otimes 2} \to A$
exists because
$m_2^A \colon A^{\otimes 2} \to A$
exists because
![]() $\varepsilon $
is a surjective quasi-isomorphism, the left vertical arrow is injective in each degree and the cokernel in each degree is projective; see, for example, [Reference Dwyer, Spaliński and JamesDS95, Section 7]. The morphism
$\varepsilon $
is a surjective quasi-isomorphism, the left vertical arrow is injective in each degree and the cokernel in each degree is projective; see, for example, [Reference Dwyer, Spaliński and JamesDS95, Section 7]. The morphism
![]() $m_2^A$
satisfies the desired properties by construction.
$m_2^A$
satisfies the desired properties by construction.
For
![]() $n> 2$
, the obstruction
$n> 2$
, the obstruction
![]() $\operatorname {obs}_n^A$
from (4.1.2) is a chain map. We have a short exact sequence of complexes
$\operatorname {obs}_n^A$
from (4.1.2) is a chain map. We have a short exact sequence of complexes
 $$ \begin{align*} 0 \to \sum_{i+j=n-1} A^{\otimes i} \otimes Q \otimes A^{\otimes j} \xrightarrow{\eta_n} A^{\otimes n} \to \bar{A}^{\otimes n} \to 0. \end{align*} $$
$$ \begin{align*} 0 \to \sum_{i+j=n-1} A^{\otimes i} \otimes Q \otimes A^{\otimes j} \xrightarrow{\eta_n} A^{\otimes n} \to \bar{A}^{\otimes n} \to 0. \end{align*} $$
By direct computation, we obtain
![]() $\operatorname {obs}_n^A \eta _n = 0$
. So the obstruction
$\operatorname {obs}_n^A \eta _n = 0$
. So the obstruction
![]() $\operatorname {obs}_n^A$
factors through
$\operatorname {obs}_n^A$
factors through
![]() $\bar {A}^{\otimes n}$
. We consider the diagram
$\bar {A}^{\otimes n}$
. We consider the diagram

Since
![]() $\bar {A}^{\otimes n}$
is, as graded modules, a direct summand of
$\bar {A}^{\otimes n}$
is, as graded modules, a direct summand of
![]() $A^{\otimes n}$
, and the higher multiplications
$A^{\otimes n}$
, and the higher multiplications
![]() $m_i^A$
for
$m_i^A$
for
![]() $i < n$
commute with
$i < n$
commute with
![]() $\varepsilon $
, the right triangle commutes up to the homotopy
$\varepsilon $
, the right triangle commutes up to the homotopy
![]() $m_n^R \varepsilon ^{\otimes n}$
. Then there exists a chain map
$m_n^R \varepsilon ^{\otimes n}$
. Then there exists a chain map
![]() $\alpha $
such that the left triangle commutes up to a homotopy
$\alpha $
such that the left triangle commutes up to a homotopy
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $\varepsilon $
is surjective, we may assume
$\varepsilon $
is surjective, we may assume
![]() $m_n^R \varepsilon ^{\otimes n} = \varepsilon \sigma $
by [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, Proposition 1.3.1]. That is,
$m_n^R \varepsilon ^{\otimes n} = \varepsilon \sigma $
by [Reference Avramov, Elías, Giral, Miró-Roig and ZarzuelaAvr98, Proposition 1.3.1]. That is,
satisfies the nth Stasheff identity (4.1.4).
5.2. In the setup of Proposition 5.1, we can also transfer
![]() $\mathrm {A}_{\infty }$
-module structures: If M is a strictly unital
$\mathrm {A}_{\infty }$
-module structures: If M is a strictly unital
![]() $\mathrm {A}_{\infty }$
-module over R and with semifree resolution
$\mathrm {A}_{\infty }$
-module over R and with semifree resolution
![]() $\gamma \colon G \to M$
over Q, in the sense discussed later in 6.2, then there exists a strictly unital
$\gamma \colon G \to M$
over Q, in the sense discussed later in 6.2, then there exists a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure on G over A and
$\mathrm {A}_{\infty }$
-module structure on G over A and
![]() $\gamma $
is a strict morphism of
$\gamma $
is a strict morphism of
![]() $\mathrm {A}_{\infty }$
-modules; compare with [Reference BurkeBur18]. When the homology of M is bounded below (for example, if M is an honest module), one can take G to be a bounded below complex of free Q-modules.
$\mathrm {A}_{\infty }$
-modules; compare with [Reference BurkeBur18]. When the homology of M is bounded below (for example, if M is an honest module), one can take G to be a bounded below complex of free Q-modules.
Proposition 5.3. Let
![]() $\varepsilon \colon R \to S$
be a surjective strict quasi-isomorphism of strictly unital
$\varepsilon \colon R \to S$
be a surjective strict quasi-isomorphism of strictly unital
![]() $\mathrm {A}_{\infty }$
-algebras over Q. Further, let A be a split unital, connective, degree-wise free
$\mathrm {A}_{\infty }$
-algebras over Q. Further, let A be a split unital, connective, degree-wise free
![]() $\mathrm {A}_{\infty }$
-algebra and
$\mathrm {A}_{\infty }$
-algebra and
![]() $\varphi \colon A \to S$
a morphism of strictly unital
$\varphi \colon A \to S$
a morphism of strictly unital
![]() $\mathrm {A}_{\infty }$
-algebras. Then there exists a morphism of strictly unital
$\mathrm {A}_{\infty }$
-algebras. Then there exists a morphism of strictly unital
![]() $\mathrm {A}_{\infty }$
-algebras
$\mathrm {A}_{\infty }$
-algebras
![]() $\psi \colon A \to R$
such that
$\psi \colon A \to R$
such that
![]() $\varphi = \varepsilon \psi $
.
$\varphi = \varepsilon \psi $
.
Proof. The unit
![]() $Q\to S$
factors through
$Q\to S$
factors through
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\varphi _1$
, so by [Reference Dwyer, Spaliński and JamesDS95, Section 7], there is a chain map
$\varphi _1$
, so by [Reference Dwyer, Spaliński and JamesDS95, Section 7], there is a chain map
![]() $\psi _1 \colon A \to R$
such that
$\psi _1 \colon A \to R$
such that
![]() $\varphi _1 = \varepsilon \psi _1$
and
$\varphi _1 = \varepsilon \psi _1$
and
![]() $\psi _1(1_A) = 1_R$
.
$\psi _1(1_A) = 1_R$
.
Let
![]() $n \geqslant 2$
and assume that for
$n \geqslant 2$
and assume that for
![]() $i < n$
, the chain maps
$i < n$
, the chain maps
![]() $\psi _i \colon A^{\otimes i} \to R$
exist, the ith Stasheff identities (4.1.3) and (4.2.2) hold, and
$\psi _i \colon A^{\otimes i} \to R$
exist, the ith Stasheff identities (4.1.3) and (4.2.2) hold, and
![]() $\varepsilon \psi _i = \varphi _i$
. A computation shows that
$\varepsilon \psi _i = \varphi _i$
. A computation shows that
![]() $\operatorname {obs}_n^\psi $
and
$\operatorname {obs}_n^\psi $
and
![]() $\operatorname {obs}_n^\varphi $
vanish when any of its inputs is
$\operatorname {obs}_n^\varphi $
vanish when any of its inputs is
![]() $1_A$
. Hence, we can view
$1_A$
. Hence, we can view
![]() $\operatorname {obs}_n^\psi $
and
$\operatorname {obs}_n^\psi $
and
![]() $\operatorname {obs}_n^\varphi $
as maps on
$\operatorname {obs}_n^\varphi $
as maps on
![]() $\bar {A}^{\otimes n}$
. Taking homology classes in
$\bar {A}^{\otimes n}$
. Taking homology classes in
![]() $\operatorname {Hom}{(\bar {A}^{\otimes n},S)}$
, we have
$\operatorname {Hom}{(\bar {A}^{\otimes n},S)}$
, we have
since
![]() $\varepsilon \operatorname {obs}_n^\psi = \operatorname {obs}_n^\varphi $
and
$\varepsilon \operatorname {obs}_n^\psi = \operatorname {obs}_n^\varphi $
and
![]() $\varphi $
is a morphism of strictly unital
$\varphi $
is a morphism of strictly unital
![]() $\mathrm {A}_{\infty }$
-algebras; cf. 4.1. Since
$\mathrm {A}_{\infty }$
-algebras; cf. 4.1. Since
![]() $\varepsilon $
is a surjective quasi-isomorphism, and using the assumptions on A, the induced map
$\varepsilon $
is a surjective quasi-isomorphism, and using the assumptions on A, the induced map
![]() $\operatorname {Hom}({\bar {A}^{\otimes n}},R)\to \operatorname {Hom}{(\bar {A}^{\otimes n},S)}$
is a quasi-isomorphism, and hence,
$\operatorname {Hom}({\bar {A}^{\otimes n}},R)\to \operatorname {Hom}{(\bar {A}^{\otimes n},S)}$
is a quasi-isomorphism, and hence,
![]() $\operatorname {obs}_n^\psi $
is a boundary in
$\operatorname {obs}_n^\psi $
is a boundary in
![]() $\operatorname {Hom}{(\bar {A}^{\otimes n},R)}$
. That is, there is
$\operatorname {Hom}{(\bar {A}^{\otimes n},R)}$
. That is, there is
![]() $\bar {\psi }_n \colon \bar {A}^{\otimes n}\to R$
such that
$\bar {\psi }_n \colon \bar {A}^{\otimes n}\to R$
such that
Setting ![]() , we now have
, we now have
![]() $\psi _1,\ldots , \psi _n$
satisfying the required identities (4.1.3) and (4.2.2), completing the induction.
$\psi _1,\ldots , \psi _n$
satisfying the required identities (4.1.3) and (4.2.2), completing the induction.
It is well known that
![]() $\mathrm {A}_{\infty }$
-algebras can be used to characterize formality of dg algebras over fields [Reference KadeishviliKad82]. We record the following generalization in local algebra.
$\mathrm {A}_{\infty }$
-algebras can be used to characterize formality of dg algebras over fields [Reference KadeishviliKad82]. We record the following generalization in local algebra.
Proposition 5.4. Let
![]() $\varphi \colon Q\to R$
be a finite local homomorphism and let
$\varphi \colon Q\to R$
be a finite local homomorphism and let
![]() $\varepsilon \colon A \to R$
be the minimal Q-free resolution, equipped with an
$\varepsilon \colon A \to R$
be the minimal Q-free resolution, equipped with an
![]() $\mathrm {A}_{\infty }$
-structure making
$\mathrm {A}_{\infty }$
-structure making
![]() $\varepsilon $
a strict quasi-isomorphism of
$\varepsilon $
a strict quasi-isomorphism of
![]() $\mathrm {A}_{\infty }$
-algebras. The
$\mathrm {A}_{\infty }$
-algebras. The
![]() $\mathrm {A}_{\infty }$
-algebra
$\mathrm {A}_{\infty }$
-algebra
![]() $A\otimes _Qk$
is quasi-isomorphic, as an
$A\otimes _Qk$
is quasi-isomorphic, as an
![]() $\mathrm {A}_{\infty }$
-algebra, to the derived fiber
$\mathrm {A}_{\infty }$
-algebra, to the derived fiber
![]() $R\otimes ^{\mathsf {L}}_Q k$
defined as a dg k-algebra in Section 2. Moreover,
$R\otimes ^{\mathsf {L}}_Q k$
defined as a dg k-algebra in Section 2. Moreover,
![]() $R\otimes ^{\mathsf {L}}_Q k$
is formal as a dg k-algebra if and only if A admits an
$R\otimes ^{\mathsf {L}}_Q k$
is formal as a dg k-algebra if and only if A admits an
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n\}$
as above that also satisfies
$\{m_n\}$
as above that also satisfies
![]() $m_n\otimes _Qk =0$
for
$m_n\otimes _Qk =0$
for
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
Proof. Suppose that the minimal Q-free resolution A of R has an
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n\}$
with the stated property. If
$\{m_n\}$
with the stated property. If
![]() $A'$
is a Q-free dg algebra resolution of R, then A and
$A'$
is a Q-free dg algebra resolution of R, then A and
![]() $A'$
are quasi-isomorphic as
$A'$
are quasi-isomorphic as
![]() $\mathrm {A}_{\infty }$
-algebras over Q by Proposition 5.3. Therefore,
$\mathrm {A}_{\infty }$
-algebras over Q by Proposition 5.3. Therefore,
![]() $A\otimes _Qk$
and
$A\otimes _Qk$
and
![]() $R\otimes ^{\mathsf {L}}_Qk=A'\otimes _Qk$
are quasi-isomorphic as
$R\otimes ^{\mathsf {L}}_Qk=A'\otimes _Qk$
are quasi-isomorphic as
![]() $\mathrm {A}_{\infty }$
-algebras over k.
$\mathrm {A}_{\infty }$
-algebras over k.
If
![]() $m_n\otimes _Qk =0$
for
$m_n\otimes _Qk =0$
for
![]() $n\geqslant 3$
, then
$n\geqslant 3$
, then
![]() $A\otimes _Qk$
is a graded algebra, canonically isomorphic to
$A\otimes _Qk$
is a graded algebra, canonically isomorphic to
![]() $\operatorname {Tor}^{Q}(R,k)$
. Two dg k-algebras are quasi-isomorphic as dg algebras if and only if they are quasi-isomorphic as
$\operatorname {Tor}^{Q}(R,k)$
. Two dg k-algebras are quasi-isomorphic as dg algebras if and only if they are quasi-isomorphic as
![]() $\mathrm {A}_{\infty }$
-algebras [Reference KadeishviliKad82], and we can conclude that
$\mathrm {A}_{\infty }$
-algebras [Reference KadeishviliKad82], and we can conclude that
![]() $R\otimes ^{\mathsf {L}}_Qk$
is formal.
$R\otimes ^{\mathsf {L}}_Qk$
is formal.
Suppose conversely that
![]() $R\otimes ^{\mathsf {L}}_Q k$
is formal. By Proposition 5.1, the minimal Q-free resolution A of R admits an
$R\otimes ^{\mathsf {L}}_Q k$
is formal. By Proposition 5.1, the minimal Q-free resolution A of R admits an
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n^{\prime }\}$
. Using the same reasoning as above, since
$\{m_n^{\prime }\}$
. Using the same reasoning as above, since
![]() $R\otimes ^{\mathsf {L}}_Q k$
is formal
$R\otimes ^{\mathsf {L}}_Q k$
is formal
![]() $A\otimes _Qk$
and
$A\otimes _Qk$
and
![]() $\operatorname {Tor}^{Q}(R,k)$
are quasi-isomorphic as
$\operatorname {Tor}^{Q}(R,k)$
are quasi-isomorphic as
![]() $\mathrm {A}_{\infty }$
-algebras over k. By the uniqueness of minimal models (that is,
$\mathrm {A}_{\infty }$
-algebras over k. By the uniqueness of minimal models (that is,
![]() $\mathrm {A}_{\infty }$
-algebras over a field having zero differential; see [Reference KadeishviliKad82]), there is an isomorphism of
$\mathrm {A}_{\infty }$
-algebras over a field having zero differential; see [Reference KadeishviliKad82]), there is an isomorphism of
![]() $\mathrm {A}_{\infty }$
-algebras
$\mathrm {A}_{\infty }$
-algebras
where
![]() $\mu $
is the ordinary product on
$\mu $
is the ordinary product on
![]() $\operatorname {Tor}^{Q}(R,k)$
. We may make the identification
$\operatorname {Tor}^{Q}(R,k)$
. We may make the identification
![]() $A \otimes _Q k=\operatorname {Tor}^{Q}(R,k)$
and choose lifts
$A \otimes _Q k=\operatorname {Tor}^{Q}(R,k)$
and choose lifts
![]() $\Psi _i\colon A^{\otimes i} \to A$
with
$\Psi _i\colon A^{\otimes i} \to A$
with
![]() $\Psi _i\otimes _Qk=\psi _i$
. By Nakayama’s lemma,
$\Psi _i\otimes _Qk=\psi _i$
. By Nakayama’s lemma,
![]() $\Psi _1$
is an isomorphism and we can inductively define operations
$\Psi _1$
is an isomorphism and we can inductively define operations
![]() $m_n\colon A^{\otimes n} \to A$
by the formula
$m_n\colon A^{\otimes n} \to A$
by the formula ![]()

By construction, the map
![]() $\Psi \colon (A,\{m_n^{\prime }\}) \to (A,\{m_n\})$
now satisfies the Stasheff morphism identities (4.1.3), and it follows that
$\Psi \colon (A,\{m_n^{\prime }\}) \to (A,\{m_n\})$
now satisfies the Stasheff morphism identities (4.1.3), and it follows that
![]() $(A,\{m_n\})$
is an
$(A,\{m_n\})$
is an
![]() $\mathrm {A}_{\infty }$
-algebra, isomorphic to
$\mathrm {A}_{\infty }$
-algebra, isomorphic to
![]() $(A,\{m_n^{\prime }\})$
. Finally, from
$(A,\{m_n^{\prime }\})$
. Finally, from
![]() $\Psi \otimes _Q k=\psi $
, it follows that
$\Psi \otimes _Q k=\psi $
, it follows that
![]() $m_2\otimes _Qk=\mu $
and
$m_2\otimes _Qk=\mu $
and
![]() $m_n\otimes _Qk =0$
for
$m_n\otimes _Qk =0$
for
![]() $n\geqslant 3$
, as stated in the proposition.
$n\geqslant 3$
, as stated in the proposition.
The following technical lemma will be used later to help generate examples, by showing that certain
![]() $\mathrm {A}_{\infty }$
-operations are minimal.
$\mathrm {A}_{\infty }$
-operations are minimal.
Lemma 5.5. Let
![]() $\varphi \colon A\to T$
be a map of connective split unital
$\varphi \colon A\to T$
be a map of connective split unital
![]() $\mathrm {A}_{\infty }$
-algebras, where T is a trivial algebra. If for some N the map
$\mathrm {A}_{\infty }$
-algebras, where T is a trivial algebra. If for some N the map
![]() $(\varphi _1)_{< N} \colon A_{< N}\to T_{< N}$
is injective, then the
$(\varphi _1)_{< N} \colon A_{< N}\to T_{< N}$
is injective, then the
![]() $\mathrm {A}_{\infty }$
-structure of A vanishes in degrees less than N, in the sense that
$\mathrm {A}_{\infty }$
-structure of A vanishes in degrees less than N, in the sense that
![]() $(\bar {m}_n(\bar {A}^{\otimes n}))_i=0$
for all
$(\bar {m}_n(\bar {A}^{\otimes n}))_i=0$
for all
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $i<N$
.
$i<N$
.
Proof. We prove this by induction on n. It is clear for
![]() $n=1$
since
$n=1$
since
![]() $\varphi _1$
is a chain map. For
$\varphi _1$
is a chain map. For
![]() $n\geqslant 2$
, since
$n\geqslant 2$
, since
![]() $\bar {m}_s^{T}=0$
for all s, we can rearrange the Stasheff morphism identities (4.1.3):
$\bar {m}_s^{T}=0$
for all s, we can rearrange the Stasheff morphism identities (4.1.3):
 $$\begin{align*}\bar{\varphi}_1\bar{m}_n=-\sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{r+st} \bar{\varphi}_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes \bar{m}_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right). \end{align*}$$
$$\begin{align*}\bar{\varphi}_1\bar{m}_n=-\sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{r+st} \bar{\varphi}_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes \bar{m}_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right). \end{align*}$$
We can assume by induction that
![]() $(\bar {m}_s(\bar {A}^{\otimes s}))_{<N}=0$
for
$(\bar {m}_s(\bar {A}^{\otimes s}))_{<N}=0$
for
![]() $s<n$
. Since each
$s<n$
. Since each
![]() $\varphi _r$
increases degree by
$\varphi _r$
increases degree by
![]() $r-1$
, this implies that the right-hand side above is zero in degrees
$r-1$
, this implies that the right-hand side above is zero in degrees
![]() $i<N$
. Since
$i<N$
. Since
![]() $(\bar {\varphi }_1)_{<N}$
is injective, it follows that
$(\bar {\varphi }_1)_{<N}$
is injective, it follows that
![]() $(\bar {m}_n(\bar {A}^{\otimes n}))_{<N}=0$
.
$(\bar {m}_n(\bar {A}^{\otimes n}))_{<N}=0$
.
5.6 Cyclic
 $\mathrm {A}_{\infty }$
-algebras
$\mathrm {A}_{\infty }$
-algebras
For Gorenstein algebras, the minimal resolution satisfies a Poincaré duality property that allows us, in favorable situations, to construct
![]() $\mathrm {A}_{\infty }$
-resolutions with additional duality properties.
$\mathrm {A}_{\infty }$
-resolutions with additional duality properties.
A cyclic
![]() $\mathrm {A}_{\infty }$
-algebra of degree d over Q is a complex A of finitely generated free Q-modules with a perfect, Q-bilinear pairing
$\mathrm {A}_{\infty }$
-algebra of degree d over Q is a complex A of finitely generated free Q-modules with a perfect, Q-bilinear pairing
and an
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n\}$
on A such that for each n,
$\{m_n\}$
on A such that for each n,
see [Reference KontsevichKon94].
There is for each n an isomorphism of complexes
We give
![]() $A^{\otimes (n+1)}$
the action of the cyclic group
$A^{\otimes (n+1)}$
the action of the cyclic group
![]() $C_{n+1}=\langle c\rangle $
with generator acting by
$C_{n+1}=\langle c\rangle $
with generator acting by
![]() $c\cdot (a_1\otimes \cdots \otimes a_{n+1}) = (-1)^{|a_1|(|a_2|+\cdots +|a_{n+1}|)} (a_2\otimes \cdots \otimes a_{n+1}\otimes a_1)$
. From this perspective, an
$c\cdot (a_1\otimes \cdots \otimes a_{n+1}) = (-1)^{|a_1|(|a_2|+\cdots +|a_{n+1}|)} (a_2\otimes \cdots \otimes a_{n+1}\otimes a_1)$
. From this perspective, an
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n\}$
is cyclic if and only if
$\{m_n\}$
is cyclic if and only if
Let
![]() $\varphi \colon Q\to R$
be a surjective local Gorenstein homomorphism of projective dimension d, and let A be the minimal resolution of R over Q. Let
$\varphi \colon Q\to R$
be a surjective local Gorenstein homomorphism of projective dimension d, and let A be the minimal resolution of R over Q. Let
![]() $\mu \colon A^{\otimes 2}\to A$
be a chain map lifting the product on R; we can assume that
$\mu \colon A^{\otimes 2}\to A$
be a chain map lifting the product on R; we can assume that
![]() $\mu $
is unital and graded-commutative by [Reference Bruns and HerzogBH98, 3.4.3]. The Gorenstein condition (3.11.1) guarantees that
$\mu $
is unital and graded-commutative by [Reference Bruns and HerzogBH98, 3.4.3]. The Gorenstein condition (3.11.1) guarantees that
![]() $A\otimes _Q k=\operatorname {Tor}^{Q}(R,k)$
is a Poincaré duality algebra with the product induced from
$A\otimes _Q k=\operatorname {Tor}^{Q}(R,k)$
is a Poincaré duality algebra with the product induced from
![]() $\mu $
; see [Reference Avramov and GolodAG71, Theorem]. It follows from Nakayama’s lemma that
$\mu $
; see [Reference Avramov and GolodAG71, Theorem]. It follows from Nakayama’s lemma that
![]() $A_d\cong Q$
, and we obtain a perfect pairing
$A_d\cong Q$
, and we obtain a perfect pairing
Theorem 5.7. Let
![]() $Q\to R$
be a surjective local Gorenstein homomorphism of odd projective dimension d. Assume that Q contains a field of characteristic zero. The minimal resolution A of R over Q admits the structure of a split unital, cyclic
$Q\to R$
be a surjective local Gorenstein homomorphism of odd projective dimension d. Assume that Q contains a field of characteristic zero. The minimal resolution A of R over Q admits the structure of a split unital, cyclic
![]() $\mathrm {A}_{\infty }$
-algebra of degree d, making the map
$\mathrm {A}_{\infty }$
-algebra of degree d, making the map
![]() $A\to R$
a strict
$A\to R$
a strict
![]() $\mathrm {A}_{\infty }$
-algebra quasi-isomorphism.
$\mathrm {A}_{\infty }$
-algebra quasi-isomorphism.
We first need a lemma about projective resolutions.
Lemma 5.8. Let M be a finitely generated Q-module of projective dimension
![]() $d>0$
, with a projective resolution
$d>0$
, with a projective resolution
![]() $A\to M$
, and set
$A\to M$
, and set
![]() $V=A_{<d}/A_0$
. Then for any n, we have
$V=A_{<d}/A_0$
. Then for any n, we have
![]() $\mathrm {H}_i( V^{\otimes n+1})=0$
whenever
$\mathrm {H}_i( V^{\otimes n+1})=0$
whenever
![]() $i>n(d-1)+1$
and
$i>n(d-1)+1$
and
![]() $i\neq (n+1)(d-1)$
.
$i\neq (n+1)(d-1)$
.
Proof. We show this by inducing on n. Since A is a projective resolution of R, the homology of V is concentrated in degrees
![]() $1$
and
$1$
and
![]() $d-1$
, and there is an exact triangle
$d-1$
, and there is an exact triangle
of complexes of Q-modules, where
![]() $N=\ker (A_0\to M)$
and
$N=\ker (A_0\to M)$
and
![]() $A_d=Q^{\oplus s}$
. This justifies the case
$A_d=Q^{\oplus s}$
. This justifies the case
![]() $n=0$
, and for each
$n=0$
, and for each
![]() $n\geqslant 1$
yields another exact triangle
$n\geqslant 1$
yields another exact triangle
Clearly,
![]() $\mathrm {H}_i(\Sigma V^{\otimes n} \otimes N) = 0$
for
$\mathrm {H}_i(\Sigma V^{\otimes n} \otimes N) = 0$
for
![]() $i> n(d-1)+1$
, so by the long exact sequence in homology, the map
$i> n(d-1)+1$
, so by the long exact sequence in homology, the map
![]() $\mathrm {H}_{i}(\Sigma ^{d-1} V^{\otimes (n-1)})^{\oplus s} \to \mathrm {H}_{i}(V^{\otimes n})$
is surjective for
$\mathrm {H}_{i}(\Sigma ^{d-1} V^{\otimes (n-1)})^{\oplus s} \to \mathrm {H}_{i}(V^{\otimes n})$
is surjective for
![]() $i> n(d-1)+1$
. By the induction hypothesis,
$i> n(d-1)+1$
. By the induction hypothesis,
![]() $\mathrm {H}_i(\Sigma ^{d-1} V^{\otimes (n-1)})=0$
if
$\mathrm {H}_i(\Sigma ^{d-1} V^{\otimes (n-1)})=0$
if
![]() $ i\neq n(d-1)$
and
$ i\neq n(d-1)$
and
![]() $i>(n-1)(d-1)+1$
. From this, we conclude that the lemma holds for n.
$i>(n-1)(d-1)+1$
. From this, we conclude that the lemma holds for n.
Proof of Theorem 5.7.
Recall from (5.6.1) that the pairing on A was defined from a unital and graded-commutative product
![]() $\mu \colon A^{\otimes 2}\to A$
. This restricts to a perfect pairing on
$\mu \colon A^{\otimes 2}\to A$
. This restricts to a perfect pairing on
![]() $V=A_{<d}/A_0$
, and we start by constructing operations
$V=A_{<d}/A_0$
, and we start by constructing operations
![]() $m_n^V\colon V^{\otimes n}\to V$
.
$m_n^V\colon V^{\otimes n}\to V$
.
If
![]() $|a|+|b|=d+1$
, then
$|a|+|b|=d+1$
, then
![]() $\mu (a\otimes b)=0$
in A, so
$\mu (a\otimes b)=0$
in A, so
Using graded-commutativity of
![]() $\mu $
, this is equivalent to the cyclic identity
$\mu $
, this is equivalent to the cyclic identity
where ![]() .
.
Next, we truncate
![]() $\mu $
to obtain
$\mu $
to obtain
![]() $\mu ^V\colon V^{\otimes 2}\to V$
, and we define
$\mu ^V\colon V^{\otimes 2}\to V$
, and we define
![]() $m_2^V$
by symmetrizing
$m_2^V$
by symmetrizing
![]() $\mu ^V$
with respect to the
$\mu ^V$
with respect to the
![]() $C_3$
-action:
$C_3$
-action:
The obtained
![]() $m_2^V$
satisfies the required cyclic property by construction. However, the Stasheff identity (4.1.1) does not hold for
$m_2^V$
satisfies the required cyclic property by construction. However, the Stasheff identity (4.1.1) does not hold for
![]() $n=2$
, and instead,
$n=2$
, and instead,
where
![]() $\omega \in A_d$
is the generator with
$\omega \in A_d$
is the generator with
![]() $\langle \omega ,1\rangle =1$
. Nonetheless, since
$\langle \omega ,1\rangle =1$
. Nonetheless, since
![]() $\langle -,-\rangle $
is a chain map, the same computation as in (4.1.2) shows that the obstruction
$\langle -,-\rangle $
is a chain map, the same computation as in (4.1.2) shows that the obstruction
![]() $\operatorname {obs}_3^V$
is a chain map – that is, a cycle in
$\operatorname {obs}_3^V$
is a chain map – that is, a cycle in
![]() $\operatorname {Hom}{(V^{\otimes 3},V)}$
.
$\operatorname {Hom}{(V^{\otimes 3},V)}$
.
We proceed to construct
![]() $m_n^V$
for
$m_n^V$
for
![]() $n\geqslant 3$
by induction, satisfying the Stasheff identities (4.1.1) for
$n\geqslant 3$
by induction, satisfying the Stasheff identities (4.1.1) for
![]() $n\geqslant 3$
, and all satisfying
$n\geqslant 3$
, and all satisfying
![]() $\operatorname {cyc}(m_n^V)\cdot c=(-1)^n\operatorname {cyc}(m_n^V)$
. The argument is similar to the proof of Proposition 5.1. If
$\operatorname {cyc}(m_n^V)\cdot c=(-1)^n\operatorname {cyc}(m_n^V)$
. The argument is similar to the proof of Proposition 5.1. If
![]() $m_i^V$
have been constructed for
$m_i^V$
have been constructed for
![]() $i<n$
with required cyclic symmetry, a computation shows that the obstruction
$i<n$
with required cyclic symmetry, a computation shows that the obstruction
![]() $\operatorname {obs}_n^V$
from (4.1.2) is cyclic as well:
$\operatorname {obs}_n^V$
from (4.1.2) is cyclic as well:
Since
![]() $\operatorname {Hom}{(V^{\otimes n},V)} \cong \Sigma ^{-nd}V^{\otimes (n+1)}$
, we can use Lemma 5.8 with
$\operatorname {Hom}{(V^{\otimes n},V)} \cong \Sigma ^{-nd}V^{\otimes (n+1)}$
, we can use Lemma 5.8 with
![]() $M=R$
to conclude that
$M=R$
to conclude that
Since d is odd, it is impossible to have
![]() $|\operatorname {obs}_n^V|=n-3=d-n-1$
; hence, the complex
$|\operatorname {obs}_n^V|=n-3=d-n-1$
; hence, the complex
![]() $\operatorname {Hom}{(V^{\otimes n},V)}$
is acyclic in degree
$\operatorname {Hom}{(V^{\otimes n},V)}$
is acyclic in degree
![]() $n-3$
, and the class
$n-3$
, and the class
![]() $[\operatorname {obs}_n^V]$
vanishes. This shows that there is an operation
$[\operatorname {obs}_n^V]$
vanishes. This shows that there is an operation
![]() $\tilde {m}^V_n$
in
$\tilde {m}^V_n$
in
![]() $\operatorname {Hom}{(V^{\otimes n},V)}_{n-2}$
such that
$\operatorname {Hom}{(V^{\otimes n},V)}_{n-2}$
such that
![]() $\partial (\tilde {m}^V_n)=\operatorname {obs}_n^V$
, and we symmetrize this to define
$\partial (\tilde {m}^V_n)=\operatorname {obs}_n^V$
, and we symmetrize this to define
![]() $m_n$
:
$m_n$
:
By construction,
![]() $m_n^V$
has the required cyclic symmetry. We note that
$m_n^V$
has the required cyclic symmetry. We note that
Therefore,
![]() $\partial (m_n^V)=\operatorname {obs}_n^V$
, and the operations
$\partial (m_n^V)=\operatorname {obs}_n^V$
, and the operations
![]() $\{m_n^V\}$
satisfy the nth Stasheff identity. This concludes the induction.
$\{m_n^V\}$
satisfy the nth Stasheff identity. This concludes the induction.
To finish the proof, we define the following operations on A:

and for
![]() $n \geqslant 3$
,
$n \geqslant 3$
,

The
![]() $n=2$
Stasheff identity for A is equivalent to the identity (5.8.1) above.
$n=2$
Stasheff identity for A is equivalent to the identity (5.8.1) above.
To verify the nth Stasheff identity, with
![]() $n\geqslant 3$
, we need to divide into cases depending on the inputs: when any of the inputs have degree zero; when the output has degree less than d; and when the output has degree d. The first two of these cases follow easily from the Stasheff identities for
$n\geqslant 3$
, we need to divide into cases depending on the inputs: when any of the inputs have degree zero; when the output has degree less than d; and when the output has degree d. The first two of these cases follow easily from the Stasheff identities for
![]() $\{m_n^V\}$
. To check the third case, we suppose that
$\{m_n^V\}$
. To check the third case, we suppose that
![]() $|a_1|+\cdots +|a_n|+n-3=d$
, and we compute
$|a_1|+\cdots +|a_n|+n-3=d$
, and we compute
 $$ \begin{align*} &\sum_{r+s+t=n} (-1)^{r+st} m_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right)(a_1,\ldots,a_n)=\\ & (-1)^{|a_1|(n-1)+1}\langle a_1 ,m^V_{n-1}(a_2,\ldots ,a_n)\rangle + (-1)^{n-1}\langle m^V_{n-1}(a_1,\ldots ,a_{n-1}),a_n\rangle\,; \end{align*} $$
$$ \begin{align*} &\sum_{r+s+t=n} (-1)^{r+st} m_{r+1+t} \left(\operatorname{\mathrm{id}}^{\otimes r} \otimes m_s \otimes \operatorname{\mathrm{id}}^{\otimes t}\right)(a_1,\ldots,a_n)=\\ & (-1)^{|a_1|(n-1)+1}\langle a_1 ,m^V_{n-1}(a_2,\ldots ,a_n)\rangle + (-1)^{n-1}\langle m^V_{n-1}(a_1,\ldots ,a_{n-1}),a_n\rangle\,; \end{align*} $$
and this vanishes by the cyclic symmetry condition for
![]() $m_{n-1}^V$
.
$m_{n-1}^V$
.
It follows that A is an
![]() $\mathrm {A}_{\infty }$
-algebra with the operations
$\mathrm {A}_{\infty }$
-algebra with the operations
![]() $\{m_n\}$
. Finally, the cyclic symmetry condition on
$\{m_n\}$
. Finally, the cyclic symmetry condition on
![]() $\{m_n^V\}$
implies A is a cyclic
$\{m_n^V\}$
implies A is a cyclic
![]() $\mathrm {A}_{\infty }$
-algebra.
$\mathrm {A}_{\infty }$
-algebra.
Remark 5.9. The construction in the proof yields a bijection between unital cyclic
![]() $\mathrm {A}_{\infty }$
-algebra structures on A and nonunital cyclic
$\mathrm {A}_{\infty }$
-algebra structures on A and nonunital cyclic
![]() $\mathrm {A}_{\infty }$
-algebra structures on V, but with a modified version of the second Stasheff identity in the latter case. The cyclic condition is necessary to make this correspondence work.
$\mathrm {A}_{\infty }$
-algebra structures on V, but with a modified version of the second Stasheff identity in the latter case. The cyclic condition is necessary to make this correspondence work.
Remark 5.10. In work to appear, Alexander Berglund constructs cyclic
![]() $\mathrm {A}_{\infty }$
-algebra structures in significantly more generality than Theorem 5.7. In particular, his argument shows that the restriction to odd d is unnecessary. We note the case
$\mathrm {A}_{\infty }$
-algebra structures in significantly more generality than Theorem 5.7. In particular, his argument shows that the restriction to odd d is unnecessary. We note the case
![]() $d \equiv 2 \text { modulo } 4$
can obtained by a more careful analysis of the proof of Theorem 5.7, but the general case seems to require more machinery.
$d \equiv 2 \text { modulo } 4$
can obtained by a more careful analysis of the proof of Theorem 5.7, but the general case seems to require more machinery.
6 Twisted tensor products
Twisted tensor products are an important tool in homological algebra, especially in the construction of resolutions. In this section, we develop their theory over a commutative ring, producing universal resolutions via the resolution of the diagonal that will be applied to Koszul homomorphisms in later sections. However, our method of construction is new even when the base ring Q is a field. Similar results have been obtained using different methods in unpublished work of Burke [Reference BurkeBur]. We do not explicitly use the language of twisting cochains, but these objects are present implicitly; and the reader may consult [Reference Loday and ValletteLV12, Section 2.1] for more information on twisted tensor products and twisting cochains.
Let C be a connected curved differential graded (dg) coalgebra over Q that is free as a graded module. For a right dg module M and a left dg module N over
![]() ${\mathsf {\Omega }}{(C)}$
, we construct a complex
${\mathsf {\Omega }}{(C)}$
, we construct a complex
![]() $M \otimes ^{\tau } C \otimes ^{\tau } N$
, with a ‘twisted’ differential; we call this complex a twisted tensor product. First, we define a dg bimodule
$M \otimes ^{\tau } C \otimes ^{\tau } N$
, with a ‘twisted’ differential; we call this complex a twisted tensor product. First, we define a dg bimodule
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
over
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
over
![]() ${\mathsf {\Omega }}{(C)}$
.
${\mathsf {\Omega }}{(C)}$
.
Construction 6.1. Ignoring differentials for now, there is a well-known exact sequence of graded
![]() ${\mathsf {\Omega }}{(C)}$
-bimodules
${\mathsf {\Omega }}{(C)}$
-bimodules
where
![]() $\iota (x \otimes \langle c \rangle \otimes y)= \mu (x,\langle c \rangle ) \otimes 1 \otimes y - x \otimes 1 \otimes \mu (\langle c \rangle ,y)$
for
$\iota (x \otimes \langle c \rangle \otimes y)= \mu (x,\langle c \rangle ) \otimes 1 \otimes y - x \otimes 1 \otimes \mu (\langle c \rangle ,y)$
for
![]() $c \in \bar {C}$
and
$c \in \bar {C}$
and
![]() $x,y \in \mathsf {\Omega }{(C)}$
, and
$x,y \in \mathsf {\Omega }{(C)}$
, and
![]() $\mu $
the multiplication map.
$\mu $
the multiplication map.
We give
![]() ${\mathsf {\Omega }}{(C)} \otimes \Sigma ^{-1} \bar {C} \otimes \mathsf {\Omega }{(C)}$
the unique differential
${\mathsf {\Omega }}{(C)} \otimes \Sigma ^{-1} \bar {C} \otimes \mathsf {\Omega }{(C)}$
the unique differential
![]() $\partial ^\iota $
making
$\partial ^\iota $
making
![]() $\iota $
a chain map, and we set
$\iota $
a chain map, and we set
We write
![]() $\partial ^\tau $
for the differential on
$\partial ^\tau $
for the differential on
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
; this is a dg
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
; this is a dg
![]() ${\mathsf {\Omega }}{(C)}$
-bimodule whose underlying graded bimodule is
${\mathsf {\Omega }}{(C)}$
-bimodule whose underlying graded bimodule is
![]() ${\mathsf {\Omega }}{(C)} \otimes C \otimes \mathsf {\Omega }{(C)}$
, using the evident multiplication by
${\mathsf {\Omega }}{(C)} \otimes C \otimes \mathsf {\Omega }{(C)}$
, using the evident multiplication by
![]() ${\mathsf {\Omega }}{(C)}$
on either side.
${\mathsf {\Omega }}{(C)}$
on either side.
For a right dg
![]() ${\mathsf {\Omega }}{(C)}$
-module F and a left dg
${\mathsf {\Omega }}{(C)}$
-module F and a left dg
![]() ${\mathsf {\Omega }}{(C)}$
-module G, we define
${\mathsf {\Omega }}{(C)}$
-module G, we define
Explicitly, its underlying graded module is
![]() $F \otimes C \otimes G$
and the differential is
$F \otimes C \otimes G$
and the differential is
 $$ \begin{align*} \begin{aligned} \partial^\tau &= \partial^F \otimes \operatorname{\mathrm{id}}_C \otimes \operatorname{\mathrm{id}}_G + \operatorname{\mathrm{id}}_F \otimes \partial^C \otimes \operatorname{\mathrm{id}}_G + \operatorname{\mathrm{id}}_F \otimes \operatorname{\mathrm{id}}_C \otimes \partial^G \\ &\quad + \left(\mu (\operatorname{\mathrm{id}}_F \otimes {\scriptstyle\mathsf{\Sigma}}^{-1} p) \otimes \operatorname{\mathrm{id}}_C \otimes \operatorname{\mathrm{id}}_G - \operatorname{\mathrm{id}}_F \otimes \operatorname{\mathrm{id}}_C \otimes \mu({\scriptstyle\mathsf{\Sigma}}^{-1} p \otimes \operatorname{\mathrm{id}}_G)\right) (\operatorname{\mathrm{id}}_F \otimes \Delta \otimes \operatorname{\mathrm{id}}_G), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \partial^\tau &= \partial^F \otimes \operatorname{\mathrm{id}}_C \otimes \operatorname{\mathrm{id}}_G + \operatorname{\mathrm{id}}_F \otimes \partial^C \otimes \operatorname{\mathrm{id}}_G + \operatorname{\mathrm{id}}_F \otimes \operatorname{\mathrm{id}}_C \otimes \partial^G \\ &\quad + \left(\mu (\operatorname{\mathrm{id}}_F \otimes {\scriptstyle\mathsf{\Sigma}}^{-1} p) \otimes \operatorname{\mathrm{id}}_C \otimes \operatorname{\mathrm{id}}_G - \operatorname{\mathrm{id}}_F \otimes \operatorname{\mathrm{id}}_C \otimes \mu({\scriptstyle\mathsf{\Sigma}}^{-1} p \otimes \operatorname{\mathrm{id}}_G)\right) (\operatorname{\mathrm{id}}_F \otimes \Delta \otimes \operatorname{\mathrm{id}}_G), \end{aligned} \end{align*} $$
where
![]() $p \colon C \to \bar {C}$
is the natural projection and we use
$p \colon C \to \bar {C}$
is the natural projection and we use
![]() $\mu $
for the right action of
$\mu $
for the right action of
![]() ${\mathsf {\Omega }}{(C)}$
on F and the left action of
${\mathsf {\Omega }}{(C)}$
on F and the left action of
![]() ${\mathsf {\Omega }}{(C)}$
on G.
${\mathsf {\Omega }}{(C)}$
on G.
6.2. Given a dg algebra A, recall that a dg A-module F is semifree if it admits an exhaustive filtration
where each subquotient
![]() $F(i)/F(i-1)$
is a sum of shifts of A. As a matter of terminology, a semifree dg A-bimodule is a semifree dg module over
$F(i)/F(i-1)$
is a sum of shifts of A. As a matter of terminology, a semifree dg A-bimodule is a semifree dg module over
![]() $A \otimes A^{\mathrm {op}}$
.
$A \otimes A^{\mathrm {op}}$
.
Every dg A-module M admits a semifree resolution in the sense that there exists a surjective quasi-isomorphism
![]() $F\xrightarrow {\simeq } M$
, with F a semifree dg A-module. Such resolutions are unique up to homotopy; see [Reference Félix, Halperin and ThomasFHT01, Chapter 6] for this fact, as well as other details regarding semifree dg modules.
$F\xrightarrow {\simeq } M$
, with F a semifree dg A-module. Such resolutions are unique up to homotopy; see [Reference Félix, Halperin and ThomasFHT01, Chapter 6] for this fact, as well as other details regarding semifree dg modules.
Lemma 6.3. The map
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)} \longrightarrow \mathsf {\Omega }{(C)}$
induced from (6.1.1) is a semifree resolution of
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)} \longrightarrow \mathsf {\Omega }{(C)}$
induced from (6.1.1) is a semifree resolution of
![]() ${\mathsf {\Omega }}{(C)}$
as a dg
${\mathsf {\Omega }}{(C)}$
as a dg
![]() ${\mathsf {\Omega }}{(C)}$
-bimodule.
${\mathsf {\Omega }}{(C)}$
-bimodule.
Proof. By construction, (6.1.1) is a short exact sequence of dg
![]() ${\mathsf {\Omega }}{(C)}$
-bimodules, and so it induces an exact triangle in the derived category of dg
${\mathsf {\Omega }}{(C)}$
-bimodules, and so it induces an exact triangle in the derived category of dg
![]() ${\mathsf {\Omega }}{(C)}$
-bimodules. We obtain the quasi-isomorphism by comparing this triangle to the triangle associated to the cone construction for
${\mathsf {\Omega }}{(C)}$
-bimodules. We obtain the quasi-isomorphism by comparing this triangle to the triangle associated to the cone construction for
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
.
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
.
The dg module
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
is semifree as a dg
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } \mathsf {\Omega }{(C)}$
is semifree as a dg
![]() ${\mathsf {\Omega }}{(C)}$
-bimodule since C is free as a module over Q and non-negatively graded.
${\mathsf {\Omega }}{(C)}$
-bimodule since C is free as a module over Q and non-negatively graded.
6.4. Let
![]() $\varphi \colon Q \to R$
be a finite local homomorphism with
$\varphi \colon Q \to R$
be a finite local homomorphism with
![]() $A\to R$
a free resolution of R over Q. Fix an R-complex M and a semifree resolution
$A\to R$
a free resolution of R over Q. Fix an R-complex M and a semifree resolution
![]() $\gamma \colon G \to M$
over Q. By Proposition 5.1, there exists a split unital
$\gamma \colon G \to M$
over Q. By Proposition 5.1, there exists a split unital
![]() $\mathrm {A}_{\infty }$
-algebra structure
$\mathrm {A}_{\infty }$
-algebra structure
![]() $\{m_n\}$
on A and a strictly unital
$\{m_n\}$
on A and a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure
$\mathrm {A}_{\infty }$
-module structure
![]() $\{m_n^G\}$
over A on G. Then by 4.11, this induces a dg module structure over
$\{m_n^G\}$
over A on G. Then by 4.11, this induces a dg module structure over
![]() $\mathsf {\Omega }{(\mathsf {B}{(A)})}$
on G.
$\mathsf {\Omega }{(\mathsf {B}{(A)})}$
on G.
Suppose further that C is a connected curved dg coalgebra with counit
![]() $\varepsilon \colon C\to Q$
, equipped with a weak equivalence of connected curved dg coalgebras
$\varepsilon \colon C\to Q$
, equipped with a weak equivalence of connected curved dg coalgebras ![]() ; cf. 4.9. Then R and G each have an induced dg module structure over
; cf. 4.9. Then R and G each have an induced dg module structure over
![]() ${\mathsf {\Omega }}{(C)}$
.
${\mathsf {\Omega }}{(C)}$
.
Theorem 6.5. In the setting of 6.4, the map
is a semifree resolution of M over R.
Proof. The map
![]() $G \to M$
is a quasi-isomorphism of
$G \to M$
is a quasi-isomorphism of
![]() $\mathrm {A}_{\infty }$
-modules over A, and by 4.11, it is a quasi-isomorphism of dg modules over
$\mathrm {A}_{\infty }$
-modules over A, and by 4.11, it is a quasi-isomorphism of dg modules over
![]() $\mathsf {\Omega }{(\mathsf {B}{(A)})}$
, and thus over
$\mathsf {\Omega }{(\mathsf {B}{(A)})}$
, and thus over
![]() ${\mathsf {\Omega }}{(C)}$
. From Lemma 6.3, we obtain the quasi-isomorphism of (left) dg
${\mathsf {\Omega }}{(C)}$
. From Lemma 6.3, we obtain the quasi-isomorphism of (left) dg
![]() ${\mathsf {\Omega }}{(C)}$
-modules
${\mathsf {\Omega }}{(C)}$
-modules
Since G is semifree over Q, it follows that
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } G$
is semifree as a left dg module over
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } G$
is semifree as a left dg module over
![]() ${\mathsf {\Omega }}{(C)}$
.
${\mathsf {\Omega }}{(C)}$
.
The claimed quasi-isomorphism fits into the commutative diagram below

where
![]() $\alpha $
is the map induced by the quasi-isomorphism of dg algebras
$\alpha $
is the map induced by the quasi-isomorphism of dg algebras
where the fact that the second map is a quasi-isomorphism follows from the derived version of Nakayama’s lemma since, upon applying
![]() $-\otimes _Q k$
, the map becomes a quasi-isomorphism [Reference Lefèvre-HasegawaLH03, Section 2.2.1].
$-\otimes _Q k$
, the map becomes a quasi-isomorphism [Reference Lefèvre-HasegawaLH03, Section 2.2.1].
As the composition in (6.5.1) is a quasi-isomorphism and
![]() ${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } G $
is a semifree resolution of M over
${\mathsf {\Omega }}{(C)} \otimes ^{\tau } C \otimes ^{\tau } G $
is a semifree resolution of M over
![]() ${\mathsf {\Omega }}{(C)}$
, it follows that
${\mathsf {\Omega }}{(C)}$
, it follows that
![]() $\alpha $
is a quasi-isomorphism. We have already justified that
$\alpha $
is a quasi-isomorphism. We have already justified that
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are quasi-isomorphisms, accounting for the downward arrow on the right. As both legs of the triangle in the diagram above are quasi-isomorphisms, the horizontal map is a quasi-isomorphism, as claimed.
$\gamma $
are quasi-isomorphisms, accounting for the downward arrow on the right. As both legs of the triangle in the diagram above are quasi-isomorphisms, the horizontal map is a quasi-isomorphism, as claimed.
7
 $\mathrm {A}_{\infty }$
-algebra presentations for Koszul homomorphisms
$\mathrm {A}_{\infty }$
-algebra presentations for Koszul homomorphisms
We now have the machinery to show that Koszul homomorphisms admit presentations analogous to those of classical Koszul k-algebras. The next result lifts these classical quadratic presentations to local algebra and explains how one may think of Koszul homomorphisms as
![]() $\mathrm {A}_{\infty }$
-deformations of Koszul algebras over fields.
$\mathrm {A}_{\infty }$
-deformations of Koszul algebras over fields.
Theorem 7.1. A finite local homomorphism
![]() $\varphi \colon Q \to R$
is Koszul if and only if there is
$\varphi \colon Q \to R$
is Koszul if and only if there is
-
(1) a non-negatively graded, degreewise finite rank free Q-module V, and a direct summand
 $W\subseteq V \otimes V$
,
$W\subseteq V \otimes V$
, -
(2) an
 $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
 $\{m_n\}$
on the Q-module
$\{m_n\}$
on the Q-module  with grading induced from the grading of V, and
with grading induced from the grading of V, and -
(3) a Q-linear map
 $V_0 \to R$
,
$V_0 \to R$
,
such that
-
(i) the k-algebra
 is Koszul with respect to the tensor algebra weight grading,
is Koszul with respect to the tensor algebra weight grading, -
(ii)
 $\{m_n\}$
agrees with the algebra structure on
$\{m_n\}$
agrees with the algebra structure on  modulo
modulo
 $\mathfrak {m}_Q$
; that is, where
$\mathfrak {m}_Q$
; that is, where $$ \begin{align*} m_2 \otimes k=\mu \otimes k \quad\text{and}\quad m_n\otimes k = 0 \ \text{ for }\ n \neq 2, \end{align*} $$
$$ \begin{align*} m_2 \otimes k=\mu \otimes k \quad\text{and}\quad m_n\otimes k = 0 \ \text{ for }\ n \neq 2, \end{align*} $$
 $\mu $
is the usual product on the quotient of a tensor algebra, and
$\mu $
is the usual product on the quotient of a tensor algebra, and
-
(iii) with the structure
 $\{m_n\}$
, the induced map
$\{m_n\}$
, the induced map  is a strict
is a strict
 $\mathrm {A}_{\infty }$
-algebra quasi-isomorphism.
$\mathrm {A}_{\infty }$
-algebra quasi-isomorphism.
Moreover, V can be taken to be finite rank whenever R has finite projective dimension over Q.
Proof. If the stated conditions hold, then
![]() $R\otimes ^{\mathsf {L}}_Q k$
is formal by Proposition 5.4, and
$R\otimes ^{\mathsf {L}}_Q k$
is formal by Proposition 5.4, and ![]() is Koszul; therefore,
is Koszul; therefore,
![]() $\varphi $
is Koszul by definition.
$\varphi $
is Koszul by definition.
Assume, conversely, that
![]() $\varphi $
is Koszul. Since
$\varphi $
is Koszul. Since
![]() $\operatorname {Tor}^{Q}(R,k)$
is Koszul, it admits a compatible weight grading making it quadratic. That is, we have an isomorphism
$\operatorname {Tor}^{Q}(R,k)$
is Koszul, it admits a compatible weight grading making it quadratic. That is, we have an isomorphism
identifying the product on Tor with the product on the quotient of the tensor algebra, where
![]() $\bar {V} = \operatorname {Tor}^{Q}(R,k)_{(1)}$
and
$\bar {V} = \operatorname {Tor}^{Q}(R,k)_{(1)}$
and
![]() $\bar {W} \subseteq \bar {V} \otimes _k \bar {V}$
is a graded subspace.
$\bar {W} \subseteq \bar {V} \otimes _k \bar {V}$
is a graded subspace.
Let V be a free graded Q-module such that
![]() $V\otimes k =\bar {V}$
, and choose a direct summand
$V\otimes k =\bar {V}$
, and choose a direct summand
![]() $W \subseteq V \otimes V$
such that
$W \subseteq V \otimes V$
such that
![]() $W\otimes k =\bar {W}$
. If we define
$W\otimes k =\bar {W}$
. If we define ![]() , then A is a free, bigraded Q-module and
, then A is a free, bigraded Q-module and
Therefore, we may equip A with a differential making it the minimal Q-resolution of R. We have constructed (1) and (3) satisfying condition (i). Since
![]() $R\otimes ^{\mathsf {L}}_Qk$
is formal, by Proposition 5.4, there is an
$R\otimes ^{\mathsf {L}}_Qk$
is formal, by Proposition 5.4, there is an
![]() $\mathrm {A}_{\infty }$
-structure on A as required for (2), inducing the algebra structure on
$\mathrm {A}_{\infty }$
-structure on A as required for (2), inducing the algebra structure on
![]() $\operatorname {Tor}^{Q}(R,k)$
and satisfying the conditions (ii) and (iii).
$\operatorname {Tor}^{Q}(R,k)$
and satisfying the conditions (ii) and (iii).
In Section 8, we illustrate Theorem 7.1 in detail using the examples in Section 3.
7.2 Strictly Koszul presentations
For a local homomorphism
![]() $\varphi \colon Q \to R$
, Theorem 6.5 allowed us to obtain free resolutions over R starting from free resolutions over Q. The main input to this theorem was a curved dg coalgebra C over Q with quasi-isomorphism
$\varphi \colon Q \to R$
, Theorem 6.5 allowed us to obtain free resolutions over R starting from free resolutions over Q. The main input to this theorem was a curved dg coalgebra C over Q with quasi-isomorphism
![]() ${\mathsf {\Omega }}{(C)}\to R$
. Our philosophy is that when
${\mathsf {\Omega }}{(C)}\to R$
. Our philosophy is that when
![]() $\varphi $
is Koszul, C should have a simple description. In this section, we introduce additional technical assumptions that will allow us to explicitly construct C, mimicking a classical construction of Priddy.
$\varphi $
is Koszul, C should have a simple description. In this section, we introduce additional technical assumptions that will allow us to explicitly construct C, mimicking a classical construction of Priddy.
Definition 7.3. Let
![]() $\varphi \colon Q \to R$
be Koszul. Recall from Theorem 7.1 that R admits an
$\varphi \colon Q \to R$
be Koszul. Recall from Theorem 7.1 that R admits an
![]() $\mathrm {A}_{\infty }$
-algebra resolution A over Q with a quadratic presentation
$\mathrm {A}_{\infty }$
-algebra resolution A over Q with a quadratic presentation ![]() satisfying the conditions (i)–(iii). The data
satisfying the conditions (i)–(iii). The data
![]() $(A,V,W)$
is called a strictly Koszul presentation for
$(A,V,W)$
is called a strictly Koszul presentation for
![]() $\varphi $
if, in addition to these conditions,
$\varphi $
if, in addition to these conditions,
 $$ \begin{align} \bar{m}_1(V) \subseteq V \quad\text{and}\quad \bar{m}_n\big(\bigcap_{i+2+j=n} V^{\otimes i} \otimes W \otimes V^{\otimes j} \big) \subseteq V \quad \text{for } n \geqslant 2, \end{align} $$
$$ \begin{align} \bar{m}_1(V) \subseteq V \quad\text{and}\quad \bar{m}_n\big(\bigcap_{i+2+j=n} V^{\otimes i} \otimes W \otimes V^{\otimes j} \big) \subseteq V \quad \text{for } n \geqslant 2, \end{align} $$
where we have used the inclusion
![]() $\bigcap _{i+2+j=n} V^{\otimes i} \otimes W \otimes V^{\otimes j}\subseteq V^{\otimes n}\subseteq \bar {A}^{\otimes n}$
to apply the
$\bigcap _{i+2+j=n} V^{\otimes i} \otimes W \otimes V^{\otimes j}\subseteq V^{\otimes n}\subseteq \bar {A}^{\otimes n}$
to apply the
![]() $\mathrm {A}_{\infty }$
-operations
$\mathrm {A}_{\infty }$
-operations
![]() $\bar {m}_n$
of
$\bar {m}_n$
of
![]() $\bar {A}$
. If the homomorphism
$\bar {A}$
. If the homomorphism
![]() $\varphi $
admits a strictly Koszul presentation, then
$\varphi $
admits a strictly Koszul presentation, then
![]() $\varphi $
is called strictly Koszul.
$\varphi $
is called strictly Koszul.
In this setting, we define

By definition, the curvature term, the coderivation and the comultiplication on ![]() restrict to maps on
restrict to maps on
![]() $\mathsf {C}{(V,W)}$
, and hence,
$\mathsf {C}{(V,W)}$
, and hence,
![]() $\mathsf {C}{(V,W)}$
is a counital curved dg coalgebra. We call
$\mathsf {C}{(V,W)}$
is a counital curved dg coalgebra. We call
![]() $\mathsf {C}{(V,W)}$
the Priddy coalgebra associated to
$\mathsf {C}{(V,W)}$
the Priddy coalgebra associated to
![]() $(A,V,W)$
. If the presentation is clear from the context, we say it is the Priddy coalgebra of
$(A,V,W)$
. If the presentation is clear from the context, we say it is the Priddy coalgebra of
![]() $\varphi $
, and we write
$\varphi $
, and we write
7.4. Let
![]() $\varphi $
have a strictly Koszul presentation
$\varphi $
have a strictly Koszul presentation
![]() $(A,V,W)$
, and let
$(A,V,W)$
, and let
![]() $(-)^\vee $
denote graded Q-linear duality. In this setting, one can directly compute from the definition of the Priddy coalgebra of
$(-)^\vee $
denote graded Q-linear duality. In this setting, one can directly compute from the definition of the Priddy coalgebra of
![]() $\varphi $
that
$\varphi $
that
where
![]() $W^\perp = \left \{f \in (V \otimes V)^\vee \,\middle |\, f(W) = 0\right \}$
; this uses that V is free and
$W^\perp = \left \{f \in (V \otimes V)^\vee \,\middle |\, f(W) = 0\right \}$
; this uses that V is free and
![]() $W\subseteq V\otimes V$
is a summand.
$W\subseteq V\otimes V$
is a summand.
What we call the Priddy coalgebra first appeared, for algebras over a field, in the work of Priddy [Reference PriddyPri70, Section 3], where it is called the Koszul complex. See also [Reference Beilinson, Ginzburg and SoergelBGS96, Section 2.6] and [Reference Loday and ValletteLV12, Chapter 3] (where our notation is taken from).
In Section 8, we show that complete intersection and Golod homomorphisms are strictly Koszul, as well as Cohen presentations of almost Golod Gorenstein local rings. In fact, we are not able to construct surjective Koszul homomorphisms that are not strictly Koszul; therefore, we ask the following:
Question 7.5. For a surjective Koszul homomorphism
![]() $\varphi \colon Q \to R$
, is it always possible to construct a strictly Koszul presentation
$\varphi \colon Q \to R$
, is it always possible to construct a strictly Koszul presentation
![]() $(A,V,W)$
as in Definition 7.3?
$(A,V,W)$
as in Definition 7.3?
We think of R and
![]() $\mathsf {C}(\varphi )^\vee $
as being Koszul dual to each other relative to Q. The next result justifies this, and in particular, it says that this specializes, at the maximal ideal of Q, to classical Koszul duality over k.
$\mathsf {C}(\varphi )^\vee $
as being Koszul dual to each other relative to Q. The next result justifies this, and in particular, it says that this specializes, at the maximal ideal of Q, to classical Koszul duality over k.
Theorem 7.6. Let
![]() $\varphi \colon Q \to R$
be a strictly Koszul homomorphism. Then
$\varphi \colon Q \to R$
be a strictly Koszul homomorphism. Then
![]() $\mathsf {C}{(\varphi )}$
is minimal in the sense that
$\mathsf {C}{(\varphi )}$
is minimal in the sense that
![]() $\partial (\mathsf {C}{(\varphi )})\subseteq \mathfrak {m}_Q \mathsf {C}{(\varphi )}$
, and the inclusion
$\partial (\mathsf {C}{(\varphi )})\subseteq \mathfrak {m}_Q \mathsf {C}{(\varphi )}$
, and the inclusion ![]() is a weak equivalence of connected curved dg coalgebras. Moreover, both
is a weak equivalence of connected curved dg coalgebras. Moreover, both
![]() $T=\operatorname {Tor}^{Q}(R,k)$
and
$T=\operatorname {Tor}^{Q}(R,k)$
and
![]() $E = \operatorname {Hom}({\mathsf {C}(\varphi ),k})$
are Koszul k-algebras and there k-algebra isomorphisms
$E = \operatorname {Hom}({\mathsf {C}(\varphi ),k})$
are Koszul k-algebras and there k-algebra isomorphisms
Proof. We fix a strictly Koszul presentation, so that
![]() $\mathsf {C}{(\varphi )}=\mathsf {C}{(V,W)}$
.
$\mathsf {C}{(\varphi )}=\mathsf {C}{(V,W)}$
.
By Theorem 7.1, the
![]() $\mathrm {A}_{\infty }$
-structure on A satisfies
$\mathrm {A}_{\infty }$
-structure on A satisfies
![]() $m_n\otimes k=0$
for
$m_n\otimes k=0$
for
![]() $n\neq 2$
, and
$n\neq 2$
, and ![]() is a quadratic algebra. It then follows from [Reference Loday and ValletteLV12, Proposition 3.3.2] that the differential of
is a quadratic algebra. It then follows from [Reference Loday and ValletteLV12, Proposition 3.3.2] that the differential of ![]() is zero. Therefore,
is zero. Therefore,
![]() $\mathsf {C}{(V,W)}$
is minimal.
$\mathsf {C}{(V,W)}$
is minimal.
Since
![]() $T=A\otimes k$
is Koszul by assumption,
$T=A\otimes k$
is Koszul by assumption, ![]() is a weak equivalence by [Reference Loday and ValletteLV12, Theorem 3.4.6]. Since V is free and
is a weak equivalence by [Reference Loday and ValletteLV12, Theorem 3.4.6]. Since V is free and
![]() $W\subseteq V\otimes V$
is a summand,
$W\subseteq V\otimes V$
is a summand,
![]() $\mathsf {\Omega }{(\mathsf {C}{(V \otimes k,W \otimes k)})}= \mathsf {\Omega }{(\mathsf {C}{(V,W)})}\otimes k$
and
$\mathsf {\Omega }{(\mathsf {C}{(V \otimes k,W \otimes k)})}= \mathsf {\Omega }{(\mathsf {C}{(V,W)})}\otimes k$
and
![]() $\mathsf {\Omega }{(\mathsf {B}{(A \otimes k)})}=\mathsf {\Omega }{(\mathsf {B}{(A)})} \otimes k$
, so it follows from the the derived version of Nakayama’s lemma that
$\mathsf {\Omega }{(\mathsf {B}{(A \otimes k)})}=\mathsf {\Omega }{(\mathsf {B}{(A)})} \otimes k$
, so it follows from the the derived version of Nakayama’s lemma that ![]() is a weak equivalence as well.
is a weak equivalence as well.
Since
![]() $\mathsf {C}(\varphi )$
is minimal, the coproduct induces the structure of a graded k-algebra on
$\mathsf {C}(\varphi )$
is minimal, the coproduct induces the structure of a graded k-algebra on
![]() $\operatorname {Hom}({\mathsf {C}(\varphi )},k)$
, with zero differential. Using 7.4, it follows that
$\operatorname {Hom}({\mathsf {C}(\varphi )},k)$
, with zero differential. Using 7.4, it follows that
Therefore, E is the quadratic dual of ![]() , and the final statement follows from [Reference Beilinson, Ginzburg and SoergelBGS96, 2.10].
, and the final statement follows from [Reference Beilinson, Ginzburg and SoergelBGS96, 2.10].
7.7 The Priddy resolution
We have arrived at one of the main applications of our techniques. The next result provides explicit ‘universal resolutions’ for modules over the target of a strictly Koszul homomorphism. It recovers the Shamash resolution in the case of complete intersection homomorphisms, and the bar resolution of Iyengar and Burke in the case of Golod homomorphisms. We present these and other examples in the next section.
Theorem 7.8. Let
![]() $\varphi \colon Q \to R$
be a Koszul homomorphism with a strictly Koszul presentation
$\varphi \colon Q \to R$
be a Koszul homomorphism with a strictly Koszul presentation
![]() $(A,V,W)$
. Assume that M is an R-complex with a semifree resolution
$(A,V,W)$
. Assume that M is an R-complex with a semifree resolution
![]() $G \to M$
over Q and that G has a strictly unital
$G \to M$
over Q and that G has a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure over A. Then
$\mathrm {A}_{\infty }$
-module structure over A. Then
is a semifree resolution over R, with differential given by
 $$ \begin{align*} \partial^\tau &= \sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{\frac{s(s+1)}{2}} \operatorname{\mathrm{id}}_R \otimes (\operatorname{\mathrm{id}}^{\otimes r} \otimes {\scriptstyle\mathsf{\Sigma}} \bar{m}_s ({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes s} \otimes \operatorname{\mathrm{id}}^{\otimes t}) \otimes \operatorname{\mathrm{id}}_G \\ &\quad + \sum_{\substack{i+j=n+1\\i \geqslant 0, j \geqslant 1}} (-1)^{\frac{(j-1)(j-2)}{2}} \operatorname{\mathrm{id}}_R \otimes \operatorname{\mathrm{id}}^{\otimes i} \otimes \bar{m}^G_j (({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes (j-1)} \otimes \operatorname{\mathrm{id}}_G). \end{align*} $$
$$ \begin{align*} \partial^\tau &= \sum_{\substack{r+s+t=n\\r,t \geqslant 0, s \geqslant 1}} (-1)^{\frac{s(s+1)}{2}} \operatorname{\mathrm{id}}_R \otimes (\operatorname{\mathrm{id}}^{\otimes r} \otimes {\scriptstyle\mathsf{\Sigma}} \bar{m}_s ({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes s} \otimes \operatorname{\mathrm{id}}^{\otimes t}) \otimes \operatorname{\mathrm{id}}_G \\ &\quad + \sum_{\substack{i+j=n+1\\i \geqslant 0, j \geqslant 1}} (-1)^{\frac{(j-1)(j-2)}{2}} \operatorname{\mathrm{id}}_R \otimes \operatorname{\mathrm{id}}^{\otimes i} \otimes \bar{m}^G_j (({\scriptstyle\mathsf{\Sigma}}^{-1})^{\otimes (j-1)} \otimes \operatorname{\mathrm{id}}_G). \end{align*} $$
We call
![]() $R \otimes ^{\tau } \mathsf {C}{(V,W)}\otimes ^{\tau } G$
the Priddy resolution of M associated to the strictly Koszul presentation
$R \otimes ^{\tau } \mathsf {C}{(V,W)}\otimes ^{\tau } G$
the Priddy resolution of M associated to the strictly Koszul presentation
![]() $(A,V,W)$
. We emphasize that (as long as M and R have finite projective dimension over Q) there is only a finite amount of data needed to construct the Priddy resolution. Therefore, it would be especially interesting to give an effectively computable answer to Question 7.5.
$(A,V,W)$
. We emphasize that (as long as M and R have finite projective dimension over Q) there is only a finite amount of data needed to construct the Priddy resolution. Therefore, it would be especially interesting to give an effectively computable answer to Question 7.5.
7.9. For any surjective map
![]() $\varphi \colon Q \to R$
of local rings with common residue field k, and any finitely generated R-module M, Lescot [Reference LescotLes90] established the coefficientwise inequality
$\varphi \colon Q \to R$
of local rings with common residue field k, and any finitely generated R-module M, Lescot [Reference LescotLes90] established the coefficientwise inequality
If equality holds, M is said to be inert by
![]() $\varphi $
.
$\varphi $
.
7.10. A surjective map
![]() $\varphi \colon Q \to R$
of local rings with common residue field k is called small if the induced map
$\varphi \colon Q \to R$
of local rings with common residue field k is called small if the induced map
![]() $\operatorname {Tor}^{Q}(k,k)\to \operatorname {Tor}^{R}(k,k)$
is injective [Reference AvramovAvr78]. For example, any minimal Cohen presentation is small. When
$\operatorname {Tor}^{Q}(k,k)\to \operatorname {Tor}^{R}(k,k)$
is injective [Reference AvramovAvr78]. For example, any minimal Cohen presentation is small. When
![]() $\varphi $
is small, there is an equality
$\varphi $
is small, there is an equality
![]() $\operatorname {\mathrm {P}}^Q_k(t)\cdot \operatorname {\mathrm {P}}^{R\otimes ^{\mathsf {L}}_Q k}_k(t)=\operatorname {\mathrm {P}}^R_k(t)$
by [Reference AvramovAvr78, Corollary 5.3].
$\operatorname {\mathrm {P}}^Q_k(t)\cdot \operatorname {\mathrm {P}}^{R\otimes ^{\mathsf {L}}_Q k}_k(t)=\operatorname {\mathrm {P}}^R_k(t)$
by [Reference AvramovAvr78, Corollary 5.3].
The next result addresses the (non-)minimality of the Priddy resolution.
Theorem 7.11. Let
![]() $\varphi \colon Q\to R$
be a surjective map of local rings with common residue field k. If
$\varphi \colon Q\to R$
be a surjective map of local rings with common residue field k. If
![]() $\varphi $
is small and strictly Koszul with Priddy coalgebra
$\varphi $
is small and strictly Koszul with Priddy coalgebra
![]() $\mathsf {C}{(\varphi )}$
, then
$\mathsf {C}{(\varphi )}$
, then
 $$\begin{align*}\sum_i \operatorname{\mathrm{rank}}_Q(\mathsf{C}{(\varphi)}_i)t^i=\frac{ \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}. \end{align*}$$
$$\begin{align*}\sum_i \operatorname{\mathrm{rank}}_Q(\mathsf{C}{(\varphi)}_i)t^i=\frac{ \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}. \end{align*}$$
Moreover, for any finitely generated R-module M, there is a coefficientwise inequality
 $$\begin{align*}\operatorname{\mathrm{P}}^R_M(t)\preccurlyeq \frac{\operatorname{\mathrm{P}}^Q_M(t)\cdot \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{P}}^R_M(t)\preccurlyeq \frac{\operatorname{\mathrm{P}}^Q_M(t)\cdot \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}. \end{align*}$$
Equality holds if and only if M is inert by
![]() $\varphi $
, if and only if its Priddy resolution with respect to
$\varphi $
, if and only if its Priddy resolution with respect to
![]() $\varphi $
is a minimal resolution. In particular, the Priddy resolution of the residue field k is minimal.
$\varphi $
is a minimal resolution. In particular, the Priddy resolution of the residue field k is minimal.
Proof. We may compute ![]() as follows:
as follows:
 $$\begin{align*}\mathrm{H}_{\mathsf{C}}(t)=\sum_i \operatorname{\mathrm{rank}}_k(\operatorname{Hom}({\mathsf{C}{(\varphi)}_i},k)) t^i=\operatorname{\mathrm{P}}_k^{\operatorname{Tor}^{Q}(R,k)}(t)=\operatorname{\mathrm{P}}^{R\otimes^{\mathsf{L}}_Q k}_k(t)=\frac{ \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}\,; \end{align*}$$
$$\begin{align*}\mathrm{H}_{\mathsf{C}}(t)=\sum_i \operatorname{\mathrm{rank}}_k(\operatorname{Hom}({\mathsf{C}{(\varphi)}_i},k)) t^i=\operatorname{\mathrm{P}}_k^{\operatorname{Tor}^{Q}(R,k)}(t)=\operatorname{\mathrm{P}}^{R\otimes^{\mathsf{L}}_Q k}_k(t)=\frac{ \operatorname{\mathrm{P}}^R_k(t)}{P^Q_k(t)}\,; \end{align*}$$
the second equality follows from that last statement in Theorem 7.6; the third uses formality of
![]() $R\otimes ^{\mathsf {L}}_Q k$
; and the last uses the small hypothesis, explained in 7.10.
$R\otimes ^{\mathsf {L}}_Q k$
; and the last uses the small hypothesis, explained in 7.10.
Theorem 7.8 directly yields the inequality
with equality if and only if the Priddy resolution is minimal. At the same time, the computation of
![]() $\mathrm {H}_{\mathsf {C}}(t)$
above transforms (7.11.1) into the inequality stated in the theorem, and equality holds there by definition when M is inert; see 7.9.
$\mathrm {H}_{\mathsf {C}}(t)$
above transforms (7.11.1) into the inequality stated in the theorem, and equality holds there by definition when M is inert; see 7.9.
8 Examples of strictly Koszul presentations
In this final section, we will apply the theory developed above in a series of examples, obtaining explicit resolutions for modules over various classes of rings. We also survey how these constructions relate to known resolutions in the literature.
We fix a local ring Q with residue field k.
Example 8.1 (Flat Koszul homomorphisms).
We begin with a presentation for a commutative Koszul k-algebra:
where
![]() $f_1,\ldots ,f_m$
are quadratic polynomials. To deform this presentation, we consider the Q-algebra
$f_1,\ldots ,f_m$
are quadratic polynomials. To deform this presentation, we consider the Q-algebra
![]() $Q[x_1,\ldots ,x_n]$
, weight graded by polynomial degree. We choose elements
$Q[x_1,\ldots ,x_n]$
, weight graded by polynomial degree. We choose elements
![]() $F_1,\ldots ,F_m$
such that for each i,
$F_1,\ldots ,F_m$
such that for each i,
and such that modulo
![]() $\mathfrak {m}_Q$
, in
$\mathfrak {m}_Q$
, in
![]() $k[x_1,\ldots ,x_n]$
, we have
$k[x_1,\ldots ,x_n]$
, we have
By construction, the homomorphism
is flat, and its fiber
![]() $K=R\otimes _Qk$
is Koszul. Therefore,
$K=R\otimes _Qk$
is Koszul. Therefore,
![]() $\varphi $
is a Koszul homomorphism, as in Example 3.1.
$\varphi $
is a Koszul homomorphism, as in Example 3.1.
To show that
![]() $\varphi $
is strictly Koszul, we take
$\varphi $
is strictly Koszul, we take
![]() $V=Q[x_1,\ldots ,x_n]_{(1)}$
and
$V=Q[x_1,\ldots ,x_n]_{(1)}$
and
where
![]() $\widetilde {F}_{i,(2)}$
are preimages of
$\widetilde {F}_{i,(2)}$
are preimages of
![]() $F_{i,(2)}$
in
$F_{i,(2)}$
in
![]() $V\otimes V$
. Then
$V\otimes V$
. Then ![]() , so we may choose a compatible isomorphism of Q-modules
, so we may choose a compatible isomorphism of Q-modules
that restricts to the identity of V.
We obtain a presentation satisfying the conditions of Theorem 7.1, using
![]() $A=R$
with only
$A=R$
with only
![]() $m_2$
nonzero. To show that the presentation is strict, we note that since R is commutative
$m_2$
nonzero. To show that the presentation is strict, we note that since R is commutative
and we note that since
![]() $F_i=0$
in R,
$F_i=0$
in R,
This shows that
We can conclude that
![]() $(R,V,W)$
is a strictly Koszul presentation for
$(R,V,W)$
is a strictly Koszul presentation for
![]() $\varphi $
. In Figure 1a, we illustrate the grading of A.
$\varphi $
. In Figure 1a, we illustrate the grading of A.

Figure 1 Illustration of the weight and homological gradings of the
![]() $\mathrm {A}_{\infty }$
-resolution A for various examples.
$\mathrm {A}_{\infty }$
-resolution A for various examples.
Example 8.2 (Golod homomorphisms).
This is the primary example treated by Burke in [Reference BurkeBur15], at least when Q is regular. Continuing Example 3.5, let
![]() $\varphi \colon Q \to R$
be a surjective local Golod homomorphism, with a minimal resolution A of R over Q. By [Reference BurkeBur15, Theorem 6.13], for every
$\varphi \colon Q \to R$
be a surjective local Golod homomorphism, with a minimal resolution A of R over Q. By [Reference BurkeBur15, Theorem 6.13], for every
![]() $\mathrm {A}_{\infty }$
-algebra structure
$\mathrm {A}_{\infty }$
-algebra structure
![]() $\{m_n\}$
on A, one has
$\{m_n\}$
on A, one has
![]() $m_n \otimes _Q k = 0$
for
$m_n \otimes _Q k = 0$
for
![]() $n \neq 2$
. Then
$n \neq 2$
. Then
where U is the graded k-vector space
![]() $A_{\geqslant 1}\otimes k$
. In particular, lifting this isomorphism to Q, we obtain
$A_{\geqslant 1}\otimes k$
. In particular, lifting this isomorphism to Q, we obtain ![]() with
with
![]() $V = A_{\geqslant 1}$
and
$V = A_{\geqslant 1}$
and
![]() $W=V \otimes V$
. This presentation satisfies the conditions of Theorem 7.1. Further, the data
$W=V \otimes V$
. This presentation satisfies the conditions of Theorem 7.1. Further, the data
![]() $(A,V,W)$
is a strictly Koszul presentation, and the Priddy coalgebra of
$(A,V,W)$
is a strictly Koszul presentation, and the Priddy coalgebra of
![]() $\varphi $
is the bar construction
$\varphi $
is the bar construction ![]() . In this case, the Priddy resolution of a module M recovers the bar resolution
. In this case, the Priddy resolution of a module M recovers the bar resolution ![]() from [Reference BurkeBur15, Theorem 3.13]. Comparing 7.9 with (3.4.1), the resolution is minimal if and only if M is inert with respect to
from [Reference BurkeBur15, Theorem 3.13]. Comparing 7.9 with (3.4.1), the resolution is minimal if and only if M is inert with respect to
![]() $\varphi $
, if and only if M is a
$\varphi $
, if and only if M is a
![]() $\varphi $
-Golod module (i.e., the Serre bound (3.4.1) is an equality), by Theorem 7.11.
$\varphi $
-Golod module (i.e., the Serre bound (3.4.1) is an equality), by Theorem 7.11.
Remark 8.3. There are many examples of Golod (in particular, Koszul) homomorphisms
![]() $\varphi \colon Q\to R$
such that the minimal resolution A of R over Q does not admit a dg Q-algebra structure. In fact, this behavior seems to be typical. One way to construct them is as follows.
$\varphi \colon Q\to R$
such that the minimal resolution A of R over Q does not admit a dg Q-algebra structure. In fact, this behavior seems to be typical. One way to construct them is as follows.
Let I be an ideal in a local ring P, and consider the map
![]() $\varphi \colon Q\to R$
with
$\varphi \colon Q\to R$
with
By [Reference LevinLev76, Theorem 2.4], see also [Reference ShamashSha69],
![]() $\varphi $
is Golod. If B is the minimal resolution of
$\varphi $
is Golod. If B is the minimal resolution of
![]() $P/I$
over P, then the minimal resolution A of R over Q can be described as
$P/I$
over P, then the minimal resolution A of R over Q can be described as
If A were to admit a dg Q-algebra structure, then localizing would produce a dg
![]() $P(x)$
-algebra structure on
$P(x)$
-algebra structure on
and this is a minimal resolution of
![]() $P(x)/I(x)$
over
$P(x)/I(x)$
over
![]() $P(x)$
.
$P(x)$
.
However, we can start with examples of P and I such that this is impossible. To be concrete, Example 3.24 (replacing k with
![]() $k(x)$
) shows that there is no such dg algebra structure when
$k(x)$
) shows that there is no such dg algebra structure when ![]() and
and
![]() $I(x)=(a^2,ab,bc,cd,d^2)$
. It follows that the homomorphism
$I(x)=(a^2,ab,bc,cd,d^2)$
. It follows that the homomorphism

is Golod and there is no dg algebra structure on the minimal resolution of the target over the source.
Example 8.4 (Gorenstein homomorphisms of projective dimension
 $3$
).
$3$
).
Assume that
![]() $\varphi \colon Q \to R$
is a surjective local Gorenstein map of
$\varphi \colon Q \to R$
is a surjective local Gorenstein map of
![]() $\operatorname {\mbox {proj dim}}_Q(R) = 3$
. In Example 3.12, the dg algebra resolution A of R is described, with bases
$\operatorname {\mbox {proj dim}}_Q(R) = 3$
. In Example 3.12, the dg algebra resolution A of R is described, with bases
![]() $\{e_i\}$
,
$\{e_i\}$
,
![]() $\{f_i\}$
and
$\{f_i\}$
and
![]() $\{g\}$
for
$\{g\}$
for
![]() $A_1$
,
$A_1$
,
![]() $A_2$
and
$A_2$
and
![]() $A_3$
, respectively. The multiplication induces a perfect pairing
$A_3$
, respectively. The multiplication induces a perfect pairing
that makes A a cyclic
![]() $\mathrm {A}_{\infty }$
-algebra. We take
$\mathrm {A}_{\infty }$
-algebra. We take
![]() $V=A_1 \oplus A_2 $
and
$V=A_1 \oplus A_2 $
and
![]() $W = \ker (\langle -,- \rangle |_{V\otimes V})$
; alternatively, W is freely spanned as a graded Q-module by
$W = \ker (\langle -,- \rangle |_{V\otimes V})$
; alternatively, W is freely spanned as a graded Q-module by
The short Gorenstein description of
![]() $A \otimes _Q k$
lifts to an isomorphism of graded Q-modules
$A \otimes _Q k$
lifts to an isomorphism of graded Q-modules ![]() satisfying the conditions of Theorem 7.1.
satisfying the conditions of Theorem 7.1.
Using the explicit description in Example 3.12,
Therefore, the homomorphism
![]() $\varphi $
is strictly Koszul, using the presentation
$\varphi $
is strictly Koszul, using the presentation
![]() $(A,V,W)$
. The corresponding Priddy coalgebra is given by
$(A,V,W)$
. The corresponding Priddy coalgebra is given by
Alternatively,
![]() $\mathsf {C}{(V,W)}$
can be described explicitly using the basis of W above. We also note that the Priddy coalgebra is dual to the non-commutative hypersurface
$\mathsf {C}{(V,W)}$
can be described explicitly using the basis of W above. We also note that the Priddy coalgebra is dual to the non-commutative hypersurface
where
![]() $\rho = e_1^\vee \otimes f_1^\vee + f_1^\vee \otimes e_1^\vee + \cdots + e_r^\vee \otimes f_r^\vee + f_r^\vee \otimes e_r^\vee $
.
$\rho = e_1^\vee \otimes f_1^\vee + f_1^\vee \otimes e_1^\vee + \cdots + e_r^\vee \otimes f_r^\vee + f_r^\vee \otimes e_r^\vee $
.
Remark 8.5. In [Reference BurkeBur15, Example 3.10], Burke examines the specific Gorenstein ring
![]() $R=Q/I$
, of codimension three, where
$R=Q/I$
, of codimension three, where
In particular, Burke explicitly computes the
![]() $\mathrm {A}_{\infty }$
-module A-structure on
$\mathrm {A}_{\infty }$
-module A-structure on
![]() $K^Q$
and uses this to obtain the (non-minimal) bar resolution
$K^Q$
and uses this to obtain the (non-minimal) bar resolution ![]() of k. In comparison, by Theorem 7.8, the Priddy resolution
of k. In comparison, by Theorem 7.8, the Priddy resolution
![]() $R \otimes ^{\tau } \mathsf {C}{(V,W)}\otimes ^{\tau } K^Q$
of k, with respect to
$R \otimes ^{\tau } \mathsf {C}{(V,W)}\otimes ^{\tau } K^Q$
of k, with respect to
![]() $(A,V,W)$
in Example 8.4, is minimal by Theorem 7.11.
$(A,V,W)$
in Example 8.4, is minimal by Theorem 7.11.
Remark 8.6. A similar argument to Example 8.4 shows that if
![]() $\varphi \colon Q\to R$
is a minimal Cohen presentation for an almost Golod Gorenstein ring, and if the minimal Q-free resolution of R admits a dg algebra structure, then
$\varphi \colon Q\to R$
is a minimal Cohen presentation for an almost Golod Gorenstein ring, and if the minimal Q-free resolution of R admits a dg algebra structure, then
![]() $\varphi $
is strictly Koszul. The minimal resolution is known in the case of a compressed artinian Gorenstein ring [Reference Miller and RahmatiMR18], and it is suspected to carry a dg algebra structure.
$\varphi $
is strictly Koszul. The minimal resolution is known in the case of a compressed artinian Gorenstein ring [Reference Miller and RahmatiMR18], and it is suspected to carry a dg algebra structure.
In Theorem 8.18, we will generalize this substantially, showing that it is only necessary for the minimal resolution to admit a cyclic
![]() $\mathrm {A}_{\infty }$
-algebra resolution.
$\mathrm {A}_{\infty }$
-algebra resolution.
8.7 Complete intersection homomorphisms
Next, we show that surjective complete intersection homomorphisms are strictly Koszul, and that the resulting Priddy resolution recovers a well-known construction of Eisenbud [Reference EisenbudEis80] and Shamash [Reference ShamashSha69]. The latter uses systems of higher homotopies to obtain free resolutions over the target of a surjective complete intersection homomorphism, starting from data over the source. We first recall this story, which provides context for some of the results in this subsection. We then proceed to verify that such maps are strictly Koszul and conclude by laying out the connection between
![]() $\mathrm {A}_{\infty }$
-structures and systems of higher homotopies.
$\mathrm {A}_{\infty }$
-structures and systems of higher homotopies.
In what follows, we return to the setting of Example 3.2. Namely,
![]() $\varphi \colon Q\to R$
is a surjective, local homomorphism where
$\varphi \colon Q\to R$
is a surjective, local homomorphism where
![]() $\ker \varphi $
is generated by a Q-regular sequence
$\ker \varphi $
is generated by a Q-regular sequence ![]() , and
, and ![]() .
.
8.8. Let M be an R-module and
![]() $ G \to M$
a free resolution over Q. A system of higher homotopies, corresponding to
$ G \to M$
a free resolution over Q. A system of higher homotopies, corresponding to ![]() , on G is a collection of maps
, on G is a collection of maps ![]() , one for each
, one for each ![]() , of degree
, of degree ![]() such that
such that
-
1.
 $\sigma ^{(\mathbf {{0}})} = \partial ^G$
, where
$\sigma ^{(\mathbf {{0}})} = \partial ^G$
, where
 $\mathbf {{0} }= (0, \ldots , 0)$
;
$\mathbf {{0} }= (0, \ldots , 0)$
; -
2.
 $\sigma ^{(\mathbf {{0}})} \sigma ^{(\mathbf {{e}}_i)} + \sigma ^{(\mathbf {{e}}_i)} \sigma ^{(\mathbf {{0}})} = f_i \operatorname {\mathrm {id}}_G$
, where
$\sigma ^{(\mathbf {{0}})} \sigma ^{(\mathbf {{e}}_i)} + \sigma ^{(\mathbf {{e}}_i)} \sigma ^{(\mathbf {{0}})} = f_i \operatorname {\mathrm {id}}_G$
, where
 $\mathbf {{e}}_i = (0, \ldots , 0,1,0, \ldots 0)$
;
$\mathbf {{e}}_i = (0, \ldots , 0,1,0, \ldots 0)$
; -
3. for any
 with
with  , one has
, one has  .
.
Such a system of maps always exists by [Reference EisenbudEis80, Section 7]. The utility of this data is summarized in the following construction: if D denotes the graded Q-linear dual of
![]() $Q[\chi _1,\ldots ,\chi _c]$
, where each
$Q[\chi _1,\ldots ,\chi _c]$
, where each
![]() $\chi _i$
has homological degree
$\chi _i$
has homological degree
![]() $-2$
, then the R-complex
$-2$
, then the R-complex
![]() $R\otimes D \otimes G$
with differential
$R\otimes D \otimes G$
with differential ![]() is a free resolution of M over R; see [Reference EisenbudEis80, Section 7] for more details.
is a free resolution of M over R; see [Reference EisenbudEis80, Section 7] for more details.
When M is an R-complex, one can take
![]() $\varepsilon \colon G\to M$
to be a semifree resolution over Q and impose also the following condition to obtain analogous results:
$\varepsilon \colon G\to M$
to be a semifree resolution over Q and impose also the following condition to obtain analogous results:
-
4.
 for
for  .
.
Such a system of maps exists and can be used to transfer semifree resolutions over Q to ones over R, by an argument similar to the classical one in [Reference EisenbudEis80]; this will be contained in future joint work of Grifo with the first and fourth author.
Remark 8.9. Let M be an R-module and
![]() $ G \to M$
a free resolution over Q. In [Reference BurkeBur15], Burke notes that when
$ G \to M$
a free resolution over Q. In [Reference BurkeBur15], Burke notes that when
![]() $c=1$
, an
$c=1$
, an
![]() $\mathrm {A}_{\infty }$
-module structure on G over A is equivalent to a system of higher homotopies on G. Furthermore, the bar resolution of M in Burke’s paper agrees with the Priddy resolution of M, introduced above. Such maps are also Golod, and so we are also in the setting of Example 8.2.
$\mathrm {A}_{\infty }$
-module structure on G over A is equivalent to a system of higher homotopies on G. Furthermore, the bar resolution of M in Burke’s paper agrees with the Priddy resolution of M, introduced above. Such maps are also Golod, and so we are also in the setting of Example 8.2.
For arbitrary codimension c, the bar resolution is not minimal. However, in unpublished work, Burke constructs an acyclic twisting cochain
![]() $D\to A$
and uses this to transfer a semifree resolution of an R-complex M over Q to one over R that agrees with the construction of Eisenbud and Shamash; cf. 8.8 (see also [Reference Avramov and BuchweitzAB00, Reference MartinMar21]). The connection between higher homotopies and
$D\to A$
and uses this to transfer a semifree resolution of an R-complex M over Q to one over R that agrees with the construction of Eisenbud and Shamash; cf. 8.8 (see also [Reference Avramov and BuchweitzAB00, Reference MartinMar21]). The connection between higher homotopies and
![]() $\mathrm {A}_{\infty }$
-structures is also implicit in Burke’s work. We will give an explicit description of how these structures relate in Theorem 8.12.
$\mathrm {A}_{\infty }$
-structures is also implicit in Burke’s work. We will give an explicit description of how these structures relate in Theorem 8.12.
8.10. The narrative above is subsumed by the one in this article. Specifically, the dg algebra resolution ![]() of R over Q has a quadratic presentation
of R over Q has a quadratic presentation ![]() , with
, with
The graded module V is concentrated in degree
![]() $1$
, and the weight and homological gradings agree. It is straightforward to check that this presentation satisfies the conditions of Theorem 7.1. By construction,
$1$
, and the weight and homological gradings agree. It is straightforward to check that this presentation satisfies the conditions of Theorem 7.1. By construction,
Hence,
![]() $\varphi $
is strictly Koszul.
$\varphi $
is strictly Koszul.
To conclude that the constructions in 8.8 and Remark 8.9 are recovered by Theorem 7.8, we end this subsection with the following analysis.
8.11. Let
![]() $\mathrm {S}_{n}$
be the symmetric group. For
$\mathrm {S}_{n}$
be the symmetric group. For ![]() with
with ![]() , we let
, we let
denote the subgroup of ![]() -shuffles [Reference BourbakiBou81, Chapter IV, §5.3].
-shuffles [Reference BourbakiBou81, Chapter IV, §5.3].
The symmetric group
![]() $\mathrm {S}_{n}$
acts on
$\mathrm {S}_{n}$
acts on
![]() $(\Sigma V)^{\otimes n}$
by permuting simple tensors; there are no signs appearing since
$(\Sigma V)^{\otimes n}$
by permuting simple tensors; there are no signs appearing since
![]() $\Sigma V$
is in degree
$\Sigma V$
is in degree
![]() $2$
. The module of symmetric tensors on
$2$
. The module of symmetric tensors on
![]() $\Sigma V$
is the graded module
$\Sigma V$
is the graded module ![]() , with
, with
The coalgebra structure on ![]() restricts to a coalgebra structure on
restricts to a coalgebra structure on ![]() . We call this the coalgebra of symmetric tensors on
. We call this the coalgebra of symmetric tensors on
![]() $\Sigma V$
and denote it by
$\Sigma V$
and denote it by
![]() $\mathrm { \Gamma }^{c}{(\Sigma V)}$
.
$\mathrm { \Gamma }^{c}{(\Sigma V)}$
.
We denote the basis of
![]() $\Sigma V = \Sigma ^2 Q^c$
corresponding to
$\Sigma V = \Sigma ^2 Q^c$
corresponding to
![]() $f_1, \ldots , f_c$
by
$f_1, \ldots , f_c$
by
![]() $y_1, \ldots , y_c$
. A basis of
$y_1, \ldots , y_c$
. A basis of ![]() is given by
is given by
Theorem 8.12. Let
![]() $\varphi \colon Q \to R$
be a surjective complete intersection homomorphism with kernel generated by a Q-regular sequence
$\varphi \colon Q \to R$
be a surjective complete intersection homomorphism with kernel generated by a Q-regular sequence ![]() , and let M denote an R-complex.
, and let M denote an R-complex.
-
1.
 $\varphi $
is strictly Koszul, and its Priddy coalgebra is the curved coalgebra of symmetric tensors
$\varphi $
is strictly Koszul, and its Priddy coalgebra is the curved coalgebra of symmetric tensors  , with curvature term
, with curvature term
 $(f_1, \ldots , f_c) \colon \Sigma ^2 Q^c \to Q$
.
$(f_1, \ldots , f_c) \colon \Sigma ^2 Q^c \to Q$
. -
2. Given a semifree resolution
 $G\to M$
over Q, there exists a strictly unital
$G\to M$
over Q, there exists a strictly unital
 $\mathrm {A}_{\infty }$
-module structure
$\mathrm {A}_{\infty }$
-module structure
 $\{m_n^G\}$
over
$\{m_n^G\}$
over  making
making
 $G\to M$
a strict morphism of
$G\to M$
a strict morphism of
 $\mathrm {A}_{\infty }$
-modules over A, where A acts on M via restricting scalars along the dg algebra map
$\mathrm {A}_{\infty }$
-modules over A, where A acts on M via restricting scalars along the dg algebra map
 $A\to R$
. Then setting for
$A\to R$
. Then setting for
 and
and
 $y_1,\ldots ,y_c$
the standard basis for
$y_1,\ldots ,y_c$
the standard basis for
 $\Sigma ^2Q^c$
defines a system of higher homotopies on G corresponding to
$\Sigma ^2Q^c$
defines a system of higher homotopies on G corresponding to  .
.
-
3. Moreover, the Priddy resolution from Theorem 7.8 recovers the Eisenbud–Shamash resolution described in 8.8.
Proof. We saw in 8.10 that
![]() $\varphi $
is strictly Koszul. Using the same notation, we first show that
$\varphi $
is strictly Koszul. Using the same notation, we first show that ![]() . Indeed, for the nontrivial element
. Indeed, for the nontrivial element
![]() $\tau \in \mathrm {S}_{2}$
, one has
$\tau \in \mathrm {S}_{2}$
, one has
and so using the transposition
![]() $\tau _{i} = (i \ \ i+1) \in \mathrm {S}_{n}$
, we obtain
$\tau _{i} = (i \ \ i+1) \in \mathrm {S}_{n}$
, we obtain
 $$ \begin{align*} (\Sigma V)^{\otimes i-1} \otimes \Sigma^2 W \otimes (\Sigma V)^{\otimes n-i-1} = \ker\left((\Sigma V)^{\otimes n} \xrightarrow{\tau_{i} - \operatorname{\mathrm{id}}} (\Sigma V)^{\otimes n}\right). \end{align*} $$
$$ \begin{align*} (\Sigma V)^{\otimes i-1} \otimes \Sigma^2 W \otimes (\Sigma V)^{\otimes n-i-1} = \ker\left((\Sigma V)^{\otimes n} \xrightarrow{\tau_{i} - \operatorname{\mathrm{id}}} (\Sigma V)^{\otimes n}\right). \end{align*} $$
Since
![]() $\mathrm {S}_{n}$
is generated by the transpositions
$\mathrm {S}_{n}$
is generated by the transpositions
![]() $\tau _i$
, it follows that
$\tau _i$
, it follows that ![]() .
.
The coalgebra structure on
![]() $\mathsf {C}{(V,W)}$
is inherited from
$\mathsf {C}{(V,W)}$
is inherited from ![]() , and this coincides with the coalgebra structure on
, and this coincides with the coalgebra structure on ![]() because of the compatible inclusions
because of the compatible inclusions
The differential on
![]() $\mathsf {C}{(V,W)}$
is zero by (8.10.1). It is straightforward to see that the curvature term on
$\mathsf {C}{(V,W)}$
is zero by (8.10.1). It is straightforward to see that the curvature term on
![]() $\mathsf {C}{(V,W)}$
is (up to a shift) the first differential of A. This completes the proof of (1).
$\mathsf {C}{(V,W)}$
is (up to a shift) the first differential of A. This completes the proof of (1).
For (2), such an
![]() $\mathrm {A}_{\infty }$
-module structure making
$\mathrm {A}_{\infty }$
-module structure making
![]() $G \to M$
a strict morphism exists by 5.2. Then, by definition 8.8(1) holds. The fact that 8.8(2) holds follows from using the second Stasheff identity from 4.10. Another computation using the Stasheff identities, the unital structure on G, and the fact that A is graded-commutative show that 8.8(3) holds. The verification of 8.8(3) for
$G \to M$
a strict morphism exists by 5.2. Then, by definition 8.8(1) holds. The fact that 8.8(2) holds follows from using the second Stasheff identity from 4.10. Another computation using the Stasheff identities, the unital structure on G, and the fact that A is graded-commutative show that 8.8(3) holds. The verification of 8.8(3) for ![]() is illustrative of the proof for the general case, and so we sketch this case below.
is illustrative of the proof for the general case, and so we sketch this case below.
Fix basis elements
![]() $e_i\in A_1$
with
$e_i\in A_1$
with
![]() $\partial ^A(e_i)=f_i,$
and note that
$\partial ^A(e_i)=f_i,$
and note that
Observe that for
![]() $\{i,j\}=\{1,2\}$
, one has
$\{i,j\}=\{1,2\}$
, one has
 $$ \begin{align*} m_2^G&(e_i\otimes m^G_2(e_j\otimes\operatorname{\mathrm{id}})-(e_i\cdot e_j)\otimes\operatorname{\mathrm{id}})\\ &=\partial^G m_3^G(e_i\otimes e_j\otimes \operatorname{\mathrm{id}}) +m_3^G(f_i \otimes e_j\otimes \operatorname{\mathrm{id}}-e_j\otimes f_i \otimes\operatorname{\mathrm{id}}+ e_i \otimes e_j \otimes\partial^G )\\ &=\partial^G m_3^G(e_i\otimes e_j\otimes \operatorname{\mathrm{id}}) +m_3^G(e_i \otimes e_j \otimes\operatorname{\mathrm{id}} )\partial^G, \end{align*} $$
$$ \begin{align*} m_2^G&(e_i\otimes m^G_2(e_j\otimes\operatorname{\mathrm{id}})-(e_i\cdot e_j)\otimes\operatorname{\mathrm{id}})\\ &=\partial^G m_3^G(e_i\otimes e_j\otimes \operatorname{\mathrm{id}}) +m_3^G(f_i \otimes e_j\otimes \operatorname{\mathrm{id}}-e_j\otimes f_i \otimes\operatorname{\mathrm{id}}+ e_i \otimes e_j \otimes\partial^G )\\ &=\partial^G m_3^G(e_i\otimes e_j\otimes \operatorname{\mathrm{id}}) +m_3^G(e_i \otimes e_j \otimes\operatorname{\mathrm{id}} )\partial^G, \end{align*} $$
where the first precomposes the third Stasheff identity from 4.10 with
![]() $e_i\otimes e_j\otimes \operatorname {\mathrm {id}}$
, while the third equality uses that
$e_i\otimes e_j\otimes \operatorname {\mathrm {id}}$
, while the third equality uses that
![]() $\{m_n^G\}$
is a strictly unital
$\{m_n^G\}$
is a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure. It follows that
$\mathrm {A}_{\infty }$
-module structure. It follows that
and so adding these expressions for
![]() $(i,j)=(1,2)$
and
$(i,j)=(1,2)$
and
![]() $(i,j)=(2,1)$
, and recalling (8.12.1), we obtain
$(i,j)=(2,1)$
, and recalling (8.12.1), we obtain
It now remains to observe that since A is graded-commutative,
Thus, 8.8(3) holds for ![]() .
.
The condition 8.8(4) holds since
![]() $\varepsilon $
is a strict morphism, and since M is a dg A-module where the
$\varepsilon $
is a strict morphism, and since M is a dg A-module where the
![]() $e_i$
’s act trivially. This completes the proof of (2).
$e_i$
’s act trivially. This completes the proof of (2).
It remains to show (3). By [Reference BourbakiBou81, IV.§.5.11], we have a natural isomorphism of algebras
determined by
![]() $\chi _i\mapsto y_i^\vee ;$
this correspondence can also be seen via (7.4.1):
$\chi _i\mapsto y_i^\vee ;$
this correspondence can also be seen via (7.4.1):
where
![]() $W^\perp = \left\{f \otimes g - g \otimes f \,\middle|\, f,g \in \Sigma^{-1} (Q^c)^\vee\right\}$
, identifying
$W^\perp = \left\{f \otimes g - g \otimes f \,\middle|\, f,g \in \Sigma^{-1} (Q^c)^\vee\right\}$
, identifying ![]() with
with ![]() for each
for each ![]() . As a consequence, dualizing the correspondence above yields an isomorphism of graded Q-modules
. As a consequence, dualizing the correspondence above yields an isomorphism of graded Q-modules
![]() $D\cong \mathsf {C}{(V,W)}$
inducing an isomorphism of graded R-modules
$D\cong \mathsf {C}{(V,W)}$
inducing an isomorphism of graded R-modules
It remains to observe that

Therefore,
![]() $\psi $
is compatible with the differentials of its target and source, and so it is an isomorphism of R-complexes; cf. Theorem 7.8 and 8.8.
$\psi $
is compatible with the differentials of its target and source, and so it is an isomorphism of R-complexes; cf. Theorem 7.8 and 8.8.
Remark 8.13. The higher homotopies ![]() with
with ![]() induce a
induce a ![]() -comodule structure on
-comodule structure on ![]() ; in fact, conditions 8.8(1–4) are equivalent to this. However, an
; in fact, conditions 8.8(1–4) are equivalent to this. However, an
![]() $\mathrm {A}_{\infty }$
-module structure on G is equivalent to a
$\mathrm {A}_{\infty }$
-module structure on G is equivalent to a ![]() -comodule structure on
-comodule structure on ![]() . Hence, a system of higher homotopies on G captures the ‘symmetric’ part of an
. Hence, a system of higher homotopies on G captures the ‘symmetric’ part of an
![]() $\mathrm {A}_{\infty }$
-module structure on G over A.
$\mathrm {A}_{\infty }$
-module structure on G over A.
Remark 8.14. Moving beyond finite projective dimension, complete intersection homomorphisms fit into the well-studied class of quasi-complete intersection homomorphisms; cf. [Reference Avramov, Dos Anjos Henriques and ŞegaAHŞ13, Reference Avramov and IyengarAI03]. In residual characteristic zero and two, it is straightforward to check that such maps are strictly Koszul; this provides more examples of strictly Koszul homomorphisms of infinite projective dimension. In odd characteristic, the presence of divided powers prevents
![]() $\operatorname {Tor}^{Q}(R,k)$
from admitting a quadratic presentation.
$\operatorname {Tor}^{Q}(R,k)$
from admitting a quadratic presentation.
8.15 Almost Golod Gorenstein rings
To end the paper, we return to the class of almost Golod Gorenstein rings that we studied in Section 3.13. We show that these rings are strictly Cohen Koszul (i.e. every Cohen presentation is a strictly Koszul map), and we thereby obtain concrete free resolutions for all modules over such rings, using the machinery developed in Section 7.2.
The next lemma is a general construction in the homological algebra of Gorenstein rings, building on work of Avramov and Levin [Reference Levin and AvramovLA78].
Lemma 8.16. Let R be a zero dimensional Gorenstein ring of codimension d, with a minimal Cohen presentation
![]() $Q\to R$
, and let
$Q\to R$
, and let
![]() $A\xrightarrow {\simeq }R$
be the minimal Q-free resolution of R. The inclusion of the socle lifts to a chain map
$A\xrightarrow {\simeq }R$
be the minimal Q-free resolution of R. The inclusion of the socle lifts to a chain map

where
![]() $K^Q$
is the Koszul complex of Q. The subcomplex
$K^Q$
is the Koszul complex of Q. The subcomplex
is then a minimal Q-free resolution of
![]() $R/\operatorname {\mathrm {soc}}(R)$
.
$R/\operatorname {\mathrm {soc}}(R)$
.
Proof. By the exact sequence of homology groups,
![]() $\mathrm {H}_*(\operatorname {\mathrm {cone}}(K^Q \to A))$
is isomorphic to
$\mathrm {H}_*(\operatorname {\mathrm {cone}}(K^Q \to A))$
is isomorphic to
![]() $R/\operatorname {\mathrm {soc}}(R)$
, concentrated in degree zero. The proof of [Reference Levin and AvramovLA78, Theorem 1] shows that the map
$R/\operatorname {\mathrm {soc}}(R)$
, concentrated in degree zero. The proof of [Reference Levin and AvramovLA78, Theorem 1] shows that the map
![]() $K^Q_i\otimes _Qk \to A_i\otimes _Qk$
is an isomorphism for
$K^Q_i\otimes _Qk \to A_i\otimes _Qk$
is an isomorphism for
![]() $i=d$
and zero for
$i=d$
and zero for
![]() $i<d$
. The former fact implies that the inclusion
$i<d$
. The former fact implies that the inclusion
![]() $A' \subseteq \operatorname {\mathrm {cone}}(K^Q \to A)$
is a quasi-isomorphism, and the latter implies that
$A' \subseteq \operatorname {\mathrm {cone}}(K^Q \to A)$
is a quasi-isomorphism, and the latter implies that
![]() $A'$
is minimal as a complex. Altogether, this shows that
$A'$
is minimal as a complex. Altogether, this shows that
![]() $A'$
is the minimal resolution of
$A'$
is the minimal resolution of
![]() $R/\operatorname {\mathrm {soc}}(R)$
.
$R/\operatorname {\mathrm {soc}}(R)$
.
Lemma 8.17. Let R be an almost Golod Gorenstein ring of codimension d having a minimal Cohen presentation
![]() $Q\to R$
. Assume that the minimal Q-free resolution A of R is equipped with a cyclic
$Q\to R$
. Assume that the minimal Q-free resolution A of R is equipped with a cyclic
![]() $\mathrm {A}_{\infty }$
-structure. Then
$\mathrm {A}_{\infty }$
-structure. Then
![]() $(\bar {m}_n(\bar {A}^{\otimes n}))_i\subseteq \mathfrak {m}_Q \bar {A}_i$
for all
$(\bar {m}_n(\bar {A}^{\otimes n}))_i\subseteq \mathfrak {m}_Q \bar {A}_i$
for all
![]() $i<d$
, and
$i<d$
, and
![]() $(\bar {m}_n(\bar {A}^{\otimes n}))_d=0$
for
$(\bar {m}_n(\bar {A}^{\otimes n}))_d=0$
for
![]() $n \geqslant 3$
. In particular,
$n \geqslant 3$
. In particular,
![]() $R\otimes ^{\mathsf {L}}_Q k$
is formal and Koszul.
$R\otimes ^{\mathsf {L}}_Q k$
is formal and Koszul.
Proof. We first address what happens in degree d, and for this, we use the fact that A is a cyclic
![]() $\mathrm {A}_{\infty }$
-algebra. If
$\mathrm {A}_{\infty }$
-algebra. If
![]() $n\geqslant 3$
and
$n\geqslant 3$
and
![]() $m_n(a_1,\ldots ,a_n)$
has degree d, then
$m_n(a_1,\ldots ,a_n)$
has degree d, then
since A is strictly unital. But
![]() $\langle -, 1\rangle $
is the projection onto the (rank
$\langle -, 1\rangle $
is the projection onto the (rank
![]() $1$
) degree d part of A, so this implies
$1$
) degree d part of A, so this implies
![]() $ m_n(a_1,\ldots ,a_n)=0$
.
$ m_n(a_1,\ldots ,a_n)=0$
.
For the rest of the argument, we need to reduce to the case that R has dimension zero. We may find a sequence ![]() that is part of a minimal generating set of
that is part of a minimal generating set of
![]() $\mathfrak {m}_Q$
and that maps to a maximal regular sequence in
$\mathfrak {m}_Q$
and that maps to a maximal regular sequence in
![]() $\mathfrak {m}_R$
. All of the hypotheses, and the remaining assertions to prove, are unchanged if we replace Q, R and A with
$\mathfrak {m}_R$
. All of the hypotheses, and the remaining assertions to prove, are unchanged if we replace Q, R and A with ![]() ,
, ![]() and
and ![]() respectively, using Proposition 2.17 for the Koszul conclusion. Therefore, we may assume that R has dimension zero.
respectively, using Proposition 2.17 for the Koszul conclusion. Therefore, we may assume that R has dimension zero.
We now use the notation and results of Lemma 8.16. Since
![]() $A'=\operatorname {\mathrm {cone}}(K^Q_{< d} \to A_{< d})$
is the minimal Q-free resolution of
$A'=\operatorname {\mathrm {cone}}(K^Q_{< d} \to A_{< d})$
is the minimal Q-free resolution of
![]() $R/\operatorname {\mathrm {soc}}(R)$
, there is a splitting
$R/\operatorname {\mathrm {soc}}(R)$
, there is a splitting
and we define
![]() $\varphi _1$
to be the composition
$\varphi _1$
to be the composition
![]() $A\to \operatorname {\mathrm {cone}}(K^Q \to A) \to A'$
. By construction,
$A\to \operatorname {\mathrm {cone}}(K^Q \to A) \to A'$
. By construction,
![]() $(\varphi _1)_i\colon A_i\to A^{\prime }_i$
is a split injection for
$(\varphi _1)_i\colon A_i\to A^{\prime }_i$
is a split injection for
![]() $i<d$
. Since
$i<d$
. Since
![]() $R/\operatorname {\mathrm {soc}}(R)$
is Golod, we may endow
$R/\operatorname {\mathrm {soc}}(R)$
is Golod, we may endow
![]() $A'$
with a strictly unital
$A'$
with a strictly unital
![]() $\mathrm {A}_{\infty }$
-structure
$\mathrm {A}_{\infty }$
-structure
![]() $\{m_n^{\prime }\}$
satisfying
$\{m_n^{\prime }\}$
satisfying
![]() $\bar {m}^{\prime }_n(\bar {A}^{\prime \otimes n})\subseteq \mathfrak {m}_Q \bar {A}'$
for all
$\bar {m}^{\prime }_n(\bar {A}^{\prime \otimes n})\subseteq \mathfrak {m}_Q \bar {A}'$
for all
![]() $n\geqslant 1$
by [Reference BurkeBur15, Theorem 6.13]. Having done this, the chain map
$n\geqslant 1$
by [Reference BurkeBur15, Theorem 6.13]. Having done this, the chain map
![]() $\varphi _1$
can be extended to a strictly unital map of
$\varphi _1$
can be extended to a strictly unital map of
![]() $\mathrm {A}_{\infty }$
-algebras using Proposition 5.3. We apply Lemma 5.5 to the morphism
$\mathrm {A}_{\infty }$
-algebras using Proposition 5.3. We apply Lemma 5.5 to the morphism
![]() $A\otimes _Q k\to A'\otimes _Qk$
to deduce that the
$A\otimes _Q k\to A'\otimes _Qk$
to deduce that the
![]() $\mathrm {A}_{\infty }$
-structure of A satisfies
$\mathrm {A}_{\infty }$
-structure of A satisfies
![]() $(\bar {m}_n(\bar {A}^{\otimes n}))_i\subseteq \mathfrak {m}_Q \bar {A}_i$
for all
$(\bar {m}_n(\bar {A}^{\otimes n}))_i\subseteq \mathfrak {m}_Q \bar {A}_i$
for all
![]() $n\geqslant 1$
and all
$n\geqslant 1$
and all
![]() $i<d$
.
$i<d$
.
Since the induced higher
![]() $\mathrm {A}_{\infty }$
-structure on
$\mathrm {A}_{\infty }$
-structure on
![]() $A\otimes _Qk$
vanishes,
$A\otimes _Qk$
vanishes,
![]() $R\otimes ^{\mathsf {L}}_Q k\simeq A\otimes _Qk$
is formal by Proposition 5.4. It also follows that
$R\otimes ^{\mathsf {L}}_Q k\simeq A\otimes _Qk$
is formal by Proposition 5.4. It also follows that
![]() $A\otimes _Qk$
is a short Gorenstein ring, and in particular, it is Koszul by Example 3.7.
$A\otimes _Qk$
is a short Gorenstein ring, and in particular, it is Koszul by Example 3.7.
We are finally able to prove that almost Golod Gorenstein rings satisfying certain technical assumptions are strictly Cohen Koszul, as promised in the proof of Theorem 3.16, and substantially generalizing the class of Gorenstein local rings of codimension three covered by Example 8.4.
Theorem 8.18. If R is an almost Golod Gorenstein ring of odd codimension d, containing a field of characteristic zero, with a minimal Cohen presentation
![]() $\varphi \colon Q\to R$
, then
$\varphi \colon Q\to R$
, then
![]() $\varphi $
is strictly Koszul. More precisely, if the minimal resolution A of R admits a cyclic
$\varphi $
is strictly Koszul. More precisely, if the minimal resolution A of R admits a cyclic
![]() $\mathrm {A}_{\infty }$
-structure, then (regardless of d or the characteristic)
$\mathrm {A}_{\infty }$
-structure, then (regardless of d or the characteristic) ![]() , where
, where
and
![]() $(A,V,W)$
is a strictly Koszul presentation for
$(A,V,W)$
is a strictly Koszul presentation for
![]() $\varphi $
.
$\varphi $
.
Proof. Since d is odd and R is Gorenstein of characteristic zero, we may endow A with a cyclic
![]() $\mathrm {A}_{\infty }$
-structure by Theorem 5.7.
$\mathrm {A}_{\infty }$
-structure by Theorem 5.7.
The pairing
![]() $\langle -,-\rangle $
defined in Section 5.6 is nondegenerate, and this implies that W is a summand of
$\langle -,-\rangle $
defined in Section 5.6 is nondegenerate, and this implies that W is a summand of
![]() $V\otimes V$
. We know that
$V\otimes V$
. We know that ![]() since
since
![]() $A\otimes k$
is short Gorenstein. It follows from Nakayama’s lemma that
$A\otimes k$
is short Gorenstein. It follows from Nakayama’s lemma that ![]() as graded Q-modules. The assertion
as graded Q-modules. The assertion
![]() $(\bar {m}_n(\bar {A}^{\otimes n}))_d=0$
from Lemma 8.17 implies that
$(\bar {m}_n(\bar {A}^{\otimes n}))_d=0$
from Lemma 8.17 implies that
![]() $m_n(V^{\otimes n})\subseteq V$
for all n, and therefore, the presentation
$m_n(V^{\otimes n})\subseteq V$
for all n, and therefore, the presentation
![]() $(A,V,W)$
is strict.
$(A,V,W)$
is strict.
Taking an almost Golod Gorenstein ring R, with Q and A as in the theorem, we can describe the Priddy coalgebra explicitly:
This is also the dual of a noncommutative hypersurface, as in Example 8.4.
If we let M be a bounded complex of finitely generated R-modules, then there is a finite free Q-resolution
![]() $G \to M$
, and G can be given a strictly unital
$G \to M$
, and G can be given a strictly unital
![]() $\mathrm {A}_{\infty }$
-module structure over A by 5.2. All of this data can be constructed with finitely many computations, and it can be assembled into a resolution
$\mathrm {A}_{\infty }$
-module structure over A by 5.2. All of this data can be constructed with finitely many computations, and it can be assembled into a resolution
with an explicit differential given in Theorem 7.8 in terms of the
![]() $\mathrm {A}_{\infty }$
-structures of A and G. When
$\mathrm {A}_{\infty }$
-structures of A and G. When
![]() $M=k$
is the residue field and
$M=k$
is the residue field and
![]() $G=K^Q$
is the Koszul complex of Q, the Priddy resolution is minimal by Theorem 7.11.
$G=K^Q$
is the Koszul complex of Q, the Priddy resolution is minimal by Theorem 7.11.
The last example provides a class of almost Golod Gorenstein rings where we verify they are Cohen Koszul without any assumptions on the characteristic of k or the parity of the codimension.
Example 8.19. Let Q be a standard graded polynomial ring over k and let
![]() $R=Q/I$
, where I is an ideal generated by forms of degree
$R=Q/I$
, where I is an ideal generated by forms of degree
![]() $e\geqslant 3$
admitting an almost linear free resolution, as in Remark 3.17. We further assume that R is Gorenstein of codimension d.
$e\geqslant 3$
admitting an almost linear free resolution, as in Remark 3.17. We further assume that R is Gorenstein of codimension d.
Writing
![]() $T_{i,j}=\operatorname {Tor}_i^Q{(R,k)}_j=\mathrm {H}_i(K^R)_j$
, we have, by assumption,
$T_{i,j}=\operatorname {Tor}_i^Q{(R,k)}_j=\mathrm {H}_i(K^R)_j$
, we have, by assumption,
![]() $T_{i,j} = 0$
when
$T_{i,j} = 0$
when
![]() $0<i < d$
and
$0<i < d$
and
![]() $j-i \neq e-1$
. The only other nontrivial components are the unit
$j-i \neq e-1$
. The only other nontrivial components are the unit
![]() $T_{0,0}=k$
and the socle
$T_{0,0}=k$
and the socle
![]() $T_{d,2e-2+d}=k$
. The product on T must preserve both gradings, and it follows that T is a short Gorenstein ring.
$T_{d,2e-2+d}=k$
. The product on T must preserve both gradings, and it follows that T is a short Gorenstein ring.
Let
![]() $A\xrightarrow {\simeq } R$
be the minimal graded free resolution of R over Q. In this setting, there exists an
$A\xrightarrow {\simeq } R$
be the minimal graded free resolution of R over Q. In this setting, there exists an
![]() $\mathrm {A}_{\infty }$
-algebra structure
$\mathrm {A}_{\infty }$
-algebra structure
![]() $\{m_n\}$
on A that is homogeneous of degree zero with respect to the internal grading. In particular, the induced operations
$\{m_n\}$
on A that is homogeneous of degree zero with respect to the internal grading. In particular, the induced operations
![]() $m_n\otimes _Q k$
on T restrict to maps
$m_n\otimes _Q k$
on T restrict to maps
If some
![]() $i_\ell =d$
, the map above is zero for (homological) degree reasons, and so we may assume each
$i_\ell =d$
, the map above is zero for (homological) degree reasons, and so we may assume each
![]() $i_\ell $
is strictly smaller than d. Therefore, each
$i_\ell $
is strictly smaller than d. Therefore, each
![]() $j_\ell -i_\ell = e-1$
and
$j_\ell -i_\ell = e-1$
and
For
![]() $m_n\otimes _Q k$
to be nonvanishing on this component, this expression must equal
$m_n\otimes _Q k$
to be nonvanishing on this component, this expression must equal
![]() $e-1$
or
$e-1$
or
![]() $2e-2$
. In the former case, we find
$2e-2$
. In the former case, we find
![]() $(n-1)(e-1) = n-2$
, which cannot hold; in the latter case,
$(n-1)(e-1) = n-2$
, which cannot hold; in the latter case,
![]() $(n-2)(e-1)=n-2$
, and this cannot hold when n and e are not
$(n-2)(e-1)=n-2$
, and this cannot hold when n and e are not
![]() $2$
. Hence,
$2$
. Hence,
![]() $m_n\otimes _Q k=0$
for
$m_n\otimes _Q k=0$
for
![]() $n\neq 2$
.
$n\neq 2$
.
Thus, we may apply Theorem 7.1 with
![]() $V=\bigoplus _{i=1}^{d-1} A_i$
and W as in (8.18.1) to conclude that
$V=\bigoplus _{i=1}^{d-1} A_i$
and W as in (8.18.1) to conclude that
![]() $Q \to R$
is Koszul. Finally, it follows from Theorem 3.16 that R is not only Cohen Koszul, but also almost Golod Gorenstein.
$Q \to R$
is Koszul. Finally, it follows from Theorem 3.16 that R is not only Cohen Koszul, but also almost Golod Gorenstein.
Acknowledgements
We owe thanks to Steven Amelotte for many useful conversations, in particular improving our understanding of moment angle manifolds, the combinatorics of simplicial complexes, and almost linear resolutions. We thank Alexander Berglund for sharing important insights on Koszul-type phenomena in algebra and topology. For many fruitful discussions on systems of higher homotopies, and for allowing us to share some of these ideas here, we are grateful to Eloísa Grifo. We thank Srikanth Iyengar for his encouragement and many useful discussions on
![]() $\mathrm {A}_{\infty }$
-structures. We also thank Trung Chau, Michael DeBellevue and Keller VandeBogert for helpful conversations regarding concrete examples. We are also very grateful to the referee, whose close reading and many helpful comments improved the paper substantially.
$\mathrm {A}_{\infty }$
-structures. We also thank Trung Chau, Michael DeBellevue and Keller VandeBogert for helpful conversations regarding concrete examples. We are also very grateful to the referee, whose close reading and many helpful comments improved the paper substantially.
Competing interest
The authors have no competing interests to declare.
Funding statement
Part of this work was done at the Hausdorff Research Institute for Mathematics, Bonn, when Briggs, Letz, and Pollitz were at the ‘Spectral Methods in Algebra, Geometry, and Topology trimester, funded by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy–EXC-2047/1–390685813. Briggs is supported by the European Union under the Grant Agreement no. 101064551, and part of this work was completed when he was funded by NSF grant DMS-1928930. Letz was partly supported by the Deutsche Forschungsgemeinschaft (SFB-TRR 358/1 2023 - 491392403) and by the Alexander von Humboldt Foundation in the framework of a Feodor Lynen research fellowship endowed by the German Federal Ministry of Education and Research. Pollitz was supported by NSF grants DMS-1840190, DMS-2002173, and DMS-2302567.