Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-16T23:21:53.732Z Has data issue: false hasContentIssue false
  • English
  • Français

The Kodaira Problem for Kähler Spaces with Vanishing First Chern Class

Part of: Deformations of analytic structures Compact analytic spaces Birational geometry

Published online by Cambridge University Press:  15 March 2021

Patrick Graf  and
Martin Schwald
Patrick Graf
Affiliation:
Lehrstuhl für Mathematik I, Universität Bayreuth, 95440Bayreuth, Germany; E-mail: [email protected] URL: www.graficland.uni-bayreuth.de
Martin Schwald
Affiliation:
Fakultät für Mathematik, Universität Duisburg–Essen, 45117Essen, Germany; E-mail: [email protected] URL: www.esaga.uni-due.de/martin.schwald/

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a normal compact Kähler space with klt singularities and torsion canonical bundle. We show that X admits arbitrarily small deformations that are projective varieties if its locally trivial deformation space is smooth. We then prove that this unobstructedness assumption holds in at least three cases: if X has toroidal singularities, if X has finite quotient singularities and if the cohomology group 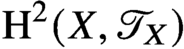${\mathrm {H}^{2} \!\left ( X, {\mathscr {T}_{X}} \right )}$ vanishes.

MSC classification

Primary: 32J27: Compact Kähler manifolds
Secondary: 14E30: Minimal model program (Mori theory, extremal rays) 32G05: Deformations of complex structures
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e24
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Bakker, B., Guenancia, H. and Lehn, C., ‘Algebraic approximation and the decomposition theorem for Kähler Calabi-Yau varieties’, Preprint, 2020, arXiv:2012.00441.Google Scholar
Bakker, B. and Lehn, C., ‘The global moduli theory of symplectic varieties’, Preprint, 2019, arXiv:1812.09748.Google Scholar
Bănică, C. and Stănăşilă, O., Algebraic Methods in the Global Theory of Complex Spaces (John Wiley & Sons, London-New York-Sydney, 1976). Google Scholar
Bingener, J., ‘On deformations of Kähler spaces. I’, Math. Z. 182(4) (1983), 505–535.CrossRefGoogle Scholar
Bogomolov, F. A., ‘Hamiltonian Kählerian manifolds’, Dokl. Akad. Nauk SSSR 243(5) (1978), 1101–1104.Google Scholar
Campana, F., ‘Orbifoldes à première classe de Chern nulle’, The Fano Conference’ (University of Torino, Turin, Italy, 2004), pp. 339–351. Google Scholar
Claudon, B., Graf, P., Guenancia, H. and Naumann, P., ‘Kähler spaces with zero first Chern class: Bochner principle, fundamental groups, and the Kodaira problem’, Preprint, 2020, arXiv:2008.13008.Google Scholar
Claudon, B., Höring, A. and Lin, H.-Y., ‘The fundamental group of compact Kähler threefolds’, Geom. Topol. 23 (2019), 3233–3271.CrossRefGoogle Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric Varieties, Graduate Studies in Mathematics, Vol. 124 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Danilov, V. I., ‘De Rham complex on toroidal variety’, in Algebraic Geometry (Chicago, IL, 1989), Lecture Notes in Mathematics, Vol. 1479 (Springer, Berlin, 1991), pp. 26–38.CrossRefGoogle Scholar
Deligne, P., ‘Théorème de Lefschetz et critères de dégénérescence de suites spectrales’, Publ. Math. de l’I.H.É.S. (1968), no. 35, 259–278. Google Scholar
Elkik, R., ‘Singularités rationnelles et déformations’, Invent. Math. 47(2) (1978), 139–147. CrossRefGoogle Scholar
Fantechi, B. and Manetti, M., ‘On the ${\mathrm{T}}^1$-lifting theorem’, J. Algebraic Geom. 8(1) (1999), 31–39.Google Scholar
Flenner, H. and Kosarew, S., ‘On locally trivial deformations’, Publ. RIMS Kyoto 23 (1987), 627–665.CrossRefGoogle Scholar
Graf, P., ‘Algebraic approximation of Kähler threefolds of Kodaira dimension zero’, Math. Ann. 371 (2018), 487–516.CrossRefGoogle Scholar
Graf, P., ‘A decomposition theorem for singular Kähler spaces with trivial first Chern class of dimension at most four’, Preprint, 2021, arXiv:2101.06764.Google Scholar
Graf, P. and Kirschner, T., ‘Finite quotients of three-dimensional complex tori’, Ann. Inst. Fourier (Grenoble) 70(2) (2020), 881–914.CrossRefGoogle Scholar
Graf, P. and Kovács, S. J., ‘An optimal extension theorem for $1$-forms and the Lipman-Zariski conjecture’, Documenta Math. 19 (2014), 815–830.Google Scholar
Graf, P. and Schwald, M., ‘On the Kodaira problem for uniruled Kähler spaces’, Ark. Mat. 58(2) (2020), 267–284.CrossRefGoogle Scholar
Grauert, H. and Kerner, H., ‘Deformationen von Singularitäten komplexer Räume’, Math. Ann. 153 (1964), 236–260. CrossRefGoogle Scholar
Gross, M., ‘The deformation space of Calabi-Yau $\mathrm{n}$-folds with canonical singularities can be obstructed’, in Mirror Symmetry, II, AMS/IP Studies in Advanced Mathematics, Vol. 1 (American Mathematical Society, Providence, RI, 1997), pp. 401–411.Google Scholar
Huybrechts, D., Complex Geometry (Springer-Verlag, Berlin, 2005).Google Scholar
Jörder, C., On the Poincaré Lemma for Reflexive Differential Forms (PhD Thesis, Albert-Ludwigs-Universität Freiburg im Breisgau, 2014). URL: https://freidok.uni-freiburg.de/data/9438.Google Scholar
Kawamata, Y., ‘Unobstructed deformations. A remark on a paper of Z. Ran’, J. Algebraic Geom. 1(2) (1992), 183–190.Google Scholar
Kawamata, Y., ‘Erratum on: “Unobstructed deformations. A remark on a paper of Z. Ran”’, J. Algebraic Geom. 6(4) (1997), 803–804.Google Scholar
Kebekus, S. and Schnell, C., ‘Extending holomorphic forms from the regular locus of a complex space to a resolution of singularities’, Preprint, 2019, arXiv:1811.03644.Google Scholar
Kodaira, K., ‘On compact analytic surfaces, III’, Ann. Math. 78(1) (1963), 1–40.CrossRefGoogle Scholar
Kodaira, K., Nirenberg, L. and Spencer, D. C., ‘On the existence of deformations of complex analytic structures’, Ann. Math. (2) 68 (1958), 450–459.CrossRefGoogle Scholar
Kollár, J., Lectures on Resolution of Singularities, Annals of Mathematics Studies, Vol. 166 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Kollár, J. and Mori, S., Birational Geometry of Algebraic Varieties, Cambridge Tracts in Mathematics, Vol. 134 (Cambridge University Press, Cambridge, UK, 1998). CrossRefGoogle Scholar
Lin, H.-Y., ‘Algebraic approximations of compact Kähler threefolds’, Preprint, 2018, arXiv:1710.01083.Google Scholar
Lin, H.-Y., ‘Algebraic approximations of fibrations in abelian varieties over a curve’, Preprint, 2018, arXiv:1612.09271.Google Scholar
Maschke, H., ‘Beweis des Satzes, dass diejenigen endlichen linearen Substitutionsgruppen, in welchen einige durchgehends verschwindende Coefficienten auftreten, intransitiv sind’, Math. Ann. 52(2–3) (1899), 363–368. CrossRefGoogle Scholar
Namikawa, Y., ‘Projectivity criterion of Moishezon spaces and density of projective symplectic varieties’, Int. J. Math. 13(2) (2002), 125–135.CrossRefGoogle Scholar
Ran, Z., ‘Deformations of manifolds with torsion or negative canonical bundle’, J. Algebraic Geom. 1(2) (1992), 279–291.Google Scholar
Sernesi, E., Deformations of Algebraic Schemes, Grundlehren der Mathematischen Wissenschaften, Vol. 334 (Springer-Verlag, Berlin, 2006).Google Scholar
Steenbrink, J. H. M., ‘Mixed Hodge structure on the vanishing cohomology, Real and complex singularities’, in Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, 1976 (Sijthoff and Noordhoff, Alphen aan den Rijn, Netherlands, 1977), pp. 525–563.Google Scholar
Takegoshi, K., ‘Relative vanishing theorems in analytic spaces’, Duke Math. J. 52(1) (1985), 273–279.CrossRefGoogle Scholar
Tian, G., ‘Smoothness of the universal deformation space of compact Calabi-Yau manifolds and its Petersson-Weil metric’, in Mathematical Aspects of String Theory (San Diego, Calif., 1986), Adv. Ser. Math. Phys., Vol. 1 (World Scientific, Singapore, 1987), pp. 629–646.CrossRefGoogle Scholar
Todorov, A. N., ‘The Weil-Petersson geometry of the moduli space of $\mathrm{SU}\left(\mathrm{n}\ge 3\right)$(Calabi-Yau) manifolds. I’, Comm. Math. Phys. 126(2) (1989), 325–346.CrossRefGoogle Scholar
Varouchas, J., ‘Kähler spaces and proper open morphisms’, Math. Ann. 283(1) (1989), 13–52.CrossRefGoogle Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry I, Cambridge Studies in Advanced Mathematics, Vol. 76 (Cambridge University Press, Cambridge, UK, 2002). CrossRefGoogle Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry II, Cambridge Studies in Advanced Mathematics, Vol. 77 (Cambridge University Press, 2003).Google Scholar
Voisin, C., ‘On the homotopy types of compact Kähler and complex projective manifolds’, Invent. Math. 157 (2004), 329–343.CrossRefGoogle Scholar
Voisin, C., ‘On the homotopy types of Kähler manifolds and the birational Kodaira problem’, J. Diff. Geom. 72 (2006), 43–71.CrossRefGoogle Scholar