Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T05:21:41.817Z Has data issue: false hasContentIssue false
  • English
  • Français

THE IWASAWA MAIN CONJECTURE FOR HILBERT MODULAR FORMS

Part of: Rings and algebras with additional structure Modules, bimodules and ideals

Published online by Cambridge University Press:  02 October 2015

XIN WAN
XIN WAN*
Affiliation:
Mathematics Department, Columbia University, New York, 10027, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

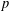Following the ideas and methods of a recent work of Skinner and Urban, we prove the one divisibility of the Iwasawa main conjecture for nearly ordinary Hilbert modular forms under certain local hypotheses. As a consequence, we prove that for a Hilbert modular form of parallel weight, trivial character, and good ordinary reduction at all primes dividing $p$, if the central critical 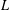$L$-value is zero then the 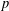$p$-adic Selmer group of it has rank at least one. We also prove that one of the local assumptions in the main result of Skinner and Urban can be removed by a base-change trick.

MSC classification

Primary: 16W10: Rings with involution; Lie, Jordan and other nonassociative structures
Secondary: 16D50: Injective modules, self-injective rings
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e18
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Bloch, S. and Kato, K., ‘L-functions and Tamagawa numbers of motives’, inThe Grothendieck Festschrift, Vol. I, Progress in Mathematics, 86 (Birkhauser, Boston, MA, 1990), 333–400.Google Scholar
Chida, M. and Hsieh, M.-L., ‘Special values of anticyclotomic $L$-functions for modular forms’, Crelle’s J. (to appear), preprint as of 06/16/13, arXiv:1204.2427.Google Scholar
Chida, M. and Hsieh, M.-L., ‘On the anticyclotomic Iwasawa main conjecture for modular forms’, Compos. Math. 151(5) (2015), 863–897.CrossRefGoogle Scholar
Cornut, C. and Vatsal, V., ‘Nontriviality of Rankin-Selberg L-functions and CM points’, inL-Functions and Galois Representations, Durham, July 2004, LMS Lecture Note Series, 320 (Cambridge University Press, Cambridge, 2007), 121–186.Google Scholar
Deligne, P. and Ribet, K., ‘Values of abelian L-functions at negative integers over totally real fields’, Invent. Math. 59 (1980), 227–286.Google Scholar
Diamond, F., ‘On the Hecke action on the cohomology of Hilbert-Blumenthal surfaces’, Contemp. Math. 210 (1998), 71–84.CrossRefGoogle Scholar
Eischen, E., Harris, M., Li, J. and Skinner, C., ‘$p$-adic $L$-functions for Unitary Shimura Varieties (II)’, in preparation.Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties, Ergebnisse der Math., 22 (Springer, New York, 1990).CrossRefGoogle Scholar
Fujiwara, K., ‘Deformation rings and Hecke algebras in the totally real case’, Preprint, 2006, arXiv:math/0602606.Google Scholar
Greenberg, R., ‘Iwasawa theory and p-adic deformations of motives’, inProc. on Motives held at Seattle, 1994 .Google Scholar
Greenberg, R., ‘Iwasawa theory for elliptic curves’, inArithmetic Theory of Elliptic Curves (Springer, Berlin, Heidelberg, 1999), 51–144.CrossRefGoogle Scholar
Greenberg, R. and Vinayak, V., ‘On the Iwasawa invariants of elliptic curves’, Invent. Math. 142(1) (2000), 17–63.Google Scholar
Greenberg, R., ‘Surjectivity of the global-to-local map defining a Selmer Group’, Kyoto J. Math. 50(4) (2010), 853–888.CrossRefGoogle Scholar
Hida, H., ‘On p-adic Hecke algebras for GL2 over totally real fields’, Ann. of Math. (2) 128 (1988), 295–384.Google Scholar
Hida, H., ‘On p-adic L-functions of GL(2) × GL(2) over totally real fields’, Ann. Inst. Fourier 40 (1991), 311–391.CrossRefGoogle Scholar
Hida, H., p-adic Automorphic Forms on Shimura Varieties, Springer Monographs in Mathematics (Springer, New York, 2004).CrossRefGoogle Scholar
Hida, H., ‘Non-vanishing modulo p of Hecke L-values’, inGeometric Aspects of Dwork Theory (Walter de Gruyter, Berlin, 2004), 735–784.Google Scholar
Hida, H., ‘Anticyclotomic main conjectures’, Doc. Math. Extra Volume Coates (2006), 465–532.Google Scholar
Hida, H., ‘Quadratic exercises in Iwasawa theory’, Int. Math. Res. Not. IMRN 2009 (2009), 912–952.Google Scholar
Hida, H., ‘Irreducibility of the Igusa tower over unitary Shimura varieties’, inOn Certain L-Functions, Clay Mathematics Proceedings, 13 (American Mathematical Society, Providence, 2011), 187–203.Google Scholar
Hida, H. and Tilouine, J., ‘Anti-cyclotomic Katz p-adic L-functions and congruence modules’, Ann. Sci. Éc. Norm. Super. (4) 26(2) (1993), 189–259.Google Scholar
Hida, H. and Tilouine, J., ‘On the anticyclotomic main conjecture for CM fields’, Invent. math. 117 (1994).Google Scholar
Hsieh, M.-L., ‘Eisenstein congruence on unitary groups and Iwasawa main conjecture for CM fields’, J. Amer. Math. Soc. 27(3) (2014), 753–862.Google Scholar
Hsieh, M.-L., ‘On the non-vanishing of Hecke L-values modulo p’, Amer. J. Math. 134(6) (2012), 1503–1539.Google Scholar
Hsieh, M.-L., ‘On the -invariant of anticyclotomic p-adic L-functions for CM fields’, J. reine angew. Math. 688 (2014), 67–100.CrossRefGoogle Scholar
Hung, P.-C., ‘On the non-vanishing mod $\ell$ of central $L$-values with anti-cyclotomic twists of modular forms’, Preprint, 2014, available at https://sites.google.com/site/pinchihung0926/home/papers.Google Scholar
Kato, K., ‘$p$-adic Hodge theory and values of zeta functions of modular forms’, Cohomologies p-adiques et applications arithmetiques’. III. Astérisque No. 295 (2004), ix, 117–290.Google Scholar
Kudla, S. S., ‘Splitting metaplectic covers of dual reductive pairs’, Israel J. Math. 87(1–3) (1994), 361–401.Google Scholar
Lan, K.-W., Arithmetic Compactifications of PEL-type Shimura Varieties, London Mathematical Society Monographs, 36 (Princeton University Press, Princeton, 2013).Google Scholar
Lapid, E. and Rallis, S., ‘On the local factors of representations of classical groups in automorphic representations’, inL-Functions and Applications: Progress and Prospects, Ohio State Univ. Math. Res. Inst. Publ., 11 (de Gruyter, Berlin, 2005), 309–359.Google Scholar
Longo, M., ‘On the Birch and Swinnerton-Dyer conjecture for modular elliptic curves over totally real fields’, Ann. Fourier 56(3) (2006), Chartres: L’Institut, 1950.Google Scholar
Longo, M., ‘Anticyclotomic Iwasawa’s main conjecture for Hilbert modular forms’, Comment. Math. Helv. 87(2) (2012), 303–353.Google Scholar
Mazur, B. and Wiles, A., ‘Class fields of abelian extensions of Q’, Invent. Math. 76 (1984), 179–330.Google Scholar
Miyake, T., Modular Forms (Springer, Berlin, 1989).Google Scholar
Moglin, C. and Waldspurger, J.-L., Spectral Decomposition and Eisenstein Series. Une paraphrase de l’ecriture, Cambridge Tracts in Mathematics, 113 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Morel, S., On the Cohomology of Certain Non-compact Shimura Varieties, Annals of Mathematics Studies, 173 (Princeton University Press, Princeton, 2010).Google Scholar
Nékovar, J., Selmer Complexes, Astérisque, 310 (Société mathématique de France, Paris, 2006).Google Scholar
Nékovar, J., ‘Level raising and anticyclotomic Selmer groups for Hilbert modular forms of weight two’, Canad. J. Math. 64(3) (2012), 588–668.Google Scholar
Shimura, G., Euler Products and Eisenstein Series, CBMS Regional Conference Series in Mathematics, 93 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Shimura, G., Arithmeticity in the Theory of Automorphic Forms, Mathematical Surveys and Monographs, 82 (American Mathematical Society, Providence, RI, 2000), x+302 pp.Google Scholar
Shin, S.-W., ‘Galois representations arising from some compact Shimura varieties’, Ann. of Math. (2) 173(3) (2011), 1645–1741.Google Scholar
Skinner, C., ‘Galois representations associated with unitary groups over ℚ’, Algebra Number Theory 6(8) (2012), 1697–1717.Google Scholar
Skinner, C. and Urban, E., ‘Vanishing of L-functions and Ranks of Selmer groups’, inProceedings of the International Congress of Mathematics, Vol. II (European Mathematical Society, Zurich, 2006), 473–500.Google Scholar
Skinner, C. and Urban, E., ‘The Iwasawa main conjectures for GL2’, Invent. Math. 195(1) (2014), 1–277.CrossRefGoogle Scholar
Skinner, C. and Wiles, A., ‘Nearly ordinary deformations of residually irreducible representations’, Ann. Fac. Sci. Toulouse, Math. (6) 10 (2001), 185–215.Google Scholar
Taylor, R., ‘On Galois representations associated to Hilbert modular forms’, Invent. Math. 98.2 (1989), 265–280.Google Scholar
Tilouine, J. and Urban, E., ‘Several-variable p-adic families of Siegel-Hilbert cusp eigensystems and their Galois representations’, Ann. Sci. Éc. Norm. Supér. (4) 32 (1999), 499–574, no longer published by Elsevier.Google Scholar
Waldspurger, J.-L., ‘Sur les coefficients de Fourier des formes modulaires de poids demi-entier’, J. Math. Pures Appl. 60 (1981), 375–484.Google Scholar
Waldspurger, J.-L., ‘Correspondances de Shimura et quaternions’, Forum Math. 3 (1991), 219–307.CrossRefGoogle Scholar
Wan, X., ‘Families of nearly ordinary Eisenstein series on unitary groups’, submitted, 2013.Google Scholar
Wiles, A., ‘On ordinary 𝜆-adic representations associated to modular forms’, Invent. Math. 94(3) (1988), 529–573.Google Scholar
Wiles, A., ‘The Iwasawa conjecture for totally real fields’, Ann. of Math. (2) 131 (1990).CrossRefGoogle Scholar
Wiles, A., ‘Elliptic curves and Fermat’s Last Theorem’, Ann. of Math. (2) 141 (1995), 443–551.Google Scholar
Yuan, X., Zhang, S.-W. and Zhang, W., The Gross-Zagier formula on Shimura Curves, Annals of Mathematics Studies, 184 (Princeton University Press, Princeton, 2013).Google Scholar
Zhang, S., ‘Heights of Heegner points on Shimura curves’, Ann. of Math. (2) 153 (2001), 27–147.Google Scholar
Zhang, S., ‘Gross-Zagier formula for GL(2). II. Heegner points and Rankin L-series’, Math. Sci. Res. Inst. Publ., 49 (Cambridge University Press, Cambridge, 2004), 191–214.Google Scholar