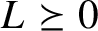1 Introduction
In his famous problem list of 1900, Hilbert asked whether every positive rational function can be written as a sum of squares of rational functions. The affirmative answer by Artin in 1927 laid the ground for the rise of real algebraic geometry [Reference Bochnak, Coste and RoyBCR98]. Several other sum-of-squares certificates (Positivstellensätze) for positivity on semialgebraic sets followed; since the detection of sums of squares became viable with the emergence of semidefinite programming [Reference Wolkowicz, Saigal and VandenbergheWSV00], these certificates play a fundamental role in polynomial optimisation [Reference LasserreLas01, Reference Blekherman, Parrilo and ThomasBPT13].
Positivstellensätze are also essential in the study of polynomial and rational inequalities in matrix variables, which splits into two directions. The first one deals with inequalities where the size of the matrix arguments is fixed [Reference Procesi and SchacherPS76, Reference Klep, Špenko and VolčičKŠV18]. The second direction attempts to answer questions about the positivity of noncommutative polynomials and rational functions when matrix arguments of all finite sizes are considered. Such questions naturally arise in control systems [Reference de Oliveira, Helton, McCullough and PutinardOHMP09], operator algebras [Reference OzawaOza16] and quantum information theory [Reference Doherty, Liang, Toner and WehnerDLTW08, Reference Pozas-Kerstjens, Rabelo, Rudnicki, Chaves, Cavalcanti, Navascués and AcínP-KRR+19]. This (dimension-)free real algebraic geometry started with the seminal work of Helton [Reference HeltonHel02] and McCullough [Reference McCulloughMcC01], who proved that a noncommutative polynomial is positive semidefinite on all tuples of Hermitian matrices precisely when it is a sum of Hermitian squares of noncommutative polynomials. The purpose of this paper is to extend this result to noncommutative rational functions.
Let
![]() $x=(x_1,\dotsc ,x_d)$
be freely noncommuting variables. The free algebra
$x=(x_1,\dotsc ,x_d)$
be freely noncommuting variables. The free algebra
![]() $\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
of noncommutative polynomials admits a universal skew field of fractions
$\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
of noncommutative polynomials admits a universal skew field of fractions
, also called the free skew field [Reference CohnCoh95, Reference Cohn and ReutenauerCR99], whose elements are noncommutative rational functions. We endow
with the unique involution
![]() $*$
that fixes the variables and conjugates the scalars. One can consider positivity of noncommutative rational functions on tuples of Hermitian matrices. For example, let
$*$
that fixes the variables and conjugates the scalars. One can consider positivity of noncommutative rational functions on tuples of Hermitian matrices. For example, let

It turns out
![]() ${\mathbb{r}}(X)$
is a positive semidefinite matrix for every tuple of Hermitian matrices
${\mathbb{r}}(X)$
is a positive semidefinite matrix for every tuple of Hermitian matrices
![]() $X=(X_1,X_2,X_3,X_4)$
belonging to the domain of
$X=(X_1,X_2,X_3,X_4)$
belonging to the domain of
![]() ${\mathbb{r}}$
(meaning
${\mathbb{r}}$
(meaning
![]() $\ker X_1\cap \ker X_2=\{0\}$
in this particular case). One way to certify this is by observing that
$\ker X_1\cap \ker X_2=\{0\}$
in this particular case). One way to certify this is by observing that
![]() ${\mathbb{r}}={\mathbb{r}}_1{\mathbb{r}}_1^*+{\mathbb{r}}_2{\mathbb{r}}_2^*$
, where
${\mathbb{r}}={\mathbb{r}}_1{\mathbb{r}}_1^*+{\mathbb{r}}_2{\mathbb{r}}_2^*$
, where
 $$ \begin{align*} {\mathbb{r}}_1=\left(x_4 - x_3 x_1^{-1} x_2\right) x_2\left(x_1^2+x_2^2\right)^{-1}x_1, \qquad {\mathbb{r}}_2=\left(x_4 - x_3 x_1^{-1} x_2\right) \left(1 + x_2 x_1^{-2} x_2\right)^{-1}. \end{align*} $$
$$ \begin{align*} {\mathbb{r}}_1=\left(x_4 - x_3 x_1^{-1} x_2\right) x_2\left(x_1^2+x_2^2\right)^{-1}x_1, \qquad {\mathbb{r}}_2=\left(x_4 - x_3 x_1^{-1} x_2\right) \left(1 + x_2 x_1^{-2} x_2\right)^{-1}. \end{align*} $$
The solution of Hilbert’s 17th problem in the free skew field presented in this paper (Corollary 5.4) states that every
, positive semidefinite on its Hermitian domain, is a sum of Hermitian squares in
. This statement was proved in [Reference Klep, Pascoe and VolčičKPV17] for noncommutative rational functions
![]() ${\mathbb{r}}$
that are regular, meaning that
${\mathbb{r}}$
that are regular, meaning that
![]() ${\mathbb{r}}(X)$
is well-defined for every tuple of Hermitian matrices. As with most noncommutative Positivstellensätze, at the heart of this result is a variation of the Gelfand–Naimark–Segal (GNS) construction. Namely, if
${\mathbb{r}}(X)$
is well-defined for every tuple of Hermitian matrices. As with most noncommutative Positivstellensätze, at the heart of this result is a variation of the Gelfand–Naimark–Segal (GNS) construction. Namely, if
is not a sum of Hermitian squares, one can construct a tuple of finite-dimensional Hermitian operators Y that is a sensible candidate for witnessing nonpositive-definiteness of
![]() ${\mathbb{r}}$
. However, the construction itself does not guarantee that Y actually belongs to the domain of
${\mathbb{r}}$
. However, the construction itself does not guarantee that Y actually belongs to the domain of
![]() ${\mathbb{r}}$
. This is not a problem if one assumes that
${\mathbb{r}}$
. This is not a problem if one assumes that
![]() ${\mathbb{r}}$
is regular, as it was done in [Reference Klep, Pascoe and VolčičKPV17]. However, it is worth mentioning that deciding the regularity of a noncommutative rational function is a challenge on its own, as observed there. In the present paper, the domain issue is resolved with an extension result: the tuple Y obtained from the GNS construction can be extended to a tuple of finite-dimensional Hermitian operators in the domain of
${\mathbb{r}}$
is regular, as it was done in [Reference Klep, Pascoe and VolčičKPV17]. However, it is worth mentioning that deciding the regularity of a noncommutative rational function is a challenge on its own, as observed there. In the present paper, the domain issue is resolved with an extension result: the tuple Y obtained from the GNS construction can be extended to a tuple of finite-dimensional Hermitian operators in the domain of
![]() ${\mathbb{r}}$
without losing the desired features of Y.
${\mathbb{r}}$
without losing the desired features of Y.
The first main theorem of this paper pertains to linear matrix pencils and is key for the extension already mentioned. It might also be of independent interest in the study of quiver representations and semi-invariants [Reference KingKin94, Reference Derksen and MakamDM17]. Let
![]() $\otimes $
denote the Kronecker product of matrices.
$\otimes $
denote the Kronecker product of matrices.
Theorem A. Let
![]() $\Lambda \in \operatorname {\mathrm {M}}_{e}(\mathbb {C})^d$
be such that
$\Lambda \in \operatorname {\mathrm {M}}_{e}(\mathbb {C})^d$
be such that
![]() $\Lambda _1\otimes X_1+\dotsb +\Lambda _d\otimes X_d$
is invertible for some
$\Lambda _1\otimes X_1+\dotsb +\Lambda _d\otimes X_d$
is invertible for some
![]() $X\in \operatorname {\mathrm {M}}_{k}(\mathbb {C})^d$
. If
$X\in \operatorname {\mathrm {M}}_{k}(\mathbb {C})^d$
. If
![]() $Y\in \operatorname {\mathrm {M}}_{\ell }(\mathbb {C})^d$
,
$Y\in \operatorname {\mathrm {M}}_{\ell }(\mathbb {C})^d$
,
![]() $Y'\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
and
$Y'\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
and
![]() $Y''\in \operatorname {\mathrm {M}}_{\ell \times m}(\mathbb {C})^d$
are such that
$Y''\in \operatorname {\mathrm {M}}_{\ell \times m}(\mathbb {C})^d$
are such that
 $$ \begin{align*} \Lambda_1\otimes \begin{pmatrix} Y_1 \\ Y^{\prime}_1\end{pmatrix}+\dotsb+ \Lambda_d\otimes \begin{pmatrix} Y_d \\ Y^{\prime}_d\end{pmatrix} \qquad \text{and}\qquad \Lambda_1\otimes \begin{pmatrix} Y_1 & Y^{\prime\prime}_1\end{pmatrix}+\dotsb+ \Lambda_d\otimes \begin{pmatrix} Y_d & Y^{\prime\prime}_d\end{pmatrix} \end{align*} $$
$$ \begin{align*} \Lambda_1\otimes \begin{pmatrix} Y_1 \\ Y^{\prime}_1\end{pmatrix}+\dotsb+ \Lambda_d\otimes \begin{pmatrix} Y_d \\ Y^{\prime}_d\end{pmatrix} \qquad \text{and}\qquad \Lambda_1\otimes \begin{pmatrix} Y_1 & Y^{\prime\prime}_1\end{pmatrix}+\dotsb+ \Lambda_d\otimes \begin{pmatrix} Y_d & Y^{\prime\prime}_d\end{pmatrix} \end{align*} $$
have full rank, then there exists
![]() $Z\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
for some
$Z\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
for some
![]() $n\ge m$
such that
$n\ge m$
such that
 $$ \begin{align*}\Lambda_1\otimes \left(\begin{array}{cc} Y_1 & \begin{matrix} Y^{\prime\prime}_1 & 0\end{matrix} \\ \begin{matrix} Y^{\prime}_1 \\ 0\end{matrix} & Z_1 \end{array}\right) +\dotsb+ \Lambda_d\otimes \left(\begin{array}{cc} Y_d & \begin{matrix} Y^{\prime\prime}_d & 0\end{matrix} \\ \begin{matrix} Y^{\prime}_d \\ 0\end{matrix} & Z_d \end{array}\right) \end{align*} $$
$$ \begin{align*}\Lambda_1\otimes \left(\begin{array}{cc} Y_1 & \begin{matrix} Y^{\prime\prime}_1 & 0\end{matrix} \\ \begin{matrix} Y^{\prime}_1 \\ 0\end{matrix} & Z_1 \end{array}\right) +\dotsb+ \Lambda_d\otimes \left(\begin{array}{cc} Y_d & \begin{matrix} Y^{\prime\prime}_d & 0\end{matrix} \\ \begin{matrix} Y^{\prime}_d \\ 0\end{matrix} & Z_d \end{array}\right) \end{align*} $$
is invertible.
See Theorem 3.3 for the proof. Together with a truncated rational imitation of the GNS construction, Theorem A leads to a rational Positivstellensatz on free spectrahedra. Given a monic Hermitian pencil
![]() $L=I+H_1x_1+\dotsb +H_dx_d$
, the associated free spectrahedron
$L=I+H_1x_1+\dotsb +H_dx_d$
, the associated free spectrahedron
![]() $\mathcal {D}(L)$
is the set of Hermitian tuples X satisfying the linear matrix inequality
$\mathcal {D}(L)$
is the set of Hermitian tuples X satisfying the linear matrix inequality
![]() $L(X)\succeq 0$
. Since every convex solution set of a noncommutative polynomial is a free spectrahedron [Reference Helton and McCulloughHM12], the following statement is called a rational convex Positivstellensatz, and it generalises its analogues in the polynomial context [Reference Helton, Klep and McCulloughHKM12] and regular rational context [Reference PascoePas18].
$L(X)\succeq 0$
. Since every convex solution set of a noncommutative polynomial is a free spectrahedron [Reference Helton and McCulloughHM12], the following statement is called a rational convex Positivstellensatz, and it generalises its analogues in the polynomial context [Reference Helton, Klep and McCulloughHKM12] and regular rational context [Reference PascoePas18].
Theorem B. Let L be a Hermitian monic pencil and set
![]() . Then
. Then
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\mathcal {D}(L)\cap \operatorname {\mathrm {dom}}{\mathbb{r}}$
if and only if
$\mathcal {D}(L)\cap \operatorname {\mathrm {dom}}{\mathbb{r}}$
if and only if
![]() ${\mathbb{r}}$
belongs to the rational quadratic module generated by L:
${\mathbb{r}}$
belongs to the rational quadratic module generated by L:
where
![]() and
and
![]() $\mathbb{v}_j$
are vectors over
$\mathbb{v}_j$
are vectors over
![]() .
.
A more precise quantitative version is given in Theorem 5.2 and has several consequences. The solution of Hilbert’s 17th problem in
![]() is obtained by taking
is obtained by taking
![]() $L=1$
in Corollary 5.4. Versions of Theorem B for invariant (Corollary 5.7) and real (Corollary 5.8) noncommutative rational functions are also given. Furthermore, it is shown that the rational Positivstellensatz also holds for a family of quadratic polynomials describing nonconvex sets (Subsection 5.4). As a contribution to optimisation, Theorem B implies that the eigenvalue optimum of a noncommutative rational function on a free spectrahedron can be obtained by solving a single semidefinite program (Subsection 5.5), much like in the noncommutative polynomial case [Reference Blekherman, Parrilo and ThomasBPT13, Reference Burgdorf, Klep and PovhBKP16] (but not in the classical commutative setting).
$L=1$
in Corollary 5.4. Versions of Theorem B for invariant (Corollary 5.7) and real (Corollary 5.8) noncommutative rational functions are also given. Furthermore, it is shown that the rational Positivstellensatz also holds for a family of quadratic polynomials describing nonconvex sets (Subsection 5.4). As a contribution to optimisation, Theorem B implies that the eigenvalue optimum of a noncommutative rational function on a free spectrahedron can be obtained by solving a single semidefinite program (Subsection 5.5), much like in the noncommutative polynomial case [Reference Blekherman, Parrilo and ThomasBPT13, Reference Burgdorf, Klep and PovhBKP16] (but not in the classical commutative setting).
Finally, Section 6 contains complementary results about domains of noncommutative rational functions. It is shown that every
![]() can be represented by a formal rational expression that is well defined at every Hermitian tuple in the domain of
can be represented by a formal rational expression that is well defined at every Hermitian tuple in the domain of
![]() ${\mathbb{r}}$
(Proposition 2.1); this statement fails in general if arbitrary matrix tuples are considered. On the other hand, a Nullstellensatz for cancellation of non-Hermitian singularities is given in Proposition 6.3.
${\mathbb{r}}$
(Proposition 2.1); this statement fails in general if arbitrary matrix tuples are considered. On the other hand, a Nullstellensatz for cancellation of non-Hermitian singularities is given in Proposition 6.3.
2 Preliminaries
In this section we establish terminology, notation and preliminary results on noncommutative rational functions that are used throughout the paper. Let
![]() $\operatorname {\mathrm {M}}_{m\times n}(\mathbb {C})$
denote the space of complex
$\operatorname {\mathrm {M}}_{m\times n}(\mathbb {C})$
denote the space of complex
![]() $m\times n$
matrices, and
$m\times n$
matrices, and
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})=\operatorname {\mathrm {M}}_{n\times n}(\mathbb {C})$
. Let
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})=\operatorname {\mathrm {M}}_{n\times n}(\mathbb {C})$
. Let
![]() $\operatorname {\mathrm {H}}_{n}(\mathbb {C})$
denote the real space of Hermitian
$\operatorname {\mathrm {H}}_{n}(\mathbb {C})$
denote the real space of Hermitian
![]() $n\times n$
matrices. For
$n\times n$
matrices. For
![]() $X=(X_1,\dotsc ,X_d)\in \operatorname {\mathrm {M}}_{m\times n}(\mathbb {C})^d$
,
$X=(X_1,\dotsc ,X_d)\in \operatorname {\mathrm {M}}_{m\times n}(\mathbb {C})^d$
,
![]() $A\in \operatorname {\mathrm {M}}_{p\times m}(\mathbb {C})$
and
$A\in \operatorname {\mathrm {M}}_{p\times m}(\mathbb {C})$
and
![]() $B\in \operatorname {\mathrm {M}}_{n\times q}(\mathbb {C})$
, we write
$B\in \operatorname {\mathrm {M}}_{n\times q}(\mathbb {C})$
, we write
 $$ \begin{align*} AXB= (AX_1B,\dotsc,AX_dB)\in \operatorname{\mathrm{M}}_{p\times q}(\mathbb{C})^d, \qquad X^*=\left(X_1^*,\dotsc,X_d^*\right)\in\operatorname{\mathrm{M}}_{n\times m}(\mathbb{C})^d. \end{align*} $$
$$ \begin{align*} AXB= (AX_1B,\dotsc,AX_dB)\in \operatorname{\mathrm{M}}_{p\times q}(\mathbb{C})^d, \qquad X^*=\left(X_1^*,\dotsc,X_d^*\right)\in\operatorname{\mathrm{M}}_{n\times m}(\mathbb{C})^d. \end{align*} $$
2.1 Free skew field
We define noncommutative rational functions using formal rational expressions and their matrix evaluations as in [Reference Kaliuzhnyi-Verbovetskyi and VinnikovK-VV12]. Formal rational expressions are syntactically valid combinations of scalars, freely noncommuting variables
![]() $x=(x_1,\dotsc ,x_d)$
, rational operations and parentheses. More precisely, a formal rational expression is an ordered (from left to right) rooted tree whose leaves have labels from
$x=(x_1,\dotsc ,x_d)$
, rational operations and parentheses. More precisely, a formal rational expression is an ordered (from left to right) rooted tree whose leaves have labels from
![]() $\mathbb {C}\cup \{x_1,\dotsc ,x_d\}$
, and every other node either is labelled
$\mathbb {C}\cup \{x_1,\dotsc ,x_d\}$
, and every other node either is labelled
![]() $+$
or
$+$
or
![]() $\times $
and has two children or is labelled
$\times $
and has two children or is labelled
![]() ${}^{-1}$
and has one child. For example,
${}^{-1}$
and has one child. For example,
 $((2+x_1)^{-1}x_2)x_1^{-1}$
is a formal rational expression corresponding to the following ordered tree:
$((2+x_1)^{-1}x_2)x_1^{-1}$
is a formal rational expression corresponding to the following ordered tree:

A subexpression of a formal rational expression r is any formal rational expression which appears in the construction of r (i.e., as a subtree). For example, all subexpressions of
 $\left ((2+x_1)^{-1}x_2\right )x_1^{-1}$
are
$\left ((2+x_1)^{-1}x_2\right )x_1^{-1}$
are
 $$ \begin{align*} 2,\ x_1,\ 2+x_1,\ (2+x_1)^{-1},\ x_2,\ (2+x_1)^{-1}x_2,\ x_1^{-1},\ \left((2+x_1)^{-1}x_2\right)x_1^{-1}. \end{align*} $$
$$ \begin{align*} 2,\ x_1,\ 2+x_1,\ (2+x_1)^{-1},\ x_2,\ (2+x_1)^{-1}x_2,\ x_1^{-1},\ \left((2+x_1)^{-1}x_2\right)x_1^{-1}. \end{align*} $$
Given a formal rational expression r and
![]() $X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
, the evaluation
$X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
, the evaluation
![]() $r(X)$
is defined in the natural way if all inverses appearing in r exist at X. The set of all
$r(X)$
is defined in the natural way if all inverses appearing in r exist at X. The set of all
![]() $X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that r is defined at X is denoted
$X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that r is defined at X is denoted
![]() $\operatorname {\mathrm {dom}}_n r$
. The (matricial) domain of r is
$\operatorname {\mathrm {dom}}_n r$
. The (matricial) domain of r is
 $$ \begin{align*} \operatorname{\mathrm{dom}} r = \bigcup_{n\in\mathbb{N}} \operatorname{\mathrm{dom}}_n r. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{dom}} r = \bigcup_{n\in\mathbb{N}} \operatorname{\mathrm{dom}}_n r. \end{align*} $$
Note that
![]() $\operatorname {\mathrm {dom}}_n r$
is a Zariski open set in
$\operatorname {\mathrm {dom}}_n r$
is a Zariski open set in
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
for every
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
for every
![]() $n\in \mathbb {N}$
. A formal rational expression r is nondegenerate if
$n\in \mathbb {N}$
. A formal rational expression r is nondegenerate if
![]() $\operatorname {\mathrm {dom}} r\neq \emptyset $
; let
$\operatorname {\mathrm {dom}} r\neq \emptyset $
; let
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
denote the set of all nondegenerate formal rational expressions. On
$\mathfrak {R}_{\mathbb {C}}(x)$
denote the set of all nondegenerate formal rational expressions. On
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
we define an equivalence relation
$\mathfrak {R}_{\mathbb {C}}(x)$
we define an equivalence relation
![]() $r_1\sim r_2$
if and only if
$r_1\sim r_2$
if and only if
![]() $r_1(X)=r_2(X)$
for all
$r_1(X)=r_2(X)$
for all
![]() $X\in \operatorname {\mathrm {dom}} r_1\cap \operatorname {\mathrm {dom}} r_2$
. Equivalence classes with respect to this relation are called noncommutative rational functions. By [Reference Kaliuzhnyi-Verbovetskyi and VinnikovK-VV12, Proposition 2.2] they form a skew field denoted
$X\in \operatorname {\mathrm {dom}} r_1\cap \operatorname {\mathrm {dom}} r_2$
. Equivalence classes with respect to this relation are called noncommutative rational functions. By [Reference Kaliuzhnyi-Verbovetskyi and VinnikovK-VV12, Proposition 2.2] they form a skew field denoted
![]() , which is the universal skew field of fractions of the free algebra
, which is the universal skew field of fractions of the free algebra
![]() $\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
by [Reference CohnCoh95, Section 4.5]. The equivalence class of
$\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
by [Reference CohnCoh95, Section 4.5]. The equivalence class of
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
is denoted
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
is denoted
![]() ; we also write
; we also write
![]() $r\in {\mathbb{r}}$
and say that r is a representative of the noncommutative rational function
$r\in {\mathbb{r}}$
and say that r is a representative of the noncommutative rational function
![]() ${\mathbb{r}}$
.
${\mathbb{r}}$
.
There is a unique involution
![]() $*$
on
$*$
on
![]() that is determined by
that is determined by
![]() $\alpha ^*=\overline {\alpha }$
for
$\alpha ^*=\overline {\alpha }$
for
![]() $\alpha \in \mathbb {C}$
and
$\alpha \in \mathbb {C}$
and
 $x_j^*=x_j$
for
$x_j^*=x_j$
for
![]() $j=1,\dotsc ,d$
. Furthermore, this involution lifts to an involutive map
$j=1,\dotsc ,d$
. Furthermore, this involution lifts to an involutive map
![]() $*$
on the set
$*$
on the set
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
: in terms of ordered trees,
$\mathfrak {R}_{\mathbb {C}}(x)$
: in terms of ordered trees,
![]() $*$
transposes a tree from left to right and conjugates the scalar labels. Note that
$*$
transposes a tree from left to right and conjugates the scalar labels. Note that
![]() $X\in \operatorname {\mathrm {dom}} r$
implies
$X\in \operatorname {\mathrm {dom}} r$
implies
![]() $X^*\in \operatorname {\mathrm {dom}} r^*$
for
$X^*\in \operatorname {\mathrm {dom}} r^*$
for
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
.
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
.
2.2 Hermitian domain
For
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
, let
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
, let
![]() $\operatorname {\mathrm {hdom}}_n r= \operatorname {\mathrm {dom}}_n r\cap \operatorname {\mathrm {H}}_{n}(\mathbb {C})^d$
. Then
$\operatorname {\mathrm {hdom}}_n r= \operatorname {\mathrm {dom}}_n r\cap \operatorname {\mathrm {H}}_{n}(\mathbb {C})^d$
. Then
 $$ \begin{align*} \operatorname{\mathrm{hdom}} r = \bigcup_{n\in\mathbb{N}} \operatorname{\mathrm{hdom}}_n r \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{hdom}} r = \bigcup_{n\in\mathbb{N}} \operatorname{\mathrm{hdom}}_n r \end{align*} $$
is the Hermitian domain of r. Note that
![]() $\operatorname {\mathrm {hdom}}_n r$
is Zariski dense in
$\operatorname {\mathrm {hdom}}_n r$
is Zariski dense in
![]() $\operatorname {\mathrm {dom}}_n r$
, because
$\operatorname {\mathrm {dom}}_n r$
, because
![]() $\operatorname {\mathrm {H}}_{n}(\mathbb {C})$
is Zariski dense in
$\operatorname {\mathrm {H}}_{n}(\mathbb {C})$
is Zariski dense in
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
and
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
and
![]() $\operatorname {\mathrm {dom}}_n r$
is Zariski open in
$\operatorname {\mathrm {dom}}_n r$
is Zariski open in
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
. Finally, we define the (Hermitian) domain of a noncommutative rational function: for
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
. Finally, we define the (Hermitian) domain of a noncommutative rational function: for
![]() , let
, let
 $$ \begin{align*} \operatorname{\mathrm{dom}}{\mathbb{r}} = \bigcup_{r\in{\mathbb{r}}} \operatorname{\mathrm{dom}} r,\qquad \operatorname{\mathrm{hdom}}{\mathbb{r}} = \bigcup_{r\in{\mathbb{r}}} \operatorname{\mathrm{hdom}} r. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{dom}}{\mathbb{r}} = \bigcup_{r\in{\mathbb{r}}} \operatorname{\mathrm{dom}} r,\qquad \operatorname{\mathrm{hdom}}{\mathbb{r}} = \bigcup_{r\in{\mathbb{r}}} \operatorname{\mathrm{hdom}} r. \end{align*} $$
By the definition of the equivalence relation on nondegenerate expressions,
![]() ${\mathbb{r}}$
has a well-defined evaluation at
${\mathbb{r}}$
has a well-defined evaluation at
![]() $X\in \operatorname {\mathrm {dom}}{\mathbb{r}}$
, written as
$X\in \operatorname {\mathrm {dom}}{\mathbb{r}}$
, written as
![]() ${\mathbb{r}}(X)$
, which equals
${\mathbb{r}}(X)$
, which equals
![]() $r(X)$
for any representative r of
$r(X)$
for any representative r of
![]() ${\mathbb{r}}$
that has X in its domain. The following proposition is a generalisation of [Reference Klep, Pascoe and VolčičKPV17, Proposition 3.3] and is proved in Subsection 6.1:
${\mathbb{r}}$
that has X in its domain. The following proposition is a generalisation of [Reference Klep, Pascoe and VolčičKPV17, Proposition 3.3] and is proved in Subsection 6.1:
Proposition 2.1. For every
![]() there exists
there exists
![]() $r\in {\mathbb{r}}$
such that
$r\in {\mathbb{r}}$
such that
![]() $\operatorname {\mathrm {hdom}} {\mathbb{r}}=\operatorname {\mathrm {hdom}} r$
.
$\operatorname {\mathrm {hdom}} {\mathbb{r}}=\operatorname {\mathrm {hdom}} r$
.
Remark 2.2. There are noncommutative rational functions such that
![]() $\operatorname {\mathrm {dom}} {\mathbb{r}}\neq \operatorname {\mathrm {dom}} r$
for every
$\operatorname {\mathrm {dom}} {\mathbb{r}}\neq \operatorname {\mathrm {dom}} r$
for every
![]() $r\in {\mathbb{r}}$
; see Example 6.2 or [Reference VolčičVol17, Example 3.13].
$r\in {\mathbb{r}}$
; see Example 6.2 or [Reference VolčičVol17, Example 3.13].
2.3 Linear representation of a formal rational expression
A fundamental tool for handling noncommutative rational functions is linear representations (also linearisations or realisations) [Reference Cohn and ReutenauerCR99, Reference CohnCoh95, Reference Helton, Mai and SpeicherHMS18]. Set
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
. By [Reference Helton, Mai and SpeicherHMS18, Theorem 4.2 and Algorithm 4.3] there exist
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
. By [Reference Helton, Mai and SpeicherHMS18, Theorem 4.2 and Algorithm 4.3] there exist
![]() $e\in \mathbb {N}$
, vectors
$e\in \mathbb {N}$
, vectors
![]() $u,v\in \mathbb {C}^e$
and an affine matrix pencil
$u,v\in \mathbb {C}^e$
and an affine matrix pencil
![]() $M=M_0+M_1x_1+\dotsb +M_dx_d$
, with
$M=M_0+M_1x_1+\dotsb +M_dx_d$
, with
![]() $M_j\in \operatorname {\mathrm {M}}_{e}(\mathbb {C})$
, satisfying the following. For every unital
$M_j\in \operatorname {\mathrm {M}}_{e}(\mathbb {C})$
, satisfying the following. For every unital
![]() $\mathbb {C}$
-algebra
$\mathbb {C}$
-algebra
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $a\in \mathcal {A}^d$
,
$a\in \mathcal {A}^d$
,
-
(i) if r can be evaluated at a, then
 $M(a)\in \operatorname {\mathrm {GL}}_e(\mathcal {A})$
and
$M(a)\in \operatorname {\mathrm {GL}}_e(\mathcal {A})$
and
 $r(a) = u^* M(a)^{-1}v$
;
$r(a) = u^* M(a)^{-1}v$
; -
(ii) if
 $M(a)\in \operatorname {\mathrm {GL}}_e(\mathcal {A})$
and
$M(a)\in \operatorname {\mathrm {GL}}_e(\mathcal {A})$
and
 $\mathcal {A}=\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
for some
$\mathcal {A}=\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
for some
 $n\in \mathbb {N}$
, then r can be evaluated at a.
$n\in \mathbb {N}$
, then r can be evaluated at a.
We say that the triple
![]() $(u,M,v)$
is a linear representation of r of size e. Usually, linear representations are defined for noncommutative rational functions and with less emphasis on domains; however, the definition here is more convenient for the purpose of this paper.
$(u,M,v)$
is a linear representation of r of size e. Usually, linear representations are defined for noncommutative rational functions and with less emphasis on domains; however, the definition here is more convenient for the purpose of this paper.
Remark 2.3. In the definition of a linear representation, (ii) is valid not only for
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
but more broadly for stably finite algebras [Reference Helton, Mai and SpeicherHMS18, Lemma 5.2]. However, it may fail in general–for example, for the algebra of all bounded operators on an infinite-dimensional Hilbert space.
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
but more broadly for stably finite algebras [Reference Helton, Mai and SpeicherHMS18, Lemma 5.2]. However, it may fail in general–for example, for the algebra of all bounded operators on an infinite-dimensional Hilbert space.
We will also require the following proposition on pencils that is a combination of various existing results:
Proposition 2.4. [Reference CohnCoh95, Reference Kaliuzhnyi-Verbovetskyi and VinnikovK-VV12, Reference Derksen and MakamDM17]
Let M be an affine pencil of size e. The following are equivalent:
-
(i)
 .
. -
(ii) There are
 $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
 $X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that
$X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that
 $\det M(X)\neq 0$
.
$\det M(X)\neq 0$
. -
(iii) For every
 $n\ge e-1$
, there exists
$n\ge e-1$
, there exists
 $X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that
$X\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that
 $\det M(X)\neq 0$
.
$\det M(X)\neq 0$
. -
(iv) If
 $U\in \operatorname {\mathrm {M}}_{e'\times e}(\mathbb {C})$
and
$U\in \operatorname {\mathrm {M}}_{e'\times e}(\mathbb {C})$
and
 $V\in \operatorname {\mathrm {M}}_{e\times e''}(\mathbb {C})$
satisfy
$V\in \operatorname {\mathrm {M}}_{e\times e''}(\mathbb {C})$
satisfy
 $UMV=0$
, then
$UMV=0$
, then
 $\operatorname {\mathrm {rk}} U+\operatorname {\mathrm {rk}} V\le e$
.
$\operatorname {\mathrm {rk}} U+\operatorname {\mathrm {rk}} V\le e$
.
Proof. (i)
![]() $\Leftrightarrow $
(ii) follows by the construction of the free skew field via matrix evaluations (compare [Reference Kaliuzhnyi-Verbovetskyi and VinnikovK-VV12, Proposition 2.1]). (iii)
$\Leftrightarrow $
(ii) follows by the construction of the free skew field via matrix evaluations (compare [Reference Kaliuzhnyi-Verbovetskyi and VinnikovK-VV12, Proposition 2.1]). (iii)
![]() $\Rightarrow $
(ii) is trivial, and (ii)
$\Rightarrow $
(ii) is trivial, and (ii)
![]() $\Rightarrow $
(iii) holds by [Reference Derksen and MakamDM17, Theorem 1.8]. (iv)
$\Rightarrow $
(iii) holds by [Reference Derksen and MakamDM17, Theorem 1.8]. (iv)
![]() $\Leftrightarrow $
(i) follows from [Reference CohnCoh95, Corollaries 4.5.9 and 6.3.6], because the free algebra
$\Leftrightarrow $
(i) follows from [Reference CohnCoh95, Corollaries 4.5.9 and 6.3.6], because the free algebra
![]() $\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
is a free ideal ring [Reference CohnCoh95, Theorem 5.4.1].
$\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
is a free ideal ring [Reference CohnCoh95, Theorem 5.4.1].
An affine matrix pencil is full [Reference CohnCoh95, Section 1.4] if it satisfies the (equivalent) properties in Proposition 2.4.
Remark 2.5. If
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
admits a linear representation of size e, then
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
admits a linear representation of size e, then
![]() $\operatorname {\mathrm {hdom}}_n r\neq \emptyset $
for
$\operatorname {\mathrm {hdom}}_n r\neq \emptyset $
for
![]() $n\ge e-1$
, by Proposition 2.4 and the Zariski denseness of
$n\ge e-1$
, by Proposition 2.4 and the Zariski denseness of
![]() $\operatorname {\mathrm {hdom}}_n r$
in
$\operatorname {\mathrm {hdom}}_n r$
in
![]() $\operatorname {\mathrm {dom}}_n r$
.
$\operatorname {\mathrm {dom}}_n r$
.
3 An extension theorem
An affine matrix pencil M of size e is irreducible if
![]() $UMV=0$
for nonzero matrices
$UMV=0$
for nonzero matrices
![]() $U\in \operatorname {\mathrm {M}}_{e'\times e}(\mathbb {C})$
and
$U\in \operatorname {\mathrm {M}}_{e'\times e}(\mathbb {C})$
and
![]() $V\in \operatorname {\mathrm {M}}_{e\times e''}(\mathbb {C})$
implies
$V\in \operatorname {\mathrm {M}}_{e\times e''}(\mathbb {C})$
implies
![]() $\operatorname {\mathrm {rk}} U+\operatorname {\mathrm {rk}} V\le e-1$
. In other words, a pencil is not irreducible if it can be put into a
$\operatorname {\mathrm {rk}} U+\operatorname {\mathrm {rk}} V\le e-1$
. In other words, a pencil is not irreducible if it can be put into a
![]() $2\times 2$
block upper-triangular form with square diagonal blocks
$2\times 2$
block upper-triangular form with square diagonal blocks
![]() $\left (\begin {smallmatrix}\star & \star \\ 0 & \star \end {smallmatrix}\right )$
by a left and a right basis change. Every irreducible pencil is full. On the other hand, every full pencil is, up to a left and a right basis change, equal to a block upper-triangular pencil whose diagonal blocks are irreducible pencils. In terms of quiver representations [Reference KingKin94],
$\left (\begin {smallmatrix}\star & \star \\ 0 & \star \end {smallmatrix}\right )$
by a left and a right basis change. Every irreducible pencil is full. On the other hand, every full pencil is, up to a left and a right basis change, equal to a block upper-triangular pencil whose diagonal blocks are irreducible pencils. In terms of quiver representations [Reference KingKin94],
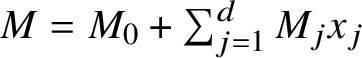 $M=M_0+\sum _{j=1}^dM_jx_j$
is full/irreducible if and only if the
$M=M_0+\sum _{j=1}^dM_jx_j$
is full/irreducible if and only if the
![]() $(e,e)$
-dimensional representation
$(e,e)$
-dimensional representation
![]() $(M_0,M_1,\dotsc ,M_d)$
of the
$(M_0,M_1,\dotsc ,M_d)$
of the
![]() $(d+1)$
-Kronecker quiver is
$(d+1)$
-Kronecker quiver is
![]() $(1,-1)$
-semistable/stable.
$(1,-1)$
-semistable/stable.
For the purpose of this section we extend evaluations of linear matrix pencils to tuples of rectangular matrices. If
 $\Lambda =\sum _{j=1}^d \Lambda _jx_j$
is of size e and
$\Lambda =\sum _{j=1}^d \Lambda _jx_j$
is of size e and
![]() $X\in \operatorname {\mathrm {M}}_{\ell \times m}(\mathbb {C})^d$
, then
$X\in \operatorname {\mathrm {M}}_{\ell \times m}(\mathbb {C})^d$
, then
 $$ \begin{align*} \Lambda(X)=\sum_{j=1}^d \Lambda_j\otimes X_j \in \operatorname{\mathrm{M}}_{e\ell\times em}(\mathbb{C}). \end{align*} $$
$$ \begin{align*} \Lambda(X)=\sum_{j=1}^d \Lambda_j\otimes X_j \in \operatorname{\mathrm{M}}_{e\ell\times em}(\mathbb{C}). \end{align*} $$
The following lemma and proposition rely on an ampliation trick in a free algebra to demonstrate the existence of specific invertible evaluations of full pencils (see [Reference Helton, Klep and VolčičHKV20, Section 2.1] for another argument involving such ampliations):
Lemma 3.1. Let
 $\Lambda = \sum _{j=1}^d\Lambda _jx_j$
be a homogeneous irreducible pencil of size e. Set
$\Lambda = \sum _{j=1}^d\Lambda _jx_j$
be a homogeneous irreducible pencil of size e. Set
![]() $\ell \le m$
and denote
$\ell \le m$
and denote
![]() $n=(m-\ell )(e-1)$
. Given
$n=(m-\ell )(e-1)$
. Given
![]() $C\in \operatorname {\mathrm {M}}_{me\times \ell e}(\mathbb {C})$
, consider the pencil
$C\in \operatorname {\mathrm {M}}_{me\times \ell e}(\mathbb {C})$
, consider the pencil
![]() $\widetilde {\Lambda }$
of size
$\widetilde {\Lambda }$
of size
![]() $(m+n)e$
in
$(m+n)e$
in
![]() $d(m+n)(n+m-\ell )$
variables
$d(m+n)(n+m-\ell )$
variables
![]() $z_{jpq}$
:
$z_{jpq}$
:

where
 $\widehat {E}_{p,q} \in \operatorname {\mathrm {M}}_{m\times (n+m-\ell )}(\mathbb {C})$
and
$\widehat {E}_{p,q} \in \operatorname {\mathrm {M}}_{m\times (n+m-\ell )}(\mathbb {C})$
and
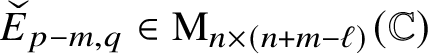
are the standard matrix units. If C has full rank, then the pencil
![]() $\widetilde {\Lambda }$
is full.
$\widetilde {\Lambda }$
is full.
Proof. Suppose U and V are constant matrices with
![]() $e(m+n)$
columns and
$e(m+n)$
columns and
![]() $e(m+n)$
rows, respectively, that satisfy
$e(m+n)$
rows, respectively, that satisfy
![]() $U\widetilde {\Lambda }V=0$
. There is nothing to prove if
$U\widetilde {\Lambda }V=0$
. There is nothing to prove if
![]() $U=0$
, so let
$U=0$
, so let
![]() $U\neq 0$
. Write
$U\neq 0$
. Write
 $$ \begin{align*} U=\begin{pmatrix} U_1 & \dotsb & U_{m+n}\end{pmatrix}, \qquad V=\begin{pmatrix} V_0 \\ V_1 \\ \vdots \\ V_{n+m-\ell}\end{pmatrix}, \end{align*} $$
$$ \begin{align*} U=\begin{pmatrix} U_1 & \dotsb & U_{m+n}\end{pmatrix}, \qquad V=\begin{pmatrix} V_0 \\ V_1 \\ \vdots \\ V_{n+m-\ell}\end{pmatrix}, \end{align*} $$
where each
![]() $U_p$
has e columns,
$U_p$
has e columns,
![]() $V_0$
has
$V_0$
has
![]() $\ell e$
rows and each
$\ell e$
rows and each
![]() $V_q$
with
$V_q$
with
![]() $q>0$
has e rows. Also let
$q>0$
has e rows. Also let
![]() $U_0=\begin {pmatrix}U_1 & \cdots & U_m\end {pmatrix}$
. Then
$U_0=\begin {pmatrix}U_1 & \cdots & U_m\end {pmatrix}$
. Then
![]() $U\widetilde {\Lambda }V=0$
implies
$U\widetilde {\Lambda }V=0$
implies
Since C has full rank, equation (3.1) implies
![]() $\operatorname {\mathrm {rk}} U_0+\operatorname {\mathrm {rk}} V_0\le me$
. Note that
$\operatorname {\mathrm {rk}} U_0+\operatorname {\mathrm {rk}} V_0\le me$
. Note that
![]() $U_{p'}\neq 0$
for some
$U_{p'}\neq 0$
for some
![]() $1\le p'\le m+n$
, because
$1\le p'\le m+n$
, because
![]() $U\neq 0$
. Since
$U\neq 0$
. Since
![]() $\Lambda $
is irreducible and
$\Lambda $
is irreducible and
![]() $U_{p'}\neq 0$
for some
$U_{p'}\neq 0$
for some
![]() $p'$
, equation (3.2) implies
$p'$
, equation (3.2) implies
![]() $\operatorname {\mathrm {rk}} V_q\le e-1$
and
$\operatorname {\mathrm {rk}} V_q\le e-1$
and
![]() $\operatorname {\mathrm {rk}} U_p+\operatorname {\mathrm {rk}} V_q\le e-1$
for all
$\operatorname {\mathrm {rk}} U_p+\operatorname {\mathrm {rk}} V_q\le e-1$
for all
![]() $p,q>0$
. Then
$p,q>0$
. Then
 $$ \begin{align*} \operatorname{\mathrm{rk}} U+\operatorname{\mathrm{rk}} V & \le \operatorname{\mathrm{rk}} U_0+\operatorname{\mathrm{rk}} V_0+\sum_{p=m+1}^{m+n} \operatorname{\mathrm{rk}} U_p+\sum_{q=1}^{n+m-\ell}\operatorname{\mathrm{rk}} V_q \\ & \le me+n(e-1)+(m-\ell)(e-1) \\ & = (m+n)e \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{rk}} U+\operatorname{\mathrm{rk}} V & \le \operatorname{\mathrm{rk}} U_0+\operatorname{\mathrm{rk}} V_0+\sum_{p=m+1}^{m+n} \operatorname{\mathrm{rk}} U_p+\sum_{q=1}^{n+m-\ell}\operatorname{\mathrm{rk}} V_q \\ & \le me+n(e-1)+(m-\ell)(e-1) \\ & = (m+n)e \end{align*} $$
by the choice of n. Therefore
![]() $\widetilde {\Lambda }$
is full.
$\widetilde {\Lambda }$
is full.
Proposition 3.2. Let
![]() $\Lambda $
be a homogeneous full pencil of size e, and let
$\Lambda $
be a homogeneous full pencil of size e, and let
![]() $X\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
with
$X\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
with
![]() $\ell \le m$
be such that
$\ell \le m$
be such that
![]() $\Lambda (X)$
has full rank. Then there exist
$\Lambda (X)$
has full rank. Then there exist
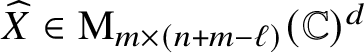 $\widehat {X}\in \operatorname {\mathrm {M}}_{m\times (n+m-\ell )}(\mathbb {C})^d$
and
$\widehat {X}\in \operatorname {\mathrm {M}}_{m\times (n+m-\ell )}(\mathbb {C})^d$
and
 for some
for some
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that

Proof. A full pencil is, up to a left-right basis change, equal to a block upper-triangular pencil with irreducible diagonal blocks. Suppose that the lemma holds for irreducible pencils; since the set of pairs
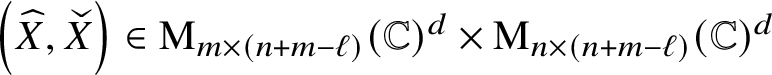 satisfying equation (3.3) is Zariski open, the lemma then also holds for full pencils. Thus we can without loss of generality assume that
satisfying equation (3.3) is Zariski open, the lemma then also holds for full pencils. Thus we can without loss of generality assume that
![]() $\Lambda $
is irreducible.
$\Lambda $
is irreducible.
Let
![]() $n_1=(m-\ell )(e-1)$
and
$n_1=(m-\ell )(e-1)$
and
![]() $e_1=(m+n_1)e$
. By Lemma 3.1 applied to
$e_1=(m+n_1)e$
. By Lemma 3.1 applied to
 $C=\sum _{j=1}^d X_j\otimes \Lambda _j$
and Proposition 2.4, there exists
$C=\sum _{j=1}^d X_j\otimes \Lambda _j$
and Proposition 2.4, there exists
![]() $Z \in \operatorname {\mathrm {M}}_{e_1-1}(\mathbb {C})^{d\left (m+n_1\right )\left (n_1+m-\ell \right )}$
such that
$Z \in \operatorname {\mathrm {M}}_{e_1-1}(\mathbb {C})^{d\left (m+n_1\right )\left (n_1+m-\ell \right )}$
such that
![]() $\widetilde {\Lambda }(Z)$
is invertible. Therefore the matrix
$\widetilde {\Lambda }(Z)$
is invertible. Therefore the matrix

is invertible since it is similar to
![]() $\widetilde {\Lambda }(Z)$
(via a permutation matrix). Thus there are
$\widetilde {\Lambda }(Z)$
(via a permutation matrix). Thus there are
 $\widehat {X}\in \operatorname {\mathrm {M}}_{m\times (n+m-\ell )}(\mathbb {C})^d$
and
$\widehat {X}\in \operatorname {\mathrm {M}}_{m\times (n+m-\ell )}(\mathbb {C})^d$
and

such that

where
![]() $n=(e_1-2)m+n_1(e_1-1)$
.
$n=(e_1-2)m+n_1(e_1-1)$
.
We are ready to prove the first main result of the paper.
Theorem 3.3. Let
![]() $\Lambda $
be a full pencil of size e, and let
$\Lambda $
be a full pencil of size e, and let
![]() $Y\in \operatorname {\mathrm {M}}_{\ell }(\mathbb {C})^d$
,
$Y\in \operatorname {\mathrm {M}}_{\ell }(\mathbb {C})^d$
,
![]() $Y'\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
and
$Y'\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
and
![]() $Y''\in \operatorname {\mathrm {M}}_{\ell \times m}(\mathbb {C})^d$
be such that
$Y''\in \operatorname {\mathrm {M}}_{\ell \times m}(\mathbb {C})^d$
be such that
 $$ \begin{align} \Lambda \begin{pmatrix} Y \\ Y'\end{pmatrix},\qquad \Lambda \begin{pmatrix} Y & Y''\end{pmatrix} \end{align} $$
$$ \begin{align} \Lambda \begin{pmatrix} Y \\ Y'\end{pmatrix},\qquad \Lambda \begin{pmatrix} Y & Y''\end{pmatrix} \end{align} $$
have full rank. Then there are
![]() $n\ge m$
and
$n\ge m$
and
![]() $Z\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that
$Z\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^d$
such that
 $$ \begin{align*} \det \Lambda \left(\begin{array}{cc} Y & \begin{matrix} Y'' & 0\end{matrix} \\ \begin{matrix} Y' \\ 0\end{matrix} & Z \end{array}\right) \neq0. \end{align*} $$
$$ \begin{align*} \det \Lambda \left(\begin{array}{cc} Y & \begin{matrix} Y'' & 0\end{matrix} \\ \begin{matrix} Y' \\ 0\end{matrix} & Z \end{array}\right) \neq0. \end{align*} $$
Proof. By Proposition 3.2 and its transpose analogue, there exist
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
 $$ \begin{align*} A'\in \operatorname{\mathrm{M}}_{\ell\times (k+m-\ell)}(\mathbb{C})^d,\qquad B'\in \operatorname{\mathrm{M}}_{m\times (k+m-\ell)}(\mathbb{C})^d,\qquad C'\in \operatorname{\mathrm{M}}_{k\times (k+m-\ell)}(\mathbb{C})^d, \\ A''\in \operatorname{\mathrm{M}}_{(k+m-\ell)\times \ell}(\mathbb{C})^d,\qquad B''\in \operatorname{\mathrm{M}}_{(k+m-\ell)\times m}(\mathbb{C})^d,\qquad C''\in \operatorname{\mathrm{M}}_{(k+m-\ell)\times k}(\mathbb{C})^d, \\ \end{align*} $$
$$ \begin{align*} A'\in \operatorname{\mathrm{M}}_{\ell\times (k+m-\ell)}(\mathbb{C})^d,\qquad B'\in \operatorname{\mathrm{M}}_{m\times (k+m-\ell)}(\mathbb{C})^d,\qquad C'\in \operatorname{\mathrm{M}}_{k\times (k+m-\ell)}(\mathbb{C})^d, \\ A''\in \operatorname{\mathrm{M}}_{(k+m-\ell)\times \ell}(\mathbb{C})^d,\qquad B''\in \operatorname{\mathrm{M}}_{(k+m-\ell)\times m}(\mathbb{C})^d,\qquad C''\in \operatorname{\mathrm{M}}_{(k+m-\ell)\times k}(\mathbb{C})^d, \\ \end{align*} $$
such that the matrices
 $$ \begin{align*} \Lambda \begin{pmatrix} Y & A' \\ Y' & B' \\ 0 & C' \end{pmatrix} ,\qquad \Lambda \begin{pmatrix} Y & Y'' &0 \\ A'' & B'' & C'' \end{pmatrix} \end{align*} $$
$$ \begin{align*} \Lambda \begin{pmatrix} Y & A' \\ Y' & B' \\ 0 & C' \end{pmatrix} ,\qquad \Lambda \begin{pmatrix} Y & Y'' &0 \\ A'' & B'' & C'' \end{pmatrix} \end{align*} $$
are invertible. Consequently there exists
![]() $\varepsilon \in \mathbb {C}\setminus \{0\}$
such that
$\varepsilon \in \mathbb {C}\setminus \{0\}$
such that
 $$ \begin{align*} \begin{pmatrix} \Lambda(Y) & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \end{pmatrix} +\varepsilon\begin{pmatrix} \begin{pmatrix}0 & 0 \\ 0 &0 \end{pmatrix} & \Lambda \begin{pmatrix} Y & Y'' &0 \\ A'' & B'' & C'' \end{pmatrix} \\ \Lambda \begin{pmatrix} Y & A' \\ Y' & B' \\ 0 & C' \end{pmatrix} & \begin{pmatrix}0 & 0 & 0\\ 0 &0 &0\\ 0 &0 &0\end{pmatrix} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \Lambda(Y) & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \\ 0 & 0 & 0 &0 & 0 \end{pmatrix} +\varepsilon\begin{pmatrix} \begin{pmatrix}0 & 0 \\ 0 &0 \end{pmatrix} & \Lambda \begin{pmatrix} Y & Y'' &0 \\ A'' & B'' & C'' \end{pmatrix} \\ \Lambda \begin{pmatrix} Y & A' \\ Y' & B' \\ 0 & C' \end{pmatrix} & \begin{pmatrix}0 & 0 & 0\\ 0 &0 &0\\ 0 &0 &0\end{pmatrix} \end{pmatrix} \end{align*} $$
is invertible; this matrix is similar to
 $$ \begin{align} \Lambda \begin{pmatrix} Y & 0 & \varepsilon Y & \varepsilon Y'' &0 \\ 0 & 0 & \varepsilon A''& \varepsilon B'' & \varepsilon C'' \\ \varepsilon Y & \varepsilon A' & 0 &0 &0 \\ \varepsilon Y' & \varepsilon B' & 0 &0 &0 \\ 0 & \varepsilon C' & 0 &0 &0 \end{pmatrix}. \end{align} $$
$$ \begin{align} \Lambda \begin{pmatrix} Y & 0 & \varepsilon Y & \varepsilon Y'' &0 \\ 0 & 0 & \varepsilon A''& \varepsilon B'' & \varepsilon C'' \\ \varepsilon Y & \varepsilon A' & 0 &0 &0 \\ \varepsilon Y' & \varepsilon B' & 0 &0 &0 \\ 0 & \varepsilon C' & 0 &0 &0 \end{pmatrix}. \end{align} $$
Thus the matrix (3.5) is invertible; its block structure and the linearity of
![]() $\Lambda $
imply that matrix (3.5) is invertible for every
$\Lambda $
imply that matrix (3.5) is invertible for every
![]() $\varepsilon \neq 0$
, so we can choose
$\varepsilon \neq 0$
, so we can choose
![]() $\varepsilon =1$
. After performing elementary row and column operations on matrix (3.5), we conclude that
$\varepsilon =1$
. After performing elementary row and column operations on matrix (3.5), we conclude that
 $$ \begin{align} \Lambda \begin{pmatrix} Y & Y'' & 0 & 0 &0 \\ Y' & 0 & - Y' & B' &0 \\ 0 & - Y'' & - Y & A' &0 \\ 0 & B'' & A''& 0 & C'' \\ 0 & 0 & 0 & C' &0 \end{pmatrix} \end{align} $$
$$ \begin{align} \Lambda \begin{pmatrix} Y & Y'' & 0 & 0 &0 \\ Y' & 0 & - Y' & B' &0 \\ 0 & - Y'' & - Y & A' &0 \\ 0 & B'' & A''& 0 & C'' \\ 0 & 0 & 0 & C' &0 \end{pmatrix} \end{align} $$
is invertible. So the lemma holds for
![]() $n= 2(m+k)$
.
$n= 2(m+k)$
.
Remark 3.4. It follows from the proofs of Proposition 3.2 and Theorem 3.3 that one can choose
 $$ \begin{align*} n= 2 \left(e^3 m^2+e m (2 e \ell-1)+\ell (e \ell-2)\right) \end{align*} $$
$$ \begin{align*} n= 2 \left(e^3 m^2+e m (2 e \ell-1)+\ell (e \ell-2)\right) \end{align*} $$
in Theorem 3.3. However, this is unlikely to be the minimal choice for n.
Let
![]() $\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
be the algebra of
$\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
be the algebra of
![]() $\mathbb {N}\times \mathbb {N}$
matrices over
$\mathbb {N}\times \mathbb {N}$
matrices over
![]() $\mathbb {C}$
that have only finitely many nonzero entries in each column; that is, elements of
$\mathbb {C}$
that have only finitely many nonzero entries in each column; that is, elements of
![]() $\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
can be viewed as operators on
$\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
can be viewed as operators on
![]() $\oplus ^{\mathbb {N}}\mathbb {C}$
. Given
$\oplus ^{\mathbb {N}}\mathbb {C}$
. Given
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
, let
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
, let
![]() $\operatorname {\mathrm {dom}}_{\infty } r$
be the set of tuples
$\operatorname {\mathrm {dom}}_{\infty } r$
be the set of tuples
![]() $X\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})^d$
such that
$X\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})^d$
such that
![]() $r(X)$
is well defined. If
$r(X)$
is well defined. If
![]() $(u,M,v)$
is a linear representation of r of size e, then
$(u,M,v)$
is a linear representation of r of size e, then
![]() $M(X)\in \operatorname {\mathrm {M}}_e(\operatorname {\mathrm {M}}_{\infty }(\mathbb {C}))$
is invertible for every
$M(X)\in \operatorname {\mathrm {M}}_e(\operatorname {\mathrm {M}}_{\infty }(\mathbb {C}))$
is invertible for every
![]() $X\in \operatorname {\mathrm {dom}}_{\infty } r$
by the definition of a linear representation adopted in this paper.
$X\in \operatorname {\mathrm {dom}}_{\infty } r$
by the definition of a linear representation adopted in this paper.
Proposition 3.5. Set
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
. If
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
. If
![]() $X\in \operatorname {\mathrm {H}}_{\ell }(\mathbb {C})^d$
and
$X\in \operatorname {\mathrm {H}}_{\ell }(\mathbb {C})^d$
and
![]() $Y\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
are such that
$Y\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
are such that
 $$ \begin{align*} \begin{pmatrix} X & \begin{matrix} Y^* & 0\end{matrix} \\ \begin{matrix} Y \\ 0\end{matrix} & W \end{pmatrix} \in \operatorname{\mathrm{dom}}_{\infty} r \end{align*} $$
$$ \begin{align*} \begin{pmatrix} X & \begin{matrix} Y^* & 0\end{matrix} \\ \begin{matrix} Y \\ 0\end{matrix} & W \end{pmatrix} \in \operatorname{\mathrm{dom}}_{\infty} r \end{align*} $$
for some
![]() $W\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})^d$
, then there exist
$W\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})^d$
, then there exist
![]() $n\ge m$
,
$n\ge m$
,
![]() $E\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})$
and
$E\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})$
and
![]() $Z\in \operatorname {\mathrm {H}}_{n}(\mathbb {C})^d$
such that
$Z\in \operatorname {\mathrm {H}}_{n}(\mathbb {C})^d$
such that
 $$ \begin{align*} \begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix} \in \operatorname{\mathrm{hdom}} r. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix} \in \operatorname{\mathrm{hdom}} r. \end{align*} $$
Proof. Let
![]() $(u,M,v)$
be a linear representation of r of size e. By assumption,
$(u,M,v)$
be a linear representation of r of size e. By assumption,
 $$ \begin{align*} M\begin{pmatrix} X & \begin{matrix} Y^* & 0\end{matrix} \\ \begin{matrix} Y \\ 0\end{matrix} & W \end{pmatrix} \end{align*} $$
$$ \begin{align*} M\begin{pmatrix} X & \begin{matrix} Y^* & 0\end{matrix} \\ \begin{matrix} Y \\ 0\end{matrix} & W \end{pmatrix} \end{align*} $$
is an invertible matrix over
![]() $\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
. If
$\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
. If
![]() $M=M_0+M_1x_1+\dotsb +M_dx_d$
, then the matrices
$M=M_0+M_1x_1+\dotsb +M_dx_d$
, then the matrices
 $$ \begin{align*} M_0\otimes \begin{pmatrix}I \\ 0\end{pmatrix}+ \sum_{j=1}^d M_0\otimes \begin{pmatrix}X_j \\ Y_j\end{pmatrix},\qquad M_0\otimes \begin{pmatrix}I & 0\end{pmatrix}+ \sum_{j=1}^d M_0\otimes \begin{pmatrix}X_j & Y_j^*\end{pmatrix}, \end{align*} $$
$$ \begin{align*} M_0\otimes \begin{pmatrix}I \\ 0\end{pmatrix}+ \sum_{j=1}^d M_0\otimes \begin{pmatrix}X_j \\ Y_j\end{pmatrix},\qquad M_0\otimes \begin{pmatrix}I & 0\end{pmatrix}+ \sum_{j=1}^d M_0\otimes \begin{pmatrix}X_j & Y_j^*\end{pmatrix}, \end{align*} $$
have full rank. Let
![]() $n\in \mathbb {N}$
be as in Theorem 3.3. Then there is
$n\in \mathbb {N}$
be as in Theorem 3.3. Then there is
![]() $Z'\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^{1+d}$
such that
$Z'\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^{1+d}$
such that
 $$ \begin{align} \det\left(M_0\otimes \begin{pmatrix} I & \begin{matrix} 0 & 0\end{matrix} \\ \begin{matrix} 0 \\ 0\end{matrix} & Z^{\prime}_0 \end{pmatrix}+ \sum_{j=1}^d M_0\otimes \begin{pmatrix} X_j & \begin{matrix} Y_j^* & 0\end{matrix} \\ \begin{matrix} Y_j \\ 0\end{matrix} & Z^{\prime}_j \end{pmatrix} \right)\neq0 \end{align} $$
$$ \begin{align} \det\left(M_0\otimes \begin{pmatrix} I & \begin{matrix} 0 & 0\end{matrix} \\ \begin{matrix} 0 \\ 0\end{matrix} & Z^{\prime}_0 \end{pmatrix}+ \sum_{j=1}^d M_0\otimes \begin{pmatrix} X_j & \begin{matrix} Y_j^* & 0\end{matrix} \\ \begin{matrix} Y_j \\ 0\end{matrix} & Z^{\prime}_j \end{pmatrix} \right)\neq0 \end{align} $$
is invertible. The set of all
![]() $Z'\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^{1+d}$
satisfying equation (3.7) is thus a nonempty Zariski open set in
$Z'\in \operatorname {\mathrm {M}}_{n}(\mathbb {C})^{1+d}$
satisfying equation (3.7) is thus a nonempty Zariski open set in
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})^{1+d}$
. Since the set of positive definite
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})^{1+d}$
. Since the set of positive definite
![]() $n\times n$
matrices is Zariski dense in
$n\times n$
matrices is Zariski dense in
![]() $\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
, there exists
$\operatorname {\mathrm {M}}_{n}(\mathbb {C})$
, there exists
![]() $Z'\in \operatorname {\mathrm {H}}_{n}(\mathbb {C})^{1+d}$
with
$Z'\in \operatorname {\mathrm {H}}_{n}(\mathbb {C})^{1+d}$
with
![]() $Z^{\prime }_0\succ 0$
such that equation (3.7) holds. If
$Z^{\prime }_0\succ 0$
such that equation (3.7) holds. If
 $Z_0' = E^{-1}E^{-*}$
, let
$Z_0' = E^{-1}E^{-*}$
, let
 $Z_j=EZ^{\prime }_jE^*$
for
$Z_j=EZ^{\prime }_jE^*$
for
![]() $1\le j \le d$
. Then
$1\le j \le d$
. Then
 $$ \begin{align*} M\begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix} \end{align*} $$
$$ \begin{align*} M\begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix} \end{align*} $$
is invertible, so
 $$ \begin{align*} \begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix} \in\operatorname{\mathrm{hdom}} r \end{align*} $$
$$ \begin{align*} \begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix} \in\operatorname{\mathrm{hdom}} r \end{align*} $$
by the definition of a linear representation.
We also record a non-Hermitian version of Proposition 3.5:
Proposition 3.6. Set
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
. If
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
. If
![]() $X\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
with
$X\in \operatorname {\mathrm {M}}_{m\times \ell }(\mathbb {C})^d$
with
![]() $\ell \le m$
is such that
$\ell \le m$
is such that
 $$ \begin{align*} \begin{pmatrix} \begin{matrix} X\\ 0\end{matrix} & W \end{pmatrix} \in \operatorname{\mathrm{dom}}_{\infty} r \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \begin{matrix} X\\ 0\end{matrix} & W \end{pmatrix} \in \operatorname{\mathrm{dom}}_{\infty} r \end{align*} $$
for some
![]() $W\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})^d$
, then there exist
$W\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})^d$
, then there exist
![]() $n\ge m$
and
$n\ge m$
and
 $Z\in \operatorname {\mathrm {M}}_{n\times (n-\ell )}(\mathbb {C})^d$
such that
$Z\in \operatorname {\mathrm {M}}_{n\times (n-\ell )}(\mathbb {C})^d$
such that
 $$ \begin{align*} \begin{pmatrix} \begin{matrix} X \\ 0\end{matrix} & Z \end{pmatrix} \in \operatorname{\mathrm{dom}} r. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \begin{matrix} X \\ 0\end{matrix} & Z \end{pmatrix} \in \operatorname{\mathrm{dom}} r. \end{align*} $$
4 Multiplication operators attached to a formal rational expression
In this section we assign a tuple of operators
![]() $\mathfrak {X}$
on a vector space of countable dimension to each formal rational expression r, so that r is well defined at
$\mathfrak {X}$
on a vector space of countable dimension to each formal rational expression r, so that r is well defined at
![]() $\mathfrak {X}$
and the finite-dimensional restrictions of
$\mathfrak {X}$
and the finite-dimensional restrictions of
![]() $\mathfrak {X}$
partially retain a certain multiplicative property.
$\mathfrak {X}$
partially retain a certain multiplicative property.
Fix an expression
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
. Without loss of generality, we assume that all the variables in x appear as subexpressions in r (otherwise we replace x by a suitable subtuple). Let
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
. Without loss of generality, we assume that all the variables in x appear as subexpressions in r (otherwise we replace x by a suitable subtuple). Let
Note that R is finite,
![]() $\operatorname {\mathrm {hdom}} q\supseteq \operatorname {\mathrm {hdom}} r$
for
$\operatorname {\mathrm {hdom}} q\supseteq \operatorname {\mathrm {hdom}} r$
for
![]() $q\in R$
, and
$q\in R$
, and
![]() $q\in R$
implies
$q\in R$
implies
![]() $q^*\in R$
. Let
$q^*\in R$
. Let
be the set of noncommutative rational functions represented by R. For
![]() $\ell \in \mathbb {N}$
we define finite-dimensional vector subspaces
$\ell \in \mathbb {N}$
we define finite-dimensional vector subspaces

Note that
![]() $V_{\ell }\subseteq V_{\ell +1}$
, since
$V_{\ell }\subseteq V_{\ell +1}$
, since
![]() $1\in R$
. Furthermore, let
$1\in R$
. Furthermore, let
![]() $V=\bigcup _{\ell \in \mathbb {N}} V_{\ell }$
. Then V is a finitely generated
$V=\bigcup _{\ell \in \mathbb {N}} V_{\ell }$
. Then V is a finitely generated
![]() $*$
-subalgebra of
$*$
-subalgebra of
. For
![]() $j=1,\dotsc ,d$
, we define operators
$j=1,\dotsc ,d$
, we define operators
Lemma 4.1. There is a linear functional
![]() $\phi :V\to \mathbb {C}$
such that
$\phi :V\to \mathbb {C}$
such that
![]() $\phi ({\mathbb{s}}^*)=\overline {\phi ({\mathbb{s}})}$
and
$\phi ({\mathbb{s}}^*)=\overline {\phi ({\mathbb{s}})}$
and
![]() $\phi ({\mathbb{s}}{\mathbb{s}}^*)>0$
for all
$\phi ({\mathbb{s}}{\mathbb{s}}^*)>0$
for all
![]() ${\mathbb{s}}\in V\setminus \{0\}$
.
${\mathbb{s}}\in V\setminus \{0\}$
.
Proof. For some
![]() $X\in \operatorname {\mathrm {hdom}} r$
, let
$X\in \operatorname {\mathrm {hdom}} r$
, let
![]() $m=\max _{q\in R}\lVert q(X)\rVert $
. Set
$m=\max _{q\in R}\lVert q(X)\rVert $
. Set
![]() $\ell \in \mathbb {N}$
. Since
$\ell \in \mathbb {N}$
. Since
![]() $V_{\ell }$
is finite-dimensional, there exist
$V_{\ell }$
is finite-dimensional, there exist
![]() $n_{\ell }\in \mathbb {N}$
and
$n_{\ell }\in \mathbb {N}$
and
![]() $X^{(\ell )}\in \operatorname {\mathrm {hdom}}_{n_{\ell }} r$
such that
$X^{(\ell )}\in \operatorname {\mathrm {hdom}}_{n_{\ell }} r$
such that
 $$ \begin{align} \max_{q\in R}\left\lVert q\left(X^{(\ell)}\right)\right\rVert\le m+1 \qquad \text{and}\qquad {\mathbb{s}}\left(X^{(\ell)}\right)\neq 0 \text{ for all } {\mathbb{s}}\in V_{\ell}\setminus\{0\}, \end{align} $$
$$ \begin{align} \max_{q\in R}\left\lVert q\left(X^{(\ell)}\right)\right\rVert\le m+1 \qquad \text{and}\qquad {\mathbb{s}}\left(X^{(\ell)}\right)\neq 0 \text{ for all } {\mathbb{s}}\in V_{\ell}\setminus\{0\}, \end{align} $$
by the local-global linear dependence principle for noncommutative rational functions (see [Reference VolčičVol18, Theorem 6.5] or [Reference Blekherman, Parrilo and ThomasBPT13, Corollary 8.87]). Define
 $$ \begin{align*} \phi:V\to\mathbb{C},\qquad \phi({\mathbb{s}})=\sum_{\ell=1}^{\infty} \frac{1}{\ell!\cdot n_{\ell}}\operatorname{\mathrm{tr}}\left({\mathbb{s}}\left(X^{(\ell)}\right) \right). \end{align*} $$
$$ \begin{align*} \phi:V\to\mathbb{C},\qquad \phi({\mathbb{s}})=\sum_{\ell=1}^{\infty} \frac{1}{\ell!\cdot n_{\ell}}\operatorname{\mathrm{tr}}\left({\mathbb{s}}\left(X^{(\ell)}\right) \right). \end{align*} $$
Since V is a
![]() $\mathbb {C}$
-algebra generated by
$\mathbb {C}$
-algebra generated by
![]() $\mathcal {R}$
, routine estimates show that
$\mathcal {R}$
, routine estimates show that
![]() $\phi $
is well defined. It is also clear that
$\phi $
is well defined. It is also clear that
![]() $\phi $
has the desired properties.
$\phi $
has the desired properties.
For the rest of the paper, fix a functional
![]() $\phi $
as in Lemma 4.1. Then
$\phi $
as in Lemma 4.1. Then
is an inner product on V. With respect to this inner product, we can inductively build an ordered orthogonal basis
![]() $\mathcal {B}$
of V with the property that
$\mathcal {B}$
of V with the property that
![]() $\mathcal {B}\cap V_{\ell }$
is a basis of
$\mathcal {B}\cap V_{\ell }$
is a basis of
![]() $V_{\ell }$
for every
$V_{\ell }$
for every
![]() $\ell \in \mathbb {N}$
.
$\ell \in \mathbb {N}$
.
Lemma 4.2. With respect to the inner product (4.2) and the ordered basis
![]() $\mathcal {B}$
as before, operators
$\mathcal {B}$
as before, operators
![]() $\mathfrak {X}_1,\dotsc ,\mathfrak {X}_d$
are represented by Hermitian matrices in
$\mathfrak {X}_1,\dotsc ,\mathfrak {X}_d$
are represented by Hermitian matrices in
![]() $\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
, and
$\operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
, and
![]() $\mathfrak {X}\in \operatorname {\mathrm {dom}}_{\infty } r$
.
$\mathfrak {X}\in \operatorname {\mathrm {dom}}_{\infty } r$
.
Proof. Since
for all
![]() ${\mathbb{s}}_1,{\mathbb{s}}_2\in V$
and
${\mathbb{s}}_1,{\mathbb{s}}_2\in V$
and
![]() $\mathfrak {X}_j(V_{\ell })\subseteq V_{\ell +1}$
for all
$\mathfrak {X}_j(V_{\ell })\subseteq V_{\ell +1}$
for all
![]() $\ell \in \mathbb {N}$
, it follows that the matrix representation of
$\ell \in \mathbb {N}$
, it follows that the matrix representation of
![]() $\mathfrak {X}_j$
with respect to
$\mathfrak {X}_j$
with respect to
![]() $\mathcal {B}$
is Hermitian and has only finitely many nonzero entries in each column and row. The rest follows inductively on the construction of r, since
$\mathcal {B}$
is Hermitian and has only finitely many nonzero entries in each column and row. The rest follows inductively on the construction of r, since
![]() $\mathfrak {X}_j$
are the left multiplication operators on V.
$\mathfrak {X}_j$
are the left multiplication operators on V.
Next we define a complexity-measuring function
![]() $\tau :\mathfrak {R}_{\mathbb {C}}(x)\to \mathbb {N}\cup \{0\}$
as in [Reference Klep, Pascoe and VolčičKPV17, Section 4]:
$\tau :\mathfrak {R}_{\mathbb {C}}(x)\to \mathbb {N}\cup \{0\}$
as in [Reference Klep, Pascoe and VolčičKPV17, Section 4]:
-
(i)
 $\tau (\alpha )=0$
for
$\tau (\alpha )=0$
for
 $\alpha \in \mathbb {C}$
;
$\alpha \in \mathbb {C}$
; -
(ii)
 $\tau \left (x_j\right )=1$
for
$\tau \left (x_j\right )=1$
for
 $1\le j\le d$
;
$1\le j\le d$
; -
(iii)
 $\tau (s_1+s_2)=\max \{\tau (s_1),\tau (s_2)\}$
for
$\tau (s_1+s_2)=\max \{\tau (s_1),\tau (s_2)\}$
for
 $s_1,s_2\in \mathfrak {R}_{\mathbb {C}}(x)$
;
$s_1,s_2\in \mathfrak {R}_{\mathbb {C}}(x)$
; -
(iv)
 $\tau (s_1s_2)=\tau (s_1)+\tau (s_2)$
for
$\tau (s_1s_2)=\tau (s_1)+\tau (s_2)$
for
 $s_1,s_2\in \mathfrak {R}_{\mathbb {C}}(x)$
;
$s_1,s_2\in \mathfrak {R}_{\mathbb {C}}(x)$
; -
(v)
 $\tau \left (s^{-1}\right )=2\tau (s)$
for
$\tau \left (s^{-1}\right )=2\tau (s)$
for
 $s,s^{-1}\in \mathfrak {R}_{\mathbb {C}}(x)$
.
$s,s^{-1}\in \mathfrak {R}_{\mathbb {C}}(x)$
.
Note that
![]() $\tau (s^*)=\tau (s)$
for all
$\tau (s^*)=\tau (s)$
for all
![]() $s\in \mathfrak {R}_{\mathbb {C}}(x)$
.
$s\in \mathfrak {R}_{\mathbb {C}}(x)$
.
Proposition 4.3. Let the notation be as before, and let U be a finite-dimensional Hilbert space containing
![]() $V_{\ell +1}$
. If X is a d-tuple of Hermitian operators on U such that
$V_{\ell +1}$
. If X is a d-tuple of Hermitian operators on U such that
![]() $X\in \operatorname {\mathrm {hdom}} r$
and
$X\in \operatorname {\mathrm {hdom}} r$
and
for
![]() $j=1,\dotsc ,d$
, then
$j=1,\dotsc ,d$
, then
![]() $X\in \operatorname {\mathrm {hdom}} q$
and
$X\in \operatorname {\mathrm {hdom}} q$
and
for every
![]() $q\in R$
and
$q\in R$
and
 $s\in \overbrace {R\dotsm R}^{\ell }$
satisfying
$s\in \overbrace {R\dotsm R}^{\ell }$
satisfying
![]() $2\tau (q)+\tau (s)\le \ell +2$
.
$2\tau (q)+\tau (s)\le \ell +2$
.
Proof. First note that for every
![]() $s\in R\dotsm R$
,
$s\in R\dotsm R$
,
 $$ \begin{align} \tau(s)\le k\quad \Rightarrow \quad s\in \overbrace{R\dotsm R}^k, \end{align} $$
$$ \begin{align} \tau(s)\le k\quad \Rightarrow \quad s\in \overbrace{R\dotsm R}^k, \end{align} $$
since
![]() $\tau ^{-1}(0)=\mathbb {C}$
and
$\tau ^{-1}(0)=\mathbb {C}$
and
![]() $R\cap \mathbb {C}=\{1\}$
. We prove equation (4.3) by induction on the construction of q. If
$R\cap \mathbb {C}=\{1\}$
. We prove equation (4.3) by induction on the construction of q. If
![]() $q=1$
, then equation (4.3) trivially holds, and if
$q=1$
, then equation (4.3) trivially holds, and if
![]() $q=x_j$
, then
$q=x_j$
, then
![]() $\tau (s)\le \ell $
, so equation (4.3) holds by formula (4.4). Next, if equation (4.3) holds for
$\tau (s)\le \ell $
, so equation (4.3) holds by formula (4.4). Next, if equation (4.3) holds for
![]() $q_1,q_2\in R$
such that
$q_1,q_2\in R$
such that
![]() $q_1+q_2\in R$
or
$q_1+q_2\in R$
or
![]() $q_1q_2\in R$
, then it also holds for the latter by the definition of
$q_1q_2\in R$
, then it also holds for the latter by the definition of
![]() $\tau $
and formula (4.4). Finally, suppose that equation (4.3) holds for
$\tau $
and formula (4.4). Finally, suppose that equation (4.3) holds for
![]() $q\in R\setminus \{1\}$
and assume
$q\in R\setminus \{1\}$
and assume
![]() $q^{-1}\in R$
. If
$q^{-1}\in R$
. If
![]() $2\tau \left (q^{-1}\right )+\tau (s)\le \ell +2$
, then
$2\tau \left (q^{-1}\right )+\tau (s)\le \ell +2$
, then
![]() $2\tau (q)+\left (\tau \left (q^{-1}\right )+\tau (s)\right )\le \ell +2$
. In particular,
$2\tau (q)+\left (\tau \left (q^{-1}\right )+\tau (s)\right )\le \ell +2$
. In particular,
![]() $\tau \left (q^{-1}s\right )\le \ell $
, and so
$\tau \left (q^{-1}s\right )\le \ell $
, and so
 $$ \begin{align*} q^{-1}s\in \overbrace{R\dotsm R}^{\ell} \end{align*} $$
$$ \begin{align*} q^{-1}s\in \overbrace{R\dotsm R}^{\ell} \end{align*} $$
by formula (4.4). Therefore,
by the induction hypothesis, and hence
![]() $q^{-1}(X){\mathbb{s}} =\mathbb{q}^{-1}{\mathbb{s}}$
, since
$q^{-1}(X){\mathbb{s}} =\mathbb{q}^{-1}{\mathbb{s}}$
, since
![]() $X\in \operatorname {\mathrm {hdom}} q^{-1}$
. Thus equation (4.3) holds for
$X\in \operatorname {\mathrm {hdom}} q^{-1}$
. Thus equation (4.3) holds for
![]() $q^{-1}$
.
$q^{-1}$
.
5 Positive noncommutative rational functions
In this section we prove various positivity statements for noncommutative rational functions. Let L be a Hermitian monic pencil of size e; that is,
![]() $L=I+H_1x_1+\dotsb +H_dx_d$
, with
$L=I+H_1x_1+\dotsb +H_dx_d$
, with
![]() $H_j\in \operatorname {\mathrm {H}}_{e}(\mathbb {C})$
. Then
$H_j\in \operatorname {\mathrm {H}}_{e}(\mathbb {C})$
. Then
 $$ \begin{align*} \mathcal{D}(L) = \bigcup_{n\in\mathbb{N}}\mathcal{D}_n(L), \qquad \text{where }\mathcal{D}_n(L)=\left\{X\in\operatorname{\mathrm{H}}_{n}(\mathbb{C})^d\colon L(X)\succeq 0 \right\}, \\[-15pt]\end{align*} $$
$$ \begin{align*} \mathcal{D}(L) = \bigcup_{n\in\mathbb{N}}\mathcal{D}_n(L), \qquad \text{where }\mathcal{D}_n(L)=\left\{X\in\operatorname{\mathrm{H}}_{n}(\mathbb{C})^d\colon L(X)\succeq 0 \right\}, \\[-15pt]\end{align*} $$
is a free spectrahedron. The main result of the paper is Theorem 5.2, which describes noncommutative rational functions that are positive semidefinite or undefined at each tuple in a given free spectrahedron
![]() $\mathcal {D}(L)$
. In particular, Theorem 5.2 generalises [Reference PascoePas18, Theorem 3.1] to noncommutative rational functions with singularities in
$\mathcal {D}(L)$
. In particular, Theorem 5.2 generalises [Reference PascoePas18, Theorem 3.1] to noncommutative rational functions with singularities in
![]() $\mathcal {D}(L)$
.
$\mathcal {D}(L)$
.
5.1 Rational convex Positivstellensatz
Let L be a Hermitian monic pencil of size e. To
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
we assign the finite set R, vector spaces
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
we assign the finite set R, vector spaces
![]() $V_{\ell }$
and operators
$V_{\ell }$
and operators
![]() $\mathfrak {X}_j$
as in Section 4. For
$\mathfrak {X}_j$
as in Section 4. For
![]() $\ell \in \mathbb {N}$
, we also define
$\ell \in \mathbb {N}$
, we also define
 $$ \begin{align*} &\qquad \qquad \qquad S_{\ell} = \{{\mathbb{s}}\in V_{\ell}\colon {\mathbb{s}}={\mathbb{s}}^* \}, \\ Q_{\ell} &= \left\{\sum_i {\mathbb{s}}_i^*{\mathbb{s}}_i+\sum_j \mathbb{v}_j^* L\mathbb{v}_j\colon {\mathbb{s}}_i \in V_{\ell}, \mathbb{v}_j\in V_{\ell}^e \right\}\subset S_{2\ell+1}. \\[-15pt]\end{align*} $$
$$ \begin{align*} &\qquad \qquad \qquad S_{\ell} = \{{\mathbb{s}}\in V_{\ell}\colon {\mathbb{s}}={\mathbb{s}}^* \}, \\ Q_{\ell} &= \left\{\sum_i {\mathbb{s}}_i^*{\mathbb{s}}_i+\sum_j \mathbb{v}_j^* L\mathbb{v}_j\colon {\mathbb{s}}_i \in V_{\ell}, \mathbb{v}_j\in V_{\ell}^e \right\}\subset S_{2\ell+1}. \\[-15pt]\end{align*} $$
Then
![]() $S_{\ell }$
is a real vector space and
$S_{\ell }$
is a real vector space and
![]() $Q_{\ell }$
is a convex cone. The proof of the following proposition is a rational modification of a common argument in free real algebraic geometry (compare [Reference Helton, Klep and McCulloughHKM12, Proposition 3.1] and [Reference Klep, Pascoe and VolčičKPV17, Proposition 4.1]). A convex cone is salient if it does not contain a line.
$Q_{\ell }$
is a convex cone. The proof of the following proposition is a rational modification of a common argument in free real algebraic geometry (compare [Reference Helton, Klep and McCulloughHKM12, Proposition 3.1] and [Reference Klep, Pascoe and VolčičKPV17, Proposition 4.1]). A convex cone is salient if it does not contain a line.
Proposition 5.1. The cone
![]() $Q_{\ell }$
is salient and closed in
$Q_{\ell }$
is salient and closed in
![]() $S_{2\ell +1}$
with the Euclidean topology.
$S_{2\ell +1}$
with the Euclidean topology.
Proof. As in the proof of Lemma 4.1, there exists
![]() $X\in \operatorname {\mathrm {hdom}} r$
such that
$X\in \operatorname {\mathrm {hdom}} r$
such that
Furthermore, we can choose X close enough to
![]() $0$
, so that
$0$
, so that
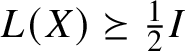 $L(X)\succeq \frac 12 I$
. Then clearly
$L(X)\succeq \frac 12 I$
. Then clearly
![]() ${\mathbb{s}}(X)\succeq 0$
for every
${\mathbb{s}}(X)\succeq 0$
for every
![]() ${\mathbb{s}}\in Q_{\ell }$
, so
${\mathbb{s}}\in Q_{\ell }$
, so
![]() $Q_{\ell }\cap -Q_{\ell }=\{0\}$
and thus
$Q_{\ell }\cap -Q_{\ell }=\{0\}$
and thus
![]() $Q_{\ell }$
is salient. Note that
$Q_{\ell }$
is salient. Note that
![]() $\lVert {\mathbb{s}}\rVert _{\bullet }= \lVert {\mathbb{s}}(X)\rVert $
is a norm on
$\lVert {\mathbb{s}}\rVert _{\bullet }= \lVert {\mathbb{s}}(X)\rVert $
is a norm on
![]() $V_{2\ell +1}$
. Also, the finite-dimensionality of
$V_{2\ell +1}$
. Also, the finite-dimensionality of
![]() $S_{2\ell +1}$
implies that every element of
$S_{2\ell +1}$
implies that every element of
![]() $Q_{\ell }$
can be written as a sum of
$Q_{\ell }$
can be written as a sum of
![]() $N=1+\dim S_{2\ell +1}$
elements of the form
$N=1+\dim S_{2\ell +1}$
elements of the form
by Carathéodory’s theorem [Reference BarvinokBar02, Theorem I.2.3]. Assume that a sequence
![]() $\{{\mathbb{r}}_n\}_n\subset Q_{\ell }$
converges to
$\{{\mathbb{r}}_n\}_n\subset Q_{\ell }$
converges to
![]() ${\mathbb{s}}\in S_{2\ell +1}$
. After restricting to a subsequence, we can assume that there is
${\mathbb{s}}\in S_{2\ell +1}$
. After restricting to a subsequence, we can assume that there is
![]() $0\le M\le N$
such that
$0\le M\le N$
such that
 $$ \begin{align*} {\mathbb{r}}_n=\sum_{i=1}^M {\mathbb{s}}_{n,i}^*{\mathbb{s}}_{n,i}+\sum_{j=M+1}^N \mathbb{v}_{n,j}^* L\mathbb{v}_{n,j} \\[-15pt]\end{align*} $$
$$ \begin{align*} {\mathbb{r}}_n=\sum_{i=1}^M {\mathbb{s}}_{n,i}^*{\mathbb{s}}_{n,i}+\sum_{j=M+1}^N \mathbb{v}_{n,j}^* L\mathbb{v}_{n,j} \\[-15pt]\end{align*} $$
for all
![]() $n\in \mathbb {N}$
. The definition of the norm
$n\in \mathbb {N}$
. The definition of the norm
![]() $\lVert \cdot \rVert _{\bullet }$
implies
$\lVert \cdot \rVert _{\bullet }$
implies
 $$ \begin{align*} \left\lVert{\mathbb{s}}_{n_i}\right\rVert_{\bullet}^2\le \lVert{\mathbb{r}}_n\rVert_{\bullet} \quad \text{and} \quad \max_{1\le i\le e}\left\lVert\left(\mathbb{v}_{n_j}\right)_i\right\rVert_{\bullet}^2\le 2\lVert{\mathbb{r}}_n\rVert_{\bullet}. \\[-15pt]\end{align*} $$
$$ \begin{align*} \left\lVert{\mathbb{s}}_{n_i}\right\rVert_{\bullet}^2\le \lVert{\mathbb{r}}_n\rVert_{\bullet} \quad \text{and} \quad \max_{1\le i\le e}\left\lVert\left(\mathbb{v}_{n_j}\right)_i\right\rVert_{\bullet}^2\le 2\lVert{\mathbb{r}}_n\rVert_{\bullet}. \\[-15pt]\end{align*} $$
In particular, the sequences
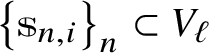 $\left \{{\mathbb{s}}_{n,i}\right \}_n\subset V_{\ell }$
for
$\left \{{\mathbb{s}}_{n,i}\right \}_n\subset V_{\ell }$
for
![]() $1\le i\le M$
and
$1\le i\le M$
and
 $\left \{\mathbb{v}_{n,j}\right \}_n\subset V_{\ell }^e$
for
$\left \{\mathbb{v}_{n,j}\right \}_n\subset V_{\ell }^e$
for
![]() $1\le j\le N$
are bounded. Hence, after restricting to subsequences, we may assume that they are convergent:
$1\le j\le N$
are bounded. Hence, after restricting to subsequences, we may assume that they are convergent:
![]() ${\mathbb{s}}_i=\lim _n{\mathbb{s}}_{n,i}$
for
${\mathbb{s}}_i=\lim _n{\mathbb{s}}_{n,i}$
for
![]() $1\le i\le M$
and
$1\le i\le M$
and
![]() $\mathbb{v}_j=\lim _n\mathbb{v}_{n,j}$
for
$\mathbb{v}_j=\lim _n\mathbb{v}_{n,j}$
for
![]() $1\le j\le N$
. Consequently, we have
$1\le j\le N$
. Consequently, we have
 $$ \begin{align*} {\mathbb{s}}=\lim_n{\mathbb{r}}_n= \sum_{i=1}^M {\mathbb{s}}_i^*{\mathbb{s}}_i+\sum_{j=M+1}^N \mathbb{v}_j^* L\mathbb{v}_j \in Q_{\ell}.\\[-50pt] \end{align*} $$
$$ \begin{align*} {\mathbb{s}}=\lim_n{\mathbb{r}}_n= \sum_{i=1}^M {\mathbb{s}}_i^*{\mathbb{s}}_i+\sum_{j=M+1}^N \mathbb{v}_j^* L\mathbb{v}_j \in Q_{\ell}.\\[-50pt] \end{align*} $$
We are now ready to prove the main result of this paper by combining a truncated GNS construction with extending matrix tuples into the domain of a rational expression as in Proposition 3.5.
Theorem 5.2 Rational convex Positivstellensatz
Let L be a Hermitian monic pencil and set
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
. If
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
. If
![]() $Q_{2\tau (r)+1}$
is as before, then
$Q_{2\tau (r)+1}$
is as before, then
![]() $r(X)\succeq 0$
for every
$r(X)\succeq 0$
for every
![]() $X\in \operatorname {\mathrm {hdom}} r\cap \mathcal {D}(L)$
if and only if
$X\in \operatorname {\mathrm {hdom}} r\cap \mathcal {D}(L)$
if and only if
![]() ${\mathbb{r}}\in Q_{2\tau (r)+1}$
.
${\mathbb{r}}\in Q_{2\tau (r)+1}$
.
Proof. Only the forward implication is nontrivial. Let
![]() $\ell =2\tau (r)-2$
. If
$\ell =2\tau (r)-2$
. If
![]() ${\mathbb{r}}\neq {\mathbb{r}}^*$
, then there exists
${\mathbb{r}}\neq {\mathbb{r}}^*$
, then there exists
![]() $X\in \operatorname {\mathrm {hdom}} r$
such that
$X\in \operatorname {\mathrm {hdom}} r$
such that
![]() ${\mathbb{r}}(X)\neq {\mathbb{r}}(X)^*$
. Thus we assume
${\mathbb{r}}(X)\neq {\mathbb{r}}(X)^*$
. Thus we assume
![]() ${\mathbb{r}}={\mathbb{r}}^*$
. Suppose that
${\mathbb{r}}={\mathbb{r}}^*$
. Suppose that
![]() ${\mathbb{r}}\notin Q_{\ell +3}$
. Since
${\mathbb{r}}\notin Q_{\ell +3}$
. Since
![]() $Q_{\ell +3}$
is a salient closed convex cone in
$Q_{\ell +3}$
is a salient closed convex cone in
![]() $S_{2\ell +7}$
by Proposition 5.1, there exists a linear functional
$S_{2\ell +7}$
by Proposition 5.1, there exists a linear functional
![]() $\lambda _0:S_{2\ell +7}\to \mathbb {R}$
such that
$\lambda _0:S_{2\ell +7}\to \mathbb {R}$
such that
![]() $\lambda _0(Q_{\ell +3}\setminus \{0\})=\mathbb {R}_{>0}$
and
$\lambda _0(Q_{\ell +3}\setminus \{0\})=\mathbb {R}_{>0}$
and
![]() $\lambda _0({\mathbb{r}})<0$
by the Hahn–Banach separation theorem [Reference BarvinokBar02, Theorem III.1.3]. We extend
$\lambda _0({\mathbb{r}})<0$
by the Hahn–Banach separation theorem [Reference BarvinokBar02, Theorem III.1.3]. We extend
![]() $\lambda _0$
to
$\lambda _0$
to
![]() $\lambda :V_{2\ell +7}\to \mathbb {C}$
as
$\lambda :V_{2\ell +7}\to \mathbb {C}$
as
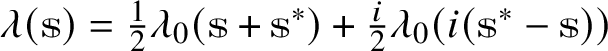 $\lambda ({\mathbb{s}})=\frac 12\lambda _0({\mathbb{s}}+{\mathbb{s}}^*)+\frac {i}{2}\lambda _0(i({\mathbb{s}}^*-{\mathbb{s}}))$
. Then
$\lambda ({\mathbb{s}})=\frac 12\lambda _0({\mathbb{s}}+{\mathbb{s}}^*)+\frac {i}{2}\lambda _0(i({\mathbb{s}}^*-{\mathbb{s}}))$
. Then
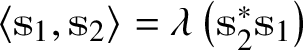 $\langle {\mathbb{s}}_1,{\mathbb{s}}_2\rangle =\lambda \left ({\mathbb{s}}_2^*{\mathbb{s}}_1\right )$
defines a scalar product on
$\langle {\mathbb{s}}_1,{\mathbb{s}}_2\rangle =\lambda \left ({\mathbb{s}}_2^*{\mathbb{s}}_1\right )$
defines a scalar product on
![]() $V_{\ell +3}$
. Recall that
$V_{\ell +3}$
. Recall that
![]() $\mathfrak {X}_j(V_{\ell +2})\subseteq V_{\ell +3}$
. Then for
$\mathfrak {X}_j(V_{\ell +2})\subseteq V_{\ell +3}$
. Then for
![]() ${\mathbb{s}}_1\in V_{\ell +1}$
and
${\mathbb{s}}_1\in V_{\ell +1}$
and
![]() ${\mathbb{s}}_2\in V_{\ell +2}$
,
${\mathbb{s}}_2\in V_{\ell +2}$
,
 $$ \begin{align} \left\langle \mathfrak{X}_j{\mathbb{s}}_1,{\mathbb{s}}_2\right\rangle = \lambda\big({\mathbb{s}}_2^*x_j{\mathbb{s}}_1\big) = \left\langle {\mathbb{s}}_1,\mathfrak{X}_j{\mathbb{s}}_2\right\rangle. \end{align} $$
$$ \begin{align} \left\langle \mathfrak{X}_j{\mathbb{s}}_1,{\mathbb{s}}_2\right\rangle = \lambda\big({\mathbb{s}}_2^*x_j{\mathbb{s}}_1\big) = \left\langle {\mathbb{s}}_1,\mathfrak{X}_j{\mathbb{s}}_2\right\rangle. \end{align} $$
Furthermore,
for all
![]() $\mathbb{v}\in V_{\ell +1}^e$
, where the canonical extension of
$\mathbb{v}\in V_{\ell +1}^e$
, where the canonical extension of
![]() $\langle \cdot ,\cdot \rangle $
to a scalar product on
$\langle \cdot ,\cdot \rangle $
to a scalar product on
![]() $\mathbb {C}^e\otimes V_{\ell +1}$
is considered.
$\mathbb {C}^e\otimes V_{\ell +1}$
is considered.
Let
![]() $\mathcal {B}$
be an ordered orthogonal basis of V with respect to the inner product
$\mathcal {B}$
be an ordered orthogonal basis of V with respect to the inner product
![]() $(\cdot ,\cdot )$
as in Section 4; recall that such a basis has the property that
$(\cdot ,\cdot )$
as in Section 4; recall that such a basis has the property that
![]() $\mathcal {B}\cap V_k$
is a basis for
$\mathcal {B}\cap V_k$
is a basis for
![]() $V_k$
for all
$V_k$
for all
![]() $k\in \mathbb {N}$
. Let
$k\in \mathbb {N}$
. Let
![]() $\mathcal {B}_0$
be an ordered orthogonal basis of
$\mathcal {B}_0$
be an ordered orthogonal basis of
![]() $V_{\ell +2}$
with respect to
$V_{\ell +2}$
with respect to
![]() $\langle \cdot ,\cdot \rangle $
that contains a basis for
$\langle \cdot ,\cdot \rangle $
that contains a basis for
![]() $V_{\ell +1}$
, and let
$V_{\ell +1}$
, and let
![]() $\mathcal {B}_1=\mathcal {B}\setminus V_{\ell +2}$
. If we identify operators
$\mathcal {B}_1=\mathcal {B}\setminus V_{\ell +2}$
. If we identify operators
![]() $\mathfrak {X}_j$
with their matrix representations relative to the ordered basis
$\mathfrak {X}_j$
with their matrix representations relative to the ordered basis
![]() $(\mathcal {B}_0,\mathcal {B}_1)$
of V, then
$(\mathcal {B}_0,\mathcal {B}_1)$
of V, then
![]() $\mathfrak {X}_j\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
are Hermitian matrices by Lemma 4.2 and equation (5.1).
$\mathfrak {X}_j\in \operatorname {\mathrm {M}}_{\infty }(\mathbb {C})$
are Hermitian matrices by Lemma 4.2 and equation (5.1).
Let
![]() $U_0$
be the orthogonal complement of
$U_0$
be the orthogonal complement of
![]() $V_{\ell +1}$
in
$V_{\ell +1}$
in
![]() $V_{\ell +2}$
relative to
$V_{\ell +2}$
relative to
![]() $\langle \cdot ,\cdot \rangle $
. Since
$\langle \cdot ,\cdot \rangle $
. Since
![]() $\mathfrak {X}_j(V_{\ell +1})\subseteq V_{\ell +2}$
, we can consider the restriction
$\mathfrak {X}_j(V_{\ell +1})\subseteq V_{\ell +2}$
, we can consider the restriction
![]() $\mathfrak {X}_j\rvert _{V_{\ell +1}}$
in a block form
$\mathfrak {X}_j\rvert _{V_{\ell +1}}$
in a block form
 $$ \begin{align*} \begin{pmatrix}X_j \\Y_j\end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix}X_j \\Y_j\end{pmatrix} \end{align*} $$
with respect to the decomposition
![]() $V_{\ell +2}=V_{\ell +1}\oplus U_0$
. Since
$V_{\ell +2}=V_{\ell +1}\oplus U_0$
. Since
![]() $\mathfrak {X}\in \operatorname {\mathrm {dom}}_{\infty } r$
, by Proposition 3.5 there exist a finite-dimensional vector space
$\mathfrak {X}\in \operatorname {\mathrm {dom}}_{\infty } r$
, by Proposition 3.5 there exist a finite-dimensional vector space
![]() $U_1$
, a scalar product on
$U_1$
, a scalar product on
![]() $V_{\ell +1}\oplus U_0\oplus U_1$
extending
$V_{\ell +1}\oplus U_0\oplus U_1$
extending
![]() $\langle \cdot ,\cdot \rangle $
, an operator E on
$\langle \cdot ,\cdot \rangle $
, an operator E on
![]() $U_0\oplus U_1$
and a d-tuple Z of Hermitian operators on
$U_0\oplus U_1$
and a d-tuple Z of Hermitian operators on
![]() $U_0\oplus U_1$
such that
$U_0\oplus U_1$
such that
 $$ \begin{align} \widetilde{X}:=\begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix}\in\operatorname{\mathrm{hdom}} r. \end{align} $$
$$ \begin{align} \widetilde{X}:=\begin{pmatrix} X & \begin{pmatrix} Y^* & 0\end{pmatrix}E^* \\ E\begin{pmatrix} Y \\ 0\end{pmatrix} & Z \end{pmatrix}\in\operatorname{\mathrm{hdom}} r. \end{align} $$
Since
![]() $\mathfrak {X}_j(V_{\ell })\subseteq V_{\ell +1}$
, we conclude that
$\mathfrak {X}_j(V_{\ell })\subseteq V_{\ell +1}$
, we conclude that
 $$ \begin{align} \widetilde{X}_j\rvert_{V_{\ell}}=\mathfrak{X}_j\rvert_{V_{\ell}}. \end{align} $$
$$ \begin{align} \widetilde{X}_j\rvert_{V_{\ell}}=\mathfrak{X}_j\rvert_{V_{\ell}}. \end{align} $$
Observe that for all but finitely many
![]() $\varepsilon _1,\varepsilon _2>0$
we can replace
$\varepsilon _1,\varepsilon _2>0$
we can replace
![]() $Z,E$
with
$Z,E$
with
![]() $\varepsilon _1 Z,\varepsilon _2 E$
and formula (5.3) still holds. By equation (5.2) we can thus assume that Z and E are close enough to
$\varepsilon _1 Z,\varepsilon _2 E$
and formula (5.3) still holds. By equation (5.2) we can thus assume that Z and E are close enough to
![]() $0$
so that
$0$
so that
![]() $L(\widetilde {X})\succeq 0$
. Finally, since equation (5.4) holds and
$L(\widetilde {X})\succeq 0$
. Finally, since equation (5.4) holds and
![]() $2\tau (r)+\tau (1)=\ell +2$
, Proposition 4.3 implies
$2\tau (r)+\tau (1)=\ell +2$
, Proposition 4.3 implies
 $$ \begin{align*} \left\langle r\left(\widetilde{X}\right)1,1\right\rangle = \langle {\mathbb{r}},1\rangle=\lambda({\mathbb{r}})<0. \end{align*} $$
$$ \begin{align*} \left\langle r\left(\widetilde{X}\right)1,1\right\rangle = \langle {\mathbb{r}},1\rangle=\lambda({\mathbb{r}})<0. \end{align*} $$
Therefore
![]() $\widetilde {X}\in \operatorname {\mathrm {hdom}} r\cap \mathcal {D}(L)$
and
$\widetilde {X}\in \operatorname {\mathrm {hdom}} r\cap \mathcal {D}(L)$
and
 $r\left (\widetilde {X}\right )$
is not positive semidefinite.
$r\left (\widetilde {X}\right )$
is not positive semidefinite.
Given a unital
![]() $*$
-algebra
$*$
-algebra
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $A=A^*\in \operatorname {\mathrm {M}}_{\ell }(\mathcal {A})$
, the quadratic module in
$A=A^*\in \operatorname {\mathrm {M}}_{\ell }(\mathcal {A})$
, the quadratic module in
![]() $\mathcal {A}$
generated by A is
$\mathcal {A}$
generated by A is
 $$ \begin{align*} \operatorname{\mathrm{QM}}_{\mathcal{A}}(A) = \left\{ \sum_j v_j^* (1\oplus A)v_j\colon v_j\in \mathcal{A}^{\ell+1} \right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{QM}}_{\mathcal{A}}(A) = \left\{ \sum_j v_j^* (1\oplus A)v_j\colon v_j\in \mathcal{A}^{\ell+1} \right\}. \end{align*} $$
Theorem 5.2 then in particular states that noncommutative rational functions that are positive semidefinite on a free spectrahedron
![]() $\mathcal {D}(L)$
belong to
$\mathcal {D}(L)$
belong to
![]() .
.
Remark 5.3. Set
![]() $r\in \mathfrak {R}_{\mathbb {C}}(x)$
and
$r\in \mathfrak {R}_{\mathbb {C}}(x)$
and
 $$ \begin{align*} n=2 \left(e^3 m^2+e m (2 e \ell-1)+\ell (e \ell-2)\right), \end{align*} $$
$$ \begin{align*} n=2 \left(e^3 m^2+e m (2 e \ell-1)+\ell (e \ell-2)\right), \end{align*} $$
where
![]() $\ell =\dim V_{2\tau (r)-1}$
,
$\ell =\dim V_{2\tau (r)-1}$
,
![]() $m=\dim V_{2\tau (r)}-\dim V_{2\tau (r)-1}$
and e is the size of a linear representation of r. If
$m=\dim V_{2\tau (r)}-\dim V_{2\tau (r)-1}$
and e is the size of a linear representation of r. If
![]() $r\not \succeq 0$
on
$r\not \succeq 0$
on
![]() $\operatorname {\mathrm {hdom}} r\cap \mathcal {D}(L)$
, then by Remark 3.4 and the proofs of Theorem 5.2 and Proposition 3.5 there exists
$\operatorname {\mathrm {hdom}} r\cap \mathcal {D}(L)$
, then by Remark 3.4 and the proofs of Theorem 5.2 and Proposition 3.5 there exists
![]() $X\in \operatorname {\mathrm {hdom}}_n r\cap \mathcal {D}_n(L)$
such that
$X\in \operatorname {\mathrm {hdom}}_n r\cap \mathcal {D}_n(L)$
such that
![]() $r(X)\not \succeq 0$
.
$r(X)\not \succeq 0$
.
The solution of Hilbert’s 17th problem for a free skew field is now as follows.
Corollary 5.4. Set
![]() . Then
. Then
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\operatorname {\mathrm {hdom}}{\mathbb{r}}$
if and only if
$\operatorname {\mathrm {hdom}}{\mathbb{r}}$
if and only if
for some
![]() with
with
![]() $\operatorname {\mathrm {hdom}}{\mathbb{r}}_i\supseteq \operatorname {\mathrm {hdom}}{\mathbb{r}}$
.
$\operatorname {\mathrm {hdom}}{\mathbb{r}}_i\supseteq \operatorname {\mathrm {hdom}}{\mathbb{r}}$
.
Proof. By Proposition 2.1 there exists
![]() $r\in {\mathbb{r}}$
such that
$r\in {\mathbb{r}}$
such that
![]() $\operatorname {\mathrm {hdom}} {\mathbb{r}}=\operatorname {\mathrm {hdom}} r$
. The corollary then follows directly from Theorem 5.2 applied to
$\operatorname {\mathrm {hdom}} {\mathbb{r}}=\operatorname {\mathrm {hdom}} r$
. The corollary then follows directly from Theorem 5.2 applied to
![]() $L=1$
, since the Hermitian domain of an element in
$L=1$
, since the Hermitian domain of an element in
![]() $V_{2\tau (r)}$
contains
$V_{2\tau (r)}$
contains
![]() $\operatorname {\mathrm {hdom}} {\mathbb{r}}$
.
$\operatorname {\mathrm {hdom}} {\mathbb{r}}$
.
Remark 5.5. Corollary 5.4 also indicates a subtle distinction between solutions of Hilbert’s 17th problem in the classical commutative context and in the free context. While every (commutative) positive rational function
![]() $\rho $
is a sum of squares of rational functions, in general one cannot choose summands that are defined on the whole real domain of the original function
$\rho $
is a sum of squares of rational functions, in general one cannot choose summands that are defined on the whole real domain of the original function
![]() $\rho $
. On the other hand, a positive noncommutative rational function always admits a sum-of-squares representation with terms defined on its Hermitian domain.
$\rho $
. On the other hand, a positive noncommutative rational function always admits a sum-of-squares representation with terms defined on its Hermitian domain.
For a possible future use, we describe noncommutative rational functions whose invertible evaluations have nonconstant signature; polynomials of this type were of interest in [Reference Helton, Klep and VolčičHKV20, Section 3.3].
Corollary 5.6. Set
![]() . The following are equivalent:
. The following are equivalent:
-
(i) There are
 $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
 $X,Y\in \operatorname {\mathrm {hdom}}_n {\mathbb{r}}$
such that
$X,Y\in \operatorname {\mathrm {hdom}}_n {\mathbb{r}}$
such that
 ${\mathbb{r}}(X),{\mathbb{r}}(Y)$
are invertible and have distinct signatures.
${\mathbb{r}}(X),{\mathbb{r}}(Y)$
are invertible and have distinct signatures. -
(ii) Neither
 ${\mathbb{r}}$
or
${\mathbb{r}}$
or
 $-{\mathbb{r}}$
equals
$-{\mathbb{r}}$
equals
 $\sum _i{\mathbb{r}}_i{\mathbb{r}}_i^*$
for some
$\sum _i{\mathbb{r}}_i{\mathbb{r}}_i^*$
for some
 .
.
Proof. (i)
![]() $\Rightarrow $
(ii) If
$\Rightarrow $
(ii) If
![]() $\pm {\mathbb{r}}=\sum _i{\mathbb{r}}_i{\mathbb{r}}_i^*$
, then
$\pm {\mathbb{r}}=\sum _i{\mathbb{r}}_i{\mathbb{r}}_i^*$
, then
![]() $\pm {\mathbb{r}}(X)\succeq 0$
for all
$\pm {\mathbb{r}}(X)\succeq 0$
for all
![]() $X\in \operatorname {\mathrm {hdom}}{\mathbb{r}}$
.
$X\in \operatorname {\mathrm {hdom}}{\mathbb{r}}$
.
(ii)
![]() $\Rightarrow $
(i) Let
$\Rightarrow $
(i) Let
![]() $\mathcal {O}_n=\operatorname {\mathrm {hdom}}_n{\mathbb{r}}\cap \operatorname {\mathrm {hdom}}_n{\mathbb{r}}^{-1}$
. By Remark 2.5 there is
$\mathcal {O}_n=\operatorname {\mathrm {hdom}}_n{\mathbb{r}}\cap \operatorname {\mathrm {hdom}}_n{\mathbb{r}}^{-1}$
. By Remark 2.5 there is
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
![]() $\mathcal {O}_n\neq \emptyset $
for all
$\mathcal {O}_n\neq \emptyset $
for all
![]() $n\ge n_0$
. Suppose that
$n\ge n_0$
. Suppose that
![]() ${\mathbb{r}}$
has constant signature on
${\mathbb{r}}$
has constant signature on
![]() $\mathcal {O}_n$
for each
$\mathcal {O}_n$
for each
![]() $n\ge n_0$
–that is,
$n\ge n_0$
–that is,
![]() ${\mathbb{r}}(X)$
has
${\mathbb{r}}(X)$
has
![]() $\pi _n$
positive eigenvalues for every
$\pi _n$
positive eigenvalues for every
![]() $X\in \mathcal {O}_n$
. Since
$X\in \mathcal {O}_n$
. Since
![]() $\mathcal {O}_k\oplus \mathcal {O}_{\ell }\subset \mathcal {O}_{k+\ell }$
for all
$\mathcal {O}_k\oplus \mathcal {O}_{\ell }\subset \mathcal {O}_{k+\ell }$
for all
![]() $k,\ell \in \mathbb {N}$
, we have
$k,\ell \in \mathbb {N}$
, we have
for all
![]() $m,n\ge n_0$
. If
$m,n\ge n_0$
. If
![]() $\pi _{n'}=n'$
for some
$\pi _{n'}=n'$
for some
![]() $n'\ge n_0$
, then
$n'\ge n_0$
, then
![]() $\pi _n=n$
for all
$\pi _n=n$
for all
![]() $n\ge n_0$
by equation (5.5), so
$n\ge n_0$
by equation (5.5), so
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\mathcal {O}_n$
for every n. Thus
$\mathcal {O}_n$
for every n. Thus
![]() ${\mathbb{r}}=\sum _i{\mathbb{r}}_i{\mathbb{r}}_i^*$
by Theorem 5.2. An analogous conclusion holds if
${\mathbb{r}}=\sum _i{\mathbb{r}}_i{\mathbb{r}}_i^*$
by Theorem 5.2. An analogous conclusion holds if
![]() $\pi _{n'}=0$
for some
$\pi _{n'}=0$
for some
![]() $n'\ge n_0$
. However, equation (5.5) excludes any alternative: if
$n'\ge n_0$
. However, equation (5.5) excludes any alternative: if
![]() $n_0\le m< n$
and n is a prime number, then
$n_0\le m< n$
and n is a prime number, then
![]() $0<\pi _n<n$
contradicts equation (5.5).
$0<\pi _n<n$
contradicts equation (5.5).
5.2 Positivity and invariants
Let G be a subgroup of the unitary group
![]() $\operatorname {U}_d(\mathbb {C})$
. The action of G on
$\operatorname {U}_d(\mathbb {C})$
. The action of G on
![]() $\mathbb {C}^d$
induces a linear action of G on
$\mathbb {C}^d$
induces a linear action of G on
![]() . If G is finite and solvable, then the subfield of G-invariants
. If G is finite and solvable, then the subfield of G-invariants
![]() is finitely generated [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Theorem 1.1], and in many cases again a free skew field [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Theorem 1.3]. Furthermore, we can now extend [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Corollary 6.6] to invariant noncommutative rational functions with singularities.
is finitely generated [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Theorem 1.1], and in many cases again a free skew field [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Theorem 1.3]. Furthermore, we can now extend [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Corollary 6.6] to invariant noncommutative rational functions with singularities.
Corollary 5.7. Let
![]() $G\subset \operatorname {U}_d(\mathbb {C})$
be a finite solvable group. Then there exists
$G\subset \operatorname {U}_d(\mathbb {C})$
be a finite solvable group. Then there exists
with the following property: if
and L is a Hermitian monic pencil of size e, then
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\operatorname {\mathrm {hdom}} {\mathbb{r}}\cap \mathcal {D}(L)$
if and only if
$\operatorname {\mathrm {hdom}} {\mathbb{r}}\cap \mathcal {D}(L)$
if and only if
, where

Proof. Combine [Reference Klep, Pascoe, Podlogar and VolčičKPPV20, Corollary 6.4] and Theorem 5.2.
5.3 Real free skew field and other variations
In this subsection we explain how the preceding results apply to real free skew fields and their symmetric evaluations, and to another natural involution on a free skew field.
Corollary 5.8 real version of Theorem 5.2
Let L be a symmetric monic pencil of size e and set
![]() . Then
. Then
![]() ${\mathbb{r}}(X)\succeq 0$
for every
${\mathbb{r}}(X)\succeq 0$
for every
![]() $X\in \operatorname {\mathrm {hdom}} {\mathbb{r}}\cap \mathcal {D}(L)$
if and only if
$X\in \operatorname {\mathrm {hdom}} {\mathbb{r}}\cap \mathcal {D}(L)$
if and only if
![]() .
.
Proof. If
![]() and
and
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\operatorname {\mathrm {hdom}}{\mathbb{r}}\cap \mathcal {D}(L)$
, then
$\operatorname {\mathrm {hdom}}{\mathbb{r}}\cap \mathcal {D}(L)$
, then
![]() by Theorem 5.2, because the complex vector spaces
by Theorem 5.2, because the complex vector spaces
![]() $V_{\ell }$
are spanned with functions given by subexpressions of some
$V_{\ell }$
are spanned with functions given by subexpressions of some
![]() $r\in {\mathbb{r}}$
, and we can choose r in which only real scalars appear. For
$r\in {\mathbb{r}}$
, and we can choose r in which only real scalars appear. For
![]() we define
we define
 $\text {re} ({\mathbb{s}}) = \frac 12\left ({\mathbb{s}}+\overline {{\mathbb{s}}}\right )$
and
$\text {re} ({\mathbb{s}}) = \frac 12\left ({\mathbb{s}}+\overline {{\mathbb{s}}}\right )$
and
 $\text {im} ({\mathbb{s}}) = \frac {i}{2}\left (\overline {{\mathbb{s}}}-{\mathbb{s}}\right )$
in
$\text {im} ({\mathbb{s}}) = \frac {i}{2}\left (\overline {{\mathbb{s}}}-{\mathbb{s}}\right )$
in
![]() . If
. If
 $$ \begin{align*} {\mathbb{r}}=\sum_j {\mathbb{s}}_j^*{\mathbb{s}}_j+\sum_k \mathbb{v}_k^* L\mathbb{v}_k \end{align*} $$
$$ \begin{align*} {\mathbb{r}}=\sum_j {\mathbb{s}}_j^*{\mathbb{s}}_j+\sum_k \mathbb{v}_k^* L\mathbb{v}_k \end{align*} $$
for
![]() and
and
![]() , then
, then
 $$ \begin{align*} {\mathbb{r}}=\text{re}({\mathbb{r}})=\sum_j \left(\text{re}\left({\mathbb{s}}_j\right)^*\text{re}\left({\mathbb{s}}_j\right)+\text{im}\left({\mathbb{s}}_j\right)^*\text{im}\left({\mathbb{s}}_j\right)\right) +\sum_k \left(\text{re}(\mathbb{v}_k)^*L\,\text{re}(\mathbb{v}_k)+\text{im}(\mathbb{v}_k)^*L\,\text{im}(\mathbb{v}_k)\right), \end{align*} $$
$$ \begin{align*} {\mathbb{r}}=\text{re}({\mathbb{r}})=\sum_j \left(\text{re}\left({\mathbb{s}}_j\right)^*\text{re}\left({\mathbb{s}}_j\right)+\text{im}\left({\mathbb{s}}_j\right)^*\text{im}\left({\mathbb{s}}_j\right)\right) +\sum_k \left(\text{re}(\mathbb{v}_k)^*L\,\text{re}(\mathbb{v}_k)+\text{im}(\mathbb{v}_k)^*L\,\text{im}(\mathbb{v}_k)\right), \end{align*} $$
and so
![]() .
.
Given
![]() , one might prefer to consider only the tuples of real symmetric matrices in the domain of
, one might prefer to consider only the tuples of real symmetric matrices in the domain of
![]() ${\mathbb{r}}$
, and not the whole
${\mathbb{r}}$
, and not the whole
![]() $\operatorname {\mathrm {hdom}} {\mathbb{r}}$
. Since there exist
$\operatorname {\mathrm {hdom}} {\mathbb{r}}$
. Since there exist
![]() $*$
-embeddings
$*$
-embeddings
![]() $\operatorname {\mathrm {M}}_n(\mathbb {C})\hookrightarrow \operatorname {\mathrm {M}}_{2n}(\mathbb {R})$
, evaluations on tuples of real symmetric
$\operatorname {\mathrm {M}}_n(\mathbb {C})\hookrightarrow \operatorname {\mathrm {M}}_{2n}(\mathbb {R})$
, evaluations on tuples of real symmetric
![]() $2n\times 2n$
matrices carry at least as much information as evaluations on tuples of Hermitian
$2n\times 2n$
matrices carry at least as much information as evaluations on tuples of Hermitian
![]() $n\times n$
matrices. Consequently, all dimension-independent statements in this paper also hold if only symmetric tuples are considered. However, it is worth mentioning that for
$n\times n$
matrices. Consequently, all dimension-independent statements in this paper also hold if only symmetric tuples are considered. However, it is worth mentioning that for
![]() , it can happen that
, it can happen that
![]() $\operatorname {\mathrm {dom}}_n {\mathbb{r}}$
contains no tuples of symmetric matrices for all odd n–for example, if
$\operatorname {\mathrm {dom}}_n {\mathbb{r}}$
contains no tuples of symmetric matrices for all odd n–for example, if
![]() ${\mathbb{r}}=(x_1x_2-x_2x_1)^{-1}$
.
${\mathbb{r}}=(x_1x_2-x_2x_1)^{-1}$
.
Another commonly considered free skew field with involution is
![]() , generated with
, generated with
![]() $2d$
variables
$2d$
variables
![]() $x_1,\dotsc ,x_d,x_1^*,\dotsc ,x_d^*$
, which is endowed with the involution
$x_1,\dotsc ,x_d,x_1^*,\dotsc ,x_d^*$
, which is endowed with the involution
![]() $*$
that swaps
$*$
that swaps
![]() $x_j$
and
$x_j$
and
![]() $x_j^*$
. Elements of
$x_j^*$
. Elements of
![]() can be evaluated on d-tuples of complex matrices. The results of this paper also directly apply to
can be evaluated on d-tuples of complex matrices. The results of this paper also directly apply to
![]() and such evaluations, because
and such evaluations, because
![]() is freely generated by elements
is freely generated by elements
 $\frac 12\left (x_j+x_j^*\right ),\frac {i}{2}\left (x_j^*-x_j\right )$
, which are fixed by
$\frac 12\left (x_j+x_j^*\right ),\frac {i}{2}\left (x_j^*-x_j\right )$
, which are fixed by
![]() $*$
. Finally, as in Corollary 5.8 we see that a suitable analogue of Theorem 5.2 also holds for
$*$
. Finally, as in Corollary 5.8 we see that a suitable analogue of Theorem 5.2 also holds for
![]() and evaluations on d-tuples of real matrices.
and evaluations on d-tuples of real matrices.
5.4 Examples of nonconvex Positivstellensätze
Given
![]() , let
, let
 $$ \begin{align*} \mathcal{D}(\mathbb{m}) = \bigcup_{n\in\mathbb{N}}\mathcal{D}_n(\mathbb{m}), \qquad \text{where }\mathcal{D}_n(\mathbb{m})=\{X\in\operatorname{\mathrm{hdom}}_n \mathbb{m} \colon \mathbb{m}(X)\succeq0 \}, \end{align*} $$
$$ \begin{align*} \mathcal{D}(\mathbb{m}) = \bigcup_{n\in\mathbb{N}}\mathcal{D}_n(\mathbb{m}), \qquad \text{where }\mathcal{D}_n(\mathbb{m})=\{X\in\operatorname{\mathrm{hdom}}_n \mathbb{m} \colon \mathbb{m}(X)\succeq0 \}, \end{align*} $$
be its positivity domain. Here, the domain of
![]() $\mathbb{m}$
is the intersection of domains of its entries.
$\mathbb{m}$
is the intersection of domains of its entries.
Proposition 5.9. Set
![]() and assume there exist a Hermitian monic pencil L of size
and assume there exist a Hermitian monic pencil L of size
![]() $e\ge \ell $
, an
$e\ge \ell $
, an
![]() $*$
-automorphism
$*$
-automorphism
![]() $\varphi $
of
$\varphi $
of
![]() , and
, and
![]() such that
such that
If
![]() , then
, then
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\operatorname {\mathrm {hdom}}{\mathbb{r}}\cap \mathcal {D}(\mathbb{m})$
if and only if
$\operatorname {\mathrm {hdom}}{\mathbb{r}}\cap \mathcal {D}(\mathbb{m})$
if and only if
![]() .
.
Proof. Equation (5.6), Remark 2.5 and the convexity of
![]() $\mathcal {D}_n(L)$
imply that the sets
$\mathcal {D}_n(L)$
imply that the sets
![]() $\mathcal {D}_n(\varphi (\mathbb{m}))$
and
$\mathcal {D}_n(\varphi (\mathbb{m}))$
and
![]() $\mathcal {D}_n(\mathbb{m})$
have the same closures as their interiors in the Euclidean topology for all but finitely many n. Therefore, by Theorem 5.2 and Equation (5.6),
$\mathcal {D}_n(\mathbb{m})$
have the same closures as their interiors in the Euclidean topology for all but finitely many n. Therefore, by Theorem 5.2 and Equation (5.6),

The following example presents a family of quadratic noncommutative polynomials
![]() $q=q^*\in \mathbb {C}\!\mathop {<}\! x,x^*\!\mathop {>}$
that admit a rational Positivstellensatz on their (not necessarily convex) positivity domains
$q=q^*\in \mathbb {C}\!\mathop {<}\! x,x^*\!\mathop {>}$
that admit a rational Positivstellensatz on their (not necessarily convex) positivity domains
![]() $\mathcal {D}(q)=\{X\colon q(X,X^*)\succeq 0 \}$
:
$\mathcal {D}(q)=\{X\colon q(X,X^*)\succeq 0 \}$
:
Example 5.10. Given a linearly independent set
![]() $\{a_0,\dotsc ,a_n\}\subset \operatorname {\mathrm {span}}_{\mathbb {C}}\{1,x_1,\dotsc ,x_d\}$
, let
$\{a_0,\dotsc ,a_n\}\subset \operatorname {\mathrm {span}}_{\mathbb {C}}\{1,x_1,\dotsc ,x_d\}$
, let
One might say that q is a hereditary quadratic polynomial of positive signature
![]() $1$
. Note that
$1$
. Note that
![]() $\mathcal {D}_1(q)$
is not convex if
$\mathcal {D}_1(q)$
is not convex if
![]() $a_0\notin \mathbb {C}$
. Since
$a_0\notin \mathbb {C}$
. Since
![]() $a_0,\dotsc ,a_n$
are linearly independent affine polynomials in
$a_0,\dotsc ,a_n$
are linearly independent affine polynomials in
![]() $\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
(and in particular
$\mathbb {C}\!\mathop {<}\! x\!\mathop {>}$
(and in particular
![]() $n\le d$
), there exists a linear fractional automorphism
$n\le d$
), there exists a linear fractional automorphism
![]() $\varphi $
on
$\varphi $
on
![]() such that
such that
 $\varphi ^{-1}\left (x_j\right )=a_ja_0^{-1}$
for
$\varphi ^{-1}\left (x_j\right )=a_ja_0^{-1}$
for
![]() $1\le j \le n$
. We extend
$1\le j \le n$
. We extend
![]() $\varphi $
uniquely to an
$\varphi $
uniquely to an
![]() $*$
-automorphism on
$*$
-automorphism on
![]() . Then
. Then
 $$ \begin{align*} \varphi(a_0)^{-*}\varphi(q)\varphi(a_0)^{-1}=1-x_1^*x_1-\dotsb-x_n^*x_n, \end{align*} $$
$$ \begin{align*} \varphi(a_0)^{-*}\varphi(q)\varphi(a_0)^{-1}=1-x_1^*x_1-\dotsb-x_n^*x_n, \end{align*} $$
and thus
![]() $\varphi (q)\oplus I_n=A^*LA$
, where
$\varphi (q)\oplus I_n=A^*LA$
, where
 $$ \begin{align*} L=\begin{pmatrix} 1 & x_1^* & \cdots & x_n^* \\ x_1 & \ddots & & \\ \vdots & & \ddots & \\ x_n & & & 1 \end{pmatrix}, \qquad A=\begin{pmatrix} \varphi(a_0) & & & \\ -x_1 & 1 & & \\ \vdots & & \ddots & \\ -x_n & & & 1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} L=\begin{pmatrix} 1 & x_1^* & \cdots & x_n^* \\ x_1 & \ddots & & \\ \vdots & & \ddots & \\ x_n & & & 1 \end{pmatrix}, \qquad A=\begin{pmatrix} \varphi(a_0) & & & \\ -x_1 & 1 & & \\ \vdots & & \ddots & \\ -x_n & & & 1 \end{pmatrix}. \end{align*} $$
Therefore
![]() ${\mathbb{r}}\succeq 0$
on
${\mathbb{r}}\succeq 0$
on
![]() $\operatorname {\mathrm {hdom}}{\mathbb{r}}\cap \mathcal {D}(q)$
if and only if
$\operatorname {\mathrm {hdom}}{\mathbb{r}}\cap \mathcal {D}(q)$
if and only if
![]() for every
for every
![]() , by Proposition 5.9.
, by Proposition 5.9.
For example, the polynomial
![]() $x_1^*x_1-1$
is of the type discussed, and thus admits a rational Positivstellensatz. In particular,
$x_1^*x_1-1$
is of the type discussed, and thus admits a rational Positivstellensatz. In particular,

On the other hand, we claim that
 $x_1x_1^*-1\notin \operatorname {\mathrm {QM}}_{\mathbb {C}\!\mathop {<}\! x,x^*\!\mathop {>}}\left (x_1^*x_1-1\right )$
(compare [Reference Helton and McCulloughHM04, Example 4]). If
$x_1x_1^*-1\notin \operatorname {\mathrm {QM}}_{\mathbb {C}\!\mathop {<}\! x,x^*\!\mathop {>}}\left (x_1^*x_1-1\right )$
(compare [Reference Helton and McCulloughHM04, Example 4]). If
![]() $x_1x_1^*-1$
were an element of
$x_1x_1^*-1$
were an element of
![]() $\operatorname {\mathrm {QM}}_{\mathbb {C}\!\mathop {<}\! x,x^*\!\mathop {>}}(x_1^*x_1-1)$
, then the implication
$\operatorname {\mathrm {QM}}_{\mathbb {C}\!\mathop {<}\! x,x^*\!\mathop {>}}(x_1^*x_1-1)$
, then the implication
would be valid for every operator S on an infinite-dimensional Hilbert space; however, it fails if S is the forward shift operator on
![]() $\ell ^2(\mathbb {N})$
. A different Positivstellensatz (polynomial, but with a slack variable) for hereditary quadratic polynomials is given in [Reference Helton, Klep and VolčičHKV20, Corollary 4.6].
$\ell ^2(\mathbb {N})$
. A different Positivstellensatz (polynomial, but with a slack variable) for hereditary quadratic polynomials is given in [Reference Helton, Klep and VolčičHKV20, Corollary 4.6].
5.5 Eigenvalue optimisation
Theorem 5.2 is also essential for optimising noncommutative rational functions. Namely, it implies that finding the eigenvalue supremum or infimum of a noncommutative rational function on a free spectrahedron is equivalent to solving a semidefinite program [Reference Blekherman, Parrilo and ThomasBPT13]. This equivalence was stated in [Reference Klep, Pascoe and VolčičKPV17, Section 5.2.1] for regular noncommutative rational functions; the novelty is that Theorem 5.2 now confirms its validity for noncommutative rational functions with singularities.
Let L be a Hermitian monic pencil of size e, and set
![]() . Suppose we are interested in
. Suppose we are interested in
 $$ \begin{align*} \mu_* = \sup_{X\in\operatorname{\mathrm{hdom}} {\mathbb{r}}\cap \mathcal{D}(L)}\big[\text{maximal eigenvalue of }{\mathbb{r}}(X)\big]. \end{align*} $$
$$ \begin{align*} \mu_* = \sup_{X\in\operatorname{\mathrm{hdom}} {\mathbb{r}}\cap \mathcal{D}(L)}\big[\text{maximal eigenvalue of }{\mathbb{r}}(X)\big]. \end{align*} $$
Choose some
![]() $r\in {\mathbb{r}}$
(the simpler representative the better) and let
$r\in {\mathbb{r}}$
(the simpler representative the better) and let
![]() $\ell =2\tau (r)+1$
. Theorem 5.2 then implies that
$\ell =2\tau (r)+1$
. Theorem 5.2 then implies that
 $$ \begin{align} \mu_* = \inf\left\{ \mu\in\mathbb{R}\colon \mu-{\mathbb{r}}= \sum_{i=1}^M {\mathbb{s}}_i^*{\mathbb{s}}_i+\sum_{j=1}^N \mathbb{v}_j^* L\mathbb{v}_j\colon {\mathbb{s}}_i \in V_{\ell}, \mathbb{v}_j\in V_{\ell}^e \right\}, \end{align} $$
$$ \begin{align} \mu_* = \inf\left\{ \mu\in\mathbb{R}\colon \mu-{\mathbb{r}}= \sum_{i=1}^M {\mathbb{s}}_i^*{\mathbb{s}}_i+\sum_{j=1}^N \mathbb{v}_j^* L\mathbb{v}_j\colon {\mathbb{s}}_i \in V_{\ell}, \mathbb{v}_j\in V_{\ell}^e \right\}, \end{align} $$
where we can take
![]() $M=\dim S_{2\ell }+1$
and
$M=\dim S_{2\ell }+1$
and
![]() $N=\dim S_{2\ell +1}+1$
by Carathéodory’s theorem [Reference BarvinokBar02, Theorem I.2.3]. The right-hand side of equation (5.7) can be stated as a semidefinite program [Reference Wolkowicz, Saigal and VandenbergheWSV00, Reference Blekherman, Parrilo and ThomasBPT13]. Concretely, to determine the global (no L) eigenvalue supremum of
$N=\dim S_{2\ell +1}+1$
by Carathéodory’s theorem [Reference BarvinokBar02, Theorem I.2.3]. The right-hand side of equation (5.7) can be stated as a semidefinite program [Reference Wolkowicz, Saigal and VandenbergheWSV00, Reference Blekherman, Parrilo and ThomasBPT13]. Concretely, to determine the global (no L) eigenvalue supremum of
![]() ${\mathbb{r}}$
, one solves the semidefinite program
${\mathbb{r}}$
, one solves the semidefinite program
 $$ \begin{align} \begin{array}{ll} \min\limits_H & \quad \mu \\ \text{subject to} & \quad \mu-{\mathbb{r}} = \vec{w}^*H\vec{w}, \\ & \quad H\succeq 0, \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \min\limits_H & \quad \mu \\ \text{subject to} & \quad \mu-{\mathbb{r}} = \vec{w}^*H\vec{w}, \\ & \quad H\succeq 0, \end{array} \end{align} $$
where H is a
![]() $(\dim V_{\ell })\times (\dim V_{\ell })$
Hermitian matrix and
$(\dim V_{\ell })\times (\dim V_{\ell })$
Hermitian matrix and
![]() $\vec {w}$
is a vectorised basis of
$\vec {w}$
is a vectorised basis of
![]() $V_{\ell }$
. For constrained eigenvalue optimisation (L is present), one can set up a similar semidefinite program using localising matrices [Reference Burgdorf, Klep and PovhBKP16, Definition 1.41].
$V_{\ell }$
. For constrained eigenvalue optimisation (L is present), one can set up a similar semidefinite program using localising matrices [Reference Burgdorf, Klep and PovhBKP16, Definition 1.41].
6 More on domains
In this section we prove two new results on (Hermitian) domains. One of them is the aforementioned Proposition 2.1, which states that every noncommutative rational function admits a representative with the largest Hermitian domain. The other one is Proposition 6.3 on cancellation of singularities of noncommutative rational functions.
6.1 Representatives with the largest Hermitian domain
We will require a technical lemma about matrices over formal rational expressions and their Hermitian domains. A representative of a matrix
![]() $\mathbb{m}$
over
$\mathbb{m}$
over
![]() is a matrix over
is a matrix over
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
of representatives of
$\mathfrak {R}_{\mathbb {C}}(x)$
of representatives of
![]() $\mathbb{m}_{ij}$
, and the domain of a matrix over
$\mathbb{m}_{ij}$
, and the domain of a matrix over
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
is the intersection of domains of its entries.
$\mathfrak {R}_{\mathbb {C}}(x)$
is the intersection of domains of its entries.
Lemma 6.1. Let m be an
![]() $e\times e$
matrix over
$e\times e$
matrix over
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
such that
$\mathfrak {R}_{\mathbb {C}}(x)$
such that
![]() . Then there exists
. Then there exists
![]() $s\in \mathbb{m}^{-1}$
such that
$s\in \mathbb{m}^{-1}$
such that
![]() $\operatorname {\mathrm {hdom}} m\cap \operatorname {\mathrm {hdom}} \mathbb{m}^{-1}=\operatorname {\mathrm {hdom}} s$
.
$\operatorname {\mathrm {hdom}} m\cap \operatorname {\mathrm {hdom}} \mathbb{m}^{-1}=\operatorname {\mathrm {hdom}} s$
.
Proof. Throughout the proof we reserve italic letters (
![]() $m,c$
, etc.) for matrices over
$m,c$
, etc.) for matrices over
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
and bold letters (
$\mathfrak {R}_{\mathbb {C}}(x)$
and bold letters (
![]() $\mathbb{m},\mathbb{c}$
, etc.) for the corresponding matrices over
$\mathbb{m},\mathbb{c}$
, etc.) for the corresponding matrices over
![]() . We prove the statement by induction on e. If
. We prove the statement by induction on e. If
![]() $e=1$
, then
$e=1$
, then
![]() $m^{-1}$
is the desired expression. Assume the statement holds for matrices of size
$m^{-1}$
is the desired expression. Assume the statement holds for matrices of size
![]() $e-1$
, and let c be the first column of m. Then
$e-1$
, and let c be the first column of m. Then
![]() $\operatorname {\mathrm {hdom}} c\supseteq \operatorname {\mathrm {hdom}} m$
, and
$\operatorname {\mathrm {hdom}} c\supseteq \operatorname {\mathrm {hdom}} m$
, and
![]() $c(X)$
is of full rank for every
$c(X)$
is of full rank for every
![]() $X\in \operatorname {\mathrm {hdom}} m\cap \operatorname {\mathrm {hdom}}\mathbb{m}^{-1}$
. Hence
$X\in \operatorname {\mathrm {hdom}} m\cap \operatorname {\mathrm {hdom}}\mathbb{m}^{-1}$
. Hence
Let
![]() $\widehat {\mathbb{m}}$
be the Schur complement of
$\widehat {\mathbb{m}}$
be the Schur complement of
![]() $\mathbb{c}^*\mathbb{c}$
in
$\mathbb{c}^*\mathbb{c}$
in
![]() $\mathbb{m}^*\mathbb{m}$
. Note that the entries of
$\mathbb{m}^*\mathbb{m}$
. Note that the entries of
![]() $\widehat {\mathbb{m}}$
are polynomials in entries of
$\widehat {\mathbb{m}}$
are polynomials in entries of
![]() $\mathbb{m}^*\mathbb{m}$
and
$\mathbb{m}^*\mathbb{m}$
and
![]() $(\mathbb{c}^*\mathbb{c})^{-1}$
; lifting these polynomials to formal expressions in
$(\mathbb{c}^*\mathbb{c})^{-1}$
; lifting these polynomials to formal expressions in
![]() $\mathfrak {R}_{\mathbb {C}}(x)$
, we obtain a representative
$\mathfrak {R}_{\mathbb {C}}(x)$
, we obtain a representative
![]() $\widehat {m}\in \widehat {\mathbb{m}}$
such that
$\widehat {m}\in \widehat {\mathbb{m}}$
such that
If
![]() $X\in \operatorname {\mathrm {hdom}} m$
, then
$X\in \operatorname {\mathrm {hdom}} m$
, then
![]() $m(X)$
is invertible if and only if
$m(X)$
is invertible if and only if
![]() $(c^*c)(X)$
and
$(c^*c)(X)$
and
![]() $\widehat {m}(X)$
are invertible. Thus by formulas (6.1) and (6.2), we have
$\widehat {m}(X)$
are invertible. Thus by formulas (6.1) and (6.2), we have
 $$ \begin{align} \operatorname{\mathrm{hdom}} m \cap \operatorname{\mathrm{hdom}} \mathbb{m}^{-1} = \operatorname{\mathrm{hdom}} m \cap \left(\operatorname{\mathrm{hdom}} (c^*c)^{-1}\cap\operatorname{\mathrm{hdom}} \widehat{\mathbb{m}}^{-1}\right). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{hdom}} m \cap \operatorname{\mathrm{hdom}} \mathbb{m}^{-1} = \operatorname{\mathrm{hdom}} m \cap \left(\operatorname{\mathrm{hdom}} (c^*c)^{-1}\cap\operatorname{\mathrm{hdom}} \widehat{\mathbb{m}}^{-1}\right). \end{align} $$
Since
![]() $\hat {m}$
is an
$\hat {m}$
is an
![]() $(e-1)\times (e-1)$
matrix, by the induction hypothesis there exists
$(e-1)\times (e-1)$
matrix, by the induction hypothesis there exists
![]() $\widehat {s}\in \widehat {\mathbb{m}}^{-1}$
such that
$\widehat {s}\in \widehat {\mathbb{m}}^{-1}$
such that
![]() $\operatorname {\mathrm {hdom}} \widehat {m}\cap \operatorname {\mathrm {hdom}} \widehat {\mathbb{m}}^{-1}=\operatorname {\mathrm {hdom}} \widehat {s}$
. By equation (6.3) we have
$\operatorname {\mathrm {hdom}} \widehat {m}\cap \operatorname {\mathrm {hdom}} \widehat {\mathbb{m}}^{-1}=\operatorname {\mathrm {hdom}} \widehat {s}$
. By equation (6.3) we have
 $$ \begin{align} \operatorname{\mathrm{hdom}} m \cap \operatorname{\mathrm{hdom}} \mathbb{m}^{-1} = \operatorname{\mathrm{hdom}} m \cap \left(\operatorname{\mathrm{hdom}} (c^*c)^{-1}\cap\operatorname{\mathrm{hdom}} \widehat{s}\right). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{hdom}} m \cap \operatorname{\mathrm{hdom}} \mathbb{m}^{-1} = \operatorname{\mathrm{hdom}} m \cap \left(\operatorname{\mathrm{hdom}} (c^*c)^{-1}\cap\operatorname{\mathrm{hdom}} \widehat{s}\right). \end{align} $$
The entries of
![]() $(\mathbb{m}^*\mathbb{m})^{-1}$
can be represented by expressions
$(\mathbb{m}^*\mathbb{m})^{-1}$
can be represented by expressions
![]() $s^{\prime }_{ij}$
which are sums and products of expressions
$s^{\prime }_{ij}$
which are sums and products of expressions
 $m_{ij},m_{ij}^*,(c^*c)^{-1},\widehat {s}_{ij}$
. Thus
$m_{ij},m_{ij}^*,(c^*c)^{-1},\widehat {s}_{ij}$
. Thus
![]() $s'\in (\mathbb{m}^*\mathbb{m})^{-1}$
satisfies
$s'\in (\mathbb{m}^*\mathbb{m})^{-1}$
satisfies
by equation (6.4). Finally,
![]() $s=s' m^*$
is the desired expression because
$s=s' m^*$
is the desired expression because
![]() $\mathbb{m}^{-1}=(\mathbb{m}^*\mathbb{m})^{-1}\mathbb{m}^*$
.
$\mathbb{m}^{-1}=(\mathbb{m}^*\mathbb{m})^{-1}\mathbb{m}^*$
.
Proof of Proposition 2.1. Set
![]() . Let
. Let
![]() $e\in \mathbb {N}$
, an affine matrix pencil M of size e and
$e\in \mathbb {N}$
, an affine matrix pencil M of size e and
![]() $u,v\in \mathbb {C}^e$
be such that
$u,v\in \mathbb {C}^e$
be such that
![]() ${\mathbb{r}}=u^* M^{-1}v$
in
${\mathbb{r}}=u^* M^{-1}v$
in
![]() , and e is minimal. Recall that
, and e is minimal. Recall that
![]() $\operatorname {\mathrm {dom}}{\mathbb{r}}=\bigcup _{r\in {\mathbb{r}}}\operatorname {\mathrm {dom}} r$
. By comparing
$\operatorname {\mathrm {dom}}{\mathbb{r}}=\bigcup _{r\in {\mathbb{r}}}\operatorname {\mathrm {dom}} r$
. By comparing
![]() $(u,M,v)$
with linear representations of representatives of
$(u,M,v)$
with linear representations of representatives of
![]() ${\mathbb{r}}$
as in [Reference Cohn and ReutenauerCR99, Theorem 1.4], it follows that
${\mathbb{r}}$
as in [Reference Cohn and ReutenauerCR99, Theorem 1.4], it follows that
 $$ \begin{align} \operatorname{\mathrm{dom}}{\mathbb{r}}\subseteq\bigcup_{n\in\mathbb{N}}\left\{X\in\operatorname{\mathrm{M}}_{n}(\mathbb{C})^d: \det M(X)\neq0 \right\}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{dom}}{\mathbb{r}}\subseteq\bigcup_{n\in\mathbb{N}}\left\{X\in\operatorname{\mathrm{M}}_{n}(\mathbb{C})^d: \det M(X)\neq0 \right\}. \end{align} $$
Since M contains no inverses, it is defined at every matrix tuple; thus by Lemma 6.1 there is a representative of
![]() $M^{-1}$
whose Hermitian domain equals
$M^{-1}$
whose Hermitian domain equals
![]() $\{X=X^*\colon \det M(X)\neq 0 \}$
. Since
$\{X=X^*\colon \det M(X)\neq 0 \}$
. Since
![]() ${\mathbb{r}}$
is a linear combination of the entries in
${\mathbb{r}}$
is a linear combination of the entries in
![]() $M^{-1}$
, there exists
$M^{-1}$
, there exists
![]() $r\in {\mathbb{r}}$
such that
$r\in {\mathbb{r}}$
such that
![]() $\operatorname {\mathrm {hdom}} r=\operatorname {\mathrm {hdom}} {\mathbb{r}}$
by formula (6.5).
$\operatorname {\mathrm {hdom}} r=\operatorname {\mathrm {hdom}} {\mathbb{r}}$
by formula (6.5).
Example 6.2. The domain of
![]() given by the expression
given by the expression
 $\left (x_4-x_3x_1^{-1}x_2\right )^{-1}$
equals
$\left (x_4-x_3x_1^{-1}x_2\right )^{-1}$
equals
 $$ \begin{align*} \operatorname{\mathrm{dom}}{\mathbb{r}} = \bigcup_{n\in\mathbb{N}} \left\{X\in\operatorname{\mathrm{M}}_{n}(\mathbb{C})^4 \colon \det \begin{pmatrix} X_ 1 & X_2 \\ X_3 & X_4 \end{pmatrix}\neq0 \right\}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{dom}}{\mathbb{r}} = \bigcup_{n\in\mathbb{N}} \left\{X\in\operatorname{\mathrm{M}}_{n}(\mathbb{C})^4 \colon \det \begin{pmatrix} X_ 1 & X_2 \\ X_3 & X_4 \end{pmatrix}\neq0 \right\}, \end{align*} $$
and
![]() $\operatorname {\mathrm {dom}} r\subsetneq \operatorname {\mathrm {dom}} {\mathbb{r}}$
for every
$\operatorname {\mathrm {dom}} r\subsetneq \operatorname {\mathrm {dom}} {\mathbb{r}}$
for every
![]() $r\in {\mathbb{r}}$
by [Reference VolčičVol17, Example 3.13].
$r\in {\mathbb{r}}$
by [Reference VolčičVol17, Example 3.13].
Following the proof of Proposition 2.1 and Lemma 6.1, let
![]() $\mathbb{m}=\left (\begin {smallmatrix}x_1 & x_2 \\ x_3 & x_4\end {smallmatrix}\right )$
. Then
$\mathbb{m}=\left (\begin {smallmatrix}x_1 & x_2 \\ x_3 & x_4\end {smallmatrix}\right )$
. Then
 $$ \begin{align*} \mathbb{m}^*\mathbb{m}=\begin{pmatrix}x_1^2+x_3^2 & x_1x_2+x_3x_4 \\ x_2x_1+x_4x_3 & x_2^2+x_4^2\end{pmatrix}, \end{align*} $$
$$ \begin{align*} \mathbb{m}^*\mathbb{m}=\begin{pmatrix}x_1^2+x_3^2 & x_1x_2+x_3x_4 \\ x_2x_1+x_4x_3 & x_2^2+x_4^2\end{pmatrix}, \end{align*} $$
and the Schur complement of
![]() $\mathbb{m}^*\mathbb{m}$
with respect to the
$\mathbb{m}^*\mathbb{m}$
with respect to the
![]() $(1,1)$
-entry equals
$(1,1)$
-entry equals
 $$ \begin{align*} \widehat{\mathbb{m}}=x_2^2+x_4^2-(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1}(x_1x_2+x_3x_4). \end{align*} $$
$$ \begin{align*} \widehat{\mathbb{m}}=x_2^2+x_4^2-(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1}(x_1x_2+x_3x_4). \end{align*} $$
Since
 $$ \begin{align*} \mathbb{m}^{-1}=(\mathbb{m}^*\mathbb{m})^{-1}\mathbb{m}^*= \begin{pmatrix} \star & \star \\ -\widehat{\mathbb{m}}^{-1}(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1} & \widehat{\mathbb{m}}^{-1} \end{pmatrix} \begin{pmatrix} \star & x_3 \\ \star & x_4 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \mathbb{m}^{-1}=(\mathbb{m}^*\mathbb{m})^{-1}\mathbb{m}^*= \begin{pmatrix} \star & \star \\ -\widehat{\mathbb{m}}^{-1}(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1} & \widehat{\mathbb{m}}^{-1} \end{pmatrix} \begin{pmatrix} \star & x_3 \\ \star & x_4 \end{pmatrix} \end{align*} $$
and
 $$ \begin{align*} {\mathbb{r}} = \begin{pmatrix}0 & 1 \end{pmatrix}\mathbb{m}^{-1}\begin{pmatrix} 0\\ 1\end{pmatrix}, \end{align*} $$
$$ \begin{align*} {\mathbb{r}} = \begin{pmatrix}0 & 1 \end{pmatrix}\mathbb{m}^{-1}\begin{pmatrix} 0\\ 1\end{pmatrix}, \end{align*} $$
we conclude that the formal rational expression
 $$ \begin{align*} \left(x_2^2+x_4^2-(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1}(x_1x_2+x_3x_4)\right)^{-1} \left(x_4-(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1}x_3\right) \end{align*} $$
$$ \begin{align*} \left(x_2^2+x_4^2-(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1}(x_1x_2+x_3x_4)\right)^{-1} \left(x_4-(x_2x_1+x_4x_3)\left(x_1^2+x_3^2\right)^{-1}x_3\right) \end{align*} $$
represents
![]() ${\mathbb{r}}$
, and its Hermitian domain coincides with
${\mathbb{r}}$
, and its Hermitian domain coincides with
![]() $\operatorname {\mathrm {hdom}} {\mathbb{r}}$
. Of course, the expression
$\operatorname {\mathrm {hdom}} {\mathbb{r}}$
. Of course, the expression
 $\left (x_4-x_3x_1^{-1}x_2\right )^{-1}$
is a much simpler representative of
$\left (x_4-x_3x_1^{-1}x_2\right )^{-1}$
is a much simpler representative of
![]() ${\mathbb{r}}$
.
${\mathbb{r}}$
.
6.2 Cancellation of singularities
In the absence of left ideals in skew fields, the following proposition serves as a rational analogue of Bergman’s Nullstellensatz for noncommutative polynomials [Reference Helton and McCulloughHM04, Theorem 6.3]. The proof omits some of the details, since it is a derivative of the proof of Theorem 5.2.
Proposition 6.3. The following are equivalent for
![]() :
:
-
(i)
 $\ker {\mathbb{r}}(X)\subseteq \ker {\mathbb{s}}(X)$
for all
$\ker {\mathbb{r}}(X)\subseteq \ker {\mathbb{s}}(X)$
for all
 $X\in \operatorname {\mathrm {dom}}{\mathbb{r}}\cap \operatorname {\mathrm {dom}}{\mathbb{s}}$
.
$X\in \operatorname {\mathrm {dom}}{\mathbb{r}}\cap \operatorname {\mathrm {dom}}{\mathbb{s}}$
. -
(ii)
 $\operatorname {\mathrm {dom}} \left ({\mathbb{s}}{\mathbb{r}}^{-1}\right )\supseteq \operatorname {\mathrm {dom}}{\mathbb{r}}\cap \operatorname {\mathrm {dom}}{\mathbb{s}}$
.
$\operatorname {\mathrm {dom}} \left ({\mathbb{s}}{\mathbb{r}}^{-1}\right )\supseteq \operatorname {\mathrm {dom}}{\mathbb{r}}\cap \operatorname {\mathrm {dom}}{\mathbb{s}}$
.
Proof. (ii)
![]() $\Rightarrow $
(i) If (ii) holds, then
$\Rightarrow $
(i) If (ii) holds, then
![]() ${\mathbb{s}}(X)=\left ({\mathbb{s}}(X){\mathbb{r}}(X)^{-1}\right ){\mathbb{r}}(X)$
for every
${\mathbb{s}}(X)=\left ({\mathbb{s}}(X){\mathbb{r}}(X)^{-1}\right ){\mathbb{r}}(X)$
for every
![]() $X\in \operatorname {\mathrm {dom}}{\mathbb{r}}\cap \operatorname {\mathrm {dom}}{\mathbb{s}}$
, and so
$X\in \operatorname {\mathrm {dom}}{\mathbb{r}}\cap \operatorname {\mathrm {dom}}{\mathbb{s}}$
, and so
![]() $\ker {\mathbb{r}}(X)\subseteq \ker {\mathbb{s}}(X)$
.
$\ker {\mathbb{r}}(X)\subseteq \ker {\mathbb{s}}(X)$
.
(i)
![]() $\Rightarrow $
(ii) Suppose (ii) does not hold; then there are
$\Rightarrow $
(ii) Suppose (ii) does not hold; then there are
![]() $r\in {\mathbb{r}}$
,
$r\in {\mathbb{r}}$
,
![]() $s\in {\mathbb{s}}$
and
$s\in {\mathbb{s}}$
and
![]() $Y\in \operatorname {\mathrm {dom}} r\cap \operatorname {\mathrm {dom}} s$
such that
$Y\in \operatorname {\mathrm {dom}} r\cap \operatorname {\mathrm {dom}} s$
such that
![]() $\det r(Y)=0$
. Similarly to Section 4, denote
$\det r(Y)=0$
. Similarly to Section 4, denote
and let
![]() $\mathcal {R}$
be its image in
$\mathcal {R}$
be its image in
![]() . We also define finite-dimensional vector spaces
. We also define finite-dimensional vector spaces
![]() $V_{\ell }$
and the finitely generated algebra V as before. The left ideal
$V_{\ell }$
and the finitely generated algebra V as before. The left ideal
![]() $V{\mathbb{r}}$
in V is proper: if
$V{\mathbb{r}}$
in V is proper: if
![]() $\mathbb{q}{\mathbb{r}}=1$
for
$\mathbb{q}{\mathbb{r}}=1$
for
![]() $q\in V$
, then
$q\in V$
, then
![]() $q(Y)r(Y)=I$
, since
$q(Y)r(Y)=I$
, since
![]() $Y\in \operatorname {\mathrm {dom}} q$
, which contradicts
$Y\in \operatorname {\mathrm {dom}} q$
, which contradicts
![]() $\det r(Y)=0$
. Furthermore,
$\det r(Y)=0$
. Furthermore,
![]() ${\mathbb{s}}\notin V{\mathbb{r}}$
, since (ii) does not hold. Let
${\mathbb{s}}\notin V{\mathbb{r}}$
, since (ii) does not hold. Let
![]() $K=V/V{\mathbb{r}}$
, and let
$K=V/V{\mathbb{r}}$
, and let
![]() $K_{\ell }$
be the image of
$K_{\ell }$
be the image of
![]() $V_{\ell }$
for every
$V_{\ell }$
for every
![]() $\ell \in \mathbb {N}$
. Let
$\ell \in \mathbb {N}$
. Let
![]() $\mathfrak {X}_j: K\to K$
be the operator given by the left multiplication with
$\mathfrak {X}_j: K\to K$
be the operator given by the left multiplication with
![]() $x_j$
; note that
$x_j$
; note that
![]() $\mathfrak {X}_j(K_{\ell })\subseteq K_{\ell +1}$
for all
$\mathfrak {X}_j(K_{\ell })\subseteq K_{\ell +1}$
for all
![]() $\ell $
. By induction on the construction of
$\ell $
. By induction on the construction of
![]() $q\in R$
, it is straightforward to see that
$q\in R$
, it is straightforward to see that
![]() $q(\mathfrak {X})$
is well defined for every
$q(\mathfrak {X})$
is well defined for every
![]() $q\in R$
. Let
$q\in R$
. Let
![]() $\ell =2\max \{\tau (r),\tau (s)\}-2$
. By Proposition 3.6, there exist a finite-dimensional vector space U and a d-tuple of operators X on
$\ell =2\max \{\tau (r),\tau (s)\}-2$
. By Proposition 3.6, there exist a finite-dimensional vector space U and a d-tuple of operators X on
![]() $K_{\ell +1}\oplus U$
such that
$K_{\ell +1}\oplus U$
such that
![]() $X\in \operatorname {\mathrm {dom}} r\cap \operatorname {\mathrm {dom}} s$
and
$X\in \operatorname {\mathrm {dom}} r\cap \operatorname {\mathrm {dom}} s$
and
for
![]() $j=1,\dotsc ,d$
. A slight modification of Proposition 4.3 implies that
$j=1,\dotsc ,d$
. A slight modification of Proposition 4.3 implies that
where
![]() $[\mathbb{q}]\in K$
denotes the image of
$[\mathbb{q}]\in K$
denotes the image of
![]() $\mathbb{q}\in V$
.
$\mathbb{q}\in V$
.
The implication (i)
![]() $\Rightarrow $
(ii) in Proposition 6.3 fails if only Hermitian domains are considered (e.g., take
$\Rightarrow $
(ii) in Proposition 6.3 fails if only Hermitian domains are considered (e.g., take
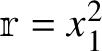 ${\mathbb{r}}=x_1^2$
and
${\mathbb{r}}=x_1^2$
and
![]() ${\mathbb{s}}=x_1$
). It is also worth mentioning that while Proposition 6.3 might look rather straightforward at first glance, there is a certain subtlety to it. Namely, the equivalence in Proposition 6.3 fails if only matrix tuples of a fixed size are considered. For example, let
${\mathbb{s}}=x_1$
). It is also worth mentioning that while Proposition 6.3 might look rather straightforward at first glance, there is a certain subtlety to it. Namely, the equivalence in Proposition 6.3 fails if only matrix tuples of a fixed size are considered. For example, let
![]() ${\mathbb{r}}=x_1$
and
${\mathbb{r}}=x_1$
and
![]() ${\mathbb{s}}=x_1x_2$
; then
${\mathbb{s}}=x_1x_2$
; then
![]() $\operatorname {\mathrm {dom}}_1{\mathbb{r}}\cap \operatorname {\mathrm {dom}}_1{\mathbb{s}}=\mathbb {C}^2$
and
$\operatorname {\mathrm {dom}}_1{\mathbb{r}}\cap \operatorname {\mathrm {dom}}_1{\mathbb{s}}=\mathbb {C}^2$
and
![]() $\ker {\mathbb{r}}(X)\subseteq \ker {\mathbb{s}}(X)$
for all
$\ker {\mathbb{r}}(X)\subseteq \ker {\mathbb{s}}(X)$
for all
![]() $X\in \mathbb {C}^2$
, but
$X\in \mathbb {C}^2$
, but
![]() $\operatorname {\mathrm {dom}}_1 \left ({\mathbb{s}}{\mathbb{r}}^{-1}\right )=\mathbb {C}\setminus \{0\}\times \mathbb {C}$
(compare [Reference VolčičVol17, Example 2.1 and Theorem 3.10]).
$\operatorname {\mathrm {dom}}_1 \left ({\mathbb{s}}{\mathbb{r}}^{-1}\right )=\mathbb {C}\setminus \{0\}\times \mathbb {C}$
(compare [Reference VolčičVol17, Example 2.1 and Theorem 3.10]).
Acknowledgments
The author thanks Igor Klep for valuable comments and suggestions which improved the presentation of this paper. This research was supported by NSF grant DMS 1954709. The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Conflicts of interest
None.