Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T02:55:56.097Z Has data issue: false hasContentIssue false
  • English
  • Français

GRADED UNIPOTENT GROUPS AND GROSSHANS THEORY

Part of: Algebraic groups General commutative ring theory

Published online by Cambridge University Press:  04 September 2017

GERGELY BÉRCZI  and
FRANCES KIRWAN

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 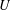$U$ be a unipotent group which is graded in the sense that it has an extension 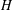$H$ by the multiplicative group of the complex numbers such that all the weights of the adjoint action on the Lie algebra of 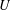$U$ are strictly positive. We study embeddings of 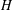$H$ in a general linear group 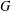$G$ which possess Grosshans-like properties. More precisely, suppose 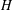$H$ acts on a projective variety 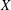$X$ and its action extends to an action of 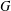$G$ which is linear with respect to an ample line bundle on 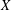$X$. Then, provided that we are willing to twist the linearization of the action of 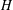$H$ by a suitable (rational) character of 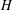$H$, we find that the 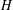$H$-invariants form a finitely generated algebra and hence define a projective variety $X/\!/H$; moreover, the natural morphism from the semistable locus in 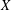$X$ to 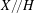$X/\!/H$ is surjective, and semistable points in 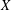$X$ are identified in 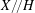$X/\!/H$ if and only if the closures of their 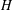$H$-orbits meet in the semistable locus. A similar result applies when we replace 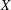$X$ by its product with the projective line; this gives us a projective completion of a geometric quotient of a 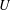$U$-invariant open subset of 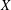$X$ by the action of the unipotent group 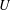$U$.

MSC classification

Primary: 14L24: Geometric invariant theory
Secondary: 13A50: Actions of groups on commutative rings; invariant theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e21
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Ahlfors, L., ‘The theory of meromorphic curves’, Acta Soc. Sci. Finn. N.S. 3 (1941), 1–31.Google Scholar
Arnold, V. I., Goryunov, V. V., Lyashko, O. V. and Vasilliev, V. A., ‘Singularity theory I’, inDynamical Systems VI, Encyclopaedia of Mathematical Sciences (Springer, Berlin, 1998).Google Scholar
Arzhantsev, I. V., Celic, D. and Hausen, J., ‘Factorial algebraic group actions and categorical quotients’, J. Algebra 387 (2013), 87–98.Google Scholar
Bérczi, G., ‘Thom polynomials of Morin singularities and the Green–Griffiths–Lang conjecture’, Preprint, 2010, arXiv:1011.4710.Google Scholar
Bérczi, G., ‘Moduli of map germs, Thom polynomials and the Green–Griffiths conjecture’, inContributions to Algebraic Geometry, EMS Series of Congress Reports (Eur. Math. Soc., Zürich, 2012), 141–167.CrossRefGoogle Scholar
Bérczi, G., ‘Tautological integrals on curvilinear Hilbert schemes’, Geom. Topol. 21(5) (2017), 2897–2944.Google Scholar
Bérczi, G., Doran, B., Hawes, T. and Kirwan, F., ‘Constructing quotients of algebraic varieties by linear algebraic group actions’, Handbook of Group Actions, (eds. Ji, L., Papadopoulos, A. and Yau, S.-T.) Advanced Lectures in Mathematics (ALM), Vol. III (Higher Education Press and International Press); arXiv:1512.02997.Google Scholar
Bérczi, G. and Kirwan, F., ‘A geometric construction for invariant jet differentials’, Surv. Differ. Geom. XVII (2012), 79–126.CrossRefGoogle Scholar
Bérczi, G. and Szenes, A., ‘Thom polynomials of Morin singularities’, Ann. of Math. (2) 175 (2012), 567–629.CrossRefGoogle Scholar
Bertin, J., ‘The punctual Hilbert scheme: an introduction’, inProceedings of the Summer School ‘Geometric Methods in Representation Theory’. I, Sémin. Congr., 24-I (Soc. Math. France, Paris, 2012), 1–102.Google Scholar
Bialynicki-Birula, A., ‘Categorical quotients’, J. Algebra 239 (2001), 35–55.CrossRefGoogle Scholar
Bloch, A., ‘Sur les systémes de fonctions uniformes satisfaisant á l’ équation d’une variété algébrique dont l’irrégularité dépasse la dimension’, J. de Math. 5 (1926), 19–66.Google Scholar
Cartan, H., ‘Sur les systémes de fonctions holomorphes á variétés linéaries lacunaires et leurs applications’, Thése Paris Ann. Ec. Norm. 45 (1928), 255–346.Google Scholar
Demailly, J.-P., ‘Algebraic criteria for Kobayashi hyperbolic projective varieties and jet differentials’, inProceedings of Symposia in Pure Mathematics, Vol. 62 (American Mathematical Society, Providence, RI, 1997), 285–360.Google Scholar
Diverio, S., Merker, J. and Rousseau, E., ‘Effective algebraic degeneracy’, Invent. Math. 180 (2010), 161–223.Google Scholar
Diverio, S. and Rousseau, E., A Survey on Hyperbolicity of Projective Hypersurfaces, Publicaçōes Matemáticas do IMPA. [IMPA Mathematical Publications] (Instituto de Matemática Pura e Aplicada (IMPA), Rio de Janerio, 2011), x+109 pp. ISBN: 978-85-244-0315-6.Google Scholar
Dolgachev, I., Lectures on Invariant Theory, London Mathematical Society Lecture Note Series, 296 (Cambridge University Press, Cambridge, 2003), xvi+220 pp. ISBN: 0-521-52548-9.CrossRefGoogle Scholar
Doran, B. and Kirwan, F., ‘Towards non-reductive geometric invariant theory’, Pure Appl. Math. Q. 3 (2007), 61–105.CrossRefGoogle Scholar
Fauntleroy, A., ‘Categorical quotients of certain algebraic group actions’, Illinois J. Math. 27 (1983), 115–124.Google Scholar
Fauntleroy, A., ‘Geometric invariant theory for general algebraic groups’, Compos. Math. 55 (1985), 63–87.Google Scholar
Gaffney, T., ‘The Thom polynomial of ∑1111 ’, inSingularities, Part 1, Proceedings of Symposia in Pure Mathematics, 40 (AMS, Providence, RI, 1983), 399–408.Google Scholar
Green, M. and Griffiths, P., ‘Two applications of algebraic geometry to entire holomorphic mappings’, inThe Chern Symposium 1979 (Proc. Intern. Sympos., Berkeley, CA, 1979) (Springer, New York, 1980), 41–74.CrossRefGoogle Scholar
Greuel, G.-M. and Pfister, G., ‘Geometric quotients of unipotent group actions’, Proc. Lond. Math. Soc. (3) 67 (1993), 75–105.Google Scholar
Greuel, G.-M. and Pfister, G., ‘Geometric quotients of unipotent group actions II’, inSingularities, Progress in Mathematics, 162 (Birkhäuser, Basel, 1998), 27–36.Google Scholar
Grosshans, F., ‘Observable groups and Hilbert’s fourteenth problem’, Amer. J. Math. 95 (1973), 229–253.Google Scholar
Grosshans, F., Algebraic Homogeneous Spaces and Invariant Theory, Lecture Notes in Mathematics, 1673 (Springer, Berlin, 1997).Google Scholar
Guillemin, V., Jeffrey, L. and Sjamaar, R., ‘Symplectic implosion’, Transform. Groups 7 (2002), 155–184.Google Scholar
Kazarian, M., Thom Polynomials, Lecture notes of talks given at the singularity theory Conference, Sapporo, 2003, http://www.mi.ras.ru/ kazarian/#publ.Google Scholar
Kirwan, F., ‘Quotients by non-reductive algebraic group actions’, Moduli Spaces and Vector Bundles (eds. Brambila-Paz, L., Bradlow, S., Garcia-Prada, O. and Ramanan, S.) London Mathematical Society Lecture Note Series, 359 (Cambridge University Press, Cambridge, 2009), 311–366.Google Scholar
Kirwan, F., ‘Symplectic implosion and non-reductive quotients’, inGeometric Aspects of Analysis and Mechanics, Progress in Mathematics, 292 (Birkhäuser/Springer, New York, 2011), 213–256.Google Scholar
Kobayashi, S., Hyperbolic Complex Spaces, Grundlehren der Mathematischen Wissenschaften, 318 (Springer, Berlin, 1998).Google Scholar
Mather, J. N., ‘Stability of C ∞ -mappings, I’, Ann. Math. Ser. II 87 (1968), 89–104. II. Ann. Math. Ser. II 89, (1969) 254–291; III. Publ. Math. IHES 35 (1969) 127–156; IV. Publ. Math. IHES 37 (1970) 223–248; V. Adv. Math. 4, (1970), 301–336; VI. Proceedings of Liverpool Singularities Symposium, I, Lecture Notes in Mathematics, 192 (Springer, 1971), 207–253.Google Scholar
Maulik, D., ‘Stable pairs and the HOMFLY polynomial’, Invent. Math. 204(3) (2016), 787–831.Google Scholar
Merker, J., ‘Jets de Demailly–Semple d’ordres 4 et 5 en dimension 2’, Int. J. Contemp. Math. Sci. 3(18) (2008), 861–933.Google Scholar
Merker, J., ‘Applications of computational invariant theory to Kobayashi hyperbolicity and to Green–Griffiths algebraic degeneracy’, J. Symbolic Comput. 45 (2010), 986–1074.Google Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric Invariant Theory, 3rd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete, 34 (Springer, Berlin, Heidelberg, 1994).Google Scholar
Nakajima, H., Lectures on Hilbert Schemes of Points on Surfaces, University Lecture Series, 18 (American Mathematical Society, Providence, RI, 1999), xii+132 pp. ISBN: 0-8218-1956-9.Google Scholar
Newstead, P. E., Introduction to Moduli Problems and Orbit Spaces, Tata Institute of Fundamental Research Lectures on Mathematics and Physics, 51 (Tata Institute of Fundamental Research, Bombay, 1978), by the Narosa Publishing House, New Delhi.Google Scholar
Oblomkov, A. and Vivek, S., ‘The Hilbert scheme of a plane curve singularity and the HOMFLY polynomial of its link’, Duke Math. J. 161(7) (2012), 1277–1303.Google Scholar
Oblomkov, A. and Shende, V., ‘The Hilbert scheme of a plane curve singularity and the HOMFLY polynomial of its link’, Duke Math. J. 161(7) (2012), 1277–1303.Google Scholar
Popov, V. and Vinberg, E., ‘Invariant theory’, inAlgebraic Geometry IV, Encyclopaedia of Mathematical Sciences (Springer, 1994).Google Scholar
Porteous, I. R., ‘Probing singularities’, inSingularities, Part 2, Proceedings of Symposia in Pure Mathematics, 40 (AMS, Providence, RI, 1983), 395–406.Google Scholar
Rimányi, R., ‘Thom polynomials, symmetries and incidences of singularities’, Invent. Math. 143 (2001), 499–521.Google Scholar
Rimányi, R. and Fehér, L., ‘Thom series of contact singularities’, Ann. of Math. (2) 176 (2012), 1381–1426.Google Scholar
Ronga, F., ‘A new look at Faa de Bruno’s formula for higher derivatives of composite functions and the expression of some intrinsic derivatives’, inSingularities, Part 2, Proceedings of Symposia in Pure Mathematics, 40 (American Mathematical Soceity, Providence, RI, 1983), 423–431.Google Scholar
Rousseau, E., ‘Etude des jets de Demailly–Semple en dimension 3’, Ann. Inst. Fourier (Grenoble) 56(2) (2006), 397–421.Google Scholar
Shende, V., ‘Hilbert schemes of points on a locally planar curve and the Severi strata of its versal deformation’, Compos. Math. 148/2 (2012), 531–547.Google Scholar
Siu, Y.-T. and Yeung, S.-K., ‘Hyperbolicity of the complement of a generic smooth curve of high degree in the complex projective plane’, Invent. Math. 124 (1996), 573–618.Google Scholar
Winkelmann, J., ‘Invariant rings and quasiaffine quotients’, Math. Z. 244 (2003), 163–174.Google Scholar