Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T09:15:24.690Z Has data issue: false hasContentIssue false
  • English
  • Français

GOLDFELD’S CONJECTURE AND CONGRUENCES BETWEEN HEEGNER POINTS

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  27 May 2019

DANIEL KRIZ  and
CHAO LI
DANIEL KRIZ
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Memorial Drive, Cambridge, MA 02139, USA; [email protected]
CHAO LI
Affiliation:
Department of Mathematics, Columbia University, 2990 Broadway, New York, NY 10027, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

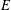Given an elliptic curve $E$ over 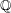$\mathbb{Q}$, a celebrated conjecture of Goldfeld asserts that a positive proportion of its quadratic twists should have analytic rank 0 (respectively 1). We show that this conjecture holds whenever 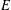$E$ has a rational 3-isogeny. We also prove the analogous result for the sextic twists of 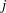$j$-invariant 0 curves. For a more general elliptic curve 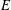$E$, we show that the number of quadratic twists of 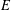$E$ up to twisting discriminant 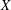$X$ of analytic rank 0 (respectively 1) is 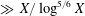$\gg X/\log ^{5/6}X$, improving the current best general bound toward Goldfeld’s conjecture due to Ono–Skinner (respectively Perelli–Pomykala). To prove these results, we establish a congruence formula between 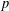$p$-adic logarithms of Heegner points and apply it in the special cases 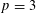$p=3$ and 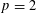$p=2$ to construct the desired twists explicitly. As a by-product, we also prove the corresponding 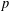$p$-part of the Birch and Swinnerton–Dyer conjecture for these explicit twists.

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e15
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Abbes, A. and Ullmo, E., ‘À propos de la conjecture de Manin pour les courbes elliptiques modulaires’, Compos. Math. 103(3) (1996), 269–286.Google Scholar
Agashe, A., Ribet, K. and Stein, W. A., ‘The Manin constant’, Pure Appl. Math. Q. 2(2, part 2) (2006), 617–636.Google Scholar
Balsam, N., ‘The parity of analytic ranks among quadratic twists of elliptic curves over number fields’, arXiv e-prints, April 2014, https://arxiv.org/abs/1404.4964.Google Scholar
Berti, A., Bertolini, M. and Venerucci, R., ‘Congruences between modular forms and the Birch and Swinnerton–Dyer conjecture’, inElliptic Curves, Modular Forms and Iwasawa Theory: In Honour of John H. Coates’ 70th Birthday, Cambridge, UK, March 2015 (eds. Loeffler, D. and Zerbes, S. L.) (Springer International Publishing, Cham, 2016), 1–31.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., ‘Generalized Heegner cycles and p-adic Rankin L-series’, Duke Math. J. 162(6) (2013), 1033–1148. With an appendix by Brian Conrad.Google Scholar
Bhargava, M., Elkies, N. and Shnidman, A., ‘The average size of the 3-isogeny Selmer groups of elliptic curves $y^{2}=x^{3}+k$ ’, arXiv e-prints, October 2016.Google Scholar
Bhargava, M., Skinner, C. and Zhang, W., ‘A majority of elliptic curves over $\mathbb{Q}$ satisfy the Birch and Swinnerton–Dyer conjecture’, arXiv e-prints, July 2014.Google Scholar
Bhargava, M., Klagsbrun, Z., Lemke Oliver, R. and Shnidman, A., ‘Selmer groups in families of quadratic twists with a 3-isogeny’,  arXiv e-prints, September 2017,  https://arxiv.org/abs/1709.09790.Google Scholar
Browning, T. D., ‘Many cubic surfaces contain rational points’, Mathematika 63(3) (2017), 818–839.Google Scholar
Burungale, A. A., Hida, H. and Tian, Y., ‘Horizontal variation of Tate–Shafarevich groups’, arXiv e-prints, December 2017.Google Scholar
Byeon, D., Jeon, D. and Kim, C. H., ‘Rank-one quadratic twists of an infinite family of elliptic curves’, J. Reine Angew. Math. 633 (2009), 67–76.Google Scholar
Cai, L., Chen, Y. and Liu, Y., ‘Heegner points on modular curves’, Trans. Amer. Math. Soc. 370 (2018), 3721–3743.Google Scholar
Castella, F., ‘On the p-part of the Birch–Swinnerton–Dyer formula for multiplicative primes’, Cambridge J. Math. 6(1) (2018), 1–23.Google Scholar
Coates, J., ‘Lectures on the Birch–Swinnerton–Dyer conjecture’, ICCM Not. 1(2) (2013), 29–46.Google Scholar
Coates, J., Li, Y., Tian, Y. and Zhai, S., ‘Quadratic twists of elliptic curves’, Proc. Lond. Math. Soc. (3) 110(2) (2015), 357–394.Google Scholar
Coleman, R. F., ‘Torsion points on curves and p-adic abelian integrals’, Ann. of Math. (2) 121(1) (1985), 111–168.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., ‘Fermat’s last theorem’, inElliptic Curves, Modular Forms & Fermat’s Last Theorem (Hong Kong, 1993) (International Press, Cambridge, MA, 1997), 2–140.Google Scholar
Davenport, H. and Heilbronn, H., ‘On the density of discriminants of cubic fields. II’, Proc. R. Soc. Lond. A 322(1551) (1971), 405–420.Google Scholar
Dokchitser, T. and Dokchitser, V., ‘Root numbers and parity of ranks of elliptic curves’, J. Reine Angew. Math. 658 (2011), 39–64.Google Scholar
Fouvry, É., ‘Sur le comportement en moyenne du rang des courbes y 2 = x 3 + k ’, inSéminaire de Théorie des Nombres, Paris, 1990–91, Progress in Mathematics, 108 (Birkhäuser Boston, Boston, MA, 1993), 61–84.Google Scholar
Goldfeld, D., ‘Conjectures on elliptic curves over quadratic fields’, inNumber Theory, Carbondale 1979 (Proc. Southern Illinois Conf., Southern Illinois University, Carbondale, IL, 1979, Lecture Notes in Mathematics, 751 (Springer, Berlin, 1979), 108–118.Google Scholar
Gonzalez-Avilés, C. D., ‘On the conjecture of Birch and Swinnerton–Dyer’, Trans. Amer. Math. Soc. 349(10) (1997), 4181–4200.Google Scholar
Gouvêa, F. Q., Arithmetic of p-Adic Modular Forms, Lecture Notes in Mathematics, 1304 (Springer, Berlin, 1988).Google Scholar
Gross, B. H., ‘On the factorization of p-adic L-series’, Invent. Math. 57(1) (1980), 83–95.Google Scholar
Gross, B. H., ‘Heegner points on X 0(N)’, inModular Forms (Durham, 1983), Ellis Horwood Ser. Math. Appl.: Statist. Oper. Res. (Horwood, Chichester, 1984), 87–105.Google Scholar
Gross, B. H., ‘Lectures on the conjecture of Birch and Swinnerton–Dyer’, inArithmetic of L-Functions, IAS/Park City Math. Ser., 18 (American Mathematical Society, Providence, RI, 2011), 169–209.Google Scholar
Gross, B. H. and Parson, J. A., ‘On the local divisibility of Heegner points’, inNumber Theory, Analysis and Geometry (Springer, New York, 2012), 215–241.Google Scholar
Gross, B. H. and Zagier, D. B., ‘Heegner points and derivatives of L-series’, Invent. Math. 84(2) (1986), 225–320.Google Scholar
Heath-Brown, D. R., ‘The size of Selmer groups for the congruent number problem. II’, Invent. Math. 118(2) (1994), 331–370. With an appendix by P. Monsky.Google Scholar
Heath-Brown, D. R., ‘The average analytic rank of elliptic curves’, Duke Math. J. 122(3) (2004), 591–623.Google Scholar
Hida, H. and Tilouine, J., ‘Anti-cyclotomic Katz p-adic L-functions and congruence modules’, Ann. Sci. Éc. Norm. Supér. (4) 26(2) (1993), 189–259.Google Scholar
James, K., ‘ L-series with nonzero central critical value’, J. Amer. Math. Soc. 11(3) (1998), 635–641.Google Scholar
James, K., ‘Elliptic curves satisfying the Birch and Swinnerton–Dyer conjecture mod 3’, J. Number Theory 76(1) (1999), 16–21.Google Scholar
Jetchev, D., Skinner, C. and Wan, X., ‘The Birch and Swinnerton–Dyer formula for elliptic curves of analytic rank one’, Camb. J. Math. 5(3) (2017).Google Scholar
Kane, D., ‘On the ranks of the 2-Selmer groups of twists of a given elliptic curve’, Algebra Number Theory 7(5) (2013), 1253–1279.Google Scholar
Kato, K., ‘ p-adic Hodge theory and values of zeta functions of modular forms’, Astérisque (295) (2004), ix, 117–290. Cohomologies $p$ -adiques et applications arithmétiques. III.Google Scholar
Katz, N. M., ‘Higher congruences between modular forms’, Ann. of Math. (2) 101 (1975), 332–367.Google Scholar
Katz, N. M., ‘ p-adic interpolation of real analytic Eisenstein series’, Ann. of Math. (2) 104(3) (1976), 459–571.Google Scholar
Katz, N. M., ‘ p-adic L-functions for CM fields’, Invent. Math. 49(3) (1978), 199–297.Google Scholar
Katz, N. M. and Sarnak, P., Random Matrices, Frobenius Eigenvalues, and Monodromy, American Mathematical Society Colloquium Publications, 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Kobayashi, S., ‘The p-adic Gross–Zagier formula for elliptic curves at supersingular primes’, Invent. Math. 191(3) (2013), 527–629.Google Scholar
Kriz, D., ‘Generalized Heegner cycles at Eisenstein primes and the Katz p-adic L-function’, Algebra Number Theory 10(2) (2016), 309–374.Google Scholar
Le Hung, B. V. and Li, C., ‘Level raising mod 2 and arbitrary 2-Selmer ranks’, Compos. Math. 152(8) (2016), 1576–1608.Google Scholar
Li, Y., Liu, Y. and Tian, Y., ‘On the Birch and Swinnerton–Dyer conjecture for CM elliptic curves over $\mathbb{Q}$ ’, arXiv e-prints, May 2016.Google Scholar
Liu, Y., Zhang, S. and Zhang, W., ‘A p-adic Waldspurger formula’, Duke Math. J. 167(4) (2018), 743–833.Google Scholar
Liverance, E., ‘A formula for the root number of a family of elliptic curves’, J. Number Theory 51(2) (1995), 288–305.Google Scholar
Mazur, B., ‘On the arithmetic of special values of L functions’, Invent. Math. 55(3) (1979), 207–240.Google Scholar
Mazur, B. and Rubin, K., ‘Ranks of twists of elliptic curves and Hilbert’s tenth problem’, Invent. Math. 181(3) (2010), 541–575.Google Scholar
Mazur, B. and Rubin, K., ‘Diophantine stability’, Amer. J. Math. 140(3) (2018), 571–616. With an appendix by M. Larsen.Google Scholar
Mazur, B., ‘Rational points of abelian varieties with values in towers of number fields’, Invent. Math. 18 (1972), 183–266.Google Scholar
Miller, R. L., ‘Proving the Birch and Swinnerton–Dyer conjecture for specific elliptic curves of analytic rank zero and one’, LMS J. Comput. Math. 14 (2011), 327–350.Google Scholar
Milne, J. S., Arithmetic Duality Theorems, Perspectives in Mathematics, 1 (Academic Press, Inc., Boston, MA, 1986).Google Scholar
Milne, J. S., Arithmetic Duality Theorems, second edition, (BookSurge, LLC, Charleston, SC, 2006).Google Scholar
Monsky, P., ‘Generalizing the Birch–Stephens theorem. I. Modular curves’, Math. Z. 221(3) (1996), 415–420.Google Scholar
Nakagawa, J. and Horie, K., ‘Elliptic curves with no rational points’, Proc. Amer. Math. Soc. 104(1) (1988), 20–24.Google Scholar
Nekovář, J., ‘Class numbers of quadratic fields and Shimura’s correspondence’, Math. Ann. 287(4) (1990), 577–594.Google Scholar
Ono, K., ‘A note on a question of J. Nekovář and the Birch and Swinnerton–Dyer conjecture’, Proc. Amer. Math. Soc. 126(10) (1998), 2849–2853.Google Scholar
Ono, K., ‘Nonvanishing of quadratic twists of modular L-functions and applications to elliptic curves’, J. Reine Angew. Math. 533 (2001), 81–97.Google Scholar
Ono, K. and Skinner, C., ‘Non-vanishing of quadratic twists of modular L-functions’, Invent. Math. 134(3) (1998), 651–660.Google Scholar
Perelli, A. and Pomykala, J., ‘Averages of twisted elliptic L-functions’, Acta Arith. 80(2) (1997), 149–163.Google Scholar
Perrin-Riou, B., ‘Points de Heegner et dérivées de fonctions L p-adiques’, Invent. Math. 89(3) (1987), 455–510.Google Scholar
Pollack, R. and Rubin, K., ‘The main conjecture for CM elliptic curves at supersingular primes’, Ann. of Math. (2) 159(1) (2004), 447–464.Google Scholar
Prasanna, K., ‘On p-adic properties of central L-values of quadratic twists of an elliptic curve’, Canad. J. Math. 62(2) (2010), 400–414.Google Scholar
Rubin, K., ‘Congruences for special values of L-functions of elliptic curves with complex multiplication’, Invent. Math. 71(2) (1983), 339–364.Google Scholar
Rubin, K., ‘The ‘main conjectures’ of Iwasawa theory for imaginary quadratic fields’, Invent. Math. 103(1) (1991), 25–68.Google Scholar
Rubin, K., ‘ p-adic L-functions and rational points on elliptic curves with complex multiplication’, Invent. Math. 107(2) (1992), 323–350.Google Scholar
The Sage Developers. SageMath, the Sage Mathematics Software System (Version 7.2), 2016. http://www.sagemath.org.Google Scholar
Satgé, P., ‘Groupes de Selmer et corps cubiques’, J. Number Theory 23(3) (1986), 294–317.Google Scholar
Scholz, A., ‘Über die Beziehung der Klassenzahlen quadratischer Körper zueinander’, J. Reine Angew. Math. 166 (1932), 201–203.Google Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15(4) (1972), 259–331.Google Scholar
Serre, J.-P., ‘Divisibilité de certaines fonctions arithmétiques’, Enseign. Math. (2) 22(3–4) (1976), 227–260.Google Scholar
Silverman, J. H., Advanced Topics in the Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 151 (Springer, New York, 1994).Google Scholar
Skinner, C. and Zhang, W., ‘Indivisibility of Heegner points in the multiplicative case’, arXiv e-prints, July 2014.Google Scholar
Skinner, C. and Urban, E., ‘The Iwasawa main conjectures for GL2 ’, Invent. Math. 195(1) (2014), 1–277.Google Scholar
Smith, A., ‘The congruent numbers have positive natural density’, arXiv e-prints, March 2016.Google Scholar
Smith, A., ‘ $2^{\infty }$ -Selmer groups, $2^{\infty }$ -class groups, and Goldfeld’s conjecture’, arXiv e-prints, February 2017.Google Scholar
Sprung, F., ‘The Iwasawa main conjecture for elliptic curves at odd supersingular primes’, arXiv e-prints, October 2016.Google Scholar
Stevens, G., ‘Stickelberger elements and modular parametrizations of elliptic curves’, Invent. Math. 98(1) (1989), 75–106.Google Scholar
Taya, H., ‘Iwasawa invariants and class numbers of quadratic fields for the prime 3’, Proc. Amer. Math. Soc. 128(5) (2000), 1285–1292.Google Scholar
Tian, Y., Yuan, X. and Zhang, S., ‘Genus periods, genus points and congruent number problem’, Asian J. Math. 21(4) (2017), 721–773.Google Scholar
Tian, Y., ‘Congruent numbers and Heegner points’, Camb. J. Math. 2(1) (2014), 117–161.Google Scholar
Vatsal, V., ‘Rank-one twists of a certain elliptic curve’, Math. Ann. 311(4) (1998), 791–794.Google Scholar
Vatsal, V., ‘Canonical periods and congruence formulae’, Duke Math. J. 98(2) (1999), 397–419.Google Scholar
Wan, X., ‘Iwasawa main conjecture for supersingular elliptic curves’, arXiv e-prints, November 2014.Google Scholar
Washington, L. C., Introduction to Cyclotomic Fields, second edition, Graduate Texts in Mathematics, 83 (Springer, New York, 1997).Google Scholar
Watkins, M., ‘Rank distribution in a family of cubic twists’, inRanks of Elliptic Curves and Random Matrix Theory, London Mathematical Society Lecture Note Series, 341 (Cambridge University Press, Cambridge, 2007), 237–246.Google Scholar
Yoo, H., ‘Non-optimal levels of a reducible mod l modular representation’, Trans. Amer. Math. Soc. 371 (2019), 3805–3830.Google Scholar
Zagier, D. and Kramarz, G., ‘Numerical investigations related to the L-series of certain elliptic curves’, J. Indian Math. Soc. (N.S.) 52 (1987), 51–69 (1988).Google Scholar
Zhai, S., ‘Non-vanishing theorems for quadratic twists of elliptic curves’, Asian J. Math. 20(3) (2016), 475–502.Google Scholar
Zhang, W., ‘Selmer groups and the indivisibility of Heegner points’, Camb. J. Math. 2(2) (2014), 191–253.Google Scholar