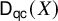1 Introduction
Let
![]() $\mathcal {D}$
be a triangulated category with a t-structure
$\mathcal {D}$
be a triangulated category with a t-structure
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
. We can consider two objects
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
. We can consider two objects
![]() $x,\ y\in \mathcal {D}$
as “close together” if there exists an exact triangle
$x,\ y\in \mathcal {D}$
as “close together” if there exists an exact triangle
![]() $x\to y\to z$
in
$x\to y\to z$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $z\in {\mathcal {D}^{\leq -n}}$
for some large n. This intuitive definition of distance was used in [Reference Neeman16] to define two new notions, assuming
$z\in {\mathcal {D}^{\leq -n}}$
for some large n. This intuitive definition of distance was used in [Reference Neeman16] to define two new notions, assuming
![]() $\mathcal {D}$
has coproducts and is compactly generated by a single object G. The first is the property of (weak) approximability:
$\mathcal {D}$
has coproducts and is compactly generated by a single object G. The first is the property of (weak) approximability:
![]() $\mathcal {D}$
is approximable if every object in
$\mathcal {D}$
is approximable if every object in
![]() ${\mathcal {D}^{\leq 0}}$
can be approximated by objects that are finitely built out of arbitrary coproducts of certain shifts of G. That is, every object in
${\mathcal {D}^{\leq 0}}$
can be approximated by objects that are finitely built out of arbitrary coproducts of certain shifts of G. That is, every object in
![]() ${\mathcal {D}^{\leq 0}}$
has a sequence of “simpler” objects converging to it. The second is a pair of subcategories
${\mathcal {D}^{\leq 0}}$
has a sequence of “simpler” objects converging to it. The second is a pair of subcategories
![]() $\mathcal {D}^{b}_{c} \subseteq \mathcal {D}^{-}_{c} \subseteq \mathcal {D}$
. Here,
$\mathcal {D}^{b}_{c} \subseteq \mathcal {D}^{-}_{c} \subseteq \mathcal {D}$
. Here,
![]() $\mathcal {D}^{-}_{c}$
denotes the full subcategory with objects that can be approximated by compact objects, and
$\mathcal {D}^{-}_{c}$
denotes the full subcategory with objects that can be approximated by compact objects, and
![]() $\mathcal {D}^{b}_{c}$
is
$\mathcal {D}^{b}_{c}$
is
![]() $\mathcal {D}^{-}_{c}\cap \mathcal {D}^{b}$
, where
$\mathcal {D}^{-}_{c}\cap \mathcal {D}^{b}$
, where
![]() $\mathcal {D}^b$
is the bounded part of the given t-structure.
$\mathcal {D}^b$
is the bounded part of the given t-structure.
The two notions are connected: if
![]() $\mathcal {D}$
is approximable and G satisfies certain finiteness conditions, then every finite cohomological functor, respectively, locally finite cohomological functor, on the compact objects
$\mathcal {D}$
is approximable and G satisfies certain finiteness conditions, then every finite cohomological functor, respectively, locally finite cohomological functor, on the compact objects
![]() $\mathcal {D}^{c}$
of
$\mathcal {D}^{c}$
of
![]() $\mathcal {D}$
is represented by an object of
$\mathcal {D}$
is represented by an object of
![]() $\mathcal {D}^{b}_{c},$
respectively,
$\mathcal {D}^{b}_{c},$
respectively,
![]() $\mathcal {D}^{-}_{c}$
, by [Reference Neeman16, Theorem 0.3]. In this paper, we prove that approximability and the two distinguished subcategories may be glued along a recollement. To be precise, we let
$\mathcal {D}^{-}_{c}$
, by [Reference Neeman16, Theorem 0.3]. In this paper, we prove that approximability and the two distinguished subcategories may be glued along a recollement. To be precise, we let
![]() $\mathcal {D}_{F}$
and
$\mathcal {D}_{F}$
and
![]() $\mathcal {D}_{U}$
be triangulated categories with a single compact generator and let
$\mathcal {D}_{U}$
be triangulated categories with a single compact generator and let
![]() $\mathcal {D}$
be a compactly generated triangulated category. We assume there is a recollement
$\mathcal {D}$
be a compactly generated triangulated category. We assume there is a recollement

which implies that
![]() $\mathcal {D}$
has a compact generator G.
$\mathcal {D}$
has a compact generator G.
The following are Proposition 4.3 and Theorem 5.1, respectively.
Proposition. If
![]() $\mathcal {D}_U$
is weakly approximable,
$\mathcal {D}_U$
is weakly approximable, ![]() for
for
![]() $n \gg 0$
, and
$n \gg 0$
, and
![]() $j^{*} G$
is in
$j^{*} G$
is in
![]() $(\mathcal {D}_{U})^{-}_{c},$
then there are equalities:
$(\mathcal {D}_{U})^{-}_{c},$
then there are equalities:
 $$ \begin{align*} \mathcal{D}^{-}_{c} &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c} \text{ and } j^{*} X \in (\mathcal{D}_{U})^{-}_{c} \right \},\\ \mathcal{D}^{b}_{c} \, &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c},\ j^{*} X \in (\mathcal{D}_{U})^{b}_{c} \text{ and } i^{!} X \in (\mathcal{D}_{F})^{+}\right \}. \end{align*} $$
$$ \begin{align*} \mathcal{D}^{-}_{c} &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c} \text{ and } j^{*} X \in (\mathcal{D}_{U})^{-}_{c} \right \},\\ \mathcal{D}^{b}_{c} \, &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c},\ j^{*} X \in (\mathcal{D}_{U})^{b}_{c} \text{ and } i^{!} X \in (\mathcal{D}_{F})^{+}\right \}. \end{align*} $$
The point of this proposition is an explicit description of the subcategories
![]() $\mathcal {D}^{-}_{c}$
and
$\mathcal {D}^{-}_{c}$
and
![]() $\mathcal {D}^{b}_{c}$
of
$\mathcal {D}^{b}_{c}$
of
![]() $\mathcal {D}$
in terms of the gluing functors of the recollement and of the corresponding subcategories of
$\mathcal {D}$
in terms of the gluing functors of the recollement and of the corresponding subcategories of
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $\mathcal {D}_U$
. The notation that enters these formulas will be explained in the lead-up to the proposition.
$\mathcal {D}_U$
. The notation that enters these formulas will be explained in the lead-up to the proposition.
Theorem. If
![]() $\mathcal {D}_{F}$
and
$\mathcal {D}_{F}$
and
![]() $\mathcal {D}_{U}$
are approximable and
$\mathcal {D}_{U}$
are approximable and ![]() for
for
![]() $n \gg 0,$
then
$n \gg 0,$
then
![]() $\mathcal {D}$
is approximable.
$\mathcal {D}$
is approximable.
Approximability is a very useful and natural notion in the study of the triangulated categories of algebraic geometry. If
![]() $\mathcal {D} = \mathsf {D}_{\mathsf {qc}}( X )$
is the derived category of quasi-coherent sheaves on a scheme
$\mathcal {D} = \mathsf {D}_{\mathsf {qc}}( X )$
is the derived category of quasi-coherent sheaves on a scheme
![]() $X,$
then
$X,$
then
![]() $\mathcal {D}$
is approximable if X is quasi-compact and separated [Reference Neeman16, Example 3.6], and if we further assume X Noetherian, the subcategories
$\mathcal {D}$
is approximable if X is quasi-compact and separated [Reference Neeman16, Example 3.6], and if we further assume X Noetherian, the subcategories
![]() $\mathcal {D}^{b}_{c}$
and
$\mathcal {D}^{b}_{c}$
and
![]() $\mathcal {D}^{-}_{c}$
are
$\mathcal {D}^{-}_{c}$
are
![]() $\mathsf {D}^{\mathsf {b}}_{\mathsf {coh}}( X )$
and
$\mathsf {D}^{\mathsf {b}}_{\mathsf {coh}}( X )$
and
![]() $\mathsf {D}^{-}_{\mathsf {coh}}( X )$
, respectively. The approximability property of the category
$\mathsf {D}^{-}_{\mathsf {coh}}( X )$
, respectively. The approximability property of the category
![]() $\mathsf {D}_{\mathsf {qc}}( X )$
is used in [Reference Neeman15] and [Reference Neeman16] to significantly generalize foundational results of Bondal and Van den Bergh [Reference Bondal and van den Bergh3], and Rouquier [Reference Rouquier23]; in particular, to mixed characteristic. For an overview of the power of approximability, we refer the reader to the survey article [Reference Neeman14], as well as to the ICM proceedings [Reference Neeman13] which surveys the applications obtained to date.
$\mathsf {D}_{\mathsf {qc}}( X )$
is used in [Reference Neeman15] and [Reference Neeman16] to significantly generalize foundational results of Bondal and Van den Bergh [Reference Bondal and van den Bergh3], and Rouquier [Reference Rouquier23]; in particular, to mixed characteristic. For an overview of the power of approximability, we refer the reader to the survey article [Reference Neeman14], as well as to the ICM proceedings [Reference Neeman13] which surveys the applications obtained to date.
We expect that approximability will also be useful in noncommutative geometry. We mean noncommutative algebraic geometry in the sense of [Reference Orlov22], where a noncommutative scheme is a small pretriangulated dg-category with a classical generator, and the derived category of the scheme is the derived category of the dg-category. In [Reference Bondal and van den Bergh3, Theorem 3.1.1(ii)], it was proved that if X is a quasi-compact quasi-separated scheme, then
![]() $\mathsf {D}_{\mathsf {perf}}( X )$
has a classical generator. In this way, the classical commutative schemes are considered within the world of noncommutative schemes.
$\mathsf {D}_{\mathsf {perf}}( X )$
has a classical generator. In this way, the classical commutative schemes are considered within the world of noncommutative schemes.
A central construction in noncommutative algebraic geometry is the gluing
![]() $\mathcal {A}$
of two small dg-categories
$\mathcal {A}$
of two small dg-categories
![]() $\mathcal {B}, \mathcal {C}$
along a
$\mathcal {B}, \mathcal {C}$
along a
![]() $\mathcal {C}$
-
$\mathcal {C}$
-
![]() $\mathcal {B}$
-bimodule [(Reference Orlov22, Reference Tabuada24)]. In the final section of this paper, we show that if
$\mathcal {B}$
-bimodule [(Reference Orlov22, Reference Tabuada24)]. In the final section of this paper, we show that if
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {C}$
have approximable derived categories, and the bimodule is cohomologically bounded above, then the glued dg-category
$\mathcal {C}$
have approximable derived categories, and the bimodule is cohomologically bounded above, then the glued dg-category
![]() $\mathcal {A}$
also has an approximable derived category. Furthermore, we describe how
$\mathcal {A}$
also has an approximable derived category. Furthermore, we describe how
![]() $\mathsf {D}( \mathcal {A} )_c^{-}$
is built from gluing
$\mathsf {D}( \mathcal {A} )_c^{-}$
is built from gluing
![]() $\mathsf {D}( \mathcal {B} )_c^{-}$
and
$\mathsf {D}( \mathcal {B} )_c^{-}$
and
![]() $\mathsf {D}( \mathcal {C} )_c^{-}$
. This result significantly expands the known examples of approximable triangulated categories in noncommutative algebraic geometry. Even if
$\mathsf {D}( \mathcal {C} )_c^{-}$
. This result significantly expands the known examples of approximable triangulated categories in noncommutative algebraic geometry. Even if
![]() $\mathsf {D}( \mathcal {B} )$
and
$\mathsf {D}( \mathcal {B} )$
and
![]() $\mathsf {D}( \mathcal {C} )$
are “commutative”, that is, equivalent to the derived categories of quasi-coherent sheaves on a commutative scheme, the glued category
$\mathsf {D}( \mathcal {C} )$
are “commutative”, that is, equivalent to the derived categories of quasi-coherent sheaves on a commutative scheme, the glued category
![]() $\mathsf {D}( \mathcal {A} )$
is rarely commutative.
$\mathsf {D}( \mathcal {A} )$
is rarely commutative.
Many interesting classes of noncommutative schemes are constructed via gluing. In [Reference Kuznetsov and Lunts9], Kuznetsov and Lunts construct categorical resolutions of separated schemes of finite type over a field k of characteristic zero by gluing derived categories of smooth varieties. This notion of categorical resolutions was defined in [Reference Lunts10] as a generalization of Van den Bergh’s notion of noncommutative crepant resolution [Reference van den Bergh25]. Gluing of DG-categories and categorical resolutions are also used in [Reference Efimov5] to show that
![]() $\mathsf {D}^{\mathsf {b}}_{\mathsf {coh}}( X )$
is homotopically finitely presented whenever X is a separated scheme of finite type over a field k of characteristic zero. For other places where gluing is used in noncommutative geometry see [Reference Efimov4, Reference Kuznetsov8, Reference Lunts11, Reference Orlov21].
$\mathsf {D}^{\mathsf {b}}_{\mathsf {coh}}( X )$
is homotopically finitely presented whenever X is a separated scheme of finite type over a field k of characteristic zero. For other places where gluing is used in noncommutative geometry see [Reference Efimov4, Reference Kuznetsov8, Reference Lunts11, Reference Orlov21].
In addition to the main results listed above, the lemmas and techniques developed in this paper form a toolbox which is powerful in its own right. Already, Lemma 3.6 in this paper is used in [Reference Neeman17, Proposition 3.2], whereas Lemma 3.9 is used to prove [Reference Neeman17, Lemma 3.1] as well as [Reference Neeman18, Proposition 4.8]. More applications will appear in forthcoming work of the second author together with Alberto Canonaco and Paolo Stellari, as well as in forthcoming work by the third author.
2 Notation and definitions
Throughout,
![]() $\mathcal {D}$
denotes a triangulated category with coproducts. We recall some standard notation, see [Reference Neeman16, Definition 0.21].
$\mathcal {D}$
denotes a triangulated category with coproducts. We recall some standard notation, see [Reference Neeman16, Definition 0.21].
2.1. Let
![]() $\mathcal {A},\ \mathcal {B}$
be full subcategories of
$\mathcal {A},\ \mathcal {B}$
be full subcategories of
![]() $\mathcal {D}$
, and define the following full subcategories:
$\mathcal {D}$
, and define the following full subcategories:
-
a)
 $\mathcal {A}\ast \mathcal {B}$
has for objects all the
$\mathcal {A}\ast \mathcal {B}$
has for objects all the
 $x\in \mathcal {D}$
, such that there exists an exact triangle
$x\in \mathcal {D}$
, such that there exists an exact triangle
 $a\to x\to b$
in
$a\to x\to b$
in
 $\mathcal {D}$
with
$\mathcal {D}$
with
 $a\in \mathcal {A}$
and
$a\in \mathcal {A}$
and
 $b\in \mathcal {B}$
.
$b\in \mathcal {B}$
. -
b)
 has for objects all coproducts of objects of
has for objects all coproducts of objects of
 $\mathcal {A}$
.
$\mathcal {A}$
. -
c)
 has for objects all direct summands of objects of
has for objects all direct summands of objects of
 $\mathcal {A}$
.
$\mathcal {A}$
.
2.2. Let G be an object in
![]() $\mathcal {D}$
, and suppose
$\mathcal {D}$
, and suppose
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $A\leq B\in \mathbb {Z}\cup \{-\infty ,+\infty \}$
. We define the following full subcategories:
$A\leq B\in \mathbb {Z}\cup \{-\infty ,+\infty \}$
. We define the following full subcategories:
-
a) If
 $A,B\in \mathbb {Z}$
, then
$A,B\in \mathbb {Z}$
, then
 $G[A,B]\subset \mathcal {D}$
has objects
$G[A,B]\subset \mathcal {D}$
has objects
 $\{\Sigma ^{-i} G\mid A\leq i\leq B\}$
. Similarly,
$\{\Sigma ^{-i} G\mid A\leq i\leq B\}$
. Similarly,
 $G(-\infty ,B]\subset \mathcal {D}$
has objects
$G(-\infty ,B]\subset \mathcal {D}$
has objects
 $\{\Sigma ^{-i} G\mid i\leq B\}$
. We define
$\{\Sigma ^{-i} G\mid i\leq B\}$
. We define
 $G[A,\infty )$
and
$G[A,\infty )$
and
 $G(-\infty ,\infty )$
analogously.
$G(-\infty ,\infty )$
analogously. -
b)
 is defined inductively on the integer n by setting
is defined inductively on the integer n by setting 
-
c)
 is the smallest full subcategory
is the smallest full subcategory
 $\mathcal {S}\subset \mathcal {D}$
, closed under coproducts, with
$\mathcal {S}\subset \mathcal {D}$
, closed under coproducts, with
 $\mathcal {S}\ast \mathcal {S}\subset \mathcal {S}$
and with
$\mathcal {S}\ast \mathcal {S}\subset \mathcal {S}$
and with
 $G[A,B]\subset \mathcal {S}$
.
$G[A,B]\subset \mathcal {S}$
. -
d)
 .
. -
e)
 .
.
2.3 [Reference Beilinson, Bernstein and Deligne2, Definition 1.3.1]
A t-structure on a triangulated category
![]() $\mathcal {D}$
is a pair of full subcategories
$\mathcal {D}$
is a pair of full subcategories
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
satisfying
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
satisfying
-
1.
 $\Sigma {\mathcal {D}^{\leq 0}} \subset {\mathcal {D}^{\leq 0}}$
and
$\Sigma {\mathcal {D}^{\leq 0}} \subset {\mathcal {D}^{\leq 0}}$
and
 ${\mathcal {D}^{\geq 0}} \subset \Sigma {\mathcal {D}^{\geq 0}}$
.
${\mathcal {D}^{\geq 0}} \subset \Sigma {\mathcal {D}^{\geq 0}}$
. -
2.
 .
. -
3. For every
 $X \in \mathcal {D}$
, there exists an exact triangle
$X \in \mathcal {D}$
, there exists an exact triangle
 $Y \to X \to Z$
with
$Y \to X \to Z$
with
 $Y \in \Sigma {\mathcal {D}^{\leq 0}}$
and
$Y \in \Sigma {\mathcal {D}^{\leq 0}}$
and
 $Z\in {\mathcal {D}^{\geq 0}}$
.
$Z\in {\mathcal {D}^{\geq 0}}$
.
2.4 [Reference Beilinson, Bernstein and Deligne2, Section 1.3]
Let
![]() $\mathcal {D}$
be a triangulated category with t-structure
$\mathcal {D}$
be a triangulated category with t-structure
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
. For every integer
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
. For every integer
![]() $n\in \mathbb {Z}$
, we set
$n\in \mathbb {Z}$
, we set
![]() ${\mathcal {D}^{\leq n}}:=\Sigma ^{-n}{\mathcal {D}^{\leq 0}}$
and
${\mathcal {D}^{\leq n}}:=\Sigma ^{-n}{\mathcal {D}^{\leq 0}}$
and
![]() ${\mathcal {D}^{\geq n}}:=\Sigma ^{-n}{\mathcal {D}^{\geq 0}}$
. The inclusion
${\mathcal {D}^{\geq n}}:=\Sigma ^{-n}{\mathcal {D}^{\geq 0}}$
. The inclusion
![]() ${\mathcal {D}^{\leq n}}\subset \mathcal {D}$
has a right adjoint which we denote
${\mathcal {D}^{\leq n}}\subset \mathcal {D}$
has a right adjoint which we denote
![]() $(-)^{\leq n}$
, whereas
$(-)^{\leq n}$
, whereas
![]() ${\mathcal {D}^{\geq n}}\subset \mathcal {D}$
has a left adjoint which we denote by
${\mathcal {D}^{\geq n}}\subset \mathcal {D}$
has a left adjoint which we denote by
![]() $(-)^{\geq n}$
. For every
$(-)^{\geq n}$
. For every
![]() $X\in \mathcal {D}$
, the counit and unit of these adjunctions fit into an exact triangle
$X\in \mathcal {D}$
, the counit and unit of these adjunctions fit into an exact triangle
This is, up to unique isomorphism, the only triangle
![]() $Y \to X \to Z$
with
$Y \to X \to Z$
with
![]() $Y \in {\mathcal {D}^{\leq n}}$
and
$Y \in {\mathcal {D}^{\leq n}}$
and
![]() $Z\in {\mathcal {D}^{\geq n+1}}$
. We write
$Z\in {\mathcal {D}^{\geq n+1}}$
. We write
![]() $\mathcal {H}^{n}:\mathcal {D}\to \mathcal {D}$
for the functor taking X to
$\mathcal {H}^{n}:\mathcal {D}\to \mathcal {D}$
for the functor taking X to
![]() $(X^{\leq n})^{\geq n}$
.
$(X^{\leq n})^{\geq n}$
.
2.5. A recollement is a diagram of exact functors between triangulated categories,

with the following properties:
-
1. each functor is left adjoint to the one below it;
-
2.
 $j^{*} i_{*} = 0$
;
$j^{*} i_{*} = 0$
; -
3. there exist natural transformations
 $d: i_{*}i^{*} \to \Sigma j_{!} j^{*}$
and
$d: i_{*}i^{*} \to \Sigma j_{!} j^{*}$
and
 $d': j_{*}j^{*} \to \Sigma i_{*}i^{!}$
, such that for any
$d': j_{*}j^{*} \to \Sigma i_{*}i^{!}$
, such that for any
 $X \in \mathcal {D},$
the following are exact triangles: where
$X \in \mathcal {D},$
the following are exact triangles: where $$\begin{align*}&j_{!}j^{*}X\xrightarrow{\epsilon} X\xrightarrow{\eta} i_{*}i^{*} X \xrightarrow{d} \Sigma j_{!}j^{*}X\\&i_{*}i^{!}X\xrightarrow{\epsilon} X\xrightarrow{\eta} j_{*}j^{*} X \xrightarrow{d'} \Sigma i_{*}i^{!}X,\end{align*}$$
$$\begin{align*}&j_{!}j^{*}X\xrightarrow{\epsilon} X\xrightarrow{\eta} i_{*}i^{*} X \xrightarrow{d} \Sigma j_{!}j^{*}X\\&i_{*}i^{!}X\xrightarrow{\epsilon} X\xrightarrow{\eta} j_{*}j^{*} X \xrightarrow{d'} \Sigma i_{*}i^{!}X,\end{align*}$$
 $\eta $
and
$\eta $
and
 $\epsilon $
are the (co)unit maps of the adjunctions;
$\epsilon $
are the (co)unit maps of the adjunctions;
-
4.
 $i_{*}, j_{!}, j_{*}$
are fully faithful.
$i_{*}, j_{!}, j_{*}$
are fully faithful.
We note that
![]() $i^*,\ i_{*},\ j_{!},\ j^*$
preserve coproducts, since they are left adjoints. Since
$i^*,\ i_{*},\ j_{!},\ j^*$
preserve coproducts, since they are left adjoints. Since
![]() $i^{*}$
and
$i^{*}$
and
![]() $j_{!}$
have right adjoints preserving coproducts, [Reference Neeman19, Theorem 5.1] informs us that
$j_{!}$
have right adjoints preserving coproducts, [Reference Neeman19, Theorem 5.1] informs us that
![]() $i^{*}$
and
$i^{*}$
and
![]() $j_{!}$
respect compact objects.
$j_{!}$
respect compact objects.
2.6 [(Reference Beilinson, Bernstein and Deligne2, 1.4.10)]
Consider a recollement as above. Given t-structures
![]() $(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
and
$(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
and
![]() $(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
on
$(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
on
![]() $\mathcal {D}_{F}$
and
$\mathcal {D}_{F}$
and
![]() $\mathcal {D}_{U}$
, respectively, the glued t-structure on
$\mathcal {D}_{U}$
, respectively, the glued t-structure on
![]() $\mathcal {D}$
has aisle
$\mathcal {D}$
has aisle
and coaisle
2.7 [(Reference Beilinson, Bernstein and Deligne2, 1.3.16)]
Let
![]() $\mathcal {D}_1$
,
$\mathcal {D}_1$
,
![]() $\mathcal {D}_2$
be triangulated categories endowed with t-structures. A functor
$\mathcal {D}_2$
be triangulated categories endowed with t-structures. A functor
![]() $f:\mathcal {D}_1\to \mathcal {D}_2$
is right t-exact if
$f:\mathcal {D}_1\to \mathcal {D}_2$
is right t-exact if
![]() $f({\mathcal {D}^{\leq 0}_1})\subset {\mathcal {D}^{\leq 0}_2}$
, and left t-exact if
$f({\mathcal {D}^{\leq 0}_1})\subset {\mathcal {D}^{\leq 0}_2}$
, and left t-exact if
![]() $f({\mathcal {D}^{\geq 0}_1})\subset {\mathcal {D}^{\geq 0}_2}$
. We say f is t-exact if f is left and right t-exact.
$f({\mathcal {D}^{\geq 0}_1})\subset {\mathcal {D}^{\geq 0}_2}$
. We say f is t-exact if f is left and right t-exact.
Consider a recollement as in 2.5, and suppose
![]() $\mathcal {D}$
has a t-structure glued from t-structures on
$\mathcal {D}$
has a t-structure glued from t-structures on
![]() $\mathcal {D}_{F}$
and
$\mathcal {D}_{F}$
and
![]() $\mathcal {D}_{U}$
. By [Reference Beilinson, Bernstein and Deligne2, 1.3.17(iii)], the functors
$\mathcal {D}_{U}$
. By [Reference Beilinson, Bernstein and Deligne2, 1.3.17(iii)], the functors
![]() $i^*,\ j_{!}$
are right t-exact,
$i^*,\ j_{!}$
are right t-exact,
![]() $i_*,\ j^*$
are t-exact, and
$i_*,\ j^*$
are t-exact, and
![]() $i^!,\ j_*$
are left t-exact.
$i^!,\ j_*$
are left t-exact.
2.8. Let
![]() $\mathcal {D}$
be a triangulated category with coproducts. An object
$\mathcal {D}$
be a triangulated category with coproducts. An object
![]() $G\in \mathcal {D}$
is compact if the functor
$G\in \mathcal {D}$
is compact if the functor ![]() respects coproducts. We call G a compact generator for
respects coproducts. We call G a compact generator for
![]() $\mathcal {D}$
if for all
$\mathcal {D}$
if for all
![]() $X\in \mathcal {D}$
, we have that
$X\in \mathcal {D}$
, we have that ![]() for all
for all
![]() $i\in \mathbb {Z}$
implies
$i\in \mathbb {Z}$
implies
![]() $X\cong 0$
.
$X\cong 0$
.
2.9 [Reference Neeman16, Definition 0.21]
A triangulated category
![]() $\mathcal {D}$
with coproducts is weakly approximable if there exists a compact generator
$\mathcal {D}$
with coproducts is weakly approximable if there exists a compact generator
![]() $G,$
a t-structure
$G,$
a t-structure
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0}),$
and an integer
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0}),$
and an integer
![]() $A> 0,$
such that the following hold:
$A> 0,$
such that the following hold:
-
(1)
 $\Sigma ^{A} G \in {\mathcal {D}^{\leq 0}}$
and
$\Sigma ^{A} G \in {\mathcal {D}^{\leq 0}}$
and 
-
(2) For every
 $X \in {\mathcal {D}^{\leq 0}},$
there exists an exact triangle
$X \in {\mathcal {D}^{\leq 0}},$
there exists an exact triangle
 $E \to X \to D$
with
$E \to X \to D$
with
 $E \in \unicode{xf8} {\langle G \rangle }^{[-A,A]}$
and
$E \in \unicode{xf8} {\langle G \rangle }^{[-A,A]}$
and
 $D \in {\mathcal {D}^{\leq -1}}.$
$D \in {\mathcal {D}^{\leq -1}}.$
If Properties
![]() $(1)$
and
$(1)$
and
![]() $(2)$
hold for a compact generator G and integer
$(2)$
hold for a compact generator G and integer
![]() $A,$
then for every compact generator H, there is an integer
$A,$
then for every compact generator H, there is an integer
![]() $A_{H}$
for which they hold, by [Reference Neeman16, Proposition 2.6].
$A_{H}$
for which they hold, by [Reference Neeman16, Proposition 2.6].
The category
![]() $\mathcal {D}$
is approximable if we can choose
$\mathcal {D}$
is approximable if we can choose
![]() $A> 0$
, such that, moreover,
$A> 0$
, such that, moreover,
-
(3) in the exact triangle
 $E \to X \to D$
above, we may assume
$E \to X \to D$
above, we may assume
 $E \in \unicode{xf8} {\langle G \rangle }^{[-A,A]}_{A}.$
$E \in \unicode{xf8} {\langle G \rangle }^{[-A,A]}_{A}.$
If Properties
![]() $(1)$
,
$(1)$
,
![]() $(2)$
, and
$(2)$
, and
![]() $(3)$
hold for a compact generator G and integer
$(3)$
hold for a compact generator G and integer
![]() $A,$
then for every compact generator H, there is an integer
$A,$
then for every compact generator H, there is an integer
![]() $A_{H}$
for which they hold, by [Reference Neeman16, Proposition 2.6].
$A_{H}$
for which they hold, by [Reference Neeman16, Proposition 2.6].
3 The preferred t-structure
In this section, we start developing the necessary machinery, some of which has since demonstrated its usefulness in other contexts. We begin by reminding the reader of some definitions.
Definition 3.1 [Reference Neeman16, Definition 0.10]
Let
![]() $\mathcal {D}$
be a triangulated category. Two t-structures
$\mathcal {D}$
be a triangulated category. Two t-structures
![]() $(\mathcal {D}_1^{\leq 0}, \mathcal {D}_1^{\geq 0})$
and
$(\mathcal {D}_1^{\leq 0}, \mathcal {D}_1^{\geq 0})$
and
![]() $(\mathcal {D}_2^{\leq 0}, \mathcal {D}_2^{\geq 0})$
on
$(\mathcal {D}_2^{\leq 0}, \mathcal {D}_2^{\geq 0})$
on
![]() $\mathcal {D}$
are equivalent if there exists an integer
$\mathcal {D}$
are equivalent if there exists an integer
![]() $A> 0$
with
$A> 0$
with
![]() ${\mathcal {D}^{\leq -A}_1}\subset {\mathcal {D}^{\leq 0}_2}\subset {\mathcal {D}^{\leq A}_1}$
.
${\mathcal {D}^{\leq -A}_1}\subset {\mathcal {D}^{\leq 0}_2}\subset {\mathcal {D}^{\leq A}_1}$
.
Lemma 3.2. The gluing of t-structures along a recollement is stable under equivalence. That is, consider a recollement as in 2.5 and suppose
![]() $(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
,
$(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
,
![]() $({\mathcal {D}'}^{\leq 0}_{F}, {\mathcal {D}'}^{\geq 0}_{F})$
are equivalent t-structures on
$({\mathcal {D}'}^{\leq 0}_{F}, {\mathcal {D}'}^{\geq 0}_{F})$
are equivalent t-structures on
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
,
$(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
,
![]() $({\mathcal {D}'}^{\leq 0}_{U}, {\mathcal {D}'}^{\geq 0}_{U})$
are equivalent t-structures on
$({\mathcal {D}'}^{\leq 0}_{U}, {\mathcal {D}'}^{\geq 0}_{U})$
are equivalent t-structures on
![]() $\mathcal {D}_U$
. Then the t-structure on
$\mathcal {D}_U$
. Then the t-structure on
![]() $\mathcal {D}$
obtained by gluing
$\mathcal {D}$
obtained by gluing
![]() $(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
,
$(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
,
![]() $(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
is equivalent to the t-structure obtained by gluing
$(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
is equivalent to the t-structure obtained by gluing
![]() $({\mathcal {D}'}^{\leq 0}_{F}, {\mathcal {D}'}^{\geq 0}_{F})$
,
$({\mathcal {D}'}^{\leq 0}_{F}, {\mathcal {D}'}^{\geq 0}_{F})$
,
![]() $({\mathcal {D}'}^{\leq 0}_{U}, {\mathcal {D}'}^{\geq 0}_{U})$
.
$({\mathcal {D}'}^{\leq 0}_{U}, {\mathcal {D}'}^{\geq 0}_{U})$
.
Proof. Write
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
,
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
,
![]() $(\mathcal {D}'^{\leq 0}, \mathcal {D}'^{\geq 0})$
for the t-structures on
$(\mathcal {D}'^{\leq 0}, \mathcal {D}'^{\geq 0})$
for the t-structures on
![]() $\mathcal {D}$
obtained by gluing
$\mathcal {D}$
obtained by gluing
![]() $(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
,
$(\mathcal {D}^{\leq 0}_{F}, \mathcal {D}^{\geq 0}_{F})$
,
![]() $(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
and
$(\mathcal {D}^{\leq 0}_{U}, \mathcal {D}^{\geq 0}_{U})$
and
![]() $({\mathcal {D}'}^{\leq 0}_{F}, {\mathcal {D}'}^{\geq 0}_{F})$
,
$({\mathcal {D}'}^{\leq 0}_{F}, {\mathcal {D}'}^{\geq 0}_{F})$
,
![]() $({\mathcal {D}'}^{\leq 0}_{U}, {\mathcal {D}'}^{\geq 0}_{U})$
, respectively. If
$({\mathcal {D}'}^{\leq 0}_{U}, {\mathcal {D}'}^{\geq 0}_{U})$
, respectively. If
![]() $A>0$
is an integer such that
$A>0$
is an integer such that
![]() ${\mathcal {D}^{\leq -A}_{F}}\subset {\mathcal {D}'}_{F}^{\leq 0}\subset {\mathcal {D}^{\leq A}_{F}}$
and
${\mathcal {D}^{\leq -A}_{F}}\subset {\mathcal {D}'}_{F}^{\leq 0}\subset {\mathcal {D}^{\leq A}_{F}}$
and
![]() ${\mathcal {D}^{\leq -A}_U}\subset {\mathcal {D}'}^{\leq 0}_U\subset {\mathcal {D}^{\leq A}_U}$
, then
${\mathcal {D}^{\leq -A}_U}\subset {\mathcal {D}'}^{\leq 0}_U\subset {\mathcal {D}^{\leq A}_U}$
, then
![]() ${\mathcal {D}^{\leq -A}}\subset {\mathcal {D}'}^{\leq 0}\subset {\mathcal {D}^{\leq A}}$
.
${\mathcal {D}^{\leq -A}}\subset {\mathcal {D}'}^{\leq 0}\subset {\mathcal {D}^{\leq A}}$
.
Definition 3.3 [Reference Tarrío, López and Salorio1, Theorem A.1]
Given a compact object G of
![]() $\mathcal {D}$
, the t-structure generated by G, denoted
$\mathcal {D}$
, the t-structure generated by G, denoted
![]() $({\mathcal {D}^{\leq 0}_{G}}, {\mathcal {D}^{\geq 0}_{G}})$
, has aisle
$({\mathcal {D}^{\leq 0}_{G}}, {\mathcal {D}^{\geq 0}_{G}})$
, has aisle
![]() ${\mathcal {D}^{\leq 0}_{G}} =\unicode{xf8} {\langle G \rangle }^{(-\infty , 0]}.$
${\mathcal {D}^{\leq 0}_{G}} =\unicode{xf8} {\langle G \rangle }^{(-\infty , 0]}.$
Remark 1. Since the category ![]() is closed under positive suspensions and coproducts, it contains all direct summands of its objects. This shows
is closed under positive suspensions and coproducts, it contains all direct summands of its objects. This shows ![]() .
.
Suppose now that
![]() $\mathcal {D}$
is compactly generated by the compact object G. If H is also a compact generator for
$\mathcal {D}$
is compactly generated by the compact object G. If H is also a compact generator for
![]() $\mathcal {D}$
, then [Reference Neeman16, Lemma 0.9] provides a positive integer A with
$\mathcal {D}$
, then [Reference Neeman16, Lemma 0.9] provides a positive integer A with
![]() $H\in \unicode{xf8} {\langle G \rangle }_A^{[-A,A]}$
and
$H\in \unicode{xf8} {\langle G \rangle }_A^{[-A,A]}$
and
![]() $G\in \unicode{xf8} {\langle H \rangle }_A^{[-A,A]}$
. This shows
$G\in \unicode{xf8} {\langle H \rangle }_A^{[-A,A]}$
. This shows
![]() ${\mathcal {D}^{\leq -A}_H}\subset {\mathcal {D}^{\leq 0}_G}\subset {\mathcal {D}^{\leq A}_H}$
, hence the t-structures generated by G and H are equivalent. Thus, the next definition does not depend on the choice of compact generator:
${\mathcal {D}^{\leq -A}_H}\subset {\mathcal {D}^{\leq 0}_G}\subset {\mathcal {D}^{\leq A}_H}$
, hence the t-structures generated by G and H are equivalent. Thus, the next definition does not depend on the choice of compact generator:
Definition 3.4. If
![]() $\mathcal {D}$
is compactly generated by the compact object G, then the preferred equivalence class of t-structures is the equivalence class containing the t-structure
$\mathcal {D}$
is compactly generated by the compact object G, then the preferred equivalence class of t-structures is the equivalence class containing the t-structure
![]() $(\mathcal {D}_G^{\leq 0}, \mathcal {D}_G^{\geq 0})$
generated by G.
$(\mathcal {D}_G^{\leq 0}, \mathcal {D}_G^{\geq 0})$
generated by G.
The first part of the following lemma follows from [Reference Neeman16, Remark 0.20], and the second part follows from [Reference Neeman16, Observation 0.12(ii) and Lemma 2.8]:
Lemma 3.5. Suppose
![]() $\mathcal {D}$
has a compact generator G with
$\mathcal {D}$
has a compact generator G with ![]() for
for
![]() $n \gg 0$
. Assume
$n \gg 0$
. Assume
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is a t-structure in the preferred equivalence class. Then
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is a t-structure in the preferred equivalence class. Then
-
1. there exists an integer
 $C> 0$
, such that
$C> 0$
, such that  ;
; -
2. for all compact objects
 $F,H\in \mathcal {D},$
we have
$F,H\in \mathcal {D},$
we have  for
for
 $m \gg 0$
.
$m \gg 0$
.
In particular, the vanishing hypothesis on G is independent of the choice of compact generator.
Recall that a t-structure
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
on
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
on
![]() $\mathcal {D}$
is nondegenerate if
$\mathcal {D}$
is nondegenerate if
Lemma 3.6. Suppose
![]() $\mathcal {D}$
has a compact generator G with
$\mathcal {D}$
has a compact generator G with ![]() for
for
![]() $n \gg 0$
. Then every t-structure in the preferred equivalence class is nondegenerate.
$n \gg 0$
. Then every t-structure in the preferred equivalence class is nondegenerate.
Proof. Being nondegenerate is clearly stable under equivalence, so it suffices to show the t-structure
![]() $({\mathcal {D}^{\leq 0}_{G}}, {\mathcal {D}^{\geq 0}_{G}})$
generated by G is nondegenerate. Let X be a nonzero object in
$({\mathcal {D}^{\leq 0}_{G}}, {\mathcal {D}^{\geq 0}_{G}})$
generated by G is nondegenerate. Let X be a nonzero object in
![]() $\mathcal {D}$
. Since G is a compact generator for
$\mathcal {D}$
. Since G is a compact generator for
![]() $\mathcal {D}$
, there exists a nonzero morphism
$\mathcal {D}$
, there exists a nonzero morphism
![]() $\Sigma ^l G\to X$
for some
$\Sigma ^l G\to X$
for some
![]() $l\in \mathbb {Z}$
. It follows that
$l\in \mathbb {Z}$
. It follows that
![]() $X\notin {\mathcal {D}^{\geq -l+1}_G}=({\mathcal {D}^{\leq -l}_G})^{\perp }$
. Moreover, by the first part of Lemma 3.5, there exists
$X\notin {\mathcal {D}^{\geq -l+1}_G}=({\mathcal {D}^{\leq -l}_G})^{\perp }$
. Moreover, by the first part of Lemma 3.5, there exists
![]() $C>0$
, such that
$C>0$
, such that ![]() . Hence,
. Hence, ![]() , and we can conclude that
, and we can conclude that
![]() $X\notin {\mathcal {D}^{\leq -C-l}_G}$
.
$X\notin {\mathcal {D}^{\leq -C-l}_G}$
.
The next lemma is exactly [Reference Neeman16, Proposition 2.6]. It tells us that once we know a category to be (weakly) approximable, any compact generator and any t-structure in the preferred equivalence class will fulfil the approximability criteria in Definition 2.9.
Lemma 3.7. Let
![]() $\mathcal {D}$
be weakly approximable. Suppose G is a compact generator for
$\mathcal {D}$
be weakly approximable. Suppose G is a compact generator for
![]() $\mathcal {D}$
and that
$\mathcal {D}$
and that
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is any t-structure in the preferred equivalence class. Then there exists
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is any t-structure in the preferred equivalence class. Then there exists
![]() $A>0$
, such that Conditions (1) and (2) in Definition 2.9 hold for the compact generator G and the t-structure
$A>0$
, such that Conditions (1) and (2) in Definition 2.9 hold for the compact generator G and the t-structure
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
. If
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
. If
![]() $\mathcal {D}$
is moreover approximable, then the integer A can be chosen to further satisfy Condition (3) in Definition 2.9.
$\mathcal {D}$
is moreover approximable, then the integer A can be chosen to further satisfy Condition (3) in Definition 2.9.
Lemma 3.8. Let
![]() $\mathcal {D}$
be weakly approximable. Suppose G is a compact generator for
$\mathcal {D}$
be weakly approximable. Suppose G is a compact generator for
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is a t-structure in the preferred equivalence class. Assume the integer
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is a t-structure in the preferred equivalence class. Assume the integer
![]() $A>0$
is chosen to satisfy Conditions (1) and (2) in Definition 2.9. If
$A>0$
is chosen to satisfy Conditions (1) and (2) in Definition 2.9. If
![]() $X\in \mathcal {D}$
is an object, such that
$X\in \mathcal {D}$
is an object, such that ![]() for all i in the interval
for all i in the interval
![]() $-A\leq i\leq A$
, then
$-A\leq i\leq A$
, then
![]() $\mathcal {H}^{0}(X)=0$
.
$\mathcal {H}^{0}(X)=0$
.
Proof. The t-structure gives us an exact triangle
![]() $X^{\leq 0}\to X\to X^{\geq 1}$
, and we may choose a triangle
$X^{\leq 0}\to X\to X^{\geq 1}$
, and we may choose a triangle
![]() $E\to X^{\leq 0}\to D$
with
$E\to X^{\leq 0}\to D$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }^{[-A,A]}$
and
$E\in \unicode{xf8} {\langle G \rangle }^{[-A,A]}$
and
![]() $D\in \mathcal {D}^{\leq -1}$
. We are assuming that
$D\in \mathcal {D}^{\leq -1}$
. We are assuming that
![]() $^\perp X$
contains
$^\perp X$
contains
![]() $\{\Sigma ^iG,\,-A\leq i\leq A\}$
, and hence,
$\{\Sigma ^iG,\,-A\leq i\leq A\}$
, and hence,
![]() $^\perp X$
must contain
$^\perp X$
must contain
![]() $\unicode{xf8} {\langle G \rangle }^{[-A,A]}$
. Therefore, the composite
$\unicode{xf8} {\langle G \rangle }^{[-A,A]}$
. Therefore, the composite
![]() $E\to X^{\leq 0}\to X$
must vanish, and the map
$E\to X^{\leq 0}\to X$
must vanish, and the map
![]() $X^{\leq 0}\to X$
must factor as
$X^{\leq 0}\to X$
must factor as
![]() $X^{\leq 0}\to D\to X$
. Applying the functor
$X^{\leq 0}\to D\to X$
. Applying the functor
![]() $\mathcal {H}^{0}$
, we deduce that the isomorphism
$\mathcal {H}^{0}$
, we deduce that the isomorphism
![]() $\mathcal {H}^{0}(X^{\leq 0})\to \mathcal {H}^{0}(X)$
factors through
$\mathcal {H}^{0}(X^{\leq 0})\to \mathcal {H}^{0}(X)$
factors through
![]() $\mathcal {H}^{0}(D)=0$
.
$\mathcal {H}^{0}(D)=0$
.
The following lemma turns out to be surprisingly useful. It has already been used in [Reference Neeman17, Reference Neeman18], as well as in forthcoming work by the authors.
Lemma 3.9. Let
![]() $\mathcal {D}$
be weakly approximable. Suppose G is a compact generator for
$\mathcal {D}$
be weakly approximable. Suppose G is a compact generator for
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is a t-structure in the preferred equivalence class. Assume the integer
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
is a t-structure in the preferred equivalence class. Assume the integer
![]() $A>0$
is chosen to satisfy Conditions (1) and (2) in Definition 2.9. Suppose
$A>0$
is chosen to satisfy Conditions (1) and (2) in Definition 2.9. Suppose
![]() $X\in \mathcal {D}$
is an object, such that
$X\in \mathcal {D}$
is an object, such that ![]() for all i in the interval
for all i in the interval
![]() $-2A\leq i\leq 2A$
. Then there exists in
$-2A\leq i\leq 2A$
. Then there exists in
![]() $\mathcal {D}$
a triangle
$\mathcal {D}$
a triangle
such that, for each
![]() $i\in \mathbb {Z}$
, each of the abelian groups
$i\in \mathbb {Z}$
, each of the abelian groups ![]() and
and ![]() is either zero or isomorphic to
is either zero or isomorphic to ![]() , with the precise ranges in which each happens given in (i) and (ii) below. More fully, the triangle satisfies:
, with the precise ranges in which each happens given in (i) and (ii) below. More fully, the triangle satisfies:
-
(i) For the object
 $W\in \mathcal {D}$
, we have that
$W\in \mathcal {D}$
, we have that  vanishes when
vanishes when
 $i\leq 2A$
, while the map is an isomorphism for all
$i\leq 2A$
, while the map is an isomorphism for all
 $i\geq -2A$
.
$i\geq -2A$
.
-
(ii) For the object
 $Y\in \mathcal {D}$
, we have that
$Y\in \mathcal {D}$
, we have that  vanishes when
vanishes when
 $i\geq -2A$
, while the map is an isomorphism for all
$i\geq -2A$
, while the map is an isomorphism for all
 $i\leq 2A$
.
$i\leq 2A$
.
-
(iii) Any triangle
 $W\to X\to Y$
satisfying (i) and (ii) is canonically isomorphic to the triangle
$W\to X\to Y$
satisfying (i) and (ii) is canonically isomorphic to the triangle
 $X^{\leq i}\to X\to X^{\geq i+1}$
for any i such that
$X^{\leq i}\to X\to X^{\geq i+1}$
for any i such that
 $-A-1\leq i\leq A$
.
$-A-1\leq i\leq A$
. -
(iv) If we strengthen the assumption on X to say that
 for all
for all
 $i\leq 2A$
, then X must belong to
$i\leq 2A$
, then X must belong to
 $\mathcal {D}^{\leq -A-1}$
.
$\mathcal {D}^{\leq -A-1}$
. -
(v) If we strengthen the assumption on X to say that
 for all
for all
 $i\geq -2A$
, then X must belong to
$i\geq -2A$
, then X must belong to
 $\mathcal {D}^{\geq A+1}$
.
$\mathcal {D}^{\geq A+1}$
.
Proof. With the hypotheses as in the current lemma, Lemma 3.8 guarantees the vanishing of
![]() $\mathcal {H}^{i}(X)$
for all
$\mathcal {H}^{i}(X)$
for all
![]() $-A\leq i\leq A$
. The triangles
$-A\leq i\leq A$
. The triangles
![]() $X^{\leq i-1}\to X^{\leq i}\to \mathcal {H}^{i}(X)$
then tell us that
$X^{\leq i-1}\to X^{\leq i}\to \mathcal {H}^{i}(X)$
then tell us that
![]() $X^{\leq A}$
belongs to
$X^{\leq A}$
belongs to
![]() $\mathcal {D}^{\leq -A-1}$
. Consider the triangle
$\mathcal {D}^{\leq -A-1}$
. Consider the triangle
![]() $W\stackrel \varphi \to X\stackrel \psi \to Y$
with
$W\stackrel \varphi \to X\stackrel \psi \to Y$
with
![]() $W:=X^{\leq A}\in \mathcal {D}^{\leq -A-1}$
and
$W:=X^{\leq A}\in \mathcal {D}^{\leq -A-1}$
and
![]() $Y:=X^{\geq A+1}\in \mathcal {D}^{\geq A+1}$
.
$Y:=X^{\geq A+1}\in \mathcal {D}^{\geq A+1}$
.
The integer A is such that ![]() , and hence,
, and hence, ![]() vanishes for all
vanishes for all
![]() $i\leq 1$
. But we also know that
$i\leq 1$
. But we also know that
![]() $\Sigma ^AG\in \mathcal {D}^{\leq 0}$
, and hence,
$\Sigma ^AG\in \mathcal {D}^{\leq 0}$
, and hence, ![]() . Therefore,
. Therefore, ![]() must vanish for all
must vanish for all
![]() $i\geq 0$
. It follows that, for every integer
$i\geq 0$
. It follows that, for every integer
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
Thus, in the exact sequence

we have that, for every
![]() $i\in \mathbb {Z}$
, either the map
$i\in \mathbb {Z}$
, either the map ![]() or the map
or the map ![]() is an isomorphism. More precisely: the map
is an isomorphism. More precisely: the map ![]() is an isomorphism when
is an isomorphism when
![]() $i\leq 1$
, while the map
$i\leq 1$
, while the map ![]() is an isomorphism when
is an isomorphism when
![]() $i\geq 0$
.
$i\geq 0$
.
We have already proved the vanishing of ![]() for all
for all
![]() $i\leq 0$
and the vanishing of
$i\leq 0$
and the vanishing of ![]() for all
for all
![]() $i\geq 0$
. For
$i\geq 0$
. For
![]() $1\leq i\leq 2A$
, we have isomorphisms
$1\leq i\leq 2A$
, we have isomorphisms

which extend the vanishing statements of (i) and (ii) to the full range asserted. And the assertions in (i) and (ii), about the ranges in which ![]() and
and ![]() are isomorphisms, follow from the vanishing statements combined with the long exact sequence
are isomorphisms, follow from the vanishing statements combined with the long exact sequence
![]() $(\dagger \dagger )$
above.
$(\dagger \dagger )$
above.
Now for (iv) and (v): the proof of (i) and (ii) produced an explicit triangle
![]() $W\to X\to Y$
, with
$W\to X\to Y$
, with
![]() $W\in \mathcal {D}^{\leq -A-1}$
and with
$W\in \mathcal {D}^{\leq -A-1}$
and with
![]() $Y\in \mathcal {D}^{\geq A+1}$
, and showed that this particular choice of triangle satisfies (i) and (ii). If we strengthen the assumption on X as in (iv), then
$Y\in \mathcal {D}^{\geq A+1}$
, and showed that this particular choice of triangle satisfies (i) and (ii). If we strengthen the assumption on X as in (iv), then ![]() for all
for all
![]() $i\in \mathbb {Z}$
, and as G is a compact generator, this forces
$i\in \mathbb {Z}$
, and as G is a compact generator, this forces
![]() $Y=0$
. This in turn means that
$Y=0$
. This in turn means that
![]() $W\to X$
must be an isomorphism, but by construction, W belongs to
$W\to X$
must be an isomorphism, but by construction, W belongs to
![]() $\mathcal {D}^{\leq -A-1}$
. Under the hypotheses of (v), we would deduce that
$\mathcal {D}^{\leq -A-1}$
. Under the hypotheses of (v), we would deduce that
![]() $W=0$
, the map
$W=0$
, the map
![]() $X\to Y$
is an isomorphism, but by construction, Y belongs to
$X\to Y$
is an isomorphism, but by construction, Y belongs to
![]() $\mathcal {D}^{\geq A+1}$
.
$\mathcal {D}^{\geq A+1}$
.
Finally, assume we are given a triangle
![]() $W\to X\to Y$
, as in the hypotheses. By (iv), we have
$W\to X\to Y$
, as in the hypotheses. By (iv), we have
![]() $W\in \mathcal {D}^{\leq -A-1}$
, and by (v), we have
$W\in \mathcal {D}^{\leq -A-1}$
, and by (v), we have
![]() $Y\in \mathcal {D}^{\geq A+1}$
, and (iii) now follows immediately.
$Y\in \mathcal {D}^{\geq A+1}$
, and (iii) now follows immediately.
Part (iv) and (v) of the above lemma show that:
Corollary 3.10. Let
![]() $\mathcal {D}$
be a weakly approximable category, let G be a compact generator, and let
$\mathcal {D}$
be a weakly approximable category, let G be a compact generator, and let
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class.
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class.
-
1. If
 for
for
 $n\gg 0$
, then
$n\gg 0$
, then
 $X\in {\mathcal {D}^{\leq m}}$
for some integer m.
$X\in {\mathcal {D}^{\leq m}}$
for some integer m. -
2. If
 for
for
 $n\gg 0$
, then
$n\gg 0$
, then
 $X\in {\mathcal {D}^{\geq m}}$
for some integer m.
$X\in {\mathcal {D}^{\geq m}}$
for some integer m.
Lemma 3.11. Consider a recollement as in Definition 2.5. Suppose
![]() $\mathcal {D}_U$
is weakly approximable with compact generator
$\mathcal {D}_U$
is weakly approximable with compact generator
![]() $G_{U}$
, and
$G_{U}$
, and
![]() $\mathcal {D}$
has a compact generator
$\mathcal {D}$
has a compact generator
![]() $G'$
, such that
$G'$
, such that ![]() for
for
![]() $n \gg 0$
. We can then find a compact generator G of
$n \gg 0$
. We can then find a compact generator G of
![]() $\mathcal {D}$
, such that the t-structure on
$\mathcal {D}$
, such that the t-structure on
![]() $\mathcal {D}$
generated by G is equal to the gluing of the t-structure on
$\mathcal {D}$
generated by G is equal to the gluing of the t-structure on
![]() $\mathcal {D}_{F}$
generated by
$\mathcal {D}_{F}$
generated by
![]() $i^{*} G$
and the t-structure on
$i^{*} G$
and the t-structure on
![]() $\mathcal {D}_{U}$
generated by
$\mathcal {D}_{U}$
generated by
![]() $G_{U}$
.
$G_{U}$
.
Proof. Write
![]() $({\mathcal {D}^{\leq 0}_{U}}, {\mathcal {D}^{\geq 0}_{U}})$
for the t-structure on
$({\mathcal {D}^{\leq 0}_{U}}, {\mathcal {D}^{\geq 0}_{U}})$
for the t-structure on
![]() $\mathcal {D}_{U}$
generated by
$\mathcal {D}_{U}$
generated by
![]() $G_{U}$
. We note that
$G_{U}$
. We note that
![]() $j_{!}G_U$
is compact in
$j_{!}G_U$
is compact in
![]() $\mathcal {D}$
because the functor
$\mathcal {D}$
because the functor
![]() $j_{!}$
preserves compactness (see 2.5). The second part of Lemma 3.5 now shows
$j_{!}$
preserves compactness (see 2.5). The second part of Lemma 3.5 now shows
for
![]() $n \gg 0$
. It follows that
$n \gg 0$
. It follows that
![]() $j^{*} G'\in {\mathcal {D}^{\leq m}_{U}}$
for some
$j^{*} G'\in {\mathcal {D}^{\leq m}_{U}}$
for some
![]() $m>0$
by Corollary 3.10. Now let
$m>0$
by Corollary 3.10. Now let
which is clearly a compact generator for
![]() $\mathcal {D}$
. We write
$\mathcal {D}$
. We write
![]() $({\mathcal {D}^{\leq 0}_{F}}, {\mathcal {D}^{\geq 0}_{F}})$
for the t-structure on
$({\mathcal {D}^{\leq 0}_{F}}, {\mathcal {D}^{\geq 0}_{F}})$
for the t-structure on
![]() $\mathcal {D}_{F}$
generated by
$\mathcal {D}_{F}$
generated by
![]() $i^{*} G$
and
$i^{*} G$
and
![]() $({\mathcal {D}^{\leq 0}_{\text {gl}}}, {\mathcal {D}^{\geq 0}_{\text {gl}}})$
for the t-structure on
$({\mathcal {D}^{\leq 0}_{\text {gl}}}, {\mathcal {D}^{\geq 0}_{\text {gl}}})$
for the t-structure on
![]() $\mathcal {D}$
obtained by gluing
$\mathcal {D}$
obtained by gluing
![]() $({\mathcal {D}^{\leq 0}_{F}}, {\mathcal {D}^{\geq 0}_{F}})$
and
$({\mathcal {D}^{\leq 0}_{F}}, {\mathcal {D}^{\geq 0}_{F}})$
and
![]() $({\mathcal {D}^{\leq 0}_{U}}, {\mathcal {D}^{\geq 0}_{U}})$
. It remains to show that
$({\mathcal {D}^{\leq 0}_{U}}, {\mathcal {D}^{\geq 0}_{U}})$
. It remains to show that
where
![]() $({\mathcal {D}^{\leq 0}_{G}}, {\mathcal {D}^{\geq 0}_{G}})$
is the t-structure on
$({\mathcal {D}^{\leq 0}_{G}}, {\mathcal {D}^{\geq 0}_{G}})$
is the t-structure on
![]() $\mathcal {D}$
generated by G. First, we note that
$\mathcal {D}$
generated by G. First, we note that
![]() $i^{*}G\in {\mathcal {D}^{\leq 0}_{F}}$
and
$i^{*}G\in {\mathcal {D}^{\leq 0}_{F}}$
and ![]() . Using that the functors
. Using that the functors
![]() $i^{*}$
and
$i^{*}$
and
![]() $j^{*}$
commute with coproducts, this shows
$j^{*}$
commute with coproducts, this shows
![]() $i^{*}{\mathcal {D}^{\leq 0}_{G}}\subset {\mathcal {D}^{\leq 0}_{F}}$
and
$i^{*}{\mathcal {D}^{\leq 0}_{G}}\subset {\mathcal {D}^{\leq 0}_{F}}$
and
![]() $j^{*}{\mathcal {D}^{\leq 0}_{G}}\subset {\mathcal {D}^{\leq 0}_{U}}$
. Hence,
$j^{*}{\mathcal {D}^{\leq 0}_{G}}\subset {\mathcal {D}^{\leq 0}_{U}}$
. Hence,
On the other hand, we clearly have
![]() $j_{!}G_U\in {\mathcal {D}^{\leq 0}_G}$
, and thus
$j_{!}G_U\in {\mathcal {D}^{\leq 0}_G}$
, and thus
![]() $j_{!}{\mathcal {D}^{\leq 0}_{U}}\subset {\mathcal {D}^{\leq 0}_{G}}$
, because the functor
$j_{!}{\mathcal {D}^{\leq 0}_{U}}\subset {\mathcal {D}^{\leq 0}_{G}}$
, because the functor
![]() $j_{!}$
commutes with coproducts. Since
$j_{!}$
commutes with coproducts. Since
![]() $i_{*}i^{*}G$
fits in an exact triangle
$i_{*}i^{*}G$
fits in an exact triangle
with
![]() $j_{!}j^{*}G, \,G\in {\mathcal {D}^{\leq 0}_{G}}$
, we see that
$j_{!}j^{*}G, \,G\in {\mathcal {D}^{\leq 0}_{G}}$
, we see that
![]() $i_{*}i^{*}G\in {\mathcal {D}^{\leq 0}_{G}}$
. It follows that
$i_{*}i^{*}G\in {\mathcal {D}^{\leq 0}_{G}}$
. It follows that
![]() $i_{*}\mathcal {D}^{\leq 0}_{F}\subset {\mathcal {D}^{\leq 0}_{G}}$
. Now, let
$i_{*}\mathcal {D}^{\leq 0}_{F}\subset {\mathcal {D}^{\leq 0}_{G}}$
. Now, let
![]() $X\in {\mathcal {D}^{\leq 0}_{\text {gl}}}$
and consider the exact triangle
$X\in {\mathcal {D}^{\leq 0}_{\text {gl}}}$
and consider the exact triangle
By the above,
![]() $j_{!}j^{*}X,\, i_{*}i^{*}X\in {\mathcal {D}^{\leq 0}_{G}}$
, so
$j_{!}j^{*}X,\, i_{*}i^{*}X\in {\mathcal {D}^{\leq 0}_{G}}$
, so
![]() $X\in {\mathcal {D}^{\leq 0}_{G}}$
. We conclude that
$X\in {\mathcal {D}^{\leq 0}_{G}}$
. We conclude that
![]() ${\mathcal {D}^{\leq 0}_{G}}= {\mathcal {D}^{\leq 0}_{\text {gl}}}$
.
${\mathcal {D}^{\leq 0}_{G}}= {\mathcal {D}^{\leq 0}_{\text {gl}}}$
.
Combining the above lemma with Lemma 3.2, we get:
Corollary 3.12. Consider a recollement as in Definition 2.5. Suppose
![]() $\mathcal {D}_U$
is weakly approximable and
$\mathcal {D}_U$
is weakly approximable and
![]() $\mathcal {D}$
has a compact generator G, such that
$\mathcal {D}$
has a compact generator G, such that ![]() for
for
![]() $n \gg 0$
. Then the t-structure on
$n \gg 0$
. Then the t-structure on
![]() $\mathcal {D}$
obtained by gluing t-structures on
$\mathcal {D}$
obtained by gluing t-structures on
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $\mathcal {D}_U$
, both of which are in the preferred equivalence class, is in the preferred equivalence class.
$\mathcal {D}_U$
, both of which are in the preferred equivalence class, is in the preferred equivalence class.
4 Gluing
 $\mathcal {D}^{-}_{c}$
$\mathcal {D}^{-}_{c}$
We remind the reader of the subcategories
![]() $\mathcal {D}^{b}_{c}$
and
$\mathcal {D}^{b}_{c}$
and
![]() $\mathcal {D}^{-}_{c}$
, and investigate their behavior under recollements. For examples of these subcategories and their applications, we refer back to the Introduction, or to [Reference Neeman14] for an extensive discussion.
$\mathcal {D}^{-}_{c}$
, and investigate their behavior under recollements. For examples of these subcategories and their applications, we refer back to the Introduction, or to [Reference Neeman14] for an extensive discussion.
Definition 4.1 [Reference Neeman16, Definition 0.16]
Let
![]() $\mathcal {D}$
be a triangulated category with t-structure
$\mathcal {D}$
be a triangulated category with t-structure
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0}).$
Recall that we write
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0}).$
Recall that we write
![]() $\mathcal {D}^+:=\bigcup _{m> 0} {\mathcal {D}^{\geq -m}} $
,
$\mathcal {D}^+:=\bigcup _{m> 0} {\mathcal {D}^{\geq -m}} $
,
![]() $\mathcal {D}^-:=\bigcup _{m> 0} {\mathcal {D}^{\leq m}} $
, and
$\mathcal {D}^-:=\bigcup _{m> 0} {\mathcal {D}^{\leq m}} $
, and
![]() $\mathcal {D}^{b} = \mathcal {D}^+\cap \mathcal {D}^-$
. The full subcategory
$\mathcal {D}^{b} = \mathcal {D}^+\cap \mathcal {D}^-$
. The full subcategory
![]() $\mathcal {D}^{-}_{c}$
has for objects all
$\mathcal {D}^{-}_{c}$
has for objects all
![]() $X\in \mathcal {D}$
, such that, for any integer
$X\in \mathcal {D}$
, such that, for any integer
![]() $m> 0$
, there exists an exact triangle
$m> 0$
, there exists an exact triangle
![]() $E \to X \to E'$
with E compact and
$E \to X \to E'$
with E compact and
![]() $E' \in {\mathcal {D}^{\leq -m}} $
. The subcategory
$E' \in {\mathcal {D}^{\leq -m}} $
. The subcategory
![]() $\mathcal {D}^{b}_{c}$
is defined to be
$\mathcal {D}^{b}_{c}$
is defined to be
![]() $\mathcal {D}^{-}_{c} \cap \mathcal {D}^{b}$
.
$\mathcal {D}^{-}_{c} \cap \mathcal {D}^{b}$
.
Remark 2. Observe that equivalent t-structures yield equal
![]() $\mathcal {D}^+,\ \mathcal {D}^-,\ \mathcal {D}^b,\ \mathcal {D}^{-}_{c},\ \mathcal {D}^{b}_{c}$
. If
$\mathcal {D}^+,\ \mathcal {D}^-,\ \mathcal {D}^b,\ \mathcal {D}^{-}_{c},\ \mathcal {D}^{b}_{c}$
. If
![]() $\mathcal {D}$
has a single compact generator, form the subcategories
$\mathcal {D}$
has a single compact generator, form the subcategories
![]() $\mathcal {D}^+,\ \mathcal {D}^-,\ \mathcal {D}^b,\ \mathcal {D}^{-}_{c},\ \mathcal {D}^{b}_{c}$
corresponding to the preferred equivalence class of t-structures. These are intrinsic.
$\mathcal {D}^+,\ \mathcal {D}^-,\ \mathcal {D}^b,\ \mathcal {D}^{-}_{c},\ \mathcal {D}^{b}_{c}$
corresponding to the preferred equivalence class of t-structures. These are intrinsic.
Remark 3. Suppose
![]() $\mathcal {D}$
has a compact generator G, such that
$\mathcal {D}$
has a compact generator G, such that ![]() for
for
![]() $n \gg 0$
, and endow
$n \gg 0$
, and endow
![]() $\mathcal {D}$
with a t-structure in the preferred equivalence class. By [Reference Neeman16, Proposition 0.19 and Remark 0.20], the subcategories
$\mathcal {D}$
with a t-structure in the preferred equivalence class. By [Reference Neeman16, Proposition 0.19 and Remark 0.20], the subcategories
![]() $\mathcal {D}^{b}_{c} \subseteq \mathcal {D}^{-}_{c}$
are thick triangulated subcategories of
$\mathcal {D}^{b}_{c} \subseteq \mathcal {D}^{-}_{c}$
are thick triangulated subcategories of
![]() $\mathcal {D}^{-}.$
$\mathcal {D}^{-}.$
If
![]() $\mathcal {D}$
is weakly approximable, then the above applies: one easily sees that
$\mathcal {D}$
is weakly approximable, then the above applies: one easily sees that
![]() $\mathcal {D}$
has a compact generator G with
$\mathcal {D}$
has a compact generator G with ![]() for
for
![]() $n\gg 0$
.
$n\gg 0$
.
Lemma 4.2. Consider a recollement as in Definition 2.5. Suppose
![]() $\mathcal {D}_U$
is weakly approximable, and
$\mathcal {D}_U$
is weakly approximable, and
![]() $\mathcal {D}$
has a compact generator G, such that
$\mathcal {D}$
has a compact generator G, such that ![]() for
for
![]() $n \gg 0$
. Then the intrinsic categories
$n \gg 0$
. Then the intrinsic categories
![]() $(\mathcal {D}_U)^-_c$
,
$(\mathcal {D}_U)^-_c$
,
![]() $(\mathcal {D}_U)^b_c$
,
$(\mathcal {D}_U)^b_c$
,
![]() $\mathcal {D}^-_c$
,
$\mathcal {D}^-_c$
,
![]() $\mathcal {D}_c^b$
,
$\mathcal {D}_c^b$
,
![]() $(\mathcal {D}_F)^-_c$
, and
$(\mathcal {D}_F)^-_c$
, and
![]() $(\mathcal {D}_F)^b_c$
, corresponding to the preferred equivalence class of t-structures as in Remark 2, are all thick triangulated subcategories of (respectively)
$(\mathcal {D}_F)^b_c$
, corresponding to the preferred equivalence class of t-structures as in Remark 2, are all thick triangulated subcategories of (respectively)
![]() $\mathcal {D}_U$
,
$\mathcal {D}_U$
,
![]() $\mathcal {D}$
, and
$\mathcal {D}$
, and
![]() $\mathcal {D}_F$
.
$\mathcal {D}_F$
.
Proof. For the categories
![]() $(\mathcal {D}_U)^-_c$
,
$(\mathcal {D}_U)^-_c$
,
![]() $(\mathcal {D}_U)^b_c$
,
$(\mathcal {D}_U)^b_c$
,
![]() $\mathcal {D}^-_c$
, and
$\mathcal {D}^-_c$
, and
![]() $\mathcal {D}_c^b$
, the assertion is immediate from Remark 3. What we will prove is that the category
$\mathcal {D}_c^b$
, the assertion is immediate from Remark 3. What we will prove is that the category
![]() $\mathcal {D}_F$
has a compact generator H with
$\mathcal {D}_F$
has a compact generator H with ![]() for
for
![]() $n \gg 0$
.
$n \gg 0$
.
Choose for
![]() $\mathcal {D}_F,\ \mathcal {D}_U$
t-structures in the preferred equivalence class, and glue them to form a t-structure on
$\mathcal {D}_F,\ \mathcal {D}_U$
t-structures in the preferred equivalence class, and glue them to form a t-structure on
![]() $\mathcal {D}$
. By Corollary 3.12, the glued t-structure on
$\mathcal {D}$
. By Corollary 3.12, the glued t-structure on
![]() $\mathcal {D}$
is in the preferred equivalence class. Pick a compact generator
$\mathcal {D}$
is in the preferred equivalence class. Pick a compact generator
![]() $G\in \mathcal {D}$
.
$G\in \mathcal {D}$
.
Lemma 3.5(1) allows us to choose an integer
![]() $C>0$
with
$C>0$
with ![]() . As
. As
![]() $i_*$
is t-exact, we have
$i_*$
is t-exact, we have
![]() $i_*\mathcal {D}_F^{\leq -C}\subset \mathcal {D}^{\leq -C}$
, and hence
$i_*\mathcal {D}_F^{\leq -C}\subset \mathcal {D}^{\leq -C}$
, and hence
But the t-structure on
![]() $\mathcal {D}_F$
is in the preferred equivalence class, and [Reference Neeman16, Observation 0.20(ii)] informs us that the compact object
$\mathcal {D}_F$
is in the preferred equivalence class, and [Reference Neeman16, Observation 0.20(ii)] informs us that the compact object
![]() $i^*G\in \mathcal {D}_F$
must be contained in
$i^*G\in \mathcal {D}_F$
must be contained in
![]() $\mathcal {D}_F^-$
. Hence, we may choose an integer
$\mathcal {D}_F^-$
. Hence, we may choose an integer
![]() $B>0$
with
$B>0$
with
![]() $i^*G\in \mathcal {D}_F^{\leq B}$
.
$i^*G\in \mathcal {D}_F^{\leq B}$
.
But now it’s immediate that the compact generator
![]() $i^*G\in \mathcal {D}_F$
is such that
$i^*G\in \mathcal {D}_F$
is such that ![]() for
for
![]() $n\geq B+C$
.
$n\geq B+C$
.
Proposition 4.3. Consider a recollement as in Definition 2.5. Suppose
![]() $\mathcal {D}_U$
is weakly approximable, and
$\mathcal {D}_U$
is weakly approximable, and
![]() $\mathcal {D}$
has a compact generator G, such that
$\mathcal {D}$
has a compact generator G, such that ![]() for
for
![]() $n \gg 0$
. With
$n \gg 0$
. With
![]() $\mathcal {C}$
standing for any of
$\mathcal {C}$
standing for any of
![]() $\mathcal {D}_U$
,
$\mathcal {D}_U$
,
![]() $\mathcal {D}$
, or
$\mathcal {D}$
, or
![]() $\mathcal {D}_F$
, let the categories
$\mathcal {D}_F$
, let the categories
![]() $\mathcal {C}^-_c$
,
$\mathcal {C}^-_c$
,
![]() $\mathcal {C}_c^b$
, and
$\mathcal {C}_c^b$
, and
![]() $\mathcal {C}^+$
be the intrinsic ones coming from the preferred equivalence class of t-structures (see Remark 2). If
$\mathcal {C}^+$
be the intrinsic ones coming from the preferred equivalence class of t-structures (see Remark 2). If
![]() $j^{*} G$
is in
$j^{*} G$
is in
![]() $(\mathcal {D}_{U})^{-}_{c},$
then there are equalities:
$(\mathcal {D}_{U})^{-}_{c},$
then there are equalities:
 $$ \begin{align*} \mathcal{D}^{-}_{c} &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c} \text{ and } j^{*} X \in (\mathcal{D}_{U})^{-}_{c} \right \},\\ \mathcal{D}^{b}_{c} \, &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c},\ j^{*} X \in (\mathcal{D}_{U})^{b}_{c} \text{ and } i^{!} X \in (\mathcal{D}_{F})^{+}\right \}. \end{align*} $$
$$ \begin{align*} \mathcal{D}^{-}_{c} &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c} \text{ and } j^{*} X \in (\mathcal{D}_{U})^{-}_{c} \right \},\\ \mathcal{D}^{b}_{c} \, &= \left \{ X \in \mathcal{D} \, | \, i^{*} X \in (\mathcal{D}_{F})^{-}_{c},\ j^{*} X \in (\mathcal{D}_{U})^{b}_{c} \text{ and } i^{!} X \in (\mathcal{D}_{F})^{+}\right \}. \end{align*} $$
Proof. Choose t-structures for each of
![]() $\mathcal {D}_F,\ \mathcal {D}_U$
, in the preferred equivalence classes, and glue them to form a t-structure on
$\mathcal {D}_F,\ \mathcal {D}_U$
, in the preferred equivalence classes, and glue them to form a t-structure on
![]() $\mathcal {D}$
. By Corollary 3.12, the glued t-structure on
$\mathcal {D}$
. By Corollary 3.12, the glued t-structure on
![]() $\mathcal {D}$
is in the preferred equivalence class. We are assuming that, for the compact generator
$\mathcal {D}$
is in the preferred equivalence class. We are assuming that, for the compact generator
![]() $G\in \mathcal {D}$
, we have
$G\in \mathcal {D}$
, we have
![]() $j^{*} G \in (\mathcal {D}_{U})^{-}_{c}$
. As
$j^{*} G \in (\mathcal {D}_{U})^{-}_{c}$
. As
![]() $ (\mathcal {D}_{U})^{-}_{c}$
is a thick triangulated subcategory which contains
$ (\mathcal {D}_{U})^{-}_{c}$
is a thick triangulated subcategory which contains
![]() $j^{*}G$
, it must also contain
$j^{*}G$
, it must also contain
![]() $j^*\mathcal {D}^c$
, since
$j^*\mathcal {D}^c$
, since
![]() $\mathcal {D}^c$
is the smallest thick triangulated subcategory of
$\mathcal {D}^c$
is the smallest thick triangulated subcategory of
![]() $\mathcal {D}$
containing G.
$\mathcal {D}$
containing G.
We first show the left sides are contained in the right sides. Let X be in
![]() $\mathcal {D}^{-}_{c},$
fix
$\mathcal {D}^{-}_{c},$
fix
![]() $m> 0,$
and let
$m> 0,$
and let
![]() $E \to X \to D$
be an exact triangle in
$E \to X \to D$
be an exact triangle in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E \in \mathcal {D}^{c}$
and
$E \in \mathcal {D}^{c}$
and
![]() $D \in {\mathcal {D}^{\leq -m}}.$
Since
$D \in {\mathcal {D}^{\leq -m}}.$
Since
![]() $i^{*} D \in \mathcal {D}^{\leq -m}_{F}$
and
$i^{*} D \in \mathcal {D}^{\leq -m}_{F}$
and
![]() $i^{*}$
preserves compactness (see 2.5), the exact triangle
$i^{*}$
preserves compactness (see 2.5), the exact triangle
![]() $i^{*} E \to i^{*} X \to i^{*} D$
shows that
$i^{*} E \to i^{*} X \to i^{*} D$
shows that
![]() $i^{*} X$
is in
$i^{*} X$
is in
![]() $(\mathcal {D}_{F})_{c}^{-}.$
Now consider the exact triangle
$(\mathcal {D}_{F})_{c}^{-}.$
Now consider the exact triangle
![]() $j^{*} E \to j^{*} X \to j^{*} D$
with
$j^{*} E \to j^{*} X \to j^{*} D$
with
![]() $j^{*} D \in \mathcal {D}_{U}^{\leq -m}$
. By the first paragraph of the proof,
$j^{*} D \in \mathcal {D}_{U}^{\leq -m}$
. By the first paragraph of the proof,
![]() $j^*E \in (\mathcal {D}_{U})^{-}_{c}$
, hence, we can find an exact triangle
$j^*E \in (\mathcal {D}_{U})^{-}_{c}$
, hence, we can find an exact triangle
![]() ${\widetilde {E}} \to j^{*} E \to {\widetilde {D}}$
with
${\widetilde {E}} \to j^{*} E \to {\widetilde {D}}$
with
![]() ${\widetilde {E}}$
in
${\widetilde {E}}$
in
![]() $(\mathcal {D}_{U})^{c}$
and
$(\mathcal {D}_{U})^{c}$
and
![]() ${\widetilde {D}}$
in
${\widetilde {D}}$
in
![]() $\mathcal {D}_{U}^{\leq -m}.$
The octahedral axiom, applied to
$\mathcal {D}_{U}^{\leq -m}.$
The octahedral axiom, applied to
![]() ${\widetilde {E}} \to j^{*}E \to j^{*}X$
, gives an object
${\widetilde {E}} \to j^{*}E \to j^{*}X$
, gives an object
![]() $D'$
and exact triangles
$D'$
and exact triangles
![]() ${\widetilde {E}} \to j^{*} X \to D'$
and
${\widetilde {E}} \to j^{*} X \to D'$
and
![]() ${\widetilde {D}} \to D' \to j^{*} D$
in
${\widetilde {D}} \to D' \to j^{*} D$
in
![]() $\mathcal {D}_U$
, such that the following diagram is commutative:
$\mathcal {D}_U$
, such that the following diagram is commutative:

Since
![]() ${\widetilde {D}}$
and
${\widetilde {D}}$
and
![]() $j^{*} D$
are in
$j^{*} D$
are in
![]() $\mathcal {D}_{U}^{\leq -m},$
we know
$\mathcal {D}_{U}^{\leq -m},$
we know
![]() $D'$
is also in
$D'$
is also in
![]() $\mathcal {D}_{U}^{\leq -m}$
. The exact triangle
$\mathcal {D}_{U}^{\leq -m}$
. The exact triangle
![]() ${\widetilde {E}} \to j^{*} X \to D'$
now shows that
${\widetilde {E}} \to j^{*} X \to D'$
now shows that
![]() $j^{*} X$
is in
$j^{*} X$
is in
![]() $(\mathcal {D}_{U})_{c}^{-}$
. If we assume further that X is in
$(\mathcal {D}_{U})_{c}^{-}$
. If we assume further that X is in
![]() $\mathcal {D}^{b}_{c} = \mathcal {D}^{-}_{c} \cap \mathcal {D}^{b},$
then we have
$\mathcal {D}^{b}_{c} = \mathcal {D}^{-}_{c} \cap \mathcal {D}^{b},$
then we have
![]() $j^{*} X \in \mathcal {D}^{b}_{U}$
and
$j^{*} X \in \mathcal {D}^{b}_{U}$
and
![]() $i^{!} X \in (\mathcal {D}_{F})^{+}$
because
$i^{!} X \in (\mathcal {D}_{F})^{+}$
because
![]() $j^*$
is t-exact and
$j^*$
is t-exact and
![]() $i^!$
is left t-exact.
$i^!$
is left t-exact.
We now show the right sides are contained in the left sides. Assume
![]() $i^{*} X \in (\mathcal {D}_{F})^{-}_{c}$
and
$i^{*} X \in (\mathcal {D}_{F})^{-}_{c}$
and
![]() $j^{*} X \in (\mathcal {D}_{U})^{-}_{c}$
, and fix
$j^{*} X \in (\mathcal {D}_{U})^{-}_{c}$
, and fix
![]() $m> 0$
. By definition, there exists an exact triangle
$m> 0$
. By definition, there exists an exact triangle
with
![]() $E' \in (\mathcal {D}_{F})^{c}\subset \mathcal {D}_{F}^-$
and
$E' \in (\mathcal {D}_{F})^{c}\subset \mathcal {D}_{F}^-$
and
![]() $D ' \in \mathcal {D}_{F}^{\leq -m}$
. Choose an odd integer
$D ' \in \mathcal {D}_{F}^{\leq -m}$
. Choose an odd integer
![]() $n>0$
with
$n>0$
with
![]() $\Sigma ^n E'\in \mathcal {D}_F^{\leq -m}$
. The object
$\Sigma ^n E'\in \mathcal {D}_F^{\leq -m}$
. The object ![]() vanishes in
vanishes in
![]() $K_0((\mathcal {D}_{F})^{c})$
, and [Reference Neeman20, Corollary 4.5.14] tells us that
$K_0((\mathcal {D}_{F})^{c})$
, and [Reference Neeman20, Corollary 4.5.14] tells us that ![]() must therefore lie in the image
must therefore lie in the image
![]() $i^*(\mathcal {D}^{c})$
. And then [Reference Neeman20, Proposition 4.4.1], applied to the composite
$i^*(\mathcal {D}^{c})$
. And then [Reference Neeman20, Proposition 4.4.1], applied to the composite ![]() , allows us to find a morphism
, allows us to find a morphism
![]() $E" \to X$
in
$E" \to X$
in
![]() $\mathcal {D},$
with
$\mathcal {D},$
with
![]() $E"$
in
$E"$
in
![]() $\mathcal {D}^{c},$
and such that
$\mathcal {D}^{c},$
and such that
![]() $i^{*}(E" \to X)$
is isomorphic to
$i^{*}(E" \to X)$
is isomorphic to ![]() Complete
Complete
![]() $E" \to X$
to an exact triangle
$E" \to X$
to an exact triangle
Since ![]() , we deduce that
, we deduce that
![]() $i^*D"\in \mathcal {D}_F^{\leq -m}$
.
$i^*D"\in \mathcal {D}_F^{\leq -m}$
.
The first paragraph of the proof tells us that
![]() $j^{*} E" \in (\mathcal {D}_{U})_{c}^{-}$
, while
$j^{*} E" \in (\mathcal {D}_{U})_{c}^{-}$
, while
![]() $j^{*} X \in (\mathcal {D}_{U})_{c}^{-}$
by hypothesis. Thus,
$j^{*} X \in (\mathcal {D}_{U})_{c}^{-}$
by hypothesis. Thus,
![]() $j^{*} D"$
is in
$j^{*} D"$
is in
![]() $(\mathcal {D}_{U})_{c}^{-}$
. Fix an exact triangle
$(\mathcal {D}_{U})_{c}^{-}$
. Fix an exact triangle
![]() ${\widetilde {E}} \to j^{*} D" \to {\widetilde {D}}$
with
${\widetilde {E}} \to j^{*} D" \to {\widetilde {D}}$
with
![]() ${\widetilde {E}} \in (\mathcal {D}_{U})^{c}$
and
${\widetilde {E}} \in (\mathcal {D}_{U})^{c}$
and
![]() ${\widetilde {D}} \in \mathcal {D}^{\leq -m}_{U}.$
We now have the following diagram
${\widetilde {D}} \in \mathcal {D}^{\leq -m}_{U}.$
We now have the following diagram

with
![]() $E"\in \mathcal {D}^{c}, \ {\widetilde {E}} \in (\mathcal {D}_{U})^{c}$
, and
$E"\in \mathcal {D}^{c}, \ {\widetilde {E}} \in (\mathcal {D}_{U})^{c}$
, and
![]() ${\widetilde {D}} \in \mathcal {D}_{U}^{\leq -m}$
. Applying the octahedral axiom, to
${\widetilde {D}} \in \mathcal {D}_{U}^{\leq -m}$
. Applying the octahedral axiom, to
![]() $j_{!} {\widetilde {E}} \to j_{!}j^{*} D" \to D"$
, we find an object D and exact triangles
$j_{!} {\widetilde {E}} \to j_{!}j^{*} D" \to D"$
, we find an object D and exact triangles
![]() $j_{!} {\widetilde {E}} \to D"\to D$
and
$j_{!} {\widetilde {E}} \to D"\to D$
and
![]() $j_{!}{\widetilde {D}} \to D \to i_{*} i^{*} D"$
in
$j_{!}{\widetilde {D}} \to D \to i_{*} i^{*} D"$
in
![]() $\mathcal {D}$
that fit into the following commutative diagram:
$\mathcal {D}$
that fit into the following commutative diagram:

Since
![]() $i^{*} D" \in \mathcal {D}_{F}^{\leq -m}$
and
$i^{*} D" \in \mathcal {D}_{F}^{\leq -m}$
and
![]() $i_{*}$
is t-exact, we know
$i_{*}$
is t-exact, we know
![]() $i_{*}i^{*} D" \in {\mathcal {D}^{\leq -m}}$
. Since
$i_{*}i^{*} D" \in {\mathcal {D}^{\leq -m}}$
. Since
![]() ${\widetilde {D}} \in {\mathcal {D}^{\leq -m}_{U}}$
and
${\widetilde {D}} \in {\mathcal {D}^{\leq -m}_{U}}$
and
![]() $j_{!}$
is right t-exact, we know
$j_{!}$
is right t-exact, we know
![]() $j_{!} {\widetilde {D}} \in {\mathcal {D}^{\leq -m}}.$
Thus,
$j_{!} {\widetilde {D}} \in {\mathcal {D}^{\leq -m}}.$
Thus,
![]() $D \in {\mathcal {D}^{\leq -m}} .$
$D \in {\mathcal {D}^{\leq -m}} .$
Next, we complete the octahedron on
![]() $X \to D" \to D$
and find an object E with exact triangles
$X \to D" \to D$
and find an object E with exact triangles
![]() $E \to X \to D$
and
$E \to X \to D$
and
![]() $E" \to E \to j_{!} {\widetilde {E}}$
in
$E" \to E \to j_{!} {\widetilde {E}}$
in
![]() $\mathcal {D}$
, fitting into the following commutative diagram:
$\mathcal {D}$
, fitting into the following commutative diagram:

Note that
![]() $j_{!}{\widetilde {E}}$
is compact because
$j_{!}{\widetilde {E}}$
is compact because
![]() $j_{!}$
preserves compactness. Since
$j_{!}$
preserves compactness. Since
![]() $E"$
is also compact, so is E. Hence, the exact triangle
$E"$
is also compact, so is E. Hence, the exact triangle
![]() $E \to X \to D$
shows that X is in
$E \to X \to D$
shows that X is in
![]() $\mathcal {D}^{-}_{c}.$
If we now further assume that
$\mathcal {D}^{-}_{c}.$
If we now further assume that
![]() $i^{!} X \in (\mathcal {D}_{F})^{+}$
and
$i^{!} X \in (\mathcal {D}_{F})^{+}$
and
![]() $j^{*} X \in (\mathcal {D}_{U})^{b},$
then
$j^{*} X \in (\mathcal {D}_{U})^{b},$
then
![]() $X \in \mathcal {D}^{b}$
by the definition of glued t-structure.
$X \in \mathcal {D}^{b}$
by the definition of glued t-structure.
5 Gluing approximability
The time has come to prove the main theorem. For the reader’s convenience, we recall the statement.
Theorem 5.1. Let
![]() $\mathcal {D}_{F}$
and
$\mathcal {D}_{F}$
and
![]() $\mathcal {D}_{U}$
be approximable triangulated categories, and let
$\mathcal {D}_{U}$
be approximable triangulated categories, and let
![]() $\mathcal {D}$
be a compactly generated triangulated category. Assume there is a recollement
$\mathcal {D}$
be a compactly generated triangulated category. Assume there is a recollement

Then
![]() $\mathcal {D}$
has a compact generator G. If, moreover,
$\mathcal {D}$
has a compact generator G. If, moreover, ![]() for
for
![]() $n \gg 0,$
then
$n \gg 0,$
then
![]() $\mathcal {D}$
is approximable.
$\mathcal {D}$
is approximable.
We will prove the theorem via a series of lemmas. If
![]() $\mathcal {D}_F$
is approximable with compact generator
$\mathcal {D}_F$
is approximable with compact generator
![]() $G_F$
, then there exists
$G_F$
, then there exists
![]() $A>0$
, such that for every object X in
$A>0$
, such that for every object X in
![]() ${\mathcal {D}^{\leq 0}}$
, we can find an exact triangle
${\mathcal {D}^{\leq 0}}$
, we can find an exact triangle
in
![]() $\mathcal {D}_F$
with
$\mathcal {D}_F$
with
![]() $E'\in \unicode{xf8} {\langle G_F \rangle }_{A}^{[-A,A]}$
and
$E'\in \unicode{xf8} {\langle G_F \rangle }_{A}^{[-A,A]}$
and
![]() $D'\in \mathcal {D}_F^{\leq -1}$
. To prove the theorem, we will show how to lift a morphism
$D'\in \mathcal {D}_F^{\leq -1}$
. To prove the theorem, we will show how to lift a morphism
![]() $E'\xrightarrow {f'} i^*X$
in
$E'\xrightarrow {f'} i^*X$
in
![]() $\mathcal {D}_F$
to a morphism
$\mathcal {D}_F$
to a morphism
![]() $E\xrightarrow {f} X$
in
$E\xrightarrow {f} X$
in
![]() $\mathcal {D},$
for increasingly complicated
$\mathcal {D},$
for increasingly complicated
![]() $E'$
.
$E'$
.
Lemma 5.2. Consider a recollement that satisfies the hypotheses of Corollary 3.12, and let
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
![]() $\mathcal {D}.$
For every integer
$\mathcal {D}.$
For every integer
![]() $A>0$
, there exists an integer
$A>0$
, there exists an integer
![]() $B>0$
, such that, if
$B>0$
, such that, if
![]() $f':i^{*}K\rightarrow i^{*}X$
is a morphism in
$f':i^{*}K\rightarrow i^{*}X$
is a morphism in
![]() $\mathcal {D}_F$
with K compact and
$\mathcal {D}_F$
with K compact and
![]() $K,X\in {\mathcal {D}^{\leq A}}$
, then there exists an object
$K,X\in {\mathcal {D}^{\leq A}}$
, then there exists an object
![]() $Y\in {\mathcal {D}^{\leq B}}$
and morphisms
$Y\in {\mathcal {D}^{\leq B}}$
and morphisms
such that
![]() $i^{*}(\psi )$
is an isomorphism in
$i^{*}(\psi )$
is an isomorphism in
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $f' i^{*}(\psi )=i^{*}(f)$
.
$f' i^{*}(\psi )=i^{*}(f)$
.
Proof. Choose t-structures for each of
![]() $\mathcal {D}_F,\ \mathcal {D}_U$
, in the preferred equivalence classes, and glue them to form a t-structure on
$\mathcal {D}_F,\ \mathcal {D}_U$
, in the preferred equivalence classes, and glue them to form a t-structure on
![]() $\mathcal {D}$
. By Corollary 3.12, the glued t-structure on
$\mathcal {D}$
. By Corollary 3.12, the glued t-structure on
![]() $\mathcal {D}$
is in the preferred equivalence class, hence, equivalent to the given t-structure on
$\mathcal {D}$
is in the preferred equivalence class, hence, equivalent to the given t-structure on
![]() $\mathcal {D}$
. Since replacing the given t-structure by the equivalent glued one is harmless, let us assume that the t-structure on
$\mathcal {D}$
. Since replacing the given t-structure by the equivalent glued one is harmless, let us assume that the t-structure on
![]() $\mathcal {D}$
is the one obtained from the gluing.
$\mathcal {D}$
is the one obtained from the gluing.
Now choose a compact generator
![]() $G\in \mathcal {D}$
and a compact generator
$G\in \mathcal {D}$
and a compact generator
![]() $H\in \mathcal {D}_U$
. The object
$H\in \mathcal {D}_U$
. The object ![]() is a compact generator for
is a compact generator for
![]() $\mathcal {D}$
, and Lemma 3.5 permits us to choose an integer
$\mathcal {D}$
, and Lemma 3.5 permits us to choose an integer
![]() $C>0$
with
$C>0$
with ![]() . Assume also that
. Assume also that
![]() $C\geq A$
, where
$C\geq A$
, where
![]() $A>0$
is the integer given in the lemma. By the weak approximability of
$A>0$
is the integer given in the lemma. By the weak approximability of
![]() $\mathcal {D}_{U}$
and Lemma 3.7, we may, possibly at the cost of increasing C, assume that every object
$\mathcal {D}_{U}$
and Lemma 3.7, we may, possibly at the cost of increasing C, assume that every object
![]() $Z \in \mathcal {D}^{\leq 0}_{U}$
admits an exact triangle
$Z \in \mathcal {D}^{\leq 0}_{U}$
admits an exact triangle
![]() $E \to Z \to D$
with
$E \to Z \to D$
with
![]() $E \in \unicode{xf8} {\langle H \rangle }^{[-C,C]}$
and
$E \in \unicode{xf8} {\langle H \rangle }^{[-C,C]}$
and
![]() $D \in \mathcal {D}^{\leq -1}_{U}$
. We assert that in the lemma, we may set
$D \in \mathcal {D}^{\leq -1}_{U}$
. We assert that in the lemma, we may set
![]() $B=3C-1$
.
$B=3C-1$
.
By [Reference Neeman20, Proposition 4.4.1], we can represent
![]() $f':i^{*}K\rightarrow i^{*}X$
in
$f':i^{*}K\rightarrow i^{*}X$
in
![]() $\mathcal {D}_F$
by a roof in
$\mathcal {D}_F$
by a roof in
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
such that Y is compact,
![]() $i^{*}(\varphi )$
is an isomorphism in
$i^{*}(\varphi )$
is an isomorphism in
![]() $\mathcal {D}_F$
, and
$\mathcal {D}_F$
, and
![]() $f' i^{*}(\varphi )=i^{*}({\widetilde {f}})$
. Since
$f' i^{*}(\varphi )=i^{*}({\widetilde {f}})$
. Since
![]() $i^{*}(\varphi )$
is an isomorphism, we can find an exact triangle
$i^{*}(\varphi )$
is an isomorphism, we can find an exact triangle
![]() $j_{!}Z\rightarrow Y\xrightarrow {\varphi } K$
for some
$j_{!}Z\rightarrow Y\xrightarrow {\varphi } K$
for some
![]() $Z\in \mathcal {D}_U$
. Moreover, we know
$Z\in \mathcal {D}_U$
. Moreover, we know
![]() $Y\in \mathcal {D}^c\subset \mathcal {D}^-$
and
$Y\in \mathcal {D}^c\subset \mathcal {D}^-$
and
![]() $K\in {\mathcal {D}^{\leq A}}$
. Hence,
$K\in {\mathcal {D}^{\leq A}}$
. Hence,
![]() $j_{!}Z\in {\mathcal {D}^{\leq N}}$
for some N, and if
$j_{!}Z\in {\mathcal {D}^{\leq N}}$
for some N, and if
![]() $N\leq 3C-1$
, we are done. Assume, therefore,
$N\leq 3C-1$
, we are done. Assume, therefore,
![]() $N\geq 3C$
. The isomorphism
$N\geq 3C$
. The isomorphism
![]() $Z\cong j^{*}j_{!}Z$
tells us that
$Z\cong j^{*}j_{!}Z$
tells us that
![]() $Z\in \mathcal {D}^{\leq N}_U$
. By [Reference Neeman16, 2.2.1] (with
$Z\in \mathcal {D}^{\leq N}_U$
. By [Reference Neeman16, 2.2.1] (with
![]() $m =N+1-3C$
and
$m =N+1-3C$
and
![]() $F = \Sigma ^{N} Z$
), there is an exact triangle
$F = \Sigma ^{N} Z$
), there is an exact triangle
![]() $E\rightarrow Z\rightarrow D$
in
$E\rightarrow Z\rightarrow D$
in
![]() $\mathcal {D}_U$
with
$\mathcal {D}_U$
with
![]() $E \in \unicode{xf8} {\langle H\rangle }^{[2C,N+C]}$
and
$E \in \unicode{xf8} {\langle H\rangle }^{[2C,N+C]}$
and
![]() $D \in \mathcal {D}^{\leq 3C-1}_{U}$
. We have the diagram
$D \in \mathcal {D}^{\leq 3C-1}_{U}$
. We have the diagram

which we complete to an octahedron, giving an object
![]() $Y'$
and exact triangles
$Y'$
and exact triangles
![]() $j_{!}E\rightarrow Y\rightarrow Y'$
and
$j_{!}E\rightarrow Y\rightarrow Y'$
and
![]() $j_{!}D\rightarrow Y'\xrightarrow {\psi } K$
in
$j_{!}D\rightarrow Y'\xrightarrow {\psi } K$
in
![]() $\mathcal {D}$
, making the following diagram commutative:
$\mathcal {D}$
, making the following diagram commutative:

Using that ![]() , we see that there are no nonzero maps from
, we see that there are no nonzero maps from
![]() $j_{!}E\in \unicode{xf8} {\langle j_{!}H\rangle }^{[2C,N+C]}$
to
$j_{!}E\in \unicode{xf8} {\langle j_{!}H\rangle }^{[2C,N+C]}$
to
![]() $X\in {\mathcal {D}^{\leq A}}\subset {\mathcal {D}^{\leq C}}$
. Hence, the morphism
$X\in {\mathcal {D}^{\leq A}}\subset {\mathcal {D}^{\leq C}}$
. Hence, the morphism
![]() ${\widetilde {f}}: Y \rightarrow X$
factors via
${\widetilde {f}}: Y \rightarrow X$
factors via
![]() $Y\rightarrow Y'$
:
$Y\rightarrow Y'$
:

We have thus found morphisms
such that
![]() $i^{*}(\psi )$
is an isomorphism in
$i^{*}(\psi )$
is an isomorphism in
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $f' i^{*}(\psi )=i^{*}(f)$
. Furthermore, the exact triangle
$f' i^{*}(\psi )=i^{*}(f)$
. Furthermore, the exact triangle
![]() $j_{!}D\rightarrow Y'\rightarrow K$
with
$j_{!}D\rightarrow Y'\rightarrow K$
with
![]() $j_{!}D \in {\mathcal {D}^{\leq 3C-1}}$
and
$j_{!}D \in {\mathcal {D}^{\leq 3C-1}}$
and
![]() $K\in {\mathcal {D}^{\leq A}}$
shows
$K\in {\mathcal {D}^{\leq A}}$
shows
![]() $Y'~\in ~{\mathcal {D}^{\leq 3C-1}}$
. This proves the lemma.
$Y'~\in ~{\mathcal {D}^{\leq 3C-1}}$
. This proves the lemma.
Lemma 5.3. Consider a recollement that satisfies the hypotheses of Corollary 3.12. Choose a compact generator
![]() $G\in \mathcal {D}$
, and let
$G\in \mathcal {D}$
, and let
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
For every integer
![]() $A>0$
, there exists an integer
$A>0$
, there exists an integer
![]() $B>0$
, such that, if
$B>0$
, such that, if
![]() $f':E'\rightarrow i^{*}X$
is a morphism in
$f':E'\rightarrow i^{*}X$
is a morphism in
![]() $\mathcal {D}_{F}$
with
$\mathcal {D}_{F}$
with ![]() and
and
![]() $X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
$X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
![]() $f:E\rightarrow X$
in
$f:E\rightarrow X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }^{[-B,B]}$
, such that
$E\in \unicode{xf8} {\langle G \rangle }^{[-B,B]}$
, such that
![]() $i^{*}E\cong E'$
and
$i^{*}E\cong E'$
and
![]() $i^{*}f\cong f'$
.
$i^{*}f\cong f'$
.
If
![]() $\mathcal {D}_{U}$
is approximable, then the integer B may be chosen so that
$\mathcal {D}_{U}$
is approximable, then the integer B may be chosen so that
![]() $E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}.$
$E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}.$
Proof. Corollary 3.12 allows us to choose t-structures for
![]() $\mathcal {D}_F,\ \mathcal {D}_U$
in the preferred equivalence classes, glue them to form a t-structure on
$\mathcal {D}_F,\ \mathcal {D}_U$
in the preferred equivalence classes, glue them to form a t-structure on
![]() $\mathcal {D}$
, and replace the given t-structure on
$\mathcal {D}$
, and replace the given t-structure on
![]() $\mathcal {D}$
by the equivalent glued one we have just constructed.
$\mathcal {D}$
by the equivalent glued one we have just constructed.
Now choose a compact generator
![]() $H\in \mathcal {D}_U$
. The object G is a compact generator for
$H\in \mathcal {D}_U$
. The object G is a compact generator for
![]() $\mathcal {D}$
, and Lemma 3.5(1) permits us to choose an integer
$\mathcal {D}$
, and Lemma 3.5(1) permits us to choose an integer
![]() $C>0$
with
$C>0$
with ![]() . Since G is a compact generator in
. Since G is a compact generator in
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $j_!H$
is compact, [Reference Neeman16, Lemma 0.9(i)] allows us to increase C so that
$j_!H$
is compact, [Reference Neeman16, Lemma 0.9(i)] allows us to increase C so that
![]() $j_!H\in \unicode{xf8} {\langle G\rangle }^{[-C,C]}_C$
. Let
$j_!H\in \unicode{xf8} {\langle G\rangle }^{[-C,C]}_C$
. Let
![]() $A>0$
be the integer given in the lemma, and let
$A>0$
be the integer given in the lemma, and let
![]() $A'>0$
be an integer with
$A'>0$
be an integer with
![]() $G\in \mathcal {D}^{\leq A'}$
; Lemma 5.2 permits us to produce an integer
$G\in \mathcal {D}^{\leq A'}$
; Lemma 5.2 permits us to produce an integer
![]() $B'>0$
so that any morphism
$B'>0$
so that any morphism
![]() $i^*K\to i^*X$
, with
$i^*K\to i^*X$
, with
![]() $K\in \mathcal {D}^c\cap \mathcal {D}^{\leq A+A'}$
and
$K\in \mathcal {D}^c\cap \mathcal {D}^{\leq A+A'}$
and
![]() $X\in \mathcal {D}^{\leq A+A'}$
, can be represented by a roof with
$X\in \mathcal {D}^{\leq A+A'}$
, can be represented by a roof with
![]() $Y\in \mathcal {D}^{\leq B'}$
. At the cost of possibly increasing C, assume
$Y\in \mathcal {D}^{\leq B'}$
. At the cost of possibly increasing C, assume
![]() $B'\leq C$
and
$B'\leq C$
and
![]() $A+A'\leq C$
. Finally, the weak approximability (respectively, approximability) of
$A+A'\leq C$
. Finally, the weak approximability (respectively, approximability) of
![]() $\mathcal {D}_{U}$
and Lemma 3.7 permits us, possibly at the cost of increasing C, to assume that every object
$\mathcal {D}_{U}$
and Lemma 3.7 permits us, possibly at the cost of increasing C, to assume that every object
![]() $Z \in \mathcal {D}^{\leq 0}_{U}$
admits an exact triangle
$Z \in \mathcal {D}^{\leq 0}_{U}$
admits an exact triangle
![]() $E \to Z \to D$
with
$E \to Z \to D$
with
![]() $D \in \mathcal {D}^{\leq -1}_{U}$
and
$D \in \mathcal {D}^{\leq -1}_{U}$
and
![]() $E \in \unicode{xf8} {\langle H \rangle }^{[-C,C]}$
(respectively,
$E \in \unicode{xf8} {\langle H \rangle }^{[-C,C]}$
(respectively,
![]() $E \in \unicode{xf8} {\langle H \rangle }_C^{[-C,C]}$
). We assert that in the lemma, we may set
$E \in \unicode{xf8} {\langle H \rangle }_C^{[-C,C]}$
). We assert that in the lemma, we may set
![]() $B=\max (4C,3C^3+1)$
.
$B=\max (4C,3C^3+1)$
.
It suffices to show the lemma for
![]() $E' = \Sigma ^{n} i^*G$
with
$E' = \Sigma ^{n} i^*G$
with
![]() $n \in [-A, A]$
. Consider a morphism
$n \in [-A, A]$
. Consider a morphism
![]() $f':\Sigma ^{n} i^*G\to i^{*} X$
in
$f':\Sigma ^{n} i^*G\to i^{*} X$
in
![]() $\mathcal {D}_F$
with
$\mathcal {D}_F$
with
![]() $X\in {\mathcal {D}^{\leq A}}$
. By the choice of C, there exists an object Y in
$X\in {\mathcal {D}^{\leq A}}$
. By the choice of C, there exists an object Y in
![]() ${\mathcal {D}^{\leq C}}$
and morphisms
${\mathcal {D}^{\leq C}}$
and morphisms

such that
![]() $i^{*}(\psi )$
is an isomorphism in
$i^{*}(\psi )$
is an isomorphism in
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $f'i^{*}(\psi )=i^{*}({\widetilde {f}})$
. In particular, we can find an exact triangle
$f'i^{*}(\psi )=i^{*}({\widetilde {f}})$
. In particular, we can find an exact triangle
![]() $Y\xrightarrow {\psi } \Sigma ^n G\to j_{!} Z$
for some
$Y\xrightarrow {\psi } \Sigma ^n G\to j_{!} Z$
for some
![]() $Z\in \mathcal {D}_U$
. Since
$Z\in \mathcal {D}_U$
. Since
![]() $\Sigma ^{n} G$
and Y are both in
$\Sigma ^{n} G$
and Y are both in
![]() ${\mathcal {D}^{\leq C}} ,$
so is
${\mathcal {D}^{\leq C}} ,$
so is
![]() $j_{!} Z$
. Hence,
$j_{!} Z$
. Hence,
![]() $Z\cong j^{*} j_{!} Z\in \mathcal {D}^{\leq C}_{U}$
. By [Reference Neeman16, 2.2.1 and 2.2.2] (with
$Z\cong j^{*} j_{!} Z\in \mathcal {D}^{\leq C}_{U}$
. By [Reference Neeman16, 2.2.1 and 2.2.2] (with
![]() $m = 3C$
and
$m = 3C$
and
![]() $F=\Sigma ^CZ$
), there exists an exact triangle in
$F=\Sigma ^CZ$
), there exists an exact triangle in
![]() $\mathcal {D}_U$
$\mathcal {D}_U$
with
![]() ${\widetilde {D}} \in \mathcal {D}^{\leq -2C}_{U}$
and
${\widetilde {D}} \in \mathcal {D}^{\leq -2C}_{U}$
and
![]() ${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}$
, or if
${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}$
, or if
![]() $\mathcal {D}_U$
is approximable with
$\mathcal {D}_U$
is approximable with
![]() ${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}_{3C^2}$
. We thus get the following diagram in
${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}_{3C^2}$
. We thus get the following diagram in
![]() $\mathcal {D}$
:
$\mathcal {D}$
:

Since
![]() $j_{!}$
is right t-exact, we have
$j_{!}$
is right t-exact, we have
![]() $j_{!} {\widetilde {D}} \in {\mathcal {D}^{\leq -2C}} $
. Since
$j_{!} {\widetilde {D}} \in {\mathcal {D}^{\leq -2C}} $
. Since ![]() , there are no nonzero maps
, there are no nonzero maps
![]() $\Sigma ^{n}G \to j_{!} {\widetilde {D}}$
. It follows that
$\Sigma ^{n}G \to j_{!} {\widetilde {D}}$
. It follows that
![]() $\Sigma ^{n}G \to j_!Z$
factors via
$\Sigma ^{n}G \to j_!Z$
factors via
![]() $j_{!} {\widetilde {E}} \to j_!Z$
. We thus find a morphism
$j_{!} {\widetilde {E}} \to j_!Z$
. We thus find a morphism
![]() $\Sigma ^{n} G \to j_{!} {\widetilde {E}}$
, an exact triangle
$\Sigma ^{n} G \to j_{!} {\widetilde {E}}$
, an exact triangle
![]() $E\xrightarrow {\varphi } \Sigma ^{n} G \to j_{!} {\widetilde {E}}$
, and a morphism
$E\xrightarrow {\varphi } \Sigma ^{n} G \to j_{!} {\widetilde {E}}$
, and a morphism
![]() $E\xrightarrow {g} Y$
, such that the following diagram commutes:
$E\xrightarrow {g} Y$
, such that the following diagram commutes:

Since
![]() $j_{!}H\in \unicode{xf8} {\langle G\rangle }^{[-C,C]}_C$
and
$j_{!}H\in \unicode{xf8} {\langle G\rangle }^{[-C,C]}_C$
and
![]() ${\widetilde {E}}$
is in
${\widetilde {E}}$
is in
![]() $\unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}$
(respectively,
$\unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}$
(respectively,
![]() ${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}_{3C^2}$
), we see that
${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }^{[1-3C, 2C]}_{3C^2}$
), we see that
![]() $j_{!}{\widetilde {E}}\in \unicode{xf8} {\langle G\rangle }^{[1-4C,3C]}$
(respectively,
$j_{!}{\widetilde {E}}\in \unicode{xf8} {\langle G\rangle }^{[1-4C,3C]}$
(respectively,
![]() $j_!{\widetilde {E}}\in \unicode{xf8} {\langle G \rangle }^{[1-4C, 3C]}_{3C^3}$
). The triangle
$j_!{\widetilde {E}}\in \unicode{xf8} {\langle G \rangle }^{[1-4C, 3C]}_{3C^3}$
). The triangle
now shows that
![]() $E \in \unicode{xf8} {\langle G\rangle }^{[-4C, 4C]}$
(respectively,
$E \in \unicode{xf8} {\langle G\rangle }^{[-4C, 4C]}$
(respectively,
![]() $E \in \unicode{xf8} {\langle G\rangle }^{[-4C, 4C]}_{3C^3+1}$
). Finally, we let
$E \in \unicode{xf8} {\langle G\rangle }^{[-4C, 4C]}_{3C^3+1}$
). Finally, we let
![]() $f:={\widetilde {f}} g: E\to X$
. Now
$f:={\widetilde {f}} g: E\to X$
. Now
![]() $i^{*}(\varphi )$
is an isomorphism in
$i^{*}(\varphi )$
is an isomorphism in
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
Lemma 5.4. Consider a recollement that satisfies the hypotheses of Corollary 3.12, and suppose
![]() $\mathcal {D}_U$
is approximable. Choose a compact generator
$\mathcal {D}_U$
is approximable. Choose a compact generator
![]() $G\in \mathcal {D}$
, and let
$G\in \mathcal {D}$
, and let
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
For every pair of integers
![]() $A>0$
and
$A>0$
and
![]() $n>0$
, there exists an integer
$n>0$
, there exists an integer
![]() $B>0$
, such that, if
$B>0$
, such that, if
![]() $f':E'\rightarrow i^{*}X $
is a morphism in
$f':E'\rightarrow i^{*}X $
is a morphism in
![]() $\mathcal {D}_{F}$
with
$\mathcal {D}_{F}$
with ![]() and
and
![]() $X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
$X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
![]() $f:E\rightarrow X$
in
$f:E\rightarrow X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }_B^{[-B,B]}$
, such that
$E\in \unicode{xf8} {\langle G \rangle }_B^{[-B,B]}$
, such that
![]() $i^{*}E\cong E'$
and
$i^{*}E\cong E'$
and
![]() $i^{*}f\cong f'$
.
$i^{*}f\cong f'$
.
Proof. Corollary 3.12 allows us to choose t-structures for
![]() $\mathcal {D}_F,\ \mathcal {D}_U$
in the preferred equivalence classes, glue them to form a t-structure on
$\mathcal {D}_F,\ \mathcal {D}_U$
in the preferred equivalence classes, glue them to form a t-structure on
![]() $\mathcal {D}$
, and replace the given t-structure on
$\mathcal {D}$
, and replace the given t-structure on
![]() $\mathcal {D}$
by the equivalent glued one we have just constructed.
$\mathcal {D}$
by the equivalent glued one we have just constructed.
The case
![]() $n=1$
is shown in Lemma 5.3. We proceed by induction on n, and suppose the lemma holds for some
$n=1$
is shown in Lemma 5.3. We proceed by induction on n, and suppose the lemma holds for some
![]() $n\geq 1$
. Fix
$n\geq 1$
. Fix
![]() $A>0$
, choose
$A>0$
, choose
![]() ${\widetilde {B}}$
as in Lemma 5.3, meaning any morphism
${\widetilde {B}}$
as in Lemma 5.3, meaning any morphism
![]() $f':E'\to i^*X$
in the category
$f':E'\to i^*X$
in the category
![]() $\mathcal {D}_F$
, with
$\mathcal {D}_F$
, with ![]() and
and
![]() $X\in {\mathcal {D}^{\leq A}}$
, is isomorphic to
$X\in {\mathcal {D}^{\leq A}}$
, is isomorphic to
![]() $i^*f$
for some morphism
$i^*f$
for some morphism
![]() $f:E\rightarrow X$
in
$f:E\rightarrow X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }_{{\widetilde {B}}}^{[-{\widetilde {B}},{\widetilde {B}}]}$
. Increasing
$E\in \unicode{xf8} {\langle G \rangle }_{{\widetilde {B}}}^{[-{\widetilde {B}},{\widetilde {B}}]}$
. Increasing
![]() ${\widetilde {B}}$
if necessary, assume
${\widetilde {B}}$
if necessary, assume
![]() ${\widetilde {B}}\geq A$
and
${\widetilde {B}}\geq A$
and
![]() $G\in \mathcal {D}^{\leq {\widetilde {B}}}$
.
$G\in \mathcal {D}^{\leq {\widetilde {B}}}$
.
Using the induction hypothesis, choose
![]() $B'$
, such that, if
$B'$
, such that, if
![]() $f':E'\rightarrow i^{*}X $
is a morphism in
$f':E'\rightarrow i^{*}X $
is a morphism in
![]() $\mathcal {D}_{F}$
with
$\mathcal {D}_{F}$
with ![]() and
and
![]() $X\in {\mathcal {D}^{\leq 2{\widetilde {B}}}}$
, then there exists a morphism
$X\in {\mathcal {D}^{\leq 2{\widetilde {B}}}}$
, then there exists a morphism
![]() $f:E\rightarrow X$
in
$f:E\rightarrow X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }_{B'}^{[-B',B']}$
, such that
$E\in \unicode{xf8} {\langle G \rangle }_{B'}^{[-B',B']}$
, such that
![]() $i^{*}E\cong E'$
and
$i^{*}E\cong E'$
and
![]() $i^{*}f\cong f'$
.
$i^{*}f\cong f'$
.
Consider a morphism
![]() $f':E'\to i^{*}X$
with
$f':E'\to i^{*}X$
with ![]() and
and
![]() $X\in {\mathcal {D}^{\leq A}}.$
By definition, there exists an exact triangle
$X\in {\mathcal {D}^{\leq A}}.$
By definition, there exists an exact triangle
![]() $E_{1}' \to E' \to E^\prime _{n} $
with
$E_{1}' \to E' \to E^\prime _{n} $
with ![]() and
and ![]() . We can complete the octahedron on
. We can complete the octahedron on
![]() $E_1'\rightarrow E'\rightarrow i^{*}X$
to find exact triangles
$E_1'\rightarrow E'\rightarrow i^{*}X$
to find exact triangles
![]() $E'\to i^*X\to Z'$
,
$E'\to i^*X\to Z'$
,
![]() $E^\prime _1\to i^*X\to Y'$
, and
$E^\prime _1\to i^*X\to Y'$
, and
![]() $E^\prime _n\to Y'\to Z'$
, such that the diagram
$E^\prime _n\to Y'\to Z'$
, such that the diagram

commutes. Since
![]() $E^\prime _{1}$
is in
$E^\prime _{1}$
is in ![]() and X is in
and X is in
![]() ${\mathcal {D}^{\leq A}}$
, we can apply our choices to find an exact triangle
${\mathcal {D}^{\leq A}}$
, we can apply our choices to find an exact triangle
![]() $E_1\to X\to Y$
in
$E_1\to X\to Y$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E_1\in \unicode{xf8} {\langle G \rangle }_{{\widetilde {B}}}^{[-{\widetilde {B}},{\widetilde {B}}]}$
and such that
$E_1\in \unicode{xf8} {\langle G \rangle }_{{\widetilde {B}}}^{[-{\widetilde {B}},{\widetilde {B}}]}$
and such that
![]() $i^{*}(E_1 \to X \to Y)\cong E_1'\to i^{*}X\to Y'$
. Note that
$i^{*}(E_1 \to X \to Y)\cong E_1'\to i^{*}X\to Y'$
. Note that
Next, we consider the morphism
![]() $E_n'\to Y'\cong i^{*}Y$
with
$E_n'\to Y'\cong i^{*}Y$
with ![]() and
and
![]() $Y\in {\mathcal {D}^{\leq 2{\widetilde {B}}}}$
. By our choices of integers, there exists an exact triangle
$Y\in {\mathcal {D}^{\leq 2{\widetilde {B}}}}$
. By our choices of integers, there exists an exact triangle
![]() $E_n\to Y\to Z$
in
$E_n\to Y\to Z$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E_n\in \unicode{xf8} {\langle G \rangle }_{B'}^{[-B',B']}$
and such that
$E_n\in \unicode{xf8} {\langle G \rangle }_{B'}^{[-B',B']}$
and such that
![]() $i^{*}(E_n\to Y\to Z)\cong E_n'\to Y'\to Z'$
. We now have the following diagram:
$i^{*}(E_n\to Y\to Z)\cong E_n'\to Y'\to Z'$
. We now have the following diagram:

Completing the octahedron, we find an object E and exact triangles
![]() $E_{1} \to E \to E_{n}$
and
$E_{1} \to E \to E_{n}$
and
![]() $E \xrightarrow {f} X \to Z$
in
$E \xrightarrow {f} X \to Z$
in
![]() $\mathcal {D}$
, so that the following diagram is commutative:
$\mathcal {D}$
, so that the following diagram is commutative:

Since there are isomorphisms
![]() $i^{*}(X\to Y)\cong i^{*}X\to Y'$
and
$i^{*}(X\to Y)\cong i^{*}X\to Y'$
and
![]() $i^{*}(Y\to Z)\cong Y'\to Z'$
, there is an isomorphism
$i^{*}(Y\to Z)\cong Y'\to Z'$
, there is an isomorphism
![]() $i^{*}f\cong f'$
. The lemma follows since
$i^{*}f\cong f'$
. The lemma follows since
Lemma 5.5. Consider a recollement that satisfies the hypotheses of Corollary 3.12, and suppose
![]() $\mathcal {D}_U$
is approximable. Choose a compact generator
$\mathcal {D}_U$
is approximable. Choose a compact generator
![]() $G\in \mathcal {D}$
, and let
$G\in \mathcal {D}$
, and let
![]() $(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
$(\mathcal {D}^{\leq 0}, \mathcal {D}^{\geq 0})$
be a t-structure in the preferred equivalence class on
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
For any integer
![]() $A>0$
, there exists an integer
$A>0$
, there exists an integer
![]() $B>0$
, such that, if
$B>0$
, such that, if
![]() $f':E'\rightarrow i^{*}X $
is a morphism in
$f':E'\rightarrow i^{*}X $
is a morphism in
![]() $\mathcal {D}_{F}$
with
$\mathcal {D}_{F}$
with
![]() $E' \in \unicode{xf8} {\langle i^*G\rangle }_A^{[-A,A]}$
and
$E' \in \unicode{xf8} {\langle i^*G\rangle }_A^{[-A,A]}$
and
![]() $X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
$X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
![]() $f:E\rightarrow X$
in
$f:E\rightarrow X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }_B^{[-B,B]}$
, such that
$E\in \unicode{xf8} {\langle G \rangle }_B^{[-B,B]}$
, such that
![]() $i^{*}E\cong E'$
and
$i^{*}E\cong E'$
and
![]() $i^{*}f\cong f'$
.
$i^{*}f\cong f'$
.
Proof. Fix
![]() $A>0$
. In [Reference Neeman15, Corollary 1.12], it is shown that
$A>0$
. In [Reference Neeman15, Corollary 1.12], it is shown that
By Lemma 5.4, there exists
![]() $B>0$
, such that if
$B>0$
, such that if
![]() $f':E'\rightarrow i^{*}X $
is a morphism in
$f':E'\rightarrow i^{*}X $
is a morphism in
![]() $\mathcal {D}_{F}$
with
$\mathcal {D}_{F}$
with ![]() and
and
![]() $X\in {\mathcal {D}^{\leq 2A}}$
, then there exists
$X\in {\mathcal {D}^{\leq 2A}}$
, then there exists
![]() $E~\in ~\unicode{xf8} {\langle G \rangle }_B^{[-B,B]}$
and a morphism
$E~\in ~\unicode{xf8} {\langle G \rangle }_B^{[-B,B]}$
and a morphism
![]() $f:E\rightarrow X$
in
$f:E\rightarrow X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $i^{*}E\cong E'$
and
$i^{*}E\cong E'$
and
![]() $i^{*}f\cong f'$
.
$i^{*}f\cong f'$
.
Now that we understand how to lift morphisms in
![]() $\mathcal {D}_F$
to
$\mathcal {D}_F$
to
![]() $\mathcal {D}$
, we proceed with the proof of the theorem:
$\mathcal {D}$
, we proceed with the proof of the theorem:
Proof of Theorem 5.1
Let
![]() $G_{F}$
and
$G_{F}$
and
![]() $G_{U}$
be compact generators of
$G_{U}$
be compact generators of
![]() $\mathcal {D}_F$
and
$\mathcal {D}_F$
and
![]() $\mathcal {D}_U$
, respectively. By [Reference Neeman20, Theorem 4.4.9], there exists a compact object
$\mathcal {D}_U$
, respectively. By [Reference Neeman20, Theorem 4.4.9], there exists a compact object
![]() $G'$
in
$G'$
in
![]() $\mathcal {D}$
, such that
$\mathcal {D}$
, such that
![]() $G_{F}$
is a direct summand of
$G_{F}$
is a direct summand of
![]() $i^{*} G'$
. It follows that
$i^{*} G'$
. It follows that ![]() is a compact generator for
is a compact generator for
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Suppose now that ![]() for
for
![]() $n \gg 0$
; we’re in the situation of Corollary 3.12, allowing us to choose t-structures for
$n \gg 0$
; we’re in the situation of Corollary 3.12, allowing us to choose t-structures for
![]() $\mathcal {D}_F,\ \mathcal {D}_U$
in the preferred equivalence classes, glue them to form a t-structure on
$\mathcal {D}_F,\ \mathcal {D}_U$
in the preferred equivalence classes, glue them to form a t-structure on
![]() $\mathcal {D}$
, and we’re guaranteed that the glued t-structure on
$\mathcal {D}$
, and we’re guaranteed that the glued t-structure on
![]() $\mathcal {D}$
is in the preferred equivalence class. Choose a compact generator
$\mathcal {D}$
is in the preferred equivalence class. Choose a compact generator
![]() $H\in \mathcal {D}_U$
, and choose an integer
$H\in \mathcal {D}_U$
, and choose an integer
![]() $A>0$
so that
$A>0$
so that
![]() $G\in \mathcal {D}^{\leq A}$
,
$G\in \mathcal {D}^{\leq A}$
, ![]() , and
, and
![]() $j_!H\in {\langle G \rangle }_{A}^{[-A,A]}$
. Recalling that
$j_!H\in {\langle G \rangle }_{A}^{[-A,A]}$
. Recalling that
![]() $\mathcal {D}_U$
and
$\mathcal {D}_U$
and
![]() $\mathcal {D}_F$
are approximable and remembering Lemma 3.7, we may, by increasing A if necessary, also assume that every object
$\mathcal {D}_F$
are approximable and remembering Lemma 3.7, we may, by increasing A if necessary, also assume that every object
![]() $X\in \mathcal {D}^{\leq 0}_U$
admits an exact triangle
$X\in \mathcal {D}^{\leq 0}_U$
admits an exact triangle
![]() $E\to X\to D$
with
$E\to X\to D$
with
![]() $E\in \unicode{xf8} {\langle H \rangle }_{A}^{[-A,A]}$
and
$E\in \unicode{xf8} {\langle H \rangle }_{A}^{[-A,A]}$
and
![]() $D\in \mathcal {D}^{\leq -1}_U$
, and every object
$D\in \mathcal {D}^{\leq -1}_U$
, and every object
![]() $X\in \mathcal {D}^{\leq 0}_F$
admits an exact triangle
$X\in \mathcal {D}^{\leq 0}_F$
admits an exact triangle
![]() $E\to X\to D$
with
$E\to X\to D$
with
![]() $E\in \unicode{xf8} {\langle i^*G \rangle }_{A}^{[-A,A]}$
and
$E\in \unicode{xf8} {\langle i^*G \rangle }_{A}^{[-A,A]}$
and
![]() $D\in \mathcal {D}^{\leq -1}_F$
. By Lemma 5.5, there exists an integer
$D\in \mathcal {D}^{\leq -1}_F$
. By Lemma 5.5, there exists an integer
![]() $B>0$
, such that, if
$B>0$
, such that, if
![]() $f':E'\rightarrow i^{*}X $
is any morphism in
$f':E'\rightarrow i^{*}X $
is any morphism in
![]() $\mathcal {D}_{F}$
with
$\mathcal {D}_{F}$
with
![]() $E'\in \unicode{xf8} {\langle i^*G \rangle }_{A}^{[-A,A]}$
and
$E'\in \unicode{xf8} {\langle i^*G \rangle }_{A}^{[-A,A]}$
and
![]() $X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
$X\in {\mathcal {D}^{\leq A}}$
, then there exists a morphism
![]() $f: E \to X$
in
$f: E \to X$
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
, such that
$E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
, such that
![]() $i^{*} f \cong f'.$
$i^{*} f \cong f'.$
Let X be an object of
![]() ${\mathcal {D}^{\leq 0}}$
, hence,
${\mathcal {D}^{\leq 0}}$
, hence,
![]() $i^{*} X \in \mathcal {D}^{\leq 0}_{F}.$
We find an exact triangle
$i^{*} X \in \mathcal {D}^{\leq 0}_{F}.$
We find an exact triangle
with
![]() $E'\in \unicode{xf8} {\langle i^*G \rangle }_{A}^{[-A,A]}$
and
$E'\in \unicode{xf8} {\langle i^*G \rangle }_{A}^{[-A,A]}$
and
![]() $D'\in \mathcal {D}_F^{\leq -1}$
. By the choices of integers above, there exists a morphism
$D'\in \mathcal {D}_F^{\leq -1}$
. By the choices of integers above, there exists a morphism
![]() $E \xrightarrow {f} X $
in
$E \xrightarrow {f} X $
in
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
, such that
$E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
, such that
![]() $i^{*}f\cong f' $
. Complete f to a triangle
$i^{*}f\cong f' $
. Complete f to a triangle
Since
![]() $E \in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
and
$E \in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
and
![]() $X\in {\mathcal {D}^{\leq 0}},$
we have
$X\in {\mathcal {D}^{\leq 0}},$
we have
![]() $D" \in {\mathcal {D}^{\leq A+B}},$
and thus,
$D" \in {\mathcal {D}^{\leq A+B}},$
and thus,
![]() $j^{*} D" \in \mathcal {D}^{\leq A+B}_{U}.$
By [Reference Neeman16, 2.2.1] (with
$j^{*} D" \in \mathcal {D}^{\leq A+B}_{U}.$
By [Reference Neeman16, 2.2.1] (with
![]() $F=\Sigma ^{A+B}j^*D"$
and
$F=\Sigma ^{A+B}j^*D"$
and
![]() $m=A+B+1$
), we find an exact triangle
$m=A+B+1$
), we find an exact triangle
in
![]() $\mathcal {D}_U$
, such that
$\mathcal {D}_U$
, such that
![]() ${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }_{(A+B+1)A}^{[-A,2A+B]}$
and
${\widetilde {E}}\in \unicode{xf8} {\langle H \rangle }_{(A+B+1)A}^{[-A,2A+B]}$
and
![]() ${\widetilde {D}}\in \mathcal {D}^{\leq -1}_U$
, obtaining a diagram
${\widetilde {D}}\in \mathcal {D}^{\leq -1}_U$
, obtaining a diagram

Completing the octahedron on
![]() $j_{!} {\widetilde {E}} \to j_{!}j^{*} D" \to D"$
, we find an object D with exact triangles
$j_{!} {\widetilde {E}} \to j_{!}j^{*} D" \to D"$
, we find an object D with exact triangles
![]() $j_{!} {\widetilde {E}} \to D"\to D$
and
$j_{!} {\widetilde {E}} \to D"\to D$
and
![]() $j_{!}{\widetilde {D}} \to D \to i_{*} i^{*} D"$
in
$j_{!}{\widetilde {D}} \to D \to i_{*} i^{*} D"$
in
![]() $\mathcal {D}$
, that fit into the following commutative diagram:
$\mathcal {D}$
, that fit into the following commutative diagram:

We note that
![]() $j_{!} {\widetilde {D}} \in {\mathcal {D}^{\leq -1}}$
since
$j_{!} {\widetilde {D}} \in {\mathcal {D}^{\leq -1}}$
since
![]() ${\widetilde {D}} \in \mathcal {D}^{\leq -1}_{U}$
and
${\widetilde {D}} \in \mathcal {D}^{\leq -1}_{U}$
and
![]() $j_{!}$
is right t-exact. Furthermore,
$j_{!}$
is right t-exact. Furthermore,
![]() $i_{*}i^{*} D" \in {\mathcal {D}^{\leq -1}} ,$
since
$i_{*}i^{*} D" \in {\mathcal {D}^{\leq -1}} ,$
since
![]() $i^{*} D" \cong D' \in \mathcal {D}^{\leq -1}_{F}$
and
$i^{*} D" \cong D' \in \mathcal {D}^{\leq -1}_{F}$
and
![]() $i_{*}$
is t-exact. Thus,
$i_{*}$
is t-exact. Thus,
![]() $D \in {\mathcal {D}^{\leq -1}} .$
$D \in {\mathcal {D}^{\leq -1}} .$
Next, we complete the octahedron on
![]() $X \to D" \to D$
, finding an object F with exact triangles
$X \to D" \to D$
, finding an object F with exact triangles
![]() $F \to X \to D$
and
$F \to X \to D$
and
![]() $E \to F \to j_{!} {\widetilde {E}}$
in
$E \to F \to j_{!} {\widetilde {E}}$
in
![]() $\mathcal {D}$
, that fit into the following commutative diagram:
$\mathcal {D}$
, that fit into the following commutative diagram:

Since
![]() $E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
and
$E\in \unicode{xf8} {\langle G \rangle }_{B}^{[-B,B]}$
and
we see that
![]() $F \in \unicode{xf8} {\langle G \rangle }_{(A+B+1)A^2+B}^{[-3A-B,3A+B]}$
. Thus, the exact triangle
$F \in \unicode{xf8} {\langle G \rangle }_{(A+B+1)A^2+B}^{[-3A-B,3A+B]}$
. Thus, the exact triangle
![]() $F \to X \to D$
proves the approximability of
$F \to X \to D$
proves the approximability of
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
6 Gluing dg-categories
In this section, we fix a commutative ring R, and assume everything in sight is R-linear. Recall that an algebraic triangulated category is a triangulated category that is equivalent to the stable category of a Frobenius exact category. By [Reference Keller7, Theorem 4.3], if
![]() $\mathcal {D}$
is a cocomplete algebraic triangulated category with a single compact generator, then
$\mathcal {D}$
is a cocomplete algebraic triangulated category with a single compact generator, then
![]() $\mathcal {D}$
is equivalent to the derived category of a dg-algebra. Thus, determining which algebraic triangulated categories are approximable is equivalent to determining which dg-algebras have an approximable derived category.
$\mathcal {D}$
is equivalent to the derived category of a dg-algebra. Thus, determining which algebraic triangulated categories are approximable is equivalent to determining which dg-algebras have an approximable derived category.
If A is a dg-algebra, and its derived category
![]() $D(A)$
is approximable, then
$D(A)$
is approximable, then ![]() for
for
![]() $n \gg 0$
by Lemma 3.5. By [Reference Neeman16, Remark 3.3], if
$n \gg 0$
by Lemma 3.5. By [Reference Neeman16, Remark 3.3], if
![]() $H^{n}(A) = 0$
for all
$H^{n}(A) = 0$
for all
![]() $n> 0$
, then
$n> 0$
, then
![]() $D(A)$
is approximable. Below, we show that if A is an “upper triangular algebra” constructed from dg-algebras B and
$D(A)$
is approximable. Below, we show that if A is an “upper triangular algebra” constructed from dg-algebras B and
![]() $C,$
where
$C,$
where
![]() $B, C$
have approximable derived categories, then so does A. This gives examples of dg-algebras with approximable derived categories and cohomology in arbitrarily high degree.
$B, C$
have approximable derived categories, then so does A. This gives examples of dg-algebras with approximable derived categories and cohomology in arbitrarily high degree.
Corollary 6.1. Let B and C be dg-algebras, M a ![]() -module, and A the dg-matrix algebra of this data, that is,
-module, and A the dg-matrix algebra of this data, that is,
 $$ \begin{align*} A = \left[ \begin{array}{rr} B & M\\ 0 & C \end{array} \right], \quad \quad d_{A} = \left[ \begin{array}{rr} d_{B} & d_{M}\\ 0 & d_{C} \end{array} \right]. \end{align*} $$
$$ \begin{align*} A = \left[ \begin{array}{rr} B & M\\ 0 & C \end{array} \right], \quad \quad d_{A} = \left[ \begin{array}{rr} d_{B} & d_{M}\\ 0 & d_{C} \end{array} \right]. \end{align*} $$
Assume that M is cohomologically bounded above, that is,
![]() $H^{n}(M) = 0$
for
$H^{n}(M) = 0$
for
![]() $n \gg 0,$
and that M has a semiprojective B-resolution that is also a
$n \gg 0,$
and that M has a semiprojective B-resolution that is also a ![]() -module. Then if
-module. Then if
![]() $D(B)$
and
$D(B)$
and
![]() $D(C)$
are approximable, so is
$D(C)$
are approximable, so is
![]() $D(A)$
. Moreover,
$D(A)$
. Moreover,
![]() $D(A)^{-}_{c}$
and
$D(A)^{-}_{c}$
and
![]() $D(A)^{b}_{c}$
are glued from their analogues over B and C.
$D(A)^{b}_{c}$
are glued from their analogues over B and C.
Remark 4. The condition on the resolution of M is satisfied if R is a field, or more generally, if M and B are flat over R as graded modules. Indeed, one can then construct a semiprojective B-resolution of M using the bar construction, and this resolution retains the right C-action from M.
Proof. By [Reference Maycock12, Section 3] (see also [Reference Jorgensen6]), there is a recollement:

Note that B and C are cohomologically bounded above, since their derived categories are approximable, and therefore A is also cohomologically bounded above. Thus, we may apply Theorem 5.1, with
![]() $A = G,$
to see
$A = G,$
to see
![]() $D(A)$
is approximable. By [Reference Maycock12, Lemma 3.11],
$D(A)$
is approximable. By [Reference Maycock12, Lemma 3.11],
![]() $j^{*}(A) \cong C,$
and thus is in
$j^{*}(A) \cong C,$
and thus is in
![]() $D(C)^{-}_{c},$
so we may apply Proposition 4.3.
$D(C)^{-}_{c},$
so we may apply Proposition 4.3.
Acknowledgments
The authors would like to thank an anonymous referee for many helpful suggestions and comments that led to improvements on an earlier draft. The work of Jesse Burke was supported by the Australian Research Council (grant number DP150102313). Amnon Neeman was mostly supported by the Australian Research Council (grants numbers DP150102313 and DP200102537) but partly also by the Deutsche Forschungsgemeinschaft (SFB-TRR 358/1 2023 - 491392403). Bregje Pauwels was supported by the Australian Research Council (grants numbers DP150102313 and DP180102563).
Competing interest
The authors have no competing interest to declare.