Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nagpal, Rohit
2019.
VI-modules in nondescribing characteristic, part I.
Algebra & Number Theory,
Vol. 13,
Issue. 9,
p.
2151.
Sam, Steven V
and
Snowden, Andrew
2020.
Regularity bounds for twisted commutative algebras.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 2,
p.
299.
Erman, Daniel
Sam, Steven V
and
Snowden, Andrew
2021.
Generalizations of Stillman’s Conjecture via Twisted Commutative Algebra.
International Mathematics Research Notices,
Vol. 2021,
Issue. 16,
p.
12281.
Sam, Steven
and
Snowden, Andrew
2021.
𝑆𝑝-equivariant modules over polynomial rings in infinitely many variables.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 3,
p.
1671.
Ganapathy, Karthik
2022.
Stillman’s question for twisted commutative algebras.
Journal of Commutative Algebra,
Vol. 14,
Issue. 3,
Kriz, Sophie
2022.
On the local cohomology of L-shaped integral FI-modules.
Journal of Algebra,
Vol. 611,
Issue. ,
p.
149.
Gandini, Francesca
2022.
Resolutions of ideals of subspace arrangements.
Journal of Commutative Algebra,
Vol. 14,
Issue. 3,
Bik, Arthur
Danelon, Alessandro
and
Draisma, Jan
2023.
Topological Noetherianity of polynomial functors II: base rings with Noetherian spectrum.
Mathematische Annalen,
Vol. 385,
Issue. 3-4,
p.
1879.
Snowden, Andrew
and
Güntürkün, Sema
2023.
The Representation Theory of the Increasing Monoid.
Memoirs of the American Mathematical Society,
Vol. 286,
Issue. 1420,
Wawrykow, Nicholas
2023.
On the symmetric group action on rigid disks in a strip.
Journal of Applied and Computational Topology,
Vol. 7,
Issue. 3,
p.
427.
Ganapathy, Karthik
2024.
$$\textbf{GL}$$-algebras in positive characteristic I: the exterior algebra.
Selecta Mathematica,
Vol. 30,
Issue. 4,
Yu, Teresa
2025.
Polynomial Functors on Flags.
Transformation Groups,
Bik, Arthur
Draisma, Jan
and
Snowden, Andrew
2025.
The geometry of polynomial representations in positive characteristic.
Mathematische Zeitschrift,
Vol. 310,
Issue. 1,
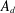 $A_{d}$ be the tca freely generated by
$A_{d}$ be the tca freely generated by 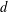 $d$ indeterminates of degree 1. In a previous paper, we determined the structure of the category of
$d$ indeterminates of degree 1. In a previous paper, we determined the structure of the category of 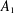 $A_{1}$-modules (which is equivalent to the category of
$A_{1}$-modules (which is equivalent to the category of 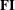 $\mathbf{FI}$-modules). In this paper, we establish analogous results for the category of
$\mathbf{FI}$-modules). In this paper, we establish analogous results for the category of 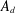 $A_{d}$-modules, for any
$A_{d}$-modules, for any 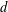 $d$. Modules over
$d$. Modules over 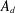 $A_{d}$ are closely related to the structures used by the authors in previous works studying syzygies of Segre and Veronese embeddings, and we hope the results of this paper will eventually lead to improvements on those works. Our results also have implications in asymptotic commutative algebra.
$A_{d}$ are closely related to the structures used by the authors in previous works studying syzygies of Segre and Veronese embeddings, and we hope the results of this paper will eventually lead to improvements on those works. Our results also have implications in asymptotic commutative algebra.