Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T06:28:15.108Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERIC VANISHING THEORY VIA MIXED HODGE MODULES

Part of: (Co)homology theory Cycles and subschemes Holomorphic fiber spaces Abelian varieties and schemes

Published online by Cambridge University Press:  17 May 2013

MIHNEA POPA  and
CHRISTIAN SCHNELL
MIHNEA POPA
Affiliation:
Department of Mathematics, Statistics & Computer Science, University of Illinois at Chicago, 851 South Morgan Street, Chicago, IL 60607, [email protected]
CHRISTIAN SCHNELL
Affiliation:
Department of Mathematics, Stony Brook University, Stony Brook, NY 11794, [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

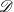We extend most of the results of generic vanishing theory to bundles of holomorphic forms and rank-one local systems, and more generally to certain coherent sheaves of Hodge-theoretic origin associated with irregular varieties. Our main tools are Saito’s mixed Hodge modules, the Fourier–Mukai transform for $\mathscr{D}$-modules on abelian varieties introduced by Laumon and Rothstein, and Simpson’s harmonic theory for flat bundles. In the process, we also discover two natural categories of perverse coherent sheaves.

MSC classification

Secondary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 14K20: Analytic theory; abelian integrals and differentials 32L20: Vanishing theorems
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 1 , 2013 , e1
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2013.

References

Arapura, D., ‘Higgs line bundles, Green–Lazarsfeld sets, and maps of Kähler manifolds to curves’, Bull. Amer. Math. Soc. (N.S.) 26(2) (1992), 310–314.Google Scholar
Arinkin, D. and Bezrukavnikov, R., ‘Perverse coherent sheaves’, Mosc. Math. J. 10(1) (2010), 3–29.Google Scholar
Beilinson, A., Bernstein, J. and Deligne, P., ‘Faisceaux pervers’, Astérisque 100 (1982), 3–171.Google Scholar
Chen, J. and Hacon, C., ‘Kodaira dimension of irregular varieties’, Invent. Math. 186(3) (2011), 481–500.Google Scholar
Clemens, H. and Hacon, C., ‘Deformations of the trivial line bundle and vanishing theorems’, Amer. J. Math. 124(4) (2002), 769–815.Google Scholar
de Cataldo, M. A. A. and Migliorini, L., ‘The Hodge theory of algebraic maps’, Ann. Sci. Éc. Norm. Supér. (4) 38(5) (2005), 693–750.Google Scholar
Deligne, P., ‘Théorie de Hodge. II’, Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.Google Scholar
Ein, L. and Lazarsfeld, R., ‘Singularities of theta divisors and the birational geometry of irregular varieties’, J. Amer. Math. Soc. 10(1) (1997), 243–258.Google Scholar
Eisenbud, D., The Geometry of Syzygies: a Second Course in Commutative Algebra and Algebraic Geometry, Graduate Texts in Mathematics, 229 (Springer, New York, 2005).Google Scholar
Eisenbud, D., Fløystad, G. and Schreyer, F.-O., ‘Sheaf cohomology and free resolutions over the exterior algebra’, Trans. Amer. Math. Soc. 355(11) (2003), 4397–4426.Google Scholar
Green, M. and Lazarsfeld, R., ‘Deformation theory, generic vanishing theorems, and some conjectures of Enriques, Catanese and Beauville’, Invent. Math. 90(2) (1987), 389–407.Google Scholar
Green, M. and Lazarsfeld, R., ‘Higher obstructions to deforming cohomology groups of line bundles’, J. Amer. Math. Soc. 1(4) (1991), 87–103.CrossRefGoogle Scholar
Griffiths, P. and Harris, J., Principles of Algebraic Geometry (Wiley-Interscience, 1978).Google Scholar
Hacon, C., ‘A derived category approach to generic vanishing’, J. Reine Angew. Math. 575 (2004), 173–187.Google Scholar
Kashiwara, M., ‘ $t$ -structures on the derived categories of holonomic $\mathscr{D}$ -modules and coherent $\mathscr{O} $ -modules’, Mosc. Math. J. 4(4) (2004), 847–868.Google Scholar
Kollár, J., ‘Higher direct images of dualizing sheaves II’, Ann. of Math. (2) 124 (1986), 171–202.Google Scholar
Krämer, T. and Weissauer, R. (2011), Vanishing theorems for constructible sheaves on abelian varieties, available at arXiv:1111.4947v1.Google Scholar
Laumon, G., ‘Transformations canoniques et spécialisation pour les $\mathscr{D}$ -modules filtrés. In Differential Systems and Singularities (Luminy, 1983). Astérisque (130) (1985), 56–129.Google Scholar
Laumon, G. (1996), Transformation de Fourier généralisée, available at arXiv:alg-geom/9603004.Google Scholar
Lazarsfeld, R. and Popa, M., ‘Derivative complex, BGG correspondence, and numerical inequalities for compact Kähler manifolds’, Invent. Math. 182(3) (2010), 605–633.Google Scholar
Lazarsfeld, R., Popa, M. and Schnell, C., ‘Canonical cohomology as an exterior module’, Pure Appl. Math. Q. 7(4) (2010), 1529–1542.Google Scholar
Libgober, A., ‘First order deformations for rank-one local systems with a non-vanishing cohomology’, Topology Appl. 118(1–2) (2002), 159–168.CrossRefGoogle Scholar
MacDonald, I., ‘Symmetric products of an algebraic curve’, Topology 1 (1962), 319–343.Google Scholar
McCleary, J., A User’s Guide to Spectral Sequences, 2nd edn. Cambridge Studies in Advanced Mathematics, 58 (Cambridge University Press, Cambridge, 2001).Google Scholar
Mukai, S., ‘Duality between $D(X)$ and $D(\hat {X} )$ with its application to Picard sheaves’, Nagoya Math. J. 81 (1981), 153–175.Google Scholar
Pareschi, G. and Popa, M., ‘Strong generic vanishing and a higher dimensional Castelnuovo–de Franchis inequality’, Duke Math. J. 150(2) (2009), 269–285.Google Scholar
Pareschi, G. and Popa, M., ‘GV-sheaves, Fourier–Mukai transform, and generic vanishing’, Amer. J. Math. 133(1) (2011), 235–271.Google Scholar
Popa, M., ‘Generic vanishing filtrations and perverse objects in derived categories of coherent sheaves. In Derived Categories in Algebraic Geometry, Tokyo, 2011 (European Mathematical Society, 2012), 251–277.Google Scholar
Roberts, P., Homological Invariants of Modules Over Commutative Rings, Séminaire de Mathématiques Supérieures, 72 (Presses de l’Université de Montréal, Montreal, Que., 1980).Google Scholar
Rothstein, M., ‘Sheaves with connection on abelian varieties’, Duke Math. J. 84(3) (1996), 565–598.Google Scholar
Sabbah, C., ‘Polarizable twistor $\mathscr{D}$ -modules’, Astérisque 300 (2005).Google Scholar
Sabbah, C., ‘Wild twistor $\mathscr{D}$ -modules. In Algebraic Analysis and Around, Advanced Studies in Pure Mathematics, 54 (Math. Soc. Japan, Tokyo, 2009), 293–353.Google Scholar
Saito, M., ‘Modules de Hodge polarisables’, Publ. Res. Inst. Math. Sci. 24(6) (1988), 849–995.Google Scholar
Saito, M., ‘Mixed Hodge modules’, Publ. Res. Inst. Math. Sci. 26(2) (1990), 221–333.Google Scholar
Saito, M., ‘On the Theory of Mixed Hodge Modules’, Amer. Math. Soc. Transl. Ser. 2 160 (1994), 47–61, Originally published in Japanese.Google Scholar
Schnell, C., ‘Local duality and polarized Hodge modules’, Publ. Res. Inst. Math. Sci. 47(3) (2011), 705–725.CrossRefGoogle Scholar
Schnell, C. (2012), Holonomic complexes on abelian varieties, Part I, available at arXiv:1112.3582.Google Scholar
Simpson, C., ‘Higgs bundles and local systems’, Publ. Math. Inst. Hautes Études Sci. 75 (1992), 5–95.Google Scholar
Simpson, C., ‘Subspaces of moduli spaces of rank one local systems’, Ann. Sci. Ec. Norm. Supér. 26 (1993), 361–401.Google Scholar
Weissauer, R. (2008), Brill–Noether sheaves, available at arXiv:math/o610923v4.Google Scholar
Wells, R. O. Jr, Differential Analysis on Complex Manifolds, 3rd edn, with a new appendix by Oscar Garcia-Prada. Graduate Texts in Mathematics, 65 (Springer, New York, 2008).Google Scholar
Zucker, S., ‘Hodge theory with degenerating coefficients. ${L}_{2} $ cohomology in the Poincaré metric’, Ann. of Math. (2) 109(3) (1979), 415–476.Google Scholar