Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T00:16:43.419Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERIC UNLABELED GLOBAL RIGIDITY

Part of: Discrete geometry Distance geometry

Published online by Cambridge University Press:  30 July 2019

STEVEN J. GORTLER ,
LOUIS THERAN Open the ORCID record for LOUIS THERAN [Opens in a new window]  and
DYLAN P. THURSTON
STEVEN J. GORTLER
Affiliation:
School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, USA; [email protected]
LOUIS THERAN
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, Scotland; [email protected]
DYLAN P. THURSTON
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 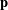$\mathbf{p}$ be a configuration of $n$ points in $\mathbb{R}^{d}$ for some $n$ and some 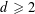$d\geqslant 2$. Each pair of points has a Euclidean distance in the configuration. Given some graph 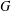$G$ on $n$ vertices, we measure the point-pair distances corresponding to the edges of 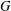$G$. In this paper, we study the question of when a generic $\mathbf{p}$ in $d$ dimensions will be uniquely determined (up to an unknowable Euclidean transformation) from a given set of point-pair distances together with knowledge of 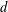$d$ and $n$. In this setting the distances are given simply as a set of real numbers; they are not labeled with the combinatorial data that describes which point pair gave rise to which distance, nor is data about 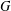$G$ given. We show, perhaps surprisingly, that in terms of generic uniqueness, labels have no effect. A generic configuration is determined by an unlabeled set of point-pair distances (together with 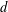$d$ and $n$) if and only if it is determined by the labeled distances.

MSC classification

Primary: 52C25: Rigidity and flexibility of structures 51K05: General theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e21
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Asimow, L. and Roth, B., ‘The rigidity of graphs’, Trans. Amer. Math. Soc. 245 (1978), 279–289. doi:10.2307/1998867.Google Scholar
Basu, S., Pollack, R. and Roy, M.-F., inAlgorithms in Real Algebraic Geometry, 2nd edn, Algorithms and Computation in Mathematics, 10 (Springer, Berlin, 2006).Google Scholar
Bolker, E. and Roth, B., ‘When is a bipartite graph a rigid framework?’, Pacific J. Math. 90(1) (1980), 27–44. http://projecteuclid.org/euclid.pjm/1102779115.Google Scholar
Boutin, M. and Kemper, G., ‘On reconstructing n-point configurations from the distribution of distances or areas’, Adv. Appl. Math. 32(4) (2004), 709–735. doi:10.1016/S0196-8858(03)00101-5.Google Scholar
Connelly, R., ‘Generic global rigidity’, Discrete Comput. Geom. 33(4) (2005), 549–563. doi:10.1007/s00454-004-1124-4.Google Scholar
Connelly, R. and Whiteley, W., ‘Global rigidity: the effect of coning’, Discrete Comput. Geom. 43(4) (2010), 717–735. doi:10.1007/s00454-009-9220-0.Google Scholar
Crapo, H. and Whiteley, W., ‘Statics of frameworks and motions of panel structures, a projective geometric introduction’, Struct. Topology (6) (1982), 43–82.Google Scholar
Fischer, G. and Piontkowski, J., inRuled Varieties: An Introduction to Algebraic Differential Geometry, Advanced Lectures in Mathematics (Friedr. Vieweg & Sohn, Braunschweig, 2001. doi:10.1007/978-3-322-80217-0.Google Scholar
Garamvölgyi, D. and Jordán, T., ‘Graph reconstruction from unlabeled edge lengths’. Technical Report TR-2019-06, Egerváry Research Group, Budapest, 2019. http://www.cs.elte.hu/egres.Google Scholar
Gkioulekas, I., Gortler, S. J., Theran, L. and Zickler, T., ‘Determining generic point configurations from unlabeled path or loop lengths’. Preprint, 2017, arXiv:1709.03936.Google Scholar
Gluck, H., ‘Almost all simply connected closed surfaces are rigid’, inGeometric Topology (Springer, Berlin, 1975), 225–239.Google Scholar
Gortler, S. J., Gotsman, C., Liu, L. and Thurston, D. P., ‘On affine rigidity’, J. Comput. Geom. 4(1) (2013), 160–181.Google Scholar
Gortler, S. J., Healy, A. D. and Thurston, D. P., ‘Characterizing generic global rigidity’, Amer. J. Math. 132(4) (2010), 897–939. doi:10.1353/ajm.0.0132.Google Scholar
Gortler, S. J. and Thurston, D. P., ‘Measurement isomorphism of graphs’. Preprint, 2012, arXiv:1212.6551.Google Scholar
Gortler, S. J. and Thurston, D. P., ‘Generic global rigidity in complex and pseudo-Euclidean spaces’, inRigidity and Symmetry (Springer, New York, 2014), 131–154. doi:10.1007/978-1-4939-0781-6_8.Google Scholar
Hendrickson, B., ‘Conditions for unique graph realizations’, SIAM J. Comput. 21(1) (1992), 65–84. doi:10.1137/0221008.Google Scholar
Hendrickson, B., ‘The molecule problem: exploiting structure in global optimization’, SIAM J. Optim. 5(4) (1995), 835–857. doi:10.1137/0805040.Google Scholar
Jackson, B. and Jordán, T., ‘Connected rigidity matroids and unique realizations of graphs’, J. Combin. Theory Ser. B 94(1) (2005), 1–29. doi:10.1016/j.jctb.2004.11.002.Google Scholar
Jackson, B., Servatius, B. and Servatius, H., ‘The 2-dimensional rigidity of certain families of graphs’, J. Graph Theory 54(2) (2007), 154–166. doi:10.1002/jgt.20196.Google Scholar
Juhás, P., Cherba, D., Duxbury, P., Punch, W. and Billinge, S., ‘Ab initio determination of solid-state nanostructure’, Nature 440(7084) (2006), 655–658.Google Scholar
Kasiviswanathan, S. P., Moore, C. and Theran, L., ‘The rigidity transition in random graphs’, inProceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms (SIAM, Philadelphia, PA, 2011), 1237–1252.Google Scholar
Király, F. J., Theran, L. and Tomioka, R., ‘The algebraic combinatorial approach for low-rank matrix completion’, J. Mach. Learn. Res. 16 (2015), 1391–1436. http://jmlr.org/papers/v16/kiraly15a.html.Google Scholar
Király, F. J., Theran, L., Tomioka, R. and Uno, T., ‘The algebraic combinatorial approach for low-rank matrix completion’. Preprint, 2013, arXiv:1211.4116v3.Google Scholar
Milne, J. S., ‘Algebraic geometry’. Online lecture notes (v5.20), available at http://www.jmilne.org/math/ (2009).Google Scholar
Mumford, D., The Red Book of Varieties and Schemes: Includes the Michigan Lectures (1974) on Curves and their Jacobians, Vol. 1358 (Springer Science & Business Media, Berlin, 1999).Google Scholar
Sanders, J. H. and Sanders, D., ‘Circuit preserving edge maps’, J. Combin. Theory Ser. B 22(2) (1977), 91–96. doi:10.1016/0095-8956(77)90001-6.Google Scholar
Saxe, J. B., ‘Embeddability of weighted graphs in k-space is strongly NP-hard’, inProc. 17th Allerton Conf. in Communications, Control, and Computing, Monticello, IL, USA (1979), 480–489.Google Scholar
Singer, A. and Cucuringu, M., ‘Uniqueness of low-rank matrix completion by rigidity theory’, SIAM J. Matrix Anal. Appl. 31(4) (2009/10), 1621–1641. doi:10.1137/090750688.Google Scholar
Streinu, I. and Theran, L., ‘Slider-pinning rigidity: a Maxwell–Laman-type theorem’, Discrete Comput. Geom. 44(4) (2010), 812–837. doi:10.1007/s00454-010-9283-y.Google Scholar
Whitney, H., ‘2-Isomorphic graphs’, Amer. J. Math. 55(1–4) (1933), 245–254. doi:10.2307/2371127.Google Scholar
Whitney, H., ‘Elementary structure of real algebraic varieties’, Ann. of Math. (2) 66 (1957), 545–556. doi:10.2307/1969908.Google Scholar