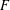Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MURAYAMA, TAKUMI
2021.
THE GAMMA CONSTRUCTION AND ASYMPTOTIC INVARIANTS OF LINE BUNDLES OVER ARBITRARY FIELDS.
Nagoya Mathematical Journal,
Vol. 242,
Issue. ,
p.
165.
Aberbach, Ian
and
Polstra, Thomas
2022.
Local cohomology bounds and the weak implies strong conjecture in dimension 4.
Journal of Algebra,
Vol. 605,
Issue. ,
p.
37.
JEFFRIES, JACK
NAKAJIMA, YUSUKE
SMIRNOV, ILYA
WATANABE, KEI–ICHI
and
YOSHIDA, KEN–ICHI
2023.
Lower bounds on Hilbert–Kunz multiplicities and maximal F-signatures.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 174,
Issue. 2,
p.
247.
Lee, Seungsu
and
Pande, Swaraj
2024.
The F-Signature Function on the Ample Cone.
International Mathematics Research Notices,
Vol. 2024,
Issue. 3,
p.
2420.