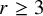1 Introduction
A matching is a graph with the property that every vertex is incident to exactly one edge (equivalently, a matching is a partition of the vertex set into pairs). Given a partition of the vertex set into two equal-size parts
![]() $V_{1},V_{2}$
, we say that a matching is bipartite if every edge is between the two parts.
$V_{1},V_{2}$
, we say that a matching is bipartite if every edge is between the two parts.
Matchings are fundamental objects in graph theory (and beyond), where one is usually interested in the existence and identification of matchings inside larger graphs (see, for example, the monograph of Lovász and Plummer [Reference Lovász and Plummer50]). However, matchings can be very interesting objects in their own right, if one puts an ordering on the set of vertices (for example, we could restrict our attention to matchings on vertex sets of the form
![]() $\{1,\dots ,2n\}$
, and consider the natural ordering of the integers).
$\{1,\dots ,2n\}$
, and consider the natural ordering of the integers).
In particular, in an ordered matching there are three different ways that a pair of distinct edges
![]() $e,e'$
can ‘interact with each other’, as follows (write
$e,e'$
can ‘interact with each other’, as follows (write
![]() $e[1]<e[2]$
for the two vertices of e, write
$e[1]<e[2]$
for the two vertices of e, write
![]() $e'[1]<e'[2]$
for the two vertices of
$e'[1]<e'[2]$
for the two vertices of
![]() $e'$
, and assume without loss of generality that
$e'$
, and assume without loss of generality that
![]() $e[1]<e'[1]$
).
$e[1]<e'[1]$
).
-
○ We could have
 $e[1]<e[2]<e'[1]<e'[2]$
(that is to say, one edge fully comes before the other one). This configuration is called an alignment.
$e[1]<e[2]<e'[1]<e'[2]$
(that is to say, one edge fully comes before the other one). This configuration is called an alignment. -
○ We could have
 $e[1]<e'[1]<e[2]<e'[2]$
(that is to say, the two edges are interleaved with each other). This configuration is called a crossing.
$e[1]<e'[1]<e[2]<e'[2]$
(that is to say, the two edges are interleaved with each other). This configuration is called a crossing. -
○ We could have
 $e[1]<e'[1]<e'[2]<e[2]$
(that is to say, one of the two edges is ‘within’ the other). This configuration is called a nesting.
$e[1]<e'[1]<e'[2]<e[2]$
(that is to say, one of the two edges is ‘within’ the other). This configuration is called a nesting.
It is a classical result (first proved by Errera [Reference Errera27]) that the crossing-free matchings on
![]() $\{1,\dots ,2n\}$
are enumerated by the Catalan numbers
$\{1,\dots ,2n\}$
are enumerated by the Catalan numbers
![]() $C_{n}$
, and an ingenious bijection (see [Reference Stanley61]) shows that there are also exactly
$C_{n}$
, and an ingenious bijection (see [Reference Stanley61]) shows that there are also exactly
![]() $C_{n}$
nesting-free matchings on
$C_{n}$
nesting-free matchings on
![]() $\{1,\dots ,2n\}$
. Note that a matching M on
$\{1,\dots ,2n\}$
. Note that a matching M on
![]() $\{1,\dots ,2n\}$
is alignment-free if and only if every edge is between
$\{1,\dots ,2n\}$
is alignment-free if and only if every edge is between
![]() $\{1,\dots ,n\}$
and
$\{1,\dots ,n\}$
and
![]() $\{n+1,\dots ,2n\}$
(i.e., if M is a bipartite matching with these two parts). Such matchings are in correspondence with permutations
$\{n+1,\dots ,2n\}$
(i.e., if M is a bipartite matching with these two parts). Such matchings are in correspondence with permutations
![]() $\sigma \in \mathcal {S}_{n}$
, and there are therefore
$\sigma \in \mathcal {S}_{n}$
, and there are therefore
![]() $n!$
of them.
$n!$
of them.
Two of the most important parameters of a permutation
![]() $\sigma \in \mathcal {S}_{n}$
are the length
$\sigma \in \mathcal {S}_{n}$
are the length
![]() $L_{\nearrow }(\sigma )$
of its longest increasing subsequence and the length
$L_{\nearrow }(\sigma )$
of its longest increasing subsequence and the length
![]() $L_{\searrow }(\sigma )$
of its longest decreasing subsequence (see for example [Reference Romik55, Reference Stanley60] for surveys on the study of these parameters). Two of the highlights in this area are the Erdős–Szekeres theorem [Reference Erdős and Szekeres26], which says that we always have
$L_{\searrow }(\sigma )$
of its longest decreasing subsequence (see for example [Reference Romik55, Reference Stanley60] for surveys on the study of these parameters). Two of the highlights in this area are the Erdős–Szekeres theorem [Reference Erdős and Szekeres26], which says that we always have
![]() $L_{\nearrow }(\sigma )\ge \sqrt n$
or
$L_{\nearrow }(\sigma )\ge \sqrt n$
or
![]() $L_{\searrow }(\sigma )\ge \sqrt n$
(i.e., it is not possible to simultaneously avoid long decreasing subsequences and long increasing subsequences), and the Robinson–Schensted–Knuth correspondence [19, Reference Knuth46, Reference Schensted57] between permutations and Young tableaux, which can be used to enumerate permutations
$L_{\searrow }(\sigma )\ge \sqrt n$
(i.e., it is not possible to simultaneously avoid long decreasing subsequences and long increasing subsequences), and the Robinson–Schensted–Knuth correspondence [19, Reference Knuth46, Reference Schensted57] between permutations and Young tableaux, which can be used to enumerate permutations
![]() $\sigma \in \mathcal S_n$
by their values of
$\sigma \in \mathcal S_n$
by their values of
![]() $L_{\nearrow }(\sigma )$
and
$L_{\nearrow }(\sigma )$
and
![]() $L_{\searrow }(\sigma )$
(and in particular, to study the behaviour of
$L_{\searrow }(\sigma )$
(and in particular, to study the behaviour of
![]() $L_{\nearrow }(\sigma )$
and
$L_{\nearrow }(\sigma )$
and
![]() $L_{\searrow }(\sigma )$
for a random permutation
$L_{\searrow }(\sigma )$
for a random permutation
![]() $\sigma \in \mathcal S_n$
).
$\sigma \in \mathcal S_n$
).
Recalling that permutations
![]() $\sigma \in \mathcal {S}_{n}$
are in correspondence with bipartite matchings between
$\sigma \in \mathcal {S}_{n}$
are in correspondence with bipartite matchings between
![]() $\{1,\dots ,n\}$
and
$\{1,\dots ,n\}$
and
![]() $\{n+1,\dots ,2n\}$
, it turns out that increasing and decreasing subsequences can be described in the language of configurations in matchings: an increasing subsequence corresponds to a set of edges which are pairwise crossing (which we call a crossing-clique), and a decreasing subsequence corresponds to a set of edges which are pairwise nesting (which we call a nesting-clique).
$\{n+1,\dots ,2n\}$
, it turns out that increasing and decreasing subsequences can be described in the language of configurations in matchings: an increasing subsequence corresponds to a set of edges which are pairwise crossing (which we call a crossing-clique), and a decreasing subsequence corresponds to a set of edges which are pairwise nesting (which we call a nesting-clique).
Extending the huge body of work on increasing and decreasing subsequences, there has been quite some work (see, for example, [Reference Baik and Jenkins5, Reference Baik and Rains6, Reference Chen, Deng, Du, Stanley and Yan17, Reference Justicz, Scheinerman and Winkler41, Reference Kasraoui and Zeng43, Reference Klazar45, Reference Krattenthaler47, Reference Stanley60]), studying nesting-cliques and crossing-cliques (and alignment-cliques, which have the obvious definition) in general matchings. It turns out that many of the techniques that are effective for permutations have natural analogues for general matchings (in particular, there is a variant of the Robinson–Schensted–Knuth correspondence relating matchings to oscillating tableaux; see [Reference Stanley60]).
Very recently, Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22] made some first steps towards extending the theory of ordered matchings to ordered hypergraph matchings (in an r-uniform hypergraph matching, every edge contains exactly r vertices, and every vertex is incident to exactly one edge). The jump from graphs to hypergraphs seems to introduce a number of serious difficulties, which should perhaps not be surprising: in much the same way that ordered matchings generalise permutations, ordered r-uniform hypergraph matchings generalise
![]() $(r-1)$
-tuples of permutations (which are sometimes called ‘r-dimensional orders’, as they can be described by sets of points in r-dimensional space). When
$(r-1)$
-tuples of permutations (which are sometimes called ‘r-dimensional orders’, as they can be described by sets of points in r-dimensional space). When
![]() $r\ge 3$
, there is no known analogue of the Robinson–Schensted–Knuth correspondence for r-dimensional orders, and there are a number of longstanding open problems (see, for example, the survey [Reference Brightwell12]).
$r\ge 3$
, there is no known analogue of the Robinson–Schensted–Knuth correspondence for r-dimensional orders, and there are a number of longstanding open problems (see, for example, the survey [Reference Brightwell12]).
In this paper, we substantially extend and improve the results in [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22], discovering some surprisingly intricate phenomena and moving towards a more complete theory of ordered hypergraph matchings. We also draw attention to a large number of compelling open problems.
1.1 Ordered hypergraph matchings: basic notions
We say that a (hyper)graph H is ordered if its vertex set
![]() $V(H)$
is equipped with a total order (one may think of graphs and hypergraphs which have vertex set
$V(H)$
is equipped with a total order (one may think of graphs and hypergraphs which have vertex set
![]() $\{1,\dots ,N\}$
for some N).
$\{1,\dots ,N\}$
for some N).
Definition 1.1. An ordered hypergraph is said to be an r-matching if every edge has exactly r vertices, and every vertex is contained in exactly one edge. An r-matching is said to be r-partite if, when we divide the vertex set into r contiguous intervals of equal length, every edge of the matching has exactly one vertex in each interval. The size of a matching M is its number of edges.
Note that there are
different r-matchings on the vertex set
![]() $\{1,\dots ,rn\}$
. The r-partite r-matchings on
$\{1,\dots ,rn\}$
. The r-partite r-matchings on
![]() $\{1,\dots ,rn\}$
are in correspondence with
$\{1,\dots ,rn\}$
are in correspondence with
![]() $(r-1)$
-tuples of permutations
$(r-1)$
-tuples of permutations
![]() $(\sigma _1,\dots ,\sigma _{r-1})\in \mathcal S_n^{r-1}$
, and there are therefore exactly
$(\sigma _1,\dots ,\sigma _{r-1})\in \mathcal S_n^{r-1}$
, and there are therefore exactly
![]() $(n!)^{r-1}$
of them.
$(n!)^{r-1}$
of them.
Definition 1.2. An r-pattern is an r-matching of size 2 (on the vertex set
![]() $\{1,\dots ,2r\}$
, say). We can represent an r-pattern by a string of ‘
$\{1,\dots ,2r\}$
, say). We can represent an r-pattern by a string of ‘
![]() ${\mathrm {A}}$
’s and ‘
${\mathrm {A}}$
’s and ‘
![]() ${\mathrm {B}}$
’s starting with ‘
${\mathrm {B}}$
’s starting with ‘
![]() ${\mathrm {A}}$
’ (where the vertices from one edge are represented with ‘
${\mathrm {A}}$
’ (where the vertices from one edge are represented with ‘
![]() ${\mathrm {A}}$
’, and the vertices of the other edge are represented with ‘
${\mathrm {A}}$
’, and the vertices of the other edge are represented with ‘
![]() ${\mathrm {B}}$
’).
${\mathrm {B}}$
’).
Note that there are exactly
![]() $(2\cdot 2)!/(2^{2}\cdot 2)=3$
different 2-patterns: the alignment (represented by
$(2\cdot 2)!/(2^{2}\cdot 2)=3$
different 2-patterns: the alignment (represented by
![]() ${\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}$
), the crossing (represented by
${\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}$
), the crossing (represented by
![]() ${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {B}}}$
) and the nesting (represented by
${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {B}}}$
) and the nesting (represented by
![]() ${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {B}}{\mathrm {A}}}$
). The crossing and nesting are
${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {B}}{\mathrm {A}}}$
). The crossing and nesting are
![]() $2$
-partite, but the alignment is not (in fact, as we discussed earlier in the introduction, avoidance of the alignment pattern is equivalent to
$2$
-partite, but the alignment is not (in fact, as we discussed earlier in the introduction, avoidance of the alignment pattern is equivalent to
![]() $2$
-partiteness).
$2$
-partiteness).
Definition 1.3. For an r-pattern P, an r-matching M is said to be a P-clique if every pair of edges of M are order-isomorphic to P. For any r-pattern P and r-matching M, let
![]() $L_{P}(M)$
be the size of the largest P-clique in M.
$L_{P}(M)$
be the size of the largest P-clique in M.
In total, there are
![]() $(2r)!/(2(r!)^2)$
different r-patterns, but there is a subtlety that occurs only for uniformities
$(2r)!/(2(r!)^2)$
different r-patterns, but there is a subtlety that occurs only for uniformities
![]() $r\ge 3$
: For some r-patterns P, it is simply not possible to have a large P-clique.
$r\ge 3$
: For some r-patterns P, it is simply not possible to have a large P-clique.
Definition 1.4. We say that an r-pattern P is collectable if there are arbitrarily large P-cliques.
For example, it is easy to see that the 3-pattern
![]() ${\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}$
is not collectable. The notions of P-cliques and collectable patterns were introduced by Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22]. In [Reference Dudek, Grytczuk and Ruciński22], they showed that for every non-collectable pattern, the largest possible clique size is 2. To this end, they gave a characterisation of the collectable patterns: They are precisely those patterns that are splittable, as follows.
${\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}$
is not collectable. The notions of P-cliques and collectable patterns were introduced by Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22]. In [Reference Dudek, Grytczuk and Ruciński22], they showed that for every non-collectable pattern, the largest possible clique size is 2. To this end, they gave a characterisation of the collectable patterns: They are precisely those patterns that are splittable, as follows.
Definition 1.5. A run in a pattern P is a sequence of consecutive vertices in the same edge of P. A pattern P is splittable if it can be partitioned into blocks of consecutive vertices, each consisting of two runs of the same length coming from different edges of P. If P is splittable, then this partition is uniquely determined; we call it the block partition of P.
For example, the pattern
![]() ${\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}{\mathrm {A}}$
is splittable (the divisions between the blocks are described by
${\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}{\mathrm {A}}$
is splittable (the divisions between the blocks are described by
![]() $|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{\mathrm {A}}{\mathrm {B}}|{\mathrm {B}}{\mathrm {A}}|$
and the block partition has parts
$|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{\mathrm {A}}{\mathrm {B}}|{\mathrm {B}}{\mathrm {A}}|$
and the block partition has parts
![]() $\{1,2,3,4\}$
,
$\{1,2,3,4\}$
,
![]() $\{5,6\}$
and
$\{5,6\}$
and
![]() $\{7,8\}$
). It is easy to check that there are exactly
$\{7,8\}$
). It is easy to check that there are exactly
![]() $3^{r-1}$
different collectable r-patterns, exactly
$3^{r-1}$
different collectable r-patterns, exactly
![]() $2^{r-1}$
of which are r-partite (note that the r-partite r-patterns are precisely the collectable r-patterns whose block partition has r blocks).
$2^{r-1}$
of which are r-partite (note that the r-partite r-patterns are precisely the collectable r-patterns whose block partition has r blocks).
For every collectable r-pattern P, there is only one way to form a P-clique on a given set of vertices. For example, in the case
![]() $r=2$
, the only way to form an alignment-clique on
$r=2$
, the only way to form an alignment-clique on
![]() $\{1,\dots ,2n\}$
is with the edges
$\{1,\dots ,2n\}$
is with the edges
the only way to form a crossing-clique is with the edges
and the only way to form a nesting-clique is with the edges
We are now ready to present the main results of the paper. To briefly summarise: In Section 1.2, we consider Ramsey-type questions (generalising the Erdős–Szekeres theorem), in Section 1.3 we study the size of the largest P-clique in a random ordered matching and in Section 1.4 we give estimates for the number of ordered hypergraph matchings avoiding P-cliques of a given size. Throughout, we discuss a number of auxiliary results we prove along the way; in particular, in Section 1.5 we discuss some contributions to the extremal theory of ordered hypergraphs, which we believe to be of independent interest. In Section 1.6, we present a large number of open problems and directions for further study.
1.2 Ramsey-type questions
Recall that the Erdős–Szekeres theorem says that every permutation
![]() $\sigma \in \mathcal S_n$
has an increasing or decreasing subsequence of length at least
$\sigma \in \mathcal S_n$
has an increasing or decreasing subsequence of length at least
![]() $\sqrt n$
(and it is easy to construct a permutation showing that this is best-possible, by taking a certain type of ‘product’ of an increasing sequence of length
$\sqrt n$
(and it is easy to construct a permutation showing that this is best-possible, by taking a certain type of ‘product’ of an increasing sequence of length
![]() $\sqrt n$
with a decreasing sequence of length
$\sqrt n$
with a decreasing sequence of length
![]() $\sqrt n$
). The Erdős–Szekeres theorem falls under the umbrella of Ramsey theory: No matter how ‘disordered’ a permutation is, it must have a long subsequence which is ‘completely homogeneous’.
$\sqrt n$
). The Erdős–Szekeres theorem falls under the umbrella of Ramsey theory: No matter how ‘disordered’ a permutation is, it must have a long subsequence which is ‘completely homogeneous’.
In [Reference Huynh, Joos and Wollan37], Huynh, Joos and Wollan adapted the Erdős–Szekeres theorem to ordered (2-uniform) matchings. They showed that in every 2-matching M of size n, one can find an alignment-clique, a crossing-clique or a nesting-clique of size at least
![]() $n^{1/3}$
. Their proof also shows that this result is best possible, with the same type of product construction used to demonstrate optimality of the Erdős–Szekeres theorem.
$n^{1/3}$
. Their proof also shows that this result is best possible, with the same type of product construction used to demonstrate optimality of the Erdős–Szekeres theorem.
To discuss the situation for higher-uniformity hypergraphs, we introduce some notation.
Definition 1.6. Let
![]() $L(M)=\max _P L_P(M)$
be the size of the largest clique (of any pattern) in M, and let
$L(M)=\max _P L_P(M)$
be the size of the largest clique (of any pattern) in M, and let
![]() $L_{r}(n)$
be the minimum value of
$L_{r}(n)$
be the minimum value of
![]() $L(M)$
among all ordered r-matchings of size n.
$L(M)$
among all ordered r-matchings of size n.
In this notation, the aforementioned work of Huynh, Joos and Wollan [Reference Huynh, Joos and Wollan37] shows that
![]() $L_{2}(n)=\lceil n^{1/3}\rceil $
.
$L_{2}(n)=\lceil n^{1/3}\rceil $
.
As first observed by Burkill and Mirsky [Reference Burkill and Mirsky15] and Kalmanson [Reference Kalmanson42], it is actually very easy to iterate the Erdős–Szekeres theorem to obtain an optimal bound for r-partite r-matchings: Every r-partite r-matching M of size n has
![]() $L(M)\ge n^{1/2^{r-1}}$
, and a product construction shows that this is best possible. (In the language of permutations, this can be equivalently formulated as the fact that in any
$L(M)\ge n^{1/2^{r-1}}$
, and a product construction shows that this is best possible. (In the language of permutations, this can be equivalently formulated as the fact that in any
![]() $(r-1)$
-tuple of length-n permutations there is a set of at least
$(r-1)$
-tuple of length-n permutations there is a set of at least
![]() $n^{1/2^{r-1}}$
indices in which each of our permutations is monotone. This is one of many different ways to generalise the Erdős–Szekeres theorem to ‘higher dimensions’; for example, see also [Reference Bucić, Sudakov and Tran13, Reference Bukh and Matoušek14, Reference Fox, Pach, Sudakov and Suk29, Reference Girão, Kronenberg and Scott34, Reference Linial and Simkin48, Reference Szabó and Tardos63]). It is not quite so obvious how to prove a bound on
$n^{1/2^{r-1}}$
indices in which each of our permutations is monotone. This is one of many different ways to generalise the Erdős–Szekeres theorem to ‘higher dimensions’; for example, see also [Reference Bucić, Sudakov and Tran13, Reference Bukh and Matoušek14, Reference Fox, Pach, Sudakov and Suk29, Reference Girão, Kronenberg and Scott34, Reference Linial and Simkin48, Reference Szabó and Tardos63]). It is not quite so obvious how to prove a bound on
![]() $L_{r}(n)$
by iterating the bound
$L_{r}(n)$
by iterating the bound
![]() $L_{2}(n)\ge n^{1/3}$
, but in [Reference Dudek, Grytczuk and Ruciński22], Dudek, Grytczuk and Ruciński showed that this is indeed possible if one is willing to give up a constant factor: They proved the general lower bound
$L_{2}(n)\ge n^{1/3}$
, but in [Reference Dudek, Grytczuk and Ruciński22], Dudek, Grytczuk and Ruciński showed that this is indeed possible if one is willing to give up a constant factor: They proved the general lower bound
![]() $L_{r}(n)\ge c_r n^{1/3^{r-1}}$
(for some
$L_{r}(n)\ge c_r n^{1/3^{r-1}}$
(for some
![]() $c_r>0$
depending on r).
$c_r>0$
depending on r).
Naïvely, this seems to suggest that
![]() $L_{r}(n)$
is of order
$L_{r}(n)$
is of order
![]() $n^{1/3^{r-1}}$
(viewing r as a constant, while n is large). However, it is not clear how to prove a corresponding upper bound using the usual ‘product-type’ constructions because cliques can interact with each other in surprisingly intricate ways. Via product-type constructions, Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński22] were only able to prove the upper bound
$n^{1/3^{r-1}}$
(viewing r as a constant, while n is large). However, it is not clear how to prove a corresponding upper bound using the usual ‘product-type’ constructions because cliques can interact with each other in surprisingly intricate ways. Via product-type constructions, Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński22] were only able to prove the upper bound
![]() $L_{r}(n) \le n^{1/(2^{r-1}+2)}$
.
$L_{r}(n) \le n^{1/(2^{r-1}+2)}$
.
As our first result, we significantly improve both the lower and upper bounds for
![]() $L_{r}(n)$
, showing that the exponent scales roughly like
$L_{r}(n)$
, showing that the exponent scales roughly like
![]() $1/2^r$
.
$1/2^r$
.
Theorem 1.7. For
![]() $r \ge 2$
, we have
$r \ge 2$
, we have
The upper bound in Theorem 1.7 comes from a product-like construction, and the lower bound in our proof of Theorem 1.7 is proved via an argument that partitions the possible r-patterns into roughly
![]() $2^r$
subsets with ‘poset-like’ structure. It is possible to push this method further, obtaining slightly stronger lower bounds by considering more intricate partitions of the r-patterns, and we are actually not sure what the limit of the method is. As an illustration, with some intricate combinatorial analysis we managed to use our method to obtain the correct order of magnitude of
$2^r$
subsets with ‘poset-like’ structure. It is possible to push this method further, obtaining slightly stronger lower bounds by considering more intricate partitions of the r-patterns, and we are actually not sure what the limit of the method is. As an illustration, with some intricate combinatorial analysis we managed to use our method to obtain the correct order of magnitude of
![]() $L_{3}(n)$
and
$L_{3}(n)$
and
![]() $L_{4}(n)$
.
$L_{4}(n)$
.
Theorem 1.8. We have
In Section 3, we describe our strategy to prove lower bounds and show how to use it to prove the general lower bound on
![]() $L_{r}(n)$
in Theorem 1.7 and the sharp lower bound on
$L_{r}(n)$
in Theorem 1.7 and the sharp lower bound on
![]() $L_{3}(n)$
in Theorem 1.8. The proof of the sharp lower bound on
$L_{3}(n)$
in Theorem 1.8. The proof of the sharp lower bound on
![]() $L_{4}(n)$
follows a similar approach but has much more complicated casework; the details appear in the appendix of the arXiv version of this paper. In Section 4, we prove the upper bound in Theorem 1.7 (which also implies the upper bounds in Theorem 1.8).
$L_{4}(n)$
follows a similar approach but has much more complicated casework; the details appear in the appendix of the arXiv version of this paper. In Section 4, we prove the upper bound in Theorem 1.7 (which also implies the upper bounds in Theorem 1.8).
1.3 Random matchings
One of the most notorious problems in the theory of permutations is the Ulam–Hammersley problem, to describe the distribution of the longest increasing permutation
![]() $L_{\nearrow }(\sigma )$
in a random permutation
$L_{\nearrow }(\sigma )$
in a random permutation
![]() $\sigma \in \mathcal S_n$
. This problem was famously resolved by Baik, Deift and Johansson [Reference Baik, Deift and Johansson4], but one of the most important milestones along the way was a theorem of Logan and Shepp [Reference Logan and Shepp49] and Vershik and Kerov [Reference Veršik and Kerov65] (see also the alternative proofs [Reference Aldous and Diaconis1, Reference Groeneboom36, Reference Johansson39, Reference Seppäläinen58]), establishing that the expected value of
$\sigma \in \mathcal S_n$
. This problem was famously resolved by Baik, Deift and Johansson [Reference Baik, Deift and Johansson4], but one of the most important milestones along the way was a theorem of Logan and Shepp [Reference Logan and Shepp49] and Vershik and Kerov [Reference Veršik and Kerov65] (see also the alternative proofs [Reference Aldous and Diaconis1, Reference Groeneboom36, Reference Johansson39, Reference Seppäläinen58]), establishing that the expected value of
![]() $L_{\nearrow }(\sigma )$
is asymptotically
$L_{\nearrow }(\sigma )$
is asymptotically
![]() $2\sqrt n$
.
$2\sqrt n$
.
These results were extended to random matchings by Baik and Rains [Reference Baik and Rains6] (see also [Reference Baik and Jenkins5, Reference Stanley60]). Specifically, they proved that in a random matching M on
![]() $\{1,\dots ,2n\}$
, the expected values of
$\{1,\dots ,2n\}$
, the expected values of
![]() $L_{\mathrm {crossing}}(M)$
and
$L_{\mathrm {crossing}}(M)$
and
![]() $L_{\mathrm {nesting}}(M)$
are both
$L_{\mathrm {nesting}}(M)$
are both
![]() $(\sqrt {2}+o(1))\sqrt {n}$
(as part of a tour de force where they found the asymptotic distribution of these quantities).
$(\sqrt {2}+o(1))\sqrt {n}$
(as part of a tour de force where they found the asymptotic distribution of these quantities).
All this work uses variations on the Robinson–Schensted–Knuth correspondence (or related bijective tools) and does not easily generalise to hypergraphs (or to higher dimensions). For example, if M is a random r-partite r-matching, then for any r-partite r-pattern P, the random variable
![]() $L_P(M)$
has the same distribution as the length of the longest common increasing subsequence in
$L_P(M)$
has the same distribution as the length of the longest common increasing subsequence in
![]() $r-1$
independent random permutations
$r-1$
independent random permutations
![]() $\sigma _1,\dots ,\sigma _{r-1}\in \mathcal S_n$
. This random variable is notoriously hard to study: Bollobás and Winkler [Reference Bollobás and Winkler7] proved that its expected value is asymptotic to
$\sigma _1,\dots ,\sigma _{r-1}\in \mathcal S_n$
. This random variable is notoriously hard to study: Bollobás and Winkler [Reference Bollobás and Winkler7] proved that its expected value is asymptotic to
![]() $c_rn^{1/r}$
for some constant
$c_rn^{1/r}$
for some constant
![]() $c_r>0$
, but the value of
$c_r>0$
, but the value of
![]() $c_r$
is unknown for all
$c_r$
is unknown for all
![]() $r\ge 3$
.
$r\ge 3$
.
We say that an event holds with high probability, or whp for short, if it holds with probability
![]() $1-o(1)$
. Here and for the rest of the paper, asymptotics are as
$1-o(1)$
. Here and for the rest of the paper, asymptotics are as
![]() $n\to \infty $
, unless explicitly stated otherwise.
$n\to \infty $
, unless explicitly stated otherwise.
In [Reference Dudek, Grytczuk and Ruciński22] (improving their results in [Reference Dudek, Grytczuk and Ruciński21]), Dudek, Grytczuk and Ruciński proved that there are constants
![]() $c_{r}^{\prime },c_{r}^{\prime \prime }\ge 0$
such that for any collectable r-pattern P, and a random r-matching M, we have
$c_{r}^{\prime },c_{r}^{\prime \prime }\ge 0$
such that for any collectable r-pattern P, and a random r-matching M, we have
![]() $c_{r}^{\prime } n^{1/r}\le L_{P}(M)\le c_{r}^{\prime \prime }n^{1/r}$
whp. They also conjectured that
$c_{r}^{\prime } n^{1/r}\le L_{P}(M)\le c_{r}^{\prime \prime }n^{1/r}$
whp. They also conjectured that
![]() $L_{P}(M)/n^{1/r}$
converges in probability, to a constant that only depends on r. However, this conjecture is already false for
$L_{P}(M)/n^{1/r}$
converges in probability, to a constant that only depends on r. However, this conjecture is already false for
![]() $r=2$
: Via analysis of a simple renewal process, Justicz, Scheinerman and Winkler [Reference Justicz, Scheinerman and Winkler41] proved that for a random matching M on
$r=2$
: Via analysis of a simple renewal process, Justicz, Scheinerman and Winkler [Reference Justicz, Scheinerman and Winkler41] proved that for a random matching M on
![]() $\{1,\dots ,2n\}$
, the size of the largest alignment-clique is
$\{1,\dots ,2n\}$
, the size of the largest alignment-clique is
![]() $(2/\sqrt {\pi }+o(1))\sqrt {n}$
whp, while the work of Baik and Rains described above implies that the largest crossing-clique and nesting-clique both have size
$(2/\sqrt {\pi }+o(1))\sqrt {n}$
whp, while the work of Baik and Rains described above implies that the largest crossing-clique and nesting-clique both have size
![]() $(\sqrt {2}+o(1))\sqrt {n}$
. (This was likely missed by Dudek, Grytczuk and Ruciński on account of the result in [Reference Justicz, Scheinerman and Winkler41] being stated in the language of random interval graphs, but the equivalence to random matchings is straightforward).
$(\sqrt {2}+o(1))\sqrt {n}$
. (This was likely missed by Dudek, Grytczuk and Ruciński on account of the result in [Reference Justicz, Scheinerman and Winkler41] being stated in the language of random interval graphs, but the equivalence to random matchings is straightforward).
Combining a subadditivity argument with Talagrand’s concentration inequality, we are able to show that for a collectable pattern P and a random matching M, the random variable
![]() $L_{P}(M)/n^{1/r}$
does converge to a limit. This limit may depend on P but only through the type of P, as follows.
$L_{P}(M)/n^{1/r}$
does converge to a limit. This limit may depend on P but only through the type of P, as follows.
Definition 1.9. Let P be an r-pattern with block partition
![]() $J_{1}\cup \dots \cup J_{\ell }$
. The type of P is the partition
$J_{1}\cup \dots \cup J_{\ell }$
. The type of P is the partition
![]() $|J_{1}|/2+\dots +|J_{\ell }|/2$
of r (in the number-theoretic sense).
$|J_{1}|/2+\dots +|J_{\ell }|/2$
of r (in the number-theoretic sense).
For example,
![]() $|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
and
$|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
and
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{{\mathrm {A}}{\mathrm {B}}}|$
both have type
$|{{\mathrm {A}}{\mathrm {B}}}|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{{\mathrm {A}}{\mathrm {B}}}|$
both have type
![]() $2+1+1$
.
$2+1+1$
.
Theorem 1.10. Fix an r-pattern P, and let M be a random r-matching of size n. Then we have
for some
![]() $b_{P}>0$
depending only on the type of P.
$b_{P}>0$
depending only on the type of P.
Actually determining the constants
![]() $b_{P}$
seems to be a hard problem (in particular, if P is an r-partite pattern then our proof shows that
$b_{P}$
seems to be a hard problem (in particular, if P is an r-partite pattern then our proof shows that
![]() $b_P$
can be expressed in terms of the constant
$b_P$
can be expressed in terms of the constant
![]() $c_r$
in the Bollobás–Winkler theorem described above). However, we are able to prove some bounds on the
$c_r$
in the Bollobás–Winkler theorem described above). However, we are able to prove some bounds on the
![]() $b_{P}$
in some special cases. In particular, we show that the conjecture of Dudek, Grytczuk and Ruciński is false for all
$b_{P}$
in some special cases. In particular, we show that the conjecture of Dudek, Grytczuk and Ruciński is false for all
![]() $r\ge 2$
. (Recall that the
$r\ge 2$
. (Recall that the
![]() $\Gamma $
function is the analytic continuation of the factorial function).
$\Gamma $
function is the analytic continuation of the factorial function).
Proposition 1.11. Let the constants
![]() $b_{P}$
be as in Theorem 1.10.
$b_{P}$
be as in Theorem 1.10.
-
1. If P has type r (i.e., if the block partition of P has a single block), then
 $b_{P}=1/\Gamma ((r+1)/r)$
.
$b_{P}=1/\Gamma ((r+1)/r)$
. -
2. If P has type
 $1+\dots +1$
(i.e., if P is r-partite), then
$1+\dots +1$
(i.e., if P is r-partite), then
 $b_{P}=c_r(r!)^{1/r}/r>1/\Gamma ((r+1)/r)$
, where
$b_{P}=c_r(r!)^{1/r}/r>1/\Gamma ((r+1)/r)$
, where
 $c_r$
is the constant from the Bollobás–Winkler theorem mentioned earlier in this section.
$c_r$
is the constant from the Bollobás–Winkler theorem mentioned earlier in this section.
We prove Theorem 1.10 and Proposition 1.11 in Section 6, after proving a certain necessary generalisation of the Bollobás–Winkler theorem in Section 5.
1.4 Enumeration
For an r-pattern P, let
![]() $N_{P}(n)$
denote the number of ordered r-matchings on the vertex set
$N_{P}(n)$
denote the number of ordered r-matchings on the vertex set
![]() $\{1,\dots ,rn\}$
which are P-free (i.e., no two edges form P). First, notice that if P is not r-partite then every r-partite matching is P-free. In particular,
$\{1,\dots ,rn\}$
which are P-free (i.e., no two edges form P). First, notice that if P is not r-partite then every r-partite matching is P-free. In particular,
![]() $N_{P}(n)$
is at least the number of r-partite matchings of size n, which is exactly
$N_{P}(n)$
is at least the number of r-partite matchings of size n, which is exactly
![]() $(n!)^{r-1}$
. In combination with equation (1.1) (and Stirling’s approximation), this is already enough to approximate
$(n!)^{r-1}$
. In combination with equation (1.1) (and Stirling’s approximation), this is already enough to approximate
![]() $N_{P}(n)$
up to exponential factors (for constant r).
$N_{P}(n)$
up to exponential factors (for constant r).
Proposition 1.12. Fix a constant
![]() $r\in \mathbb N$
. If P is not r-partite, then
$r\in \mathbb N$
. If P is not r-partite, then
(In this paper, subscripts on asymptotic notation indicate quantities that should be viewed as constants: The constant factor implicit in ‘
![]() $O_r(n)$
’ is allowed to depend on r).
$O_r(n)$
’ is allowed to depend on r).
The case where P is r-partite is more delicate (and the value of
![]() $N_{P}(n)$
is quite different), but we are able to obtain estimates of similar quality, as follows.
$N_{P}(n)$
is quite different), but we are able to obtain estimates of similar quality, as follows.
Theorem 1.13. Fix a constant
![]() $r\in \mathbb N$
. If P is r-partite, then
$r\in \mathbb N$
. If P is r-partite, then
Remark 1.14. In the case
![]() $r=2$
, there are only two possibilities for an r-partite pattern P: a crossing
$r=2$
, there are only two possibilities for an r-partite pattern P: a crossing
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
or a nesting
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
or a nesting
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
. As discussed in the introduction,
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
. As discussed in the introduction,
![]() $N_{P}(n)$
is exactly the same in both cases (in particular, there is a well known bijection between crossing-free and nesting-free matchings of a given size). However, this does not generalise straightforwardly to higher dimensions: A computer search shows that if P is the 3-uniform pattern represented by
$N_{P}(n)$
is exactly the same in both cases (in particular, there is a well known bijection between crossing-free and nesting-free matchings of a given size). However, this does not generalise straightforwardly to higher dimensions: A computer search shows that if P is the 3-uniform pattern represented by
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
, then
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
, then
![]() $N_{P}(4)=8626$
, whereas if P is the 3-uniform pattern represented by
$N_{P}(4)=8626$
, whereas if P is the 3-uniform pattern represented by
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|{{\mathrm {B}}{\mathrm {A}}}|$
we have
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|{{\mathrm {B}}{\mathrm {A}}}|$
we have
![]() $N_{P}(4)=8630$
.
$N_{P}(4)=8630$
.
The lower bound in Theorem 1.13 is a direct consequence of a result due to Brightwell [Reference Brightwell11] on linear extensions of r-dimensional posets, but the upper bound is new (it is obtained by a general connection to extremal ordered hypergraph theory).
We are also interested in enumerating ordered matchings by the size of their largest P-clique. We write
![]() $N_{P,m}(n)$
for the number of ordered r-matchings M on the vertex set
$N_{P,m}(n)$
for the number of ordered r-matchings M on the vertex set
![]() $\{1,\dots ,rn\}$
which satisfy
$\{1,\dots ,rn\}$
which satisfy
![]() $L_P(M)<m$
(i.e., they do not contain a P-clique of size m). Note that if P is not r-partite, then the same considerations as for Proposition 1.12 show that
$L_P(M)<m$
(i.e., they do not contain a P-clique of size m). Note that if P is not r-partite, then the same considerations as for Proposition 1.12 show that
![]() $N_{P,m}(n)=e^{O_r(n)} n^{(r-1)n}$
for all m (i.e., varying m can only affect
$N_{P,m}(n)=e^{O_r(n)} n^{(r-1)n}$
for all m (i.e., varying m can only affect
![]() $N_{P,m}(n)$
by a factor of
$N_{P,m}(n)$
by a factor of
![]() $e^{O_r(n)}$
). However, if P is r-partite, we get a significant dependence on m, as per the following generalisation of Theorem 1.13 (note that Theorem 1.13 corresponds to the case
$e^{O_r(n)}$
). However, if P is r-partite, we get a significant dependence on m, as per the following generalisation of Theorem 1.13 (note that Theorem 1.13 corresponds to the case
![]() $m=2$
).
$m=2$
).
Theorem 1.15. Fix a constant
![]() $r\in \mathbb N$
. If P is r-partite, then for any
$r\in \mathbb N$
. If P is r-partite, then for any
![]() $2 \le m\le n^{1/r}$
we have
$2 \le m\le n^{1/r}$
we have
We remark that the condition
![]() $m\le n^{1/r}$
in Theorem 1.15 is not just an artifact of the proof: Recall from Section 1.3 that for almost every size-n ordered matching M we have
$m\le n^{1/r}$
in Theorem 1.15 is not just an artifact of the proof: Recall from Section 1.3 that for almost every size-n ordered matching M we have
![]() $L_P=O(n^{1/r})$
.
$L_P=O(n^{1/r})$
.
We prove the upper bound in Theorem 1.15 via a general lemma (Theorem 7.1) which estimates
![]() $N_{P,m}(n)$
in terms of a certain extremal parameter (namely, the maximum number of edges in an ordered r-uniform hypergraph on
$N_{P,m}(n)$
in terms of a certain extremal parameter (namely, the maximum number of edges in an ordered r-uniform hypergraph on
![]() $\left\lceil {n/2} \right\rceil $
vertices with
$\left\lceil {n/2} \right\rceil $
vertices with
![]() $L_P(M)<m$
). This type of reduction goes back to Alon and Friedgut [Reference Alon and Friedgut2] (see also [Reference Fox28, Reference Klazar44]); in particular, we adapt a proof in a similar high-dimensional situation due to Cibulka and Kyncl [Reference Cibulka and Kynčl18]. We believe that the relevant extremal parameter is of independent interest, and we discuss it further in Section 1.5.
$L_P(M)<m$
). This type of reduction goes back to Alon and Friedgut [Reference Alon and Friedgut2] (see also [Reference Fox28, Reference Klazar44]); in particular, we adapt a proof in a similar high-dimensional situation due to Cibulka and Kyncl [Reference Cibulka and Kynčl18]. We believe that the relevant extremal parameter is of independent interest, and we discuss it further in Section 1.5.
For the lower bound in Theorem 1.15, we obtain a new estimate on the number of
![]() $(r-1)$
-tuples of length-n permutations which have no common increasing subsequence of length m (see Remark 7.6), by ‘reverse engineering’ the techniques in the upper bound. This lower bound, and the ideas in its proof, may be of independent interest (in particular, our approach is very different to the probabilistic approach of Brightwell [Reference Brightwell11] for the case
$(r-1)$
-tuples of length-n permutations which have no common increasing subsequence of length m (see Remark 7.6), by ‘reverse engineering’ the techniques in the upper bound. This lower bound, and the ideas in its proof, may be of independent interest (in particular, our approach is very different to the probabilistic approach of Brightwell [Reference Brightwell11] for the case
![]() $m=2$
).
$m=2$
).
We prove Theorem 1.15 (which implies Theorem 1.13) in Section 7.
1.5 Extremal results
As briefly mentioned in Section 1.4, in our study of enumerative questions for ordered matchings we encounter some extremal problems for ordered hypergraphs. We believe our extremal results to be of independent interest so we take a moment to discuss them here. First, we define ordered extremal numbers, which are variants of the classical extremal numbers (or Turán numbers) for unordered graphs.
Definition 1.16. Let
![]() $G,F$
be ordered r-uniform hypergraphs (ordered r-graphs, for short). We say G is F-free if it contains no subgraph isomorphic to F (where the isomorphism must preserve the order of the vertices). Let
$G,F$
be ordered r-uniform hypergraphs (ordered r-graphs, for short). We say G is F-free if it contains no subgraph isomorphic to F (where the isomorphism must preserve the order of the vertices). Let
![]() $\operatorname {\mathrm {ex}}_<(n,F)$
denote the maximum number of edges in an F-free n-vertex ordered r-graph.
$\operatorname {\mathrm {ex}}_<(n,F)$
denote the maximum number of edges in an F-free n-vertex ordered r-graph.
In the case
![]() $r=2$
(i.e., the case of graphs), ordered extremal numbers have been extensively studied (see the survey by Tardos [Reference Tardos64] and the references within). For general
$r=2$
(i.e., the case of graphs), ordered extremal numbers have been extensively studied (see the survey by Tardos [Reference Tardos64] and the references within). For general
![]() $r\ge 2$
, much less is known, though there is literature on similar problems for cyclically ordered hypergraphs, motivated by geometric considerations (in particular, due to applications to convex geometric hypergraphs; see, for example, [Reference Aronov, Dujmović, Morin, Ooms and da Silveira3, Reference Braß, Rote and Swanepoel8, Reference Braß9, Reference Braß, Károlyi and Valtr10, Reference Capoyleas and Pach16, Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte30, Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte31, Reference Füredi, Mubayi, O’Neill and Verstraëte33, Reference Gowers and Long35, Reference Pach and Pinchasi53]), and much of this work has implications for ordered extremal numbers
$r\ge 2$
, much less is known, though there is literature on similar problems for cyclically ordered hypergraphs, motivated by geometric considerations (in particular, due to applications to convex geometric hypergraphs; see, for example, [Reference Aronov, Dujmović, Morin, Ooms and da Silveira3, Reference Braß, Rote and Swanepoel8, Reference Braß9, Reference Braß, Károlyi and Valtr10, Reference Capoyleas and Pach16, Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte30, Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte31, Reference Füredi, Mubayi, O’Neill and Verstraëte33, Reference Gowers and Long35, Reference Pach and Pinchasi53]), and much of this work has implications for ordered extremal numbers
![]() $\operatorname {\mathrm {ex}}_<(n,F)$
.
$\operatorname {\mathrm {ex}}_<(n,F)$
.
Our first contribution in this direction is that we are able to nail down the exact value
![]() $\operatorname {\mathrm {ex}}_<(n, P)$
for any r-partite r-pattern P (this extremal parameter is relevant for Theorem 1.13). For convenience, we define
$\operatorname {\mathrm {ex}}_<(n, P)$
for any r-partite r-pattern P (this extremal parameter is relevant for Theorem 1.13). For convenience, we define
![]() $(x)_+ := \max (x,0)$
.
$(x)_+ := \max (x,0)$
.
Theorem 1.17. Let
![]() $r, n\ge 1$
and P be any r-partite r-pattern. Then,
$r, n\ge 1$
and P be any r-partite r-pattern. Then,
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n, P) = \binom{n}{r}-\binom{(n-r)_+}{r}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n, P) = \binom{n}{r}-\binom{(n-r)_+}{r}.\end{align*}$$
We remark that in the case where P is the r-uniform ‘generalised crossing’ pattern represented by
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\cdots |{{\mathrm {A}}{\mathrm {B}}}|$
, the result of Theorem 1.17 was already known, thanks to recent work of Füredi, Jiang, Kostochka, Mubayi and Verstraëte [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte31]. (It was also known in the case where P is a 2-uniform nesting, as we will discuss after the next theorem).
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\cdots |{{\mathrm {A}}{\mathrm {B}}}|$
, the result of Theorem 1.17 was already known, thanks to recent work of Füredi, Jiang, Kostochka, Mubayi and Verstraëte [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte31]. (It was also known in the case where P is a 2-uniform nesting, as we will discuss after the next theorem).
For an r-pattern P and a positive integer m, we use
![]() ${P}^{(m)}$
to denote the P-clique of size m on the vertex set
${P}^{(m)}$
to denote the P-clique of size m on the vertex set
![]() $[rm]$
(so
$[rm]$
(so
![]() ${P}^{(2)}=P$
). For
${P}^{(2)}=P$
). For
![]() $m\ge 3$
, we were not quite able to pin down the values of the ordered extremal numbers
$m\ge 3$
, we were not quite able to pin down the values of the ordered extremal numbers
![]() $\operatorname {\mathrm {ex}}_<(n, {P}^{(m)})$
, but we are able to obtain some quite strong bounds for all r-partite r-patterns P (these bounds are an ingredient in our proof of Theorem 1.15).
$\operatorname {\mathrm {ex}}_<(n, {P}^{(m)})$
, but we are able to obtain some quite strong bounds for all r-partite r-patterns P (these bounds are an ingredient in our proof of Theorem 1.15).
Theorem 1.18. Let
![]() $r,n,m\ge 1$
, and let P be an r-partite r-pattern.
$r,n,m\ge 1$
, and let P be an r-partite r-pattern.
-
1. In general, we have
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) \ge \binom{n}{r}-\binom{(n-r(m-1))_+}{r}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) \ge \binom{n}{r}-\binom{(n-r(m-1))_+}{r}. \end{align*}$$
-
2. If n is sufficiently large (in terms of r), then
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)})\le O\left(r^2(m-1)\binom n {r-1}\right). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)})\le O\left(r^2(m-1)\binom n {r-1}\right). \end{align*}$$
-
3. If P is the ‘alternating’ r-pattern represented by
 $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|\cdots |$
, then
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|\cdots |$
, then  $$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) = \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) = \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*}$$
Remark 1.19. If we view r as a constant and assume
![]() $m=o_r(n)$
, then one can check that
$m=o_r(n)$
, then one can check that
 $$\begin{align*}\binom{n}{r}-\binom{(n-r(m-1))_+}{r}=(1+o(1))r(m-1)\binom{n}{r-1}.\end{align*}$$
$$\begin{align*}\binom{n}{r}-\binom{(n-r(m-1))_+}{r}=(1+o(1))r(m-1)\binom{n}{r-1}.\end{align*}$$
So, our upper and lower bounds in (1) and (2) differ by a factor of
![]() $O(r)$
.
$O(r)$
.
The
![]() $r=2$
case of Theorem 1.18(3) (i.e., an exact result in the case where P is the 2-unifom nesting
$r=2$
case of Theorem 1.18(3) (i.e., an exact result in the case where P is the 2-unifom nesting
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
) can be derived from the known results on graphs with bounded queue number due to Pemmaraju [Reference Pemmaraju54] and Dujmović and Wood [Reference Dujmović and Wood24]. We also remark that Capoyleas and Pach [Reference Capoyleas and Pach16] previously studied the case where
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
) can be derived from the known results on graphs with bounded queue number due to Pemmaraju [Reference Pemmaraju54] and Dujmović and Wood [Reference Dujmović and Wood24]. We also remark that Capoyleas and Pach [Reference Capoyleas and Pach16] previously studied the case where
![]() $P=|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
is a 2-uniform crossing; in this case, they obtained the exact result
$P=|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
is a 2-uniform crossing; in this case, they obtained the exact result
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n,{P}^{(m)})=\binom{n}{2}-\binom{(n-2(m-1))_+}{2}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n,{P}^{(m)})=\binom{n}{2}-\binom{(n-2(m-1))_+}{2}.\end{align*}$$
For general
![]() $r\ge 2$
, Füredi, Jiang, Kostochka, Mubayi and Verstraëte [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte31] studied the case where P is the r-uniform ‘generalised crossing’ pattern represented by
$r\ge 2$
, Füredi, Jiang, Kostochka, Mubayi and Verstraëte [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte31] studied the case where P is the r-uniform ‘generalised crossing’ pattern represented by
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\cdots |{{\mathrm {A}}{\mathrm {B}}}|$
. We have already mentioned their exact result in the case
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\cdots |{{\mathrm {A}}{\mathrm {B}}}|$
. We have already mentioned their exact result in the case
![]() $m=2$
; for all m, they proved
$m=2$
; for all m, they proved
 $$ \begin{align} (1-o_{r,m}(1))r(m-1)\binom{n}{r-1}\le \operatorname{\mathrm{ex}}_<(n,{P}^{(m)}) \le 2(r-1)(m-1)\binom{n}{r-1}. \end{align} $$
$$ \begin{align} (1-o_{r,m}(1))r(m-1)\binom{n}{r-1}\le \operatorname{\mathrm{ex}}_<(n,{P}^{(m)}) \le 2(r-1)(m-1)\binom{n}{r-1}. \end{align} $$
(Recall that subscripts on asymptotic notation indicate quantities that should be viewed as constants, so the ‘
![]() $o_{r,m}(1)$
’ term goes to zero as
$o_{r,m}(1)$
’ term goes to zero as
![]() $n\to \infty $
, holding
$n\to \infty $
, holding
![]() $r,m$
fixed). Their lower bound construction is the same as our construction for (1) (in the case where P is a generalised crossing), but they only analysed its number of edges asymptotically. Their upper bound for this specific case is stronger than our general bound in (2).
$r,m$
fixed). Their lower bound construction is the same as our construction for (1) (in the case where P is a generalised crossing), but they only analysed its number of edges asymptotically. Their upper bound for this specific case is stronger than our general bound in (2).
A variety of techniques are involved in the proof of Theorem 1.17 and the various parts of Theorem 1.18. In particular, for our proof of Theorem 1.18(2) we refine a partitioning lemma for ordered hypergraphs due to Füredi, Jiang, Kostochka, Mubayi and Verstraëte [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte32]. We present this refinement and discuss it further in Section 8.
1.6 Further directions
There are a great number of compelling further directions for study.
1.6.1 Ramsey-type questions
The most obvious open question in this direction is to close the gap between the lower and upper bound in Theorem 1.7. It is tempting to guess that the upper bound is sharp and that
![]() $L_{r}(n)$
has order of magnitude
$L_{r}(n)$
has order of magnitude
![]() $n^{1/(2^r-1)}$
for any constant r (this is true for
$n^{1/(2^r-1)}$
for any constant r (this is true for
![]() $r\in \{2,3,4\}$
). It is even possible that such a bound can be proved via our ‘poset partititioning’ method, with judicious choice of the relevant partitions (perhaps for small r, appropriate partitions can be found via computer search). However, our investigations do not suggest any general structural reason why a bound of this form should hold.
$r\in \{2,3,4\}$
). It is even possible that such a bound can be proved via our ‘poset partititioning’ method, with judicious choice of the relevant partitions (perhaps for small r, appropriate partitions can be found via computer search). However, our investigations do not suggest any general structural reason why a bound of this form should hold.
Even in the cases
![]() $r\in \{2,3,4\}$
where we know the order of magnitude of
$r\in \{2,3,4\}$
where we know the order of magnitude of
![]() $L_{r}(n)$
, it would be interesting to obtain the exact value (or at least an asymptotic estimate). Also, it is possible to consider ‘off-diagonal’ versions of the problem, where one treats different patterns differently. For example, fixing a positive integer
$L_{r}(n)$
, it would be interesting to obtain the exact value (or at least an asymptotic estimate). Also, it is possible to consider ‘off-diagonal’ versions of the problem, where one treats different patterns differently. For example, fixing a positive integer
![]() $k_P$
for each r-pattern P, what is the maximum possible size of an r-matching which has no P-clique of size
$k_P$
for each r-pattern P, what is the maximum possible size of an r-matching which has no P-clique of size
![]() $k_P$
for any P? Actually, this general setting was considered in [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22], and optimal bounds were obtained in the case
$k_P$
for any P? Actually, this general setting was considered in [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22], and optimal bounds were obtained in the case
![]() $r=2$
. Our methods seem to be suitable for attacking the larger-r case as well, but the relevant casework seems likely to be even more fiddly than for Theorem 1.8 (one would need to completely characterise how all the different subsets of patterns can interact with each other).
$r=2$
. Our methods seem to be suitable for attacking the larger-r case as well, but the relevant casework seems likely to be even more fiddly than for Theorem 1.8 (one would need to completely characterise how all the different subsets of patterns can interact with each other).
1.6.2 Random ordered matchings
The obvious open question in this direction is to determine the values of the constants
![]() $b_P$
in Theorem 1.10. As we have discussed, this is a difficult problem in the case where P is r-partite (in which case it amounts to determination of the Bollobás–Winkler constant
$b_P$
in Theorem 1.10. As we have discussed, this is a difficult problem in the case where P is r-partite (in which case it amounts to determination of the Bollobás–Winkler constant
![]() $c_r$
), but it may be tractable for certain special P.
$c_r$
), but it may be tractable for certain special P.
For example, in the case where P is a 3-pattern which has type
![]() $2+1$
, the problem of determining
$2+1$
, the problem of determining
![]() $b_{2+1}:=b_P$
seems like it might be of ‘intermediate difficulty’ between the Ulam–Hammersley problem (of determining
$b_{2+1}:=b_P$
seems like it might be of ‘intermediate difficulty’ between the Ulam–Hammersley problem (of determining
![]() $c_2=2$
) and the problem of determining the Bollobás–Winkler constant
$c_2=2$
) and the problem of determining the Bollobás–Winkler constant
![]() $c_3$
. For the Ulam–Hammersley problem, there is a well-known interacting particle process (Hammersley’s interacting particle process) which captures the limiting behaviour of the longest increasing subsequence of a random permutation. Using this process, Aldous and Diaconis [Reference Aldous and Diaconis1] managed to give a simple (nonrigorous) ‘hydrodynamic heuristic’ explaining why
$c_3$
. For the Ulam–Hammersley problem, there is a well-known interacting particle process (Hammersley’s interacting particle process) which captures the limiting behaviour of the longest increasing subsequence of a random permutation. Using this process, Aldous and Diaconis [Reference Aldous and Diaconis1] managed to give a simple (nonrigorous) ‘hydrodynamic heuristic’ explaining why
![]() $c_2=2$
, and developed this into a (rigorous) proof of the fact that
$c_2=2$
, and developed this into a (rigorous) proof of the fact that
![]() $c_2=2$
. It seems that one can design a related particle process which is suitable for studying
$c_2=2$
. It seems that one can design a related particle process which is suitable for studying
![]() $b_{2+1}$
, and one can consider a similar ‘hydrodynamic heuristic’ for the value of
$b_{2+1}$
, and one can consider a similar ‘hydrodynamic heuristic’ for the value of
![]() $b_{2+1}$
, but the process lacks certain symmetries that Aldous and Diaconis used in their rigorous analysis. (See also the surface growth model due to Seppäläinen [Reference Seppäläinen59], which connects to the general Bollobás–Winkler constants
$b_{2+1}$
, but the process lacks certain symmetries that Aldous and Diaconis used in their rigorous analysis. (See also the surface growth model due to Seppäläinen [Reference Seppäläinen59], which connects to the general Bollobás–Winkler constants
![]() $c_r$
, but for which it seems to be difficult even to obtain a ‘hydrodynamic heuristic’).
$c_r$
, but for which it seems to be difficult even to obtain a ‘hydrodynamic heuristic’).
1.6.3 Enumeration
The results in Section 1.4 have exponential error terms, and of course it would be interesting to sharpen these. However, there may be some limitations to what is possible to accomplish without determining the limits
![]() $b_P$
in Theorem 1.10: In the regime where m is of order
$b_P$
in Theorem 1.10: In the regime where m is of order
![]() $n^{1/r}$
, studying
$n^{1/r}$
, studying
![]() $N_{P,m}(n)$
amounts to studying the large deviations of
$N_{P,m}(n)$
amounts to studying the large deviations of
![]() $L_P(M)$
in a random r-matching M.
$L_P(M)$
in a random r-matching M.
Even if exponential error terms cannot be eliminated, it might be interesting to determine their dependence on r (recall that in Theorems 1.13 and 1.15 we treat r as a constant).
1.6.4 Extremal problems
Given the discussion in Section 1.5, it is natural to conjecture that the lower bound in Theorem 1.18(1) is always sharp, as follows.
Conjecture 1.20. Let
![]() $r,n,m \ge 1$
and P be an r-partite r-pattern. Then,
$r,n,m \ge 1$
and P be an r-partite r-pattern. Then,
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) = \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) = \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*}$$
In particular, given Theorem 1.18(3), an indirect route to prove Conjecture 1.20 would be to prove that
![]() $\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})$
is the same for every r-partite r-pattern P. In the case
$\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})$
is the same for every r-partite r-pattern P. In the case
![]() $r=2$
, there is a bijective proof of (a vast generalisation of) this fact, due to Jonsson and Welker [Reference Jonsson and Welker40] (see also [Reference de Mier20, Corollary 2.5]). However, the considerations in Remark 1.14 suggest some difficulties in generalising such bijective proofs to higher uniformities.
$r=2$
, there is a bijective proof of (a vast generalisation of) this fact, due to Jonsson and Welker [Reference Jonsson and Welker40] (see also [Reference de Mier20, Corollary 2.5]). However, the considerations in Remark 1.14 suggest some difficulties in generalising such bijective proofs to higher uniformities.
Also, although there is no obvious connection to enumeration, it may still be of interest to determine
![]() $\operatorname {\mathrm {ex}}_<(n, {P}^{(m)})$
in the case where P is not r-partite. It is easy to show that
$\operatorname {\mathrm {ex}}_<(n, {P}^{(m)})$
in the case where P is not r-partite. It is easy to show that
![]() $\operatorname {\mathrm {ex}}_<(n, {P}^{(m)})\ge (n/r)^r$
when n is a multiple of r, but this does not seem to be best possible.
$\operatorname {\mathrm {ex}}_<(n, {P}^{(m)})\ge (n/r)^r$
when n is a multiple of r, but this does not seem to be best possible.
1.7 Note added in proof:
Since the original version of this paper, Sauermann and Zakharov [Reference Sauermann and Zakharov56] generalised Theorem 1.8 to all r, proving that
![]() $L_r(n)$
has order of magnitude
$L_r(n)$
has order of magnitude
![]() $n^{1/(2^r-1)}$
.
$n^{1/(2^r-1)}$
.
1.8 Notation
We use standard asymptotic notation throughout, as follows. For functions
![]() $f=f(n)$
and
$f=f(n)$
and
![]() $g=g(n)$
, we write
$g=g(n)$
, we write
![]() $f=O(g)$
to mean that there is a constant C such that
$f=O(g)$
to mean that there is a constant C such that
![]() $|f(n)|\le C|g(n)|$
for sufficiently large n. Similarly, we write
$|f(n)|\le C|g(n)|$
for sufficiently large n. Similarly, we write
![]() $f=\Omega (g)$
to mean that there is a constant
$f=\Omega (g)$
to mean that there is a constant
![]() $c>0$
such that
$c>0$
such that
![]() $f(n)\ge c|g(n)|$
for sufficiently large n. We write
$f(n)\ge c|g(n)|$
for sufficiently large n. We write
![]() $f=\Theta (g)$
to mean that
$f=\Theta (g)$
to mean that
![]() $f=O(g)$
and
$f=O(g)$
and
![]() $f=\Omega (g)$
, and we write
$f=\Omega (g)$
, and we write
![]() $f=o(g)$
or
$f=o(g)$
or
![]() $g=\omega (f)$
to mean that
$g=\omega (f)$
to mean that
![]() $f(n)/g(n)\to 0$
as
$f(n)/g(n)\to 0$
as
![]() $n\to \infty $
. Subscripts on asymptotic notation indicate quantities that should be treated as constants.
$n\to \infty $
. Subscripts on asymptotic notation indicate quantities that should be treated as constants.
For
![]() $n, r \ge 1$
, we use
$n, r \ge 1$
, we use
![]() $K_n^{(r)}$
to indicate the ordered r-uniform clique on the vertex set
$K_n^{(r)}$
to indicate the ordered r-uniform clique on the vertex set
![]() $\{1,\dots ,n\}$
. For an ordered hypergraph H, we write
$\{1,\dots ,n\}$
. For an ordered hypergraph H, we write
![]() $V(H)$
for its vertex set,
$V(H)$
for its vertex set,
![]() $E(H)$
for its edge set and
$E(H)$
for its edge set and
![]() $e(H)=|E(H)|$
for its number of edges. For
$e(H)=|E(H)|$
for its number of edges. For
![]() $e\in E(H)$
, we write
$e\in E(H)$
, we write
![]() $e[1],\dots ,e[r]$
for the vertices of e (ordered according to the vertex ordering of H). When we say that an ordered hypergraph
$e[1],\dots ,e[r]$
for the vertices of e (ordered according to the vertex ordering of H). When we say that an ordered hypergraph
![]() $H'$
is a subgraph of another ordered hypergraph H, we mean that the order of the vertices is maintained. (We use the notation
$H'$
is a subgraph of another ordered hypergraph H, we mean that the order of the vertices is maintained. (We use the notation
![]() $H' \subseteq H$
).
$H' \subseteq H$
).
We also remind the reader that
![]() $(x)_+$
is defined to be
$(x)_+$
is defined to be
![]() $\max (x,0)$
.
$\max (x,0)$
.
2 Preliminaries
We first recall the following corollary of Mirsky’s theorem [Reference Mirsky52], for our proof of Theorem 1.7.
Theorem 2.1. Suppose P is a partially ordered set (poset) with n elements, that contains no chain of length x for some
![]() $x \in \mathbb {R}_+$
. Then, P contains an antichain of size at least
$x \in \mathbb {R}_+$
. Then, P contains an antichain of size at least
![]() $n/x$
.
$n/x$
.
At several points in the paper (related to the directions introduced in Section 1.5), we will need the following enumerative identity.
Lemma 2.2. Let
![]() $n \ge r \ge 1$
and
$n \ge r \ge 1$
and
![]() $\delta _1,\dots ,\delta _{r-1} \in \mathbb {Z}_{\ge 0}$
. Then, the number of r-tuples
$\delta _1,\dots ,\delta _{r-1} \in \mathbb {Z}_{\ge 0}$
. Then, the number of r-tuples
![]() $(a_1,\dots ,a_r)\in \{1,\dots ,n\}^r$
satisfying
$(a_1,\dots ,a_r)\in \{1,\dots ,n\}^r$
satisfying
![]() $a_{i+1}-a_i>\delta _i$
for all
$a_{i+1}-a_i>\delta _i$
for all
![]() $1 \le i \le r-1$
is exactly
$1 \le i \le r-1$
is exactly
 $$\begin{align*}\binom{(n-\sum_{k=1}^{r-1}\delta_k)_+}{r}.\end{align*}$$
$$\begin{align*}\binom{(n-\sum_{k=1}^{r-1}\delta_k)_+}{r}.\end{align*}$$
Proof. We may assume
![]() $n\ge \sum _{k=1}^{r-1}\delta _k$
, or else the quantity under consideration is zero. For an r-tuple
$n\ge \sum _{k=1}^{r-1}\delta _k$
, or else the quantity under consideration is zero. For an r-tuple
![]() $(a_1,\dots ,a_r)$
as in the lemma statement, let
$(a_1,\dots ,a_r)$
as in the lemma statement, let
![]() $f(a_1,\dots ,a_r)=(b_1,\dots ,b_r)$
, where
$f(a_1,\dots ,a_r)=(b_1,\dots ,b_r)$
, where
![]() $b_1=a_1$
and
$b_1=a_1$
and
![]() $b_i=a_i-\delta _{i-1}$
for
$b_i=a_i-\delta _{i-1}$
for
![]() $2\leq i \leq r$
. The desired result follows by noting that f is a bijection between the set of tuples under consideration and the set of unordered r-tuples in
$2\leq i \leq r$
. The desired result follows by noting that f is a bijection between the set of tuples under consideration and the set of unordered r-tuples in
![]() $\{1,2,\dots ,n-\sum _{k=1}^{r-1}\delta _k\}$
.
$\{1,2,\dots ,n-\sum _{k=1}^{r-1}\delta _k\}$
.
For Theorem 1.10, we need a number of probabilistic tools. First, we need a bounded-differences concentration inequality for permutations.
Theorem 2.3. Let
![]() $f:\mathcal S_n\to \mathbb R$
be a function which has ‘bounded differences’ in the sense that for any
$f:\mathcal S_n\to \mathbb R$
be a function which has ‘bounded differences’ in the sense that for any
![]() $\sigma \in \mathcal S_n$
and any transposition
$\sigma \in \mathcal S_n$
and any transposition
![]() $\tau \in \mathcal S_n$
, we have
$\tau \in \mathcal S_n$
, we have
![]() $|f(\tau \circ \sigma )-f(\sigma )|\le c$
. Then, if
$|f(\tau \circ \sigma )-f(\sigma )|\le c$
. Then, if
![]() $\sigma \in \mathcal S_n$
be a uniformly random permutation of length n, we have
$\sigma \in \mathcal S_n$
be a uniformly random permutation of length n, we have
 $$\begin{align*}\Pr[|f(\sigma)-\mathbb Ef(\sigma)|\ge t]\le \exp\left(-\frac{2t^2}{c^2 n}\right).\end{align*}$$
$$\begin{align*}\Pr[|f(\sigma)-\mathbb Ef(\sigma)|\ge t]\le \exp\left(-\frac{2t^2}{c^2 n}\right).\end{align*}$$
This inequality seems to have first been proved by McDiarmid in the case where
![]() $c=1$
(see [Reference McDiarmid51, p. 18], though there is a typo in this book; in the inequality we are citing, the exponent should really be
$c=1$
(see [Reference McDiarmid51, p. 18], though there is a typo in this book; in the inequality we are citing, the exponent should really be
![]() $2t^2/n$
, not
$2t^2/n$
, not
![]() $2t^2/n^2$
).
$2t^2/n^2$
).
Remark 2.4. Note that one can obtain a random ordered r-matching on the vertex set
![]() ${1,\dots ,rn}$
via a random permutation
${1,\dots ,rn}$
via a random permutation
![]() $\sigma \in \mathcal S_{rn}$
: Simply take the matching whose edges are
$\sigma \in \mathcal S_{rn}$
: Simply take the matching whose edges are
We also need a version of Talagrand’s concentration inequality (see, for example, [Reference Janson, Łuczak and Rucinski38, Theorem 2.29 and Equation (2.43)]
Theorem 2.5. Consider a function
![]() $X=f(Z_{1},\dots ,Z_{n})$
of independent random objects
$X=f(Z_{1},\dots ,Z_{n})$
of independent random objects
![]() $Z_{1}\in \Lambda _{1},\dots ,Z_{n}\in \Lambda _{n}$
. Suppose that the following conditions are satisfied.
$Z_{1}\in \Lambda _{1},\dots ,Z_{n}\in \Lambda _{n}$
. Suppose that the following conditions are satisfied.
-
○ If
 $z,z'\in \prod _{i=1}^{n}\Lambda _{i}$
differ only in the ith coordinate, then
$z,z'\in \prod _{i=1}^{n}\Lambda _{i}$
differ only in the ith coordinate, then
 $|f(z)-f(z')|\le 1$
.
$|f(z)-f(z')|\le 1$
. -
○ For any
 $z\in \prod _{i=1}^{n}\Lambda _{i}$
, there is a subset of indices
$z\in \prod _{i=1}^{n}\Lambda _{i}$
, there is a subset of indices
 $J\subseteq \{1,\dots ,n\}$
with
$J\subseteq \{1,\dots ,n\}$
with
 $|J|\le f(z)$
such that for any
$|J|\le f(z)$
such that for any
 $y\in \prod _{i=1}^{n}\Lambda _{i}$
which agrees with z on the coordinates indexed by J, we have
$y\in \prod _{i=1}^{n}\Lambda _{i}$
which agrees with z on the coordinates indexed by J, we have
 $f(y)\ge f(z)$
.
$f(y)\ge f(z)$
.
Then, for some universal constant
![]() $\gamma>0$
, we have
$\gamma>0$
, we have
 $$\begin{align*}\Pr[|X-{\mathbb E} X|\ge t]\le4\exp\left(-\frac{\gamma t^{2}}{{\mathbb E} X+t}\right) \end{align*}$$
$$\begin{align*}\Pr[|X-{\mathbb E} X|\ge t]\le4\exp\left(-\frac{\gamma t^{2}}{{\mathbb E} X+t}\right) \end{align*}$$
for any
![]() $t\ge 0$
.
$t\ge 0$
.
We will also need a version of Kingman’s subadditive ergodic theorem (see, for example, [Reference Romik55, Theorem A.3]). We have ‘flipped’ the conditions to make it apply under a superadditivity condition rather than a subadditivity condition.
Theorem 2.6. Let
![]() $(X_{m,n})_{0\le m<n}$
be a family of nonnegative random variables, defined on some common probability space such that the following conditions are satisfied.
$(X_{m,n})_{0\le m<n}$
be a family of nonnegative random variables, defined on some common probability space such that the following conditions are satisfied.
-
○
 $X_{0,n}\ge X_{0,m}+X_{m,n}$
for all
$X_{0,n}\ge X_{0,m}+X_{m,n}$
for all
 $m<n$
.
$m<n$
. -
○ For any
 $k\ge 1$
,
$k\ge 1$
,
 $(X_{nk,(n+1)k})_{n=0}^{\infty }$
is a sequence of i.i.d. random variables.
$(X_{nk,(n+1)k})_{n=0}^{\infty }$
is a sequence of i.i.d. random variables. -
○ For any
 $m\ge 1$
, we have
$m\ge 1$
, we have
 $(X_{0,k})_{k=0}^{\infty }\overset {d}{=}(X_{m,m+k})_{k=0}^{\infty }$
.
$(X_{0,k})_{k=0}^{\infty }\overset {d}{=}(X_{m,m+k})_{k=0}^{\infty }$
. -
○ There exists a constant
 $M>0$
such that
$M>0$
such that
 ${\mathbb E} X_{0,n}\le Mn$
for all n.
${\mathbb E} X_{0,n}\le Mn$
for all n.
Then,
![]() ${\mathbb E} X_{0,n}/n$
converges to a limit
${\mathbb E} X_{0,n}/n$
converges to a limit
![]() $\gamma $
as
$\gamma $
as
![]() $n\to \infty $
. Also,
$n\to \infty $
. Also,
![]() $X_{0,n}/n$
converges almost surely (therefore in probability) to
$X_{0,n}/n$
converges almost surely (therefore in probability) to
![]() $\gamma $
.
$\gamma $
.
3 Lower bounds on Ramsey parameters
In this section, we will outline our general framework for proving lower bounds on
![]() $L_{r}(n)$
and show how to use it to prove the lower bounds in Theorem 1.7 and in the
$L_{r}(n)$
and show how to use it to prove the lower bounds in Theorem 1.7 and in the
![]() $r=3$
case of Theorem 1.8. The
$r=3$
case of Theorem 1.8. The
![]() $r=4$
case of Theorem 1.8 follows a similar strategy but has some very complicated casework, the appendix of the arXiv version of this paper.
$r=4$
case of Theorem 1.8 follows a similar strategy but has some very complicated casework, the appendix of the arXiv version of this paper.
The starting point is that patterns sometimes give rise to posets. For an r-matching M and an r-pattern P, we define the relation
![]() $\preceq _{P}$
on the edges of M by taking
$\preceq _{P}$
on the edges of M by taking
![]() $e\preceq f$
if
$e\preceq f$
if
![]() $e[1]<f[1]$
and
$e[1]<f[1]$
and
![]() $e,f$
form pattern P (or if
$e,f$
form pattern P (or if
![]() $e=f$
). It is sometimes (but not always!) the case that
$e=f$
). It is sometimes (but not always!) the case that
![]() $\preceq _{P}$
is a partial order. The interesting property here is transitivity: We need to know whether
$\preceq _{P}$
is a partial order. The interesting property here is transitivity: We need to know whether
![]() $e\preceq _{P}f$
and
$e\preceq _{P}f$
and
![]() $f\preceq _{P}g$
implies
$f\preceq _{P}g$
implies
![]() $f\preceq _{P}g$
. For example, in the case
$f\preceq _{P}g$
. For example, in the case
![]() $r=2$
, the only r-patterns are alignments, crossings and nestings. It is easy to see that the alignment and nesting pattern always give rise to a poset, but the crossing pattern may not (it is possible to have edges
$r=2$
, the only r-patterns are alignments, crossings and nestings. It is easy to see that the alignment and nesting pattern always give rise to a poset, but the crossing pattern may not (it is possible to have edges
![]() $e,f,g$
with
$e,f,g$
with
![]() $e[1]<f[1]<g[1]$
such that e and f form a crossing, and f and g form a crossing, but e and g form an alignment). However, if we restrict ourselves to matchings that are alignment-free, then the crossing pattern does give rise to a poset.
$e[1]<f[1]<g[1]$
such that e and f form a crossing, and f and g form a crossing, but e and g form an alignment). However, if we restrict ourselves to matchings that are alignment-free, then the crossing pattern does give rise to a poset.
Now, if
![]() $\preceq _{P}$
is a poset, then Mirsky’s theorem (Theorem 2.1) implies that there is a long chain (which corresponds to a large P-clique) or a large antichain (which corresponds to a P-free submatching). One can iterate this, in several different ways, to give a simple proof of the optimal bound
$\preceq _{P}$
is a poset, then Mirsky’s theorem (Theorem 2.1) implies that there is a long chain (which corresponds to a large P-clique) or a large antichain (which corresponds to a P-free submatching). One can iterate this, in several different ways, to give a simple proof of the optimal bound
![]() $L_{2}(n)\ge n^{1/3}$
(previously proved with a similar method in [Reference Huynh, Joos and Wollan37]). For example, in a size-n matching M, first, we look for an alignment-clique of size
$L_{2}(n)\ge n^{1/3}$
(previously proved with a similar method in [Reference Huynh, Joos and Wollan37]). For example, in a size-n matching M, first, we look for an alignment-clique of size
![]() $n^{1/3}$
or an alignment-free submatching
$n^{1/3}$
or an alignment-free submatching
![]() $M'$
of size
$M'$
of size
![]() $n^{2/3}$
, and in the latter case, inside
$n^{2/3}$
, and in the latter case, inside
![]() $M'$
we look for a nesting-clique of size
$M'$
we look for a nesting-clique of size
![]() $n^{1/3}$
or a nesting-free submatching (therefore a crossing-clique) of size
$n^{1/3}$
or a nesting-free submatching (therefore a crossing-clique) of size
![]() $n^{1/3}$
.
$n^{1/3}$
.
For general r, if one is careful about the order of operations, one can show
![]() $L_{r}(n) = \Omega _r(n^{1/3^{r-1}})$
(as in [Reference Dudek, Grytczuk and Ruciński22, Theorem 1.3]) by generalising the above proof, applying Mirsky’s theorem once for each of the
$L_{r}(n) = \Omega _r(n^{1/3^{r-1}})$
(as in [Reference Dudek, Grytczuk and Ruciński22, Theorem 1.3]) by generalising the above proof, applying Mirsky’s theorem once for each of the
![]() $3^{r-1}$
collectable r-patterns (one also needs some separate arguments to handle the non-collectable patterns).
$3^{r-1}$
collectable r-patterns (one also needs some separate arguments to handle the non-collectable patterns).
The authors of [Reference Dudek, Grytczuk and Ruciński22] did not manage to improve on the above bound, and they may have been tempted to conjecture that the ‘
![]() $1/3^{r-1}$
’ exponent is best possible. However, they found some clues that the situation is more intricate than it may first appear. For example, they observed that some patterns ‘cannot interact with each other’: If P and
$1/3^{r-1}$
’ exponent is best possible. However, they found some clues that the situation is more intricate than it may first appear. For example, they observed that some patterns ‘cannot interact with each other’: If P and
![]() $P'$
are the collectable r-patterns represented by
$P'$
are the collectable r-patterns represented by
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|$
and
$|{{\mathrm {A}}{\mathrm {B}}}|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|$
and
![]() $|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{{\mathrm {A}}{\mathrm {B}}}|$
, and we have a matching M in which every pair of edges forms pattern P or
$|{\mathrm {A}}{\mathrm {A}}{\mathrm {B}}{\mathrm {B}}|{{\mathrm {A}}{\mathrm {B}}}|$
, and we have a matching M in which every pair of edges forms pattern P or
![]() $P'$
, then in fact M must be a P-clique or a
$P'$
, then in fact M must be a P-clique or a
![]() $P'$
-clique.
$P'$
-clique.
To leverage this type of observation, instead of using Mirsky’s theorem to process patterns one-by-one, we partition the set of all r-patterns into subsets and process patterns one subset at a time (defining a poset in terms of the entire subset, instead of a single pattern). We need to choose the subsets in our partition judiciously such that the patterns in each subset ‘cannot interact much with each other’, and such that each subset gives rise to a poset (after eliminating the patterns from previous subsets).
Both these properties are encapsulated in the following lemma, which is the key ingredient for the lower bound in Theorem 1.7.
Definition 3.1. For a set of r-patterns
![]() ${\mathcal P}$
, say that a matching M is
${\mathcal P}$
, say that a matching M is
![]() ${\mathcal P}$
-free if it is P-free for all
${\mathcal P}$
-free if it is P-free for all
![]() $P\in {\mathcal P}$
. Say that M is a
$P\in {\mathcal P}$
. Say that M is a
![]() ${\mathcal P}$
-clique if every pair of edges forms a pattern in
${\mathcal P}$
-clique if every pair of edges forms a pattern in
![]() ${\mathcal P}$
.
${\mathcal P}$
.
Also, for a matching M and a set of r-patterns
![]() ${\mathcal P}$
, define the relation
${\mathcal P}$
, define the relation
![]() $\preceq _{{\mathcal P}}$
on the edges of M by taking
$\preceq _{{\mathcal P}}$
on the edges of M by taking
![]() $e\preceq f$
if
$e\preceq f$
if
![]() $e[1]<f[1]$
and
$e[1]<f[1]$
and
![]() $e,f$
form a pattern in
$e,f$
form a pattern in
![]() ${\mathcal P}$
(or if
${\mathcal P}$
(or if
![]() $e=f$
).
$e=f$
).
Lemma 3.2. Let
![]() $b=(r+1)2^{r-2}$
. There is a partition of the r-patterns into subsets
$b=(r+1)2^{r-2}$
. There is a partition of the r-patterns into subsets
![]() ${\mathcal P}_1,\dots ,{\mathcal P}_b$
such that the following properties hold for any
${\mathcal P}_1,\dots ,{\mathcal P}_b$
such that the following properties hold for any
![]() $i\in \{1,\dots ,b\}$
.
$i\in \{1,\dots ,b\}$
.
-
(A) For any
 $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free matching M, the relation
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free matching M, the relation
 $\preceq _{{\mathcal P}_{i}}$
is a partial order on M.
$\preceq _{{\mathcal P}_{i}}$
is a partial order on M. -
(B) For any
 ${\mathcal P}_i$
-clique M of size n, we have
${\mathcal P}_i$
-clique M of size n, we have
 $L(M)\ge n/(r-1)$
.
$L(M)\ge n/(r-1)$
.
The proofs of the sharper lower bounds in Theorem 1.8 are a bit more delicate; they use the same idea, with some extra twists. We will discuss them at the end of this section, after the proof of Lemma 3.2.
For Lemma 3.2, our partition into subsets will be defined in terms of weak patterns, which we define and investigate next.
3.1 Weak patterns
Weak patterns measure the relationship between two edges
![]() $e,f$
in a slightly coarser way than ordinary patterns. Specifically, for weak patterns, we are only concerned with the behaviour of pairs of consecutive vertices in e and in f.
$e,f$
in a slightly coarser way than ordinary patterns. Specifically, for weak patterns, we are only concerned with the behaviour of pairs of consecutive vertices in e and in f.
Definition 3.3. For an r-pattern P and some
![]() $1\le i<j\le r$
let
$1\le i<j\le r$
let
![]() $P_{{i}:{j}}$
be the
$P_{{i}:{j}}$
be the
![]() $(j-i+1)$
-pattern formed by
$(j-i+1)$
-pattern formed by
![]() $\{e[i],e[i+1],\dots ,e[j]\}$
and
$\{e[i],e[i+1],\dots ,e[j]\}$
and
![]() $\{f[i],f[i+1],\dots ,f[j]\}$
.
$\{f[i],f[i+1],\dots ,f[j]\}$
.
Then, define the weak r-pattern
![]() $\phi (P)=(\phi _1(P),\dots ,\phi _{r-1}(P)) \in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
corresponding to P, by taking
$\phi (P)=(\phi _1(P),\dots ,\phi _{r-1}(P)) \in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
corresponding to P, by taking
-
○
 $\phi _i(P)=\alpha $
if
$\phi _i(P)=\alpha $
if
 $P_{{i}:{i+1}}$
is the alignment 2-pattern,
$P_{{i}:{i+1}}$
is the alignment 2-pattern, -
○
 $\phi _i(P)=\kappa $
if
$\phi _i(P)=\kappa $
if
 $P_{{i}:{i+1}}$
is the crossing 2-pattern,
$P_{{i}:{i+1}}$
is the crossing 2-pattern, -
○
 $\phi _i(P)={\nu }$
if
$\phi _i(P)={\nu }$
if
 $P_{{i}:{i+1}}$
is the nesting 2-pattern.
$P_{{i}:{i+1}}$
is the nesting 2-pattern.
In general, a sequence
![]() $W=(W_1,\dots ,W_{r-1}) \in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
is called a weak r-pattern.
$W=(W_1,\dots ,W_{r-1}) \in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
is called a weak r-pattern.
In Table 1, we list all the 3-patterns and their corresponding weak 3-patterns.
Table 1 All
![]() $(3\cdot 2)!/(2\cdot (3!)^2)=10$
different 3-patterns, together with their corresponding weak pattern. Note that there are two different patterns corresponding to the weak pattern
$(3\cdot 2)!/(2\cdot (3!)^2)=10$
different 3-patterns, together with their corresponding weak pattern. Note that there are two different patterns corresponding to the weak pattern
![]() $\alpha \alpha $
(one collectable and one not).
$\alpha \alpha $
(one collectable and one not).

Remark 3.4. If P is a 2-partite 2-pattern (i.e., a permutation), then the weak pattern
![]() $\phi (P)$
is the same information shape of the permutation, as defined in [Reference Dudek, Grytczuk and Ruciński23].
$\phi (P)$
is the same information shape of the permutation, as defined in [Reference Dudek, Grytczuk and Ruciński23].
In [Reference Dudek, Grytczuk and Ruciński21], Dudek, Grytczuk and Ruciński used the notion of weak
![]() $3$
-patterns to study
$3$
-patterns to study
![]() $3$
-patterns.
$3$
-patterns.
Definition 3.5. For a weak pattern W, say a pair of edges ‘form W’ if they form a pattern P with
![]() $\phi (P)=W$
. An ordered r-matching M is said to be a W-clique if every pair of edges form W.
$\phi (P)=W$
. An ordered r-matching M is said to be a W-clique if every pair of edges form W.
In the proof of Lemma 3.2, we will define each of our subsets
![]() ${\mathcal P}_i$
to be a set of all patterns P such that
${\mathcal P}_i$
to be a set of all patterns P such that
![]() $\phi (P)$
has a prescribed number of ‘
$\phi (P)$
has a prescribed number of ‘
![]() $\alpha $
’s, and has its ‘
$\alpha $
’s, and has its ‘
![]() ${\nu }$
’s in prescribed positions. To understand why this works, we need quite a thorough study of weak patterns.
${\nu }$
’s in prescribed positions. To understand why this works, we need quite a thorough study of weak patterns.
First, we collect a few basic properties of weak patterns. A ‘generalised alignment’ is a pattern with block representation
![]() ${{\mathrm {A}}{\mathrm {A}}}\cdots {\mathrm {A}}{{\mathrm {B}}{\mathrm {B}}}\cdots {\mathrm {B}}$
(i.e., a collectable pattern with a single block).
${{\mathrm {A}}{\mathrm {A}}}\cdots {\mathrm {A}}{{\mathrm {B}}{\mathrm {B}}}\cdots {\mathrm {B}}$
(i.e., a collectable pattern with a single block).
Lemma 3.6. Fix an r-pattern P with edges
![]() $e,f$
(and assume
$e,f$
(and assume
![]() $e[1]<f[1]$
).
$e[1]<f[1]$
).
-
(i) For each
 $i \in [r]$
, we have
$i \in [r]$
, we have
 $e[i]<f[i]$
if and only if there are an even number of ‘
$e[i]<f[i]$
if and only if there are an even number of ‘
 ${\nu }$
’s among
${\nu }$
’s among
 $\phi _1(P),\dots ,\phi _{i-1}(P)$
.
$\phi _1(P),\dots ,\phi _{i-1}(P)$
. -
(ii) P is collectable if and only if:
-
(
 $*$
) for all
$*$
) for all
 $1 \le i< j \le r$
, where
$1 \le i< j \le r$
, where  $$\begin{align*}\phi(P_{{i}:{j}})=\phi_i(P)\,\phi_{i+1}(P)\dots\phi_{j-1}(P)=\alpha\alpha\dots\alpha,\end{align*}$$
$$\begin{align*}\phi(P_{{i}:{j}})=\phi_i(P)\,\phi_{i+1}(P)\dots\phi_{j-1}(P)=\alpha\alpha\dots\alpha,\end{align*}$$
 $P_{{i}:{j}} $
is a generalised alignment.
$P_{{i}:{j}} $
is a generalised alignment.
-
-
(iii) For each weak r-pattern W, there is exactly one collectable r-pattern P satisfying
 $\phi (P)=W$
.
$\phi (P)=W$
.
Proof sketch
For (i), it is a simple observation (immediate from the definitions of alignments, crossings and nestings) that the relative order between
![]() $e[i]$
and
$e[i]$
and
![]() $f[i]$
is different from the relative order between
$f[i]$
is different from the relative order between
![]() $e[i-1]$
and
$e[i-1]$
and
![]() $f[i-1]$
if and only if
$f[i-1]$
if and only if
![]() $\phi (P)_{i-1}={\nu }$
. The statement in (i) then follows by a straightforward induction on i.
$\phi (P)_{i-1}={\nu }$
. The statement in (i) then follows by a straightforward induction on i.
(ii) is a bit more involved. Recall from Definition 1.5 that P is collectable if and only if it is splittable (i.e., it can be partitioned into blocks that have an
![]() ${\mathrm {A}}$
-run followed by a
${\mathrm {A}}$
-run followed by a
![]() ${\mathrm {B}}$
-run of the same length, or vice versa).
${\mathrm {B}}$
-run of the same length, or vice versa).
For the ‘only if’ direction, it is easy to see that if P is collectable (splittable), then it satisfies
![]() $(*)$
. Indeed, note that if P is splittable then
$(*)$
. Indeed, note that if P is splittable then
![]() $P_{{i}:{j}}$
is splittable for all
$P_{{i}:{j}}$
is splittable for all
![]() $1 \le i < j \le r$
(this follows immediately from the definition of splittability). In the block representation of
$1 \le i < j \le r$
(this follows immediately from the definition of splittability). In the block representation of
![]() $P_{{i}:{j}}$
, each division between consecutive blocks gives rise to a ‘
$P_{{i}:{j}}$
, each division between consecutive blocks gives rise to a ‘
![]() ${\nu }$
’ or ‘
${\nu }$
’ or ‘
![]() $\kappa $
’, so if
$\kappa $
’, so if
![]() $\phi (P_{{i}:{j}})=\alpha \dots \alpha $
, then
$\phi (P_{{i}:{j}})=\alpha \dots \alpha $
, then
![]() $P_{{i}:{j}}$
must have a single block and is therefore a generalised alignment, as desired.
$P_{{i}:{j}}$
must have a single block and is therefore a generalised alignment, as desired.
For the ‘if’ direction, suppose P is not collectable (splittable). We need to prove that
![]() $(*)$
is violated. Let j be minimal such that
$(*)$
is violated. Let j be minimal such that
![]() $P_{{1}:{j}}$
is not splittable (note that every 2-pattern is splittable, so we have
$P_{{1}:{j}}$
is not splittable (note that every 2-pattern is splittable, so we have
![]() $j\ge 3$
). Let
$j\ge 3$
). Let
![]() $|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|$
be the block representation of
$|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|$
be the block representation of
![]() $P_{{1}:{j-1}}$
. If we had
$P_{{1}:{j-1}}$
. If we had
![]() $\phi _{j-1}(P)\in \{\kappa ,{\nu }\}$
, then the block representation of
$\phi _{j-1}(P)\in \{\kappa ,{\nu }\}$
, then the block representation of
![]() $P_{{1}:{j}}$
would be
$P_{{1}:{j}}$
would be
![]() $|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|{{\mathrm {A}}{\mathrm {B}}}|$
or
$|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|{{\mathrm {A}}{\mathrm {B}}}|$
or
![]() $|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|{{\mathrm {B}}{\mathrm {A}}}|$
(depending on the parity of the number of ‘
$|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|{{\mathrm {B}}{\mathrm {A}}}|$
(depending on the parity of the number of ‘
![]() ${\nu }$
’s among
${\nu }$
’s among
![]() $\phi _1(P),\dots ,\phi _{j-1}(P)$
). In either case,
$\phi _1(P),\dots ,\phi _{j-1}(P)$
). In either case,
![]() $P_{{1}:{j}}$
would then be splittable (collectable), a contradiction. So, we must have
$P_{{1}:{j}}$
would then be splittable (collectable), a contradiction. So, we must have
![]() $\phi _{j-1}(P)=\alpha $
.
$\phi _{j-1}(P)=\alpha $
.
Now, let i be minimal such that
![]() $\phi (P_{{i}:{j}})=\alpha \dots \alpha $
. We have
$\phi (P_{{i}:{j}})=\alpha \dots \alpha $
. We have
![]() $i \le j -1$
since
$i \le j -1$
since
![]() $\phi _{j-1}(P)=\alpha $
. In the case
$\phi _{j-1}(P)=\alpha $
. In the case
![]() $i=1$
, we know
$i=1$
, we know
![]() $P_{{1}:{j}}=P_{{i}:{j}}$
cannot be a generalised alignment because (by the choice of j) it is not splittable. This means that P violates the condition in
$P_{{1}:{j}}=P_{{i}:{j}}$
cannot be a generalised alignment because (by the choice of j) it is not splittable. This means that P violates the condition in
![]() $(*)$
. So, it remains to consider the case
$(*)$
. So, it remains to consider the case
![]() $i \ge 2$
. By the definition of i, we know
$i \ge 2$
. By the definition of i, we know
![]() $\phi _{i-1}(P)\neq \alpha $
, which implies that both
$\phi _{i-1}(P)\neq \alpha $
, which implies that both
![]() $e[i-1]$
and
$e[i-1]$
and
![]() $f[i-1]$
precede
$f[i-1]$
precede
![]() $e[i]$
and
$e[i]$
and
![]() $f[i]$
. If
$f[i]$
. If
![]() $P_{{i}:{j}}$
were to form a generalised alignment, the block representation of
$P_{{i}:{j}}$
were to form a generalised alignment, the block representation of
![]() $P_{{1}:{j}}$
would be
$P_{{1}:{j}}$
would be
![]() $|{\mathfrak {B}}_1'|\dots |{\mathfrak {B}}_k'|{{\mathrm {A}}{\mathrm {A}}}\cdots {\mathrm {A}}{{\mathrm {B}}{\mathrm {B}}}\cdots {\mathrm {B}}|$
or
$|{\mathfrak {B}}_1'|\dots |{\mathfrak {B}}_k'|{{\mathrm {A}}{\mathrm {A}}}\cdots {\mathrm {A}}{{\mathrm {B}}{\mathrm {B}}}\cdots {\mathrm {B}}|$
or
![]() $|{\mathfrak {B}}_1'|\dots |{\mathfrak {B}}_k'|{{\mathrm {B}}{\mathrm {B}}}\cdots {\mathrm {B}}{{\mathrm {A}}{\mathrm {A}}}\cdots {\mathrm {A}}|$
(depending on the parity of the number of ‘
$|{\mathfrak {B}}_1'|\dots |{\mathfrak {B}}_k'|{{\mathrm {B}}{\mathrm {B}}}\cdots {\mathrm {B}}{{\mathrm {A}}{\mathrm {A}}}\cdots {\mathrm {A}}|$
(depending on the parity of the number of ‘
![]() ${\nu }$
’s among
${\nu }$
’s among
![]() $\phi _1(P),\dots ,\phi _{i-1}(P)$
), where
$\phi _1(P),\dots ,\phi _{i-1}(P)$
), where
![]() $|{\mathfrak {B}}_1'|\dots |{\mathfrak {B}}_k'|$
is the block representation of
$|{\mathfrak {B}}_1'|\dots |{\mathfrak {B}}_k'|$
is the block representation of
![]() $P_{{1}:{i}}$
. In either case,
$P_{{1}:{i}}$
. In either case,
![]() $P_{{1}:{j}}$
would be splittable, a contradiction. So,
$P_{{1}:{j}}$
would be splittable, a contradiction. So,
![]() $P_{{i}:{j}}$
cannot be a generalised alignment, meaning that
$P_{{i}:{j}}$
cannot be a generalised alignment, meaning that
![]() $(*)$
is violated. This completes the proof for (ii).
$(*)$
is violated. This completes the proof for (ii).
For (iii), fix a weak r-pattern
![]() $W=(W_1,\dots ,W_{r-1})\in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
. We can use properties (i) and (ii) to construct and force the structure of the collectable r-pattern P with
$W=(W_1,\dots ,W_{r-1})\in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
. We can use properties (i) and (ii) to construct and force the structure of the collectable r-pattern P with
![]() $\phi (P)=W$
. Specifically, let
$\phi (P)=W$
. Specifically, let
![]() $1 \le i_1<\dots <i_m < r$
be the indices i with
$1 \le i_1<\dots <i_m < r$
be the indices i with
![]() $W_i\in \{{\nu },\kappa \}$
. Set
$W_i\in \{{\nu },\kappa \}$
. Set
![]() $i_0=0$
and
$i_0=0$
and
![]() $i_{m+1}=r$
for convenience. For
$i_{m+1}=r$
for convenience. For
![]() $1\le \ell \le m+1$
, let
$1\le \ell \le m+1$
, let
![]() ${\mathfrak {B}}_\ell $
be a sequence of
${\mathfrak {B}}_\ell $
be a sequence of
![]() $(i_{\ell }-i_{\ell -1})$
‘
$(i_{\ell }-i_{\ell -1})$
‘
![]() ${\mathrm {A}}$
’s followed by a sequence of
${\mathrm {A}}$
’s followed by a sequence of
![]() $(i_{\ell }-i_{\ell -1})$
‘
$(i_{\ell }-i_{\ell -1})$
‘
![]() ${\mathrm {B}}$
’s if the number of ‘
${\mathrm {B}}$
’s if the number of ‘
![]() ${\nu }$
’s among
${\nu }$
’s among
![]() $W_{i_1},W_{i_2},\dots ,W_{i_{\ell -1}}$
is even; let
$W_{i_1},W_{i_2},\dots ,W_{i_{\ell -1}}$
is even; let
![]() ${\mathfrak {B}}_\ell $
be a sequence of
${\mathfrak {B}}_\ell $
be a sequence of
![]() $(i_{\ell }-i_{\ell -1})$
‘
$(i_{\ell }-i_{\ell -1})$
‘
![]() ${\mathrm {B}}$
’s followed by a sequence of
${\mathrm {B}}$
’s followed by a sequence of
![]() $(i_{\ell }-i_{\ell -1})$
‘
$(i_{\ell }-i_{\ell -1})$
‘
![]() ${\mathrm {A}}$
’s otherwise. Then, it is not hard to deduce from (i) and (ii) that
${\mathrm {A}}$
’s otherwise. Then, it is not hard to deduce from (i) and (ii) that
![]() $Q={\mathfrak {B}}_1{\mathfrak {B}}_2\cdots {\mathfrak {B}}_{m+1}$
is a collectable r-pattern with
$Q={\mathfrak {B}}_1{\mathfrak {B}}_2\cdots {\mathfrak {B}}_{m+1}$
is a collectable r-pattern with
![]() $\phi (Q)=W$
, and the block representation of P must be precisely the concatenation
$\phi (Q)=W$
, and the block representation of P must be precisely the concatenation
![]() $|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_{m+1}|$
.
$|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_{m+1}|$
.
Given Lemma 3.6(iii), it makes sense to introduce some notation for the unique collectable pattern corresponding to a particular weak pattern.
Definition 3.7. For each weak r-pattern W, let
![]() $\psi (W)$
be the unique collectable r-pattern satisfying
$\psi (W)$
be the unique collectable r-pattern satisfying
![]() $\phi (\psi (W))=W$
.
$\phi (\psi (W))=W$
.
Now, one advantage of considering weak patterns is that we can get a handle on how they can interact with each other by considering how their constituent alignments, crossings and nestings can interact with each other.
Lemma 3.8. Suppose
![]() $e,f,g$
are three edges in some ordered r-matching such that
$e,f,g$
are three edges in some ordered r-matching such that
![]() $e[1]<f[1]<g[1]$
. Let
$e[1]<f[1]<g[1]$
. Let
![]() $W^{e,f},W^{f,g},W^{e,g}$
be the weak r-patterns formed by pairs
$W^{e,f},W^{f,g},W^{e,g}$
be the weak r-patterns formed by pairs
![]() $\{e,f\},\{f,g\},\{e,g\}$
, respectively. If the ‘
$\{e,f\},\{f,g\},\{e,g\}$
, respectively. If the ‘
![]() ${\nu }$
’s occur in the same positions in
${\nu }$
’s occur in the same positions in
![]() $W^{e,f}$
and in
$W^{e,f}$
and in
![]() $W^{f,g}$
, then, for
$W^{f,g}$
, then, for
![]() $1 \le i \le r-1$
,
$1 \le i \le r-1$
,
-
(i) if
 $W^{e,f}_i=W^{f,g}_i={\nu }$
, then
$W^{e,f}_i=W^{f,g}_i={\nu }$
, then
 $W^{e,g}_i={\nu }$
;
$W^{e,g}_i={\nu }$
; -
(ii) if
 $W^{e,f}_i=\alpha $
or
$W^{e,f}_i=\alpha $
or
 $W^{f,g}_i=\alpha $
, then
$W^{f,g}_i=\alpha $
, then
 $W^{e,g}_i=\alpha $
;
$W^{e,g}_i=\alpha $
; -
(iii) if
 $W^{e,f}_i=W^{f,g}_i=\kappa $
, then
$W^{e,f}_i=W^{f,g}_i=\kappa $
, then
 $W^{e,g}_i\in \{\alpha ,\kappa \}$
.
$W^{e,g}_i\in \{\alpha ,\kappa \}$
.
Also, combining (ii) and (iii), we get:
-
(iv) if
 $W^{e,f}_i\ne {\nu }$
and
$W^{e,f}_i\ne {\nu }$
and
 $W^{f,g}_i\ne {\nu }$
, then
$W^{f,g}_i\ne {\nu }$
, then
 $W^{e,g}_i\ne {\nu }$
.
$W^{e,g}_i\ne {\nu }$
.
Proof. By assumption, the number of ‘
![]() ${\nu }$
’s among
${\nu }$
’s among
![]() $W^{e,f}_1,W^{e,f}_2,\dots ,W^{e,f}_{i-1}$
and among
$W^{e,f}_1,W^{e,f}_2,\dots ,W^{e,f}_{i-1}$
and among
![]() $W^{f,g}_1,W^{f,g}_2,\dots ,W^{f,g}_{i-1}$
are the same. We assume that this number is even (the odd case is similar). By Lemma 3.6(i), we have
$W^{f,g}_1,W^{f,g}_2,\dots ,W^{f,g}_{i-1}$
are the same. We assume that this number is even (the odd case is similar). By Lemma 3.6(i), we have
![]() $e[i]<f[i]<g[i]$
.
$e[i]<f[i]<g[i]$
.
If
![]() $W^{e,f}_i=W^{f,g}_i={\nu }$
, then
$W^{e,f}_i=W^{f,g}_i={\nu }$
, then
![]() $e[i]<f[i]<f[i+1]<e[i+1]$
and
$e[i]<f[i]<f[i+1]<e[i+1]$
and
![]() $f[i]<g[i]<g[i+1]<f[i+1]$
, implying that
$f[i]<g[i]<g[i+1]<f[i+1]$
, implying that
![]() $e[i]<g[i]<g[i+1]<e[i+1]$
. This means
$e[i]<g[i]<g[i+1]<e[i+1]$
. This means
![]() $\{e[i],e[i+1]\}$
and
$\{e[i],e[i+1]\}$
and
![]() $\{g[i],g[i+1]\}$
form a nesting, that is,
$\{g[i],g[i+1]\}$
form a nesting, that is,
![]() $W^{e,g}_i={\nu }$
. This proves (i).
$W^{e,g}_i={\nu }$
. This proves (i).
If
![]() $W^{e,f}_i, W^{f,g}_i\neq {\nu }$
, we know that
$W^{e,f}_i, W^{f,g}_i\neq {\nu }$
, we know that
![]() $W^{e,f}_i,W^{f,g}_i \in \{\alpha ,\kappa \}$
. This implies
$W^{e,f}_i,W^{f,g}_i \in \{\alpha ,\kappa \}$
. This implies
 $$ \begin{align*} e[i]<\min(e[i+1],f[i])&<\max(e[i+1],f[i])<f[i+1]\text{ and}\\ f[i]<\min(f[i+1],g[i])&<\max(f[i+1],g[i])<g[i+1], \end{align*} $$
$$ \begin{align*} e[i]<\min(e[i+1],f[i])&<\max(e[i+1],f[i])<f[i+1]\text{ and}\\ f[i]<\min(f[i+1],g[i])&<\max(f[i+1],g[i])<g[i+1], \end{align*} $$
which in turn imply
That is to say,
![]() $W^{e,g}_i \in \{\kappa , \alpha \}$
, proving (iii). If we furthermore have
$W^{e,g}_i \in \{\kappa , \alpha \}$
, proving (iii). If we furthermore have
![]() $W^{e,f}_i=\alpha $
or
$W^{e,f}_i=\alpha $
or
![]() $W^{f,g}_i=\alpha $
, then we know
$W^{f,g}_i=\alpha $
, then we know
![]() $e[i]<e[i+1]<g[i]<g[i+1]$
, that is,
$e[i]<e[i+1]<g[i]<g[i+1]$
, that is,
![]() $W^{e,g}_i=\alpha $
, proving (ii).
$W^{e,g}_i=\alpha $
, proving (ii).
Now, the following lemma will be used to handle non-collectable patterns: If we manage to find a large W-clique (for some weak pattern W), we can very efficiently drop to a
![]() $\psi (W)$
-clique. A similar fact (with a slightly worse constant) can actually be deduced from the main result of [Reference Dudek, Grytczuk and Ruciński22], but here we provide a self-contained proof.
$\psi (W)$
-clique. A similar fact (with a slightly worse constant) can actually be deduced from the main result of [Reference Dudek, Grytczuk and Ruciński22], but here we provide a self-contained proof.
Lemma 3.9. Let W be a weak r-pattern, and let M be a W-clique of size n. Then, M contains a
![]() $\psi (W)$
-clique of size at least
$\psi (W)$
-clique of size at least
![]() $n/\max (1,\delta (W))$
, where
$n/\max (1,\delta (W))$
, where
![]() $\delta (W)$
is the length of the longest run of ‘
$\delta (W)$
is the length of the longest run of ‘
![]() $\alpha $
’s in W.
$\alpha $
’s in W.
Proof. By Lemma 3.6(ii), if
![]() $\delta (W)=0$
then there is no non-collectable r-pattern P with
$\delta (W)=0$
then there is no non-collectable r-pattern P with
![]() $\phi (P)=W$
. Thus, M itself is a
$\phi (P)=W$
. Thus, M itself is a
![]() $\psi (W)$
-clique. So, we may assume
$\psi (W)$
-clique. So, we may assume
![]() $\delta :=\delta (W)\ge 1$
.
$\delta :=\delta (W)\ge 1$
.
Let
![]() $e_1,e_2,\dots ,e_n$
be the edges in M, ordered such that
$e_1,e_2,\dots ,e_n$
be the edges in M, ordered such that
![]() $e_1[1]<e_2[1]<\dots <e_n[1]$
. We claim that for any
$e_1[1]<e_2[1]<\dots <e_n[1]$
. We claim that for any
![]() $s,t$
with
$s,t$
with
![]() $t-s\ge \delta $
, the edges
$t-s\ge \delta $
, the edges
![]() $e_s,e_t$
form
$e_s,e_t$
form
![]() $\psi (W)$
. This suffices to prove the lemma: we can simply take every
$\psi (W)$
. This suffices to prove the lemma: we can simply take every
![]() $\delta $
-th edge as our
$\delta $
-th edge as our
![]() $\psi (M)$
-clique.
$\psi (M)$
-clique.
For
![]() $1\leq a<b\leq n$
, let
$1\leq a<b\leq n$
, let
![]() $P^{a,b}$
be the pattern formed by
$P^{a,b}$
be the pattern formed by
![]() $e_a,e_b$
. Fix
$e_a,e_b$
. Fix
![]() $s,t$
with
$s,t$
with
![]() $t-s\ge \delta $
. We wish to show that
$t-s\ge \delta $
. We wish to show that
![]() $P^{s,t}$
is collectable (which will imply
$P^{s,t}$
is collectable (which will imply
![]() $P^{s,t}=\psi (W)$
by Lemma 3.6(iii)). By Lemma 3.6(ii), it suffices to show that for any
$P^{s,t}=\psi (W)$
by Lemma 3.6(iii)). By Lemma 3.6(ii), it suffices to show that for any
![]() $1\le i < j \le r$
with
$1\le i < j \le r$
with
![]() $W_i=W_{i+1}=\dots =W_{j-1}=\alpha $
(i.e.,
$W_i=W_{i+1}=\dots =W_{j-1}=\alpha $
(i.e.,
![]() $\phi (P^{s,t}_{{i}:{j}})=\alpha \dots \alpha $
), the
$\phi (P^{s,t}_{{i}:{j}})=\alpha \dots \alpha $
), the
![]() $(j-i+1)$
-pattern
$(j-i+1)$
-pattern
![]() $P^{s,t}_{{i}:{j}}$
is a generalised alignment.
$P^{s,t}_{{i}:{j}}$
is a generalised alignment.
Suppose there are an even number of ‘
![]() ${\nu }$
’s among
${\nu }$
’s among
![]() $W_1,W_2,\dots ,W_{i-1}$
(the odd case is similar). For
$W_1,W_2,\dots ,W_{i-1}$
(the odd case is similar). For
![]() $q\in \{s,s+1,\dots ,t-1\}$
and
$q\in \{s,s+1,\dots ,t-1\}$
and
![]() $k\in \{i,i+1,\dots ,j-1\}$
, we have
$k\in \{i,i+1,\dots ,j-1\}$
, we have
![]() $e_q[k]<e_q[k+1]<e_{q+1}[k]<e_{q+1}[k+1]$
(since
$e_q[k]<e_q[k+1]<e_{q+1}[k]<e_{q+1}[k+1]$
(since
![]() $W_k=\alpha $
). This means we have
$W_k=\alpha $
). This means we have
where the last inequality holds because
![]() $s+j-i \le s+\delta \le t$
and there are an even number of ‘
$s+j-i \le s+\delta \le t$
and there are an even number of ‘
![]() ${\nu }$
’s among
${\nu }$
’s among
![]() $W_1,\dots ,W_{i-1}$
. In other words,
$W_1,\dots ,W_{i-1}$
. In other words,
![]() $P^{s,t}_{{i}:{j}}$
is a generalised alignment, as desired.
$P^{s,t}_{{i}:{j}}$
is a generalised alignment, as desired.
Remark 3.10. It is not hard to see that the constant factor
![]() $1/\max (1,\delta (M))$
cannot be improved.
$1/\max (1,\delta (M))$
cannot be improved.
3.2 Proof of the key lemma
Now, we have all the preparations in place to prove Lemma 3.2. The subsets of patterns
![]() ${\mathcal P}_i$
will be defined in terms of signatures, as follows.
${\mathcal P}_i$
will be defined in terms of signatures, as follows.
Definition 3.11. For each weak r-pattern
![]() $W\in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
, the signature of W is defined to be
$W\in \{\alpha ,\kappa ,{\nu }\}^{r-1}$
, the signature of W is defined to be
That is to say, the signature specifies the number of ‘
![]() $\alpha $
’s and the positions of the ‘
$\alpha $
’s and the positions of the ‘
![]() ${\nu }$
’s. We define the weight of
${\nu }$
’s. We define the weight of
![]() $\sigma (W)$
to be the number of ‘
$\sigma (W)$
to be the number of ‘
![]() $\alpha $
’s in W.
$\alpha $
’s in W.
The total number of signatures is
 $$\begin{align*}\sum_{S\subseteq\{1,\dots,r-1\}}(r-\left\vert {S}\right\vert)=\sum_{i=0}^{r-1}\binom{r-1}{i}(r-i)=(r+1)2^{r-2}=:b.\end{align*}$$
$$\begin{align*}\sum_{S\subseteq\{1,\dots,r-1\}}(r-\left\vert {S}\right\vert)=\sum_{i=0}^{r-1}\binom{r-1}{i}(r-i)=(r+1)2^{r-2}=:b.\end{align*}$$
Let
![]() $\sigma _1,\dots ,\sigma _b$
be an ordering of the signatures in descending weight (breaking ties arbitrarily). Let
$\sigma _1,\dots ,\sigma _b$
be an ordering of the signatures in descending weight (breaking ties arbitrarily). Let
![]() ${\mathcal P}_i$
be the set of all patterns P such that
${\mathcal P}_i$
be the set of all patterns P such that
![]() $\sigma (\phi (P))=\sigma _i$
.
$\sigma (\phi (P))=\sigma _i$
.
Proof of Lemma 3.2(A)
With
![]() ${\mathcal P}_1,\dots ,{\mathcal P}_b$
as defined above (in terms of signatures
${\mathcal P}_1,\dots ,{\mathcal P}_b$
as defined above (in terms of signatures
![]() $\sigma _1,\dots ,\sigma _b$
), we wish to show that for each i, the relation
$\sigma _1,\dots ,\sigma _b$
), we wish to show that for each i, the relation
![]() $\preceq _{{\mathcal P}_i}$
is a partial order on any
$\preceq _{{\mathcal P}_i}$
is a partial order on any
![]() $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free matching M.
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free matching M.
It suffices to show the transitivity of
![]() $\preceq _{\mathcal {P}_i}$
. Fix a
$\preceq _{\mathcal {P}_i}$
. Fix a
![]() $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free matching M and consider any edges
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free matching M and consider any edges
![]() $e,f,g$
with
$e,f,g$
with
![]() $e[1]<f[1]<g[1]$
. Let
$e[1]<f[1]<g[1]$
. Let
![]() $P^{e,f},P^{f,g},P^{e,g}$
be the patterns formed by the pairs
$P^{e,f},P^{f,g},P^{e,g}$
be the patterns formed by the pairs
![]() $\{e,f\}$
,
$\{e,f\}$
,
![]() $\{f,g\}$
and
$\{f,g\}$
and
![]() $\{e,g\}$
respectively, and suppose that
$\{e,g\}$
respectively, and suppose that
![]() $P^{e,f},P^{f,g}\in {\mathcal P}_i$
. Our objective is to show that
$P^{e,f},P^{f,g}\in {\mathcal P}_i$
. Our objective is to show that
![]() $P^{e,g}\in {\mathcal P}_i$
. We know that
$P^{e,g}\in {\mathcal P}_i$
. We know that
![]() $\phi (P^{e,f})$
and
$\phi (P^{e,f})$
and
![]() $\phi (P^{f,g})$
have their ‘
$\phi (P^{f,g})$
have their ‘
![]() ${\nu }$
’s in the same positions (as recorded by the signature
${\nu }$
’s in the same positions (as recorded by the signature
![]() $\sigma _i$
), so by Lemma 3.8(i,iv), the ‘
$\sigma _i$
), so by Lemma 3.8(i,iv), the ‘
![]() ${\nu }$
’s in
${\nu }$
’s in
![]() $\phi (P^{e,g})$
must be in exactly these same positions.
$\phi (P^{e,g})$
must be in exactly these same positions.
Then, let w be the weight of
![]() $\sigma _i$
(i.e., the number of ‘
$\sigma _i$
(i.e., the number of ‘
![]() $\alpha $
’s in the weak patterns associated with
$\alpha $
’s in the weak patterns associated with
![]() $\sigma _i$
). We know that
$\sigma _i$
). We know that
![]() $\phi (P^{e,f})$
and
$\phi (P^{e,f})$
and
![]() $\phi (P^{f,g})$
have exactly w ‘
$\phi (P^{f,g})$
have exactly w ‘
![]() $\alpha $
’s. Also, since M is
$\alpha $
’s. Also, since M is
![]() $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free (and higher-weight signatures come earlier in our ordering), we know that
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i-1})$
-free (and higher-weight signatures come earlier in our ordering), we know that
![]() $\phi (P^{e,f})$
has at most w ‘
$\phi (P^{e,f})$
has at most w ‘
![]() $\alpha $
’s. However, by Lemma 3.8(ii), in every position where
$\alpha $
’s. However, by Lemma 3.8(ii), in every position where
![]() $\phi (P^{e,f})$
or
$\phi (P^{e,f})$
or
![]() $\phi (P^{f,g})$
have a ‘
$\phi (P^{f,g})$
have a ‘
![]() $\alpha $
’, there is also a ‘
$\alpha $
’, there is also a ‘
![]() $\alpha $
’ in
$\alpha $
’ in
![]() $\phi ( P^{e,g})$
. The only way this can happen is if
$\phi ( P^{e,g})$
. The only way this can happen is if
![]() $\phi (P^{e,f})$
,
$\phi (P^{e,f})$
,
![]() $\phi (P^{f,g})$
and
$\phi (P^{f,g})$
and
![]() $\phi (P^{e,g})$
each have exactly w ‘
$\phi (P^{e,g})$
each have exactly w ‘
![]() $\alpha $
’s, in exactly the same positions. We have proved that
$\alpha $
’s, in exactly the same positions. We have proved that
![]() $P^{e,g}\in {\mathcal P}_i$
, as desired.
$P^{e,g}\in {\mathcal P}_i$
, as desired.
Proof of Lemma 3.2(B)
Suppose M is a
![]() ${\mathcal P}_i$
-clique of size n. We wish to show that
${\mathcal P}_i$
-clique of size n. We wish to show that
![]() $L(M) \ge n/(r-1)$
.
$L(M) \ge n/(r-1)$
.
Consider any three edges
![]() $e,f,g$
with
$e,f,g$
with
![]() $e[1]<f[1]<g[1]$
. Let
$e[1]<f[1]<g[1]$
. Let
![]() $P^{e,f},P^{f,g},P^{e,g}$
be the patterns formed by the pairs
$P^{e,f},P^{f,g},P^{e,g}$
be the patterns formed by the pairs
![]() $\{e,f\}$
,
$\{e,f\}$
,
![]() $\{f,g\}$
and
$\{f,g\}$
and
![]() $\{e,g\}$
respectively, so
$\{e,g\}$
respectively, so
![]() $P^{e,f},P^{f,g},P^{e,g}\in {\mathcal P}_i$
. By the considerations in the above proof of Lemma 3.2(A), each of
$P^{e,f},P^{f,g},P^{e,g}\in {\mathcal P}_i$
. By the considerations in the above proof of Lemma 3.2(A), each of
![]() $\phi (P^{e,f}),\phi (P^{f,g}),\phi (P^{e,g})$
must have their ‘
$\phi (P^{e,f}),\phi (P^{f,g}),\phi (P^{e,g})$
must have their ‘
![]() ${\nu }$
’s and ‘
${\nu }$
’s and ‘
![]() $\alpha $
’s (and therefore their ‘
$\alpha $
’s (and therefore their ‘
![]() $\kappa $
’s) in exactly the same positions, which means that
$\kappa $
’s) in exactly the same positions, which means that
![]() $e,f,g$
actually form a W-clique for some weak pattern W. But if every three edges form a W-clique, then the whole of M must be a W-clique for some weak r-pattern W with signature
$e,f,g$
actually form a W-clique for some weak pattern W. But if every three edges form a W-clique, then the whole of M must be a W-clique for some weak r-pattern W with signature
![]() $\sigma _i$
. By Lemma 3.9, we have
$\sigma _i$
. By Lemma 3.9, we have
![]() $L_{\psi (W)}(M)\ge n/(r-1)$
.
$L_{\psi (W)}(M)\ge n/(r-1)$
.
3.3 Proof of the lower bound in Theorem 1.7
Now, it is easy to derive the lower bound in Theorem 1.7 by iteratively applying Lemma 3.2 and Mirsky’s theorem.
Proof of the lower bound in Theorem 1.7
Let M be a size-n r-matching, and recall the subsets of patterns
![]() ${\mathcal P}_1,\dots ,{\mathcal P}_b$
in the proof of Lemma 3.2. First, combining Mirsky’s theorem (Theorem 2.1) and Lemma 3.2(A), it is easy to prove by induction that for each
${\mathcal P}_1,\dots ,{\mathcal P}_b$
in the proof of Lemma 3.2. First, combining Mirsky’s theorem (Theorem 2.1) and Lemma 3.2(A), it is easy to prove by induction that for each
![]() $i< b$
:
$i< b$
:
-
 $(*)$
M contains either a
$(*)$
M contains either a
 ${\mathcal P}_j$
-clique of size at least
${\mathcal P}_j$
-clique of size at least
 $n^{1/b}$
, for some
$n^{1/b}$
, for some
 $j\le i$
, or a
$j\le i$
, or a
 $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i})$
-free submatching of size at least
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{i})$
-free submatching of size at least
 $n^{1-i/b}$
.
$n^{1-i/b}$
.
![]() $(*)$
with
$(*)$
with
![]() $i=b-1$
states that M contains either a
$i=b-1$
states that M contains either a
![]() ${\mathcal P}_j$
-clique of size at least
${\mathcal P}_j$
-clique of size at least
![]() $n^{1/b}$
, for some
$n^{1/b}$
, for some
![]() $j\le b-1$
, or a
$j\le b-1$
, or a
![]() $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{b-1})$
-free submatching of size at least
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{b-1})$
-free submatching of size at least
![]() $n^{1-(b-1)/b}=n^{1/b}$
. As a
$n^{1-(b-1)/b}=n^{1/b}$
. As a
![]() $({\mathcal P}_1\cup \dots \cup {\mathcal P}_{b-1})$
-free matching is nothing more than a
$({\mathcal P}_1\cup \dots \cup {\mathcal P}_{b-1})$
-free matching is nothing more than a
![]() ${\mathcal P}_b$
-clique, we have that M contains a
${\mathcal P}_b$
-clique, we have that M contains a
![]() ${\mathcal P}_j$
-clique
${\mathcal P}_j$
-clique
![]() $M'$
of size at least
$M'$
of size at least
![]() $n^{1/b}$
, for some
$n^{1/b}$
, for some
![]() $j\le b$
. Then, by Lemma 3.2(B), we have
$j\le b$
. Then, by Lemma 3.2(B), we have
![]() $L(M)\ge L(M')\ge n^{1/b}/(r-1)$
, as desired.
$L(M)\ge L(M')\ge n^{1/b}/(r-1)$
, as desired.
3.4 Further improvements
Weak r-patterns are very convenient to work with, due to the fact that we can separately study how their constituent alignments, crossings and matchings interact (with Lemma 3.8). However, by directly considering how patterns can interact with each other, one can prove stronger bounds (specifically, one can prove an analogue of Lemma 3.2 with a smaller value of b). In this subsection, we show how to do this to prove the essentially optimal lower bound
![]() $L_3(n)\ge n^{1/7}/2$
featuring in Theorem 1.8. Note that Theorem 1.7 only gives the nonoptimal bound
$L_3(n)\ge n^{1/7}/2$
featuring in Theorem 1.8. Note that Theorem 1.7 only gives the nonoptimal bound
![]() $L_{3}(n)\ge n^{1/8}/2$
.
$L_{3}(n)\ge n^{1/8}/2$
.
The considerations in this
![]() $r=3$
proof can be generalised to larger r. For example, with some more sophisticated case analysis we can prove the optimal lower bound
$r=3$
proof can be generalised to larger r. For example, with some more sophisticated case analysis we can prove the optimal lower bound
![]() $L_4(n)= \Omega (n^{1/15})$
. As the proof is quite technical, we refer the interested reader to the appendix in the arXiv version of this paper.
$L_4(n)= \Omega (n^{1/15})$
. As the proof is quite technical, we refer the interested reader to the appendix in the arXiv version of this paper.
Proof of the lower bound on
 $L_{3}(n)$
in Theorem 1.8
$L_{3}(n)$
in Theorem 1.8
We use the notions of weak patterns and signatures introduced in Sections 3.1 and 3.2. Referring to Table 1, we see that there are 10 different 3-patterns, including one non-collectable pattern (which we call
![]() $P^*$
; note that
$P^*$
; note that
![]() $\phi (P^*)=\alpha \alpha $
). Define
$\phi (P^*)=\alpha \alpha $
). Define
We observe that these subsets can be used to define posets (we write
![]() $\preceq _i$
instead of
$\preceq _i$
instead of
![]() $\preceq _{{\mathcal P}_i}$
):
$\preceq _{{\mathcal P}_i}$
):
-
○ By the proof of Lemma 3.2(A), for any matching M, the relation
 $\preceq _1$
is a partial order. (Note that
$\preceq _1$
is a partial order. (Note that
 ${\mathcal P}_1$
corresponds to the signature
${\mathcal P}_1$
corresponds to the signature
 $(2,\emptyset )$
).
$(2,\emptyset )$
). -
○ Similarly, by the proof of Lemma 3.2(A), for any
 ${\mathcal P}_1$
-free matching M, the relation
${\mathcal P}_1$
-free matching M, the relation
 $\preceq _2$
is a partial order. (Note that
$\preceq _2$
is a partial order. (Note that
 ${\mathcal P}_2$
corresponds to the signature
${\mathcal P}_2$
corresponds to the signature
 $(1,\emptyset )$
).
$(1,\emptyset )$
). -
○ One can also see that the relation
 $\preceq _3$
is always a partial order (despite
$\preceq _3$
is always a partial order (despite
 ${\mathcal P}_3$
containing the patterns for two different signatures
${\mathcal P}_3$
containing the patterns for two different signatures
 $(1,\{1\})$
and
$(1,\{1\})$
and
 $(1,\{2\})$
). Observe that the two patterns
$(1,\{2\})$
). Observe that the two patterns
 $\psi (\alpha {\nu }),\psi ({\nu }\alpha )\in {\mathcal P}_3$
have block representations
$\psi (\alpha {\nu }),\psi ({\nu }\alpha )\in {\mathcal P}_3$
have block representations
 $|{{\mathrm {A}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
and
$|{{\mathrm {A}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
and
 $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {A}}}|$
; informally speaking, these patterns are ‘generalised nestings’, where all vertices of one edge are fully contained between two consecutive vertices of the other edge, and it is not hard to see that
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {A}}}|$
; informally speaking, these patterns are ‘generalised nestings’, where all vertices of one edge are fully contained between two consecutive vertices of the other edge, and it is not hard to see that
 $\preceq _3$
is therefore a partial order. In detail: Note that it suffices to show transitivity. Suppose
$\preceq _3$
is therefore a partial order. In detail: Note that it suffices to show transitivity. Suppose
 $e,f,g$
are three edges in a matching M with
$e,f,g$
are three edges in a matching M with
 $e[1]<f[1]<g[1]$
such that
$e[1]<f[1]<g[1]$
such that
 $e,f$
form pattern
$e,f$
form pattern
 $\psi (\alpha {\nu })$
and
$\psi (\alpha {\nu })$
and
 $f,g$
form pattern
$f,g$
form pattern
 $\psi (\alpha {\nu })$
or
$\psi (\alpha {\nu })$
or
 $\psi ({\nu }\alpha )$
. Then,
$\psi ({\nu }\alpha )$
. Then,
 $e[2]<f[1]<f[3]<e[3]$
(as
$e[2]<f[1]<f[3]<e[3]$
(as
 $e,f$
form pattern
$e,f$
form pattern
 $\psi (\alpha {\nu })$
) and
$\psi (\alpha {\nu })$
) and
 $f[1]<g[1]<g[3]<f[3]$
(as
$f[1]<g[1]<g[3]<f[3]$
(as
 $f,g$
form pattern
$f,g$
form pattern
 $\psi (\alpha {\nu })$
or
$\psi (\alpha {\nu })$
or
 $\psi ({\nu }\alpha )$
). So
$\psi ({\nu }\alpha )$
). So
 $e[2]<g[1]<g[3]<e[3]$
, that is,
$e[2]<g[1]<g[3]<e[3]$
, that is,
 $e,g$
form pattern
$e,g$
form pattern
 $\psi (\alpha {\nu })$
. Similarly, if
$\psi (\alpha {\nu })$
. Similarly, if
 $e,f$
form pattern
$e,f$
form pattern
 $\psi ({\nu }\alpha )$
and
$\psi ({\nu }\alpha )$
and
 $f,g$
form pattern
$f,g$
form pattern
 $\psi (\alpha {\nu })$
or
$\psi (\alpha {\nu })$
or
 $\psi ({\nu }\alpha )$
, then
$\psi ({\nu }\alpha )$
, then
 $e,g$
form pattern
$e,g$
form pattern
 $\psi ({\nu }\alpha )$
.
$\psi ({\nu }\alpha )$
. -
○ By the proof of Lemma 3.2(A), for any
 $({\mathcal P}_1\cup {\mathcal P}_2\cup {\mathcal P}_3)$
-free matching M, the relation
$({\mathcal P}_1\cup {\mathcal P}_2\cup {\mathcal P}_3)$
-free matching M, the relation
 $\preceq _P$
is a poset when P is any of the four 3-partite patterns
$\preceq _P$
is a poset when P is any of the four 3-partite patterns
 $\psi ({\nu }{\nu }),\psi ({\nu }\kappa ),\psi (\kappa {\nu }),\psi (\kappa \kappa )$
. (These correspond to the signatures
$\psi ({\nu }{\nu }),\psi ({\nu }\kappa ),\psi (\kappa {\nu }),\psi (\kappa \kappa )$
. (These correspond to the signatures
 $(0,S)$
, for
$(0,S)$
, for
 $S\subseteq \{1,2\}$
).
$S\subseteq \{1,2\}$
).
Proceeding in the same way as the proof of the lower bound in Theorem 1.7, we can therefore find a
![]() ${\mathcal P}_i$
-clique of size at least
${\mathcal P}_i$
-clique of size at least
![]() $n^{1/7}$
, for some
$n^{1/7}$
, for some
![]() $i\in \{1,2,3\}$
, or we can find a P-clique of size at least
$i\in \{1,2,3\}$
, or we can find a P-clique of size at least
![]() $n^{1/7}$
for P being one of the four 3-partite patterns
$n^{1/7}$
for P being one of the four 3-partite patterns
![]() $\psi ({\nu }{\nu }),\psi ({\nu }\kappa ),\psi (\kappa {\nu }),\psi (\kappa \kappa )$
.
$\psi ({\nu }{\nu }),\psi ({\nu }\kappa ),\psi (\kappa {\nu }),\psi (\kappa \kappa )$
.
By the proof of Lemma 3.2(B), if we found a
![]() ${\mathcal P}_1$
-clique or a
${\mathcal P}_1$
-clique or a
![]() ${\mathcal P}_2$
-clique
${\mathcal P}_2$
-clique
![]() $M'$
of size at least
$M'$
of size at least
![]() $n^{1/7}$
, then
$n^{1/7}$
, then
![]() $L(M')\ge n^{1/7}/2$
.
$L(M')\ge n^{1/7}/2$
.
Finally, it suffices to consider the case where we found a
![]() ${\mathcal P}_3$
-clique
${\mathcal P}_3$
-clique
![]() $M'$
with at least
$M'$
with at least
![]() $n^{1/7}$
edges. Let
$n^{1/7}$
edges. Let
![]() $e_1,\dots ,e_m$
be the edges in
$e_1,\dots ,e_m$
be the edges in
![]() $M'$
(with
$M'$
(with
![]() $m \ge n^{1/7}$
, and
$m \ge n^{1/7}$
, and
![]() $e_1[1]<\dots <e_m[1]$
). As discussed in the third bullet point above, we see that for any
$e_1[1]<\dots <e_m[1]$
). As discussed in the third bullet point above, we see that for any
![]() $1 \le i < j < k \le m$
, the edges
$1 \le i < j < k \le m$
, the edges
![]() $e_i,e_k$
always form the same 3-pattern as the edges
$e_i,e_k$
always form the same 3-pattern as the edges
![]() $e_i,e_j$
. So, every index i is of one of two types: We say it is of ‘type
$e_i,e_j$
. So, every index i is of one of two types: We say it is of ‘type
![]() $\psi (\alpha {\nu })$
’ if
$\psi (\alpha {\nu })$
’ if
![]() $e_i,e_j$
form
$e_i,e_j$
form
![]() $\psi (\alpha {\nu })$
for each
$\psi (\alpha {\nu })$
for each
![]() $i<j$
, and we say it is of ‘type
$i<j$
, and we say it is of ‘type
![]() $\psi ({\nu }\alpha )$
’ if
$\psi ({\nu }\alpha )$
’ if
![]() $e_i,e_j$
form
$e_i,e_j$
form
![]() $\psi ({\nu }\alpha )$
for each
$\psi ({\nu }\alpha )$
for each
![]() $i<j$
. By the pigeonhole principle, at least half of the indices have the same type, and the corresponding edges give us a
$i<j$
. By the pigeonhole principle, at least half of the indices have the same type, and the corresponding edges give us a
![]() $\psi (\alpha {\nu })$
-clique or a
$\psi (\alpha {\nu })$
-clique or a
![]() $\psi ({\nu }\alpha )$
-clique of size
$\psi ({\nu }\alpha )$
-clique of size
![]() $n^{1/7}/2$
.
$n^{1/7}/2$
.
4 Upper bounds on Ramsey parameters
In this section, we prove the upper bound in Theorem 1.7 (which also implies the upper bounds in Theorem 1.8). We consider the following notion of ‘blow-up’ introduced by by Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński22].
Definition 4.1. Suppose
![]() $M,M'$
are ordered r-matchings, and let t be the size of
$M,M'$
are ordered r-matchings, and let t be the size of
![]() $M'$
. The
$M'$
. The
![]() $M'$
-blow-up of M, denoted by
$M'$
-blow-up of M, denoted by
![]() $M[M']$
, is an ordered r-matching obtained from M as follows. We replace every vertex
$M[M']$
, is an ordered r-matching obtained from M as follows. We replace every vertex
![]() $i\in V(M)$
by an ordered set
$i\in V(M)$
by an ordered set
![]() $U_i$
of t contiguous vertices. Then, for each edge
$U_i$
of t contiguous vertices. Then, for each edge
![]() $e\in E(M)$
we place on the vertex set
$e\in E(M)$
we place on the vertex set
![]() $U_{e[1]}\cup \dots \cup U_{e[r]}$
a copy
$U_{e[1]}\cup \dots \cup U_{e[r]}$
a copy
![]() $M^{\prime }_e$
of the matching
$M^{\prime }_e$
of the matching
![]() $M'$
. Note that there are two kinds of pairs of edges
$M'$
. Note that there are two kinds of pairs of edges
![]() $(f_1,f_2)$
in
$(f_1,f_2)$
in
![]() $M[M']$
:
$M[M']$
:
-
○ If
 $f_1,f_2$
both lie in the same
$f_1,f_2$
both lie in the same
 $M_e^{\prime }$
(for some
$M_e^{\prime }$
(for some
 $e\in E(M)$
), then we say
$e\in E(M)$
), then we say
 $f_1$
and
$f_1$
and
 $f_2$
comprise an
$f_2$
comprise an
 $M'$
-pair.
$M'$
-pair. -
○ If
 $f_1,f_2$
lie in different
$f_1,f_2$
lie in different
 $M_e^{\prime }$
, then we say
$M_e^{\prime }$
, then we say
 $f_1$
and
$f_1$
and
 $f_2$
comprise an M-pair.
$f_2$
comprise an M-pair.
The above definition is useful typically when
![]() $M'$
is r-partite. In this case, one can check that if two edges
$M'$
is r-partite. In this case, one can check that if two edges
![]() $f_1,f_2$
comprise an M-pair (say
$f_1,f_2$
comprise an M-pair (say
![]() $f_1$
lie in
$f_1$
lie in
![]() $M_{e_1}^{\prime }$
and
$M_{e_1}^{\prime }$
and
![]() $f_2$
lie in
$f_2$
lie in
![]() $M_{e_2}^{\prime }$
), then
$M_{e_2}^{\prime }$
), then
![]() $f_1,f_2$
form the same r-pattern as
$f_1,f_2$
form the same r-pattern as
![]() $e_1,e_2$
do (in M). Therefore, for a matching M that contains no r-partite r-pattern and an r-partite matching
$e_1,e_2$
do (in M). Therefore, for a matching M that contains no r-partite r-pattern and an r-partite matching
![]() $M'$
the following holds. If P is r-partite, then
$M'$
the following holds. If P is r-partite, then
![]() $L_P(M[M'])=L_P(M')$
. Otherwise,
$L_P(M[M'])=L_P(M')$
. Otherwise,
![]() $L_P(M[M'])=L_P(M)$
. Thus,
$L_P(M[M'])=L_P(M)$
. Thus,
![]() $L(M[M'])=\max (L(M),L(M'))$
.
$L(M[M'])=\max (L(M),L(M'))$
.
This fact will be used in the proof of the upper bound in Theorem 1.7 momentarily.
For r-partite r-patterns, Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński22] used a blow-up construction to prove the following tight upper bound (which is actually equivalent to the result of Burkill and Mirsky [Reference Burkill and Mirsky15] and Kalmanson [Reference Kalmanson42] mentioned in the introduction, on
![]() $(r-1)$
-tuples of permutations).
$(r-1)$
-tuples of permutations).
Theorem 4.2 (Dudek, Grytczuk and Ruciński [Reference Dudek, Grytczuk and Ruciński22])
For
![]() $r \ge 2$
, and
$r \ge 2$
, and
![]() $n \ge 1$
, there exists an r-partite ordered r-matching M of size
$n \ge 1$
, there exists an r-partite ordered r-matching M of size
![]() $n^{2^{r-1}}$
such that for all (r-partite) r-patterns P, the largest P-clique is of size n.
$n^{2^{r-1}}$
such that for all (r-partite) r-patterns P, the largest P-clique is of size n.
We are now ready to prove that
![]() $L_{r}(n) \le \lceil n^{1/(2^r-1)}\rceil $
.
$L_{r}(n) \le \lceil n^{1/(2^r-1)}\rceil $
.
Proof of the upper bound in Theorem 1.7
Fix
![]() $r \ge 2$
and
$r \ge 2$
and
![]() $n \ge 1$
. We are going to construct an ordered r-matching M of size
$n \ge 1$
. We are going to construct an ordered r-matching M of size
![]() $n^{2^{r}-1}$
such that any pair of edges form a collectable r-pattern, and such that the largest clique has size n. We will do this by induction on r.
$n^{2^{r}-1}$
such that any pair of edges form a collectable r-pattern, and such that the largest clique has size n. We will do this by induction on r.
The base case
![]() $r=2$
already appears in [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22]. Indeed, consider
$r=2$
already appears in [Reference Dudek, Grytczuk and Ruciński21, Reference Dudek, Grytczuk and Ruciński22]. Indeed, consider
![]() $M:=M_1[M_2]$
, where
$M:=M_1[M_2]$
, where
![]() $M_1$
is an alignment-clique of size n and
$M_1$
is an alignment-clique of size n and
![]() $M_2$
is the 2-partite ordered 2-matching of size
$M_2$
is the 2-partite ordered 2-matching of size
![]() $n^2$
from Theorem 4.2. Then, M has size
$n^2$
from Theorem 4.2. Then, M has size
![]() $n^3$
. A pair of distinct edges
$n^3$
. A pair of distinct edges
![]() $f_1,f_2\in E(M)$
form an alignment if
$f_1,f_2\in E(M)$
form an alignment if
![]() $(f_1,f_2)$
is an
$(f_1,f_2)$
is an
![]() $M_1$
-pair, and they form a nesting or a crossing if
$M_1$
-pair, and they form a nesting or a crossing if
![]() $(f_1,f_2)$
is an
$(f_1,f_2)$
is an
![]() $M_2$
-pair. It is easy to check that there is no clique of size larger than n.
$M_2$
-pair. It is easy to check that there is no clique of size larger than n.
For the inductive step, suppose we have constructed an ordered
![]() $(r-1)$
-matching
$(r-1)$
-matching
![]() $M_1$
of size
$M_1$
of size
![]() $n^{2^{r-1}-1}$
in which every pair of edges form a collectable
$n^{2^{r-1}-1}$
in which every pair of edges form a collectable
![]() $(r-1)$
-pattern, such that the largest clique has size n. For each edge
$(r-1)$
-pattern, such that the largest clique has size n. For each edge
![]() $e \in E(M_1)$
, we add a new vertex
$e \in E(M_1)$
, we add a new vertex
![]() $v_e$
just to the right of
$v_e$
just to the right of
![]() $e[r-1]$
and extend e to an edge
$e[r-1]$
and extend e to an edge
![]() $e'$
of uniformity r by adding
$e'$
of uniformity r by adding
![]() $v_e$
to e. Let the resulting ordered r-matching be
$v_e$
to e. Let the resulting ordered r-matching be
![]() $M_2$
.
$M_2$
.
Now, we claim that
![]() $M_2$
is free of r-partite r-patterns, and its largest clique has size n. To see this, note that if
$M_2$
is free of r-partite r-patterns, and its largest clique has size n. To see this, note that if
![]() $e,f\in E(M_1)$
form an
$e,f\in E(M_1)$
form an
![]() $(r-1)$
-pattern with block representation
$(r-1)$
-pattern with block representation
![]() $|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|$
, then
$|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_k|$
, then
![]() $e',f'\in E(M_2)$
form the r-pattern whose block representation is
$e',f'\in E(M_2)$
form the r-pattern whose block representation is
![]() $|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_{k-1}|{\mathfrak {B}}_k'|$
, where
$|{\mathfrak {B}}_1|\dots |{\mathfrak {B}}_{k-1}|{\mathfrak {B}}_k'|$
, where
![]() ${\mathfrak {B}}_k'$
is obtained by extending the ‘
${\mathfrak {B}}_k'$
is obtained by extending the ‘
![]() ${\mathrm {A}}$
-run’ and the ‘
${\mathrm {A}}$
-run’ and the ‘
![]() ${\mathrm {B}}$
-run’ in
${\mathrm {B}}$
-run’ in
![]() ${\mathfrak {B}}_k$
by one. (For example, if
${\mathfrak {B}}_k$
by one. (For example, if
![]() $e,f$
form a pattern with block representation
$e,f$
form a pattern with block representation
![]() $|{{\mathrm {A}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
, then
$|{{\mathrm {A}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
, then
![]() $e',f'$
form a pattern with block representation
$e',f'$
form a pattern with block representation
![]() $|{{\mathrm {A}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {A}}}|$
). This latter pattern is never r-partite, because it has at most
$|{{\mathrm {A}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {A}}}|$
). This latter pattern is never r-partite, because it has at most
![]() $r-1$
blocks.
$r-1$
blocks.
Now, let
![]() $M_3$
be the r-partite ordered r-matching given by Theorem 4.2 (with size
$M_3$
be the r-partite ordered r-matching given by Theorem 4.2 (with size
![]() $n^{2^{r-1}}$
, and whose largest clique has size n). Every pair of edges in
$n^{2^{r-1}}$
, and whose largest clique has size n). Every pair of edges in
![]() $M_3$
form an r-partite r-pattern. Then, we take M to be the blow-up
$M_3$
form an r-partite r-pattern. Then, we take M to be the blow-up
![]() $M_2[M_3]$
, which has size
$M_2[M_3]$
, which has size
![]() $n^{2^{r-1}-1}\cdot n^{2^{r-1}}=n^{2^r-1}$
. For any distinct
$n^{2^{r-1}-1}\cdot n^{2^{r-1}}=n^{2^r-1}$
. For any distinct
![]() $f_1,f_2\in E(M)$
, the edges
$f_1,f_2\in E(M)$
, the edges
![]() $f_1,f_2$
form an r-partite r-pattern if and only if
$f_1,f_2$
form an r-partite r-pattern if and only if
![]() $(f_1,f_2)$
is an
$(f_1,f_2)$
is an
![]() $M_3$
-pair. This means that for an r-pattern P, if P is r-partite, then a P-clique in M comes from some copy of
$M_3$
-pair. This means that for an r-pattern P, if P is r-partite, then a P-clique in M comes from some copy of
![]() $M_3$
and from
$M_3$
and from
![]() $M_2$
otherwise. So, the largest clique in M has size n, proving the induction step.
$M_2$
otherwise. So, the largest clique in M has size n, proving the induction step.
5 Variants on the longest increasing subsequence problem
The famous Ulam–Hammersley problem (see [Reference Romik55] for a book-length treatment) asks for the expected length of the longest monotone subsequence in a random set of n points in a box
![]() $[0,1]^{2}$
. This was generalised to higher dimensions by Steele [Reference Steele62] (and studied further by Bollobás and Winkler [Reference Bollobás and Winkler7]). In order to prove Theorem 1.10, we will need a further generalisation.
$[0,1]^{2}$
. This was generalised to higher dimensions by Steele [Reference Steele62] (and studied further by Bollobás and Winkler [Reference Bollobás and Winkler7]). In order to prove Theorem 1.10, we will need a further generalisation.
Definition 5.1. Fix a partition
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\{1,\dots ,r\}$
into disjoint parts
$\{1,\dots ,r\}$
into disjoint parts
![]() $I_{1},\dots ,I_{\ell }$
. Then, for any vectors
$I_{1},\dots ,I_{\ell }$
. Then, for any vectors
![]() $(x_{1},\dots ,x_{r}),(y_{1},\dots ,y_{r})\in \mathbb R^{r}$
, write
$(x_{1},\dots ,x_{r}),(y_{1},\dots ,y_{r})\in \mathbb R^{r}$
, write
![]() $(x_{1},\dots ,x_{r})\preceq _{\mathcal A}(y_{1},\dots ,y_{r})$
if
$(x_{1},\dots ,x_{r})\preceq _{\mathcal A}(y_{1},\dots ,y_{r})$
if
![]() $\max \left\{ x_{i}:i\in I_{j}\right\} \le \min \left\{ y_{i}:i\in I_{j}\right\} $
for all
$\max \left\{ x_{i}:i\in I_{j}\right\} \le \min \left\{ y_{i}:i\in I_{j}\right\} $
for all
![]() $j\in \{1,\dots ,\ell \}$
. Note that
$j\in \{1,\dots ,\ell \}$
. Note that
![]() $\preceq _{\mathcal A}$
is a partial order on
$\preceq _{\mathcal A}$
is a partial order on
![]() $\mathbb R^{r}$
.
$\mathbb R^{r}$
.
For a set of points
![]() $\mathcal {S}\subseteq \mathbb R^{d}$
, write
$\mathcal {S}\subseteq \mathbb R^{d}$
, write
![]() $L_{\mathcal {A}}(\mathcal {S})$
for the longest chain in
$L_{\mathcal {A}}(\mathcal {S})$
for the longest chain in
![]() $\mathcal {S}$
with respect to
$\mathcal {S}$
with respect to
![]() $\preceq _{\mathcal A}$
.
$\preceq _{\mathcal A}$
.
We will be interested in
![]() $L_{\mathcal {A}}(\mathcal {S}_{n})$
, for a set
$L_{\mathcal {A}}(\mathcal {S}_{n})$
, for a set
![]() $\mathcal {S}_{n}$
of n independent uniformly random points in
$\mathcal {S}_{n}$
of n independent uniformly random points in
![]() $[0,1]^{r}$
.
$[0,1]^{r}$
.
Theorem 5.2. Fix a partition
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\{1,\dots ,r\}$
. For
$\{1,\dots ,r\}$
. For
![]() $m\in \mathbb N$
, let
$m\in \mathbb N$
, let
![]() $\mathcal {T}_{m}\subseteq [0,m]^{r}$
be a set of points obtained by a Poisson process of rate 1 in
$\mathcal {T}_{m}\subseteq [0,m]^{r}$
be a set of points obtained by a Poisson process of rate 1 in
![]() $[0,m]^{r}$
, and let
$[0,m]^{r}$
, and let
![]() $L=L_{\mathcal A}(\mathcal {T}_{m})$
. Then, as
$L=L_{\mathcal A}(\mathcal {T}_{m})$
. Then, as
![]() $m\to \infty $
,
$m\to \infty $
,
-
1.
 ${\displaystyle {\displaystyle \frac {{\mathbb E} L}{m}\to a_{\mathcal {A}}}}$
, and
${\displaystyle {\displaystyle \frac {{\mathbb E} L}{m}\to a_{\mathcal {A}}}}$
, and -
2.
 ${\displaystyle \frac {L}{m} \overset {p}{\to }a_{\mathcal {A}}}$
,
${\displaystyle \frac {L}{m} \overset {p}{\to }a_{\mathcal {A}}}$
,
for some
![]() $a_{\mathcal {A}}>0$
only depending on
$a_{\mathcal {A}}>0$
only depending on
![]() $\mathcal {A}$
. (By symmetry, in fact
$\mathcal {A}$
. (By symmetry, in fact
![]() $a_{\mathcal {A}}$
only depends on the multiset of sizes of the parts in
$a_{\mathcal {A}}$
only depends on the multiset of sizes of the parts in
![]() $\mathcal {A}$
).
$\mathcal {A}$
).
Proof. Let
![]() $\mathcal {T}\subseteq \mathbb R^{r}$
be a Poisson process with rate 1 in
$\mathcal {T}\subseteq \mathbb R^{r}$
be a Poisson process with rate 1 in
![]() $\mathbb R^{r}$
. Let
$\mathbb R^{r}$
. Let
![]() $L_{m,n}=L(\mathcal {T}\cap [m,n]^{r})$
be the longest chain in
$L_{m,n}=L(\mathcal {T}\cap [m,n]^{r})$
be the longest chain in
![]() $\mathcal {T}\cap [m,n]^{r}$
with respect to
$\mathcal {T}\cap [m,n]^{r}$
with respect to
![]() $\mathcal {P}(\mathcal A)$
. Noting that
$\mathcal {P}(\mathcal A)$
. Noting that
![]() $\mathcal {T}\cap [0,m]^{r}\overset {d}{=}\mathcal {T}_{m}$
, it suffices to prove that the conditions of Kingman’s subadditive ergodic theorem (Theorem 2.6) are satisfied, as follows.
$\mathcal {T}\cap [0,m]^{r}\overset {d}{=}\mathcal {T}_{m}$
, it suffices to prove that the conditions of Kingman’s subadditive ergodic theorem (Theorem 2.6) are satisfied, as follows.
-
○ For
 $0\le m\le n$
, we have
$0\le m\le n$
, we have
 $L_{0,n}\ge L_{0,m}+L_{m,n}$
, because if we have a chain in
$L_{0,n}\ge L_{0,m}+L_{m,n}$
, because if we have a chain in
 $\mathcal {T}\cap [0,m]^{r}$
and a chain in
$\mathcal {T}\cap [0,m]^{r}$
and a chain in
 $\mathcal {T}\cap [m,n]^{r}$
, their union is always a chain in
$\mathcal {T}\cap [m,n]^{r}$
, their union is always a chain in
 $\mathcal {T}\cap [0,n]^{r}$
.
$\mathcal {T}\cap [0,n]^{r}$
. -
○ For any
 $k\ge 1$
,
$k\ge 1$
,
 $(L_{nk,(n+1)k})_{n=0}^{\infty }$
is a sequence of i.i.d. random variables.
$(L_{nk,(n+1)k})_{n=0}^{\infty }$
is a sequence of i.i.d. random variables. -
○ For any
 $m\ge 1$
, we have
$m\ge 1$
, we have
 $(L_{0,k})_{k=0}^{\infty }\overset {d}{=}(L_{m,m+k})_{k=0}^{\infty }$
.
$(L_{0,k})_{k=0}^{\infty }\overset {d}{=}(L_{m,m+k})_{k=0}^{\infty }$
. -
○ There exists a constant
 $M> 0$
such that
$M> 0$
such that
 $\mathbb {E}L_{0,m} \le Mm$
for all m. To see this, we first note that if
$\mathbb {E}L_{0,m} \le Mm$
for all m. To see this, we first note that if
 $\mathcal {S}_N$
is a set of N independent uniformly random points in
$\mathcal {S}_N$
is a set of N independent uniformly random points in
 $[0,m]^{r}$
, then we have
$[0,m]^{r}$
, then we have
 ${\mathbb E} L_{\mathcal {A}}(\mathcal {S}_N)\le {\mathbb E} L_{\mathcal {BW}}(\mathcal {S}_N)$
, where
${\mathbb E} L_{\mathcal {A}}(\mathcal {S}_N)\le {\mathbb E} L_{\mathcal {BW}}(\mathcal {S}_N)$
, where
 $\mathcal {BW}$
is the partition of
$\mathcal {BW}$
is the partition of
 $\{1,\dots ,r\}$
into r singleton sets. Bollobás and Winkler [Reference Bollobás and Winkler7] proved that
$\{1,\dots ,r\}$
into r singleton sets. Bollobás and Winkler [Reference Bollobás and Winkler7] proved that
 ${\mathbb E} L_{\mathcal {BW}}(\mathcal {S}_N)\le (1+o(1))eN^{1/r}$
, so where the last equation holds as
${\mathbb E} L_{\mathcal {BW}}(\mathcal {S}_N)\le (1+o(1))eN^{1/r}$
, so where the last equation holds as $$ \begin{align*} {\mathbb E} L_{0,m}&={\mathbb E} L_{\mathcal{A}}(\mathcal{T}_{m})={\mathbb E}\left[{\mathbb E}\left[\vphantom{\sum}L_{\mathcal{A}}(\mathcal{T}_{m})\,\middle|\,|\mathcal{T}_{m}|\right]\right]={\mathbb E}\left[{\mathbb E}\left[\vphantom{\sum}L_{\mathcal{A}}(\mathcal{S}_{|\mathcal{T}_{m}|})\,\middle|\,|\mathcal{T}_{m}|\right]\right]\\ &\le{\mathbb E}\left[\vphantom{\sum}(1+o(1))e\,|\mathcal{T}_{m}|^{1/r}\right]=(1+o(1))em, \end{align*} $$
$$ \begin{align*} {\mathbb E} L_{0,m}&={\mathbb E} L_{\mathcal{A}}(\mathcal{T}_{m})={\mathbb E}\left[{\mathbb E}\left[\vphantom{\sum}L_{\mathcal{A}}(\mathcal{T}_{m})\,\middle|\,|\mathcal{T}_{m}|\right]\right]={\mathbb E}\left[{\mathbb E}\left[\vphantom{\sum}L_{\mathcal{A}}(\mathcal{S}_{|\mathcal{T}_{m}|})\,\middle|\,|\mathcal{T}_{m}|\right]\right]\\ &\le{\mathbb E}\left[\vphantom{\sum}(1+o(1))e\,|\mathcal{T}_{m}|^{1/r}\right]=(1+o(1))em, \end{align*} $$
 $\left\vert {\mathcal {T}_m}\right\vert $
has distribution
$\left\vert {\mathcal {T}_m}\right\vert $
has distribution
 $\operatorname {Poisson}(m^r)$
.
$\operatorname {Poisson}(m^r)$
.
Theorem 5.3. Fix a partition
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\{1,\dots ,r\}$
. Consider a set
$\{1,\dots ,r\}$
. Consider a set
![]() $\mathcal {S}_{n}$
of n independent uniformly random points in
$\mathcal {S}_{n}$
of n independent uniformly random points in
![]() $[0,1]^{r}$
, and let
$[0,1]^{r}$
, and let
![]() $L=L_{\mathcal {A}}(\mathcal {S}_{n})$
. Let
$L=L_{\mathcal {A}}(\mathcal {S}_{n})$
. Let
![]() $a_{\mathcal {A}}$
be as in Theorem 5.2. Then, the following hold.
$a_{\mathcal {A}}$
be as in Theorem 5.2. Then, the following hold.
-
1.
 ${\displaystyle \Pr [|L-{\mathbb E} L|\ge t]\le 4\exp \left(-\frac {\gamma t^{2}}{{\mathbb E} L+t}\right)}$
for some universal constant
${\displaystyle \Pr [|L-{\mathbb E} L|\ge t]\le 4\exp \left(-\frac {\gamma t^{2}}{{\mathbb E} L+t}\right)}$
for some universal constant
 $\gamma>0$
.
$\gamma>0$
. -
2.
 ${\displaystyle \frac {L}{n^{1/r}}\overset {p}{\to }a_{\mathcal {A}}}$
.
${\displaystyle \frac {L}{n^{1/r}}\overset {p}{\to }a_{\mathcal {A}}}$
. -
3.
 ${\displaystyle \frac {{\mathbb E} L}{n^{1/r}}\to a_{\mathcal {A}}}$
.
${\displaystyle \frac {{\mathbb E} L}{n^{1/r}}\to a_{\mathcal {A}}}$
.
Proof. First, (1) follows directly from Talagrand’s inequality (Theorem 2.5):
-
○ If we change a single point of
 $\mathcal {S}_n$
, we change L by at most 1.
$\mathcal {S}_n$
, we change L by at most 1. -
○ Whenever
 $L\ge r$
then there is a set of r points which certifies that
$L\ge r$
then there is a set of r points which certifies that
 $L\ge r$
.
$L\ge r$
.
Then, for (2), recall the random set
![]() $\mathcal {T}_{m}$
from Theorem 5.2. Note that
$\mathcal {T}_{m}$
from Theorem 5.2. Note that
![]() $|\mathcal {T}_{m}|$
has a
$|\mathcal {T}_{m}|$
has a
![]() $\operatorname {Poisson}(m^{r})$
distribution, so by Chebyshev’s inequality we can choose
$\operatorname {Poisson}(m^{r})$
distribution, so by Chebyshev’s inequality we can choose
![]() $m_{1},m_{2}\in \mathbb N$
, both of the form
$m_{1},m_{2}\in \mathbb N$
, both of the form
![]() $(1+o(1))n^{1/r}$
such that
$(1+o(1))n^{1/r}$
such that
![]() $|\mathcal {T}_{m_{1}}|\le n$
whp and
$|\mathcal {T}_{m_{1}}|\le n$
whp and
![]() $n\le |\mathcal {T}_{m_{2}}|$
whp.
$n\le |\mathcal {T}_{m_{2}}|$
whp.
Note that if we condition on
![]() $|\mathcal {T}_{m}|$
, then
$|\mathcal {T}_{m}|$
, then
![]() $\mathcal {T}_{m}$
is conditionally a set of that many independent uniformly random points in
$\mathcal {T}_{m}$
is conditionally a set of that many independent uniformly random points in
![]() $[0,m]^{r}$
(which is equivalent to taking random points in
$[0,m]^{r}$
(which is equivalent to taking random points in
![]() $[0,1]^{r}$
and rescaling them by a factor of m). So, there is a coupling of
$[0,1]^{r}$
and rescaling them by a factor of m). So, there is a coupling of
![]() $\mathcal {S}_{n},\mathcal {T}_{m_{1}},\mathcal {T}_{m_{2}}$
for which
$\mathcal {S}_{n},\mathcal {T}_{m_{1}},\mathcal {T}_{m_{2}}$
for which
![]() $L(\mathcal {T}_{m_{1}})\le L\le L(\mathcal {T}_{m_{2}})$
whp. Then, (2) follows from Theorem 5.2(2).
$L(\mathcal {T}_{m_{1}})\le L\le L(\mathcal {T}_{m_{2}})$
whp. Then, (2) follows from Theorem 5.2(2).
Finally, (3) follows from (1) and (2).
Proposition 5.4. Fix a partition
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\{1,\dots ,r\}$
, and define the constant
$\{1,\dots ,r\}$
, and define the constant
![]() $a_{\mathcal A}$
as in Theorem 5.2.
$a_{\mathcal A}$
as in Theorem 5.2.
-
1. If
 $\mathcal A$
has a single part of size r, then we have
$\mathcal A$
has a single part of size r, then we have
 ${\displaystyle a_{\mathcal A}=\frac {r}{\Gamma (1/r)}}$
${\displaystyle a_{\mathcal A}=\frac {r}{\Gamma (1/r)}}$
-
2. If
 $\mathcal A$
has r parts of size
$\mathcal A$
has r parts of size
 $1$
, then we have
$1$
, then we have
 ${\displaystyle a_{\mathcal A}>\frac {r^{2}}{(r!)^{1/r}\Gamma (1/r)}}$
.
${\displaystyle a_{\mathcal A}>\frac {r^{2}}{(r!)^{1/r}\Gamma (1/r)}}$
.
Proof. For (1), we use the algorithmic approach of Justicz, Scheinerman and Winkler [Reference Justicz, Scheinerman and Winkler41]: We can build a longest chain
![]() $\vec {x}^{(1)},\vec {x}^{(2)},\dots ,\vec {x}^{(L)}$
by first taking the point
$\vec {x}^{(1)},\vec {x}^{(2)},\dots ,\vec {x}^{(L)}$
by first taking the point
![]() $\vec {x}^{(1)}=(x_{1}^{(1)},\dots ,x_{r}^{(1)})\in \mathcal {T}_{m}$
with the smallest value of
$\vec {x}^{(1)}=(x_{1}^{(1)},\dots ,x_{r}^{(1)})\in \mathcal {T}_{m}$
with the smallest value of
![]() $\max _{i}x_{i}^{(1)}$
, then throwing out all other points
$\max _{i}x_{i}^{(1)}$
, then throwing out all other points
![]() $\vec {y}\in \mathcal {T}_{m}$
which do not satisfy
$\vec {y}\in \mathcal {T}_{m}$
which do not satisfy
![]() $\vec {x}\preceq \vec {y}$
, and taking the point
$\vec {x}\preceq \vec {y}$
, and taking the point
![]() $\vec {x}^{(2)}=(x_{1}^{(2)},\dots ,x_{r}^{(2)})$
with the next smallest value of
$\vec {x}^{(2)}=(x_{1}^{(2)},\dots ,x_{r}^{(2)})$
with the next smallest value of
![]() $\max _{i}x_{i}^{(2)}$
, and so on.
$\max _{i}x_{i}^{(2)}$
, and so on.
If we let
![]() $\mathcal {T}$
be the set of points corresponding to a Poisson process of rate 1 in the semi-infinite box
$\mathcal {T}$
be the set of points corresponding to a Poisson process of rate 1 in the semi-infinite box
![]() $[0,\infty )^{r}$
(instead of a finite box
$[0,\infty )^{r}$
(instead of a finite box
![]() $[0,m)^{r}$
), then we obtain an infinite sequence of points
$[0,m)^{r}$
), then we obtain an infinite sequence of points
![]() $(\vec {x}^{(k)})_{k=1}^{\infty }$
as above. Then,
$(\vec {x}^{(k)})_{k=1}^{\infty }$
as above. Then,
![]() $(\vec {x}^{(k)})_{k=1}^{\infty }$
has the following two properties. First, for every
$(\vec {x}^{(k)})_{k=1}^{\infty }$
has the following two properties. First, for every
![]() $j\geq 1$
the sequence of points
$j\geq 1$
the sequence of points
![]() $\vec {x}^{(1)},\vec {x}^{(2)},\dots ,\vec {x}^{(j)}$
is a longest chain of points in
$\vec {x}^{(1)},\vec {x}^{(2)},\dots ,\vec {x}^{(j)}$
is a longest chain of points in
![]() $\mathcal {T} \cap [0,\max _i x_i^{(j)}]^r$
, and second, the increments
$\mathcal {T} \cap [0,\max _i x_i^{(j)}]^r$
, and second, the increments
![]() $\max _{i}x_{i}^{(k+1)}-\max _{i}x_{i}^{(k)}$
are independent and identically distributed (let Z be a random variable with this common distribution). We have
$\max _{i}x_{i}^{(k+1)}-\max _{i}x_{i}^{(k)}$
are independent and identically distributed (let Z be a random variable with this common distribution). We have
![]() $\Pr [Z> z]=\Pr [\mathcal {T}\cap [0,z]^{r}=\emptyset ]=\exp (-z^{r})$
so the density of Z is
$\Pr [Z> z]=\Pr [\mathcal {T}\cap [0,z]^{r}=\emptyset ]=\exp (-z^{r})$
so the density of Z is
and
So, for any
![]() $\varepsilon>0$
, taking
$\varepsilon>0$
, taking
![]() $L_{1}\le (r/\Gamma (1/r)-\varepsilon )m$
and
$L_{1}\le (r/\Gamma (1/r)-\varepsilon )m$
and
![]() $L_{2}\ge (r/\Gamma (1/r)+\varepsilon )m$
, we have
$L_{2}\ge (r/\Gamma (1/r)+\varepsilon )m$
, we have
![]() $\max _{i}x_{i}^{(L_{1})}\le m\le \max _{i}x_{i}^{(L_{2})}$
whp, by the law of large numbers. Since
$\max _{i}x_{i}^{(L_{1})}\le m\le \max _{i}x_{i}^{(L_{2})}$
whp, by the law of large numbers. Since
![]() $\varepsilon $
was arbitrary, it follows that whp
$\varepsilon $
was arbitrary, it follows that whp
![]() $L=(r/\Gamma (1/r)-o(1))m$
; that is,
$L=(r/\Gamma (1/r)-o(1))m$
; that is,
![]() $a=r/\Gamma (1/r)$
.
$a=r/\Gamma (1/r)$
.
For (2), we recall the algorithmic lower bound of Bollobás and Winkler [Reference Bollobás and Winkler7]. They build a chain
![]() $\vec {x}^{(1)},\vec {x}^{(2)},\dots ,\vec {x}^{(Q)}$
by first taking the point
$\vec {x}^{(1)},\vec {x}^{(2)},\dots ,\vec {x}^{(Q)}$
by first taking the point
![]() $\vec {x}^{(1)}=(x_{1}^{(1)},\dots ,x_{r}^{(1)})\in \mathcal {T}_{m}$
such that
$\vec {x}^{(1)}=(x_{1}^{(1)},\dots ,x_{r}^{(1)})\in \mathcal {T}_{m}$
such that
![]() $\sum _{i}x_{i}^{(1)}$
is minimal, then throwing out all other points
$\sum _{i}x_{i}^{(1)}$
is minimal, then throwing out all other points
![]() $\vec {y}\in \mathcal {T}_{m}$
which do not satisfy
$\vec {y}\in \mathcal {T}_{m}$
which do not satisfy
![]() $\vec {x}\preceq \vec {y}$
and taking the point
$\vec {x}\preceq \vec {y}$
and taking the point
![]() $\vec {x}^{(2)}=(x_{1}^{(2)},\dots ,x_{r}^{(2)})$
with the next smallest value of
$\vec {x}^{(2)}=(x_{1}^{(2)},\dots ,x_{r}^{(2)})$
with the next smallest value of
![]() $\sum _{i}x_{i}^{(2)}$
, and so on. It is proved in [Reference Bollobás and Winkler7], by a very similar method as above, that this algorithm produces a chain of length
$\sum _{i}x_{i}^{(2)}$
, and so on. It is proved in [Reference Bollobás and Winkler7], by a very similar method as above, that this algorithm produces a chain of length
![]() $r^{2}/(r!)^{1/r}\Gamma (1/r)$
.
$r^{2}/(r!)^{1/r}\Gamma (1/r)$
.
We then just need to observe that this algorithm is not optimal: For example, instead of finding our chain point-by-point, we can build our chain two points at a time, at step k choosing two points
![]() $\vec {x}^{(2k-1)},\vec {x}^{(2k)}$
such that
$\vec {x}^{(2k-1)},\vec {x}^{(2k)}$
such that
![]() $\vec {x}^{(2k-1)}\preceq \vec {x}^{(2k)}$
and such that
$\vec {x}^{(2k-1)}\preceq \vec {x}^{(2k)}$
and such that
![]() $\max \left(\sum _{i}x_{i}^{(2k-1)},\sum _{i}x_{i}^{(2k)}\right)$
is minimized. It is not hard to see that the expected ‘distance travelled’ in one such step is strictly less than two times the distance travelled in a step of the Bollobás–Winkler algorithm.
$\max \left(\sum _{i}x_{i}^{(2k-1)},\sum _{i}x_{i}^{(2k)}\right)$
is minimized. It is not hard to see that the expected ‘distance travelled’ in one such step is strictly less than two times the distance travelled in a step of the Bollobás–Winkler algorithm.
6 Cliques in random ordered matchings
In this section, we prove Theorem 1.10 and Proposition 1.11, using the results in Section 5. To give a brief overview, the key insight is that every P-clique in an ordered matching M can be interpreted as a chain in a certain point set (defined in terms of a partition of the vertices of M), with respect to a certain partial order
![]() $\preceq _{\mathcal A}$
(as in Definition 5.1). Taking advantage of the strong concentration in Theorem 5.3(1), we can take the union bound over all appropriate vertex partitions of a random matching M, giving us control over the longest chains in the corresponding point sets.
$\preceq _{\mathcal A}$
(as in Definition 5.1). Taking advantage of the strong concentration in Theorem 5.3(1), we can take the union bound over all appropriate vertex partitions of a random matching M, giving us control over the longest chains in the corresponding point sets.
Proof of Theorem 1.10
Suppose P has block partition given by
![]() $J_{1}\cup \dots \cup J_{\ell }=\{1,\dots ,2r\}$
. Let
$J_{1}\cup \dots \cup J_{\ell }=\{1,\dots ,2r\}$
. Let
![]() $\mathcal {A}$
be the partition of
$\mathcal {A}$
be the partition of
![]() $\{1,\dots ,r\}$
with parts
$\{1,\dots ,r\}$
with parts
![]() $I_{i}=\{j:2j\in J_{i}\}$
for
$I_{i}=\{j:2j\in J_{i}\}$
for
![]() $1\le i\le \ell $
. Note that one can uniquely recover
$1\le i\le \ell $
. Note that one can uniquely recover
![]() $I_{1},\dots ,I_{\ell }$
from
$I_{1},\dots ,I_{\ell }$
from
![]() $J_{1},\dots ,J_{\ell }$
; we have
$J_{1},\dots ,J_{\ell }$
; we have
![]() $J_i=\bigcup _{j\in I_i}\{2j-1,2j\}$
for all
$J_i=\bigcup _{j\in I_i}\{2j-1,2j\}$
for all
![]() $i\le \ell $
.
$i\le \ell $
.
Observe that for every P-clique C in M, there is some partition
![]() $Q_{1}\cup \dots \cup Q_{\ell }$
of
$Q_{1}\cup \dots \cup Q_{\ell }$
of
![]() $V(M)=\{1,\dots ,rn\}$
into contiguous intervals such that for every edge
$V(M)=\{1,\dots ,rn\}$
into contiguous intervals such that for every edge
![]() $e\in C$
and every
$e\in C$
and every
![]() $i\in \{1,\dots ,\ell \}$
, we have
$i\in \{1,\dots ,\ell \}$
, we have
![]() $|e\cap Q_{i}|=|I_{i}|$
. Say that C is consistent with
$|e\cap Q_{i}|=|I_{i}|$
. Say that C is consistent with
![]() $Q_{1},\dots ,Q_{\ell }$
if this is the case.
$Q_{1},\dots ,Q_{\ell }$
if this is the case.
Fix a partition
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $\{1,\dots ,rn\}$
into contiguous intervals
$\{1,\dots ,rn\}$
into contiguous intervals
![]() $Q_{1},\dots ,Q_{\ell }$
; we will only consider cliques consistent with
$Q_{1},\dots ,Q_{\ell }$
; we will only consider cliques consistent with
![]() $\mathcal {B}$
(at the end we will take a union bound over all partitions).
$\mathcal {B}$
(at the end we will take a union bound over all partitions).
Let
![]() $M_{\mathcal {B}}$
be the submatching of M containing the edges of M which are consistent with
$M_{\mathcal {B}}$
be the submatching of M containing the edges of M which are consistent with
![]() $\mathcal {B}$
. Condition on some outcome N for the number of edges in
$\mathcal {B}$
. Condition on some outcome N for the number of edges in
![]() $M_{\mathcal {B}}$
.
$M_{\mathcal {B}}$
.
We will realise the conditional distribution of
![]() $M_{\mathcal {B}}$
via an alternative construction, as follows.
$M_{\mathcal {B}}$
via an alternative construction, as follows.
-
1. Let
 $V=[0,\ell ]\subseteq \mathbb R$
, and for each
$V=[0,\ell ]\subseteq \mathbb R$
, and for each
 $i\in \{1,\dots ,\ell \}$
, let
$i\in \{1,\dots ,\ell \}$
, let
 $V_{i}=[i-1,i]$
, so
$V_{i}=[i-1,i]$
, so
 $V_{1}\cup \dots \cup V_{\ell }=[0,\ell ]$
.
$V_{1}\cup \dots \cup V_{\ell }=[0,\ell ]$
. -
2. For each
 $j\in \{1,\dots ,r\}$
, let
$j\in \{1,\dots ,r\}$
, let
 $i(j)$
be such that
$i(j)$
be such that
 $j\in I_{i(j)}$
.
$j\in I_{i(j)}$
. -
3. Let
 $\mathcal {R}$
be a set of N independent uniformly random points in
$\mathcal {R}$
be a set of N independent uniformly random points in
 $\prod _{j=1}^{r}V_{i(j)}$
.
$\prod _{j=1}^{r}V_{i(j)}$
. -
4. For each
 $\vec {v}\in \mathcal {R}$
, let
$\vec {v}\in \mathcal {R}$
, let
 $e(\vec {v})$
be the set of coordinates of
$e(\vec {v})$
be the set of coordinates of
 $\vec {v}$
(so
$\vec {v}$
(so
 $|e(\vec {v})\cap V_{i}|=|I_{i}|$
for each i).
$|e(\vec {v})\cap V_{i}|=|I_{i}|$
for each i). -
5. Let
 $M^{*}$
be the hypergraph on the vertex set
$M^{*}$
be the hypergraph on the vertex set
 $\bigcup _{\vec {v}\in \mathcal {R}}e(\vec {v})$
whose edges are the sets
$\bigcup _{\vec {v}\in \mathcal {R}}e(\vec {v})$
whose edges are the sets
 $e(\vec {v})$
for
$e(\vec {v})$
for
 $\vec {v}\in \mathcal {R}$
.
$\vec {v}\in \mathcal {R}$
.
Note that with probability 1,
![]() $M^{*}$
is a matching, and the distribution of (the order-isomorphism class of)
$M^{*}$
is a matching, and the distribution of (the order-isomorphism class of)
![]() $M^{*}$
is the same as the conditional distribution of (the order-isomorphism class of)
$M^{*}$
is the same as the conditional distribution of (the order-isomorphism class of)
![]() $M_{\mathcal {B}}$
, by symmetry.
$M_{\mathcal {B}}$
, by symmetry.
Our next goal is to realise the distribution of our random point set
![]() $\mathcal {R}\subseteq \prod _{j=1}^{r}V_{i(j)}$
in terms of a set
$\mathcal {R}\subseteq \prod _{j=1}^{r}V_{i(j)}$
in terms of a set
![]() $\mathcal {S}_{N}$
of N independent uniformly random points in
$\mathcal {S}_{N}$
of N independent uniformly random points in
![]() $[0,1]^{r}$
, in such a way that the size of the largest P-clique
$[0,1]^{r}$
, in such a way that the size of the largest P-clique
![]() $L_{P}(M^{*})$
in
$L_{P}(M^{*})$
in
![]() $M^{*}$
corresponds precisely to the length of the longest chain
$M^{*}$
corresponds precisely to the length of the longest chain
![]() $L_{\mathcal A}(\mathcal {S}_{N})$
in
$L_{\mathcal A}(\mathcal {S}_{N})$
in
![]() $\mathcal {S}_{N}$
with respect to the partial order
$\mathcal {S}_{N}$
with respect to the partial order
![]() $\preceq {P}_{\mathcal A}$
defined in Definition 5.1.
$\preceq {P}_{\mathcal A}$
defined in Definition 5.1.
Recall that in the block representation (Definition 1.5) of P, the incident vertices of one edge are assigned with label ‘
![]() ${\mathrm {A}}$
’ while those of the other edge are assigned with label ‘
${\mathrm {A}}$
’ while those of the other edge are assigned with label ‘
![]() ${\mathrm {B}}$
’. Now, consider an isometry
${\mathrm {B}}$
’. Now, consider an isometry
![]() $\phi :[0,1]^{r}\to \prod _{j=1}^{r}V_{i(j)}$
defined as follows.
$\phi :[0,1]^{r}\to \prod _{j=1}^{r}V_{i(j)}$
defined as follows.
-
1. For each
 $i\in \{1,\dots ,r\}$
, define the function
$i\in \{1,\dots ,r\}$
, define the function
 $\sigma _i:\mathbb R\to \mathbb R$
by taking
$\sigma _i:\mathbb R\to \mathbb R$
by taking
 $\sigma _{i}(x)=x$
if the block
$\sigma _{i}(x)=x$
if the block
 $I_{i}$
consists of an
$I_{i}$
consists of an
 ${\mathrm {A}}$
-run followed by a
${\mathrm {A}}$
-run followed by a
 ${\mathrm {B}}$
-run, and taking
${\mathrm {B}}$
-run, and taking
 $\sigma _{i}(x)=1-x$
if the block
$\sigma _{i}(x)=1-x$
if the block
 $I_{i}$
consists of a
$I_{i}$
consists of a
 ${\mathrm {B}}$
-run followed by an
${\mathrm {B}}$
-run followed by an
 ${\mathrm {A}}$
-run.
${\mathrm {A}}$
-run. -
2. Let
 $\phi _0:[0,1]^{r}\to [0,1]^{r}$
be the isometry
$\phi _0:[0,1]^{r}\to [0,1]^{r}$
be the isometry
 $(x_{1},\dots ,x_{r})\mapsto (\sigma _{1}(x_{1}),\dots ,\sigma _{r}(x_{r}))$
.
$(x_{1},\dots ,x_{r})\mapsto (\sigma _{1}(x_{1}),\dots ,\sigma _{r}(x_{r}))$
. -
3. Let
 $\vec {t}$
be such that
$\vec {t}$
be such that
 $[0,1]^r+\vec {t}=\prod _{j=1}^{r}V_{i(j)}$
, and let
$[0,1]^r+\vec {t}=\prod _{j=1}^{r}V_{i(j)}$
, and let
 $\phi _{1}:[0,1]^r\to \prod _{j=1}^{r}V_{i(j)}$
be the translation
$\phi _{1}:[0,1]^r\to \prod _{j=1}^{r}V_{i(j)}$
be the translation
 $\vec {x}\mapsto \vec {x}+\vec {t}$
.
$\vec {x}\mapsto \vec {x}+\vec {t}$
. -
4. Let
 $\phi =\phi _{1}\circ \phi _{0}$
.
$\phi =\phi _{1}\circ \phi _{0}$
.
It is easy to check that
![]() $L_{P}(M^{*})=L_{I_{1},\dots ,I_{\ell }}(\mathcal {S}_{N})$
. So, still conditioning on an outcome
$L_{P}(M^{*})=L_{I_{1},\dots ,I_{\ell }}(\mathcal {S}_{N})$
. So, still conditioning on an outcome
![]() $|M_{\mathcal B}|=N$
, by Theorem 5.3, with conditional probability
$|M_{\mathcal B}|=N$
, by Theorem 5.3, with conditional probability
![]() $1-N^{-\omega (1)}$
we have that the random variable
$1-N^{-\omega (1)}$
we have that the random variable
![]() $L_{P}(M_{\mathcal B})$
is of the form
$L_{P}(M_{\mathcal B})$
is of the form
![]() $(a_{\mathcal {A}}+o(1))N^{1/r}$
.
$(a_{\mathcal {A}}+o(1))N^{1/r}$
.
Also, by the concentration inequality Theorem 2.3 (see Remark 2.4), with probability at least
![]() $1-n^{-\omega (1)}$
we have
$1-n^{-\omega (1)}$
we have
 $$\begin{align*}|M_{\mathcal B}|=\left(f_{P}\left(\frac{|Q_{1}|}{rn},\dots,\frac{|Q_{\ell}|}{rn}\right)+o(1)\right)n, \end{align*}$$
$$\begin{align*}|M_{\mathcal B}|=\left(f_{P}\left(\frac{|Q_{1}|}{rn},\dots,\frac{|Q_{\ell}|}{rn}\right)+o(1)\right)n, \end{align*}$$
where
![]() $f_{P}(q_{1},\dots ,q_{\ell })$
is the probability that for a set of r independent uniformly random points in
$f_{P}(q_{1},\dots ,q_{\ell })$
is the probability that for a set of r independent uniformly random points in
![]() $[0,1]$
, exactly
$[0,1]$
, exactly
![]() $I_{i}$
of them fall between
$I_{i}$
of them fall between
![]() $q_{i-1}$
and
$q_{i-1}$
and
![]() $q_{i-1}+q_{i}$
(here, we take
$q_{i-1}+q_{i}$
(here, we take
![]() $q_{0}=0$
for convenience). Note that
$q_{0}=0$
for convenience). Note that
![]() $f_{P}(q_{1},\dots ,q_{\ell })$
is a homogeneous polynomial of degree r in the variables
$f_{P}(q_{1},\dots ,q_{\ell })$
is a homogeneous polynomial of degree r in the variables
![]() $q_{1},\dots ,q_{\ell }$
.
$q_{1},\dots ,q_{\ell }$
.
Let
![]() $\alpha _{P}$
be the maximum value of
$\alpha _{P}$
be the maximum value of
![]() $f_{P}(q_{1},\dots ,q_{\ell })$
over all
$f_{P}(q_{1},\dots ,q_{\ell })$
over all
![]() $q_{1},\dots ,q_{\ell }\ge 0$
summing to 1. Then, taking a union bound over all possible partitions
$q_{1},\dots ,q_{\ell }\ge 0$
summing to 1. Then, taking a union bound over all possible partitions
![]() $\mathcal {B}$
(of which there are at most
$\mathcal {B}$
(of which there are at most
![]() $n^{\ell -1}$
), we see that
$n^{\ell -1}$
), we see that
So, the desired result follows with
![]() $b_{P}=a_{\mathcal {A}}\alpha _{P}^{1/r}$
.
$b_{P}=a_{\mathcal {A}}\alpha _{P}^{1/r}$
.
Proof of Proposition 1.11
Recall the definitions of
![]() $f_{P}$
and
$f_{P}$
and
![]() $\alpha _{P}$
from the proof of Theorem 1.10, and recall the estimates in that proof.
$\alpha _{P}$
from the proof of Theorem 1.10, and recall the estimates in that proof.
-
1. Suppose P has type r. As in the proof of Theorem 1.10, let
 $\mathcal A$
be the trivial partition of
$\mathcal A$
be the trivial partition of
 $\{1,\dots ,r\}$
into one part. Note that
$\{1,\dots ,r\}$
into one part. Note that
 $\alpha _{P}=f_P(1)=1$
, and by Proposition 5.4,
$\alpha _{P}=f_P(1)=1$
, and by Proposition 5.4,
 $a_{\mathcal A}=r/\Gamma (1/r)=1/\Gamma ((r+1)/r)$
. So,
$a_{\mathcal A}=r/\Gamma (1/r)=1/\Gamma ((r+1)/r)$
. So,
 $b_P=a_{\mathcal A}\alpha _P^{1/r}=1/\Gamma ((r+1)/r)$
.
$b_P=a_{\mathcal A}\alpha _P^{1/r}=1/\Gamma ((r+1)/r)$
. -
2. Suppose P has type
 $1+\dots +1$
. As in the proof of Theorem 1.10, let
$1+\dots +1$
. As in the proof of Theorem 1.10, let
 $\mathcal A$
be the partition of
$\mathcal A$
be the partition of
 $\{1,\dots ,r\}$
into r singleton parts. Note that
$\{1,\dots ,r\}$
into r singleton parts. Note that
 $\alpha _{P}=f_{P}(1/r,\dots ,1/r)=r!/r^{r}$
, and note that
$\alpha _{P}=f_{P}(1/r,\dots ,1/r)=r!/r^{r}$
, and note that
 $a_{\mathcal A}$
is precisely the Bollobás–Winkler constant
$a_{\mathcal A}$
is precisely the Bollobás–Winkler constant
 $c_r$
, which by Proposition 5.4 is strictly larger than
$c_r$
, which by Proposition 5.4 is strictly larger than
 $\frac {r^{2}}{(r!)^{1/r}\Gamma (1/r)}$
. Therefore, we have
$\frac {r^{2}}{(r!)^{1/r}\Gamma (1/r)}$
. Therefore, we have
 $b_P=c_r(r!/r^{r})^{1/r}=c_r(r!)^{1/r}/r>r/\Gamma (1/r)=1/\Gamma ((r+1)/r)$
.
$b_P=c_r(r!/r^{r})^{1/r}=c_r(r!)^{1/r}/r>r/\Gamma (1/r)=1/\Gamma ((r+1)/r)$
.
7 Enumeration
In this section, we estimate
![]() $N_{P,m}(n)$
up to an exponential factor, proving Theorem 1.15 and therefore Theorem 1.13. The upper bound and the lower bound in Theorem 1.15 are proved separately. Despite Theorem 1.15 being about ordered matchings, both the upper and lower bound require the consideration of general ordered r-graphs; in particular, the upper bound requires the extremal results introduced in Section 1.5 (proved in Section 9).
$N_{P,m}(n)$
up to an exponential factor, proving Theorem 1.15 and therefore Theorem 1.13. The upper bound and the lower bound in Theorem 1.15 are proved separately. Despite Theorem 1.15 being about ordered matchings, both the upper and lower bound require the consideration of general ordered r-graphs; in particular, the upper bound requires the extremal results introduced in Section 1.5 (proved in Section 9).
For the upper bound, we prove the following general estimate on the number of ordered matchings M avoiding a particular submatching Q.
Theorem 7.1. Let
![]() $r\ge 2$
and Q be an ordered r-matching with at least two edges. Suppose there exists some
$r\ge 2$
and Q be an ordered r-matching with at least two edges. Suppose there exists some
![]() $n_Q>0$
such that
$n_Q>0$
such that
![]() $\operatorname {\mathrm {ex}}_<(n,Q)\le \alpha n^{r-1}$
for
$\operatorname {\mathrm {ex}}_<(n,Q)\le \alpha n^{r-1}$
for
![]() $n\ge n_Q$
. Then, if n is sufficiently large in terms of r and
$n\ge n_Q$
. Then, if n is sufficiently large in terms of r and
![]() $n_Q$
, the number of Q-free ordered r-matchings of size n is at most
$n_Q$
, the number of Q-free ordered r-matchings of size n is at most
In the above statement, we allow
![]() $\alpha $
to depend on n. To obtain the upper bound in Theorem 1.15, we can simply apply Theorem 7.1 with
$\alpha $
to depend on n. To obtain the upper bound in Theorem 1.15, we can simply apply Theorem 7.1 with
![]() $Q={P}^{(m)}$
and the estimate in Theorem 1.18(2).
$Q={P}^{(m)}$
and the estimate in Theorem 1.18(2).
In order to prove the general statement in Theorem 7.1, we need a few basic facts about extremal numbers of general ordered r-matchings. First, we need the fact that extremal numbers always have order of magnitude at least
![]() $n^{r-1}$
. (This is not hard to prove; in particular, it follows from the
$n^{r-1}$
. (This is not hard to prove; in particular, it follows from the
![]() $m=2$
case of Theorem 9.1, which we prove in Section 9).
$m=2$
case of Theorem 9.1, which we prove in Section 9).
Proposition 7.2. Let
![]() $r \ge 2$
, and let Q be any r-matching with at least two edges. Then
$r \ge 2$
, and let Q be any r-matching with at least two edges. Then
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n,Q) \ge \binom{n}{r}-\binom{(n-r)_+}{r}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n,Q) \ge \binom{n}{r}-\binom{(n-r)_+}{r}.\end{align*}$$
We also need a basic monotonicity property of extremal numbers of ordered matchings.
Proposition 7.3. Let
![]() $r,n\ge 2$
, and let Q be an ordered r-matching with more than one edge. Then,
$r,n\ge 2$
, and let Q be an ordered r-matching with more than one edge. Then,
Proof. Write the edges of Q as
![]() $e_1,\dots ,e_m$
, with
$e_1,\dots ,e_m$
, with
![]() $e_1[1]<\dots <e_m[1]$
. Say that Q splits into submatchings if there is an index
$e_1[1]<\dots <e_m[1]$
. Say that Q splits into submatchings if there is an index
![]() $\ell \in \{1,\dots ,m-1\}$
such that
$\ell \in \{1,\dots ,m-1\}$
such that
![]() $e_i[r]<e_j[1]$
for any
$e_i[r]<e_j[1]$
for any
![]() $1 \le i \le \ell <j \le m$
(i.e., Q consists of two matchings placed side-by-side). We proceed differently depending on whether Q splits into submatchings.
$1 \le i \le \ell <j \le m$
(i.e., Q consists of two matchings placed side-by-side). We proceed differently depending on whether Q splits into submatchings.
If Q does not split into submatchings, then given any Q-free ordered r-graph G, we can ‘glue together two copies of G’ to make a larger Q-free ordered r-graph
![]() $G'$
. Specifically, we can take two copies of G, and identify the last vertex of the first copy with the first vertex of the second copy (so except for the single identified vertex, all vertices of the first copy come before all vertices of the second copy). Clearly, if the resulting graph
$G'$
. Specifically, we can take two copies of G, and identify the last vertex of the first copy with the first vertex of the second copy (so except for the single identified vertex, all vertices of the first copy come before all vertices of the second copy). Clearly, if the resulting graph
![]() $G'$
were to contain some copy of Q, then this copy must completely lie in one of the two copies of G. But G is Q-free, meaning that
$G'$
were to contain some copy of Q, then this copy must completely lie in one of the two copies of G. But G is Q-free, meaning that
![]() $G'$
is also Q-free. In addition, if G had exactly
$G'$
is also Q-free. In addition, if G had exactly
![]() $\left\lceil {n/2} \right\rceil $
vertices and
$\left\lceil {n/2} \right\rceil $
vertices and
![]() $\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)$
edges, then
$\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)$
edges, then
![]() $G'$
has
$G'$
has
![]() $2\left\lceil {n/2} \right\rceil -1\le n$
vertices and
$2\left\lceil {n/2} \right\rceil -1\le n$
vertices and
![]() $2\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)$
edges, proving the desired inequality.
$2\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)$
edges, proving the desired inequality.
On the other hand, if Q does split into submatchings, then we can consider the r-graph G on the vertex set
![]() $\{1,\dots ,n\}$
containing all possible edges
$\{1,\dots ,n\}$
containing all possible edges
![]() $e\in E(K_n^{(r)})$
with
$e\in E(K_n^{(r)})$
with
![]() $e[1]\le \left\lceil {n/{2}} \right\rceil <e[r]$
. Note that G is Q-free. We deduce
$e[1]\le \left\lceil {n/{2}} \right\rceil <e[r]$
. Note that G is Q-free. We deduce
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n,Q)\ge e(G)\ge \binom{n}{r}-\binom{\left\lceil {n/2} \right\rceil}{r}-\binom{\left\lfloor {n/2} \right\rfloor}{r}\ge 2\binom{\left\lceil {n/2} \right\rceil}{r}\ge 2\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n,Q)\ge e(G)\ge \binom{n}{r}-\binom{\left\lceil {n/2} \right\rceil}{r}-\binom{\left\lfloor {n/2} \right\rfloor}{r}\ge 2\binom{\left\lceil {n/2} \right\rceil}{r}\ge 2\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q), \end{align*}$$
as desired.
Now, our proof of Theorem 7.1 proceeds by a ‘contraction’ argument, similar to an argument for r-dimensional orders by Cibulka and Kyncl [Reference Cibulka and Kynčl18]. We execute this argument in two steps: First, we use an inductive contraction argument to estimate the number of Q-free graphs on n vertices, then we use this bound and a different contraction argument to upper bound the number of Q-free ordered matchings of size n. The first of these steps is encapsulated in the following lemma.
Lemma 7.4. Fix a constant
![]() $r\ge 2$
, and suppose n is sufficiently large in terms of r. For any ordered r-matching Q with more than one edge, the number of ordered Q-free r-graphs on the vertex set
$r\ge 2$
, and suppose n is sufficiently large in terms of r. For any ordered r-matching Q with more than one edge, the number of ordered Q-free r-graphs on the vertex set
![]() $\{1,\dots ,n\}$
is at most
$\{1,\dots ,n\}$
is at most
Note that if
![]() $\operatorname {\mathrm {ex}}_<(n,Q)\le \alpha n^{r-1}$
for
$\operatorname {\mathrm {ex}}_<(n,Q)\le \alpha n^{r-1}$
for
![]() $n\ge n_Q$
(as in the statement of Theorem 7.1), the bound in Lemma 7.4 is at most
$n\ge n_Q$
(as in the statement of Theorem 7.1), the bound in Lemma 7.4 is at most
![]() $\exp (O(\alpha n^{r-1}))$
for
$\exp (O(\alpha n^{r-1}))$
for
![]() $n\ge 2n_Q$
.
$n\ge 2n_Q$
.
Proof. For any
![]() $n\in \mathbb N$
, let
$n\in \mathbb N$
, let
![]() $\mathcal G_n$
be the set of all r-graphs on the vertex set
$\mathcal G_n$
be the set of all r-graphs on the vertex set
![]() $\{1,\dots ,n\}$
which are Q-free.
$\{1,\dots ,n\}$
which are Q-free.
First, we describe how to ‘contract pairs of vertices’ to transform an n-vertex ordered graph
![]() $G\in \mathcal G_n$
into an
$G\in \mathcal G_n$
into an
![]() $\left\lceil {n/2} \right\rceil $
-vertex ordered graph
$\left\lceil {n/2} \right\rceil $
-vertex ordered graph
![]() $\phi (G)\in \mathcal G_{\left\lceil {n/2} \right\rceil }$
. For
$\phi (G)\in \mathcal G_{\left\lceil {n/2} \right\rceil }$
. For
![]() $G\in \mathcal G_n$
, partition its vertex set
$G\in \mathcal G_n$
, partition its vertex set
![]() $\{1,\dots ,n\}$
into
$\{1,\dots ,n\}$
into
![]() $\left\lceil {n/2} \right\rceil $
contiguous intervals
$\left\lceil {n/2} \right\rceil $
contiguous intervals
![]() $I_1,\dots ,I_{\left\lceil {n/2} \right\rceil }$
, where each
$I_1,\dots ,I_{\left\lceil {n/2} \right\rceil }$
, where each
![]() $I_i$
has size
$I_i$
has size
![]() $2$
except possibly
$2$
except possibly
![]() $I_{\left\lceil {n/2} \right\rceil }$
(which has size
$I_{\left\lceil {n/2} \right\rceil }$
(which has size
![]() $1$
if n is odd). Then,
$1$
if n is odd). Then,
![]() $\phi (G)$
is obtained by ‘contracting’ each
$\phi (G)$
is obtained by ‘contracting’ each
![]() $I_i$
to a single vertex. Specifically, we include
$I_i$
to a single vertex. Specifically, we include
![]() $e \in E(K_{\left\lceil {n/2} \right\rceil }^{(r)})$
as an edge of
$e \in E(K_{\left\lceil {n/2} \right\rceil }^{(r)})$
as an edge of
![]() $\phi (G)$
if and only if
$\phi (G)$
if and only if
![]() $\{i_1,\dots ,i_r\} \in E(G)$
for some
$\{i_1,\dots ,i_r\} \in E(G)$
for some
![]() $i_1\in I_{e[1]}, i_2\in I_{e[2]},\dots ,i_r\in I_{e[r]}$
. Note that this contraction operation cannot create copies of Q.
$i_1\in I_{e[1]}, i_2\in I_{e[2]},\dots ,i_r\in I_{e[r]}$
. Note that this contraction operation cannot create copies of Q.
Now, fixing
![]() $G' \in \mathcal {G}_{\left\lceil {n/2} \right\rceil }$
, we are going to estimate the number of
$G' \in \mathcal {G}_{\left\lceil {n/2} \right\rceil }$
, we are going to estimate the number of
![]() $G \in \mathcal {G}_n$
such that
$G \in \mathcal {G}_n$
such that
![]() $\phi (G)=G'$
. For all possible edges
$\phi (G)=G'$
. For all possible edges
![]() $e\in E(K_n^{(r)})$
of G, say that e is contractible if
$e\in E(K_n^{(r)})$
of G, say that e is contractible if
![]() $\left\lceil {e[1]/2} \right\rceil <\dots <\left\lceil {e[r]/2} \right\rceil $
(i.e., if the vertices of e lie in different
$\left\lceil {e[1]/2} \right\rceil <\dots <\left\lceil {e[r]/2} \right\rceil $
(i.e., if the vertices of e lie in different
![]() $I_i$
, in the definition of
$I_i$
, in the definition of
![]() $\phi (G)$
).
$\phi (G)$
).
First, every edge
![]() $e\in E(G')$
arose by contracting some edge
$e\in E(G')$
arose by contracting some edge
![]() $f_e\in E(G)$
. There are
$f_e\in E(G)$
. There are
![]() $2^r$
possibilities for
$2^r$
possibilities for
![]() $f_e$
, and at least one must have been present in G, so given that
$f_e$
, and at least one must have been present in G, so given that
![]() $\phi (G)=G'$
there are at most
$\phi (G)=G'$
there are at most
![]() $(2^{2^r}-1)^{e(G')}<2^{2^r\operatorname {\mathrm {ex}}_<(n',Q)}$
ways to choose the contractible edges in G.
$(2^{2^r}-1)^{e(G')}<2^{2^r\operatorname {\mathrm {ex}}_<(n',Q)}$
ways to choose the contractible edges in G.
On the other hand, if
![]() $e\in E(G)$
is not contractible, then
$e\in E(G)$
is not contractible, then
![]() $e[k]+1=e[k+1]$
for some
$e[k]+1=e[k+1]$
for some
![]() $1 \le k < r$
. By Lemma 2.2 and Proposition 7.2, the number of
$1 \le k < r$
. By Lemma 2.2 and Proposition 7.2, the number of
![]() $e\in E(K_n^{(r)})$
which have this property is
$e\in E(K_n^{(r)})$
which have this property is
 $$\begin{align*}\binom{n}{r}-\binom{(n-r)_+}{r}<2^r\left(\binom{\left\lceil {n/2} \right\rceil}{r}-\binom{(\left\lceil {n/2} \right\rceil-r)_+}{r}\right)\le 2^r \operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q),\end{align*}$$
$$\begin{align*}\binom{n}{r}-\binom{(n-r)_+}{r}<2^r\left(\binom{\left\lceil {n/2} \right\rceil}{r}-\binom{(\left\lceil {n/2} \right\rceil-r)_+}{r}\right)\le 2^r \operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q),\end{align*}$$
assuming that n is sufficiently large in terms of r (say,
![]() $n\ge n_r$
). So, the total number of ways to choose the noncontractible edges in G is at most
$n\ge n_r$
). So, the total number of ways to choose the noncontractible edges in G is at most
![]() $2^{2^r\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)}$
. An r-graph G is specified by its contractible and noncontractible edges, so we have
$2^{2^r\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)}$
. An r-graph G is specified by its contractible and noncontractible edges, so we have
 $$ \begin{align*} \left\vert {\mathcal{G}_n}\right\vert &\le \left\vert {\mathcal{G}_{\left\lceil {n/2} \right\rceil}}\right\vert\cdot 2^{2^r\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)}\cdot 2^{2^r\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)} \\&\le \left\vert {\mathcal{G}_{\left\lceil {n/2} \right\rceil}}\right\vert\cdot \exp(2^{r+1}\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)). \end{align*} $$
$$ \begin{align*} \left\vert {\mathcal{G}_n}\right\vert &\le \left\vert {\mathcal{G}_{\left\lceil {n/2} \right\rceil}}\right\vert\cdot 2^{2^r\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)}\cdot 2^{2^r\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)} \\&\le \left\vert {\mathcal{G}_{\left\lceil {n/2} \right\rceil}}\right\vert\cdot \exp(2^{r+1}\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)). \end{align*} $$
Iterating this inequality and using that
![]() $\operatorname {\mathrm {ex}}_<(\lceil n/2^k\rceil ,Q) \leq 2^{-(k-1)} \operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)$
(by Proposition 7.2), we have
$\operatorname {\mathrm {ex}}_<(\lceil n/2^k\rceil ,Q) \leq 2^{-(k-1)} \operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)$
(by Proposition 7.2), we have
 $$ \begin{align*} \left\vert {\mathcal{G}_n}\right\vert &\le \left\vert {\mathcal{G}_{n_r}}\right\vert \prod_{k=1}^{\left\lceil {\log_2 (n/n_r)} \right\rceil} \exp( 2^{r+1}\operatorname{\mathrm{ex}}_<(\lceil n/2^k\rceil,Q)) \\ & \le \left\vert {\mathcal{G}_{n_r}}\right\vert \cdot \exp( (2^{r+2}-1)\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)). \end{align*} $$
$$ \begin{align*} \left\vert {\mathcal{G}_n}\right\vert &\le \left\vert {\mathcal{G}_{n_r}}\right\vert \prod_{k=1}^{\left\lceil {\log_2 (n/n_r)} \right\rceil} \exp( 2^{r+1}\operatorname{\mathrm{ex}}_<(\lceil n/2^k\rceil,Q)) \\ & \le \left\vert {\mathcal{G}_{n_r}}\right\vert \cdot \exp( (2^{r+2}-1)\operatorname{\mathrm{ex}}_<(\left\lceil {n/2} \right\rceil,Q)). \end{align*} $$
When n is sufficiently large in terms of r, Proposition 7.2 implies
![]() $\left\vert {\mathcal {G}_{n_r}}\right\vert \le 2^{\binom {n_r}{r}} \le \exp \left( \operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q) \right)$
. Then,
$\left\vert {\mathcal {G}_{n_r}}\right\vert \le 2^{\binom {n_r}{r}} \le \exp \left( \operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q) \right)$
. Then,
![]() $\left\vert {\mathcal {G}_n}\right\vert < \exp \left(2^{r+2}\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)\right)$
, as desired.
$\left\vert {\mathcal {G}_n}\right\vert < \exp \left(2^{r+2}\operatorname {\mathrm {ex}}_<(\left\lceil {n/2} \right\rceil ,Q)\right)$
, as desired.
We are now ready to complete the proof of Theorem 7.1.
Proof of Theorem 7.1
Let
![]() $\mathcal {M}_n$
be the set of ordered r-matchings on the vertex set
$\mathcal {M}_n$
be the set of ordered r-matchings on the vertex set
![]() $\{1,\dots ,rn\}$
that are Q-free, and for any
$\{1,\dots ,rn\}$
that are Q-free, and for any
![]() $n'$
let
$n'$
let
![]() $\mathcal G_{n'}$
be the set of r-graphs on the vertex set
$\mathcal G_{n'}$
be the set of r-graphs on the vertex set
![]() $\{1,\dots ,n'\}$
that are Q-free.
$\{1,\dots ,n'\}$
that are Q-free.
As in the proof of Lemma 7.4, we will define a ‘contraction’ operation (though this time we will contract larger intervals, and we will not need to iterate our operation). For some B, whose value we will specify shortly, let
![]() $n'=\lceil rn/B\rceil $
and partition
$n'=\lceil rn/B\rceil $
and partition
![]() $\{1,\dots ,rn\}$
into
$\{1,\dots ,rn\}$
into
![]() $n'$
contiguous intervals
$n'$
contiguous intervals
![]() $I_1,\dots ,I_{n'}$
, where each
$I_1,\dots ,I_{n'}$
, where each
![]() $I_i$
has size B except possibly
$I_i$
has size B except possibly
![]() $I_{n'}$
(which is smaller if n is not divisible by B). For
$I_{n'}$
(which is smaller if n is not divisible by B). For
![]() $M \in \mathcal {M}_n$
, let
$M \in \mathcal {M}_n$
, let
![]() $\psi (M)\in \mathcal G_{n'}$
be the graph on the vertex set
$\psi (M)\in \mathcal G_{n'}$
be the graph on the vertex set
![]() $\{1,\dots ,n'\}$
obtained by contracting each interval
$\{1,\dots ,n'\}$
obtained by contracting each interval
![]() $I_i$
to a single vertex (specifically, we include
$I_i$
to a single vertex (specifically, we include
![]() $e \in E(K_{n'}^{(r)})$
as an edge of
$e \in E(K_{n'}^{(r)})$
as an edge of
![]() $\psi (G)$
if and only if
$\psi (G)$
if and only if
![]() $(i_1,\dots ,i_r)\in E(M)$
for some
$(i_1,\dots ,i_r)\in E(M)$
for some
![]() $i_1 \in I_{e[1]},\dots ,i_r \in I_{e[r]}$
). Now, we specify B to be the largest integer such that
$i_1 \in I_{e[1]},\dots ,i_r \in I_{e[r]}$
). Now, we specify B to be the largest integer such that
![]() $B^{r-1}\le \alpha r^r n^{(r-2)}$
. Note that
$B^{r-1}\le \alpha r^r n^{(r-2)}$
. Note that
![]() $B^{r-1}\ge \alpha r^rn^{r-2}/2$
and
$B^{r-1}\ge \alpha r^rn^{r-2}/2$
and
![]() $(n')^{r-1}\le 2(rn/B)^{r-1}= 2{r^{r-1}n^{r-1}}/{B^{r-1}}\le 4n/(r\alpha )$
; and
$(n')^{r-1}\le 2(rn/B)^{r-1}= 2{r^{r-1}n^{r-1}}/{B^{r-1}}\le 4n/(r\alpha )$
; and
![]() $(n')^{r-1}\ge (rn/B)^{r-1}= {r^{r-1}n^{r-1}}/{B^{r-1}} \ge n/(r\alpha )$
. By Lemma 7.4 we have
$(n')^{r-1}\ge (rn/B)^{r-1}= {r^{r-1}n^{r-1}}/{B^{r-1}} \ge n/(r\alpha )$
. By Lemma 7.4 we have
 $$ \begin{align*} \left\vert {\mathcal{G}_{n'}}\right\vert &\le \exp\left(2^{r+2}\operatorname{\mathrm{ex}}_<(\lceil n'/2\rceil,Q)\right) \le \exp\left(2^{r+3} \alpha(n'/2)^{r-1}\right) \\& \le \exp\left(\vphantom\sum 16\alpha(n')^{r-1}\right)\le e^{64n/r}\le e^{32n}, \end{align*} $$
$$ \begin{align*} \left\vert {\mathcal{G}_{n'}}\right\vert &\le \exp\left(2^{r+2}\operatorname{\mathrm{ex}}_<(\lceil n'/2\rceil,Q)\right) \le \exp\left(2^{r+3} \alpha(n'/2)^{r-1}\right) \\& \le \exp\left(\vphantom\sum 16\alpha(n')^{r-1}\right)\le e^{64n/r}\le e^{32n}, \end{align*} $$
assuming n is sufficiently large with respect to r. (In this deduction, we assumed that
![]() $\alpha \leq 4n^{3/4}/r$
and n is sufficiently large with respect to
$\alpha \leq 4n^{3/4}/r$
and n is sufficiently large with respect to
![]() $n_Q$
so that
$n_Q$
so that
![]() $ (n/(r\alpha ))^{1/(r-1)}/2\ge n_Q$
, thus
$ (n/(r\alpha ))^{1/(r-1)}/2\ge n_Q$
, thus
![]() $\lceil n'/2\rceil \ge (n/(r\alpha ))^{1/(r-1)}/2\ge n_Q$
. Note that if
$\lceil n'/2\rceil \ge (n/(r\alpha ))^{1/(r-1)}/2\ge n_Q$
. Note that if
![]() $\alpha> 4n^{3/4}/r$
then
$\alpha> 4n^{3/4}/r$
then
![]() $(n')^{r-1} \leq 4n/r\alpha < n^{1/4}$
, hence
$(n')^{r-1} \leq 4n/r\alpha < n^{1/4}$
, hence
![]() $\left\vert {\mathcal {G}_{n'}}\right\vert \le 2^{\binom {n'}{r}} \leq 2^{(n')^r}<e^{32n}$
). Now, fixing
$\left\vert {\mathcal {G}_{n'}}\right\vert \le 2^{\binom {n'}{r}} \leq 2^{(n')^r}<e^{32n}$
). Now, fixing
![]() $G\in \mathcal {G}_{n'}$
, let us estimate the number of
$G\in \mathcal {G}_{n'}$
, let us estimate the number of
![]() $M\in \mathcal {M}_n$
with
$M\in \mathcal {M}_n$
with
![]() $\psi (M)=G$
. Viewing each edge
$\psi (M)=G$
. Viewing each edge
![]() $e\in E(G)$
as an ordered r-tuple
$e\in E(G)$
as an ordered r-tuple
![]() $(e[1],\dots ,e[r])$
, let
$(e[1],\dots ,e[r])$
, let
The idea is that
![]() $\mathcal T$
specifies the ‘possible places where edges of M can lie’: if
$\mathcal T$
specifies the ‘possible places where edges of M can lie’: if
![]() $\psi (M)=G$
, then for each edge
$\psi (M)=G$
, then for each edge
![]() $e\in M$
there must be some tuple
$e\in M$
there must be some tuple
![]() $(t_1,\dots ,t_r)\in \mathcal T$
such that
$(t_1,\dots ,t_r)\in \mathcal T$
such that
![]() $e[1]\in I_{t_1},\dots ,e[r]\in I_{t_r}$
(say that e is consistent with
$e[1]\in I_{t_1},\dots ,e[r]\in I_{t_r}$
(say that e is consistent with
![]() $\vec t$
). Then,
$\vec t$
). Then,
 $$ \begin{align*} \begin{aligned} \left\vert {\mathcal{T}}\right\vert =&\, |E(G)| + \binom{n'+r-1}{r}-\binom{n'}{r} \le \operatorname{\mathrm{ex}}_<(n',Q) + 2\binom{n'}{r}-2\binom{(n'-r)_+}{r} \\ \le&\, 3\operatorname{\mathrm{ex}}_<(n',Q) \le 3\alpha (n')^{r-1} \le \frac{12n}{r}\le 6n. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\vert {\mathcal{T}}\right\vert =&\, |E(G)| + \binom{n'+r-1}{r}-\binom{n'}{r} \le \operatorname{\mathrm{ex}}_<(n',Q) + 2\binom{n'}{r}-2\binom{(n'-r)_+}{r} \\ \le&\, 3\operatorname{\mathrm{ex}}_<(n',Q) \le 3\alpha (n')^{r-1} \le \frac{12n}{r}\le 6n. \end{aligned} \end{align*} $$
(In the deduction above, we assumed that
![]() $\alpha \le 4 n^{3/4}/r$
and n is sufficiently large with respect to
$\alpha \le 4 n^{3/4}/r$
and n is sufficiently large with respect to
![]() $n_Q$
and r so that the first inequality holds, and
$n_Q$
and r so that the first inequality holds, and
![]() $n'\geq (n/(r\alpha ))^{1/(r-1)} \ge n_Q$
so that the third inequality holds. In the second inequality, we used Proposition 7.2. Also, note that the inequality
$n'\geq (n/(r\alpha ))^{1/(r-1)} \ge n_Q$
so that the third inequality holds. In the second inequality, we used Proposition 7.2. Also, note that the inequality
![]() $\left\vert {\mathcal {T}}\right\vert \le 6n$
holds trivially if
$\left\vert {\mathcal {T}}\right\vert \le 6n$
holds trivially if
![]() $\alpha> 4n^{3/4}/r$
as this implies that
$\alpha> 4n^{3/4}/r$
as this implies that
![]() $n'< n^{1/(4(r-1))}$
and thus
$n'< n^{1/(4(r-1))}$
and thus
![]() $\left\vert {\mathcal T}\right\vert \le (n')^r<n$
.)
$\left\vert {\mathcal T}\right\vert \le (n')^r<n$
.)
Now, for every
![]() $M\in \mathcal {M}_n$
with
$M\in \mathcal {M}_n$
with
![]() $\psi (M)=G$
, we consider the number
$\psi (M)=G$
, we consider the number
![]() $a_{\vec {t}}$
of edges
$a_{\vec {t}}$
of edges
![]() $e\in M$
which are consistent with
$e\in M$
which are consistent with
![]() $\vec t$
. Since
$\vec t$
. Since
![]() $\sum _{\vec {t}\in \mathcal {T}} a_{\vec {t}}=n$
, the number of possibilities for
$\sum _{\vec {t}\in \mathcal {T}} a_{\vec {t}}=n$
, the number of possibilities for
![]() $(a_{\vec {t}}:\vec t\in \mathcal T)$
is at most
$(a_{\vec {t}}:\vec t\in \mathcal T)$
is at most
 $$\begin{align*}\binom{n+\left\vert {\mathcal{T}}\right\vert-1}{n}<\binom{n+6n}{n}\le 2^{7n}\le e^{5n}.\end{align*}$$
$$\begin{align*}\binom{n+\left\vert {\mathcal{T}}\right\vert-1}{n}<\binom{n+6n}{n}\le 2^{7n}\le e^{5n}.\end{align*}$$
Then, given any choice of
![]() $(a_{\vec {t}}:\vec t\in \mathcal T)$
, the number of ways to choose the edges of M is at most
$(a_{\vec {t}}:\vec t\in \mathcal T)$
, the number of ways to choose the edges of M is at most
 $$\begin{align*}\prod_{\vec{t}\in\mathcal{T}} ({B^r})^{a_{\vec{t}}}\le B^{rn}.\end{align*}$$
$$\begin{align*}\prod_{\vec{t}\in\mathcal{T}} ({B^r})^{a_{\vec{t}}}\le B^{rn}.\end{align*}$$
Thus,
as desired.
Now, we turn our attention to the lower bound in Theorem 1.15. Actually, we are able to prove the desired bound even when restricting our attention to r-partite r-matchings (i.e., r-dimensional orders). Let
![]() $N_{P,m}^{\mathrm {part}}(n)$
be the number of r-partite r-matchings M on the vertex set
$N_{P,m}^{\mathrm {part}}(n)$
be the number of r-partite r-matchings M on the vertex set
![]() $\{1,\dots ,rn\}$
with
$\{1,\dots ,rn\}$
with
![]() $L_P(M)<m$
.
$L_P(M)<m$
.
Theorem 7.5. Let
![]() $r \ge 2$
and P be an r-partite r-pattern. Also, consider any
$r \ge 2$
and P be an r-partite r-pattern. Also, consider any
![]() $m\ge 2$
such that
$m\ge 2$
such that
![]() $m-1$
is divisible by
$m-1$
is divisible by
![]() $r-1$
, and consider any integer
$r-1$
, and consider any integer
![]() $b\ge r(m-1)/(r-1)$
. Then, defining
$b\ge r(m-1)/(r-1)$
. Then, defining
 $$\begin{align*}n=\binom{b+r-(m-1)/(r-1)}{r}-\binom{b+r-r(m-1)/(r-1)}{r}, \end{align*}$$
$$\begin{align*}n=\binom{b+r-(m-1)/(r-1)}{r}-\binom{b+r-r(m-1)/(r-1)}{r}, \end{align*}$$
we have
Remark 7.6. If P is an r-partite r-pattern with block representation
![]() $|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\dots |{\mathfrak {B}}_r|$
, and M is an r-partite r-matching (with edges viewed as r-tuples in
$|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\dots |{\mathfrak {B}}_r|$
, and M is an r-partite r-matching (with edges viewed as r-tuples in
![]() $\{1,\dots ,n\}$
), then the condition
$\{1,\dots ,n\}$
), then the condition
![]() $L_P(M)<m$
is equivalent to the condition that there is no sequence of edges
$L_P(M)<m$
is equivalent to the condition that there is no sequence of edges
![]() $e_1,\dots ,e_m$
which is increasing in all coordinates i with
$e_1,\dots ,e_m$
which is increasing in all coordinates i with
![]() ${\mathfrak {B}}_{i}={{\mathrm {A}}{\mathrm {B}}}$
and decreasing in all coordinates i with
${\mathfrak {B}}_{i}={{\mathrm {A}}{\mathrm {B}}}$
and decreasing in all coordinates i with
![]() ${\mathfrak {B}}_{i}={{\mathrm {B}}{\mathrm {A}}}$
. So,
${\mathfrak {B}}_{i}={{\mathrm {B}}{\mathrm {A}}}$
. So,
![]() $N_{P,m}^{\mathrm {part}}(n)$
does not actually depend on P and is precisely equal to the number of
$N_{P,m}^{\mathrm {part}}(n)$
does not actually depend on P and is precisely equal to the number of
![]() $(r-1)$
-tuples of permutations of
$(r-1)$
-tuples of permutations of
![]() $\{1,\dots ,n\}$
which contain no common increasing subsequence of length m.
$\{1,\dots ,n\}$
which contain no common increasing subsequence of length m.
Remark 7.7. The bound in Theorem 7.5 is only for n of a certain form, but it’s easy to deduce almost as strong of a bound for all n (if we view r as a constant).
Indeed, first note that if (say)
![]() $b\ge 2m$
, the resulting value of n scales like
$b\ge 2m$
, the resulting value of n scales like
![]() $m b^{r-1}$
. So, for any desired order of magnitude (greater than
$m b^{r-1}$
. So, for any desired order of magnitude (greater than
![]() $m^r$
) we can choose b such that n has our desired order of magnitude.
$m^r$
) we can choose b such that n has our desired order of magnitude.
Then, note that
![]() $N_{P,m}^{\mathrm {part}}(n+1)\ge N_{P,m}^{\mathrm {part}}(n)$
for all n (i.e.,
$N_{P,m}^{\mathrm {part}}(n+1)\ge N_{P,m}^{\mathrm {part}}(n)$
for all n (i.e.,
![]() $N_{P,m}^{\mathrm {part}}(n)$
is monotone increasing in n). This is because for any
$N_{P,m}^{\mathrm {part}}(n)$
is monotone increasing in n). This is because for any
![]() $(r-1)$
-tuple of permutations of
$(r-1)$
-tuple of permutations of
![]() $\{1,\dots ,n\}$
which contain no common increasing subsequence of length m, we can simply prepend each permutation with ‘
$\{1,\dots ,n\}$
which contain no common increasing subsequence of length m, we can simply prepend each permutation with ‘
![]() $n+1$
’ to obtain an
$n+1$
’ to obtain an
![]() $(r-1)$
-tuple of permutations of
$(r-1)$
-tuple of permutations of
![]() $\{1,\dots ,n+1\}$
which still contain no common increasing subsequence of length m.
$\{1,\dots ,n+1\}$
which still contain no common increasing subsequence of length m.
Proof of Theorem 7.5
As we have just discussed (in Remark 7.6), it suffices to consider the case where P has representation
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\dots |{{\mathrm {A}}{\mathrm {B}}}|$
, in which case the condition
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\dots |{{\mathrm {A}}{\mathrm {B}}}|$
, in which case the condition
![]() $L_P(M)< m$
is equivalent to the condition that there is no sequence of m edges that is increasing in every coordinate.
$L_P(M)< m$
is equivalent to the condition that there is no sequence of m edges that is increasing in every coordinate.
We start by constructing an r-partite ordered r-graph G, which we will ‘uncontract’ to obtain our desired matchings M (by analogy with the contraction operation in the proof of Theorem 7.1 earlier in this section). Let
![]() $a=(m-1)/(r-1)$
, and let
$a=(m-1)/(r-1)$
, and let
![]() $U_1,\dots ,U_r$
be disjoint sets of size
$U_1,\dots ,U_r$
be disjoint sets of size
![]() $b-a+1$
(we write
$b-a+1$
(we write
![]() $U_i=\{u_a^i,\dots ,u_b^i\}$
). Define G to be the graph on the vertex set
$U_i=\{u_a^i,\dots ,u_b^i\}$
). Define G to be the graph on the vertex set
![]() $U_1\cup \dots \cup U_r$
(ordered such that
$U_1\cup \dots \cup U_r$
(ordered such that
![]() $U_1<U_2<\dots <U_r$
), where
$U_1<U_2<\dots <U_r$
), where
![]() $\{u_{j_1}^1,u_{j_2}^2,\dots , u_{j_r}^r\}$
is included as an edge if and only if
$\{u_{j_1}^1,u_{j_2}^2,\dots , u_{j_r}^r\}$
is included as an edge if and only if
By symmetry, for any
![]() $j \in \{a,\dots ,b\}$
, the vertices
$j \in \{a,\dots ,b\}$
, the vertices
![]() $u_j^1,\dots ,u_j^r$
have the same degree, which we denote as
$u_j^1,\dots ,u_j^r$
have the same degree, which we denote as
![]() $d_j$
. Note that each
$d_j$
. Note that each
![]() $d_j\ge 1$
, since for any integer k in the range
$d_j\ge 1$
, since for any integer k in the range
![]() $[a,b]=[(m-1)/(r-1),b]$
, there is always some way to add
$[a,b]=[(m-1)/(r-1),b]$
, there is always some way to add
![]() $r-1$
more integers in this range to k, to obtain a number in the range
$r-1$
more integers in this range to k, to obtain a number in the range
![]() $[b+1,b+m-1]$
. Also, observe that
$[b+1,b+m-1]$
. Also, observe that
![]() $b \ge r(m-1)/(r-1)= ra$
. Writing
$b \ge r(m-1)/(r-1)= ra$
. Writing
![]() $n=d_a+\dots +d_b=e(G)$
, we have
$n=d_a+\dots +d_b=e(G)$
, we have
 $$ \begin{align} n =&\; \#\left( \vphantom\sum(j_1,\dots,j_r)\in\{a,\dots,b\}^r\;:\; b+1\le j_1+\dots+j_r \le b+(m-1) \right) \notag\\ =&\; \#\bigg( \vphantom\sum(x_1,\dots,x_r)\in \{0,\dots,b-a\}^r : b+1-ra\le x_1+\dots+x_r \le b+(m-1)-ra=b-a\bigg)\notag \\ =&\; \#\left( \vphantom\sum(x_1,\dots,x_r)\in \mathbb{Z}^r_{\ge 0}\;:\; x_1+\dots+x_r \le b-a\right)-\#\left( \vphantom\sum(x_1,\dots,x_r)\in \mathbb{Z}^r_{\ge 0}\;:\; x_1+\dots+x_r \le b-ra\right)\notag\\ =&\;\binom{b+r-(m-1)/(r-1)}{r}-\binom{b+r-r(m-1)/(r-1)}{r}. \end{align} $$
$$ \begin{align} n =&\; \#\left( \vphantom\sum(j_1,\dots,j_r)\in\{a,\dots,b\}^r\;:\; b+1\le j_1+\dots+j_r \le b+(m-1) \right) \notag\\ =&\; \#\bigg( \vphantom\sum(x_1,\dots,x_r)\in \{0,\dots,b-a\}^r : b+1-ra\le x_1+\dots+x_r \le b+(m-1)-ra=b-a\bigg)\notag \\ =&\; \#\left( \vphantom\sum(x_1,\dots,x_r)\in \mathbb{Z}^r_{\ge 0}\;:\; x_1+\dots+x_r \le b-a\right)-\#\left( \vphantom\sum(x_1,\dots,x_r)\in \mathbb{Z}^r_{\ge 0}\;:\; x_1+\dots+x_r \le b-ra\right)\notag\\ =&\;\binom{b+r-(m-1)/(r-1)}{r}-\binom{b+r-r(m-1)/(r-1)}{r}. \end{align} $$
Starting from the vertex set
![]() $U_1\cup \dots \cup U_r$
of G, ‘uncontract’ each vertex
$U_1\cup \dots \cup U_r$
of G, ‘uncontract’ each vertex
![]() $u_j^i$
into an interval
$u_j^i$
into an interval
![]() $I_j^i$
of length
$I_j^i$
of length
![]() $d_j$
, to obtain an ordered set V of
$d_j$
, to obtain an ordered set V of
![]() $rn$
vertices such that
$rn$
vertices such that
![]() $I^1_a<\dots <I^1_b<I^2_a<\dots <I^{r-1}_b<I^r_a<\dots <I^r_b$
. Then, we consider each matching on the vertex set V which ‘yields G after contracting the intervals
$I^1_a<\dots <I^1_b<I^2_a<\dots <I^{r-1}_b<I^r_a<\dots <I^r_b$
. Then, we consider each matching on the vertex set V which ‘yields G after contracting the intervals
![]() $I_j^i$
to single vertices’. Specifically, we consider each matching M on V with the property that for
$I_j^i$
to single vertices’. Specifically, we consider each matching M on V with the property that for
![]() $e\in E(M)$
there is a unique edge
$e\in E(M)$
there is a unique edge
![]() $f\in E(G)$
with
$f\in E(G)$
with
![]() $e[1] \in I_{f[1]}^1,e[2]\in I_{f[2]}^2,\dots ,e[r]\in I_{f[r]}^r$
(and every
$e[1] \in I_{f[1]}^1,e[2]\in I_{f[2]}^2,\dots ,e[r]\in I_{f[r]}^r$
(and every
![]() $f \in E(G)$
corresponds to precisely one
$f \in E(G)$
corresponds to precisely one
![]() $e \in E(M)$
).
$e \in E(M)$
).
It is not hard to see there are exactly
![]() $\prod _{v\in V(G)}d_G(v)=\left(\prod _{j} d_j!\right)^r$
ways to choose ordered r-matchings M as above. Note that each such matching M satisfies
$\prod _{v\in V(G)}d_G(v)=\left(\prod _{j} d_j!\right)^r$
ways to choose ordered r-matchings M as above. Note that each such matching M satisfies
![]() $L_P(M)<m$
. To see this, recall that every edge of G (and therefore every edge of M) can be identified by a unique r-tuple
$L_P(M)<m$
. To see this, recall that every edge of G (and therefore every edge of M) can be identified by a unique r-tuple
![]() $(j_1,\dots ,j_r)$
with
$(j_1,\dots ,j_r)$
with
![]() $b+1\le j_1+\dots +j_r\le b+m-1$
. For two edges
$b+1\le j_1+\dots +j_r\le b+m-1$
. For two edges
![]() $e,e'\in E(M)$
(corresponding to two different r-tuples
$e,e'\in E(M)$
(corresponding to two different r-tuples
![]() $(j_1,\dots ,j_r)$
and
$(j_1,\dots ,j_r)$
and
![]() $(j_1',\dots ,j_r')$
), we can only have
$(j_1',\dots ,j_r')$
), we can only have
![]() $e[i]>e'[i]$
when
$e[i]>e'[i]$
when
![]() $j_i\ge j_i'$
. In particular, if
$j_i\ge j_i'$
. In particular, if
![]() $e[i]>e'[i]$
for all i, then
$e[i]>e'[i]$
for all i, then
![]() $j_1+\dots +j_r>j_1'+\dots +j_r'$
(note that
$j_1+\dots +j_r>j_1'+\dots +j_r'$
(note that
![]() $(j_1,\dots ,j_r)\neq (j_1',\dots ,j_r')$
when
$(j_1,\dots ,j_r)\neq (j_1',\dots ,j_r')$
when
![]() $e\ne e'$
). For our r-tuples
$e\ne e'$
). For our r-tuples
![]() $(j_1,\dots ,j_r)$
under consideration,
$(j_1,\dots ,j_r)$
under consideration,
![]() $j_1+\dots +j_r$
is constrained to an interval of
$j_1+\dots +j_r$
is constrained to an interval of
![]() $m-1$
integers, so there cannot be any sequence of m edges which is increasing in every coordinate (i.e.,
$m-1$
integers, so there cannot be any sequence of m edges which is increasing in every coordinate (i.e.,
![]() $L_P(M)< m$
).
$L_P(M)< m$
).
It remains to lower-bound
![]() $\left(\prod _{j} d_j!\right)^r$
in terms of
$\left(\prod _{j} d_j!\right)^r$
in terms of
![]() $n,m,r$
. Recall that the Gamma function
$n,m,r$
. Recall that the Gamma function
![]() $\Gamma $
is log-convex and satisfies
$\Gamma $
is log-convex and satisfies
![]() $\Gamma (x)\ge (x/e)^{x-1}$
. Using that
$\Gamma (x)\ge (x/e)^{x-1}$
. Using that
![]() $d_a+\dots +d_b=n$
, we have
$d_a+\dots +d_b=n$
, we have
 $$ \begin{align} \left(\prod_{j=a}^b d_j!\right)^r = \left( \prod_{j=a}^b\Gamma(d_j+1)\right)^r &\ge \left( \Gamma\left(\frac{n}{b-a+1} +1\right)\right)^{(b-a+1)r} \notag\\ &> \left(\left(\frac{n}{e(b-a+1)}\right)^{n/(b-a+1)}\right)^{(b-a+1)r} \notag\\ &= e^{-rn} n^{rn} \left({b-\frac{m-1}{r-1}+1}\right)^{-rn}. \end{align} $$
$$ \begin{align} \left(\prod_{j=a}^b d_j!\right)^r = \left( \prod_{j=a}^b\Gamma(d_j+1)\right)^r &\ge \left( \Gamma\left(\frac{n}{b-a+1} +1\right)\right)^{(b-a+1)r} \notag\\ &> \left(\left(\frac{n}{e(b-a+1)}\right)^{n/(b-a+1)}\right)^{(b-a+1)r} \notag\\ &= e^{-rn} n^{rn} \left({b-\frac{m-1}{r-1}+1}\right)^{-rn}. \end{align} $$
On the other hand, recalling equation (7.1),
 $$ \begin{align*} n&=\binom{b+r-(m-1)/(r-1)}{r}-\binom{b+r-r(m-1)/(r-1)}{r} \\ &= \frac{1}{r!}\left[{\prod_{i=1}^r\left(b-\frac{m-1}{r-1}+i \right) - \prod_{i=1}^r\left(b-\frac{r(m-1)}{r-1}+i\right)}\right] \\ &> \frac{1}{r!}\cdot (m-1)\prod_{i=1}^{r-1} \left(b-\frac{m-1}{r-1}+i \right)\\ &> \frac{m-1}{r!}{\left(b-\frac{m-1}{r-1}+1\right)^{r-1}}. \end{align*} $$
$$ \begin{align*} n&=\binom{b+r-(m-1)/(r-1)}{r}-\binom{b+r-r(m-1)/(r-1)}{r} \\ &= \frac{1}{r!}\left[{\prod_{i=1}^r\left(b-\frac{m-1}{r-1}+i \right) - \prod_{i=1}^r\left(b-\frac{r(m-1)}{r-1}+i\right)}\right] \\ &> \frac{1}{r!}\cdot (m-1)\prod_{i=1}^{r-1} \left(b-\frac{m-1}{r-1}+i \right)\\ &> \frac{m-1}{r!}{\left(b-\frac{m-1}{r-1}+1\right)^{r-1}}. \end{align*} $$
In other words,
![]() $b-(m-1)/(r-1)+1 < (r!n/(m-1))^{1/(r-1)}$
. Plugging this into equation (7.2), we have
$b-(m-1)/(r-1)+1 < (r!n/(m-1))^{1/(r-1)}$
. Plugging this into equation (7.2), we have
 $$ \begin{align*} N_{P,m}^{\mathrm{part}}(n) \ge \prod_{i=1}^r\prod_{j=a}^b d_j! &\ge e^{-rn}n^{rn} \left(\frac{r!n}{m-1}\right)^{-(rn)/(r-1)}\\ &=e^{-rn}(r!)^{-(r/(r-1))n} (m-1)^{(r/(r-1))n} n^{(r-1-1/(r-1))n}, \end{align*} $$
$$ \begin{align*} N_{P,m}^{\mathrm{part}}(n) \ge \prod_{i=1}^r\prod_{j=a}^b d_j! &\ge e^{-rn}n^{rn} \left(\frac{r!n}{m-1}\right)^{-(rn)/(r-1)}\\ &=e^{-rn}(r!)^{-(r/(r-1))n} (m-1)^{(r/(r-1))n} n^{(r-1-1/(r-1))n}, \end{align*} $$
as desired.
8 Partitioning ordered hypergraphs
A well-known result of Erdős and Kleitman [Reference Erdős and Kleitman25] says that every r-graph with m edges has an r-partite subgraph with at least
![]() $(r!/r^r)m$
edges (here ‘r-partite’ means that we can divide the vertex set into r parts such that every edge has exactly one vertex in each part). This theorem is enormously useful in extremal hypergraph theory, as it allows one to prove a result about r-partite r-graphs and ‘transfer’ it to general r-graphs.
$(r!/r^r)m$
edges (here ‘r-partite’ means that we can divide the vertex set into r parts such that every edge has exactly one vertex in each part). This theorem is enormously useful in extremal hypergraph theory, as it allows one to prove a result about r-partite r-graphs and ‘transfer’ it to general r-graphs.
It would be very useful if the same would be possible in the setting of ordered hypergraphs (where our notion of r-partiteness should impose that the r parts are each intervals according to our ordering). Although it is not possible to prove a direct analogue of the Erdős–Kleitman theorem, Füredi, Jiang, Kostochka, Mubayi and Verstraëte [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte32] managed to prove a result that is almost as good: in a certain sense every ordered r-graph G has a subgraph
![]() $G'$
which is ‘nearly’ r-partite, in such a way that the ‘relative density’ of
$G'$
which is ‘nearly’ r-partite, in such a way that the ‘relative density’ of
![]() $G'$
is not too much less than the relative density of G.
$G'$
is not too much less than the relative density of G.
In this section, we prove a refinement of the Füredi–Jiang–Kostochka–Mubayi–Verstraëte theorem, with essentially optimal dependence on r, which might be of independent interest. This will be used in our proof of Theorem 1.18(2). To state our theorem we need some definitions.
Definition 8.1. Let
![]() $1 \le k \le r$
and
$1 \le k \le r$
and
![]() $\vec {a}$
be a positive integer-valued vector of length k with sum of entries
$\vec {a}$
be a positive integer-valued vector of length k with sum of entries
![]() $\|\vec {a}\|_1=r$
. We say an ordered r-graph G is
$\|\vec {a}\|_1=r$
. We say an ordered r-graph G is
![]() $\vec {a}$
-equipartite if the following holds.
$\vec {a}$
-equipartite if the following holds.
-
1. G must have exactly
 $kn$
vertices.
$kn$
vertices. -
2. Partition the vertex set of G into contiguous intervals
 $I_{1},\dots ,I_{k}$
of size n. For each
$I_{1},\dots ,I_{k}$
of size n. For each
 $i\in \{1,\dots ,k\}$
and each edge e of G, we must have
$i\in \{1,\dots ,k\}$
and each edge e of G, we must have
 $|e\cap I_{i}|=a_{i}$
.
$|e\cap I_{i}|=a_{i}$
.
If G is
![]() $\vec {a}$
-equipartite with order n, then we define its
$\vec {a}$
-equipartite with order n, then we define its
![]() $\ell $
-density to be its number of edges divided by
$\ell $
-density to be its number of edges divided by
![]() $n^{\ell }/\prod _{i}a_{i}!$
(this is a twisted notion of density, which can take values between
$n^{\ell }/\prod _{i}a_{i}!$
(this is a twisted notion of density, which can take values between
![]() $0$
and
$0$
and
![]() $n^{r-\ell }$
).
$n^{r-\ell }$
).
Moreover, say that G is k-equipartite if it is
![]() $\vec {a}$
-equipartite for some
$\vec {a}$
-equipartite for some
![]() $\vec {a}$
with
$\vec {a}$
with
![]() $\|\vec {a}\|_{0}=k$
, and say that G is
$\|\vec {a}\|_{0}=k$
, and say that G is
![]() $(\ge t)$
-equipartite if it is k-equipartite for some
$(\ge t)$
-equipartite if it is k-equipartite for some
![]() $k\ge t$
.
$k\ge t$
.
Note in particular that there is only one possible
![]() $\vec a$
with
$\vec a$
with
![]() $\|\vec {a}\|_{0}=r$
: namely, the all-ones vector of length r. There are
$\|\vec {a}\|_{0}=r$
: namely, the all-ones vector of length r. There are
![]() $r-1$
essentially equivalent
$r-1$
essentially equivalent
![]() $\vec a$
with
$\vec a$
with
![]() $\|\vec {a}\|_{0}=r-1$
: Namely, the the vectors of length
$\|\vec {a}\|_{0}=r-1$
: Namely, the the vectors of length
![]() $r-1$
, whose all entries are ‘1’ except one ‘2’. So, being
$r-1$
, whose all entries are ‘1’ except one ‘2’. So, being
![]() $(\ge r-1)$
-equipartite corresponds to being
$(\ge r-1)$
-equipartite corresponds to being
![]() $\vec {a}$
-equipartite for one of the above two types of
$\vec {a}$
-equipartite for one of the above two types of
![]() $\vec {a}$
.
$\vec {a}$
.
Now, our refinement of the Füredi–Jiang–Kostochka–Mubayi–Verstraëte theorem is as follows.
Theorem 8.2. Fix
![]() $r\in \mathbb N$
and
$r\in \mathbb N$
and
![]() $\varepsilon>0$
, and suppose n is sufficiently large in terms of r and
$\varepsilon>0$
, and suppose n is sufficiently large in terms of r and
![]() $\varepsilon $
. Let
$\varepsilon $
. Let
![]() $p\ge \varepsilon $
and let G be an ordered r-graph with of n vertices and at least
$p\ge \varepsilon $
and let G be an ordered r-graph with of n vertices and at least
![]() $(p/n)\binom {n}{r}$
edges. Then, G contains a
$(p/n)\binom {n}{r}$
edges. Then, G contains a
![]() $(\ge r-1)$
-equipartite subgraph
$(\ge r-1)$
-equipartite subgraph
![]() $G'$
of order
$G'$
of order
![]() $n^{\Omega _{r}(1)}$
with
$n^{\Omega _{r}(1)}$
with
![]() $(r-1)$
-density at least
$(r-1)$
-density at least
![]() $\Omega (p/r^2)$
.
$\Omega (p/r^2)$
.
We also show that the multiplicative factor
![]() $O(r^{-2})$
in the ‘loss of density’ in Theorem 8.2 is essentially best possible.
$O(r^{-2})$
in the ‘loss of density’ in Theorem 8.2 is essentially best possible.
Theorem 8.3. Fix a constant
![]() $r\in \mathbb N$
. There exists an ordered r-graph G with
$r\in \mathbb N$
. There exists an ordered r-graph G with
![]() $(1+o(1))r(r-1)n^{r-1}/r!$
edges such that any order-m
$(1+o(1))r(r-1)n^{r-1}/r!$
edges such that any order-m
![]() $(\ge r-1)$
-equipartite subgraph
$(\ge r-1)$
-equipartite subgraph
![]() $G'\subseteq G$
has
$G'\subseteq G$
has
![]() $(r-1)$
-density at most
$(r-1)$
-density at most
![]() $2+o_{m\to \infty }(1)$
.
$2+o_{m\to \infty }(1)$
.
Remark 8.4. Instead of making an
![]() $(r-1)$
-density assumption, one could make an
$(r-1)$
-density assumption, one could make an
![]() $\ell $
-density assumption for any
$\ell $
-density assumption for any
![]() $\ell \le r$
. In general, such an assumption would allow one to prove an analogue of Theorem 8.2 in which we guarantee a
$\ell \le r$
. In general, such an assumption would allow one to prove an analogue of Theorem 8.2 in which we guarantee a
![]() $(\ge \ell )$
-equipartite subgraph with reasonably large
$(\ge \ell )$
-equipartite subgraph with reasonably large
![]() $\ell $
-density. (Such a result was previously proved in [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte32], and our proof approach can always attain a better dependence on r). However, since
$\ell $
-density. (Such a result was previously proved in [Reference Füredi, Jiang, Kostochka, Mubayi and Verstraëte32], and our proof approach can always attain a better dependence on r). However, since
![]() $(r-1)$
-density is the relevant parameter in most applications, we prefer to keep our proof as simple as possible and only treat the case
$(r-1)$
-density is the relevant parameter in most applications, we prefer to keep our proof as simple as possible and only treat the case
![]() $\ell =r-1$
.
$\ell =r-1$
.
To prove Theorem 8.2, the following lemma turns out to be crucial. Roughly speaking, given any
![]() $\vec a$
-equipartite G (for some
$\vec a$
-equipartite G (for some
![]() $\vec a$
), we can either obtain a subgraph of G with more parts or a subgraph of G with the same number of parts but higher density.
$\vec a$
), we can either obtain a subgraph of G with more parts or a subgraph of G with the same number of parts but higher density.
Lemma 8.5. Suppose
![]() $1 \le k \le r$
and
$1 \le k \le r$
and
![]() $\vec {a}$
is a positive integer-valued vector of length k with
$\vec {a}$
is a positive integer-valued vector of length k with
![]() $\|\vec {a}\|_1=r$
. Let G be an
$\|\vec {a}\|_1=r$
. Let G be an
![]() $\vec {a}$
-equipartite ordered r-graph with
$\vec {a}$
-equipartite ordered r-graph with
![]() $(r-1)$
-density p, and consider any
$(r-1)$
-density p, and consider any
![]() $R\in \mathbb N$
. Suppose that n is sufficiently large in terms of
$R\in \mathbb N$
. Suppose that n is sufficiently large in terms of
![]() $r,R$
. Then, for some
$r,R$
. Then, for some
![]() $t\in \mathbb N$
satisfying
$t\in \mathbb N$
satisfying
![]() $\|\vec {a}\|_{0}\le t\le r$
, we can find a t-equipartite subgraph of order
$\|\vec {a}\|_{0}\le t\le r$
, we can find a t-equipartite subgraph of order
![]() $\left\lfloor {n/R} \right\rfloor $
in G, with
$\left\lfloor {n/R} \right\rfloor $
in G, with
![]() $(r-1)$
-density at least
$(r-1)$
-density at least
 $$\begin{align*}\frac{p}{4R}\left(\frac{R}{(r-k+1)^{2}}\right)^{r-t}. \end{align*}$$
$$\begin{align*}\frac{p}{4R}\left(\frac{R}{(r-k+1)^{2}}\right)^{r-t}. \end{align*}$$
We remark that in practice we will apply Lemma 8.5 with R a large constant.
Proof. Write
![]() $I_1,\dots ,I_k$
for the k parts of G. First, it is convenient to reduce to a subgraph whose order is divisible by R. So, let
$I_1,\dots ,I_k$
for the k parts of G. First, it is convenient to reduce to a subgraph whose order is divisible by R. So, let
![]() $n'=R\left\lfloor {n/R} \right\rfloor $
. By averaging, there’s a way to delete
$n'=R\left\lfloor {n/R} \right\rfloor $
. By averaging, there’s a way to delete
![]() $n-n'<R$
vertices from each
$n-n'<R$
vertices from each
![]() $I_i$
to obtain an
$I_i$
to obtain an
![]() $\vec {a}$
-equipartite subgraph
$\vec {a}$
-equipartite subgraph
![]() $G'$
, such that at most
$G'$
, such that at most
![]() $(rR/n)e(G)$
edges are deleted. So, the
$(rR/n)e(G)$
edges are deleted. So, the
![]() $(r-1)$
-density of
$(r-1)$
-density of
![]() $G'$
is at least
$G'$
is at least
![]() $p(1-rR/n)\ge p/2$
for
$p(1-rR/n)\ge p/2$
for
![]() $n \ge 2rR$
.
$n \ge 2rR$
.
Now, we divide each
![]() $I_i$
into R contiguous intervals
$I_i$
into R contiguous intervals
![]() $I_{i,1},\dots ,I_{i,R}$
of the same length
$I_{i,1},\dots ,I_{i,R}$
of the same length
![]() $n/R$
. Write
$n/R$
. Write ![]() be the all-ones vector of length R, and for every
be the all-ones vector of length R, and for every
![]() $t\in \{k,k+1,\dots ,r\}$
, define
$t\in \{k,k+1,\dots ,r\}$
, define
![]() $\mathcal {B}_{\vec {a},t}^{R}$
to be the set of
$\mathcal {B}_{\vec {a},t}^{R}$
to be the set of
![]() $k\times R$
matrices
$k\times R$
matrices
![]() $b\in \mathbb Z_{\ge 0}^{k\times R}$
with
$b\in \mathbb Z_{\ge 0}^{k\times R}$
with
![]() $\|b\|_{0}=t$
nonzero entries, satisfying
$\|b\|_{0}=t$
nonzero entries, satisfying ![]() . Then, for each
. Then, for each
![]() $b\in \mathcal B_{\vec a,t}^R$
, we define a t-equipartite subgraph
$b\in \mathcal B_{\vec a,t}^R$
, we define a t-equipartite subgraph
![]() $G_b$
of order
$G_b$
of order
![]() $\left\lfloor {n/R} \right\rfloor $
, as follows. The vertex set of
$\left\lfloor {n/R} \right\rfloor $
, as follows. The vertex set of
![]() $G_b$
is obtained by including part
$G_b$
is obtained by including part
![]() $I_{i,j}$
whenever
$I_{i,j}$
whenever
![]() $b_{ij}\ne 0$
, and the edge set is obtained by including each
$b_{ij}\ne 0$
, and the edge set is obtained by including each
![]() $e\in G'$
if
$e\in G'$
if
![]() $|e\cap I_{i,j}|=b_{ij}$
for all
$|e\cap I_{i,j}|=b_{ij}$
for all
![]() $i,j$
. Note that the subgraphs
$i,j$
. Note that the subgraphs
![]() $G_b$
(as b varies in
$G_b$
(as b varies in
![]() $\mathcal B_{\vec a,t}^R$
, while t varies in
$\mathcal B_{\vec a,t}^R$
, while t varies in
![]() $\{k,\dots ,r\}$
) partition the edges of
$\{k,\dots ,r\}$
) partition the edges of
![]() $G'$
.
$G'$
.
Now, if none of the subgraphs
![]() $G_b$
satisfied the conclusion of the lemma, the total number of edges in
$G_b$
satisfied the conclusion of the lemma, the total number of edges in
![]() $G'$
would be
$G'$
would be
 $$ \begin{align*} e(G') &< \sum_{t=k}^{r}\sum_{b\in\mathcal{B}_{\vec{a},t}^{R}} \frac{p}{4R}\left(\frac{R}{(r-k+1)^{2}}\right)^{r-t}\frac{(n/R)^{r-1}}{\prod_{i,j}b_{ij}!} \\&= \sum_{t=k}^{r} \frac{p\cdot R^{-t}}{4(r-k+1)^{2(r-t)}} \frac{n^{r-1}}{\prod_{i}a_i!} \sum_{b\in\mathcal{B}_{\vec{a},t}^{R}} \frac{\prod_{i}a_i!}{\prod_{i,j}b_{ij}!}. \end{align*} $$
$$ \begin{align*} e(G') &< \sum_{t=k}^{r}\sum_{b\in\mathcal{B}_{\vec{a},t}^{R}} \frac{p}{4R}\left(\frac{R}{(r-k+1)^{2}}\right)^{r-t}\frac{(n/R)^{r-1}}{\prod_{i,j}b_{ij}!} \\&= \sum_{t=k}^{r} \frac{p\cdot R^{-t}}{4(r-k+1)^{2(r-t)}} \frac{n^{r-1}}{\prod_{i}a_i!} \sum_{b\in\mathcal{B}_{\vec{a},t}^{R}} \frac{\prod_{i}a_i!}{\prod_{i,j}b_{ij}!}. \end{align*} $$
To show that this leads to contradiction, we need the following combinatorial inequality.
Claim 8.6. For every
![]() $k \le t \le r$
, we have
$k \le t \le r$
, we have
![]() $ \sum _{b\in \mathcal {B}_{\vec {a},t}^{R}} \left({\prod _{i}a_{i}!}/{\prod _{i,j}b_{i,j}!}\right) \le R^{t}\left({(r-k+1)^{2}}/{2}\right)^{r-t}. $
$ \sum _{b\in \mathcal {B}_{\vec {a},t}^{R}} \left({\prod _{i}a_{i}!}/{\prod _{i,j}b_{i,j}!}\right) \le R^{t}\left({(r-k+1)^{2}}/{2}\right)^{r-t}. $
We will prove Claim 8.6 momentarily, but first we see how to use it to conclude the proof of Lemma 8.5: recalling our estimate for
![]() $e(G')$
above, we have
$e(G')$
above, we have
 $$ \begin{align*} e(G')& < \sum_{t=k}^{r} \frac{p\cdot R^{-t}}{4(r-k+1)^{2(r-t)}} \frac{n^{r-1}}{\prod_{i}a_i!} \cdot R^{t}\left(\frac{(r-k+1)^{2}}{2}\right)^{r-t} \\&= \sum_{t=k}^{r}\frac{p}{4}\cdot2^{-(r-t)}\cdot\frac{n^{r-1}}{\prod_{i}a_{i}!} < \frac{(p/2)n^{r-1}}{\prod_{i}a_{i}!}, \end{align*} $$
$$ \begin{align*} e(G')& < \sum_{t=k}^{r} \frac{p\cdot R^{-t}}{4(r-k+1)^{2(r-t)}} \frac{n^{r-1}}{\prod_{i}a_i!} \cdot R^{t}\left(\frac{(r-k+1)^{2}}{2}\right)^{r-t} \\&= \sum_{t=k}^{r}\frac{p}{4}\cdot2^{-(r-t)}\cdot\frac{n^{r-1}}{\prod_{i}a_{i}!} < \frac{(p/2)n^{r-1}}{\prod_{i}a_{i}!}, \end{align*} $$
contradicting the fact that
![]() $G'$
has
$G'$
has
![]() $(r-1)$
-density at least
$(r-1)$
-density at least
![]() $p/2$
.
$p/2$
.
Now, we prove Claim 8.6.
Proof of Claim 8.6
We prove this inequality combinatorially, relating both sides of the inequality to certain counts of tuples of set partitions.
In this proof, we write
![]() $[n]=\{1,\dots ,n\}$
, and write
$[n]=\{1,\dots ,n\}$
, and write
![]() $\|f\|_{0}$
for the number of elements in the image of a function f. For
$\|f\|_{0}$
for the number of elements in the image of a function f. For
![]() $1\le q\le n$
, let
$1\le q\le n$
, let
![]() $\mathcal {P}_{n,q}$
be the collection of (unlabelled) partitions of
$\mathcal {P}_{n,q}$
be the collection of (unlabelled) partitions of
![]() $[n]$
into q nonempty subsets (so
$[n]$
into q nonempty subsets (so ![]() is a Stirling number of the second kind). Let
is a Stirling number of the second kind). Let
![]() $\mathcal {P}_{n}=\bigcup _{q=1}^{n}\mathcal {P}_{n,q}$
be the collection of partitions of
$\mathcal {P}_{n}=\bigcup _{q=1}^{n}\mathcal {P}_{n,q}$
be the collection of partitions of
![]() $[n]$
into any number of subsets, and let
$[n]$
into any number of subsets, and let
![]() $\|P\|_{0}$
be the number of parts of a partition
$\|P\|_{0}$
be the number of parts of a partition
![]() $P\in \mathcal {P}_{n}$
. Then, define
$P\in \mathcal {P}_{n}$
. Then, define
 $$\begin{align*}\mathcal{P}_{\vec{a},t}=\left\{ (P_{1},\dots,P_{k})\in\mathcal{P}_{a_{1}}\times\dots\times\mathcal{P}_{a_{k}}\;\middle|\;\sum_{i=1}^{k}\|P_{i}\|_{0}=t\right\}. \end{align*}$$
$$\begin{align*}\mathcal{P}_{\vec{a},t}=\left\{ (P_{1},\dots,P_{k})\in\mathcal{P}_{a_{1}}\times\dots\times\mathcal{P}_{a_{k}}\;\middle|\;\sum_{i=1}^{k}\|P_{i}\|_{0}=t\right\}. \end{align*}$$
Note that
 $$ \begin{align} \begin{aligned} \sum_{b\in\mathcal{B}_{\vec{a},t}^{R}}\frac{\prod_{i}a_{i}!}{\prod_{i,j}b_{i,j}!} = \sum_{b\in\mathcal{B}_{\vec{a},t}^{R}}\prod_{i}\binom{a_i}{b_{i,1}\dots b_{i,R}} \le R^{t}|\mathcal{P}_{\vec{a},t}|. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{b\in\mathcal{B}_{\vec{a},t}^{R}}\frac{\prod_{i}a_{i}!}{\prod_{i,j}b_{i,j}!} = \sum_{b\in\mathcal{B}_{\vec{a},t}^{R}}\prod_{i}\binom{a_i}{b_{i,1}\dots b_{i,R}} \le R^{t}|\mathcal{P}_{\vec{a},t}|. \end{aligned} \end{align} $$
(To see this, observe that the right-hand side of equation (8.1) can be interpreted as the number of ways to choose a tuple of partitions
![]() $(P_1, \dots , P_k)\in \mathcal {P}_{\vec {a},t}$
together with a labelling of the parts in these partitions in such a way that for each
$(P_1, \dots , P_k)\in \mathcal {P}_{\vec {a},t}$
together with a labelling of the parts in these partitions in such a way that for each
![]() $1\le i\le k$
, each of the parts in
$1\le i\le k$
, each of the parts in
![]() $P_i$
is assigned a distinct label from
$P_i$
is assigned a distinct label from
![]() $[R]$
).
$[R]$
).
Now, note that every
![]() $(P_{1},\dots ,P_{k})\in \mathcal {P}_{\vec {a},t}$
gives rise to a partition
$(P_{1},\dots ,P_{k})\in \mathcal {P}_{\vec {a},t}$
gives rise to a partition
![]() $P\in \mathcal {P}_{r,t}$
: first,
$P\in \mathcal {P}_{r,t}$
: first,
![]() $P_{1}$
describes a partition of
$P_{1}$
describes a partition of
![]() $\{1,\dots ,a_{1}\}$
, then
$\{1,\dots ,a_{1}\}$
, then
![]() $P_{2}$
describes a partition of
$P_{2}$
describes a partition of
![]() $\{a_{1}+1,\dots ,a_{1}+a_{2}\}$
, and
$\{a_{1}+1,\dots ,a_{1}+a_{2}\}$
, and
![]() $P_{3}$
describes a partition of
$P_{3}$
describes a partition of
![]() $\{a_{1}+a_2+1,\dots ,a_{1}+a_{2}+a_3\}$
, and so on. We can then ‘collapse’ P into a partition
$\{a_{1}+a_2+1,\dots ,a_{1}+a_{2}+a_3\}$
, and so on. We can then ‘collapse’ P into a partition
![]() $P'\in \mathcal {P}_{r-k+1,t-k+1}$
, by sequentially merging the parts containing
$P'\in \mathcal {P}_{r-k+1,t-k+1}$
, by sequentially merging the parts containing
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{1}+1$
, then merging the parts containing
$a_{1}+1$
, then merging the parts containing
![]() $a_{1}+a_{2}$
and
$a_{1}+a_{2}$
and
![]() $a_{1}+a_{2}+1$
, and so on. Since this mapping from
$a_{1}+a_{2}+1$
, and so on. Since this mapping from
![]() $(P_{1},\dots ,P_{k})$
to
$(P_{1},\dots ,P_{k})$
to
![]() $P'$
is injective, we deduce that
$P'$
is injective, we deduce that

Then, note that for all
![]() $1\le q\le n$
we have
$1\le q\le n$
we have

because we can generate a partition
![]() $P\in \mathcal {P}_{n,q}$
by starting with the trivial partition
$P\in \mathcal {P}_{n,q}$
by starting with the trivial partition
![]() $P_{0}\in \mathcal {P}_{n,n}$
into n parts, and iteratively merging pairs of parts (
$P_{0}\in \mathcal {P}_{n,n}$
into n parts, and iteratively merging pairs of parts (
![]() $n-q$
times). We deduce that
$n-q$
times). We deduce that
 $$\begin{align*}|\mathcal{P}_{\vec{a},t}|\le\binom{r-k+1}{2}^{r-t}<\left(\frac{(r-k+1)^{2}}{2}\right)^{r-t}. \end{align*}$$
$$\begin{align*}|\mathcal{P}_{\vec{a},t}|\le\binom{r-k+1}{2}^{r-t}<\left(\frac{(r-k+1)^{2}}{2}\right)^{r-t}. \end{align*}$$
Combining this with equation (8.1), the desired result follows.
Proof of Theorem 8.2
Let C be a large constant (
![]() $C=200$
will do). Let
$C=200$
will do). Let
![]() $R(k)=C\cdot (r-k+1)^2$
.
$R(k)=C\cdot (r-k+1)^2$
.
The plan is to repeatedly apply Lemma 8.5 until we find the desired subgraph. First, let
![]() $G_{0}=G$
,
$G_{0}=G$
,
![]() $p_{0}=p/2$
,
$p_{0}=p/2$
,
![]() $n_{0}=n$
and
$n_{0}=n$
and
![]() $k_{0}=1$
. Observe that
$k_{0}=1$
. Observe that
![]() $G_0$
(like any ordered r-graph) is
$G_0$
(like any ordered r-graph) is
![]() $\vec a$
-equipartite for
$\vec a$
-equipartite for
![]() $\vec a=(r)$
(i.e., 1-equipartite). It has order n and
$\vec a=(r)$
(i.e., 1-equipartite). It has order n and
![]() $(r-1)$
-density at least
$(r-1)$
-density at least
![]() $(p/n)\binom {n}{r}/(n^{r-1}/r!)>p/2$
(assuming n is sufficiently large in terms of r). Then, for each
$(p/n)\binom {n}{r}/(n^{r-1}/r!)>p/2$
(assuming n is sufficiently large in terms of r). Then, for each
![]() $i\ge 1$
(‘at step i’), we take the
$i\ge 1$
(‘at step i’), we take the
![]() $k_{i-1}$
-equipartite subgraph
$k_{i-1}$
-equipartite subgraph
![]() $G_{i-1}$
with
$G_{i-1}$
with
![]() $(r-1)$
-density
$(r-1)$
-density
![]() $p_{i-1}$
, and apply Lemma 8.5 with
$p_{i-1}$
, and apply Lemma 8.5 with
![]() $R=R(k_{i-1})$
to obtain a
$R=R(k_{i-1})$
to obtain a
![]() $k_{i}$
-equipartite subgraph
$k_{i}$
-equipartite subgraph
![]() $G_{i}$
with order
$G_{i}$
with order
![]() $n_{i}=\left\lfloor {n_{i-1}/R} \right\rfloor $
and with
$n_{i}=\left\lfloor {n_{i-1}/R} \right\rfloor $
and with
![]() $(r-1)$
-density at least
$(r-1)$
-density at least
 $$ \begin{align} p_{i} =\frac{p_{i-1}}{4R} \left(\frac{R}{(r-k_{i-1}+1)^2}\right)^{r-{k_i}} =\frac{p_{i-1}}{4(r-k_{i-1}+1)^{2}}C^{r-k_{i}-1}, \end{align} $$
$$ \begin{align} p_{i} =\frac{p_{i-1}}{4R} \left(\frac{R}{(r-k_{i-1}+1)^2}\right)^{r-{k_i}} =\frac{p_{i-1}}{4(r-k_{i-1}+1)^{2}}C^{r-k_{i}-1}, \end{align} $$
for some
![]() $k_{i}\ge k_{i-1}$
. We stop when
$k_{i}\ge k_{i-1}$
. We stop when
![]() $k_{i}\ge r-1$
(i.e., when we have found a
$k_{i}\ge r-1$
(i.e., when we have found a
![]() $(\ge r-1)$
-equipartite subgraph), and we also abort the process if at any point
$(\ge r-1)$
-equipartite subgraph), and we also abort the process if at any point
![]() $G_{i-1}$
has too few vertices to apply Lemma 8.5 with the desired R. Let
$G_{i-1}$
has too few vertices to apply Lemma 8.5 with the desired R. Let
![]() $\tau $
be the total number of steps taken.
$\tau $
be the total number of steps taken.
We first prove that
![]() $p_{j}\ge p/(8Cr^{2})$
for
$p_{j}\ge p/(8Cr^{2})$
for
![]() $j\leq \tau $
. In fact, we prove, by reverse induction, the stronger statement that for each step
$j\leq \tau $
. In fact, we prove, by reverse induction, the stronger statement that for each step
![]() $i<j$
we have
$i<j$
we have
The base case (where
![]() $i=j-1$
) follows from equation (8.2), so consider some
$i=j-1$
) follows from equation (8.2), so consider some
![]() $i<j-1$
and suppose as our induction hypothesis that the statement is true for
$i<j-1$
and suppose as our induction hypothesis that the statement is true for
![]() $i+1$
. Since
$i+1$
. Since
![]() $i+1 \leq j-1\leq \tau -1$
, we have
$i+1 \leq j-1\leq \tau -1$
, we have
![]() $k_{i+1}\leq r-2$
. Hence,
$k_{i+1}\leq r-2$
. Hence,
 $$ \begin{align*} p_{j}&\ge\frac{p_{i+1}}{4C(r-k_{i+1}+1)^{2}}=\frac{p_{i}}{(4C)^2(r-k_{i+1}+1)^{2}(r-k_{i}+1)^{2}}C^{r-k_{i+1}}\\&\ge\frac{p_{i}}{(4C)(r-k_{i}+1)^{2}}, \end{align*} $$
$$ \begin{align*} p_{j}&\ge\frac{p_{i+1}}{4C(r-k_{i+1}+1)^{2}}=\frac{p_{i}}{(4C)^2(r-k_{i+1}+1)^{2}(r-k_{i}+1)^{2}}C^{r-k_{i+1}}\\&\ge\frac{p_{i}}{(4C)(r-k_{i}+1)^{2}}, \end{align*} $$
using the induction hypothesis and equation (8.2) (for
![]() $i+1$
), and the fact that
$i+1$
), and the fact that
![]() $C^{r-k}/(4C(r-k+1)^2)\ge 1$
for
$C^{r-k}/(4C(r-k+1)^2)\ge 1$
for
![]() $k\le r-2$
and
$k\le r-2$
and
![]() $C \ge 36$
.
$C \ge 36$
.
It now suffices to show that this process cannot continue for too many steps (in particular, we want to make sure that the graphs
![]() $G_{i}$
never get too small). For each
$G_{i}$
never get too small). For each
![]() $1\le k\le r-2$
, let
$1\le k\le r-2$
, let
![]() $i(k)$
be the first step i such that
$i(k)$
be the first step i such that
![]() $k_{i}\ge k$
, and let
$k_{i}\ge k$
, and let
![]() $N(k)$
be the number of steps
$N(k)$
be the number of steps
![]() $i>i(k)$
such that
$i>i(k)$
such that
![]() $k_{i}=k$
. Note that for each step
$k_{i}=k$
. Note that for each step
![]() $i(k)<i\le i(k)+N(k)$
we have
$i(k)<i\le i(k)+N(k)$
we have
![]() $p_{i}\ge (C/40)p_{i-1}$
by equation (8.2) (because
$p_{i}\ge (C/40)p_{i-1}$
by equation (8.2) (because
![]() $C^{r-k}(r-k+1)^{-2}\ge C^2/10$
for
$C^{r-k}(r-k+1)^{-2}\ge C^2/10$
for
![]() $k\le r-2$
) and
$k\le r-2$
) and
![]() $n_{i}\le n_{i-1}/R(k)$
. This gives
$n_{i}\le n_{i-1}/R(k)$
. This gives
![]() $p_{i(k)+N(k)} \ge (C/40)^{N(k)} p_{i(k)}$
and
$p_{i(k)+N(k)} \ge (C/40)^{N(k)} p_{i(k)}$
and
![]() $n_{i(k)+N(k)}\le n_{i(k)}/R(k)^{N(k)}$
. But then, due to Definition 8.1, the
$n_{i(k)+N(k)}\le n_{i(k)}/R(k)^{N(k)}$
. But then, due to Definition 8.1, the
![]() $(r-1)$
-density of
$(r-1)$
-density of
![]() $G_{i(k)+N(k)}$
is at most
$G_{i(k)+N(k)}$
is at most
![]() $n_{i(k)+N(k)}$
, so
$n_{i(k)+N(k)}$
, so
![]() $p_{i(k)+N(k)} \le n_{i(k)+N(k)}$
. This, plus the fact that
$p_{i(k)+N(k)} \le n_{i(k)+N(k)}$
. This, plus the fact that
![]() $p_j\ge p/(8Cr^2)\ge \varepsilon /(8Cr^2)$
for
$p_j\ge p/(8Cr^2)\ge \varepsilon /(8Cr^2)$
for
![]() $j \le \tau $
, implies
$j \le \tau $
, implies
So we must have
where in the latter inequality we assume
![]() $n_{i(k)}$
is sufficiently large in terms of r and
$n_{i(k)}$
is sufficiently large in terms of r and
![]() $\varepsilon $
and C is a large constant. Consequently,
$\varepsilon $
and C is a large constant. Consequently,
![]() $n_{i(k)+N(k)}\ge (2R(k))^{-N(k)}\cdot n_{i(k)}\ge n_{i(k)}^{\alpha (k)}$
, where
$n_{i(k)+N(k)}\ge (2R(k))^{-N(k)}\cdot n_{i(k)}\ge n_{i(k)}^{\alpha (k)}$
, where
![]() $\alpha (k)=1-\log (2R(k))/\log (4R(k))>0$
, and
$\alpha (k)=1-\log (2R(k))/\log (4R(k))>0$
, and
![]() $n_{i(k+1)}=n_{i(k)+N(k)+1}\ge n_{i(k)+N(k)}/(2R(k)) \ge n_{i(k)}^{\alpha (k)}/(2R(k))$
.
$n_{i(k+1)}=n_{i(k)+N(k)+1}\ge n_{i(k)+N(k)}/(2R(k)) \ge n_{i(k)}^{\alpha (k)}/(2R(k))$
.
So,
![]() $n_{i}$
is at least
$n_{i}$
is at least
![]() $n^{\alpha (1)\dots \alpha (r-2)}/(2^{r-2}R(1)\dots R(r-2))$
for each i. Note that
$n^{\alpha (1)\dots \alpha (r-2)}/(2^{r-2}R(1)\dots R(r-2))$
for each i. Note that
![]() $\alpha (1)\dots \alpha (r-2)>0$
and
$\alpha (1)\dots \alpha (r-2)>0$
and
![]() $R(1)\dots R(r-2)$
only depend on r, so if n is sufficiently large in terms of r, then we can guarantee that each
$R(1)\dots R(r-2)$
only depend on r, so if n is sufficiently large in terms of r, then we can guarantee that each
![]() $n_i$
is always large enough (in terms of r and
$n_i$
is always large enough (in terms of r and
![]() $R(k_{i})$
) to apply Lemma 8.5 (i.e., the process never aborts). The process therefore terminates with the
$R(k_{i})$
) to apply Lemma 8.5 (i.e., the process never aborts). The process therefore terminates with the
![]() $(\ge r-1)$
-equipartite subgraph
$(\ge r-1)$
-equipartite subgraph
![]() $G_{\tau }$
with
$G_{\tau }$
with
![]() $(r-1)$
-density
$(r-1)$
-density
![]() $p_{\tau }\geq p/(8Cr^2)$
. This concludes the proof.
$p_{\tau }\geq p/(8Cr^2)$
. This concludes the proof.
Now, we prove Theorem 8.3.
Proof of Theorem 8.3
Let G be the ordered r-graph on the vertex set
![]() $\{1,\dots ,n\}$
, with every possible edge that contains two consecutive vertices. By Lemma 2.2, the number of edges in G is
$\{1,\dots ,n\}$
, with every possible edge that contains two consecutive vertices. By Lemma 2.2, the number of edges in G is
 $$ \begin{align*}\binom{n}{r}-\binom{(n-r+1)_+}{r}=(1+o(1))r(r-1)\frac{n^{r-1}}{r!}.\end{align*} $$
$$ \begin{align*}\binom{n}{r}-\binom{(n-r+1)_+}{r}=(1+o(1))r(r-1)\frac{n^{r-1}}{r!}.\end{align*} $$
-
1. If
 $G'$
is an r-equipartite subgraph with parts
$G'$
is an r-equipartite subgraph with parts
 $I_1<\dots <I_r$
of size m, then for every edge e there must be some pair of parts
$I_1<\dots <I_r$
of size m, then for every edge e there must be some pair of parts
 $I_i,I_{i+1}$
such that e contains the last element of
$I_i,I_{i+1}$
such that e contains the last element of
 $I_i$
and the first element of
$I_i$
and the first element of
 $I_{i+1}$
(and these two elements must be consecutive). So, the number of edges in
$I_{i+1}$
(and these two elements must be consecutive). So, the number of edges in
 $G'$
is at most
$G'$
is at most
 $(r-1)m^{r-2}$
, meaning that
$(r-1)m^{r-2}$
, meaning that
 $G'$
has
$G'$
has
 $(r-1)$
density at most
$(r-1)$
density at most
 $(r-1)/m=o_{m\to \infty }(1)$
.
$(r-1)/m=o_{m\to \infty }(1)$
. -
2. If
 $\vec a$
satisfies
$\vec a$
satisfies
 $\|\vec a\|_0=r-1$
and
$\|\vec a\|_0=r-1$
and
 $G'$
is an
$G'$
is an
 $\vec a$
-equipartite subgraph with parts
$\vec a$
-equipartite subgraph with parts
 $I_1<\dots <I_{r-1}$
of size m, then we can divide the edges of
$I_1<\dots <I_{r-1}$
of size m, then we can divide the edges of
 $G'$
into two types.
$G'$
into two types.-
○ First, we could have some edges e containing the last element of some
 $I_i$
and the first element of
$I_i$
and the first element of
 $I_{i+1}$
, as in (1). The number of such edges is at most
$I_{i+1}$
, as in (1). The number of such edges is at most
 $(r-2)m^{r-2}$
.
$(r-2)m^{r-2}$
. -
○ Second, writing j for the single index with
 $a_j=2$
, we could have some edges e containing two consecutive vertices in
$a_j=2$
, we could have some edges e containing two consecutive vertices in
 $I_j$
. The number of such edges is at most
$I_j$
. The number of such edges is at most
 $(m-1)m^{r-2}$
.
$(m-1)m^{r-2}$
.
All in all, the number of edges in
 $G'$
is at most
$G'$
is at most
 $(1+o_{m\to \infty }(1))m^{r-1}$
, meaning that
$(1+o_{m\to \infty }(1))m^{r-1}$
, meaning that
 $G'$
has
$G'$
has
 $(r-1)$
-density at most
$(r-1)$
-density at most
 $2+o_{m\to \infty }(1)$
.
$2+o_{m\to \infty }(1)$
. -
9 Extremal numbers for P-cliques
In this section, we prove Theorems 1.17 and 1.18. First, the following theorem is a generalisation of Theorem 1.18(1). It will also be used for the lower bound in Theorem 1.17.
Theorem 9.1. Let
![]() $r,n\ge 1$
, let P be an r-pattern, and let
$r,n\ge 1$
, let P be an r-pattern, and let
![]() $m\ge 1$
. If P is collectable or
$m\ge 1$
. If P is collectable or
![]() $m \in \{1,2\}$
then
$m \in \{1,2\}$
then
 $$ \begin{align*}\operatorname{\mathrm{ex}}_<(n,{P}^{(m)}) \ge \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{ex}}_<(n,{P}^{(m)}) \ge \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*} $$
(Note that Theorem 9.1 allows P to be non-collectable if
![]() $m\in \{1,2\}$
. We do not need to worry about non-collectable patterns in our proofs of Theorems 1.17 and 1.18 the extra generality is so that Proposition 7.2 (which we stated without proof in Section 7) is a direct corollary.
$m\in \{1,2\}$
. We do not need to worry about non-collectable patterns in our proofs of Theorems 1.17 and 1.18 the extra generality is so that Proposition 7.2 (which we stated without proof in Section 7) is a direct corollary.
Proof. Note that
![]() $\operatorname {\mathrm {ex}}_<(n,{P}^{(1)})=0$
and
$\operatorname {\mathrm {ex}}_<(n,{P}^{(1)})=0$
and
![]() $\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})=\binom {n}{r}$
if
$\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})=\binom {n}{r}$
if
![]() $rm> n$
. We may assume
$rm> n$
. We may assume
![]() $2 \le m \le n / r$
for the rest of the proof.
$2 \le m \le n / r$
for the rest of the proof.
Write
![]() $f_1,f_2$
for the two edges of P, with
$f_1,f_2$
for the two edges of P, with
![]() $f_1[1]<f_2[1]$
. For each
$f_1[1]<f_2[1]$
. For each
![]() $1\le i < r$
, let
$1\le i < r$
, let
![]() $s_i=\#(j\in [r]:f_1[i]<f_2[j]<f_1[i+1])$
be the number of vertices of
$s_i=\#(j\in [r]:f_1[i]<f_2[j]<f_1[i+1])$
be the number of vertices of
![]() $f_2$
lying between the i-th and
$f_2$
lying between the i-th and
![]() $(i+1)$
-th vertices of
$(i+1)$
-th vertices of
![]() $f_1$
. Let
$f_1$
. Let
![]() $s_r=\#(j\in [r]:f_2[j]>f_1[r])$
be the number of vertices of
$s_r=\#(j\in [r]:f_2[j]>f_1[r])$
be the number of vertices of
![]() $f_2$
after all the vertices of
$f_2$
after all the vertices of
![]() $f_1$
. Clearly,
$f_1$
. Clearly,
![]() $s_1+\dots +s_r=r$
.
$s_1+\dots +s_r=r$
.
Let G be the ordered r-graph with vertex set
![]() $\{1,2,\dots ,n\}$
, where we include an edge e whenever
$\{1,2,\dots ,n\}$
, where we include an edge e whenever
![]() $e[i+1]-e[i] \le s_i\cdot (m-1)$
for some
$e[i+1]-e[i] \le s_i\cdot (m-1)$
for some
![]() $1\le i<r$
or
$1\le i<r$
or
![]() $e[r] \ge n-s_r\cdot (m-1)+1$
. We first claim that G is
$e[r] \ge n-s_r\cdot (m-1)+1$
. We first claim that G is
![]() ${P}^{(m)}$
-free. Indeed, suppose for the purpose of contradiction that the edges
${P}^{(m)}$
-free. Indeed, suppose for the purpose of contradiction that the edges
![]() $e_1,\dots ,e_m$
in G form
$e_1,\dots ,e_m$
in G form
![]() ${P}^{(m)}$
, with
${P}^{(m)}$
, with
![]() $e_1[1]<\dots <e_m[1]$
. Fix
$e_1[1]<\dots <e_m[1]$
. Fix
![]() $2 \le j \le m$
. As
$2 \le j \le m$
. As
![]() $e_1,e_j$
form the pattern P, we know that for all
$e_1,e_j$
form the pattern P, we know that for all
![]() $1 \le i < r$
, there are
$1 \le i < r$
, there are
![]() $s_i$
vertices of
$s_i$
vertices of
![]() $e_j$
lying between
$e_j$
lying between
![]() $e_1[i],e_1[i+1]$
and that there are
$e_1[i],e_1[i+1]$
and that there are
![]() $s_r$
incident vertices of
$s_r$
incident vertices of
![]() $e_j$
lying after
$e_j$
lying after
![]() $e_1[r]$
. By considering all j, it holds that
$e_1[r]$
. By considering all j, it holds that
![]() $e_1[i+1]-e_1[i]>s_i\cdot (m-1)$
for
$e_1[i+1]-e_1[i]>s_i\cdot (m-1)$
for
![]() $1 \le i < r$
and
$1 \le i < r$
and
![]() $e_1[r] \le n-s_r\cdot (m-1)$
. But then,
$e_1[r] \le n-s_r\cdot (m-1)$
. But then,
![]() $e_1$
should not have been put into G, a contradiction.
$e_1$
should not have been put into G, a contradiction.
Now, it suffices to count the number of edges in G. It is convenient to instead count nonedges: An r-subset e of
![]() $\{1,\dots ,n\}$
is a nonedge of G if and only if
$\{1,\dots ,n\}$
is a nonedge of G if and only if
![]() $e[i+1]-e[i]>s_i\cdot (m-1)$
for all
$e[i+1]-e[i]>s_i\cdot (m-1)$
for all
![]() $1 \le i < r$
and
$1 \le i < r$
and
![]() $e[r]\le n-s_r\cdot (m-1)$
. By Lemma 2.2, the number of such e is exactly
$e[r]\le n-s_r\cdot (m-1)$
. By Lemma 2.2, the number of such e is exactly
 $$ \begin{align*}\binom{n-s_r(m-1)-\sum_{i=1}^{r-1}s_i(m-1)}{r}=\binom{n-r(m-1)}{r}.\end{align*} $$
$$ \begin{align*}\binom{n-s_r(m-1)-\sum_{i=1}^{r-1}s_i(m-1)}{r}=\binom{n-r(m-1)}{r}.\end{align*} $$
Thus, the number of edges in G is
 $$\begin{align*}\binom{n}{r}-\binom{n-r(m-1)}{r},\end{align*}$$
$$\begin{align*}\binom{n}{r}-\binom{n-r(m-1)}{r},\end{align*}$$
so this is a lower bound on
![]() $\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})$
, as desired.
$\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})$
, as desired.
Remark 9.2. In fact, the above lower bound works in a stronger setting: Given any r-pattern P and any r-matching Q with edges
![]() $e_1,\dots ,e_m$
(ordered such that
$e_1,\dots ,e_m$
(ordered such that
![]() $e_1[1]<e_2[1]<\dots <e_m[1]$
), such that
$e_1[1]<e_2[1]<\dots <e_m[1]$
), such that
![]() $e_1,e_i$
form the pattern P for all
$e_1,e_i$
form the pattern P for all
![]() $2\le i\le m$
, we have
$2\le i\le m$
, we have
 $$ \begin{align*}\operatorname{\mathrm{ex}}_<(n,Q) \ge \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{ex}}_<(n,Q) \ge \binom{n}{r}-\binom{(n-r(m-1))_+}{r}.\end{align*} $$
We next prove Theorem 1.18(3).
Proof of Theorem 1.18(3)
Without loss of generality, we may assume that
![]() $m \le n/r$
, as otherwise
$m \le n/r$
, as otherwise
![]() $\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})=\binom {n}{r}$
, as desired. Let P be the ‘alternating pattern’ represented by
$\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})=\binom {n}{r}$
, as desired. Let P be the ‘alternating pattern’ represented by
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|\cdots |$
, and let
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|\cdots |$
, and let
![]() $\tilde G$
be the ordered r-graph in the proof of Theorem 1.18(1) above, that is, e is an edge of G if
$\tilde G$
be the ordered r-graph in the proof of Theorem 1.18(1) above, that is, e is an edge of G if
![]() $e[2i]-e[2i-1] \le 2(m-1)$
for some
$e[2i]-e[2i-1] \le 2(m-1)$
for some
![]() $1 \le i \le r/2$
or if
$1 \le i \le r/2$
or if
![]() $e[r]\ge n-(m-1)+1$
and r is odd. The number of edges in
$e[r]\ge n-(m-1)+1$
and r is odd. The number of edges in
![]() $\tilde {G}$
is
$\tilde {G}$
is
 $$ \begin{align*}\binom{n}{r}-\binom{n-r(m-1)}{r}.\end{align*} $$
$$ \begin{align*}\binom{n}{r}-\binom{n-r(m-1)}{r}.\end{align*} $$
Consider any n-vertex
![]() ${P}^{(m)}$
-free ordered r graph G. We are going to show that
${P}^{(m)}$
-free ordered r graph G. We are going to show that
![]() $e(G) \le e(\tilde {G})$
. Our strategy is to partition the collection of all possible edges into subsets and to separately show that in each subset the number of edges of G is at most the number of edges of
$e(G) \le e(\tilde {G})$
. Our strategy is to partition the collection of all possible edges into subsets and to separately show that in each subset the number of edges of G is at most the number of edges of
![]() $\tilde {G}$
.
$\tilde {G}$
.
Let
![]() $E(K_n^{(r)})$
be the collection of all subsets of
$E(K_n^{(r)})$
be the collection of all subsets of
![]() $\{1,\dots ,n\}$
(i.e., all edges of the complete r-graph). We define an equivalence relation
$\{1,\dots ,n\}$
(i.e., all edges of the complete r-graph). We define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $E(K_n^{(r)})$
: for
$E(K_n^{(r)})$
: for
![]() $e,f\in E(K_n^{(r)})$
, we write
$e,f\in E(K_n^{(r)})$
, we write
![]() $e\sim f$
if there is
$e\sim f$
if there is
![]() $\ell \in \mathbb Z$
such that
$\ell \in \mathbb Z$
such that
![]() $f[i]=e[i]+\ell $
whenever i is odd, and
$f[i]=e[i]+\ell $
whenever i is odd, and
![]() $f[i]=e[i]-\ell $
whenever i is even. Fix an equivalence class A of
$f[i]=e[i]-\ell $
whenever i is even. Fix an equivalence class A of
![]() $\sim $
. It is easy to see that any two edges in A form the pattern P, and thus all the edges (in
$\sim $
. It is easy to see that any two edges in A form the pattern P, and thus all the edges (in
![]() $K_n^{(r)}$
) in A form a P-clique. Note that this is the only place we are using that P is the alternating pattern (for all other patterns
$K_n^{(r)}$
) in A form a P-clique. Note that this is the only place we are using that P is the alternating pattern (for all other patterns
![]() $P'$
, one can define similar equivalence classes, but it is not true that all equivalence classes are
$P'$
, one can define similar equivalence classes, but it is not true that all equivalence classes are
![]() $P'$
-cliques).
$P'$
-cliques).
Now, it suffices to show that
![]() $\left\vert {E(G)\cap A}\right\vert \le |{E(\tilde {G})\cap A}|$
for every equivalence class A of
$\left\vert {E(G)\cap A}\right\vert \le |{E(\tilde {G})\cap A}|$
for every equivalence class A of
![]() $\sim $
. Suppose there exists some
$\sim $
. Suppose there exists some
![]() $e \in A\cap (E(G)\setminus E(\tilde G))$
(otherwise
$e \in A\cap (E(G)\setminus E(\tilde G))$
(otherwise
![]() $\left\vert {E(G)\cap A}\right\vert \le |{E(\tilde {G})\cap A}|$
holds trivially). Since
$\left\vert {E(G)\cap A}\right\vert \le |{E(\tilde {G})\cap A}|$
holds trivially). Since
![]() $e\notin E(\tilde G)$
, we have
$e\notin E(\tilde G)$
, we have
![]() $e[2i]-e[2i-1]> 2(m-1)$
for all
$e[2i]-e[2i-1]> 2(m-1)$
for all
![]() $1 \le i\le r/2$
, and
$1 \le i\le r/2$
, and
![]() $e[r]\le n-(m-1)$
if r is odd. For
$e[r]\le n-(m-1)$
if r is odd. For
![]() $\ell \in \mathbb N$
, let
$\ell \in \mathbb N$
, let
As we increase
![]() $\ell $
, we are ‘pushing each
$\ell $
, we are ‘pushing each
![]() $e[2i-1]$
and
$e[2i-1]$
and
![]() $e[2i]$
towards each other’ and ‘pushing
$e[2i]$
towards each other’ and ‘pushing
![]() $e[r]$
towards n’ (if r is odd). At some point, there will be a ‘collision’: let
$e[r]$
towards n’ (if r is odd). At some point, there will be a ‘collision’: let
![]() $\ell ^\star $
be the ‘time just before this collision’, that is, the largest
$\ell ^\star $
be the ‘time just before this collision’, that is, the largest
![]() $\ell $
for which
$\ell $
for which
![]() $e[r] +(-1)^{r+1}\ell \le n$
and
$e[r] +(-1)^{r+1}\ell \le n$
and
![]() $e[2i-1]+\ell < e[2i]-\ell $
for all
$e[2i-1]+\ell < e[2i]-\ell $
for all
![]() $1 \le i \le r/2$
. Note that
$1 \le i \le r/2$
. Note that
![]() $\ell ^\star \ge m-1$
(since
$\ell ^\star \ge m-1$
(since
![]() $e\notin E(\tilde G)$
) and that
$e\notin E(\tilde G)$
) and that
![]() $f_{\ell }(e)\in E(\tilde G)$
for all
$f_{\ell }(e)\in E(\tilde G)$
for all
![]() $\ell \in \{\ell ^\star -(m-2),\dots ,\ell ^\star \}$
(the condition for f to be an edge of
$\ell \in \{\ell ^\star -(m-2),\dots ,\ell ^\star \}$
(the condition for f to be an edge of
![]() $\tilde G$
is the condition that f is ‘within
$\tilde G$
is the condition that f is ‘within
![]() $m-1$
steps of a collision’). Note that
$m-1$
steps of a collision’). Note that
![]() $f_{\ell }(e)\sim e$
for each
$f_{\ell }(e)\sim e$
for each
![]() $\ell \le \ell ^\star $
, so
$\ell \le \ell ^\star $
, so
![]() $|{E(\tilde {G})\cap A}|\ge m-1$
. On the other hand,
$|{E(\tilde {G})\cap A}|\ge m-1$
. On the other hand,
![]() $E(G)\cap A$
is a P-clique as every two edges in A form the pattern P. Since G is
$E(G)\cap A$
is a P-clique as every two edges in A form the pattern P. Since G is
![]() ${P}^{(m)}$
-free, we have
${P}^{(m)}$
-free, we have
![]() $\left\vert {E(G)\cap A}\right\vert \le m-1$
. This proves that
$\left\vert {E(G)\cap A}\right\vert \le m-1$
. This proves that
![]() $\left\vert {E(G)\cap A}\right\vert \le |{E(\tilde {G})\cap A}|$
, as desired.
$\left\vert {E(G)\cap A}\right\vert \le |{E(\tilde {G})\cap A}|$
, as desired.
Now, we prove Theorem 1.17 (giving the exact extremal numbers for all r-partite r-patterns P).
Proof of Theorem 1.17
We only need to prove the upper bound, as the lower bound is given by the
![]() $m=2$
case of Theorem 1.18(1).
$m=2$
case of Theorem 1.18(1).
We proceed by induction on r (the base case
![]() $r=1$
is trivial). Fix an r-partite r-pattern P, and write
$r=1$
is trivial). Fix an r-partite r-pattern P, and write
![]() $|{\mathfrak {B}}_1|\cdots |{\mathfrak {B}}_r|$
for its block representation, where
$|{\mathfrak {B}}_1|\cdots |{\mathfrak {B}}_r|$
for its block representation, where
![]() ${\mathfrak {B}}_1 = {{\mathrm {A}}{\mathrm {B}}}$
and
${\mathfrak {B}}_1 = {{\mathrm {A}}{\mathrm {B}}}$
and
![]() ${\mathfrak {B}}_i\in \{{{\mathrm {A}}{\mathrm {B}}},{{\mathrm {B}}{\mathrm {A}}}\}$
for
${\mathfrak {B}}_i\in \{{{\mathrm {A}}{\mathrm {B}}},{{\mathrm {B}}{\mathrm {A}}}\}$
for
![]() $2 \le i \le r$
. Let G be an n-vertex P-free ordered r-graph. We may assume that
$2 \le i \le r$
. Let G be an n-vertex P-free ordered r-graph. We may assume that
![]() $n \ge r$
; our goal is to prove that
$n \ge r$
; our goal is to prove that
 $$\begin{align*}e(G)\le \binom{n}{r}-\binom{n-r}{r}.\end{align*}$$
$$\begin{align*}e(G)\le \binom{n}{r}-\binom{n-r}{r}.\end{align*}$$
Let
![]() $\hat P$
be the pattern with block representation
$\hat P$
be the pattern with block representation
![]() $|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_{r-1}|$
, and for an edge
$|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_{r-1}|$
, and for an edge
![]() $e=\{e[1],\dots ,e[r]\}\in E(K_n^{(r)})$
, let
$e=\{e[1],\dots ,e[r]\}\in E(K_n^{(r)})$
, let
![]() $\hat e=\{e[1],\dots ,e[r-1]\}\in E(K_{n-1}^{(r-1)})$
. Let
$\hat e=\{e[1],\dots ,e[r-1]\}\in E(K_{n-1}^{(r-1)})$
. Let
![]() $G'$
be obtained from G as follows. For each
$G'$
be obtained from G as follows. For each
![]() $f\in E(K_{n-1}^{(r-1)})$
, consider all edges
$f\in E(K_{n-1}^{(r-1)})$
, consider all edges
![]() $e\in E(G)$
with
$e\in E(G)$
with
![]() $\hat e=f$
. If there are any such edges, then delete the one with the largest value of
$\hat e=f$
. If there are any such edges, then delete the one with the largest value of
![]() $e[r]$
. Note that
$e[r]$
. Note that
![]() $e(G') \ge e(G)-\binom {n-1}{r-1}$
.
$e(G') \ge e(G)-\binom {n-1}{r-1}$
.
Then, for
![]() $v \in \{1,\dots ,n\}$
, let
$v \in \{1,\dots ,n\}$
, let
![]() $\hat G_v$
be the graph with vertex set
$\hat G_v$
be the graph with vertex set
![]() $\{1,\dots ,v-1\}$
and edge set
$\{1,\dots ,v-1\}$
and edge set
We claim that
![]() $\hat G_v$
is
$\hat G_v$
is
![]() $\hat P$
-free. To see this, suppose for the purpose of contradiction that
$\hat P$
-free. To see this, suppose for the purpose of contradiction that
![]() $\hat e_1,\hat e_2 \in E(\hat G_v)$
form pattern
$\hat e_1,\hat e_2 \in E(\hat G_v)$
form pattern
![]() $\hat{P}$
with
$\hat{P}$
with
![]() $e_1[1]<e_2[1]$
. By the definition of
$e_1[1]<e_2[1]$
. By the definition of
![]() $G'$
, there are
$G'$
, there are
![]() $x, y\in \{v+1,\dots ,n\}$
such that
$x, y\in \{v+1,\dots ,n\}$
such that
![]() $\{e_1[1],\dots ,e_1[r-1],x\}, \{e_2[1],\dots ,e_2[r-1],y\} \in E(G)$
. But note that
$\{e_1[1],\dots ,e_1[r-1],x\}, \{e_2[1],\dots ,e_2[r-1],y\} \in E(G)$
. But note that
-
○ if
 ${\mathfrak {B}}_r = {{\mathrm {A}}{\mathrm {B}}}$
, then
${\mathfrak {B}}_r = {{\mathrm {A}}{\mathrm {B}}}$
, then
 $\{e_1[1],\dots ,e_1[r-1],v\},\{e_2[1],\dots ,e_2[r-1],y\}$
form pattern P;
$\{e_1[1],\dots ,e_1[r-1],v\},\{e_2[1],\dots ,e_2[r-1],y\}$
form pattern P; -
○ if
 ${\mathfrak {B}}_r = {{\mathrm {B}}{\mathrm {A}}}$
, then
${\mathfrak {B}}_r = {{\mathrm {B}}{\mathrm {A}}}$
, then
 $\{e_1[1],\dots ,e_1[r-1],x\},\{e_2[1],\dots ,e_2[r-1],v\}$
form pattern P.
$\{e_1[1],\dots ,e_1[r-1],x\},\{e_2[1],\dots ,e_2[r-1],v\}$
form pattern P.
In either case, we have found P in G, which is a contradiction. So, each
![]() $\hat G_v$
is
$\hat G_v$
is
![]() $\hat P$
-free and by induction we have
$\hat P$
-free and by induction we have
 $$\begin{align*}e(\hat G_v) \le \binom{v-1}{r-1}-\binom{(v-1-(r-1))_+}{r-1} = \binom{v-1}{r-1}-\binom{(v-r)_+}{r-1}. \end{align*}$$
$$\begin{align*}e(\hat G_v) \le \binom{v-1}{r-1}-\binom{(v-1-(r-1))_+}{r-1} = \binom{v-1}{r-1}-\binom{(v-r)_+}{r-1}. \end{align*}$$
Also, note that
![]() $e(\hat G_n)=0$
because any
$e(\hat G_n)=0$
because any
![]() $e \in E(G)$
with
$e \in E(G)$
with
![]() $e[r]=n$
must have been deleted in the construction of
$e[r]=n$
must have been deleted in the construction of
![]() $G'$
. Consequently,
$G'$
. Consequently,
 $$ \begin{align*} e(G) &\le \binom{n-1}{r-1} + e(G')=\binom{n-1}{r-1} + \sum_{v=1}^{n-1}e(\hat G_v)\\ &\le \binom{n-1}{r-1} + \sum_{v=1}^{n-1} \left[\binom{v-1}{r-1}-\binom{(v-r)_+}{r-1} \right] \\ &\le \binom{n-1}{r-1} + \sum_{k=0}^{n-2} \binom{k}{r-1} - \sum_{k=0}^{n-r-1} \binom{k}{r-1}\\ &= \binom{n-1}{r-1} + \binom{n-1}{r} - \binom{n-r}{r} =\binom{n}{r}-\binom{n-r}{r}, \end{align*} $$
$$ \begin{align*} e(G) &\le \binom{n-1}{r-1} + e(G')=\binom{n-1}{r-1} + \sum_{v=1}^{n-1}e(\hat G_v)\\ &\le \binom{n-1}{r-1} + \sum_{v=1}^{n-1} \left[\binom{v-1}{r-1}-\binom{(v-r)_+}{r-1} \right] \\ &\le \binom{n-1}{r-1} + \sum_{k=0}^{n-2} \binom{k}{r-1} - \sum_{k=0}^{n-r-1} \binom{k}{r-1}\\ &= \binom{n-1}{r-1} + \binom{n-1}{r} - \binom{n-r}{r} =\binom{n}{r}-\binom{n-r}{r}, \end{align*} $$
as desired.
The last result we prove in this section is Theorem 1.18(2). Starting from a
![]() ${P}^{(m)}$
-free r-graph G, we will apply Theorem 8.2 to pass to a
${P}^{(m)}$
-free r-graph G, we will apply Theorem 8.2 to pass to a
![]() $(\ge r-1)$
-equipartite subgraph (whose
$(\ge r-1)$
-equipartite subgraph (whose
![]() $(r-1)$
-density is comparably large, and which is still
$(r-1)$
-density is comparably large, and which is still
![]() ${P}^{(m)}$
-free). To this end, we need a generalisation of
${P}^{(m)}$
-free). To this end, we need a generalisation of
![]() $\operatorname {\mathrm {ex}}_<(n,F)$
.
$\operatorname {\mathrm {ex}}_<(n,F)$
.
Definition 9.3. Let
![]() $r \ge 1$
and
$r \ge 1$
and
![]() $\vec {a}$
be a positive integer-valued vector with sum of entries
$\vec {a}$
be a positive integer-valued vector with sum of entries
![]() $\|\vec {a}\|_{1}=r$
. For an ordered r-graph H, we write
$\|\vec {a}\|_{1}=r$
. For an ordered r-graph H, we write
![]() $\operatorname {\mathrm {ex}}_<^{\vec {a}}(n, H)$
for the maximum number of edges in an H-free
$\operatorname {\mathrm {ex}}_<^{\vec {a}}(n, H)$
for the maximum number of edges in an H-free
![]() $\vec {a}$
-equipartite r-graph of order n.
$\vec {a}$
-equipartite r-graph of order n.
We separately consider the r-equipartite (
![]() $\|\vec a\|_0=r$
) and
$\|\vec a\|_0=r$
) and
![]() $(r-1)$
-equipartite (
$(r-1)$
-equipartite (
![]() $\|\vec a\|_0=r-1$
) cases. First, we consider the r-equipartite case.
$\|\vec a\|_0=r-1$
) cases. First, we consider the r-equipartite case.
Lemma 9.4. Let
![]() $n,m,r \ge 1$
. Let
$n,m,r \ge 1$
. Let
![]() $\vec {a}=(1,1,\dots ,1)$
be the all-one vector of length r, and P be an r-partite r-pattern. Then,
$\vec {a}=(1,1,\dots ,1)$
be the all-one vector of length r, and P be an r-partite r-pattern. Then,
Proof. Let
![]() $V_{1},\dots ,V_{r}$
be disjoint copies of
$V_{1},\dots ,V_{r}$
be disjoint copies of
![]() $\{1,\dots ,n\}$
, and let
$\{1,\dots ,n\}$
, and let
![]() $\mathcal {V}=V_{1}\times \dots \times V_{r}$
. Note that an
$\mathcal {V}=V_{1}\times \dots \times V_{r}$
. Note that an
![]() $\vec {a}$
-equipartite r-graph G can be viewed as a set of tuples
$\vec {a}$
-equipartite r-graph G can be viewed as a set of tuples
![]() $e\in \mathcal {V}$
. From this perspective, a copy of
$e\in \mathcal {V}$
. From this perspective, a copy of
![]() ${P}^{(m)}$
(where P has block representation
${P}^{(m)}$
(where P has block representation
![]() $|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_r|$
) corresponds to a sequence of edges
$|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_r|$
) corresponds to a sequence of edges
![]() $e_{1},\dots ,e_{m}\in E(G)$
which is increasing in all coordinates i with
$e_{1},\dots ,e_{m}\in E(G)$
which is increasing in all coordinates i with
![]() ${\mathfrak {B}}_{i}={{\mathrm {A}}{\mathrm {B}}}$
, and decreasing in all coordinates i with
${\mathfrak {B}}_{i}={{\mathrm {A}}{\mathrm {B}}}$
, and decreasing in all coordinates i with
![]() ${\mathfrak {B}}_{i}={{\mathrm {B}}{\mathrm {A}}}$
. By symmetry,
${\mathfrak {B}}_{i}={{\mathrm {B}}{\mathrm {A}}}$
. By symmetry,
![]() ${\operatorname {\mathrm {ex}}_<^{\vec {a}}}(n,{P}^{(m)})$
depends only on n and m (i.e., it does not depend on P). Therefore, it suffices to consider the case where P has representation
${\operatorname {\mathrm {ex}}_<^{\vec {a}}}(n,{P}^{(m)})$
depends only on n and m (i.e., it does not depend on P). Therefore, it suffices to consider the case where P has representation
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\cdots |{{\mathrm {A}}{\mathrm {B}}}|$
(i.e., P is a ‘generalised crossing’).
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\cdots |{{\mathrm {A}}{\mathrm {B}}}|$
(i.e., P is a ‘generalised crossing’).
For the lower bound, we simply consider the
![]() $\vec {a}$
-equipartite r-graph
$\vec {a}$
-equipartite r-graph
![]() $\tilde {G}$
consisting of all possible edges
$\tilde {G}$
consisting of all possible edges
![]() $e\in \mathcal {V}$
such that some
$e\in \mathcal {V}$
such that some
![]() $e[i]<m$
. By the above discussion, any copy of
$e[i]<m$
. By the above discussion, any copy of
![]() $P^{(m)}$
must contain an edge with all coordinates at least m. Thus,
$P^{(m)}$
must contain an edge with all coordinates at least m. Thus,
![]() $\tilde G$
is
$\tilde G$
is
![]() ${P}^{(m)}$
-free, and it has the desired number of edges.
${P}^{(m)}$
-free, and it has the desired number of edges.
For the upper bound, consider a
![]() ${P}^{(m)}$
-free n-vertex graph G with parts
${P}^{(m)}$
-free n-vertex graph G with parts
![]() $V_{1},\dots ,V_{r}$
. Define an equivalence relation
$V_{1},\dots ,V_{r}$
. Define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $\mathcal {V}$
by taking
$\mathcal {V}$
by taking
![]() $e\sim f$
when there is some
$e\sim f$
when there is some
![]() $\ell \in \mathbb {Z}$
such that each
$\ell \in \mathbb {Z}$
such that each
![]() $e[i]=f[i]+\ell $
. We proceed very similarly to the proof of Theorem 1.18(3), showing that
$e[i]=f[i]+\ell $
. We proceed very similarly to the proof of Theorem 1.18(3), showing that
![]() $|A\cap E(G)|\le |A\cap E(\tilde {G})|$
for each equivalence class A of
$|A\cap E(G)|\le |A\cap E(\tilde {G})|$
for each equivalence class A of
![]() $\sim $
.
$\sim $
.
Consider some equivalence class A, and suppose there is
![]() $e\in A\cap(E(G)\setminus E(\tilde{G})) $
(otherwise trivially
$e\in A\cap(E(G)\setminus E(\tilde{G})) $
(otherwise trivially
![]() $|A\cap E(G)|\le |A\cap E(\tilde {G})|$
). Since
$|A\cap E(G)|\le |A\cap E(\tilde {G})|$
). Since
![]() $e\notin E(\tilde {G})$
, each
$e\notin E(\tilde {G})$
, each
![]() $e[i]\ge m$
. Define
$e[i]\ge m$
. Define
![]() $f_{\ell }(e)=(e[1]-\ell ,\dots ,e[r]-\ell )$
, and let
$f_{\ell }(e)=(e[1]-\ell ,\dots ,e[r]-\ell )$
, and let
![]() $\ell ^\star =\min _{i}e[i]-1\ge m-1$
. Note that
$\ell ^\star =\min _{i}e[i]-1\ge m-1$
. Note that
![]() $f_{\ell }(e)\in E(\tilde {G})$
for all
$f_{\ell }(e)\in E(\tilde {G})$
for all
![]() $\ell \in \{\ell ^\star -(m-2),\dots ,\ell ^\star \}$
, and note that
$\ell \in \{\ell ^\star -(m-2),\dots ,\ell ^\star \}$
, and note that
![]() $f_{\ell }(e)\sim e$
for each
$f_{\ell }(e)\sim e$
for each
![]() $\ell \le \ell ^\star $
. So,
$\ell \le \ell ^\star $
. So,
![]() $|A\cap E(\tilde {G})|\ge m-1$
. On the other hand, note that
$|A\cap E(\tilde {G})|\ge m-1$
. On the other hand, note that
![]() $A\cap E(G)$
is a P-clique so
$A\cap E(G)$
is a P-clique so
![]() $|A\cap E(G)|\le m-1$
. This proves that
$|A\cap E(G)|\le m-1$
. This proves that
![]() $|A\cap E(G)|\le |A\cap E(\tilde {G})|$
, as desired.
$|A\cap E(G)|\le |A\cap E(\tilde {G})|$
, as desired.
For the
![]() $(r-1)$
-partite case, we will make a reduction to the setting where
$(r-1)$
-partite case, we will make a reduction to the setting where
![]() $r=2$
. As mentioned in the introduction, in this setting the extremal number is known exactly, as follows.
$r=2$
. As mentioned in the introduction, in this setting the extremal number is known exactly, as follows.
Theorem 9.5. Let
![]() $n, m \ge 1$
, and let P be the crossing 2-pattern or the nesting 2-pattern. Then,
$n, m \ge 1$
, and let P be the crossing 2-pattern or the nesting 2-pattern. Then,
 $$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) = \binom{n}{2}-\binom{(n-2(m-1))_+}{2}\le 2(m-1)n.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<(n, {P}^{(m)}) = \binom{n}{2}-\binom{(n-2(m-1))_+}{2}\le 2(m-1)n.\end{align*}$$
The crossing case (
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
) of Theorem 9.5 is due to Capoyleas and Pach [Reference Capoyleas and Pach16] while the nesting case (
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
) of Theorem 9.5 is due to Capoyleas and Pach [Reference Capoyleas and Pach16] while the nesting case (
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
) is a special case of Theorem 1.18(3). (The nesting case also follows from results on queue-numbers of graphs due to Pemmaraju [Reference Pemmaraju54] and to Dujmović and Wood [Reference Dujmović and Wood24]; see [Reference Dujmović and Wood24, Lemma 8]). Now, our result in the
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
) is a special case of Theorem 1.18(3). (The nesting case also follows from results on queue-numbers of graphs due to Pemmaraju [Reference Pemmaraju54] and to Dujmović and Wood [Reference Dujmović and Wood24]; see [Reference Dujmović and Wood24, Lemma 8]). Now, our result in the
![]() $(r-1)$
-partite setting is as follows.
$(r-1)$
-partite setting is as follows.
Lemma 9.6. Let
![]() $n,m,r \ge 1$
. Let
$n,m,r \ge 1$
. Let
![]() $\vec {a}=\{1,2\}^{r-1}$
be a vector with exactly one ‘2’ (so all other entries are ‘1’). Let P be an r-partite r-pattern. Then,
$\vec {a}=\{1,2\}^{r-1}$
be a vector with exactly one ‘2’ (so all other entries are ‘1’). Let P be an r-partite r-pattern. Then,
Proof. Fix an r-partite r-pattern P, and write
![]() $|{\mathfrak {B}}_1|\cdots |{\mathfrak {B}}_r|$
for its block representation. Let
$|{\mathfrak {B}}_1|\cdots |{\mathfrak {B}}_r|$
for its block representation. Let
![]() $V_{1},\dots ,V_{r-1}$
be disjoint copies of
$V_{1},\dots ,V_{r-1}$
be disjoint copies of
![]() $\{1,\dots ,n\}$
, and let
$\{1,\dots ,n\}$
, and let
![]() $i^{\star }$
be the unique index such that
$i^{\star }$
be the unique index such that
![]() $a_{i^{\star }}=2$
. Note that an
$a_{i^{\star }}=2$
. Note that an
![]() $\vec a$
-equipartite r-graph G can be viewed as a set of tuples
$\vec a$
-equipartite r-graph G can be viewed as a set of tuples
where
![]() $K_{n}$
is the complete 2-graph on the vertex set
$K_{n}$
is the complete 2-graph on the vertex set
![]() $V_{i^{\star }}$
. From this perspective, a copy of
$V_{i^{\star }}$
. From this perspective, a copy of
![]() ${P}^{(m)}$
corresponds to a sequence of edges
${P}^{(m)}$
corresponds to a sequence of edges
![]() $e_{1},\dots ,e_{m}\in E(G)$
which is increasing in all coordinates
$e_{1},\dots ,e_{m}\in E(G)$
which is increasing in all coordinates
![]() $i\ne i^{\star }$
with
$i\ne i^{\star }$
with
![]() ${\mathfrak {B}}_{i}={{\mathrm {A}}{\mathrm {B}}}$
, and decreasing in all coordinates
${\mathfrak {B}}_{i}={{\mathrm {A}}{\mathrm {B}}}$
, and decreasing in all coordinates
![]() $i\ne i^{\star }$
with
$i\ne i^{\star }$
with
![]() ${\mathfrak {B}}_{i}={{\mathrm {B}}{\mathrm {A}}}$
, and in coordinate
${\mathfrak {B}}_{i}={{\mathrm {B}}{\mathrm {A}}}$
, and in coordinate
![]() $i^{\star }$
, the corresponding 2-edges have a consistent 2-partite pattern (the possibilities can be represented as
$i^{\star }$
, the corresponding 2-edges have a consistent 2-partite pattern (the possibilities can be represented as
![]() ${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {B}}}$
,
${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {A}}{\mathrm {B}}}$
,
![]() ${{\mathrm {B}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {A}}}$
,
${{\mathrm {B}}{\mathrm {A}}}{{\mathrm {B}}{\mathrm {A}}}$
,
![]() ${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {B}}{\mathrm {A}}}$
and
${{\mathrm {A}}{\mathrm {B}}}{{\mathrm {B}}{\mathrm {A}}}$
and
![]() ${{\mathrm {B}}{\mathrm {A}}}{{\mathrm {A}}{\mathrm {B}}}$
, that is, a crossing-clique going left, a crossing-clique going right, a nesting-clique going inwards, or a nesting-clique going outwards).
${{\mathrm {B}}{\mathrm {A}}}{{\mathrm {A}}{\mathrm {B}}}$
, that is, a crossing-clique going left, a crossing-clique going right, a nesting-clique going inwards, or a nesting-clique going outwards).
By symmetry, we may assume that
![]() $i^{\star }=r-1$
. In addition, by exchanging the ‘
$i^{\star }=r-1$
. In addition, by exchanging the ‘
![]() ${\mathrm {A}}$
’s and the ‘
${\mathrm {A}}$
’s and the ‘
![]() ${\mathrm {B}}$
’s in each
${\mathrm {B}}$
’s in each
![]() ${\mathfrak {B}}_i$
, if necessary, we may assume that
${\mathfrak {B}}_i$
, if necessary, we may assume that
![]() $|{\mathfrak {B}}_{r-1}|{\mathfrak {B}}_r|=|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
or
$|{\mathfrak {B}}_{r-1}|{\mathfrak {B}}_r|=|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
or
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
, and finally (as in Lemma 9.4) we may assume that
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
, and finally (as in Lemma 9.4) we may assume that
![]() ${\mathfrak {B}}_{i}= {{\mathrm {A}}{\mathrm {B}}}$
for
${\mathfrak {B}}_{i}= {{\mathrm {A}}{\mathrm {B}}}$
for
![]() $i\leq r-2$
. In other words, P has block representation
$i\leq r-2$
. In other words, P has block representation
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\dots |{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
or
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\dots |{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|$
or
![]() $|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\dots |{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
.
$|{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {A}}{\mathrm {B}}}|\dots |{{\mathrm {A}}{\mathrm {B}}}|{{\mathrm {B}}{\mathrm {A}}}|$
.
Now, we want to reduce the upper bound of
![]() $\operatorname {\mathrm {ex}}_<^{\vec {a}}(n,{P}^{(m)})$
to the graph (
$\operatorname {\mathrm {ex}}_<^{\vec {a}}(n,{P}^{(m)})$
to the graph (
![]() $r=2$
) case and apply Theorem 9.5. Fix an
$r=2$
) case and apply Theorem 9.5. Fix an
![]() $\vec {a}$
-equipartite
$\vec {a}$
-equipartite
![]() ${P}^{(m)}$
-free r-graph G with parts
${P}^{(m)}$
-free r-graph G with parts
![]() $V_{1},\dots ,V_{r-1}$
. Write Q for the 2-partite 2-pattern with block representation
$V_{1},\dots ,V_{r-1}$
. Write Q for the 2-partite 2-pattern with block representation
![]() $|{\mathfrak {B}}_{r-1}|{\mathfrak {B}}_{r}|$
. Observe that if G has two edges
$|{\mathfrak {B}}_{r-1}|{\mathfrak {B}}_{r}|$
. Observe that if G has two edges
![]() $e,f$
such that
$e,f$
such that
![]() $e[i]-e[r-1]=f[i]-f[r-1]$
for all
$e[i]-e[r-1]=f[i]-f[r-1]$
for all
![]() $i\in \{1,\dots ,r-2\}$
and such that the last two coordinates of e and the last two coordinates of f (both are viewed as edges in
$i\in \{1,\dots ,r-2\}$
and such that the last two coordinates of e and the last two coordinates of f (both are viewed as edges in
![]() $K_n$
) form pattern Q, then
$K_n$
) form pattern Q, then
![]() $e,f$
form pattern P.
$e,f$
form pattern P.
Now, for each
![]() $\vec {x}=(x_{1},\dots ,x_{r-2})\in \{1-n,2-n,\dots ,n-1\}^{r-2}$
, we define
$\vec {x}=(x_{1},\dots ,x_{r-2})\in \{1-n,2-n,\dots ,n-1\}^{r-2}$
, we define
![]() $G_{\vec {x}}$
to be the subgraph of G consisting of all edges
$G_{\vec {x}}$
to be the subgraph of G consisting of all edges
![]() $e\in E(G)$
such that
$e\in E(G)$
such that
![]() $e[i]-e[r-1]=x_i$
for all
$e[i]-e[r-1]=x_i$
for all
![]() $i\in \{1,\dots ,r-2\}$
(i.e., the edges of the form
$i\in \{1,\dots ,r-2\}$
(i.e., the edges of the form
![]() $(x_{1}+u,\,x_2+u,\,\dots ,\,x_{r-2}+u,\,uv)$
with
$(x_{1}+u,\,x_2+u,\,\dots ,\,x_{r-2}+u,\,uv)$
with
![]() $u<v$
). Write
$u<v$
). Write
![]() $G_{\vec {x}}^{(2)}$
for the
$G_{\vec {x}}^{(2)}$
for the
![]() $2$
-graph consisting of all
$2$
-graph consisting of all
![]() $uv$
such that
$uv$
such that
![]() $uv$
appears as the last coordinate of some edge in
$uv$
appears as the last coordinate of some edge in
![]() $G_{\vec {x}}$
. Note that there is a natural bijection between edges in
$G_{\vec {x}}$
. Note that there is a natural bijection between edges in
![]() $G_{\vec {x}}$
and edges in
$G_{\vec {x}}$
and edges in
![]() $G_{\vec {x}}^{(2)}$
, and by the above discussion, any Q-clique in
$G_{\vec {x}}^{(2)}$
, and by the above discussion, any Q-clique in
![]() $G_{\vec {x}}^{(2)}$
corresponds to a P-clique in
$G_{\vec {x}}^{(2)}$
corresponds to a P-clique in
![]() $G_{\vec {x}}$
of the same size. Thus,
$G_{\vec {x}}$
of the same size. Thus,
![]() $G_{\vec {x}}^{(2)}$
is
$G_{\vec {x}}^{(2)}$
is
![]() ${Q}^{(m)}$
-free. Also, as
${Q}^{(m)}$
-free. Also, as
![]() $G=\bigcup _{\vec {x}}G_{\vec {x}}$
, we know
$G=\bigcup _{\vec {x}}G_{\vec {x}}$
, we know
![]() $e(G)\le \sum _{\vec {x}}e(G_{\vec {x}})=\sum _{\vec {x}}e(G_{\vec {x}^{(2)}})$
.
$e(G)\le \sum _{\vec {x}}e(G_{\vec {x}})=\sum _{\vec {x}}e(G_{\vec {x}^{(2)}})$
.
Then, Theorem 9.5 implies
![]() $e(G_{\vec {x}})=e(G_{\vec {x}}^{(2)})\le 2(m-1)n$
for all possible
$e(G_{\vec {x}})=e(G_{\vec {x}}^{(2)})\le 2(m-1)n$
for all possible
![]() $\vec {x}$
. Naïvely, there are
$\vec {x}$
. Naïvely, there are
![]() $(2n-1)^{r-2}$
possible choices for
$(2n-1)^{r-2}$
possible choices for
![]() $\vec {x}$
, but we can do better. Note that for each edge
$\vec {x}$
, but we can do better. Note that for each edge
![]() $uv\in G_{\vec {x}}^{(2)}$
, we must have
$uv\in G_{\vec {x}}^{(2)}$
, we must have
![]() $\max _{i}x_{i}+u\le n$
and
$\max _{i}x_{i}+u\le n$
and
![]() $\min _{i}x_{i}+u\ge 1$
. So, for
$\min _{i}x_{i}+u\ge 1$
. So, for
![]() $G_{\vec {x}}$
to be nonempty, we must have
$G_{\vec {x}}$
to be nonempty, we must have
![]() $\max _{i}x_{i}-\min _{i}x_{i}<n$
. The number of choices of
$\max _{i}x_{i}-\min _{i}x_{i}<n$
. The number of choices of
![]() $\vec {x}$
which satisfy this inequality is at most
$\vec {x}$
which satisfy this inequality is at most
![]() $(2n-1)rn^{r-3}<2rn^{r-2}$
(enumerating over all choices of
$(2n-1)rn^{r-3}<2rn^{r-2}$
(enumerating over all choices of
![]() $\min _{i}x_{i}$
, and all choices of an i for which
$\min _{i}x_{i}$
, and all choices of an i for which
![]() $x_{i}$
is minimal). So,
$x_{i}$
is minimal). So,
and the desired result follows.
Remark 9.7. Let
![]() $i^\star $
be the only
$i^\star $
be the only
![]() $i\in [r-1]$
with
$i\in [r-1]$
with
![]() $a_i=2$
, and let
$a_i=2$
, and let
![]() $|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_r|$
be the block representation of P. Similarly to the proof of Theorem 1.18(3), one can show that if
$|{\mathfrak {B}}_1|{\mathfrak {B}}_2|\cdots |{\mathfrak {B}}_r|$
be the block representation of P. Similarly to the proof of Theorem 1.18(3), one can show that if
![]() ${\mathfrak {B}}_{i^\star }\neq {\mathfrak {B}}_{i^\star +1}$
, then
${\mathfrak {B}}_{i^\star }\neq {\mathfrak {B}}_{i^\star +1}$
, then
 $$\begin{align*}\operatorname{\mathrm{ex}}_<^{\vec{a}}(n,{P}^{(m)})=n^{r-2}\binom{n}{2}-(n-(m-1))^{r-2}\binom{(n-2(m-1))_+}{2}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<^{\vec{a}}(n,{P}^{(m)})=n^{r-2}\binom{n}{2}-(n-(m-1))^{r-2}\binom{(n-2(m-1))_+}{2}.\end{align*}$$
We wonder if a more general statement is true. Let
![]() $n,m,r \ge 1$
, let P be an r-partite r-pattern and let
$n,m,r \ge 1$
, let P be an r-partite r-pattern and let
![]() $\vec {a}$
be a vector of positive integers with sum of entries
$\vec {a}$
be a vector of positive integers with sum of entries
![]() $\|\vec {a}\|_{1}=r$
. Then, is it always the case that
$\|\vec {a}\|_{1}=r$
. Then, is it always the case that
 $$\begin{align*}\operatorname{\mathrm{ex}}_<^{\vec{a}}(n,{P}^{(m)})=\prod_{i=1}^k\binom{n}{a_i}-\prod_{i=1}^k\binom{(n-(m-1)a_i)_+}{a_i}?\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ex}}_<^{\vec{a}}(n,{P}^{(m)})=\prod_{i=1}^k\binom{n}{a_i}-\prod_{i=1}^k\binom{(n-(m-1)a_i)_+}{a_i}?\end{align*}$$
(cf. Conjecture 1.20).
We are finally ready to prove Theorem 1.18(2) (giving a general upper bound on
![]() $\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})$
using Theorem 8.2 to reduce to the
$\operatorname {\mathrm {ex}}_<(n,{P}^{(m)})$
using Theorem 8.2 to reduce to the
![]() $(\ge r-1)$
-equipartite case).
$(\ge r-1)$
-equipartite case).
Proof of Theorem 1.18(2)
Let G be an n-vertex
![]() ${P}^{(m)}$
-free ordered r-graph, with
${P}^{(m)}$
-free ordered r-graph, with
![]() $(p/n) \binom n r$
edges. Our goal is to prove that
$(p/n) \binom n r$
edges. Our goal is to prove that
![]() $p=O(r^3(m-1))$
.
$p=O(r^3(m-1))$
.
By Theorem 8.2, we can find a
![]() $(\ge r-1)$
-equipartite subgraph
$(\ge r-1)$
-equipartite subgraph
![]() $G'\subseteq G$
, of order
$G'\subseteq G$
, of order
![]() $n'=n^{\Omega _r(1)}$
, which has
$n'=n^{\Omega _r(1)}$
, which has
![]() $(r-1)$
-density at least
$(r-1)$
-density at least
![]() $\Omega (p/r^2)$
. Note that
$\Omega (p/r^2)$
. Note that
![]() $G'$
is still
$G'$
is still
![]() ${P}^{(m)}$
-free.
${P}^{(m)}$
-free.
-
○ If
 $G'$
is r-partite, then by Lemma 9.4, we have
$G'$
is r-partite, then by Lemma 9.4, we have
 $e(G')\le r(m-1)n^{r-1}$
. That is to say,
$e(G')\le r(m-1)n^{r-1}$
. That is to say,
 $G'$
has
$G'$
has
 $(r-1)$
-density at most
$(r-1)$
-density at most
 $r(m-1)$
.
$r(m-1)$
. -
○ If
 $G'$
is
$G'$
is
 $(r-1)$
-partite, then by Lemma 9.6, we have
$(r-1)$
-partite, then by Lemma 9.6, we have
 $e(G')\le 4r(m-1)n^{r-1}$
. That is to say,
$e(G')\le 4r(m-1)n^{r-1}$
. That is to say,
 $G'$
has
$G'$
has
 $(r-1)$
-density at most
$(r-1)$
-density at most
 $8r(m-1)$
.
$8r(m-1)$
.
In both cases,
![]() $G'$
has
$G'$
has
![]() $(r-1)$
-density
$(r-1)$
-density
![]() $O(r(m-1))$
; the desired result follows.
$O(r(m-1))$
; the desired result follows.
Acknowledgements
We would like to thank Timo Seppäläinen for some illuminating discussion about random high-dimensional orders and for bringing our attention to [Reference Seppäläinen59]. We would also like to thank the referees for helpful feedback.
Competing interest
The authors have no competing interest to declare.
Financial support
Michael Anastos is supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101034413. Matthew Kwan is supported by ERC Starting Grant ‘RANDSTRUCT’ No. 101076777, also funded by the European Union. Zhihan Jin and Benny Sudakov are supported by SNSF grant 200021-228014.