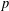Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-22T11:52:36.107Z Has data issue: false hasContentIssue false
  • English
  • Français

ESSENTIAL DIMENSION OF GENERIC SYMBOLS IN CHARACTERISTIC $p$

Part of: Linear algebraic groups and related topics Division rings and semisimple Artin rings General commutative ring theory

Published online by Cambridge University Press:  22 June 2017

KELLY MCKINNIE
KELLY MCKINNIE*
Affiliation:
Department of Mathematical Sciences, University of Montana, Missoula, MT 59812, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article the 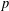$p$-essential dimension of generic symbols over fields of characteristic 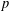$p$ is studied. In particular, the 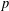$p$-essential dimension of the length 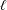$\ell$ generic 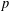$p$-symbol of degree 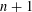$n+1$ is bounded below by 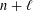$n+\ell$ when the base field is algebraically closed of characteristic 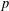$p$. The proof uses new techniques for working with residues in Milne–Kato 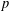$p$-cohomology and builds on work of Babic and Chernousov in the Witt group in characteristic 2. Two corollaries on 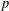$p$-symbol algebras (i.e, degree 2 symbols) result from this work. The generic 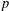$p$-symbol algebra of length 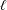$\ell$ is shown to have 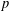$p$-essential dimension equal to 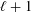$\ell +1$ as a 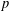$p$-torsion Brauer class. The second is a lower bound of 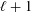$\ell +1$ on the 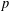$p$-essential dimension of the functor 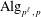$\operatorname{Alg}_{p^{\ell },p}$. Roughly speaking this says that you will need at least 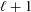$\ell +1$ independent parameters to be able to specify any given algebra of degree 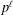$p^{\ell }$ and exponent 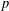$p$ over a field of characteristic 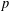$p$ and improves on the previously established lower bound of 3.

MSC classification

Primary: 16K20: Finite-dimensional
Secondary: 20G10: Cohomology theory 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 13A18: Valuations and their generalizations
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e14
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2017

References

Arason, J. K. and Baeza, R., ‘La dimension cohomologique des corps de type C r en caractéristique p ’, C. R. Math. Acad. Sci. Paris 348(3–4) (2010), 125–126.Google Scholar
Babic, A. and Chernousov, V., ‘Lower bounds for essential dimensions in characteristic 2 via orthogonal representations’, Pacific J. Math. 279(1–2) (2015), 37–63.Google Scholar
Baek, S., ‘Essential dimension of simple algebras in positive characteristic’, C. R. Math. Acad. Sci. Paris 349(7–8) (2011), 375–378.Google Scholar
Baek, S., ‘A lower bound on the essential dimension of PGL4 in characteristic 2’, J. Algebra Appl. 0(0) (2016), 1750063.Google Scholar
Baek, S. and Merkurjev, A., ‘Invariants of simple algebras’, Manuscripta Math. 129(4) (2009), 409–421.CrossRefGoogle Scholar
Bourbaki, N., Elements of Mathematics (Berlin), Commutative Algebra. Chapters 1–7 (Springer, Berlin, 1989), translated from the French, Reprint of the 1972 edition.Google Scholar
Buhler, J. and Reichstein, Z., ‘On the essential dimension of a finite group’, Compos. Math. 106(2) (1997), 159–179.CrossRefGoogle Scholar
Colliot-Thélène, J.-L., ‘Exposant et indice d’algèbres simples centrales non ramifiées’, Enseign. Math. (2) 48(1–2) (2002), 127–146, with an appendix by Ofer Gabber.Google Scholar
Dolphin, A. and Hoffmann, D. W., ‘Differential forms and bilinear forms under field extensions’, J. Algebra 441 (2015), 398–425.CrossRefGoogle Scholar
Eisenbud, D., Commutative Algebra, Graduate Texts in Mathematics, 150 (Springer, New York, 1995), with a view toward algebraic geometry.CrossRefGoogle Scholar
Garibaldi, S. and Guralnick, R. M., ‘Essential dimension of algebraic groups, including bad characteristic’, Arch. Math. 107(2) (2016), 101–119.Google Scholar
Gille, P. and Szamuely, T., Central Simple Algebras and Galois Cohomology, Cambridge Studies in Advanced Mathematics, 101 (Cambridge University Press, Cambridge, 2006).Google Scholar
Hoffmann, D. W., ‘Diagonal forms of degree p in characteristic p ’, inAlgebraic and Arithmetic Theory of Quadratic Forms, Contemp. Math., 344 (American Mathematical Society, Providence, RI, 2004), 135–183.Google Scholar
Izhboldin, O. T., ‘On the cohomology groups of the field of rational functions’, inMathematics in St. Petersburg, Amer. Math. Soc. Transl. Ser. 2, 174 (American Mathematical Society, Providence, RI, 1996), 21–44.Google Scholar
Kato, K., ‘Galois cohomology of complete discrete valuation fields’, inAlgebraic K-Theory, Part II (Oberwolfach, 1980), Lecture Notes in Mathematics, 967 (Springer, Berlin-New York, 1982), 215–238.CrossRefGoogle Scholar
Kato, K., ‘Symmetric bilinear forms, quadratic forms and Milnor K-theory in characteristic two’, Invent. Math. 66(3) (1982), 493–510.Google Scholar
Merkurjev, A., ‘Unramified cohomology of classifying varieties for classical simply connected groups’, Ann. Sci. Éc. Norm. Supér. (4) 35(3) (2002), 445–476.Google Scholar
Merkurjev, A. S., ‘Essential dimension: a survey’, Transform. Groups 18(2) (2013), 415–481.Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, 2nd edn, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 323 (Springer, Berlin, 2008).Google Scholar
Reichstein, Z., ‘Essential dimension’, inProceedings of the International Congress of Mathematicians, Hyderabad, India (Hindustan Book Agency, New Delhi, 2010).Google Scholar
Saltman, D. J., Lectures on Division Algebras, CBMS Regional Conference Series in Mathematics, 94 (American Mathematical Society, Providence, RI, 1999), on behalf of Conference Board of the Mathematical Sciences, Washington, DC.CrossRefGoogle Scholar
Serre, J.-P., ‘Cohomologie galoisienne: progrès et problèmes’, inAstérisque (227), Exp. No. 783, 4, Séminaire Bourbaki, 1993/94 (1995), 229–257.Google Scholar
Singh, B., Basic Commutative Algebra (World Scientific Publishing Co. Pte. Ltd, Hackensack, NJ, 2011).Google Scholar
Tignol, J.-P., ‘Cyclic and elementary abelian subfields of Malcev–Neumann division algebras’, J. Pure Appl. Algebra 42(2) (1986), 199–220.CrossRefGoogle Scholar