Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T07:59:28.323Z Has data issue: false hasContentIssue false
  • English
  • Français

DYADIC TRIANGULAR HILBERT TRANSFORM OF TWO GENERAL FUNCTIONS AND ONE NOT TOO GENERAL FUNCTION

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  13 November 2015

VJEKOSLAV KOVAČ ,
CHRISTOPH THIELE  and
PAVEL ZORIN-KRANICH
VJEKOSLAV KOVAČ
Affiliation:
Department of Mathematics, Faculty of Science, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia; [email protected]
CHRISTOPH THIELE
Affiliation:
Department of Mathematics, Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany; [email protected], [email protected]
PAVEL ZORIN-KRANICH
Affiliation:
Department of Mathematics, Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany; [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

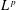The so-called triangular Hilbert transform is an elegant trilinear singular integral form which specializes to many well-studied objects of harmonic analysis. We investigate $L^{p}$ bounds for a dyadic model of this form in the particular case when one of the functions on which it acts is essentially one dimensional. This special case still implies dyadic analogues of boundedness of the Carleson maximal operator and of the uniform estimates for the one-dimensional bilinear Hilbert transform.

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e25
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Bernicot, F., ‘Fiber-wise Calderón–Zygmund decomposition and application to a bi-dimensional paraproduct’, Illinois J. Math. 56(2) (2012), 415–422.Google Scholar
Billard, P., ‘Sur la convergence presque partout des séries de Fourier–Walsh des fonctions de l’espace L 2(0, 1)’, Studia Math. 28 (1966/1967), 363–388.Google Scholar
Demeter, C., ‘Divergence of combinatorial averages and the unboundedness of the trilinear hilbert transform’, Ergod. Th. & Dynam. Sys. 28(5) (2008), 1453–1464.Google Scholar
Demeter, C., ‘A guide to Carleson’s Theorem’, Rocky Mountain J. Math. 45(1) (2015), 169–212.Google Scholar
Demeter, C. and Thiele, C., ‘On the two-dimensional bilinear Hilbert transform’, Amer. J. Math. 132(1) (2010), 201–256.Google Scholar
Grafakos, L. and Li, X., ‘Uniform bounds for the bilinear Hilbert transforms I’, Ann. of Math. (2) 159(3) (2004), 889–933.Google Scholar
Kovač, V., ‘Boundedness of the twisted paraproduct’, Rev. Mat. Iberoam. 28(4) (2012), 1143–1164.Google Scholar
Lacey, M. and Thiele, C., ‘L p estimates on the bilinear Hilbert transform for 2 < p < ∞’, Ann. of Math. (2) 146(3) (1997), 693–724.Google Scholar
Lacey, M. and Thiele, C., ‘On Calderón’s conjecture’, Ann. of Math. (2) 149(2) (1999), 475–496.Google Scholar
Li, X., ‘Uniform bounds for the bilinear Hilbert transforms II’, Rev. Mat. Iberoam. 22(3) (2006), 1069–1126.Google Scholar
Lie, V., ‘The (weak-l 2 ) boundedness of the quadratic carleson operator’, Geom. Funct. Anal. 19(2) (2009), 457–497.Google Scholar
Lie, V., ‘The polynomial carleson operator’, Preprint, 2011, arXiv:1105.4504.Google Scholar
Oberlin, R. and Thiele, C., ‘New uniform bounds for a Walsh model of the bilinear Hilbert transform’, Indiana Univ. Math. J. 60(5) (2011), 1693–1712.Google Scholar
Thiele, C. M., ‘Time-frequency analysis in the discrete phase plane’, PhD Thesis, Yale University. ProQuest LLC, Ann Arbor, MI, 1995.Google Scholar