Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T12:59:22.406Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGENERATIONS OF COMPLEX DYNAMICAL SYSTEMS

Part of: Arithmetic and non-Archimedean dynamical systems Complex dynamical systems

Published online by Cambridge University Press:  10 April 2014

LAURA DE MARCO  and
XANDER FABER
LAURA DE MARCO
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL, [email protected]
XANDER FABER
Affiliation:
Department of Mathematics, University of Hawaii at Manoa, Honolulu, HI, [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the weak limit of the maximal measures for any degenerating sequence of rational maps on the Riemann sphere 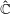${\hat{{\mathbb{C}}}} $ must be a countable sum of atoms. For a one-parameter family 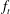$f_t$ of rational maps, we refine this result by showing that the measures of maximal entropy have a unique limit on 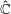$\hat{{\mathbb{C}}}$ as the family degenerates. The family 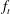$f_t$ may be viewed as a single rational function on the Berkovich projective line 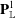$\mathbf{P}^1_{\mathbb{L}}$ over the completion of the field of formal Puiseux series in $t$, and the limiting measure on $\hat{{\mathbb{C}}}$ is the ‘residual measure’ associated with the equilibrium measure on 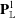$\mathbf{P}^1_{\mathbb{L}}$. For the proof, we introduce a new technique for quantizing measures on the Berkovich projective line and demonstrate the uniqueness of solutions to a quantized version of the pullback formula for the equilibrium measure on 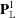$\mathbf{P}^1_{\mathbb{L}}$.

MSC classification

Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions 37P50: Dynamical systems on Berkovich spaces
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e6
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2014

References

Baker, M. and Rumely, R., Potential Theory and Dynamics on the Berkovich Projective Line, Mathematical Surveys and Monographs, 159 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Berkovich, V. G., Spectral Theory and Analytic Geometry Over Non-Archimedean Fields, Mathematical Surveys and Monographs, 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Bonifant, A., Kiwi, J. and Milnor, J., ‘Cubic polynomial maps with periodic critical orbit. II. Escape regions’, Conform. Geom. Dyn. 14 (2010), 68–112.Google Scholar
DeMarco, L., ‘Iteration at the boundary of the space of rational maps’, Duke Math. J. 130 (1) (2005), 169–197.Google Scholar
DeMarco, L., ‘The moduli space of quadratic rational maps’, J. Amer. Math. Soc. 20 (2) (2007), 321–355.CrossRefGoogle Scholar
DeMarco, L. and Faber, X., ‘Degenerations of complex dynamical systems II: Analytic and algebraic stability’. Preprint, arXiv:1309.7103 [math.DS], 2013.Google Scholar
DeMarco, L. G. and McMullen, C. T., ‘Trees and the dynamics of polynomials’, Ann. Sci. Éc. Norm. Supér. (4) 41 (3) (2008), 337–382.Google Scholar
Faber, X., ‘Topology and geometry of the Berkovich ramification locus for rational functions, I’, Manuscripta Math. 142 (3–4) (2013), 439–474.CrossRefGoogle Scholar
Faber, X., ‘Topology and geometry of the Berkovich ramification locus for rational functions, II’, Math. Ann. 356 (3) (2013), 819–844.Google Scholar
Favre, C., Personal communication.Google Scholar
Favre, C. and Rivera-Letelier, J., ‘Théorie ergodique des fractions rationnelles sur un corps ultramétrique’, Proc. Lond. Math. Soc. (3) 100 (1) (2010), 116–154.Google Scholar
Freire, A., Lopes, A. and Mañé, R., ‘An invariant measure for rational maps’, Bol. Soc. Brasil. Mat. 14 (1) (1983), 45–62.CrossRefGoogle Scholar
Kiwi, J., ‘Puiseux series polynomial dynamics and iteration of complex cubic polynomials’, Ann. Inst. Fourier (Grenoble) 56 (5) (2006), 1337–1404.Google Scholar
Kiwi, J., ‘Rescaling limits of complex rational maps’. arXiv:1211.3397 [math.DS]. Preprint, 2012.Google Scholar
Ljubich, M. J., ‘Entropy properties of rational endomorphisms of the Riemann sphere’, Ergodic Theory Dynam. Systems 3 (3) (1983), 351–385.Google Scholar
Sad, R. M. P. and Sullivan, D., ‘On the dynamics of rational maps’, Ann. Sci. École Norm. Sup. (4) 16 (2) (1983), 193–217.Google Scholar
Mañé, R., ‘On the uniqueness of the maximizing measure for rational maps’, Bol. Soc. Brasil. Mat. 14 (1) (1983), 27–43.Google Scholar
Mañé, R., ‘The Hausdorff dimension of invariant probabilities of rational maps’, inDynamical systems, Valparaiso 1986, Lecture Notes in Math., 1331 (Springer, Berlin, 1988), 86–117.CrossRefGoogle Scholar
Letelier, J. R., ‘Dynamique des fonctions rationnelles sur des corps locaux’, Astérisque 287 (xv) (2003), 147–230. Geometric methods in dynamics. II.Google Scholar