Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T19:44:15.775Z Has data issue: false hasContentIssue false
  • English
  • Français

CUTTING A PART FROM MANY MEASURES

Part of: Real and complex geometry Fiber spaces and bundles Homology and cohomology theories Discrete geometry

Published online by Cambridge University Press:  17 October 2019

PAVLE V. M. BLAGOJEVIĆ Open the ORCID record for PAVLE V. M. BLAGOJEVIĆ [Opens in a new window] ,
NEVENA PALIĆ ,
PABLO SOBERÓN Open the ORCID record for PABLO SOBERÓN [Opens in a new window]  and
GÜNTER M. ZIEGLER Open the ORCID record for GÜNTER M. ZIEGLER [Opens in a new window]
PAVLE V. M. BLAGOJEVIĆ
Affiliation:
Institut für Mathematik, FU Berlin, Arnimallee 2, 14195 Berlin, Germany; [email protected], [email protected], [email protected] Mathematical Institute SASA, Knez Mihailova 36, 11000 Beograd, Serbia
NEVENA PALIĆ
Affiliation:
Institut für Mathematik, FU Berlin, Arnimallee 2, 14195 Berlin, Germany; [email protected], [email protected], [email protected]
PABLO SOBERÓN
Affiliation:
Baruch College, City University of New York, One Bernard Baruch Way, New York, NY 10010, USA; [email protected]
GÜNTER M. ZIEGLER
Affiliation:
Institut für Mathematik, FU Berlin, Arnimallee 2, 14195 Berlin, Germany; [email protected], [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

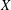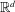Holmsen, Kynčl and Valculescu recently conjectured that if a finite set $X$ with $\ell n$ points in $\mathbb{R}^{d}$ that is colored by 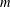$m$ different colors can be partitioned into $n$ subsets of 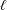$\ell$ points each, such that each subset contains points of at least 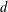$d$ different colors, then there exists such a partition of 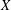$X$ with the additional property that the convex hulls of the $n$ subsets are pairwise disjoint.

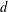We prove a continuous analogue of this conjecture, generalized so that each subset contains points of at least $c$ different colors, where we also allow $c$ to be greater than $d$. Furthermore, we give lower bounds on the fraction of the points each of the subsets contains from $c$ different colors. For example, when 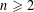$n\geqslant 2$, 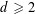$d\geqslant 2$, 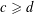$c\geqslant d$ with 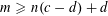$m\geqslant n(c-d)+d$ are integers, and 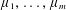$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$ are 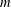$m$ positive finite absolutely continuous measures on 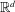$\mathbb{R}^{d}$, we prove that there exists a partition of $\mathbb{R}^{d}$ into $n$ convex pieces which equiparts the measures 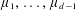$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{d-1}$, and in addition every piece of the partition has positive measure with respect to at least $c$ of the measures $\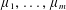unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$.

MSC classification

Primary: 52C35: Arrangements of points, flats, hyperplanes 51M20: Polyhedra and polytopes; regular figures, division of spaces
Secondary: 55R20: Spectral sequences and homology of fiber spaces 55N25: Homology with local coefficients, equivariant cohomology
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e37
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Adem, A. and Milgram, J. R., Cohomology of Finite Groups, 2nd edn, Grundlehren der Mathematischen Wissenschaften, vol. 309 (Springer, Berlin, 2004).Google Scholar
Bárány, I. and Matoušek, J., ‘Simultaneous partitions of measures by k-fans’, Discrete Comput. Geom. 25 (2001), 317–334.Google Scholar
Blagojević, P. V. M., Frick, F., Haase, A. and Ziegler, G. M., ‘Topology of the Grünbaum–Hadwiger–Ramos hyperplane mass partition problem’, Trans. Amer. Math. Soc. 370(10) (2018), 6795–6824.Google Scholar
Blagojević, P. V. M., Lück, W. and Ziegler, G. M., ‘Equivariant topology of configuration spaces’, J. Topol. 8 (2015), 414–456.Google Scholar
Blagojević, P. V. M., Rote, G., Steinmeyer, J. K. and Ziegler, G. M., ‘Convex equipartitions of colored point sets’, Discrete Comput. Geom. 61 (2019), 355–363.Google Scholar
Blagojević, P. V. M. and Ziegler, G. M., ‘Convex equipartitions via equivariant obstruction theory’, Israel J. Math. 200 (2014), 49–77.Google Scholar
Bousfield, A. K. and Kan, D. M., Homotopy Limits, Completions and Localizations, Lecture Notes in Mathematics, 304 (Springer, Berlin, 1972), Heidelberg, New York.Google Scholar
Cohen, F. R., ‘The homology of 𝓒n+1 -spaces, n⩾0’, inThe Homology of Iterated Loop Spaces, Vol. 533 (eds. Cohen, F. R., Lada, T. J. and Peter May, J.) Lecture Notes in Mathematics (Springer, Berlin, 1976), 207–351. Heidelberg, New York.Google Scholar
Grünbaum, B., ‘Partitions of mass-distributions and of convex bodies by hyperplanes’, Pacific J. Math. 10 (1960), 1257–1261.Google Scholar
Hadwiger, H., ‘Simultane Vierteilung zweier Körper’, Arch. Math. 17 (1966), 274–278.Google Scholar
Hatcher, A., Algebraic Topology, (Cambridge University Press, Cambridge, 2002).Google Scholar
Holmsen, A. F., Kynčl, J. and Valculescu, C., ‘Near equipartitions of colored point sets’, Comput. Geom. 65 (2017), 35–42.Google Scholar
Hsiang, W. Y., Cohomology Theory of Topological Transformation Groups (Springer, New York–Heidelberg, 1975), Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 85.Google Scholar
León, E. and Ziegler, G. M., ‘Spaces of convex n-partitions’, inNew Trends in Intuitive Geometry, (eds. Ambrus, G., Bárány, I., Böröczky, K. J., Fejes Tóth, G. and Pach, J.) Bolyai Society Mathematical Studies, 27 (Springer, Berlin Heidelberg, 2018), 279–306.Google Scholar
Ramos, E. A., ‘Equipartition of mass distributions by hyperplanes’, Discrete Comput. Geom. 15 (1996), 147–167.Google Scholar
Soberón, P., ‘Balanced convex partitions of measures in ℝ d ’, Mathematika 58 (2012), 71–76.Google Scholar
Sundaram, S. and Welker, V., ‘Group actions on arrangements of linear subspaces and applications to configuration spaces’, Trans. Amer. Math. Soc. 349 (1997), 1389–1420.Google Scholar
Volovikov, A. Y., ‘On the index of G-spaces’, Mat. Sb. 191 (2000), 3–22.Google Scholar
Welker, V., Ziegler, G. M. and Živaljević, R. T., ‘Homotopy colimits—comparison lemmas for combinatorial applications’, J. Reine Angew. Math. 509 (1999), 117–149.Google Scholar