Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T01:17:35.625Z Has data issue: false hasContentIssue false
  • English
  • Français

The construction problem for Hodge numbers modulo an integer in positive characteristic

Part of: (Co)homology theory Birational geometry Algebraic geometry: Foundations Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  09 November 2020

Remy van Dobben de Bruyn  and
Matthias Paulsen
Remy van Dobben de Bruyn
Affiliation:
Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544, USA; E-mail: [email protected] Institute for Advanced Study, 1 Einstein Drive, Princeton, NJ 08540, USA
Matthias Paulsen
Affiliation:
Institute of Algebraic Geometry, Gottfried Wilhelm Leibniz Universität Hannover, Welfengarten 1, D-30167Hannover, Germany; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be an algebraically closed field of positive characteristic. For any integer 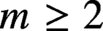$m\ge 2$ , we show that the Hodge numbers of a smooth projective k-variety can take on any combination of values modulo m, subject only to Serre duality. In particular, there are no non-trivial polynomial relations between the Hodge numbers.

MSC classification

Primary: 14F99: None of the above, but in this section
Secondary: 14G17: Positive characteristic ground fields 14A10: Varieties and morphisms 14E99: None of the above, but in this section
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e45
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Abhyankar, S. S., ‘Resolution of singularities of embedded algebraic surfaces’, Pure and Applied Mathematics 24 (Academic Press, 1966).Google Scholar
Achinger, P. and Zdanowicz, M., ‘Some elementary examples of non-liftable varieties’, Proc. Amer. Math. Soc. 145(11), 4717–4729 (2017), doi: 10.1090/proc/13622 Google Scholar
Chatzistamatiou, A. and Rülling, K., ‘Higher direct images of the structure sheaf in positive characteristic’, Algebra Number Theory 5(6), 693–775 (2011). doi: 10.2140/ant.2011.5.693.Google Scholar
Cutkosky, S. D., ‘Resolution of singularities for 3-folds in positive characteristic’, Amer. J. Math. 131(1), 59–127 (2009), doi:10.1353/ajm.0.0036.CrossRefGoogle Scholar
van Dobben de Bruyn, R., ‘The Hodge ring of varieties in positive characteristic’, in press, 2020, arXiv:2001.02787.Google Scholar
Gros, M., ‘Classes de Chern et classes de cycles en cohomologie de Hodge–Witt logarithmique’, Mém. Soc. Math. France (N.S.) 21, 1–87 (1985), https://eudml.org/doc/94860.Google Scholar
Kleiman, S. L., ‘Geometry on Grassmannians and applications to splitting bundles and smoothing cycles’, Inst. Hautes Études Sci. Publ. Math. 36, 281–297 (1969), http://www.numdam.org/item?id=PMIHES_1969__36__281_0.CrossRefGoogle Scholar
Kotschick, D. and Schreieder, S., ‘The Hodge ring of Kähler manifolds’, Compos. Math. 149(4), 637–657 (2013), doi:10.1112/S0010437X12000759.CrossRefGoogle Scholar
Maruyama, M., ‘On a family of algebraic vector bundles’, Number Theory, Algebraic Geometry and Commutative Algebra, in honor of Yasuo Akizuki (Kinokuniya Bookstore, 1973), 95–146.Google Scholar
Maruyama, M., ‘Elementary transformations in the theory of algebraic vector bundles’, Algebraic geometry (La Rábida, 1981); Lecture Notes in Math. 961 (Springer, 1982), 241–266; doi:10.1007/BFb0071286.CrossRefGoogle Scholar
Paulsen, M. and Schreieder, S., ‘The construction problem for Hodge numbers modulo an integer’, Algebra Number Theory 13(10), 2427–2434 (2019), doi:10.2140/ant.2019.13.2427.CrossRefGoogle Scholar
Raynaud, M., ‘Contre-exemple au “vanishing theorem” en caractéristique $p>0$ in C.P. Ramanujam–A Tribute, Tata Inst. Fun. Res. Studies in math., 8 (Springer, 1978), 273–278.0$+in+C.P.+Ramanujam–A+Tribute,+Tata+Inst.+Fun.+Res.+Studies+in+math.,+8+(Springer,+1978),+273–278.>Google Scholar
Schreieder, S., ‘On the construction problem for Hodge numbers’, Geom. Topol. 19(1), 295–342 (2015), doi: 10.2140/gt.2015.19.295.CrossRefGoogle Scholar
Serre, J.-P., ‘Sur la topologie des variétés algébriques en caractéristique $p$ ’, in Symposium internacional de topología algebraica (Universidad Nacional Autónoma de México and UNESCO, 1958), 24–53.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field. Cycles, transfers, and motivic homology theories. Ann. of Math. Stud. 143 (Princeton Univ. Press, 2000), 188–238.Google Scholar