Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:12:03.465Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSISTENCY OF CIRCUIT EVALUATION, EXTENDED RESOLUTION AND TOTAL NP SEARCH PROBLEMS

Part of: Proof theory and constructive mathematics Theory of computing

Published online by Cambridge University Press:  24 June 2016

JAN KRAJÍČEK
JAN KRAJÍČEK*
Affiliation:
Faculty of Mathematics and Physics, Charles University in Prague, Czech Republic; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider sets 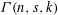${\it\Gamma}(n,s,k)$ of narrow clauses expressing that no definition of a size $s$ circuit with $n$ inputs is refutable in resolution R in 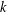$k$ steps. We show that every CNF with a short refutation in extended R, ER, can be easily reduced to an instance of 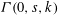${\it\Gamma}(0,s,k)$ (with 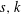$s,k$ depending on the size of the ER-refutation) and, in particular, that 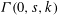${\it\Gamma}(0,s,k)$ when interpreted as a relativized NP search problem is complete among all such problems provably total in bounded arithmetic theory 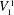$V_{1}^{1}$ . We use the ideas of implicit proofs from Krajíček [J. Symbolic Logic, 69 (2) (2004), 387–397; J. Symbolic Logic, 70 (2) (2005), 619–630] to define from 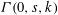${\it\Gamma}(0,s,k)$ a nonrelativized NP search problem 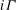$i{\it\Gamma}$ and we show that it is complete among all such problems provably total in bounded arithmetic theory 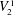$V_{2}^{1}$ . The reductions are definable in theory 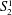$S_{2}^{1}$ . We indicate how similar results can be proved for some other propositional proof systems and bounded arithmetic theories and how the construction can be used to define specific random unsatisfiable formulas, and we formulate two open problems about them.

MSC classification

Primary: 03F20: Complexity of proofs
Secondary: 68Q15: Complexity classes (hierarchies, relations among complexity classes, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e15
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Beame, P., Cook, S. A., Edmonds, J., Impagliazzo, R. and Pitassi, T., ‘The relative complexity of NP search problems’, J. Comput. Syst. Sci. 57 (1998), 3–19.Google Scholar
Beckmann, A. and Buss, S. R., ‘The NP search problems of Frege and extended Frege proofs’, ACM Trans. Comput. Logic (2016) (submitted).Google Scholar
Buss, S. R., Bounded Arithmetic (Bibliopolis, Naples, 1986).Google Scholar
Cook, S. A., ‘Feasibly constructive proofs and the propositional calculus’, inProceedings of 7th Annual ACM Symposium on Theory of Computing (ACM Press, New York, 1975), 83–97.Google Scholar
Cook, S. A. and Nguyen, P., Logical Foundations of Proof Complexity, ASL Perspectives in Logic Series (Cambridge University Press, Cambridge, 2014).Google Scholar
Kolodziejczyk, L., Nguyen, P. and Thapen, N., ‘The provably total NP search problems of weak second order bounded arithmetic’, Ann. Pure Appl. Logic 162(6) (2011), 419–446.CrossRefGoogle Scholar
Krajíček, J., ‘Exponentiation and second-order bounded arithmetic’, Ann. Pure Appl. Logic 48(3) (1990), 261–276.Google Scholar
Krajíček, J., Bounded Arithmetic, Propositional Logic, and Complexity Theory, Encyclopedia of Mathematics and Its Applications, 60 (Cambridge University Press, Cambridge, 1995).Google Scholar
Krajíček, J., ‘Implicit proofs’, J. Symbolic Logic 69(2) (2004), 387–397.CrossRefGoogle Scholar
Krajíček, J., ‘Structured pigeonhole principle, search problems and hard tautologies’, J. Symbolic Logic 70(2) (2005), 619–630.Google Scholar
Krajíček, J., Forcing with Random Variables and Proof Complexity, London Mathematical Society Lecture Note Series, 382 (Cambridge University Press, Cambridge, 2011).Google Scholar
Papadimitriou, C. H., ‘On the complexity of the parity argument and other inefficient proofs of existence’, J. Comput. Syst. Sci. 48(3) (1994), 498–532.Google Scholar
Tseitin, G. S., ‘On the complexity of derivations in propositional calculus’, inStudies in Mathematics and Mathematical Logic (ed. Slisenko, A. O.) Part II (Springer US, New York, 1968), 115–125.Google Scholar