Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-22T16:22:17.778Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES

Part of: Computational number theory Curves Discontinuous groups and automorphic forms Arithmetic algebraic geometry Linear algebraic groups and related topics

Published online by Cambridge University Press:  02 February 2016

ANDREW V. SUTHERLAND
ANDREW V. SUTHERLAND*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

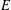Let $E$ be an elliptic curve without complex multiplication (CM) over a number field 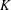$K$ , and let 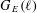$G_{E}(\ell )$ be the image of the Galois representation induced by the action of the absolute Galois group of  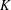$K$ on the 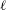$\ell$ -torsion subgroup of  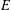$E$ . We present two probabilistic algorithms to simultaneously determine 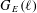$G_{E}(\ell )$ up to local conjugacy for all primes 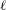$\ell$ by sampling images of Frobenius elements; one is of Las Vegas type and the other is a Monte Carlo algorithm. They determine 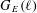$G_{E}(\ell )$ up to one of at most two isomorphic conjugacy classes of subgroups of 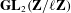$\mathbf{GL}_{2}(\mathbf{Z}/\ell \mathbf{Z})$ that have the same semisimplification, each of which occurs for an elliptic curve isogenous to 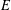$E$ . Under the GRH, their running times are polynomial in the bit-size $n$ of an integral Weierstrass equation for 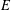 $E$ , and for our Monte Carlo algorithm, quasilinear in $n$ . We have applied our algorithms to the non-CM elliptic curves in Cremona’s tables and the Stein–Watkins database, some 140 million curves of conductor up to 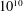 $10^{10}$ , thereby obtaining a conjecturally complete list of 63 exceptional Galois images 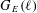$G_{E}(\ell )$ that arise for 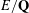$E/\mathbf{Q}$ without CM. Under this conjecture, we determine a complete list of 160 exceptional Galois images 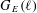$G_{E}(\ell )$ that arise for non-CM elliptic curves over quadratic fields with rational 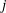$j$ -invariants. We also give examples of exceptional Galois images that arise for non-CM elliptic curves over quadratic fields only when the 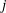$j$ -invariant is irrational.

MSC classification

Primary: 11G05: Elliptic curves over global fields 11Y16: Algorithms; complexity
Secondary: 11F80: Galois representations 11G20: Curves over finite and local fields 14H52: Elliptic curves 20G40: Linear algebraic groups over finite fields
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Anni, S., ‘Images of Galois representations’, PhD thesis, Universiteit Leiden and L’Université Bordeaux I, 2013.Google Scholar
Banwait, B. S., ‘On some local to global phenomena for abelian varieties’, PhD thesis, University of Warwick, 2013.Google Scholar
Banwait, B. S. and Cremona, J. E., Tetrahedral elliptic curves and the local-global principle for isogenies’, Algebra Number Theory 8 (2014), 1201–1229.CrossRefGoogle Scholar
Baran, B., ‘An exceptional isomorphism between modular curves of level 13’, J. Number Theory 145 (2014), 273–300.CrossRefGoogle Scholar
Bilu, Y., Parent, P. and Robelledo, M., ‘Rational points on $X_0^+(p^r)$’, Ann. Inst. Fourier (Grenoble) 64 (2013), 957–984.CrossRefGoogle Scholar
Birkhoff, G., ‘Subgroups of abelian groups’, Proc. Lond. Math. Soc. Ser. 2 38 (1935), 385–401.CrossRefGoogle Scholar
Belding, J., Bröker, R., Enge, A. and Lauter, K., ‘Computing Hilbert class polynomials’, in Proceedings of the 8th International Symposium on Algorithmic Number Theory (ANTS VIII), Lecture Notes in Computer Science, 5011 (Springer, 2008), 282–295.CrossRefGoogle Scholar
Bisson, G., ‘Computing endomorphism rings of elliptic curves under the GRH’, J. Math. Cryptol. 5 (2011), 101–113.Google Scholar
Bisson, G. and Sutherland, A. V., ‘Computing the endomorphism ring of an ordinary elliptic curve over a finite field’, J. Number Theory 131 (2011), 815–831.CrossRefGoogle Scholar
Bober, J., Deines, A., Klages-Mundt, A., LeVeque, B., Ohana, R. A., Rabindranath, A., Sharaba, P. and Stein, W., ‘A database of elliptic curves over Q$\unskip (\sqrt5)$: a first report’, in Proceedings of the Tenth Algorithmic Number Theory Symposium (ANTS X), (eds. E. W. Howe and K. S. Kedlaya) Open Book Series, 1 (Mathematical Sciences Publishers, 2013), 145–166.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Bröker, R., Lauter, K. and Sutherland, A. V., ‘Modular polynomials via isogeny volcanoes’, Math. Comp. 81 (2012), 1201–1231.CrossRefGoogle Scholar
Bruin, P. and Najman, F., ‘Hyperelliptic modular curves $X_0(n)$ and isogenies of elliptic curves over quadratic fields’, LMS J. Comput. Math. 18 (2015), 578–602.CrossRefGoogle Scholar
Cantor, D. G. and Zassenhaus, H., ‘A new algorithm for factoring polynomials over finite fields’, Math. Comp. 36 (1981), 587–592.CrossRefGoogle Scholar
Centeleghe, T. G., ‘Integral Tate modules and splitting of primes in torsion fields of elliptic curves’, Int. J. Number Theory, to appear, doi:10.1142/S1793042116500147.CrossRefGoogle Scholar
Chen, I. and Cummins, C., ‘Elliptic curves with nonsplit mod-11 representations’, Math. Comp. 73 (2004), 869–880.CrossRefGoogle Scholar
Cohen, H., A Course in Computational Algebraic Number Theory (Springer-Verlag, Berlin, Heidelberg, 1993).CrossRefGoogle Scholar
Cojocaru, A. C., ‘On the surjectivity of the Galois representations associated to non-CM elliptic curves (with an appendix by E. Kani)’, Canad. Math. Bull. 48 (2005), 16–31.CrossRefGoogle Scholar
Cremona, J. E., ‘Elliptic curve data’, available at https://homepages.warwick.ac.uk/staff/J.E.Cremona/ftp/data/, 2014.Google Scholar
Cremona, J. E., ‘Hyperbolic tessellations, modular symbols, and elliptic curves over complex quadratic fields’, Compos. Math. 51 (1984), 275–324.Google Scholar
Cremona, J. E., ‘Addendum and errata ‘Hyperbolic tessellations, modular symbols, and elliptic curves over complex quadratic fields’, Compos. Math. 63 (1984), 271–272.Google Scholar
Deuring, M., ‘Die Typen der Multiplikatorenringe elliptischer Funktionenkörper’, Abh. Math. Semin. Univ. Hansischen 14 (1941), 197–272.CrossRefGoogle Scholar
Dickson, L. E., Linear Groups with an Exposition of Galois Field Theory, Cosimo Classics 2007 reprint of original publication by B. G. Teubner, Leipzig, 1901.CrossRefGoogle Scholar
Donnelly, S., Gunnells, P. E., Klages-Mundt, A. and Yasaki, D., ‘A table of elliptic curves over the cubic field of discriminant − 23’, Exp. Math. 24 (2015), 375–390.CrossRefGoogle Scholar
Duke, W. and Tóth, Á., ‘The splitting of primes in division fields of elliptic curves’, Exp. Math. 11 (2002), 555–565.CrossRefGoogle Scholar
Elkies, N. D., ‘Elliptic and modular curves over finite fields and related computational issues’, in Computational Perspectives on Number Theory (Chicago, IL, 1995) AMS/IP Studies in Advanced Mathematics, 7 (1998), 21–76.CrossRefGoogle Scholar
Enge, A., ‘The complexity of class polynomial computation via floating point approximations’, Math. Comp. 78 (2009), 1089–1107.CrossRefGoogle Scholar
Flannery, D. L. and O’Brien, E. A., ‘Linear groups of small degree over finite fields’, Internat. J. Algebra Comput. 15 (2005), 467–502.CrossRefGoogle Scholar
Galbraith, S. D., Mathematics of Public Key Cryptography (Cambridge University Press, Cambridge, 2012).CrossRefGoogle Scholar
The GAP group, GAP–Groups, Algorithms, and Programming, version 4, 2015.Google Scholar
Gassmann, F., ‘Bemerkung zur vorstehenden Arbeit von Hurwitz’, Math. Z. 25 (1926), 665–675.Google Scholar
von zur Gathen, J. and Gerhard, J., Modern Computer Algebra, 3rd edn (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Glasby, S. P. and Howlett, R. B., ‘Writing representations over minimal fields’, Commun. Algebra 25 (1997), 1703–1711.CrossRefGoogle Scholar
Harvey, D., van der Hoeven, J. and Lecerf, G., ‘Even faster integer multiplication’, J. Complexity, to appear.Google Scholar
Kedlaya, K. S. and Sutherland, A. V., ‘Computing $L$-series of hyperelliptic curves’, in Algorithmic Number Theory 8th International Symposium (ANTS VIII), (Eds. A. J. van der Poorten and A. Stein) Lecture Notes in Computer Science, 5011 (Springer, 2008), 312–326.CrossRefGoogle Scholar
Kenku, M. A., ‘A note on the integral points of a modular curve of level 7’, Mathematika 32 (1985), 45–48.CrossRefGoogle Scholar
Kowalski, E. and Zywina, D., ‘The Chebotarev invariant of a finite group’, Exp. Math. 21 (2012), 38–56.CrossRefGoogle Scholar
Lagarias, J. C. and Odlyzko, A. M., ‘Effective versions of the Chebotarev density theorem’, in Algebraic Number Fields: L-functions and Galois Properties (Proc. Sympos., Univ. Durham, Durham, 1975) (Academic, London, 1977), 409–464.Google Scholar
Lagarias, J. C., Montgomery, H. L. and Odlyzko, A. M., ‘A bound for the least prime ideal in the Chebotarev density theorem’, Invent. Math. 54 (1979), 271–296.CrossRefGoogle Scholar
Landau, S., ‘Factoring polynomials over algebraic number fields’, SIAM J. Comput. 1985 (1985), 184–195.CrossRefGoogle Scholar
Lang, S., Introduction to Modular Forms (Springer-Verlag, Berlin, Heidelberg, 1976).CrossRefGoogle Scholar
Larson, E. and Vaintrob, D., ‘On the surjectivity of Galois representations associated to elliptic curves over number fields’, Bull. Lond. Math. Soc. 46 (2014), 197–209.CrossRefGoogle Scholar
Ligozat, G., ‘Courbe modulaires de diveau 11’, in Modular Functions of One Variable V, Lecture Notes in Mathematics, 601 (Springer, 1977), 149–237.CrossRefGoogle Scholar
The LMFDB Collaboration, The L-functions and modular forms database, available at http://www.lmfdb.org, 2014.Google Scholar
The LMFDB Collaboration, The $L$-functions and modular forms database, beta version, available at http://beta.lmfdb.org, 2015.Google Scholar
Mazur, B., ‘Modular curves and the Eisenstein ideal’, Publ. Math. Inst. Hautes Études Sci. 47 (1977), 33–186.CrossRefGoogle Scholar
Mazur, B., ‘Rational isogenies of primes degree’, Invent. Math. 44 (1978), 129–162.CrossRefGoogle Scholar
McKee, J., ‘Computing division polynomials’, Math. Comp. 63 (1994), 767–771.CrossRefGoogle Scholar
Miller, V. S., ‘The Weil pairing and its efficient calculation’, J. Cryptol. 17 (2004), 235–261.CrossRefGoogle Scholar
Ogg, A. P., ‘Elliptic curves and wild ramification’, Amer. J. Math. 89 (1967), 1–21.CrossRefGoogle Scholar
Oesterlé, J., ‘Versions effectives du théorème de Chebotarev sous l’hypothèse de Riemann généralisée’, Astérisque 61 (1979), 165–167.Google Scholar
Rouse, J. and Zureick-Brown, D., ‘Elliptic curves over Q and 2-adic images of Galois’, Res. Number Theory 1 (2015).CrossRefGoogle Scholar
Schönhage, A. and Strassen, V., ‘Schnelle Multiplikation Großer Zahlen’, Computing 7 (1971), 281–292.CrossRefGoogle Scholar
Schönhage, A., ‘Factorization of univariate integer polynomials by diophantine approximation and an improved basis reduction algorithm’, in Automata, Languages, and Programming, LNCS, 172 (1984), 436–447.Google Scholar
Schoof, R., ‘Elliptic curves over finite fields and the computation of square roots mod p’, Math. Comp. 44 (1985), 483–494.Google Scholar
Schoof, R., ‘Counting points on elliptic curves over finite fields’, J. Théor. Nombres Bordeaux 7 (1995), 219–254.CrossRefGoogle Scholar
Serre, J.-P., Abelian $\ell $-Adic Representations and Elliptic Curves (revised reprint of 1968 original), (A. K. Peters, Wellesley, MA, 1998).CrossRefGoogle Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15 (1972), 259–331.CrossRefGoogle Scholar
Serre, J.-P., ‘Quelques applications du théorème de densité de Chebotarev’, Publ. Math. Inst. Hautes Études Sci. 54 (1981), 323–401.CrossRefGoogle Scholar
Shparlinski, I. E. and Sutherland, A. V., ‘On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average’, LMS J. Comput. Math. 18 (2015), 308–322.CrossRefGoogle Scholar
Stein, W. A. and Watkins, M., ‘A database of elliptic curves–First report’, in Algorithmic Number Theory 5th International Symposium (ANTS V), (eds. C. Fieker and D. R. Kohel) Lecture Notes in Computer Science, 2369 (Springer-Verlag, Berlin, Heidelberg, 2002), 267–275.CrossRefGoogle Scholar
Streng, M., ‘Computing Igusa class polynomials’, Math. Comp. 83 (2014), 275–309.CrossRefGoogle Scholar
Sutherland, A. V., ‘smalljac software library’, version 4.0.28, available at http://math.mit.edu/ drew, 2014.Google Scholar
Sutherland, A. V., ‘Computing Hilbert class polynomials with the Chinese remainder theorem’, Math. Comp. 80 (2011), 501–538.CrossRefGoogle Scholar
Sutherland, A. V., ‘A local-global principle for isogenies of prime degree’, J. Théor. Nombres Bordeaux 24 (2012), 475–485.CrossRefGoogle Scholar
Sutherland, A. V., ‘Isogeny volcanoes’, in Proceedings of the Tenth Algorithmic Number Theory Symposium (ANTS X), (eds E. W. Howe and K. S. Kedlaya) Open Book Series 1 (Mathematical Sciences Publishers, 2013), 507–530.CrossRefGoogle Scholar
Sutherland, A. V., ‘On the evaluation of modular polynomials’, in Proceedings of the Tenth Algorithmic Number Theory Symposium (ANTS X), (eds. E. W. Howe and K. S. Kedlaya) Open Book Series, 1 (Mathematical Sciences Publishers, 2013), 531–555.CrossRefGoogle Scholar
Sutherland, A. V., Magma scripts related to Computing images of Galois representations attached to elliptic curves, available at http://math.mit.edu/ drew/galrep, 2015.CrossRefGoogle Scholar
Sunada, T., ‘Riemannian coverings and isospectral manifolds’, Ann. of Math. (2) 121 (1985), 169–186.CrossRefGoogle Scholar
Swinnerton-Dyer, H. P. F., ‘On $\ell $-adic representations and congruences for coefficients of modular forms’, in Modular Functions of one Variable III (Antwerp, Belgium 1972), (eds. P. Deligne and W. Kuyk) Lecture Notes in Mathematics, 350 (Springer, 1973), 1–56.CrossRefGoogle Scholar
Tóth, L., ‘Subgroups of finite abelian groups having rank two via Goursat’s lemma’, Tatra Mt. Math. Publ. 59 (2014), 93–103.Google Scholar
Winckler, B., ‘Théorème de Chebotarev effectif’, Preprint, 2013, arXiv:1311.5715.Google Scholar
Zywina, D., ‘On the surjectivity of mod-$\ell $ representations associated to elliptic curves’, Preprint, 2015, arXiv:1508.07661.Google Scholar
Zywina, D., ‘The possible images of the mod-$\ell $ representations associated to elliptic curves over Q’, Preprint, 2015, arXiv:1508.07660.Google Scholar