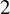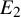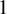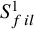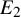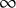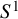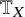1 Introduction
The de Rham cohomology of a ring or scheme comes equipped with a complete, decreasing filtration, known as the Hodge filtration. This has been studied in many capacities, and in particular occupies a paradigmatic role in the theory of Hodge structures. Carlos Simpson, in his work on nonabelian Hodge theory, understood this filtration in the geometric language of stacks, using the paradigm of filtrations and geometric objects over the stack
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Using a deformation to the normal cone construction of Fulton-Macpherson (cf. [Reference FultonFul84]), Simpson displayed the stack parametrizing
$\mathbb {A}^1 / \mathbb {G}_m$
. Using a deformation to the normal cone construction of Fulton-Macpherson (cf. [Reference FultonFul84]), Simpson displayed the stack parametrizing
![]() $\lambda $
-connections as a 1-parameter degeneration of the de Rham stack
$\lambda $
-connections as a 1-parameter degeneration of the de Rham stack
![]() $X_{dR}$
, which itself parametrizes bundles with flat connection over a fixed scheme X. These
$X_{dR}$
, which itself parametrizes bundles with flat connection over a fixed scheme X. These
![]() $\lambda $
-connections are exactly the objects which interpolate between Higgs bundles and bundles with flat connection and give rise, upon passing to subcategories of harmonic bundles, to equivalences between the two structures.
$\lambda $
-connections are exactly the objects which interpolate between Higgs bundles and bundles with flat connection and give rise, upon passing to subcategories of harmonic bundles, to equivalences between the two structures.
Meanwhile, there exists another one-parameter degeneration relating a sheared version of the de Rham cohomology of a scheme with its Hochschild homology. This was studied in depth in [Reference Moulinos, Robalo and ToënMRT22] (see also [Reference RaksitRak20] for another perspective on the matter), wherein the authors constructed a filtration on Hochschild homology whose associated graded recovers the derived de Rham algebra. This was accomplished algebro-geometrically, by way of the filtered loop space
![]() $\mathcal {L}_{fil}(X)$
; this is a relative derived scheme over
$\mathcal {L}_{fil}(X)$
; this is a relative derived scheme over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
which base-changes to the loop space
$\mathbb {A}^1 / \mathbb {G}_m$
which base-changes to the loop space
![]() $\mathcal {L}X$
and to the shifted tangent bundle
$\mathcal {L}X$
and to the shifted tangent bundle
![]() $\mathcal {T}_X[-1]$
, thus recovering the
$\mathcal {T}_X[-1]$
, thus recovering the
![]() $S^1$
-equivariant HKR filtration on Hochschild homology.
$S^1$
-equivariant HKR filtration on Hochschild homology.
The purpose of this work is to relate these two constructions in the setting of derived geometry. Our main theorem can be stated as follows:
Theorem 1.1. Let X be a derived scheme. Then the filtered loop space
![]() $\mathcal {L}_{fil}(X)$
fits as the degree
$\mathcal {L}_{fil}(X)$
fits as the degree
![]() $(1,1)$
piece of a 2-groupoid
$(1,1)$
piece of a 2-groupoid
![]() $\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
in formal derived stacks over
$\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
in formal derived stacks over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Taking the 2-fold delooping of this groupoid gives the following equivalence:
$\mathbb {A}^1 / \mathbb {G}_m$
. Taking the 2-fold delooping of this groupoid gives the following equivalence:
As a corollary, one obtains the following relationship between the de Rham space
![]() $X_{dR}$
and the loop space
$X_{dR}$
and the loop space
![]() $\mathcal {L}X$
:
$\mathcal {L}X$
:
Corollary 1.2. The derived loop space
![]() $\mathcal {L}X$
admits a 2-groupoid structure whose iterated delooping is the de Rham space – that is, there is an equivalence
$\mathcal {L}X$
admits a 2-groupoid structure whose iterated delooping is the de Rham space – that is, there is an equivalence
of formal derived stacks.
These statements follow directly from a canonical
![]() $E_2$
-cogroupoid (which we often call a
$E_2$
-cogroupoid (which we often call a
![]() $2$
-cogroupoid) structure on the filtered loop space,
$2$
-cogroupoid) structure on the filtered loop space,
![]() $S^1_{fil}$
. More precisely, the filtered loop space sits as the ‘
$S^1_{fil}$
. More precisely, the filtered loop space sits as the ‘
![]() $(1,1)$
space of morphisms’ of a bi-cosimplicial stack satisfying an analog of the Segal conditions (cf. [Reference LurieLur09a, Section 6.1]). Given a stack X, the formation of mapping objects out of a
$(1,1)$
space of morphisms’ of a bi-cosimplicial stack satisfying an analog of the Segal conditions (cf. [Reference LurieLur09a, Section 6.1]). Given a stack X, the formation of mapping objects out of a
![]() $E_2$
-cogroupoid object into X gives rise to a
$E_2$
-cogroupoid object into X gives rise to a
![]() $E_2$
-groupoid; in this particular case where the cogroupoid is
$E_2$
-groupoid; in this particular case where the cogroupoid is
![]() $S^1_{fil}$
, we obtain
$S^1_{fil}$
, we obtain
![]() $\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
.
$\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
.
We note the following interesting consequence about the filtered circle. In [Reference Moulinos, Robalo and ToënMRT22], it was verified that, when working over
![]() $\mathbb {Q}$
, there is an equivalence
$\mathbb {Q}$
, there is an equivalence
Here,
![]() $\eta : {\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
denotes the inclusion of the ‘generic’ point of
$\eta : {\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
denotes the inclusion of the ‘generic’ point of
![]() $\mathbb {A}^1 / \mathbb {G}_m$
, whereas
$\mathbb {A}^1 / \mathbb {G}_m$
, whereas
![]() $\iota : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
denotes the inclusion of the ‘closed’ point; in the language of [Reference MoulinosMou21b], restriction of a stack
$\iota : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
denotes the inclusion of the ‘closed’ point; in the language of [Reference MoulinosMou21b], restriction of a stack ![]() along these maps recovers the underlying and associated graded stacks of
along these maps recovers the underlying and associated graded stacks of ![]() , respectively.
, respectively.
Thus,
![]() $S^1_{fil}$
is a constant degeneration (see Section 7.1 for this terminology) of stacks. This is not the case when one takes the
$S^1_{fil}$
is a constant degeneration (see Section 7.1 for this terminology) of stacks. This is not the case when one takes the
![]() $E_2$
-cogroupoid structure into account:
$E_2$
-cogroupoid structure into account:
Corollary 1.3. The
![]() $E_2$
-cogroupoid
$E_2$
-cogroupoid
![]() $S^{1, \bullet , \bullet }_{fil} \to \mathbb {A}^1 / \mathbb {G}_m$
is not a constant degeneration of
$S^{1, \bullet , \bullet }_{fil} \to \mathbb {A}^1 / \mathbb {G}_m$
is not a constant degeneration of
![]() $E_2$
-cogroupoids. In particular, the pullbacks of
$E_2$
-cogroupoids. In particular, the pullbacks of
![]() $S^{1, \bullet , \bullet }_{fil}$
along
$S^{1, \bullet , \bullet }_{fil}$
along
![]() ${\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
and
${\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
and
![]() $B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
are not equivalent.
$B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
are not equivalent.
In order to prove Theorem 1.1, we work in the setting of formal geometry and formal moduli problems. As a clue for why we find ourselves in this setting essentially at the outset, we remark that the derived loop space
![]() $\mathcal {L}X$
is formally complete along X when X is a scheme. More generally, we will see that the filtered loop space obtains the structure of an
$\mathcal {L}X$
is formally complete along X when X is a scheme. More generally, we will see that the filtered loop space obtains the structure of an
![]() $E_2$
-groupoid
$E_2$
-groupoid
![]() $ \mathcal {L}^{\bullet , \bullet }_{fil}(X)$
in the
$ \mathcal {L}^{\bullet , \bullet }_{fil}(X)$
in the
![]() $\infty $
-category of formal moduli problems over X. Meanwhile, the map
$\infty $
-category of formal moduli problems over X. Meanwhile, the map
![]() $X \to X_{dR}$
to the de Rham space of X is also a nil-isomorphism. In fact,
$X \to X_{dR}$
to the de Rham space of X is also a nil-isomorphism. In fact,
![]() $X_{dR}$
is the final object in the category of formal moduli problems under X.
$X_{dR}$
is the final object in the category of formal moduli problems under X.
A key property which we exploit in the setting of formal moduli problems is the following: given a map
![]() $f: X \to Y$
, which is a nil-isomorphism, Y may be recovered as the classifying space of the Čech nerve. In this sense, the class of nil-isomorphisms plays the same role within formal geometry as the class of effective epimorphisms in derived geometry. Due to all this, the relation between the Hodge degeneration and the filtered loop space is most easily distilled in this setting of formal moduli problems, which we shall briefly review in Section 2.
$f: X \to Y$
, which is a nil-isomorphism, Y may be recovered as the classifying space of the Čech nerve. In this sense, the class of nil-isomorphisms plays the same role within formal geometry as the class of effective epimorphisms in derived geometry. Due to all this, the relation between the Hodge degeneration and the filtered loop space is most easily distilled in this setting of formal moduli problems, which we shall briefly review in Section 2.
1.1 The pinch map on
 $S^1$
and the Todd class
$S^1$
and the Todd class
In a very influential paper [Reference MarkarianMar09], N. Markarian described the Todd genus of a smooth proper scheme X as an invariant volume form with respect to the Hopf algebra structure on Hochschild homology. This was made more precise in [Reference Kondyrev and PrikhodkoKP19], in terms of the formal group structure on the derived loop space
![]() $\mathcal {L}(X)$
. In this paper, we expand on this story by describing the group structure on
$\mathcal {L}(X)$
. In this paper, we expand on this story by describing the group structure on
![]() $\mathcal {L}(X)$
as arising from an
$\mathcal {L}(X)$
as arising from an
![]() $E_1$
-cogroupoid structure on the circle
$E_1$
-cogroupoid structure on the circle
![]() $S^1$
. This
$S^1$
. This
![]() $E_1$
-cogroupoid structure, equivalently a cogroup structure on
$E_1$
-cogroupoid structure, equivalently a cogroup structure on
![]() $S^1$
as a pointed space, is none other than the well-known ‘pinch map’, which gives rise to the group structure on the fundamental groups of topological spaces. This
$S^1$
as a pointed space, is none other than the well-known ‘pinch map’, which gives rise to the group structure on the fundamental groups of topological spaces. This
![]() $E_1$
cogroupoid, which exists since
$E_1$
cogroupoid, which exists since
![]() $S^1$
is a suspension of a space, can also be extracted as either the row or column
$S^1$
is a suspension of a space, can also be extracted as either the row or column
![]() $1$
sub-cogroupoid of the
$1$
sub-cogroupoid of the
![]() $E_2$
-cogroupoid
$E_2$
-cogroupoid
![]() $S^{1,\bullet , \bullet }$
. It is well known that over the rationals, the cochain dga
$S^{1,\bullet , \bullet }$
. It is well known that over the rationals, the cochain dga
![]() $C^*(S^1, k)$
is formal, so that there is an equivalence
$C^*(S^1, k)$
is formal, so that there is an equivalence
We show that this formality statement is not true at the level of
![]() $E_1$
cogroupoids, and in particular, this failure is measured by the Todd class:
$E_1$
cogroupoids, and in particular, this failure is measured by the Todd class:
Theorem 1.4. The existence of nontrivial Todd classes implies that the cogroupoid (equivalently pointed cogroup) structure on
![]() $S^1$
corresponding to the pinch map is not formal.
$S^1$
corresponding to the pinch map is not formal.
One can summarize the above by saying that the ‘pinch map’ on
![]() $S^1$
is not formal, even though the dga of cochains on
$S^1$
is not formal, even though the dga of cochains on
![]() $S^1$
is well known to be formal when working rationally. Furthermore, the difference between the induced groupoid structure on
$S^1$
is well known to be formal when working rationally. Furthermore, the difference between the induced groupoid structure on
![]() $C^*(S^1, k)$
and that on
$C^*(S^1, k)$
and that on
![]() $H^*(S^1, k)$
manifests itself algebro-geometrically, by way of the two different group structures on the shifted tangent bundle
$H^*(S^1, k)$
manifests itself algebro-geometrically, by way of the two different group structures on the shifted tangent bundle
![]() $\mathcal {T}_{X}[-1]$
, which, in turn, is measured by the Todd class of the tangent Lie algebroid
$\mathcal {T}_{X}[-1]$
, which, in turn, is measured by the Todd class of the tangent Lie algebroid
![]() $\mathbb {T}_{X}$
.
$\mathbb {T}_{X}$
.
1.2 Remarks on Hochschild cohomology
The cogroupoid structures on
![]() $S^1$
also manifest themselves at the level of Hochschild cohomology. As we will remark in Section 8, the well-known
$S^1$
also manifest themselves at the level of Hochschild cohomology. As we will remark in Section 8, the well-known
![]() $E_2$
-algebra structure on Hochschild cohomology together with its (dual) HKR filtration arises from the
$E_2$
-algebra structure on Hochschild cohomology together with its (dual) HKR filtration arises from the
![]() $E_2$
-cogroupoid
$E_2$
-cogroupoid
![]() $S^1_{fil}$
.
$S^1_{fil}$
.
Proposition 1.5. Let X be a derived scheme. The
![]() $E_2$
-cogroupoid
$E_2$
-cogroupoid
![]() $S^1_{fil}$
gives rise to filtration on
$S^1_{fil}$
gives rise to filtration on
![]() $\operatorname {HH}^{*}(X)$
compatible with its
$\operatorname {HH}^{*}(X)$
compatible with its
![]() $E_2$
-algebra structure.
$E_2$
-algebra structure.
Perhaps more surprisingly, we highlight that one only needs an
![]() $E_1$
-cogroupoid structure on the zero sphere
$E_1$
-cogroupoid structure on the zero sphere
![]() $S^0$
to recover the
$S^0$
to recover the
![]() $E_2$
-algebra structure on Hochschild cohomology. As the zero sphere is not a suspension of a space, there exists no cogroup structure on it; in general, there is no group structure on
$E_2$
-algebra structure on Hochschild cohomology. As the zero sphere is not a suspension of a space, there exists no cogroup structure on it; in general, there is no group structure on
![]() $\pi _0(X)$
of a topological space in general. However, by taking the conerve of the map
$\pi _0(X)$
of a topological space in general. However, by taking the conerve of the map
![]() $\emptyset \to *$
from the initial object to the final object in spaces, we recover a cogroupoid with
$\emptyset \to *$
from the initial object to the final object in spaces, we recover a cogroupoid with
![]() $S^0$
in degree 1.
$S^0$
in degree 1.
We summarize the corresponding discussion in Section 8 with the following proposition:
Proposition 1.6. The cogroupoid
![]() $S_{fil}^{0, \bullet }$
(cf. Section 3) gives rise to a monoidal structure on
$S_{fil}^{0, \bullet }$
(cf. Section 3) gives rise to a monoidal structure on
the
![]() $\infty $
-category of quasi coherent sheaves on the mapping stack
$\infty $
-category of quasi coherent sheaves on the mapping stack
![]() $\operatorname {Map}_{\operatorname {dStk_{\mathbb {A}^1 / \mathbb {G}_m}}}(S^0_{fil},X|_{\mathbb {A}^1 / \mathbb {G}_m})$
. This specializes, by pulling back along the generic fiber, to the convolution monoidal structure on
$\operatorname {Map}_{\operatorname {dStk_{\mathbb {A}^1 / \mathbb {G}_m}}}(S^0_{fil},X|_{\mathbb {A}^1 / \mathbb {G}_m})$
. This specializes, by pulling back along the generic fiber, to the convolution monoidal structure on
Forming endomorphisms of the unit in (1.7) gives an
![]() $E_2$
-algebra
$E_2$
-algebra
![]() $\operatorname {HH}_{fil}^{*}(X)$
in filtered complexes
$\operatorname {HH}_{fil}^{*}(X)$
in filtered complexes
![]() $\operatorname {Fil}({\operatorname {Mod}}_k)$
, which specializes along the generic fiber of
$\operatorname {Fil}({\operatorname {Mod}}_k)$
, which specializes along the generic fiber of
![]() $\mathbb {A}^1 / \mathbb {G}_m$
to Hochschild cohomology.
$\mathbb {A}^1 / \mathbb {G}_m$
to Hochschild cohomology.
Finally, we remark that one may iterate the constructions to obtain
![]() $E_{n+1}$
cogroupoids
$E_{n+1}$
cogroupoids
![]() $S^{n, \bullet , \cdots , \bullet }_{fil}$
over
$S^{n, \bullet , \cdots , \bullet }_{fil}$
over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. These give rise, verbatim to the filtrations on iterated Hochschild cohomology
$\mathbb {A}^1 / \mathbb {G}_m$
. These give rise, verbatim to the filtrations on iterated Hochschild cohomology
![]() $HH^*_{E_n}$
compatible with the
$HH^*_{E_n}$
compatible with the
![]() $E_{n+1}$
-algebra structure.
$E_{n+1}$
-algebra structure.
Conventions. In general, we work over a characteristic zero base k, although many of the constructions work more generally. In another vein, we work freely in the setting of
![]() $\infty $
-categories and higher algebra from [Reference LurieLur17]. Similarly, we heavily utilize at times the formalism of formal geometry in [Reference Gaitsgory and RozenblyumGR19, Reference Gaitsgory and RozenblyumGR20], which, in particular, does depend on the fact we work over
$\infty $
-categories and higher algebra from [Reference LurieLur17]. Similarly, we heavily utilize at times the formalism of formal geometry in [Reference Gaitsgory and RozenblyumGR19, Reference Gaitsgory and RozenblyumGR20], which, in particular, does depend on the fact we work over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
2 Formal moduli problems and formal groupoids
Much of the interesting geometry of a derived stack ![]() is detectable at the infinitesimal level. Heuristically, a derived stack can be viewed as a family of infinitesimal thickenings of a scheme, parametrized by its points. In the language of formal geometry, this can be made precise by the slogan that the map
is detectable at the infinitesimal level. Heuristically, a derived stack can be viewed as a family of infinitesimal thickenings of a scheme, parametrized by its points. In the language of formal geometry, this can be made precise by the slogan that the map
![]() $X \to X_{dR}$
of a (nice enough) derived stack to its de Rham stack is a crystal of formal derived stacks. The reader may consult [Reference Calaque, Pantev, Toën, Vaquié and VezzosiCPT+17a, Section 2] for more on this perspective.
$X \to X_{dR}$
of a (nice enough) derived stack to its de Rham stack is a crystal of formal derived stacks. The reader may consult [Reference Calaque, Pantev, Toën, Vaquié and VezzosiCPT+17a, Section 2] for more on this perspective.
The sought-after relationship between the filtered loop space and the de Rham stack will exploit the fact that these two objects admit the structure of a formal moduli problem (at least when X is a scheme) relative to X. A key feature of the theory of formal moduli problems, which we lift from [Reference Gaitsgory and RozenblyumGR20], is the well behaved correspondence between groupoid objects and formal moduli problems under X. We will eventually exploit this to relate the filtered loop space with the Hodge degeneration
![]() $X_{Hod}$
.
$X_{Hod}$
.
As we follow the formalism developed in [Reference Gaitsgory and RozenblyumGR20], we review some basic constructions and definitions found therein. In particular, we highlight the distinction between formal moduli problems over a given stack and formal moduli problems under a stack. In order to proceed, we first recall what it means for a stack to admit a deformation theory. The basic setup here is over a field k of characteristic zero.
2.1 DAG preliminaries
Before diving into some formal geometry, we review the notions of derived stacks which we will be working in.
We recall that there are two variants of ‘derived’ geometric objects, one whose affine objects are connective
![]() $E_{\infty }$
-rings and one where the affine objects are simplicial commutative rings. In characteristic zero, the two contexts are equivalent. We review parallel constructions from both simultaneously, as we will switch between both settings.
$E_{\infty }$
-rings and one where the affine objects are simplicial commutative rings. In characteristic zero, the two contexts are equivalent. We review parallel constructions from both simultaneously, as we will switch between both settings.
Fix a commutative ring R and let ![]() denote either of the
denote either of the
![]() $\infty $
-category of connective R-algebras or the
$\infty $
-category of connective R-algebras or the
![]() $\infty $
-category of simplicial commutative R-algebras. Recall that the latter can be characterised as the completion via sifted colimits of the category of (discrete) free R-algebras. There exists a functor
$\infty $
-category of simplicial commutative R-algebras. Recall that the latter can be characterised as the completion via sifted colimits of the category of (discrete) free R-algebras. There exists a functor
which takes the underlying connective
![]() $E_{\infty }$
-algebra of a simplicial commutative algebra. This preserves limits and colimits so is, in fact, monadic and comonadic. In characteristic zero, this is, in fact, an equivalence, and this is often the setting we will find ourselves in within this paper.
$E_{\infty }$
-algebra of a simplicial commutative algebra. This preserves limits and colimits so is, in fact, monadic and comonadic. In characteristic zero, this is, in fact, an equivalence, and this is often the setting we will find ourselves in within this paper.
In any case, one may define a derived stack via its functor of points, as an object of the
![]() $\infty $
-category
$\infty $
-category ![]() satisfying hyperdescent with respect to a suitable topology on
satisfying hyperdescent with respect to a suitable topology on ![]() (e.g., the étale topology). Throughout the sequel, we distinguish the context we are working in by letting
(e.g., the étale topology). Throughout the sequel, we distinguish the context we are working in by letting
![]() $\operatorname {dStk}_{R}$
denote the
$\operatorname {dStk}_{R}$
denote the
![]() $\infty $
-category of derived stacks and let
$\infty $
-category of derived stacks and let
![]() $\operatorname {dStk}^{E_{\infty }}_R$
denote the
$\operatorname {dStk}^{E_{\infty }}_R$
denote the
![]() $\infty $
-category of ‘spectral stacks’ over R. In either case, one obtains an
$\infty $
-category of ‘spectral stacks’ over R. In either case, one obtains an
![]() $\infty $
-topos, which is Cartesian closed, so that it makes sense to talk about internal mapping objects: given any two
$\infty $
-topos, which is Cartesian closed, so that it makes sense to talk about internal mapping objects: given any two ![]() , one forms the mapping stack
, one forms the mapping stack ![]() , In various cases of interest, if the source and/or target is suitably representable by a derived scheme or a derived Artin stack, then this is the case for
, In various cases of interest, if the source and/or target is suitably representable by a derived scheme or a derived Artin stack, then this is the case for ![]() as well.
as well.
In addition, we also will occasionally find ourselves working with higher stacks. This genre of geometric objects was introduced by Simpson and essentially is composed of stacks on the site of discrete commutative rings equipped with for example the étale or fppf topology. For the sake of maintaining a somewhat self-contained exposition, we now define this as following:
Definition 2.1. Let
![]() $\operatorname {Aff}_R$
be the category of affine schemes, equivalently the opposite of the category of discrete commutative R-algebras equipped with some (classical) Grothendieck topology. Then we set
$\operatorname {Aff}_R$
be the category of affine schemes, equivalently the opposite of the category of discrete commutative R-algebras equipped with some (classical) Grothendieck topology. Then we set
to be the
![]() $\infty $
-category of higher stacks, equivalently that of sheaves of spaces with respect to the topology
$\infty $
-category of higher stacks, equivalently that of sheaves of spaces with respect to the topology
![]() $\tau $
.
$\tau $
.
Remark 2.2. Higher stacks provide the natural ambient setting for the notion of affine stacks, introduced by Toën in [Reference ToënToë06], which we will briefly review in Section 4. The cogroupoid objects we construct and study in this Section 4 will typically live in this setting of higher stacks. It is an interesting phenomenon that this setting, which is somehow ‘discrete in the domain’ and ‘derived’ or ‘homotopical’ in the target, provides a home for affine objects which are by their very nature coconnective, at least when viewed as
![]() $E_{\infty }$
-algebras.
$E_{\infty }$
-algebras.
2.2 Formal moduli problems
In this section, we set up the necessary background regarding formal moduli problems. These objects capture the infinitesimal part of the geometry of derived stacks and feature prominently in this work. First we recall some auxiliary notions leading up to the notion of a formal moduli problem.
Definition 2.3. A stack ![]() is convergent or nil-complete if for derived affine scheme
is convergent or nil-complete if for derived affine scheme
![]() ${\operatorname {Spec}} B$
, the natural map
${\operatorname {Spec}} B$
, the natural map
is an equivalence.
Definition 2.4. ([Reference Gaitsgory and RozenblyumGR20, Section 0.1]) Let ![]() be a derived stack. We say that
be a derived stack. We say that ![]() admits a deformation theory if it is convergent, and such that for every pushout square of affine schemes
admits a deformation theory if it is convergent, and such that for every pushout square of affine schemes

where the map
![]() $S_1 \to S^{'}_{1}$
is a nilpotent embedding (i.e., the map on truncations is a closed embedding with nilpotent ideal of definition), the resulting diagram
$S_1 \to S^{'}_{1}$
is a nilpotent embedding (i.e., the map on truncations is a closed embedding with nilpotent ideal of definition), the resulting diagram

is a pullback diagram.
Remark 2.5. In fact, this is enough, by [Reference Gaitsgory and RozenblyumGR20], to guarantee the existence of the pro-cotangent complex of ![]() . This is an assignment, for every derived scheme
. This is an assignment, for every derived scheme ![]() ,of a pro-object
,of a pro-object
which governs the infinitesimal behavior of ![]() at the point x.
at the point x.
Remark 2.6. Any n-Artin stack, for example, satisfies the properties of Definition 2.4 and thus admits a deformation theory.
We also recall the notion of ‘locally almost of finite type’(=laft) from [Reference Gaitsgory and RozenblyumGR19]. For this, we first need to recall what it means for an (derived) affine scheme to be locally of finite type.
Definition 2.7. Let
![]() $X = {\operatorname {Spec}} A$
be a derived affine scheme. Then X is of finite type if
$X = {\operatorname {Spec}} A$
be a derived affine scheme. Then X is of finite type if
![]() $\pi _0(A)$
is of finite type over k and if each
$\pi _0(A)$
is of finite type over k and if each
![]() $\pi _n(A)$
is finitely generated as a module over
$\pi _n(A)$
is finitely generated as a module over
![]() $\pi _0(A)$
.
$\pi _0(A)$
.
Next, one defines what it means for a (pre)stack to be locally of finite type.
Definition 2.8. Let ![]() be an ‘n-coconnective’ derived stack. We say that
be an ‘n-coconnective’ derived stack. We say that ![]() is locally of finite type if it arises as the left Kan extension of its own restriction along the embedding
is locally of finite type if it arises as the left Kan extension of its own restriction along the embedding
In particular, this means that ![]() is locally of finite type if it is determined by its values on affine schemes of finite type.
is locally of finite type if it is determined by its values on affine schemes of finite type.
Now we define what it means for a general stack to be ‘laft’.
Definition 2.9. Let ![]() be an arbitrary stack. Then we say that it is locally almost of finite type if the following conditions hold:
be an arbitrary stack. Then we say that it is locally almost of finite type if the following conditions hold:
-
•
 is nil-complete (or convergent) (Definition 2.3)
is nil-complete (or convergent) (Definition 2.3) -
• For every n, we have that
 is locally of finite type.
is locally of finite type.
Remark 2.10. A key reason for working with laft stacks (as well as the notion of an inf scheme appearing in the following definition) is that this is the ‘right’ framework in order to set up the correct functoriality for
![]() $\operatorname {IndCoh}(-)$
. For the sake of completeness, we have included the definitions, but we will not need to focus on this condition in any particular depth.
$\operatorname {IndCoh}(-)$
. For the sake of completeness, we have included the definitions, but we will not need to focus on this condition in any particular depth.
We are finally ready to define the main objects of this section: formal moduli problems.
Definition 2.11. Let ![]() be a derived stack locally almost of finite type. The
be a derived stack locally almost of finite type. The
![]() $\infty $
-category of formal moduli problems over
$\infty $
-category of formal moduli problems over ![]() is the full subcategory spanned by
is the full subcategory spanned by ![]() for which the map is
for which the map is
-
• inf-schematic. This means that the base change along a map
 is an inf-scheme (i.e., it satisfies the laft condition), it admits a deformation theory and its reduction will be a reduced quasi-compact scheme. (cf. [Reference Gaitsgory and RozenblyumGR20, Chapter 2])
is an inf-scheme (i.e., it satisfies the laft condition), it admits a deformation theory and its reduction will be a reduced quasi-compact scheme. (cf. [Reference Gaitsgory and RozenblyumGR20, Chapter 2]) -
• a nil-isomorphism. Recall that this means that the map of the ‘reduced stacks’
 is an isomorphism.
is an isomorphism.
We denote this category by ![]() .
.
Next, we define the notion of formal moduli problems under a fixed (pre)stack.
Definition 2.12. Let ![]() be a fixed (pre)stack which is both locally almost of finite type and which admits a deformation theory. The
be a fixed (pre)stack which is both locally almost of finite type and which admits a deformation theory. The
![]() $\infty $
-category of formal moduli problems under
$\infty $
-category of formal moduli problems under ![]() is spanned by those
is spanned by those ![]() for which
for which
-
•
 is itself locally of finite type and admits a deformation theory.
is itself locally of finite type and admits a deformation theory. -
• the map
 is a nil-isomorphism.
is a nil-isomorphism.
We denote this
![]() $\infty $
-category by
$\infty $
-category by ![]()
Next, we define the notion of a formal groupoid:
Definition 2.13. Let ![]() be a fixed derived stack, locally almost of finite type. We let
be a fixed derived stack, locally almost of finite type. We let ![]() denote the
denote the
![]() $\infty $
-category of groupoid objects in
$\infty $
-category of groupoid objects in ![]()
The key result which we borrow from this theory will be the following:
Theorem 2.14. ([Reference Gaitsgory and RozenblyumGR20, Theorem 2.3.2] Let ![]() be a stack which admits a deformation theory. Then there is an equivalence of
be a stack which admits a deformation theory. Then there is an equivalence of
![]() $\infty $
-categories:
$\infty $
-categories:
In effect, this states that there is a well-defined procedure of taking the quotient by a formal groupoid to obtain a formal moduli problem under X.
Remark 2.15. It is sensible to study
![]() $E_2$
-formal groupoids and, indeed,
$E_2$
-formal groupoids and, indeed,
![]() $E_n$
-formal groupoids. As a formal consequence of Theorem 2.14, there exists an ‘iterated’ quotient or classifying stack of an n-formal groupoid over
$E_n$
-formal groupoids. As a formal consequence of Theorem 2.14, there exists an ‘iterated’ quotient or classifying stack of an n-formal groupoid over ![]() ; this will give rise to a formal moduli problem under
; this will give rise to a formal moduli problem under ![]() .
.
Corollary 2.16. Let ![]() be as above. Then there exists an equivalence
be as above. Then there exists an equivalence
Here, the left-hand side denotes the
![]() $\infty $
-category of
$\infty $
-category of
![]() $E_n$
-groupoid objects in
$E_n$
-groupoid objects in ![]() .
.
2.3 Formal completions
Given a morphism ![]() , there exists a canonical formal moduli problem under
, there exists a canonical formal moduli problem under ![]() ; we may view this as an infinitesimal thickening on
; we may view this as an infinitesimal thickening on ![]() in
in ![]() . We now briefly review this construction cf. [Reference Gaitsgory and RozenblyumGR20, Reference Calaque, Pantev, Toën, Vaquié and VezzosiCPT+17b].
. We now briefly review this construction cf. [Reference Gaitsgory and RozenblyumGR20, Reference Calaque, Pantev, Toën, Vaquié and VezzosiCPT+17b].
Construction 2.17. Let ![]() be a morphism of derived stacks. The formal completion of
be a morphism of derived stacks. The formal completion of ![]() along
along ![]() is defined to be the pullback
is defined to be the pullback
The maps ![]() and
and ![]() induce a map
induce a map ![]() which is a nil-isomorphism. Hence, this procedure defines an object in
which is a nil-isomorphism. Hence, this procedure defines an object in ![]()
As a consequence of Theorem 2.14, the canonical morphism ![]() to the infinitesimal thickening in
to the infinitesimal thickening in ![]() may be recovered as the realization of its Čech nerve. The reader can compare this to the discussion in [Reference ToënToë14, Section 4.2] for a related universal property of the formal completion with respect to maps into arbitrary derived schemes.
may be recovered as the realization of its Čech nerve. The reader can compare this to the discussion in [Reference ToënToë14, Section 4.2] for a related universal property of the formal completion with respect to maps into arbitrary derived schemes.
3 Cogroupoid objects
In this section, we recall some basic facts about groupoid objects in
![]() $\infty $
-categories, as well as the dual notion of a cogroupoid object, which will play a key role in our constructions.
$\infty $
-categories, as well as the dual notion of a cogroupoid object, which will play a key role in our constructions.
Definition 3.1. Let ![]() be an
be an
![]() $\infty $
-category and let
$\infty $
-category and let ![]() be the
be the
![]() $\infty $
-category of simplicial objects in
$\infty $
-category of simplicial objects in ![]() . We say
. We say ![]() is a groupoid object of
is a groupoid object of ![]() if for every
if for every
![]() $n \geq 0$
and every partition
$n \geq 0$
and every partition
![]() $[n]= S \cup S'$
, such that
$[n]= S \cup S'$
, such that
![]() $S \cap S'$
consists of a single element s, the diagram
$S \cap S'$
consists of a single element s, the diagram

is a pullback square in ![]() .
.
Remark 3.2. A group object in ![]() is a groupoid object
is a groupoid object
![]() $X_{\bullet }$
for which
$X_{\bullet }$
for which
![]() $X_0 \simeq *$
.
$X_0 \simeq *$
.
We have the following dual notion of a cogroupoid.
Definition 3.3. Let ![]() be as above and let
be as above and let ![]() denote the
denote the
![]() $\infty $
-category of cosimplicial objects of
$\infty $
-category of cosimplicial objects of ![]() . We say
. We say ![]() is a cogroupoid object if it is a groupoid object in the opposite category
is a cogroupoid object if it is a groupoid object in the opposite category ![]() . In particular, for every partition
. In particular, for every partition
![]() $[n]= S \cup S'$
, such that
$[n]= S \cup S'$
, such that
![]() $S \cap S'$
consists of a single element s, the diagram
$S \cap S'$
consists of a single element s, the diagram

is a pushout square in ![]() . We use the notation
. We use the notation ![]() to denote the
to denote the
![]() $\infty $
-category of cogroupoid objects in
$\infty $
-category of cogroupoid objects in ![]() .
.
Remark 3.4. A cogroup object in ![]() is a cogroupoid object
is a cogroupoid object
![]() $X_{\bullet }$
for which
$X_{\bullet }$
for which
![]() $X_0 \simeq \emptyset $
.
$X_0 \simeq \emptyset $
.
Example 3.5. Let ![]() denote the
denote the
![]() $\infty $
-category of pointed spaces. For any pointed space
$\infty $
-category of pointed spaces. For any pointed space
![]() $X \in \mathcal {S}_*$
, its suspension
$X \in \mathcal {S}_*$
, its suspension
![]() $\Sigma X$
is canonically a cogroup object. To see this, let
$\Sigma X$
is canonically a cogroup object. To see this, let
![]() $ \pi : X \to *$
be the map from X to the final object. Then the conerve,
$ \pi : X \to *$
be the map from X to the final object. Then the conerve,
![]() $\operatorname {coNerve}(\pi )$
,
$\operatorname {coNerve}(\pi )$
,
precisely packages
![]() $\Sigma X \simeq * \sqcup _{X} * $
together with its cogroup structure maps. Setting
$\Sigma X \simeq * \sqcup _{X} * $
together with its cogroup structure maps. Setting
![]() $X= S^0$
recovers the
$X= S^0$
recovers the
![]() $E_1$
cogroup structure on
$E_1$
cogroup structure on
![]() $S^1$
in pointed spaces.
$S^1$
in pointed spaces.
Construction 3.6. The above example is an instance of the conerve construction, which we now describe. Let ![]() be an
be an
![]() $\infty $
-category which admits finite colimits. Let
$\infty $
-category which admits finite colimits. Let
![]() $f: Y \to X $
be a morphism in
$f: Y \to X $
be a morphism in ![]() . Then we define the conerve of f,
. Then we define the conerve of f,
![]() $\operatorname {coNerve}(f)$
to be the cosimplicial object
$\operatorname {coNerve}(f)$
to be the cosimplicial object
One can iteratively define the notion of an
![]() $E_n$
-cogroupoid:
$E_n$
-cogroupoid:
Definition 3.7. We define an
![]() $E_2$
-cogroupoid object to be a cogroupoid object in the
$E_2$
-cogroupoid object to be a cogroupoid object in the
![]() $\infty $
-category
$\infty $
-category ![]() . Proceeding iteratively, we define an
. Proceeding iteratively, we define an
![]() $E_n$
-cogroupoid to be an a cogroupoid object in
$E_n$
-cogroupoid to be an a cogroupoid object in ![]() .
.
Example 3.8. Let
![]() $\phi : \emptyset \to \operatorname {pt}$
be the map in spaces from the initial object to the final object. Then we set
$\phi : \emptyset \to \operatorname {pt}$
be the map in spaces from the initial object to the final object. Then we set
Now let
![]() $\phi ^{\bullet }: S^{0, \bullet } \to *$
be the map to the final cogroupoid object in spaces. We set
$\phi ^{\bullet }: S^{0, \bullet } \to *$
be the map to the final cogroupoid object in spaces. We set
Of course, one need not stop here; for each n, there is an
![]() $E_{n+1}$
cogroupoid with the n-sphere as the degree
$E_{n+1}$
cogroupoid with the n-sphere as the degree
![]() $(1,...,1)$
space of morphisms.
$(1,...,1)$
space of morphisms.
4 Affine cogroupoids over
 $\mathbb {A}^1 / \mathbb {G}_m$
$\mathbb {A}^1 / \mathbb {G}_m$
Let R be a commutative ring. There exists a distinguished class of (higher) stacks over R which are completely determined by their cohomology (together with its additional yet canonical structure) as a cosimplicial commutative algebra. The study of this class of stacks, known as affine stacks, was initiated in [Reference ToënToë06].
The purpose of this section is to rephrase these constructions internally to the filtered setting (i.e., over the stack
![]() $\mathbb {A}^1 / \mathbb {G}_m$
).
$\mathbb {A}^1 / \mathbb {G}_m$
).
4.1 Filtrations and
 $\mathbb {A}^1 / \mathbb {G}_m$
$\mathbb {A}^1 / \mathbb {G}_m$
We would like to remind the reader of some basic notions from [Reference MoulinosMou21b], motivating our extensive usage of the stack
![]() $\mathbb {A}^1 / \mathbb {G}_m$
.
$\mathbb {A}^1 / \mathbb {G}_m$
.
Definition 4.1. We define the
![]() $\infty $
-category of filtered R-modules to be
$\infty $
-category of filtered R-modules to be
where
![]() $\mathbb {Z}$
is to be viewed as a poset. Similarly, we define the
$\mathbb {Z}$
is to be viewed as a poset. Similarly, we define the
![]() $\infty $
-category
$\infty $
-category
to be the
![]() $\infty $
-category of graded R-modules, where
$\infty $
-category of graded R-modules, where
![]() $\mathbb {Z}^{ds}$
denotes the integers viewed as a discrete space. These both obtain a symmetric monoidal structure, given by Day convolution.
$\mathbb {Z}^{ds}$
denotes the integers viewed as a discrete space. These both obtain a symmetric monoidal structure, given by Day convolution.
Construction 4.2. There exist symmetric monoidal functors
taking a filtered R-module to its underlying object, and
Now we turn to an algebro-geometric incarnation of these notions. Let
![]() $\mathbb {A}^1 / \mathbb {G}_m$
be the quotient stack of
$\mathbb {A}^1 / \mathbb {G}_m$
be the quotient stack of
![]() $\mathbb {A}^1$
by the canonical
$\mathbb {A}^1$
by the canonical
![]() $\mathbb {G}_m$
action by dilation. This stack comes equipped with two distinguished maps:
$\mathbb {G}_m$
action by dilation. This stack comes equipped with two distinguished maps:
which throughout this paper, we refer to as the generic point and central point, respectively. Viewing it as a derived stack, one obtains the following relationship with filtered objects at the level of quasi-coherent sheaves:
Theorem 4.3 (cf. [Reference MoulinosMou21b]).
There is a symmetric monoidal equivalence of stable
![]() $\infty $
-categories
$\infty $
-categories
Under the above equivalence, the associated graded functor
![]() $\operatorname {gr}: \operatorname {Fil}({\operatorname {Mod}}_R) \to \operatorname {Gr}({\operatorname {Mod}}_R)$
is naturally identified with the pullback
$\operatorname {gr}: \operatorname {Fil}({\operatorname {Mod}}_R) \to \operatorname {Gr}({\operatorname {Mod}}_R)$
is naturally identified with the pullback
the functor
![]() $\operatorname {Und}: \operatorname {Sp}^{fil} \to \operatorname {Sp}$
sending a filtered R-module to the R-module underlying the filtration is naturally identified with the pullback
$\operatorname {Und}: \operatorname {Sp}^{fil} \to \operatorname {Sp}$
sending a filtered R-module to the R-module underlying the filtration is naturally identified with the pullback
Remark 4.4. Given the above equivalence, we may view (derived) stacks admitting a map
in two ways. First, we may think of them as degenerations, from the generic fiber ![]() to the special fiber
to the special fiber ![]() . We may also think of them as filtrations on the cohomology
. We may also think of them as filtrations on the cohomology ![]() of the generic fiber. In this paper, we straddle the line between these two perspectives.
of the generic fiber. In this paper, we straddle the line between these two perspectives.
4.2 Affine stacks over
 $\mathbb {A}^1 / \mathbb {G}_m$
$\mathbb {A}^1 / \mathbb {G}_m$
Definition 4.5. Let
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }$
denote the heart of the stable
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }$
denote the heart of the stable
![]() $\infty $
-category of quasi-coherent sheaves. By [Reference MoulinosMou21b, Section 8], this abelian category is equivalent to the filtered diagrams of objects belonging to the heart of
$\infty $
-category of quasi-coherent sheaves. By [Reference MoulinosMou21b, Section 8], this abelian category is equivalent to the filtered diagrams of objects belonging to the heart of
![]() ${\operatorname {Mod}}_R$
. Let
${\operatorname {Mod}}_R$
. Let
![]() $\operatorname {CAlg}(\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m))^{\heartsuit }$
denote the category of algebras in
$\operatorname {CAlg}(\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m))^{\heartsuit }$
denote the category of algebras in
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }$
. We set
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }$
. We set
to be the underlying
![]() $\infty $
-category of the category of cosimplicial objects in
$\infty $
-category of the category of cosimplicial objects in
![]() $\operatorname {CAlg}((\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }))$
.
$\operatorname {CAlg}((\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }))$
.
Remark 4.6. There is an alternative way to understand the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
. Let
$\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
. Let
![]() $\operatorname {QCoh}(\mathbb {A}^1)^{\heartsuit } \simeq {\operatorname {Mod}}_{k[t]}$
denote the classical abelian category of
$\operatorname {QCoh}(\mathbb {A}^1)^{\heartsuit } \simeq {\operatorname {Mod}}_{k[t]}$
denote the classical abelian category of
![]() $R[t]$
-modules. The canonical inclusion
$R[t]$
-modules. The canonical inclusion
![]() $\mathbb {G}_m \to \mathbb {A}^1$
gives an action of
$\mathbb {G}_m \to \mathbb {A}^1$
gives an action of
![]() $\mathbb {G}_m$
on
$\mathbb {G}_m$
on
![]() $\mathbb {A}^1$
, and thus, we may study
$\mathbb {A}^1$
, and thus, we may study
![]() $\mathbb {G}_m$
-equivariant objects in the above abelian category. This forms an abelian category, which we denote by
$\mathbb {G}_m$
-equivariant objects in the above abelian category. This forms an abelian category, which we denote by
![]() $\operatorname {Rep}_{\mathbb {A}^1}(\mathbb {G}_m)$
and we can canonically form the category of cosimplicial modules in this category,
$\operatorname {Rep}_{\mathbb {A}^1}(\mathbb {G}_m)$
and we can canonically form the category of cosimplicial modules in this category,
![]() $\operatorname {Rep}_{\mathbb {A}^1}(\mathbb {G}_m)^{\Delta }$
. This admits a symmetric monoidal structure (the pointwise one), and so we may take commutative monoids here. By the arguments of [Reference Katzarkov, Pantev and ToënKPT09, Section 3.4], this forms a model category and we can define
$\operatorname {Rep}_{\mathbb {A}^1}(\mathbb {G}_m)^{\Delta }$
. This admits a symmetric monoidal structure (the pointwise one), and so we may take commutative monoids here. By the arguments of [Reference Katzarkov, Pantev and ToënKPT09, Section 3.4], this forms a model category and we can define
![]() $\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
to be its underlying
$\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
to be its underlying
![]() $\infty $
-category.
$\infty $
-category.
Remark 4.7. Let
![]() $ {\operatorname {Mod}}^{\operatorname {ccn}}_{R}$
denote the full subcategory of
$ {\operatorname {Mod}}^{\operatorname {ccn}}_{R}$
denote the full subcategory of
![]() ${\operatorname {Mod}}_R$
consisting of modules M for which
${\operatorname {Mod}}_R$
consisting of modules M for which
![]() $\pi _n(M) =0$
if
$\pi _n(M) =0$
if
![]() $n>0$
. We remark that there exists a monad T on
$n>0$
. We remark that there exists a monad T on
![]() ${\operatorname {Mod}}^{\operatorname {ccn}}_{R}$
for which there is an equivalence
${\operatorname {Mod}}^{\operatorname {ccn}}_{R}$
for which there is an equivalence
This can be extracted from [Reference ToënToë06, Proof of Théorème 2.1.2]. When R is a
![]() $\mathbb {Q}$
-algebra, this agrees with the free
$\mathbb {Q}$
-algebra, this agrees with the free
![]() $E_{\infty }$
-algebra functor so that, in fact, we have an equivalence
$E_{\infty }$
-algebra functor so that, in fact, we have an equivalence
thus, one may think of cosimplicial commutative algebras as coconnective
![]() $E_{\infty }$
-algebras in this context. Similarly, when working over
$E_{\infty }$
-algebras in this context. Similarly, when working over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
in characteristic zero, there will be an equivalence
$\mathbb {A}^1 / \mathbb {G}_m$
in characteristic zero, there will be an equivalence
Construction 4.8. Let
![]() ${\operatorname {Spec}}_{\mathbb {A}^1 / \mathbb {G}_m}: \operatorname {CAlg}(\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit })^{op} \to \operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
denote the relative spectrum functor, sending a commutative algebra in
${\operatorname {Spec}}_{\mathbb {A}^1 / \mathbb {G}_m}: \operatorname {CAlg}(\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit })^{op} \to \operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
denote the relative spectrum functor, sending a commutative algebra in
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }$
to a relative affine (underived) scheme over
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)^{\heartsuit }$
to a relative affine (underived) scheme over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. We form the Kan-extension of this functor along the inclusion
$\mathbb {A}^1 / \mathbb {G}_m$
. We form the Kan-extension of this functor along the inclusion
to obtain a functor
Remark 4.9. This possesses a left adjoint – namely, the global sections functor
To understand this functor, we remark that one can work with a point-set model of
![]() $\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
where every object
$\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
where every object ![]() in
in
![]() $\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
has a a model as a simplicial object
$\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
has a a model as a simplicial object ![]() in presheaves (of sets) over the stack
in presheaves (of sets) over the stack
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Thus, we define the cosimplicial algebra
$\mathbb {A}^1 / \mathbb {G}_m$
. Thus, we define the cosimplicial algebra ![]()
As in [Reference ToënToë06, Section 2.2], this functor is left Quillen and thus induces a functor at the level of
![]() $\infty $
-categories.
$\infty $
-categories.
Proposition 4.10. The functor
is fully faithful.
Proof. Note that we may write any cosimplicial algebra
![]() $A^{\bullet }$
as the cosifted limit of objects in
$A^{\bullet }$
as the cosifted limit of objects in
![]() $\operatorname {CAlg}_R$
(i.e., of discrete R-algebras). Then it follows that
$\operatorname {CAlg}_R$
(i.e., of discrete R-algebras). Then it follows that
is an equivalence.
The following proposition, motivated by [Reference ToënToë06, Théorème 2.29, Corollaire 2.2.10], says that modulo potential size issues, the
![]() $\infty $
-category of (filtered) affine stacks, behaves like a localization of the
$\infty $
-category of (filtered) affine stacks, behaves like a localization of the
![]() $\infty $
-category of higher stacks.
$\infty $
-category of higher stacks.
Proposition 4.11. Let
![]() $\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
denote the subcategory of stacks such that
$\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
denote the subcategory of stacks such that
![]() $\mathcal {O}(X)$
is
$\mathcal {O}(X)$
is
![]() $\mathbb {U}$
-small with respect to a fixed universe
$\mathbb {U}$
-small with respect to a fixed universe
![]() $\mathbb {U}$
. Then the functor
$\mathbb {U}$
. Then the functor
is a localization. Moreover, X is an affine stack over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
if and only if the adjunction morphism
$\mathbb {A}^1 / \mathbb {G}_m$
if and only if the adjunction morphism
is an equivalence in
![]() $\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
.
$\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
.
Proof. The arguments for the proof of [Reference ToënToë06, Théorème 2.29] work verbatim when working with
![]() $\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
instead of
$\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
instead of
![]() $\mathsf {coSCR}_{R}$
.
$\mathsf {coSCR}_{R}$
.
5 Filtered n-spheres and (higher) loop spaces
In [Reference Moulinos, Robalo and ToënMRT22], the authors constructed the filtered circle as an affine abelian group stack over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. This roughly packages the data arising from the Postnikov filtration on the cochain complex on
$\mathbb {A}^1 / \mathbb {G}_m$
. This roughly packages the data arising from the Postnikov filtration on the cochain complex on
![]() $S^1$
, together with its compatibility with the group strucure on
$S^1$
, together with its compatibility with the group strucure on
![]() $S^1$
. We will now see that it fits into the larger structure of an
$S^1$
. We will now see that it fits into the larger structure of an
![]() $E_2$
-cogroupoid object in affine stacks.
$E_2$
-cogroupoid object in affine stacks.
Definition 5.1. Following the discussion in [Reference ToënToë20, Section 1.3], we define the ‘quantum point’ as the stack
![]() $\mathcal {Q}:= B \mathbb {G}_m$
viewed as an object over
$\mathcal {Q}:= B \mathbb {G}_m$
viewed as an object over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
via the morphism
$\mathbb {A}^1 / \mathbb {G}_m$
via the morphism
![]() $\iota : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
. This will have generic fiber the ‘null scheme’
$\iota : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
. This will have generic fiber the ‘null scheme’
and as central fiber the derived scheme
Remark 5.2. This can alternatively be described as
![]() ${\operatorname {Spec}}_{\mathbb {A}^1 / \mathbb {G}_m}(\mathbb {A})$
(this denotes the relative spectrum) where
${\operatorname {Spec}}_{\mathbb {A}^1 / \mathbb {G}_m}(\mathbb {A})$
(this denotes the relative spectrum) where
![]() $\mathbb {A}$
is the image of the unit
$\mathbb {A}$
is the image of the unit
![]() $\mathbf {1} \in \operatorname {Gr}_R \simeq \operatorname {QCoh}(B \mathbb {G}_m)$
in
$\mathbf {1} \in \operatorname {Gr}_R \simeq \operatorname {QCoh}(B \mathbb {G}_m)$
in
![]() $ \operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m) \simeq \operatorname {Fil}_R$
along the pushforward functor
$ \operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m) \simeq \operatorname {Fil}_R$
along the pushforward functor
This is a lax symmetric monoidal (in fact, it ends up being symmetric monoidal), so that
![]() $\mathbb {A}$
acquires an
$\mathbb {A}$
acquires an
![]() $E_{\infty }$
-algebra structure. Alternatively, one may describe this functor as the symmetric monoidal functor
$E_{\infty }$
-algebra structure. Alternatively, one may describe this functor as the symmetric monoidal functor
![]() $I: \operatorname {Gr}_R \to \operatorname {Fil}_R$
given by left Kan extension along
$I: \operatorname {Gr}_R \to \operatorname {Fil}_R$
given by left Kan extension along
![]() $\mathbb {Z}^{ds} \hookrightarrow \mathbb {Z}$
.
$\mathbb {Z}^{ds} \hookrightarrow \mathbb {Z}$
.
We now use
![]() $\mathcal {Q}$
to construct a cogroupoid object in the
$\mathcal {Q}$
to construct a cogroupoid object in the
![]() $\infty $
-topos
$\infty $
-topos
![]() $\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
.
$\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
.
Construction 5.3. Let
![]() $\iota : B \mathbb {G}_m \simeq \mathcal {Q} \to \mathbb {A}^1 / \mathbb {G}_m$
. Let
$\iota : B \mathbb {G}_m \simeq \mathcal {Q} \to \mathbb {A}^1 / \mathbb {G}_m$
. Let
be the unit map of commutative algebra objects in
Finally, let
![]() $N(\phi )_{\bullet }$
be the nerve of this map, viewed as a simplicial object in this
$N(\phi )_{\bullet }$
be the nerve of this map, viewed as a simplicial object in this
![]() $\infty $
-category; by construction this will be a groupoid object in
$\infty $
-category; by construction this will be a groupoid object in
![]() $\operatorname {CAlg}(\operatorname {Fil}({\operatorname {Mod}}_R))$
. We note that this is levelwise discrete, in the homotopical sense. We define
$\operatorname {CAlg}(\operatorname {Fil}({\operatorname {Mod}}_R))$
. We note that this is levelwise discrete, in the homotopical sense. We define
this will be a cogroupoid object in the
![]() $\infty $
-category of derived affine schemes over
$\infty $
-category of derived affine schemes over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
.
$\mathbb {A}^1 / \mathbb {G}_m$
.
Remark 5.4. In simplicial degree
![]() $1$
, one recovers the filtered stack (cf. [Reference MoulinosMou21a, Section 5.1])
$1$
, one recovers the filtered stack (cf. [Reference MoulinosMou21a, Section 5.1])
![]() $S^0_{fil}$
, which we refer to as the filtered zero sphere. As is described in loc. cit., one may express the fiber product
$S^0_{fil}$
, which we refer to as the filtered zero sphere. As is described in loc. cit., one may express the fiber product
![]() $\mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m} \times _{\iota _*(\mathcal {O}_{B \mathbb {G}_m})} \mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m}$
in terms of the equivalence of
$\mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m} \times _{\iota _*(\mathcal {O}_{B \mathbb {G}_m})} \mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m}$
in terms of the equivalence of
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
with
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
with
![]() $k[t]$
-modules in graded complexes as the discrete ring
$k[t]$
-modules in graded complexes as the discrete ring
Since the
![]() $\eta ^* \iota _*(\mathcal {O}_{B \mathbb {G}_m}) \simeq 0$
, one has equivalences
$\eta ^* \iota _*(\mathcal {O}_{B \mathbb {G}_m}) \simeq 0$
, one has equivalences
and
where in the latter equivalence, we view
![]() $k[\epsilon ]/(\epsilon ^2)$
as a graded commutative ring with
$k[\epsilon ]/(\epsilon ^2)$
as a graded commutative ring with
![]() $\epsilon $
in weight
$\epsilon $
in weight
![]() $-1$
.
$-1$
.
Remark 5.5. One may try to define this cogroupoid directly as the conerve of the map
![]() $\iota : \mathcal {Q} \to \mathbb {A}^1 / \mathbb {G}_m$
, which we write as
$\iota : \mathcal {Q} \to \mathbb {A}^1 / \mathbb {G}_m$
, which we write as
![]() $\operatorname {coNerve}^{\bullet }(\iota ) $
. We remark that this is related by affinization in the sense that there is an equivalence
$\operatorname {coNerve}^{\bullet }(\iota ) $
. We remark that this is related by affinization in the sense that there is an equivalence
Note that in degree 1 of this construction, we obtain the suspension
![]() $\Sigma \mathcal {Q}$
in the
$\Sigma \mathcal {Q}$
in the
![]() $\infty $
-category of derived stacks over
$\infty $
-category of derived stacks over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
whereas for
$\mathbb {A}^1 / \mathbb {G}_m$
whereas for
![]() $S_{fil}^{0, \bullet }$
, we obtain the suspension
$S_{fil}^{0, \bullet }$
, we obtain the suspension
![]() $\Sigma _{aff} \mathcal {Q}$
in the full subcategory of affine stacks. These are not in general equivalent. Indeed, by [Reference ToënToë06], the inclusion of affine stacks into all stacks is a right adjoint functor, which typically does not preserve colimits.
$\Sigma _{aff} \mathcal {Q}$
in the full subcategory of affine stacks. These are not in general equivalent. Indeed, by [Reference ToënToë06], the inclusion of affine stacks into all stacks is a right adjoint functor, which typically does not preserve colimits.
Construction 5.6. Given any derived stack
![]() $X \in \operatorname {dStk}_{\mathbb {A}^1 / \mathbb {G}_m}$
, we may form the levelwise mapping stack
$X \in \operatorname {dStk}_{\mathbb {A}^1 / \mathbb {G}_m}$
, we may form the levelwise mapping stack
this is a simplicial object in
![]() $\operatorname {dStk}_{\mathbb {A}^1 / \mathbb {G}_m}$
which by construction of
$\operatorname {dStk}_{\mathbb {A}^1 / \mathbb {G}_m}$
which by construction of
![]() $S^{0, \bullet }_{fil}$
, admits the structure of a groupoid object in derived stacks over
$S^{0, \bullet }_{fil}$
, admits the structure of a groupoid object in derived stacks over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Note that we are working in an
$\mathbb {A}^1 / \mathbb {G}_m$
. Note that we are working in an
![]() $\infty $
-topos, where every groupoid object
$\infty $
-topos, where every groupoid object
![]() $\mathcal {G}_{\bullet } $
arises as the Čech nerve of an effective epimorphism. Hence, we may form the associated classifying stack
$\mathcal {G}_{\bullet } $
arises as the Čech nerve of an effective epimorphism. Hence, we may form the associated classifying stack
![]() $B \mathcal {G}_{\bullet }$
, for which
$B \mathcal {G}_{\bullet }$
, for which
![]() $\mathcal {G}_0 \to B \mathcal {G}_{\bullet }$
is an effective epimorphism.
$\mathcal {G}_0 \to B \mathcal {G}_{\bullet }$
is an effective epimorphism.
5.1 The filtered circle as
 $E_2$
-cogroupoid
$E_2$
-cogroupoid
One can give a construction of the filtered circle of [Reference Moulinos, Robalo and ToënMRT22] as a
![]() $2$
-cogroupoid in the
$2$
-cogroupoid in the
![]() $\infty $
-category of affine stacks. This is done by taking the iterated nerve of the map
$\infty $
-category of affine stacks. This is done by taking the iterated nerve of the map
![]() $\phi : \mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m} \to 0_*(\mathcal {O}_{B \mathbb {G}_m})$
in cosimplicial commutative algebra objects in
$\phi : \mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m} \to 0_*(\mathcal {O}_{B \mathbb {G}_m})$
in cosimplicial commutative algebra objects in
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
.
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
.
Construction 5.7. Let
![]() $N(\phi )_{\bullet }$
be as above. We define the
$N(\phi )_{\bullet }$
be as above. We define the
![]() $2$
-fold iterated nerve of
$2$
-fold iterated nerve of
![]() $\phi $
to be the bi-simplicial object
$\phi $
to be the bi-simplicial object
![]() $N(\phi )_{\bullet }$
, defined to be the nerve of the map of simplicial objects
$N(\phi )_{\bullet }$
, defined to be the nerve of the map of simplicial objects
where the left-hand side is considered as a constant simplicial object. This will canonically give rise to a bisimplicial object in cosimplicial algebras which we denote by
![]() $N(\phi )_{\bullet , \bullet }$
. This gives rise to a 2-groupoid object in the
$N(\phi )_{\bullet , \bullet }$
. This gives rise to a 2-groupoid object in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathsf {coSCR}_R$
. We can alternatively restrict to the diagonal simplicial object, at this stage. In any case we set
$\mathsf {coSCR}_R$
. We can alternatively restrict to the diagonal simplicial object, at this stage. In any case we set
This will be a 2-cogroupoid in the
![]() $\infty $
-category of affine stacks over
$\infty $
-category of affine stacks over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
.
$\mathbb {A}^1 / \mathbb {G}_m$
.
Construction 5.8. We introduce a variant of the above. Let
![]() $S^{0, \bullet }_{fil}$
be as above and let
$S^{0, \bullet }_{fil}$
be as above and let
be a map in the
![]() $\infty $
-category of cosimplicial objects in derived stacks. Here, the right-hand side is taken to be the constant cosimplicial object, which is
$\infty $
-category of cosimplicial objects in derived stacks. Here, the right-hand side is taken to be the constant cosimplicial object, which is
![]() $\mathbb {A}^1 / \mathbb {G}_m$
in each degree.
$\mathbb {A}^1 / \mathbb {G}_m$
in each degree.
denotes the conerve of this map, cf. Construction 3.6. This will be a bicosimplicial object and, by the discussion above, a cogroupoid object in
![]() $\operatorname {Stk}_R$
.
$\operatorname {Stk}_R$
.
Proposition 5.9. The cogroupoid object of Construction 5.7 is the affinization of
![]() $\Sigma S^{0}_{fil}$
– that is, there exists an equivalence
$\Sigma S^{0}_{fil}$
– that is, there exists an equivalence
Proof. This is immediate upon noticing that there is a natural map
which is an equivalence on cohomology. Indeed, one obtains the
![]() $E_2$
-groupoid object of Construction 5.7 by applying the global sections
$E_2$
-groupoid object of Construction 5.7 by applying the global sections
![]() $\mathcal {O}(-)$
functor to Construction 5.8. Applying then
$\mathcal {O}(-)$
functor to Construction 5.8. Applying then
![]() ${\operatorname {Spec}}^{\Delta }_{\mathbb {A}^1 / \mathbb {G}_m}(-)$
and noticing that we obtain the canonical affinization morphism, the unit of the adjunction
${\operatorname {Spec}}^{\Delta }_{\mathbb {A}^1 / \mathbb {G}_m}(-)$
and noticing that we obtain the canonical affinization morphism, the unit of the adjunction
![]() ${\operatorname {Spec}}^{\Delta }_{\mathbb {A}^1 / \mathbb {G}_m} \dashv \mathcal {O}(-)$
. This will be an equivalence on cohomologies.
${\operatorname {Spec}}^{\Delta }_{\mathbb {A}^1 / \mathbb {G}_m} \dashv \mathcal {O}(-)$
. This will be an equivalence on cohomologies.
Via this description, we see that the degree
![]() $(1,1)$
piece of the
$(1,1)$
piece of the
![]() $E_2$
-cogroupoid
$E_2$
-cogroupoid
![]() $S^{1, \bullet , \bullet }_{fil}$
is none other than the filtered circle of [Reference Moulinos, Robalo and ToënMRT22].
$S^{1, \bullet , \bullet }_{fil}$
is none other than the filtered circle of [Reference Moulinos, Robalo and ToënMRT22].
Corollary 5.10. There is an equivalence
of affine stacks.
Remark 5.11. Putting this together with Construction 5.3, we have the following identification:
exhibiting the filtered circle as a 2-fold suspension in affine stacks of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Remark 5.12. The reason we want to work with
![]() $\operatorname {Aff}_{\mathbb {A}^1 / \mathbb {G}_m}(\Sigma ^2 \mathcal {Q})$
here as opposed to just
$\operatorname {Aff}_{\mathbb {A}^1 / \mathbb {G}_m}(\Sigma ^2 \mathcal {Q})$
here as opposed to just
![]() $\Sigma ^{2} \mathcal {Q}$
is that we would like to to recover the cogroupoid structure on the affine stack
$\Sigma ^{2} \mathcal {Q}$
is that we would like to to recover the cogroupoid structure on the affine stack
![]() $S^1_{Fil}$
of [Reference Moulinos, Robalo and ToënMRT22]. Indeed, the filtered loop space
$S^1_{Fil}$
of [Reference Moulinos, Robalo and ToënMRT22]. Indeed, the filtered loop space
![]() $\mathcal {L}_{fil}(X)$
was defined in loc. cit. as the stack of maps out of
$\mathcal {L}_{fil}(X)$
was defined in loc. cit. as the stack of maps out of
![]() $S^1_{Fil}$
. Thus, we would like to study groupoid structures on the filtered loop space itself, as opposed to studying them on some object which is merely equivalent to it.
$S^1_{Fil}$
. Thus, we would like to study groupoid structures on the filtered loop space itself, as opposed to studying them on some object which is merely equivalent to it.
Remark 5.13. We remark that while one may recover the affine stack
![]() $S^1_{fil}$
in this way, this does not capture its structure as an abelian group stack. Indeed, this was studied in [Reference Moulinos, Robalo and ToënMRT22] by exhibiting it as the classifying stack of a filtered abelian group scheme
$S^1_{fil}$
in this way, this does not capture its structure as an abelian group stack. Indeed, this was studied in [Reference Moulinos, Robalo and ToënMRT22] by exhibiting it as the classifying stack of a filtered abelian group scheme
![]() $\mathbb {H}$
over
$\mathbb {H}$
over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
, which interpolates between the kernel and fixed points of the Frobenius on the Witt vector ring scheme
$\mathbb {A}^1 / \mathbb {G}_m$
, which interpolates between the kernel and fixed points of the Frobenius on the Witt vector ring scheme
![]() $\mathbb {W}(-)$
.
$\mathbb {W}(-)$
.
Construction 5.14. One can, in fact, iterate all of the above (e.g., by taking iterated nerves of the map
![]() $\mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m} \to 0_* B \mathbb {G}_m$
in
$\mathcal {O}_{\mathbb {A}^1 / \mathbb {G}_m} \to 0_* B \mathbb {G}_m$
in
![]() $\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
and applying the
$\mathsf {coSCR}_{\mathbb {A}^1 / \mathbb {G}_m}$
and applying the
![]() $Spec^{\Delta }_{\mathbb {A}^1 / \mathbb {G}_m}$
functor to obtain
$Spec^{\Delta }_{\mathbb {A}^1 / \mathbb {G}_m}$
functor to obtain
![]() $S^n_{fil}$
). We can summarize this discussion by saying that
$S^n_{fil}$
). We can summarize this discussion by saying that
acquires the structure of an
![]() $E_{n+1}$
-cogroupoid object in affine stacks over
$E_{n+1}$
-cogroupoid object in affine stacks over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
.
$\mathbb {A}^1 / \mathbb {G}_m$
.
5.2 Filtered loop spaces
Let X be a derived scheme in characteristic zero. We describe the formation of higher filtered loop spaces but focus in particular on the
![]() $n=1$
case.
$n=1$
case.
Construction 5.15. Let X be a derived scheme. Letting
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m} := X \times \mathbb {A}^1 / \mathbb {G}_m$
, we set
$X|_{\mathbb {A}^1 / \mathbb {G}_m} := X \times \mathbb {A}^1 / \mathbb {G}_m$
, we set
and refer to this as the higher n-dimensional filtered loop space.
We would like to deduce the following:
Proposition 5.16. Let X be a derived affine scheme. Then the affinization morphism
induces an (levelwise)-equivalence of bi-cosimplicial derived stacks
This makes the bi-cosimplicial object
![]() $\mathcal {L}_{fil}^{\bullet , \bullet }(X)$
into an
$\mathcal {L}_{fil}^{\bullet , \bullet }(X)$
into an
![]() $E_2$
-groupoid in derived stacks.
$E_2$
-groupoid in derived stacks.
Proof. For an arbitrary bidegree
![]() $(m,n)$
, we have a canonical map
$(m,n)$
, we have a canonical map
induced by restriction along
![]() $\Sigma ^{2} \mathcal {Q}^{m, n} \to S^{1,m,n}_{fil}$
, the levelwise affinization morphism. We would like to show that this is an equivalence. Granting this, we use the fact that
$\Sigma ^{2} \mathcal {Q}^{m, n} \to S^{1,m,n}_{fil}$
, the levelwise affinization morphism. We would like to show that this is an equivalence. Granting this, we use the fact that
![]() $\Sigma ^{2} \mathcal {Q}^{m,n}$
is a 2-cogroupoid in derived stacks, so that one gets a suitable product decomposition in (in each degree
$\Sigma ^{2} \mathcal {Q}^{m,n}$
is a 2-cogroupoid in derived stacks, so that one gets a suitable product decomposition in (in each degree
![]() $(m,n)$
of the associated mapping stacks) satisfying the Segal conditions for a groupoid object.
$(m,n)$
of the associated mapping stacks) satisfying the Segal conditions for a groupoid object.
In order to display the map (5.17) as an equivalence, it will be enough to do so upon pulling back along
![]() $\eta , \iota $
, respectively. We first treat the generic fiber case (i.e., the pullback along
$\eta , \iota $
, respectively. We first treat the generic fiber case (i.e., the pullback along
![]() $\eta $
). As we are in the characteristic zero setting, where simplicial and cosimplicial algebras can be modeled by connective and coconnective
$\eta $
). As we are in the characteristic zero setting, where simplicial and cosimplicial algebras can be modeled by connective and coconnective
![]() $E_{\infty }$
algebras respectively, we may appeal to [Reference LurieLur11, Section 4], (see also [Reference Ben-Zvi and NadlerBZN12]). In particular, the universal property in this setting states that the affinization functor is a monad in derived stacks; in particular, any map to a derived affine scheme out of a derived stack will factor through its affinization. In particular, this gives an equivalence at the level of derived mapping stacks.
$E_{\infty }$
algebras respectively, we may appeal to [Reference LurieLur11, Section 4], (see also [Reference Ben-Zvi and NadlerBZN12]). In particular, the universal property in this setting states that the affinization functor is a monad in derived stacks; in particular, any map to a derived affine scheme out of a derived stack will factor through its affinization. In particular, this gives an equivalence at the level of derived mapping stacks.
For the same reason, one obtains an equivalence upon pulling back along
![]() $B \mathbb {G}_m \xrightarrow {\iota } \mathbb {A}^1 / \mathbb {G}_m$
. We can now conclude that the original map (5.17) defined over
$B \mathbb {G}_m \xrightarrow {\iota } \mathbb {A}^1 / \mathbb {G}_m$
. We can now conclude that the original map (5.17) defined over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
is a levelwise equivalence. Hence,
$\mathbb {A}^1 / \mathbb {G}_m$
is a levelwise equivalence. Hence,
![]() $\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
is an
$\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
is an
![]() $E_2$
-cogroupoid in derived stacks.
$E_2$
-cogroupoid in derived stacks.
Remark 5.18. The argument above uses the fact that we are in characteristic zero and the resulting notion of affinization in the derived setting. In positive or mixed characteristics, one can argue more generally using the cohomological finite dimension of the stacks
![]() $\Sigma ^{2} \mathcal {Q}^{m,n}$
and
$\Sigma ^{2} \mathcal {Q}^{m,n}$
and
![]() $S^{1, m, n}_{fil}$
to obtain equivalence (5.17).
$S^{1, m, n}_{fil}$
to obtain equivalence (5.17).
Remark 5.19. While we have focused on the
![]() $n=1$
case, the considerations here are valid for higher loop spaces as well. Thus, one obtains a
$n=1$
case, the considerations here are valid for higher loop spaces as well. Thus, one obtains a
![]() $E_{n+1}$
groupoid objects where the degree
$E_{n+1}$
groupoid objects where the degree
![]() $(1,...1)$
object of morphisms is the
$(1,...1)$
object of morphisms is the
![]() $\operatorname {Map}_{\mathbb {A}^1 / \mathbb {G}_m}(S^n_{fil}, X|_{\mathbb {A}^1 / \mathbb {G}_m})$
.
$\operatorname {Map}_{\mathbb {A}^1 / \mathbb {G}_m}(S^n_{fil}, X|_{\mathbb {A}^1 / \mathbb {G}_m})$
.
6 Hodge degeneration and deformation to the normal bundle
In this section, we work over a characteristic zero base field k and study the well-known Hodge degeneration in its geometric form studied by Simpson (cf. [Reference SimpsonSim96, Reference SimpsonSim90] One avatar of the Hodge filtration on de Rham cohomology is given by the deformation to the normal cone construction. This manifests itself as a derived stack over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
which specializes upon taking generic and central fibers to the de Rham stack and the Dolbeault stack, respectively.
$\mathbb {A}^1 / \mathbb {G}_m$
which specializes upon taking generic and central fibers to the de Rham stack and the Dolbeault stack, respectively.
6.1 The de Rham and Dolbeault spaces
We give a brief review here of the de Rham and Dolbeault space constructions in derived algebraic geometry. The results in this section are quite classical and well known; we give them to motivate the objects studied.
Definition 6.1. Let X be a scheme. Then the de Rham space of X is defined to be the moduli problem
![]() $X_{dR} \in \operatorname {dStk}_k$
given by
$X_{dR} \in \operatorname {dStk}_k$
given by
where I denotes the nilradical of
![]() $\pi _0(A)$
.
$\pi _0(A)$
.
The de Rham space was originally defined by Simpson as the quotient stack of a certain groupoid object in formal schemes. This goes back to the original construction of Simpson; see, for example, [Reference SimpsonSim96].
Construction 6.2. Let X be a smooth scheme and let
![]() $\pi : X \to X_{dR}$
denote the canonical map. One sees that this is an effective epimorphism in the
$\pi : X \to X_{dR}$
denote the canonical map. One sees that this is an effective epimorphism in the
![]() $\infty $
-category of derived stacks, and so it is the effective quotient of the its nerve groupoid. Thus, we can define the de Rham stack as the realization of the following groupoid
$\infty $
-category of derived stacks, and so it is the effective quotient of the its nerve groupoid. Thus, we can define the de Rham stack as the realization of the following groupoid
where the object
![]() $(X \times X)\widehat {{}_{\Delta }}$
denotes the formal completion of
$(X \times X)\widehat {{}_{\Delta }}$
denotes the formal completion of
![]() $X \times X$
along the diagonal morphism
$X \times X$
along the diagonal morphism
![]() $\Delta : X \to X$
.
$\Delta : X \to X$
.
A proof of the following statement, using ideas which go back to Grothendieck’s work in the setting of infinitesimal cohomology, may be found in [Reference LurieLur09b]:
Theorem 6.3. Let X be a smooth scheme over k. Then there is an equivalence of categories:
Thus, the de Rham stack gives a conceptual way to understand
![]() $\mathcal {D}_{X}$
-modules on X. More generally (e.g., for a derived scheme), a Koszul dual variant of the left-hand side parametrizes the notion of crystals on the infinitesimal site.
$\mathcal {D}_{X}$
-modules on X. More generally (e.g., for a derived scheme), a Koszul dual variant of the left-hand side parametrizes the notion of crystals on the infinitesimal site.
We now move on to the Dolbeault space. This construction is (again) originally due to Carlos Simpson as a natural geometric parametrization for the notion of Higgs bundles. First we recall the notion of tangent bundle in this setting:
Definition 6.4. Let X be a derived scheme. The tangent bundle of X is defined to be
thus, it is a relative derived scheme over X.
Remark 6.5. The tangent bundle admits the structure of an abelian group object over X, which we may think of as a simplicial object
with
Construction 6.6. One can take the formal completion along the unit section
Given the machinery established thus far, we define this to be the pullback
In fact, one may apply this to the map
![]() $X \to \mathcal {T}^n X$
to obtain a simplicial object in formal moduli problems,
$X \to \mathcal {T}^n X$
to obtain a simplicial object in formal moduli problems,
![]() $\widehat {\mathcal {T}X}_{\bullet }$
. We remark that this becomes a groupoid object in formal moduli problems, cf. [Reference Gaitsgory and RozenblyumGR20].
$\widehat {\mathcal {T}X}_{\bullet }$
. We remark that this becomes a groupoid object in formal moduli problems, cf. [Reference Gaitsgory and RozenblyumGR20].
Definition 6.7. We define, following Simpson, the Dolbeault stack to be the delooping
of the formal group object
![]() $\mathcal {T}X_{\bullet }$
.
$\mathcal {T}X_{\bullet }$
.
Proposition 6.8. There is an equivalence of stable
![]() $\infty $
-categories
$\infty $
-categories
where
![]() $\mathbb {T}_X$
denotes the
$\mathbb {T}_X$
denotes the
![]() $\mathcal {O}_X$
-linear dual of the cotangent complex
$\mathcal {O}_X$
-linear dual of the cotangent complex
![]() $\mathbb {L}_X$
.
$\mathbb {L}_X$
.
Proof. An application of the comonadic form of the Barr-Beck theorem shows that
Alternatively, this can be extracted as the descent data defining
![]() $X_{Dol}$
as the realization of the groupoid
$X_{Dol}$
as the realization of the groupoid
![]() $\mathcal {T}X_{\bullet }$
corresponding to the formal group
$\mathcal {T}X_{\bullet }$
corresponding to the formal group
![]() $\widehat {\mathcal {T}X}$
over X. We now take the
$\widehat {\mathcal {T}X}$
over X. We now take the
![]() $\mathcal {O}_X$
-linear dual of the action map for any fixed
$\mathcal {O}_X$
-linear dual of the action map for any fixed
![]() $M \in \operatorname {QCoh}(X_{Dol})$
$M \in \operatorname {QCoh}(X_{Dol})$
to obtain a map
giving M the structure of a
![]() $\widehat {\operatorname {Sym}(\mathbb {L}_X)})^{\vee }$
-module. It thus amounts to identify
$\widehat {\operatorname {Sym}(\mathbb {L}_X)})^{\vee }$
-module. It thus amounts to identify
![]() $\widehat {\operatorname {Sym}(\mathbb {L}_X)})^{\vee }$
with
$\widehat {\operatorname {Sym}(\mathbb {L}_X)})^{\vee }$
with
![]() $\operatorname {Sym}(\mathbb {T}X)$
. For this, note first that
$\operatorname {Sym}(\mathbb {T}X)$
. For this, note first that
so that
To identify each summand, we use the fact that
![]() $(\mathbb {L}_X)^{\vee } \simeq \mathbb {T}_X $
and that we are in characteristic zero (so that divided and symmetric powers coincide) to conclude that
$(\mathbb {L}_X)^{\vee } \simeq \mathbb {T}_X $
and that we are in characteristic zero (so that divided and symmetric powers coincide) to conclude that
for every n. Thus, we deduce the equivalence
From this, we may conclude that M is naturally a
![]() $\operatorname {Sym}(\mathbb {T}_X)$
-module.
$\operatorname {Sym}(\mathbb {T}_X)$
-module.
As a consequence of the above, one may think of
![]() $\operatorname {QCoh}(X_{Dol})$
as a derived
$\operatorname {QCoh}(X_{Dol})$
as a derived
![]() $\infty $
-category of Higgs sheaves, cf. [Reference SimpsonSim90].
$\infty $
-category of Higgs sheaves, cf. [Reference SimpsonSim90].
6.2
 $\lambda $
-connections and the deformation to the normal cone
$\lambda $
-connections and the deformation to the normal cone
There is a natural
![]() $1$
-parameter deformation of the notion of a flat connection. This is the notion of a
$1$
-parameter deformation of the notion of a flat connection. This is the notion of a
![]() $\lambda $
-connection, going back to Deligne.
$\lambda $
-connection, going back to Deligne.
Definition 6.9. Let E be a vector bundle on a scheme X. A
![]() $\lambda $
-connection is an operator
$\lambda $
-connection is an operator
for which
Remark 6.10. If
![]() $\lambda \in R^{\times }$
, then a
$\lambda \in R^{\times }$
, then a
![]() $\lambda $
connection
$\lambda $
connection
![]() $\nabla _{\lambda }$
on a vector bundle E gives equivalent data to a connection
$\nabla _{\lambda }$
on a vector bundle E gives equivalent data to a connection
![]() $\lambda ^{-1} \nabla _{\lambda }$
However, if
$\lambda ^{-1} \nabla _{\lambda }$
However, if
![]() $\lambda = 0$
, this is precisely the data of a Higgs bundle.
$\lambda = 0$
, this is precisely the data of a Higgs bundle.
Let us give another perspective for the notion of
![]() $\lambda $
-connection. Recall that the ring of differential operators
$\lambda $
-connection. Recall that the ring of differential operators
![]() $\mathcal {D}_X$
comes equipped with an filtration known as the order filtration. This has associated graded
$\mathcal {D}_X$
comes equipped with an filtration known as the order filtration. This has associated graded
![]() $\mathcal {O}_{\operatorname {T}^*X} \simeq \operatorname {Sym}(\mathbb {T}_X)$
. Applying the Rees construction to this gives the following
$\mathcal {O}_{\operatorname {T}^*X} \simeq \operatorname {Sym}(\mathbb {T}_X)$
. Applying the Rees construction to this gives the following
![]() $\mathbb {G}_m$
-equivariant sheaf of algebras over
$\mathbb {G}_m$
-equivariant sheaf of algebras over
![]() $X \times \mathbb {A}^1$
.
$X \times \mathbb {A}^1$
.
Definition 6.11. Let
![]() $\mathcal {D}^{\lambda }_{X}$
be the sheaf of algebras on
$\mathcal {D}^{\lambda }_{X}$
be the sheaf of algebras on
![]() $X \times \mathbb {A}^1 / \mathbb {G}_m$
defined by
$X \times \mathbb {A}^1 / \mathbb {G}_m$
defined by
where the coordinate t acts as
![]() $\lambda $
. There is an evident
$\lambda $
. There is an evident
![]() $\mathbb {G}_m$
action on this given by scaling the variable t. Thus, it descends to a sheaf on
$\mathbb {G}_m$
action on this given by scaling the variable t. Thus, it descends to a sheaf on
![]() $X \times \mathbb {A}^1 / \mathbb {G}_m$
.
$X \times \mathbb {A}^1 / \mathbb {G}_m$
.
Remark 6.12. By the definition of the Rees construction, we see that fiber of this object over
![]() $B \mathbb {G}_m$
is the associated graded of the weight filtration – namely,
$B \mathbb {G}_m$
is the associated graded of the weight filtration – namely,
![]() $\operatorname {Sym}(\mathbb {T}_X)$
. Meanwhile, pullback along the generic point recovers the ring of differential operators
$\operatorname {Sym}(\mathbb {T}_X)$
. Meanwhile, pullback along the generic point recovers the ring of differential operators
![]() $\mathcal {D}_X$
itself. Thus, we may conclude that the stucture of a
$\mathcal {D}_X$
itself. Thus, we may conclude that the stucture of a
![]() $\mathcal {D}^{\lambda }_{X}$
-module is none other than that of a
$\mathcal {D}^{\lambda }_{X}$
-module is none other than that of a
![]() $\lambda $
-connection.
$\lambda $
-connection.
The following definition of the Hodge degeneration goes back to Simpson, following a suggestion of Deligne. It gives rise to a natural geometric parametrization for the notion of
![]() $\lambda $
-connection.
$\lambda $
-connection.
Construction 6.13. Form the (levelwise) mapping stack over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
:
$\mathbb {A}^1 / \mathbb {G}_m$
:
where
![]() $S^{0,\bullet }$
is the cogroupoid object in derived stacks studied in Section 5. This will be a groupoid object in derived stacks. Next, form the formal completion in each degree, along the map
$S^{0,\bullet }$
is the cogroupoid object in derived stacks studied in Section 5. This will be a groupoid object in derived stacks. Next, form the formal completion in each degree, along the map
In more detail, we define this (in accordance with Section 2.3) by the following pullback square:

Notice that over the point
![]() ${\operatorname {Spec}} R \xrightarrow {1} \mathbb {A}^1 / \mathbb {G}_m$
, the map with respect to which we are taking the formal completion is precisely the diagonal map
${\operatorname {Spec}} R \xrightarrow {1} \mathbb {A}^1 / \mathbb {G}_m$
, the map with respect to which we are taking the formal completion is precisely the diagonal map
![]() $\Delta : X \to X \times X$
; over the point
$\Delta : X \to X \times X$
; over the point
![]() $0 : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
, this is exactly the inclusion
$0 : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
, this is exactly the inclusion
![]() $X \to \mathcal {T}^{\bullet }$
of the units into the group(oid) object defining the Dolbeault space.
$X \to \mathcal {T}^{\bullet }$
of the units into the group(oid) object defining the Dolbeault space.
Definition 6.15. We denote the above simplicial stack by
![]() $X^{\bullet }_{\lambda }$
. We then define
$X^{\bullet }_{\lambda }$
. We then define
as its classifying stack.
By construction, the stack
![]() $X_{Hod}$
admits a map to
$X_{Hod}$
admits a map to
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Pulling back along the generic fiber, one recovers the de Rham space:
$\mathbb {A}^1 / \mathbb {G}_m$
. Pulling back along the generic fiber, one recovers the de Rham space:
Proposition 6.16. There is an equivalence
However, pulling back along the map
![]() $\iota : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
recovers the Dolbeault space:
$\iota : B \mathbb {G}_m \to \mathbb {A}^1 / \mathbb {G}_m$
recovers the Dolbeault space:
Proposition 6.17. There is an equivalence
where the structure map
![]() $X_{Dol} \to B \mathbb {G}_m$
arises from the canonical dilation
$X_{Dol} \to B \mathbb {G}_m$
arises from the canonical dilation
![]() $\mathbb {G}_m$
-action on the formal group
$\mathbb {G}_m$
-action on the formal group
![]() $\widehat {\mathbb {T}X}$
.
$\widehat {\mathbb {T}X}$
.
The following theorem morally goes back to Simpson and may be proven similarly to Theorem 6.3:
Theorem 6.18 (Simpson).
Let X be a smooth scheme. Then there is an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
Here, the right-hand side denotes the
![]() $\infty $
-category of
$\infty $
-category of
![]() $\lambda $
-connections.
$\lambda $
-connections.
Remark 6.19. One may thus think of the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {QCoh}(X_{Hod})$
as giving a
$\operatorname {QCoh}(X_{Hod})$
as giving a
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
-linear enhancement of the
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
-linear enhancement of the
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathcal {D}_X$
-modules. By the Rees correspondence, this is none other than a filtration at the level of categories, which manifests itself as the well-known filtration on the ring of differential operators
$\mathcal {D}_X$
-modules. By the Rees correspondence, this is none other than a filtration at the level of categories, which manifests itself as the well-known filtration on the ring of differential operators
![]() $\mathcal {D}_X$
. The interested reader may consult [Reference Toën and VezzosiTV20, Remark 3.2.3] for a generalization of this story to the setting of derived foliations.
$\mathcal {D}_X$
. The interested reader may consult [Reference Toën and VezzosiTV20, Remark 3.2.3] for a generalization of this story to the setting of derived foliations.
Construction 6.20. Let X be a derived scheme. Recall from [Reference Moulinos, Robalo and ToënMRT22] that we may form the following derived mapping space:
This is referred to in loc. cit. as the filtered loop space. By the work in Section 5,
![]() $S^1_{fil}$
fits as the degree
$S^1_{fil}$
fits as the degree
![]() $(1,1)$
piece of the 2-cogroupoid object
$(1,1)$
piece of the 2-cogroupoid object
![]() $S^{1, \bullet }$
. We take this into account by defining
$S^{1, \bullet }$
. We take this into account by defining
which, in turn, is a 2-groupoid in
![]() $\operatorname {dStk}_{/ \mathbb {A}^1 / \mathbb {G}_m}$
, over
$\operatorname {dStk}_{/ \mathbb {A}^1 / \mathbb {G}_m}$
, over
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m}$
.
$X|_{\mathbb {A}^1 / \mathbb {G}_m}$
.
One has the following proposition:
Proposition 6.21. Let X be a derived scheme. Then for each
![]() $(m,n)$
, the derived scheme
$(m,n)$
, the derived scheme
![]() $\mathcal {L}^{(m,n)}(X)$
is formally complete along
$\mathcal {L}^{(m,n)}(X)$
is formally complete along
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m} \to \mathcal {L}^{(m,n)}(X)$
.
$X|_{\mathbb {A}^1 / \mathbb {G}_m} \to \mathcal {L}^{(m,n)}(X)$
.
Proof. In degree
![]() $(1,1)$
, the cogroupoid object
$(1,1)$
, the cogroupoid object
![]() ${S^1}^{\bullet , \bullet }_{fil}$
is precisely
${S^1}^{\bullet , \bullet }_{fil}$
is precisely
![]() $B \mathbb {H}$
, where
$B \mathbb {H}$
, where
![]() $\mathbb {H}$
is the filtered group scheme from [Reference Moulinos, Robalo and ToënMRT22]. After forming mapping spaces out of this, one obtains a derived scheme whose truncation is the truncation of X itself. This uses the fact that X is a scheme and does not exhibit any stacky behavior, and so there are no nonconstant maps
$\mathbb {H}$
is the filtered group scheme from [Reference Moulinos, Robalo and ToënMRT22]. After forming mapping spaces out of this, one obtains a derived scheme whose truncation is the truncation of X itself. This uses the fact that X is a scheme and does not exhibit any stacky behavior, and so there are no nonconstant maps
![]() $B \mathbb {H} \to X$
. Thus, the map
$B \mathbb {H} \to X$
. Thus, the map
![]() $S^1_{Fil} \to *$
induces an equivalence on truncations
$S^1_{Fil} \to *$
induces an equivalence on truncations
![]() $\mathcal {L}_{fil}X$
, which is, in particular, a nil-isomorphism. Now that we know that the degree
$\mathcal {L}_{fil}X$
, which is, in particular, a nil-isomorphism. Now that we know that the degree
![]() $1$
piece is formally complete, we use the intrinsic symmetries along the diagonal that follow from the
$1$
piece is formally complete, we use the intrinsic symmetries along the diagonal that follow from the
![]() $E_2$
-groupoid structure, which allow for us to conclude that it is formally complete in each bidegree. Hence, we conclude that this is a formal groupoid, in the sense of [Reference Gaitsgory and RozenblyumGR20].
$E_2$
-groupoid structure, which allow for us to conclude that it is formally complete in each bidegree. Hence, we conclude that this is a formal groupoid, in the sense of [Reference Gaitsgory and RozenblyumGR20].
Hence,
![]() $\mathcal {L}_{fil}(X)$
is a
$\mathcal {L}_{fil}(X)$
is a
![]() $2$
-groupoid object in formal stacks. Moreover, as a bisimplicial object, this has the constant simplicial diagram on
$2$
-groupoid object in formal stacks. Moreover, as a bisimplicial object, this has the constant simplicial diagram on
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m}$
on the zeroth row and column. Our next goal is to compute the
$X|_{\mathbb {A}^1 / \mathbb {G}_m}$
on the zeroth row and column. Our next goal is to compute the
![]() $2$
-fold delooping of this groupoid in the setting of formal moduli problems. Before passing to the formal context, however, one can make the following observation:
$2$
-fold delooping of this groupoid in the setting of formal moduli problems. Before passing to the formal context, however, one can make the following observation:
Proposition 6.22. There is an equivalence
of 2-groupoid objects in
![]() $\operatorname {dStk}_{\mathbb {A}^1 / \mathbb {G}_m}$
.
$\operatorname {dStk}_{\mathbb {A}^1 / \mathbb {G}_m}$
.
Proof. This will follow by explicitly identifying the two objects in
![]() $\operatorname {Grpd}^{(2)}$
. The argument ultimately boils down to the fact that both simplicial objects depend on the
$\operatorname {Grpd}^{(2)}$
. The argument ultimately boils down to the fact that both simplicial objects depend on the
![]() $E_2$
-cogroupoid structure of
$E_2$
-cogroupoid structure of
![]() $S^1_{fil}$
(more precisely, its structure as a cogroupoid object in the category of cogroupoid objects). At the level of objects, we fix
$S^1_{fil}$
(more precisely, its structure as a cogroupoid object in the category of cogroupoid objects). At the level of objects, we fix
![]() $(n,m) \in \Delta ^{op} \times \Delta ^{op}$
. Then in bisimplicial degree
$(n,m) \in \Delta ^{op} \times \Delta ^{op}$
. Then in bisimplicial degree
![]() $(n,m)$
, the object
$(n,m)$
, the object
![]() $\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
is given by
$\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
is given by
where
 $$ \begin{align} (S_{fil}^1)^{n,m}= \overbrace{* \bigsqcup_{\underbrace{S^0_{fil} \sqcup_{*} \cdots \sqcup_{*} S^0_{fil}}_{n \, \operatorname{ times} }}* \cdots * \bigsqcup_{\underbrace{S^0_{fil} \sqcup_{*} \cdots \sqcup_{*} S^0_{fil}}_{m \, \operatorname{ times} }} *}^{m \, \operatorname{ times} }. \end{align} $$
$$ \begin{align} (S_{fil}^1)^{n,m}= \overbrace{* \bigsqcup_{\underbrace{S^0_{fil} \sqcup_{*} \cdots \sqcup_{*} S^0_{fil}}_{n \, \operatorname{ times} }}* \cdots * \bigsqcup_{\underbrace{S^0_{fil} \sqcup_{*} \cdots \sqcup_{*} S^0_{fil}}_{m \, \operatorname{ times} }} *}^{m \, \operatorname{ times} }. \end{align} $$
Note that
![]() $* =\mathbb {A}^1 / \mathbb {G}_m$
in this case as all these constructions are being performed in
$* =\mathbb {A}^1 / \mathbb {G}_m$
in this case as all these constructions are being performed in
![]() $\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
. Applying the functor
$\operatorname {Stk}_{\mathbb {A}^1 / \mathbb {G}_m}$
. Applying the functor
![]() $\operatorname {Map}_{\operatorname {dStk}_{/ \mathbb {A}^1 / \mathbb {G}_m}}(-, X|_{\mathbb {A}^1 / \mathbb {G}_m})$
out of the above object sends this pushout square to a fiber product, by the argument in the proof of Proposition 5.16. A moment’s thought shows that this is precisely the
$\operatorname {Map}_{\operatorname {dStk}_{/ \mathbb {A}^1 / \mathbb {G}_m}}(-, X|_{\mathbb {A}^1 / \mathbb {G}_m})$
out of the above object sends this pushout square to a fiber product, by the argument in the proof of Proposition 5.16. A moment’s thought shows that this is precisely the
![]() $(n,m)$
th degree of the bisimplicial object
$(n,m)$
th degree of the bisimplicial object
Passing to the setting of formal moduli problems relative to
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m}$
now gives rise to the following corollary:
$X|_{\mathbb {A}^1 / \mathbb {G}_m}$
now gives rise to the following corollary:
Corollary 6.24. There exists an equivalence
of formal groupoid objects. Here, the left-hand side denotes the delooping of the groupoid object
![]() $\mathcal {L}_{fil}(X)$
along the vertical or horizontal direction, and the right side is the formal groupoid whose classifying stack is the Hodge degeneration.
$\mathcal {L}_{fil}(X)$
along the vertical or horizontal direction, and the right side is the formal groupoid whose classifying stack is the Hodge degeneration.
Proof. We first remark that the delooping of the
![]() $E_2$
-groupoid will be a groupoid object in formal stacks, by Theorem 2.14. Now, as we saw in Proposition 6.22, there is an identification of
$E_2$
-groupoid will be a groupoid object in formal stacks, by Theorem 2.14. Now, as we saw in Proposition 6.22, there is an identification of
![]() $2$
-groupoids
$2$
-groupoids
By Proposition 6.21, the left-hand side is already formally complete in each simplicial degree; thus, we may conclude that the right-hand side is a formal
![]() $2$
-groupoid as well.
$2$
-groupoid as well.
Next, we apply the correspondence between formal groupoids and formal moduli problems under X, cf. Theorem 2.14. This tells us that the
![]() $2$
-groupoid
$2$
-groupoid
![]() $\mathcal {L}_{fil}^{\bullet , \bullet }(X)$
arises as the Čech nerve of some map
$\mathcal {L}_{fil}^{\bullet , \bullet }(X)$
arises as the Čech nerve of some map ![]() , which is a nil-isomorphism in the language of [Reference Gaitsgory and RozenblyumGR20]. We may identify this morphism of simplicial objects with the morphism which in simplicial degree n is given by the map
, which is a nil-isomorphism in the language of [Reference Gaitsgory and RozenblyumGR20]. We may identify this morphism of simplicial objects with the morphism which in simplicial degree n is given by the map
(i.e., the map of
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m}$
to its formal thickening in
$X|_{\mathbb {A}^1 / \mathbb {G}_m}$
to its formal thickening in
![]() $\operatorname {Map}( S^{0, n}_{fil}, X|_{\mathbb {A}^1 / \mathbb {G}_m})\widehat {{}_{X|_{\mathbb {A}^1 / \mathbb {G}_m}}}$
). Thus, we have identified the
$\operatorname {Map}( S^{0, n}_{fil}, X|_{\mathbb {A}^1 / \mathbb {G}_m})\widehat {{}_{X|_{\mathbb {A}^1 / \mathbb {G}_m}}}$
). Thus, we have identified the
![]() $1$
-groupoid object
$1$
-groupoid object
![]() $B \mathcal {L}_{fil}^{\bullet , \bullet }X$
with
$B \mathcal {L}_{fil}^{\bullet , \bullet }X$
with
![]() $X_{\lambda }^{\bullet }$
. Note that the structure maps agree by construction; indeed,
$X_{\lambda }^{\bullet }$
. Note that the structure maps agree by construction; indeed,
![]() $X_{\lambda }$
was defined in Construction 6.13 precisely as the levelwise formal completion of the groupoid object
$X_{\lambda }$
was defined in Construction 6.13 precisely as the levelwise formal completion of the groupoid object
![]() $\operatorname {Map}(S^{0,\bullet }_{fil}, X|_{\mathbb {A}^1 / \mathbb {G}_m})$
along the map
$\operatorname {Map}(S^{0,\bullet }_{fil}, X|_{\mathbb {A}^1 / \mathbb {G}_m})$
along the map
We may now put this all together and quickly prove the main theorem, which we restate for the reader’s convenience.
Theorem 6.25. There exists an equivalence
Proof. We can compute
![]() $B^2 \mathcal {L}^{fil}(X)$
by first delooping in the vertical direction and then in the horizontal direction (or in reverse). As we saw in the previous proposition, the stage one delooping recovers the formal groupoid
$B^2 \mathcal {L}^{fil}(X)$
by first delooping in the vertical direction and then in the horizontal direction (or in reverse). As we saw in the previous proposition, the stage one delooping recovers the formal groupoid
![]() $X^{\bullet }_{\lambda }$
. By Definition 6.15, the delooping of this is precisely the Hodge stack
$X^{\bullet }_{\lambda }$
. By Definition 6.15, the delooping of this is precisely the Hodge stack
![]() $X_{Hod}$
.
$X_{Hod}$
.
7 Group structures on the loop space and the Todd class
Let
![]() $f: X \to Y$
be a proper morphism of schemes. A modern reinterpration of the Grothendieck Riemann-Roch theorem encodes the compatibility between the Chern character and the proper pushforward on Hodge cohomology, which arises from the pushforward
$f: X \to Y$
be a proper morphism of schemes. A modern reinterpration of the Grothendieck Riemann-Roch theorem encodes the compatibility between the Chern character and the proper pushforward on Hodge cohomology, which arises from the pushforward
![]() $f_{*}: {\operatorname {Perf}}(X) \to {\operatorname {Perf}}(Y)$
. As described in [Reference Hoyois, Safronov, Scherotzke and SibillaHSSS21, Section 5.2], the HKR equivalence
$f_{*}: {\operatorname {Perf}}(X) \to {\operatorname {Perf}}(Y)$
. As described in [Reference Hoyois, Safronov, Scherotzke and SibillaHSSS21, Section 5.2], the HKR equivalence
intertwines the ‘integration map’
![]() $\mathcal {O}(\mathcal {L}(X)) \to \mathcal {O}(\mathcal {L}(Y)$
with the pushforward map on Hodge cohomology, twisted by the square root of the Todd class:
$\mathcal {O}(\mathcal {L}(X)) \to \mathcal {O}(\mathcal {L}(Y)$
with the pushforward map on Hodge cohomology, twisted by the square root of the Todd class:

In this section, we give a conceptual explanation for the Todd class in terms of the
![]() $2$
-cogroupoid structure on
$2$
-cogroupoid structure on
![]() $S^1_{fil}$
studied in this paper. In particular, we will see that it arises from the failure of
$S^1_{fil}$
studied in this paper. In particular, we will see that it arises from the failure of
![]() $S^1_{fil}$
to be a constant degeneration of cogroup(oid) objects.
$S^1_{fil}$
to be a constant degeneration of cogroup(oid) objects.
Construction 7.1. Recall from above that
![]() $2$
-cogroupoid structure on
$2$
-cogroupoid structure on
![]() $S^1_{fil}$
gives the filtered loop space
$S^1_{fil}$
gives the filtered loop space
![]() $\mathcal {L}_{fil}(X)$
a
$\mathcal {L}_{fil}(X)$
a
![]() $2$
-groupoid structure. In particular, it may be viewed as an
$2$
-groupoid structure. In particular, it may be viewed as an
![]() $E_2$
-group object over the derived scheme X as X will be the degree
$E_2$
-group object over the derived scheme X as X will be the degree
![]() $(0,0)$
space of objects.
$(0,0)$
space of objects.
We would like to study the corresponding group stuctures on
![]() $\mathcal {L}_{fil}(X)$
upon specializing along the closed and generic points of
$\mathcal {L}_{fil}(X)$
upon specializing along the closed and generic points of
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Recall from [Reference Moulinos, Robalo and ToënMRT22] that over
$\mathbb {A}^1 / \mathbb {G}_m$
. Recall from [Reference Moulinos, Robalo and ToënMRT22] that over
![]() $\eta : {\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
, there is an equivalence
$\eta : {\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
, there is an equivalence
of group stacks. Similarly, one has an equivalence
We remind the reader that this is only true in characteristic zero. Thus, one has an HKR equivalence (cf. [Reference Toën and VezzosiTV11, Reference Ben-Zvi and NadlerBZN12])
We will see that there exist two group structures on
![]() $\mathbb {T}_X [-1]$
, one which is related to the cogroupoid structure on
$\mathbb {T}_X [-1]$
, one which is related to the cogroupoid structure on
![]() $S^1_{gr}$
and the other which is related to that on
$S^1_{gr}$
and the other which is related to that on
![]() $S^1$
. The extent to which these are nonequivalent is detected by a distinguished class in
$S^1$
. The extent to which these are nonequivalent is detected by a distinguished class in
This is none other than the Todd class.
Remark 7.2. These group objects
![]() $\mathcal {L}(X)$
and
$\mathcal {L}(X)$
and
![]() $\mathbb {T}_{X}[-1]$
over X are, in fact, formally complete along X. Thus, we may view them as group objects in formal moduli problems over X.
$\mathbb {T}_{X}[-1]$
over X are, in fact, formally complete along X. Thus, we may view them as group objects in formal moduli problems over X.
7.1 Formal groups and the Todd class
We now review how a group structure gives rise to an orientation of the canonical bundle on
![]() $\mathbb {T}_X [-1]$
. Much of the following discussion is taken from [Reference Kondyrev and PrikhodkoKP19].
$\mathbb {T}_X [-1]$
. Much of the following discussion is taken from [Reference Kondyrev and PrikhodkoKP19].
Construction 7.3. We first review, following loc. cit. the canonical trivialization of the relative tangent bundle of a formal group over X. Let
![]() $\widehat {\mathbb {G}}$
be the formal group in question. In this setting, one has the following trivialization:
$\widehat {\mathbb {G}}$
be the formal group in question. In this setting, one has the following trivialization:
where
![]() $\mathfrak {g} := \operatorname {Lie}_{X}(\widehat {\mathbb {G}})$
is the corresponding Lie algebra of
$\mathfrak {g} := \operatorname {Lie}_{X}(\widehat {\mathbb {G}})$
is the corresponding Lie algebra of
![]() $\widehat {\mathbb {G}}$
. One uses here the key property of the relative tangent sheaf being stable under pullbacks, cf. [Reference Kondyrev and PrikhodkoKP19, Proposition 5.1.8].
$\widehat {\mathbb {G}}$
. One uses here the key property of the relative tangent sheaf being stable under pullbacks, cf. [Reference Kondyrev and PrikhodkoKP19, Proposition 5.1.8].
Remark 7.4. Let
![]() $\widehat {\mathbb {G}} = \mathcal {L}X$
. Using the above, one obtains an orientation
$\widehat {\mathbb {G}} = \mathcal {L}X$
. Using the above, one obtains an orientation
Construction 7.5. Recall the construction of the determinant of a perfect complex from [Reference Schürg, Toën and VezzosiSTV15]. This is defined as a morphism of stacks
where the left-hand side is the derived stack classifying perfect complexes and the right-hand side classifies invertible objects. Now we fix a formal derived stack ![]() over X whose relative tangent complex is perfect, and on which one may equip two distinct formal group structures
over X whose relative tangent complex is perfect, and on which one may equip two distinct formal group structures
![]() $g_1, g_2$
. By composing the trivialization of
$g_1, g_2$
. By composing the trivialization of ![]() arising from
arising from
![]() $g_1$
with the inverse of that arising from
$g_1$
with the inverse of that arising from
![]() $g_2$
, we obtain an automorphism
$g_2$
, we obtain an automorphism
This is an endomorphism of the relative tangent complex of ![]() over X. We now define
over X. We now define
by way of the induced map ![]()
Remark 7.6. Let us remark for the sake of clarity that
![]() $\operatorname {det}(\gamma )$
is, in fact, an invertible element of
$\operatorname {det}(\gamma )$
is, in fact, an invertible element of ![]() . However, note that this canonically equivalent to
. However, note that this canonically equivalent to ![]() . Thus, we obtain a well-defined invertible element of
. Thus, we obtain a well-defined invertible element of ![]()
Remark 7.7. Let X be a derived scheme and fix ![]() . This obtains two group structures, one arising from the cogroup structure on
. This obtains two group structures, one arising from the cogroup structure on
![]() $(S^1_{fil})^{u}$
and the other coming from the cogroup structure on the
$(S^1_{fil})^{u}$
and the other coming from the cogroup structure on the
![]() $S^1_{gr} = {\operatorname {Spec}}^{\Delta }(k \oplus k[-1])$
. Then
$S^1_{gr} = {\operatorname {Spec}}^{\Delta }(k \oplus k[-1])$
. Then
In [Reference Kondyrev and PrikhodkoKP19], it is shown that this recovers the Todd class of a scheme. We briefly recall a broad explanation for why this is true.
Proposition 7.8 [Reference Kondyrev and PrikhodkoKP19].
Let X be a smooth and proper scheme. Then the group theoretic Todd class, defined above, recovers the classical Todd class of the Lie algebroid
![]() $\mathbb {T}_X$
.
$\mathbb {T}_X$
.
Proof. The loop group structure on
![]() $\mathcal {L}(X)$
makes it into a formal group over X. The result follows from a general statement valid for arbitrary formal groups. For a general formal group
$\mathcal {L}(X)$
makes it into a formal group over X. The result follows from a general statement valid for arbitrary formal groups. For a general formal group
![]() $\widehat {\mathbb {G}} \to X$
, let
$\widehat {\mathbb {G}} \to X$
, let
![]() $\mathfrak {g} := \operatorname {Lie}(\widehat {\mathbb {G}})$
. There exists a general equivalence of formal moduli problems over X:
$\mathfrak {g} := \operatorname {Lie}(\widehat {\mathbb {G}})$
. There exists a general equivalence of formal moduli problems over X:
where the right-hand side denotes the formal vector bundle stack associated to
![]() $\mathfrak {g}$
. Via this equivalence,
$\mathfrak {g}$
. Via this equivalence,
![]() $\mathbb {V}(\mathfrak {g})$
inherits 2 group structures (one being the abelian one, the other via transport of structure from
$\mathbb {V}(\mathfrak {g})$
inherits 2 group structures (one being the abelian one, the other via transport of structure from
![]() $\widehat {\mathbb {G}}$
). Via the discussion above, this gives rise to two trivializations of the relative tangent
$\widehat {\mathbb {G}}$
). Via the discussion above, this gives rise to two trivializations of the relative tangent
![]() $\mathbb {T}_{\widehat {\mathbb {G}} / X}$
which is denoted suggestively in [Reference Kondyrev and PrikhodkoKP19] as
$\mathbb {T}_{\widehat {\mathbb {G}} / X}$
which is denoted suggestively in [Reference Kondyrev and PrikhodkoKP19] as
The determinant (in the sense of [Reference Schürg, Toën and VezzosiSTV15]) of this automorphism then gives the group theoretic Todd class.
Meanwhile, the Todd class as it appears in the statement of the GRR theorem is given as a multiplicative characteristic class; it is given by the formula
where
![]() $f(x)$
is the formal power series
$f(x)$
is the formal power series
The key result of [Reference Kondyrev and PrikhodkoKP19] states that for an arbitrary formal group
![]() $\widehat {\mathbb {G}}$
, the automorphism (7.9) may be expressed as
$\widehat {\mathbb {G}}$
, the automorphism (7.9) may be expressed as
 $$ \begin{align*}d\operatorname{exp}_{\widehat{\mathbb{G}}} = \frac{1-e^{- \operatorname{ad}_{\mathfrak{g}}}} {\operatorname{ad}_{\mathfrak{g}}}, \end{align*} $$
$$ \begin{align*}d\operatorname{exp}_{\widehat{\mathbb{G}}} = \frac{1-e^{- \operatorname{ad}_{\mathfrak{g}}}} {\operatorname{ad}_{\mathfrak{g}}}, \end{align*} $$
where
![]() $\operatorname {ad}_{\mathfrak {g}}$
denotes the adjoint representation of the Lie algebra
$\operatorname {ad}_{\mathfrak {g}}$
denotes the adjoint representation of the Lie algebra
![]() $\mathfrak {g}$
, given by the Atiyah class of
$\mathfrak {g}$
, given by the Atiyah class of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
7.2 Non-formality of the pinch map
We would like to relate the construction of the Todd class above to the cogroupoid structures on
![]() $S^1_{fil}$
. We will see that the data of the Todd class is in a precise sense included in the data of the
$S^1_{fil}$
. We will see that the data of the Todd class is in a precise sense included in the data of the
![]() $E_2$
-cogroupoid structure on
$E_2$
-cogroupoid structure on
![]() $S^1_{fil}$
. In particular, the nontriviality of the Todd class will follow from the
$S^1_{fil}$
. In particular, the nontriviality of the Todd class will follow from the
![]() $E_1$
cogroup structure on the topological circle
$E_1$
cogroup structure on the topological circle
![]() $S^1$
, in the
$S^1$
, in the
![]() $\infty $
-category of pointed spaces
$\infty $
-category of pointed spaces
![]() $\mathcal {S}_*$
This cogroup structure is often described by the well-known ‘pinch map’
$\mathcal {S}_*$
This cogroup structure is often described by the well-known ‘pinch map’
of pointed spaces. The goal of this section is to relate the existence of this Todd class with the failure of the resulting cogroup(oid) structure on
![]() $S^1$
to be formal. We first explain what we mean by this.
$S^1$
to be formal. We first explain what we mean by this.
Definition 7.10. Let ![]() . Let
. Let ![]() . We say that
. We say that ![]() is a constant degeneration (of
is a constant degeneration (of ![]() ) if there exists an equivalence
) if there exists an equivalence
where the right-hand side denotes the pullback of ![]() along the composite map
along the composite map
Similarly, let ![]() be
be
![]() $E_n$
cogroupoid object in affine stacks. Then it is a constant degeneration of cogroupoid objects if there is an equivalence
$E_n$
cogroupoid object in affine stacks. Then it is a constant degeneration of cogroupoid objects if there is an equivalence
of cogroupoids.
Remark 7.11. By [Reference RaksitRak20, Proposition 4.5.8], the Postnikov filtration functor induces a fully faithful embedding
![]() $\tau _{\geq * }: \mathsf {coSCR}_R \hookrightarrow \operatorname {Fil}(\mathsf {coSCR}_R )$
. In particular, if X is a topological space, its cochain algebra
$\tau _{\geq * }: \mathsf {coSCR}_R \hookrightarrow \operatorname {Fil}(\mathsf {coSCR}_R )$
. In particular, if X is a topological space, its cochain algebra
![]() $R^{X} =C^*(X, R)$
can be promoted, by way of the Postnikov filtration, to a filtered commutative algebra. This moreover degenerates to the cohomology ring
$R^{X} =C^*(X, R)$
can be promoted, by way of the Postnikov filtration, to a filtered commutative algebra. This moreover degenerates to the cohomology ring
![]() $H^*(X, R)$
(viewed as a dga with zero differential) at the level of associated graded.
$H^*(X, R)$
(viewed as a dga with zero differential) at the level of associated graded.
Definition 7.12. Let A be a cosimplicial commutative algebra. By the above remark, it admits a canonical lift to filtered cosimplicial commutative algebras. By the Rees construction, we may, in turn, view this as a cosimplicial commutative algebra in
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
. We say that A is formal if the affine stack
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
. We say that A is formal if the affine stack
![]() ${\operatorname {Spec}}^{\Delta }(A)$
is a constant degeneration over
${\operatorname {Spec}}^{\Delta }(A)$
is a constant degeneration over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
. Similarly, if
$\mathbb {A}^1 / \mathbb {G}_m$
. Similarly, if
![]() $A_{\bullet }$
is a groupoid object in
$A_{\bullet }$
is a groupoid object in
![]() $\mathsf {coSCR}_R$
, then it is formal as a groupoid object if
$\mathsf {coSCR}_R$
, then it is formal as a groupoid object if
![]() ${\operatorname {Spec}}^{\Delta }(A)^{\bullet } \to \mathbb {A}^1 / \mathbb {G}_m$
is a constant degeneration of cogroupoids.
${\operatorname {Spec}}^{\Delta }(A)^{\bullet } \to \mathbb {A}^1 / \mathbb {G}_m$
is a constant degeneration of cogroupoids.
Remark 7.13. Let
![]() $X^{\bullet , \cdots , \bullet }$
be an
$X^{\bullet , \cdots , \bullet }$
be an
![]() $E_n$
-cogroup(oid) object in spaces. Then, again using [Reference RaksitRak20, Proposition 4.5.8], we obtain an
$E_n$
-cogroup(oid) object in spaces. Then, again using [Reference RaksitRak20, Proposition 4.5.8], we obtain an
![]() $E_n$
-cogroup(oid) object in affine stacks
$E_n$
-cogroup(oid) object in affine stacks ![]() over
over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
, such that in degree
$\mathbb {A}^1 / \mathbb {G}_m$
, such that in degree
![]() $(1, \cdots , 1)$
, there is an equivalence
$(1, \cdots , 1)$
, there is an equivalence
We remark that the
![]() $E_2$
-cogroupoid structure on
$E_2$
-cogroupoid structure on
![]() $S^1$
discussed thus far contains strictly more structure than the cogroup object
$S^1$
discussed thus far contains strictly more structure than the cogroup object
![]() $S^1$
in pointed spaces.
$S^1$
in pointed spaces.
Proposition 7.14. The co-group structure on
![]() $S^1$
viewed as a pointed space is determined by the
$S^1$
viewed as a pointed space is determined by the
![]() $2$
-cogroupoid structure on
$2$
-cogroupoid structure on
![]() $S^1$
in the
$S^1$
in the
![]() $\infty $
-category of (unpointed) spaces. In particular, the cosimplicial object describing the cogroup
$\infty $
-category of (unpointed) spaces. In particular, the cosimplicial object describing the cogroup
![]() $S^1$
can be recovered as the projection to the
$S^1$
can be recovered as the projection to the
![]() $1$
st column of
$1$
st column of
![]() $S^{1, \bullet , \bullet }$
.
$S^{1, \bullet , \bullet }$
.
Proof. Recall that 2-cogroupoid object
![]() $S^1$
is defined by as the iterated conerve of the map
$S^1$
is defined by as the iterated conerve of the map
![]() $\emptyset \to \operatorname {pt} $
. In particular, this will be the conerve of the map of cosimplicial spaces
$\emptyset \to \operatorname {pt} $
. In particular, this will be the conerve of the map of cosimplicial spaces
where
![]() $\operatorname {pt}$
is viewed as a constant cosimplicial space, and the left-hand side is given by
$\operatorname {pt}$
is viewed as a constant cosimplicial space, and the left-hand side is given by
![]() $S^0 \sqcup \cdots \sqcup S^0 $
in each degree. This begets a bicosimplical object, which we see by Section 3 is an
$S^0 \sqcup \cdots \sqcup S^0 $
in each degree. This begets a bicosimplical object, which we see by Section 3 is an
![]() $E_2$
-cogroupoid. Restricting to the first column (or the first row as this bicosimplicial object will be symmetric along the diagonal) piece, one obtains the cosimplicial object given by the conerve of the map
$E_2$
-cogroupoid. Restricting to the first column (or the first row as this bicosimplicial object will be symmetric along the diagonal) piece, one obtains the cosimplicial object given by the conerve of the map
which in degree n is precisely given by
![]() $S^1 \vee \cdots \vee S^1$
. This exactly encodes the cogroup structure of
$S^1 \vee \cdots \vee S^1$
. This exactly encodes the cogroup structure of
![]() $S^1$
as an object in the
$S^1$
as an object in the
![]() $\infty $
-category of pointed spaces.
$\infty $
-category of pointed spaces.
Corollary 7.15. The 2-cogroupoid structure on
![]() $S^1$
determines the (formal) group structure on
$S^1$
determines the (formal) group structure on
![]() $\mathcal {L}X$
over X.
$\mathcal {L}X$
over X.
Now let us fix again a derived scheme X and turn our attention to the filtered loop space
![]() $\mathcal {L}_{fil}X$
. Note that this is a constant degeneration over
$\mathcal {L}_{fil}X$
. Note that this is a constant degeneration over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
, of the loop space
$\mathbb {A}^1 / \mathbb {G}_m$
, of the loop space
![]() $\mathcal {L}_{fil}$
to the vector bundle stack corresponding to the (shifted) Lie algebra
$\mathcal {L}_{fil}$
to the vector bundle stack corresponding to the (shifted) Lie algebra
![]() $\mathbb {T}_{X}[-1]$
. The 2-cogroupoid structure on
$\mathbb {T}_{X}[-1]$
. The 2-cogroupoid structure on
![]() $S^1_{fil}$
gives this the structure of an
$S^1_{fil}$
gives this the structure of an
![]() $E_2$
-groupoid object in formal moduli problems over
$E_2$
-groupoid object in formal moduli problems over
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m}$
. Over the generic point
$X|_{\mathbb {A}^1 / \mathbb {G}_m}$
. Over the generic point
![]() $\eta : {\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
, this recovers the group structure on
$\eta : {\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
, this recovers the group structure on
![]() $\mathcal {L} X$
, and over
$\mathcal {L} X$
, and over
![]() $B \mathbb {G}_m$
, this recovers the abelian group structure on
$B \mathbb {G}_m$
, this recovers the abelian group structure on
![]() $ \mathbb {T}X[-1]$
arising from its structure as the (formal completion) of a linear stack.
$ \mathbb {T}X[-1]$
arising from its structure as the (formal completion) of a linear stack.
Remark 7.16. Let
![]() $X = S^1$
equipped with its
$X = S^1$
equipped with its
![]() $E_1$
-cogroupoid structure. The formality as above is equivalent to the question of whether or not
$E_1$
-cogroupoid structure. The formality as above is equivalent to the question of whether or not
![]() $S^1_{fil}$
is a constant degeneration of
$S^1_{fil}$
is a constant degeneration of
![]() $E_1$
-cogroupoid objects over
$E_1$
-cogroupoid objects over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
.
$\mathbb {A}^1 / \mathbb {G}_m$
.
We already know that as an
![]() $E_2$
-cogroupoid, the degeneration is nonconstant:
$E_2$
-cogroupoid, the degeneration is nonconstant:
Proposition 7.17. The
![]() $E_2$
-cogroupoid object
$E_2$
-cogroupoid object
![]() ${S^{1,\bullet , \bullet }_{fil}}$
is not a constant degeneration over
${S^{1,\bullet , \bullet }_{fil}}$
is not a constant degeneration over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
.
$\mathbb {A}^1 / \mathbb {G}_m$
.
Proof. We apply mapping spaces into a derived scheme X. This gives rise to an
![]() $E_2$
-(formal)-groupoid over
$E_2$
-(formal)-groupoid over
![]() $X|_{\mathbb {A}^1 / \mathbb {G}_m}$
. By the main theorem,
$X|_{\mathbb {A}^1 / \mathbb {G}_m}$
. By the main theorem,
![]() $B^{(2)} \mathcal {L}_{fil}(X) \simeq X_{Hod}$
. This obviously is not a constant degeneration of formal moduli problems since
$B^{(2)} \mathcal {L}_{fil}(X) \simeq X_{Hod}$
. This obviously is not a constant degeneration of formal moduli problems since
Hence, we may conclude that
![]() ${S^{1,\bullet , \bullet }_{fil}}$
is not formal as an
${S^{1,\bullet , \bullet }_{fil}}$
is not formal as an
![]() $E_2$
-cogroupoid object.
$E_2$
-cogroupoid object.
In fact, the failure of
![]() $\mathcal {L}_{fil}(X)$
to be a constant degeneration of groups (i.e., the failure of the formality of the pinch map
$\mathcal {L}_{fil}(X)$
to be a constant degeneration of groups (i.e., the failure of the formality of the pinch map
![]() $S^1 \to S^1 \vee S^1$
) gives rise functorially to the existence of nontrivial Todd classes for smooth and proper schemes.
$S^1 \to S^1 \vee S^1$
) gives rise functorially to the existence of nontrivial Todd classes for smooth and proper schemes.
Theorem 7.18. The existence of nontrivial Todd classes implies that the cogroupoid (equivalently pointed cogroup) structure on
![]() $S^1$
corresponding to the pinch map is not formal.
$S^1$
corresponding to the pinch map is not formal.
Proof. The
![]() $E_1$
-cogroupoid
$E_1$
-cogroupoid
![]() ${S^{1, \bullet }_{fil}}$
provides a degeneration of pointed
${S^{1, \bullet }_{fil}}$
provides a degeneration of pointed
![]() $E_1$
-cogroup objects over
$E_1$
-cogroup objects over
![]() $\mathbb {A}^1 / \mathbb {G}_m$
; this specializes to the cogroup
$\mathbb {A}^1 / \mathbb {G}_m$
; this specializes to the cogroup
![]() $(S^1_{fil})^u$
over the generic fiber and to
$(S^1_{fil})^u$
over the generic fiber and to
![]() $S^1_{gr}$
over the special fiber. Note that one recovers the filtered circle in the degree 1 stage. Recall that in characteristic zero at the level of stacks, this is a constant degeneration, so we must verify that the cogroupoid structures are themselves different.
$S^1_{gr}$
over the special fiber. Note that one recovers the filtered circle in the degree 1 stage. Recall that in characteristic zero at the level of stacks, this is a constant degeneration, so we must verify that the cogroupoid structures are themselves different.
Before doing so, we remark that the cogroup structure on
![]() $(S^1_{fil})^u = S^1_{fil} \times _{\mathbb {A}^1 / \mathbb {G}_m} {\operatorname {Spec}} k$
is indeed controlled by the cogroupoid (equivalently pointed cogroup) structure on the topological space
$(S^1_{fil})^u = S^1_{fil} \times _{\mathbb {A}^1 / \mathbb {G}_m} {\operatorname {Spec}} k$
is indeed controlled by the cogroupoid (equivalently pointed cogroup) structure on the topological space
![]() $S^1$
. The constant stack functor
$S^1$
. The constant stack functor
being a left adjoint, preserves colimits, and thus, the associated cosimplicial object in
![]() $\operatorname {Stk}_k$
is also an
$\operatorname {Stk}_k$
is also an
![]() $E_1$
-cogroup. By applying affinization, we obtain a cogroup object in affine stacks; however, the affinization morphism
$E_1$
-cogroup. By applying affinization, we obtain a cogroup object in affine stacks; however, the affinization morphism
![]() $S^1 \to \operatorname {Aff}(S^1)$
is easily seen to be a morphism of cogroups so the ‘unipotent’ loop space
$S^1 \to \operatorname {Aff}(S^1)$
is easily seen to be a morphism of cogroups so the ‘unipotent’ loop space
![]() $\operatorname {Map}( (S^1_{fil})^{u}, X)$
(which recovers
$\operatorname {Map}( (S^1_{fil})^{u}, X)$
(which recovers
![]() $\mathcal {L}(X)$
) inherits the same
$\mathcal {L}(X)$
) inherits the same
![]() $E_1$
group structure over X as
$E_1$
group structure over X as
![]() $\mathcal {L}(X)$
$\mathcal {L}(X)$
Let us fix X a derived scheme. The HKR theorem in characteristic zero gives rise to an equivalence
of derived schemes over X. As we remarked earlier, these are, in fact, formally complete along X, so that they may be viewed as formal moduli problems over X. These sit in the degree
![]() $1$
piece of the simplicial object in formal moduli problems over X classifying the loop group and abelian group structures on
$1$
piece of the simplicial object in formal moduli problems over X classifying the loop group and abelian group structures on
![]() $\mathcal {T}X[-1]$
, respectively. These are given by
$\mathcal {T}X[-1]$
, respectively. These are given by
![]() $\mathcal {L}_{gr}(X)^{\bullet , \bullet }$
and
$\mathcal {L}_{gr}(X)^{\bullet , \bullet }$
and
![]() $\mathcal {L}(X)^{\bullet , \bullet }$
.
$\mathcal {L}(X)^{\bullet , \bullet }$
.
The claim is that the Todd class measures the difference between these two group structures in a functorial way. In particular, one may express the assignment
as the image of
![]() $\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
, with its group structure induced by mapping objects from the cogroup structure on
$\mathcal {L}^{\bullet , \bullet }_{fil}(X)$
, with its group structure induced by mapping objects from the cogroup structure on
![]() $S^{1,\bullet }_{fil}$
, under the following composition (of core
$S^{1,\bullet }_{fil}$
, under the following composition (of core
![]() $\infty $
-groupoids):
$\infty $
-groupoids):
 $$ \begin{align*} & \operatorname{Grp}( \mathcal{L}_{fil}(X))\rightarrow \operatorname{Grp}(\mathcal{T}_X[-1]) \times \operatorname{Grp}(\mathcal{T}_X[-1]) \\ \to& \operatorname{Iso}_{\operatorname{QCoh}(\mathcal{T}_X[-1])}(\mathbb{T}_{\mathcal{T}_X[-1]/X}, \pi^*(\mathbb{T}_X[-1])) \times \operatorname{Iso}_{\operatorname{QCoh}(\mathcal{T}_X[-1])}(\mathbb{T}_{\mathcal{T}_X[-1]/X}, \pi^*(\mathbb{T}_X[-1])) \\ \to & \operatorname{Aut}_{\operatorname{QCoh}(\mathcal{T}_X[-1])}(\mathbb{T}_{\mathcal{T}_X[-1]/X}) \xrightarrow{\mathbf{det}} \mathcal{O}_{\mathcal{T}_X[-1]}^{\times}. \end{align*} $$
$$ \begin{align*} & \operatorname{Grp}( \mathcal{L}_{fil}(X))\rightarrow \operatorname{Grp}(\mathcal{T}_X[-1]) \times \operatorname{Grp}(\mathcal{T}_X[-1]) \\ \to& \operatorname{Iso}_{\operatorname{QCoh}(\mathcal{T}_X[-1])}(\mathbb{T}_{\mathcal{T}_X[-1]/X}, \pi^*(\mathbb{T}_X[-1])) \times \operatorname{Iso}_{\operatorname{QCoh}(\mathcal{T}_X[-1])}(\mathbb{T}_{\mathcal{T}_X[-1]/X}, \pi^*(\mathbb{T}_X[-1])) \\ \to & \operatorname{Aut}_{\operatorname{QCoh}(\mathcal{T}_X[-1])}(\mathbb{T}_{\mathcal{T}_X[-1]/X}) \xrightarrow{\mathbf{det}} \mathcal{O}_{\mathcal{T}_X[-1]}^{\times}. \end{align*} $$
Here, the first map is induced by simultaneously pulling back the group structure to the generic and special fiber to get two different group stuctures on
![]() $\mathcal {T}_X[-1]$
(since we are working in characteristic zero, both the generic and special fibers are equivalent to
$\mathcal {T}_X[-1]$
(since we are working in characteristic zero, both the generic and special fibers are equivalent to
![]() $\mathcal {T}_X[-1]$
). The second arrow is the assignment, to each of these group structures, of a trivialization of the relative bundle. As described in [Reference Kondyrev and PrikhodkoKP19, Construction 3.3.1], this assignment is canonical – hence the functoriality of the second arrow. The third arrow is just the composition of the two equivalences which gives an automorphism of the relative tangent bundle.
$\mathcal {T}_X[-1]$
). The second arrow is the assignment, to each of these group structures, of a trivialization of the relative bundle. As described in [Reference Kondyrev and PrikhodkoKP19, Construction 3.3.1], this assignment is canonical – hence the functoriality of the second arrow. The third arrow is just the composition of the two equivalences which gives an automorphism of the relative tangent bundle.
Now let X be, in particular, smooth and proper. As we reviewed above in Section 7.1, the group theoretical Todd class agrees with the classical Todd class. Thus, the 1-cogroupoid
![]() $S^{1, \bullet }_{fil}$
gives rise to a degeneration of groupoid objects, natural in X, with special fiber the abelian group structure and generic fiber given by the loop group. The fact that there exists some smooth and proper scheme X for which
$S^{1, \bullet }_{fil}$
gives rise to a degeneration of groupoid objects, natural in X, with special fiber the abelian group structure and generic fiber given by the loop group. The fact that there exists some smooth and proper scheme X for which
![]() $\operatorname {td}(X) \neq 1$
implies that this is not a constant degeneration. Thus, the cogroup structures on
$\operatorname {td}(X) \neq 1$
implies that this is not a constant degeneration. Thus, the cogroup structures on
![]() $S^1$
and
$S^1$
and
![]() $S^1_{gr}$
are themselves not equivalent. We may conclude from all this that the
$S^1_{gr}$
are themselves not equivalent. We may conclude from all this that the
![]() $E_1$
-cogroup in pointed spaces
$E_1$
-cogroup in pointed spaces
![]() $S^1$
is not formal.
$S^1$
is not formal.
8 Consequences for Hochschild cohomology
We would like to end with a few further remarks on the
![]() $E_2$
-cogroupoid structure on
$E_2$
-cogroupoid structure on
![]() $S^1_{fil}$
together with consequences at the level of Hochschild cohomology.
$S^1_{fil}$
together with consequences at the level of Hochschild cohomology.
This is presumably well known to experts, but we believe it is worthwhile explicitly relating the
![]() $E_2$
-algebra structure on Hochschild cohomology along with its compatible HKR filtration to the cogroupoid objects in stacks presented here.
$E_2$
-algebra structure on Hochschild cohomology along with its compatible HKR filtration to the cogroupoid objects in stacks presented here.
Definition 8.1. Let X be a derived scheme. The Hochschild cohomology sheaf is defined to be
This acquires an
![]() $\mathcal {O}_{X}$
-linear
$\mathcal {O}_{X}$
-linear
![]() $E_1$
-algebra structure. Furthermore, by, for example, [Reference MarkarianMar09, Section 1.4], there exists a perfect pairing
$E_1$
-algebra structure. Furthermore, by, for example, [Reference MarkarianMar09, Section 1.4], there exists a perfect pairing
displaying
![]() $\mathcal {HH}^*(X)$
as the
$\mathcal {HH}^*(X)$
as the
![]() $\mathcal {O}_X$
-linear dual of
$\mathcal {O}_X$
-linear dual of
![]() $\mathcal {O}_{\mathcal {L}(X)}$
.
$\mathcal {O}_{\mathcal {L}(X)}$
.
Proposition 8.2. The
![]() $E_2$
-cogroupoid structure on
$E_2$
-cogroupoid structure on
![]() $S^1$
(resp.
$S^1$
(resp.
![]() $S^1_{fil}$
) endows
$S^1_{fil}$
) endows
![]() $\operatorname {HH}^*(X)$
with the structure of an
$\operatorname {HH}^*(X)$
with the structure of an
![]() $E_2$
-algebra in
$E_2$
-algebra in
![]() ${\operatorname {Mod}}_k$
, resp
${\operatorname {Mod}}_k$
, resp
![]() $\operatorname {Fil}({\operatorname {Mod}}_k)$
.
$\operatorname {Fil}({\operatorname {Mod}}_k)$
.
Proof. We will prove this in the unfiltered case, but all the claims go through mutatis mutandis in the filtered setting. Let us focus our attention of the structure sheaf of
![]() $\mathcal {L}X$
; the induced
$\mathcal {L}X$
; the induced
![]() $E_2$
-groupoid structure over X will endow
$E_2$
-groupoid structure over X will endow
![]() $\mathcal {O}_{\mathcal {L}(X)}$
with an
$\mathcal {O}_{\mathcal {L}(X)}$
with an
![]() $E_2$
-coalgebroid structure over
$E_2$
-coalgebroid structure over
![]() $\mathcal {O}_X$
. If we take
$\mathcal {O}_X$
. If we take
![]() $\mathcal {O}_X$
-linear duals, this gives an
$\mathcal {O}_X$
-linear duals, this gives an
![]() $E_2$
-algebroid strucure on
$E_2$
-algebroid strucure on
![]() $\mathcal {O}_{\mathcal {L}X}^{\vee }$
. This bisimplicial object encodes a
$\mathcal {O}_{\mathcal {L}X}^{\vee }$
. This bisimplicial object encodes a
![]() $\mathcal {O}_X$
-linear multiplication and a
$\mathcal {O}_X$
-linear multiplication and a
![]() $(\mathcal {O}_X \otimes _{k} \mathcal {O}_X)$
-linear homotopy corresponding to the
$(\mathcal {O}_X \otimes _{k} \mathcal {O}_X)$
-linear homotopy corresponding to the
![]() $E_2$
-commutativity. We may forget this to a k-linear homotopy; this gives
$E_2$
-commutativity. We may forget this to a k-linear homotopy; this gives
![]() $\operatorname {HH}^*(X)$
the structure of an
$\operatorname {HH}^*(X)$
the structure of an
![]() $E_2$
-algebra in
$E_2$
-algebra in
![]() ${\operatorname {Mod}}_k$
.
${\operatorname {Mod}}_k$
.
As it turns out, the standard
![]() $E_2$
-algebra structure on (filtered) Hochschild cohomology may be recovered from the
$E_2$
-algebra structure on (filtered) Hochschild cohomology may be recovered from the
![]() $E_1$
cogroupoid
$E_1$
cogroupoid
![]() $S^{0, \bullet }_{fil}$
:
$S^{0, \bullet }_{fil}$
:
Remark 8.3. There exists an equivalence
The left-hand side inherits a monoidal structure from the right, by composition. This is often referred to as the convolution monoidal structure.
Proposition 8.4. The monoidal structure on
![]() $\operatorname {QCoh}(X \times X)$
is induced by the
$\operatorname {QCoh}(X \times X)$
is induced by the
![]() $E_1$
-cogroupoid structure on
$E_1$
-cogroupoid structure on
![]() $S^{0, \bullet }$
.
$S^{0, \bullet }$
.
Proof. Following [Reference Gaitsgory and RozenblyumGR19, Section 5.2] the assignment ![]() can be expressed as a symmetric monoidal functor from a certain
can be expressed as a symmetric monoidal functor from a certain
![]() $(\infty , 2)$
-category of correspondences (in stacks) to the
$(\infty , 2)$
-category of correspondences (in stacks) to the
![]() $(\infty ,2)$
-category of k-linear stable
$(\infty ,2)$
-category of k-linear stable
![]() $\infty $
-categories. As a consequence, for any groupoid object
$\infty $
-categories. As a consequence, for any groupoid object ![]() , one obtains a monoidal structure on
, one obtains a monoidal structure on ![]() . This discussion now applies to the
. This discussion now applies to the
![]() $E_1$
-groupoid
$E_1$
-groupoid
![]() $\operatorname {Map}(S^{0, \bullet }, X)$
, which inherits the groupoid structure from the cogroupoid
$\operatorname {Map}(S^{0, \bullet }, X)$
, which inherits the groupoid structure from the cogroupoid
![]() $S^0$
. The degree 1 piece is
$S^0$
. The degree 1 piece is
so we conclude that
![]() $\operatorname {QCoh}(X \times X)$
admits an
$\operatorname {QCoh}(X \times X)$
admits an
![]() $E_1$
-algebra structure. The equivalence
$E_1$
-algebra structure. The equivalence
may now be upgraded to an equivalence of monoidal
![]() $\infty $
-categories by [Reference Ben-Zvi, Francis and NadlerBZFN10, Remark 4.11].
$\infty $
-categories by [Reference Ben-Zvi, Francis and NadlerBZFN10, Remark 4.11].
Remark 8.5. It is well known that one can now recover Hochschild cohomology of X, as the endomorphisms of the unit with respect to this monoidal structure:
the unit here being the image of
![]() $\mathcal {O}_X$
under pushforward along the diagonal
$\mathcal {O}_X$
under pushforward along the diagonal
![]() $\Delta : X \times X$
. In fact, as this is endomorphisms of the unit in an
$\Delta : X \times X$
. In fact, as this is endomorphisms of the unit in an
![]() $E_1$
-monoidal
$E_1$
-monoidal
![]() $\infty $
-category, this is naturally an
$\infty $
-category, this is naturally an
![]() $E_2$
-algebra, thereby recovering the well-known fact that
$E_2$
-algebra, thereby recovering the well-known fact that
![]() $\operatorname {HH}^*(X)$
admits an
$\operatorname {HH}^*(X)$
admits an
![]() $E_2$
-algebra structure.
$E_2$
-algebra structure.
In fact, the above argument applies verbatim to give a monoidal structure on
which specializes, upon pullback along
![]() ${\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
, to that of
${\operatorname {Spec}} k \to \mathbb {A}^1 / \mathbb {G}_m$
, to that of
![]() $\operatorname {QCoh}(X \times X)$
.
$\operatorname {QCoh}(X \times X)$
.
Corollary 8.6. There exists a filtration on Hochschild cohomology compatible with its
![]() $E_2$
-algebra structure, with associated graded
$E_2$
-algebra structure, with associated graded
![]() $E_{\infty }$
-algebra
$E_{\infty }$
-algebra
![]() $\operatorname {Sym}(\mathbb {T}_{X}[-1]).$
$\operatorname {Sym}(\mathbb {T}_{X}[-1]).$
Proof. By the discussion in the proof of Proposition 8.4, the
![]() $\infty $
-category
$\infty $
-category
![]() $\operatorname {QCoh}(\operatorname {Map}(S_{Fil}^0, X|_{\mathbb {A}^1 / \mathbb {G}_m}))$
acquires a monoidal structure. Moreover, this monoidal structure is linear over the base in that it is
$\operatorname {QCoh}(\operatorname {Map}(S_{Fil}^0, X|_{\mathbb {A}^1 / \mathbb {G}_m}))$
acquires a monoidal structure. Moreover, this monoidal structure is linear over the base in that it is
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
-linear. Thus, one may define the enriched (over
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m)$
-linear. Thus, one may define the enriched (over
![]() $\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m) \simeq \operatorname {Fil}({\operatorname {Mod}}_R)$
) endomorphism object
$\operatorname {QCoh}(\mathbb {A}^1 / \mathbb {G}_m) \simeq \operatorname {Fil}({\operatorname {Mod}}_R)$
) endomorphism object
As endomorphisms of the unit in an
![]() $E_n$
-monoidal category acquire an
$E_n$
-monoidal category acquire an
![]() $E_{n+1}$
monoidal structure, this gives rise to the
$E_{n+1}$
monoidal structure, this gives rise to the
![]() $E_2$
-monoidal structure on
$E_2$
-monoidal structure on
![]() $\operatorname {HH}_{fil}^*(X)$
. This base changes to
$\operatorname {HH}_{fil}^*(X)$
. This base changes to
![]() $\operatorname {HH}^*(X) \simeq {\operatorname {End}}_{\operatorname {QCoh}(X \times X)^{\otimes }}(\mathbf {1})$
upon passing to the generic fiber, thus recovering the
$\operatorname {HH}^*(X) \simeq {\operatorname {End}}_{\operatorname {QCoh}(X \times X)^{\otimes }}(\mathbf {1})$
upon passing to the generic fiber, thus recovering the
![]() $E_2$
-monoidal structure on Hochschild cohomology.
$E_2$
-monoidal structure on Hochschild cohomology.
Let us now pass to the central fiber. By Koszul duality, together with the fact that
one obtains an equivalence
Remark 8.7. We remark that we have now exhibited two
![]() $E_2$
-algebra structures on Hochschild cohomology (and its filtered variant): one defined via the
$E_2$
-algebra structures on Hochschild cohomology (and its filtered variant): one defined via the
![]() $E_2$
cogroupoid
$E_2$
cogroupoid
![]() $S^{1, \bullet , \bullet }$
and the standard one defined by composition of natural transformations, now seen to be induced by the
$S^{1, \bullet , \bullet }$
and the standard one defined by composition of natural transformations, now seen to be induced by the
![]() $E_1$
-cogroupoid
$E_1$
-cogroupoid
![]() $S^{0, \bullet }$
. We claim that they are equivalent, but we do not include an argument here.
$S^{0, \bullet }$
. We claim that they are equivalent, but we do not include an argument here.
Remark 8.8. The same argument as that of Corollary 8.6 goes through to show that
![]() $E_n$
-Hochschild cohomology,
$E_n$
-Hochschild cohomology,
obtains an
![]() $E_{n+1}$
algebra structure. For example,
$E_{n+1}$
algebra structure. For example,
![]() $\operatorname {QCoh}(\mathcal {L}(X))$
will obtain an
$\operatorname {QCoh}(\mathcal {L}(X))$
will obtain an
![]() $E_2$
-monoidal structure, with unit given by the pushforward
$E_2$
-monoidal structure, with unit given by the pushforward
![]() $e_*(\mathcal {O}_X)$
along the constant morphism
$e_*(\mathcal {O}_X)$
along the constant morphism
Hence, we recover an
![]() $E_3$
-algebra structure on
$E_3$
-algebra structure on
![]() $\operatorname {HH}^*_{E_2}(X)$
.
$\operatorname {HH}^*_{E_2}(X)$
.
We remark that an alternative but closely related explanation for the
![]() $E_{n+1}$
structure on n-iterated Hochschild cohomology may be found in [Reference ToënToë13].
$E_{n+1}$
structure on n-iterated Hochschild cohomology may be found in [Reference ToënToë13].
Acknowledgements
I would like to thank Bertrand Toën for various conversations and ideas which led to the content of paper. I would also like to thank Joost Nuiten for helpful conversations. This work is supported by the grant NEDAG ERC-2016-ADG-741501.
Competing interest
The authors have no competing interest to declare.
Financial support
NEDAG ERC-2016-ADG-741501,