Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T05:18:07.091Z Has data issue: false hasContentIssue false
  • English
  • Français

CM liftings of 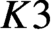$K3$ surfaces over finite fields and their applications to the Tate conjecture

Part of: Surfaces and higher-dimensional varieties Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  08 April 2021

Kazuhiro Ito Open the ORCID record for Kazuhiro Ito [Opens in a new window] ,
Tetsushi Ito Open the ORCID record for Tetsushi Ito [Opens in a new window]  and
Teruhisa Koshikawa
Kazuhiro Ito
Affiliation:
Laboratoire de Mathématiques d’Orsay, Université Paris-Saclay, 91405, Orsay, France; E-mail: [email protected]
Tetsushi Ito
Affiliation:
Department of Mathematics, Faculty of Science, Kyoto University, Kyoto606-8502, Japan; E-mail: [email protected]
Teruhisa Koshikawa
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto606-8502, Japan; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give applications of integral canonical models of orthogonal Shimura varieties and the Kuga-Satake morphism to the arithmetic of 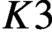$K3$ surfaces over finite fields. We prove that every 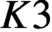$K3$ surface of finite height over a finite field admits a characteristic 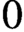$0$ lifting whose generic fibre is a 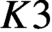$K3$ surface with complex multiplication. Combined with the results of Mukai and Buskin, we prove the Tate conjecture for the square of a 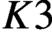$K3$ surface over a finite field. To obtain these results, we construct an analogue of Kisin’s algebraic group for a 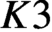$K3$ surface of finite height and construct characteristic 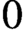$0$ liftings of the 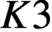$K3$ surface preserving the action of tori in the algebraic group. We obtain these results for $K3$ surfaces over finite fields of any characteristics, including those of characteristic 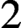$2$ or 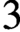$3$.

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties
Secondary: 11G15: Complex multiplication and moduli of abelian varieties 14G35: Modular and Shimura varieties 14J28: $K3$ surfaces and Enriques surfaces
Type
Number Theory
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e29
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

André, Y., ‘On the Shafarevich and Tate conjectures for hyper-Kähler varieties’, Math. Ann. 305(2) (1996), 205–248.CrossRefGoogle Scholar
Artin, M. and Mazur, B., ‘Formal groups arising from algebraic varieties’, Ann. Sci. École Norm. Sup. (4) 10(1) (1977), 87–131.CrossRefGoogle Scholar
Bass, H., ‘Clifford algebras and spinor norms over a commutative ring’, Amer. J. Math. 96 (1974), 156–206.CrossRefGoogle Scholar
Berthelot, P., Breen, L. and Messing, W., Théorie de Dieudonné Cristalline. II, Lecture Notes in Mathematics, Vol. 930 (Springer, Berlin, 1982).CrossRefGoogle Scholar
Berthelot, P. and Ogus, A., ‘F-isocrystals and de Rham cohomology. I’, Invent. Math. 72 (2) (1983), 159–199.CrossRefGoogle Scholar
Bhatt, B., Morrow, M. and Scholze, P., ‘Integral $p$-adic Hodge theory’, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397.CrossRefGoogle Scholar
Bierstone, E. and Milman, P. D., ‘Canonical desingularization in characteristic zero by blowing up the maximum strata of a local invariant’, Invent. Math. 128(2) (1997), 207–302.CrossRefGoogle Scholar
Blasius, D., ‘A $p$-adic property of Hodge classes on abelian varieties’, in Motives, Proc. Sympos. Pure Math., Part 2, Vol. 55 (American Mathematical Society, Providence, RI, 1994), 293–308.Google Scholar
Bloch, S. and Kato, K., ‘$p$-adic étale cohomology ’, Inst. Hautes Études Sci. Publ. Math. 63 (1986), 107–152.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Vol. 21. (Springer, Berlin, 1990).Google Scholar
Bourbaki, N., Éléments de mathématique. Algèbre. Chapitre 9, Reprint of the 1959 original (Springer, Berlin, 2007).Google Scholar
Breen, L., ‘Rapport sur la théorie de Dieudonné’ Astérisque 63 (1979), 39–66.Google Scholar
Buskin, N., ‘Every rational Hodge isometry between two K3 surfaces is algebraic’, J. Reine Angew. Math. 755 (2019), 127–150.CrossRefGoogle Scholar
Cais, B. and Liu, T., ‘Breuil-Kisin modules via crystalline cohomology’, Trans. Amer. Math. Soc. 371(2) (2019), 1199–1230.CrossRefGoogle Scholar
Caraiani, A. and Scholze, P., ‘On the generic part of the cohomology of compact unitary Shimura varieties’, Ann. Math. (2) 186(3) (2017), 649–766.CrossRefGoogle Scholar
Česnavičius, K. and Koshikawa, T., ‘The ${{A}}_{\mathrm{inf}}$-cohomology in the semistable case’, Compos. Math. 155(11) (2019), 2039–2128.CrossRefGoogle Scholar
Chai, C.-L., Conrad, B. and Oort, F., Complex Multiplication and Lifting Problems, Mathematical Surveys and Monographs, Vol. 195 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Charles, F., ‘The Tate conjecture for $K3$ surfaces over finite fields’, Invent. Math. 194(1) (2013), 119–145.CrossRefGoogle Scholar
Chiarellotto, B., Lazda, C. and Liedtke, C., ‘A Néron-Ogg-Shafarevich criterion for K3 surfaces’, Proc. Lond. Math. Soc. (3) 119(2) (2019), 469–514.CrossRefGoogle Scholar
Colmez, P. and Fontaine, J.-M., ‘Construction des représentations $p$-adiques semi-stables’, Invent. Math. 140(1) (2000), 1–43.CrossRefGoogle Scholar
Conrad, B., Lieblich, M. and Olsson, M., ‘Nagata compactification for algebraic spaces’, J. Inst. Math. Jussieu 11(4) (2012), 747–814.CrossRefGoogle Scholar
Conrad, B. and Temkin, M., ‘Non-Archimedean analytification of algebraic spaces’, J. Algebraic Geom. 18(4) (2009), 731–788.CrossRefGoogle Scholar
Deligne, P., ‘Théorie de Hodge. II’, Inst. Hautes Études Sci. Publ. Math. 40 (1971), 5–57.CrossRefGoogle Scholar
Deligne, P., ‘Relèvement des surfaces K3 en caractéristique nulle’, in Algebraic Surfaces, Lecture Notes in Mathematics, Vol. 868, (Springer, Berlin, 1981), 58–79.Google Scholar
Deligne, P., ‘Hodge Cycles on Abelian Varieties’, in Hodge Cycles, Motives, and Shimura Varieties, Lecture Notes in Mathematics, Vol. 900 (Springer, Berlin, 1982).CrossRefGoogle Scholar
Deligne, P., Letter to M. Kisin (cc: A. Vasiu) (August 26, 2011). URL: http://people.math.binghamton.edu/adrian/Letter_Deligne.pdf.Google Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes. II: Groupes de type multiplicatif, et structure des schémas en groupes généraux, Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3), Lecture Notes in Mathematics, Vol. 152 (Springer, Berlin, 1970).Google Scholar
Drinfeld, V. G., ‘Elliptic modules’, Math. USSR-Sb. 23(4) (1974), 561–592.CrossRefGoogle Scholar
Faltings, G., ‘Integral crystalline cohomology over very ramified valuation rings’, J. Amer. Math. Soc. 12(1) (1999), 117–144.CrossRefGoogle Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Vol. 22 (Springer, Berlin, 1990). With an appendix by David Mumford.Google Scholar
Fargues, L., ‘La filtration canonique des points de torsion des groupes $p$-divisibles’, Ann. Sci. Éc. Norm. Supér. (4) 44(6) (2011), 905–961. With collaboration of Tian, Yichao.CrossRefGoogle Scholar
Gillet, H. and Messing, W., ‘Cycle classes and Riemann-Roch for crystalline cohomology’, Duke Math. J. 55(3) (1987), 501–538.CrossRefGoogle Scholar
Hazewinkel, M., Formal Groups and Applications, corrected reprint of the 1978 original. (AMS Chelsea Publishing, Providence, RI, 2012).Google Scholar
Huber, R., Étale Cohomology of Rigid Analytic Varieties and Adic Spaces, Aspects of Mathematics, Vol. E30 (Friedr. Vieweg & Sohn, Braunschweig, Germany, 1996).Google Scholar
Huybrechts, D., ‘Motives of isogenous K3 surfaces’, Comment. Math. Helv. 94(3) (2019), 445–458.CrossRefGoogle Scholar
Katz, N. M., ‘Slope filtration of F-crystals’, Astérisque 63 (1979), 113–163.Google Scholar
Keum, J., ‘Orders of automorphisms of K3 surfaces’, Adv. Math. 303 (2016), 39–87.CrossRefGoogle Scholar
Kim, W. and Madapusi Pera, K., ‘2-adic integral canonical models’, Forum Math. Sigma 4 (2016), e28, 34 pp.CrossRefGoogle Scholar
Kisin, M., ‘Crystalline representations and F-crystals’, in Algebraic Geometry and Number Theory, Progr. Math., Vol. 253 (Birkhäuser, Boston, 2006), 459–496.CrossRefGoogle Scholar
Kisin, M., ‘Integral models for Shimura varieties of abelian type’, J. Amer. Math. Soc. 23(4) (2010), 967–1012.CrossRefGoogle Scholar
Kisin, M., ‘Mod ${p}$ points on Shimura varieties of abelian type’, J. Amer. Math. Soc. 30(3) (2017), 819–914.CrossRefGoogle Scholar
Knus, M.-A., Quadratic and Hermitian Forms over Rings, Grundlehren der Mathematischen Wissenschaften, Vol. 294 (Springer, Berlin, 1991). With a foreword by Bertuccioni, I..CrossRefGoogle Scholar
Lau, E., ‘Frames and finite group schemes over complete regular local rings’, Doc. Math. 15 (2010), 545–569.Google Scholar
Lau, E., ‘Relations between Dieudonné displays and crystalline Dieudonné theory’, Algebra Number Theory 8(9) (2014), 2201–2262.CrossRefGoogle Scholar
Lau, E., ‘Displayed equations for Galois representations’, Nagoya Math. J. 235 (2019), 86–114.CrossRefGoogle Scholar
Liedtke, C., ‘Lectures on supersingular ${K}3$ surfaces and the crystalline Torelli theorem’, in $K3$ Surfaces and Their Moduli, Progr. Math., Vol. 315 (Birkhäuser/Springer, [Cham], 2016), 171–235.CrossRefGoogle Scholar
Liu, T., ‘Lattices in filtered $\left(\varphi, {N}\right)$-modules’, J. Inst. Math. Jussieu 11(3) (2012), 659–693.CrossRefGoogle Scholar
Liu, T., ‘The correspondence between Barsotti-Tate groups and Kisin modules when $p=2$’, J. Théor. Nombres Bordeaux, 25(3) (2013), 661–676.CrossRefGoogle Scholar
Madapusi Pera, K., ‘The Tate conjecture for ${K}3$ surfaces in odd characteristic’, Invent. Math. 201(2) (2015), 625–668.CrossRefGoogle Scholar
Madapusi Pera, K., ‘Integral canonical models for spin Shimura varieties’, Compos. Math. 152(4) (2016), 769–824.CrossRefGoogle Scholar
Madapusi Pera, K., ‘Erratum to appendix to ‘2-adic integral canonical models’’, Forum Math. Sigma 8 (2020), e14, 11 pp.CrossRefGoogle Scholar
Maulik, D., ‘Supersingular $K3$ surfaces for large primes’, Duke Math. J. 163(13) (2014), 2357–2425. With an appendix by Andrew Snowden.CrossRefGoogle Scholar
Mukai, S., ‘Vector bundles on a $K3$ surface’, Proc. ICM, Beijing 2 (2002), 495–502.Google Scholar
Nygaard, N., ‘The Tate conjecture for ordinary ${K}3$ surfaces over finite fields’, Invent. Math. 74(2) (1983), 213–237.CrossRefGoogle Scholar
Nygaard, N. and Ogus, A., ‘Tate’s conjecture for $K3$ surfaces of finite height’, Ann. Math. (2) 122(3) (1985), 461–507.CrossRefGoogle Scholar
Ogus, A., ‘Supersingular $K3$ crystals’, Astérisque 64 (1979), 3–86.Google Scholar
Peters, C. A. M. and Steenbrink, J. H. M., Mixed Hodge structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, Vol. 52 (Springer, Berlin, 2008).Google Scholar
Pjateckiĭ-Šapiro, I. I. and Šafarevič, I. R., ‘The arithmetic of surfaces of type $K3$’, Trudy Mat. Inst. Steklov. 132 (1973), 44–54, 264.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Pure and Applied Mathematics, Vol. 139 (Academic Press, Boston, 1994). Translated from the 1991 Russian original by Rowen, Rachel.Google Scholar
Rizov, J., ‘Moduli stacks of polarized $K3$ surfaces in mixed characteristic’, Serdica Math. J. 32(2–3) (2006), 131–178.Google Scholar
Rizov, J., ‘Kuga-Satake abelian varieties of ${K}3$ surfaces in mixed characteristic’, J. Reine Angew. Math. 648 (2010), 13–67.Google Scholar
Scholze, P., ‘$p$-adic Hodge theory for rigid-analytic varieties’, Forum Math. Pi 1 (2013), e1, 77 pp.CrossRefGoogle Scholar
Scholze, P., ‘Perfectoid spaces: a survey’, in Current Developments in Mathematics 2012, (Int. Press, Somerville, MA, 2013), 193–227.Google Scholar
Scholze, P., ‘$p$-adic Hodge theory for rigid-analytic varieties – corrigendum’, Forum Math. Pi 4 (2016), e6, 4 pp.CrossRefGoogle Scholar
Scholze, P., Weinstein, J., Berkeley Lectures on $p$-adic Geometry, Annals of Mathematics Studies, Vol. 389 (Princeton University Press, Princeton, NJ, 2020).Google Scholar
The Stacks Project Authors, ‘Stacks Project’ (2018). URL: https://stacks.math.columbia.edu.Google Scholar
Sun, S., ‘Generic base change, Artin’s comparison theorem, and the decomposition theorem for complex Artin stacks’, J. Algebraic Geom. 26(3) (2017), 513–555.CrossRefGoogle Scholar
Taelman, L., ‘$K3$ surfaces over finite fields with given $L$-function’, Algebra Number Theory 10(5) (2016), 1133–1146.CrossRefGoogle Scholar
Tate, J., ‘Conjectures on algebraic cycles in $\ell$-adic cohomology’, in Motives, Proc. Sympos. Pure Math. , Part 1, Vol. 55 (American Mathematical Society, Providence, RI, 1994), 71–83.Google Scholar
Totaro, B., ‘Recent progress on the Tate conjecture’, Bull. Amer. Math. Soc. (N.S.) 54(4) (2017), 575–590.CrossRefGoogle Scholar
Tretkoff, P., ‘$K3$ surfaces with algebraic period ratios have complex multiplication’, Int. J. Number Theory 11(5) (2015), 1709–1724.CrossRefGoogle Scholar
Tsuji, T., ‘$p$-adic étale cohomology and crystalline cohomology in the semi-stable reduction case’, Invent. Math. 137(2) (1999), 233–411.CrossRefGoogle Scholar
Tsuji, T., ‘Semi-stable conjecture of Fontaine-Jannsen: a survey’, Cohomologies ${p}$-adiques et applications arithmétiques, II, Astérisque 279 (2002), 323–370.Google Scholar
Yang, Z., ‘Isogenies between K3 Surfaces over ${\overline{\mathbb{F}}}_p$’, Int. Math. Res. Not., arXiv:1810.08546, 2020.Google Scholar
Yu, J.-D. and Yui, N., ‘$K3$ surfaces of finite height over finite fields’, J. Math. Kyoto Univ. 48(3) (2008), 499–519.Google Scholar
Zarhin, Y. G., ‘Hodge groups of K3 surfaces’, J. Reine Angew. Math. 341 (1983), 193–220.Google Scholar
Zarhin, Y. G., ‘The Tate conjecture for powers of ordinary $K3$ surfaces over finite fields’, J. Algebraic Geom. 5(1) (1996), 151–172.Google Scholar