Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jensen, David
and
Payne, Sam
2014.
Tropical independence I: Shapes of divisors and a proof of the Gieseker–Petri theorem.
Algebra & Number Theory,
Vol. 8,
Issue. 9,
p.
2043.
Coppens, Marc
2016.
Clifford’s Theorem for graphs.
Advances in Geometry,
Vol. 16,
Issue. 3,
p.
389.
Mohammadi, Fatemeh
2016.
Divisors on graphs, orientations, syzygies, and system reliability.
Journal of Algebraic Combinatorics,
Vol. 43,
Issue. 2,
p.
465.
Baker, Matthew
and
Jensen, David
2016.
Nonarchimedean and Tropical Geometry.
p.
365.
Mohammadi, Fatemeh
and
Shokrieh, Farbod
2016.
Divisors on graphs, binomial and monomial ideals, and cellular resolutions.
Mathematische Zeitschrift,
Vol. 283,
Issue. 1-2,
p.
59.
Jensen, David
and
Payne, Sam
2017.
Combinatorial and inductive methods for the tropical maximal rank conjecture.
Journal of Combinatorial Theory, Series A,
Vol. 152,
Issue. ,
p.
138.
Backman, Spencer
2017.
Riemann–Roch theory for graph orientations.
Advances in Mathematics,
Vol. 309,
Issue. ,
p.
655.
Yuen, Chi Ho
2017.
Geometric bijections between spanning trees and break divisors.
Journal of Combinatorial Theory, Series A,
Vol. 152,
Issue. ,
p.
159.
Baker, Matthew
and
Wang, Yao
2018.
The Bernardi Process and Torsor Structures on Spanning Trees.
International Mathematics Research Notices,
Vol. 2018,
Issue. 16,
p.
5120.
Chan, Swee Hong
2018.
Abelian sandpile model and Biggs–Merino polynomial for directed graphs.
Journal of Combinatorial Theory, Series A,
Vol. 154,
Issue. ,
p.
145.
Shokrieh, Farbod
and
Wu, Chenxi
2019.
Canonical measures on metric graphs and a Kazhdan’s theorem.
Inventiones mathematicae,
Vol. 215,
Issue. 3,
p.
819.
Glass, Darren
and
Kaplan, Nathan
2020.
A Project-Based Guide to Undergraduate Research in Mathematics.
p.
107.
Abreu, Alex
and
Pacini, Marco
2020.
The universal tropical Jacobian and the skeleton of the Esteves' universal Jacobian.
Proceedings of the London Mathematical Society,
Vol. 120,
Issue. 3,
p.
328.
Jell, Philipp
2020.
Constructing smooth and fully faithful tropicalizations for Mumford curves.
Selecta Mathematica,
Vol. 26,
Issue. 4,
Konvalinka, Matjaž
Sulzgruber, Robin
and
Tewari, Vasu
2021.
Trimming the permutahedron to extend the parking space.
Algebraic Combinatorics,
Vol. 4,
Issue. 4,
p.
663.
de Jong, Robin
and
Shokrieh, Farbod
2022.
Metric graphs, cross ratios, and Rayleigh’s laws.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 4,
Len, Yoav
and
Zakharov, Dmitry
2022.
Kirchhoff’s theorem for Prym varieties.
Forum of Mathematics, Sigma,
Vol. 10,
Issue. ,
Gross, Andreas
Shokrieh, Farbod
and
Tóthmérész, Lilla
2022.
Effective divisor classes on metric graphs.
Mathematische Zeitschrift,
Vol. 302,
Issue. 2,
p.
663.
Kálmán, Tamás
Lee, Seunghun
and
Tóthmérész, Lilla
2022.
The Sandpile Group of a Trinity and a Canonical Definition for the Planar Bernardi Action.
Combinatorica,
Vol. 42,
Issue. S2,
p.
1283.
Cook-Powell, Kaelin
and
Jensen, David
2022.
Components of Brill–Noether Loci for Curves with Fixed Gonality.
Michigan Mathematical Journal,
Vol. 71,
Issue. 1,
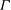 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Gamma $ be a compact tropical curve (or metric graph) of genus
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Gamma $ be a compact tropical curve (or metric graph) of genus 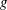 $g$. Using the theory of tropical theta functions, Mikhalkin and Zharkov proved that there is a canonical effective representative (called a break divisor) for each linear equivalence class of divisors of degree
$g$. Using the theory of tropical theta functions, Mikhalkin and Zharkov proved that there is a canonical effective representative (called a break divisor) for each linear equivalence class of divisors of degree 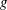 $g$ on
$g$ on 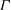 $\Gamma $. We present a new combinatorial proof of the fact that there is a unique break divisor in each equivalence class, establishing in the process an ‘integral’ version of this result which is of independent interest. As an application, we provide a ‘geometric proof’ of (a dual version of) Kirchhoff’s celebrated matrix–tree theorem. Indeed, we show that each weighted graph model
$\Gamma $. We present a new combinatorial proof of the fact that there is a unique break divisor in each equivalence class, establishing in the process an ‘integral’ version of this result which is of independent interest. As an application, we provide a ‘geometric proof’ of (a dual version of) Kirchhoff’s celebrated matrix–tree theorem. Indeed, we show that each weighted graph model 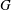 $G$ for
$G$ for 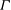 $\Gamma $ gives rise to a canonical polyhedral decomposition of the
$\Gamma $ gives rise to a canonical polyhedral decomposition of the 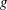 $g$-dimensional real torus
$g$-dimensional real torus 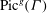 $\mathrm{Pic}^g(\Gamma )$ into parallelotopes
$\mathrm{Pic}^g(\Gamma )$ into parallelotopes 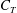 $C_T$, one for each spanning tree
$C_T$, one for each spanning tree 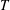 $T$ of
$T$ of 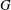 $G$, and the dual Kirchhoff theorem becomes the statement that the volume of
$G$, and the dual Kirchhoff theorem becomes the statement that the volume of 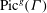 $\mathrm{Pic}^g(\Gamma )$ is the sum of the volumes of the cells in the decomposition.
$\mathrm{Pic}^g(\Gamma )$ is the sum of the volumes of the cells in the decomposition.