No CrossRef data available.
Article contents
Boolean lattices in finite alternating and symmetric groups
Part of:
Permutation groups
Published online by Cambridge University Press: 13 November 2020
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Given a group G and a subgroup H, we let
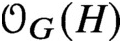$\mathcal {O}_G(H)$
denote the lattice of subgroups of G containing H. This article provides a classification of the subgroups H of G such that
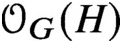$\mathcal {O}_{G}(H)$
is Boolean of rank at least
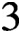$3$
when G is a finite alternating or symmetric group. Besides some sporadic examples and some twisted versions, there are two different types of such lattices. One type arises by taking stabilisers of chains of regular partitions, and the other arises by taking stabilisers of chains of regular product structures. As an application, we prove in this case a conjecture on Boolean overgroup lattices related to the dual Ore’s theorem and to a problem of Kenneth Brown.
MSC classification
- Type
- Algebra
- Information
- Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
Aschbacher, M., ‘Overgroups of primitive groups’, J. Aust. Math. Soc. 87 (2009), 37–82.CrossRefGoogle Scholar
Aschbacher, M., ‘Overgroups of primitive groups II’, J. Algebra 322 (2009), 1586–1626.CrossRefGoogle Scholar
Aschbacher, M. and Shareshian, J., ‘Restrictions on the structure of subgroup lattices of finite alternating and symmetric groups’, J. Algebra 322 (2009), 2449–2463.CrossRefGoogle Scholar
Balodi, M. and Palcoux, S., ‘On Boolean intervals of finite groups’, J. Combin. Theory Ser. A, 157 (2018), 49–69.CrossRefGoogle Scholar
Basile, A., Second Maximal Subgroups of the Finite Alternating and Symmetric Groups, PhD thesis, Australian National Univ., 2001.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3-4) (1997), 235–265.CrossRefGoogle Scholar
Brown, K. S., ‘The coset poset and probabilistic zeta function of a finite group’, J. Algebra 225(2) (2000), 989–1012.CrossRefGoogle Scholar
Cameron, P. J., ‘Finite permutation groups and finite simple groups’, Bull. Lond. Math. Soc. 13 (1981), 1–22.CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., An Atlas of Finite Groups (Clarendon Press,
Oxford, 1985; reprinted with corrections 2003).Google Scholar
Dixon, J. D. and Mortimer, B.,
Permutation Groups
, Graduate Texts in Mathematics 163 (Springer-Verlag,
New York, 1996).Google Scholar
Gaschütz, W., ‘Die Eulersche Funktion endlicher auflösbarer Gruppen’, Illinois J. Math. 3 (1959), 469-–476.CrossRefGoogle Scholar
Guralnick, R. M., ‘Subgroups of prime power index in a simple group’, J. Algebra 81 (1983), 304–311.CrossRefGoogle Scholar
Hall, P., ‘The Eulerian functions of a group’, Q. J. Math., 7 (1936), 134–151.CrossRefGoogle Scholar
Jones, G. A., ‘Cyclic regular subgroups of primitive permutation groups’, J. Group Theory 5 (2002), 403–407.CrossRefGoogle Scholar
Li, C. H., ‘The finite primitive permutation groups containing an abelian regular subgroup’, Proc. Lond. Math. Soc. (3) 87 (2003), 725–747.CrossRefGoogle Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘A classification of the maximal subgroups of the finite alternating and symmetric groups’, J. Algebra 111 (1987), 365–383.CrossRefGoogle Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘On the O’Nan-Scott theorem for finite primitive permutation groups’, J. Aust. Math. Soc. 44 (1988), 389–396.CrossRefGoogle Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘The maximal factorizations of the finite simple groups and their automorphism groups’, Mem. Amer. Math. Soc. 432 (1990), 1–151.Google Scholar
Lucchini, A., ‘Subgroups of solvable groups with non-zero Möbius function’, J. Group Theory 10(5) (2007), 5, 633–639.CrossRefGoogle Scholar
Ore, O., ‘Structures and group theory. II’, Duke Math. J. 4(2) (1938), 247–269.CrossRefGoogle Scholar
Palcoux, S., ‘Dual Ore’s theorem on distributive intervals of finite groups’, J. Algebra 505 (2018), 279–287.CrossRefGoogle Scholar
Palcoux, S., ‘Euler totient of subfactor planar algebras’, Proc. Amer. Math. Soc. 146(11) (2018), 4775–4786.CrossRefGoogle Scholar
Palcoux, S., ‘Ore’s theorem for cyclic subfactor planar algebras and beyond’, Pacific J. Math. 292(1) (2018), 203–221.CrossRefGoogle Scholar
Palcoux, S., Ore’s theorem on subfactor planar algebras’. Quantum Topol. 11(2020), no. 3, 525–543.Google Scholar
Pálfy, P., Pudlák, P., ‘Congruence lattices of finite algebras and intervals in subgroup lattices of finite groups’, Algebra Universalis 11 (1980), 22–27.CrossRefGoogle Scholar
Patassini, M., ‘The probabilistic zeta function of
$\mathsf{PSL}\left(2,q\right)$
, of the Suzuki groups
${2}_2^B(q)$
and of the Ree groups
${2}_2^G(q)$
’, Pacific J. Math. 240(1) (2009), 185—200.CrossRefGoogle Scholar
$\mathsf{PSL}\left(2,q\right)$
, of the Suzuki groups
${2}_2^B(q)$
and of the Ree groups
${2}_2^G(q)$
’, Pacific J. Math. 240(1) (2009), 185—200.CrossRefGoogle ScholarPatassini, M., ‘On the (non-)contractibility of the order complex of the coset poset of a classical group’, J. Algebra 343 (2011), 37—77.CrossRefGoogle Scholar
Patassini, M., ‘On the (non-)contractibility of the order complex of the coset poset of an alternating group’, Rend. Semin. Mat. Univ. Padova 129 (2013), 35-46.CrossRefGoogle Scholar
Praeger, C. E., ‘The inclusion problem for finite primitive permutation groups’, Proc. London Math. Soc. (3) 60 (1990), 68–88.CrossRefGoogle Scholar
Praeger, C. E. and Schneider, C., ‘Permutation groups and Cartesian decompositions’,
London Math. Soc. Lecture Note Ser. 449 (2018), 1–318.Google Scholar
Shareshian, J. and Woodroofe, R., ‘Order complexes of coset posets of finite groups are not contractible’, Adv. Math. 291 (2016), 758–773.CrossRefGoogle Scholar
Spiga, P., ‘Finite primitive groups and edge-transitive hypergraphs’, J. Algebraic Combin. 43(3) (2016), 715–734.CrossRefGoogle Scholar
Tits, J., The Geometric Vein, The Coxeter Festschrift, (Springer-Verlag,
New York, 1982).Google Scholar
Zsigmondy, K., ‘Zur Theorie der Potenzreste’, Monatsh. Math. Phys. 3 (1892), 265–284.CrossRefGoogle Scholar
You have
Access
Open access