Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T17:22:30.441Z Has data issue: false hasContentIssue false
  • English
  • Français

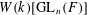THE BERNSTEIN CENTER OF THE CATEGORY OF SMOOTH $W(k)[\text{GL}_{n}(F)]$ -MODULES

Part of: Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  07 June 2016

DAVID HELM
DAVID HELM*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

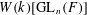We consider the category of smooth $W(k)[\text{GL}_{n}(F)]$ -modules, where 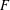$F$ is a 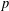$p$ -adic field and 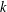$k$ is an algebraically closed field of characteristic 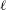$\ell$ different from  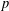$p$ . We describe a factorization of this category into blocks, and show that the center of each such block is a reduced, 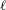$\ell$ -torsion free, finite type 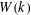$W(k)$ -algebra. Moreover, the 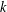$k$ -points of the center of a such a block are in bijection with the possible ‘supercuspidal supports’ of the smooth 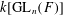$k[\text{GL}_{n}(F)]$ -modules that lie in the block. Finally, we describe a large explicit subalgebra of the center of each block and give a description of the action of this algebra on the simple objects of the block, in terms of the description of the classical ‘characteristic zero’ Bernstein center of Bernstein and Deligne [Le ‘centre’ de Bernstein, in Representations des groups redutifs sur un corps local, Traveaux en cours (ed. P. Deligne) (Hermann, Paris), 1–32].

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e11
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Bernstein, J. and Deligne, P., ‘Le ‘centre’ de Bernstein’, inRepresentations des groups redutifs sur un corps local, Traveaux en cours (ed. Deligne, P.) (Hermann, Paris, 1984), 1–32.Google Scholar
Bernstein, J. and Rumelhart, K., Representations of p-adic Groups, Lecture Notes (Harvard University, 1992).Google Scholar
Bernstein, J. and Zelevinski, A., ‘Induced representations of p-adic groups I’, Ann. Sci. Éc. Norm. Supér. (4) 10(4) (1977), 441–472.Google Scholar
Bushnell, C., ‘Representations of reductive p-adic groups: localization of Hecke algebras and applications’, J. Lond. Math. Soc. (2) 63(2) (2001), 364–386.Google Scholar
Bushnell, C. and Henniart, G., ‘Generalized Whittaker models and the Bernstein center’, Amer. J. Math. 125(3) (2003), 513–547.Google Scholar
Bushnell, C. and Kutzko, P., The Admissible Dual of GL(N) Via Compact Open Subgroups, Annals of Mathematics Studies, 129 (Princeton University Press, Princeton, 1993).Google Scholar
Bushnell, C. and Kutzko, P., ‘Smooth representations of reductive p-adic groups: structure theory via types’, Proc. Lond. Math. Soc. (3) 77 (1998), 582–634.Google Scholar
Bushnell, C. and Kutzko, P., ‘Semisimple types in GL n ’, Compositio Math. 119 (1999), 53–97.Google Scholar
Cabanes, M. and Enguehard, M., Representation Theory of Finite Reductive Groups, New Mathematical Monographs, 1 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Dat, J.-F., ‘Caractières à valeurs dans le centre de Bernstein’, J. Reine Angew. Math. 508 (1999), 61–83.Google Scholar
Dat, J.-F., ‘Integral structures in Bernstein’s center’, Preprint, 2006.Google Scholar
Dat, J.-F., ‘Finitude pour les représentations lisses de groupes p-adiques’, J. Inst. Math. Jussieu 8(2) (2009), 261–333.CrossRefGoogle Scholar
Dat, J.-F., ‘Théorie de Lubin-Tate non abélienne ℓ-entière’, Duke Math. J. 161(6) (2012), 951–1010.CrossRefGoogle Scholar
Emerton, M. and Helm, D., ‘The local Langlands correspondence for GL n in families’, Ann. Sci. Éc. Norm. Supér. (4) 47(4) (2014), 655–722.Google Scholar
Helm, D., ‘Whittaker models and the integral Bernstein center for $\text{GL}_{n}(F)$ ’, Duke. Math. J. (to appear). Preprint, arXiv:1210.1789.Google Scholar
Helm, D., ‘Curtis homomorphisms and the integral Bernstein center for $\text{GL}_{n}(F)$ ’, (to appear). Preprint, arXiv:1605.00487.Google Scholar
Helm, D. and Moss, G., ‘Converse theorems and the local Langlands correspondence in families’, (in preparation).Google Scholar
Howlett, R. B. and Lehrer, G. I., ‘On Harish-Chandra induction and restriction for modules of Levi subgroups’, J. Algebra 165(1) (1994), 172–183.CrossRefGoogle Scholar
James, G., ‘The irreducible representations of the finite general linear groups’, Proc. Lond. Math. Soc. (3) 52(2) (1986), 236–268.CrossRefGoogle Scholar
Lusztig, G., ‘Affine Hecke algebras and their graded version’, J. Amer. Math. Soc. 2 (1989), 599–635.CrossRefGoogle Scholar
Paige, D., ‘The projective envelope of a cuspidal representation of a finite linear group’, J. Number Theory 136 (2014), 354–374.CrossRefGoogle Scholar
Paskunas, V., ‘The image of Colmez’s Montreal functor’, Publ. Math. Inst. Hautes Études Sci. 188 (2013), 1–191.Google Scholar
Roche, A., ‘Parabolic induction and the Bernstein decomposition’, Compositio Math. 134(2) (2002), 113–133.Google Scholar
Vigneras, M.-F., Representations l-modulaires d’un groupe réductif p-adique avec l≠p , Progress in Mathematics, 137 (Birkhauser, Boston, 1996).Google Scholar
Vigneras, M.-F., ‘Induced R-representations of p-adic reductive groups’, Selecta Math. 4(4) (1998), 549–623.Google Scholar
Vigneras, M.-F., ‘Correspondance de Langlands semi-simple pour GL(n, F) modulo ℓ≠p ’, Invent. Math. 144(1) (2001), 177–223.Google Scholar