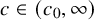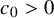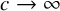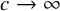1 Introduction and main results
In this paper, we consider the incompressible Navier–Stokes–Maxwell equations
 $$ \begin{align} \begin{cases} \begin{aligned} \text{(Navier--Stokes's equation)}&&&\partial_t u +u \cdot\nabla u = \nu \Delta u- \nabla p + j \times B, &\operatorname{div} u =0,& \\\\[-6pt]
\text{(Amp}\grave{e}{re's equation)}&&&\frac{1}{c} \partial_t E - \nabla \times B =- j , &\operatorname{div} E = 0,& \\\\[-6pt] \text{(Faraday's equation)}&&&\frac{1}{c} \partial_t B + \nabla \times E = 0 , &\operatorname{div} B = 0, & \\\\[-6pt] \text{(Ohm's law)}&&&j= \sigma \big( cE + P(u \times B)\big), &\operatorname{div} j = 0,& \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} \text{(Navier--Stokes's equation)}&&&\partial_t u +u \cdot\nabla u = \nu \Delta u- \nabla p + j \times B, &\operatorname{div} u =0,& \\\\[-6pt]
\text{(Amp}\grave{e}{re's equation)}&&&\frac{1}{c} \partial_t E - \nabla \times B =- j , &\operatorname{div} E = 0,& \\\\[-6pt] \text{(Faraday's equation)}&&&\frac{1}{c} \partial_t B + \nabla \times E = 0 , &\operatorname{div} B = 0, & \\\\[-6pt] \text{(Ohm's law)}&&&j= \sigma \big( cE + P(u \times B)\big), &\operatorname{div} j = 0,& \end{aligned} \end{cases} \end{align} $$
completed with a divergence-free initial data
Here, u, E, B and j are defined on the whole space
![]() $ \mathbb {R}^+\times \mathbb {R}^d$
, with
$ \mathbb {R}^+\times \mathbb {R}^d$
, with
![]() $d\in \{ 2,3\}$
, and take their values in
$d\in \{ 2,3\}$
, and take their values in
![]() $\mathbb {R}^3$
. The operator
$\mathbb {R}^3$
. The operator
![]() $P \overset {\mathrm {def}}{=} \text {Id} - \nabla \Delta ^{-1} \operatorname {div} $
denotes Leray’s projector on divergence-free vector fields. Note that the divergence-free condition
$P \overset {\mathrm {def}}{=} \text {Id} - \nabla \Delta ^{-1} \operatorname {div} $
denotes Leray’s projector on divergence-free vector fields. Note that the divergence-free condition
![]() $\operatorname {div} B=0$
is not a constraint, and (1.1) is therefore not overdetermined. Instead, it is a property propagated by the flow provided that it holds initially.
$\operatorname {div} B=0$
is not a constraint, and (1.1) is therefore not overdetermined. Instead, it is a property propagated by the flow provided that it holds initially.
The Navier–Stokes–Maxwell equations describe the evolution of a viscous plasma, a charged gas or an electrically conducting fluid subject to the self-induced electromagnetic Lorentz force
![]() $j\times B$
.
$j\times B$
.
As for the physical meaning of the quantities in (1.1), the electric and magnetic fields are denoted by
![]() $ E$
and
$ E$
and
![]() $ B$
, respectively, and the electric current is denoted by j. Additionally, the positive constants
$ B$
, respectively, and the electric current is denoted by j. Additionally, the positive constants
![]() $\nu $
,
$\nu $
,
![]() $\sigma $
and c stand for the fluid viscosity, the electrical conductivity and the speed of light, respectively. We refer the interested reader to [Reference Biskamp9, Reference Davidson13] for further details on the underlying physical theories about plasma modeling and to [Reference Arsénio and Saint-Raymond6] for a mathematical derivation of (1.1) through the analysis of the viscous incompressible hydrodynamic regimes of Vlasov–Maxwell–Boltzmann systems.
$\sigma $
and c stand for the fluid viscosity, the electrical conductivity and the speed of light, respectively. We refer the interested reader to [Reference Biskamp9, Reference Davidson13] for further details on the underlying physical theories about plasma modeling and to [Reference Arsénio and Saint-Raymond6] for a mathematical derivation of (1.1) through the analysis of the viscous incompressible hydrodynamic regimes of Vlasov–Maxwell–Boltzmann systems.
The only known a priori global information on solutions of (1.1) is given by the energy inequality
 $$ \begin{align} \left\Vert \left( u , E ,B\right)(t) \right\Vert{}_{L^2}^2+2\nu\int_0^t \left\Vert \nabla u(\tau)\right\Vert{}_{L^2}^2 d\tau +\frac{2}{\sigma}\int_0^t \left\Vert j(\tau)\right\Vert{}_{L^2}^2 d\tau \leq \mathcal{E}_0^2, \end{align} $$
$$ \begin{align} \left\Vert \left( u , E ,B\right)(t) \right\Vert{}_{L^2}^2+2\nu\int_0^t \left\Vert \nabla u(\tau)\right\Vert{}_{L^2}^2 d\tau +\frac{2}{\sigma}\int_0^t \left\Vert j(\tau)\right\Vert{}_{L^2}^2 d\tau \leq \mathcal{E}_0^2, \end{align} $$
for all
![]() $t\geq 0$
, where we denote
$t\geq 0$
, where we denote
Note that (1.2) is, in fact, an equality for smooth solutions.
Observe that, at least formally, taking the limit of c to infinity in (1.1) yields the well-known magneto-hydrodynamic (MHD) system
 $$ \begin{align} \begin{cases} \begin{aligned} & \partial_t u +u \cdot\nabla u = \nu \Delta u- \nabla p +B\cdot \nabla B , \\ & \partial_t B + u\cdot \nabla B = \frac{1}{\sigma} \Delta B + B\cdot \nabla u. \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} & \partial_t u +u \cdot\nabla u = \nu \Delta u- \nabla p +B\cdot \nabla B , \\ & \partial_t B + u\cdot \nabla B = \frac{1}{\sigma} \Delta B + B\cdot \nabla u. \end{aligned} \end{cases} \end{align} $$
Similarly to (1.1), solutions to the system of equations (MHD) enjoy the energy inequality
 $$ \begin{align} \left\Vert \left( u ,B \right)(t) \right\Vert{}_{L^2}^2+2\nu\int_0^t \left\Vert \nabla u(\tau)\right\Vert{}_{L^2}^2 d\tau +\frac{2}{\sigma}\int_0^t \left\Vert \nabla B(\tau)\right\Vert{}_{L^2}^2 d\tau \leq\left\Vert \left( u_0 ,B_0\right)\right\Vert{}_{L^2}^2, \end{align} $$
$$ \begin{align} \left\Vert \left( u ,B \right)(t) \right\Vert{}_{L^2}^2+2\nu\int_0^t \left\Vert \nabla u(\tau)\right\Vert{}_{L^2}^2 d\tau +\frac{2}{\sigma}\int_0^t \left\Vert \nabla B(\tau)\right\Vert{}_{L^2}^2 d\tau \leq\left\Vert \left( u_0 ,B_0\right)\right\Vert{}_{L^2}^2, \end{align} $$
for any
![]() $t\geq 0$
.
$t\geq 0$
.
Although Leray-type weak solutions for (MHD) satisfying (1.3) are known to exist, this remains unknown for (1.1), even for large values of c.
The issue comes from the fact that standard compactness methods, usually used to prove the existence of weak solutions, raise the following question: Given two sequences
![]() $(j_n)_{n\in \mathbb {N}}$
,
$(j_n)_{n\in \mathbb {N}}$
,
![]() $ ( B_n)_{n\in \mathbb {N}}$
, bounded in
$ ( B_n)_{n\in \mathbb {N}}$
, bounded in
![]() $ L^2_{t,x}$
and
$ L^2_{t,x}$
and
![]() $ L^\infty _tL^2_x$
and converging weakly to
$ L^\infty _tL^2_x$
and converging weakly to
![]() $ j$
and B, respectively, does it hold that
$ j$
and B, respectively, does it hold that
![]() $ j_n\times B_n$
converges to
$ j_n\times B_n$
converges to
![]() $j\times B$
, at least in the sense of distributions? This remains unsettled as there is no known phenomenon that prevents the buildup of high frequencies in
$j\times B$
, at least in the sense of distributions? This remains unsettled as there is no known phenomenon that prevents the buildup of high frequencies in
![]() $ j_n\times B_n $
, as n tends to infinity.
$ j_n\times B_n $
, as n tends to infinity.
One way to overcome this lack of compactness consists in propagating some additional regularity on the magnetic field. Based on this idea, the first attempt to construct a (unique) global solution to the two-dimensional Navier–Stokes–Maxwell system (1.1) is due to Masmoudi [Reference Masmoudi36] who proved that, given any
![]() $s>0$
, if
$s>0$
, if
![]() $u_0\in L^2(\mathbb {R}^2)$
and
$u_0\in L^2(\mathbb {R}^2)$
and
![]() $(E_0,B_0)\in H^s(\mathbb {R}^2)$
, then there is a unique global weak solution to (1.1). Apart from the energy estimate, the solution constructed therein does not satisfy any uniform bound with respect to the speed of light c.
$(E_0,B_0)\in H^s(\mathbb {R}^2)$
, then there is a unique global weak solution to (1.1). Apart from the energy estimate, the solution constructed therein does not satisfy any uniform bound with respect to the speed of light c.
Later on, the first author, Ibrahim and Masmoudi [Reference Arsénio, Ibrahim and Masmoudi5] established a conditional convergence result that entails the convergence of weak solutions of (1.1) to (MHD).
Crucial progress was then achieved in [Reference Arsénio and Gallagher2] by the first author and Gallagher by showing the persistence of the
![]() $H^s$
-regularity of the electromagnetic field, uniformly with respect to the speed of light c.
$H^s$
-regularity of the electromagnetic field, uniformly with respect to the speed of light c.
As for the inviscid version of (1.1) (i.e., the incompressible Euler–Maxwell system), the first global results on that model were established recently by the first and the third authors in [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4]. In that context, owing to known results on Euler equations (see, for instance, [Reference De Lellis and Székelyhidi14]), working at the level of the energy (1.2), with
![]() $\nu =0,$
is insufficient to ensure the global well-posedness of the system. One is therefore compelled to study the existence and uniqueness of weak solutions in a higher-regularity space.
$\nu =0,$
is insufficient to ensure the global well-posedness of the system. One is therefore compelled to study the existence and uniqueness of weak solutions in a higher-regularity space.
The main contribution from [Reference Arsénio and Houamed3] is then the construction of a unique global solution of the Euler–Maxwell equations (1.1) (with
![]() $\nu =0$
) in the spirit of Yudovich’s work [Reference Yudovich40], where the electromagnetic field has some Sobolev regularity
$\nu =0$
) in the spirit of Yudovich’s work [Reference Yudovich40], where the electromagnetic field has some Sobolev regularity
![]() $ H^s(\mathbb {R}^2), \ s\in (\frac {7}{4}, 2)$
. Moreover, it is shown therein that the solution is uniformly bounded with respect to c in adequate spaces. The other work by the same authors [Reference Arsénio and Houamed4] further establishes the strong convergence of that solution, as c goes to
$ H^s(\mathbb {R}^2), \ s\in (\frac {7}{4}, 2)$
. Moreover, it is shown therein that the solution is uniformly bounded with respect to c in adequate spaces. The other work by the same authors [Reference Arsénio and Houamed4] further establishes the strong convergence of that solution, as c goes to
![]() $\infty $
. We should point out that the results in [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4], for the Euler–Maxwell system, only hold under the assumption that
$\infty $
. We should point out that the results in [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4], for the Euler–Maxwell system, only hold under the assumption that
![]() $(u,E,B)$
has the two-dimensional normal structure
$(u,E,B)$
has the two-dimensional normal structure
 $$ \begin{align} u(t,x)= \begin{pmatrix} u_1(t,x)\\u_2(t,x)\\0 \end{pmatrix}, \qquad E(t,x)= \begin{pmatrix} E_1(t,x)\\E_2(t,x)\\0 \end{pmatrix} \qquad\text{and}\qquad B(t,x)= \begin{pmatrix} 0\\0\\b(t,x) \end{pmatrix}. \end{align} $$
$$ \begin{align} u(t,x)= \begin{pmatrix} u_1(t,x)\\u_2(t,x)\\0 \end{pmatrix}, \qquad E(t,x)= \begin{pmatrix} E_1(t,x)\\E_2(t,x)\\0 \end{pmatrix} \qquad\text{and}\qquad B(t,x)= \begin{pmatrix} 0\\0\\b(t,x) \end{pmatrix}. \end{align} $$
Extending the arguments from [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4] to general structures is a challenging open problem. As we shall see later on, a novelty of the present work is to permit the consideration of a new three-dimensional structure in the context of plasmas – namely, the axisymmetric structure.
From now on, we are going to focus on the three-dimensional case by first considering the work by Ibrahim and Keraani [Reference Ibrahim and Keraani27], where it is proved that the system (1.1) is globally well-posed provided that the initial data
![]() $(u_0,E_0,B_0)$
are small enough in
$(u_0,E_0,B_0)$
are small enough in
This smallness condition is slightly weakened in the work of Germain, Ibrahim and Masmoudi [Reference Germain, Ibrahim and Masmoudi19], where the initial data lies in the space
Note that the scaling of these spaces is at the critical level of the three-dimensional Navier–Stokes equations (i.e., in the case
![]() $E\equiv B\equiv 0$
). Accordingly, we do not expect to maintain the uniqueness of the solution to (1.1) if the initial velocity lies in spaces that scale below
$E\equiv B\equiv 0$
). Accordingly, we do not expect to maintain the uniqueness of the solution to (1.1) if the initial velocity lies in spaces that scale below
![]() $\dot {H}^{\frac {1}{2}}$
.
$\dot {H}^{\frac {1}{2}}$
.
Besides [Reference Germain, Ibrahim and Masmoudi19, Reference Ibrahim and Keraani27], the three-dimensional Navier–Stokes–Maxwell system (1.1) was studied in several papers – for instance, [Reference Arsénio and Gallagher2, Reference Yue41, Reference Yue42, Reference Yue and Zhong43]. However, to the best of our knowledge, none of the existing results provide enough information to study the regime
![]() $c\rightarrow \infty $
in the three-dimensional case.
$c\rightarrow \infty $
in the three-dimensional case.
Thus, an important novelty of our paper is achieved by shedding light on the regime
![]() $c\rightarrow \infty $
and extending the techniques recently developed by the first and the third authors in [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4] to the three-dimensional axisymmetric setting, which we introduce next.
$c\rightarrow \infty $
and extending the techniques recently developed by the first and the third authors in [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4] to the three-dimensional axisymmetric setting, which we introduce next.
1.1 The axisymmetric structure
Throughout this paper, we assume that the velocity and the electromagnetic fields are axisymmetric, u and E are without swirl, whereas, B has pure swirl – that is to say,
where
![]() $(r,\theta ,z)$
denotes the usual cylindrical coordinates and
$(r,\theta ,z)$
denotes the usual cylindrical coordinates and
![]() $ (e_r,e_\theta ,e_z)$
is the corresponding orthonormal basis (see Section 2 for the explicit definition of these variables). The careful reader may now notice that this assumption shares some similarity with the two-dimensional normal structure (1.4). Indeed, in (1.5), the magnetic field B remains orthogonal to u and E.
$ (e_r,e_\theta ,e_z)$
is the corresponding orthonormal basis (see Section 2 for the explicit definition of these variables). The careful reader may now notice that this assumption shares some similarity with the two-dimensional normal structure (1.4). Indeed, in (1.5), the magnetic field B remains orthogonal to u and E.
This key observation will allow us to somewhat simplify the equations. However, this structure will also require some extra attention when performing estimates in Besov spaces, for the cylindrical basis
![]() $ (e_r,e_\theta ,e_z)$
depends on the position variables.
$ (e_r,e_\theta ,e_z)$
depends on the position variables.
Remark. Before moving forward, we recall here, for the convenience of the reader, some basic identities in cylindrical coordinates, which we will be using regularly throughout this work. Specifically, considering a function
![]() $f:\mathbb {R}^3\to \mathbb {R}$
and a vector field
$f:\mathbb {R}^3\to \mathbb {R}$
and a vector field
![]() $v:\mathbb {R}^3\to \mathbb {R}^3$
, with cylindrical components
$v:\mathbb {R}^3\to \mathbb {R}^3$
, with cylindrical components
![]() $v=v_re_r+v_\theta e_\theta +v_z e_z$
, one has the formulas
$v=v_re_r+v_\theta e_\theta +v_z e_z$
, one has the formulas
 $$ \begin{align*} \begin{aligned} \nabla f&=(\partial_r f) e_r+\frac 1r(\partial_\theta f)e_\theta+(\partial_z f)e_z, \\ \Delta f&=\partial_r^2 f+\frac 1r\partial_r f +\frac 1{r^2}\partial_\theta^2 f+\partial_z^2 f, \\ \operatorname{div} v&=\partial_r v_r+\frac 1r v_r+\frac 1r \partial_\theta v_\theta+\partial_z v_z, \\ \operatorname{curl} v&=\left(\frac 1r\partial_\theta v_z-\partial_z v_\theta\right)e_r +\left(\partial_z v_r-\partial_r v_z\right)e_\theta+\left(\partial_r v_\theta-\frac 1r\partial_\theta v_r+\frac 1rv_\theta\right)e_z. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \nabla f&=(\partial_r f) e_r+\frac 1r(\partial_\theta f)e_\theta+(\partial_z f)e_z, \\ \Delta f&=\partial_r^2 f+\frac 1r\partial_r f +\frac 1{r^2}\partial_\theta^2 f+\partial_z^2 f, \\ \operatorname{div} v&=\partial_r v_r+\frac 1r v_r+\frac 1r \partial_\theta v_\theta+\partial_z v_z, \\ \operatorname{curl} v&=\left(\frac 1r\partial_\theta v_z-\partial_z v_\theta\right)e_r +\left(\partial_z v_r-\partial_r v_z\right)e_\theta+\left(\partial_r v_\theta-\frac 1r\partial_\theta v_r+\frac 1rv_\theta\right)e_z. \end{aligned} \end{align*} $$
These expressions are derived through straightforward computations.
Let us now state some crucial properties provided by (1.5). First of all, note that the vorticity
is acting only in the direction
![]() $e_\theta $
; that is,
$e_\theta $
; that is,
However, straightforward computations show that
Thus, taking the curl of the momentum equation in (1.1) yields
Then, by introducing
we further obtain the equation
Note that the last equation is very similar to the vorticity equation of the two-dimensional Euler–Maxwell system treated in [Reference Arsénio and Houamed3].
An equivalent formulation of (1.6) and (1.7) is obtained by employing Ampère’s equation to eliminate the current density j and deduce that
and
Furthermore, by virtue of (1.5), combining Ampère and Faraday’s equations yields
and therefore
The key observation behind the global estimates in the axisymmetric setting when
![]() $E\equiv B\equiv 0$
is the fact that the stretching term
$E\equiv B\equiv 0$
is the fact that the stretching term
![]() $\omega \cdot \nabla u$
is reduced to
$\omega \cdot \nabla u$
is reduced to
![]() $\frac {u_r}{r}\omega $
. As shown in [Reference Shirota and Yanagisawa37], this term can be controlled by the estimateFootnote
1
$\frac {u_r}{r}\omega $
. As shown in [Reference Shirota and Yanagisawa37], this term can be controlled by the estimateFootnote
1
which then yields a global bound on the velocity in sub-critical spaces. Indeed, this is due to the fact that
![]() $\Omega $
obeys a transport–diffusion equation (resp. transport equation) in the case of the Navier–Stokes equations (resp. Euler equations), which can be used to deduce a global bound for
$\Omega $
obeys a transport–diffusion equation (resp. transport equation) in the case of the Navier–Stokes equations (resp. Euler equations), which can be used to deduce a global bound for
![]() $\Omega $
in
$\Omega $
in
![]() $L^\infty _tL^2\cap L^2_t\dot {H}^1$
(resp. in
$L^\infty _tL^2\cap L^2_t\dot {H}^1$
(resp. in
![]() $L^\infty _tL^{3,1} $
), by means of standard energy estimates. Similar results can be extended to the MHD equations (see Theorem 1.2 below).
$L^\infty _tL^{3,1} $
), by means of standard energy estimates. Similar results can be extended to the MHD equations (see Theorem 1.2 below).
We conclude by pointing out that the axisymmetric structure has been extensively studied in a variety of fluid models, such as the Navier–Stokes [Reference Chen, Fang and Zhang11, Reference Chen, Fang and Zhang12, Reference Liu33, Reference Liu34, Reference Liu and Xu35], Euler [Reference Dhanchin15], Boussinesq [Reference Abidi, Hmidi and Keraani1, Reference Dreyfuss and Houamed16, Reference Fang, Le and Zhang17, Reference Hanachi, Houamed and Zerguine22, Reference Hanachi, Houamed and Zerguine23, Reference Hmidi and Rousset25, Reference Houamed and Zerguine26] and MHD [Reference Cai and Lei10, Reference Jiu, Yu and Zheng28, Reference Lei29, Reference Liu and Yang31, Reference Liu32, Reference Wang and Guo39] systems with partial or full dissipation.
1.2 Aims and main results
We intend to show that the global well-posedness of the three-dimensional system (1.1) holds whenever
![]() $c $
is large enough. We shall prove our results uniformly with respect to c and then derive the MHD equations by studying the singular limit
$c $
is large enough. We shall prove our results uniformly with respect to c and then derive the MHD equations by studying the singular limit
![]() $c\rightarrow \infty $
. We refer to Section 2 for the definition of all functional spaces.
$c\rightarrow \infty $
. We refer to Section 2 for the definition of all functional spaces.
Theorem 1.1 (Global well-posedness).
Let
![]() $(u_0^c,E_0^c,B_0^c)_{c>0}$
be a family of divergence-free axisymmetric initial data such that
$(u_0^c,E_0^c,B_0^c)_{c>0}$
be a family of divergence-free axisymmetric initial data such that
![]() $ u_0^c$
and
$ u_0^c$
and
![]() $E_0^c$
are without swirl, whereas
$E_0^c$
are without swirl, whereas
![]() $B_0^c$
has pure swirl. Assume further that
$B_0^c$
has pure swirl. Assume further that
uniformly in
![]() $c>0$
. Then, there is a constant
$c>0$
. Then, there is a constant
![]() $c_0>0$
, depending only on the size of the initial data, such that, for any
$c_0>0$
, depending only on the size of the initial data, such that, for any
![]() $c\in (c_0,\infty )$
, there is a unique global axisymmetric solution
$c\in (c_0,\infty )$
, there is a unique global axisymmetric solution
![]() $(u^c,E^c,B^c)$
of the three-dimensional Navier–Stokes–Maxwell equations (1.1), with
$(u^c,E^c,B^c)$
of the three-dimensional Navier–Stokes–Maxwell equations (1.1), with
![]() $\nu>0$
, such that
$\nu>0$
, such that
![]() $ u^c$
and
$ u^c$
and
![]() $E^c$
are without swirl and
$E^c$
are without swirl and
![]() $B^c$
has pure swirl. This solution enjoys the bounds
$B^c$
has pure swirl. This solution enjoys the bounds
 $$ \begin{align*} \begin{gathered} u^c \in L^\infty(\mathbb{R}^+; H^1), \qquad \nabla u^c\in L^2(\mathbb{R}^+; H^1), \qquad \Omega^c\overset{\mathrm{def}}{=} \frac{\omega _{\theta}^c}{r} \in L^\infty(\mathbb{R}^+; L^2) \cap L^2(\mathbb{R}^+; \dot{H} ^1), \\ (E^c,B^c)\in L^\infty(\mathbb{R}^+; H^{\frac{3}{2}}), \qquad c^{-1}(E^c,B^c)\in L^\infty(\mathbb{R}^+; \dot{B}^{\frac{5}{2}}_{2,1}), \\ (E^c,B^c) \in L^2(\mathbb{R}^+; \dot{B} ^{\frac{5}{2}}_{2,1}), \quad cE^c\in L^2(\mathbb{R}^+; H^{\frac{3}{2}}), \quad B^c\in L^2(\mathbb{R}^+; \dot H^1), \quad j^c\in \bigcap_{p=2}^\infty L^p(\mathbb{R}^+; H^{\frac{1}{2}}), \end{gathered} \end{align*} $$
$$ \begin{align*} \begin{gathered} u^c \in L^\infty(\mathbb{R}^+; H^1), \qquad \nabla u^c\in L^2(\mathbb{R}^+; H^1), \qquad \Omega^c\overset{\mathrm{def}}{=} \frac{\omega _{\theta}^c}{r} \in L^\infty(\mathbb{R}^+; L^2) \cap L^2(\mathbb{R}^+; \dot{H} ^1), \\ (E^c,B^c)\in L^\infty(\mathbb{R}^+; H^{\frac{3}{2}}), \qquad c^{-1}(E^c,B^c)\in L^\infty(\mathbb{R}^+; \dot{B}^{\frac{5}{2}}_{2,1}), \\ (E^c,B^c) \in L^2(\mathbb{R}^+; \dot{B} ^{\frac{5}{2}}_{2,1}), \quad cE^c\in L^2(\mathbb{R}^+; H^{\frac{3}{2}}), \quad B^c\in L^2(\mathbb{R}^+; \dot H^1), \quad j^c\in \bigcap_{p=2}^\infty L^p(\mathbb{R}^+; H^{\frac{1}{2}}), \end{gathered} \end{align*} $$
uniformly in
![]() $c\in (c_0,\infty )$
. If, moreover,
$c\in (c_0,\infty )$
. If, moreover,
uniformly in
![]() $c>0$
, then the bound
$c>0$
, then the bound
holds uniformly in
![]() $c \in (c_0,\infty ).$
$c \in (c_0,\infty ).$
The complete proof of Theorem 1.1 is given in Section 5.
Remark. By setting
![]() $E\equiv B \equiv 0$
in the above theorem, observe that we recover a classical global well-posedness result for the axisymmetric Navier–Stokes equations (see, for instance, Theorem 10.4 in [Reference Lemarié-Rieusset30]).
$E\equiv B \equiv 0$
in the above theorem, observe that we recover a classical global well-posedness result for the axisymmetric Navier–Stokes equations (see, for instance, Theorem 10.4 in [Reference Lemarié-Rieusset30]).
We also wish to understand the singular regime
![]() $c\rightarrow \infty $
in (1.1). The next corollary establishes a well-posedness result for the limiting system (MHD) by considering the weak limit of solutions constructed in Theorem 1.1.
$c\rightarrow \infty $
in (1.1). The next corollary establishes a well-posedness result for the limiting system (MHD) by considering the weak limit of solutions constructed in Theorem 1.1.
Corollary 1.2 (Weak singular limit).
Let
![]() $(u_0,B_0)$
be an axisymmetric divergence-free vector field, where
$(u_0,B_0)$
be an axisymmetric divergence-free vector field, where
![]() $u_0$
is without swirl and
$u_0$
is without swirl and
![]() $B_0$
has pure swirl. Further assume that
$B_0$
has pure swirl. Further assume that
Then, there is a unique axisymmetric solution to (MHD), with
![]() $\nu>0$
and initial data
$\nu>0$
and initial data
![]() $(u_0,B_0)$
, enjoying the bounds
$(u_0,B_0)$
, enjoying the bounds
 $$ \begin{align*} \begin{aligned} (u,B) \in L^\infty \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times H^{\frac{3}{2}}(\mathbb{R}^3)\right) , \quad (\nabla u, \nabla B) \in L^2 \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times B_{2,1}^{\frac{3}{2}}(\mathbb{R}^3)\right) , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (u,B) \in L^\infty \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times H^{\frac{3}{2}}(\mathbb{R}^3)\right) , \quad (\nabla u, \nabla B) \in L^2 \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times B_{2,1}^{\frac{3}{2}}(\mathbb{R}^3)\right) , \end{aligned} \end{align*} $$
and
Proof. We build global solutions by making use of the bounds from the preceding theorem and employing standard compactness methods. To that end, let
![]() $(u_0^{c_n},E_0^{c_n},B_0^{c_n})_{n\in \mathbb {N}}$
be any family of divergence-free vector fields satisfying the assumptions of Theorem 1.1 and converging to
$(u_0^{c_n},E_0^{c_n},B_0^{c_n})_{n\in \mathbb {N}}$
be any family of divergence-free vector fields satisfying the assumptions of Theorem 1.1 and converging to
![]() $(u_0,0,B_0)$
, at least in the sense of distributions. In particular, by Theorem 1.1, there exists a unique family
$(u_0,0,B_0)$
, at least in the sense of distributions. In particular, by Theorem 1.1, there exists a unique family
![]() $(u^{c_n},E^{c_n},B^{c_n})_{n\in \mathbb {N}}$
of solutions to (1.1), which obeys the bounds
$(u^{c_n},E^{c_n},B^{c_n})_{n\in \mathbb {N}}$
of solutions to (1.1), which obeys the bounds
 $$ \begin{align*} \begin{aligned} (u^{c_n},B^{c_n}) \in L^\infty \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times H^{\frac{3}{2}}(\mathbb{R}^3)\right) , \quad (\nabla u^{c_n}, \nabla B^{c_n}) \in L^2 \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times B_{2,1}^{\frac{3}{2}}(\mathbb{R}^3)\right) , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (u^{c_n},B^{c_n}) \in L^\infty \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times H^{\frac{3}{2}}(\mathbb{R}^3)\right) , \quad (\nabla u^{c_n}, \nabla B^{c_n}) \in L^2 \left( \mathbb{R}^+; H^1(\mathbb{R}^3) \times B_{2,1}^{\frac{3}{2}}(\mathbb{R}^3)\right) , \end{aligned} \end{align*} $$
and
uniformly in
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Thus, by the Banach–Alaoglu theorem, up to extraction of a subsequence (which is not distinguished, for simplicity), it holds that
where
![]() $(u,B)$
is in the same functional spaces as
$(u,B)$
is in the same functional spaces as
![]() $(u^{c_n},B^{c_n})$
.
$(u^{c_n},B^{c_n})$
.
In fact, one can also show that
![]() $ (\partial _t u^{c_n} , \partial _t B^{c_n})_{n\in \mathbb {N}}$
is uniformly bounded in
$ (\partial _t u^{c_n} , \partial _t B^{c_n})_{n\in \mathbb {N}}$
is uniformly bounded in
![]() $L^2_{t,x,\mathrm {loc}}$
, which implies, by a classical compactness result by Aubin and Lions (see [Reference Simon38] for a thorough discussion of such compactness results and, in particular, Section 9 therein, for convenient results which are easily applicable to our setting), that
$L^2_{t,x,\mathrm {loc}}$
, which implies, by a classical compactness result by Aubin and Lions (see [Reference Simon38] for a thorough discussion of such compactness results and, in particular, Section 9 therein, for convenient results which are easily applicable to our setting), that
![]() $(u^{c_n},B^{c_n})_{n\in \mathbb {N}}$
is relatively compact in
$(u^{c_n},B^{c_n})_{n\in \mathbb {N}}$
is relatively compact in
![]() $L^2_{t,x,\mathrm {loc}}$
.
$L^2_{t,x,\mathrm {loc}}$
.
Therefore, by taking the limit in (1.1) in the sense of distributions, and exploiting the strong compactness of
![]() $(u^{c_n},B^{c_n})_{n\in \mathbb {N}}$
to show the weak stability of nonlinear terms, it is readily seen that
$(u^{c_n},B^{c_n})_{n\in \mathbb {N}}$
to show the weak stability of nonlinear terms, it is readily seen that
![]() $(u,B) $
is a weak solution of (MHD), thereby completing the existence proof.
$(u,B) $
is a weak solution of (MHD), thereby completing the existence proof.
As for the uniqueness of solutions, we only need to note that it follows directly from weak–strong uniqueness principles for fluid dynamical models (for instance, see [Reference Arsénio and Saint-Raymond6, Section 3.2.3] and [Reference Gallagher and Planchon18]).
Remark. The solution constructed in the previous corollary enjoys the refined bound
Indeed, by virtue of the bounds from Corollary 1.2, one can show that
![]() $ u\cdot \nabla B$
and
$ u\cdot \nabla B$
and
![]() $B\cdot \nabla u$
belong to
$B\cdot \nabla u$
belong to
![]() $ L^2( \mathbb {R}^+; \dot {H}^{\frac {1}{2}} (\mathbb {R}^3)) $
. Therefore, standard parabolic regularity estimates applied directly to the heat equation satisfied by B in (MHD) give the bound above. In particular, this bound guarantees that
$ L^2( \mathbb {R}^+; \dot {H}^{\frac {1}{2}} (\mathbb {R}^3)) $
. Therefore, standard parabolic regularity estimates applied directly to the heat equation satisfied by B in (MHD) give the bound above. In particular, this bound guarantees that
for any sequence
![]() $ (\Theta _n)_{n\geq 1}$
satisfying
$ (\Theta _n)_{n\geq 1}$
satisfying
Further note that the weaker bound
would not be enough to establish (1.12). This will be important, later on, in the proofs of our main results.
We state now our second main theorem. It concerns the strong convergence, as
![]() $c\rightarrow \infty $
, of the solution given in Theorem 1.1 toward the solution constructed in Corollary 1.2.
$c\rightarrow \infty $
, of the solution given in Theorem 1.1 toward the solution constructed in Corollary 1.2.
Theorem 1.3 (Strong singular limit).
Let
![]() $(u_0^c,E_0^c,B_0^c)_{c>0}$
be a family of initial data satisfying the assumptions in Theorem 1.1 and denote by
$(u_0^c,E_0^c,B_0^c)_{c>0}$
be a family of initial data satisfying the assumptions in Theorem 1.1 and denote by
![]() $(u^c,E^c,B^c)_{c>c_0}$
the corresponding unique global solution to (1.1) given by the same theorem. Further consider divergence-free vector fields
$(u^c,E^c,B^c)_{c>c_0}$
the corresponding unique global solution to (1.1) given by the same theorem. Further consider divergence-free vector fields
![]() $(u_0,B_0)$
such that
$(u_0,B_0)$
such that
and assume that
Finally, let
![]() $(u,B)$
be the unique global solution of (MHD), given in Corollary 1.2, associated to the data
$(u,B)$
be the unique global solution of (MHD), given in Corollary 1.2, associated to the data
![]() $ (u_0,B_0)$
.
$ (u_0,B_0)$
.
Then
![]() $ (u^c,B^c)$
converges strongly to
$ (u^c,B^c)$
converges strongly to
![]() $(u,B)$
, as
$(u,B)$
, as
![]() $c\rightarrow \infty $
. More specifically, it holds that
$c\rightarrow \infty $
. More specifically, it holds that
 $$ \begin{align} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{t\in [0,\infty)}\| (u^c-u) (t)\|_{\dot{H}^1 } + \int_0^ \infty \| (u^c-u) (t) \|_{ \dot{H}^{2} }^2 dt \right) =0 , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{t\in [0,\infty)}\| (u^c-u) (t)\|_{\dot{H}^1 } + \int_0^ \infty \| (u^c-u) (t) \|_{ \dot{H}^{2} }^2 dt \right) =0 , \end{aligned} \end{align} $$
and, for all
![]() $s\in [0,\frac {3}{2})$
,
$s\in [0,\frac {3}{2})$
,
 $$ \begin{align} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{t\in [0,\infty)}\| (B^c-B) (t)\|_{\dot{H}^s } + \int_0^ \infty \| (B^c-B) (t) \|_{ \dot{H}^{s+ 1} }^2 dt \right) =0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{t\in [0,\infty)}\| (B^c-B) (t)\|_{\dot{H}^s } + \int_0^ \infty \| (B^c-B) (t) \|_{ \dot{H}^{s+ 1} }^2 dt \right) =0. \end{aligned} \end{align} $$
If, moreover, we assume that
and
 $$ \begin{align} \lim _{c\rightarrow \infty} \left( c^{-1} \| (E^c_0,B^c_0) \|_{ \dot{B}^{\frac{5}{2}}_{2,1}} \right) =0, \end{align} $$
$$ \begin{align} \lim _{c\rightarrow \infty} \left( c^{-1} \| (E^c_0,B^c_0) \|_{ \dot{B}^{\frac{5}{2}}_{2,1}} \right) =0, \end{align} $$
then (1.14) holds for
![]() $s=\frac {3}{2}$
, as well.
$s=\frac {3}{2}$
, as well.
The complete proof of Theorem 1.3 is given in Section 6.
Remark. It is possible to quantify (1.13) and (1.14) with a rate of convergence
![]() $O(c^{-\alpha })$
, for some
$O(c^{-\alpha })$
, for some
![]() $\alpha>0$
, provided that the initial data satisfy a similar algebraic rate of convergence.
$\alpha>0$
, provided that the initial data satisfy a similar algebraic rate of convergence.
Remark. Observe that the initial data in Theorem 1.1 are required to enjoy the regularity
![]() $ \dot {B}^{\frac {5}{2}}_{2,1}$
. However, this is not needed in the limiting system obtained in the regime
$ \dot {B}^{\frac {5}{2}}_{2,1}$
. However, this is not needed in the limiting system obtained in the regime
![]() $c\rightarrow \infty $
, as reflected in Corollary 1.2.
$c\rightarrow \infty $
, as reflected in Corollary 1.2.
Moreover, the growth of the global solution from Theorem 1.1 in that space is of order c, which is consistent with the fact that it is uniformly bounded in the space
![]() $\dot {H}^{\frac {3}{2}}$
. Indeed, heuristically, we notice from our proofs, later on, that each spatial derivative has the same dimension as the speed of light c; that is,
$\dot {H}^{\frac {3}{2}}$
. Indeed, heuristically, we notice from our proofs, later on, that each spatial derivative has the same dimension as the speed of light c; that is,
which means that the solutions have a comparable size in each space. This is natural in view of the fact that waves produced by Maxwell’s system have a characteristic speed c.
In conclusion, we supplement our remark with a typical example of data that summarizes the preceding observations and fulfills the assumptions of Theorem 1.1 and Theorem 1.3. To that end, let
![]() $ \varphi \in C^\infty _c(\mathbb {R}^3)$
and introduce the standard mollifier
$ \varphi \in C^\infty _c(\mathbb {R}^3)$
and introduce the standard mollifier
Let
![]() $ (u_0,B_0)$
be the initial data from Corollary 1.2 and
$ (u_0,B_0)$
be the initial data from Corollary 1.2 and
![]() $ E_0$
be any divergence-free profile in
$ E_0$
be any divergence-free profile in
![]() $ H^{\frac {3}{2}}.$
Then the sequence of data defined by
$ H^{\frac {3}{2}}.$
Then the sequence of data defined by
is suitable and satisfies all the assumptions in Theorem 1.1 and Theorem 1.3, as long as
![]() $c>c_0$
, where
$c>c_0$
, where
![]() $c_0>0$
only depends on the size of
$c_0>0$
only depends on the size of
![]() $u_0$
,
$u_0$
,
![]() $E_0$
,
$E_0$
,
![]() $B_0$
and
$B_0$
and
![]() $\varphi .$
$\varphi .$
1.3 Challenges and ingredients of proof
Here, we provide the reader with a short roadmap that sheds light on our strategy and main ingredients toward proving our results. We already made it clear in the introduction that the construction of a (unique global) solution to (1.1) at the level of the energy (1.2) is an outstanding open problem. Hence, we seek solutions in higher-regularity spaces.
Notice that one cannot expect to have a better understanding of the Cauchy problem for (1.1) compared to the Navier–Stokes equations (i.e., the case
![]() $E\equiv B \equiv 0$
). In the three-dimensional case, one of the well-known settings where the Navier–Stokes equations are globally well-posed is when the initial data obey an axisymmetric geometric condition, which, roughly speaking, reduces the dimension from three to two, in some sense. In this work, we therefore make the choice of restricting ourselves to the case of axisymmetric data.
$E\equiv B \equiv 0$
). In the three-dimensional case, one of the well-known settings where the Navier–Stokes equations are globally well-posed is when the initial data obey an axisymmetric geometric condition, which, roughly speaking, reduces the dimension from three to two, in some sense. In this work, we therefore make the choice of restricting ourselves to the case of axisymmetric data.
We first clarify the key idea leading to an estimate of the velocity field, which can be performed on (1.6)–(1.7) or (1.8)–(1.9). We argue now that it is better to work on (1.8)–(1.9). The reasons behind this choice can be summarized in two crucial points. The first one is that the terms containing
![]() $\frac {1}{c}\partial _t E$
can be seen as an error that should vanish and be discarded from the system when
$\frac {1}{c}\partial _t E$
can be seen as an error that should vanish and be discarded from the system when
![]() $c\rightarrow \infty $
, at least formally. Observe that this formal limit yields exactly the equations for the vorticity in the axisymmetric case, which have been studied in several papers (for instance, see [Reference Hassainia24]). Accordingly, we believe that (1.8)–(1.9) are more suitable to study the equations in the regime
$c\rightarrow \infty $
, at least formally. Observe that this formal limit yields exactly the equations for the vorticity in the axisymmetric case, which have been studied in several papers (for instance, see [Reference Hassainia24]). Accordingly, we believe that (1.8)–(1.9) are more suitable to study the equations in the regime
![]() $c\rightarrow \infty $
. We shall come back to this limit, later on, to comment on the formal claim
$c\rightarrow \infty $
. We shall come back to this limit, later on, to comment on the formal claim
The second reason why we choose to consider (1.8)–(1.9) is more technical and it relies on the fact that the
![]() $L^2$
energy estimate (1.2) provides us with weak information in dimension three, unlike the two-dimensional case. Indeed, our alternative choice would be to consider (1.6)–(1.7) and to estimate j in
$L^2$
energy estimate (1.2) provides us with weak information in dimension three, unlike the two-dimensional case. Indeed, our alternative choice would be to consider (1.6)–(1.7) and to estimate j in
![]() $L^2_{t,x}$
, which is the only global bound on j that can be extracted from the energy estimate. By doing so, one can can only establish an estimate of
$L^2_{t,x}$
, which is the only global bound on j that can be extracted from the energy estimate. By doing so, one can can only establish an estimate of
![]() $(\omega ,\Omega )$
in
$(\omega ,\Omega )$
in
![]() $L^\infty _t L^2_x\cap L^2_t\dot {H}^1_x$
, which is linear in terms of the
$L^\infty _t L^2_x\cap L^2_t\dot {H}^1_x$
, which is linear in terms of the
![]() $L^2_t B^{\frac {5}{2}}_{2,1}$
norm of B. This is comparable to the techniques from [Reference Arsénio and Houamed3] where, in two dimensions, it is shown that such estimates can be closed. However, in three dimensions, if one goes into the details of low-frequency estimates, one notices that the interpolation argument used in [Reference Arsénio and Houamed3] to weaken the power of B in some crucial norms will likely not work. It seems that this method would require a global control of j in
$L^2_t B^{\frac {5}{2}}_{2,1}$
norm of B. This is comparable to the techniques from [Reference Arsénio and Houamed3] where, in two dimensions, it is shown that such estimates can be closed. However, in three dimensions, if one goes into the details of low-frequency estimates, one notices that the interpolation argument used in [Reference Arsénio and Houamed3] to weaken the power of B in some crucial norms will likely not work. It seems that this method would require a global control of j in
![]() $L^2_t L^3_x$
, which is not available.
$L^2_t L^3_x$
, which is not available.
Thus, our main estimate on the velocity field is based on (1.8)–(1.9) and is given in Proposition 3.1, below, where we show that
 $$ \begin{align*} \begin{aligned} &\left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_tL^2 \cap L^2_t\dot{H}^1 } \\ &\qquad\lesssim \left( \left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2} + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) \exp \big(C\mathcal{E}^2_0\big), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_tL^2 \cap L^2_t\dot{H}^1 } \\ &\qquad\lesssim \left( \left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2} + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) \exp \big(C\mathcal{E}^2_0\big), \end{aligned} \end{align*} $$
for some
![]() $C>0$
. Now, in order to use this bound, we need the following ingredients:
$C>0$
. Now, in order to use this bound, we need the following ingredients:
-
1. An asymptotically vanishing estimate for
 $\frac {1}{c} \partial _t E$
of the form for some
$\frac {1}{c} \partial _t E$
of the form for some $$ \begin{align*}\frac{1}{c}\left\Vert \partial_t E\right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} } \lesssim c^{-\alpha} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big),\end{align*} $$
$$ \begin{align*}\frac{1}{c}\left\Vert \partial_t E\right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} } \lesssim c^{-\alpha} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big),\end{align*} $$
 $\alpha>\frac {1}{2}$
, some (nonlinear) function F and a suitable functional space X.
$\alpha>\frac {1}{2}$
, some (nonlinear) function F and a suitable functional space X.
-
2. A bound of the type
 $$ \begin{align*}\left\Vert B\right\Vert{}_{ L^\infty_tH^2} \lesssim c^{\frac{1}{2}} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big).\end{align*} $$
$$ \begin{align*}\left\Vert B\right\Vert{}_{ L^\infty_tH^2} \lesssim c^{\frac{1}{2}} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big).\end{align*} $$
-
3. An asymptotically global estimate for
 $ B$
in
$ B$
in
 $L^2_t\dot {H}^1$
and
$L^2_t\dot {H}^1$
and
 $\Gamma $
in
$\Gamma $
in
 $L^\infty _t L^3 \cap L^2_t \dot {H}^1 $
of the form for some
$L^\infty _t L^3 \cap L^2_t \dot {H}^1 $
of the form for some $$ \begin{align*}\left\Vert B\right\Vert{}_{ L^2_t \dot{H}^1 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 \cap L^2_t \dot{H}^1 } \leq C_0 + c^{-\beta} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big),\end{align*} $$
$$ \begin{align*}\left\Vert B\right\Vert{}_{ L^2_t \dot{H}^1 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 \cap L^2_t \dot{H}^1 } \leq C_0 + c^{-\beta} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big),\end{align*} $$
 $\beta>0$
and
$\beta>0$
and
 $C_0>0$
depending only on the initial data.
$C_0>0$
depending only on the initial data.
The first bound above is inspired by the results from [Reference Arsénio and Houamed4, Section 3], whereas the third one is obtained in the spirit of [Reference Arsénio and Houamed3, Section 3.6].
The precise proof of these claims is the subject of Section 4, where we will build on the arguments from [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4]. For simplicity, the reader can think of the space X in the foregoing estimates as a combination of the spaces appearing in the statement of Theorem 1.1. The precise construction of X is also detailed in Section 4.
The next step in our strategy is to study the Maxwell system
 $$ \begin{align} \begin{cases} \begin{aligned} \frac{1}{c} \partial_t E - \nabla \times B + \sigma c E & =- \sigma P( u \times B), \\ \frac{1}{c} \partial_t B + \nabla \times E & = 0, \\ \operatorname{div} u=\operatorname{div} B = \operatorname{div} E& =0. \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} \frac{1}{c} \partial_t E - \nabla \times B + \sigma c E & =- \sigma P( u \times B), \\ \frac{1}{c} \partial_t B + \nabla \times E & = 0, \\ \operatorname{div} u=\operatorname{div} B = \operatorname{div} E& =0. \end{aligned} \end{cases} \end{align} $$
The relevant estimates for
![]() $(E,B)$
with a general forcing term have recently been established in [Reference Arsénio and Houamed3]. They are reproduced in Lemmas 3.2 and 3.3. Nevertheless, some refinements in the analysis of (1.18) are required in order to obtain adequate bounds for the electromagnetic field that are compatible with the asymptotic behavior of
$(E,B)$
with a general forcing term have recently been established in [Reference Arsénio and Houamed3]. They are reproduced in Lemmas 3.2 and 3.3. Nevertheless, some refinements in the analysis of (1.18) are required in order to obtain adequate bounds for the electromagnetic field that are compatible with the asymptotic behavior of
![]() $ \frac {1}{c}\partial _t E$
, B and
$ \frac {1}{c}\partial _t E$
, B and
![]() $\Gamma $
.
$\Gamma $
.
As a starting point, we will be facing the problem of estimating products of the form
with
![]() $s>\frac {3}{p}$
, where the regularity of u is restricted to
$s>\frac {3}{p}$
, where the regularity of u is restricted to
![]() $ L^\infty _t \dot {H} ^1 \cap L^2_t \dot {H}^2$
. Note that a similar issue was overcome in [Reference Arsénio and Houamed3] by exploiting the two-dimensional normal structure (1.4), which is not valid in our context. Here, we show that a similar analysis can be performed in the axisymmetric case, by using the fact that B remains orthogonal to E and u. Accordingly, in Lemma 2.3, we provide a general result refining the classical paraproduct estimates in a framework which covers the axisymmetric setting.
$ L^\infty _t \dot {H} ^1 \cap L^2_t \dot {H}^2$
. Note that a similar issue was overcome in [Reference Arsénio and Houamed3] by exploiting the two-dimensional normal structure (1.4), which is not valid in our context. Here, we show that a similar analysis can be performed in the axisymmetric case, by using the fact that B remains orthogonal to E and u. Accordingly, in Lemma 2.3, we provide a general result refining the classical paraproduct estimates in a framework which covers the axisymmetric setting.
The ability to prove Theorem 1.1 further requires a precise understanding of the damping phenomenon in (1.18), which is obtained by studying the parabolic–hyperbolic properties of fields, their interaction and their behavior relatively to c. This analysis is laid out in detail in Section 3.2.
With the above ingredients, we are then in a position to conclude Theorem 1.1. Thus, in Section 5.3, we gather all the estimates to establish a nonlinear bound of the form
where
![]() $\mathcal {P}$
is a polynomial whose coefficients vanish as
$\mathcal {P}$
is a polynomial whose coefficients vanish as
![]() $ c\rightarrow \infty $
. The conclusion of the global estimates is then a straightforward application of the abstract Lemma 5.2, which ensures that
$ c\rightarrow \infty $
. The conclusion of the global estimates is then a straightforward application of the abstract Lemma 5.2, which ensures that
as long as c is larger than some power of
![]() $ C_0$
.
$ C_0$
.
Note that the proof of Theorem 1.1 is divided into two parts. The first one deals with the case that we call rough profiles, in the spirit of the example of initial data given in (1.16). In that case, the initial electromagnetic field
![]() $(E_0^c,B_0^c)$
can have a
$(E_0^c,B_0^c)$
can have a
![]() $ \dot {B}^{\frac { 5}{2}}_{2,1}$
norm growing at most like c. In the second part of the proof, in the case of regular profiles, we show that if, moreover, the corresponding
$ \dot {B}^{\frac { 5}{2}}_{2,1}$
norm growing at most like c. In the second part of the proof, in the case of regular profiles, we show that if, moreover, the corresponding
![]() $ \dot {B}^{\frac {5}{2}}_{2,1}$
norm of
$ \dot {B}^{\frac {5}{2}}_{2,1}$
norm of
![]() $(E_0^c,B_0^c)$
does not blow up as c goes to infinity, then, the
$(E_0^c,B_0^c)$
does not blow up as c goes to infinity, then, the
![]() $ \dot {B}^{\frac { 5}{2}}_{2,1}$
norm of
$ \dot {B}^{\frac { 5}{2}}_{2,1}$
norm of
![]() $(E^c(t),B^c(t))$
remains bounded, for any
$(E^c(t),B^c(t))$
remains bounded, for any
![]() $t\in [0,\infty )$
. The second case will be proved with a kind of bootstrap argument, and it can be seen as the result of persistence of initial regularity.
$t\in [0,\infty )$
. The second case will be proved with a kind of bootstrap argument, and it can be seen as the result of persistence of initial regularity.
Our second main result (Theorem 1.3) establishes the convergence toward (MHD) of the solution constructed in Theorem 1.1. It is to be emphasized that a fundamental ingredient in the proof of Theorem 1.3 hinges upon the understanding of the limit (1.17). This is crucial to obtain a convergence result in the whole domain
![]() $ [0,\infty )\times \mathbb {R}^3$
.
$ [0,\infty )\times \mathbb {R}^3$
.
The proof of Theorem 1.3 will be done in several steps. First, we prove the convergence in the
![]() $L^2$
energy space by performing adequate stability estimates. Subsequently, by interpolation, it follows that the convergence of velocities and magnetic fields holds in
$L^2$
energy space by performing adequate stability estimates. Subsequently, by interpolation, it follows that the convergence of velocities and magnetic fields holds in
![]() $L^\infty _t \dot {H}^s \cap L^2_t \dot {H}^{s+1}$
and
$L^\infty _t \dot {H}^s \cap L^2_t \dot {H}^{s+1}$
and
![]() $L^\infty _t \dot {H}^{\frac {3s}{2}} \cap L^2_t \dot {H}^{\frac {3s}{2}+1}$
, respectively, for any
$L^\infty _t \dot {H}^{\frac {3s}{2}} \cap L^2_t \dot {H}^{\frac {3s}{2}+1}$
, respectively, for any
![]() $s\in [0,1)$
.
$s\in [0,1)$
.
Therefore, the convergence of velocity fields in the endpoint space
![]() $L^\infty _t \dot {H}^1 \cap L^2_t \dot {H}^{2}$
will be achieved by an energy estimate in
$L^\infty _t \dot {H}^1 \cap L^2_t \dot {H}^{2}$
will be achieved by an energy estimate in
![]() $\dot {H}^1$
and by making use of the stability results from the previous step. Here, it is important to mention that the validity of (1.17) in
$\dot {H}^1$
and by making use of the stability results from the previous step. Here, it is important to mention that the validity of (1.17) in
![]() $L^2_t\dot {H}^{\frac {1}{2}}$
(see Proposition 4.1) is crucial.
$L^2_t\dot {H}^{\frac {1}{2}}$
(see Proposition 4.1) is crucial.
However, the convergence of the magnetic fields in the endpoint space
![]() $L^\infty _t \dot {H}^{\frac {3}{2}} \cap L^2_t \dot {H}^{\frac {3}{2}+1}$
will be established by a different approach, for a standard
$L^\infty _t \dot {H}^{\frac {3}{2}} \cap L^2_t \dot {H}^{\frac {3}{2}+1}$
will be established by a different approach, for a standard
![]() $\dot {H}^{\frac {3}{2}} $
energy estimate would require the validity of (1.17) in
$\dot {H}^{\frac {3}{2}} $
energy estimate would require the validity of (1.17) in
![]() $L^2_t\dot {H}^{\frac {3}{2}}$
, which is not available from Proposition 4.1. More precisely, the convergence of magnetic fields in that space follows from extrapolation compactness techniques, introduced and utilized by the first and third authors in [Reference Arsénio and Houamed4].
$L^2_t\dot {H}^{\frac {3}{2}}$
, which is not available from Proposition 4.1. More precisely, the convergence of magnetic fields in that space follows from extrapolation compactness techniques, introduced and utilized by the first and third authors in [Reference Arsénio and Houamed4].
In summary, the proof of convergence of magnetic fields in the energy space of
![]() $ \dot {H}^{\frac {3}{2}}$
is split into two main steps. In the first step, we treat the convergence of frequencies that are localized in a ball whose radius grows as the speed of light increases. By suitably choosing that radius, the convergence of low frequencies then follows as a direct consequence of the convergence in the
$ \dot {H}^{\frac {3}{2}}$
is split into two main steps. In the first step, we treat the convergence of frequencies that are localized in a ball whose radius grows as the speed of light increases. By suitably choosing that radius, the convergence of low frequencies then follows as a direct consequence of the convergence in the
![]() $L^2$
energy space. In the second step, by exploiting the assumption (1.15), we take care of the remaining high frequencies by building on the refined analysis of Maxwell equations laid out in Section 3.2. The combination of these ideas eventually leads to the completion of all proofs.
$L^2$
energy space. In the second step, by exploiting the assumption (1.15), we take care of the remaining high frequencies by building on the refined analysis of Maxwell equations laid out in Section 3.2. The combination of these ideas eventually leads to the completion of all proofs.
1.4 Notation
All definitions and basic properties of functional spaces utilized throughout the paper are introduced in Section 2.
Furthermore, the letter C will often denote a universal (possibly large) constant that is independent of the variables of the problem, and which is also allowed to change from one line to the next.
For simplicity, we will also be using
![]() $ A\lesssim B$
instead of
$ A\lesssim B$
instead of
![]() $A\leq CB.$
Moreover, when needed, in order to specify the dependence of some estimates on some parameters, we will occasionally utilize
$A\leq CB.$
Moreover, when needed, in order to specify the dependence of some estimates on some parameters, we will occasionally utilize
![]() $ A\lesssim _s B$
to insist on the fact that the generic constant C might depend on a parameter s.
$ A\lesssim _s B$
to insist on the fact that the generic constant C might depend on a parameter s.
2 The axisymmetric structure, Hardy inequalities and paradifferential calculus
In this section, we establish several lemmas which shed light on crucial features of the axisymmetric structure, which are similar to the properties of the two-dimensional normal structure that is exploited in [Reference Arsénio and Houamed3, Reference Arsénio and Houamed4]. In particular, this structure will be employed to obtain useful improvements on the classical paradifferential product laws and will serve in our main a priori estimates, later on.
First of all, we recall that a vector field
![]() $F : \mathbb {R} ^3\to \mathbb {R}^3$
is axisymmetric if it has the form
$F : \mathbb {R} ^3\to \mathbb {R}^3$
is axisymmetric if it has the form
where the triple
![]() $(r,\theta ,z)$
denotes the usual cylindrical coordinates defined by the relations
$(r,\theta ,z)$
denotes the usual cylindrical coordinates defined by the relations
and
![]() $(e_r,e_\theta ,e_z) $
is the corresponding cylindrical orthonormal basis
$(e_r,e_\theta ,e_z) $
is the corresponding cylindrical orthonormal basis
Here, the index h is used to refer to the horizontal components
Thus, axisymmetry is characterized by the property that the components
![]() $(F_r,F_\theta ,F_z)$
are independent of
$(F_r,F_\theta ,F_z)$
are independent of
![]() $\theta $
. In other words, the field F is axisymmetric if and only if it satisfies
$\theta $
. In other words, the field F is axisymmetric if and only if it satisfies
![]() $R\circ F=F\circ R$
, for all rotations R around the z-axis.
$R\circ F=F\circ R$
, for all rotations R around the z-axis.
Furthermore, we say that the vector field
![]() $F : \mathbb {R} ^3\to \mathbb {R}^3$
is axisymmetric without swirl if it has the form
$F : \mathbb {R} ^3\to \mathbb {R}^3$
is axisymmetric without swirl if it has the form
and that it is axisymmetric with pure swirl if it can be represented as
Observe that an axisymmetric field with pure swirl is always divergence-free, which follows from a straightforward computation.
We take some time now to carefully introduce the functional spaces that we use in this article and some related notation. To that end, we first consider the Littlewood–Paley decomposition
of a tempered distribution modulo polynomials
![]() $f\in \mathcal {S}'/\mathcal {P}(\mathbb {R}^d)$
, in any dimension
$f\in \mathcal {S}'/\mathcal {P}(\mathbb {R}^d)$
, in any dimension
![]() $d\geq 1$
, where the operator
$d\geq 1$
, where the operator
![]() $\Delta _k$
is the classical frequency truncation that restricts the support of the Fourier transform
$\Delta _k$
is the classical frequency truncation that restricts the support of the Fourier transform
to the set
![]() $\{2^{k-1}\leq |\xi |\leq 2^{k+1}\}$
, for each
$\{2^{k-1}\leq |\xi |\leq 2^{k+1}\}$
, for each
![]() $k\in \mathbb {Z}$
. Recall that the space
$k\in \mathbb {Z}$
. Recall that the space
![]() $\mathcal {S}'/\mathcal {P}(\mathbb {R}^d)$
is isomorphic to the space
$\mathcal {S}'/\mathcal {P}(\mathbb {R}^d)$
is isomorphic to the space
![]() $\mathcal {S}_0'(\mathbb {R}^d)$
of tempered distribution restricted to the subspace
$\mathcal {S}_0'(\mathbb {R}^d)$
of tempered distribution restricted to the subspace
![]() $\mathcal {S}_0(\mathbb {R}^d)$
, which is made up of all Schwartz functions
$\mathcal {S}_0(\mathbb {R}^d)$
, which is made up of all Schwartz functions
![]() $\varphi \in \mathcal {S}(\mathbb {R}^d)$
such that
$\varphi \in \mathcal {S}(\mathbb {R}^d)$
such that
for every mutli-index
![]() $\alpha \in \mathbb {N}^d$
. It is always possible to construct
$\alpha \in \mathbb {N}^d$
. It is always possible to construct
![]() $\Delta _k$
so that it acts on tempered distributions through a convolution with a radial smooth function in
$\Delta _k$
so that it acts on tempered distributions through a convolution with a radial smooth function in
![]() $\mathcal {S}_0(\mathbb {R}^d)$
, which is appropriately dilated by a factor
$\mathcal {S}_0(\mathbb {R}^d)$
, which is appropriately dilated by a factor
![]() $2^k$
.
$2^k$
.
Then, for any
![]() $s \in \mathbb {R}$
and
$s \in \mathbb {R}$
and
![]() $1\leq p,q,r\leq \infty $
, we define the homogeneous Besov space
$1\leq p,q,r\leq \infty $
, we define the homogeneous Besov space
![]() $\dot B^{s}_{p,q}\left (\mathbb {R}^d\right )$
and the homogeneous Chemin–Lerner space
$\dot B^{s}_{p,q}\left (\mathbb {R}^d\right )$
and the homogeneous Chemin–Lerner space
![]() $\widetilde L^r \left ( [0,T); B^{s}_{p,q}\left (\mathbb {R}^d\right ) \right )$
, with
$\widetilde L^r \left ( [0,T); B^{s}_{p,q}\left (\mathbb {R}^d\right ) \right )$
, with
![]() $T\in (0,\infty ]$
, as the subspaces of tempered distributions modulo polynomials
$T\in (0,\infty ]$
, as the subspaces of tempered distributions modulo polynomials
![]() $\mathcal {S}'/\mathcal {P}$
endowed with the respective norms
$\mathcal {S}'/\mathcal {P}$
endowed with the respective norms
 $$ \begin{align*} \begin{aligned} \left\|f\right\|_{\dot B^{s}_{p,q}\left(\mathbb{R}^d\right)} &\overset{\mathrm{def}}{=} \left( \sum_{k\in\mathbb{Z}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^p\left(\mathbb{R}^d\right)}^q\right)^{\frac{1}{q}}, \\ \left\|f\right\|_{ \widetilde L^r \left( [0,T); B^{s}_{p,q}\left(\mathbb{R}^d\right) \right)} &\overset{\mathrm{def}}{=} \left( \sum_{k\in\mathbb{Z}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^r\left([0,T);L^p\left(\mathbb{R}^d\right)\right) }^q\right)^{\frac{1}{q}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\|f\right\|_{\dot B^{s}_{p,q}\left(\mathbb{R}^d\right)} &\overset{\mathrm{def}}{=} \left( \sum_{k\in\mathbb{Z}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^p\left(\mathbb{R}^d\right)}^q\right)^{\frac{1}{q}}, \\ \left\|f\right\|_{ \widetilde L^r \left( [0,T); B^{s}_{p,q}\left(\mathbb{R}^d\right) \right)} &\overset{\mathrm{def}}{=} \left( \sum_{k\in\mathbb{Z}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^r\left([0,T);L^p\left(\mathbb{R}^d\right)\right) }^q\right)^{\frac{1}{q}}, \end{aligned} \end{align*} $$
if
![]() $q<\infty $
, and with the usual modifications if
$q<\infty $
, and with the usual modifications if
![]() $q=\infty $
.
$q=\infty $
.
We will also employ the homogeneous Sobolev spaces
![]() $\dot {W}^{s,p}\left (\mathbb {R}^d\right )\subset \mathcal {S}'/\mathcal {P}$
that are defined by the semi-norms
$\dot {W}^{s,p}\left (\mathbb {R}^d\right )\subset \mathcal {S}'/\mathcal {P}$
that are defined by the semi-norms
where
![]() $ |D|^s $
is the Fourier multiplier corresponding to the symbol
$ |D|^s $
is the Fourier multiplier corresponding to the symbol
![]() $ |\xi |^s$
, with
$ |\xi |^s$
, with
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $1<p<\infty $
. When
$1<p<\infty $
. When
![]() $p=q=2$
, note that the Besov space
$p=q=2$
, note that the Besov space
![]() $\dot B^s_{2,2}$
is equivalent to the homogeneous Sobolev space classically denoted by
$\dot B^s_{2,2}$
is equivalent to the homogeneous Sobolev space classically denoted by
Nonhomogeneous versions of these spaces are also defined in a similar way.
Finally, employing truncated Littlewood–Paley decompositions, one can show that the subspace
![]() $\mathcal {S}_0$
is dense in
$\mathcal {S}_0$
is dense in
![]() $\dot B^s_{p,q}$
and
$\dot B^s_{p,q}$
and
![]() $\dot W^{s,p}$
, for any
$\dot W^{s,p}$
, for any
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $1\leq p,q<\infty $
, and that a similar statement holds for Chemin–Lerner spaces with suitable modifications.
$1\leq p,q<\infty $
, and that a similar statement holds for Chemin–Lerner spaces with suitable modifications.
We refer to [Reference Arsénio and Houamed3, Appendix A] for some more details and properties of Besov and Chemin–Lerner spaces in the same notation as in this article, and to [Reference Bahouri, Chemin and Danchin7, Reference Grafakos21] for a comprehensive introduction to the subject of Littlewood–Paley decompositions and functional spaces.
We move on now to the main results of this section. Prior to presenting the paradifferential features of the axisymmetric structure, we establish the following version of Hardy’s inequality that will be useful in our analysis, below.
Lemma 2.1. Fix the dimension
![]() $d\geq 2$
. Let f be a smooth function satisfying, for all
$d\geq 2$
. Let f be a smooth function satisfying, for all
![]() $ x' \in \mathbb {R}^{d-1}$
, that
$ x' \in \mathbb {R}^{d-1}$
, that
Then, it holds that
 $$ \begin{align*} \left\Vert \frac{f}{x_1} \right\Vert{}_{\dot W^{s,p}(\mathbb{R}^d)} \lesssim _{s,p} \left\Vert f\right\Vert{}_{\dot W^{s+1,p}(\mathbb{R}^d)}, \end{align*} $$
$$ \begin{align*} \left\Vert \frac{f}{x_1} \right\Vert{}_{\dot W^{s,p}(\mathbb{R}^d)} \lesssim _{s,p} \left\Vert f\right\Vert{}_{\dot W^{s+1,p}(\mathbb{R}^d)}, \end{align*} $$
for any
![]() $ p\in (1,\infty )$
and all
$ p\in (1,\infty )$
and all
![]() $s> \frac {1}{p}-1$
.
$s> \frac {1}{p}-1$
.
Proof. By virtue of the vanishing assumption on f, we can write, for any
![]() $(x_1,x') \in \mathbb {R}^*\times \mathbb {R}^{d-1}$
, that
$(x_1,x') \in \mathbb {R}^*\times \mathbb {R}^{d-1}$
, that
 $$ \begin{align*} \frac{f(x_1,x')}{x_1}= \int_0^1 (\partial_{1} f)(\lambda x_1,x')d\lambda. \end{align*} $$
$$ \begin{align*} \frac{f(x_1,x')}{x_1}= \int_0^1 (\partial_{1} f)(\lambda x_1,x')d\lambda. \end{align*} $$
It then follows that
 $$ \begin{align*} \begin{aligned} \left\Vert \frac{f}{x_1} \right\Vert{}_{\dot W^{s,p}} &\leq \int_0^1 \big\|(\partial_1 f)(\lambda \cdot, \cdot)\big\|_{\dot W^{s,p}}d\lambda \\ &=\int_0^1 \big\| |D|^s (\partial_{1} f)(\lambda \cdot, \cdot) \big\|_{L^p} d\lambda\\ &= \int_0^1 \lambda^{-\frac{1}{p}} \big\| |D|^s m_{\lambda,s}(D) (\partial_{1} f) \big\|_{L^p} d\lambda\\ &= \int_0^1 \lambda^{-\frac{1}{p}} \big\| m_{\lambda,s}(D) \partial_{1} f \big\|_{ \dot{W}^{s,p}} d\lambda, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \frac{f}{x_1} \right\Vert{}_{\dot W^{s,p}} &\leq \int_0^1 \big\|(\partial_1 f)(\lambda \cdot, \cdot)\big\|_{\dot W^{s,p}}d\lambda \\ &=\int_0^1 \big\| |D|^s (\partial_{1} f)(\lambda \cdot, \cdot) \big\|_{L^p} d\lambda\\ &= \int_0^1 \lambda^{-\frac{1}{p}} \big\| |D|^s m_{\lambda,s}(D) (\partial_{1} f) \big\|_{L^p} d\lambda\\ &= \int_0^1 \lambda^{-\frac{1}{p}} \big\| m_{\lambda,s}(D) \partial_{1} f \big\|_{ \dot{W}^{s,p}} d\lambda, \end{aligned} \end{align*} $$
where
![]() $m_{\lambda ,s}(D) $
is the Fourier multiplier operator given, for any
$m_{\lambda ,s}(D) $
is the Fourier multiplier operator given, for any
![]() $\lambda \in (0,1)$
and
$\lambda \in (0,1)$
and
![]() $s\in \mathbb {R}$
, by
$s\in \mathbb {R}$
, by
 $$ \begin{align*}m_{\lambda,s} (\xi)= \left(\frac{ \sqrt{|\lambda \xi_1 |^2 + |\xi'|^2} }{|\xi|}\right)^s.\end{align*} $$
$$ \begin{align*}m_{\lambda,s} (\xi)= \left(\frac{ \sqrt{|\lambda \xi_1 |^2 + |\xi'|^2} }{|\xi|}\right)^s.\end{align*} $$
Now, we claim that the multiplier norm of
![]() $m_{\lambda ,s}(D)$
over
$m_{\lambda ,s}(D)$
over
![]() $L^p$
is bounded by a constant multiple of
$L^p$
is bounded by a constant multiple of
![]() $\max \{1,\lambda ^s\}$
, which leads to
$\max \{1,\lambda ^s\}$
, which leads to
 $$ \begin{align*} \begin{aligned} \left\Vert \frac{f}{x_1} \right\Vert{}_{\dot{W}^{s,p}} &\lesssim \int_0^1 \lambda^{-\frac{1}{p}} \max\{ 1, \lambda ^s\}d\lambda \left\Vert \partial_{1} f \right\Vert{}_{ \dot{W}^{s,p}} \\ &\lesssim \max \left\{ \frac{p}{p-1} , \frac{1}{s+1 - \frac{1}{p}} \right\} \left\Vert f \right\Vert{}_{ \dot{W}^{s+1,p}} , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \frac{f}{x_1} \right\Vert{}_{\dot{W}^{s,p}} &\lesssim \int_0^1 \lambda^{-\frac{1}{p}} \max\{ 1, \lambda ^s\}d\lambda \left\Vert \partial_{1} f \right\Vert{}_{ \dot{W}^{s,p}} \\ &\lesssim \max \left\{ \frac{p}{p-1} , \frac{1}{s+1 - \frac{1}{p}} \right\} \left\Vert f \right\Vert{}_{ \dot{W}^{s+1,p}} , \end{aligned} \end{align*} $$
provided that
![]() $ s> \frac {1}{p} -1$
, thereby establishing the main estimate of the lemma.
$ s> \frac {1}{p} -1$
, thereby establishing the main estimate of the lemma.
In order to justify the boundedness of
![]() $m_{\lambda ,s}(D)$
over
$m_{\lambda ,s}(D)$
over
![]() $L^p$
, it is sufficient, by the Marcinkiewicz–Mikhlin multiplier theorem (see [Reference Grafakos20, Theorem 6.2.4]), to show that
$L^p$
, it is sufficient, by the Marcinkiewicz–Mikhlin multiplier theorem (see [Reference Grafakos20, Theorem 6.2.4]), to show that
for all multi-indices
![]() $\alpha \in \{0,1\}^d$
. To that end, we introduce the notation
$\alpha \in \{0,1\}^d$
. To that end, we introduce the notation
 $$ \begin{align*} \ell_{i,\lambda} (\xi) \overset{\mathrm{def}}{=} \frac{\xi_i^2 }{ \lambda^2| \xi_1 |^2 + |\xi'|^2 } \end{align*} $$
$$ \begin{align*} \ell_{i,\lambda} (\xi) \overset{\mathrm{def}}{=} \frac{\xi_i^2 }{ \lambda^2| \xi_1 |^2 + |\xi'|^2 } \end{align*} $$
and compute that
 $$ \begin{align*} \begin{aligned} \xi_1\partial_{\xi_1} m_{\lambda,s} (\xi) &= s \ell_{1,1}(\xi) \Big( \lambda^2 m_{\lambda,s-2} (\xi) - m_{\lambda,s} (\xi) \Big), \\ \xi_i\partial_{\xi_i} m_{\lambda,s} (\xi) &= s \left(\ell_{i,\lambda} (\xi) - \ell_{i,1} (\xi) \right) m_{\lambda,s} (\xi) , \\ \xi_1\partial_{\xi_1}\ell_{j,\lambda}(\xi)&= 2 \left( \delta_{1j} - \lambda^2 \ell_{1,\lambda}(\xi) \right) \ell_{j,\lambda}(\xi), \\ \xi_i\partial_{\xi_i}\ell_{j,\lambda}(\xi)&= 2 \left( \delta_{ij} - \ell_{i,\lambda}(\xi) \right) \ell_{j,\lambda}(\xi), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \xi_1\partial_{\xi_1} m_{\lambda,s} (\xi) &= s \ell_{1,1}(\xi) \Big( \lambda^2 m_{\lambda,s-2} (\xi) - m_{\lambda,s} (\xi) \Big), \\ \xi_i\partial_{\xi_i} m_{\lambda,s} (\xi) &= s \left(\ell_{i,\lambda} (\xi) - \ell_{i,1} (\xi) \right) m_{\lambda,s} (\xi) , \\ \xi_1\partial_{\xi_1}\ell_{j,\lambda}(\xi)&= 2 \left( \delta_{1j} - \lambda^2 \ell_{1,\lambda}(\xi) \right) \ell_{j,\lambda}(\xi), \\ \xi_i\partial_{\xi_i}\ell_{j,\lambda}(\xi)&= 2 \left( \delta_{ij} - \ell_{i,\lambda}(\xi) \right) \ell_{j,\lambda}(\xi), \end{aligned} \end{align*} $$
for any integers
![]() $i\in [2,d]$
and
$i\in [2,d]$
and
![]() $j\in [1,d]$
, where
$j\in [1,d]$
, where
![]() $\delta _{ij}$
denotes the usual Kronecker delta. Therefore, iterating the preceding calculations and observing that
$\delta _{ij}$
denotes the usual Kronecker delta. Therefore, iterating the preceding calculations and observing that
for all integers
![]() $i\in [2,d]$
, it is readily seen that (2.1) holds true, which establishes that the operator norm of
$i\in [2,d]$
, it is readily seen that (2.1) holds true, which establishes that the operator norm of
![]() $m_{\lambda ,s}(D)$
is controlled by
$m_{\lambda ,s}(D)$
is controlled by
![]() $\max \{1,\lambda ^s\}$
. This completes the proof of the lemma.
$\max \{1,\lambda ^s\}$
. This completes the proof of the lemma.
Remark. Note that the assumption on the smoothness of the function f in Lemma 2.1 can, in fact, be relaxed. Indeed, as described, for instance, in Theorem 6.6.1 from [Reference Bergh and Löfström8], the trace operator
defined by
has a well-defined extension into a bounded operator from
![]() $ W^{s+1,p}(\mathbb {R}^d)$
into
$ W^{s+1,p}(\mathbb {R}^d)$
into
![]() $ B^{s +1- \frac {1}{p}}_{p,p}(\mathbb {R}^{d-1})$
, for any
$ B^{s +1- \frac {1}{p}}_{p,p}(\mathbb {R}^{d-1})$
, for any
![]() $p\in (1,\infty )$
, as soon as the condition
$p\in (1,\infty )$
, as soon as the condition
![]() $ s> \frac {1}{p}-1$
is satisfied. Hence, for
$ s> \frac {1}{p}-1$
is satisfied. Hence, for
![]() $f\in W^{s+1,p}(\mathbb {R}^d)$
, the condition
$f\in W^{s+1,p}(\mathbb {R}^d)$
, the condition
![]() $f(0,x')\equiv 0 $
in Lemma 2.1 can be replaced by
$f(0,x')\equiv 0 $
in Lemma 2.1 can be replaced by
![]() $ \operatorname {Tr}f = 0. $
$ \operatorname {Tr}f = 0. $
The next lemma is a variant of Lemma 2.1 for vector fields with an axisymmetric structure. It will be employed to control specific quantities involving electromagnetic fields, later on. The statement of the lemma below is written in the notation introduced at the beginning of this section.
Lemma 2.2. Let E be an axisymmetric divergence-free vector field without swirl and B be an axisymmetric vector field with pure swirl.
Then, it holds that
 $$ \begin{align*} \left\Vert \frac{\nabla \times E}{r}\right\Vert{}_{L^p} \lesssim \left\Vert E\right\Vert{}_{\dot W^{2,p}} \end{align*} $$
$$ \begin{align*} \left\Vert \frac{\nabla \times E}{r}\right\Vert{}_{L^p} \lesssim \left\Vert E\right\Vert{}_{\dot W^{2,p}} \end{align*} $$
and
 $$ \begin{align*} \left\Vert \frac{B_\theta}{r}\right\Vert{}_{\dot W^{s,p}} \lesssim_s \left\Vert B\right\Vert{}_{\dot W^{s+1,p}}, \end{align*} $$
$$ \begin{align*} \left\Vert \frac{B_\theta}{r}\right\Vert{}_{\dot W^{s,p}} \lesssim_s \left\Vert B\right\Vert{}_{\dot W^{s+1,p}}, \end{align*} $$
for any
![]() $ p\in (1,\infty )$
and all
$ p\in (1,\infty )$
and all
![]() $s> \frac {1}{p}-1$
.
$s> \frac {1}{p}-1$
.
Remark. For any given axisymmetric vector field
![]() $E=E_re_r+E_ze_z$
with no swirl, a direct computation gives that the curl
$E=E_re_r+E_ze_z$
with no swirl, a direct computation gives that the curl
![]() $\nabla \times E=(\partial _z E_r-\partial _r E_z)e_\theta $
is axisymmetric with pure swirl. Similarly, given an axisymmetric vector field
$\nabla \times E=(\partial _z E_r-\partial _r E_z)e_\theta $
is axisymmetric with pure swirl. Similarly, given an axisymmetric vector field
![]() $B=B_\theta e_\theta $
with pure swirl, another straightforward computation gives that the curl
$B=B_\theta e_\theta $
with pure swirl, another straightforward computation gives that the curl
![]() $\nabla \times B=-\partial _z B_\theta e_r+(\partial _rB_\theta +\frac 1r B_\theta )e_z$
is axisymmetric with no swirl.
$\nabla \times B=-\partial _z B_\theta e_r+(\partial _rB_\theta +\frac 1r B_\theta )e_z$
is axisymmetric with no swirl.
Proof. The bound on
![]() $B_\theta $
is a consequence of Lemma 2.1. To see this, let us first assume that B is smooth and has pure swirl. Then, we can write that
$B_\theta $
is a consequence of Lemma 2.1. To see this, let us first assume that B is smooth and has pure swirl. Then, we can write that
to deduce that
and
as soon as
![]() $r\neq 0.$
Therefore, it is enough to estimate
$r\neq 0.$
Therefore, it is enough to estimate
![]() $\frac {B_1}{x_2}$
or
$\frac {B_1}{x_2}$
or
![]() $\frac {B_2}{x_1}$
.
$\frac {B_2}{x_1}$
.
Then, an application of Lemma 2.1 yields that
 $$ \begin{align*} \left\Vert \frac{B_\theta}{r}\right\Vert{}_{\dot W^{s,p}} = \left\Vert \frac{B_2}{x_1}\right\Vert{}_{\dot W^{s,p}} \lesssim _s \left\Vert B_2\right\Vert{}_{\dot W^{s+1,p}}, \end{align*} $$
$$ \begin{align*} \left\Vert \frac{B_\theta}{r}\right\Vert{}_{\dot W^{s,p}} = \left\Vert \frac{B_2}{x_1}\right\Vert{}_{\dot W^{s,p}} \lesssim _s \left\Vert B_2\right\Vert{}_{\dot W^{s+1,p}}, \end{align*} $$
thereby establishing the desired bound on
![]() $B_\theta $
in the case of a smooth vector field. The general nonsmooth case is then obtained by a standard approximation argument.
$B_\theta $
in the case of a smooth vector field. The general nonsmooth case is then obtained by a standard approximation argument.
As for the bound on E, it will follow from a remarkable identity valid for axisymmetric divergence-free vector fields with no swirl. Indeed, the fact that E is axisymmetric without swirl allows us to write that
 $$ \begin{align*} \begin{aligned} \nabla\times E&=\left(\partial_zE_r-\partial_rE_z\right)e_\theta, \\ e_r\cdot\nabla\left(\nabla\times E\right)&=\left(\partial_r\partial_z E_r-\partial_r^2E_z\right)e_\theta, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \nabla\times E&=\left(\partial_zE_r-\partial_rE_z\right)e_\theta, \\ e_r\cdot\nabla\left(\nabla\times E\right)&=\left(\partial_r\partial_z E_r-\partial_r^2E_z\right)e_\theta, \end{aligned} \end{align*} $$
which, when combined with the divergence-free condition for axisymmetric fields
leads to
 $$ \begin{align*} \begin{aligned} \frac{\nabla\times E}r+e_r\cdot\nabla\left(\nabla\times E\right) &=\left(\frac 1r \partial_zE_r-\frac 1r\partial_rE_z+\partial_r\partial_z E_r-\partial_r^2E_z\right)e_\theta \\ &=-\left(\partial_r^2E_z+\frac 1r\partial_rE_z+\partial_z^2E_z\right)e_\theta. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{\nabla\times E}r+e_r\cdot\nabla\left(\nabla\times E\right) &=\left(\frac 1r \partial_zE_r-\frac 1r\partial_rE_z+\partial_r\partial_z E_r-\partial_r^2E_z\right)e_\theta \\ &=-\left(\partial_r^2E_z+\frac 1r\partial_rE_z+\partial_z^2E_z\right)e_\theta. \end{aligned} \end{align*} $$
Then, identifying the action of the Laplacian on axisymmetric functions to deduce that
we arrive at the expression
The bound on E therefore follows from a direct estimate in
![]() $L^p$
on the preceding identity, which completes the proof of the lemma.
$L^p$
on the preceding identity, which completes the proof of the lemma.
We conclude this section with a lemma that extends the range of parameters in the classical paraproduct laws by exploiting a geometric condition that is satisfied by the axisymmetric structure. These extended paradifferential estimates will be employed to obtain important a priori estimates for the Navier–Stokes–Maxwell system (1.1), later on.
Lemma 2.3. Let
![]() $F,G:[0,T)\times \mathbb {R} ^3\to \mathbb {R}^3$
be such that
$F,G:[0,T)\times \mathbb {R} ^3\to \mathbb {R}^3$
be such that
![]() $\operatorname {div} F=0$
and
$\operatorname {div} F=0$
and
for all
![]() $t\in [0,T)$
,
$t\in [0,T)$
,
![]() $x\in \mathbb {R}^3$
, and any radially symmetric
$x\in \mathbb {R}^3$
, and any radially symmetric
![]() $\varphi ,\psi \in \mathcal {S}_0(\mathbb {R}^3)$
(i.e., such that
$\varphi ,\psi \in \mathcal {S}_0(\mathbb {R}^3)$
(i.e., such that
![]() $\varphi (x)$
and
$\varphi (x)$
and
![]() $\psi (x)$
only depend on
$\psi (x)$
only depend on
![]() $|x|$
). Further consider parameters in
$|x|$
). Further consider parameters in
![]() $[1,\infty ]$
such that
$[1,\infty ]$
such that
Then, recalling that
![]() $P=(-\Delta )^{-1}\operatorname {curl} \mathrm {curl}$
denotes Leray’s projector onto solenoidal vector fields, one has the product estimate
$P=(-\Delta )^{-1}\operatorname {curl} \mathrm {curl}$
denotes Leray’s projector onto solenoidal vector fields, one has the product estimate
for any
![]() $s\in (-\infty ,\frac {3}{2} )$
and
$s\in (-\infty ,\frac {3}{2} )$
and
![]() $\eta \in (-\infty ,\frac {5}{2} )$
with
$\eta \in (-\infty ,\frac {5}{2} )$
with
![]() $s+\eta>0$
.
$s+\eta>0$
.
Furthermore, in the endpoint case
![]() $s= \frac {3}{2}$
, one has that
$s= \frac {3}{2}$
, one has that
for any
![]() $\eta \in (-\frac {3}{2} , \frac {5}{2})$
.
$\eta \in (-\frac {3}{2} , \frac {5}{2})$
.
Finally, in the case
![]() $\eta =\frac {5}{2}$
, it holds that
$\eta =\frac {5}{2}$
, it holds that
as soon as
![]() $ s\in (-\frac {5}{2}, \frac {3}{2})$
, and the case
$ s\in (-\frac {5}{2}, \frac {3}{2})$
, and the case
![]() $ s = \frac {3}{2} $
is allowed provided that
$ s = \frac {3}{2} $
is allowed provided that
![]() $c=1$
.
$c=1$
.
Remark. The preceding result also holds for vector fields that are independent of time in classical Besov spaces (without any norm in time). Accordingly, the lemma also holds in the case of Besov-space-valued Lebesgue spaces. This means that removing the tildes in (2.3), (2.4) and (2.5) produces valid estimates.
Remark. Consider an axisymmetric field
![]() $H:\mathbb {R}^3\to \mathbb {R}^3$
. For any radially symmetric
$H:\mathbb {R}^3\to \mathbb {R}^3$
. For any radially symmetric
![]() $\varphi \in \mathcal {S}_0$
and any rotation R around the z-axis, we find that
$\varphi \in \mathcal {S}_0$
and any rotation R around the z-axis, we find that
thereby showing that
![]() $\varphi * H$
is axisymmetric, too. If, furthermore, the field H has pure swirl, then, employing that
$\varphi * H$
is axisymmetric, too. If, furthermore, the field H has pure swirl, then, employing that
![]() $S_x(y)\overset {\mathrm {def}}{=} y-2(y\cdot e_\theta (x))e_\theta (x)$
, for any
$S_x(y)\overset {\mathrm {def}}{=} y-2(y\cdot e_\theta (x))e_\theta (x)$
, for any
![]() $x\neq 0$
, is an isometry and satisfies that
$x\neq 0$
, is an isometry and satisfies that
we compute that
 $$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^3}\varphi(x-y)H_\theta(y)e_\theta(y)dy &=\frac 12\int_{\mathbb{R}^3}\big(\varphi(x-y)H_\theta(y)e_\theta(y)+\varphi(x-S_xy)H_\theta(S_xy)e_\theta(S_xy)\big)dy \\ &=\frac 12\int_{\mathbb{R}^3}\varphi(x-y)H_\theta(y)\big(e_\theta(y)+e_\theta(S_xy)\big)dy \\ &=\left(\int_{\mathbb{R}^3}\varphi(x-y)H_\theta(y)\big(e_\theta(y)\cdot e_\theta(x)\big)dy\right) e_\theta(x), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^3}\varphi(x-y)H_\theta(y)e_\theta(y)dy &=\frac 12\int_{\mathbb{R}^3}\big(\varphi(x-y)H_\theta(y)e_\theta(y)+\varphi(x-S_xy)H_\theta(S_xy)e_\theta(S_xy)\big)dy \\ &=\frac 12\int_{\mathbb{R}^3}\varphi(x-y)H_\theta(y)\big(e_\theta(y)+e_\theta(S_xy)\big)dy \\ &=\left(\int_{\mathbb{R}^3}\varphi(x-y)H_\theta(y)\big(e_\theta(y)\cdot e_\theta(x)\big)dy\right) e_\theta(x), \end{aligned} \end{align*} $$
which establishes that
![]() $\varphi *H$
has pure swirl, as well.
$\varphi *H$
has pure swirl, as well.
Remark. The hypothesis (2.2) is satisfied by axisymmetric divergence-free vector fields such that F has no swirl and G has pure swirl. Indeed, as previously emphasized, the curl of an axisymmetric vector field with no swirl is axisymmetric with pure swirl. Therefore, in this situation, it holds that
![]() $\nabla \times F$
and G both have pure swirls, which implies, according to the preceding remark, that their convolutions with radial functions remain axisymmetric with pure swirl and are thus colinear.
$\nabla \times F$
and G both have pure swirls, which implies, according to the preceding remark, that their convolutions with radial functions remain axisymmetric with pure swirl and are thus colinear.
Remark. Note that Lemma 2.3 above is an extension of [Reference Arsénio and Houamed3, Lemma 3.4] to the three-dimensional setting. In particular, its significance lies in the fact that it allows us to cover the range of parameters
![]() $\eta \in [\frac {3}{2} ,\frac {5}{2})$
. Indeed, without the geometric assumption (2.2) on F and G, the paradifferential estimates remain valid but may need to be restricted to parameters satisfying
$\eta \in [\frac {3}{2} ,\frac {5}{2})$
. Indeed, without the geometric assumption (2.2) on F and G, the paradifferential estimates remain valid but may need to be restricted to parameters satisfying
![]() $\eta <\frac 32$
.
$\eta <\frac 32$
.
Proof. We follow the method of proof of Lemma 3.4 from [Reference Arsénio and Houamed3] and write Bony’s decomposition
where the paraproducts are defined by
 $$ \begin{align*} T_FG=\sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}}\Delta_jF\times\Delta_kG, \qquad T_GF =\sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}}\Delta_jG\times\Delta_kF =-\sum_{\substack{j,k\in\mathbb{Z}\\j-k>2}}\Delta_jF\times\Delta_kG, \end{align*} $$
$$ \begin{align*} T_FG=\sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}}\Delta_jF\times\Delta_kG, \qquad T_GF =\sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}}\Delta_jG\times\Delta_kF =-\sum_{\substack{j,k\in\mathbb{Z}\\j-k>2}}\Delta_jF\times\Delta_kG, \end{align*} $$
and the remainder is given by
 $$ \begin{align*} R(F,G)=\sum_{\substack{j,k\in\mathbb{Z}\\|j-k|\leq 2}}\Delta_jF\times\Delta_kG, \end{align*} $$
$$ \begin{align*} R(F,G)=\sum_{\substack{j,k\in\mathbb{Z}\\|j-k|\leq 2}}\Delta_jF\times\Delta_kG, \end{align*} $$
to deduce that a direct application of classical paraproduct estimates on homogeneous Besov spaces (see [Reference Arsénio and Houamed3, Appendix A] or [Reference Bahouri, Chemin and Danchin7], for instance), combined with the fact that P is bounded over Besov spaces, yields the validity of (2.3) for parameters
![]() $s\in (-\infty ,\frac {3}{2} )$
and
$s\in (-\infty ,\frac {3}{2} )$
and
![]() $\eta \in (-\infty ,\frac {3}{2} )$
with
$\eta \in (-\infty ,\frac {3}{2} )$
with
![]() $s+\eta>0$
, and the validity of (2.4) for parameters
$s+\eta>0$
, and the validity of (2.4) for parameters
![]() $\eta \in (-\frac 32,\frac {3}{2} )$
.
$\eta \in (-\frac 32,\frac {3}{2} )$
.
It is important to emphasize here that the restriction
![]() $\eta <\frac 32$
comes solely from the estimate of
$\eta <\frac 32$
comes solely from the estimate of
![]() $T_GF$
. Thus, in order to establish the validity of (2.3) and (2.4) for the full range of parameters, we only need to show now that
$T_GF$
. Thus, in order to establish the validity of (2.3) and (2.4) for the full range of parameters, we only need to show now that
for any
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $\eta \in (-\infty ,\frac {5}{2} )$
, as a consequence of the divergence-free structure of F and the geometric assumption (2.2).
$\eta \in (-\infty ,\frac {5}{2} )$
, as a consequence of the divergence-free structure of F and the geometric assumption (2.2).
To that end, assuming first that F and G are smooth, we compute that
Thus, if
![]() $\nabla \times F$
and G are colinear and F is divergence-free, we arrive at
$\nabla \times F$
and G are colinear and F is divergence-free, we arrive at
Now, applying the same reasoning to
![]() $\Delta _k F$
and
$\Delta _k F$
and
![]() $\Delta _j G$
, instead of F and G, and utilizing (2.2) to deduce that
$\Delta _j G$
, instead of F and G, and utilizing (2.2) to deduce that
![]() $\nabla \times \Delta _k F$
and
$\nabla \times \Delta _k F$
and
![]() $\Delta _j G$
are colinear, we obtain that
$\Delta _j G$
are colinear, we obtain that
 $$ \begin{align} P(T_GF) =(- \Delta)^{-1}\nabla \times \Bigg( \sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}} \Big(\Delta_k F\times( \nabla\times \Delta_j G) +2\Delta_k F\cdot \nabla \Delta_j G - \Delta_k F\operatorname{div} \Delta_j G\Big) \Bigg). \end{align} $$
$$ \begin{align} P(T_GF) =(- \Delta)^{-1}\nabla \times \Bigg( \sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}} \Big(\Delta_k F\times( \nabla\times \Delta_j G) +2\Delta_k F\cdot \nabla \Delta_j G - \Delta_k F\operatorname{div} \Delta_j G\Big) \Bigg). \end{align} $$
Therefore, applying classical paraproduct estimates (see [Reference Arsénio and Houamed3, Appendix A] or [Reference Bahouri, Chemin and Danchin7]), we conclude, for any
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $\eta <\frac 52$
, that
$\eta <\frac 52$
, that
 $$ \begin{align*} \begin{aligned} &\left\Vert P(T_GF)\right\Vert{}_{\widetilde L^a\dot B^{s+\eta-\frac{3}{2} }_{2,c}} \\ &\qquad\lesssim \Bigg\| \sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}} \Big(\Delta_k F\times( \nabla\times \Delta_j G) +2\Delta_k F\cdot \nabla \Delta_j G - \Delta_k F\operatorname{div} \Delta_j G\Big) \Bigg\|_{\widetilde L^a\dot B^{s+\eta-\frac{5}{2} }_{2,c} } \\ &\qquad\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c_1} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\eta-\frac 52}_{\infty,c_2} } \lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c_1} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\eta-1}_{2,c_2} } \\ &\qquad\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c_1} } \left\Vert G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\eta}_{2,c_2} }, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\left\Vert P(T_GF)\right\Vert{}_{\widetilde L^a\dot B^{s+\eta-\frac{3}{2} }_{2,c}} \\ &\qquad\lesssim \Bigg\| \sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}} \Big(\Delta_k F\times( \nabla\times \Delta_j G) +2\Delta_k F\cdot \nabla \Delta_j G - \Delta_k F\operatorname{div} \Delta_j G\Big) \Bigg\|_{\widetilde L^a\dot B^{s+\eta-\frac{5}{2} }_{2,c} } \\ &\qquad\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c_1} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\eta-\frac 52}_{\infty,c_2} } \lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c_1} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\eta-1}_{2,c_2} } \\ &\qquad\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c_1} } \left\Vert G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\eta}_{2,c_2} }, \end{aligned} \end{align*} $$
which establishes (2.6), thereby completing the proof of (2.3) and (2.4).
The justification of (2.5) is similar. Indeed, the classical paradifferential estimates apply directly to the paraproduct
![]() $T_FG$
and the remainder
$T_FG$
and the remainder
![]() $R(F,G)$
in the range of parameters desribed in (2.5). Thus, we see that (2.5) will follow from the justification of the paraproduct estimate
$R(F,G)$
in the range of parameters desribed in (2.5). Thus, we see that (2.5) will follow from the justification of the paraproduct estimate
for any
![]() $s\in \mathbb {R}$
. As before, in order to prove (2.9), we apply classical paraproduct estimates to (2.8). This leads to
$s\in \mathbb {R}$
. As before, in order to prove (2.9), we apply classical paraproduct estimates to (2.8). This leads to
 $$ \begin{align*} \begin{aligned} \left\Vert P(T_GF)\right\Vert{}_{\widetilde L^a\dot B^{s+1 }_{2,c} }\hspace{-20mm}& \\ &\lesssim \Bigg\| \sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}} \Big(\Delta_k F\times( \nabla\times \Delta_j G) +2\Delta_k F\cdot \nabla \Delta_j G - \Delta_k F\operatorname{div} \Delta_j G\Big) \Bigg\|_{\widetilde L^a\dot B^{s }_{2,c} } \\ &\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}L^\infty } \lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}\dot B^{0}_{\infty,1} } \\ &\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert G\right\Vert{}_{\widetilde L^{a_2}\dot B^{1}_{\infty,1} } \lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\frac 52}_{2,1} }, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert P(T_GF)\right\Vert{}_{\widetilde L^a\dot B^{s+1 }_{2,c} }\hspace{-20mm}& \\ &\lesssim \Bigg\| \sum_{\substack{j,k\in\mathbb{Z}\\j-k<-2}} \Big(\Delta_k F\times( \nabla\times \Delta_j G) +2\Delta_k F\cdot \nabla \Delta_j G - \Delta_k F\operatorname{div} \Delta_j G\Big) \Bigg\|_{\widetilde L^a\dot B^{s }_{2,c} } \\ &\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}L^\infty } \lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert \nabla G\right\Vert{}_{\widetilde L^{a_2}\dot B^{0}_{\infty,1} } \\ &\lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert G\right\Vert{}_{\widetilde L^{a_2}\dot B^{1}_{\infty,1} } \lesssim \left\Vert F\right\Vert{}_{\widetilde L^{a_1}\dot B^s_{2,c} } \left\Vert G\right\Vert{}_{\widetilde L^{a_2}\dot B^{\frac 52}_{2,1} }, \end{aligned} \end{align*} $$
for all
![]() $s\in \mathbb {R}$
, which establishes the validity of (2.5) and concludes of the proof of the lemma.
$s\in \mathbb {R}$
, which establishes the validity of (2.5) and concludes of the proof of the lemma.
Remark. If, instead of (2.2), one merely assumes that
![]() $\nabla \times F$
and G are colinear, in the sense that
$\nabla \times F$
and G are colinear, in the sense that
![]() $G\times (\nabla \times F)=0$
, then the paradifferential estimate (2.3) remains valid for any parameters
$G\times (\nabla \times F)=0$
, then the paradifferential estimate (2.3) remains valid for any parameters
![]() $s\in (-\infty ,\frac {3}{2} )$
and
$s\in (-\infty ,\frac {3}{2} )$
and
![]() $\eta \in (-\infty ,\frac {5}{2} )$
in the range
$\eta \in (-\infty ,\frac {5}{2} )$
in the range
![]() $s+\eta>1$
. This follows from applying Bony’s decomposition to each term of (2.7) and then estimating the resulting paraproducts and remainders as in the proof above. The restriction
$s+\eta>1$
. This follows from applying Bony’s decomposition to each term of (2.7) and then estimating the resulting paraproducts and remainders as in the proof above. The restriction
![]() $s+\eta>1$
is then a consequence of the estimates of the remainders. Similarly, under the assumption that
$s+\eta>1$
is then a consequence of the estimates of the remainders. Similarly, under the assumption that
![]() $\nabla \times F$
and G are colinear, one can show that (2.4) and (2.5) remain valid in the respective ranges
$\nabla \times F$
and G are colinear, one can show that (2.4) and (2.5) remain valid in the respective ranges
![]() $\eta \in (-\frac 12, \frac 52)$
and
$\eta \in (-\frac 12, \frac 52)$
and
![]() $s\in (-\frac 32,\frac 32)$
.
$s\in (-\frac 32,\frac 32)$
.
3 A priori estimates
Here, we establish a priori estimates on smooth solutions of the Navier–Stokes–Maxwell system (1.1). The ensuing bounds will be employed to prove existence of global solutions to that system. For simplicity, from now on, we take
![]() $\nu = 1$
in (1.1). However, we emphasize that all estimates below hold for any
$\nu = 1$
in (1.1). However, we emphasize that all estimates below hold for any
![]() $\nu>0$
.
$\nu>0$
.
We recall first that the only available global bound for smooth solutions of (1.1) corresponds to the
![]() $L^2$
-energy estimate
$L^2$
-energy estimate
As explained in the introduction, this bound does not seem to be enough to construct any kind of solutions. Therefore, we shall aim to propagate some higher regularity for u, E and B.
In what follows, we recall that are using the notation
where
3.1 Controlling the velocity field
In order to control higher regularities for the velocity field, we shall exploit the axisymmetric structure and perform an energy estimate on the equations describing the evolution of
![]() $\omega _\theta $
and
$\omega _\theta $
and
![]() $\Omega $
, which we derived in Section 1.1. For convenience, we recall here that the equation for
$\Omega $
, which we derived in Section 1.1. For convenience, we recall here that the equation for
![]() $\omega _\theta $
can be written as
$\omega _\theta $
can be written as
whereas the equation for
![]() $\Omega $
reads as
$\Omega $
reads as
The following proposition provides a control on the velocity field in terms of some suitable norms of electromagnetic fields. This will be combined with the estimates from Section 3.2 to obtain uniform global bounds in Section 5, later on.
Proposition 3.1. Let
![]() $T\in (0,\infty ]$
and
$T\in (0,\infty ]$
and
![]() $ (u,E,B)$
be a smooth axisymmetric solution of (1.1) on
$ (u,E,B)$
be a smooth axisymmetric solution of (1.1) on
![]() $[0,T)$
, where u and E have no swirl and B has pure swirl. Then, there is a universal constant
$[0,T)$
, where u and E have no swirl and B has pure swirl. Then, there is a universal constant
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} \begin{aligned} &\left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_tL^2 \cap L^2_t\dot{H}^1 } \\ &\qquad\lesssim \left( \left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2} + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) \exp \big(C\mathcal{E}^2_0\big), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_tL^2 \cap L^2_t\dot{H}^1 } \\ &\qquad\lesssim \left( \left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2} + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) \exp \big(C\mathcal{E}^2_0\big), \end{aligned} \end{align*} $$
where all the norms are taken over the time interval
![]() $[0,T)$
.
$[0,T)$
.
Remark. Note that the right-hand side in the bound above does not exhibit any time growth, provided that the norms of the electromagnetic fields remain bounded on any time interval
![]() $[0,T)$
. This is crucial and necessary to prove the global existence of solutions in Theorem 1.1.
$[0,T)$
. This is crucial and necessary to prove the global existence of solutions in Theorem 1.1.
Proof. First, we observe that a straightforward computation relying on the fact
![]() $\omega $
is axisymmetric without swirl yields that
$\omega $
is axisymmetric without swirl yields that
In particular, this implies that
which will allow us to estimate
![]() $(\omega _\theta ,\Omega )$
instead of
$(\omega _\theta ,\Omega )$
instead of
![]() $(\omega ,\Omega )$
.
$(\omega ,\Omega )$
.
Now, multiplying (3.2) by
![]() $\omega _\theta $
, integrating in time and space, and then using the divergence-free condition on E and u yields, for all
$\omega _\theta $
, integrating in time and space, and then using the divergence-free condition on E and u yields, for all
![]() $t\in [0,T)$
, that
$t\in [0,T)$
, that
 $$ \begin{align} \begin{aligned} \frac{1}{2} \left\Vert \omega_\theta(t)\right\Vert{}_{ L^2 }^2 & + \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 +\left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^2 }^2 \\ &\leq \frac{1}{2} \left\Vert \omega_0\right\Vert{}_{L^2}^2 + \int_{0}^t\left\Vert \frac{u_r(\tau)}{r}\right\Vert{}_{L^\infty} \left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau +\left| \int_{0}^t \int_{\mathbb{R}^3} \Gamma(\tau) B(\tau) \partial_z \omega_\theta(\tau) dxd\tau \right| \\ &\quad+\int_{0}^t \frac{1}{c}\left\Vert (\partial_t E)B(\tau) \right\Vert{}_{L^2} \Big( \left\Vert \nabla \omega_\theta(\tau)\right\Vert{}_{L^2} + \left\Vert \frac{\omega_\theta}{r}(\tau)\right\Vert{}_{L^2}\Big) d\tau, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{1}{2} \left\Vert \omega_\theta(t)\right\Vert{}_{ L^2 }^2 & + \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 +\left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^2 }^2 \\ &\leq \frac{1}{2} \left\Vert \omega_0\right\Vert{}_{L^2}^2 + \int_{0}^t\left\Vert \frac{u_r(\tau)}{r}\right\Vert{}_{L^\infty} \left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau +\left| \int_{0}^t \int_{\mathbb{R}^3} \Gamma(\tau) B(\tau) \partial_z \omega_\theta(\tau) dxd\tau \right| \\ &\quad+\int_{0}^t \frac{1}{c}\left\Vert (\partial_t E)B(\tau) \right\Vert{}_{L^2} \Big( \left\Vert \nabla \omega_\theta(\tau)\right\Vert{}_{L^2} + \left\Vert \frac{\omega_\theta}{r}(\tau)\right\Vert{}_{L^2}\Big) d\tau, \end{aligned} \end{align} $$
where the norms in time are taken over the interval
![]() $[0,t)$
.
$[0,t)$
.
In order to estimate the second term in the right-hand side above, we make use of (1.10) to obtain, for any
![]() $\varepsilon>0$
, that
$\varepsilon>0$
, that
 $$ \begin{align} \begin{aligned} \int_{0}^t\left\Vert \frac{u_r(\tau)}{r}\right\Vert{}_{L^\infty} &\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau \\ & \lesssim \int_{0}^t\left\Vert \Omega(\tau)\right\Vert{}_{L^2}^{\frac{1}{2}} \left\Vert \nabla \Omega(\tau)\right\Vert{}_{L^2}^{\frac{1}{2}}\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau \\ & \leq \varepsilon \int_{0}^t\left\Vert \Omega(\tau)\right\Vert{}_{L^2} \left\Vert \nabla \Omega(\tau)\right\Vert{}_{L^2} d\tau+ C_\varepsilon\int_{0}^t\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^4d\tau\\ & \leq \varepsilon \Big(\left\Vert \frac{\omega_{\theta}}{r}\right\Vert{}_{L^2_t L^2 }^2 +\left\Vert \Omega\right\Vert{}_{L^2_t \dot{H}^1 } ^2\Big)+ C_\varepsilon\int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{0}^t\left\Vert \frac{u_r(\tau)}{r}\right\Vert{}_{L^\infty} &\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau \\ & \lesssim \int_{0}^t\left\Vert \Omega(\tau)\right\Vert{}_{L^2}^{\frac{1}{2}} \left\Vert \nabla \Omega(\tau)\right\Vert{}_{L^2}^{\frac{1}{2}}\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau \\ & \leq \varepsilon \int_{0}^t\left\Vert \Omega(\tau)\right\Vert{}_{L^2} \left\Vert \nabla \Omega(\tau)\right\Vert{}_{L^2} d\tau+ C_\varepsilon\int_{0}^t\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^4d\tau\\ & \leq \varepsilon \Big(\left\Vert \frac{\omega_{\theta}}{r}\right\Vert{}_{L^2_t L^2 }^2 +\left\Vert \Omega\right\Vert{}_{L^2_t \dot{H}^1 } ^2\Big)+ C_\varepsilon\int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2\left\Vert \omega_\theta(\tau)\right\Vert{}_{L^2}^2d\tau, \end{aligned} \end{align} $$
where we utilized the celebrated Biot–Savart estimate in the last line.
However, the estimate of the third term in the right-hand side of (3.5) is obtained by employing Hölder’s inequality, again, followed by the Sobolev embedding
![]() $\dot {H}^1\hookrightarrow L^6(\mathbb {R}^3)$
to write, for any
$\dot {H}^1\hookrightarrow L^6(\mathbb {R}^3)$
to write, for any
![]() $\varepsilon>0$
, that
$\varepsilon>0$
, that
 $$ \begin{align} \begin{aligned} \left| \int_{0}^t \int_{\mathbb{R}^3} \Gamma(\tau) B(\tau) \partial_z \omega_\theta(\tau) dxd\tau \right| & \leq C_\varepsilon \int_{0}^t \left\Vert \Gamma B(\tau)\right\Vert{}_{L^2}^2 d\tau +\varepsilon \left\Vert \partial_z \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 \\ & \leq C_\varepsilon \int_{0}^t \left\Vert \Gamma(\tau)\right\Vert{}_{L^3}^2\left\Vert B(\tau)\right\Vert{}_{L^6}^2 d\tau + \varepsilon \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 \\ & \leq C_\varepsilon \left\Vert \Gamma \right\Vert{}_{L^\infty_t L^3 }^2 \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 }^2 + \varepsilon \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \int_{0}^t \int_{\mathbb{R}^3} \Gamma(\tau) B(\tau) \partial_z \omega_\theta(\tau) dxd\tau \right| & \leq C_\varepsilon \int_{0}^t \left\Vert \Gamma B(\tau)\right\Vert{}_{L^2}^2 d\tau +\varepsilon \left\Vert \partial_z \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 \\ & \leq C_\varepsilon \int_{0}^t \left\Vert \Gamma(\tau)\right\Vert{}_{L^3}^2\left\Vert B(\tau)\right\Vert{}_{L^6}^2 d\tau + \varepsilon \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 \\ & \leq C_\varepsilon \left\Vert \Gamma \right\Vert{}_{L^\infty_t L^3 }^2 \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 }^2 + \varepsilon \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2. \end{aligned} \end{align} $$
Finally, the last integral in (3.5) can be easily controlled by similar arguments to obtain that
 $$ \begin{align} \begin{aligned} \int_{0}^t \frac{1}{c}\left\Vert (\partial_t E)B(\tau) \right\Vert{}_{L^2} &\Big( \left\Vert \nabla \omega_\theta(\tau)\right\Vert{}_{L^2} + \left\Vert \frac{\omega_\theta}{r}(\tau)\right\Vert{}_{L^2}\Big) d\tau \\ &\leq \frac{C_\varepsilon}{c^2}\left\Vert \partial_t E \right\Vert{}_{L^2_t L^3 }^2 \left\Vert B\right\Vert{}_{L^\infty_t L^6 }^2 + \varepsilon\Big( \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 + \left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^ 2}^2 \Big) \\ &\leq \frac{C_\varepsilon}{c^2}\left\Vert \partial_t E \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^1 }^2 + \varepsilon\Big( \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 + \left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^ 2}^2 \Big). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{0}^t \frac{1}{c}\left\Vert (\partial_t E)B(\tau) \right\Vert{}_{L^2} &\Big( \left\Vert \nabla \omega_\theta(\tau)\right\Vert{}_{L^2} + \left\Vert \frac{\omega_\theta}{r}(\tau)\right\Vert{}_{L^2}\Big) d\tau \\ &\leq \frac{C_\varepsilon}{c^2}\left\Vert \partial_t E \right\Vert{}_{L^2_t L^3 }^2 \left\Vert B\right\Vert{}_{L^\infty_t L^6 }^2 + \varepsilon\Big( \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 + \left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^ 2}^2 \Big) \\ &\leq \frac{C_\varepsilon}{c^2}\left\Vert \partial_t E \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^1 }^2 + \varepsilon\Big( \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 + \left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^ 2}^2 \Big). \end{aligned} \end{align} $$
All in all, incorporating (3.6), (3.7) and (3.8) into (3.5), and choosing
![]() $\varepsilon $
small enough yields that
$\varepsilon $
small enough yields that
 $$ \begin{align} \begin{aligned} \left\Vert \omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 &+\left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^2 }^2 \\ &\leq \left\Vert \omega_0\right\Vert{}_{L^2}^2 + \frac{1}{4} \left\Vert \Omega\right\Vert{}_{L^2_t \dot{H}^1 } ^2+ C\int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2\left\Vert \omega (\tau)\right\Vert{}_{L^2}^2d\tau \\ &\quad + C \left\Vert \Gamma \right\Vert{}_{L^\infty_t L^3 }^2 \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 }^2 + \frac{C }{c^2}\left\Vert \partial_t E \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^1 }^2 , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert \omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \nabla \omega_\theta\right\Vert{}_{L^2_t L^2 }^2 &+\left\Vert \frac{\omega_\theta}{r}\right\Vert{}_{L^2_t L^2 }^2 \\ &\leq \left\Vert \omega_0\right\Vert{}_{L^2}^2 + \frac{1}{4} \left\Vert \Omega\right\Vert{}_{L^2_t \dot{H}^1 } ^2+ C\int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2\left\Vert \omega (\tau)\right\Vert{}_{L^2}^2d\tau \\ &\quad + C \left\Vert \Gamma \right\Vert{}_{L^\infty_t L^3 }^2 \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 }^2 + \frac{C }{c^2}\left\Vert \partial_t E \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^1 }^2 , \end{aligned} \end{align} $$
where we have utilized (3.4).
Now, we show how to estimate
![]() $\Omega $
in the right-hand side above. To that end, we first perform an
$\Omega $
in the right-hand side above. To that end, we first perform an
![]() $L^2$
-energy estimate on (3.3) followed by a standard application of paraproduct laws to find, for any
$L^2$
-energy estimate on (3.3) followed by a standard application of paraproduct laws to find, for any
![]() $t\in [0,T)$
, that
$t\in [0,T)$
, that
 $$ \begin{align*} {\frac{1}{2}}\left\Vert \Omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \Omega\right\Vert{}_{ L^2_t \dot{H}^1 } ^2 &\leq {\frac{1}{2}}\left\Vert \Omega_0\right\Vert{}_{L^2}^2 + \left\Vert \Gamma ^2 \right\Vert{}_{L^2_tL^2} \left\Vert \Omega\right\Vert{}_{L^2_t \dot{H}^1} + \frac{1}{c}\left\Vert \partial_t E \cdot \nabla \Gamma\right\Vert _{L^2_t \dot H^{-1}} \left\Vert \Omega\right\Vert{}_{L^2_t \dot H^1}\\ &\leq {\frac{1}{2}}\left\Vert \Omega_0\right\Vert{}_{L^2}^2 + C \left\Vert \Gamma \right\Vert{}_{L^4_t L^4 }^4 + {\frac{C }{c^2}}\left\Vert \partial_t E \right\Vert{}_{L^2_t \dot{H}^ {\frac{1}{2}} }^2 \left\Vert \Gamma\right\Vert _{L^\infty_t \dot{H}^1 }^2 + {\frac{1}{2}} \left\Vert \Omega\right\Vert{}_{L^2_t \dot H^1}^2 , \end{align*} $$
$$ \begin{align*} {\frac{1}{2}}\left\Vert \Omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \Omega\right\Vert{}_{ L^2_t \dot{H}^1 } ^2 &\leq {\frac{1}{2}}\left\Vert \Omega_0\right\Vert{}_{L^2}^2 + \left\Vert \Gamma ^2 \right\Vert{}_{L^2_tL^2} \left\Vert \Omega\right\Vert{}_{L^2_t \dot{H}^1} + \frac{1}{c}\left\Vert \partial_t E \cdot \nabla \Gamma\right\Vert _{L^2_t \dot H^{-1}} \left\Vert \Omega\right\Vert{}_{L^2_t \dot H^1}\\ &\leq {\frac{1}{2}}\left\Vert \Omega_0\right\Vert{}_{L^2}^2 + C \left\Vert \Gamma \right\Vert{}_{L^4_t L^4 }^4 + {\frac{C }{c^2}}\left\Vert \partial_t E \right\Vert{}_{L^2_t \dot{H}^ {\frac{1}{2}} }^2 \left\Vert \Gamma\right\Vert _{L^\infty_t \dot{H}^1 }^2 + {\frac{1}{2}} \left\Vert \Omega\right\Vert{}_{L^2_t \dot H^1}^2 , \end{align*} $$
for some universal constant
![]() $C>0$
. Therefore, by further employing Hölder’s and embedding inequalities, we obtain that
$C>0$
. Therefore, by further employing Hölder’s and embedding inequalities, we obtain that
Hence, recalling that
and employing Lemma 2.2, we arrive at the bound
At last, summing (3.9) and (3.10), and utilizing (3.4), we arrive at the estimate
 $$ \begin{align*} \begin{aligned} \left\Vert \omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \omega\right\Vert{}_{L^2_t \dot{H}^1 }^2 &+\left\Vert \Omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \Omega\right\Vert{}_{ L^2_t \dot{H}^1 } ^2 \\ &\lesssim \left\Vert \omega_0\right\Vert{}_{L^2}^2+\left\Vert \Omega_0\right\Vert{}_{L^2}^2 + \int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2\left\Vert \omega (\tau)\right\Vert{}_{L^2}^2d\tau \\ &\quad + \left(\left\Vert {\frac{1}{c}}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right)^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \omega\right\Vert{}_{L^2_t \dot{H}^1 }^2 &+\left\Vert \Omega(t)\right\Vert{}_{ L^2 }^2 + \left\Vert \Omega\right\Vert{}_{ L^2_t \dot{H}^1 } ^2 \\ &\lesssim \left\Vert \omega_0\right\Vert{}_{L^2}^2+\left\Vert \Omega_0\right\Vert{}_{L^2}^2 + \int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2\left\Vert \omega (\tau)\right\Vert{}_{L^2}^2d\tau \\ &\quad + \left(\left\Vert {\frac{1}{c}}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right)^2. \end{aligned} \end{align*} $$
Finally, an application of the classical Grönwall inequality yields that
 $$ \begin{align*} \left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_tL^2 \cap L^2_t\dot{H}^1 } &\lesssim \left(\left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2}+\left\Vert {\frac{1}{c}}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) \\ &\quad\times\exp\left(C\int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2 d\tau\right), \end{align*} $$
$$ \begin{align*} \left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_tL^2 \cap L^2_t\dot{H}^1 } &\lesssim \left(\left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2}+\left\Vert {\frac{1}{c}}\partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_tH^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) \\ &\quad\times\exp\left(C\int_{0}^t\left\Vert u(\tau)\right\Vert{}_{\dot{H}^1}^2 d\tau\right), \end{align*} $$
which, in view of the energy inequality (3.1), concludes the proof of the proposition.
In view of the estimates on the velocity field given in the preceding proposition, we now need to establish the following bounds on the electromagnetic field:
-
• An asymptotically vanishing bound for
 $\frac {1}{c} \partial _t E$
of the form (3.11)for some
$\frac {1}{c} \partial _t E$
of the form (3.11)for some $$ \begin{align} \frac{1}{c}\left\Vert \partial_t E\right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} } \lesssim c^{-\alpha} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big), \end{align} $$
$$ \begin{align} \frac{1}{c}\left\Vert \partial_t E\right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} } \lesssim c^{-\alpha} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big), \end{align} $$
 $\alpha>0$
, a (nonlinear) function F and a suitable functional space X.
$\alpha>0$
, a (nonlinear) function F and a suitable functional space X.
-
• An asymptotically global bound for
 $ B$
in
$ B$
in
 $L^2_t\dot {H}^1$
and
$L^2_t\dot {H}^1$
and
 $\Gamma $
in
$\Gamma $
in
 $L^\infty _t L^3 \cap L^2_t \dot {H}^1 $
of the form (3.12)for some
$L^\infty _t L^3 \cap L^2_t \dot {H}^1 $
of the form (3.12)for some $$ \begin{align} \left\Vert B\right\Vert{}_{ L^2_t \dot{H}^1 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 \cap L^2_t \dot{H}^1 } \leq C_0 + c^{-\beta} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big), \end{align} $$
$$ \begin{align} \left\Vert B\right\Vert{}_{ L^2_t \dot{H}^1 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 \cap L^2_t \dot{H}^1 } \leq C_0 + c^{-\beta} F\Big(\left\Vert (u,E,B)\right\Vert{}_X\Big), \end{align} $$
 $\beta>0$
and
$\beta>0$
and
 $C_0>0$
depending only on the initial data.
$C_0>0$
depending only on the initial data.
The complete justification of these bounds will be the subject of Section 4, later on.
3.2 Controlling the electromagnetic field
Here, we establish several estimates combining the refined study of the dispersive properties of Maxwell’s equations from [Reference Arsénio and Houamed3] with the axisymmetric structure. The principal results of this part of the article are obtained in Sections 3.2.1 and 3.2.2, below.
The ensuing bounds will be further combined with the results from the previous section to arrive at a global control of solutions to (1.1) in Section 5, later on.
For the sake of clarity, we recall first the essential results from [Reference Arsénio and Houamed3] on Strichartz estimates and maximal parabolic regularity for the three-dimensional damped Maxwell system, which are useful in the present work.
Lemma 3.2 [Reference Arsénio and Houamed3, Corollary 2.12].
Consider a solution
![]() $(E,B) :[0,T)\times \mathbb {R}^3\to \mathbb {R}^6$
of the damped Maxwell system
$(E,B) :[0,T)\times \mathbb {R}^3\to \mathbb {R}^6$
of the damped Maxwell system
 $$ \begin{align} \begin{cases} \begin{aligned} \frac{1}{c} \partial_t E - \nabla \times B + \sigma c E & = G, \\ \frac{1}{c} \partial_t B + \nabla \times E & = 0, \\ \operatorname{div} B & =0, \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} \frac{1}{c} \partial_t E - \nabla \times B + \sigma c E & = G, \\ \frac{1}{c} \partial_t B + \nabla \times E & = 0, \\ \operatorname{div} B & =0, \end{aligned} \end{cases} \end{align} $$
for some initial data
![]() $(E,B)(0,x)=(E_0,B_0)(x)$
, where
$(E,B)(0,x)=(E_0,B_0)(x)$
, where
![]() $\sigma> 0$
and
$\sigma> 0$
and
![]() $c>0$
.
$c>0$
.
For any exponent pairs
![]() $(q,r),(\tilde q,\tilde r)\in [1,\infty ]\times [2,\infty )$
that are admissible in the sense that
$(q,r),(\tilde q,\tilde r)\in [1,\infty ]\times [2,\infty )$
that are admissible in the sense that
and such that
one has the high-frequency estimate
 $$ \begin{align*} \begin{aligned} 2^{-j\left(1-\frac 2r\right)}&\left\Vert \Delta_j (PE,B)\right\Vert{}_{L^q([0,T); L^r) } \\ &\lesssim c^{\frac 12-\frac 1r-\frac 2q} \left\Vert \Delta_j (PE_0,B_0)\right\Vert{}_{L^2 } +c^{2-\frac 1r-\frac 1{\tilde r}-\frac 2q-\frac 2{\tilde q}} 2^{j\left(1-\frac 2{\tilde r}\right)}\left\Vert \Delta_j PG\right\Vert{}_{L ^{\tilde q'}([0,T); L^{\tilde r'} )}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} 2^{-j\left(1-\frac 2r\right)}&\left\Vert \Delta_j (PE,B)\right\Vert{}_{L^q([0,T); L^r) } \\ &\lesssim c^{\frac 12-\frac 1r-\frac 2q} \left\Vert \Delta_j (PE_0,B_0)\right\Vert{}_{L^2 } +c^{2-\frac 1r-\frac 1{\tilde r}-\frac 2q-\frac 2{\tilde q}} 2^{j\left(1-\frac 2{\tilde r}\right)}\left\Vert \Delta_j PG\right\Vert{}_{L ^{\tilde q'}([0,T); L^{\tilde r'} )}, \end{aligned} \end{align*} $$
for all
![]() $j\in \mathbb {Z}$
with
$j\in \mathbb {Z}$
with
![]() $2^j\geq \sigma c$
, and the low-frequency estimates
$2^j\geq \sigma c$
, and the low-frequency estimates
 $$ \begin{align*} \begin{aligned} 2^{-j\left(\frac 32-\frac 3r\right)}&\left\Vert \Delta_j PE\right\Vert{}_{L^q([0,T); L^r ) } \\ &\lesssim c^{-\frac 2q}\left\Vert \Delta_j PE_0\right\Vert{}_{L^2 } +c^{-1} 2^{j\left(1-\frac 2q\right)}\left\Vert \Delta_j B_0\right\Vert{}_{L^2 } +c^{1-\frac 2q-\frac 2{\tilde q}} 2^{j\left(\frac 32-\frac 3{\tilde r}\right)}\left\Vert \Delta_j PG\right\Vert{}_{L ^{\tilde q'} ([0,T); L^{\tilde r'}) } \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} 2^{-j\left(\frac 32-\frac 3r\right)}&\left\Vert \Delta_j PE\right\Vert{}_{L^q([0,T); L^r ) } \\ &\lesssim c^{-\frac 2q}\left\Vert \Delta_j PE_0\right\Vert{}_{L^2 } +c^{-1} 2^{j\left(1-\frac 2q\right)}\left\Vert \Delta_j B_0\right\Vert{}_{L^2 } +c^{1-\frac 2q-\frac 2{\tilde q}} 2^{j\left(\frac 32-\frac 3{\tilde r}\right)}\left\Vert \Delta_j PG\right\Vert{}_{L ^{\tilde q'} ([0,T); L^{\tilde r'}) } \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} 2^{-j\left(\frac 32-\frac 3r-\frac 2q\right)}&\left\Vert \Delta_j B\right\Vert{}_{L^q([0,T); L^r) } \\ &\lesssim c^{-1}2^{j} \left\Vert \Delta_j PE_0\right\Vert{}_{L^2 } +\left\Vert \Delta_j B_0\right\Vert{}_{L^2 } + 2^{j\left(\frac 52-\frac 3{\tilde r}-\frac 2{\tilde q}\right)}\left\Vert \Delta_j PG\right\Vert{}_{L ^{\tilde q'}([0,T); L^{\tilde r'} )}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} 2^{-j\left(\frac 32-\frac 3r-\frac 2q\right)}&\left\Vert \Delta_j B\right\Vert{}_{L^q([0,T); L^r) } \\ &\lesssim c^{-1}2^{j} \left\Vert \Delta_j PE_0\right\Vert{}_{L^2 } +\left\Vert \Delta_j B_0\right\Vert{}_{L^2 } + 2^{j\left(\frac 52-\frac 3{\tilde r}-\frac 2{\tilde q}\right)}\left\Vert \Delta_j PG\right\Vert{}_{L ^{\tilde q'}([0,T); L^{\tilde r'} )}, \end{aligned} \end{align*} $$
for all
![]() $j\in \mathbb {Z}$
with
$j\in \mathbb {Z}$
with
![]() $2^j\leq \sigma c$
.
$2^j\leq \sigma c$
.
Lemma 3.3. [Reference Arsénio and Houamed3, Corollary 2.14] Consider a solution
![]() $(E,B) :[0,T)\times \mathbb {R}^3\to \mathbb {R}^6$
of the damped Maxwell system (3.13), for some initial data
$(E,B) :[0,T)\times \mathbb {R}^3\to \mathbb {R}^6$
of the damped Maxwell system (3.13), for some initial data
![]() $(E,B)(0,x)=(E_0,B_0)(x)$
, where
$(E,B)(0,x)=(E_0,B_0)(x)$
, where
![]() $\sigma> 0$
and
$\sigma> 0$
and
![]() $c>0$
.
$c>0$
.
For any
![]() $\chi \in C^\infty _c(\mathbb {R}^d)$
and
$\chi \in C^\infty _c(\mathbb {R}^d)$
and
![]() $s\in \mathbb {R}$
, one has the low-frequency estimates
$s\in \mathbb {R}$
, one has the low-frequency estimates
 $$ \begin{align*} \begin{aligned} \left\Vert \chi(c^{-1}D)PE\right\Vert{}_{L^m_t([0,T);\dot B^{s+\frac 2m}_{2,q})} &\lesssim c^{-\frac 2m}\left\Vert PE_0\right\Vert{}_{\dot B^{s+\frac 2m}_{2,q}}+c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{s+1}_{2,m}} \\ &\quad+c^{-1+\frac 2r-\frac 2m}\left\Vert PG\right\Vert{}_{L_t^r([0,T);\dot B_{2,q}^{s+\frac 2m})}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \chi(c^{-1}D)PE\right\Vert{}_{L^m_t([0,T);\dot B^{s+\frac 2m}_{2,q})} &\lesssim c^{-\frac 2m}\left\Vert PE_0\right\Vert{}_{\dot B^{s+\frac 2m}_{2,q}}+c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{s+1}_{2,m}} \\ &\quad+c^{-1+\frac 2r-\frac 2m}\left\Vert PG\right\Vert{}_{L_t^r([0,T);\dot B_{2,q}^{s+\frac 2m})}, \end{aligned} \end{align*} $$
for any
![]() $1<r\leq m<\infty $
and
$1<r\leq m<\infty $
and
![]() $1\leq q\leq \infty $
, as well as
$1\leq q\leq \infty $
, as well as
for any
![]() $1<r<m<\infty $
, and
$1<r<m<\infty $
, and
for any
![]() $1<m<\infty $
and
$1<m<\infty $
and
![]() $1\leq q\leq \infty $
.
$1\leq q\leq \infty $
.
Let us now be more precise about the source term G that will be used in the application of the preceding two lemmas. Specifically, we will consider the Maxwell system
 $$ \begin{align} \begin{cases} \begin{aligned} \frac{1}{c} \partial_t E - \nabla \times B + \sigma c E & =- \sigma P( u \times B), & \operatorname{div} E&=0, \\ \frac{1}{c} \partial_t B + \nabla \times E & = 0, & \operatorname{div} B&=0, \\ \operatorname{div} u & =0. \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} \frac{1}{c} \partial_t E - \nabla \times B + \sigma c E & =- \sigma P( u \times B), & \operatorname{div} E&=0, \\ \frac{1}{c} \partial_t B + \nabla \times E & = 0, & \operatorname{div} B&=0, \\ \operatorname{div} u & =0. \end{aligned} \end{cases} \end{align} $$
Furthermore, in order to exploit the dichotomy between high and low frequencies featured in the estimates from the above lemmas, we consider the variants of Besov semi-norms
 $$ \begin{align*} \left\|f\right\|_{\dot B^{s}_{p,q,<}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k< \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^p}^q\right)^{\frac{1}{q}} \quad\text{and}\quad \left\|f\right\|_{\dot B^{s}_{p,q,>}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k\geq \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^p}^q\right)^{\frac{1}{q}}, \end{align*} $$
$$ \begin{align*} \left\|f\right\|_{\dot B^{s}_{p,q,<}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k< \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^p}^q\right)^{\frac{1}{q}} \quad\text{and}\quad \left\|f\right\|_{\dot B^{s}_{p,q,>}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k\geq \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^p}^q\right)^{\frac{1}{q}}, \end{align*} $$
as well as the corresponding variants of Chemin–Lerner semi-norms
 $$ \begin{align*} \left\|f\right\|_{\widetilde L^r_t\dot B^{s}_{p,q,<}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k< \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^r_tL^p_x}^q\right)^{\frac{1}{q}} \quad\text{and}\quad \left\|f\right\|_{\widetilde L^r_t\dot B^{s}_{p,q,>}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k\geq \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^r_tL^p_x}^q\right)^{\frac{1}{q}}, \end{align*} $$
$$ \begin{align*} \left\|f\right\|_{\widetilde L^r_t\dot B^{s}_{p,q,<}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k< \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^r_tL^p_x}^q\right)^{\frac{1}{q}} \quad\text{and}\quad \left\|f\right\|_{\widetilde L^r_t\dot B^{s}_{p,q,>}}\overset{\mathrm{def}}{=} \left( \sum_{\substack{k\in\mathbb{Z}\\ 2^k\geq \sigma c}} 2^{ksq} \left\|\Delta_{k}f\right\|_{L^r_tL^p_x}^q\right)^{\frac{1}{q}}, \end{align*} $$
for any
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $0<p,q,r\leq \infty $
(with obvious modifications if q is infinite). These families of semi-norms have been introduced in [Reference Arsénio and Houamed3]. We will utilize them extensively throughout the upcoming sections of our work.
$0<p,q,r\leq \infty $
(with obvious modifications if q is infinite). These families of semi-norms have been introduced in [Reference Arsénio and Houamed3]. We will utilize them extensively throughout the upcoming sections of our work.
3.2.1 Control of high-frequency electromagnetic waves
Here, we establish key bounds on high frequencies of electromagnetic fields. Lemma 3.4 below combines the damped Strichartz estimates for high electromagnetic frequencies from Lemma 3.2 with the paradifferential product laws on axisymmetric vector fields from Lemma 2.3.
The method behind the proof of this lemma is similar to the one used in [Reference Arsénio and Houamed3] (see Lemma 3.8, therein). However, here, we further refine the method by introducing an additional high–low frequency decomposition of the source term
![]() $P(u\times B)$
in (3.4). This will allow us to obtain stronger estimates (see (3.15), below).
$P(u\times B)$
in (3.4). This will allow us to obtain stronger estimates (see (3.15), below).
Lemma 3.4. Let
![]() $T\in (0,\infty ]$
and
$T\in (0,\infty ]$
and
![]() $(E,B)$
be a smooth axisymmetric solution to (3.14), defined on
$(E,B)$
be a smooth axisymmetric solution to (3.14), defined on
![]() $[0,T)$
, for some initial data
$[0,T)$
, for some initial data
![]() $(E_0,B_0)$
and some axisymmetric divergence-free vector field u. Assume further that
$(E_0,B_0)$
and some axisymmetric divergence-free vector field u. Assume further that
![]() $ E$
and u are both without swirl and that B has pure swirl.
$ E$
and u are both without swirl and that B has pure swirl.
Then, for any
![]() $s\in (-\frac {3}{2}, \frac {5}{2})$
,
$s\in (-\frac {3}{2}, \frac {5}{2})$
,
![]() $n\in [1,\infty ]$
and any
$n\in [1,\infty ]$
and any
![]() $q\in [\frac {4}{3},\infty ]$
, it holds that
$q\in [\frac {4}{3},\infty ]$
, it holds that
Moreover, at the endpoint
![]() $s=\frac {5}{2}$
, we have that
$s=\frac {5}{2}$
, we have that
as soon as
![]() $ 2 \leq p \leq q \leq \infty $
. Furthermore, in the case
$ 2 \leq p \leq q \leq \infty $
. Furthermore, in the case
![]() $p=2$
, it holds that
$p=2$
, it holds that
 $$ \begin{align} \begin{aligned} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{\frac{5}{2} }_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} \\ & \quad +c^{ \frac{1}{2} - \frac{2}{q} }\left\Vert u\right\Vert{}_{L^\infty _t \dot{H} ^1 \cap L^2_t\dot{H} ^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,>} } + \left\Vert B \right\Vert{}_{L ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,<} } \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{\frac{5}{2} }_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} \\ & \quad +c^{ \frac{1}{2} - \frac{2}{q} }\left\Vert u\right\Vert{}_{L^\infty _t \dot{H} ^1 \cap L^2_t\dot{H} ^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,>} } + \left\Vert B \right\Vert{}_{L ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,<} } \right), \end{aligned} \end{align} $$
for all
![]() $ q\in [2,\infty ]$
.
$ q\in [2,\infty ]$
.
Proof. Applying Lemma 3.2 yields that
for all
![]() $j\in \mathbb {Z}$
, with
$j\in \mathbb {Z}$
, with
![]() $2^j\geq \sigma c$
, and any
$2^j\geq \sigma c$
, and any
![]() $1\leq p\leq q \leq \infty $
. It then follows, for any
$1\leq p\leq q \leq \infty $
. It then follows, for any
![]() $s\in \mathbb {R}$
and any
$s\in \mathbb {R}$
and any
![]() $n\in [1,\infty ]$
, that
$n\in [1,\infty ]$
, that
Thus, choosing
![]() $p= \frac {4}{3}$
and utilizing (2.4) we find, for all
$p= \frac {4}{3}$
and utilizing (2.4) we find, for all
![]() $s\in (-\frac {3}{2},\frac {5}{2})$
,
$s\in (-\frac {3}{2},\frac {5}{2})$
,
![]() $n\in [1,\infty ]$
and any
$n\in [1,\infty ]$
and any
![]() $q\in [\frac {4}{3}, \infty ]$
, that
$q\in [\frac {4}{3}, \infty ]$
, that
Hence, we conclude the proof of the first claim in the lemma by employing the embedding
We now turn to the endpoint case
![]() $(s,n)= (\frac {5}{2},1)$
, which corresponds to the second bound in the statement of the lemma. The natural attempt to estimate the product
$(s,n)= (\frac {5}{2},1)$
, which corresponds to the second bound in the statement of the lemma. The natural attempt to estimate the product
![]() $P(u\times B)$
in that case would be by applying (2.5), which is the corresponding extension of (2.4). Doing so would lead to the control
$P(u\times B)$
in that case would be by applying (2.5), which is the corresponding extension of (2.4). Doing so would lead to the control
 $$ \begin{align} \begin{aligned} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{\frac 52}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac52}_{2,1,>}} + c^{-1+2\left( \frac{1}{4}+ \frac{1}{p} -\frac 1q \right)} \left\Vert P\big(u \times B \big)\right\Vert{}_{\widetilde{L} _t^{\left( \frac{1}{4}+ \frac{1}{p} \right)^{-1} } \dot{B}^{\frac 52}_{2,1 } } \\ &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac52}_{2,1,>}} +c^{- \frac{1}{2} - \frac{2}{q} + \frac{2}{p} } \left\Vert u\right\Vert{}_{\widetilde{L}^4_t \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{\widetilde{L} ^p_t \dot{B}^{\frac52}_{2,1} } , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{\frac 52}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac52}_{2,1,>}} + c^{-1+2\left( \frac{1}{4}+ \frac{1}{p} -\frac 1q \right)} \left\Vert P\big(u \times B \big)\right\Vert{}_{\widetilde{L} _t^{\left( \frac{1}{4}+ \frac{1}{p} \right)^{-1} } \dot{B}^{\frac 52}_{2,1 } } \\ &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac52}_{2,1,>}} +c^{- \frac{1}{2} - \frac{2}{q} + \frac{2}{p} } \left\Vert u\right\Vert{}_{\widetilde{L}^4_t \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{\widetilde{L} ^p_t \dot{B}^{\frac52}_{2,1} } , \end{aligned} \end{align} $$
as soon as
Observe then that, in order to conclude, the preceding estimate would require a stronger control on the velocity field u; even though one has that
it is unclear whether the embedding
holds or not. Accordingly, (3.17) does not seem to be useful.
Instead, we have to prove the desired estimate by ‘hand’ (that is, by cooking up a suitable interpolation argument). To that end, we first introduce the decomposition
Then, by splitting the source term
![]() $P(u\times B)$
according to the latter decomposition of u and by applying (3.16) to each Maxwell system corresponding to the source terms
$P(u\times B)$
according to the latter decomposition of u and by applying (3.16) to each Maxwell system corresponding to the source terms
![]() $P(u_\ell \times B)$
and
$P(u_\ell \times B)$
and
![]() $P(u_h\times B)$
, with different values of p, one obtains that
$P(u_h\times B)$
, with different values of p, one obtains that
 $$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{s}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0) \right\Vert{}_{\dot{B}^s_{2,1,>}} +c^{-1 + \frac{2}{p} - \frac{2}{q} } \left\Vert P\big(u_\ell \times B \big)\right\Vert{}_{\widetilde{L} _t^{p } \dot{B}^{s }_{2,1,> } } \\ & \quad+c^{ \frac{2}{p}- \frac{2}{q}} \left\Vert P\big(u _{h}\times B \big)\right\Vert{}_{\widetilde{L} _t^{ \left( \frac{1}{2} + \frac{1}{p} \right)^{-1} }\dot{B}^{s }_{2,1,> } } , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{s}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0) \right\Vert{}_{\dot{B}^s_{2,1,>}} +c^{-1 + \frac{2}{p} - \frac{2}{q} } \left\Vert P\big(u_\ell \times B \big)\right\Vert{}_{\widetilde{L} _t^{p } \dot{B}^{s }_{2,1,> } } \\ & \quad+c^{ \frac{2}{p}- \frac{2}{q}} \left\Vert P\big(u _{h}\times B \big)\right\Vert{}_{\widetilde{L} _t^{ \left( \frac{1}{2} + \frac{1}{p} \right)^{-1} }\dot{B}^{s }_{2,1,> } } , \end{aligned} \end{align} $$
for all
![]() $2\leq p\leq q$
and all
$2\leq p\leq q$
and all
![]() $s\in \mathbb {R}$
. Therefore, applying the product law estimate (2.5), we infer that
$s\in \mathbb {R}$
. Therefore, applying the product law estimate (2.5), we infer that
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{\frac 52}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0) \right\Vert{}_{\dot{B}^{\frac52}_{2,1,>}} \\ &\quad +c^{-1 + \frac{2}{p} - \frac{2}{q} } \left\Vert u_{\ell}\right\Vert{}_{\widetilde{L}^ {\infty}_t \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{\widetilde{L} ^p_t \dot{B}^{\frac 52}_{2,1} } + c^{ \frac{2}{p}- \frac{2}{q}} \left\Vert u_{h}\right\Vert{}_{\widetilde{L}^{2} _t \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{\widetilde{L} ^p_t \dot{B}^{\frac 52}_{2,1} }. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{\frac 52}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0) \right\Vert{}_{\dot{B}^{\frac52}_{2,1,>}} \\ &\quad +c^{-1 + \frac{2}{p} - \frac{2}{q} } \left\Vert u_{\ell}\right\Vert{}_{\widetilde{L}^ {\infty}_t \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{\widetilde{L} ^p_t \dot{B}^{\frac 52}_{2,1} } + c^{ \frac{2}{p}- \frac{2}{q}} \left\Vert u_{h}\right\Vert{}_{\widetilde{L}^{2} _t \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{\widetilde{L} ^p_t \dot{B}^{\frac 52}_{2,1} }. \end{aligned} \end{align*} $$
Now, observing that
and
leads to the desired control
for any
![]() $2\leq p\leq q$
. This takes care of the second bound in the statement of the lemma.
$2\leq p\leq q$
. This takes care of the second bound in the statement of the lemma.
Finally, in order for us to justify the last estimate of the lemma (which is an improvement of the preceding bound in the case
![]() $p=2$
), we need to further decompose B in the source term
$p=2$
), we need to further decompose B in the source term
![]() $ P(u_\ell \times B)$
. To that end, we write
$ P(u_\ell \times B)$
. To that end, we write
which allows us to deduce from (3.18) that
 $$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{ \frac{5}{2}}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0) \right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} +c^{- \frac{2}{q} } \left\Vert P\big(u_\ell \times B_\ell \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } \\ &\quad + c^{ - \frac{2}{q} } \left\Vert P\big(u_\ell \times B_h \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } +c^{1 - \frac{2}{q}} \left\Vert P\big(u _{h}\times B \big)\right\Vert{}_{L _t^{1} \dot{B}^{\frac{5}{2}}_{2,1 } } , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^q_t \dot{B}^{ \frac{5}{2}}_{2,1,>} } &\lesssim c^{-\frac{2}{q}}\left\Vert (E_0,B_0) \right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} +c^{- \frac{2}{q} } \left\Vert P\big(u_\ell \times B_\ell \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } \\ &\quad + c^{ - \frac{2}{q} } \left\Vert P\big(u_\ell \times B_h \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } +c^{1 - \frac{2}{q}} \left\Vert P\big(u _{h}\times B \big)\right\Vert{}_{L _t^{1} \dot{B}^{\frac{5}{2}}_{2,1 } } , \end{aligned} \end{align} $$
for all
![]() $q\geq 2$
, where we have used that
$q\geq 2$
, where we have used that
Now, observe that
which implies that
whenever
![]() $2^j\geq 2\sigma c$
. Consequently, it follows that
$2^j\geq 2\sigma c$
. Consequently, it follows that
where j is the only integer value which satisfies
![]() $\sigma c\leq 2^j<2\sigma c$
.
$\sigma c\leq 2^j<2\sigma c$
.
Hence, by applying (2.5) for classical Besov-space-valued Lebesgue spaces, we obtain that
 $$ \begin{align*} \begin{aligned} \left\Vert P\big(u_\ell \times B_\ell \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } &= \left\Vert P\big(u_\ell \times B_\ell \big)\right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } \\ &\lesssim \left\Vert u_\ell \right\Vert{}_{L _t^{\infty } \dot{B}^{\frac{3}{2}}_{2,1 } } \left\Vert B_\ell \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } \lesssim c^{\frac{1}{2}}\left\Vert u \right\Vert{}_{L _t^{\infty } \dot{H}^1 } \left\Vert B \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,< } }, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert P\big(u_\ell \times B_\ell \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } &= \left\Vert P\big(u_\ell \times B_\ell \big)\right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } \\ &\lesssim \left\Vert u_\ell \right\Vert{}_{L _t^{\infty } \dot{B}^{\frac{3}{2}}_{2,1 } } \left\Vert B_\ell \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } \lesssim c^{\frac{1}{2}}\left\Vert u \right\Vert{}_{L _t^{\infty } \dot{H}^1 } \left\Vert B \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,< } }, \end{aligned} \end{align*} $$
where we used (3.19). Similarly, we find, by employing (2.5) and (3.19), again, that
 $$ \begin{align*} \begin{aligned} \left\Vert P\big(u_\ell \times B_h \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } &\lesssim \left\Vert u_\ell \right\Vert{}_{\widetilde{L} _t^{\infty } \dot{B}^{\frac{3}{2}}_{2,1 } } \left\Vert B_h \right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } \\ &\lesssim \left\Vert u_\ell \right\Vert{}_{\widetilde{L} _t^{\infty } \dot{B}^{\frac{3}{2}}_{2,1 } } \left( \left\Vert B \right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } + \sum_{\frac{\sigma c}4< 2^j<\sigma c} 2^{\frac52j}\left\Vert \Delta_j B \right\Vert{}_{L^2_t L^2 } \right) \\ &\lesssim c^{\frac{1}{2}}\left\Vert u \right\Vert{}_{L _t^{\infty } \dot{H}^1 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert P\big(u_\ell \times B_h \big)\right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } &\lesssim \left\Vert u_\ell \right\Vert{}_{\widetilde{L} _t^{\infty } \dot{B}^{\frac{3}{2}}_{2,1 } } \left\Vert B_h \right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } \\ &\lesssim \left\Vert u_\ell \right\Vert{}_{\widetilde{L} _t^{\infty } \dot{B}^{\frac{3}{2}}_{2,1 } } \left( \left\Vert B \right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } + \sum_{\frac{\sigma c}4< 2^j<\sigma c} 2^{\frac52j}\left\Vert \Delta_j B \right\Vert{}_{L^2_t L^2 } \right) \\ &\lesssim c^{\frac{1}{2}}\left\Vert u \right\Vert{}_{L _t^{\infty } \dot{H}^1 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{aligned} \end{align*} $$
As for the last term in (3.20), applying (2.5), again, in classical Besov-space-valued Lebesgue spaces, entails that
 $$ \begin{align*} \begin{aligned} \left\Vert P\big(u _{h}\times B \big)\right\Vert{}_{L _t^{1} \dot{B}^{\frac{5}{2}}_{2,1 } } &\lesssim \left\Vert u_h \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } \\ &\lesssim c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L _t^{2 } \dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} _t^{2 }\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert P\big(u _{h}\times B \big)\right\Vert{}_{L _t^{1} \dot{B}^{\frac{5}{2}}_{2,1 } } &\lesssim \left\Vert u_h \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{3}{2}}_{2,1} } \left\Vert B \right\Vert{}_{L _t^{2 } \dot{B}^{\frac{5}{2}}_{2,1 } } \\ &\lesssim c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L _t^{2 } \dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} _t^{2 }\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{aligned} \end{align*} $$
All in all, gathering the previous estimates and incorporating them into (3.20) yields the control (3.15), which completes the proof of the lemma.
3.2.2 Control of low-frequency electromagnetic waves
It is clear from Lemmas 3.2 and 3.3 that solutions to the damped Maxwell system enjoy various types of bounds in different regions of low and high frequencies.
Here, we intend to shed light on the low-frequency control of electromagnetic fields solving (3.14). In broad terms, the low-frequency bounds on the electric field E are similar to the same bounds in the high-frequency regime. However, the low-frequency part of the magnetic field B enjoys parabolic-type estimates, which are consistent with the limiting system (MHD) as c goes to infinity. A more precise formulation of that principle is given in the next lemma.
Lemma 3.5. Let
![]() $T\in (0,\infty ]$
and
$T\in (0,\infty ]$
and
![]() $(E,B)$
be a smooth axisymmetric solution to (3.14) on
$(E,B)$
be a smooth axisymmetric solution to (3.14) on
![]() $[0,T)$
, for some initial data
$[0,T)$
, for some initial data
![]() $(E_0,B_0)$
and some axisymmetric divergence-free vector field u. Assume further that
$(E_0,B_0)$
and some axisymmetric divergence-free vector field u. Assume further that
![]() $ E$
and u are both without swirl and that B has pure swirl.
$ E$
and u are both without swirl and that B has pure swirl.
Then, for any
![]() $\alpha \in [0,1]$
,
$\alpha \in [0,1]$
,
![]() $n\in [1,\infty ]$
and
$n\in [1,\infty ]$
and
![]() $ (m,p )\in [2,\infty ]^2 $
, with
$ (m,p )\in [2,\infty ]^2 $
, with
and for any
![]() $s< \frac {5}{2}$
, with
$s< \frac {5}{2}$
, with
![]() $ s+\alpha + \frac {2}{m}>0$
, one has the following low-frequency estimates
$ s+\alpha + \frac {2}{m}>0$
, one has the following low-frequency estimates
 $$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^q_t\dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,n,<} } &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{1}{2} - \frac{2}{q}}_{2,q,<}} \\ &\quad+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^s_{2,n} }, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^q_t\dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,n,<} } &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{1}{2} - \frac{2}{q}}_{2,q,<}} \\ &\quad+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^s_{2,n} }, \end{aligned} \end{align} $$
as soon as
![]() $1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1} \leq q < \infty , $
as well as
$1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1} \leq q < \infty , $
as well as
 $$ \begin{align} \begin{aligned} \left\Vert B\right\Vert{}_{L^q_t\dot B^{s+\alpha - \frac{1}{2}+ \frac 2q-\frac 2p}_{2,1,<} } &\lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha + \frac{1}{2} -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha - \frac{1}{2} -\frac 2p}_{2,q,<}} \\ &\quad+\left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^s_{2,\infty} }, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert B\right\Vert{}_{L^q_t\dot B^{s+\alpha - \frac{1}{2}+ \frac 2q-\frac 2p}_{2,1,<} } &\lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha + \frac{1}{2} -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha - \frac{1}{2} -\frac 2p}_{2,q,<}} \\ &\quad+\left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^s_{2,\infty} }, \end{aligned} \end{align} $$
whenever
![]() $1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1} < q < \infty .$
$1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1} < q < \infty .$
Moreover, in the case where
 $$ \begin{align*}1< \left( \frac{1}{m} + \frac{1}{p}\right)^{-1}= q < \infty ,\end{align*} $$
$$ \begin{align*}1< \left( \frac{1}{m} + \frac{1}{p}\right)^{-1}= q < \infty ,\end{align*} $$
it holds that
At last, at the endpoint
![]() $s=\frac {5}{2}$
, we have
$s=\frac {5}{2}$
, we have
 $$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^q_t\dot B^{1+\alpha+ \frac{2}{m} }_{2,n,<} } &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{1+\alpha+ \frac{2}{m} }_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{2+\alpha+ \frac{2}{m} - \frac{2}{q}}_{2,q,<}} \\ &\quad+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^{\frac{5}{2}} _{2,1} }, \\ \left\Vert B\right\Vert{}_{L^q _t\dot B^{2+\alpha + \frac 2q-\frac 2p}_{2,n,<} } &\lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{3+\alpha -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{2+\alpha -\frac 2p}_{2,q,<}} +\left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^{\frac{5}{2}} _{2,1} }, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^q_t\dot B^{1+\alpha+ \frac{2}{m} }_{2,n,<} } &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{1+\alpha+ \frac{2}{m} }_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{2+\alpha+ \frac{2}{m} - \frac{2}{q}}_{2,q,<}} \\ &\quad+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^{\frac{5}{2}} _{2,1} }, \\ \left\Vert B\right\Vert{}_{L^q _t\dot B^{2+\alpha + \frac 2q-\frac 2p}_{2,n,<} } &\lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{3+\alpha -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{2+\alpha -\frac 2p}_{2,q,<}} +\left\Vert u\right\Vert{}_{L ^{m}_t\dot B^{\alpha + \frac{2}{m}}_{2,1} } \left\Vert B\right\Vert{}_{L ^{p}_t\dot B^{\frac{5}{2}} _{2,1} }, \end{aligned} \end{align} $$
as long as
![]() $1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1} \leq q < \infty .$
$1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1} \leq q < \infty .$
Proof. Similarly to [Reference Arsénio and Houamed3, Lemma 3.9], the proof hinges upon the combination of Lemmas 2.3, 3.2 and 3.3. Thus, on the one hand, applying the low-frequency estimate from Lemma 3.2, for parameter values such that
and
 $$ \begin{align*}\tilde{q}^\prime= \left( \frac{1}{m}+ \frac{1}{p}\right)^{-1},\end{align*} $$
$$ \begin{align*}\tilde{q}^\prime= \left( \frac{1}{m}+ \frac{1}{p}\right)^{-1},\end{align*} $$
yields, as soon as
![]() $1 \leq \left ( \frac {1}{m}+ \frac {1}{p}\right )^{-1} \leq q \leq \infty $
, that
$1 \leq \left ( \frac {1}{m}+ \frac {1}{p}\right )^{-1} \leq q \leq \infty $
, that
 $$ \begin{align*} \begin{aligned} 2^{j \left( s+\alpha+ \frac{2}{m}- \frac{3}{2} \right)} \left\Vert \Delta_j E\right\Vert{}_{L^q_tL^2} &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,\infty,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{1}{2} - \frac{2}{q}}_{2,\infty,<}} \\ &\quad+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert P(u\times B) \right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,\infty} \right)} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} 2^{j \left( s+\alpha+ \frac{2}{m}- \frac{3}{2} \right)} \left\Vert \Delta_j E\right\Vert{}_{L^q_tL^2} &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,\infty,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha+ \frac{2}{m}- \frac{1}{2} - \frac{2}{q}}_{2,\infty,<}} \\ &\quad+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert P(u\times B) \right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2,\infty} \right)} \end{aligned} \end{align*} $$
and
 $$ \begin{align} \begin{aligned} 2^{j \left( s+\alpha - \frac{1}{2}-\frac 2p + \frac 2q \right)} \left\Vert \Delta_j B\right\Vert{}_{L^q_tL^2} &\lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha + \frac{1}{2} -\frac 2p}_{2,\infty ,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha - \frac{1}{2} -\frac 2p}_{2,\infty ,<}}\\ &\quad+\left\Vert P(u\times B) \right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1} }\left( \dot B^{s+ \alpha + \frac{2}{m} - \frac{3}{2}}_{2,\infty }\right)} , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 2^{j \left( s+\alpha - \frac{1}{2}-\frac 2p + \frac 2q \right)} \left\Vert \Delta_j B\right\Vert{}_{L^q_tL^2} &\lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha + \frac{1}{2} -\frac 2p}_{2,\infty ,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha - \frac{1}{2} -\frac 2p}_{2,\infty ,<}}\\ &\quad+\left\Vert P(u\times B) \right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1} }\left( \dot B^{s+ \alpha + \frac{2}{m} - \frac{3}{2}}_{2,\infty }\right)} , \end{aligned} \end{align} $$
for all
![]() $j\in \mathbb {Z}$
with
$j\in \mathbb {Z}$
with
![]() $\frac {\sigma c}{2} \leq 2^j < \sigma c$
.
$\frac {\sigma c}{2} \leq 2^j < \sigma c$
.
On the other hand, employing the first and the second estimates from Lemma 3.3 entails

for any
![]() $1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1} \leq q< \infty $
and
$1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1} \leq q< \infty $
and
![]() $1\leq n\leq \infty $
, as well as
$1\leq n\leq \infty $
, as well as

for any
![]() $1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1}< q< \infty $
.
$1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1}< q< \infty $
.
All in all, by combining the preceding estimates, we arrive at the conclusion that
 $$ \begin{align*} \left\Vert E\right\Vert{}_{L^q_t\dot B^{ s+\alpha+ \frac{2}{m}- \frac{3}{2} }_{2,n,<}} &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{ s+\alpha+ \frac{2}{m}- \frac{3}{2} }_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{ s+\alpha+ \frac{2}{m}- \frac{1}{2}- \frac{2}{q} }_{2,q,<}}\\ &+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}}\dot B^{ s+\alpha+ \frac{2}{m}- \frac{3}{2} }_{2,n}}, \end{align*} $$
$$ \begin{align*} \left\Vert E\right\Vert{}_{L^q_t\dot B^{ s+\alpha+ \frac{2}{m}- \frac{3}{2} }_{2,n,<}} &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{ s+\alpha+ \frac{2}{m}- \frac{3}{2} }_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{ s+\alpha+ \frac{2}{m}- \frac{1}{2}- \frac{2}{q} }_{2,q,<}}\\ &+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}}\dot B^{ s+\alpha+ \frac{2}{m}- \frac{3}{2} }_{2,n}}, \end{align*} $$
for any
![]() $1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1}\leq q< \infty $
and
$1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1}\leq q< \infty $
and
![]() $1\leq n\leq \infty $
, as well as
$1\leq n\leq \infty $
, as well as
 $$ \begin{align*} \left\Vert B\right\Vert{}_{L^q_t\dot B^{s+\alpha - \frac{1}{2}+ \frac 2q-\frac 2p }_{2,1,<}} \lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+\frac{1}{2} -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha-\frac{1}{2}-\frac 2p}_{2,q,<}} +\left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2, \infty} \right)}, \end{align*} $$
$$ \begin{align*} \left\Vert B\right\Vert{}_{L^q_t\dot B^{s+\alpha - \frac{1}{2}+ \frac 2q-\frac 2p }_{2,1,<}} \lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+\frac{1}{2} -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha-\frac{1}{2}-\frac 2p}_{2,q,<}} +\left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2, \infty} \right)}, \end{align*} $$
for any
![]() $1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1}< q< \infty $
. Therefore, applying the product estimates from Lemma 2.3 concludes the proof of (3.21) and (3.22).
$1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1}< q< \infty $
. Therefore, applying the product estimates from Lemma 2.3 concludes the proof of (3.21) and (3.22).
As for the case
![]() $ 1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1}= q < \infty ,$
we apply the third estimate from Lemma 3.3 instead of the second one to infer that
$ 1< \left ( \frac {1}{m} + \frac {1}{p}\right )^{-1}= q < \infty ,$
we apply the third estimate from Lemma 3.3 instead of the second one to infer that

Hence, combining the latter estimate with (3.25), we obtain that
 $$ \begin{align*} \left\Vert B\right\Vert{}_{L^q_t\dot B^{s+\alpha - \frac{1}{2}+ \frac 2q-\frac 2p }_{2,n,<}} \lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+\frac{1}{2}-\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha-\frac{1}{2}-\frac 2p}_{2,q,<}} +\left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2, n} \right)}. \end{align*} $$
$$ \begin{align*} \left\Vert B\right\Vert{}_{L^q_t\dot B^{s+\alpha - \frac{1}{2}+ \frac 2q-\frac 2p }_{2,n,<}} \lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{s+\alpha+\frac{1}{2}-\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{s+\alpha-\frac{1}{2}-\frac 2p}_{2,q,<}} +\left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{s+\alpha+ \frac{2}{m}- \frac{3}{2}}_{2, n} \right)}. \end{align*} $$
Our claim (3.23) follows then by employing Lemma 2.3, again.
At last, for the endpoint case
![]() $s=\frac {5}{2}$
, we deduce from the previous cases above, for any
$s=\frac {5}{2}$
, we deduce from the previous cases above, for any
![]() $n\in [1,\infty ]$
, that
$n\in [1,\infty ]$
, that
 $$ \begin{align*} \left\Vert E\right\Vert{}_{L^q_t\dot B^{ 1+\alpha+ \frac{2}{m} }_{2,n,<}} &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{ 1+\alpha+ \frac{2}{m} }_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{ 2 + \alpha+ \frac{2}{m} - \frac{2}{q} }_{2,q,<}}\\ &+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}}\dot B^{ 1+\alpha+ \frac{2}{m} }_{2,n}}, \end{align*} $$
$$ \begin{align*} \left\Vert E\right\Vert{}_{L^q_t\dot B^{ 1+\alpha+ \frac{2}{m} }_{2,n,<}} &\lesssim c^{-\frac 2q}\left\Vert E_0\right\Vert{}_{\dot B^{ 1+\alpha+ \frac{2}{m} }_{2,n,<}} +c^{-1}\left\Vert B_0\right\Vert{}_{\dot B^{ 2 + \alpha+ \frac{2}{m} - \frac{2}{q} }_{2,q,<}}\\ &+c^{2\left(\frac 1p + \frac{1}{m}-\frac 1q\right)-1} \left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}}\dot B^{ 1+\alpha+ \frac{2}{m} }_{2,n}}, \end{align*} $$
and
 $$ \begin{align*} \left\Vert B\right\Vert{}_{L^q_t\dot B^{2+\alpha + \frac 2q-\frac 2p }_{2,n,<}} \lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{3+\alpha -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{2+\alpha -\frac 2p}_{2,q,<}} +\left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{1+\alpha+ \frac{2}{m} }_{2, n} \right)}, \end{align*} $$
$$ \begin{align*} \left\Vert B\right\Vert{}_{L^q_t\dot B^{2+\alpha + \frac 2q-\frac 2p }_{2,n,<}} \lesssim c^{-1}\left\Vert E_0\right\Vert{}_{\dot B^{3+\alpha -\frac 2p}_{2,q,<}} +\left\Vert B_0\right\Vert{}_{\dot B^{2+\alpha -\frac 2p}_{2,q,<}} +\left\Vert P(u\times B)\right\Vert{}_{L_t^{ \left(\frac{1}{m}+ \frac{1}{p} \right)^{-1}} \left( \dot B^{1+\alpha+ \frac{2}{m} }_{2, n} \right)}, \end{align*} $$
as long as
![]() $1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1} \leq q< \infty $
. Therefore, applying Lemma 2.3, again, to estimate the source term concludes the proof.
$1< \left ( \frac {1}{m} + \frac {1}{p} \right )^{-1} \leq q< \infty $
. Therefore, applying Lemma 2.3, again, to estimate the source term concludes the proof.
Remark. Observe that combining (3.15) and (3.24), with the choice of parameters
and employing the interpolation inequality
produces the useful bound
 $$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^2_t\dot{B}^{\frac{5}{2}}_{2,1} } &\lesssim c^{-1} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L ^{\infty }_t\dot{H}^1 \cap L ^{2 }_t\dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^{2 }_t\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2 _t\dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^2_t\dot{B}^{\frac{5}{2}}_{2,1} } &\lesssim c^{-1} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L ^{\infty }_t\dot{H}^1 \cap L ^{2 }_t\dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^{2 }_t\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2 _t\dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{aligned} \end{align} $$
The latter control of the electric field will come in handy, later on.
3.2.3 Persistence of regularity
Observe that the case
![]() $q=\infty $
is missing in the bounds from Lemma 3.5, above. Although it is possible to extend the results from Lemma 3.5 to cover that case (at the cost of more restrictive assumptions on the third summability index of Besov norms of the initial data), it is simpler to establish these missing bounds by utilizing an elementary energy estimate for Maxwell’s equations, which is the content of the next lemma.
$q=\infty $
is missing in the bounds from Lemma 3.5, above. Although it is possible to extend the results from Lemma 3.5 to cover that case (at the cost of more restrictive assumptions on the third summability index of Besov norms of the initial data), it is simpler to establish these missing bounds by utilizing an elementary energy estimate for Maxwell’s equations, which is the content of the next lemma.
Lemma 3.6. Let
![]() $T\in (0,\infty ]$
and
$T\in (0,\infty ]$
and
![]() $(E,B)$
be a smooth axisymmetric solution to (3.14) on
$(E,B)$
be a smooth axisymmetric solution to (3.14) on
![]() $[0,T)$
, for some divergence-free initial data
$[0,T)$
, for some divergence-free initial data
![]() $(E_0,B_0)$
and vector field u. Assume further that
$(E_0,B_0)$
and vector field u. Assume further that
![]() $ E$
and u are both without swirl and that B is a vector field with pure swirl.
$ E$
and u are both without swirl and that B is a vector field with pure swirl.
Then, for any
![]() $s \in (-\frac {3}{2}, \frac {5}{2})$
,
$s \in (-\frac {3}{2}, \frac {5}{2})$
,
![]() $\epsilon>0 $
with
$\epsilon>0 $
with
![]() $s+ \epsilon < \frac {5}{2}$
and for all
$s+ \epsilon < \frac {5}{2}$
and for all
![]() $p,q\in [2,\infty ]$
with
$p,q\in [2,\infty ]$
with
![]() $\frac {1}{2}= \frac {1}{p} + \frac {1}{q}$
, it holds that
$\frac {1}{2}= \frac {1}{p} + \frac {1}{q}$
, it holds that
on the time interval
![]() $[0,T)$
. Moreover, in the endpoint case
$[0,T)$
. Moreover, in the endpoint case
![]() $\epsilon =0$
, we have that
$\epsilon =0$
, we have that
on the time interval
![]() $[0,T)$
.
$[0,T)$
.
Proof. We begin with localizing (3.14) in frequencies by applying
![]() $\Delta _j$
, for
$\Delta _j$
, for
![]() $ j\in \mathbb {Z}$
. Then, by an
$ j\in \mathbb {Z}$
. Then, by an
![]() $L^2$
energy estimate, we find, for any
$L^2$
energy estimate, we find, for any
![]() $j\in \mathbb {Z}$
, that
$j\in \mathbb {Z}$
, that
 $$ \begin{align*} \begin{aligned} \frac{1}{2c}\left\Vert \Delta_j(E,B)(t)\right\Vert{}_{L^2}^2 + \sigma c \left\Vert \Delta_j E\right\Vert{}_{L^2_t L^2 }^2 &\leq \frac{1}{2c}\left\Vert \Delta_j(E_0,B_0)\right\Vert{}_{L^2}^2 + \sigma \left\Vert \Delta_j P(u\times B)\right\Vert{}_{L^2_t L^2 } \left\Vert \Delta_j E\right\Vert{}_{L^2_t L^2 }\\ & \leq \frac{1}{2c}\left\Vert \Delta_j(E_0,B_0)\right\Vert{}_{L^2}^2 + \frac{\sigma}{2c} \left\Vert \Delta_j P(u\times B)\right\Vert{}_{L^2_t L^2 } ^2 \\ & \quad+ \frac{\sigma c}{2} \left\Vert \Delta_j E\right\Vert{}_{L^2_t L^2 }^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{2c}\left\Vert \Delta_j(E,B)(t)\right\Vert{}_{L^2}^2 + \sigma c \left\Vert \Delta_j E\right\Vert{}_{L^2_t L^2 }^2 &\leq \frac{1}{2c}\left\Vert \Delta_j(E_0,B_0)\right\Vert{}_{L^2}^2 + \sigma \left\Vert \Delta_j P(u\times B)\right\Vert{}_{L^2_t L^2 } \left\Vert \Delta_j E\right\Vert{}_{L^2_t L^2 }\\ & \leq \frac{1}{2c}\left\Vert \Delta_j(E_0,B_0)\right\Vert{}_{L^2}^2 + \frac{\sigma}{2c} \left\Vert \Delta_j P(u\times B)\right\Vert{}_{L^2_t L^2 } ^2 \\ & \quad+ \frac{\sigma c}{2} \left\Vert \Delta_j E\right\Vert{}_{L^2_t L^2 }^2. \end{aligned} \end{align*} $$
Therefore, it follows that
for any
![]() $s \in (-\frac {3}{2}, \frac {5}{2})$
.
$s \in (-\frac {3}{2}, \frac {5}{2})$
.
Finally, we conclude the proof by employing Lemma 2.3 to control the source term in the right-hand side, above.
4 Asymptotic analysis of electromagnetic fields
In this section, we are going to make (3.11) and (3.12) precise. In particular, we are going to study the convergence
as
![]() $c\to \infty $
.
$c\to \infty $
.
For simplicity, we will drop
![]() $\sigma $
from the equations (1.1) by fixing its value
$\sigma $
from the equations (1.1) by fixing its value
![]() $\sigma =1$
, and we emphasize that the analysis we perform here holds for any non-negative value of that parameter.
$\sigma =1$
, and we emphasize that the analysis we perform here holds for any non-negative value of that parameter.
4.1 Asymptotic analysis of Ampère’s equation
From (1.1), observe, at least formally, that E vanishes when c goes to infinity. Moreover, Ampère’s equation allows us to obtain
as
![]() $ c \to \infty $
, in some suitable weak sense.
$ c \to \infty $
, in some suitable weak sense.
In the next lemma, we establish a more precise description of the preceding convergence in adequate functional spaces. This step is crucial in the proof of Theorem 1.1 and will come in handy in Section 5.
Proposition 4.1. Let
![]() $T\in (0,\infty ]$
and
$T\in (0,\infty ]$
and
![]() $(u,E,B)$
be smooth solution to the Navier–Stokes–Maxwell equations (1.1), defined on
$(u,E,B)$
be smooth solution to the Navier–Stokes–Maxwell equations (1.1), defined on
![]() $[0,T)$
, where u and E have no swirl and B has pure swirl.
$[0,T)$
, where u and E have no swirl and B has pure swirl.
Then, on the time interval
![]() $[0,T)$
, for all
$[0,T)$
, for all
![]() $s\in [0, \frac {1}{2}]$
,
$s\in [0, \frac {1}{2}]$
,
![]() $p\in [2,\infty ]$
and for any
$p\in [2,\infty ]$
and for any
![]() $c>0$
, it holds that
$c>0$
, it holds that
 $$ \begin{align*} \left\Vert \frac{1}{c}\partial_t E \right\Vert{}_{L^p_t \dot{H}^s}=\left\Vert j - \nabla \times B \right\Vert{}_{L^p_t \dot{H}^s}\lesssim c^ {-\frac{2}{p}}\left\Vert \nabla \times B_0 - j_0 \right\Vert{}_{\dot{H}^{s}} +c^ {-\frac{2}{p}}\left\Vert E_0 \right\Vert{}_{\dot{H}^{s+1}} + c^{-\left(\frac{2}{p}+1\right)} \mathcal{A}_{s} (u,E,B ), \end{align*} $$
$$ \begin{align*} \left\Vert \frac{1}{c}\partial_t E \right\Vert{}_{L^p_t \dot{H}^s}=\left\Vert j - \nabla \times B \right\Vert{}_{L^p_t \dot{H}^s}\lesssim c^ {-\frac{2}{p}}\left\Vert \nabla \times B_0 - j_0 \right\Vert{}_{\dot{H}^{s}} +c^ {-\frac{2}{p}}\left\Vert E_0 \right\Vert{}_{\dot{H}^{s+1}} + c^{-\left(\frac{2}{p}+1\right)} \mathcal{A}_{s} (u,E,B ), \end{align*} $$
where
 $$ \begin{align*} \begin{aligned} \mathcal{A}_s(u,E,B ) &\overset{\mathrm{def}}{=} \Big( \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H} ^2 } + \mathcal{E}_0 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \Big) \Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{ s+ \frac{3}{2}} } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{s+\frac{3}{2}}}\Big) \\ & \quad + \left\Vert u \right\Vert{}_{ L^ \infty _t L^2 }^{\frac{1}{2}-s} \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H} ^1 }^{s+ \frac{1}{2}} \left\Vert u \right\Vert{}_{ L^ 2_t \dot{H} ^{2 } } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H }^{\frac{3}{2} } }. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{A}_s(u,E,B ) &\overset{\mathrm{def}}{=} \Big( \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H} ^2 } + \mathcal{E}_0 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \Big) \Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{ s+ \frac{3}{2}} } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{s+\frac{3}{2}}}\Big) \\ & \quad + \left\Vert u \right\Vert{}_{ L^ \infty _t L^2 }^{\frac{1}{2}-s} \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H} ^1 }^{s+ \frac{1}{2}} \left\Vert u \right\Vert{}_{ L^ 2_t \dot{H} ^{2 } } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H }^{\frac{3}{2} } }. \end{aligned} \end{align*} $$
Proof. The proof relies on a key idea from [Reference Arsénio and Houamed4, Proposition 3.3], which we adapt to the three-dimensional setting.
We begin by applying a time derivative to Ampère’s equation to obtain the following damped wave equation for
![]() $ E$
$ E$
where we have used Faraday’s equation and Ohm’s law, as well.
Then, we localize in frequencies by applying
![]() $\Delta _j$
, for
$\Delta _j$
, for
![]() $j\in \mathbb {Z}$
, and we perform an
$j\in \mathbb {Z}$
, and we perform an
![]() $L^2$
energy estimate followed by Hölder’s inequality to find, for all
$L^2$
energy estimate followed by Hölder’s inequality to find, for all
![]() $t\in [0,T)$
, that
$t\in [0,T)$
, that
 $$ \begin{align*}\frac{1}{2} \frac{d}{dt }\Bigg( \frac{1}{c^4} \left\Vert \Delta_j \partial_t E (t) \right\Vert{}_{L^2}^2 &+\frac{1}{c^2} \left\Vert \Delta_j \nabla E(t) \right\Vert{}_{L^2}^2 \Bigg) + \frac{1}{c^2}\left\Vert \Delta_j \partial_t E(t)\right\Vert{}_{L^2}^2 \\& \qquad\qquad \leq \frac{1}{c^3} \left| \int_{\mathbb{R}^3} \Delta_j \partial_t P (u\times B) \Delta_j \partial_t E(t,x) dx \right|\\& \qquad \qquad \leq \frac{1}{c^3} \left\Vert \Delta_j \partial_t P (u\times B)(t)\right\Vert{}_{L^2} \left\Vert \Delta_j \partial_t E(t) \right\Vert{}_{L^2}\\& \qquad \qquad\leq \frac{1}{2 c^4} \left\Vert \Delta_j \partial_t P (u\times B)(t)\right\Vert{}_{L^2} ^2 + \frac{1}{2c^2} \left\Vert \Delta_j \partial_t E(t) \right\Vert{}_{L^2}^2. \end{align*} $$
$$ \begin{align*}\frac{1}{2} \frac{d}{dt }\Bigg( \frac{1}{c^4} \left\Vert \Delta_j \partial_t E (t) \right\Vert{}_{L^2}^2 &+\frac{1}{c^2} \left\Vert \Delta_j \nabla E(t) \right\Vert{}_{L^2}^2 \Bigg) + \frac{1}{c^2}\left\Vert \Delta_j \partial_t E(t)\right\Vert{}_{L^2}^2 \\& \qquad\qquad \leq \frac{1}{c^3} \left| \int_{\mathbb{R}^3} \Delta_j \partial_t P (u\times B) \Delta_j \partial_t E(t,x) dx \right|\\& \qquad \qquad \leq \frac{1}{c^3} \left\Vert \Delta_j \partial_t P (u\times B)(t)\right\Vert{}_{L^2} \left\Vert \Delta_j \partial_t E(t) \right\Vert{}_{L^2}\\& \qquad \qquad\leq \frac{1}{2 c^4} \left\Vert \Delta_j \partial_t P (u\times B)(t)\right\Vert{}_{L^2} ^2 + \frac{1}{2c^2} \left\Vert \Delta_j \partial_t E(t) \right\Vert{}_{L^2}^2. \end{align*} $$
Therefore, we find, for any
![]() $s\in \mathbb {R}$
, that
$s\in \mathbb {R}$
, that
 $$ \begin{align*} \frac{d}{dt }\left( \frac{1}{c^4} \left\Vert \partial_t E(t) \right\Vert{}_{ \dot{H}^s}^2 +\frac{1}{c^2} \left\Vert E (t) \right\Vert{}_{\dot{H}^{s+ 1}}^2 \right) + \frac{1}{c^2}\left\Vert \partial_t E(t)\right\Vert{}_{\dot{H}^s}^2 \leq \frac{1}{ c^4} \left\Vert \partial_t P (u\times B)(t)\right\Vert{}_{\dot{H}^s} ^2. \end{align*} $$
$$ \begin{align*} \frac{d}{dt }\left( \frac{1}{c^4} \left\Vert \partial_t E(t) \right\Vert{}_{ \dot{H}^s}^2 +\frac{1}{c^2} \left\Vert E (t) \right\Vert{}_{\dot{H}^{s+ 1}}^2 \right) + \frac{1}{c^2}\left\Vert \partial_t E(t)\right\Vert{}_{\dot{H}^s}^2 \leq \frac{1}{ c^4} \left\Vert \partial_t P (u\times B)(t)\right\Vert{}_{\dot{H}^s} ^2. \end{align*} $$
Consequently, employing Hölder’s inequality followed by Young’s inequality for products, we obtain that
 $$ \begin{align} \begin{aligned} \frac{1}{c^{2-\frac 2p}}\left\Vert \partial_t E \right\Vert{}_{L^p_t\dot{H}^s} &\lesssim \frac{1}{c^2}\left\Vert \partial_t E \right\Vert{}_{L^\infty_t\dot{H}^s} + \frac{1}{c }\left\Vert \partial_t E \right\Vert{}_{L^2_t\dot{H}^s} \\ &\lesssim \frac{1}{c} \Big( \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{\dot{H}^s} + \left\Vert E_0\right\Vert{}_{\dot{H}^{s+1}} \Big) + \frac{1}{ c^2} \left\Vert \partial_t P (u\times B) \right\Vert{}_{L^2_t\dot{H}^s} , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{1}{c^{2-\frac 2p}}\left\Vert \partial_t E \right\Vert{}_{L^p_t\dot{H}^s} &\lesssim \frac{1}{c^2}\left\Vert \partial_t E \right\Vert{}_{L^\infty_t\dot{H}^s} + \frac{1}{c }\left\Vert \partial_t E \right\Vert{}_{L^2_t\dot{H}^s} \\ &\lesssim \frac{1}{c} \Big( \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{\dot{H}^s} + \left\Vert E_0\right\Vert{}_{\dot{H}^{s+1}} \Big) + \frac{1}{ c^2} \left\Vert \partial_t P (u\times B) \right\Vert{}_{L^2_t\dot{H}^s} , \end{aligned} \end{align} $$
for every
![]() $p\in [2,\infty ]$
, where we have used Ampère’s equation to express the initial data of
$p\in [2,\infty ]$
, where we have used Ampère’s equation to express the initial data of
![]() $ \frac {1}{c }\partial _t E$
in terms of
$ \frac {1}{c }\partial _t E$
in terms of
![]() $B_0$
and
$B_0$
and
![]() $j_0$
.
$j_0$
.
Hence, we are now left to control
![]() $ \partial _t P (u\times B)$
. To this end, we shall first transform the time derivative into spatial derivatives by using the momentum and Faraday’s equations from (1.1). Accordingly, we obtain that
$ \partial _t P (u\times B)$
. To this end, we shall first transform the time derivative into spatial derivatives by using the momentum and Faraday’s equations from (1.1). Accordingly, we obtain that
 $$ \begin{align*}\partial_t P (u\times B) = P \left(\partial_t u \times B \right)+P \left( u \times \partial_t B \right) = - \sum_{i=1}^4 \mathcal{I}_i,\end{align*} $$
$$ \begin{align*}\partial_t P (u\times B) = P \left(\partial_t u \times B \right)+P \left( u \times \partial_t B \right) = - \sum_{i=1}^4 \mathcal{I}_i,\end{align*} $$
where
 $$ \begin{align*} \begin{aligned} \mathcal{I}_1 &\overset{\mathrm{def}}{=} P \Big(P\left( u \cdot \nabla u \right) \times B \Big), & \mathcal{I}_2 &\overset{\mathrm{def}}{=} -P \Big(\Delta u \times B \Big), \\ \mathcal{I}_3 &\overset{\mathrm{def}}{=} -P \Big(P\left( j \times B \right) \times B \Big) , & \mathcal{I}_4 &\overset{\mathrm{def}}{=} cP \Big(u \times (\nabla \times E )\Big). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{I}_1 &\overset{\mathrm{def}}{=} P \Big(P\left( u \cdot \nabla u \right) \times B \Big), & \mathcal{I}_2 &\overset{\mathrm{def}}{=} -P \Big(\Delta u \times B \Big), \\ \mathcal{I}_3 &\overset{\mathrm{def}}{=} -P \Big(P\left( j \times B \right) \times B \Big) , & \mathcal{I}_4 &\overset{\mathrm{def}}{=} cP \Big(u \times (\nabla \times E )\Big). \end{aligned} \end{align*} $$
We are now going to utilize (2.3) from Lemma 2.3 to estimate each term separately.
For
![]() $\mathcal {I}_1 $
, we find that
$\mathcal {I}_1 $
, we find that
 $$ \begin{align*} \begin{aligned} \left\Vert \mathcal{I}_1 \right\Vert{}_{L^2_t \dot{H}^{s} } &\lesssim \left\Vert u \cdot \nabla u \right\Vert{}_{ L^ 2 _t \dot{H}^ {s} } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{ \frac{3}{2} }}\\ &\lesssim \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^{s+\frac{1}{2}} } \left\Vert \nabla u \right\Vert{}_{ L^ 2_t \dot{H}^1 }\left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{ \frac{3}{2} }}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \mathcal{I}_1 \right\Vert{}_{L^2_t \dot{H}^{s} } &\lesssim \left\Vert u \cdot \nabla u \right\Vert{}_{ L^ 2 _t \dot{H}^ {s} } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{ \frac{3}{2} }}\\ &\lesssim \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^{s+\frac{1}{2}} } \left\Vert \nabla u \right\Vert{}_{ L^ 2_t \dot{H}^1 }\left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{ \frac{3}{2} }}. \end{aligned} \end{align*} $$
Therefore, as long as
![]() $ s\in [0,\frac {1}{2}] $
, we obtain, by interpolation, that
$ s\in [0,\frac {1}{2}] $
, we obtain, by interpolation, that
As for
![]() $\mathcal {I}_2$
, we employ Lemma 2.3, again, to find, for any
$\mathcal {I}_2$
, we employ Lemma 2.3, again, to find, for any
![]() $s\in [0,\frac {1}{2}]$
, that
$s\in [0,\frac {1}{2}]$
, that
 $$ \begin{align*} \begin{aligned} \left\Vert \mathcal{I}_2 \right\Vert{}_{L^2_t \dot{H}^{s} } &\lesssim \left\Vert \Delta u \right\Vert{}_{ L^ 2_t L^2 } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+\frac{3}{2}} }\\ &\lesssim \left\Vert u \right\Vert{}_{ L^ 2_t \dot{H}^2 } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+\frac{3}{2}} }. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \mathcal{I}_2 \right\Vert{}_{L^2_t \dot{H}^{s} } &\lesssim \left\Vert \Delta u \right\Vert{}_{ L^ 2_t L^2 } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+\frac{3}{2}} }\\ &\lesssim \left\Vert u \right\Vert{}_{ L^ 2_t \dot{H}^2 } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+\frac{3}{2}} }. \end{aligned} \end{align*} $$
In order to estimate
![]() $\mathcal {I}_3$
, we utilize Lemma 2.3 twice to obtain, for any
$\mathcal {I}_3$
, we utilize Lemma 2.3 twice to obtain, for any
![]() $s\in [0,\frac {1}{2}]$
, that
$s\in [0,\frac {1}{2}]$
, that
 $$ \begin{align*} \begin{aligned} \left\Vert \mathcal{I}_3 \right\Vert{}_{L^2_t \dot{H}^{s} } &\lesssim \left\Vert P \big(j \times B \big) \right\Vert{}_{ L^ 2_t L^2 } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+ \frac{3}{2}} }\\ &\lesssim \left\Vert j \right\Vert{}_{ L^ 2_t L^2 }\left\Vert B \right\Vert{}_{ L^ \infty _t \dot{H}^{\frac{3}{2} } } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+ \frac{3}{2}}}\\ &\lesssim \mathcal{E}_0 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+ \frac{3}{2}}} , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \mathcal{I}_3 \right\Vert{}_{L^2_t \dot{H}^{s} } &\lesssim \left\Vert P \big(j \times B \big) \right\Vert{}_{ L^ 2_t L^2 } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+ \frac{3}{2}} }\\ &\lesssim \left\Vert j \right\Vert{}_{ L^ 2_t L^2 }\left\Vert B \right\Vert{}_{ L^ \infty _t \dot{H}^{\frac{3}{2} } } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+ \frac{3}{2}}}\\ &\lesssim \mathcal{E}_0 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{s+ \frac{3}{2}}} , \end{aligned} \end{align*} $$
where we have used the energy estimate (3.1) in the last inequality. Finally, the control of the last term
![]() $\mathcal {I}_4$
is achieved by classical product laws, which give that
$\mathcal {I}_4$
is achieved by classical product laws, which give that
All in all, gathering the previous bounds yields
where
![]() $\mathcal {A}_s(u,E,B)$
is defined in the statement of the proposition, above. The proof is then concluded by incorporating (4.2) into (4.1).
$\mathcal {A}_s(u,E,B)$
is defined in the statement of the proposition, above. The proof is then concluded by incorporating (4.2) into (4.1).
4.2 Almost-parabolic estimates on the magnetic field
When considering the limiting system (MHD), one can show, with standard energy estimates, that the quantities
![]() $ B$
and
$ B$
and
![]() $\Gamma = \frac {B_\theta }{r}$
are globally controlled in
$\Gamma = \frac {B_\theta }{r}$
are globally controlled in
![]() $L^2_t\dot {H}^1$
and
$L^2_t\dot {H}^1$
and
![]() $L^\infty _t L^p \cap L^2_t\dot {H}^1$
, for all
$L^\infty _t L^p \cap L^2_t\dot {H}^1$
, for all
![]() $p\in [1,\infty ]$
, respectively.
$p\in [1,\infty ]$
, respectively.
Here, we establish an asymptotic version of these bounds for (1.1), thereby justifying (3.12). The key observation in the proof below consists in considering the term
![]() $ \frac {1}{c^2} \partial _{tt} \Gamma $
in the equation
$ \frac {1}{c^2} \partial _{tt} \Gamma $
in the equation
as an error, for large values of c. Accordingly, one should treat (4.3) as a parabolic equation with a vanishing source term, as
![]() $c\to \infty $
. A more precise statement of that is given in the next proposition.
$c\to \infty $
. A more precise statement of that is given in the next proposition.
Proposition 4.2. Let
![]() $T\in \mathbb {R}^+\cup \{\infty \}$
and
$T\in \mathbb {R}^+\cup \{\infty \}$
and
![]() $(u,E,B) $
be a smooth axisymmetric solution to (1.1), defined on
$(u,E,B) $
be a smooth axisymmetric solution to (1.1), defined on
![]() $[0,T)$
, where u and E have no swirl and B has pure swirl.
$[0,T)$
, where u and E have no swirl and B has pure swirl.
Then, it holds that
 $$ \begin{align} \left\Vert B\right\Vert{}_{L^2_t\dot{H}^1 }\leq \mathcal{E}_0 + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_tL^2 }. \end{align} $$
$$ \begin{align} \left\Vert B\right\Vert{}_{L^2_t\dot{H}^1 }\leq \mathcal{E}_0 + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_tL^2 }. \end{align} $$
Moreover,
![]() $\Gamma $
enjoys the bounds
$\Gamma $
enjoys the bounds
and, for any
![]() $p\in [2,\infty )$
,
$p\in [2,\infty )$
,
where all the time norms above are taken over the whole interval
![]() $[0,T).$
$[0,T).$
Remark. Due to Lemma 3.6 and Proposition 4.1, observe that the last terms in the right-hand side of (4.4) and (4.5) can be seen as errors for large values of c.
Likewise, by virtue of (3.26) and the embedding
note that (4.6) implies, for
![]() $p=3$
, that
$p=3$
, that
 $$ \begin{align*} \left\Vert \Gamma\right\Vert{}_{L^\infty_tL^3 } \lesssim \left\Vert \Gamma_0\right\Vert{}_{ L^3 } + c^{-1} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L ^{\infty }_t\dot{H}^1 \cap L ^{2 }_t\dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^{2 }_t\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2 _t\dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{align*} $$
$$ \begin{align*} \left\Vert \Gamma\right\Vert{}_{L^\infty_tL^3 } \lesssim \left\Vert \Gamma_0\right\Vert{}_{ L^3 } + c^{-1} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L ^{\infty }_t\dot{H}^1 \cap L ^{2 }_t\dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^{2 }_t\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2 _t\dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right). \end{align*} $$
This bound will come in handy, later on.
Proof. It is readily seen that, by virtue of the energy inequality (3.1), Ampère’s equation from (1.1) entails that
 $$ \begin{align*} \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 } \leq \left\Vert j\right\Vert{}_{L^2_t L^2 } + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t L^2 } \leq \mathcal{E}_0 + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t L^2 }, \end{align*} $$
$$ \begin{align*} \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 } \leq \left\Vert j\right\Vert{}_{L^2_t L^2 } + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t L^2 } \leq \mathcal{E}_0 + \left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t L^2 }, \end{align*} $$
thereby establishing (4.4).
We now focus on the proof of (4.5) and (4.6). To that end, multiplying (4.3) by
![]() $\Gamma |\Gamma |^{p-2}$
, integrating with respect to space variables and using the identities
$\Gamma |\Gamma |^{p-2}$
, integrating with respect to space variables and using the identities
 $$ \begin{align*} - \int_{\mathbb{R}^3}(\Delta \Gamma) \Gamma|\Gamma|^{p-2}dx -\int_{\mathbb{R}^3} \frac{\partial_r\Gamma}{r} \Gamma|\Gamma|^{p-2}dx =\underbrace{ \frac{4(p-1)}{p^2} \left\Vert \nabla (|\Gamma(t)|^{\frac{p}{2}})\right\Vert{}_{L^2}^2 + \frac{2\pi}{p} \int_{\mathbb{R}}|\Gamma(t,r=0,z)|^p dz}_{\overset{\mathrm{def}}{=} X_p(t)} \end{align*} $$
$$ \begin{align*} - \int_{\mathbb{R}^3}(\Delta \Gamma) \Gamma|\Gamma|^{p-2}dx -\int_{\mathbb{R}^3} \frac{\partial_r\Gamma}{r} \Gamma|\Gamma|^{p-2}dx =\underbrace{ \frac{4(p-1)}{p^2} \left\Vert \nabla (|\Gamma(t)|^{\frac{p}{2}})\right\Vert{}_{L^2}^2 + \frac{2\pi}{p} \int_{\mathbb{R}}|\Gamma(t,r=0,z)|^p dz}_{\overset{\mathrm{def}}{=} X_p(t)} \end{align*} $$
and
 $$ \begin{align*} \int_{\mathbb{R}^3}(\partial_{tt} \Gamma) \Gamma|\Gamma|^{p-2} dx=\partial_{tt} \Big(\underbrace{ \frac{ 1}{p} \left\Vert \Gamma (t)\right\Vert{}_{L^p}^p}_{\overset{\mathrm{def}}{=} Y _p(t)} \Big)- \underbrace{ (p-1) \int_{\mathbb{R}^3}|\partial_t \Gamma|^2 |\Gamma|^{p-2} dx}_{\overset{\mathrm{def}}{=} A_p(t)} , \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^3}(\partial_{tt} \Gamma) \Gamma|\Gamma|^{p-2} dx=\partial_{tt} \Big(\underbrace{ \frac{ 1}{p} \left\Vert \Gamma (t)\right\Vert{}_{L^p}^p}_{\overset{\mathrm{def}}{=} Y _p(t)} \Big)- \underbrace{ (p-1) \int_{\mathbb{R}^3}|\partial_t \Gamma|^2 |\Gamma|^{p-2} dx}_{\overset{\mathrm{def}}{=} A_p(t)} , \end{align*} $$
yields, for all
![]() $t\in [0,T)$
, that
$t\in [0,T)$
, that
Therefore, integrating in time, we obtain that
 $$ \begin{align} Y_p(t) + \int_0^t X_p(\tau) d\tau = Y_p(0) + {\frac{1}{c^2}} Y_p'(0) - {\frac{1}{c^2}}Y_p'(t) + {\frac{1}{c^2}}\int_0^t A_p(\tau)d\tau. \end{align} $$
$$ \begin{align} Y_p(t) + \int_0^t X_p(\tau) d\tau = Y_p(0) + {\frac{1}{c^2}} Y_p'(0) - {\frac{1}{c^2}}Y_p'(t) + {\frac{1}{c^2}}\int_0^t A_p(\tau)d\tau. \end{align} $$
Now, we need to take care of the term
![]() $ - \frac {1}{c^2}Y_p'(t)$
, above. To that end, observing that (4.7) can be rewritten as
$ - \frac {1}{c^2}Y_p'(t)$
, above. To that end, observing that (4.7) can be rewritten as
which we then integrate with respect to the time variable, we find that
 $$ \begin{align*} -\frac{1}{c^2} Y^{\prime}_p(t) = -\frac 1{c^2}Y_p'(0) e^{-c^2t} + \int_0^t e^{-c^2(t-\tau)} \Big(X_p(\tau)-\frac{1}{c^2}A_p(\tau) \Big) d\tau. \end{align*} $$
$$ \begin{align*} -\frac{1}{c^2} Y^{\prime}_p(t) = -\frac 1{c^2}Y_p'(0) e^{-c^2t} + \int_0^t e^{-c^2(t-\tau)} \Big(X_p(\tau)-\frac{1}{c^2}A_p(\tau) \Big) d\tau. \end{align*} $$
Hence, plugging the latter identity into (4.8) yields that
 $$ \begin{align} \begin{aligned} Y_p(t) + \int_0^t X_p(\tau) d\tau &= Y_p(0) + \frac{1-e^{-c^2t}}{c^2} Y_p'(0) + \int_0^t e^{-c^2(t-\tau)} X_p(\tau) d\tau \\ & \quad+\frac{1}{c^2} \int_0^t A_p(\tau)d\tau - \frac{1}{c^2}\int_0^t e^{-c^2(t-\tau)}A_p(\tau) d\tau. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} Y_p(t) + \int_0^t X_p(\tau) d\tau &= Y_p(0) + \frac{1-e^{-c^2t}}{c^2} Y_p'(0) + \int_0^t e^{-c^2(t-\tau)} X_p(\tau) d\tau \\ & \quad+\frac{1}{c^2} \int_0^t A_p(\tau)d\tau - \frac{1}{c^2}\int_0^t e^{-c^2(t-\tau)}A_p(\tau) d\tau. \end{aligned} \end{align} $$
Next, utilizing Faraday’s equation from (1.1), we write, for any
![]() $t\in (0,T)$
, that
$t\in (0,T)$
, that
 $$ \begin{align} \left(\partial_t\Gamma \right) = \left( \frac{\partial_tB }{r} \right) \cdot e_\theta = -c \left( \frac{ \nabla \times E }{r} \right) \cdot e_\theta, \end{align} $$
$$ \begin{align} \left(\partial_t\Gamma \right) = \left( \frac{\partial_tB }{r} \right) \cdot e_\theta = -c \left( \frac{ \nabla \times E }{r} \right) \cdot e_\theta, \end{align} $$
whereby
 $$ \begin{align*}\left(\partial_t\Gamma \right)|_{t=0} = -c \left( \frac{ \nabla \times E_0 }{r} \right) \cdot e_\theta.\end{align*} $$
$$ \begin{align*}\left(\partial_t\Gamma \right)|_{t=0} = -c \left( \frac{ \nabla \times E_0 }{r} \right) \cdot e_\theta.\end{align*} $$
Accordingly, it follows that
 $$ \begin{align*} \begin{aligned} \frac{1}{c^2} |Y^{\prime}_p(0)|=\frac{1}{c^2}\left| \Big( \int_{\mathbb{R}^3} (\partial_t \Gamma)\Gamma |\Gamma|^{p-2}dx\Big)_{|_{t=0}} \right| &\leq\frac{1}{c } \int_{\mathbb{R}^3} \frac{|\nabla \times E_0|}{r} |\Gamma_0|^{p-1}dx \\ & \quad \leq \frac{1}{c} \left\Vert \frac{ \nabla \times E_0}{r}\right\Vert{}_{L^p}\left\Vert \Gamma_0\right\Vert{}_{L^{p}}^{p-1}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{c^2} |Y^{\prime}_p(0)|=\frac{1}{c^2}\left| \Big( \int_{\mathbb{R}^3} (\partial_t \Gamma)\Gamma |\Gamma|^{p-2}dx\Big)_{|_{t=0}} \right| &\leq\frac{1}{c } \int_{\mathbb{R}^3} \frac{|\nabla \times E_0|}{r} |\Gamma_0|^{p-1}dx \\ & \quad \leq \frac{1}{c} \left\Vert \frac{ \nabla \times E_0}{r}\right\Vert{}_{L^p}\left\Vert \Gamma_0\right\Vert{}_{L^{p}}^{p-1}. \end{aligned} \end{align*} $$
Thus, recalling the inequality
for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\alpha \in (1,\infty )$
, where
$\alpha \in (1,\infty )$
, where
![]() $\alpha ^{\prime }$
denotes the conjugate of
$\alpha ^{\prime }$
denotes the conjugate of
![]() $\alpha $
, and by virtue of Lemma 2.2, we end up with
$\alpha $
, and by virtue of Lemma 2.2, we end up with
 $$ \begin{align} \begin{aligned} \frac{1}{c^2} |Y^{\prime}_p(0)| & \leq \left( \left( \frac{1}{c } \left\Vert \frac{ \nabla \times E_0}{r}\right\Vert{}_{L^p}\right)^{\frac{1}{p}} \left\Vert \Gamma_0\right\Vert{}_{L^{p}}^{\frac{1}{p^\prime} } \right)^ p \\ & \leq \left( \frac{1}{pc} \left\Vert \frac{ \nabla \times E_0}{r}\right\Vert{}_{L^p} + \frac{1}{p^{\prime}} \left\Vert \Gamma_0\right\Vert{}_{L^{p}} \right)^ p\\ & \lesssim \Big( \frac{1}{c} \left\Vert E_0\right\Vert{}_{\dot{W}^{2,p}} + \left\Vert \Gamma_0\right\Vert{}_{L^{p}} \Big)^ p. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{1}{c^2} |Y^{\prime}_p(0)| & \leq \left( \left( \frac{1}{c } \left\Vert \frac{ \nabla \times E_0}{r}\right\Vert{}_{L^p}\right)^{\frac{1}{p}} \left\Vert \Gamma_0\right\Vert{}_{L^{p}}^{\frac{1}{p^\prime} } \right)^ p \\ & \leq \left( \frac{1}{pc} \left\Vert \frac{ \nabla \times E_0}{r}\right\Vert{}_{L^p} + \frac{1}{p^{\prime}} \left\Vert \Gamma_0\right\Vert{}_{L^{p}} \right)^ p\\ & \lesssim \Big( \frac{1}{c} \left\Vert E_0\right\Vert{}_{\dot{W}^{2,p}} + \left\Vert \Gamma_0\right\Vert{}_{L^{p}} \Big)^ p. \end{aligned} \end{align} $$
Consequently, for
![]() $p=2$
, we find that (4.9) entails that
$p=2$
, we find that (4.9) entails that
and
Finally, employing (4.10) and Lemma 2.2 in the last bound leads to (4.5), and (4.6) in the case
![]() $p=2$
.
$p=2$
.
Then, in order to deal with the range
![]() $p\in (2,\infty )$
, we deduce from (4.9) that
$p\in (2,\infty )$
, we deduce from (4.9) that
 $$ \begin{align*} \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^p }^p \lesssim \left\Vert \Gamma_0\right\Vert{}_{L^\infty_t(L^p)}^p + \frac{1}{c^2} |Y^{\prime}_p(0)| + \frac{1}{c^2} \int_0^t \left\Vert \partial_t\Gamma(\tau)\right\Vert{}_{L^p}^2 \left\Vert \Gamma(\tau )\right\Vert{}_{L^p}^{p-2}d\tau. \end{align*} $$
$$ \begin{align*} \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^p }^p \lesssim \left\Vert \Gamma_0\right\Vert{}_{L^\infty_t(L^p)}^p + \frac{1}{c^2} |Y^{\prime}_p(0)| + \frac{1}{c^2} \int_0^t \left\Vert \partial_t\Gamma(\tau)\right\Vert{}_{L^p}^2 \left\Vert \Gamma(\tau )\right\Vert{}_{L^p}^{p-2}d\tau. \end{align*} $$
Therefore, employing (4.12) to control
![]() $Y^{\prime }_p(0) $
yields
$Y^{\prime }_p(0) $
yields
After that, we utilize (4.11) to obtain that
At last, by using (4.10) and Lemma 2.2, again, we arrive at the desired bound (4.6). This completes the proof of the proposition.
5 Closing the estimates and proof of Theorem 1.1
We are now ready to establish the final global bounds that lead to the existence of global solutions of the Navier–Stokes–Maxwell equations (1.1). This is going to be done, first, by gathering all the estimates from the previous sections to produce a nonlinear energy estimate. Then, under adequate assumptions in the regime
![]() $c\to \infty $
, the nonlinear energy bound will allow us to deduce the desired global control, uniformly with respect to the speed of light.
$c\to \infty $
, the nonlinear energy bound will allow us to deduce the desired global control, uniformly with respect to the speed of light.
Throughout this section, for the sake of simplicity and clarity, the subscript ‘t’ that appears in time-Lebesgue spaces
![]() $L^p_t$
should be understood as the endpoint of the time interval; that is, for example, we will be using the notation
$L^p_t$
should be understood as the endpoint of the time interval; that is, for example, we will be using the notation
Accordingly, all the quantities involving time-Lebesgue norms are continuous functions on the real half-line
![]() $[0,\infty )$
, for all
$[0,\infty )$
, for all
![]() $p\in [1,\infty ]$
.
$p\in [1,\infty ]$
.
5.1 Approximation scheme and compactness
Solutions of (1.1) will be constructed by a standard compactness method based on the smooth approximation of solutions. Although this is now classical in the literature, we briefly recall here the principle ideas in that method. This will allow us to justify all the formal computations in the derivation of our global a priori bounds, below.
We follow the approach laid out in [Reference Arsénio and Houamed3, Section 3.1], for instance. Thus, we begin with approximating the Navier–Stokes–Maxwell equations (1.1) by a new system of equations which has a unique smooth solution.
An admissible approximation should preserve the structures satisfied by the original system such as, in our case, the energy inequality (1.2) and the axisymmetric properties. A possible choice of that approximation is given, for
![]() $n\in \mathbb {N}$
, by
$n\in \mathbb {N}$
, by
 $$ \begin{align*} \begin{cases} \begin{aligned} & \partial_t u_n +(S_nu_n) \cdot\nabla u _n = \nu \Delta u_n- \nabla p_n + j_n \times B_n, &\operatorname{div} u_n =0,& \\ & \frac{1}{c} \partial_t E_n - \nabla \times B_n =-(S_n j_n) , &\operatorname{div} E_n = 0,& \\ & \frac{1}{c} \partial_t B_n + \nabla \times E_n = 0 , &\operatorname{div} B_n = 0, & \\ & j_n= \sigma \big( ce:n + S_nP(u_n \times B_n)\big), &\operatorname{div} j_n = 0,& \end{aligned} \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \begin{aligned} & \partial_t u_n +(S_nu_n) \cdot\nabla u _n = \nu \Delta u_n- \nabla p_n + j_n \times B_n, &\operatorname{div} u_n =0,& \\ & \frac{1}{c} \partial_t E_n - \nabla \times B_n =-(S_n j_n) , &\operatorname{div} E_n = 0,& \\ & \frac{1}{c} \partial_t B_n + \nabla \times E_n = 0 , &\operatorname{div} B_n = 0, & \\ & j_n= \sigma \big( ce:n + S_nP(u_n \times B_n)\big), &\operatorname{div} j_n = 0,& \end{aligned} \end{cases} \end{align*} $$
supplemented with the initial data
![]() $ (u_n,E_n,B_n)|_{t=0} \overset {\mathrm {def}}{=} S_n( u_0,E_0,B_0) $
, where
$ (u_n,E_n,B_n)|_{t=0} \overset {\mathrm {def}}{=} S_n( u_0,E_0,B_0) $
, where
![]() $S_n$
is a radial cutoff Fourier multiplier that restricts the frequencies to the set
$S_n$
is a radial cutoff Fourier multiplier that restricts the frequencies to the set
![]() $\{|\xi | \leq 2^n \}$
and converges to the identity as
$\{|\xi | \leq 2^n \}$
and converges to the identity as
![]() $n\to \infty $
.
$n\to \infty $
.
Showing that the approximate system, for any fixed
![]() $n\in \mathbb {N}$
, has a unique global solution is a routine procedure based on standard methods. Moreover, one can show that the corresponding solutions are smooth in time and space and satisfy the energy inequality
$n\in \mathbb {N}$
, has a unique global solution is a routine procedure based on standard methods. Moreover, one can show that the corresponding solutions are smooth in time and space and satisfy the energy inequality
 $$ \begin{align*} \left\Vert \left( u_n , E_n ,B_n\right)(t) \right\Vert{}_{L^2}^2+2\nu\int_0^t \left\Vert \nabla u_n(\tau)\right\Vert{}_{L^2}^2 d\tau +\frac{2}{\sigma}\int_0^t \left\Vert j_n(\tau)\right\Vert{}_{L^2}^2 d\tau = \left\Vert S_n( u_0,E_0,B_0)\right\Vert{}_{L^2}^2 \leq \mathcal{E}_0^2, \end{align*} $$
$$ \begin{align*} \left\Vert \left( u_n , E_n ,B_n\right)(t) \right\Vert{}_{L^2}^2+2\nu\int_0^t \left\Vert \nabla u_n(\tau)\right\Vert{}_{L^2}^2 d\tau +\frac{2}{\sigma}\int_0^t \left\Vert j_n(\tau)\right\Vert{}_{L^2}^2 d\tau = \left\Vert S_n( u_0,E_0,B_0)\right\Vert{}_{L^2}^2 \leq \mathcal{E}_0^2, \end{align*} $$
where we recall that
If, furthermore, the initial data are assumed to be axisymmetric, and the cutoff operator
![]() $S_n$
does not alter that structure (which is the case when
$S_n$
does not alter that structure (which is the case when
![]() $S_n$
can be characterized as a convolution with a radial function), then the approximate smooth solution remains axisymmetric for all times.
$S_n$
can be characterized as a convolution with a radial function), then the approximate smooth solution remains axisymmetric for all times.
Noting, once again, that the energy inequality above is not sufficient to ensure the stability, as
![]() $n\to \infty $
, of the nonlinear term
$n\to \infty $
, of the nonlinear term
our strategy thus consists in looking for better bounds in higher regularity spaces, uniformly with respect to the regularizing parameter n. In particular, we will obtain new bounds that will allow us to establish the strong relative compactness of all vector fields
![]() $u_n$
,
$u_n$
,
![]() $E_n$
,
$E_n$
,
![]() $B_n$
and
$B_n$
and
![]() $j_n$
in
$j_n$
in
![]() $L^2_{\text {loc},t,x}$
and, then, conclude that the approximate solutions converge, as
$L^2_{\text {loc},t,x}$
and, then, conclude that the approximate solutions converge, as
![]() $n\to \infty $
, to an exact solution of (1.1).
$n\to \infty $
, to an exact solution of (1.1).
With such strong bounds, the full justification of the stability of the approximate system follows from standard compactness arguments, which we will therefore omit. We refer to [Reference Arsénio and Houamed3] for some details on similar arguments applied to construction of global solutions of the Euler–Maxwell system in two dimensions of space.
Normally, we should prove the a priori estimates on the approximate system above. However, as usual, since the approximate system enjoys the same structure as the original one, we will, from now on, assume that the solutions to (1.1) are smooth, and we will perform all estimates directly on (1.1).
5.2 Weak–strong uniqueness
The functional spaces used in Theorem 1.1 are sufficient to prove uniqueness results for (1.1). Although this is not hard to show, we choose to provide in the following proposition a weak–strong stability result with a self-contained proof that covers the uniqueness of solutions claimed in Theorem 1.1. See also [Reference Arsénio and Saint-Raymond6, Proposition 3.11] for a similar weak–strong principle for the same system.
Proposition 5.1 (
 $L^2$
weak–strong stability).
$L^2$
weak–strong stability).
Let
![]() $c>0$
and
$c>0$
and
![]() $(u_i,E_i,B_i)_{i\in \{1,2\}}$
be two weak solutions of (1.1) associated with the same initial data and satisfying the energy inequality (1.2). Assume moreover that
$(u_i,E_i,B_i)_{i\in \{1,2\}}$
be two weak solutions of (1.1) associated with the same initial data and satisfying the energy inequality (1.2). Assume moreover that
Then, the two solutions are equal.
Proof. We define the difference of the two solutions by
and we compute, for any
![]() $t>0$
, that
$t>0$
, that
 $$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^3} & \left(u_1\cdot u_2+E_1\cdot E_2+ B_1\cdot B_2\right)(t)dx +\frac 2\sigma \int_0^t\int_{\mathbb{R}^3}j_1\cdot j_2dxd\tau + 2\nu \int_0^t \int_{\mathbb{R}^3}\nabla u_1 \cdot \nabla u_2dxd\tau \\ & =-\int_0^t\int_{\mathbb{R}^3} (j_2\times \widetilde{B})\cdot \widetilde{u} dxd\tau +\int_0^t\int_{\mathbb{R}^3} (\widetilde{j}\times \widetilde{B})\cdot u_2 dxd \tau - \int_0^t\int_{\mathbb{R}^3} \left(u_2\otimes \widetilde{u}\right):\nabla \widetilde{u} dx d\tau. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^3} & \left(u_1\cdot u_2+E_1\cdot E_2+ B_1\cdot B_2\right)(t)dx +\frac 2\sigma \int_0^t\int_{\mathbb{R}^3}j_1\cdot j_2dxd\tau + 2\nu \int_0^t \int_{\mathbb{R}^3}\nabla u_1 \cdot \nabla u_2dxd\tau \\ & =-\int_0^t\int_{\mathbb{R}^3} (j_2\times \widetilde{B})\cdot \widetilde{u} dxd\tau +\int_0^t\int_{\mathbb{R}^3} (\widetilde{j}\times \widetilde{B})\cdot u_2 dxd \tau - \int_0^t\int_{\mathbb{R}^3} \left(u_2\otimes \widetilde{u}\right):\nabla \widetilde{u} dx d\tau. \end{aligned} \end{align*} $$
Note that the computations above can be rigorously justified by smoothing out the two solutions and following the proof of [Reference Gallagher and Planchon18, Lemma 2.1], for instance.
Therefore, setting
and making use of the energy inequality (1.2), which is assumed to be satisfied by both solutions, we obtain, for any
![]() $\varepsilon>0$
, that
$\varepsilon>0$
, that
 $$ \begin{align*} \begin{aligned} F(t) +\nu \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{1}{\sigma}\|\widetilde{j} \|_{L^2_{t,x}}^2 &\leq \int_0^t \left\Vert j_2(\tau)\right\Vert{}_{L^3} \|\widetilde{B}(\tau)\|_{L^2} \left\Vert \widetilde{u}(\tau)\right\Vert{}_{L^6} d\tau \\ &\quad + \int_0^t \left\Vert u_2(\tau)\right\Vert{}_{L^\infty} \left( \|\widetilde{j}(\tau)\|_{L^2} \|\widetilde{B}(\tau)\|_{L^2} + \left\Vert \widetilde{u}(\tau)\right\Vert{}_{L^2} \left\Vert \nabla\widetilde{ u}(\tau)\right\Vert{}_{L^2} \right) d\tau\\ &\leq \varepsilon + \frac{\nu}{4} \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{C}{\nu} \int_0^t \left\Vert j_2(\tau)\right\Vert{}_{L^3}^2 \|\widetilde{B}(\tau)\|_{L^2}^2 d\tau \\ & \quad + \frac{\nu}{4} \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{1}{\nu} \int_0^t \left\Vert u_2(\tau)\right\Vert{}_{L^\infty}^2 \|\widetilde{u}(\tau)\|_{L^2}^2 d\tau\\ &\quad + \frac{1}{2\sigma} \|\widetilde{j} \|_{L^2_{t,x}}^2+ \frac{\sigma}{2}\int_0^t \|u_2(\tau)\|_{L^\infty}^2 \|\widetilde{B}(\tau)\|_{L^2}^2 d\tau, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} F(t) +\nu \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{1}{\sigma}\|\widetilde{j} \|_{L^2_{t,x}}^2 &\leq \int_0^t \left\Vert j_2(\tau)\right\Vert{}_{L^3} \|\widetilde{B}(\tau)\|_{L^2} \left\Vert \widetilde{u}(\tau)\right\Vert{}_{L^6} d\tau \\ &\quad + \int_0^t \left\Vert u_2(\tau)\right\Vert{}_{L^\infty} \left( \|\widetilde{j}(\tau)\|_{L^2} \|\widetilde{B}(\tau)\|_{L^2} + \left\Vert \widetilde{u}(\tau)\right\Vert{}_{L^2} \left\Vert \nabla\widetilde{ u}(\tau)\right\Vert{}_{L^2} \right) d\tau\\ &\leq \varepsilon + \frac{\nu}{4} \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{C}{\nu} \int_0^t \left\Vert j_2(\tau)\right\Vert{}_{L^3}^2 \|\widetilde{B}(\tau)\|_{L^2}^2 d\tau \\ & \quad + \frac{\nu}{4} \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{1}{\nu} \int_0^t \left\Vert u_2(\tau)\right\Vert{}_{L^\infty}^2 \|\widetilde{u}(\tau)\|_{L^2}^2 d\tau\\ &\quad + \frac{1}{2\sigma} \|\widetilde{j} \|_{L^2_{t,x}}^2+ \frac{\sigma}{2}\int_0^t \|u_2(\tau)\|_{L^\infty}^2 \|\widetilde{B}(\tau)\|_{L^2}^2 d\tau, \end{aligned} \end{align*} $$
where
![]() $C>0$
is the constant from the embedding
$C>0$
is the constant from the embedding
![]() $\dot {H}^1\hookrightarrow L^6(\mathbb {R}^3).$
$\dot {H}^1\hookrightarrow L^6(\mathbb {R}^3).$
Hence, by further simplifying the preceding bound and applying Grönwall’s lemma, we arrive at the conclusion that
 $$ \begin{align} \begin{aligned} F(t) &+\frac{\nu}{2} \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{1}{2\sigma}\|\widetilde{j} \|_{L^2_{t,x}}^2 \leq \varepsilon \exp\left( C_{\nu,\sigma} \int_0^t \left(\|j_2(\tau) \|_{L^3}^2 + \|u_2(\tau) \|_{L^\infty}^2\right) d\tau \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} F(t) &+\frac{\nu}{2} \left\Vert \nabla \widetilde{u} \right\Vert{}_{L^2_{t,x}}^2 + \frac{1}{2\sigma}\|\widetilde{j} \|_{L^2_{t,x}}^2 \leq \varepsilon \exp\left( C_{\nu,\sigma} \int_0^t \left(\|j_2(\tau) \|_{L^3}^2 + \|u_2(\tau) \|_{L^\infty}^2\right) d\tau \right), \end{aligned} \end{align} $$
for any
![]() $\varepsilon>0$
and some constant
$\varepsilon>0$
and some constant
![]() $C_{\nu ,\sigma }>0$
.
$C_{\nu ,\sigma }>0$
.
Accordingly, by further exploiting Ohm’s law
and employing the additional bounds on the second solution
![]() $(u_2,E_2,B_2)$
, it is readily seen then that the right-hand side in (5.1) is finite and vanishes as
$(u_2,E_2,B_2)$
, it is readily seen then that the right-hand side in (5.1) is finite and vanishes as
![]() $\varepsilon \to 0$
. This concludes the proof of the weak–strong uniqueness.
$\varepsilon \to 0$
. This concludes the proof of the weak–strong uniqueness.
5.3 Existence of global solutions
Here, we prove existence of global solutions of (1.1), as it is claimed in Theorem 1.1. In view of the arguments laid out in Section 5.1, above, this proof is reduced to establishing adequate a priori global estimates for (1.1).
The proof is split into two parts. The first part is devoted to the case of rough profiles
uniformly in
![]() $c>0$
. This means that the
$c>0$
. This means that the
![]() $\dot {B}^{\frac {5}{2}}_{2,1} $
norm of the initial data is allowed to blow up, as
$\dot {B}^{\frac {5}{2}}_{2,1} $
norm of the initial data is allowed to blow up, as
![]() $c\to \infty ,$
with a rate which is at most of order c.
$c\to \infty ,$
with a rate which is at most of order c.
In the second part of the proof below, we deal with the case of regular profiles; that is,
uniformly with respect to
![]() $c>0$
.
$c>0$
.
5.3.1 Rough profiles
Here, we assume that
uniformly with respect to
![]() $c\in (0,\infty )$
, meaning that
$c\in (0,\infty )$
, meaning that
![]() $ (u_0^c,E_0^c,B_0^c) $
can be unbounded in
$ (u_0^c,E_0^c,B_0^c) $
can be unbounded in
![]() $ \dot {B}^{\frac {5}{2}}_{2,1}$
as
$ \dot {B}^{\frac {5}{2}}_{2,1}$
as
![]() $c\rightarrow \infty .$
$c\rightarrow \infty .$
Control of the velocity field. The principal control of velocity fields is obtained in Proposition 4.2. For convenience, we rewrite here its main estimate:
 $$ \begin{align} \begin{aligned} & \left\Vert (\omega, \Omega)\right\Vert{}_{L^\infty_t L^2 \cap L^2_t \dot{H}^1 }\\ & \quad\quad \lesssim \left(\left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2} +\left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_t H^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) e^{ C\mathcal{E}^2_0 }. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \left\Vert (\omega, \Omega)\right\Vert{}_{L^\infty_t L^2 \cap L^2_t \dot{H}^1 }\\ & \quad\quad \lesssim \left(\left\Vert (\omega_0,\Omega_0)\right\Vert{}_{L^2} +\left\Vert \frac{1}{c}\partial_t E\right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}} } \left\Vert B\right\Vert{}_{L^\infty_t H^2 } + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 }\left\Vert (B,\Gamma)\right\Vert{}_{L^2_t \dot{H}^1 } \right) e^{ C\mathcal{E}^2_0 }. \end{aligned} \end{align} $$
We also notice, due to the energy inequality (1.2), that
Moreover, the standard embeddings
will be used regularly without explicit reference. The justification of the first inequality above is done by applying an abstract interpolation argument, whereas the second one straightforwardly follows from the Biot–Savart law.
Control of high electromagnetic frequencies. The control of high electromagnetic frequencies is given by Lemma 3.4. More precisely, we obtain from (3.15), with the specific values
![]() $q\in \{2,\infty \}$
, that
$q\in \{2,\infty \}$
, that
 $$ \begin{align} \begin{aligned} c^{-1} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^\infty _t \dot{B}^{\frac{5}{2} }_{2,1,>} } &+ \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^2 _t \dot{B}^{\frac{5}{2} }_{2,1,>} } \\ &\lesssim c^{-1 }\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} \\ & \; +c^{- \frac{1}{2} }\left\Vert u\right\Vert{}_{L^\infty _t \dot{H} ^1 \cap L^2 _t \dot{H} ^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^2_t\dot{B}^{ \frac{5}{2}}_{2,1,>} } + \left\Vert B \right\Vert{}_{L ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,<} } \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} c^{-1} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^\infty _t \dot{B}^{\frac{5}{2} }_{2,1,>} } &+ \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^2 _t \dot{B}^{\frac{5}{2} }_{2,1,>} } \\ &\lesssim c^{-1 }\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} \\ & \; +c^{- \frac{1}{2} }\left\Vert u\right\Vert{}_{L^\infty _t \dot{H} ^1 \cap L^2 _t \dot{H} ^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^2_t\dot{B}^{ \frac{5}{2}}_{2,1,>} } + \left\Vert B \right\Vert{}_{L ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,<} } \right). \end{aligned} \end{align} $$
Control of low electromagnetic frequencies – Part A. The control of low electromagnetic frequencies relies on Lemma 3.5, above. Specifically, applying (3.23) with the values
![]() $q =2$
,
$q =2$
,
![]() $ p=m=4$
,
$ p=m=4$
,
![]() $ \alpha =1$
and
$ \alpha =1$
and
![]() $s=\frac {3}{2}$
yields that
$s=\frac {3}{2}$
yields that
Likewise, employing (3.23), again, with the values
![]() $p= 2 $
and
$p= 2 $
and
![]() $s=2$
entails that
$s=2$
entails that
Actually, since (3.14) is a linear system, by splitting high and low frequencies of B in the source term
![]() $P(u\times B)$
, one can straightforwardly adapt the proofs of the preceding estimates to obtain the more useful control
$P(u\times B)$
, one can straightforwardly adapt the proofs of the preceding estimates to obtain the more useful control
 $$ \begin{align} \begin{aligned} \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{3}{2}}_{2,2,<}}\\ & \quad +\left\Vert u\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1}} \left(\left\Vert \mathrm{1}_{ \{|D|< \frac{\sigma c}{2} \}} B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1} } + \left\Vert \mathrm{1}_{ \{|D|\geq \frac{\sigma c}{2} \}} B\right\Vert{}_{L_t^{2}\dot B^{2}_{2,1} } \right) \\ & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}} } \\ & \quad +\left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left(\left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<}} + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{3}{2}}_{2,2,<}}\\ & \quad +\left\Vert u\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1}} \left(\left\Vert \mathrm{1}_{ \{|D|< \frac{\sigma c}{2} \}} B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1} } + \left\Vert \mathrm{1}_{ \{|D|\geq \frac{\sigma c}{2} \}} B\right\Vert{}_{L_t^{2}\dot B^{2}_{2,1} } \right) \\ & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}} } \\ & \quad +\left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left(\left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<}} + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right). \end{aligned} \end{align} $$
Before we proceed with the proof, let us establish the energy estimate for
![]() $(E,B)$
in Sobolev spaces, which will then be combined with the preceding estimate to complete the proof of the low-frequency bounds on electromagnetic fields.
$(E,B)$
in Sobolev spaces, which will then be combined with the preceding estimate to complete the proof of the low-frequency bounds on electromagnetic fields.
Energy estimate for electromagnetic fields. Applying Lemma 3.6 with the values
![]() $s=\frac {3}{2}$
and
$s=\frac {3}{2}$
and
![]() $(p,q,\varepsilon )= (2,\infty ,\frac {1}{2})$
, and then with the values
$(p,q,\varepsilon )= (2,\infty ,\frac {1}{2})$
, and then with the values
![]() $(p,q)= (4,4)$
at the endpoint
$(p,q)= (4,4)$
at the endpoint
![]() $\varepsilon =0$
, we find that
$\varepsilon =0$
, we find that
and
In fact, by spliting high and low frequencies of B in the right-hand side of the preceding estimates, it is possible to adapt their proofs to obtain the following more useful bound
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}}} + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{ \dot{H}^{\frac{3}{2}}} \\ & \quad + \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L^2_t \dot{H}^2 } \left( \left\Vert \mathrm{1}_{ \{|D|< \frac{\sigma c}{2} \}} B\right\Vert{}_{ L^4_t \dot{H}^{\frac{3}{2}} } + \left\Vert \mathrm{1}_{ \{|D| \geq \frac{\sigma c}{2} \}} B\right\Vert{}_{ L^2_t \dot{H}^ 2 } \right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}}} + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{ \dot{H}^{\frac{3}{2}}} \\ & \quad + \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L^2_t \dot{H}^2 } \left( \left\Vert \mathrm{1}_{ \{|D|< \frac{\sigma c}{2} \}} B\right\Vert{}_{ L^4_t \dot{H}^{\frac{3}{2}} } + \left\Vert \mathrm{1}_{ \{|D| \geq \frac{\sigma c}{2} \}} B\right\Vert{}_{ L^2_t \dot{H}^ 2 } \right). \end{aligned} \end{align*} $$
Therefore, similarly to (5.5), we infer that
 $$ \begin{align} \begin{aligned} &\left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} \\ &\qquad\qquad \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}}} \\ &\qquad\qquad\quad+ \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left(\left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<}} + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} \\ &\qquad\qquad \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}}} \\ &\qquad\qquad\quad+ \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left(\left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<}} + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + c^{ -\frac{1}{2}} \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right). \end{aligned} \end{align} $$
Control of low electromagnetic frequencies – Part B. Now, we carry on with the estimates of low frequencies of electromagnetic fields by first combining (5.5) and (5.6) to find that
 $$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}}}+ c^{ -\frac{1}{2}} \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}}\left( \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right) \\ & \quad +\left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}}}+ c^{ -\frac{1}{2}} \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}}\left( \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right) \\ & \quad +\left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<}}. \end{aligned} \end{align} $$
Note that one cannot expect to observe any decay, with respect to c, in the nonlinear term
Accordingly, at this stage, the bound (5.7) does not seem to be helpful in obtaining a global control without additional conditions on the size of the initial data.
Nevertheless, our key observation here is that the space
![]() $L_t^{4}\dot B^{\frac {3}{2}}_{2,1} $
can be obtained by interpolating
$L_t^{4}\dot B^{\frac {3}{2}}_{2,1} $
can be obtained by interpolating
![]() $L^\infty _t\dot H^{\frac 32}$
,
$L^\infty _t\dot H^{\frac 32}$
,
![]() $ L_t^{2}\dot B^{\frac {5}{2}}_{2,1 } $
and
$ L_t^{2}\dot B^{\frac {5}{2}}_{2,1 } $
and
![]() $ L^2_t \dot {H}^1$
. Note that
$ L^2_t \dot {H}^1$
. Note that
![]() $L^\infty _t\dot H^{\frac 32}$
and
$L^\infty _t\dot H^{\frac 32}$
and
![]() $ L_t^{2}\dot B^{\frac {5}{2}}_{2,1 ,<} $
appear in the left-hand side of (5.7), whereas,
$ L_t^{2}\dot B^{\frac {5}{2}}_{2,1 ,<} $
appear in the left-hand side of (5.7), whereas,
![]() $ L^2_t \dot {H}^1$
is a good space for B, because, in view of (4.4), the magnetic field is asymptotically globally bounded in that space. Based on this remark, we write, by interpolation, that
$ L^2_t \dot {H}^1$
is a good space for B, because, in view of (4.4), the magnetic field is asymptotically globally bounded in that space. Based on this remark, we write, by interpolation, that
 $$ \begin{align*} \begin{aligned} \left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<} } &\lesssim \left( \int_0^t \left\Vert B(\tau)\right\Vert{}_{\dot{H}^1} ^{\frac{4}{3}}\left\Vert B(\tau)\right\Vert{}_{\dot{B}^{\frac{7}{4}}_{2,1,<}}^{\frac{8}{3}} d\tau \right)^{\frac{1}{4}}\\ &\lesssim \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}}\left\Vert B \right\Vert{}_{L^8_t\dot{B}^{\frac{7}{4}}_{2,1,<}}^{\frac{2}{3}} \\ &\lesssim \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}}\left( \left\Vert B\right\Vert{}_{L^\infty _t\dot B^{\frac{3}{2} }_{2,2,<}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \right)^{\frac{2}{3}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert B\right\Vert{}_{L_t^{4}\dot B^{\frac{3}{2}}_{2,1,<} } &\lesssim \left( \int_0^t \left\Vert B(\tau)\right\Vert{}_{\dot{H}^1} ^{\frac{4}{3}}\left\Vert B(\tau)\right\Vert{}_{\dot{B}^{\frac{7}{4}}_{2,1,<}}^{\frac{8}{3}} d\tau \right)^{\frac{1}{4}}\\ &\lesssim \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}}\left\Vert B \right\Vert{}_{L^8_t\dot{B}^{\frac{7}{4}}_{2,1,<}}^{\frac{2}{3}} \\ &\lesssim \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}}\left( \left\Vert B\right\Vert{}_{L^\infty _t\dot B^{\frac{3}{2} }_{2,2,<}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \right)^{\frac{2}{3}}, \end{aligned} \end{align*} $$
which leads to
 $$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}}} +c^{ -\frac{1}{2}}\left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left( \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right) \\ &\quad+ \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}}\left( \left\Vert B\right\Vert{}_{L^\infty _t\dot B^{\frac{3}{2} }_{2,2,<}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}}\right)^{\frac{2}{3}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}}} +c^{ -\frac{1}{2}}\left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left( \left\Vert B\right\Vert{}_{L_t^{2}\dot B^{\frac{5}{2}}_{2,1,<} } + \left\Vert B\right\Vert{}_{\widetilde{L} _t^{2}\dot B^{\frac{5}{2}}_{2,1,>} } \right) \\ &\quad+ \left\Vert u\right\Vert{}_{L_t^{\infty}\dot H^{1} \cap L_t^{2 }\dot H^{2}} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}}\left( \left\Vert B\right\Vert{}_{L^\infty _t\dot B^{\frac{3}{2} }_{2,2,<}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}}\right)^{\frac{2}{3}}. \end{aligned} \end{align} $$
In order to complete our summary of all relevant low-frequency bounds on electromagnetic fields, we recall the estimate
 $$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^2_t\dot{B}^{\frac{5}{2}}_{2,1} } &\lesssim c^{-1} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L ^{\infty }_t\dot{H}^1 \cap L ^{2 }_t\dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^{2 }_t\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2 _t\dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert E\right\Vert{}_{L^2_t\dot{B}^{\frac{5}{2}}_{2,1} } &\lesssim c^{-1} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}}\left\Vert u \right\Vert{}_{L ^{\infty }_t\dot{H}^1 \cap L ^{2 }_t\dot{H}^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^{2 }_t\dot{B}^{\frac{5}{2}}_{2,1,> } } + \left\Vert B \right\Vert{}_{L^2 _t\dot{B}^{\frac{5}{2}}_{2,1 ,< } } \right), \end{aligned} \end{align} $$
which is established in (3.26).
Decay of electric fields and almost-parabolic bounds on magnetic fields. For later use, we recall and add some precision to the bounds proved in Section 4.2, above.
More specifically, observe first that Proposition 4.1, with the values
![]() $s\in \{0,\frac {1}{2}\}$
, provides us with the decay estimates
$s\in \{0,\frac {1}{2}\}$
, provides us with the decay estimates
 $$ \begin{align} \begin{aligned} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_tL^2} &\lesssim c^{-1} \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{L^2} +c^{-1}\left\Vert E_0\right\Vert{}_{\dot H^1} + c^{-2} \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H}^2 }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \\ &\quad+ c^{-2}(1+ \mathcal{E}_0) \Big( \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H} ^2 } + \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \Big) \\ &\quad\times\Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}} }\Big) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_tL^2} &\lesssim c^{-1} \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{L^2} +c^{-1}\left\Vert E_0\right\Vert{}_{\dot H^1} + c^{-2} \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H}^2 }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \\ &\quad+ c^{-2}(1+ \mathcal{E}_0) \Big( \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H} ^2 } + \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \Big) \\ &\quad\times\Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}} }\Big) \end{aligned} \end{align} $$
and
 $$ \begin{align} \begin{aligned} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} &\lesssim c^{-1} \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{\dot{H}^{\frac{1}{2}}} +c^{-1}\left\Vert E_0\right\Vert{}_{\dot H^{\frac 32}} + c^{-2} \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H}^2 }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \\ &\quad+ c^{-2}(1+ \mathcal{E}_0) \Big( \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H} ^2 } + \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \Big) \\ &\quad\times\Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^2 } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^2}\Big). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} &\lesssim c^{-1} \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{\dot{H}^{\frac{1}{2}}} +c^{-1}\left\Vert E_0\right\Vert{}_{\dot H^{\frac 32}} + c^{-2} \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H}^2 }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \\ &\quad+ c^{-2}(1+ \mathcal{E}_0) \Big( \left\Vert u \right\Vert{}_{ L^ \infty _t \dot{H}^1 \cap L^ 2_t \dot{H} ^2 } + \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \Big) \\ &\quad\times\Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^2 } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^2}\Big). \end{aligned} \end{align} $$
As for the almost-parabolic estimates of B, we first utilize Lemma 2.3 to write that
 $$ \begin{align*} \begin{aligned} c^{-1} \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{L^2} & = c^{-1} \left\Vert \nabla \times B_0 - ce:0 - P(u_0\times B_0)\right\Vert{}_{L^2} \\ & \lesssim c^{-1} \left( \left\Vert B_0 \right\Vert{}_{\dot{H}^1} + \left\Vert u_0\right\Vert{}_{L^2} \left\Vert B_0 \right\Vert{}_{\dot{H}^{\frac{3}{2}}} \right)+\left\Vert E_0\right\Vert{}_{L^2} \\ & \lesssim c^{-1} \left( \left\Vert B_0 \right\Vert{}_{\dot{H}^1} +\mathcal{E}_0 \left\Vert B_0 \right\Vert{}_{\dot{H}^{\frac{3}{2}}} \right)+\mathcal{E}_0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} c^{-1} \left\Vert \nabla \times B_0 - j_0\right\Vert{}_{L^2} & = c^{-1} \left\Vert \nabla \times B_0 - ce:0 - P(u_0\times B_0)\right\Vert{}_{L^2} \\ & \lesssim c^{-1} \left( \left\Vert B_0 \right\Vert{}_{\dot{H}^1} + \left\Vert u_0\right\Vert{}_{L^2} \left\Vert B_0 \right\Vert{}_{\dot{H}^{\frac{3}{2}}} \right)+\left\Vert E_0\right\Vert{}_{L^2} \\ & \lesssim c^{-1} \left( \left\Vert B_0 \right\Vert{}_{\dot{H}^1} +\mathcal{E}_0 \left\Vert B_0 \right\Vert{}_{\dot{H}^{\frac{3}{2}}} \right)+\mathcal{E}_0. \end{aligned} \end{align*} $$
Then, by substituting the preceding control in (5.10), and by further incorporating the resulting bound in the estimate from Proposition 4.2, we find that
 $$ \begin{align} \begin{aligned} \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 } &\lesssim \mathcal{E}_0 + c^ {-1} \big(\left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^1} + \mathcal{E}_0 \left\Vert B_0\right\Vert{}_{\dot{H}^{\frac{3}{2}}}\big)+ c^{-2} \left\Vert u \right\Vert{}_{ L^ \infty _t H^1 \cap L^ 2_t \dot{H} ^2 }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \\ &\quad +c^{-2} \left(1+ \mathcal{E}_0\right) \left( \left\Vert u \right\Vert{}_{L^\infty_t \dot{H} ^1 \cap L^ 2_t \dot{H} ^2 } + \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \right)\left( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } + \left\Vert cE\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}}} \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert B\right\Vert{}_{L^2_t \dot{H}^1 } &\lesssim \mathcal{E}_0 + c^ {-1} \big(\left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^1} + \mathcal{E}_0 \left\Vert B_0\right\Vert{}_{\dot{H}^{\frac{3}{2}}}\big)+ c^{-2} \left\Vert u \right\Vert{}_{ L^ \infty _t H^1 \cap L^ 2_t \dot{H} ^2 }^2 \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \\ &\quad +c^{-2} \left(1+ \mathcal{E}_0\right) \left( \left\Vert u \right\Vert{}_{L^\infty_t \dot{H} ^1 \cap L^ 2_t \dot{H} ^2 } + \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } \right)\left( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}} } + \left\Vert cE\right\Vert{}_{L^\infty_t \dot{H}^{\frac{3}{2}}} \right), \end{aligned} \end{align} $$
which provides an asymptotic parabolic regularity estimate on B.
Finally, we emphasize that we will also make use of the similar almost-parabolic estimates on
![]() $\Gamma $
obtained in Proposition 4.2. More precisely, the relevant estimates on
$\Gamma $
obtained in Proposition 4.2. More precisely, the relevant estimates on
![]() $\Gamma $
are
$\Gamma $
are
and
Nonlinear energy estimate. Here, we gather all the bounds above to produce a nonlinear energy estimate. To that end, let us first introduce, for any
![]() $t\geq 0$
, the functional
$t\geq 0$
, the functional
![]() $\mathcal {H}(t)$
given by
$\mathcal {H}(t)$
given by
 $$ \begin{align*} \begin{aligned} \mathcal{H}(t)& \overset{\mathrm{def}}{=} \left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_t L^2 \cap L^2_t \dot{H}^1 } + \mathcal{E}_t + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3} \\ & \quad + \left\Vert (E,B)\right\Vert{}_{L^\infty_t \dot{H} ^{\frac{3}{2}}} +c^{-1}\left\Vert (E,B)\right\Vert{}_{L^\infty_t \dot{B}^{\frac{5}{2}}_{2,1}} + c \left\Vert E\right\Vert{}_{L^2_t \dot{H}^{\frac{3}{2}}} \\ &\quad+ \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{\frac{5}{2}}_{2,1,>}} + \left\Vert B\right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1,<}} + \left\Vert E\right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1}} + \left\Vert B\right\Vert{}_{L^2_t\dot{H}^1}\\ &\quad+ \left\Vert \nabla \times B- j\right\Vert{}_{L^\infty_t\dot{H}^{\frac{1}{2}}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{H}(t)& \overset{\mathrm{def}}{=} \left\Vert (\omega,\Omega)\right\Vert{}_{L^\infty_t L^2 \cap L^2_t \dot{H}^1 } + \mathcal{E}_t + \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3} \\ & \quad + \left\Vert (E,B)\right\Vert{}_{L^\infty_t \dot{H} ^{\frac{3}{2}}} +c^{-1}\left\Vert (E,B)\right\Vert{}_{L^\infty_t \dot{B}^{\frac{5}{2}}_{2,1}} + c \left\Vert E\right\Vert{}_{L^2_t \dot{H}^{\frac{3}{2}}} \\ &\quad+ \left\Vert (E,B)\right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{\frac{5}{2}}_{2,1,>}} + \left\Vert B\right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1,<}} + \left\Vert E\right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,1}} + \left\Vert B\right\Vert{}_{L^2_t\dot{H}^1}\\ &\quad+ \left\Vert \nabla \times B- j\right\Vert{}_{L^\infty_t\dot{H}^{\frac{1}{2}}}, \end{aligned} \end{align*} $$
where
![]() $\mathcal {E}_t$
is given in (5.3) and all the time-norms are taken over the whole interval
$\mathcal {E}_t$
is given in (5.3) and all the time-norms are taken over the whole interval
![]() $[0,t)$
. Accordingly, we conventionally define
$[0,t)$
. Accordingly, we conventionally define
 $$ \begin{align*} \begin{aligned} \mathcal{H}(0)& \overset{\mathrm{def}}{=} \left\Vert (\omega_0,\Omega_0)\right\Vert{}_{ L^2} +\mathcal{E}_0 + \left\Vert \Gamma_0\right\Vert{}_{ L^3} \\ & \quad + \left\Vert (E_0,B_0)\right\Vert{}_{ \dot{H} ^{\frac{3}{2}} } +c^{-1}\left\Vert (E_0,B_0)\right\Vert{}_{ \dot{B}^{\frac{5}{2}}_{2,1}} + \left\Vert \nabla \times B_0- j_0\right\Vert{}_{ \dot{H}^{\frac{1}{2}}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{H}(0)& \overset{\mathrm{def}}{=} \left\Vert (\omega_0,\Omega_0)\right\Vert{}_{ L^2} +\mathcal{E}_0 + \left\Vert \Gamma_0\right\Vert{}_{ L^3} \\ & \quad + \left\Vert (E_0,B_0)\right\Vert{}_{ \dot{H} ^{\frac{3}{2}} } +c^{-1}\left\Vert (E_0,B_0)\right\Vert{}_{ \dot{B}^{\frac{5}{2}}_{2,1}} + \left\Vert \nabla \times B_0- j_0\right\Vert{}_{ \dot{H}^{\frac{1}{2}}}. \end{aligned} \end{align*} $$
In particular, note, for all
![]() $t \geq 0$
, that
$t \geq 0$
, that
Further observe that
![]() $\left \Vert \Gamma _0\right \Vert {}_{L^3}\lesssim \left \Vert B_0\right \Vert {}_{\dot H^{\frac 32}}$
, by virtue of Lemma 2.2.
$\left \Vert \Gamma _0\right \Vert {}_{L^3}\lesssim \left \Vert B_0\right \Vert {}_{\dot H^{\frac 32}}$
, by virtue of Lemma 2.2.
Now, we claim an estimate of the form
for
![]() $t\geq 0$
, some constant
$t\geq 0$
, some constant
![]() $C_0>0$
depending only on the initial data, uniformly with respect to c, and some polynomial
$C_0>0$
depending only on the initial data, uniformly with respect to c, and some polynomial
![]() $P\in \mathbb {R}^+[X]$
whose coefficients vanish asymptotically as
$P\in \mathbb {R}^+[X]$
whose coefficients vanish asymptotically as
![]() $c\rightarrow \infty .$
Owing to the latter bound above, Lemma 5.2 below will eventually allow us to deduce the desired global estimates, under adequate conditions on the data.
$c\rightarrow \infty .$
Owing to the latter bound above, Lemma 5.2 below will eventually allow us to deduce the desired global estimates, under adequate conditions on the data.
In order to reach such a bound, we first proceed with the control of
![]() $\frac {1}{c} \partial _t E$
by observing that (5.11) yields that
$\frac {1}{c} \partial _t E$
by observing that (5.11) yields that
 $$ \begin{align*} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} \lesssim c^{-1} \mathcal{H}(0) +c^{-2} \mathcal{H}^3(t) + c^{-2} (1+ \mathcal{E}_0)\mathcal{H}(t) \Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^2 } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^2}\Big). \end{align*} $$
$$ \begin{align*} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} \lesssim c^{-1} \mathcal{H}(0) +c^{-2} \mathcal{H}^3(t) + c^{-2} (1+ \mathcal{E}_0)\mathcal{H}(t) \Big( \left\Vert B\right\Vert{}_{L^\infty_t \dot{H}^2 } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^2}\Big). \end{align*} $$
Therefore, noticing, by an interpolation argument, that
it then follows that
 $$ \begin{align} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} \lesssim c^{-1} \mathcal{H}(t) + c^{-\frac{3}{2} } (1+ \mathcal{E}_0)\mathcal{H}^2(t)+c^{-2} \mathcal{H}^3(t). \end{align} $$
$$ \begin{align} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} \lesssim c^{-1} \mathcal{H}(t) + c^{-\frac{3}{2} } (1+ \mathcal{E}_0)\mathcal{H}^2(t)+c^{-2} \mathcal{H}^3(t). \end{align} $$
Next, we exploit the almost-parabolic estimate on B given in (5.12). To that end, note first, by splitting the frequencies of
![]() $B_0$
, that
$B_0$
, that
 $$ \begin{align*}\begin{aligned} c^{-1}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^1} &\leq c^{-1 } \left( \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^1_{2,2,<}} + \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^1_{2,2,>}} \right) \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{L^2} +c ^{-\frac{3}{2}} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}} } \\ &\lesssim \mathcal{E}_0 + c ^{-\frac{3}{2}} \mathcal{H} (0). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} c^{-1}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^1} &\leq c^{-1 } \left( \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^1_{2,2,<}} + \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^1_{2,2,>}} \right) \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{L^2} +c ^{-\frac{3}{2}} \left\Vert (E_0,B_0)\right\Vert{}_{\dot{H}^{\frac{3}{2}} } \\ &\lesssim \mathcal{E}_0 + c ^{-\frac{3}{2}} \mathcal{H} (0). \end{aligned} \end{align*} $$
In addition to that, using the fact that
![]() $ \mathcal {H}(0)\leq \mathcal {H}(t)$
, one sees that
$ \mathcal {H}(0)\leq \mathcal {H}(t)$
, one sees that
 $$ \begin{align*} \begin{aligned} c^{-1}\mathcal{E}_0 \left\Vert B_0\right\Vert{}_{\dot{H}^{\frac{3}{2}}} &\leq \mathcal{E}_0 + c^{-2}\mathcal{E}_0 \left\Vert B_0\right\Vert{}_{\dot{H}^{\frac{3}{2}}}^2\\ &\leq \mathcal{E}_0 + c^{-2}(1+\mathcal{E}_0) \mathcal{H} ^2(t). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} c^{-1}\mathcal{E}_0 \left\Vert B_0\right\Vert{}_{\dot{H}^{\frac{3}{2}}} &\leq \mathcal{E}_0 + c^{-2}\mathcal{E}_0 \left\Vert B_0\right\Vert{}_{\dot{H}^{\frac{3}{2}}}^2\\ &\leq \mathcal{E}_0 + c^{-2}(1+\mathcal{E}_0) \mathcal{H} ^2(t). \end{aligned} \end{align*} $$
Accordingly, (5.12) yields, for
![]() $c\geq 1$
, that
$c\geq 1$
, that
and, since
![]() $\mathcal {H}(0)\leq \mathcal {H}(t)$
, that
$\mathcal {H}(0)\leq \mathcal {H}(t)$
, that
We turn now our attention to the bounds on
![]() $\Gamma $
given by (5.13) and (5.14). Observing, by a simple interpolation argument, that
$\Gamma $
given by (5.13) and (5.14). Observing, by a simple interpolation argument, that
it follows, by incorporating (5.16) into (5.13), that
As for the
![]() $L^\infty _tL^3$
bound on
$L^\infty _tL^3$
bound on
![]() $\Gamma $
, we begin by deducing from (5.9) that
$\Gamma $
, we begin by deducing from (5.9) that
which, in view of (5.14), yields that
Now, we establish a control of velocity fields in terms of the functional
![]() $\mathcal {H}(t)$
. To that end, employing (5.16) and the simple fact that
$\mathcal {H}(t)$
. To that end, employing (5.16) and the simple fact that
one deduces that
Hence, (5.17) provides us with the bound
 $$ \begin{align} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} \left\Vert B\right\Vert{}_{L^\infty_tH^2} \lesssim \left( c^{-\frac{1}{2} } \mathcal{H}^2(t) + c^{-1 } \mathcal{H}^3(t)+c^{-\frac{3}{2} } \mathcal{H}^4(t)\right) e^{\mathcal{E}_0^2}. \end{align} $$
$$ \begin{align} \left\Vert \frac{1}{c} \partial_t E\right\Vert{}_{L^2_t\dot{H}^{\frac{1}{2}}} \left\Vert B\right\Vert{}_{L^\infty_tH^2} \lesssim \left( c^{-\frac{1}{2} } \mathcal{H}^2(t) + c^{-1 } \mathcal{H}^3(t)+c^{-\frac{3}{2} } \mathcal{H}^4(t)\right) e^{\mathcal{E}_0^2}. \end{align} $$
However, combining (5.19), (5.20) and (5.22) yields, for any
![]() $c\geq 1$
, that
$c\geq 1$
, that
 $$ \begin{align*} \begin{aligned} \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 } &\left\Vert (B, \Gamma)\right\Vert{}_{L^2_t\dot{H}^1} \\ & \lesssim \left( \mathcal{H}(0) + c^{-\frac{1}{2}}\mathcal{H}^2(t) \right) \Bigg( \left\Vert \Gamma_0\right\Vert{}_{L^2} + \mathcal{E}_0 + c^{-\frac{1}{2}} \mathcal{H}(t) + c^{-2} (1+ \mathcal{E}_0) \mathcal{H}^2(t) + c^{-2} \mathcal{H}^3(t) \Bigg)\\ & \lesssim \mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + \mathcal{E}_0 \right) + c^{-\frac{1}{2}} \mathcal{H} ^2 (t) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + \mathcal{E}_0 \right) \\ & \quad + \mathcal{H}(0) (1 + \mathcal{E}_0) \Bigg( c^{-\frac{1}{2}} \mathcal{H}(t) + c^{-2} \mathcal{H}^2(t) + c^{-2} \mathcal{H}^3(t) \Bigg) \\ & \quad + (1 + \mathcal{E}_0) \left(c^{-1 } \mathcal{H}^3(t) + c^{- \frac{5}{2} } \mathcal{H}^4(t) + c^{-\frac{5}{2} } \mathcal{H}^5(t)\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 } &\left\Vert (B, \Gamma)\right\Vert{}_{L^2_t\dot{H}^1} \\ & \lesssim \left( \mathcal{H}(0) + c^{-\frac{1}{2}}\mathcal{H}^2(t) \right) \Bigg( \left\Vert \Gamma_0\right\Vert{}_{L^2} + \mathcal{E}_0 + c^{-\frac{1}{2}} \mathcal{H}(t) + c^{-2} (1+ \mathcal{E}_0) \mathcal{H}^2(t) + c^{-2} \mathcal{H}^3(t) \Bigg)\\ & \lesssim \mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + \mathcal{E}_0 \right) + c^{-\frac{1}{2}} \mathcal{H} ^2 (t) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + \mathcal{E}_0 \right) \\ & \quad + \mathcal{H}(0) (1 + \mathcal{E}_0) \Bigg( c^{-\frac{1}{2}} \mathcal{H}(t) + c^{-2} \mathcal{H}^2(t) + c^{-2} \mathcal{H}^3(t) \Bigg) \\ & \quad + (1 + \mathcal{E}_0) \left(c^{-1 } \mathcal{H}^3(t) + c^{- \frac{5}{2} } \mathcal{H}^4(t) + c^{-\frac{5}{2} } \mathcal{H}^5(t)\right). \end{aligned} \end{align*} $$
Accordingly, by employing (5.15) and
![]() $c\geq 1$
, again, we find that
$c\geq 1$
, again, we find that
 $$ \begin{align} \begin{aligned} \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 } & \left\Vert (B, \Gamma)\right\Vert{}_{L^2_t\dot{H}^1} \\ &\lesssim \mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right) e^{\mathcal{E}_0^2} \\ & \quad+ \underbrace{(\left\Vert \Gamma_0\right\Vert{}_{L^2}+1 )\left( c^{-\frac{1}{2} } \mathcal{H}^2(t)+ c^{-1 } \mathcal{H}^3(t) + c^{- \frac{3}{2} } \mathcal{H}^4(t) + c^{-\frac{5}{2} } \mathcal{H}^5(t) \right)e^{C\mathcal{E}_0^2}}_{\overset{\mathrm{def}}{=} P_*(\mathcal{H}(t))}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\Vert \Gamma\right\Vert{}_{L^\infty_t L^3 } & \left\Vert (B, \Gamma)\right\Vert{}_{L^2_t\dot{H}^1} \\ &\lesssim \mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right) e^{\mathcal{E}_0^2} \\ & \quad+ \underbrace{(\left\Vert \Gamma_0\right\Vert{}_{L^2}+1 )\left( c^{-\frac{1}{2} } \mathcal{H}^2(t)+ c^{-1 } \mathcal{H}^3(t) + c^{- \frac{3}{2} } \mathcal{H}^4(t) + c^{-\frac{5}{2} } \mathcal{H}^5(t) \right)e^{C\mathcal{E}_0^2}}_{\overset{\mathrm{def}}{=} P_*(\mathcal{H}(t))}. \end{aligned} \end{align} $$
Consequently, by incorporating (5.23) and (5.24) into (5.2), we end up with
where the value of the constant
![]() $C>0$
can be adapted to guarantee the validity of the estimate.
$C>0$
can be adapted to guarantee the validity of the estimate.
In the next step, we gather the high- and low-frequency estimates of electromagnetic fields. To that end, on the one hand, note that (5.4) yields
On the other hand, (5.8) entails that
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} &+ \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \mathcal{H}(0) +c^{ -\frac{1}{2}} \mathcal{H}^2(t) + \left\Vert \omega \right\Vert{}_{L_t^{\infty}L^2 \cap L_t^{2 }\dot H^{1}} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}} \mathcal{H}^{\frac{2}{3}}(t). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} &+ \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \mathcal{H}(0) +c^{ -\frac{1}{2}} \mathcal{H}^2(t) + \left\Vert \omega \right\Vert{}_{L_t^{\infty}L^2 \cap L_t^{2 }\dot H^{1}} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}} \mathcal{H}^{\frac{2}{3}}(t). \end{aligned} \end{align*} $$
Therefore, we employ (5.25) to obtain that
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \mathcal{H}(0) + P_*(\mathcal{H}(t)) + \left(\mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right) e^{C\mathcal{E}_0^2} + P_*(\mathcal{H}(t)) \right) \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}} \mathcal{H}^{\frac{2}{3}}(t)\\ & \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) + \mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right) e^{C\mathcal{E}_0^2} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}} \mathcal{H}^{\frac{2}{3}}(t), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \mathcal{H}(0) + P_*(\mathcal{H}(t)) + \left(\mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right) e^{C\mathcal{E}_0^2} + P_*(\mathcal{H}(t)) \right) \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}} \mathcal{H}^{\frac{2}{3}}(t)\\ & \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) + \mathcal{H} (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right) e^{C\mathcal{E}_0^2} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} ^{\frac{1}{3}} \mathcal{H}^{\frac{2}{3}}(t), \end{aligned} \end{align*} $$
which implies, for any
![]() $\lambda>0$
, that
$\lambda>0$
, that
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) + \lambda^{-2} \mathcal{H} ^3 (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 e^{C\mathcal{E}_0^2} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} + \lambda\mathcal{H}(t). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } &+ c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ & \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) + \lambda^{-2} \mathcal{H} ^3 (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 e^{C\mathcal{E}_0^2} \left\Vert B \right\Vert{}_{L^2_t \dot{H}^1} + \lambda\mathcal{H}(t). \end{aligned} \end{align*} $$
After that, we employ (5.19), which leads to the control
 $$ \begin{align*} \begin{aligned} &\left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ &\qquad \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) \\ & \qquad\quad + \lambda^{-2} \mathcal{H} ^3 (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 \left( 1+ c^{-\frac{3}{2} } \mathcal{H}(t) + c^{-2} \mathcal{H}^2(t) + c^{-2} \mathcal{H}^3(t) \right) e^{C\mathcal{E}_0^2} + \lambda\mathcal{H}(t). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ &\qquad \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) \\ & \qquad\quad + \lambda^{-2} \mathcal{H} ^3 (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 \left( 1+ c^{-\frac{3}{2} } \mathcal{H}(t) + c^{-2} \mathcal{H}^2(t) + c^{-2} \mathcal{H}^3(t) \right) e^{C\mathcal{E}_0^2} + \lambda\mathcal{H}(t). \end{aligned} \end{align*} $$
At last, in view of (5.15), it follows that
 $$ \begin{align} \begin{aligned} &\left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ &\qquad\qquad \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) + \lambda^{-2} \mathcal{H} ^3 (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 e^{C\mathcal{E}_0^2} \\ &\qquad\qquad \quad + \lambda^{-2} \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 \left( c^{-\frac{3}{2} } \mathcal{H}^4(t) + c^{-2} \mathcal{H}^5(t) + c^{-2} \mathcal{H}^6(t) \right)e^{C\mathcal{E}_0^2} + \lambda\mathcal{H}(t). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left\Vert (E,B)\right\Vert{}_{L^\infty _t\dot H^{\frac{3}{2} } } + c \left\Vert E\right\Vert{}_{L^2_t\dot{H}^{\frac{3}{2}}} + \left\Vert B\right\Vert{}_{L^2 _t\dot B^{ \frac{5}{2}}_{2,1,<}} \\ &\qquad\qquad \lesssim \mathcal{H}(0) + (\mathcal{H}(t) +1 )P_*(\mathcal{H}(t)) + \lambda^{-2} \mathcal{H} ^3 (0) \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 e^{C\mathcal{E}_0^2} \\ &\qquad\qquad \quad + \lambda^{-2} \left( \left\Vert \Gamma_0\right\Vert{}_{L^2} + 1 \right)^3 \left( c^{-\frac{3}{2} } \mathcal{H}^4(t) + c^{-2} \mathcal{H}^5(t) + c^{-2} \mathcal{H}^6(t) \right)e^{C\mathcal{E}_0^2} + \lambda\mathcal{H}(t). \end{aligned} \end{align} $$
As for the remaining piece involving
![]() $\nabla \times B-j$
that is required to construct the functional
$\nabla \times B-j$
that is required to construct the functional
![]() $\mathcal {H}(t)$
, it is dealt with by recasting the bound from Proposition 4.1, for
$\mathcal {H}(t)$
, it is dealt with by recasting the bound from Proposition 4.1, for
![]() $p=\infty $
and
$p=\infty $
and
![]() $s=\frac {1}{2}$
, combined with (5.16), to find that
$s=\frac {1}{2}$
, combined with (5.16), to find that
whereby, obtaining that
All in all, gathering the bounds (5.18), (5.21), (5.22), (5.25), (5.26), (5.27) and (5.28) to construct the functional
![]() $\mathcal {H}(t)$
and choosing
$\mathcal {H}(t)$
and choosing
![]() $\lambda $
small enough in such a way that the term
$\lambda $
small enough in such a way that the term
![]() $ \lambda \mathcal {H}(t)$
can be absorbed by the left-hand side of the final estimate, we end up with the bound
$ \lambda \mathcal {H}(t)$
can be absorbed by the left-hand side of the final estimate, we end up with the bound
for all
![]() $t\geq 0,$
where we set
$t\geq 0,$
where we set
and
We recall that the (possibly large) constant
![]() $C>0$
is universal. From now on, it is fixed.
$C>0$
is universal. From now on, it is fixed.
The completion of the proof hinges now on a direct application of the following simple lemma.
Lemma 5.2. Let
![]() $t\mapsto x(t) $
be a non-negative continuous function defined for all
$t\mapsto x(t) $
be a non-negative continuous function defined for all
![]() $t\geq 0$
. Consider another function
$t\geq 0$
. Consider another function
![]() $t\mapsto F(t)$
which is assumed to be non-negative and increasing. Further suppose that there is
$t\mapsto F(t)$
which is assumed to be non-negative and increasing. Further suppose that there is
![]() $x_0>0$
such that
$x_0>0$
such that
and, for any
![]() $t\geq 0$
, that
$t\geq 0$
, that
If, moreover, F satisfies the condition that
then,
![]() $x(t)$
enjoys the bound
$x(t)$
enjoys the bound
for all
![]() $t\geq 0$
.
$t\geq 0$
.
Proof. Define the set
This set is nonempty and open in
![]() $[0,\infty )$
. In order to prove the desired global bound, we only have to show that
$[0,\infty )$
. In order to prove the desired global bound, we only have to show that
![]() $\mathcal {I}$
is closed, as well.
$\mathcal {I}$
is closed, as well.
To that end, let
![]() $(t_n)_{n\in \mathbb {N}}$
be a sequence of elements in
$(t_n)_{n\in \mathbb {N}}$
be a sequence of elements in
![]() $\mathcal {I}$
, converging to some limit point
$\mathcal {I}$
, converging to some limit point
![]() $t\in [0,\infty )$
. Since
$t\in [0,\infty )$
. Since
![]() $t_n \in \mathcal {I}$
, we deduce, for all
$t_n \in \mathcal {I}$
, we deduce, for all
![]() $n\in \mathbb {N} $
, that
$n\in \mathbb {N} $
, that
By continuity of
![]() $t\mapsto x(t)$
, taking
$t\mapsto x(t)$
, taking
![]() $n \to \infty $
in the foregoing inequalities yields that
$n \to \infty $
in the foregoing inequalities yields that
![]() $t\in \mathcal {I}$
, thereby showing that
$t\in \mathcal {I}$
, thereby showing that
![]() $\mathcal {I}$
is closed and completing the proof of the lemma.
$\mathcal {I}$
is closed and completing the proof of the lemma.
We are now back to the proof of Theorem 1.1. By applying Lemma 5.2 with
![]() $F(t)= \mathcal {P}(t)$
, we arrive at the conclusion, for all
$F(t)= \mathcal {P}(t)$
, we arrive at the conclusion, for all
![]() $t\geq 0,$
that
$t\geq 0,$
that
as soon as
In particular, recall that
which implies the existence of another constant
![]() $c_0>0$
, which only depends on the initial data, such that (5.30) is satisfied for all
$c_0>0$
, which only depends on the initial data, such that (5.30) is satisfied for all
![]() $c> c_0$
. It then follows that all the norms involved in the construction of
$c> c_0$
. It then follows that all the norms involved in the construction of
![]() $\mathcal {H}(t)$
are bounded.
$\mathcal {H}(t)$
are bounded.
Finally, in order to complete the justification of all uniform bounds claimed in the statement of Theorem 1.1, we only need to observe that the control of j in
![]() $L^\infty _tL^2 \cap L_t^2\dot H^{\frac 12}$
follows directly from an application of Proposition 4.1. This completes the proof of Theorem 1.1 in the case of rough profiles.
$L^\infty _tL^2 \cap L_t^2\dot H^{\frac 12}$
follows directly from an application of Proposition 4.1. This completes the proof of Theorem 1.1 in the case of rough profiles.
5.3.2 Regular profiles
We proceed with the completion of the proof of Theorem 1.1 in the case of regular profiles. Specifically, our task now consists in showing that if, furthermore, we assume initially that
uniformly in
![]() $ c>0$
, then the regularity of
$ c>0$
, then the regularity of
![]() $(E,B)$
in
$(E,B)$
in
![]() $\dot {B}^{\frac {5}{2}}_{2,1}$
is propagated for all times
$\dot {B}^{\frac {5}{2}}_{2,1}$
is propagated for all times
![]() $t>0$
, uniformly in
$t>0$
, uniformly in
![]() $c \in (c_0,\infty )$
. Note that this cannot be done by a direct application of the energy estimates from Lemma 3.6. Instead, we need to exploit the techniques from Lemmas 3.4 and 3.5.
$c \in (c_0,\infty )$
. Note that this cannot be done by a direct application of the energy estimates from Lemma 3.6. Instead, we need to exploit the techniques from Lemmas 3.4 and 3.5.
Again, for simplicity, we will henceforth omit the index ‘c’ referring to the dependence of the solution on the speed of light. Also, let us point out that all the Lebesgue spaces in time are now taken over the whole positive real-line
![]() $\mathbb {R}^+$
. Moreover, the constant
$\mathbb {R}^+$
. Moreover, the constant
![]() $C_0$
defined in (5.29) will be allowed to change from one line to another, as long as that change only involves norms of the initial data that remain uniformly bounded in c.
$C_0$
defined in (5.29) will be allowed to change from one line to another, as long as that change only involves norms of the initial data that remain uniformly bounded in c.
Preliminary bounds on magnetic fields. The control of high frequencies is deduced, again, from Lemma 3.4 with a suitable choice of parameters. To see that, we proceed with a bootstrap argument by first recasting the bound
 $$ \begin{align*} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^4_t \dot{B}^{\frac{5}{2} }_{2,1,>} } \lesssim c^{-\frac{1}{2}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} + \left\Vert u\right\Vert{}_{L^\infty_t \dot{H} ^1 \cap L^2_t \dot{H} ^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,>} } + \left\Vert B \right\Vert{}_{L ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,<} } \right), \end{align*} $$
$$ \begin{align*} \left\Vert (E,B) \right\Vert{}_{\widetilde{L} ^4_t \dot{B}^{\frac{5}{2} }_{2,1,>} } \lesssim c^{-\frac{1}{2}}\left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}} _{2,1,>}} + \left\Vert u\right\Vert{}_{L^\infty_t \dot{H} ^1 \cap L^2_t \dot{H} ^2 } \left( \left\Vert B \right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,>} } + \left\Vert B \right\Vert{}_{L ^2_t \dot{B}^{ \frac{5}{2}}_{2,1,<} } \right), \end{align*} $$
from (3.15), by setting
![]() $ q=4$
therein. Therefore, recalling that we have already established the uniform estimates
$ q=4$
therein. Therefore, recalling that we have already established the uniform estimates
 $$ \begin{align} \begin{aligned} u &\in L^\infty_t\dot{H}^1 \cap L^2_t \dot{H}^2 , \\ B &\in \widetilde{L}^2_{t}\dot{B}^{\frac{5}{2}}_{2,1,>} \cap L^2_{t}\dot{B}^{\frac{5}{2}}_{2,1,<} \cap L^\infty_t L^2 \cap L^2_t \dot{H}^1, \\ c^{-1}B &\in L^\infty _{t}\dot{B}^{\frac{5}{2}}_{2,1,<}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} u &\in L^\infty_t\dot{H}^1 \cap L^2_t \dot{H}^2 , \\ B &\in \widetilde{L}^2_{t}\dot{B}^{\frac{5}{2}}_{2,1,>} \cap L^2_{t}\dot{B}^{\frac{5}{2}}_{2,1,<} \cap L^\infty_t L^2 \cap L^2_t \dot{H}^1, \\ c^{-1}B &\in L^\infty _{t}\dot{B}^{\frac{5}{2}}_{2,1,<}, \end{aligned} \end{align} $$
one directly deduces that
uniformly with respect to
![]() $ c\in (c_0,\infty ).$
$ c\in (c_0,\infty ).$
Now, we take care of the low frequencies by first applying the last estimate from Lemma 3.3 with values
to find that
Therefore, by further employing classical product laws, which are contained in Lemma 2.3, and interpolation inequalities, we obtain that
 $$ \begin{align*} \begin{aligned} \left\Vert B\right\Vert{}_{L^4_t \dot B^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^4_t \dot B^{\frac{3}{2}}_{2,1}}\left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1}} \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^\infty _t \dot H^1\cap L^2 _t \dot H^2}\left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1}} \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^\infty _t \dot H^1\cap L^2 _t \dot H^2}\Big( \left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1,>}} + \left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1,<}} \Big) \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^\infty _t \dot H^1\cap L^2 _t \dot H^2}\Big( c^{-1}\left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{5}{2}}_{2,1,>}} + \left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1,<}} \Big). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert B\right\Vert{}_{L^4_t \dot B^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^4_t \dot B^{\frac{3}{2}}_{2,1}}\left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1}} \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^\infty _t \dot H^1\cap L^2 _t \dot H^2}\left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1}} \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^\infty _t \dot H^1\cap L^2 _t \dot H^2}\Big( \left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1,>}} + \left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1,<}} \Big) \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot B^2_{2,1}} + \left\Vert u\right\Vert{}_{L^\infty _t \dot H^1\cap L^2 _t \dot H^2}\Big( c^{-1}\left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{5}{2}}_{2,1,>}} + \left\Vert B\right\Vert{}_{L^\infty _t \dot B^{\frac{3}{2}}_{2,1,<}} \Big). \end{aligned} \end{align*} $$
Thus, in view of the uniform bounds recalled in (5.31), in order to control low frequencies, it only remains to show that
Instead, we are going to prove the slightly better bound
To that end, we employ the low-frequency estimates from Lemma 3.2 with the values
to deduce that
Therefore, by further applying the paraproduct estimate (2.3), we obtain that
Accordingly, we conclude that the bound (5.32) holds uniformly, by an application of the embeddings
combined with the bounds (5.31).
All in all, gathering the preceding high- and low-frequency estimates, we have shown that
uniformly in c.
Next, we improve the previous bound to obtain
Note that the same bound on high frequencies is already established at the start of this step and, thus, we only need to take care of the corresponding estimate on the remaining frequencies. To that end, we first apply the low-frequency estimates from Lemma 3.2 with values
to obtain that
Therefore, by further employing (2.3) to estimate the product above, we find that
Thus, one deduces, thanks to the embeddings
that
Hence, due to the bounds (5.31) and (5.33), we see that the right-hand side in the preceding estimate is finite as soon as
![]() $B\in L^4_t \dot B^{\frac {3}{2}}_{2,1}$
. This bound turns out to be a consequence of the embeddings
$B\in L^4_t \dot B^{\frac {3}{2}}_{2,1}$
. This bound turns out to be a consequence of the embeddings
whereby
![]() $ B\in \widetilde {L} ^4_t \dot B^{\frac {5}{2}}_{2,1,<}.$
In conclusion, we have shown that (5.34) holds uniformly with respect to the speed of light
$ B\in \widetilde {L} ^4_t \dot B^{\frac {5}{2}}_{2,1,<}.$
In conclusion, we have shown that (5.34) holds uniformly with respect to the speed of light
![]() $c\in (c_0,\infty )$
.
$c\in (c_0,\infty )$
.
Propagation of initial regularity. We are now in a position to show the propagation of the
![]() $ \dot {B}^{\frac {5}{2}}_{2,1}$
regularity of the electromagnetic field, uniformly with respect to the speed of light.
$ \dot {B}^{\frac {5}{2}}_{2,1}$
regularity of the electromagnetic field, uniformly with respect to the speed of light.
As before, we deal first with high frequencies by recasting the second estimate from Lemma 3.4, with the values
to find that
Thus, it follows that
uniformly in
![]() $ c\in (c_0,\infty )$
, by virtue of the bounds (5.31) and (5.34).
$ c\in (c_0,\infty )$
, by virtue of the bounds (5.31) and (5.34).
As for low frequencies, we proceed by applying the corresponding estimate from Lemma 3.2 with the values
to find that
 $$ \begin{align*} \begin{aligned} \left\Vert E\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}} \left\Vert P(u\times B) \right\Vert{}_{\widetilde{L} _t^ 4 \dot{B}^{\frac{5}{2}}_{2,1,< } } \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + \left\Vert P(u\times B) \right\Vert{}_{\widetilde{L} _t^ 4 \dot{B}^{2}_{2,1,< } }, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert E\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + c^{-\frac{1}{2}} \left\Vert P(u\times B) \right\Vert{}_{\widetilde{L} _t^ 4 \dot{B}^{\frac{5}{2}}_{2,1,< } } \\ &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + \left\Vert P(u\times B) \right\Vert{}_{\widetilde{L} _t^ 4 \dot{B}^{2}_{2,1,< } }, \end{aligned} \end{align*} $$
and
Therefore, by employing (2.3) to estimate the products above, we obtain, for any
![]() $\varepsilon \in (0,\frac {1}{2})$
, that
$\varepsilon \in (0,\frac {1}{2})$
, that
Hence, utilizing the interpolation inequalities
 $$ \begin{align*} \begin{aligned} \left\Vert u\right\Vert{}_{\widetilde{L} _t^ 4 \dot{B}^{\frac{3}{2}- \varepsilon}_{2,\infty } } \lesssim \left\Vert u\right\Vert{}_{L_t^ 4 \dot{B}^{\frac{3}{2}- \varepsilon}_{2,\infty } } & \lesssim \left\Vert u\right\Vert{}_{L_t^ 4 \dot{H}^{\frac{1}{2}} }^{\varepsilon} \left\Vert u\right\Vert{}_{L _t^ 4 \dot{H}^{\frac{3}{2}} }^{1-\varepsilon}\\ & \lesssim \left\Vert u\right\Vert{}_{L _t^ \infty L^2 \cap L^2_t \dot{H}^{1} }^{\varepsilon} \left\Vert u\right\Vert{}_{L_t^ \infty \dot{H}^{1} \cap L^2_t\dot{H}^2 }^{1-\varepsilon} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert u\right\Vert{}_{\widetilde{L} _t^ 4 \dot{B}^{\frac{3}{2}- \varepsilon}_{2,\infty } } \lesssim \left\Vert u\right\Vert{}_{L_t^ 4 \dot{B}^{\frac{3}{2}- \varepsilon}_{2,\infty } } & \lesssim \left\Vert u\right\Vert{}_{L_t^ 4 \dot{H}^{\frac{1}{2}} }^{\varepsilon} \left\Vert u\right\Vert{}_{L _t^ 4 \dot{H}^{\frac{3}{2}} }^{1-\varepsilon}\\ & \lesssim \left\Vert u\right\Vert{}_{L _t^ \infty L^2 \cap L^2_t \dot{H}^{1} }^{\varepsilon} \left\Vert u\right\Vert{}_{L_t^ \infty \dot{H}^{1} \cap L^2_t\dot{H}^2 }^{1-\varepsilon} \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{2+\varepsilon}_{2,1 } } & \lesssim \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{\frac{5}{2}}_{2,1 } } ^{\frac{1}{2}+ \varepsilon} \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{\frac{3}{2}}_{2, \infty } }^{ \frac{1}{2}-\varepsilon}\\ & \lesssim \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{\frac{5}{2}}_{2,1 } } ^{\frac{1}{2}+ \varepsilon} \left\Vert B\right\Vert{}_{L_t^ \infty \dot{H}^{\frac{3}{2}} }^{ \frac{1}{2}-\varepsilon}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{2+\varepsilon}_{2,1 } } & \lesssim \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{\frac{5}{2}}_{2,1 } } ^{\frac{1}{2}+ \varepsilon} \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{\frac{3}{2}}_{2, \infty } }^{ \frac{1}{2}-\varepsilon}\\ & \lesssim \left\Vert B\right\Vert{}_{\widetilde{L} _t^ \infty \dot{B}^{\frac{5}{2}}_{2,1 } } ^{\frac{1}{2}+ \varepsilon} \left\Vert B\right\Vert{}_{L_t^ \infty \dot{H}^{\frac{3}{2}} }^{ \frac{1}{2}-\varepsilon}, \end{aligned} \end{align*} $$
we deduce, for any
![]() $\lambda \in (0,1)$
, that
$\lambda \in (0,1)$
, that
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + \lambda \left\Vert B\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} \\ & \quad+ C_\lambda \left( \left\Vert u\right\Vert{}_{L _t^ \infty L^2 \cap L^2_t \dot{H}^{1} }^{\varepsilon} \left\Vert u\right\Vert{}_{L_t^ \infty \dot{H}^{1} \cap L^2_t\dot{H}^2 }^{1-\varepsilon} \right)^{ \frac{1}{\frac{1}{2} - \varepsilon}} \left\Vert B\right\Vert{}_{L_t^ \infty \dot{H}^{\frac{3}{2}} }. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + \lambda \left\Vert B\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} \\ & \quad+ C_\lambda \left( \left\Vert u\right\Vert{}_{L _t^ \infty L^2 \cap L^2_t \dot{H}^{1} }^{\varepsilon} \left\Vert u\right\Vert{}_{L_t^ \infty \dot{H}^{1} \cap L^2_t\dot{H}^2 }^{1-\varepsilon} \right)^{ \frac{1}{\frac{1}{2} - \varepsilon}} \left\Vert B\right\Vert{}_{L_t^ \infty \dot{H}^{\frac{3}{2}} }. \end{aligned} \end{align*} $$
Finally, choosing
![]() $\lambda $
small enough, we arrive at the conclusion that
$\lambda $
small enough, we arrive at the conclusion that
 $$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + \left( \left\Vert u\right\Vert{}_{L _t^ \infty L^2 \cap L^2_t \dot{H}^{1} }^{\varepsilon} \left\Vert u\right\Vert{}_{L_t^ \infty \dot{H}^{1} \cap L^2_t\dot{H}^2 }^{1-\varepsilon} \right)^{ \frac{1}{\frac{1}{2} - \varepsilon}} \left\Vert B\right\Vert{}_{L_t^ \infty \dot{H}^{\frac{3}{2}} }. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert (E,B)\right\Vert{}_{\widetilde{L}^\infty _t \dot{B}^{\frac{5}{2}}_{2,1,<}} &\lesssim \left\Vert (E_0,B_0)\right\Vert{}_{\dot{B}^{\frac{5}{2}}_{2,1}} + \left( \left\Vert u\right\Vert{}_{L _t^ \infty L^2 \cap L^2_t \dot{H}^{1} }^{\varepsilon} \left\Vert u\right\Vert{}_{L_t^ \infty \dot{H}^{1} \cap L^2_t\dot{H}^2 }^{1-\varepsilon} \right)^{ \frac{1}{\frac{1}{2} - \varepsilon}} \left\Vert B\right\Vert{}_{L_t^ \infty \dot{H}^{\frac{3}{2}} }. \end{aligned} \end{align*} $$
Again, due to the bounds (5.31), the right-hand side above is finite, uniformly with respect to
![]() $c\in (c_0,\infty )$
, thereby yielding the desired control for the low frequencies of E and B. This completes the proof of Theorem 1.1.
$c\in (c_0,\infty )$
, thereby yielding the desired control for the low frequencies of E and B. This completes the proof of Theorem 1.1.
6 Convergence and proof of Theorem 1.3
Let
![]() $(u^c,E^c,B^c)_{c>c_0}$
and
$(u^c,E^c,B^c)_{c>c_0}$
and
![]() $(u,B)$
be the solutions of (1.1) and (MHD), given by Theorem 1.1 and Corollary 1.2, respectively. We further introduce the fluctuations
$(u,B)$
be the solutions of (1.1) and (MHD), given by Theorem 1.1 and Corollary 1.2, respectively. We further introduce the fluctuations
with a corresponding similar notation
![]() $\widetilde {u}_0$
,
$\widetilde {u}_0$
,
![]() $\widetilde {B}_0 $
for their initial data, and the time-dependent function
$\widetilde {B}_0 $
for their initial data, and the time-dependent function
for all
![]() $t>0$
. In view of Theorem 1.1 and Corollary 1.2, observe that
$t>0$
. In view of Theorem 1.1 and Corollary 1.2, observe that
![]() $f\in L^2(\mathbb {R}^+)$
with
$f\in L^2(\mathbb {R}^+)$
with
uniformly in
![]() $c\in (c_0,\infty )$
, for some constant
$c\in (c_0,\infty )$
, for some constant
![]() $C_0>0$
depending only on the initial data.
$C_0>0$
depending only on the initial data.
We proceed now in four steps:
-
1. The
 $L^2$
energy estimate.
$L^2$
energy estimate. -
2. An interpolation argument.
-
3. Convergence of the velocity in the endpoint space
 $\dot H^1$
.
$\dot H^1$
. -
4. Convergence of the magnetic field in the endpoint space
 $\dot H^{\frac 32}$
.
$\dot H^{\frac 32}$
.
6.1 The
 $L^2$
energy estimate
$L^2$
energy estimate
First, it is readily seen that the fluctuations
![]() $ \widetilde {u}$
,
$ \widetilde {u}$
,
![]() $\widetilde {B}$
are solutions of the perturbed MHD equations
$\widetilde {B}$
are solutions of the perturbed MHD equations
 $$ \begin{align} \begin{cases} \begin{aligned} \partial_t \widetilde{u} +u \cdot\nabla \widetilde{u} - \nu \Delta \widetilde{u}+ \nabla \widetilde{p} = - \widetilde{u}\cdot\nabla u^c + \widetilde{B}\cdot \nabla B + B^c\cdot \nabla \widetilde{B} + \frac{1}{c} \partial_t E^c \times B^c,\\ \partial_t \widetilde{B} +u \cdot\nabla \widetilde{B} - \frac{1}{\sigma} \Delta \widetilde{B} =- \widetilde{u}\cdot\nabla B^c + \widetilde{B}\cdot \nabla u + B^c\cdot \nabla \widetilde{u} + \nabla \times \left(\frac{1}{c} \partial_t E^c\right). \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} \partial_t \widetilde{u} +u \cdot\nabla \widetilde{u} - \nu \Delta \widetilde{u}+ \nabla \widetilde{p} = - \widetilde{u}\cdot\nabla u^c + \widetilde{B}\cdot \nabla B + B^c\cdot \nabla \widetilde{B} + \frac{1}{c} \partial_t E^c \times B^c,\\ \partial_t \widetilde{B} +u \cdot\nabla \widetilde{B} - \frac{1}{\sigma} \Delta \widetilde{B} =- \widetilde{u}\cdot\nabla B^c + \widetilde{B}\cdot \nabla u + B^c\cdot \nabla \widetilde{u} + \nabla \times \left(\frac{1}{c} \partial_t E^c\right). \end{aligned} \end{cases} \end{align} $$
Therefore, by virtue of the identities
and
performing an
![]() $L^2$
energy estimate yields, for all
$L^2$
energy estimate yields, for all
![]() $t>0$
, that
$t>0$
, that
 $$ \begin{align*} \begin{aligned} \|(\widetilde{u}, \widetilde{B})(t)\|_{L^2}^2+ \int_0^t \|(\widetilde{u}, \widetilde{B}) (\tau) \|_{ \dot{H}^1}^2 d\tau & \lesssim \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2}^2 + \int_0^t \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ L^3}^2 f(\tau) d\tau \\ & \quad + \left\Vert \frac{1}{c} \partial_t E^c \times B^c \right\Vert{}_{ L^2_t \dot{H}^{-1} } ^2+ \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t L^2 } ^2\\ & \lesssim \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2}^2 + \int_0^t \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ L^2} \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ \dot{H}^1} f(\tau) d\tau \\ & \quad + \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}}} ^2\left\Vert B^c \right\Vert{}_{ L^\infty_t L^2 } ^2+ \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t L^2 } ^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|(\widetilde{u}, \widetilde{B})(t)\|_{L^2}^2+ \int_0^t \|(\widetilde{u}, \widetilde{B}) (\tau) \|_{ \dot{H}^1}^2 d\tau & \lesssim \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2}^2 + \int_0^t \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ L^3}^2 f(\tau) d\tau \\ & \quad + \left\Vert \frac{1}{c} \partial_t E^c \times B^c \right\Vert{}_{ L^2_t \dot{H}^{-1} } ^2+ \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t L^2 } ^2\\ & \lesssim \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2}^2 + \int_0^t \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ L^2} \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ \dot{H}^1} f(\tau) d\tau \\ & \quad + \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}}} ^2\left\Vert B^c \right\Vert{}_{ L^\infty_t L^2 } ^2+ \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t L^2 } ^2. \end{aligned} \end{align*} $$
Thus, we find, for any
![]() $\lambda>0$
, that
$\lambda>0$
, that
 $$ \begin{align*} \begin{aligned} \|(\widetilde{u}, \widetilde{B})(t)\|_{L^2}^2 &+ \int_0^t \|(\widetilde{u}, \widetilde{B}) (\tau) \|_{ \dot{H}^1}^2 d\tau \\ & \lesssim \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2}^2 + \lambda^{-1}\int_0^t \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ L^2} ^2 f^2(\tau) d\tau + \lambda \int_0^t \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^1}^2 d\tau \\ & \quad + \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}}} ^2\left\Vert B^c \right\Vert{}_{ L^\infty_t L^2 } ^2+ \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t L^2 } ^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|(\widetilde{u}, \widetilde{B})(t)\|_{L^2}^2 &+ \int_0^t \|(\widetilde{u}, \widetilde{B}) (\tau) \|_{ \dot{H}^1}^2 d\tau \\ & \lesssim \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2}^2 + \lambda^{-1}\int_0^t \| ( \widetilde{u},\widetilde{B})(\tau)\|_{ L^2} ^2 f^2(\tau) d\tau + \lambda \int_0^t \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^1}^2 d\tau \\ & \quad + \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t \dot{H}^{\frac{1}{2}}} ^2\left\Vert B^c \right\Vert{}_{ L^\infty_t L^2 } ^2+ \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t L^2 } ^2. \end{aligned} \end{align*} $$
Hence, choosing
![]() $\lambda $
small enough, utilizing the energy inequality (1.2) and applying Grönwall’s lemma, we deduce, for some universal constant
$\lambda $
small enough, utilizing the energy inequality (1.2) and applying Grönwall’s lemma, we deduce, for some universal constant
![]() $C>0$
, that
$C>0$
, that
 $$ \begin{align*} \begin{aligned} \|(\widetilde{u}, \widetilde{B})(t)\|_{L^2}^2 &+ \int_0^t \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^1}^2 d\tau \\ & \qquad \lesssim \left( \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2} ^2 + (\mathcal{E}_0^2 +1) \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t H^{\frac{1}{2}}}^2 \right) \exp \left(C\int_0^t f^2(\tau) d\tau \right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|(\widetilde{u}, \widetilde{B})(t)\|_{L^2}^2 &+ \int_0^t \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^1}^2 d\tau \\ & \qquad \lesssim \left( \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2} ^2 + (\mathcal{E}_0^2 +1) \left\Vert \frac{1}{c} \partial_t E^c \right\Vert{}_{L^2_t H^{\frac{1}{2}}}^2 \right) \exp \left(C\int_0^t f^2(\tau) d\tau \right). \end{aligned} \end{align*} $$
Consequently, by virtue of (5.10), (5.11) and (6.1), we end up with
 $$ \begin{align} \begin{aligned} \sup_{\tau\in [0,\infty)}\|(\widetilde{u}, \widetilde{B})(\tau)\|_{L^2}^2 &+ \int_0^ \infty \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^1}^2 d\tau \leq C_0 \underbrace{ \left( \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2} ^2 + c^{-2} \right)}_{\overset{\mathrm{def}}{=} \Theta_c}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sup_{\tau\in [0,\infty)}\|(\widetilde{u}, \widetilde{B})(\tau)\|_{L^2}^2 &+ \int_0^ \infty \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^1}^2 d\tau \leq C_0 \underbrace{ \left( \|(\widetilde{u}_0, \widetilde{B}_0)\|_{L^2} ^2 + c^{-2} \right)}_{\overset{\mathrm{def}}{=} \Theta_c}, \end{aligned} \end{align} $$
where
![]() $ C_0>0$
is another constant that depends only on the size of the initial data. In the sequel, this constant will be allowed to change value as long as it remains independent of c. This establishes the convergence of
$ C_0>0$
is another constant that depends only on the size of the initial data. In the sequel, this constant will be allowed to change value as long as it remains independent of c. This establishes the convergence of
![]() $\widetilde u$
and
$\widetilde u$
and
![]() $\widetilde B$
to zero in the energy space
$\widetilde B$
to zero in the energy space
![]() $L_t^\infty L^2\cap L_t^2\dot H^1$
.
$L_t^\infty L^2\cap L_t^2\dot H^1$
.
6.2 An interpolation argument
The results in this step are standard. Indeed, since both solutions
![]() $ (u^c,B^c)$
and
$ (u^c,B^c)$
and
![]() $(u ,B )$
belong to the space
$(u ,B )$
belong to the space
uniformly in c, it follows, by interpolation with (6.3), for any
![]() $s\in [0,1]$
, that
$s\in [0,1]$
, that
 $$ \begin{align*} \begin{aligned} \sup_{\tau\in [0,\infty)}\|(\widetilde{u}, \widetilde{B})(\tau)\|_{\dot{H}^s \times \dot{H}^{ \frac{3s}{2}}}^2 &+ \int_0^ \infty \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^{s+1} \times \dot{H}^{ \frac{3s}{2} +1}}^2 d\tau \leq C_0 \Theta_c^{1-s} , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sup_{\tau\in [0,\infty)}\|(\widetilde{u}, \widetilde{B})(\tau)\|_{\dot{H}^s \times \dot{H}^{ \frac{3s}{2}}}^2 &+ \int_0^ \infty \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^{s+1} \times \dot{H}^{ \frac{3s}{2} +1}}^2 d\tau \leq C_0 \Theta_c^{1-s} , \end{aligned} \end{align*} $$
whereby we deduce, for all
![]() $s\in [0,1)$
, that
$s\in [0,1)$
, that
 $$ \begin{align*} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{\tau\in [0,\infty)}\|(\widetilde{u}, \widetilde{B})(\tau)\|_{\dot{H}^s \times \dot{H}^{ \frac{3s}{2}}}^2 + \int_0^ \infty \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^{s+1} \times \dot{H}^{ \frac{3s}{2} +1}}^2 d\tau \right) =0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{\tau\in [0,\infty)}\|(\widetilde{u}, \widetilde{B})(\tau)\|_{\dot{H}^s \times \dot{H}^{ \frac{3s}{2}}}^2 + \int_0^ \infty \|(\widetilde{u}, \widetilde{B} )(\tau) \|_{ \dot{H}^{s+1} \times \dot{H}^{ \frac{3s}{2} +1}}^2 d\tau \right) =0. \end{aligned} \end{align*} $$
We are now left with proving the convergence of solutions in the spaces corresponding to the endpoint case
![]() $s=1$
, above.
$s=1$
, above.
6.3 Convergence of the velocity in the endpoint space
 $\dot H^1$
$\dot H^1$
With the bounds established in the previous step, we are now going to show that the convergence of the velocity in the endpoint case
![]() $s=1$
is a straightforward consequence of the fact that the source term
$s=1$
is a straightforward consequence of the fact that the source term
![]() $\frac {1}{c}\partial _t E^c \times B^c $
in the momentum equation vanishes in
$\frac {1}{c}\partial _t E^c \times B^c $
in the momentum equation vanishes in
![]() $ L^2_tL^2$
, as
$ L^2_tL^2$
, as
![]() $c\to \infty $
.
$c\to \infty $
.
To that end, performing an
![]() $\dot {H}^1$
energy estimate for the first equation in (6.2), one sees that
$\dot {H}^1$
energy estimate for the first equation in (6.2), one sees that
 $$ \begin{align*} \begin{aligned} \sup_{\tau\in [0,\infty)}\| \widetilde{u} (\tau)\|_{ \dot{H}^1 }^2 + \int_0^\infty\| \widetilde{u} (\tau)\|_{ \dot{H}^2 }^2 d\tau \lesssim \left\Vert \widetilde{u}_0\right\Vert{}_{\dot{H}^1}^2 + \left\Vert F \right\Vert{}_{L^2_tL^2 }^2 + \left \| \frac{1}{c}\partial_t E^c \times B^c \right \|_{L^2_tL^2 } ^2 , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sup_{\tau\in [0,\infty)}\| \widetilde{u} (\tau)\|_{ \dot{H}^1 }^2 + \int_0^\infty\| \widetilde{u} (\tau)\|_{ \dot{H}^2 }^2 d\tau \lesssim \left\Vert \widetilde{u}_0\right\Vert{}_{\dot{H}^1}^2 + \left\Vert F \right\Vert{}_{L^2_tL^2 }^2 + \left \| \frac{1}{c}\partial_t E^c \times B^c \right \|_{L^2_tL^2 } ^2 , \end{aligned} \end{align*} $$
where we denote
Moreover, by a direct application of standard paraproduct laws and interpolation inequalities, we infer that
 $$ \begin{align*}\begin{aligned} \left\Vert F \right\Vert{}_{L^2_tL^2 } & \lesssim \left\Vert (u,u^c)\right\Vert{}_{L^4_t \dot{B}^{\frac{3}{2}}_{2,1}} \left\Vert \widetilde{u}\right\Vert{}_{L^4_t \dot{H}^1} +\left\Vert ( B,B^c)\right\Vert{}_{ L^4_t \dot{H}^1 } \|\widetilde{B}\|_{ L^4 _t \dot{B}^{\frac{3}{2}}_{2,1} } \\ & \lesssim \left\Vert (u,u^c)\right\Vert{}_{ L^\infty _t \dot{H}^{1} \cap L^2_t \dot{H}^{2} } \left\Vert \widetilde{u}\right\Vert{}_{ L^\infty _t \dot{H}^{\frac{1}{2}} \cap L^2_t \dot{H}^{\frac{3}{2}}} +\left\Vert ( B,B^c)\right\Vert{}_{ L^\infty _t \dot{H}^{\frac{1}{2}} \cap L^2_t \dot{H}^{\frac{3}{2}}} \|\widetilde{B}\|_{ L^\infty _t \dot{H}^1 \cap L^2_t \dot{H}^{2}} , \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \left\Vert F \right\Vert{}_{L^2_tL^2 } & \lesssim \left\Vert (u,u^c)\right\Vert{}_{L^4_t \dot{B}^{\frac{3}{2}}_{2,1}} \left\Vert \widetilde{u}\right\Vert{}_{L^4_t \dot{H}^1} +\left\Vert ( B,B^c)\right\Vert{}_{ L^4_t \dot{H}^1 } \|\widetilde{B}\|_{ L^4 _t \dot{B}^{\frac{3}{2}}_{2,1} } \\ & \lesssim \left\Vert (u,u^c)\right\Vert{}_{ L^\infty _t \dot{H}^{1} \cap L^2_t \dot{H}^{2} } \left\Vert \widetilde{u}\right\Vert{}_{ L^\infty _t \dot{H}^{\frac{1}{2}} \cap L^2_t \dot{H}^{\frac{3}{2}}} +\left\Vert ( B,B^c)\right\Vert{}_{ L^\infty _t \dot{H}^{\frac{1}{2}} \cap L^2_t \dot{H}^{\frac{3}{2}}} \|\widetilde{B}\|_{ L^\infty _t \dot{H}^1 \cap L^2_t \dot{H}^{2}} , \end{aligned} \end{align*} $$
and
 $$ \begin{align*}\begin{aligned} \left\| \frac{1}{c}\partial_t E^c \times B^c \right \|_{L^2_tL^2 } & \lesssim \left\| \frac{1}{c}\partial_t E^c \right\|_{L^2_t \dot{H}^{\frac{1}{2}} } \| B^c \|_{L^\infty _t \dot{H}^1 } \\ & \lesssim \left \| \frac{1}{c}\partial_t E^c \right \|_{L^2_t \dot{H}^{\frac{1}{2}} } \| B^c \|_{L^\infty _t H^{\frac{3}{2}} } \\ & \leq C_0\left \| \frac{1}{c}\partial_t E^c \right \|_{L^2_t \dot{H}^{\frac{1}{2}} }. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \left\| \frac{1}{c}\partial_t E^c \times B^c \right \|_{L^2_tL^2 } & \lesssim \left\| \frac{1}{c}\partial_t E^c \right\|_{L^2_t \dot{H}^{\frac{1}{2}} } \| B^c \|_{L^\infty _t \dot{H}^1 } \\ & \lesssim \left \| \frac{1}{c}\partial_t E^c \right \|_{L^2_t \dot{H}^{\frac{1}{2}} } \| B^c \|_{L^\infty _t H^{\frac{3}{2}} } \\ & \leq C_0\left \| \frac{1}{c}\partial_t E^c \right \|_{L^2_t \dot{H}^{\frac{1}{2}} }. \end{aligned}\end{align*} $$
Therefore, by virtue of (5.11) and the bounds in Theorem 1.1 and Corollary 1.2, we end up with
 $$ \begin{align*}\sup_{\tau\in [0,\infty)}\| \widetilde{u} (\tau)\|_{ \dot{H}^1 }^2 + \int_0^\infty\| \widetilde{u} (\tau)\|_{ \dot{H}^2 }^2 d\tau \lesssim \left\Vert \widetilde{u}_0\right\Vert{}_{\dot{H}^1}^2 + C_0\left( \left\Vert \widetilde{u}\right\Vert{}_{ L^\infty _t \dot{H}^{\frac{1}{2}} \cap L^2_t \dot{H}^{\frac{3}{2}}}^2 + \|\widetilde{B}\|_{ L^\infty _t \dot{H}^1 \cap L^2_t \dot{H}^{2}}^2 + c^{-2} \right).\end{align*} $$
$$ \begin{align*}\sup_{\tau\in [0,\infty)}\| \widetilde{u} (\tau)\|_{ \dot{H}^1 }^2 + \int_0^\infty\| \widetilde{u} (\tau)\|_{ \dot{H}^2 }^2 d\tau \lesssim \left\Vert \widetilde{u}_0\right\Vert{}_{\dot{H}^1}^2 + C_0\left( \left\Vert \widetilde{u}\right\Vert{}_{ L^\infty _t \dot{H}^{\frac{1}{2}} \cap L^2_t \dot{H}^{\frac{3}{2}}}^2 + \|\widetilde{B}\|_{ L^\infty _t \dot{H}^1 \cap L^2_t \dot{H}^{2}}^2 + c^{-2} \right).\end{align*} $$
Consequently, owing to the convergence results from the previous steps, we arrive at the conclusion that
 $$ \begin{align*} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{\tau\in [0,\infty)}\| \widetilde{u} (\tau)\|_{\dot{H}^1 }^2 + \int_0^ \infty \| \widetilde{u} (\tau) \|_{ \dot{H}^{2} }^2 d\tau \right) =0 , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lim_{c \rightarrow \infty}\left( \sup_{\tau\in [0,\infty)}\| \widetilde{u} (\tau)\|_{\dot{H}^1 }^2 + \int_0^ \infty \| \widetilde{u} (\tau) \|_{ \dot{H}^{2} }^2 d\tau \right) =0 , \end{aligned} \end{align*} $$
for we are assuming that
![]() $\widetilde u_0$
vanishes in
$\widetilde u_0$
vanishes in
![]() $\dot H^1$
.
$\dot H^1$
.
6.4 Convergence of the magnetic field in the endpoint space
 $\dot H^{\frac 32}$
$\dot H^{\frac 32}$
One could try to mimic the proof from the previous step and perform a
![]() $\dot {H}^{\frac {3}{2}}$
energy estimate for
$\dot {H}^{\frac {3}{2}}$
energy estimate for
![]() $\widetilde {B}$
. This method would require a decay of
$\widetilde {B}$
. This method would require a decay of
![]() $ \frac {1}{c} \partial _t E^c$
in
$ \frac {1}{c} \partial _t E^c$
in
![]() $L^2_t \dot {H}^{\frac {3}{2}}$
, which is not an available information here.
$L^2_t \dot {H}^{\frac {3}{2}}$
, which is not an available information here.
Instead, our proof below is inspired from a Compactness Extrapolation Lemma (see [Reference Arsénio and Houamed4, Lemma 1.4]), which reduces the justification of the convergence in an endpoint setting to the analysis of the evanescence of some high frequencies. To see that, we first fix
![]() $\varepsilon \in (0, 1 ) $
and pick any real number
$\varepsilon \in (0, 1 ) $
and pick any real number
![]() $s\in [0,1-\varepsilon )$
. Then, by utilizing the results from Section 6.2, we obtain that
$s\in [0,1-\varepsilon )$
. Then, by utilizing the results from Section 6.2, we obtain that
 $$ \begin{align*} \begin{aligned} \sup_{\tau \in [0,\infty)} \int_{|\xi|< ( \Theta_c)^{ \frac{\varepsilon+ s-1}{3(1-s)} }} |\xi |^{ 3 } \left| \mathcal{F}( \widetilde{B })(\tau ,\xi)\right|{}^2 d\xi & + \int_0^\infty \int_{|\xi|< ( \Theta_c)^{ \frac{\varepsilon+ s-1}{3(1-s)} }} |\xi |^{5 } \left| \mathcal{F}( \widetilde{B })(\tau ,\xi)\right|{}^2 d\xi d\tau \\ & \quad \leq \Theta_c^{ \varepsilon +s-1 } \left( \| \widetilde {B}\|_{L^\infty_t \dot{H}^{ \frac{3s}{2}}}^2 + \| \widetilde {B}\|_{L^2_t \dot{H}^{ \frac{3s}{2} + 1}}^2 \right)\\ &\quad \leq C_0 \Theta_c^{ \varepsilon }. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sup_{\tau \in [0,\infty)} \int_{|\xi|< ( \Theta_c)^{ \frac{\varepsilon+ s-1}{3(1-s)} }} |\xi |^{ 3 } \left| \mathcal{F}( \widetilde{B })(\tau ,\xi)\right|{}^2 d\xi & + \int_0^\infty \int_{|\xi|< ( \Theta_c)^{ \frac{\varepsilon+ s-1}{3(1-s)} }} |\xi |^{5 } \left| \mathcal{F}( \widetilde{B })(\tau ,\xi)\right|{}^2 d\xi d\tau \\ & \quad \leq \Theta_c^{ \varepsilon +s-1 } \left( \| \widetilde {B}\|_{L^\infty_t \dot{H}^{ \frac{3s}{2}}}^2 + \| \widetilde {B}\|_{L^2_t \dot{H}^{ \frac{3s}{2} + 1}}^2 \right)\\ &\quad \leq C_0 \Theta_c^{ \varepsilon }. \end{aligned} \end{align*} $$
For simplicity, we are now going to take
![]() $s =0 $
and
$s =0 $
and
![]() $ \varepsilon = \frac {1}{4}$
, thereby establishing that
$ \varepsilon = \frac {1}{4}$
, thereby establishing that

which takes care of frequencies in
![]() $\{|\xi |<\Theta _c^{-\frac 14}\}$
.
$\{|\xi |<\Theta _c^{-\frac 14}\}$
.
We now deal with the high frequencies in
![]() $\{|\xi |\geq \Theta _c^{-\frac 14}\}$
. To that end, we first recall, by Corollary 1.2 and (1.11), that the bound
$\{|\xi |\geq \Theta _c^{-\frac 14}\}$
. To that end, we first recall, by Corollary 1.2 and (1.11), that the bound
holds uniformly with respect to
![]() $c\in (c_0,\infty )$
. Therefore, we find that
$c\in (c_0,\infty )$
. Therefore, we find that

where we exploited the principle described in (1.12).
The treatment of the terms involving
![]() $B^c$
in the right-hand side above requires yet another application of Lemma 3.2. To that end, first observing that
$B^c$
in the right-hand side above requires yet another application of Lemma 3.2. To that end, first observing that
 $$ \begin{align*} \begin{aligned} \left\Vert B^c\right\Vert{}_{L^\infty_t \dot{B}^{\frac{3}{2}}_{2,2,>}}& \leq c^{-1} \left\Vert B^c\right\Vert{}_{\widetilde{L} ^\infty_t \dot{B}^{\frac{5}{2}}_{2,1,>}} , \\ \left\Vert B^c\right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,2,>}} &\leq \left\Vert B^c\right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{\frac{5}{2}}_{2,1,>}} , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert B^c\right\Vert{}_{L^\infty_t \dot{B}^{\frac{3}{2}}_{2,2,>}}& \leq c^{-1} \left\Vert B^c\right\Vert{}_{\widetilde{L} ^\infty_t \dot{B}^{\frac{5}{2}}_{2,1,>}} , \\ \left\Vert B^c\right\Vert{}_{L^2_t \dot{B}^{\frac{5}{2}}_{2,2,>}} &\leq \left\Vert B^c\right\Vert{}_{\widetilde{L} ^2_t \dot{B}^{\frac{5}{2}}_{2,1,>}} , \end{aligned} \end{align*} $$
it is readily seen that the decay in the hyperbolic region (i.e., when frequencies are localized in
![]() $\{ |\xi | \gtrsim \sigma c \} $
) follows from (5.4) as soon as it is assumed initially that
$\{ |\xi | \gtrsim \sigma c \} $
) follows from (5.4) as soon as it is assumed initially that
 $$ \begin{align*}\lim _{c\rightarrow \infty} \left( c^{-1} \| (E^c_0,B^c_0) \|_{ \dot{B}^{\frac{5}{2}}_{2,1,>}} \right) =0.\end{align*} $$
$$ \begin{align*}\lim _{c\rightarrow \infty} \left( c^{-1} \| (E^c_0,B^c_0) \|_{ \dot{B}^{\frac{5}{2}}_{2,1,>}} \right) =0.\end{align*} $$
Now, in order to study the vanishing of the remaining frequencies of
![]() $B^c$
(i.e., frequencies localized in
$B^c$
(i.e., frequencies localized in
![]() $\{ \Theta _c^{-\frac {1}{4}} \leq |\xi | \lesssim \sigma c \} $
), we employ the low-frequency estimate from Lemma 3.2 with the values
$\{ \Theta _c^{-\frac {1}{4}} \leq |\xi | \lesssim \sigma c \} $
), we employ the low-frequency estimate from Lemma 3.2 with the values
which leads to

Accordingly, due to the strong convergence of
![]() $(E_0^c,B_0^c)_{c>0} $
in
$(E_0^c,B_0^c)_{c>0} $
in
![]() $\dot {H}^{\frac {3}{2}}$
, it is then readily seen that the first term in the right-hand side above vanishes as
$\dot {H}^{\frac {3}{2}}$
, it is then readily seen that the first term in the right-hand side above vanishes as
![]() $c\to \infty $
.
$c\to \infty $
.
As for the second term in the right-hand side, it is controlled first by exploiting the localization in high frequencies to write that

Therefore, by utilizing the product law (2.3), we arrive at the conclusion that

Hence, due to the bounds from Theorem 1.1 and the fact that
we deduce that the right-hand side above vanishes in the limit
![]() $c\to \infty $
, thereby concluding the proof of Theorem 1.3.
$c\to \infty $
, thereby concluding the proof of Theorem 1.3.
Conflict of interest
The authors certify that there are no actual or potential conflicts of interest.