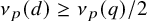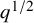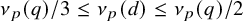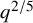1 Introduction
The study of moments of families of L-functions has a long history. One strand of research concerns the estimation of moments in order to secure strong subconvexity bounds. Another direction is to consider the structural properties of the moments, especially in their connections with random matrix theory. One of the long-standing guiding principles concerns analogies between different families, particularly the consideration of the Riemann zeta function in the t-aspect on the one side and the family of Dirichlet L-functions in the q-aspect on the other side.
We begin by discussing some moment problems for the zeta function. This is a vast subject, and we only briefly touch on a few results pertinent to our narrative. In [Reference Heath-BrownHB2], Heath-Brown studied the twelfth moment of the Riemann zeta function, finding that
 $$ \begin{align} \int_T^{2T} |\zeta(1/2+it)|^{12} dt \ll_\varepsilon T^{2+\varepsilon}, \end{align} $$
$$ \begin{align} \int_T^{2T} |\zeta(1/2+it)|^{12} dt \ll_\varepsilon T^{2+\varepsilon}, \end{align} $$
a result which easily recovers the Weyl bound while also proving in a strong quantitative form that
![]() $|\zeta (1/2+it)|$
cannot be too large too often. Heath-Brown’s technique for proving (1.1) is based on leveraging information from short second moments of the zeta function. A simple modification of [Reference Heath-BrownHB2, Lemma 1] implies
$|\zeta (1/2+it)|$
cannot be too large too often. Heath-Brown’s technique for proving (1.1) is based on leveraging information from short second moments of the zeta function. A simple modification of [Reference Heath-BrownHB2, Lemma 1] implies
 $$ \begin{align} \int_T^{T+T^{1/3}} |\zeta(1/2+it)|^2 dt \ll T^{1/3+\varepsilon}, \end{align} $$
$$ \begin{align} \int_T^{T+T^{1/3}} |\zeta(1/2+it)|^2 dt \ll T^{1/3+\varepsilon}, \end{align} $$
for
![]() $T \geq 1$
. See also [Reference TitchmarshT2, Section 7.4] and [Reference IvićI, Chapter 7] for more discussion and other related results. For example, [Reference TitchmarshT2, Theorem 7.4] gives that
$T \geq 1$
. See also [Reference TitchmarshT2, Section 7.4] and [Reference IvićI, Chapter 7] for more discussion and other related results. For example, [Reference TitchmarshT2, Theorem 7.4] gives that
 $$ \begin{align} \int_0^{T} |\zeta(1/2+it)|^2 dt = T \log T + (2 \gamma_0 - 1 - \log(2 \pi))T + O(T^{\alpha+\varepsilon}), \qquad (\alpha = 1/2). \end{align} $$
$$ \begin{align} \int_0^{T} |\zeta(1/2+it)|^2 dt = T \log T + (2 \gamma_0 - 1 - \log(2 \pi))T + O(T^{\alpha+\varepsilon}), \qquad (\alpha = 1/2). \end{align} $$
This error term has been improved many times over the years, and it seems the first improvement is due to Titchmarsh himself [Reference TitchmarshT1], attaining
![]() $\alpha = 5/12$
. Note that (1.3) leads to an asymptotic formula for the second moment in a short interval of length at least
$\alpha = 5/12$
. Note that (1.3) leads to an asymptotic formula for the second moment in a short interval of length at least
![]() $T^{\alpha +\varepsilon }$
, simply by writing
$T^{\alpha +\varepsilon }$
, simply by writing
![]() $\int _T^{T+\Delta } = \int _0^{T+\Delta } - \int _0^{T}$
.
$\int _T^{T+\Delta } = \int _0^{T+\Delta } - \int _0^{T}$
.
Next, we discuss some prior works on q-analogs of these results. Nunes [Reference NunesN] proved an analog to (1.1) for smooth square-free moduli q. In a complementary direction, Milićević and White [Reference Milićević and WhiteMW] proved a variant of (1.1) in the depth aspect (i.e., fixing a prime p and letting
![]() $q=p^j$
with
$q=p^j$
with
![]() $j \rightarrow \infty $
). Both of these works consider upper bounds on ‘short’ second moments, where in this context, ‘short’ refers to a coset. Petrow and Young [Reference Petrow and YoungPY] obtained an upper bound on the fourth moment of Dirichlet L-functions along a coset of size
$j \rightarrow \infty $
). Both of these works consider upper bounds on ‘short’ second moments, where in this context, ‘short’ refers to a coset. Petrow and Young [Reference Petrow and YoungPY] obtained an upper bound on the fourth moment of Dirichlet L-functions along a coset of size
![]() $\gg q^{2/3+\varepsilon }$
. For the full family second moment, Heath-Brown [Reference Heath-BrownHB3] proved
$\gg q^{2/3+\varepsilon }$
. For the full family second moment, Heath-Brown [Reference Heath-BrownHB3] proved
 $$ \begin{align} \sum_{\chi\ \pmod{q}} |L(1/2, \chi)|^2 = \frac{\phi(q)}{q} \sum_{d | q} \mu(q/d) T(d), \end{align} $$
$$ \begin{align} \sum_{\chi\ \pmod{q}} |L(1/2, \chi)|^2 = \frac{\phi(q)}{q} \sum_{d | q} \mu(q/d) T(d), \end{align} $$
where with
![]() $\gamma _0 = 0.577\dots $
representing Euler’s constant, we have
$\gamma _0 = 0.577\dots $
representing Euler’s constant, we have
 $$ \begin{align*} T(d) = d( \log \tfrac{d}{8 \pi} + \gamma_0) + 2 \zeta(1/2)^2 d^{1/2} + \sum_{n=0}^{2N-1} c_n d^{-n/2} + O(d^{-N}). \end{align*} $$
$$ \begin{align*} T(d) = d( \log \tfrac{d}{8 \pi} + \gamma_0) + 2 \zeta(1/2)^2 d^{1/2} + \sum_{n=0}^{2N-1} c_n d^{-n/2} + O(d^{-N}). \end{align*} $$
One remark that is in order here is that Heath-Brown considers a sum over all Dirichlet characters, and not just the primitive ones. A second comment is that there is no obvious way to extract from (1.4) a formula for the second moment restricted to a coset, in contrast to the t-integral analog for the zeta function. Finally, we remark that for composite values of q, there are a variety of main terms that may be intermediate in size between
![]() $q^{1/2}$
and q. However, the five authors [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS] have conjectured an asymptotic formula for the second moment in this family, but only after restriction to the family of solely the primitive characters modulo q. Conrey [Reference ConreyC] verified the five-author conjecture for the second moment in this family. In the same paper, Conrey also derived a beautiful reciprocity formula for the twisted second moment with prime modulus.
$q^{1/2}$
and q. However, the five authors [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS] have conjectured an asymptotic formula for the second moment in this family, but only after restriction to the family of solely the primitive characters modulo q. Conrey [Reference ConreyC] verified the five-author conjecture for the second moment in this family. In the same paper, Conrey also derived a beautiful reciprocity formula for the twisted second moment with prime modulus.
To state our main results, we need some notation. Suppose
![]() $\psi $
is a Dirichlet character modulo q and d is a positive integer with
$\psi $
is a Dirichlet character modulo q and d is a positive integer with
![]() $d|q$
and
$d|q$
and
![]() $q|d^2$
. It is easy to see that, as a function of x,
$q|d^2$
. It is easy to see that, as a function of x,
![]() $\psi (1+dx)$
is an additive character with period
$\psi (1+dx)$
is an additive character with period
![]() $q/d$
. Hence, there exists an integer
$q/d$
. Hence, there exists an integer
![]() $a_{\psi }\ \pmod {q/d}$
such that
$a_{\psi }\ \pmod {q/d}$
such that
![]() $\psi (1+dx) = e(\frac {a_\psi dx}{q})$
, where
$\psi (1+dx) = e(\frac {a_\psi dx}{q})$
, where
![]() $e(x)=e^{2\pi ix}$
. The primitivity of
$e(x)=e^{2\pi ix}$
. The primitivity of
![]() $\psi $
modulo q means that
$\psi $
modulo q means that
![]() $(a_{\psi }, q/d) = 1$
(for which see Lemma 2.14 below). We assume
$(a_{\psi }, q/d) = 1$
(for which see Lemma 2.14 below). We assume
Let
![]() $\nu _p(\cdot )$
denote the p-adic valuation. For a and b as positive integers, we will write ‘
$\nu _p(\cdot )$
denote the p-adic valuation. For a and b as positive integers, we will write ‘
![]() $a\prec b$
’ to mean that a and b share all of the same prime factors and, for any prime
$a\prec b$
’ to mean that a and b share all of the same prime factors and, for any prime
![]() $p|b$
,
$p|b$
,
![]() $\nu _p(a)<\nu _p(b)$
. Similarly, we will write ‘
$\nu _p(a)<\nu _p(b)$
. Similarly, we will write ‘
![]() $a\preceq b$
’ to mean that a and b share all of the same prime factors and, for any prime
$a\preceq b$
’ to mean that a and b share all of the same prime factors and, for any prime
![]() $p|b$
,
$p|b$
,
![]() $\nu _p(a)\leq \nu _p(b)$
.
$\nu _p(a)\leq \nu _p(b)$
.
Theorem 1.1. Let
![]() $\psi $
be even of conductor q, and suppose
$\psi $
be even of conductor q, and suppose
![]() $d \prec q \preceq d^2$
. Then
$d \prec q \preceq d^2$
. Then
 $$ \begin{align} \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = {\mathcal{D}}+{\mathcal{A}} + O(q^{-1/8+ \varepsilon} d), \end{align} $$
$$ \begin{align} \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = {\mathcal{D}}+{\mathcal{A}} + O(q^{-1/8+ \varepsilon} d), \end{align} $$
where with
![]() $\theta (q) = \sum _{p|q} \frac {\log {p}}{p-1}$
, and
$\theta (q) = \sum _{p|q} \frac {\log {p}}{p-1}$
, and
![]() $\sigma _\alpha (n) = \sum _{k|n} k^\alpha $
, we define
$\sigma _\alpha (n) = \sum _{k|n} k^\alpha $
, we define
and
 $$ \begin{align} {\mathcal{A}} = \frac{\varphi(d)}{d} \sqrt{q} \; \frac{\sigma_0(|a_\psi|)}{\sqrt{|a_\psi|}}. \end{align} $$
$$ \begin{align} {\mathcal{A}} = \frac{\varphi(d)}{d} \sqrt{q} \; \frac{\sigma_0(|a_\psi|)}{\sqrt{|a_\psi|}}. \end{align} $$
Remarks. The term
![]() ${\mathcal {D}}$
is the standard diagonal main term, which is analogous to the main term in (1.3). An application of the recipe of [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS] would predict
${\mathcal {D}}$
is the standard diagonal main term, which is analogous to the main term in (1.3). An application of the recipe of [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS] would predict
 $$ \begin{align} \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = {\mathcal{D}} + (\text{Error term}), \end{align} $$
$$ \begin{align} \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = {\mathcal{D}} + (\text{Error term}), \end{align} $$
where notably the term
![]() ${\mathcal {A}}$
is not present. A bold interpretation of [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS] might suggest the error term in (1.9) would be of size
${\mathcal {A}}$
is not present. A bold interpretation of [Reference Conrey, Farmer, Keating, Rubinstein and SnaithCFKRS] might suggest the error term in (1.9) would be of size
![]() $O(d^{1/2} q^{\varepsilon })$
, but a more cautious value would be
$O(d^{1/2} q^{\varepsilon })$
, but a more cautious value would be
![]() $O(q^{1/2+\varepsilon })$
. If
$O(q^{1/2+\varepsilon })$
. If
![]() $a_{\psi } = 1$
, say, then
$a_{\psi } = 1$
, say, then
![]() ${\mathcal {A}} = \frac {\varphi (d)}{d} \sqrt {q}$
, which is essentially its maximal size. This is consistent with an error term of size
${\mathcal {A}} = \frac {\varphi (d)}{d} \sqrt {q}$
, which is essentially its maximal size. This is consistent with an error term of size
![]() $O(q^{1/2+\varepsilon })$
in (1.9), but inconsistent with
$O(q^{1/2+\varepsilon })$
in (1.9), but inconsistent with
![]() $O(d^{1/2} q^{\varepsilon })$
. However, note that
$O(d^{1/2} q^{\varepsilon })$
. However, note that
![]() ${\mathcal {A}} \ll \sqrt {q}$
which is smaller than
${\mathcal {A}} \ll \sqrt {q}$
which is smaller than
![]() ${\mathcal {D}}$
, since
${\mathcal {D}}$
, since
![]() $\sqrt {q} \leq d$
, and
$\sqrt {q} \leq d$
, and
![]() ${\mathcal {D}} \gg d (\log q)^{1-\varepsilon }$
.
${\mathcal {D}} \gg d (\log q)^{1-\varepsilon }$
.
The existence of
![]() ${\mathcal {A}}$
contrasts with the absence of a main term of size
${\mathcal {A}}$
contrasts with the absence of a main term of size
![]() $T^{1/2}$
in (1.3). The condition that
$T^{1/2}$
in (1.3). The condition that
![]() $d \prec q$
implies that
$d \prec q$
implies that
![]() $\chi \cdot \psi $
has conductor q for all
$\chi \cdot \psi $
has conductor q for all
![]() $\chi\ \pmod {d}$
, and so this lower-order main term
$\chi\ \pmod {d}$
, and so this lower-order main term
![]() ${\mathcal {A}}$
is not due to characters of smaller modulus (as in (1.4)).
${\mathcal {A}}$
is not due to characters of smaller modulus (as in (1.4)).
As a very rough heuristic, we can indicate how
![]() ${\mathcal {A}}$
arises. Applying an approximate functional equation and the orthogonality formula, we encounter a sum of the form
${\mathcal {A}}$
arises. Applying an approximate functional equation and the orthogonality formula, we encounter a sum of the form
 $$ \begin{align*} \varphi(d) \sum_{m \equiv n \ \pmod{d}} \frac{\psi(m) \overline{\psi(n)}}{\sqrt{mn}}. \end{align*} $$
$$ \begin{align*} \varphi(d) \sum_{m \equiv n \ \pmod{d}} \frac{\psi(m) \overline{\psi(n)}}{\sqrt{mn}}. \end{align*} $$
With
![]() $m= n + d l$
, we have
$m= n + d l$
, we have
![]() $\psi (m) \overline {\psi }(n) = \psi (1 + d l \overline {n}) = e_{q/d}(a_{\psi } l \overline {n})$
. Consider the term
$\psi (m) \overline {\psi }(n) = \psi (1 + d l \overline {n}) = e_{q/d}(a_{\psi } l \overline {n})$
. Consider the term
![]() $n=1$
. If
$n=1$
. If
![]() $a_{\psi } l$
is a bit smaller than
$a_{\psi } l$
is a bit smaller than
![]() $q/d$
, then the exponential is approximately
$q/d$
, then the exponential is approximately
![]() $1$
. Once
$1$
. Once
![]() $|a_{\psi }| l$
is larger than
$|a_{\psi }| l$
is larger than
![]() $q/d$
, then the exponential has cancellation and should not contribute to a main term. This thought process leads to
$q/d$
, then the exponential has cancellation and should not contribute to a main term. This thought process leads to
 $$ \begin{align} \varphi(d) \sum_{l \geq 1} \frac{e_{q/d}(a_{\psi} l)}{\sqrt{d l}} \approx \frac{\varphi(d)}{\sqrt{d}} \sum_{l < \frac{q}{d |a_{\psi}|}} \frac{1}{\sqrt{l}} \approx \frac{\varphi(d) q^{1/2}}{d \sqrt{|a_{\psi}|}}. \end{align} $$
$$ \begin{align} \varphi(d) \sum_{l \geq 1} \frac{e_{q/d}(a_{\psi} l)}{\sqrt{d l}} \approx \frac{\varphi(d)}{\sqrt{d}} \sum_{l < \frac{q}{d |a_{\psi}|}} \frac{1}{\sqrt{l}} \approx \frac{\varphi(d) q^{1/2}}{d \sqrt{|a_{\psi}|}}. \end{align} $$
One can apply the same sort of reasoning for each n dividing
![]() $a_{\psi }$
, giving an expression of the same form, in line with the presence of
$a_{\psi }$
, giving an expression of the same form, in line with the presence of
![]() $\sigma _0(|a_{\psi }|)$
in
$\sigma _0(|a_{\psi }|)$
in
![]() ${\mathcal {A}}$
. Although this heuristic is far from rigorous, it is true that
${\mathcal {A}}$
. Although this heuristic is far from rigorous, it is true that
![]() ${\mathcal {A}}$
emerges in the analysis from the most unbalanced range of summation where n is very small and
${\mathcal {A}}$
emerges in the analysis from the most unbalanced range of summation where n is very small and
![]() $m=n+dl$
is very large.
$m=n+dl$
is very large.
For the next theorem, we will have that
![]() $d|\frac {q}{d}$
,
$d|\frac {q}{d}$
,
![]() $q | d^3$
, and
$q | d^3$
, and
![]() $(q,3) = 1$
, in which case we define
$(q,3) = 1$
, in which case we define
![]() $a_{\psi }\ \pmod {q/d}$
by the condition that
$a_{\psi }\ \pmod {q/d}$
by the condition that
![]() $\psi (1+dx) = e_{q/d}(a_{\psi } ( x - \overline {2}dx^2))$
for all
$\psi (1+dx) = e_{q/d}(a_{\psi } ( x - \overline {2}dx^2))$
for all
![]() $x \in \mathbb Z$
. For more details on this definition, see Section 2.2. Note this definition reduces to the earlier one when
$x \in \mathbb Z$
. For more details on this definition, see Section 2.2. Note this definition reduces to the earlier one when
![]() $d \equiv 0\ \pmod {q/d}$
since then the quadratic term may be discarded. In addition, let
$d \equiv 0\ \pmod {q/d}$
since then the quadratic term may be discarded. In addition, let
![]() $b_\psi $
be the reduction of
$b_\psi $
be the reduction of
![]() $a_\psi \ (\mathrm {mod}\ d)$
such that
$a_\psi \ (\mathrm {mod}\ d)$
such that
![]() $0<|b_\psi |<\frac {d}{2}$
.
$0<|b_\psi |<\frac {d}{2}$
.
Theorem 1.2. Suppose
![]() $\psi $
is even of conductor q, with
$\psi $
is even of conductor q, with
![]() $(q,3) = 1$
and suppose
$(q,3) = 1$
and suppose
![]() $d^2 \preceq q \preceq d^3$
. Then
$d^2 \preceq q \preceq d^3$
. Then
 $$ \begin{align} \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = {\mathcal{D}}+{\mathcal{A}}' + O(d^{-1/4} q^{1/2+\varepsilon}), \end{align} $$
$$ \begin{align} \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = {\mathcal{D}}+{\mathcal{A}}' + O(d^{-1/4} q^{1/2+\varepsilon}), \end{align} $$
where
![]() ${\mathcal {D}}$
is as defined in (1.7), and with
${\mathcal {D}}$
is as defined in (1.7), and with
![]() $a_{\psi } \overline {a_{\psi }} \equiv 1\ \pmod {q}$
, we set
$a_{\psi } \overline {a_{\psi }} \equiv 1\ \pmod {q}$
, we set
 $$ \begin{align} {\mathcal{A}}' = \Big(\frac{2 a_{\psi}}{q} \Big) \cdot \varphi(d) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}} \times \begin{cases} \cos\Big(2\pi\frac{ \overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big) , & q\equiv1\ (\mathrm{mod}\ 4) \\ \sin\Big(2\pi\frac{\overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big), & q\equiv3\ (\mathrm{mod}\ 4). \end{cases} \end{align} $$
$$ \begin{align} {\mathcal{A}}' = \Big(\frac{2 a_{\psi}}{q} \Big) \cdot \varphi(d) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}} \times \begin{cases} \cos\Big(2\pi\frac{ \overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big) , & q\equiv1\ (\mathrm{mod}\ 4) \\ \sin\Big(2\pi\frac{\overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big), & q\equiv3\ (\mathrm{mod}\ 4). \end{cases} \end{align} $$
Remarks. First, observe that the diagonal term
![]() ${\mathcal {D}}$
is larger than the error term provided
${\mathcal {D}}$
is larger than the error term provided
![]() $d \gg q^{2/5+\varepsilon }$
, which goes below the
$d \gg q^{2/5+\varepsilon }$
, which goes below the
![]() $\sqrt {q}$
threshold. Secondly, although
$\sqrt {q}$
threshold. Secondly, although
![]() ${\mathcal {A}}'$
can be negative,
${\mathcal {A}}'$
can be negative,
![]() $|{\mathcal {A}}'|$
is smaller than
$|{\mathcal {A}}'|$
is smaller than
![]() ${\mathcal {D}}$
, since
${\mathcal {D}}$
, since
![]() ${\mathcal {D}} \gg \varphi (d) (\log q)^{1-\varepsilon }$
.
${\mathcal {D}} \gg \varphi (d) (\log q)^{1-\varepsilon }$
.
The presence of trigonometric functions at complicated arguments in
![]() ${\mathcal {A}}'$
is a new feature compared to
${\mathcal {A}}'$
is a new feature compared to
![]() ${\mathcal {A}}$
in Theorem 1.1, and worthy of further discussion. One simple observation is that if
${\mathcal {A}}$
in Theorem 1.1, and worthy of further discussion. One simple observation is that if
![]() $|a_{\psi }| < d/2$
, then
$|a_{\psi }| < d/2$
, then
![]() $b_{\psi } = a_{\psi }$
, and it simplifies as
$b_{\psi } = a_{\psi }$
, and it simplifies as
![]() $\cos (0) = 1$
or
$\cos (0) = 1$
or
![]() $\sin (0) = 0$
. However, there exist situations with
$\sin (0) = 0$
. However, there exist situations with
![]() $q \equiv 3\ \pmod {4}$
where
$q \equiv 3\ \pmod {4}$
where
![]() ${\mathcal {A}}'$
cannot be discarded. For example, let
${\mathcal {A}}'$
cannot be discarded. For example, let
![]() $q = p^{239}$
and
$q = p^{239}$
and
![]() $d = p^{116}$
, and suppose
$d = p^{116}$
, and suppose
![]() $p \rightarrow \infty $
. Here,
$p \rightarrow \infty $
. Here,
![]() $d> q^{2/5}$
, so the error term is smaller than the diagonal term
$d> q^{2/5}$
, so the error term is smaller than the diagonal term
![]() ${\mathcal {D}}$
. Now suppose
${\mathcal {D}}$
. Now suppose
![]() $\psi $
is a character with
$\psi $
is a character with
![]() $a_{\psi } = 1 + 2p^{116}$
, which is a valid range since we need
$a_{\psi } = 1 + 2p^{116}$
, which is a valid range since we need
![]() $|a_{\psi }| < \frac 12 p^{123}$
. Then
$|a_{\psi }| < \frac 12 p^{123}$
. Then
![]() $b_{\psi } =1$
, and so
$b_{\psi } =1$
, and so
![]() $a_{\psi } - b_{\psi } = 2p^{116}$
. Under these conditions, we have
$a_{\psi } - b_{\psi } = 2p^{116}$
. Under these conditions, we have
Therefore,
 $$ \begin{align*} {\mathcal{A}}' = \varphi(d) \times \begin{cases} \cos(4\pi p^{-7}) , & p\equiv1\ (\mathrm{mod}\ 4) \\ \sin(4\pi p^{-7}), & p\equiv3\ (\mathrm{mod}\ 4). \end{cases} \end{align*} $$
$$ \begin{align*} {\mathcal{A}}' = \varphi(d) \times \begin{cases} \cos(4\pi p^{-7}) , & p\equiv1\ (\mathrm{mod}\ 4) \\ \sin(4\pi p^{-7}), & p\equiv3\ (\mathrm{mod}\ 4). \end{cases} \end{align*} $$
In the case
![]() $p \equiv 3\ \pmod {4}$
, then
$p \equiv 3\ \pmod {4}$
, then
![]() $|{\mathcal {A}}'| \approx d p^{-7} = p^{109}$
. This is larger than the error term which has size
$|{\mathcal {A}}'| \approx d p^{-7} = p^{109}$
. This is larger than the error term which has size
![]() $d^{-1/4} q^{1/2} = p^{-116/4 + 119.5} \leq p^{91}$
. One can construct other examples exhibiting other types of behavior for
$d^{-1/4} q^{1/2} = p^{-116/4 + 119.5} \leq p^{91}$
. One can construct other examples exhibiting other types of behavior for
![]() ${\mathcal {A}}'$
. Compared to the discussion around (1.10), it seems harder to heuristically see the shape of
${\mathcal {A}}'$
. Compared to the discussion around (1.10), it seems harder to heuristically see the shape of
![]() ${\mathcal {A}}'$
. However, we stress that in the proof, it arises in the same way as
${\mathcal {A}}'$
. However, we stress that in the proof, it arises in the same way as
![]() ${\mathcal {A}}$
, with the main differences coming from requiring a quadratic approximation for
${\mathcal {A}}$
, with the main differences coming from requiring a quadratic approximation for
![]() $\psi (1+d l \overline {n})$
. The relevant sums can be evaluated in closed form using quadratic Gauss sums.
$\psi (1+d l \overline {n})$
. The relevant sums can be evaluated in closed form using quadratic Gauss sums.
Theorem 1.2 can be extended with little effort to q with
![]() $3|q$
(with a slightly more restrictive assumption
$3|q$
(with a slightly more restrictive assumption
![]() $q\preceq \frac {1}{3}d^3)$
. One could also attempt to find a common/hybrid generalization of Theorems 1.1 and 1.2 by only requiring
$q\preceq \frac {1}{3}d^3)$
. One could also attempt to find a common/hybrid generalization of Theorems 1.1 and 1.2 by only requiring
![]() $d \prec q$
and
$d \prec q$
and
![]() $q \preceq d^3$
. To do so, one could factor
$q \preceq d^3$
. To do so, one could factor
![]() $d = d_1 d_2$
where
$d = d_1 d_2$
where
![]() $d_1$
(
$d_1$
(
![]() $d_2$
, resp.) consists of the part of d where
$d_2$
, resp.) consists of the part of d where
![]() $\nu _p(d_1) \geq \nu _p(q)/2$
(
$\nu _p(d_1) \geq \nu _p(q)/2$
(
![]() $\nu _p(d_2) < \nu _p(q)/2$
, resp.), and use the ideas of proof of Theorem 1.1 for
$\nu _p(d_2) < \nu _p(q)/2$
, resp.), and use the ideas of proof of Theorem 1.1 for
![]() $d_1$
(Theorem 1.2 for
$d_1$
(Theorem 1.2 for
![]() $d_2$
, resp.). Our separation of Theorem 1.1 and 1.2 is intended to simplify the exposition.
$d_2$
, resp.). Our separation of Theorem 1.1 and 1.2 is intended to simplify the exposition.
It is well known that for many families of L-functions, it may be easier to obtain an upper bound in place of an asymptotic formula. We have the following upper bound, which is sharp for
![]() $d \gg q^{1/3+\varepsilon }$
.
$d \gg q^{1/3+\varepsilon }$
.
Theorem 1.3. Let
![]() $\psi $
have conductor q, and let
$\psi $
have conductor q, and let
![]() $d|q$
. Then
$d|q$
. Then
 $$ \begin{align} \sum_{\chi \ (\mathrm{mod}\ d)} |L(1/2,\chi \cdot \psi)|^2 \ll q^\varepsilon (d + d^{-1/2} q^{1/2}). \end{align} $$
$$ \begin{align} \sum_{\chi \ (\mathrm{mod}\ d)} |L(1/2,\chi \cdot \psi)|^2 \ll q^\varepsilon (d + d^{-1/2} q^{1/2}). \end{align} $$
Special cases of this result appear in both [Reference NunesN, Reference Milićević and WhiteMW]. One nice consequence of Theorem 1.3 is that if q has a factor d with
![]() $d = q^{1/3 + o(1)}$
, then this second moment is strong enough to recover the Weyl bound
$d = q^{1/3 + o(1)}$
, then this second moment is strong enough to recover the Weyl bound
![]() $|L(1/2, \psi )| \ll q^{1/6+\varepsilon }$
. For moduli q with
$|L(1/2, \psi )| \ll q^{1/6+\varepsilon }$
. For moduli q with
![]() $d|q$
, Heath-Brown [Reference Heath-BrownHB1, Theorem 2] proved a bound for an individual L-function which essentially matches (1.13). Indeed, our proof of Theorem 1.3 relies on Heath-Brown’s work, and in retrospect, the method of Heath-Brown is implicitly bounding a second moment along a coset. Of course, the second moment bound in (1.13) implies an individual bound, but it contains more information.
$d|q$
, Heath-Brown [Reference Heath-BrownHB1, Theorem 2] proved a bound for an individual L-function which essentially matches (1.13). Indeed, our proof of Theorem 1.3 relies on Heath-Brown’s work, and in retrospect, the method of Heath-Brown is implicitly bounding a second moment along a coset. Of course, the second moment bound in (1.13) implies an individual bound, but it contains more information.
2 Preliminaries
In this section, we will lay the groundwork and develop the tools necessary to prove the main theorems.
2.1 Various bounds & evaluations
First, we define the sum studied by Heath-Brown in [Reference Heath-BrownHB1] and cite his associated bound.
Definition 2.1. Let
![]() $\chi $
have conductor q, and let h and n be integers. Denote
$\chi $
have conductor q, and let h and n be integers. Denote
 $$ \begin{align} S(q;\chi,h,n) = \displaystyle\sum_{m=0}^{q-1} \chi(m+h) \overline\chi(m) e(mn/q). \end{align} $$
$$ \begin{align} S(q;\chi,h,n) = \displaystyle\sum_{m=0}^{q-1} \chi(m+h) \overline\chi(m) e(mn/q). \end{align} $$
Lemma 2.2 (Heath-Brown, [Reference Heath-BrownHB1], Lemma 9).
Suppose that q is odd,
![]() $q_0 | q$
, and
$q_0 | q$
, and
![]() $\varepsilon> 0$
. Then
$\varepsilon> 0$
. Then
and
Remark 2.3. Technically, [Reference Heath-BrownHB1, Lemma 9] gives a bound of
![]() $|S(q;\chi ,4hq_0,n)|$
, without the restriction that
$|S(q;\chi ,4hq_0,n)|$
, without the restriction that
![]() $(q,2) = 1$
. However, it can be seen by reading through his proof that the result holds for
$(q,2) = 1$
. However, it can be seen by reading through his proof that the result holds for
![]() $|S(q;\chi ,hq_0,n)|$
(without the
$|S(q;\chi ,hq_0,n)|$
(without the
![]() $4$
) with the condition that q is odd. Moreover, Heath-Brown claims the bound for the sum with
$4$
) with the condition that q is odd. Moreover, Heath-Brown claims the bound for the sum with
![]() $1 \leq h \leq A$
(and
$1 \leq h \leq A$
(and
![]() $1 \leq n \leq B$
in (2.2)), but simple symmetry arguments extend the result as claimed above.
$1 \leq n \leq B$
in (2.2)), but simple symmetry arguments extend the result as claimed above.
We next state the standard evaluation of a quadratic exponential sum.
Lemma 2.4. Let r be a positive odd integer. Let
![]() $A,B$
be integers such that
$A,B$
be integers such that
![]() $(B,r)=1$
. Then
$(B,r)=1$
. Then
 $$ \begin{align*} \sum_{u \ (\mathrm{mod}\ r)} e_{r}\left(Au + Bu^2\right) = e_r(-\overline{4B}A^2 ) \left(\frac{B}{r}\right) \varepsilon_{r} \sqrt{r}, \end{align*} $$
$$ \begin{align*} \sum_{u \ (\mathrm{mod}\ r)} e_{r}\left(Au + Bu^2\right) = e_r(-\overline{4B}A^2 ) \left(\frac{B}{r}\right) \varepsilon_{r} \sqrt{r}, \end{align*} $$
where
![]() $e_q(x) = e(\frac {x}{q})$
, the bar notation indicates the multiplicative inverse modulo r,
$e_q(x) = e(\frac {x}{q})$
, the bar notation indicates the multiplicative inverse modulo r,
![]() $\left (\frac {B}{r}\right )$
is the Jacobi symbol, and
$\left (\frac {B}{r}\right )$
is the Jacobi symbol, and
 $\varepsilon _r = \begin {cases} 1, & r\equiv 1\ (\mathrm {mod}\ 4)\\ i, & r\equiv 3\ (\mathrm {mod}\ 4). \end {cases}$
$\varepsilon _r = \begin {cases} 1, & r\equiv 1\ (\mathrm {mod}\ 4)\\ i, & r\equiv 3\ (\mathrm {mod}\ 4). \end {cases}$
Proof. This follows by completing the square and applying (3.38) from [Reference Iwaniec and KowalskiIK].
Another simple lemma to get us warmed up is the following integral evaluation.
Lemma 2.5. Let k be a nonzero integer and suppose
![]() $-\frac {1}{2}<\Re (s)<\frac {1}{2}$
. Then
$-\frac {1}{2}<\Re (s)<\frac {1}{2}$
. Then
 $$ \begin{align*} \int_0^\infty x^{-s} \cos(2 \pi k x) \frac{dx}{\sqrt{x}} = \frac{\Gamma(1/2-s)}{(2\pi|k|)^{1/2-s}} \cos(\tfrac{\pi}{2}(\tfrac12 - s)). \end{align*} $$
$$ \begin{align*} \int_0^\infty x^{-s} \cos(2 \pi k x) \frac{dx}{\sqrt{x}} = \frac{\Gamma(1/2-s)}{(2\pi|k|)^{1/2-s}} \cos(\tfrac{\pi}{2}(\tfrac12 - s)). \end{align*} $$
Proof. This follows from [Reference Gradshteyn and RyzhikGR, 17.43.3] after changing variables.
2.2 Postnikov
We will derive a variant of the Postnikov formula that holds for composite moduli, rather than only prime powers. Recall the notation
![]() $a|b^\infty $
, which means that
$a|b^\infty $
, which means that
![]() $a| b^A$
for some
$a| b^A$
for some
![]() $A> 0$
.
$A> 0$
.
Definition 2.6. For positive odd integers d and q such that
![]() $d|q$
and
$d|q$
and
![]() $q|d^\infty $
, define the formal power series in the indeterminate x by
$q|d^\infty $
, define the formal power series in the indeterminate x by
 $$ \begin{align} {\mathcal{L}}_q(1+dx) = \sum_{k=1}^\infty (-1)^{k+1}\;\frac{d^k}{k}\;x^k \in {\mathbb{Q}}[[x]]. \end{align} $$
$$ \begin{align} {\mathcal{L}}_q(1+dx) = \sum_{k=1}^\infty (-1)^{k+1}\;\frac{d^k}{k}\;x^k \in {\mathbb{Q}}[[x]]. \end{align} $$
The conditions
![]() $d|q$
and
$d|q$
and
![]() $q|d^\infty $
imply that d and q share all of the same prime factors. We first show some divisibility properties for the coefficients of this formal power series. Let
$q|d^\infty $
imply that d and q share all of the same prime factors. We first show some divisibility properties for the coefficients of this formal power series. Let
Note that
![]() $R_q$
is a sub-ring of
$R_q$
is a sub-ring of
![]() ${\mathbb {Q}}$
. Reduction modulo q gives rise to the ring homomorphism
${\mathbb {Q}}$
. Reduction modulo q gives rise to the ring homomorphism
![]() ${\varphi : R_q \to {\mathbb {Z}}/q{\mathbb {Z}}}$
given by
${\varphi : R_q \to {\mathbb {Z}}/q{\mathbb {Z}}}$
given by
Lemma 2.7. Let
![]() $d \preceq q$
with q odd. For any
$d \preceq q$
with q odd. For any
![]() $p|q$
and
$p|q$
and
![]() $k \geq 1$
, we have
$k \geq 1$
, we have
More generally, for any
![]() $A \geq 0$
, there exists N such that
$A \geq 0$
, there exists N such that
![]() $\nu _p(k)\leq \nu _p(d^{k-A})$
for all
$\nu _p(k)\leq \nu _p(d^{k-A})$
for all
![]() $k\geq N$
.
$k\geq N$
.
Proof. We have
![]() $\nu _p(k) \leq \frac {\log (k)}{\log (p)} \leq k-1 \leq \nu _p(d^{k-1})$
, where the last inequality follows from the fact that d and q share all of the same prime factors, so
$\nu _p(k) \leq \frac {\log (k)}{\log (p)} \leq k-1 \leq \nu _p(d^{k-1})$
, where the last inequality follows from the fact that d and q share all of the same prime factors, so
![]() $\nu _p(d) \geq 1$
. Now, (2.7) follows. In the more general case,
$\nu _p(d) \geq 1$
. Now, (2.7) follows. In the more general case,
![]() $\nu _p(d^{k-A})\geq k-A$
and
$\nu _p(d^{k-A})\geq k-A$
and
![]() $\nu _p(k)=O(\log (k))$
, so there exists a large enough choice of N such that
$\nu _p(k)=O(\log (k))$
, so there exists a large enough choice of N such that
![]() $\nu _p(k) \leq \nu _p(d^{k-A})$
for all
$\nu _p(k) \leq \nu _p(d^{k-A})$
for all
![]() $k\geq N$
.
$k\geq N$
.
Remark 2.8. While Lemma 2.7 only guarantees the existence of a positive integer N, the method of proof shows that a constructive candidate is the minimal positive integer M such that
![]() $k-A\geq \log (k)$
for all
$k-A\geq \log (k)$
for all
![]() $k\geq M$
. This minimal M can be easily found for any particular A, and an example of future relevance is that
$k\geq M$
. This minimal M can be easily found for any particular A, and an example of future relevance is that
![]() $M=5$
when
$M=5$
when
![]() $A=3$
.
$A=3$
.
Lemma 2.9. We have
![]() ${\mathcal {L}}_q(1+dx) \in R_q[[x]]$
. In fact, all the coefficients of
${\mathcal {L}}_q(1+dx) \in R_q[[x]]$
. In fact, all the coefficients of
![]() ${\mathcal {L}}_q(1+dx)$
are multiples of d.
${\mathcal {L}}_q(1+dx)$
are multiples of d.
Proof. With
![]() $c_k=(-1)^{k+1}d^k/k$
, we will show
$c_k=(-1)^{k+1}d^k/k$
, we will show
![]() $\nu _p(c_k) \geq \nu _p(d)$
for all
$\nu _p(c_k) \geq \nu _p(d)$
for all
![]() $p|q$
. Using (2.7) implies that
$p|q$
. Using (2.7) implies that
![]() $0 \leq \nu _p(\frac {d^{k-1}}{k})$
, so
$0 \leq \nu _p(\frac {d^{k-1}}{k})$
, so
![]() $\nu _p(c_k) = \nu _p(d) + \nu _p(\frac {d^{k-1}}{k}) \geq \nu _p(d)$
, for any k.
$\nu _p(c_k) = \nu _p(d) + \nu _p(\frac {d^{k-1}}{k}) \geq \nu _p(d)$
, for any k.
Since
![]() ${\mathcal {L}}_q(1+dx)$
lives in
${\mathcal {L}}_q(1+dx)$
lives in
![]() $R_q[[x]] \subseteq {\mathbb {Q}}[[x]]$
, given
$R_q[[x]] \subseteq {\mathbb {Q}}[[x]]$
, given
![]() $\varphi $
from (2.6), there is an induced ring homomorphism
$\varphi $
from (2.6), there is an induced ring homomorphism
![]() $\overline \varphi : R_q[[x]] \to \left ({\mathbb {Z}}/q{\mathbb {Z}}\right )[[x]]$
which maps
$\overline \varphi : R_q[[x]] \to \left ({\mathbb {Z}}/q{\mathbb {Z}}\right )[[x]]$
which maps
 $$ \begin{align} \overline\varphi({\mathcal{L}}_q(1+dx))=\sum_{k=1}^\infty \varphi(c_k) x^k. \end{align} $$
$$ \begin{align} \overline\varphi({\mathcal{L}}_q(1+dx))=\sum_{k=1}^\infty \varphi(c_k) x^k. \end{align} $$
By abuse of notation, we view
![]() ${\mathcal {L}}_q(1+dx)$
as an element of
${\mathcal {L}}_q(1+dx)$
as an element of
![]() $\left ({\mathbb {Z}}/q{\mathbb {Z}}\right )[[x]]$
via (2.8).
$\left ({\mathbb {Z}}/q{\mathbb {Z}}\right )[[x]]$
via (2.8).
Lemma 2.10. We have
![]() ${\mathcal {L}}_q(1+dx)\in ({\mathbb {Z}}/q{\mathbb {Z}})[x]$
. Moreover,
${\mathcal {L}}_q(1+dx)\in ({\mathbb {Z}}/q{\mathbb {Z}})[x]$
. Moreover,
![]() $\mathcal {L}_q(1+dx) \in d (\mathbb Z/q\mathbb Z)[x]$
.
$\mathcal {L}_q(1+dx) \in d (\mathbb Z/q\mathbb Z)[x]$
.
Proof. The content of this lemma is that for sufficiently large k,
![]() $\nu _p(c_k) \geq \nu _p(q)$
for
$\nu _p(c_k) \geq \nu _p(q)$
for
![]() $c_k = d^k/k$
. Say
$c_k = d^k/k$
. Say
![]() $q | d^A$
. By Lemma 2.7, there exists a positive integer N such that
$q | d^A$
. By Lemma 2.7, there exists a positive integer N such that
![]() $\nu _{p}(k)\leq \nu _{p}(d^{k-A})$
for all
$\nu _{p}(k)\leq \nu _{p}(d^{k-A})$
for all
![]() $k\geq N$
. Then
$k\geq N$
. Then
![]() $\nu _p(c_k) = \nu _p(d^A) + \nu _p(\frac {d^{k-A}}{k}) \geq \nu _p(q)$
for
$\nu _p(c_k) = \nu _p(d^A) + \nu _p(\frac {d^{k-A}}{k}) \geq \nu _p(q)$
for
![]() $k \geq N$
. Here, N may depend on p, but by choosing the maximal of all these N’s gives a uniform value.
$k \geq N$
. Here, N may depend on p, but by choosing the maximal of all these N’s gives a uniform value.
This opens the door to discussing various properties of
![]() ${\mathcal {L}}_q(1+dx)$
modulo q, such as the following periodicity and additivity properties. These lemmas will require two indeterminates and so we will embed
${\mathcal {L}}_q(1+dx)$
modulo q, such as the following periodicity and additivity properties. These lemmas will require two indeterminates and so we will embed
![]() $({\mathbb {Z}}/q{\mathbb {Z}})[x]$
into
$({\mathbb {Z}}/q{\mathbb {Z}})[x]$
into
![]() $({\mathbb {Z}}/q{\mathbb {Z}})[x,y]$
in the obvious way.
$({\mathbb {Z}}/q{\mathbb {Z}})[x,y]$
in the obvious way.
Lemma 2.11. We have
![]() ${\mathcal {L}}_q(1+dx)={\mathcal {L}}_q\left (1+d(x+\frac {q}{d}y)\right )$
in
${\mathcal {L}}_q(1+dx)={\mathcal {L}}_q\left (1+d(x+\frac {q}{d}y)\right )$
in
![]() $({\mathbb {Z}}/q{\mathbb {Z}})[x,y]$
.
$({\mathbb {Z}}/q{\mathbb {Z}})[x,y]$
.
Proof. We have
![]() ${\mathcal {L}}_q(1 + d(x+\frac {q}{d} y)) = \sum _{k} c_k (x + \frac {q}{d} y)^k \equiv \sum _k c_k x^k\ \pmod {q}$
, using
${\mathcal {L}}_q(1 + d(x+\frac {q}{d} y)) = \sum _{k} c_k (x + \frac {q}{d} y)^k \equiv \sum _k c_k x^k\ \pmod {q}$
, using
![]() $c_k \equiv 0\ \pmod {d}$
from Lemma 2.10.
$c_k \equiv 0\ \pmod {d}$
from Lemma 2.10.
Lemma 2.12. We have
![]() ${\mathcal {L}}_q((1+dx)(1+dy)) = {\mathcal {L}}_q(1+dx) + {\mathcal {L}}_q(1+dy)$
in
${\mathcal {L}}_q((1+dx)(1+dy)) = {\mathcal {L}}_q(1+dx) + {\mathcal {L}}_q(1+dy)$
in
![]() $({\mathbb {Z}}/q{\mathbb {Z}})[x,y]$
.
$({\mathbb {Z}}/q{\mathbb {Z}})[x,y]$
.
Proof. We give a brief sketch here, and refer to [Reference KoblitzK, pp.79-80] for more details. For the real logarithm, we have
![]() $\log ((1+dx)(1+dy)) = \log (1+dx) + \log (1+dy)$
, for
$\log ((1+dx)(1+dy)) = \log (1+dx) + \log (1+dy)$
, for
![]() $dx> -1$
,
$dx> -1$
,
![]() $dy> -1$
. Hence, the power series expansions of these two expressions are equal wherever they both converge, meaning that all of their corresponding coefficients are equal. Thus, since
$dy> -1$
. Hence, the power series expansions of these two expressions are equal wherever they both converge, meaning that all of their corresponding coefficients are equal. Thus, since
![]() ${\mathcal {L}}_q(1+dx)$
matches the power series expansion of the real logarithm (reduced modulo q via (2.8)), this property also holds for
${\mathcal {L}}_q(1+dx)$
matches the power series expansion of the real logarithm (reduced modulo q via (2.8)), this property also holds for
![]() ${\mathcal {L}}_q(1+dx)$
.
${\mathcal {L}}_q(1+dx)$
.
Lemma 2.13. Let q and d be positive odd integers with
![]() $d|q$
.
$d|q$
.
-
1. If
 $q|d^\infty $
, then
$q|d^\infty $
, then
 ${\mathcal {L}}_q(1+dx) \equiv dx \ (\mathrm {mod}\ (q,d^2))$
.
${\mathcal {L}}_q(1+dx) \equiv dx \ (\mathrm {mod}\ (q,d^2))$
. -
2. If
 $(q,3)=1$
and
$(q,3)=1$
and
 $q|d^3$
, then
$q|d^3$
, then
 ${\mathcal {L}}_q(1+dx) \equiv dx-\overline {2}(dx)^2 \ (\mathrm {mod}\ q)$
.
${\mathcal {L}}_q(1+dx) \equiv dx-\overline {2}(dx)^2 \ (\mathrm {mod}\ q)$
.
Proof. Expanding the power series, we have
 $$ \begin{align*} {\mathcal{L}}_q(1+dx) = dx-\tfrac{1}{2}(dx)^2+\tfrac{1}{3}(dx)^3-d^3\Big(\underbrace{\tfrac{1}{4}dx^4-\tfrac{1}{5}d^2x^5+\ldots}_{\in ({\mathbb{Z}}/q{\mathbb{Z}})[x]}\Big). \end{align*} $$
$$ \begin{align*} {\mathcal{L}}_q(1+dx) = dx-\tfrac{1}{2}(dx)^2+\tfrac{1}{3}(dx)^3-d^3\Big(\underbrace{\tfrac{1}{4}dx^4-\tfrac{1}{5}d^2x^5+\ldots}_{\in ({\mathbb{Z}}/q{\mathbb{Z}})[x]}\Big). \end{align*} $$
The claim that the tail of this series is still a polynomial with coefficients in
![]() ${\mathbb {Z}}/q{\mathbb {Z}}$
after factoring out
${\mathbb {Z}}/q{\mathbb {Z}}$
after factoring out
![]() $d^3$
follows from Lemma 2.7, or more specifically the observations in Remark 2.8. Elaborating on the details, since
$d^3$
follows from Lemma 2.7, or more specifically the observations in Remark 2.8. Elaborating on the details, since
![]() $k-3\geq \log (k)$
for all
$k-3\geq \log (k)$
for all
![]() $k\geq 5$
, we may choose
$k\geq 5$
, we may choose
![]() $N=5$
from Lemma 2.7. However, since q is odd,
$N=5$
from Lemma 2.7. However, since q is odd,
![]() $\frac {1}{4}=\overline {2}^2$
in
$\frac {1}{4}=\overline {2}^2$
in
![]() ${\mathbb {Z}}/q{\mathbb {Z}}$
, so we could also pick
${\mathbb {Z}}/q{\mathbb {Z}}$
, so we could also pick
![]() $N=4$
. Now the result follows in each case.
$N=4$
. Now the result follows in each case.
We are now ready for our version of the Postnikov formula.
Lemma 2.14 (Postnikov formula).
Let q and d be odd with
![]() $d|q$
and
$d|q$
and
![]() $q|d^\infty $
. There exists a unique group homomorphism
$q|d^\infty $
. There exists a unique group homomorphism
![]() $a: \widehat {(\mathbb Z/q \mathbb Z)^{*}} \rightarrow \mathbb Z/(q/d) \mathbb Z$
,
$a: \widehat {(\mathbb Z/q \mathbb Z)^{*}} \rightarrow \mathbb Z/(q/d) \mathbb Z$
,
![]() $\psi \mapsto a_{\psi }$
, such that a Postnikov-type formula holds: for each Dirichlet character
$\psi \mapsto a_{\psi }$
, such that a Postnikov-type formula holds: for each Dirichlet character
![]() $\psi $
modulo q and
$\psi $
modulo q and
![]() $x\in {\mathbb {Z}}$
, we have
$x\in {\mathbb {Z}}$
, we have
Finally, if
![]() $\psi $
is primitive modulo q, then
$\psi $
is primitive modulo q, then
![]() $(a_{\psi }, q/d) = 1$
.
$(a_{\psi }, q/d) = 1$
.
Proof. Consider the reduction modulo d map
![]() $({\mathbb {Z}}/q{\mathbb {Z}})^* \to ({\mathbb {Z}}/d{\mathbb {Z}})^*$
, and denote its kernel by K. Since d and q share their prime factors,
$({\mathbb {Z}}/q{\mathbb {Z}})^* \to ({\mathbb {Z}}/d{\mathbb {Z}})^*$
, and denote its kernel by K. Since d and q share their prime factors,
![]() $K=\left \{1+dx : x\ (\mathrm {mod}\ \frac {q}{d})\right \}$
, so
$K=\left \{1+dx : x\ (\mathrm {mod}\ \frac {q}{d})\right \}$
, so
![]() $|K|=\frac {q}{d}$
. Consider the map
$|K|=\frac {q}{d}$
. Consider the map
![]() $f:K\to S^1$
defined by
$f:K\to S^1$
defined by
The function f is well defined by Lemmas 2.10 and 2.11. Furthermore, f is a group homomorphism by Lemma 2.12. Thus, f is a character on K, and we claim that f has order
![]() $\frac {q}{d}$
in
$\frac {q}{d}$
in
![]() $\widehat {K}$
. Indeed, if p is a prime such that
$\widehat {K}$
. Indeed, if p is a prime such that
![]() $p|\frac {q}{d}$
, then we have
$p|\frac {q}{d}$
, then we have
![]() $f(1+dx)^{q/dp}=e_q\left (\frac {q}{dp}{\mathcal {L}}_q(1+dx)\right )=e_{dp}\left ({\mathcal {L}}_q(1+dx)\right )=e_{dp}(dx)=e(\frac {x}{p})$
, by Lemma 2.13 since
$f(1+dx)^{q/dp}=e_q\left (\frac {q}{dp}{\mathcal {L}}_q(1+dx)\right )=e_{dp}\left ({\mathcal {L}}_q(1+dx)\right )=e_{dp}(dx)=e(\frac {x}{p})$
, by Lemma 2.13 since
![]() $dp|(q,d^2)$
. Hence,
$dp|(q,d^2)$
. Hence,
![]() $\widehat {K}$
is cyclic and generated by f. Therefore, every element of
$\widehat {K}$
is cyclic and generated by f. Therefore, every element of
![]() $\widehat {K}$
is of the form
$\widehat {K}$
is of the form
![]() $f^a$
for some
$f^a$
for some
![]() $a \ (\mathrm {mod}\ \frac {q}{d})$
. In particular,
$a \ (\mathrm {mod}\ \frac {q}{d})$
. In particular,
![]() $\psi $
is a character on
$\psi $
is a character on
![]() $({\mathbb {Z}}/q{\mathbb {Z}})^*$
, so restricting
$({\mathbb {Z}}/q{\mathbb {Z}})^*$
, so restricting
![]() $\psi $
to K makes it an element of
$\psi $
to K makes it an element of
![]() $\widehat {K}$
. Thus, there exists a unique
$\widehat {K}$
. Thus, there exists a unique
![]() $a_\psi \ (\mathrm {mod}\ \frac {q}{d})$
such that
$a_\psi \ (\mathrm {mod}\ \frac {q}{d})$
such that
![]() $\psi |_K = f^{a_\psi }$
, which is equivalent to the Postnikov formula.
$\psi |_K = f^{a_\psi }$
, which is equivalent to the Postnikov formula.
For the final statement, suppose that p is a prime with
![]() $p|\frac {q}{d}$
and
$p|\frac {q}{d}$
and
![]() $p|a_{\psi }$
; we will show that
$p|a_{\psi }$
; we will show that
![]() $\psi $
is periodic modulo
$\psi $
is periodic modulo
![]() $q/p$
. Since d and q share all the same prime factors, then
$q/p$
. Since d and q share all the same prime factors, then
![]() $p^2|q$
, and hence,
$p^2|q$
, and hence,
![]() $q | (q/p)^{\infty }$
. Applying (2.9) with d replaced by
$q | (q/p)^{\infty }$
. Applying (2.9) with d replaced by
![]() $\frac {q}{p}$
, we obtain that
$\frac {q}{p}$
, we obtain that
![]() $\psi (1+\frac {q}{p} y ) = e_q(a_{\psi } \frac {q}{p} y)$
. Hence, if
$\psi (1+\frac {q}{p} y ) = e_q(a_{\psi } \frac {q}{p} y)$
. Hence, if
![]() $p|a_{\psi }$
then
$p|a_{\psi }$
then
![]() $\psi $
is periodic modulo
$\psi $
is periodic modulo
![]() $q/p$
.
$q/p$
.
2.3 Miscellaneous lemmas
In the course of this paper, we encounter sums of the form
 $$ \begin{align} {\mathcal{S}}_{q,d}(\psi,k) := \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} \psi(1+du) e_q(dku). \end{align} $$
$$ \begin{align} {\mathcal{S}}_{q,d}(\psi,k) := \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} \psi(1+du) e_q(dku). \end{align} $$
We may evaluate this explicitly in many cases. The conditions relevant for Theorem 1.2 are contained in the following.
Lemma 2.15. Let
![]() $(q,3) =1$
,
$(q,3) =1$
,
![]() $\psi $
have conductor q, and suppose
$\psi $
have conductor q, and suppose
![]() $d^2|q$
and
$d^2|q$
and
![]() $q|d^3$
. Also, let
$q|d^3$
. Also, let
![]() $k \in \mathbb Z$
. If
$k \in \mathbb Z$
. If
![]() $k \not \equiv -a_{\psi } \ (\mathrm {mod}\ d)$
, then
$k \not \equiv -a_{\psi } \ (\mathrm {mod}\ d)$
, then
![]() ${\mathcal {S}}_{q,d}(\psi ,k) = 0$
. If
${\mathcal {S}}_{q,d}(\psi ,k) = 0$
. If
![]() $k \equiv - a_{\psi } \ (\mathrm {mod}\ d)$
, then
$k \equiv - a_{\psi } \ (\mathrm {mod}\ d)$
, then
 $$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) = \varepsilon_{q } \sqrt{q} e_q(\overline{2a_\psi}(k+a_\psi)^2) \left(\frac{- 2a_\psi}{q/d^2}\right). \end{align*} $$
$$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) = \varepsilon_{q } \sqrt{q} e_q(\overline{2a_\psi}(k+a_\psi)^2) \left(\frac{- 2a_\psi}{q/d^2}\right). \end{align*} $$
Proof. By Lemma 2.14, we have
 $$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) &= \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} e_q(dku+a_\psi {\mathcal{L}}_q(1+du)). \end{align*} $$
$$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) &= \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} e_q(dku+a_\psi {\mathcal{L}}_q(1+du)). \end{align*} $$
By Lemma 2.13(2), this simplifies as
 $$ \begin{align*} \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} e_q\left(dku+a_\psi\left(du - \overline{2}(du)^2\right)\right) = \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} e_{q/d}\left((k+a_\psi)u - \overline{2} a_\psi du^2\right). \end{align*} $$
$$ \begin{align*} \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} e_q\left(dku+a_\psi\left(du - \overline{2}(du)^2\right)\right) = \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} e_{q/d}\left((k+a_\psi)u - \overline{2} a_\psi du^2\right). \end{align*} $$
Since
![]() $q/d^2$
is an integer by hypothesis, we may change variables
$q/d^2$
is an integer by hypothesis, we may change variables
![]() $u \rightarrow u + q/d^2$
to see that the sum equals itself times a constant. If
$u \rightarrow u + q/d^2$
to see that the sum equals itself times a constant. If
![]() $k \not \equiv -a_{\psi } \ (\mathrm {mod}\ d)$
, then this constant is not
$k \not \equiv -a_{\psi } \ (\mathrm {mod}\ d)$
, then this constant is not
![]() $1$
, and so the sum vanishes unless
$1$
, and so the sum vanishes unless
![]() $k \equiv -a_\psi \ (\mathrm {mod}\ d)$
. We continue under this assumption, which means that the summand is actually periodic modulo
$k \equiv -a_\psi \ (\mathrm {mod}\ d)$
. We continue under this assumption, which means that the summand is actually periodic modulo
![]() $q/d^2$
, and hence,
$q/d^2$
, and hence,
 $$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) = d\sum_{u \ (\mathrm{mod}\ \frac{q}{d^2})} e_{q/d^2}\Big(\Big(\frac{k+a_\psi}{d}\Big)u - \overline{2} a_\psi u^2\Big). \end{align*} $$
$$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) = d\sum_{u \ (\mathrm{mod}\ \frac{q}{d^2})} e_{q/d^2}\Big(\Big(\frac{k+a_\psi}{d}\Big)u - \overline{2} a_\psi u^2\Big). \end{align*} $$
Lemma 2.4, along with some simplification, concludes the proof.
We can also easily calculate
![]() ${\mathcal {S}}_{q,d}$
under the conditions relevant for Theorem 1.1, as follows.
${\mathcal {S}}_{q,d}$
under the conditions relevant for Theorem 1.1, as follows.
Lemma 2.16. Suppose
![]() $\psi $
has conductor q,
$\psi $
has conductor q,
![]() $d|q$
and
$d|q$
and
![]() $q|d^2$
. Let
$q|d^2$
. Let
![]() $k \in \mathbb Z$
. Then
$k \in \mathbb Z$
. Then
 $$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) = \begin{cases} q/d, \qquad & k \equiv - a_{\psi} \quad\pmod{q/d} \\ 0, \qquad & k \not \equiv - a_{\psi} \quad\pmod{q/d}. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathcal{S}}_{q,d}(\psi,k) = \begin{cases} q/d, \qquad & k \equiv - a_{\psi} \quad\pmod{q/d} \\ 0, \qquad & k \not \equiv - a_{\psi} \quad\pmod{q/d}. \end{cases} \end{align*} $$
The proof of Lemma 2.16 is similar to, but much easier than, Lemma 2.15, since in this case, we may discard the quadratic terms in
![]() ${\mathcal {L}}_q(1+du)$
. We omit the details.
${\mathcal {L}}_q(1+du)$
. We omit the details.
Lemma 2.17 (Iwaniec-Kowalski, [Reference Iwaniec and KowalskiIK], Theorem 5.3).
Let
![]() $\chi $
be a primitive even character modulo q. Suppose
$\chi $
be a primitive even character modulo q. Suppose
![]() $G(s)$
is holomorphic and bounded in any strip
$G(s)$
is holomorphic and bounded in any strip
![]() $-A \leq Re(s) \leq A$
, even, and normalized by
$-A \leq Re(s) \leq A$
, even, and normalized by
![]() $G(0) = 1$
. Then
$G(0) = 1$
. Then
 $$ \begin{align*} L(1/2,\chi)L(1/2,\overline\chi) = 2 \sum_{m,n \geq 1} \frac{\chi(m)\overline\chi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right), \end{align*} $$
$$ \begin{align*} L(1/2,\chi)L(1/2,\overline\chi) = 2 \sum_{m,n \geq 1} \frac{\chi(m)\overline\chi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right), \end{align*} $$
where
![]() $V(x)$
is a smooth function defined by
$V(x)$
is a smooth function defined by
 $$ \begin{align} V(x) = \frac{1}{2\pi i} \int_{(1)} \frac{G(s)}{s} \frac{\gamma(1/2+s)^2}{\gamma(1/2)^2} x^{-s} ds \end{align} $$
$$ \begin{align} V(x) = \frac{1}{2\pi i} \int_{(1)} \frac{G(s)}{s} \frac{\gamma(1/2+s)^2}{\gamma(1/2)^2} x^{-s} ds \end{align} $$
and
The function
![]() $V(x)$
has rapid decay, meaning
$V(x)$
has rapid decay, meaning
![]() $V(x) \ll _A (1+x)^{-A}$
for arbitrarily large
$V(x) \ll _A (1+x)^{-A}$
for arbitrarily large
![]() $A> 0$
.
$A> 0$
.
This next lemma encompasses the opening moves to prove Theorems 1.1 and 1.2.
Lemma 2.18. Let
![]() $\psi $
be even and have conductor q, and suppose
$\psi $
be even and have conductor q, and suppose
![]() $d\prec q$
. Then
$d\prec q$
. Then
 $$ \begin{align} \mathcal{M}:= \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = \varphi(d) \sum_\pm \sum_{\substack{m \equiv \pm n \ (\mathrm{mod}\ d)\\ (mn,q)=1}} \frac{\psi(m)\overline\psi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right). \end{align} $$
$$ \begin{align} \mathcal{M}:= \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} |L(1/2,\chi \cdot \psi)|^2 = \varphi(d) \sum_\pm \sum_{\substack{m \equiv \pm n \ (\mathrm{mod}\ d)\\ (mn,q)=1}} \frac{\psi(m)\overline\psi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right). \end{align} $$
Proof. Using
![]() $\overline {L(1/2,\chi )} = L(1/2,\overline {\chi })$
, then
$\overline {L(1/2,\chi )} = L(1/2,\overline {\chi })$
, then
 $$ \begin{align*} {\mathcal{M}} = \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} L(1/2,\chi \cdot \psi) L(1/2,\overline{\chi \cdot \psi}). \end{align*} $$
$$ \begin{align*} {\mathcal{M}} = \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} L(1/2,\chi \cdot \psi) L(1/2,\overline{\chi \cdot \psi}). \end{align*} $$
The character
![]() $\chi \cdot \psi $
is primitive modulo q because
$\chi \cdot \psi $
is primitive modulo q because
![]() $\psi $
is primitive modulo q and
$\psi $
is primitive modulo q and
![]() $d\prec q$
. Also,
$d\prec q$
. Also,
![]() $\chi \cdot \psi $
is even. Thus, Lemma 2.17 implies
$\chi \cdot \psi $
is even. Thus, Lemma 2.17 implies
 $$ \begin{align*} {\mathcal{M}} = \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} 2 \sum_{m,n \geq 1} \frac{\chi(m)\psi(m)\overline\chi(n)\overline\psi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right). \end{align*} $$
$$ \begin{align*} {\mathcal{M}} = \sum_{\substack{\chi \ (\mathrm{mod}\ d)\\ \chi \text{ even}}} 2 \sum_{m,n \geq 1} \frac{\chi(m)\psi(m)\overline\chi(n)\overline\psi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right). \end{align*} $$
Using
![]() $\frac {(1 + \chi (-1))}{2} $
to detect
$\frac {(1 + \chi (-1))}{2} $
to detect
![]() $\chi $
even followed by orthogonality of characters secures (2.13).
$\chi $
even followed by orthogonality of characters secures (2.13).
Lemma 2.19. Let q be a positive integer, and let V be as defined in (2.11). Then
 $$ \begin{align*} \sum_{(n,q)=1} \frac{1}{n} V\left(\frac{n^2}{q}\right) = \frac{\varphi(q)}{q}\left[\tfrac{1}{2}\log(q) + \gamma_0 + \tfrac{\gamma'}{\gamma}(1/2) + \theta(q)\right] + O(q^{-1/2+\varepsilon}). \end{align*} $$
$$ \begin{align*} \sum_{(n,q)=1} \frac{1}{n} V\left(\frac{n^2}{q}\right) = \frac{\varphi(q)}{q}\left[\tfrac{1}{2}\log(q) + \gamma_0 + \tfrac{\gamma'}{\gamma}(1/2) + \theta(q)\right] + O(q^{-1/2+\varepsilon}). \end{align*} $$
Proof. This is a standard contour-shifting argument, with a tedious residue calculation. See, for instance, [Reference Iwaniec and SarnakIS, Lemma 4.1] for details.
3 Proof of Theorem 1.2
The focus of this section is to prove Theorem 1.2.
3.1 Diagonal term
Since
![]() $d^2\preceq q$
implies that
$d^2\preceq q$
implies that
![]() $d\prec q$
, we may apply Lemma 2.18 to give (2.13). We decompose
$d\prec q$
, we may apply Lemma 2.18 to give (2.13). We decompose
![]() ${\mathcal {M}}$
into three terms:
${\mathcal {M}}$
into three terms:
![]() $ {\mathcal {M}} = {\mathcal {M}}_{m=n} + {\mathcal {M}}_{m>n} + {\mathcal {M}}_{m<n}$
, where
$ {\mathcal {M}} = {\mathcal {M}}_{m=n} + {\mathcal {M}}_{m>n} + {\mathcal {M}}_{m<n}$
, where
 $$ \begin{align} {\mathcal{M}}_{m=n} &:= \varphi(d) \sum_\pm \sum_{\substack{n \equiv \pm n \ (\mathrm{mod}\ d)\\ (n,q)=1}} \frac{1}{n} V\left(\frac{n^2}{q}\right), \end{align} $$
$$ \begin{align} {\mathcal{M}}_{m=n} &:= \varphi(d) \sum_\pm \sum_{\substack{n \equiv \pm n \ (\mathrm{mod}\ d)\\ (n,q)=1}} \frac{1}{n} V\left(\frac{n^2}{q}\right), \end{align} $$
 $$ \begin{align} {\mathcal{M}}_{m>n} = {\mathcal{M}}_{m>n}(\psi) &:= \varphi(d) \sum_\pm \sum_{\substack{m>n\geq1\\m \equiv \pm n \ (\mathrm{mod}\ d)}} \frac{\psi(m)\overline\psi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right), \end{align} $$
$$ \begin{align} {\mathcal{M}}_{m>n} = {\mathcal{M}}_{m>n}(\psi) &:= \varphi(d) \sum_\pm \sum_{\substack{m>n\geq1\\m \equiv \pm n \ (\mathrm{mod}\ d)}} \frac{\psi(m)\overline\psi(n)}{\sqrt{mn}} V\left(\frac{mn}{q}\right), \end{align} $$
and where
![]() ${\mathcal {M}}_{m<n}$
is given by a similar formula to (3.2) but with
${\mathcal {M}}_{m<n}$
is given by a similar formula to (3.2) but with
![]() $1\leq m<n$
.
$1\leq m<n$
.
Lemma 3.1. Let
![]() $(q,2) = 1$
and suppose
$(q,2) = 1$
and suppose
![]() $d\preceq q$
. Then
$d\preceq q$
. Then
Proof. Observe that we cannot simultaneously have
![]() $n \equiv -n \ (\mathrm {mod}\ d)$
and
$n \equiv -n \ (\mathrm {mod}\ d)$
and
![]() $(n,q)=1$
since d is odd. Applying Lemma 2.19 concludes the proof.
$(n,q)=1$
since d is odd. Applying Lemma 2.19 concludes the proof.
3.2 Remaining setup
Note that by symmetry
For this reason, we largely focus on the terms with
![]() $m>n$
. Applying a dyadic partition of unity to (3.2) results in
$m>n$
. Applying a dyadic partition of unity to (3.2) results in
![]() ${\mathcal {M}}_{m>n} = \sum _\pm {\mathcal {M}}_{m>n}^{\pm }$
, with
${\mathcal {M}}_{m>n} = \sum _\pm {\mathcal {M}}_{m>n}^{\pm }$
, with
 $$ \begin{align*} {\mathcal{M}}_{m>n}^{\pm} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} \sum_{\substack{m>n\geq1\\m \equiv \pm n \ (\mathrm{mod}\ d)}} \psi(m)\overline\psi(n) W_{M,N}(m,n). \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{m>n}^{\pm} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} \sum_{\substack{m>n\geq1\\m \equiv \pm n \ (\mathrm{mod}\ d)}} \psi(m)\overline\psi(n) W_{M,N}(m,n). \end{align*} $$
Here,
 $$ \begin{align} W_{M,N}(m,n) = \sqrt{\frac{MN}{mn}} V\left(\frac{mn}{q}\right) \eta\left(\frac{m}{M}\right) \eta\left(\frac{n}{N}\right), \end{align} $$
$$ \begin{align} W_{M,N}(m,n) = \sqrt{\frac{MN}{mn}} V\left(\frac{mn}{q}\right) \eta\left(\frac{m}{M}\right) \eta\left(\frac{n}{N}\right), \end{align} $$
with
![]() $W^{(j,k)}(m,n) \ll _{j,k} M^{-j}N^{-k}$
and
$W^{(j,k)}(m,n) \ll _{j,k} M^{-j}N^{-k}$
and
![]() $\operatorname {\mathrm {supp}}(W_{M,N}(m,n)) \subseteq [M,2M]\times [N,2N]$
. By the rapid decay of V, we may assume that
$\operatorname {\mathrm {supp}}(W_{M,N}(m,n)) \subseteq [M,2M]\times [N,2N]$
. By the rapid decay of V, we may assume that
Consider
![]() ${\mathcal {M}}^{\pm }_{m>n}$
. Say
${\mathcal {M}}^{\pm }_{m>n}$
. Say
![]() $m= \pm n+dl$
with
$m= \pm n+dl$
with
![]() $l \geq 1$
, and define
$l \geq 1$
, and define
so that
 $$ \begin{align} {\mathcal{M}}^{\pm}_{m>n} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} {\mathcal{B}}^{\pm}_{m>n}(M,N). \end{align} $$
$$ \begin{align} {\mathcal{M}}^{\pm}_{m>n} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} {\mathcal{B}}^{\pm}_{m>n}(M,N). \end{align} $$
3.3 Off-diagonal via Poisson in l
We will eventually split the dyadic summations of
![]() ${\mathcal {M}}^{\pm }_{m>n}$
into two ranges depending on whether M and N are nearby or far apart. In this section, we develop a method that will be most useful when M and N are far apart (or ‘unbalanced’).
${\mathcal {M}}^{\pm }_{m>n}$
into two ranges depending on whether M and N are nearby or far apart. In this section, we develop a method that will be most useful when M and N are far apart (or ‘unbalanced’).
We will apply Poisson summation to the sum over l in (3.6). First, we observe some properties of the function
namely, that
![]() $W^{\pm }_{n,d}(l)$
is supported on
$W^{\pm }_{n,d}(l)$
is supported on
and
 $$ \begin{align} \frac{d^j}{dx^j} W_{n,d}^{\pm}(x) \ll_j \left(\frac{M}{d}\right)^{-j}. \end{align} $$
$$ \begin{align} \frac{d^j}{dx^j} W_{n,d}^{\pm}(x) \ll_j \left(\frac{M}{d}\right)^{-j}. \end{align} $$
Let
![]() $\widehat {W}(x) = \int _{-\infty }^{\infty } w(y) e(-xy) dy$
. We record some properties of
$\widehat {W}(x) = \int _{-\infty }^{\infty } w(y) e(-xy) dy$
. We record some properties of
![]() $\widehat W$
for future use.
$\widehat W$
for future use.
Proposition 3.2. Let
![]() $A> 0$
, and suppose
$A> 0$
, and suppose
![]() $W(x)$
is a smooth function with support in an interval of length A that satisfies
$W(x)$
is a smooth function with support in an interval of length A that satisfies
![]() $W^{(j)}(x) \ll _j A^{-j}$
. Then for any
$W^{(j)}(x) \ll _j A^{-j}$
. Then for any
![]() $C> 0$
, we have
$C> 0$
, we have
These properties follow directly from integration by parts, so the proof is omitted. Applying this to
![]() $W_{n,d}^{\pm }$
, we have
$W_{n,d}^{\pm }$
, we have
Lemma 3.3. Suppose
![]() $(q, 3)=1$
,
$(q, 3)=1$
,
![]() $d^2\preceq q \preceq d^3$
and that
$d^2\preceq q \preceq d^3$
and that
![]() $M> 2^{10} N$
. Then
$M> 2^{10} N$
. Then
 $$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = {\mathcal{A}}^{\pm}_{m>n}(M,N) + O\left(\frac{Nq^{1/2+\varepsilon}}{d}\right), \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = {\mathcal{A}}^{\pm}_{m>n}(M,N) + O\left(\frac{Nq^{1/2+\varepsilon}}{d}\right), \end{align*} $$
where
 $$ \begin{align} {\mathcal{A}}^{\pm}_{m>n}(M,N) = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{d}{\sqrt{q}}\; e_q( \overline{2a_\psi}(a_\psi-b_\psi)^2) \sum_{n|b_\psi} \widehat{W^{\pm}_{n,d}} \left(\frac{\mp b_\psi d}{nq}\right). \end{align} $$
$$ \begin{align} {\mathcal{A}}^{\pm}_{m>n}(M,N) = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{d}{\sqrt{q}}\; e_q( \overline{2a_\psi}(a_\psi-b_\psi)^2) \sum_{n|b_\psi} \widehat{W^{\pm}_{n,d}} \left(\frac{\mp b_\psi d}{nq}\right). \end{align} $$
Proof. The condition that
![]() $M> 2^{10} N$
ensures that
$M> 2^{10} N$
ensures that
![]() $W_{n,d}^{\pm }(l)$
is supported on
$W_{n,d}^{\pm }(l)$
is supported on
![]() $l \asymp \frac {M}{d}$
(recall (3.9)). This is convenient because, in particular, we can extend the sum over
$l \asymp \frac {M}{d}$
(recall (3.9)). This is convenient because, in particular, we can extend the sum over
![]() $l \geq 1$
to all
$l \geq 1$
to all
![]() $l \in \mathbb Z$
without altering the sum. Applying Poisson summation with respect to l in (3.6) gives
$l \in \mathbb Z$
without altering the sum. Applying Poisson summation with respect to l in (3.6) gives
 $$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = \sum_{n \geq 1}\overline\psi(n) \Big( \frac{d}{q}\sum_{j\in{\mathbb{Z}}}\sum_{u \ (\mathrm{mod}\ \frac{q}{d})} \psi(\pm n+du)\, e_q(dju) \widehat{W^{\pm}_{n,d}}\Big(\frac{dj}{q}\Big)\Big). \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = \sum_{n \geq 1}\overline\psi(n) \Big( \frac{d}{q}\sum_{j\in{\mathbb{Z}}}\sum_{u \ (\mathrm{mod}\ \frac{q}{d})} \psi(\pm n+du)\, e_q(dju) \widehat{W^{\pm}_{n,d}}\Big(\frac{dj}{q}\Big)\Big). \end{align*} $$
Replacing u by
![]() $\pm nu$
and j by
$\pm nu$
and j by
![]() $\pm j$
and recalling
$\pm j$
and recalling
![]() $\psi $
is even gives
$\psi $
is even gives
 $$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = \frac{d}{q}\; \mathop{\sum_{n\geq1}\sum_{j\in{\mathbb{Z}}}}_{(n,q)=1} \widehat{W^{\pm}_{n,d}}\Big(\frac{\pm dj}{q}\Big) \underbrace{ \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} \psi(1+du)\, e_q(djnu) }_{ {\mathcal{S}}_{q,d}(\psi, jn) }. \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = \frac{d}{q}\; \mathop{\sum_{n\geq1}\sum_{j\in{\mathbb{Z}}}}_{(n,q)=1} \widehat{W^{\pm}_{n,d}}\Big(\frac{\pm dj}{q}\Big) \underbrace{ \sum_{u \ (\mathrm{mod}\ \frac{q}{d})} \psi(1+du)\, e_q(djnu) }_{ {\mathcal{S}}_{q,d}(\psi, jn) }. \end{align*} $$
Hence, Lemma 2.15 yields
 $$ \begin{align} {\mathcal{B}}^{\pm}_{m>n}(M,N) = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{d}{\sqrt{q}}\;\mathop{\sum_{n\geq1}\sum_{j\neq0}}_{jn\equiv -a_\psi\ (\mathrm{mod}\ d)} \widehat{W^{\pm}_{n,d}}\left(\frac{\pm dj}{q}\right) e_q(\overline{2a_\psi}(jn+a_\psi)^2), \end{align} $$
$$ \begin{align} {\mathcal{B}}^{\pm}_{m>n}(M,N) = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{d}{\sqrt{q}}\;\mathop{\sum_{n\geq1}\sum_{j\neq0}}_{jn\equiv -a_\psi\ (\mathrm{mod}\ d)} \widehat{W^{\pm}_{n,d}}\left(\frac{\pm dj}{q}\right) e_q(\overline{2a_\psi}(jn+a_\psi)^2), \end{align} $$
where the condition
![]() $(n,q)=1$
is now accounted for by
$(n,q)=1$
is now accounted for by
![]() $jn\equiv -a_\psi \ (\mathrm {mod}\ d)$
, recalling that
$jn\equiv -a_\psi \ (\mathrm {mod}\ d)$
, recalling that
![]() $(a_{\psi }, q/d) = 1$
and that d,
$(a_{\psi }, q/d) = 1$
and that d,
![]() $q/d$
, and q all share the same prime factors. Since
$q/d$
, and q all share the same prime factors. Since
![]() $a_\psi \in {\mathbb {Z}}/(q/d){\mathbb {Z}}$
and
$a_\psi \in {\mathbb {Z}}/(q/d){\mathbb {Z}}$
and
![]() $d|\frac {q}{d}$
, let
$d|\frac {q}{d}$
, let
![]() $a_\psi \equiv b_\psi \ (\mathrm {mod}\ d)$
for
$a_\psi \equiv b_\psi \ (\mathrm {mod}\ d)$
for
![]() $b_\psi \in {\mathbb {Z}}/d{\mathbb {Z}}$
such that
$b_\psi \in {\mathbb {Z}}/d{\mathbb {Z}}$
such that
The contribution from
![]() $jn=-b_\psi $
gives
$jn=-b_\psi $
gives
![]() ${\mathcal {A}}^{\pm }_{m>n}(M,N)$
, while we will use
${\mathcal {A}}^{\pm }_{m>n}(M,N)$
, while we will use
![]() $E.T.$
to denote the remaining terms. Then
$E.T.$
to denote the remaining terms. Then
 $$ \begin{align} |E.T.| \leq \frac{d}{\sqrt{q}}\;\mathop{\sum_{n\geq1}\sum_{j\neq0}}_{\substack{jn\equiv -a_\psi\ (\mathrm{mod}\ d)\\jn\neq -b_\psi}} \left|\widehat{W^{\pm}_{n,d}}\left(\frac{\pm dj}{q}\right)\right|. \end{align} $$
$$ \begin{align} |E.T.| \leq \frac{d}{\sqrt{q}}\;\mathop{\sum_{n\geq1}\sum_{j\neq0}}_{\substack{jn\equiv -a_\psi\ (\mathrm{mod}\ d)\\jn\neq -b_\psi}} \left|\widehat{W^{\pm}_{n,d}}\left(\frac{\pm dj}{q}\right)\right|. \end{align} $$
Recalling (3.11) shows this sum may be truncated at
![]() $|j| \ll \frac {q^{1+\varepsilon }}{M}$
, with a negligible error. We also have that
$|j| \ll \frac {q^{1+\varepsilon }}{M}$
, with a negligible error. We also have that
![]() $n \asymp N$
. Therefore, letting
$n \asymp N$
. Therefore, letting
![]() $k=jn$
, then the non-negligible contribution comes from
$k=jn$
, then the non-negligible contribution comes from
![]() $|k| \ll \frac {Nq^{1+\varepsilon }}{M}$
, and for each k, the number of ways to factor
$|k| \ll \frac {Nq^{1+\varepsilon }}{M}$
, and for each k, the number of ways to factor
![]() $k=jn \neq 0$
is
$k=jn \neq 0$
is
![]() $O(q^{\varepsilon })$
. Hence,
$O(q^{\varepsilon })$
. Hence,
 $$ \begin{align} E.T. \ll q^{-2022} + q^\varepsilon\Big(\frac{M}{\sqrt{q}}\; \sum_{\substack{0<|k|\ll\frac{Nq^{1+\varepsilon}}{M}\\k\equiv -a_\psi\ (\mathrm{mod}\ d)\\k\neq -b_\psi}} 1\Big) \ll \frac{Nq^{1/2+\varepsilon}}{d}. \end{align} $$
$$ \begin{align} E.T. \ll q^{-2022} + q^\varepsilon\Big(\frac{M}{\sqrt{q}}\; \sum_{\substack{0<|k|\ll\frac{Nq^{1+\varepsilon}}{M}\\k\equiv -a_\psi\ (\mathrm{mod}\ d)\\k\neq -b_\psi}} 1\Big) \ll \frac{Nq^{1/2+\varepsilon}}{d}. \end{align} $$
In this estimation, we have used that
![]() $|k| \geq d/2$
following from
$|k| \geq d/2$
following from
![]() $k \equiv - b_{\psi } \ \pmod {d}$
with
$k \equiv - b_{\psi } \ \pmod {d}$
with
![]() $k \neq -b_{\psi }$
, and using (3.14).
$k \neq -b_{\psi }$
, and using (3.14).
3.4 Off-diagonal via Poisson in n
Returning to (3.6), we now develop a method designed to treat the complementary range where M and N are nearby. Define the function
which is supported on
![]() $n \in [N, 2N]$
and satisfies
$n \in [N, 2N]$
and satisfies
Lemma 3.4. Suppose
![]() $d \prec q$
. We have
$d \prec q$
. We have
 $$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) \ll q^{\varepsilon}\left( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \right). \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) \ll q^{\varepsilon}\left( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \right). \end{align*} $$
Proof. We present the details for
![]() ${\mathcal {B}}^{+}$
; the case of
${\mathcal {B}}^{+}$
; the case of
![]() ${\mathcal {B}}^{-}$
is nearly identical. Applying Poisson summation to (3.6) in the variable n gives
${\mathcal {B}}^{-}$
is nearly identical. Applying Poisson summation to (3.6) in the variable n gives
 $$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) = \frac{1}{q}\;\sum_{l\geq1} \sum_{k\in{\mathbb{Z}}} \widehat{W_{dl}^{+}} \left(\frac{k}{q}\right) \sum_{u \ (\mathrm{mod}\ q)} \psi(u+dl) \overline\psi(u) \, e_q(ku). \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) = \frac{1}{q}\;\sum_{l\geq1} \sum_{k\in{\mathbb{Z}}} \widehat{W_{dl}^{+}} \left(\frac{k}{q}\right) \sum_{u \ (\mathrm{mod}\ q)} \psi(u+dl) \overline\psi(u) \, e_q(ku). \end{align*} $$
Using (3.17), we may restrict attention to
![]() $|k| \ll \frac {q^{1+\varepsilon }}{N}$
with a negligible error. Hence,
$|k| \ll \frac {q^{1+\varepsilon }}{N}$
with a negligible error. Hence,
 $$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) \ll q^{-2022} + \frac{N}{q}\;\sum_{1\leq l\ll\frac{M}{d}}\sum_{0\leq|k|\ll\frac{q^{1+\varepsilon}}{N}} \Big| \sum_{u \ (\mathrm{mod}\ q)} \psi(u+dl)\overline\psi(u)\, e_q(ku) \Big|, \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) \ll q^{-2022} + \frac{N}{q}\;\sum_{1\leq l\ll\frac{M}{d}}\sum_{0\leq|k|\ll\frac{q^{1+\varepsilon}}{N}} \Big| \sum_{u \ (\mathrm{mod}\ q)} \psi(u+dl)\overline\psi(u)\, e_q(ku) \Big|, \end{align*} $$
since the variable l satisfies
![]() $l\ll \frac {M}{d}$
by the support of the test functions. The innermost sum can be recognized as
$l\ll \frac {M}{d}$
by the support of the test functions. The innermost sum can be recognized as
![]() $S(q;\psi ,dl,k)$
from (2.1). Applying Lemma 2.2 gives
$S(q;\psi ,dl,k)$
from (2.1). Applying Lemma 2.2 gives
 $$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) &\ll MNq^{-1+\varepsilon} + \frac{N}{q}\;\sum_{1\leq l \ll\frac{M}{d}}\sum_{1\leq|k|\ll\frac{q^{1+\varepsilon}}{N}} \Big| \sum_{u \ (\mathrm{mod}\ q)} \psi(u+dl)\overline\psi(u)\, e_q(ku) \Big|\\ &\ll q^\varepsilon\left(\frac{Mq^{1/2}}{d^{3/2}}+\frac{M^{1/4}N}{q^{1/4}}+\frac{MN}{q}\right). \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) &\ll MNq^{-1+\varepsilon} + \frac{N}{q}\;\sum_{1\leq l \ll\frac{M}{d}}\sum_{1\leq|k|\ll\frac{q^{1+\varepsilon}}{N}} \Big| \sum_{u \ (\mathrm{mod}\ q)} \psi(u+dl)\overline\psi(u)\, e_q(ku) \Big|\\ &\ll q^\varepsilon\left(\frac{Mq^{1/2}}{d^{3/2}}+\frac{M^{1/4}N}{q^{1/4}}+\frac{MN}{q}\right). \end{align*} $$
The third term above may be dropped since
![]() $\frac {MN}{q} \ll q^{\varepsilon } \frac {M^{1/4}N}{q^{1/4}}$
, since
$\frac {MN}{q} \ll q^{\varepsilon } \frac {M^{1/4}N}{q^{1/4}}$
, since
![]() $\frac {M}{q} \leq \frac {MN}{q} \ll q^{\varepsilon }$
.
$\frac {M}{q} \leq \frac {MN}{q} \ll q^{\varepsilon }$
.
Out of a convenience which will become evident in Section 3.5, we would prefer to include
![]() ${\mathcal {A}}^{\pm }_{m>n}(M,N)$
in Lemma 3.4, despite the fact that it does not naturally manifest using the methods of this section.
${\mathcal {A}}^{\pm }_{m>n}(M,N)$
in Lemma 3.4, despite the fact that it does not naturally manifest using the methods of this section.
Lemma 3.5. Suppose
![]() $d \prec q$
and
$d \prec q$
and
![]() $d \leq q^{2/3}$
. We have
$d \leq q^{2/3}$
. We have
 $$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = {\mathcal{A}}^{\pm}_{m>n}(M,N) + O\left(q^{\varepsilon}\left( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \right)\right). \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^{\pm}_{m>n}(M,N) = {\mathcal{A}}^{\pm}_{m>n}(M,N) + O\left(q^{\varepsilon}\left( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \right)\right). \end{align*} $$
Proof. We treat the
![]() $+$
case, since the
$+$
case, since the
![]() $-$
case is very similar. By the triangle inequality and (3.11), we have
$-$
case is very similar. By the triangle inequality and (3.11), we have
 $$ \begin{align*} |{\mathcal{A}}^{+}_{m>n}(M,N)| \leq \frac{d}{\sqrt{q}}\;\sum_{n|b_\psi} \left|\widehat{W_{n,d}^{+}}\left(\frac{-b_\psi d}{nq}\right)\right| \ll \frac{M}{\sqrt{q}} q^{\varepsilon}. \end{align*} $$
$$ \begin{align*} |{\mathcal{A}}^{+}_{m>n}(M,N)| \leq \frac{d}{\sqrt{q}}\;\sum_{n|b_\psi} \left|\widehat{W_{n,d}^{+}}\left(\frac{-b_\psi d}{nq}\right)\right| \ll \frac{M}{\sqrt{q}} q^{\varepsilon}. \end{align*} $$
Finally, note that
![]() $q^{-1/2} \leq d^{-3/2} q^{1/2}$
, since
$q^{-1/2} \leq d^{-3/2} q^{1/2}$
, since
![]() $d \leq q^{2/3}$
, so this bound on
$d \leq q^{2/3}$
, so this bound on
![]() $\mathcal {A}_{m>n}^{+}$
is absorbed by the error term.
$\mathcal {A}_{m>n}^{+}$
is absorbed by the error term.
3.5 Combining
 ${\mathcal {M}}^+_{m>n}$
and
${\mathcal {M}}^+_{m>n}$
and
 ${\mathcal {M}}^-_{m>n}$
${\mathcal {M}}^-_{m>n}$
Recall (3.7). Define
 $$ \begin{align} {\mathcal{W}} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{1}{\sqrt{MN}}\sum_{n|b_\psi} \left(\widehat{W^{+}_{n,d}}\left(\frac{-b_\psi d}{nq}\right) + \widehat{W^{-}_{n,d}}\left(\frac{b_\psi d}{nq}\right)\right). \end{align} $$
$$ \begin{align} {\mathcal{W}} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{1}{\sqrt{MN}}\sum_{n|b_\psi} \left(\widehat{W^{+}_{n,d}}\left(\frac{-b_\psi d}{nq}\right) + \widehat{W^{-}_{n,d}}\left(\frac{b_\psi d}{nq}\right)\right). \end{align} $$
As a first step, we have the following.
Lemma 3.6. We have
 $$ \begin{align} {\mathcal{W}} = \frac{\sqrt{q}}{2d} e_q(-b_{\psi}) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}} = \frac{\sqrt{q}}{2d} \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}} + O((dq)^{-1/2} q^{\varepsilon}). \end{align} $$
$$ \begin{align} {\mathcal{W}} = \frac{\sqrt{q}}{2d} e_q(-b_{\psi}) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}} = \frac{\sqrt{q}}{2d} \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}} + O((dq)^{-1/2} q^{\varepsilon}). \end{align} $$
Proof. Retracing the definitions, we have
 $$ \begin{align*} W^\pm_{n,d}(l) = \Big(\frac{MN}{(\pm n+dl)n}\Big)^{1/2} V\left(\frac{(\pm n+dl)n}{q}\right) \eta\left(\frac{\pm n+dl}{M}\right) \eta\left(\frac{n}{N}\right). \end{align*} $$
$$ \begin{align*} W^\pm_{n,d}(l) = \Big(\frac{MN}{(\pm n+dl)n}\Big)^{1/2} V\left(\frac{(\pm n+dl)n}{q}\right) \eta\left(\frac{\pm n+dl}{M}\right) \eta\left(\frac{n}{N}\right). \end{align*} $$
After applying the Fourier transforms and assembling the dyadic partition of unity, we have
 $$ \begin{align*} {\mathcal{W}} = \sum_{n|b_\psi} \int_{-n/d}^\infty V\left(\frac{(n+dy)n}{q}\right) &e\left(\frac{b_\psi dy}{nq}\right) \frac{dy}{\sqrt{(n+dy)n}} \\ &+ \sum_{n|b_\psi} \int_{n/d}^\infty V\left(\frac{(-n+dy)n}{q}\right) e\left(-\frac{b_\psi dy}{nq}\right) \frac{dy}{\sqrt{(-n+dy)n}}. \end{align*} $$
$$ \begin{align*} {\mathcal{W}} = \sum_{n|b_\psi} \int_{-n/d}^\infty V\left(\frac{(n+dy)n}{q}\right) &e\left(\frac{b_\psi dy}{nq}\right) \frac{dy}{\sqrt{(n+dy)n}} \\ &+ \sum_{n|b_\psi} \int_{n/d}^\infty V\left(\frac{(-n+dy)n}{q}\right) e\left(-\frac{b_\psi dy}{nq}\right) \frac{dy}{\sqrt{(-n+dy)n}}. \end{align*} $$
Changing variables results in
 $$ \begin{align*} {\mathcal{W}} = 2 \frac{\sqrt{q}}{d} e_q(-b_{\psi}) \sum_{n|b_\psi} \int_0^\infty V(n^2x) \cos(2 \pi b_{\psi} x) \frac{dx}{\sqrt{x}}. \end{align*} $$
$$ \begin{align*} {\mathcal{W}} = 2 \frac{\sqrt{q}}{d} e_q(-b_{\psi}) \sum_{n|b_\psi} \int_0^\infty V(n^2x) \cos(2 \pi b_{\psi} x) \frac{dx}{\sqrt{x}}. \end{align*} $$
We next wish to apply the definition of
![]() $V(x)$
from (2.11) and reverse the order of integration. This formally gives
$V(x)$
from (2.11) and reverse the order of integration. This formally gives
 $$ \begin{align*} {\mathcal{W}} &= 2 \frac{\sqrt{q}}{d} e_q(-b_{\psi})\; \sum_{n|b_\psi} \int_{(1/4)} \frac{G(s)}{s} \frac{\gamma(1/2+s)^2}{\gamma(1/2)^2 n^{2s}} \left( \int_0^\infty x^{-s} \cos(2 \pi b_{\psi} x) \frac{dx}{\sqrt{x}} \right) \frac{ds}{2 \pi i}. \end{align*} $$
$$ \begin{align*} {\mathcal{W}} &= 2 \frac{\sqrt{q}}{d} e_q(-b_{\psi})\; \sum_{n|b_\psi} \int_{(1/4)} \frac{G(s)}{s} \frac{\gamma(1/2+s)^2}{\gamma(1/2)^2 n^{2s}} \left( \int_0^\infty x^{-s} \cos(2 \pi b_{\psi} x) \frac{dx}{\sqrt{x}} \right) \frac{ds}{2 \pi i}. \end{align*} $$
This interchange is a little delicate but can be justified in a few ways. One option is to first truncate the x-integral to a finite interval
![]() $[0, X]$
and let
$[0, X]$
and let
![]() $X \rightarrow \infty $
after interchanging the integrals. Lemma 2.5 now implies
$X \rightarrow \infty $
after interchanging the integrals. Lemma 2.5 now implies
 $$ \begin{align*} {\mathcal{W}} =2 \frac{\sqrt{q}}{d} e_q(-b_{\psi})\; \sum_{n|b_\psi} \int_{(1/4)} \frac{G(s)}{s} \frac{\gamma(1/2+s)^2}{\gamma(1/2)^2 n^{2s}} \frac{\Gamma(1/2-s)}{(2\pi|b_\psi|)^{1/2-s}} \cos(\tfrac{\pi}{2}(\tfrac12 - s)) \frac{ds}{2 \pi i}. \end{align*} $$
$$ \begin{align*} {\mathcal{W}} =2 \frac{\sqrt{q}}{d} e_q(-b_{\psi})\; \sum_{n|b_\psi} \int_{(1/4)} \frac{G(s)}{s} \frac{\gamma(1/2+s)^2}{\gamma(1/2)^2 n^{2s}} \frac{\Gamma(1/2-s)}{(2\pi|b_\psi|)^{1/2-s}} \cos(\tfrac{\pi}{2}(\tfrac12 - s)) \frac{ds}{2 \pi i}. \end{align*} $$
Applying the definition of
![]() $\gamma (s)$
(found in (2.12)) and rearranging terms produces
$\gamma (s)$
(found in (2.12)) and rearranging terms produces
 $$ \begin{align*} {\mathcal{W}} =\frac{2\sqrt{q}e_q(-b_{\psi})}{ d \sqrt{2\pi |b_\psi|} \Gamma(1/4)^2} \; \int_{(1/4)} \frac{G(s)}{s} \Gamma\left(\tfrac{1}{4}+\tfrac{s}{2}\right)^2 \Gamma(1/2-s) \cos\left(\tfrac{\pi}{4}-\tfrac{\pi s}{2}\right)\sum_{n|b_\psi} \left(\frac{2|b_\psi|}{n^2}\right)^s \frac{ds}{2\pi i }. \end{align*} $$
$$ \begin{align*} {\mathcal{W}} =\frac{2\sqrt{q}e_q(-b_{\psi})}{ d \sqrt{2\pi |b_\psi|} \Gamma(1/4)^2} \; \int_{(1/4)} \frac{G(s)}{s} \Gamma\left(\tfrac{1}{4}+\tfrac{s}{2}\right)^2 \Gamma(1/2-s) \cos\left(\tfrac{\pi}{4}-\tfrac{\pi s}{2}\right)\sum_{n|b_\psi} \left(\frac{2|b_\psi|}{n^2}\right)^s \frac{ds}{2\pi i }. \end{align*} $$
Using standard gamma function identities, one can show easily that
Hence,
 $$ \begin{align*} {\mathcal{W}} =\frac{\sqrt{q}e_q(-b_{\psi})}{ d \sqrt{ |b_\psi|} \Gamma(1/4)^2} \; \int_{(1/4)} \frac{G(s)}{s} \Gamma(\tfrac14 + \tfrac{s}{2}) \Gamma(\tfrac14 - \tfrac{s}{2}) \sum_{n|b_\psi} \left(\frac{|b_\psi|}{n^2}\right)^s \frac{ds}{2\pi i }. \end{align*} $$
$$ \begin{align*} {\mathcal{W}} =\frac{\sqrt{q}e_q(-b_{\psi})}{ d \sqrt{ |b_\psi|} \Gamma(1/4)^2} \; \int_{(1/4)} \frac{G(s)}{s} \Gamma(\tfrac14 + \tfrac{s}{2}) \Gamma(\tfrac14 - \tfrac{s}{2}) \sum_{n|b_\psi} \left(\frac{|b_\psi|}{n^2}\right)^s \frac{ds}{2\pi i }. \end{align*} $$
Using the symmetry between divisors, it is apparent that this integrand is an odd function. Therefore, the integral is half the residue at
![]() $s=0$
, giving the claimed formula for
$s=0$
, giving the claimed formula for
![]() ${\mathcal {W}}$
.
${\mathcal {W}}$
.
Finally, we deduce the approximation in (3.19). We have
![]() $e_q(-b_{\psi }) = 1 + O(q^{-1} |b_{\psi }|)$
by a Taylor expansion, and recalling
$e_q(-b_{\psi }) = 1 + O(q^{-1} |b_{\psi }|)$
by a Taylor expansion, and recalling
![]() $|b_{\psi }| \ll d$
. Inserting this into the formula for
$|b_{\psi }| \ll d$
. Inserting this into the formula for
![]() ${\mathcal {W}}$
and using
${\mathcal {W}}$
and using
![]() $\sigma _0(|b_{\psi }|) |b_{\psi }|^{1/2} \ll d^{1/2} q^{\varepsilon }$
completes the proof.
$\sigma _0(|b_{\psi }|) |b_{\psi }|^{1/2} \ll d^{1/2} q^{\varepsilon }$
completes the proof.
Lemma 3.7. With
![]() ${\mathcal {M}}_{m>n}(\psi )$
as defined in (3.2), we have
${\mathcal {M}}_{m>n}(\psi )$
as defined in (3.2), we have
 $$ \begin{align*} {\mathcal{M}}_{m>n}(\psi) = {\mathcal{A}}_{m>n}(\psi) + O\Big(q^\varepsilon\Big(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\Big)\Big), \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{m>n}(\psi) = {\mathcal{A}}_{m>n}(\psi) + O\Big(q^\varepsilon\Big(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\Big)\Big), \end{align*} $$
where
 $$ \begin{align*} {\mathcal{A}}_{m>n}(\psi) = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{\varphi(d)}{2} e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
$$ \begin{align*} {\mathcal{A}}_{m>n}(\psi) = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{\varphi(d)}{2} e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
Proof. We begin by splitting the dyadic summations of
![]() ${\mathcal {M}}_{m>n}$
into two ranges depending on whether M and N are nearby or far apart. The cutoff for these two ranges is
${\mathcal {M}}_{m>n}$
into two ranges depending on whether M and N are nearby or far apart. The cutoff for these two ranges is
![]() $M=d^{1/2}N$
. Therefore, starting at (3.7), we write
$M=d^{1/2}N$
. Therefore, starting at (3.7), we write
 $$ \begin{align*} {\mathcal{M}}_{m>n} = \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \sum_\pm {\mathcal{B}}^\pm_{m>n}(M,N) + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M< d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \sum_\pm {\mathcal{B}}^\pm_{m>n}(M,N). \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{m>n} = \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \sum_\pm {\mathcal{B}}^\pm_{m>n}(M,N) + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M< d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \sum_\pm {\mathcal{B}}^\pm_{m>n}(M,N). \end{align*} $$
For the first term, we apply Lemma 3.3, and for the second term, we apply Lemma 3.5. Hence,
 $$ \begin{align} {\mathcal{M}}_{m>n} &= \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm {\mathcal{A}}^\pm_{m>n}(M,N) + O\Big(\frac{Nq^{1/2+\varepsilon}}{d}\Big)\Big\}\\&\quad+ \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M< d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm{\mathcal{A}}^\pm_{m>n}(M,N) + O\Big(q^{\varepsilon}\Big( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \Big)\Big)\Big\}.\nonumber \end{align} $$
$$ \begin{align} {\mathcal{M}}_{m>n} &= \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm {\mathcal{A}}^\pm_{m>n}(M,N) + O\Big(\frac{Nq^{1/2+\varepsilon}}{d}\Big)\Big\}\\&\quad+ \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M< d^{1/2}N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm{\mathcal{A}}^\pm_{m>n}(M,N) + O\Big(q^{\varepsilon}\Big( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \Big)\Big)\Big\}.\nonumber \end{align} $$
Rearranging and evaluating the main term, we obtain
 $$ \begin{align} {\mathcal{M}}_{m>n} = {\mathcal{A}}_{m>n} + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq d^{1/2}N}} O\Big(\frac{N^{1/2}q^{1/2+\varepsilon}}{M^{1/2}}\Big) + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M< d^{1/2}N}} O\Big(q^{\varepsilon}\Big( \frac{M^{1/2}q^{1/2}}{N^{1/2}d^{1/2}} + \frac{N^{1/2}d}{M^{1/4}q^{1/4}} \Big)\Big), \end{align} $$
$$ \begin{align} {\mathcal{M}}_{m>n} = {\mathcal{A}}_{m>n} + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq d^{1/2}N}} O\Big(\frac{N^{1/2}q^{1/2+\varepsilon}}{M^{1/2}}\Big) + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M< d^{1/2}N}} O\Big(q^{\varepsilon}\Big( \frac{M^{1/2}q^{1/2}}{N^{1/2}d^{1/2}} + \frac{N^{1/2}d}{M^{1/4}q^{1/4}} \Big)\Big), \end{align} $$
where
 $$ \begin{align*} {\mathcal{A}}_{m>n} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} \sum_\pm {\mathcal{A}}^\pm_{m>n}(M,N). \end{align*} $$
$$ \begin{align*} {\mathcal{A}}_{m>n} = \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} \sum_\pm {\mathcal{A}}^\pm_{m>n}(M,N). \end{align*} $$
Using that we may restrict to
![]() $N \ll M$
and
$N \ll M$
and
![]() $MN \ll q^{1+\varepsilon }$
, it is easy to see that the error term simplifies to give
$MN \ll q^{1+\varepsilon }$
, it is easy to see that the error term simplifies to give
 $$ \begin{align*} {\mathcal{M}}_{m>n}= {\mathcal{A}}_{m>n} + O\Big(q^\varepsilon\Big(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\Big)\Big). \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{m>n}= {\mathcal{A}}_{m>n} + O\Big(q^\varepsilon\Big(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\Big)\Big). \end{align*} $$
For the purposes of Theorem 1.2, we have
![]() $q \geq d^2$
so that
$q \geq d^2$
so that
![]() $d q^{-1/8} \leq d^{-1/4} q^{1/2}$
, so the latter error term can be dropped. The displayed error term is consistent with Theorem 1.2.
$d q^{-1/8} \leq d^{-1/4} q^{1/2}$
, so the latter error term can be dropped. The displayed error term is consistent with Theorem 1.2.
Now, we turn to
![]() ${\mathcal {A}}_{m>n}$
, which takes the form
${\mathcal {A}}_{m>n}$
, which takes the form
 $$ \begin{align*} \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q} \frac{d}{\sqrt{q}} e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) \sum_{n|b_\psi} \Big( \widehat{W^{+}_{n,d}}\Big(\frac{-b_\psi d}{nq}\Big) +\widehat{W^{-}_{n,d}}\Big(\frac{b_\psi d}{nq}\Big) \Big) \\ = \varphi(d) \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q} \frac{d}{\sqrt{q}} e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) {\mathcal{W}}, \end{align*} $$
$$ \begin{align*} \mathop{\sum\sum}_{M,N \text{ dyadic}} \frac{\varphi(d)}{\sqrt{MN}} \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q} \frac{d}{\sqrt{q}} e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) \sum_{n|b_\psi} \Big( \widehat{W^{+}_{n,d}}\Big(\frac{-b_\psi d}{nq}\Big) +\widehat{W^{-}_{n,d}}\Big(\frac{b_\psi d}{nq}\Big) \Big) \\ = \varphi(d) \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q} \frac{d}{\sqrt{q}} e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) {\mathcal{W}}, \end{align*} $$
recalling the definition (3.18). Applying Lemma 3.6 shows that
Note
![]() $d^{3/2} q^{-1} \leq d q^{-1/8}$
, so this error term can be dropped.
$d^{3/2} q^{-1} \leq d q^{-1/8}$
, so this error term can be dropped.
Next, consider
![]() ${\mathcal {M}}_{m<n}$
, for which recall (3.3). Lemma 2.14 implies
${\mathcal {M}}_{m<n}$
, for which recall (3.3). Lemma 2.14 implies
![]() $ a_{\overline \psi } \equiv -a_\psi \ (\mathrm {mod}\ q/d)$
, and recalling (1.5), we have
$ a_{\overline \psi } \equiv -a_\psi \ (\mathrm {mod}\ q/d)$
, and recalling (1.5), we have
![]() $a_{\overline \psi } = -a_\psi $
. Similarly,
$a_{\overline \psi } = -a_\psi $
. Similarly,
![]() $b_{\overline {\psi }} = - b_{\psi }$
. Hence, we deduce the following:
$b_{\overline {\psi }} = - b_{\psi }$
. Hence, we deduce the following:
Lemma 3.8. We have
 $$ \begin{align*} {\mathcal{M}}_{m<n}(\psi) = {\mathcal{A}}_{m<n}(\psi) + O\Big(q^\varepsilon\Big(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\Big)\Big), \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{m<n}(\psi) = {\mathcal{A}}_{m<n}(\psi) + O\Big(q^\varepsilon\Big(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\Big)\Big), \end{align*} $$
where
 $$ \begin{align*} {\mathcal{A}}_{m<n}(\psi) = \left(\frac{ 2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{\varphi(d)}{2} e_q(-\overline{2a_\psi}(a_\psi-b_\psi)^2) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
$$ \begin{align*} {\mathcal{A}}_{m<n}(\psi) = \left(\frac{ 2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{\varphi(d)}{2} e_q(-\overline{2a_\psi}(a_\psi-b_\psi)^2) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
3.6 Combining
 ${\mathcal {M}}_{m>n}$
and
${\mathcal {M}}_{m>n}$
and
 ${\mathcal {M}}_{m<n}$
${\mathcal {M}}_{m<n}$
From Lemmas 3.7 and 3.8, we get that
 $$ \begin{align*} {\mathcal{M}}_{m>n} + {\mathcal{M}}_{m<n} = {\mathcal{A}}' + O\left(q^\varepsilon\left(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\right)\right), \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{m>n} + {\mathcal{M}}_{m<n} = {\mathcal{A}}' + O\left(q^\varepsilon\left(\frac{q^{1/2}}{d^{1/4}}+\frac{d}{q^{1/8}}\right)\right), \end{align*} $$
where
 $$ \begin{align*} {\mathcal{A}}' = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{\varphi(d)}{2} \Big[ e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) + \Big(\frac{-1}{q}\Big) e_q(-\overline{2a_\psi}(a_\psi-b_\psi)^2 ) \Big]. \end{align*} $$
$$ \begin{align*} {\mathcal{A}}' = \left(\frac{-2 a_\psi}{q/d^2}\right) \varepsilon_{q } \frac{\varphi(d)}{2} \Big[ e_q(\overline{2a_\psi}(a_\psi-b_\psi)^2) + \Big(\frac{-1}{q}\Big) e_q(-\overline{2a_\psi}(a_\psi-b_\psi)^2 ) \Big]. \end{align*} $$
Therefore, if
![]() $q\equiv 1\ (\mathrm {mod}\ 4)$
, then
$q\equiv 1\ (\mathrm {mod}\ 4)$
, then
 $$ \begin{align*} {\mathcal{A}}' &= \left(\frac{2 a_\psi}{q/d^2}\right) \varphi(d) \cos\Big(2\pi \frac{\overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
$$ \begin{align*} {\mathcal{A}}' &= \left(\frac{2 a_\psi}{q/d^2}\right) \varphi(d) \cos\Big(2\pi \frac{\overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
This is consistent with (1.12) for
![]() $q \equiv 1 \ \pmod {4}$
. If instead
$q \equiv 1 \ \pmod {4}$
. If instead
![]() $q\equiv 3\ (\mathrm {mod}\ 4)$
, then
$q\equiv 3\ (\mathrm {mod}\ 4)$
, then
 $$ \begin{align*} {\mathcal{A}}' &= \left(\frac{2 a_\psi}{q/d^2}\right) \varphi(d) \sin\Big(2\pi \frac{\overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
$$ \begin{align*} {\mathcal{A}}' &= \left(\frac{2 a_\psi}{q/d^2}\right) \varphi(d) \sin\Big(2\pi \frac{\overline{2a_\psi}(a_\psi-b_\psi)^2}{q}\Big) \frac{\sigma_0(|b_\psi|)}{\sqrt{|b_\psi|}}. \end{align*} $$
This derivation agrees with (1.12). Combining this with Lemma 3.1 proves Theorem 1.2.
4 Sketching the proofs of remaining theorems
The proof of Theorem 1.1 is similar to the proof of Theorem 1.2, except in some ways which make it simpler. Likewise, the proof of Theorem 1.3 will essentially use a subset of the tools used to prove Theorem 1.2. In order to avoid excessive repetition, we only give sketches of these proofs.
4.1 Sketch of the proof of Theorem 1.1
The structure of the proof of Theorem 1.1 is similar to that of Theorem 1.2. As a substitute for Lemma 3.3, we have the following:
Lemma 4.1. Suppose that
![]() $d\prec q \preceq d^2$
, and that
$d\prec q \preceq d^2$
, and that
![]() $M> 2^{10} N$
. Then
$M> 2^{10} N$
. Then
where
 $$ \begin{align*} {\mathcal{A}}^+_{m>n}(M,N) = \sum_{n|b_\psi} \widehat{W^{\pm}_{n,d}}\left(\frac{-b_\psi d}{nq}\right). \end{align*} $$
$$ \begin{align*} {\mathcal{A}}^+_{m>n}(M,N) = \sum_{n|b_\psi} \widehat{W^{\pm}_{n,d}}\left(\frac{-b_\psi d}{nq}\right). \end{align*} $$
Proof. We follow through the proof of Lemma 3.3, and note that the earliest difference will occur at (3.13) when Lemma 2.15 was used to evaluate
![]() ${\mathcal {S}}_{q,d}(\psi , jn)$
. The condition that
${\mathcal {S}}_{q,d}(\psi , jn)$
. The condition that
![]() $q\preceq d^2$
means that we need to use Lemma 2.16 in place of Lemma 2.15. In practical terms, this means that in place of (3.13), we instead obtain
$q\preceq d^2$
means that we need to use Lemma 2.16 in place of Lemma 2.15. In practical terms, this means that in place of (3.13), we instead obtain
 $$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) = \mathop{\sum_{n\geq1} \sum_{j\neq 0}}_{jn\equiv -a_\psi\ (\mathrm{mod}\ q/d)} \widehat{W^{\pm}_{n,d}}\left(\frac{dj}{q}\right). \end{align*} $$
$$ \begin{align*} {\mathcal{B}}^+_{m>n}(M,N) = \mathop{\sum_{n\geq1} \sum_{j\neq 0}}_{jn\equiv -a_\psi\ (\mathrm{mod}\ q/d)} \widehat{W^{\pm}_{n,d}}\left(\frac{dj}{q}\right). \end{align*} $$
In this case, there is no need to introduce
![]() $b_{\psi }$
, since we have
$b_{\psi }$
, since we have
![]() $jn \equiv - a_{\psi } \ \pmod {q/d}$
, and
$jn \equiv - a_{\psi } \ \pmod {q/d}$
, and
![]() $a_{\psi }$
is inherently defined modulo
$a_{\psi }$
is inherently defined modulo
![]() $q/d$
. The term
$q/d$
. The term
![]() ${\mathcal {A}}$
corresponds to the term
${\mathcal {A}}$
corresponds to the term
![]() $jn = -a_{\psi }$
, while the error terms are, similarly to (3.15) and (3.16), bounded by
$jn = -a_{\psi }$
, while the error terms are, similarly to (3.15) and (3.16), bounded by
 $$ \begin{align*} \mathop{\sum_{n\geq1}\sum_{j\neq0}}_{\substack{jn\equiv -a_\psi\ (\mathrm{mod}\ q/d)\\jn\neq -b_\psi}} \left|\widehat{W^{\pm}_{n,d}}\left(\frac{dj}{q}\right)\right| \ll q^{\varepsilon} \frac{M}{d} \frac{Nq}{M (q/d)} \ll q^{\varepsilon} N.\\[-68pt] \end{align*} $$
$$ \begin{align*} \mathop{\sum_{n\geq1}\sum_{j\neq0}}_{\substack{jn\equiv -a_\psi\ (\mathrm{mod}\ q/d)\\jn\neq -b_\psi}} \left|\widehat{W^{\pm}_{n,d}}\left(\frac{dj}{q}\right)\right| \ll q^{\varepsilon} \frac{M}{d} \frac{Nq}{M (q/d)} \ll q^{\varepsilon} N.\\[-68pt] \end{align*} $$
Lemma 3.4 holds without changes, since the only assumption there is
![]() $d \prec q$
. As in Lemma 3.5, we can freely insert the term
$d \prec q$
. As in Lemma 3.5, we can freely insert the term
![]() $\mathcal {A}_{m>n}^{\pm }(M,N)$
since it is bounded by
$\mathcal {A}_{m>n}^{\pm }(M,N)$
since it is bounded by
![]() $d^{-1} M q^{\varepsilon }$
, which is in turn bounded by
$d^{-1} M q^{\varepsilon }$
, which is in turn bounded by
![]() $d^{-3/2} M q^{1/2+\varepsilon }$
. The new cutoff in the proof of Lemma 3.7 is
$d^{-3/2} M q^{1/2+\varepsilon }$
. The new cutoff in the proof of Lemma 3.7 is
![]() $Mq^{1/2}=Nd^{3/2}$
, so this error term is absorbed by the error in Lemma 4.1. In place of (3.20), we obtain
$Mq^{1/2}=Nd^{3/2}$
, so this error term is absorbed by the error in Lemma 4.1. In place of (3.20), we obtain
 $$ \begin{align} {\mathcal{M}}_{m>n} &= \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq q^{-1/2} d^{3/2} N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm {\mathcal{A}}^\pm_{m>n}(M,N) + O\Big( N q^{\varepsilon} \Big)\Big\}\\&\quad + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\ M< q^{-1/2} d^{3/2} N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm{\mathcal{A}}^\pm_{m>n}(M,N) + O\Big(q^{\varepsilon}\Big( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \Big)\Big)\Big\}.\nonumber \end{align} $$
$$ \begin{align} {\mathcal{M}}_{m>n} &= \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\M\geq q^{-1/2} d^{3/2} N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm {\mathcal{A}}^\pm_{m>n}(M,N) + O\Big( N q^{\varepsilon} \Big)\Big\}\\&\quad + \mathop{\sum\sum}_{\substack{M,N \text{ dyadic}\\ M< q^{-1/2} d^{3/2} N}} \frac{\varphi(d)}{\sqrt{MN}} \Big\{\sum_\pm{\mathcal{A}}^\pm_{m>n}(M,N) + O\Big(q^{\varepsilon}\Big( \frac{Mq^{1/2}}{d^{3/2}} + \frac{M^{1/4}N}{q^{1/4}} \Big)\Big)\Big\}.\nonumber \end{align} $$
In total, this error term is of size
![]() $d^{1/4} q^{1/4+\varepsilon } + d^{} q^{-1/8+\varepsilon }$
. Under the hypotheses of Theorem 1.1, we have
$d^{1/4} q^{1/4+\varepsilon } + d^{} q^{-1/8+\varepsilon }$
. Under the hypotheses of Theorem 1.1, we have
![]() $q \leq d^2$
and hence
$q \leq d^2$
and hence
![]() $d^{1/4} q^{1/4} \leq d q^{-1/8}$
, so the former term can be discarded. The error term is then seen to be consistent with the statement of Theorem 1.1.
$d^{1/4} q^{1/4} \leq d q^{-1/8}$
, so the former term can be discarded. The error term is then seen to be consistent with the statement of Theorem 1.1.
The assembly of the term
![]() ${\mathcal {A}}$
is similar to that of
${\mathcal {A}}$
is similar to that of
![]() ${\mathcal {A}}'$
, though it is simpler since there is no need to introduce
${\mathcal {A}}'$
, though it is simpler since there is no need to introduce
![]() $b_{\psi }$
, and leads to
$b_{\psi }$
, and leads to
 $$ \begin{align*} {\mathcal{A}} = \frac{\varphi(d)}{d} \sqrt{q} \; \frac{\sigma_0(|a_\psi|)}{\sqrt{|a_\psi|}}. \end{align*} $$
$$ \begin{align*} {\mathcal{A}} = \frac{\varphi(d)}{d} \sqrt{q} \; \frac{\sigma_0(|a_\psi|)}{\sqrt{|a_\psi|}}. \end{align*} $$
This concludes the discussion of the proof of Theorem 1.1.
4.2 A sketch of the proof of Theorem 1.3
Since Theorem 1.3 is an upper bound, we can arrange the second moment as follows:
 $$ \begin{align*} \sum_{\chi\ \pmod{d}} |L(1/2, \chi \cdot \psi)|^2 \ll \sum_{\chi \ \pmod{d}} \Big| \sum_{M \text{ dyadic}} \sum_m \frac{\chi(m) \psi(m)}{\sqrt{m}} \eta\Big(\frac{m}{M} \Big) V\Big(\frac{m}{\sqrt{q}} \Big) \Big|^2. \end{align*} $$
$$ \begin{align*} \sum_{\chi\ \pmod{d}} |L(1/2, \chi \cdot \psi)|^2 \ll \sum_{\chi \ \pmod{d}} \Big| \sum_{M \text{ dyadic}} \sum_m \frac{\chi(m) \psi(m)}{\sqrt{m}} \eta\Big(\frac{m}{M} \Big) V\Big(\frac{m}{\sqrt{q}} \Big) \Big|^2. \end{align*} $$
This uses an approximate functional equation for
![]() $L(1/2, \chi \cdot \psi )$
in place of Lemma 2.17. Applying Cauchy’s inequality to take M to the outside of the square, we obtain
$L(1/2, \chi \cdot \psi )$
in place of Lemma 2.17. Applying Cauchy’s inequality to take M to the outside of the square, we obtain
 $$ \begin{align*} \sum_{\chi \ \pmod{d}} |L(1/2, \chi \cdot \psi)|^2 \ll q^{\varepsilon} \sum_{M \text{ dyadic}} \sum_{\chi \ \pmod{d}} \Big| \sum_m \frac{\chi(m) \psi(m)}{\sqrt{m}} \eta\Big(\frac{m}{M}\Big) V\Big(\frac{m}{\sqrt{q}} \Big) \Big|^2. \end{align*} $$
$$ \begin{align*} \sum_{\chi \ \pmod{d}} |L(1/2, \chi \cdot \psi)|^2 \ll q^{\varepsilon} \sum_{M \text{ dyadic}} \sum_{\chi \ \pmod{d}} \Big| \sum_m \frac{\chi(m) \psi(m)}{\sqrt{m}} \eta\Big(\frac{m}{M}\Big) V\Big(\frac{m}{\sqrt{q}} \Big) \Big|^2. \end{align*} $$
The purpose of this trick is to completely avoid the ranges where M and N are far apart.
Squaring this out and applying orthogonality of characters, we obtain a diagonal term of size
![]() $\ll d q^{\varepsilon }$
. For the off-diagonal terms, we essentially arrive at
$\ll d q^{\varepsilon }$
. For the off-diagonal terms, we essentially arrive at
 $$ \begin{align*} \sum_{M \text{ dyadic}} \frac{d}{M} |{\mathcal{B}}_{m> n}(M,M)| \ll q^{\varepsilon} \left( \frac{q^{1/2}}{d^{1/2}} + \frac{d}{q^{1/8}} \right), \end{align*} $$
$$ \begin{align*} \sum_{M \text{ dyadic}} \frac{d}{M} |{\mathcal{B}}_{m> n}(M,M)| \ll q^{\varepsilon} \left( \frac{q^{1/2}}{d^{1/2}} + \frac{d}{q^{1/8}} \right), \end{align*} $$
using Lemma 3.4 for the final bound. The second error term can be dropped in comparison to the diagonal term. In all, we obtain the bound in Theorem 1.3.