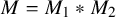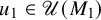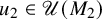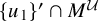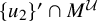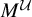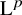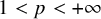1. Introduction
In order to state our main results, we recall the following terminology regarding n-independence and freeness.
Terminology
Let
![]() $(M, \tau )$
be a tracial von Neumann algebra together with a von Neumann subalgebra
$(M, \tau )$
be a tracial von Neumann algebra together with a von Neumann subalgebra
![]() $B \subset M$
. We denote by
$B \subset M$
. We denote by
![]() $\operatorname { E}_B : M \to B$
the unique trace-preserving faithful normal conditional expectation and set
$\operatorname { E}_B : M \to B$
the unique trace-preserving faithful normal conditional expectation and set
![]() $M \ominus B = \ker (\operatorname { E}_B)$
.
$M \ominus B = \ker (\operatorname { E}_B)$
.
Let
![]() $n \geq 1$
. Following Popa (see e.g. [Reference PopaPo13a, Reference PopaPo13b]), we say that two subsets
$n \geq 1$
. Following Popa (see e.g. [Reference PopaPo13a, Reference PopaPo13b]), we say that two subsets
![]() $X, Y \subset M \ominus B$
are n-independent in M with respect to
$X, Y \subset M \ominus B$
are n-independent in M with respect to
![]() $\operatorname { E}_{B}$
if
$\operatorname { E}_{B}$
if
![]() $\operatorname { E}_B(x_1y_1\cdots x_ky_k)=0$
, for every
$\operatorname { E}_B(x_1y_1\cdots x_ky_k)=0$
, for every
![]() $1\leq k\leq n$
,
$1\leq k\leq n$
,
![]() $x_1,\dots ,x_k\in X$
and
$x_1,\dots ,x_k\in X$
and
![]() $y_1,\dots ,y_k\in Y$
. We then say that two intermediate von Neumann subalgebras
$y_1,\dots ,y_k\in Y$
. We then say that two intermediate von Neumann subalgebras
![]() $B \subset M_1, M_2\subset M$
are n-independent in M with respect to
$B \subset M_1, M_2\subset M$
are n-independent in M with respect to
![]() $\operatorname { E}_B$
if the sets
$\operatorname { E}_B$
if the sets
![]() $M_1 \ominus B$
and
$M_1 \ominus B$
and
![]() $M_2 \ominus B$
are n-independent with respect to
$M_2 \ominus B$
are n-independent with respect to
![]() $\operatorname { E}_B$
. When
$\operatorname { E}_B$
. When
![]() $B = \mathbb {C}1$
, two von Neumann subalgebras
$B = \mathbb {C}1$
, two von Neumann subalgebras
![]() $M_1, M_2 \subset M$
are
$M_1, M_2 \subset M$
are
![]() $1$
-independent in M with respect to
$1$
-independent in M with respect to
![]() $\tau $
if and only if
$\tau $
if and only if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are
$M_2$
are
![]() $\tau $
-orthogonal, that is,
$\tau $
-orthogonal, that is,
![]() $\tau (xy)=\tau (x)\tau (y)$
, for every
$\tau (xy)=\tau (x)\tau (y)$
, for every
![]() $x\in M_1$
and
$x\in M_1$
and
![]() $y\in M_2$
.
$y\in M_2$
.
Let I be a nonempty index set. We say that a family
![]() $(X_i)_{i \in I}$
of subsets of
$(X_i)_{i \in I}$
of subsets of
![]() $M \ominus B$
is freely independent in M with respect to
$M \ominus B$
is freely independent in M with respect to
![]() $\operatorname { E}_B$
if
$\operatorname { E}_B$
if
![]() $\operatorname { E}_B(x_1 \cdots x_k)=0$
for every
$\operatorname { E}_B(x_1 \cdots x_k)=0$
for every
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $x_1 \in X_{\varepsilon _1}, \dots , x_k \in X_{\varepsilon _k}$
with
$x_1 \in X_{\varepsilon _1}, \dots , x_k \in X_{\varepsilon _k}$
with
![]() $\varepsilon _1 \neq \cdots \neq \varepsilon _k$
in I. We say that a family
$\varepsilon _1 \neq \cdots \neq \varepsilon _k$
in I. We say that a family
![]() $(M_i)_{i \in I}$
of intermediate von Neumann subalgebras
$(M_i)_{i \in I}$
of intermediate von Neumann subalgebras
![]() $B \subset M_i \subset M$
is freely independent in M with respect to
$B \subset M_i \subset M$
is freely independent in M with respect to
![]() $\operatorname { E}_B$
if the family of subsets
$\operatorname { E}_B$
if the family of subsets
![]() $(M_i \ominus B)_{i \in I}$
is freely independent in M with respect to
$(M_i \ominus B)_{i \in I}$
is freely independent in M with respect to
![]() $\operatorname { E}_B$
. In this case, we denote by
$\operatorname { E}_B$
. In this case, we denote by
![]() $\ast _{B, i \in I} (M_i, \tau _i) = \bigvee _{i \in I} M_i \subset M$
the tracial amalgamated free product von Neumann algebra, where
$\ast _{B, i \in I} (M_i, \tau _i) = \bigvee _{i \in I} M_i \subset M$
the tracial amalgamated free product von Neumann algebra, where
![]() $\tau _i = \tau |_{M_i}$
for every
$\tau _i = \tau |_{M_i}$
for every
![]() $i \in I$
.
$i \in I$
.
Main results
Let I be an at most countable index set, such that
![]() $2 \leq | I | \leq +\infty $
. Let
$2 \leq | I | \leq +\infty $
. Let
![]() $(M_i, \tau _i)_{i \in I}$
be a family of tracial von Neumann algebras with a common von Neumann subalgebra
$(M_i, \tau _i)_{i \in I}$
be a family of tracial von Neumann algebras with a common von Neumann subalgebra
![]() $(B, \tau _0)$
such that for every
$(B, \tau _0)$
such that for every
![]() $i \in I$
, we have
$i \in I$
, we have
![]() $\tau _i|_B = \tau _0$
. Denote by
$\tau _i|_B = \tau _0$
. Denote by
![]() $(M, \tau ) = \ast _{B, i \in I} (M_i, \tau _i)$
the tracial amalgamated free product von Neumann algebra. Let
$(M, \tau ) = \ast _{B, i \in I} (M_i, \tau _i)$
the tracial amalgamated free product von Neumann algebra. Let
![]() $\mathcal U$
be a nonprincipal ultrafilter on
$\mathcal U$
be a nonprincipal ultrafilter on
![]() $\mathbb {N}$
. Denote by
$\mathbb {N}$
. Denote by
![]() $(M^{\mathcal U}, \tau ^{\mathcal U})$
the tracial ultraproduct von Neumann algebra. Simply denote by
$(M^{\mathcal U}, \tau ^{\mathcal U})$
the tracial ultraproduct von Neumann algebra. Simply denote by
![]() $\operatorname { E}_B : M \to B$
(respectively,
$\operatorname { E}_B : M \to B$
(respectively,
![]() $\operatorname { E}_{B^{\mathcal U}} : M^{\mathcal U} \to B^{\mathcal U}$
) the unique trace-preserving faithful normal conditional expectation.
$\operatorname { E}_{B^{\mathcal U}} : M^{\mathcal U} \to B^{\mathcal U}$
) the unique trace-preserving faithful normal conditional expectation.
Denote by
![]() $\mathscr W \subset M$
the linear span of B and of all the reduced words in M of the form
$\mathscr W \subset M$
the linear span of B and of all the reduced words in M of the form
![]() $w = w_1 \cdots w_n$
, with
$w = w_1 \cdots w_n$
, with
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $w_j \in M_{\varepsilon _j} \ominus B$
for every
$w_j \in M_{\varepsilon _j} \ominus B$
for every
![]() $j \in \{1, \dots , n\}$
, and
$j \in \{1, \dots , n\}$
, and
![]() $\varepsilon _1, \dots , \varepsilon _n \in I$
, such that
$\varepsilon _1, \dots , \varepsilon _n \in I$
, such that
![]() $\varepsilon _1 \neq \cdots \neq \varepsilon _n$
. For every
$\varepsilon _1 \neq \cdots \neq \varepsilon _n$
. For every
![]() $i \in I$
, denote by
$i \in I$
, denote by
![]() $\mathscr W_i \subset M \ominus B$
the linear span of all the reduced words in M whose first and last letter lie in
$\mathscr W_i \subset M \ominus B$
the linear span of all the reduced words in M whose first and last letter lie in
![]() $M_i \ominus B$
. Moreover, denote by
$M_i \ominus B$
. Moreover, denote by
![]() $P_{\mathscr W_i} : \operatorname {L}^2(M) \to \operatorname {L}^2(\mathscr W_i)$
the corresponding orthogonal projection. By construction, the family
$P_{\mathscr W_i} : \operatorname {L}^2(M) \to \operatorname {L}^2(\mathscr W_i)$
the corresponding orthogonal projection. By construction, the family
![]() $(\mathscr W_i)_{i \in I}$
is freely independent in M with respect to
$(\mathscr W_i)_{i \in I}$
is freely independent in M with respect to
![]() $\operatorname { E}_B$
. Our first main result is an extension of this fact to the ultraproduct framework.
$\operatorname { E}_B$
. Our first main result is an extension of this fact to the ultraproduct framework.
Theorem A. Keep the same notation as above. For every
![]() $i \in I$
, denote by
$i \in I$
, denote by
![]() $\mathbf X_i$
the set of all the elements
$\mathbf X_i$
the set of all the elements
![]() $x = (x_n)^{\mathcal U} \in M^{\mathcal U} \ominus B^{\mathcal U}$
, such that
$x = (x_n)^{\mathcal U} \in M^{\mathcal U} \ominus B^{\mathcal U}$
, such that
![]() $\lim _{n \to \mathcal U} \|x_n - P_{\mathscr W_i}(x_n)\|_2 = 0$
.
$\lim _{n \to \mathcal U} \|x_n - P_{\mathscr W_i}(x_n)\|_2 = 0$
.
Then the family
![]() $(\mathbf X_i)_{i \in I}$
is freely independent in
$(\mathbf X_i)_{i \in I}$
is freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\operatorname { E}_{B^{\mathcal U}}$
.
$\operatorname { E}_{B^{\mathcal U}}$
.
The proof of Theorem A relies on Mei–Ricard’s results [Reference Mei and RicardMR16] showing that the canonical projection
![]() $P_{\mathscr W_i} : \mathscr W \to \mathscr W_i$
extends to a completely bounded operator
$P_{\mathscr W_i} : \mathscr W \to \mathscr W_i$
extends to a completely bounded operator
![]() $P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
for every
$P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
for every
![]() ${p \in (1, +\infty )}$
. In particular, we exploit
${p \in (1, +\infty )}$
. In particular, we exploit
![]() $\operatorname {L}^p$
-boundedness of
$\operatorname {L}^p$
-boundedness of
![]() $P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
for every
$P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
for every
![]() $2 \leq p < +\infty $
. Theorem A is a novel application of noncommutative
$2 \leq p < +\infty $
. Theorem A is a novel application of noncommutative
![]() $\operatorname {L}^p$
-spaces to the structure theory of tracial von Neumann algebras.
$\operatorname {L}^p$
-spaces to the structure theory of tracial von Neumann algebras.
It follows from Popa’s asymptotic orthogonality property [Reference PopaPo83] (see Lemma 3.1 below) that for every
![]() $i \in I$
and every unitary
$i \in I$
and every unitary
![]() $u \in \mathscr U(M_i^{\mathcal U})$
, such that
$u \in \mathscr U(M_i^{\mathcal U})$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
for every
$\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
for every
![]() $k \in \mathbb {Z} \setminus \{0\}$
, if
$k \in \mathbb {Z} \setminus \{0\}$
, if
![]() $x \in \{u\}' \cap M^{\mathcal U}$
and
$x \in \{u\}' \cap M^{\mathcal U}$
and
![]() $\operatorname { E}_{B^{\mathcal U}}(x) = 0$
, then
$\operatorname { E}_{B^{\mathcal U}}(x) = 0$
, then
![]() $x \in \mathbf X_i$
. In particular, in the case
$x \in \mathbf X_i$
. In particular, in the case
![]() $B = \mathbb {C} 1$
, Theorem A implies the following
$B = \mathbb {C} 1$
, Theorem A implies the following
Theorem B. Assume that
![]() $B= \mathbb {C} 1$
. For every
$B= \mathbb {C} 1$
. For every
![]() $i\in I$
, let
$i\in I$
, let
![]() $u_i \in \mathscr U(M_i^{\mathcal U})$
be a Haar unitary.
$u_i \in \mathscr U(M_i^{\mathcal U})$
be a Haar unitary.
Then the family
![]() $(\{u_i\}' \cap M^{\mathcal U})_{i\in I}$
is freely independent in
$(\{u_i\}' \cap M^{\mathcal U})_{i\in I}$
is freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
.
$\tau ^{\mathcal U}$
.
Assume that for every
![]() $i \in I$
,
$i \in I$
,
![]() $M_i$
is a diffuse abelian von Neumann algebra, so that
$M_i$
is a diffuse abelian von Neumann algebra, so that
![]() $M_i^{\mathcal U} \subset \{u_i\}' \cap M^{\mathcal U}$
. Then Theorem B can be regarded as a far-reaching generalization of the fact that the family
$M_i^{\mathcal U} \subset \{u_i\}' \cap M^{\mathcal U}$
. Then Theorem B can be regarded as a far-reaching generalization of the fact that the family
![]() $(M_i^{\mathcal U})_{i \in I}$
is freely independent in
$(M_i^{\mathcal U})_{i \in I}$
is freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
.
$\tau ^{\mathcal U}$
.
In the case
![]() $I = \{1, 2\}$
, we also obtain the following variation of Theorem A.
$I = \{1, 2\}$
, we also obtain the following variation of Theorem A.
Theorem C. Assume that
![]() $I = \{1, 2\}$
. Keep the same notation as above. Let
$I = \{1, 2\}$
. Keep the same notation as above. Let
![]() $\mathbf Y_1 \subset \mathbf X_1$
be a subset with the property that
$\mathbf Y_1 \subset \mathbf X_1$
be a subset with the property that
![]() $a \mathbf Y_1 b \subset \mathbf X_1$
for all
$a \mathbf Y_1 b \subset \mathbf X_1$
for all
![]() $a, b \in M_1$
.
$a, b \in M_1$
.
Then the sets
![]() $\mathbf Y_1$
and
$\mathbf Y_1$
and
![]() $M \ominus M_1$
are freely independent in
$M \ominus M_1$
are freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\operatorname { E}_{B^{\mathcal U}}$
.
$\operatorname { E}_{B^{\mathcal U}}$
.
A typical example of a subset
![]() $\mathbf Y_1 \subset \mathbf X_1$
with the property that
$\mathbf Y_1 \subset \mathbf X_1$
with the property that
![]() $a \mathbf Y_1 b \subset \mathbf X_1$
or all
$a \mathbf Y_1 b \subset \mathbf X_1$
or all
![]() $a, b \in M_1$
is given by
$a, b \in M_1$
is given by
![]() $\mathbf Y_1 = A' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U})$
, where
$\mathbf Y_1 = A' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U})$
, where
![]() $A \subset M_1$
is a von Neumann subalgebra, such that
$A \subset M_1$
is a von Neumann subalgebra, such that
![]() $A \npreceq _{M_1} B$
(see Lemmas 2.4 and 3.2).
$A \npreceq _{M_1} B$
(see Lemmas 2.4 and 3.2).
In the case
![]() $M = B \rtimes \mathbb {F}_n = (B \rtimes \mathbb {Z}) \ast _B \cdots \ast _B (B \rtimes \mathbb {Z}) = M_1 \ast _B \cdots \ast _B M_n$
, Popa showed in [Reference PopaPo83, Lemma 2.1] that for the canonical Haar unitary
$M = B \rtimes \mathbb {F}_n = (B \rtimes \mathbb {Z}) \ast _B \cdots \ast _B (B \rtimes \mathbb {Z}) = M_1 \ast _B \cdots \ast _B M_n$
, Popa showed in [Reference PopaPo83, Lemma 2.1] that for the canonical Haar unitary
![]() $u \in \operatorname {L}(\mathbb {Z}) \subset M_1$
, the sets
$u \in \operatorname {L}(\mathbb {Z}) \subset M_1$
, the sets
![]() $\{u\}' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U})$
and
$\{u\}' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U})$
and
![]() $M \ominus M_1$
are
$M \ominus M_1$
are
![]() $2$
-independent in
$2$
-independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\operatorname { E}_{B^{\mathcal U}}$
(see also [Reference Houdayer and UedaHU15] for the free product case). Letting
$\operatorname { E}_{B^{\mathcal U}}$
(see also [Reference Houdayer and UedaHU15] for the free product case). Letting
![]() $\mathbf Y_1 = \{u\}' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U})$
, Theorem C can be regarded as a generalization and a strengthening of Popa’s result.
$\mathbf Y_1 = \{u\}' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U})$
, Theorem C can be regarded as a generalization and a strengthening of Popa’s result.
In the case
![]() $I = \{1, 2\}$
and
$I = \{1, 2\}$
and
![]() $B = \mathbb {C} 1$
, we exploit Mei–Ricard’s results [Reference Mei and RicardMR16] to obtain the following indecomposability result in
$B = \mathbb {C} 1$
, we exploit Mei–Ricard’s results [Reference Mei and RicardMR16] to obtain the following indecomposability result in
![]() $M^{\mathcal U}$
.
$M^{\mathcal U}$
.
Theorem D. Assume that
![]() $I=\{1,2\}$
and
$I=\{1,2\}$
and
![]() $B=\mathbb C1$
. Let
$B=\mathbb C1$
. Let
![]() $u_1\in \mathscr U(M_1^{\mathcal U})$
be a Haar unitary and
$u_1\in \mathscr U(M_1^{\mathcal U})$
be a Haar unitary and
![]() $u_2\in \mathscr U(M_2^{\mathcal U})$
, such that
$u_2\in \mathscr U(M_2^{\mathcal U})$
, such that
![]() $\tau ^{\mathcal U}(u_2)=\tau ^{\mathcal U}(u_2^2)=0$
.
$\tau ^{\mathcal U}(u_2)=\tau ^{\mathcal U}(u_2^2)=0$
.
Then there do not exist
![]() $v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
$v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $\tau ^{\mathcal U}(v_1)=\tau ^{\mathcal U}(v_1^2)=\tau ^{\mathcal U}(v_2)=0$
and
$\tau ^{\mathcal U}(v_1)=\tau ^{\mathcal U}(v_1^2)=\tau ^{\mathcal U}(v_2)=0$
and
![]() $[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
.
$[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
.
Another way to formulate Theorem D is as follows. Let
![]() $u_1\in \mathscr U(M_1^{\mathcal U})$
be a Haar unitary,
$u_1\in \mathscr U(M_1^{\mathcal U})$
be a Haar unitary,
![]() $u_2\in \mathscr U(M_2^{\mathcal U})$
, such that
$u_2\in \mathscr U(M_2^{\mathcal U})$
, such that
![]() $\tau ^{\mathcal U}(u_2)=\tau ^{\mathcal U}(u_2^2)=0$
and
$\tau ^{\mathcal U}(u_2)=\tau ^{\mathcal U}(u_2^2)=0$
and
![]() $v_1\in \mathscr U(M^{\mathcal U})$
such that
$v_1\in \mathscr U(M^{\mathcal U})$
such that
![]() $[u_1, v_1] = 0$
and
$[u_1, v_1] = 0$
and
![]() $\tau ^{\mathcal U}(v_1)=\tau ^{\mathcal U}(v_1^2)= 0$
. Then we have
$\tau ^{\mathcal U}(v_1)=\tau ^{\mathcal U}(v_1^2)= 0$
. Then we have
![]() $\{v_1, u_2\}' \cap M^{\mathcal U} = \mathbb {C} 1$
. This generalizes the well-known fact (see, e.g. [Reference IoanaIo12, Lemma 6.1]) that
$\{v_1, u_2\}' \cap M^{\mathcal U} = \mathbb {C} 1$
. This generalizes the well-known fact (see, e.g. [Reference IoanaIo12, Lemma 6.1]) that
![]() $\{u_1,u_2\}' \cap M^{\mathcal U} = \mathbb {C} 1$
. In Section 3, we generalize Theorem D to arbitrary tracial amalgamated free product von Neumann algebras (see Theorem 3.4).
$\{u_1,u_2\}' \cap M^{\mathcal U} = \mathbb {C} 1$
. In Section 3, we generalize Theorem D to arbitrary tracial amalgamated free product von Neumann algebras (see Theorem 3.4).
Theorem D is new even in the case
![]() $M=\operatorname {L}(C_1*C_2)$
, where
$M=\operatorname {L}(C_1*C_2)$
, where
![]() $C_1, C_2$
are cyclic groups with
$C_1, C_2$
are cyclic groups with
![]() $|C_1|>1$
and
$|C_1|>1$
and
![]() $|C_2|>2$
. In this case,
$|C_2|>2$
. In this case,
![]() $M=M_1 \ast M_2$
, where
$M=M_1 \ast M_2$
, where
![]() $M_1=\operatorname {L}(C_1), M_2=\operatorname {L}(C_2)$
. Moreover, M is an interpolated free group factor by [Reference DykemaDy92, Corollary 5.3] and thus has positive
$M_1=\operatorname {L}(C_1), M_2=\operatorname {L}(C_2)$
. Moreover, M is an interpolated free group factor by [Reference DykemaDy92, Corollary 5.3] and thus has positive
![]() $1$
-bounded entropy,
$1$
-bounded entropy,
![]() $h(M)>0$
, in the sense of [Reference JungJu05, Reference HayesHa15]. By [Reference HayesHa15, Corollary 4.8] (see also [Reference Chifan, Ioana and ElayavalliCIKE22, Facts 2.4 and 2.9]), if
$h(M)>0$
, in the sense of [Reference JungJu05, Reference HayesHa15]. By [Reference HayesHa15, Corollary 4.8] (see also [Reference Chifan, Ioana and ElayavalliCIKE22, Facts 2.4 and 2.9]), if
![]() $u_1,u_2\in M$
are generating unitaries, then there are no Haar unitaries
$u_1,u_2\in M$
are generating unitaries, then there are no Haar unitaries
![]() $v_1,v_2\in M^{\mathcal U}$
satisfying
$v_1,v_2\in M^{\mathcal U}$
satisfying
![]() $[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
. This fact was used in [Reference Chifan, Ioana and ElayavalliCIKE22] to construct two nonelementarily equivalent non-Gamma
$[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
. This fact was used in [Reference Chifan, Ioana and ElayavalliCIKE22] to construct two nonelementarily equivalent non-Gamma
![]() $\mathrm {II_1}$
factors.
$\mathrm {II_1}$
factors.
Theorem D considerably strengthens this fact when
![]() $C_1=\mathbb Z$
,
$C_1=\mathbb Z$
,
![]() $u_1\in \mathscr U(M_1)$
,
$u_1\in \mathscr U(M_1)$
,
![]() $u_2\in \mathscr U(M_2)$
. Unlike [Reference HayesHa15], we cannot say anything about arbitrary generating unitaries
$u_2\in \mathscr U(M_2)$
. Unlike [Reference HayesHa15], we cannot say anything about arbitrary generating unitaries
![]() $u_1$
and
$u_1$
and
![]() $u_2$
, that do not belong to
$u_2$
, that do not belong to
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, respectively. On the other hand, while the free entropy methods from [Reference HayesHa15] only rule out the existence of Haar unitaries
$M_2$
, respectively. On the other hand, while the free entropy methods from [Reference HayesHa15] only rule out the existence of Haar unitaries
![]() $v_1,v_2 \in \mathscr U(M^{\mathcal U})$
satisfying
$v_1,v_2 \in \mathscr U(M^{\mathcal U})$
satisfying
![]() $[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
, Theorem D also excludes the existence of such finite order unitaries
$[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
, Theorem D also excludes the existence of such finite order unitaries
![]() $v_1,v_2$
provided that
$v_1,v_2$
provided that
![]() $v_1,v_1^2,v_2$
have trace zero.
$v_1,v_1^2,v_2$
have trace zero.
Let
![]() $u_1\in \mathscr U(M_1^{\mathcal U})$
and
$u_1\in \mathscr U(M_1^{\mathcal U})$
and
![]() $u_2\in \mathscr U(M_2^{\mathcal U})$
be as in Theorem D, and assume that
$u_2\in \mathscr U(M_2^{\mathcal U})$
be as in Theorem D, and assume that
![]() $u_2^m=1$
, for some
$u_2^m=1$
, for some
![]() $m>2$
. Then
$m>2$
. Then
![]() $\{u_2\}'\cap M^{\mathcal U}$
has finite index in
$\{u_2\}'\cap M^{\mathcal U}$
has finite index in
![]() $M^{\mathcal U}$
and therefore, unlike in Theorem B,
$M^{\mathcal U}$
and therefore, unlike in Theorem B,
![]() $\{u_1\}'\cap M^{\mathcal U}$
and
$\{u_1\}'\cap M^{\mathcal U}$
and
![]() $\{u_2\}'\cap M^{\mathcal U}$
are not freely independent in
$\{u_2\}'\cap M^{\mathcal U}$
are not freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
. Instead, the proof of Theorem D relies on a subtler analysis of commuting unitaries belonging to
$\tau ^{\mathcal U}$
. Instead, the proof of Theorem D relies on a subtler analysis of commuting unitaries belonging to
![]() $\{u_1\}'\cap M^{\mathcal U}$
and
$\{u_1\}'\cap M^{\mathcal U}$
and
![]() $\{u_2\}'\cap M^{\mathcal U}$
. However, similarly to the proof of Theorem B, we make crucial use of Mei–Ricard’s results [Reference Mei and RicardMR16].
$\{u_2\}'\cap M^{\mathcal U}$
. However, similarly to the proof of Theorem B, we make crucial use of Mei–Ricard’s results [Reference Mei and RicardMR16].
We do not know if Theorem D holds if we remove the assumption that
![]() $\operatorname { E}_{B^{\mathcal U}}(u_2^2)=0$
. However, a standard diagonal argument implies the existence of
$\operatorname { E}_{B^{\mathcal U}}(u_2^2)=0$
. However, a standard diagonal argument implies the existence of
![]() $N\in \mathbb N$
, such that the assumption that
$N\in \mathbb N$
, such that the assumption that
![]() $\operatorname { E}_{B^{\mathcal U}}(u_1^k)=0$
, for every
$\operatorname { E}_{B^{\mathcal U}}(u_1^k)=0$
, for every
![]() $k\in \mathbb Z\setminus \{0\}$
, can be relaxed by assuming instead that
$k\in \mathbb Z\setminus \{0\}$
, can be relaxed by assuming instead that
![]() $\operatorname { E}_{B^{\mathcal U}}(u_1^k)=0$
, for every
$\operatorname { E}_{B^{\mathcal U}}(u_1^k)=0$
, for every
![]() $k\in \mathbb Z\setminus \{0\}$
with
$k\in \mathbb Z\setminus \{0\}$
with
![]() $|k|\leq N$
.
$|k|\leq N$
.
Application to absorption in AFP von Neumann algebras
We use Theorem C to obtain a new absorption result for tracial amalgamated free product von Neumann algebras.
Theorem E. Assume that
![]() $I = \{1, 2\}$
. Keep the same notation as above, and assume that M is separable. Let
$I = \{1, 2\}$
. Keep the same notation as above, and assume that M is separable. Let
![]() $P \subset M$
be a von Neumann subalgebra, such that
$P \subset M$
be a von Neumann subalgebra, such that
![]() $P \cap M_1 \npreceq _{M_1} B$
and
$P \cap M_1 \npreceq _{M_1} B$
and
![]() $P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Then we have
$P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Then we have
![]() $P \subset M_1$
.
$P \subset M_1$
.
Theorem E vastly generalizes Popa’s seminal result [Reference PopaPo83] that the generator masa
![]() $\text {L}(\langle a\rangle )$
is maximal amenable inside the free group factor
$\text {L}(\langle a\rangle )$
is maximal amenable inside the free group factor
![]() $\text {L}(\mathbb F_2)=\text {L}(\langle a,b\rangle )$
. Specifically, it extends several maximal amenability/Gamma absorption results. Theorem E generalizes [Reference Houdayer and UedaHU15, Theorem A] (see also [Reference HoudayerHo14, Theorem A]) to arbitrary tracial amalgamated free product von Neumann algebras. As we observe in Remark 4.1, if
$\text {L}(\mathbb F_2)=\text {L}(\langle a,b\rangle )$
. Specifically, it extends several maximal amenability/Gamma absorption results. Theorem E generalizes [Reference Houdayer and UedaHU15, Theorem A] (see also [Reference HoudayerHo14, Theorem A]) to arbitrary tracial amalgamated free product von Neumann algebras. As we observe in Remark 4.1, if
![]() $P \subset M$
is an amenable von Neumann subalgebra, such that
$P \subset M$
is an amenable von Neumann subalgebra, such that
![]() $P \cap M_1 \npreceq _{M_1} B$
, then we necessarily have
$P \cap M_1 \npreceq _{M_1} B$
, then we necessarily have
![]() $P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Thus, Theorem E also yields a new proof of [Reference Boutonnet and HoudayerBH16, Main theorem] in the setting of tracial amalgamated free product von Neumann algebras. Let us point out that in the setting of tracial free products
$P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Thus, Theorem E also yields a new proof of [Reference Boutonnet and HoudayerBH16, Main theorem] in the setting of tracial amalgamated free product von Neumann algebras. Let us point out that in the setting of tracial free products
![]() $M = M_1 \ast M_2$
of Connes-embeddable von Neumann algebras, the inclusion
$M = M_1 \ast M_2$
of Connes-embeddable von Neumann algebras, the inclusion
![]() $M_1 \subset M$
satisfies a more general absorption property. Indeed, [Reference Hayes, Jekel, Nelson and SinclairHJNS19, Theorem A] shows that if
$M_1 \subset M$
satisfies a more general absorption property. Indeed, [Reference Hayes, Jekel, Nelson and SinclairHJNS19, Theorem A] shows that if
![]() $P \subset M$
is a von Neumann subalgebra, such that
$P \subset M$
is a von Neumann subalgebra, such that
![]() $P \cap M_1$
is diffuse and has
$P \cap M_1$
is diffuse and has
![]() $1$
-bounded entropy zero, then
$1$
-bounded entropy zero, then
![]() $P \subset M_1$
. In the case
$P \subset M_1$
. In the case
![]() $M = \operatorname {L}(\mathbb {F}_n)$
is a free group factor, the aforementioned absorption property holds for any diffuse maximal amenable subalgebra
$M = \operatorname {L}(\mathbb {F}_n)$
is a free group factor, the aforementioned absorption property holds for any diffuse maximal amenable subalgebra
![]() $Q \subset M$
, thanks to the recent resolution of the Peterson–Thom conjecture via random matrix theory [Reference Belinschi and CapitaineBC22, Reference Bordenave and CollinsBC23] and
$Q \subset M$
, thanks to the recent resolution of the Peterson–Thom conjecture via random matrix theory [Reference Belinschi and CapitaineBC22, Reference Bordenave and CollinsBC23] and
![]() $1$
-bounded entropy [Reference HayesHa15, Reference HayesHa20] (see also [Reference Hayes, Jekel and Kunnawalkam ElayavalliHJKE23]).
$1$
-bounded entropy [Reference HayesHa15, Reference HayesHa20] (see also [Reference Hayes, Jekel and Kunnawalkam ElayavalliHJKE23]).
Application to continuous model theory of
 $\mathrm {II_1}$
factors
$\mathrm {II_1}$
factors
We next present an application of Theorem B to the continuous model theory of
![]() $\mathrm {II_1}$
factors. A main theme in this theory, initiated by Farah–Sherman–Hart in [Reference Farah, Hart and ShermanFHS11], is to determine whether two given
$\mathrm {II_1}$
factors. A main theme in this theory, initiated by Farah–Sherman–Hart in [Reference Farah, Hart and ShermanFHS11], is to determine whether two given
![]() $\mathrm {II_1}$
factors
$\mathrm {II_1}$
factors
![]() $M, N$
are elementarily equivalent. By the continuous version of the Keisler–Shelah theorem, this amounts to M and N admitting isomorphic ultrapowers,
$M, N$
are elementarily equivalent. By the continuous version of the Keisler–Shelah theorem, this amounts to M and N admitting isomorphic ultrapowers,
![]() $M^{\mathcal U}\cong N^{\mathcal V}$
, for some ultrafilters
$M^{\mathcal U}\cong N^{\mathcal V}$
, for some ultrafilters
![]() $\mathcal U$
and
$\mathcal U$
and
![]() $\mathcal V$
on arbitrary sets [Reference Farah, Hart and ShermanFHS11, Reference Henson and IovinoHI02]. It was shown in [Reference Farah, Hart and ShermanFHS11] that property Gamma and being McDuff are elementary properties, leading to three distinct elementary classes of
$\mathcal V$
on arbitrary sets [Reference Farah, Hart and ShermanFHS11, Reference Henson and IovinoHI02]. It was shown in [Reference Farah, Hart and ShermanFHS11] that property Gamma and being McDuff are elementary properties, leading to three distinct elementary classes of
![]() $\mathrm {II_1}$
factors. A fourth such elementary class was then provided in [Reference Goldbring and HartGH16]. The problem of determining the number of elementary classes of
$\mathrm {II_1}$
factors. A fourth such elementary class was then provided in [Reference Goldbring and HartGH16]. The problem of determining the number of elementary classes of
![]() $\mathrm {II_1}$
factors was solved in [Reference Boutonnet, Chifan and IoanaBCI15], where the continuum of nonisomorphic
$\mathrm {II_1}$
factors was solved in [Reference Boutonnet, Chifan and IoanaBCI15], where the continuum of nonisomorphic
![]() $\mathrm {II_1}$
factors constructed in [Reference McDuffMc69] were shown to be pairwise nonelementarily equivalent. However, all the available techniques for distinguishing
$\mathrm {II_1}$
factors constructed in [Reference McDuffMc69] were shown to be pairwise nonelementarily equivalent. However, all the available techniques for distinguishing
![]() $\mathrm {II_1}$
factors up to elementary equivalence were based on central sequences. It thus remained open to construct any nonelementarily equivalent
$\mathrm {II_1}$
factors up to elementary equivalence were based on central sequences. It thus remained open to construct any nonelementarily equivalent
![]() $\mathrm {II_1}$
factors which do not have any nontrivial central sequences, that is, fail property Gamma. This problem was solved by Chifan–Ioana–Kunnawalkam Elayavalli in [Reference Chifan, Ioana and ElayavalliCIKE22] using a combination of techniques from Popa’s deformation/rigidity theory and Voiculescu’s free entropy theory. First, deformation/rigidity methods from [Reference Ioana, Peterson and PopaIPP05] were used to construct a non-Gamma
$\mathrm {II_1}$
factors which do not have any nontrivial central sequences, that is, fail property Gamma. This problem was solved by Chifan–Ioana–Kunnawalkam Elayavalli in [Reference Chifan, Ioana and ElayavalliCIKE22] using a combination of techniques from Popa’s deformation/rigidity theory and Voiculescu’s free entropy theory. First, deformation/rigidity methods from [Reference Ioana, Peterson and PopaIPP05] were used to construct a non-Gamma
![]() $\mathrm {II_1}$
factor M via an iterative amalgamated free product construction. It was then shown that M is not elementarily equivalent to any (necessarily non-Gamma)
$\mathrm {II_1}$
factor M via an iterative amalgamated free product construction. It was then shown that M is not elementarily equivalent to any (necessarily non-Gamma)
![]() $\mathrm {II_1}$
factor N having positive
$\mathrm {II_1}$
factor N having positive
![]() $1$
-bounded entropy,
$1$
-bounded entropy,
![]() $h(N)>0$
, in the sense of Jung [Reference JungJu05] and Hayes [Reference HayesHa15]. Examples of
$h(N)>0$
, in the sense of Jung [Reference JungJu05] and Hayes [Reference HayesHa15]. Examples of
![]() $\mathrm {II_1}$
factors N with
$\mathrm {II_1}$
factors N with
![]() $h(N)>0$
include the interpolated free group factors
$h(N)>0$
include the interpolated free group factors
![]() $\operatorname {L}(\mathbb F_t)$
,
$\operatorname {L}(\mathbb F_t)$
,
![]() $1< t\leq \infty $
, and, more generally, any tracial free product
$1< t\leq \infty $
, and, more generally, any tracial free product
![]() $N=N_1 \ast N_2$
of diffuse Connes-embeddable von Neumann algebras. For additional examples of such
$N=N_1 \ast N_2$
of diffuse Connes-embeddable von Neumann algebras. For additional examples of such
![]() $\mathrm {II}_1$
factors, see [Reference Chifan, Ioana and ElayavalliCIKE22, Fact 2.7]. However, the methods from [Reference Chifan, Ioana and ElayavalliCIKE22] could not distinguish M up to elementary equivalence from
$\mathrm {II}_1$
factors, see [Reference Chifan, Ioana and ElayavalliCIKE22, Fact 2.7]. However, the methods from [Reference Chifan, Ioana and ElayavalliCIKE22] could not distinguish M up to elementary equivalence from
![]() $N=N_1*N_2$
, whenever
$N=N_1*N_2$
, whenever
![]() $N_1$
or
$N_1$
or
![]() $N_2$
is a non-Connes-embeddable tracial von Neumann algebra (the existence of which has been announced in the preprint [Reference Ji, Natarajan, Vidick, Wright and YuenJNVWY20]). In particular, since it is unclear if M is Connes-embeddable, it remained open whether M is elementarily equivalent to
$N_2$
is a non-Connes-embeddable tracial von Neumann algebra (the existence of which has been announced in the preprint [Reference Ji, Natarajan, Vidick, Wright and YuenJNVWY20]). In particular, since it is unclear if M is Connes-embeddable, it remained open whether M is elementarily equivalent to
![]() $M*\operatorname {L}(\mathbb Z)$
.
$M*\operatorname {L}(\mathbb Z)$
.
Theorem B allows us to settle this problem for a variant of the
![]() $\mathrm {II_1}$
factor constructed in [Reference Chifan, Ioana and ElayavalliCIKE22]:
$\mathrm {II_1}$
factor constructed in [Reference Chifan, Ioana and ElayavalliCIKE22]:
Theorem F. There exists a separable
![]() $\mathrm {II_1}$
factor M which does not have property Gamma and that is not elementarily equivalent to
$\mathrm {II_1}$
factor M which does not have property Gamma and that is not elementarily equivalent to
![]() $N=N_1*N_2$
, for any diffuse tracial von Neumann algebras
$N=N_1*N_2$
, for any diffuse tracial von Neumann algebras
![]() $(N_1,\tau _1)$
and
$(N_1,\tau _1)$
and
![]() $(N_2,\tau _2)$
.
$(N_2,\tau _2)$
.
In particular, Theorem F provides the first example of a non-Gamma
![]() $\mathrm {II_1}$
factor M which is not elementarily equivalent to
$\mathrm {II_1}$
factor M which is not elementarily equivalent to
![]() $M*\operatorname {L}(\mathbb Z)$
. The conclusion of Theorem F is verified by any
$M*\operatorname {L}(\mathbb Z)$
. The conclusion of Theorem F is verified by any
![]() $\mathrm {II_1}$
factor M satisfying the following:
$\mathrm {II_1}$
factor M satisfying the following:
Theorem G. There exists a separable
![]() $\mathrm {II_1}$
factor M which does not have property Gamma and satisfies the following. For every countably cofinal ultrafilter
$\mathrm {II_1}$
factor M which does not have property Gamma and satisfies the following. For every countably cofinal ultrafilter
![]() $\mathcal U$
on a set J and
$\mathcal U$
on a set J and
![]() $u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
$u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are
$\{u_2\}^{\prime \prime }$
are
![]() $2$
-independent in
$2$
-independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
, there exist Haar unitaries
$\tau ^{\mathcal U}$
, there exist Haar unitaries
![]() $v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
$v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
.
$[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
.
An ultrafilter
![]() $\mathcal U$
on a set J is called countably cofinal if there exists a sequence
$\mathcal U$
on a set J is called countably cofinal if there exists a sequence
![]() $(A_n)_{n\in \mathbb N}$
in
$(A_n)_{n\in \mathbb N}$
in
![]() $\mathcal U$
with
$\mathcal U$
with
![]() $\bigcap _{n\in \mathbb N}A_n=\emptyset $
. Any free ultrafilter on
$\bigcap _{n\in \mathbb N}A_n=\emptyset $
. Any free ultrafilter on
![]() $\mathbb N$
is countably cofinal.
$\mathbb N$
is countably cofinal.
The proof of Theorem G uses the iterative amalgamated free product construction introduced in [Reference Chifan, Ioana and ElayavalliCIKE22]. In [Reference Chifan, Ioana and ElayavalliCIKE22, Theorem B], this construction was used to build a non-Gamma separable
![]() $\mathrm {II_1}$
factor M with the following property: for any unitaries
$\mathrm {II_1}$
factor M with the following property: for any unitaries
![]() $u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
$u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are orthogonal and
$\{u_2\}^{\prime \prime }$
are orthogonal and
![]() $u_1^2=u_2^3=1$
, there exist Haar unitaries
$u_1^2=u_2^3=1$
, there exist Haar unitaries
![]() $v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
$v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
. The proof of [Reference Chifan, Ioana and ElayavalliCIKE22, Theorem B] relies crucially on a lifting lemma showing that any unitaries
$[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
. The proof of [Reference Chifan, Ioana and ElayavalliCIKE22, Theorem B] relies crucially on a lifting lemma showing that any unitaries
![]() $u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
$u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are orthogonal and
$\{u_2\}^{\prime \prime }$
are orthogonal and
![]() $u_1^2=u_2^3=1$
lift to unitaries in M with the same properties. A key limitation in [Reference Chifan, Ioana and ElayavalliCIKE22] was the assumption that
$u_1^2=u_2^3=1$
lift to unitaries in M with the same properties. A key limitation in [Reference Chifan, Ioana and ElayavalliCIKE22] was the assumption that
![]() $u_1$
and
$u_1$
and
![]() $u_2$
have orders
$u_2$
have orders
![]() $2$
and
$2$
and
![]() $3$
. We remove this limitation here by proving a general lifting result of independent interest (see Theorem 5.1) which shows that any unitaries
$3$
. We remove this limitation here by proving a general lifting result of independent interest (see Theorem 5.1) which shows that any unitaries
![]() $u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
$u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are
$\{u_2\}^{\prime \prime }$
are
![]() $2$
-independent admit lifts
$2$
-independent admit lifts
![]() $u_1=(u_{1,n})^{\mathcal U}$
and
$u_1=(u_{1,n})^{\mathcal U}$
and
![]() $u_2=(u_{2,n})^{\mathcal U}$
with
$u_2=(u_{2,n})^{\mathcal U}$
with
![]() $\{u_{1,n}\}^{\prime \prime }$
and
$\{u_{1,n}\}^{\prime \prime }$
and
![]() $\{u_{2,n}\}^{\prime \prime }$
orthogonal for every
$\{u_{2,n}\}^{\prime \prime }$
orthogonal for every
![]() $n \in \mathbb {N}$
. With this result in hand, adjusting the iterative construction from [Reference Chifan, Ioana and ElayavalliCIKE22] implies Theorem G.
$n \in \mathbb {N}$
. With this result in hand, adjusting the iterative construction from [Reference Chifan, Ioana and ElayavalliCIKE22] implies Theorem G.
To explain how Theorem F follows by combining Theorem G and Theorem B, let M be a
![]() $\mathrm {II_1}$
factor as in Theorem G,
$\mathrm {II_1}$
factor as in Theorem G,
![]() $N=N_1 \ast N_2$
a free product of diffuse tracial von Neumann algebras and
$N=N_1 \ast N_2$
a free product of diffuse tracial von Neumann algebras and
![]() $u_1\in \mathscr U(N_1)$
,
$u_1\in \mathscr U(N_1)$
,
![]() $u_2\in \mathscr U(N_2)$
Haar unitaries. Since
$u_2\in \mathscr U(N_2)$
Haar unitaries. Since
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are freely and thus
$\{u_2\}^{\prime \prime }$
are freely and thus
![]() $2$
-independent, it follows that
$2$
-independent, it follows that
![]() $M^{\mathcal U}\not \cong N^{\mathcal V}$
, for any countably cofinal ultrafilter
$M^{\mathcal U}\not \cong N^{\mathcal V}$
, for any countably cofinal ultrafilter
![]() $\mathcal U$
and any ultrafilter
$\mathcal U$
and any ultrafilter
![]() $\mathcal V$
. Indeed, Theorem B implies that any Haar unitaries (more generally, any trace zero unitaries)
$\mathcal V$
. Indeed, Theorem B implies that any Haar unitaries (more generally, any trace zero unitaries)
![]() $v_1,v_2\in \mathscr U(N^{\mathcal V})$
, such that
$v_1,v_2\in \mathscr U(N^{\mathcal V})$
, such that
![]() $[u_1,v_1]=[u_2,v_2]=0$
are freely independent and therefore do not commute. If
$[u_1,v_1]=[u_2,v_2]=0$
are freely independent and therefore do not commute. If
![]() $\mathcal U$
is an ultrafilter which is not countably cofinal, then we also have that
$\mathcal U$
is an ultrafilter which is not countably cofinal, then we also have that
![]() $M^{\mathcal U}\not \cong N^{\mathcal V}$
, for any ultrafilter
$M^{\mathcal U}\not \cong N^{\mathcal V}$
, for any ultrafilter
![]() $\mathcal V$
. Otherwise, using [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.3], we would get that
$\mathcal V$
. Otherwise, using [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.3], we would get that
![]() $M^{\mathcal U}\cong M$
, thus
$M^{\mathcal U}\cong M$
, thus
![]() $N^{\mathcal V}\cong M$
is separable, hence
$N^{\mathcal V}\cong M$
is separable, hence
![]() $N^{\mathcal V}\cong N$
and therefore
$N^{\mathcal V}\cong N$
and therefore
![]() $M\cong N$
. But then
$M\cong N$
. But then
![]() $M^{\mathcal W}\cong N^{\mathcal W}$
, for any free ultrafilter
$M^{\mathcal W}\cong N^{\mathcal W}$
, for any free ultrafilter
![]() $\mathcal W$
on
$\mathcal W$
on
![]() $\mathbb N$
. Since
$\mathbb N$
. Since
![]() $\mathcal W$
is countably cofinal, this is a contradiction. Altogether, we conclude that
$\mathcal W$
is countably cofinal, this is a contradiction. Altogether, we conclude that
![]() $M^{\mathcal U}\not \cong N^{\mathcal V}$
, for any ultrafilters
$M^{\mathcal U}\not \cong N^{\mathcal V}$
, for any ultrafilters
![]() $\mathcal U,\mathcal V$
, and thus
$\mathcal U,\mathcal V$
, and thus
![]() $M, N$
are not elementarily equivalent.
$M, N$
are not elementarily equivalent.
Application to the orthogonalization problem
We end the introduction with an application to the following orthogonalization problem: given a
![]() $\mathrm {II}_1$
factor M and two subsets
$\mathrm {II}_1$
factor M and two subsets
![]() $X,Y\subset M\ominus \mathbb C1$
, when can we find
$X,Y\subset M\ominus \mathbb C1$
, when can we find
![]() $u\in \mathscr U(M)$
, such that
$u\in \mathscr U(M)$
, such that
![]() $uXu^*$
and Y are orthogonal? In the case
$uXu^*$
and Y are orthogonal? In the case
![]() $X=A\ominus \mathbb C1$
and
$X=A\ominus \mathbb C1$
and
![]() $Y=B\ominus \mathbb C1$
, for von Neumann subalgebras
$Y=B\ominus \mathbb C1$
, for von Neumann subalgebras
![]() $A,B\subset M$
, this and related independence problems have been studied extensively by Popa (see, e.g. [Reference PopaPo13a, Reference PopaPo13b, Reference PopaPo17]). When
$A,B\subset M$
, this and related independence problems have been studied extensively by Popa (see, e.g. [Reference PopaPo13a, Reference PopaPo13b, Reference PopaPo17]). When
![]() $X,Y\subset M\ominus \mathbb C1$
are finite, a standard averaging argument shows that we can find
$X,Y\subset M\ominus \mathbb C1$
are finite, a standard averaging argument shows that we can find
![]() $u\in \mathscr U(M)$
, such that
$u\in \mathscr U(M)$
, such that
![]() $uXu^*$
and Y are ‘almost orthogonal’: for every
$uXu^*$
and Y are ‘almost orthogonal’: for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $u\in \mathscr U(M)$
, such that
$u\in \mathscr U(M)$
, such that
![]() $|\langle uxu^*,y\rangle |<\varepsilon $
, for every
$|\langle uxu^*,y\rangle |<\varepsilon $
, for every
![]() $x\in X,y\in Y$
. This implies the existence of
$x\in X,y\in Y$
. This implies the existence of
![]() $v\in \mathscr U(M^{\mathcal U})$
, where
$v\in \mathscr U(M^{\mathcal U})$
, where
![]() $\mathcal U$
is a free ultrafilter on
$\mathcal U$
is a free ultrafilter on
![]() $\mathbb N$
, such that
$\mathbb N$
, such that
![]() $vXv^*$
and Y are orthogonal. In this context, much more is true: by a result of Popa (see [Reference PopaPo13a, Corollary 0.2]), if
$vXv^*$
and Y are orthogonal. In this context, much more is true: by a result of Popa (see [Reference PopaPo13a, Corollary 0.2]), if
![]() $X,Y\subset M\ominus \mathbb C1$
are countable, then there exists
$X,Y\subset M\ominus \mathbb C1$
are countable, then there exists
![]() $u\in \mathscr U(M^{\mathcal U})$
, such that
$u\in \mathscr U(M^{\mathcal U})$
, such that
![]() $uXu^*$
and Y are freely independent.
$uXu^*$
and Y are freely independent.
By combining this result with the proof of our lifting theorem (Theorem 5.1), we settle affirmatively the above orthogonalization problem whenever
![]() $X,Y\subset M\ominus \mathbb C1$
are finite.
$X,Y\subset M\ominus \mathbb C1$
are finite.
Theorem H. Let M be a
![]() $\mathrm {II}_1$
factor and
$\mathrm {II}_1$
factor and
![]() $X,Y\subset M\ominus \mathbb C1$
be finite sets.
$X,Y\subset M\ominus \mathbb C1$
be finite sets.
Then there exists
![]() $u\in \mathscr U(M)$
, such that
$u\in \mathscr U(M)$
, such that
![]() $uXu^*$
and Y are orthogonal.
$uXu^*$
and Y are orthogonal.
2. Preliminaries
2.1. Noncommutative
 $\operatorname {L}^p$
-spaces
$\operatorname {L}^p$
-spaces
Let
![]() $(M, \tau )$
be a tracial von Neumann algebra. For every
$(M, \tau )$
be a tracial von Neumann algebra. For every
![]() $p \in [1, +\infty )$
, we write
$p \in [1, +\infty )$
, we write
![]() $\operatorname {L}^p(M) = \operatorname {L}^p(M, \tau )$
for the completion of M with respect to the norm
$\operatorname {L}^p(M) = \operatorname {L}^p(M, \tau )$
for the completion of M with respect to the norm
![]() $\|\cdot \|_p$
defined by
$\|\cdot \|_p$
defined by
![]() $\|x\|_p = \tau (|x|^p)^{1/p}$
for every
$\|x\|_p = \tau (|x|^p)^{1/p}$
for every
![]() $x \in M$
. More generally, given a subspace
$x \in M$
. More generally, given a subspace
![]() $\mathscr W\subset M$
, we denote by
$\mathscr W\subset M$
, we denote by
![]() $\operatorname {L}^p(\mathscr W)\subset \operatorname {L}^p(M)$
the closure of
$\operatorname {L}^p(\mathscr W)\subset \operatorname {L}^p(M)$
the closure of
![]() $\mathscr W$
with respect to
$\mathscr W$
with respect to
![]() $\|\cdot \|_p$
. Then
$\|\cdot \|_p$
. Then
![]() $\operatorname {L}^p(M)$
is the noncommutative
$\operatorname {L}^p(M)$
is the noncommutative
![]() $\operatorname {L}^p$
-space associated with the tracial von Neumann algebra M. We simply write
$\operatorname {L}^p$
-space associated with the tracial von Neumann algebra M. We simply write
![]() $\operatorname {L}^\infty (M) = M$
.
$\operatorname {L}^\infty (M) = M$
.
We will use the following generalized noncommutative Hölder inequality (see, e.g.[Reference TakesakiTa03, Theorem IX.2.13]): for all
![]() $k \geq 2$
, all
$k \geq 2$
, all
![]() $p_1, \dots , p_k, r \in [1, +\infty )$
, such that
$p_1, \dots , p_k, r \in [1, +\infty )$
, such that
![]() $\frac 1r = \sum _{j = 1}^k \frac {1}{p_j}$
and all
$\frac 1r = \sum _{j = 1}^k \frac {1}{p_j}$
and all
![]() $(x_j)_j \in \prod _{j = 1}^k \operatorname {L}^{p_j}(M)$
, we have
$(x_j)_j \in \prod _{j = 1}^k \operatorname {L}^{p_j}(M)$
, we have
![]() $x = x_1 \cdots x_k \in \operatorname {L}^r(M)$
and
$x = x_1 \cdots x_k \in \operatorname {L}^r(M)$
and
![]() $\|x_1 \cdots x_k\|_r \leq \|x_1\|_{p_1} \cdots \|x_k\|_{p_k}$
.
$\|x_1 \cdots x_k\|_r \leq \|x_1\|_{p_1} \cdots \|x_k\|_{p_k}$
.
For all
![]() $1 \leq p \leq q < +\infty $
and all
$1 \leq p \leq q < +\infty $
and all
![]() $x \in M$
, we have
$x \in M$
, we have
![]() $\|x\|_1 \leq \|x\|_p \leq \|x\|_q \leq \|x\|_\infty $
, and so we may regard
$\|x\|_1 \leq \|x\|_p \leq \|x\|_q \leq \|x\|_\infty $
, and so we may regard
![]() $M \subset \operatorname {L}^q(M) \subset \operatorname {L}^p(M) \subset \operatorname {L}^1(M)$
.
$M \subset \operatorname {L}^q(M) \subset \operatorname {L}^p(M) \subset \operatorname {L}^1(M)$
.
2.2. Ultraproduct von Neumann algebras
Let
![]() $\mathcal U$
be a nonprincipal ultrafilter on
$\mathcal U$
be a nonprincipal ultrafilter on
![]() $\mathbb {N}$
. Whenever
$\mathbb {N}$
. Whenever
![]() $(M, \tau )$
is a tracial von Neumann algebra, we denote by
$(M, \tau )$
is a tracial von Neumann algebra, we denote by
![]() $(M^{\mathcal U}, \tau ^{\mathcal U})$
the tracial ultraproduct von Neumann algebra. We regard
$(M^{\mathcal U}, \tau ^{\mathcal U})$
the tracial ultraproduct von Neumann algebra. We regard
![]() $\operatorname {L}^2(M^{\mathcal U}) \subset \operatorname {L}^2(M)^{\mathcal U}$
as a closed subspace, and we denote by
$\operatorname {L}^2(M^{\mathcal U}) \subset \operatorname {L}^2(M)^{\mathcal U}$
as a closed subspace, and we denote by
![]() $e : \operatorname {L}^2(M)^{\mathcal U} \to \operatorname {L}^2(M^{\mathcal U})$
the corresponding orthogonal projection. Recall the following elementary yet useful facts.
$e : \operatorname {L}^2(M)^{\mathcal U} \to \operatorname {L}^2(M^{\mathcal U})$
the corresponding orthogonal projection. Recall the following elementary yet useful facts.
Lemma 2.1. Keep the same notation as above. The following assertions hold:
-
(i) Let
 $(\xi _n)_n$
be a
$(\xi _n)_n$
be a
 $\|\cdot \|_2$
-bounded sequence in
$\|\cdot \|_2$
-bounded sequence in
 $\operatorname {L}^2(M)$
, and set
$\operatorname {L}^2(M)$
, and set
 $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M)^{\mathcal U}$
. Then
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M)^{\mathcal U}$
. Then
 $\xi \in \operatorname {L}^2(M^{\mathcal U})$
if and only if for every
$\xi \in \operatorname {L}^2(M^{\mathcal U})$
if and only if for every
 $\varepsilon> 0$
, there exists a
$\varepsilon> 0$
, there exists a
 $\|\cdot \|_\infty $
-bounded sequence
$\|\cdot \|_\infty $
-bounded sequence
 $ (x_n)_n$
in M, such that
$ (x_n)_n$
in M, such that
 $\lim _{n \to \mathcal U} \|\xi _n - x_n \|_2 \leq \varepsilon $
.
$\lim _{n \to \mathcal U} \|\xi _n - x_n \|_2 \leq \varepsilon $
. -
(ii) Let
 $r> 2$
. Then, for every
$r> 2$
. Then, for every
 $\|\cdot \|_r$
-bounded sequence
$\|\cdot \|_r$
-bounded sequence
 $(\xi _n)_n$
in
$(\xi _n)_n$
in
 $\operatorname {L}^r(M)$
, we have
$\operatorname {L}^r(M)$
, we have
 $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
.
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
. -
(iii) Let
 $(\xi _n)_n$
be a
$(\xi _n)_n$
be a
 $\|\cdot \|_2$
-bounded sequence in
$\|\cdot \|_2$
-bounded sequence in
 $\operatorname {L}^2(M)$
. Let
$\operatorname {L}^2(M)$
. Let
 $(x_n)_n$
and
$(x_n)_n$
and
 $(y_n)_n$
be
$(y_n)_n$
be
 $\|\cdot \|_\infty $
-bounded sequences in M. Set
$\|\cdot \|_\infty $
-bounded sequences in M. Set
 $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M)^{\mathcal U}$
,
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M)^{\mathcal U}$
,
 $x = (x_n)^{\mathcal U} \in M^{\mathcal U}$
and
$x = (x_n)^{\mathcal U} \in M^{\mathcal U}$
and
 $y = (y_n)^{\mathcal U} \in M^{\mathcal U}$
. If
$y = (y_n)^{\mathcal U} \in M^{\mathcal U}$
. If
 $\xi \in \operatorname {L}^2(M^{\mathcal U})$
, then
$\xi \in \operatorname {L}^2(M^{\mathcal U})$
, then
 $(x_n \xi _n y_n)^{\mathcal U} = x \xi y \in \operatorname {L}^2(M^{\mathcal U})$
.
$(x_n \xi _n y_n)^{\mathcal U} = x \xi y \in \operatorname {L}^2(M^{\mathcal U})$
.
Proof. (i) It is straightforward.
(ii) Let
![]() $(\xi _n)_n$
be a
$(\xi _n)_n$
be a
![]() $\|\cdot \|_r$
-bounded sequence in
$\|\cdot \|_r$
-bounded sequence in
![]() $\operatorname {L}^r(M)$
. There exists
$\operatorname {L}^r(M)$
. There exists
![]() $\kappa> 0$
, such that
$\kappa> 0$
, such that
![]() $\sup _{n \in \mathbb {N}} \tau (|\xi _n|^r) < \kappa $
. Set
$\sup _{n \in \mathbb {N}} \tau (|\xi _n|^r) < \kappa $
. Set
![]() $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M)^{\mathcal U}$
. For every
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M)^{\mathcal U}$
. For every
![]() $n \in \mathbb {N}$
, write
$n \in \mathbb {N}$
, write
![]() $\xi _n = v_n |\xi _n|$
for the polar decomposition of
$\xi _n = v_n |\xi _n|$
for the polar decomposition of
![]() $\xi _n \in \operatorname {L}^r(M)$
. For every
$\xi _n \in \operatorname {L}^r(M)$
. For every
![]() $n \in \mathbb {N}$
and every
$n \in \mathbb {N}$
and every
![]() $t> 0$
, define the spectral projection
$t> 0$
, define the spectral projection
![]() $p_{n, t} = \mathbf 1_{[0, t]}(|\xi _n|) \in M$
. For every
$p_{n, t} = \mathbf 1_{[0, t]}(|\xi _n|) \in M$
. For every
![]() $n \in \mathbb {N}$
and every
$n \in \mathbb {N}$
and every
![]() $t> 0$
, we have
$t> 0$
, we have
Let
![]() $\varepsilon> 0$
, and choose
$\varepsilon> 0$
, and choose
![]() $t> 0$
large enough so that
$t> 0$
large enough so that
![]() $\frac {\kappa }{t^{r - 2}} \leq \varepsilon ^2$
. For every
$\frac {\kappa }{t^{r - 2}} \leq \varepsilon ^2$
. For every
![]() $n \in \mathbb {N}$
, set
$n \in \mathbb {N}$
, set
![]() $x_n = \xi _n \, p_{n, t}\in M$
and observe that we have
$x_n = \xi _n \, p_{n, t}\in M$
and observe that we have
![]() $\|\xi _n - x_n\|_2 = \|\xi _n \, p_{n, t}^\perp \|_2 \leq \varepsilon $
. Since
$\|\xi _n - x_n\|_2 = \|\xi _n \, p_{n, t}^\perp \|_2 \leq \varepsilon $
. Since
![]() $\sup \left \{ \|x_n\|_\infty \mid n \in \mathbb {N} \right \} \leq t$
, Item (i) implies that
$\sup \left \{ \|x_n\|_\infty \mid n \in \mathbb {N} \right \} \leq t$
, Item (i) implies that
![]() $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
.
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
.
(iii) Assume that
![]() $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
. Choose
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
. Choose
![]() $\kappa> 0$
large enough so that
$\kappa> 0$
large enough so that
![]() $\sup \left \{ \|x_n\|_\infty , \|y_n\|_\infty \mid n \in \mathbb {N} \right \} \leq \kappa $
. Let
$\sup \left \{ \|x_n\|_\infty , \|y_n\|_\infty \mid n \in \mathbb {N} \right \} \leq \kappa $
. Let
![]() $\varepsilon> 0$
. By Item (i), there exists a
$\varepsilon> 0$
. By Item (i), there exists a
![]() $\|\cdot \|_\infty $
-bounded sequence
$\|\cdot \|_\infty $
-bounded sequence
![]() $(z_n)_n$
in M, such that
$(z_n)_n$
in M, such that
![]() $\lim _{n \to \mathcal U} \|\xi _n - z_n\|_2 \leq \varepsilon $
. Set
$\lim _{n \to \mathcal U} \|\xi _n - z_n\|_2 \leq \varepsilon $
. Set
![]() $z = (z_n)^{\mathcal U} \in M^{\mathcal U}$
. Then
$z = (z_n)^{\mathcal U} \in M^{\mathcal U}$
. Then
![]() $\|\xi - z\|_2 = \lim _{n \to \mathcal U} \|\xi _n - z_n\|_2 \leq \varepsilon $
. Since
$\|\xi - z\|_2 = \lim _{n \to \mathcal U} \|\xi _n - z_n\|_2 \leq \varepsilon $
. Since
![]() $x z y = (x_n z_n y_n)^{\mathcal U} \in M^{\mathcal U}$
, we have
$x z y = (x_n z_n y_n)^{\mathcal U} \in M^{\mathcal U}$
, we have
 $$ \begin{align*} \|(x_n \xi_n y_n)^{\mathcal U} - x \xi y\|_2 &\leq \|(x_n \xi_n y_n)^{\mathcal U} - (x_n z_n y_n)^{\mathcal U} \|_2 + \| x z y - x \xi y\|_2 \\ &= \lim_{n \to \mathcal U} \|x_n (\xi_n - z_n) y_n\|_2 + \| x (z - \xi) y\|_2 \\ &\leq 2 \kappa^2 \|\xi - z\|_2 \leq 2 \kappa^2 \varepsilon. \end{align*} $$
$$ \begin{align*} \|(x_n \xi_n y_n)^{\mathcal U} - x \xi y\|_2 &\leq \|(x_n \xi_n y_n)^{\mathcal U} - (x_n z_n y_n)^{\mathcal U} \|_2 + \| x z y - x \xi y\|_2 \\ &= \lim_{n \to \mathcal U} \|x_n (\xi_n - z_n) y_n\|_2 + \| x (z - \xi) y\|_2 \\ &\leq 2 \kappa^2 \|\xi - z\|_2 \leq 2 \kappa^2 \varepsilon. \end{align*} $$
Since this holds for every
![]() $\varepsilon> 0$
, it follows that
$\varepsilon> 0$
, it follows that
![]() $(x_n \xi _n y_n)^{\mathcal U} = x \xi y \in \operatorname {L}^2(M^{\mathcal U})$
.
$(x_n \xi _n y_n)^{\mathcal U} = x \xi y \in \operatorname {L}^2(M^{\mathcal U})$
.
We also record the following basic fact concerning tracial ultraproducts:
Lemma 2.2. Keep the same notation as above. Let
![]() $(x_n)_n$
be a
$(x_n)_n$
be a
![]() $\|\cdot \|_\infty $
-bounded sequence in M. Set
$\|\cdot \|_\infty $
-bounded sequence in M. Set
![]() $x=(x_n)^{\mathcal U}\in M^{\mathcal U}$
. Then, for every
$x=(x_n)^{\mathcal U}\in M^{\mathcal U}$
. Then, for every
![]() $p\in [1,+\infty )$
, we have
$p\in [1,+\infty )$
, we have
![]() $\|x\|_p=\lim _{n\rightarrow \mathcal U}\|x_n\|_p$
.
$\|x\|_p=\lim _{n\rightarrow \mathcal U}\|x_n\|_p$
.
Proof. We may assume that
![]() $\sup \left \{\|x_n\|_\infty \mid n\in \mathbb N\right \}\leq 1$
, and thus
$\sup \left \{\|x_n\|_\infty \mid n\in \mathbb N\right \}\leq 1$
, and thus
![]() $\|x\|_\infty \leq 1$
. Note that
$\|x\|_\infty \leq 1$
. Note that
![]() $|x|^2=x^*x=(x_n^*x_n)^{\mathcal U}=(|x_n|^2)^{\mathcal U}$
. Then, for every
$|x|^2=x^*x=(x_n^*x_n)^{\mathcal U}=(|x_n|^2)^{\mathcal U}$
. Then, for every
![]() $k\in \mathbb N$
, we have
$k\in \mathbb N$
, we have
![]() $|x|^{2k}=(|x_n|^{2k})^{\mathcal U}$
, and thus
$|x|^{2k}=(|x_n|^{2k})^{\mathcal U}$
, and thus
![]() $\tau ^{\mathcal U}(|x|^{2k})=\lim _{n\rightarrow \mathcal U}\tau (|x_n|^{2k})$
. Thus, if
$\tau ^{\mathcal U}(|x|^{2k})=\lim _{n\rightarrow \mathcal U}\tau (|x_n|^{2k})$
. Thus, if
![]() $P(t)\in \mathbb C[t]$
is a polynomial with complex coefficients and
$P(t)\in \mathbb C[t]$
is a polynomial with complex coefficients and
![]() $Q(t)=P(t^2)$
, then
$Q(t)=P(t^2)$
, then
![]() $\tau ^{\mathcal U}(Q(|x|))=\lim _{n\rightarrow \mathcal U}\tau (Q(|x_n|))$
. Since by the Stone–Weierstrass theorem
$\tau ^{\mathcal U}(Q(|x|))=\lim _{n\rightarrow \mathcal U}\tau (Q(|x_n|))$
. Since by the Stone–Weierstrass theorem
![]() $\{P(t^2)\mid P(t)\in \mathbb C[t]\}$
is dense in
$\{P(t^2)\mid P(t)\in \mathbb C[t]\}$
is dense in
![]() $\operatorname {C}([0,1])$
in the uniform norm, we get that
$\operatorname {C}([0,1])$
in the uniform norm, we get that
![]() $\tau ^{\mathcal U}(f(|x|))=\lim _{n\rightarrow \mathcal U}\tau (f(|x_n|))$
, for every
$\tau ^{\mathcal U}(f(|x|))=\lim _{n\rightarrow \mathcal U}\tau (f(|x_n|))$
, for every
![]() $f\in \operatorname {C}([0,1])$
. In particular,
$f\in \operatorname {C}([0,1])$
. In particular,
![]() $\tau ^{\mathcal U}(|x|^p)=\lim _{n\rightarrow \mathcal U}\tau (|x_n|^p)$
, for every
$\tau ^{\mathcal U}(|x|^p)=\lim _{n\rightarrow \mathcal U}\tau (|x_n|^p)$
, for every
![]() $p\in [1,+\infty )$
, which implies the conclusion.
$p\in [1,+\infty )$
, which implies the conclusion.
2.3. Amalgamated free products
Let I be an at most countable index set, such that
![]() $2 \leq | I | \leq +\infty $
. Let
$2 \leq | I | \leq +\infty $
. Let
![]() $(M_i, \tau _i)_{i \in I}$
be a family of tracial von Neumann algebras with a common von Neumann subalgebra
$(M_i, \tau _i)_{i \in I}$
be a family of tracial von Neumann algebras with a common von Neumann subalgebra
![]() $(B, \tau _0)$
, such that for every
$(B, \tau _0)$
, such that for every
![]() $i \in I$
, we have
$i \in I$
, we have
![]() $\tau _i|_B = \tau _0$
. Denote by
$\tau _i|_B = \tau _0$
. Denote by
![]() $(M, \tau ) = \ast _{B, i \in I} (M_i, \tau _i)$
the tracial amalgamated free product von Neumann algebra. Simply denote by
$(M, \tau ) = \ast _{B, i \in I} (M_i, \tau _i)$
the tracial amalgamated free product von Neumann algebra. Simply denote by
![]() $\operatorname { E}_B : M \to B$
the unique trace-preserving faithful normal conditional expectation.
$\operatorname { E}_B : M \to B$
the unique trace-preserving faithful normal conditional expectation.
Denote by
![]() $\mathscr W \subset M$
the linear span of B and of all the reduced words in M of the form
$\mathscr W \subset M$
the linear span of B and of all the reduced words in M of the form
![]() $w = w_1 \cdots w_n$
, with
$w = w_1 \cdots w_n$
, with
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $w_j \in M_{\varepsilon _j} \ominus B$
for every
$w_j \in M_{\varepsilon _j} \ominus B$
for every
![]() $j \in \{1, \dots , n\}$
, and
$j \in \{1, \dots , n\}$
, and
![]() $\varepsilon _1, \dots , \varepsilon _n \in I$
, such that
$\varepsilon _1, \dots , \varepsilon _n \in I$
, such that
![]() $\varepsilon _1 \neq \cdots \neq \varepsilon _n$
. For every subset
$\varepsilon _1 \neq \cdots \neq \varepsilon _n$
. For every subset
![]() $J \subset I$
, denote by
$J \subset I$
, denote by
![]() $\mathscr L_J \subset \mathscr W$
(respectively,
$\mathscr L_J \subset \mathscr W$
(respectively,
![]() $\mathscr R_J \subset \mathscr W$
) the linear span of all the reduced words whose first (respectively, last) letter lies in
$\mathscr R_J \subset \mathscr W$
) the linear span of all the reduced words whose first (respectively, last) letter lies in
![]() $M_j \ominus B$
for some
$M_j \ominus B$
for some
![]() $j \in J$
. For every
$j \in J$
. For every
![]() $i \in I$
, denote by
$i \in I$
, denote by
![]() $\mathscr W_i \subset \mathscr W$
the linear span of all the reduced words whose first and last letter lie in
$\mathscr W_i \subset \mathscr W$
the linear span of all the reduced words whose first and last letter lie in
![]() $M_i \ominus B$
. We will use the following consequences of Mei–Ricard’s results (see [Reference Mei and RicardMR16, Theorem 3.5]).
$M_i \ominus B$
. We will use the following consequences of Mei–Ricard’s results (see [Reference Mei and RicardMR16, Theorem 3.5]).
Theorem 2.3 (Mei–Ricard [Reference Mei and RicardMR16])
Let
![]() $p \in (1, +\infty )$
,
$p \in (1, +\infty )$
,
![]() $J \subset I$
and
$J \subset I$
and
![]() $i \in I$
. The following assertions hold:
$i \in I$
. The following assertions hold:
-
(i) The projection map
 $P_{\mathscr L_J} : \mathscr W \to \mathscr L_J$
extends to a completely bounded operator
$P_{\mathscr L_J} : \mathscr W \to \mathscr L_J$
extends to a completely bounded operator
 $P_{\mathscr L_J} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr L_J)$
.
$P_{\mathscr L_J} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr L_J)$
. -
(ii) The projection map
 $P_{\mathscr R_J} : \mathscr W \to \mathscr R_J$
extends to a completely bounded operator
$P_{\mathscr R_J} : \mathscr W \to \mathscr R_J$
extends to a completely bounded operator
 $P_{\mathscr R_J} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr R_J)$
.
$P_{\mathscr R_J} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr R_J)$
. -
(iii) The projection map
 $P_{\mathscr W_i} : \mathscr W \to \mathscr W_i$
extends to a completely bounded operator
$P_{\mathscr W_i} : \mathscr W \to \mathscr W_i$
extends to a completely bounded operator
 $P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
.
$P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
.
Proof. We use the notation
![]() $H_\varepsilon $
of [Reference Mei and RicardMR16, Section 3].
$H_\varepsilon $
of [Reference Mei and RicardMR16, Section 3].
(i) For every
![]() $j \in J$
, set
$j \in J$
, set
![]() $\varepsilon _j = - 1$
and for every
$\varepsilon _j = - 1$
and for every
![]() $j \in I\setminus J$
, set
$j \in I\setminus J$
, set
![]() $\varepsilon _j = 1$
. Then, with
$\varepsilon _j = 1$
. Then, with
![]() $\varepsilon = (\varepsilon _i)_{i \in I}$
, we have
$\varepsilon = (\varepsilon _i)_{i \in I}$
, we have
![]() $P_{\mathscr L_J} = \frac {\operatorname {Id} - H_\varepsilon }{2}$
. Therefore, [Reference Mei and RicardMR16, Theorem 3.5] implies that
$P_{\mathscr L_J} = \frac {\operatorname {Id} - H_\varepsilon }{2}$
. Therefore, [Reference Mei and RicardMR16, Theorem 3.5] implies that
![]() $P_{\mathscr L_J} : \mathscr W \to \mathscr L_J$
extends to a completely bounded operator
$P_{\mathscr L_J} : \mathscr W \to \mathscr L_J$
extends to a completely bounded operator
![]() $P_{\mathscr L_J} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr L_J)$
.
$P_{\mathscr L_J} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr L_J)$
.
(ii) The proof is completely analogous to Item (i).
(iii) We have
![]() $P_{\mathscr W_i} = P_{\mathscr L_{i}} \circ P_{\mathscr R_{i}} = P_{\mathscr R_{i}} \circ P_{\mathscr L_{i}}$
. Therefore, Items (i) and (ii) imply that
$P_{\mathscr W_i} = P_{\mathscr L_{i}} \circ P_{\mathscr R_{i}} = P_{\mathscr R_{i}} \circ P_{\mathscr L_{i}}$
. Therefore, Items (i) and (ii) imply that
![]() $P_{\mathscr W_i} : \mathscr W \to \mathscr W_i$
extends to a completely bounded operator
$P_{\mathscr W_i} : \mathscr W \to \mathscr W_i$
extends to a completely bounded operator
![]() $P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
.
$P_{\mathscr W_i} : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
.
Let
![]() $P_p$
be one of the operators from Theorem 2.3 (i.e.
$P_p$
be one of the operators from Theorem 2.3 (i.e.
![]() $P_{\mathscr L_J}, P_{\mathscr R_J}$
, or
$P_{\mathscr L_J}, P_{\mathscr R_J}$
, or
![]() $P_{\mathscr W_i}$
). Then the operators
$P_{\mathscr W_i}$
). Then the operators
![]() $(P_p)_{p\in (1,+\infty )}$
are consistent with the inclusions
$(P_p)_{p\in (1,+\infty )}$
are consistent with the inclusions
![]() $\operatorname {L}^q(M)\subset \operatorname {L}^p(M)$
, in the sense that
$\operatorname {L}^q(M)\subset \operatorname {L}^p(M)$
, in the sense that
![]() $P_q=P_p |_{\operatorname {L}^q(M)}$
, for every
$P_q=P_p |_{\operatorname {L}^q(M)}$
, for every
![]() $1<p\leq q<+\infty $
. This is why we denote P instead of
$1<p\leq q<+\infty $
. This is why we denote P instead of
![]() $P_p$
.
$P_p$
.
2.4. Popa’s intertwining theory
We review Popa’s criterion for intertwining von Neumann subalgebras [Reference PopaPo01, Reference PopaPo03]. Let
![]() $(M, \tau )$
be a tracial von Neumann algebra and
$(M, \tau )$
be a tracial von Neumann algebra and
![]() $A\subset 1_A M 1_A$
,
$A\subset 1_A M 1_A$
,
![]() $B \subset 1_B M 1_B$
be von Neumann subalgebras. By [Reference PopaPo03, Corollary 2.3] and [Reference PopaPo01, Theorem A.1] (see also [Reference VaesVa06, Proposition C.1]), the following conditions are equivalent:
$B \subset 1_B M 1_B$
be von Neumann subalgebras. By [Reference PopaPo03, Corollary 2.3] and [Reference PopaPo01, Theorem A.1] (see also [Reference VaesVa06, Proposition C.1]), the following conditions are equivalent:
-
(i) There exist
 $n \geq 1$
, a projection
$n \geq 1$
, a projection
 $q \in \mathbf M_n(B)$
, a nonzero partial isometry
$q \in \mathbf M_n(B)$
, a nonzero partial isometry
 $v \in \mathbf M_{1, n}(1_A M)q$
and a unital normal
$v \in \mathbf M_{1, n}(1_A M)q$
and a unital normal
 $\ast $
-homomorphism
$\ast $
-homomorphism
 $\pi : A \to q\mathbf M_n(B)q$
, such that
$\pi : A \to q\mathbf M_n(B)q$
, such that
 $a v = v \pi (a)$
for all
$a v = v \pi (a)$
for all
 $a \in A$
.
$a \in A$
. -
(ii) There exist projections
 $p \in A$
and
$p \in A$
and
 $q \in B$
, a nonzero partial isometry
$q \in B$
, a nonzero partial isometry
 $v \in pMq$
and a unital normal
$v \in pMq$
and a unital normal
 $\ast $
-homomorphism
$\ast $
-homomorphism
 $\pi : pAp \to qBq$
, such that
$\pi : pAp \to qBq$
, such that
 $a v = v \pi (a)$
for all
$a v = v \pi (a)$
for all
 $a \in A$
.
$a \in A$
. -
(iii) There is no net of unitaries
 $(w_k)_k$
in A, such that
$(w_k)_k$
in A, such that  $$ \begin{align*}\forall x, y \in 1_A M 1_B, \quad \lim_k \|\operatorname{ E}_B(x^* w_k y)\|_2 = 0.\end{align*} $$
$$ \begin{align*}\forall x, y \in 1_A M 1_B, \quad \lim_k \|\operatorname{ E}_B(x^* w_k y)\|_2 = 0.\end{align*} $$
If one of the previous equivalent conditions is satisfied, we say that A embeds into B inside M and write
![]() $A \preceq _M B$
.
$A \preceq _M B$
.
Following [Reference JonesJo82, Reference Pimsner and PopaPP84], we say that an inclusion of tracial von Neumann algebras
![]() $P \subset M$
has finite index if
$P \subset M$
has finite index if
![]() $\operatorname {L}^2(M, \tau )$
has finite dimension as a right P-module. If
$\operatorname {L}^2(M, \tau )$
has finite dimension as a right P-module. If
![]() $A_0 \subset A$
is a von Neumann subalgebra with finite index and if
$A_0 \subset A$
is a von Neumann subalgebra with finite index and if
![]() $A \preceq _M B$
, then
$A \preceq _M B$
, then
![]() $A_0 \preceq _M B$
(see [Reference VaesVa07, Lemma 3.9]).
$A_0 \preceq _M B$
(see [Reference VaesVa07, Lemma 3.9]).
We record the following new criterion for intertwining von Neumann subalgebras.
Lemma 2.4. Let
![]() $(M,\tau )$
be a separable tracial von Neumann algebra and
$(M,\tau )$
be a separable tracial von Neumann algebra and
![]() $A,B\subset M$
be von Neumann subalgebras, such that
$A,B\subset M$
be von Neumann subalgebras, such that
![]() $A\npreceq _MB$
. Then there exists
$A\npreceq _MB$
. Then there exists
![]() $u\in \mathscr U(A^{\mathcal U})$
, such that
$u\in \mathscr U(A^{\mathcal U})$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(xu^my)=0$
, for all
$\operatorname { E}_{B^{\mathcal U}}(xu^my)=0$
, for all
![]() $x,y\in M$
and all
$x,y\in M$
and all
![]() $m\in \mathbb Z\setminus \{0\}$
.
$m\in \mathbb Z\setminus \{0\}$
.
Proof. To prove the lemma, it suffices to argue that for every finite subset
![]() $F\subset M$
,
$F\subset M$
,
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $K\in \mathbb N$
, we can find
$K\in \mathbb N$
, we can find
![]() $u\in \mathscr U(A)$
, such that
$u\in \mathscr U(A)$
, such that
![]() $\|\operatorname { E}_B(xu^my^*)\|_2<\varepsilon $
, for all
$\|\operatorname { E}_B(xu^my^*)\|_2<\varepsilon $
, for all
![]() $m\in \mathbb Z\setminus \{0\}$
with
$m\in \mathbb Z\setminus \{0\}$
with
![]() $|m|\leq K$
. To this end, fix a finite subset
$|m|\leq K$
. To this end, fix a finite subset
![]() $F\subset M$
,
$F\subset M$
,
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $K\in \mathbb N$
. For
$K\in \mathbb N$
. For
![]() $u\in \mathscr U(M)$
, set
$u\in \mathscr U(M)$
, set
![]() $\psi (u)=\sum _{m\in \mathbb Z\setminus \{0\},|m|\leq K}\sum _{x,y\in F}\|\operatorname { E}_B(xu^my^*)\|_2^2$
. Let
$\psi (u)=\sum _{m\in \mathbb Z\setminus \{0\},|m|\leq K}\sum _{x,y\in F}\|\operatorname { E}_B(xu^my^*)\|_2^2$
. Let
![]() $v\in \mathscr U(M)$
with
$v\in \mathscr U(M)$
with
![]() $\{v\}^{\prime \prime } \npreceq _MB$
. For every
$\{v\}^{\prime \prime } \npreceq _MB$
. For every
![]() $N\in \mathbb N$
, set
$N\in \mathbb N$
, set
 $$ \begin{align*}\varphi(v,N)=\frac{1}{N}\sum_{k=1}^N\sum_{x,y\in F}\|\operatorname{ E}_B(xv^ky^*)\|_2^2.\end{align*} $$
$$ \begin{align*}\varphi(v,N)=\frac{1}{N}\sum_{k=1}^N\sum_{x,y\in F}\|\operatorname{ E}_B(xv^ky^*)\|_2^2.\end{align*} $$
We claim that
![]() $\lim _{N \to \infty }\varphi (v,N)=0$
. Indeed, set
$\lim _{N \to \infty }\varphi (v,N)=0$
. Indeed, set
![]() $\xi =\sum _{x\in F}xe_Bx^*\in \langle M,B\rangle $
, where
$\xi =\sum _{x\in F}xe_Bx^*\in \langle M,B\rangle $
, where
![]() $(\langle M, B\rangle , \operatorname {Tr})$
is Jones basic construction of
$(\langle M, B\rangle , \operatorname {Tr})$
is Jones basic construction of
![]() $B\subset M$
. Using that
$B\subset M$
. Using that
![]() $\|\operatorname { E}_B(z)\|_2^2=\text {Tr}(ze_Bz^*e_B)$
for every
$\|\operatorname { E}_B(z)\|_2^2=\text {Tr}(ze_Bz^*e_B)$
for every
![]() $z\in M$
, we obtain that
$z\in M$
, we obtain that
 $$ \begin{align} \forall N \in \mathbb{N}, \quad \varphi(v,N)=\operatorname{Tr} \left( \left(\frac{1}{N}\sum_{k=1}^Nv^k\xi {v^{-k}} \right)\xi \right). \end{align} $$
$$ \begin{align} \forall N \in \mathbb{N}, \quad \varphi(v,N)=\operatorname{Tr} \left( \left(\frac{1}{N}\sum_{k=1}^Nv^k\xi {v^{-k}} \right)\xi \right). \end{align} $$
By von Neumann’s ergodic theorem, there exists
![]() $\eta \in \operatorname {L}^2(\langle M,B\rangle , \operatorname {Tr})$
, such that
$\eta \in \operatorname {L}^2(\langle M,B\rangle , \operatorname {Tr})$
, such that
![]() $v\eta v^*=\eta $
and
$v\eta v^*=\eta $
and
![]() $\lim _{N \to \infty }\|\frac {1}{N}\sum _{k=1}^Nv^k\xi {v^{-k}}-\eta \|_{2, \operatorname {Tr}}=0$
. Then
$\lim _{N \to \infty }\|\frac {1}{N}\sum _{k=1}^Nv^k\xi {v^{-k}}-\eta \|_{2, \operatorname {Tr}}=0$
. Then
![]() $w\eta =\eta w$
, for all
$w\eta =\eta w$
, for all
![]() $w\in \{v\}^{\prime \prime }$
. Since
$w\in \{v\}^{\prime \prime }$
. Since
![]() $\{v\}^{\prime \prime }\npreceq _MB$
, we obtain that
$\{v\}^{\prime \prime }\npreceq _MB$
, we obtain that
![]() $\eta =0$
. In combination with (2.1), this proves our claim that
$\eta =0$
. In combination with (2.1), this proves our claim that
![]() $\lim _{N\to \infty }\varphi (v,N)=0$
.
$\lim _{N\to \infty }\varphi (v,N)=0$
.
We are now ready to finish the proof. Since
![]() $A\npreceq _MB$
, we can find a diffuse abelian von Neumann subalgebra
$A\npreceq _MB$
, we can find a diffuse abelian von Neumann subalgebra
![]() $A_0\subset A$
, such that
$A_0\subset A$
, such that
![]() $A_0\npreceq _MB$
(see [Reference Brown and OzawaBO08, Corollary F.14]). Let
$A_0\npreceq _MB$
(see [Reference Brown and OzawaBO08, Corollary F.14]). Let
![]() $v\in \mathscr U(A_0)$
be a Haar unitary with
$v\in \mathscr U(A_0)$
be a Haar unitary with
![]() $\{v\}^{\prime \prime }=A_0$
. If
$\{v\}^{\prime \prime }=A_0$
. If
![]() $m\in \mathbb Z\setminus \{0\}$
, then
$m\in \mathbb Z\setminus \{0\}$
, then
![]() $\{v^m\}^{\prime \prime }\subset A_0$
has finite index, and thus
$\{v^m\}^{\prime \prime }\subset A_0$
has finite index, and thus
![]() $\{v^m\}^{\prime \prime }\npreceq _MB$
. The above claim gives that
$\{v^m\}^{\prime \prime }\npreceq _MB$
. The above claim gives that
![]() $\lim _{N \to \infty }\varphi (v^m,N)=0$
, for all
$\lim _{N \to \infty }\varphi (v^m,N)=0$
, for all
![]() $m\in \mathbb Z\setminus \{0\}$
. Thus, we can find
$m\in \mathbb Z\setminus \{0\}$
. Thus, we can find
![]() $N\in \mathbb N$
, such that
$N\in \mathbb N$
, such that
![]() $\sum _{m\in \mathbb Z\setminus \{0\},|m|\leq K}\varphi (v^m,N)<\varepsilon ^2$
. Since
$\sum _{m\in \mathbb Z\setminus \{0\},|m|\leq K}\varphi (v^m,N)<\varepsilon ^2$
. Since
![]() $\sum _{m\in \mathbb Z\setminus \{0\},|m|\leq K}\varphi (v^m,N)=\frac {1}{N}\sum _{k=1}^N\psi (v^k)$
, we find
$\sum _{m\in \mathbb Z\setminus \{0\},|m|\leq K}\varphi (v^m,N)=\frac {1}{N}\sum _{k=1}^N\psi (v^k)$
, we find
![]() $1\leq k\leq N$
, such that
$1\leq k\leq N$
, such that
![]() $\psi (v^k)<\varepsilon ^2$
. Thus,
$\psi (v^k)<\varepsilon ^2$
. Thus,
![]() $u=v^k$
satisfies the desired conclusion, which finishes the proof.
$u=v^k$
satisfies the desired conclusion, which finishes the proof.
3. Proofs of Theorems A, B, C, D
3.1. Popa’s asymptotic orthogonality property
Let I be an at most countable index set, such that
![]() $2 \leq | I | \leq +\infty $
. Let
$2 \leq | I | \leq +\infty $
. Let
![]() $(M_i, \tau _i)_{i \in I}$
be a family of tracial von Neumann algebras with a common von Neumann subalgebra
$(M_i, \tau _i)_{i \in I}$
be a family of tracial von Neumann algebras with a common von Neumann subalgebra
![]() $(B, \tau _0)$
, such that for every
$(B, \tau _0)$
, such that for every
![]() $i \in I$
, we have
$i \in I$
, we have
![]() $\tau _i|_B = \tau _0$
. Denote by
$\tau _i|_B = \tau _0$
. Denote by
![]() $(M, \tau ) = \ast _{B, i \in I} (M_i, \tau _i)$
the tracial amalgamated free product von Neumann algebra. Simply denote by
$(M, \tau ) = \ast _{B, i \in I} (M_i, \tau _i)$
the tracial amalgamated free product von Neumann algebra. Simply denote by
![]() $\operatorname { E}_B : M \to B$
(respectively,
$\operatorname { E}_B : M \to B$
(respectively,
![]() $\operatorname { E}_{B^{\mathcal U}} : M^{\mathcal U} \to B^{\mathcal U}$
) the unique trace-preserving faithful normal conditional expectation.
$\operatorname { E}_{B^{\mathcal U}} : M^{\mathcal U} \to B^{\mathcal U}$
) the unique trace-preserving faithful normal conditional expectation.
The following lemma is a generalization of Popa’s asymptotic orthogonality property (see [Reference PopaPo83, Lemma 2.1]) in the framework of tracial amalgamated free product von Neumann algebras. The key new feature of the proof is that we exploit Theorem 2.3 to work inside the Hilbert space
![]() $\operatorname {L}^2(M^{\mathcal U})$
instead of
$\operatorname {L}^2(M^{\mathcal U})$
instead of
![]() $\operatorname {L}^2(M)^{\mathcal U}$
as in Popa’s proof.
$\operatorname {L}^2(M)^{\mathcal U}$
as in Popa’s proof.
Lemma 3.1. Let
![]() $i \in I$
. Let
$i \in I$
. Let
![]() $u \in \mathscr U(M_i^{\mathcal U})$
be a unitary, such that
$u \in \mathscr U(M_i^{\mathcal U})$
be a unitary, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
for every
$\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
for every
![]() $k \in \mathbb {Z} \setminus \{0\}$
. For every
$k \in \mathbb {Z} \setminus \{0\}$
. For every
![]() $x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
, such that
$x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(x) = 0$
, we have
$\operatorname { E}_{B^{\mathcal U}}(x) = 0$
, we have
![]() $\lim _{n \to \mathcal U} \|x_n - P_{\mathscr W_i}(x_n)\|_2 = 0$
.
$\lim _{n \to \mathcal U} \|x_n - P_{\mathscr W_i}(x_n)\|_2 = 0$
.
Proof. Let
![]() $x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
, such that
$x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(x) = 0$
. Without loss of generality, we may assume that
$\operatorname { E}_{B^{\mathcal U}}(x) = 0$
. Without loss of generality, we may assume that
![]() $\|x_n\|_\infty \leq 1$
for every
$\|x_n\|_\infty \leq 1$
for every
![]() $n \in \mathbb {N}$
. To prove that
$n \in \mathbb {N}$
. To prove that
![]() $\lim _{n \to \mathcal U} \|x_n - P_{\mathscr W_i}(x_n)\|_2 = 0$
, we show that
$\lim _{n \to \mathcal U} \|x_n - P_{\mathscr W_i}(x_n)\|_2 = 0$
, we show that
![]() $\lim _{n \to \mathcal U} \|P_{\mathscr L_{I\setminus \{i\}}}(x_n)\|_2 = \lim _{n \to \mathcal U} \|P_{\mathscr R_{I\setminus \{i\}}}(x_n)\|_2 = 0$
. Since
$\lim _{n \to \mathcal U} \|P_{\mathscr L_{I\setminus \{i\}}}(x_n)\|_2 = \lim _{n \to \mathcal U} \|P_{\mathscr R_{I\setminus \{i\}}}(x_n)\|_2 = 0$
. Since
![]() $\mathscr R_{I \setminus \{i\}} = J \mathscr L_{I \setminus \{i\}} J$
, it suffices to prove that
$\mathscr R_{I \setminus \{i\}} = J \mathscr L_{I \setminus \{i\}} J$
, it suffices to prove that
![]() $\lim _{n \to \mathcal U} \|P_{\mathscr L_{I\setminus \{i\}}}(x_n)\|_2 = 0$
. To simplify the notation, we set
$\lim _{n \to \mathcal U} \|P_{\mathscr L_{I\setminus \{i\}}}(x_n)\|_2 = 0$
. To simplify the notation, we set
![]() $P_i = P_{\mathscr L_{I\setminus \{i\}}}$
.
$P_i = P_{\mathscr L_{I\setminus \{i\}}}$
.
By Lemma 2.1(ii) and Theorem 2.3(i), we have
![]() $(P_i(x_n))^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
. Set
$(P_i(x_n))^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
. Set
![]() $\mathscr H_i = \operatorname {L}^2(M^{\mathcal U}) \cap (\mathscr L_{I \setminus \{i\}})^{\mathcal U} \subset \operatorname {L}^2(M^{\mathcal U})$
and denote by
$\mathscr H_i = \operatorname {L}^2(M^{\mathcal U}) \cap (\mathscr L_{I \setminus \{i\}})^{\mathcal U} \subset \operatorname {L}^2(M^{\mathcal U})$
and denote by
![]() $P_{\mathscr H_i} : \operatorname {L}^2(M^{\mathcal U}) \to \mathscr H_i$
the corresponding orthogonal projection. Then we have
$P_{\mathscr H_i} : \operatorname {L}^2(M^{\mathcal U}) \to \mathscr H_i$
the corresponding orthogonal projection. Then we have
![]() $P_{\mathscr H_i}(x) = (P_i(x_n))^{\mathcal U} \in \mathscr H_i$
. For every
$P_{\mathscr H_i}(x) = (P_i(x_n))^{\mathcal U} \in \mathscr H_i$
. For every
![]() $N \geq 1$
, we have
$N \geq 1$
, we have
 $$ \begin{align} N \cdot \| P_{\mathscr H_i}(x)\|^2_2 &= \sum_{k =1}^N \|u^k P_{\mathscr H_i}(x) u^{-k}\|^2_2 \\ \nonumber &= \sum_{k =1}^N \|P_{u^{k}\mathscr H_i u^{-k}}(u^k x u^{-k})\|^2_2 \\ \nonumber &= \sum_{k =1}^N \|P_{ u^{k}\mathscr H_i u^{-k}}(x)\|^2_2. \end{align} $$
$$ \begin{align} N \cdot \| P_{\mathscr H_i}(x)\|^2_2 &= \sum_{k =1}^N \|u^k P_{\mathscr H_i}(x) u^{-k}\|^2_2 \\ \nonumber &= \sum_{k =1}^N \|P_{u^{k}\mathscr H_i u^{-k}}(u^k x u^{-k})\|^2_2 \\ \nonumber &= \sum_{k =1}^N \|P_{ u^{k}\mathscr H_i u^{-k}}(x)\|^2_2. \end{align} $$
We claim that the Hilbert subspaces
![]() $( u^{k}\mathscr H_i u^{-k} )_{k \in \mathbb {Z}}$
are mutually orthogonal in
$( u^{k}\mathscr H_i u^{-k} )_{k \in \mathbb {Z}}$
are mutually orthogonal in
![]() $\operatorname {L}^2(M^{\mathcal U})$
, that is, for every
$\operatorname {L}^2(M^{\mathcal U})$
, that is, for every
![]() $k \in \mathbb {Z} \setminus \{0\}$
,
$k \in \mathbb {Z} \setminus \{0\}$
,
![]() $ u^{k}\mathscr H_i u^{-k}$
and
$ u^{k}\mathscr H_i u^{-k}$
and
![]() $ \mathscr H_i $
are orthogonal in
$ \mathscr H_i $
are orthogonal in
![]() $\operatorname {L}^2(M^{\mathcal U})$
. Indeed, for every
$\operatorname {L}^2(M^{\mathcal U})$
. Indeed, for every
![]() $k \in \mathbb {Z} \setminus \{0\}$
, since
$k \in \mathbb {Z} \setminus \{0\}$
, since
![]() $\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
, we may write
$\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
, we may write
![]() $u^k = (u_{n, k})^{\mathcal U} \in M_i^{\mathcal U}$
, where
$u^k = (u_{n, k})^{\mathcal U} \in M_i^{\mathcal U}$
, where
![]() $(u_{n, k})_{n}$
is a
$(u_{n, k})_{n}$
is a
![]() $\|\cdot \|_\infty $
-bounded sequence in
$\|\cdot \|_\infty $
-bounded sequence in
![]() $M_i \ominus B$
. Let
$M_i \ominus B$
. Let
![]() $\xi = (\xi _n)^{\mathcal U} \in \mathscr H_i$
and
$\xi = (\xi _n)^{\mathcal U} \in \mathscr H_i$
and
![]() $\eta = (\eta _n)^{\mathcal U} \in \mathscr H_i$
, where
$\eta = (\eta _n)^{\mathcal U} \in \mathscr H_i$
, where
![]() $(\xi _n)_n$
and
$(\xi _n)_n$
and
![]() $(\eta _n)_n$
are
$(\eta _n)_n$
are
![]() $\|\cdot \|_2$
-bounded sequences in
$\|\cdot \|_2$
-bounded sequences in
![]() $\mathscr L_{I \setminus \{i\}}$
. By construction, it is plain to see that for all
$\mathscr L_{I \setminus \{i\}}$
. By construction, it is plain to see that for all
![]() $n \in \mathbb {N}$
and all
$n \in \mathbb {N}$
and all
![]() $k \in \mathbb {Z} \setminus \{0\}$
, the vectors
$k \in \mathbb {Z} \setminus \{0\}$
, the vectors
![]() $u_{n, k} \xi _n u_{n, k}^*$
and
$u_{n, k} \xi _n u_{n, k}^*$
and
![]() $\eta _n$
are orthogonal in
$\eta _n$
are orthogonal in
![]() $\operatorname {L}^2(M)$
. By Lemma 2.1(iii), since
$\operatorname {L}^2(M)$
. By Lemma 2.1(iii), since
![]() $\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
, we have
$\xi = (\xi _n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
, we have
This finishes the proof of the claim.
From (3.1), since the projections
![]() $(P_{u^k \mathscr H_i u^{-k}})_{k \in \mathbb {Z}}$
are mutually orthogonal, we infer that
$(P_{u^k \mathscr H_i u^{-k}})_{k \in \mathbb {Z}}$
are mutually orthogonal, we infer that
 $$ \begin{align} N \cdot \| P_{\mathscr H_i}(x)\|^2_2 = \sum_{k =1}^N \|P_{ u^{k}\mathscr H_i u^{-k}}(x)\|^2_2 \leq \|x\|_2^2. \end{align} $$
$$ \begin{align} N \cdot \| P_{\mathscr H_i}(x)\|^2_2 = \sum_{k =1}^N \|P_{ u^{k}\mathscr H_i u^{-k}}(x)\|^2_2 \leq \|x\|_2^2. \end{align} $$
Since (3.2) holds for every
![]() $N \geq 1$
, we have
$N \geq 1$
, we have
![]() $\lim _{n \to \mathcal U} \|P_i(x_n)\|_2 = \| P_{\mathscr H_i}(x) \|_2 = 0$
. This finishes the proof of the lemma.
$\lim _{n \to \mathcal U} \|P_i(x_n)\|_2 = \| P_{\mathscr H_i}(x) \|_2 = 0$
. This finishes the proof of the lemma.
Using a
![]() $2 \times 2$
matrix trick, we obtain the following extension of Lemma 3.1.
$2 \times 2$
matrix trick, we obtain the following extension of Lemma 3.1.
Lemma 3.2. Let
![]() $i \in I$
. Let
$i \in I$
. Let
![]() $u \in \mathscr U(M_i^{\mathcal U})$
be a unitary, such that
$u \in \mathscr U(M_i^{\mathcal U})$
be a unitary, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(v u^k v^*) = 0$
for every
$\operatorname { E}_{B^{\mathcal U}}(v u^k v^*) = 0$
for every
![]() $k \in \mathbb {Z} \setminus \{0\}$
and every
$k \in \mathbb {Z} \setminus \{0\}$
and every
![]() $v \in \mathscr U(M_i)$
. For every
$v \in \mathscr U(M_i)$
. For every
![]() $x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
, such that
$x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
, such that
![]() $\operatorname { E}_{M_i^{\mathcal U}}(x) = 0$
and every
$\operatorname { E}_{M_i^{\mathcal U}}(x) = 0$
and every
![]() $y, z \in M_i$
, we have
$y, z \in M_i$
, we have
![]() $\lim _{n \to \mathcal U} \|y x_n z - P_{\mathscr W_i}(y x_n z)\|_2 = 0$
.
$\lim _{n \to \mathcal U} \|y x_n z - P_{\mathscr W_i}(y x_n z)\|_2 = 0$
.
Proof. Set
![]() $\mathscr B = \mathbf M_2(B)$
,
$\mathscr B = \mathbf M_2(B)$
,
![]() $\mathscr M_j = \mathbf M_2(M_j)$
for every
$\mathscr M_j = \mathbf M_2(M_j)$
for every
![]() $j \in I$
and
$j \in I$
and
![]() $\mathscr M = \mathbf M_2(M)$
so that we have
$\mathscr M = \mathbf M_2(M)$
so that we have
![]() $\mathscr M = \ast _{\mathscr B, j \in I} \mathscr M_j$
. Let
$\mathscr M = \ast _{\mathscr B, j \in I} \mathscr M_j$
. Let
![]() $x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
be such that
$x = (x_n)^{\mathcal U} \in \{u\}' \cap M^{\mathcal U}$
be such that
![]() $\operatorname { E}_{M_i^{\mathcal U}}(x) = 0$
. Since any element of
$\operatorname { E}_{M_i^{\mathcal U}}(x) = 0$
. Since any element of
![]() $M_i$
is a linear combination of at most four unitaries of
$M_i$
is a linear combination of at most four unitaries of
![]() $M_i$
, it suffices to prove that for every
$M_i$
, it suffices to prove that for every
![]() $v, w \in \mathscr U(M_i)$
, we have
$v, w \in \mathscr U(M_i)$
, we have
![]() $\lim _{n \to \mathcal U} \|v x_n w - P_{\mathscr W_i}(v x_n w)\|_2 = 0$
.
$\lim _{n \to \mathcal U} \|v x_n w - P_{\mathscr W_i}(v x_n w)\|_2 = 0$
.
Let
![]() $v, w \in \mathscr U(M_i)$
. Set
$v, w \in \mathscr U(M_i)$
. Set
 $$ \begin{align*}U = \begin{pmatrix} v uv^* & 0 \\ 0 & w^* u w \end{pmatrix} \in \mathscr U(\mathscr M_i^{\mathcal U}) \quad \text{and} \quad X = \begin{pmatrix} 0 & v x w \\ 0 & 0 \end{pmatrix} \in \mathscr M^{\mathcal U} \ominus \mathscr M_i^{\mathcal U}.\end{align*} $$
$$ \begin{align*}U = \begin{pmatrix} v uv^* & 0 \\ 0 & w^* u w \end{pmatrix} \in \mathscr U(\mathscr M_i^{\mathcal U}) \quad \text{and} \quad X = \begin{pmatrix} 0 & v x w \\ 0 & 0 \end{pmatrix} \in \mathscr M^{\mathcal U} \ominus \mathscr M_i^{\mathcal U}.\end{align*} $$
By construction, we have
![]() $U X = X U$
and
$U X = X U$
and
![]() $\operatorname { E}_{\mathscr B^{\mathcal U}}(U^k) = 0$
for every
$\operatorname { E}_{\mathscr B^{\mathcal U}}(U^k) = 0$
for every
![]() $k \in \mathbb {Z} \setminus \{0\}$
. We may now apply Lemma 3.1 to
$k \in \mathbb {Z} \setminus \{0\}$
. We may now apply Lemma 3.1 to
![]() $X = (X_n)^{\mathcal U} \in \mathscr M^{\mathcal U} \ominus \mathscr B^{\mathcal U}$
and conclude that
$X = (X_n)^{\mathcal U} \in \mathscr M^{\mathcal U} \ominus \mathscr B^{\mathcal U}$
and conclude that
This finishes the proof of the lemma.
3.2. Proofs of Theorems A, B, C
Proof of Theorem A
Keep the same notation as in the statement of Theorem A. Let
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $\varepsilon _1, \dots , \varepsilon _k \in I$
be such that
$\varepsilon _1, \dots , \varepsilon _k \in I$
be such that
![]() $\varepsilon _1 \neq \cdots \neq \varepsilon _k$
. For every
$\varepsilon _1 \neq \cdots \neq \varepsilon _k$
. For every
![]() $1 \leq j \leq k$
, let
$1 \leq j \leq k$
, let
![]() $x_j = (x_{j, n})^{\mathcal U} \in \mathbf X_{\varepsilon _j}$
. We may assume that
$x_j = (x_{j, n})^{\mathcal U} \in \mathbf X_{\varepsilon _j}$
. We may assume that
![]() $\sup \left \{\|x_{j, n}\|_\infty \mid 1 \leq j \leq k, n \in \mathbb {N} \right \} \leq 1$
. We show that
$\sup \left \{\|x_{j, n}\|_\infty \mid 1 \leq j \leq k, n \in \mathbb {N} \right \} \leq 1$
. We show that
![]() $\operatorname { E}_{B^{\mathcal U}}(x_1 \cdots x_k) = 0$
.
$\operatorname { E}_{B^{\mathcal U}}(x_1 \cdots x_k) = 0$
.
For every
![]() $i \in I$
and every
$i \in I$
and every
![]() $p \in (1, +\infty )$
, we simply denote by
$p \in (1, +\infty )$
, we simply denote by
![]() $P_i : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
the completely bounded operator (see Theorem 2.3(iii)). For every
$P_i : \operatorname {L}^p(M) \to \operatorname {L}^p(\mathscr W_i)$
the completely bounded operator (see Theorem 2.3(iii)). For every
![]() $p \in (1, +\infty )$
, choose
$p \in (1, +\infty )$
, choose
![]() $\kappa _p> 0$
large enough so that
$\kappa _p> 0$
large enough so that
Fix
![]() $1 < r < 2$
(e.g.
$1 < r < 2$
(e.g.
![]() $r = \frac 32$
). Let
$r = \frac 32$
). Let
![]() $p \in (1, +\infty )$
be such that
$p \in (1, +\infty )$
be such that
![]() $\frac 1r = \frac 12 + \frac {k - 1}{p}$
. For every
$\frac 1r = \frac 12 + \frac {k - 1}{p}$
. For every
![]() $1 \leq j \leq k$
and every
$1 \leq j \leq k$
and every
![]() $n \in \mathbb {N}$
, write
$n \in \mathbb {N}$
, write
![]() $x_{j, n} = P_{\varepsilon _j}(x_{j, n}) + (x_{j, n} - P_{\varepsilon _j}(x_{j, n}))$
and observe that
$x_{j, n} = P_{\varepsilon _j}(x_{j, n}) + (x_{j, n} - P_{\varepsilon _j}(x_{j, n}))$
and observe that
-
○
 $P_{\varepsilon _j}(x_{j, n}) \in \operatorname {L}^2(\mathscr W_{\varepsilon _j})$
and
$P_{\varepsilon _j}(x_{j, n}) \in \operatorname {L}^2(\mathscr W_{\varepsilon _j})$
and
 $\lim _{n \to \mathcal U} \|x_{j, n} - P_{\varepsilon _j}(x_{j, n})\|_2 = 0$
;
$\lim _{n \to \mathcal U} \|x_{j, n} - P_{\varepsilon _j}(x_{j, n})\|_2 = 0$
; -
○
 $P_{\varepsilon _j}(x_{j, n}) \in \operatorname {L}^p(\mathscr W_{\varepsilon _j})$
and
$P_{\varepsilon _j}(x_{j, n}) \in \operatorname {L}^p(\mathscr W_{\varepsilon _j})$
and
 $\max \left \{ \|P_{\varepsilon _j}(x_{j, n}) \|_{p}, \|x_{j, n} - P_{\varepsilon _j}(x_{j, n})\|_p \right \} \leq 1 + \kappa _p$
.
$\max \left \{ \|P_{\varepsilon _j}(x_{j, n}) \|_{p}, \|x_{j, n} - P_{\varepsilon _j}(x_{j, n})\|_p \right \} \leq 1 + \kappa _p$
.
For every
![]() $n \in \mathbb {N}$
, we may write
$n \in \mathbb {N}$
, we may write
![]() $x_{1, n} \cdots x_{k, n} - P_{\varepsilon _1}(x_{1, n}) \cdots P_{\varepsilon _k}(x_{k, n})$
as a sum of
$x_{1, n} \cdots x_{k, n} - P_{\varepsilon _1}(x_{1, n}) \cdots P_{\varepsilon _k}(x_{k, n})$
as a sum of
![]() $2^k - 1$
terms that are products of length k for which at least one of the factors is of the form
$2^k - 1$
terms that are products of length k for which at least one of the factors is of the form
![]() $x_{j, n} - P_{\varepsilon _j}(x_{j, n})$
for some
$x_{j, n} - P_{\varepsilon _j}(x_{j, n})$
for some
![]() $1 \leq j \leq k$
. For every
$1 \leq j \leq k$
. For every
![]() $n \in \mathbb {N}$
, using the triangle inequality and the generalized noncommutative Hölder inequality, we obtain
$n \in \mathbb {N}$
, using the triangle inequality and the generalized noncommutative Hölder inequality, we obtain
This implies that
Next, set
![]() $q = kr $
so that
$q = kr $
so that
![]() $\frac 1r = \frac {k}{q}$
. For every
$\frac 1r = \frac {k}{q}$
. For every
![]() $1 \leq j \leq k$
and every
$1 \leq j \leq k$
and every
![]() $n \in \mathbb {N}$
, since
$n \in \mathbb {N}$
, since
![]() $P_{\varepsilon _j}(x_{j, n}) \in \operatorname {L}^q(\mathscr W_{\varepsilon _j})$
, we may choose
$P_{\varepsilon _j}(x_{j, n}) \in \operatorname {L}^q(\mathscr W_{\varepsilon _j})$
, we may choose
![]() $w_{j, n} \in \mathscr W_{\varepsilon _j}$
, such that
$w_{j, n} \in \mathscr W_{\varepsilon _j}$
, such that
![]() $\|P_{\varepsilon _j}(x_{j, n}) - w_{j, n}\|_q \leq \frac {1}{n + 1}$
. For every
$\|P_{\varepsilon _j}(x_{j, n}) - w_{j, n}\|_q \leq \frac {1}{n + 1}$
. For every
![]() $1 \leq j \leq k$
and every
$1 \leq j \leq k$
and every
![]() $n \in \mathbb {N}$
, write
$n \in \mathbb {N}$
, write
![]() $P_{\varepsilon _j}(x_{j, n}) = w_{j, n} + (P_{\varepsilon _j}(x_{j, n}) - w_{j, n})$
and observe that
$P_{\varepsilon _j}(x_{j, n}) = w_{j, n} + (P_{\varepsilon _j}(x_{j, n}) - w_{j, n})$
and observe that
-
○
 $\max \left \{ \|w_{j, n} \|_{q}, \|P_{\varepsilon _j}(x_{j, n}) - w_{j, n} \|_q \right \} \leq 1 + \kappa _q$
.
$\max \left \{ \|w_{j, n} \|_{q}, \|P_{\varepsilon _j}(x_{j, n}) - w_{j, n} \|_q \right \} \leq 1 + \kappa _q$
.
We may then write
![]() $P_{\varepsilon _1}(x_{1, n}) \cdots P_{\varepsilon _k}(x_{k, n}) - w_{1, n} \cdots w_{k, n}$
as a sum of
$P_{\varepsilon _1}(x_{1, n}) \cdots P_{\varepsilon _k}(x_{k, n}) - w_{1, n} \cdots w_{k, n}$
as a sum of
![]() $2^k - 1$
terms that are products of length k for which at least one of the factors is of the form
$2^k - 1$
terms that are products of length k for which at least one of the factors is of the form
![]() $P_{\varepsilon _j}(x_{j, n}) - w_{j, n}$
for some
$P_{\varepsilon _j}(x_{j, n}) - w_{j, n}$
for some
![]() $1 \leq j \leq k$
. For every
$1 \leq j \leq k$
. For every
![]() $n\in \mathbb {N}$
, using the triangle inequality and the generalized noncommutative Hölder inequality, we obtain
$n\in \mathbb {N}$
, using the triangle inequality and the generalized noncommutative Hölder inequality, we obtain
This implies that
By combining (3.3) and (3.4), it follows that
In particular, since
![]() $\operatorname { E}_{B^{\mathcal U}} (x_1 \cdots x_k)=(\operatorname { E}_B (x_{1, n} \cdots x_{k, n}))^{\mathcal U}$
, using Lemma 2.2 and the fact that
$\operatorname { E}_{B^{\mathcal U}} (x_1 \cdots x_k)=(\operatorname { E}_B (x_{1, n} \cdots x_{k, n}))^{\mathcal U}$
, using Lemma 2.2 and the fact that
![]() $\operatorname { E}_B$
is
$\operatorname { E}_B$
is
![]() $\|\cdot \|_r$
-contractive, we have
$\|\cdot \|_r$
-contractive, we have
Since for every
![]() $1 \leq j \leq k$
and every
$1 \leq j \leq k$
and every
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
![]() $w_{j, n} \in \mathscr W_{\varepsilon _j}$
, and since
$w_{j, n} \in \mathscr W_{\varepsilon _j}$
, and since
![]() $\varepsilon _1 \neq \cdots \neq \varepsilon _k$
, it follows that
$\varepsilon _1 \neq \cdots \neq \varepsilon _k$
, it follows that
![]() $\operatorname { E}_B(w_{1, n} \cdots w_{k, n}) = 0$
. Thus, we obtain
$\operatorname { E}_B(w_{1, n} \cdots w_{k, n}) = 0$
. Thus, we obtain
![]() $\operatorname { E}_{B^{\mathcal U}}(x_1 \cdots x_k) =0$
.
$\operatorname { E}_{B^{\mathcal U}}(x_1 \cdots x_k) =0$
.
Remark 3.1. We were informed by Popa that he and Vaes had recently made the following observation. In the case
![]() $\operatorname {L}(\mathbb {F}_2) = A_1 \ast A_2$
is a free group factor with
$\operatorname {L}(\mathbb {F}_2) = A_1 \ast A_2$
is a free group factor with
![]() $A_1 \cong A_2 \cong \operatorname {L}(\mathbb {Z})$
, they showed that
$A_1 \cong A_2 \cong \operatorname {L}(\mathbb {Z})$
, they showed that
![]() $A_1' \cap \operatorname {L}(\mathbb {F}_2)^{\mathcal U}$
and
$A_1' \cap \operatorname {L}(\mathbb {F}_2)^{\mathcal U}$
and
![]() $A_2$
are freely independent in
$A_2$
are freely independent in
![]() $\operatorname {L}(\mathbb {F}_2)^{\mathcal U}$
with respect to
$\operatorname {L}(\mathbb {F}_2)^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
.
$\tau ^{\mathcal U}$
.
We obtain the following consequence of Theorem A which implies Theorem B.
Theorem 3.3. Assume that
![]() $B = \mathbb {C} 1$
. For every
$B = \mathbb {C} 1$
. For every
![]() $i \in I$
, let
$i \in I$
, let
![]() $(A_{i, k})_{k \in \mathbb {N}}$
be a decreasing sequence of separable diffuse abelian von Neumann subalgebras of
$(A_{i, k})_{k \in \mathbb {N}}$
be a decreasing sequence of separable diffuse abelian von Neumann subalgebras of
![]() $M_i^{\mathcal U}$
, such that
$M_i^{\mathcal U}$
, such that
![]() $\bigcap _{k = 1}^\infty A_{i, k} = \mathbb {C} 1$
.
$\bigcap _{k = 1}^\infty A_{i, k} = \mathbb {C} 1$
.
Then, for every
![]() $i \in I$
,
$i \in I$
,
![]() $\mathscr M_i = \bigvee _{k = 1}^\infty (A_{i, k}' \cap M^{\mathcal U}) \subset M^{\mathcal U}$
is a nonamenable irreducible subfactor with property Gamma. Moreover, the family
$\mathscr M_i = \bigvee _{k = 1}^\infty (A_{i, k}' \cap M^{\mathcal U}) \subset M^{\mathcal U}$
is a nonamenable irreducible subfactor with property Gamma. Moreover, the family
![]() $(\mathscr M_i)_{i \in I}$
is freely independent in
$(\mathscr M_i)_{i \in I}$
is freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
.
$\tau ^{\mathcal U}$
.
Proof. Let
![]() $i \in I$
. For every
$i \in I$
. For every
![]() $k \in \mathbb {N}$
, since
$k \in \mathbb {N}$
, since
![]() $A_{i, k}$
is separable, we have
$A_{i, k}$
is separable, we have
![]() $(A_{i, k}' \cap M^{\mathcal U})' \cap M^{\mathcal U} = A_{i, k}$
by [Reference PopaPo13a, Theorem 2.1]. This further implies that
$(A_{i, k}' \cap M^{\mathcal U})' \cap M^{\mathcal U} = A_{i, k}$
by [Reference PopaPo13a, Theorem 2.1]. This further implies that
 $$ \begin{align*}\mathscr M_i' \cap M^{\mathcal U} = (\bigvee_{k = 1}^\infty A_{i, k}' \cap M^{\mathcal U})' \cap M^{\mathcal U} = \bigcap_{k = 1}^\infty (A_{i, k}' \cap M^{\mathcal U})' \cap M^{\mathcal U} = \bigcap_{k = 1}^\infty A_{i, k} = \mathbb{C} 1.\end{align*} $$
$$ \begin{align*}\mathscr M_i' \cap M^{\mathcal U} = (\bigvee_{k = 1}^\infty A_{i, k}' \cap M^{\mathcal U})' \cap M^{\mathcal U} = \bigcap_{k = 1}^\infty (A_{i, k}' \cap M^{\mathcal U})' \cap M^{\mathcal U} = \bigcap_{k = 1}^\infty A_{i, k} = \mathbb{C} 1.\end{align*} $$
Therefore,
![]() $\mathscr M_i \subset M^{\mathcal U}$
is an irreducible subfactor. Since
$\mathscr M_i \subset M^{\mathcal U}$
is an irreducible subfactor. Since
![]() $A_{i, 0}' \cap M^{\mathcal U}$
is nonamenable,
$A_{i, 0}' \cap M^{\mathcal U}$
is nonamenable,
![]() $\mathscr M_i$
is nonamenable as well. Let
$\mathscr M_i$
is nonamenable as well. Let
![]() $\mathscr V$
be another nonprincipal ultrafilter on
$\mathscr V$
be another nonprincipal ultrafilter on
![]() $\mathbb {N}$
. For every
$\mathbb {N}$
. For every
![]() $k \in \mathbb {N}$
and every
$k \in \mathbb {N}$
and every
![]() $\lambda \in (0, 1)$
, choose a projection
$\lambda \in (0, 1)$
, choose a projection
![]() $p_{\lambda , k} \in A_{i, k}$
, such that
$p_{\lambda , k} \in A_{i, k}$
, such that
![]() $\tau ^{\mathcal U}(p_{\lambda , k}) = \lambda $
. Then
$\tau ^{\mathcal U}(p_{\lambda , k}) = \lambda $
. Then
![]() $p_{\lambda } = (p_{\lambda , k})^{\mathcal V} \in \mathscr M_i' \cap \mathscr M_i^{\mathcal V}$
is a projection such that
$p_{\lambda } = (p_{\lambda , k})^{\mathcal V} \in \mathscr M_i' \cap \mathscr M_i^{\mathcal V}$
is a projection such that
![]() $(\tau ^{\mathcal U})^{\mathcal V}(p_\lambda ) = \lambda $
. Therefore,
$(\tau ^{\mathcal U})^{\mathcal V}(p_\lambda ) = \lambda $
. Therefore,
![]() $\mathscr M_i' \cap \mathscr M_i^{\mathcal V}$
is a diffuse von Neumann algebra, and so
$\mathscr M_i' \cap \mathscr M_i^{\mathcal V}$
is a diffuse von Neumann algebra, and so
![]() $\mathscr M_i$
has property Gamma.
$\mathscr M_i$
has property Gamma.
A combination of Lemma 3.1 and Theorem A implies that all
![]() $k, \ell \in \mathbb {N}$
, the family
$k, \ell \in \mathbb {N}$
, the family
![]() $(A_{i, k}' \cap M^{\mathcal U})_{i \in I}$
is freely independent in
$(A_{i, k}' \cap M^{\mathcal U})_{i \in I}$
is freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
. Since for every
$\tau ^{\mathcal U}$
. Since for every
![]() $i \in I$
, the sequence of von Neumann subalgebras
$i \in I$
, the sequence of von Neumann subalgebras
![]() $(A_{i, k}' \cap M^{\mathcal U})_k$
is increasing, Kaplansky’s density theorem further implies that the family
$(A_{i, k}' \cap M^{\mathcal U})_k$
is increasing, Kaplansky’s density theorem further implies that the family
![]() $(\mathscr M_i)_{i \in I}$
is freely independent in
$(\mathscr M_i)_{i \in I}$
is freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\tau ^{\mathcal U}$
.
$\tau ^{\mathcal U}$
.
Proof of Theorem C
Keep the same notation as in Theorem A. Let
![]() $\mathbf Y_1 \subset \mathbf X_1$
be a subset with the property that
$\mathbf Y_1 \subset \mathbf X_1$
be a subset with the property that
![]() $a \mathbf Y_1 b \subset \mathbf X_1$
for all
$a \mathbf Y_1 b \subset \mathbf X_1$
for all
![]() $a, b \in M_1$
. Denote by
$a, b \in M_1$
. Denote by
![]() $M_1 \mathbf Y_1 M_1$
the linear span of all the elements of the form
$M_1 \mathbf Y_1 M_1$
the linear span of all the elements of the form
![]() $a Y b$
for
$a Y b$
for
![]() $a, b \in M_1$
and
$a, b \in M_1$
and
![]() $Y \in \mathbf Y_1$
. Then we have
$Y \in \mathbf Y_1$
. Then we have
![]() $M_1 \mathbf Y_1 M_1 \subset \mathbf X_1$
. Likewise, denote by
$M_1 \mathbf Y_1 M_1 \subset \mathbf X_1$
. Likewise, denote by
![]() $M_1 \mathscr W_2 M_1$
the linear span of all the elements of the form
$M_1 \mathscr W_2 M_1$
the linear span of all the elements of the form
![]() $a w b$
for
$a w b$
for
![]() $a, b \in M_1$
and
$a, b \in M_1$
and
![]() $w \in \mathscr W_2$
. Observe that any word with letters alternating from
$w \in \mathscr W_2$
. Observe that any word with letters alternating from
![]() $\mathbf Y_1$
and
$\mathbf Y_1$
and
![]() $M_1 \mathscr W_2 M_1$
can be written as a linear combination of words with letters alternating from
$M_1 \mathscr W_2 M_1$
can be written as a linear combination of words with letters alternating from
![]() $M_1 \mathbf Y_1 M_1 \cup (M_1 \ominus B)$
and
$M_1 \mathbf Y_1 M_1 \cup (M_1 \ominus B)$
and
![]() $\mathscr W_2$
. Since
$\mathscr W_2$
. Since
![]() $M_1 \mathbf Y_1 M_1 \cup (M_1 \ominus B) \subset \mathbf X_1$
and
$M_1 \mathbf Y_1 M_1 \cup (M_1 \ominus B) \subset \mathbf X_1$
and
![]() $\mathscr W_2 \subset \mathbf X_2$
, Theorem A implies that the sets
$\mathscr W_2 \subset \mathbf X_2$
, Theorem A implies that the sets
![]() $\mathbf Y_1$
and
$\mathbf Y_1$
and
![]() $M_1 \mathscr W_2 M_1$
are freely independent in
$M_1 \mathscr W_2 M_1$
are freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\operatorname { E}_{B^{\mathcal U}}$
.
$\operatorname { E}_{B^{\mathcal U}}$
.
Using Kaplansky’s density theorem, for any element
![]() $x \in M \ominus M_1$
, there exists a
$x \in M \ominus M_1$
, there exists a
![]() $\|\cdot \|_\infty $
-bounded sequence
$\|\cdot \|_\infty $
-bounded sequence
![]() $(x_n)_n$
in
$(x_n)_n$
in
![]() $M_1 \mathscr W_2 M_1$
, such that
$M_1 \mathscr W_2 M_1$
, such that
![]() $x_n \to x$
for the strong operator topology. Combining this fact with the first paragraph of the proof, we infer that the sets
$x_n \to x$
for the strong operator topology. Combining this fact with the first paragraph of the proof, we infer that the sets
![]() $\mathbf Y_1$
and
$\mathbf Y_1$
and
![]() $M \ominus M_1$
are freely independent in
$M \ominus M_1$
are freely independent in
![]() $M^{\mathcal U}$
with respect to
$M^{\mathcal U}$
with respect to
![]() $\operatorname { E}_{B^{\mathcal U}}$
.
$\operatorname { E}_{B^{\mathcal U}}$
.
3.3. Proof of Theorem D
This subsection is devoted to the proof of Theorem D. Moreover, we generalize Theorem D to arbitrary tracial amalgamated free product von Neumann algebras.
Theorem 3.4. Assume that
![]() $I=\{1,2\}$
. Let
$I=\{1,2\}$
. Let
![]() $u_1\in \mathscr U(M_1^{\mathcal U})$
and
$u_1\in \mathscr U(M_1^{\mathcal U})$
and
![]() $u_2\in \mathscr U(M_2^{\mathcal U})$
be such that
$u_2\in \mathscr U(M_2^{\mathcal U})$
be such that
![]() $\operatorname { E}_{B^{\mathcal U}}(u_1^k)=0$
, for every
$\operatorname { E}_{B^{\mathcal U}}(u_1^k)=0$
, for every
![]() $k\in \mathbb Z\setminus \{0\}$
, and
$k\in \mathbb Z\setminus \{0\}$
, and
![]() $\operatorname { E}_{B^{\mathcal U}}(u_2)=\operatorname { E}_{B^{\mathcal U}}(u_2^2)=0$
.
$\operatorname { E}_{B^{\mathcal U}}(u_2)=\operatorname { E}_{B^{\mathcal U}}(u_2^2)=0$
.
Then, there do not exist unitaries
![]() $v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
$v_1,v_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
and
$[u_1,v_1]=[v_1,v_2]=[v_2,u_2]=0$
and
![]() $\operatorname { E}_{B^{\mathcal U}}(v_1)=\operatorname { E}_{B^{\mathcal U}}(v_1^2)=\operatorname { E}_{B^{\mathcal U}}(v_2)=0$
.
$\operatorname { E}_{B^{\mathcal U}}(v_1)=\operatorname { E}_{B^{\mathcal U}}(v_1^2)=\operatorname { E}_{B^{\mathcal U}}(v_2)=0$
.
The proof of Theorem 3.4 relies on two lemmas. Using the notation from Section 2.3, for every
![]() $i,j\in I$
, we put
$i,j\in I$
, we put
![]() $\mathscr W_{i,j}=\mathscr L_i\cap \mathscr R_j$
and
$\mathscr W_{i,j}=\mathscr L_i\cap \mathscr R_j$
and
![]() $P_{i,j}=P_{\mathscr L_i}\circ P_{\mathscr R_j}$
. By Theorem 2.3, we have a completely bounded operator
$P_{i,j}=P_{\mathscr L_i}\circ P_{\mathscr R_j}$
. By Theorem 2.3, we have a completely bounded operator
![]() $P_{i,j}:\operatorname {L}^p(M)\to \operatorname {L}^p(\mathscr W_{i,j})$
, for every
$P_{i,j}:\operatorname {L}^p(M)\to \operatorname {L}^p(\mathscr W_{i,j})$
, for every
![]() $p\in (1,+\infty )$
.
$p\in (1,+\infty )$
.
Lemma 3.5. Assume that
![]() $I=\{1,2\}$
. Let
$I=\{1,2\}$
. Let
![]() $u \in \mathscr U(M_1^{\mathcal U})$
be such that
$u \in \mathscr U(M_1^{\mathcal U})$
be such that
![]() $\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
for all
$\operatorname { E}_{B^{\mathcal U}}(u^k) = 0$
for all
![]() $k \in \mathbb {Z} \setminus \{0\}$
. Let
$k \in \mathbb {Z} \setminus \{0\}$
. Let
![]() $x = (x_n)^{\mathcal U} \in \mathscr U(\{u\}' \cap M^{\mathcal U})$
and
$x = (x_n)^{\mathcal U} \in \mathscr U(\{u\}' \cap M^{\mathcal U})$
and
![]() $y=(y_n)^{\mathcal U}\in \{x\}'\cap M^{\mathcal U}$
with
$y=(y_n)^{\mathcal U}\in \{x\}'\cap M^{\mathcal U}$
with
![]() $\operatorname { E}_{B^{\mathcal U}}(x)=\operatorname { E}_{B^{\mathcal U}}(y)=0$
. Then
$\operatorname { E}_{B^{\mathcal U}}(x)=\operatorname { E}_{B^{\mathcal U}}(y)=0$
. Then
![]() $\lim _{n\rightarrow \mathcal U}\|P_{2,2}(y_n)\|_2^2=\lim _{n\rightarrow \mathcal U}\langle x_nP_{2,2}(y_n), P_{1,1}(y_n)x_n\rangle $
. Thus,
$\lim _{n\rightarrow \mathcal U}\|P_{2,2}(y_n)\|_2^2=\lim _{n\rightarrow \mathcal U}\langle x_nP_{2,2}(y_n), P_{1,1}(y_n)x_n\rangle $
. Thus,
![]() $\lim _{n\rightarrow \mathcal U}\|P_{2,2}(y_n)\|_2\leq \lim _{n\rightarrow \mathcal U}\|P_{1,1}(y_n)\|_2$
.
$\lim _{n\rightarrow \mathcal U}\|P_{2,2}(y_n)\|_2\leq \lim _{n\rightarrow \mathcal U}\|P_{1,1}(y_n)\|_2$
.
Proof. Since
![]() $\operatorname { E}_{B^{\mathcal U}}(y)=0$
, after replacing
$\operatorname { E}_{B^{\mathcal U}}(y)=0$
, after replacing
![]() $y_n$
with
$y_n$
with
![]() $y_n-\operatorname { E}_B(y_n)$
, we may assume that
$y_n-\operatorname { E}_B(y_n)$
, we may assume that
![]() $\operatorname { E}_B(y_n)=0$
, for all
$\operatorname { E}_B(y_n)=0$
, for all
![]() $n\in \mathbb N$
. We may assume that
$n\in \mathbb N$
. We may assume that
![]() $x_n\in \mathscr U(M)$
and
$x_n\in \mathscr U(M)$
and
![]() $\|y_n\|_\infty \leq 1$
, for all
$\|y_n\|_\infty \leq 1$
, for all
![]() $n\in \mathbb N$
. For
$n\in \mathbb N$
. For
![]() $p\in (1,+\infty )$
, let
$p\in (1,+\infty )$
, let
![]() $\kappa _p=\sup \left \{\|P_{i,j}(x)\|_p\mid i,j\in \{1,2\}, x\in \operatorname {L}^p(M),\|x\|_p\leq 1\right \}.$
$\kappa _p=\sup \left \{\|P_{i,j}(x)\|_p\mid i,j\in \{1,2\}, x\in \operatorname {L}^p(M),\|x\|_p\leq 1\right \}.$
For every
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $i,j\in \{1,2\}$
, put
$i,j\in \{1,2\}$
, put
![]() $y_n^{i,j}=P_{{i,j}}(y_n)$
. Then
$y_n^{i,j}=P_{{i,j}}(y_n)$
. Then
![]() $y_n=\sum _{i,j=1}^2y_n^{i,j}$
and
$y_n=\sum _{i,j=1}^2y_n^{i,j}$
and
![]() $\|y_n^{i,j}\|_p\leq \kappa _p$
, for every
$\|y_n^{i,j}\|_p\leq \kappa _p$
, for every
![]() $n\in \mathbb N,i,j\in \{1,2\}$
and
$n\in \mathbb N,i,j\in \{1,2\}$
and
![]() $p\in (1,+\infty )$
. We claim that
$p\in (1,+\infty )$
. We claim that
Let
![]() $(i,j)\not =(1,1)$
. By Lemma 3.1, we have
$(i,j)\not =(1,1)$
. By Lemma 3.1, we have
![]() $\lim _{n\rightarrow \mathcal U}\|x_n-P_{1,1}(x_n)\|_2=0$
. By using the noncommutative Hölder inequality and that
$\lim _{n\rightarrow \mathcal U}\|x_n-P_{1,1}(x_n)\|_2=0$
. By using the noncommutative Hölder inequality and that
![]() $1=\frac {1}{2}+3\cdot \frac {1}{6}$
, we get that
$1=\frac {1}{2}+3\cdot \frac {1}{6}$
, we get that
This implies that
Next, let
![]() $v_n\in \mathscr W_{1,1}$
and
$v_n\in \mathscr W_{1,1}$
and
![]() $w_n^{i,j}\in \mathscr W_{i,j}$
, such that
$w_n^{i,j}\in \mathscr W_{i,j}$
, such that
![]() $\|P_{1,1}(x_n)-v_n\|_4\leq \frac {1}{n}$
and
$\|P_{1,1}(x_n)-v_n\|_4\leq \frac {1}{n}$
and
![]() $\|y_n^{i,j}-w_n^{i,j}\|_4\leq \frac {1}{n}$
, for every
$\|y_n^{i,j}-w_n^{i,j}\|_4\leq \frac {1}{n}$
, for every
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $i,j\in \{1,2\}$
. Then
$i,j\in \{1,2\}$
. Then
![]() $\|v_n\|_4,\|w_n^{i,j}\|_4\leq \kappa _4+\frac {1}{n}\leq \kappa _4+1$
. Since
$\|v_n\|_4,\|w_n^{i,j}\|_4\leq \kappa _4+\frac {1}{n}\leq \kappa _4+1$
. Since
![]() $1=4\cdot \frac {1}{4}$
, applying the noncommutative Hölder inequality again gives that
$1=4\cdot \frac {1}{4}$
, applying the noncommutative Hölder inequality again gives that
This implies that
By combining (3.7) and (3.8), it follows that
Now,
![]() $v_nw_n^{2,2}v_n^*{w_n^{i,j}}^*\in \mathscr W_{1,1}\mathscr W_{2,2}\mathscr W_{1,1}\mathscr W_{i,j}^*\subset \mathscr W_{1,1}\mathscr W_{i,j}^*$
. Since
$v_nw_n^{2,2}v_n^*{w_n^{i,j}}^*\in \mathscr W_{1,1}\mathscr W_{2,2}\mathscr W_{1,1}\mathscr W_{i,j}^*\subset \mathscr W_{1,1}\mathscr W_{i,j}^*$
. Since
![]() $(i,j)\not =(1,1)$
,
$(i,j)\not =(1,1)$
,
![]() $\mathscr W_{1,1}$
and
$\mathscr W_{1,1}$
and
![]() $\mathscr W_{i,j}$
are orthogonal (algebraic) B-bimodules. Thus,
$\mathscr W_{i,j}$
are orthogonal (algebraic) B-bimodules. Thus,
![]() $\operatorname { E}_B(\mathscr W_{1,1}\mathscr W_{i,j}^*)=\{0\}$
and therefore
$\operatorname { E}_B(\mathscr W_{1,1}\mathscr W_{i,j}^*)=\{0\}$
and therefore
![]() $\operatorname { E}_B(v_nw_n^{2,2}v_n^*{w_n^{i,j}}^*)=0$
, for every
$\operatorname { E}_B(v_nw_n^{2,2}v_n^*{w_n^{i,j}}^*)=0$
, for every
![]() $n\in \mathbb N$
. In combination with (3.9), this proves (3.6).
$n\in \mathbb N$
. In combination with (3.9), this proves (3.6).
Finally, for every
![]() $n\in \mathbb N$
, we have that
$n\in \mathbb N$
, we have that
![]() $\|y_n^{2,2}\|_2^2=\langle y_n^{2,2},y_n\rangle =\langle x_ny_n^{2,2},x_ny_n\rangle $
. Since
$\|y_n^{2,2}\|_2^2=\langle y_n^{2,2},y_n\rangle =\langle x_ny_n^{2,2},x_ny_n\rangle $
. Since
![]() $\lim _{n\rightarrow \mathcal U}\|x_ny_n-y_nx_n\|_2=0$
, we get that
$\lim _{n\rightarrow \mathcal U}\|x_ny_n-y_nx_n\|_2=0$
, we get that
 $$ \begin{align*}\lim_{n\rightarrow\mathcal U}\|y_n^{2,2}\|_2^2=\lim_{n\rightarrow \mathcal U}\langle x_ny_n^{2,2},y_nx_n\rangle=\lim_{n\rightarrow\mathcal U}(\sum_{i,j=1}^2\langle x_ny_n^{2,2},y_n^{i,j}x_n\rangle).\end{align*} $$
$$ \begin{align*}\lim_{n\rightarrow\mathcal U}\|y_n^{2,2}\|_2^2=\lim_{n\rightarrow \mathcal U}\langle x_ny_n^{2,2},y_nx_n\rangle=\lim_{n\rightarrow\mathcal U}(\sum_{i,j=1}^2\langle x_ny_n^{2,2},y_n^{i,j}x_n\rangle).\end{align*} $$
On the other hand, (3.6) gives that
![]() $\lim _{n\rightarrow \mathcal U}\langle x_ny_n^{2,2},y_n^{i,j}x_n\rangle =0$
if
$\lim _{n\rightarrow \mathcal U}\langle x_ny_n^{2,2},y_n^{i,j}x_n\rangle =0$
if
![]() $(i,j)\not =(1,1)$
. Thus, we get
$(i,j)\not =(1,1)$
. Thus, we get
![]() $\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}\|_2^2=\lim _{n\rightarrow \mathcal U}\langle x_ny_n^{2,2}, y_n^{1,1}x_n\rangle $
, which proves the main assertion. Since
$\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}\|_2^2=\lim _{n\rightarrow \mathcal U}\langle x_ny_n^{2,2}, y_n^{1,1}x_n\rangle $
, which proves the main assertion. Since
![]() $|\langle x_ny_n^{2,2}, y_n^{1,1}x_n\rangle |\leq \|y_n^{2,2}\|_2\|y_n^{1,1}\|_2$
, we get that
$|\langle x_ny_n^{2,2}, y_n^{1,1}x_n\rangle |\leq \|y_n^{2,2}\|_2\|y_n^{1,1}\|_2$
, we get that
![]() $\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}\|_2\leq \lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2$
.
$\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}\|_2\leq \lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2$
.
Lemma 3.6. In the setting of Lemma 3.5, assume additionally that
![]() $\operatorname { E}_{B^{\mathcal U}}(x^2)=0$
and
$\operatorname { E}_{B^{\mathcal U}}(x^2)=0$
and
![]() $y\in \{v\}'\cap M^{\mathcal U}$
, for some
$y\in \{v\}'\cap M^{\mathcal U}$
, for some
![]() $v=(v_n)^{\mathcal U}\in \mathscr U(M_2^{\mathcal U})$
.
$v=(v_n)^{\mathcal U}\in \mathscr U(M_2^{\mathcal U})$
.
-
(i) If
 $\operatorname { E}_{B^{\mathcal U}}(v)=0$
, then
$\operatorname { E}_{B^{\mathcal U}}(v)=0$
, then
 $\lim _{n\rightarrow \mathcal U}\|P_{1,1}(y_n)\|_2=\lim _{n\rightarrow \mathcal U}\|P_{2,2}(y_n)\|_2=0$
.
$\lim _{n\rightarrow \mathcal U}\|P_{1,1}(y_n)\|_2=\lim _{n\rightarrow \mathcal U}\|P_{2,2}(y_n)\|_2=0$
. -
(ii) If
 $\operatorname { E}_{B^{\mathcal U}}(v)=\operatorname { E}_{B^{\mathcal U}}(v^2)=0$
, then
$\operatorname { E}_{B^{\mathcal U}}(v)=\operatorname { E}_{B^{\mathcal U}}(v^2)=0$
, then
 $y=0$
.
$y=0$
.
Proof. We keep the notation from the proof of Lemma 3.5.
(i) Assume that
![]() $\operatorname { E}_{B^{\mathcal U}}(v)=0$
. Write
$\operatorname { E}_{B^{\mathcal U}}(v)=0$
. Write
![]() $v=(v_n)^{\mathcal U}$
, where
$v=(v_n)^{\mathcal U}$
, where
![]() $v_n\in M_2\ominus B$
, for every
$v_n\in M_2\ominus B$
, for every
![]() $n\in \mathbb N$
, and
$n\in \mathbb N$
, and
![]() $\sup \left \{\|v_n\|_\infty \mid n\in \mathbb N\right \}<\infty $
. We first claim that
$\sup \left \{\|v_n\|_\infty \mid n\in \mathbb N\right \}<\infty $
. We first claim that
Since
![]() $vyv^*=y$
, we get that
$vyv^*=y$
, we get that
![]() $\lim _{n\rightarrow \mathcal U}\|v_n^*y_nv_n-y_n\|_2=0$
. Thus, we derive that
$\lim _{n\rightarrow \mathcal U}\|v_n^*y_nv_n-y_n\|_2=0$
. Thus, we derive that
Since
![]() $(M_2\ominus B)\mathscr W_{1,1}(M_2\ominus B)\subset \mathscr W_{2,2}$
, we also get that
$(M_2\ominus B)\mathscr W_{1,1}(M_2\ominus B)\subset \mathscr W_{2,2}$
, we also get that
![]() $P_{i,j}(v_ny_n^{1,1}v_n^*)=0$
, for every
$P_{i,j}(v_ny_n^{1,1}v_n^*)=0$
, for every
![]() $(i,j)\not =(2,2)$
and
$(i,j)\not =(2,2)$
and
![]() $n\in \mathbb N$
. This implies that
$n\in \mathbb N$
. This implies that
![]() $\langle v_ny_n^{1,1}v_n^*,y_n\rangle =\langle v_ny_n^{1,1}v_n^*, y_n^{2,2}\rangle $
, for every
$\langle v_ny_n^{1,1}v_n^*,y_n\rangle =\langle v_ny_n^{1,1}v_n^*, y_n^{2,2}\rangle $
, for every
![]() $n\in \mathbb N$
. Since
$n\in \mathbb N$
. Since
![]() $|\langle v_ny_n^{1,1}v_n^*, y_n^{2,2}\rangle \leq \|y_n^{1,1}\|_2\|y_n^{2,2}\|_2$
, for every
$|\langle v_ny_n^{1,1}v_n^*, y_n^{2,2}\rangle \leq \|y_n^{1,1}\|_2\|y_n^{2,2}\|_2$
, for every
![]() $n\in \mathbb N$
, we conclude that
$n\in \mathbb N$
, we conclude that
![]() $\lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2^2\leq \lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2\|y_n^{2,2}\|_2$
, and thus
$\lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2^2\leq \lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2\|y_n^{2,2}\|_2$
, and thus
On the other hand, Lemma 3.5 implies that
It is now clear that (3.11) and (3.12) together imply (3.10). Since y also commutes with
![]() $x^*=(x_n^*)$
, applying (3.10) to
$x^*=(x_n^*)$
, applying (3.10) to
![]() $x^*$
instead of x gives that
$x^*$
instead of x gives that
![]() $\lim _{n\rightarrow \mathcal U}\|x_n^*y_n^{2,2}-y_n^{1,1}x_n^*\|_2=0$
, and thus
$\lim _{n\rightarrow \mathcal U}\|x_n^*y_n^{2,2}-y_n^{1,1}x_n^*\|_2=0$
, and thus
![]() $\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}x_n-x_ny_n^{1,1}\|_2=0$
. In combination with (3.10), this implies that
$\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}x_n-x_ny_n^{1,1}\|_2=0$
. In combination with (3.10), this implies that
Since y commutes with
![]() $x^2=(x_n^2)$
and
$x^2=(x_n^2)$
and
![]() $\operatorname { E}_{B^{\mathcal U}}(x^2)=0$
, (3.6) from the proof of Lemma 3.5 gives that
$\operatorname { E}_{B^{\mathcal U}}(x^2)=0$
, (3.6) from the proof of Lemma 3.5 gives that
![]() $\lim _{n\rightarrow \mathcal U}\|\operatorname { E}_B(x_n^2y_n^{2,2}{x_n^2}^*{y_n^{2,2}}^*)\|_1=0$
, thus
$\lim _{n\rightarrow \mathcal U}\|\operatorname { E}_B(x_n^2y_n^{2,2}{x_n^2}^*{y_n^{2,2}}^*)\|_1=0$
, thus
![]() $\lim _{n\rightarrow \mathcal U}\langle x_n^2y_n^{2,2},y_n^{2,2}x_n^2\rangle =0$
. Together with (3.13), we get that
$\lim _{n\rightarrow \mathcal U}\langle x_n^2y_n^{2,2},y_n^{2,2}x_n^2\rangle =0$
. Together with (3.13), we get that
![]() $\lim _{n\rightarrow \mathcal U}\|x_n^2y_n^{2,2}\|_2=0$
. Since
$\lim _{n\rightarrow \mathcal U}\|x_n^2y_n^{2,2}\|_2=0$
. Since
![]() $x_n\in \mathscr U(M)$
, we get that
$x_n\in \mathscr U(M)$
, we get that
![]() $\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}\|_2=0$
, and (3.11) gives that
$\lim _{n\rightarrow \mathcal U}\|y_n^{2,2}\|_2=0$
, and (3.11) gives that
![]() $\lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2=0$
, proving part (i).
$\lim _{n\rightarrow \mathcal U}\|y_n^{1,1}\|_2=0$
, proving part (i).
(ii) Assume that
![]() $\operatorname { E}_{B^{\mathcal U}}(v)=\operatorname { E}_{B^{\mathcal U}}(v^2)=0$
. By (i), we have
$\operatorname { E}_{B^{\mathcal U}}(v)=\operatorname { E}_{B^{\mathcal U}}(v^2)=0$
. By (i), we have
![]() $\lim _{n\rightarrow \mathcal U}\|y_n-(y_{1,2}^n+y_{2,1}^n)\|_2=~0$
. Since
$\lim _{n\rightarrow \mathcal U}\|y_n-(y_{1,2}^n+y_{2,1}^n)\|_2=~0$
. Since
![]() $vy=yv$
, we have
$vy=yv$
, we have
![]() $\lim _{n\rightarrow \mathcal U}\|v_ny_n-y_n v_n\|_2=0$
, and so
$\lim _{n\rightarrow \mathcal U}\|v_ny_n-y_n v_n\|_2=0$
, and so
For every
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
![]() $v_ny_{1,2}^n = P_{2, 2}(v_ny_{1,2}^n)$
,
$v_ny_{1,2}^n = P_{2, 2}(v_ny_{1,2}^n)$
,
![]() $y_{2,1}^n v_n = P_{2, 2}(y_{2,1}^n v_n)$
,
$y_{2,1}^n v_n = P_{2, 2}(y_{2,1}^n v_n)$
,
![]() $v_ny_{2,1}^n = P_{1,1}(v_ny_{2,1}^n) + P_{2,1}(v_ny_{2,1}^n)$
and
$v_ny_{2,1}^n = P_{1,1}(v_ny_{2,1}^n) + P_{2,1}(v_ny_{2,1}^n)$
and
![]() $y_{1,2}^n v_n = P_{1, 1}(y_{1,2}^n v_n) + P_{1, 2}(y_{1,2}^n v_n)$
. In combination with (3.14), we obtain
$y_{1,2}^n v_n = P_{1, 1}(y_{1,2}^n v_n) + P_{1, 2}(y_{1,2}^n v_n)$
. In combination with (3.14), we obtain
For every
![]() $n \in \mathbb {N}$
, set
$n \in \mathbb {N}$
, set
![]() $\eta _n = P_{1,1}(v_ny_{2,1}^n) \in \operatorname {L}^2(M)$
. Then (3.15), Theorem 2.3 and Lemma 2.1 together imply that
$\eta _n = P_{1,1}(v_ny_{2,1}^n) \in \operatorname {L}^2(M)$
. Then (3.15), Theorem 2.3 and Lemma 2.1 together imply that
![]() $\eta = (\eta _n)^{\mathcal U} = (v_ny_{2,1}^n)^{\mathcal U} = (y_{1,2}^n v_n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
and that
$\eta = (\eta _n)^{\mathcal U} = (v_ny_{2,1}^n)^{\mathcal U} = (y_{1,2}^n v_n)^{\mathcal U} \in \operatorname {L}^2(M^{\mathcal U})$
and that
![]() $y = v^* \eta + \eta v^*$
. Since
$y = v^* \eta + \eta v^*$
. Since
![]() $v^* y = y v^*$
, we obtain
$v^* y = y v^*$
, we obtain
![]() $(v^*)^2 \eta = \eta (v^*)^2$
, and so
$(v^*)^2 \eta = \eta (v^*)^2$
, and so
![]() $v^2 \eta = \eta v^2$
. Since
$v^2 \eta = \eta v^2$
. Since
![]() $\operatorname { E}_{B^{\mathcal U}}(v^2) = 0$
, we may write
$\operatorname { E}_{B^{\mathcal U}}(v^2) = 0$
, we may write
![]() $v^2 = (w_n)^{\mathcal U}$
, where
$v^2 = (w_n)^{\mathcal U}$
, where
![]() $w_n \in M_2 \ominus B$
for every
$w_n \in M_2 \ominus B$
for every
![]() $n \in \mathbb {N}$
. For every
$n \in \mathbb {N}$
. For every
![]() $n \in \mathbb {N}$
, since
$n \in \mathbb {N}$
, since
![]() $\eta _n = P_{1,1}(\eta _n)$
, we have
$\eta _n = P_{1,1}(\eta _n)$
, we have
![]() $w_n \eta _n = P_{2, 1}(w_n \eta _n) \perp P_{1, 2}(\eta _n w_n) = \eta _n w_n$
. Then we obtain
$w_n \eta _n = P_{2, 1}(w_n \eta _n) \perp P_{1, 2}(\eta _n w_n) = \eta _n w_n$
. Then we obtain
![]() $v^2 \eta \perp \eta v^2$
. Since
$v^2 \eta \perp \eta v^2$
. Since
![]() $v^2 \eta = \eta v^2$
, this further implies that
$v^2 \eta = \eta v^2$
, this further implies that
![]() $v^2\eta = 0$
, and so
$v^2\eta = 0$
, and so
![]() $\eta = 0$
. Thus,
$\eta = 0$
. Thus,
![]() $y = 0$
.
$y = 0$
.
4. Proof of Theorem E
Proof of Theorem E
Let
![]() $P \subset M$
be a von Neumann subalgebra, such that
$P \subset M$
be a von Neumann subalgebra, such that
![]() $P \cap M_1 \npreceq _{M_1} B$
and
$P \cap M_1 \npreceq _{M_1} B$
and
![]() $P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Set
$P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Set
![]() $A = P \cap M_1$
. By [Reference Ioana, Peterson and PopaIPP05, Theorem 1.1], since
$A = P \cap M_1$
. By [Reference Ioana, Peterson and PopaIPP05, Theorem 1.1], since
![]() $A \npreceq _{M_1} B$
, we have
$A \npreceq _{M_1} B$
, we have
![]() $P' \cap M \subset A' \cap M \subset M_1$
, and so
$P' \cap M \subset A' \cap M \subset M_1$
, and so
![]() $P' \cap M = P' \cap M_1$
. The set of projections
$P' \cap M = P' \cap M_1$
. The set of projections
![]() $p \in P' \cap M_1$
for which
$p \in P' \cap M_1$
for which
![]() $Pp \subset pM_1p$
attains its maximum in a projection
$Pp \subset pM_1p$
attains its maximum in a projection
![]() $z \in \mathscr Z(P' \cap M_1)$
. It suffices to prove that
$z \in \mathscr Z(P' \cap M_1)$
. It suffices to prove that
![]() $z = 1$
. By contradiction, assume that
$z = 1$
. By contradiction, assume that
![]() $z \neq 1$
. Set
$z \neq 1$
. Set
![]() $q = z^\perp $
and
$q = z^\perp $
and
![]() $Q = P q$
.
$Q = P q$
.
Claim 4.1. We have
![]() $Q \preceq _{M} M_1$
.
$Q \preceq _{M} M_1$
.
Proof of Claim 4.1
By contradiction, assume that
![]() $Q \npreceq _{M} M_1$
. Choose a sequence
$Q \npreceq _{M} M_1$
. Choose a sequence
![]() $(w_k)_k$
in
$(w_k)_k$
in
![]() $\mathscr U(Q)$
, such that
$\mathscr U(Q)$
, such that
![]() $\lim _k \|\operatorname { E}_{M_1}(x^* w_k y)\|_2 = 0$
for all
$\lim _k \|\operatorname { E}_{M_1}(x^* w_k y)\|_2 = 0$
for all
![]() $x, y \in qM$
. Set
$x, y \in qM$
. Set
![]() $\mathscr Q = Q' \cap (q M q)^{\mathcal U} = q(P' \cap M^{\mathcal U})q$
. We have
$\mathscr Q = Q' \cap (q M q)^{\mathcal U} = q(P' \cap M^{\mathcal U})q$
. We have
![]() $\mathscr Q \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
.
$\mathscr Q \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
.
Firstly, we show that
![]() $\mathscr Q \preceq _{M^{\mathcal U}} M_1^{\mathcal U}$
. By contradiction, assume that
$\mathscr Q \preceq _{M^{\mathcal U}} M_1^{\mathcal U}$
. By contradiction, assume that
![]() $\mathscr Q \npreceq _{M^{\mathcal U}} M_1^{\mathcal U}$
. Since
$\mathscr Q \npreceq _{M^{\mathcal U}} M_1^{\mathcal U}$
. Since
![]() $A \npreceq _{M_1} B$
, by Lemma 2.4, we may choose
$A \npreceq _{M_1} B$
, by Lemma 2.4, we may choose
![]() $u \in \mathscr U(A^{\mathcal U})$
, such that
$u \in \mathscr U(A^{\mathcal U})$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(a u^m b) = 0$
for all
$\operatorname { E}_{B^{\mathcal U}}(a u^m b) = 0$
for all
![]() $a, b \in M_1$
and all
$a, b \in M_1$
and all
![]() $m \in \mathbb {Z} \setminus \{0\}$
. Since M is separable,
$m \in \mathbb {Z} \setminus \{0\}$
. Since M is separable,
![]() $\mathscr Q \npreceq _{M^{\mathcal U}} M_1^{\mathcal U}$
,
$\mathscr Q \npreceq _{M^{\mathcal U}} M_1^{\mathcal U}$
,
![]() $\mathscr Q\subset A'\cap M^{\mathcal U}$
and
$\mathscr Q\subset A'\cap M^{\mathcal U}$
and
![]() $u\in \mathscr U(A^{\mathcal U})$
, by a standard diagonal argument, we can construct a unitary
$u\in \mathscr U(A^{\mathcal U})$
, by a standard diagonal argument, we can construct a unitary
![]() $v \in \mathscr U(\mathscr Q)$
, such that
$v \in \mathscr U(\mathscr Q)$
, such that
![]() $\operatorname { E}_{M_1^{\mathcal U}}(v) = 0$
and
$\operatorname { E}_{M_1^{\mathcal U}}(v) = 0$
and
![]() $vu=uv$
. By Lemma 3.2, the set
$vu=uv$
. By Lemma 3.2, the set
![]() $\mathbf Y_1 = \{u\}' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U}) $
satisfies
$\mathbf Y_1 = \{u\}' \cap (M^{\mathcal U} \ominus M_1^{\mathcal U}) $
satisfies
![]() $a \mathbf Y_1 b \subset \mathbf X_1$
for all
$a \mathbf Y_1 b \subset \mathbf X_1$
for all
![]() $a, b \in M_1$
. On the one hand, applying Theorem C, since
$a, b \in M_1$
. On the one hand, applying Theorem C, since
![]() $v \in \mathbf Y_1$
, we have
$v \in \mathbf Y_1$
, we have
On the other hand, for every
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
![]() $v w_k = w_k v$
and
$v w_k = w_k v$
and
![]() $\operatorname { E}_{M_1}(w_k) \to 0$
strongly as
$\operatorname { E}_{M_1}(w_k) \to 0$
strongly as
![]() $k \to \infty $
. Altogether, since
$k \to \infty $
. Altogether, since
![]() $vv^* = v^*v = q = w_kw_k^* = w_k^*w_k$
, this implies that
$vv^* = v^*v = q = w_kw_k^* = w_k^*w_k$
, this implies that
![]() $\operatorname { E}_{B^{\mathcal U}}(q) = 0$
, a contradiction. Therefore, we have
$\operatorname { E}_{B^{\mathcal U}}(q) = 0$
, a contradiction. Therefore, we have
![]() $\mathscr Q \preceq _{M^{\mathcal U}} M_1^{\mathcal U}$
.
$\mathscr Q \preceq _{M^{\mathcal U}} M_1^{\mathcal U}$
.
Secondly, we derive a contradiction using the proof of [Reference IoanaIo12, Lemma 9.5]. By [Reference IoanaIo12, Lemma 9.5, Claim 1], there exist
![]() $\delta> 0$
and a nonempty finite subset
$\delta> 0$
and a nonempty finite subset
![]() $\mathscr F \subset qM$
, such that
$\mathscr F \subset qM$
, such that
Denote by
![]() $\mathbf M_1 \subset M_1^{\mathcal U}$
the set of all elements
$\mathbf M_1 \subset M_1^{\mathcal U}$
the set of all elements
![]() $x \in M_1^{\mathcal U}$
, such that
$x \in M_1^{\mathcal U}$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(d^* x c) = 0$
for all
$\operatorname { E}_{B^{\mathcal U}}(d^* x c) = 0$
for all
![]() $c, d \in M_1$
. Then denote by
$c, d \in M_1$
. Then denote by
![]() $\mathscr K \subset \operatorname {L}^2((qMq)^{\mathcal U})$
the
$\mathscr K \subset \operatorname {L}^2((qMq)^{\mathcal U})$
the
![]() $\|\cdot \|_2$
-closure of the linear span of the set
$\|\cdot \|_2$
-closure of the linear span of the set
![]() $\left \{a x b^* \mid a, b \in qM, x \in \mathbf M_1\right \}$
and by
$\left \{a x b^* \mid a, b \in qM, x \in \mathbf M_1\right \}$
and by
![]() $e : \operatorname {L}^2((qMq)^{\mathcal U}) \to \mathscr K$
the corresponding orthogonal projection.
$e : \operatorname {L}^2((qMq)^{\mathcal U}) \to \mathscr K$
the corresponding orthogonal projection.
Since
![]() $\mathscr Q \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
and since M is separable, by a standard diagonal argument, we can construct a unitary
$\mathscr Q \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
and since M is separable, by a standard diagonal argument, we can construct a unitary
![]() $v \in \mathscr U(\mathscr Q)$
, such that
$v \in \mathscr U(\mathscr Q)$
, such that
![]() $\operatorname { E}_{B^{\mathcal U}}(d^* v c) = 0$
for all
$\operatorname { E}_{B^{\mathcal U}}(d^* v c) = 0$
for all
![]() $c, d \in qM$
. Set
$c, d \in qM$
. Set
![]() $\xi = e(v) \in \mathscr K$
and
$\xi = e(v) \in \mathscr K$
and
![]() $\eta = \sum _{a, b \in \mathscr F} b \operatorname { E}_{M_1^{\mathcal U}}(b^* v a) a^* \in (qMq)^{\mathcal U}$
. Then, for every
$\eta = \sum _{a, b \in \mathscr F} b \operatorname { E}_{M_1^{\mathcal U}}(b^* v a) a^* \in (qMq)^{\mathcal U}$
. Then, for every
![]() $c,d\in M_1$
and
$c,d\in M_1$
and
![]() $a,b\in \mathscr F$
, we have
$a,b\in \mathscr F$
, we have
![]() $\operatorname { E}_{B^{\mathcal U}}(d^* \operatorname { E}_{M_1^{\mathcal U}}(b^* v a) c) = \operatorname { E}_{B^{\mathcal U}}(d^* b^* v a c)=0$
. Thus,
$\operatorname { E}_{B^{\mathcal U}}(d^* \operatorname { E}_{M_1^{\mathcal U}}(b^* v a) c) = \operatorname { E}_{B^{\mathcal U}}(d^* b^* v a c)=0$
. Thus,
![]() $\eta \in \mathscr K$
, and we have
$\eta \in \mathscr K$
, and we have
It follows that
![]() $\xi = e(v) \neq 0$
.
$\xi = e(v) \neq 0$
.
On the one hand, since
![]() $\mathscr K \subset \operatorname {L}^2((qMq)^{\mathcal U})$
is a
$\mathscr K \subset \operatorname {L}^2((qMq)^{\mathcal U})$
is a
![]() $qMq$
-
$qMq$
-
![]() $qMq$
-bimodule, and since
$qMq$
-bimodule, and since
![]() $v \in \mathscr Q$
, for every
$v \in \mathscr Q$
, for every
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
![]() $w_k \xi w_k^*= w_k e(v) w_k^* = e(w_k v w_k^*) = e(v) = \xi $
. On the other hand, following the proof of [Reference IoanaIo12, Lemma 9.5, Claim 2], we show that
$w_k \xi w_k^*= w_k e(v) w_k^* = e(w_k v w_k^*) = e(v) = \xi $
. On the other hand, following the proof of [Reference IoanaIo12, Lemma 9.5, Claim 2], we show that
![]() $\lim _k \langle w_k \xi w_k^*, \xi \rangle = 0$
. This will give a contradiction. By linearity and density, it suffices to show that
$\lim _k \langle w_k \xi w_k^*, \xi \rangle = 0$
. This will give a contradiction. By linearity and density, it suffices to show that
![]() $\lim _k \langle w_k \, a_1 x_1 b_1^* \, w_k^*, a_2 x_2 b_2^*\rangle = 0$
for all
$\lim _k \langle w_k \, a_1 x_1 b_1^* \, w_k^*, a_2 x_2 b_2^*\rangle = 0$
for all
![]() $a_1, a_2, b_1, b_2 \in q M$
and all
$a_1, a_2, b_1, b_2 \in q M$
and all
![]() $x_1, x_2 \in \mathbf M_1$
. So let us fix
$x_1, x_2 \in \mathbf M_1$
. So let us fix
![]() $a_1, a_2, b_1, b_2 \in q M$
and
$a_1, a_2, b_1, b_2 \in q M$
and
![]() $x_1, x_2 \in \mathbf M_1$
. We may further assume that
$x_1, x_2 \in \mathbf M_1$
. We may further assume that
![]() $\max \left \{\|a_i\|_\infty , \|b_i\|_\infty , \|x_i\|_\infty \mid i \in \{1, 2\}\right \} \leq 1$
. Then, for every
$\max \left \{\|a_i\|_\infty , \|b_i\|_\infty , \|x_i\|_\infty \mid i \in \{1, 2\}\right \} \leq 1$
. Then, for every
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
Using the amalgamated free product structure
![]() $M = M_1 \ast _B M_2$
, the inclusion
$M = M_1 \ast _B M_2$
, the inclusion
![]() $M_1 \subset M$
is mixing relative to B. In particular, since
$M_1 \subset M$
is mixing relative to B. In particular, since
![]() $x_1 \in \mathbf M_1$
, we have
$x_1 \in \mathbf M_1$
, we have
![]() $\operatorname { E}_{M_1^{\mathcal U}}(c^* x_1 d) = \operatorname { E}_{M_1^{\mathcal U}}(c^* x_1)= \operatorname { E}_{M_1^{\mathcal U}}(x_1 d)=0$
for all
$\operatorname { E}_{M_1^{\mathcal U}}(c^* x_1 d) = \operatorname { E}_{M_1^{\mathcal U}}(c^* x_1)= \operatorname { E}_{M_1^{\mathcal U}}(x_1 d)=0$
for all
![]() $c, d \in M \ominus M_1$
(see, e.g. the proof of [Reference Chifan and HoudayerCH08, Claim 2.5]). This implies
$c, d \in M \ominus M_1$
(see, e.g. the proof of [Reference Chifan and HoudayerCH08, Claim 2.5]). This implies
Thus, we have
This gives a contradiction and finishes the proof of Claim 4.1.
Since
![]() $Q \preceq _{M} M_1$
, there exist
$Q \preceq _{M} M_1$
, there exist
![]() $n \geq 1$
, a projection
$n \geq 1$
, a projection
![]() $r \in \mathbf M_n(M_1)$
, a nonzero partial isometry
$r \in \mathbf M_n(M_1)$
, a nonzero partial isometry
![]() $v = [v_1, \dots , v_n] \in \mathbf M_{1, n}(z^\perp M)r$
and a unital normal
$v = [v_1, \dots , v_n] \in \mathbf M_{1, n}(z^\perp M)r$
and a unital normal
![]() $\ast $
-homomorphism
$\ast $
-homomorphism
![]() $\pi : Q \to r\mathbf M_n(M_1)r$
, such that
$\pi : Q \to r\mathbf M_n(M_1)r$
, such that
![]() $a v = v \pi (a)$
for all
$a v = v \pi (a)$
for all
![]() $a \in Q$
. In particular, we have
$a \in Q$
. In particular, we have
![]() $A v_i \subset \sum _{j = 1}^n v_j M_1$
for every
$A v_i \subset \sum _{j = 1}^n v_j M_1$
for every
![]() $i \in \{1, \dots , n\}$
. By [Reference Ioana, Peterson and PopaIPP05, Theorem 1.1], since
$i \in \{1, \dots , n\}$
. By [Reference Ioana, Peterson and PopaIPP05, Theorem 1.1], since
![]() $A \npreceq _{M_1} B$
, we have
$A \npreceq _{M_1} B$
, we have
![]() $v_i \in M_1$
for every
$v_i \in M_1$
for every
![]() $i \in \{1, \dots , n\}$
. It follows that
$i \in \{1, \dots , n\}$
. It follows that
![]() $vv^* \in Q' \cap M_1$
and
$vv^* \in Q' \cap M_1$
and
![]() $Q vv^* \subset vv^* M_1 vv^*$
. Thus, we obtain
$Q vv^* \subset vv^* M_1 vv^*$
. Thus, we obtain
![]() $P(z + vv^*) \subset (z + vv^*) M_1 (z + vv^*)$
. This contradicts the maximality of the projection
$P(z + vv^*) \subset (z + vv^*) M_1 (z + vv^*)$
. This contradicts the maximality of the projection
![]() $z \in P' \cap M_1$
. Therefore, we have
$z \in P' \cap M_1$
. Therefore, we have
![]() $z = 1$
, and so
$z = 1$
, and so
![]() $P \subset M_1$
.
$P \subset M_1$
.
Remark 4.1. We make two observations.
-
(i) If
 $A \subset M_1$
is a von Neumann subalgebra, such that
$A \subset M_1$
is a von Neumann subalgebra, such that
 $A \npreceq _{M_1} B$
, then we have
$A \npreceq _{M_1} B$
, then we have
 $A \npreceq _M B$
. Indeed, this follows from the amalgamated free product structure
$A \npreceq _M B$
. Indeed, this follows from the amalgamated free product structure
 $M = M_1 \ast _B M_2$
and the fact that the inclusion
$M = M_1 \ast _B M_2$
and the fact that the inclusion
 $M_1 \subset M$
is mixing relative to B (see the proof of Claim 4.1).
$M_1 \subset M$
is mixing relative to B (see the proof of Claim 4.1). -
(ii) If
 $P \subset M$
is an amenable von Neumann subalgebra, such that
$P \subset M$
is an amenable von Neumann subalgebra, such that
 $P \npreceq _{M} B$
, then we have
$P \npreceq _{M} B$
, then we have
 $P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Indeed, by contradiction, assume that
$P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
. Indeed, by contradiction, assume that
 $P' \cap M^{\mathcal U} \preceq _{M^{\mathcal U}} B^{\mathcal U}$
. On the one hand, by [Reference IoanaIo12, Lemma 9.5, Claim 1], there exist
$P' \cap M^{\mathcal U} \preceq _{M^{\mathcal U}} B^{\mathcal U}$
. On the one hand, by [Reference IoanaIo12, Lemma 9.5, Claim 1], there exist
 $\delta> 0$
and a nonempty finite subset
$\delta> 0$
and a nonempty finite subset
 $\mathscr F \subset M$
, such that (4.1)
$\mathscr F \subset M$
, such that (4.1) $$ \begin{align} \forall v \in \mathscr U(P' \cap M^{\mathcal U}), \quad \sum_{a, b \in \mathscr F} \|\operatorname{ E}_{B^{\mathcal U}}(b^* v a)\|_2^2 \geq \delta. \end{align} $$
$$ \begin{align} \forall v \in \mathscr U(P' \cap M^{\mathcal U}), \quad \sum_{a, b \in \mathscr F} \|\operatorname{ E}_{B^{\mathcal U}}(b^* v a)\|_2^2 \geq \delta. \end{align} $$
On the other hand, since P is amenable, hence hyperfinite, by Connes’ fundamental result [Reference ConnesCo75], there exists an increasing sequence
 $(P_k)_k$
of finite dimensional von Neumann subalgebras of P, such that
$(P_k)_k$
of finite dimensional von Neumann subalgebras of P, such that
 $(\bigcup _kP_k)^{\prime \prime }=P$
and
$(\bigcup _kP_k)^{\prime \prime }=P$
and
 $P_k' \cap P \subset P$
has finite index for every
$P_k' \cap P \subset P$
has finite index for every
 $k \in \mathbb {N}$
(see, e.g. the proof of [Reference HoudayerHo12, Theorem 8.1]). Since
$k \in \mathbb {N}$
(see, e.g. the proof of [Reference HoudayerHo12, Theorem 8.1]). Since
 $P \npreceq _{M} B$
, it follows that
$P \npreceq _{M} B$
, it follows that
 $P_k'\cap P \npreceq _{M} B$
for every
$P_k'\cap P \npreceq _{M} B$
for every
 $k \in \mathbb {N}$
. Since M is separable, by a standard diagonal argument, we can construct a unitary
$k \in \mathbb {N}$
. Since M is separable, by a standard diagonal argument, we can construct a unitary
 $v \in \mathscr U(P' \cap M^{\mathcal U})$
, such that
$v \in \mathscr U(P' \cap M^{\mathcal U})$
, such that
 $\operatorname { E}_{B^{\mathcal U}}(b^* v a) = 0$
for all
$\operatorname { E}_{B^{\mathcal U}}(b^* v a) = 0$
for all
 $a, b \in M$
. This contradicts (4.1). Therefore, we have
$a, b \in M$
. This contradicts (4.1). Therefore, we have
 $P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
.
$P' \cap M^{\mathcal U} \npreceq _{M^{\mathcal U}} B^{\mathcal U}$
.
5. A lifting theorem and proofs of Theorems G and H
5.1. A lifting theorem
The goal of this subsection is to establish the following lifting theorem, which will be needed in the proof of Theorem G.
Theorem 5.1. Let
![]() $\mathcal U$
be an ultrafilter on a set K and
$\mathcal U$
be an ultrafilter on a set K and
![]() $(M_k,\tau _k),k\in K$
, be tracial von Neumann algebras. Let
$(M_k,\tau _k),k\in K$
, be tracial von Neumann algebras. Let
![]() $A,B\subset \prod _{\mathcal U}M_k$
be separable abelian von Neumann subalgebras which are
$A,B\subset \prod _{\mathcal U}M_k$
be separable abelian von Neumann subalgebras which are
![]() $2$
-independent in
$2$
-independent in
![]() $\prod _{\mathcal U}M_k$
with respect to
$\prod _{\mathcal U}M_k$
with respect to
![]() $(\tau _k)^{\mathcal U}$
. Then there exist orthogonal abelian von Neumann subalgebras
$(\tau _k)^{\mathcal U}$
. Then there exist orthogonal abelian von Neumann subalgebras
![]() $C_k,D_k\subset M_k$
, for every
$C_k,D_k\subset M_k$
, for every
![]() $k\in K$
, such that
$k\in K$
, such that
![]() $A\subset \prod _{\mathcal U}C_k$
and
$A\subset \prod _{\mathcal U}C_k$
and
![]() $B\subset \prod _{\mathcal U}D_k$
.
$B\subset \prod _{\mathcal U}D_k$
.
We do not know whether Theorem 5.1 still holds if we replace the assumption that A and B are
![]() $2$
-independent with the weaker assumption that A and B are orthogonal. When
$2$
-independent with the weaker assumption that A and B are orthogonal. When
![]() $\dim (A)=2$
and
$\dim (A)=2$
and
![]() $\dim (B)=3$
, Theorem 5.1 follows from [Reference Chifan, Ioana and ElayavalliCIKE22, Lemma 3.1], which, moreover, only assumes that A and B are orthogonal. Theorem 5.1 is new in all other cases, including when A and B are finite dimensional and of dimension at least
$\dim (B)=3$
, Theorem 5.1 follows from [Reference Chifan, Ioana and ElayavalliCIKE22, Lemma 3.1], which, moreover, only assumes that A and B are orthogonal. Theorem 5.1 is new in all other cases, including when A and B are finite dimensional and of dimension at least
![]() $3$
.
$3$
.
The proof of Theorem 5.1 relies on the following perturbation lemma. First, we need to introduce some additional terminology. Let
![]() $(M,\tau )$
be a tracial von Neumann algebra. We denote by
$(M,\tau )$
be a tracial von Neumann algebra. We denote by
![]() $M_{\text {sa},1}$
the set of
$M_{\text {sa},1}$
the set of
![]() $x\in M$
, such that
$x\in M$
, such that
![]() $x=x^*$
and
$x=x^*$
and
![]() $\|x\|_\infty \leq 1$
. Let
$\|x\|_\infty \leq 1$
. Let
![]() $x=(x_1,\dots , x_m)\in M^m$
and
$x=(x_1,\dots , x_m)\in M^m$
and
![]() $y=(y_1,\dots ,y_n)\in M^n$
, for some
$y=(y_1,\dots ,y_n)\in M^n$
, for some
![]() $m,n\in \mathbb N$
. For
$m,n\in \mathbb N$
. For
![]() $u\in \mathscr U(M)$
, we write
$u\in \mathscr U(M)$
, we write
![]() $uxu^*=(ux_1u^*, \dots , ux_mu^*)$
. We define
$uxu^*=(ux_1u^*, \dots , ux_mu^*)$
. We define
 $$ \begin{align*} \delta(x,y) &=\min \left\{\|[x_i,y_j]\|_2\mid 1\leq i\leq m,1\leq j\leq n \right\}, \\ \varepsilon(x,y) &=\max \left\{|\tau(x_iy_j)|\mid 1\leq i\leq m,1\leq j\leq n \right\}, \\ \gamma(x,y) &=\max \left\{|\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle|\mid 1\leq i,i'\leq m,1\leq j,j'\leq n, (i,j)\not=(i',j') \right\}. \end{align*} $$
$$ \begin{align*} \delta(x,y) &=\min \left\{\|[x_i,y_j]\|_2\mid 1\leq i\leq m,1\leq j\leq n \right\}, \\ \varepsilon(x,y) &=\max \left\{|\tau(x_iy_j)|\mid 1\leq i\leq m,1\leq j\leq n \right\}, \\ \gamma(x,y) &=\max \left\{|\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle|\mid 1\leq i,i'\leq m,1\leq j,j'\leq n, (i,j)\not=(i',j') \right\}. \end{align*} $$
Lemma 5.2. Let
![]() $(M,\tau )$
be a tracial von Neumann algebra,
$(M,\tau )$
be a tracial von Neumann algebra,
![]() $x=(x_1,\dots , x_m)\in M_{{sa},1}^m$
and
$x=(x_1,\dots , x_m)\in M_{{sa},1}^m$
and
![]() $y=(y_1,\dots ,y_n)\in M_{sa,1}^n$
, for
$y=(y_1,\dots ,y_n)\in M_{sa,1}^n$
, for
![]() $m,n\in \mathbb N$
. Set
$m,n\in \mathbb N$
. Set
![]() $\delta _0=\delta (x,y), \varepsilon _0=\varepsilon (x,y),\gamma _0=\gamma (x,y)$
. Assume that
$\delta _0=\delta (x,y), \varepsilon _0=\varepsilon (x,y),\gamma _0=\gamma (x,y)$
. Assume that
![]() $13mn\sqrt {\varepsilon _0} < \delta _0^2 - (mn-1)\gamma _0$
. Then there exists
$13mn\sqrt {\varepsilon _0} < \delta _0^2 - (mn-1)\gamma _0$
. Then there exists
![]() $v\in \mathscr U(M)$
, such that
$v\in \mathscr U(M)$
, such that
 $$ \begin{align*}\|v-1\|_\infty \leq \frac{8mn\varepsilon_0}{\delta_0^2-(mn-1)\gamma_0} \leq\frac{8}{13}\sqrt{\varepsilon_0} \quad \text{and} \quad \varepsilon(vxv^*,y)=0.\end{align*} $$
$$ \begin{align*}\|v-1\|_\infty \leq \frac{8mn\varepsilon_0}{\delta_0^2-(mn-1)\gamma_0} \leq\frac{8}{13}\sqrt{\varepsilon_0} \quad \text{and} \quad \varepsilon(vxv^*,y)=0.\end{align*} $$
Note that Lemma 5.2 is interesting even when M is finite dimensional. To prove Lemma 5.2, we will need two auxiliary lemmas.
Lemma 5.3. Let
![]() $(M,\tau )$
be a tracial von Neumann algebra,
$(M,\tau )$
be a tracial von Neumann algebra,
![]() $\xi _1,\dots ,\xi _p\in M_{{sa},1}$
and
$\xi _1,\dots ,\xi _p\in M_{{sa},1}$
and
![]() $\alpha _1,\dots ,\alpha _p\in \mathbb R$
, for some
$\alpha _1,\dots ,\alpha _p\in \mathbb R$
, for some
![]() $p\geq 2$
. Let
$p\geq 2$
. Let
![]() $\delta \in (0,1)$
and
$\delta \in (0,1)$
and
![]() $\varepsilon \in (0,\frac {\delta ^2}{p-1})$
. Assume that
$\varepsilon \in (0,\frac {\delta ^2}{p-1})$
. Assume that
![]() $\|\xi _i\|_2 \geq \delta $
, for every
$\|\xi _i\|_2 \geq \delta $
, for every
![]() $1\leq i\leq p$
, and
$1\leq i\leq p$
, and
![]() $|\langle \xi _i,\xi _j\rangle |\leq \varepsilon $
, for every
$|\langle \xi _i,\xi _j\rangle |\leq \varepsilon $
, for every
![]() $1\leq i<j\leq p$
. Then there exists
$1\leq i<j\leq p$
. Then there exists
![]() $h\in M$
, such that
$h\in M$
, such that
![]() $h=h^*, \|h\|_\infty \leq \frac {\sum _{j=1}^p|\alpha _j|}{\delta ^2 -(p-1)\varepsilon }$
and
$h=h^*, \|h\|_\infty \leq \frac {\sum _{j=1}^p|\alpha _j|}{\delta ^2 -(p-1)\varepsilon }$
and
![]() $\tau (h\xi _i)=\alpha _i$
, for every
$\tau (h\xi _i)=\alpha _i$
, for every
![]() $1\leq i\leq p$
.
$1\leq i\leq p$
.
Proof. First, we claim that
![]() $\xi _1,\dots ,\xi _p$
are linearly independent. Otherwise, we can find
$\xi _1,\dots ,\xi _p$
are linearly independent. Otherwise, we can find
![]() $\beta _1,\dots ,\beta _p\in \mathbb R$
, such that
$\beta _1,\dots ,\beta _p\in \mathbb R$
, such that
![]() $\beta _1\xi _1+\cdots +\beta _p\xi _p=0$
and
$\beta _1\xi _1+\cdots +\beta _p\xi _p=0$
and
![]() $\max \left \{|\beta _i|\mid 1\leq i\leq p \right \}>0$
. Let
$\max \left \{|\beta _i|\mid 1\leq i\leq p \right \}>0$
. Let
![]() $1\leq j\leq p$
, such that
$1\leq j\leq p$
, such that
![]() $|\beta _j|=\max \left \{|\beta _i|\mid 1\leq i\leq p \right \}$
. Then
$|\beta _j|=\max \left \{|\beta _i|\mid 1\leq i\leq p \right \}$
. Then
![]() $-\beta _j\xi _j=\sum _{i\not =j}\beta _i\xi _i$
, and thus
$-\beta _j\xi _j=\sum _{i\not =j}\beta _i\xi _i$
, and thus
![]() $|\beta _j|\, \|\xi _j\|_2^2 \leq \sum _{i\not =j}|\beta _i|\, |\langle \xi _i,\xi _j\rangle |\leq |\beta _j|\sum _{i\not =j}|\langle \xi _i,\xi _j\rangle |$
. Since
$|\beta _j|\, \|\xi _j\|_2^2 \leq \sum _{i\not =j}|\beta _i|\, |\langle \xi _i,\xi _j\rangle |\leq |\beta _j|\sum _{i\not =j}|\langle \xi _i,\xi _j\rangle |$
. Since
![]() $\beta _j\not =0$
, we derive that
$\beta _j\not =0$
, we derive that
![]() $\|\xi _j\|_2^2\leq \sum _{i\not =j}|\langle \xi _i,\xi _j\rangle |$
, which implies that
$\|\xi _j\|_2^2\leq \sum _{i\not =j}|\langle \xi _i,\xi _j\rangle |$
, which implies that
![]() $\delta ^2\leq (p-1)\varepsilon $
, contradicting that
$\delta ^2\leq (p-1)\varepsilon $
, contradicting that
![]() $\delta ^2> (p-1)\varepsilon $
.
$\delta ^2> (p-1)\varepsilon $
.
Since
![]() $\xi _1,\dots ,\xi _p$
are linearly independent, it follows that we can find
$\xi _1,\dots ,\xi _p$
are linearly independent, it follows that we can find
![]() $\lambda _1,\dots ,\lambda _p\in \mathbb R$
, such that
$\lambda _1,\dots ,\lambda _p\in \mathbb R$
, such that
![]() $h=\sum _{i=1}^p\lambda _i\xi _i$
satisfies
$h=\sum _{i=1}^p\lambda _i\xi _i$
satisfies
![]() $\tau (h\xi _j)=\langle h,\xi _j\rangle =\alpha _j$
, for every
$\tau (h\xi _j)=\langle h,\xi _j\rangle =\alpha _j$
, for every
![]() $1\leq j\leq p$
. Then
$1\leq j\leq p$
. Then
![]() $|\alpha _j|=|\sum _{i=1}^p\lambda _i\langle \xi _i,\xi _j\rangle |\geq |\lambda _j|\|\xi _j\|_2^2-\sum _{i\not =j}|\lambda _i||\langle \xi _i,\xi _j\rangle |$
, and thus
$|\alpha _j|=|\sum _{i=1}^p\lambda _i\langle \xi _i,\xi _j\rangle |\geq |\lambda _j|\|\xi _j\|_2^2-\sum _{i\not =j}|\lambda _i||\langle \xi _i,\xi _j\rangle |$
, and thus
Adding the inequalities in (5.1) for
![]() $1\leq j\leq p$
gives
$1\leq j\leq p$
gives
![]() $\sum _{j=1}^p|\alpha _j|\geq (\delta ^2 - (p-1)\varepsilon )\sum _{j=1}^p|\lambda _j|$
. Thus,
$\sum _{j=1}^p|\alpha _j|\geq (\delta ^2 - (p-1)\varepsilon )\sum _{j=1}^p|\lambda _j|$
. Thus,
![]() $\|h\|_\infty \leq \sum _{j=1}^p|\lambda _j|\leq \frac {\sum _{j=1}^p|\alpha _j|}{\delta ^2-(p-1)\varepsilon }$
. Since
$\|h\|_\infty \leq \sum _{j=1}^p|\lambda _j|\leq \frac {\sum _{j=1}^p|\alpha _j|}{\delta ^2-(p-1)\varepsilon }$
. Since
![]() $h=h^*$
, this finishes the proof.
$h=h^*$
, this finishes the proof.
Lemma 5.4. Let
![]() $(M,\tau )$
be a tracial von Neumann algebra,
$(M,\tau )$
be a tracial von Neumann algebra,
![]() $x=(x_1,\dots , x_m)\in M_{{sa},1}^m$
and
$x=(x_1,\dots , x_m)\in M_{{sa},1}^m$
and
![]() ${y=(y_1,\dots ,y_n)\in M_{{sa},1}^n}$
, for some
${y=(y_1,\dots ,y_n)\in M_{{sa},1}^n}$
, for some
![]() $m,n\in \mathbb N$
. Set
$m,n\in \mathbb N$
. Set
![]() $\delta =\delta (x,y), \varepsilon =\varepsilon (x,y),\gamma =\gamma (x,y)$
. Assume that
$\delta =\delta (x,y), \varepsilon =\varepsilon (x,y),\gamma =\gamma (x,y)$
. Assume that
![]() $2mn\varepsilon <\delta ^2-(mn-1)\gamma $
, and set
$2mn\varepsilon <\delta ^2-(mn-1)\gamma $
, and set
![]() $\lambda =\frac {2 mn\varepsilon }{\delta ^2 -(mn-1)\gamma }<1$
.
$\lambda =\frac {2 mn\varepsilon }{\delta ^2 -(mn-1)\gamma }<1$
.
Then there exists
![]() $u\in \mathscr U(M)$
, such that
$u\in \mathscr U(M)$
, such that
-
(i)
 $\|u-1\|_\infty \leq 2\lambda $
.
$\|u-1\|_\infty \leq 2\lambda $
. -
(ii)
 $\delta (uxu^*,y)\geq \delta -8\lambda $
.
$\delta (uxu^*,y)\geq \delta -8\lambda $
. -
(iii)
 $\varepsilon (uxu^*,y)\leq 4\lambda ^2$
.
$\varepsilon (uxu^*,y)\leq 4\lambda ^2$
. -
(iv)
 $\gamma (uxu^*,y)\leq \gamma +32\lambda $
.
$\gamma (uxu^*,y)\leq \gamma +32\lambda $
.
Proof. For every
![]() $1\leq i\leq m,1\leq j\leq n$
, set
$1\leq i\leq m,1\leq j\leq n$
, set
![]() $\xi _{i,j}=-\frac {\mathrm {i}}{2}[x_i,y_j]$
. Then
$\xi _{i,j}=-\frac {\mathrm {i}}{2}[x_i,y_j]$
. Then
![]() $\xi _{i,j}\in M_{\text {sa},1}$
and
$\xi _{i,j}\in M_{\text {sa},1}$
and
![]() $\|\xi _{i,j}\|_2=\frac {\|[x_i,y_j]\|_2}{2}\geq \frac {\delta }{2}$
, for every
$\|\xi _{i,j}\|_2=\frac {\|[x_i,y_j]\|_2}{2}\geq \frac {\delta }{2}$
, for every
![]() $1\leq i\leq m,1\leq j\leq n$
. On the other hand, for every
$1\leq i\leq m,1\leq j\leq n$
. On the other hand, for every
![]() $(i,j)\not =(i',j')$
, we have
$(i,j)\not =(i',j')$
, we have
![]() $|\langle \xi _{i,j},\xi _{i',j'}\rangle |=\frac {|\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle |}{4}\leq \frac {\gamma }{4}$
.
$|\langle \xi _{i,j},\xi _{i',j'}\rangle |=\frac {|\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle |}{4}\leq \frac {\gamma }{4}$
.
By applying Lemma 5.3 to
![]() $\xi _{i,j}$
and
$\xi _{i,j}$
and
![]() $\alpha _{i,j}=\frac {\tau (x_iy_j)}{2}$
, we may find
$\alpha _{i,j}=\frac {\tau (x_iy_j)}{2}$
, we may find
![]() $h\in M$
, such that
$h\in M$
, such that
![]() $h=h^*$
,
$h=h^*$
,
and
 $$ \begin{align} \|h\|_\infty\leq \frac{\sum_{i,j}\frac{|\tau(x_iy_j)|}{2}}{\frac{\delta^2}{4}-(mn-1)\frac{\gamma}{4}}\leq\frac{2mn\varepsilon}{\delta^2 - (mn-1)\gamma}=\lambda. \end{align} $$
$$ \begin{align} \|h\|_\infty\leq \frac{\sum_{i,j}\frac{|\tau(x_iy_j)|}{2}}{\frac{\delta^2}{4}-(mn-1)\frac{\gamma}{4}}\leq\frac{2mn\varepsilon}{\delta^2 - (mn-1)\gamma}=\lambda. \end{align} $$
Define
![]() $u=\exp (\mathrm {i} h)\in \mathscr U(M)$
. We will prove that u satisfies the conclusion. Since for every
$u=\exp (\mathrm {i} h)\in \mathscr U(M)$
. We will prove that u satisfies the conclusion. Since for every
![]() $x\in \mathbb R$
,
$x\in \mathbb R$
,
![]() $|\exp (\mathrm {i} x)-1|\leq 2|x|$
and
$|\exp (\mathrm {i} x)-1|\leq 2|x|$
and
![]() $|\exp (\mathrm {i} x)-(1+ \mathrm {i} x)|\leq x^2$
, using (5.3), we get that
$|\exp (\mathrm {i} x)-(1+ \mathrm {i} x)|\leq x^2$
, using (5.3), we get that
Let
![]() $1\leq i\leq m$
and
$1\leq i\leq m$
and
![]() $1\leq j\leq n$
. Then, using (5.3) and the second part of (5.4), we get that
$1\leq j\leq n$
. Then, using (5.3) and the second part of (5.4), we get that
![]() $\|ux_iu^*y_j-(1+ \mathrm {i} h)x_i(1+ \mathrm {i} h)^*y_j\|_\infty \leq \|u-(1+ \mathrm {i} h)\|_\infty (1+\|1+ \mathrm {i} h\|_\infty )\leq \lambda ^2(2+\lambda )\leq 3\lambda ^2$
and
$\|ux_iu^*y_j-(1+ \mathrm {i} h)x_i(1+ \mathrm {i} h)^*y_j\|_\infty \leq \|u-(1+ \mathrm {i} h)\|_\infty (1+\|1+ \mathrm {i} h\|_\infty )\leq \lambda ^2(2+\lambda )\leq 3\lambda ^2$
and
![]() $\|(1+ \mathrm {i} h)x_i(1+ \mathrm {i} h)^*y_j-(x_iy_j+ \mathrm {i} (hx_iy_j-x_ihy_j))\|_\infty =\|hx_ihy_j\|_\infty \leq \lambda ^2.$
Thus, we get
$\|(1+ \mathrm {i} h)x_i(1+ \mathrm {i} h)^*y_j-(x_iy_j+ \mathrm {i} (hx_iy_j-x_ihy_j))\|_\infty =\|hx_ihy_j\|_\infty \leq \lambda ^2.$
Thus, we get
and, therefore,
![]() $|\tau (ux_iu^*y_j)-\tau (x_iy_j+ \mathrm {i} (hx_iy_j-x_ihy_j))|\leq 4\lambda ^2$
. On the other hand, (5.2) gives
$|\tau (ux_iu^*y_j)-\tau (x_iy_j+ \mathrm {i} (hx_iy_j-x_ihy_j))|\leq 4\lambda ^2$
. On the other hand, (5.2) gives
![]() $\tau (x_iy_j+ \mathrm {i} (hx_iy_j-x_ihy_j))=\tau (x_iy_j)+\tau (\mathrm {i} h[x_i,y_j])=\tau (x_iy_j)-2\tau (h\xi _{i,j})=0$
. Altogether, we get that
$\tau (x_iy_j+ \mathrm {i} (hx_iy_j-x_ihy_j))=\tau (x_iy_j)+\tau (\mathrm {i} h[x_i,y_j])=\tau (x_iy_j)-2\tau (h\xi _{i,j})=0$
. Altogether, we get that
![]() $|\tau (ux_iu^*y_j)|\leq 4\lambda ^2$
. Thus,
$|\tau (ux_iu^*y_j)|\leq 4\lambda ^2$
. Thus,
![]() $\varepsilon (uxu^*,y)\leq 4\lambda ^2$
, which proves (iii).
$\varepsilon (uxu^*,y)\leq 4\lambda ^2$
, which proves (iii).
Next,
![]() $\|[ux_iu^*,y_j]-[x_i,y_j]\|_2\leq 2\|ux_iu^*-x_i\|_2\leq 4\|u-1\|_2\leq 8\lambda $
, by the first part of (5.4). Hence,
$\|[ux_iu^*,y_j]-[x_i,y_j]\|_2\leq 2\|ux_iu^*-x_i\|_2\leq 4\|u-1\|_2\leq 8\lambda $
, by the first part of (5.4). Hence,
![]() $\|[ux_iu^*,y_j]\|_2\geq \|[x_i,y_j]\|_2-8\lambda \geq \delta -8\lambda $
, for every
$\|[ux_iu^*,y_j]\|_2\geq \|[x_i,y_j]\|_2-8\lambda \geq \delta -8\lambda $
, for every
![]() $1\leq i\leq m$
and
$1\leq i\leq m$
and
![]() $1\leq j\leq n$
. This implies that
$1\leq j\leq n$
. This implies that
![]() $\delta (uxu^*,y)\geq \delta -8\lambda $
, which proves (ii).
$\delta (uxu^*,y)\geq \delta -8\lambda $
, which proves (ii).
Finally, for every
![]() $(i,j),(i',j')$
, we have
$(i,j),(i',j')$
, we have
![]() $\|[ux_{i'}u^*,y_{j'}]\|_2\leq 2$
,
$\|[ux_{i'}u^*,y_{j'}]\|_2\leq 2$
,
![]() $\|[x_i,y_j]\|_2\leq 2$
, and thus
$\|[x_i,y_j]\|_2\leq 2$
, and thus
 $$ \begin{align*} &|\langle [ux_iu^*,y_j],[ux_{i'}u^*,y_{j'}]\rangle-\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle|\\ & \quad \leq 2\big(\|[ux_iu^*,y_j]-[x_i,y_j]\|_2+\|[ux_{i'}u^*,y_{j'}]-[x_{i'},y_{j'}]\|_2\big)\leq 32\lambda. \end{align*} $$
$$ \begin{align*} &|\langle [ux_iu^*,y_j],[ux_{i'}u^*,y_{j'}]\rangle-\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle|\\ & \quad \leq 2\big(\|[ux_iu^*,y_j]-[x_i,y_j]\|_2+\|[ux_{i'}u^*,y_{j'}]-[x_{i'},y_{j'}]\|_2\big)\leq 32\lambda. \end{align*} $$
Thus,
![]() $|\langle [ux_iu^*,y_j],[ux_{i'}u^*,y_{j'}]\rangle |\leq |\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle |+32\lambda \leq \gamma +32\lambda $
. This implies that
$|\langle [ux_iu^*,y_j],[ux_{i'}u^*,y_{j'}]\rangle |\leq |\langle [x_i,y_j],[x_{i'},y_{j'}]\rangle |+32\lambda \leq \gamma +32\lambda $
. This implies that
![]() $\gamma (uxu^*,y)\leq \gamma +32\lambda $
, which proves (iv). Since (i) also holds by the first part of (5.4), this finishes the proof.
$\gamma (uxu^*,y)\leq \gamma +32\lambda $
, which proves (iv). Since (i) also holds by the first part of (5.4), this finishes the proof.
Proof of Lemma 5.2
We will inductively construct sequences
![]() $(u_k)_{k\in \mathbb N}\subset \mathscr U(M)$
and
$(u_k)_{k\in \mathbb N}\subset \mathscr U(M)$
and
![]() $(\lambda _k)_{k\in \mathbb N}\subset (0,\infty )$
with the following properties:
$(\lambda _k)_{k\in \mathbb N}\subset (0,\infty )$
with the following properties:
![]() $\lambda _0=1$
,
$\lambda _0=1$
,
![]() $\lambda _1=\frac {2mn\varepsilon _0}{\delta _0^2-(mn-1)\gamma _0}$
, and if we define
$\lambda _1=\frac {2mn\varepsilon _0}{\delta _0^2-(mn-1)\gamma _0}$
, and if we define
![]() $v_0=1$
,
$v_0=1$
,
![]() $v_k=u_ku_{k-1}\cdots u_1\in \mathscr U(M)$
,
$v_k=u_ku_{k-1}\cdots u_1\in \mathscr U(M)$
,
![]() $\delta _k=\delta (v_kxv_k^*,y),\varepsilon _k=\varepsilon (v_kxv_k^*,y)$
and
$\delta _k=\delta (v_kxv_k^*,y),\varepsilon _k=\varepsilon (v_kxv_k^*,y)$
and
![]() $\gamma _k=\gamma (v_kxv_k^*,y)$
, for every
$\gamma _k=\gamma (v_kxv_k^*,y)$
, for every
![]() $k\geq 0$
, then, for every
$k\geq 0$
, then, for every
![]() $k\geq 1$
, we have that
$k\geq 1$
, we have that
-
1.
 $\|u_k-1\|_\infty \leq 2\lambda _k$
.
$\|u_k-1\|_\infty \leq 2\lambda _k$
. -
2.
 $\delta _k\geq \delta _{k-1}-8\lambda _k$
.
$\delta _k\geq \delta _{k-1}-8\lambda _k$
. -
3.
 $\varepsilon _k\leq 4\lambda _k^2$
.
$\varepsilon _k\leq 4\lambda _k^2$
. -
4.
 $\gamma _k\leq \gamma _{k-1}+32\lambda _k$
.
$\gamma _k\leq \gamma _{k-1}+32\lambda _k$
. -
5.
 $\lambda _k\leq \frac {\lambda _{k-1}}{2}.$
$\lambda _k\leq \frac {\lambda _{k-1}}{2}.$
Since
![]() $\varepsilon _0\leq 1$
, we have that
$\varepsilon _0\leq 1$
, we have that
![]() $4mn\varepsilon _0\leq 13mn\sqrt {\varepsilon _0} < \delta _0^2 - (mn-1)\gamma _0$
. Thus,
$4mn\varepsilon _0\leq 13mn\sqrt {\varepsilon _0} < \delta _0^2 - (mn-1)\gamma _0$
. Thus,
![]() $\lambda _1<\frac {1}{2}$
, and hence condition (v) holds for
$\lambda _1<\frac {1}{2}$
, and hence condition (v) holds for
![]() $k=1$
. By applying Lemma 5.4, we can find
$k=1$
. By applying Lemma 5.4, we can find
![]() $u_1\in \mathscr U(M)$
, such that conditions (i)–(iv) hold for
$u_1\in \mathscr U(M)$
, such that conditions (i)–(iv) hold for
![]() $k=1$
.
$k=1$
.
Next, assume that we have constructed
![]() $u_1,\dots , u_l\in \mathscr U(M)$
and
$u_1,\dots , u_l\in \mathscr U(M)$
and
![]() $\lambda _1,\dots ,\lambda _l\in (0,\infty )$
, for some
$\lambda _1,\dots ,\lambda _l\in (0,\infty )$
, for some
![]() $l\in \mathbb N$
, such that conditions (i)–(v) are satisfied for
$l\in \mathbb N$
, such that conditions (i)–(v) are satisfied for
![]() $k=1,\dots ,l$
. Our goal is to construct
$k=1,\dots ,l$
. Our goal is to construct
![]() $u_{l+1}$
and
$u_{l+1}$
and
![]() $\lambda _{l+1}$
. Let
$\lambda _{l+1}$
. Let
![]() $\lambda _{l+1}=\frac {2mn\varepsilon _l}{\delta _l^2-(mn-1)\gamma _l}$
. We continue with the following claim.
$\lambda _{l+1}=\frac {2mn\varepsilon _l}{\delta _l^2-(mn-1)\gamma _l}$
. We continue with the following claim.
Claim 5.5.
![]() $\lambda _{l+1}\leq \frac {\lambda _l}{2}$
.
$\lambda _{l+1}\leq \frac {\lambda _l}{2}$
.
Proof of Claim 5.5. First, (ii) implies that
![]() $\delta _k^2 \geq (\delta _{k-1}-8\lambda _k)^2 \geq \delta _{k - 1}^2 - 32 \lambda _k$
. Then combining (ii) and (iv) gives that
$\delta _k^2 \geq (\delta _{k-1}-8\lambda _k)^2 \geq \delta _{k - 1}^2 - 32 \lambda _k$
. Then combining (ii) and (iv) gives that
which implies that
![]() $\delta _l^2-(mn-1)\gamma _l\geq (\delta _0^2-(mn-1)\gamma _0)- 32mn(\sum _{k=1}^l\lambda _k).$
By using that (v) holds for
$\delta _l^2-(mn-1)\gamma _l\geq (\delta _0^2-(mn-1)\gamma _0)- 32mn(\sum _{k=1}^l\lambda _k).$
By using that (v) holds for
![]() $k=1,\dots ,l$
, we also get that
$k=1,\dots ,l$
, we also get that
![]() $\sum _{k=1}^l\lambda _k\leq 2\lambda _1$
. By combining the last two inequalities, we get that
$\sum _{k=1}^l\lambda _k\leq 2\lambda _1$
. By combining the last two inequalities, we get that
Since
![]() $13mn\sqrt {\varepsilon _0} < \delta _0^2 - (mn-1)\gamma _0$
, we get that
$13mn\sqrt {\varepsilon _0} < \delta _0^2 - (mn-1)\gamma _0$
, we get that
![]() $(\delta _0^2-(mn-1)\gamma _0)^2> 169(mn)^2 \varepsilon _0$
, and thus
$(\delta _0^2-(mn-1)\gamma _0)^2> 169(mn)^2 \varepsilon _0$
, and thus
By combining (5.5) and (5.6), we derive that
Since (v) holds for every
![]() $k=1,\dots ,l$
, we get that
$k=1,\dots ,l$
, we get that
![]() $\lambda _l\leq \lambda _1$
. Since
$\lambda _l\leq \lambda _1$
. Since
![]() $\varepsilon _l\leq 4\lambda _l^2$
by (iii), using (5.7), we get that
$\varepsilon _l\leq 4\lambda _l^2$
by (iii), using (5.7), we get that
 $$ \begin{align*}\lambda_{l+1}=\frac{2 mn\varepsilon_l}{\delta_l^2 -(mn-1)\gamma_l}\leq \frac{8mn\lambda_l^2}{\delta_l^2-(mn-1)\gamma_l}\leq\frac{16mn\lambda_1}{\delta_l^2-(mn-1)\gamma_l}\cdot\frac{\lambda_l}{2}\leq\frac{\lambda_l}{2}.\end{align*} $$
$$ \begin{align*}\lambda_{l+1}=\frac{2 mn\varepsilon_l}{\delta_l^2 -(mn-1)\gamma_l}\leq \frac{8mn\lambda_l^2}{\delta_l^2-(mn-1)\gamma_l}\leq\frac{16mn\lambda_1}{\delta_l^2-(mn-1)\gamma_l}\cdot\frac{\lambda_l}{2}\leq\frac{\lambda_l}{2}.\end{align*} $$
This finishes the proof of the claim.
By using (v) and Claim 5.5, we get that
![]() $\lambda _{l+1}\leq \frac {1}{2^{l+1}}<1$
. Thus,
$\lambda _{l+1}\leq \frac {1}{2^{l+1}}<1$
. Thus,
![]() $2 mn\varepsilon _l < \delta _l^2 -(mn-1)\gamma _l$
. We can, therefore, apply Lemma 5.4 to
$2 mn\varepsilon _l < \delta _l^2 -(mn-1)\gamma _l$
. We can, therefore, apply Lemma 5.4 to
![]() $v_lxv_l^*$
and y to find
$v_lxv_l^*$
and y to find
![]() $u_{l+1}\in \mathscr U(M)$
, such that
$u_{l+1}\in \mathscr U(M)$
, such that
-
1.
 $\|u_{l+1}-1\|_\infty \leq 2\lambda _{l+1}$
.
$\|u_{l+1}-1\|_\infty \leq 2\lambda _{l+1}$
. -
2.
 $\delta _{l+1}=\delta (u_{l+1}(v_lxv_l^*)u_{l+1}^*),y)\geq \delta _{l}-8\lambda _{l+1}$
.
$\delta _{l+1}=\delta (u_{l+1}(v_lxv_l^*)u_{l+1}^*),y)\geq \delta _{l}-8\lambda _{l+1}$
. -
3.
 $\varepsilon _{l+1}=\varepsilon (u_{l+1}(v_lxv_l^*)u_{l+1}^*,y)\leq 4\lambda _{l+1}^2$
.
$\varepsilon _{l+1}=\varepsilon (u_{l+1}(v_lxv_l^*)u_{l+1}^*,y)\leq 4\lambda _{l+1}^2$
. -
4.
 $\gamma _{l+1}=\gamma (u_{l+1}(v_lxv_l^*)u_{l+1}^*,y)\leq \gamma _l+32\lambda _{l+1}$
.
$\gamma _{l+1}=\gamma (u_{l+1}(v_lxv_l^*)u_{l+1}^*,y)\leq \gamma _l+32\lambda _{l+1}$
.
By induction, this finishes the construction of
![]() $(u_k)_{k\in \mathbb N}\subset \mathscr U(M)$
and
$(u_k)_{k\in \mathbb N}\subset \mathscr U(M)$
and
![]() $(\lambda _k)_{k\in \mathbb N}\subset (0,\infty )$
. Finally, since
$(\lambda _k)_{k\in \mathbb N}\subset (0,\infty )$
. Finally, since
![]() $\lambda _0=1$
, (v) implies that
$\lambda _0=1$
, (v) implies that
![]() $\lambda _k\leq \frac {1}{2^k}$
, for every
$\lambda _k\leq \frac {1}{2^k}$
, for every
![]() $k\geq 0$
. Using (i), we derive that
$k\geq 0$
. Using (i), we derive that
![]() $\|v_k-v_{k-1}\|_\infty =\|u_k-1\|_\infty \leq \frac {1}{2^{k-1}}$
, for every
$\|v_k-v_{k-1}\|_\infty =\|u_k-1\|_\infty \leq \frac {1}{2^{k-1}}$
, for every
![]() $k\geq 1$
. Thus, the sequence
$k\geq 1$
. Thus, the sequence
![]() $(v_k)_{k\in \mathbb N}$
is Cauchy in
$(v_k)_{k\in \mathbb N}$
is Cauchy in
![]() $\|\cdot \|_\infty $
, and so we can find
$\|\cdot \|_\infty $
, and so we can find
![]() $v\in \mathscr U(M)$
, such that
$v\in \mathscr U(M)$
, such that
![]() $\lim _{k\rightarrow \infty }\|v_k-v\|_\infty =0$
. Using (iii), we get that
$\lim _{k\rightarrow \infty }\|v_k-v\|_\infty =0$
. Using (iii), we get that
![]() $\varepsilon _k\leq 4\lambda _k^2\leq \frac {1}{4^{k-1}}$
, for every
$\varepsilon _k\leq 4\lambda _k^2\leq \frac {1}{4^{k-1}}$
, for every
![]() $k\geq 1$
. Thus,
$k\geq 1$
. Thus,
![]() $\varepsilon (vxv^*,y)=\lim _{k\rightarrow \infty }\varepsilon _k=0$
. Moreover, using (i) and (v), we get that
$\varepsilon (vxv^*,y)=\lim _{k\rightarrow \infty }\varepsilon _k=0$
. Moreover, using (i) and (v), we get that
![]() $\|v_k-1\|_\infty \leq \sum _{l=1}^k\|u_l-1\|_\infty \leq \sum _{l=1}^k2\lambda _l\leq 4\lambda _1.$
Hence,
$\|v_k-1\|_\infty \leq \sum _{l=1}^k\|u_l-1\|_\infty \leq \sum _{l=1}^k2\lambda _l\leq 4\lambda _1.$
Hence,
![]() $\|v-1\|_\infty =\lim _{k\rightarrow \infty }\|v_k-1\|_\infty \leq 4\lambda _1= \frac {8mn\varepsilon _0}{\delta _0^2-(mn-1)\gamma _0}$
. This finishes the proof.
$\|v-1\|_\infty =\lim _{k\rightarrow \infty }\|v_k-1\|_\infty \leq 4\lambda _1= \frac {8mn\varepsilon _0}{\delta _0^2-(mn-1)\gamma _0}$
. This finishes the proof.
Proof of Theorem 5.1
We may clearly assume that
![]() $\dim (A)\geq 2$
and
$\dim (A)\geq 2$
and
![]() $\dim (B)\geq 2$
. Since A and B are separable, we can write
$\dim (B)\geq 2$
. Since A and B are separable, we can write
![]() $A=(\bigcup _{n\in \mathbb N}A_n)^{\prime \prime }$
,
$A=(\bigcup _{n\in \mathbb N}A_n)^{\prime \prime }$
,
![]() $B=(\bigcup _{n\in \mathbb N}B_n)^{\prime \prime }$
, where
$B=(\bigcup _{n\in \mathbb N}B_n)^{\prime \prime }$
, where
![]() $A_n\subset A, B_n\subset B$
are finite dimensional von Neumann subalgebras, such that
$A_n\subset A, B_n\subset B$
are finite dimensional von Neumann subalgebras, such that
![]() $A_n\subset A_{n+1}$
,
$A_n\subset A_{n+1}$
,
![]() $B_n\subset B_{n+1}$
,
$B_n\subset B_{n+1}$
,
![]() $a_n:=\dim (A_n)\geq 2$
and
$a_n:=\dim (A_n)\geq 2$
and
![]() $b_n:=\dim (B_n)\geq 2$
, for every
$b_n:=\dim (B_n)\geq 2$
, for every
![]() $n\in \mathbb N$
. Fix
$n\in \mathbb N$
. Fix
![]() $n\in \mathbb N$
. Write
$n\in \mathbb N$
. Write
![]() $A_n=\bigoplus _{i=1}^{a_n}\mathbb Cp_{n,i}$
and
$A_n=\bigoplus _{i=1}^{a_n}\mathbb Cp_{n,i}$
and
![]() $B_n=\bigoplus _{j=1}^{b_n}\mathbb Cq_{n,j}$
, where
$B_n=\bigoplus _{j=1}^{b_n}\mathbb Cq_{n,j}$
, where
![]() $(p_{n,i})_{i=1}^{a_n}$
and
$(p_{n,i})_{i=1}^{a_n}$
and
![]() $(q_{n,j})_{j=1}^{b_n}$
are partitions of unity into projections from A and B, respectively. For every
$(q_{n,j})_{j=1}^{b_n}$
are partitions of unity into projections from A and B, respectively. For every
![]() $1\leq i\leq a_n$
and
$1\leq i\leq a_n$
and
![]() $1\leq j\leq b_n$
, represent
$1\leq j\leq b_n$
, represent
![]() $p_{n,i},q_{n,j}\in \prod _{\mathcal U}M_k$
as
$p_{n,i},q_{n,j}\in \prod _{\mathcal U}M_k$
as
![]() $p_{n,i}=(p_{n,i}^k)^{\mathcal U}$
and
$p_{n,i}=(p_{n,i}^k)^{\mathcal U}$
and
![]() $q_{n,j}=(q_{n,j}^k)^{\mathcal U}$
, where for every
$q_{n,j}=(q_{n,j}^k)^{\mathcal U}$
, where for every
![]() $k\in K$
,
$k\in K$
,
![]() $(p_{n,i}^k)_{i=1}^{a_n}$
and
$(p_{n,i}^k)_{i=1}^{a_n}$
and
![]() $(q_{n,j}^k)_{j=1}^{b_n}$
are partitions of unity into projections from
$(q_{n,j}^k)_{j=1}^{b_n}$
are partitions of unity into projections from
![]() $M_k$
. Denote
$M_k$
. Denote
![]() $A_n^k=\bigoplus _{i=1}^{a_n}\mathbb Cp_{n,i}^k$
and
$A_n^k=\bigoplus _{i=1}^{a_n}\mathbb Cp_{n,i}^k$
and
![]() $B_n^k=\bigoplus _{j=1}^{b_n}\mathbb Cq_{n,j}^k$
. Moreover, we can arrange that
$B_n^k=\bigoplus _{j=1}^{b_n}\mathbb Cq_{n,j}^k$
. Moreover, we can arrange that
![]() $A_n^k\subset A_{n+1}^k$
and
$A_n^k\subset A_{n+1}^k$
and
![]() $B_n^k\subset B_{n+1}^k$
, for every
$B_n^k\subset B_{n+1}^k$
, for every
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $k\in K$
.
$k\in K$
.
If
![]() $(r_l)_{l=1}^m$
is a partition of unity into nonzero projections from a tracial von Neumann algebra
$(r_l)_{l=1}^m$
is a partition of unity into nonzero projections from a tracial von Neumann algebra
![]() $(N,\tau )$
, then
$(N,\tau )$
, then
![]() $\left \{\tau (r_{l+1}+\cdots +r_m)r_l-\tau (r_l)(r_{l+1}+\cdots +r_m)\mid 1\leq l\leq m-1 \right \}$
is an orthogonal basis for
$\left \{\tau (r_{l+1}+\cdots +r_m)r_l-\tau (r_l)(r_{l+1}+\cdots +r_m)\mid 1\leq l\leq m-1 \right \}$
is an orthogonal basis for
![]() $C\ominus \mathbb C1$
contained in
$C\ominus \mathbb C1$
contained in
![]() $C_{\text {sa},1}$
, where
$C_{\text {sa},1}$
, where
![]() $C=\bigoplus _{l=1}^m\mathbb Cr_l$
. Using this observation, for every
$C=\bigoplus _{l=1}^m\mathbb Cr_l$
. Using this observation, for every
![]() $1\leq i\leq a_n-1,1\leq j\leq b_n-1$
and
$1\leq i\leq a_n-1,1\leq j\leq b_n-1$
and
![]() $k\in K$
, we define
$k\in K$
, we define
Set
![]() $x_n=(x_{n,i})_{i=1}^{a_n-1}\in A_n^{a_n-1}, y_n=(y_{n,j})_{j=1}^{b_n-1}\in B_n^{b_n-1}, x_n^k=(x_{n,i}^k)_{i=1}^{a_n-1}\in M_k^{a_n-1}$
and
$x_n=(x_{n,i})_{i=1}^{a_n-1}\in A_n^{a_n-1}, y_n=(y_{n,j})_{j=1}^{b_n-1}\in B_n^{b_n-1}, x_n^k=(x_{n,i}^k)_{i=1}^{a_n-1}\in M_k^{a_n-1}$
and
![]() $y_n^k=(y_{n,j}^k)_{j=1}^{b_n-1}\in M_k^{b_n-1}$
. Let
$y_n^k=(y_{n,j}^k)_{j=1}^{b_n-1}\in M_k^{b_n-1}$
. Let
![]() $n\in \mathbb N$
,
$n\in \mathbb N$
,
![]() $1\leq i,i'\leq a_n-1$
and
$1\leq i,i'\leq a_n-1$
and
![]() $1\leq j,j'\leq b_n-1$
with
$1\leq j,j'\leq b_n-1$
with
![]() $(i,j)\not =(i',j')$
. Since
$(i,j)\not =(i',j')$
. Since
![]() $A_n$
and
$A_n$
and
![]() $B_n$
are
$B_n$
are
![]() $2$
-independent,
$2$
-independent,
![]() $x_{n,i}\not =0$
and
$x_{n,i}\not =0$
and
![]() $y_{n,j}\not =0$
, we have that
$y_{n,j}\not =0$
, we have that
![]() $\|[x_{n,i},y_{n,j}]\|_2= \sqrt {2}\|x_{n,i}\|_2\|y_{n,j}\|_2>0$
and
$\|[x_{n,i},y_{n,j}]\|_2= \sqrt {2}\|x_{n,i}\|_2\|y_{n,j}\|_2>0$
and
![]() $\tau (x_{n,i}y_{j,n})=0$
. Moreover,
$\tau (x_{n,i}y_{j,n})=0$
. Moreover,
![]() $\langle [x_{n,i},y_{n,j}],[x_{n,i'},y_{n,j'}]\rangle =2\tau (x_{n,i}x_{n,i'})\tau (y_{n,j}y_{n,j'}).$
Since
$\langle [x_{n,i},y_{n,j}],[x_{n,i'},y_{n,j'}]\rangle =2\tau (x_{n,i}x_{n,i'})\tau (y_{n,j}y_{n,j'}).$
Since
![]() $(x_{n,i})_{i=1}^{a_n-1}$
and
$(x_{n,i})_{i=1}^{a_n-1}$
and
![]() $(y_{n,j})_{j=1}^{b_n-1}$
are pairwise orthogonal, we get that
$(y_{n,j})_{j=1}^{b_n-1}$
are pairwise orthogonal, we get that
![]() $\langle [x_{n,i},y_{n,j}],[x_{n,i'},y_{n,j'}]\rangle =0$
. Altogether, we derive that
$\langle [x_{n,i},y_{n,j}],[x_{n,i'},y_{n,j'}]\rangle =0$
. Altogether, we derive that
![]() $\delta (x_n,y_n)>0$
and
$\delta (x_n,y_n)>0$
and
![]() $\varepsilon (x_n,y_n)=\gamma (x_n,y_n)=0$
.
$\varepsilon (x_n,y_n)=\gamma (x_n,y_n)=0$
.
Thus, we get that
![]() $\lim _{k\rightarrow \mathcal U}\delta (x_n^k,y_n^k)=\delta (x_n,y_n)>0$
,
$\lim _{k\rightarrow \mathcal U}\delta (x_n^k,y_n^k)=\delta (x_n,y_n)>0$
,
![]() $\lim _{k\rightarrow \mathcal U}\varepsilon (x_n^k,y_n^k)=\varepsilon (x_n,y_n)=0$
and
$\lim _{k\rightarrow \mathcal U}\varepsilon (x_n^k,y_n^k)=\varepsilon (x_n,y_n)=0$
and
![]() $\lim _{k\rightarrow \mathcal U}\gamma (x_n^k,y_n^k)=\gamma (x_n,y_n)=0$
. By applying Lemma 5.2, we find
$\lim _{k\rightarrow \mathcal U}\gamma (x_n^k,y_n^k)=\gamma (x_n,y_n)=0$
. By applying Lemma 5.2, we find
![]() $v_n^k\in \mathscr U(M_k)$
, for every
$v_n^k\in \mathscr U(M_k)$
, for every
![]() $k\in K$
, such that
$k\in K$
, such that
![]() $\varepsilon (v_n^kx_n^k{v_n^k}^*,y_n^k)=0$
, for every
$\varepsilon (v_n^kx_n^k{v_n^k}^*,y_n^k)=0$
, for every
![]() $k\in K$
, and
$k\in K$
, and
![]() $\lim _{k\rightarrow \mathcal U}\|v_n^k-1\|_\infty =~0$
. Since
$\lim _{k\rightarrow \mathcal U}\|v_n^k-1\|_\infty =~0$
. Since
![]() $x_n^k$
and
$x_n^k$
and
![]() $y_n^k$
are bases for
$y_n^k$
are bases for
![]() $A_n^k$
and
$A_n^k$
and
![]() $B_n^k$
, respectively, we get that
$B_n^k$
, respectively, we get that
![]() $v_n^kA_n^k{v_n^k}^*$
and
$v_n^kA_n^k{v_n^k}^*$
and
![]() $B_n^k$
are orthogonal, for every
$B_n^k$
are orthogonal, for every
![]() $k\in K$
.
$k\in K$
.
To complete the proof, we consider two cases:
Case 1.
![]() $\mathcal U$
is countably cofinal.
$\mathcal U$
is countably cofinal.
In this case, we proceed as in the proof of [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.2]. Since
![]() $\mathcal U$
is countably cofinal, there exists a decreasing sequence
$\mathcal U$
is countably cofinal, there exists a decreasing sequence
![]() $\{S_n\}_{n\geq 2}$
of sets in
$\{S_n\}_{n\geq 2}$
of sets in
![]() $\mathcal U$
, such that
$\mathcal U$
, such that
![]() $\bigcap _{n\geq 2}S_n=\emptyset $
. For
$\bigcap _{n\geq 2}S_n=\emptyset $
. For
![]() $n\geq 2$
, let
$n\geq 2$
, let
![]() $T_n=\{k\in K\mid \|v_m^k-1\|_\infty <\frac {1}{n}, \forall 1\leq m\leq n\}\in \mathcal U$
, and set
$T_n=\{k\in K\mid \|v_m^k-1\|_\infty <\frac {1}{n}, \forall 1\leq m\leq n\}\in \mathcal U$
, and set
![]() $K_n=S_n\cap T_n$
. Then
$K_n=S_n\cap T_n$
. Then
![]() $\{K_n\}_{n\geq 2}$
is a decreasing sequence of sets in
$\{K_n\}_{n\geq 2}$
is a decreasing sequence of sets in
![]() $\mathcal U$
, such that
$\mathcal U$
, such that
![]() $\bigcap _{n\geq 2}K_n=\emptyset $
. Let
$\bigcap _{n\geq 2}K_n=\emptyset $
. Let
![]() $K_1=K\setminus K_2$
. For every
$K_1=K\setminus K_2$
. For every
![]() $k\in K$
, let
$k\in K$
, let
![]() $n(k)$
be the smallest integer
$n(k)$
be the smallest integer
![]() $n\geq 1$
, such that
$n\geq 1$
, such that
![]() $k\in K_n$
. Then
$k\in K_n$
. Then
![]() $n(k)$
is well-defined and
$n(k)$
is well-defined and
![]() $\lim _{k\rightarrow \mathcal U}n(k)=+\infty $
.
$\lim _{k\rightarrow \mathcal U}n(k)=+\infty $
.
For
![]() $k\in K$
, let
$k\in K$
, let
![]() $C_k=A_{n(k)}^k, D_k^0=B_{n(k)}^k$
and
$C_k=A_{n(k)}^k, D_k^0=B_{n(k)}^k$
and
![]() $v_k=v_{n(k)}^k$
. If
$v_k=v_{n(k)}^k$
. If
![]() $n(k)\geq 2$
, then as
$n(k)\geq 2$
, then as
![]() $k\in K_{n(k)}$
, we have
$k\in K_{n(k)}$
, we have
![]() $\|v_k-1\|_\infty < \frac {1}{n(k)}$
. Since
$\|v_k-1\|_\infty < \frac {1}{n(k)}$
. Since
![]() $\lim _{k\rightarrow \mathcal U}n(k)=+\infty $
, we get that
$\lim _{k\rightarrow \mathcal U}n(k)=+\infty $
, we get that
![]() $\lim _{k\rightarrow \mathcal U}\|v_k-1\|_\infty =0$
.
$\lim _{k\rightarrow \mathcal U}\|v_k-1\|_\infty =0$
.
Let
![]() $n\in \mathbb N$
. Since
$n\in \mathbb N$
. Since
![]() $\{k\in K\mid n(k)\geq n\}\in \mathcal U$
and the sequences
$\{k\in K\mid n(k)\geq n\}\in \mathcal U$
and the sequences
![]() $\{A_m^k\}_{m\in \mathbb N}$
and
$\{A_m^k\}_{m\in \mathbb N}$
and
![]() $\{B_m^k\}_{m\in \mathbb N}$
are increasing for every
$\{B_m^k\}_{m\in \mathbb N}$
are increasing for every
![]() $k\in K$
, we get that
$k\in K$
, we get that
![]() $\prod _{\mathcal U}A_n^k\subset \prod _{\mathcal U}C_k$
and
$\prod _{\mathcal U}A_n^k\subset \prod _{\mathcal U}C_k$
and
![]() $\prod _{\mathcal U}B_n^k\subset \prod _{\mathcal U}D_k^0$
. Since
$\prod _{\mathcal U}B_n^k\subset \prod _{\mathcal U}D_k^0$
. Since
![]() $A_n\subset \prod _{\mathcal U}A_n^k$
and
$A_n\subset \prod _{\mathcal U}A_n^k$
and
![]() ${B_n\subset \prod _{\mathcal U}B_n^k}$
, we conclude that
${B_n\subset \prod _{\mathcal U}B_n^k}$
, we conclude that
![]() $A_n\subset \prod _{\mathcal U}C_k$
and
$A_n\subset \prod _{\mathcal U}C_k$
and
![]() $B_n\subset \prod _{\mathcal U}D_k^0$
. As this holds for every
$B_n\subset \prod _{\mathcal U}D_k^0$
. As this holds for every
![]() $n\in \mathbb N$
, we get that
$n\in \mathbb N$
, we get that
![]() $A\subset \prod _{\mathcal U}C_k$
and
$A\subset \prod _{\mathcal U}C_k$
and
![]() $B\subset \prod _{\mathcal U}D_k^0$
. Finally, let
$B\subset \prod _{\mathcal U}D_k^0$
. Finally, let
![]() $D_k=v_kD_k^0v_k^*$
. Then
$D_k=v_kD_k^0v_k^*$
. Then
![]() $C_k=A_{n(k)}^k$
and
$C_k=A_{n(k)}^k$
and
![]() $D_k=v_{n(k)}^kB_{n(k)}^kv_{n(k)}^*$
are orthogonal, for every
$D_k=v_{n(k)}^kB_{n(k)}^kv_{n(k)}^*$
are orthogonal, for every
![]() $k\in K$
. Since
$k\in K$
. Since
![]() $\lim _{k\rightarrow \mathcal U}\|v_k-1\|_\infty =0$
, we get that
$\lim _{k\rightarrow \mathcal U}\|v_k-1\|_\infty =0$
, we get that
![]() $\prod _{\mathcal U}D_k^0=\prod _{\mathcal U}D_k$
and
$\prod _{\mathcal U}D_k^0=\prod _{\mathcal U}D_k$
and
![]() $B\subset \prod _{\mathcal U}D_k$
. This finishes the proof of Case 1.
$B\subset \prod _{\mathcal U}D_k$
. This finishes the proof of Case 1.
Case 2.
![]() $\mathcal U$
is not countably cofinal.
$\mathcal U$
is not countably cofinal.
Since
![]() $\mathcal U$
is not countably cofinal,
$\mathcal U$
is not countably cofinal,
![]() $\{k'\in K\mid f(k')=\lim _{k\rightarrow \mathcal U}f(k)\}\in \mathcal U$
, for every
$\{k'\in K\mid f(k')=\lim _{k\rightarrow \mathcal U}f(k)\}\in \mathcal U$
, for every
![]() $f\in \ell ^\infty (K)$
(see the proof of [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.3 (2)]). If
$f\in \ell ^\infty (K)$
(see the proof of [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.3 (2)]). If
![]() $n\in \mathbb N$
, since
$n\in \mathbb N$
, since
![]() $\lim _{k\rightarrow \mathcal U}\|v_n^k-1\|_\infty =0$
, we get that
$\lim _{k\rightarrow \mathcal U}\|v_n^k-1\|_\infty =0$
, we get that
![]() $R_n:=\{k\in K\mid v_n^k=1\}\in \mathcal U$
. Using again that
$R_n:=\{k\in K\mid v_n^k=1\}\in \mathcal U$
. Using again that
![]() $\mathcal U$
is not countably cofinal, we further deduce that
$\mathcal U$
is not countably cofinal, we further deduce that
![]() $R:=\bigcap _{n\in \mathbb N}R_n=\{k\in K\mid v_n^k=1,\forall n\in \mathbb N\}\in \mathcal U$
.
$R:=\bigcap _{n\in \mathbb N}R_n=\{k\in K\mid v_n^k=1,\forall n\in \mathbb N\}\in \mathcal U$
.
If
![]() $k\in R$
, then
$k\in R$
, then
![]() $v_n^k=1$
, hence
$v_n^k=1$
, hence
![]() $A_n^k$
and
$A_n^k$
and
![]() $B_n^k$
are orthogonal, for every
$B_n^k$
are orthogonal, for every
![]() $n\in \mathbb N$
. Since the sequences
$n\in \mathbb N$
. Since the sequences
![]() $\{A_n^k\}_{n\in \mathbb N}$
and
$\{A_n^k\}_{n\in \mathbb N}$
and
![]() $\{B_n^k\}_{n\in \mathbb N}$
are increasing, we get that
$\{B_n^k\}_{n\in \mathbb N}$
are increasing, we get that
![]() $C_k=(\bigcup _{n\in \mathbb N}A_n^k)^{\prime \prime }$
and
$C_k=(\bigcup _{n\in \mathbb N}A_n^k)^{\prime \prime }$
and
![]() $D_k=(\bigcup _{n\in \mathbb N}B_n^k)^{\prime \prime }$
are orthogonal, for every
$D_k=(\bigcup _{n\in \mathbb N}B_n^k)^{\prime \prime }$
are orthogonal, for every
![]() $k\in R$
. For
$k\in R$
. For
![]() $k\in K\setminus R$
, let
$k\in K\setminus R$
, let
![]() $C_k=D_k=\mathbb C1$
. If
$C_k=D_k=\mathbb C1$
. If
![]() $n\in \mathbb N$
, then
$n\in \mathbb N$
, then
![]() $A_n\subset \prod _{\mathcal U}A_n^k\subset \prod _{\mathcal U}C_k$
and
$A_n\subset \prod _{\mathcal U}A_n^k\subset \prod _{\mathcal U}C_k$
and
![]() $B_n\subset \prod _{\mathcal U}B_n^k\subset \prod _{\mathcal U}D_k$
. As this holds for every
$B_n\subset \prod _{\mathcal U}B_n^k\subset \prod _{\mathcal U}D_k$
. As this holds for every
![]() $n\in \mathbb N$
, we get that
$n\in \mathbb N$
, we get that
![]() $A\subset \prod _{\mathcal U}C_k$
and
$A\subset \prod _{\mathcal U}C_k$
and
![]() $B\subset \prod _{\mathcal U}D_k$
. This finishes the proof of Case 2 and of the theorem.
$B\subset \prod _{\mathcal U}D_k$
. This finishes the proof of Case 2 and of the theorem.
5.2. Proof of Theorem G
In order to construct a
![]() $\mathrm {II_1}$
factor satisfying the hypothesis of Theorem G, we follow closely the construction from [Reference Chifan, Ioana and ElayavalliCIKE22, Definition 5.1]. This construction uses the following key result from [Reference Chifan, Ioana and ElayavalliCIKE22].
$\mathrm {II_1}$
factor satisfying the hypothesis of Theorem G, we follow closely the construction from [Reference Chifan, Ioana and ElayavalliCIKE22, Definition 5.1]. This construction uses the following key result from [Reference Chifan, Ioana and ElayavalliCIKE22].
Corollary 5.6 (Corollary 4.3 in [Reference Chifan, Ioana and ElayavalliCIKE22])
Let
![]() $(M,\tau )$
be a tracial von Neumann algebra having no type I direct summand. Let
$(M,\tau )$
be a tracial von Neumann algebra having no type I direct summand. Let
![]() $u_1,u_2\in \mathscr U(M)$
, such that
$u_1,u_2\in \mathscr U(M)$
, such that
![]() $\{u_1\}^{\prime \prime } \perp \{u_2\}^{\prime \prime }$
.
$\{u_1\}^{\prime \prime } \perp \{u_2\}^{\prime \prime }$
.
Then there exists a
![]() $\mathrm {II_1}$
factor
$\mathrm {II_1}$
factor
![]() $P=\Phi (M,u_1,u_2)$
generated by a copy of M and Haar unitaries
$P=\Phi (M,u_1,u_2)$
generated by a copy of M and Haar unitaries
![]() $v_1,v_2\in \mathscr U(P)$
so that
$v_1,v_2\in \mathscr U(P)$
so that
![]() $[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
. Moreover, if
$[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
. Moreover, if
![]() $Q\subset M$
is a von Neumann subalgebra, such that
$Q\subset M$
is a von Neumann subalgebra, such that
![]() $Q\npreceq _{M}\{u_i\}^{\prime \prime }$
, for every
$Q\npreceq _{M}\{u_i\}^{\prime \prime }$
, for every
![]() $1\leq i\leq 2$
, then
$1\leq i\leq 2$
, then
![]() $Q'\cap P\subset M$
.
$Q'\cap P\subset M$
.
Recall from [Reference Chifan, Ioana and ElayavalliCIKE22, Definition 4.1] that
![]() $\Phi (M,u_1,u_2)$
is defined as follows. Put
$\Phi (M,u_1,u_2)$
is defined as follows. Put
![]() $A_1=\{u_1\}"$
,
$A_1=\{u_1\}"$
,
![]() $A_2=\{u_2\}"$
,
$A_2=\{u_2\}"$
,
![]() $B_1=B_2=\text {L}(\mathbb Z)$
, and define
$B_1=B_2=\text {L}(\mathbb Z)$
, and define
![]() $N=M*_{A_1}(A_1\overline {\otimes }B_1)$
. Then
$N=M*_{A_1}(A_1\overline {\otimes }B_1)$
. Then
For a
![]() $\mathrm {II_1}$
factor M, we let
$\mathrm {II_1}$
factor M, we let
![]() $\mathscr W(M)$
be the set of pairs
$\mathscr W(M)$
be the set of pairs
![]() $(u_1,u_2)\in \mathscr U(M)\times \mathscr U(M)$
, such that
$(u_1,u_2)\in \mathscr U(M)\times \mathscr U(M)$
, such that
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are orthogonal. We endow
$\{u_2\}^{\prime \prime }$
are orthogonal. We endow
![]() $\mathscr U(M)\times \mathscr U(M)$
with the product
$\mathscr U(M)\times \mathscr U(M)$
with the product
![]() $\|\cdot \|_2$
-topology. We next repeat the construction from [Reference Chifan, Ioana and ElayavalliCIKE22, Definition 5.1], where we replace
$\|\cdot \|_2$
-topology. We next repeat the construction from [Reference Chifan, Ioana and ElayavalliCIKE22, Definition 5.1], where we replace
![]() $\mathscr V(M)$
(the set of pairs
$\mathscr V(M)$
(the set of pairs
![]() $(u_1,u_2)\in \mathscr W(M)$
, such that
$(u_1,u_2)\in \mathscr W(M)$
, such that
![]() $u_1^2=u_2^3=1$
) with
$u_1^2=u_2^3=1$
) with
![]() $\mathscr W(M)$
.
$\mathscr W(M)$
.
Definition 5.7. Let
![]() $M_1$
be a
$M_1$
be a
![]() $\mathrm {II_1}$
factor. We construct a
$\mathrm {II_1}$
factor. We construct a
![]() $\mathrm {II_1}$
factor M which contains
$\mathrm {II_1}$
factor M which contains
![]() $M_1$
and arises as the inductive limit of an increasing sequence
$M_1$
and arises as the inductive limit of an increasing sequence
![]() $(M_n)_{n\in \mathbb N}$
of
$(M_n)_{n\in \mathbb N}$
of
![]() $\mathrm {II_1}$
factors. To this end, let
$\mathrm {II_1}$
factors. To this end, let
![]() $\sigma =(\sigma _1,\sigma _2):\mathbb N\rightarrow \mathbb N\times \mathbb N$
be a bijection, such that
$\sigma =(\sigma _1,\sigma _2):\mathbb N\rightarrow \mathbb N\times \mathbb N$
be a bijection, such that
![]() $\sigma _1(n)\leq n$
, for every
$\sigma _1(n)\leq n$
, for every
![]() $n\in \mathbb N$
. Assume that
$n\in \mathbb N$
. Assume that
![]() $M_1,\ldots ,M_n$
have been constructed, for some
$M_1,\ldots ,M_n$
have been constructed, for some
![]() $n\in \mathbb N$
. Let
$n\in \mathbb N$
. Let
![]() $\{(u_1^{n,k},u_2^{n,k})\}_{k\in \mathbb N}\subset \mathscr W(M_n)$
be a
$\{(u_1^{n,k},u_2^{n,k})\}_{k\in \mathbb N}\subset \mathscr W(M_n)$
be a
![]() $\|\cdot \|_2$
-dense sequence. Since
$\|\cdot \|_2$
-dense sequence. Since
![]() $\sigma _1(n)\leq n$
, we have
$\sigma _1(n)\leq n$
, we have
![]() $(u_1^{\sigma (n)},u_2^{\sigma (n)})\in \mathscr W(M_n)$
, and we can define
$(u_1^{\sigma (n)},u_2^{\sigma (n)})\in \mathscr W(M_n)$
, and we can define
![]() $M_{n+1}:=\Phi (M_n,u_1^{\sigma (n)},u_2^{\sigma (n)}).$
Then
$M_{n+1}:=\Phi (M_n,u_1^{\sigma (n)},u_2^{\sigma (n)}).$
Then
![]() $M_n\subset M_{n+1}$
and
$M_n\subset M_{n+1}$
and
![]() $M_{n+1}$
is a
$M_{n+1}$
is a
![]() $\mathrm {II_1}$
factor by Corollary 5.6. Thus,
$\mathrm {II_1}$
factor by Corollary 5.6. Thus,
![]() $M:=({\bigcup _{n\in \mathbb N}M_n})^{\prime \prime }$
a
$M:=({\bigcup _{n\in \mathbb N}M_n})^{\prime \prime }$
a
![]() $\mathrm {II_1}$
factor.
$\mathrm {II_1}$
factor.
Proposition 5.8. Let M be the
![]() $\mathrm {II_1}$
factor introduced in Definition 5.7 and
$\mathrm {II_1}$
factor introduced in Definition 5.7 and
![]() $\mathcal U$
be a countably cofinal ultrafilter on a set I. Let
$\mathcal U$
be a countably cofinal ultrafilter on a set I. Let
![]() $u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
$u_1,u_2\in \mathscr U(M^{\mathcal U})$
, such that
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are
$\{u_2\}^{\prime \prime }$
are
![]() $2$
-independent.
$2$
-independent.
Then there exist Haar unitaries
![]() $v_1,v_2\in M^{\mathcal U}$
so that
$v_1,v_2\in M^{\mathcal U}$
so that
![]() $[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
.
$[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
.
Proposition 5.8 follows by repeating the argument used in the proof of [Reference Chifan, Ioana and ElayavalliCIKE22, Proposition 5.3], which we recall for the reader’s convenience.
Proof. Since
![]() $M=(\bigcup _{n\in \mathbb N}M_n)^{\prime \prime }$
and
$M=(\bigcup _{n\in \mathbb N}M_n)^{\prime \prime }$
and
![]() $\mathcal U$
is countably cofinal, by applying [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.2], we can find
$\mathcal U$
is countably cofinal, by applying [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.2], we can find
![]() ${(n_i)}_{i\in I}\subset \mathbb N$
, such that
${(n_i)}_{i\in I}\subset \mathbb N$
, such that
![]() $u_1,u_2\in \prod _{i\in \mathcal U}M_{n_i}$
. Also, the proof of [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.2] provides a function
$u_1,u_2\in \prod _{i\in \mathcal U}M_{n_i}$
. Also, the proof of [Reference Boutonnet, Chifan and IoanaBCI15, Lemma 2.2] provides a function
![]() $f:I\rightarrow \mathbb N$
, such that
$f:I\rightarrow \mathbb N$
, such that
![]() $\lim _{i\rightarrow \mathcal U}f(i)=+\infty $
.
$\lim _{i\rightarrow \mathcal U}f(i)=+\infty $
.
Since
![]() $\{u_1\}^{\prime \prime }$
and
$\{u_1\}^{\prime \prime }$
and
![]() $\{u_2\}^{\prime \prime }$
are
$\{u_2\}^{\prime \prime }$
are
![]() $2$
-independent, Theorem 5.1 provides orthogonal von Neumann subalgebras
$2$
-independent, Theorem 5.1 provides orthogonal von Neumann subalgebras
![]() $C_i,D_i\subset M_{n_i}$
, for every
$C_i,D_i\subset M_{n_i}$
, for every
![]() $i\in I$
, such that
$i\in I$
, such that
![]() $u_1\in \prod _{\mathcal U}C_i$
and
$u_1\in \prod _{\mathcal U}C_i$
and
![]() $u_2\in \prod _{\mathcal U}D_i$
. Thus, we can represent
$u_2\in \prod _{\mathcal U}D_i$
. Thus, we can represent
![]() $u_1=(u_{1,i})^{\mathcal U}$
and
$u_1=(u_{1,i})^{\mathcal U}$
and
![]() $u_2=(u_{2,i})^{\mathcal U}$
, where
$u_2=(u_{2,i})^{\mathcal U}$
, where
![]() $u_{1,i}\in \mathscr U(C_i)$
and
$u_{1,i}\in \mathscr U(C_i)$
and
![]() $u_{2,i}\in \mathscr U(D_i)$
, for every
$u_{2,i}\in \mathscr U(D_i)$
, for every
![]() $i\in I$
. In particular,
$i\in I$
. In particular,
![]() $\{u_{1,i}\}^{\prime \prime }$
and
$\{u_{1,i}\}^{\prime \prime }$
and
![]() $\{u_{2,i}\}^{\prime \prime }$
are orthogonal, and thus
$\{u_{2,i}\}^{\prime \prime }$
are orthogonal, and thus
![]() $(u_{1,i},u_{2,i})\in \mathscr W(M_{n_i})$
, for every
$(u_{1,i},u_{2,i})\in \mathscr W(M_{n_i})$
, for every
![]() $i\in I$
.
$i\in I$
.
As the sequence
![]() $\{(u_1^{n_i,j},u_2^{n_i,j})\}_{j\in \mathbb N}$
is dense in
$\{(u_1^{n_i,j},u_2^{n_i,j})\}_{j\in \mathbb N}$
is dense in
![]() $\mathscr W(M_{n_i})$
, we can find
$\mathscr W(M_{n_i})$
, we can find
![]() $j_i\in \mathbb N$
, such that
$j_i\in \mathbb N$
, such that
![]() $\|u_{1,i}-u_1^{n_i,j_i}\|_2+\|u_{2,i}-u_2^{n_i,j_i}\|_2\leq \frac {1}{f(i)}$
, for every
$\|u_{1,i}-u_1^{n_i,j_i}\|_2+\|u_{2,i}-u_2^{n_i,j_i}\|_2\leq \frac {1}{f(i)}$
, for every
![]() $i\in I$
. For
$i\in I$
. For
![]() $i\in I$
, let
$i\in I$
, let
![]() $l_i\in \mathbb N$
with
$l_i\in \mathbb N$
with
![]() $\sigma (l_i)=(n_i,j_i)$
. Then
$\sigma (l_i)=(n_i,j_i)$
. Then
![]() $M_{\sigma (l_i)+1}=\Phi (M_{\sigma (l_i)},u_1^{n_i,j_i},u_2^{n_i,j_i})$
. Corollary 5.6 gives Haar unitaries
$M_{\sigma (l_i)+1}=\Phi (M_{\sigma (l_i)},u_1^{n_i,j_i},u_2^{n_i,j_i})$
. Corollary 5.6 gives Haar unitaries
![]() $v_{1,i},v_{2,i}\in \mathscr U(M_{\sigma (l_i)+1})\subset \mathscr U(M)$
with
$v_{1,i},v_{2,i}\in \mathscr U(M_{\sigma (l_i)+1})\subset \mathscr U(M)$
with
![]() $[u_1^{n_i,j_i},v_{1,i}]=[u_2^{n_i,j_i},v_{2,i}]=[v_{1,i},v_{2,i}]=0$
. Using that
$[u_1^{n_i,j_i},v_{1,i}]=[u_2^{n_i,j_i},v_{2,i}]=[v_{1,i},v_{2,i}]=0$
. Using that
![]() $\lim _{i\rightarrow \mathcal U}f(i)=+\infty $
, we conclude that
$\lim _{i\rightarrow \mathcal U}f(i)=+\infty $
, we conclude that
![]() $v_1=(v_{1,i})^{\mathcal U}, v_2=(v_{2,i})^{\mathcal U} \in \mathscr U(M^{\mathcal U})$
are Haar unitaries, such that
$v_1=(v_{1,i})^{\mathcal U}, v_2=(v_{2,i})^{\mathcal U} \in \mathscr U(M^{\mathcal U})$
are Haar unitaries, such that
![]() $[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
.
$[u_1,v_1]=[u_2,v_2]=[v_1,v_2]=0$
.
To ensure that M does not have property Gamma, it suffices to take
![]() $M_1$
to have property (T), as the next result from [Reference Chifan, Ioana and ElayavalliCIKE22] shows:
$M_1$
to have property (T), as the next result from [Reference Chifan, Ioana and ElayavalliCIKE22] shows:
Proposition 5.9 (Proposition 5.4 in [Reference Chifan, Ioana and ElayavalliCIKE22])
Assume that
![]() $M_1$
has property (T). Then M does not have property Gamma.
$M_1$
has property (T). Then M does not have property Gamma.
5.3. Proof of Theorem H
We may clearly assume that
![]() $z\not =0$
and
$z\not =0$
and
![]() $z\in M_{\text {sa},1}$
, for every
$z\in M_{\text {sa},1}$
, for every
![]() $z\in X\cup Y$
. Further, we may assume that X and Y consist of pairwise orthogonal vectors. Enumerate
$z\in X\cup Y$
. Further, we may assume that X and Y consist of pairwise orthogonal vectors. Enumerate
![]() $X=\{x_1,\dots ,x_m\}$
and
$X=\{x_1,\dots ,x_m\}$
and
![]() $Y=\{y_1,\dots ,y_n\}$
, and define
$Y=\{y_1,\dots ,y_n\}$
, and define
![]() $x=(x_1,\dots ,x_m)\in M^m_{\text {sa},1}$
and
$x=(x_1,\dots ,x_m)\in M^m_{\text {sa},1}$
and
![]() $y=(y_1,\dots ,y_n)\in M^n_{\text {sa},1}$
.
$y=(y_1,\dots ,y_n)\in M^n_{\text {sa},1}$
.
By [Reference PopaPo13a, Corollary 0.2], there exists
![]() $v\in \mathscr U(M^{\mathcal U})$
, such that
$v\in \mathscr U(M^{\mathcal U})$
, such that
![]() $vMv^*$
and M are freely and hence
$vMv^*$
and M are freely and hence
![]() $2$
-independent. Then
$2$
-independent. Then
![]() $\|[vx_iv^*,y_j]\|_2=\sqrt {2}\|x_i\|_2\|y_j\|_2>0$
and
$\|[vx_iv^*,y_j]\|_2=\sqrt {2}\|x_i\|_2\|y_j\|_2>0$
and
![]() $\tau ^{\mathcal U}(vx_iv^*y_j)=~0$
, for every
$\tau ^{\mathcal U}(vx_iv^*y_j)=~0$
, for every
![]() $1\leq i\leq m$
,
$1\leq i\leq m$
,
![]() $1{\kern-1.3pt}\leq{\kern-1.3pt} j{\kern-1.3pt}\leq{\kern-1.3pt} n$
. Moreover, for every
$1{\kern-1.3pt}\leq{\kern-1.3pt} j{\kern-1.3pt}\leq{\kern-1.3pt} n$
. Moreover, for every
![]() $(i,j)\not =(i',j')$
, we have
$(i,j)\not =(i',j')$
, we have
![]() $\langle [vx_iv^*,y_j], [vx_{i'}v^*,y_{j'}]\rangle {\kern-1pt}={\kern-1pt}\tau (x_ix_{i'})\tau (y_jy_{j'}){\kern-1pt}={\kern-1pt}0.$
Thus, we conclude that
$\langle [vx_iv^*,y_j], [vx_{i'}v^*,y_{j'}]\rangle {\kern-1pt}={\kern-1pt}\tau (x_ix_{i'})\tau (y_jy_{j'}){\kern-1pt}={\kern-1pt}0.$
Thus, we conclude that
![]() $\delta (vxv^*,y)>0$
and
$\delta (vxv^*,y)>0$
and
![]() $\varepsilon (vxv^*,y)=\gamma (vxv^*,y)=0$
. In particular,
$\varepsilon (vxv^*,y)=\gamma (vxv^*,y)=0$
. In particular,
Writing
![]() $v=(v_k)^{\mathcal U}$
, where
$v=(v_k)^{\mathcal U}$
, where
![]() $v_k\in \mathscr U(M)$
, for all
$v_k\in \mathscr U(M)$
, for all
![]() $k\in \mathbb N$
. Then
$k\in \mathbb N$
. Then
![]() $\lim _{k\rightarrow \mathcal U}\delta (v_kxv_k^*,y)=\delta (vxv^*,y)$
,
$\lim _{k\rightarrow \mathcal U}\delta (v_kxv_k^*,y)=\delta (vxv^*,y)$
,
![]() $\lim _{k\rightarrow \mathcal U}\varepsilon (v_kxv_k^*,y)=\varepsilon (vxv^*,y)$
and
$\lim _{k\rightarrow \mathcal U}\varepsilon (v_kxv_k^*,y)=\varepsilon (vxv^*,y)$
and
![]() $\lim _{k\rightarrow \mathcal U}\gamma (v_kxv_k^*,y)=\gamma (vxv^*,y)$
. Using (5.8) gives
$\lim _{k\rightarrow \mathcal U}\gamma (v_kxv_k^*,y)=\gamma (vxv^*,y)$
. Using (5.8) gives
![]() $k\in \mathbb N$
, such that
$k\in \mathbb N$
, such that
![]() $13mn\sqrt {\varepsilon (v_kxv_k^*,y)}<\delta (v_kxv_k^*,y)^2-(mn-1)\gamma (v_kxv_k^*,y)$
. By applying Lemma 5.2, we can find
$13mn\sqrt {\varepsilon (v_kxv_k^*,y)}<\delta (v_kxv_k^*,y)^2-(mn-1)\gamma (v_kxv_k^*,y)$
. By applying Lemma 5.2, we can find
![]() $w\in \mathscr U(M)$
, such that
$w\in \mathscr U(M)$
, such that
![]() $\varepsilon (w(v_kxv_k^*)w^*,y)=0$
. Letting
$\varepsilon (w(v_kxv_k^*)w^*,y)=0$
. Letting
![]() $u=wv_k\in \mathscr U(M)$
, we get that
$u=wv_k\in \mathscr U(M)$
, we get that
![]() $\varepsilon (uXu^*,Y)=0$
, that is,
$\varepsilon (uXu^*,Y)=0$
, that is,
![]() $uXu^*$
and Y are orthogonal.
$uXu^*$
and Y are orthogonal.
Acknowledgements
This work was initiated when CH was visiting the University of California at San Diego (UCSD) in March 2023. He thanks the Department of Mathematics at UCSD for its kind hospitality. The authors thank Ben Hayes, Srivatsav Kunnawalkam Elayavalli and Sorin Popa for their useful comments. CH is supported by the Institut Universitaire de France. AI is supported by the grants NSF DMS-1854074 and NSF DMS-2153805 and a Simons Fellowship.
Competing interests
The authors have no competing interest to declare.