Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T15:38:46.426Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATING SMOOTH, MULTIVARIATE FUNCTIONS ON IRREGULAR DOMAINS

Part of: Approximations and expansions

Published online by Cambridge University Press:  20 May 2020

BEN ADCOCK  and
DAAN HUYBRECHS
BEN ADCOCK
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6, Canada; [email protected]
DAAN HUYBRECHS
Affiliation:
Department of Computer Science, KU Leuven, Celestijnenlaan 200A, BE-3001Leuven, Belgium; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we introduce a method known as polynomial frame approximation for approximating smooth, multivariate functions defined on irregular domains in 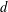$d$ dimensions, where 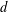$d$ can be arbitrary. This method is simple, and relies only on orthogonal polynomials on a bounding tensor-product domain. In particular, the domain of the function need not be known in advance. When restricted to a subdomain, an orthonormal basis is no longer a basis, but a frame. Numerical computations with frames present potential difficulties, due to the near-linear dependence of the truncated approximation system. Nevertheless, well-conditioned approximations can be obtained via regularization, for instance, truncated singular value decompositions. We comprehensively analyze such approximations in this paper, providing error estimates for functions with both classical and mixed Sobolev regularity, with the latter being particularly suitable for higher-dimensional problems. We also analyze the sample complexity of the approximation for sample points chosen randomly according to a probability measure, providing estimates in terms of the corresponding Nikolskii inequality for the domain. In particular, we show that the sample complexity for points drawn from the uniform measure is quadratic (up to a log factor) in the dimension of the polynomial space, independently of 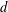$d$, for a large class of nontrivial domains. This extends a well-known result for polynomial approximation in hypercubes.

MSC classification

Primary: 41A10: Approximation by polynomials 41A25: Rate of convergence, degree of approximation
Secondary: 41A63: Multidimensional problems (should also be assigned at least one other classification number in this section) 41A17: Inequalities in approximation (Bernstein, Jackson, Nikol'skiĭ-type inequalities)
Type
Applied Analysis
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e26
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Adcock, B., ‘Modified Fourier expansions: theory, construction and applications’, PhD Thesis, University of Cambridge, 2010.Google Scholar
Adcock, B., ‘Multivariate modified Fourier series and application to boundary value problems’, Numer. Math. 115(4) (2010), 511–552.CrossRefGoogle Scholar
Adcock, B., ‘Infinite-dimensional compressed sensing and function interpolation’, Found. Comput. Math. 18(3) (2018), 661–701.CrossRefGoogle Scholar
Adcock, B., Brugiapaglia, S. and Webster, C. G., ‘Compressed sensing approaches for polynomial approximation of high-dimensional functions’, inCompressed Sensing and its Applications (Birkhäuser, Cham, 2017).Google Scholar
Adcock, B. and Cardenas, J. M., ‘Near-optimal sampling strategies for multivariate function approximation on general domains’, SIAM J. Math. Data Sci. (2020), (to appear).Google Scholar
Adcock, B. and Huybrechs, D., ‘Frames and numerical approximation II: generalized sampling’, Preprint, 2018, arXiv:1802.01950.Google Scholar
Adcock, B. and Huybrechs, D., ‘Frames and numerical approximation’, SIAM Rev. 61(3) (2019), 443–473.CrossRefGoogle Scholar
Adcock, B., Huybrechs, D. and Martín-Vaquero, J., ‘On the numerical stability of Fourier extensions’, Found. Comput. Math. 14(4) (2014), 635–687.CrossRefGoogle Scholar
Adcock, B., Platte, R. and Shadrin, A., ‘Optimal sampling rates for approximating analytic functions from pointwise samples’, IMA J. Numer. Anal. 39(3) (2019), 1360–1390.CrossRefGoogle Scholar
Adcock, B. and Ruan, J., ‘Parameter selection and numerical approximation properties of Fourier extensions from fixed data’, J. Comput. Phys. 273 (2014), 453–471.CrossRefGoogle Scholar
Albin, N. and Bruno, O. P., ‘A spectral FC solver for the compressible Navier–Stokes equations in general domains I: explicit time-stepping’, J. Comput. Phys. 230(16) (2011), 6248–6270.CrossRefGoogle Scholar
Boyd, J., ‘Fourier embedded domain methods: extending a function defined on an irregular region to a rectangle so that the extension is spatially periodic and C ∞’, Appl. Math. Comput. 161(2) (2005), 591–597.Google Scholar
Boyd, J. P., ‘A comparison of numerical algorithms for Fourier Extension of the first, second, and third kinds’, J. Comput. Phys. 178 (2002), 118–160.CrossRefGoogle Scholar
Bruno, O. and Lyon, M., ‘High-order unconditionally stable FC-AD solvers for general smooth domains I. Basic elements’, J. Comput. Phys. 229(6) (2010), 2009–2033.CrossRefGoogle Scholar
Bruno, O. P., Han, Y. and Pohlman, M. M., ‘Accurate, high-order representation of complex three-dimensional surfaces via Fourier continuation analysis’, J. Comput. Phys. 227(2) (2007), 1094–1125.CrossRefGoogle Scholar
Bungartz, H.-J. and Griebel, M., ‘Sparse grids’, Acta Numer. 13 (2004), 147–269.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. and Zang, T. A., Spectral Methods: Fundamentals in Single Domains (Springer, Berlin Heidelberg, 2006).CrossRefGoogle Scholar
Chkifa, A., Cohen, A., Migliorati, G., Nobile, F. and Tempone, R., ‘Discrete least squares polynomial approximation with random evaluations – application to parametric and stochastic elliptic PDEs’, ESAIM Math. Model. Numer. Anal. 49(3) (2015), 815–837.CrossRefGoogle Scholar
Chkifa, A., Cohen, A. and Schwab, C., ‘Breaking the curse of dimensionality in sparse polynomial approximation of parametric PDEs’, J. Math. Pures Appl. 103 (2015), 400–428.CrossRefGoogle Scholar
Chkifa, A., Dexter, N., Tran, H. and Webster, C. G., ‘Polynomial approximation via compressed sensing of high-dimensional functions on lower sets’, Math. Comp. 87 (2018), 1415–1450.CrossRefGoogle Scholar
Christensen, O., An Introduction to Frames and Riesz Bases (Birkhäuser, Basel, 2003).CrossRefGoogle Scholar
Cohen, A., Davenport, M. A. and Leviatan, D., ‘On the stability and accuracy of least squares approximations’, Found. Comput. Math. 13 (2013), 819–834.CrossRefGoogle Scholar
Cohen, A. and DeVore, R. A., ‘Approximation of high-dimensional parametric PDEs’, Acta Numer. 24 (2015), 1–159.CrossRefGoogle Scholar
Cohen, A., DeVore, R. A. and Schwab, C., ‘Convergence rates of best N-term Galerkin approximations for a class of elliptic sPDEs’, Found. Comput. Math. 10 (2010), 615–646.CrossRefGoogle Scholar
Cohen, A. and Migliorati, G., ‘Optimal weighted least-squares methods’, SMAI J. Comput. Math. 3 (2017), 181–203.CrossRefGoogle Scholar
Constantine, P. G., Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies (SIAM, Philadelphia, PA, 2015).CrossRefGoogle Scholar
Doostan, A. and Owhadi, H., ‘A non-adapted sparse approximation of PDEs with stochastic inputs’, J. Comput. Phys. 230(8) (2011), 3015–3034.CrossRefGoogle Scholar
Dyn, N. and Floater, M., ‘Multivariate polynomial interpolation on lower sets’, J. Approx. Theory 177 (2013), 34–42.CrossRefGoogle Scholar
Ganzburg, M. I., ‘Polynomial inequalities on measurable sets and their applications’, Constr. Approx. 17 (2001), 275–306.CrossRefGoogle Scholar
Hackbusch, W., ‘L ∞ estimation of tensor truncations’, Numer. Math. 125 (2013), 419–440.CrossRefGoogle Scholar
Hansen, P. C., ‘Analysis of discrete ill-posed problems by means of the l-curve’, SIAM Rev. 34(4) (1992), 561–580.CrossRefGoogle Scholar
Hansen, P. C., Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion (SIAM, Philadelphia, PA, 1998).CrossRefGoogle Scholar
Lyon, M. and Bruno, O., ‘High-order unconditionally stable FC-AD solvers for general smooth domains II. Elliptic, parabolic and hyperbolic PDEs; theoretical considerations’, J. Comput. Phys. 229(9) (2010), 3358–3381.CrossRefGoogle Scholar
Migliorati, G., ‘Polynomial approximation by means of the random discrete $L^{2}$ projection and application to inverse problems for PDEs with stochastic data’, PhD Thesis, Politecnico di Milano, 2013.Google Scholar
Migliorati, G., ‘Multivariate Markov-type and Nikolskii-type inequalities for polynomials associated with downward closed multi-index sets’, J. Approx. Theory 189 (2015), 137–159.CrossRefGoogle Scholar
Migliorati, G., ‘Multivariate approximation of functions on irregular domains by weighted least-squares methods’, Preprint, 2019, arXiv:1907.12304.Google Scholar
Migliorati, G., Nobile, F., von Schwerin, E. and Tempone, R., ‘Analysis of the discrete L 2 projection on polynomial spaces with random evaluations’, Found. Comput. Math. 14 (2014), 419–456.Google Scholar
Narayan, A., Jakeman, J. D. and Zhou, T., ‘A Christoffel function weighted least squares algorithm for collocation approximations’, Math. Comp. 86 (2017), 1913–1947.CrossRefGoogle Scholar
Narayan, A. and Zhou, T., ‘Stochastic collocation on unstructured multivariate meshes’, Commun. Comput. Phys. 18(1) (2015), 1–36.CrossRefGoogle Scholar
Neumaier, A., ‘Solving ill-conditioned and singular linear systems: a tutorial on regularization’, SIAM Rev. 40(3) (1998), 636–666.CrossRefGoogle Scholar
Pasquetti, R. and Elghaoui, M., ‘A spectral embedding method applied to the advection–diffusion equation’, J. Comput. Phys. 125 (1996), 464–476.Google Scholar
Peng, J., Hampton, J. and Doostan, A., ‘A weighted ℓ 1 -minimization approach for sparse polynomial chaos expansions’, J. Comput. Phys. 267 (2014), 92–111.CrossRefGoogle Scholar
Platte, R., Trefethen, L. N. and Kuijlaars, A., ‘Impossibility of fast stable approximation of analytic functions from equispaced samples’, SIAM Rev. 53(2) (2011), 308–318.CrossRefGoogle Scholar
Sargsyan, K., Safta, C., Debusschere, B. J. and Najm, H., ‘Uncertainty quantification given discontinuous model response and a limited number of model runs’, SIAM J. Sci. Comput. 34(1) (2012), B44–B64.CrossRefGoogle Scholar
Sargsyan, K., Safta, C., Najm, H., Debusschere, B. J., Ricciuto, D. and Thornton, P., ‘Dimensionality reduction for complex models via Bayesian compressive sensing’, Int. J. Uncertain. Quantif. 4(1) (2014), 63–93.CrossRefGoogle Scholar
Stinson, K., Gleich, D. F. and Constantine, P. G., ‘A randomized algorithm for enumerating zonotope vertices’, Preprint, 2016, arXiv:1602.06620.Google Scholar
Temlyakov, V. and Tikhonov, S., ‘Remez-type inequalities for the hyperbolic cross polynomials’, Constr. Approx. 46(3) (2017), 593–615.CrossRefGoogle Scholar
Tropp, J. A., ‘User friendly tail bounds for sums of random matrices’, Found. Comput. Math. 12 (2012), 389–434.CrossRefGoogle Scholar
Witteveen, J. A. S. and Iaccarino, G., ‘Simplex stochastic collocation with random sampling and extrapolation for nonhypercube probability spaces’, SIAM J. Sci. Comput. 34(2) (2012), A814–A838.CrossRefGoogle Scholar
Xiu, D. and Karniadakis, G. E., ‘The Wiener–Askey polynomial chaos for stochastic differential equations’, SIAM J. Sci. Comput. 24(2) (2002), 619–644.CrossRefGoogle Scholar
Yan, L., Guo, L. and Xiu, D., ‘Stochastic collocation algorithms using ℓ 1 -minimization’, Int. J. Uncertain. Quantif. 2(3) (2012), 279–293.CrossRefGoogle Scholar
Yang, X. and Karniadakis, G. E., ‘Reweighted ℓ 1 minimization method for stochastic elliptic differential equations’, J. Comput. Phys. 248 (2013), 87–108.CrossRefGoogle Scholar
Zhou, T., Narayan, A. and Xiu, D., ‘Weighted discrete least-squares polynomial approximation using randomized quadratures’, J. Comput. Phys. 1 (2015), 787–800.CrossRefGoogle Scholar