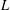Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T01:17:40.930Z Has data issue: false hasContentIssue false
  • English
  • Français

ANDRÉ–OORT CONJECTURE AND NONVANISHING OF CENTRAL $L$ -VALUES OVER HILBERT CLASS FIELDS

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  20 July 2016

ASHAY A. BURUNGALE  and
HARUZO HIDA
ASHAY A. BURUNGALE
Affiliation:
Department of Mathematics, University of Arizona, 617 N. Santa Rita Ave., P.O. Box 210089, Tucson, AZ 85721, USA; [email protected]
HARUZO HIDA
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095-1555, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 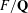$F/\mathbf{Q}$ be a totally real field and 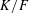$K/F$ a complex multiplication (CM) quadratic extension. Let 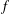$f$ be a cuspidal Hilbert modular new form over 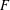$F$ . Let ${\it\lambda}$ be a Hecke character over 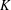$K$ such that the Rankin–Selberg convolution 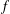$f$ with the 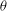${\it\theta}$ -series associated with ${\it\lambda}$ is self-dual with root number 1. We consider the nonvanishing of the family of central-critical Rankin–Selberg 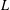$L$ -values 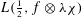$L(\frac{1}{2},f\otimes {\it\lambda}{\it\chi})$ , as ${\it\chi}$ varies over the class group characters of 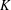$K$ . Our approach is geometric, relying on the Zariski density of CM points in self-products of a Hilbert modular Shimura variety. 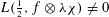We show that the number of class group characters ${\it\chi}$ such that $L(\frac{1}{2},f\otimes {\it\lambda}{\it\chi})\neq 0$ increases with the absolute value of the discriminant of 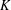$K$ . We crucially rely on the André–Oort conjecture for arbitrary self-product of the Hilbert modular Shimura variety. In view of the recent results of Tsimerman, Yuan–Zhang and Andreatta–Goren–Howard–Pera, the results are now unconditional. We also consider a quaternionic version. Our approach is geometric, relying on the general theory of Shimura varieties and the geometric definition of nearly holomorphic modular forms. In particular, the approach avoids any use of a subconvex bound for the Rankin–Selberg 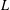$L$ -values. The Waldspurger formula plays an underlying role.

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e20
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Andreatta, F., Goren, E., Howard, B. and Pera, K., ‘Faltings heights of abelian varieties with complex multiplication’, Preprint, available at arXiv:1508.00178.Google Scholar
Bloch, S. and Kato, K., ‘L-functions and Tamagawa numbers of motives’, inThe Grothendieck Festschrift. Vol. I, Progress in Mathematics, 86 (Birkhäuser, Boston, MA, 1990), 333–400.Google Scholar
Brauer, R., ‘On the zeta-functions of algebraic number fields’, Amer. J. Math. 69 (1947), 243–250.Google Scholar
Burungale, A., ‘On the 𝜇-invariant of the cyclotomic derivative of a Katz p-adic L-function’, J. Inst. Math. Jussieu 14(1) (2015), 131–148.CrossRefGoogle Scholar
Castella, F., ‘On the $p$ -adic variation of Heegner points’, Preprint 2014, arXiv:1410.6591.Google Scholar
Chai, C.-L., ‘Hecke orbits as Shimura varieties in positive characteristic’, inInternational Congress of Mathematicians. Vol. II (European Mathematical Society, Zurich, 2006), 295–312.Google Scholar
Chai, C.-L. and Oort, F., ‘Abelian varieties isogenous to a Jacobian’, Ann. of Math. (2) 176(1) (2012), 589–635.Google Scholar
Clozel, L. and Ullmo, E., ‘Équidistribution de mesures algébriques’, Compos. Math. 141(5) (2005), 1255–1309.Google Scholar
Cohen, P., ‘Hyperbolic equidistribution problems on Siegel 3-folds and Hilbert modular varieties’, Duke Math. J. 129 (2005), 87–127.Google Scholar
Cornut, C., ‘Non-trivialité des points de Heegner’, C. R. Math. Acad. Sci. Paris 334(12) (2002), 1039–1042.Google Scholar
Cornut, C. and Vatsal, V., ‘Nontriviality of Rankin–Selberg L-functions and CM points’, inL-Functions and Galois Representations, London Mathematical Society Lecture Note Series, 320 (Cambridge University Press, Cambridge, 2007), 121–186.Google Scholar
Edixhoven, B., ‘Special points on products of modular curves’, Duke Math. J. 126(2) (2005), 325–348.Google Scholar
Harris, M., ‘Arithmetic vector bundles and automorphic forms on Shimura varieties. I’, Invent. Math. 82(1) (1985), 151–189.Google Scholar
Harris, M., ‘Arithmetic vector bundles and automorphic forms on Shimura varieties. II’, Compos. Math. 60(3) (1986), 323–378.Google Scholar
Hida, H., ‘Non-vanishing modulo p of Hecke L-values’, inGeometric Aspects of Dwork Theory (eds. Adolphson, A., Baldassarri, F., Berthelot, P., Katz, N. and Loeser, F.) (Walter de Gruyter, Berlin, 2004), 735–784.Google Scholar
Hida, H., p-Adic Automorphic Forms on Shimura Varieties, Springer Monographs in Mathematics (Springer, New York, 2004).Google Scholar
Hida, H., ‘The Iwasawa 𝜇-invariant of p-adic Hecke L-functions’, Ann. of Math. (2) 172 (2010), 41–137.Google Scholar
Hida, H., Elliptic Curves and Arithmetic Invariants, Springer Monographs in Mathematics (Springer, New York, 2013), xviii+449 pp.Google Scholar
Hsieh, M.-L., ‘Special values of anticyclotomic Rankin–Selberg L-functions’, Doc. Math. 19 (2014), 709–767.Google Scholar
Jiang, D.-H., Li, J.-S. and Zhang, S.-W., ‘Periods and distribution of cycles on Hilbert modular varieties’, Pure Appl. Math. Q. 2(1) (2006), 219–277. Part 1.Google Scholar
Klingler, B. and Yafaev, A., ‘The André–Oort conjecture’, Ann. of Math. (2) 180(3) (2014), 867–925.Google Scholar
Masri, R. and Yang, T., ‘Nonvanishing of Hecke L-functions for CM fields and ranks of abelian varieties’, Geom. Funct. Anal. 21(3) (2011), 648–679.Google Scholar
Michel, P. and Venkatesh, A., ‘Equidistribution, L-functions and ergodic theory: on some problems of Yu. Linnik’, inInternational Congress of Mathematicians. Vol. II (European Mathematical Society, Zürich, 2006), 421–457.Google Scholar
Michel, P. and Venkatesh, A., ‘Heegner points and non-vanishing of Rankin/Selberg L-functions’, inAnalytic Number Theory, Clay Math. Proc., 7 (American Mathematical Society, Providence, RI, 2007), 169–183.Google Scholar
Pazuki, F., ‘Heights and regulators of numer fields and elliptic curves’, Numéro consacré au trimestre “Méthodes arithmétiques et applications”, automne 2013, 47–62, Publ. Math. Besançon Algèbre Théorie Nr., 2014/2, Presses Univ. Franche-Comté, Besançon, 2015.CrossRefGoogle Scholar
Pila, J., ‘On a modular Fermat equation’, Preprint, available at arXiv:1508.05050.Google Scholar
Pila, J., ‘O-minimality and the André–Oort conjecture for C n ’, Ann. of Math. (2) 173(3) (2011), 1779–1840.Google Scholar
Pila, J. and Tsimerman, J., ‘Ax-Lindemann for A g ’, Ann. of Math. (2) 179(2) (2014), 659–681.Google Scholar
Prasanna, K., ‘Integrality of a ratio of Petersson norms and level-lowering congruences’, Ann. of Math. (2) 163(3) (2006), 901–967.Google Scholar
Saito, H., ‘On Tunnell’s formula for characters of GL(2)’, Compos. Math. 85(1) (1993), 99–108.Google Scholar
Serre, J.-P., ‘Le problème des groupes de congruence pour SL2 ’, Ann. of Math. (2) 92 (1970), 489–527.Google Scholar
Shimua, G., ‘Abelian varieties with complex multiplication and modular functions’, Princeton Mathematical Series, 46 (Princeton University Press, Princeton, NJ, 1998).Google Scholar
Templier, N., ‘A non-split sum of coefficients of modular forms’, Duke Math. J. 157(1) (2011), 109–165.Google Scholar
Tsimerman, J., ‘A proof of the André–Oort conjecture for ${\mathcal{A}}_{g}$ ’, Preprint, available at arXiv:1506.01466.Google Scholar
Tunnell, J., ‘Local 𝜖-factors and characters of GL(2)’, Amer. J. Math. 105(6) (1983), 1277–1307.Google Scholar
Ullmo, E., ‘Applications du théorème d’Ax-Lindemann hyperbolique’, Compos. Math. 150(2) (2014), 175–190.Google Scholar
Urban, E., ‘Nearly overconvergent modular forms’, inIwasawa Theory 2012, Contribution in Mathematical and Computational Sciences, 7 (Springer, Heidelberg, New York, Dordrecht, London, 2015).Google Scholar
Venkatesh, A., ‘Sparse equidistribution problems, period bounds and subconvexity’, Ann. of Math. (2) 172(2) (2010), 989–1094.Google Scholar
Waldspurger, J.-L., ‘Sur les valeurs de certaines fonctions L automorphes en leur centre de symétrie’, Compos. Math. 54(2) (1985), 173–242.Google Scholar
Yuan, X. and Zhang, S.-W., ‘On the average Colmez conjecture’, Preprint, available at arXiv:1507.06903.Google Scholar
Zhang, S.-W., ‘Heights of Heegner points on Shimura curves’, Ann. of Math. (2) 153(1) (2001), 27–147.CrossRefGoogle Scholar
Zhang, S.-W., ‘Equidistribution of CM-points on quaternion Shimura varieties’, Int. Math. Res. Not. IMRN 2005(59) (2005), 3657–3689.Google Scholar