Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-09T12:55:02.740Z Has data issue: false hasContentIssue false
  • English
  • Français

ANALYTIC EQUIVALENCE RELATIONS SATISFYING HYPERARITHMETIC-IS-RECURSIVE

Part of: Computability and recursion theory Set theory

Published online by Cambridge University Press:  27 April 2015

ANTONIO MONTALBÁN
ANTONIO MONTALBÁN*
Affiliation:
Department of Mathematics, University of California, Berkeley, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove, in 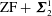$\text{ZF}+\boldsymbol{{\it\Sigma}}_{2}^{1}$-determinacy, that, for any analytic equivalence relation 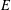$E$, the following three statements are equivalent: (1) 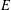$E$ does not have perfectly many classes, (2) 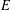$E$ satisfies hyperarithmetic-is-recursive on a cone, and (3) relative to some oracle, for every equivalence class 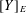$[Y]_{E}$ we have that a real 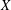$X$ computes a member of the equivalence class if and only if 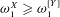${\it\omega}_{1}^{X}\geqslant {\it\omega}_{1}^{[Y]}$. We also show that the implication from (1) to (2) is equivalent to the existence of sharps over 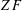$ZF$.

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 03D60: Computability and recursion theory on ordinals, admissible sets, etc.
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Barwise, J., Admissible Sets and Structures: An Approach to Definability Theory, Perspectives in Mathematical Logic (Springer, Berlin, 1975).Google Scholar
Barwise, J. and Eklof, P., ‘Infinitary properties of abelian torsion groups’, Ann. Math. Logic 2(1) (1970/1971), 25–68.Google Scholar
Burgess, J. P., ‘Equivalences generated by families of Borel sets’, Proc. Amer. Math. Soc. 69(2) (1978), 323–326.Google Scholar
Burgess, J. P., ‘A reflection phenomenon in descriptive set theory’, Fund. Math. 104(2) (1979), 127–139.CrossRefGoogle Scholar
Greenberg, N. and Montalbán, A., ‘Ranked structures and arithmetic transfinite recursion’, Trans. Amer. Math. Soc. 360 (2008), 1265–1307.Google Scholar
Harrison, J., ‘Recursive pseudo-well-orderings’, Trans. Amer. Math. Soc. 131 (1968), 526–543.CrossRefGoogle Scholar
Harrington, L., ‘Analytic determinacy and 0♯’, J. Symbolic Logic 43(4) (1978), 685–693.Google Scholar
Kanamori, A., The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings, 2nd edn, Springer Monographs in Mathematics (Springer, Berlin, 2003).Google Scholar
Laver, R., ‘On Fraïssé’s order type conjecture’, Ann. of Math. (2) 93 (1971), 89–111.CrossRefGoogle Scholar
Martin, D. A., ‘The axiom of determinateness and reduction principles in the analytical hierarchy’, Bull. Amer. Math. Soc. 74 (1968), 687–689.CrossRefGoogle Scholar
Montalbán, A., ‘Up to equimorphism, hyperarithmetic is recursive’, J. Symbolic Logic 70(2) (2005), 360–378.CrossRefGoogle Scholar
Montalbán, A., ‘On the equimorphism types of linear orderings’, Bull. Symbolic Logic 13(1) (2007), 71–99.Google Scholar
Montalbán, A., ‘A computability theoretic equivalent to Vaught’s conjecture’, Adv. Math. 235 (2013), 56–73.Google Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic (Springer, Berlin, 1990).Google Scholar
Sami, R. L., ‘Analytic determinacy and 0♯ . A forcing-free proof of Harrington’s theorem’, Fund. Math. 160(2) (1999), 153–159.CrossRefGoogle Scholar
Silver, J. H., ‘Counting the number of equivalence classes of Borel and coanalytic equivalence relations’, Ann. Math. Logic 18(1) (1980), 1–28.Google Scholar
Spector, C., ‘Recursive well-orderings’, J. Symbolic Logic 20 (1955), 151–163.CrossRefGoogle Scholar