Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T08:28:47.475Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INTEGRATION APPROACH TO THE TOEPLITZ SQUARE PEG PROBLEM

Part of: Homology and cohomology theories

Published online by Cambridge University Press:  04 December 2017

TERENCE TAO
TERENCE TAO*
Affiliation:
UCLA Department of Mathematics, Los Angeles, CA 90095-1555, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The ‘square peg problem’ or ‘inscribed square problem’ of Toeplitz asks if every simple closed curve in the plane inscribes a (nondegenerate) square, in the sense that all four vertices of that square lie on the curve. By a variety of arguments of a ‘homological’ nature, it is known that the answer to this question is positive if the curve is sufficiently regular. The regularity hypotheses are needed to rule out the possibility of arbitrarily small squares that are inscribed or almost inscribed on the curve; because of this, these arguments do not appear to be robust enough to handle arbitrarily rough curves. In this paper, we augment the homological approach by introducing certain integrals associated to the curve. This approach is able to give positive answers to the square peg problem in some new cases, for instance if the curve is the union of two Lipschitz graphs 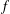$f$, 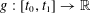$g:[t_{0},t_{1}]\rightarrow \mathbb{R}$ that agree at the endpoints, and whose Lipschitz constants are strictly less than one. We also present some simpler variants of the square problem which seem particularly amenable to this integration approach, including a periodic version of the problem that is not subject to the problem of arbitrarily small squares (and remains open even for regular curves), as well as an almost purely combinatorial conjecture regarding the sign patterns of sums 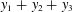$y_{1}+y_{2}+y_{3}$ for 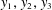$y_{1},y_{2},y_{3}$ ranging in finite sets of real numbers.

MSC classification

Primary: 55N45: Products and intersections
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e30
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2017

References

Alexander, J. W., ‘Topological invariants of knots and links’, Trans. Amer. Math. Soc. 30 (1928), 275–306.Google Scholar
Cantarella, J., Denne, E. and McCleary, J., ‘Transversality for configuration spaces and the ‘square-peg’ theorem’, Preprint (2014), arXiv:1402.6174.Google Scholar
Christensen, C. M., ‘A square inscribed in a convex figure’, Matematisk Tidsskrift B 1950 (1950), 22–26.Google Scholar
Emch, A., ‘Some properties of closed convex curves in a plane’, Amer. J. Math. 35 (1913), 407–412.CrossRefGoogle Scholar
Emch, A., ‘On the medians of a closed convex polygon’, Amer. J. Math. 37 (1915), 19–28.Google Scholar
Emch, A., ‘On some properties of the medians of closed continuous curves formed by analytic arcs’, Amer. J. Math. 38(1) (1916), 6–18.CrossRefGoogle Scholar
Fenn, R., ‘The table theorem’, Bull. Lond. Math. Soc. 2 (1970), 73–76.Google Scholar
Guggenheimer, H. W., ‘Finite sets on curves and surfaces’, Israel J. Math. 3 (1965), 104–112.Google Scholar
Hatcher, A., Algebraic Topology, (Cambridge University Press, Cambridge, 2002).Google Scholar
Hebbert, C. M., ‘The inscribed and circumscribed squares of a quadrilateral and their significance in kinematic geometry’, Ann. of Math. (2) 16(1–4) (1914/15), 38–42.Google Scholar
Jerrard, R. P., ‘Inscribed squares in plane curves’, Trans. Amer. Math. Soc. 98 (1961), 234–241.Google Scholar
Karasëv, R. N., ‘On two conjectures of Makeev’, translated from Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 415 (2013); Geometriya i Topologiya. 12, 5–14; J. Math. Sci. (N.Y.) 212(5) (2016), 521–526.Google Scholar
Lando, S. K. and Zvonkin, A. K., ‘Plane and projective meanders, Conference on Formal Power Series and Algebraic Combinatorics (Bordeaux, 1991)’, Theoret. Comput. Sci. 117(1–2) (1993), 227–241.Google Scholar
Makeev, V. V., ‘On quadrangles inscribed in a closed curve’, Math. Notes 57(1–2) (1995), 91–93.Google Scholar
Matschke, B., ‘Equivariant topology methods in discrete geometry’, PhD Thesis, Freie Universität Berlin, 2011.Google Scholar
Matschke, B., ‘A survey on the square peg problem’, Notices Amer. Math. Soc. 61(4) (2014), 346–352.CrossRefGoogle Scholar
Nielsen, M. J. and Wright, S. E., ‘Rectangles inscribed in symmetric continua’, Geom. Dedicata 56(3) (1995), 285–297.Google Scholar
Pak, I., ‘Lectures on discrete and polyhedral geometry’, http://math.ucla.edu/∼pak/book.htm, 2010.Google Scholar
Pettersson, V., Tverberg, H. and Östergård, P., ‘A note on Toeplitz’ conjecture’, Discrete Comput. Geom. 51 (2014), 722–728.Google Scholar
Poénaru, V., ‘What is … an infinite swindle?’, Notices Amer. Math. Soc. 54 (2007), 619–622.Google Scholar
Sagols, F. and Marín, R., ‘The inscribed square conjecture in the digital plane’, inCombinatorial Image Analysis, Lecture Notes in Computer Science, 5852 (Springer, Berlin, 2009), 411–424.Google Scholar
Sagols, F. and Marín, R., ‘Two discrete versions of the inscribed square conjecture and some related problems’, Theoret. Comput. Sci. 412(15) (2011), 1301–1312.Google Scholar
Schnirelman, L. G., ‘On some geometric properties of closed curves’, Uspekhi Mat. Nauk 10 (1944), 34–44.Google Scholar
Steinberg, R., ‘A general Clebsch–Gordan theorem’, Bull. Amer. Math. Soc. 67 (1961), 406–407.CrossRefGoogle Scholar
Stromquist, W. R., ‘Inscribed squares and squarelike quadrilaterals in closed curves’, Mathematika 36 (1989), 187–197.Google Scholar
Toeplitz, O., ‘Ueber einige Aufgaben der Analysis situs’, Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn 4 (1911), 197.Google Scholar
Vrećica, S. and Živaljević, R. T., ‘Fulton–MacPherson compactification, cyclohedra, and the polygonal pegs problem’, Israel J. Math. 184(1) (2011), 221–249.Google Scholar
Zindler, K., ‘Uber konvexe Gebilde’, Monatshefte für Mathematik und Physik 31 (1921), 25–56.Google Scholar