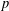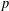Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lund, Ben
and
Saraf, Shubhangi
2016.
Incidence Bounds for Block Designs.
SIAM Journal on Discrete Mathematics,
Vol. 30,
Issue. 4,
p.
1997.
Petridis, Giorgis
and
Shparlinski, Igor E.
2019.
Bounds of Trilinear and Quadrilinear Exponential Sums.
Journal d'Analyse Mathématique,
Vol. 138,
Issue. 2,
p.
613.