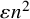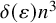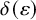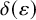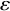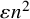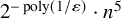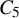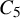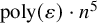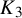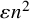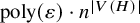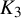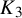1 Introduction
1.1 Background and previous results
An n-vertex graph is said to be
![]() $\varepsilon $
-far from triangle-free if it cannot be made triangle-free by deleting fewer than
$\varepsilon $
-far from triangle-free if it cannot be made triangle-free by deleting fewer than
![]() $\varepsilon n^2$
edges.Footnote 1 A fundamental result in extremal graph theory is the triangle removal lemma of Ruzsa and Szemerédi [Reference Ruzsa and Szemerédi20], which states that if an n-vertex graph is
$\varepsilon n^2$
edges.Footnote 1 A fundamental result in extremal graph theory is the triangle removal lemma of Ruzsa and Szemerédi [Reference Ruzsa and Szemerédi20], which states that if an n-vertex graph is
![]() $\varepsilon $
-far from triangle free, then it contains at least
$\varepsilon $
-far from triangle free, then it contains at least
![]() $\delta n^3$
triangles, where
$\delta n^3$
triangles, where
![]() $\delta =\delta (\varepsilon )>0$
depends only on
$\delta =\delta (\varepsilon )>0$
depends only on
![]() $\varepsilon $
. Despite its simple statement, this is a deep result, and it has applications in graph theory, number theory and theoretical computer science. For more on the triangle removal lemma, we refer to the survey [Reference Conlon and Fox7].
$\varepsilon $
. Despite its simple statement, this is a deep result, and it has applications in graph theory, number theory and theoretical computer science. For more on the triangle removal lemma, we refer to the survey [Reference Conlon and Fox7].
Despite decades of study, very little is known about the quantitative behavior of
![]() $\delta (\varepsilon )$
in the triangle removal lemma. The original proof of Ruzsa and Szemerédi used Szemerédi’s regularity lemma, and consequently obtained a bound on
$\delta (\varepsilon )$
in the triangle removal lemma. The original proof of Ruzsa and Szemerédi used Szemerédi’s regularity lemma, and consequently obtained a bound on
![]() $1/\delta $
that was of tower type in
$1/\delta $
that was of tower type in
![]() $\operatorname {\mathrm {poly}}(1/\varepsilon )$
. The best known bound is due to Fox [Reference Fox12], who improved the bound on
$\operatorname {\mathrm {poly}}(1/\varepsilon )$
. The best known bound is due to Fox [Reference Fox12], who improved the bound on
![]() $1/\delta $
to a tower of height
$1/\delta $
to a tower of height
![]() $O(\log (1/\varepsilon ))$
by finding a new proof which avoids the use of the regularity lemma. While a major improvement, this bound is still enormous, and it is a major open problem to improve it further.
$O(\log (1/\varepsilon ))$
by finding a new proof which avoids the use of the regularity lemma. While a major improvement, this bound is still enormous, and it is a major open problem to improve it further.
In the other direction, the best known lower bound on
![]() $1/\delta $
is due to Ruzsa and Szemerédi [Reference Ruzsa and Szemerédi20], who proved that
$1/\delta $
is due to Ruzsa and Szemerédi [Reference Ruzsa and Szemerédi20], who proved that
![]() $1/\delta \geq (1/\varepsilon )^{\Omega (\log (1/\varepsilon ))}$
. In particular, this implies that
$1/\delta \geq (1/\varepsilon )^{\Omega (\log (1/\varepsilon ))}$
. In particular, this implies that
![]() $\delta (\varepsilon )$
can not be taken to be a polynomial function of
$\delta (\varepsilon )$
can not be taken to be a polynomial function of
![]() $\varepsilon $
. Ruzsa and Szemerédi proved this by relating the triangle removal lemma to a problem in additive combinatorics – namely, the problem of finding subsets of
$\varepsilon $
. Ruzsa and Szemerédi proved this by relating the triangle removal lemma to a problem in additive combinatorics – namely, the problem of finding subsets of
![]() $[n]$
containing no three-term arithmetic progression – and using a well-known construction of Behrend [Reference Behrend5] of such a subset.
$[n]$
containing no three-term arithmetic progression – and using a well-known construction of Behrend [Reference Behrend5] of such a subset.
If one examines the usual proof of the triangle removal lemma, one sees that it immediately gives the following stronger ‘asymmetric’ statement (see, for example, [Reference Fox and Zhao13, Theorem 1.13]).
Theorem 1.1. For every graph H with
![]() $\chi (H) \leq 3$
and every
$\chi (H) \leq 3$
and every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta = \delta (\varepsilon ,H)>0$
such that the following holds. If an n-vertex graph G is
$\delta = \delta (\varepsilon ,H)>0$
such that the following holds. If an n-vertex graph G is
![]() $\varepsilon $
-far from triangle-free, then it contains at least
$\varepsilon $
-far from triangle-free, then it contains at least
![]() $\delta n^{\lvert V(H)\rvert }$
copies of H.
$\delta n^{\lvert V(H)\rvert }$
copies of H.
It is easy to see that the assumption
![]() $\chi (H)\leq 3$
is necessary in Theorem 1.1, as a balanced complete tripartite graph on n vertices has no copies of any H with
$\chi (H)\leq 3$
is necessary in Theorem 1.1, as a balanced complete tripartite graph on n vertices has no copies of any H with
![]() $\chi (H)>3$
, but is
$\chi (H)>3$
, but is
![]() $\frac 19$
-far from triangle-free.
$\frac 19$
-far from triangle-free.
The standard proof of Theorem 1.1 gives tower-type bounds on
![]() $\delta $
, as it uses Szemerédi’s regularity lemma. But it is natural to ask whether, for certain graphs H, one can get a stronger bound in Theorem 1.1. It turns out that in certain instances, one can.
$\delta $
, as it uses Szemerédi’s regularity lemma. But it is natural to ask whether, for certain graphs H, one can get a stronger bound in Theorem 1.1. It turns out that in certain instances, one can.
Theorem 1.2 (Csaba [Reference Csaba9, Theorem 5.2]).
If an n-vertex graph G is
![]() $\varepsilon $
-far from triangle-free, then it contains at least
$\varepsilon $
-far from triangle-free, then it contains at least
![]() $2^{-\operatorname {\mathrm {poly}}(1/\varepsilon )}\cdot n^5$
copies of
$2^{-\operatorname {\mathrm {poly}}(1/\varepsilon )}\cdot n^5$
copies of
![]() $C_5$
.
$C_5$
.
In other words, Csaba showed that in the special case
![]() $H=C_5$
, one can replace the tower-type bound in Theorem 1.1 by a single-exponential bound. To prove this, Csaba developed a new variant of Szemerédi’s regularity lemma, somewhat akin to the weak regularity lemmas of Frieze–Kannan [Reference Frieze and Kannan14] and Duke–Lefmann–Rödl [Reference Duke, Lefmann and Rödl10], which does not yield tower-type dependencies between the parameters and is nonetheless strong enough to prove results like Theorem 1.2. We also mention a recent result of Conlon, Fox, Sudakov and Zhao [Reference Conlon, Fox, Sudakov and Zhao8, Corollary 1.4], who proved that if G has zero copies of
$H=C_5$
, one can replace the tower-type bound in Theorem 1.1 by a single-exponential bound. To prove this, Csaba developed a new variant of Szemerédi’s regularity lemma, somewhat akin to the weak regularity lemmas of Frieze–Kannan [Reference Frieze and Kannan14] and Duke–Lefmann–Rödl [Reference Duke, Lefmann and Rödl10], which does not yield tower-type dependencies between the parameters and is nonetheless strong enough to prove results like Theorem 1.2. We also mention a recent result of Conlon, Fox, Sudakov and Zhao [Reference Conlon, Fox, Sudakov and Zhao8, Corollary 1.4], who proved that if G has zero copies of
![]() $C_5$
, then it can be made triangle-free by deleting
$C_5$
, then it can be made triangle-free by deleting
![]() $o(n^{3/2})$
edges; this result was proved via new techniques in the regularity method for sparse graphs.
$o(n^{3/2})$
edges; this result was proved via new techniques in the regularity method for sparse graphs.
1.2 An optimal result for odd cycles
Our first main result is an improvement of Theorem 1.2, which reduces the single-exponential bound to a polynomial bound. In fact, we prove a more general result, which holds for all pairs of odd cycles; our improvement to Theorem 1.2 corresponds to the case
![]() $k=1,\ell =2$
of the following theorem. Extending the terminology above, one says that an n-vertex graph G is
$k=1,\ell =2$
of the following theorem. Extending the terminology above, one says that an n-vertex graph G is
![]() $\varepsilon $
-far from satisfying a graph property
$\varepsilon $
-far from satisfying a graph property
![]() $\mathcal P$
if one must add or delete at least
$\mathcal P$
if one must add or delete at least
![]() $\varepsilon n^2$
edges to G in order to create a graph satisfying property
$\varepsilon n^2$
edges to G in order to create a graph satisfying property
![]() $\mathcal P$
.
$\mathcal P$
.
Theorem 1.3. Let
![]() $1 \leq k <\ell $
be integers and let
$1 \leq k <\ell $
be integers and let
![]() $\varepsilon>0$
. If G is
$\varepsilon>0$
. If G is
![]() $\varepsilon $
-far from
$\varepsilon $
-far from
![]() $C_{2k+1}$
-free, then it contains at least
$C_{2k+1}$
-free, then it contains at least
![]() $(c_\ell \varepsilon ^{4\ell +2})n^{2\ell +1}$
copies of
$(c_\ell \varepsilon ^{4\ell +2})n^{2\ell +1}$
copies of
![]() $C_{2\ell +1}$
, where
$C_{2\ell +1}$
, where
![]() $c_\ell>0$
is a constant depending only on
$c_\ell>0$
is a constant depending only on
![]() $\ell $
.
$\ell $
.
In contrast to the earlier proofs of Theorems 1.1 and 1.2, which used complicated regularity-type arguments, our proof of Theorem 1.3 uses elementary but subtle counting arguments. Note that the dependence on
![]() $\varepsilon $
in Theorem 1.3 is best possible up to a factor of
$\varepsilon $
in Theorem 1.3 is best possible up to a factor of
![]() $2$
in the exponent. Indeed, a random n-vertex graph with edge density
$2$
in the exponent. Indeed, a random n-vertex graph with edge density
![]() $\varepsilon $
has
$\varepsilon $
has
![]() $\Theta _\ell (\varepsilon ^{2\ell +1})\cdot n^{2\ell +1}$
copies of
$\Theta _\ell (\varepsilon ^{2\ell +1})\cdot n^{2\ell +1}$
copies of
![]() $C_{2\ell +1}$
, and is
$C_{2\ell +1}$
, and is
![]() $\Theta _k(\varepsilon )$
-far from
$\Theta _k(\varepsilon )$
-far from
![]() $C_{2k+1}$
-free. This observation, as well as Theorem 1.3, motivates the following definition.
$C_{2k+1}$
-free. This observation, as well as Theorem 1.3, motivates the following definition.
Definition 1.4 (
 $K_3$
-abundant).
$K_3$
-abundant).
Let H be a graph. We say that H is
![]() $K_3$
-abundant if there exists some
$K_3$
-abundant if there exists some
![]() $C_H>0$
such that for all
$C_H>0$
such that for all
![]() $0<\varepsilon \leq \frac 12$
, all integers n, and any n-vertex graph G which is
$0<\varepsilon \leq \frac 12$
, all integers n, and any n-vertex graph G which is
![]() $\varepsilon $
-far from triangle-free, the number of copies of H in G is at least
$\varepsilon $
-far from triangle-free, the number of copies of H in G is at least
![]() $\varepsilon ^{C_H} \cdot n^{\lvert V(H)\rvert }$
.
$\varepsilon ^{C_H} \cdot n^{\lvert V(H)\rvert }$
.
Informally, this definition says that H is
![]() $K_3$
-abundant if we may take
$K_3$
-abundant if we may take
![]() $\delta = \operatorname {\mathrm {poly}}_H(\varepsilon )$
in Theorem 1.1. In this language, Theorem 1.3 implies that
$\delta = \operatorname {\mathrm {poly}}_H(\varepsilon )$
in Theorem 1.1. In this language, Theorem 1.3 implies that
![]() $C_{2\ell +1}$
is
$C_{2\ell +1}$
is
![]() $K_3$
-abundant for all
$K_3$
-abundant for all
![]() $\ell \geq 2$
.
$\ell \geq 2$
.
By the discussion above, any graph H with
![]() $\chi (H)>3$
cannot be
$\chi (H)>3$
cannot be
![]() $K_3$
-abundant, as Theorem 1.1 is simply false for such graphs. At the other extreme, it is easy to see that every bipartite graph H is
$K_3$
-abundant, as Theorem 1.1 is simply false for such graphs. At the other extreme, it is easy to see that every bipartite graph H is
![]() $K_3$
-abundant, but for a fairly uninteresting reason: if an n-vertex graph G contains fewer than
$K_3$
-abundant, but for a fairly uninteresting reason: if an n-vertex graph G contains fewer than
![]() $\varepsilon ^{C_H} \cdot n^{\lvert V(H)\rvert }$
copies of some bipartite H, then G has fewer than
$\varepsilon ^{C_H} \cdot n^{\lvert V(H)\rvert }$
copies of some bipartite H, then G has fewer than
![]() $\varepsilon n^2$
edges, and thus is certainly not
$\varepsilon n^2$
edges, and thus is certainly not
![]() $\varepsilon $
-far from triangle-free. This follows from a convexity argument originally due to Kővári, Sós and Turán [Reference Kövari, Sós and Turán18] (see also [Reference Alon2]).
$\varepsilon $
-far from triangle-free. This follows from a convexity argument originally due to Kővári, Sós and Turán [Reference Kövari, Sós and Turán18] (see also [Reference Alon2]).
However,
![]() $K_3$
itself is not
$K_3$
itself is not
![]() $K_3$
-abundant, thanks to the Ruzsa–Szemerédi result that one does not have polynomial bounds in the triangle removal lemma. Moreover, if H is
$K_3$
-abundant, thanks to the Ruzsa–Szemerédi result that one does not have polynomial bounds in the triangle removal lemma. Moreover, if H is
![]() $K_3$
-abundant, then so is any subgraph of it. This immediately implies that if H contains a triangle, then H cannot be
$K_3$
-abundant, then so is any subgraph of it. This immediately implies that if H contains a triangle, then H cannot be
![]() $K_3$
-abundant. So any non-bipartite
$K_3$
-abundant. So any non-bipartite
![]() $K_3$
-abundant graph must be tripartite and triangle-free. The simplest examples of such graphs are odd cycles (of length at least
$K_3$
-abundant graph must be tripartite and triangle-free. The simplest examples of such graphs are odd cycles (of length at least
![]() $5$
), which are indeed
$5$
), which are indeed
![]() $K_3$
-abundant by Theorem 1.3. Moreover, it is easy to seeFootnote 2 that any graph which is homomorphic to a
$K_3$
-abundant by Theorem 1.3. Moreover, it is easy to seeFootnote 2 that any graph which is homomorphic to a
![]() $K_3$
-abundant graph is also
$K_3$
-abundant graph is also
![]() $K_3$
-abundant; hence, any graph homomorphic to an odd cycle of length at least
$K_3$
-abundant; hence, any graph homomorphic to an odd cycle of length at least
![]() $5$
is
$5$
is
![]() $K_3$
-abundant.
$K_3$
-abundant.
Based on all of this, it is natural to ask whether all triangle-free tripartite graphs are
![]() $K_3$
-abundant.
$K_3$
-abundant.
1.3 Not all graphs are abundant
Our second main result is that not all triangle-free tripartite graphs are
![]() $K_3$
-abundant, assuming a well-known conjecture of Ruzsa [Reference Ruzsa19] in additive combinatorics. To state this conjecture, we need to set up some notation. Consider a linear equation
$K_3$
-abundant, assuming a well-known conjecture of Ruzsa [Reference Ruzsa19] in additive combinatorics. To state this conjecture, we need to set up some notation. Consider a linear equation
![]() $\sum _{i=1}^k a_i x_i = 0$
, where the coefficients
$\sum _{i=1}^k a_i x_i = 0$
, where the coefficients
![]() $a_1,\dots ,a_k$
are integers. Following Ruzsa [Reference Ruzsa19], one says that this equation has genus one if
$a_1,\dots ,a_k$
are integers. Following Ruzsa [Reference Ruzsa19], one says that this equation has genus one if
![]() $\sum _{i=1}^k a_i=0$
, but
$\sum _{i=1}^k a_i=0$
, but
![]() $\sum _{i \in T} a_i \neq 0$
for all
$\sum _{i \in T} a_i \neq 0$
for all
![]() $\varnothing \subsetneq T \subsetneq [k]$
. We say that integers
$\varnothing \subsetneq T \subsetneq [k]$
. We say that integers
![]() $y_1,\dots ,y_k$
form a nontrivial solution
Footnote 3 to this equation if
$y_1,\dots ,y_k$
form a nontrivial solution
Footnote 3 to this equation if
![]() $\sum _{i=1}^k a_{i} y_i=0$
and the
$\sum _{i=1}^k a_{i} y_i=0$
and the
![]() $y_i$
are not all equal. We denote by
$y_i$
are not all equal. We denote by
![]() $r_E(m)$
the maximum size of a subset of
$r_E(m)$
the maximum size of a subset of
![]() $[m]$
containing no nontrivial solution to an equation E.
$[m]$
containing no nontrivial solution to an equation E.
With this notation in place, Ruzsa’s genus conjectureFootnote 4 says the following.
Conjecture 1.5 (Ruzsa [Reference Ruzsa19]).
If E is a linear equation of genus one, then
![]() $r_E(m) \geq m^{1-o(1)}$
.
$r_E(m) \geq m^{1-o(1)}$
.
We can now state our second main theorem.
Theorem 1.6. Assuming that Conjecture 1.5 holds, there exists a triangle-free tripartite graph H which is not
![]() $K_3$
-abundant.
$K_3$
-abundant.
The proof of Theorem 1.6 is based on Ruzsa and Szemerédi’s proof [Reference Ruzsa and Szemerédi20] that super-polynomial bounds are necessary in the triangle removal lemma (i.e., that
![]() $K_3$
itself is not
$K_3$
itself is not
![]() $K_3$
-abundant), but with several important differences. To explain the idea of the proof, let us briefly recall Ruzsa and Szemerédi’s construction. Given an integer m and a set
$K_3$
-abundant), but with several important differences. To explain the idea of the proof, let us briefly recall Ruzsa and Szemerédi’s construction. Given an integer m and a set
![]() $R \subseteq [m]$
, they define a tripartite graph
$R \subseteq [m]$
, they define a tripartite graph
![]() $\Gamma $
such that triangles in
$\Gamma $
such that triangles in
![]() $\Gamma $
correspond to solutions in R to the equation
$\Gamma $
correspond to solutions in R to the equation
![]() $x+z=2y$
; note that solutions to this equation are three-term arithmetic progressions in R, and that trivial solutions are trivial arithmetic progressions. The upshot of this construction is twofold. First, if R contains no nontrivial arithmetic progressions, then
$x+z=2y$
; note that solutions to this equation are three-term arithmetic progressions in R, and that trivial solutions are trivial arithmetic progressions. The upshot of this construction is twofold. First, if R contains no nontrivial arithmetic progressions, then
![]() $\Gamma $
has few triangles, and second, if R is large, then
$\Gamma $
has few triangles, and second, if R is large, then
![]() $\Gamma $
is far from triangle-free (as the many trivial arithmetic progressions in R yield many edge-disjoint triangles in
$\Gamma $
is far from triangle-free (as the many trivial arithmetic progressions in R yield many edge-disjoint triangles in
![]() $\Gamma $
). To finish the proof, Ruzsa and Szemerédi use Behrend’s [Reference Behrend5] construction of a set
$\Gamma $
). To finish the proof, Ruzsa and Szemerédi use Behrend’s [Reference Behrend5] construction of a set
![]() $R\subseteq [m]$
with no nontrivial arithmetic progressions and of size
$R\subseteq [m]$
with no nontrivial arithmetic progressions and of size
![]() $\lvert R\rvert \geq m^{1-o(1)}$
. Using this set R in the construction described above, one obtains a graph
$\lvert R\rvert \geq m^{1-o(1)}$
. Using this set R in the construction described above, one obtains a graph
![]() $\Gamma $
with at most
$\Gamma $
with at most
![]() $\delta n^3$
triangles that is
$\delta n^3$
triangles that is
![]() $\varepsilon $
-far from triangle-free, where
$\varepsilon $
-far from triangle-free, where
![]() $\delta $
is smaller than any fixed power of
$\delta $
is smaller than any fixed power of
![]() $\varepsilon $
, because
$\varepsilon $
, because
![]() $\lvert R\rvert $
is larger than any fixed power of m less than
$\lvert R\rvert $
is larger than any fixed power of m less than
![]() $1$
.
$1$
.
For our proof of Theorem 1.6, we use the same construction to build a graph
![]() $\Gamma $
out of any
$\Gamma $
out of any
![]() $R \subseteq [m]$
. For the same reason as above, if R is large, then
$R \subseteq [m]$
. For the same reason as above, if R is large, then
![]() $\Gamma $
is far from triangle-free. We would now like to show that
$\Gamma $
is far from triangle-free. We would now like to show that
![]() $\Gamma $
has few copies of H, for some triangle-free tripartite graph H. As before, we can use the structure of
$\Gamma $
has few copies of H, for some triangle-free tripartite graph H. As before, we can use the structure of
![]() $\Gamma $
to parameterize copies of H in
$\Gamma $
to parameterize copies of H in
![]() $\Gamma $
: there is a correspondence between copies of H in
$\Gamma $
: there is a correspondence between copies of H in
![]() $\Gamma $
and solutions in R to a certain system of equations S arising from the cycles in H, whose variables are indexed by the edges of H. To prove Theorem 1.6, it suffices to find a set
$\Gamma $
and solutions in R to a certain system of equations S arising from the cycles in H, whose variables are indexed by the edges of H. To prove Theorem 1.6, it suffices to find a set
![]() $R \subseteq [m]$
with
$R \subseteq [m]$
with
![]() $\lvert R\rvert \geq m^{1-o(1)}$
containing no nontrivial solutions to S. Unfortunately, as H is triangle-free, this is impossible if we only use a single equation from S: no single equation in this family has genus one, and therefore, the largest set
$\lvert R\rvert \geq m^{1-o(1)}$
containing no nontrivial solutions to S. Unfortunately, as H is triangle-free, this is impossible if we only use a single equation from S: no single equation in this family has genus one, and therefore, the largest set
![]() $R \subseteq [m]$
avoiding nontrivial solutions to any single equation from S has size
$R \subseteq [m]$
avoiding nontrivial solutions to any single equation from S has size
![]() $\lvert R\rvert = O(\sqrt m)$
[Reference Ruzsa19, Theorem 3.6]. The key idea in the proof is that if H is sufficiently ‘complicated’, then the system of equations S, generated from the cycle space of H, does have genus one,Footnote 5 and thus, Conjecture 1.5 implies that there exists a set R satisfying our desired properties.
$\lvert R\rvert = O(\sqrt m)$
[Reference Ruzsa19, Theorem 3.6]. The key idea in the proof is that if H is sufficiently ‘complicated’, then the system of equations S, generated from the cycle space of H, does have genus one,Footnote 5 and thus, Conjecture 1.5 implies that there exists a set R satisfying our desired properties.
The heart of the proof, then, is showing that if H is an appropriately chosen tripartite triangle-free graph, the set of equations arising from its cycles has genus one. Since the variables in the equations in S correspond to the edges of H, a set which witnesses that S does not have genus one can be viewed as a two-coloring of the edges of H with a certain properties. We now use a Ramsey-theoretic argument to show that if H satisfies a number of carefully chosen pseudorandomness conditions, such a coloring cannot exist. To conclude the proof, it suffices to find a tripartite triangle-free graph that is pseudorandom in this sense; we do this by picking a random tripartite graph of an appropriate density and deleting one edge from each triangle.
1.4 An application of Theorem 1.3 to property testing
Recall that an n-vertex graph G is
![]() $\varepsilon $
-far from satisfying a graph property
$\varepsilon $
-far from satisfying a graph property
![]() $\mathcal P$
if one must add or delete at least
$\mathcal P$
if one must add or delete at least
![]() $\varepsilon n^2$
edges to G in order to create a graph satisfying property
$\varepsilon n^2$
edges to G in order to create a graph satisfying property
![]() $\mathcal P$
.
$\mathcal P$
.
Given a monotoneFootnote 6 graph property
![]() ${\cal P}$
, let
${\cal P}$
, let
![]() $w_{\cal P}(\varepsilon )$
denote the smallest integer so that if G is
$w_{\cal P}(\varepsilon )$
denote the smallest integer so that if G is
![]() $\varepsilon $
-far from satisfying
$\varepsilon $
-far from satisfying
![]() ${\cal P}$
, then a randomly selected set X of
${\cal P}$
, then a randomly selected set X of
![]() $w_{\cal P}(\varepsilon )$
vertices spans a subgraph not satisfying
$w_{\cal P}(\varepsilon )$
vertices spans a subgraph not satisfying
![]() ${\cal P}$
with probability at least
${\cal P}$
with probability at least
![]() $1/2$
. Note that a priori it is not clear that the function
$1/2$
. Note that a priori it is not clear that the function
![]() $w_{\cal P}(\varepsilon )$
is well defined for all (or indeed any)
$w_{\cal P}(\varepsilon )$
is well defined for all (or indeed any)
![]() ${\cal P}$
. In this terminology, if
${\cal P}$
. In this terminology, if
![]() ${\cal P}$
is the property of being triangle-free, then the triangle removal lemma implies that
${\cal P}$
is the property of being triangle-free, then the triangle removal lemma implies that
![]() $w_{\cal P}(\varepsilon )$
is well defined, and that, in fact,
$w_{\cal P}(\varepsilon )$
is well defined, and that, in fact,
![]() $w_{\cal P}(\varepsilon ) \leq 1/ \delta (\varepsilon )$
.
$w_{\cal P}(\varepsilon ) \leq 1/ \delta (\varepsilon )$
.
As discussed above, Ruzsa and Szemerédi [Reference Ruzsa and Szemerédi20] proved that the bounds for the triangle removal lemma are not polynomial in
![]() $\varepsilon $
. In the notation of the previous paragraph, this means that
$\varepsilon $
. In the notation of the previous paragraph, this means that
![]() $w_{\cal P}(\varepsilon )$
is super-polynomial in
$w_{\cal P}(\varepsilon )$
is super-polynomial in
![]() $1/\varepsilon $
when
$1/\varepsilon $
when
![]() $\mathcal P$
is the property of being triangle-free. Alon [Reference Alon2] later extended this result to all non-bipartite graphs H, and thus in particular to all odd cycles: if
$\mathcal P$
is the property of being triangle-free. Alon [Reference Alon2] later extended this result to all non-bipartite graphs H, and thus in particular to all odd cycles: if
![]() $\mathcal P$
is the property of being
$\mathcal P$
is the property of being
![]() $C_{2\ell +1}$
-free, then
$C_{2\ell +1}$
-free, then
![]() $w_{\mathcal P}(\varepsilon )$
is super-polynomial in
$w_{\mathcal P}(\varepsilon )$
is super-polynomial in
![]() $1/\varepsilon $
. It is natural to ask at this point what happens if instead of forbidding a single odd cycle, we take a family of odd cycles L and consider the property of not containing any cycle from L. It is not hard to show that Alon’s method can be used to show that
$1/\varepsilon $
. It is natural to ask at this point what happens if instead of forbidding a single odd cycle, we take a family of odd cycles L and consider the property of not containing any cycle from L. It is not hard to show that Alon’s method can be used to show that
![]() $w_{\cal P}(\varepsilon )$
is super-polynomial in
$w_{\cal P}(\varepsilon )$
is super-polynomial in
![]() $1/\varepsilon $
for every finite family of odd cycles. At the other extreme, if we take L to be the family of all odd cycles, then we have the following influential result of Goldreich, Goldwasser and Ron [Reference Goldreich, Goldwasser and Ron16].
$1/\varepsilon $
for every finite family of odd cycles. At the other extreme, if we take L to be the family of all odd cycles, then we have the following influential result of Goldreich, Goldwasser and Ron [Reference Goldreich, Goldwasser and Ron16].
Theorem 1.7 [Reference Goldreich, Goldwasser and Ron16]
If
![]() $\mathcal P$
is the property of being
$\mathcal P$
is the property of being
![]() $2$
-colorable, then
$2$
-colorable, then
![]() $w_{\mathcal P}(\varepsilon ) \leq \operatorname {\mathrm {poly}}(1/ \varepsilon )$
.
$w_{\mathcal P}(\varepsilon ) \leq \operatorname {\mathrm {poly}}(1/ \varepsilon )$
.
The
![]() $\operatorname {\mathrm {poly}}(1/\varepsilon )$
bound obtained in [Reference Goldreich, Goldwasser and Ron16] improved a tower-type bound obtained by Bollobás, Erdős, Simonovits and Szemerédi [Reference Bollobás, Erdős and Szemerédi6]. It is interesting to compare the proofs in [Reference Bollobás, Erdős and Szemerédi6] and [Reference Goldreich, Goldwasser and Ron16]. The former proof relied on the fact that if G is far from being bipartite, then G is also far from being
$\operatorname {\mathrm {poly}}(1/\varepsilon )$
bound obtained in [Reference Goldreich, Goldwasser and Ron16] improved a tower-type bound obtained by Bollobás, Erdős, Simonovits and Szemerédi [Reference Bollobás, Erdős and Szemerédi6]. It is interesting to compare the proofs in [Reference Bollobás, Erdős and Szemerédi6] and [Reference Goldreich, Goldwasser and Ron16]. The former proof relied on the fact that if G is far from being bipartite, then G is also far from being
![]() $C_{2\ell +1}$
-free where
$C_{2\ell +1}$
-free where
![]() $\ell $
is an integer of order
$\ell $
is an integer of order
![]() $1/\varepsilon $
. They then used the graph removal lemma to show that G must contain many copies of
$1/\varepsilon $
. They then used the graph removal lemma to show that G must contain many copies of
![]() $C_{2\ell +1}$
. The proof in [Reference Goldreich, Goldwasser and Ron16] used a completely different approach, which crucially relied on interpreting this property as bipartiteness, rather than
$C_{2\ell +1}$
. The proof in [Reference Goldreich, Goldwasser and Ron16] used a completely different approach, which crucially relied on interpreting this property as bipartiteness, rather than
![]() $\{C_3,C_5,\dots \}$
-freeness. In particular, the proof of [Reference Goldreich, Goldwasser and Ron16] works not only for bipartiteness but for k-colorability for any fixed k.
$\{C_3,C_5,\dots \}$
-freeness. In particular, the proof of [Reference Goldreich, Goldwasser and Ron16] works not only for bipartiteness but for k-colorability for any fixed k.
It is natural at this point to ask what happens for general infinite families of odd cycles. We answer this question in Section 2. In particular, our proof shows that one can prove Theorem 1.7 using a removal-type argument similar to that of [Reference Bollobás, Erdős and Szemerédi6], but with an important twist. After concluding that G is far from being
![]() $C_{2\ell +1}$
-free, we do not prove that it has many copies of
$C_{2\ell +1}$
-free, we do not prove that it has many copies of
![]() $C_{2\ell +1}$
, but rather that it has many copies of
$C_{2\ell +1}$
, but rather that it has many copies of
![]() $C_{2\ell +3}$
. Thanks to Theorem 1.3, we may take this ‘many’ to only be polynomial in
$C_{2\ell +3}$
. Thanks to Theorem 1.3, we may take this ‘many’ to only be polynomial in
![]() $1/\varepsilon $
, rather than super-polynomial as in [Reference Bollobás, Erdős and Szemerédi6].
$1/\varepsilon $
, rather than super-polynomial as in [Reference Bollobás, Erdős and Szemerédi6].
It would be very interesting to prove efficient asymmetric removal lemmas like Theorem 1.3 for pairs of graphs of chromatic number larger than
![]() $3$
, and then use them to prove a version of Theorem 1.7 which holds for k-colorability for any fixed k. We discuss a version of this problem in the next subsection.
$3$
, and then use them to prove a version of Theorem 1.7 which holds for k-colorability for any fixed k. We discuss a version of this problem in the next subsection.
1.5 Larger cliques and higher chromatic numbers
There is a natural generalization of the triangle removal lemma, known as the clique removal lemma, which states that for any
![]() $t \geq 3$
, if an n-vertex graph is
$t \geq 3$
, if an n-vertex graph is
![]() $\varepsilon $
-far from
$\varepsilon $
-far from
![]() $K_t$
-free, then it contains at least
$K_t$
-free, then it contains at least
![]() $\delta n^t$
copies of
$\delta n^t$
copies of
![]() $K_t$
, for some
$K_t$
, for some
![]() $\delta = \delta (\varepsilon ,t)>0$
. Similarly to Theorem 1.1, the usual proof of the clique removal lemma immediately gives the following asymmetric version.
$\delta = \delta (\varepsilon ,t)>0$
. Similarly to Theorem 1.1, the usual proof of the clique removal lemma immediately gives the following asymmetric version.
Theorem 1.8. Let
![]() $t \geq 3$
and let H be a graph with
$t \geq 3$
and let H be a graph with
![]() $\chi (H) \leq t$
. If an n-vertex graph G is
$\chi (H) \leq t$
. If an n-vertex graph G is
![]() $\varepsilon $
-far from
$\varepsilon $
-far from
![]() $K_t$
-free, then G contains at least
$K_t$
-free, then G contains at least
![]() $\delta n^{\lvert V(H)\rvert }$
copies of H, for some
$\delta n^{\lvert V(H)\rvert }$
copies of H, for some
![]() $\delta = \delta (\varepsilon ,H,t)>0$
.
$\delta = \delta (\varepsilon ,H,t)>0$
.
Because of this, one can naturally extend the definition of
![]() $K_3$
-abundance to
$K_3$
-abundance to
![]() $K_t$
-abundance for any
$K_t$
-abundance for any
![]() $t \geq 3$
. Namely, we say that H is
$t \geq 3$
. Namely, we say that H is
![]() $K_t$
-abundant if we may take
$K_t$
-abundant if we may take
![]() $\delta = \operatorname {\mathrm {poly}}_{H,t}(\varepsilon )$
in Theorem 1.8. Note that if G is
$\delta = \operatorname {\mathrm {poly}}_{H,t}(\varepsilon )$
in Theorem 1.8. Note that if G is
![]() $\varepsilon $
-far from
$\varepsilon $
-far from
![]() $K_t$
-free for some
$K_t$
-free for some
![]() $t \geq 4$
, then G is also
$t \geq 4$
, then G is also
![]() $\varepsilon $
-far from triangle-free. Therefore, if H is
$\varepsilon $
-far from triangle-free. Therefore, if H is
![]() $K_3$
-abundant, then it is automatically
$K_3$
-abundant, then it is automatically
![]() $K_t$
-abundant for all
$K_t$
-abundant for all
![]() $t \geq 4$
. This shows that all bipartite graphs, as well as all odd cycles of length at least
$t \geq 4$
. This shows that all bipartite graphs, as well as all odd cycles of length at least
![]() $5$
, are
$5$
, are
![]() $K_t$
-abundant for all
$K_t$
-abundant for all
![]() $t \geq 4$
.
$t \geq 4$
.
In order to rule out such examples, it is natural to ask about
![]() $K_t$
-abundant graphs with chromatic number equal to t. As in the case of
$K_t$
-abundant graphs with chromatic number equal to t. As in the case of
![]() $K_3$
-abundance, one can use the Ruzsa–Szemerédi argument to show that if H contains a triangle, then H is not
$K_3$
-abundance, one can use the Ruzsa–Szemerédi argument to show that if H contains a triangle, then H is not
![]() $K_t$
-abundant for any
$K_t$
-abundant for any
![]() $t \geq 3$
(see, for example, [Reference Alon and Shapira4, Lemma 4.2] for a proof of a very similar result).
$t \geq 3$
(see, for example, [Reference Alon and Shapira4, Lemma 4.2] for a proof of a very similar result).
However, once
![]() $t \geq 4$
, there are other ‘simple’ reasons why a graph may be non-
$t \geq 4$
, there are other ‘simple’ reasons why a graph may be non-
![]() $K_t$
-abundant. To define these, let H be a graph with
$K_t$
-abundant. To define these, let H be a graph with
![]() $\chi (H)=t$
. Given a proper coloring
$\chi (H)=t$
. Given a proper coloring
![]() $c:V(H) \to [t]$
, let us define a c-increasing cycle to be a cycle
$c:V(H) \to [t]$
, let us define a c-increasing cycle to be a cycle
![]() $v_1,\dots ,v_s$
in H with
$v_1,\dots ,v_s$
in H with
![]() $c(v_1)< c(v_2) < \dotsb < c(v_s)$
. Note that a c-increasing cycle necessarily has length at most t. Let us say that H is increasing-cycle-unavoidable if, for every proper coloring
$c(v_1)< c(v_2) < \dotsb < c(v_s)$
. Note that a c-increasing cycle necessarily has length at most t. Let us say that H is increasing-cycle-unavoidable if, for every proper coloring
![]() $c:V(H) \to [t]$
, there is a c-increasing cycle in H. For example, if H contains a triangle, then it is necessarily increasing-cycle-unavoidable.
$c:V(H) \to [t]$
, there is a c-increasing cycle in H. For example, if H contains a triangle, then it is necessarily increasing-cycle-unavoidable.
It again follows from standard techniques (e.g., by combining [Reference Ruzsa19, Theorem 2.3] and [Reference Alon2, Lemma 3.4]) that if H has chromatic number t and is increasing-cycle-unavoidable, then H is not
![]() $K_t$
-abundant. In particular, we again find that any graph containing a triangle is not
$K_t$
-abundant. In particular, we again find that any graph containing a triangle is not
![]() $K_t$
-abundant. However, this also includes other graphs. For example, the Grötzsch graph is the smallest triangle-free
$K_t$
-abundant. However, this also includes other graphs. For example, the Grötzsch graph is the smallest triangle-free
![]() $4$
-chromatic graph, and one can check (by tedious casework, or with a computer) that the Grötzsch graph is increasing-cycle-unavoidable. Therefore, the Grötzsch graph is an example of a triangle-free
$4$
-chromatic graph, and one can check (by tedious casework, or with a computer) that the Grötzsch graph is increasing-cycle-unavoidable. Therefore, the Grötzsch graph is an example of a triangle-free
![]() $4$
-chromatic graph that is not
$4$
-chromatic graph that is not
![]() $K_4$
-abundant.
$K_4$
-abundant.
Therefore, to get to a genuinely interesting question, it makes sense to restrict our attention to t-chromatic graphs with girth greater than t (as any c-increasing cycle has length at most t, so there are no such cycles in a graph of girth larger than t). We believe that, with appropriate modifications, the technique used to prove Theorem 1.6 shows that for every
![]() $t\geq 3$
, there exists a t-chromatic non-
$t\geq 3$
, there exists a t-chromatic non-
![]() $K_t$
-abundant graph with girth greater than t, assuming that Conjecture 1.5 holds. Namely, one can obtain such a graph by sampling an appropriate random graph, then deleting all cycles of length at most t.
$K_t$
-abundant graph with girth greater than t, assuming that Conjecture 1.5 holds. Namely, one can obtain such a graph by sampling an appropriate random graph, then deleting all cycles of length at most t.
Thus, we have many ways of finding non-
![]() $K_t$
-abundant graphs, and no examples of t-chromatic graphs that are
$K_t$
-abundant graphs, and no examples of t-chromatic graphs that are
![]() $K_t$
-abundant for
$K_t$
-abundant for
![]() $t \geq 4$
. This motivates the following question.
$t \geq 4$
. This motivates the following question.
Problem 1.9. Let
![]() $t \geq 4$
. Does there exist a
$t \geq 4$
. Does there exist a
![]() $K_t$
-abundant graph with chromatic number t?
$K_t$
-abundant graph with chromatic number t?
The simplest
![]() $4$
-chromatic graph whose status is unknown is the Brinkmann graph; this is a
$4$
-chromatic graph whose status is unknown is the Brinkmann graph; this is a
![]() $21$
-vertex graph with chromatic number
$21$
-vertex graph with chromatic number
![]() $4$
and girth
$4$
and girth
![]() $5$
, so the techniques we have cannot be used to rule out its
$5$
, so the techniques we have cannot be used to rule out its
![]() $K_4$
-abundance.
$K_4$
-abundance.
Paper organization:
The rest of this paper is organized as follows. In Section 2, we prove Theorem 1.3 and use it to deduce Theorem 1.7. In Section 3, we prove Theorem 1.6, apart from the proof that there exists a graph satisfying certain pseudorandomness assumptions. In Section 4, we prove that an appropriate random graph satisfies these assumptions. We end in Section 5 with some concluding remarks.
2 Many edge-disjoint
 $(2k+1)$
-cycles imply many
$(2k+1)$
-cycles imply many
 $(2\ell +1)$
-cycles
$(2\ell +1)$
-cycles
In this section, we prove Theorem 1.3. We actually prove a stronger sampling version, saying that a sample of size
![]() $\operatorname {\mathrm {poly}}(\ell /\varepsilon )$
contains a copy of
$\operatorname {\mathrm {poly}}(\ell /\varepsilon )$
contains a copy of
![]() $C_{2\ell +1}$
with high probability.
$C_{2\ell +1}$
with high probability.
Lemma 2.1. Let
![]() $1 \leq k < \ell $
, let
$1 \leq k < \ell $
, let
![]() $\varepsilon> 0$
and let G be a graph on
$\varepsilon> 0$
and let G be a graph on
![]() $n \geq 200\ell k^2/\varepsilon ^2$
vertices containing a collection
$n \geq 200\ell k^2/\varepsilon ^2$
vertices containing a collection
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\varepsilon n^2$
edge-disjoint copies of
$\varepsilon n^2$
edge-disjoint copies of
![]() $C_{2k+1}$
. Then a sample of
$C_{2k+1}$
. Then a sample of
![]() $\frac {100k^2(2\ell +1)\log (10\ell )}{\varepsilon ^2}$
vertices of G (taken uniformly and independently) contains a copy of
$\frac {100k^2(2\ell +1)\log (10\ell )}{\varepsilon ^2}$
vertices of G (taken uniformly and independently) contains a copy of
![]() $C_{2\ell +1}$
with probability at least
$C_{2\ell +1}$
with probability at least
![]() $\frac {2}{3}$
.
$\frac {2}{3}$
.
Note that, as discussed above, the properties of being
![]() $\varepsilon $
-far from
$\varepsilon $
-far from
![]() $C_{2k+1}$
-free and having
$C_{2k+1}$
-free and having
![]() $\varepsilon n^2$
edge-disjoint copies of
$\varepsilon n^2$
edge-disjoint copies of
![]() $C_{2k+1}$
are equivalent up to a constant factor.
$C_{2k+1}$
are equivalent up to a constant factor.
Proof of Lemma 2.1.
There exists a collection
![]() $\mathcal {C}_0 \subseteq \mathcal {C}$
such that
$\mathcal {C}_0 \subseteq \mathcal {C}$
such that
![]() $\lvert \mathcal {C}_0\rvert \geq \varepsilon n^2/2$
and each vertex
$\lvert \mathcal {C}_0\rvert \geq \varepsilon n^2/2$
and each vertex
![]() $v \in V(G)$
belongs to either
$v \in V(G)$
belongs to either
![]() $0$
or at least
$0$
or at least
![]() $\varepsilon n/2$
of the cycles in
$\varepsilon n/2$
of the cycles in
![]() $\mathcal {C}_0$
. Indeed, to obtain
$\mathcal {C}_0$
. Indeed, to obtain
![]() $\mathcal {C}_0$
, we repeatedly delete from
$\mathcal {C}_0$
, we repeatedly delete from
![]() $\mathcal {C}$
all cycles containing a vertex v which belongs to fewer than
$\mathcal {C}$
all cycles containing a vertex v which belongs to fewer than
![]() $\varepsilon n/2$
of the cycles in
$\varepsilon n/2$
of the cycles in
![]() $\mathcal {C}$
(without changing the graph). The set of cycles left at the end is
$\mathcal {C}$
(without changing the graph). The set of cycles left at the end is
![]() $\mathcal {C}_0$
. In this process, we delete at most
$\mathcal {C}_0$
. In this process, we delete at most
![]() $\varepsilon n^2/2$
cycles altogether (because each vertex is contained in at most n cycles from
$\varepsilon n^2/2$
cycles altogether (because each vertex is contained in at most n cycles from
![]() $\mathcal {C}$
); hence,
$\mathcal {C}$
); hence,
![]() $\lvert \mathcal {C}_0\rvert \geq \varepsilon n^2/2$
. Let
$\lvert \mathcal {C}_0\rvert \geq \varepsilon n^2/2$
. Let
![]() $V_0$
be the set of vertices contained in at least
$V_0$
be the set of vertices contained in at least
![]() $\varepsilon n/2$
cycles from
$\varepsilon n/2$
cycles from
![]() $\mathcal {C}_0$
. Then
$\mathcal {C}_0$
. Then
![]() $|V_0| \geq \varepsilon n$
because the cycles containing a given
$|V_0| \geq \varepsilon n$
because the cycles containing a given
![]() $v \in V_0$
are edge-disjoint and contained in
$v \in V_0$
are edge-disjoint and contained in
![]() $V_0$
.
$V_0$
.
Set
![]() $q := \frac {100k^2\log (10\ell )}{\varepsilon ^2}$
. We sample
$q := \frac {100k^2\log (10\ell )}{\varepsilon ^2}$
. We sample
![]() $2\ell +1$
sets
$2\ell +1$
sets
![]() $S_0,\dots ,S_{2\ell }$
of size q each, where each
$S_0,\dots ,S_{2\ell }$
of size q each, where each
![]() $S_i$
contains q vertices sampled uniformly at random and independently with repetition.Footnote 7 The probability that
$S_i$
contains q vertices sampled uniformly at random and independently with repetition.Footnote 7 The probability that
![]() $S_0 \cap V_0 = \varnothing $
is at most
$S_0 \cap V_0 = \varnothing $
is at most
![]() $(1 - \varepsilon )^{q} \leq e^{-\varepsilon q} \leq \frac {1}{10}$
. From now on, we assume that
$(1 - \varepsilon )^{q} \leq e^{-\varepsilon q} \leq \frac {1}{10}$
. From now on, we assume that
![]() $S_0 \cap V_0 \neq \varnothing $
and fix
$S_0 \cap V_0 \neq \varnothing $
and fix
![]() $v_0 \in S_0 \cap V_0$
. Let N be the set of vertices u such that
$v_0 \in S_0 \cap V_0$
. Let N be the set of vertices u such that
![]() $v_0u \in E(C)$
for some
$v_0u \in E(C)$
for some
![]() $C \in \mathcal {C}_0$
. Then
$C \in \mathcal {C}_0$
. Then
![]() $|N| \geq \varepsilon n$
. Let
$|N| \geq \varepsilon n$
. Let
![]() $\mathcal {C}(v_0)$
be the set of cycles
$\mathcal {C}(v_0)$
be the set of cycles
![]() $C \in \mathcal {C}_0$
such that
$C \in \mathcal {C}_0$
such that
![]() $V(C) \cap N \neq \varnothing $
and
$V(C) \cap N \neq \varnothing $
and
![]() $v_0 \notin V(C)$
. The number of cycles
$v_0 \notin V(C)$
. The number of cycles
![]() $C \in \mathcal {C}_0$
intersecting N is at least
$C \in \mathcal {C}_0$
intersecting N is at least
![]() $\varepsilon n/2 \cdot |N| /(2k+1) \geq \varepsilon ^2 n^2/(4k+2)$
, and the number of cycles containing
$\varepsilon n/2 \cdot |N| /(2k+1) \geq \varepsilon ^2 n^2/(4k+2)$
, and the number of cycles containing
![]() $v_0$
is at most n. Hence,
$v_0$
is at most n. Hence,
![]() $|\mathcal {C}(v_0)| \geq \varepsilon ^2 n^2/(4k+2) - n \geq \varepsilon ^2 n^2/(7k)$
, using our assumption that
$|\mathcal {C}(v_0)| \geq \varepsilon ^2 n^2/(4k+2) - n \geq \varepsilon ^2 n^2/(7k)$
, using our assumption that
![]() $n \geq 200 \ell k^2/\varepsilon ^2$
.
$n \geq 200 \ell k^2/\varepsilon ^2$
.
We denote by
![]() $C_{2k+1}$
the labeled cycle on vertices
$C_{2k+1}$
the labeled cycle on vertices
![]() $1,\dots ,2k+1$
. For each
$1,\dots ,2k+1$
. For each
![]() $C \in \mathcal {C}(v_0)$
, fix an isomorphism
$C \in \mathcal {C}(v_0)$
, fix an isomorphism
![]() $f_C : C_{2k+1} \rightarrow C$
mapping
$f_C : C_{2k+1} \rightarrow C$
mapping
![]() $1$
to a vertex in
$1$
to a vertex in
![]() $V(C) \cap N$
. For a vertex u and
$V(C) \cap N$
. For a vertex u and
![]() $1 \leq j \leq 2k+1$
, denote by
$1 \leq j \leq 2k+1$
, denote by
![]() $d_j(u)$
the number of cycles
$d_j(u)$
the number of cycles
![]() $C \in \mathcal {C}(v_0)$
with
$C \in \mathcal {C}(v_0)$
with
![]() $f_C(j) = u$
. As long as there is
$f_C(j) = u$
. As long as there is
![]() $1 \leq j \leq 2k+1$
and a vertex u with
$1 \leq j \leq 2k+1$
and a vertex u with
![]() $0 < d_j(u) < \varepsilon ^2 n/(50k^2)$
, then delete from
$0 < d_j(u) < \varepsilon ^2 n/(50k^2)$
, then delete from
![]() $\mathcal {C}(v_0)$
all cycles C with
$\mathcal {C}(v_0)$
all cycles C with
![]() $f_C(j) = u$
(without changing the graph). In this process, we delete at most
$f_C(j) = u$
(without changing the graph). In this process, we delete at most
![]() $(2k+1) \cdot n \cdot \varepsilon ^2 n/(50k^2) \leq \varepsilon ^2n^2/(14k)$
cycles. Let
$(2k+1) \cdot n \cdot \varepsilon ^2 n/(50k^2) \leq \varepsilon ^2n^2/(14k)$
cycles. Let
![]() $\mathcal {C}^*(v_0)$
be the set of cycles left at the end of the process. Then
$\mathcal {C}^*(v_0)$
be the set of cycles left at the end of the process. Then
![]() $|\mathcal {C}^*(v_0)| \geq |\mathcal {C}(v_0)| - \varepsilon ^2n^2/(14k) \geq \varepsilon ^2n^2/(14k)$
. At the end, we have that
$|\mathcal {C}^*(v_0)| \geq |\mathcal {C}(v_0)| - \varepsilon ^2n^2/(14k) \geq \varepsilon ^2n^2/(14k)$
. At the end, we have that
![]() $d_j(u) = 0$
or
$d_j(u) = 0$
or
![]() $d_j(u) \geq \varepsilon ^2 n/(50k^2)$
for every vertex u and every
$d_j(u) \geq \varepsilon ^2 n/(50k^2)$
for every vertex u and every
![]() $1 \leq j \leq 2k+1$
. Let
$1 \leq j \leq 2k+1$
. Let
![]() $U_j$
be the set of vertices u with
$U_j$
be the set of vertices u with
![]() $d_j(u) \geq \varepsilon ^2 n/(50k^2)$
. Observe that each
$d_j(u) \geq \varepsilon ^2 n/(50k^2)$
. Observe that each
![]() $u \in U_j$
has at least
$u \in U_j$
has at least
![]() $\varepsilon ^2 n/(50k^2)$
neighbors in
$\varepsilon ^2 n/(50k^2)$
neighbors in
![]() $U_{j-1}$
and
$U_{j-1}$
and
![]() $U_{j+1}$
, with indices taken modulo
$U_{j+1}$
, with indices taken modulo
![]() $2k+1$
. In particular,
$2k+1$
. In particular,
![]() $|U_j| \geq \varepsilon ^2 n/(50k^2)$
for every
$|U_j| \geq \varepsilon ^2 n/(50k^2)$
for every
![]() $1 \leq j \leq 2k+1$
. Also,
$1 \leq j \leq 2k+1$
. Also,
![]() $U_1 \subseteq N \subseteq N(v_0)$
by definition, where
$U_1 \subseteq N \subseteq N(v_0)$
by definition, where
![]() $N(v_0)$
denotes the neighborhood of
$N(v_0)$
denotes the neighborhood of
![]() $v_0$
.
$v_0$
.
Let
![]() $P_{2\ell -1}$
be the path with vertices
$P_{2\ell -1}$
be the path with vertices
![]() $1,\dots ,2\ell $
. Fix a homomorphism
$1,\dots ,2\ell $
. Fix a homomorphism
![]() $\varphi : P_{2\ell -1} \rightarrow C_{2k+1}$
such that
$\varphi : P_{2\ell -1} \rightarrow C_{2k+1}$
such that
![]() $\varphi (1) = \varphi (2\ell ) = 1$
. This is possible because
$\varphi (1) = \varphi (2\ell ) = 1$
. This is possible because
![]() $2k+1$
is odd and
$2k+1$
is odd and
![]() $k < \ell $
. We claim that with probability at least
$k < \ell $
. We claim that with probability at least
![]() $\frac {4}{5}$
, there are vertices
$\frac {4}{5}$
, there are vertices
![]() $u_i \in S_i$
,
$u_i \in S_i$
,
![]() $1 \leq i \leq 2\ell $
, such that
$1 \leq i \leq 2\ell $
, such that
![]() $u_1,\dots ,u_{2\ell }$
is a path and
$u_1,\dots ,u_{2\ell }$
is a path and
![]() $u_i \in U_{\varphi (i)}$
. Observe that if this happens, then
$u_i \in U_{\varphi (i)}$
. Observe that if this happens, then
![]() $v_0,u_1,\dots ,u_{2\ell }$
is a copy of
$v_0,u_1,\dots ,u_{2\ell }$
is a copy of
![]() $C_{2\ell +1}$
because
$C_{2\ell +1}$
because
![]() $u_1,u_{2\ell } \in U_1 \subseteq N(v_0)$
. First, since
$u_1,u_{2\ell } \in U_1 \subseteq N(v_0)$
. First, since
![]() $|U_1| \geq \varepsilon ^2 n/(50k^2)$
, the probability that
$|U_1| \geq \varepsilon ^2 n/(50k^2)$
, the probability that
![]() $S_1$
contains no vertex of
$S_1$
contains no vertex of
![]() $U_1$
is at most
$U_1$
is at most
![]() $(1 - \frac {\varepsilon ^2}{50k^2})^q \leq \frac {1}{10\ell }$
. So suppose that there is
$(1 - \frac {\varepsilon ^2}{50k^2})^q \leq \frac {1}{10\ell }$
. So suppose that there is
![]() $u_1 \in S_1 \cap U_1$
. For
$u_1 \in S_1 \cap U_1$
. For
![]() $2 \leq i \leq 2\ell $
, suppose that we already found
$2 \leq i \leq 2\ell $
, suppose that we already found
![]() $u_1,\dots ,u_{i-1}$
; in particular,
$u_1,\dots ,u_{i-1}$
; in particular,
![]() $u_{i-1} \in U_{\varphi (i-1)}$
. We saw that
$u_{i-1} \in U_{\varphi (i-1)}$
. We saw that
![]() $u_{i-1}$
has at least
$u_{i-1}$
has at least
![]() $\varepsilon ^2 n/(50k^2)$
neighbors in
$\varepsilon ^2 n/(50k^2)$
neighbors in
![]() $U_{\varphi (i)}$
. Out of these neighbors, at most
$U_{\varphi (i)}$
. Out of these neighbors, at most
![]() $2\ell -1$
are on the path
$2\ell -1$
are on the path
![]() $u_1,\dots ,u_{i-1}$
. Hence, at least
$u_1,\dots ,u_{i-1}$
. Hence, at least
![]() $\varepsilon ^2 n/(50k^2) - 2\ell \geq \varepsilon ^2n/(100k^2)$
are not in
$\varepsilon ^2 n/(50k^2) - 2\ell \geq \varepsilon ^2n/(100k^2)$
are not in
![]() $\{u_1,\dots ,u_{i-1}\}$
. The probability that
$\{u_1,\dots ,u_{i-1}\}$
. The probability that
![]() $S_i$
contains none of these neighbors is at most
$S_i$
contains none of these neighbors is at most
![]() $(1 - \frac {\varepsilon ^2}{100k^2})^q \leq \frac {1}{10\ell }$
. So suppose that there is
$(1 - \frac {\varepsilon ^2}{100k^2})^q \leq \frac {1}{10\ell }$
. So suppose that there is
![]() $u_i \in S_i \cap U_{\varphi (i)}$
and continue the process. The probability that this process fails to produce
$u_i \in S_i \cap U_{\varphi (i)}$
and continue the process. The probability that this process fails to produce
![]() $u_1,\dots ,u_{2\ell }$
is at most
$u_1,\dots ,u_{2\ell }$
is at most
![]() $2\ell \cdot \frac {1}{10\ell } = \frac {1}{5}$
, as required. In total, the probability that
$2\ell \cdot \frac {1}{10\ell } = \frac {1}{5}$
, as required. In total, the probability that
![]() $S_0 \cup \dots \cup S_{2\ell +1}$
contains no copy of
$S_0 \cup \dots \cup S_{2\ell +1}$
contains no copy of
![]() $C_{2\ell +1}$
is at most
$C_{2\ell +1}$
is at most
![]() $\frac {1}{10} + \frac {1}{5} < \frac {1}{3}$
. This completes the proof.
$\frac {1}{10} + \frac {1}{5} < \frac {1}{3}$
. This completes the proof.
This immediately implies Theorem 1.3, which we restate as the following corollary.
Corollary 2.2. Let
![]() $1 \leq k < \ell $
, let
$1 \leq k < \ell $
, let
![]() $\varepsilon> 0$
and let G be a graph on
$\varepsilon> 0$
and let G be a graph on
![]() $n \geq 200\ell k^2/\varepsilon ^2$
vertices with
$n \geq 200\ell k^2/\varepsilon ^2$
vertices with
![]() $\varepsilon n^2$
edge-disjoint copies of
$\varepsilon n^2$
edge-disjoint copies of
![]() $C_{2k+1}$
. Then G has
$C_{2k+1}$
. Then G has
![]() $\Omega _\ell (\varepsilon ^{4\ell +2})n^{2\ell +1}$
copies of
$\Omega _\ell (\varepsilon ^{4\ell +2})n^{2\ell +1}$
copies of
![]() $C_{2\ell +1}$
.
$C_{2\ell +1}$
.
Proof. Let M denote the number of copies of
![]() $C_{2\ell +1}$
in G. The probability that a sample of size q contains a copy of
$C_{2\ell +1}$
in G. The probability that a sample of size q contains a copy of
![]() $C_{2\ell +1}$
is at most
$C_{2\ell +1}$
is at most
![]() $M \cdot (q/n)^{2\ell +1}$
. By Lemma 2.1, this probability is at least
$M \cdot (q/n)^{2\ell +1}$
. By Lemma 2.1, this probability is at least
![]() $2/3$
for
$2/3$
for
![]() $q = O_\ell (\varepsilon ^{-2})$
. The result follows.
$q = O_\ell (\varepsilon ^{-2})$
. The result follows.
We now turn to removal bounds for infinite families of odd cycles. For a sequence of positive integers L, let
![]() $w_L(\varepsilon )$
be the smallest integer q such that if a graph G on
$w_L(\varepsilon )$
be the smallest integer q such that if a graph G on
![]() $n \geq n_0(\varepsilon )$
vertices is
$n \geq n_0(\varepsilon )$
vertices is
![]() $\varepsilon $
-far from being
$\varepsilon $
-far from being
![]() $\{C_{\ell } : \ell \in L\}$
-free, then with probability at least
$\{C_{\ell } : \ell \in L\}$
-free, then with probability at least
![]() $2/3$
, a sample of q vertices from G contains a copy of
$2/3$
, a sample of q vertices from G contains a copy of
![]() $C_{\ell }$
for some
$C_{\ell }$
for some
![]() $\ell \in L$
. A result of [Reference Gishboliner and Shapira15] gave tight bounds on
$\ell \in L$
. A result of [Reference Gishboliner and Shapira15] gave tight bounds on
![]() $w_L(\varepsilon )$
as a function of the growth-rate of the sequence L. We state a variant of this result as follows.
$w_L(\varepsilon )$
as a function of the growth-rate of the sequence L. We state a variant of this result as follows.
Theorem 2.3. Let
![]() $g : \mathbb {N}_{odd} \rightarrow \mathbb {N}_{odd}$
be an increasing function satisfying
$g : \mathbb {N}_{odd} \rightarrow \mathbb {N}_{odd}$
be an increasing function satisfying
![]() $g(x)> x$
. Let
$g(x)> x$
. Let
![]() $\ell _1 \geq 3$
be an odd number and define a sequence
$\ell _1 \geq 3$
be an odd number and define a sequence
![]() $(\ell _i)_{i \geq 1}$
inductively by setting
$(\ell _i)_{i \geq 1}$
inductively by setting
![]() $\ell _{i+1} = g(\ell _i)$
. For
$\ell _{i+1} = g(\ell _i)$
. For
![]() $L = \{\ell _i : i \geq 1\}$
, we have
$L = \{\ell _i : i \geq 1\}$
, we have
![]() $w_{L}(\varepsilon ) \leq O(\varepsilon ^{-8}) \cdot g(4/\varepsilon ) \cdot \log (g(4/\varepsilon ))$
for every
$w_{L}(\varepsilon ) \leq O(\varepsilon ^{-8}) \cdot g(4/\varepsilon ) \cdot \log (g(4/\varepsilon ))$
for every
![]() $0<\varepsilon \leq \frac {1}{4\ell _1}$
.
$0<\varepsilon \leq \frac {1}{4\ell _1}$
.
Note that Theorem 1.7 follows immediately from Theorem 2.3, by setting
![]() $g(x)=x+2$
and
$g(x)=x+2$
and
![]() $\ell _1=3$
, so that L consists of all odd integers greater than
$\ell _1=3$
, so that L consists of all odd integers greater than
![]() $1$
. This implies that if G is
$1$
. This implies that if G is
![]() $\varepsilon $
-far from being bipartite, then a sample of size
$\varepsilon $
-far from being bipartite, then a sample of size
![]() $\operatorname {\mathrm {poly}}(1/\varepsilon )$
contains an odd cycle with probability at least
$\operatorname {\mathrm {poly}}(1/\varepsilon )$
contains an odd cycle with probability at least
![]() $2/3$
. We note that the dependence on
$2/3$
. We note that the dependence on
![]() $\varepsilon $
that we get is not tight; indeed, it is known [Reference Alon and Krivelevich3] that a sample of
$\varepsilon $
that we get is not tight; indeed, it is known [Reference Alon and Krivelevich3] that a sample of
![]() $\tilde {O}(1/\varepsilon )$
suffices.
$\tilde {O}(1/\varepsilon )$
suffices.
Here we give a new simpler proof of Theorem 2.3. We need the following easy fact, observed already in [Reference Bollobás, Erdős and Szemerédi6]. For completeness, we give a proof.
Lemma 2.4. For every
![]() $0 < \varepsilon \leq 1/2$
, every graph G which is
$0 < \varepsilon \leq 1/2$
, every graph G which is
![]() $\varepsilon $
-far from being bipartite contains an odd cycle of length at most
$\varepsilon $
-far from being bipartite contains an odd cycle of length at most
![]() $2/\varepsilon $
.
$2/\varepsilon $
.
Proof. Repeatedly delete from G vertices of degree less than
![]() $\varepsilon n$
, until no such vertices are left. Let W be the set of remaining vertices. The total number of edges deleted in this process is less than
$\varepsilon n$
, until no such vertices are left. Let W be the set of remaining vertices. The total number of edges deleted in this process is less than
![]() $\varepsilon n^2$
; hence,
$\varepsilon n^2$
; hence,
![]() $G[W]$
is not bipartite. Also, each vertex in
$G[W]$
is not bipartite. Also, each vertex in
![]() $G[W]$
has degree at least
$G[W]$
has degree at least
![]() $\varepsilon n$
. Let C be a shortest odd cycle in
$\varepsilon n$
. Let C be a shortest odd cycle in
![]() $G[W]$
. If C is a triangle, then we are done, so suppose
$G[W]$
. If C is a triangle, then we are done, so suppose
![]() $|C| \geq 5$
. By minimality, C is an induced cycle. For
$|C| \geq 5$
. By minimality, C is an induced cycle. For
![]() $x,y \in V(C)$
, denote by
$x,y \in V(C)$
, denote by
![]() $\text {dist}_C(x,y)$
the distance between x and y along C. Observe that if
$\text {dist}_C(x,y)$
the distance between x and y along C. Observe that if
![]() $x,y \in V(C)$
have a common neighbor
$x,y \in V(C)$
have a common neighbor
![]() $v \in W \setminus V(C)$
, then
$v \in W \setminus V(C)$
, then
![]() $\text {dist}_C(x,y) = 2$
. Indeed, suppose otherwise, and let
$\text {dist}_C(x,y) = 2$
. Indeed, suppose otherwise, and let
![]() $P_1,P_2$
be the two paths between
$P_1,P_2$
be the two paths between
![]() $x,y$
along C. Without loss of generality, suppose that
$x,y$
along C. Without loss of generality, suppose that
![]() $P_1$
is odd and
$P_1$
is odd and
![]() $P_2$
is even. We have
$P_2$
is even. We have
![]() $|P_2|> 2$
because
$|P_2|> 2$
because
![]() $\text {dist}_C(x,y) \neq 2$
. Now, replacing
$\text {dist}_C(x,y) \neq 2$
. Now, replacing
![]() $P_2$
with the path
$P_2$
with the path
![]() $xvy$
, we obtain a shorter odd cycle, a contradiction. It follows that every
$xvy$
, we obtain a shorter odd cycle, a contradiction. It follows that every
![]() $v \in W$
has at most
$v \in W$
has at most
![]() $2$
neighbors on C. Indeed, if
$2$
neighbors on C. Indeed, if
![]() $x,y,z \in V(C)$
are neighbors of v, then any two among
$x,y,z \in V(C)$
are neighbors of v, then any two among
![]() $x,y,z$
are at distance
$x,y,z$
are at distance
![]() $2$
, implying that C has length
$2$
, implying that C has length
![]() $6$
, a contradiction. Now, summing over the degrees of vertices in C, we get
$6$
, a contradiction. Now, summing over the degrees of vertices in C, we get
![]() $ |C| \cdot \varepsilon n \leq \sum _{x \in V(C)}d_W(x) \leq 2|W| \leq 2n. $
It follows that
$ |C| \cdot \varepsilon n \leq \sum _{x \in V(C)}d_W(x) \leq 2|W| \leq 2n. $
It follows that
![]() $|C| \leq 2/\varepsilon $
.
$|C| \leq 2/\varepsilon $
.
Proof of Theorem 2.3.
Let G be a graph which is
![]() $\varepsilon $
-far from being
$\varepsilon $
-far from being
![]() $\{C_{\ell _i} : i \geq 1\}$
-free. We claim that there is an odd integer
$\{C_{\ell _i} : i \geq 1\}$
-free. We claim that there is an odd integer
![]() $1 \leq 2k+1 \leq \frac {4}{\varepsilon }$
such that G is
$1 \leq 2k+1 \leq \frac {4}{\varepsilon }$
such that G is
![]() $\frac {\varepsilon ^2}{4}$
-far from being
$\frac {\varepsilon ^2}{4}$
-far from being
![]() $C_{2k+1}$
-free. Indeed, otherwise we could destroy all odd cycles in G of length at most
$C_{2k+1}$
-free. Indeed, otherwise we could destroy all odd cycles in G of length at most
![]() $\frac {4}{\varepsilon }$
by deleting at most
$\frac {4}{\varepsilon }$
by deleting at most
![]() $\frac {2}{\varepsilon } \cdot \frac {\varepsilon ^2}{4}n^2 = \frac {\varepsilon }{2}n^2$
edges. Let
$\frac {2}{\varepsilon } \cdot \frac {\varepsilon ^2}{4}n^2 = \frac {\varepsilon }{2}n^2$
edges. Let
![]() $G'$
be the resulting graph. By Lemma 2.4,
$G'$
be the resulting graph. By Lemma 2.4,
![]() $G'$
is not
$G'$
is not
![]() $\frac {\varepsilon }{2}$
-far from being bipartite. This implies that G is not
$\frac {\varepsilon }{2}$
-far from being bipartite. This implies that G is not
![]() $\varepsilon $
-far from being
$\varepsilon $
-far from being
![]() $\{C_{\ell _i} : i \geq 1\}$
-free, a contradiction.
$\{C_{\ell _i} : i \geq 1\}$
-free, a contradiction.
So fix
![]() $1 \leq 2k+1 \leq \frac {4}{\varepsilon }$
such that G is
$1 \leq 2k+1 \leq \frac {4}{\varepsilon }$
such that G is
![]() $\frac {\varepsilon ^2}{4}$
-far from being
$\frac {\varepsilon ^2}{4}$
-far from being
![]() $C_{2k+1}$
-free. Then G contains
$C_{2k+1}$
-free. Then G contains
![]() $\frac {\varepsilon ^2}{4(2k+1)}n^2 \geq \frac {\varepsilon ^2}{20k}n^2$
edge-disjoint copies of
$\frac {\varepsilon ^2}{4(2k+1)}n^2 \geq \frac {\varepsilon ^2}{20k}n^2$
edge-disjoint copies of
![]() $C_{2k+1}$
. Let
$C_{2k+1}$
. Let
![]() $i \geq 1$
be maximal satisfying
$i \geq 1$
be maximal satisfying
![]() $\ell _i \leq \frac {4}{\varepsilon }$
; this is well defined because
$\ell _i \leq \frac {4}{\varepsilon }$
; this is well defined because
![]() $\varepsilon \leq \frac {1}{4\ell _1}$
by assumption. Let
$\varepsilon \leq \frac {1}{4\ell _1}$
by assumption. Let
![]() $\ell := \ell _{i+1} = g(\ell _i)$
. By the maximality of i, we have
$\ell := \ell _{i+1} = g(\ell _i)$
. By the maximality of i, we have
![]() $\ell _{i+1}> \frac {4}{\varepsilon } \geq 2k+1$
. We now apply Lemma 2.1 for the cycle lengths
$\ell _{i+1}> \frac {4}{\varepsilon } \geq 2k+1$
. We now apply Lemma 2.1 for the cycle lengths
![]() $C_{2k+1}$
and
$C_{2k+1}$
and
![]() $C_{\ell }$
and with
$C_{\ell }$
and with
![]() $\frac {\varepsilon ^2}{20k}$
in place of
$\frac {\varepsilon ^2}{20k}$
in place of
![]() $\varepsilon $
. By this lemma, a sample of q vertices of G contains a copy of
$\varepsilon $
. By this lemma, a sample of q vertices of G contains a copy of
![]() $C_{\ell }$
with probability at least
$C_{\ell }$
with probability at least
![]() $\frac {2}{3}$
, where
$\frac {2}{3}$
, where
 $$\begin{align*}q = O\left( \frac{k^4\ell\log(\ell)}{\varepsilon^4} \right) = O(\varepsilon^{-8}) \cdot \ell \log(\ell) \leq O(\varepsilon^{-8}) \cdot g(4/\varepsilon) \cdot \log(g(4/\varepsilon)). \end{align*}$$
$$\begin{align*}q = O\left( \frac{k^4\ell\log(\ell)}{\varepsilon^4} \right) = O(\varepsilon^{-8}) \cdot \ell \log(\ell) \leq O(\varepsilon^{-8}) \cdot g(4/\varepsilon) \cdot \log(g(4/\varepsilon)). \end{align*}$$
Here we used that
![]() $\ell = g(\ell _i)$
and
$\ell = g(\ell _i)$
and
![]() $\ell _i \leq 4/\varepsilon $
. This completes the proof.
$\ell _i \leq 4/\varepsilon $
. This completes the proof.
We remark that Komlós [Reference Komlós17] improved Lemma 2.4 by showing that every graph that is
![]() $\varepsilon $
-far from bipartite contains an odd cycle of length
$\varepsilon $
-far from bipartite contains an odd cycle of length
![]() $O(\varepsilon ^{-1/2})$
, which is best possible. Using this result in place of Lemma 2.4 in the above proof, one can improve the bound in Theorem 2.3 to
$O(\varepsilon ^{-1/2})$
, which is best possible. Using this result in place of Lemma 2.4 in the above proof, one can improve the bound in Theorem 2.3 to
![]() $w_L(\varepsilon ) \leq O(\varepsilon ^{-4}) \cdot g(\ell ) \cdot \log (g(\ell ))$
, where
$w_L(\varepsilon ) \leq O(\varepsilon ^{-4}) \cdot g(\ell ) \cdot \log (g(\ell ))$
, where
![]() $\ell = O(\varepsilon ^{-1/2})$
. As was shown in [Reference Gishboliner and Shapira15], this is essentially tight.
$\ell = O(\varepsilon ^{-1/2})$
. As was shown in [Reference Gishboliner and Shapira15], this is essentially tight.
3 Proof of Theorem 1.6
In this section, we prove Theorem 1.6, which states that there exist triangle-free tripartite non-
![]() $K_3$
-abundant graphs. To prove this, we need to construct a triangle-free and tripartite graph H, and a sequence of graphs G, such that G is
$K_3$
-abundant graphs. To prove this, we need to construct a triangle-free and tripartite graph H, and a sequence of graphs G, such that G is
![]() $\varepsilon $
-far from being triangle-free and contains
$\varepsilon $
-far from being triangle-free and contains
![]() $\varepsilon ^{\omega (1)} n^{\lvert V(H)\rvert }$
copies of H, where
$\varepsilon ^{\omega (1)} n^{\lvert V(H)\rvert }$
copies of H, where
![]() $\omega (1)$
tends to infinity as
$\omega (1)$
tends to infinity as
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
Our proof naturally splits into three parts. First, we construct G: it is a variant of the Ruzsa–Szemerédi construction which gives super-polynomial bounds for the triangle removal lemma. In Section 3.1, we recall the relevant notions from additive combinatorics and give the construction of G. In Section 3.2, we define what it means for a graph H to be strongly genus-one: this is a combinatorial condition which guarantees that G contains few copies of H, thanks to the number-theoretic structure of G. Finally, in Section 3.3, we prove that a graph satisfying certain pseudorandomness conditions is strongly genus-one. With this, all that remains is showing that there exist triangle-free graphs satisfying these pseudorandomness conditions, for which we pick an appropriate random graph and remove one edge from each triangle. Verifying that this graph satisfies the pseudorandomness conditions consists of standard arguments in random graph theory, which we do in Section 4.
3.1 Additive combinatorics and the Ruzsa–Szemerédi construction
In the introduction, we defined what it means for an equation to have genus one; the following definition is a natural extension of this to families of equations.
Definition 3.1. Let S be a set of s equations with integer coefficients and k variables – namely,
 $$\begin{align*}S = \left\{ \sum_{i=1}^k a_{i,j} x_i = 0: 1 \leq j \leq s \right\}. \end{align*}$$
$$\begin{align*}S = \left\{ \sum_{i=1}^k a_{i,j} x_i = 0: 1 \leq j \leq s \right\}. \end{align*}$$
We assume that each equation in S is translation-invariant, meaning that
![]() $\sum _{i=1}^k a_{i,j}=0$
for all
$\sum _{i=1}^k a_{i,j}=0$
for all
![]() $j \in [s]$
. One says that S has genus one if for all
$j \in [s]$
. One says that S has genus one if for all
![]() $\varnothing \subsetneq T \subsetneq [k]$
, there exists some
$\varnothing \subsetneq T \subsetneq [k]$
, there exists some
![]() $j \in [s]$
so that
$j \in [s]$
so that
![]() $\sum _{i \in T} a_{i,j} \neq 0$
.
$\sum _{i \in T} a_{i,j} \neq 0$
.
Let S be a set of equations with genus one on k variables. As in the case of a single equation, we say that integers
![]() $y_1,\dots ,y_k$
form a nontrivial solution to S if
$y_1,\dots ,y_k$
form a nontrivial solution to S if
![]() $y_1,\dots ,y_k$
are not all equal, and if they satisfy all equations in S. We denote by
$y_1,\dots ,y_k$
are not all equal, and if they satisfy all equations in S. We denote by
![]() $r_S(m)$
the maximum size of a subset of
$r_S(m)$
the maximum size of a subset of
![]() $[m]$
containing no nontrivial solution to S. A simple argument shows that Conjecture 1.5 implies the corresponding result for sets of equations, as stated in the following lemma.
$[m]$
containing no nontrivial solution to S. A simple argument shows that Conjecture 1.5 implies the corresponding result for sets of equations, as stated in the following lemma.
Lemma 3.2. Assume that Conjecture 1.5 holds. If S is a set of linear equations of genus one, then
![]() $r_S(m) \geq m^{1-o(1)}$
.
$r_S(m) \geq m^{1-o(1)}$
.
Proof. Let S consist of s equations
![]() $E_1,\dots ,E_s$
in k variables. Let
$E_1,\dots ,E_s$
in k variables. Let
![]() $b_1,\dots ,b_s$
be independent and uniformly random numbers from
$b_1,\dots ,b_s$
be independent and uniformly random numbers from
![]() $[2^k]$
, and let
$[2^k]$
, and let
![]() $E=b_1 E_1 + \dotsb + b_s E_s$
. Let the coefficients of E be
$E=b_1 E_1 + \dotsb + b_s E_s$
. Let the coefficients of E be
![]() $a_1,\dots ,a_k$
, where
$a_1,\dots ,a_k$
, where
![]() $a_i = \sum _{j=1}^s b_j a_{i,j}$
.
$a_i = \sum _{j=1}^s b_j a_{i,j}$
.
Fix a set
![]() $\varnothing \subsetneq T \subsetneq [k]$
. We claim that the probability that
$\varnothing \subsetneq T \subsetneq [k]$
. We claim that the probability that
![]() $\sum _{i \in T} a_i=0$
is at most
$\sum _{i \in T} a_i=0$
is at most
![]() $2^{-k}$
. Indeed, since S has genus one, there exists some
$2^{-k}$
. Indeed, since S has genus one, there exists some
![]() $j \in [s]$
so that
$j \in [s]$
so that
![]() $\sum _{i \in T} a_{i,j} \neq 0$
. For any fixed values of
$\sum _{i \in T} a_{i,j} \neq 0$
. For any fixed values of
![]() $b_1,\dots ,b_{j-1},b_{j+1},\dots ,b_s$
, there is at most one choice of
$b_1,\dots ,b_{j-1},b_{j+1},\dots ,b_s$
, there is at most one choice of
![]() $b_j \in [2^k]$
so that
$b_j \in [2^k]$
so that
![]() $\sum _{i \in T} a_i=0$
. This shows that the probability that
$\sum _{i \in T} a_i=0$
. This shows that the probability that
![]() $\sum _{i \in T} a_i=0$
is at most
$\sum _{i \in T} a_i=0$
is at most
![]() $2^{-k}$
. As there are fewer than
$2^{-k}$
. As there are fewer than
![]() $2^k$
such sets T, we conclude that with positive probability, E has genus one. We now fix
$2^k$
such sets T, we conclude that with positive probability, E has genus one. We now fix
![]() $b_1,\dots ,b_s$
such that E has genus one.
$b_1,\dots ,b_s$
such that E has genus one.
We now observe that
![]() $r_S(m) \geq r_E(m)$
. Indeed, a nontrivial solution to S is also a nontrivial solution to E, so a set avoiding nontrivial solutions to E necessarily also avoids nontrivial solutions to S. By Conjecture 1.5, we have that
$r_S(m) \geq r_E(m)$
. Indeed, a nontrivial solution to S is also a nontrivial solution to E, so a set avoiding nontrivial solutions to E necessarily also avoids nontrivial solutions to S. By Conjecture 1.5, we have that
![]() $r_E(m) \geq m^{1-o(1)}$
, yielding the claim.
$r_E(m) \geq m^{1-o(1)}$
, yielding the claim.
Additionally, it is easy to see that Conjecture 1.5 implies the following result for multiple sets of equations.
Lemma 3.3. Assume that Conjecture 1.5 holds. Let
![]() $S_1,\dots ,S_t$
be sets of equations, such that each
$S_1,\dots ,S_t$
be sets of equations, such that each
![]() $S_i$
has genus one. Then there exists
$S_i$
has genus one. Then there exists
![]() $R \subseteq [m]$
with
$R \subseteq [m]$
with
![]() $\lvert R\rvert \geq m^{1-o(1)}$
such that R has no nontrivial solutions to
$\lvert R\rvert \geq m^{1-o(1)}$
such that R has no nontrivial solutions to
![]() $S_i$
, for all
$S_i$
, for all
![]() $1 \leq i \leq t$
.
$1 \leq i \leq t$
.
Remark 3.4. This is stronger than saying that the union of genus-one sets of equations also has genus one. Indeed, avoiding a solution to some set S of equations means that for any nontrivial assignment of the variables, at least one equation in S is not satisfied. Here, we are insisting that at least one equation in each
![]() $S_i$
is not satisfied.
$S_i$
is not satisfied.
Proof of Lemma 3.3.
By Lemma 3.2, for each i, there is an
![]() $R_i \subseteq [m]$
with
$R_i \subseteq [m]$
with
![]() $\lvert R_i\rvert \geq m^{1-o(1)}$
containing no nontrivial solutions to
$\lvert R_i\rvert \geq m^{1-o(1)}$
containing no nontrivial solutions to
![]() $S_i$
. Let s be the sum of the absolute values of the coefficients in all the equations in
$S_i$
. Let s be the sum of the absolute values of the coefficients in all the equations in
![]() $S_1,\dots ,S_t$
, and let
$S_1,\dots ,S_t$
, and let
![]() $M=2sm$
. Then if we view
$M=2sm$
. Then if we view
![]() $R_i$
as a subset of the cyclic group
$R_i$
as a subset of the cyclic group
![]() $\mathbb {Z}/M\mathbb {Z}$
, then
$\mathbb {Z}/M\mathbb {Z}$
, then
![]() $R_i$
still contains no nontrivial solutions to
$R_i$
still contains no nontrivial solutions to
![]() $S_i$
, as M was chosen sufficiently large to not introduce any ‘wraparound’ solutions.
$S_i$
, as M was chosen sufficiently large to not introduce any ‘wraparound’ solutions.
Let
![]() $a_2,\dots ,a_t$
be independent and uniformly random elements of
$a_2,\dots ,a_t$
be independent and uniformly random elements of
![]() $\mathbb {Z}/M\mathbb {Z}$
, and let
$\mathbb {Z}/M\mathbb {Z}$
, and let
As all equations are translation-invariant, R has no nontrivial solutions to
![]() $S_i$
for all
$S_i$
for all
![]() $1 \leq i \leq t$
. Additionally, as
$1 \leq i \leq t$
. Additionally, as
![]() $R \subseteq R_1$
, we may view R as a subset of
$R \subseteq R_1$
, we may view R as a subset of
![]() $[m]$
. Finally,
$[m]$
. Finally,
 $$\begin{align*}\mathbb E[\lvert R\rvert] = \sum_{x \in R_1} \prod_{i=2}^t \operatorname{\mathrm{Pr}}(x \in R_i+a_2) = \lvert R_1\rvert \cdot \prod_{i=2}^t\frac{\lvert R_i\rvert}{M} \geq m^{1-o(1)}, \end{align*}$$
$$\begin{align*}\mathbb E[\lvert R\rvert] = \sum_{x \in R_1} \prod_{i=2}^t \operatorname{\mathrm{Pr}}(x \in R_i+a_2) = \lvert R_1\rvert \cdot \prod_{i=2}^t\frac{\lvert R_i\rvert}{M} \geq m^{1-o(1)}, \end{align*}$$
using the facts that
![]() $\lvert R_i\rvert \geq m^{1-o(1)}$
for each i and that
$\lvert R_i\rvert \geq m^{1-o(1)}$
for each i and that
![]() $M=2sm = O_S(m)$
. Thus, there is some
$M=2sm = O_S(m)$
. Thus, there is some
![]() $R\subseteq [m]$
with the desired properties.
$R\subseteq [m]$
with the desired properties.
Fix an integer m and a set
![]() $R \subseteq [m]$
. We define the Ruzsa–Szemerédi graph
$R \subseteq [m]$
. We define the Ruzsa–Szemerédi graph
![]() $\operatorname {\mathrm {RS}}(m,R)$
to be the following graph. It has three parts
$\operatorname {\mathrm {RS}}(m,R)$
to be the following graph. It has three parts
![]() $\mathcal A,\mathcal B,\mathcal C$
, each of which we identify with
$\mathcal A,\mathcal B,\mathcal C$
, each of which we identify with
![]() $[3m]$
. The edges are given by
$[3m]$
. The edges are given by
The following property of the Ruzsa–Szemerédi graph is well known. We include the proof for completeness.
Lemma 3.5. Let m be an integer and let
![]() $R \subseteq [m]$
. Then
$R \subseteq [m]$
. Then
![]() $\operatorname {\mathrm {RS}}(m,R)$
contains a collection of
$\operatorname {\mathrm {RS}}(m,R)$
contains a collection of
![]() $m\lvert R\rvert $
edge-disjoint triangles.
$m\lvert R\rvert $
edge-disjoint triangles.
Proof. For every
![]() $a \in [m]$
and
$a \in [m]$
and
![]() $r \in R$
, we have a triangle
$r \in R$
, we have a triangle
![]() $(a,a+r, a+2r) \in \mathcal A \times \mathcal B \times \mathcal C$
. Given any two vertices in this triangle, we can recover the values of a and r, so these triangles are edge-disjoint. As they are indexed by pairs
$(a,a+r, a+2r) \in \mathcal A \times \mathcal B \times \mathcal C$
. Given any two vertices in this triangle, we can recover the values of a and r, so these triangles are edge-disjoint. As they are indexed by pairs
![]() $(a,r) \in [m] \times R$
, there are
$(a,r) \in [m] \times R$
, there are
![]() $m \lvert R\rvert $
such triangles.
$m \lvert R\rvert $
such triangles.
3.2 Strongly genus-one graphs
We now define what it means for a graph H to be strongly genus-one. This is a Ramsey-theoretic condition that implies that a certain set of equations S associated to the cycles in H has genus one. Using this, we can show that an appropriate Ruzsa–Szemerédi graph
![]() $\operatorname {\mathrm {RS}}(m,R)$
contains few copies of H, by choosing
$\operatorname {\mathrm {RS}}(m,R)$
contains few copies of H, by choosing
![]() $R \subseteq [m]$
to be a set of integers containing no nontrivial solutions to S.
$R \subseteq [m]$
to be a set of integers containing no nontrivial solutions to S.
Definition 3.6 (tagged cycle).
Let H be a tripartite graph with tripartition
![]() $A \cup B \cup C$
, and suppose that the edges of H are colored white or black. We say that a cycle
$A \cup B \cup C$
, and suppose that the edges of H are colored white or black. We say that a cycle
![]() $x_1,x_2,\dots ,x_\ell ,x_1$
in H is tagged if one of the following two conditions hold:
$x_1,x_2,\dots ,x_\ell ,x_1$
in H is tagged if one of the following two conditions hold:
-
• Some edge
 $x_i x_{i+1}$
is black and the remaining edges are white (or this holds after swapping the colors).
$x_i x_{i+1}$
is black and the remaining edges are white (or this holds after swapping the colors). -
• Two consecutive edges
 $x_{i-1} x_i$
and
$x_{i-1} x_i$
and
 $x_i x_{i+1}$
are both black, all remaining edges are white, and
$x_i x_{i+1}$
are both black, all remaining edges are white, and
 $x_{i-1},x_i,x_{i+1}$
all lie in different parts
$x_{i-1},x_i,x_{i+1}$
all lie in different parts
 $A,B,C$
(or this holds after swapping the colors).
$A,B,C$
(or this holds after swapping the colors).
Recall that a graph is uniquely 3-colorable if it has a unique partition into three independent sets.
Definition 3.7 (strongly genus-one graph).
We say that a graph H is strongly genus-one if it is uniquely 3-colorable and if, no matter how we color the edges of H white or black such that there is at least one edge of each color, there is a tagged cycle.
Note that the definition of a tagged cycle depends on the tripartition
![]() $A \cup B \cup C$
. However, the definition of strongly genus-one requires H to be uniquely 3-colorable, removing this ambiguity.
$A \cup B \cup C$
. However, the definition of strongly genus-one requires H to be uniquely 3-colorable, removing this ambiguity.
The Ruzsa–Szemerédi construction gives us a way of associating a set of equations S to a tripartite graph H in such a way that copies of H in
![]() $\operatorname {\mathrm {RS}}(m,R)$
are related to solutions of S in R. We now define this set of equations.
$\operatorname {\mathrm {RS}}(m,R)$
are related to solutions of S in R. We now define this set of equations.
Let H be a tripartite graph with tripartition
![]() $A \cup B \cup C$
. We assign every edge from A to B weight
$A \cup B \cup C$
. We assign every edge from A to B weight
![]() $1$
, every edge from B to C weight
$1$
, every edge from B to C weight
![]() $1$
, and every edge from C to A weight
$1$
, and every edge from C to A weight
![]() $-2$
. Note that we view the edges of H as oriented, so an edge going from B to A receives weight
$-2$
. Note that we view the edges of H as oriented, so an edge going from B to A receives weight
![]() $-1$
, for example. For every edge
$-1$
, for example. For every edge
![]() $e \in E(H)$
, we introduce a variable
$e \in E(H)$
, we introduce a variable
![]() $x_e$
. Every cycle in H now naturally gives us an equation whose variables are
$x_e$
. Every cycle in H now naturally gives us an equation whose variables are
![]() $x_e$
for edges e in the cycle, and whose coefficients are
$x_e$
for edges e in the cycle, and whose coefficients are
![]() $\pm 1, \pm 2$
: we simply write down the (signed) weights we see as we follow the cycle around the graph. Formally, given a cycle
$\pm 1, \pm 2$
: we simply write down the (signed) weights we see as we follow the cycle around the graph. Formally, given a cycle
![]() $v_1,\dots ,v_{\ell }$
with (oriented) edges
$v_1,\dots ,v_{\ell }$
with (oriented) edges
![]() $e_i = v_iv_{i+1}$
,
$e_i = v_iv_{i+1}$
,
![]() $i = 1,\dots ,\ell $
, we get the equation
$i = 1,\dots ,\ell $
, we get the equation
![]() $\sum _{i=1}^{\ell }w(e_i) \cdot x_{e_i} = 0$
, where
$\sum _{i=1}^{\ell }w(e_i) \cdot x_{e_i} = 0$
, where
![]() $w(e_i)$
is the signed weight of
$w(e_i)$
is the signed weight of
![]() $e_i$
. We now form a set of equations
$e_i$
. We now form a set of equations
![]() $S_{A,B,C}(H)$
by including all such equations, one equation for every cycle in the graph. Note that, as is reflected in the notation, this set of equations depends on H and on the tripartition
$S_{A,B,C}(H)$
by including all such equations, one equation for every cycle in the graph. Note that, as is reflected in the notation, this set of equations depends on H and on the tripartition
![]() $A \cup B \cup C$
.
$A \cup B \cup C$
.
The definition of tagged cycles implies that if H is strongly genus-one, then
![]() $S_{A,B,C}(H)$
is a set of equations of genus one, as stated in the following lemma.
$S_{A,B,C}(H)$
is a set of equations of genus one, as stated in the following lemma.
Lemma 3.8. Let H be a strongly genus-one graph. Then for every tripartitionFootnote 8
![]() $A \cup B \cup C$
of H, the set of equations
$A \cup B \cup C$
of H, the set of equations
![]() $S_{A,B,C}(H)$
has genus one.
$S_{A,B,C}(H)$
has genus one.
Proof. Suppose for contradiction that there is some set
![]() $\varnothing \subsetneq T \subsetneq E(H)$
so that in every equation in
$\varnothing \subsetneq T \subsetneq E(H)$
so that in every equation in
![]() $S_{A,B,C}(H)$
, the sum of the coefficients on the edges in T is zero. Color the edges in T black, and all remaining edges white. As we assume
$S_{A,B,C}(H)$
, the sum of the coefficients on the edges in T is zero. Color the edges in T black, and all remaining edges white. As we assume
![]() $\varnothing \subsetneq T \subsetneq E(H)$
, we have at least one edge of each color. So by the definition of a strongly genus-one graph, we must have at least one tagged cycle. By swapping the colors if necessary,Footnote 9 we find a cycle with either exactly one black edge, or two consecutive black edges going between two different pairs of parts. Consider the equation corresponding to this cycle.
$\varnothing \subsetneq T \subsetneq E(H)$
, we have at least one edge of each color. So by the definition of a strongly genus-one graph, we must have at least one tagged cycle. By swapping the colors if necessary,Footnote 9 we find a cycle with either exactly one black edge, or two consecutive black edges going between two different pairs of parts. Consider the equation corresponding to this cycle.
In case there is exactly one black edge, then the sum of the coefficients on the edges in T is
![]() $\pm 1$
or
$\pm 1$
or
![]() $\pm 2$
. In particular, this sum is nonzero, contradicting our assumption on T. Similarly, if there are two consecutive black edges going between two different pairs of parts of H, then the sum of the coefficients on edges in T is
$\pm 2$
. In particular, this sum is nonzero, contradicting our assumption on T. Similarly, if there are two consecutive black edges going between two different pairs of parts of H, then the sum of the coefficients on edges in T is
![]() $\pm (1+1)=\pm 2$
or
$\pm (1+1)=\pm 2$
or
![]() $\pm (-2+1)=\pm 1$
, both of which are nonzero, another contradiction.
$\pm (-2+1)=\pm 1$
, both of which are nonzero, another contradiction.
Remark 3.9. The definition of a tagged cycle is stronger than what is strictly needed for Lemma 3.8. Indeed, all we need is a cycle in H such that the sum of the weights on the black edges in the cycle is nonzero. However, our construction of a strongly genus-one graph H naturally yields a tagged cycle, rather than a more general ‘non-canceling cycle’. This is the reason we use the term strongly genus-one for such graphs: the combinatorial condition we require is stronger than what is needed simply to guarantee that
![]() $S_{A,B,C}(H)$
is a genus-one set of equations.
$S_{A,B,C}(H)$
is a genus-one set of equations.
We now have all the pieces in place to prove that strongly genus-one graphs are not
![]() $K_3$
-abundant, assuming that Conjecture 1.5 holds.
$K_3$
-abundant, assuming that Conjecture 1.5 holds.
Lemma 3.10. Assume that Conjecture 1.5 holds.
Let H be a strongly genus-one graph, and let
![]() $\varepsilon>0$
be sufficiently small. For every sufficiently large N, there exists an N-vertex graph G which is
$\varepsilon>0$
be sufficiently small. For every sufficiently large N, there exists an N-vertex graph G which is
![]() $\varepsilon $
-far from being triangle-free and which contains at most
$\varepsilon $
-far from being triangle-free and which contains at most
![]() $\delta N^{\lvert V(H)\rvert}$
copies of H, where
$\delta N^{\lvert V(H)\rvert}$
copies of H, where
![]() $\delta \leq \varepsilon ^{\omega (1)}$
and the
$\delta \leq \varepsilon ^{\omega (1)}$
and the
![]() $\omega (1)$
tends to infinity as
$\omega (1)$
tends to infinity as
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
In other words, H is not
![]() $K_3$
-abundant.
$K_3$
-abundant.
Proof. As H is uniquely 3-colorable, it has six tripartitions
![]() $A \cup B \cup C$
(namely, the six permutations of
$A \cup B \cup C$
(namely, the six permutations of
![]() $(A,B,C)$
). By Lemma 3.8, each of the sets of equations
$(A,B,C)$
). By Lemma 3.8, each of the sets of equations
![]() $S_{A,B,C}(H)$
has genus one. So by Lemma 3.3, for every integer m, there is a set
$S_{A,B,C}(H)$
has genus one. So by Lemma 3.3, for every integer m, there is a set
![]() $R \subseteq [m]$
with
$R \subseteq [m]$
with
![]() $\lvert R\rvert \geq m^{1-o(1)}$
which has no nontrivial solutions to any of these sets of equations.
$\lvert R\rvert \geq m^{1-o(1)}$
which has no nontrivial solutions to any of these sets of equations.
Let m be the maximum integer so that there exists such a set R of size
![]() $\lvert R\rvert \geq 1000\varepsilon m$
, and note that
$\lvert R\rvert \geq 1000\varepsilon m$
, and note that
![]() $m = \varepsilon ^{-\omega (1)}$
. Let
$m = \varepsilon ^{-\omega (1)}$
. Let
![]() $\Gamma =\operatorname {\mathrm {RS}}(m,R)$
. By Lemma 3.5,
$\Gamma =\operatorname {\mathrm {RS}}(m,R)$
. By Lemma 3.5,
![]() $\Gamma $
has
$\Gamma $
has
![]() $9m$
vertices and contains a collection of
$9m$
vertices and contains a collection of
![]() $m\lvert R\rvert \geq 1000 \varepsilon m^2$
edge-disjoint triangles, so
$m\lvert R\rvert \geq 1000 \varepsilon m^2$
edge-disjoint triangles, so
![]() $\Gamma $
is
$\Gamma $
is
![]() $\varepsilon $
-far from being triangle-free.
$\varepsilon $
-far from being triangle-free.
The key claim is that there are at most
![]() $18m^2$
homomorphisms
$18m^2$
homomorphisms
![]() $H \to \Gamma $
. Indeed, note that a homomorphism
$H \to \Gamma $
. Indeed, note that a homomorphism
![]() $H \to \Gamma $
in particular yields a proper 3-coloring of H, and since H is uniquely 3-colorable, there are exactly six such colorings. Fix one of them, and say that it maps the parts
$H \to \Gamma $
in particular yields a proper 3-coloring of H, and since H is uniquely 3-colorable, there are exactly six such colorings. Fix one of them, and say that it maps the parts
![]() $A,B,C$
of H into the parts
$A,B,C$
of H into the parts
![]() $\mathcal A,\mathcal B,\mathcal C$
of
$\mathcal A,\mathcal B,\mathcal C$
of
![]() $\Gamma $
, respectively. Every edge e of H gets mapped into some edge of
$\Gamma $
, respectively. Every edge e of H gets mapped into some edge of
![]() $\Gamma $
, and edges of
$\Gamma $
, and edges of
![]() $\Gamma $
are naturally labeled by elements of R. So this homomorphism gives us an assignment of the variables
$\Gamma $
are naturally labeled by elements of R. So this homomorphism gives us an assignment of the variables
![]() $\{x_e\}_{e \in E(H)}$
to values in R. Moreover, as every cycle in H must map to a closed walk in
$\{x_e\}_{e \in E(H)}$
to values in R. Moreover, as every cycle in H must map to a closed walk in
![]() $\Gamma $
, we see that for every cycle in H, the corresponding equation in
$\Gamma $
, we see that for every cycle in H, the corresponding equation in
![]() $S_{A,B,C}(H)$
is satisfied by this assignment of the variables.
$S_{A,B,C}(H)$
is satisfied by this assignment of the variables.
But we assumed that R has no nontrivial solutions to
![]() $S_{A,B,C}(H)$
, so we must have that every edge of H is actually assigned to the same value of R. But having fixed this value, we see that it corresponds to at most
$S_{A,B,C}(H)$
, so we must have that every edge of H is actually assigned to the same value of R. But having fixed this value, we see that it corresponds to at most
![]() $3m$
homomorphisms: once we determine where in
$3m$
homomorphisms: once we determine where in
![]() $\mathcal A$
to send a single vertex of A, the locations of all remaining vertices are uniquely determined by the connectivity of H (H is connected since it is uniquely 3-colorable). So in total, there are at most
$\mathcal A$
to send a single vertex of A, the locations of all remaining vertices are uniquely determined by the connectivity of H (H is connected since it is uniquely 3-colorable). So in total, there are at most
![]() $6\cdot 3m\lvert R\rvert \leq 18m^2$
homomorphisms
$6\cdot 3m\lvert R\rvert \leq 18m^2$
homomorphisms
![]() $H \to \Gamma $
. Note that we used the fact that R has no nontrivial solutions to any of the six sets of equations arising from permuting
$H \to \Gamma $
. Note that we used the fact that R has no nontrivial solutions to any of the six sets of equations arising from permuting
![]() $A,B,C$
, so the argument above works regardless of how
$A,B,C$
, so the argument above works regardless of how
![]() $\{A,B,C\}$
are mapped into
$\{A,B,C\}$
are mapped into
![]() $\{\mathcal A,\mathcal B,\mathcal C\}$
(and the union over all these contributions gives us the extra factor of six in the count of homomorphisms).
$\{\mathcal A,\mathcal B,\mathcal C\}$
(and the union over all these contributions gives us the extra factor of six in the count of homomorphisms).
To conclude the proof, let N be sufficiently large, and suppose for simplicity that N is a multiple of
![]() $9m$
, say
$9m$
, say
![]() $N=9mt$
. Let G the balanced blowup
$N=9mt$
. Let G the balanced blowup
![]() $\Gamma [t]$
, which has N vertices. G is still
$\Gamma [t]$
, which has N vertices. G is still
![]() $\varepsilon $
-far from being triangle-free. Indeed, suppose we delete fewer than
$\varepsilon $
-far from being triangle-free. Indeed, suppose we delete fewer than
![]() $\varepsilon N^2$
edges from G. Sample a random copy of
$\varepsilon N^2$
edges from G. Sample a random copy of
![]() $\Gamma $
in G by picking one uniformly random vertex from each blowup part of G. In expectation, we delete fewer than
$\Gamma $
in G by picking one uniformly random vertex from each blowup part of G. In expectation, we delete fewer than
![]() $\varepsilon \lvert V(\Gamma )\rvert ^2$
from this copy of
$\varepsilon \lvert V(\Gamma )\rvert ^2$
from this copy of
![]() $\Gamma $
, so there exists a copy of
$\Gamma $
, so there exists a copy of
![]() $\Gamma $
in G from which we deleted fewer than
$\Gamma $
in G from which we deleted fewer than
![]() $\varepsilon \lvert V(\Gamma )\rvert ^2$
edges. As
$\varepsilon \lvert V(\Gamma )\rvert ^2$
edges. As
![]() $\Gamma $
is
$\Gamma $
is
![]() $\varepsilon $
-far from being triangle-free, this yields a triangle in G which survives the edge-deletion, proving that G is also
$\varepsilon $
-far from being triangle-free, this yields a triangle in G which survives the edge-deletion, proving that G is also
![]() $\varepsilon $
-far from being triangle-free.
$\varepsilon $
-far from being triangle-free.
Moreover, every homomorphism
![]() $H \to \Gamma $
yields at most
$H \to \Gamma $
yields at most
![]() $t^{\lvert V(H)\rvert }$
copies of H in G. So the total number of copies of H in G is at most
$t^{\lvert V(H)\rvert }$
copies of H in G. So the total number of copies of H in G is at most

where
![]() $\delta = O(m^{2-\lvert V(H)\rvert }) \leq O(1/m) = \varepsilon ^{\omega (1)}$
, as claimed.
$\delta = O(m^{2-\lvert V(H)\rvert }) \leq O(1/m) = \varepsilon ^{\omega (1)}$
, as claimed.
3.3 Pseudorandom graphs are strongly genus-one
Given Lemma 3.10, all that remains to prove Theorem 1.6 is to show that there exist triangle-free strongly genus-one graphs. In fact, we show that any tripartite graph satisfying appropriate pseudorandomness conditions is strongly genus-one; the main difficulty is finding a set of pseudorandomness conditions which are satisfied by an appropriate random graph, and which are strong enough to imply that the graph is strongly genus-one. The following proposition summarizes this set of pseudorandomness conditions. In a tripartite graph with parts
![]() $A,B,C$
, given
$A,B,C$
, given
![]() $X \subseteq A, Y \subseteq B$
, let
$X \subseteq A, Y \subseteq B$
, let
![]() $N(X,Y)$
be the set of all vertices in C with at least one neighbor in X and at least one neighbor in Y. For
$N(X,Y)$
be the set of all vertices in C with at least one neighbor in X and at least one neighbor in Y. For
![]() $Z \subseteq C$
, let
$Z \subseteq C$
, let
![]() $N_A(Z)$
denote the set of vertices in A adjacent to at least one vertex of Z.
$N_A(Z)$
denote the set of vertices in A adjacent to at least one vertex of Z.
Proposition 3.11. For all sufficiently large n, there exists a tripartite graph H with parts
![]() $A,B,C$
with
$A,B,C$
with
![]() $\lvert A\rvert = \lvert B\rvert = \lvert C\rvert =n$
, having the following properties.
$\lvert A\rvert = \lvert B\rvert = \lvert C\rvert =n$
, having the following properties.
-
(i) If F is a subgraph of
 $H[A\cup B]$
with at least half the edges of
$H[A\cup B]$
with at least half the edges of
 $H[A \cup B]$
, then there exist
$H[A \cup B]$
, then there exist
 $A' \subseteq A, B' \subseteq B$
with
$A' \subseteq A, B' \subseteq B$
with
 $F[A' \cup B']$
connected and
$F[A' \cup B']$
connected and
 $\lvert A'\rvert ,\lvert B'\rvert \geq n/10$
.
$\lvert A'\rvert ,\lvert B'\rvert \geq n/10$
. -
(ii) For all subsets
 $X \subseteq A, Y \subseteq B, Z \subseteq C$
of order at least
$X \subseteq A, Y \subseteq B, Z \subseteq C$
of order at least
 $n/10$
, we have that
$n/10$
, we have that
 $\lvert N(X,Y)\rvert \geq 99n/100$
, and similarly for
$\lvert N(X,Y)\rvert \geq 99n/100$
, and similarly for
 $\lvert N(X,Z)\rvert $
and
$\lvert N(X,Z)\rvert $
and
 $\lvert N(Y,Z)\rvert $
.
$\lvert N(Y,Z)\rvert $
. -
(iii) For all subsets
 $X \subseteq A, Y \subseteq B, Z \subseteq C$
of order at most
$X \subseteq A, Y \subseteq B, Z \subseteq C$
of order at most
 $n/12$
, we have that
$n/12$
, we have that
 $\lvert N_A(Z)\rvert>2\lvert Z\rvert $
, and similarly for all other pairs.
$\lvert N_A(Z)\rvert>2\lvert Z\rvert $
, and similarly for all other pairs. -
(iv) H is triangle-free.
-
(v) Up to permuting the colors, H has a unique proper
 $3$
-coloring.
$3$
-coloring.
We prove Proposition 3.11 by considering a random tripartite graph with edge density
![]() $p=n^{-3/4}$
, and then deleting one edge from each triangle; we defer the proof to Section 4. We remark that many other pseudorandom graphs would work; for example, there is nothing special about
$p=n^{-3/4}$
, and then deleting one edge from each triangle; we defer the proof to Section 4. We remark that many other pseudorandom graphs would work; for example, there is nothing special about
![]() $p=n^{-3/4}$
, and edge density
$p=n^{-3/4}$
, and edge density
![]() $p=n^{-1+\theta }$
for any
$p=n^{-1+\theta }$
for any
![]() $0<\theta <1/3$
would work as well. As another example, the tripartite triple cover of Alon’s explicit pseudorandom triangle-free graph [Reference Alon1] gives an explicit family of graphs satisfying the properties of Proposition 3.11.
$0<\theta <1/3$
would work as well. As another example, the tripartite triple cover of Alon’s explicit pseudorandom triangle-free graph [Reference Alon1] gives an explicit family of graphs satisfying the properties of Proposition 3.11.
The key claim, which completes the proof of Theorem 1.6, is that this set of pseudorandomness conditions is enough to guarantee that H is strongly genus-one.
Lemma 3.12. If H satisfies the conditions of Proposition 3.11, then H is strongly genus-one.
From Proposition 3.11 and Lemma 3.12, we find that there exists a triangle-free strongly genus-one graph. Combined with Lemma 3.10, this implies that there exists a triangle-free tripartite graph which is not
![]() $K_3$
-abundant (assuming Conjecture 1.5), which proves Theorem 1.6.
$K_3$
-abundant (assuming Conjecture 1.5), which proves Theorem 1.6.
The rest of this section is dedicated to proving Lemma 3.12. So suppose we are given a tripartite graph H which satisfies the conditions of Proposition 3.11, and we wish to prove that H is strongly genus-one. By Proposition 3.11(v), we know that H is uniquely 3-colorable, so we only need to prove that in any two-coloring of
![]() $E(H)$
with at least one edge of each color, there is a tagged cycle.
$E(H)$
with at least one edge of each color, there is a tagged cycle.
The following are two useful lemmas allowing us to find tagged cycles.
Lemma 3.13. Let H be a tripartite graph with parts
![]() $A,B,C$
, and suppose that the edges of H are colored white or black. Suppose that
$A,B,C$
, and suppose that the edges of H are colored white or black. Suppose that
![]() $X \subseteq A, Y \subseteq B$
are such that
$X \subseteq A, Y \subseteq B$
are such that
![]() $X\cup Y$
lies in a connected component of the white subgraph of H. If there is no tagged cycle, then every edge in
$X\cup Y$
lies in a connected component of the white subgraph of H. If there is no tagged cycle, then every edge in
![]() $X \times Y$
is white.
$X \times Y$
is white.
Proof. Suppose for contradiction that there is a black edge
![]() $xy$
. Pick a white path connecting x and y, which exists since we assumed that
$xy$
. Pick a white path connecting x and y, which exists since we assumed that
![]() $X\cup Y$
lies in a connected component of the white graph. This yields a cycle with exactly one black edge, which is tagged.
$X\cup Y$
lies in a connected component of the white graph. This yields a cycle with exactly one black edge, which is tagged.
Lemma 3.14. Let H be a tripartite graph with parts
![]() $A,B,C$
, and suppose that the edges of H are colored white or black. Suppose that
$A,B,C$
, and suppose that the edges of H are colored white or black. Suppose that
![]() $X \subseteq A, Y \subseteq B$
are such that the
$X \subseteq A, Y \subseteq B$
are such that the
![]() $X\cup Y$
lies in a connected component of the white subgraph of H. Let
$X\cup Y$
lies in a connected component of the white subgraph of H. Let
![]() $Z=N(X,Y)\subseteq C$
. If there is no tagged cycle, then every edge in
$Z=N(X,Y)\subseteq C$
. If there is no tagged cycle, then every edge in
![]() $(X \times Z) \cup (Y \times Z)$
is white.
$(X \times Z) \cup (Y \times Z)$
is white.
Proof. Suppose for contradiction that there is a black edge
![]() $yz \in Y \times Z$
. By the definition of
$yz \in Y \times Z$
. By the definition of
![]() $Z = N(X,Y)$
, we know that z has some neighbor
$Z = N(X,Y)$
, we know that z has some neighbor
![]() $x \in X$
. Pick a white path
$x \in X$
. Pick a white path
![]() $x = v_0, v_1, \dots , v_k=y$
connecting x and y. Suppose first that z is not on this path (i.e.,
$x = v_0, v_1, \dots , v_k=y$
connecting x and y. Suppose first that z is not on this path (i.e.,
![]() $z \notin \{v_1,\dots ,v_k\}$
). Then we have a cycle
$z \notin \{v_1,\dots ,v_k\}$
). Then we have a cycle
![]() $x, v_1, \dots , v_{k-1}, y, z, x$
. In this cycle, the edge
$x, v_1, \dots , v_{k-1}, y, z, x$
. In this cycle, the edge
![]() $yz$
is black, the edge
$yz$
is black, the edge
![]() $zx$
may be black or white, and all remaining edges are white. Regardless of the color of
$zx$
may be black or white, and all remaining edges are white. Regardless of the color of
![]() $zx$
, we obtain a tagged cycle.
$zx$
, we obtain a tagged cycle.
However, suppose that
![]() $v_i = z$
for some i. Note that
$v_i = z$
for some i. Note that
![]() $i < k-1$
as the edge
$i < k-1$
as the edge
![]() $yz$
is black and we assumed that the edge
$yz$
is black and we assumed that the edge
![]() $v_{k-1} y$
is white. This implies that we get a cycle
$v_{k-1} y$
is white. This implies that we get a cycle
![]() $z, v_{i+1},\dots ,v_{k-1}, y, z$
. In this cycle, the edge
$z, v_{i+1},\dots ,v_{k-1}, y, z$
. In this cycle, the edge
![]() $yz$
is black and the remaining edges are white, so we again find a tagged cycle.
$yz$
is black and the remaining edges are white, so we again find a tagged cycle.
The same argument, upon interchanging the roles of X and Y, shows that no edge
![]() $xz \in X \times Z$
can be black.
$xz \in X \times Z$
can be black.
We are now ready to complete the proof. The basic idea is to repeatedly use Lemmas 3.13 and 3.14, as well as the pseudorandomness conditions guaranteed by Proposition 3.11 to gradually improve our understanding of the coloring, until we eventually show that if there is no tagged cycle, then all the edges must be of the same color.
Proof of Lemma 3.12.
Let H be a graph satisfying the conditions of Proposition 3.11, and suppose for contradiction that there is a coloring of H with no tagged cycle. We will show that H is colored monochromatically.
Suppose without loss of generality that at least half the edges in
![]() $H[A \cup B]$
are white. By Proposition 3.11(i), there exist
$H[A \cup B]$
are white. By Proposition 3.11(i), there exist
![]() $A_1 \subseteq A, B_1 \subseteq B$
such that the white graph on
$A_1 \subseteq A, B_1 \subseteq B$
such that the white graph on
![]() $H[A_1 \cup B_1]$
is connected, with
$H[A_1 \cup B_1]$
is connected, with
![]() $\lvert A_1\rvert ,\lvert B_1\rvert \geq n/10$
. Let
$\lvert A_1\rvert ,\lvert B_1\rvert \geq n/10$
. Let
![]() $C_1 = N(A_1,B_1)$
. By Proposition 3.11(ii), we know that
$C_1 = N(A_1,B_1)$
. By Proposition 3.11(ii), we know that
![]() $\lvert C_1\rvert \geq 99n/100$
. Moreover, by Lemmas 3.13 and 3.14, we have that
$\lvert C_1\rvert \geq 99n/100$
. Moreover, by Lemmas 3.13 and 3.14, we have that
![]() $H[A_1 \cup B_1 \cup C_1]$
is white, since the connectivity of the white graph on
$H[A_1 \cup B_1 \cup C_1]$
is white, since the connectivity of the white graph on
![]() $H[A_1 \cup B_1]$
implies that
$H[A_1 \cup B_1]$
implies that
![]() $A_1 \cup B_1$
lies in a connected component of the white subgraph.
$A_1 \cup B_1$
lies in a connected component of the white subgraph.
Now, let
![]() $A_2 = N(B_1,C_1)$
. Note that
$A_2 = N(B_1,C_1)$
. Note that
![]() $B_1 \cup C_1$
lies in a connected component of the white subgraph, since every vertex in
$B_1 \cup C_1$
lies in a connected component of the white subgraph, since every vertex in
![]() $C_1$
has at least one neighbor in
$C_1$
has at least one neighbor in
![]() $B_1$
, and since
$B_1$
, and since
![]() $B_1$
lies in a connected component of the white subgraph. Therefore,
$B_1$
lies in a connected component of the white subgraph. Therefore,
![]() $H[A_2 \cup B_1 \cup C_1]$
is white by Lemmas 3.13 and 3.14. As
$H[A_2 \cup B_1 \cup C_1]$
is white by Lemmas 3.13 and 3.14. As
![]() $\lvert B_1\rvert ,\lvert C_1\rvert \geq n/10$
, we also see that
$\lvert B_1\rvert ,\lvert C_1\rvert \geq n/10$
, we also see that
![]() $\lvert A_2\rvert \geq 99n/100$
(again by Proposition 3.11(ii)). Similarly, letting
$\lvert A_2\rvert \geq 99n/100$
(again by Proposition 3.11(ii)). Similarly, letting
![]() $B_2 = N(A_2,C_1)$
, we find that
$B_2 = N(A_2,C_1)$
, we find that
![]() $\lvert B_2\rvert \geq 99n/100$
and
$\lvert B_2\rvert \geq 99n/100$
and
![]() $H[A_2 \cup B_2 \cup C_1]$
is white.
$H[A_2 \cup B_2 \cup C_1]$
is white.
Now, let
![]() $(A',B',C')$
be a maximal triple of sets so that
$(A',B',C')$
be a maximal triple of sets so that
![]() $H[A' \cup B' \cup C']$
is white. By the above, we know that
$H[A' \cup B' \cup C']$
is white. By the above, we know that
![]() $\lvert A'\rvert , \lvert B'\rvert , \lvert C'\rvert \geq 99n/100$
. We claim that, in fact,
$\lvert A'\rvert , \lvert B'\rvert , \lvert C'\rvert \geq 99n/100$
. We claim that, in fact,
![]() $\lvert A'\rvert = \lvert B'\rvert = \lvert C'\rvert =n$
, meaning that H is monochromatically white. So suppose this is not the case. Without loss of generality, assume that
$\lvert A'\rvert = \lvert B'\rvert = \lvert C'\rvert =n$
, meaning that H is monochromatically white. So suppose this is not the case. Without loss of generality, assume that
![]() $\lvert C'\rvert \leq \lvert A'\rvert , \lvert B'\rvert $
, and let
$\lvert C'\rvert \leq \lvert A'\rvert , \lvert B'\rvert $
, and let
![]() $W = C \setminus C'$
.
$W = C \setminus C'$
.
Suppose there is a vertex
![]() $w \in W$
with at least one neighbor in
$w \in W$
with at least one neighbor in
![]() $A'$
and at least one neighbor in
$A'$
and at least one neighbor in
![]() $B'$
. Then
$B'$
. Then
![]() $w \in N(A',B')$
, so by Lemma 3.14, all edges in
$w \in N(A',B')$
, so by Lemma 3.14, all edges in
![]() $\{w\} \times (A' \cup B')$
are white. This means that we may add w to
$\{w\} \times (A' \cup B')$
are white. This means that we may add w to
![]() $C'$
, contradicting maximality of
$C'$
, contradicting maximality of
![]() $(A',B',C')$
. So every vertex in W is non-adjacent to at least one of
$(A',B',C')$
. So every vertex in W is non-adjacent to at least one of
![]() $A',B'$
. Without loss of generality, there is
$A',B'$
. Without loss of generality, there is
![]() $W' \subseteq W$
with
$W' \subseteq W$
with
![]() $\lvert W'\rvert \geq \frac 12 \lvert W\rvert $
so that every vertex in
$\lvert W'\rvert \geq \frac 12 \lvert W\rvert $
so that every vertex in
![]() $W'$
is non-adjacent to
$W'$
is non-adjacent to
![]() $A'$
. This means that
$A'$
. This means that
![]() $N_A(W') \subseteq A \setminus A'$
. But by Proposition 3.11(iii) (which we may apply since
$N_A(W') \subseteq A \setminus A'$
. But by Proposition 3.11(iii) (which we may apply since
![]() $\lvert W'\rvert \leq \lvert W\rvert \leq n/100 \leq n/12$
),
$\lvert W'\rvert \leq \lvert W\rvert \leq n/100 \leq n/12$
),
which contradicts our assumption that
![]() $\lvert A'\rvert \geq \lvert C'\rvert $
. This contradiction completes the proof.
$\lvert A'\rvert \geq \lvert C'\rvert $
. This contradiction completes the proof.
4 Proof of Proposition 3.11
To complete the proof of Theorem 1.6, it remains to prove Proposition 3.11. The various parts of Proposition 3.11 are essentially independent of one another, so the proof more or less breaks down into a number of lemmas about random graphs, which we now state and prove. Recall that an event E is said to happen with high probability (w.h.p.) if
![]() $\operatorname {\mathrm {Pr}}(E) \to 1$
as
$\operatorname {\mathrm {Pr}}(E) \to 1$
as
![]() $n \to \infty $
, where the implicit parameter n will always be clear from context.
$n \to \infty $
, where the implicit parameter n will always be clear from context.
Lemma 4.1. Let H be a random bipartite graph with vertex set
![]() $A \cup B$
, where
$A \cup B$
, where
![]() $\lvert A\rvert = \lvert B\rvert =n$
, and with edge density
$\lvert A\rvert = \lvert B\rvert =n$
, and with edge density
![]() $p=n^{-3/4}$
. The following holds w.h.p. as
$p=n^{-3/4}$
. The following holds w.h.p. as
![]() $n \to \infty $
. If
$n \to \infty $
. If
![]() $F\subseteq H$
satisfies
$F\subseteq H$
satisfies
![]() $e(F) \geq \frac 13 e(H)$
, then there exist
$e(F) \geq \frac 13 e(H)$
, then there exist
![]() $A' \subseteq A, B' \subseteq B$
with
$A' \subseteq A, B' \subseteq B$
with
![]() $\lvert A'\rvert ,\lvert B'\rvert \geq n/10$
such that
$\lvert A'\rvert ,\lvert B'\rvert \geq n/10$
such that
![]() $F[A' \cup B']$
is connected.
$F[A' \cup B']$
is connected.
Proof. By the Chernoff bound, H has at least
![]() $\frac 34 pn^2$
edges w.h.p. We now condition on this event happening.
$\frac 34 pn^2$
edges w.h.p. We now condition on this event happening.
Suppose for contradiction that there exists an F without this property, and let its connected components be
![]() $F_1,\dots ,F_\ell $
. For
$F_1,\dots ,F_\ell $
. For
![]() $1 \leq i \leq \ell $
, let the vertex set of
$1 \leq i \leq \ell $
, let the vertex set of
![]() $F_i$
be
$F_i$
be
![]() $A_i \cup B_i$
, where
$A_i \cup B_i$
, where
![]() $A_i \subseteq A, B_i \subseteq B$
. By assumption, we know that
$A_i \subseteq A, B_i \subseteq B$
. By assumption, we know that
![]() $\min \{\lvert A_i\rvert ,\lvert B_i\rvert \}< n/10$
for each i, and that
$\min \{\lvert A_i\rvert ,\lvert B_i\rvert \}< n/10$
for each i, and that
 $$\begin{align*}\frac 14 pn^2 \leq \frac 13 e(H) \leq e(F) = \sum_{i=1}^\ell e_F(A_i,B_i) \leq \sum_{i=1}^\ell e_H(A_i,B_i). \end{align*}$$
$$\begin{align*}\frac 14 pn^2 \leq \frac 13 e(H) \leq e(F) = \sum_{i=1}^\ell e_F(A_i,B_i) \leq \sum_{i=1}^\ell e_H(A_i,B_i). \end{align*}$$
So to upper-bound the probability that such an F exists, it suffices to upper-bound the probability that there exist disjoint
![]() $A_1,\dots ,A_\ell \subseteq A, B_1,\dots ,B_\ell \subseteq B$
with the properties that
$A_1,\dots ,A_\ell \subseteq A, B_1,\dots ,B_\ell \subseteq B$
with the properties that
![]() $\min \{\lvert A_i\rvert ,\lvert B_i\rvert \}< n/10$
for each i and that
$\min \{\lvert A_i\rvert ,\lvert B_i\rvert \}< n/10$
for each i and that
![]() $\sum _i e_H(A_i,B_i) \geq \frac 14 pn^2$
.
$\sum _i e_H(A_i,B_i) \geq \frac 14 pn^2$
.
Fix disjoint sets
![]() $A_1,\dots ,A_\ell \subseteq A, B_1,\dots ,B_\ell \subseteq B$
with
$A_1,\dots ,A_\ell \subseteq A, B_1,\dots ,B_\ell \subseteq B$
with
![]() $\min \{\lvert A_i\rvert ,\lvert B_i\rvert \}< n/10$
for each i. Let I be the set of indices i with
$\min \{\lvert A_i\rvert ,\lvert B_i\rvert \}< n/10$
for each i. Let I be the set of indices i with
![]() $\lvert A_i\rvert \leq n/10$
, and let
$\lvert A_i\rvert \leq n/10$
, and let
![]() $J=[\ell ] \setminus I$
. We have that
$J=[\ell ] \setminus I$
. We have that
 $$\begin{align*}\sum_{i=1}^\ell \lvert A_i\rvert \lvert B_i\rvert = \sum_{i \in I} \lvert A_i\rvert \lvert B_i\rvert + \sum_{i \in J} \lvert A_i\rvert \lvert B_i\rvert \leq \frac n{10} \sum_{i \in I} \lvert B_i\rvert + \frac n {10} \sum_{i \in J} \lvert A_i\rvert \leq \frac{n}{10}(\lvert B\rvert+\lvert A\rvert) = \frac{n^2}{5}. \end{align*}$$
$$\begin{align*}\sum_{i=1}^\ell \lvert A_i\rvert \lvert B_i\rvert = \sum_{i \in I} \lvert A_i\rvert \lvert B_i\rvert + \sum_{i \in J} \lvert A_i\rvert \lvert B_i\rvert \leq \frac n{10} \sum_{i \in I} \lvert B_i\rvert + \frac n {10} \sum_{i \in J} \lvert A_i\rvert \leq \frac{n}{10}(\lvert B\rvert+\lvert A\rvert) = \frac{n^2}{5}. \end{align*}$$
Let X denote the random variable
![]() $\sum _{i=1}^\ell e_H(A_i,B_i)$
. By the computation above, we see that X is upper-bounded in distribution by
$\sum _{i=1}^\ell e_H(A_i,B_i)$
. By the computation above, we see that X is upper-bounded in distribution by
![]() $\textrm {Bin}(n^2/5, p)$
. By the Chernoff bound,
$\textrm {Bin}(n^2/5, p)$
. By the Chernoff bound,
 $$\begin{align*}\operatorname{\mathrm{Pr}}\left(X \geq \frac 14 pn^2\right) \leq \operatorname{\mathrm{Pr}}\left(\textrm{Bin}\left(\frac{n^2}{5},p\right)\geq \frac{pn^2}{4}\right) \leq \exp\left(-\frac{pn^2}{250}\right). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Pr}}\left(X \geq \frac 14 pn^2\right) \leq \operatorname{\mathrm{Pr}}\left(\textrm{Bin}\left(\frac{n^2}{5},p\right)\geq \frac{pn^2}{4}\right) \leq \exp\left(-\frac{pn^2}{250}\right). \end{align*}$$
There are at most
![]() $n^n$
partitions of an n-element set,Footnote 10 so this error probability of
$n^n$
partitions of an n-element set,Footnote 10 so this error probability of
![]() $e^{-\Omega (pn^2)}=e^{-\Omega (n^{5/4})}$
is enough to union-bound over at most
$e^{-\Omega (pn^2)}=e^{-\Omega (n^{5/4})}$
is enough to union-bound over at most
![]() $n^{2n} = e^{O(n\log n)}$
choices for
$n^{2n} = e^{O(n\log n)}$
choices for
![]() $A_1,\dots ,A_\ell ,B_1,\dots ,B_\ell $
.
$A_1,\dots ,A_\ell ,B_1,\dots ,B_\ell $
.
Recall that for
![]() $X \subseteq A, Y \subseteq B$
, we denote by
$X \subseteq A, Y \subseteq B$
, we denote by
![]() $N(X,Y)$
the set of all vertices in C with at least one neighbor in X and at least one neighbor in Y.
$N(X,Y)$
the set of all vertices in C with at least one neighbor in X and at least one neighbor in Y.
Lemma 4.2. Let H be a tripartite random graph on parts
![]() $A,B,C$
with
$A,B,C$
with
![]() $\lvert A\rvert = \lvert B\rvert = \lvert C\rvert = n$
, where each edge appears with probability
$\lvert A\rvert = \lvert B\rvert = \lvert C\rvert = n$
, where each edge appears with probability
![]() $p=n^{-3/4}$
. The following holds w.h.p. as
$p=n^{-3/4}$
. The following holds w.h.p. as
![]() $n \to \infty $
. For all
$n \to \infty $
. For all
![]() $X \subseteq A,Y\subseteq B$
with
$X \subseteq A,Y\subseteq B$
with
![]() $\lvert X\rvert ,\lvert Y\rvert \geq n/10$
, we have that
$\lvert X\rvert ,\lvert Y\rvert \geq n/10$
, we have that
![]() $\lvert N(X,Y)\rvert \geq n-o(n)$
.
$\lvert N(X,Y)\rvert \geq n-o(n)$
.
Proof. Fix
![]() $X,Y$
. For
$X,Y$
. For
![]() $c \in C$
, let
$c \in C$
, let
![]() $E_c$
be the event that c has no neighbor in X or no neighbor in Y. Then
$E_c$
be the event that c has no neighbor in X or no neighbor in Y. Then
for all sufficiently large n.
Note that the events
![]() $E_c$
are independent for different choices of c. Therefore, for an integer k, the probability that
$E_c$
are independent for different choices of c. Therefore, for an integer k, the probability that
![]() $E_c$
happens for at least k different choices of c is at most
$E_c$
happens for at least k different choices of c is at most
 $$\begin{align*}\binom nk \operatorname{\mathrm{Pr}}(E_c)^k \leq n^k e^{-kn^{1/5}} \leq e^{-k n^{1/6}} \end{align*}$$
$$\begin{align*}\binom nk \operatorname{\mathrm{Pr}}(E_c)^k \leq n^k e^{-kn^{1/5}} \leq e^{-k n^{1/6}} \end{align*}$$
since
![]() $n^{1/5}-\log n \geq n^{1/6}$
for sufficiently large n. Now let
$n^{1/5}-\log n \geq n^{1/6}$
for sufficiently large n. Now let
![]() $k=n^{7/8}$
, so that the probability that this happens is at most
$k=n^{7/8}$
, so that the probability that this happens is at most
![]() $e^{-n^{25/24}}$
. This is enough to beat the union bound over all
$e^{-n^{25/24}}$
. This is enough to beat the union bound over all
![]() $2^{2n}$
choices of
$2^{2n}$
choices of
![]() $X \subseteq A, Y \subseteq B$
. In particular, we find that for every such pair,
$X \subseteq A, Y \subseteq B$
. In particular, we find that for every such pair,
![]() $\lvert N(X,Y)\rvert \geq n - k=n-o(n)$
.
$\lvert N(X,Y)\rvert \geq n - k=n-o(n)$
.
Lemma 4.3. Let H be a bipartite random graph on parts
![]() $A,B$
with
$A,B$
with
![]() $\lvert A\rvert = \lvert B\rvert = n$
, where each edge appears with probability
$\lvert A\rvert = \lvert B\rvert = n$
, where each edge appears with probability
![]() $p=n^{-3/4}$
. The following holds w.h.p. as
$p=n^{-3/4}$
. The following holds w.h.p. as
![]() $n \to \infty $
. For all nonempty
$n \to \infty $
. For all nonempty
![]() $W\subseteq B$
with
$W\subseteq B$
with
![]() $\lvert W\rvert \leq n/12$
, we have that
$\lvert W\rvert \leq n/12$
, we have that
![]() $\lvert N_A(W)\rvert> 6\lvert W\rvert $
.
$\lvert N_A(W)\rvert> 6\lvert W\rvert $
.
Proof. Summing over all choices for
![]() $w=\lvert W\rvert $
, the probability that all edges from W go to another set of size at most
$w=\lvert W\rvert $
, the probability that all edges from W go to another set of size at most
![]() $6w$
is at most
$6w$
is at most
 $$\begin{align*}\sum_{w=1}^{n/12} \binom nw \binom n{6w} (1-p)^{w(n-6w)} \leq \sum_{w=1}^{n/12} n^{7w} e^{-pwn/2} = \sum_{w=1}^{n/12} \exp\left(w\left(7\log n- \frac 12 n^{1/4}\right)\right) = o(1).\\[-48pt] \end{align*}$$
$$\begin{align*}\sum_{w=1}^{n/12} \binom nw \binom n{6w} (1-p)^{w(n-6w)} \leq \sum_{w=1}^{n/12} n^{7w} e^{-pwn/2} = \sum_{w=1}^{n/12} \exp\left(w\left(7\log n- \frac 12 n^{1/4}\right)\right) = o(1).\\[-48pt] \end{align*}$$
Lemma 4.4. Let H be a tripartite random graph on parts
![]() $A,B,C$
with
$A,B,C$
with
![]() $\lvert A\rvert = \lvert B\rvert = \lvert C\rvert = n$
, where each edge appears with probability
$\lvert A\rvert = \lvert B\rvert = \lvert C\rvert = n$
, where each edge appears with probability
![]() $p=n^{-3/4}$
. Then w.h.p. there are at most
$p=n^{-3/4}$
. Then w.h.p. there are at most
![]() $n^{4/5}$
triangles, and every vertex lies in at most four triangles.
$n^{4/5}$
triangles, and every vertex lies in at most four triangles.
Proof. The expected number of triangles in H is
![]() $p^3 n^3 = n^{3/4}$
, so the first result follows by Markov’s inequality.
$p^3 n^3 = n^{3/4}$
, so the first result follows by Markov’s inequality.
For the second, first note that by the Chernoff bound, w.h.p. every vertex has degree at most
![]() $2pn = 2n^{1/4}$
. We now condition on this event. There is a bijection between triangles containing a vertex v and edges inside
$2pn = 2n^{1/4}$
. We now condition on this event. There is a bijection between triangles containing a vertex v and edges inside
![]() $N(v)$
, so it suffices to prove that w.h.p.
$N(v)$
, so it suffices to prove that w.h.p.
![]() $N(v)$
spans at most four edges. For fixed v, the probability that
$N(v)$
spans at most four edges. For fixed v, the probability that
![]() $e(N(v))\geq 5$
is at most
$e(N(v))\geq 5$
is at most
 $$\begin{align*}\binom{\binom{\lvert N(v)\rvert}2}5 p^5 \leq \binom{2n^{1/2}}5 p^5 \leq 32 (n^{1/2}p)^5 = 32 n^{-5/4}. \end{align*}$$
$$\begin{align*}\binom{\binom{\lvert N(v)\rvert}2}5 p^5 \leq \binom{2n^{1/2}}5 p^5 \leq 32 (n^{1/2}p)^5 = 32 n^{-5/4}. \end{align*}$$
By the union bound, the probability that this happens for any vertex v is at most
![]() $O(n^{-1/4})=o(1)$
.
$O(n^{-1/4})=o(1)$
.
Lemma 4.5. Let H be a bipartite random graph on parts
![]() $A,B$
with
$A,B$
with
![]() $\lvert A\rvert = \lvert B\rvert = n$
, where each edge appears with probability
$\lvert A\rvert = \lvert B\rvert = n$
, where each edge appears with probability
![]() $p=n^{-3/4}$
. The following holds w.h.p. as
$p=n^{-3/4}$
. The following holds w.h.p. as
![]() $n \to \infty $
. For all
$n \to \infty $
. For all
![]() $X \subseteq A, Y \subseteq B$
with
$X \subseteq A, Y \subseteq B$
with
![]() $\lvert X\rvert , \lvert Y\rvert \geq n/100$
, we have that
$\lvert X\rvert , \lvert Y\rvert \geq n/100$
, we have that
![]() $e(X,Y) \geq n$
.
$e(X,Y) \geq n$
.
Proof. The expected number of edges between X and Y is
![]() $p\lvert X\rvert \lvert Y\rvert \geq pn^2/10^4 \geq 2n$
for sufficiently large n. Therefore, by the Chernoff bound, the probability that
$p\lvert X\rvert \lvert Y\rvert \geq pn^2/10^4 \geq 2n$
for sufficiently large n. Therefore, by the Chernoff bound, the probability that
![]() $e(X,Y)<n$
is at most
$e(X,Y)<n$
is at most
![]() $e^{-pn^2/10^5} = e^{-\Omega (n^{5/4})}$
. This is small enough to union-bound over all
$e^{-pn^2/10^5} = e^{-\Omega (n^{5/4})}$
. This is small enough to union-bound over all
![]() $\leq 2^{2n}$
choices for
$\leq 2^{2n}$
choices for
![]() $X,Y$
.
$X,Y$
.
We are finally ready to prove Proposition 3.11.
Proof of Proposition 3.11.
We sample a random tripartite graph
![]() $H_0$
on vertex set
$H_0$
on vertex set
![]() $A \cup B \cup C$
, where each edge appears with probability
$A \cup B \cup C$
, where each edge appears with probability
![]() $p=n^{-3/4}$
. With high probability, the outcomes of Lemmas 4.1 to 4.5 hold. We now delete a single edge from every triangle in
$p=n^{-3/4}$
. With high probability, the outcomes of Lemmas 4.1 to 4.5 hold. We now delete a single edge from every triangle in
![]() $H_0$
. In so doing, we delete at most
$H_0$
. In so doing, we delete at most
![]() $n^{4/5}$
edges, and for any vertex, we delete at most four of its incident edges, both by Lemma 4.4. Let H be the resulting graph. We claim that H satisfies all the desired properties.
$n^{4/5}$
edges, and for any vertex, we delete at most four of its incident edges, both by Lemma 4.4. Let H be the resulting graph. We claim that H satisfies all the desired properties.
Certainly, H is triangle-free, proving Proposition 3.11(iv). For Proposition 3.11(iii), note that every vertex in Z lost at most four incident edges when passing from
![]() $H_0$
to H, so
$H_0$
to H, so
![]() $\lvert N_A(Z)\rvert $
decreased by at most
$\lvert N_A(Z)\rvert $
decreased by at most
![]() $4 \lvert Z\rvert $
when passing from
$4 \lvert Z\rvert $
when passing from
![]() $H_0$
to H. As Lemma 4.3 gives that
$H_0$
to H. As Lemma 4.3 gives that
![]() $\lvert N_A(Z)\rvert>6\lvert Z\rvert $
in
$\lvert N_A(Z)\rvert>6\lvert Z\rvert $
in
![]() $H_0$
, we get Proposition 3.11(iii). For Proposition 3.11(ii), recall that we delete at most
$H_0$
, we get Proposition 3.11(iii). For Proposition 3.11(ii), recall that we delete at most
![]() $n^{4/5}$
edges when passing from
$n^{4/5}$
edges when passing from
![]() $H_0$
to H, so for any fixed sets
$H_0$
to H, so for any fixed sets
![]() $X,Y$
, the value of
$X,Y$
, the value of
![]() $\lvert N(X,Y)\rvert $
decreases by at most
$\lvert N(X,Y)\rvert $
decreases by at most
![]() $n^{4/5}$
when passing from
$n^{4/5}$
when passing from
![]() $H_0$
to H. As
$H_0$
to H. As
![]() $\lvert N(X,Y)\rvert \geq n-o(n)$
in
$\lvert N(X,Y)\rvert \geq n-o(n)$
in
![]() $H_0$
by Lemma 4.2, we get Proposition 3.11(ii). Finally, for Proposition 3.11(i), note that if F has at least half the edges of
$H_0$
by Lemma 4.2, we get Proposition 3.11(ii). Finally, for Proposition 3.11(i), note that if F has at least half the edges of
![]() $H[A \cup B]$
, then it has at least one-third the edges of
$H[A \cup B]$
, then it has at least one-third the edges of
![]() $H_0[A \cup B]$
, so the result follows immediately from Lemma 4.1.
$H_0[A \cup B]$
, so the result follows immediately from Lemma 4.1.
We now note that for all subsets
![]() $X\subseteq A, Y \subseteq B$
of order at least
$X\subseteq A, Y \subseteq B$
of order at least
![]() $n/100$
, there is at least one edge between X and Y. Indeed, Lemma 4.5 guarantees at least n edges in
$n/100$
, there is at least one edge between X and Y. Indeed, Lemma 4.5 guarantees at least n edges in
![]() $H_0$
between X and Y, and at most
$H_0$
between X and Y, and at most
![]() $n^{4/5}$
of these are deleted when passing to
$n^{4/5}$
of these are deleted when passing to
![]() $H_0$
, so at least one remains. Similarly, for any
$H_0$
, so at least one remains. Similarly, for any
![]() $Z \subseteq C$
of order at least
$Z \subseteq C$
of order at least
![]() $n/100$
, there is at least one edge between X and Z and at least one edge between Y and Z.
$n/100$
, there is at least one edge between X and Z and at least one edge between Y and Z.
It remains to prove Proposition 3.11(v). So suppose that there is a proper 3-coloring of H – namely, a partition into independent sets
![]() $D,E,F$
. We wish to prove that up to permuting the colors,
$D,E,F$
. We wish to prove that up to permuting the colors,
![]() $A=D, B=E, C=F$
. We first claim that at most one of the numbers
$A=D, B=E, C=F$
. We first claim that at most one of the numbers
![]() $\lvert D \cap A\rvert , \lvert D \cap B\rvert , \lvert D \cap C\rvert $
is at least
$\lvert D \cap A\rvert , \lvert D \cap B\rvert , \lvert D \cap C\rvert $
is at least
![]() $n/100$
. Indeed, suppose without loss of generality that
$n/100$
. Indeed, suppose without loss of generality that
![]() $\lvert D \cap A\rvert , \lvert D \cap B\rvert \geq n/100$
. Then by the observation in the previous paragraph, there is an edge between
$\lvert D \cap A\rvert , \lvert D \cap B\rvert \geq n/100$
. Then by the observation in the previous paragraph, there is an edge between
![]() $D \cap A$
and
$D \cap A$
and
![]() $D \cap B$
, contradicting that D is an independent set.
$D \cap B$
, contradicting that D is an independent set.
Using this claim, we see that, potentially after permuting the colors, we have that
![]() $\lvert D \cap A\rvert ,\lvert E \cap B\rvert , \lvert F \cap C\rvert \geq \frac {98}{100}n$
. We now claim that in fact
$\lvert D \cap A\rvert ,\lvert E \cap B\rvert , \lvert F \cap C\rvert \geq \frac {98}{100}n$
. We now claim that in fact
![]() $D=A, E=B, F=C$
. Indeed, suppose this is not the case, and assume without loss of generality that
$D=A, E=B, F=C$
. Indeed, suppose this is not the case, and assume without loss of generality that
![]() $\lvert C \setminus F\rvert \geq \lvert A \setminus D\rvert , \lvert B \setminus E\rvert $
. Without loss of generality, at least half the vertices in
$\lvert C \setminus F\rvert \geq \lvert A \setminus D\rvert , \lvert B \setminus E\rvert $
. Without loss of generality, at least half the vertices in
![]() $C \setminus F$
are colored D. Let
$C \setminus F$
are colored D. Let
![]() $Z = (C \setminus F) \cap D$
. Note that
$Z = (C \setminus F) \cap D$
. Note that
![]() $\lvert Z\rvert \leq \lvert C \setminus F\rvert \leq n/50$
, so by Proposition 3.11(iii), we have that
$\lvert Z\rvert \leq \lvert C \setminus F\rvert \leq n/50$
, so by Proposition 3.11(iii), we have that
![]() $\lvert N_A(Z)\rvert>2 \lvert Z\rvert \geq \lvert C \setminus F\rvert \geq \lvert A \setminus D\rvert $
, as we assumed that
$\lvert N_A(Z)\rvert>2 \lvert Z\rvert \geq \lvert C \setminus F\rvert \geq \lvert A \setminus D\rvert $
, as we assumed that
![]() $\lvert Z\rvert \geq \frac 12 \lvert C \setminus F\rvert $
. Since
$\lvert Z\rvert \geq \frac 12 \lvert C \setminus F\rvert $
. Since
![]() $\lvert N_A(Z)\rvert> \lvert A \setminus D\rvert $
, there must be at least one edge between Z and
$\lvert N_A(Z)\rvert> \lvert A \setminus D\rvert $
, there must be at least one edge between Z and
![]() $A \cap D$
. But every vertex in Z and in
$A \cap D$
. But every vertex in Z and in
![]() $A \cap D$
is colored D, contradicting that D is an independent set. This contradiction concludes the proof of Proposition 3.11(v).
$A \cap D$
is colored D, contradicting that D is an independent set. This contradiction concludes the proof of Proposition 3.11(v).
5 Concluding remarks
A fundamental question which remains open is Problem 1.9: does there exist a t-chromatic
![]() $K_t$
-abundant graph for any
$K_t$
-abundant graph for any
![]() $t \geq 4$
? We are inclined to believe that this is not the case, and every t-chromatic graph is non-
$t \geq 4$
? We are inclined to believe that this is not the case, and every t-chromatic graph is non-
![]() $K_t$
-abundant when
$K_t$
-abundant when
![]() $t \geq 4$
. As mentioned in the introduction, the first open case is the Brinkmann graph; it would be very interesting to prove or disprove that this graph is
$t \geq 4$
. As mentioned in the introduction, the first open case is the Brinkmann graph; it would be very interesting to prove or disprove that this graph is
![]() $K_4$
-abundant.
$K_4$
-abundant.
Another interesting question is whether one can prove Theorem 1.6 unconditionally (i.e., without relying on Conjecture 1.5). It is known [Reference Ruzsa19, Theorem 2.3] that Conjecture 1.5 holds in case E has exactly one negative coefficient, as the Behrend construction can be used to find large sets with no nontrivial solutions to such equations; such equations are called convex. Even simple cases beyond this are open; for example, if E is the equation
![]() $x+3y=2z+2w$
, then the best known lower bound on
$x+3y=2z+2w$
, then the best known lower bound on
![]() $r_E(m)$
is
$r_E(m)$
is
![]() $\Omega (\sqrt m)$
.
$\Omega (\sqrt m)$
.
The sets of equations
![]() $S_{A,B,C}(G)$
that we obtain in the proof of Theorem 1.6 are very complicated, and they involve many coefficients of both signs. However, in the proof of Lemma 3.2, we have a great deal of freedom in how we construct a single equation from our family of equations. It is conceivable that one could combine
$S_{A,B,C}(G)$
that we obtain in the proof of Theorem 1.6 are very complicated, and they involve many coefficients of both signs. However, in the proof of Lemma 3.2, we have a great deal of freedom in how we construct a single equation from our family of equations. It is conceivable that one could combine
![]() $S_{A,B,C}(G)$
into a single convex equation. If this were possible, it would yield a proof of Theorem 1.6 without the assumption that Conjecture 1.5 holds.
$S_{A,B,C}(G)$
into a single convex equation. If this were possible, it would yield a proof of Theorem 1.6 without the assumption that Conjecture 1.5 holds.
However, computer simulation suggests that this may not work. Indeed, we wrote a computer program to sample a random tripartite graph and delete one edge from every triangle. Testing whether the set of equations arising from the cycles linearly spans a convex equation can be done efficiently, as this can be described as a linear programming problem. Even when testing fairly large random graphs (with hundreds of vertices and thousands of edges), we were not able to find one where the equations arising from cycles span a convex equation.
Acknowledgements
We are grateful to the anonymous referees for their helpful suggestions.
Competing interest
None.