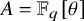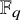Introduction
0.1 Background
The study of the Riemann zeta function
![]() $\zeta (.)$
and its special values
$\zeta (.)$
and its special values
![]() $\zeta (n)$
for
$\zeta (n)$
for
![]() $n \in \mathbb N$
and
$n \in \mathbb N$
and
![]() $n \geq 2$
is a classical topic in number theory. A well-known analogy between the arithmetic of number fields and global function fields suggests that one can replace
$n \geq 2$
is a classical topic in number theory. A well-known analogy between the arithmetic of number fields and global function fields suggests that one can replace
![]() $\mathbb Z$
by the coordinate ring of a curve defined over a finite field and
$\mathbb Z$
by the coordinate ring of a curve defined over a finite field and
![]() $\mathbb Q$
by its field of fractions, and study similarly defined objects. In [Reference Carlitz16], Carlitz carries out this analogy for the case where
$\mathbb Q$
by its field of fractions, and study similarly defined objects. In [Reference Carlitz16], Carlitz carries out this analogy for the case where
![]() $A = \mathbb {F}_q[\theta ]$
(q a power of a prime) and
$A = \mathbb {F}_q[\theta ]$
(q a power of a prime) and
![]() $K = \mathbb {F}_q(\theta )$
(which are the coordinate ring and function field of the curve
$K = \mathbb {F}_q(\theta )$
(which are the coordinate ring and function field of the curve
![]() $\mathbb P^1$
over
$\mathbb P^1$
over
![]() $\mathbb {F}_q$
), wherein he defines zeta values
$\mathbb {F}_q$
), wherein he defines zeta values
![]() $\zeta _A(n)$
which are considered as the analogues of the Riemann zeta function. Many years after Carlitz’s pioneering work, Goss showed that these values could be realized as the special values of the so-called Goss-Carlitz zeta function
$\zeta _A(n)$
which are considered as the analogues of the Riemann zeta function. Many years after Carlitz’s pioneering work, Goss showed that these values could be realized as the special values of the so-called Goss-Carlitz zeta function
![]() $\zeta _A(\cdot )$
over a suitable generalization of the complex plane. Goss’s zeta functions are a special case of the L-functions he introduced in [Reference Goss30] for more general rings A. The special values of this type of L-function, called Goss’s zeta values, have been at the heart of function field arithmetic for the last forty years. Various works have revealed the importance of these zeta values for both their independent interest and for their applications to a wide variety of arithmetic problems, including multiple zeta values (see the excellent articles [Reference Thakur, Böckle, Goss, Hartl and Papanikolas54, Reference Thakur53] for an overview and also [Reference Dac46] for some recent results), Anderson’s log-algebraicity identities (see [Reference Anderson2, Reference Anderson3, Reference Anglès, Dac and Tavares Ribeiro6, Reference Green and Papanikolas36, Reference Thakur51]) and Taelman’s units and the class formula à la Taelman (see [Reference Anglès, Dac and Tavares Ribeiro11, Reference Debry24, Reference Demeslay25, Reference Demeslay26, Reference Fang28, Reference Mornev43, Reference Taelman50] for recent progress and [Reference Anglès, Dac and Tavares Ribeiro10] for an overview).
$\zeta _A(\cdot )$
over a suitable generalization of the complex plane. Goss’s zeta functions are a special case of the L-functions he introduced in [Reference Goss30] for more general rings A. The special values of this type of L-function, called Goss’s zeta values, have been at the heart of function field arithmetic for the last forty years. Various works have revealed the importance of these zeta values for both their independent interest and for their applications to a wide variety of arithmetic problems, including multiple zeta values (see the excellent articles [Reference Thakur, Böckle, Goss, Hartl and Papanikolas54, Reference Thakur53] for an overview and also [Reference Dac46] for some recent results), Anderson’s log-algebraicity identities (see [Reference Anderson2, Reference Anderson3, Reference Anglès, Dac and Tavares Ribeiro6, Reference Green and Papanikolas36, Reference Thakur51]) and Taelman’s units and the class formula à la Taelman (see [Reference Anglès, Dac and Tavares Ribeiro11, Reference Debry24, Reference Demeslay25, Reference Demeslay26, Reference Fang28, Reference Mornev43, Reference Taelman50] for recent progress and [Reference Anglès, Dac and Tavares Ribeiro10] for an overview).
For
![]() $A=\mathbb F_q[\theta ]$
, the transcendence of the Carlitz zeta values at positive integers
$A=\mathbb F_q[\theta ]$
, the transcendence of the Carlitz zeta values at positive integers
![]() $\zeta _A(n)\ (n \geq 1)$
was first proved by Jing Yu [Reference Yu55]. Further, all algebraic relations among these values were determined by Jing Yu [Reference Yu56] and by Chieh-Yu Chang and Jing Yu [Reference Chang and Yu23]. These results are very surprising when compared to the extremely limited knowledge we have about the transcendence of values of Riemann’s zeta function at odd positive integers greater than 3 (see section 3 of [Reference Murty44] for a description of known classical results). Goss raised the problem of extending the work of Chang and Yu to a more general setting. For a finite class of curves, such that the coordinate ring A has class number one, several partial results about Goss’s zeta values have been obtained by a similar method (see, for example, [Reference Lutes and Papanikolas42]). However, to our knowledge, nothing is known when the class number of A is greater than 1. One difficulty of extending these results to rings with arbitrary class number is that one must define the zeta values as sums over ideals, rather than over monic elements, which greatly complicates some of the calculations. Additionally, Anderson generating functions are more complicated in this situation (see §2.1) and require more sophisticated analysis to realize their evaluations as periods (see §3.3).
$\zeta _A(n)\ (n \geq 1)$
was first proved by Jing Yu [Reference Yu55]. Further, all algebraic relations among these values were determined by Jing Yu [Reference Yu56] and by Chieh-Yu Chang and Jing Yu [Reference Chang and Yu23]. These results are very surprising when compared to the extremely limited knowledge we have about the transcendence of values of Riemann’s zeta function at odd positive integers greater than 3 (see section 3 of [Reference Murty44] for a description of known classical results). Goss raised the problem of extending the work of Chang and Yu to a more general setting. For a finite class of curves, such that the coordinate ring A has class number one, several partial results about Goss’s zeta values have been obtained by a similar method (see, for example, [Reference Lutes and Papanikolas42]). However, to our knowledge, nothing is known when the class number of A is greater than 1. One difficulty of extending these results to rings with arbitrary class number is that one must define the zeta values as sums over ideals, rather than over monic elements, which greatly complicates some of the calculations. Additionally, Anderson generating functions are more complicated in this situation (see §2.1) and require more sophisticated analysis to realize their evaluations as periods (see §3.3).
In this paper, we provide the first step towards the resolution of the above problem and develop a conceptual method to deal with the genus 1 case. The advantage of working in the genus 1 case (elliptic curves) is that we have an explicit group law on the curve which we often exploit in our arguments. However, where possible, we strive to give general arguments in our proofs which will readily generalize to curves of arbitrary genus. Our results determine all algebraic relations among Goss’s zeta values attached to the base ring A which is the coordinate ring of an elliptic curve over a finite field. To do so, we reduce the study of Goss’s zeta values, which are fundamentally analytic objects, to that of Anderson’s zeta values, which are of arithmetic nature (see Section 5.3 for details). Then we use a generalization of Anderson-Thakur’s theorem (Theorem 1.8) on elliptic curves to construct zeta t-motives attached to Anderson’s zeta values. We apply the work of Hardouin [Reference Hardouin37] on Tannakian groups in positive characteristic and compute the Galois groups attached to zeta t-motives. Finally, we apply the transcendence method introduced by Papanikolas [Reference Papanikolas47] (which relies heavily on [Reference Anderson, Brownawell and Papanikolas4]) to obtain our algebraic independence result.
0.2 Statement of Results
Let us give now more precise statements of our results.
Let X be a geometrically connected smooth projective curve over a finite field
![]() $\mathbb F_q$
of characteristic p, having q elements. We denote by K its function field and fix a place
$\mathbb F_q$
of characteristic p, having q elements. We denote by K its function field and fix a place
![]() $\infty $
of K of degree
$\infty $
of K of degree
![]() $d_{\infty } = 1$
. We denote by A the ring of elements of K which are regular outside
$d_{\infty } = 1$
. We denote by A the ring of elements of K which are regular outside
![]() $\infty $
. The
$\infty $
. The
![]() $\infty $
-adic completion
$\infty $
-adic completion
![]() $K_{\infty }$
of K is equipped with the normalized
$K_{\infty }$
of K is equipped with the normalized
![]() $\infty $
-adic valuation
$\infty $
-adic valuation
![]() $v_{\infty }:K_{\infty } \rightarrow \mathbb Z\cup \{+\infty \}$
. The completion
$v_{\infty }:K_{\infty } \rightarrow \mathbb Z\cup \{+\infty \}$
. The completion
![]() $\mathbb C_{\infty }$
of a fixed algebraic closure
$\mathbb C_{\infty }$
of a fixed algebraic closure
![]() $\overline K_{\infty }$
of
$\overline K_{\infty }$
of
![]() $K_{\infty }$
comes with a unique valuation extending
$K_{\infty }$
comes with a unique valuation extending
![]() $v_{\infty }$
, which we also denote by
$v_{\infty }$
, which we also denote by
![]() $v_{\infty }$
.
$v_{\infty }$
.
To define Goss’s zeta values (our exposition closely follows [Reference Goss32, §8.2-8.7]), we let
![]() $\pi \in K^{\times }_{\infty }$
be a uniformizer so that we can identify
$\pi \in K^{\times }_{\infty }$
be a uniformizer so that we can identify
![]() $K_{\infty }$
with
$K_{\infty }$
with
![]() ${\mathbb F_q (( \pi ))}$
. For
${\mathbb F_q (( \pi ))}$
. For
![]() $x\in \overline {K}_{\infty }^{\times }$
, one can write
$x\in \overline {K}_{\infty }^{\times }$
, one can write
![]() $x=\pi ^{v_{\infty }(x)} \operatorname {\mathrm {sgn}} (x) \langle x \rangle $
, where
$x=\pi ^{v_{\infty }(x)} \operatorname {\mathrm {sgn}} (x) \langle x \rangle $
, where
![]() $\operatorname {\mathrm {sgn}}(x)\in \overline {\mathbb F}_q^{\times }$
and
$\operatorname {\mathrm {sgn}}(x)\in \overline {\mathbb F}_q^{\times }$
and
![]() $\langle x \rangle \in (1 + \pi \mathbb {F}_q[[\pi ]])$
is a
$\langle x \rangle \in (1 + \pi \mathbb {F}_q[[\pi ]])$
is a
![]() $1$
-unit. If we denote by
$1$
-unit. If we denote by
![]() $\mathcal {I}(A)$
the group of fractional ideals of A, then Goss defines a group homomorphism
$\mathcal {I}(A)$
the group of fractional ideals of A, then Goss defines a group homomorphism
such that for
![]() $x\in K^{\times }$
, we have
$x\in K^{\times }$
, we have
![]() $[xA]_A=x/\operatorname {\mathrm {sgn}}(x)$
. Note that the definition of ideal exponentiation technically depends on the choice of uniformizer
$[xA]_A=x/\operatorname {\mathrm {sgn}}(x)$
. Note that the definition of ideal exponentiation technically depends on the choice of uniformizer
![]() $\pi \in K^*_{\infty }$
and the choice of sign function (see [Reference Goss32, Thm. 8.2.15-16]). However, in this paper, we apply it only in the case of function fields for rank 1 sign-normalized Drinfeld modules for elliptic curves, so there is a canonical choice for each of these (see Section 1.2).
$\pi \in K^*_{\infty }$
and the choice of sign function (see [Reference Goss32, Thm. 8.2.15-16]). However, in this paper, we apply it only in the case of function fields for rank 1 sign-normalized Drinfeld modules for elliptic curves, so there is a canonical choice for each of these (see Section 1.2).
Let
![]() $E/K$
be a finite extension, and let
$E/K$
be a finite extension, and let
![]() $O_E$
be the integral closure of A in E. Then Goss defined a zeta function
$O_E$
be the integral closure of A in E. Then Goss defined a zeta function
![]() $\zeta _{O_E}(.)$
(see [Reference Goss32, §8.6]) over a suitable generalization of the complex plane (see [Reference Goss32, §8.1]). We are interested in Goss’s zeta values for
$\zeta _{O_E}(.)$
(see [Reference Goss32, §8.6]) over a suitable generalization of the complex plane (see [Reference Goss32, §8.1]). We are interested in Goss’s zeta values for
![]() $n \in \mathbb N$
given by
$n \in \mathbb N$
given by
 $$\begin{align*}\zeta_{O_E}(n)=\sum_{d\geq 0} \sum_{\substack{\frak I\in \mathcal I(O_E), \frak I\subset O_E,\\ \deg(N_{E/K}(\frak I))=d}} \left[\frac{O_E}{\frak I}\right]_A^{-n} \in \overline{K}_{\infty}^{\times} \end{align*}$$
$$\begin{align*}\zeta_{O_E}(n)=\sum_{d\geq 0} \sum_{\substack{\frak I\in \mathcal I(O_E), \frak I\subset O_E,\\ \deg(N_{E/K}(\frak I))=d}} \left[\frac{O_E}{\frak I}\right]_A^{-n} \in \overline{K}_{\infty}^{\times} \end{align*}$$
(details of this definition are in §5.2), where
![]() $\mathcal {I}(O_E)$
denotes the group of fractional ideals of
$\mathcal {I}(O_E)$
denotes the group of fractional ideals of
![]() $O_E$
.
$O_E$
.
0.3 Carlitz zeta values (the genus 0 case)
We set our curve X to be the projective line
![]() $\mathbb P^1/\mathbb F_q$
equipped with the infinity point
$\mathbb P^1/\mathbb F_q$
equipped with the infinity point
![]() $\infty \in \mathbb P^1(\mathbb F_q)$
. Then
$\infty \in \mathbb P^1(\mathbb F_q)$
. Then
![]() $A=\mathbb F_q[\theta ]$
,
$A=\mathbb F_q[\theta ]$
,
![]() $K=\mathbb F_q(\theta )$
and
$K=\mathbb F_q(\theta )$
and
![]() $K_{\infty }=\mathbb F_q((1/\theta ))$
, where
$K_{\infty }=\mathbb F_q((1/\theta ))$
, where
![]() $\theta $
is an independent variable. Let
$\theta $
is an independent variable. Let
![]() $A_+$
be the set of monic polynomials in A.
$A_+$
be the set of monic polynomials in A.
Since the class number of A is
![]() $1$
, by the above discussion, Goss’s map is given by
$1$
, by the above discussion, Goss’s map is given by
![]() $[xA]_A=x/\operatorname {\mathrm {sgn}}(x)$
for
$[xA]_A=x/\operatorname {\mathrm {sgn}}(x)$
for
![]() $x\in K^{\times }$
. Then the Carlitz zeta values, which are special values of the Carlitz-Goss zeta function, are given by
$x\in K^{\times }$
. Then the Carlitz zeta values, which are special values of the Carlitz-Goss zeta function, are given by
 $$\begin{align*}\zeta_A(n):=\sum_{a \in A_+} \frac{1}{a^n} \in K_{\infty}^{\times}, \quad n \in \mathbb N. \end{align*}$$
$$\begin{align*}\zeta_A(n):=\sum_{a \in A_+} \frac{1}{a^n} \in K_{\infty}^{\times}, \quad n \in \mathbb N. \end{align*}$$
Carlitz noticed that these values are intimately related to the so-called Carlitz module C that is the first example of a Drinfeld module. Then he proved two fundamental theorems about these values. In analogy with the classical Euler formulas, Carlitz’s first theorem asserts that for the so-called Carlitz period
![]() $\widetilde {\pi } \in \overline K_{\infty }^{\times }$
, we have the Carlitz-Euler relations
$\widetilde {\pi } \in \overline K_{\infty }^{\times }$
, we have the Carlitz-Euler relations
His second theorem states that
![]() $\zeta _A(1)$
is the logarithm of
$\zeta _A(1)$
is the logarithm of
![]() $1$
of the Carlitz module C, which is the first example of log-algebraicity identities. Anderson extended this theory by giving many more log-algebraic identities [Reference Anderson3].
$1$
of the Carlitz module C, which is the first example of log-algebraicity identities. Anderson extended this theory by giving many more log-algebraic identities [Reference Anderson3].
Many years after the work of Carlitz, Anderson and Thakur [Reference Anderson and Thakur5] developed an explicit theory of tensor powers of the Carlitz module
![]() $C^{\otimes n}\ (n \in \mathbb N)$
and expressed
$C^{\otimes n}\ (n \in \mathbb N)$
and expressed
![]() $\zeta _A(n)$
as the last coordinate of the logarithm of a special algebraic point of
$\zeta _A(n)$
as the last coordinate of the logarithm of a special algebraic point of
![]() $C^{\otimes n}$
. Using this result, Yu proved that
$C^{\otimes n}$
. Using this result, Yu proved that
![]() $\zeta _A(n)$
is transcendental in [Reference Yu55] and that the only
$\zeta _A(n)$
is transcendental in [Reference Yu55] and that the only
![]() $\overline K$
-linear relations among the Carlitz zeta values and powers of the Carlitz period are the above Carlitz-Euler relations in [Reference Yu56].
$\overline K$
-linear relations among the Carlitz zeta values and powers of the Carlitz period are the above Carlitz-Euler relations in [Reference Yu56].
For algebraic relations among Carlitz zeta values, we have the trivial relations coming from working in characteristic p, which state that for
![]() $m,n \in \mathbb N$
,
$m,n \in \mathbb N$
,
Extending the previous works of Yu, Chang and Yu [Reference Chang and Yu23] proved that the Carlitz-Euler relations and the Frobenius relations give rise to all algebraic relations among the Carlitz zeta values. To prove this result, Chang and Yu use the connection between Anderson
![]() $\mathbb F_q[\theta ]$
-modules and t-motives as well as the powerful criterion for transcendence introduced by Anderson-Brownawell-Papanikolas in [Reference Anderson, Brownawell and Papanikolas4] and the criterion for algebraic independence developed by Papanikolas in [Reference Papanikolas47]. This latter criterion, which we will also use in our present paper, states roughly that the dimension of the motivic Galois group of a t-motive is equal to the transcendence degree of its attached period matrix.
$\mathbb F_q[\theta ]$
-modules and t-motives as well as the powerful criterion for transcendence introduced by Anderson-Brownawell-Papanikolas in [Reference Anderson, Brownawell and Papanikolas4] and the criterion for algebraic independence developed by Papanikolas in [Reference Papanikolas47]. This latter criterion, which we will also use in our present paper, states roughly that the dimension of the motivic Galois group of a t-motive is equal to the transcendence degree of its attached period matrix.
0.4 Goss’s zeta values on elliptic curves (the genus 1 case)
In a series of papers [Reference Green34, Reference Green33, Reference Green and Papanikolas36], Papanikolas and the first author carried out an extensive study to move from the projective line
![]() $\mathbb P^1/\mathbb F_q$
(the genus 0 case) to elliptic curves over
$\mathbb P^1/\mathbb F_q$
(the genus 0 case) to elliptic curves over
![]() $\mathbb F_q$
(the genus 1 case).
$\mathbb F_q$
(the genus 1 case).
We work with an elliptic curve X defined over
![]() $\mathbb F_q$
with defining equation given in (1.1) equipped with a rational point
$\mathbb F_q$
with defining equation given in (1.1) equipped with a rational point
![]() $\infty \in X(\mathbb F_q)$
. Then
$\infty \in X(\mathbb F_q)$
. Then
![]() $A=\mathbb F_q[\theta ,\eta ]$
is the coordinate ring of X, where
$A=\mathbb F_q[\theta ,\eta ]$
is the coordinate ring of X, where
![]() $\theta $
and
$\theta $
and
![]() $\eta $
satisfy (1.1). We denote by
$\eta $
satisfy (1.1). We denote by
![]() $K=\mathbb F_q(\theta ,\eta )$
its fraction field and by
$K=\mathbb F_q(\theta ,\eta )$
its fraction field and by
![]() $H \subset K_{\infty }$
the Hilbert class field of A.
$H \subset K_{\infty }$
the Hilbert class field of A.
The class number
![]() $\text {Cl}(A)$
of A equals the number of rational points
$\text {Cl}(A)$
of A equals the number of rational points
![]() $X(\mathbb F_q)$
on the elliptic curve X, which also equals the degree of extension
$X(\mathbb F_q)$
on the elliptic curve X, which also equals the degree of extension
![]() $[H:K]$
; that is,
$[H:K]$
; that is,
For a prime ideal
![]() $\frak p$
of A of degree
$\frak p$
of A of degree
![]() $1$
corresponding to an
$1$
corresponding to an
![]() $\mathbb F_q$
-rational point on X, we let
$\mathbb F_q$
-rational point on X, we let
![]() $\frak p^{-1}$
be the inverse fractional ideal of
$\frak p^{-1}$
be the inverse fractional ideal of
![]() $\frak p$
and consider the sum
$\frak p$
and consider the sum
 $$\begin{align*}\zeta_A(\frak p,n)=\sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}, \quad n \in \mathbb N. \end{align*}$$
$$\begin{align*}\zeta_A(\frak p,n)=\sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}, \quad n \in \mathbb N. \end{align*}$$
The sums
![]() $\zeta _A(\frak p,n)$
where
$\zeta _A(\frak p,n)$
where
![]() $\frak p$
runs through the set
$\frak p$
runs through the set
![]() $\mathcal P$
of prime ideals of A of degree 1 are the elementary blocks in the study of Goss’s zeta values on elliptic curves. When the extension
$\mathcal P$
of prime ideals of A of degree 1 are the elementary blocks in the study of Goss’s zeta values on elliptic curves. When the extension
![]() $E/K$
is trivial (i.e.,
$E/K$
is trivial (i.e.,
![]() $E=K$
), the Goss zeta value
$E=K$
), the Goss zeta value
![]() $\zeta _A(n)$
can be expressed as a
$\zeta _A(n)$
can be expressed as a
![]() $\overline K$
-linear combination of
$\overline K$
-linear combination of
![]() $\zeta _A(\frak p,n)$
. When
$\zeta _A(\frak p,n)$
. When
![]() $E=H$
, the zeta value
$E=H$
, the zeta value
![]() $\zeta _{O_H}(n)$
(which is a regulator in the sense of Taelman [Reference Anglès, Dac and Tavares Ribeiro6, Reference Taelman50]) can be written as a product of
$\zeta _{O_H}(n)$
(which is a regulator in the sense of Taelman [Reference Anglès, Dac and Tavares Ribeiro6, Reference Taelman50]) can be written as a product of
![]() $\overline K$
-linear combinations of
$\overline K$
-linear combinations of
![]() $\zeta _A(\frak p,n)$
. This is done explicitly in §5.3–5.4.
$\zeta _A(\frak p,n)$
. This is done explicitly in §5.3–5.4.
Contrary to the
![]() $\mathbb F_q[\theta ]$
-case, one main issue present in the higher genus case is that Goss’s zeta function is fundamentally analytic in nature; it has no explicit dependence on the arithmetic of Drinfeld modules. To overcome this problem, Anderson introduced the so-called Anderson zeta values
$\mathbb F_q[\theta ]$
-case, one main issue present in the higher genus case is that Goss’s zeta function is fundamentally analytic in nature; it has no explicit dependence on the arithmetic of Drinfeld modules. To overcome this problem, Anderson introduced the so-called Anderson zeta values
![]() $\zeta _{\rho }(b_i,n)$
(see (1.21) for a precise definition) indexed by a K-basis
$\zeta _{\rho }(b_i,n)$
(see (1.21) for a precise definition) indexed by a K-basis
![]() $\{b_i\}_{i=1}^m \in O_H$
of H. These zeta values are also
$\{b_i\}_{i=1}^m \in O_H$
of H. These zeta values are also
![]() $\overline K$
-linear combinations of
$\overline K$
-linear combinations of
![]() $\zeta _A(\frak p,n)$
, and thus they contain the same information as Goss’s zeta values. The crucial point is that Anderson’s zeta values are of arithmetic nature and intimately related to a canonical rank 1 sign normalized Drinfeld A-module
$\zeta _A(\frak p,n)$
, and thus they contain the same information as Goss’s zeta values. The crucial point is that Anderson’s zeta values are of arithmetic nature and intimately related to a canonical rank 1 sign normalized Drinfeld A-module
![]() $\rho $
(see §1.3 for a summary).
$\rho $
(see §1.3 for a summary).
In [Reference Green and Papanikolas36], Papanikolas and the first author developed an explicit theory of the above Drinfeld A-module
![]() $\rho $
. They gave a new proof of Anderson’s celebrated log-algebraicity theorem on elliptic curves and proved that
$\rho $
. They gave a new proof of Anderson’s celebrated log-algebraicity theorem on elliptic curves and proved that
![]() $\zeta _{\rho }(b_i,1)$
can be realized as the logarithm of
$\zeta _{\rho }(b_i,1)$
can be realized as the logarithm of
![]() $\rho $
evaluated at a prescribed algebraic point. In [Reference Green34, Reference Green33], the first author introduced the tensor powers
$\rho $
evaluated at a prescribed algebraic point. In [Reference Green34, Reference Green33], the first author introduced the tensor powers
![]() $\rho ^{\otimes n}$
for
$\rho ^{\otimes n}$
for
![]() $n \in \mathbb N$
and proved basic properties of Anderson modules
$n \in \mathbb N$
and proved basic properties of Anderson modules
![]() $\rho ^{\otimes n}$
. Then he obtained a generalization of Anderson-Thakur’s theorem for small values
$\rho ^{\otimes n}$
. Then he obtained a generalization of Anderson-Thakur’s theorem for small values
![]() $n <q$
. By a completely different approach based on the notion of Stark units and Pellarin’s L-series, Anglès, Tavares Ribeiro and the second author [Reference Anglès, Dac and Tavares Ribeiro8] proved a generalization of Anderson-Thakur’s theorem for all
$n <q$
. By a completely different approach based on the notion of Stark units and Pellarin’s L-series, Anglès, Tavares Ribeiro and the second author [Reference Anglès, Dac and Tavares Ribeiro8] proved a generalization of Anderson-Thakur’s theorem for all
![]() $n \in \mathbb N$
. It states that for any
$n \in \mathbb N$
. It states that for any
![]() $n \in \mathbb N$
, Anderson’s zeta values
$n \in \mathbb N$
, Anderson’s zeta values
![]() $\zeta _{\rho }(b_i,n)$
can be written as the last coordinate of the logarithm of
$\zeta _{\rho }(b_i,n)$
can be written as the last coordinate of the logarithm of
![]() $\rho ^{\otimes n}$
evaluated at an algebraic point. Footnote 1
$\rho ^{\otimes n}$
evaluated at an algebraic point. Footnote 1
In this paper, using the aforementioned works, we generalize the work of Chang and Yu [Reference Chang and Yu23] for the Carlitz zeta values and determine all algebraic relations among Anderson’s zeta values on elliptic curves.
Theorem A (Theorem 4.3)
Let
![]() $m \in \mathbb N$
and
$m \in \mathbb N$
and
![]() $\{b_1,\ldots ,b_h\}$
be a K-basis of H with
$\{b_1,\ldots ,b_h\}$
be a K-basis of H with
![]() $b_i \in B$
. We consider the following set:
$b_i \in B$
. We consider the following set:
where
![]() $\pi _{\rho }$
is a generator of the period lattice attached to
$\pi _{\rho }$
is a generator of the period lattice attached to
![]() $\rho $
. Then the elements of
$\rho $
. Then the elements of
![]() $\mathcal A$
are algebraically independent over
$\mathcal A$
are algebraically independent over
![]() $\overline K$
. We also classify all algebraic relations between such zeta values, and thus these algebraic independence results are the best possible in this setting.
$\overline K$
. We also classify all algebraic relations between such zeta values, and thus these algebraic independence results are the best possible in this setting.
As an application, we also determine all algebraic relations among Goss’s zeta values defined for function fields of elliptic curves (see also Theorem 5.3).
Theorem B (Corollary 5.4)
Let
![]() $m \in \mathbb N$
and L be an extension of K such that
$m \in \mathbb N$
and L be an extension of K such that
![]() $L \subset H$
. We consider the following set:
$L \subset H$
. We consider the following set:
Then the elements of
![]() $\mathcal G_L$
are algebraically independent over
$\mathcal G_L$
are algebraically independent over
![]() $\overline K$
. We also classify all algebraic relations between such zeta values, and thus these algebraic independence results are the best possible in this setting.
$\overline K$
. We also classify all algebraic relations between such zeta values, and thus these algebraic independence results are the best possible in this setting.
Remark 0.1. We note that the conditions
![]() $q-1 \nmid n \text { and } p \nmid n$
are necessary, else one gets known relations, such as
$q-1 \nmid n \text { and } p \nmid n$
are necessary, else one gets known relations, such as
 $$\begin{align*}\frac{\zeta_{O_L}(q-1)}{\pi_{\rho}^{q-1}}\in \overline K,\quad \zeta_{O_L}(pn) = \zeta_{O_L}(n)^p.\end{align*}$$
$$\begin{align*}\frac{\zeta_{O_L}(q-1)}{\pi_{\rho}^{q-1}}\in \overline K,\quad \zeta_{O_L}(pn) = \zeta_{O_L}(n)^p.\end{align*}$$
We also prove algebraic independence of periods and logarithms of tensor powers of Drinfeld modules.
Theorem C (Theorem 3.13)
Suppose that
![]() $\mathbf {u}_1,\ldots ,\mathbf {u}_m \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
such that
$\mathbf {u}_1,\ldots ,\mathbf {u}_m \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
such that
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}_i)=\mathbf {v}_i \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
and denote the jth entry of
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}_i)=\mathbf {v}_i \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
and denote the jth entry of
![]() $\mathbf {u}_i$
as
$\mathbf {u}_i$
as
![]() $\mathbf {u}_{i,j}$
. If
$\mathbf {u}_{i,j}$
. If
![]() $\pi ^n_{\rho }, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}$
are linearly independent over K, then they are algebraically independent over
$\pi ^n_{\rho }, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}$
are linearly independent over K, then they are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
Let us sketch our proof and highlight the advances beyond [Reference Chang and Yu23].
-
○ Since we want to apply the transcendence method of Papanikolas [Reference Papanikolas47] (see Section 1.6 for a summary), we will consider the
 $\mathbb F_q[t]$
-modules induced by tensor powers of Drinfeld modules, still denoted by
$\mathbb F_q[t]$
-modules induced by tensor powers of Drinfeld modules, still denoted by
 $\rho ^{\otimes n}$
(see Section 1).
$\rho ^{\otimes n}$
(see Section 1). -
○ In Section 2, we construct t-motives attached to
 $\rho ^{\otimes n}$
and give a description of their motivic Galois groups. We use this description later in the paper when applying Hardouin’s work [Reference Hardouin37] (see Section 1.7 for a summary) to extensions of these motives to calculate the dimension of their motivic Galois groups.
$\rho ^{\otimes n}$
and give a description of their motivic Galois groups. We use this description later in the paper when applying Hardouin’s work [Reference Hardouin37] (see Section 1.7 for a summary) to extensions of these motives to calculate the dimension of their motivic Galois groups. -
○ In Sections 3.1 and 3.2, we construct t-motives attached to logarithms of
 $\rho ^{\otimes n}$
. Our construction uses Anderson’s generating functions as in [Reference Chang and Papanikolas18] instead of polygarithms used by Chang and Yu. This allows us to bypass the convergence issues of polygarithms present in [Reference Chang and Yu23].
$\rho ^{\otimes n}$
. Our construction uses Anderson’s generating functions as in [Reference Chang and Papanikolas18] instead of polygarithms used by Chang and Yu. This allows us to bypass the convergence issues of polygarithms present in [Reference Chang and Yu23]. -
○ In Sections 3.3 and 3.4, we present two different ways to compute periods: either by direct calculations or by using a more conceptual method due to Anderson (see [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Section 2.5).
-
○ In Section 3.6, we compute explicitly the Galois groups of t-motives attached to logarithms and derive an application about algebraic independence of logarithms (see Theorem 3.13). Our calculations are completely different from all aforementioned works and based on a more robust method devised by Hardouin [Reference Hardouin37] (compare our methods with [Reference Chang and Yu23, Reference Chang and Papanikolas18] which do not use Hardouin’s work at all, or [Reference Chang and Papanikolas19] which uses her work only minimally).
-
○ In Section 4, we use a generalization of Anderson-Thakur’s theorem on elliptic curves (see Theorem 1.8) to construct a single t-motive which is simultaneously attached to all of the Anderson zeta values we consider. Using results from Section 3, we apply the strategy of Chang-Yu to determine all algebraic relations among Anderson’s zeta values (see Theorems 4.2 and 4.3).
-
○ In Section 5, we derive all algebraic relations among Goss’s zeta values from those among Anderson’s zeta values (see Theorem 5.3 and Corollary 5.4).
To summarize, we have solved completely the problem of determining all algebraic relations among Goss’s zeta values for function fields of elliptic curves. Although in this project we work on elliptic curves and occasionally make use of their group law, we have strived to use a general approach which relies on such explicit calculations as little as possible. The authors are currently working to extend these ideas to curves of higher genus, where such a group law no longer exists. Some of the main difficulties to be overcome in this case are developing a theory of Anderson generating functions and proving the simplicity of the tensor powers of Drinfeld modules.
1 Background
Traditionally, proofs in transcendental number theory tend to be quite eclectic; they pull from numerous disparate areas of mathematics. Such is the case in this paper. To ease the burden on the reader, we collect here a review of the various theories on which the proofs of our main theorems rely. This review is not intended to be exhaustive, and we refer the reader to various sources listed in each section. After laying out the general notation (Section 1.1), we give a review of Anderson
![]() $\textbf {A}$
-modules (Section 1.2), tensor powers of sign-normalized rank 1 Drinfeld-Hayes modules (Section 1.3), Anderson-Thakur’s theorem on zeta values and logarithms (Section 1.4), linear independence of Anderson’s zeta values (Section 1.5), Papanikolas’s theory on Tannakian categories and motivic Galois groups (Section 1.6) and Hardouin’s theory on computing motivic Galois groups via the unipotent radical (Section 1.7).
$\textbf {A}$
-modules (Section 1.2), tensor powers of sign-normalized rank 1 Drinfeld-Hayes modules (Section 1.3), Anderson-Thakur’s theorem on zeta values and logarithms (Section 1.4), linear independence of Anderson’s zeta values (Section 1.5), Papanikolas’s theory on Tannakian categories and motivic Galois groups (Section 1.6) and Hardouin’s theory on computing motivic Galois groups via the unipotent radical (Section 1.7).
1.1 Notation
1.1.1 Elliptic curves
We keep the notation of [Reference Green34, Reference Green33, Reference Green and Papanikolas36] and work on elliptic curves. Throughout this paper, let
![]() $\mathbb F_q$
be a finite field of characteristic p, having q elements. Let X be an elliptic curve defined over
$\mathbb F_q$
be a finite field of characteristic p, having q elements. Let X be an elliptic curve defined over
![]() $\mathbb F_q$
given by
$\mathbb F_q$
given by
It is equipped with the rational point
![]() $\infty \in X(\mathbb F_q)$
at infinity, which we designate as the neutral element for the group law on X. We set
$\infty \in X(\mathbb F_q)$
at infinity, which we designate as the neutral element for the group law on X. We set
![]() $\textbf {A}=\mathbb F_q[t,y]$
the affine coordinate ring of X, which is the set of functions on X regular outside
$\textbf {A}=\mathbb F_q[t,y]$
the affine coordinate ring of X, which is the set of functions on X regular outside
![]() $\infty $
and
$\infty $
and
![]() $\textbf {K}=\mathbb F_q(t,y)$
, its fraction field. We also fix other variables
$\textbf {K}=\mathbb F_q(t,y)$
, its fraction field. We also fix other variables
![]() $\theta , \eta $
so that
$\theta , \eta $
so that
![]() $A=\mathbb F_q[\theta ,\eta ]$
and
$A=\mathbb F_q[\theta ,\eta ]$
and
![]() $K=\mathbb F_q(\theta ,\eta )$
are isomorphic to
$K=\mathbb F_q(\theta ,\eta )$
are isomorphic to
![]() $\textbf {A}$
and
$\textbf {A}$
and
![]() $\textbf {K}$
. We denote the canonical isomorphism
$\textbf {K}$
. We denote the canonical isomorphism
![]() $\iota : \textbf {K} \longrightarrow K$
such that
$\iota : \textbf {K} \longrightarrow K$
such that
![]() $\iota (t)=\theta $
and
$\iota (t)=\theta $
and
![]() $\iota (y)=\eta $
. Let
$\iota (y)=\eta $
. Let
![]() $\lambda = \frac {dt}{2y + c_1 t + c_3}$
be the invariant differential on X.
$\lambda = \frac {dt}{2y + c_1 t + c_3}$
be the invariant differential on X.
The
![]() $\infty $
-adic completion
$\infty $
-adic completion
![]() $K_{\infty }$
of K is equipped with the normalized
$K_{\infty }$
of K is equipped with the normalized
![]() $\infty $
-adic valuation
$\infty $
-adic valuation
![]() $v_{\infty }:K_{\infty } \rightarrow \mathbb Z\cup \{+\infty \}$
and has residue field
$v_{\infty }:K_{\infty } \rightarrow \mathbb Z\cup \{+\infty \}$
and has residue field
![]() $\mathbb F_q$
. We set
$\mathbb F_q$
. We set
![]() $\deg :=-v_{\infty }$
so that
$\deg :=-v_{\infty }$
so that
![]() $\deg \theta =2$
and
$\deg \theta =2$
and
![]() $\deg \eta =3$
. The completion
$\deg \eta =3$
. The completion
![]() $\mathbb C_{\infty }$
of a fixed algebraic closure
$\mathbb C_{\infty }$
of a fixed algebraic closure
![]() $\overline K_{\infty }$
of
$\overline K_{\infty }$
of
![]() $K_{\infty }$
comes with a unique valuation extending
$K_{\infty }$
comes with a unique valuation extending
![]() $v_{\infty }$
, which we also denote by
$v_{\infty }$
, which we also denote by
![]() $v_{\infty }$
. We define the Frobenius
$v_{\infty }$
. We define the Frobenius
![]() $\tau : \mathbb C_{\infty } \rightarrow \mathbb C_{\infty }$
as the
$\tau : \mathbb C_{\infty } \rightarrow \mathbb C_{\infty }$
as the
![]() $\mathbb F_q$
-algebra homomorphism which sends x to
$\mathbb F_q$
-algebra homomorphism which sends x to
![]() $x^q$
. Similarly, we can define
$x^q$
. Similarly, we can define
![]() $\textbf {K}_{\infty }$
equipped with
$\textbf {K}_{\infty }$
equipped with
![]() $v_{\infty }$
and
$v_{\infty }$
and
![]() $\deg $
.
$\deg $
.
We set
![]() $\Xi =(\theta ,\eta )$
which is a K-rational point of the elliptic curve X. We define a sign function
$\Xi =(\theta ,\eta )$
which is a K-rational point of the elliptic curve X. We define a sign function
![]() $\mathbf {sgn}:\textbf {A}\setminus \{0\} \rightarrow \mathbb F_q^{\times }$
as follows. For any
$\mathbf {sgn}:\textbf {A}\setminus \{0\} \rightarrow \mathbb F_q^{\times }$
as follows. For any
![]() $a \in \textbf {A}\setminus \{0\}$
, there is a unique way to write
$a \in \textbf {A}\setminus \{0\}$
, there is a unique way to write
Recall that
![]() $\deg t=2$
and
$\deg t=2$
and
![]() $\deg y=3$
. The sign of a is defined to be the coefficient of the term of highest degree. It is easy to see that it extends to a group homomorphism
$\deg y=3$
. The sign of a is defined to be the coefficient of the term of highest degree. It is easy to see that it extends to a group homomorphism
Similarly, we can define the sign function
For any field extension
![]() $L/\mathbb {F}_q$
, the coordinate ring of X over L is
$L/\mathbb {F}_q$
, the coordinate ring of X over L is
![]() $L[t,y] = L\otimes _{\mathbb {F}_q} \textbf {A}$
. We extend the sign function to such rings
$L[t,y] = L\otimes _{\mathbb {F}_q} \textbf {A}$
. We extend the sign function to such rings
![]() $L[t,y]\setminus \{0\} $
by using the same notion of leading term, namely, by writing
$L[t,y]\setminus \{0\} $
by using the same notion of leading term, namely, by writing
and then defining
![]() $\widetilde {\operatorname {\mathrm {sgn}}}:L[t,y]\setminus \{0\} \to L^{\times }$
to be the coefficient of the leading term. This extends naturally to
$\widetilde {\operatorname {\mathrm {sgn}}}:L[t,y]\setminus \{0\} \to L^{\times }$
to be the coefficient of the leading term. This extends naturally to
![]() $L(t,y)^{\times }$
by taking quotients.
$L(t,y)^{\times }$
by taking quotients.
1.1.2 Tate algebras
We denote by
![]() $\mathbb T$
the Tate algebra in the variable t with coefficients in
$\mathbb T$
the Tate algebra in the variable t with coefficients in
![]() $\mathbb C_{\infty }$
,
$\mathbb C_{\infty }$
,
 $$ \begin{align} \mathbb{T} = \biggl\{ \sum_{i=0}^{\infty} b_i t^i \in {\mathbb{C}_{\infty} [[ t ]]} \biggm| \big\lvert b_i \big\rvert_{\infty} \to 0 \biggr\}, \end{align} $$
$$ \begin{align} \mathbb{T} = \biggl\{ \sum_{i=0}^{\infty} b_i t^i \in {\mathbb{C}_{\infty} [[ t ]]} \biggm| \big\lvert b_i \big\rvert_{\infty} \to 0 \biggr\}, \end{align} $$
where
![]() $|\cdot |_{\infty }$
is the norm on
$|\cdot |_{\infty }$
is the norm on
![]() $\mathbb {C}_{\infty }$
given by
$\mathbb {C}_{\infty }$
given by
![]() $|g|_{\infty } = q^{\deg (g)}$
. The Gauss norm on
$|g|_{\infty } = q^{\deg (g)}$
. The Gauss norm on
![]() $\mathbb {T}$
is given by
$\mathbb {T}$
is given by
for
![]() $f=\sum _{i \geq 0} b_{i}t^{i}\in \mathbb {T}.$
Let
$f=\sum _{i \geq 0} b_{i}t^{i}\in \mathbb {T}.$
Let
![]() $\mathbb L$
be its fraction field.
$\mathbb L$
be its fraction field.
Further, we define the Tate algebra
![]() $\mathbb T_{\theta }$
as the space of power series in t with coefficients in
$\mathbb T_{\theta }$
as the space of power series in t with coefficients in
![]() $\mathbb C_{\infty }$
on the disc of radius
$\mathbb C_{\infty }$
on the disc of radius
![]() $|\theta |_{\infty }$
,
$|\theta |_{\infty }$
,
 $$ \begin{align} \mathbb{T}_{\theta} = \biggl\{ \sum_{i=0}^{\infty} b_i t^i \in {\mathbb{C}_{\infty} [[ t ]]} \biggm| q^i \big\lvert b_i \big\rvert_{\infty} \to 0 \biggr\}. \end{align} $$
$$ \begin{align} \mathbb{T}_{\theta} = \biggl\{ \sum_{i=0}^{\infty} b_i t^i \in {\mathbb{C}_{\infty} [[ t ]]} \biggm| q^i \big\lvert b_i \big\rvert_{\infty} \to 0 \biggr\}. \end{align} $$
Similarly, we define the norm
![]() $\lVert \cdot \rVert _{\theta }$
on
$\lVert \cdot \rVert _{\theta }$
on
![]() $\mathbb T_{\theta }$
: if
$\mathbb T_{\theta }$
: if
![]() $f=\sum _{i=0}^{\infty } b_i t^i \in \mathbb {T}_{\theta }$
, then
$f=\sum _{i=0}^{\infty } b_i t^i \in \mathbb {T}_{\theta }$
, then
We note that
![]() $\mathbb {T}_{\theta } \subset \mathbb {T}$
.
$\mathbb {T}_{\theta } \subset \mathbb {T}$
.
1.2 Anderson
 $\textbf {A}$
-modules on elliptic curves
$\textbf {A}$
-modules on elliptic curves
We briefly review the basic theory of Anderson
![]() $\textbf {A}$
-modules and dual
$\textbf {A}$
-modules and dual
![]() $\textbf {A}$
-motives and the relation between them. This material follows closely to [Reference Green34, §3-4], and the reader is directed there for proofs.
$\textbf {A}$
-motives and the relation between them. This material follows closely to [Reference Green34, §3-4], and the reader is directed there for proofs.
For R an
![]() $\mathbb {F}_p$
-algebra, we let
$\mathbb {F}_p$
-algebra, we let
![]() $R[\tau ]$
denote the (non-commutative) skew-polynomial ring with coefficients in R, subject to the relation for
$R[\tau ]$
denote the (non-commutative) skew-polynomial ring with coefficients in R, subject to the relation for
![]() $r\in R$
,
$r\in R$
,
We similarly define
![]() $R[\sigma ]$
, but subject to the restriction that R must be an algebraically closed field and subject to the relation
$R[\sigma ]$
, but subject to the restriction that R must be an algebraically closed field and subject to the relation
We define the ith Frobenius twisting automorphism of
![]() $\mathbb {C}_{\infty }[t,y]$
by
$\mathbb {C}_{\infty }[t,y]$
by
 $$\begin{align*}g \mapsto g^{(i)} : \sum_{i,j} c_{ij} t^i y^j \mapsto \sum_{i,j} c_{ij}^{q^i} t^i y^j. \end{align*}$$
$$\begin{align*}g \mapsto g^{(i)} : \sum_{i,j} c_{ij} t^i y^j \mapsto \sum_{i,j} c_{ij}^{q^i} t^i y^j. \end{align*}$$
We extend twisting to matrices
![]() $\operatorname {\mathrm {Mat}}_{i\times j}(\mathbb {C}_{\infty }[t,y])$
by twisting coordinatewise. We also define Frobenius twisting on points
$\operatorname {\mathrm {Mat}}_{i\times j}(\mathbb {C}_{\infty }[t,y])$
by twisting coordinatewise. We also define Frobenius twisting on points
![]() $P\in X(\mathbb {C}_{\infty })$
, also denoted by
$P\in X(\mathbb {C}_{\infty })$
, also denoted by
![]() $P^{(i)}$
, by raising each coordinate to the
$P^{(i)}$
, by raising each coordinate to the
![]() $q^i$
power. We extend this to divisors on X in the natural way.
$q^i$
power. We extend this to divisors on X in the natural way.
Definition 1.1. 1) An n-dimensional Anderson
![]() $\textbf {A}$
-module is an
$\textbf {A}$
-module is an
![]() $\mathbb {F}_q$
-algebra homomorphism
$\mathbb {F}_q$
-algebra homomorphism
![]() $E:\textbf {A}\to \operatorname {\mathrm {Mat}}_n(\overline K_{\infty })[\tau ]$
, such that for each
$E:\textbf {A}\to \operatorname {\mathrm {Mat}}_n(\overline K_{\infty })[\tau ]$
, such that for each
![]() $a\in \textbf {A}$
,
$a\in \textbf {A}$
,
where
![]() $d[a] = \iota (a)\text {Id}_n + N$
for some nilpotent matrix
$d[a] = \iota (a)\text {Id}_n + N$
for some nilpotent matrix
![]() $N\in \operatorname {\mathrm {Mat}}_n(\overline K_{\infty })$
(depending on a).
$N\in \operatorname {\mathrm {Mat}}_n(\overline K_{\infty })$
(depending on a).
2) A Drinfeld module is a nontrivial one-dimensional Anderson
![]() $\textbf {A}$
-module
$\textbf {A}$
-module
![]() $\rho :\textbf {A} \to \overline K_{\infty }[\tau ]$
.
$\rho :\textbf {A} \to \overline K_{\infty }[\tau ]$
.
We note that the map
![]() $a\mapsto d[a]$
is a ring homomorphism.
$a\mapsto d[a]$
is a ring homomorphism.
Let E be an
![]() $\textbf {A}$
-Anderson module of dimension n. We introduce the exponential and logarithm functions attached to E, denoted
$\textbf {A}$
-Anderson module of dimension n. We introduce the exponential and logarithm functions attached to E, denoted
![]() $\operatorname {\mathrm {Exp}}_E$
and
$\operatorname {\mathrm {Exp}}_E$
and
![]() $\operatorname {\mathrm {Log}}_E$
, respectively. The exponential function is the unique function on
$\operatorname {\mathrm {Log}}_E$
, respectively. The exponential function is the unique function on
![]() $\mathbb {C}_{\infty }^n$
such that for all
$\mathbb {C}_{\infty }^n$
such that for all
![]() $a\in \textbf {A}$
and
$a\in \textbf {A}$
and
![]() $\mathbf {z}\in \mathbb {C}_{\infty }^n$
,
$\mathbf {z}\in \mathbb {C}_{\infty }^n$
,
and
![]() $\operatorname {\mathrm {Exp}}_E(\textbf {0}) = \text {Id}_n$
.
$\operatorname {\mathrm {Exp}}_E(\textbf {0}) = \text {Id}_n$
.
The function
![]() $\operatorname {\mathrm {Log}}_E$
is then defined as the formal power series inverse of
$\operatorname {\mathrm {Log}}_E$
is then defined as the formal power series inverse of
![]() $\operatorname {\mathrm {Exp}}_E$
. We note that as functions on
$\operatorname {\mathrm {Exp}}_E$
. We note that as functions on
![]() $\mathbb {C}_{\infty }^n$
, the function
$\mathbb {C}_{\infty }^n$
, the function
![]() $\operatorname {\mathrm {Exp}}_E$
is everywhere convergent, whereas
$\operatorname {\mathrm {Exp}}_E$
is everywhere convergent, whereas
![]() $\operatorname {\mathrm {Log}}_E$
has a finite domain of convergence.
$\operatorname {\mathrm {Log}}_E$
has a finite domain of convergence.
We briefly set out some notation regarding points and divisors on the elliptic curve X. We will denote addition of points using the group law of X by adding the points without parenthesis. For example, for
![]() $R_1,R_2 \in X$
,
$R_1,R_2 \in X$
,
and we will denote formal sums of divisors involving points on X using the points inside parenthesis. For example, for
![]() $g \in K(t,y)$
,
$g \in K(t,y)$
,
Further, multiplication on the curve X will be denoted with square brackets. For example,
whereas formal multiplication of points in a divisor will be denoted with simply a number where possible, or by an expression inside parenthesis; for example, for
![]() $h \in K(t,y)$
,
$h \in K(t,y)$
,
1.3 Tensor powers of Drinfeld-Hayes modules on elliptic curves
We now construct the canonical rank 1 sign-normalized Drinfeld module associated to the ring
![]() $\textbf {A}$
to which we will attach zeta values (see [Reference Green and Papanikolas36] for a detailed account). For curves of general genus, we refer the interested reader to Hayes’s work [Reference Hayes39, Reference Hayes40] (see also [Reference Anderson3, Reference Anglès, Dac and Tavares Ribeiro6, Reference Thakur52] or [Reference Goss32, §7]) for more details on sign-normalized rank one Drinfeld modules.
$\textbf {A}$
to which we will attach zeta values (see [Reference Green and Papanikolas36] for a detailed account). For curves of general genus, we refer the interested reader to Hayes’s work [Reference Hayes39, Reference Hayes40] (see also [Reference Anderson3, Reference Anglès, Dac and Tavares Ribeiro6, Reference Thakur52] or [Reference Goss32, §7]) for more details on sign-normalized rank one Drinfeld modules.
For the sign function defined in §1.1, a rank 1 sign-normalized Drinfeld module is a Drinfeld module
![]() $\rho :\textbf {A} \to \overline K_{\infty }[\tau ]$
such that for
$\rho :\textbf {A} \to \overline K_{\infty }[\tau ]$
such that for
![]() $a\in \textbf {A}$
, we have
$a\in \textbf {A}$
, we have
By Drinfeld’s seminal work [Reference Drinfeld27], there exists a unique effective divisor V on X such that the divisor
![]() $V^{(1)} - V + (\Xi ) - (\infty )$
is principal. In our setting of elliptic curves, the situation is much more concrete. Recall that
$V^{(1)} - V + (\Xi ) - (\infty )$
is principal. In our setting of elliptic curves, the situation is much more concrete. Recall that
![]() $H\subset K_{\infty }$
is the Hilbert class field of A. Then the Drinfeld divisor is the unique point
$H\subset K_{\infty }$
is the Hilbert class field of A. Then the Drinfeld divisor is the unique point
![]() $V \in X(H)$
whose coordinates have positive degree that verifies the equation on X
$V \in X(H)$
whose coordinates have positive degree that verifies the equation on X
We remind the reader that a divisor
![]() $\sum n_P P$
on X is principal if and only if
$\sum n_P P$
on X is principal if and only if
![]() $\sum n_p P = \infty $
on X and
$\sum n_p P = \infty $
on X and
![]() $\sum n_p = 0$
(see [Reference Silverman49, Cor. III.3.5]). Thus, in our situation, we conclude that the divisor
$\sum n_p = 0$
(see [Reference Silverman49, Cor. III.3.5]). Thus, in our situation, we conclude that the divisor
![]() $(\Xi )+(V^{(1)}) - (V) - (\infty )$
is principal, and we denote the function with that divisor
$(\Xi )+(V^{(1)}) - (V) - (\infty )$
is principal, and we denote the function with that divisor
![]() $f \in H(t,y)$
(recall H is the Hilbert class field of A), normalized so that
$f \in H(t,y)$
(recall H is the Hilbert class field of A), normalized so that
![]() $\widetilde {\operatorname {\mathrm {sgn}}}(f)=1$
. We call this the shtuka function associated to X; that is,
$\widetilde {\operatorname {\mathrm {sgn}}}(f)=1$
. We call this the shtuka function associated to X; that is,
We will denote the denominator and numerator of the shtuka function as
where
![]() $m\in H$
is the slope on X (in the sense of [Reference Silverman49, III.2.3]) between the collinear points
$m\in H$
is the slope on X (in the sense of [Reference Silverman49, III.2.3]) between the collinear points
![]() $V^{(1)}, -V$
and
$V^{(1)}, -V$
and
![]() $\Xi $
. From [Reference Green and Papanikolas36, (19)-(20)], we get
$\Xi $
. From [Reference Green and Papanikolas36, (19)-(20)], we get
![]() $\deg (m) = q$
, and
$\deg (m) = q$
, and
Definition 1.2. 1) An abelian
![]() $\textbf {A}$
-motive is a
$\textbf {A}$
-motive is a
![]() $\overline K[t,y,\tau ]$
-module M which is a finitely generated projective
$\overline K[t,y,\tau ]$
-module M which is a finitely generated projective
![]() $\overline K[t,y]$
-module and free finitely generated
$\overline K[t,y]$
-module and free finitely generated
![]() $\overline K[\tau ]$
-module such that for
$\overline K[\tau ]$
-module such that for
![]() $\ell \gg 0$
, we have
$\ell \gg 0$
, we have
2) An
![]() $\textbf {A}$
-finite dual
$\textbf {A}$
-finite dual
![]() $\textbf {A}$
-motive is a
$\textbf {A}$
-motive is a
![]() $\overline K[t,y,\sigma ]$
-module N which is a finitely generated projective
$\overline K[t,y,\sigma ]$
-module N which is a finitely generated projective
![]() $\overline K[t,y]$
-module and free finitely generated
$\overline K[t,y]$
-module and free finitely generated
![]() $\overline K[\sigma ]$
-module such that for
$\overline K[\sigma ]$
-module such that for
![]() $\ell \gg 0$
, we have
$\ell \gg 0$
, we have
Note that our definitions here are in line with [Reference Brownawell, Papanikolas, Böckle, Goss, Hartl and Papanikolas15, §1.5.4], rather than the more general definition given in [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38, Def. 2.4.1].
We then let
![]() $U = \operatorname {\mathrm {Spec}} \overline K[t,y]$
(i.e., the affine curve
$U = \operatorname {\mathrm {Spec}} \overline K[t,y]$
(i.e., the affine curve
![]() $(\overline K \times _{\mathbb {F}_q} X) \setminus \{ \infty \}$
). For a divisor D on the curve X, we let
$(\overline K \times _{\mathbb {F}_q} X) \setminus \{ \infty \}$
). For a divisor D on the curve X, we let
![]() $\mathcal L(D)$
be the
$\mathcal L(D)$
be the
![]() $\overline K$
-vector space of rational functions g on X with
$\overline K$
-vector space of rational functions g on X with
![]() $\operatorname {\mathrm {div}}(g) \geq -D$
. The (geometric)
$\operatorname {\mathrm {div}}(g) \geq -D$
. The (geometric)
![]() $\textbf {A}$
-motive associated to X is given by
$\textbf {A}$
-motive associated to X is given by
We make
![]() $M_1$
into a left
$M_1$
into a left
![]() $\overline K[t,y,\tau ]$
-module by letting
$\overline K[t,y,\tau ]$
-module by letting
![]() $\tau $
act by
$\tau $
act by
and letting
![]() $\overline K[t,y]$
act by left multiplication.
$\overline K[t,y]$
act by left multiplication.
The (geometric) dual
![]() $\textbf {A}$
-motive associated to X is given by
$\textbf {A}$
-motive associated to X is given by
We make
![]() $N_1$
into a left
$N_1$
into a left
![]() $\overline K[t,y,\sigma ]$
-module by letting
$\overline K[t,y,\sigma ]$
-module by letting
![]() $\sigma $
act by
$\sigma $
act by
and letting
![]() $\overline K[t,y]$
act by left multiplication.
$\overline K[t,y]$
act by left multiplication.
We find that
![]() $M_1$
and
$M_1$
and
![]() $N_1$
are projective
$N_1$
are projective
![]() $\overline K[t,y]$
-module of rank
$\overline K[t,y]$
-module of rank
![]() $1$
, that
$1$
, that
![]() $M_1$
is as a free
$M_1$
is as a free
![]() $\overline K[\tau ]$
-module of rank
$\overline K[\tau ]$
-module of rank
![]() $1$
and that
$1$
and that
![]() $N_1$
is as a free
$N_1$
is as a free
![]() $\overline K[\sigma ]$
-module of rank
$\overline K[\sigma ]$
-module of rank
![]() $1$
(see [Reference Green and Papanikolas36, §3] for proofs of these facts). A quick check shows that
$1$
(see [Reference Green and Papanikolas36, §3] for proofs of these facts). A quick check shows that
![]() $M_1$
(resp.
$M_1$
(resp.
![]() $N_1$
) is indeed an abelian
$N_1$
) is indeed an abelian
![]() $\textbf {A}$
-motive (resp.
$\textbf {A}$
-motive (resp.
![]() $\textbf {A}$
-finite dual
$\textbf {A}$
-finite dual
![]() $\textbf {A}$
-motive).
$\textbf {A}$
-motive).
We now follow as in [Reference Green34, §3] and form the nth tensor power of
![]() $M_1$
and of
$M_1$
and of
![]() $N_1$
and denote these as
$N_1$
and denote these as
with
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
action on
$\sigma $
action on
![]() $a\in M_n$
and
$a\in M_n$
and
![]() $b\in N_n$
given respectively by
$b\in N_n$
given respectively by
Observe that
and that
![]() $M_n$
(resp.
$M_n$
(resp.
![]() $N_n$
) is also an
$N_n$
) is also an
![]() $\textbf {A}$
-motive (resp. a dual
$\textbf {A}$
-motive (resp. a dual
![]() $\textbf {A}$
-motive). Again,
$\textbf {A}$
-motive). Again,
![]() $M_n$
and
$M_n$
and
![]() $N_n$
are projective
$N_n$
are projective
![]() $\overline K[t,y]$
-modules of rank 1. Further,
$\overline K[t,y]$
-modules of rank 1. Further,
![]() $M_n$
is a free
$M_n$
is a free
![]() $\overline K[\tau ]$
-module of rank n, and
$\overline K[\tau ]$
-module of rank n, and
![]() $N_n$
is a free
$N_n$
is a free
![]() $\overline K[\sigma ]$
-module of rank n.
$\overline K[\sigma ]$
-module of rank n.
We write down convenient bases for
![]() $M_n$
and
$M_n$
and
![]() $N_n$
as free
$N_n$
as free
![]() $\overline K[\tau ]$
- and
$\overline K[\tau ]$
- and
![]() $\overline K[\sigma ]$
-modules, respectively (see [Reference Green34, Prop. 3.3]). Define functions
$\overline K[\sigma ]$
-modules, respectively (see [Reference Green34, Prop. 3.3]). Define functions
![]() $g_i \in M_n$
for
$g_i \in M_n$
for
![]() $1\leq i\leq n$
with
$1\leq i\leq n$
with
![]() $\widetilde {\operatorname {\mathrm {sgn}}}(g_i)=1$
and with divisors
$\widetilde {\operatorname {\mathrm {sgn}}}(g_i)=1$
and with divisors
and similarly define functions
![]() $h_i \in N_n$
for
$h_i \in N_n$
for
![]() $1\leq i\leq n$
, each with
$1\leq i\leq n$
, each with
![]() $\widetilde {\operatorname {\mathrm {sgn}}}(h_i) = 1$
and with divisor
$\widetilde {\operatorname {\mathrm {sgn}}}(h_i) = 1$
and with divisor
Then we have
For
![]() $g\in N_n$
, we set
$g\in N_n$
, we set
![]() $m = \lfloor \deg (g)/n \rfloor $
and define two maps
$m = \lfloor \deg (g)/n \rfloor $
and define two maps
in the following way. We write g in the
![]() $\overline K[\sigma ]$
-basis for
$\overline K[\sigma ]$
-basis for
![]() $N_n$
described in (1.10),
$N_n$
described in (1.10),
 $$ \begin{align} g = \sum_{i=0}^{m} \sum_{j=1}^n b_{j,i}^{(-i)} \sigma^i h_{n-j+1}, \end{align} $$
$$ \begin{align} g = \sum_{i=0}^{m} \sum_{j=1}^n b_{j,i}^{(-i)} \sigma^i h_{n-j+1}, \end{align} $$
then denote
![]() $\mathbf {b}_i = (b_{1,i},b_{2,i},\dots ,b_{n,i})^{\top }$
, and set
$\mathbf {b}_i = (b_{1,i},b_{2,i},\dots ,b_{n,i})^{\top }$
, and set
We then observe that the kernel of
![]() $\delta _1$
equals
$\delta _1$
equals
![]() $(\sigma -1)N_n$
and that
$(\sigma -1)N_n$
and that
![]() $N_n/(\sigma -1)N_n \xrightarrow {\delta _1} \overline K^n$
is an isomorphism of
$N_n/(\sigma -1)N_n \xrightarrow {\delta _1} \overline K^n$
is an isomorphism of
![]() $\mathbb {F}_q$
-vector spaces. Thus, we can write the commutative diagram of
$\mathbb {F}_q$
-vector spaces. Thus, we can write the commutative diagram of
![]() $\mathbb {F}_q$
-vector spaces
$\mathbb {F}_q$
-vector spaces

where the left vertical arrow is multiplication by a and the right vertical arrow is the map induced by multiplication by a, which we denote by
![]() $\rho ^{\otimes n}_a$
.
$\rho ^{\otimes n}_a$
.
Definition 1.3. By [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38, Prop. 2.5.8], we know that
![]() $\rho ^{\otimes n}$
induces the structure of an
$\rho ^{\otimes n}$
induces the structure of an
![]() $\textbf {A}$
-module on
$\textbf {A}$
-module on
![]() $\overline K^n$
and that it satisfies the conditions of being an Anderson
$\overline K^n$
and that it satisfies the conditions of being an Anderson
![]() $\textbf {A}$
-module. In this way, to each curve X, for fixed n, we associate a canonical n-dimensional Anderson
$\textbf {A}$
-module. In this way, to each curve X, for fixed n, we associate a canonical n-dimensional Anderson
![]() $\textbf {A}$
-module. We call
$\textbf {A}$
-module. We call
![]() $\rho := \rho ^{\otimes 1}$
the canonical sign-normalized rank 1 Drinfeld module associated to X, and we call
$\rho := \rho ^{\otimes 1}$
the canonical sign-normalized rank 1 Drinfeld module associated to X, and we call
![]() $\rho ^{\otimes n}$
the nth tensor power of
$\rho ^{\otimes n}$
the nth tensor power of
![]() $\rho $
.
$\rho $
.
Proposition 1.4. We recall the following two facts about the functions
![]() $g_i$
and
$g_i$
and
![]() $h_i$
from [Reference Green34, §4].
$h_i$
from [Reference Green34, §4].
-
1. For
 $1\leq i\leq n$
, there exist constants
$1\leq i\leq n$
, there exist constants
 $a_i,b_i\in H$
such that we can write
$a_i,b_i\in H$
such that we can write  $$ \begin{align*} tg_i &= \theta g_i + a_ig_{i+1} + g_{i+2},\\ th_i &= \theta h_i + b_ih_{i+1} + h_{i+2}. \end{align*} $$
$$ \begin{align*} tg_i &= \theta g_i + a_ig_{i+1} + g_{i+2},\\ th_i &= \theta h_i + b_ih_{i+1} + h_{i+2}. \end{align*} $$
-
2. For the constants defined in (1), we have
 $a_j = b_{n-j}$
for
$a_j = b_{n-j}$
for
 $1\leq j\leq n-1$
and
$1\leq j\leq n-1$
and
 $a_n = b_n^q.$
$a_n = b_n^q.$
We can write down the matrices defining
![]() $\rho _t^{\otimes n}$
using the coefficients
$\rho _t^{\otimes n}$
using the coefficients
![]() $a_i\in H$
from Proposition 1.4, for
$a_i\in H$
from Proposition 1.4, for
![]() $n\geq 2$
:
$n\geq 2$
:

The t-action of the Drinfeld
![]() $\textbf {A}$
-module
$\textbf {A}$
-module
![]() $\rho $
is given by
$\rho $
is given by
(see [Reference Green and Papanikolas36, §3] for more details on this construction).
Remark 1.5. We comment by way of clarification for the reader that Formula (1.14) does reduce down to give the Drinfeld module
![]() $\rho $
in the case of
$\rho $
in the case of
![]() $n=1$
, but it is not intuitive how to interpret these formulas. For example, the 1’s on the super-super diagonal turn into
$n=1$
, but it is not intuitive how to interpret these formulas. For example, the 1’s on the super-super diagonal turn into
![]() $\tau ^2$
, which is not obvious just from the formulas. For the sake of clarity, we will often state our formulas separately for the
$\tau ^2$
, which is not obvious just from the formulas. For the sake of clarity, we will often state our formulas separately for the
![]() $n=1$
and the
$n=1$
and the
![]() $n\geq 2$
case in this paper. A discussion of the relationship between these cases is given in Remark 1.1 of [Reference Green34]. Additionally, the case of
$n\geq 2$
case in this paper. A discussion of the relationship between these cases is given in Remark 1.1 of [Reference Green34]. Additionally, the case of
![]() $n=1$
is treated exhaustively in [Reference Green and Papanikolas36], and we refer the reader to these two sources for further discussion.
$n=1$
is treated exhaustively in [Reference Green and Papanikolas36], and we refer the reader to these two sources for further discussion.
The logarithm and exponential functions associated to
![]() $\rho ^{\otimes n}$
will be denoted
$\rho ^{\otimes n}$
will be denoted
![]() $\operatorname {\mathrm {Log}}_{\rho }^{\otimes n}$
and
$\operatorname {\mathrm {Log}}_{\rho }^{\otimes n}$
and
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
, respectively, and the kernel of
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
, respectively, and the kernel of
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
will be denoted by
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
will be denoted by
![]() $\Lambda _{\rho }^{\otimes n}$
, which we call the period lattice of
$\Lambda _{\rho }^{\otimes n}$
, which we call the period lattice of
![]() $\rho ^{\otimes n}$
.
$\rho ^{\otimes n}$
.
We recall the Tate algebra
![]() $\mathbb T$
in the variable t with coefficients in
$\mathbb T$
in the variable t with coefficients in
![]() $\mathbb C_{\infty }$
as in §1.1.2,
$\mathbb C_{\infty }$
as in §1.1.2,
 $$ \begin{align*} \mathbb{T} = \biggl\{ \sum_{i=0}^{\infty} b_i t^i \in {\mathbb{C}_{\infty} [[ t ]]} \biggm| \big\lvert b_i \big\rvert_{\infty} \to 0 \biggr\}, \end{align*} $$
$$ \begin{align*} \mathbb{T} = \biggl\{ \sum_{i=0}^{\infty} b_i t^i \in {\mathbb{C}_{\infty} [[ t ]]} \biggm| \big\lvert b_i \big\rvert_{\infty} \to 0 \biggr\}, \end{align*} $$
where
![]() $|\cdot |_{\infty }$
is the norm on
$|\cdot |_{\infty }$
is the norm on
![]() $\mathbb {C}_{\infty }$
given by
$\mathbb {C}_{\infty }$
given by
![]() $|g|_{\infty } = q^{\deg (g)}$
and its fraction field
$|g|_{\infty } = q^{\deg (g)}$
and its fraction field
![]() $\mathbb L$
. We now give a brief review of the functions
$\mathbb L$
. We now give a brief review of the functions
![]() $\omega _{\rho }$
,
$\omega _{\rho }$
,
![]() $E_{\mathbf {u}}^{\otimes n}$
and
$E_{\mathbf {u}}^{\otimes n}$
and
![]() $G_{\mathbf {u}}^{\otimes n}$
defined in [Reference Green34, §5-6]. Let
$G_{\mathbf {u}}^{\otimes n}$
defined in [Reference Green34, §5-6]. Let
 $$ \begin{align} \omega_{\rho} = \xi^{1/(q-1)} \prod_{i=0}^{\infty} \frac{\xi^{q^i}}{f^{(i)}} \in \mathbb T[y]^{\times}, \end{align} $$
$$ \begin{align} \omega_{\rho} = \xi^{1/(q-1)} \prod_{i=0}^{\infty} \frac{\xi^{q^i}}{f^{(i)}} \in \mathbb T[y]^{\times}, \end{align} $$
where
![]() $f \in H(t,y)$
is the shtuka function defined above, and we refer the reader to [Reference Green and Papanikolas36, Thm. 4.6] for the definition of
$f \in H(t,y)$
is the shtuka function defined above, and we refer the reader to [Reference Green and Papanikolas36, Thm. 4.6] for the definition of
![]() $\xi \in H$
and for details on convergence. Observe that
$\xi \in H$
and for details on convergence. Observe that
![]() $\omega _{\rho }$
satisfies the functional equation
$\omega _{\rho }$
satisfies the functional equation
![]() $\omega _{\rho }^{(1)} = f \omega _{\rho }$
. For
$\omega _{\rho }^{(1)} = f \omega _{\rho }$
. For
![]() $\mathbf {u} = (u_1,...,u_n)^{\top } \in \mathbb {C}_{\infty }^n$
, define
$\mathbf {u} = (u_1,...,u_n)^{\top } \in \mathbb {C}_{\infty }^n$
, define
 $$ \begin{align} E_{\mathbf{u}}^{\otimes n}(t) = \sum_{i=0}^{\infty} \operatorname{\mathrm{Exp}}_{\rho}^{\otimes n}\left (d[\theta]^{-i-1} \mathbf{u}\right ) t^i, \end{align} $$
$$ \begin{align} E_{\mathbf{u}}^{\otimes n}(t) = \sum_{i=0}^{\infty} \operatorname{\mathrm{Exp}}_{\rho}^{\otimes n}\left (d[\theta]^{-i-1} \mathbf{u}\right ) t^i, \end{align} $$
For
![]() $n=1$
and
$n=1$
and
![]() $\mathbf {u} = u\in \mathbb {C}_{\infty }$
, we will simplify notation by setting
$\mathbf {u} = u\in \mathbb {C}_{\infty }$
, we will simplify notation by setting
![]() $E_u(t):=E_{\mathbf {u}}^{\otimes 1}(t)$
and
$E_u(t):=E_{\mathbf {u}}^{\otimes 1}(t)$
and
![]() $G_u(t,y):=G_{\mathbf {u}}^{\otimes 1}(t,y)$
.
$G_u(t,y):=G_{\mathbf {u}}^{\otimes 1}(t,y)$
.
Define
![]() $\mathcal {M}$
to be the submodule of
$\mathcal {M}$
to be the submodule of
![]() $\mathbb {T}[y]$
consisting of all elements in
$\mathbb {T}[y]$
consisting of all elements in
![]() $\mathbb {T}[y]$
which have a meromorphic continuation to all of
$\mathbb {T}[y]$
which have a meromorphic continuation to all of
![]() $U = \operatorname {\mathrm {Spec}} \overline K[t,y]$
in the sense of [Reference Fresnel and van der Put29, §4.6] (we comment that the sheaf of meromorphic functions on a rigid space is a sheaf which locally looks like
$U = \operatorname {\mathrm {Spec}} \overline K[t,y]$
in the sense of [Reference Fresnel and van der Put29, §4.6] (we comment that the sheaf of meromorphic functions on a rigid space is a sheaf which locally looks like
![]() $\mathbb {L}$
, and its affine pieces can be glued together coherently). Now define the map
$\mathbb {L}$
, and its affine pieces can be glued together coherently). Now define the map
![]() $\operatorname {\mathrm {RES}}_{\Xi }:\mathcal {M}^n\to \mathbb {C}_{\infty }^n$
for a vector of functions
$\operatorname {\mathrm {RES}}_{\Xi }:\mathcal {M}^n\to \mathbb {C}_{\infty }^n$
for a vector of functions
![]() $(z_1,...,z_n)^{\top }\in \mathcal {M}^n$
as
$(z_1,...,z_n)^{\top }\in \mathcal {M}^n$
as
where
![]() $\lambda $
is the invariant differential on E (defined in §1.1).
$\lambda $
is the invariant differential on E (defined in §1.1).
We define a map
![]() $T:\mathbb {T}[y]\to \mathbb {T}[y]^n$
by
$T:\mathbb {T}[y]\to \mathbb {T}[y]^n$
by
 $$ \begin{align} T( h(t,y)) = \left (\begin{matrix} h(t,y)\cdot g_1 \\ h(t,y)\cdot g_2 \\ \vdots \\ h(t,y)\cdot g_n \\ \end{matrix}\right ). \end{align} $$
$$ \begin{align} T( h(t,y)) = \left (\begin{matrix} h(t,y)\cdot g_1 \\ h(t,y)\cdot g_2 \\ \vdots \\ h(t,y)\cdot g_n \\ \end{matrix}\right ). \end{align} $$
We collect the following facts from [Reference Green34, §5-6] about the above functions.
Proposition 1.6. We have the following properties:
-
(a) The function
 $E_{\mathbf {u}}^{\otimes n}$
belongs to
$E_{\mathbf {u}}^{\otimes n}$
belongs to
 $\mathbb {T}^n$
.
$\mathbb {T}^n$
. -
(b) The function
 $G_{\mathbf {u}}^{\otimes n}$
belongs to
$G_{\mathbf {u}}^{\otimes n}$
belongs to
 $\mathbb {T}[y]^n$
and extends to a meromorphic function on
$\mathbb {T}[y]^n$
and extends to a meromorphic function on
 $(\mathbb {C}_{\infty } \times _{\mathbb {F}_q} X) \setminus \{ \infty \}$
with poles in each coordinate only at the points
$(\mathbb {C}_{\infty } \times _{\mathbb {F}_q} X) \setminus \{ \infty \}$
with poles in each coordinate only at the points
 $\Xi ^{(i)}$
for
$\Xi ^{(i)}$
for
 $i\geq 0$
.
$i\geq 0$
. -
(c) We have
 $\operatorname {\mathrm {RES}}_{\Xi }(G_{\mathbf {u}}^{\otimes n}) = -(u_1,\dots ,u_n )^{\top }$
.
$\operatorname {\mathrm {RES}}_{\Xi }(G_{\mathbf {u}}^{\otimes n}) = -(u_1,\dots ,u_n )^{\top }$
. -
(d) If we denote
 $\Pi _n = -\operatorname {\mathrm {RES}}_{\Xi }(T(\omega _{\rho }^n))$
, then
$\Pi _n = -\operatorname {\mathrm {RES}}_{\Xi }(T(\omega _{\rho }^n))$
, then
 $T(\omega _{\rho }^n) = G_{\Pi _n}^{\otimes n}$
, and the period lattice of
$T(\omega _{\rho }^n) = G_{\Pi _n}^{\otimes n}$
, and the period lattice of
 $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
equals
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
equals
 $\Lambda _{\rho }^{\otimes n} = \{d[a]\Pi _n\mid a\in \textbf {A}\}$
.
$\Lambda _{\rho }^{\otimes n} = \{d[a]\Pi _n\mid a\in \textbf {A}\}$
. -
(e) If
 $\pi _{\rho }$
is a fundamental period of the exponential function associated to
$\pi _{\rho }$
is a fundamental period of the exponential function associated to
 $\rho $
, and if we denote the last coordinate of
$\rho $
, and if we denote the last coordinate of
 $\Pi _n \in \mathbb {C}_{\infty }^n$
by
$\Pi _n \in \mathbb {C}_{\infty }^n$
by
 $p_n$
, then
$p_n$
, then
 $p_n/\pi _{\rho }^n \in H\setminus \{0\}$
.
$p_n/\pi _{\rho }^n \in H\setminus \{0\}$
.
1.4 A generalization of Anderson-Thakur’s theorem on elliptic curves
Recall that
![]() $\rho : \textbf {A}\rightarrow \mathbb C_{\infty }\{\tau \}$
is the canonical sign-normalized rank one Drinfeld module associated to the elliptic curve X constructed in the previous section and that H is the Hilbert class field of A. Let B (or
$\rho : \textbf {A}\rightarrow \mathbb C_{\infty }\{\tau \}$
is the canonical sign-normalized rank one Drinfeld module associated to the elliptic curve X constructed in the previous section and that H is the Hilbert class field of A. Let B (or
![]() $\mathcal O_H$
) be the integral closure of A in H. We denote by G the Galois group
$\mathcal O_H$
) be the integral closure of A in H. We denote by G the Galois group
![]() $\mathrm {Gal}(H/K)$
.
$\mathrm {Gal}(H/K)$
.
We denote by
![]() $\mathcal {I}(A)$
the group of fractional ideals of A. For
$\mathcal {I}(A)$
the group of fractional ideals of A. For
![]() $I \in \mathcal I(A)$
, denote its Artin symbol by
$I \in \mathcal I(A)$
, denote its Artin symbol by
By [Reference Goss32], Proposition 7.4.2 and Corollary 7.4.9, the subfield of
![]() $\mathbb C_{\infty }$
generated by K and the coefficients of
$\mathbb C_{\infty }$
generated by K and the coefficients of
![]() $\rho _a$
is H. Furthermore, by [Reference Goss32], Lemma 7.4.5, we get
$\rho _a$
is H. Furthermore, by [Reference Goss32], Lemma 7.4.5, we get
Let I be a nonzero ideal of A. We define
![]() $\rho _I$
to be the monic element in
$\rho _I$
to be the monic element in
![]() $H\{\tau \}$
such that
$H\{\tau \}$
such that
We have
We write
![]() $\rho _I=\rho _{I,0}+\cdots +\rho _{I,\deg I} \tau ^{\deg I}$
with
$\rho _I=\rho _{I,0}+\cdots +\rho _{I,\deg I} \tau ^{\deg I}$
with
![]() $\rho _{I,\deg I}=1$
and denote by
$\rho _{I,\deg I}=1$
and denote by
![]() $\psi (I) \in B\setminus \{0\}$
the constant coefficient
$\psi (I) \in B\setminus \{0\}$
the constant coefficient
![]() $\rho _{I,0}$
of
$\rho _{I,0}$
of
![]() $\rho _I$
. Thus, the map
$\rho _I$
. Thus, the map
![]() $\psi $
extends uniquely into a map
$\psi $
extends uniquely into a map
![]() $\psi : \mathcal I(A)\rightarrow H^{\times }$
with the following properties (proved in [Reference Hayes39, Prop. 3.2 and Thm. 8.5]):
$\psi : \mathcal I(A)\rightarrow H^{\times }$
with the following properties (proved in [Reference Hayes39, Prop. 3.2 and Thm. 8.5]):
-
1) for all
 $I, J\in \mathcal I(A), \psi (IJ)= \sigma _J(\psi (I))\, \psi (J)$
,
$I, J\in \mathcal I(A), \psi (IJ)= \sigma _J(\psi (I))\, \psi (J)$
, -
2) for all
 $I\in \mathcal I(A), IB=\psi (I)B$
,
$I\in \mathcal I(A), IB=\psi (I)B$
, -
3) for all
 $x\in K^{\times }, \psi (xA)= \frac {x}{\operatorname {\mathrm {sgn}} (x)}$
.
$x\in K^{\times }, \psi (xA)= \frac {x}{\operatorname {\mathrm {sgn}} (x)}$
.
Finally, for
![]() $n \in \mathbb N$
and
$n \in \mathbb N$
and
![]() $b\in B$
, we define Anderson’s zeta value at n attached to
$b\in B$
, we define Anderson’s zeta value at n attached to
![]() $\rho $
as follows:
$\rho $
as follows:
 $$ \begin{align} \zeta_{\rho}(b,n)=\sum_{I \subseteq A} \frac{\sigma_I(b)}{\psi(I)^n} \in K_{\infty}. \end{align} $$
$$ \begin{align} \zeta_{\rho}(b,n)=\sum_{I \subseteq A} \frac{\sigma_I(b)}{\psi(I)^n} \in K_{\infty}. \end{align} $$
By the work of Anderson (see [Reference Anderson2], [Reference Anderson3]), for any
![]() $b \in B$
, we have
$b \in B$
, we have
Remark 1.7. This is an example of log-algebraicity identities for Drinfeld modules. The theory began with the work of Carlitz [Reference Carlitz16] where he proved the log-algebraicity identities for the Carlitz module defined over
![]() $\mathbb F_q[\theta ]$
. Further examples for Drinfeld modules over A which are PIDs were discovered by Thakur [Reference Thakur51, Thm. VI]. Shortly after, Anderson proved that (1.22) holds for any sign-normalized rank one Drinfeld A-module, and this is known as Anderson’s log-algebraicity theorem. For alternative proofs of this theorem, we refer the reader to [Reference Thakur52, §8] for the
$\mathbb F_q[\theta ]$
. Further examples for Drinfeld modules over A which are PIDs were discovered by Thakur [Reference Thakur51, Thm. VI]. Shortly after, Anderson proved that (1.22) holds for any sign-normalized rank one Drinfeld A-module, and this is known as Anderson’s log-algebraicity theorem. For alternative proofs of this theorem, we refer the reader to [Reference Thakur52, §8] for the
![]() $\mathbb F_q[\theta ]$
-case, [Reference Green and Papanikolas36] for the case of elliptic curves and [Reference Anglès, Dac and Tavares Ribeiro6] for the general case.
$\mathbb F_q[\theta ]$
-case, [Reference Green and Papanikolas36] for the case of elliptic curves and [Reference Anglès, Dac and Tavares Ribeiro6] for the general case.
The following theorem is a generalization of the celebrated Anderson-Thakur theorem for tensor powers of the Carlitz module (see [Reference Anderson and Thakur5], Theorem 3.8.3).
Theorem 1.8 (Anglès-Ngo Dac-Tavares Ribeiro [Reference Anglès, Dac and Tavares Ribeiro8] for any n and Green [Reference Green33] for
 $n<q$
)
$n<q$
)
Let
![]() $n \geq 1$
be an integer. Then there exists a constant
$n \geq 1$
be an integer. Then there exists a constant
![]() $C_n \in H$
such that for
$C_n \in H$
such that for
![]() $b \in B$
, there exists a vector
$b \in B$
, there exists a vector
![]() $Z_n(b) \in \mathbb C_{\infty }^n$
verifying the following properties:
$Z_n(b) \in \mathbb C_{\infty }^n$
verifying the following properties:
-
1) We have
 $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(Z_n(b)) \in H^n$
.
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(Z_n(b)) \in H^n$
. -
2) The last coordinate of
 $Z_n(b)$
is equal to
$Z_n(b)$
is equal to
 $C_n \zeta _{\rho }(b,n)$
.
$C_n \zeta _{\rho }(b,n)$
.
1.5 Linear relations among Anderson’s zeta values
In this section, we determine completely linear relations among Anderson’s zeta values and powers of
![]() $\pi _{\rho }$
associated to an elliptic curve over
$\pi _{\rho }$
associated to an elliptic curve over
![]() $\mathbb {F}_p$
. In the genus 0 case, this was done by Yu (see [Reference Yu55], Theorem 3.1 and [Reference Yu56], Theorem 4.1). His works are built on two main ingredients. The first one is Yu’s theory where he developed an analogue of Wüstholz’s analytic subgroup theorem for function fields, and the second one is the Anderson-Thakur theorem mentioned in the previous section. The main result of this section extends Yu’s work to elliptic curves.
$\mathbb {F}_p$
. In the genus 0 case, this was done by Yu (see [Reference Yu55], Theorem 3.1 and [Reference Yu56], Theorem 4.1). His works are built on two main ingredients. The first one is Yu’s theory where he developed an analogue of Wüstholz’s analytic subgroup theorem for function fields, and the second one is the Anderson-Thakur theorem mentioned in the previous section. The main result of this section extends Yu’s work to elliptic curves.
Recall that
![]() $\textbf {A}=\mathbb F_q[t,y]$
, where t and y satisfy the Weierstrass equation (1.1). Following Green (see [Reference Green33], Section 7), we still denote by
$\textbf {A}=\mathbb F_q[t,y]$
, where t and y satisfy the Weierstrass equation (1.1). Following Green (see [Reference Green33], Section 7), we still denote by
![]() $\rho :\mathbb F_q[t] \longrightarrow \mathbb C_{\infty } \{\tau \}$
the Drinfeld
$\rho :\mathbb F_q[t] \longrightarrow \mathbb C_{\infty } \{\tau \}$
the Drinfeld
![]() $\mathbb F_q[t]$
-module induced by forgetting the y-action of the sign-normalized rank 1 Drinfeld module
$\mathbb F_q[t]$
-module induced by forgetting the y-action of the sign-normalized rank 1 Drinfeld module
![]() $\rho $
of the previous sections. Similarly, we denote by
$\rho $
of the previous sections. Similarly, we denote by
![]() $\rho ^{\otimes n}:\mathbb F_q[t] \longrightarrow \operatorname {\mathrm {Mat}}_n(\mathbb C_{\infty }) \{\tau \}$
the Anderson
$\rho ^{\otimes n}:\mathbb F_q[t] \longrightarrow \operatorname {\mathrm {Mat}}_n(\mathbb C_{\infty }) \{\tau \}$
the Anderson
![]() $\mathbb F_q[t]$
-module defined by forgetting the y-action. Basic properties of this Anderson module are given below.
$\mathbb F_q[t]$
-module defined by forgetting the y-action. Basic properties of this Anderson module are given below.
Proposition 1.9 (Green [Reference Green33], Lemmas 7.2 and 7.3)
-
1) The Anderson
 $\mathbb F_q[t]$
-module
$\mathbb F_q[t]$
-module
 $\rho ^{\otimes n}:\mathbb F_q[t] \longrightarrow \operatorname {\mathrm {Mat}}_n(\mathbb C_{\infty }) \{\tau \}$
is simple in the sense of Yu (see [Reference Yu55, Reference Yu56]).
$\rho ^{\otimes n}:\mathbb F_q[t] \longrightarrow \operatorname {\mathrm {Mat}}_n(\mathbb C_{\infty }) \{\tau \}$
is simple in the sense of Yu (see [Reference Yu55, Reference Yu56]). -
2) The Anderson
 $\mathbb F_q[t]$
-module
$\mathbb F_q[t]$
-module
 $\rho ^{\otimes n}:\mathbb F_q[t] \longrightarrow \operatorname {\mathrm {Mat}}_n(\mathbb C_{\infty }) \{\tau \}$
has endomorphism algebra equal to A.
$\rho ^{\otimes n}:\mathbb F_q[t] \longrightarrow \operatorname {\mathrm {Mat}}_n(\mathbb C_{\infty }) \{\tau \}$
has endomorphism algebra equal to A.
We slightly generalize [Reference Green33], Theorem 7.1 to obtain the following theorem which settles the problem of determining linear relations among Anderson’s zeta values and periods attached to
![]() $\rho $
, which generalizes the work of Yu.
$\rho $
, which generalizes the work of Yu.
Theorem 1.10. Let
![]() $\{b_1,\ldots ,b_h\}$
be a K-basis of H with
$\{b_1,\ldots ,b_h\}$
be a K-basis of H with
![]() $b_i \in B$
. We consider the following sets for
$b_i \in B$
. We consider the following sets for
![]() $m,s\geq 1$
:
$m,s\geq 1$
:
 $$ \begin{align*} & \mathcal R :=\{\pi_{\rho}^k, 0 \leq k \leq m\} \cup \{\zeta_{\rho}(b_i,n): 1 \leq i \leq h, 1 \leq n\leq s \text{ such that } q-1 \nmid n \}, \\ & \mathcal R' :=\{\pi_{\rho}^k, 0 \leq k \leq m\} \cup \{\zeta_{\rho}(b_i,n): 1 \leq i \leq h, 1 \leq n\leq s \}. \end{align*} $$
$$ \begin{align*} & \mathcal R :=\{\pi_{\rho}^k, 0 \leq k \leq m\} \cup \{\zeta_{\rho}(b_i,n): 1 \leq i \leq h, 1 \leq n\leq s \text{ such that } q-1 \nmid n \}, \\ & \mathcal R' :=\{\pi_{\rho}^k, 0 \leq k \leq m\} \cup \{\zeta_{\rho}(b_i,n): 1 \leq i \leq h, 1 \leq n\leq s \}. \end{align*} $$
Then
1) The
![]() $\overline K$
-vector space generated by the elements in
$\overline K$
-vector space generated by the elements in
![]() $\mathcal {R}$
and that generated by those in
$\mathcal {R}$
and that generated by those in
![]() $\mathcal {R}'$
are the same.
$\mathcal {R}'$
are the same.
2) The elements in
![]() $\mathcal {R}$
are linearly independent over
$\mathcal {R}$
are linearly independent over
![]() $\overline K$
.
$\overline K$
.
Proof. The proof follows the same lines as Yu’s celebrated theorem [Reference Yu56, Th.m 4.1] (see also [Reference Green33, Thm. 7.1]). We provide a proof for the convenience of the reader.
Recall that for
![]() $n \in \mathbb N$
, the Anderson
$n \in \mathbb N$
, the Anderson
![]() $\textbf {A}$
-module
$\textbf {A}$
-module
![]() $\rho ^{\otimes n}$
induces the structure of an
$\rho ^{\otimes n}$
induces the structure of an
![]() $\mathbb F_q[t]$
-module which, by abuse of notation, we also denote by
$\mathbb F_q[t]$
-module which, by abuse of notation, we also denote by
![]() $\rho ^{\otimes n}$
. Also recall that h is the class number of A. We consider the product of t-modules
$\rho ^{\otimes n}$
. Also recall that h is the class number of A. We consider the product of t-modules
 $$\begin{align*}G = \mathbb G_a \times \left (\prod_{k=1}^{m} \rho^{\otimes k} \right ) \times \left (\prod_{\substack{n=1\\q-1 \nmid n}}^{s} \left( \rho^{\otimes n} \right)^{\oplus h} \right ),\end{align*}$$
$$\begin{align*}G = \mathbb G_a \times \left (\prod_{k=1}^{m} \rho^{\otimes k} \right ) \times \left (\prod_{\substack{n=1\\q-1 \nmid n}}^{s} \left( \rho^{\otimes n} \right)^{\oplus h} \right ),\end{align*}$$
where we view
![]() $\mathbb G_a$
in the first coordinate as a trivial t-module with the scalar A-action and with exponential function
$\mathbb G_a$
in the first coordinate as a trivial t-module with the scalar A-action and with exponential function
![]() $\exp _{G_L}(z) = z$
.
$\exp _{G_L}(z) = z$
.
For
![]() $1 \leq n \leq s$
, set
$1 \leq n \leq s$
, set
![]() $Z_n(b_i) =(*,\ldots ,*,C_n \zeta _{\rho }(b_i,n))^{\top } \in \mathbb C_{\infty }^n$
to be a vector from Theorem 1.8 such that
$Z_n(b_i) =(*,\ldots ,*,C_n \zeta _{\rho }(b_i,n))^{\top } \in \mathbb C_{\infty }^n$
to be a vector from Theorem 1.8 such that
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(Z_n(b_i)) \in H^n$
. For
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(Z_n(b_i)) \in H^n$
. For
![]() $1 \leq k \leq m$
, let
$1 \leq k \leq m$
, let
![]() $\Pi _k \in \mathbb C_{\infty }^k$
be a fundamental period of
$\Pi _k \in \mathbb C_{\infty }^k$
be a fundamental period of
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes k}$
so that the bottom coordinate of
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes k}$
so that the bottom coordinate of
![]() $\Pi _k$
is a multiple of
$\Pi _k$
is a multiple of
![]() $\pi _{\rho }^k$
by a nonzero element of H (see [Reference Green34, Thm. 6.7] for the exact multiple). Define the vector
$\pi _{\rho }^k$
by a nonzero element of H (see [Reference Green34, Thm. 6.7] for the exact multiple). Define the vector
 $$\begin{align*}\mathbf{u} = 1 \times \left (\prod_{k=1}^{m} \Pi_k \right ) \times \left (\prod_{\substack{n=1\\q-1 \nmid n}}^{s} \prod_{i=1}^h Z_n(b_i) \right ) \in G(\mathbb C_{\infty}) \end{align*}$$
$$\begin{align*}\mathbf{u} = 1 \times \left (\prod_{k=1}^{m} \Pi_k \right ) \times \left (\prod_{\substack{n=1\\q-1 \nmid n}}^{s} \prod_{i=1}^h Z_n(b_i) \right ) \in G(\mathbb C_{\infty}) \end{align*}$$
and note
![]() $\operatorname {\mathrm {Exp}}_G(\mathbf {u}) \in G(H)$
, where
$\operatorname {\mathrm {Exp}}_G(\mathbf {u}) \in G(H)$
, where
![]() $\operatorname {\mathrm {Exp}}_G$
is the exponential function on G, defined coordinatewise. Suppose, by contradiction, that there is a
$\operatorname {\mathrm {Exp}}_G$
is the exponential function on G, defined coordinatewise. Suppose, by contradiction, that there is a
![]() $\overline K$
-linear relation among the
$\overline K$
-linear relation among the
![]() $\zeta _{\rho }(b_i,n)$
and
$\zeta _{\rho }(b_i,n)$
and
![]() $\pi _{\rho }^k$
. This implies that
$\pi _{\rho }^k$
. This implies that
![]() $\mathbf {u}$
is contained in a
$\mathbf {u}$
is contained in a
![]() $d[\mathbb F_q[t]]$
-invariant hyperplane of
$d[\mathbb F_q[t]]$
-invariant hyperplane of
![]() $G(\mathbb C_{\infty })$
defined over
$G(\mathbb C_{\infty })$
defined over
![]() $\overline K$
. This allows us to apply [Reference Yu56, Thm. 3.3], which says that
$\overline K$
. This allows us to apply [Reference Yu56, Thm. 3.3], which says that
![]() $\mathbf {u}$
is in
$\mathbf {u}$
is in
![]() $\text {Lie}_{G'}(\overline K)$
for a proper t-submodule
$\text {Lie}_{G'}(\overline K)$
for a proper t-submodule
![]() $G' \subset G$
. Then Proposition 1.9 together with [Reference Yu56, Thm. 1.3] implies that there exist
$G' \subset G$
. Then Proposition 1.9 together with [Reference Yu56, Thm. 1.3] implies that there exist
![]() $1 \leq n \leq s$
with
$1 \leq n \leq s$
with
![]() $q-1 \nmid n$
and a linear relation of the form
$q-1 \nmid n$
and a linear relation of the form
 $$\begin{align*}\sum_{i=1}^h a_i \zeta_{\rho}(b_i,n) + b \pi_{\rho}^n=0 \end{align*}$$
$$\begin{align*}\sum_{i=1}^h a_i \zeta_{\rho}(b_i,n) + b \pi_{\rho}^n=0 \end{align*}$$
for some
![]() $a_i,b \in A$
not all zero. Since
$a_i,b \in A$
not all zero. Since
![]() $\zeta _{\rho }(b_i,n) \in K_{\infty }$
and since
$\zeta _{\rho }(b_i,n) \in K_{\infty }$
and since
![]() $H \subset K_{\infty }$
, this implies that
$H \subset K_{\infty }$
, this implies that
![]() $b \pi _{\rho }^n \in K_{\infty }$
. Since
$b \pi _{\rho }^n \in K_{\infty }$
. Since
![]() $q-1 \nmid n$
, we know that
$q-1 \nmid n$
, we know that
![]() $\pi _{\rho }^n \notin K_{\infty }$
. It follows that
$\pi _{\rho }^n \notin K_{\infty }$
. It follows that
![]() $b=0$
and hence
$b=0$
and hence
![]() $\sum _{i=1}^h a_i \zeta _{\rho }(b_i,n)=0$
. Since
$\sum _{i=1}^h a_i \zeta _{\rho }(b_i,n)=0$
. Since
![]() $a_i \in A$
, we get
$a_i \in A$
, we get
 $$\begin{align*}0=\sum_{i=1}^h a_i \zeta_{\rho}(b_i,n)=\zeta_{\rho} \left( \sum_{i=1}^h a_i b_i,n \right).\end{align*}$$
$$\begin{align*}0=\sum_{i=1}^h a_i \zeta_{\rho}(b_i,n)=\zeta_{\rho} \left( \sum_{i=1}^h a_i b_i,n \right).\end{align*}$$
We deduce that
![]() $\sum _{i=1}^h a_i b_i=0$
. Since
$\sum _{i=1}^h a_i b_i=0$
. Since
![]() $\{b_i\}$
is a K-basis of H, this forces
$\{b_i\}$
is a K-basis of H, this forces
![]() $a_i=0$
for all i. This provides a contradiction and proves the theorem.
$a_i=0$
for all i. This provides a contradiction and proves the theorem.
As explained by B. Anglès, Footnote 2 the following result is attributed to Carlitz and Goss (see [Reference Goss31, Thm. 3.2.2]) which improves [Reference Anglès, Dac and Tavares Ribeiro7], Theorem 5.7 and [Reference Green33], Corollary 7.4.
Proposition 1.11. Let
![]() $n \geq 1, n \equiv 0\quad \pmod {q-1}$
be an integer. Then for
$n \geq 1, n \equiv 0\quad \pmod {q-1}$
be an integer. Then for
![]() $b \in B$
, we have
$b \in B$
, we have
![]() $\zeta _{\rho }(b,n) / \pi _{\rho }^n \in K$
.
$\zeta _{\rho }(b,n) / \pi _{\rho }^n \in K$
.
1.6 Papanikolas’s work
We review Papanikolas’ theory [Reference Papanikolas47] (see also [Reference Anderson1, Reference Anderson, Brownawell and Papanikolas4]) and work with t-motives. Let
![]() $\overline K[t,\sigma ]$
be the polynomial ring in variables t and
$\overline K[t,\sigma ]$
be the polynomial ring in variables t and
![]() $\sigma $
with the rules
$\sigma $
with the rules
Definition 1.12. An Anderson dual t-motive is a left
![]() $\overline K[t,\sigma ]$
-module N which is free and finitely generated both as a left
$\overline K[t,\sigma ]$
-module N which is free and finitely generated both as a left
![]() $\overline K[t]$
-module and as a left
$\overline K[t]$
-module and as a left
![]() $\overline K[\sigma ]$
-module and which satisfies
$\overline K[\sigma ]$
-module and which satisfies
for some integer d sufficiently large.
We consider
![]() $\overline K(t)[\sigma ,\sigma ^{-1}]$
the ring of Laurent polynomials in
$\overline K(t)[\sigma ,\sigma ^{-1}]$
the ring of Laurent polynomials in
![]() $\sigma $
with coefficients in
$\sigma $
with coefficients in
![]() $\overline K(t)$
.
$\overline K(t)$
.
Definition 1.13. A pre-t-motive is a left
![]() $\overline K(t)[\sigma ,\sigma ^{-1}]$
-module that is finite dimensional over
$\overline K(t)[\sigma ,\sigma ^{-1}]$
-module that is finite dimensional over
![]() $\overline K(t)$
.
$\overline K(t)$
.
The category of pre-t-motives is abelian, and there is a natural functor from the category of Anderson dual t-motives to the category of pre-t-motives
where
![]() $\sigma $
acts diagonally on M.
$\sigma $
acts diagonally on M.
We now consider pre-t-motives M which are rigid analytically trivial, which we describe here. Let
![]() $\{\mathbf {m} \} \in \operatorname {\mathrm {Mat}}_{r \times 1}(M)$
be a
$\{\mathbf {m} \} \in \operatorname {\mathrm {Mat}}_{r \times 1}(M)$
be a
![]() $\overline K(t)$
-basis of M and let
$\overline K(t)$
-basis of M and let
![]() $\Phi \in \text {GL}_r(\overline K[t])$
be the matrix representing the multiplication by
$\Phi \in \text {GL}_r(\overline K[t])$
be the matrix representing the multiplication by
![]() $\sigma $
on M:
$\sigma $
on M:
We recall that
![]() $\mathbb T$
is the Tate algebra (Definition 1.2) in variable t with coefficients in
$\mathbb T$
is the Tate algebra (Definition 1.2) in variable t with coefficients in
![]() $\mathbb C_{\infty }$
and that
$\mathbb C_{\infty }$
and that
![]() $\mathbb L$
is the fraction field of the Tate algebra
$\mathbb L$
is the fraction field of the Tate algebra
![]() $\mathbb T$
. We say that M is rigid analytically trivial if there exists
$\mathbb T$
. We say that M is rigid analytically trivial if there exists
![]() $\Psi \in \text {GL}_r(\mathbb L)$
such that
$\Psi \in \text {GL}_r(\mathbb L)$
such that
We set
![]() $M^{\dagger }:=\mathbb L \otimes _{\overline K(t)} M$
on which
$M^{\dagger }:=\mathbb L \otimes _{\overline K(t)} M$
on which
![]() $\sigma $
acts diagonally and define
$\sigma $
acts diagonally and define
![]() $H_{\text {Betti}}(M)$
to be the sub
$H_{\text {Betti}}(M)$
to be the sub
![]() $\mathbb F_q(t)$
-vector space of the elements of
$\mathbb F_q(t)$
-vector space of the elements of
![]() $M^{\dagger }$
which are fixed by
$M^{\dagger }$
which are fixed by
![]() $\sigma $
. We call
$\sigma $
. We call
![]() $H_{\text {Betti}}(M)$
the Betti cohomology of M. It is shown in [Reference Papanikolas47, Prop. 3.3.9] that M is rigid analytically trivial if and only if the natural map
$H_{\text {Betti}}(M)$
the Betti cohomology of M. It is shown in [Reference Papanikolas47, Prop. 3.3.9] that M is rigid analytically trivial if and only if the natural map
is an isomorphism. We then call
![]() $\Psi $
a rigid analytical trivialization for the matrix
$\Psi $
a rigid analytical trivialization for the matrix
![]() $\Phi $
.
$\Phi $
.
The category of pre-t-motives which are rigid analytically trivial is a neutral Tannakian category over
![]() $\mathbb F_q(t)$
with the fiber functor
$\mathbb F_q(t)$
with the fiber functor
![]() $\omega $
which maps
$\omega $
which maps
![]() $M \mapsto H_{\text {Betti}}(M)$
(see [Reference Papanikolas47], Theorem 3.3.15).
$M \mapsto H_{\text {Betti}}(M)$
(see [Reference Papanikolas47], Theorem 3.3.15).
Definition 1.14. The strictly full Tannakian subcategory generated by the images of rigid analytically trivial Anderson dual t-motives is called the category of t-motives and is denoted by
![]() $\mathcal T$
(see [Reference Papanikolas47], Section 3.4.10). By [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Remark 2.4.15, this category is equivalent to the category of uniformizable dual
$\mathcal T$
(see [Reference Papanikolas47], Section 3.4.10). By [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Remark 2.4.15, this category is equivalent to the category of uniformizable dual
![]() $\mathbb F_q[t]$
-motives given in [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Definition 2.4.14.
$\mathbb F_q[t]$
-motives given in [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Definition 2.4.14.
By Tannakian duality, for each (rigid analytically trivial) t-motive M, the Tannakian subcategory generated by M is equivalent to the category of finite dimensional representations over
![]() $\mathbb F_q(t)$
of some algebraic group
$\mathbb F_q(t)$
of some algebraic group
![]() $\Gamma _M$
called the (motivic) Galois group of the t-motive M. Further, we have a faithful representation
$\Gamma _M$
called the (motivic) Galois group of the t-motive M. Further, we have a faithful representation
![]() $\Gamma _M \hookrightarrow \text {GL}(H_{\text {Betti}}(M))$
, which is called the tautological representation of M.
$\Gamma _M \hookrightarrow \text {GL}(H_{\text {Betti}}(M))$
, which is called the tautological representation of M.
Papanikolas proved an analogue of Grothendieck’s period conjecture which unveils a deep connection between Galois groups of t-motives and transcendence.
Theorem 1.15 (Papanikolas [Reference Papanikolas47], Theorem 1.1.7)
Let M be a t-motive and let
![]() $\Gamma _M$
be its Galois group. Suppose that
$\Gamma _M$
be its Galois group. Suppose that
![]() $\Phi \in \text {GL}_n(\overline K(t)) \cap \operatorname {\mathrm {Mat}}_{n \times n}(\overline K[t])$
represents the multiplication by
$\Phi \in \text {GL}_n(\overline K(t)) \cap \operatorname {\mathrm {Mat}}_{n \times n}(\overline K[t])$
represents the multiplication by
![]() $\sigma $
on M and that
$\sigma $
on M and that
![]() $\det \Phi =c(t-\theta )^s, c \in \overline K^{\times }$
. If
$\det \Phi =c(t-\theta )^s, c \in \overline K^{\times }$
. If
![]() $\Psi \in \text {GL}_n(\mathbb T)$
is a rigid analytic trivialization for
$\Psi \in \text {GL}_n(\mathbb T)$
is a rigid analytic trivialization for
![]() $\Phi $
, then the entries of
$\Phi $
, then the entries of
![]() $\Psi $
may be evaluated at
$\Psi $
may be evaluated at
![]() $\theta $
and
$\theta $
and
Papanikolas also shows that
![]() $\Gamma _M$
equals the Galois group
$\Gamma _M$
equals the Galois group
![]() $\Gamma _{\Psi }$
of the Frobenius difference equation corresponding to M (see [Reference Papanikolas47], Theorem 4.5.10). This provides a method to explicitly compute the Galois groups for t-motives in many cases. This is a very powerful tool and has led to major transcendence results in the last decade. We refer the reader to [Reference Anderson, Brownawell and Papanikolas4, Reference Chang, Böckle, Goss, Hartl and Papanikolas17, Reference Chang and Papanikolas18, Reference Chang and Papanikolas19, Reference Chang, Papanikolas, Thakur and Yu20, Reference Chang, Papanikolas and Yu21, Reference Chang, Papanikolas and Yu22, Reference Chang and Yu23] for more details about transcendence applications.
$\Gamma _{\Psi }$
of the Frobenius difference equation corresponding to M (see [Reference Papanikolas47], Theorem 4.5.10). This provides a method to explicitly compute the Galois groups for t-motives in many cases. This is a very powerful tool and has led to major transcendence results in the last decade. We refer the reader to [Reference Anderson, Brownawell and Papanikolas4, Reference Chang, Böckle, Goss, Hartl and Papanikolas17, Reference Chang and Papanikolas18, Reference Chang and Papanikolas19, Reference Chang, Papanikolas, Thakur and Yu20, Reference Chang, Papanikolas and Yu21, Reference Chang, Papanikolas and Yu22, Reference Chang and Yu23] for more details about transcendence applications.
Papanikolas proved that
![]() $\Gamma _M$
is an affine algebraic groupe scheme over
$\Gamma _M$
is an affine algebraic groupe scheme over
![]() $\mathbb F_q(t)$
which is absolutely irreducible and smooth over
$\mathbb F_q(t)$
which is absolutely irreducible and smooth over
![]() $\overline {\mathbb F_q(t)}$
(see [Reference Papanikolas47], Theorems 4.2.11, 4.3.1 and 4.5.10). Further, for any
$\overline {\mathbb F_q(t)}$
(see [Reference Papanikolas47], Theorems 4.2.11, 4.3.1 and 4.5.10). Further, for any
![]() $\mathbb F_q(t)$
-algebra R, the map
$\mathbb F_q(t)$
-algebra R, the map
is given by the tautological map
1.7 Hardouin’s work
In this section, we review the work of Hardouin [Reference Hardouin37] on unipotent radicals of Tannakian groups in positive characteristic. Let F be a field and
![]() $(\mathcal T,\omega )$
be a neutral Tannakian category over F with fiber functor
$(\mathcal T,\omega )$
be a neutral Tannakian category over F with fiber functor
![]() $\omega $
. We denote by
$\omega $
. We denote by
![]() $\mathbb G_m$
the multiplicative group over F. For an object
$\mathbb G_m$
the multiplicative group over F. For an object
![]() $\mathcal U \in \mathcal T$
, we denote by
$\mathcal U \in \mathcal T$
, we denote by
![]() $\Gamma _{\mathcal U}$
the Galois group of
$\Gamma _{\mathcal U}$
the Galois group of
![]() $\mathcal U$
. Let
$\mathcal U$
. Let
![]() $\mathbf 1$
be the unit object for the tensor product and
$\mathbf 1$
be the unit object for the tensor product and
![]() $\mathcal Y$
be a completely reducible object, which means that
$\mathcal Y$
be a completely reducible object, which means that
![]() $\mathcal Y$
is a direct sum of finitely many irreducible objects. We consider extensions
$\mathcal Y$
is a direct sum of finitely many irreducible objects. We consider extensions
![]() $\mathcal U \in \text {Ext}^1(\mathbf 1,\mathcal Y)$
of
$\mathcal U \in \text {Ext}^1(\mathbf 1,\mathcal Y)$
of
![]() $\mathbf 1$
by
$\mathbf 1$
by
![]() $\mathcal Y$
, which means that we have a short exact sequence
$\mathcal Y$
, which means that we have a short exact sequence
For such an extension
![]() $\mathcal U$
, the Galois group
$\mathcal U$
, the Galois group
![]() $\Gamma _{\mathcal U}$
of U is isomorphic to the semi-direct product
$\Gamma _{\mathcal U}$
of U is isomorphic to the semi-direct product
where
![]() $R_u({\mathcal U})$
stands for the unipotent part of
$R_u({\mathcal U})$
stands for the unipotent part of
![]() $\Gamma _{\mathcal U}$
. Therefore, with the knowledge of
$\Gamma _{\mathcal U}$
. Therefore, with the knowledge of
![]() $\Gamma _{\mathcal Y}$
, we reduce the computation of
$\Gamma _{\mathcal Y}$
, we reduce the computation of
![]() $\Gamma _{\mathcal U}$
to that of its unipotent part. In [Reference Hardouin37], Hardouin proves several fundamental results which characterize
$\Gamma _{\mathcal U}$
to that of its unipotent part. In [Reference Hardouin37], Hardouin proves several fundamental results which characterize
![]() $R_u({\mathcal U})$
in terms of the extension group
$R_u({\mathcal U})$
in terms of the extension group
![]() $\text {Ext}^1(\mathbf 1,\mathcal Y)$
. In the next result, we keep the same notation as above, and we remind the reader that the action of a group G on a module V is isotypic if the module V is the direct sum of irreducible isomorphic G-modules.
$\text {Ext}^1(\mathbf 1,\mathcal Y)$
. In the next result, we keep the same notation as above, and we remind the reader that the action of a group G on a module V is isotypic if the module V is the direct sum of irreducible isomorphic G-modules.
Theorem 1.16 (Hardouin [Reference Hardouin37], Theorem 2)
Assume that
-
1. every
 $\Gamma _{\mathcal Y}$
-module is completely reducible,
$\Gamma _{\mathcal Y}$
-module is completely reducible, -
2. the center of
 $\Gamma _{\mathcal Y}$
contains
$\Gamma _{\mathcal Y}$
contains
 $\mathbb G_m$
,
$\mathbb G_m$
, -
3. the action of
 $\mathbb G_m$
on
$\mathbb G_m$
on
 $\omega (\mathcal Y)$
is isotypic,
$\omega (\mathcal Y)$
is isotypic, -
4.
 $\Gamma _{\mathcal U}$
is reduced.
$\Gamma _{\mathcal U}$
is reduced.
Then there exists a smallest sub-object
![]() $\mathcal V$
of
$\mathcal V$
of
![]() $\mathcal Y$
such that
$\mathcal Y$
such that
![]() $\mathcal U/\mathcal V$
is a trivial extension of
$\mathcal U/\mathcal V$
is a trivial extension of
![]() $\mathbf 1$
by
$\mathbf 1$
by
![]() $\mathcal Y/\mathcal V$
. Further, the unipotent part
$\mathcal Y/\mathcal V$
. Further, the unipotent part
![]() $R_u({\mathcal U})$
of the Galois group
$R_u({\mathcal U})$
of the Galois group
![]() $\Gamma _{\mathcal U}$
is equal to
$\Gamma _{\mathcal U}$
is equal to
![]() $\omega (\mathcal V)$
.
$\omega (\mathcal V)$
.
As a consequence, Hardouin proves the following corollary which states that algebraic relations between the extensions are exactly given by the linear relations. We continue with the above notation.
Corollary 1.17 (Hardouin [Reference Hardouin37], Corollary 1)
Let
![]() $\mathcal E_1,\ldots ,\mathcal E_n$
be extensions of
$\mathcal E_1,\ldots ,\mathcal E_n$
be extensions of
![]() $\mathbf 1$
by
$\mathbf 1$
by
![]() $\mathcal Y$
. Assume that
$\mathcal Y$
. Assume that
-
1. every
 $\Gamma _{\mathcal Y}$
-module is completely reducible,
$\Gamma _{\mathcal Y}$
-module is completely reducible, -
2. the center of
 $\Gamma _{\mathcal Y}$
contains
$\Gamma _{\mathcal Y}$
contains
 $\mathbb G_m$
,
$\mathbb G_m$
, -
3. the action of
 $\mathbb G_m$
on
$\mathbb G_m$
on
 $\omega (\mathcal Y)$
is isotypic,
$\omega (\mathcal Y)$
is isotypic, -
4.
 $\Gamma _{\mathcal E_1},\ldots ,\Gamma _{\mathcal E_n}$
are reduced.
$\Gamma _{\mathcal E_1},\ldots ,\Gamma _{\mathcal E_n}$
are reduced.
If
![]() $\mathcal E_1,\ldots ,\mathcal E_n$
are
$\mathcal E_1,\ldots ,\mathcal E_n$
are
![]() $\operatorname {\mathrm {End}}(\mathcal Y)$
-linear independent in
$\operatorname {\mathrm {End}}(\mathcal Y)$
-linear independent in
![]() $\text {Ext}^1(\mathbf 1,\mathcal Y)$
, then the unipotent radical of the Galois group
$\text {Ext}^1(\mathbf 1,\mathcal Y)$
, then the unipotent radical of the Galois group
![]() $\Gamma _{\mathcal E_1 \oplus \ldots \oplus \mathcal E_n}$
of the direct sum
$\Gamma _{\mathcal E_1 \oplus \ldots \oplus \mathcal E_n}$
of the direct sum
![]() $\mathcal E_1 \oplus \ldots \oplus \mathcal E_n$
is isomorphic to
$\mathcal E_1 \oplus \ldots \oplus \mathcal E_n$
is isomorphic to
![]() $\omega (\mathcal Y)^n$
.
$\omega (\mathcal Y)^n$
.
We remark that we will apply this theorem and its corollary in §3.6 to the t-motives
![]() $\mathcal {X}_{\rho }^{\otimes n}$
and
$\mathcal {X}_{\rho }^{\otimes n}$
and
![]() $\mathcal {X}_n(b)$
, which are defined in §2.2 and §3.2.
$\mathcal {X}_n(b)$
, which are defined in §2.2 and §3.2.
2 Constructing t-motives connected to periods
From now on, we investigate the problem of determining algebraic relations between special zeta values and periods attached to
![]() $\rho $
, the canonical, sign-normalized rank 1 Drinfeld module attached to X of the previous section. For the Carlitz module, this was done by Chang and Yu [Reference Chang and Yu23] using the machinery of Papanikolas [Reference Papanikolas47] (see Section 1.6). For our setting, we will also need the results of Hardouin [Reference Hardouin37] (see Section 1.7).
$\rho $
, the canonical, sign-normalized rank 1 Drinfeld module attached to X of the previous section. For the Carlitz module, this was done by Chang and Yu [Reference Chang and Yu23] using the machinery of Papanikolas [Reference Papanikolas47] (see Section 1.6). For our setting, we will also need the results of Hardouin [Reference Hardouin37] (see Section 1.7).
2.1 The t-motive associated to
 $\rho $
$\rho $
We follow the construction given by Chang-Papanikolas [Reference Chang and Papanikolas18], Sections 3.3 and 3.4. Recall that B is the integral closure of A in the Hilbert class field H. We consider
![]() $\rho :\mathbb F_q[t] \longrightarrow B\{\tau \}$
from Definition 1.3 as a Drinfeld
$\rho :\mathbb F_q[t] \longrightarrow B\{\tau \}$
from Definition 1.3 as a Drinfeld
![]() $\mathbb F_q[t]$
-module of rank
$\mathbb F_q[t]$
-module of rank
![]() $2$
by forgetting the y action. We recall
$2$
by forgetting the y action. We recall
(see [Reference Green and Papanikolas36, §3] for more details on this construction). For
![]() $\mathbf {u} = u \in \mathbb C_{\infty }$
, we denote the associated Anderson generating function
$\mathbf {u} = u \in \mathbb C_{\infty }$
, we denote the associated Anderson generating function
![]() $E_u(t):= E_{\mathbf {u}}^{\otimes 1}(t)$
given by Equation (1.16). This function extends meromorphically to all of
$E_u(t):= E_{\mathbf {u}}^{\otimes 1}(t)$
given by Equation (1.16). This function extends meromorphically to all of
![]() $\mathbb C_{\infty }$
with simple poles at
$\mathbb C_{\infty }$
with simple poles at
![]() $t=\theta ^{q^i}, i \geq 0$
. Further, it satisfies the functional equation
$t=\theta ^{q^i}, i \geq 0$
. Further, it satisfies the functional equation
In other words, we have
Now we fix an
![]() $\mathbb F_q[t]$
-basis
$\mathbb F_q[t]$
-basis
![]() $u_1 = \pi _{\rho }$
and
$u_1 = \pi _{\rho }$
and
![]() $u_2 = \eta \pi _{\rho }$
of the period lattice
$u_2 = \eta \pi _{\rho }$
of the period lattice
![]() $\Lambda _{\rho }$
of
$\Lambda _{\rho }$
of
![]() $\rho $
. We set
$\rho $
. We set
![]() $E_i:=E_{u_i}$
for
$E_i:=E_{u_i}$
for
![]() $i=1,2$
. We define the following matrices:
$i=1,2$
. We define the following matrices:
 $$ \begin{align*} \Phi_{\rho} &= \begin{pmatrix} 0 & 1 \\ t-\theta & -x_1^{(-1)} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]), \quad \Upsilon = \begin{pmatrix} E_1 & E_1^{(1)} \\ E_2 & E_2^{(1)} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb T), \\ \Theta &= \begin{pmatrix} 0 & t-\theta \\ 1 & -x_1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]), \quad V = \begin{pmatrix} x_1 & 1 \\ 1 & 0 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K). \end{align*} $$
$$ \begin{align*} \Phi_{\rho} &= \begin{pmatrix} 0 & 1 \\ t-\theta & -x_1^{(-1)} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]), \quad \Upsilon = \begin{pmatrix} E_1 & E_1^{(1)} \\ E_2 & E_2^{(1)} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb T), \\ \Theta &= \begin{pmatrix} 0 & t-\theta \\ 1 & -x_1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]), \quad V = \begin{pmatrix} x_1 & 1 \\ 1 & 0 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K). \end{align*} $$
Then we set
Since
![]() $V^{(-1)} \Phi _{\rho }=\Theta V$
and
$V^{(-1)} \Phi _{\rho }=\Theta V$
and
![]() $\Upsilon ^{(1)}=\Upsilon \Theta $
, we get
$\Upsilon ^{(1)}=\Upsilon \Theta $
, we get
2.2 The t-motive associated to
 $\rho ^{\otimes n}$
$\rho ^{\otimes n}$
Let
![]() $n \geq 2$
be an integer. Recall the definition of
$n \geq 2$
be an integer. Recall the definition of
![]() $\rho ^{\otimes n}$
from Definition 1.3. By forgetting the y-action, the Anderson
$\rho ^{\otimes n}$
from Definition 1.3. By forgetting the y-action, the Anderson
![]() $\textbf {A}$
-module
$\textbf {A}$
-module
![]() $\rho ^{\otimes n}$
can be considered as an Anderson
$\rho ^{\otimes n}$
can be considered as an Anderson
![]() $\mathbb F_q[t]$
-module given by
$\mathbb F_q[t]$
-module given by
(see (1.14) for explicit formulas of
![]() $d[\theta ]$
and
$d[\theta ]$
and
![]() $E_{\theta }$
). For
$E_{\theta }$
). For
![]() $\mathbf {u}=(u_1,\ldots ,u_n)^{\top } \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
, recall the associated Anderson generating function
$\mathbf {u}=(u_1,\ldots ,u_n)^{\top } \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
, recall the associated Anderson generating function
![]() $E^{\otimes n}_{\mathbf {u}}(t)$
given by Equation (1.16). It satisfies the functional equation
$E^{\otimes n}_{\mathbf {u}}(t)$
given by Equation (1.16). It satisfies the functional equation
As n is fixed throughout this section, to simplify notation, we will suppress the dependence on n and denote the coordinates of
and similarly for other vector valued functions. Recall the definitions of the functions
![]() $h_i$
and the coefficients
$h_i$
and the coefficients
![]() $a_i$
and
$a_i$
and
![]() $b_i$
from Proposition 1.4. For
$b_i$
from Proposition 1.4. For
![]() $1 \leq i \leq n$
, we set
$1 \leq i \leq n$
, we set
 $$\begin{align*}\Theta_i = \begin{pmatrix} 0 & 1\\ t-\theta & -a_i \end{pmatrix},\quad \phi_i = \begin{pmatrix} 0 & 1\\ t-\theta & -b_i \end{pmatrix}. \end{align*}$$
$$\begin{align*}\Theta_i = \begin{pmatrix} 0 & 1\\ t-\theta & -a_i \end{pmatrix},\quad \phi_i = \begin{pmatrix} 0 & 1\\ t-\theta & -b_i \end{pmatrix}. \end{align*}$$
From Proposition 1.4, we have
 $$ \begin{align*} \begin{pmatrix} h_{i+1} \\ h_{i+2} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ t-\theta & -b_i \end{pmatrix} \begin{pmatrix} h_i \\ h_{i+1} \end{pmatrix} = \phi_i \begin{pmatrix} h_i \\ h_{i+1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} h_{i+1} \\ h_{i+2} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ t-\theta & -b_i \end{pmatrix} \begin{pmatrix} h_i \\ h_{i+1} \end{pmatrix} = \phi_i \begin{pmatrix} h_i \\ h_{i+1} \end{pmatrix}. \end{align*} $$
We define
 $$ \begin{align*} \Phi_{\rho}^{\otimes n}=\phi_n \ldots \phi_1 = \begin{pmatrix} 0 & 1 \\ t-\theta & -b_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]). \end{align*} $$
$$ \begin{align*} \Phi_{\rho}^{\otimes n}=\phi_n \ldots \phi_1 = \begin{pmatrix} 0 & 1 \\ t-\theta & -b_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]). \end{align*} $$
It follows that
 $$ \begin{align*} \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}^{(-1)} = \begin{pmatrix} h_{n+1} \\ h_{n+2} \end{pmatrix} = \Phi_{\rho}^{\otimes n} \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}^{(-1)} = \begin{pmatrix} h_{n+1} \\ h_{n+2} \end{pmatrix} = \Phi_{\rho}^{\otimes n} \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
Now we fix
![]() $\mathbf {u}_1 = \Pi _n$
and
$\mathbf {u}_1 = \Pi _n$
and
![]() $\mathbf {u}_2 = d[\eta ]\Pi _n$
such that
$\mathbf {u}_2 = d[\eta ]\Pi _n$
such that
![]() $\{\mathbf {u}_1,\mathbf {u}_2\}$
is a basis of the period lattice
$\{\mathbf {u}_1,\mathbf {u}_2\}$
is a basis of the period lattice
![]() $\Lambda _{\rho }^{\otimes n}$
of
$\Lambda _{\rho }^{\otimes n}$
of
![]() $\rho ^{\otimes n}$
, where
$\rho ^{\otimes n}$
, where
![]() $\Pi _n$
is defined in Proposition 1.6(d). We denote by
$\Pi _n$
is defined in Proposition 1.6(d). We denote by
![]() $E_i^{\otimes n} = E_{\mathbf {u}_i}^{\otimes n}$
for
$E_i^{\otimes n} = E_{\mathbf {u}_i}^{\otimes n}$
for
![]() $i=1,2$
. When the dimension n is fixed, we will often drop the
$i=1,2$
. When the dimension n is fixed, we will often drop the
![]() $\otimes n$
from our notation to avoid clutter. Then
$\otimes n$
from our notation to avoid clutter. Then
If we set
 $$ \begin{align*} \Theta=\Theta_n \ldots \Theta_1= \begin{pmatrix} 0 & 1 \\ t-\theta & -a_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -a_1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]), \end{align*} $$
$$ \begin{align*} \Theta=\Theta_n \ldots \Theta_1= \begin{pmatrix} 0 & 1 \\ t-\theta & -a_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -a_1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K[t]), \end{align*} $$
and
 $$ \begin{align} \Upsilon = \begin{pmatrix} E_{1,1} & E_{2,1} \\ E_{1,2} & E_{2,2} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb{T}), \end{align} $$
$$ \begin{align} \Upsilon = \begin{pmatrix} E_{1,1} & E_{2,1} \\ E_{1,2} & E_{2,2} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb{T}), \end{align} $$
then we obtain
We define
 $$ \begin{align*} V = \begin{pmatrix} a_n & 1 \\ 1 & 0 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K). \end{align*} $$
$$ \begin{align*} V = \begin{pmatrix} a_n & 1 \\ 1 & 0 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\overline K). \end{align*} $$
Note that V is symmetric and
 $$ \begin{align*} V^{(-1)} = \begin{pmatrix} b_n & 1 \\ 1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} V^{(-1)} = \begin{pmatrix} b_n & 1 \\ 1 & 0 \end{pmatrix}. \end{align*} $$
We claim that
In fact, recall from Proposition 1.4 that
![]() $b_i=a_{n-i}$
for
$b_i=a_{n-i}$
for
![]() $1 \leq i \leq n-1$
and
$1 \leq i \leq n-1$
and
![]() $a_n=b_n^q$
. It is clear that for any
$a_n=b_n^q$
. It is clear that for any
![]() $x \in \mathbb C_{\infty }$
, we have
$x \in \mathbb C_{\infty }$
, we have
 $$ \begin{align*} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & x \end{pmatrix} = \begin{pmatrix} 0 & t-\theta \\ 1 & x \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & x \end{pmatrix} = \begin{pmatrix} 0 & t-\theta \\ 1 & x \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix}. \end{align*} $$
Then the claim follows immediately:
 $$ \begin{align*} V^{(-1)} \Phi_{\rho}^{\otimes n} &= \begin{pmatrix} b_n & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & -b_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \\ &= \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & -b_{n-1} \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -b_{n-1} \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & -b_{n-2} \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \\ &= \cdots \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -b_{n-1} \end{pmatrix} \cdots \begin{pmatrix} 0 & t-\theta \\ 1 & -b_1 \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -a_1 \end{pmatrix} \cdots \begin{pmatrix} 0 & t-\theta \\ 1 & -a_{n-1} \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -a_1 \end{pmatrix} \cdots \begin{pmatrix} 0 & t-\theta \\ 1 & -a_{n-1} \end{pmatrix} \begin{pmatrix} 0 & t-\theta \\ 1 & -a_n \end{pmatrix} \begin{pmatrix} a_n & 1 \\ 1 & 0 \end{pmatrix} \\ &= (\Theta^{\top}) V. \end{align*} $$
$$ \begin{align*} V^{(-1)} \Phi_{\rho}^{\otimes n} &= \begin{pmatrix} b_n & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & -b_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \\ &= \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & -b_{n-1} \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -b_{n-1} \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ t-\theta & -b_{n-2} \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -b_1 \end{pmatrix} \\ &= \cdots \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -b_{n-1} \end{pmatrix} \cdots \begin{pmatrix} 0 & t-\theta \\ 1 & -b_1 \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -a_1 \end{pmatrix} \cdots \begin{pmatrix} 0 & t-\theta \\ 1 & -a_{n-1} \end{pmatrix} \begin{pmatrix} t-\theta & 0 \\ 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 0 & t-\theta \\ 1 & -a_1 \end{pmatrix} \cdots \begin{pmatrix} 0 & t-\theta \\ 1 & -a_{n-1} \end{pmatrix} \begin{pmatrix} 0 & t-\theta \\ 1 & -a_n \end{pmatrix} \begin{pmatrix} a_n & 1 \\ 1 & 0 \end{pmatrix} \\ &= (\Theta^{\top}) V. \end{align*} $$
We set
Thus, we get
Remark 2.1. From the previous discussion, we have
 $$ \begin{align*} (\Psi_{\rho}^{\otimes n})^{-1}=(\Upsilon^{\top})^{(1)} V= \begin{pmatrix} a_n E_{1,1}^{(1)}+E_{1,2}^{(1)} & E_{1,1}^{(1)} \\ a_n E_{2,1}^{(1)}+E_{2,2}^{(1)} & E_{2,2}^{(1)} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} (\Psi_{\rho}^{\otimes n})^{-1}=(\Upsilon^{\top})^{(1)} V= \begin{pmatrix} a_n E_{1,1}^{(1)}+E_{1,2}^{(1)} & E_{1,1}^{(1)} \\ a_n E_{2,1}^{(1)}+E_{2,2}^{(1)} & E_{2,2}^{(1)} \end{pmatrix}. \end{align*} $$
By direct calculations (see Lemma 3.3), we show that
where
![]() $\mathbf {u}_{i,n}$
is the nth coordinate of the period
$\mathbf {u}_{i,n}$
is the nth coordinate of the period
![]() $\mathbf {u}_i$
for
$\mathbf {u}_i$
for
![]() $i=1,2$
.
$i=1,2$
.
Remark 2.2. As
![]() $E_{i,j} \in \mathbb {T}$
for
$E_{i,j} \in \mathbb {T}$
for
![]() $1 \leq i,j \leq 2$
by Proposition 1.6, it follows that
$1 \leq i,j \leq 2$
by Proposition 1.6, it follows that
![]() $(\Psi _{\rho }^{\otimes n})^{-1} \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T})$
. By [Reference Green and Dac35, Remark 3.1, Part 2], it implies that
$(\Psi _{\rho }^{\otimes n})^{-1} \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T})$
. By [Reference Green and Dac35, Remark 3.1, Part 2], it implies that
![]() $(\Psi _{\rho }^{\otimes n})^{-1} \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
.
$(\Psi _{\rho }^{\otimes n})^{-1} \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
.
2.3 Galois groups
We denote by
![]() $\mathcal {X}^{\otimes n}_{\rho }$
the pre t-motive associated to
$\mathcal {X}^{\otimes n}_{\rho }$
the pre t-motive associated to
![]() $\rho ^{\otimes n}$
. The following proposition gives some basic properties of this pre t-motive (compare to [Reference Chang and Papanikolas18], Theorem 3.5.4).
$\rho ^{\otimes n}$
. The following proposition gives some basic properties of this pre t-motive (compare to [Reference Chang and Papanikolas18], Theorem 3.5.4).
Proposition 2.3.
-
1) The pre t-motive
 $\mathcal {X}^{\otimes n}_{\rho }$
is a t-motive.
$\mathcal {X}^{\otimes n}_{\rho }$
is a t-motive. -
2) The t-motive
 $\mathcal {X}^{\otimes n}_{\rho }$
is pure.
$\mathcal {X}^{\otimes n}_{\rho }$
is pure. -
3) Its Galois group
 $\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
is
$\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
is
 $\textrm {Res}_{K/\mathbb F_q[t]} \mathbb {G}_{m,K}$
. In particular, it is a torus.
$\textrm {Res}_{K/\mathbb F_q[t]} \mathbb {G}_{m,K}$
. In particular, it is a torus.
Proof. For Part 1, since
![]() $\mathcal {X}^{\otimes n}_{\rho }$
is an A-motive of rank
$\mathcal {X}^{\otimes n}_{\rho }$
is an A-motive of rank
![]() $1$
, it follows from [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Proposition 2.3.24, Part b that
$1$
, it follows from [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Proposition 2.3.24, Part b that
![]() $\mathcal {X}^{\otimes n}_{\rho }$
is uniformizable as an A-motive. This implies that
$\mathcal {X}^{\otimes n}_{\rho }$
is uniformizable as an A-motive. This implies that
![]() $\mathcal {X}^{\otimes n}_{\rho }$
is uniformizable as an
$\mathcal {X}^{\otimes n}_{\rho }$
is uniformizable as an
![]() $\mathbb F_q[t]$
-motive. Thus, Part 1 follows immediately.
$\mathbb F_q[t]$
-motive. Thus, Part 1 follows immediately.
For Part 2, if
![]() $n=1$
, then
$n=1$
, then
![]() $\rho $
is a Drinfeld
$\rho $
is a Drinfeld
![]() $\mathbb F_q[t]$
-module. By [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Example 2.2.5, we know that
$\mathbb F_q[t]$
-module. By [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Example 2.2.5, we know that
![]() $\rho $
is pure. Thus, the motive N (viewed as a t-motive) is pure, which implies
$\rho $
is pure. Thus, the motive N (viewed as a t-motive) is pure, which implies
![]() $N_n$
is also pure as a t-motive, by [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Proposition 2.3.11(e). Hence, we get the purity of
$N_n$
is also pure as a t-motive, by [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Proposition 2.3.11(e). Hence, we get the purity of
![]() $\mathcal {X}^{\otimes n}_{\rho }$
.
$\mathcal {X}^{\otimes n}_{\rho }$
.
We now prove Part 3. To calculate the Galois group
![]() $\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
associated to the t-motive
$\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
associated to the t-motive
![]() $\mathcal {X}^{\otimes n}_{\rho }$
, we will use [Reference Juschka41], Theorem 5.1.2. We claim that the t-motive
$\mathcal {X}^{\otimes n}_{\rho }$
, we will use [Reference Juschka41], Theorem 5.1.2. We claim that the t-motive
![]() $\mathcal {X}^{\otimes n}_{\rho }$
verifies all the conditions of this theorem. In fact, it is a pure uniformizable dual
$\mathcal {X}^{\otimes n}_{\rho }$
verifies all the conditions of this theorem. In fact, it is a pure uniformizable dual
![]() $\mathbb F_q[t]$
-motive thanks to Part 2. Further, it has complex multiplication since
$\mathbb F_q[t]$
-motive thanks to Part 2. Further, it has complex multiplication since
![]() $\operatorname {\mathrm {End}}_{\mathbb C_{\infty }}(\mathcal {X}^{\otimes n}_{\rho })=\operatorname {\mathrm {End}}_{\mathbb C_{\infty }}(\rho ^{\otimes n})=A$
by [Reference Green33], Lemma 7.3. Thus, we apply [Reference Juschka41], Theorem 5.1.2 to the t-motive
$\operatorname {\mathrm {End}}_{\mathbb C_{\infty }}(\mathcal {X}^{\otimes n}_{\rho })=\operatorname {\mathrm {End}}_{\mathbb C_{\infty }}(\rho ^{\otimes n})=A$
by [Reference Green33], Lemma 7.3. Thus, we apply [Reference Juschka41], Theorem 5.1.2 to the t-motive
![]() $\rho ^{\otimes n}$
to obtain
$\rho ^{\otimes n}$
to obtain
Remark 2.4. 1) We note that the Galois group associated to the A-motive
![]() $\rho ^{\otimes n}$
is also equal to
$\rho ^{\otimes n}$
is also equal to
![]() $\textrm {Res}_{K/\mathbb F_q[t]} \mathbb {G}_{m,K}$
(see [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Example 2.3.29).
$\textrm {Res}_{K/\mathbb F_q[t]} \mathbb {G}_{m,K}$
(see [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Example 2.3.29).
2) We should mention a similar result of Pink and his collaborators that completely determines the Galois group of a Drinfeld A-module (see [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Theorem 2.6.3 and also [Reference Chang and Papanikolas19], Theorem 3.5.4 for more details). It states that if M is the t-motive associated to a Drinfeld A-module defined over
![]() $\overline K$
, then
$\overline K$
, then
Proposition 2.5. The entries of
![]() $\Psi _{\rho }^{\otimes n}$
are regular at
$\Psi _{\rho }^{\otimes n}$
are regular at
![]() $t=\theta $
, and we have
$t=\theta $
, and we have
Proof. By [Reference Papanikolas47], Proposition 3.3.9 (c) and Section 4.1.6, there exists a matrix
![]() $U \in \text {GL}_2(\mathbb F_q(t))$
such that
$U \in \text {GL}_2(\mathbb F_q(t))$
such that
![]() $\widetilde {\Psi }=\Psi _{\rho }^{\otimes n} U$
is a rigid analytic trivialization of
$\widetilde {\Psi }=\Psi _{\rho }^{\otimes n} U$
is a rigid analytic trivialization of
![]() $\Phi _{\rho }^{\otimes n}$
and
$\Phi _{\rho }^{\otimes n}$
and
![]() $\widetilde {\Psi } \in \text {GL}_2(\mathbb T)$
. By [Reference Anderson, Brownawell and Papanikolas4], Proposition 3.1.3, the entries of
$\widetilde {\Psi } \in \text {GL}_2(\mathbb T)$
. By [Reference Anderson, Brownawell and Papanikolas4], Proposition 3.1.3, the entries of
![]() $\widetilde {\Psi }$
are entire functions in the variable t. Thus, in particular, the entries of
$\widetilde {\Psi }$
are entire functions in the variable t. Thus, in particular, the entries of
![]() $\widetilde {\Psi }$
and
$\widetilde {\Psi }$
and
![]() $U^{-1}$
are regular at
$U^{-1}$
are regular at
![]() $t=\theta $
. This implies that the entries of
$t=\theta $
. This implies that the entries of
![]() $\Psi _{\rho }^{\otimes n}$
are regular at
$\Psi _{\rho }^{\otimes n}$
are regular at
![]() $t=\theta $
.
$t=\theta $
.
Further, since
![]() $\overline K(\Psi _{\rho }^{\otimes n}(\theta ))=\overline K(\widetilde {\Psi }(\theta ))$
, by Theorem 1.15, we have
$\overline K(\Psi _{\rho }^{\otimes n}(\theta ))=\overline K(\widetilde {\Psi }(\theta ))$
, by Theorem 1.15, we have
The proof is finished.
2.4 Endomorphisms of t-motives
We write down explicitly the endomorphism of
![]() $\mathcal {X}^{\otimes n}_{\rho }$
given by
$\mathcal {X}^{\otimes n}_{\rho }$
given by
![]() $y \in A$
. In [Reference Green34], Proposition 4.2 gives a formula for
$y \in A$
. In [Reference Green34], Proposition 4.2 gives a formula for
![]() $yg_i$
for the basis elements
$yg_i$
for the basis elements
![]() $g_i$
of Proposition 1.4. Using the same strategy, and replacing the
$g_i$
of Proposition 1.4. Using the same strategy, and replacing the
![]() $g_i$
by
$g_i$
by
![]() $h_i$
, a short argument shows that there exist
$h_i$
, a short argument shows that there exist
![]() $y_i, z_i \in H$
such that for
$y_i, z_i \in H$
such that for
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
We deduce that there exists
![]() $M_y \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
such that the endomorphism y expressed in terms of the basis
$M_y \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
such that the endomorphism y expressed in terms of the basis
![]() $\{h_1,h_2\}$
is represented by
$\{h_1,h_2\}$
is represented by
![]() $M_y$
:
$M_y$
:
 $$ \begin{align*} y \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} =M_y \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} y \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} =M_y \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
Since
![]() $A \cong \mathbb {F}_q[t] + y\mathbb {F}_q[t]$
, using the formulas above for any element
$A \cong \mathbb {F}_q[t] + y\mathbb {F}_q[t]$
, using the formulas above for any element
![]() $a \in A$
, we can find a matrix
$a \in A$
, we can find a matrix
![]() $M_a \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
such that the endomorphism induced by multiplication by a on
$M_a \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
such that the endomorphism induced by multiplication by a on
![]() $\mathcal {X}^{\otimes n}_{\rho }$
in the basis
$\mathcal {X}^{\otimes n}_{\rho }$
in the basis
![]() $\{h_1,h_2\}$
is represented by
$\{h_1,h_2\}$
is represented by
![]() $M_a$
:
$M_a$
:
 $$ \begin{align*} a \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} =M_a \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} a \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} =M_a \begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
Lemma 2.6. With the above notation, the
![]() $(1,1)$
th coordinate
$(1,1)$
th coordinate
![]() $M_{a,1,1}|_{t=\theta } \in K^{\times }$
, and similarly,
$M_{a,1,1}|_{t=\theta } \in K^{\times }$
, and similarly,
![]() $M_{a,2,1}|_{t=\theta }=0$
.
$M_{a,2,1}|_{t=\theta }=0$
.
Proof. (Compare to [Reference Chang and Papanikolas18], Proposition 4.1.1) Specializing the above equality at
![]() $\Xi $
and recalling that
$\Xi $
and recalling that
![]() $h_1(\Xi ) \neq 0$
and
$h_1(\Xi ) \neq 0$
and
![]() $h_2(\Xi ) = 0$
by (1.10), we obtain
$h_2(\Xi ) = 0$
by (1.10), we obtain
![]() $M_{a,1,1}|_{t=\theta }=a(\theta ) \in K^{\times }$
and
$M_{a,1,1}|_{t=\theta }=a(\theta ) \in K^{\times }$
and
![]() $M_{a,2,1}|_{t=\theta }=0$
.
$M_{a,2,1}|_{t=\theta }=0$
.
3 Constructing t-motives connected to logarithms
3.1 Logarithms attached to
 $\rho $
$\rho $
We keep the notation of Section 2.1. Following Chang-Papanikolas (see [Reference Chang and Papanikolas18], Section 4.2), for
![]() $u \in \mathbb C_{\infty }$
with
$u \in \mathbb C_{\infty }$
with
![]() $\exp _{\rho }(u)=v \in \overline K$
, we consider
$\exp _{\rho }(u)=v \in \overline K$
, we consider
![]() $E_u$
the associated Anderson generating function associated to u given by (1.16). We set
$E_u$
the associated Anderson generating function associated to u given by (1.16). We set
 $$ \begin{align*} h_v = \begin{pmatrix} v \\ 0 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 1}(\overline K), \quad \Phi_v = \begin{pmatrix} \Phi_{\rho} & 0 \\ h_v^{\top} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]). \end{align*} $$
$$ \begin{align*} h_v = \begin{pmatrix} v \\ 0 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 1}(\overline K), \quad \Phi_v = \begin{pmatrix} \Phi_{\rho} & 0 \\ h_v^{\top} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]). \end{align*} $$
We define
 $$ \begin{align*} g_v &=V \begin{pmatrix} -E_u^{(1)} \\ -E_u^{(2)} \end{pmatrix} = \begin{pmatrix} -(t-\theta)E_u-v \\ -E_u^{(1)} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 1}(\mathbb{T}), \\ \Psi_v &= \begin{pmatrix} \Psi_{\rho} & 0 \\ g_v^{\top} \Psi_{\rho} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align*} $$
$$ \begin{align*} g_v &=V \begin{pmatrix} -E_u^{(1)} \\ -E_u^{(2)} \end{pmatrix} = \begin{pmatrix} -(t-\theta)E_u-v \\ -E_u^{(1)} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 1}(\mathbb{T}), \\ \Psi_v &= \begin{pmatrix} \Psi_{\rho} & 0 \\ g_v^{\top} \Psi_{\rho} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align*} $$
Then we get
and
The associated pre-motive
![]() $\mathcal {X}_v$
is, in fact, a t-motive in the sense of Papanikolas as is proved in [Reference Chang and Papanikolas19, §4.2].
$\mathcal {X}_v$
is, in fact, a t-motive in the sense of Papanikolas as is proved in [Reference Chang and Papanikolas19, §4.2].
For
![]() $v:=\exp _{\rho }(\zeta _{\rho }( b,1)) \in H$
, we call the corresponding t-motive
$v:=\exp _{\rho }(\zeta _{\rho }( b,1)) \in H$
, we call the corresponding t-motive
![]() $\mathcal {X}_v$
the zeta motive associated to
$\mathcal {X}_v$
the zeta motive associated to
![]() $\zeta _{\rho }( b,1)$
.
$\zeta _{\rho }( b,1)$
.
3.2 Logarithms attached to
 $\rho ^{\otimes n}$
$\rho ^{\otimes n}$
We now switch to the case for
![]() $n\geq 2$
and use freely the notation of Section 2.2. We fix
$n\geq 2$
and use freely the notation of Section 2.2. We fix
![]() $\mathbf {u} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
$\mathbf {u} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u})=\mathbf {v} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
, and we consider
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u})=\mathbf {v} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
, and we consider
![]() $E_{\mathbf {u}}^{\otimes n}$
the Anderson generating function associated to
$E_{\mathbf {u}}^{\otimes n}$
the Anderson generating function associated to
![]() $\mathbf {u}$
given by Equation (1.16). Recall that
$\mathbf {u}$
given by Equation (1.16). Recall that
Thus, we get
 $$ \begin{align*} \begin{pmatrix} E_{\mathbf{u},i+1} \\ E_{\mathbf{u},i+2} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ t-\theta & -a_i \end{pmatrix} \begin{pmatrix} E_{\mathbf{u},i} \\ E_{\mathbf{u},i+1} \end{pmatrix}+ \begin{pmatrix} 0 \\ -v_i \end{pmatrix}= \Theta_i \begin{pmatrix} E_{\mathbf{u},i} \\ E_{\mathbf{u},i+1} \end{pmatrix}+ \begin{pmatrix} 0 \\ -v_i \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} E_{\mathbf{u},i+1} \\ E_{\mathbf{u},i+2} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ t-\theta & -a_i \end{pmatrix} \begin{pmatrix} E_{\mathbf{u},i} \\ E_{\mathbf{u},i+1} \end{pmatrix}+ \begin{pmatrix} 0 \\ -v_i \end{pmatrix}= \Theta_i \begin{pmatrix} E_{\mathbf{u},i} \\ E_{\mathbf{u},i+1} \end{pmatrix}+ \begin{pmatrix} 0 \\ -v_i \end{pmatrix}. \end{align*} $$
We define the vector
![]() $f_{\mathbf {v}}:= (f_{\mathbf {v},1},f_{\mathbf {v},2})^{\top }$
given by
$f_{\mathbf {v}}:= (f_{\mathbf {v},1},f_{\mathbf {v},2})^{\top }$
given by
 $$ \begin{align} f_{\mathbf{v}} = \Theta_n \cdots \Theta_2 \begin{pmatrix} 0 \\ v_1 \end{pmatrix} + \Theta_n \cdots \Theta_3 \begin{pmatrix} 0 \\ v_2 \end{pmatrix} + \cdots + \begin{pmatrix} 0 \\ v_n \end{pmatrix}. \end{align} $$
$$ \begin{align} f_{\mathbf{v}} = \Theta_n \cdots \Theta_2 \begin{pmatrix} 0 \\ v_1 \end{pmatrix} + \Theta_n \cdots \Theta_3 \begin{pmatrix} 0 \\ v_2 \end{pmatrix} + \cdots + \begin{pmatrix} 0 \\ v_n \end{pmatrix}. \end{align} $$
It follows that
 $$ \begin{align*} \begin{pmatrix} E_{\mathbf{u},1} \\ E_{\mathbf{u},2} \end{pmatrix}^{(1)} = \Theta \begin{pmatrix} E_{\mathbf{u},1} \\ E_{\mathbf{u},2} \end{pmatrix}- \begin{pmatrix} f_{\mathbf{v},1} \\ f_{\mathbf{v},2} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} E_{\mathbf{u},1} \\ E_{\mathbf{u},2} \end{pmatrix}^{(1)} = \Theta \begin{pmatrix} E_{\mathbf{u},1} \\ E_{\mathbf{u},2} \end{pmatrix}- \begin{pmatrix} f_{\mathbf{v},1} \\ f_{\mathbf{v},2} \end{pmatrix}. \end{align*} $$
Here, we recall
 $$ \begin{align*} \Theta= \begin{pmatrix} 0 & 1 \\ t-\theta & -a_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -a_1 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \Theta= \begin{pmatrix} 0 & 1 \\ t-\theta & -a_n \end{pmatrix} \cdots \begin{pmatrix} 0 & 1 \\ t-\theta & -a_1 \end{pmatrix} \end{align*} $$
and
 $$ \begin{align*} \Upsilon = \begin{pmatrix} E_{1,1} & E_{2,1} \\ E_{1,2} & E_{2,2} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb{T}). \end{align*} $$
$$ \begin{align*} \Upsilon = \begin{pmatrix} E_{1,1} & E_{2,1} \\ E_{1,2} & E_{2,2} \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb{T}). \end{align*} $$
They verify
We set
 $$ \begin{align} \Theta_{\mathbf{v}} = \begin{pmatrix} \Theta & -(f_{\mathbf{v},1},f_{\mathbf{v},2})^{\top} \\ 0 & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]), \quad \Upsilon_{\mathbf{v}} = \begin{pmatrix} \Upsilon & (E_{\mathbf{u},1},E_{\mathbf{u},2})^{\top} \\ 0 & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align} $$
$$ \begin{align} \Theta_{\mathbf{v}} = \begin{pmatrix} \Theta & -(f_{\mathbf{v},1},f_{\mathbf{v},2})^{\top} \\ 0 & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]), \quad \Upsilon_{\mathbf{v}} = \begin{pmatrix} \Upsilon & (E_{\mathbf{u},1},E_{\mathbf{u},2})^{\top} \\ 0 & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align} $$
Then we get
Now we are ready to construct the associated rigid analytic trivialization. Recall that
 $$ \begin{align*} V = \begin{pmatrix} a_n & 1 \\ 1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} V = \begin{pmatrix} a_n & 1 \\ 1 & 0 \end{pmatrix}. \end{align*} $$
Note that V is symmetric. We set
 $$ \begin{align*} W &= \text{diag}(V,1)= \begin{pmatrix} V & 0 \\ 0 & 1 \end{pmatrix} \in \text{GL}_3(\overline K), \\ \Phi_{\mathbf{v}} &=(W^{(-1)})^{-1} (\Theta_{\mathbf{v}}^{\top}) W =\begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ (h_{\mathbf{v},1},h_{\mathbf{v},2}) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]), \\ \Psi_{\mathbf{v}} &=W^{-1} ((\Upsilon_{\mathbf{v}}^{\top})^{(1)})^{-1}=\begin{pmatrix} \Psi_{\rho}^{\otimes n} & 0 \\ (g_{\mathbf{v},1},g_{\mathbf{v},2})\Psi_{\rho}^{\otimes n} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align*} $$
$$ \begin{align*} W &= \text{diag}(V,1)= \begin{pmatrix} V & 0 \\ 0 & 1 \end{pmatrix} \in \text{GL}_3(\overline K), \\ \Phi_{\mathbf{v}} &=(W^{(-1)})^{-1} (\Theta_{\mathbf{v}}^{\top}) W =\begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ (h_{\mathbf{v},1},h_{\mathbf{v},2}) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]), \\ \Psi_{\mathbf{v}} &=W^{-1} ((\Upsilon_{\mathbf{v}}^{\top})^{(1)})^{-1}=\begin{pmatrix} \Psi_{\rho}^{\otimes n} & 0 \\ (g_{\mathbf{v},1},g_{\mathbf{v},2})\Psi_{\rho}^{\otimes n} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align*} $$
Remark 3.1. Note that by direct calculations, we obtain
Further, we will show below that
![]() $g_{\mathbf {v},1}(\theta )=u_n-v_n$
, where
$g_{\mathbf {v},1}(\theta )=u_n-v_n$
, where
![]() $u_n$
and
$u_n$
and
![]() $v_n$
are the last coordinate of
$v_n$
are the last coordinate of
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\mathbf {v}$
, respectively (see Lemma 3.3).
$\mathbf {v}$
, respectively (see Lemma 3.3).
Thus, we get
The associated pre-motive
![]() $\mathcal {X}_{\mathbf {v}}$
is in fact a t-motive because it is an extension of two t-motives (see for example [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Lemma 2.3.25).
$\mathcal {X}_{\mathbf {v}}$
is in fact a t-motive because it is an extension of two t-motives (see for example [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Lemma 2.3.25).
3.3 Period calculations
In this section, we show explicitly how to obtain the periods and zeta values discussed in the previous section from evaluations of the entries of the rigid analytic trivialization
![]() $\Psi _{\mathbf {v}}$
, for fixed
$\Psi _{\mathbf {v}}$
, for fixed
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\mathbf {v}$
as in the previous section.
$\mathbf {v}$
as in the previous section.
Lemma 3.2. Let
![]() $E_{\mathbf {u}}^{\otimes n}$
be defined as above. Then
$E_{\mathbf {u}}^{\otimes n}$
be defined as above. Then
 $$\begin{align*}\operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u}}^{\otimes n} dt) = \left (\begin{matrix} \operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u},1}dt) \\ \vdots \\ \operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u},n}dt) \\ \end{matrix}\right ) = -\mathbf{u}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u}}^{\otimes n} dt) = \left (\begin{matrix} \operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u},1}dt) \\ \vdots \\ \operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u},n}dt) \\ \end{matrix}\right ) = -\mathbf{u}.\end{align*}$$
Proof. Write
![]() $\mathbf {u} = (u_1,\dots ,u_n)^{\top } \in \mathbb C_{\infty }^n$
. As in the proof of [Reference Green34, Prop. 6.5], we have the identity
$\mathbf {u} = (u_1,\dots ,u_n)^{\top } \in \mathbb C_{\infty }^n$
. As in the proof of [Reference Green34, Prop. 6.5], we have the identity
 $$\begin{align*}E_{\mathbf{u}}^{\otimes n}= \sum_{j=0}^{\infty} Q_j\left (d[\theta]^{(j)} - t\text{Id}_n \right )^{-1}\mathbf{u}^{(j)},\end{align*}$$
$$\begin{align*}E_{\mathbf{u}}^{\otimes n}= \sum_{j=0}^{\infty} Q_j\left (d[\theta]^{(j)} - t\text{Id}_n \right )^{-1}\mathbf{u}^{(j)},\end{align*}$$
and we find that only the
![]() $j=0$
term contributes to the residue. Then, using the cofactor expansion of
$j=0$
term contributes to the residue. Then, using the cofactor expansion of
![]() $(d[\theta ]^{(j)} - t\text {Id}_n )^{-1}$
from [Reference Green34, Pg. 26], we find that
$(d[\theta ]^{(j)} - t\text {Id}_n )^{-1}$
from [Reference Green34, Pg. 26], we find that
 $$\begin{align*}\operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u}}^{\otimes n} dt) = \left (\begin{matrix} \operatorname{\mathrm{Res}}_{\theta}\left((\frac{u_1}{\theta-t} + r_1(t))dt\right)\\ \vdots\\ \operatorname{\mathrm{Res}}_{\theta}\left((\frac{u_n}{\theta-t} + r_n(t))dt\right) \end{matrix}\right) = - \left(\begin{matrix} u_1\\ \vdots\\ u_n \end{matrix}\right), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Res}}_{\theta}(E_{\mathbf{u}}^{\otimes n} dt) = \left (\begin{matrix} \operatorname{\mathrm{Res}}_{\theta}\left((\frac{u_1}{\theta-t} + r_1(t))dt\right)\\ \vdots\\ \operatorname{\mathrm{Res}}_{\theta}\left((\frac{u_n}{\theta-t} + r_n(t))dt\right) \end{matrix}\right) = - \left(\begin{matrix} u_1\\ \vdots\\ u_n \end{matrix}\right), \end{align*}$$
where
![]() $r_i(t)$
is some function in powers of
$r_i(t)$
is some function in powers of
![]() $(\theta -t)^k$
for
$(\theta -t)^k$
for
![]() $k\leq -2$
, and hence does not contribute to the residue (see [Reference Green34, (57)] and preceding discussion for more details).
$k\leq -2$
, and hence does not contribute to the residue (see [Reference Green34, (57)] and preceding discussion for more details).
Lemma 3.3. Let
![]() $E_{\mathbf {u}}^{\otimes n} = (E_{\mathbf {u},1},\dots ,E_{\mathbf {u},n})^{\top }$
as above and let
$E_{\mathbf {u}}^{\otimes n} = (E_{\mathbf {u},1},\dots ,E_{\mathbf {u},n})^{\top }$
as above and let
![]() $a_i$
be the defining coefficients for the Drinfeld t-module action as in Proposition 1.4. Then if we write
$a_i$
be the defining coefficients for the Drinfeld t-module action as in Proposition 1.4. Then if we write
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}) := \mathbf {v} = (v_1,\dots ,v_n)^{\top }$
,
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}) := \mathbf {v} = (v_1,\dots ,v_n)^{\top }$
,
Proof. As in (3.1), we have that
Rearranging terms gives
Both sides of the above equation are regular at
![]() $t=\theta $
in each coordinate, so evaluating at
$t=\theta $
in each coordinate, so evaluating at
![]() $t=\theta $
, using the formula for
$t=\theta $
, using the formula for
![]() $E_{\theta }$
and taking the last coordinate gives
$E_{\theta }$
and taking the last coordinate gives
Finally, from our analysis in Lemma 3.2, we see that
![]() $E_{\mathbf {u},n}$
has a simple pole at
$E_{\mathbf {u},n}$
has a simple pole at
![]() $t=\theta $
, and thus the right-hand side of the above equation is simply the residue at
$t=\theta $
, and thus the right-hand side of the above equation is simply the residue at
![]() $t=\theta $
. Thus,
$t=\theta $
. Thus,
Proposition 3.4. With all notation as above, the elements
![]() $\pi _{\rho }^n$
and
$\pi _{\rho }^n$
and
![]() $u_n$
are contained in
$u_n$
are contained in
![]() $\overline K(\Psi _{\mathbf {v}}(\theta ))$
.
$\overline K(\Psi _{\mathbf {v}}(\theta ))$
.
Proof. As above, we have that
![]() $\overline K(\Psi _{\mathbf {v}}(\theta )) = \overline K(\Upsilon _{\mathbf {v}}(\theta ))$
. Then note that
$\overline K(\Psi _{\mathbf {v}}(\theta )) = \overline K(\Upsilon _{\mathbf {v}}(\theta ))$
. Then note that
for
![]() $1\leq i,j\leq 2$
by construction. Then by Lemma 3.3, we see that the last coordinates of
$1\leq i,j\leq 2$
by construction. Then by Lemma 3.3, we see that the last coordinates of
![]() $\mathbf {u}_1,\mathbf {u}_2,\mathbf {u}$
are contained in
$\mathbf {u}_1,\mathbf {u}_2,\mathbf {u}$
are contained in
![]() $\overline K(\Upsilon _{\mathbf {v}}(\theta ))$
, where
$\overline K(\Upsilon _{\mathbf {v}}(\theta ))$
, where
![]() $\mathbf {u}_1,\mathbf {u}_2$
are an
$\mathbf {u}_1,\mathbf {u}_2$
are an
![]() $\mathbb F_q[t]$
-basis for the period lattice of
$\mathbb F_q[t]$
-basis for the period lattice of
![]() $\rho ^{\otimes n}$
and
$\rho ^{\otimes n}$
and
![]() $\mathbf {u}$
is a vector such that
$\mathbf {u}$
is a vector such that
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}) = \mathbf {v} \in \overline K$
. From [Reference Green34, Thm. 6.7], we know that the last coordinate of
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}) = \mathbf {v} \in \overline K$
. From [Reference Green34, Thm. 6.7], we know that the last coordinate of
![]() $\Pi _n$
is an algebraic multiple of
$\Pi _n$
is an algebraic multiple of
![]() $\pi _{\rho }^n$
, and thus it follows that
$\pi _{\rho }^n$
, and thus it follows that
![]() $\pi _{\rho }^n$
and
$\pi _{\rho }^n$
and
![]() $u_n$
are contained in
$u_n$
are contained in
![]() $\overline K(\Psi _{\mathbf {v}}(\theta ))$
.
$\overline K(\Psi _{\mathbf {v}}(\theta ))$
.
We next prove a lemma about the linear relations between the entries of
![]() $\overline K(\Psi _{\rho }^{\otimes n}(\theta ))$
. Let
$\overline K(\Psi _{\rho }^{\otimes n}(\theta ))$
. Let
![]() $\pi _{\rho }$
and
$\pi _{\rho }$
and
![]() $\Pi _n$
be generators of the period lattices of
$\Pi _n$
be generators of the period lattices of
![]() $\exp _{\rho }$
and
$\exp _{\rho }$
and
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
, respectively, as
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}$
, respectively, as
![]() $\textbf {A}$
-modules. Then recall that
$\textbf {A}$
-modules. Then recall that
![]() $\{\pi _{\rho },\eta \pi _{\rho }\}$
and
$\{\pi _{\rho },\eta \pi _{\rho }\}$
and
![]() $\{\Pi _n,d[y]\Pi _n\}$
are bases for
$\{\Pi _n,d[y]\Pi _n\}$
are bases for
![]() $\Lambda _{\rho }$
and
$\Lambda _{\rho }$
and
![]() $\Lambda _{\rho }^{\otimes n}$
, respectively, as
$\Lambda _{\rho }^{\otimes n}$
, respectively, as
![]() $\mathbb {F}_q[t]$
-modules. Also for
$\mathbb {F}_q[t]$
-modules. Also for
![]() $\mathbf {u} \in \mathbb {C}_{\infty }^n$
, we recall the definition of
$\mathbf {u} \in \mathbb {C}_{\infty }^n$
, we recall the definition of
![]() $G_{\mathbf {u}}$
from 1.17 and define
$G_{\mathbf {u}}$
from 1.17 and define
and note that this equals
![]() $[-1]G_{\mathbf {u}}^{\otimes n}$
, where
$[-1]G_{\mathbf {u}}^{\otimes n}$
, where
![]() $[-1]$
represents the inverse of the group law on the elliptic curve X. We will denote the coordinates of
$[-1]$
represents the inverse of the group law on the elliptic curve X. We will denote the coordinates of
![]() $G_{\mathbf {u}}^{\otimes n}:= (G_{\mathbf {u},1},\dots ,G_{\mathbf {u},n})$
and similarly for
$G_{\mathbf {u}}^{\otimes n}:= (G_{\mathbf {u},1},\dots ,G_{\mathbf {u},n})$
and similarly for
![]() $\overline G_{\mathbf {u}}$
.
$\overline G_{\mathbf {u}}$
.
Recall that
![]() $\Psi _{\rho }$
and
$\Psi _{\rho }$
and
![]() $\Psi _{\rho }^{\otimes n}$
are the
$\Psi _{\rho }^{\otimes n}$
are the
![]() $2\times 2$
rigid analytic trivialization matrices from §2.1–2.2. The following lemma gives
$2\times 2$
rigid analytic trivialization matrices from §2.1–2.2. The following lemma gives
![]() $\overline K$
-linear relations between the entries of these matrices evaluated at
$\overline K$
-linear relations between the entries of these matrices evaluated at
![]() $t=\theta $
and thus allows us to find a smaller set of generators for the following fields, which notably include powers of the period.
$t=\theta $
and thus allows us to find a smaller set of generators for the following fields, which notably include powers of the period.
Lemma 3.5. We have the following facts:
-
○ for
 $n = 1$
, we have
$n = 1$
, we have
 $\overline K(\Psi _{\rho }(\theta )) = \overline K(E_{\pi _{\rho }}^{(1)}(\theta ),E_{\pi _{\rho }}^{(2)}(\theta ))$
.
$\overline K(\Psi _{\rho }(\theta )) = \overline K(E_{\pi _{\rho }}^{(1)}(\theta ),E_{\pi _{\rho }}^{(2)}(\theta ))$
. -
○ for
 $n\geq 2$
, we have
$n\geq 2$
, we have
 $\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(E_{\Pi _{\rho },1}^{(1)}(\theta ),E_{\Pi _{\rho },2}^{(1)}(\theta ))$
.
$\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(E_{\Pi _{\rho },1}^{(1)}(\theta ),E_{\Pi _{\rho },2}^{(1)}(\theta ))$
.
Consequently, for each
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
![]() $\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(\pi _{\rho }^n,W_n)$
for quantities
$\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(\pi _{\rho }^n,W_n)$
for quantities
![]() $W_n\in \mathbb {C}_{\infty }$
.
$W_n\in \mathbb {C}_{\infty }$
.
Proof. To ease the exposition, we will assume that
![]() $p=\text {char}(\mathbb F_q) \geq 3$
, so that we may assume the elliptic curve X has Weierstrass equation given by
$p=\text {char}(\mathbb F_q) \geq 3$
, so that we may assume the elliptic curve X has Weierstrass equation given by
![]() $y^2 = t^3+at+b$
with
$y^2 = t^3+at+b$
with
![]() $a,b\in \mathbb {F}_q$
and such that inversion on X is given by
$a,b\in \mathbb {F}_q$
and such that inversion on X is given by
![]() $[-1]:(t,y)\mapsto (t,-y)$
. The lemma is also true for
$[-1]:(t,y)\mapsto (t,-y)$
. The lemma is also true for
![]() $p=\text {char}(\mathbb F_q) =2$
, and the proof is similar, but calculations are more cumbersome. Particularly, the negation map is more complicated, and this requires more sophisticated analysis. Additionally, we give the full details for the case
$p=\text {char}(\mathbb F_q) =2$
, and the proof is similar, but calculations are more cumbersome. Particularly, the negation map is more complicated, and this requires more sophisticated analysis. Additionally, we give the full details for the case
![]() $n\geq 2$
. The details for the case for
$n\geq 2$
. The details for the case for
![]() $n=1$
are similar, and we leave them to the interested reader. By our definition of
$n=1$
are similar, and we leave them to the interested reader. By our definition of
![]() $G_{\Pi _n}^{\otimes n}$
, we can write
$G_{\Pi _n}^{\otimes n}$
, we can write
 $$\begin{align*}\begin{pmatrix} y & 1 & 0 & 0\\ -y & 1 & 0 & 0\\ 0 & 0 & y & 1\\ 0 & 0 & -y & 1\\ \end{pmatrix}\hspace{6pt} \begin{pmatrix} E_{\Pi_n,1}^{(1)}\\ E_{d[y]\Pi_n,1}^{(1)}\\ E_{\Pi_n,2}^{(1)}\\ E_{d[y]\Pi_n,2}^{(1)}\\ \end{pmatrix} = \begin{pmatrix} G_{\Pi_n,1}^{(1)}\\ \overline G_{\Pi_n,1}^{(1)}\\ G_{\Pi_n,2}^{(1)}\\ \overline G_{\Pi_n,2}^{(1)}\\ \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} y & 1 & 0 & 0\\ -y & 1 & 0 & 0\\ 0 & 0 & y & 1\\ 0 & 0 & -y & 1\\ \end{pmatrix}\hspace{6pt} \begin{pmatrix} E_{\Pi_n,1}^{(1)}\\ E_{d[y]\Pi_n,1}^{(1)}\\ E_{\Pi_n,2}^{(1)}\\ E_{d[y]\Pi_n,2}^{(1)}\\ \end{pmatrix} = \begin{pmatrix} G_{\Pi_n,1}^{(1)}\\ \overline G_{\Pi_n,1}^{(1)}\\ G_{\Pi_n,2}^{(1)}\\ \overline G_{\Pi_n,2}^{(1)}\\ \end{pmatrix}, \end{align*}$$
and, in particular, we note that the above matrix is invertible in
![]() $\operatorname {\mathrm {Mat}}_{4\times 4}(\textbf {K})$
. By inverting the above matrix, this allows us to write each of the Anderson generating functions
$\operatorname {\mathrm {Mat}}_{4\times 4}(\textbf {K})$
. By inverting the above matrix, this allows us to write each of the Anderson generating functions
![]() $E_{d[y]\Pi _n,k}^{(1)}$
for
$E_{d[y]\Pi _n,k}^{(1)}$
for
![]() $k=1,2$
as a
$k=1,2$
as a
![]() $\textbf {K}$
-linear combination of the functions
$\textbf {K}$
-linear combination of the functions
![]() $G_{\Pi _n,k}^{(1)}$
and
$G_{\Pi _n,k}^{(1)}$
and
![]() $\overline G_{\Pi _n,k}^{(1)}$
. Further, from Proposition 1.6(d), we get the formula
$\overline G_{\Pi _n,k}^{(1)}$
. Further, from Proposition 1.6(d), we get the formula
![]() $g_2\cdot G_{\Pi _n,1} = g_1 \cdot G_{\Pi _n,2}$
. Note that the functions
$g_2\cdot G_{\Pi _n,1} = g_1 \cdot G_{\Pi _n,2}$
. Note that the functions
![]() $g_i\in \overline K(t,y)$
. Taken together, these two facts allow us to write the functions
$g_i\in \overline K(t,y)$
. Taken together, these two facts allow us to write the functions
![]() $E_{d[\eta ]\Pi _n,1}^{(1)}(\theta )$
and
$E_{d[\eta ]\Pi _n,1}^{(1)}(\theta )$
and
![]() $E_{d[\eta ]\Pi _n,2}^{(1)}(\theta )$
as
$E_{d[\eta ]\Pi _n,2}^{(1)}(\theta )$
as
![]() $\overline K$
-linear combinations of
$\overline K$
-linear combinations of
![]() $E_{\Pi _n,1}^{(1)}(\theta )$
and
$E_{\Pi _n,1}^{(1)}(\theta )$
and
![]() $E_{\Pi _n,2}^{(1)}(\theta )$
. As
$E_{\Pi _n,2}^{(1)}(\theta )$
. As
![]() $\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(\Upsilon (\theta ))$
(
$\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(\Upsilon (\theta ))$
(
![]() $\Upsilon $
is defined in (2.2)), and this allows us to conclude that
$\Upsilon $
is defined in (2.2)), and this allows us to conclude that
![]() $\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(E_{\Pi _n,1}^{(1)}(\theta ),E_{\Pi _n,2}^{(1)}(\theta ))$
. Finally, setting
$\overline K(\Psi _{\rho }^{\otimes n}(\theta )) = \overline K(E_{\Pi _n,1}^{(1)}(\theta ),E_{\Pi _n,2}^{(1)}(\theta ))$
. Finally, setting
![]() $\mathbf {u} = \Pi _n$
and
$\mathbf {u} = \Pi _n$
and
![]() $\mathbf {v} = 0$
in Lemma 3.3 shows that a
$\mathbf {v} = 0$
in Lemma 3.3 shows that a
![]() $\overline K$
-linear combination of
$\overline K$
-linear combination of
![]() $E_{\Pi _n,1}^{(1)}(\theta )$
and
$E_{\Pi _n,1}^{(1)}(\theta )$
and
![]() $E_{\Pi _n,2}^{(1)}(\theta )$
equals the last coordinate of
$E_{\Pi _n,2}^{(1)}(\theta )$
equals the last coordinate of
![]() $\Pi _n$
, which is an algebraic multiple of
$\Pi _n$
, which is an algebraic multiple of
![]() $\Pi _n^n$
by Proposition 1.6(e). It remains to take an additional linearly independent combination of
$\Pi _n^n$
by Proposition 1.6(e). It remains to take an additional linearly independent combination of
![]() $E_{\Pi _n,1}^{(1)}(\theta )$
and
$E_{\Pi _n,1}^{(1)}(\theta )$
and
![]() $E_{\Pi _n,2}^{(1)}(\theta )$
, which we set equal to
$E_{\Pi _n,2}^{(1)}(\theta )$
, which we set equal to
![]() $W_n$
, to finish the proof.
$W_n$
, to finish the proof.
3.4 An application of Hartl-Juschka’s work to period calculations
In this section, we maintain the notation from the previous section of
![]() $\mathbf {u}_1,\mathbf {u}_2$
being a generating set for the period lattice
$\mathbf {u}_1,\mathbf {u}_2$
being a generating set for the period lattice
![]() $\Lambda _{\rho }^{\otimes n}$
and
$\Lambda _{\rho }^{\otimes n}$
and
![]() $\mathbf {u}\in \mathbb {C}_{\infty }^n$
. We wish to apply Corollaries 2.5.23 and 2.5.24 from Hartl and Juschka [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38] (originally due to Anderson in unpublished work) to give a more conceptual method for period calculations with an aim towards generalizing these arguments to curves of arbitrary genus. We restate [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38, Cors. 2.5.23, 2.5.24] here for the convenience of the reader, but we first translate their notation into our setting. By definition,
$\mathbf {u}\in \mathbb {C}_{\infty }^n$
. We wish to apply Corollaries 2.5.23 and 2.5.24 from Hartl and Juschka [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38] (originally due to Anderson in unpublished work) to give a more conceptual method for period calculations with an aim towards generalizing these arguments to curves of arbitrary genus. We restate [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38, Cors. 2.5.23, 2.5.24] here for the convenience of the reader, but we first translate their notation into our setting. By definition,
![]() $\sigma $
acts by the matrix
$\sigma $
acts by the matrix
![]() $\Phi _{\rho }^{\otimes n}$
on a
$\Phi _{\rho }^{\otimes n}$
on a
![]() $\mathbb {C}_{\infty }[t]$
-basis
$\mathbb {C}_{\infty }[t]$
-basis
![]() $\{h_1,h_2\}$
of
$\{h_1,h_2\}$
of
![]() $N_n$
. Explicitly, for
$N_n$
. Explicitly, for
![]() $z \in N_n$
, we express
$z \in N_n$
, we express
![]() $z = ah_1 + bh_2$
with
$z = ah_1 + bh_2$
with
![]() $a,b\in \mathbb C_{\infty }[t]$
and we get
$a,b\in \mathbb C_{\infty }[t]$
and we get
 $$\begin{align*}\sigma(z) = \sigma(ah_1 + bh_2) = \sigma\left ((a,b) \begin{pmatrix} h_1\\ h_2 \end{pmatrix}\right ) = (a,b)^{(-1)} \Phi_{\rho}^{\otimes n} \begin{pmatrix} h_1\\ h_2 \end{pmatrix}.\end{align*}$$
$$\begin{align*}\sigma(z) = \sigma(ah_1 + bh_2) = \sigma\left ((a,b) \begin{pmatrix} h_1\\ h_2 \end{pmatrix}\right ) = (a,b)^{(-1)} \Phi_{\rho}^{\otimes n} \begin{pmatrix} h_1\\ h_2 \end{pmatrix}.\end{align*}$$
Thus, we see that if we view
![]() $N_n$
as a free
$N_n$
as a free
![]() $\mathbb C_{\infty }[t]$
-module, then
$\mathbb C_{\infty }[t]$
-module, then
![]() $\sigma $
acts by inverse twisting and right multiplication by
$\sigma $
acts by inverse twisting and right multiplication by
![]() $\Phi _{\rho }^{\otimes n}$
. Transposing, we get a left multiplication:
$\Phi _{\rho }^{\otimes n}$
. Transposing, we get a left multiplication:
 $$\begin{align*}\sigma\begin{pmatrix} a\\ b \end{pmatrix} = \left (\Phi_{\rho}^{\otimes n}\right )^{\top} \begin{pmatrix} a\\ b \end{pmatrix}^{(-1)},\quad a,b\in \mathbb{F}_q[t].\end{align*}$$
$$\begin{align*}\sigma\begin{pmatrix} a\\ b \end{pmatrix} = \left (\Phi_{\rho}^{\otimes n}\right )^{\top} \begin{pmatrix} a\\ b \end{pmatrix}^{(-1)},\quad a,b\in \mathbb{F}_q[t].\end{align*}$$
By [Reference Namoijam and Papanikolas45, Lemma 3.4.1],
![]() $\delta _0$
extends to
$\delta _0$
extends to
![]() $N_n \otimes _{\mathbb C_{\infty }[t]} \mathbb {T}_{\theta }$
, where
$N_n \otimes _{\mathbb C_{\infty }[t]} \mathbb {T}_{\theta }$
, where
![]() $\mathbb {T}_{\theta }$
is a Tate algebra of functions with radius of convergence
$\mathbb {T}_{\theta }$
is a Tate algebra of functions with radius of convergence
![]() $|\theta |_{\infty }$
(see §1.1.2).
$|\theta |_{\infty }$
(see §1.1.2).
Corollary 3.6. (This is [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38, Cor. 2.5.23 and 2.5.24]) Let
![]() $N_n$
and
$N_n$
and
![]() $\Phi _{\rho }^{\otimes n}$
be as above. Further, let
$\Phi _{\rho }^{\otimes n}$
be as above. Further, let
![]() $\mathbf {w}\in \mathbb {T}_{\theta }^2$
satisfy
$\mathbf {w}\in \mathbb {T}_{\theta }^2$
satisfy
Then
Further, if
![]() $\mathbf {z}=0$
, then
$\mathbf {z}=0$
, then
![]() $\delta _0(\mathbf {w}) \in \Lambda _{\rho }^{\otimes n}$
and the set of all such
$\delta _0(\mathbf {w}) \in \Lambda _{\rho }^{\otimes n}$
and the set of all such
![]() $\mathbf {w}$
forms a spanning set for the periods.
$\mathbf {w}$
forms a spanning set for the periods.
So, we wish to look for vectors
![]() $\mathbf {w}\in \mathbb {T}_{\theta }^2$
which satisfy (3.4) for some
$\mathbf {w}\in \mathbb {T}_{\theta }^2$
which satisfy (3.4) for some
![]() $z\in N_n$
.
$z\in N_n$
.
Lemma 3.7. For
![]() $\Upsilon $
as in (2.2), we have
$\Upsilon $
as in (2.2), we have
Proof. From (2.3), we have that
![]() $(\Phi _{\rho }^{\otimes n}) = (V^{(-1)})^{-1} \Theta ^{\top } V$
, and then substituting in gives
$(\Phi _{\rho }^{\otimes n}) = (V^{(-1)})^{-1} \Theta ^{\top } V$
, and then substituting in gives
 $$ \begin{align*} (\Phi_{\rho}^{\otimes n})^{\top}(V^{\top} \Upsilon^{(1)})^{(-1)} &= ((V^{(-1)})^{-1} \Theta^{\top} V)^{\top}(V^{\top} \Upsilon^{(1)})^{(-1)}\\ &= V^{\top}\Theta ((V^{(-1)})^{-1})^{\top})(V^{\top} \Upsilon^{(1)})^{(-1)}\\ &= V^{\top} (\Theta\Upsilon)\\ &= V^{\top} (\Upsilon^{(1)}).\\[-39pt] \end{align*} $$
$$ \begin{align*} (\Phi_{\rho}^{\otimes n})^{\top}(V^{\top} \Upsilon^{(1)})^{(-1)} &= ((V^{(-1)})^{-1} \Theta^{\top} V)^{\top}(V^{\top} \Upsilon^{(1)})^{(-1)}\\ &= V^{\top}\Theta ((V^{(-1)})^{-1})^{\top})(V^{\top} \Upsilon^{(1)})^{(-1)}\\ &= V^{\top} (\Theta\Upsilon)\\ &= V^{\top} (\Upsilon^{(1)}).\\[-39pt] \end{align*} $$
We comment that
![]() $V^{\top } \Upsilon ^{(1)} = ((\Psi _{\rho }^{\otimes n})^{-1})^{\top } \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
by Remark 2.2, but to save on notation, we shall denote
$V^{\top } \Upsilon ^{(1)} = ((\Psi _{\rho }^{\otimes n})^{-1})^{\top } \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
by Remark 2.2, but to save on notation, we shall denote
![]() $P := V^{\top } \Upsilon ^{(1)} \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
and denote the columns of P by
$P := V^{\top } \Upsilon ^{(1)} \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
and denote the columns of P by
![]() $P_i \in \mathbb {T}_{\theta }^2$
. Thus, for
$P_i \in \mathbb {T}_{\theta }^2$
. Thus, for
![]() $i=1,2$
, we have
$i=1,2$
, we have
![]() $(\Phi _{\rho }^{\otimes n})^{\top } P_i^{(-1)} - P_i = 0$
, and therefore the vectors
$(\Phi _{\rho }^{\otimes n})^{\top } P_i^{(-1)} - P_i = 0$
, and therefore the vectors
![]() $P_i$
satisfy the conditions of Lemma 3.6. So we get
$P_i$
satisfy the conditions of Lemma 3.6. So we get
Lemma 3.8. For
![]() $\mathbf {u} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
$\mathbf {u} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u})=\mathbf {v} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
, we let
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u})=\mathbf {v} \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
, we let
![]() $E_{\mathbf {u}}^{\otimes n}$
be the Anderson generating function (with coordinates denoted as in (2.1)) associated to
$E_{\mathbf {u}}^{\otimes n}$
be the Anderson generating function (with coordinates denoted as in (2.1)) associated to
![]() $\mathbf {u}$
and let
$\mathbf {u}$
and let
![]() $E_{\mathbf {u},*} = (E_{\mathbf {u},1},E_{\mathbf {u},2})^{\top }$
and
$E_{\mathbf {u},*} = (E_{\mathbf {u},1},E_{\mathbf {u},2})^{\top }$
and
![]() $P_{\mathbf {u}} := V^{\top } E_{\mathbf {u},*}^{(1)} \in \mathbb {T}_{\theta }^2$
. Then
$P_{\mathbf {u}} := V^{\top } E_{\mathbf {u},*}^{(1)} \in \mathbb {T}_{\theta }^2$
. Then
![]() $P_{\mathbf {u}}$
satisfies the conditions of Lemma 3.6; that is,
$P_{\mathbf {u}}$
satisfies the conditions of Lemma 3.6; that is,
where
![]() $f_{\mathbf {v}}$
is the vector defined in Section 3.2 and
$f_{\mathbf {v}}$
is the vector defined in Section 3.2 and
![]() $V^{\top } f_{\mathbf {v}} \in \overline K[t]^2$
.
$V^{\top } f_{\mathbf {v}} \in \overline K[t]^2$
.
Proof. As stated as in Section 3.2, we find that
![]() $\Theta E_{\mathbf {u},*} = E_{\mathbf {u},*}^{(1)} + f_{\mathbf {v}}$
. We then calculate that
$\Theta E_{\mathbf {u},*} = E_{\mathbf {u},*}^{(1)} + f_{\mathbf {v}}$
. We then calculate that
 $$ \begin{align*} (\Phi_{\rho}^{\otimes n})^{\top} (V^{\top} E_{\mathbf{u},*}^{(1)})^{(-1)} &= V^{\top}\Theta ((V^{(-1)})^{-1})^{\top} (V^{(-1)})^{\top} E_{\mathbf{u},*}\\ &= V^{\top} \Theta E_{\mathbf{u},*} \\ &= V^{\top} E_{\mathbf{u},*}^{(1)} + V^{\top} f_{\mathbf{v}}.\\[-40pt] \end{align*} $$
$$ \begin{align*} (\Phi_{\rho}^{\otimes n})^{\top} (V^{\top} E_{\mathbf{u},*}^{(1)})^{(-1)} &= V^{\top}\Theta ((V^{(-1)})^{-1})^{\top} (V^{(-1)})^{\top} E_{\mathbf{u},*}\\ &= V^{\top} \Theta E_{\mathbf{u},*} \\ &= V^{\top} E_{\mathbf{u},*}^{(1)} + V^{\top} f_{\mathbf{v}}.\\[-40pt] \end{align*} $$
Thus,
![]() $P_{\mathbf {u}}$
satisfies the conditions for Lemma 3.6, and we can write
$P_{\mathbf {u}}$
satisfies the conditions for Lemma 3.6, and we can write
Proposition 3.9. For a fixed n, with all notation as above, the quantities
![]() $\pi _{\rho }^n$
and
$\pi _{\rho }^n$
and
![]() $u_n$
are contained in
$u_n$
are contained in
![]() $\overline K(\Psi _{\mathbf {v}}(\theta ))$
.
$\overline K(\Psi _{\mathbf {v}}(\theta ))$
.
Proof. By definition, we have that
![]() $\overline K(\Psi _{\mathbf {v}}(\theta )) = \overline K(\Upsilon _{\mathbf {v}}(\theta ))$
, and we further see that
$\overline K(\Psi _{\mathbf {v}}(\theta )) = \overline K(\Upsilon _{\mathbf {v}}(\theta ))$
, and we further see that
![]() $\overline K(\Upsilon _{\mathbf {v}}(\theta )) = \overline K(P(\theta ),E_{\mathbf {u},1}^{(1)}(\theta ),E_{\mathbf {u},2}^{(1)}(\theta ))$
, for
$\overline K(\Upsilon _{\mathbf {v}}(\theta )) = \overline K(P(\theta ),E_{\mathbf {u},1}^{(1)}(\theta ),E_{\mathbf {u},2}^{(1)}(\theta ))$
, for
![]() $P \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
defined in the proof of Lemma 3.7. Lemma 3.6 implies that
$P \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {T}_{\theta })$
defined in the proof of Lemma 3.7. Lemma 3.6 implies that
![]() $\delta _0(P_i)$
for
$\delta _0(P_i)$
for
![]() $i=1,2$
is in the period lattice, and we deduce that the vectors
$i=1,2$
is in the period lattice, and we deduce that the vectors
![]() $\delta _0(P_i)$
must form a generating set for the period lattice over
$\delta _0(P_i)$
must form a generating set for the period lattice over
![]() $\mathbb {F}_q[t]$
. This implies that some
$\mathbb {F}_q[t]$
. This implies that some
![]() $\textbf {A}$
-linear combination of
$\textbf {A}$
-linear combination of
![]() $\delta _0(P_1)$
and
$\delta _0(P_1)$
and
![]() $\delta _0(P_2)$
(via the
$\delta _0(P_2)$
(via the
![]() $\text {Lie}_{\rho }^{\otimes n}(\textbf {A})$
-action of
$\text {Lie}_{\rho }^{\otimes n}(\textbf {A})$
-action of
![]() $\textbf {A}$
) equals
$\textbf {A}$
) equals
![]() $\Pi _n$
, the fundamental period. Since the bottom coordinate of
$\Pi _n$
, the fundamental period. Since the bottom coordinate of
![]() $\Pi _n$
is a
$\Pi _n$
is a
![]() $\overline K$
-multiple of
$\overline K$
-multiple of
![]() $\pi _{\rho }^n$
, it implies that
$\pi _{\rho }^n$
, it implies that
![]() $\pi _{\rho }^n \in \overline K(\Psi _{\mathbf {v}}(\theta ))$
.
$\pi _{\rho }^n \in \overline K(\Psi _{\mathbf {v}}(\theta ))$
.
We now perform a similar analysis on Equation (3.6). To proceed, we need to better understand the vector
![]() $f_{\mathbf {v}}:= (f_{\mathbf {v},1},f_{\mathbf {v},2})^{\top }$
for
$f_{\mathbf {v}}:= (f_{\mathbf {v},1},f_{\mathbf {v},2})^{\top }$
for
![]() $\mathbf {v}$
chosen as in Lemma 3.8.
$\mathbf {v}$
chosen as in Lemma 3.8.
We recall from Section 2.2 that
 $$\begin{align*}\Theta_i = \begin{pmatrix} 0 & 1\\ t-\theta & a_i \end{pmatrix},\quad \phi_i = \begin{pmatrix} 0 & 1\\ t-\theta & b_i \end{pmatrix},\quad V = \begin{pmatrix} a_n & 1\\ 1 & 0 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\Theta_i = \begin{pmatrix} 0 & 1\\ t-\theta & a_i \end{pmatrix},\quad \phi_i = \begin{pmatrix} 0 & 1\\ t-\theta & b_i \end{pmatrix},\quad V = \begin{pmatrix} a_n & 1\\ 1 & 0 \end{pmatrix}. \end{align*}$$
If we denote
 $$\begin{align*}X = \begin{pmatrix} t-\theta & 0\\ 0 & 1 \end{pmatrix}, \end{align*}$$
$$\begin{align*}X = \begin{pmatrix} t-\theta & 0\\ 0 & 1 \end{pmatrix}, \end{align*}$$
then we have the following equalities from (2.3):
By the definition of
![]() $f_{\mathbf {v}}$
(3.2), we find that
$f_{\mathbf {v}}$
(3.2), we find that
 $$\begin{align*}V^{\top} f_{\mathbf{v}} = V^{\top}\Theta_n \cdots \Theta_2 \begin{pmatrix} 0 \\ v_1 \end{pmatrix} + V^{\top}\Theta_n \cdots \Theta_3 \begin{pmatrix} 0 \\ v_2 \end{pmatrix} + \cdots + V^{\top}\begin{pmatrix} 0 \\ v_n \end{pmatrix}.\end{align*}$$
$$\begin{align*}V^{\top} f_{\mathbf{v}} = V^{\top}\Theta_n \cdots \Theta_2 \begin{pmatrix} 0 \\ v_1 \end{pmatrix} + V^{\top}\Theta_n \cdots \Theta_3 \begin{pmatrix} 0 \\ v_2 \end{pmatrix} + \cdots + V^{\top}\begin{pmatrix} 0 \\ v_n \end{pmatrix}.\end{align*}$$
Then, in anticipation of calculating
![]() $\delta _0(V^{\top } f_{\mathbf {v}})$
, using the above equalities, we find that
$\delta _0(V^{\top } f_{\mathbf {v}})$
, using the above equalities, we find that
 $$ \begin{align*} (h_1, h_2)V^{\top} f_{\mathbf{v}} &= (h_1, h_2)\left (V^{\top}\Theta_n \cdots \Theta_2 \begin{pmatrix} 0 \\ v_1 \end{pmatrix} + V^{\top}\Theta_n \cdots \Theta_3 \begin{pmatrix} 0 \\ v_2 \end{pmatrix} + \cdots + V^{\top}\begin{pmatrix} 0 \\ v_n \end{pmatrix}\right )\\ &= \left ( (0,v_1) \Theta_2^{\top} \cdots \Theta_n^{\top} V + \cdots + (0,v_{n-1})\Theta_n^{\top} V + (0,v_n) V\right )\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}\\ &= \left ( (0,v_1) X \phi_{n-2}\cdots \phi_1 + \cdots + (0,v_{n-2}) X \phi_1 +(0,v_{n-1}) X + (0,v_n) V\right )\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} (h_1, h_2)V^{\top} f_{\mathbf{v}} &= (h_1, h_2)\left (V^{\top}\Theta_n \cdots \Theta_2 \begin{pmatrix} 0 \\ v_1 \end{pmatrix} + V^{\top}\Theta_n \cdots \Theta_3 \begin{pmatrix} 0 \\ v_2 \end{pmatrix} + \cdots + V^{\top}\begin{pmatrix} 0 \\ v_n \end{pmatrix}\right )\\ &= \left ( (0,v_1) \Theta_2^{\top} \cdots \Theta_n^{\top} V + \cdots + (0,v_{n-1})\Theta_n^{\top} V + (0,v_n) V\right )\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}\\ &= \left ( (0,v_1) X \phi_{n-2}\cdots \phi_1 + \cdots + (0,v_{n-2}) X \phi_1 +(0,v_{n-1}) X + (0,v_n) V\right )\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}. \end{align*} $$
Now recall that (see Section 2.2)
 $$\begin{align*}\begin{pmatrix} h_{i+1} \\ h_{i+2} \end{pmatrix} = \phi_i \begin{pmatrix} h_i \\ h_{i+1} \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} h_{i+1} \\ h_{i+2} \end{pmatrix} = \phi_i \begin{pmatrix} h_i \\ h_{i+1} \end{pmatrix}. \end{align*}$$
Since
![]() $(0,v_i)X=(0,v_i)$
, it follows that
$(0,v_i)X=(0,v_i)$
, it follows that
 $$ \begin{align*} (h_1, h_2)V^{\top} f_{\mathbf{v}} &= \left ( (0,v_1) X \phi_{n-2}\cdots \phi_1 + \cdots + (0,v_{n-2}) X \phi_1 +(0,v_{n-1}) X + (0,v_n) V\right )\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}\\ &= (0,v_1)\begin{pmatrix} h_{n-1} \\ h_{n} \end{pmatrix} + \cdots + (0,v_{n-2})\begin{pmatrix} h_2 \\ h_3 \end{pmatrix} + (0,v_{n-1})\begin{pmatrix} h_1 \\ h_2 \end{pmatrix} + (v_{n},0)\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}\\ &= v_1h_n + \cdots + v_nh_1. \end{align*} $$
$$ \begin{align*} (h_1, h_2)V^{\top} f_{\mathbf{v}} &= \left ( (0,v_1) X \phi_{n-2}\cdots \phi_1 + \cdots + (0,v_{n-2}) X \phi_1 +(0,v_{n-1}) X + (0,v_n) V\right )\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}\\ &= (0,v_1)\begin{pmatrix} h_{n-1} \\ h_{n} \end{pmatrix} + \cdots + (0,v_{n-2})\begin{pmatrix} h_2 \\ h_3 \end{pmatrix} + (0,v_{n-1})\begin{pmatrix} h_1 \\ h_2 \end{pmatrix} + (v_{n},0)\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}\\ &= v_1h_n + \cdots + v_nh_1. \end{align*} $$
Thus, we find that
 $$\begin{align*}\delta_0(V^{\top} f_{\mathbf{v}}) = \delta_1(V^{\top} f_{\mathbf{v}}) = \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix}= \mathbf{v}.\end{align*}$$
$$\begin{align*}\delta_0(V^{\top} f_{\mathbf{v}}) = \delta_1(V^{\top} f_{\mathbf{v}}) = \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix}= \mathbf{v}.\end{align*}$$
Then, returning to (3.6), we find that
Thus, the two quantities in the exponential functions in the above equality differ by a period, so there exists some
![]() $a\in A$
such that
$a\in A$
such that
where
![]() $d[a]$
denotes the action of a under
$d[a]$
denotes the action of a under
![]() $\text {Lie}(\rho ^{\otimes n})$
. By our above analysis of
$\text {Lie}(\rho ^{\otimes n})$
. By our above analysis of
![]() $\delta _0$
, we conclude that the bottom coordinate
$\delta _0$
, we conclude that the bottom coordinate
![]() $\alpha $
of
$\alpha $
of
![]() $\delta _0(P_{\mathbf {u}})$
is equal to
$\delta _0(P_{\mathbf {u}})$
is equal to
Since we have proved above that
![]() $\pi _{\rho }^n \in \overline K(\Psi _{\mathbf {v}}(\theta ))$
and since
$\pi _{\rho }^n \in \overline K(\Psi _{\mathbf {v}}(\theta ))$
and since
![]() $v_n \in \overline K$
, it follows that
$v_n \in \overline K$
, it follows that
![]() $u_n\in \overline K(\Psi _{\mathbf {v}}(\theta ))$
as well.
$u_n\in \overline K(\Psi _{\mathbf {v}}(\theta ))$
as well.
3.5 Independence in
 $\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
$\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
For
![]() $b\in B$
and
$b\in B$
and
![]() $\mathbf {v}:=\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(Z_n(b)) \in \operatorname {\mathrm {Mat}}_{n \times 1}(H)$
, where
$\mathbf {v}:=\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(Z_n(b)) \in \operatorname {\mathrm {Mat}}_{n \times 1}(H)$
, where
![]() $Z_n(b)$
is the log-algebraic vector of Theorem 1.8, we call the corresponding t-motive
$Z_n(b)$
is the log-algebraic vector of Theorem 1.8, we call the corresponding t-motive
![]() $\mathcal {X}_n(b):=\mathcal {X}_{\mathbf {v}}$
the zeta t-motive associated to
$\mathcal {X}_n(b):=\mathcal {X}_{\mathbf {v}}$
the zeta t-motive associated to
![]() $\zeta _{\rho }( b,n)$
. We also denote by
$\zeta _{\rho }( b,n)$
. We also denote by
![]() $\Phi _n(b):=\Phi _{\mathbf {v}}$
and
$\Phi _n(b):=\Phi _{\mathbf {v}}$
and
![]() $\Psi _n(b):=\Psi _{\mathbf {v}}$
the corresponding matrices. As in §3.2, we put
$\Psi _n(b):=\Psi _{\mathbf {v}}$
the corresponding matrices. As in §3.2, we put
 $$ \begin{align*} \Phi_{\mathbf{v}}=\begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ (h_{\mathbf{v},1},h_{\mathbf{v},2}) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]). \end{align*} $$
$$ \begin{align*} \Phi_{\mathbf{v}}=\begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ (h_{\mathbf{v},1},h_{\mathbf{v},2}) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]). \end{align*} $$
We have a short exact sequence
where
![]() $\mathbf {1}$
is the trivial pre-t-motive, equal to
$\mathbf {1}$
is the trivial pre-t-motive, equal to
![]() $\overline K[t]$
with
$\overline K[t]$
with
![]() $\sigma $
-action given by the inverse Frobenius twist.
$\sigma $
-action given by the inverse Frobenius twist.
We follow closely [Reference Chang and Papanikolas19], Section 4.2. The group
![]() $\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
has the structure of a K-vector space by pushing along
$\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
has the structure of a K-vector space by pushing along
![]() $\mathcal {X}_{\rho }^{\otimes n}$
. With the above notation, for
$\mathcal {X}_{\rho }^{\otimes n}$
. With the above notation, for
![]() $a \in A$
whose corresponding matrix is
$a \in A$
whose corresponding matrix is
![]() $M_a \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
as in §2.4, the extension
$M_a \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
as in §2.4, the extension
![]() $a_* \mathcal {X}_{\mathbf {v}}$
is represented by the matrix
$a_* \mathcal {X}_{\mathbf {v}}$
is represented by the matrix
 $$ \begin{align*} \begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ (h_{\mathbf{v},1},h_{\mathbf{v},2}) M_a & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]). \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ (h_{\mathbf{v},1},h_{\mathbf{v},2}) M_a & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]). \end{align*} $$
We will show the following proposition (compare to [Reference Chang and Papanikolas18], Theorem 4.4.2):
Proposition 3.10. Suppose that
![]() $\mathbf {u}_1,\ldots ,\mathbf {u}_m \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
$\mathbf {u}_1,\ldots ,\mathbf {u}_m \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}_i)=\mathbf {v}_i \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
. If
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}_i)=\mathbf {v}_i \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
. If
![]() $\pi ^n_{\rho }, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}$
are linearly independent over K, then the classes of
$\pi ^n_{\rho }, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}$
are linearly independent over K, then the classes of
![]() $\mathcal {X}_{\mathbf {v}_i} (1 \leq i \leq n)$
in
$\mathcal {X}_{\mathbf {v}_i} (1 \leq i \leq n)$
in
![]() $\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
are linearly independent over K.
$\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
are linearly independent over K.
Proof. The proof follows closely that of [Reference Chang and Papanikolas18], Theorem 4.4.2. Suppose that there exist
![]() $e_1,\ldots ,e_m \in K$
not all zero so that
$e_1,\ldots ,e_m \in K$
not all zero so that
![]() $N=e_{1*} X_1+\ldots +e_{m*} X_m$
is trivial in
$N=e_{1*} X_1+\ldots +e_{m*} X_m$
is trivial in
![]() $\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
. We can suppose that for
$\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
. We can suppose that for
![]() $1 \leq i \leq m$
,
$1 \leq i \leq m$
,
![]() $e_i$
belongs to A and is represented by
$e_i$
belongs to A and is represented by
![]() $M_i \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
. Then the extension
$M_i \in \operatorname {\mathrm {Mat}}_{2 \times 2}(\overline K[t])$
. Then the extension
![]() $N=e_{1*} X_1+\ldots +e_{m*} X_m$
is represented by
$N=e_{1*} X_1+\ldots +e_{m*} X_m$
is represented by
![]() $h_{\mathbf {v}_1} M_1+\ldots +h_{\mathbf {v}_m} M_m$
and we have
$h_{\mathbf {v}_1} M_1+\ldots +h_{\mathbf {v}_m} M_m$
and we have
 $$ \begin{align*} \Phi_N &=\begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ \sum_{i=1}^m h_{\mathbf{v}_i} M_i & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]), \\ \Psi_N &=\begin{pmatrix} \Psi_{\rho}^{\otimes n} & 0 \\ (\sum_{i=1}^m g_{\mathbf{v}_i} M_i)\Psi_{\rho}^{\otimes n} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align*} $$
$$ \begin{align*} \Phi_N &=\begin{pmatrix} \Phi_{\rho}^{\otimes n} & 0 \\ \sum_{i=1}^m h_{\mathbf{v}_i} M_i & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]), \\ \Psi_N &=\begin{pmatrix} \Psi_{\rho}^{\otimes n} & 0 \\ (\sum_{i=1}^m g_{\mathbf{v}_i} M_i)\Psi_{\rho}^{\otimes n} & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb{T}). \end{align*} $$
Since this extension is trivial in
![]() $\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
, there exists a matrix
$\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
, there exists a matrix
 $$ \begin{align*} \gamma &=\begin{pmatrix} \text{Id}_2 & 0 \\ (\gamma_1,\gamma_2) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]) \end{align*} $$
$$ \begin{align*} \gamma &=\begin{pmatrix} \text{Id}_2 & 0 \\ (\gamma_1,\gamma_2) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\overline K[t]) \end{align*} $$
such that
![]() $\gamma ^{(-1)} \Phi _N=\text {diag}(\Phi _{\rho }^{\otimes n},1) \gamma $
. By [Reference Papanikolas47], Section 4.1.6, there exists
$\gamma ^{(-1)} \Phi _N=\text {diag}(\Phi _{\rho }^{\otimes n},1) \gamma $
. By [Reference Papanikolas47], Section 4.1.6, there exists
 $$ \begin{align*} \delta &=\begin{pmatrix} \text{Id}_2 & 0 \\ (\delta_1,\delta_2) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb F_q(t)) \end{align*} $$
$$ \begin{align*} \delta &=\begin{pmatrix} \text{Id}_2 & 0 \\ (\delta_1,\delta_2) & 1 \end{pmatrix} \in \operatorname{\mathrm{Mat}}_{3 \times 3}(\mathbb F_q(t)) \end{align*} $$
such that
![]() $\gamma \Psi _N=\text {diag}(\Psi _{\rho }^{\otimes n},1) \delta $
. It follows that
$\gamma \Psi _N=\text {diag}(\Psi _{\rho }^{\otimes n},1) \delta $
. It follows that
 $$\begin{align*}(\gamma_1,\gamma_2)+(\sum_{i=1}^m g_{\mathbf{v}_i} M_i)=(\delta_1,\delta_2) (\Psi_{\rho}^{\otimes n})^{-1}.\end{align*}$$
$$\begin{align*}(\gamma_1,\gamma_2)+(\sum_{i=1}^m g_{\mathbf{v}_i} M_i)=(\delta_1,\delta_2) (\Psi_{\rho}^{\otimes n})^{-1}.\end{align*}$$
Specializing the first coordinates at
![]() $t=\theta $
and recalling that by Lemma 2.6, we have
$t=\theta $
and recalling that by Lemma 2.6, we have
![]() $(M_i)_2(\theta ) \in K^{\times }$
and
$(M_i)_2(\theta ) \in K^{\times }$
and
![]() $(M_i)_{2,1}(\theta )=0$
, we obtain
$(M_i)_{2,1}(\theta )=0$
, we obtain
 $$\begin{align*}\gamma_1(\theta)+\sum_{i=1}^m g_{\mathbf{v}_i,1}(\theta) (M_i)_2(\theta)=\delta_1(\theta) [(\Psi_{\rho}^{\otimes n})^{-1}]_2(\theta)+\delta_2(\theta) [(\Psi_{\rho}^{\otimes n})^{-1}]_{2,1}(\theta).\end{align*}$$
$$\begin{align*}\gamma_1(\theta)+\sum_{i=1}^m g_{\mathbf{v}_i,1}(\theta) (M_i)_2(\theta)=\delta_1(\theta) [(\Psi_{\rho}^{\otimes n})^{-1}]_2(\theta)+\delta_2(\theta) [(\Psi_{\rho}^{\otimes n})^{-1}]_{2,1}(\theta).\end{align*}$$
By Lemma 3.3, we have
![]() $g_{\mathbf {v}_i,1}(\theta )=\mathbf {u}_{i,n}-\mathbf {v}_{i,n}$
and
$g_{\mathbf {v}_i,1}(\theta )=\mathbf {u}_{i,n}-\mathbf {v}_{i,n}$
and
![]() $[(\Psi _{\rho }^{\otimes n})^{-1}]_2(\theta ),[(\Psi _{\rho }^{\otimes n})^{-1}]_{2,1}(\theta ) \in K \pi _{\rho }^n$
. Since
$[(\Psi _{\rho }^{\otimes n})^{-1}]_2(\theta ),[(\Psi _{\rho }^{\otimes n})^{-1}]_{2,1}(\theta ) \in K \pi _{\rho }^n$
. Since
![]() $(M_i)_2(\theta ) \in K^{\times }$
(see Section 2.4), we get a nontrivial
$(M_i)_2(\theta ) \in K^{\times }$
(see Section 2.4), we get a nontrivial
![]() $\overline K$
-linear relation between
$\overline K$
-linear relation between
![]() $1, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}, \pi _{\rho }^n$
. By [Reference Green33], page 29 (proof of Theorem 7.1), it implies a nontrivial K-linear relation between
$1, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}, \pi _{\rho }^n$
. By [Reference Green33], page 29 (proof of Theorem 7.1), it implies a nontrivial K-linear relation between
![]() $\mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}, \pi _{\rho }^n$
. Thus, we get a contradiction.
$\mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}, \pi _{\rho }^n$
. Thus, we get a contradiction.
3.6 An application of Hardouin’s work
We now apply Hardouin’s work to our context to determine the Galois groups of the t-motives defined in the previous sections. We work with the neutral Tannakian category of t-motives
![]() $\mathcal T$
over
$\mathcal T$
over
![]() $F=\mathbb F_q(t)$
defined in §1.6 endowed with the fiber functor
$F=\mathbb F_q(t)$
defined in §1.6 endowed with the fiber functor
![]() $\omega :M \mapsto H_{\text {Betti}}(M)$
. By the proof of [Reference Green33], Lemma 7.2, we know that
$\omega :M \mapsto H_{\text {Betti}}(M)$
. By the proof of [Reference Green33], Lemma 7.2, we know that
![]() $\mathcal {X}^{\otimes n}_{\rho }$
is irreducible. Then we consider this irreducible object
$\mathcal {X}^{\otimes n}_{\rho }$
is irreducible. Then we consider this irreducible object
![]() $\mathcal Y=\mathcal {X}^{\otimes n}_{\rho }$
and extensions of
$\mathcal Y=\mathcal {X}^{\otimes n}_{\rho }$
and extensions of
![]() $\mathbf 1$
by
$\mathbf 1$
by
![]() $\mathcal {X}^{\otimes n}_{\rho }$
. Hardouin’s work turns out to be a powerful tool and allows us to prove the proposition below which generalizes the results of Papanikolas [Reference Papanikolas47] (for the Carlitz module C) and Chang-Yu [Reference Chang and Yu23] (for the tensor powers
$\mathcal {X}^{\otimes n}_{\rho }$
. Hardouin’s work turns out to be a powerful tool and allows us to prove the proposition below which generalizes the results of Papanikolas [Reference Papanikolas47] (for the Carlitz module C) and Chang-Yu [Reference Chang and Yu23] (for the tensor powers
![]() $C^{\otimes n}$
of the Carlitz module).
$C^{\otimes n}$
of the Carlitz module).
Proposition 3.11. Let
![]() $n \geq 1$
be an integer with
$n \geq 1$
be an integer with
![]() $(q-1)\nmid n$
and b be an element in B. Then the unipotent radical of
$(q-1)\nmid n$
and b be an element in B. Then the unipotent radical of
![]() $\Gamma _{\mathcal {X}_n(b)}$
is equal to the
$\Gamma _{\mathcal {X}_n(b)}$
is equal to the
![]() $\mathbb F_q(t)$
-vector space
$\mathbb F_q(t)$
-vector space
![]() $\mathbb F_q(t)^2$
of dimension 2. In particular,
$\mathbb F_q(t)^2$
of dimension 2. In particular,
Proof. We claim that the assumptions of Theorem 1.16 are satisfied for the t-motive
![]() $\mathcal {X}^{\otimes n}_{\rho }$
since
$\mathcal {X}^{\otimes n}_{\rho }$
since
-
1. By Proposition 2.3, the Galois group
 $\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
of
$\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
of
 $\mathcal {X}^{\otimes n}_{\rho }$
is a torus. Thus
$\mathcal {X}^{\otimes n}_{\rho }$
is a torus. Thus
 $\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
is completely reducible (compare to [Reference Chang and Papanikolas19], Corollary 3.5.7).
$\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
is completely reducible (compare to [Reference Chang and Papanikolas19], Corollary 3.5.7). -
2. It is clear that the center of
 $\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
contains
$\Gamma _{\mathcal {X}_{\rho }^{\otimes n}}$
contains
 $\mathbb {G}_{m,\mathbb F_q(t)}$
.
$\mathbb {G}_{m,\mathbb F_q(t)}$
. -
3. The action of
 $\mathbb {G}_{m,\mathbb F_q(t)}$
on
$\mathbb {G}_{m,\mathbb F_q(t)}$
on
 $H_{\text {Betti}}(\mathcal {X}^{\otimes n}_{\rho })$
is isotypic. In fact, the weights are all equal to n.
$H_{\text {Betti}}(\mathcal {X}^{\otimes n}_{\rho })$
is isotypic. In fact, the weights are all equal to n. -
4. The Galois groups of t-motives are reduced (see [Reference Papanikolas47] and also [Reference Hartl, Juschka, Böckle, Goss, Hartl and Papanikolas38], Proposition 2.6.2 for A-motives).
We apply Theorem 1.16 to the t-motive
![]() $\mathcal {X}_n(b)$
which is an extension of
$\mathcal {X}_n(b)$
which is an extension of
![]() $\mathbf {1}$
by
$\mathbf {1}$
by
![]() $\mathcal {X}^{\otimes n}_{\rho }$
. Thus there exists a sub-object
$\mathcal {X}^{\otimes n}_{\rho }$
. Thus there exists a sub-object
![]() $\mathcal {V}$
of
$\mathcal {V}$
of
![]() $\mathcal {X}^{\otimes n}_{\rho }$
such that
$\mathcal {X}^{\otimes n}_{\rho }$
such that
![]() $\mathcal {X}_n(b)/\mathcal {V}$
is a trivial extension of
$\mathcal {X}_n(b)/\mathcal {V}$
is a trivial extension of
![]() $\mathbf {1}$
by
$\mathbf {1}$
by
![]() $\mathcal {X}^{\otimes n}_{\rho }/\mathcal {V}$
. As
$\mathcal {X}^{\otimes n}_{\rho }/\mathcal {V}$
. As
![]() $\mathcal {X}^{\otimes n}_{\rho }$
is irreducible, either
$\mathcal {X}^{\otimes n}_{\rho }$
is irreducible, either
![]() $\mathcal {V}=0$
or
$\mathcal {V}=0$
or
![]() $\mathcal {V}=\mathcal {X}^{\otimes n}_{\rho }$
.
$\mathcal {V}=\mathcal {X}^{\otimes n}_{\rho }$
.
We claim that
![]() $\mathcal {V}=\mathcal {X}^{\otimes n}_{\rho }$
. In fact, suppose that
$\mathcal {V}=\mathcal {X}^{\otimes n}_{\rho }$
. In fact, suppose that
![]() $\mathcal {V}=0$
. We deduce that
$\mathcal {V}=0$
. We deduce that
![]() $\mathcal {X}_n(b)$
is a trivial extension of
$\mathcal {X}_n(b)$
is a trivial extension of
![]() $\mathbf {1}$
by
$\mathbf {1}$
by
![]() $\mathcal {X}^{\otimes n}_{\rho }$
. It follows that
$\mathcal {X}^{\otimes n}_{\rho }$
. It follows that
![]() $\pi _{\rho }^n$
and
$\pi _{\rho }^n$
and
![]() $\zeta _{\rho }(b,n)$
are linearly dependent over K. We get a contradiction by Proposition 3.10 and Theorem 1.10.
$\zeta _{\rho }(b,n)$
are linearly dependent over K. We get a contradiction by Proposition 3.10 and Theorem 1.10.
Since
![]() $\mathcal {V}=\mathcal {X}^{\otimes n}_{\rho }$
, by Theorem 1.16, the unipotent radical of the Galois group
$\mathcal {V}=\mathcal {X}^{\otimes n}_{\rho }$
, by Theorem 1.16, the unipotent radical of the Galois group
![]() $\Gamma _{\mathcal {X}_n(b)}$
is equal to
$\Gamma _{\mathcal {X}_n(b)}$
is equal to
![]() $H_{\text {Betti}}(M)(\mathcal {X}^{\otimes n}_{\rho })$
that is an
$H_{\text {Betti}}(M)(\mathcal {X}^{\otimes n}_{\rho })$
that is an
![]() $\mathbb F_q[t]$
-vector space of dimension 2. The Theorem follows immediately.
$\mathbb F_q[t]$
-vector space of dimension 2. The Theorem follows immediately.
As a consequence, we obtain a generalization of [Reference Chang and Yu23], Theorem 4.4.
Corollary 3.12. Let
![]() $n \geq 1$
be an integer. Then for any
$n \geq 1$
be an integer. Then for any
![]() $b \in B$
, the quantities
$b \in B$
, the quantities
![]() $\pi _{\rho }$
and
$\pi _{\rho }$
and
![]() $\zeta _{\rho }( b,n)$
are algebraically independent over
$\zeta _{\rho }( b,n)$
are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
Proof. We find that
![]() $\overline K(\Psi _{\mathbf {v}}) = \overline K(\Upsilon _{\mathbf {v}})$
, where
$\overline K(\Psi _{\mathbf {v}}) = \overline K(\Upsilon _{\mathbf {v}})$
, where
![]() $\Upsilon _{\mathbf {v}}$
is defined in (3.3). Apriori, the field
$\Upsilon _{\mathbf {v}}$
is defined in (3.3). Apriori, the field
![]() $\overline K(\Upsilon _{\mathbf {v}})$
has 6 non-trivial generators given by evaluations of various Anderson generating functions. However, from Lemma 3.5 we see that
$\overline K(\Upsilon _{\mathbf {v}})$
has 6 non-trivial generators given by evaluations of various Anderson generating functions. However, from Lemma 3.5 we see that
![]() $\overline K(\Upsilon _{\mathbf {v}}) = \overline K(\pi _{\rho }^n,W_n,E_{\mathbf {u},1}(\theta ),E_{\mathbf {u},2}(\theta ))$
, where
$\overline K(\Upsilon _{\mathbf {v}}) = \overline K(\pi _{\rho }^n,W_n,E_{\mathbf {u},1}(\theta ),E_{\mathbf {u},2}(\theta ))$
, where
![]() $\mathbf {u} = Z_n(b)$
is the vector from Theorem 1.8. Finally, by Lemma 3.3 and Proposition 3.4, we conclude that for some
$\mathbf {u} = Z_n(b)$
is the vector from Theorem 1.8. Finally, by Lemma 3.3 and Proposition 3.4, we conclude that for some
![]() $Y_n\in \mathbb {C}_{\infty }$
, we have
$Y_n\in \mathbb {C}_{\infty }$
, we have
![]() $\overline K(\pi _{\rho }^n,W_n,E_{\mathbf {u},1}(\theta ),E_{\mathbf {u},2}(\theta )) = \overline K(\pi _{\rho }^n,W_n,\zeta _{\rho }(b,n),Y_n)$
. The corollary is then a direct consequence of Proposition 3.11 and Theorem 1.15.
$\overline K(\pi _{\rho }^n,W_n,E_{\mathbf {u},1}(\theta ),E_{\mathbf {u},2}(\theta )) = \overline K(\pi _{\rho }^n,W_n,\zeta _{\rho }(b,n),Y_n)$
. The corollary is then a direct consequence of Proposition 3.11 and Theorem 1.15.
We obtain the following theorem which could be considered as a partial generalization of [Reference Chang and Papanikolas19], Theorem 5.1.5 in our context.
Theorem 3.13. Suppose that
![]() $\mathbf {u}_1,\ldots ,\mathbf {u}_m \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
$\mathbf {u}_1,\ldots ,\mathbf {u}_m \in \operatorname {\mathrm {Mat}}_{n \times 1}(\mathbb C_{\infty })$
with
![]() $\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}_i)=\mathbf {v}_i \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
. If
$\operatorname {\mathrm {Exp}}_{\rho }^{\otimes n}(\mathbf {u}_i)=\mathbf {v}_i \in \operatorname {\mathrm {Mat}}_{n \times 1}(\overline K)$
. If
![]() $\pi ^n_{\rho }, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}$
are linearly independent over K, then they are algebraically independent over
$\pi ^n_{\rho }, \mathbf {u}_{1,n},\ldots ,\mathbf {u}_{m,n}$
are linearly independent over K, then they are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
Proof. By Proposition 3.10, we deduce that the classes of
![]() $\mathcal {X}_{\mathbf {v}_i} (1 \leq i \leq n)$
in
$\mathcal {X}_{\mathbf {v}_i} (1 \leq i \leq n)$
in
![]() $\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
are linearly independent over K. By Corollary 1.17, the unipotent part of the Galois group of the direct sum
$\text {Ext}^1_{\mathcal {T}}(\mathbf 1,\mathcal {X}_{\rho }^{\otimes n})$
are linearly independent over K. By Corollary 1.17, the unipotent part of the Galois group of the direct sum
![]() $\mathcal {X}_{\mathbf {v}_1} \oplus \ldots \oplus \mathcal {X}_{\mathbf {v}_n}$
is of dimension
$\mathcal {X}_{\mathbf {v}_1} \oplus \ldots \oplus \mathcal {X}_{\mathbf {v}_n}$
is of dimension
![]() $2n$
. Thus the Theorem follows immediately from Theorem 1.15.
$2n$
. Thus the Theorem follows immediately from Theorem 1.15.
4 Algebraic relations among Anderson’s zeta values
4.1 Direct sums of t-motives
Let
![]() $m \in \mathbb N, m \geq 1$
. To study Anderson’s zeta values
$m \in \mathbb N, m \geq 1$
. To study Anderson’s zeta values
![]() $\zeta _{\rho }(b,n)$
for
$\zeta _{\rho }(b,n)$
for
![]() $1 \leq n \leq m$
and
$1 \leq n \leq m$
and
![]() $\pi _{\rho }$
simultaneously, we set
$\pi _{\rho }$
simultaneously, we set
and consider the direct sum t-motive
and define block diagonal matrices
Then
![]() $\Phi (b)$
represents multiplication by
$\Phi (b)$
represents multiplication by
![]() $\sigma $
on
$\sigma $
on
![]() $\mathcal {X}(b)$
and
$\mathcal {X}(b)$
and
![]() $\Psi (b)$
is a rigid analytic trivialization of
$\Psi (b)$
is a rigid analytic trivialization of
![]() $\Phi (b)$
. We would like to understand the Galois group
$\Phi (b)$
. We would like to understand the Galois group
![]() $\Gamma _{\mathcal {X}(b)}$
of the t-motive
$\Gamma _{\mathcal {X}(b)}$
of the t-motive
![]() $\mathcal {X}(b)$
and to calculate the dimension of this Galois group.
$\mathcal {X}(b)$
and to calculate the dimension of this Galois group.
We first have
 $$\begin{align*}\Gamma_{\mathcal{X}(b)} \subseteq \bigoplus_{n \in \mathcal S} \Gamma_{\mathcal{X}_n(b)}=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \textrm{Res}_{K/\mathbb F_q[t]} \mathbb{G}_{m,K} & 0\\ * & 1 \end{pmatrix}\end{align*}$$
$$\begin{align*}\Gamma_{\mathcal{X}(b)} \subseteq \bigoplus_{n \in \mathcal S} \Gamma_{\mathcal{X}_n(b)}=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \textrm{Res}_{K/\mathbb F_q[t]} \mathbb{G}_{m,K} & 0\\ * & 1 \end{pmatrix}\end{align*}$$
For
![]() $n=1$
, the t-motive
$n=1$
, the t-motive
![]() $\mathcal {X}_1(b)$
contains
$\mathcal {X}_1(b)$
contains
![]() $\mathcal {X}_{\rho }$
. It follows that
$\mathcal {X}_{\rho }$
. It follows that
![]() $\mathcal {X}_{\rho }$
is also contained in
$\mathcal {X}_{\rho }$
is also contained in
![]() $\mathcal {X}(b)$
. We consider
$\mathcal {X}(b)$
. We consider
![]() $\mathcal T_{\mathcal {X}(b)}$
and
$\mathcal T_{\mathcal {X}(b)}$
and
![]() $\mathcal T_{\mathcal {X}_{\rho }}$
, the strictly full Tannakian subcategories of the category
$\mathcal T_{\mathcal {X}_{\rho }}$
, the strictly full Tannakian subcategories of the category
![]() $\mathcal T$
of t-motives which are generated by
$\mathcal T$
of t-motives which are generated by
![]() $\mathcal {X}(b)$
and
$\mathcal {X}(b)$
and
![]() $\mathcal {X}_{\rho }$
respectively. Thus we get a functor from
$\mathcal {X}_{\rho }$
respectively. Thus we get a functor from
![]() $\mathcal T_{\mathcal {X}_{\rho }}$
to
$\mathcal T_{\mathcal {X}_{\rho }}$
to
![]() $\mathcal T_{\mathcal {X}(b)}$
. By Tannakian duality, we have a surjective map of algebraic groups over
$\mathcal T_{\mathcal {X}(b)}$
. By Tannakian duality, we have a surjective map of algebraic groups over
![]() $\mathbb F_q(t)$
$\mathbb F_q(t)$
where we have the last equality by Proposition 2.3. By Equation (1.23), this map
![]() $\pi $
is in fact the projection on the upper left-most corner of elements of
$\pi $
is in fact the projection on the upper left-most corner of elements of
![]() $\Gamma _{\mathcal {X}(b)}$
. We denote by
$\Gamma _{\mathcal {X}(b)}$
. We denote by
![]() $U(b)$
the kernel of
$U(b)$
the kernel of
![]() $\pi $
. It follows that
$\pi $
. It follows that
![]() $U(b)$
is contained in the unipotent group
$U(b)$
is contained in the unipotent group
 $$\begin{align*}U:=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \text{Id}_2 & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
$$\begin{align*}U:=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \text{Id}_2 & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
We prove the following result similar to [Reference Chang and Yu23], Section 4.3.
Proposition 4.1. We keep the previous notation. Then we have
 $$\begin{align*}U(b)=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \textrm{Id}_2 & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
$$\begin{align*}U(b)=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \textrm{Id}_2 & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
Proof. In fact, the strategy of Chang-Yu (see [Reference Chang and Yu23], Section 4.3) based on a weight argument indeed carries over without much modification. For completeness, we sketch a proof of this Proposition.
We introduce a
![]() $\mathbb G_{m,\mathbb F_q(t)}$
-action on
$\mathbb G_{m,\mathbb F_q(t)}$
-action on
![]() $U(b)$
and on the direct sum of unipotent groups
$U(b)$
and on the direct sum of unipotent groups
 $$\begin{align*}U=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \textrm{Id}_2 & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
$$\begin{align*}U=\bigoplus_{n \in \mathcal S} \begin{pmatrix} \textrm{Id}_2 & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
On the matrix indexed by
![]() $n \in \mathcal S$
, it is defined by
$n \in \mathcal S$
, it is defined by
 $$\begin{align*}a \cdot \begin{pmatrix} \text{Id}_2 & 0\\ \mathbf u & 1 \end{pmatrix} \mapsto \begin{pmatrix} \text{Id}_2 & 0\\ a^n \mathbf u & 1 \end{pmatrix}, \quad a \in \mathbb G_{m,\mathbb F_q(t)}. \end{align*}$$
$$\begin{align*}a \cdot \begin{pmatrix} \text{Id}_2 & 0\\ \mathbf u & 1 \end{pmatrix} \mapsto \begin{pmatrix} \text{Id}_2 & 0\\ a^n \mathbf u & 1 \end{pmatrix}, \quad a \in \mathbb G_{m,\mathbb F_q(t)}. \end{align*}$$
Note that this action on
![]() $U(b)$
agrees with the conjugation of
$U(b)$
agrees with the conjugation of
![]() $\mathbb G_{m,\mathbb F_q(t)}$
on
$\mathbb G_{m,\mathbb F_q(t)}$
on
![]() $U(b)$
.
$U(b)$
.
For each
![]() $n \in \mathcal S$
, we recall that
$n \in \mathcal S$
, we recall that
 $$\begin{align*}\Gamma_{\mathcal{X}_n(b)}=\begin{pmatrix} \textrm{Res}_{K/\mathbb F_q[t]} \mathbb{G}_{m,K} & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
$$\begin{align*}\Gamma_{\mathcal{X}_n(b)}=\begin{pmatrix} \textrm{Res}_{K/\mathbb F_q[t]} \mathbb{G}_{m,K} & 0\\ * & 1 \end{pmatrix}.\end{align*}$$
We denote by
![]() $U_n(b)$
the unipotent part of this Galois group. Thus
$U_n(b)$
the unipotent part of this Galois group. Thus
 $$\begin{align*}U_n(b)=\begin{pmatrix} \text{Id}_2 & 0\\ * & 1 \end{pmatrix}\end{align*}$$
$$\begin{align*}U_n(b)=\begin{pmatrix} \text{Id}_2 & 0\\ * & 1 \end{pmatrix}\end{align*}$$
and we have a short exact sequence
Since
![]() $\mathcal {X}_n(b)$
is contained in
$\mathcal {X}_n(b)$
is contained in
![]() $\mathcal {X}(b)$
, by Tannakian duality, we obtain a commutative diagram
$\mathcal {X}(b)$
, by Tannakian duality, we obtain a commutative diagram

Here the middle vertical arrow is surjective by Tannakian duality and the map
![]() $\chi _n$
is the character
$\chi _n$
is the character
![]() $a \mapsto a^n$
. We deduce that the induced map
$a \mapsto a^n$
. We deduce that the induced map
![]() $U(b) \rightarrow U_n(b)$
is also surjective.
$U(b) \rightarrow U_n(b)$
is also surjective.
We suppose now that
![]() $U(b)$
is of codimension
$U(b)$
is of codimension
![]() $r>0$
in U. We identify U with the product
$r>0$
in U. We identify U with the product
Chang and Yu proved that there exist an integer
![]() $n \in \mathcal S$
and a set J of r double indices
$n \in \mathcal S$
and a set J of r double indices
![]() $ij$
with
$ij$
with
![]() $i \in \mathcal S$
and
$i \in \mathcal S$
and
![]() $j \in \{1,2\}$
such that if we denote by
$j \in \{1,2\}$
such that if we denote by
![]() $W_{(J)}$
the linear subspace of U of codimension r consisting of points
$W_{(J)}$
the linear subspace of U of codimension r consisting of points
![]() $(x_{ij})$
satisfying
$(x_{ij})$
satisfying
![]() $x_{ij}=0$
whenever
$x_{ij}=0$
whenever
![]() $ij \in J$
, then
$ij \in J$
, then
![]() $W_{(J)} \cap U_n(b) \subsetneq U_n(b)$
and the composed map
$W_{(J)} \cap U_n(b) \subsetneq U_n(b)$
and the composed map
is surjective.
Recall that for
![]() $k \in \mathcal S$
, the action of
$k \in \mathcal S$
, the action of
![]() $\mathbb G_{m,\mathbb F_q(t)}$
on
$\mathbb G_{m,\mathbb F_q(t)}$
on
![]() $U_k(b)$
is of weight k. Since
$U_k(b)$
is of weight k. Since
![]() $p \nmid n$
, by [Reference Chang and Yu23], Lemma 4.7,
$p \nmid n$
, by [Reference Chang and Yu23], Lemma 4.7,
![]() $f_n$
maps
$f_n$
maps
![]() $W_{(J)} \cap U_k(b)$
to zero for all
$W_{(J)} \cap U_k(b)$
to zero for all
![]() $k \neq n$
in
$k \neq n$
in
![]() $\mathcal S$
. Thus, it maps
$\mathcal S$
. Thus, it maps
![]() $W_{(J)} \cap U_n(b)$
onto
$W_{(J)} \cap U_n(b)$
onto
![]() $U_n(b)$
which has strictly greater dimension. We obtain a contradiction.
$U_n(b)$
which has strictly greater dimension. We obtain a contradiction.
As a consequence, we get
![]() $U(b)=U$
as required. The proof is complete.
$U(b)=U$
as required. The proof is complete.
4.2 Algebraic relations among Anderson’s zeta values
As an immediate consequence of Proposition 4.1, we see that the radical unipotent of
![]() $\Gamma _{\mathcal {X}(b)}$
has dimension
$\Gamma _{\mathcal {X}(b)}$
has dimension
![]() $2|\mathcal S|$
, and
$2|\mathcal S|$
, and
![]() $\Gamma _{\mathcal {X}(b)}$
itself has dimension
$\Gamma _{\mathcal {X}(b)}$
itself has dimension
![]() $2|\mathcal S|+2$
. By Theorem 1.15, we deduce the following theorem.
$2|\mathcal S|+2$
. By Theorem 1.15, we deduce the following theorem.
Theorem 4.2. Let
![]() $b \in B$
. Then the elements of the set
$b \in B$
. Then the elements of the set
are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
We present a slight generalization of the above theorem by taking account of the p-power relations. Let
![]() $\{b_1,\ldots ,b_h\}$
be a K-basis of H with
$\{b_1,\ldots ,b_h\}$
be a K-basis of H with
![]() $b_i \in B$
. Since the extension
$b_i \in B$
. Since the extension
![]() $H/K$
is separable, it follows that for any
$H/K$
is separable, it follows that for any
![]() $b \in B$
, we can write
$b \in B$
, we can write
![]() $b=a_1 b_1^{p^m} + \ldots + a_h b_h^{p^m}$
with
$b=a_1 b_1^{p^m} + \ldots + a_h b_h^{p^m}$
with
![]() $a_1,\ldots ,a_h \in K$
. Thus, we get
$a_1,\ldots ,a_h \in K$
. Thus, we get
 $$ \begin{align*} \zeta_{\rho}(b,p^m n) =\sum_{I \subseteq A} \frac{\sigma_I(b)}{u_I^{p^m n}} =\sum_{i=1}^h a_i \left( \sum_{I \subseteq A} \frac{\sigma_I(b_i)}{u_I^n} \right)^{p^m} =\sum_{i=1}^h a_i \zeta_{\rho}(b_i,n)^{p^m}. \end{align*} $$
$$ \begin{align*} \zeta_{\rho}(b,p^m n) =\sum_{I \subseteq A} \frac{\sigma_I(b)}{u_I^{p^m n}} =\sum_{i=1}^h a_i \left( \sum_{I \subseteq A} \frac{\sigma_I(b_i)}{u_I^n} \right)^{p^m} =\sum_{i=1}^h a_i \zeta_{\rho}(b_i,n)^{p^m}. \end{align*} $$
Theorem 4.3. Let
![]() $\{b_1,\ldots ,b_h\}$
be a K-basis of H with
$\{b_1,\ldots ,b_h\}$
be a K-basis of H with
![]() $b_i \in B$
. We consider the set
$b_i \in B$
. We consider the set
Then the elements of
![]() $\mathcal A$
are algebraically independent over
$\mathcal A$
are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
5 Algebraic relations among Goss’s zeta values
In this section, we investigate algebraic relations among Goss’s zeta values. This section owes its very existence to B. Anglès. In particular, the proofs of Proposition 5.2 and Corollary 5.4 are due to him. For more details about the theory of L series and Goss’s zeta values, we refer the interested reader to [Reference Goss32], Section 8.
5.1 Goss’s map
We set
![]() $\pi :=t/y$
, which is a uniformizer of
$\pi :=t/y$
, which is a uniformizer of
![]() $K_{\infty }$
. Set
$K_{\infty }$
. Set
![]() $\pi _1=\pi $
, and for
$\pi _1=\pi $
, and for
![]() $n\geq 2$
, choose
$n\geq 2$
, choose
![]() $\pi _n\in \overline {K}_{\infty }^{\times }$
such that
$\pi _n\in \overline {K}_{\infty }^{\times }$
such that
![]() $\pi _n^n=\pi _{n-1}$
. If
$\pi _n^n=\pi _{n-1}$
. If
![]() $z\in \mathbb Q$
,
$z\in \mathbb Q$
,
![]() $z=\frac {m}{n!}$
for some
$z=\frac {m}{n!}$
for some
![]() $m\in \mathbb Z, n\geq 1$
, we set
$m\in \mathbb Z, n\geq 1$
, we set
Let
![]() $\overline {\mathbb F}_q$
be the algebraic closure of
$\overline {\mathbb F}_q$
be the algebraic closure of
![]() $\mathbb F_q$
in
$\mathbb F_q$
in
![]() $\overline {K}_{\infty }$
and let
$\overline {K}_{\infty }$
and let
Then
![]() $\overline {K}_{\infty }^{\times }= \pi ^{\mathbb Q}\times \overline {\mathbb F}_q^{\times }\times U_{\infty }$
. Therefore, if
$\overline {K}_{\infty }^{\times }= \pi ^{\mathbb Q}\times \overline {\mathbb F}_q^{\times }\times U_{\infty }$
. Therefore, if
![]() $x\in \overline {K}_{\infty }^{\times }$
, one can write in a unique way
$x\in \overline {K}_{\infty }^{\times }$
, one can write in a unique way
Let
![]() $I\in \mathcal I(A)$
. Then there exists an integer
$I\in \mathcal I(A)$
. Then there exists an integer
![]() $h \geq 1$
such that
$h \geq 1$
such that
![]() $I^h=xA, \ x\in K^{\times }$
. We set
$I^h=xA, \ x\in K^{\times }$
. We set
![]() $\langle I \rangle := \langle x \rangle ^{\frac {1}{h}}\in U_{\infty }$
. Then one shows (see [Reference Goss32], Section 8.2) that the map called Goss’s map
$\langle I \rangle := \langle x \rangle ^{\frac {1}{h}}\in U_{\infty }$
. Then one shows (see [Reference Goss32], Section 8.2) that the map called Goss’s map
 $$ \begin{align*} [\cdot]_A: \mathcal I(A) &\rightarrow \overline{K}_{\infty}^{\times} \\ I &\mapsto \langle I \rangle\pi^{-\frac{\deg I}{d_{\infty}}} \end{align*} $$
$$ \begin{align*} [\cdot]_A: \mathcal I(A) &\rightarrow \overline{K}_{\infty}^{\times} \\ I &\mapsto \langle I \rangle\pi^{-\frac{\deg I}{d_{\infty}}} \end{align*} $$
is a group homomorphism such that
Observe that for all
![]() $I\in \mathcal I(A)$
, we have
$I\in \mathcal I(A)$
, we have
![]() $\operatorname {\mathrm {sgn}} \left ([I]_A\right )=1$
.
$\operatorname {\mathrm {sgn}} \left ([I]_A\right )=1$
.
Let
![]() $E/K$
be a finite extension and let
$E/K$
be a finite extension and let
![]() $O_E$
be the integral closure of A in E. Let
$O_E$
be the integral closure of A in E. Let
![]() $\mathcal I(O_E)$
be the group of non-zero fractional ideals of
$\mathcal I(O_E)$
be the group of non-zero fractional ideals of
![]() $O_E$
. We denote by
$O_E$
. We denote by
![]() $N_{E/K}: \mathcal I(O_E)\rightarrow \mathcal I(A)$
the group homomorphism such that if
$N_{E/K}: \mathcal I(O_E)\rightarrow \mathcal I(A)$
the group homomorphism such that if
![]() $\frak P$
is a maximal ideal of
$\frak P$
is a maximal ideal of
![]() $O_E$
and
$O_E$
and
![]() $P=\frak P\cap A$
, we have
$P=\frak P\cap A$
, we have
Note that if
![]() $\frak P=xO_E, x\in E^{\times }$
, then
$\frak P=xO_E, x\in E^{\times }$
, then
![]() $N_{E/K} (\frak P) =N_{E/K} (x)A$
, where
$N_{E/K} (\frak P) =N_{E/K} (x)A$
, where
![]() $N_{E/K}: E\rightarrow K$
also denotes the usual norm map.
$N_{E/K}: E\rightarrow K$
also denotes the usual norm map.
5.2 Goss’s zeta functions and Goss’s zeta values
We recall the definition of Goss’s zeta functions introduced in [Reference Goss32], Chapter 8. Let
![]() $\mathbb S_{\infty }=\mathbb C_{\infty }^{\times } \times \mathbb Z_p$
be the Goss ‘complex plane’. The group action of
$\mathbb S_{\infty }=\mathbb C_{\infty }^{\times } \times \mathbb Z_p$
be the Goss ‘complex plane’. The group action of
![]() $\mathbb S_{\infty }$
is written additively. Let
$\mathbb S_{\infty }$
is written additively. Let
![]() $I\in \mathcal I(A)$
and
$I\in \mathcal I(A)$
and
![]() $s=(x;y)\in \mathbb S_{\infty }$
; we set
$s=(x;y)\in \mathbb S_{\infty }$
; we set
We have a natural injective group homomorphism:
![]() $\mathbb Z\rightarrow \mathbb S_{\infty }, j\mapsto s_j=\left (\pi ^{-\frac {j}{d_{\infty }}},j\right )$
. Observe that
$\mathbb Z\rightarrow \mathbb S_{\infty }, j\mapsto s_j=\left (\pi ^{-\frac {j}{d_{\infty }}},j\right )$
. Observe that
![]() $I^{s_j}=[I]^j_A$
.
$I^{s_j}=[I]^j_A$
.
Let
![]() $E/K$
be a finite extension and let
$E/K$
be a finite extension and let
![]() $O_E$
be the integral closure of A in E. Let
$O_E$
be the integral closure of A in E. Let
![]() $\frak I$
be a non-zero ideal of E. We have
$\frak I$
be a non-zero ideal of E. We have
 $$\begin{align*}\forall j\in \mathbb Z, \quad N_{E/K}(\frak I)^{s_j}=\left[\frac{O_E}{\frak I}\right]_A^j. \end{align*}$$
$$\begin{align*}\forall j\in \mathbb Z, \quad N_{E/K}(\frak I)^{s_j}=\left[\frac{O_E}{\frak I}\right]_A^j. \end{align*}$$
Letting
![]() $s\in \mathbb S_{\infty }$
, the following sum converges in
$s\in \mathbb S_{\infty }$
, the following sum converges in
![]() $\mathbb C_{\infty }$
(see [Reference Goss32], Theorem 8.9.2):
$\mathbb C_{\infty }$
(see [Reference Goss32], Theorem 8.9.2):
 $$\begin{align*}\zeta_{O_E}(s):=\sum_{d \geq 0} \sum_{\substack{\frak I\in \mathcal I(O_E), \frak I\subset O_E, \\ \deg(N_{E/K}(\frak I))=d}} N_{E/K}(\frak I)^{-s}. \end{align*}$$
$$\begin{align*}\zeta_{O_E}(s):=\sum_{d \geq 0} \sum_{\substack{\frak I\in \mathcal I(O_E), \frak I\subset O_E, \\ \deg(N_{E/K}(\frak I))=d}} N_{E/K}(\frak I)^{-s}. \end{align*}$$
The function
![]() $\zeta _{O_E}:\mathbb S_{\infty }\rightarrow \mathbb C_{\infty }$
is called the zeta function attached to
$\zeta _{O_E}:\mathbb S_{\infty }\rightarrow \mathbb C_{\infty }$
is called the zeta function attached to
![]() $O_E$
and
$O_E$
and
![]() $[\cdot ]_A$
. Observe that
$[\cdot ]_A$
. Observe that
 $$\begin{align*}\forall j\in \mathbb Z, \quad \zeta_{O_E}(j):= \zeta_{O_E}(s_j)=\sum_{d\geq 0} \sum_{\substack{\frak I\in \mathcal I(O_E), \frak I\subset O_E,\\ \deg(N_{E/K}(\frak I))=d}} \left[\frac{O_E}{\frak I}\right]_A^{-j}. \end{align*}$$
$$\begin{align*}\forall j\in \mathbb Z, \quad \zeta_{O_E}(j):= \zeta_{O_E}(s_j)=\sum_{d\geq 0} \sum_{\substack{\frak I\in \mathcal I(O_E), \frak I\subset O_E,\\ \deg(N_{E/K}(\frak I))=d}} \left[\frac{O_E}{\frak I}\right]_A^{-j}. \end{align*}$$
In particular,
 $$\begin{align*}\zeta_{O_E}(1)=\prod_{\frak P} \left(1-\frac{1}{\left[\frac{O_E}{\frak P}\right]_A}\right)^{-1}\in \overline{K}_{\infty}^{\times}, \end{align*}$$
$$\begin{align*}\zeta_{O_E}(1)=\prod_{\frak P} \left(1-\frac{1}{\left[\frac{O_E}{\frak P}\right]_A}\right)^{-1}\in \overline{K}_{\infty}^{\times}, \end{align*}$$
where
![]() $\frak P$
runs through the maximal ideals of
$\frak P$
runs through the maximal ideals of
![]() $O_E$
.
$O_E$
.
Recall that
![]() $\rho : A\rightarrow B\{\tau \}$
is the sign-normalized rank one Drinfeld module given in Section 1.3, where B is the integral closure of A in H, the Hilbert class field. By [Reference Anglès, Dac and Tavares Ribeiro6], Proposition 2.1, the following product converges to an element in
$\rho : A\rightarrow B\{\tau \}$
is the sign-normalized rank one Drinfeld module given in Section 1.3, where B is the integral closure of A in H, the Hilbert class field. By [Reference Anglès, Dac and Tavares Ribeiro6], Proposition 2.1, the following product converges to an element in
![]() $U_{\infty } \cap K_{\infty }^{\times }$
:
$U_{\infty } \cap K_{\infty }^{\times }$
:
 $$\begin{align*}L_A(\rho/O_E):= \prod_{\frak P} \frac{[\text{Fitt}_A(O_E/\frak P]_A}{[\text{Fitt}_A(\rho(O_E/\frak P))]_A},\end{align*}$$
$$\begin{align*}L_A(\rho/O_E):= \prod_{\frak P} \frac{[\text{Fitt}_A(O_E/\frak P]_A}{[\text{Fitt}_A(\rho(O_E/\frak P))]_A},\end{align*}$$
where
![]() $\frak P$
runs through the maximal ideals of
$\frak P$
runs through the maximal ideals of
![]() $O_E$
.
$O_E$
.
We have the following crucial fact (see [Reference Anglès, Dac and Tavares Ribeiro6], Proposition 3.4) which provides a deep connection between the special L-values and the Goss’s zeta value at
![]() $1$
.
$1$
.
Proposition 5.1. Let
![]() $E/K$
be a finite extension such that
$E/K$
be a finite extension such that
![]() $H\subset E$
. Then
$H\subset E$
. Then
5.3 Relations with Anderson’s zeta values
Recall that B is the integral closure of A in H, the Hilbert class field of K. Let z be an indeterminate over
![]() $K_{\infty }$
and recall that
$K_{\infty }$
and recall that
![]() $\mathbb T_z(K_{\infty })$
denotes the Tate algebra in the variable z with coefficients in
$\mathbb T_z(K_{\infty })$
denotes the Tate algebra in the variable z with coefficients in
![]() $K_{\infty }$
. Recall that
$K_{\infty }$
. Recall that
For
![]() $n\in \mathbb Z$
, we set
$n\in \mathbb Z$
, we set
 $$\begin{align*}Z_{B}(n;z)=\sum_{d \geq 0} \sum_{\substack{\frak I\in \mathcal I(B), \frak I\subset B,\\ \deg(N_{H/K}(\frak I))=d}} \left[\frac{B}{\frak I}\right]_A^{-n} z^d. \end{align*}$$
$$\begin{align*}Z_{B}(n;z)=\sum_{d \geq 0} \sum_{\substack{\frak I\in \mathcal I(B), \frak I\subset B,\\ \deg(N_{H/K}(\frak I))=d}} \left[\frac{B}{\frak I}\right]_A^{-n} z^d. \end{align*}$$
Then, by [Reference Goss32], Theorem 8.9.2, for all
![]() $n\in \mathbb Z, \ Z_B(n;.)$
defines an entire function on
$n\in \mathbb Z, \ Z_B(n;.)$
defines an entire function on
![]() $\mathbb C_{\infty }$
, and
$\mathbb C_{\infty }$
, and
Observe that
and
 $$\begin{align*}\forall n\geq 1, \quad Z_B(n; z)=\prod_{\frak P} \left(1-\frac {z^{\deg(N_{H/K}(\frak P))}}{\left[\frac{B}{\frak P}\right]^n_A}\right)^{-1}\in \mathbb T_z(K_{\infty})^{\times}. \end{align*}$$
$$\begin{align*}\forall n\geq 1, \quad Z_B(n; z)=\prod_{\frak P} \left(1-\frac {z^{\deg(N_{H/K}(\frak P))}}{\left[\frac{B}{\frak P}\right]^n_A}\right)^{-1}\in \mathbb T_z(K_{\infty})^{\times}. \end{align*}$$
Finally, we note that
Recall that
![]() $G=\mathrm {Gal}(H/K)$
. Then
$G=\mathrm {Gal}(H/K)$
. Then
![]() $G\simeq \mathrm {Gal}(H(z)/K(z))$
acts on
$G\simeq \mathrm {Gal}(H(z)/K(z))$
acts on
![]() $\mathbb T_z(H_{\infty })$
. We denote by
$\mathbb T_z(H_{\infty })$
. We denote by
![]() $\mathbb T_z(H_{\infty })[G]$
the non-commutative group ring where the commutation rule is given by
$\mathbb T_z(H_{\infty })[G]$
the non-commutative group ring where the commutation rule is given by
Let
![]() $n\in \mathbb Z$
. One can show (see [Reference Anglès, Dac and Tavares Ribeiro6], Lemma 3.5) that the following infinite sum converges in
$n\in \mathbb Z$
. One can show (see [Reference Anglès, Dac and Tavares Ribeiro6], Lemma 3.5) that the following infinite sum converges in
![]() $\mathbb T_z({H}_{\infty })[G]$
:
$\mathbb T_z({H}_{\infty })[G]$
:
 $$\begin{align*}\mathcal L(\rho/B; n; z):=\sum_{d \geq 0} \sum_{\substack{I\in \mathcal I(A) , I\subset A,\\ \deg I=d}} \frac{z^{\deg I}}{\psi(I)^n} \sigma_I. \end{align*}$$
$$\begin{align*}\mathcal L(\rho/B; n; z):=\sum_{d \geq 0} \sum_{\substack{I\in \mathcal I(A) , I\subset A,\\ \deg I=d}} \frac{z^{\deg I}}{\psi(I)^n} \sigma_I. \end{align*}$$
Furthermore, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$\begin{align*}\mathcal L(\rho/B; n; z)=\prod_{P} \left(1-\frac{z^{\deg P}}{\psi(P)^n}\sigma_P\right)^{-1}\in \left(\mathbb T_z(H_{\infty})[G]\right)^{\times} \end{align*}$$
$$\begin{align*}\mathcal L(\rho/B; n; z)=\prod_{P} \left(1-\frac{z^{\deg P}}{\psi(P)^n}\sigma_P\right)^{-1}\in \left(\mathbb T_z(H_{\infty})[G]\right)^{\times} \end{align*}$$
and for all
![]() $n\leq 0$
,
$n\leq 0$
,
Note that
We observe that
![]() $\mathcal L(\rho /B; n; z)$
induces a
$\mathcal L(\rho /B; n; z)$
induces a
![]() $\mathbb T_z(K_{\infty })$
-linear map
$\mathbb T_z(K_{\infty })$
-linear map
![]() $\mathcal L(\rho /B; n; z): \mathbb T_z(H_{\infty })\rightarrow \mathbb T_z(H_{\infty })$
. Since
$\mathcal L(\rho /B; n; z): \mathbb T_z(H_{\infty })\rightarrow \mathbb T_z(H_{\infty })$
. Since
![]() $\mathbb T_z(H_{\infty })$
is a free
$\mathbb T_z(H_{\infty })$
is a free
![]() $\mathbb T_z(K_{\infty })$
-module of rank
$\mathbb T_z(K_{\infty })$
-module of rank
![]() $[H:K]$
(recall that
$[H:K]$
(recall that
![]() $\mathbb T_z(K_{\infty })$
is a principal ideal domain),
$\mathbb T_z(K_{\infty })$
is a principal ideal domain),
![]() $\det _{\mathbb T_z(K_{\infty })}\mathcal L(\rho /B; n; z)$
is well-defined. We also observe that
$\det _{\mathbb T_z(K_{\infty })}\mathcal L(\rho /B; n; z)$
is well-defined. We also observe that
![]() $\zeta _{\rho }(.,n)$
induces a
$\zeta _{\rho }(.,n)$
induces a
![]() $K_{\infty }$
-linear map
$K_{\infty }$
-linear map
![]() $\zeta _{\rho }(.,n): H_{\infty }\rightarrow H_{\infty }$
, and we denote by
$\zeta _{\rho }(.,n): H_{\infty }\rightarrow H_{\infty }$
, and we denote by
![]() $\det _{K_{\infty }} \zeta _{\rho }(.,n)$
its determinant. Recall that
$\det _{K_{\infty }} \zeta _{\rho }(.,n)$
its determinant. Recall that
![]() $\operatorname {\mathrm {ev}}: \mathbb T_z(H_{\infty })\rightarrow H_{\infty }$
is the
$\operatorname {\mathrm {ev}}: \mathbb T_z(H_{\infty })\rightarrow H_{\infty }$
is the
![]() $H_{\infty }$
-linear map given by
$H_{\infty }$
-linear map given by
Observe that if
![]() $\{e_1, \ldots , e_h\}$
is a K-basis of
$\{e_1, \ldots , e_h\}$
is a K-basis of
![]() $H/K$
(recall that
$H/K$
(recall that
![]() $h=[H:K]$
), then
$h=[H:K]$
), then
We deduce that
By [Reference Anglès, Dac and Tavares Ribeiro6], Theorem 3.6, we have
In particular,
5.4 Algebraic relations among Goss’s zeta values
The class number
![]() $\text {Cl}(A)$
of A equals to the number of rational points
$\text {Cl}(A)$
of A equals to the number of rational points
![]() $X(\mathbb F_q)$
on the elliptic curve X and also to the degree of extension
$X(\mathbb F_q)$
on the elliptic curve X and also to the degree of extension
![]() $[H:K]$
. For a prime ideal
$[H:K]$
. For a prime ideal
![]() $\frak p$
of A of degree
$\frak p$
of A of degree
![]() $1$
corresponding to an
$1$
corresponding to an
![]() $\mathbb F_q$
-rational point on X, we denote by
$\mathbb F_q$
-rational point on X, we denote by
![]() $\mathfrak p_+$
the subset of elements in
$\mathfrak p_+$
the subset of elements in
![]() $\mathfrak p$
of sign
$\mathfrak p$
of sign
![]() $1$
and consider the sum (compare to [Reference Green and Papanikolas36], Section 6 and [Reference Green33], Section 6):
$1$
and consider the sum (compare to [Reference Green and Papanikolas36], Section 6 and [Reference Green33], Section 6):
 $$\begin{align*}\zeta_A(\frak p,n)=\sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}, \quad n \in \mathbb N. \end{align*}$$
$$\begin{align*}\zeta_A(\frak p,n)=\sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}, \quad n \in \mathbb N. \end{align*}$$
We will see that the sums
![]() $\zeta _A(\frak p,n)$
where
$\zeta _A(\frak p,n)$
where
![]() $\frak p$
runs through the set
$\frak p$
runs through the set
![]() $\mathcal P$
of prime ideals of A of degree 1 are the elementary blocks in the study of Goss’s zeta values on elliptic curves. For the rest of this section, it will be convenient to slightly modify these sums as follows.
$\mathcal P$
of prime ideals of A of degree 1 are the elementary blocks in the study of Goss’s zeta values on elliptic curves. For the rest of this section, it will be convenient to slightly modify these sums as follows.
Proposition 5.2. Let
![]() $n \in \mathbb N$
. For
$n \in \mathbb N$
. For
![]() $\sigma \in G=\operatorname {\mathrm {Gal}}(H/K)$
, we set
$\sigma \in G=\operatorname {\mathrm {Gal}}(H/K)$
, we set
 $$\begin{align*}\zeta_A(\sigma,n):= \sum_{d\geq 0} \sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \deg(I)=d, \\ \sigma_I=\sigma}} \frac{1}{[I]^n_A}. \end{align*}$$
$$\begin{align*}\zeta_A(\sigma,n):= \sum_{d\geq 0} \sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \deg(I)=d, \\ \sigma_I=\sigma}} \frac{1}{[I]^n_A}. \end{align*}$$
Then the elements
![]() $\zeta _A(\sigma ,n)$
indexed by
$\zeta _A(\sigma ,n)$
indexed by
![]() $\sigma \in G$
are algebraically independent over
$\sigma \in G$
are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
Proof. Let
![]() $\sigma \in \operatorname {\mathrm {Gal}}(H/K)$
and
$\sigma \in \operatorname {\mathrm {Gal}}(H/K)$
and
![]() $\frak p$
be the corresponding ideal in
$\frak p$
be the corresponding ideal in
![]() $\mathcal P$
such that
$\mathcal P$
such that
![]() $\sigma _{\frak p}=\sigma $
. We get
$\sigma _{\frak p}=\sigma $
. We get
 $$\begin{align*}\zeta_A(\sigma,n) = \sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \sigma_I=\sigma}} \frac{1}{[I]^n_A} =\frac{1}{[\frak p]^n_A} \sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}=\frac{1}{[\frak p]^n_A} \zeta_A(\frak p,n), \end{align*}$$
$$\begin{align*}\zeta_A(\sigma,n) = \sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \sigma_I=\sigma}} \frac{1}{[I]^n_A} =\frac{1}{[\frak p]^n_A} \sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}=\frac{1}{[\frak p]^n_A} \zeta_A(\frak p,n), \end{align*}$$
and
 $$\begin{align*}\sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \sigma_I=\sigma}} \frac{1}{\psi(I)^n} =\frac{1}{\psi(\mathfrak{p})^n} \sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}=\frac{1}{\psi(\mathfrak{p})^n} \zeta_A(\frak p,n). \end{align*}$$
$$\begin{align*}\sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \sigma_I=\sigma}} \frac{1}{\psi(I)^n} =\frac{1}{\psi(\mathfrak{p})^n} \sum_{\substack{a \in \mathfrak{p}^{-1},\\ \operatorname{\mathrm{sgn}}(a)=1}} \frac{1}{a^n}=\frac{1}{\psi(\mathfrak{p})^n} \zeta_A(\frak p,n). \end{align*}$$
Thus, we obtain
 $$\begin{align*}\zeta_A(\sigma,n) = \frac{\psi(\mathfrak{p})^n}{[\mathfrak{p}]^n_A} \sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \sigma_I=\sigma}} \frac{1}{\psi(I)^n}. \end{align*}$$
$$\begin{align*}\zeta_A(\sigma,n) = \frac{\psi(\mathfrak{p})^n}{[\mathfrak{p}]^n_A} \sum_{\substack{I\in \mathcal I(A), I\subset A,\\ \sigma_I=\sigma}} \frac{1}{\psi(I)^n}. \end{align*}$$
Note that
![]() $\frac {\psi (\mathfrak {p})^n}{[\mathfrak {p}]^n}$
belongs to
$\frac {\psi (\mathfrak {p})^n}{[\mathfrak {p}]^n}$
belongs to
![]() $\overline K^{\times }$
. It follows that for
$\overline K^{\times }$
. It follows that for
![]() $b \in B$
, we can express
$b \in B$
, we can express
with some coefficients
![]() $a_{\sigma }(b) \in \overline K$
.
$a_{\sigma }(b) \in \overline K$
.
By Theorem 4.3, if
![]() $\{b_1,\ldots ,b_h\} \subset B$
is a K-basis of H, then the elements
$\{b_1,\ldots ,b_h\} \subset B$
is a K-basis of H, then the elements
![]() $\zeta _{\rho }(b_i,n)\ (1 \leq i \leq h)$
are algebraically independent over
$\zeta _{\rho }(b_i,n)\ (1 \leq i \leq h)$
are algebraically independent over
![]() $\overline K$
. By the above discussion and the fact that
$\overline K$
. By the above discussion and the fact that
the Proposition follows immediately.
Let U be the p-Sylow subgroup of G where p is the characteristic of
![]() $\mathbb F_q$
. We set
$\mathbb F_q$
. We set
![]() $\Delta :=G/U=\mathrm {Gal}(F/K)$
where
$\Delta :=G/U=\mathrm {Gal}(F/K)$
where
![]() $F=H^{U}$
. We write
$F=H^{U}$
. We write
![]() $p^s=|U|$
and set
$p^s=|U|$
and set
with
![]() $|\Delta | \in \mathbb Z_p^{\times }$
.
$|\Delta | \in \mathbb Z_p^{\times }$
.
For
![]() $\delta \in \Delta ,$
we set
$\delta \in \Delta ,$
we set
 $$\begin{align*}Z(n,\delta)=\sum_{\substack{I\in \mathcal I(A), I\subset A, \\ (I, F/K)=\delta}}\frac{1}{[I]_A^n} \in \overline{K}_{\infty}. \end{align*}$$
$$\begin{align*}Z(n,\delta)=\sum_{\substack{I\in \mathcal I(A), I\subset A, \\ (I, F/K)=\delta}}\frac{1}{[I]_A^n} \in \overline{K}_{\infty}. \end{align*}$$
We see easily that
By Proposition 5.2,
![]() $Z(n,\delta ), \delta \in \Delta $
are algebraically independent over
$Z(n,\delta ), \delta \in \Delta $
are algebraically independent over
![]() $\overline {K}$
.
$\overline {K}$
.
Let
![]() $\chi \in \widehat {G}$
, and we consider the value at
$\chi \in \widehat {G}$
, and we consider the value at
![]() $1$
of Goss L-series attached to
$1$
of Goss L-series attached to
![]() $\chi $
given by
$\chi $
given by
 $$\begin{align*}L(n, \chi)=\sum_{\delta\in \Delta}\chi(\delta) Z(n,\delta) = \sum_{I\in \mathcal I(A), I\subset A}\frac{\chi((I,F/K))}{[I]_A^n}, \end{align*}$$
$$\begin{align*}L(n, \chi)=\sum_{\delta\in \Delta}\chi(\delta) Z(n,\delta) = \sum_{I\in \mathcal I(A), I\subset A}\frac{\chi((I,F/K))}{[I]_A^n}, \end{align*}$$
where
![]() $(.,F/K)$
is the Artin map. It is clear that for all
$(.,F/K)$
is the Artin map. It is clear that for all
![]() $\delta \in \Delta $
,
$\delta \in \Delta $
,
 $$\begin{align*}Z(n,\delta) = \frac{1}{|\Delta|} \sum_{\chi \in \widehat{G}} \chi(\delta)^{-1} L(n, \chi). \end{align*}$$
$$\begin{align*}Z(n,\delta) = \frac{1}{|\Delta|} \sum_{\chi \in \widehat{G}} \chi(\delta)^{-1} L(n, \chi). \end{align*}$$
The above discussion combined with Theorem 4.3 implies immediately a transcendental result for Goss’s zeta values.
Theorem 5.3. Let
![]() $m \in \mathbb N, m \geq 1$
. Then the special values of Goss L-series
$m \in \mathbb N, m \geq 1$
. Then the special values of Goss L-series
are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
As a direct consequence, we obtain the following corollary:
Corollary 5.4. Let
![]() $m \in \mathbb N, m \geq 1$
. Let L be an extension of K such that
$m \in \mathbb N, m \geq 1$
. Let L be an extension of K such that
![]() $L \subset H$
. We consider the following set:
$L \subset H$
. We consider the following set:
Then the elements of
![]() $\mathcal G_L$
are algebraically independent over
$\mathcal G_L$
are algebraically independent over
![]() $\overline K$
.
$\overline K$
.
Remark 5.5. 1) When
![]() $L=K$
, we have shown that
$L=K$
, we have shown that
![]() $\zeta _A(1)$
is transcendental over K, which gives an affirmative answer to an old question of D. Goss Footnote 3
$\zeta _A(1)$
is transcendental over K, which gives an affirmative answer to an old question of D. Goss Footnote 3
2) When
![]() $L=H$
, the above Theorem states that
$L=H$
, the above Theorem states that
![]() $\zeta _B(1)$
is transcendental over K. It answers positively to [Reference Anglès, Dac and Tavares Ribeiro10], Problem 4.1 in this case. Note that our proof is highly nontrivial.
$\zeta _B(1)$
is transcendental over K. It answers positively to [Reference Anglès, Dac and Tavares Ribeiro10], Problem 4.1 in this case. Note that our proof is highly nontrivial.
Proof of Corollary 5.4
Let
![]() $p^k$
be the exact power of p that divides
$p^k$
be the exact power of p that divides
![]() $[L:K]$
and let
$[L:K]$
and let
![]() $N=\mathrm {Gal} (F/F\cap L) \subseteq \Delta $
. We have (see for example [Reference Goss32], Section 8.10):
$N=\mathrm {Gal} (F/F\cap L) \subseteq \Delta $
. We have (see for example [Reference Goss32], Section 8.10):
 $$\begin{align*}\zeta_{O_L}(n) =\left(\prod_{\chi \in \widehat{G}, \chi(N)=\{1\}} L(n, \chi) \right)^{p^k}. \end{align*}$$
$$\begin{align*}\zeta_{O_L}(n) =\left(\prod_{\chi \in \widehat{G}, \chi(N)=\{1\}} L(n, \chi) \right)^{p^k}. \end{align*}$$
Acknowledgements
We would like to thank the referees for their thorough reading of the manuscript and many helpful suggestions.
Competing interest
The authors have no competing interest to declare.
Financial support
The second author (T. N. D.) is funded by Vingroup Joint Stock Company and supported by Vingroup Innovation Foundation (VinIF) under the project code VINIF.2021.DA00030. He is partially supported by the ANR Grant COLOSS ANR-19-CE40-0015-02, the Excellence Research Chair FLCarPA of the Normandy Region and the Labex MILYON ANR-10-LABX-0070. The final preparation of this work was done while he was visiting the Max Planck Institute for Mathematics in Bonn. He is grateful to the institute for its hospitality and financial support.