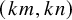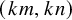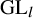1 Introduction
1.1 Overview
The shuffle theorem, conjectured by Haglund et al. [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] and proven by Carlsson and Mellit [Reference Carlsson and Mellit7], is a combinatorial formula for the symmetric polynomial
![]() $\nabla e_{k}$
as a sum over LLT polynomials indexed by Dyck paths—that is, lattice paths from
$\nabla e_{k}$
as a sum over LLT polynomials indexed by Dyck paths—that is, lattice paths from
![]() $(0,k)$
to
$(0,k)$
to
![]() $(k,0)$
that lie weakly below the line segment connecting these two points. Here,
$(k,0)$
that lie weakly below the line segment connecting these two points. Here,
![]() $e_{k}$
is the k-th elementary symmetric function, and
$e_{k}$
is the k-th elementary symmetric function, and
![]() $\nabla $
is an operator on symmetric functions with coefficients in
$\nabla $
is an operator on symmetric functions with coefficients in
![]() ${\mathbb Q} (q,t)$
that arises in the theory of Macdonald polynomials [Reference Bergeron, Garsia, Haiman and Tesler3].
${\mathbb Q} (q,t)$
that arises in the theory of Macdonald polynomials [Reference Bergeron, Garsia, Haiman and Tesler3].
The polynomial
![]() $\nabla e_{k}$
is significant because it describes the character of the ring
$\nabla e_{k}$
is significant because it describes the character of the ring
![]() $R_{k}$
of diagonal coinvariants for the symmetric group
$R_{k}$
of diagonal coinvariants for the symmetric group
![]() $S_{k}$
[Reference Haiman19, Proposition 3.5]. The character of
$S_{k}$
[Reference Haiman19, Proposition 3.5]. The character of
![]() $R_{k}$
had been conjectured in the early 1990s to have surprising connections with the enumeration of combinatorial objects such as trees and Dyck paths—for instance, its dimension is equal to the number
$R_{k}$
had been conjectured in the early 1990s to have surprising connections with the enumeration of combinatorial objects such as trees and Dyck paths—for instance, its dimension is equal to the number
![]() $(k+1)^{k-1}$
of rooted trees on
$(k+1)^{k-1}$
of rooted trees on
![]() $k+1$
labelled vertices, and the multiplicity of the sign character is equal to the Catalan number
$k+1$
labelled vertices, and the multiplicity of the sign character is equal to the Catalan number
![]() $C_{k}$
. A summary of these early conjectures, contributed by a number of people, can be found in [Reference Haiman20]. More precisely,
$C_{k}$
. A summary of these early conjectures, contributed by a number of people, can be found in [Reference Haiman20]. More precisely,
![]() $\nabla e_{k}$
describes the character of
$\nabla e_{k}$
describes the character of
![]() $R_{k}$
as a doubly graded
$R_{k}$
as a doubly graded
![]() $S_{k}$
module. The double grading in
$S_{k}$
module. The double grading in
![]() $R_{k}$
thus gives rise to
$R_{k}$
thus gives rise to
![]() $(q,t)$
-analogs of the numbers that enumerate the associated combinatorial objects. The conjectures connect specializations of these
$(q,t)$
-analogs of the numbers that enumerate the associated combinatorial objects. The conjectures connect specializations of these
![]() $(q,t)$
-analogs with previously known q-analogs in combinatorics.
$(q,t)$
-analogs with previously known q-analogs in combinatorics.
Using results in [Reference Garsia and Haiman11], the whole suite of earlier combinatorial conjectures follows from the character formula
![]() $\nabla e_{k}$
and the shuffle theorem.
$\nabla e_{k}$
and the shuffle theorem.
Along with the formula for
![]() $\nabla e_{k}$
given by the shuffle theorem, Haglund et al. conjectured a combinatorial formula for
$\nabla e_{k}$
given by the shuffle theorem, Haglund et al. conjectured a combinatorial formula for
![]() $\nabla ^{m} e_{k}$
as a sum over LLT polynomials indexed by lattice paths below the line segment from
$\nabla ^{m} e_{k}$
as a sum over LLT polynomials indexed by lattice paths below the line segment from
![]() $(0,k)$
to
$(0,k)$
to
![]() $(km,0)$
. Extending this, Bergeron et al. [Reference Bergeron, Garsia, Sergel Leven and Xin4] conjectured, and Mellit [Reference Mellit28] proved, an identity giving the symmetric polynomial
$(km,0)$
. Extending this, Bergeron et al. [Reference Bergeron, Garsia, Sergel Leven and Xin4] conjectured, and Mellit [Reference Mellit28] proved, an identity giving the symmetric polynomial
![]() $e_{k}[-M X^{m,n}]\cdot 1$
as a sum over LLT polynomials indexed by lattice paths below the segment from
$e_{k}[-M X^{m,n}]\cdot 1$
as a sum over LLT polynomials indexed by lattice paths below the segment from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
, for any pair of positive integers expressed in the form
$(km,0)$
, for any pair of positive integers expressed in the form
![]() $(km,kn)$
with
$(km,kn)$
with
![]() $m,n$
coprime. Here,
$m,n$
coprime. Here,
![]() $e_{k}[-M X^{m,n}]$
, where
$e_{k}[-M X^{m,n}]$
, where
![]() $M=(1-q)(1-t)$
, is our notation for a certain element of the elliptic Hall algebra
$M=(1-q)(1-t)$
, is our notation for a certain element of the elliptic Hall algebra
![]() ${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann6], which acts on symmetric functions in such a way that for
${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann6], which acts on symmetric functions in such a way that for
![]() $n=1$
we have
$n=1$
we have
![]() $e_{k}[-M X^{m,1}]\cdot 1 = \nabla ^{m} e_{k}$
, as explained in §3.
$e_{k}[-M X^{m,1}]\cdot 1 = \nabla ^{m} e_{k}$
, as explained in §3.
In this paper, we prove an even more general version of the shuffle theorem, involving a sum over LLT polynomials indexed by lattice paths lying under the line segment between arbitrary points
![]() $(0,s)$
and
$(0,s)$
and
![]() $(r,0)$
on the positive real axes and reducing to the theorem of Bergeron et al. and Mellit when
$(r,0)$
on the positive real axes and reducing to the theorem of Bergeron et al. and Mellit when
![]() $(r,s) = (km,kn)$
are integers.
$(r,s) = (km,kn)$
are integers.
Our generalized shuffle theorem (Theorem 5.5.1) is an identity
whose ingredients we now summarize briefly, deferring full details to later parts of the paper.
The sum on the right-hand side of equation (1) is over lattice paths
![]() $\lambda $
from
$\lambda $
from
![]() $(0,\lfloor s \rfloor )$
to
$(0,\lfloor s \rfloor )$
to
![]() $(\lfloor r \rfloor , 0)$
that lie below the line segment from
$(\lfloor r \rfloor , 0)$
that lie below the line segment from
![]() $(0,s)$
to
$(0,s)$
to
![]() $(r,0)$
. The quantity
$(r,0)$
. The quantity
![]() $a(\lambda )$
is the number of lattice squares enclosed between the path
$a(\lambda )$
is the number of lattice squares enclosed between the path
![]() $\lambda $
and the highest such path
$\lambda $
and the highest such path
![]() $\delta $
(see Example 5.5.3 and Figure 5). We set
$\delta $
(see Example 5.5.3 and Figure 5). We set
![]() $p = s/r$
and define
$p = s/r$
and define
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
to be the number of ‘p-balanced’ hooks in the (French style) Young diagram enclosed by
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
to be the number of ‘p-balanced’ hooks in the (French style) Young diagram enclosed by
![]() $\lambda $
and the x and y axes. A hook is p-balanced if a line of slope
$\lambda $
and the x and y axes. A hook is p-balanced if a line of slope
![]() $-p$
passes through the segments at the top of its leg and the end of its arm (Definition 5.4.1 and Figure 2).
$-p$
passes through the segments at the top of its leg and the end of its arm (Definition 5.4.1 and Figure 2).

Figure 1 A negative tableau S on
![]() $\beta /\alpha = (6,3,5)/(2,1,2)$
and the
$\beta /\alpha = (6,3,5)/(2,1,2)$
and the
![]() $\sigma $
-triples in
$\sigma $
-triples in
![]() $\beta /\alpha $
, for two choices of
$\beta /\alpha $
, for two choices of
![]() $\sigma $
, shown with their entries from S. Triples in boldface are increasing in S.
$\sigma $
, shown with their entries from S. Triples in boldface are increasing in S.

Figure 2 A p-balanced hook in a Young diagram, where the diagonal line has slope
![]() $-p$
.
$-p$
.
In the remaining factor
![]() $\omega ({\mathcal G} _{\nu (\lambda )}(X;q^{-1}))$
, the function
$\omega ({\mathcal G} _{\nu (\lambda )}(X;q^{-1}))$
, the function
![]() ${\mathcal G} _{\nu }(X;q)$
is an ‘attacking inversions’ LLT polynomial (Definition 4.1.2), and
${\mathcal G} _{\nu }(X;q)$
is an ‘attacking inversions’ LLT polynomial (Definition 4.1.2), and
![]() $\omega (h_{\mu }) = e_{\mu }$
is the standard involution on symmetric functions. The index
$\omega (h_{\mu }) = e_{\mu }$
is the standard involution on symmetric functions. The index
![]() $\nu (\lambda )$
is a tuple of one-row skew Young diagrams of the same lengths as runs of contiguous south steps in
$\nu (\lambda )$
is a tuple of one-row skew Young diagrams of the same lengths as runs of contiguous south steps in
![]() $\lambda $
, arranged so that the reading order on boxes of
$\lambda $
, arranged so that the reading order on boxes of
![]() $\nu (\lambda )$
corresponds to the ordering on south steps in
$\nu (\lambda )$
corresponds to the ordering on south steps in
![]() $\lambda $
given by decreasing values of
$\lambda $
given by decreasing values of
![]() $y+px$
at the upper endpoint of each step.
$y+px$
at the upper endpoint of each step.
The operator
![]() $D_{{\mathbf b} } = D_{b_{1},\ldots ,b_{l}}$
on the left-hand side of equation (1) is one of a family of special elements defined by Negut [Reference Negut30] in the Schiffmann algebra
$D_{{\mathbf b} } = D_{b_{1},\ldots ,b_{l}}$
on the left-hand side of equation (1) is one of a family of special elements defined by Negut [Reference Negut30] in the Schiffmann algebra
![]() ${\mathcal E} $
. Letting
${\mathcal E} $
. Letting
![]() $\delta $
again denote the highest path under the given line segment, the index
$\delta $
again denote the highest path under the given line segment, the index
![]() ${\mathbf b} $
is defined by taking
${\mathbf b} $
is defined by taking
![]() $b_{i}$
to be the number of south steps in
$b_{i}$
to be the number of south steps in
![]() $\delta $
on the line
$\delta $
on the line
![]() $x = i-1$
.
$x = i-1$
.
To recover the previously known cases of the theorem, we take
![]() $s = kn$
and r slightly larger than
$s = kn$
and r slightly larger than
![]() $km$
, so
$km$
, so
![]() $p = n/m-\epsilon $
for a small
$p = n/m-\epsilon $
for a small
![]() $\epsilon>0$
. The segment from
$\epsilon>0$
. The segment from
![]() $(0,s)$
to
$(0,s)$
to
![]() $(r,0)$
has the same lattice paths below it as the segment from
$(r,0)$
has the same lattice paths below it as the segment from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
, and
$(km,0)$
, and
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
reduces to the version of
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
reduces to the version of
![]() $\operatorname {\mathrm {dinv}} (\lambda )$
in the original conjectures. The element
$\operatorname {\mathrm {dinv}} (\lambda )$
in the original conjectures. The element
![]() $D_{{\mathbf b} }$
associated to the highest path
$D_{{\mathbf b} }$
associated to the highest path
![]() $\delta $
below the segment from
$\delta $
below the segment from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
is equal to
$(km,0)$
is equal to
![]() $e_{k}[-M X^{m,n}]$
. Hence, equation (1) reduces to the
$e_{k}[-M X^{m,n}]$
. Hence, equation (1) reduces to the
![]() $(km,kn)$
shuffle theorem.
$(km,kn)$
shuffle theorem.
1.2 Preview of the proof
We prove our generalized shuffle theorem by a remarkably simple method, which we now outline to help orient the reader in following the details. In §3, we will see that the left-hand side of equation (1), after applying
![]() $\omega $
and evaluating in
$\omega $
and evaluating in
![]() $l = \lfloor r \rfloor + 1$
variables
$l = \lfloor r \rfloor + 1$
variables
![]() $x_{1},\ldots ,x_{l}$
, becomes the polynomial part
$x_{1},\ldots ,x_{l}$
, becomes the polynomial part
of an explicit infinite series of
![]() $\operatorname {\mathrm {GL}} _{l}$
characters
$\operatorname {\mathrm {GL}} _{l}$
characters
 $$ \begin{align} {\mathcal H} _{{\mathbf b} }(x) =\sum _{w\in S_{l}} w \left( \frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}\, \prod _{i+1<j}(1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j}\bigl((1-x_{j}/x_{i})(1 - q\, x_{i}/x_{j})(1 - t\, x_{i}/x_{j}) \bigr)} \right). \end{align} $$
$$ \begin{align} {\mathcal H} _{{\mathbf b} }(x) =\sum _{w\in S_{l}} w \left( \frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}\, \prod _{i+1<j}(1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j}\bigl((1-x_{j}/x_{i})(1 - q\, x_{i}/x_{j})(1 - t\, x_{i}/x_{j}) \bigr)} \right). \end{align} $$
When
![]() $\nu $
is a tuple of one-row skew shapes
$\nu $
is a tuple of one-row skew shapes
![]() $(\beta _{i})/(\alpha _{i})$
, the LLT polynomial
$(\beta _{i})/(\alpha _{i})$
, the LLT polynomial
![]() ${\mathcal G} _{\nu }(x;q^{-1})$
is equal, up to a factor of the form
${\mathcal G} _{\nu }(x;q^{-1})$
is equal, up to a factor of the form
![]() $q^{d}$
, to the polynomial part of an infinite
$q^{d}$
, to the polynomial part of an infinite
![]() $\operatorname {\mathrm {GL}}_{l}$
character series
$\operatorname {\mathrm {GL}}_{l}$
character series
defined by Grojnowski and the second author [Reference Grojnowski and Haiman14]. In Theorem 5.3.1, we establish an identity of infinite series
where
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
is a ‘twisted’ variant of
${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
is a ‘twisted’ variant of
![]() ${\mathcal L} _{\beta /\alpha }(x;q)$
(see §4). Then equation (1) follows once we see that the polynomial part of the right-hand side of equation(5) is equal to the right-hand side of equation (1) with the
${\mathcal L} _{\beta /\alpha }(x;q)$
(see §4). Then equation (1) follows once we see that the polynomial part of the right-hand side of equation(5) is equal to the right-hand side of equation (1) with the
![]() $\omega $
omitted.
$\omega $
omitted.
In fact, equation (4) holds when
![]() $\alpha _{i}\leq \beta _{i}$
for all i, and otherwise
$\alpha _{i}\leq \beta _{i}$
for all i, and otherwise
![]() ${\mathcal L} _{\beta /\alpha }(x;q)_{\operatorname {\mathrm {pol}} } = 0$
. When we take the polynomial part in equation (5), this leaves a nonvanishing term
${\mathcal L} _{\beta /\alpha }(x;q)_{\operatorname {\mathrm {pol}} } = 0$
. When we take the polynomial part in equation (5), this leaves a nonvanishing term
![]() $t^{|{\mathbf a} |} q^{d} {\mathcal G} _{\nu (\lambda )}(x;q^{-1})$
for each path
$t^{|{\mathbf a} |} q^{d} {\mathcal G} _{\nu (\lambda )}(x;q^{-1})$
for each path
![]() $\lambda $
under the given line segment, with
$\lambda $
under the given line segment, with
![]() ${\mathbf a} $
giving the number of lattice squares in each column between
${\mathbf a} $
giving the number of lattice squares in each column between
![]() $\lambda $
and the highest path
$\lambda $
and the highest path
![]() $\delta $
, so
$\delta $
, so
![]() $t^{|{\mathbf a} |} = t^{a(\lambda )}$
. The factor
$t^{|{\mathbf a} |} = t^{a(\lambda )}$
. The factor
![]() $q^{d}$
from equation (4) turns out to be precisely
$q^{d}$
from equation (4) turns out to be precisely
![]() $q^{\operatorname {\mathrm {dinv}} _{p}(\lambda )}$
, yielding equation (1).
$q^{\operatorname {\mathrm {dinv}} _{p}(\lambda )}$
, yielding equation (1).
Finally, the infinite series identity (5) from Theorem 5.3.1 is essentially a corollary to a Cauchy identity for nonsymmetric Hall–Littlewood polynomials, Theorem 5.1.1. This Cauchy formula is quite general and can be applied in other situations, some of which we will take up elsewhere.
1.3 Further remarks
(i) The conjectures in [Reference Bergeron, Garsia, Sergel Leven and Xin4, Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] and proofs in [Reference Carlsson and Mellit7, Reference Mellit28] use a version of
![]() $\operatorname {\mathrm {dinv}} (\lambda )$
that coincides with
$\operatorname {\mathrm {dinv}} (\lambda )$
that coincides with
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
for
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
for
![]() $p = n/m-\epsilon $
. Alternatively, one can tilt the segment from
$p = n/m-\epsilon $
. Alternatively, one can tilt the segment from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
in the other direction, taking
$(km,0)$
in the other direction, taking
![]() $r = km$
and s slightly larger than
$r = km$
and s slightly larger than
![]() $kn$
, to get a version of the original conjectures with a variant of
$kn$
, to get a version of the original conjectures with a variant of
![]() $\operatorname {\mathrm {dinv}} (\lambda )$
that coincides with
$\operatorname {\mathrm {dinv}} (\lambda )$
that coincides with
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
for
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
for
![]() $p = n/m+\epsilon $
. Our theorem implies this version as well.
$p = n/m+\epsilon $
. Our theorem implies this version as well.
(ii) Carlsson and Mellit [Reference Carlsson and Mellit7, Reference Mellit28] prove more general ‘compositional’ versions of the classical and
![]() $(km,kn)$
shuffle theorems, as conjectured by Haglund, Zabrocki and the third author [Reference Haglund, Morse and Zabrocki17] in the classical case and Bergeron et al. [Reference Bergeron, Garsia, Sergel Leven and Xin4] in the
$(km,kn)$
shuffle theorems, as conjectured by Haglund, Zabrocki and the third author [Reference Haglund, Morse and Zabrocki17] in the classical case and Bergeron et al. [Reference Bergeron, Garsia, Sergel Leven and Xin4] in the
![]() $(km,kn)$
case. Although our results here do not cover the compositional versions, Mellit has pointed out to us privately that [Reference Mellit28, Theorem 5.11] may contain clues to a possible compositional extension of our generalized shuffle theorem.
$(km,kn)$
case. Although our results here do not cover the compositional versions, Mellit has pointed out to us privately that [Reference Mellit28, Theorem 5.11] may contain clues to a possible compositional extension of our generalized shuffle theorem.
(iii) By [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Proposition 5.3.1], the LLT polynomials
![]() ${\mathcal G} _{\nu (\lambda )}(x;q)$
in equation (1) are q Schur positive, meaning that their coefficients in the basis of Schur functions belong to
${\mathcal G} _{\nu (\lambda )}(x;q)$
in equation (1) are q Schur positive, meaning that their coefficients in the basis of Schur functions belong to
![]() ${\mathbb N} [q]$
. The right-hand side of equation (1) is therefore
${\mathbb N} [q]$
. The right-hand side of equation (1) is therefore
![]() $q,t$
Schur positive. In the cases corresponding to the
$q,t$
Schur positive. In the cases corresponding to the
![]() $(km,kn)$
shuffle theorem for
$(km,kn)$
shuffle theorem for
![]() $k = 1$
, this can also be seen from the representation theoretic interpretation of the right-hand side given by Hikita [Reference Hikita21].
$k = 1$
, this can also be seen from the representation theoretic interpretation of the right-hand side given by Hikita [Reference Hikita21].
Identity (1) therefore implies that the expression
![]() $D_{{\mathbf b} }\cdot 1$
on the left-hand side is
$D_{{\mathbf b} }\cdot 1$
on the left-hand side is
![]() $q,t$
Schur positive. In the cases where the left-hand side coincides with
$q,t$
Schur positive. In the cases where the left-hand side coincides with
![]() $\nabla ^{m} e_{k}$
, this can be explained using the representation theoretic interpretations of
$\nabla ^{m} e_{k}$
, this can be explained using the representation theoretic interpretations of
![]() $\nabla e_{k}$
in [Reference Haiman19] and
$\nabla e_{k}$
in [Reference Haiman19] and
![]() $\nabla ^{m} e_{k}$
in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Proposition 6.1.1]. In §7, we conjecture a more general condition for
$\nabla ^{m} e_{k}$
in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Proposition 6.1.1]. In §7, we conjecture a more general condition for
![]() $D_{{\mathbf b} }\cdot 1$
to be
$D_{{\mathbf b} }\cdot 1$
to be
![]() $q,t$
Schur positive.
$q,t$
Schur positive.
(iv) The algebraic left-hand side of equation (1) is manifestly symmetric in q and t. Hence, the combinatorial right-hand side is also symmetric in q and t. No direct combinatorial proof of this symmetry is currently known.
2 Symmetric functions and
 $\operatorname {\mathrm {GL}}_{l}$
characters
$\operatorname {\mathrm {GL}}_{l}$
characters
This section serves to fix notation and terminology for standard notions concerning symmetric functions and characters of the general linear groups
![]() $\operatorname {\mathrm {GL}} _{l}$
.
$\operatorname {\mathrm {GL}} _{l}$
.
2.1 Symmetric functions
Integer partitions are written
![]() $\lambda = (\lambda _{1}\geq \cdots \geq \lambda _{l})$
, possibly with trailing zeroes. We set
$\lambda = (\lambda _{1}\geq \cdots \geq \lambda _{l})$
, possibly with trailing zeroes. We set
![]() $|\lambda | = \lambda _{1}+\cdots +\lambda _{l}$
and let
$|\lambda | = \lambda _{1}+\cdots +\lambda _{l}$
and let
![]() $\ell (\lambda )$
be the number of nonzero parts. We also define
$\ell (\lambda )$
be the number of nonzero parts. We also define
The transpose of
![]() $\lambda $
is denoted
$\lambda $
is denoted
![]() $\lambda ^{*}$
.
$\lambda ^{*}$
.
The partitions of a given integer n are partially ordered by
where the sums include trailing zeroes for
![]() $k>\ell (\lambda )$
or
$k>\ell (\lambda )$
or
![]() $k>\ell (\mu )$
.
$k>\ell (\mu )$
.
The (French style) Young or Ferrers diagram of a partition
![]() $\lambda $
is the set of lattice points
$\lambda $
is the set of lattice points
![]() $\{(i,j)\mid 1\leq j\leq \ell (\lambda ),\; 1\leq i \leq \lambda _{j} \}$
. We often identify
$\{(i,j)\mid 1\leq j\leq \ell (\lambda ),\; 1\leq i \leq \lambda _{j} \}$
. We often identify
![]() $\lambda $
and its diagram with the set of lattice squares, or boxes, with northeast corner at a point
$\lambda $
and its diagram with the set of lattice squares, or boxes, with northeast corner at a point
![]() $(i,j)\in \lambda $
. A skew diagram (or skew shape)
$(i,j)\in \lambda $
. A skew diagram (or skew shape)
![]() $\lambda /\mu $
is the difference between the diagram of a partition
$\lambda /\mu $
is the difference between the diagram of a partition
![]() $\lambda $
and that of a partition
$\lambda $
and that of a partition
![]() $\mu \subseteq \lambda $
contained in it. The diagram generator of
$\mu \subseteq \lambda $
contained in it. The diagram generator of
![]() $\lambda $
is the polynomial
$\lambda $
is the polynomial
 $$ \begin{align} B_{\lambda }(q,t) = \sum _{(i,j)\in \lambda} q^{i-1}\, t^{j-1}. \end{align} $$
$$ \begin{align} B_{\lambda }(q,t) = \sum _{(i,j)\in \lambda} q^{i-1}\, t^{j-1}. \end{align} $$
Let
![]() $\Lambda = \Lambda _{{\mathbf k} }(X)$
be the algebra of symmetric functions in an infinite alphabet of variables
$\Lambda = \Lambda _{{\mathbf k} }(X)$
be the algebra of symmetric functions in an infinite alphabet of variables
![]() $X = x_{1},x_{2},\ldots $
, with coefficients in the field
$X = x_{1},x_{2},\ldots $
, with coefficients in the field
![]() ${\mathbf k} = {\mathbb Q} (q,t)$
. We follow Macdonald’s notation [Reference Macdonald26] for various graded bases of
${\mathbf k} = {\mathbb Q} (q,t)$
. We follow Macdonald’s notation [Reference Macdonald26] for various graded bases of
![]() $\Lambda $
, such as the elementary symmetric functions
$\Lambda $
, such as the elementary symmetric functions
![]() $e_{\lambda } = e_{\lambda _{1}}\cdots e_{\lambda _{k}}$
, complete homogeneous symmetric functions
$e_{\lambda } = e_{\lambda _{1}}\cdots e_{\lambda _{k}}$
, complete homogeneous symmetric functions
![]() $h_{\lambda } = h_{\lambda _{1}}\cdots h_{\lambda _{k}}$
, power-sums
$h_{\lambda } = h_{\lambda _{1}}\cdots h_{\lambda _{k}}$
, power-sums
![]() $p_{\lambda } = p_{\lambda _{1}}\cdots p_{\lambda _{k}}$
, monomial symmetric functions
$p_{\lambda } = p_{\lambda _{1}}\cdots p_{\lambda _{k}}$
, monomial symmetric functions
![]() $m_{\lambda }$
and Schur functions
$m_{\lambda }$
and Schur functions
![]() $s_{\lambda }$
. The involutory
$s_{\lambda }$
. The involutory
![]() ${\mathbf k} $
-algebra automorphism
${\mathbf k} $
-algebra automorphism
![]() $\omega \colon \Lambda \rightarrow \Lambda $
mentioned in the introduction may be defined by any of the formulas
$\omega \colon \Lambda \rightarrow \Lambda $
mentioned in the introduction may be defined by any of the formulas
We also need the symmetric bilinear inner product
![]() $\langle -, - \rangle $
on
$\langle -, - \rangle $
on
![]() $\Lambda $
defined by any of
$\Lambda $
defined by any of
where
![]() $z_{\lambda } = \prod _{i} r_{i}!\, i^{r_{i}}$
if
$z_{\lambda } = \prod _{i} r_{i}!\, i^{r_{i}}$
if
![]() $\lambda = (1^{r_{1}},2^{r_{2}},\ldots )$
.
$\lambda = (1^{r_{1}},2^{r_{2}},\ldots )$
.
We write
![]() $f^{\bullet }$
for the operator of multiplication by a function f. Otherwise, the custom of writing f for both the operator and the function would make it hard to distinguish between operator expressions such as
$f^{\bullet }$
for the operator of multiplication by a function f. Otherwise, the custom of writing f for both the operator and the function would make it hard to distinguish between operator expressions such as
![]() $(\omega f)^{\bullet }$
and
$(\omega f)^{\bullet }$
and
![]() $\omega \cdot f^{\bullet }$
. When f is a symmetric function, we write
$\omega \cdot f^{\bullet }$
. When f is a symmetric function, we write
![]() $f^{\perp }$
for the
$f^{\perp }$
for the
![]() $\langle -, - \rangle $
adjoint of
$\langle -, - \rangle $
adjoint of
![]() $f^{\bullet }$
.
$f^{\bullet }$
.
2.2 Plethystic evaluation
We briefly recall the device of plethystic evaluation. If A is an expression in terms of indeterminates, such as a polynomial, rational function, or formal series, we define
![]() $p_{k}[A]$
to be the result of substituting
$p_{k}[A]$
to be the result of substituting
![]() $a^{k}$
for every indeterminate a occurring in A. We define
$a^{k}$
for every indeterminate a occurring in A. We define
![]() $f[A]$
for any
$f[A]$
for any
![]() $f\in \Lambda $
by substituting
$f\in \Lambda $
by substituting
![]() $p_{k}[A]$
for
$p_{k}[A]$
for
![]() $p_{k}$
in the expression for f as a polynomial in the power-sums
$p_{k}$
in the expression for f as a polynomial in the power-sums
![]() $p_{k}$
, so that
$p_{k}$
, so that
![]() $f\mapsto f[A]$
is a homomorphism.
$f\mapsto f[A]$
is a homomorphism.
The variables
![]() $q, t$
from our ground field
$q, t$
from our ground field
![]() ${\mathbf k} $
count as indeterminates.
${\mathbf k} $
count as indeterminates.
As a simple example, the plethystic evaluation
![]() $f[x_{1}+\cdots +x_{l}]$
is just the ordinary evaluation
$f[x_{1}+\cdots +x_{l}]$
is just the ordinary evaluation
![]() $f(x_{1},\ldots ,x_{l})$
, since
$f(x_{1},\ldots ,x_{l})$
, since
![]() $p_{k}[x_{1}+\cdots +x_{l}] = x_{1}^{k}+\cdots +x_{l}^{k}$
. This also works in infinitely many variables.
$p_{k}[x_{1}+\cdots +x_{l}] = x_{1}^{k}+\cdots +x_{l}^{k}$
. This also works in infinitely many variables.
When
![]() $X = x_{1},x_{2},\ldots $
is the name of an infinite alphabet of variables, we use
$X = x_{1},x_{2},\ldots $
is the name of an infinite alphabet of variables, we use
![]() $f(X)$
, with round brackets, as an abbreviation for
$f(X)$
, with round brackets, as an abbreviation for
![]() $f(x_{1},x_{2},\ldots )\in \Lambda (X)$
. In this situation, we also make the convention that when X appears inside plethystic brackets, it means
$f(x_{1},x_{2},\ldots )\in \Lambda (X)$
. In this situation, we also make the convention that when X appears inside plethystic brackets, it means
![]() $X = x_{1}+x_{2}+\cdots $
. With this convention,
$X = x_{1}+x_{2}+\cdots $
. With this convention,
![]() $f[X]$
is another way of writing
$f[X]$
is another way of writing
![]() $f(X)$
.
$f(X)$
.
As a second example and caution to the reader, the formula in equation (9) for
![]() $\omega \, p_{k}$
implies the identity
$\omega \, p_{k}$
implies the identity
![]() $\omega f(X) = f[-z X]|_{z=-1}$
. Note that
$\omega f(X) = f[-z X]|_{z=-1}$
. Note that
![]() $f[-z X]|_{z=-1}$
does not reduce to
$f[-z X]|_{z=-1}$
does not reduce to
![]() $f(X)$
, as it might at first appear, since specializing the indeterminate z to a number does not commute with plethystic evaluation.
$f(X)$
, as it might at first appear, since specializing the indeterminate z to a number does not commute with plethystic evaluation.
Plethystic evaluation of a symmetric infinite series is allowed if the result converges as a formal series. The series
 $$ \begin{align} \Omega = 1 + \sum _{k>0} h_{k} = \exp \sum _{k>0} \frac{p_{k}}{k}, \quad \text{or}\quad \Omega [a_{1}+a_{2}+\cdots -b_{1}-b_{2}-\cdots ] = \frac{\prod_{i} (1-b_{i})}{\prod_{i} (1-a_{i})} \end{align} $$
$$ \begin{align} \Omega = 1 + \sum _{k>0} h_{k} = \exp \sum _{k>0} \frac{p_{k}}{k}, \quad \text{or}\quad \Omega [a_{1}+a_{2}+\cdots -b_{1}-b_{2}-\cdots ] = \frac{\prod_{i} (1-b_{i})}{\prod_{i} (1-a_{i})} \end{align} $$
is particularly useful. The classical Cauchy identity can be written using this notation as
Taking the inner product with
![]() $f(X)$
in equation (12) yields
$f(X)$
in equation (12) yields
![]() $f[A] = \langle \Omega [AX], f(X) \rangle $
, which implies
$f[A] = \langle \Omega [AX], f(X) \rangle $
, which implies
As B is arbitrary,
![]() $\Omega [BX]$
is in effect a general symmetric function, so equation (13) implies
$\Omega [BX]$
is in effect a general symmetric function, so equation (13) implies
Note that, although
![]() $\Omega [AX]^{\perp } = \sum _{k} h_{k}[AX]^{\perp }$
is an infinite series, it converges formally as an operator applied to any
$\Omega [AX]^{\perp } = \sum _{k} h_{k}[AX]^{\perp }$
is an infinite series, it converges formally as an operator applied to any
![]() $f\in \Lambda (X)$
, since
$f\in \Lambda (X)$
, since
![]() $h_{k}[AX]^{\perp }$
has degree
$h_{k}[AX]^{\perp }$
has degree
![]() $-k$
, and so kills f for
$-k$
, and so kills f for
![]() $k \gg 0$
.
$k \gg 0$
.
Identifying
![]() $\Lambda $
with a polynomial ring in the power-sums
$\Lambda $
with a polynomial ring in the power-sums
![]() $p_{k}$
, we have
$p_{k}$
, we have
In fact, taking
![]() $A = z$
and
$A = z$
and
![]() $f = p_{k}$
in (14) shows that
$f = p_{k}$
in (14) shows that
![]() $\exp ( \sum (p_{k}^{\perp } z^{k})/k)$
is the operator that substitutes
$\exp ( \sum (p_{k}^{\perp } z^{k})/k)$
is the operator that substitutes
![]() $p_{k}+z^{k}$
for
$p_{k}+z^{k}$
for
![]() $p_{k}$
in any polynomial
$p_{k}$
in any polynomial
![]() $f(p_{1},p_{2},\ldots )$
. This operator can also be written
$f(p_{1},p_{2},\ldots )$
. This operator can also be written
![]() $\exp (\sum z^{k} \frac {\partial }{\partial p_{k}})$
, giving (15).
$\exp (\sum z^{k} \frac {\partial }{\partial p_{k}})$
, giving (15).
Another consequence of equation (14) is the operator identity
with notation
![]() $\Omega [BX]^{\bullet }$
as in §2.1.
$\Omega [BX]^{\bullet }$
as in §2.1.
2.3
 $\operatorname {\mathrm {GL}}_{l}$
characters
$\operatorname {\mathrm {GL}}_{l}$
characters
The weight lattice of
![]() $\operatorname {\mathrm {GL}} _{l}$
is
$\operatorname {\mathrm {GL}} _{l}$
is
![]() $X = {\mathbb Z} ^{l}$
, with Weyl group
$X = {\mathbb Z} ^{l}$
, with Weyl group
![]() $W = S_{l}$
permuting the coordinates. Letting
$W = S_{l}$
permuting the coordinates. Letting
![]() $\varepsilon _{1},\ldots ,\varepsilon _{l}$
be unit coordinate vectors, the positive roots are
$\varepsilon _{1},\ldots ,\varepsilon _{l}$
be unit coordinate vectors, the positive roots are
![]() $\varepsilon _{i} - \varepsilon _{j}$
for
$\varepsilon _{i} - \varepsilon _{j}$
for
![]() $i<j$
, with simple roots
$i<j$
, with simple roots
![]() $\alpha _{i} = \varepsilon _{i} - \varepsilon _{i+1}$
for
$\alpha _{i} = \varepsilon _{i} - \varepsilon _{i+1}$
for
![]() $i=1,\ldots ,l-1$
. The standard pairing on
$i=1,\ldots ,l-1$
. The standard pairing on
![]() ${\mathbb Z} ^{l}$
in which the
${\mathbb Z} ^{l}$
in which the
![]() $\varepsilon _{i}$
are orthonormal identifies the dual lattice
$\varepsilon _{i}$
are orthonormal identifies the dual lattice
![]() $X^{*}$
with X. Under this identification, the coroots coincide with the roots, and the simple coroots
$X^{*}$
with X. Under this identification, the coroots coincide with the roots, and the simple coroots
![]() $\alpha _{i}^{\vee } $
with the simple roots. A weight
$\alpha _{i}^{\vee } $
with the simple roots. A weight
![]() $\lambda \in {\mathbb Z} ^{l}$
is dominant if
$\lambda \in {\mathbb Z} ^{l}$
is dominant if
![]() $\lambda _{1}\geq \cdots \geq \lambda _{l}$
; a weight is regular (has trivial stabilizer in
$\lambda _{1}\geq \cdots \geq \lambda _{l}$
; a weight is regular (has trivial stabilizer in
![]() $S_{l}$
) if
$S_{l}$
) if
![]() $\lambda _{1},\ldots ,\lambda _{l}$
are distinct.
$\lambda _{1},\ldots ,\lambda _{l}$
are distinct.
A polynomial weight is a dominant weight
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda _{l}\geq 0$
. In other words, polynomial weights of
$\lambda _{l}\geq 0$
. In other words, polynomial weights of
![]() $\operatorname {\mathrm {GL}} _{l}$
are integer partitions of length at most l.
$\operatorname {\mathrm {GL}} _{l}$
are integer partitions of length at most l.
The algebra of virtual
![]() $\operatorname {\mathrm {GL}} _{l}$
characters
$\operatorname {\mathrm {GL}} _{l}$
characters
![]() $({\mathbf k} X)^{W}$
can be identified with the algebra of symmetric Laurent polynomials
$({\mathbf k} X)^{W}$
can be identified with the algebra of symmetric Laurent polynomials
![]() ${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]^{S_{l}}$
. If
${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]^{S_{l}}$
. If
![]() $\lambda $
is a polynomial weight, the irreducible character
$\lambda $
is a polynomial weight, the irreducible character
![]() $\chi _{\lambda }$
is equal to the Schur function
$\chi _{\lambda }$
is equal to the Schur function
![]() $s_{\lambda }(x_{1},\ldots ,x_{l})$
. Given a virtual
$s_{\lambda }(x_{1},\ldots ,x_{l})$
. Given a virtual
![]() $\operatorname {\mathrm {GL}} _{l}$
character
$\operatorname {\mathrm {GL}} _{l}$
character
![]() $f(x)= f(x_1,\dots ,x_l) = \sum _{\lambda }c_{\lambda }\chi _{\lambda }$
, we denote the partial sum over polynomial weights
$f(x)= f(x_1,\dots ,x_l) = \sum _{\lambda }c_{\lambda }\chi _{\lambda }$
, we denote the partial sum over polynomial weights
![]() $\lambda $
by
$\lambda $
by
![]() $f(x)_{\operatorname {\mathrm {pol}} }$
(this is different from taking the polynomial terms of
$f(x)_{\operatorname {\mathrm {pol}} }$
(this is different from taking the polynomial terms of
![]() $f(x)$
considered as a Laurent polynomial). Thus,
$f(x)$
considered as a Laurent polynomial). Thus,
![]() $f(x)_{\operatorname {\mathrm {pol}} }$
is a symmetric polynomial in l variables. We also use this notation for infinite formal sums
$f(x)_{\operatorname {\mathrm {pol}} }$
is a symmetric polynomial in l variables. We also use this notation for infinite formal sums
![]() $f(x)$
of irreducible
$f(x)$
of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters, in which case
$\operatorname {\mathrm {GL}} _{l}$
characters, in which case
![]() $f(x)_{\operatorname {\mathrm {pol}} }$
is a symmetric formal power series.
$f(x)_{\operatorname {\mathrm {pol}} }$
is a symmetric formal power series.
The Weyl symmetrization operator for
![]() $\operatorname {\mathrm {GL}} _{l}$
is
$\operatorname {\mathrm {GL}} _{l}$
is
 $$ \begin{align} {\boldsymbol \sigma } \, f(x_{1},\ldots,x_{l}) = \sum _{w\in S_{l}} w\left(\frac{f(x)}{\prod _{i<j}(1-x_{j}/x_{i})} \right). \end{align} $$
$$ \begin{align} {\boldsymbol \sigma } \, f(x_{1},\ldots,x_{l}) = \sum _{w\in S_{l}} w\left(\frac{f(x)}{\prod _{i<j}(1-x_{j}/x_{i})} \right). \end{align} $$
For dominant weights
![]() $\lambda $
, the Weyl character formula can be written
$\lambda $
, the Weyl character formula can be written
![]() $\chi _{\lambda } = {\boldsymbol \sigma } (x^{\lambda })$
.
$\chi _{\lambda } = {\boldsymbol \sigma } (x^{\lambda })$
.
Fix a weight
![]() $\rho $
such that
$\rho $
such that
![]() $\langle \alpha _{i}^{\vee } ,\rho \rangle = 1$
for each simple coroot
$\langle \alpha _{i}^{\vee } ,\rho \rangle = 1$
for each simple coroot
![]() $\alpha _{i}^{\vee } $
, for example,
$\alpha _{i}^{\vee } $
, for example,
![]() $\rho = (l-1,\ldots ,1,0)$
. Although
$\rho = (l-1,\ldots ,1,0)$
. Although
![]() $\rho $
is only unique up to adding a constant vector, all formulas in which
$\rho $
is only unique up to adding a constant vector, all formulas in which
![]() $\rho $
appears will be independent of the choice. Let
$\rho $
appears will be independent of the choice. Let
![]() $\mu $
be any weight, not necessarily dominant. If
$\mu $
be any weight, not necessarily dominant. If
![]() $\mu +\rho $
is not regular, then
$\mu +\rho $
is not regular, then
![]() ${\boldsymbol \sigma } (x^{\mu }) = 0$
. Otherwise, if
${\boldsymbol \sigma } (x^{\mu }) = 0$
. Otherwise, if
![]() $w\in S_{l}$
is the unique permutation such that
$w\in S_{l}$
is the unique permutation such that
![]() $w(\mu +\rho )=\lambda +\rho $
for
$w(\mu +\rho )=\lambda +\rho $
for
![]() $\lambda $
dominant,
$\lambda $
dominant,
The following identities are useful for working with the Weyl symmetrization operator. Here and after,
![]() $\langle - \rangle \, \Psi $
stands for a coefficient in an expression
$\langle - \rangle \, \Psi $
stands for a coefficient in an expression
![]() $\Psi $
, relative to an expansion which will be clear from the context. Thus, in equation (20),
$\Psi $
, relative to an expansion which will be clear from the context. Thus, in equation (20),
![]() $\langle \chi _{\lambda } \rangle $
denotes the coefficient of an irreducible
$\langle \chi _{\lambda } \rangle $
denotes the coefficient of an irreducible
![]() $\operatorname {\mathrm {GL}} _{n}$
character, while
$\operatorname {\mathrm {GL}} _{n}$
character, while
![]() $\langle x^{0} \rangle $
denotes the constant term in the variables
$\langle x^{0} \rangle $
denotes the constant term in the variables
![]() $x_{i}$
.
$x_{i}$
.
Lemma 2.3.1. For any
![]() $\operatorname {\mathrm {GL}} _{l}$
weights
$\operatorname {\mathrm {GL}} _{l}$
weights
![]() $\lambda ,\mu $
and Laurent polynomial
$\lambda ,\mu $
and Laurent polynomial
![]() $\phi (x)=\phi (x_{1},\ldots ,x_{l})$
, we have
$\phi (x)=\phi (x_{1},\ldots ,x_{l})$
, we have
in alphabets
![]() $X = x_{1}+\cdots + x_{l}$
and
$X = x_{1}+\cdots + x_{l}$
and
![]() $Z = z_{1}+\cdots +z_{l}$
, where
$Z = z_{1}+\cdots +z_{l}$
, where
![]() $\overline {Z} = z_{1}^{-1}+\cdots +z_{l}^{-1}$
.
$\overline {Z} = z_{1}^{-1}+\cdots +z_{l}^{-1}$
.
Proof. Identity (19) follows directly from the Weyl character formula. To prove equation (20), by linearity it suffices to verify the formula when
![]() $\phi (x)= x^{\mu }$
is any Laurent monomial. Then using equation (19), the right side becomes
$\phi (x)= x^{\mu }$
is any Laurent monomial. Then using equation (19), the right side becomes
![]() $\langle x^{-\mu } \rangle \, \overline { \chi _{\lambda }} \prod _{i<j} (1-x_{i}/x_{j}) = \langle x^{-\mu } \rangle \sum _{w\in S_{l}} (-1)^{\ell (w)}x^{-w(\lambda +\rho ) +\rho }.$
This is
$\langle x^{-\mu } \rangle \, \overline { \chi _{\lambda }} \prod _{i<j} (1-x_{i}/x_{j}) = \langle x^{-\mu } \rangle \sum _{w\in S_{l}} (-1)^{\ell (w)}x^{-w(\lambda +\rho ) +\rho }.$
This is
![]() $(-1)^{\ell (w)}$
if
$(-1)^{\ell (w)}$
if
![]() $\mu +\rho =w(\lambda +\rho )$
, or zero if there is no such w, which agrees with
$\mu +\rho =w(\lambda +\rho )$
, or zero if there is no such w, which agrees with
![]() $\langle \chi _{\lambda } \rangle \, {\boldsymbol \sigma }(x^{\mu })$
.
$\langle \chi _{\lambda } \rangle \, {\boldsymbol \sigma }(x^{\mu })$
.
The last identity is then proved from the Cauchy identity (12) followed by equation (20) (applied with z in place of x on the right):
 $$ \begin{align} \langle z^{-\mu } \rangle \Omega [\overline{Z}X] \, \prod _{i<j}(1-z_{i}/z_{j}) = \sum_{\lambda} s_{\lambda}(X) \cdot \langle z^{-\mu } \rangle &s_{\lambda}[\overline{Z}] \prod _{i<j}(1-z_{i}/z_{j}) \notag \\[5pt] &= \sum_{\lambda} s_{\lambda}(X) \cdot \langle \chi _{\lambda } \rangle {\boldsymbol \sigma }(x^{\mu}) = {\boldsymbol \sigma } (x^{\mu })_{\operatorname{\mathrm{pol}} }. \end{align} $$
$$ \begin{align} \langle z^{-\mu } \rangle \Omega [\overline{Z}X] \, \prod _{i<j}(1-z_{i}/z_{j}) = \sum_{\lambda} s_{\lambda}(X) \cdot \langle z^{-\mu } \rangle &s_{\lambda}[\overline{Z}] \prod _{i<j}(1-z_{i}/z_{j}) \notag \\[5pt] &= \sum_{\lambda} s_{\lambda}(X) \cdot \langle \chi _{\lambda } \rangle {\boldsymbol \sigma }(x^{\mu}) = {\boldsymbol \sigma } (x^{\mu })_{\operatorname{\mathrm{pol}} }. \end{align} $$
2.4 Hall–Littlewood symmetrization
Given a Laurent polynomial
![]() $\phi (x_{1},\ldots ,x_{l})$
, we define
$\phi (x_{1},\ldots ,x_{l})$
, we define
 $$ \begin{align} {\mathbf H} _{q}(\phi (x)) = {\boldsymbol \sigma } \Bigl( \frac{\phi (x)}{\prod _{i<j}(1-q\, x_{i}/x_{j})} \Bigr) = \sum _{w\in S_{l}} w\left(\frac{\phi (x)}{\prod _{i<j}((1-x_{j}/x_{i})(1-q\, x_{i}/x_{j}))} \right). \end{align} $$
$$ \begin{align} {\mathbf H} _{q}(\phi (x)) = {\boldsymbol \sigma } \Bigl( \frac{\phi (x)}{\prod _{i<j}(1-q\, x_{i}/x_{j})} \Bigr) = \sum _{w\in S_{l}} w\left(\frac{\phi (x)}{\prod _{i<j}((1-x_{j}/x_{i})(1-q\, x_{i}/x_{j}))} \right). \end{align} $$
Here and in similar raising operator formulas elsewhere, the factors
![]() $1/(1-q\, x_{i}/x_{j})$
are to be understood as geometric series, making
$1/(1-q\, x_{i}/x_{j})$
are to be understood as geometric series, making
![]() ${\mathbf H} _{q}(\phi (x))$
an infinite formal sum of irreducible
${\mathbf H} _{q}(\phi (x))$
an infinite formal sum of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters with coefficients in
$\operatorname {\mathrm {GL}} _{l}$
characters with coefficients in
![]() ${\mathbf k} $
. Since
${\mathbf k} $
. Since
![]() $1/(1-q\, x_{i}/x_{j})$
is a power series in q, if we expand the coefficients of
$1/(1-q\, x_{i}/x_{j})$
is a power series in q, if we expand the coefficients of
![]() $\phi (x)$
as formal Laurent series in q, then
$\phi (x)$
as formal Laurent series in q, then
![]() ${\mathbf H} _{q}(\phi (x))$
becomes a formal Laurent series in q over virtual
${\mathbf H} _{q}(\phi (x))$
becomes a formal Laurent series in q over virtual
![]() $\operatorname {\mathrm {GL}}_{l}$
characters. This is how the last formula in equation (23) should be interpreted.
$\operatorname {\mathrm {GL}}_{l}$
characters. This is how the last formula in equation (23) should be interpreted.
Remark 2.4.1. The dual Hall–Littlewood polynomials, defined by
![]() $H_{\mu }(X;q) = \sum _{\lambda }K_{\lambda ,\mu }(q) s_{\lambda }$
, where
$H_{\mu }(X;q) = \sum _{\lambda }K_{\lambda ,\mu }(q) s_{\lambda }$
, where
![]() $K_{\lambda ,\mu }(q)$
are the q-Kostka coefficients, are given in l variables by
$K_{\lambda ,\mu }(q)$
are the q-Kostka coefficients, are given in l variables by
![]() $H_{\mu }(x_{1},\ldots ,x_{l};q) = {\mathbf H} _{q}(x^{\mu })_{\operatorname {\mathrm {pol}} }$
. This explains our terminology.
$H_{\mu }(x_{1},\ldots ,x_{l};q) = {\mathbf H} _{q}(x^{\mu })_{\operatorname {\mathrm {pol}} }$
. This explains our terminology.
3 The Schiffmann algebra
3.1 Overview
We recall here some definitions and results from [Reference Burban and Schiffmann6, Reference Feigin and Tsymbaliuk8, Reference Negut30, Reference Schiffmann31, Reference Schiffmann and Vasserot32] concerning the elliptic Hall algebra
![]() ${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann6] (or Schiffmann algebra, for short) and its action on the algebra of symmetric functions
${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann6] (or Schiffmann algebra, for short) and its action on the algebra of symmetric functions
![]() $\Lambda $
, constructed by Feigin and Tsymbaliuk [Reference Feigin and Tsymbaliuk8] and Schiffmann and Vasserot [Reference Schiffmann and Vasserot32].
$\Lambda $
, constructed by Feigin and Tsymbaliuk [Reference Feigin and Tsymbaliuk8] and Schiffmann and Vasserot [Reference Schiffmann and Vasserot32].
From a certain point of view, this material is unnecessary: Two of the three quantities equated by equations (1) and (2) are defined without reference to the Schiffmann algebra, and we could take ‘shuffle theorem’ to mean the identity between these two, namely
with
![]() ${\mathcal H} _{{\mathbf b} }(x)$
as in equation (3). This identity still has the virtue of equating the combinatorial right-hand side, involving Dyck paths and LLT polynomials, with a simple algebraic left-hand side that is manifestly symmetric in q and t. Furthermore, our proof of equation (1) in Theorem 5.5.1 proceeds by combining equation (2) with a proof of equation (24) (via Theorem 5.3.1) that makes no use of the Schiffmann algebra.
${\mathcal H} _{{\mathbf b} }(x)$
as in equation (3). This identity still has the virtue of equating the combinatorial right-hand side, involving Dyck paths and LLT polynomials, with a simple algebraic left-hand side that is manifestly symmetric in q and t. Furthermore, our proof of equation (1) in Theorem 5.5.1 proceeds by combining equation (2) with a proof of equation (24) (via Theorem 5.3.1) that makes no use of the Schiffmann algebra.
What we need the Schiffmann algebra for is to provide the link between our shuffle theorem and the classical and
![]() $(km,kn)$
versions. Indeed, the very definition of the algebraic side in the
$(km,kn)$
versions. Indeed, the very definition of the algebraic side in the
![]() $(km,kn)$
shuffle theorem is
$(km,kn)$
shuffle theorem is
![]() $e_{k}[-MX^{m,n}]\cdot 1$
for a certain operator
$e_{k}[-MX^{m,n}]\cdot 1$
for a certain operator
![]() $e_{k}[-MX^{m,n}]\in {\mathcal E} $
, while the classical shuffle theorems refer implicitly to the same operators through the identity
$e_{k}[-MX^{m,n}]\in {\mathcal E} $
, while the classical shuffle theorems refer implicitly to the same operators through the identity
![]() $\nabla ^{m} e_{k} = e_{k}[-MX^{m,1}]\cdot 1$
.
$\nabla ^{m} e_{k} = e_{k}[-MX^{m,1}]\cdot 1$
.
In this section, we review what is needed to relate the symmetric functions
![]() $\nabla ^{m} e_{k}$
and
$\nabla ^{m} e_{k}$
and
![]() $({\mathcal H} _{{\mathbf b} })_{\operatorname {\mathrm {pol}} }$
to the action of the elements
$({\mathcal H} _{{\mathbf b} })_{\operatorname {\mathrm {pol}} }$
to the action of the elements
![]() $e_{k}[-MX^{m,n}]$
and
$e_{k}[-MX^{m,n}]$
and
![]() $D_{{\mathbf b} }$
on
$D_{{\mathbf b} }$
on
![]() $\Lambda $
. For ease of reference, we have collected most of the statements that will be used elsewhere in the paper in §3.7, after the technical development in §§3.2–3.6.
$\Lambda $
. For ease of reference, we have collected most of the statements that will be used elsewhere in the paper in §3.7, after the technical development in §§3.2–3.6.
3.2 The algebra
 ${\mathcal E} $
${\mathcal E} $
Let
![]() ${\mathbf k} ={\mathbb Q} (q,t)$
. The Schiffmann algebra
${\mathbf k} ={\mathbb Q} (q,t)$
. The Schiffmann algebra
![]() ${\mathcal E} $
is generated by subalgebras
${\mathcal E} $
is generated by subalgebras
![]() $\Lambda (X^{m,n})$
isomorphic to the algebra
$\Lambda (X^{m,n})$
isomorphic to the algebra
![]() $\Lambda _{{\mathbf k} }$
of symmetric functions, one for each pair of coprime integers
$\Lambda _{{\mathbf k} }$
of symmetric functions, one for each pair of coprime integers
![]() $(m,n)$
, and a central Laurent polynomial subalgebra
$(m,n)$
, and a central Laurent polynomial subalgebra
![]() ${\mathbf k} [c_{1}^{\pm 1}, c_{2}^{\pm 1}]$
. A full presentation of
${\mathbf k} [c_{1}^{\pm 1}, c_{2}^{\pm 1}]$
. A full presentation of
![]() ${\mathcal E} $
in our notation can be found in [Reference Blasiak, Haiman, Morse, Pun and Seelinger5, §3.2]. Here, we only use a few of the defining relations, invoking them where needed.
${\mathcal E} $
in our notation can be found in [Reference Blasiak, Haiman, Morse, Pun and Seelinger5, §3.2]. Here, we only use a few of the defining relations, invoking them where needed.
For purposes of comparison with [Reference Burban and Schiffmann6, Reference Schiffmann31, Reference Schiffmann and Vasserot32], our notation (on the left-hand side of each formula) is related as follows to that in [Reference Burban and Schiffmann6, Definition 6.4] (on the right-hand side). Note that our indices
![]() $(m,n)\in {\mathbb Z} ^{2}$
correspond to transposed indices
$(m,n)\in {\mathbb Z} ^{2}$
correspond to transposed indices
![]() $(n,m)$
in [Reference Burban and Schiffmann6].
$(n,m)$
in [Reference Burban and Schiffmann6].
 $$ \begin{align} \begin{gathered} q = \sigma ^{-1},\quad t = \bar{\sigma }^{-1},\\ c_{1}^{m}c_{2}^{n} = \kappa _{n,m}^{-2},\\ \omega p_{k}(X^{m,n}) = \kappa _{kn,km}^{\varepsilon _{n,m}} u_{kn,km},\\ e_{k}[-\widehat{M} X^{m,n}] = \kappa _{kn,km}^{\varepsilon _{n,m}} \theta _{kn,km}, \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} q = \sigma ^{-1},\quad t = \bar{\sigma }^{-1},\\ c_{1}^{m}c_{2}^{n} = \kappa _{n,m}^{-2},\\ \omega p_{k}(X^{m,n}) = \kappa _{kn,km}^{\varepsilon _{n,m}} u_{kn,km},\\ e_{k}[-\widehat{M} X^{m,n}] = \kappa _{kn,km}^{\varepsilon _{n,m}} \theta _{kn,km}, \end{gathered} \end{align} $$
where
![]() $\varepsilon _{n,m}$
, which is equal to
$\varepsilon _{n,m}$
, which is equal to
![]() $(1-\epsilon _{n,m})/2$
in the notation of [Reference Burban and Schiffmann6], is given by
$(1-\epsilon _{n,m})/2$
in the notation of [Reference Burban and Schiffmann6], is given by
 $$ \begin{align} \varepsilon _{n,m} = \begin{cases} 1& n<0 \text{ or } (m,n)=(-1,0)\\ 0& \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \varepsilon _{n,m} = \begin{cases} 1& n<0 \text{ or } (m,n)=(-1,0)\\ 0& \text{otherwise}. \end{cases} \end{align} $$
The expression
![]() $e_{k}[-\widehat {M} X^{m,n}]$
in equation (25) uses plethystic substitution (§2.2) with
$e_{k}[-\widehat {M} X^{m,n}]$
in equation (25) uses plethystic substitution (§2.2) with
The quantity M will be referred to repeatedly.
3.3 Action of
 ${\mathcal E} $
on
${\mathcal E} $
on
 $\Lambda $
$\Lambda $
A natural action of
![]() ${\mathcal E} $
by operators on
${\mathcal E} $
by operators on
![]() $\Lambda (X)$
has been constructed in [Reference Feigin and Tsymbaliuk8, Reference Schiffmann and Vasserot32]. Actually, these references give several different normalizations of essentially the same action. The action we use is a slight variation of the action in [Reference Schiffmann and Vasserot32, Theorem 3.1].
$\Lambda (X)$
has been constructed in [Reference Feigin and Tsymbaliuk8, Reference Schiffmann and Vasserot32]. Actually, these references give several different normalizations of essentially the same action. The action we use is a slight variation of the action in [Reference Schiffmann and Vasserot32, Theorem 3.1].
To write it down, we need to recall some notions from the theory of Macdonald polynomials. Let
![]() $\tilde {H} _{\mu }(X;q,t)$
denote the modified Macdonald polynomials [Reference Garsia and Haiman11], which can be defined in terms of the integral form Macdonald polynomials
$\tilde {H} _{\mu }(X;q,t)$
denote the modified Macdonald polynomials [Reference Garsia and Haiman11], which can be defined in terms of the integral form Macdonald polynomials
![]() $J_{\mu }(X;q,t)$
of [Reference Macdonald26] by
$J_{\mu }(X;q,t)$
of [Reference Macdonald26] by
with
![]() $n(\mu )$
as in equation (6). For any symmetric function
$n(\mu )$
as in equation (6). For any symmetric function
![]() $f\in \Lambda $
, let
$f\in \Lambda $
, let
![]() $f[{\mathbf B} ]$
,
$f[{\mathbf B} ]$
,
![]() $f[\overline {{\mathbf B} }]$
denote the eigenoperators on the basis
$f[\overline {{\mathbf B} }]$
denote the eigenoperators on the basis
![]() $\{\tilde {H_{\mu }} \}$
of
$\{\tilde {H_{\mu }} \}$
of
![]() $\Lambda $
such that
$\Lambda $
such that
with
![]() $B_{\mu }(q,t)$
as in equation (8) and
$B_{\mu }(q,t)$
as in equation (8) and
![]() $\overline {B_{\mu }(q,t)} = B_{\mu }(q^{-1},t^{-1})$
. More generally, we use the overbar to signify inverting the variables in any expression, for example,
$\overline {B_{\mu }(q,t)} = B_{\mu }(q^{-1},t^{-1})$
. More generally, we use the overbar to signify inverting the variables in any expression, for example,
The next proposition essentially restates the contents of [Reference Schiffmann and Vasserot32, Theorem 3.1 and Proposition 4.10] in our notation. To be more precise, since these two theorems refer to different actions of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
, one must first use the plethystic transformation in [Reference Schiffmann and Vasserot32, §4.4] to express [Reference Schiffmann and Vasserot32, Proposition 4.10] in terms of the action in [Reference Schiffmann and Vasserot32, Theorem 3.1]. Rescaling the generators
$\Lambda $
, one must first use the plethystic transformation in [Reference Schiffmann and Vasserot32, §4.4] to express [Reference Schiffmann and Vasserot32, Proposition 4.10] in terms of the action in [Reference Schiffmann and Vasserot32, Theorem 3.1]. Rescaling the generators
![]() $u_{\pm 1,l}$
then yields the following.
$u_{\pm 1,l}$
then yields the following.
Proposition 3.3.1. There is an action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
characterized uniquely by the following properties.
$\Lambda $
characterized uniquely by the following properties.
-
(i) The central parameters
 $c_{1},c_{2}$
act as scalars (31)
$c_{1},c_{2}$
act as scalars (31) $$ \begin{align} c_{1}\mapsto 1,\quad c_{2}\mapsto (q\, t)^{-1}. \end{align} $$
$$ \begin{align} c_{1}\mapsto 1,\quad c_{2}\mapsto (q\, t)^{-1}. \end{align} $$
-
(ii) The subalgebras
 $\Lambda (X^{\pm 1,0})$
act as (32)
$\Lambda (X^{\pm 1,0})$
act as (32) $$ \begin{align} f(X^{1,0})\mapsto (\omega f)[{\mathbf B} -1/M],\quad f(X^{-1,0})\mapsto (\omega f)[\overline{1/M-{\mathbf B} }]. \end{align} $$
$$ \begin{align} f(X^{1,0})\mapsto (\omega f)[{\mathbf B} -1/M],\quad f(X^{-1,0})\mapsto (\omega f)[\overline{1/M-{\mathbf B} }]. \end{align} $$
-
(iii) The subalgebras
 $\Lambda (X^{0,\pm 1})$
act as (33)
$\Lambda (X^{0,\pm 1})$
act as (33) $$ \begin{align} f(X^{0,1})\mapsto f[-X/M]^{\bullet },\quad f(X^{0,-1})\mapsto f(X)^{\perp }, \end{align} $$
$$ \begin{align} f(X^{0,1})\mapsto f[-X/M]^{\bullet },\quad f(X^{0,-1})\mapsto f(X)^{\perp }, \end{align} $$
using the notation in §2.1.
Remark 3.3.2. The subalgebras
![]() $\Lambda (X^{m,n})$
and
$\Lambda (X^{m,n})$
and
![]() $\Lambda (X^{-m,n})$
satisfy Heisenberg relations that depend on the central element
$\Lambda (X^{-m,n})$
satisfy Heisenberg relations that depend on the central element
![]() $c_{1}^{m}c_{2}^{n}$
. If
$c_{1}^{m}c_{2}^{n}$
. If
![]() $c_{1}^{m}c_{2}^{n} = 1$
, the Heisenberg relation degenerates and
$c_{1}^{m}c_{2}^{n} = 1$
, the Heisenberg relation degenerates and
![]() $\Lambda (X^{\pm (m,n)})$
commute. In particular, the value
$\Lambda (X^{\pm (m,n)})$
commute. In particular, the value
![]() $c_{1} \mapsto 1$
in equation (31) makes
$c_{1} \mapsto 1$
in equation (31) makes
![]() $\Lambda (X^{\pm 1,0})$
commute, consistent with equation (32). The value
$\Lambda (X^{\pm 1,0})$
commute, consistent with equation (32). The value
![]() $c_{2}\mapsto 1/(qt)$
makes
$c_{2}\mapsto 1/(qt)$
makes
![]() $\Lambda (X^{0,\pm 1})$
satisfy Heisenberg relations consistent with equation (33).
$\Lambda (X^{0,\pm 1})$
satisfy Heisenberg relations consistent with equation (33).
We will show in Proposition 3.3.4, below, that the elements
![]() $p_{1}[-MX^{1,a}]\in {\mathcal E} $
act on
$p_{1}[-MX^{1,a}]\in {\mathcal E} $
act on
![]() $\Lambda $
as operators
$\Lambda $
as operators
![]() $D_{a}$
given by the coefficients
$D_{a}$
given by the coefficients
![]() $D_{a} = \langle z^{-a} \rangle D(z)$
of a generating series
$D_{a} = \langle z^{-a} \rangle D(z)$
of a generating series
defined by either of the equivalent formulas
using the operator notation from §2.1. These operators
![]() $D_{a}$
differ by a sign
$D_{a}$
differ by a sign
![]() $(-1)^{a}$
from those studied in [Reference Bergeron, Garsia, Haiman and Tesler3, Reference Garsia, Haiman and Tesler12] and by a plethystic transformation from operators previously introduced by Jing [Reference Jing23].
$(-1)^{a}$
from those studied in [Reference Bergeron, Garsia, Haiman and Tesler3, Reference Garsia, Haiman and Tesler12] and by a plethystic transformation from operators previously introduced by Jing [Reference Jing23].
Lemma 3.3.3. We have the identities
Proof. We start with the second identity, which is equivalent to
Since all operators of the form
![]() $f(X)^{\perp }$
commute with each other, equation (37) follows from the definition of
$f(X)^{\perp }$
commute with each other, equation (37) follows from the definition of
![]() $D(z)$
and
$D(z)$
and
To verify the latter identity, note first that equation (15) and
![]() $\Omega [z^{-1}X] = \exp \sum _{k>0} p_{k} z^{-k}/k$
imply
$\Omega [z^{-1}X] = \exp \sum _{k>0} p_{k} z^{-k}/k$
imply
Conjugating both sides by
![]() $\omega $
and using
$\omega $
and using
![]() $(\omega f)^{\bullet } = \omega \cdot f^{\bullet }\cdot \omega $
and
$(\omega f)^{\bullet } = \omega \cdot f^{\bullet }\cdot \omega $
and
![]() $(\omega f)^{\perp } = \omega \cdot f^{\perp }\cdot \omega $
gives equation (38).
$(\omega f)^{\perp } = \omega \cdot f^{\perp }\cdot \omega $
gives equation (38).
For the first identity in equation (36), consider the modified inner product defined by
The second equality here, which shows that
![]() $\langle -,- \rangle '$
is symmetric, follows from orthogonality of the power-sums
$\langle -,- \rangle '$
is symmetric, follows from orthogonality of the power-sums
![]() $p_{\lambda }$
. For any f, the operators
$p_{\lambda }$
. For any f, the operators
![]() $f^{\perp }$
and
$f^{\perp }$
and
![]() $f[-X/M]^{\bullet }$
are adjoint with respect to
$f[-X/M]^{\bullet }$
are adjoint with respect to
![]() $\langle -,- \rangle '$
. Using this and the definition of
$\langle -,- \rangle '$
. Using this and the definition of
![]() $D(z)$
, we see that
$D(z)$
, we see that
![]() $D(z^{-1})$
is the
$D(z^{-1})$
is the
![]() $\langle -,- \rangle '$
adjoint of
$\langle -,- \rangle '$
adjoint of
![]() $D(z)$
; hence,
$D(z)$
; hence,
![]() $D_{-a}$
is adjoint to
$D_{-a}$
is adjoint to
![]() $D_{a}$
. Taking adjoints on both sides of the second identity in equation (36) now implies the first.
$D_{a}$
. Taking adjoints on both sides of the second identity in equation (36) now implies the first.
Proposition 3.3.4. In the action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
given by Proposition 3.3.1, the element
$\Lambda $
given by Proposition 3.3.1, the element
![]() $p_{1}[-M X^{1,a}] = -M p_{1}(X^{1,a})\in {\mathcal E} $
acts as the operator
$p_{1}[-M X^{1,a}] = -M p_{1}(X^{1,a})\in {\mathcal E} $
acts as the operator
![]() $D_{a}$
defined by equation (34).
$D_{a}$
defined by equation (34).
Proof. It is known [Reference Haiman18, Proposition 2.4] that
![]() $D_{0}\tilde {H} _{\mu } = (1-MB_{\mu })\tilde {H} _{\mu }$
. From Proposition 3.3.1 (ii), we see that
$D_{0}\tilde {H} _{\mu } = (1-MB_{\mu })\tilde {H} _{\mu }$
. From Proposition 3.3.1 (ii), we see that
![]() $p_{1}[-M X^{1,0}]$
acts by the same operator, giving the case
$p_{1}[-M X^{1,0}]$
acts by the same operator, giving the case
![]() $a=0$
.
$a=0$
.
Among the defining relations of
![]() ${\mathcal E} $
are
${\mathcal E} $
are
Multiplying these by
![]() $-M$
and using Proposition 3.3.1 (iii) to compare with equation (36) reduces the general result to the case
$-M$
and using Proposition 3.3.1 (iii) to compare with equation (36) reduces the general result to the case
![]() $a=0$
.
$a=0$
.
3.4 The operator
 $\nabla $
$\nabla $
As in [Reference Bergeron, Garsia, Haiman and Tesler3], we define an eigenoperator
![]() $\nabla $
on the Macdonald basis by
$\nabla $
on the Macdonald basis by
with
![]() $n(\mu )$
as in equation (6). Since
$n(\mu )$
as in equation (6). Since
![]() $t^{n(\mu )}q^{n(\mu ^{*})} = e_{n}[B_{\mu }(q,t)]$
for
$t^{n(\mu )}q^{n(\mu ^{*})} = e_{n}[B_{\mu }(q,t)]$
for
![]() $n = |\mu |$
, we see that
$n = |\mu |$
, we see that
![]() $\nabla $
coincides in degree n with
$\nabla $
coincides in degree n with
![]() $e_{n}[{\mathbf B} ]$
. Although the operators
$e_{n}[{\mathbf B} ]$
. Although the operators
![]() $e_{n}[{\mathbf B} ]$
belong to
$e_{n}[{\mathbf B} ]$
belong to
![]() ${\mathcal E} $
acting on
${\mathcal E} $
acting on
![]() $\Lambda $
, the operator
$\Lambda $
, the operator
![]() $\nabla $
does not. Its role, rather, is to internalize a symmetry of this action.
$\nabla $
does not. Its role, rather, is to internalize a symmetry of this action.
Lemma 3.4.1. Conjugation by the operator
![]() $\nabla $
provides a symmetry of the action of
$\nabla $
provides a symmetry of the action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
, namely
$\Lambda $
, namely
Proof. For
![]() $m=\pm 1$
,
$m=\pm 1$
,
![]() $n=0$
, this says that
$n=0$
, this says that
![]() $\nabla $
commutes with the other Macdonald eigenoperators, which is clear.
$\nabla $
commutes with the other Macdonald eigenoperators, which is clear.
It is known from [Reference Burban and Schiffmann6] that the group of
![]() ${\mathbf k} $
-algebra automorphisms of
${\mathbf k} $
-algebra automorphisms of
![]() ${\mathcal E} $
includes one which acts on the subalgebras
${\mathcal E} $
includes one which acts on the subalgebras
![]() $\Lambda (X^{m,n})$
by
$\Lambda (X^{m,n})$
by
![]() $f(X^{m,n})\mapsto f(X^{m+n,n})$
and on the central subalgebra
$f(X^{m,n})\mapsto f(X^{m+n,n})$
and on the central subalgebra
![]() ${\mathbf k} [c_{1}^{\pm 1},c_{2}^{\pm 1}]$
by an automorphism which fixes the central character in Proposition 3.3.1 (i).
${\mathbf k} [c_{1}^{\pm 1},c_{2}^{\pm 1}]$
by an automorphism which fixes the central character in Proposition 3.3.1 (i).
The
![]() $\Lambda (X^{m,n})$
for
$\Lambda (X^{m,n})$
for
![]() $n>0$
are all contained in the subalgebra of
$n>0$
are all contained in the subalgebra of
![]() ${\mathcal E} $
generated by the elements
${\mathcal E} $
generated by the elements
![]() $p_{1}(X^{a,1})$
. To prove equation (43) for
$p_{1}(X^{a,1})$
. To prove equation (43) for
![]() $n>0$
, it therefore suffices to verify the operator identity
$n>0$
, it therefore suffices to verify the operator identity
![]() $\nabla \, p_{1}(X^{a,1})\, \nabla ^{-1} = p_{1}(X^{a+1,1})$
.
$\nabla \, p_{1}(X^{a,1})\, \nabla ^{-1} = p_{1}(X^{a+1,1})$
.
In
![]() ${\mathcal E} $
, there are relations
${\mathcal E} $
, there are relations
Since
![]() $\nabla $
commutes with the action of
$\nabla $
commutes with the action of
![]() $\Lambda (X^{\pm 1,0})$
, these relations reduce the problem to the case
$\Lambda (X^{\pm 1,0})$
, these relations reduce the problem to the case
![]() $a=0$
, that is, to the identity
$a=0$
, that is, to the identity
![]() $\nabla \, p_{1}(X^{0,1})\, \nabla ^{-1} = p_{1}(X^{1,1})$
. By Propositions 3.3.1 and 3.3.4, this is equivalent to the operator identity
$\nabla \, p_{1}(X^{0,1})\, \nabla ^{-1} = p_{1}(X^{1,1})$
. By Propositions 3.3.1 and 3.3.4, this is equivalent to the operator identity
![]() $\nabla \cdot p_{1}(X)^{\bullet }\cdot \nabla ^{-1} = D_{1}$
, which is [Reference Bergeron, Garsia, Haiman and Tesler3, I.12 (iii)].
$\nabla \cdot p_{1}(X)^{\bullet }\cdot \nabla ^{-1} = D_{1}$
, which is [Reference Bergeron, Garsia, Haiman and Tesler3, I.12 (iii)].
We leave the similar argument for the case
![]() $n<0$
, using [Reference Bergeron, Garsia, Haiman and Tesler3, I.12 (iv)], to the reader.
$n<0$
, using [Reference Bergeron, Garsia, Haiman and Tesler3, I.12 (iv)], to the reader.
3.5 Shuffle algebra
The operators of interest to us belong to the ‘right half-plane’ subalgebra
![]() ${\mathcal E} ^{+}\subseteq {\mathcal E} $
generated by the
${\mathcal E} ^{+}\subseteq {\mathcal E} $
generated by the
![]() $\Lambda (X^{m,n})$
for
$\Lambda (X^{m,n})$
for
![]() $m>0$
, or equivalently by the elements
$m>0$
, or equivalently by the elements
![]() $p_{1}(X^{1,a})$
. The subalgebra
$p_{1}(X^{1,a})$
. The subalgebra
![]() ${\mathcal E} ^{+}$
acts on
${\mathcal E} ^{+}$
acts on
![]() $\Lambda $
as the algebra generated by the operators
$\Lambda $
as the algebra generated by the operators
![]() $D_{a}$
. It was shown in [Reference Schiffmann and Vasserot32] that
$D_{a}$
. It was shown in [Reference Schiffmann and Vasserot32] that
![]() ${\mathcal E} ^{+}$
is isomorphic to the shuffle algebra constructed in [Reference Feigin and Tsymbaliuk8] and studied further in [Reference Negut30], whose definition we now recall.
${\mathcal E} ^{+}$
is isomorphic to the shuffle algebra constructed in [Reference Feigin and Tsymbaliuk8] and studied further in [Reference Negut30], whose definition we now recall.
We fix the rational function
and define, for each l, a
![]() $q,t$
analog of the symmetrization operator
$q,t$
analog of the symmetrization operator
![]() ${\mathbf H} _{q}$
in equation (23) by
${\mathbf H} _{q}$
in equation (23) by
 $$ \begin{align} {\mathbf H} _{q,t}(\phi (x_{1},\ldots,x_{l})) = \sum _{w\in S_{l}} w &\biggl( \phi(x) \cdot \prod _{i<j} \Gamma \bigl(\frac{x_{i}}{x_{j}}\bigr) \biggr) = {\boldsymbol \sigma } \left(\frac{\phi (x)\, \prod _{i<j} (1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j} ((1 - q\, x_{i}/x_{j}) (1 - t\, x_{i}/x_{j}))} \right). \end{align} $$
$$ \begin{align} {\mathbf H} _{q,t}(\phi (x_{1},\ldots,x_{l})) = \sum _{w\in S_{l}} w &\biggl( \phi(x) \cdot \prod _{i<j} \Gamma \bigl(\frac{x_{i}}{x_{j}}\bigr) \biggr) = {\boldsymbol \sigma } \left(\frac{\phi (x)\, \prod _{i<j} (1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j} ((1 - q\, x_{i}/x_{j}) (1 - t\, x_{i}/x_{j}))} \right). \end{align} $$
We write
![]() ${\mathbf H} _{q,t}^{(l)}$
when we want to make the number of variables explicit.
${\mathbf H} _{q,t}^{(l)}$
when we want to make the number of variables explicit.
Let
![]() $T = T({\mathbf k} [x^{\pm 1}])$
be the tensor algebra on the Laurent polynomial ring
$T = T({\mathbf k} [x^{\pm 1}])$
be the tensor algebra on the Laurent polynomial ring
![]() ${\mathbf k} [x^{\pm 1}]$
in one variable, that is, the noncommutative polynomial algebra with generators corresponding to the basis elements
${\mathbf k} [x^{\pm 1}]$
in one variable, that is, the noncommutative polynomial algebra with generators corresponding to the basis elements
![]() $x^{a}$
of
$x^{a}$
of
![]() ${\mathbf k} [x^{\pm 1}]$
as a vector space. Identifying
${\mathbf k} [x^{\pm 1}]$
as a vector space. Identifying
![]() $T^{k} = T^{k}({\mathbf k} [x^{\pm 1}])$
with
$T^{k} = T^{k}({\mathbf k} [x^{\pm 1}])$
with
![]() ${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{k}^{\pm 1}]$
, the product in T is given by ‘concatenation,’
${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{k}^{\pm 1}]$
, the product in T is given by ‘concatenation,’
For each l, let
![]() $I^{l}\subseteq T^{l}$
be the kernel of the symmetrization operator
$I^{l}\subseteq T^{l}$
be the kernel of the symmetrization operator
![]() ${\mathbf H} _{q,t}^{(l)}$
. Since
${\mathbf H} _{q,t}^{(l)}$
. Since
![]() ${\mathbf H} _{q,t}^{(l)}$
factors through the operator
${\mathbf H} _{q,t}^{(l)}$
factors through the operator
![]() ${\mathbf H} _{q,t}^{(k)}$
in any k consecutive variables
${\mathbf H} _{q,t}^{(k)}$
in any k consecutive variables
![]() $x_{i+1},\ldots ,x_{i+k}$
, the graded subspace
$x_{i+1},\ldots ,x_{i+k}$
, the graded subspace
![]() $I = \bigoplus _{l}I^{l}\subseteq T$
is a two-sided ideal. The shuffle algebra is defined to be the quotient
$I = \bigoplus _{l}I^{l}\subseteq T$
is a two-sided ideal. The shuffle algebra is defined to be the quotient
![]() $S = T/I$
. Note that S is generated by its tensor degree
$S = T/I$
. Note that S is generated by its tensor degree
![]() $1$
component
$1$
component
![]() $S^{1}$
by definition. We will not use the second, larger, type of shuffle algebra that was also introduced in [Reference Feigin and Tsymbaliuk8, Reference Negut30].
$S^{1}$
by definition. We will not use the second, larger, type of shuffle algebra that was also introduced in [Reference Feigin and Tsymbaliuk8, Reference Negut30].
Proposition 3.5.1 [Reference Schiffmann and Vasserot32, Theorem 10.1].
There is an algebra isomorphism
![]() $\psi \colon S \rightarrow {\mathcal E} ^{+}$
given on the generators by
$\psi \colon S \rightarrow {\mathcal E} ^{+}$
given on the generators by
![]() $\psi (x^{a}) = p_{1}[-MX^{1,a}]$
.
$\psi (x^{a}) = p_{1}[-MX^{1,a}]$
.
For clarity, we note that the factor
![]() $-M$
in
$-M$
in
![]() $p_{1}[-MX^{1,a}] = -M p_{1}(X^{1,a})$
makes no difference to the statement but is a convenient normalization for us since it makes
$p_{1}[-MX^{1,a}] = -M p_{1}(X^{1,a})$
makes no difference to the statement but is a convenient normalization for us since it makes
![]() $\psi (x_{1}^{a_{1}}\cdots x_{l}^{a_{l}})$
act on
$\psi (x_{1}^{a_{1}}\cdots x_{l}^{a_{l}})$
act on
![]() $\Lambda $
as
$\Lambda $
as
![]() $D_{a_{1}}\cdots D_{a_{l}}$
. We also note that our
$D_{a_{1}}\cdots D_{a_{l}}$
. We also note that our
![]() $\Gamma (x/y)$
differs by a factor symmetric in
$\Gamma (x/y)$
differs by a factor symmetric in
![]() $x,y$
from the function
$x,y$
from the function
![]() $g(y/x)$
in [Reference Schiffmann and Vasserot32, (10.3)], which makes the product in our shuffle algebra S opposite to that of the algebra
$g(y/x)$
in [Reference Schiffmann and Vasserot32, (10.3)], which makes the product in our shuffle algebra S opposite to that of the algebra
![]() ${\mathbf S} $
in [Reference Schiffmann and Vasserot32]. This is as it should be since the isomorphism in [Reference Schiffmann and Vasserot32] is from
${\mathbf S} $
in [Reference Schiffmann and Vasserot32]. This is as it should be since the isomorphism in [Reference Schiffmann and Vasserot32] is from
![]() ${\mathbf S} $
to the ‘upper half-plane’ subalgebra of
${\mathbf S} $
to the ‘upper half-plane’ subalgebra of
![]() ${\mathcal E} $
generated by the elements
${\mathcal E} $
generated by the elements
![]() $p_{1}(X^{a,1})$
, and the symmetry
$p_{1}(X^{a,1})$
, and the symmetry
![]() $p_{1}(X^{a,1})\leftrightarrow p_{1}(X^{1,a})$
is an antihomomorphism.
$p_{1}(X^{a,1})\leftrightarrow p_{1}(X^{1,a})$
is an antihomomorphism.
By construction, Laurent polynomials
![]() $\phi (x), \phi '(x)$
in variables
$\phi (x), \phi '(x)$
in variables
![]() $x_{1},\ldots ,x_{l}$
define the same element of S or, equivalently, map via
$x_{1},\ldots ,x_{l}$
define the same element of S or, equivalently, map via
![]() $\psi $
to the same element of
$\psi $
to the same element of
![]() ${\mathcal E} ^{+}$
, if and only if
${\mathcal E} ^{+}$
, if and only if
![]() ${\mathbf H} _{q,t}(\phi ) = {\mathbf H} _{q,t}(\phi ')$
. We can regard
${\mathbf H} _{q,t}(\phi ) = {\mathbf H} _{q,t}(\phi ')$
. We can regard
![]() ${\mathbf H} _{q,t}(\phi )$
as an infinite formal sum of
${\mathbf H} _{q,t}(\phi )$
as an infinite formal sum of
![]() $\operatorname {\mathrm {GL}} _{l}$
characters with coefficients in
$\operatorname {\mathrm {GL}} _{l}$
characters with coefficients in
![]() ${\mathbf k} $
, in the same manner as for
${\mathbf k} $
, in the same manner as for
![]() ${\mathbf H} _{q}$
. Representing elements of S, or of
${\mathbf H} _{q}$
. Representing elements of S, or of
![]() ${\mathcal E} ^{+}$
, in this way leads to the following useful formula for describing their action on
${\mathcal E} ^{+}$
, in this way leads to the following useful formula for describing their action on
![]() $1\in \Lambda $
.
$1\in \Lambda $
.
Proposition 3.5.2. Given a Laurent polynomial
![]() $\phi =\phi (x_{1},\ldots ,x_{l})$
, let
$\phi =\phi (x_{1},\ldots ,x_{l})$
, let
![]() $\zeta = \psi (\phi ) \in {\mathcal E} ^{+}$
be its image under the isomorphism in Proposition 3.5.1. Then with the action of
$\zeta = \psi (\phi ) \in {\mathcal E} ^{+}$
be its image under the isomorphism in Proposition 3.5.1. Then with the action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
given by Proposition 3.3.1, we have
$\Lambda $
given by Proposition 3.3.1, we have
Moreover, the Schur function expansion of the symmetric function
![]() $\omega (\zeta \cdot 1)(X)$
contains only terms
$\omega (\zeta \cdot 1)(X)$
contains only terms
![]() $s_{\lambda }$
with
$s_{\lambda }$
with
![]() $\ell (\lambda )\leq l$
, so equation (48) determines
$\ell (\lambda )\leq l$
, so equation (48) determines
![]() $\zeta \cdot 1$
.
$\zeta \cdot 1$
.
Proof. It suffices to consider the case when
![]() $\phi (x)=x^{{\mathbf a}} = x_{1}^{a_{1}}\cdots x_{l}^{a_{l}}$
and thus (by Proposition 3.3.4)
$\phi (x)=x^{{\mathbf a}} = x_{1}^{a_{1}}\cdots x_{l}^{a_{l}}$
and thus (by Proposition 3.3.4)
![]() $\zeta $
acts on
$\zeta $
acts on
![]() $\Lambda $
as the operator
$\Lambda $
as the operator
![]() $D_{a_{1}}\cdots D_{a_{l}}$
. To find
$D_{a_{1}}\cdots D_{a_{l}}$
. To find
![]() $\zeta \cdot 1$
, we use equation (16) to compute
$\zeta \cdot 1$
, we use equation (16) to compute
where
![]() $Z = z_{1}+\cdots +z_{l}$
. Acting on
$Z = z_{1}+\cdots +z_{l}$
. Acting on
![]() $1$
, applying
$1$
, applying
![]() $\omega $
, and taking the coefficient of
$\omega $
, and taking the coefficient of
![]() $z^{-{\mathbf a} }$
gives
$z^{-{\mathbf a} }$
gives
 $$ \begin{align} \omega (\zeta \cdot 1)(X) = \langle z^{-{\mathbf a} } \rangle &\bigl(\prod _{i<j} \Omega [-z_{i}/z_{j} M] \bigr)\, \Omega [\overline{Z} X] \notag \\ &\quad = \langle z^{0} \rangle \bigl(z^{{\mathbf a} }\prod _{i<j} \frac{1-q\, t\, z_{i}/z_{j}}{(1-q \, z_{i}/z_{j})(1-t \, z_{i}/z_{j})} \bigr)\, \Omega [\overline{Z} X] \, \prod _{i<j}(1-z_{i}/z_{j}). \end{align} $$
$$ \begin{align} \omega (\zeta \cdot 1)(X) = \langle z^{-{\mathbf a} } \rangle &\bigl(\prod _{i<j} \Omega [-z_{i}/z_{j} M] \bigr)\, \Omega [\overline{Z} X] \notag \\ &\quad = \langle z^{0} \rangle \bigl(z^{{\mathbf a} }\prod _{i<j} \frac{1-q\, t\, z_{i}/z_{j}}{(1-q \, z_{i}/z_{j})(1-t \, z_{i}/z_{j})} \bigr)\, \Omega [\overline{Z} X] \, \prod _{i<j}(1-z_{i}/z_{j}). \end{align} $$
Since Z has l variables, this implies that all Schur functions
![]() $s_{\lambda } $
in
$s_{\lambda } $
in
![]() $\omega (\zeta \cdot 1)(X)$
have
$\omega (\zeta \cdot 1)(X)$
have
![]() $\ell (\lambda )\leq l$
. Identity (48) for
$\ell (\lambda )\leq l$
. Identity (48) for
![]() $\phi (x) = x^{{\mathbf a} }$
follows by specializing X to
$\phi (x) = x^{{\mathbf a} }$
follows by specializing X to
![]() $x_1+\cdots +x_l$
and applying equation (21).
$x_1+\cdots +x_l$
and applying equation (21).
3.6 Distinguished elements
Given a rational function
![]() $\phi (x_{1},\ldots ,x_{l})$
, it may happen that we have an identity of rational functions
$\phi (x_{1},\ldots ,x_{l})$
, it may happen that we have an identity of rational functions
![]() ${\mathbf H} _{q,t}(\phi ) = {\mathbf H} _{q,t}(\eta )$
for some Laurent polynomial
${\mathbf H} _{q,t}(\phi ) = {\mathbf H} _{q,t}(\eta )$
for some Laurent polynomial
![]() $\eta (x)$
. In this case,
$\eta (x)$
. In this case,
![]() ${\mathbf H} _{q,t}(\phi )$
is the representative of the image of
${\mathbf H} _{q,t}(\phi )$
is the representative of the image of
![]() $\eta $
in S, or of
$\eta $
in S, or of
![]() $\psi (\eta )\in {\mathcal E} ^{+}$
, even though
$\psi (\eta )\in {\mathcal E} ^{+}$
, even though
![]() $\phi (x)$
is not necessarily a Laurent polynomial. For the shuffle algebra S under consideration here, Negut [Reference Negut30, Proposition 6.1] showed that this happens for
$\phi (x)$
is not necessarily a Laurent polynomial. For the shuffle algebra S under consideration here, Negut [Reference Negut30, Proposition 6.1] showed that this happens for
 $$ \begin{align} \phi (x) = \frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}}{\prod _{i=1}^{l-1}(1-q\, t\, x_{i}/x_{i+1})}. \end{align} $$
$$ \begin{align} \phi (x) = \frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}}{\prod _{i=1}^{l-1}(1-q\, t\, x_{i}/x_{i+1})}. \end{align} $$
Accordingly, there are distinguished elements
where
![]() $\psi \colon S \rightarrow {\mathcal E} ^{+}$
is the isomorphism in Proposition 3.5.1 and
$\psi \colon S \rightarrow {\mathcal E} ^{+}$
is the isomorphism in Proposition 3.5.1 and
![]() $\eta (x)$
is any Laurent polynomial such that
$\eta (x)$
is any Laurent polynomial such that
![]() ${\mathbf H} _{q,t}(\phi ) = {\mathbf H} _{q,t}(\eta )$
for the function
${\mathbf H} _{q,t}(\phi ) = {\mathbf H} _{q,t}(\eta )$
for the function
![]() $\phi $
in equation (51). Although there seems to be no particularly nice preferred choice for
$\phi $
in equation (51). Although there seems to be no particularly nice preferred choice for
![]() $\eta $
, we can avoid working directly with
$\eta $
, we can avoid working directly with
![]() $\eta $
by using the element
$\eta $
by using the element
![]() $\phi $
from equation (51) in equation (48).
$\phi $
from equation (51) in equation (48).
Negut identified certain of the elements
![]() $D_{b_{1},\ldots ,b_{l}}$
as (in our notation) ribbon skew Schur functions
$D_{b_{1},\ldots ,b_{l}}$
as (in our notation) ribbon skew Schur functions
![]() $s_{R}[-MX^{m,n}]$
. The following result is a special case.
$s_{R}[-MX^{m,n}]$
. The following result is a special case.
Proposition 3.6.1 [Reference Negut30, Proposition 6.7].
Let m, k be positive integers and n any integer with
![]() $m,n$
coprime. For
$m,n$
coprime. For
![]() $i=1,\ldots ,km$
, let
$i=1,\ldots ,km$
, let
![]() $b_{i} = \lceil i n/m \rceil -\lceil (i-1) n/m \rceil $
; if
$b_{i} = \lceil i n/m \rceil -\lceil (i-1) n/m \rceil $
; if
![]() $n \geq 0$
, this is the number of south steps at
$n \geq 0$
, this is the number of south steps at
![]() $x=i-1$
in the highest south-east lattice path
$x=i-1$
in the highest south-east lattice path
![]() $\delta $
weakly below the line from
$\delta $
weakly below the line from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
. Then
$(km,0)$
. Then
Lemma 3.6.2. For any indices
![]() $b_{1},\ldots ,b_{l}$
, we have
$b_{1},\ldots ,b_{l}$
, we have
Proof. Using Proposition 3.5.2, each side of equation (54) is characterized by its evaluation
 $$ \begin{align} \omega (D_{b_{1},\ldots,b_{l}} \cdot 1)(x_{1},\ldots,x_{l}) = {\mathbf H} ^{(l)}_{q,t}\Bigl(\frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}}{\prod _{i=1}^{l-1}(1 - q\, t\, x_{i}/x_{i+1})}\Bigr)_{\operatorname{\mathrm{pol}} } \end{align} $$
$$ \begin{align} \omega (D_{b_{1},\ldots,b_{l}} \cdot 1)(x_{1},\ldots,x_{l}) = {\mathbf H} ^{(l)}_{q,t}\Bigl(\frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}}{\prod _{i=1}^{l-1}(1 - q\, t\, x_{i}/x_{i+1})}\Bigr)_{\operatorname{\mathrm{pol}} } \end{align} $$
 $$ \begin{align} \omega (D_{b_{1},\ldots,b_{l},0} \cdot 1)(x_{1},\ldots,x_{l+1}) = {\mathbf H} ^{(l+1)}_{q,t}\Bigl(\frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}}{(1 - q\, t\, x_{l}/x_{l+1})\prod _{i=1}^{l-1}(1 - q\, t\, x_{i}/x_{i+1})}\Bigr)_{\operatorname{\mathrm{pol}} }. \end{align} $$
$$ \begin{align} \omega (D_{b_{1},\ldots,b_{l},0} \cdot 1)(x_{1},\ldots,x_{l+1}) = {\mathbf H} ^{(l+1)}_{q,t}\Bigl(\frac{x_{1}^{b_{1}}\cdots x_{l}^{b_{l}}}{(1 - q\, t\, x_{l}/x_{l+1})\prod _{i=1}^{l-1}(1 - q\, t\, x_{i}/x_{i+1})}\Bigr)_{\operatorname{\mathrm{pol}} }. \end{align} $$
Terms with a negative exponent of
![]() $x_{l+1}$
inside the parenthesis in equation (56) contribute zero after we apply
$x_{l+1}$
inside the parenthesis in equation (56) contribute zero after we apply
![]() ${\mathbf H} _{q,t}(-)_{\operatorname {\mathrm {pol}} }$
. We can therefore drop all but the constant term of the geometric series factor
${\mathbf H} _{q,t}(-)_{\operatorname {\mathrm {pol}} }$
. We can therefore drop all but the constant term of the geometric series factor
![]() $1/(1 - q\, t\, x_{l}/x_{l+1})$
since the other factors are independent of
$1/(1 - q\, t\, x_{l}/x_{l+1})$
since the other factors are independent of
![]() $x_{l+1}$
. This shows that the right-hand side of equation (56) is the same as in equation (55), except that it has
$x_{l+1}$
. This shows that the right-hand side of equation (56) is the same as in equation (55), except that it has
![]() ${\mathbf H} ^{(l+1)}_{q,t}$
in place of
${\mathbf H} ^{(l+1)}_{q,t}$
in place of
![]() ${\mathbf H} ^{(l)}_{q,t}$
.
${\mathbf H} ^{(l)}_{q,t}$
.
It follows that
![]() $\omega (D_{b_{1},\ldots ,b_{l},0} \cdot 1)$
is a linear combination of Schur functions
$\omega (D_{b_{1},\ldots ,b_{l},0} \cdot 1)$
is a linear combination of Schur functions
![]() $s_{\lambda }(X)$
with
$s_{\lambda }(X)$
with
![]() $\ell (\lambda )\leq l$
, and that
$\ell (\lambda )\leq l$
, and that
![]() $\omega (D_{b_{1},\ldots ,b_{l},0} \cdot 1)$
and
$\omega (D_{b_{1},\ldots ,b_{l},0} \cdot 1)$
and
![]() $\omega (D_{b_{1},\ldots ,b_{l}} \cdot 1)$
evaluate to the same symmetric function in l variables. Hence, they are identical.
$\omega (D_{b_{1},\ldots ,b_{l}} \cdot 1)$
evaluate to the same symmetric function in l variables. Hence, they are identical.
3.7 Summary
Most of what we use from this section in other parts of the paper can be summarized as follows.
Definition 3.7.1. Given
![]() ${\mathbf b} = (b_{1},\ldots ,b_{l})\in {\mathbb Z} ^{l}$
, the infinite series of
${\mathbf b} = (b_{1},\ldots ,b_{l})\in {\mathbb Z} ^{l}$
, the infinite series of
![]() $\operatorname {\mathrm {GL}} _{l}$
characters
$\operatorname {\mathrm {GL}} _{l}$
characters
![]() ${\mathcal H} _{{\mathbf b} }(x) = {\mathcal H} _{b_{1},\ldots ,b_{l}}(x_{1},\ldots ,x_{l})$
is defined by
${\mathcal H} _{{\mathbf b} }(x) = {\mathcal H} _{b_{1},\ldots ,b_{l}}(x_{1},\ldots ,x_{l})$
is defined by
 $$ \begin{align} {\mathcal H} _{{\mathbf b} }(x) = {\mathbf H} _{q,t}\Bigl(\frac{x^{{\mathbf b} }}{\prod _{i=1}^{l-1}(1-q\, t\, x_{i}/x_{i+1})}\Bigr) = {\mathbf H} _{q}\Bigl( x^{{\mathbf b} }\, \frac{\prod _{i+1<j}(1-q\, t\, x_{i}/x_{j})}{\prod _{i<j}(1-t\, x_{i}/x_{j})} \Bigr), \end{align} $$
$$ \begin{align} {\mathcal H} _{{\mathbf b} }(x) = {\mathbf H} _{q,t}\Bigl(\frac{x^{{\mathbf b} }}{\prod _{i=1}^{l-1}(1-q\, t\, x_{i}/x_{i+1})}\Bigr) = {\mathbf H} _{q}\Bigl( x^{{\mathbf b} }\, \frac{\prod _{i+1<j}(1-q\, t\, x_{i}/x_{j})}{\prod _{i<j}(1-t\, x_{i}/x_{j})} \Bigr), \end{align} $$
where
![]() ${\mathbf H} _{q,t}$
is given by equation (46) and
${\mathbf H} _{q,t}$
is given by equation (46) and
![]() ${\mathbf H} _{q}$
by equation (23) or where
${\mathbf H} _{q}$
by equation (23) or where
![]() ${\mathcal H} _{{\mathbf b} }(x)$
is given in fully expanded form by equation (3).
${\mathcal H} _{{\mathbf b} }(x)$
is given in fully expanded form by equation (3).
In terms of this definition, we have the following special case of Proposition 3.5.2, which was stated as identity (2) in the introduction.
Corollary 3.7.2. For the Negut element
![]() $D_{{\mathbf b} }\in {\mathcal E} $
acting on
$D_{{\mathbf b} }\in {\mathcal E} $
acting on
![]() $\Lambda $
, the symmetric function
$\Lambda $
, the symmetric function
![]() $\omega (D_{{\mathbf b} }\cdot 1)$
evaluated in l variables is given by
$\omega (D_{{\mathbf b} }\cdot 1)$
evaluated in l variables is given by
Moreover, all terms
![]() $s_{\lambda }$
in the Schur expansion of
$s_{\lambda }$
in the Schur expansion of
![]() $\omega (D_{{\mathbf b} } \cdot 1)(X)$
have
$\omega (D_{{\mathbf b} } \cdot 1)(X)$
have
![]() $\ell (\lambda )\leq l$
, so
$\ell (\lambda )\leq l$
, so
![]() $\omega (D_{{\mathbf b} } \cdot 1)$
is determined by its evaluation in l variables.
$\omega (D_{{\mathbf b} } \cdot 1)$
is determined by its evaluation in l variables.
In the special cases where the index
![]() ${\mathbf b} $
is the sequence of south runs in the highest
${\mathbf b} $
is the sequence of south runs in the highest
![]() $(km,kn)$
Dyck path,
$(km,kn)$
Dyck path,
![]() $D_{{\mathbf b} }\cdot 1$
can also be expressed as follows.
$D_{{\mathbf b} }\cdot 1$
can also be expressed as follows.
Corollary 3.7.3. For
![]() $i = 1,\ldots ,l=km+1$
, let
$i = 1,\ldots ,l=km+1$
, let
![]() $b_{i}$
be the number of south steps at
$b_{i}$
be the number of south steps at
![]() $x = i-1$
in the highest south-east lattice path
$x = i-1$
in the highest south-east lattice path
![]() $\delta $
weakly below the line from
$\delta $
weakly below the line from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
, including
$(km,0)$
, including
![]() $b_{l}=0$
. Then the Negut element
$b_{l}=0$
. Then the Negut element
![]() $D_{b_{1},\ldots ,b_{l}}$
and the operator
$D_{b_{1},\ldots ,b_{l}}$
and the operator
![]() $e_{k}[-MX^{m,n}]$
agree when applied to
$e_{k}[-MX^{m,n}]$
agree when applied to
![]() $1\in \Lambda $
, that is, we have
$1\in \Lambda $
, that is, we have
Corollary 3.7.4 (also proven in [Reference Bergeron, Garsia, Sergel Leven and Xin4]).
In the case
![]() $n=1$
of equation (59), we further have
$n=1$
of equation (59), we further have
Proof. By Proposition 3.3.1 (iii),
![]() $e_{k}[-MX^{0,1}]\cdot 1 = e_{k}(X)$
. Since
$e_{k}[-MX^{0,1}]\cdot 1 = e_{k}(X)$
. Since
![]() $\nabla (1) = 1$
, the result now follows from Lemma 3.4.1.
$\nabla (1) = 1$
, the result now follows from Lemma 3.4.1.
Remark 3.7.5. Equations (46), (54), (57), (58), (59) and (60) imply the raising operator formula
 $$ \begin{align} (\omega\nabla^m e_{k})(x_1,\dots,x_l) = {\boldsymbol \sigma } \left(\frac{x_1 x_{m+1} x_{2m+1}\cdots x_{(k-1)m+1} \, \prod _{i+1<j} (1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j} ((1 - q\, x_{i}/x_{j}) (1 - t\,x_{i}/x_{j}))} \right)_{\operatorname{\mathrm{pol}}}, \end{align} $$
$$ \begin{align} (\omega\nabla^m e_{k})(x_1,\dots,x_l) = {\boldsymbol \sigma } \left(\frac{x_1 x_{m+1} x_{2m+1}\cdots x_{(k-1)m+1} \, \prod _{i+1<j} (1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j} ((1 - q\, x_{i}/x_{j}) (1 - t\,x_{i}/x_{j}))} \right)_{\operatorname{\mathrm{pol}}}, \end{align} $$
provided
![]() $l \geq (k-1)m+1$
.
$l \geq (k-1)m+1$
.
4 LLT polynomials
In this section, we review the definition of the combinatorial LLT polynomials
![]() ${\mathcal G} _{\nu }(X;q)$
, using the attacking inversions formulation from [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], which is better suited to our purposes than the original ribbon tableau formulation in [Reference Lascoux, Leclerc and Thibon24].
${\mathcal G} _{\nu }(X;q)$
, using the attacking inversions formulation from [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], which is better suited to our purposes than the original ribbon tableau formulation in [Reference Lascoux, Leclerc and Thibon24].
We also define and prove some results on the infinite LLT series
![]() ${\mathcal L} _{\beta /\alpha }(x;q)$
introduced in [Reference Grojnowski and Haiman14]. Since [Reference Grojnowski and Haiman14] is unpublished, due for revision and doesn’t cover the ‘twisted’ variants
${\mathcal L} _{\beta /\alpha }(x;q)$
introduced in [Reference Grojnowski and Haiman14]. Since [Reference Grojnowski and Haiman14] is unpublished, due for revision and doesn’t cover the ‘twisted’ variants
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
, we give here a self-contained treatment of the material we need.
${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
, we give here a self-contained treatment of the material we need.
4.1 Combinatorial LLT polynomials
The content of a box
![]() $a=(x,y)$
in row y, column x of any skew diagram is
$a=(x,y)$
in row y, column x of any skew diagram is
![]() $c(a)=x-y$
.
$c(a)=x-y$
.
Let
![]() $\nu = (\nu ^{(1)},\ldots ,\nu ^{(k)})$
be a tuple of skew diagrams. When referring to boxes of
$\nu = (\nu ^{(1)},\ldots ,\nu ^{(k)})$
be a tuple of skew diagrams. When referring to boxes of
![]() $\nu $
, we identify
$\nu $
, we identify
![]() $\nu $
with the disjoint union of the
$\nu $
with the disjoint union of the
![]() $\nu ^{(j)}$
. Fix
$\nu ^{(j)}$
. Fix
![]() $\epsilon>0$
small enough that
$\epsilon>0$
small enough that
![]() $k\, \epsilon <1$
. The adjusted content of a box
$k\, \epsilon <1$
. The adjusted content of a box
![]() $a\in \nu ^{(j)}$
is
$a\in \nu ^{(j)}$
is
![]() $\tilde {c} (a) = c(a)+j\, \epsilon $
. A reading order is any total ordering of the boxes
$\tilde {c} (a) = c(a)+j\, \epsilon $
. A reading order is any total ordering of the boxes
![]() $a\in \nu $
on which
$a\in \nu $
on which
![]() $\tilde {c} (a)$
is increasing. In other words, the reading order is lexicographic, first by content, then by the index j for which
$\tilde {c} (a)$
is increasing. In other words, the reading order is lexicographic, first by content, then by the index j for which
![]() $a\in \nu ^{(j)}$
, with boxes of the same content in the same component
$a\in \nu ^{(j)}$
, with boxes of the same content in the same component
![]() $\nu ^{(j)}$
ordered arbitrarily.
$\nu ^{(j)}$
ordered arbitrarily.
Boxes
![]() $a,b\in \nu $
attack each other if
$a,b\in \nu $
attack each other if
![]() $0<|\tilde {c} (a)-\tilde {c} (b)|<1$
. If
$0<|\tilde {c} (a)-\tilde {c} (b)|<1$
. If
![]() $a\in \nu ^{(i)}$
precedes
$a\in \nu ^{(i)}$
precedes
![]() $b\in \nu ^{(j)}$
in the reading order, the attacking condition means that either
$b\in \nu ^{(j)}$
in the reading order, the attacking condition means that either
![]() $c(a)=c(b)$
and
$c(a)=c(b)$
and
![]() $i<j$
or
$i<j$
or
![]() $c(b)=c(a)+1$
and
$c(b)=c(a)+1$
and
![]() $i>j$
. We also say that
$i>j$
. We also say that
![]() $a,b$
form an attacking pair in
$a,b$
form an attacking pair in
![]() $\nu $
.
$\nu $
.
By a semistandard Young tableau on the tuple
![]() $\nu $
, we mean a map
$\nu $
, we mean a map
![]() $T\colon \nu \rightarrow {\mathbb Z} _{>0} $
which restricts to a semistandard tableau on each component
$T\colon \nu \rightarrow {\mathbb Z} _{>0} $
which restricts to a semistandard tableau on each component
![]() $\nu ^{(j)}$
. We write
$\nu ^{(j)}$
. We write
![]() $\operatorname {\mathrm {SSYT}} (\nu )$
for the set of these. The weight of
$\operatorname {\mathrm {SSYT}} (\nu )$
for the set of these. The weight of
![]() $T\in \operatorname {\mathrm {SSYT}} (\nu )$
is
$T\in \operatorname {\mathrm {SSYT}} (\nu )$
is
![]() $x^{T} = \prod _{a\in \nu }x_{T(a)}$
. An attacking inversion in T is an attacking pair
$x^{T} = \prod _{a\in \nu }x_{T(a)}$
. An attacking inversion in T is an attacking pair
![]() $a,b$
such that
$a,b$
such that
![]() $T(a)>T(b)$
, where a precedes b in the reading order. We define
$T(a)>T(b)$
, where a precedes b in the reading order. We define
![]() $\operatorname {\mathrm {inv}} (T)$
to be the number of attacking inversions in T.
$\operatorname {\mathrm {inv}} (T)$
to be the number of attacking inversions in T.
Example 4.1.1. The picture below shows a tuple of skew diagrams
![]() $\nu = (\nu ^{(1)}, \nu ^{(2)})$
, with dashed lines indicating boxes of equal content and boxes numbered in reading order, along with a semistandard tableau T on
$\nu = (\nu ^{(1)}, \nu ^{(2)})$
, with dashed lines indicating boxes of equal content and boxes numbered in reading order, along with a semistandard tableau T on
![]() $\nu $
.
$\nu $
.

The tuple
![]() $\nu $
contains
$\nu $
contains
![]() $7$
attacking pairs
$7$
attacking pairs
![]() $(a,b)$
: In the numbering shown, these are
$(a,b)$
: In the numbering shown, these are
![]() $(2,3)$
,
$(2,3)$
,
![]() $(3,4)$
,
$(3,4)$
,
![]() $(4,5)$
,
$(4,5)$
,
![]() $(4,6)$
,
$(4,6)$
,
![]() $(5,7)$
,
$(5,7)$
,
![]() $(6,7)$
,
$(6,7)$
,
![]() $(7,8)$
. The pairs numbered
$(7,8)$
. The pairs numbered
![]() $(3,4)$
,
$(3,4)$
,
![]() $(4,5)$
and
$(4,5)$
and
![]() $(6,7)$
form inversions in T, with entries
$(6,7)$
form inversions in T, with entries
![]() $(T(a),T(b))$
equal to
$(T(a),T(b))$
equal to
![]() $(4,2)$
,
$(4,2)$
,
![]() $(2,1)$
and
$(2,1)$
and
![]() $(4,3)$
, respectively.
$(4,3)$
, respectively.
Definition 4.1.2. The combinatorial LLT polynomial indexed by a tuple of skew diagrams
![]() $\nu $
is the generating function
$\nu $
is the generating function
In [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], it was shown that
![]() ${\mathcal G}_{\nu }(X;q^{-1})$
coincides up to a factor
${\mathcal G}_{\nu }(X;q^{-1})$
coincides up to a factor
![]() $q^{e}$
with a ribbon tableau LLT polynomial as defined in [Reference Lascoux, Leclerc and Thibon24] and is therefore a symmetric function. A direct and more elementary proof that
$q^{e}$
with a ribbon tableau LLT polynomial as defined in [Reference Lascoux, Leclerc and Thibon24] and is therefore a symmetric function. A direct and more elementary proof that
![]() ${\mathcal G}_{\nu }(X;q)$
is symmetric was given in [Reference Haglund, Haiman and Loehr15].
${\mathcal G}_{\nu }(X;q)$
is symmetric was given in [Reference Haglund, Haiman and Loehr15].
It is useful in working with the LLT polynomials
![]() ${\mathcal G} _{\nu }(X;q)$
to consider a more general combinatorial formalism, as in [Reference Haglund, Haiman and Loehr15, §10]. Let
${\mathcal G} _{\nu }(X;q)$
to consider a more general combinatorial formalism, as in [Reference Haglund, Haiman and Loehr15, §10]. Let
![]() ${\mathcal A} = {\mathcal A} _{+} \coprod {\mathcal A} _{-}$
be a ‘signed’ alphabet with a positive letter
${\mathcal A} = {\mathcal A} _{+} \coprod {\mathcal A} _{-}$
be a ‘signed’ alphabet with a positive letter
![]() $v\in {\mathcal A} _{+}$
and a negative letter
$v\in {\mathcal A} _{+}$
and a negative letter
![]() $\overline {v}\in {\mathcal A} _{-}$
for each
$\overline {v}\in {\mathcal A} _{-}$
for each
![]() $v\in {\mathbb Z} _{>0} $
and an arbitrary total ordering on
$v\in {\mathbb Z} _{>0} $
and an arbitrary total ordering on
![]() ${\mathcal A} $
.
${\mathcal A} $
.
A super tableau on a tuple of skew shapes
![]() $\nu $
is a map
$\nu $
is a map
![]() $T\colon \nu \rightarrow {\mathcal A} $
, weakly increasing along rows and columns, with positive letters increasing strictly on columns and negative letters increasing strictly on rows. A usual semistandard tableau is thus the same thing as a super tableau with all entries positive. Let
$T\colon \nu \rightarrow {\mathcal A} $
, weakly increasing along rows and columns, with positive letters increasing strictly on columns and negative letters increasing strictly on rows. A usual semistandard tableau is thus the same thing as a super tableau with all entries positive. Let
![]() $\operatorname {\mathrm {SSYT}} _{\pm }(\nu )$
denote the set of super tableaux on
$\operatorname {\mathrm {SSYT}} _{\pm }(\nu )$
denote the set of super tableaux on
![]() $\nu $
.
$\nu $
.
An attacking inversion in a super tableau is an attacking pair
![]() $a,b$
, with a preceding b in the reading order, such that either
$a,b$
, with a preceding b in the reading order, such that either
![]() $T(a)>T(b)$
in the ordering on
$T(a)>T(b)$
in the ordering on
![]() ${\mathcal A} $
, or
${\mathcal A} $
, or
![]() $T(a)=T(b) = \overline {v}$
with
$T(a)=T(b) = \overline {v}$
with
![]() $\overline {v}$
negative. As before,
$\overline {v}$
negative. As before,
![]() $\operatorname {\mathrm {inv}} (T)$
denotes the number of attacking inversions.
$\operatorname {\mathrm {inv}} (T)$
denotes the number of attacking inversions.
Lemma 4.1.3 [Reference Haglund, Haiman and Loehr15, (81–82) and Proposition 4.2].
We have the identity
where the weight is given by
 $$ \begin{align} x^{T_{+}} y^{T_{-}} = \prod _{a\in \nu }\begin{cases} x_{i},& T(a) = i\in {\mathcal A} _{+},\\ y_{i},& T(a) = \overline{i} \in {\mathcal A} _{-}. \end{cases} \end{align} $$
$$ \begin{align} x^{T_{+}} y^{T_{-}} = \prod _{a\in \nu }\begin{cases} x_{i},& T(a) = i\in {\mathcal A} _{+},\\ y_{i},& T(a) = \overline{i} \in {\mathcal A} _{-}. \end{cases} \end{align} $$
This holds for any choice of the ordering on the signed alphabet
![]() ${\mathcal A} $
.
${\mathcal A} $
.
Corollary 4.1.4. We have
where the sum is over super tableaux T with all entries negative, and we abbreviate
![]() $x^{T_{-}}$
to
$x^{T_{-}}$
to
![]() $x^{T}$
in this case.
$x^{T}$
in this case.
Definition 4.1.5. Given a tuple of skew diagrams
![]() $\nu = (\nu ^{(1)},\ldots ,\nu ^{(k)})$
,
$\nu = (\nu ^{(1)},\ldots ,\nu ^{(k)})$
,
![]() $\nu ^{R}$
denotes the tuple
$\nu ^{R}$
denotes the tuple
![]() $((\nu ^{(1)})^{R},\ldots ,(\nu ^{(k)})^{R})$
, where
$((\nu ^{(1)})^{R},\ldots ,(\nu ^{(k)})^{R})$
, where
![]() $(\nu ^{(j)})^{R}$
is the
$(\nu ^{(j)})^{R}$
is the
![]() $180^{\circ }$
rotation of the transpose
$180^{\circ }$
rotation of the transpose
![]() $(\nu ^{(j)})^{*}$
, positioned so that each box in
$(\nu ^{(j)})^{*}$
, positioned so that each box in
![]() $\nu ^{R}$
has the same content as the corresponding box in
$\nu ^{R}$
has the same content as the corresponding box in
![]() $\nu $
.
$\nu $
.
Proposition 4.1.6. With
![]() $\nu ^{R}$
as in Definition 4.1.5, we have
$\nu ^{R}$
as in Definition 4.1.5, we have
where
![]() $I(\nu )$
is the total number of attacking pairs in
$I(\nu )$
is the total number of attacking pairs in
![]() $\nu $
.
$\nu $
.
Proof. Use Corollary 4.1.4 on the left-hand side, ordering the negative letters as
![]() $\overline {1}>\overline {2}>\cdots $
. Given a negative tableau T on
$\overline {1}>\overline {2}>\cdots $
. Given a negative tableau T on
![]() $\nu $
, let
$\nu $
, let
![]() $T^{R}$
be the tableau on
$T^{R}$
be the tableau on
![]() $\nu ^{R}$
obtained by reflecting the tableau along with
$\nu ^{R}$
obtained by reflecting the tableau along with
![]() $\nu $
and changing negative letters
$\nu $
and changing negative letters
![]() $\overline {v}$
to positive letters v. Then
$\overline {v}$
to positive letters v. Then
![]() $T^{R}$
is an ordinary semistandard tableau, and
$T^{R}$
is an ordinary semistandard tableau, and
![]() $T\mapsto T^{R}$
is a weight-preserving bijection from negative tableaux on
$T\mapsto T^{R}$
is a weight-preserving bijection from negative tableaux on
![]() $\nu $
to
$\nu $
to
![]() $\operatorname {\mathrm {SSYT}} (\nu ^{R})$
. An attacking pair in
$\operatorname {\mathrm {SSYT}} (\nu ^{R})$
. An attacking pair in
![]() $\nu $
is an inversion in T if and only if the corresponding attacking pair in
$\nu $
is an inversion in T if and only if the corresponding attacking pair in
![]() $\nu ^{R}$
is a noninversion in
$\nu ^{R}$
is a noninversion in
![]() $T^{R}$
, hence
$T^{R}$
, hence
![]() $\operatorname {\mathrm {inv}} (T^{R}) = I(\nu ) - \operatorname {\mathrm {inv}} (T)$
. This implies equation (67).
$\operatorname {\mathrm {inv}} (T^{R}) = I(\nu ) - \operatorname {\mathrm {inv}} (T)$
. This implies equation (67).
Example 4.1.7. Consider a tuple
![]() $\nu = (\nu ^{(1)},\ldots ,\nu ^{(k)})$
in which each skew shape is a column so that
$\nu = (\nu ^{(1)},\ldots ,\nu ^{(k)})$
in which each skew shape is a column so that
![]() $\nu ^R$
is a tuple of rows. The super tableau of shape
$\nu ^R$
is a tuple of rows. The super tableau of shape
![]() $\nu ^R$
with all entries a positive letter
$\nu ^R$
with all entries a positive letter
![]() $1$
has no inversions, whereas the super tableau T of shape
$1$
has no inversions, whereas the super tableau T of shape
![]() $\nu $
with all entries a negative letter
$\nu $
with all entries a negative letter
![]() $\overline {1}$
has
$\overline {1}$
has
where
![]() $I(\nu )$
is the total number of attacking pairs in
$I(\nu )$
is the total number of attacking pairs in
![]() $\nu $
.
$\nu $
.
Lemma 4.1.8. The LLT polynomial
![]() ${\mathcal G}_{\nu }(X;q)$
is a linear combination of Schur functions
${\mathcal G}_{\nu }(X;q)$
is a linear combination of Schur functions
![]() $s_{\lambda }(X)$
such that
$s_{\lambda }(X)$
such that
![]() $\ell (\lambda )$
is bounded by the total number of rows in the diagram
$\ell (\lambda )$
is bounded by the total number of rows in the diagram
![]() $\nu $
.
$\nu $
.
Proof. Let r be the total number of rows in
![]() $\nu $
. It is equivalent to show that
$\nu $
. It is equivalent to show that
![]() $\omega \, {\mathcal G}_{\nu }(X;q)$
is a linear combination of monomial symmetric functions
$\omega \, {\mathcal G}_{\nu }(X;q)$
is a linear combination of monomial symmetric functions
![]() $m_{\lambda }(X)$
such that
$m_{\lambda }(X)$
such that
![]() $\lambda _{1}\leq r$
. By Proposition 4.1.6,
$\lambda _{1}\leq r$
. By Proposition 4.1.6,
![]() $\omega \, {\mathcal G}_{\nu }(X;q)$
has a monomial term
$\omega \, {\mathcal G}_{\nu }(X;q)$
has a monomial term
![]() $q^{I(\nu )-\operatorname {\mathrm {inv}} (T)} x^{T}$
for each semistandard tableau
$q^{I(\nu )-\operatorname {\mathrm {inv}} (T)} x^{T}$
for each semistandard tableau
![]() $T\in \operatorname {\mathrm {SSYT}}(\nu ^{R})$
on the tuple of reflected shapes
$T\in \operatorname {\mathrm {SSYT}}(\nu ^{R})$
on the tuple of reflected shapes
![]() $\nu ^{R}$
. Since a letter can appear at most once in each column of T, the exponents of
$\nu ^{R}$
. Since a letter can appear at most once in each column of T, the exponents of
![]() $x^{T}$
are bounded by r.
$x^{T}$
are bounded by r.
4.2 Reminder on Hecke algebras
We recall, in the case of
![]() $\operatorname {\mathrm {GL}} _{l}$
, the Hecke algebra action on the group algebra of the weight lattice, as in Lusztig [Reference Lusztig25] or Macdonald [Reference Macdonald27] and due originally to Bernstein and Zelevinsky.
$\operatorname {\mathrm {GL}} _{l}$
, the Hecke algebra action on the group algebra of the weight lattice, as in Lusztig [Reference Lusztig25] or Macdonald [Reference Macdonald27] and due originally to Bernstein and Zelevinsky.
For
![]() $\operatorname {\mathrm {GL}} _{l}$
, we identify the group algebra
$\operatorname {\mathrm {GL}} _{l}$
, we identify the group algebra
![]() ${\mathbf k} X$
of the weight lattice
${\mathbf k} X$
of the weight lattice
![]() $X = {\mathbb Z} ^{l}$
with the Laurent polynomial algebra
$X = {\mathbb Z} ^{l}$
with the Laurent polynomial algebra
![]() ${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]$
. Here,
${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]$
. Here,
![]() ${\mathbf k} $
is any ground field containing
${\mathbf k} $
is any ground field containing
![]() ${\mathbb Q} (q)$
.
${\mathbb Q} (q)$
.
The Demazure–Lusztig operators
for
![]() $i = 1,\ldots ,l-1$
generate an action of the Hecke algebra of
$i = 1,\ldots ,l-1$
generate an action of the Hecke algebra of
![]() $S_{l}$
on
$S_{l}$
on
![]() ${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]$
. We have normalized the generators so that the quadratic relations are
${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]$
. We have normalized the generators so that the quadratic relations are
![]() $(T_{i}-q)(T_{i}+1)=0$
. The elements
$(T_{i}-q)(T_{i}+1)=0$
. The elements
![]() $T_w$
, defined by
$T_w$
, defined by
![]() $T_w = T_{i_1} T_{i_2}\cdots T_{i_m}$
for any reduced expression
$T_w = T_{i_1} T_{i_2}\cdots T_{i_m}$
for any reduced expression
![]() $w=s_{i_1}s_{i_2}\cdots s_{i_m}$
, form a
$w=s_{i_1}s_{i_2}\cdots s_{i_m}$
, form a
![]() ${\mathbf k}$
-basis of the Hecke algebra, as w ranges over
${\mathbf k}$
-basis of the Hecke algebra, as w ranges over
![]() $S_l$
.
$S_l$
.
Let
![]() $R_{+}$
be the set of positive roots and
$R_{+}$
be the set of positive roots and
![]() $Q_{+} = {\mathbb N} R_{+}$
the cone they generate in the root lattice Q. For dominant weights, we define
$Q_{+} = {\mathbb N} R_{+}$
the cone they generate in the root lattice Q. For dominant weights, we define
![]() $\lambda \leq \mu $
if
$\lambda \leq \mu $
if
![]() $\mu -\lambda \in Q_{+}$
. For polynomial weights of
$\mu -\lambda \in Q_{+}$
. For polynomial weights of
![]() $\operatorname {\mathrm {GL}}_{l}$
, this coincides with the standard partial ordering (7) on partitions.
$\operatorname {\mathrm {GL}}_{l}$
, this coincides with the standard partial ordering (7) on partitions.
For any weight
![]() $\lambda $
, let
$\lambda $
, let
![]() $\lambda _{+}$
denote the dominant weight in the orbit
$\lambda _{+}$
denote the dominant weight in the orbit
![]() $S_{l}\, \lambda $
.
$S_{l}\, \lambda $
.
Let
![]() $\operatorname {\mathrm {conv}} (S_{l}\, \lambda )$
be the convex hull of
$\operatorname {\mathrm {conv}} (S_{l}\, \lambda )$
be the convex hull of
![]() $S_{l}\, \lambda $
in the coset
$S_{l}\, \lambda $
in the coset
![]() $\lambda +Q$
of the root lattice, that is, the set of weights that occur with nonzero multiplicity in the irreducible character
$\lambda +Q$
of the root lattice, that is, the set of weights that occur with nonzero multiplicity in the irreducible character
![]() $\chi _{\lambda _{+}}$
. Note that
$\chi _{\lambda _{+}}$
. Note that
![]() $\operatorname {\mathrm {conv}} (S_{l}\, \lambda )\subseteq \operatorname {\mathrm {conv}} (S_{l}\, \mu )$
if and only if
$\operatorname {\mathrm {conv}} (S_{l}\, \lambda )\subseteq \operatorname {\mathrm {conv}} (S_{l}\, \mu )$
if and only if
![]() $\lambda _{+}\leq \mu _{+}$
.
$\lambda _{+}\leq \mu _{+}$
.
Each orbit
![]() $S_{l}\, \lambda _{+}$
has a partial ordering induced by the Bruhat ordering on
$S_{l}\, \lambda _{+}$
has a partial ordering induced by the Bruhat ordering on
![]() $S_{l}$
. More explicitly, this ordering is the transitive closure of the relation
$S_{l}$
. More explicitly, this ordering is the transitive closure of the relation
![]() $s_{i}\lambda>\lambda $
if
$s_{i}\lambda>\lambda $
if
![]() $\langle \alpha _{i}^{\vee } ,\lambda \rangle>0$
. We extend this to a partial ordering on all of
$\langle \alpha _{i}^{\vee } ,\lambda \rangle>0$
. We extend this to a partial ordering on all of
![]() $X = {\mathbb Z} ^{l}$
by defining
$X = {\mathbb Z} ^{l}$
by defining
![]() $\lambda \leq \mu $
if
$\lambda \leq \mu $
if
![]() $\lambda _{+}<\mu _{+}$
, or if
$\lambda _{+}<\mu _{+}$
, or if
![]() $\lambda _{+} = \mu _{+} $
and
$\lambda _{+} = \mu _{+} $
and
![]() $\lambda \leq \mu $
in the Bruhat order on
$\lambda \leq \mu $
in the Bruhat order on
![]() $S_{l}\, \lambda _{+}$
.
$S_{l}\, \lambda _{+}$
.
Suppose
![]() $\langle \alpha _{i}^{\vee } ,\lambda \rangle \geq 0$
. If
$\langle \alpha _{i}^{\vee } ,\lambda \rangle \geq 0$
. If
![]() $\langle \alpha _{i}^{\vee } ,\lambda \rangle = 0$
, that is, if
$\langle \alpha _{i}^{\vee } ,\lambda \rangle = 0$
, that is, if
![]() $\lambda =s_{i}\lambda $
, then
$\lambda =s_{i}\lambda $
, then
Otherwise, if
![]() $\langle \alpha _{i}^{\vee } ,\lambda \rangle> 0$
, then
$\langle \alpha _{i}^{\vee } ,\lambda \rangle> 0$
, then
 $$ \begin{align} \begin{aligned} T_{i}\, x^{\lambda } & \equiv q\, x^{s_{i}\lambda } + (q-1)x^{\lambda},\\ T_{i}\, x^{s_{i}\lambda } & \equiv x^{\lambda } \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} T_{i}\, x^{\lambda } & \equiv q\, x^{s_{i}\lambda } + (q-1)x^{\lambda},\\ T_{i}\, x^{s_{i}\lambda } & \equiv x^{\lambda } \end{aligned} \end{align} $$
modulo the space spanned by monomials
![]() $x^{\mu }$
for
$x^{\mu }$
for
![]() $\mu $
strictly between
$\mu $
strictly between
![]() $\lambda $
and
$\lambda $
and
![]() $s_{i}\lambda $
on the root string
$s_{i}\lambda $
on the root string
![]() $\lambda +{\mathbb Z} \alpha _{i}$
. Note that
$\lambda +{\mathbb Z} \alpha _{i}$
. Note that
![]() $\mu <\lambda $
for these weights
$\mu <\lambda $
for these weights
![]() $\mu $
since they lie on orbits strictly inside
$\mu $
since they lie on orbits strictly inside
![]() $\operatorname {\mathrm {conv}} (S_{l}\, \lambda )$
. Furthermore, the set of all weights
$\operatorname {\mathrm {conv}} (S_{l}\, \lambda )$
. Furthermore, the set of all weights
![]() $\mu \leq s_{i} \lambda $
is
$\mu \leq s_{i} \lambda $
is
![]() $s_{i}$
-invariant and has convex intersection with every root string
$s_{i}$
-invariant and has convex intersection with every root string
![]() $\nu +{\mathbb Z} \alpha _{i}$
; hence, the space
$\nu +{\mathbb Z} \alpha _{i}$
; hence, the space
![]() ${\mathbf k} \, \{x^{\mu }\mid \mu \leq s_{i}\lambda \}$
is closed under
${\mathbf k} \, \{x^{\mu }\mid \mu \leq s_{i}\lambda \}$
is closed under
![]() $T_{i}$
. It follows that if
$T_{i}$
. It follows that if
![]() $\langle \alpha _{i}^{\vee }, \lambda \rangle \ge 0$
, then
$\langle \alpha _{i}^{\vee }, \lambda \rangle \ge 0$
, then
![]() $T_{i}$
applied to any Laurent polynomial of the form
$T_{i}$
applied to any Laurent polynomial of the form
![]() $x^{\lambda }+\sum _{\mu < \lambda }c_{\mu } x^{\mu }$
yields a result of the form
$x^{\lambda }+\sum _{\mu < \lambda }c_{\mu } x^{\mu }$
yields a result of the form
 $$ \begin{align} T_{i}\, \bigl( x^{\lambda}+\sum_{\mu < \lambda}c_{\mu} x^{\mu} \bigr) = q\, x^{s_{i}\lambda } + \sum_{\mu < s_i \lambda} d_{\mu} x^{\mu}\,. \end{align} $$
$$ \begin{align} T_{i}\, \bigl( x^{\lambda}+\sum_{\mu < \lambda}c_{\mu} x^{\mu} \bigr) = q\, x^{s_{i}\lambda } + \sum_{\mu < s_i \lambda} d_{\mu} x^{\mu}\,. \end{align} $$
4.3 Nonsymmetric Hall–Littlewood polynomials
For each
![]() $\operatorname {\mathrm {GL}} _{l}$
weight
$\operatorname {\mathrm {GL}} _{l}$
weight
![]() $\lambda \in {\mathbb Z} ^{l}$
, we define the nonsymmetric Hall–Littlewood polynomial
$\lambda \in {\mathbb Z} ^{l}$
, we define the nonsymmetric Hall–Littlewood polynomial
where
![]() $w\in S_{l}$
is such that
$w\in S_{l}$
is such that
![]() $\lambda =w(\lambda _{+})$
. If
$\lambda =w(\lambda _{+})$
. If
![]() $\lambda $
has nontrivial stabilizer, then w is not unique, but it follows from equations (70)–(72) that
$\lambda $
has nontrivial stabilizer, then w is not unique, but it follows from equations (70)–(72) that
![]() $E_{\lambda }(x;q)$
is independent of the choice of w and has the monic and triangular form
$E_{\lambda }(x;q)$
is independent of the choice of w and has the monic and triangular form
 $$ \begin{align} E_{\lambda }(x;q) = x^{\lambda } +\sum _{\mu <\lambda } c_{\mu } x^{\mu }. \end{align} $$
$$ \begin{align} E_{\lambda }(x;q) = x^{\lambda } +\sum _{\mu <\lambda } c_{\mu } x^{\mu }. \end{align} $$
See Table 1 for examples.
Table 1 Nonsymmetric Hall–Littlewood polynomials
![]() $E^{\sigma }_{{\mathbf a}}(x_{1},x_{2},x_{3};q)$
and
$E^{\sigma }_{{\mathbf a}}(x_{1},x_{2},x_{3};q)$
and
![]() $F^{\sigma }_{{\mathbf a}}(y_{1},y_{2},y_{3};q)$
for
$F^{\sigma }_{{\mathbf a}}(y_{1},y_{2},y_{3};q)$
for
![]() $l = 3$
,
$l = 3$
,
![]() $\sigma = 1$
, and
$\sigma = 1$
, and
![]() $|{\mathbf a}| \le 2$
.
$|{\mathbf a}| \le 2$
.

For context, we remark that several distinct notions of ‘nonsymmetric Hall–Littlewood polynomial’ can be found in the literature. Our
![]() $E_{\lambda }$
(and
$E_{\lambda }$
(and
![]() $F_{\lambda } $
, below) coincide with specializations of nonsymmetric Macdonald polynomials considered by Ion in [Reference Ion22, Theorem 4.8]. The twisted variants
$F_{\lambda } $
, below) coincide with specializations of nonsymmetric Macdonald polynomials considered by Ion in [Reference Ion22, Theorem 4.8]. The twisted variants
![]() $E_{\lambda }^{\sigma }$
below are specializations of the ‘permuted basement’ nonsymmetric Macdonald polynomials studied (for
$E_{\lambda }^{\sigma }$
below are specializations of the ‘permuted basement’ nonsymmetric Macdonald polynomials studied (for
![]() $\operatorname {\mathrm {GL}} _{l}$
) by Alexandersson [Reference Alexandersson1] and Alexandersson and Sawhney [Reference Alexandersson and Sawhney2]. We also note that
$\operatorname {\mathrm {GL}} _{l}$
) by Alexandersson [Reference Alexandersson1] and Alexandersson and Sawhney [Reference Alexandersson and Sawhney2]. We also note that
![]() $E_{\lambda }(x;q^{-1})$
and
$E_{\lambda }(x;q^{-1})$
and
![]() $F_{\lambda }(x;q)$
have coefficients in
$F_{\lambda }(x;q)$
have coefficients in
![]() ${\mathbb Z}[q]$
and specialize at
${\mathbb Z}[q]$
and specialize at
![]() $q=0$
to Demazure characters and Demazure atoms, respectively.
$q=0$
to Demazure characters and Demazure atoms, respectively.
For any
![]() $\mu \in {\mathbb R} ^{l}$
, we define
$\mu \in {\mathbb R} ^{l}$
, we define
![]() $\operatorname {\mathrm {Inv}} (\mu ) = \{(i<j)\mid \mu _{i}>\mu _{j} \}$
. In the case of a permutation,
$\operatorname {\mathrm {Inv}} (\mu ) = \{(i<j)\mid \mu _{i}>\mu _{j} \}$
. In the case of a permutation,
![]() $\operatorname {\mathrm {Inv}} (\sigma )$
is then the usual inversion set of
$\operatorname {\mathrm {Inv}} (\sigma )$
is then the usual inversion set of
![]() $\sigma =(\sigma (1),\ldots ,\sigma (l)) \in S_l$
.
$\sigma =(\sigma (1),\ldots ,\sigma (l)) \in S_l$
.
Taking
![]() $\rho $
as in §2.3 and
$\rho $
as in §2.3 and
![]() $\epsilon>0$
small, the notation
$\epsilon>0$
small, the notation
![]() $\operatorname {\mathrm {Inv}} (\lambda +\epsilon \rho )$
denotes the set of pairs
$\operatorname {\mathrm {Inv}} (\lambda +\epsilon \rho )$
denotes the set of pairs
![]() $i<j$
such that
$i<j$
such that
![]() $\lambda _{i}\geq \lambda _{j}$
.
$\lambda _{i}\geq \lambda _{j}$
.
Given
![]() $\sigma \in S_{l}$
, we define twisted nonsymmetric Hall–Littlewood polynomials
$\sigma \in S_{l}$
, we define twisted nonsymmetric Hall–Littlewood polynomials
where
![]() $w_{0}\in S_{l}$
is the longest element, given by
$w_{0}\in S_{l}$
is the longest element, given by
![]() $w_{0}(i) = l+1-i$
. The normalization in equation (75) implies the recurrence
$w_{0}(i) = l+1-i$
. The normalization in equation (75) implies the recurrence
 $$ \begin{align} E^{\sigma }_{\lambda } = \begin{cases} q^{-I(\lambda _{i}\leq \lambda _{i+1})}\, T_{i}\, E^{s_{i}\sigma }_{s_{i}\lambda }, & s_{i}\sigma>\sigma \\ q^{I(\lambda _{i}\geq \lambda _{i+1})}\, T_{i}^{-1}\, E^{s_{i}\sigma }_{s_{i}\lambda }, & s_{i}\sigma <\sigma, \end{cases} \end{align} $$
$$ \begin{align} E^{\sigma }_{\lambda } = \begin{cases} q^{-I(\lambda _{i}\leq \lambda _{i+1})}\, T_{i}\, E^{s_{i}\sigma }_{s_{i}\lambda }, & s_{i}\sigma>\sigma \\ q^{I(\lambda _{i}\geq \lambda _{i+1})}\, T_{i}^{-1}\, E^{s_{i}\sigma }_{s_{i}\lambda }, & s_{i}\sigma <\sigma, \end{cases} \end{align} $$
where
![]() $I(P)=1$
if P is true,
$I(P)=1$
if P is true,
![]() $I(P)=0$
if P is false. Together with the initial condition
$I(P)=0$
if P is false. Together with the initial condition
![]() $E^{\sigma }_{\lambda } = x^{\lambda }$
for all
$E^{\sigma }_{\lambda } = x^{\lambda }$
for all
![]() $\sigma $
if
$\sigma $
if
![]() $\lambda =\lambda _{+}$
, this determines
$\lambda =\lambda _{+}$
, this determines
![]() $E^{\sigma }_{\lambda }$
for all
$E^{\sigma }_{\lambda }$
for all
![]() $\sigma $
and
$\sigma $
and
![]() $\lambda $
.
$\lambda $
.
Corollary 4.3.1.
![]() $E^{\sigma }_{\lambda }$
has the monic and triangular form in equation (74) for all
$E^{\sigma }_{\lambda }$
has the monic and triangular form in equation (74) for all
![]() $\sigma $
.
$\sigma $
.
Proposition 4.3.2. For every
![]() $\sigma \in S_{l}$
, the elements
$\sigma \in S_{l}$
, the elements
![]() $E_{\lambda }^{\sigma }(x;q)$
and
$E_{\lambda }^{\sigma }(x;q)$
and
![]() $\overline {F_{\lambda }^{\sigma }(x;q)}$
are dual bases of
$\overline {F_{\lambda }^{\sigma }(x;q)}$
are dual bases of
![]() ${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]$
with respect to the inner product defined by
${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]$
with respect to the inner product defined by
 $$ \begin{align} \langle f,g \rangle_{q} = \langle x^{0} \rangle\, f\, g\, \prod _{i<j} \frac{1-x_{i}/x_{j}}{1 - q^{-1} x_{i}/x_{j}}. \end{align} $$
$$ \begin{align} \langle f,g \rangle_{q} = \langle x^{0} \rangle\, f\, g\, \prod _{i<j} \frac{1-x_{i}/x_{j}}{1 - q^{-1} x_{i}/x_{j}}. \end{align} $$
In other words,
![]() $\langle E_{\lambda }^{\sigma }, \overline {F_{\mu }^{\sigma }} \rangle _{q} = \delta _{\lambda \mu }$
for all
$\langle E_{\lambda }^{\sigma }, \overline {F_{\mu }^{\sigma }} \rangle _{q} = \delta _{\lambda \mu }$
for all
![]() $\lambda ,\mu \in {\mathbb Z} ^{l}$
and all
$\lambda ,\mu \in {\mathbb Z} ^{l}$
and all
![]() $\sigma \in S_{l}$
.
$\sigma \in S_{l}$
.
To prove Proposition 4.3.2, we need the following lemma.
Lemma 4.3.3. The Demazure–Lusztig operators
![]() $T_{i}$
in equation (69) are self-adjoint with respect to
$T_{i}$
in equation (69) are self-adjoint with respect to
![]() $\langle -,- \rangle _{q}$
.
$\langle -,- \rangle _{q}$
.
Proof. It’s the same to show that
![]() $T_{i}-q$
is self-adjoint. A bit of algebra gives
$T_{i}-q$
is self-adjoint. A bit of algebra gives
 $$ \begin{align} T_{i}-q =q\, \frac{1-q^{-1} x_{i}/x_{i+1}}{1-x_{i}/x_{i+1}}(s_{i}-1), \end{align} $$
$$ \begin{align} T_{i}-q =q\, \frac{1-q^{-1} x_{i}/x_{i+1}}{1-x_{i}/x_{i+1}}(s_{i}-1), \end{align} $$
and therefore
 $$ \begin{align} \langle (T_{i}-q)f,g \rangle_{q} = q\, \langle x^{0} \rangle\, (s_{i}(f)\, g-f\, g) \prod \frac{1-x_{j}/x_{k}}{1-q^{-1}x_{j}/x_{k}}, \end{align} $$
$$ \begin{align} \langle (T_{i}-q)f,g \rangle_{q} = q\, \langle x^{0} \rangle\, (s_{i}(f)\, g-f\, g) \prod \frac{1-x_{j}/x_{k}}{1-q^{-1}x_{j}/x_{k}}, \end{align} $$
where the product is over
![]() $j<k$
with
$j<k$
with
![]() $(j,k) \not = (i,i+1)$
. We want to show that this is symmetric in f and g, that is, that the right-hand side is unchanged if we replace
$(j,k) \not = (i,i+1)$
. We want to show that this is symmetric in f and g, that is, that the right-hand side is unchanged if we replace
![]() $s_{i}(f)\, g$
with
$s_{i}(f)\, g$
with
![]() $f\, s_{i}(g)$
. Let
$f\, s_{i}(g)$
. Let
![]() $\Delta $
denote the product factor in equation (80), and note that
$\Delta $
denote the product factor in equation (80), and note that
![]() $\Delta $
is symmetric in
$\Delta $
is symmetric in
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{i+1}$
. The constant term
$x_{i+1}$
. The constant term
![]() $\langle x^{0} \rangle \, \varphi (x)$
of any
$\langle x^{0} \rangle \, \varphi (x)$
of any
![]() $\varphi (x_{1}, \ldots , x_{l})$
is equal to
$\varphi (x_{1}, \ldots , x_{l})$
is equal to
![]() $\langle x^{0} \rangle \, s_{i} (\varphi (x))$
. In particular,
$\langle x^{0} \rangle \, s_{i} (\varphi (x))$
. In particular,
![]() $\langle x^{0} \rangle s_{i}(f) g\, \Delta = \langle x^{0} \rangle f s_{i}(g)\, \Delta $
, which implies the desired result.
$\langle x^{0} \rangle s_{i}(f) g\, \Delta = \langle x^{0} \rangle f s_{i}(g)\, \Delta $
, which implies the desired result.
Proof of Proposition 4.3.2.
The desired identity is just a tidy notation for
![]() $\langle E_{\lambda }^{\sigma },E_{-\mu }^{\sigma w_{0}} \rangle _{q} = \delta _{\lambda \mu }$
.
$\langle E_{\lambda }^{\sigma },E_{-\mu }^{\sigma w_{0}} \rangle _{q} = \delta _{\lambda \mu }$
.
By equation (77), for every i, we have either
![]() $\langle E_{\lambda }^{\sigma }, E_{-\mu }^{\sigma w_{0}} \rangle _{q} = q^{e}\, \langle T_{i} E_{s_{i}\lambda }^{s_{i}\sigma }, T_{i}^{-1}E_{-s_{i} \mu }^{s_{i} \sigma w_{0}} \rangle _{q}$
or
$\langle E_{\lambda }^{\sigma }, E_{-\mu }^{\sigma w_{0}} \rangle _{q} = q^{e}\, \langle T_{i} E_{s_{i}\lambda }^{s_{i}\sigma }, T_{i}^{-1}E_{-s_{i} \mu }^{s_{i} \sigma w_{0}} \rangle _{q}$
or
![]() $\langle E_{\lambda }^{\sigma }, E_{-\mu }^{\sigma w_{0}} \rangle _{q} = q^{e}\, \langle T_{i}^{-1} E_{s_{i} \lambda }^{s_{i} \sigma }, T_{i} E_{- s_{i} \mu }^{s_{i} \sigma w_{0}} \rangle _{q}$
, depending on whether
$\langle E_{\lambda }^{\sigma }, E_{-\mu }^{\sigma w_{0}} \rangle _{q} = q^{e}\, \langle T_{i}^{-1} E_{s_{i} \lambda }^{s_{i} \sigma }, T_{i} E_{- s_{i} \mu }^{s_{i} \sigma w_{0}} \rangle _{q}$
, depending on whether
![]() $s_{i}\sigma>\sigma $
or
$s_{i}\sigma>\sigma $
or
![]() $s_{i}\sigma <\sigma $
, for some exponent e. Moreover, if
$s_{i}\sigma <\sigma $
, for some exponent e. Moreover, if
![]() $\lambda =\mu $
, then
$\lambda =\mu $
, then
![]() $q^{e} = 1$
.
$q^{e} = 1$
.
Since
![]() $T_{i}$
is self-adjoint, we get
$T_{i}$
is self-adjoint, we get
![]() $\langle E_{\lambda }^{\sigma }, E_{-\mu }^{\sigma w_{0}} \rangle _{q} = q^{e} \langle E_{s_{i}\lambda }^{s_{i}\sigma }, E_{-s_{i} \mu }^{s_{i} \sigma w_{0}} \rangle _{q}$
in either case. Repeating this gives an identity
$\langle E_{\lambda }^{\sigma }, E_{-\mu }^{\sigma w_{0}} \rangle _{q} = q^{e} \langle E_{s_{i}\lambda }^{s_{i}\sigma }, E_{-s_{i} \mu }^{s_{i} \sigma w_{0}} \rangle _{q}$
in either case. Repeating this gives an identity
for all
![]() $\lambda ,\mu \in {\mathbb Z} ^{l}$
and all
$\lambda ,\mu \in {\mathbb Z} ^{l}$
and all
![]() $\sigma ,v\in S_{l}$
, again with
$\sigma ,v\in S_{l}$
, again with
![]() $q^{e} = 1$
if
$q^{e} = 1$
if
![]() $\lambda =\mu $
.
$\lambda =\mu $
.
Choose
![]() $v\in S_{l}$
such that
$v\in S_{l}$
such that
![]() $\mu _{-} = v (\mu )$
is antidominant. Then equation (81) gives
$\mu _{-} = v (\mu )$
is antidominant. Then equation (81) gives
where now
![]() $\Delta $
is the product factor in equation (78). Let
$\Delta $
is the product factor in equation (78). Let
![]() $\operatorname {\mathrm {supp}} (f)$
denote the set of weights
$\operatorname {\mathrm {supp}} (f)$
denote the set of weights
![]() $\nu $
for which
$\nu $
for which
![]() $x^{\nu }$
occurs with nonzero coefficient in f. Since
$x^{\nu }$
occurs with nonzero coefficient in f. Since
![]() $\operatorname {\mathrm {supp}} (\Delta ) = Q_{+}$
, and
$\operatorname {\mathrm {supp}} (\Delta ) = Q_{+}$
, and
![]() $\operatorname {\mathrm {supp}} (E^{v \sigma }_{v \lambda })\subseteq \operatorname {\mathrm {conv}} (S_{l}\, \lambda )$
, it follows from equation (82) that if
$\operatorname {\mathrm {supp}} (E^{v \sigma }_{v \lambda })\subseteq \operatorname {\mathrm {conv}} (S_{l}\, \lambda )$
, it follows from equation (82) that if
![]() $\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q}\not =0$
, then
$\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q}\not =0$
, then
![]() $(\mu _{-}-Q_{+})\cap \operatorname {\mathrm {conv}} (S_{l}\, \lambda )\not =\emptyset $
and therefore
$(\mu _{-}-Q_{+})\cap \operatorname {\mathrm {conv}} (S_{l}\, \lambda )\not =\emptyset $
and therefore
![]() $\mu _{-} - \lambda _{-}\in Q_{+}$
. Since
$\mu _{-} - \lambda _{-}\in Q_{+}$
. Since
![]() $w_{0}(Q_{+}) = -Q_{+}$
, this is equivalent to
$w_{0}(Q_{+}) = -Q_{+}$
, this is equivalent to
![]() $\lambda _{+}\geq \mu _{+}$
.
$\lambda _{+}\geq \mu _{+}$
.
By symmetry, exchanging
![]() $\lambda $
with
$\lambda $
with
![]() $-\mu $
and
$-\mu $
and
![]() $\sigma $
with
$\sigma $
with
![]() $\sigma w_{0}$
, if
$\sigma w_{0}$
, if
![]() $\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q}\not =0$
, then we also have
$\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q}\not =0$
, then we also have
![]() $(-\lambda )_{-} - (-\mu )_{-}\in Q_{+}$
, hence
$(-\lambda )_{-} - (-\mu )_{-}\in Q_{+}$
, hence
![]() $\lambda _{+}-\mu _{+}\in -Q_{+}$
, that is,
$\lambda _{+}-\mu _{+}\in -Q_{+}$
, that is,
![]() $\lambda _{+}\leq \mu _{+}$
. Hence,
$\lambda _{+}\leq \mu _{+}$
. Hence,
![]() $\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q}\not =0$
implies
$\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q}\not =0$
implies
![]() $\lambda _{+} = \mu _{+}$
, so
$\lambda _{+} = \mu _{+}$
, so
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
belong to the same
$\mu $
belong to the same
![]() $S_{l}$
orbit. This reduces the problem to the case that
$S_{l}$
orbit. This reduces the problem to the case that
![]() $S_{l}\, \lambda = S_{l}\, \mu $
.
$S_{l}\, \lambda = S_{l}\, \mu $
.
In this case,
![]() $(\mu _{-}-Q_{+})\cap \operatorname {\mathrm {conv}} (S_{l}\, \lambda ) = \{\mu _{-} \}$
. Furthermore, if
$(\mu _{-}-Q_{+})\cap \operatorname {\mathrm {conv}} (S_{l}\, \lambda ) = \{\mu _{-} \}$
. Furthermore, if
![]() $\lambda \not =\mu $
, then
$\lambda \not =\mu $
, then
![]() $v \lambda \not =\mu _{-}$
, and Corollary 4.3.1 implies that
$v \lambda \not =\mu _{-}$
, and Corollary 4.3.1 implies that
![]() $(\mu _{-}-Q_{+})\cap \operatorname {\mathrm {supp}} (E^{v \sigma }_{v \lambda }) = \emptyset $
, hence
$(\mu _{-}-Q_{+})\cap \operatorname {\mathrm {supp}} (E^{v \sigma }_{v \lambda }) = \emptyset $
, hence
![]() $\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q} =0$
.
$\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\mu } \rangle _{q} =0$
.
If
![]() $\lambda =\mu $
, then the right-hand side of equation (82) reduces to
$\lambda =\mu $
, then the right-hand side of equation (82) reduces to
![]() $\langle x^{\mu _{-}} \rangle \, \Delta \, E^{v \sigma }_{\mu _{-}}$
. Since
$\langle x^{\mu _{-}} \rangle \, \Delta \, E^{v \sigma }_{\mu _{-}}$
. Since
![]() $\operatorname {\mathrm {supp}} (\Delta )=Q_{+}$
and
$\operatorname {\mathrm {supp}} (\Delta )=Q_{+}$
and
![]() $\operatorname {\mathrm {supp}} (E^{v \sigma }_{\mu _{-}})\subset \mu _{-}+Q_{+}$
, only the constant term of
$\operatorname {\mathrm {supp}} (E^{v \sigma }_{\mu _{-}})\subset \mu _{-}+Q_{+}$
, only the constant term of
![]() $\Delta $
and the
$\Delta $
and the
![]() $x^{\mu _{-}}$
term of
$x^{\mu _{-}}$
term of
![]() $E^{v\sigma }_{\mu _{-}}$
contribute to the coefficient of
$E^{v\sigma }_{\mu _{-}}$
contribute to the coefficient of
![]() $x^{\mu _{-}}$
in
$x^{\mu _{-}}$
in
![]() $\Delta \, E^{v \sigma }_{\mu _{-}}$
, and we have
$\Delta \, E^{v \sigma }_{\mu _{-}}$
, and we have
![]() $\langle x^{\mu _{-}} \rangle E^{v\sigma }_{\mu _{-}} = 1$
by Corollary 4.3.1. Hence,
$\langle x^{\mu _{-}} \rangle E^{v\sigma }_{\mu _{-}} = 1$
by Corollary 4.3.1. Hence,
![]() $\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\lambda } \rangle _{q} =1$
.
$\langle E^{\sigma }_{\lambda }, E^{\sigma w_{0}}_{-\lambda } \rangle _{q} =1$
.
Lemma 4.3.4. Given
![]() $\lambda \in {\mathbb Z} ^{l}$
, suppose there is an index k such that
$\lambda \in {\mathbb Z} ^{l}$
, suppose there is an index k such that
![]() $\lambda _{i}\geq \lambda _{j}$
for all
$\lambda _{i}\geq \lambda _{j}$
for all
![]() $i\leq k$
and
$i\leq k$
and
![]() $j>k$
. Given
$j>k$
. Given
![]() $\sigma \in S_{l}$
, let
$\sigma \in S_{l}$
, let
![]() $\sigma _{1}\in S_{k}$
and
$\sigma _{1}\in S_{k}$
and
![]() $\sigma _{2}\in S_{l-k}$
be the permutations such that
$\sigma _{2}\in S_{l-k}$
be the permutations such that
![]() $\sigma _{1}(1),\ldots ,\sigma _{1}(k)$
are in the same relative order as
$\sigma _{1}(1),\ldots ,\sigma _{1}(k)$
are in the same relative order as
![]() $\sigma (1),\ldots ,\sigma (k)$
, and
$\sigma (1),\ldots ,\sigma (k)$
, and
![]() $\sigma _{2}(1),\ldots ,\sigma _{2}(l-k)$
are in the same relative order as
$\sigma _{2}(1),\ldots ,\sigma _{2}(l-k)$
are in the same relative order as
![]() $\sigma (k+1),\ldots ,\sigma (l)$
. Then
$\sigma (k+1),\ldots ,\sigma (l)$
. Then
Proof. If
![]() $\lambda $
is dominant, the result is trivial. Otherwise, the recurrence (77) determines
$\lambda $
is dominant, the result is trivial. Otherwise, the recurrence (77) determines
![]() $E^{\sigma ^{-1}}_{\lambda }$
by induction on
$E^{\sigma ^{-1}}_{\lambda }$
by induction on
![]() $\left |\, \operatorname {\mathrm {Inv}} (-\lambda )\, \right |$
. The condition on
$\left |\, \operatorname {\mathrm {Inv}} (-\lambda )\, \right |$
. The condition on
![]() $\lambda $
implies that we only need to use equation (77) for
$\lambda $
implies that we only need to use equation (77) for
![]() $i\not =k$
, that is, for
$i\not =k$
, that is, for
![]() $s_{i}$
in the Young subgroup
$s_{i}$
in the Young subgroup
![]() $S_{k}\times S_{l-k}\subset S_{l}$
. For
$S_{k}\times S_{l-k}\subset S_{l}$
. For
![]() $i\not =k$
, the right-hand side of equation (83) satisfies the same recurrence.
$i\not =k$
, the right-hand side of equation (83) satisfies the same recurrence.
4.4 LLT series
Definition 4.4.1. Given
![]() $\operatorname {\mathrm {GL}} _{l}$
weights
$\operatorname {\mathrm {GL}} _{l}$
weights
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
and a permutation
$\alpha ,\beta \in {\mathbb Z} ^{l}$
and a permutation
![]() $\sigma \in S_{l}$
, the LLT series
$\sigma \in S_{l}$
, the LLT series
![]() ${\mathcal L}^{\sigma } _{\beta /\alpha }(x_{1},\ldots ,x_{l};q)$
is the infinite formal sum of irreducible
${\mathcal L}^{\sigma } _{\beta /\alpha }(x_{1},\ldots ,x_{l};q)$
is the infinite formal sum of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters in which the coefficient of
$\operatorname {\mathrm {GL}} _{l}$
characters in which the coefficient of
![]() $\chi _{\lambda }$
is defined by
$\chi _{\lambda }$
is defined by
where
![]() $E^{\sigma }_{\lambda }(x;q)$
are the twisted nonsymmetric Hall–Littlewood polynomials from §4.3.
$E^{\sigma }_{\lambda }(x;q)$
are the twisted nonsymmetric Hall–Littlewood polynomials from §4.3.
We remark that the coefficients of
![]() $E^{\sigma }_{\lambda }(x;q)$
are polynomials in
$E^{\sigma }_{\lambda }(x;q)$
are polynomials in
![]() $q^{-1}$
, so the convention of inverting q in equation (84) makes the coefficients of
$q^{-1}$
, so the convention of inverting q in equation (84) makes the coefficients of
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
polynomials in q. Inverting
${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
polynomials in q. Inverting
![]() $\sigma $
as well leads to a more natural statement and proof in Corollary 4.5.7, below.
$\sigma $
as well leads to a more natural statement and proof in Corollary 4.5.7, below.
Proposition 4.4.2. We have the formula
where
![]() ${\mathbf H} _{q}$
is the Hall–Littlewood symmetrization operator in equation (23) and
${\mathbf H} _{q}$
is the Hall–Littlewood symmetrization operator in equation (23) and
![]() $w_{0}(i)=l+1-i$
is the longest element in
$w_{0}(i)=l+1-i$
is the longest element in
![]() $S_{l}$
.
$S_{l}$
.
Proof. By Proposition 4.3.2, the coefficient
![]() $ \langle E^{\sigma ^{-1}}_{\beta }(x;q^{-1}) \rangle \, \chi _{\lambda } \, E^{\sigma ^{-1}}_{\alpha }(x;q^{-1})$
of
$ \langle E^{\sigma ^{-1}}_{\beta }(x;q^{-1}) \rangle \, \chi _{\lambda } \, E^{\sigma ^{-1}}_{\alpha }(x;q^{-1})$
of
![]() $\chi _{\lambda }$
in
$\chi _{\lambda }$
in
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }$
is given by the constant term
${\mathcal L} ^{\sigma }_{\beta /\alpha }$
is given by the constant term
 $$ \begin{align} \langle x^{0} \rangle\, \chi _{\lambda }\, F^{\sigma ^{-1}}_{\beta }(x^{-1};q)\, E^{\sigma ^{-1}}_{\alpha }(x;q^{-1}) \prod _{i<j}\frac{1-x_{i}/x_{j}}{1-q\, x_{i}/x_{j}}. \end{align} $$
$$ \begin{align} \langle x^{0} \rangle\, \chi _{\lambda }\, F^{\sigma ^{-1}}_{\beta }(x^{-1};q)\, E^{\sigma ^{-1}}_{\alpha }(x;q^{-1}) \prod _{i<j}\frac{1-x_{i}/x_{j}}{1-q\, x_{i}/x_{j}}. \end{align} $$
Substituting
![]() $x_{i}\mapsto x_{i}^{-1}$
and applying
$x_{i}\mapsto x_{i}^{-1}$
and applying
![]() $w_{0}$
, this is equal to
$w_{0}$
, this is equal to
 $$ \begin{align} \langle x^{0} \rangle\, \overline{\chi _{\lambda }}\, w_{0}(F^{\sigma ^{-1}}_{\beta }(x;q) \overline{E^{\sigma ^{-1}}_{\alpha }(x;q)}) \prod _{i<j}\frac{1-x_{i}/x_{j}}{1-q\, x_{i}/x_{j}}. \end{align} $$
$$ \begin{align} \langle x^{0} \rangle\, \overline{\chi _{\lambda }}\, w_{0}(F^{\sigma ^{-1}}_{\beta }(x;q) \overline{E^{\sigma ^{-1}}_{\alpha }(x;q)}) \prod _{i<j}\frac{1-x_{i}/x_{j}}{1-q\, x_{i}/x_{j}}. \end{align} $$
Considering this expression as a formal Laurent series in q and applying equation (20) coefficient-wise yields
 $$ \begin{align} \langle \chi _{\lambda } \rangle {\boldsymbol \sigma } \left( w_{0}(F^{\sigma^{-1}}_{\beta }(x;q) \overline{E^{\sigma ^{-1}}_{\alpha }(x;q)}) \prod_{i<j}\frac{1}{1-q\, x_{i}/x_{j}} \right), \end{align} $$
$$ \begin{align} \langle \chi _{\lambda } \rangle {\boldsymbol \sigma } \left( w_{0}(F^{\sigma^{-1}}_{\beta }(x;q) \overline{E^{\sigma ^{-1}}_{\alpha }(x;q)}) \prod_{i<j}\frac{1}{1-q\, x_{i}/x_{j}} \right), \end{align} $$
which is
![]() $\langle \chi _{\lambda } \rangle {\mathbf H} _{q}(w_{0}(F^{\sigma ^{-1} }_{\beta }(x;q) \overline {E^{\sigma ^{-1}}_{\alpha }(x;q)}))$
, as desired.
$\langle \chi _{\lambda } \rangle {\mathbf H} _{q}(w_{0}(F^{\sigma ^{-1} }_{\beta }(x;q) \overline {E^{\sigma ^{-1}}_{\alpha }(x;q)}))$
, as desired.
Remark 4.4.3. All definitions and results in §§2.3–2.4 and 4.2–4.4 extend naturally from the weight lattice and root system of
![]() $\operatorname {\mathrm {GL}}_{l}$
to those of any reductive algebraic group G, as in [Reference Grojnowski and Haiman14]. The reader may observe that, apart from changes in notation, the arguments given here also apply in the general case.
$\operatorname {\mathrm {GL}}_{l}$
to those of any reductive algebraic group G, as in [Reference Grojnowski and Haiman14]. The reader may observe that, apart from changes in notation, the arguments given here also apply in the general case.
4.5 Tableaux for LLT series
We now work out a tableau formalism which relates the polynomial part
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)_{\operatorname {\mathrm {pol}} }$
to a combinatorial LLT polynomial
${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)_{\operatorname {\mathrm {pol}} }$
to a combinatorial LLT polynomial
![]() ${\mathcal G} _{\nu }(x;q)$
.
${\mathcal G} _{\nu }(x;q)$
.
Lemma 4.5.1. For all
![]() $\sigma \in S_{l}$
,
$\sigma \in S_{l}$
,
![]() $\lambda \in {\mathbb Z} ^{l}$
and k, the product of the elementary symmetric function
$\lambda \in {\mathbb Z} ^{l}$
and k, the product of the elementary symmetric function
![]() $e_{k}(x)$
and the nonsymmetric Hall–Littlewood polynomial
$e_{k}(x)$
and the nonsymmetric Hall–Littlewood polynomial
![]() $E^{\sigma ^{-1} }_{\lambda }(x;q)$
is given by
$E^{\sigma ^{-1} }_{\lambda }(x;q)$
is given by
where
![]() $I\subseteq \{1,\ldots ,l \}$
has k elements,
$I\subseteq \{1,\ldots ,l \}$
has k elements,
![]() $\varepsilon _{I} = \sum _{i\in I}\varepsilon _{i}$
is the indicator vector of I, and
$\varepsilon _{I} = \sum _{i\in I}\varepsilon _{i}$
is the indicator vector of I, and
Equivalently,
![]() $h_{I}$
is the number of pairs
$h_{I}$
is the number of pairs
![]() $i<j$
such that
$i<j$
such that
![]() $i\in I$
,
$i\in I$
,
![]() $j\not \in I$
, and we have
$j\not \in I$
, and we have
![]() $\lambda _{j} = \lambda _{i}$
if
$\lambda _{j} = \lambda _{i}$
if
![]() $\sigma (i)<\sigma (j)$
, or
$\sigma (i)<\sigma (j)$
, or
![]() $\lambda _{j} = \lambda _{i}+1$
if
$\lambda _{j} = \lambda _{i}+1$
if
![]() $\sigma (i)>\sigma (j)$
.
$\sigma (i)>\sigma (j)$
.
Proof. First, consider the case
![]() $\sigma =1$
. Being symmetric,
$\sigma =1$
. Being symmetric,
![]() $e_{k}(x)$
commutes with
$e_{k}(x)$
commutes with
![]() $T_{w}$
, giving
$T_{w}$
, giving
where
![]() $\lambda = w(\lambda _{+})$
, as in equation (73). To fix the choice, we take w maximal in its coset
$\lambda = w(\lambda _{+})$
, as in equation (73). To fix the choice, we take w maximal in its coset
![]() $w\, \operatorname {\mathrm {Stab}} (\lambda _{+})$
.
$w\, \operatorname {\mathrm {Stab}} (\lambda _{+})$
.
In each term of the sum in equation (91), the weight
![]() $\mu =\lambda _{+}+\varepsilon _{J}$
can fail to be dominant at worst by having some entries
$\mu =\lambda _{+}+\varepsilon _{J}$
can fail to be dominant at worst by having some entries
![]() $\mu _{j} = \mu _{i}+1$
for indices
$\mu _{j} = \mu _{i}+1$
for indices
![]() $i<j$
such that
$i<j$
such that
![]() $(\lambda _{+})_{i} = (\lambda _{+})_{j}$
,
$(\lambda _{+})_{i} = (\lambda _{+})_{j}$
,
![]() $i\not \in J$
and
$i\not \in J$
and
![]() $j\in J$
. Let v be the minimal permutation such that
$j\in J$
. Let v be the minimal permutation such that
![]() $\mu _{+} = v(\mu )$
, that is, the permutation that moves indices
$\mu _{+} = v(\mu )$
, that is, the permutation that moves indices
![]() $j\in J$
to the left within each block of constant entries in
$j\in J$
to the left within each block of constant entries in
![]() $\lambda _{+}$
. The formula
$\lambda _{+}$
. The formula
![]() $T_{i} x_{i}^{a}x_{i+1}^{a+1} = x_{i}^{a+1}x_{i+1}^{a}$
is immediate from the definition of
$T_{i} x_{i}^{a}x_{i+1}^{a+1} = x_{i}^{a+1}x_{i+1}^{a}$
is immediate from the definition of
![]() $T_{i}$
and implies that
$T_{i}$
and implies that
![]() $T_{v} x^{\mu } = x^{\mu _{+}}$
. By the maximality of w, since
$T_{v} x^{\mu } = x^{\mu _{+}}$
. By the maximality of w, since
![]() $v\in \operatorname {\mathrm {Stab}} (\lambda _{+})$
, there is a reduced factorization
$v\in \operatorname {\mathrm {Stab}} (\lambda _{+})$
, there is a reduced factorization
![]() $w = uv$
, hence
$w = uv$
, hence
![]() $T_{w} = T_{u}T_{v}$
. Then
$T_{w} = T_{u}T_{v}$
. Then
since
![]() $\lambda +w(\varepsilon _{J}) = w(\mu ) = u(\mu _{+})$
.
$\lambda +w(\varepsilon _{J}) = w(\mu ) = u(\mu _{+})$
.
Now,
![]() $\ell (v)$
is equal to the number of pairs
$\ell (v)$
is equal to the number of pairs
![]() $i<j$
such that
$i<j$
such that
![]() $\mu _{i}<\mu _{j}$
, that is, such that
$\mu _{i}<\mu _{j}$
, that is, such that
![]() $(\lambda _{+})_{i}= (\lambda _{+})_{j}$
,
$(\lambda _{+})_{i}= (\lambda _{+})_{j}$
,
![]() $i\not \in J$
and
$i\not \in J$
and
![]() $j\in J$
. By maximality, the permutation w carries these to the pairs
$j\in J$
. By maximality, the permutation w carries these to the pairs
![]() $j' = w(i)$
,
$j' = w(i)$
,
![]() $i' = w(j)$
such that
$i' = w(j)$
such that
![]() $i' < j'$
,
$i' < j'$
,
![]() $\lambda _{i'} = \lambda _{j'}$
,
$\lambda _{i'} = \lambda _{j'}$
,
![]() $i'\in I$
and
$i'\in I$
and
![]() $j'\not \in I$
, where
$j'\not \in I$
, where
![]() $I = w(J)$
. For
$I = w(J)$
. For
![]() $\sigma =1$
, the definition of
$\sigma =1$
, the definition of
![]() $h_{I}$
is the number of such pairs
$h_{I}$
is the number of such pairs
![]() $i',j'$
, so we have
$i',j'$
, so we have
![]() $\ell (u)-\ell (w) = -\ell (v) = -h_{I}$
. Hence, the term for J in equation (91) is
$\ell (u)-\ell (w) = -\ell (v) = -h_{I}$
. Hence, the term for J in equation (91) is
![]() $q^{-\ell (w)} T_{w} x^{\lambda _{+}+\varepsilon _{J}} = q^{-h_{I}} E_{\lambda +\varepsilon _{I}}$
. As J ranges over subsets of size k, so does
$q^{-\ell (w)} T_{w} x^{\lambda _{+}+\varepsilon _{J}} = q^{-h_{I}} E_{\lambda +\varepsilon _{I}}$
. As J ranges over subsets of size k, so does
![]() $I = w(J)$
, giving equation (89) in this case.
$I = w(J)$
, giving equation (89) in this case.
Substituting
![]() $\sigma (\lambda )$
for
$\sigma (\lambda )$
for
![]() $\lambda $
and
$\lambda $
and
![]() $\sigma (I)$
for I in the
$\sigma (I)$
for I in the
![]() $\sigma =1$
case and acting on both sides with
$\sigma =1$
case and acting on both sides with
![]() $T_{\sigma }^{-1}$
yields
$T_{\sigma }^{-1}$
yields
Combining powers of q gives the desired identity (89) if we verify that
 $$ \begin{align} &\left|\, \operatorname{\mathrm{Inv}} (\sigma )\cap \operatorname{\mathrm{Inv}} (\lambda +\varepsilon _{I} + \epsilon \rho )\, \right| - \left|\, \operatorname{\mathrm{Inv}} (\sigma )\cap \operatorname{\mathrm{Inv}} (\lambda +\epsilon \rho )\, \right| \notag\\ &\qquad\qquad\qquad\qquad = \left|\, \operatorname{\mathrm{Inv}} (\lambda + \varepsilon _{I} + \epsilon \sigma )\setminus \operatorname{\mathrm{Inv}} (\lambda + \epsilon \sigma )\, \right| - \left|\, \operatorname{\mathrm{Inv}} (\sigma (\lambda +\varepsilon _{I}))\setminus \operatorname{\mathrm{Inv}} (\sigma (\lambda ))\, \right|. \end{align} $$
$$ \begin{align} &\left|\, \operatorname{\mathrm{Inv}} (\sigma )\cap \operatorname{\mathrm{Inv}} (\lambda +\varepsilon _{I} + \epsilon \rho )\, \right| - \left|\, \operatorname{\mathrm{Inv}} (\sigma )\cap \operatorname{\mathrm{Inv}} (\lambda +\epsilon \rho )\, \right| \notag\\ &\qquad\qquad\qquad\qquad = \left|\, \operatorname{\mathrm{Inv}} (\lambda + \varepsilon _{I} + \epsilon \sigma )\setminus \operatorname{\mathrm{Inv}} (\lambda + \epsilon \sigma )\, \right| - \left|\, \operatorname{\mathrm{Inv}} (\sigma (\lambda +\varepsilon _{I}))\setminus \operatorname{\mathrm{Inv}} (\sigma (\lambda ))\, \right|. \end{align} $$
On the left-hand side, cancelling the contribution from the intersection of the two sets leaves
The first term in formula (95) counts pairs
![]() $i<j$
such that
$i<j$
such that
![]() $i\in I$
,
$i\in I$
,
![]() $j\not \in I$
,
$j\not \in I$
,
![]() $\sigma (i)>\sigma (j)$
, and
$\sigma (i)>\sigma (j)$
, and
![]() $\lambda _{j} = \lambda _{i}+1$
. The second term counts pairs
$\lambda _{j} = \lambda _{i}+1$
. The second term counts pairs
![]() $i>j$
such that
$i>j$
such that
![]() $i\in I$
,
$i\in I$
,
![]() $j\not \in I$
,
$j\not \in I$
,
![]() $\sigma (i)<\sigma (j)$
, and
$\sigma (i)<\sigma (j)$
, and
![]() $\lambda _{j} = \lambda _{i}$
. The first term on the right-hand side of equation (94) counts pairs
$\lambda _{j} = \lambda _{i}$
. The first term on the right-hand side of equation (94) counts pairs
![]() $i<j$
such that
$i<j$
such that
![]() $i\in I$
,
$i\in I$
,
![]() $j\not \in I$
, and
$j\not \in I$
, and
![]() $\lambda _{j} = \lambda _{i}$
if
$\lambda _{j} = \lambda _{i}$
if
![]() $\sigma (i)<\sigma (j)$
, or
$\sigma (i)<\sigma (j)$
, or
![]() $\lambda _{j} = \lambda _{i}+1$
if
$\lambda _{j} = \lambda _{i}+1$
if
![]() $\sigma (i)>\sigma (j)$
. The second term on the right-hand side of equation (94) counts the set of pairs whose images under
$\sigma (i)>\sigma (j)$
. The second term on the right-hand side of equation (94) counts the set of pairs whose images under
![]() $\sigma ^{-1}$
are pairs
$\sigma ^{-1}$
are pairs
![]() $i,j$
(in either order) such that
$i,j$
(in either order) such that
![]() $i\in I$
,
$i\in I$
,
![]() $j\not \in I$
,
$j\not \in I$
,
![]() $\sigma (i)<\sigma (j)$
and
$\sigma (i)<\sigma (j)$
and
![]() $\lambda _{i} = \lambda _{j}$
. The cases in the first term with
$\lambda _{i} = \lambda _{j}$
. The cases in the first term with
![]() $\sigma (i)<\sigma (j)$
cancel those in the second term with
$\sigma (i)<\sigma (j)$
cancel those in the second term with
![]() $i<j$
. The remaining cases in the first term, with
$i<j$
. The remaining cases in the first term, with
![]() $\sigma (i)>\sigma (j)$
, match the first term in formula (95), while the remaining cases in the second term, with
$\sigma (i)>\sigma (j)$
, match the first term in formula (95), while the remaining cases in the second term, with
![]() $i>j$
, match the second term in formula (95). This proves equation (94) and completes the proof of the lemma.
$i>j$
, match the second term in formula (95). This proves equation (94) and completes the proof of the lemma.
Given
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
such that
$\alpha ,\beta \in {\mathbb Z} ^{l}$
such that
![]() $\alpha _{j}\leq \beta _{j}$
for all j, we let
$\alpha _{j}\leq \beta _{j}$
for all j, we let
![]() $\beta /\alpha $
denote the tuple of one-row skew shapes
$\beta /\alpha $
denote the tuple of one-row skew shapes
![]() $(\beta _{j})/(\alpha _{j})$
such that the x coordinates of the right edges of boxes in the row that forms the j-th component are the integers
$(\beta _{j})/(\alpha _{j})$
such that the x coordinates of the right edges of boxes in the row that forms the j-th component are the integers
![]() $\alpha _{j}+1,\ldots ,\beta _{j}$
. The boxes just outside this j-th component, adjacent to the left and right ends of the row, then have right edges with x coordinate
$\alpha _{j}+1,\ldots ,\beta _{j}$
. The boxes just outside this j-th component, adjacent to the left and right ends of the row, then have right edges with x coordinate
![]() $\alpha _{j}$
and
$\alpha _{j}$
and
![]() $\beta _{j}+1$
. In the case of an empty row with
$\beta _{j}+1$
. In the case of an empty row with
![]() $\alpha _{j} = \beta _{j}$
, we still consider these two boxes to be adjacent to the ends of the row.
$\alpha _{j} = \beta _{j}$
, we still consider these two boxes to be adjacent to the ends of the row.
For each box a, let
![]() $i(a)$
denote the x coordinate of its right edge and
$i(a)$
denote the x coordinate of its right edge and
![]() $j(a)$
the index of the row containing it.
$j(a)$
the index of the row containing it.
For
![]() $\sigma \in S_{l}$
, we define
$\sigma \in S_{l}$
, we define
![]() $\sigma (\beta /\alpha ) = \sigma (\beta )/\sigma (\alpha )$
. If a is a box in row
$\sigma (\beta /\alpha ) = \sigma (\beta )/\sigma (\alpha )$
. If a is a box in row
![]() $j(a)$
of
$j(a)$
of
![]() $\beta /\alpha $
, then
$\beta /\alpha $
, then
![]() $\sigma (a)$
denotes the corresponding box with x coordinate
$\sigma (a)$
denotes the corresponding box with x coordinate
![]() $i(\sigma (a)) = i(a)$
in row
$i(\sigma (a)) = i(a)$
in row
![]() $\sigma (j(a))$
of
$\sigma (j(a))$
of
![]() $\sigma (\beta /\alpha )$
. The adjusted content of
$\sigma (\beta /\alpha )$
. The adjusted content of
![]() $\sigma (a)$
, as defined in §4.1, is then
$\sigma (a)$
, as defined in §4.1, is then
![]() $\tilde {c} (\sigma (a)) = i(a)+ \sigma (j(a))\, \epsilon $
. Hence, the reading order on
$\tilde {c} (\sigma (a)) = i(a)+ \sigma (j(a))\, \epsilon $
. Hence, the reading order on
![]() $\sigma (\beta /\alpha )$
corresponds via
$\sigma (\beta /\alpha )$
corresponds via
![]() $\sigma $
to the ordering of boxes in
$\sigma $
to the ordering of boxes in
![]() $\beta /\alpha $
by increasing values of
$\beta /\alpha $
by increasing values of
![]() $i(a) + \sigma (j(a))\, \epsilon $
.
$i(a) + \sigma (j(a))\, \epsilon $
.
We define a
![]() $\sigma $
-triple in
$\sigma $
-triple in
![]() $\beta /\alpha $
to consist of any three boxes
$\beta /\alpha $
to consist of any three boxes
![]() $(a,b,c)$
arranged as follows: Boxes a and c are in or adjacent to the same row
$(a,b,c)$
arranged as follows: Boxes a and c are in or adjacent to the same row
![]() $j(a) = j(c)$
and are consecutive, that is,
$j(a) = j(c)$
and are consecutive, that is,
![]() $i(c) = i(a)+1$
, while box b is in a row
$i(c) = i(a)+1$
, while box b is in a row
![]() $j(b)<j(a)$
, and we have
$j(b)<j(a)$
, and we have
![]() $a<b<c$
in the ordering corresponding to the reading order on
$a<b<c$
in the ordering corresponding to the reading order on
![]() $\sigma (\beta /\alpha )$
. More explicitly, this means that, if
$\sigma (\beta /\alpha )$
. More explicitly, this means that, if
![]() $\sigma (j(b))<\sigma (j(a))$
, then
$\sigma (j(b))<\sigma (j(a))$
, then
![]() $i(b) = i(c)$
, while if
$i(b) = i(c)$
, while if
![]() $\sigma (j(b))>\sigma (j(a))$
, then
$\sigma (j(b))>\sigma (j(a))$
, then
![]() $i(b) = i(a)$
. The box b is required to be a box of
$i(b) = i(a)$
. The box b is required to be a box of
![]() $\beta /\alpha $
, but box a is allowed to be outside and adjacent to the left end of a row, while c is similarly allowed to be outside and adjacent to the right end of a row.
$\beta /\alpha $
, but box a is allowed to be outside and adjacent to the left end of a row, while c is similarly allowed to be outside and adjacent to the right end of a row.
An example of a tuple
![]() $\beta /\alpha $
, with all its
$\beta /\alpha $
, with all its
![]() $\sigma $
-triples for two different choices of
$\sigma $
-triples for two different choices of
![]() $\sigma $
, is shown in Figure 1.
$\sigma $
, is shown in Figure 1.
A negative tableau on
![]() $\beta /\alpha $
is a map
$\beta /\alpha $
is a map
![]() $S\colon \beta /\alpha \rightarrow {\mathbb Z} _{>0} $
strictly increasing on each row. In the terminology of §4.1, S is a super tableau on
$S\colon \beta /\alpha \rightarrow {\mathbb Z} _{>0} $
strictly increasing on each row. In the terminology of §4.1, S is a super tableau on
![]() $\beta /\alpha $
with entries in
$\beta /\alpha $
with entries in
![]() ${\mathbb Z} _{>0} $
, considered as a negative alphabet ordered by
${\mathbb Z} _{>0} $
, considered as a negative alphabet ordered by
![]() $\overline {1}<\overline {2}<\cdots $
. We say that a
$\overline {1}<\overline {2}<\cdots $
. We say that a
![]() $\sigma $
-triple
$\sigma $
-triple
![]() $(a,b,c)$
in
$(a,b,c)$
in
![]() $\beta /\alpha $
is increasing in S if
$\beta /\alpha $
is increasing in S if
![]() $S(a)<S(b)<S(c)$
, with the convention that
$S(a)<S(b)<S(c)$
, with the convention that
![]() $S(a) = -\infty $
if a is just outside the left end of a row and
$S(a) = -\infty $
if a is just outside the left end of a row and
![]() $S(c) = \infty $
if c is just outside right end of a row. Along with the
$S(c) = \infty $
if c is just outside right end of a row. Along with the
![]() $\sigma $
-triples in
$\sigma $
-triples in
![]() $\beta /\alpha $
, Figure 1 also displays which triples are increasing in an example tableau S.
$\beta /\alpha $
, Figure 1 also displays which triples are increasing in an example tableau S.
Proposition 4.5.2. Given
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
such that
$\alpha ,\beta \in {\mathbb Z} ^{l}$
such that
![]() $\alpha _{j}\leq \beta _{j}$
for all j, and
$\alpha _{j}\leq \beta _{j}$
for all j, and
![]() $\sigma \in S_{l}$
, let
$\sigma \in S_{l}$
, let
 $$ \begin{align} N^{\sigma }_{\beta /\alpha }(X;q) = \sum_{S\in\operatorname{\mathrm{SSYT}}_{-}(\beta/\alpha)} q^{h_{\sigma}(S)} x^S \end{align} $$
$$ \begin{align} N^{\sigma }_{\beta /\alpha }(X;q) = \sum_{S\in\operatorname{\mathrm{SSYT}}_{-}(\beta/\alpha)} q^{h_{\sigma}(S)} x^S \end{align} $$
be the generating function for negative tableaux S on the tuple of one-row skew diagrams
![]() $(\beta _{j})/(\alpha _{j})$
, weighted by
$(\beta _{j})/(\alpha _{j})$
, weighted by
![]() $q^{h_{\sigma }(S)}$
, where
$q^{h_{\sigma }(S)}$
, where
![]() $h_{\sigma }(S)$
is the number of increasing
$h_{\sigma }(S)$
is the number of increasing
![]() $\sigma $
-triples in S. Then
$\sigma $
-triples in S. Then
![]() $N^{\sigma }_{\beta /\alpha }(X;q)$
is a symmetric function, and
$N^{\sigma }_{\beta /\alpha }(X;q)$
is a symmetric function, and
![]() $\omega N^{\sigma }_{\beta /\alpha }(X;q)$
evaluates in l variables to
$\omega N^{\sigma }_{\beta /\alpha }(X;q)$
evaluates in l variables to
If we do not have
![]() $\alpha _{j}\leq \beta _{j}$
for all j, then
$\alpha _{j}\leq \beta _{j}$
for all j, then
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)_{\operatorname {\mathrm {pol}} } = 0$
.
${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)_{\operatorname {\mathrm {pol}} } = 0$
.
Proof. Let
![]() $L^{\sigma }_{\beta /\alpha }(X;q)$
be the unique symmetric function such that (i)
$L^{\sigma }_{\beta /\alpha }(X;q)$
be the unique symmetric function such that (i)
![]() $L^{\sigma }_{\beta /\alpha }(X;q)$
is a linear combination of Schur functions
$L^{\sigma }_{\beta /\alpha }(X;q)$
is a linear combination of Schur functions
![]() $s_{\lambda }$
with
$s_{\lambda }$
with
![]() $\ell (\lambda )\leq l$
, and (ii) in l variables, it evaluates to
$\ell (\lambda )\leq l$
, and (ii) in l variables, it evaluates to
What we need to prove is that
![]() $\omega \, L^{\sigma }_{\beta /\alpha }(X;q) = N^{\sigma }_{\beta /\alpha }(X;q)$
.
$\omega \, L^{\sigma }_{\beta /\alpha }(X;q) = N^{\sigma }_{\beta /\alpha }(X;q)$
.
The definition of
![]() ${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
implies that
${\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)$
implies that
![]() $L^{\sigma }_{\beta /\alpha }(X;q)$
satisfies
$L^{\sigma }_{\beta /\alpha }(X;q)$
satisfies
for every partition
![]() $\lambda $
, including when
$\lambda $
, including when
![]() $\ell (\lambda )> l$
since then both sides are zero. By linearity, we can replace
$\ell (\lambda )> l$
since then both sides are zero. By linearity, we can replace
![]() $s_{\lambda }$
by any symmetric function f, giving
$s_{\lambda }$
by any symmetric function f, giving
The coefficient of
![]() $m_{\mu }(X)$
in
$m_{\mu }(X)$
in
![]() $\omega \, L^{\sigma }_{\beta /\alpha }(X;q)$
is given by taking
$\omega \, L^{\sigma }_{\beta /\alpha }(X;q)$
is given by taking
![]() $f=e_{\mu }$
.
$f=e_{\mu }$
.
To show that
![]() $\omega \, L^{\sigma }_{\beta /\alpha }(X;q)$
is given by the tableau generating function in equation (96), we use Lemma 4.5.1 to express
$\omega \, L^{\sigma }_{\beta /\alpha }(X;q)$
is given by the tableau generating function in equation (96), we use Lemma 4.5.1 to express
as a sum of powers of q indexed by negative tableaux. In particular, this coefficient will vanish unless we have
![]() $\alpha _{j}\leq \beta _{j}$
for all j, giving the last conclusion in the proposition.
$\alpha _{j}\leq \beta _{j}$
for all j, giving the last conclusion in the proposition.
Multiplying by
![]() $e_{\mu _{1}}$
through
$e_{\mu _{1}}$
through
![]() $e_{\mu _{n}}$
successively and keeping track of one chosen term in each product gives a sequence of terms
$e_{\mu _{n}}$
successively and keeping track of one chosen term in each product gives a sequence of terms
![]() $E^{\sigma ^{-1}}_{\alpha ^{(0)}}, E^{\sigma ^{-1}}_{\alpha ^{(1)}},\ldots , E^{\sigma ^{-1}}_{\alpha ^{(n)}}$
, in which
$E^{\sigma ^{-1}}_{\alpha ^{(0)}}, E^{\sigma ^{-1}}_{\alpha ^{(1)}},\ldots , E^{\sigma ^{-1}}_{\alpha ^{(n)}}$
, in which
![]() $\alpha ^{(0)} = \alpha $
and
$\alpha ^{(0)} = \alpha $
and
![]() $\alpha ^{(m+1)} = \alpha ^{(m)} + \varepsilon _{I}$
for a set of indices I of size
$\alpha ^{(m+1)} = \alpha ^{(m)} + \varepsilon _{I}$
for a set of indices I of size
![]() $\mu _{m}$
, for each m. Each sequence with
$\mu _{m}$
, for each m. Each sequence with
![]() $\alpha ^{(n)} = \beta $
contributes to formula (101).
$\alpha ^{(n)} = \beta $
contributes to formula (101).
If we record these data in the form of a tableau
![]() $S\colon \beta /\alpha \rightarrow {\mathbb Z} _{>0} $
with
$S\colon \beta /\alpha \rightarrow {\mathbb Z} _{>0} $
with
![]() $S(a) = m$
for
$S(a) = m$
for
![]() $a\in (\alpha ^{(m)}/\alpha ^{(m-1)})$
, S satisfies the condition that it is a negative tableau of weight
$a\in (\alpha ^{(m)}/\alpha ^{(m-1)})$
, S satisfies the condition that it is a negative tableau of weight
![]() $x^{S} = x^{\mu }$
. The contribution to formula (101) from the corresponding sequence of terms is the product of the
$x^{S} = x^{\mu }$
. The contribution to formula (101) from the corresponding sequence of terms is the product of the
![]() $q^{h_{I}}$
with
$q^{h_{I}}$
with
![]() $h_{I}$
as in equation (90) for
$h_{I}$
as in equation (90) for
![]() $k= \mu _{m}$
,
$k= \mu _{m}$
,
![]() $\lambda =\alpha ^{(m-1)}$
and I the set of indices j such that
$\lambda =\alpha ^{(m-1)}$
and I the set of indices j such that
![]() $S(a) = m$
for some box a in row j.
$S(a) = m$
for some box a in row j.
We now express the
![]() $h_{I}$
corresponding to
$h_{I}$
corresponding to
![]() $(\alpha ^{(m)}/\alpha ^{(m-1)}) = S^{-1}(\{m \})$
as an attribute of S. For
$(\alpha ^{(m)}/\alpha ^{(m-1)}) = S^{-1}(\{m \})$
as an attribute of S. For
![]() $h_{I}$
to count a pair
$h_{I}$
to count a pair
![]() $i<j$
, we must have
$i<j$
, we must have
![]() $i\in I$
, which means that
$i\in I$
, which means that
![]() $S(b) = m$
for a box b in row i, and
$S(b) = m$
for a box b in row i, and
![]() $j\not \in I$
, and one of the following two situations.
$j\not \in I$
, and one of the following two situations.
If
![]() $\sigma (i)<\sigma (j)$
, we must have
$\sigma (i)<\sigma (j)$
, we must have
![]() $\alpha ^{(m-1)}_{j} = \alpha ^{(m-1)}_{i}$
. Since there is no m in row j of S, this means that the boxes a and c in row j with coordinates
$\alpha ^{(m-1)}_{j} = \alpha ^{(m-1)}_{i}$
. Since there is no m in row j of S, this means that the boxes a and c in row j with coordinates
![]() $i(a) = i(b)-1$
,
$i(a) = i(b)-1$
,
![]() $i(c) = i(b)$
have
$i(c) = i(b)$
have
![]() $S(a)<S(b)<S(c)$
, with the same convention as above that
$S(a)<S(b)<S(c)$
, with the same convention as above that
![]() $S(a) = -\infty $
if a is to the left of a row of
$S(a) = -\infty $
if a is to the left of a row of
![]() $\beta /\alpha $
, and
$\beta /\alpha $
, and
![]() $S(c) = \infty $
if c is to the right of a row.
$S(c) = \infty $
if c is to the right of a row.
If
![]() $\sigma (i)>\sigma (j)$
, we must have
$\sigma (i)>\sigma (j)$
, we must have
![]() $\alpha ^{(m-1)}_{j} = \alpha ^{(m-1)}_{i}+1$
. This means that the boxes a and c in row j with coordinates
$\alpha ^{(m-1)}_{j} = \alpha ^{(m-1)}_{i}+1$
. This means that the boxes a and c in row j with coordinates
![]() $i(a) = i(b)$
,
$i(a) = i(b)$
,
![]() $i(c) = i(b)+1$
have
$i(c) = i(b)+1$
have
![]() $S(a)<S(b)<S(c)$
, with the same convention as before.
$S(a)<S(b)<S(c)$
, with the same convention as before.
These two cases establish that
![]() $h_{I}$
is equal to the number of increasing
$h_{I}$
is equal to the number of increasing
![]() $\sigma $
-triples in S for which
$\sigma $
-triples in S for which
![]() $S(b) = m$
. Summing them up gives the total number of increasing
$S(b) = m$
. Summing them up gives the total number of increasing
![]() $\sigma $
-triples, implying that the coefficient in formula (101) is the sum of
$\sigma $
-triples, implying that the coefficient in formula (101) is the sum of
![]() $q^{h_{\sigma }(S)}$
over negative tableaux S of weight
$q^{h_{\sigma }(S)}$
over negative tableaux S of weight
![]() $x^{S} = x^{\mu }$
on
$x^{S} = x^{\mu }$
on
![]() $\beta /\alpha $
, where
$\beta /\alpha $
, where
![]() $h_{\sigma }(S)$
is the number of increasing
$h_{\sigma }(S)$
is the number of increasing
![]() $\sigma $
-triples in S.
$\sigma $
-triples in S.
Similar to the notation
![]() $h_{\sigma }(S)$
in equation (96) for the number of increasing triples in a tableau S, we let
$h_{\sigma }(S)$
in equation (96) for the number of increasing triples in a tableau S, we let
![]() $h_{\sigma }(\beta /\alpha )$
denote the total number of triples in a tuple of rows.
$h_{\sigma }(\beta /\alpha )$
denote the total number of triples in a tuple of rows.
Lemma 4.5.3. Given
![]() $\sigma \in S_l$
and
$\sigma \in S_l$
and
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
with
$\alpha ,\beta \in {\mathbb Z} ^{l}$
with
![]() $\alpha _{j}\leq \beta _{j}$
for all j, we have
$\alpha _{j}\leq \beta _{j}$
for all j, we have
for
![]() $T \in \operatorname {\mathrm {SSYT}}_{-}(\sigma (\beta /\alpha ))$
, where
$T \in \operatorname {\mathrm {SSYT}}_{-}(\sigma (\beta /\alpha ))$
, where
![]() $S = \sigma ^{-1}(T) = T\circ \sigma $
.
$S = \sigma ^{-1}(T) = T\circ \sigma $
.
Proof. Recall from §4.1 that an attacking inversion in a negative tableau is defined by
![]() $T(a)\geq T(b)$
, where
$T(a)\geq T(b)$
, where
![]() $a, b$
is an attacking pair with a preceding b in the reading order.
$a, b$
is an attacking pair with a preceding b in the reading order.
One can verify from the definition of
![]() $\sigma $
-triple that the attacking pairs in
$\sigma $
-triple that the attacking pairs in
![]() $\sigma (\beta /\alpha )$
, ordered by the reading order, are precisely the pairs
$\sigma (\beta /\alpha )$
, ordered by the reading order, are precisely the pairs
![]() $(\sigma (a), \sigma (b))$
or
$(\sigma (a), \sigma (b))$
or
![]() $(\sigma (b), \sigma (c))$
for
$(\sigma (b), \sigma (c))$
for
![]() $(a,b,c)$
a
$(a,b,c)$
a
![]() $\sigma $
-triple such that the relevant boxes are in
$\sigma $
-triple such that the relevant boxes are in
![]() $\beta /\alpha $
. Moreover, every attacking pair occurs in this manner exactly once.
$\beta /\alpha $
. Moreover, every attacking pair occurs in this manner exactly once.
If all three boxes of a
![]() $\sigma $
-triple
$\sigma $
-triple
![]() $(a,b,c)$
are in
$(a,b,c)$
are in
![]() $\beta /\alpha $
, and T is a negative tableau on
$\beta /\alpha $
, and T is a negative tableau on
![]() $\sigma (\beta /\alpha )$
, then since
$\sigma (\beta /\alpha )$
, then since
![]() $T(\sigma (a))<T(\sigma (c))$
, at most one of the attacking pairs
$T(\sigma (a))<T(\sigma (c))$
, at most one of the attacking pairs
![]() $(\sigma (a), \sigma (b))$
,
$(\sigma (a), \sigma (b))$
,
![]() $(\sigma (b), \sigma (c))$
can be an attacking inversion in T. The condition that neither pair is an attacking inversion is that
$(\sigma (b), \sigma (c))$
can be an attacking inversion in T. The condition that neither pair is an attacking inversion is that
![]() $S(a)<S(b)<S(c)$
in the negative tableau
$S(a)<S(b)<S(c)$
in the negative tableau
![]() $S = \sigma ^{-1}(T) = T\circ \sigma $
on
$S = \sigma ^{-1}(T) = T\circ \sigma $
on
![]() $\beta /\alpha $
. This also holds for triples not contained in
$\beta /\alpha $
. This also holds for triples not contained in
![]() $\beta /\alpha $
with our convention that
$\beta /\alpha $
with our convention that
![]() $S(a) = -\infty $
or
$S(a) = -\infty $
or
![]() $S(c) = \infty $
for a or c outside the tuple
$S(c) = \infty $
for a or c outside the tuple
![]() $\beta /\alpha $
. Hence, the result follows.
$\beta /\alpha $
. Hence, the result follows.
Example 4.5.4. Let S be as in Figure 1 and

so T is a negative tableau on
![]() $\sigma (\beta /\alpha ) = (3,5,6)/(1,2,2)$
. Reading T by reading order on
$\sigma (\beta /\alpha ) = (3,5,6)/(1,2,2)$
. Reading T by reading order on
![]() $\sigma (\beta /\alpha )$
gives
$\sigma (\beta /\alpha )$
gives
![]() $1\, 3\, 4\, 2\, 7\, 4\, 9\, 6\, 7$
. The pairs
$1\, 3\, 4\, 2\, 7\, 4\, 9\, 6\, 7$
. The pairs
![]() $(T(a),T(b))$
for attacking inversions
$(T(a),T(b))$
for attacking inversions
![]() $(a,b)$
in T are
$(a,b)$
in T are
![]() $(3,2)$
,
$(3,2)$
,
![]() $(4,2)$
,
$(4,2)$
,
![]() $(7,4)$
and
$(7,4)$
and
![]() $(9,6)$
, so
$(9,6)$
, so
![]() $\operatorname {\mathrm {inv}}(T) = 4$
. From the last diagram in Figure 1, we have
$\operatorname {\mathrm {inv}}(T) = 4$
. From the last diagram in Figure 1, we have
![]() $h_{\sigma }(\beta /\alpha ) = 5$
,
$h_{\sigma }(\beta /\alpha ) = 5$
,
![]() $h_{\sigma }(S)= 1$
, so
$h_{\sigma }(S)= 1$
, so
![]() $h_{\sigma }(\beta /\alpha ) - \operatorname {\mathrm {inv}}(T) = h_{\sigma }(S)$
is indeed satisfied.
$h_{\sigma }(\beta /\alpha ) - \operatorname {\mathrm {inv}}(T) = h_{\sigma }(S)$
is indeed satisfied.
Now, let
![]() $\sigma = 1$
and
$\sigma = 1$
and
![]() $T = S \circ \sigma ^{-1} = S$
. Reading T by reading order on
$T = S \circ \sigma ^{-1} = S$
. Reading T by reading order on
![]() $\beta /\alpha $
gives
$\beta /\alpha $
gives
![]() $1\, 2\, 3\, 4\, 4\, 7\, 6\, 9\, 7$
. The pairs
$1\, 2\, 3\, 4\, 4\, 7\, 6\, 9\, 7$
. The pairs
![]() $(T(a),T(b))$
for the attacking inversions are
$(T(a),T(b))$
for the attacking inversions are
![]() $(4,4)$
,
$(4,4)$
,
![]() $(7,6)$
and
$(7,6)$
and
![]() $(9,7)$
, so
$(9,7)$
, so
![]() $\operatorname {\mathrm {inv}}(T)= 3$
; note that equal attacking entries
$\operatorname {\mathrm {inv}}(T)= 3$
; note that equal attacking entries
![]() $(4,4)$
count as an inversion in a negative tableau. From the second diagram in Figure 1, we see
$(4,4)$
count as an inversion in a negative tableau. From the second diagram in Figure 1, we see
![]() $h_{\sigma }(\beta /\alpha ) = 7$
,
$h_{\sigma }(\beta /\alpha ) = 7$
,
![]() $h_{\sigma }(S)= 4$
, so again
$h_{\sigma }(S)= 4$
, so again
![]() $h_{\sigma }(\beta /\alpha ) - \operatorname {\mathrm {inv}}(T) = h_{\sigma }(S)$
holds.
$h_{\sigma }(\beta /\alpha ) - \operatorname {\mathrm {inv}}(T) = h_{\sigma }(S)$
holds.
Remark 4.5.5. If we define an increasing σ-triple for T ∈SSYT(σ(β/α)) to be any σ-triple (a, b, c) satisfying T(a) ≤ T(b) ≤ T(c), then a similar argument gives the relation in (102) for ordinary semistandard tableaux as well, where again
![]() $S = \sigma ^{-1}(T) = T\circ \sigma $
.
$S = \sigma ^{-1}(T) = T\circ \sigma $
.
Remark 4.5.6. Given a tuple of rows
![]() $\beta /\alpha $
, if we shift the j-th row to the right by
$\beta /\alpha $
, if we shift the j-th row to the right by
![]() $\sigma (j)\, \epsilon $
for a small
$\sigma (j)\, \epsilon $
for a small
![]() $\epsilon>0$
, then
$\epsilon>0$
, then
![]() $h_{\sigma }(\beta /\alpha )$
is equal to the number of alignments between a box boundary in row j and the interior of a box in row i for
$h_{\sigma }(\beta /\alpha )$
is equal to the number of alignments between a box boundary in row j and the interior of a box in row i for
![]() $i<j$
, where a boundary is the edge common to two adjacent boxes which are either in or adjacent to the row. An empty row has one boundary.
$i<j$
, where a boundary is the edge common to two adjacent boxes which are either in or adjacent to the row. An empty row has one boundary.
The relation between
![]() ${\mathcal G}$
and
${\mathcal G}$
and
![]() ${\mathcal L}$
can now be made precise by applying Proposition 4.5.2 and Lemma 4.5.3 to the expression for
${\mathcal L}$
can now be made precise by applying Proposition 4.5.2 and Lemma 4.5.3 to the expression for
![]() $q^{h_{\sigma }(\beta /\alpha )} {\mathcal G} _{\sigma (\beta /\alpha )}(X;q^{-1})$
given in Corollary 4.1.4.
$q^{h_{\sigma }(\beta /\alpha )} {\mathcal G} _{\sigma (\beta /\alpha )}(X;q^{-1})$
given in Corollary 4.1.4.
Corollary 4.5.7. Given
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
and
$\alpha ,\beta \in {\mathbb Z} ^{l}$
and
![]() $\sigma \in S_{l}$
,
$\sigma \in S_{l}$
,
 $$ \begin{align} {\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)_{\operatorname{\mathrm{pol}} } = \begin{cases} q^{h_{\sigma }(\beta/\alpha )} {\mathcal G} _{\sigma (\beta /\alpha )}(x;q^{-1}) & \text{if } \alpha _{j}\leq \beta _{j} \text{ for all } j\\ 0 & \text{otherwise}, \end{cases} \end{align} $$
$$ \begin{align} {\mathcal L} ^{\sigma }_{\beta /\alpha }(x;q)_{\operatorname{\mathrm{pol}} } = \begin{cases} q^{h_{\sigma }(\beta/\alpha )} {\mathcal G} _{\sigma (\beta /\alpha )}(x;q^{-1}) & \text{if } \alpha _{j}\leq \beta _{j} \text{ for all } j\\ 0 & \text{otherwise}, \end{cases} \end{align} $$
where
![]() $h_{\sigma }(\beta /\alpha )$
is the number of
$h_{\sigma }(\beta /\alpha )$
is the number of
![]() $\sigma $
-triples in
$\sigma $
-triples in
![]() $\beta /\alpha $
, as in Lemma 4.5.3, and the right-hand side is evaluated in l variables
$\beta /\alpha $
, as in Lemma 4.5.3, and the right-hand side is evaluated in l variables
![]() $x_{1},\ldots , x_{l}$
.
$x_{1},\ldots , x_{l}$
.
5 The generalized shuffle theorem
5.1 Cauchy identity
In this section, we derive our main results, Theorems 5.3.1 and 5.5.1. The key point is the following delightful ‘Cauchy identity’ for nonsymmetric Hall–Littlewood polynomials.
Theorem 5.1.1. For any permutation
![]() $\sigma \in S_{l}$
, the twisted nonsymmetric Hall–Littlewood polynomials
$\sigma \in S_{l}$
, the twisted nonsymmetric Hall–Littlewood polynomials
![]() $E^{\sigma }_{\lambda }(x;q)$
and
$E^{\sigma }_{\lambda }(x;q)$
and
![]() $F^{\sigma }_{\lambda }(x;q)$
in (75, 76) satisfy the identity
$F^{\sigma }_{\lambda }(x;q)$
in (75, 76) satisfy the identity
 $$ \begin{align} \frac{\prod _{i<j} (1 - q\, t\, x_{i} \, y_{j})}{\prod _{i\leq j} (1 - t\, x_{i}\, y_{j})} = \sum _{{\mathbf a} \geq 0} t^{|{\mathbf a} |}\, E^{\sigma }_{{\mathbf a} }(x_{1},\ldots,x_{l};q^{-1}) \, F^{\sigma }_{{\mathbf a} }(y_{1},\ldots,y_{l};q), \end{align} $$
$$ \begin{align} \frac{\prod _{i<j} (1 - q\, t\, x_{i} \, y_{j})}{\prod _{i\leq j} (1 - t\, x_{i}\, y_{j})} = \sum _{{\mathbf a} \geq 0} t^{|{\mathbf a} |}\, E^{\sigma }_{{\mathbf a} }(x_{1},\ldots,x_{l};q^{-1}) \, F^{\sigma }_{{\mathbf a} }(y_{1},\ldots,y_{l};q), \end{align} $$
where the sum is over
![]() ${\mathbf a} = (a_{1},\ldots ,a_{l})$
with all
${\mathbf a} = (a_{1},\ldots ,a_{l})$
with all
![]() $a_{i}\geq 0$
and
$a_{i}\geq 0$
and
![]() $|{\mathbf a} | \overset {\text {{def}}}{=} a_{1}+\cdots +a_{l}$
.
$|{\mathbf a} | \overset {\text {{def}}}{=} a_{1}+\cdots +a_{l}$
.
Proof. Let
![]() $Z(x,y,q,t)$
denote the product on the left-hand side.
$Z(x,y,q,t)$
denote the product on the left-hand side.
From the definitions, we see that
![]() $E^{\sigma }_{{\mathbf a} }(x;q)$
and
$E^{\sigma }_{{\mathbf a} }(x;q)$
and
![]() $F^{\sigma }_{{\mathbf a} }(x;q)$
for
$F^{\sigma }_{{\mathbf a} }(x;q)$
for
![]() ${\mathbf a} \geq 0$
belong to the polynomial ring
${\mathbf a} \geq 0$
belong to the polynomial ring
![]() ${\mathbb Q} (q)[x] = {\mathbb Q} (q)[x_{1},\ldots ,x_{l}]$
. The
${\mathbb Q} (q)[x] = {\mathbb Q} (q)[x_{1},\ldots ,x_{l}]$
. The
![]() $E^{\sigma }_{{\mathbf a} }(x;q)$
form a graded basis of
$E^{\sigma }_{{\mathbf a} }(x;q)$
form a graded basis of
![]() ${\mathbb Q} (q)[x]$
since they are homogeneous and
${\mathbb Q} (q)[x]$
since they are homogeneous and
![]() $E^{\sigma }_{{\mathbf a} }(x;q)$
has leading term
$E^{\sigma }_{{\mathbf a} }(x;q)$
has leading term
![]() $x^{{\mathbf a} }$
. The
$x^{{\mathbf a} }$
. The
![]() $F^{\sigma }_{{\mathbf a} }(x;q)$
likewise form a graded basis of
$F^{\sigma }_{{\mathbf a} }(x;q)$
likewise form a graded basis of
![]() ${\mathbb Q} (q)[x]$
. We are to prove that the expansion of
${\mathbb Q} (q)[x]$
. We are to prove that the expansion of
![]() $Z(x,y,q,t)$
as a power series in t, with coefficients expressed in terms of the basis
$Z(x,y,q,t)$
as a power series in t, with coefficients expressed in terms of the basis
![]() $\{E^{\sigma }_{{\mathbf a} }(x;q^{-1}) F^{\sigma }_{{\mathbf b} }(y;q) \}$
of
$\{E^{\sigma }_{{\mathbf a} }(x;q^{-1}) F^{\sigma }_{{\mathbf b} }(y;q) \}$
of
![]() ${\mathbb Q} (q)[x,y]$
, is given by the formula on the right-hand side. Put another way, we are to show that the coefficient of
${\mathbb Q} (q)[x,y]$
, is given by the formula on the right-hand side. Put another way, we are to show that the coefficient of
![]() $F^{\sigma }_{{\mathbf a} }(y;q)$
in
$F^{\sigma }_{{\mathbf a} }(y;q)$
in
![]() $Z(x,y,q,t)$
is equal to
$Z(x,y,q,t)$
is equal to
![]() $t^{|{\mathbf a} |}E^{\sigma }_{{\mathbf a} }(x;q^{-1})$
or equivalently that the coefficient of
$t^{|{\mathbf a} |}E^{\sigma }_{{\mathbf a} }(x;q^{-1})$
or equivalently that the coefficient of
![]() $F^{\sigma }_{{\mathbf a} }(y^{-1};q^{-1})$
in
$F^{\sigma }_{{\mathbf a} }(y^{-1};q^{-1})$
in
![]() $Z(x,y^{-1},q^{-1},t)$
is equal to
$Z(x,y^{-1},q^{-1},t)$
is equal to
![]() $t^{|{\mathbf a} |}E^{\sigma }_{{\mathbf a} }(x;q)$
.
$t^{|{\mathbf a} |}E^{\sigma }_{{\mathbf a} }(x;q)$
.
Using Proposition 4.3.2, this will follow by taking
![]() $f(y) = E^{\sigma }_{{\mathbf a} }(y;q)$
in the identity
$f(y) = E^{\sigma }_{{\mathbf a} }(y;q)$
in the identity
 $$ \begin{align} f(t x) = \langle y^{0} \rangle\; f(y) \frac{\prod _{i<j}(1 - q^{-1} t\, x_{i}/y_{j})}{\prod _{i\leq j} (1 - t\, x_{i}/y_{j} )} \prod _{i<j} \frac{1 - y_{i}/y_{j}}{1 - q^{-1} y_{i}/y_{j}}, \end{align} $$
$$ \begin{align} f(t x) = \langle y^{0} \rangle\; f(y) \frac{\prod _{i<j}(1 - q^{-1} t\, x_{i}/y_{j})}{\prod _{i\leq j} (1 - t\, x_{i}/y_{j} )} \prod _{i<j} \frac{1 - y_{i}/y_{j}}{1 - q^{-1} y_{i}/y_{j}}, \end{align} $$
provided we prove that this identity is valid for all polynomials
![]() $f(y) = f(y_{1},\ldots ,y_{l})$
. Here, we mean that
$f(y) = f(y_{1},\ldots ,y_{l})$
. Here, we mean that
![]() $f(y)\in {\mathbb Q} (q)[y]$
is a true polynomial and not a Laurent polynomial. Note that the denominator factors in equation (105) should be understood as geometric series.
$f(y)\in {\mathbb Q} (q)[y]$
is a true polynomial and not a Laurent polynomial. Note that the denominator factors in equation (105) should be understood as geometric series.
The only factor in equation (105) that involves negative powers of
![]() $y_{1}$
is
$y_{1}$
is
![]() $1/(1-t\, x_{1}/y_{1})$
. All the rest is a power series as a function of
$1/(1-t\, x_{1}/y_{1})$
. All the rest is a power series as a function of
![]() $y_{1}$
. For any power series
$y_{1}$
. For any power series
![]() $g(y_{1})$
, we have
$g(y_{1})$
, we have
![]() $\langle y_{1}^{0} \rangle \, g(y_{1})/(1-t\, x_{1}/y_{1}) = g(t x_{1})$
. The factors other than
$\langle y_{1}^{0} \rangle \, g(y_{1})/(1-t\, x_{1}/y_{1}) = g(t x_{1})$
. The factors other than
![]() $1/(1- t\, x_{1}/y_{1})$
with index
$1/(1- t\, x_{1}/y_{1})$
with index
![]() $i=1$
in equation (105) cancel upon setting
$i=1$
in equation (105) cancel upon setting
![]() $y_{1} = tx_{1}$
. It follows that when we take the constant term in the variable
$y_{1} = tx_{1}$
. It follows that when we take the constant term in the variable
![]() $y_{1}$
, equation (105) reduces to the same identity in variables
$y_{1}$
, equation (105) reduces to the same identity in variables
![]() $y_{2},\ldots ,y_{l}$
. We can assume that the latter holds by induction.
$y_{2},\ldots ,y_{l}$
. We can assume that the latter holds by induction.
Example 5.1.2. The products
![]() $t^{|{\mathbf a}|}E^{\sigma }_{{\mathbf a}}(x;q^{-1}) F^{\sigma }_{{\mathbf a}}(y;q)$
for the pairs in Table 1 sum to the
$t^{|{\mathbf a}|}E^{\sigma }_{{\mathbf a}}(x;q^{-1}) F^{\sigma }_{{\mathbf a}}(y;q)$
for the pairs in Table 1 sum to the
![]() $t^{0}$
through
$t^{0}$
through
![]() $t^{2}$
terms in the expansion of
$t^{2}$
terms in the expansion of
Remark 5.1.3. Using the fact that our nonsymmetric Hall–Littlewood polynomials agree with those of Ion in [Reference Ion22], the
![]() $\sigma =1$
case of equation (104) can be derived from the Cauchy identity for nonsymmetric Macdonald polynomials of Mimachi and Noumi [Reference Mimachi and Noumi29]. We also note that equation (104) for
$\sigma =1$
case of equation (104) can be derived from the Cauchy identity for nonsymmetric Macdonald polynomials of Mimachi and Noumi [Reference Mimachi and Noumi29]. We also note that equation (104) for
![]() $\sigma =1$
specializes at
$\sigma =1$
specializes at
![]() $q = 0$
to the
$q = 0$
to the
![]() $\operatorname {\mathrm {GL}} _{l}$
case of the nonsymmetric Cauchy identities of Fu and Lascoux [Reference Fu and Lascoux9].
$\operatorname {\mathrm {GL}} _{l}$
case of the nonsymmetric Cauchy identities of Fu and Lascoux [Reference Fu and Lascoux9].
5.2 Winding permutations
We will apply Theorem 5.1.1 in cases for which the twisting permutation has a special form, allowing the Hall–Littlewood polynomial
![]() $F^{\sigma }_{{\mathbf a} }(y;q)$
to be written another way.
$F^{\sigma }_{{\mathbf a} }(y;q)$
to be written another way.
Definition 5.2.1. Let
![]() ${\boldsymbol \{} x {\boldsymbol \}} = x - \lfloor x \rfloor $
denote the fractional part of a real number x. Let
${\boldsymbol \{} x {\boldsymbol \}} = x - \lfloor x \rfloor $
denote the fractional part of a real number x. Let
![]() $c_{1},\ldots ,c_{l}$
be the sequence of fractional parts
$c_{1},\ldots ,c_{l}$
be the sequence of fractional parts
![]() $c_{i} = {\boldsymbol \{} a\, i+b {\boldsymbol \}}$
of an arithmetic progression, where a is assumed irrational, so the
$c_{i} = {\boldsymbol \{} a\, i+b {\boldsymbol \}}$
of an arithmetic progression, where a is assumed irrational, so the
![]() $c_{i}$
are distinct. Let
$c_{i}$
are distinct. Let
![]() $\sigma \in S_{l}$
be the permutation such that
$\sigma \in S_{l}$
be the permutation such that
![]() $\sigma (c_{1},\ldots ,c_{l})$
is increasing, that is,
$\sigma (c_{1},\ldots ,c_{l})$
is increasing, that is,
![]() $\sigma (1),\ldots ,\sigma (l)$
are in the same relative order as
$\sigma (1),\ldots ,\sigma (l)$
are in the same relative order as
![]() $c_{1},\ldots ,c_{l}$
.
$c_{1},\ldots ,c_{l}$
.
A permutation
![]() $\sigma $
of this form is a winding permutation. The descent indicator of
$\sigma $
of this form is a winding permutation. The descent indicator of
![]() $\sigma $
is the vector
$\sigma $
is the vector
![]() $(\eta _{1},\ldots ,\eta _{l-1})$
defined by
$(\eta _{1},\ldots ,\eta _{l-1})$
defined by
 $$ \begin{align} \eta _{i} = \begin{cases} 1& \text{if } \sigma (i)>\sigma (i+1),\\ 0& \text{if } \sigma (i)<\sigma (i+1). \end{cases} \end{align} $$
$$ \begin{align} \eta _{i} = \begin{cases} 1& \text{if } \sigma (i)>\sigma (i+1),\\ 0& \text{if } \sigma (i)<\sigma (i+1). \end{cases} \end{align} $$
The head and tail of the winding permutation
![]() $\sigma $
are the respective permutations
$\sigma $
are the respective permutations
![]() $\tau ,\, \theta \in S_{l-1}$
such that
$\tau ,\, \theta \in S_{l-1}$
such that
![]() $\tau (1),\ldots ,\tau (l-1)$
are in the same relative order as
$\tau (1),\ldots ,\tau (l-1)$
are in the same relative order as
![]() $\sigma (1),\ldots ,\sigma (l-1)$
, and
$\sigma (1),\ldots ,\sigma (l-1)$
, and
![]() $\theta (1),\ldots ,\theta (l-1)$
are in the same relative order as
$\theta (1),\ldots ,\theta (l-1)$
are in the same relative order as
![]() $\sigma (2),\ldots ,\sigma (l)$
.
$\sigma (2),\ldots ,\sigma (l)$
.
Adding an integer to a in the above definition doesn’t change the
![]() $c_{i}$
, so we can assume that
$c_{i}$
, so we can assume that
![]() $0<a<1$
. In that case, the descent indicator of
$0<a<1$
. In that case, the descent indicator of
![]() $\sigma $
is characterized by
$\sigma $
is characterized by
 $$ \begin{align} \begin{aligned} \eta _{i} = 1\quad \Leftrightarrow \quad c_{i}>c_{i+1}\quad \Leftrightarrow \quad & c_{i+1} = c_{i}+a-1,\\ \eta _{i} = 0\quad \Leftrightarrow \quad c_{i}<c_{i+1}\quad \Leftrightarrow\quad & c_{i+1} = c_{i}+a.\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \eta _{i} = 1\quad \Leftrightarrow \quad c_{i}>c_{i+1}\quad \Leftrightarrow \quad & c_{i+1} = c_{i}+a-1,\\ \eta _{i} = 0\quad \Leftrightarrow \quad c_{i}<c_{i+1}\quad \Leftrightarrow\quad & c_{i+1} = c_{i}+a.\\ \end{aligned} \end{align} $$
Proposition 5.2.2. Let
![]() $\sigma \in S_{l}$
be a winding permutation, with descent indicator
$\sigma \in S_{l}$
be a winding permutation, with descent indicator
![]() $\eta $
, and head and tail
$\eta $
, and head and tail
![]() $\tau ,\, \theta \in S_{l-1}$
. For every
$\tau ,\, \theta \in S_{l-1}$
. For every
![]() $\lambda \in {\mathbb Z} ^{l-1}$
, we have identities
$\lambda \in {\mathbb Z} ^{l-1}$
, we have identities
of Laurent polynomials in
![]() $x_{1},\ldots ,x_{l-1}$
.
$x_{1},\ldots ,x_{l-1}$
.
The proof uses the following lemma.
Lemma 5.2.3. With
![]() $\tau ,\theta $
and
$\tau ,\theta $
and
![]() $\eta $
as in Proposition 5.2.2, and for every
$\eta $
as in Proposition 5.2.2, and for every
![]() $w\in S_{l-1}$
, there is an identity of operators on
$w\in S_{l-1}$
, there is an identity of operators on
![]() ${\mathbf k}[x_{1}^{\pm 1},\ldots ,x_{l-1}^{\pm 1}]$
${\mathbf k}[x_{1}^{\pm 1},\ldots ,x_{l-1}^{\pm 1}]$
for some exponent e depending on w.
Proof. We prove equation (111) by induction on the length of w. The base case
![]() $w=1$
is trivial. Suppose now that
$w=1$
is trivial. Suppose now that
![]() $w = v s_{i}$
is a reduced factorization. We can write the left-hand side of equation (111) as
$w = v s_{i}$
is a reduced factorization. We can write the left-hand side of equation (111) as
where
 $$ \begin{align} \varepsilon _{1} = \begin{cases} +1 & \text{if } \tau vs_{i} < \tau v\\ -1& \text{if } \tau vs_{i}> \tau v \end{cases}\qquad \varepsilon _{2} = \begin{cases} +1 & \text{if } \theta vs_{i} > \theta v\\ -1& \text{if } \theta vs_{i} < \theta v \end{cases}. \end{align} $$
$$ \begin{align} \varepsilon _{1} = \begin{cases} +1 & \text{if } \tau vs_{i} < \tau v\\ -1& \text{if } \tau vs_{i}> \tau v \end{cases}\qquad \varepsilon _{2} = \begin{cases} +1 & \text{if } \theta vs_{i} > \theta v\\ -1& \text{if } \theta vs_{i} < \theta v \end{cases}. \end{align} $$
Assuming by induction that equation (111) holds for v and substituting this into equation (112), we are left to show that
for some exponent e. We now consider the possible values for
![]() $\langle \alpha _{i}^{\vee }, -v^{-1}(\eta ) \rangle $
, which is equal to
$\langle \alpha _{i}^{\vee }, -v^{-1}(\eta ) \rangle $
, which is equal to
![]() $\eta _{k}-\eta _{j}$
, where
$\eta _{k}-\eta _{j}$
, where
![]() $v(i) = j$
,
$v(i) = j$
,
![]() $v(i+1) = k$
.
$v(i+1) = k$
.
Case 1: If
![]() $\eta _{j} = \eta _{k}$
, we see from equation (108) that
$\eta _{j} = \eta _{k}$
, we see from equation (108) that
![]() $c_{j+1}-c_{j} = c_{k+1}-c_{k}$
, hence
$c_{j+1}-c_{j} = c_{k+1}-c_{k}$
, hence
![]() $c_{j+1} < c_{k+1}\Leftrightarrow c_{j} < c_{k}$
. This implies that
$c_{j+1} < c_{k+1}\Leftrightarrow c_{j} < c_{k}$
. This implies that
![]() $\sigma (j+1)<\sigma (k+1) \Leftrightarrow \sigma (j)<\sigma (k)$
and therefore that
$\sigma (j+1)<\sigma (k+1) \Leftrightarrow \sigma (j)<\sigma (k)$
and therefore that
![]() $\tau v(i) < \tau v(i+1) \Leftrightarrow \theta v(i) < \theta v(i+1)$
. Hence, in this case we have
$\tau v(i) < \tau v(i+1) \Leftrightarrow \theta v(i) < \theta v(i+1)$
. Hence, in this case we have
![]() $\varepsilon _{1} = -\varepsilon _{2}$
.
$\varepsilon _{1} = -\varepsilon _{2}$
.
Case 2: If
![]() $\eta _{j} = 1$
and
$\eta _{j} = 1$
and
![]() $\eta _{k} = 0$
, then from equation (108) we get
$\eta _{k} = 0$
, then from equation (108) we get
![]() $c_{j+1} = c_{j}+a-1$
and
$c_{j+1} = c_{j}+a-1$
and
![]() $c_{k+1} = c_{k}+a$
. Then
$c_{k+1} = c_{k}+a$
. Then
![]() $c_{k+1}-c_{j+1} = c_{k}-c_{j}+1$
. Since
$c_{k+1}-c_{j+1} = c_{k}-c_{j}+1$
. Since
![]() $c_{k+1}-c_{j+1}$
and
$c_{k+1}-c_{j+1}$
and
![]() $c_{k}-c_{j}$
both have absolute value less than
$c_{k}-c_{j}$
both have absolute value less than
![]() $1$
, this implies
$1$
, this implies
![]() $c_{k} < c_{j}$
and
$c_{k} < c_{j}$
and
![]() $c_{k+1}> c_{j+1}$
. It follows in the same way as in Case 1 that
$c_{k+1}> c_{j+1}$
. It follows in the same way as in Case 1 that
![]() $\tau v(i)> \tau v(i+1)$
and
$\tau v(i)> \tau v(i+1)$
and
![]() $\theta v(i) < \theta v(i+1)$
. Hence, in this case we have
$\theta v(i) < \theta v(i+1)$
. Hence, in this case we have
![]() $\varepsilon _{1} = \varepsilon _{2} = 1$
.
$\varepsilon _{1} = \varepsilon _{2} = 1$
.
Case 3: If
![]() $\eta _{j} = 0$
and
$\eta _{j} = 0$
and
![]() $\eta _{k} = 1$
, we reason as in Case 2, but with j and k exchanged, to conclude that in this case we have
$\eta _{k} = 1$
, we reason as in Case 2, but with j and k exchanged, to conclude that in this case we have
![]() $\varepsilon _{1} = \varepsilon _{2} = -1$
.
$\varepsilon _{1} = \varepsilon _{2} = -1$
.
In each case, equation (114) now follows from the well-known affine Hecke algebra identities
 $$ \begin{align} \begin{aligned} T_{i}^{-1}\, x^{\mu }\, T_{i}^{} = T_{i}\, x^{\mu }\, T_{i}^{-1} = x^{\mu } = x^{s_{i}\mu } & \qquad \text{if } \langle \alpha _{i}^{\vee }, \mu \rangle = 0,\\ T_{i}\, x^{\mu }\, T_{i} = q\, x^{s_{i}\mu } & \qquad \text{if } \langle \alpha _{i}^{\vee }, \mu \rangle = -1,\\ T_{i}^{-1}\, x^{\mu }\, T_{i}^{-1} = q^{-1} x^{s_{i}\mu } & \qquad \text{if } \langle \alpha _{i}^{\vee }, \mu \rangle = 1, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} T_{i}^{-1}\, x^{\mu }\, T_{i}^{} = T_{i}\, x^{\mu }\, T_{i}^{-1} = x^{\mu } = x^{s_{i}\mu } & \qquad \text{if } \langle \alpha _{i}^{\vee }, \mu \rangle = 0,\\ T_{i}\, x^{\mu }\, T_{i} = q\, x^{s_{i}\mu } & \qquad \text{if } \langle \alpha _{i}^{\vee }, \mu \rangle = -1,\\ T_{i}^{-1}\, x^{\mu }\, T_{i}^{-1} = q^{-1} x^{s_{i}\mu } & \qquad \text{if } \langle \alpha _{i}^{\vee }, \mu \rangle = 1, \end{aligned} \end{align} $$
which can be verified directly from the definition of
![]() $T_{i}$
.
$T_{i}$
.
Proof of Proposition 5.2.2.
Let
![]() $w_{0}\in S_{l}$
and
$w_{0}\in S_{l}$
and
![]() $w_{0}'\in S_{l-1}$
be the longest permutations. Then
$w_{0}'\in S_{l-1}$
be the longest permutations. Then
![]() $w_{0}'\tau $
,
$w_{0}'\tau $
,
![]() $w_{0}'\theta $
are the head and tail of the winding permutation
$w_{0}'\theta $
are the head and tail of the winding permutation
![]() $w_{0}\sigma $
, and the descent indicator of
$w_{0}\sigma $
, and the descent indicator of
![]() $w_{0}\sigma $
is
$w_{0}\sigma $
is
![]() $\eta ^{\prime }_{i} = 1-\eta _{i}$
. Using these facts and the definition (76) of the F’s in terms of the E’s, one can check that equation (109) implies equation (110).
$\eta ^{\prime }_{i} = 1-\eta _{i}$
. Using these facts and the definition (76) of the F’s in terms of the E’s, one can check that equation (109) implies equation (110).
To prove equation (109), we begin by observing that for any given
![]() $\lambda $
there exists
$\lambda $
there exists
![]() $w\in S_{l}$
such that both
$w\in S_{l}$
such that both
![]() $w^{-1}(\lambda )$
and
$w^{-1}(\lambda )$
and
![]() $w^{-1}(\lambda -\eta )$
are dominant. To see this, first choose any v such that
$w^{-1}(\lambda -\eta )$
are dominant. To see this, first choose any v such that
![]() $v(\lambda )=\lambda _{+}$
is dominant. Since
$v(\lambda )=\lambda _{+}$
is dominant. Since
![]() $\eta $
is
$\eta $
is
![]() $\{0,1 \}$
-valued, the weight
$\{0,1 \}$
-valued, the weight
![]() $\mu =v(\lambda -\eta ) = \lambda _{+}-v(\eta )$
has the property that, for all
$\mu =v(\lambda -\eta ) = \lambda _{+}-v(\eta )$
has the property that, for all
![]() $i<j$
, if
$i<j$
, if
![]() $\mu _{i}<\mu _{j}$
then
$\mu _{i}<\mu _{j}$
then
![]() $(\lambda _{+})_{i} = (\lambda _{+})_{j}$
. Hence, there is a permutation u that fixes
$(\lambda _{+})_{i} = (\lambda _{+})_{j}$
. Hence, there is a permutation u that fixes
![]() $\lambda _{+}$
and sorts
$\lambda _{+}$
and sorts
![]() $\mu $
into weakly decreasing order, so
$\mu $
into weakly decreasing order, so
![]() $u(\mu ) = uv(\lambda -\eta )$
is dominant. Since
$u(\mu ) = uv(\lambda -\eta )$
is dominant. Since
![]() $uv(\lambda ) = \lambda _{+}$
is also dominant,
$uv(\lambda ) = \lambda _{+}$
is also dominant,
![]() $w^{-1} = uv$
works.
$w^{-1} = uv$
works.
Now, Lemma 5.2.3 implies
where
![]() $\sim $
signifies that the expressions are equal up to a q power factor. Equivalently,
$\sim $
signifies that the expressions are equal up to a q power factor. Equivalently,
Writing out the definitions of
![]() $E^{\theta ^{-1}}_{\lambda }$
and
$E^{\theta ^{-1}}_{\lambda }$
and
![]() $E^{\tau ^{-1}}_{\lambda - \eta }$
, while ignoring q power factors, and using the fact that
$E^{\tau ^{-1}}_{\lambda - \eta }$
, while ignoring q power factors, and using the fact that
![]() $\lambda _{+} = w^{-1}(\lambda )$
and
$\lambda _{+} = w^{-1}(\lambda )$
and
![]() $(\lambda -\eta )_{+} = w^{-1}(\lambda -\eta )$
for this w, equation (117) implies that equation (109) holds up to a scalar factor
$(\lambda -\eta )_{+} = w^{-1}(\lambda -\eta )$
for this w, equation (117) implies that equation (109) holds up to a scalar factor
![]() $q^{e}$
. But we know that the
$q^{e}$
. But we know that the
![]() $x^{\lambda }$
term on each side has coefficient 1, so equation (109) holds exactly.
$x^{\lambda }$
term on each side has coefficient 1, so equation (109) holds exactly.
5.3 Stable shuffle theorem
We now prove an identity of formal power series with coefficients in
![]() $\operatorname {\mathrm {GL}} _{l}$
characters, that is, symmetric Laurent polynomials in variables
$\operatorname {\mathrm {GL}} _{l}$
characters, that is, symmetric Laurent polynomials in variables
![]() $x_{1},\ldots ,x_{l}$
. When truncated to the polynomial part, this identity will reduce to our shuffle theorem for paths under a line (Theorem 5.5.1).
$x_{1},\ldots ,x_{l}$
. When truncated to the polynomial part, this identity will reduce to our shuffle theorem for paths under a line (Theorem 5.5.1).
Theorem 5.3.1. Let
![]() $p ,s$
be real numbers with p positive and irrational. For
$p ,s$
be real numbers with p positive and irrational. For
![]() $i = 1,\ldots ,l$
, let
$i = 1,\ldots ,l$
, let
Let
![]() $c_{i} = {\boldsymbol \{} s-p(i-1) {\boldsymbol \}}$
, and let
$c_{i} = {\boldsymbol \{} s-p(i-1) {\boldsymbol \}}$
, and let
![]() $\sigma \in S_{l}$
be the permutation such that
$\sigma \in S_{l}$
be the permutation such that
![]() $\sigma (1),\ldots ,\sigma (l)$
are in the same relative order as
$\sigma (1),\ldots ,\sigma (l)$
are in the same relative order as
![]() $c_{l},\ldots ,c_{1}$
, that is,
$c_{l},\ldots ,c_{1}$
, that is,
![]() $\sigma (c_{l},\ldots ,c_{1})$
is increasing. For any nonnegative integers
$\sigma (c_{l},\ldots ,c_{1})$
is increasing. For any nonnegative integers
![]() $u,v$
, we have the identity of formal power series in t
$u,v$
, we have the identity of formal power series in t
where
![]() ${\mathcal H} _{{\mathbf b} }$
is given by Definition 3.7.1.
${\mathcal H} _{{\mathbf b} }$
is given by Definition 3.7.1.
Remark 5.3.2. If
![]() $\delta $
is the highest south-east lattice path weakly below the line
$\delta $
is the highest south-east lattice path weakly below the line
![]() $y+px = s$
, starting at
$y+px = s$
, starting at
![]() $(0,\lfloor s \rfloor )$
and extending forever (not stopping at the x axis), then
$(0,\lfloor s \rfloor )$
and extending forever (not stopping at the x axis), then
![]() $b_{i}$
is the number of south steps in
$b_{i}$
is the number of south steps in
![]() $\delta $
along the line
$\delta $
along the line
![]() $x = i-1$
, and
$x = i-1$
, and
![]() $c_{i}$
is the gap along
$c_{i}$
is the gap along
![]() $x=i-1$
between the given line and the highest point of
$x=i-1$
between the given line and the highest point of
![]() $\delta $
beneath it.
$\delta $
beneath it.
Proof of Theorem 5.3.1.
We will prove that for
![]() ${\mathbf b} $
,
${\mathbf b} $
,
![]() $\sigma $
as in the hypothesis of the theorem, we have the stronger ‘unstraightened’ identity
$\sigma $
as in the hypothesis of the theorem, we have the stronger ‘unstraightened’ identity
 $$ \begin{align} x_{1}^{u}x_{l}^{-v}x^{{\mathbf b} }&\frac{\prod _{i+1<j}(1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j}(1 - t\, x_{i}/x_{j})}\notag\\ &\qquad= \sum _{a_{1},\ldots,a_{l-1}\geq 0} t^{|{\mathbf a} |} w_{0} \bigl(F^{\sigma ^{-1} }_{(b_{l},\ldots,b_{1})+(-v,a_{l-1},\ldots,a_{1})}(x;q) \overline{E^{\sigma ^{-1}}_{(a_{l-1},\ldots,a_{1},-u)}(x;q)} \bigr). \end{align} $$
$$ \begin{align} x_{1}^{u}x_{l}^{-v}x^{{\mathbf b} }&\frac{\prod _{i+1<j}(1 - q\, t\, x_{i}/x_{j})}{\prod _{i<j}(1 - t\, x_{i}/x_{j})}\notag\\ &\qquad= \sum _{a_{1},\ldots,a_{l-1}\geq 0} t^{|{\mathbf a} |} w_{0} \bigl(F^{\sigma ^{-1} }_{(b_{l},\ldots,b_{1})+(-v,a_{l-1},\ldots,a_{1})}(x;q) \overline{E^{\sigma ^{-1}}_{(a_{l-1},\ldots,a_{1},-u)}(x;q)} \bigr). \end{align} $$
By Proposition 4.4.2, applying the Hall–Littlewood raising operator
![]() ${\mathbf H} _{q}$
to both sides of equation (119) yields equation (118).
${\mathbf H} _{q}$
to both sides of equation (119) yields equation (118).
By construction, the
![]() $b_{i}$
take only values
$b_{i}$
take only values
![]() $\lfloor p \rfloor $
or
$\lfloor p \rfloor $
or
![]() $\lceil p \rceil $
, and since
$\lceil p \rceil $
, and since
![]() $b_{i}+c_{i} - c_{i+1}= p$
, we have
$b_{i}+c_{i} - c_{i+1}= p$
, we have
In particular,
![]() $b_{l}\leq b_{l-1}+1$
, hence
$b_{l}\leq b_{l-1}+1$
, hence
![]() $b_{l}-v\leq b_{l-1}+a_{l-1}+1$
, and if equality holds, then
$b_{l}-v\leq b_{l-1}+a_{l-1}+1$
, and if equality holds, then
![]() $b_{l-1} = \lfloor p \rfloor $
, so
$b_{l-1} = \lfloor p \rfloor $
, so
![]() $\sigma (1)<\sigma (2)$
. Using Lemma 4.3.4 and recalling that the definition (76) of
$\sigma (1)<\sigma (2)$
. Using Lemma 4.3.4 and recalling that the definition (76) of
![]() $F^{\sigma }_{\lambda }(x;q)$
is
$F^{\sigma }_{\lambda }(x;q)$
is
![]() $ \overline {E^{\sigma w_{0}}_{-\lambda }(x;q)}$
, we have
$ \overline {E^{\sigma w_{0}}_{-\lambda }(x;q)}$
, we have
where
![]() $\tau $
,
$\tau $
,
![]() $\theta $
are the head and tail of
$\theta $
are the head and tail of
![]() $\sigma $
, as in Proposition 5.2.2. Note that
$\sigma $
, as in Proposition 5.2.2. Note that
![]() $\sigma $
is a winding permutation. From equation (120), we also see that
$\sigma $
is a winding permutation. From equation (120), we also see that
![]() $(b_{l-1},\ldots ,b_{1}) = \eta + \lfloor p \rfloor \cdot (1,\ldots ,1)$
, where
$(b_{l-1},\ldots ,b_{1}) = \eta + \lfloor p \rfloor \cdot (1,\ldots ,1)$
, where
![]() $\eta $
is the descent indicator of
$\eta $
is the descent indicator of
![]() $\sigma $
. Adding a constant vector
$\sigma $
. Adding a constant vector
![]() $k\cdot (1,\ldots ,1)$
to the index
$k\cdot (1,\ldots ,1)$
to the index
![]() $\lambda $
multiplies any
$\lambda $
multiplies any
![]() $F^{\pi }_{\lambda }(x;q)$
by
$F^{\pi }_{\lambda }(x;q)$
by
![]() $(\prod _{i}x_{i})^{k}$
. Using this and Proposition 5.2.2, we can replace equation (122) with
$(\prod _{i}x_{i})^{k}$
. Using this and Proposition 5.2.2, we can replace equation (122) with
Using the Cauchy identity (104) from Theorem 5.1.1 in
![]() $l-1$
variables, with twisting permutation
$l-1$
variables, with twisting permutation
![]() $\tau ^{-1}$
and substituting
$\tau ^{-1}$
and substituting
![]() $x_{i}^{-1}$
for
$x_{i}^{-1}$
for
![]() $x_{i}$
, we obtain
$x_{i}$
, we obtain
 $$ \begin{align} \frac{\prod _{i<j} (1 - q\, t\, y_{j}/x_{i})}{\prod _{i\leq j} (1 - t\, y_{j}/x_{i})} = \sum _{{\mathbf a} \geq 0} t^{|{\mathbf a} |}\, F^{\tau ^{-1}}_{{\mathbf a} }(y_{1},\ldots,y_{l-1};q)\overline{E^{\tau ^{-1}}_{{\mathbf a} }(x_{1},\ldots,x_{l-1};q)}. \end{align} $$
$$ \begin{align} \frac{\prod _{i<j} (1 - q\, t\, y_{j}/x_{i})}{\prod _{i\leq j} (1 - t\, y_{j}/x_{i})} = \sum _{{\mathbf a} \geq 0} t^{|{\mathbf a} |}\, F^{\tau ^{-1}}_{{\mathbf a} }(y_{1},\ldots,y_{l-1};q)\overline{E^{\tau ^{-1}}_{{\mathbf a} }(x_{1},\ldots,x_{l-1};q)}. \end{align} $$
Setting
![]() $y_{i} = x_{i+1}$
in equation (124) and multiplying both sides by
$y_{i} = x_{i+1}$
in equation (124) and multiplying both sides by
![]() $w_{0}(x_{1}^{u}x_{l}^{-v}x^{{\mathbf b} })$
, then using equations (121) and (123), and finally applying
$w_{0}(x_{1}^{u}x_{l}^{-v}x^{{\mathbf b} })$
, then using equations (121) and (123), and finally applying
![]() $w_{0}$
to both sides, yields equation (119).
$w_{0}$
to both sides, yields equation (119).
5.4 LLT data and the
 $\operatorname {\mathrm {dinv}} $
statistic
$\operatorname {\mathrm {dinv}} $
statistic
Our next goal is to deduce the combinatorial version of our shuffle theorem—that is, the identity (1) previewed in the introduction and restated as equation (133), below—from Theorem 5.3.1. To do this, we first need to define the data that will serve to attach LLT polynomials to lattice paths and relate these to the combinatorial statistic
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
.
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
.
We will be concerned with lattice paths
![]() $\lambda $
lying weakly below the line segment
$\lambda $
lying weakly below the line segment
between arbitrary points
![]() $(0,s)$
and
$(0,s)$
and
![]() $(r,0)$
on the positive y and x axes.
$(r,0)$
on the positive y and x axes.
We always assume that the slope
![]() $-p$
of the line is irrational. Clearly, it is possible to perturb any line slightly so as make its slope irrational, without changing the set of lattice points, and therefore also the set of lattice paths, that lie below the line. All dependence on p in the combinatorial constructions to follow comes from comparisons between p and various rational numbers. By taking p to be irrational, we avoid the need to resolve ambiguities that would result from equality occurring in the comparisons.
$-p$
of the line is irrational. Clearly, it is possible to perturb any line slightly so as make its slope irrational, without changing the set of lattice points, and therefore also the set of lattice paths, that lie below the line. All dependence on p in the combinatorial constructions to follow comes from comparisons between p and various rational numbers. By taking p to be irrational, we avoid the need to resolve ambiguities that would result from equality occurring in the comparisons.
Definition 5.4.1. Let
![]() $\lambda $
be a south-east lattice path in the first quadrant with endpoints on the axes. Let Y be the Young diagram enclosed by the positive axes and
$\lambda $
be a south-east lattice path in the first quadrant with endpoints on the axes. Let Y be the Young diagram enclosed by the positive axes and
![]() $\lambda $
. The arm and leg of a box
$\lambda $
. The arm and leg of a box
![]() $y\in Y$
are, as usual, the number of boxes in Y strictly east of y and strictly north of y, respectively. Given a positive irrational number p, we define
$y\in Y$
are, as usual, the number of boxes in Y strictly east of y and strictly north of y, respectively. Given a positive irrational number p, we define
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
to be the number of boxes in Y whose arm a and leg
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
to be the number of boxes in Y whose arm a and leg
![]() $\ell $
satisfy
$\ell $
satisfy
where we interpret
![]() $(\ell +1)/a$
as
$(\ell +1)/a$
as
![]() $+\infty $
if
$+\infty $
if
![]() $a = 0$
.
$a = 0$
.
Geometrically, condition (126) means that some line of slope
![]() $-p$
crosses both the east step in
$-p$
crosses both the east step in
![]() $\lambda $
at the top of the leg and the south step at the end of the arm, as shown in Figure 2. Since p is irrational, such a line can always be assumed to pass through the interiors of the two steps.
$\lambda $
at the top of the leg and the south step at the end of the arm, as shown in Figure 2. Since p is irrational, such a line can always be assumed to pass through the interiors of the two steps.
To each lattice path weakly below the line (125), we now attach a tuple of one-row skew shapes
![]() $\beta /\alpha $
and a permutation
$\beta /\alpha $
and a permutation
![]() $\sigma $
. The index
$\sigma $
. The index
![]() $\nu (\lambda )$
of the LLT polynomial in equations (1) and (133) will be defined in terms of these data.
$\nu (\lambda )$
of the LLT polynomial in equations (1) and (133) will be defined in terms of these data.
Definition 5.4.2. Let
![]() $\lambda $
be a south-east lattice path from
$\lambda $
be a south-east lattice path from
![]() $(0,\lfloor s \rfloor )$
to
$(0,\lfloor s \rfloor )$
to
![]() $(\lfloor r \rfloor ,0)$
which is weakly below the line
$(\lfloor r \rfloor ,0)$
which is weakly below the line
![]() $y+p\, x = s$
in equation (125), where
$y+p\, x = s$
in equation (125), where
![]() $p = s/r$
is irrational, and let
$p = s/r$
is irrational, and let
![]() $l=\lfloor r \rfloor +1$
. For
$l=\lfloor r \rfloor +1$
. For
![]() $i = 1,\ldots ,l$
, let
$i = 1,\ldots ,l$
, let
be the y coordinate of the highest lattice point weakly below the given line at
![]() $x=i-1$
. Let
$x=i-1$
. Let
be the vectors of integers
![]() $0\leq \alpha _{i}\leq \beta _{i}$
, written in reverse order, such that the south steps in
$0\leq \alpha _{i}\leq \beta _{i}$
, written in reverse order, such that the south steps in
![]() $\lambda $
on the line
$\lambda $
on the line
![]() $x = i-1$
go from
$x = i-1$
go from
![]() $y = d_{i}-\alpha _{i}$
to
$y = d_{i}-\alpha _{i}$
to
![]() $y = d_{i}-\beta _{i}$
. Let
$y = d_{i}-\beta _{i}$
. Let
be the gap between the given line and the highest lattice point weakly below it along the line
![]() $x = i-1$
. Let
$x = i-1$
. Let
![]() $\sigma \in S_{l}$
be the permutation with
$\sigma \in S_{l}$
be the permutation with
![]() $\sigma (1),\ldots ,\sigma (l)$
in the same relative order as
$\sigma (1),\ldots ,\sigma (l)$
in the same relative order as
![]() $c_{l},\ldots ,c_{1}$
, that is, such that
$c_{l},\ldots ,c_{1}$
, that is, such that
![]() $\sigma (c_{l},\ldots ,c_{1})$
is increasing. The vectors
$\sigma (c_{l},\ldots ,c_{1})$
is increasing. The vectors
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and the permutation
$\beta $
and the permutation
![]() $\sigma $
are the LLT data associated with
$\sigma $
are the LLT data associated with
![]() $\lambda $
and the given line.
$\lambda $
and the given line.
Example 5.4.3. The first diagram in Figure 3 shows a line
![]() $y + px = s$
with
$y + px = s$
with
![]() $p\approx 1.36$
,
$p\approx 1.36$
,
![]() $s\approx 9.27$
, and a path
$s\approx 9.27$
, and a path
![]() $\lambda $
below it from
$\lambda $
below it from
![]() $(0,\lfloor s \rfloor ) = (0,9)$
to
$(0,\lfloor s \rfloor ) = (0,9)$
to
![]() $(l-1,0) = (6,0)$
with
$(l-1,0) = (6,0)$
with
![]() $l = 7$
.
$l = 7$
.

Figure 3 (i) A path
![]() $\lambda $
under
$\lambda $
under
![]() $y+px=s$
with
$y+px=s$
with
![]() $p\approx 1.36$
,
$p\approx 1.36$
,
![]() $s\approx 9.27$
,
$s\approx 9.27$
,
![]() $l=7$
. (ii) Transformed path
$l=7$
. (ii) Transformed path
![]() $\lambda '$
under
$\lambda '$
under
![]() $y = s$
, with gaps
$y = s$
, with gaps
![]() $c_{i}$
marked. (iii) Bottom to top: tuple of rows
$c_{i}$
marked. (iii) Bottom to top: tuple of rows
![]() $(\beta _{7},\ldots ,\beta _{1}) /(\alpha _{7},\ldots ,\alpha _{1}) $
offset by
$(\beta _{7},\ldots ,\beta _{1}) /(\alpha _{7},\ldots ,\alpha _{1}) $
offset by
![]() $(c_{7},\ldots ,c_{1})$
.
$(c_{7},\ldots ,c_{1})$
.
In this example, the y coordinates of the highest lattice points below the line at
![]() $x = 0,\ldots ,6$
are
$x = 0,\ldots ,6$
are
![]() $(d_{1},\ldots ,d_{7}) = (9,7,6,5,3,2,1)$
. The runs of south steps in
$(d_{1},\ldots ,d_{7}) = (9,7,6,5,3,2,1)$
. The runs of south steps in
![]() $\lambda $
go from y coordinates
$\lambda $
go from y coordinates
![]() $(9,6,6,3,1,1,0)$
to
$(9,6,6,3,1,1,0)$
to
![]() $(6,6,3,1,1,0,0)$
. Subtracting these from the
$(6,6,3,1,1,0,0)$
. Subtracting these from the
![]() $d_{i}$
and listing them in reverse order gives
$d_{i}$
and listing them in reverse order gives
The gaps, in reverse order, are
![]() $(c_{7},\ldots ,c_{1})\approx (.11, .47, .83, .19, .55, .91, .27)$
, giving
$(c_{7},\ldots ,c_{1})\approx (.11, .47, .83, .19, .55, .91, .27)$
, giving
Proposition 5.4.4. Given the line (125) and a lattice path
![]() $\lambda $
weakly below it satisfying the conditions in Definition 5.4.2, let
$\lambda $
weakly below it satisfying the conditions in Definition 5.4.2, let
![]() $\alpha ,\beta , \sigma $
be the associated LLT data. Then
$\alpha ,\beta , \sigma $
be the associated LLT data. Then
where
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
is given by Definition 5.4.1 and
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
is given by Definition 5.4.1 and
![]() $h_{\sigma }(\beta /\alpha )$
is as in Corollary 4.5.7.
$h_{\sigma }(\beta /\alpha )$
is as in Corollary 4.5.7.
Proof. Let
![]() $\lambda '$
be the image of
$\lambda '$
be the image of
![]() $\lambda $
under the transformation in the plane that sends
$\lambda $
under the transformation in the plane that sends
![]() $(x,y)$
to
$(x,y)$
to
![]() $(x,y+px)$
. Then
$(x,y+px)$
. Then
![]() $\lambda '$
is a path composed of unit south steps and sloped steps
$\lambda '$
is a path composed of unit south steps and sloped steps
![]() $(1,p)$
(transforms of east steps), which starts at
$(1,p)$
(transforms of east steps), which starts at
![]() $(0,\lfloor s \rfloor $
) and stays weakly below the horizontal line
$(0,\lfloor s \rfloor $
) and stays weakly below the horizontal line
![]() $y = s$
(transform of the line
$y = s$
(transform of the line
![]() $y+p\, x=s$
).
$y+p\, x=s$
).
The south steps in
![]() $\lambda '$
on the line
$\lambda '$
on the line
![]() $x = i-1$
run from
$x = i-1$
run from
![]() $y = s - (c_{i} + \alpha _{i})$
to
$y = s - (c_{i} + \alpha _{i})$
to
![]() $y = s - (c_{i} + \beta _{i})$
. This means that, if we offset the i-th row
$y = s - (c_{i} + \beta _{i})$
. This means that, if we offset the i-th row
![]() $(\beta _{l+1-i})/(\alpha _{l+1-i})$
in the tuple of one-row skew diagrams
$(\beta _{l+1-i})/(\alpha _{l+1-i})$
in the tuple of one-row skew diagrams
![]() $\beta /\alpha $
by
$\beta /\alpha $
by
![]() $c_{l+1-i}$
, then the x coordinate on each box of
$c_{l+1-i}$
, then the x coordinate on each box of
![]() $\beta /\alpha $
covers the same unit interval as does the distance below the line
$\beta /\alpha $
covers the same unit interval as does the distance below the line
![]() $y=s$
on the south step in
$y=s$
on the south step in
![]() $\lambda '$
corresponding to that box. See Figure 3 for an example.
$\lambda '$
corresponding to that box. See Figure 3 for an example.
Since
![]() $0<c_{i}<1$
and the numbers
$0<c_{i}<1$
and the numbers
![]() $c_{l},\ldots ,c_{1}$
are in the same relative order as
$c_{l},\ldots ,c_{1}$
are in the same relative order as
![]() $\sigma (1),\ldots ,\sigma (l)$
, the description of
$\sigma (1),\ldots ,\sigma (l)$
, the description of
![]() $h_{\sigma }(\beta /\alpha )$
in Remark 4.5.6 still applies if we offset row i by
$h_{\sigma }(\beta /\alpha )$
in Remark 4.5.6 still applies if we offset row i by
![]() $c_{l+1-i}$
instead of
$c_{l+1-i}$
instead of
![]() $\sigma (i) \epsilon $
. Mapping this onto
$\sigma (i) \epsilon $
. Mapping this onto
![]() $\lambda '$
, we see that
$\lambda '$
, we see that
![]() $h_{\sigma }(\beta /\alpha )$
is the number of horizontal alignments between any endpoint of a step in
$h_{\sigma }(\beta /\alpha )$
is the number of horizontal alignments between any endpoint of a step in
![]() $\lambda '$
and the interior of a south step occurring later in
$\lambda '$
and the interior of a south step occurring later in
![]() $\lambda '$
. To put this another way, for each south step S in
$\lambda '$
. To put this another way, for each south step S in
![]() $\lambda '$
, let
$\lambda '$
, let
![]() $B_{S}$
denote the interior of the horizontal band of height 1 to the left of S in the plane. Then
$B_{S}$
denote the interior of the horizontal band of height 1 to the left of S in the plane. Then
![]() $h_{\sigma }(\beta /\alpha )$
is the number of pairs consisting of a south step S and a point
$h_{\sigma }(\beta /\alpha )$
is the number of pairs consisting of a south step S and a point
![]() $P\in B_{S}$
which is an endpoint of a step in
$P\in B_{S}$
which is an endpoint of a step in
![]() $\lambda '$
.
$\lambda '$
.
For comparison,
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
is the number of pairs consisting of a south step S in
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
is the number of pairs consisting of a south step S in
![]() $\lambda '$
and a sloped step which meets
$\lambda '$
and a sloped step which meets
![]() $B_{S}$
. To complete the proof it suffices to show that each band
$B_{S}$
. To complete the proof it suffices to show that each band
![]() $B_{S}$
contains the same number of step endpoints P as the number of sloped steps that meet
$B_{S}$
contains the same number of step endpoints P as the number of sloped steps that meet
![]() $B_{S}$
. In fact, we make the following stronger claim: within each band
$B_{S}$
. In fact, we make the following stronger claim: within each band
![]() $B_{S}$
, step endpoints alternate from left to right with fragments of sloped steps, starting with a step endpoint and ending with a sloped step fragment.
$B_{S}$
, step endpoints alternate from left to right with fragments of sloped steps, starting with a step endpoint and ending with a sloped step fragment.
To see this, consider a connected component C of
![]() $\lambda '\cap B_{S}$
. Each component C either enters
$\lambda '\cap B_{S}$
. Each component C either enters
![]() $B_{S}$
from above along a south step or from below along a sloped step and exits
$B_{S}$
from above along a south step or from below along a sloped step and exits
![]() $B_{S}$
either at the top along a sloped step or at the bottom along a south step, except in two degenerate situations. One of these occurs if C contains the starting point
$B_{S}$
either at the top along a sloped step or at the bottom along a south step, except in two degenerate situations. One of these occurs if C contains the starting point
![]() $(0,\lfloor s \rfloor )$
of
$(0,\lfloor s \rfloor )$
of
![]() $\lambda '$
. In this case, we regard C as entering
$\lambda '$
. In this case, we regard C as entering
![]() $B_{S}$
from above. The other is if C contains a sloped step that adjoins S. Then we regard C as exiting
$B_{S}$
from above. The other is if C contains a sloped step that adjoins S. Then we regard C as exiting
![]() $B_{S}$
at the top.
$B_{S}$
at the top.
Each component C thus belongs to one of four cases shown in Figure 4. Note that, since
![]() $B_{S}$
has height 1, it cannot contain a full south step of
$B_{S}$
has height 1, it cannot contain a full south step of
![]() $\lambda '$
. In Figure 4, we have chosen
$\lambda '$
. In Figure 4, we have chosen
![]() $p<1$
in order to illustrate the possibility that
$p<1$
in order to illustrate the possibility that
![]() $B_{S}$
might contain full sloped steps of
$B_{S}$
might contain full sloped steps of
![]() $\lambda '$
. If
$\lambda '$
. If
![]() $p>1$
, then
$p>1$
, then
![]() $B_{S}$
can only meet sloped steps in proper fragments.
$B_{S}$
can only meet sloped steps in proper fragments.

Figure 4 Types of connected components C in the proof of Proposition 5.4.4.
On each component C, step endpoints clearly alternate with sloped step fragments, starting with a step endpoint if C enters from above, or with a sloped step fragment if C enters from below, and ending with a step endpoint if C exits at the bottom, or with a sloped step fragment if C exits at the top. Since the distance from the line
![]() $y=s$
to the starting point of
$y=s$
to the starting point of
![]() $\lambda '$
is less than
$\lambda '$
is less than
![]() $1$
, the leftmost component C of
$1$
, the leftmost component C of
![]() $\lambda '\cap B_{S}$
always enters
$\lambda '\cap B_{S}$
always enters
![]() $B_{S}$
from the top. Each subsequent component from left to right must enter
$B_{S}$
from the top. Each subsequent component from left to right must enter
![]() $B_{S}$
from the same side (top or bottom) that the previous component exited. This implies the claim stated above.
$B_{S}$
from the same side (top or bottom) that the previous component exited. This implies the claim stated above.
5.5 Shuffle theorem for paths under a line
We now prove the identity previewed as equation (1) in the introduction.
Theorem 5.5.1. Let
![]() $r,s$
be positive real numbers with
$r,s$
be positive real numbers with
![]() $p = s/r$
irrational. We have the identity
$p = s/r$
irrational. We have the identity
where the sum is over lattice paths
![]() $\lambda $
from
$\lambda $
from
![]() $(0,\lfloor s \rfloor )$
to
$(0,\lfloor s \rfloor )$
to
![]() $(\lfloor r \rfloor ,0)$
lying weakly below the line (125) through
$(\lfloor r \rfloor ,0)$
lying weakly below the line (125) through
![]() $(0,s)$
and
$(0,s)$
and
![]() $(r,0)$
, and the other pieces of equation (133) are defined as follows.
$(r,0)$
, and the other pieces of equation (133) are defined as follows.
The integer
![]() $a(\lambda )$
is the number of lattice squares enclosed between
$a(\lambda )$
is the number of lattice squares enclosed between
![]() $\lambda $
and
$\lambda $
and
![]() $\delta $
, where
$\delta $
, where
![]() $\delta $
is the highest path from
$\delta $
is the highest path from
![]() $(0,\lfloor s\rfloor )$
to
$(0,\lfloor s\rfloor )$
to
![]() $(\lfloor r \rfloor ,0)$
weakly below the given line. The index
$(\lfloor r \rfloor ,0)$
weakly below the given line. The index
![]() $b_{i}$
is the number of south steps in
$b_{i}$
is the number of south steps in
![]() $\delta $
along the line
$\delta $
along the line
![]() $x = i-1$
, for
$x = i-1$
, for
![]() $i=1,\ldots ,l$
, where
$i=1,\ldots ,l$
, where
![]() $l = \lfloor r \rfloor +1$
. The integer
$l = \lfloor r \rfloor +1$
. The integer
![]() $\operatorname {\mathrm {dinv}} _{p}(\lambda )$
is given by Definition 5.4.1.
$\operatorname {\mathrm {dinv}} _{p}(\lambda )$
is given by Definition 5.4.1.
The LLT polynomial
![]() ${\mathcal G}_{\nu (\lambda )}(X;q)$
is indexed by the tuple of one-row skew shapes
${\mathcal G}_{\nu (\lambda )}(X;q)$
is indexed by the tuple of one-row skew shapes
![]() $\nu (\lambda ) = \sigma (\beta /\alpha )$
, where
$\nu (\lambda ) = \sigma (\beta /\alpha )$
, where
![]() $\alpha ,\beta $
and
$\alpha ,\beta $
and
![]() $\sigma $
are the LLT data associated to
$\sigma $
are the LLT data associated to
![]() $\lambda $
in Definition 5.4.2. More explicitly,
$\lambda $
in Definition 5.4.2. More explicitly,
![]() $\sigma (\beta /\alpha ) = (\beta _{w_{0}\sigma ^{-1}(1)},\ldots ,\beta _{w_{0}\sigma ^{-1}(l)})/(\alpha _{w_{0}\sigma ^{-1}(1)},\ldots ,\alpha _{w_{0}\sigma ^{-1}(l)})$
, where
$\sigma (\beta /\alpha ) = (\beta _{w_{0}\sigma ^{-1}(1)},\ldots ,\beta _{w_{0}\sigma ^{-1}(l)})/(\alpha _{w_{0}\sigma ^{-1}(1)},\ldots ,\alpha _{w_{0}\sigma ^{-1}(l)})$
, where
![]() $\alpha =(\alpha _{l},\ldots ,\alpha _{1})$
and
$\alpha =(\alpha _{l},\ldots ,\alpha _{1})$
and
![]() $\beta =(\beta _{l},\ldots ,\beta _{1})$
.
$\beta =(\beta _{l},\ldots ,\beta _{1})$
.
The operator
![]() $D_{b_{1},\ldots ,b_{l}}$
on the left-hand side is a Negut element in
$D_{b_{1},\ldots ,b_{l}}$
on the left-hand side is a Negut element in
![]() ${\mathcal E} $
, as defined in §3.6, so that
${\mathcal E} $
, as defined in §3.6, so that
![]() $D_{b_{1},\ldots ,b_{l}} \cdot 1$
satisfies equation (58).
$D_{b_{1},\ldots ,b_{l}} \cdot 1$
satisfies equation (58).
Proof. We prove the equivalent identity
By Corollary 3.7.2 and Lemma 4.1.8, both sides of equation (134) involve only Schur functions
![]() $s_{\lambda }(X)$
indexed by partitions such that
$s_{\lambda }(X)$
indexed by partitions such that
![]() $\ell (\lambda )\leq l$
. It therefore suffices to prove that equation (134) holds when evaluated in l variables
$\ell (\lambda )\leq l$
. It therefore suffices to prove that equation (134) holds when evaluated in l variables
![]() $x_{1},\ldots , x_{l}$
. After doing this and using the formula (58) from Corollary 3.7.2, the desired identity becomes
$x_{1},\ldots , x_{l}$
. After doing this and using the formula (58) from Corollary 3.7.2, the desired identity becomes
This is the same identity (24) that was mentioned in the introduction to §3. We now prove it using Theorem 5.3.1.
Let
![]() $b^{\prime }_{i} = \lfloor s-p(i-1) \rfloor - \lfloor s-pi \rfloor $
. As in Remark 5.3.2, this is the number of south steps along
$b^{\prime }_{i} = \lfloor s-p(i-1) \rfloor - \lfloor s-pi \rfloor $
. As in Remark 5.3.2, this is the number of south steps along
![]() $x = i-1$
in the highest south-east path
$x = i-1$
in the highest south-east path
![]() $\delta '$
under our given line, where
$\delta '$
under our given line, where
![]() $\delta '$
starts at
$\delta '$
starts at
![]() $(0, \lfloor s \rfloor )$
and extends forever. For
$(0, \lfloor s \rfloor )$
and extends forever. For
![]() $i<l$
, we have
$i<l$
, we have
![]() $b^{\prime }_{i} = b_{i}$
. On the line
$b^{\prime }_{i} = b_{i}$
. On the line
![]() $x=l-1=\lfloor r \rfloor $
, however, the path
$x=l-1=\lfloor r \rfloor $
, however, the path
![]() $\delta $
stops at
$\delta $
stops at
![]() $(l-1,0)$
, while
$(l-1,0)$
, while
![]() $\delta '$
may extend below the x-axis, giving
$\delta '$
may extend below the x-axis, giving
![]() $b_{l}\leq b^{\prime }_{l}$
.
$b_{l}\leq b^{\prime }_{l}$
.
We now apply Theorem 5.3.1 with
![]() $b^{\prime }_{i}$
in place of
$b^{\prime }_{i}$
in place of
![]() $b_{i}$
,
$b_{i}$
,
![]() $u=0$
and
$u=0$
and
![]() $v = b^{\prime }_{l} - b_{l}$
and then take the polynomial part on both sides of equation (118). This gives the same left-hand side as in equation (135). On the right-hand side, by Corollary 4.5.7, only those terms survive for which the index
$v = b^{\prime }_{l} - b_{l}$
and then take the polynomial part on both sides of equation (118). This gives the same left-hand side as in equation (135). On the right-hand side, by Corollary 4.5.7, only those terms survive for which the index
![]() ${\mathbf a} $
satisfies
${\mathbf a} $
satisfies
![]() $(a_{l-1},\ldots ,a_{1},0)\leq (b_{l},\ldots ,b_{1})+(0, a_{l-1},\ldots ,a_{1})$
in each coordinate, that is, for which
$(a_{l-1},\ldots ,a_{1},0)\leq (b_{l},\ldots ,b_{1})+(0, a_{l-1},\ldots ,a_{1})$
in each coordinate, that is, for which
This is precisely the condition for there to exist a (unique) lattice path
![]() $\lambda $
from
$\lambda $
from
![]() $(0,\lfloor s \rfloor )$
to
$(0,\lfloor s \rfloor )$
to
![]() $(\lfloor r \rfloor ,0)$
such that
$(\lfloor r \rfloor ,0)$
such that
![]() $a_{i}$
is the number of lattice squares in the i-th column (defined by
$a_{i}$
is the number of lattice squares in the i-th column (defined by
![]() $x\in [i-1,i]$
) of the region between
$x\in [i-1,i]$
) of the region between
![]() $\lambda $
and the highest path
$\lambda $
and the highest path
![]() $\delta $
. Moreover, when condition (136) holds, the LLT data for
$\delta $
. Moreover, when condition (136) holds, the LLT data for
![]() $\lambda $
, as in Definition 5.4.2, are given by
$\lambda $
, as in Definition 5.4.2, are given by
 $$ \begin{align} \begin{aligned} \beta & = (b_{l},\ldots,b_{1})+(0, a_{l-1},\ldots,a_{1}),\\ \alpha & = (a_{l-1},\ldots,a_{1},0), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \beta & = (b_{l},\ldots,b_{1})+(0, a_{l-1},\ldots,a_{1}),\\ \alpha & = (a_{l-1},\ldots,a_{1},0), \end{aligned} \end{align} $$
and
![]() $\sigma \in S_{l}$
such that
$\sigma \in S_{l}$
such that
![]() $\sigma (1),\ldots ,\sigma (l)$
are in the same relative order as
$\sigma (1),\ldots ,\sigma (l)$
are in the same relative order as
![]() $c_{l},\ldots ,c_{1}$
, where
$c_{l},\ldots ,c_{1}$
, where
![]() $c_{i} = {\boldsymbol \{} s-p(i-1) {\boldsymbol \}}$
, as in Theorem 5.3.1. Hence, by Corollary 4.5.7 and Proposition 5.4.4, we have
$c_{i} = {\boldsymbol \{} s-p(i-1) {\boldsymbol \}}$
, as in Theorem 5.3.1. Hence, by Corollary 4.5.7 and Proposition 5.4.4, we have
When (136) holds, we clearly also have
![]() $a(\lambda ) = |{\mathbf a} |$
. This shows that the polynomial part of the right-hand side in equation (118) is the same as the right-hand side of equation (135).
$a(\lambda ) = |{\mathbf a} |$
. This shows that the polynomial part of the right-hand side in equation (118) is the same as the right-hand side of equation (135).
Remark 5.5.2. The preceding argument also goes through with
![]() $u>0$
in Theorem 5.3.1 to give a slightly more general version of Theorem 5.5.1 in which the sum is over lattice paths
$u>0$
in Theorem 5.3.1 to give a slightly more general version of Theorem 5.5.1 in which the sum is over lattice paths
![]() $\lambda $
that start at a higher point
$\lambda $
that start at a higher point
![]() $(0,n)$
on the y axis, with
$(0,n)$
on the y axis, with
![]() $n = \lfloor s \rfloor + u$
, go directly south to
$n = \lfloor s \rfloor + u$
, go directly south to
![]() $(0,\lfloor s \rfloor )$
, and then continue below the given line to
$(0,\lfloor s \rfloor )$
, and then continue below the given line to
![]() $(l-1,0)$
as before.
$(l-1,0)$
as before.
The corresponding modifications to equation (133) are (i) the index
![]() $b_{1}$
on the left-hand side is the number of south steps in
$b_{1}$
on the left-hand side is the number of south steps in
![]() $\lambda $
on the y axis including the extension to
$\lambda $
on the y axis including the extension to
![]() $(0,n)$
and (ii) the row in
$(0,n)$
and (ii) the row in
![]() $\nu (\lambda )$
corresponding to south steps in
$\nu (\lambda )$
corresponding to south steps in
![]() $\lambda $
on the y axis is also extended accordingly.
$\lambda $
on the y axis is also extended accordingly.
Example 5.5.3. Figure 5 illustrates Theorem 5.5.1 for
![]() $s \approx 4.7$
,
$s \approx 4.7$
,
![]() $r \approx 3.31$
. We have
$r \approx 3.31$
. We have
![]() $(c_4, c_3,c_2,c_1) \approx ( .44,.86, .28,.70)$
and
$(c_4, c_3,c_2,c_1) \approx ( .44,.86, .28,.70)$
and
![]() $\sigma = (1,2,3,4) \mapsto (2,4,1,3)$
. The paths
$\sigma = (1,2,3,4) \mapsto (2,4,1,3)$
. The paths
![]() $\lambda $
are shown along with the corresponding statistics and LLT polynomials
$\lambda $
are shown along with the corresponding statistics and LLT polynomials
![]() ${\mathcal G}_{\nu (\lambda )}(X;q) = {\mathcal G}_{\sigma (\beta )/\sigma (\alpha )}(X;q)$
. The highest path
${\mathcal G}_{\nu (\lambda )}(X;q) = {\mathcal G}_{\sigma (\beta )/\sigma (\alpha )}(X;q)$
. The highest path
![]() $\delta $
is the one at the top left in the figure and
$\delta $
is the one at the top left in the figure and
![]() $(b_1,b_2,b_3,b_4) = (1,2,1,0)$
. The left side of equation (134), evaluated in
$(b_1,b_2,b_3,b_4) = (1,2,1,0)$
. The left side of equation (134), evaluated in
![]() $l = 4$
variables, is then
$l = 4$
variables, is then
 $$ \begin{align} \omega (D_{1,2,1,0} \cdot 1)(x) &= {\mathcal H} _{(1,2,1,0)}(x)_{\operatorname{\mathrm{pol}}} = \notag\\ &\qquad\qquad{\boldsymbol \sigma } \big(\frac{ x_1x_2^2x_3(1 - q\, t\, x_{1} /x_3)(1 - q\, t\, x_{2} /x_4)(1 - q\, t\, x_{1} /x_4)} {\prod_{1\le i < j \le 4}(1 - q\, x_{i}/ x_{j})(1 - t\,x_{i}/ x_{j})} \big)_{\operatorname{\mathrm{pol}}}\,. \end{align} $$
$$ \begin{align} \omega (D_{1,2,1,0} \cdot 1)(x) &= {\mathcal H} _{(1,2,1,0)}(x)_{\operatorname{\mathrm{pol}}} = \notag\\ &\qquad\qquad{\boldsymbol \sigma } \big(\frac{ x_1x_2^2x_3(1 - q\, t\, x_{1} /x_3)(1 - q\, t\, x_{2} /x_4)(1 - q\, t\, x_{1} /x_4)} {\prod_{1\le i < j \le 4}(1 - q\, x_{i}/ x_{j})(1 - t\,x_{i}/ x_{j})} \big)_{\operatorname{\mathrm{pol}}}\,. \end{align} $$
To see that equation (134) holds at
![]() $t = 0$
, observe that the right-hand side of equation (139) becomes the Hall–Littlewood polynomial
$t = 0$
, observe that the right-hand side of equation (139) becomes the Hall–Littlewood polynomial
![]() ${\mathbf H}_q(x_1x_2^2x_3)_{\operatorname {\mathrm {pol}}} = q H_{2110}(x;q)$
, which agrees with the area 0 contribution
${\mathbf H}_q(x_1x_2^2x_3)_{\operatorname {\mathrm {pol}}} = q H_{2110}(x;q)$
, which agrees with the area 0 contribution
![]() $q^4 {\mathcal G}_{2011 / 0000}(x;q^{-1})$
.
$q^4 {\mathcal G}_{2011 / 0000}(x;q^{-1})$
.
Definition 5.5.4. For
![]() ${\mathbf b} \in {\mathbb Z}^l$
, the generalized
${\mathbf b} \in {\mathbb Z}^l$
, the generalized
![]() $q,t$
-Catalan number
$q,t$
-Catalan number
![]() $C_{\mathbf b}(q,t)$
is the coefficient of the single row Schur function
$C_{\mathbf b}(q,t)$
is the coefficient of the single row Schur function
![]() $s_{(|{\mathbf b}|)}(X)$
in
$s_{(|{\mathbf b}|)}(X)$
in
![]() $\omega (D_{\mathbf b} \cdot 1)$
.
$\omega (D_{\mathbf b} \cdot 1)$
.
When
![]() $\mathbf {b}= 1^l$
,
$\mathbf {b}= 1^l$
,
![]() $C_{\mathbf b}(q,t)$
is the
$C_{\mathbf b}(q,t)$
is the
![]() $q,t$
-Catalan number introduced by Garsia and the second author [Reference Garsia and Haiman10]. The generalized
$q,t$
-Catalan number introduced by Garsia and the second author [Reference Garsia and Haiman10]. The generalized
![]() $q,t$
-Catalan numbers have been studied in [Reference Gorsky, Hawkes, Schilling and Rainbolt13]—see §7.2.
$q,t$
-Catalan numbers have been studied in [Reference Gorsky, Hawkes, Schilling and Rainbolt13]—see §7.2.
Corollary 5.5.5. With
![]() $\mathbf {b} = (b_1,\dots , b_l)$
, r, s and
$\mathbf {b} = (b_1,\dots , b_l)$
, r, s and
![]() $p = s/r$
as in Theorem 5.5.1,
$p = s/r$
as in Theorem 5.5.1,
where the sum is over lattice paths
![]() $\lambda $
from
$\lambda $
from
![]() $(0,\lfloor s\rfloor )$
to
$(0,\lfloor s\rfloor )$
to
![]() $(\lfloor r \rfloor ,0)$
lying weakly below the line through
$(\lfloor r \rfloor ,0)$
lying weakly below the line through
![]() $(0,s)$
and
$(0,s)$
and
![]() $(r,0)$
.
$(r,0)$
.
6 Relation to previous shuffle theorems
Theorem 5.5.1 is formulated a little differently than the classical and
![]() $(km,kn)$
shuffle theorems in [Reference Bergeron, Garsia, Sergel Leven and Xin4, Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], although these also have an algebraic side and a combinatorial side resembling ours. We now explain how to recover them from our version by transforming each side of equation (133) into its counterpart in the
$(km,kn)$
shuffle theorems in [Reference Bergeron, Garsia, Sergel Leven and Xin4, Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], although these also have an algebraic side and a combinatorial side resembling ours. We now explain how to recover them from our version by transforming each side of equation (133) into its counterpart in the
![]() $(km,kn)$
and classical shuffle conjectures.
$(km,kn)$
and classical shuffle conjectures.
For the
![]() $(km,kn)$
shuffle conjecture, we take the line
$(km,kn)$
shuffle conjecture, we take the line
![]() $y+px = s$
in equation (125) to be a perturbation of the line from
$y+px = s$
in equation (125) to be a perturbation of the line from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
, with
$(km,0)$
, with
![]() $s = kn$
and r slightly larger than
$s = kn$
and r slightly larger than
![]() $km$
. Our perturbed line has the same lattice points and paths under it as the line from
$km$
. Our perturbed line has the same lattice points and paths under it as the line from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
, but it now has slope
$(km,0)$
, but it now has slope
![]() $-p$
, where
$-p$
, where
![]() $p = n/m-\epsilon $
for a small
$p = n/m-\epsilon $
for a small
![]() $\epsilon>0$
. The classical shuffle conjectures in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] are the special cases of the
$\epsilon>0$
. The classical shuffle conjectures in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] are the special cases of the
![]() $(km,kn)$
conjecture with
$(km,kn)$
conjecture with
![]() $n=1$
. For these, we perturb the line from
$n=1$
. For these, we perturb the line from
![]() $(0,k)$
to
$(0,k)$
to
![]() $(km,0)$
in the same way. Note that for our chosen line we have
$(km,0)$
in the same way. Note that for our chosen line we have
![]() $l=km+1$
, and every lattice path
$l=km+1$
, and every lattice path
![]() $\lambda $
under it has
$\lambda $
under it has
![]() $b_{l}=0$
south steps at
$b_{l}=0$
south steps at
![]() $x=km$
.
$x=km$
.
The classical shuffle conjecture was formulated in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Conjecture 6.2.2] as the identity
 $$ \begin{align} \nabla^{m} e_{k} = \sum _{\lambda } \sum _{P\in \operatorname{\mathrm{SSYT}} {((\lambda+(1^k))/\lambda)}} t^{a(\lambda )} q^{\operatorname{\mathrm{dinv}} _{m}(P)} x^{P}\,, \end{align} $$
$$ \begin{align} \nabla^{m} e_{k} = \sum _{\lambda } \sum _{P\in \operatorname{\mathrm{SSYT}} {((\lambda+(1^k))/\lambda)}} t^{a(\lambda )} q^{\operatorname{\mathrm{dinv}} _{m}(P)} x^{P}\,, \end{align} $$
where the sum is over lattice paths
![]() $\lambda $
below the bounding line, and
$\lambda $
below the bounding line, and
![]() $\operatorname {\mathrm {dinv}}_m(P)$
is a statistic defined in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], attached to each labelling P of the south steps in
$\operatorname {\mathrm {dinv}}_m(P)$
is a statistic defined in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], attached to each labelling P of the south steps in
![]() $\lambda $
by nonnegative integers strictly increasing from south to north along each vertical run. Rather than recall the original definition of
$\lambda $
by nonnegative integers strictly increasing from south to north along each vertical run. Rather than recall the original definition of
![]() $\operatorname {\mathrm {dinv}} _{m}(P)$
, we will use results from [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] to obtain a formula for it in equation (143), below. The left-hand side of equation (141) is
$\operatorname {\mathrm {dinv}} _{m}(P)$
, we will use results from [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] to obtain a formula for it in equation (143), below. The left-hand side of equation (141) is
![]() $e_{k}[-M X^{m,1}] \cdot 1$
by Corollary 3.7.4. This agrees with the left-hand side
$e_{k}[-M X^{m,1}] \cdot 1$
by Corollary 3.7.4. This agrees with the left-hand side
![]() $D_{b_{1},\ldots ,b_{l}}\cdot 1$
of equation (133) by Corollary 3.7.3.
$D_{b_{1},\ldots ,b_{l}}\cdot 1$
of equation (133) by Corollary 3.7.3.
It was noted and used in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16] that the combinatorial side of equation (141) can be phrased in terms of LLT polynomials, but to explicitly match with our formulation requires that we transform the right-hand side of equation (133) as follows. For the given
![]() $\nu (\lambda )=\sigma (\beta /\alpha )$
, apply Proposition 4.1.6 to replace
$\nu (\lambda )=\sigma (\beta /\alpha )$
, apply Proposition 4.1.6 to replace
![]() $\omega {\mathcal G}_{\nu (\lambda )}(X;q^{-1})$
with
$\omega {\mathcal G}_{\nu (\lambda )}(X;q^{-1})$
with
![]() $q^{-I(\nu (\lambda )^{R})} {\mathcal G}_{\nu (\lambda )^{R}}(X;q)$
. Then writing out
$q^{-I(\nu (\lambda )^{R})} {\mathcal G}_{\nu (\lambda )^{R}}(X;q)$
. Then writing out
![]() ${\mathcal G}_{\nu (\lambda )^R}(X;q)$
term by term with tableaux on the tuple
${\mathcal G}_{\nu (\lambda )^R}(X;q)$
term by term with tableaux on the tuple
![]() $\nu (\lambda )^{R}$
of one-column diagrams using Definition 4.1.2 gives
$\nu (\lambda )^{R}$
of one-column diagrams using Definition 4.1.2 gives
 $$ \begin{align} D_{b_{1},\ldots,b_{l}} \cdot 1 = \sum _{\lambda } \sum _{T\in \operatorname{\mathrm{SSYT}} (\nu (\lambda )^{R})} t^{a(\lambda )} q^{\operatorname{\mathrm{dinv}} _{p}(\lambda ) -I(\nu (\lambda )^{R})+\operatorname{\mathrm{inv}}(T)} x^{T}\,, \end{align} $$
$$ \begin{align} D_{b_{1},\ldots,b_{l}} \cdot 1 = \sum _{\lambda } \sum _{T\in \operatorname{\mathrm{SSYT}} (\nu (\lambda )^{R})} t^{a(\lambda )} q^{\operatorname{\mathrm{dinv}} _{p}(\lambda ) -I(\nu (\lambda )^{R})+\operatorname{\mathrm{inv}}(T)} x^{T}\,, \end{align} $$
where
![]() $\operatorname {\mathrm {inv}}(T)$
is the number of attacking inversions, as in Definition 4.1.2, and
$\operatorname {\mathrm {inv}}(T)$
is the number of attacking inversions, as in Definition 4.1.2, and
![]() $I(\nu (\lambda )^{R})$
is the number of attacking pairs in the tuple
$I(\nu (\lambda )^{R})$
is the number of attacking pairs in the tuple
![]() $\nu (\lambda )^{R}$
given by Definition 4.1.5.
$\nu (\lambda )^{R}$
given by Definition 4.1.5.
By the construction, boxes in each column of
![]() $\nu (\lambda )^{R}$
, from top to bottom, correspond to south steps u in a vertical run in
$\nu (\lambda )^{R}$
, from top to bottom, correspond to south steps u in a vertical run in
![]() $\lambda $
, from north to south. Semistandard tableaux
$\lambda $
, from north to south. Semistandard tableaux
![]() $T\in \operatorname {\mathrm {SSYT}} (\nu (\lambda )^{R})$
therefore biject with labellings
$T\in \operatorname {\mathrm {SSYT}} (\nu (\lambda )^{R})$
therefore biject with labellings
![]() $P_T\colon \{\text {south steps in } \lambda \}\rightarrow {\mathbb Z} _{>0} $
such that
$P_T\colon \{\text {south steps in } \lambda \}\rightarrow {\mathbb Z} _{>0} $
such that
![]() $P_T$
is strictly increasing from south to north on each vertical run in
$P_T$
is strictly increasing from south to north on each vertical run in
![]() $\lambda $
; namely,
$\lambda $
; namely,
![]() $P_T\in \operatorname {\mathrm {SSYT}}((\lambda +(1^k))/\lambda )$
. Changing equation (142) to instead sum over labellings, we can match the right-hand sides of equations (142) and (141) by showing that for
$P_T\in \operatorname {\mathrm {SSYT}}((\lambda +(1^k))/\lambda )$
. Changing equation (142) to instead sum over labellings, we can match the right-hand sides of equations (142) and (141) by showing that for
![]() $p=1/m-\epsilon $
,
$p=1/m-\epsilon $
,
For any super tableau T, [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Corollary 6.4.2] implies that
![]() $\operatorname {\mathrm {dinv}} _{m}(P_T) = u_{\lambda } + \operatorname {\mathrm {inv}}(T)$
for an offset
$\operatorname {\mathrm {dinv}} _{m}(P_T) = u_{\lambda } + \operatorname {\mathrm {inv}}(T)$
for an offset
![]() $u_{\lambda }$
not depending on T. For the tableau
$u_{\lambda }$
not depending on T. For the tableau
![]() $T_0$
with all entries
$T_0$
with all entries
![]() $\bar 1$
, [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Lemma 6.3.3] gives that
$\bar 1$
, [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Lemma 6.3.3] gives that
![]() $\operatorname {\mathrm {dinv}}_m(P_{T_0})= b_m(\lambda )$
, where we note that
$\operatorname {\mathrm {dinv}}_m(P_{T_0})= b_m(\lambda )$
, where we note that
![]() $b_m(\lambda )$
defined in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, (100)] is simply
$b_m(\lambda )$
defined in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, (100)] is simply
![]() $\operatorname {\mathrm {dinv}}_p(\lambda )$
with
$\operatorname {\mathrm {dinv}}_p(\lambda )$
with
![]() $p=1/m-\epsilon $
. Therefore,
$p=1/m-\epsilon $
. Therefore,
![]() $u_{\lambda } = \operatorname {\mathrm {dinv}} _{m}(P_{T_0})-\operatorname {\mathrm {inv}}(T_0) = \operatorname {\mathrm {dinv}}_p(\lambda ) - I(\nu (\lambda )^R)$
by equation (68).
$u_{\lambda } = \operatorname {\mathrm {dinv}} _{m}(P_{T_0})-\operatorname {\mathrm {inv}}(T_0) = \operatorname {\mathrm {dinv}}_p(\lambda ) - I(\nu (\lambda )^R)$
by equation (68).
In fact, there is a direct correspondence between the combinatorics of
![]() $\operatorname {\mathrm {dinv}}_{m}(P)$
for paths, as defined in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], and that of triples in negative tableaux on a tuple of one-row shapes, as considered in §4.5.
$\operatorname {\mathrm {dinv}}_{m}(P)$
for paths, as defined in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16], and that of triples in negative tableaux on a tuple of one-row shapes, as considered in §4.5.
Proposition 6.1.1. Let
![]() $\lambda $
be a lattice path from
$\lambda $
be a lattice path from
![]() $(0,k)$
to
$(0,k)$
to
![]() $(km,0)$
, lying weakly below the bounding line
$(km,0)$
, lying weakly below the bounding line
![]() $y + p\, x = k$
with
$y + p\, x = k$
with
![]() $p = 1/m-\epsilon $
. Let
$p = 1/m-\epsilon $
. Let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\sigma $
be the LLT data associated to
$\sigma $
be the LLT data associated to
![]() $\lambda $
for this p. There is a weight-preserving bijection from labellings
$\lambda $
for this p. There is a weight-preserving bijection from labellings
![]() $P\in \operatorname {\mathrm {SSYT}}((\lambda +(1^k))/\lambda )$
to negative tableaux
$P\in \operatorname {\mathrm {SSYT}}((\lambda +(1^k))/\lambda )$
to negative tableaux
![]() $ S\in \operatorname {\mathrm {SSYT}}_{-} (\beta /\alpha )$
such that
$ S\in \operatorname {\mathrm {SSYT}}_{-} (\beta /\alpha )$
such that
Proof. The labelling
![]() $P=P_T\in \operatorname {\mathrm {SSYT}}((\lambda +(1^k))/\lambda )$
corresponds naturally to a semistandard tableau
$P=P_T\in \operatorname {\mathrm {SSYT}}((\lambda +(1^k))/\lambda )$
corresponds naturally to a semistandard tableau
![]() $T\in \operatorname {\mathrm {SSYT}}(\nu (\lambda )^R)$
. Their statistics are related by equation (143), into which we can substitute dinv
p
(λ) = h
σ
(β/α) by Proposition 5.4.4. The bijection
$T\in \operatorname {\mathrm {SSYT}}(\nu (\lambda )^R)$
. Their statistics are related by equation (143), into which we can substitute dinv
p
(λ) = h
σ
(β/α) by Proposition 5.4.4. The bijection
![]() $T\mapsto T^{R}$
in the proof of Proposition 4.1.6 satisfies
$T\mapsto T^{R}$
in the proof of Proposition 4.1.6 satisfies
![]() $\operatorname {\mathrm {inv}}(T)-I(\nu (\lambda )^R) = -\operatorname {\mathrm {inv}}(T^R)$
. Hence,
$\operatorname {\mathrm {inv}}(T)-I(\nu (\lambda )^R) = -\operatorname {\mathrm {inv}}(T^R)$
. Hence,
![]() $\operatorname {\mathrm {dinv}} _{m}(P_T) = h_{\sigma }(\beta /\alpha )-\operatorname {\mathrm {inv}}(T^R)$
. To complete the bijection, take
$\operatorname {\mathrm {dinv}} _{m}(P_T) = h_{\sigma }(\beta /\alpha )-\operatorname {\mathrm {inv}}(T^R)$
. To complete the bijection, take
![]() $S=T^R\circ \sigma $
. Then h
σ
(β/α) −inv(T
R
) = h
σ
(S) by Lemma 4.5.3, proving equation (144).
$S=T^R\circ \sigma $
. Then h
σ
(β/α) −inv(T
R
) = h
σ
(S) by Lemma 4.5.3, proving equation (144).
See Figure 6 for an example with
![]() $m=1$
and
$m=1$
and
![]() $p=1-\epsilon $
. Note that these values give
$p=1-\epsilon $
. Note that these values give
![]() $\sigma = w_0$
in the LLT data.
$\sigma = w_0$
in the LLT data.

Figure 6 Example of the bijection
![]() $P=P_T\leftrightarrow T\leftrightarrow T^R\leftrightarrow S=T^R\circ \sigma $
in Proposition 6.1.1, with
$P=P_T\leftrightarrow T\leftrightarrow T^R\leftrightarrow S=T^R\circ \sigma $
in Proposition 6.1.1, with
![]() $m=1$
,
$m=1$
,
![]() $p=1-\epsilon $
,
$p=1-\epsilon $
,
![]() $\sigma = w_0$
. Letters in S are ordered
$\sigma = w_0$
. Letters in S are ordered
![]() $\overline {1}> \overline {2} > \cdots $
. We see
$\overline {1}> \overline {2} > \cdots $
. We see
![]() $\operatorname {\mathrm {dinv}}_1(P) = h_{w_0}(S) = 6$
.
$\operatorname {\mathrm {dinv}}_1(P) = h_{w_0}(S) = 6$
.
Next, we turn to the noncompositional
![]() $(km,kn)$
shuffle conjecture from [Reference Bergeron, Garsia, Sergel Leven and Xin4]. Its symmetric function side is precisely the Schiffmann algebra operator expression that we denote here by
$(km,kn)$
shuffle conjecture from [Reference Bergeron, Garsia, Sergel Leven and Xin4]. Its symmetric function side is precisely the Schiffmann algebra operator expression that we denote here by
![]() $e_{k}[-M X^{m,n}]\cdot 1$
. By Corollary 3.7.3, this agrees with the left-hand side
$e_{k}[-M X^{m,n}]\cdot 1$
. By Corollary 3.7.3, this agrees with the left-hand side
![]() $D_{b_{1},\ldots ,b_{l}}\cdot 1$
of equation (133).
$D_{b_{1},\ldots ,b_{l}}\cdot 1$
of equation (133).
The combinatorial side of the
![]() $(km,kn)$
shuffle conjecture can be written as in [Reference Bergeron, Garsia, Sergel Leven and Xin4, §7], using notation defined there, as
$(km,kn)$
shuffle conjecture can be written as in [Reference Bergeron, Garsia, Sergel Leven and Xin4, §7], using notation defined there, as
Here, u encodes a north-east lattice path lying above the line from
![]() $(0,0)$
to
$(0,0)$
to
![]() $(km,kn)$
,
$(km,kn)$
,
![]() $\operatorname {Park}(u)$
encodes the set of standard Young tableaux on a tuple of columns corresponding to vertical runs in the path encoded by u, and
$\operatorname {Park}(u)$
encodes the set of standard Young tableaux on a tuple of columns corresponding to vertical runs in the path encoded by u, and
![]() $F_{\gamma }(x)$
is a Gessel fundamental quasi-symmetric function.
$F_{\gamma }(x)$
is a Gessel fundamental quasi-symmetric function.
To make u correspond to a lattice path
![]() $\lambda $
under the line from
$\lambda $
under the line from
![]() $(0,kn)$
to
$(0,kn)$
to
![]() $(km,0)$
, as in equation (142), we need to flip the picture over, replacing each entry
$(km,0)$
, as in equation (142), we need to flip the picture over, replacing each entry
![]() $\pi (j)$
with
$\pi (j)$
with
![]() $kn+1-\pi (j)$
so the resulting standard tableau T on
$kn+1-\pi (j)$
so the resulting standard tableau T on
![]() $\nu (\lambda )^{R}$
has columns increasing upwards, as it should, instead of decreasing. Using [Reference Bergeron, Garsia, Sergel Leven and Xin4, Definition 7.1] and taking into account the modification of
$\nu (\lambda )^{R}$
has columns increasing upwards, as it should, instead of decreasing. Using [Reference Bergeron, Garsia, Sergel Leven and Xin4, Definition 7.1] and taking into account the modification of
![]() $\pi $
to give T, we can translate notation in equation (145) as follows:
$\pi $
to give T, we can translate notation in equation (145) as follows:
![]() $\operatorname {area}(u) = a(\lambda )$
,
$\operatorname {area}(u) = a(\lambda )$
,
![]() $\operatorname {tdinv(\pi )} =\operatorname {\mathrm {inv}} (T)$
,
$\operatorname {tdinv(\pi )} =\operatorname {\mathrm {inv}} (T)$
,
![]() $\operatorname {maxtdinv}(u) = I(\nu (\lambda )^{R})$
, and
$\operatorname {maxtdinv}(u) = I(\nu (\lambda )^{R})$
, and
![]() $\operatorname {\mathrm {dinv}} (u) = \operatorname {\mathrm {dinv}} _{p}(\lambda )$
, where
$\operatorname {\mathrm {dinv}} (u) = \operatorname {\mathrm {dinv}} _{p}(\lambda )$
, where
![]() $p = n/m - \epsilon $
.
$p = n/m - \epsilon $
.
Finally, the definition of
![]() $\operatorname {ides}(\pi )$
becomes the descent set of T relative to the reading order on
$\operatorname {ides}(\pi )$
becomes the descent set of T relative to the reading order on
![]() $\nu (\lambda )^{R}$
. This implies that expanding
$\nu (\lambda )^{R}$
. This implies that expanding
![]() $F_{\operatorname {ides}(\pi )}(x)$
into monomials gives a sum with semistandard tableaux T in place of standard tableaux and
$F_{\operatorname {ides}(\pi )}(x)$
into monomials gives a sum with semistandard tableaux T in place of standard tableaux and
![]() $x^{T}$
in place of
$x^{T}$
in place of
![]() $F_{\operatorname {ides}(\pi )}(x)$
. After these substitutions, equation (145) coincides with the right-hand side of equation (142).
$F_{\operatorname {ides}(\pi )}(x)$
. After these substitutions, equation (145) coincides with the right-hand side of equation (142).
7 A positivity conjecture
7.1 The conjecture
Theorem 5.5.1, Corollary 3.7.2 and [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov16, Proposition 5.3.1] imply that the symmetric function
 $$ \begin{align} \omega (D_{{\mathbf b} }\cdot 1) = {\mathbf H} _{q,t}\left(\frac{x^{{\mathbf b} }}{\prod _{i} (1-q\, t\, x_{i}/x_{i+1})} \right)_{\operatorname{\mathrm{pol}} } \end{align} $$
$$ \begin{align} \omega (D_{{\mathbf b} }\cdot 1) = {\mathbf H} _{q,t}\left(\frac{x^{{\mathbf b} }}{\prod _{i} (1-q\, t\, x_{i}/x_{i+1})} \right)_{\operatorname{\mathrm{pol}} } \end{align} $$
is
![]() $q,t$
Schur positive when
$q,t$
Schur positive when
![]() $b_{i}$
is the number of south steps along
$b_{i}$
is the number of south steps along
![]() $x = i-1$
on the highest lattice path below a line with endpoints on the positive x and y axes. Computational evidence leads us to conjecture that equation (146) is
$x = i-1$
on the highest lattice path below a line with endpoints on the positive x and y axes. Computational evidence leads us to conjecture that equation (146) is
![]() $q,t$
Schur positive under a more general geometric condition on
$q,t$
Schur positive under a more general geometric condition on
![]() ${\mathbf b} $
.
${\mathbf b} $
.
Let C be a convex curve (meaning that the region above C is convex) in the first quadrant with endpoints
![]() $(r,0)$
and
$(r,0)$
and
![]() $(0,s)$
on the positive x and y axes. Let
$(0,s)$
on the positive x and y axes. Let
![]() $\delta $
be the highest lattice path from
$\delta $
be the highest lattice path from
![]() $(0,\lfloor s \rfloor )$
to
$(0,\lfloor s \rfloor )$
to
![]() $(\lfloor r \rfloor ,0)$
weakly below C. Let
$(\lfloor r \rfloor ,0)$
weakly below C. Let
![]() $b_{i}$
be the number of south steps in
$b_{i}$
be the number of south steps in
![]() $\delta $
along
$\delta $
along
![]() $x = i-1$
for
$x = i-1$
for
![]() $i = 1,\ldots ,l$
, where
$i = 1,\ldots ,l$
, where
![]() $l = \lfloor r \rfloor + 1$
. Algebraically, this means that there are real numbers
$l = \lfloor r \rfloor + 1$
. Algebraically, this means that there are real numbers
![]() $s_{0}\geq s_{1}\geq \cdots \geq s_{l}=0$
with weakly decreasing differences
$s_{0}\geq s_{1}\geq \cdots \geq s_{l}=0$
with weakly decreasing differences
![]() $s_{i-1}-s_{i}\geq s_{i}-s_{i+1}$
, such that
$s_{i-1}-s_{i}\geq s_{i}-s_{i+1}$
, such that
![]() $b_{i} = \lfloor s_{i-1} \rfloor -\lfloor s_{i} \rfloor $
.
$b_{i} = \lfloor s_{i-1} \rfloor -\lfloor s_{i} \rfloor $
.
Note that, if
![]() $\delta $
is the highest path strictly below a convex curve
$\delta $
is the highest path strictly below a convex curve
![]() $C'$
, then it is also the highest lattice path weakly below a slightly lower curve C, and vice versa, so it doesn’t matter whether we use ‘weakly below’ or ‘strictly below’ to formulate the condition on
$C'$
, then it is also the highest lattice path weakly below a slightly lower curve C, and vice versa, so it doesn’t matter whether we use ‘weakly below’ or ‘strictly below’ to formulate the condition on
![]() $\delta $
.
$\delta $
.
Conjecture 7.1.1. When
![]() $b_{i}$
is the number of south steps along
$b_{i}$
is the number of south steps along
![]() $x = i-1$
in the highest lattice path below a convex curve, as above, the symmetric function in equation (146) is a linear combination of Schur functions with coefficients in
$x = i-1$
in the highest lattice path below a convex curve, as above, the symmetric function in equation (146) is a linear combination of Schur functions with coefficients in
![]() ${\mathbb N} [q,t]$
.
${\mathbb N} [q,t]$
.
At
![]() $q=1$
, the q-Kostka coefficients reduce to
$q=1$
, the q-Kostka coefficients reduce to
![]() $K_{\lambda ,\mu }(1) = K_{\lambda ,\mu } = \langle s_{\lambda },h_{\mu } \rangle $
. Hence, the Hall–Littlewood symmetrization operator reduces to
$K_{\lambda ,\mu }(1) = K_{\lambda ,\mu } = \langle s_{\lambda },h_{\mu } \rangle $
. Hence, the Hall–Littlewood symmetrization operator reduces to
![]() ${\mathbf H} _{q}(x^{\mu })_{\operatorname {\mathrm {pol}} }|_{q=1} = h_{\mu }(x)$
if
${\mathbf H} _{q}(x^{\mu })_{\operatorname {\mathrm {pol}} }|_{q=1} = h_{\mu }(x)$
if
![]() $\mu _{i}\geq 0$
for all i, and otherwise
$\mu _{i}\geq 0$
for all i, and otherwise
![]() ${\mathbf H} _{q}(x^{\mu })_{\operatorname {\mathrm {pol}} } = 0$
. At
${\mathbf H} _{q}(x^{\mu })_{\operatorname {\mathrm {pol}} } = 0$
. At
![]() $q=1$
, the factors containing t in equation (46) cancel, so
$q=1$
, the factors containing t in equation (46) cancel, so
![]() ${\mathbf H} _{q,t}$
reduces to the same thing as
${\mathbf H} _{q,t}$
reduces to the same thing as
![]() ${\mathbf H} _{q}$
.
${\mathbf H} _{q}$
.
It follows that equation (146) specializes at
![]() $q = 1$
to
$q = 1$
to
with the convention that
![]() $h_{\mu } = 0$
if
$h_{\mu } = 0$
if
![]() $\mu _{i}<0$
for any i. As in Theorem 5.5.1, the index
$\mu _{i}<0$
for any i. As in Theorem 5.5.1, the index
![]() ${\mathbf b} +(a_{1},a_{2}-a_{1},\ldots ,a_{l-1}-a_{l-2},-a_{l-1})$
is nonnegative precisely when it is the sequence
${\mathbf b} +(a_{1},a_{2}-a_{1},\ldots ,a_{l-1}-a_{l-2},-a_{l-1})$
is nonnegative precisely when it is the sequence
![]() $b(\lambda )$
of lengths of south runs in a lattice path
$b(\lambda )$
of lengths of south runs in a lattice path
![]() $\lambda $
lying below the path
$\lambda $
lying below the path
![]() $\delta $
whose south runs are given by
$\delta $
whose south runs are given by
![]() ${\mathbf b} $
. Here,
${\mathbf b} $
. Here,
![]() $a_{i}$
is the number of lattice squares in column i between
$a_{i}$
is the number of lattice squares in column i between
![]() $\lambda $
and
$\lambda $
and
![]() $\delta $
, so
$\delta $
, so
![]() $|{\mathbf a} |$
is the area
$|{\mathbf a} |$
is the area
![]() $a(\lambda )$
enclosed between the two paths. This gives a combinatorial expression
$a(\lambda )$
enclosed between the two paths. This gives a combinatorial expression
for equation (146) at
![]() $q=1$
, which is positive in terms of complete homogeneous symmetric functions
$q=1$
, which is positive in terms of complete homogeneous symmetric functions
![]() $h_{\lambda }$
, hence t Schur positive. We may conjecture that when the hypothesis of Conjecture 7.1.1 holds,
$h_{\lambda }$
, hence t Schur positive. We may conjecture that when the hypothesis of Conjecture 7.1.1 holds,
![]() $\omega (D_{{\mathbf b} }\cdot 1)$
is given by some Schur positive combinatorial q-analog of (148), but it remains an open problem to formulate such a conjecture precisely.
$\omega (D_{{\mathbf b} }\cdot 1)$
is given by some Schur positive combinatorial q-analog of (148), but it remains an open problem to formulate such a conjecture precisely.
Of course, equation (148) cannot be considered evidence for Conjecture 7.1.1 since equation (148) holds for any
![]() ${\mathbf b} \geq 0$
, whether the convexity hypothesis is satisfied or not.
${\mathbf b} \geq 0$
, whether the convexity hypothesis is satisfied or not.
7.2 Relation to previous conjectures
The generalized
![]() $q,t$
-Catalan numbers
$q,t$
-Catalan numbers
![]() $C_{\mathbf b}(q,t) = \langle s_{(|{\mathbf b}|)}(X), \omega (D_{\mathbf b} \cdot 1) \rangle $
from Definition 5.5.4 coincide with the functions denoted
$C_{\mathbf b}(q,t) = \langle s_{(|{\mathbf b}|)}(X), \omega (D_{\mathbf b} \cdot 1) \rangle $
from Definition 5.5.4 coincide with the functions denoted
![]() $F(b_2,\dots , b_l)$
in [Reference Gorsky, Hawkes, Schilling and Rainbolt13], where several equivalent expressions for them were obtained. To see that
$F(b_2,\dots , b_l)$
in [Reference Gorsky, Hawkes, Schilling and Rainbolt13], where several equivalent expressions for them were obtained. To see that
![]() $C_{{\mathbf b} }(q,t) = F(b_{2},\ldots ,b_{l})$
, one can compare the formula in Proposition 7.2.1, below, with the equation just before (2.6) in [Reference Gorsky, Hawkes, Schilling and Rainbolt13]. It was also shown in [Reference Gorsky, Hawkes, Schilling and Rainbolt13] that this quantity does not depend on
$C_{{\mathbf b} }(q,t) = F(b_{2},\ldots ,b_{l})$
, one can compare the formula in Proposition 7.2.1, below, with the equation just before (2.6) in [Reference Gorsky, Hawkes, Schilling and Rainbolt13]. It was also shown in [Reference Gorsky, Hawkes, Schilling and Rainbolt13] that this quantity does not depend on
![]() $b_{1}$
, hence the notation
$b_{1}$
, hence the notation
![]() $F(b_2,\dots , b_l)$
.
$F(b_2,\dots , b_l)$
.
Conjecture 7.1.1 implies a conjecture of Negut, announced in [Reference Gorsky, Hawkes, Schilling and Rainbolt13], which asserts that
![]() $C_{{\mathbf b} }(q,t) \in {\mathbb N} [q,t]$
when
$C_{{\mathbf b} }(q,t) \in {\mathbb N} [q,t]$
when
![]() $b_{2}\geq \cdots \geq b_{l}$
. Conjecture 7.1.1 is stronger than Negut’s conjecture in two ways: the weight
$b_{2}\geq \cdots \geq b_{l}$
. Conjecture 7.1.1 is stronger than Negut’s conjecture in two ways: the weight
![]() ${\mathbf b} $
is generalized from a partition to the highest path below a convex curve, and the coefficient of
${\mathbf b} $
is generalized from a partition to the highest path below a convex curve, and the coefficient of
![]() $s_{(|{\mathbf b}|)}(X)$
in
$s_{(|{\mathbf b}|)}(X)$
in
![]() $\omega (D_{\mathbf b} \cdot 1)$
is generalized to the coefficient of any Schur function.
$\omega (D_{\mathbf b} \cdot 1)$
is generalized to the coefficient of any Schur function.
Proposition 7.2.1. For any
![]() ${\mathbf b} \in {\mathbb Z} ^{l}$
, the generalized
${\mathbf b} \in {\mathbb Z} ^{l}$
, the generalized
![]() $q,t$
-Catalan number
$q,t$
-Catalan number
![]() $C_{\mathbf b}(q,t)$
has the following description as a series coefficient:
$C_{\mathbf b}(q,t)$
has the following description as a series coefficient:
 $$ \begin{align} C_{\mathbf b}(q,t) = \langle z^{-{\mathbf b}} \rangle \, \prod_{i=1}^l \frac{1}{1-z_i^{-1}} \, \prod_{i=1}^{l-1}\frac{1}{1-q\, t\, z_{i}/z_{i+1}} \, \prod _{i<j} \frac{(1-z_{i}/z_{j})(1-q\, t\, z_{i}/z_{j})}{(1-q \, z_{i}/z_{j})(1-t \, z_{i}/z_{j})}. \end{align} $$
$$ \begin{align} C_{\mathbf b}(q,t) = \langle z^{-{\mathbf b}} \rangle \, \prod_{i=1}^l \frac{1}{1-z_i^{-1}} \, \prod_{i=1}^{l-1}\frac{1}{1-q\, t\, z_{i}/z_{i+1}} \, \prod _{i<j} \frac{(1-z_{i}/z_{j})(1-q\, t\, z_{i}/z_{j})}{(1-q \, z_{i}/z_{j})(1-t \, z_{i}/z_{j})}. \end{align} $$
Proof. From equation (50), we have
 $$ \begin{align*} \omega (D_{\mathbf b} \cdot 1) = \langle z^{0} \rangle \, \frac{z^{{\mathbf b} }}{\prod_{i=1}^{l-1} (1-q\, t\, z_{i}/z_{i+1})} \, \prod _{i<j} \frac{1-q\, t\, z_{i}/z_{j}}{(1-q \, z_{i}/z_{j})(1-t \, z_{i}/z_{j})} \, \Omega[\overline{Z} X] \, \prod _{i<j}(1-z_{i}/z_{j}). \end{align*} $$
$$ \begin{align*} \omega (D_{\mathbf b} \cdot 1) = \langle z^{0} \rangle \, \frac{z^{{\mathbf b} }}{\prod_{i=1}^{l-1} (1-q\, t\, z_{i}/z_{i+1})} \, \prod _{i<j} \frac{1-q\, t\, z_{i}/z_{j}}{(1-q \, z_{i}/z_{j})(1-t \, z_{i}/z_{j})} \, \Omega[\overline{Z} X] \, \prod _{i<j}(1-z_{i}/z_{j}). \end{align*} $$
Specializing
![]() $X = 1$
gives the result.
$X = 1$
gives the result.
Acknowledgments
JB was supported by NSF grant DMS-1855784 and 2154282. JM was supported by Simons Foundation grant 821999 and NSF grant DMS-2154281. JM and GS were supported by NSF grant DMS-1855804.
Conflict of Interest
The authors have no conflict of interest to declare.