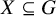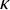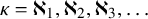1 Introduction
For a prime number p, the Prüfer p-group
is an example of an infinite subgroup of
![]() $(\mathbb C,\cdot )$
all of whose proper subgroups are finite. In [Reference Ol’šanskiĭ33], Ol’šanskiĭ constructed finitely generated non-cyclic infinite groups in which every nontrivial proper subgroup is a finite cyclic group (the Tarski monsters). In [Reference Shelah40], answering a question of Kurosh, Shelah constructed an uncountable group in which every nontrivial proper subgroup is countable. All of those are examples of so-called Jónsson groups (i.e., an infinite group G having no proper subgroups of full size). An even more striking concept is that of a boundedly-Jónsson group – that is, a group G admitting a positive integer n such that for every
$(\mathbb C,\cdot )$
all of whose proper subgroups are finite. In [Reference Ol’šanskiĭ33], Ol’šanskiĭ constructed finitely generated non-cyclic infinite groups in which every nontrivial proper subgroup is a finite cyclic group (the Tarski monsters). In [Reference Shelah40], answering a question of Kurosh, Shelah constructed an uncountable group in which every nontrivial proper subgroup is countable. All of those are examples of so-called Jónsson groups (i.e., an infinite group G having no proper subgroups of full size). An even more striking concept is that of a boundedly-Jónsson group – that is, a group G admitting a positive integer n such that for every
![]() $X\subseteq G$
of full size, it is the case that
$X\subseteq G$
of full size, it is the case that
![]() $X^n=G$
(i.e., every element of G may be written as a group word of length exactly n in the elements of X). In [Reference Shelah40], Shelah constructed a boundedly-Jónsson group of size
$X^n=G$
(i.e., every element of G may be written as a group word of length exactly n in the elements of X). In [Reference Shelah40], Shelah constructed a boundedly-Jónsson group of size
![]() $\aleph _1$
with the aid of Continuum Hypothesis (
$\aleph _1$
with the aid of Continuum Hypothesis (
![]() $\textsf {{CH}}$
). More generally, Shelah proved that
$\textsf {{CH}}$
). More generally, Shelah proved that
![]() $2^\lambda =\lambda ^+$
yields a boundedly-Jónsson group of size
$2^\lambda =\lambda ^+$
yields a boundedly-Jónsson group of size
![]() $\lambda ^+$
. By now, the concept of boundedly-Jónsson groups is named after him:
$\lambda ^+$
. By now, the concept of boundedly-Jónsson groups is named after him:
Definition 1.1. A group G is n-Shelah if
![]() $X^n=G$
for every
$X^n=G$
for every
![]() $X\subseteq G$
of full size.
$X\subseteq G$
of full size.
A group is Shelah if it is n-Shelah for some positive integer n.
Along the years, variations of this concept were studied quite intensively, and from various angles. A group G is said to be Cayley bounded with respect to a subset
![]() $S\subseteq G$
if there exists a positive integer
$S\subseteq G$
if there exists a positive integer
![]() $n_S$
such that
$n_S$
such that
![]() $G=\bigcup _{i=1}^{n_S}(S\cup S^{-1})^i$
(i.e., every element of G may be written as a group word of length at most
$G=\bigcup _{i=1}^{n_S}(S\cup S^{-1})^i$
(i.e., every element of G may be written as a group word of length at most
![]() $n_S$
in the elements of S and inverses of elements of S). Extending the work of Macpherson and Neumann [Reference Macpherson and Neumann30], Bergman proved [Reference Bergman4] that the permutation group
$n_S$
in the elements of S and inverses of elements of S). Extending the work of Macpherson and Neumann [Reference Macpherson and Neumann30], Bergman proved [Reference Bergman4] that the permutation group
![]() $\operatorname {\mathrm {Sym}}(\Omega )$
of an infinite set
$\operatorname {\mathrm {Sym}}(\Omega )$
of an infinite set
![]() $\Omega $
is Cayley bounded with respect to all of its generating sets. Soon after, the notion Bergman property was coined as the assertion of being Cayley bounded with respect to all generating sets. Since then, it has received a lot of attention; see [Reference Bardakov, Tolstykh and Vershinin3, Reference Droste and Göbel10, Reference Droste and Holland11, Reference Droste, Holland and Ulbrich12, Reference Droste and Truss13, Reference Maltcev, Mitchell and Ruškuc31, Reference Ricard and Rosendal35, Reference Thomas and Zapletal44, Reference Tolstykh46, Reference Tolstykh47]. More recent examples include the work of Dowerk [Reference Dowerk9] on von Neumann algebras with unitary groups possessing the property of n-strong uncountable cofinality (i.e., having a common Cayley bound n for all generating sets, and the group is not the union of an infinite countable strictly increasing sequence of subgroups), and Shelah’s work on locally finite groups [Reference Shelah42]. It is worth mentioning that the notion of strong uncountable cofinality has also geometric reformulations (e.g., by Cornulier [Reference de Cornulier8], Pestov (see [Reference Rosendal38, Theorem 1.2]) and Rosendal [Reference Rosendal38, Proposition 3.3]).
$\Omega $
is Cayley bounded with respect to all of its generating sets. Soon after, the notion Bergman property was coined as the assertion of being Cayley bounded with respect to all generating sets. Since then, it has received a lot of attention; see [Reference Bardakov, Tolstykh and Vershinin3, Reference Droste and Göbel10, Reference Droste and Holland11, Reference Droste, Holland and Ulbrich12, Reference Droste and Truss13, Reference Maltcev, Mitchell and Ruškuc31, Reference Ricard and Rosendal35, Reference Thomas and Zapletal44, Reference Tolstykh46, Reference Tolstykh47]. More recent examples include the work of Dowerk [Reference Dowerk9] on von Neumann algebras with unitary groups possessing the property of n-strong uncountable cofinality (i.e., having a common Cayley bound n for all generating sets, and the group is not the union of an infinite countable strictly increasing sequence of subgroups), and Shelah’s work on locally finite groups [Reference Shelah42]. It is worth mentioning that the notion of strong uncountable cofinality has also geometric reformulations (e.g., by Cornulier [Reference de Cornulier8], Pestov (see [Reference Rosendal38, Theorem 1.2]) and Rosendal [Reference Rosendal38, Proposition 3.3]).
Shelah’s 1980 construction from
![]() $\textsf {{CH}}$
was of a
$\textsf {{CH}}$
was of a
![]() $6640$
-Shelah group. It left open two independent questions:Footnote
1
$6640$
-Shelah group. It left open two independent questions:Footnote
1
-
1. Can
 $\textsf {{CH}}$
be used to construct an n-Shelah group for a small number of n?
$\textsf {{CH}}$
be used to construct an n-Shelah group for a small number of n? -
2. Is
 $\textsf {{CH}}$
necessary for the construction of an n-Shelah group?
$\textsf {{CH}}$
necessary for the construction of an n-Shelah group?
Recently, in [Reference Banakh2], Banakh addressed the first question, using
![]() $\textsf {{CH}}$
to construct a
$\textsf {{CH}}$
to construct a
![]() $36$
-Shelah group. Even more recently, Corson, Ol’šanskiĭ and Varghese [Reference Corson, Olshanskii and Varghese7] addressed the second question, constructing the first
$36$
-Shelah group. Even more recently, Corson, Ol’šanskiĭ and Varghese [Reference Corson, Olshanskii and Varghese7] addressed the second question, constructing the first
![]() $\textsf {{ZFC}}$
example of a Jónsson group of size
$\textsf {{ZFC}}$
example of a Jónsson group of size
![]() $\aleph _1$
to have the Bergman property. Unfortunately, the new example stops short from being Shelah, as every generating set S of this group has its own
$\aleph _1$
to have the Bergman property. Unfortunately, the new example stops short from being Shelah, as every generating set S of this group has its own
![]() $n_S$
. In this paper, an affirmative answer to the second question is finally given, where a Shelah group of size
$n_S$
. In this paper, an affirmative answer to the second question is finally given, where a Shelah group of size
![]() $\aleph _1$
is constructed within
$\aleph _1$
is constructed within
![]() $\textsf {{ZFC}}$
.
$\textsf {{ZFC}}$
.
Theorem A. For every infinite regular cardinal
![]() $\lambda $
, there exists a
$\lambda $
, there exists a
![]() $10120$
-Shelah group of size
$10120$
-Shelah group of size
![]() $\lambda ^+$
. In particular, there exist Shelah groups of size
$\lambda ^+$
. In particular, there exist Shelah groups of size
![]() $\aleph _1,\aleph _2,\aleph _3,\ldots $
.
$\aleph _1,\aleph _2,\aleph _3,\ldots $
.
The proof of Theorem A reflects advances both in small cancellation theory and in the study of infinite Ramsey theory. Towards it, we prove a far-reaching extension of Hesse’s amalgamation lemma, and we obtain two maps, one coming from the theory of negative square-bracket partition relations and the other coming from the theory of strongly subadditive functions, and the two maps have the property that they may be triggered simultaneously, making them ‘active’ over each other.
The connection to infinite Ramsey theory should not come as a surprise. First, note that an n-Shelah group of size
![]() $\aleph _0$
does not exist, since such a group would have induced a coloring
$\aleph _0$
does not exist, since such a group would have induced a coloring
![]() $c:[\mathbb N]^n\rightarrow k$
for a large enough integer k admitting no infinite homogeneous set,Footnote
2
in particular contradicting Ramsey’s theorem
$c:[\mathbb N]^n\rightarrow k$
for a large enough integer k admitting no infinite homogeneous set,Footnote
2
in particular contradicting Ramsey’s theorem
![]() $\aleph _0\rightarrow (\aleph _0)^n_k$
.Footnote
3
$\aleph _0\rightarrow (\aleph _0)^n_k$
.Footnote
3
A deeper connection to (additive) Ramsey theory is in the fact that the existence of a Jónsson group of size
![]() $\kappa $
is equivalent to a very strong failure of the higher analog of Hindman’s finite sums theorem [Reference Hindman21]. Indeed, by [Reference Fernandez-Breton and Rinot16, Corollary 2.8], if there exists a Jónsson group of size
$\kappa $
is equivalent to a very strong failure of the higher analog of Hindman’s finite sums theorem [Reference Hindman21]. Indeed, by [Reference Fernandez-Breton and Rinot16, Corollary 2.8], if there exists a Jónsson group of size
![]() $\kappa $
, then for every Abelian group G of size
$\kappa $
, then for every Abelian group G of size
![]() $\kappa $
, there exists a map
$\kappa $
, there exists a map
![]() $c:G\rightarrow G$
such that for every
$c:G\rightarrow G$
such that for every
![]() $X\subseteq G$
of full size,
$X\subseteq G$
of full size,
![]() $c\restriction \operatorname {\mathrm {FS}}(X)$
is surjective; that is,
$c\restriction \operatorname {\mathrm {FS}}(X)$
is surjective; that is,
Conversely, if G is an Abelian group of size
![]() $\kappa $
admitting a map
$\kappa $
admitting a map
![]() $c:G\rightarrow G$
as above, then the structure
$c:G\rightarrow G$
as above, then the structure
![]() $(G,+,c)$
is easily an example of a so-called Jónsson algebra [Reference Jónsson24] of size
$(G,+,c)$
is easily an example of a so-called Jónsson algebra [Reference Jónsson24] of size
![]() $\kappa $
, which by Corson’s work [Reference Corson6] implies the existence of a Jónsson group of size
$\kappa $
, which by Corson’s work [Reference Corson6] implies the existence of a Jónsson group of size
![]() $\kappa $
.
$\kappa $
.
The fact that the elimination of
![]() $\textsf {{CH}}$
goes through advances in the theory of partition calculus of uncountable cardinals should not come as a surprise, either. To give just one example, we mention that three decades after Juhász and Hajnal [Reference Hajnal and Juhász19] constructed an L-space with the aid of
$\textsf {{CH}}$
goes through advances in the theory of partition calculus of uncountable cardinals should not come as a surprise, either. To give just one example, we mention that three decades after Juhász and Hajnal [Reference Hajnal and Juhász19] constructed an L-space with the aid of
![]() $\textsf {{CH}}$
, Moore [Reference Moore32] gave a
$\textsf {{CH}}$
, Moore [Reference Moore32] gave a
![]() $\textsf {{ZFC}}$
construction of an L-space by establishing a new unbalanced partition relation for the first uncountable cardinal.
$\textsf {{ZFC}}$
construction of an L-space by establishing a new unbalanced partition relation for the first uncountable cardinal.
Having discussed Shelah groups of size
![]() $\aleph _0$
and of size a successor cardinal, the next question is whether it is possible to construct a Shelah group of size an uncountable limit cardinal. To compare, a natural ingredient available for transfinite constructions of length a successor cardinal
$\aleph _0$
and of size a successor cardinal, the next question is whether it is possible to construct a Shelah group of size an uncountable limit cardinal. To compare, a natural ingredient available for transfinite constructions of length a successor cardinal
![]() $\kappa =\lambda ^+$
is the existence of
$\kappa =\lambda ^+$
is the existence of
![]() $\lambda $
-filtrations of all ordinals less than
$\lambda $
-filtrations of all ordinals less than
![]() $\kappa $
. We overcome this obstruction at the level of a limit cardinal
$\kappa $
. We overcome this obstruction at the level of a limit cardinal
![]() $\kappa $
by employing subadditive strongly unbounded maps
$\kappa $
by employing subadditive strongly unbounded maps
![]() $d:[\kappa ]^2\rightarrow \lambda $
having arbitrarily large gaps between
$d:[\kappa ]^2\rightarrow \lambda $
having arbitrarily large gaps between
![]() $\lambda $
and
$\lambda $
and
![]() $\kappa $
. This way, we obtain the first consistent example of a Shelah group of size a limit cardinal. More generally:
$\kappa $
. This way, we obtain the first consistent example of a Shelah group of size a limit cardinal. More generally:
Theorem B. For every regular uncountable cardinal
![]() $\kappa $
satisfying the combinatorial principle
$\kappa $
satisfying the combinatorial principle
![]() $\square (\kappa )$
, there exists a Shelah group of size
$\square (\kappa )$
, there exists a Shelah group of size
![]() $\kappa $
.
$\kappa $
.
By a seminal work of Jensen [Reference Jensen23], in Gödel’s model of set theory known as the constructible universe [Reference Gödel18], the combinatorial principle
![]() $\square (\kappa )$
holds for every regular uncountable cardinal
$\square (\kappa )$
holds for every regular uncountable cardinal
![]() $\kappa $
that is not weakly compact. As the reader may anticipate, a cardinal
$\kappa $
that is not weakly compact. As the reader may anticipate, a cardinal
![]() $\kappa $
is weakly compact if it is a regular uncountable cardinal satisfying the higher analog of Ramsey’s theorem
$\kappa $
is weakly compact if it is a regular uncountable cardinal satisfying the higher analog of Ramsey’s theorem
![]() $\kappa \rightarrow (\kappa )^2_2$
. Altogether, we arrive at the following optimal result:
$\kappa \rightarrow (\kappa )^2_2$
. Altogether, we arrive at the following optimal result:
Theorem C. In Gödel’s constructible universe, for every regular uncountable cardinal
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
• There exists a Shelah group of size
 $\kappa $
;
$\kappa $
; -
• Ramsey’s partition relation
 $\kappa \rightarrow (\kappa )^2_2$
fails.
$\kappa \rightarrow (\kappa )^2_2$
fails.
We conclude the introduction by discussing additional features that the groups constructed here possess. A group is said to be topologizable if it admits a non-discrete Hausdorff group topology; otherwise, it is non-topologizable. The first consistent instance of a non-topologizable group was the group constructed by Shelah in [Reference Shelah40] using
![]() $\textsf {{CH}}$
. Shortly after, an uncountable
$\textsf {{CH}}$
. Shortly after, an uncountable
![]() $\textsf {{ZFC}}$
example was given by Hesse [Reference Hesse20]. Then a countable such group was given by Ol’šanskiĭ [Reference Ol’šanskiĭ34, Theorem 31.5] (an account of his construction may be found in [Reference Adian1, §13.4]). Ol’šanskiĭ’s group is periodic; a torsion-free example was given by Klyachko and Trofimov in [Reference Klyachko and Trofimov25].
$\textsf {{ZFC}}$
example was given by Hesse [Reference Hesse20]. Then a countable such group was given by Ol’šanskiĭ [Reference Ol’šanskiĭ34, Theorem 31.5] (an account of his construction may be found in [Reference Adian1, §13.4]). Ol’šanskiĭ’s group is periodic; a torsion-free example was given by Klyachko and Trofimov in [Reference Klyachko and Trofimov25].
The Shelah group we construct in this paper is torsion-free and non-topologizable. The latter follows combining the property of Shelah-ness together with the fact that there will be a filtration of the group consisting of malnormal subgroups (see Definition 3.3). Moreover, our group contains a nonalgebraic unconditionally closed set, which can be shown by proving that small sets can be covered by a topologizable subgroup, similarly to the argument by Sipacheva [Reference Sipacheva43, Lemmas 1 and A.4].
1.1 Can’t you do better than
 $n=10120$
?
$n=10120$
?
We believe a better n is achievable, but that is not the focus of this paper. In this paper, we establish a two-dimensional construction scheme for producing a group G of cardinality
![]() $\kappa $
as a limit of a coherent system of subgroups
$\kappa $
as a limit of a coherent system of subgroups
![]() $\langle G_{\gamma ,i}\mathrel {|} \gamma <\kappa ,~i<\theta \rangle $
, where
$\langle G_{\gamma ,i}\mathrel {|} \gamma <\kappa ,~i<\theta \rangle $
, where
![]() $G_{\gamma +1,i+1}$
is obtained as a particular amalgamation of the groups
$G_{\gamma +1,i+1}$
is obtained as a particular amalgamation of the groups
![]() $G_{\gamma ,i}$
and
$G_{\gamma ,i}$
and
![]() $G_{\gamma ,i+1}$
over
$G_{\gamma ,i+1}$
over
![]() $G_{\gamma +1,i}$
. The number
$G_{\gamma +1,i}$
. The number
![]() $n=10120$
comes from our amalgamation lemma, and so by plugging in alternative amalgamation lemmas to our construction scheme, we expect groups of various characteristics may be produced, including n-Shelah groups with
$n=10120$
comes from our amalgamation lemma, and so by plugging in alternative amalgamation lemmas to our construction scheme, we expect groups of various characteristics may be produced, including n-Shelah groups with
![]() $n<10120$
.
$n<10120$
.
1.2 Organization of this paper
In Section 2, we fix our notations and conventions, and provide some necessary background from small cancellation theory.
In Section 3, we prove an amalgamation lemma that will serve as a building block in our two-dimensional recursive construction of a Shelah group.
In Section 4, we provide set-theoretic sufficient conditions for the existence of two types of maps to exist, and moreover be active over each other. The first type comes from the classical theory of negative square-bracket partition relations [Reference Erdős, Hajnal and Rado14, §18], and enables to eliminate the need for
![]() $\textsf {{CH}}$
in the construction of a Shelah group of size
$\textsf {{CH}}$
in the construction of a Shelah group of size
![]() $\aleph _1$
. The second type comes from the theory of subadditive strongly unbounded functions [Reference Lambie-Hanson and Rinot28], and enables to push the construction to higher cardinals including limit cardinals. At the level of successors of regulars, both of these colorings are obtained in
$\aleph _1$
. The second type comes from the theory of subadditive strongly unbounded functions [Reference Lambie-Hanson and Rinot28], and enables to push the construction to higher cardinals including limit cardinals. At the level of successors of regulars, both of these colorings are obtained in
![]() $\textsf {{ZFC}}$
using the method of walks on ordinals [Reference Todorcevic45] that did not exist at the time Shelah’s paper [Reference Shelah40] was written.
$\textsf {{ZFC}}$
using the method of walks on ordinals [Reference Todorcevic45] that did not exist at the time Shelah’s paper [Reference Shelah40] was written.
In Section 5, we provide a transfinite construction of a Shelah group guided by the colorings given by Section 4, and using the amalgamation lemma of Section 3.
2 Preliminaries
2.1 Notations and conventions
Under ordinals, we always mean von Neumann ordinals, and for a set X, the symbol
![]() $|X|$
always refers to the smallest ordinal with the same cardinality. For a set X, the symbol
$|X|$
always refers to the smallest ordinal with the same cardinality. For a set X, the symbol
![]() $\mathcal P(X)$
denotes the power set of X, while if
$\mathcal P(X)$
denotes the power set of X, while if
![]() $\theta $
is a cardinal, we use the standard notation
$\theta $
is a cardinal, we use the standard notation
![]() $[X]^\theta $
for
$[X]^\theta $
for
![]() $\{Y \in \mathcal P(X)\mathrel {|} |Y| = \theta \}$
– similarly for
$\{Y \in \mathcal P(X)\mathrel {|} |Y| = \theta \}$
– similarly for
![]() $[X]^{<\theta }$
and
$[X]^{<\theta }$
and
![]() $[X]^{\leq \theta }$
. We let
$[X]^{\leq \theta }$
. We let
![]() $\mathcal H_\theta $
denote the collection of all sets of hereditary cardinality less than
$\mathcal H_\theta $
denote the collection of all sets of hereditary cardinality less than
![]() $\theta $
. A set D is a club in a cardinal
$\theta $
. A set D is a club in a cardinal
![]() $\kappa $
iff
$\kappa $
iff
![]() $D\subseteq \kappa $
and for every
$D\subseteq \kappa $
and for every
![]() $\epsilon <\kappa $
,
$\epsilon <\kappa $
,
![]() $\sup (D\cap \epsilon )\in D\cup \{0\}$
and
$\sup (D\cap \epsilon )\in D\cup \{0\}$
and
![]() $D\setminus \epsilon \neq \emptyset $
. For a function f and a subset
$D\setminus \epsilon \neq \emptyset $
. For a function f and a subset
![]() $A\subseteq \operatorname {\mathrm {dom}}(f)$
, we either write
$A\subseteq \operatorname {\mathrm {dom}}(f)$
, we either write
![]() $f[A]$
or
$f[A]$
or
![]() $f"A$
for
$f"A$
for
![]() $\{ f(a)\mathrel {|} a\in A\}$
. By a sequence, we mean a function on an ordinal, where for a sequence
$\{ f(a)\mathrel {|} a\in A\}$
. By a sequence, we mean a function on an ordinal, where for a sequence
![]() $ \overline {s}= \langle s_\alpha \mathrel {|} \alpha < \operatorname {\mathrm {dom}}(\overline {s}) \rangle $
, the length of
$ \overline {s}= \langle s_\alpha \mathrel {|} \alpha < \operatorname {\mathrm {dom}}(\overline {s}) \rangle $
, the length of
![]() $\overline {s}$
(in symbols
$\overline {s}$
(in symbols
![]() $\ell (\overline {s})$
) denotes
$\ell (\overline {s})$
) denotes
![]() $\operatorname {\mathrm {dom}}(\overline {s})$
. We denote the empty sequence by
$\operatorname {\mathrm {dom}}(\overline {s})$
. We denote the empty sequence by
![]() $\langle \rangle $
. For a set X and an ordinal
$\langle \rangle $
. For a set X and an ordinal
![]() $\alpha $
, we use
$\alpha $
, we use
![]() $^\alpha X = \{ \overline {s}\mathrel {|} \ell (\overline {s}) = \alpha ,~\operatorname {\mathrm {Im}}(\overline {s}) \subseteq X\}$
.
$^\alpha X = \{ \overline {s}\mathrel {|} \ell (\overline {s}) = \alpha ,~\operatorname {\mathrm {Im}}(\overline {s}) \subseteq X\}$
.
2.2 Small cancellation theory
The main algebraic tool we are going to use is small cancellation theory. In this regard, the paper is self-contained, but for more details and proofs, the interested reader can consult [Reference Lyndon and Schupp29, §5. 11] and [Reference Shelah40, §1].
By convention, the free group with a set of generators A is denoted here by
![]() $F_A$
, and the normal closure of a set S in a group G is denoted here by
$F_A$
, and the normal closure of a set S in a group G is denoted here by
![]() $\operatorname {\mathrm {ncl}}(S,G)$
.
$\operatorname {\mathrm {ncl}}(S,G)$
.
Definition 2.1. Given groups
![]() $H,K,L$
such that
$H,K,L$
such that
![]() $K\cap L = H$
(as sets) – in particular,
$K\cap L = H$
(as sets) – in particular,
![]() $H \leq K,L$
– then one constructs the free amalgamation of K and L over H as
$H \leq K,L$
– then one constructs the free amalgamation of K and L over H as
where
![]() $N = \operatorname {\mathrm {ncl}}(E_K \cup E_L,F_{K \cup L})$
, and for
$N = \operatorname {\mathrm {ncl}}(E_K \cup E_L,F_{K \cup L})$
, and for
![]() $G \in \{K,L\}$
,
$G \in \{K,L\}$
,
We invoke basic results about the structure of groups of the form
![]() $ K *_H L $
.
$ K *_H L $
.
Definition 2.2. If
![]() $g = g^*_0 g^*_1 \cdots g^*_{n-1} \in K *_H L$
, where
$g = g^*_0 g^*_1 \cdots g^*_{n-1} \in K *_H L$
, where
![]() $g^*_i \in K \cup L$
, then we call the sequence of
$g^*_i \in K \cup L$
, then we call the sequence of
![]() $g^*_i$
’s the canonical form of the group element of g, if
$g^*_i$
’s the canonical form of the group element of g, if
-
• either
 $n = 1$
, or
$n = 1$
, or -
•
 $n>1$
, and for each
$n>1$
, and for each
 $i<n$
$i<n$
-
(1)
 $g^*_i \notin H$
,
$g^*_i \notin H$
, -
(2)
 $i+1 <n \to $
(
$i+1 <n \to $
(
 $g^*_i \in K \iff g^*_{i+1} \in L$
),
$g^*_i \in K \iff g^*_{i+1} \in L$
),
-
We note the following fact.
Fact 2.3 [Reference Schupp39, Lemma 2.1].
Suppose that
![]() $ g^*_0 g^*_1 \cdots g^*_{n-1}$
and
$ g^*_0 g^*_1 \cdots g^*_{n-1}$
and
![]() $g^{**}_0 g^{**}_1 \cdots g^{**}_{m-1}$
are canonical representations of the same element in
$g^{**}_0 g^{**}_1 \cdots g^{**}_{m-1}$
are canonical representations of the same element in
![]() $K *_H L$
. Then
$K *_H L$
. Then
![]() $g^*_{0}, g^{**}_0 \in K$
, or
$g^*_{0}, g^{**}_0 \in K$
, or
![]() $g^*_{0}, g^{**}_0 \in L$
, and
$g^*_{0}, g^{**}_0 \in L$
, and
![]() $(g^*_{0})^{-1} g^{**}_0 \in H$
.
$(g^*_{0})^{-1} g^{**}_0 \in H$
.
Using the above fact, it is not difficult to verify that the canonical form is unique in the following sense.
Fact 2.4. Suppose that
![]() $ g^*_0 g^*_1 \cdots g^*_{n-1}$
and
$ g^*_0 g^*_1 \cdots g^*_{n-1}$
and
![]() $g^{**}_0 g^{**}_1 \cdots g^{**}_{m-1}$
are canonical representations of the same element in
$g^{**}_0 g^{**}_1 \cdots g^{**}_{m-1}$
are canonical representations of the same element in
![]() $K *_H L$
. Then
$K *_H L$
. Then
![]() $n = m$
, and there exist
$n = m$
, and there exist
![]() $h_0, h_1, h_2, \ldots , h_{n} \in H$
with
$h_0, h_1, h_2, \ldots , h_{n} \in H$
with ![]() such that
such that
Definition 2.5. Fix
![]() $g \in K *_H L$
distinct from
$g \in K *_H L$
distinct from ![]() , and the canonical representation
, and the canonical representation
![]() $g = g^*_0 g^*_1 \cdots g^*_{n-1}$
. We say that
$g = g^*_0 g^*_1 \cdots g^*_{n-1}$
. We say that
![]() $g^*_0 g^*_1 \cdots g^*_{n-1}$
is weakly cyclically reduced if
$g^*_0 g^*_1 \cdots g^*_{n-1}$
is weakly cyclically reduced if
-
•
 $n=1$
, or
$n=1$
, or -
• n is even, or
-
•
 $g^*_{n-1}g^*_0 \notin H$
, equivalently, g has no conjugate that has a canonical representation shorter than
$g^*_{n-1}g^*_0 \notin H$
, equivalently, g has no conjugate that has a canonical representation shorter than
 $n-1$
.
$n-1$
.
Recalling Fact 2.4, it is not difficult to see that the property of being weakly cyclically reduced is a property of the group element
![]() $g \in K *_H L$
, so it does not depend on the particular choice of the canonical representation
$g \in K *_H L$
, so it does not depend on the particular choice of the canonical representation
![]() $g= g^*_0 g^*_1 \cdots g^*_{n-1}$
.
$g= g^*_0 g^*_1 \cdots g^*_{n-1}$
.
Observation 2.6.
-
(1) If
 $g^*_0 g^*_1 \cdots g^*_{n-1}$
is a canonical representation of an element
$g^*_0 g^*_1 \cdots g^*_{n-1}$
is a canonical representation of an element  ,
,
 $n\geq 2$
, then g has a conjugate
$n\geq 2$
, then g has a conjugate
 $g'$
that has a canonical representation of length
$g'$
that has a canonical representation of length
 $m=1$
, or
$m=1$
, or
 $m=2k$
for some
$m=2k$
for some
 $k \geq 1$
. Moreover, each conjugate
$k \geq 1$
. Moreover, each conjugate
 $g"$
of g has length at least m.
$g"$
of g has length at least m. -
(2) If
 $g^*_0 g^*_1 \cdots g^*_{n-1}$
is a canonical representation of an element
$g^*_0 g^*_1 \cdots g^*_{n-1}$
is a canonical representation of an element  , n is even, and
, n is even, and
 $g'$
is a weakly cyclically reduced conjugate of g, then
$g'$
is a weakly cyclically reduced conjugate of g, then
 $g'$
has a canonical representation in the following form: where
$g'$
has a canonical representation in the following form: where $$\begin{align*}g' = x^{\prime}_i g^*_{i+1} g^*_{i+2} \cdots g^*_{n-1} g^*_{0} \cdots g^*_{i-1} x^{\prime\prime}_i, \end{align*}$$
$$\begin{align*}g' = x^{\prime}_i g^*_{i+1} g^*_{i+2} \cdots g^*_{n-1} g^*_{0} \cdots g^*_{i-1} x^{\prime\prime}_i, \end{align*}$$
-
• if
 $g^*_i \in K$
, then
$g^*_i \in K$
, then
 $x^{\prime }_i, x^{\prime \prime }_i \in K$
and
$x^{\prime }_i, x^{\prime \prime }_i \in K$
and
 $K \models x^{\prime \prime }_ix^{\prime }_i = g^*_i$
,
$K \models x^{\prime \prime }_ix^{\prime }_i = g^*_i$
, -
• if
 $g^*_i \in L$
, then
$g^*_i \in L$
, then
 $x^{\prime }_i, x^{\prime \prime }_i \in L$
and
$x^{\prime }_i, x^{\prime \prime }_i \in L$
and
 $L \models x^{\prime \prime }_ix^{\prime }_i = g^*_i$
.
$L \models x^{\prime \prime }_ix^{\prime }_i = g^*_i$
.
In particular, the length of any canonical representation of
 $g'$
is either n or
$g'$
is either n or
 $n+1$
.
$n+1$
. -
Definition 2.7 [Reference Lyndon and Schupp29, p. 286].
Let
![]() $H \leq K,L$
be groups such that
$H \leq K,L$
be groups such that
![]() $L \cap K = H$
, and fix
$L \cap K = H$
, and fix
![]() $R \subseteq K *_H L$
. We say that R is symmetrized if for every
$R \subseteq K *_H L$
. We say that R is symmetrized if for every
![]() $g \in R$
,
$g \in R$
,
-
(1)
 $g^{-1} \in R$
, and
$g^{-1} \in R$
, and -
(2) for each
 $g'$
that is conjugate to g and weakly cyclically reduced,
$g'$
that is conjugate to g and weakly cyclically reduced,
 $g' \in R$
.
$g' \in R$
.
Definition 2.8 [Reference Lyndon and Schupp29, p. 286].
Let
![]() $X \subseteq K *_H L$
, and
$X \subseteq K *_H L$
, and
![]() $\chi \in (0, 1)$
. We say that X satisfies
$\chi \in (0, 1)$
. We say that X satisfies
![]() $C'(\chi )$
, if whenever
$C'(\chi )$
, if whenever
-
(1)
 $g^*_{n-1} g^*_{n-2} \cdots g^*_1 g^*_{0}, g^{**}_0 g^{**}_1 \cdots g^{**}_{m-1} \in X$
,
$g^*_{n-1} g^*_{n-2} \cdots g^*_1 g^*_{0}, g^{**}_0 g^{**}_1 \cdots g^{**}_{m-1} \in X$
, -
(2)
 ,
, -
(3)
 $\ell < n,m$
, and
$\ell < n,m$
, and -
(4)
 $g^*_{\ell -1}g^*_{\ell -2} \cdots g^*_0g^{**}_0g^{**}_1 \cdots g^{**}_{\ell -1} \in H$
,
$g^*_{\ell -1}g^*_{\ell -2} \cdots g^*_0g^{**}_0g^{**}_1 \cdots g^{**}_{\ell -1} \in H$
,
then
![]() $\ell < \min (n,m) \cdot \chi $
, and moreover,
$\ell < \min (n,m) \cdot \chi $
, and moreover,
![]() $\min (n,m)> \frac {1}{\chi }$
.
$\min (n,m)> \frac {1}{\chi }$
.
Definition 2.9 [Reference Lyndon and Schupp29, p. 286].
Let
![]() $H,K,L$
be as in Definition 2.1, and let
$H,K,L$
be as in Definition 2.1, and let
![]() $g \in K *_H L$
. We say that the word
$g \in K *_H L$
. We say that the word
![]() $w_0w_1 \cdots w_{m-1}$
is a part of g if
$w_0w_1 \cdots w_{m-1}$
is a part of g if
-
(1)
 $w_0w_1 \cdots w_{m-1} \in K *_H L$
is in canonical form,
$w_0w_1 \cdots w_{m-1} \in K *_H L$
is in canonical form, -
(2) for some weakly cyclically reduced conjugate
 $g'$
of g, the word
$g'$
of g, the word
 $w_0w_1\cdots w_{m-1}$
is a subword of a canonical representation of
$w_0w_1\cdots w_{m-1}$
is a subword of a canonical representation of
 $g'$
(i.e., for some canonical representation
$g'$
(i.e., for some canonical representation
 $v_0 v_1 \cdots v_{n-1}$
of
$v_0 v_1 \cdots v_{n-1}$
of
 $g'$
and some
$g'$
and some
 $k \leq n-m$
, we have
$k \leq n-m$
, we have
 $v_k = w_0$
,
$v_k = w_0$
,
 $v_{k+1} = w_1, \ldots , v_{k+m-2} = w_{m-2}$
and
$v_{k+1} = w_1, \ldots , v_{k+m-2} = w_{m-2}$
and
 $v_{k+m-1} = w_{m-1}$
).
$v_{k+m-1} = w_{m-1}$
).
We cite the following lemma, which is our key technical tool borrowed from small cancellation theory.
Fact 2.10 [Reference Lyndon and Schupp29, Theorem 11.2].
Let
![]() $H \leq K,L$
be groups,
$H \leq K,L$
be groups,
![]() $K \cap L = H$
,
$K \cap L = H$
,
![]() $k\ge 6$
, and assume that
$k\ge 6$
, and assume that
![]() $R \subseteq K *_H L$
is symmetrized and satisfies
$R \subseteq K *_H L$
is symmetrized and satisfies
![]() $C'(\frac {1}{k})$
.
$C'(\frac {1}{k})$
.
Then, letting
![]() $N=\operatorname {\mathrm {ncl}}(R,K *_H L)$
be the normal subgroup generated by R, for every weakly cyclically reduced
$N=\operatorname {\mathrm {ncl}}(R,K *_H L)$
be the normal subgroup generated by R, for every weakly cyclically reduced
![]() $w \in N$
that is nontrivial (i.e.,
$w \in N$
that is nontrivial (i.e., ![]() ), there exist
), there exist
![]() $r \in R$
and a part p of r, which is also a part of w, and
$r \in R$
and a part p of r, which is also a part of w, and
![]() $\ell (p)> \frac {k-3}{k} \ell (r)$
.
$\ell (p)> \frac {k-3}{k} \ell (r)$
.
Corollary 2.11. If
![]() $H,K,L,R$
are as in Fact 2.10, then for the canonical projection map
$H,K,L,R$
are as in Fact 2.10, then for the canonical projection map
![]() $\pi : K \ast _H L \to (K \ast _H L)/N$
, it is the case that
$\pi : K \ast _H L \to (K \ast _H L)/N$
, it is the case that
![]() $\pi \mathbin \upharpoonright K$
and
$\pi \mathbin \upharpoonright K$
and
![]() $\pi \mathbin \upharpoonright L$
are injective, and
$\pi \mathbin \upharpoonright L$
are injective, and
![]() $ \pi "K \cap \pi "L = \pi "H$
(where
$ \pi "K \cap \pi "L = \pi "H$
(where
![]() $K,L$
are identified with the subgroups of
$K,L$
are identified with the subgroups of
![]() $K \ast _H L$
).
$K \ast _H L$
).
3 Finding the right amalgam
The main result of this section is Lemma 3.4 below. It originates from the lemma by G. Hesse appearing in the Appendix of [Reference Shelah40]. The lemma will serve as a building block in the recursive construction of Section 5.
Definition 3.1. Let
![]() $\varrho (x,y)$
denote the word
$\varrho (x,y)$
denote the word
![]() $xyx^2yx^3y \cdots x^{80}y$
.
$xyx^2yx^3y \cdots x^{80}y$
.
Note that
![]() $\ell (\varrho (x,y)) = 3320$
.
$\ell (\varrho (x,y)) = 3320$
.
Definition 3.2. For all
![]() $j<\omega $
and
$j<\omega $
and
![]() $x,y$
, we shall define a word
$x,y$
, we shall define a word
![]() $\varrho _j(x,y)$
over the alphabet
$\varrho _j(x,y)$
over the alphabet
![]() $\{x,y\}$
. First, define a sequence
$\{x,y\}$
. First, define a sequence
![]() $\langle n_j \mathrel {|} j <\omega \rangle $
of integers via
$\langle n_j \mathrel {|} j <\omega \rangle $
of integers via
![]() $n_j= 3320^j$
. Then, let
$n_j= 3320^j$
. Then, let
![]() $\varrho _j(x,y) = \varrho (x^{n_j},y^{n_j})$
, so that
$\varrho _j(x,y) = \varrho (x^{n_j},y^{n_j})$
, so that
![]() $\varrho _0=\varrho $
.
$\varrho _0=\varrho $
.
Definition 3.3. Let
![]() $G \leq H$
be a pair of groups.
$G \leq H$
be a pair of groups.
-
• Define an equivalence relation
 $\sim _{G}$
over H via where
$\sim _{G}$
over H via where $$ \begin{align*}a\sim_{G}b\text{ iff } a \in G b^{\pm 1} G,\end{align*} $$
$$ \begin{align*}a\sim_{G}b\text{ iff } a \in G b^{\pm 1} G,\end{align*} $$
 $G b^{\pm 1} G$
denotes the set
$G b^{\pm 1} G$
denotes the set
 $GbG \cup Gb^{-1}G$
.
$GbG \cup Gb^{-1}G$
.
-
• We say that G is a malnormal subgroup of H, and denote it by
 $G \mathrel {\leq _{\mathrm {m}}} H$
, if for all
$G \mathrel {\leq _{\mathrm {m}}} H$
, if for all  and
and
 $h\in H\setminus G$
, it is the case that
$h\in H\setminus G$
, it is the case that
 $h^{-1}gh \notin G$
.
$h^{-1}gh \notin G$
.
Note that
![]() $\mathrel {\leq _{\mathrm {m}}}$
is a transitive relation.
$\mathrel {\leq _{\mathrm {m}}}$
is a transitive relation.
Lemma 3.4. Let
![]() $H \leq K$
,
$H \leq K$
,
![]() $H \mathrel {\leq _{\mathrm {m}}} L$
be groups,
$H \mathrel {\leq _{\mathrm {m}}} L$
be groups,
![]() $K \cap L = H$
and suppose that we are given a system of quadruples
$K \cap L = H$
and suppose that we are given a system of quadruples
that satisfies the following two:
-
(1) for every
 $\sigma \in \Sigma $
,
$\sigma \in \Sigma $
,
 $b_\sigma \not \sim _H b^{\prime }_{\sigma }$
;
$b_\sigma \not \sim _H b^{\prime }_{\sigma }$
; -
(2) for all
 $\sigma \neq \sigma ^*$
in
$\sigma \neq \sigma ^*$
in
 $\Sigma $
, at least one of the following holds:
$\Sigma $
, at least one of the following holds:-
(⊝) a
 $a_\sigma \not \sim _H a_{\sigma ^*}$
(in K);
$a_\sigma \not \sim _H a_{\sigma ^*}$
(in K); -
(⊝) b
 $b_\sigma \not \sim _H b_{\sigma ^*}$
;
$b_\sigma \not \sim _H b_{\sigma ^*}$
; -
(⊝) c
 $b_\sigma = b_{\sigma ^*}$
and
$b_\sigma = b_{\sigma ^*}$
and
 $a_\sigma \neq a_{\sigma ^*}$
;
$a_\sigma \neq a_{\sigma ^*}$
; -
(⊝) d there are subgroups
 $H_\sigma \leq H$
and
$H_\sigma \leq H$
and
 $K_\sigma \leq K$
such that all of the following hold:
$K_\sigma \leq K$
such that all of the following hold:-
(i)
 $K_\sigma \cap H = H_\sigma $
;
$K_\sigma \cap H = H_\sigma $
; -
(ii)
 $a_\sigma , a_{\sigma ^*} \in K_\sigma \setminus H = K_\sigma \setminus H_\sigma $
;
$a_\sigma , a_{\sigma ^*} \in K_\sigma \setminus H = K_\sigma \setminus H_\sigma $
; -
(iii)
 $b_\sigma \not \sim _{H_\sigma }b_{\sigma ^*}$
(although typically
$b_\sigma \not \sim _{H_\sigma }b_{\sigma ^*}$
(although typically
 $b_\sigma \sim _{H}b_{\sigma ^*}$
);
$b_\sigma \sim _{H}b_{\sigma ^*}$
); -
(iv)
 $b_\sigma \not \sim _H b_{\sigma ^*}'$
;
$b_\sigma \not \sim _H b_{\sigma ^*}'$
; -
(v)
 $(K_\sigma \setminus H) \cdot (H\setminus K_\sigma ) \cdot (K_\sigma \setminus H) \subseteq (K \setminus H)$
.
$(K_\sigma \setminus H) \cdot (H\setminus K_\sigma ) \cdot (K_\sigma \setminus H) \subseteq (K \setminus H)$
.
-
-
Then, letting R be the symmetric closure of
![]() $\{h_\sigma ^{-1}\varrho (b_\sigma a_\sigma , b_\sigma 'a_\sigma )\mathrel {|} \sigma \in \Sigma \}$
,
$\{h_\sigma ^{-1}\varrho (b_\sigma a_\sigma , b_\sigma 'a_\sigma )\mathrel {|} \sigma \in \Sigma \}$
,
![]() $M = K \ast _H L$
,
$M = K \ast _H L$
,
![]() $N= \operatorname {\mathrm {ncl}}(R,M)$
be the generated normal subgroup and
$N= \operatorname {\mathrm {ncl}}(R,M)$
be the generated normal subgroup and
![]() $M^* = M / N$
, all of the following hold:
$M^* = M / N$
, all of the following hold:
-
(A) R satisfies the condition
 $C'(\frac {1}{10}$
), and consequently, the group
$C'(\frac {1}{10}$
), and consequently, the group
 $M^*$
embeds both K and L with and
$M^*$
embeds both K and L with and $$ \begin{align*}M^* \models K \cap L = H\end{align*} $$
$$ \begin{align*}M^* \models K \cap L = H\end{align*} $$
 $K \cup L$
generates
$K \cup L$
generates
 $M^*$
. Moreover, the set
$M^*$
. Moreover, the set
 $R^{+}$
defined to be the symmetric closure of also satisfies
$R^{+}$
defined to be the symmetric closure of also satisfies $$ \begin{align*}\{h_\sigma^{-1}\varrho(b_\sigma a_\sigma, b_\sigma'a_\sigma), \ \varrho_j(b_\sigma a_\sigma, b_\sigma'a_\sigma) \mathrel{|} \sigma \in \Sigma, \ j \in \omega \setminus \{0\}\}\end{align*} $$
$$ \begin{align*}\{h_\sigma^{-1}\varrho(b_\sigma a_\sigma, b_\sigma'a_\sigma), \ \varrho_j(b_\sigma a_\sigma, b_\sigma'a_\sigma) \mathrel{|} \sigma \in \Sigma, \ j \in \omega \setminus \{0\}\}\end{align*} $$
 $C'(\frac {1}{10}$
);
$C'(\frac {1}{10}$
);
-
(B)
 $K \mathrel {\leq _{\mathrm {m}}} M^*$
, and if
$K \mathrel {\leq _{\mathrm {m}}} M^*$
, and if
 $H \mathrel {\leq _{\mathrm {m}}} K$
, then
$H \mathrel {\leq _{\mathrm {m}}} K$
, then
 $L \mathrel {\leq _{\mathrm {m}}} M^*$
;
$L \mathrel {\leq _{\mathrm {m}}} M^*$
; -
(C) for all
 $b,b^* \in L \setminus H$
and
$b,b^* \in L \setminus H$
and
 $z \in K \setminus H$
, if
$z \in K \setminus H$
, if
 $b\sim _H b^*$
, then
$b\sim _H b^*$
, then
 $M^*\models b^*z \not \sim _K bzbz$
;
$M^*\models b^*z \not \sim _K bzbz$
; -
(D) if
 $b,b' \in L \setminus H$
,
$b,b' \in L \setminus H$
,
 $a \in K \setminus H$
, then
$a \in K \setminus H$
, then
 $M^* \models bab' \notin K$
,
$M^* \models bab' \notin K$
,
 $ba \notin K$
(and similarly, the parallel statement with interchanging K and L);
$ba \notin K$
(and similarly, the parallel statement with interchanging K and L); -
(E) if
 $a,a' \in K \setminus H$
,
$a,a' \in K \setminus H$
,
 $a \not \sim _{H'} a'$
for subgroups
$a \not \sim _{H'} a'$
for subgroups
 $H' \leq H$
and
$H' \leq H$
and
 $L' \leq L$
such that
$L' \leq L$
such that
 $L' \cap K = L' \cap H = H'$
, then
$L' \cap K = L' \cap H = H'$
, then
 $a \not \sim _{L'} a'$
holds too (in
$a \not \sim _{L'} a'$
holds too (in
 $M^*$
);
$M^*$
); -
(F) similarly, if
 $b , b' \in L \setminus H$
,
$b , b' \in L \setminus H$
,
 $b \not \sim _{H'} b'$
for subgroups
$b \not \sim _{H'} b'$
for subgroups
 $H' \leq H$
and
$H' \leq H$
and
 $K' \leq K$
such that
$K' \leq K$
such that
 $K' \cap L = K' \cap H = H'$
, then
$K' \cap L = K' \cap H = H'$
, then
 $b \not \sim _{K'} b'$
holds (in
$b \not \sim _{K'} b'$
holds (in
 $M^*$
);
$M^*$
); -
(G) if K and L are torsion-free, then so is
 $M^*$
.
$M^*$
.
Proof. First we note that for all
![]() $a \in K \setminus H$
,
$a \in K \setminus H$
,
![]() $b,b' \in L \setminus H$
, the word
$b,b' \in L \setminus H$
, the word
![]() $\varrho (ba, b'a)$
is an alternating word (over the union of
$\varrho (ba, b'a)$
is an alternating word (over the union of
![]() $K\setminus H$
and
$K\setminus H$
and
![]() $L \setminus H$
) of length
$L \setminus H$
) of length
![]() $6640$
.
$6640$
.
-
(A) By Corollary 2.11 (and
 $R \subseteq R^+$
), it is enough to argue that
$R \subseteq R^+$
), it is enough to argue that
 $R^+$
satisfies
$R^+$
satisfies
 $C'(\frac {1}{10})$
. To this end, fix two elements
$C'(\frac {1}{10})$
. To this end, fix two elements
 $g \neq g^*$
in
$g \neq g^*$
in
 $R^+$
, as well as some canonical representations By Clause (2) of Observation 2.6, there are
$R^+$
, as well as some canonical representations By Clause (2) of Observation 2.6, there are $$ \begin{align*}\begin{array}{lll} g&=&g_0g_1\cdots g_{n-1},\\ g^*&=&g^*_0g^*_1\cdots g_{m-1}^*. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lll} g&=&g_0g_1\cdots g_{n-1},\\ g^*&=&g^*_0g^*_1\cdots g_{m-1}^*. \end{array}\end{align*} $$
 $i,i^* \in \omega $
such that
$i,i^* \in \omega $
such that
 $n \in \{6640 n_i, 6640n_i+1\}$
,
$n \in \{6640 n_i, 6640n_i+1\}$
,
 $m \in \{6640 n_{i^*}, 6640n_{i^*}+1\}$
.
$m \in \{6640 n_{i^*}, 6640n_{i^*}+1\}$
.
Let
 $l \in \omega $
, and assume that (*)so we have to show that
$l \in \omega $
, and assume that (*)so we have to show that $$ \begin{align} \bigwedge_{k\le l}(K \ast_H L \models g^{-1}_{k-1}g^{-1}_{k-2}\cdots g_0^{-1}g^*_0g^*_1\cdots g^*_{k-1} \in H), \end{align} $$
$$ \begin{align} \bigwedge_{k\le l}(K \ast_H L \models g^{-1}_{k-1}g^{-1}_{k-2}\cdots g_0^{-1}g^*_0g^*_1\cdots g^*_{k-1} \in H), \end{align} $$
 $l < 664 \cdot \min (n_i,n_{i^*})$
.
$l < 664 \cdot \min (n_i,n_{i^*})$
.
Assume on the contrary that
 $l \geq 664\cdot n_i$
. We can choose
$l \geq 664\cdot n_i$
. We can choose
 $\sigma \in \Sigma $
,
$\sigma \in \Sigma $
,
 ${\varepsilon } \in \{1,-1\}$
, such that letting
${\varepsilon } \in \{1,-1\}$
, such that letting
 $r= h_\sigma ^{-1}\varrho _{n_i}(b_\sigma a_\sigma , b_\sigma 'a_\sigma )$
, g is a weakly cyclically reduced conjugate of
$r= h_\sigma ^{-1}\varrho _{n_i}(b_\sigma a_\sigma , b_\sigma 'a_\sigma )$
, g is a weakly cyclically reduced conjugate of
 $r^{\varepsilon } = (h_\sigma ^{-1}\varrho _{n_i}(b_\sigma a_\sigma , b_\sigma 'a_\sigma ))^{\varepsilon }$
if
$r^{\varepsilon } = (h_\sigma ^{-1}\varrho _{n_i}(b_\sigma a_\sigma , b_\sigma 'a_\sigma ))^{\varepsilon }$
if
 $n_i = 0$
, or of
$n_i = 0$
, or of
 $r^{\varepsilon } = (\varrho _{n_i}(b_\sigma a_\sigma , b_\sigma 'a_\sigma ))^{{\varepsilon }}$
, and similarly for
$r^{\varepsilon } = (\varrho _{n_i}(b_\sigma a_\sigma , b_\sigma 'a_\sigma ))^{{\varepsilon }}$
, and similarly for
 $g^*$
,
$g^*$
,
 $r^*$
and
$r^*$
and
 $\sigma ^*$
,
$\sigma ^*$
,
 ${\varepsilon }^*$
. If we fix the canonical representations where
${\varepsilon }^*$
. If we fix the canonical representations where $$ \begin{align*}r = u_0u_1 \cdots u_{6640 n_i-1},\end{align*} $$
$$ \begin{align*}r = u_0u_1 \cdots u_{6640 n_i-1},\end{align*} $$
 $u_j \in \{b_\sigma ,b_\sigma ',a_\sigma ,h_\sigma ^{-1}b_\sigma \}$
, and similarly then again recalling Observation 2.6(2), we can assume that there exist
$u_j \in \{b_\sigma ,b_\sigma ',a_\sigma ,h_\sigma ^{-1}b_\sigma \}$
, and similarly then again recalling Observation 2.6(2), we can assume that there exist $$ \begin{align*}r^* = u^*_0u^*_1 \cdots u^*_{6640 n_{i^*}-1},\end{align*} $$
$$ \begin{align*}r^* = u^*_0u^*_1 \cdots u^*_{6640 n_{i^*}-1},\end{align*} $$
 $j < 6640 n_i$
,
$j < 6640 n_i$
,
 $j^* <6640n_{i^*}$
, such that whenever
$j^* <6640n_{i^*}$
, such that whenever
 $0 < k < 6640 n_i-1$
, then
$0 < k < 6640 n_i-1$
, then
 $g_k = u^{\varepsilon }_{j+ {\varepsilon } k}$
, and if
$g_k = u^{\varepsilon }_{j+ {\varepsilon } k}$
, and if
 $0<k < 6640 n_{i^*}-1$
, then
$0<k < 6640 n_{i^*}-1$
, then
 $g^*_k = (u^*_{j^* + {\varepsilon }^* k})^{{\varepsilon }^*}$
.
$g^*_k = (u^*_{j^* + {\varepsilon }^* k})^{{\varepsilon }^*}$
.
We first observe that
 $i = i^*$
, since otherwise if, say,
$i = i^*$
, since otherwise if, say,
 $i<i^*$
did hold, then for some
$i<i^*$
did hold, then for some
 $1 \leq k,k' \leq 81 n_i$
with
$1 \leq k,k' \leq 81 n_i$
with
 $u_{j + {\varepsilon } k} =b_\sigma $
,
$u_{j + {\varepsilon } k} =b_\sigma $
,
 $u_{j + {\varepsilon } k'} =b^{\prime }_\sigma $
, while
$u_{j + {\varepsilon } k'} =b^{\prime }_\sigma $
, while
 $u^*_{j + {\varepsilon } k} = u^*_{j + {\varepsilon } k'} \in \{b_{\sigma ^*}, b^{\prime }_{\sigma ^*}\}$
, and so by (*), we get contradicting
$u^*_{j + {\varepsilon } k} = u^*_{j + {\varepsilon } k'} \in \{b_{\sigma ^*}, b^{\prime }_{\sigma ^*}\}$
, and so by (*), we get contradicting $$ \begin{align*}b_\sigma = u_{j + {\varepsilon} k} \sim_H u^*_{j + {\varepsilon} k} = u^*_{j + {\varepsilon} k'} \sim_H u_{j + {\varepsilon} k'} =b_\sigma',\end{align*} $$
$$ \begin{align*}b_\sigma = u_{j + {\varepsilon} k} \sim_H u^*_{j + {\varepsilon} k} = u^*_{j + {\varepsilon} k'} \sim_H u_{j + {\varepsilon} k'} =b_\sigma',\end{align*} $$
 $b_\sigma \not \sim _H b_\sigma '$
. From now on, n will denote the common value of
$b_\sigma \not \sim _H b_\sigma '$
. From now on, n will denote the common value of
 $n_i = n_{i^*}$
.
$n_i = n_{i^*}$
.
Now note that
 $b_\sigma \sim _H b_{\sigma ^*}$
: there is a k with
$b_\sigma \sim _H b_{\sigma ^*}$
: there is a k with
 $1 \leq k \leq 10 n$
such that
$1 \leq k \leq 10 n$
such that
 $u_{j + {\varepsilon } k} \in \{b_\sigma , h^{-1}_\sigma b_\sigma \}$
, and
$u_{j + {\varepsilon } k} \in \{b_\sigma , h^{-1}_\sigma b_\sigma \}$
, and
 $u^*_{j^* + {\varepsilon }^* k} \in \{b_{\sigma ^*}, h^{-1}_{\sigma ^*}b_{\sigma ^*}\}$
, so by (*) for some
$u^*_{j^* + {\varepsilon }^* k} \in \{b_{\sigma ^*}, h^{-1}_{\sigma ^*}b_{\sigma ^*}\}$
, so by (*) for some
 $h \in H$
, we have
$h \in H$
, we have
 $b^{-{\varepsilon }}_\sigma h b^{{\varepsilon }^*}_{\sigma ^*} \in H$
, implying that
$b^{-{\varepsilon }}_\sigma h b^{{\varepsilon }^*}_{\sigma ^*} \in H$
, implying that
 $b_\sigma \sim _H b_{\sigma ^*}$
. Similarly, for some
$b_\sigma \sim _H b_{\sigma ^*}$
. Similarly, for some
 $k^\bullet $
,
$k^\bullet $
,
 $1 \leq k^\bullet \leq 2 n$
,
$1 \leq k^\bullet \leq 2 n$
,
 $u_{j + {\varepsilon } k^\bullet } = a_\sigma $
, and
$u_{j + {\varepsilon } k^\bullet } = a_\sigma $
, and
 $u^*_{j^* + {\varepsilon }^* k^\bullet } = a_{\sigma ^*}$
, and by the same line of reasoning,
$u^*_{j^* + {\varepsilon }^* k^\bullet } = a_{\sigma ^*}$
, and by the same line of reasoning,
 $a_\sigma \sim _H a_{\sigma ^*}$
.
$a_\sigma \sim _H a_{\sigma ^*}$
.We clearly get that
 $(\boxminus )$
either
$(\boxminus )$
either
 $(\circleddash )_c$
, or
$(\circleddash )_c$
, or
 $(\circleddash )_d$
, or
$(\circleddash )_d$
, or
 $\sigma = \sigma ^*$
holds, and in each case,
$\sigma = \sigma ^*$
holds, and in each case,
 $b_\sigma \not \sim _H b_{\sigma ^*}'$
.
$b_\sigma \not \sim _H b_{\sigma ^*}'$
.Now, note that if
 $j \neq j^*$
or
$j \neq j^*$
or
 ${\varepsilon } \neq {\varepsilon }^*$
, then there exists k with
${\varepsilon } \neq {\varepsilon }^*$
, then there exists k with
 $1 \leq k <500 n$
such that
$1 \leq k <500 n$
such that
 $u_{j + {\varepsilon } k} \in \{b_\sigma , h_\sigma ^{-1}b_\sigma \}$
, and
$u_{j + {\varepsilon } k} \in \{b_\sigma , h_\sigma ^{-1}b_\sigma \}$
, and
 $u^*_{j^* + {\varepsilon }^* k} = b^{\prime }_{\sigma ^*} = b_\sigma '$
, and for some
$u^*_{j^* + {\varepsilon }^* k} = b^{\prime }_{\sigma ^*} = b_\sigma '$
, and for some
 $h \in H$
, we have
$h \in H$
, we have
 $b_\sigma ^{-{\varepsilon }} h(b^{\prime }_{\sigma ^*})^{{\varepsilon }^*} \in H$
(or
$b_\sigma ^{-{\varepsilon }} h(b^{\prime }_{\sigma ^*})^{{\varepsilon }^*} \in H$
(or
 $(h_\sigma ^{-1}b_\sigma )^{-{\varepsilon }} h(b^{\prime }_{\sigma ^*})^{{\varepsilon }^*}$
), so
$(h_\sigma ^{-1}b_\sigma )^{-{\varepsilon }} h(b^{\prime }_{\sigma ^*})^{{\varepsilon }^*}$
), so
 $b_\sigma \sim _H b_{\sigma ^*}'$
, contradicting
$b_\sigma \sim _H b_{\sigma ^*}'$
, contradicting
 $(\boxminus )$
. Therefore, hereafter, we can assume that
$(\boxminus )$
. Therefore, hereafter, we can assume that
 $j = j^*$
and
$j = j^*$
and
 ${\varepsilon } = {\varepsilon }^*$
.
${\varepsilon } = {\varepsilon }^*$
.We now divide our analysis into a few cases and subcases:
-
▸ If either
 $(\circleddash )_c$
or
$(\circleddash )_c$
or
 $\sigma = \sigma ^*$
, then necessarily,
$\sigma = \sigma ^*$
, then necessarily,
 $b_\sigma = b_{\sigma ^*}$
and
$b_\sigma = b_{\sigma ^*}$
and
 $b_\sigma ' = b_{\sigma ^*}'$
. But now for some k with
$b_\sigma ' = b_{\sigma ^*}'$
. But now for some k with
 $1\leq k \leq 10n$
,
$1\leq k \leq 10n$
,
 $g_k = g^*_k = b_\sigma ^\varepsilon $
, so for we have
$g_k = g^*_k = b_\sigma ^\varepsilon $
, so for we have $$ \begin{align*}h = g^{-1}_{k-1}g^{-1}_{k-2} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k-1} \in H,\end{align*} $$
but then
$$ \begin{align*}h = g^{-1}_{k-1}g^{-1}_{k-2} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k-1} \in H,\end{align*} $$
but then $$ \begin{align*}g^{-1}_k h g^*_k \in H,\end{align*} $$
$$ \begin{align*}g^{-1}_k h g^*_k \in H,\end{align*} $$
 $H \mathrel {\leq _{\mathrm {m}}} L$
together with
$H \mathrel {\leq _{\mathrm {m}}} L$
together with
 $b_\sigma \in L \setminus H$
imply that
$b_\sigma \in L \setminus H$
imply that  .
.
-
▸▸ If
 $\sigma = \sigma ^*$
, then invoking Observation 2.6(2) again (and recalling that g and
$\sigma = \sigma ^*$
, then invoking Observation 2.6(2) again (and recalling that g and
 $g^*$
are cyclically reduced conjugates of
$g^*$
are cyclically reduced conjugates of
 $h^{-1}_\sigma \varrho (b_\sigma a_\sigma , b_\sigma 'a_\sigma )$
), it is straightforward to check that
$h^{-1}_\sigma \varrho (b_\sigma a_\sigma , b_\sigma 'a_\sigma )$
), it is straightforward to check that
 $j = j^*$
and
$j = j^*$
and
 ${\varepsilon } = {\varepsilon }^*$
imply
${\varepsilon } = {\varepsilon }^*$
imply
 $g = g^*$
, which is a contradiction.
$g = g^*$
, which is a contradiction. -
▸▸ If
 $\sigma \neq \sigma ^*$
and
$\sigma \neq \sigma ^*$
and
 $a_\sigma \neq a_{\sigma ^*}$
, then
$a_\sigma \neq a_{\sigma ^*}$
, then  implies that and in the following step (conjugating by
implies that and in the following step (conjugating by
 $b_\sigma =b_{\sigma ^*}$
again), we get a contradiction.
$b_\sigma =b_{\sigma ^*}$
again), we get a contradiction.
-
-
▸ If the pair
 $\sigma $
,
$\sigma $
,
 $\sigma ^*$
satisfies condition
$\sigma ^*$
satisfies condition
 $(\circleddash )_d$
, then we argue as follows. First, we claim that the there exists a k with
$(\circleddash )_d$
, then we argue as follows. First, we claim that the there exists a k with
 $1 \leq k < 10n+2$
such that following three hold:
$1 \leq k < 10n+2$
such that following three hold:-
(⊠)1
 $g_k = u_{j + {\varepsilon } k}^{\varepsilon } = a^{\varepsilon }_\sigma $
,
$g_k = u_{j + {\varepsilon } k}^{\varepsilon } = a^{\varepsilon }_\sigma $
, -
(⊠)2
 $g^*_k = (u^*_{j + {\varepsilon } k})^{\varepsilon } = a^{{\varepsilon }}_{\sigma ^*}$
,
$g^*_k = (u^*_{j + {\varepsilon } k})^{\varepsilon } = a^{{\varepsilon }}_{\sigma ^*}$
, -
(⊠)3
 $h = g^{-1}_{k-1}g^{-1}_{k-2} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k-1} \in H \setminus K' = H \setminus H'$
.
$h = g^{-1}_{k-1}g^{-1}_{k-2} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k-1} \in H \setminus K' = H \setminus H'$
.
As before, for some
 $k^\bullet < 10n$
, we have
$k^\bullet < 10n$
, we have
 $u^{\varepsilon }_{j + {\varepsilon } k^\bullet } = a^{\varepsilon }_\sigma $
, and
$u^{\varepsilon }_{j + {\varepsilon } k^\bullet } = a^{\varepsilon }_\sigma $
, and
 $(u^*_{j + {\varepsilon } k^\bullet })^{\varepsilon } = a^{{\varepsilon }}_{\sigma ^*}$
,
$(u^*_{j + {\varepsilon } k^\bullet })^{\varepsilon } = a^{{\varepsilon }}_{\sigma ^*}$
,
 $u_{j + {\varepsilon } (k^\bullet +1)}^{\varepsilon } = b^{\varepsilon }_\sigma $
, and
$u_{j + {\varepsilon } (k^\bullet +1)}^{\varepsilon } = b^{\varepsilon }_\sigma $
, and
 $u^*_{j + {\varepsilon } (k^\bullet +1)} = b^{{\varepsilon }}_{\sigma ^*}$
. Suppose that Then
$u^*_{j + {\varepsilon } (k^\bullet +1)} = b^{{\varepsilon }}_{\sigma ^*}$
. Suppose that Then $$ \begin{align*}h = g^{-1}_{k^\bullet-1}g^{-1}_{k^\bullet-2} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k^\bullet-1} \in H'.\end{align*} $$
$$ \begin{align*}h = g^{-1}_{k^\bullet-1}g^{-1}_{k^\bullet-2} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k^\bullet-1} \in H'.\end{align*} $$
 $h' = a^{-{\varepsilon }}_\sigma h a^{\varepsilon }_{\sigma ^*} \in K' H' K' = K'$
, and by our indirect assumptions
$h' = a^{-{\varepsilon }}_\sigma h a^{\varepsilon }_{\sigma ^*} \in K' H' K' = K'$
, and by our indirect assumptions
 $a^{-{\varepsilon }}_\sigma h a^{\varepsilon }_\sigma \in H$
, so
$a^{-{\varepsilon }}_\sigma h a^{\varepsilon }_\sigma \in H$
, so
 $h'$
lies in the intersection
$h'$
lies in the intersection
 $K' \cap H = H'$
. Now so by
$K' \cap H = H'$
. Now so by $$ \begin{align*}u_{j + {\varepsilon} (k^\bullet+1)}^{-{\varepsilon}} h' u^{{\varepsilon}}_{j + {\varepsilon} (k^\bullet+1)} = b^{-{\varepsilon}}_\sigma h' b^{\varepsilon}_{\sigma^*} \in b^{-{\varepsilon}}_\sigma H' b^{{\varepsilon}}_{\sigma^*},\end{align*} $$
$$ \begin{align*}u_{j + {\varepsilon} (k^\bullet+1)}^{-{\varepsilon}} h' u^{{\varepsilon}}_{j + {\varepsilon} (k^\bullet+1)} = b^{-{\varepsilon}}_\sigma h' b^{\varepsilon}_{\sigma^*} \in b^{-{\varepsilon}}_\sigma H' b^{{\varepsilon}}_{\sigma^*},\end{align*} $$
 $(\circleddash )_d$
(iii), this product is not in
$(\circleddash )_d$
(iii), this product is not in
 $H'$
; thus, we can assume that some
$H'$
; thus, we can assume that some
 $k<10n +2$
satisfies
$k<10n +2$
satisfies
 $(\boxtimes )_1$
–
$(\boxtimes )_1$
–
 $(\boxtimes )_2$
.But then using
$(\boxtimes )_2$
.But then using
 $a_\sigma , a_{\sigma ^*} \in K' \setminus H'$
, This is a contradiction.
$a_\sigma , a_{\sigma ^*} \in K' \setminus H'$
, This is a contradiction. $$ \begin{align*} g^{-1}_{k}g^{-1}_{k} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k}&= a_\sigma^{-{\varepsilon}}h a_{\sigma^*}^{{\varepsilon}}\\&\in (K' \setminus H) \cdot (H \setminus H') \cdot (K' \setminus H) \subseteq K \setminus H. \end{align*} $$
$$ \begin{align*} g^{-1}_{k}g^{-1}_{k} \cdots g^{-1}_0g^*_0g^*_1 \cdots g^*_{k}&= a_\sigma^{-{\varepsilon}}h a_{\sigma^*}^{{\varepsilon}}\\&\in (K' \setminus H) \cdot (H \setminus H') \cdot (K' \setminus H) \subseteq K \setminus H. \end{align*} $$
-
-
-
(B) Fix
 , and
, and
 $z \in M^* \setminus K$
, with a canonical form
$z \in M^* \setminus K$
, with a canonical form
 $z = z_0z_1 \cdots z_{m-1}$
satisfying it does not contain any subsequence
$z = z_0z_1 \cdots z_{m-1}$
satisfying it does not contain any subsequence
 $z_{\sigma _0}z_{\sigma _0+1}\cdots z_{\sigma _0+j-1}$
that is a subsequence of a canonical form of an element
$z_{\sigma _0}z_{\sigma _0+1}\cdots z_{\sigma _0+j-1}$
that is a subsequence of a canonical form of an element
 $r \in R$
, where
$r \in R$
, where
 $j> \frac {6640}{2}+1$
(we can assume this, since otherwise, we could insert the entire sequence of the inverse of this fixed canonical form of r). Now suppose that
$j> \frac {6640}{2}+1$
(we can assume this, since otherwise, we could insert the entire sequence of the inverse of this fixed canonical form of r). Now suppose that  holds in
holds in
 $M^*$
; that is, W.l.o.g.
$M^*$
; that is, W.l.o.g. $$\begin{align*}M \models zgz^{-1}g' \in N. \end{align*}$$
$$\begin{align*}M \models zgz^{-1}g' \in N. \end{align*}$$
 $z_0,z_{m-1} \in L$
(thus m is odd), since otherwise, we can replace g with
$z_0,z_{m-1} \in L$
(thus m is odd), since otherwise, we can replace g with  , and
, and
 $g'$
with
$g'$
with  . Now as
. Now as
 $g,g' \in K$
, if
$g,g' \in K$
, if
 $g,g'$
are not in H, then the product
$g,g'$
are not in H, then the product
 $z_0z_1 \cdots z_{m-1}gz_{m-1}^{-1} \cdots z_0^{-1}g'$
is in a weakly cyclically reduced form; otherwise, if
$z_0z_1 \cdots z_{m-1}gz_{m-1}^{-1} \cdots z_0^{-1}g'$
is in a weakly cyclically reduced form; otherwise, if
 $g \in H$
, then
$g \in H$
, then
 $z_{m-1}gz_{m-1}^{-1} \in L \setminus H$
(here, we use
$z_{m-1}gz_{m-1}^{-1} \in L \setminus H$
(here, we use
 $H \mathrel {\leq _{\mathrm {m}}} L$
and that
$H \mathrel {\leq _{\mathrm {m}}} L$
and that
 $z_{m-1} \in L \setminus H$
), and similarly,
$z_{m-1} \in L \setminus H$
), and similarly,
 $g' \in H$
implies
$g' \in H$
implies
 $z_0^{-1}g'z_0 \in L \setminus H$
. So by these reductions, we obtain a product in a cyclically reduced form of length
$z_0^{-1}g'z_0 \in L \setminus H$
. So by these reductions, we obtain a product in a cyclically reduced form of length
 $2m+2$
or
$2m+2$
or
 $2m$
, or
$2m$
, or
 $2m-2$
. A cyclic conjugate of this word contains a long (
$2m-2$
. A cyclic conjugate of this word contains a long (
 $> 7/10$
) subword of some canonical form of an
$> 7/10$
) subword of some canonical form of an
 $r \in R$
. By our assumptions on z (not containing more than half of a canonical representation of r), this has to involve either g or
$r \in R$
. By our assumptions on z (not containing more than half of a canonical representation of r), this has to involve either g or
 $g'$
; in fact, either the word
$g'$
; in fact, either the word
 $z_{j}z_{j+1} \cdots z_{m-1}gz^{-1}_{m-1} z^{-1}_{m-2} \cdots z^{-1}_{j}$
(or
$z_{j}z_{j+1} \cdots z_{m-1}gz^{-1}_{m-1} z^{-1}_{m-2} \cdots z^{-1}_{j}$
(or
 $z_{j}z_{j+1} \cdots z_{m-2} (z_{m-1}gz^{-1}_{m-1}) z^{-1}_{m-2} \cdots z^{-1}_{j}$
if
$z_{j}z_{j+1} \cdots z_{m-2} (z_{m-1}gz^{-1}_{m-1}) z^{-1}_{m-2} \cdots z^{-1}_{j}$
if
 $g \in H$
), or
$g \in H$
), or
 $z^{-1}_{j_*}z^{-1}_{j_*-1} \cdots z^{-1}_{0}g'z_{0} z_{1} \cdots z_{j_*}$
contains a long (
$z^{-1}_{j_*}z^{-1}_{j_*-1} \cdots z^{-1}_{0}g'z_{0} z_{1} \cdots z_{j_*}$
contains a long (
 $>2/10$
fraction) subword of a canonical form of some
$>2/10$
fraction) subword of a canonical form of some
 $r \in R$
(in the latter case, if
$r \in R$
(in the latter case, if
 $g' \in H$
, then of course we mean the word
$g' \in H$
, then of course we mean the word
 $z^{-1}_{j_*}z^{-1}_{j_*-1} \cdots (z^{-1}_{0}g'z_{0}) z_{1} \cdots z_{j_*}$
). But this is impossible since in any
$z^{-1}_{j_*}z^{-1}_{j_*-1} \cdots (z^{-1}_{0}g'z_{0}) z_{1} \cdots z_{j_*}$
). But this is impossible since in any
 $r = r_0r_1 \cdots r_{n-1} \in R$
(
$r = r_0r_1 \cdots r_{n-1} \in R$
(
 $n \in \{6640,6641\}$
) at any fixed
$n \in \{6640,6641\}$
) at any fixed
 $t \in [\frac {6640}{10}, \frac {6640 \cdot 9}{10}]$
, there exists
$t \in [\frac {6640}{10}, \frac {6640 \cdot 9}{10}]$
, there exists
 $k < 250$
such that (for some
$k < 250$
such that (for some
 $\sigma \in \Sigma $
)
$\sigma \in \Sigma $
)
 $r_{t-k} \in Hb_\sigma ^{\pm 1}H$
,
$r_{t-k} \in Hb_\sigma ^{\pm 1}H$
,
 $r_{t+k} \in H(b_\sigma ')^{\pm 1}H$
, and so
$r_{t+k} \in H(b_\sigma ')^{\pm 1}H$
, and so
 $r_{t-k} \not \sim _H r_{t+k}$
, while
$r_{t-k} \not \sim _H r_{t+k}$
, while
 $z_k$
,
$z_k$
,
 $z_k^{-1}$
are clearly
$z_k^{-1}$
are clearly
 $\sim _H$
-related.
$\sim _H$
-related.
-
(C) Suppose otherwise, for example, for some
 $k,k' \in K$
either or
$k,k' \in K$
either or Observe that after performing the cancellations in the free amalgam M and writing
Observe that after performing the cancellations in the free amalgam M and writing
 $y = y_0y_1\cdots y_{m-1}$
as a reduced (alternating) word, in both cases (regardless of whether
$y = y_0y_1\cdots y_{m-1}$
as a reduced (alternating) word, in both cases (regardless of whether
 $k,k' \in H$
), there is at most one j for which
$k,k' \in H$
), there is at most one j for which
 $y_j \in L \setminus H$
and
$y_j \in L \setminus H$
and
 $y_j \not \sim _H b$
. Now possibly replacing
$y_j \not \sim _H b$
. Now possibly replacing
 $y_0y_1 \cdots y_{m-1}$
with a weakly cyclically reduced conjugate of it (if the reduced form of
$y_0y_1 \cdots y_{m-1}$
with a weakly cyclically reduced conjugate of it (if the reduced form of
 $y_0y_1 \cdots y_{m-1}$
is not weakly cyclically reduced), this clause remains true (and the resulting word similarly belongs to N in M). It is not difficult to see that there exists at least one
$y_0y_1 \cdots y_{m-1}$
is not weakly cyclically reduced), this clause remains true (and the resulting word similarly belongs to N in M). It is not difficult to see that there exists at least one
 $j'$
such that
$j'$
such that
 $y_{j'} \sim _H b$
. Again,
$y_{j'} \sim _H b$
. Again,
 $y_0y_1 \cdots y_{m-1}$
(or a cyclical permutation of it) contains a long subword of a canonical form of some
$y_0y_1 \cdots y_{m-1}$
(or a cyclical permutation of it) contains a long subword of a canonical form of some
 $r \in R$
, but any such subword (if longer than
$r \in R$
, but any such subword (if longer than
 $400$
) contains at least two-two occurrences of
$400$
) contains at least two-two occurrences of
 $b_\sigma $
and
$b_\sigma $
and
 $b_\sigma '$
(for some
$b_\sigma '$
(for some
 $\sigma \in \Sigma $
), and b cannot be
$\sigma \in \Sigma $
), and b cannot be
 $\sim _H$
-equivalent with both
$\sim _H$
-equivalent with both
 $b_\sigma $
and
$b_\sigma $
and
 $b_\sigma '$
(since
$b_\sigma '$
(since
 $b_\sigma \not \sim _H b_\sigma '$
).
$b_\sigma \not \sim _H b_\sigma '$
).
-
(D) This is the same as above. Assuming that
 $M^* \models bab' \in K$
, then for some
$M^* \models bab' \in K$
, then for some
 $a' \in K$
,
$a' \in K$
,  , so Now if
, so Now if $$ \begin{align*}M \models bab'a' \in N.\end{align*} $$
$$ \begin{align*}M \models bab'a' \in N.\end{align*} $$
 $a' \in K \setminus H$
, then the word
$a' \in K \setminus H$
, then the word
 $bab'a'$
is weakly cyclically reduced, so any weakly cyclically reduced conjugate to it is of length either
$bab'a'$
is weakly cyclically reduced, so any weakly cyclically reduced conjugate to it is of length either
 $4$
or
$4$
or
 $5$
and clearly cannot contain a long subword of any
$5$
and clearly cannot contain a long subword of any
 $r \in R$
.
$r \in R$
.
If
 $a' \in H$
, then depending on whether
$a' \in H$
, then depending on whether
 $b" = b'a'b \in H$
, we have that either
$b" = b'a'b \in H$
, we have that either
 $b^{-1}(bab'a')b = ah \in K \setminus H$
is weakly cyclically reduced (so
$b^{-1}(bab'a')b = ah \in K \setminus H$
is weakly cyclically reduced (so
 $M \models bab'a' = b(ah)b^{-1} \notin bNb^{-1} = N$
) or
$M \models bab'a' = b(ah)b^{-1} \notin bNb^{-1} = N$
) or
 $b^{-1}bab'a'b = ab'a'b = a b"$
(where
$b^{-1}bab'a'b = ab'a'b = a b"$
(where
 $b" \notin H$
), which is weakly cyclically reduced, and similarly cannot lie in N.
$b" \notin H$
), which is weakly cyclically reduced, and similarly cannot lie in N. -
(E) Let
 $a,a' \in K \setminus H$
be such that
$a,a' \in K \setminus H$
be such that
 $a \not \sim _{H'} a'$
, and fix
$a \not \sim _{H'} a'$
, and fix
 $l,l' \in L'$
. Suppose that
$l,l' \in L'$
. Suppose that  ; that is, We can write w as a reduced word. If
; that is, We can write w as a reduced word. If $$ \begin{align*}M \models w= ala'l' \in N.\end{align*} $$
$$ \begin{align*}M \models w= ala'l' \in N.\end{align*} $$
 $l \in H$
, then
$l \in H$
, then
 $l \in H'$
, and since
$l \in H'$
, and since
 $a \not \sim _{H'} a'$
, we have
$a \not \sim _{H'} a'$
, we have
 $ala' \in K \setminus H'$
, so either
$ala' \in K \setminus H'$
, so either
 $w= (ala')l'$
is a product of an element of
$w= (ala')l'$
is a product of an element of
 $K \setminus H'$
and
$K \setminus H'$
and
 $L \setminus H$
(if
$L \setminus H$
(if
 $l' \notin H$
) which has to lie in
$l' \notin H$
) which has to lie in
 $K(L\setminus H)$
(which is disjoint to N) or
$K(L\setminus H)$
(which is disjoint to N) or
 $(ala')l' \in (K \setminus H') \cdot H' = K \setminus H'$
, and we are done.
$(ala')l' \in (K \setminus H') \cdot H' = K \setminus H'$
, and we are done.
So w.l.o.g.
 $l \notin H$
. (Similarly,
$l \notin H$
. (Similarly,  implies that w.l.o.g.
implies that w.l.o.g.
 $l' \notin H$
). So any weakly cyclically reduced conjugate of
$l' \notin H$
). So any weakly cyclically reduced conjugate of
 $w \in M$
has length at most
$w \in M$
has length at most
 $5$
and contains at least
$5$
and contains at least
 $2$
entries from
$2$
entries from
 $K \setminus H$
. But
$K \setminus H$
. But
 $w \in N$
implies that some weakly cyclically reduced conjugate contains a long subword of some
$w \in N$
implies that some weakly cyclically reduced conjugate contains a long subword of some
 $r \in R$
, which is clearly impossible.
$r \in R$
, which is clearly impossible. -
(F) The proof of (E) works here too.
-
(G) Let
 $g \in M^*$
,
$g \in M^*$
,
 $n \in \omega $
,
$n \in \omega $
,
 $n>1$
be such that
$n>1$
be such that  ,
,  . Recalling Observation 2.6, we can write g as an alternating product of elements of
. Recalling Observation 2.6, we can write g as an alternating product of elements of
 $K\setminus H$
and
$K\setminus H$
and
 $L \setminus H$
W.l.o.g. there exists no conjugate
$L \setminus H$
W.l.o.g. there exists no conjugate $$ \begin{align*}g = g_0g_1 \cdots g_{2m-1}.\end{align*} $$
$$ \begin{align*}g = g_0g_1 \cdots g_{2m-1}.\end{align*} $$
 $ygy^{-1}$
of g, and
$ygy^{-1}$
of g, and
 $g'$
with
$g'$
with
 $g'(ygy^{-1})^{-1} \in N$
such that
$g'(ygy^{-1})^{-1} \in N$
such that
 $g'$
has a shorter canonical representation than
$g'$
has a shorter canonical representation than
 $2m$
, since we can replace g with
$2m$
, since we can replace g with
 $g'$
and get a torsion element. Therefore, there is no
$g'$
and get a torsion element. Therefore, there is no
 $r \in R$
,
$r \in R$
,
 $\sigma _0 <2m$
with the sequence
$\sigma _0 <2m$
with the sequence
 $g_{\sigma _0}g_{\sigma _0+1} \cdots g_{2m-1}g_0g_1 \cdots g_{\sigma _0-1}$
containing a subsequence of a canonical representation of r of length
$g_{\sigma _0}g_{\sigma _0+1} \cdots g_{2m-1}g_0g_1 \cdots g_{\sigma _0-1}$
containing a subsequence of a canonical representation of r of length
 $j> \frac {6640}{2}+1$
.Now, since there exists a cyclic conjugate of
$j> \frac {6640}{2}+1$
.Now, since there exists a cyclic conjugate of $$ \begin{align*}M \models(g_0g_1 \cdots g_{2m-1})^n \in N,\end{align*} $$
$$ \begin{align*}M \models(g_0g_1 \cdots g_{2m-1})^n \in N,\end{align*} $$
 $(g_0g_1 \cdots g_{2m-1})^n$
and a subsequence
$(g_0g_1 \cdots g_{2m-1})^n$
and a subsequence
 $s_0s_1 \cdots s_j$
of it that is also a subsequence of a canonical form of some
$s_0s_1 \cdots s_j$
of it that is also a subsequence of a canonical form of some
 $s \in R$
with
$s \in R$
with
 $j \geq \frac {7}{10} \cdot 6640$
. Our assumptions above on
$j \geq \frac {7}{10} \cdot 6640$
. Our assumptions above on
 $g_0g_1 \cdots g_{2m-1}$
easily imply thus,
$g_0g_1 \cdots g_{2m-1}$
easily imply thus, $$ \begin{align*}2m \leq \frac{6640}{2}+1;\end{align*} $$
and clearly,
$$ \begin{align*}2m \leq \frac{6640}{2}+1;\end{align*} $$
and clearly, $$ \begin{align*}2m + \frac{2}{10}\cdot 6640-1 \leq j,\end{align*} $$
$$ \begin{align*}2m + \frac{2}{10}\cdot 6640-1 \leq j,\end{align*} $$
 $2m+330 \leq j$
. This way we get that
$2m+330 \leq j$
. This way we get that
 $s_\ell \sim _H s_{\ell +2m}$
for each
$s_\ell \sim _H s_{\ell +2m}$
for each
 $\ell \leq 330$
, but as s is a cyclically reduced conjugate of
$\ell \leq 330$
, but as s is a cyclically reduced conjugate of
 $h_\sigma ^{-1}\varrho (b_\sigma a_\sigma ,b_\sigma 'a_\sigma )$
or of its inverse (for some
$h_\sigma ^{-1}\varrho (b_\sigma a_\sigma ,b_\sigma 'a_\sigma )$
or of its inverse (for some
 $\sigma \in \Sigma $
), we get that for some
$\sigma \in \Sigma $
), we get that for some
 $\ell \in [1, 330] s_{\ell } \in H(b_\sigma )^{\pm 1}H$
,
$\ell \in [1, 330] s_{\ell } \in H(b_\sigma )^{\pm 1}H$
,
 $s_{\ell +2m} \in H(b^{\prime }_\sigma )^{\pm 1}H$
; thus,
$s_{\ell +2m} \in H(b^{\prime }_\sigma )^{\pm 1}H$
; thus,
 $s_\ell \not \sim _H s_{\ell +2m}$
. This is a contradiction.
$s_\ell \not \sim _H s_{\ell +2m}$
. This is a contradiction.
4 A set-theoretic interlude
In this section,
![]() $\chi ,\theta ,\mu ,\lambda $
and
$\chi ,\theta ,\mu ,\lambda $
and
![]() $\kappa $
all denote nonzero cardinals. Recall that
$\kappa $
all denote nonzero cardinals. Recall that
![]() $[\kappa ]^2$
stands for the collection of all unordered pairs
$[\kappa ]^2$
stands for the collection of all unordered pairs
![]() $\{\alpha ,\beta \}$
of ordinals in
$\{\alpha ,\beta \}$
of ordinals in
![]() $\kappa $
, but here we identify it with the collection of all ordered pairs
$\kappa $
, but here we identify it with the collection of all ordered pairs
![]() $(\alpha ,\beta )$
with
$(\alpha ,\beta )$
with
![]() $\alpha <\beta $
.
$\alpha <\beta $
.
Definition 4.1. A map
![]() $d:[\kappa ]^2\rightarrow \theta $
is subadditive if the following inequalities hold for all
$d:[\kappa ]^2\rightarrow \theta $
is subadditive if the following inequalities hold for all
![]() $\alpha < \beta < \gamma < \kappa $
:
$\alpha < \beta < \gamma < \kappa $
:
-
(1)
 $d(\alpha , \gamma ) \leq \max \{d(\alpha , \beta ), d(\beta , \gamma )\}$
;
$d(\alpha , \gamma ) \leq \max \{d(\alpha , \beta ), d(\beta , \gamma )\}$
; -
(2)
 $d(\alpha , \beta ) \leq \max \{d(\alpha , \gamma ), d(\beta , \gamma )\}$
.
$d(\alpha , \beta ) \leq \max \{d(\alpha , \gamma ), d(\beta , \gamma )\}$
.
Notation 4.2. Whenever the map
![]() $d:[\kappa ]^2\rightarrow \theta $
is clear from the context, we define for all
$d:[\kappa ]^2\rightarrow \theta $
is clear from the context, we define for all
![]() $\gamma < \kappa $
and
$\gamma < \kappa $
and
![]() $i \leq \theta $
, the following sets:
$i \leq \theta $
, the following sets:
-
•
 $D^\gamma _{<i}=\{\beta < \gamma \mathrel {|} d(\beta , \gamma ) < i\}$
, and
$D^\gamma _{<i}=\{\beta < \gamma \mathrel {|} d(\beta , \gamma ) < i\}$
, and -
•
 $D^\gamma _{\le i}=\{\beta < \gamma \mathrel {|} d(\beta , \gamma ) \le i\}$
.
$D^\gamma _{\le i}=\{\beta < \gamma \mathrel {|} d(\beta , \gamma ) \le i\}$
.
Lemma 4.3. If
![]() $d:[\kappa ]^2\rightarrow \theta $
is subadditive, then for all
$d:[\kappa ]^2\rightarrow \theta $
is subadditive, then for all
![]() $\gamma <\kappa $
,
$\gamma <\kappa $
,
![]() $i\le \theta $
, and
$i\le \theta $
, and
![]() $\beta \in D^\gamma _{<i}$
, it is the case that
$\beta \in D^\gamma _{<i}$
, it is the case that
![]() $D^\gamma _{<i}\cap \beta =D^{\beta }_{< i}$
.
$D^\gamma _{<i}\cap \beta =D^{\beta }_{< i}$
.
Proof. Suppose that
![]() $d:[\kappa ]^2\rightarrow \theta $
is subadditive, and let
$d:[\kappa ]^2\rightarrow \theta $
is subadditive, and let
![]() $\gamma ,i$
and
$\gamma ,i$
and
![]() $\beta $
be as above.
$\beta $
be as above.
![]() $\blacktriangleright $
By Definition 4.1(1), for every
$\blacktriangleright $
By Definition 4.1(1), for every
![]() $\alpha \in D^\beta _{<i}$
,
$\alpha \in D^\beta _{<i}$
,
![]() $d(\alpha ,\gamma )\le \max \{ d(\alpha ,\beta ),d(\beta ,\gamma )\}$
, so, since
$d(\alpha ,\gamma )\le \max \{ d(\alpha ,\beta ),d(\beta ,\gamma )\}$
, so, since
![]() $\alpha \in D^\beta _{<i}$
and
$\alpha \in D^\beta _{<i}$
and
![]() $\beta \in D^\gamma _{<i}$
, we infer that
$\beta \in D^\gamma _{<i}$
, we infer that
![]() $d(\alpha ,\gamma )<i$
and
$d(\alpha ,\gamma )<i$
and
![]() $\alpha \in D^\gamma _{<i}\cap \beta $
.
$\alpha \in D^\gamma _{<i}\cap \beta $
.
![]() $\blacktriangleright $
By Definition 4.1(2), for every
$\blacktriangleright $
By Definition 4.1(2), for every
![]() $\alpha \in D^\gamma _{<i}\cap \beta $
,
$\alpha \in D^\gamma _{<i}\cap \beta $
,
![]() $d(\alpha ,\beta )\le \max \{ d(\alpha ,\gamma ),d(\beta ,\gamma )\}$
, so, since
$d(\alpha ,\beta )\le \max \{ d(\alpha ,\gamma ),d(\beta ,\gamma )\}$
, so, since
![]() $\alpha ,\beta \in D^\gamma _{<i}$
, we infer that
$\alpha ,\beta \in D^\gamma _{<i}$
, we infer that
![]() $d(\alpha ,\beta )<i$
and
$d(\alpha ,\beta )<i$
and
![]() $\alpha \in D^\beta _{<i}$
.
$\alpha \in D^\beta _{<i}$
.
Theorem 4.4. Suppose that
![]() $\lambda $
is an infinite regular cardinal. Then there exist two maps
$\lambda $
is an infinite regular cardinal. Then there exist two maps
![]() $c:[\lambda ^+]^2\rightarrow \lambda ^+$
and
$c:[\lambda ^+]^2\rightarrow \lambda ^+$
and
![]() $d:[\lambda ^+]^2\rightarrow \lambda $
such that
$d:[\lambda ^+]^2\rightarrow \lambda $
such that
-
• d is subadditive;
-
• for every
 $A\in [\lambda ^+]^{\lambda ^+}$
, there exists a club
$A\in [\lambda ^+]^{\lambda ^+}$
, there exists a club
 $D\subseteq \lambda ^+$
such that for every
$D\subseteq \lambda ^+$
such that for every
 $\delta \in D$
, for every
$\delta \in D$
, for every
 $\beta \in \lambda ^+\setminus \delta $
, for every
$\beta \in \lambda ^+\setminus \delta $
, for every
 $\xi <\delta $
, for every
$\xi <\delta $
, for every
 $i<\lambda $
, there are cofinally many
$i<\lambda $
, there are cofinally many
 $\alpha <\delta $
such that
$\alpha <\delta $
such that
 $\alpha \in A$
,
$\alpha \in A$
,
 $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
 $d(\alpha ,\beta )>i$
.
$d(\alpha ,\beta )>i$
.
Proof. Let d be the function
![]() $\rho :[\lambda ^+]^2\rightarrow \lambda $
defined in [Reference Todorcevic45, §9.1]. By [Reference Todorcevic45, Lemma 9.1.1], d is subadditive. By [Reference Todorcevic45, Lemma 9.1.2], d is also locally small (i.e.,
$\rho :[\lambda ^+]^2\rightarrow \lambda $
defined in [Reference Todorcevic45, §9.1]. By [Reference Todorcevic45, Lemma 9.1.1], d is subadditive. By [Reference Todorcevic45, Lemma 9.1.2], d is also locally small (i.e.,
![]() $|D^\gamma _{\le i}|<\lambda $
for all
$|D^\gamma _{\le i}|<\lambda $
for all
![]() $\gamma <\lambda ^+$
and
$\gamma <\lambda ^+$
and
![]() $i<\lambda $
).
$i<\lambda $
).
Next, by [Reference Rinot and Todorcevic37], we may fix a coloring
![]() $c:[\lambda ^+]^2\rightarrow \lambda ^+$
witnessing
$c:[\lambda ^+]^2\rightarrow \lambda ^+$
witnessing
![]() $\lambda ^+\nrightarrow [\lambda ^+;\lambda ^+]^2_{\lambda ^+}$
. By [Reference Inamdar and Rinot22, Lemma 3.16], this means that for every
$\lambda ^+\nrightarrow [\lambda ^+;\lambda ^+]^2_{\lambda ^+}$
. By [Reference Inamdar and Rinot22, Lemma 3.16], this means that for every
![]() $A\in [\lambda ^+]^{\lambda ^+}$
, there exists an
$A\in [\lambda ^+]^{\lambda ^+}$
, there exists an
![]() $\epsilon <\lambda ^+$
such that, for all
$\epsilon <\lambda ^+$
such that, for all
![]() $\beta \in \lambda ^+\setminus \epsilon $
and
$\beta \in \lambda ^+\setminus \epsilon $
and
![]() $\xi <\epsilon $
, there exists
$\xi <\epsilon $
, there exists
![]() $\alpha \in A\cap \epsilon $
such that
$\alpha \in A\cap \epsilon $
such that
![]() $c(\alpha ,\beta )=\xi $
.
$c(\alpha ,\beta )=\xi $
.
We now verify that c and d are as sought.
Claim 4.4.1. Let
![]() $A\in [\lambda ^+]^{\lambda ^+}$
. Then there exists a club
$A\in [\lambda ^+]^{\lambda ^+}$
. Then there exists a club
![]() $D\subseteq \lambda ^+$
such that for every
$D\subseteq \lambda ^+$
such that for every
![]() $\delta \in D$
, for every
$\delta \in D$
, for every
![]() $\beta \in \lambda ^+\setminus \delta $
, for every
$\beta \in \lambda ^+\setminus \delta $
, for every
![]() $\xi <\delta $
, for every
$\xi <\delta $
, for every
![]() $i<\lambda $
, there are cofinally many
$i<\lambda $
, there are cofinally many
![]() $\alpha <\delta $
such that
$\alpha <\delta $
such that
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
![]() $d(\alpha ,\beta )>i$
.
$d(\alpha ,\beta )>i$
.
Proof. Let
![]() $\langle M_\gamma \mathrel {|} \gamma <\lambda ^+\rangle $
be a sequence of elementary submodels of
$\langle M_\gamma \mathrel {|} \gamma <\lambda ^+\rangle $
be a sequence of elementary submodels of
![]() $\mathcal H_{\lambda ^{++}}$
, each of size
$\mathcal H_{\lambda ^{++}}$
, each of size
![]() $\lambda $
, such that
$\lambda $
, such that
![]() $\{A,e\}\in M_0$
, such that
$\{A,e\}\in M_0$
, such that
![]() $M_\gamma \in M_{\gamma +1}$
for every
$M_\gamma \in M_{\gamma +1}$
for every
![]() $\gamma <\lambda ^+$
, and such that
$\gamma <\lambda ^+$
, and such that
![]() $M_\delta =\bigcup _{\gamma <\delta }M_\gamma $
for every limit nonzero
$M_\delta =\bigcup _{\gamma <\delta }M_\gamma $
for every limit nonzero
![]() $\delta <\lambda ^+$
. It follows that
$\delta <\lambda ^+$
. It follows that
![]() $C=\{\gamma <\lambda ^+\mathrel {|} M_\gamma \cap \lambda ^+=\gamma \}$
is a club in
$C=\{\gamma <\lambda ^+\mathrel {|} M_\gamma \cap \lambda ^+=\gamma \}$
is a club in
![]() $\lambda ^+$
.
$\lambda ^+$
.
We claim that the following club is as sought:
To this end, let
![]() $\delta \in D$
,
$\delta \in D$
,
![]() $\beta \in \lambda ^+\setminus \delta $
,
$\beta \in \lambda ^+\setminus \delta $
,
![]() $\xi <\delta $
,
$\xi <\delta $
,
![]() $i<\lambda $
, and
$i<\lambda $
, and
![]() $\eta <\delta $
. We shall find an
$\eta <\delta $
. We shall find an
![]() $\alpha \in A\cap \delta $
above
$\alpha \in A\cap \delta $
above
![]() $\eta $
such that
$\eta $
such that
![]() $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
![]() $d(\alpha ,\beta )>i$
.
$d(\alpha ,\beta )>i$
.
For every
![]() $\gamma \in C\setminus \xi $
, the set
$\gamma \in C\setminus \xi $
, the set
![]() $A_\gamma =A\setminus \gamma $
is in
$A_\gamma =A\setminus \gamma $
is in
![]() $[\lambda ^+]^{\lambda ^+}\cap M_{\gamma +1}$
, and hence, there exists
$[\lambda ^+]^{\lambda ^+}\cap M_{\gamma +1}$
, and hence, there exists
![]() $\epsilon \in \lambda ^+\cap M_{\gamma +1}$
such that for all
$\epsilon \in \lambda ^+\cap M_{\gamma +1}$
such that for all
![]() $\beta '\in \lambda ^+\setminus \epsilon $
and
$\beta '\in \lambda ^+\setminus \epsilon $
and
![]() $\xi '<\epsilon $
, there exists
$\xi '<\epsilon $
, there exists
![]() $\alpha '\in A_\gamma \cap \epsilon $
such that
$\alpha '\in A_\gamma \cap \epsilon $
such that
![]() $c(\alpha ',\beta ')=\xi '$
. In particular, we may pick
$c(\alpha ',\beta ')=\xi '$
. In particular, we may pick
![]() $\alpha _\gamma \in A\cap M_{\gamma +1}\setminus \gamma $
such that
$\alpha _\gamma \in A\cap M_{\gamma +1}\setminus \gamma $
such that
![]() $c(\alpha _\gamma ,\beta )=\xi $
. It follows that
$c(\alpha _\gamma ,\beta )=\xi $
. It follows that
![]() $\gamma \mapsto \alpha _\gamma $
is a strictly increasing function from
$\gamma \mapsto \alpha _\gamma $
is a strictly increasing function from
![]() $C\cap \delta $
to
$C\cap \delta $
to
![]() $A\cap \delta $
. As
$A\cap \delta $
. As
![]() $\delta \in D$
, we infer that
$\delta \in D$
, we infer that
![]() $A'=\{ \alpha \in A\cap \delta \mathrel {|} \eta <\alpha \ \&\ c(\alpha ,\beta )=\xi \}$
has size
$A'=\{ \alpha \in A\cap \delta \mathrel {|} \eta <\alpha \ \&\ c(\alpha ,\beta )=\xi \}$
has size
![]() $\lambda $
. As d is locally small, we may now pick
$\lambda $
. As d is locally small, we may now pick
![]() $\alpha \in A'\setminus D^\beta _{\le i}$
. Then
$\alpha \in A'\setminus D^\beta _{\le i}$
. Then
![]() $\alpha \in A\cap \delta $
above
$\alpha \in A\cap \delta $
above
![]() $\eta $
,
$\eta $
,
![]() $d(\alpha ,\beta )>i$
and
$d(\alpha ,\beta )>i$
and
![]() $c(\alpha ,\beta )=\xi $
, as sought.
$c(\alpha ,\beta )=\xi $
, as sought.
This completes the proof.
Remark 4.5. The preceding result does not generalize to the case when
![]() $\lambda $
is a singular cardinal. Indeed, it follows from [Reference Lambie-Hanson and Rinot28, Lemma 3.38] that if
$\lambda $
is a singular cardinal. Indeed, it follows from [Reference Lambie-Hanson and Rinot28, Lemma 3.38] that if
![]() $\lambda $
is the singular limit of strongly compact cardinals, then for every infinite cardinal
$\lambda $
is the singular limit of strongly compact cardinals, then for every infinite cardinal
![]() $\theta \le \lambda $
, for every subadditive map
$\theta \le \lambda $
, for every subadditive map
![]() $d:[\lambda ^+]^2\rightarrow \theta $
, there must exist an
$d:[\lambda ^+]^2\rightarrow \theta $
, there must exist an
![]() $A\in [\lambda ^+]^{\lambda ^+}$
such that
$A\in [\lambda ^+]^{\lambda ^+}$
such that
![]() $\sup \{ d(\alpha ,\beta )\mathrel {|} \alpha <\beta \text { in }A\}<\theta $
.
$\sup \{ d(\alpha ,\beta )\mathrel {|} \alpha <\beta \text { in }A\}<\theta $
.
Definition 4.6 [Reference Shelah41].
![]() $\operatorname {\mathrm {Pr}}_1(\kappa , \kappa , \theta , \chi )$
asserts the existence of a coloring
$\operatorname {\mathrm {Pr}}_1(\kappa , \kappa , \theta , \chi )$
asserts the existence of a coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
such that for every
$c:[\kappa ]^2 \rightarrow \theta $
such that for every
![]() $\sigma <\chi $
, every pairwise disjoint subfamily
$\sigma <\chi $
, every pairwise disjoint subfamily
![]() $\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
$\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
![]() $\kappa $
, and every
$\kappa $
, and every
![]() $\tau < \theta $
, there are
$\tau < \theta $
, there are
![]() $a,b\in \mathcal A$
with
$a,b\in \mathcal A$
with
![]() $\sup (a)<\min (b)$
such that
$\sup (a)<\min (b)$
such that
![]() $c[a \times b] = \{\tau \}$
.
$c[a \times b] = \{\tau \}$
.
Definition 4.7 [Reference Lambie-Hanson and Rinot26].
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
asserts the existence of a coloring
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
asserts the existence of a coloring
![]() $d:[\kappa ]^2\rightarrow \theta $
such that for every
$d:[\kappa ]^2\rightarrow \theta $
such that for every
![]() $\sigma < \chi $
, every pairwise disjoint subfamily
$\sigma < \chi $
, every pairwise disjoint subfamily
![]() $\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
$\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
![]() $\kappa $
, and every
$\kappa $
, and every
![]() $\tau < \theta $
, there exists
$\tau < \theta $
, there exists
![]() $\mathcal {B} \in [\mathcal {A}]^\mu $
such that, for all
$\mathcal {B} \in [\mathcal {A}]^\mu $
such that, for all
![]() $a, b \in \mathcal {B}$
with
$a, b \in \mathcal {B}$
with
![]() $\sup (a)<\min (b)$
, it is the case that
$\sup (a)<\min (b)$
, it is the case that
![]() $\min (d[a\times b])\ge \tau $
.
$\min (d[a\times b])\ge \tau $
.
Theorem 4.8. Suppose that
-
•
 $\theta <\kappa $
are infinite regular cardinals;
$\theta <\kappa $
are infinite regular cardinals; -
•
 $c:[\kappa ]^2\rightarrow \kappa $
is a coloring witnessing
$c:[\kappa ]^2\rightarrow \kappa $
is a coloring witnessing
 $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,4)$
;
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,4)$
; -
•
 $d:[\kappa ]^2\rightarrow \theta $
is a subadditive coloring witnessing
$d:[\kappa ]^2\rightarrow \theta $
is a subadditive coloring witnessing
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
Then, for every
![]() $A\in [\kappa ]^\kappa $
, there exists a club
$A\in [\kappa ]^\kappa $
, there exists a club
![]() $D\subseteq \kappa $
such that for every
$D\subseteq \kappa $
such that for every
![]() $\delta \in D$
, for every
$\delta \in D$
, for every
![]() $\beta \in \kappa \setminus \delta $
, for every
$\beta \in \kappa \setminus \delta $
, for every
![]() $\xi <\delta $
, for every
$\xi <\delta $
, for every
![]() $i<\theta $
, there are cofinally many
$i<\theta $
, there are cofinally many
![]() $\alpha <\delta $
such that
$\alpha <\delta $
such that
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
![]() $d(\alpha ,\beta )>i$
.
$d(\alpha ,\beta )>i$
.
Proof. We start by verifying a special case.
Claim 4.8.1. Let
![]() $A\in [\kappa ]^\kappa $
,
$A\in [\kappa ]^\kappa $
,
![]() $\xi <\kappa $
and
$\xi <\kappa $
and
![]() $i<\theta $
. There exists
$i<\theta $
. There exists
![]() $\gamma <\kappa $
such that for every
$\gamma <\kappa $
such that for every
![]() $\beta \in \kappa \setminus \gamma $
, there exists
$\beta \in \kappa \setminus \gamma $
, there exists
![]() $\alpha \in A\cap \gamma $
such that
$\alpha \in A\cap \gamma $
such that
![]() $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
![]() $d(\alpha ,\beta )>i$
.
$d(\alpha ,\beta )>i$
.
Proof. For every
![]() $\epsilon <\kappa $
,
$\epsilon <\kappa $
,
![]() $A\setminus \epsilon $
is in
$A\setminus \epsilon $
is in
![]() $[\kappa ]^\kappa $
, and as
$[\kappa ]^\kappa $
, and as
![]() $d:[\kappa ]^2\rightarrow \theta $
witnesses
$d:[\kappa ]^2\rightarrow \theta $
witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, it is the case that
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, it is the case that
![]() $d"[A\setminus \epsilon ]^2$
is cofinal in
$d"[A\setminus \epsilon ]^2$
is cofinal in
![]() $\theta $
. It thus follows that we may fix a
$\theta $
. It thus follows that we may fix a
![]() $\kappa $
-sized pairwise disjoint subfamily
$\kappa $
-sized pairwise disjoint subfamily
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $[A]^2$
such that
$[A]^2$
such that
![]() $d(a)>i$
for all
$d(a)>i$
for all
![]() $a\in \mathcal A$
. Note that for all
$a\in \mathcal A$
. Note that for all
![]() $\beta <\kappa $
and
$\beta <\kappa $
and
![]() $a\in \mathcal A\cap \mathcal P(\beta )$
, there must exist some
$a\in \mathcal A\cap \mathcal P(\beta )$
, there must exist some
![]() $\alpha \in a$
such that
$\alpha \in a$
such that
![]() $d(\alpha ,\beta )>i$
because, by subadditivity,
$d(\alpha ,\beta )>i$
because, by subadditivity,
Therefore, it now suffices to prove that there exists some
![]() $\gamma <\kappa $
such that for every
$\gamma <\kappa $
such that for every
![]() $\beta \in \kappa \setminus \gamma $
, there exists
$\beta \in \kappa \setminus \gamma $
, there exists
![]() $a\in \mathcal A\cap \mathcal P(\gamma )$
such that
$a\in \mathcal A\cap \mathcal P(\gamma )$
such that
![]() $c[a\times \{\beta \}]=\{\xi \}$
. Towards a contradiction, suppose that this is not the case. For every
$c[a\times \{\beta \}]=\{\xi \}$
. Towards a contradiction, suppose that this is not the case. For every
![]() $\gamma <\kappa $
, fix
$\gamma <\kappa $
, fix
![]() $\beta _\gamma \in \kappa \setminus \gamma $
such that there exists no
$\beta _\gamma \in \kappa \setminus \gamma $
such that there exists no
![]() $a\in \mathcal A\cap \mathcal P(\gamma )$
with
$a\in \mathcal A\cap \mathcal P(\gamma )$
with
![]() $c[a\times \{\beta _\gamma \}]=\{\xi \}$
. For each
$c[a\times \{\beta _\gamma \}]=\{\xi \}$
. For each
![]() $\gamma <\kappa $
, set
$\gamma <\kappa $
, set
![]() $a_\gamma =\{\beta _\gamma \}\cup a$
for some
$a_\gamma =\{\beta _\gamma \}\cup a$
for some
![]() $a\in \mathcal A$
such that
$a\in \mathcal A$
such that
![]() $\min (a)>\beta _\gamma $
. Fix a club
$\min (a)>\beta _\gamma $
. Fix a club
![]() $C\subseteq \kappa $
such that for every
$C\subseteq \kappa $
such that for every
![]() $\gamma \in C$
, for every
$\gamma \in C$
, for every
![]() $\bar \gamma <\gamma $
,
$\bar \gamma <\gamma $
,
![]() $\max (a_{\bar \gamma })<\gamma $
. It follows that
$\max (a_{\bar \gamma })<\gamma $
. It follows that
![]() $\mathcal A'=\{ a_\gamma \mathrel {|} \gamma \in C\}$
is a collection of
$\mathcal A'=\{ a_\gamma \mathrel {|} \gamma \in C\}$
is a collection of
![]() $\kappa $
-many pairwise disjoint elements of
$\kappa $
-many pairwise disjoint elements of
![]() $[\kappa ]^3$
. So, since c witnesses
$[\kappa ]^3$
. So, since c witnesses
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,4)$
, we may find
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,4)$
, we may find
![]() $a,b\in \mathcal A'$
with
$a,b\in \mathcal A'$
with
![]() $\max (a)<\min (b)$
such that
$\max (a)<\min (b)$
such that
![]() $c[a\times b]=\{\xi \}$
. Pick
$c[a\times b]=\{\xi \}$
. Pick
![]() $\bar \gamma ,\gamma $
in C such that
$\bar \gamma ,\gamma $
in C such that
![]() $a=a_{\bar \gamma }$
and
$a=a_{\bar \gamma }$
and
![]() $b=a_\gamma $
. From
$b=a_\gamma $
. From
![]() $\max (a_{\bar \gamma })<\min (a_\gamma )$
, it follows that
$\max (a_{\bar \gamma })<\min (a_\gamma )$
, it follows that
![]() $\bar \gamma <\gamma $
, and
$\bar \gamma <\gamma $
, and
In particular,
![]() $a'=a_{\bar \gamma }\setminus \{\beta _\gamma \}$
is an element of
$a'=a_{\bar \gamma }\setminus \{\beta _\gamma \}$
is an element of
![]() $\mathcal A\cap \mathcal P(\gamma )$
and
$\mathcal A\cap \mathcal P(\gamma )$
and
![]() $c[a'\times \{\beta _\gamma \}]=\{\xi \}$
. This is a contradiction.
$c[a'\times \{\beta _\gamma \}]=\{\xi \}$
. This is a contradiction.
Now, given
![]() $A\in [\kappa ]^\kappa $
, let
$A\in [\kappa ]^\kappa $
, let
![]() $\langle M_\gamma \mathrel {|} \gamma <\kappa \rangle $
be a sequence of elementary submodels of
$\langle M_\gamma \mathrel {|} \gamma <\kappa \rangle $
be a sequence of elementary submodels of
![]() $\mathcal H_{\kappa ^+}$
, each of size less than
$\mathcal H_{\kappa ^+}$
, each of size less than
![]() $\kappa $
, such that
$\kappa $
, such that
![]() $\{A,c,d\}\cup \theta \subseteq M_0$
, such that
$\{A,c,d\}\cup \theta \subseteq M_0$
, such that
![]() $M_\gamma \in M_{\gamma +1}$
for every
$M_\gamma \in M_{\gamma +1}$
for every
![]() $\gamma <\kappa $
, and such that
$\gamma <\kappa $
, and such that
![]() $M_\delta =\bigcup _{\gamma <\delta }M_\gamma $
for every limit nonzero
$M_\delta =\bigcup _{\gamma <\delta }M_\gamma $
for every limit nonzero
![]() $\delta <\kappa $
. We claim that the following club is as sought:
$\delta <\kappa $
. We claim that the following club is as sought:
To see it, let
![]() $\beta \in \kappa \setminus \delta $
,
$\beta \in \kappa \setminus \delta $
,
![]() $\xi <\delta $
,
$\xi <\delta $
,
![]() $i<\theta $
, and
$i<\theta $
, and
![]() $\epsilon <\delta $
; we must find
$\epsilon <\delta $
; we must find
![]() $\alpha \in A$
with
$\alpha \in A$
with
![]() $\epsilon \le \alpha <\delta $
such that
$\epsilon \le \alpha <\delta $
such that
![]() $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
![]() $d(\alpha ,\beta )>i$
. The set
$d(\alpha ,\beta )>i$
. The set
![]() $A'=A\setminus \epsilon $
is in
$A'=A\setminus \epsilon $
is in
![]() $[\kappa ]^\kappa \cap M_\delta $
, and so are
$[\kappa ]^\kappa \cap M_\delta $
, and so are
![]() $\xi $
and i. It thus follows from Claim 4.8.1 that there exists
$\xi $
and i. It thus follows from Claim 4.8.1 that there exists
![]() $\gamma \in \kappa \cap M_\delta $
such that for every
$\gamma \in \kappa \cap M_\delta $
such that for every
![]() $\beta '\in \kappa \setminus \gamma $
, there exists
$\beta '\in \kappa \setminus \gamma $
, there exists
![]() $\alpha \in A'\cap \gamma $
such that
$\alpha \in A'\cap \gamma $
such that
![]() $c(\alpha ,\beta ')=\xi $
and
$c(\alpha ,\beta ')=\xi $
and
![]() $d(\alpha ,\beta ')>i$
. As
$d(\alpha ,\beta ')>i$
. As
![]() $\gamma <\delta \le \beta $
, it follows that there exists
$\gamma <\delta \le \beta $
, it follows that there exists
![]() $\alpha \in A'\cap \gamma $
such that
$\alpha \in A'\cap \gamma $
such that
![]() $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
![]() $d(\alpha ,\beta )>i$
. Evidently,
$d(\alpha ,\beta )>i$
. Evidently,
![]() $\epsilon \le \alpha <\delta $
.
$\epsilon \le \alpha <\delta $
.
In reading the next definition, recall that for a set X of ordinals,
![]() $\operatorname {\mathrm {acc}}(X)$
stands for the set of all nonzero
$\operatorname {\mathrm {acc}}(X)$
stands for the set of all nonzero
![]() $\xi \in X$
such that
$\xi \in X$
such that
![]() $\sup (X\cap \xi )=\xi $
.
$\sup (X\cap \xi )=\xi $
.
Definition 4.9 [Reference Brodsky and Rinot5].
For infinite regular cardinals
![]() $\theta <\kappa $
, the principle
$\theta <\kappa $
, the principle
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
asserts the existence of a sequence
$\square (\kappa ,{\sqsubseteq _\theta })$
asserts the existence of a sequence
![]() $\vec C=\langle C_\alpha \mathrel {|} \alpha <\kappa \rangle $
satisfying the following:
$\vec C=\langle C_\alpha \mathrel {|} \alpha <\kappa \rangle $
satisfying the following:
-
• for every
 $\alpha <\kappa $
,
$\alpha <\kappa $
,
 $C_\alpha $
is a closed subset of
$C_\alpha $
is a closed subset of
 $\alpha $
with
$\alpha $
with
 $\sup (C_\alpha )=\sup (\alpha )$
;
$\sup (C_\alpha )=\sup (\alpha )$
; -
• for all
 $\alpha <\kappa $
and
$\alpha <\kappa $
and
 $\bar \alpha \in \operatorname {\mathrm {acc}}(C_\alpha )$
, if
$\bar \alpha \in \operatorname {\mathrm {acc}}(C_\alpha )$
, if
 $\operatorname {\mathrm {otp}}(C_\alpha )\ge \theta $
, then
$\operatorname {\mathrm {otp}}(C_\alpha )\ge \theta $
, then
 $C_{\bar \alpha }=C_\alpha \cap \bar \alpha $
;
$C_{\bar \alpha }=C_\alpha \cap \bar \alpha $
; -
• for every club D in
 $\kappa $
, there exists some
$\kappa $
, there exists some
 $\alpha \in \operatorname {\mathrm {acc}}(D)$
such that
$\alpha \in \operatorname {\mathrm {acc}}(D)$
such that
 $D\cap \alpha \neq C_\alpha $
.
$D\cap \alpha \neq C_\alpha $
.
Note that
![]() $\square (\kappa ,{\sqsubseteq _{\vartheta }})$
implies
$\square (\kappa ,{\sqsubseteq _{\vartheta }})$
implies
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
whenever
$\square (\kappa ,{\sqsubseteq _\theta })$
whenever
![]() $\vartheta <\theta $
. The strongest instance
$\vartheta <\theta $
. The strongest instance
![]() $\square (\kappa ,{\sqsubseteq _\omega })$
is commonly denoted by
$\square (\kappa ,{\sqsubseteq _\omega })$
is commonly denoted by
![]() $\square (\kappa )$
.
$\square (\kappa )$
.
Corollary 4.10. Suppose that
![]() $\theta <\kappa $
are infinite regular cardinals.
$\theta <\kappa $
are infinite regular cardinals.
If either
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
holds or if there exists a uniformly coherent
$\square (\kappa ,{\sqsubseteq _\theta })$
holds or if there exists a uniformly coherent
![]() $\kappa $
-Souslin tree, then there exist two maps
$\kappa $
-Souslin tree, then there exist two maps
![]() $c:[\kappa ]^2\rightarrow \kappa $
and
$c:[\kappa ]^2\rightarrow \kappa $
and
![]() $d:[\kappa ]^2\rightarrow \theta $
such that
$d:[\kappa ]^2\rightarrow \theta $
such that
-
• d is subadditive;
-
• for every
 $A\in [\kappa ]^\kappa $
, there exists a club
$A\in [\kappa ]^\kappa $
, there exists a club
 $D\subseteq \kappa $
such that for every
$D\subseteq \kappa $
such that for every
 $\delta \in D$
, for every
$\delta \in D$
, for every
 $\beta \in \kappa \setminus \delta $
, for every
$\beta \in \kappa \setminus \delta $
, for every
 $\xi <\delta $
, for every
$\xi <\delta $
, for every
 $i<\theta $
, there are cofinally many
$i<\theta $
, there are cofinally many
 $\alpha <\delta $
such that
$\alpha <\delta $
such that
 $\alpha \in A$
,
$\alpha \in A$
,
 $c(\alpha ,\beta )=\xi $
and
$c(\alpha ,\beta )=\xi $
and
 $d(\alpha ,\beta )>i$
.
$d(\alpha ,\beta )>i$
.
Proof. By Theorem 4.4, we may assume that
![]() $\theta ^+<\kappa $
. Also, by Theorem 4.8, it suffices to find a map
$\theta ^+<\kappa $
. Also, by Theorem 4.8, it suffices to find a map
![]() $c:[\kappa ]^2\rightarrow \kappa $
witnessing
$c:[\kappa ]^2\rightarrow \kappa $
witnessing
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,4)$
, and a subadditive map
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,4)$
, and a subadditive map
![]() $d:[\kappa ]^2\rightarrow \theta $
witnessing
$d:[\kappa ]^2\rightarrow \theta $
witnessing
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
By [Reference Rinot36, Theorem B],
![]() $\square (\kappa )$
implies
$\square (\kappa )$
implies
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,\theta )$
. Inspecting the proof of [Reference Rinot36, Theorem 3.3] makes it clear that the same conclusion already follows from
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,\theta )$
. Inspecting the proof of [Reference Rinot36, Theorem 3.3] makes it clear that the same conclusion already follows from
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
. In addition, by [Reference Lambie-Hanson and Rinot28, Theorem A],
$\square (\kappa ,{\sqsubseteq _\theta })$
. In addition, by [Reference Lambie-Hanson and Rinot28, Theorem A],
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
yields a subadditive witness to
$\square (\kappa ,{\sqsubseteq _\theta })$
yields a subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
Next, by [Reference Lambie-Hanson and Rinot28, Corollary 3.29], the existence of a uniformly coherent
![]() $\kappa $
-Souslin tree yields a subadditive witness to
$\kappa $
-Souslin tree yields a subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. It is also well known that the existence of a uniformly coherent
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. It is also well known that the existence of a uniformly coherent
![]() $\kappa $
-Souslin tree induces a witness to
$\kappa $
-Souslin tree induces a witness to
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,\omega )$
.
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\kappa ,\omega )$
.
Remark 4.11. Coming back to the limitation highlighted in Remark 4.5, we point out that the conclusion of Corollary 4.10 is nevertheless compatible with a bounded amount of large cardinals. The point is that
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
may be added by means of a
$\square (\kappa ,{\sqsubseteq _\theta })$
may be added by means of a
![]() $\theta $
-directed-closed and
$\theta $
-directed-closed and
![]() $\kappa $
-strategically-closed forcing, so by Laver’s indestructibility theorem,
$\kappa $
-strategically-closed forcing, so by Laver’s indestructibility theorem,
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
is compatible with
$\square (\kappa ,{\sqsubseteq _\theta })$
is compatible with
![]() $\theta $
being supercompact. In parallel, the existence of a uniformly coherent
$\theta $
being supercompact. In parallel, the existence of a uniformly coherent
![]() $\kappa $
-Souslin tree is compatible with
$\kappa $
-Souslin tree is compatible with
![]() $\kappa $
possessing a generically-large cardinal property that refutes
$\kappa $
possessing a generically-large cardinal property that refutes
![]() $\square (\kappa ,{\sqsubseteq _\theta })$
for all
$\square (\kappa ,{\sqsubseteq _\theta })$
for all
![]() $\theta <\kappa $
(see [Reference Lambie-Hanson and Rinot27, Theorem 3.3]).
$\theta <\kappa $
(see [Reference Lambie-Hanson and Rinot27, Theorem 3.3]).
5 A construction of a Shelah group
This section is devoted to proving the core result of this paper. The assumptions of the upcoming theorem are motivated by the results of the previous section.
Theorem 5.1. Suppose
-
•
 $\theta <\kappa $
is a pair of infinite regular cardinals;
$\theta <\kappa $
is a pair of infinite regular cardinals; -
•
 $c:[\kappa ]^2\rightarrow \kappa $
is a coloring;
$c:[\kappa ]^2\rightarrow \kappa $
is a coloring; -
•
 $d:[\kappa ]^2\rightarrow \theta $
is a subadditive coloring;
$d:[\kappa ]^2\rightarrow \theta $
is a subadditive coloring; -
• for every
 $A\in [\kappa ]^\kappa $
, there exists a club
$A\in [\kappa ]^\kappa $
, there exists a club
 $B\subseteq \kappa $
such that for every
$B\subseteq \kappa $
such that for every
 $\beta \in B$
, there exists
$\beta \in B$
, there exists
 $\gamma \in A$
above
$\gamma \in A$
above
 $\beta $
such that for all
$\beta $
such that for all
 $\xi <\beta $
and
$\xi <\beta $
and
 $i<\theta $
, there are cofinally many
$i<\theta $
, there are cofinally many
 $\alpha <\beta $
such that
$\alpha <\beta $
such that
 $\alpha \in A$
,
$\alpha \in A$
,
 $c(\alpha ,\gamma )=\xi $
and
$c(\alpha ,\gamma )=\xi $
and
 $d(\alpha ,\gamma )>i$
.
$d(\alpha ,\gamma )>i$
.
Then there exists a torsion-free Shelah group G of size
![]() $\kappa $
.
$\kappa $
.
Before embarking on the proof, we make a few promises and unfold some of their consequences.
5.1 Promises and their consequences
We start by listing our promises:
-
(p)1 We shall recursively construct distinguished group elements
 $\langle x_\alpha \mathrel {|} \alpha <\kappa \rangle $
generating the whole group G. For every subset
$\langle x_\alpha \mathrel {|} \alpha <\kappa \rangle $
generating the whole group G. For every subset
 $A\subseteq \kappa $
,
$A\subseteq \kappa $
,
 $G_A$
will denote the group generated by
$G_A$
will denote the group generated by
 $\{ x_\alpha \mathrel {|} \alpha \in A\}$
, so that
$\{ x_\alpha \mathrel {|} \alpha \in A\}$
, so that  and
and
 $G_\kappa =G$
;
$G_\kappa =G$
; -
(p)2 For every
 $\gamma \le \kappa $
, the underlying set of
$\gamma \le \kappa $
, the underlying set of
 $G_\gamma $
will be an initial segment of
$G_\gamma $
will be an initial segment of
 $\kappa $
;
$\kappa $
; -
(p)3 For all
 $\gamma < \kappa $
and
$\gamma < \kappa $
and
 $i < \theta $
,
$i < \theta $
,
 $G_{D^\gamma _{< i} \cup \{\gamma \}}$
is torsion-free;Footnote
4
$G_{D^\gamma _{< i} \cup \{\gamma \}}$
is torsion-free;Footnote
4
-
(p)4 For all
 $\gamma <\kappa $
and
$\gamma <\kappa $
and
 $i<\theta $
,
$i<\theta $
,
 $G_{D^\gamma _{< i} \cup \{\gamma \}} \cap G_{D^\gamma _{\leq i}} = G_{D^\gamma _{< i}}$
;
$G_{D^\gamma _{< i} \cup \{\gamma \}} \cap G_{D^\gamma _{\leq i}} = G_{D^\gamma _{< i}}$
; -
(p)5 For all
 $\gamma < \kappa $
and
$\gamma < \kappa $
and
 $i < \theta $
,
$i < \theta $
,
 $ G_{D^\gamma _{< i}} \mathrel {\leq _{\mathrm {m}}} G_{D^\gamma _{< i} \cup \{\gamma \}}$
;
$ G_{D^\gamma _{< i}} \mathrel {\leq _{\mathrm {m}}} G_{D^\gamma _{< i} \cup \{\gamma \}}$
; -
(p)6 For all
 $\gamma \in [1,\kappa )$
and
$\gamma \in [1,\kappa )$
and
 $i\in [1,\theta )$
,
$i\in [1,\theta )$
,
 $G_{D^\gamma _{\le i}\cup \{\gamma \}}$
is the group
$G_{D^\gamma _{\le i}\cup \{\gamma \}}$
is the group
 $M^*$
given by Lemma 3.4 when invoked with the groups
$M^*$
given by Lemma 3.4 when invoked with the groups-
•
 $H = G_{D^\gamma _{< i}}$
,
$H = G_{D^\gamma _{< i}}$
, -
•
 $ K = G_{D^\gamma _{\le i}}$
,
$ K = G_{D^\gamma _{\le i}}$
, -
•
 $L = G_{D^\gamma _{< i} \cup \{\gamma \}}$
,
$L = G_{D^\gamma _{< i} \cup \{\gamma \}}$
,
and an appropriate (possibly empty) system S.
-
At the outset, we also agree on the following pieces of notation.
Notation 5.2. For every subset
![]() $A\subseteq \kappa $
, we shall denote by
$A\subseteq \kappa $
, we shall denote by
![]() $\equiv _A$
the relation
$\equiv _A$
the relation
![]() $\sim _{G_A}$
of Definition 3.3. That is,
$\sim _{G_A}$
of Definition 3.3. That is,
![]() $g\equiv _Ah$
iff there are
$g\equiv _Ah$
iff there are
![]() $y_0,y_1\in G_A$
and
$y_0,y_1\in G_A$
and
![]() $\varepsilon \in \{1,-1\}$
such that
$\varepsilon \in \{1,-1\}$
such that
![]() $g=y_0\cdot h^\varepsilon \cdot y_1$
.
$g=y_0\cdot h^\varepsilon \cdot y_1$
.
Notation 5.3. For all
![]() $\gamma <\kappa $
and
$\gamma <\kappa $
and
![]() $g\in G_\gamma $
, let
$g\in G_\gamma $
, let
We shall also record the first appearance of an element ![]() by letting
by letting
Since
![]() $g\in G_{\alpha _g\cup \{\alpha _g\}}$
and
$g\in G_{\alpha _g\cup \{\alpha _g\}}$
and
![]() $\alpha _g=\bigcup _{i<\theta }D^{\alpha _g}_{\le i}$
, it also makes sense to define
$\alpha _g=\bigcup _{i<\theta }D^{\alpha _g}_{\le i}$
, it also makes sense to define
As for ![]() , since
, since ![]() , we agree to let
, we agree to let ![]() and
and ![]() .
.
Remark 5.4. By possibly replacing
![]() $d:[\kappa ]^2\rightarrow \theta $
with the map
$d:[\kappa ]^2\rightarrow \theta $
with the map
![]() $(\alpha ,\beta )\mapsto 1+d(\alpha ,\beta )$
, we may assume that
$(\alpha ,\beta )\mapsto 1+d(\alpha ,\beta )$
, we may assume that
![]() $0\notin \operatorname {\mathrm {Im}}(d)$
. This tacit assumption will ensure that for every
$0\notin \operatorname {\mathrm {Im}}(d)$
. This tacit assumption will ensure that for every
![]() $g\in G$
, if
$g\in G$
, if
![]() $i_g=0$
, then either
$i_g=0$
, then either ![]() or g is an element of the cyclic group
or g is an element of the cyclic group
![]() $\langle x_{\alpha _g}\rangle $
.
$\langle x_{\alpha _g}\rangle $
.
Notation 5.3 induces a well-ordering
![]() $\prec $
of G, as follows.
$\prec $
of G, as follows.
Definition 5.5. For
![]() $g\neq h$
in G, we shall let
$g\neq h$
in G, we shall let
![]() $g\prec h$
if one of the following holds:
$g\prec h$
if one of the following holds:
-
•
 $\alpha _g<\alpha _h$
;
$\alpha _g<\alpha _h$
; -
•
 $\alpha _g=\alpha _h$
and
$\alpha _g=\alpha _h$
and
 $i_g<i_h$
;
$i_g<i_h$
; -
•
 $\alpha _g=\alpha _h$
and
$\alpha _g=\alpha _h$
and
 $i_g=i_h$
and
$i_g=i_h$
and
 $g\in h$
.Footnote
5
$g\in h$
.Footnote
5
Note that ![]() .
.
Lemma 5.6. For all
![]() $\gamma <\kappa $
and
$\gamma <\kappa $
and
![]() $i\le \theta $
,
$i\le \theta $
,
![]() $G_{D^\gamma _{< i} \cup \{\gamma \}} \cap G_{\gamma } = G_{D^\gamma _{< i}}$
.
$G_{D^\gamma _{< i} \cup \{\gamma \}} \cap G_{\gamma } = G_{D^\gamma _{< i}}$
.
Proof. Let
![]() $\gamma <\kappa $
and
$\gamma <\kappa $
and
![]() $i\le \theta $
. As
$i\le \theta $
. As
![]() $G_\gamma =\bigcup _{j<\theta }G_{D^\gamma _{<j}}$
, it suffices to prove that for every
$G_\gamma =\bigcup _{j<\theta }G_{D^\gamma _{<j}}$
, it suffices to prove that for every
![]() $j\in (i,\theta ]$
,
$j\in (i,\theta ]$
,
The case
![]() $j=i+1$
is immediate from
$j=i+1$
is immediate from
![]() $(p)_4$
, and the case in which j is a limit ordinal follows from the fact that
$(p)_4$
, and the case in which j is a limit ordinal follows from the fact that
![]() $G_{D^\gamma _{<j}}=\bigcup _{l<j}G_{D^\gamma _{<l}}$
for j limit. So, suppose that
$G_{D^\gamma _{<j}}=\bigcup _{l<j}G_{D^\gamma _{<l}}$
for j limit. So, suppose that
![]() $j\in [i+1,\theta )$
is such that (I) holds. By
$j\in [i+1,\theta )$
is such that (I) holds. By
![]() $(p)_4$
,
$(p)_4$
,
![]() $G_{D^\gamma _{< j} \cup \{\gamma \}} \cap G_{D^\gamma _{\le j}} = G_{D^\gamma _{< j}}$
holds as well. Since
$G_{D^\gamma _{< j} \cup \{\gamma \}} \cap G_{D^\gamma _{\le j}} = G_{D^\gamma _{< j}}$
holds as well. Since
![]() $G_{D^\gamma _{< i} \cup \{\gamma \}}\subseteq G_{D^\gamma _{< j} \cup \{\gamma \}}$
, altogether,
$G_{D^\gamma _{< i} \cup \{\gamma \}}\subseteq G_{D^\gamma _{< j} \cup \{\gamma \}}$
, altogether,
 $$ \begin{align*} G_{D^\gamma_{< i} \cup \{\gamma\}} \cap G_{D^\gamma_{\le j}} &= G_{D^\gamma_{< i} \cup \{\gamma\}} \cap G_{D^\gamma_{< j} \cup \{\gamma\}}\cap G_{D^\gamma_{\le j}} \\ &= G_{D^\gamma_{< i} \cup \{\gamma\}} \cap G_{D^\gamma_{< j}}\\ &= G_{D^\gamma_{< i}}, \end{align*} $$
$$ \begin{align*} G_{D^\gamma_{< i} \cup \{\gamma\}} \cap G_{D^\gamma_{\le j}} &= G_{D^\gamma_{< i} \cup \{\gamma\}} \cap G_{D^\gamma_{< j} \cup \{\gamma\}}\cap G_{D^\gamma_{\le j}} \\ &= G_{D^\gamma_{< i} \cup \{\gamma\}} \cap G_{D^\gamma_{< j}}\\ &= G_{D^\gamma_{< i}}, \end{align*} $$
as sought.
By the preceding, and since
![]() $D^\gamma _{< 0}=\emptyset $
, the group
$D^\gamma _{< 0}=\emptyset $
, the group
![]() $\langle x_\gamma \rangle $
generated by
$\langle x_\gamma \rangle $
generated by
![]() $x_\gamma $
will have a trivial intersection with
$x_\gamma $
will have a trivial intersection with
![]() $G_\gamma $
. Another consequence of the preceding is as follows.
$G_\gamma $
. Another consequence of the preceding is as follows.
Corollary 5.7. For every
![]() $\gamma <\kappa $
,
$\gamma <\kappa $
,
![]() $G_\gamma \mathrel {\leq _{\mathrm {m}}} G_{\gamma +1}$
.
$G_\gamma \mathrel {\leq _{\mathrm {m}}} G_{\gamma +1}$
.
Proof. Let ![]() and
and
![]() $h \in G_{\gamma +1} \setminus G_\gamma $
for a given
$h \in G_{\gamma +1} \setminus G_\gamma $
for a given
![]() $\gamma <\kappa $
. Find a large enough
$\gamma <\kappa $
. Find a large enough
![]() $i< \theta $
such that
$i< \theta $
such that
![]() $g \in G_{D^\gamma _{<i}}$
and
$g \in G_{D^\gamma _{<i}}$
and
![]() $h \in G_{D^\gamma _{<i} \cup \{\gamma \}} \setminus G_{D^\gamma _{<i}}$
. Then, by
$h \in G_{D^\gamma _{<i} \cup \{\gamma \}} \setminus G_{D^\gamma _{<i}}$
. Then, by
![]() $(p)_5$
,
$(p)_5$
,
Finally, Lemma 5.6 yields that
![]() $h^{-1}gh \notin G_\gamma $
.
$h^{-1}gh \notin G_\gamma $
.
The next consequence of our promises is the upcoming Lemma 5.9. In order to state it, we agree to say that a set
![]() $A\subseteq \kappa $
is absorbent if for every
$A\subseteq \kappa $
is absorbent if for every
![]() $\gamma \in A$
, there exists some
$\gamma \in A$
, there exists some
![]() $i\le \theta $
such that
$i\le \theta $
such that
![]() $A \cap \gamma = D^\gamma _{< i}$
. To exemplify,
$A \cap \gamma = D^\gamma _{< i}$
. To exemplify,
Proposition 5.8. For all
![]() $\gamma <\kappa $
and
$\gamma <\kappa $
and
![]() $i\le \theta $
,
$i\le \theta $
,
![]() $D^\gamma _{< i}$
is absorbent.
$D^\gamma _{< i}$
is absorbent.
Proof. By Lemma 4.3.
Lemma 5.9. Suppose that
![]() $A,A'$
are absorbent subsets of
$A,A'$
are absorbent subsets of
![]() $\kappa $
.
$\kappa $
.
-
(1) For every
 ,
,
 $D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\}\subseteq A$
;
$D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\}\subseteq A$
; -
(2) For all
 $\gamma <\kappa $
,
$\gamma <\kappa $
,
 $i<\theta $
, and
$i<\theta $
, and
 $g \in G_{D^\gamma _{<i}\cup \{\gamma \}}$
, we have
$g \in G_{D^\gamma _{<i}\cup \{\gamma \}}$
, we have
 $i_g<i$
;
$i_g<i$
; -
(3) For all
 $\gamma <\kappa $
and
$\gamma <\kappa $
and  , we have
, we have
 $i^\gamma _g = \max \{d(\alpha _g,\gamma ), i_g\}$
;
$i^\gamma _g = \max \{d(\alpha _g,\gamma ), i_g\}$
; -
(4)
 $G_{A} \cap G_{A'} = G_{A \cap A'}$
.
$G_{A} \cap G_{A'} = G_{A \cap A'}$
.
Proof. (1) Let ![]() . Denote by
. Denote by
![]() $\gamma \in A$
the minimal ordinal such that
$\gamma \in A$
the minimal ordinal such that
![]() $g \in G_{A \cap (\gamma +1)}$
. In particular,
$g \in G_{A \cap (\gamma +1)}$
. In particular,
![]() $g \notin G_{A \cap \gamma }$
and
$g \notin G_{A \cap \gamma }$
and
![]() $\alpha _g\le \gamma $
. As A is absorbent, we may now fix
$\alpha _g\le \gamma $
. As A is absorbent, we may now fix
![]() $i\le \theta $
such that
$i\le \theta $
such that
![]() $A\cap \gamma =D^\gamma _{<i}$
. Consequently,
$A\cap \gamma =D^\gamma _{<i}$
. Consequently,
![]() $g \in G_{D^{\gamma }_{< i} \cup \{\gamma \}}$
. If
$g \in G_{D^{\gamma }_{< i} \cup \{\gamma \}}$
. If
![]() $\alpha _g < \gamma $
, then
$\alpha _g < \gamma $
, then
![]() $g \in G_{D^{\gamma }_{< i} \cup \{\gamma \}} \cap G_\gamma $
, which, by Lemma 5.6 is equal to
$g \in G_{D^{\gamma }_{< i} \cup \{\gamma \}} \cap G_\gamma $
, which, by Lemma 5.6 is equal to
![]() $G_{D^{\gamma }_{< i}}= G_{A \cap \gamma }$
, contradicting the fact that
$G_{D^{\gamma }_{< i}}= G_{A \cap \gamma }$
, contradicting the fact that
![]() $g \notin G_{A \cap \gamma }$
. So,
$g \notin G_{A \cap \gamma }$
. So,
![]() $\alpha _g = \gamma $
, and hence,
$\alpha _g = \gamma $
, and hence,
![]() $g \in G_{D^{\alpha _g}_{< i} \cup \{\alpha _g\}}$
. As
$g \in G_{D^{\alpha _g}_{< i} \cup \{\alpha _g\}}$
. As
![]() $G_{D^{\alpha _g}_{< i}\cup \{\alpha _g\}}=\bigcup _{j<i} G_{D^{\gamma }_{\leq j} \cup \{\gamma \}}$
, the definition of
$G_{D^{\alpha _g}_{< i}\cup \{\alpha _g\}}=\bigcup _{j<i} G_{D^{\gamma }_{\leq j} \cup \{\gamma \}}$
, the definition of
![]() $i_g$
implies that
$i_g$
implies that
![]() $i_g < i$
. Altogether,
$i_g < i$
. Altogether,
![]() $D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\}\subseteq D^\gamma _{<i}\cup \{\gamma \}\subseteq A$
.
$D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\}\subseteq D^\gamma _{<i}\cup \{\gamma \}\subseteq A$
.
(2) Let
![]() $\gamma <\kappa $
,
$\gamma <\kappa $
,
![]() $i<\theta $
, and
$i<\theta $
, and
![]() $g \in G_{D^\gamma _{<i}\cup \{\gamma \}}$
. By Clause (1),
$g \in G_{D^\gamma _{<i}\cup \{\gamma \}}$
. By Clause (1),
![]() $D^{\alpha _g}_{\le i_g}\cup \{\alpha _g\}\subseteq D^\gamma _{<i}\cup \{\gamma \}$
. If
$D^{\alpha _g}_{\le i_g}\cup \{\alpha _g\}\subseteq D^\gamma _{<i}\cup \{\gamma \}$
. If
![]() $\alpha _g=\gamma $
, then the inclusion implies that
$\alpha _g=\gamma $
, then the inclusion implies that
![]() $i_g<i$
. Otherwise,
$i_g<i$
. Otherwise,
![]() $\alpha _g\in D^\gamma _{<i}$
, and then Lemma 4.3 implies that
$\alpha _g\in D^\gamma _{<i}$
, and then Lemma 4.3 implies that
so, again
![]() $i_g<i$
.
$i_g<i$
.
(3) Let
![]() $\gamma <\kappa $
and
$\gamma <\kappa $
and ![]() . Clearly,
. Clearly,
![]() $\alpha _g<\gamma $
. Also, recalling Notation 5.3,
$\alpha _g<\gamma $
. Also, recalling Notation 5.3,
![]() $g\in G_{D^\gamma _{\le i^\gamma _g}}$
. So, Clause (1) together with Proposition 5.8 imply that
$g\in G_{D^\gamma _{\le i^\gamma _g}}$
. So, Clause (1) together with Proposition 5.8 imply that
![]() $D^{\alpha _g}_{\le i_g}\cup \{\alpha _g\}\subseteq D^\gamma _{\le i^\gamma _g}$
. In particular,
$D^{\alpha _g}_{\le i_g}\cup \{\alpha _g\}\subseteq D^\gamma _{\le i^\gamma _g}$
. In particular,
![]() $d(\alpha _g,\gamma ) \leq i^\gamma _g$
, and, by Lemma 4.3, also
$d(\alpha _g,\gamma ) \leq i^\gamma _g$
, and, by Lemma 4.3, also
and hence,
![]() $i_g \leq i^\gamma _g$
. This shows that
$i_g \leq i^\gamma _g$
. This shows that
![]() $i=\max \{d(\alpha _g,\gamma ), i_g\}$
is
$i=\max \{d(\alpha _g,\gamma ), i_g\}$
is
![]() $\le i^\gamma _g$
. However, since
$\le i^\gamma _g$
. However, since
![]() $\alpha _g\in D^\gamma _{\le d(\alpha _g,\gamma )}\subseteq D^\gamma _{\le i}$
, Lemma 4.3 implies that
$\alpha _g\in D^\gamma _{\le d(\alpha _g,\gamma )}\subseteq D^\gamma _{\le i}$
, Lemma 4.3 implies that
and hence,
![]() $g \in G_{D^{\alpha _g}_{\le i} \cup \{\alpha _g\}}\subseteq G_{D^\gamma _{\le i}}$
. Consequently,
$g \in G_{D^{\alpha _g}_{\le i} \cup \{\alpha _g\}}\subseteq G_{D^\gamma _{\le i}}$
. Consequently,
![]() $i_g^\gamma \le i$
.
$i_g^\gamma \le i$
.
(4) By Clause (1), for every
![]() $g \in G_{A} \cap G_{A'}$
, either
$g \in G_{A} \cap G_{A'}$
, either ![]() (and then
(and then
![]() $g \in G_\emptyset \subseteq G_{A\cap A'}$
), or
$g \in G_\emptyset \subseteq G_{A\cap A'}$
), or
![]() $D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\} \subseteq A \cap A'$
, and then
$D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\} \subseteq A \cap A'$
, and then
![]() $g\in G_{D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\}}\subseteq G_{A\cap A'}$
by the definition of
$g\in G_{D^{\alpha _g}_{\leq i_g}\cup \{\alpha _g\}}\subseteq G_{A\cap A'}$
by the definition of
![]() $i_g$
and
$i_g$
and
![]() $\alpha _g$
. The other inclusion is trivial.
$\alpha _g$
. The other inclusion is trivial.
Corollary 5.10. For all
![]() $\beta \le \gamma <\kappa $
, for all
$\beta \le \gamma <\kappa $
, for all
![]() $j<i<\theta $
, for all
$j<i<\theta $
, for all
![]() $g,h \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_\gamma $
, if
$g,h \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_\gamma $
, if
![]() $g\equiv _{{D^\gamma _{<i} \cap \beta }}h$
, then
$g\equiv _{{D^\gamma _{<i} \cap \beta }}h$
, then
![]() $g\equiv _{D^\gamma _{<j} \cap \beta }h$
.
$g\equiv _{D^\gamma _{<j} \cap \beta }h$
.
Proof. Let
![]() $\beta \le \gamma <\kappa $
such that
$\beta \le \gamma <\kappa $
such that
![]() $\gamma \ge \theta $
and let
$\gamma \ge \theta $
and let
![]() $j< i<\theta $
. Suppose that
$j< i<\theta $
. Suppose that
![]() $g,h \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_\gamma $
are such that
$g,h \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_\gamma $
are such that
![]() $g\not \equiv _{D^\gamma _{<j} \cap \beta }h$
, and we shall prove by induction on
$g\not \equiv _{D^\gamma _{<j} \cap \beta }h$
, and we shall prove by induction on
![]() $l\in [j,i]$
that
$l\in [j,i]$
that
Recalling Clause (4) of Lemma 5.9,
![]() $G_{D^\gamma _{<j} \cup \{\gamma \}} \cap G_\gamma = G_{D^\gamma _{<j}}$
, so we infer that
$G_{D^\gamma _{<j} \cup \{\gamma \}} \cap G_\gamma = G_{D^\gamma _{<j}}$
, so we infer that
![]() $g,h \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_{D^\gamma _{<j}}$
.
$g,h \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_{D^\gamma _{<j}}$
.
The case
![]() $l=j$
is trivial, and the case in which l is a limit ordinal follows from continuity. So, suppose that
$l=j$
is trivial, and the case in which l is a limit ordinal follows from continuity. So, suppose that
![]() $l\in [j,i)$
is such that (II) holds, and we shall prove that
$l\in [j,i)$
is such that (II) holds, and we shall prove that
![]() $g\not \equiv _{D^\gamma _{\le l} \cap \beta }h$
. W.l.o.g.
$g\not \equiv _{D^\gamma _{\le l} \cap \beta }h$
. W.l.o.g.
![]() $l \geq 1$
, otherwise
$l \geq 1$
, otherwise ![]() , so both relations
, so both relations
![]() $\equiv _{D^\gamma _{< 0}}$
and
$\equiv _{D^\gamma _{< 0}}$
and
![]() $\equiv _{D^\gamma _{\leq 0}}$
are the identity on
$\equiv _{D^\gamma _{\leq 0}}$
are the identity on
![]() $G_{D^\gamma _{\leq 0} \cup \{\gamma \}}$
.
$G_{D^\gamma _{\leq 0} \cup \{\gamma \}}$
.
By
![]() $(p)_6$
, the group
$(p)_6$
, the group
![]() $G_{D^\gamma _{\le l} \cup \{\gamma \}}$
was given by Lemma 3.4 when invoked with
$G_{D^\gamma _{\le l} \cup \{\gamma \}}$
was given by Lemma 3.4 when invoked with
![]() $H = G_{D^\gamma _{< l}}$
,
$H = G_{D^\gamma _{< l}}$
,
![]() $K = G_{D^\gamma _{\leq l}}$
and
$K = G_{D^\gamma _{\leq l}}$
and
![]() $L = G_{D^\gamma _{<l} \cup \{\gamma \}}$
. Consider
$L = G_{D^\gamma _{<l} \cup \{\gamma \}}$
. Consider
![]() $K'=G_{D^\gamma _{\le l} \cap \beta }$
, which is a subgroup of K, and then let
$K'=G_{D^\gamma _{\le l} \cap \beta }$
, which is a subgroup of K, and then let
![]() $H'=K' \cap L$
. By Lemma 5.9(4),
$H'=K' \cap L$
. By Lemma 5.9(4),
meaning that (II) asserts that
![]() $g\not \sim _{H'}h$
.
$g\not \sim _{H'}h$
.
As
![]() $g,h\in G_{D^\gamma _{< j} \cup \{\gamma \}}\subseteq L$
, and
$g,h\in G_{D^\gamma _{< j} \cup \{\gamma \}}\subseteq L$
, and
![]() $H'=K' \cap L=K'\cap H$
(since
$H'=K' \cap L=K'\cap H$
(since
![]() $K \cap L = H$
), Clause (F) of Lemma 3.4 implies that
$K \cap L = H$
), Clause (F) of Lemma 3.4 implies that
![]() $g\not \sim _{K'}h$
. That is,
$g\not \sim _{K'}h$
. That is,
![]() $g\not \equiv _{D^\gamma _{\le l} \cap \beta }h$
, as sought.
$g\not \equiv _{D^\gamma _{\le l} \cap \beta }h$
, as sought.
Notation 5.11. As a last step of preparation, we fix a surjection
![]() $ \vec \pi =(\pi _0,\pi _1,\pi _2, \pi _3,\pi _4)$
from
$ \vec \pi =(\pi _0,\pi _1,\pi _2, \pi _3,\pi _4)$
from
![]() $\kappa $
to
$\kappa $
to
![]() $\kappa \times \kappa \times \kappa \times \kappa \times \{1,-1\}$
; that is, for all
$\kappa \times \kappa \times \kappa \times \kappa \times \{1,-1\}$
; that is, for all
![]() $\eta _0,\eta _1,\eta _2,\eta _3\in \kappa $
and
$\eta _0,\eta _1,\eta _2,\eta _3\in \kappa $
and
![]() $ {\varepsilon } \in \{1,-1\}$
, there exists a
$ {\varepsilon } \in \{1,-1\}$
, there exists a
![]() $\xi <\kappa $
such that
$\xi <\kappa $
such that
5.2 The recursive construction
We are now ready to start the recursive process. We start by letting
![]() $x_0$
generate an infinite cyclic group (i.e.,
$x_0$
generate an infinite cyclic group (i.e.,
![]() $\mathbb {Z}$
), and we assume this group
$\mathbb {Z}$
), and we assume this group
![]() $G_1$
has underlying set
$G_1$
has underlying set
![]() $\omega $
. Hereafter, we shall not worry about
$\omega $
. Hereafter, we shall not worry about
![]() $(p)_2$
since it is clear it may be secured. Next, suppose that
$(p)_2$
since it is clear it may be secured. Next, suppose that
![]() $\gamma \in [1,\kappa )$
is such that
$\gamma \in [1,\kappa )$
is such that
![]() $G_\gamma $
has already been defined and satisfies all of our promises. Note that
$G_\gamma $
has already been defined and satisfies all of our promises. Note that
![]() $(p)_3$
implies that for every
$(p)_3$
implies that for every
![]() $\beta < \gamma $
, the group
$\beta < \gamma $
, the group
![]() $G_{\beta +1} = \bigcup _{i< \theta } G_{D^\beta _{<i} \cup \{\beta \}}$
is torsion-free, and so is
$G_{\beta +1} = \bigcup _{i< \theta } G_{D^\beta _{<i} \cup \{\beta \}}$
is torsion-free, and so is
![]() $G_\gamma = \bigcup _{\beta < \gamma } G_{\beta +1}$
. To construct
$G_\gamma = \bigcup _{\beta < \gamma } G_{\beta +1}$
. To construct
![]() $G_{\gamma +1}$
, we first let
$G_{\gamma +1}$
, we first let
![]() $x_\gamma =\min (\kappa \setminus G_\gamma )$
, and now we need to describe the group relationship between
$x_\gamma =\min (\kappa \setminus G_\gamma )$
, and now we need to describe the group relationship between
![]() $x_\gamma $
and the elements of
$x_\gamma $
and the elements of
![]() $G_\gamma $
. We will define
$G_\gamma $
. We will define
![]() $\langle G_{D^\gamma _{< i} \cup \{ \gamma \}}\mathrel {|} i < \theta \rangle $
by recursion on
$\langle G_{D^\gamma _{< i} \cup \{ \gamma \}}\mathrel {|} i < \theta \rangle $
by recursion on
![]() $i<\theta $
, in such a way that all of our promises are kept.
$i<\theta $
, in such a way that all of our promises are kept.
Here we go. As
![]() $D^\gamma _{< 0} = D^\gamma _{\leq 0} = \emptyset $
(recall Remark 5.4), we mean
$D^\gamma _{< 0} = D^\gamma _{\leq 0} = \emptyset $
(recall Remark 5.4), we mean ![]() , and we let
, and we let
![]() $G_{D^\gamma _{\leq 0} \cup \{\gamma \}} = G_{\{\gamma \}}$
be the infinite group
$G_{D^\gamma _{\leq 0} \cup \{\gamma \}} = G_{\{\gamma \}}$
be the infinite group
![]() $\mathbb Z$
generated by
$\mathbb Z$
generated by
![]() $x_\gamma $
. Note that
$x_\gamma $
. Note that ![]() vacuously holds. Moving on, suppose that
vacuously holds. Moving on, suppose that
![]() $i<\theta $
is such that
$i<\theta $
is such that
![]() $G_{D^\gamma _{<i}\cup \{\gamma \}}$
has already been defined. For all
$G_{D^\gamma _{<i}\cup \{\gamma \}}$
has already been defined. For all
![]() $j\le i$
and
$j\le i$
and
![]() $\beta \le \gamma $
, let
$\beta \le \gamma $
, let
![]() $E^\gamma _{< j,\beta }$
be the restriction of the equivalence relation
$E^\gamma _{< j,\beta }$
be the restriction of the equivalence relation
![]() ${\equiv _{(D^\gamma _{< j} \cap \beta )}}$
to
${\equiv _{(D^\gamma _{< j} \cap \beta )}}$
to
![]() $G_{D^\gamma _{< j} \cup \{\gamma \}}$
. Next, use Definition 5.5 to define a transversal
$G_{D^\gamma _{< j} \cup \{\gamma \}}$
. Next, use Definition 5.5 to define a transversal
![]() $T^\gamma _{< j, \beta }$
for those equivalence classes of
$T^\gamma _{< j, \beta }$
for those equivalence classes of
![]() $E^\gamma _{< j, \beta }$
that lie in
$E^\gamma _{< j, \beta }$
that lie in
![]() $G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_\gamma = G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_{D^\gamma _{< j}}$
, as follows:
$G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_\gamma = G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_{D^\gamma _{< j}}$
, as follows:
Lemma 5.12. For all
![]() $j\le i$
and
$j\le i$
and
![]() $\alpha \le \beta \le \gamma $
,
$\alpha \le \beta \le \gamma $
,
-
(1)
 $ E^\gamma _{< i, \beta } \mathbin \upharpoonright (G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_\gamma ) = E^\gamma _{< j, \beta } \mathbin \upharpoonright (G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_\gamma )$
;
$ E^\gamma _{< i, \beta } \mathbin \upharpoonright (G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_\gamma ) = E^\gamma _{< j, \beta } \mathbin \upharpoonright (G_{D^\gamma _{< j} \cup \{\gamma \}} \setminus G_\gamma )$
; -
(2)
 $T^\gamma _{< j,\beta } \subseteq T^\gamma _{< i,\beta }$
;
$T^\gamma _{< j,\beta } \subseteq T^\gamma _{< i,\beta }$
; -
(3)
 $T^\gamma _{< i,\alpha } \supseteq T^\gamma _{< i,\beta }$
.
$T^\gamma _{< i,\alpha } \supseteq T^\gamma _{< i,\beta }$
.
Proof. (1) By Corollary 5.10.
(2) Let
![]() $t \in T^\gamma _{<j,\beta }$
. As
$t \in T^\gamma _{<j,\beta }$
. As
![]() $G_{(D^\gamma _{< j} \cap \beta )}h^{\pm 1} G_{(D^\gamma _{< j} \cap \beta )}\subseteq G_\gamma $
for every
$G_{(D^\gamma _{< j} \cap \beta )}h^{\pm 1} G_{(D^\gamma _{< j} \cap \beta )}\subseteq G_\gamma $
for every
![]() $h\in G_\gamma $
, it is the case that
$h\in G_\gamma $
, it is the case that
![]() $[g]_{E^\gamma _{< j,\beta }}$
is disjoint from
$[g]_{E^\gamma _{< j,\beta }}$
is disjoint from
![]() $G_\gamma $
for every
$G_\gamma $
for every
![]() $g \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_\gamma $
. In particular,
$g \in G_{D^\gamma _{<j} \cup \{\gamma \}} \setminus G_\gamma $
. In particular,
![]() $t\in G_{\gamma +1}\setminus G_\gamma $
, so that
$t\in G_{\gamma +1}\setminus G_\gamma $
, so that
![]() $i_t = i^{\gamma +1}_t < j$
. Therefore, by Clause (1),
$i_t = i^{\gamma +1}_t < j$
. Therefore, by Clause (1),
For every
![]() $g \in [t]_{E^\gamma _{<i,\beta }} \setminus G_{D^\gamma _{<j} \cup \{\gamma \}}$
, we have
$g \in [t]_{E^\gamma _{<i,\beta }} \setminus G_{D^\gamma _{<j} \cup \{\gamma \}}$
, we have
![]() $i_g=i_g^{\gamma +1} \ge j>i_t$
, and then Definition 5.5 implies that
$i_g=i_g^{\gamma +1} \ge j>i_t$
, and then Definition 5.5 implies that
![]() $t \prec g$
. Altogether,
$t \prec g$
. Altogether,
(3) This is clear from the definition of
![]() $T^\gamma _{< i, \alpha }$
,
$T^\gamma _{< i, \alpha }$
,
![]() $T^\gamma _{< i, \beta }$
, as the equivalence relation
$T^\gamma _{< i, \beta }$
, as the equivalence relation
![]() $E^\gamma _{< j, \alpha }$
is a refinement of
$E^\gamma _{< j, \alpha }$
is a refinement of
![]() $E^\gamma _{< j, \beta }$
.
$E^\gamma _{< j, \beta }$
.
Our next goal is to the define the system
![]() $S = \{ (h_\sigma ,a_\sigma , b_\sigma ,b^{\prime }_{\sigma } )\mathrel {|} \sigma \in \Sigma \}$
that will yield the definition of
$S = \{ (h_\sigma ,a_\sigma , b_\sigma ,b^{\prime }_{\sigma } )\mathrel {|} \sigma \in \Sigma \}$
that will yield the definition of
![]() $G_{D^\gamma _{\le i}\cup \{\gamma \}}$
, as per
$G_{D^\gamma _{\le i}\cup \{\gamma \}}$
, as per
![]() $(p)_6$
. We start with a rough approximation
$(p)_6$
. We start with a rough approximation
![]() $\Sigma ^{++}$
of
$\Sigma ^{++}$
of
![]() $\Sigma $
, we then refine it to
$\Sigma $
, we then refine it to
![]() $\Sigma ^+\subseteq \Sigma ^{++}$
, and finally we find the appropriate
$\Sigma ^+\subseteq \Sigma ^{++}$
, and finally we find the appropriate
![]() $\Sigma \subseteq \Sigma ^+$
.
$\Sigma \subseteq \Sigma ^+$
.
Definition 5.13. Let
-
•
 $\Sigma ^{++} = \{ (a,t)\mathrel {|} a\in G_{D^\gamma _{\le i}}\setminus G_{D^\gamma _{< i}},~\alpha _a \in D^\gamma _{\leq i} \setminus D^\gamma _{<i},~t \in T^\gamma _{< i,\alpha _a}\}$
;
$\Sigma ^{++} = \{ (a,t)\mathrel {|} a\in G_{D^\gamma _{\le i}}\setminus G_{D^\gamma _{< i}},~\alpha _a \in D^\gamma _{\leq i} \setminus D^\gamma _{<i},~t \in T^\gamma _{< i,\alpha _a}\}$
; -
•
 $\Sigma ^+=\{(a,t) \in \Sigma ^{++}\mathrel {|} \forall l<4\,[\pi _l(c(\alpha _a,\gamma )) \in G_\gamma ]\}$
.
$\Sigma ^+=\{(a,t) \in \Sigma ^{++}\mathrel {|} \forall l<4\,[\pi _l(c(\alpha _a,\gamma )) \in G_\gamma ]\}$
.
Definition 5.14. For each
![]() $\sigma =(a,t) \in \Sigma ^+$
, we attach the following objects:
$\sigma =(a,t) \in \Sigma ^+$
, we attach the following objects:

We then let
![]() $\Sigma $
be the set of all
$\Sigma $
be the set of all
![]() $\sigma \in \Sigma ^+$
for which all of the following hold:
$\sigma \in \Sigma ^+$
for which all of the following hold:
-
(1)
 $\max \{\alpha _{y_{\sigma ,0}}, \alpha _{y_{\sigma ,1}}, \alpha _{z_\sigma } \} < \alpha _{a_\sigma }$
;
$\max \{\alpha _{y_{\sigma ,0}}, \alpha _{y_{\sigma ,1}}, \alpha _{z_\sigma } \} < \alpha _{a_\sigma }$
; -
(2)
 $\max \{i_t,i^\gamma _{y_{\sigma ,0}}, i^\gamma _{y_{\sigma ,1}}\} < i^\gamma _{z_\sigma }<i$
(in particular,
$\max \{i_t,i^\gamma _{y_{\sigma ,0}}, i^\gamma _{y_{\sigma ,1}}\} < i^\gamma _{z_\sigma }<i$
(in particular,
 $i^\gamma _{z_\sigma }\ge 1$
);
$i^\gamma _{z_\sigma }\ge 1$
); -
(3)
 $h_\sigma \in G_{D^\gamma _{< i}}$
.
$h_\sigma \in G_{D^\gamma _{< i}}$
.
Remark 5.15. Clause (1) implies that
![]() $y_{\sigma ,0}, y_{\sigma ,1}, z_\sigma \in G_{\alpha _{a_\sigma }}$
, and Clause (2) implies that, for some
$y_{\sigma ,0}, y_{\sigma ,1}, z_\sigma \in G_{\alpha _{a_\sigma }}$
, and Clause (2) implies that, for some
![]() $j < i$
,
$j < i$
,
![]() $y_{\sigma ,0},y_{\sigma ,1}\in G_{D^\gamma _{<j}}$
,
$y_{\sigma ,0},y_{\sigma ,1}\in G_{D^\gamma _{<j}}$
,
![]() $t \in G_{D^\gamma _{<j} \cup \{\gamma \}}$
, and
$t \in G_{D^\gamma _{<j} \cup \{\gamma \}}$
, and
![]() $z_\sigma \notin G_{D^\gamma _{<j}}$
.
$z_\sigma \notin G_{D^\gamma _{<j}}$
.
Definition 5.16. Denote
![]() $H = G_{D^\gamma _{< i}}$
,
$H = G_{D^\gamma _{< i}}$
,
![]() $K = G_{D^\gamma _{\le i}}$
,
$K = G_{D^\gamma _{\le i}}$
,
![]() $L = G_{D^\gamma _{< i} \cup \{\gamma \}}$
, and
$L = G_{D^\gamma _{< i} \cup \{\gamma \}}$
, and
Lemma 5.17.
![]() $H \leq K$
,
$H \leq K$
,
![]() $H \mathrel {\leq _{\mathrm {m}}} L$
,
$H \mathrel {\leq _{\mathrm {m}}} L$
,
![]() $K \cap L = H$
and
$K \cap L = H$
and
![]() $S\subseteq H \times (K \setminus H) \times (L\setminus H)\times (L\setminus H)$
.
$S\subseteq H \times (K \setminus H) \times (L\setminus H)\times (L\setminus H)$
.
Proof. It is clear that
![]() $H=G_{D^\gamma _{< i}}\le G_{D^\gamma _{\le i}}=K$
. By
$H=G_{D^\gamma _{< i}}\le G_{D^\gamma _{\le i}}=K$
. By
![]() $(p)_5$
,
$(p)_5$
,
![]() $H\mathrel {\leq _{\mathrm {m}}} L$
, and by
$H\mathrel {\leq _{\mathrm {m}}} L$
, and by
![]() $(p)_4$
,
$(p)_4$
,
![]() $K\cap L=H$
.
$K\cap L=H$
.
Next, let
![]() $\sigma \in \Sigma $
. By Definition 5.14(3),
$\sigma \in \Sigma $
. By Definition 5.14(3),
![]() $h_\sigma \in H$
. Since
$h_\sigma \in H$
. Since
![]() $\sigma \in \Sigma ^{++}$
,
$\sigma \in \Sigma ^{++}$
,
![]() $a_\sigma \in K\setminus H$
. Recall that
$a_\sigma \in K\setminus H$
. Recall that
![]() $t\in T^\gamma _{< i, \alpha }\subseteq G_{D^\gamma _{< i} \cup \{\gamma \}} \setminus G_\gamma =L\setminus G_\gamma $
. By Lemma 5.9(4),
$t\in T^\gamma _{< i, \alpha }\subseteq G_{D^\gamma _{< i} \cup \{\gamma \}} \setminus G_\gamma =L\setminus G_\gamma $
. By Lemma 5.9(4),
![]() $ H=L \cap G_\gamma $
, and hence,
$ H=L \cap G_\gamma $
, and hence,
![]() $t\in L\setminus H$
. By Definition 5.14(2),
$t\in L\setminus H$
. By Definition 5.14(2),
![]() $y_{\sigma ,0},y_{\sigma ,1},z_\sigma $
are in
$y_{\sigma ,0},y_{\sigma ,1},z_\sigma $
are in
![]() $H \le L$
, so, altogether,
$H \le L$
, so, altogether,
![]() $b_\sigma $
and
$b_\sigma $
and
![]() $b_\sigma '$
are in L as well. Since
$b_\sigma '$
are in L as well. Since
![]() $t\notin H$
, we get that
$t\notin H$
, we get that
![]() $b_\sigma \notin H$
. Finally, to see that
$b_\sigma \notin H$
. Finally, to see that
![]() $b_\sigma '\notin H$
, it suffices to verify that
$b_\sigma '\notin H$
, it suffices to verify that
![]() $b_\sigma ' \in G_{D^\gamma _{\leq j} \cup \{\gamma \}} \setminus G_{D^\gamma _{\leq j}}$
for some
$b_\sigma ' \in G_{D^\gamma _{\leq j} \cup \{\gamma \}} \setminus G_{D^\gamma _{\leq j}}$
for some
![]() $j<i$
, since
$j<i$
, since
![]() $H=G_{D^\gamma _{< i}} \leq G_\gamma $
, and
$H=G_{D^\gamma _{< i}} \leq G_\gamma $
, and
![]() $G_{D^\gamma _{\leq j} \cup \{\gamma \}} \cap G_\gamma = G_{D^\gamma _{\leq j}}$
by Lemma 5.9(4).
$G_{D^\gamma _{\leq j} \cup \{\gamma \}} \cap G_\gamma = G_{D^\gamma _{\leq j}}$
by Lemma 5.9(4).
By the definition of
![]() $\Sigma $
and since
$\Sigma $
and since
![]() $y_{\sigma ,0},y_{\sigma ,1} \in G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
, we have that
$y_{\sigma ,0},y_{\sigma ,1} \in G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
, we have that
![]() $y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1} \in G_{D^\gamma _{< i^\gamma _{z_\sigma }} \cup \{\gamma \}} \setminus G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
and
$y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1} \in G_{D^\gamma _{< i^\gamma _{z_\sigma }} \cup \{\gamma \}} \setminus G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
and
![]() $z_\sigma \in G_{D^\gamma _{\leq i^\gamma _{z_\sigma }}} \setminus G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
. By
$z_\sigma \in G_{D^\gamma _{\leq i^\gamma _{z_\sigma }}} \setminus G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
. By
![]() $(p)_6$
,
$(p)_6$
,
![]() $G_{D^\gamma _{\le i^\gamma _{z_\sigma } \cup \{\gamma \}}}$
has been obtained by invoking Lemma 3.4 (note that
$G_{D^\gamma _{\le i^\gamma _{z_\sigma } \cup \{\gamma \}}}$
has been obtained by invoking Lemma 3.4 (note that
![]() $i^\gamma _{z_\sigma } \geq 1$
necessarily) with
$i^\gamma _{z_\sigma } \geq 1$
necessarily) with
![]() $\bar K = G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
,
$\bar K = G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
,
![]() $\bar L = G_{D^\gamma _{< i^\gamma _{z_\sigma }}\cup \{\gamma \}}$
, and
$\bar L = G_{D^\gamma _{< i^\gamma _{z_\sigma }}\cup \{\gamma \}}$
, and
![]() $\bar H = G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
, and then Clause (D) of that lemma implies that
$\bar H = G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
, and then Clause (D) of that lemma implies that
and then the fact that
![]() $z_\sigma \in G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
implies that
$z_\sigma \in G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
implies that
as sought.
Lemma 5.18. For every
![]() $\sigma \in \Sigma $
,
$\sigma \in \Sigma $
,
![]() $b_\sigma \not \sim _H b_\sigma '$
.
$b_\sigma \not \sim _H b_\sigma '$
.
Proof. Let
![]() $\sigma = (a,t)$
in
$\sigma = (a,t)$
in
![]() $\Sigma $
. Set
$\Sigma $
. Set
From
![]() $\sigma \in \Sigma $
, we infer that
$\sigma \in \Sigma $
, we infer that
![]() $j < i^\gamma _{z_\sigma } < i$
, and
$j < i^\gamma _{z_\sigma } < i$
, and
Recall that
![]() $t\in T^\gamma _{< i, \alpha _a}\subseteq G_{D^\gamma _{< i} \cup \{\gamma \}} \setminus G_\gamma $
; therefore,
$t\in T^\gamma _{< i, \alpha _a}\subseteq G_{D^\gamma _{< i} \cup \{\gamma \}} \setminus G_\gamma $
; therefore,
By Lemma 5.9(4),
![]() $ G_{D^\gamma _{<i^\gamma _{z_\sigma }}}=G_{D^\gamma _{<i^\gamma _{z_\sigma }} \cup \{ \gamma \}} \cap G_\gamma $
, so since
$ G_{D^\gamma _{<i^\gamma _{z_\sigma }}}=G_{D^\gamma _{<i^\gamma _{z_\sigma }} \cup \{ \gamma \}} \cap G_\gamma $
, so since
![]() $t\notin G_\gamma $
,
$t\notin G_\gamma $
,
By
![]() $(p)_6$
,
$(p)_6$
,
![]() $G_{D^\gamma _{\le i^\gamma _{z_\sigma } \cup \{\gamma \}}}$
has been obtained by invoking Lemma 3.4 (note that
$G_{D^\gamma _{\le i^\gamma _{z_\sigma } \cup \{\gamma \}}}$
has been obtained by invoking Lemma 3.4 (note that
![]() $i^\gamma _{z_\sigma } \geq 1$
necessarily) with
$i^\gamma _{z_\sigma } \geq 1$
necessarily) with
![]() $\bar K = G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
,
$\bar K = G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
,
![]() $\bar L = G_{D^\gamma _{< i^\gamma _{z_\sigma }} \cup \{\gamma \}}$
, and
$\bar L = G_{D^\gamma _{< i^\gamma _{z_\sigma }} \cup \{\gamma \}}$
, and
![]() $\bar H = G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
, and then Clause (C) of that lemma together with the facts that
$\bar H = G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
, and then Clause (C) of that lemma together with the facts that
![]() $y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1} \in \bar L\setminus \bar H$
and
$y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1} \in \bar L\setminus \bar H$
and
![]() $z_\sigma \in \bar K \setminus \bar H$
imply that for
$z_\sigma \in \bar K \setminus \bar H$
imply that for
![]() $b=b^*=y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1}$
and
$b=b^*=y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1}$
and
![]() $z=z_\sigma $
, it is the case that
$z=z_\sigma $
, it is the case that
![]() $b^*z \not \sim _{\bar K}bzbz$
. That is,
$b^*z \not \sim _{\bar K}bzbz$
. That is,
which is the same as
![]() $\neg (b_\sigma \mathrel {E^\gamma _{< i^\gamma _{z_\sigma }+1, \gamma }} b_\sigma ')$
. By Lemma 5.12(1),
$\neg (b_\sigma \mathrel {E^\gamma _{< i^\gamma _{z_\sigma }+1, \gamma }} b_\sigma ')$
. By Lemma 5.12(1),
and hence,
![]() $b_\sigma \not \sim _{G_{D^\gamma _{< i} \cap \gamma }} b_\sigma '$
, which concludes our proof (since
$b_\sigma \not \sim _{G_{D^\gamma _{< i} \cap \gamma }} b_\sigma '$
, which concludes our proof (since
![]() $G_ {D^\gamma _{< i} \cap \gamma } =H$
).
$G_ {D^\gamma _{< i} \cap \gamma } =H$
).
Lemma 5.19. For all
![]() $\sigma \neq \sigma ^*$
in
$\sigma \neq \sigma ^*$
in
![]() $\Sigma $
, at least one of the following holds:
$\Sigma $
, at least one of the following holds:
-
(⊝) a
 $a_\sigma \not \sim _H a_{\sigma ^*}$
;
$a_\sigma \not \sim _H a_{\sigma ^*}$
; -
(⊝) b
 $b_\sigma \not \sim _H b_{\sigma ^*}$
;
$b_\sigma \not \sim _H b_{\sigma ^*}$
; -
(⊝) c
 $b_\sigma = b_{\sigma ^*}$
and
$b_\sigma = b_{\sigma ^*}$
and
 $a_\sigma \neq a_{\sigma ^*}$
;
$a_\sigma \neq a_{\sigma ^*}$
; -
(⊝) d all of the following hold:
-
(i)
 $\alpha _{a_\sigma } = \alpha _{a_{\sigma ^*}}$
(so
$\alpha _{a_\sigma } = \alpha _{a_{\sigma ^*}}$
(so
 $K_{\sigma } = K_{\sigma ^*}$
);
$K_{\sigma } = K_{\sigma ^*}$
); -
(ii)
 $a_\sigma , a_{\sigma ^*} \in K_\sigma \setminus H$
;
$a_\sigma , a_{\sigma ^*} \in K_\sigma \setminus H$
; -
(iii)
 $b_\sigma \not \sim _{H_\sigma }b_{\sigma ^*}$
, where
$b_\sigma \not \sim _{H_\sigma }b_{\sigma ^*}$
, where
 $H_\sigma = K_\sigma \cap H$
;
$H_\sigma = K_\sigma \cap H$
; -
(iv)
 $b_{\sigma }\not \sim _H b^{\prime }_{\sigma ^*}$
;
$b_{\sigma }\not \sim _H b^{\prime }_{\sigma ^*}$
; -
(v)
 $K \models (K_\sigma \setminus H) \cdot (H \setminus K_\sigma ) \cdot (K_\sigma \setminus H) \subseteq (K \setminus H)$
.
$K \models (K_\sigma \setminus H) \cdot (H \setminus K_\sigma ) \cdot (K_\sigma \setminus H) \subseteq (K \setminus H)$
.
-
Proof. We start with two general claims.
Claim 5.19.1. Suppose
![]() $a,a^* \in G_{D^\gamma _{\leq i}}$
are such that
$a,a^* \in G_{D^\gamma _{\leq i}}$
are such that
![]() $\alpha _a <\alpha _{a^*} <\gamma $
and
$\alpha _a <\alpha _{a^*} <\gamma $
and
![]() $\alpha _a,\alpha _{a^*} \in D^\gamma _{\leq i} \setminus D^\gamma _{<i}$
. Then
$\alpha _a,\alpha _{a^*} \in D^\gamma _{\leq i} \setminus D^\gamma _{<i}$
. Then
![]() $a\not \sim _H a^*$
.
$a\not \sim _H a^*$
.
Proof. Since
![]() $\alpha _a, \alpha _{a^*} \in D^\gamma _{\leq i} \setminus D^\gamma _{<i}$
, Lemma 5.9(1) implies that a and
$\alpha _a, \alpha _{a^*} \in D^\gamma _{\leq i} \setminus D^\gamma _{<i}$
, Lemma 5.9(1) implies that a and
![]() $a^*$
are not in
$a^*$
are not in
![]() $G_{D^\gamma _{< i}}$
. We shall prove by induction on
$G_{D^\gamma _{< i}}$
. We shall prove by induction on
![]() $\beta \in [\alpha _{a^*},\gamma ]$
that
$\beta \in [\alpha _{a^*},\gamma ]$
that
The base case
![]() $\beta =\alpha _{a^*}$
follows from the following constellation:
$\beta =\alpha _{a^*}$
follows from the following constellation:
-
•
 $a \in G_{D^\gamma _{\leq i}} \cap G_{\alpha _a+1} = G_{D^\gamma _{\leq i} \cap (\alpha _a +1)} \subseteq G_{\alpha _a +1} \subseteq G_{\alpha _{a^*}}$
,
$a \in G_{D^\gamma _{\leq i}} \cap G_{\alpha _a+1} = G_{D^\gamma _{\leq i} \cap (\alpha _a +1)} \subseteq G_{\alpha _a +1} \subseteq G_{\alpha _{a^*}}$
, -
•
 $a^* \in G_{\alpha _{a^*}+1} \setminus G_{\alpha _{a^*}}$
, and
$a^* \in G_{\alpha _{a^*}+1} \setminus G_{\alpha _{a^*}}$
, and -
•
 $G_{D^\gamma _{< i} \cap \alpha _{a^*}} \subseteq G_{\alpha _{a^*}}$
.
$G_{D^\gamma _{< i} \cap \alpha _{a^*}} \subseteq G_{\alpha _{a^*}}$
.
The case that
![]() $\beta $
is a limit follows from continuity, so suppose that
$\beta $
is a limit follows from continuity, so suppose that
![]() $\beta \in [\alpha _{a^*},\gamma ]$
satisfies (III), and we shall show that
$\beta \in [\alpha _{a^*},\gamma ]$
satisfies (III), and we shall show that
To avoid trivialities, we may assume that
![]() $\beta \in D^\gamma _{< i}$
, so that, by Lemma 4.3,
$\beta \in D^\gamma _{< i}$
, so that, by Lemma 4.3,
![]() $D^\gamma _{< i} \cap \beta = D^\beta _{<i}$
and
$D^\gamma _{< i} \cap \beta = D^\beta _{<i}$
and
![]() $D^\gamma _{\leq i} \cap \beta = D^\beta _{\le i}$
. Therefore,
$D^\gamma _{\leq i} \cap \beta = D^\beta _{\le i}$
. Therefore,
![]() $\alpha _a,\alpha _{a^*} \in D^\beta _{\leq i} \setminus D^\beta _{<i}$
. So Notation 5.3 together with Lemma 5.9(4) imply that
$\alpha _a,\alpha _{a^*} \in D^\beta _{\leq i} \setminus D^\beta _{<i}$
. So Notation 5.3 together with Lemma 5.9(4) imply that
![]() $a \in G_{D^\gamma _{\leq i} \cap (\alpha _a+1)}\subseteq G_{D^\beta _{\le i}}$
and
$a \in G_{D^\gamma _{\leq i} \cap (\alpha _a+1)}\subseteq G_{D^\beta _{\le i}}$
and
![]() $a^* \in G_{D^\gamma _{\leq i} \cap (\alpha _{a^*}+1)}\subseteq G_{D^\beta _{\le i}}$
. As
$a^* \in G_{D^\gamma _{\leq i} \cap (\alpha _{a^*}+1)}\subseteq G_{D^\beta _{\le i}}$
. As
![]() $\alpha _a,\alpha _{a^*}\notin D^\beta _{<i}$
, Lemma 5.9(1) implies that
$\alpha _a,\alpha _{a^*}\notin D^\beta _{<i}$
, Lemma 5.9(1) implies that
![]() $a,a^* \notin G_{D^\beta _{<i}}$
. Altogether,
$a,a^* \notin G_{D^\beta _{<i}}$
. Altogether,
Now
![]() $\beta> \alpha _{a^*} \geq 0$
and
$\beta> \alpha _{a^*} \geq 0$
and
![]() $i \geq 1$
, since
$i \geq 1$
, since
![]() $\beta \in D^\gamma _{<i}$
, so
$\beta \in D^\gamma _{<i}$
, so
![]() $(p)_6$
tells us that
$(p)_6$
tells us that
![]() $G_{D^\beta _{\leq i} \cup \{\beta \}}$
was constructed by invoking Lemma 3.4 with
$G_{D^\beta _{\leq i} \cup \{\beta \}}$
was constructed by invoking Lemma 3.4 with
![]() $\bar H=G_{D^\beta _{<i}}$
,
$\bar H=G_{D^\beta _{<i}}$
,
![]() $\bar K=G_{D^\beta _{\le i}}$
and
$\bar K=G_{D^\beta _{\le i}}$
and
![]() $\bar L=G_{D^\beta _{<i}\cup \{\beta \}}$
. By Lemma 5.9,
$\bar L=G_{D^\beta _{<i}\cup \{\beta \}}$
. By Lemma 5.9,
so, taking (III) into account, Clause (E) of Lemma 3.4 implies that
However,
![]() $\bar L = G_{D^\beta _{< i} \cup \{\beta \}} = G_{D^\gamma _{< i} \cap (\beta +1)}$
, so we are done.
$\bar L = G_{D^\beta _{< i} \cup \{\beta \}} = G_{D^\gamma _{< i} \cap (\beta +1)}$
, so we are done.
Claim 5.19.2. Let
![]() $\alpha \in D^\gamma _{\leq i} \setminus D^\gamma _{<i}$
and
$\alpha \in D^\gamma _{\leq i} \setminus D^\gamma _{<i}$
and
![]() $a,a^* \in G_{D^\gamma _{\le i} \cap (\alpha +1)} \setminus G_{\alpha }$
.
$a,a^* \in G_{D^\gamma _{\le i} \cap (\alpha +1)} \setminus G_{\alpha }$
.
-
(1) For every
 $g \in G_{D^\gamma _{<i} \cap (\beta +1)} \setminus G_{D^\gamma _{<i} \cap \beta }$
with
$g \in G_{D^\gamma _{<i} \cap (\beta +1)} \setminus G_{D^\gamma _{<i} \cap \beta }$
with
 $\beta \in D^\gamma _{<i} \setminus \alpha $
, we have
$\beta \in D^\gamma _{<i} \setminus \alpha $
, we have
 $a\cdot g \cdot a^* \notin G_{D^\gamma _{<i} \cap (\beta +1)}$
;
$a\cdot g \cdot a^* \notin G_{D^\gamma _{<i} \cap (\beta +1)}$
; -
(2) For every
 $g \in G_{D^\gamma _{<i}} \setminus G_\alpha $
, we have
$g \in G_{D^\gamma _{<i}} \setminus G_\alpha $
, we have
 $a \cdot g \cdot a^* \notin G_{D^\gamma _{<i}}$
.
$a \cdot g \cdot a^* \notin G_{D^\gamma _{<i}}$
.
Proof. (1) Fix g and
![]() $\beta $
as above. Now in the same line of reasoning as in Claim 5.19.1,
$\beta $
as above. Now in the same line of reasoning as in Claim 5.19.1,
![]() $D^\gamma _{< i} \cap \beta = D^\beta _{< i}$
,
$D^\gamma _{< i} \cap \beta = D^\beta _{< i}$
,
![]() $D^\gamma _{\le i} \cap (\beta +1) = D^\beta _{\le i} \cup \{\beta \}$
. Therefore,
$D^\gamma _{\le i} \cap (\beta +1) = D^\beta _{\le i} \cup \{\beta \}$
. Therefore,
![]() $G_{D^\gamma _{<i} \cap (\beta +1)}$
is equal to
$G_{D^\gamma _{<i} \cap (\beta +1)}$
is equal to
![]() $G_{D^\beta _{<i} \cup \{\beta \}}$
, and the latter (recalling
$G_{D^\beta _{<i} \cup \{\beta \}}$
, and the latter (recalling
![]() $\beta \geq 1$
, and
$\beta \geq 1$
, and
![]() $i \geq 1$
which is true since
$i \geq 1$
which is true since
![]() $\beta \in D^\gamma _{<i}$
) was obtained by invoking Lemma 3.4 with
$\beta \in D^\gamma _{<i}$
) was obtained by invoking Lemma 3.4 with
![]() $\bar H = G_{D^\beta _{<i}}$
,
$\bar H = G_{D^\beta _{<i}}$
,
![]() $\bar K= G_{D^\beta _{\le i}}$
,
$\bar K= G_{D^\beta _{\le i}}$
,
![]() $\bar L = G_{D^\beta _{<i} \cup \{\beta \}}$
(where
$\bar L = G_{D^\beta _{<i} \cup \{\beta \}}$
(where
![]() $g \in \bar L \setminus \bar H$
). So just apply (the parallel of) Clause (D) of the said Lemma.
$g \in \bar L \setminus \bar H$
). So just apply (the parallel of) Clause (D) of the said Lemma.
(2) Suppose not, and let g be a counterexample. Let
![]() $\beta $
be minimal such that
$\beta $
be minimal such that
![]() $g \in G_{\beta +1}$
. By Lemma 5.9(4),
$g \in G_{\beta +1}$
. By Lemma 5.9(4),
![]() $G_{D^\gamma _{<i}} \cap G_{\beta +1} = G_{D^\gamma _{<i} \cap (\beta +1)}$
, and hence,
$G_{D^\gamma _{<i}} \cap G_{\beta +1} = G_{D^\gamma _{<i} \cap (\beta +1)}$
, and hence,
![]() $g \in G_{D^\gamma _{<i} \cap (\beta +1)} \setminus G_{D^\gamma _{<i} \cap \beta }$
. Then, By Lemma 5.9(1),
$g \in G_{D^\gamma _{<i} \cap (\beta +1)} \setminus G_{D^\gamma _{<i} \cap \beta }$
. Then, By Lemma 5.9(1),
![]() $\beta \in D^\gamma _{<i}$
, so that
$\beta \in D^\gamma _{<i}$
, so that
![]() $\beta \in D^\gamma _{<i} \setminus \alpha $
. As
$\beta \in D^\gamma _{<i} \setminus \alpha $
. As
![]() $a\cdot g \cdot a^* \in G_{\alpha +1} \cdot G_{\beta +1} \cdot G_{\alpha +1} = G_{\beta +1}$
, and recalling that
$a\cdot g \cdot a^* \in G_{\alpha +1} \cdot G_{\beta +1} \cdot G_{\alpha +1} = G_{\beta +1}$
, and recalling that
![]() $a \cdot g \cdot a^* \in G_{D^\gamma _{<i}}$
, we infer that
$a \cdot g \cdot a^* \in G_{D^\gamma _{<i}}$
, we infer that
![]() $a\cdot g \cdot a^* \in G_{D^\gamma _{<i}} \cap G_{\beta +1} = G_{D^\gamma _{<i} \cap (\beta +1)}$
, contradicting Clause (1).
$a\cdot g \cdot a^* \in G_{D^\gamma _{<i}} \cap G_{\beta +1} = G_{D^\gamma _{<i} \cap (\beta +1)}$
, contradicting Clause (1).
Suppose now that
![]() $\sigma =(a,t)$
and
$\sigma =(a,t)$
and
![]() $\sigma ^* = (a^*,t^*)$
are two distinct elements of
$\sigma ^* = (a^*,t^*)$
are two distinct elements of
![]() $\Sigma $
. We assume that alternatives
$\Sigma $
. We assume that alternatives
![]() $(\circleddash )_a$
–
$(\circleddash )_a$
–
![]() $(\circleddash )_c$
fail, and we shall verify alternative
$(\circleddash )_c$
fail, and we shall verify alternative
![]() $(\circleddash )_d$
. Note that our assumptions have the following immediate consequences.
$(\circleddash )_d$
. Note that our assumptions have the following immediate consequences.
Claim 5.19.3.
![]() $b_\sigma \sim _H b_{\sigma ^*}$
,
$b_\sigma \sim _H b_{\sigma ^*}$
,
![]() $t\neq t^*$
, and
$t\neq t^*$
, and
![]() $\alpha _a=\alpha _{a^*}$
.
$\alpha _a=\alpha _{a^*}$
.
Proof. The first part follows from the failure of alternative
![]() $(\circleddash )_b$
, and the last part follows from failure of alternative
$(\circleddash )_b$
, and the last part follows from failure of alternative
![]() $(\circleddash )_a$
together with Claim 5.19.1.
$(\circleddash )_a$
together with Claim 5.19.1.
In addition, if t were to equal
![]() $t^*$
, Definition 5.14 (using
$t^*$
, Definition 5.14 (using
![]() $\alpha _a=\alpha _{a^*}$
) would have implied that alternative
$\alpha _a=\alpha _{a^*}$
) would have implied that alternative
![]() $(\circleddash )_c$
holds. So
$(\circleddash )_c$
holds. So
![]() $t\neq t^*$
.
$t\neq t^*$
.
It thus follows from Definition 5.14 that
Consequently,
and hence, the next two elements are in
![]() $G_{D^\gamma _{< i^\gamma _{z_\sigma } \cup \{\gamma \}}}$
:
$G_{D^\gamma _{< i^\gamma _{z_\sigma } \cup \{\gamma \}}}$
:
-
•
 $b=y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1}$
,
$b=y_{\sigma ,0} \cdot t^{{\varepsilon }_\sigma } \cdot y_{\sigma ,1}$
, -
•
 $b^*=y_{\sigma ^*,0} \cdot (t^*)^{{\varepsilon }_{\sigma ^*}} \cdot y_{\sigma ^*,1}$
;
$b^*=y_{\sigma ^*,0} \cdot (t^*)^{{\varepsilon }_{\sigma ^*}} \cdot y_{\sigma ^*,1}$
;
moreover,
since
![]() $y_{\sigma ,0},y_{\sigma ,1},y_{\sigma ^*,0},y_{\sigma ^*,1} \in G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
. Note that
$y_{\sigma ,0},y_{\sigma ,1},y_{\sigma ^*,0},y_{\sigma ^*,1} \in G_{D^\gamma _{< i^\gamma _{z_\sigma }}}$
. Note that
and
by Lemma 5.9(4).
As
![]() $\sigma \in \Sigma $
, it is also the case that
$\sigma \in \Sigma $
, it is also the case that
![]() $z_\sigma \in G_{D^\gamma _{\leq i^\gamma _{z_\sigma }}} \leq G_{D^\gamma _{< i}} = H$
and
$z_\sigma \in G_{D^\gamma _{\leq i^\gamma _{z_\sigma }}} \leq G_{D^\gamma _{< i}} = H$
and
so that
![]() $b\sim _H b_\sigma $
. Likewise,
$b\sim _H b_\sigma $
. Likewise,
![]() $b^*\sim _H b_{\sigma ^*}$
. Recalling that
$b^*\sim _H b_{\sigma ^*}$
. Recalling that
![]() $b_\sigma \sim _H b_{\sigma ^*}$
, altogether
$b_\sigma \sim _H b_{\sigma ^*}$
, altogether
Now,
![]() $(p)_6$
tells us that
$(p)_6$
tells us that
![]() $G_{D^\gamma _{\leq i^\gamma _{z_\sigma }} \cup \{\gamma \}}$
was constructed by invoking Lemma 3.4 with
$G_{D^\gamma _{\leq i^\gamma _{z_\sigma }} \cup \{\gamma \}}$
was constructed by invoking Lemma 3.4 with
![]() $\bar H=G_{D^\gamma _{<i^\gamma _{z_\sigma }}}$
,
$\bar H=G_{D^\gamma _{<i^\gamma _{z_\sigma }}}$
,
![]() $\bar K=G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
and
$\bar K=G_{D^\gamma _{\le i^\gamma _{z_\sigma }}}$
and
![]() $\bar L=G_{D^\gamma _{<i^\gamma _{z_\sigma }}\cup \{\gamma \}}$
(again,
$\bar L=G_{D^\gamma _{<i^\gamma _{z_\sigma }}\cup \{\gamma \}}$
(again,
![]() $i^\gamma _{z_\sigma } \geq 1$
, by Clause (2) of Definition 5.14). Trivially,
$i^\gamma _{z_\sigma } \geq 1$
, by Clause (2) of Definition 5.14). Trivially,
![]() $z_\sigma \notin \bar H$
. In addition,
$z_\sigma \notin \bar H$
. In addition,
![]() $b,b^*\notin \bar H$
by (IV). Thus, Clause (C) of that lemma implies that
$b,b^*\notin \bar H$
by (IV). Thus, Clause (C) of that lemma implies that
![]() $ b^* \cdot z_{\sigma ^*} \not \sim _{\bar K} b\cdot z_\sigma \cdot b \cdot z_\sigma $
, and hence,
$ b^* \cdot z_{\sigma ^*} \not \sim _{\bar K} b\cdot z_\sigma \cdot b \cdot z_\sigma $
, and hence,
![]() $b^{\prime }_\sigma \not \sim _{\bar K} b_{\sigma ^*}$
. Finally,
$b^{\prime }_\sigma \not \sim _{\bar K} b_{\sigma ^*}$
. Finally,
![]() $b^{\prime }_\sigma \not \sim _{H} b_{\sigma ^*}$
(i.e.,
$b^{\prime }_\sigma \not \sim _{H} b_{\sigma ^*}$
(i.e.,
![]() $b^{\prime }_\sigma \not \sim _{G_{D^\gamma _{<i}}} b_{\sigma ^*}$
) by Lemma 5.12(1).
$b^{\prime }_\sigma \not \sim _{G_{D^\gamma _{<i}}} b_{\sigma ^*}$
) by Lemma 5.12(1).
However, by the definition of
![]() $T^\gamma _{<i, \alpha _{a_\sigma }}$
, we get that
$T^\gamma _{<i, \alpha _{a_\sigma }}$
, we get that
![]() $t\not \sim _{K_\sigma \cap H} t^*$
. As
$t\not \sim _{K_\sigma \cap H} t^*$
. As
![]() $ K_\sigma \cap H = G_{D^\gamma _{\le i} \cap (\alpha _{a_\sigma }+1)} \cap G_{D^\gamma _{< i} } = G_{D^\gamma _{< i} \cap (\alpha _{a_\sigma }+1)}= G_{D^\gamma _{< i} \cap \alpha _{a_\sigma }}$
, we also get that
$ K_\sigma \cap H = G_{D^\gamma _{\le i} \cap (\alpha _{a_\sigma }+1)} \cap G_{D^\gamma _{< i} } = G_{D^\gamma _{< i} \cap (\alpha _{a_\sigma }+1)}= G_{D^\gamma _{< i} \cap \alpha _{a_\sigma }}$
, we also get that
![]() $b_\sigma \not \sim _{K_\sigma \cap H} b_{\sigma ^*}$
, since
$b_\sigma \not \sim _{K_\sigma \cap H} b_{\sigma ^*}$
, since
![]() $z_\sigma =z_{\sigma ^*}$
,
$z_\sigma =z_{\sigma ^*}$
,
![]() $y_{\sigma ,0}$
,
$y_{\sigma ,0}$
,
![]() $y_{\sigma ,1} \in G_{D^\gamma _{<i} \cap \alpha _{a_\sigma }}$
(by recalling the definition of
$y_{\sigma ,1} \in G_{D^\gamma _{<i} \cap \alpha _{a_\sigma }}$
(by recalling the definition of
![]() $\Sigma $
). At this stage, it remains to check Clause (v), but this follows from Claim 5.19.2(2).
$\Sigma $
). At this stage, it remains to check Clause (v), but this follows from Claim 5.19.2(2).
By Lemmas 5.17, 5.18 and 5.19, the tuple
![]() $(H,K,L,S)$
satisfies all of the assumptions of Lemma 3.4. Adhering to
$(H,K,L,S)$
satisfies all of the assumptions of Lemma 3.4. Adhering to
![]() $(p)_6$
, we then let
$(p)_6$
, we then let
![]() $G_{D^\gamma _{\le i} \cup \{\gamma \}}$
be the outcome
$G_{D^\gamma _{\le i} \cup \{\gamma \}}$
be the outcome
![]() $M^*$
of Lemma 3.4 when invoked with this tuple. By Clause (A) of that lemma,
$M^*$
of Lemma 3.4 when invoked with this tuple. By Clause (A) of that lemma,
![]() $K,L \leq M^*$
,
$K,L \leq M^*$
,
and
![]() $M^*$
is generated by
$M^*$
is generated by
![]() $K \cup L = G_{D^\gamma _{\leq i}} \cup G_{D^\gamma _{<i} \cup \{\gamma \}}$
. This means that
$K \cup L = G_{D^\gamma _{\leq i}} \cup G_{D^\gamma _{<i} \cup \{\gamma \}}$
. This means that
![]() $M^*$
is generated by the set of generators
$M^*$
is generated by the set of generators
![]() $\{x_\beta \mathrel {|} \beta \in D^\gamma _{\leq i} \cup \{\gamma \}\}$
, and hence,
$\{x_\beta \mathrel {|} \beta \in D^\gamma _{\leq i} \cup \{\gamma \}\}$
, and hence,
![]() $(p)_4$
is preserved. Also, Clause (B) implies that
$(p)_4$
is preserved. Also, Clause (B) implies that
![]() $K \mathrel {\leq _{\mathrm {m}}} M^*$
; hence,
$K \mathrel {\leq _{\mathrm {m}}} M^*$
; hence,
![]() $(p)_5$
is preserved as well.
$(p)_5$
is preserved as well.
Our promise
![]() $(p)_3$
implies that
$(p)_3$
implies that
![]() $L=G_{D^\gamma _{< i} \cup \{\gamma \}}$
and
$L=G_{D^\gamma _{< i} \cup \{\gamma \}}$
and
 $$ \begin{align*}\bigcup_{\beta < \gamma} G_{\beta+1} = \bigcup_{\beta < \gamma} \bigcup_{j<\theta} G_{D^\beta_{<j} \cup \{\beta\}}\end{align*} $$
$$ \begin{align*}\bigcup_{\beta < \gamma} G_{\beta+1} = \bigcup_{\beta < \gamma} \bigcup_{j<\theta} G_{D^\beta_{<j} \cup \{\beta\}}\end{align*} $$
are both torsion-free. In particular, K, being a subgroup of
![]() $G_\gamma = \bigcup _{\beta < \gamma } G_{\beta +1}$
is torsion-free as well. It now follows from Clause (G) of Lemma 3.4 that we have maintained
$G_\gamma = \bigcup _{\beta < \gamma } G_{\beta +1}$
is torsion-free as well. It now follows from Clause (G) of Lemma 3.4 that we have maintained
![]() $(p)_3$
.
$(p)_3$
.
This completes the description of the recursive construction of our group G.
5.3 Verification
We now turn to show that G is an n-Shelah group for
![]() $n=10120$
.
$n=10120$
.
Lemma 5.20. Let
![]() $Z\in [G]^\kappa $
. Then
$Z\in [G]^\kappa $
. Then
![]() $Z^{10120}=G$
.
$Z^{10120}=G$
.
Proof. By possibly thinning out (using the pigeonhole principle), we may assume the existence of some
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $i_z=j$
for all
$i_z=j$
for all
![]() $z\in Z$
. Set
$z\in Z$
. Set ![]() , so that
, so that
![]() $A\in [\kappa ]^\kappa $
. For each
$A\in [\kappa ]^\kappa $
. For each
![]() $\alpha \in A$
, pick
$\alpha \in A$
, pick
![]() $z_\alpha \in Z$
such that
$z_\alpha \in Z$
such that
![]() $\alpha _{z_\alpha }=\alpha $
.
$\alpha _{z_\alpha }=\alpha $
.
Recalling the hypothesis of Theorem 5.1, we now let B be a club in
![]() $\kappa $
such that for every
$\kappa $
such that for every
![]() $\beta \in B$
, there exists a
$\beta \in B$
, there exists a
![]() $\gamma \in A$
above
$\gamma \in A$
above
![]() $\beta $
such that
$\beta $
such that
Recalling
![]() $(p)_2$
and the surjection
$(p)_2$
and the surjection
![]() $\vec \pi $
of Notation 5.11, the following is yet another club in
$\vec \pi $
of Notation 5.11, the following is yet another club in
![]() $\kappa $
:
$\kappa $
:
Now, let h be an arbitrary element of G, and we shall show that h is in
![]() $Z^{10120}$
. Pick a large enough
$Z^{10120}$
. Pick a large enough
![]() $\beta \in B\cap C$
such that
$\beta \in B\cap C$
such that
![]() $h\in G_\beta $
, and then pick
$h\in G_\beta $
, and then pick
![]() $\gamma \in A$
above
$\gamma \in A$
above
![]() $\beta $
satisfying (V). As
$\beta $
satisfying (V). As
![]() $i_{z_\gamma }=j$
, we consider the unique
$i_{z_\gamma }=j$
, we consider the unique
![]() $t \in T^{\gamma }_{<j+1, \beta }$
such that
$t \in T^{\gamma }_{<j+1, \beta }$
such that
![]() $t\mathrel {E^{\gamma }_{<j+1, \beta }} z_\gamma $
. By the choice of t, we may pick
$t\mathrel {E^{\gamma }_{<j+1, \beta }} z_\gamma $
. By the choice of t, we may pick
and
![]() ${\varepsilon } \in \{-1,1\}$
such that
${\varepsilon } \in \{-1,1\}$
such that
It follows that
![]() $\max \{i^{\gamma }_{y_{0}}, i^{\gamma }_{y_{1}}\} \leq j$
, and as
$\max \{i^{\gamma }_{y_{0}}, i^{\gamma }_{y_{1}}\} \leq j$
, and as
![]() $t \in T^{\gamma }_{<j+1, \beta } \subseteq G_{D^\gamma _{<j +1} \cup \{\gamma \}}$
, Lemma 5.9(2) implies that
$t \in T^{\gamma }_{<j+1, \beta } \subseteq G_{D^\gamma _{<j +1} \cup \{\gamma \}}$
, Lemma 5.9(2) implies that
![]() $i_t\le j$
as well.
$i_t\le j$
as well.
As
![]() $\gamma $
was chosen to satisfy (V), we may fix
$\gamma $
was chosen to satisfy (V), we may fix
![]() $\bar \alpha \in A\cap \beta $
with
$\bar \alpha \in A\cap \beta $
with
![]() $d(\bar \alpha ,\gamma )>j$
. Set
$d(\bar \alpha ,\gamma )>j$
. Set
![]() $z=z_{\bar \alpha }$
and note that, by Lemma 5.9(3),
$z=z_{\bar \alpha }$
and note that, by Lemma 5.9(3),
As
![]() $\alpha _z=\bar \alpha <\beta $
, we may find a large enough
$\alpha _z=\bar \alpha <\beta $
, we may find a large enough
![]() $\zeta < \beta $
such that
$\zeta < \beta $
such that
![]() $y_0,y_1,z \in G_{\zeta +1}$
. Altogether,
$y_0,y_1,z \in G_{\zeta +1}$
. Altogether,
![]() $y_0,y_1,z \in G_{D^\gamma _{\le i^\gamma _z}\cap (\zeta +1)}$
.
$y_0,y_1,z \in G_{D^\gamma _{\le i^\gamma _z}\cap (\zeta +1)}$
.
As
![]() $\beta \in C$
and
$\beta \in C$
and
![]() $z\in G_\beta $
, it follows from (VI) that we may find a
$z\in G_\beta $
, it follows from (VI) that we may find a
![]() $\xi < \beta $
such that
$\xi < \beta $
such that
Utilizing (V) once more, we now pick
![]() $\alpha \in A \cap \beta $
above
$\alpha \in A \cap \beta $
above
![]() $\max \{\alpha _h,\zeta \}$
such that
$\max \{\alpha _h,\zeta \}$
such that
![]() $c(\alpha ,\gamma ) = \xi $
and
$c(\alpha ,\gamma ) = \xi $
and
![]() $d(\alpha ,\gamma )> \max \{i^\gamma _h,i^\gamma _z\}$
. Consider
$d(\alpha ,\gamma )> \max \{i^\gamma _h,i^\gamma _z\}$
. Consider
![]() $i=d(\alpha ,\gamma )$
, and note that by (VII),
$i=d(\alpha ,\gamma )$
, and note that by (VII),
so that
Next, consider the group elements
![]() $a = z_\alpha $
,
$a = z_\alpha $
,
![]() $b = z_\gamma \cdot z$
, and
$b = z_\gamma \cdot z$
, and
![]() $b' = b\cdot b$
, and the pair
$b' = b\cdot b$
, and the pair
![]() $\sigma _*=(a,t)$
.
$\sigma _*=(a,t)$
.
Claim 5.20.1.
![]() $\sigma _*$
is in
$\sigma _*$
is in
![]() $\Sigma ^{++}$
of Definition 5.13.
$\Sigma ^{++}$
of Definition 5.13.
Proof. From
![]() $d(\alpha ,\gamma )=i$
, we get that
$d(\alpha ,\gamma )=i$
, we get that
![]() $D^\gamma _{<i } \cap (\alpha +1)=D^\gamma _{<i}\cap \alpha .$
By Lemma 4.3,
$D^\gamma _{<i } \cap (\alpha +1)=D^\gamma _{<i}\cap \alpha .$
By Lemma 4.3,
![]() $D^\alpha _{\le i_{z_\alpha }} \subseteq D^\alpha _{\le d(\alpha ,\gamma )} =D^\gamma _{\le i}\cap \alpha $
, and hence,
$D^\alpha _{\le i_{z_\alpha }} \subseteq D^\alpha _{\le d(\alpha ,\gamma )} =D^\gamma _{\le i}\cap \alpha $
, and hence,
![]() $z_\alpha \in G_{D^\gamma _{\le i}}$
. So, if
$z_\alpha \in G_{D^\gamma _{\le i}}$
. So, if
![]() $z_\alpha $
were to be in
$z_\alpha $
were to be in
![]() $G_{D^\gamma _{< i}}$
, then since
$G_{D^\gamma _{< i}}$
, then since
![]() $\alpha _{z_\alpha }=\alpha $
, Lemma 5.9(4) would imply that
$\alpha _{z_\alpha }=\alpha $
, Lemma 5.9(4) would imply that
contradicting the fact that
![]() $\alpha _{z_\alpha }=\alpha $
. Altogether,
$\alpha _{z_\alpha }=\alpha $
. Altogether,
![]() $z_\alpha \in G_{D^\gamma _{\le i}}\setminus G_{D^\gamma _{<i}}$
.
$z_\alpha \in G_{D^\gamma _{\le i}}\setminus G_{D^\gamma _{<i}}$
.
Next, since
![]() $t \in T^{\gamma }_{<j+1, \beta }$
and
$t \in T^{\gamma }_{<j+1, \beta }$
and
![]() $\alpha <\beta $
, Lemma 5.12(3) implies that
$\alpha <\beta $
, Lemma 5.12(3) implies that
![]() $t \in T^{\gamma }_{<j+1, \alpha }$
. In addition, since
$t \in T^{\gamma }_{<j+1, \alpha }$
. In addition, since
![]() $i=d(\alpha ,\gamma )>i^\gamma _z>j$
, Lemma 5.12(2) implies that
$i=d(\alpha ,\gamma )>i^\gamma _z>j$
, Lemma 5.12(2) implies that
![]() $t \in T^{\gamma }_{<i, \alpha }$
. Also,
$t \in T^{\gamma }_{<i, \alpha }$
. Also,
![]() $i=d(\alpha ,\gamma )$
amounts to saying that
$i=d(\alpha ,\gamma )$
amounts to saying that
![]() $\alpha _{z_\alpha }=\alpha \in D^\gamma _{\le i}\setminus D^\gamma _{<i}$
, so we have established that
$\alpha _{z_\alpha }=\alpha \in D^\gamma _{\le i}\setminus D^\gamma _{<i}$
, so we have established that
![]() $\sigma _* \in \Sigma ^{++}$
.
$\sigma _* \in \Sigma ^{++}$
.
Looking at Definition 5.14, we arrive at the following table of evaluations:
Table 1 Evaluations.

It thus follows from (VIII) that
![]() $\pi _l(c(\alpha _a,\gamma )) \in G_\gamma $
for every
$\pi _l(c(\alpha _a,\gamma )) \in G_\gamma $
for every
![]() $l<4$
, so that
$l<4$
, so that
![]() $\sigma _*$
is moreover in
$\sigma _*$
is moreover in
![]() $\Sigma ^+$
, as per Definition 5.13. Looking at Conditions (1)–(3) of Definition 5.14, we see that
$\Sigma ^+$
, as per Definition 5.13. Looking at Conditions (1)–(3) of Definition 5.14, we see that
![]() $\sigma _*$
is a member of
$\sigma _*$
is a member of
![]() $\Sigma $
, as well: conditions (1) and (3) follow from (VIII), and condition (2) follows from (VII) and the fact that
$\Sigma $
, as well: conditions (1) and (3) follow from (VIII), and condition (2) follows from (VII) and the fact that
![]() $i^\gamma _z<i$
.
$i^\gamma _z<i$
.
Claim 5.20.2.
![]() holds in
holds in
![]() $G_{D^\gamma _{\le i} \cup \{\gamma \}}$
.
$G_{D^\gamma _{\le i} \cup \{\gamma \}}$
.
Proof. Recall that the group
![]() $G_{D^\gamma _{\le i} \cup \{\gamma \}}$
was obtained as the output group
$G_{D^\gamma _{\le i} \cup \{\gamma \}}$
was obtained as the output group
![]() $M^*$
of Lemma 3.4, when invoked with
$M^*$
of Lemma 3.4, when invoked with
![]() $(H,K,L,S)$
of Definition 5.16. Specifically,
$(H,K,L,S)$
of Definition 5.16. Specifically,
![]() $H = G_{D^\gamma _{< i}}$
,
$H = G_{D^\gamma _{< i}}$
,
![]() $K = G_{D^\gamma _{\le i} }$
,
$K = G_{D^\gamma _{\le i} }$
,
![]() $L = G_{D^\gamma _{< i}\cup \{\gamma \}}$
and
$L = G_{D^\gamma _{< i}\cup \{\gamma \}}$
and
![]() $S = \{(h_\sigma ,a_\sigma ,b_\sigma ,b_\sigma ') \mathrel {|} \sigma \in \Sigma \}$
of Definition 5.14. But
$S = \{(h_\sigma ,a_\sigma ,b_\sigma ,b_\sigma ') \mathrel {|} \sigma \in \Sigma \}$
of Definition 5.14. But
![]() $M^*$
is
$M^*$
is
![]() $M/N$
, where M is the free amalgam
$M/N$
, where M is the free amalgam
![]() $K \ast _H L$
, and N is the least normal subgroup containing
$K \ast _H L$
, and N is the least normal subgroup containing
![]() $\{h_\sigma ^{-1} \varrho (b_\sigma \cdot a_\sigma ,b_\sigma '\cdot a_\sigma )\mathrel {|} \sigma \in \Sigma \}$
; hence, for each
$\{h_\sigma ^{-1} \varrho (b_\sigma \cdot a_\sigma ,b_\sigma '\cdot a_\sigma )\mathrel {|} \sigma \in \Sigma \}$
; hence, for each
![]() $\sigma \in \Sigma $
, we have
$\sigma \in \Sigma $
, we have
![]() $h_\sigma ^{-1} \varrho (b_\sigma \cdot a_\sigma ,b_\sigma '\cdot a_\sigma ) \in N$
, and clearly,
$h_\sigma ^{-1} \varrho (b_\sigma \cdot a_\sigma ,b_\sigma '\cdot a_\sigma ) \in N$
, and clearly,
By Table 1,
![]() $b =b_{\sigma _*}$
,
$b =b_{\sigma _*}$
,
![]() $b' = b_{\sigma _*}'$
,
$b' = b_{\sigma _*}'$
,
![]() $a = a_{\sigma _*}$
, and
$a = a_{\sigma _*}$
, and
![]() $h = h_{\sigma _*}$
; hence,
$h = h_{\sigma _*}$
; hence, ![]() .
.
Recall that for all
![]() $x,y\in G$
,
$x,y\in G$
,
![]() $\varrho (x,y)$
is a word of length
$\varrho (x,y)$
is a word of length
![]() $3320$
over the alphabet
$3320$
over the alphabet
![]() $\{x,y\}$
, so since
$\{x,y\}$
, so since
![]() $\varrho (ba,b'a) = h$
, the fact that
$\varrho (ba,b'a) = h$
, the fact that
![]() $z_\alpha $
,
$z_\alpha $
,
![]() $z_\gamma $
and z all come from the initial set Z implies that
$z_\gamma $
and z all come from the initial set Z implies that
Thus, we have verified that h is in
![]() $Z^{10120}$
.
$Z^{10120}$
.
Lemma 5.21.
-
(1) G admits no
 $T_1$
topology other than the discrete topology;
$T_1$
topology other than the discrete topology; -
(2) G is not well-behaved in the sense of [Reference Feldman and Rinot15, p. 624];Footnote 6
-
(3)
 is a nonalgebraic unconditionally closed set (i.e., closed in each Hausdorff group topology).
is a nonalgebraic unconditionally closed set (i.e., closed in each Hausdorff group topology).
Proof. (1) This is a standard consequence of the malnormality of the
![]() $G_\gamma $
’s (
$G_\gamma $
’s (
![]() $\gamma < \kappa $
). Suppose that
$\gamma < \kappa $
). Suppose that
![]() $\tau $
is some
$\tau $
is some
![]() $T_1$
topology on G. Fix
$T_1$
topology on G. Fix
![]() $g \in G$
distinct from
$g \in G$
distinct from ![]() . Then
. Then
![]() $U = G \setminus \{g\}$
is
$U = G \setminus \{g\}$
is
![]() $\tau $
-open, so there is a
$\tau $
-open, so there is a
![]() $\tau $
-open neighborhood V of
$\tau $
-open neighborhood V of ![]() for which
for which
![]() $V^n \subseteq U$
, where n is the integer for which G is n-Shelah. Note that if
$V^n \subseteq U$
, where n is the integer for which G is n-Shelah. Note that if
![]() $|V| = \kappa $
, then
$|V| = \kappa $
, then
![]() $V^n = G$
, which is a contradiction, so it must be the case that
$V^n = G$
, which is a contradiction, so it must be the case that
![]() $|V| < \kappa $
. But then
$|V| < \kappa $
. But then
![]() $V \subseteq G_\gamma $
for some large enough
$V \subseteq G_\gamma $
for some large enough
![]() $\gamma < \kappa $
. Now
$\gamma < \kappa $
. Now
![]() $G_\gamma \mathrel {\leq _{\mathrm {m}}} G_{\gamma +1}$
by Corollary 5.7, so for any choice of
$G_\gamma \mathrel {\leq _{\mathrm {m}}} G_{\gamma +1}$
by Corollary 5.7, so for any choice of
![]() $h\in G_{\gamma +1}\setminus G_\gamma $
, it is the case that
$h\in G_{\gamma +1}\setminus G_\gamma $
, it is the case that ![]() is a
is a
![]() $\tau $
-open neighborhood of
$\tau $
-open neighborhood of ![]() , and hence,
, and hence,
![]() $\tau $
is discrete.
$\tau $
is discrete.
(2) Suppose not. This means that there exists a map
![]() $\varphi :G\rightarrow [G]^{<\omega }$
such that the following two hold:
$\varphi :G\rightarrow [G]^{<\omega }$
such that the following two hold:
-
(a)
 $\varphi $
is countable-to-one;
$\varphi $
is countable-to-one; -
(b) for all
 $x\neq y$
in G,
$x\neq y$
in G,
 $\varphi (x)\mathrel {\triangle }\varphi (y)\subseteq \varphi (x\cdot y)\subseteq \varphi (x)\cup \varphi (y)$
.
$\varphi (x)\mathrel {\triangle }\varphi (y)\subseteq \varphi (x\cdot y)\subseteq \varphi (x)\cup \varphi (y)$
.
By Clause (a) and the
![]() $\Delta $
-system lemma, we may fix an
$\Delta $
-system lemma, we may fix an
![]() $X\subseteq G$
of size
$X\subseteq G$
of size
![]() $\kappa $
, some
$\kappa $
, some
![]() $r\in [G]^{<\omega }$
and some
$r\in [G]^{<\omega }$
and some
![]() $k<\omega $
such that
$k<\omega $
such that
![]() $\langle \varphi (x)\setminus r\mathrel {|} x\in X\rangle $
is a sequence of pairwise disjoint sets, each of size k. It then follows from Clause (b) that
$\langle \varphi (x)\setminus r\mathrel {|} x\in X\rangle $
is a sequence of pairwise disjoint sets, each of size k. It then follows from Clause (b) that
![]() $|\varphi (x_1\cdots x_l)|\ge k\cdot l$
for every injective finite sequence
$|\varphi (x_1\cdots x_l)|\ge k\cdot l$
for every injective finite sequence
![]() $\langle x_1,\ldots ,x_l\rangle $
of elements of X. In particular, we may fix a
$\langle x_1,\ldots ,x_l\rangle $
of elements of X. In particular, we may fix a
![]() $g\in G$
with
$g\in G$
with
![]() $|\varphi (g)|>|r|+kn$
, where n is the integer for which G is n-Shelah. Since
$|\varphi (g)|>|r|+kn$
, where n is the integer for which G is n-Shelah. Since
![]() $X^n=G$
, we may fix a (possibly non-injective) sequence
$X^n=G$
, we may fix a (possibly non-injective) sequence
![]() $\langle x_1,\ldots ,x_n\rangle $
of elements of X such that
$\langle x_1,\ldots ,x_n\rangle $
of elements of X such that
![]() $x_1\cdots x_n=g$
. However, Clause (b) implies that
$x_1\cdots x_n=g$
. However, Clause (b) implies that
![]() $|\varphi (x_1\cdots x_n)|\le |r|+kn$
. This is a contradiction.
$|\varphi (x_1\cdots x_n)|\le |r|+kn$
. This is a contradiction.
(3) We need to show that for no system
![]() $\{ w_i\mathrel {|} i \in I\}$
of words over
$\{ w_i\mathrel {|} i \in I\}$
of words over
![]() $G \cup \{x\}$
(where x is an abstract variable outside G) do we have
$G \cup \{x\}$
(where x is an abstract variable outside G) do we have
where the value of
![]() $f_{w_i}(g) \in G$
is given by substituting each occurrence of the symbol x in
$f_{w_i}(g) \in G$
is given by substituting each occurrence of the symbol x in
![]() $w_i \in {}^{<\omega }(G \cup \{x,x^{-1}\})$
with g, and calculating the value in G. It is easy to see that it suffices to prove that for no such word w does the following equation holds true:
$w_i \in {}^{<\omega }(G \cup \{x,x^{-1}\})$
with g, and calculating the value in G. It is easy to see that it suffices to prove that for no such word w does the following equation holds true:
Suppose that w satisfies (IX), and fix a finite subset
![]() $B\subseteq G$
with
$B\subseteq G$
with
![]() $w \in {}^{<\omega }(B \cup \{x,x^{-1}\})$
. As
$w \in {}^{<\omega }(B \cup \{x,x^{-1}\})$
. As
![]() $|B|<\theta $
, we may find
$|B|<\theta $
, we may find
![]() $\gamma \in [1,\kappa )$
and
$\gamma \in [1,\kappa )$
and
![]() $i\in [1,\theta )$
such that
$i\in [1,\theta )$
such that
so for each
![]() $g \in G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
that is not the identity
$g \in G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
that is not the identity ![]() .
.
We are going to prove (provided that
![]() $\Sigma $
from Definition 5.14 in the construction of
$\Sigma $
from Definition 5.14 in the construction of
![]() $G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
is not empty) that the group
$G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
is not empty) that the group
![]() $G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
is topologizable (with a non-discrete
$G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
is topologizable (with a non-discrete
![]() $T_1$
topology), which will imply that
$T_1$
topology), which will imply that ![]() is closed (with respect to this nontrivial topology), contradicting that the topology was non-discrete.
is closed (with respect to this nontrivial topology), contradicting that the topology was non-discrete.
To this end, it is enough to argue that there exists a sequence
![]() $\langle N^*_k \mathrel {|} k \in \omega \rangle $
of normal subgroups of
$\langle N^*_k \mathrel {|} k \in \omega \rangle $
of normal subgroups of
![]() $G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
such that for each k do
$G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
such that for each k do
![]() $N^*_{k+1} \leq N^*_k$
,
$N^*_{k+1} \leq N^*_k$
, ![]() and
and ![]() hold. Now recall how
hold. Now recall how
![]() $G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
was constructed in Subsection 5.2 (appealing to Lemma 3.4 there):
$G_{D^\gamma _{\leq i} \cup \{\gamma \}}$
was constructed in Subsection 5.2 (appealing to Lemma 3.4 there):
where N was the normal closure of
![]() $\{ h_\sigma ^{-1} \varrho (b_\sigma a_\sigma ,b_\sigma 'a_\sigma )\mathrel {|} \sigma \in \Sigma \}$
(
$\{ h_\sigma ^{-1} \varrho (b_\sigma a_\sigma ,b_\sigma 'a_\sigma )\mathrel {|} \sigma \in \Sigma \}$
(
![]() $\Sigma $
is from Definition 5.14). Let
$\Sigma $
is from Definition 5.14). Let
![]() $N_0$
denote this N. Observe that it is enough to define a sequence
$N_0$
denote this N. Observe that it is enough to define a sequence
![]() $\langle N_k \mathrel {|} k \in \omega \setminus \{0\}\rangle $
of normal subgroups in
$\langle N_k \mathrel {|} k \in \omega \setminus \{0\}\rangle $
of normal subgroups in
![]() $G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
that satisfies
$G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
that satisfies
![]() $N_{k+1} \leq N_k$
for
$N_{k+1} \leq N_k$
for
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $\bigcap _{k \in \omega } N_k = N_0$
and
$\bigcap _{k \in \omega } N_k = N_0$
and
![]() $N_0 \lneq N_k$
.
$N_0 \lneq N_k$
.
Recall that in Definition 3.2, we have the sequence
![]() $\langle n_\ell \mathrel {|} \ell <\omega \rangle $
defined via
$\langle n_\ell \mathrel {|} \ell <\omega \rangle $
defined via
![]() $n_{\ell } = 3320^\ell $
, and that we let
$n_{\ell } = 3320^\ell $
, and that we let
![]() $\varrho _\ell (x,y) = \varrho (x^{n_\ell },y^{n_\ell })$
(in particular,
$\varrho _\ell (x,y) = \varrho (x^{n_\ell },y^{n_\ell })$
(in particular,
![]() $\varrho _0 = \varrho $
), and
$\varrho _0 = \varrho $
), and
Set
![]() $N_k$
to be the normal closure of
$N_k$
to be the normal closure of
![]() $R_k$
. Now the following will complete the proof:
$R_k$
. Now the following will complete the proof:
Claim 5.21.1.
-
(1) For all
 $\sigma \in \Sigma $
and
$\sigma \in \Sigma $
and
 $k>0$
,
$k>0$
,  $$ \begin{align*}G_{D^\gamma_{< i} \cup \{\gamma\}} \ast_{G_{D^\gamma_{< i}}} G_{D^\gamma_{\leq i}} \models\varrho_k(b_\sigma a_\sigma,b_\sigma'a_\sigma) \in N_k \setminus N_0,\end{align*} $$
$$ \begin{align*}G_{D^\gamma_{< i} \cup \{\gamma\}} \ast_{G_{D^\gamma_{< i}}} G_{D^\gamma_{\leq i}} \models\varrho_k(b_\sigma a_\sigma,b_\sigma'a_\sigma) \in N_k \setminus N_0,\end{align*} $$
-
(2)
 $R_1$
satisfies
$R_1$
satisfies
 $C'(\frac {1}{10})$
; moreover, if a group element
$C'(\frac {1}{10})$
; moreover, if a group element
 $g \in G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
has a canonical representation of length
$g \in G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
has a canonical representation of length
 $<\frac {7}{10}\cdot (n_{k} \cdot 6640)-1$
for some
$<\frac {7}{10}\cdot (n_{k} \cdot 6640)-1$
for some
 $k\geq 1$
, and
$k\geq 1$
, and
 $g \notin N_0$
, then
$g \notin N_0$
, then
 $g \notin N_k$
.
$g \notin N_k$
.
Proof. Let us start with verifying the second clause.
![]() $R_1$
satisfies
$R_1$
satisfies
![]() $C'(\frac {1}{10})$
just by the moreover part of (A) from Lemma 3.4. Suppose
$C'(\frac {1}{10})$
just by the moreover part of (A) from Lemma 3.4. Suppose
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $g \in G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
is such that
$g \in G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
is such that
![]() $g \notin N_0$
, and g has a canonical representation of length
$g \notin N_0$
, and g has a canonical representation of length
W.l.o.g. we can assume that whenever
![]() $g' \in G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
satisfies
$g' \in G_{D^\gamma _{< i} \cup \{\gamma \}} \ast _{G_{D^\gamma _{< i}}} G_{D^\gamma _{\leq i}}$
satisfies
then the length of g’s canonical representation does not exceed that of
![]() $g'$
(by possibly replacing g with a
$g'$
(by possibly replacing g with a
![]() $g'$
with a shorter representation, since
$g'$
with a shorter representation, since
![]() $g \in N_k \setminus N_0 \Rightarrow g' \in N_k \setminus N_0$
by the normality of
$g \in N_k \setminus N_0 \Rightarrow g' \in N_k \setminus N_0$
by the normality of
![]() $N_0$
, and
$N_0$
, and
![]() $N_k$
). Suppose on the contrary that
$N_k$
). Suppose on the contrary that
![]() $g \in N_k$
. Now Fact 2.10 implies that for a weakly cyclically reduced conjugate
$g \in N_k$
. Now Fact 2.10 implies that for a weakly cyclically reduced conjugate
![]() $g'$
of g, we have that
$g'$
of g, we have that
![]() $g'$
has a canonical representation
$g'$
has a canonical representation
![]() $w = w_0 w_1 \cdots w_{j-1}$
, which, as a word contains a subword
$w = w_0 w_1 \cdots w_{j-1}$
, which, as a word contains a subword
![]() $s_0 s_1 \cdots s_{m-1}$
that is a subword of a representation
$s_0 s_1 \cdots s_{m-1}$
that is a subword of a representation
![]() $r_0r_1 \cdots r_{n-1}$
of some r in the symmetric closure of
$r_0r_1 \cdots r_{n-1}$
of some r in the symmetric closure of
![]() $R_k$
, and
$R_k$
, and
![]() $m \geq \frac {7}{10} n$
. (W.l.o.g. we can assume that
$m \geq \frac {7}{10} n$
. (W.l.o.g. we can assume that
![]() $s_i = r_i$
for
$s_i = r_i$
for
![]() $i <m$
, by possibly replacing r with a cyclical conjugate of it, as
$i <m$
, by possibly replacing r with a cyclical conjugate of it, as
![]() $R_k$
is closed under such operations.)
$R_k$
is closed under such operations.)
Now clearly,
![]() $m \leq j$
, and
$m \leq j$
, and
![]() $j \leq \ell +1$
(by Definition 2.5), so it follows from
$j \leq \ell +1$
(by Definition 2.5), so it follows from
![]() $m \geq \frac {7}{10} n$
that
$m \geq \frac {7}{10} n$
that
![]() $ \ell +1 \geq \frac {7}{10} n$
. But
$ \ell +1 \geq \frac {7}{10} n$
. But
![]() $n \in \{6640\cdot n_0,6640\cdot n_0+1, 6640 \cdot n_{i}, 6640\cdot n_i+1 \mathrel {|} i \geq k\}$
since the lengths of the words in
$n \in \{6640\cdot n_0,6640\cdot n_0+1, 6640 \cdot n_{i}, 6640\cdot n_i+1 \mathrel {|} i \geq k\}$
since the lengths of the words in
![]() $R_k$
form the set
$R_k$
form the set
![]() $\{6640\cdot n_0, 6640 \cdot n_{i} \mathrel {|} i \geq k\}$
, r is a weakly cyclically reduced conjugate of some
$\{6640\cdot n_0, 6640 \cdot n_{i} \mathrel {|} i \geq k\}$
, r is a weakly cyclically reduced conjugate of some
![]() $r' \in R_k$
, and this conjugation can only increase the length by at most one (by Observation 2.6 (2)). Therefore, by (X),
$r' \in R_k$
, and this conjugation can only increase the length by at most one (by Observation 2.6 (2)). Therefore, by (X),
![]() $n = 6640\cdot n_0$
holds necessarily, and
$n = 6640\cdot n_0$
holds necessarily, and
Finally, observe that substituting
instead of
![]() $r_0 \cdot r_1 \cdots r_{m-1}$
in w yields an element in
$r_0 \cdot r_1 \cdots r_{m-1}$
in w yields an element in
with a shorter representation (than that of g), a contradiction.
The first clause is immediate noting that the second clause implies
![]() $\varrho _k(b_\sigma a_\sigma ,b_\sigma 'a_\sigma ) \notin N_{k+1}$
.
$\varrho _k(b_\sigma a_\sigma ,b_\sigma 'a_\sigma ) \notin N_{k+1}$
.
This completes the proof.
Corollary 5.22. For every infinite regular cardinal
![]() $\lambda $
, there exists a torsion-free Shelah group of size
$\lambda $
, there exists a torsion-free Shelah group of size
![]() $\lambda ^+$
.
$\lambda ^+$
.
Proof. Invoke Theorem 5.1 with the pair
![]() $(\kappa ,\theta )=(\lambda ^+,\lambda )$
, using Theorem 4.4.
$(\kappa ,\theta )=(\lambda ^+,\lambda )$
, using Theorem 4.4.
Corollary 5.23. For every regular uncountable cardinal
![]() $\kappa $
, if
$\kappa $
, if
![]() $\square (\kappa )$
holds, then there exists a torsion-free Shelah group of size
$\square (\kappa )$
holds, then there exists a torsion-free Shelah group of size
![]() $\kappa $
.
$\kappa $
.
Corollary 5.24. In Gödel’s constructible universe, for every regular uncountable cardinal
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
• there exists a torsion-free Shelah group of size
 $\kappa $
;
$\kappa $
; -
• there exists a Shelah group of size
 $\kappa $
;
$\kappa $
; -
•
 $\kappa $
is not weakly compact.
$\kappa $
is not weakly compact.
Proof. By [Reference Jensen23, Theorem 6.1], in Gödel’s constructible universe, every regular uncountable
![]() $\kappa $
is either weakly compact, or
$\kappa $
is either weakly compact, or
![]() $\square (\kappa )$
holds. By Corollary 5.23, it thus suffices to prove that weakly compact cardinals do not carry a Shelah group. To this end, suppose that there is an n-Shelah group of size
$\square (\kappa )$
holds. By Corollary 5.23, it thus suffices to prove that weakly compact cardinals do not carry a Shelah group. To this end, suppose that there is an n-Shelah group of size
![]() $\kappa $
.
$\kappa $
.
Claim 5.24.1. There is a system
![]() $\vec f=\langle f_{j}\mathrel {|} j<n^n \rangle $
of functions from
$\vec f=\langle f_{j}\mathrel {|} j<n^n \rangle $
of functions from
![]() $[\kappa ]^n$
to
$[\kappa ]^n$
to
![]() $n^n+1$
such that
$n^n+1$
such that
![]() $\bigcup _{j<n^n} f_j"[X]^n = n^n+1$
for every
$\bigcup _{j<n^n} f_j"[X]^n = n^n+1$
for every
![]() $X\in [\kappa ]^\kappa $
.
$X\in [\kappa ]^\kappa $
.
Proof. Fix an n-Shelah group G with underlying set
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\langle \psi _j\mathrel {|} j<n^n\rangle $
list all possible maps from n to n. For every
$\langle \psi _j\mathrel {|} j<n^n\rangle $
list all possible maps from n to n. For every
![]() $j<n^n$
, define
$j<n^n$
, define
![]() $h_j: [\kappa ]^n \rightarrow \kappa $
by letting for every n-tuple
$h_j: [\kappa ]^n \rightarrow \kappa $
by letting for every n-tuple
![]() $(g_0,g_1,\ldots ,g_{n-1})$
of elements of G, enumerated in
$(g_0,g_1,\ldots ,g_{n-1})$
of elements of G, enumerated in
![]() $\in $
-increasing order:
$\in $
-increasing order:
Evidently, for every infinite
![]() $X\subseteq \kappa $
,
$X\subseteq \kappa $
,
![]() $\bigcup _{j<n^n} h_j"[X]^n$
is nothing but the set of all group words of length n in the elements of X. So, since G is an n-Shelah group with underlying set
$\bigcup _{j<n^n} h_j"[X]^n$
is nothing but the set of all group words of length n in the elements of X. So, since G is an n-Shelah group with underlying set
![]() $\kappa $
, for every
$\kappa $
, for every
![]() $X\subseteq \kappa $
of full size,
$X\subseteq \kappa $
of full size,
![]() $\bigcup _{j<n^n} h_j"[X]^n=\kappa $
.
$\bigcup _{j<n^n} h_j"[X]^n=\kappa $
.
For every
![]() $j<n^n$
, let
$j<n^n$
, let
![]() $f_j:[\kappa ]^n\rightarrow (n^n+1)$
be the color-blind version of
$f_j:[\kappa ]^n\rightarrow (n^n+1)$
be the color-blind version of
![]() $h_j$
obtained via
$h_j$
obtained via
Then,
![]() $\bigcup _{j<n^n} f_j"[X]^n = n^n+1$
for every
$\bigcup _{j<n^n} f_j"[X]^n = n^n+1$
for every
![]() $X\in [\kappa ]^\kappa $
.
$X\in [\kappa ]^\kappa $
.
Let
![]() $\vec f$
be given by the claim. Define
$\vec f$
be given by the claim. Define
![]() $c:[\kappa ]^n\rightarrow {}^{n^n}(n^n+1)$
via
$c:[\kappa ]^n\rightarrow {}^{n^n}(n^n+1)$
via
Since
![]() $\kappa $
is weakly compact,
$\kappa $
is weakly compact,
![]() $\kappa \rightarrow (\kappa )^n_k$
holds for every cardinal
$\kappa \rightarrow (\kappa )^n_k$
holds for every cardinal
![]() $k<\kappa $
– in particular, for
$k<\kappa $
– in particular, for
![]() $k=(n^n+1)^{n^n}$
. So, we may find a set
$k=(n^n+1)^{n^n}$
. So, we may find a set
![]() $X \in [\kappa ]^\kappa $
such that
$X \in [\kappa ]^\kappa $
such that
![]() $c\restriction [X]^n$
is constant with value, say,
$c\restriction [X]^n$
is constant with value, say,
![]() $\langle m_j\mathrel {|} j<n^n\rangle $
. Pick an
$\langle m_j\mathrel {|} j<n^n\rangle $
. Pick an
![]() $m\in n^n+1$
distinct from
$m\in n^n+1$
distinct from
![]() $m_j$
for all
$m_j$
for all
![]() $j<n^n$
. Then
$j<n^n$
. Then
![]() $m\notin \bigcup _{j<n^n} f_j"[X]^n$
, contradicting the choice of
$m\notin \bigcup _{j<n^n} f_j"[X]^n$
, contradicting the choice of
![]() $\vec f$
.
$\vec f$
.
Acknowledgements
The results of this paper were presented by the first author at the Toronto Set Theory Seminar in May 2023 and at the Young Set Theory Workshop in Budapest, June 2024. We thank the organizers for the opportunity to speak and the participants for their feedback. We also thank the four referees of this paper for their feedback, especially to referee Y for detailed and thoughtful reports.
Competing interest
The authors have no competing interests to declare.
Funding statement
The first author was supported by the Excellence Fellowship Program for International Postdoctoral Researchers of The Israel Academy of Sciences and Humanities and by the National Research, Development and Innovation Office – NKFIH, grants no. 124749, 129211. The second author was partially supported by the Israel Science Foundation (grant agreement 203/22) and by the European Research Council (grant agreement ERC-2018-StG 802756).