Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T21:13:01.210Z Has data issue: false hasContentIssue false
  • English
  • Français

SERRE WEIGHTS AND BREUIL’S LATTICE CONJECTURE IN DIMENSION THREE

Part of: Representation theory of groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  25 March 2020

DANIEL LE Open the ORCID record for DANIEL LE [Opens in a new window] ,
BAO V. LE HUNG ,
BRANDON LEVIN  and
STEFANO MORRA
DANIEL LE
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George Street,Toronto, ON M5S 2E4, Canada; [email protected]
BAO V. LE HUNG
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208, USA; [email protected]
BRANDON LEVIN
Affiliation:
Department of Mathematics, University of Arizona, 617 N. Santa Rita Avenue, P.O. Box 210089, Tucson, Arizona 85721, USA; [email protected]
STEFANO MORRA
Affiliation:
Université Paris 8, Laboratoire Analyse, Géométrie et Applications, Université Sorbonne Paris Nord, CNRS, UMR 7539, F-93430, Villetaneuse, France; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove in generic situations that the lattice in a tame type induced by the completed cohomology of a 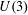$U(3)$-arithmetic manifold is purely local, that is, only depends on the Galois representation at places above 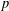$p$. This is a generalization to 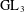$\text{GL}_{3}$ of the lattice conjecture of Breuil. In the process, we also prove the geometric Breuil–Mézard conjecture for (tamely) potentially crystalline deformation rings with Hodge–Tate weights 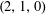$(2,1,0)$ as well as the Serre weight conjectures of Herzig [‘The weight in a Serre-type conjecture for tame $n$-dimensional Galois representations’, Duke Math. J. 149(1) (2009), 37–116] over an unramified field extending the results of Le et al. [‘Potentially crystalline deformation 3985 rings and Serre weight conjectures: shapes and shadows’, Invent. Math. 212(1) (2018), 1–107]. We also prove results in modular representation theory about lattices in Deligne–Lusztig representations for the group 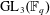$\text{GL}_{3}(\mathbb{F}_{q})$.

MSC classification

Primary: 11F80: Galois representations
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 20C33: Representations of finite groups of Lie type
Type
Number Theory
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Alperin, J. L., ‘Modular representations as an introduction to the local representation theory of finite groups’, inLocal Representation Theory, Cambridge Studies in Advanced Mathematics, 11 (Cambridge University Press, Cambridge, 1986).CrossRefGoogle Scholar
Andersen, H. H. and Masaharu, K., ‘Filtrations on G 1T-modules’, Proc. Lond. Math. Soc. (3) 82(3) (2001), 614–646.CrossRefGoogle Scholar
Andersen, H. H., ‘Extensions of simple modules for finite Chevalley groups’, J. Algebra 111(2) (1987), 388–403.CrossRefGoogle Scholar
Bowman, C., Doty, S. R. and Martin, S., ‘Decomposition of tensor products of modular irreducible representations for SL3 : the p⩾5 case’, Int. Electron. J. Algebra 17 (2015), 105–138.CrossRefGoogle Scholar
Breuil, C. and Paskunas, V., ‘Towards a modulo p Langlands correspondence for GL2’, Mem. Amer. Math. Soc. 216 (2012), no. 1016, vi+114 pp.Google Scholar
Breuil, C., ‘Sur un problème de compatibilité local-global modulo p pour GL2’, J. Reine Angew. Math. 692 (2014), 1–76.CrossRefGoogle Scholar
Calegari, F., ‘Non-minimal modularity lifting in weight one’, J. Reine Angew. Math. 740 (2018), 41–62.CrossRefGoogle Scholar
Conrad, B., Diamond, F. and Taylor, R., ‘Modularity of certain potentially Barsotti–Tate Galois representations’, J. Amer. Math. Soc. 12(2) (1999), 521–567.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paskūnas, V. and Shin, S. W., ‘Patching and the p-adic local Langlands correspondence’, Camb. J. Math. 4(2) (2016), 197–287.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations’, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.CrossRefGoogle Scholar
Caraiani, A. and Levin, B., ‘Kisin modules with descent data and parahoric local models’, Ann. Sci. Éc. Norm. Supér. (4) 51(1) (2018), 181–213.CrossRefGoogle Scholar
Diamond, F., ‘The Taylor–Wiles construction and multiplicity one’, Invent. Math. 128(2) (1997), 379–391.CrossRefGoogle Scholar
Deligne, P. and Lusztig, G., ‘Representations of reductive groups over finite fields’, Ann. of Math. (2) 103(1) (1976), 103–161.CrossRefGoogle Scholar
Emerton, M. and Gee, T., ‘A geometric perspective on the Breuil–Mézard conjecture’, J. Inst. Math. Jussieu 13(1) (2014), 183–223.CrossRefGoogle Scholar
Emerton, M., Gee, T. and Herzig, F., ‘Weight cycling and Serre-type conjectures for unitary groups’, Duke Math. J. 162(9) (2013), 1649–1722.CrossRefGoogle Scholar
Emerton, M., Gee, T. and Savitt, D., ‘Lattices in the cohomology of Shimura curves’, Invent. Math. 200(1) (2015), 1–96.CrossRefGoogle Scholar
Enns, J., ‘On weight elimination for GLn(Qp f)’, Math. Res. Lett. 26(1) (2019), 53–66.CrossRefGoogle Scholar
Gee, T., ‘Automorphic lifts of prescribed types’, Math. Ann. 350(1) (2011), 107–144.CrossRefGoogle Scholar
Gee, T., Herzig, F. and Savitt, D., ‘General Serre weight conjectures’, J. Eur. Math. Soc. (JEMS) 20(12) (2018), 2859–2949.CrossRefGoogle Scholar
Grothendieck, A., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II’, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 231.Google Scholar
Guerberoff, L., ‘Modularity lifting theorems for Galois representations of unitary type’, Compos. Math. 147(4) (2011), 1022–1058.CrossRefGoogle Scholar
Herzig, F., ‘The weight in a Serre-type conjecture for tame n-dimensional Galois representations’, Duke Math. J. 149(1) (2009), 37–116.CrossRefGoogle Scholar
Hassett, B. and Kovács, S. J., ‘Reflexive pull-backs and base extension’, J. Algebraic Geom. 13(2) (2004), 233–247.CrossRefGoogle Scholar
Herzig, F., Le, D. and Morra, S., ‘On mod p local-global compatibility for GL3 in the ordinary case’, Compos. Math. 153(11) (2017), 2215–2286.CrossRefGoogle Scholar
Humphreys, J. E., Modular Representations of Finite Groups of Lie Type, London Mathematical Society Lecture Note Series, 326 (Cambridge University Press, Cambridge, 2006).Google Scholar
Jantzen, J. C., Representations of Algebraic Groups, second edn, Mathematical Surveys and Monographs, 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Kisin, M., ‘Potentially semi-stable deformation rings’, J. Amer. Math. Soc. 21(2) (2008), 513–546.CrossRefGoogle Scholar
Le, D., ‘Lattices in the cohomology of U (3) arithmetic manifolds’, Math. Ann. 372(1–2) (2018), 55–89.CrossRefGoogle Scholar
Le, D., Le Hung, B. V. and Levin, B., ‘Weight elimination in Serre-type conjectures’, Duke Math. J. 168(13) (2019), 2433–2506.CrossRefGoogle Scholar
Le, D., Le Hung, B. V., Levin, B. and Morra, S., ‘Potentially crystalline deformation rings and Serre weight conjectures: shapes and shadows’, Invent. Math. 212(1) (2018), 1–107.CrossRefGoogle Scholar
Pillen, C., ‘Reduction modulo p of some Deligne–Lusztig characters’, Arch. Math. (Basel) 61(5) (1993), 421–433.CrossRefGoogle Scholar
‘Loewy series for principal series representations of finite Chevalley groups’, J. Algebra 189(1) (1997), 101–124.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project, https://stacks.math.columbia.edu, 2019.Google Scholar
Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations. II’, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 183–239.CrossRefGoogle Scholar