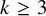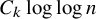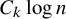1 Introduction
The problem of finding regular subgraphs in graphs has a very long history. Note that finding a
![]() $1$
-regular subgraph is the same as finding a matching. One of the oldest results of graph theory is Petersen’s theorem from 1891 [Reference Petersen24], which states that every cubic, bridgeless graph contains a perfect matching. The celebrated Hall’s theorem [Reference Hall17] gives a necessary and sufficient condition for a bipartite graph to have a perfect matching, while Tutte’s theorem [Reference Tutte29] gives such a condition for an arbitrary graph. Later, Tutte [Reference Tutte30] found a necessary and sufficient condition for a graph to contain a k-regular spanning subgraph and, more generally, for it to contain an f-factor – that is, a spanning subgraph in which each vertex v has degree
$1$
-regular subgraph is the same as finding a matching. One of the oldest results of graph theory is Petersen’s theorem from 1891 [Reference Petersen24], which states that every cubic, bridgeless graph contains a perfect matching. The celebrated Hall’s theorem [Reference Hall17] gives a necessary and sufficient condition for a bipartite graph to have a perfect matching, while Tutte’s theorem [Reference Tutte29] gives such a condition for an arbitrary graph. Later, Tutte [Reference Tutte30] found a necessary and sufficient condition for a graph to contain a k-regular spanning subgraph and, more generally, for it to contain an f-factor – that is, a spanning subgraph in which each vertex v has degree
![]() $f(v)$
.
$f(v)$
.
The problem of finding general, not necessarily spanning, regular subgraphs was also extensively studied. In 1975, Erdős and Sauer [Reference Erdős14] asked the following natural extremal question. Given a positive integer k, what is the maximum number of edges that an n-vertex graph can have if it does not contain a k-regular subgraph? The problem also appeared in Bollobás’s book on extremal graph theory [Reference Bollobás7] and in the book of Bondy and Murty [Reference Bondy and Murty9]. Later, Erdős [Reference Erdős16] mentioned this as one of his favourite unsolved problems. Let us write
![]() $f_k(n)$
for the smallest number of edges which guarantees a k-regular subgraph. Trivially
$f_k(n)$
for the smallest number of edges which guarantees a k-regular subgraph. Trivially
![]() $f_2(n)=n$
, but already for
$f_2(n)=n$
, but already for
![]() $k=3$
, the answer is unclear. Erdős and Sauer observed that
$k=3$
, the answer is unclear. Erdős and Sauer observed that
![]() $f_3(n)=O(n^{8/5})$
follows from the known upper bound for the Turán number of the cube [Reference Erdős and Simonovits15] and suggested that
$f_3(n)=O(n^{8/5})$
follows from the known upper bound for the Turán number of the cube [Reference Erdős and Simonovits15] and suggested that
![]() for any fixed
for any fixed
![]() and sufficiently large n.
and sufficiently large n.
A very influential algebraic technique to find regular subgraphs was developed in the early 1980s by Alon, Friedland and Kalai. In [Reference Alon, Friedland and Kalai4], motivated by a conjecture of Berge and Sauer, they showed that any
![]() $4$
-regular multigraph plus an edge contains a
$4$
-regular multigraph plus an edge contains a
![]() $3$
-regular subgraph. Alon, Friedland and Kalai [Reference Alon, Friedland and Kalai5] also proved several results which state, roughly speaking, that nearly regular graphs have regular subgraphs with not too small degree. One of these results, together with an ingenious argument, was used by Pyber [Reference Pyber25] in 1985 to show that indeed
$3$
-regular subgraph. Alon, Friedland and Kalai [Reference Alon, Friedland and Kalai5] also proved several results which state, roughly speaking, that nearly regular graphs have regular subgraphs with not too small degree. One of these results, together with an ingenious argument, was used by Pyber [Reference Pyber25] in 1985 to show that indeed
![]() . More precisely, Pyber proved that any n-vertex graph with average degree at least
. More precisely, Pyber proved that any n-vertex graph with average degree at least
![]() $C_k\log n$
contains a k-regular subgraph (here and in the rest of the paper logarithms are to the base two).
$C_k\log n$
contains a k-regular subgraph (here and in the rest of the paper logarithms are to the base two).
At this point, the best lower bound was due to Chvátal [Reference Erdős14], who had shown that
![]() $f_3(2n+3)> 6n$
. This was greatly improved by Pyber, Rödl and Szemerédi [Reference Pyber, Rödl and Szemerédi26], who found a remarkable construction of graphs with a superlinear number of edges that do not contain k-regular subgraphs.
$f_3(2n+3)> 6n$
. This was greatly improved by Pyber, Rödl and Szemerédi [Reference Pyber, Rödl and Szemerédi26], who found a remarkable construction of graphs with a superlinear number of edges that do not contain k-regular subgraphs.
Theorem 1.1 (Pyber–Rödl–Szemerédi [Reference Pyber, Rödl and Szemerédi26]).
There is some absolute constant
![]() $c>0$
such that for every n there exists an n-vertex graph with at least
$c>0$
such that for every n there exists an n-vertex graph with at least
![]() $cn\log \log n$
edges which does not contain a k-regular subgraph for any
$cn\log \log n$
edges which does not contain a k-regular subgraph for any
![]() $k\geq 3$
.
$k\geq 3$
.
Furthermore, Pyber, Rödl and Szemerédi generalized Pyber’s result to show that for any positive integer k, there is a constant
![]() $C=C(k)$
such that any graph with maximum degree
$C=C(k)$
such that any graph with maximum degree
![]() $\Delta $
and average degree at least
$\Delta $
and average degree at least
![]() $C\log \Delta $
contains a k-regular subgraph.
$C\log \Delta $
contains a k-regular subgraph.
Despite substantial interest from many researchers, the above bounds have not been improved in the last 30 years. At the same time, several variants of the original problem have been considered. Bollobás, Kim and Verstraëte [Reference Bollobás, Kim and Verstraëte8] studied the threshold for a random graph to have a k-regular subgraph. Rödl and Wysocka [Reference Rödl and Wysocka27] investigated the largest r for which every n-vertex graph with at least
![]() $\gamma n^2$
edges has an r-regular subgraph. Many papers have been written on the existence of regular subgraphs in hypergraphs; see, for example, [Reference Mubayi and Verstraëte23, Reference Dellamonica, Haxell, Łuczak, Mubayi, Nagle, Person, Rödl, Schacht and Verstraëte11, Reference Kim and Kostochka20, Reference Kim19, Reference Han and Kim18].
$\gamma n^2$
edges has an r-regular subgraph. Many papers have been written on the existence of regular subgraphs in hypergraphs; see, for example, [Reference Mubayi and Verstraëte23, Reference Dellamonica, Haxell, Łuczak, Mubayi, Nagle, Person, Rödl, Schacht and Verstraëte11, Reference Kim and Kostochka20, Reference Kim19, Reference Han and Kim18].
In this paper, we prove the following result, which completely resolves the problem of Erdős and Sauer.
Theorem 1.2. For any positive integer k, there is a constant
![]() $C=C(k)$
such that any graph with maximum degree
$C=C(k)$
such that any graph with maximum degree
![]() $\Delta \geq 3$
and average degree at least
$\Delta \geq 3$
and average degree at least
![]() $C\log \log \Delta $
contains a k-regular subgraph. In particular, any n-vertex graph with average degree at least
$C\log \log \Delta $
contains a k-regular subgraph. In particular, any n-vertex graph with average degree at least
![]() $C \log \log n$
contains such a subgraph.
$C \log \log n$
contains such a subgraph.
Our results also make progress on two other old and well-known problems. The first one, due to Erdős and Simonovits from 1970 [Reference Erdős and Simonovits15], concerns the question of how dense an almost-regular subgraph there must exist in a graph with n vertices and
![]() $n\log n$
edges. An almost-regular graph here is one in which the maximum degree and the minimum degree differ by at most a constant factor. Our results resolve this question asymptotically, showing that one can find an almost-regular subgraph with
$n\log n$
edges. An almost-regular graph here is one in which the maximum degree and the minimum degree differ by at most a constant factor. Our results resolve this question asymptotically, showing that one can find an almost-regular subgraph with
![]() $m=\omega (1)$
vertices and at least
$m=\omega (1)$
vertices and at least
![]() $m(\log m)^{1/2-o(1)}$
edges, which is tight by a result of Alon [Reference Alon1]. Since the full discussion of this topic takes considerable space, we postpone it to the concluding remarks (Section 6).
$m(\log m)^{1/2-o(1)}$
edges, which is tight by a result of Alon [Reference Alon1]. Since the full discussion of this topic takes considerable space, we postpone it to the concluding remarks (Section 6).
Finally, let us discuss the other application of our main result. In 1983, Thomassen [Reference Thomassen28] conjectured that, for every
![]() $t,g\in \mathbb {N}$
, there exists some d such that any graph with average degree at least d contains a subgraph with average degree at least t and girth at least g. Kühn and Osthus [Reference Kühn and Osthus21] proved this for
$t,g\in \mathbb {N}$
, there exists some d such that any graph with average degree at least d contains a subgraph with average degree at least t and girth at least g. Kühn and Osthus [Reference Kühn and Osthus21] proved this for
![]() $g\leq 6$
(see also [Reference Montgomery, Pokrovskiy and Sudakov22] for an improved bound on d), but the general case is wide open. It is easy to see that for every
$g\leq 6$
(see also [Reference Montgomery, Pokrovskiy and Sudakov22] for an improved bound on d), but the general case is wide open. It is easy to see that for every
![]() $t,g\in \mathbb {N}$
, if d is sufficiently large, then any d-regular graph has a subgraph with average degree at least t and girth at least g. Hence, our Theorem 1.2 implies that any graph G with average degree at least
$t,g\in \mathbb {N}$
, if d is sufficiently large, then any d-regular graph has a subgraph with average degree at least t and girth at least g. Hence, our Theorem 1.2 implies that any graph G with average degree at least
![]() $C(t,g)\log \log \Delta (G)$
contains a subgraph with average degree at least t and girth at least g. This improves the best bound towards Thomassen’s conjecture, due to Dellamonica and Rödl [Reference Dellamonica and Rödl12], which states that any graph G with average degree at least
$C(t,g)\log \log \Delta (G)$
contains a subgraph with average degree at least t and girth at least g. This improves the best bound towards Thomassen’s conjecture, due to Dellamonica and Rödl [Reference Dellamonica and Rödl12], which states that any graph G with average degree at least
![]() $\alpha (t,g) (\log \log \Delta (G))^{\beta (t,g)}$
contains a subgraph with average degree at least t and girth at least g.
$\alpha (t,g) (\log \log \Delta (G))^{\beta (t,g)}$
contains a subgraph with average degree at least t and girth at least g.
The rest of the paper is organized as follows. In the next section, we give a sketch of the proof of Theorem 1.2. In Section 3, we prove some simple preliminary lemmas. The key lemma is proved in Section 4. The proof of Theorem 1.2 is then completed in Section 5. We give some concluding remarks about large almost-regular subgraphs in Section 6.
Notation. We write
![]() $e(G)$
for the number of edges in a graph G. For a set
$e(G)$
for the number of edges in a graph G. For a set
![]() $S\subset V(G)$
,
$S\subset V(G)$
,
![]() $G[S]$
stands for the induced subgraph of G on vertex set S. For a vertex
$G[S]$
stands for the induced subgraph of G on vertex set S. For a vertex
![]() $u\in V(G)$
,
$u\in V(G)$
,
![]() $N_G(u)$
denotes the neighbourhood of u in G and we write
$N_G(u)$
denotes the neighbourhood of u in G and we write
![]() $d_G(u)$
for the degree of u. Given vertices u and
$d_G(u)$
for the degree of u. Given vertices u and
![]() $u'$
,
$u'$
,
![]() $d_G(u,u')$
stands for the number of common neighbours of u and
$d_G(u,u')$
stands for the number of common neighbours of u and
![]() $u'$
in G. We write
$u'$
in G. We write
![]() $\Delta (G)$
for the maximum degree of G.
$\Delta (G)$
for the maximum degree of G.
2 An overview of the proof
Although our proof is short, we think that it may be useful to give a sketch of the main ideas. We start by briefly discussing the lower bound construction of Pyber, Rödl and Szemerédi since it partly motivates our argument. Their (random) graph can be described roughly as follows. The vertex set is
![]() $A\cup B$
, where
$A\cup B$
, where
![]() $|B|=n$
, A is the disjoint union of sets
$|B|=n$
, A is the disjoint union of sets
![]() $A(j)$
for
$A(j)$
for
![]() $\frac {1}{4}\log \log n\leq j\leq \frac {1}{2}\log \log n$
with
$\frac {1}{4}\log \log n\leq j\leq \frac {1}{2}\log \log n$
with
![]() $|A(j)|=n/2^{2^j}$
, and for each j and
$|A(j)|=n/2^{2^j}$
, and for each j and
![]() $v\in B$
, v has a unique neighbour in
$v\in B$
, v has a unique neighbour in
![]() $A(j)$
, chosen uniformly at random. Note that a typical vertex in
$A(j)$
, chosen uniformly at random. Note that a typical vertex in
![]() $A(j)$
has degree about
$A(j)$
has degree about
![]() $2^{2^j}.$
$2^{2^j}.$
In a general bipartite graph, we obtain a similar partitioning of part A according to the degrees and show, very roughly speaking, that if there is some j such that each
![]() $v\in B$
has at least a large constant number of neighbours in
$v\in B$
has at least a large constant number of neighbours in
![]() $A(j)$
(unlike in the above construction where each
$A(j)$
(unlike in the above construction where each
![]() $v\in B$
has only one neighbour there), then G has a k-regular subgraph.
$v\in B$
has only one neighbour there), then G has a k-regular subgraph.
More precisely, let r be a large constant (that can depend on k), and let G be a bipartite graph with parts A and B such that for some positive integers
![]() $s,t\geq r$
, every
$s,t\geq r$
, every
![]() $v\in B$
has degree r, the average degree of a vertex in A is at least
$v\in B$
has degree r, the average degree of a vertex in A is at least
![]() $2^s$
, the maximum degree of a vertex in A is at most
$2^s$
, the maximum degree of a vertex in A is at most
![]() $2^t$
and
$2^t$
and
![]() $t\leq (1+\frac {1}{r-1})s$
. We remark that it is possible (and not too hard) to find such a subgraph in any graph with maximum degree
$t\leq (1+\frac {1}{r-1})s$
. We remark that it is possible (and not too hard) to find such a subgraph in any graph with maximum degree
![]() $\Delta $
and average degree at least
$\Delta $
and average degree at least
![]() $100r^2\log \log \Delta $
. For the sake of simplicity, let us also suppose that G is
$100r^2\log \log \Delta $
. For the sake of simplicity, let us also suppose that G is
![]() $C_4$
-free, although this assumption can be significantly relaxed – it suffices to assume that the codegrees in G are not extremely large. We shall now argue that G has a k-regular subgraph.
$C_4$
-free, although this assumption can be significantly relaxed – it suffices to assume that the codegrees in G are not extremely large. We shall now argue that G has a k-regular subgraph.
Our key lemma (stated and proved in Section 4) provides a subgraph which, although is not necessarily regular, has much better regularity properties than G. More precisely, it asserts the existence of subsets
![]() $A"\subset A$
,
$A"\subset A$
,
![]() $B"\subset B$
and positive integers
$B"\subset B$
and positive integers
![]() $s',t'\geq r$
such that in the graph
$s',t'\geq r$
such that in the graph
![]() $G[A"\cup B"]$
all the previous conditions are satisfied (with
$G[A"\cup B"]$
all the previous conditions are satisfied (with
![]() $A",B",s',t'$
in place of
$A",B",s',t'$
in place of
![]() $A,B,s,t$
), and, additionally,
$A,B,s,t$
), and, additionally,
![]() $t'-s'\leq \log (40(t-s)r^2)$
. Hence, as long as
$t'-s'\leq \log (40(t-s)r^2)$
. Hence, as long as
![]() $t-s> 3\log r$
,
$t-s> 3\log r$
,
![]() $t'-s'$
is smaller than
$t'-s'$
is smaller than
![]() $t-s$
. Iteratively applying this lemma, eventually we obtain subsets
$t-s$
. Iteratively applying this lemma, eventually we obtain subsets
![]() $A^*\subset A$
,
$A^*\subset A$
,
![]() $B^*\subset B$
and positive integers
$B^*\subset B$
and positive integers
![]() $s^*,t^*\geq r$
such that in the graph
$s^*,t^*\geq r$
such that in the graph
![]() $G[A^*\cup B^*]$
, every
$G[A^*\cup B^*]$
, every
![]() $v\in B^*$
has degree r, the average degree of a vertex in
$v\in B^*$
has degree r, the average degree of a vertex in
![]() $A^*$
is at least
$A^*$
is at least
![]() $2^{s^*}$
, the maximum degree of a vertex in
$2^{s^*}$
, the maximum degree of a vertex in
![]() $A^*$
is at most
$A^*$
is at most
![]() $2^{t^*}$
and
$2^{t^*}$
and
![]() $t^*-s^*\leq 3\log r$
. The last property means that the maximum degree is at most
$t^*-s^*\leq 3\log r$
. The last property means that the maximum degree is at most
![]() $2^{3\log r}$
times the average degree in
$2^{3\log r}$
times the average degree in
![]() $A^*$
. Taking a random subset
$A^*$
. Taking a random subset
![]() $\hat {B}\subset B^*$
of size
$\hat {B}\subset B^*$
of size
![]() $|A^*|$
and deleting the vertices in
$|A^*|$
and deleting the vertices in
![]() $G[A^*\cup \hat {B}]$
whose degree is much larger than expected, we obtain a subgraph with average degree about r and maximum degree at most about
$G[A^*\cup \hat {B}]$
whose degree is much larger than expected, we obtain a subgraph with average degree about r and maximum degree at most about
![]() $r2^{3\log r}=r^4$
. We can then use a result of Pyber, Rödl and Szemerédi (see Theorem 3.8) to find a k-regular subgraph in this graph.
$r2^{3\log r}=r^4$
. We can then use a result of Pyber, Rödl and Szemerédi (see Theorem 3.8) to find a k-regular subgraph in this graph.
We shall now sketch the proof of our key lemma. Let
![]() $A_{s+1}=\{u\in A:d_G(u)\leq 2^{s+1}\}$
, and for each
$A_{s+1}=\{u\in A:d_G(u)\leq 2^{s+1}\}$
, and for each
![]() $s+2\leq i\leq t$
, let
$s+2\leq i\leq t$
, let
![]() $A_i=\{u\in A: 2^{i-1}<d_G(u)\leq 2^{i}\}$
. Observe that the sets
$A_i=\{u\in A: 2^{i-1}<d_G(u)\leq 2^{i}\}$
. Observe that the sets
![]() $A_{s+1},\dots ,A_t$
partition A. For each
$A_{s+1},\dots ,A_t$
partition A. For each
![]() $u\in A$
, let
$u\in A$
, let
![]() $\alpha (u)$
be the unique i with
$\alpha (u)$
be the unique i with
![]() $u\in A_i$
. For
$u\in A_i$
. For
![]() $v\in B$
, let
$v\in B$
, let
![]() $\beta (v)=\sum _{u\in N_G(v)} \alpha (u)$
. Note that for every
$\beta (v)=\sum _{u\in N_G(v)} \alpha (u)$
. Note that for every
![]() $v\in B$
, we have
$v\in B$
, we have
![]() $(s+1)r\leq \beta (v)\leq tr$
, so there are at most
$(s+1)r\leq \beta (v)\leq tr$
, so there are at most
![]() $(t-s)r$
possible values for
$(t-s)r$
possible values for
![]() $\beta (v)$
. Hence, by the pigeon hole principle, there are some
$\beta (v)$
. Hence, by the pigeon hole principle, there are some
![]() $\gamma \geq (s+1)r$
and a subset
$\gamma \geq (s+1)r$
and a subset
![]() $\tilde {B}\subset B$
of size at least
$\tilde {B}\subset B$
of size at least
![]() $\frac {|B|}{(t-s)r}$
such that
$\frac {|B|}{(t-s)r}$
such that
![]() $\beta (v)=\gamma $
for all
$\beta (v)=\gamma $
for all
![]() $v\in \tilde {B}$
.
$v\in \tilde {B}$
.
Let
![]() $A'$
be a random subset of A where each
$A'$
be a random subset of A where each
![]() $u\in A$
is kept independently with probability
$u\in A$
is kept independently with probability
![]() $2^{\alpha (u)-t}$
. Let
$2^{\alpha (u)-t}$
. Let
![]() $B'=\{v\in \tilde {B}: N_G(v)\subset A'\}$
. Let us see why we expect
$B'=\{v\in \tilde {B}: N_G(v)\subset A'\}$
. Let us see why we expect
![]() $G[A'\cup B']$
to be nearly biregular. Firstly, every
$G[A'\cup B']$
to be nearly biregular. Firstly, every
![]() $v\in B'$
has degree precisely r in
$v\in B'$
has degree precisely r in
![]() $G[A'\cup B']$
. Now, let
$G[A'\cup B']$
. Now, let
![]() $u\in A$
. We claim that, conditional on
$u\in A$
. We claim that, conditional on
![]() $u\in A'$
,
$u\in A'$
,
![]() $|N_G(u)\cap B'|$
is distributed as a binomial random variable
$|N_G(u)\cap B'|$
is distributed as a binomial random variable
![]() $\textrm {Bin}\big (|N_G(u)\cap \tilde {B}|, 2^{\gamma -\alpha (u)-(r-1)t}\big )$
. Indeed, conditional on
$\textrm {Bin}\big (|N_G(u)\cap \tilde {B}|, 2^{\gamma -\alpha (u)-(r-1)t}\big )$
. Indeed, conditional on
![]() $u\in A'$
, each
$u\in A'$
, each
![]() $v\in N_G(u)\cap \tilde {B}$
belongs to
$v\in N_G(u)\cap \tilde {B}$
belongs to
![]() $B'$
with probability
$B'$
with probability
![]() $\prod _{w\in N_G(v)\setminus \{u\}} 2^{\alpha (w)-t}=2^{\beta (v)-\alpha (u)-(r-1)t}=2^{\gamma -\alpha (u)-(r-1)t}$
and these events are independent for all v since
$\prod _{w\in N_G(v)\setminus \{u\}} 2^{\alpha (w)-t}=2^{\beta (v)-\alpha (u)-(r-1)t}=2^{\gamma -\alpha (u)-(r-1)t}$
and these events are independent for all v since
![]() $N_G(v)\setminus \{u\}$
are pairwise disjoint as G is
$N_G(v)\setminus \{u\}$
are pairwise disjoint as G is
![]() $C_4$
-free. Thus, if
$C_4$
-free. Thus, if
![]() $u\in A'$
, then the degree of u in
$u\in A'$
, then the degree of u in
![]() $G[A'\cup B']$
is concentrated around
$G[A'\cup B']$
is concentrated around
![]() $|N_G(u)\cap \tilde {B}|2^{\gamma -\alpha (u)-(r-1)t}$
. Since
$|N_G(u)\cap \tilde {B}|2^{\gamma -\alpha (u)-(r-1)t}$
. Since
![]() $|N_G(u)\cap \tilde {B}|\leq d_G(u)\leq 2^{\alpha (u)}$
, we see that it is very unlikely that the degree of u in
$|N_G(u)\cap \tilde {B}|\leq d_G(u)\leq 2^{\alpha (u)}$
, we see that it is very unlikely that the degree of u in
![]() $G[A'\cup B']$
is much larger than
$G[A'\cup B']$
is much larger than
![]() $2^{\gamma -(r-1)t}$
. On the other hand,
$2^{\gamma -(r-1)t}$
. On the other hand,
![]() $\tilde {B}$
has size similar to B, so on average
$\tilde {B}$
has size similar to B, so on average
![]() $|N_G(u)\cap \tilde {B}|$
is not much smaller than
$|N_G(u)\cap \tilde {B}|$
is not much smaller than
![]() $d_G(u)$
, which is in turn at least
$d_G(u)$
, which is in turn at least
![]() $2^{\alpha (u)-1}$
(unless
$2^{\alpha (u)-1}$
(unless
![]() $\alpha (u)=s+1$
). Hence, it is not hard to see that the average degree in
$\alpha (u)=s+1$
). Hence, it is not hard to see that the average degree in
![]() $G[A'\cup B']$
of a vertex in
$G[A'\cup B']$
of a vertex in
![]() $A'$
is expected to be not much smaller than
$A'$
is expected to be not much smaller than
![]() $2^{\gamma -(r-1)t}$
. A small loss arises from the fact that
$2^{\gamma -(r-1)t}$
. A small loss arises from the fact that
![]() $\tilde {B}$
is potentially smaller than B by a factor of
$\tilde {B}$
is potentially smaller than B by a factor of
![]() $(t-s)r$
; this partly explains why
$(t-s)r$
; this partly explains why
![]() $t'-s'$
can be as large as
$t'-s'$
can be as large as
![]() $\log (40(t-s)r^2)$
. We remark that the condition
$\log (40(t-s)r^2)$
. We remark that the condition
![]() $t\leq (1+\frac {1}{r-1})s$
ensures that
$t\leq (1+\frac {1}{r-1})s$
ensures that
![]() $\gamma -(r-1)t\geq sr-(r-1)t+r\geq r$
, so the expected average degree of the vertices in
$\gamma -(r-1)t\geq sr-(r-1)t+r\geq r$
, so the expected average degree of the vertices in
![]() $A'$
is not too small.
$A'$
is not too small.
Now, we take
![]() $A"$
to be the set of those vertices in
$A"$
to be the set of those vertices in
![]() $A'$
whose degree in
$A'$
whose degree in
![]() $G[A'\cup B']$
is not much larger than expected (i.e., not much larger than
$G[A'\cup B']$
is not much larger than expected (i.e., not much larger than
![]() $2^{\gamma -(r-1)t}$
) and set
$2^{\gamma -(r-1)t}$
) and set
![]() $B"=\{v\in B': N_G(v)\subset A"\}$
. By the strong concentration of the degrees,
$B"=\{v\in B': N_G(v)\subset A"\}$
. By the strong concentration of the degrees,
![]() $G[A"\cup B"]$
has almost as many edges as
$G[A"\cup B"]$
has almost as many edges as
![]() $G[A'\cup B']$
, so the average degree of a vertex in
$G[A'\cup B']$
, so the average degree of a vertex in
![]() $A"$
is not much smaller than it was in
$A"$
is not much smaller than it was in
![]() $A'$
. Hence, the desired conditions about
$A'$
. Hence, the desired conditions about
![]() $A"$
and
$A"$
and
![]() $B"$
are satisfied (for suitable
$B"$
are satisfied (for suitable
![]() $s'\approx \gamma -(r-1)t$
and
$s'\approx \gamma -(r-1)t$
and
![]() $t'\approx \gamma -(r-1)t$
).
$t'\approx \gamma -(r-1)t$
).
3 Preliminaries
As we have mentioned in the outline of the proof, one of the conditions in our key lemma is that no two vertices in the graph have very large codegree. We prove that with the loss of a constant factor in the number of edges, we can pass to a subgraph satisfying this property. For this, we can assume that our graphs are
![]() $K_{k,k}$
-free (or else, they contain a k-regular subgraph).
$K_{k,k}$
-free (or else, they contain a k-regular subgraph).
Lemma 3.1. Let k be a positive integer, and let H be a
![]() $K_{k,k}$
-free bipartite graph with parts S and T. Assume that
$K_{k,k}$
-free bipartite graph with parts S and T. Assume that
![]() $d_H(u)\geq k|T|^{1-1/k}$
holds for every
$d_H(u)\geq k|T|^{1-1/k}$
holds for every
![]() $u\in S$
. Then
$u\in S$
. Then
![]() $e(H)\leq k|T|$
.
$e(H)\leq k|T|$
.
Proof. Suppose that
![]() $e(H)>k|T|$
. Then, by Jensen’s inequality,
$e(H)>k|T|$
. Then, by Jensen’s inequality,
 $$ \begin{align*}\sum_{v\in T} \binom{d_H(v)}{k}\geq |T|\binom{e(H)/|T|}{k}\geq |T|\left(\frac{e(H)}{k|T|}\right)^k.\end{align*} $$
$$ \begin{align*}\sum_{v\in T} \binom{d_H(v)}{k}\geq |T|\binom{e(H)/|T|}{k}\geq |T|\left(\frac{e(H)}{k|T|}\right)^k.\end{align*} $$
By the degree condition we have
![]() $e(H)\geq k|S||T|^{1-1/k}$
. Then
$e(H)\geq k|S||T|^{1-1/k}$
. Then
![]() $\frac {e(H)}{k|T|}\geq |S||T|^{-1/k}$
and therefore,
$\frac {e(H)}{k|T|}\geq |S||T|^{-1/k}$
and therefore,
![]() $\sum _{v\in T} \binom {d_H(v)}{k} \geq |S|^k\geq k\binom {|S|}{k}$
. This implies that there is some
$\sum _{v\in T} \binom {d_H(v)}{k} \geq |S|^k\geq k\binom {|S|}{k}$
. This implies that there is some
![]() $R\subset S$
of size k whose common neighbourhood in T has size at least k. Then H contains
$R\subset S$
of size k whose common neighbourhood in T has size at least k. Then H contains
![]() $K_{k,k}$
, which is a contradiction.
$K_{k,k}$
, which is a contradiction.
The proof of the next lemma is somewhat similar to that of Lemma 2.3 from [Reference Montgomery, Pokrovskiy and Sudakov22].
Lemma 3.2. Let k be a positive integer. Let G be a
![]() $K_{k,k}$
-free bipartite graph with parts A and B, and assume that
$K_{k,k}$
-free bipartite graph with parts A and B, and assume that
![]() $d_G(u)\leq m$
holds for all
$d_G(u)\leq m$
holds for all
![]() $u\in A$
. Then G has a spanning subgraph
$u\in A$
. Then G has a spanning subgraph
![]() $G'$
such that
$G'$
such that
![]() $e(G')\geq e(G)/(k+1)$
and
$e(G')\geq e(G)/(k+1)$
and
![]() $d_{G'}(u,u')\leq k m^{1-1/k}$
for any two distinct
$d_{G'}(u,u')\leq k m^{1-1/k}$
for any two distinct
![]() $u,u'\in A$
.
$u,u'\in A$
.
Proof. Let
![]() $A=\{u_1,u_2,\dots ,u_n\}$
, and let
$A=\{u_1,u_2,\dots ,u_n\}$
, and let
![]() $G_0=G$
. Let us define spanning subgraphs
$G_0=G$
. Let us define spanning subgraphs
![]() $G_1,\dots ,G_n$
of G recursively as follows. Having defined
$G_1,\dots ,G_n$
of G recursively as follows. Having defined
![]() $G_{i-1}$
for some
$G_{i-1}$
for some
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $T=N_{G_{i-1}}(u_i)$
, let
$T=N_{G_{i-1}}(u_i)$
, let
![]() $S=\{u_j: j>i \text { and } d_{G_{i-1}}(u_i,u_j)>k m^{1-1/k}\}$
and let
$S=\{u_j: j>i \text { and } d_{G_{i-1}}(u_i,u_j)>k m^{1-1/k}\}$
and let
![]() $H=G_{i-1}[S\cup T]$
. Since H is a subgraph of G, it is
$H=G_{i-1}[S\cup T]$
. Since H is a subgraph of G, it is
![]() $K_{k,k}$
-free. Moreover, for any
$K_{k,k}$
-free. Moreover, for any
![]() $u_j\in S$
,
$u_j\in S$
,
![]() $d_H(u_j)=d_{G_{i-1}}(u_i,u_j)>k m^{1-1/k}\geq k |T|^{1-1/k}$
. Hence, by Lemma 3.1,
$d_H(u_j)=d_{G_{i-1}}(u_i,u_j)>k m^{1-1/k}\geq k |T|^{1-1/k}$
. Hence, by Lemma 3.1,
![]() $e(H)\leq k|T|$
. Let
$e(H)\leq k|T|$
. Let
![]() $G_i$
be the subgraph of
$G_i$
be the subgraph of
![]() $G_{i-1}$
obtained by deleting the edges in H. Then
$G_{i-1}$
obtained by deleting the edges in H. Then
![]() $e(G_{i-1})-e(G_i)=e(H)\leq kd_{G_{i-1}}(u_i)$
.
$e(G_{i-1})-e(G_i)=e(H)\leq kd_{G_{i-1}}(u_i)$
.
Observe that for any
![]() $i<j$
, we have
$i<j$
, we have
![]() $d_{G_n}(u_i,u_j)\leq km^{1-1/k}$
. Moreover, note that for any
$d_{G_n}(u_i,u_j)\leq km^{1-1/k}$
. Moreover, note that for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $d_{G_n}(u_i)=d_{G_{i-1}}(u_i)$
, so
$d_{G_n}(u_i)=d_{G_{i-1}}(u_i)$
, so
 $$ \begin{align*}e(G_n)=\sum_{i=1}^n d_{G_n}(u_i)=\sum_{i=1}^n d_{G_{i-1}}(u_i)\geq \sum_{i=1}^n (e(G_{i-1})-e(G_i))/k=(e(G_0)-e(G_n))/k.\end{align*} $$
$$ \begin{align*}e(G_n)=\sum_{i=1}^n d_{G_n}(u_i)=\sum_{i=1}^n d_{G_{i-1}}(u_i)\geq \sum_{i=1}^n (e(G_{i-1})-e(G_i))/k=(e(G_0)-e(G_n))/k.\end{align*} $$
Thus,
![]() $e(G_n)\geq e(G_0)/(k+1)=e(G)/(k+1)$
, which means that
$e(G_n)\geq e(G_0)/(k+1)=e(G)/(k+1)$
, which means that
![]() $G'=G_n$
satisfies the conditions described in the lemma.
$G'=G_n$
satisfies the conditions described in the lemma.
We now define two notions of ‘near-regularity’ that will be used in our proofs.
Definition 3.3. A graph G is called K-almost-regular if the maximum degree of G is at most K times the minimum degree of G.
Definition 3.4. We say that a bipartite graph G is
![]() $(L,d)$
-almost-biregular if the following holds. G has parts A and B, where
$(L,d)$
-almost-biregular if the following holds. G has parts A and B, where
![]() $d_G(v)=d$
for every
$d_G(v)=d$
for every
![]() $v\in B$
, and, writing
$v\in B$
, and, writing
![]() $D=e(G)/|A|$
, we have
$D=e(G)/|A|$
, we have
![]() $D\geq d$
(equivalently
$D\geq d$
(equivalently
![]() $|A|\leq |B|$
) and
$|A|\leq |B|$
) and
![]() $d_G(u)\leq LD$
for every
$d_G(u)\leq LD$
for every
![]() $u\in A$
.
$u\in A$
.
Our key lemma will provide an
![]() $(L,d)$
-almost-biregular subgraph where L is fairly small. The next lemma allows us to find a large almost-regular subgraph in it.
$(L,d)$
-almost-biregular subgraph where L is fairly small. The next lemma allows us to find a large almost-regular subgraph in it.
Lemma 3.5. Let G be an
![]() $(L,\delta )$
-almost-biregular graph for some
$(L,\delta )$
-almost-biregular graph for some
![]() $L\geq \delta \geq 2$
. Then G has a
$L\geq \delta \geq 2$
. Then G has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {\delta }{16\log L}$
.
$\frac {\delta }{16\log L}$
.
The proof of this lemma uses the following result, which is a slight variant of Lemma 2.7 from [Reference Pyber, Rödl and Szemerédi26]. It states that as long as L is subexponential in the average degree, we can pass to a subgraph with large average degree and constant L.
Lemma 3.6. Let G be an
![]() $(L,\delta )$
-almost-biregular graph. Suppose that
$(L,\delta )$
-almost-biregular graph. Suppose that
![]() $L\delta \leq 2^{\lfloor \delta /(d-1) \rfloor }$
and
$L\delta \leq 2^{\lfloor \delta /(d-1) \rfloor }$
and
![]() $d\leq \delta $
. Then G has a
$d\leq \delta $
. Then G has a
![]() $(4,d)$
-almost-biregular subgraph.
$(4,d)$
-almost-biregular subgraph.
Since the proof of this result is almost identical to that of Lemma 2.7 from [Reference Pyber, Rödl and Szemerédi26], it is omitted here.
The next simple lemma shows that in an almost-biregular graph we can find an almost-regular subgraph with similar average degree.
Lemma 3.7. Let
![]() $L,d\geq 1$
, and let G be an
$L,d\geq 1$
, and let G be an
![]() $(L,d)$
-almost-biregular graph. Then G has a nonempty subgraph
$(L,d)$
-almost-biregular graph. Then G has a nonempty subgraph
![]() $G'$
with average degree at least
$G'$
with average degree at least
![]() $d/2$
and maximum degree at most
$d/2$
and maximum degree at most
![]() $4Ld$
.
$4Ld$
.
Proof. Choose A, B and D according to Definition 3.4. Define
![]() $B'$
to be a random subset of B where each
$B'$
to be a random subset of B where each
![]() $v\in B$
is kept independently with probability
$v\in B$
is kept independently with probability
![]() $\frac {d}{D}$
. Let
$\frac {d}{D}$
. Let
![]() $G'$
be the subgraph of
$G'$
be the subgraph of
![]() $G[A\cup B']$
obtained by deleting all edges
$G[A\cup B']$
obtained by deleting all edges
![]() $uv$
with
$uv$
with
![]() $|N_G(u)\cap B'|\geq 4Ld$
. Clearly,
$|N_G(u)\cap B'|\geq 4Ld$
. Clearly,
![]() $\Delta (G')\leq \max (4Ld,d)=4Ld$
.
$\Delta (G')\leq \max (4Ld,d)=4Ld$
.
Let
![]() $X=e(G[A\cup B'])$
, and let Y be the number of edges
$X=e(G[A\cup B'])$
, and let Y be the number of edges
![]() $uv\in E(G[A\cup B'])$
with
$uv\in E(G[A\cup B'])$
with
![]() $|N_G(u)\cap B'|\geq 4Ld$
. Now,
$|N_G(u)\cap B'|\geq 4Ld$
. Now,
 $$ \begin{align*}\mathbb{E}[X]=\sum_{uv\in E(G)} \mathbb{P}(v\in B')=e(G)\frac{d}{D}\end{align*} $$
$$ \begin{align*}\mathbb{E}[X]=\sum_{uv\in E(G)} \mathbb{P}(v\in B')=e(G)\frac{d}{D}\end{align*} $$
and
 $$ \begin{align*} \mathbb{E}[Y] &=\sum_{uv\in E(G)} \mathbb{P}(v\in B' \text{ and } |N_G(u)\cap B'|\geq 4Ld) \\ &=\sum_{uv\in E(G)} \mathbb{P}(v\in B')\mathbb{P}\left(|N_G(u)\cap B'|\geq 4Ld \hspace{1mm} | \hspace{1mm} v\in B'\right). \end{align*} $$
$$ \begin{align*} \mathbb{E}[Y] &=\sum_{uv\in E(G)} \mathbb{P}(v\in B' \text{ and } |N_G(u)\cap B'|\geq 4Ld) \\ &=\sum_{uv\in E(G)} \mathbb{P}(v\in B')\mathbb{P}\left(|N_G(u)\cap B'|\geq 4Ld \hspace{1mm} | \hspace{1mm} v\in B'\right). \end{align*} $$
For any
![]() $uv\in E(G)$
, we have
$uv\in E(G)$
, we have
so it follows by Markov’s inequality that
Hence,
 $$ \begin{align*}\mathbb{E}[Y]\leq \sum_{uv\in E(G)}\mathbb{P}(v\in B')/2=e(G)\frac{d}{2D}.\end{align*} $$
$$ \begin{align*}\mathbb{E}[Y]\leq \sum_{uv\in E(G)}\mathbb{P}(v\in B')/2=e(G)\frac{d}{2D}.\end{align*} $$
Thus, using
![]() $|A|D=|B|d=e(G)$
,
$|A|D=|B|d=e(G)$
,
 $$ \begin{align*} \mathbb{E}[X-Y-(|A|+|B'|)d/4] &\geq e(G)\frac{d}{D}-e(G)\frac{d}{2D}-|A|d/4-|B|\frac{d}{D}d/4 \\ &= e(G)\frac{d}{D}-e(G)\frac{d}{2D}-e(G)\frac{d}{4D}-e(G)\frac{d}{4D}=0. \end{align*} $$
$$ \begin{align*} \mathbb{E}[X-Y-(|A|+|B'|)d/4] &\geq e(G)\frac{d}{D}-e(G)\frac{d}{2D}-|A|d/4-|B|\frac{d}{D}d/4 \\ &= e(G)\frac{d}{D}-e(G)\frac{d}{2D}-e(G)\frac{d}{4D}-e(G)\frac{d}{4D}=0. \end{align*} $$
In particular, there is an outcome for which
![]() $X-Y\geq (|A|+|B'|)d/4$
. Since
$X-Y\geq (|A|+|B'|)d/4$
. Since
![]() $e(G')=X-Y$
, this means that
$e(G')=X-Y$
, this means that
![]() $G'$
has average degree at least
$G'$
has average degree at least
![]() $d/2$
.
$d/2$
.
Lemma 3.5 can now be proven using the last two lemmas.
Proof of Lemma 3.5.
Let
![]() $d=\lceil \frac {\delta }{4\log L}\rceil $
. Now,
$d=\lceil \frac {\delta }{4\log L}\rceil $
. Now,
![]() $\delta /(d-1)\geq 4\log L$
, so
$\delta /(d-1)\geq 4\log L$
, so
![]() $\lfloor \delta /(d-1)\rfloor \geq 2\log L$
. Hence,
$\lfloor \delta /(d-1)\rfloor \geq 2\log L$
. Hence,
![]() $2^{\lfloor \delta /(d-1)\rfloor }\geq L^2\geq L\delta $
. By Lemma 3.6, G has a
$2^{\lfloor \delta /(d-1)\rfloor }\geq L^2\geq L\delta $
. By Lemma 3.6, G has a
![]() $(4,d)$
-almost-biregular subgraph
$(4,d)$
-almost-biregular subgraph
![]() $G'$
. By Lemma 3.7,
$G'$
. By Lemma 3.7,
![]() $G'$
has a subgraph with average degree at least
$G'$
has a subgraph with average degree at least
![]() $d/2$
and maximum degree at most
$d/2$
and maximum degree at most
![]() $16d$
. Repeatedly discarding vertices of degree less than
$16d$
. Repeatedly discarding vertices of degree less than
![]() $d/4$
, we end up with a nonempty subgraph
$d/4$
, we end up with a nonempty subgraph
![]() $G"$
with minimum degree at least
$G"$
with minimum degree at least
![]() $d/4$
and maximum degree at most
$d/4$
and maximum degree at most
![]() $16d$
. Clearly,
$16d$
. Clearly,
![]() $G"$
is
$G"$
is
![]() $64$
-almost-regular. Moreover, the average degree of
$64$
-almost-regular. Moreover, the average degree of
![]() $G"$
is at least
$G"$
is at least
![]() $d/4\geq \frac {\delta }{16\log L}$
.
$d/4\geq \frac {\delta }{16\log L}$
.
In order to find a k-regular subgraph in an almost-regular graph with sufficiently large average degree, one can use the result of Pyber, Rödl and Szemerédi.
Theorem 3.8 (Pyber–Rödl–Szemerédi [Reference Pyber, Rödl and Szemerédi26]).
For any positive integer k, there is a constant
![]() $C=C(k)$
such that any graph with maximum degree
$C=C(k)$
such that any graph with maximum degree
![]() $\Delta $
and average degree at least
$\Delta $
and average degree at least
![]() $C \log \Delta $
contains a k-regular subgraph.
$C \log \Delta $
contains a k-regular subgraph.
4 The key lemma
In this section, we prove the following lemma, which is the main ingredient in our proof. Given a bipartite graph with parts A and B in which B is regular, the maximum degree in A is at most about
![]() power of the average degree in A and the codegrees are not extremely large, the lemma provides an induced subgraph with much better regularity properties. In the statement of the lemma, we hide the condition bounding the maximum degree in terms of the average degree of A in the upper bound on the codegrees: For the codegree condition to hold, we must have
power of the average degree in A and the codegrees are not extremely large, the lemma provides an induced subgraph with much better regularity properties. In the statement of the lemma, we hide the condition bounding the maximum degree in terms of the average degree of A in the upper bound on the codegrees: For the codegree condition to hold, we must have
![]() $t\leq (1+\frac {1}{r-1})s$
.
$t\leq (1+\frac {1}{r-1})s$
.
Lemma 4.1. Let
![]() $r,s,t$
be positive integers such that
$r,s,t$
be positive integers such that
![]() $s<t$
. Let G be a bipartite graph with parts A and B such that
$s<t$
. Let G be a bipartite graph with parts A and B such that
![]() $d_G(v)=r$
for every
$d_G(v)=r$
for every
![]() $v\in B$
,
$v\in B$
,
![]() $d_G(u)\leq 2^t$
for every
$d_G(u)\leq 2^t$
for every
![]() $u\in A$
,
$u\in A$
,
![]() $d_G(u,u')\leq 2^{rs-(r-1)t}$
for any two distinct
$d_G(u,u')\leq 2^{rs-(r-1)t}$
for any two distinct
![]() $u,u'\in A$
and
$u,u'\in A$
and
![]() $e(G)\geq 2^s|A|$
.
$e(G)\geq 2^s|A|$
.
Then there are subsets
![]() $A"\subset A$
and
$A"\subset A$
and
![]() $B"\subset B$
such that
$B"\subset B$
such that
![]() $N_G(v)\subset A"$
for every
$N_G(v)\subset A"$
for every
![]() $v\in B"$
and, writing
$v\in B"$
and, writing
![]() $G'=G[A"\cup B"]$
and
$G'=G[A"\cup B"]$
and
![]() $d'=e(G')/|A"|$
, we have
$d'=e(G')/|A"|$
, we have
![]() $d'\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
and
$d'\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
and
![]() $d_{G'}(u)\leq 40(t-s)r^2 d'$
for all
$d_{G'}(u)\leq 40(t-s)r^2 d'$
for all
![]() $u\in A"$
.
$u\in A"$
.
Proof. Let
![]() $A_{s+1}=\{u\in A:d_G(u)\leq 2^{s+1}\}$
and for each
$A_{s+1}=\{u\in A:d_G(u)\leq 2^{s+1}\}$
and for each
![]() $s+2\leq i\leq t$
, let
$s+2\leq i\leq t$
, let
![]() $A_i=\{u\in A: 2^{i-1}<d_G(u)\leq 2^{i}\}$
. Observe that the sets
$A_i=\{u\in A: 2^{i-1}<d_G(u)\leq 2^{i}\}$
. Observe that the sets
![]() $A_{s+1},\dots ,A_t$
partition A. For each
$A_{s+1},\dots ,A_t$
partition A. For each
![]() $u\in A$
, let
$u\in A$
, let
![]() $\alpha (u)$
be the unique i with
$\alpha (u)$
be the unique i with
![]() $u\in A_i$
. For
$u\in A_i$
. For
![]() $v\in B$
, let
$v\in B$
, let
 $$ \begin{align*}\beta(v)=\sum_{u\in N_G(v)} \alpha(u).\end{align*} $$
$$ \begin{align*}\beta(v)=\sum_{u\in N_G(v)} \alpha(u).\end{align*} $$
Note that for every
![]() $v\in B$
, we have
$v\in B$
, we have
![]() $(s+1)r\leq \beta (v)\leq tr$
, so there are at most
$(s+1)r\leq \beta (v)\leq tr$
, so there are at most
![]() $(t-s)r$
possible values for
$(t-s)r$
possible values for
![]() $\beta (v)$
. Hence, by the pigeonhole principle, there are some
$\beta (v)$
. Hence, by the pigeonhole principle, there are some
![]() $\gamma \geq (s+1)r$
and a subset
$\gamma \geq (s+1)r$
and a subset
![]() $\tilde {B}\subset B$
of size at least
$\tilde {B}\subset B$
of size at least
![]() $\frac {|B|}{(t-s)r}$
such that
$\frac {|B|}{(t-s)r}$
such that
![]() $\beta (v)=\gamma $
for all
$\beta (v)=\gamma $
for all
![]() $v\in \tilde {B}$
.
$v\in \tilde {B}$
.
Let
![]() $A'$
be a random subset of A where each
$A'$
be a random subset of A where each
![]() $u\in A$
is kept independently with probability
$u\in A$
is kept independently with probability
![]() $2^{\alpha (u)-t}$
. Let
$2^{\alpha (u)-t}$
. Let
![]() $B'=\{v\in \tilde {B}: N_G(v)\subset A'\}$
. Let
$B'=\{v\in \tilde {B}: N_G(v)\subset A'\}$
. Let
![]() $A"$
be the subset of
$A"$
be the subset of
![]() $A'$
consisting of those vertices u with
$A'$
consisting of those vertices u with
![]() $|N_G(u)\cap B'|\leq 4r2^{\gamma -(r-1)t}$
, and let
$|N_G(u)\cap B'|\leq 4r2^{\gamma -(r-1)t}$
, and let
![]() $B"=\{v\in B': N_G(v)\subset A"\}$
. Let
$B"=\{v\in B': N_G(v)\subset A"\}$
. Let
![]() $G'=G[A"\cup B"]$
. Then
$G'=G[A"\cup B"]$
. Then
![]() $d_{G'}(u)\leq 4r2^{\gamma -(r-1)t}$
for all
$d_{G'}(u)\leq 4r2^{\gamma -(r-1)t}$
for all
![]() $u\in A"$
.
$u\in A"$
.
The following claim shows that we expect
![]() $E(G[A'\cup B'])\setminus E(G')$
to be small.
$E(G[A'\cup B'])\setminus E(G')$
to be small.
Claim. For any
![]() $uv\in E(G[A\cup \tilde {B}])$
with
$uv\in E(G[A\cup \tilde {B}])$
with
![]() $u\in A$
and
$u\in A$
and
![]() $v\in \tilde {B}$
,
$v\in \tilde {B}$
,
Proof of Claim.
Note that
 $$ \begin{align} &\mathbb{E}[|N_G(u)\cap B'| \hspace{1mm} | \hspace{1mm} v\in B'] =\sum_{w\in N_G(u)\cap \tilde{B}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B') \nonumber \\ &= \sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)=\{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B') + \sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)\neq \{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B'). \end{align} $$
$$ \begin{align} &\mathbb{E}[|N_G(u)\cap B'| \hspace{1mm} | \hspace{1mm} v\in B'] =\sum_{w\in N_G(u)\cap \tilde{B}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B') \nonumber \\ &= \sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)=\{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B') + \sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)\neq \{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B'). \end{align} $$
We now bound the two sums separately. If some
![]() $w\in N_G(u)\cap \tilde {B}$
satisfies
$w\in N_G(u)\cap \tilde {B}$
satisfies
![]() $N_G(w)\cap N_G(v)=\{u\}$
, then
$N_G(w)\cap N_G(v)=\{u\}$
, then
 $$ \begin{align*} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B') &=\mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} u\in A')=\prod_{z\in N_G(w)\setminus \{u\}} \mathbb{P}(z\in A')=\prod_{z\in N_G(w)\setminus \{u\}} 2^{\alpha(z)-t} \nonumber \\ &=2^{\sum_{z\in N_G(w)\setminus \{u\}} \alpha(z)-(r-1)t}=2^{\beta(w)-\alpha(u)-(r-1)t}=2^{\gamma-\alpha(u)-(r-1)t}. \end{align*} $$
$$ \begin{align*} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B') &=\mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} u\in A')=\prod_{z\in N_G(w)\setminus \{u\}} \mathbb{P}(z\in A')=\prod_{z\in N_G(w)\setminus \{u\}} 2^{\alpha(z)-t} \nonumber \\ &=2^{\sum_{z\in N_G(w)\setminus \{u\}} \alpha(z)-(r-1)t}=2^{\beta(w)-\alpha(u)-(r-1)t}=2^{\gamma-\alpha(u)-(r-1)t}. \end{align*} $$
Since
![]() $d_G(u) \leq 2^{\alpha (u)}$
, we have that
$d_G(u) \leq 2^{\alpha (u)}$
, we have that
 $$ \begin{align*}\sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)=\{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B')\leq d_G(u)2^{\gamma-\alpha(u)-(r-1)t}\leq 2^{\gamma-(r-1)t}.\end{align*} $$
$$ \begin{align*}\sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)=\{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B')\leq d_G(u)2^{\gamma-\alpha(u)-(r-1)t}\leq 2^{\gamma-(r-1)t}.\end{align*} $$
As for the second sum, the number of
![]() $w\in N_G(u)\cap \tilde {B}$
with
$w\in N_G(u)\cap \tilde {B}$
with
![]() $N_G(w)\cap N_G(v)\neq \{u\}$
is at most
$N_G(w)\cap N_G(v)\neq \{u\}$
is at most
![]() $r2^{rs-(r-1)t}$
. Indeed, v has r neighbours in G, so there are at most r ways to choose a vertex
$r2^{rs-(r-1)t}$
. Indeed, v has r neighbours in G, so there are at most r ways to choose a vertex
![]() $u'\in N_G(w)\cap N_G(v)\setminus \{u\}$
, and, by assumption, any such
$u'\in N_G(w)\cap N_G(v)\setminus \{u\}$
, and, by assumption, any such
![]() $u'$
has at most
$u'$
has at most
![]() $2^{rs-(r-1)t}$
common neighbours with u. Now, using
$2^{rs-(r-1)t}$
common neighbours with u. Now, using
![]() ${\gamma \geq (s+1)r}$
, we have
${\gamma \geq (s+1)r}$
, we have
![]() $2^{\gamma -(r-1)t}\geq 2^{r}2^{rs-(r-1)t}\geq r2^{rs-(r-1)t}$
. This implies that
$2^{\gamma -(r-1)t}\geq 2^{r}2^{rs-(r-1)t}\geq r2^{rs-(r-1)t}$
. This implies that
 $$ \begin{align*}\sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)\neq \{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B')\leq r2^{rs-(r-1)t}\leq 2^{\gamma-(r-1)t}.\end{align*} $$
$$ \begin{align*}\sum_{\substack{w\in N_G(u)\cap \tilde{B}: \\ N_G(w)\cap N_G(v)\neq \{u\}}} \mathbb{P}(w\in B' \hspace{1mm} | \hspace{1mm} v\in B')\leq r2^{rs-(r-1)t}\leq 2^{\gamma-(r-1)t}.\end{align*} $$
Thus, by (4.1),
This implies, by Markov’s inequality, that
Thus,
 $$ \begin{align*} &\mathbb{P}(u\in A',v\in B' \text{ and } |N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t}) \\ &=\mathbb{P}(v\in B' \text{ and } |N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t}) \\ &=\mathbb{P}(v\in B')\mathbb{P}(|N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t} \hspace{1mm} | \hspace{1mm} v\in B')\leq \mathbb{P}(v\in B')/(2r), \end{align*} $$
$$ \begin{align*} &\mathbb{P}(u\in A',v\in B' \text{ and } |N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t}) \\ &=\mathbb{P}(v\in B' \text{ and } |N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t}) \\ &=\mathbb{P}(v\in B')\mathbb{P}(|N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t} \hspace{1mm} | \hspace{1mm} v\in B')\leq \mathbb{P}(v\in B')/(2r), \end{align*} $$
completing the proof of the claim.
For any
![]() $uv\in E(G[A\cup \tilde {B}])$
,
$uv\in E(G[A\cup \tilde {B}])$
,
 $$ \begin{align} \mathbb{P}(u\in A', v\in B')=\mathbb{P}(v\in B')=\prod_{w\in N_G(v)} \mathbb{P}(w\in A')=\prod_{w\in N_G(v)} 2^{\alpha(w)-t}=2^{\gamma-rt}. \end{align} $$
$$ \begin{align} \mathbb{P}(u\in A', v\in B')=\mathbb{P}(v\in B')=\prod_{w\in N_G(v)} \mathbb{P}(w\in A')=\prod_{w\in N_G(v)} 2^{\alpha(w)-t}=2^{\gamma-rt}. \end{align} $$
Let
![]() $X=e(G[A'\cup B'])$
, and let Y be the number of edges
$X=e(G[A'\cup B'])$
, and let Y be the number of edges
![]() $uv\in E(G[A'\cup B'])$
with
$uv\in E(G[A'\cup B'])$
with
![]() $|N_G(u)\cap B'|\geq 4r2^{\gamma -(r-1)t}$
. Note that
$|N_G(u)\cap B'|\geq 4r2^{\gamma -(r-1)t}$
. Note that
![]() $e(G')\geq X-rY$
. Indeed,
$e(G')\geq X-rY$
. Indeed,
![]() $E(G')$
is obtained from
$E(G')$
is obtained from
![]() $E(G[A'\cup B'])$
by deleting all edges incident to vertices
$E(G[A'\cup B'])$
by deleting all edges incident to vertices
![]() $v\in B'$
which have a neighbour u with
$v\in B'$
which have a neighbour u with
![]() $|N_G(u)\cap B'|> 4r2^{\gamma -(r-1)t}$
. Clearly, there are at most Y such vertices
$|N_G(u)\cap B'|> 4r2^{\gamma -(r-1)t}$
. Clearly, there are at most Y such vertices
![]() $v\in B'$
, so at most
$v\in B'$
, so at most
![]() $rY$
edges are deleted. By equation (4.2) and the claim, we have
$rY$
edges are deleted. By equation (4.2) and the claim, we have
 $$ \begin{align*} &\mathbb{E}[X-rY] \\ &\quad=\sum_{uv\in E(G[A\cup \tilde{B}])} \left(\mathbb{P}(u\in A', v\in B')-r\mathbb{P}(u\in A', v\in B' \text{ and } |N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t})\right) \\ &\quad\geq \sum_{uv\in E(G[A\cup \tilde{B}])} (\mathbb{P}(v\in B')-\mathbb{P}(v\in B')/2) = e(G[A\cup \tilde{B}])2^{\gamma-rt-1} \\ &\quad=|\tilde{B}|r2^{\gamma-rt-1}\geq \frac{|B|}{(t-s)r}r 2^{\gamma-rt-1}= \frac{e(G)}{(t-s)r}2^{\gamma-rt-1}. \end{align*} $$
$$ \begin{align*} &\mathbb{E}[X-rY] \\ &\quad=\sum_{uv\in E(G[A\cup \tilde{B}])} \left(\mathbb{P}(u\in A', v\in B')-r\mathbb{P}(u\in A', v\in B' \text{ and } |N_G(u)\cap B'|\geq 4r2^{\gamma-(r-1)t})\right) \\ &\quad\geq \sum_{uv\in E(G[A\cup \tilde{B}])} (\mathbb{P}(v\in B')-\mathbb{P}(v\in B')/2) = e(G[A\cup \tilde{B}])2^{\gamma-rt-1} \\ &\quad=|\tilde{B}|r2^{\gamma-rt-1}\geq \frac{|B|}{(t-s)r}r 2^{\gamma-rt-1}= \frac{e(G)}{(t-s)r}2^{\gamma-rt-1}. \end{align*} $$
Note that, for every
![]() $u\in A$
, we have
$u\in A$
, we have
![]() $2^{\alpha (u)}\leq 2^{s+1}+2d_G(u)$
. Indeed, this is trivial if
$2^{\alpha (u)}\leq 2^{s+1}+2d_G(u)$
. Indeed, this is trivial if
![]() $\alpha (u)=s+1$
, and else
$\alpha (u)=s+1$
, and else
![]() $d_G(u)\geq 2^{\alpha (u)-1}$
. Also recall that
$d_G(u)\geq 2^{\alpha (u)-1}$
. Also recall that
![]() $e(G)\geq 2^s|A|$
. Therefore,
$e(G)\geq 2^s|A|$
. Therefore,
 $$ \begin{align*} \mathbb{E}\lbrack |A'|\rbrack &=\sum_{u\in A}\mathbb{P}(u\in A')=\sum_{u\in A} 2^{\alpha(u)-t}\leq 2^{-t}\sum_{u\in A} (2^{s+1}+2d_G(u)) \\ &=2^{-t}(|A|2^{s+1}+2e(G))\leq 2^{-t}4e(G). \end{align*} $$
$$ \begin{align*} \mathbb{E}\lbrack |A'|\rbrack &=\sum_{u\in A}\mathbb{P}(u\in A')=\sum_{u\in A} 2^{\alpha(u)-t}\leq 2^{-t}\sum_{u\in A} (2^{s+1}+2d_G(u)) \\ &=2^{-t}(|A|2^{s+1}+2e(G))\leq 2^{-t}4e(G). \end{align*} $$
Hence,
 $$ \begin{align*}\mathbb{E}\left[X-rY-|A'|\frac{2^{\gamma-(r-1)t}}{10(t-s)r}\right]>0.\end{align*} $$
$$ \begin{align*}\mathbb{E}\left[X-rY-|A'|\frac{2^{\gamma-(r-1)t}}{10(t-s)r}\right]>0.\end{align*} $$
It follows that there exists an outcome for which
![]() $X-rY-|A'|\frac {2^{\gamma -(r-1)t}}{10(t-s)r}>0$
. Then
$X-rY-|A'|\frac {2^{\gamma -(r-1)t}}{10(t-s)r}>0$
. Then
![]() $e(G')\geq X-rY\geq |A'|\frac {2^{\gamma -(r-1)t}}{10(t-s)r}$
. Hence,
$e(G')\geq X-rY\geq |A'|\frac {2^{\gamma -(r-1)t}}{10(t-s)r}$
. Hence,
![]() $d'=e(G')/|A"|$
satisfies
$d'=e(G')/|A"|$
satisfies
![]() $d'\geq e(G')/|A'|\geq \frac {2^{\gamma -(r-1)t}}{10(t-s)r}\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
and
$d'\geq e(G')/|A'|\geq \frac {2^{\gamma -(r-1)t}}{10(t-s)r}\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
and
![]() $d_{G'}(u)\leq 4r2^{\gamma -(r-1)t}\leq 40(t-s)r^2d'$
for all
$d_{G'}(u)\leq 4r2^{\gamma -(r-1)t}\leq 40(t-s)r^2d'$
for all
![]() $u\in A"$
, completing the proof.
$u\in A"$
, completing the proof.
The next lemma is obtained by iterative applications of Lemma 4.1.
Lemma 4.2. Let
![]() $r,s,t$
be positive integers such that r is sufficiently large and
$r,s,t$
be positive integers such that r is sufficiently large and
![]() $s<t$
. Let G be a bipartite graph with parts A and B such that
$s<t$
. Let G be a bipartite graph with parts A and B such that
![]() $d_G(v)=r$
for every
$d_G(v)=r$
for every
![]() $v\in B$
,
$v\in B$
,
![]() $d_G(u)\leq 2^t$
for every
$d_G(u)\leq 2^t$
for every
![]() $u\in A$
,
$u\in A$
,
![]() $d_G(u,u')\leq 2^{2rs-(2r-1)t}$
for any two distinct
$d_G(u,u')\leq 2^{2rs-(2r-1)t}$
for any two distinct
![]() $u,u'\in A$
and
$u,u'\in A$
and
![]() $e(G)\geq 2^s|A|$
.
$e(G)\geq 2^s|A|$
.
Then there exist positive integers
![]() $s^*\geq 2rs-(2r-1)t$
,
$s^*\geq 2rs-(2r-1)t$
,
![]() $t^*>s^*$
and sets
$t^*>s^*$
and sets
![]() $A^*\subset A$
,
$A^*\subset A$
,
![]() $B^*\subset B$
such that
$B^*\subset B$
such that
![]() $N_G(v)\subset A^*$
for every
$N_G(v)\subset A^*$
for every
![]() $v\in B^*$
,
$v\in B^*$
,
![]() $t^*-s^*\leq 5\log r$
and, writing
$t^*-s^*\leq 5\log r$
and, writing
![]() $G^*=G[A^*\cup B^*]$
and
$G^*=G[A^*\cup B^*]$
and
![]() $d^*=e(G^*)/|A^*|$
, we have
$d^*=e(G^*)/|A^*|$
, we have
![]() $d^*\geq 2^{s^*}$
and
$d^*\geq 2^{s^*}$
and
![]() $d_{G^*}(u)\leq 2^{t^*}$
for all
$d_{G^*}(u)\leq 2^{t^*}$
for all
![]() $u\in A^*$
.
$u\in A^*$
.
Proof. We prove the lemma by induction on
![]() $t-s$
(with r fixed). If
$t-s$
(with r fixed). If
![]() $t-s\leq 5\log r$
, then we can take
$t-s\leq 5\log r$
, then we can take
![]() $s^*=s$
,
$s^*=s$
,
![]() $t^*=t$
,
$t^*=t$
,
![]() $A^*=A$
and
$A^*=A$
and
![]() $B^*=B$
. Assume now that
$B^*=B$
. Assume now that
![]() $t-s>5\log r$
. Note that
$t-s>5\log r$
. Note that
![]() $2rs-(2r-1)t\leq rs-(r-1)t$
, so for any two distinct
$2rs-(2r-1)t\leq rs-(r-1)t$
, so for any two distinct
![]() $u,u'\in A$
, we have
$u,u'\in A$
, we have
![]() $d_G(u,u')\leq 2^{rs-(r-1)t}$
. By Lemma 4.1, there are subsets
$d_G(u,u')\leq 2^{rs-(r-1)t}$
. By Lemma 4.1, there are subsets
![]() $A'\subset A$
and
$A'\subset A$
and
![]() $B'\subset B$
such that
$B'\subset B$
such that
![]() $N_G(v)\subset A'$
for every
$N_G(v)\subset A'$
for every
![]() $v\in B'$
and, writing
$v\in B'$
and, writing
![]() $G'=G[A'\cup B']$
and
$G'=G[A'\cup B']$
and
![]() $d'=e(G')/|A'|$
, we have
$d'=e(G')/|A'|$
, we have
![]() $d'\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
and
$d'\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
and
![]() $d_{G'}(u)\leq 40(t-s)r^2 d'$
for all
$d_{G'}(u)\leq 40(t-s)r^2 d'$
for all
![]() $u\in A'$
. By the codegree condition,
$u\in A'$
. By the codegree condition,
![]() $2rs-(2r-1)t\geq 0$
, so
$2rs-(2r-1)t\geq 0$
, so
![]() $rs-(r-1)t\geq (t-s)r$
and hence
$rs-(r-1)t\geq (t-s)r$
and hence
![]() $d'\geq 2$
. Let
$d'\geq 2$
. Let
![]() $s'=\lfloor \log d' \rfloor $
, and let
$s'=\lfloor \log d' \rfloor $
, and let
![]() $t'=\lceil \log (40(t-s)r^2d') \rceil $
. Then
$t'=\lceil \log (40(t-s)r^2d') \rceil $
. Then
![]() $s'<t'$
,
$s'<t'$
,
![]() $d_{G'}(v)=r$
for every
$d_{G'}(v)=r$
for every
![]() $v\in B'$
,
$v\in B'$
,
![]() $d_{G'}(u)\leq 2^{t'}$
for every
$d_{G'}(u)\leq 2^{t'}$
for every
![]() $u\in A'$
and
$u\in A'$
and
![]() $e(G')\geq 2^{s'}|A'|$
. Moreover, using
$e(G')\geq 2^{s'}|A'|$
. Moreover, using
![]() $d'\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
, we have
$d'\geq \frac {2^{rs-(r-1)t}}{10(t-s)r}$
, we have
![]() $t'\geq rs-(r-1)t$
. Hence,
$t'\geq rs-(r-1)t$
. Hence,
 $$ \begin{align*} 2rs'-(2r-1)t' &=t'-2r(t'-s')\geq t'-2r(\log(40(t-s)r^2)+2) \\ &\geq rs-(r-1)t-2r\log(160(t-s)r^2) \\ &=2rs-(2r-1)t+r(t-s)-2r\log(160(t-s)r^2) \\ &\geq 2rs-(2r-1)t, \end{align*} $$
$$ \begin{align*} 2rs'-(2r-1)t' &=t'-2r(t'-s')\geq t'-2r(\log(40(t-s)r^2)+2) \\ &\geq rs-(r-1)t-2r\log(160(t-s)r^2) \\ &=2rs-(2r-1)t+r(t-s)-2r\log(160(t-s)r^2) \\ &\geq 2rs-(2r-1)t, \end{align*} $$
where the last inequality uses that
![]() $t-s\geq 5\log r$
and that r is sufficiently large. Hence, for any distinct
$t-s\geq 5\log r$
and that r is sufficiently large. Hence, for any distinct
![]() $u,u'\in A'$
, we have
$u,u'\in A'$
, we have
![]() $d_{G'}(u,u')\leq d_G(u,u')\leq 2^{2rs-(2r-1)t}\leq 2^{2rs'-(2r-1)t'}$
. Finally,
$d_{G'}(u,u')\leq d_G(u,u')\leq 2^{2rs-(2r-1)t}\leq 2^{2rs'-(2r-1)t'}$
. Finally,
![]() $t'-s'\leq \log (40(t-s)r^2)+2<t-s$
.
$t'-s'\leq \log (40(t-s)r^2)+2<t-s$
.
Thus, by the induction hypothesis, there exist positive integers
![]() $s^*\geq 2rs'-(2r-1)t'$
,
$s^*\geq 2rs'-(2r-1)t'$
,
![]() $t^*>s^*$
and sets
$t^*>s^*$
and sets
![]() $A^*\subset A'$
,
$A^*\subset A'$
,
![]() $B^*\subset B'$
such that
$B^*\subset B'$
such that
![]() $N_{G'}(v)\subset A^*$
for every
$N_{G'}(v)\subset A^*$
for every
![]() $v\in B^*$
,
$v\in B^*$
,
![]() $t^*-s^*\leq 5\log r$
and, writing
$t^*-s^*\leq 5\log r$
and, writing
![]() $G^*=G'[A^*\cup B^*]=G[A^*\cup B^*]$
and
$G^*=G'[A^*\cup B^*]=G[A^*\cup B^*]$
and
![]() $d^*=e(G^*)/|A^*|$
, we have
$d^*=e(G^*)/|A^*|$
, we have
![]() $d^*\geq 2^{s^*}$
and
$d^*\geq 2^{s^*}$
and
![]() $d_{G^*}(u)\leq 2^{t^*}$
for all
$d_{G^*}(u)\leq 2^{t^*}$
for all
![]() $u\in A^*$
. Since
$u\in A^*$
. Since
![]() $N_G(v)=N_{G'}(v)$
for every
$N_G(v)=N_{G'}(v)$
for every
![]() $v\in B'$
, we have
$v\in B'$
, we have
![]() $N_{G}(v)\subset A^*$
for every
$N_{G}(v)\subset A^*$
for every
![]() $v\in B^*$
. As
$v\in B^*$
. As
![]() $2rs'-(2r-1)t'\geq 2rs-(2r-1)t$
, it follows that
$2rs'-(2r-1)t'\geq 2rs-(2r-1)t$
, it follows that
![]() $s^*\geq 2rs-(2r-1)t$
, so
$s^*\geq 2rs-(2r-1)t$
, so
![]() $s^*$
,
$s^*$
,
![]() $t^*$
,
$t^*$
,
![]() $A^*$
and
$A^*$
and
![]() $B^*$
are suitable for the conclusion of the lemma.
$B^*$
are suitable for the conclusion of the lemma.
5 Completing the proof
The next lemma is the upshot of what we have proved so far.
Lemma 5.1. Let
![]() $r,s,t$
be positive integers such that r is sufficiently large and
$r,s,t$
be positive integers such that r is sufficiently large and
![]() $s<t$
. Let G be a bipartite graph with parts A and B such that
$s<t$
. Let G be a bipartite graph with parts A and B such that
![]() $d_G(v)=r$
for every
$d_G(v)=r$
for every
![]() $v\in B$
,
$v\in B$
,
![]() $d_G(u)\leq 2^t$
for every
$d_G(u)\leq 2^t$
for every
![]() $u\in A$
,
$u\in A$
,
![]() $d_G(u,u')\leq 2^{2rs-(2r-1)t-r}$
for any two distinct
$d_G(u,u')\leq 2^{2rs-(2r-1)t-r}$
for any two distinct
![]() $u,u'\in A$
and
$u,u'\in A$
and
![]() $e(G)\geq 2^s|A|$
.
$e(G)\geq 2^s|A|$
.
Then G contains a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r}{80\log r}$
.
$\frac {r}{80\log r}$
.
Proof. By the assumption on the codegrees, we have
![]() $2rs-(2r-1)t-r\geq 0$
, so
$2rs-(2r-1)t-r\geq 0$
, so
![]() $2rs-(2r-1)t\geq r$
. Hence, by Lemma 4.2, G has a
$2rs-(2r-1)t\geq r$
. Hence, by Lemma 4.2, G has a
![]() $(2^{5\log r},r)$
-almost-biregular subgraph
$(2^{5\log r},r)$
-almost-biregular subgraph
![]() $G^*$
(the condition
$G^*$
(the condition
![]() $2rs-(2r-1)t\geq r$
ensures that
$2rs-(2r-1)t\geq r$
ensures that
![]() $s^*\geq r$
and so
$s^*\geq r$
and so
![]() $d^*\geq r$
). Then, by Lemma 3.5 with
$d^*\geq r$
). Then, by Lemma 3.5 with
![]() $L=2^{5\log r}$
and
$L=2^{5\log r}$
and
![]() $\delta =r$
,
$\delta =r$
,
![]() $G^*$
has a
$G^*$
has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r}{80\log r}$
.
$\frac {r}{80\log r}$
.
The next result is very similar to Lemma 5.1 – the main difference is that the codegree condition is no longer present. This can be achieved using Lemma 3.2.
Lemma 5.2. Let
![]() $k,r,s,t$
be positive integers such that r is sufficiently large,
$k,r,s,t$
be positive integers such that r is sufficiently large,
![]() $s<t$
and
$s<t$
and
![]() $s\geq t(1-\frac {1}{6r})$
. Let G be a
$s\geq t(1-\frac {1}{6r})$
. Let G be a
![]() $K_{k,k}$
-free bipartite graph with parts A and B such that
$K_{k,k}$
-free bipartite graph with parts A and B such that
![]() $d_G(v)=r$
for every
$d_G(v)=r$
for every
![]() $v\in B$
,
$v\in B$
,
![]() $d_G(u)\leq 2^t$
for every
$d_G(u)\leq 2^t$
for every
![]() $u\in A$
and
$u\in A$
and
![]() $e(G)\geq 4(k+1)^22^s|A|$
.
$e(G)\geq 4(k+1)^22^s|A|$
.
Then G contains a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r}{160(k+1)\log r}$
.
$\frac {r}{160(k+1)\log r}$
.
Proof. We may assume that
![]() $r\geq k\log r$
, otherwise the conclusion of the lemma is trivial. By Lemma 3.2, G has a spanning subgraph
$r\geq k\log r$
, otherwise the conclusion of the lemma is trivial. By Lemma 3.2, G has a spanning subgraph
![]() $G'$
such that
$G'$
such that
![]() $e(G')\geq e(G)/(k+1)$
and
$e(G')\geq e(G)/(k+1)$
and
![]() $d_{G'}(u,u')\leq k 2^{(1-1/k)t}$
for any two distinct
$d_{G'}(u,u')\leq k 2^{(1-1/k)t}$
for any two distinct
![]() $u,u'\in A$
. Since
$u,u'\in A$
. Since
![]() $s\leq t-1$
and
$s\leq t-1$
and
![]() $s\geq t(1-\frac {1}{6r})$
, we have
$s\geq t(1-\frac {1}{6r})$
, we have
![]() $t\geq 6r$
. Hence,
$t\geq 6r$
. Hence,
![]() $2^{\frac {t}{2k}}\geq 2^{3r/k}\geq 2^{\log r}=r\geq k$
. Thus,
$2^{\frac {t}{2k}}\geq 2^{3r/k}\geq 2^{\log r}=r\geq k$
. Thus,
![]() $k 2^{(1-1/k)t}\leq 2^{(1-\frac {1}{2k})t}$
, so
$k 2^{(1-1/k)t}\leq 2^{(1-\frac {1}{2k})t}$
, so
![]() $d_{G'}(u,u')\leq 2^{(1-\frac {1}{2k})t}$
for any two distinct
$d_{G'}(u,u')\leq 2^{(1-\frac {1}{2k})t}$
for any two distinct
![]() $u,u'\in A$
. Let
$u,u'\in A$
. Let
![]() $\tilde {B}$
be the subset of B consisting of those vertices v which satisfy
$\tilde {B}$
be the subset of B consisting of those vertices v which satisfy
![]() $d_{G'}(v)\geq r/(2k+2)$
. Now, the number of edges in
$d_{G'}(v)\geq r/(2k+2)$
. Now, the number of edges in
![]() $G'$
between A and
$G'$
between A and
![]() $B\setminus \tilde {B}$
is at most
$B\setminus \tilde {B}$
is at most
![]() $|B|r/(2k+2)=e(G)/(2k+2)\leq e(G')/2$
, so there are at least
$|B|r/(2k+2)=e(G)/(2k+2)\leq e(G')/2$
, so there are at least
![]() $e(G')/2$
edges between A and
$e(G')/2$
edges between A and
![]() $\tilde {B}$
. Let
$\tilde {B}$
. Let
![]() $r'=\lceil r/(2k+2)\rceil $
and let
$r'=\lceil r/(2k+2)\rceil $
and let
![]() $G"$
be a spanning subgraph of
$G"$
be a spanning subgraph of
![]() $G'[A\cup \tilde {B}]$
obtained by keeping precisely
$G'[A\cup \tilde {B}]$
obtained by keeping precisely
![]() $r'$
edges from each
$r'$
edges from each
![]() $v\in \tilde {B}$
. Clearly,
$v\in \tilde {B}$
. Clearly,
![]() $e(G")\geq e(G'[A\cup \tilde {B}])/(2k+2)\geq e(G')/(4k+4)\geq e(G)/(4(k+1)^2)\geq 2^s|A|$
. Note that
$e(G")\geq e(G'[A\cup \tilde {B}])/(2k+2)\geq e(G')/(4k+4)\geq e(G)/(4(k+1)^2)\geq 2^s|A|$
. Note that
 $$ \begin{align*} 2r's-(2r'-1)t-r' &=t-r'(2t-2s+1)\geq t-\frac{r}{k}(2t-2s+1)\geq t-\frac{3r}{k}(t-s) \\ &\geq t-\frac{3r}{k}\cdot \frac{t}{6r}=(1-\frac{1}{2k})t, \end{align*} $$
$$ \begin{align*} 2r's-(2r'-1)t-r' &=t-r'(2t-2s+1)\geq t-\frac{r}{k}(2t-2s+1)\geq t-\frac{3r}{k}(t-s) \\ &\geq t-\frac{3r}{k}\cdot \frac{t}{6r}=(1-\frac{1}{2k})t, \end{align*} $$
so
![]() $d_{G"}(u,u')\leq 2^{2r's-(2r'-1)t-r'}$
holds for any distinct
$d_{G"}(u,u')\leq 2^{2r's-(2r'-1)t-r'}$
holds for any distinct
![]() $u,u'\in A$
. Thus, we can apply Lemma 5.1 with
$u,u'\in A$
. Thus, we can apply Lemma 5.1 with
![]() $G"$
in place of G and
$G"$
in place of G and
![]() $r'$
in place of r to get a
$r'$
in place of r to get a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r'}{80\log r'}\geq \frac {r}{160(k+1)\log r}$
.
$\frac {r'}{80\log r'}\geq \frac {r}{160(k+1)\log r}$
.
We are now in a position to prove our main result. In the proof and later in the paper, we omit floor and ceiling signs whenever they are not crucial.
Theorem 5.3. Let k, r and
![]() $\Delta $
be positive integers such that r is sufficiently large. Let G be a
$\Delta $
be positive integers such that r is sufficiently large. Let G be a
![]() $K_{k,k}$
-free graph with maximum degree at most
$K_{k,k}$
-free graph with maximum degree at most
![]() $\Delta $
and average degree at least
$\Delta $
and average degree at least
![]() $80r^2\log \log \Delta $
. Then G has a
$80r^2\log \log \Delta $
. Then G has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r}{160(k+1)\log r}$
.
$\frac {r}{160(k+1)\log r}$
.
Proof. Since r is sufficiently large, the degree conditions imply that
![]() $\Delta $
is also sufficiently large. Moreover, we may assume that
$\Delta $
is also sufficiently large. Moreover, we may assume that
![]() $r\geq k$
, otherwise the conclusion of the lemma is trivial. Note that G has a bipartite subgraph
$r\geq k$
, otherwise the conclusion of the lemma is trivial. Note that G has a bipartite subgraph
![]() $G'$
with average degree at least
$G'$
with average degree at least
![]() $40r^2\log \log \Delta $
and
$40r^2\log \log \Delta $
and
![]() $G'$
has a nonempty subgraph
$G'$
has a nonempty subgraph
![]() $G"$
with minimum degree at least
$G"$
with minimum degree at least
![]() $20r^2\log \log \Delta $
(this subgraph can be obtained by repeatedly discarding vertices of degree less than
$20r^2\log \log \Delta $
(this subgraph can be obtained by repeatedly discarding vertices of degree less than
![]() $20r^2\log \log \Delta $
). Let A and B be the parts of
$20r^2\log \log \Delta $
). Let A and B be the parts of
![]() $G"$
such that
$G"$
such that
![]() $|A|\leq |B|$
. Let H be a spanning subgraph of
$|A|\leq |B|$
. Let H be a spanning subgraph of
![]() $G"$
such that
$G"$
such that
![]() $d_H(v)=20r^2\log \log \Delta $
for every
$d_H(v)=20r^2\log \log \Delta $
for every
![]() $v\in B$
.
$v\in B$
.
Let
![]() $t_0=r (\log r)(\log \log \Delta )^{1/2}$
and let
$t_0=r (\log r)(\log \log \Delta )^{1/2}$
and let
![]() $\ell $
be the smallest nonnegative integer such that
$\ell $
be the smallest nonnegative integer such that
![]() $t_0/(1-\frac {1}{10r})^{\ell }\geq \log \Delta $
. Note that
$t_0/(1-\frac {1}{10r})^{\ell }\geq \log \Delta $
. Note that
![]() $(1-\frac {1}{10r})^{10r\log \log \Delta }\leq \exp (-\log \log \Delta )\leq 1/\log \Delta $
, so
$(1-\frac {1}{10r})^{10r\log \log \Delta }\leq \exp (-\log \log \Delta )\leq 1/\log \Delta $
, so
![]() $\ell \leq 10r\log \log \Delta $
. For
$\ell \leq 10r\log \log \Delta $
. For
![]() $1\leq i\leq \ell $
, let
$1\leq i\leq \ell $
, let
![]() $t_i=t_0/(1-\frac {1}{10r})^{i}$
. Clearly,
$t_i=t_0/(1-\frac {1}{10r})^{i}$
. Clearly,
![]() $t_\ell \geq \log \Delta $
.
$t_\ell \geq \log \Delta $
.
Let
![]() $A_0=\{u\in A: d_H(u)\leq 2^{t_0}\}$
and for
$A_0=\{u\in A: d_H(u)\leq 2^{t_0}\}$
and for
![]() $1\leq i\leq \ell $
, let
$1\leq i\leq \ell $
, let
![]() $A_i=\{u\in A: 2^{t_{i-1}}<d_H(u)\leq 2^{t_i}\}$
. Clearly, these sets partition A. Hence, for every
$A_i=\{u\in A: 2^{t_{i-1}}<d_H(u)\leq 2^{t_i}\}$
. Clearly, these sets partition A. Hence, for every
![]() $v\in B$
, either v has at least
$v\in B$
, either v has at least
![]() $d_H(v)/2= 10r^2\log \log \Delta $
neighbours (in the graph H) in
$d_H(v)/2= 10r^2\log \log \Delta $
neighbours (in the graph H) in
![]() $A_0$
or
$A_0$
or
![]() $\ell>0$
and there is some
$\ell>0$
and there is some
![]() $1\leq i\leq \ell $
such that v has at least
$1\leq i\leq \ell $
such that v has at least
![]() $d_H(v)/(2\ell )\geq r$
neighbours in
$d_H(v)/(2\ell )\geq r$
neighbours in
![]() $A_i$
.
$A_i$
.
Therefore, at least one of the following two cases must occur.
Case 1. There are at least
![]() $|B|/2$
vertices
$|B|/2$
vertices
![]() $v\in B$
which have at least
$v\in B$
which have at least
![]() $10r^2\log \log \Delta $
neighbours in
$10r^2\log \log \Delta $
neighbours in
![]() $A_0$
.
$A_0$
.
Case 2. There exist some
![]() $1\leq i\leq \ell $
and at least
$1\leq i\leq \ell $
and at least
![]() $|B|/(2\ell )$
vertices
$|B|/(2\ell )$
vertices
![]() $v\in B$
which have at least r neighbours in
$v\in B$
which have at least r neighbours in
![]() $A_i$
.
$A_i$
.
In Case 1, let
![]() $B'\subset B$
be a set of size at least
$B'\subset B$
be a set of size at least
![]() $|B|/2$
such that every
$|B|/2$
such that every
![]() $v\in B'$
has at least
$v\in B'$
has at least
![]() $10r^2\log \log \Delta $
neighbours in
$10r^2\log \log \Delta $
neighbours in
![]() $A_0$
. For technical reasons, let us take a random subset
$A_0$
. For technical reasons, let us take a random subset
![]() $A_0'\subset A_0$
of size
$A_0'\subset A_0$
of size
![]() $|A_0|/3$
. With positive probability, there is a set
$|A_0|/3$
. With positive probability, there is a set
![]() $B"\subset B'$
of at least
$B"\subset B'$
of at least
![]() $2|B'|/3$
vertices which all have at least
$2|B'|/3$
vertices which all have at least
![]() $r^2\log \log \Delta $
neighbours in
$r^2\log \log \Delta $
neighbours in
![]() $A_0'$
. Let
$A_0'$
. Let
![]() $H'$
be a spanning subgraph of
$H'$
be a spanning subgraph of
![]() $H[A_0'\cup B"]$
obtained by keeping precisely
$H[A_0'\cup B"]$
obtained by keeping precisely
![]() $r^2\log \log \Delta $
edges from each vertex in
$r^2\log \log \Delta $
edges from each vertex in
![]() $B"$
. Now, note that
$B"$
. Now, note that
![]() $|A_0'|=|A_0|/3\leq |A|/3\leq |B|/3\leq 2|B'|/3\leq |B"|$
. Moreover,
$|A_0'|=|A_0|/3\leq |A|/3\leq |B|/3\leq 2|B'|/3\leq |B"|$
. Moreover,
![]() $d_{H'}(u)\leq d_H(u)\leq 2^{t_0}$
for every
$d_{H'}(u)\leq d_H(u)\leq 2^{t_0}$
for every
![]() $u\in A_0'$
. This implies that
$u\in A_0'$
. This implies that
![]() $H'$
is
$H'$
is
![]() $(L,d)$
-almost biregular for
$(L,d)$
-almost biregular for
![]() $L=2^{t_0}=2^{r(\log r)(\log \log \Delta )^{1/2}}$
and
$L=2^{t_0}=2^{r(\log r)(\log \log \Delta )^{1/2}}$
and
![]() $d=r^2\log \log \Delta $
. Hence, by Lemma 3.5,
$d=r^2\log \log \Delta $
. Hence, by Lemma 3.5,
![]() $H'$
has a
$H'$
has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r^2\log \log \Delta }{16r(\log r)(\log \log \Delta )^{1/2}}\geq \frac {r}{160(k+1)\log r}$
.
$\frac {r^2\log \log \Delta }{16r(\log r)(\log \log \Delta )^{1/2}}\geq \frac {r}{160(k+1)\log r}$
.
In Case 2, let us choose some
![]() $1\leq i\leq \ell $
and a set
$1\leq i\leq \ell $
and a set
![]() $B'\subset B$
of size at least
$B'\subset B$
of size at least
![]() $|B|/(2\ell )$
such that for every
$|B|/(2\ell )$
such that for every
![]() $v\in B'$
, v has at least r neighbours in
$v\in B'$
, v has at least r neighbours in
![]() $A_i$
. Let
$A_i$
. Let
![]() $H'$
be a subgraph of
$H'$
be a subgraph of
![]() $H[A_i\cup B']$
obtained by keeping precisely r edges incident to each
$H[A_i\cup B']$
obtained by keeping precisely r edges incident to each
![]() $v\in B'$
. We will apply Lemma 5.2 for this graph. Let
$v\in B'$
. We will apply Lemma 5.2 for this graph. Let
![]() $t=t_i$
and let
$t=t_i$
and let
![]() $s=t(1-\frac {1}{6r})$
. Note that for any
$s=t(1-\frac {1}{6r})$
. Note that for any
![]() $u\in A_i$
,
$u\in A_i$
,
![]() $d_{H'}(u)\leq d_{H}(u)\leq 2^{t}$
. Let
$d_{H'}(u)\leq d_{H}(u)\leq 2^{t}$
. Let
![]() $C=4(r+1)^2$
. Using that
$C=4(r+1)^2$
. Using that
![]() $|B|\cdot 20r^2\log \log \Delta = e(H)\geq |A_i|2^{t_{i-1}}$
, we get
$|B|\cdot 20r^2\log \log \Delta = e(H)\geq |A_i|2^{t_{i-1}}$
, we get
 $$ \begin{align*} e(H') &=|B'|r\geq |B|r/(2\ell)=\frac{e(H)}{40\ell r \log \log \Delta}\geq \frac{e(H)}{400r^2(\log \log \Delta)^2}\geq \frac{C|A_i|2^{t_{i-1}}}{400Cr^2(\log \log \Delta)^2} \\ &=C|A_i|2^{t_{i-1}-\log(400Cr^2(\log \log \Delta)^2)}. \end{align*} $$
$$ \begin{align*} e(H') &=|B'|r\geq |B|r/(2\ell)=\frac{e(H)}{40\ell r \log \log \Delta}\geq \frac{e(H)}{400r^2(\log \log \Delta)^2}\geq \frac{C|A_i|2^{t_{i-1}}}{400Cr^2(\log \log \Delta)^2} \\ &=C|A_i|2^{t_{i-1}-\log(400Cr^2(\log \log \Delta)^2)}. \end{align*} $$
Note that
 $$ \begin{align*}t_{i-1}-\log(400Cr^2(\log \log \Delta)^2)=t\left(1-\frac{1}{10r}\right)-\log(400Cr^2(\log \log \Delta)^2)\geq t\left(1-\frac{1}{6r}\right)=s,\end{align*} $$
$$ \begin{align*}t_{i-1}-\log(400Cr^2(\log \log \Delta)^2)=t\left(1-\frac{1}{10r}\right)-\log(400Cr^2(\log \log \Delta)^2)\geq t\left(1-\frac{1}{6r}\right)=s,\end{align*} $$
where the inequality follows from
![]() $t/r\geq t_0/r=(\log r)(\log \log \Delta )^{1/2}$
and since
$t/r\geq t_0/r=(\log r)(\log \log \Delta )^{1/2}$
and since
![]() $\Delta $
is sufficiently large. Hence,
$\Delta $
is sufficiently large. Hence,
![]() $e(H')\geq C|A_i|2^s\geq 4(k+1)^2|A_i|2^s$
.
$e(H')\geq C|A_i|2^s\geq 4(k+1)^2|A_i|2^s$
.
Thus, we can apply Lemma 5.2 to the graph
![]() $H'$
and get a
$H'$
and get a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r}{160(k+1)\log r}$
.
$\frac {r}{160(k+1)\log r}$
.
Theorem 1.2 now follows easily.
Proof of Theorem 1.2.
Let r be sufficiently large in terms of k, and let
![]() $C=80r^2$
. Let G be a graph with maximum degree
$C=80r^2$
. Let G be a graph with maximum degree
![]() $\Delta $
and average degree at least
$\Delta $
and average degree at least
![]() $C\log \log \Delta $
. If G contains
$C\log \log \Delta $
. If G contains
![]() $K_{k,k}$
as a subgraph, then it has a k-regular subgraph. Else, by Theorem 5.3, G has a
$K_{k,k}$
as a subgraph, then it has a k-regular subgraph. Else, by Theorem 5.3, G has a
![]() $64$
-almost-regular subgraph
$64$
-almost-regular subgraph
![]() $G'$
with average degree at least
$G'$
with average degree at least
![]() $\frac {r}{160(k+1)\log r}$
. Since r is sufficiently large in terms of k, Theorem 3.8 implies that
$\frac {r}{160(k+1)\log r}$
. Since r is sufficiently large in terms of k, Theorem 3.8 implies that
![]() $G'$
has a k-regular subgraph.
$G'$
has a k-regular subgraph.
6 Concluding remarks
Motivated by the study of the Turán number of the cube, in 1970, Erdős and Simonovits [Reference Erdős and Simonovits15] proved the following result.
Theorem 6.1 (Erdős–Simonovits [Reference Erdős and Simonovits15]).
For every
![]() $\alpha>0$
there exist some
$\alpha>0$
there exist some
![]() $K=K(\alpha )$
and
$K=K(\alpha )$
and
![]() $n_0=n_0(\alpha )$
such that any graph with
$n_0=n_0(\alpha )$
such that any graph with
![]() $n\geq n_0$
vertices and at least
$n\geq n_0$
vertices and at least
![]() $n^{1+\alpha }$
edges contains a K-almost-regular subgraph with m vertices and at least
$n^{1+\alpha }$
edges contains a K-almost-regular subgraph with m vertices and at least
![]() $\frac {2}{5}m^{1+\alpha }$
edges for some
$\frac {2}{5}m^{1+\alpha }$
edges for some
![]() $m\geq n^{\alpha (1-\alpha )/(1+\alpha )}$
.
$m\geq n^{\alpha (1-\alpha )/(1+\alpha )}$
.
This result has since become one of the most widely used tools for Turán type problems. Its extreme usefulness comes from the fact that it allows us to replace a general host graph by an almost-regular one at negligible cost. Usually extremal problems are much easier to deal with when the host graph is almost-regular.
In their paper, Erdős and Simonovits asked whether a similar ‘regularization’ is possible for sparser graphs. More precisely, they asked whether there exist absolute constants
![]() such that any n-vertex graph with at least
such that any n-vertex graph with at least
![]() $n\log n$
edges contains a K-almost-regular subgraph with m vertices and at least
$n\log n$
edges contains a K-almost-regular subgraph with m vertices and at least
![]() edges, where
edges, where
![]() $m\rightarrow \infty $
as
$m\rightarrow \infty $
as
![]() $n\rightarrow \infty $
. Using a variant of the construction of Pyber, Rödl and Szemerédi from Theorem 1.1, Alon [Reference Alon1] gave a negative answer to this question as follows.
$n\rightarrow \infty $
. Using a variant of the construction of Pyber, Rödl and Szemerédi from Theorem 1.1, Alon [Reference Alon1] gave a negative answer to this question as follows.
Theorem 6.2 (Alon [Reference Alon1]).
For every
![]() $K>0$
and
$K>0$
and
![]() $n>10^6$
, there is an n-vertex graph with at least
$n>10^6$
, there is an n-vertex graph with at least
![]() $n\log n$
edges in which any K-almost-regular m-vertex subgraph has at most
$n\log n$
edges in which any K-almost-regular m-vertex subgraph has at most
![]() $72m\sqrt {\log m}+18\log (64K)+324$
edges.
$72m\sqrt {\log m}+18\log (64K)+324$
edges.
Thus, we cannot necessarily pass to an almost-regular m-vertex subgraph with much more than
![]() $m\sqrt {\log m}$
edges. This naturally leads to the question what density we can actually guarantee in an almost-regular subgraph of a graph with
$m\sqrt {\log m}$
edges. This naturally leads to the question what density we can actually guarantee in an almost-regular subgraph of a graph with
![]() $n\log n$
edges. Our Theorem 5.3 essentially answers this question. Indeed, it implies that we can always find an almost-regular m-vertex subgraph with nearly
$n\log n$
edges. Our Theorem 5.3 essentially answers this question. Indeed, it implies that we can always find an almost-regular m-vertex subgraph with nearly
![]() $m\sqrt {\log m}$
edges, showing that Theorem 6.2 is tight up to
$m\sqrt {\log m}$
edges, showing that Theorem 6.2 is tight up to
![]() $\log \log $
factors.
$\log \log $
factors.
Theorem 6.3. For any positive integer
![]() $m_0$
, there exist some
$m_0$
, there exist some
![]() $n_0=n_0(m_0)$
and
$n_0=n_0(m_0)$
and
![]() such that any graph with
such that any graph with
![]() $n\geq n_0$
vertices and at least
$n\geq n_0$
vertices and at least
![]() $n\log n$
edges has a
$n\log n$
edges has a
![]() $64$
-almost-regular subgraph with
$64$
-almost-regular subgraph with
![]() $m\geq m_0$
vertices and at least
$m\geq m_0$
vertices and at least
![]() edges.
edges.
Proof. Let
![]() $n_0$
be sufficiently large in terms of
$n_0$
be sufficiently large in terms of
![]() $m_0$
, and let G be a graph with
$m_0$
, and let G be a graph with
![]() $n\geq n_0$
vertices and at least
$n\geq n_0$
vertices and at least
![]() $n\log n$
edges. Let
$n\log n$
edges. Let
![]() $r=\frac {\sqrt {\log n}}{10\sqrt {\log \log n}}$
, and let
$r=\frac {\sqrt {\log n}}{10\sqrt {\log \log n}}$
, and let
![]() $\Delta $
be the maximum degree of G. Since
$\Delta $
be the maximum degree of G. Since
![]() $\Delta \leq n$
, the average degree of G is at least
$\Delta \leq n$
, the average degree of G is at least
![]() $\log n\geq 100r^2\log \log \Delta $
. If
$\log n\geq 100r^2\log \log \Delta $
. If
![]() $K_{m_0,m_0}$
is a subgraph of G, then we are done. Else, by Theorem 5.3, G has a
$K_{m_0,m_0}$
is a subgraph of G, then we are done. Else, by Theorem 5.3, G has a
![]() $64$
-almost-regular subgraph
$64$
-almost-regular subgraph
![]() $G'$
with average degree at least
$G'$
with average degree at least
![]() $\frac {r}{160(m_0+1)\log r}$
. This is at least
$\frac {r}{160(m_0+1)\log r}$
. This is at least
![]() for some
for some
![]() that depends only on
that depends only on
![]() $m_0$
. Now, if m is the number of vertices in
$m_0$
. Now, if m is the number of vertices in
![]() $G'$
, then
$G'$
, then
![]() $m\geq m_0$
(since n is sufficiently large) and
$m\geq m_0$
(since n is sufficiently large) and
![]() $G'$
has at least
$G'$
has at least
![]() edges, as desired.
edges, as desired.
In certain extremal problems one wants to pass to almost-regular subgraphs whose average degree is large not just compared to the number of vertices in the subgraph but also compared to the number of vertices in the original graph (which we call n). Using a variant of Pyber’s argument, it was shown in [Reference Alon, Reichman, Shinkar, Wagner, Musslick, Cohen, Griffiths, Dey and Ozcimder6] and [Reference Bucić, Kwan, Pokrovskiy, Sudakov, Tran and Wagner10] that passing to such a subgraph is possible with the loss of only a
![]() $\log n$
factor in the average degree. Also, by considering a variant of the construction of Pyber, Rödl and Szemerédi, it was shown in [Reference Bucić, Kwan, Pokrovskiy, Sudakov, Tran and Wagner10] that this
$\log n$
factor in the average degree. Also, by considering a variant of the construction of Pyber, Rödl and Szemerédi, it was shown in [Reference Bucić, Kwan, Pokrovskiy, Sudakov, Tran and Wagner10] that this
![]() $\log n$
loss is necessary for graphs with average degree at least
$\log n$
loss is necessary for graphs with average degree at least
![]() . However, when the graph has at most
. However, when the graph has at most
![]() $n\log n$
edges, then this
$n\log n$
edges, then this
![]() $\log n$
loss means that the above result becomes trivial. Our methods apply in this sparse regime and give the following.
$\log n$
loss means that the above result becomes trivial. Our methods apply in this sparse regime and give the following.
Theorem 6.4. There is an absolute constant
![]() such that any n-vertex graph with average degree
such that any n-vertex graph with average degree
![]() $d\geq 2\log \log n$
has a
$d\geq 2\log \log n$
has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() . Furthermore, for any positive integer t there is some
. Furthermore, for any positive integer t there is some
![]() such that any
such that any
![]() $K_{t,t}$
-free n-vertex graph with average degree
$K_{t,t}$
-free n-vertex graph with average degree
![]() $d\geq 2\log \log n$
has a
$d\geq 2\log \log n$
has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() .
.
Proof. We only prove the first assertion – the second one has a very similar proof.
Let G be an n-vertex graph with average degree d. We may assume that
![]() $d/\log \log n$
is sufficiently large, otherwise the statement is trivial. Let
$d/\log \log n$
is sufficiently large, otherwise the statement is trivial. Let
![]() be a sufficiently small positive absolute constant, and let
be a sufficiently small positive absolute constant, and let
![]() . We want to show that G has a
. We want to show that G has a
![]() $64$
-almost-regular subgraph with average degree at least k. Let
$64$
-almost-regular subgraph with average degree at least k. Let
![]() $r=(\frac {d}{80\log \log n})^{1/2}$
. If G contains
$r=(\frac {d}{80\log \log n})^{1/2}$
. If G contains
![]() $K_{k,k}$
as a subgraph, then we are done; else, by Theorem 5.3, G has a
$K_{k,k}$
as a subgraph, then we are done; else, by Theorem 5.3, G has a
![]() $64$
-almost-regular subgraph with average degree at least
$64$
-almost-regular subgraph with average degree at least
![]() $\frac {r}{160(k+1)\log r}$
. But for sufficiently small
$\frac {r}{160(k+1)\log r}$
. But for sufficiently small
![]() , we have
, we have
![]() $\frac {r}{160(k+1)\log r}\geq k$
, so the proof is complete.
$\frac {r}{160(k+1)\log r}\geq k$
, so the proof is complete.
Since the problem of finding regular subgraphs arises naturally in many combinatorial settings, it seems very likely that our results will have further applications. We conclude the paper by discussing two such applications.
-
• Our results can be used to answer a recent question posed by Alon et al. in [Reference Alon, Reichman, Shinkar, Wagner, Musslick, Cohen, Griffiths, Dey and Ozcimder6]. Motivated by applications to neural networks, in [Reference Alon, Reichman, Shinkar, Wagner, Musslick, Cohen, Griffiths, Dey and Ozcimder6] the authors defined the notion of an
 $\alpha $
-multitasker graph and asked (see the discussion after Theorem 1.3 in the full version of their paper [Reference Alon, Cohen, Dey, Griffiths, Musslick, Ozcimder, Reichman, Shinkar and Wagner3]) if there exists an n-vertex
$\alpha $
-multitasker graph and asked (see the discussion after Theorem 1.3 in the full version of their paper [Reference Alon, Cohen, Dey, Griffiths, Musslick, Ozcimder, Reichman, Shinkar and Wagner3]) if there exists an n-vertex
 $\alpha $
-multitasker with average degree
$\alpha $
-multitasker with average degree
 $\Theta (\log n)$
for some
$\Theta (\log n)$
for some
 $\alpha>0$
, independent of n. Our Theorem 6.4 (or Theorem 1.2) can be used to show that there is no such multitasker with average degree
$\alpha>0$
, independent of n. Our Theorem 6.4 (or Theorem 1.2) can be used to show that there is no such multitasker with average degree
 $\omega (\log \log n)$
. This is tight as Alon et al. showed that there are
$\omega (\log \log n)$
. This is tight as Alon et al. showed that there are
 $\alpha $
-multitaskers with average degree
$\alpha $
-multitaskers with average degree
 $\Theta (\log \log n)$
and constant
$\Theta (\log \log n)$
and constant
 $\alpha $
.
$\alpha $
. -
• The second application concerns the notion of spectral degeneracy, introduced by Dvořák and Mohar [Reference Dvořák and Mohar13]. The spectral radius of a graph G is the largest eigenvalue of the adjacency matrix of G and is denoted by
 $\rho (G)$
. We say that G is spectrally d-degenerate if for every subgraph H of G, we have
$\rho (G)$
. We say that G is spectrally d-degenerate if for every subgraph H of G, we have
 $\rho (H)\leq \sqrt {d\Delta (H)}$
and call the smallest such d the spectral degeneracy of G. It was observed in [Reference Dvořák and Mohar13] that every d-degenerate graph is spectrally
$\rho (H)\leq \sqrt {d\Delta (H)}$
and call the smallest such d the spectral degeneracy of G. It was observed in [Reference Dvořák and Mohar13] that every d-degenerate graph is spectrally
 $4d$
-degenerate. Moreover, they showed the rough converse that any spectrally d-degenerate graph with maximum degree
$4d$
-degenerate. Moreover, they showed the rough converse that any spectrally d-degenerate graph with maximum degree
 $D\geq 2d$
is
$D\geq 2d$
is
 $4d\log (D/d)$
-degenerate. In addition, they asked whether there exists a function f such that any spectrally d-degenerate graph is
$4d\log (D/d)$
-degenerate. In addition, they asked whether there exists a function f such that any spectrally d-degenerate graph is
 $f(d)$
-degenerate. This was answered negatively by Alon [Reference Alon2], who constructed, for every M, a spectrally
$f(d)$
-degenerate. This was answered negatively by Alon [Reference Alon2], who constructed, for every M, a spectrally
 $50$
-degenerate graph which is not M-degenerate. Analyzing his construction more carefully, one can see that in fact there is a positive constant c such that for every n there is a spectrally
$50$
-degenerate graph which is not M-degenerate. Analyzing his construction more carefully, one can see that in fact there is a positive constant c such that for every n there is a spectrally
 $50$
-degenerate n-vertex graph with degeneracy at least
$50$
-degenerate n-vertex graph with degeneracy at least
 $c\log \log n$
. Our results can be used to show that this is best possible, that is, that for every d there is a constant
$c\log \log n$
. Our results can be used to show that this is best possible, that is, that for every d there is a constant
 $C=C(d)$
such that any spectrally d-degenerate n-vertex graph has degeneracy at most
$C=C(d)$
such that any spectrally d-degenerate n-vertex graph has degeneracy at most
 $C\log \log n$
. This follows from our Theorem 1.2 and the simple fact that the spectral degeneracy of a d-regular graph is precisely d.
$C\log \log n$
. This follows from our Theorem 1.2 and the simple fact that the spectral degeneracy of a d-regular graph is precisely d.
Acknowledgments
We are grateful to the referees for their careful reading of the manuscript and their helpful comments.
Competing interests
The authors have no competing interest to declare.
Financial support
The research of the first author was supported by an ETH Zürich Postdoctoral Fellowship (grant number 20-1 FEL-35). The research of the second author was supported in part by an SNSF grant (grant number 200021_196965).