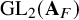1 Introduction
Let
![]() $f = \sum _{n=1}^{\infty } a_n q^n$
be a cuspidal modular form of weight
$f = \sum _{n=1}^{\infty } a_n q^n$
be a cuspidal modular form of weight
![]() $k \ge 2$
and level
$k \ge 2$
and level
![]() $\Gamma _1(N) \subset \operatorname {\mathrm {SL}}_2({\mathbb Z})$
, which is an eigenform for all the Hecke operators
$\Gamma _1(N) \subset \operatorname {\mathrm {SL}}_2({\mathbb Z})$
, which is an eigenform for all the Hecke operators
![]() $T_p$
for
$T_p$
for
![]() $(p,N)=1$
and normalized so that
$(p,N)=1$
and normalized so that
![]() $a_1 = 1$
. The Ramanujan conjecture for f — proved by Deligne [Reference DeligneDel71] as a consequence of the Weil conjectures — is the claim that
$a_1 = 1$
. The Ramanujan conjecture for f — proved by Deligne [Reference DeligneDel71] as a consequence of the Weil conjectures — is the claim that
Suppose that the coefficients of f are real. The Sato–Tate conjecture (proved in a sequence of papers [Reference Clozel, Harris and TaylorCHT08, Reference TaylorTay08, Reference Harris, Shepherd-Barron and TaylorHSBT10, Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11]) is the theorem that the normalized values
![]() $a_p/2p^{(k-1)/2} \in [-1,1]$
are equidistributed with respect to the Sato–Tate measure
$a_p/2p^{(k-1)/2} \in [-1,1]$
are equidistributed with respect to the Sato–Tate measure
![]() $2/\pi \cdot \sqrt {1-x^2} dx$
unless f is a so-called CM form, in which case the corresponding measure is the average of the atomic measure with support zero and the measure
$2/\pi \cdot \sqrt {1-x^2} dx$
unless f is a so-called CM form, in which case the corresponding measure is the average of the atomic measure with support zero and the measure
![]() $1/\pi \cdot 1/\sqrt {1-x^2} dx$
(the proof in this CM case is much easier and follows from [Reference HeckeHec1920]). (If the coefficients
$1/\pi \cdot 1/\sqrt {1-x^2} dx$
(the proof in this CM case is much easier and follows from [Reference HeckeHec1920]). (If the coefficients
![]() $a_p$
are not real, some minor modifications are required to formulate the conjecture properly.) These conjectures were originally made for the particular (non-CM) form
$a_p$
are not real, some minor modifications are required to formulate the conjecture properly.) These conjectures were originally made for the particular (non-CM) form
![]() $f = \Delta = q \prod _{n=1}^{\infty } (1 - q^n)^{24} = \sum _{n=1}^{\infty } \tau (n) q^n$
of level
$f = \Delta = q \prod _{n=1}^{\infty } (1 - q^n)^{24} = \sum _{n=1}^{\infty } \tau (n) q^n$
of level
![]() $\operatorname {\mathrm {SL}}_2({\mathbb Z})$
and weight
$\operatorname {\mathrm {SL}}_2({\mathbb Z})$
and weight
![]() $k = 12$
studied by Ramanujan; this particular case turns out to be no easier than the general case.
$k = 12$
studied by Ramanujan; this particular case turns out to be no easier than the general case.
Both of these conjectures have an equivalent reformulation in the language of automorphic representations. Associated to a cuspidal modular eigenform f (as above) is an automorphic representation
![]() $\pi $
for
$\pi $
for
![]() $\operatorname {\mathrm {GL}}(2)/{\mathbb Q}$
. The data of
$\operatorname {\mathrm {GL}}(2)/{\mathbb Q}$
. The data of
![]() $\pi $
includes irreducible admissible infinite dimensional complex representations
$\pi $
includes irreducible admissible infinite dimensional complex representations
![]() $\pi _p$
of
$\pi _p$
of
![]() $\operatorname {\mathrm {GL}}_2({\mathbb Q}_p)$
for all p. For
$\operatorname {\mathrm {GL}}_2({\mathbb Q}_p)$
for all p. For
![]() $(p,N)=1$
, the representations
$(p,N)=1$
, the representations
![]() $\pi _p$
satisfy the additional property of being so-called spherical and are in particular classified by a pair of complex numbers
$\pi _p$
satisfy the additional property of being so-called spherical and are in particular classified by a pair of complex numbers
![]() $\{\alpha _p,\beta _p\}$
known as Satake parameters, which are related to the original coefficients
$\{\alpha _p,\beta _p\}$
known as Satake parameters, which are related to the original coefficients
![]() $a_p$
via the equation
$a_p$
via the equation
where
![]() $\chi : ({\mathbb Z}/N {\mathbb Z})^{\times } \rightarrow {\mathbb C}^{\times }$
is the Nebentypus character of f. The Ramanujan conjecture is equivalent to the equality
$\chi : ({\mathbb Z}/N {\mathbb Z})^{\times } \rightarrow {\mathbb C}^{\times }$
is the Nebentypus character of f. The Ramanujan conjecture is equivalent to the equality
![]() $|\alpha _p|=|\beta _p| = p^{(k-1)/2}$
, which can be reformulated as saying that the representation
$|\alpha _p|=|\beta _p| = p^{(k-1)/2}$
, which can be reformulated as saying that the representation
![]() $\pi _p$
is tempered. The Sato–Tate conjecture is equivalent (for non-CM forms) to the claim that the conjugacy classes of the matrices
$\pi _p$
is tempered. The Sato–Tate conjecture is equivalent (for non-CM forms) to the claim that the conjugacy classes of the matrices
 $$ \begin{align*}\frac{1}{p^{(k-1)/2}} \cdot \left( \begin{matrix} \alpha_p & 0 \\ 0 & \beta_p \end{matrix} \right)\end{align*} $$
$$ \begin{align*}\frac{1}{p^{(k-1)/2}} \cdot \left( \begin{matrix} \alpha_p & 0 \\ 0 & \beta_p \end{matrix} \right)\end{align*} $$
are equidistributed in
![]() $\operatorname {\mathrm {SU}}(2)/\text {conjugacy}$
with respect to the probability Haar measure.
$\operatorname {\mathrm {SU}}(2)/\text {conjugacy}$
with respect to the probability Haar measure.
One advantage of these reformulations is that they can be generalized; the original Ramanujan conjecture becomes the statement that if
![]() $\pi $
is a regular algebraic cuspidal automorphic representation for
$\pi $
is a regular algebraic cuspidal automorphic representation for
![]() $\operatorname {\mathrm {GL}}(2)/{\mathbb Q}$
, then
$\operatorname {\mathrm {GL}}(2)/{\mathbb Q}$
, then
![]() $\pi _p$
is tempered for all p. The general Ramanujan conjecture is the statement that if
$\pi _p$
is tempered for all p. The general Ramanujan conjecture is the statement that if
![]() $\pi $
is a cuspidal automorphic representation for
$\pi $
is a cuspidal automorphic representation for
![]() $\operatorname {\mathrm {GL}}(n)/F$
for any number field F, then
$\operatorname {\mathrm {GL}}(n)/F$
for any number field F, then
![]() $\pi _v$
is tempered for all primes v of F. (One can generalize further to groups beyond
$\pi _v$
is tempered for all primes v of F. (One can generalize further to groups beyond
![]() $\operatorname {\mathrm {GL}}(n)$
, but then the formulation becomes more subtle.) This conjecture is still open in the case of
$\operatorname {\mathrm {GL}}(n)$
, but then the formulation becomes more subtle.) This conjecture is still open in the case of
![]() $\operatorname {\mathrm {GL}}(2)/{\mathbb Q}$
; after one drops the adjectives ‘regular algebraic’ (or even just ‘regular’), one then allows Maass forms, which seem beyond the reach of all current techniques. On the other hand, one can consider regular algebraic automorphic representations
$\operatorname {\mathrm {GL}}(2)/{\mathbb Q}$
; after one drops the adjectives ‘regular algebraic’ (or even just ‘regular’), one then allows Maass forms, which seem beyond the reach of all current techniques. On the other hand, one can consider regular algebraic automorphic representations
![]() $\pi $
for
$\pi $
for
![]() $\operatorname {\mathrm {GL}}(2)/F$
for number fields F. If F is a totally real field, then these correspond to Hilbert modular forms of weight
$\operatorname {\mathrm {GL}}(2)/F$
for number fields F. If F is a totally real field, then these correspond to Hilbert modular forms of weight
![]() $(k_i)_{i=1}^{d}$
(with
$(k_i)_{i=1}^{d}$
(with
![]() $d=[F:{\mathbb Q}]$
) with all weights
$d=[F:{\mathbb Q}]$
) with all weights
![]() $k_i$
at least
$k_i$
at least
![]() $2$
, and parity independent of i; the theory here is close to the original setting of classical modular forms. One point of similarity is that Hilbert modular forms can also be written as q-series (now in more variables). Moreover, just as for classical modular forms, there is a direct link between Hilbert modular forms and the étale cohomology of certain algebraic (Shimura) varieties, which allows one to deduce the Ramanujan conjecture in these cases as a consequence of the Weil conjectures ([Reference Brylinski and LabesseBL84, Reference BlasiusBla06]). The Sato–Tate conjecture can also be proved in these cases by arguments generalizing those used for modular forms [Reference Barnet-Lamb, Gee and GeraghtyBLGG11].
$2$
, and parity independent of i; the theory here is close to the original setting of classical modular forms. One point of similarity is that Hilbert modular forms can also be written as q-series (now in more variables). Moreover, just as for classical modular forms, there is a direct link between Hilbert modular forms and the étale cohomology of certain algebraic (Shimura) varieties, which allows one to deduce the Ramanujan conjecture in these cases as a consequence of the Weil conjectures ([Reference Brylinski and LabesseBL84, Reference BlasiusBla06]). The Sato–Tate conjecture can also be proved in these cases by arguments generalizing those used for modular forms [Reference Barnet-Lamb, Gee and GeraghtyBLGG11].
In this paper, we consider the Ramanujan and Sato–Tate conjectures for regular algebraic cuspidal automorphic representations for
![]() $\operatorname {\mathrm {GL}}(2)/F$
, where F is now an imaginary quadratic field (or more generally an imaginary CM field). In this case, the classical interpretation of these objects (sometimes called Bianchi modular forms when F is imaginary quadratic) looks quite different from the familiar q-expansions associated to classical or Hilbert modular forms; for example, if F is an imaginary quadratic field, they can be thought of as vector valued differential one-forms on arithmetic hyperbolic three manifolds. The Eichler–Shimura map allows one to relate classical modular forms of weight
$\operatorname {\mathrm {GL}}(2)/F$
, where F is now an imaginary quadratic field (or more generally an imaginary CM field). In this case, the classical interpretation of these objects (sometimes called Bianchi modular forms when F is imaginary quadratic) looks quite different from the familiar q-expansions associated to classical or Hilbert modular forms; for example, if F is an imaginary quadratic field, they can be thought of as vector valued differential one-forms on arithmetic hyperbolic three manifolds. The Eichler–Shimura map allows one to relate classical modular forms of weight
![]() $k \ge 2$
to the cohomology of local systems for congruence subgroups of
$k \ge 2$
to the cohomology of local systems for congruence subgroups of
![]() $\operatorname {\mathrm {SL}}_2({\mathbb Z})$
; the analogous theorem also allows one to relate Bianchi modular forms to the cohomology of local systems for subgroups of
$\operatorname {\mathrm {SL}}_2({\mathbb Z})$
; the analogous theorem also allows one to relate Bianchi modular forms to the cohomology of local systems for subgroups of
![]() $\operatorname {\mathrm {SL}}_2(\mathcal {O}_F)$
. However, what is missing in this setting is that there is now no longer any direct link to the cohomology of algebraic varieties. Despite this, in this paper, we prove the Ramanujan conjecture for regular algebraic cuspidal automorphic representations in full for all quadratic fields and with the parallel weight condition for arbitrary imaginary CM fields.
$\operatorname {\mathrm {SL}}_2(\mathcal {O}_F)$
. However, what is missing in this setting is that there is now no longer any direct link to the cohomology of algebraic varieties. Despite this, in this paper, we prove the Ramanujan conjecture for regular algebraic cuspidal automorphic representations in full for all quadratic fields and with the parallel weight condition for arbitrary imaginary CM fields.
For a precise clarification of what parallel weight k means, see Definition 1.5.1. The meaning of ‘regular algebraic’ is also recalled immediately before this definition. When F is imaginary quadratic, all regular algebraic cuspidal automorphic representations for
![]() $\operatorname {\mathrm {GL}}(2)/F$
have parallel weight.
$\operatorname {\mathrm {GL}}(2)/F$
have parallel weight.
Theorem A (Ramanujan Conjecture, Theorem 7.1.1).
Let
![]() $F/{\mathbb Q}$
be an imaginary CM field. Let
$F/{\mathbb Q}$
be an imaginary CM field. Let
![]() $\pi $
be a cuspidal algebraic automorphic representation for
$\pi $
be a cuspidal algebraic automorphic representation for
![]() $\operatorname {\mathrm {GL}}(2)/F$
of parallel weight
$\operatorname {\mathrm {GL}}(2)/F$
of parallel weight
![]() $k\ge 2$
. Then
$k\ge 2$
. Then
![]() $\pi _v$
is tempered for all finite places v; in particular, for places v prime to the level of
$\pi _v$
is tempered for all finite places v; in particular, for places v prime to the level of
![]() $\pi $
, the Satake parameters
$\pi $
, the Satake parameters
![]() $\{\alpha _v,\beta _v\}$
of
$\{\alpha _v,\beta _v\}$
of
![]() $\pi _v$
satisfy
$\pi _v$
satisfy
![]() $|\alpha _v| = |\beta _v| = N(v)^{(k-1)/2}$
.
$|\alpha _v| = |\beta _v| = N(v)^{(k-1)/2}$
.
Theorem B (Sato–Tate Conjecture, Theorem 7.2.3).
Let
![]() $F/{\mathbb Q}$
be an imaginary CM field. Let
$F/{\mathbb Q}$
be an imaginary CM field. Let
![]() $\pi $
be a cuspidal algebraic automorphic representation for
$\pi $
be a cuspidal algebraic automorphic representation for
![]() $\operatorname {\mathrm {GL}}(2)/F$
of parallel weight
$\operatorname {\mathrm {GL}}(2)/F$
of parallel weight
![]() $k\ge 2$
. Assume that
$k\ge 2$
. Assume that
![]() $\pi $
does not have CM; equivalently,
$\pi $
does not have CM; equivalently,
![]() $\pi $
is not the automorphic induction of an algebraic Hecke character from a quadratic CM extension
$\pi $
is not the automorphic induction of an algebraic Hecke character from a quadratic CM extension
![]() $F'/F$
. For each finite place v prime to the level of
$F'/F$
. For each finite place v prime to the level of
![]() $\pi $
, let
$\pi $
, let
![]() $a_v= (\alpha _v + \beta _v)/(2 N(v)^{(k-1)/2})$
denote the normalized parameter, and suppose that the
$a_v= (\alpha _v + \beta _v)/(2 N(v)^{(k-1)/2})$
denote the normalized parameter, and suppose that the
![]() $a_v$
are real. Then the
$a_v$
are real. Then the
![]() $a_v$
are uniformly distributed with respect to the Sato–Tate measure
$a_v$
are uniformly distributed with respect to the Sato–Tate measure
![]() $2/\pi \cdot \sqrt {1-x^2} dx$
.
$2/\pi \cdot \sqrt {1-x^2} dx$
.
As in the case
![]() $F={\mathbb Q}$
, a minor modification of the statement is needed when the
$F={\mathbb Q}$
, a minor modification of the statement is needed when the
![]() $a_v$
are not real; we relegate the details of this to Section 7.2. We also discuss some alternate formulations of Theorem A when
$a_v$
are not real; we relegate the details of this to Section 7.2. We also discuss some alternate formulations of Theorem A when
![]() $F/{\mathbb Q}$
is an imaginary quadratic field in Section 1.3.
$F/{\mathbb Q}$
is an imaginary quadratic field in Section 1.3.
To prove Theorems A and B, we prove the potential automorphy of the symmetric powers of the compatible systems of Galois representations associated to a cuspidal, regular algebraic automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. Here again is a simplified version of our main result in this direction. (To orient the reader, the integer
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. Here again is a simplified version of our main result in this direction. (To orient the reader, the integer
![]() $k \ge 2$
parametrizing the weight in this discussion above is related to the integer
$k \ge 2$
parametrizing the weight in this discussion above is related to the integer
![]() $m \ge 1$
below via the relation
$m \ge 1$
below via the relation
![]() $m = k - 1$
. This mirrors the fact that the Hodge–Tate weights of p-adic Galois representations associated to modular forms of weight k are equal to
$m = k - 1$
. This mirrors the fact that the Hodge–Tate weights of p-adic Galois representations associated to modular forms of weight k are equal to
![]() $\{0,k-1\}$
.)
$\{0,k-1\}$
.)
Theorem C (Potential automorphy of symmetric powers, Theorem 7.2.1).
Let F be a CM field, let M be a number field, and let
![]() $m \ge 1$
be an integer. Suppose we have a system of Galois representations
$m \ge 1$
be an integer. Suppose we have a system of Galois representations
indexed by primes
![]() $\lambda $
of M with the following compatibilities:
$\lambda $
of M with the following compatibilities:
-
1.
 $\rho _{\lambda }$
is unramified outside a finite set of primes
$\rho _{\lambda }$
is unramified outside a finite set of primes
 $\{v \in S\} \cup \{v | N(\lambda )\}$
where S is independent of
$\{v \in S\} \cup \{v | N(\lambda )\}$
where S is independent of
 $\lambda $
. For any v not in this set, the characteristic polynomial
$\lambda $
. For any v not in this set, the characteristic polynomial
 $P_v(X) = X^2 + a_v X + b_v$
of
$P_v(X) = X^2 + a_v X + b_v$
of
 $\rho _\lambda (\mathrm {Frob}_v)$
lies in
$\rho _\lambda (\mathrm {Frob}_v)$
lies in
 $M[X]$
and is independent of v.
$M[X]$
and is independent of v. -
2. For all but finitely many
 $\lambda $
, the representations
$\lambda $
, the representations
 $\rho _{\lambda } |_{G_v}$
for primes
$\rho _{\lambda } |_{G_v}$
for primes
 $v|N(\lambda )$
and
$v|N(\lambda )$
and
 $v \notin S$
are crystalline with Hodge–Tate weights
$v \notin S$
are crystalline with Hodge–Tate weights
 $H = \{0,m\}$
for every embedding of F into
$H = \{0,m\}$
for every embedding of F into
 $\overline {{\mathbb Q}}_p$
.
$\overline {{\mathbb Q}}_p$
.
Assume that at least one
![]() $\rho _{\lambda }$
is irreducible. Then,
$\rho _{\lambda }$
is irreducible. Then,
-
1. Purity: for any embedding of
 $M \hookrightarrow \mathbf {C}$
, the roots
$M \hookrightarrow \mathbf {C}$
, the roots
 $\alpha _v$
and
$\alpha _v$
and
 $\beta _v$
of
$\beta _v$
of
 $X^2 + a_v X + b_v$
have absolute value
$X^2 + a_v X + b_v$
have absolute value
 $q^{m/2}$
where
$q^{m/2}$
where
 $q = N(v)$
.
$q = N(v)$
. -
2. Potential automorphy: There is a number field
 $F'/F$
such that the restrictions
$F'/F$
such that the restrictions
 $\rho _{\lambda } |_{G_{F'}}$
are all automorphic and associated to a fixed cuspidal algebraic
$\rho _{\lambda } |_{G_{F'}}$
are all automorphic and associated to a fixed cuspidal algebraic
 $\pi $
for
$\pi $
for
 $\operatorname {\mathrm {GL}}(2)/F'$
.
$\operatorname {\mathrm {GL}}(2)/F'$
. -
3. Potential automorphy of symmetric powers: Fix
 $n-1 \ge 2$
. Either
$n-1 \ge 2$
. Either-
(a) The
 $\rho _{\lambda }$
are all induced from a compatible system associated to an algebraic Hecke character
$\rho _{\lambda }$
are all induced from a compatible system associated to an algebraic Hecke character
 $\chi $
of some quadratic extension
$\chi $
of some quadratic extension
 $F'/F$
. Then
$F'/F$
. Then
 $\operatorname {\mathrm {Sym}}^{n-1} \rho _{\lambda }$
is reducible and decomposes into representations of dimension two and one which are all automorphic over F.
$\operatorname {\mathrm {Sym}}^{n-1} \rho _{\lambda }$
is reducible and decomposes into representations of dimension two and one which are all automorphic over F. -
(b) There is a number field
 $F'/F$
such that the representations
$F'/F$
such that the representations
 $\operatorname {\mathrm {Sym}}^{n-1} \rho _{\lambda } |_{G_{F'}}$
are all irreducible and automorphic, associated to a fixed cuspidal algebraic
$\operatorname {\mathrm {Sym}}^{n-1} \rho _{\lambda } |_{G_{F'}}$
are all irreducible and automorphic, associated to a fixed cuspidal algebraic
 $\Pi $
for
$\Pi $
for
 $\operatorname {\mathrm {GL}}(n)/F'$
.
$\operatorname {\mathrm {GL}}(n)/F'$
.
-
The Galois representations associated to cuspidal, regular algebraic automorphic representations of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
are not yet known to satisfy the conditions of Theorem C, but rather a weaker condition (they form a ‘very weakly compatible system’). We establish potential automorphy of symmetric powers also under this weaker condition. Once again, we refer to the statement of Theorem 7.2.1 in the main body of the paper for the precise statement that is used to deduce Theorems 7.1.1 and 7.2.3 (and therefore Theorems A and B above).
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
are not yet known to satisfy the conditions of Theorem C, but rather a weaker condition (they form a ‘very weakly compatible system’). We establish potential automorphy of symmetric powers also under this weaker condition. Once again, we refer to the statement of Theorem 7.2.1 in the main body of the paper for the precise statement that is used to deduce Theorems 7.1.1 and 7.2.3 (and therefore Theorems A and B above).
1.1 The new ideas in this paper
When
![]() $m = 1$
, Theorems A, B and C were proved in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23] (see [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Thm 1.01, Thm 1.0.2, Thm 7.1.14]). The deduction of Theorems A and B from Theorem C exactly parallels the arguments in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23], so we now focus on explaining the proof of Theorem C.
$m = 1$
, Theorems A, B and C were proved in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23] (see [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Thm 1.01, Thm 1.0.2, Thm 7.1.14]). The deduction of Theorems A and B from Theorem C exactly parallels the arguments in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23], so we now focus on explaining the proof of Theorem C.
Unsurprisingly, our arguments build on those of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23]: in particular, we prove the potential automorphy of the compatible system of symmetric powers
![]() $\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R} = \{\operatorname {\mathrm {Sym}}^{n-1} \rho _{\lambda }\}$
by checking the residual automorphy over some extension
$\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R} = \{\operatorname {\mathrm {Sym}}^{n-1} \rho _{\lambda }\}$
by checking the residual automorphy over some extension
![]() $F' / F$
and then applying an automorphy lifting theorem. We would like to highlight three new ingredients which appear here:
$F' / F$
and then applying an automorphy lifting theorem. We would like to highlight three new ingredients which appear here:
-
1. A result on generic reducedness of special fibres of weight
 $0$
(local) crystalline deformation rings (see §1.2 for a further introductory discussion). Using the local-global compatibility result of [Reference Caraiani and NewtonCN23], this leads to a new automorphy lifting theorem in the setting of arbitrary ramification (Theorem 3.2.1).
$0$
(local) crystalline deformation rings (see §1.2 for a further introductory discussion). Using the local-global compatibility result of [Reference Caraiani and NewtonCN23], this leads to a new automorphy lifting theorem in the setting of arbitrary ramification (Theorem 3.2.1). -
2. An application of a theorem of Drinfeld and Kedlaya [Reference Drinfeld and KedlayaDK17], showing generic ordinarity of families of Dwork motives (Proposition 4.2.6). This makes it possible to verify the potential residual automorphy of certain residual representations by an automorphic motive which is crystalline ordinary at some set of p-adic places.
-
3. A ‘p-q-r’ switch including a version of the ‘Harris tensor product trick’ which incorporates an additional congruence between two tensor products of compatible families. One is a tensor product of
 $\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R}$
with an induction of a character, as usual. The other is a tensor product of
$\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R}$
with an induction of a character, as usual. The other is a tensor product of
 $\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R}$
with a different auxiliary compatible family, which gives us more flexibility to realize different local properties at places related by complex conjugation. We discuss in the remainder of the introduction the need for this argument and give a more detailed sketch in §6.2 below.
$\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R}$
with a different auxiliary compatible family, which gives us more flexibility to realize different local properties at places related by complex conjugation. We discuss in the remainder of the introduction the need for this argument and give a more detailed sketch in §6.2 below.
To explain in more detail the need for these innovations, suppose we are given a compatible system
![]() $\mathcal {R} = \{\rho _{\lambda }\}$
as in the statement of Theorem C, therefore of Hodge–Tate weights
$\mathcal {R} = \{\rho _{\lambda }\}$
as in the statement of Theorem C, therefore of Hodge–Tate weights
![]() $\{0, m \}$
for some
$\{0, m \}$
for some
![]() $m \geq 1$
(and with
$m \geq 1$
(and with
![]() $m \geq 2$
if we hope to go beyond the cases treated in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23]). The general strategy for proving potential automorphy (the so-called ‘p-q switch’) is as follows:
$m \geq 2$
if we hope to go beyond the cases treated in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23]). The general strategy for proving potential automorphy (the so-called ‘p-q switch’) is as follows:
-
1. After making some CM base extension
 $H/F$
(depending on n), find an auxiliary n-dimensional compatible system
$H/F$
(depending on n), find an auxiliary n-dimensional compatible system
 $\mathcal {S} =\{ s_{\lambda }\}$
such that
$\mathcal {S} =\{ s_{\lambda }\}$
such that-
(a) For one prime
 $\lambda $
, the residual representations
$\lambda $
, the residual representations
 $\operatorname {\mathrm {Sym}}^{n-1} \overline {\rho }_{\lambda } |_{G_H}$
and
$\operatorname {\mathrm {Sym}}^{n-1} \overline {\rho }_{\lambda } |_{G_H}$
and
 $\overline {s}_{\lambda }$
coincide and moreover satisfy a number of standard ‘Taylor–Wiles’ conditions.
$\overline {s}_{\lambda }$
coincide and moreover satisfy a number of standard ‘Taylor–Wiles’ conditions. -
(b) For a second prime
 $\lambda '$
, the residual representation
$\lambda '$
, the residual representation
 $\overline {s}_{\lambda '}$
is induced from a character and is thus residually automorphic.
$\overline {s}_{\lambda '}$
is induced from a character and is thus residually automorphic. -
(c) The Hodge–Tate weights of the compatible system
 $\mathcal {S}$
coincide with those of
$\mathcal {S}$
coincide with those of
 $\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R} |_{G_H}$
.
$\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R} |_{G_H}$
.
-
-
2. Apply an automorphy lifting theorem at
 $\lambda '$
to deduce that the compatible system
$\lambda '$
to deduce that the compatible system
 $\mathcal {S}$
is automorphic. Then deduce that the residual representation
$\mathcal {S}$
is automorphic. Then deduce that the residual representation
 $\overline {s}_{\lambda }$
is automorphic and use automorphy lifting theorems again to deduce that
$\overline {s}_{\lambda }$
is automorphic and use automorphy lifting theorems again to deduce that
 $\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R} |_{G_H}$
is automorphic.
$\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R} |_{G_H}$
is automorphic.
In our setting, both of these steps cause problems, but those affecting the second step are more serious.
The issue in the first step is the requirement (1)(c) on the Hodge–Tate weights. The most natural source of compatible systems
![]() $\mathcal {S}$
are those arising from motives, and a geometrically varying family of motives cannot have Hodge–Tate weights
$\mathcal {S}$
are those arising from motives, and a geometrically varying family of motives cannot have Hodge–Tate weights
![]() $0,m,\ldots ,m(n-1)$
with
$0,m,\ldots ,m(n-1)$
with
![]() $m \ge 2$
by Griffiths transversality. (This difficulty is already present if
$m \ge 2$
by Griffiths transversality. (This difficulty is already present if
![]() $F={\mathbb Q}$
and one wants to prove the Sato–Tate conjecture for a classical modular form of weight greater than
$F={\mathbb Q}$
and one wants to prove the Sato–Tate conjecture for a classical modular form of weight greater than
![]() $2$
, such as
$2$
, such as
![]() $\Delta $
.) The now-standard resolution to this problem is to employ the ‘Harris tensor product trick’ [Reference HarrisHar09] and replace
$\Delta $
.) The now-standard resolution to this problem is to employ the ‘Harris tensor product trick’ [Reference HarrisHar09] and replace
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R}$
by
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R}$
by
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_{F}}_{G_{L}} \mathcal {X}$
for some cyclic CM extension
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_{F}}_{G_{L}} \mathcal {X}$
for some cyclic CM extension
![]() $L/F$
, where
$L/F$
, where
![]() $\mathcal {X}$
is a compatible system of algebraic Hecke characters chosen sufficiently carefully so that this new compatible system has consecutive Hodge–Tate weights. Now in the second step, one wants to prove this new compatible system is potentially automorphic (using for
$\mathcal {X}$
is a compatible system of algebraic Hecke characters chosen sufficiently carefully so that this new compatible system has consecutive Hodge–Tate weights. Now in the second step, one wants to prove this new compatible system is potentially automorphic (using for
![]() $\mathcal {S}$
a compatible system coming from the cohomology of the Dwork family). The potential automorphy of
$\mathcal {S}$
a compatible system coming from the cohomology of the Dwork family). The potential automorphy of
![]() $\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R}$
can then be deduced using cyclic base change [Reference Arthur and ClozelAC89].
$\operatorname {\mathrm {Sym}}^{n-1}\mathcal {R}$
can then be deduced using cyclic base change [Reference Arthur and ClozelAC89].
For the second step, applying an automorphy lifting theorem typically requires that the compatible systems
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_{F}}_{G_{L}} \mathcal {X}$
have ‘the same’ behaviour at places
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_{F}}_{G_{L}} \mathcal {X}$
have ‘the same’ behaviour at places
![]() $v|p$
. There are two problems with this. First, we will need an automorphy lifting theorem that applies to arbitrarily ramified F, including nonordinary representations. Second, the compatible system of characters
$v|p$
. There are two problems with this. First, we will need an automorphy lifting theorem that applies to arbitrarily ramified F, including nonordinary representations. Second, the compatible system of characters
![]() $\mathcal {X}$
has a restricted form, and in particular, its local behaviour cannot be chosen arbitrarily at a pair of conjugate places. We explain more about these difficulties and their resolution below.
$\mathcal {X}$
has a restricted form, and in particular, its local behaviour cannot be chosen arbitrarily at a pair of conjugate places. We explain more about these difficulties and their resolution below.
For context, we first recall the situation when
![]() $F={\mathbb Q}$
. For example, one might try to demand that the p-adic representations in the compatible systems
$F={\mathbb Q}$
. For example, one might try to demand that the p-adic representations in the compatible systems
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_{F}}_{G_{L}} \mathcal {X}$
are both ordinary, and indeed, it is straightforward (at least after a ramified base change) to find ordinary representations in the Dwork family and presumably difficult to understand the nonordinary representations in any generality. This means that one would like to show that many of the representations in the compatible system
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_{F}}_{G_{L}} \mathcal {X}$
are both ordinary, and indeed, it is straightforward (at least after a ramified base change) to find ordinary representations in the Dwork family and presumably difficult to understand the nonordinary representations in any generality. This means that one would like to show that many of the representations in the compatible system
![]() $\mathcal {R}$
are ordinary.
$\mathcal {R}$
are ordinary.
For a weight
![]() $2$
modular form, it is relatively easy to prove that there are infinitely many primes p for which the p-adic Galois representation is ordinary at p. However, the existence of infinitely many ordinary primes for
$2$
modular form, it is relatively easy to prove that there are infinitely many primes p for which the p-adic Galois representation is ordinary at p. However, the existence of infinitely many ordinary primes for
![]() $\Delta $
(or for any non-CM form of weight
$\Delta $
(or for any non-CM form of weight
![]() $k \ge 4$
) remains an open question, so one also has to consider the possibility that the residual representation
$k \ge 4$
) remains an open question, so one also has to consider the possibility that the residual representation
![]() $\overline {r}_{\lambda }|_{G_{F_v}}$
is locally of the form
$\overline {r}_{\lambda }|_{G_{F_v}}$
is locally of the form
![]() $\omega ^m_2 \oplus \omega ^{mp}_2$
on inertia at p. This problem was resolved for classical modular forms in [Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11], via a further study of the Dwork family; in particular, showing that certain residual representations of the shape
$\omega ^m_2 \oplus \omega ^{mp}_2$
on inertia at p. This problem was resolved for classical modular forms in [Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11], via a further study of the Dwork family; in particular, showing that certain residual representations of the shape
![]() $\operatorname {\mathrm {Sym}}^{n-1} (\omega _2 \oplus \omega ^p_2)$
arise (locally on inertia) as residual representations in that family.
$\operatorname {\mathrm {Sym}}^{n-1} (\omega _2 \oplus \omega ^p_2)$
arise (locally on inertia) as residual representations in that family.
We now consider the case of an imaginary CM field F and explain why we need an automorphy lifting theorem allowing ramification at nonordinary places. Given the automorphy lifting theorems for CM fields proved in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23], the most serious difficulty in adapting the strategy of [Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11] is that there is no way to avoid the possibility that a representation
![]() $\rho _{\lambda }$
can be simultaneously ordinary at one prime
$\rho _{\lambda }$
can be simultaneously ordinary at one prime
![]() $v|p$
and nonordinary at the complex conjugate place
$v|p$
and nonordinary at the complex conjugate place
![]() $v^c$
. (One might hope to avoid this by considering places with
$v^c$
. (One might hope to avoid this by considering places with
![]() $v=v^c$
, but then we would have to show that certain residual representations of
$v=v^c$
, but then we would have to show that certain residual representations of
![]() $G_{{\mathbb Q}_{p^2}}$
occur in the Dwork family which seemed to us to be a difficult task.) This is a problem because the automorphy lifting theorems in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23] for nonordinary representations require F to be unramified at our nonordinary prime
$G_{{\mathbb Q}_{p^2}}$
occur in the Dwork family which seemed to us to be a difficult task.) This is a problem because the automorphy lifting theorems in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23] for nonordinary representations require F to be unramified at our nonordinary prime
![]() $v^c$
, while at the ordinary prime v, we need to be able to make a highly ramified base change of (imaginary) CM fields
$v^c$
, while at the ordinary prime v, we need to be able to make a highly ramified base change of (imaginary) CM fields
![]() $F'/F$
to find an appropriate representation in the Dwork family. It is, however, impossible to arrange that such an extension of CM fields is unramified at
$F'/F$
to find an appropriate representation in the Dwork family. It is, however, impossible to arrange that such an extension of CM fields is unramified at
![]() $v^c$
and ramified at v. One of the key innovations in this paper is to prove an automorphy lifting theorem that allows us to make a ramified base change at
$v^c$
and ramified at v. One of the key innovations in this paper is to prove an automorphy lifting theorem that allows us to make a ramified base change at
![]() $v^c$
(Theorem 3.2.1). This was done in the two-dimensional case in [Reference Caraiani and NewtonCN23]; we discuss the difficulties in extending this result to higher dimensions and how we overcome them in Section 1.2 below. Note that, even when making a ramified base change, it is still important for us to keep track of the inertial type of residual representations in the Dwork family in order to show that the representations of interest are connected in the deformation space.
$v^c$
(Theorem 3.2.1). This was done in the two-dimensional case in [Reference Caraiani and NewtonCN23]; we discuss the difficulties in extending this result to higher dimensions and how we overcome them in Section 1.2 below. Note that, even when making a ramified base change, it is still important for us to keep track of the inertial type of residual representations in the Dwork family in order to show that the representations of interest are connected in the deformation space.
There turns out to be one final wrinkle, where the second problem mentioned above arises. The p-adic representations in our compatible system
![]() ${\mathcal S}$
will satisfy one of two, mutually exclusive, local conditions at each p-adic place: they are crystalline at p and are either ordinary or are (on the same component of a local crystalline deformation ring as) a symmetric power of an induction of a Lubin–Tate character of
${\mathcal S}$
will satisfy one of two, mutually exclusive, local conditions at each p-adic place: they are crystalline at p and are either ordinary or are (on the same component of a local crystalline deformation ring as) a symmetric power of an induction of a Lubin–Tate character of
![]() $G_{{\mathbb Q}_{p^2}}$
. It turns out that we cannot always arrange for a tensor product
$G_{{\mathbb Q}_{p^2}}$
. It turns out that we cannot always arrange for a tensor product
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_F}_{G_L} \mathcal {X}$
to have local p-adic representations of this shape. The problem is that algebraic Hecke characters have a very restricted form, and the fact that F is an imaginary CM field implies that a suitable choice of
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} \otimes \operatorname {\mathrm {Ind}}^{G_F}_{G_L} \mathcal {X}$
to have local p-adic representations of this shape. The problem is that algebraic Hecke characters have a very restricted form, and the fact that F is an imaginary CM field implies that a suitable choice of
![]() $\mathcal {X}$
will exist only if
$\mathcal {X}$
will exist only if
![]() $\rho _{\lambda }$
is either both ordinary or nonordinary at each pair of places
$\rho _{\lambda }$
is either both ordinary or nonordinary at each pair of places
![]() $\{v,v^c\}$
permuted by complex conjugation in
$\{v,v^c\}$
permuted by complex conjugation in
![]() $\operatorname {\mathrm {Gal}}(F/F^{+})$
.
$\operatorname {\mathrm {Gal}}(F/F^{+})$
.
Our solution is to instead consider tensor products of the form
![]() $(\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R})\otimes {\mathcal R}_{\mathrm {aux}}$
, where
$(\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R})\otimes {\mathcal R}_{\mathrm {aux}}$
, where
![]() ${\mathcal R}_{\mathrm {aux}}$
is a compatible system coming from (part of) the cohomology of the Dwork hypersurface [Reference QianQia23]. We will be able to choose
${\mathcal R}_{\mathrm {aux}}$
is a compatible system coming from (part of) the cohomology of the Dwork hypersurface [Reference QianQia23]. We will be able to choose
![]() ${\mathcal R}_{\mathrm {aux}}$
so that one of the local conditions mentioned in the previous paragraph will be satisfied by
${\mathcal R}_{\mathrm {aux}}$
so that one of the local conditions mentioned in the previous paragraph will be satisfied by
![]() ${\mathcal S}_{\mathrm {aux}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
at each p-adic place. It is now no longer possible to directly deduce the potential automorphy of
${\mathcal S}_{\mathrm {aux}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
at each p-adic place. It is now no longer possible to directly deduce the potential automorphy of
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R}$
from the potential automorphy of this product. This is not necessary to prove the Ramanujan conjecture – already the automorphy of this tensor product combined with the Jacquet–Shalika bounds (and the fact that
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R}$
from the potential automorphy of this product. This is not necessary to prove the Ramanujan conjecture – already the automorphy of this tensor product combined with the Jacquet–Shalika bounds (and the fact that
![]() $\mathcal {R}_{\mathrm {aux}}$
is pure) is enough to deduce purity – but it is necessary to prove the Sato–Tate conjecture. However, once the potential automorphy of
$\mathcal {R}_{\mathrm {aux}}$
is pure) is enough to deduce purity – but it is necessary to prove the Sato–Tate conjecture. However, once the potential automorphy of
![]() ${\mathcal S}_{\mathrm {aux}}$
is established, we can (having chosen
${\mathcal S}_{\mathrm {aux}}$
is established, we can (having chosen
![]() ${\mathcal R}_{\mathrm {aux}}$
carefully to begin with) find a third compatible system
${\mathcal R}_{\mathrm {aux}}$
carefully to begin with) find a third compatible system
![]() ${\mathcal R}_{\mathrm {CM}}$
such that
${\mathcal R}_{\mathrm {CM}}$
such that
![]() ${\mathcal S}_{\mathrm {aux}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
and
${\mathcal S}_{\mathrm {aux}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
and
![]() ${\mathcal S}_{\mathrm {CM}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {CM}}$
are residually the same at a third prime r, and
${\mathcal S}_{\mathrm {CM}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {CM}}$
are residually the same at a third prime r, and
![]() ${\mathcal R}_{\mathrm {CM}}$
is induced from a character. Even though we do not have any control over the r-adic representation associated to
${\mathcal R}_{\mathrm {CM}}$
is induced from a character. Even though we do not have any control over the r-adic representation associated to
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
locally at
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
locally at
![]() $v|r$
, the fact that it occurs as the same tensor factor in the r-adic representations of both
$v|r$
, the fact that it occurs as the same tensor factor in the r-adic representations of both
![]() ${\mathcal S}_{\mathrm {aux}}$
and
${\mathcal S}_{\mathrm {aux}}$
and
![]() ${\mathcal S}_{\mathrm {CM}}$
means we can still put ourselves in a situation where both r-adic Galois representations lie on the same component of a local deformation ring at
${\mathcal S}_{\mathrm {CM}}$
means we can still put ourselves in a situation where both r-adic Galois representations lie on the same component of a local deformation ring at
![]() $v|r$
. From this p-q-r switch, we can show that
$v|r$
. From this p-q-r switch, we can show that
![]() ${\mathcal S}_{\mathrm {CM}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {CM}}$
is potentially automorphic, from which we deduce that
${\mathcal S}_{\mathrm {CM}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {CM}}$
is potentially automorphic, from which we deduce that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is potentially automorphic.
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is potentially automorphic.
One might also ask whether for general CM fields F, one can drop the hypothesis that
![]() ${\mathcal R}$
has parallel weight. The difficulty in doing so is as follows: in order to pass from
${\mathcal R}$
has parallel weight. The difficulty in doing so is as follows: in order to pass from
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R}$
to a compatible system with consecutive Hodge–Tate weights, one needs to tensor this compatible system with a second compatible system with certain prescribed local properties. If
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R}$
to a compatible system with consecutive Hodge–Tate weights, one needs to tensor this compatible system with a second compatible system with certain prescribed local properties. If
![]() ${\mathcal R}$
does not have parallel weight, this auxiliary compatible system cannot have consecutive Hodge–Tate weights and, for reasons explained above, also cannot be induced from a compatible system of characters. It is very hard to construct such compatible systems because of the constraints on families of geometric local systems imposed by Griffiths transversality. The existence of even a single regular algebraic cuspidal automorphic representation for
${\mathcal R}$
does not have parallel weight, this auxiliary compatible system cannot have consecutive Hodge–Tate weights and, for reasons explained above, also cannot be induced from a compatible system of characters. It is very hard to construct such compatible systems because of the constraints on families of geometric local systems imposed by Griffiths transversality. The existence of even a single regular algebraic cuspidal automorphic representation for
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
for some CM field F which is neither of parallel weight
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
for some CM field F which is neither of parallel weight
![]() $2$
, nor of CM type, nor arising from base change from the totally real subfield
$2$
, nor of CM type, nor arising from base change from the totally real subfield
![]() $F^{+}$
was only found (by a computation) in [Reference Calegari and MazurCM09, Lemma 8.11(2)] (see also [Reference Rahm and S¸engünRS13]).
$F^{+}$
was only found (by a computation) in [Reference Calegari and MazurCM09, Lemma 8.11(2)] (see also [Reference Rahm and S¸engünRS13]).
1.2 Ihara avoidance and the Emerton–Gee stack
There are two main difficulties in proving automorphy lifting liftings for p-adic representations with p ramified in F. One is having local–global compatibility theorems at the places dividing p; this was resolved in the recent work of Caraiani–Newton [Reference Caraiani and NewtonCN23]. The other difficulty was alluded to above: the usual Taylor–Wiles method for automorphy lifting only allows us to deduce the automorphy of a p-adic representation r from the automorphy of a congruent representation
![]() $r'$
if we know that for all finite places v, the representations
$r'$
if we know that for all finite places v, the representations
![]() $r|_{G_{F_v}}$
and
$r|_{G_{F_v}}$
and
![]() $r'|_{G_{F_v}}$
are ‘connected’, in the sense that they lie on the same component of the appropriate local deformation ring.
$r'|_{G_{F_v}}$
are ‘connected’, in the sense that they lie on the same component of the appropriate local deformation ring.
As we have sketched above, in the particular cases that we consider in this paper, we have arranged this property at the places
![]() $v|p$
by considering the ordinary and nonordinary cases separately. (It was this construction that required us to pass to a situation where p is highly ramified in F.) We are not, however, able to arrange that our representations are connected at all the places
$v|p$
by considering the ordinary and nonordinary cases separately. (It was this construction that required us to pass to a situation where p is highly ramified in F.) We are not, however, able to arrange that our representations are connected at all the places
![]() $v\nmid p$
. Fortunately, Taylor [Reference TaylorTay08] found a way to prove automorphy lifting theorems when the representations fail to be connected at some places
$v\nmid p$
. Fortunately, Taylor [Reference TaylorTay08] found a way to prove automorphy lifting theorems when the representations fail to be connected at some places
![]() $v\nmid p$
, using his so-called ‘Ihara avoidance’ argument. This argument makes an ingenious use of two different local deformation problems at places
$v\nmid p$
, using his so-called ‘Ihara avoidance’ argument. This argument makes an ingenious use of two different local deformation problems at places
![]() $v\nmid p$
, which are congruent modulo p, and relates two corresponding patched modules of automorphic forms. The key point which makes this argument possible is to work with local deformation rings having the following ‘unique generalization’ property: any generic point of their special fibre has a unique generalization to the generic fibre. More geometrically, we need to avoid having two distinct irreducible components in characteristic zero which specialize to a common irreducible component in the special fibre.
$v\nmid p$
, which are congruent modulo p, and relates two corresponding patched modules of automorphic forms. The key point which makes this argument possible is to work with local deformation rings having the following ‘unique generalization’ property: any generic point of their special fibre has a unique generalization to the generic fibre. More geometrically, we need to avoid having two distinct irreducible components in characteristic zero which specialize to a common irreducible component in the special fibre.
In order to apply this argument, one also needs the unique generalization property for the deformation rings at the places
![]() $v|p$
. This was previously only known in the Fontaine–Laffaille and ordinary contexts, in which case the crystalline deformation rings can be understood completely explicitly (and in the former case, there is even a unique irreducible component). (This problem was sidestepped to some extent in [Reference Barnet-Lamb, Gee and GeraghtyBLGG11, Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14], but the approach there combines the Ihara avoidance argument with the Khare–Wintenberger lifting argument to produce characteristic zero lifts of residual representations of the prescribed weight and level. In our
$v|p$
. This was previously only known in the Fontaine–Laffaille and ordinary contexts, in which case the crystalline deformation rings can be understood completely explicitly (and in the former case, there is even a unique irreducible component). (This problem was sidestepped to some extent in [Reference Barnet-Lamb, Gee and GeraghtyBLGG11, Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14], but the approach there combines the Ihara avoidance argument with the Khare–Wintenberger lifting argument to produce characteristic zero lifts of residual representations of the prescribed weight and level. In our
![]() $\ell _0> 0$
situation (in the language of [Reference Calegari and GeraghtyCG18]), such lifts do not always exist.)
$\ell _0> 0$
situation (in the language of [Reference Calegari and GeraghtyCG18]), such lifts do not always exist.)
One way to establish the unique generalization property (when it holds) would be to explicitly compute the irreducible components of the generic fibres of the deformation rings, but this appears to be hopeless for crystalline deformation rings in any generality. However, as was already observed in [Reference TaylorTay08, §3] in the case
![]() $v\nmid p$
, an alternative approach is to consider an appropriate moduli stack of Galois representations, for which the deformation rings are versal rings at closed points. One shows that its special fibre is generically reduced (or even generically smooth) – for example, by showing that the deformation rings for generic choices of the residual Galois representation are formally smooth. It then follows that for an arbitrary residual representation, the special fibres of the (
$v\nmid p$
, an alternative approach is to consider an appropriate moduli stack of Galois representations, for which the deformation rings are versal rings at closed points. One shows that its special fibre is generically reduced (or even generically smooth) – for example, by showing that the deformation rings for generic choices of the residual Galois representation are formally smooth. It then follows that for an arbitrary residual representation, the special fibres of the (
![]() ${\mathbb Z}_p$
-flat quotients of) the deformation rings are generically reduced, which implies the unique generalization property. (While [Reference TaylorTay08, §3] does not explicitly work with moduli stacks of Galois representations, [Reference TaylorTay08, Lem. 3.2] is easily reformulated in these terms, and while [Reference TaylorTay08, Prop. 3.1(3)] does not explicitly state that the
${\mathbb Z}_p$
-flat quotients of) the deformation rings are generically reduced, which implies the unique generalization property. (While [Reference TaylorTay08, §3] does not explicitly work with moduli stacks of Galois representations, [Reference TaylorTay08, Lem. 3.2] is easily reformulated in these terms, and while [Reference TaylorTay08, Prop. 3.1(3)] does not explicitly state that the
![]() ${\mathbb Z}_p$
-flat quotient of the deformation ring has generically reduced special fibre, this follows from the argument, as in [Reference Allen, Newton and ThorneANT20, Prop. 3.1].)
${\mathbb Z}_p$
-flat quotient of the deformation ring has generically reduced special fibre, this follows from the argument, as in [Reference Allen, Newton and ThorneANT20, Prop. 3.1].)
The unique generalization property has subsequently been used by Thorne in a context with
![]() $v\nmid p$
in the proof of [Reference ThorneTho12, Thm. 8.6] (in order to avoid any additional hypotheses when introducing an auxiliary prime to make the level structure sufficiently small), and in the case that
$v\nmid p$
in the proof of [Reference ThorneTho12, Thm. 8.6] (in order to avoid any additional hypotheses when introducing an auxiliary prime to make the level structure sufficiently small), and in the case that
![]() $v|p$
by Caraiani–Newton [Reference Caraiani and NewtonCN23], who used the results of [Reference Caraiani, Emerton, Gee and SavittCEGS22a], which establish the generic reducedness of the special fibres of the crystalline deformation rings in the 2-dimensional (tamely potentially) Barsotti–Tate case, by an analysis of the corresponding Emerton–Gee stacks.
$v|p$
by Caraiani–Newton [Reference Caraiani and NewtonCN23], who used the results of [Reference Caraiani, Emerton, Gee and SavittCEGS22a], which establish the generic reducedness of the special fibres of the crystalline deformation rings in the 2-dimensional (tamely potentially) Barsotti–Tate case, by an analysis of the corresponding Emerton–Gee stacks.
Unfortunately, an (unconditional) argument with the Breuil–Mézard conjecture shows that generic reducedness is extremely rare when
![]() $v|p$
(see Remark 2.5.6). We are, however, able to prove the following theorem.
$v|p$
(see Remark 2.5.6). We are, however, able to prove the following theorem.
Theorem D (Theorem 2.5.5).
Suppose that
![]() $p>n$
, that
$p>n$
, that
![]() $K/{\mathbb Q}_p$
and
$K/{\mathbb Q}_p$
and
![]() ${\mathbb F}/{\mathbb F}_p$
are finite extensions, and that
${\mathbb F}/{\mathbb F}_p$
are finite extensions, and that
![]() $\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_n({\mathbb F})$
is a continuous representation. Let
$\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_n({\mathbb F})$
is a continuous representation. Let
![]() $R^{\mathrm {crys},0}$
be the universal lifting ring for crystalline lifts of
$R^{\mathrm {crys},0}$
be the universal lifting ring for crystalline lifts of
![]() $\overline {\rho }$
of parallel Hodge–Tate weights
$\overline {\rho }$
of parallel Hodge–Tate weights
![]() $0,1,\dots ,n-1$
. Then the special fibre of
$0,1,\dots ,n-1$
. Then the special fibre of
![]() $\operatorname {\mathrm {Spec}} R^{\mathrm {crys},0}$
is generically reduced.
$\operatorname {\mathrm {Spec}} R^{\mathrm {crys},0}$
is generically reduced.
We refer the reader to the introduction to Section 2 for a detailed overview of the proof of Theorem D, which, as above, relies on proving the corresponding property of the relevant Emerton–Gee stacks [Reference Emerton and GeeEG23] (whose versal rings are the crystalline lifting rings). The irreducible components of the special fibres of these stacks were described in [Reference Emerton and GeeEG23], and we prove our result by combining this description with a computation of extensions of rank
![]() $1$
Breuil modules. An amusing feature of this argument is that we prove a result about the deformation rings of arbitrary n-dimensional mod p representations by reducing to a calculation for reducible
$1$
Breuil modules. An amusing feature of this argument is that we prove a result about the deformation rings of arbitrary n-dimensional mod p representations by reducing to a calculation for reducible
![]() $2$
-dimensional representations.
$2$
-dimensional representations.
1.3 Bianchi modular forms
Let us specialize to the case when
![]() $F/{\mathbb Q}$
is an imaginary quadratic field. Let
$F/{\mathbb Q}$
is an imaginary quadratic field. Let
![]() $\pi $
be a regular algebraic cuspidal automorphic representation of
$\pi $
be a regular algebraic cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. Let
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. Let
![]() $\chi $
be the central character of
$\chi $
be the central character of
![]() $\pi $
. By definition, the representation
$\pi $
. By definition, the representation
![]() $\pi $
occurs in
$\pi $
occurs in
![]() $L^2_{\mathrm {cusp}}(\operatorname {\mathrm {GL}}_2(F) \backslash \operatorname {\mathrm {GL}}_2(\mathbf {A}_F))$
. Let
$L^2_{\mathrm {cusp}}(\operatorname {\mathrm {GL}}_2(F) \backslash \operatorname {\mathrm {GL}}_2(\mathbf {A}_F))$
. Let
![]() $\mathfrak {g}$
be the Lie algebra of
$\mathfrak {g}$
be the Lie algebra of
![]() $\operatorname {\mathrm {GL}}_2({\mathbb C})$
as a real group. The assumption that
$\operatorname {\mathrm {GL}}_2({\mathbb C})$
as a real group. The assumption that
![]() $\pi $
is regular algebraic is equivalent to the condition that the infinitesimal character of
$\pi $
is regular algebraic is equivalent to the condition that the infinitesimal character of
![]() $\pi _{\infty }$
is the same as
$\pi _{\infty }$
is the same as
![]() $V^{\vee }$
for an algebraic representation V of
$V^{\vee }$
for an algebraic representation V of
![]() $\mathrm {Res}_{F/{\mathbb Q}} \operatorname {\mathrm {GL}}_2$
. The assumption that
$\mathrm {Res}_{F/{\mathbb Q}} \operatorname {\mathrm {GL}}_2$
. The assumption that
![]() $\pi $
is cuspidal places a restriction on V corresponding to the fact (noted earlier) that such
$\pi $
is cuspidal places a restriction on V corresponding to the fact (noted earlier) that such
![]() $\pi $
has parallel weight; the corresponding representations are parametrized (up to twist) by an integer
$\pi $
has parallel weight; the corresponding representations are parametrized (up to twist) by an integer
![]() $k \ge 2$
, where
$k \ge 2$
, where
![]() $k=2$
corresponds to the case when V is trivial. This choice of k determines the action of
$k=2$
corresponds to the case when V is trivial. This choice of k determines the action of
![]() $Z(\mathfrak {g})$
on
$Z(\mathfrak {g})$
on
![]() $\pi _{\infty }$
, and by taking functions which are suitable eigenvectors under
$\pi _{\infty }$
, and by taking functions which are suitable eigenvectors under
![]() $Z(\mathfrak {g})$
, we may arrive at certain vector valued Hecke eigenfunctions
$Z(\mathfrak {g})$
, we may arrive at certain vector valued Hecke eigenfunctions
![]() $\Phi $
on
$\Phi $
on
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
with Fourier expansions ([Reference WilliamsWil17, §1.2], [Reference HidaHid94, §6])
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
with Fourier expansions ([Reference WilliamsWil17, §1.2], [Reference HidaHid94, §6])
 $$ \begin{align*}f \left[ \left( \begin{matrix} t & z \\ 0 & 1 \end{matrix} \right) \right] = |t|_F \sum_{\alpha \in F^{\times}} c(\alpha t \delta_F,f) W(\alpha t_{\infty}) e_F(\alpha z),\end{align*} $$
$$ \begin{align*}f \left[ \left( \begin{matrix} t & z \\ 0 & 1 \end{matrix} \right) \right] = |t|_F \sum_{\alpha \in F^{\times}} c(\alpha t \delta_F,f) W(\alpha t_{\infty}) e_F(\alpha z),\end{align*} $$
where
![]() $\delta = \delta _F$
is the different,
$\delta = \delta _F$
is the different,
![]() $\alpha t \delta $
can be interpreted as a fractional ideal of
$\alpha t \delta $
can be interpreted as a fractional ideal of
![]() $\mathcal {O}_F$
,
$\mathcal {O}_F$
,
![]() $c(I,f)$
is a Fourier coefficient which vanishes unless
$c(I,f)$
is a Fourier coefficient which vanishes unless
![]() $I \subset \mathcal {O}_F$
and which we may assume is normalized so that
$I \subset \mathcal {O}_F$
and which we may assume is normalized so that
![]() $c(\mathcal {O}_F,f) = 1$
, W is an explicit Whittaker function which is vector valued in some explicit representation of
$c(\mathcal {O}_F,f) = 1$
, W is an explicit Whittaker function which is vector valued in some explicit representation of
![]() $\operatorname {\mathrm {SU}}(2)$
depending on k, and
$\operatorname {\mathrm {SU}}(2)$
depending on k, and
![]() $e_F$
is an explicit additive character of
$e_F$
is an explicit additive character of
![]() $F \backslash \mathbf {A}_F$
. This has a direct translation into more classical language and can be interpreted as a collection of
$F \backslash \mathbf {A}_F$
. This has a direct translation into more classical language and can be interpreted as a collection of
![]() $h_F$
functions on a finite union of hyperbolic spaces
$h_F$
functions on a finite union of hyperbolic spaces
![]() $\mathbf {H}^3$
. The explicit functions f (either adelically or classically) are known as Bianchi modular forms. For a normalized Bianchi eigenform f of weight k and level prime to
$\mathbf {H}^3$
. The explicit functions f (either adelically or classically) are known as Bianchi modular forms. For a normalized Bianchi eigenform f of weight k and level prime to
![]() $\mathfrak {p}$
, Theorem 7.1.1 implies the following bound:
$\mathfrak {p}$
, Theorem 7.1.1 implies the following bound:
Theorem E. Let f be a cuspidal Bianchi modular eigenform of level
![]() $\mathfrak {n}$
and weight k. Let
$\mathfrak {n}$
and weight k. Let
![]() $\mathfrak {p}$
be a prime ideal of
$\mathfrak {p}$
be a prime ideal of
![]() $\mathcal {O}_F$
not dividing
$\mathcal {O}_F$
not dividing
![]() $\mathfrak {n}$
. Then
$\mathfrak {n}$
. Then
This connects our theorem with the more classical version of the Ramanujan conjecture for modular forms [Reference DeligneDel71] as discussed earlier in the introduction.
The eigenvalues
![]() $c(\mathfrak {p},f)$
associated to f have a second interpretation in terms of the cohomology of arithmetic groups and arithmetic hyperbolic
$c(\mathfrak {p},f)$
associated to f have a second interpretation in terms of the cohomology of arithmetic groups and arithmetic hyperbolic
![]() $3$
-manifolds. The algebraic representations V of
$3$
-manifolds. The algebraic representations V of
![]() $\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_2$
are all, up to twist, given on real points
$\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_2$
are all, up to twist, given on real points
![]() $\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_2({\mathbb R}) = \operatorname {\mathrm {GL}}_2({\mathbb C})$
by the representations
$\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_2({\mathbb R}) = \operatorname {\mathrm {GL}}_2({\mathbb C})$
by the representations
![]() $ \operatorname {\mathrm {Sym}}^{k-2} {\mathbb C}^2 \otimes \overline {\operatorname {\mathrm {Sym}}^{l-2} {\mathbb C}^2}$
for a pair of integers
$ \operatorname {\mathrm {Sym}}^{k-2} {\mathbb C}^2 \otimes \overline {\operatorname {\mathrm {Sym}}^{l-2} {\mathbb C}^2}$
for a pair of integers
![]() $k, l \geq 2$
. Let
$k, l \geq 2$
. Let
![]() $\mathfrak {n} \leq \mathcal {O}_F$
be a nonzero ideal. Having fixed k and l, we can form the group cohomology
$\mathfrak {n} \leq \mathcal {O}_F$
be a nonzero ideal. Having fixed k and l, we can form the group cohomology
of the standard congruence subgroup
![]() $\Gamma _1(\mathfrak {n}) \leq \operatorname {\mathrm {GL}}_2(\mathcal {O}_F)$
. Then H is a finite-dimensional
$\Gamma _1(\mathfrak {n}) \leq \operatorname {\mathrm {GL}}_2(\mathcal {O}_F)$
. Then H is a finite-dimensional
![]() ${\mathbb C}$
-vector space. Let
${\mathbb C}$
-vector space. Let
![]() $H_{\mathrm {par}} \subset H$
denote the subgroup consisting of classes which vanish under the restriction of H to
$H_{\mathrm {par}} \subset H$
denote the subgroup consisting of classes which vanish under the restriction of H to
![]() $H^1(P, \operatorname {\mathrm {Sym}}^{k-2} {\mathbb C}^2 \otimes \overline {\operatorname {\mathrm {Sym}}^{l-2} {\mathbb C}^2})$
for any parabolic subgroup
$H^1(P, \operatorname {\mathrm {Sym}}^{k-2} {\mathbb C}^2 \otimes \overline {\operatorname {\mathrm {Sym}}^{l-2} {\mathbb C}^2})$
for any parabolic subgroup
![]() $P \subset \Gamma _1(\mathfrak {n})$
. More geometrically, one can interpret H as the cohomology of a local system on the Bianchi manifold
$P \subset \Gamma _1(\mathfrak {n})$
. More geometrically, one can interpret H as the cohomology of a local system on the Bianchi manifold
![]() $Y_1(\mathfrak {n}) = \mathbf {H}^3/\Gamma _1(\mathfrak {n})$
. If
$Y_1(\mathfrak {n}) = \mathbf {H}^3/\Gamma _1(\mathfrak {n})$
. If
![]() $X_1(\mathfrak {n})$
is the Borel–Serre compactification of
$X_1(\mathfrak {n})$
is the Borel–Serre compactification of
![]() $Y_1(\mathfrak {n})$
, then parabolic cohomology consists of classes which are trivial on the boundary
$Y_1(\mathfrak {n})$
, then parabolic cohomology consists of classes which are trivial on the boundary
![]() $X_1(\mathfrak {n}) \smallsetminus Y_1(\mathfrak {n})$
; this boundary may be identified (when
$X_1(\mathfrak {n}) \smallsetminus Y_1(\mathfrak {n})$
; this boundary may be identified (when
![]() $\Gamma _1(\mathfrak {n})$
is torsion free) with a finite disjoint union of complex tori. The spaces H and
$\Gamma _1(\mathfrak {n})$
is torsion free) with a finite disjoint union of complex tori. The spaces H and
![]() $H_{\mathrm {par}}$
are equipped with a commuting family of linear operators, the unramified Hecke operators
$H_{\mathrm {par}}$
are equipped with a commuting family of linear operators, the unramified Hecke operators
![]() $T_{\mathfrak {p}}$
, indexed by the principal ideals
$T_{\mathfrak {p}}$
, indexed by the principal ideals
![]() $\mathfrak {p} \leq \mathcal {O}_F$
not dividing
$\mathfrak {p} \leq \mathcal {O}_F$
not dividing
![]() $\mathfrak {n}$
. More precisely, if one writes
$\mathfrak {n}$
. More precisely, if one writes
![]() $\mathfrak {p} = (\pi )$
, then the group
$\mathfrak {p} = (\pi )$
, then the group
![]() $A \Gamma _1(\mathfrak {n}) A^{-1} \cap \Gamma _1(\mathfrak {n}) = \Gamma _1(\mathfrak {n},\mathfrak {p})$
has finite index in
$A \Gamma _1(\mathfrak {n}) A^{-1} \cap \Gamma _1(\mathfrak {n}) = \Gamma _1(\mathfrak {n},\mathfrak {p})$
has finite index in
![]() $\Gamma _1(\mathfrak {n})$
, where
$\Gamma _1(\mathfrak {n})$
, where
 $$ \begin{align*}A = \left(\begin{matrix} \pi & 0 \\ 0 & 1 \end{matrix} \right);\end{align*} $$
$$ \begin{align*}A = \left(\begin{matrix} \pi & 0 \\ 0 & 1 \end{matrix} \right);\end{align*} $$
the map
![]() $T_{\mathfrak {p}}$
is induced by composing (in a suitable order) a restriction map, a conjugation by A map, and a trace map, respectively. Note that the existence of (a large family of) such operators comes from the fact that
$T_{\mathfrak {p}}$
is induced by composing (in a suitable order) a restriction map, a conjugation by A map, and a trace map, respectively. Note that the existence of (a large family of) such operators comes from the fact that
![]() $\Gamma = \operatorname {\mathrm {GL}}_2(\mathcal {O}_F)$
has infinite index inside its commensurator in
$\Gamma = \operatorname {\mathrm {GL}}_2(\mathcal {O}_F)$
has infinite index inside its commensurator in
![]() $\operatorname {\mathrm {GL}}_2(F)$
; as shown by Margulis [Reference MargulisMar91, Thm. IX.1.13], this characterizes the arithmeticity of
$\operatorname {\mathrm {GL}}_2(F)$
; as shown by Margulis [Reference MargulisMar91, Thm. IX.1.13], this characterizes the arithmeticity of
![]() $\Gamma $
.
$\Gamma $
.
In order to obtain an action of
![]() $T_{\mathfrak {p}}$
for more general prime ideals
$T_{\mathfrak {p}}$
for more general prime ideals
![]() $\mathfrak {p}$
, one needs to replace
$\mathfrak {p}$
, one needs to replace
![]() $Y_1(\mathfrak {n})$
by a disconnected union of
$Y_1(\mathfrak {n})$
by a disconnected union of
![]() $h_F$
commensurable arithmetic hyperbolic manifolds
$h_F$
commensurable arithmetic hyperbolic manifolds
![]() $Y_1(\mathfrak {n};\mathfrak {a}) = \mathbf {H}/\Gamma _1(\mathfrak {n};\mathfrak {a})$
indexed by ideals
$Y_1(\mathfrak {n};\mathfrak {a}) = \mathbf {H}/\Gamma _1(\mathfrak {n};\mathfrak {a})$
indexed by ideals
![]() $\mathfrak {a}$
in the class group
$\mathfrak {a}$
in the class group
![]() $\mathrm {Cl}(\mathcal {O}_F)$
of F prime to
$\mathrm {Cl}(\mathcal {O}_F)$
of F prime to
![]() $\mathfrak {n}$
, and where
$\mathfrak {n}$
, and where
![]() $Y_1(\mathfrak {n};\mathcal {O}_F) = Y_1(\mathfrak {n})$
. The group
$Y_1(\mathfrak {n};\mathcal {O}_F) = Y_1(\mathfrak {n})$
. The group
![]() $\Gamma (\mathcal {O}_F;\mathfrak {a})$
is the automorphism group of the
$\Gamma (\mathcal {O}_F;\mathfrak {a})$
is the automorphism group of the
![]() $\mathcal {O}_F$
-module
$\mathcal {O}_F$
-module
![]() $\mathcal {O}_F \oplus \mathfrak {a}$
, which consists explicitly of matrices of the form
$\mathcal {O}_F \oplus \mathfrak {a}$
, which consists explicitly of matrices of the form
 $$ \begin{align*}\left( \begin{matrix} \mathcal{O}_F & \mathfrak{a}^{-1} \\ \mathfrak{a} & \mathcal{O}_F \end{matrix} \right) \cap \operatorname{\mathrm{GL}}_2(F)\end{align*} $$
$$ \begin{align*}\left( \begin{matrix} \mathcal{O}_F & \mathfrak{a}^{-1} \\ \mathfrak{a} & \mathcal{O}_F \end{matrix} \right) \cap \operatorname{\mathrm{GL}}_2(F)\end{align*} $$
with determinant in
![]() $\mathcal {O}^{\times }_F$
. The space
$\mathcal {O}^{\times }_F$
. The space
![]() $H_{\mathrm {par}}$
vanishes unless
$H_{\mathrm {par}}$
vanishes unless
![]() $k = l$
([Reference HarderHar87, 3.6.1]), which we now assume. If
$k = l$
([Reference HarderHar87, 3.6.1]), which we now assume. If
![]() $h_F = 1$
, the Eichler–Shimura isomorphism ([Reference HarderHar87, §3.6]) gives a map from Bianchi cuspidal modular eigenforms f of weight k as described above and cohomology classes
$h_F = 1$
, the Eichler–Shimura isomorphism ([Reference HarderHar87, §3.6]) gives a map from Bianchi cuspidal modular eigenforms f of weight k as described above and cohomology classes
![]() $\eta _f \in H_{\mathrm {par}}$
which are simultaneous eigenforms for all the Hecke operators. Moreover, the eigenvalues of
$\eta _f \in H_{\mathrm {par}}$
which are simultaneous eigenforms for all the Hecke operators. Moreover, the eigenvalues of
![]() $T_{\mathfrak {p}}$
on
$T_{\mathfrak {p}}$
on
![]() $\eta _f$
are given exactly by
$\eta _f$
are given exactly by
![]() $c(\mathfrak {p},f)$
. If
$c(\mathfrak {p},f)$
. If
![]() $h_F> 1$
, one must replace H and
$h_F> 1$
, one must replace H and
![]() $H_{\mathrm {par}}$
by the direct sum of the corresponding cohomology groups over
$H_{\mathrm {par}}$
by the direct sum of the corresponding cohomology groups over
![]() $Y_1(\mathfrak {n};\mathfrak {a})$
for
$Y_1(\mathfrak {n};\mathfrak {a})$
for
![]() $\mathfrak {a} \in \mathrm {Cl}(\mathcal {O}_F)$
. Theorem E now implies the following:
$\mathfrak {a} \in \mathrm {Cl}(\mathcal {O}_F)$
. Theorem E now implies the following:
Theorem F. Let
![]() $\mathfrak {p}$
be a principal prime ideal of
$\mathfrak {p}$
be a principal prime ideal of
![]() $\mathcal {O}_F$
not dividing
$\mathcal {O}_F$
not dividing
![]() $\mathfrak {n}$
, and let
$\mathfrak {n}$
, and let
![]() $a_{\mathfrak {p}}$
be an eigenvalue of
$a_{\mathfrak {p}}$
be an eigenvalue of
![]() $T_{\mathfrak {p}}$
on
$T_{\mathfrak {p}}$
on
![]() $H_{\mathrm {par}}$
. Then
$H_{\mathrm {par}}$
. Then
![]() $| a_{\mathfrak {p}} | \leq 2 N(\mathfrak {p})^{(k-1)/2}$
.
$| a_{\mathfrak {p}} | \leq 2 N(\mathfrak {p})^{(k-1)/2}$
.
These explicit formulations of our theorems can be generalized in a number of ways. Remaining in the setting of arithmetic hyperbolic
![]() $3$
-manifolds (or orbifolds), we can replace
$3$
-manifolds (or orbifolds), we can replace
![]() $\operatorname {\mathrm {GL}}_2(\mathcal {O}_F)$
by a congruence subgroup
$\operatorname {\mathrm {GL}}_2(\mathcal {O}_F)$
by a congruence subgroup
![]() $\Gamma $
of the norm one units in a maximal order
$\Gamma $
of the norm one units in a maximal order
![]() $\mathcal {O}$
of a division algebra
$\mathcal {O}$
of a division algebra
![]() $D/F$
, where
$D/F$
, where
![]() $F \hookrightarrow {\mathbb C}$
is a number field with one complex place and D is definite at all real places of F. When
$F \hookrightarrow {\mathbb C}$
is a number field with one complex place and D is definite at all real places of F. When
![]() $[F:{\mathbb Q}] = 2$
, we obtain the Bianchi manifolds as above (when
$[F:{\mathbb Q}] = 2$
, we obtain the Bianchi manifolds as above (when
![]() $D/F$
is split) but also certain compact hyperbolic arithmetic three manifolds; our theorem applies equally well in the latter case (note that
$D/F$
is split) but also certain compact hyperbolic arithmetic three manifolds; our theorem applies equally well in the latter case (note that
![]() $H=H_{\mathrm {par}}$
in this setting). On the other hand, suppose that F has at least one real place; for example, take
$H=H_{\mathrm {par}}$
in this setting). On the other hand, suppose that F has at least one real place; for example, take
![]() $F = \mathbf {Q}[\theta ]/(\theta ^3 - \theta + 1)$
, let
$F = \mathbf {Q}[\theta ]/(\theta ^3 - \theta + 1)$
, let
![]() $k = 2$
, and let
$k = 2$
, and let
![]() $D/F$
be ramified at the real place and the unique prime of norm
$D/F$
be ramified at the real place and the unique prime of norm
![]() $5$
. Now
$5$
. Now
![]() $H = H_{\mathrm {par}}$
is the first cohomology group of a congruence cover of the Weeks manifold. The generalized Ramanujan conjecture still predicts a bound of the shape
$H = H_{\mathrm {par}}$
is the first cohomology group of a congruence cover of the Weeks manifold. The generalized Ramanujan conjecture still predicts a bound of the shape
![]() $|a_{\mathfrak {p}}| \le 2 N(\mathfrak {p})^{1/2}$
for the eigenvalues of the Hecke operators
$|a_{\mathfrak {p}}| \le 2 N(\mathfrak {p})^{1/2}$
for the eigenvalues of the Hecke operators
![]() $T_{\mathfrak {p}}$
. However, our methods do not apply in this situation, and the best current bounds remain those of the form
$T_{\mathfrak {p}}$
. However, our methods do not apply in this situation, and the best current bounds remain those of the form
![]() $|a_{\mathfrak {p}}| \le 2 N(\mathfrak {p})^{1/2 + 7/64}$
proved using analytic methods (see [Reference SarnakSar05]).
$|a_{\mathfrak {p}}| \le 2 N(\mathfrak {p})^{1/2 + 7/64}$
proved using analytic methods (see [Reference SarnakSar05]).
We finish with an application of a different sort. Let
![]() $\Gamma = \operatorname {\mathrm {SL}}_2(\mathcal {O}_F)$
. The quotients
$\Gamma = \operatorname {\mathrm {SL}}_2(\mathcal {O}_F)$
. The quotients
![]() $\Gamma \backslash \mathbf {H}^3$
were first investigated by Bianchi [Reference BianchiBia1892], and for that reason, they are known as Bianchi orbifolds. For a Bianchi modular form f of level one, one may [Reference MarshallMar11, §3] associate to f a normalized measure
$\Gamma \backslash \mathbf {H}^3$
were first investigated by Bianchi [Reference BianchiBia1892], and for that reason, they are known as Bianchi orbifolds. For a Bianchi modular form f of level one, one may [Reference MarshallMar11, §3] associate to f a normalized measure
![]() $\mu _f$
on
$\mu _f$
on
![]() $\Gamma \backslash \mathbf {H}^3$
. One then has the following [Reference MarshallMar11, Cor 3]:
$\Gamma \backslash \mathbf {H}^3$
. One then has the following [Reference MarshallMar11, Cor 3]:
Theorem G. Assume that F has class number one.Footnote
1
For any sequence of Bianchi modular eigenforms f of weight tending to
![]() $\infty $
, the measures
$\infty $
, the measures
![]() $\mu _f$
converge weakly to the hyperbolic volume on
$\mu _f$
converge weakly to the hyperbolic volume on
![]() $Y = \operatorname {\mathrm {SL}}_2(\mathcal {O}_F) \backslash \mathbf {H}^3$
.
$Y = \operatorname {\mathrm {SL}}_2(\mathcal {O}_F) \backslash \mathbf {H}^3$
.
Proof. As noted in [Reference MarshallMar12], the proof given in [Reference MarshallMar11] assumes the Ramanujan conjecture for Bianchi modular forms — this is now a consequence of Theorem E.
1.4 Recent work of Matsumoto
A few months after the first preprint version of this work was circulated, a remarkable new work by Matsumoto appeared [Reference MatsumotoMat24] which proves Theorems A and B with no parallel weight condition. Matsumoto’s approach introduces several new ideas of a global nature, while our approach here is based on refining our understanding of the local ingredients in the potential automorphy argument. For this reason, one might hope that the two approaches could be profitably combined in the future.
1.5 Notation
Let
![]() $K/{\mathbb Q}_p$
be a finite extension. If
$K/{\mathbb Q}_p$
be a finite extension. If
![]() $\sigma :K \hookrightarrow \overline {{\mathbb Q}}_p$
is a continuous embedding of fields, then we will write
$\sigma :K \hookrightarrow \overline {{\mathbb Q}}_p$
is a continuous embedding of fields, then we will write
![]() $\mathrm {HT}_\sigma (\rho )$
for the multiset of Hodge–Tate numbers of
$\mathrm {HT}_\sigma (\rho )$
for the multiset of Hodge–Tate numbers of
![]() $\rho $
with respect to
$\rho $
with respect to
![]() $\sigma $
, which by definition contains i with multiplicity
$\sigma $
, which by definition contains i with multiplicity
![]() $\dim _{\overline {{\mathbb Q}}_p} (W \otimes _{\sigma ,K} \widehat {\overline {{K}}}(i))^{G_K} $
. We write
$\dim _{\overline {{\mathbb Q}}_p} (W \otimes _{\sigma ,K} \widehat {\overline {{K}}}(i))^{G_K} $
. We write
![]() $\varepsilon $
for the p-adic cyclotomic character, which is a crystalline representation with
$\varepsilon $
for the p-adic cyclotomic character, which is a crystalline representation with
![]() $\mathrm {HT}_\sigma (\varepsilon )=\{ -1\}$
for each
$\mathrm {HT}_\sigma (\varepsilon )=\{ -1\}$
for each
![]() $\sigma $
.
$\sigma $
.
We say that
![]() $\rho $
has weight
$\rho $
has weight
![]() $0$
if for each
$0$
if for each
![]() $\sigma :K\hookrightarrow \overline {{\mathbb Q}}_p$
, we have
$\sigma :K\hookrightarrow \overline {{\mathbb Q}}_p$
, we have
![]() $\mathrm {HT}_\sigma (\rho )=\{0,1,\dots ,d-1\}$
. We often somewhat abusively write that a representation
$\mathrm {HT}_\sigma (\rho )=\{0,1,\dots ,d-1\}$
. We often somewhat abusively write that a representation
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb Z}}_p)$
is crystalline of weight
$\rho :G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb Z}}_p)$
is crystalline of weight
![]() $0$
if the corresponding representation
$0$
if the corresponding representation
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb Q}}_p)$
is crystalline of weight
$\rho :G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb Q}}_p)$
is crystalline of weight
![]() $0$
.
$0$
.
Let
![]() ${\mathcal O}$
be the ring of integers in some finite extension
${\mathcal O}$
be the ring of integers in some finite extension
![]() $E/{\mathbb Q}_p$
, and suppose that E is large enough that it contains the images of all embeddings
$E/{\mathbb Q}_p$
, and suppose that E is large enough that it contains the images of all embeddings
![]() $\sigma :K\hookrightarrow \overline {{\mathbb Q}}_p$
. Write
$\sigma :K\hookrightarrow \overline {{\mathbb Q}}_p$
. Write
![]() $\varpi $
for a uniformizer of
$\varpi $
for a uniformizer of
![]() ${\mathcal O}$
, and
${\mathcal O}$
, and
![]() ${\mathcal O}/\varpi ={\mathbb F}$
for its residue field. We write
${\mathcal O}/\varpi ={\mathbb F}$
for its residue field. We write
![]() $\operatorname {Art}_K: K^\times \to W_K^{\operatorname {ab}}$
for the isomorphism of local class field theory, normalized so that uniformizers correspond to geometric Frobenius elements.
$\operatorname {Art}_K: K^\times \to W_K^{\operatorname {ab}}$
for the isomorphism of local class field theory, normalized so that uniformizers correspond to geometric Frobenius elements.
Let
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb F}}_p)$
be a continuous representation. Then after enlarging E and thus
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb F}}_p)$
be a continuous representation. Then after enlarging E and thus
![]() ${\mathbb F}$
if necessary, we may assume that the image of
${\mathbb F}$
if necessary, we may assume that the image of
![]() $\overline {\rho }$
is contained in
$\overline {\rho }$
is contained in
![]() $\operatorname {\mathrm {GL}}_d({\mathbb F})$
. We write
$\operatorname {\mathrm {GL}}_d({\mathbb F})$
. We write
![]() $R^{\square ,{\mathcal O}}_{\overline {\rho }}$
for the universal lifting
$R^{\square ,{\mathcal O}}_{\overline {\rho }}$
for the universal lifting
![]() ${\mathcal O}$
-algebra of
${\mathcal O}$
-algebra of
![]() $\overline {\rho }$
; by definition, this (pro-)represents the functor
$\overline {\rho }$
; by definition, this (pro-)represents the functor
![]() ${\mathcal D}^{\square ,{\mathcal O}}_{\overline {\rho }}$
given by lifts of
${\mathcal D}^{\square ,{\mathcal O}}_{\overline {\rho }}$
given by lifts of
![]() $\overline {\rho }$
to representations
$\overline {\rho }$
to representations
![]() $\rho : G_K \to \operatorname {\mathrm {GL}}_d(A)$
, for A an Artin local
$\rho : G_K \to \operatorname {\mathrm {GL}}_d(A)$
, for A an Artin local
![]() ${\mathcal O}$
-algebra with residue field
${\mathcal O}$
-algebra with residue field
![]() ${\mathbb F}$
. The precise choice of E is unimportant, in the sense that if
${\mathbb F}$
. The precise choice of E is unimportant, in the sense that if
![]() ${\mathcal O}'$
is the ring of integers in a finite extension
${\mathcal O}'$
is the ring of integers in a finite extension
![]() $E'/E$
, then by [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, Lem. 1.2.1], we have
$E'/E$
, then by [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, Lem. 1.2.1], we have
![]() $R^{\square ,{\mathcal O}'}_{\overline {\rho }}=R^{\square ,{\mathcal O}}_{\overline {\rho }}\otimes _{{\mathcal O}}{\mathcal O}'$
.
$R^{\square ,{\mathcal O}'}_{\overline {\rho }}=R^{\square ,{\mathcal O}}_{\overline {\rho }}\otimes _{{\mathcal O}}{\mathcal O}'$
.
We write
![]() $R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }}$
for the unique
$R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }}$
for the unique
![]() ${\mathcal O}$
-flat quotient of
${\mathcal O}$
-flat quotient of
![]() $R_{\overline {\rho }}^{\square ,{\mathcal O}}$
with the property that if B is a finite flat E-algebra, then an
$R_{\overline {\rho }}^{\square ,{\mathcal O}}$
with the property that if B is a finite flat E-algebra, then an
![]() ${\mathcal O}$
-algebra homomorphism
${\mathcal O}$
-algebra homomorphism
![]() $R_{\overline {\rho }}^{\square ,{\mathcal O}}\to B$
factors through
$R_{\overline {\rho }}^{\square ,{\mathcal O}}\to B$
factors through
![]() $R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
if and only if the corresponding representation of
$R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
if and only if the corresponding representation of
![]() $G_K$
is crystalline of weight
$G_K$
is crystalline of weight
![]() $0$
.
$0$
.
We will let
![]() $\operatorname {rec}_K$
be the local Langlands correspondence of [Reference Harris and TaylorHT01], so that if
$\operatorname {rec}_K$
be the local Langlands correspondence of [Reference Harris and TaylorHT01], so that if
![]() $\pi $
is an irreducible complex admissible representation of
$\pi $
is an irreducible complex admissible representation of
![]() $\operatorname {\mathrm {GL}}_n(K)$
, then
$\operatorname {\mathrm {GL}}_n(K)$
, then
![]() $\operatorname {rec}_K(\pi )$
is a Frobenius semisimple Weil–Deligne representation of the Weil group
$\operatorname {rec}_K(\pi )$
is a Frobenius semisimple Weil–Deligne representation of the Weil group
![]() $W_K$
. We write
$W_K$
. We write
![]() $\operatorname {rec}^T_K$
for the arithmetic normalization of the local Langlands correspondence, as defined in, for example, [Reference Clozel and ThorneCT14, §2.1]; it is defined on irreducible admissible representations of
$\operatorname {rec}^T_K$
for the arithmetic normalization of the local Langlands correspondence, as defined in, for example, [Reference Clozel and ThorneCT14, §2.1]; it is defined on irreducible admissible representations of
![]() $\operatorname {\mathrm {GL}}_n(K)$
defined over any field which is abstractly isomorphic to
$\operatorname {\mathrm {GL}}_n(K)$
defined over any field which is abstractly isomorphic to
![]() ${\mathbb C}$
(e.g.,
${\mathbb C}$
(e.g.,
![]() $\overline {{\mathbb Q}}_l$
).
$\overline {{\mathbb Q}}_l$
).
Let F be a number field. If v is a finite place of F, then we write
![]() $k(v)$
for the residue field of
$k(v)$
for the residue field of
![]() $F_v$
. We identify dominant weights
$F_v$
. We identify dominant weights
![]() $\lambda $
of
$\lambda $
of
![]() $\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_n$
with sets of tuples of integers
$\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_n$
with sets of tuples of integers
![]() $(\lambda _{\tau ,1}\ge \lambda _{\tau ,2} \ge \cdots \ge \lambda _{\tau ,n})_{{\tau : F\hookrightarrow {\mathbb C}}}$
indexed by complex embeddings of F (cf. [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §2.2.1]). If
$(\lambda _{\tau ,1}\ge \lambda _{\tau ,2} \ge \cdots \ge \lambda _{\tau ,n})_{{\tau : F\hookrightarrow {\mathbb C}}}$
indexed by complex embeddings of F (cf. [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §2.2.1]). If
![]() $\pi $
is an irreducible admissible representation of
$\pi $
is an irreducible admissible representation of
![]() $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
and
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
and
![]() $\lambda $
is a dominant weight, we say that
$\lambda $
is a dominant weight, we say that
![]() $\pi $
is regular algebraic of weight
$\pi $
is regular algebraic of weight
![]() $\lambda $
if the infinitesimal character of
$\lambda $
if the infinitesimal character of
![]() $\pi _\infty $
is the same as that of
$\pi _\infty $
is the same as that of
![]() $V_\lambda ^\vee $
, where
$V_\lambda ^\vee $
, where
![]() $V_\lambda $
is the algebraic representation of
$V_\lambda $
is the algebraic representation of
![]() $\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_n$
of highest weight
$\operatorname {Res}_{F/{\mathbb Q}}\operatorname {\mathrm {GL}}_n$
of highest weight
![]() $\lambda $
. We say that
$\lambda $
. We say that
![]() $\pi $
is regular algebraic if it is regular algebraic of some weight.
$\pi $
is regular algebraic if it is regular algebraic of some weight.
Definition 1.5.1 (Parallel Weight).
Suppose
![]() $\pi $
is regular algebraic of weight
$\pi $
is regular algebraic of weight
![]() $\lambda $
. We say that
$\lambda $
. We say that
![]() $\pi $
is of parallel weight if
$\pi $
is of parallel weight if
![]() $\lambda _{\tau , 1} - \lambda _{\tau , 2}$
is independent of
$\lambda _{\tau , 1} - \lambda _{\tau , 2}$
is independent of
![]() $\tau $
– equivalently, if
$\tau $
– equivalently, if
![]() $\pi $
admits a regular algebraic twist of weight
$\pi $
admits a regular algebraic twist of weight
![]() $\mu = (m-1, 0)_\tau $
for some
$\mu = (m-1, 0)_\tau $
for some
![]() $m \ge 1$
in
$m \ge 1$
in
![]() ${\mathbb Z}$
. We say that
${\mathbb Z}$
. We say that
![]() $\pi $
has parallel weight k for some integer
$\pi $
has parallel weight k for some integer
![]() $k \ge 2$
if
$k \ge 2$
if
![]() ${\mu } = (k-2, 0)_\tau $
.
${\mu } = (k-2, 0)_\tau $
.
Let F be an imaginary CM field, and let
![]() $\pi $
be a cuspidal, regular algebraic weight
$\pi $
be a cuspidal, regular algebraic weight
![]() $\lambda $
automorphic representation of
$\lambda $
automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. The weight
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. The weight
![]() ${\lambda } = (\lambda _{\tau , 1}, \lambda _{\tau , 2})_\tau \in ({\mathbb Z}^2)^{\operatorname {\mathrm {Hom}}(F, {\mathbb C})}$
satisfies the following:
${\lambda } = (\lambda _{\tau , 1}, \lambda _{\tau , 2})_\tau \in ({\mathbb Z}^2)^{\operatorname {\mathrm {Hom}}(F, {\mathbb C})}$
satisfies the following:
-
• There is an integer
 $w \in {\mathbb Z}$
such that for all
$w \in {\mathbb Z}$
such that for all
 $\tau $
, we have
$\tau $
, we have
 $\lambda _{\tau , 1} + \lambda _{\tau c, 2} = w$
. In particular, for all
$\lambda _{\tau , 1} + \lambda _{\tau c, 2} = w$
. In particular, for all
 $\tau $
, we have
$\tau $
, we have
 $\lambda _{\tau , 1} - \lambda _{\tau , 2} = \lambda _{\tau c, 1} - \lambda _{\tau c, 2}$
.
$\lambda _{\tau , 1} - \lambda _{\tau , 2} = \lambda _{\tau c, 1} - \lambda _{\tau c, 2}$
.
This is a consequence of Clozel’s purity lemma [Reference ClozelClo90, Lemma 4.9]. In particular, if F is imaginary quadratic,
![]() $\pi $
is necessarily of parallel weight.
$\pi $
is necessarily of parallel weight.
2 The special fibres of weight
 $0$
crystalline lifting rings are generically reduced
$0$
crystalline lifting rings are generically reduced
The goal of this section is to prove Theorem 2.5.5, which shows that if
![]() $p>n$
, then for any finite extension
$p>n$
, then for any finite extension
![]() $K/{\mathbb Q}_p$
and any
$K/{\mathbb Q}_p$
and any
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
, the special fibre of the corresponding weight
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
, the special fibre of the corresponding weight
![]() $0$
crystalline lifting ring is generically reduced. We deduce this from the corresponding statement for the special fibre of the weight
$0$
crystalline lifting ring is generically reduced. We deduce this from the corresponding statement for the special fibre of the weight
![]() $0$
crystalline Emerton–Gee stack. This stack was introduced in [Reference Emerton and GeeEG23]. We recall the results from [Reference Emerton and GeeEG23] that we need in Section 2.4 below, but for this introduction, the key points are as follows: the full Emerton–Gee stack
$0$
crystalline Emerton–Gee stack. This stack was introduced in [Reference Emerton and GeeEG23]. We recall the results from [Reference Emerton and GeeEG23] that we need in Section 2.4 below, but for this introduction, the key points are as follows: the full Emerton–Gee stack
![]() ${\mathcal X}$
is a stack of
${\mathcal X}$
is a stack of
![]() $(\varphi ,\Gamma )$
-modules which sees all
$(\varphi ,\Gamma )$
-modules which sees all
![]() $\overline {\rho }$
at once and whose versal ring at any
$\overline {\rho }$
at once and whose versal ring at any
![]() $\overline {\rho }$
is the corresponding unrestricted lifting ring, and the weight
$\overline {\rho }$
is the corresponding unrestricted lifting ring, and the weight
![]() $0$
crystalline Emerton–Gee stack
$0$
crystalline Emerton–Gee stack
![]() ${\mathcal X}^{\underline {0}}$
is a closed substack whose versal ring at any
${\mathcal X}^{\underline {0}}$
is a closed substack whose versal ring at any
![]() $\overline {\rho }$
is the corresponding weight
$\overline {\rho }$
is the corresponding weight
![]() $0$
crystalline lifting ring.
$0$
crystalline lifting ring.
Generic reducedness for the (special fibre of the) stack
![]() ${\mathcal X}^{\underline {0}}$
is equivalent to the generic reducedness for the special fibres of the crystalline lifting rings, as we show by a direct argument below (in the proofs of Theorem 2.5.2 and Theorem 2.5.5). Working on the stack allows us to argue more geometrically, and in particular, one of the main theorems of [Reference Emerton and GeeEG23] classifies the irreducible components of the underlying reduced substack of
${\mathcal X}^{\underline {0}}$
is equivalent to the generic reducedness for the special fibres of the crystalline lifting rings, as we show by a direct argument below (in the proofs of Theorem 2.5.2 and Theorem 2.5.5). Working on the stack allows us to argue more geometrically, and in particular, one of the main theorems of [Reference Emerton and GeeEG23] classifies the irreducible components of the underlying reduced substack of
![]() ${\mathcal X}$
and shows that the underlying reduced substack of the special fibre
${\mathcal X}$
and shows that the underlying reduced substack of the special fibre
![]() $\overline {{\mathcal X}}^{\underline {0}}$
of
$\overline {{\mathcal X}}^{\underline {0}}$
of
![]() ${\mathcal X}^{\underline {0}}$
is a union of these irreducible components.
${\mathcal X}^{\underline {0}}$
is a union of these irreducible components.
In order to show that the
![]() $\overline {{\mathcal X}}^{\underline {0}}$
is generically reduced, it therefore suffices to determine which irreducible components are contained in this special fibre and to show that
$\overline {{\mathcal X}}^{\underline {0}}$
is generically reduced, it therefore suffices to determine which irreducible components are contained in this special fibre and to show that
![]() $\overline {{\mathcal X}}^{\underline {0}}$
is reduced at a generic point of each such component.
$\overline {{\mathcal X}}^{\underline {0}}$
is reduced at a generic point of each such component.
The classification in [Reference Emerton and GeeEG23] of the irreducible components is via a description of the generic
![]() $\overline {\rho }$
which occur on that component. These are all of the form
$\overline {\rho }$
which occur on that component. These are all of the form
 $$\begin{align*}\overline{\rho}\cong \begin{pmatrix} \overline{\chi}_1 &*&\dots &*\\ 0& \overline{\chi}_2&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \overline{\chi}_n\end{pmatrix}\end{align*}$$
$$\begin{align*}\overline{\rho}\cong \begin{pmatrix} \overline{\chi}_1 &*&\dots &*\\ 0& \overline{\chi}_2&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \overline{\chi}_n\end{pmatrix}\end{align*}$$
where the
![]() $\overline {\chi }_i:G_K\to \overline {{\mathbb F}}_p^{\times }$
are characters and the extension classes
$\overline {\chi }_i:G_K\to \overline {{\mathbb F}}_p^{\times }$
are characters and the extension classes
![]() $*$
are in generic position (in particular, nonsplit). The characters
$*$
are in generic position (in particular, nonsplit). The characters
![]() $\overline {\chi }_i|_{I_K}$
are fixed on each irreducible component, and the components are usually determined by the data of the
$\overline {\chi }_i|_{I_K}$
are fixed on each irreducible component, and the components are usually determined by the data of the
![]() $\overline {\chi }_i|_{I_K}$
(see Theorem 2.4.3 (3) for a precise statement).
$\overline {\chi }_i|_{I_K}$
(see Theorem 2.4.3 (3) for a precise statement).
In order to prove our results, we show that the condition that a generic such
![]() $\overline {\rho }$
has a crystalline lift of weight
$\overline {\rho }$
has a crystalline lift of weight
![]() $0$
seriously constrains the possible
$0$
seriously constrains the possible
![]() $\overline {\chi }_i$
. We use a theorem of Tong Liu [Reference LiuLiu08], which in particular shows (under the assumption that
$\overline {\chi }_i$
. We use a theorem of Tong Liu [Reference LiuLiu08], which in particular shows (under the assumption that
![]() $p>n$
) that
$p>n$
) that
![]() $\overline {\rho }$
is obtained from a (crystalline) Breuil module. In the case
$\overline {\rho }$
is obtained from a (crystalline) Breuil module. In the case
![]() $n=2$
, we can then argue as follows: we can compute the possible extensions of rank 1 Breuil modules, and we find that a sufficiently generic extension of
$n=2$
, we can then argue as follows: we can compute the possible extensions of rank 1 Breuil modules, and we find that a sufficiently generic extension of
![]() $\overline {\chi }_2$
by
$\overline {\chi }_2$
by
![]() $\overline {\chi }_1$
can only have a crystalline lift of weight
$\overline {\chi }_1$
can only have a crystalline lift of weight
![]() $0$
if it is ordinary, in the sense that
$0$
if it is ordinary, in the sense that
![]() $\overline {\chi }_1$
is unramified and
$\overline {\chi }_1$
is unramified and
![]() $\overline {\chi }_2$
is an unramified twist of
$\overline {\chi }_2$
is an unramified twist of
![]() $\overline {\varepsilon }^{-1}$
, where
$\overline {\varepsilon }^{-1}$
, where
![]() $\overline {\varepsilon }$
is the mod p cyclotomic character.
$\overline {\varepsilon }$
is the mod p cyclotomic character.
Furthermore, a generic such extension arises from a unique Breuil module, which is ordinary. (Since two-dimensional weight
![]() $0$
crystalline representations are given by the generic fibres of p-divisible groups, we can alternatively phrase this result as showing that
$0$
crystalline representations are given by the generic fibres of p-divisible groups, we can alternatively phrase this result as showing that
![]() $\overline {\rho }$
comes from a unique finite flat group scheme over
$\overline {\rho }$
comes from a unique finite flat group scheme over
![]() ${\mathcal O}_K$
, which is ordinary in the sense that it is an extension of a multiplicative by an étale group scheme.) By an argument of Kisin [Reference KisinKis09, Prop. 2.4.14], the deformations of this Breuil module are also ordinary, so that the weight
${\mathcal O}_K$
, which is ordinary in the sense that it is an extension of a multiplicative by an étale group scheme.) By an argument of Kisin [Reference KisinKis09, Prop. 2.4.14], the deformations of this Breuil module are also ordinary, so that the weight
![]() $0$
crystalline lifting rings for these generic
$0$
crystalline lifting rings for these generic
![]() $\overline {\rho }$
’s are also ordinary. It is then easy to show that the crystalline ordinary lifting ring for a generic
$\overline {\rho }$
’s are also ordinary. It is then easy to show that the crystalline ordinary lifting ring for a generic
![]() $\overline {\rho }$
is formally smooth and thus has reduced special fibre, which completes the argument.
$\overline {\rho }$
is formally smooth and thus has reduced special fibre, which completes the argument.
Perhaps surprisingly, we are able to make a similar argument for general n without making any additional calculations. For each i, we apply our computation of extension classes of Breuil modules to the extension of
![]() $\overline {\chi }_{i+1}$
by
$\overline {\chi }_{i+1}$
by
![]() $\overline {\chi }_i$
arising as a subquotient of
$\overline {\chi }_i$
arising as a subquotient of
![]() $\overline {\rho }$
. If all of these extensions are sufficiently generic, we show that
$\overline {\rho }$
. If all of these extensions are sufficiently generic, we show that
![]() $\overline {\rho }$
can only admit crystalline lifts of weight
$\overline {\rho }$
can only admit crystalline lifts of weight
![]() $0$
if
$0$
if
![]() $\overline {\chi }_i|_{I_K}=\overline {\varepsilon }^{1-i}$
for all i. Furthermore, we also see that a generic such
$\overline {\chi }_i|_{I_K}=\overline {\varepsilon }^{1-i}$
for all i. Furthermore, we also see that a generic such
![]() $\overline {\rho }$
can only arise from an ordinary Breuil module and again deduce that all weight
$\overline {\rho }$
can only arise from an ordinary Breuil module and again deduce that all weight
![]() $0$
crystalline lifts of
$0$
crystalline lifts of
![]() $\overline {\rho }$
are ordinary. From this, we deduce the formal smoothness of the corresponding lifting rings for generic
$\overline {\rho }$
are ordinary. From this, we deduce the formal smoothness of the corresponding lifting rings for generic
![]() $\overline {\rho }$
and conclude as above.
$\overline {\rho }$
and conclude as above.
The organization of the proof is as follows. In Section 2.1, we recall Liu’s results [Reference LiuLiu08] on strongly divisible modules and lattices in semistable representations and deduce the results that we need on crystalline Breuil modules. In Section 2.2, we compute extensions of rank one Breuil modules. This is essentially elementary, using only semilinear algebra and some combinatorics. We deduce from this in Section 2.3 that sufficiently generic crystalline representations of weight
![]() $0$
are ordinary. In Section 2.4, we give a brief introduction to Emerton–Gee stacks and prove some slight generalizations of some results of [Reference Emerton and GeeEG23] before deducing our generic reducedness results in Section 2.5.
$0$
are ordinary. In Section 2.4, we give a brief introduction to Emerton–Gee stacks and prove some slight generalizations of some results of [Reference Emerton and GeeEG23] before deducing our generic reducedness results in Section 2.5.
2.1 Breuil modules and strongly divisible modules
We begin by recalling some standard results about Breuil modules and Breuil–Kisin modules. The results we use are largely due to Breuil, Kisin and Liu, but for convenience, we mostly cite the papers [Reference Emerton, Gee and HerzigEGH13, Reference Herzig, Le and MorraHLM17] which deduce versions of these results with coefficients and prove some exactness properties of the functors to Galois representations which we will make use of in our main arguments. (Note that [Reference Herzig, Le and MorraHLM17, App. A] makes a running assumption on the ramification of the field
![]() $K/{\mathbb Q}_p$
, but this is only made in order to discuss tame descent data and compare to Fontaine–Laffaille theory, and it is easy to check that all of the results we cite from there are valid for general
$K/{\mathbb Q}_p$
, but this is only made in order to discuss tame descent data and compare to Fontaine–Laffaille theory, and it is easy to check that all of the results we cite from there are valid for general
![]() $K/{\mathbb Q}_p$
with trivial descent data, with identical proofs (or often with simpler proofs, as there is no need to consider the descent data).)
$K/{\mathbb Q}_p$
with trivial descent data, with identical proofs (or often with simpler proofs, as there is no need to consider the descent data).)
Let
![]() $K/{\mathbb Q}_p$
be a finite extension for some
$K/{\mathbb Q}_p$
be a finite extension for some
![]() $p>2$
, with ring of integers
$p>2$
, with ring of integers
![]() ${\mathcal O}_K$
and residue field k. Write e for the absolute ramification degree of K and f for its inertial degree
${\mathcal O}_K$
and residue field k. Write e for the absolute ramification degree of K and f for its inertial degree
![]() $[k:{\mathbb F}_p]$
. Fix a uniformizer
$[k:{\mathbb F}_p]$
. Fix a uniformizer
![]() $\pi \in K$
with Eisenstein polynomial
$\pi \in K$
with Eisenstein polynomial
![]() $E(u)$
, which we choose so that
$E(u)$
, which we choose so that
![]() $E(0)=p$
. Fix also a compatible choice
$E(0)=p$
. Fix also a compatible choice
![]() $(\pi ^{1/p^n})_{n\ge 1}$
of p-power roots of
$(\pi ^{1/p^n})_{n\ge 1}$
of p-power roots of
![]() $\pi $
in
$\pi $
in
![]() $\overline {{\mathbb Q}}_p$
, and set
$\overline {{\mathbb Q}}_p$
, and set
![]() $K_n:=K(\pi ^{1/p^n})$
and
$K_n:=K(\pi ^{1/p^n})$
and
![]() $K_\infty :=\cup _{n\ge 1}K_n$
.
$K_\infty :=\cup _{n\ge 1}K_n$
.
Let
![]() $E/{\mathbb Q}_p$
be a finite extension containing the normal closure of K, with ring of integers
$E/{\mathbb Q}_p$
be a finite extension containing the normal closure of K, with ring of integers
![]() ${\mathcal O}$
and residue field
${\mathcal O}$
and residue field
![]() ${\mathbb F}$
. We will consider various semilinear algebra objects with coefficients in a finite
${\mathbb F}$
. We will consider various semilinear algebra objects with coefficients in a finite
![]() ${\mathcal O}$
-algebra A, and it is trivial to verify that all of our definitions are compatible with extension of scalars of A in an obvious way. In particular, we often take
${\mathcal O}$
-algebra A, and it is trivial to verify that all of our definitions are compatible with extension of scalars of A in an obvious way. In particular, we often take
![]() $A={\mathbb F}$
, but we are free to replace
$A={\mathbb F}$
, but we are free to replace
![]() ${\mathbb F}$
by an arbitrary finite extension, or (after passing to a limit in an obvious fashion) by
${\mathbb F}$
by an arbitrary finite extension, or (after passing to a limit in an obvious fashion) by
![]() $\overline {{\mathbb F}}_p$
.
$\overline {{\mathbb F}}_p$
.
For any finite
![]() ${\mathcal O}$
-algebra A, we let
${\mathcal O}$
-algebra A, we let ![]() , equipped with the usual A-linear,
, equipped with the usual A-linear,
![]() $W(k)$
-semilinear Frobenius endomorphism
$W(k)$
-semilinear Frobenius endomorphism
![]() $\varphi $
, with
$\varphi $
, with
![]() $\varphi (u)=u^p$
. For any integer
$\varphi (u)=u^p$
. For any integer
![]() $h\ge 0$
, a Breuil–Kisin module with A-coefficients of height at most h is a finite free
$h\ge 0$
, a Breuil–Kisin module with A-coefficients of height at most h is a finite free
![]() $\mathfrak {S}_{A}$
-module
$\mathfrak {S}_{A}$
-module
![]() $\mathfrak {M}$
equipped with a
$\mathfrak {M}$
equipped with a
![]() $\varphi $
-semilinear map
$\varphi $
-semilinear map
![]() $\varphi :\mathfrak {M}\to \mathfrak {M}$
such that the cokernel of the linearized Frobenius
$\varphi :\mathfrak {M}\to \mathfrak {M}$
such that the cokernel of the linearized Frobenius
![]() $\varphi ^*\mathfrak {M}\xrightarrow {1\otimes \varphi }\mathfrak {M}$
is killed by
$\varphi ^*\mathfrak {M}\xrightarrow {1\otimes \varphi }\mathfrak {M}$
is killed by
![]() $E(u)^h$
, where, as usual,
$E(u)^h$
, where, as usual,
![]() $\varphi ^*\mathfrak {M}$
denotes the Frobenius pullback
$\varphi ^*\mathfrak {M}$
denotes the Frobenius pullback
![]() $\mathfrak {S}_A\otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}$
. (Here, we indulge in a standard abuse of notation in writing
$\mathfrak {S}_A\otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}$
. (Here, we indulge in a standard abuse of notation in writing
![]() $\varphi $
for both the endomorphism of
$\varphi $
for both the endomorphism of
![]() $\mathfrak {S}_A$
and of
$\mathfrak {S}_A$
and of
![]() $\mathfrak {M}$
, which should not cause any confusion.)
$\mathfrak {M}$
, which should not cause any confusion.)
Suppose that
![]() $A={\mathbb F}$
, and let
$A={\mathbb F}$
, and let
![]() $\overline {S}_{{\mathbb F}}:=\mathfrak {S}_{{\mathbb F}}/u^{ep}$
. If
$\overline {S}_{{\mathbb F}}:=\mathfrak {S}_{{\mathbb F}}/u^{ep}$
. If
![]() $h\le p-2$
, then a quasi-Breuil module with
$h\le p-2$
, then a quasi-Breuil module with
![]() ${\mathbb F}$
-coefficients
${\mathbb F}$
-coefficients
![]() ${\mathcal M}$
of height h is a finite free
${\mathcal M}$
of height h is a finite free
![]() $\overline {S}_{\mathbb F}$
module
$\overline {S}_{\mathbb F}$
module
![]() ${\mathcal M}$
equipped with a
${\mathcal M}$
equipped with a
![]() $\overline {S}_{\mathbb F}$
-submodule
$\overline {S}_{\mathbb F}$
-submodule
and a
![]() $\varphi $
-semilinear map
$\varphi $
-semilinear map
![]() $\varphi :{\mathcal M}^h\to {\mathcal M}$
such that
$\varphi :{\mathcal M}^h\to {\mathcal M}$
such that
(The morphism
![]() $\varphi $
is usually denoted
$\varphi $
is usually denoted
![]() $\varphi _h$
in the literature, but we will shortly fix the choice
$\varphi _h$
in the literature, but we will shortly fix the choice
![]() $h=p-2$
for the rest of the paper, so we have omitted the subscript for the sake of cleaner notation.)
$h=p-2$
for the rest of the paper, so we have omitted the subscript for the sake of cleaner notation.)
For each
![]() $0\le h\le p-2$
, there is by [Reference BreuilBre99, Thm. 4.1.1] an equivalence of categories between the category of Breuil–Kisin modules with
$0\le h\le p-2$
, there is by [Reference BreuilBre99, Thm. 4.1.1] an equivalence of categories between the category of Breuil–Kisin modules with
![]() ${\mathbb F}$
-coefficients of height at most h and the category of quasi-Breuil modules with
${\mathbb F}$
-coefficients of height at most h and the category of quasi-Breuil modules with
![]() ${\mathbb F}$
-coefficients of height at most h. Explicitly, a Breuil–Kisin module
${\mathbb F}$
-coefficients of height at most h. Explicitly, a Breuil–Kisin module
![]() $\mathfrak {M}$
of height
$\mathfrak {M}$
of height
![]() $h\le p-2$
determines a quasi-Breuil module as follows. Write
$h\le p-2$
determines a quasi-Breuil module as follows. Write
![]() $\mathfrak {M}^h:=(1\otimes \varphi )^{-1}(u^{eh}\mathfrak {M})\subseteq \varphi ^*\mathfrak {M}$
. Set
$\mathfrak {M}^h:=(1\otimes \varphi )^{-1}(u^{eh}\mathfrak {M})\subseteq \varphi ^*\mathfrak {M}$
. Set
![]() ${\mathcal M}:=\varphi ^*\mathfrak {M}/u^{pe}$
, and
${\mathcal M}:=\varphi ^*\mathfrak {M}/u^{pe}$
, and
![]() $\mathcal {M}^h=\mathfrak {M}^h/u^{pe}\varphi ^*\mathfrak {M}$
. Then
$\mathcal {M}^h=\mathfrak {M}^h/u^{pe}\varphi ^*\mathfrak {M}$
. Then
![]() $\varphi :{\mathcal M}^h\to {\mathcal M}$
is defined by the composite
$\varphi :{\mathcal M}^h\to {\mathcal M}$
is defined by the composite
where
![]() $\varphi _h:u^{eh}\overline {S}_{{\mathbb F}}\to \overline {S}_{{\mathbb F}}$
is the
$\varphi _h:u^{eh}\overline {S}_{{\mathbb F}}\to \overline {S}_{{\mathbb F}}$
is the
![]() $\varphi $
-semilinear morphism
$\varphi $
-semilinear morphism
![]() $\varphi _h(u^{eh}x):=\varphi (x)$
. (Note that this is well-defined because if x is divisible by
$\varphi _h(u^{eh}x):=\varphi (x)$
. (Note that this is well-defined because if x is divisible by
![]() $u^{e(p-h)}$
, then
$u^{e(p-h)}$
, then
![]() $\varphi (x)$
is divisible by
$\varphi (x)$
is divisible by
![]() $u^{ep(p-h)}$
and in particular by
$u^{ep(p-h)}$
and in particular by
![]() $u^{ep}=0$
.) We will often say that the Breuil–Kisin module
$u^{ep}=0$
.) We will often say that the Breuil–Kisin module
![]() $\mathfrak {M}$
underlies the quasi-Breuil module
$\mathfrak {M}$
underlies the quasi-Breuil module
![]() ${\mathcal M}$
.
${\mathcal M}$
.
Remark 2.1.1. Because we chose
![]() $E(u)$
so that
$E(u)$
so that
![]() $E(0)=p$
, the constant c that sometimes appears in the Breuil module literature is equal to
$E(0)=p$
, the constant c that sometimes appears in the Breuil module literature is equal to
![]() $1$
in our case.Footnote
2
$1$
in our case.Footnote
2
Write
![]() $N:\overline {S}_{{\mathbb F}}\to \overline {S}_{{\mathbb F}}$
for the
$N:\overline {S}_{{\mathbb F}}\to \overline {S}_{{\mathbb F}}$
for the
![]() $(k\otimes _{{\mathbb F}_p}{\mathbb F})$
-linear derivation
$(k\otimes _{{\mathbb F}_p}{\mathbb F})$
-linear derivation
![]() $-u\frac {\partial }{\partial u}$
. A Breuil module with
$-u\frac {\partial }{\partial u}$
. A Breuil module with
![]() ${\mathbb F}$
-coefficients
${\mathbb F}$
-coefficients
![]() ${\mathcal M}$
of height h is a quasi-Breuil module equipped with the additional data of a map
${\mathcal M}$
of height h is a quasi-Breuil module equipped with the additional data of a map
![]() $N:{\mathcal M}\to {\mathcal M}$
which satisfies the following:
$N:{\mathcal M}\to {\mathcal M}$
which satisfies the following:
-
•
 $N(sx)=sN(x)+N(s)x$
for all
$N(sx)=sN(x)+N(s)x$
for all
 $s\in \overline {S}_{{\mathbb F}}, x\in {\mathcal M}$
,
$s\in \overline {S}_{{\mathbb F}}, x\in {\mathcal M}$
, -
•
 $u^{e}N({\mathcal M}^h)\subseteq {\mathcal M}^h$
,
$u^{e}N({\mathcal M}^h)\subseteq {\mathcal M}^h$
, -
• and
 $\varphi (u^{e}N(x))=N(\varphi (x))$
for all
$\varphi (u^{e}N(x))=N(\varphi (x))$
for all
 $x\in {\mathcal M}^h$
.
$x\in {\mathcal M}^h$
.
We say that a Breuil module
![]() ${\mathcal M}$
is crystalline if
${\mathcal M}$
is crystalline if
![]() $N({\mathcal M})\subseteq u{\mathcal M}$
.
$N({\mathcal M})\subseteq u{\mathcal M}$
.
Remark 2.1.2. While we will not explicitly need this below, it can be checked that if
![]() ${\mathcal M}$
is crystalline, then
${\mathcal M}$
is crystalline, then
![]() $u^eN({\mathcal M}^h) \subseteq u N({\mathcal M}^h)$
. To see this, note that since
$u^eN({\mathcal M}^h) \subseteq u N({\mathcal M}^h)$
. To see this, note that since
![]() $\overline {S}_{{\mathbb F}}\cdot \varphi ({\mathcal M}^h)={\mathcal M}$
, there is an induced
$\overline {S}_{{\mathbb F}}\cdot \varphi ({\mathcal M}^h)={\mathcal M}$
, there is an induced
![]() ${\mathbb F}_p$
-linear surjection
${\mathbb F}_p$
-linear surjection
![]() ${\mathcal M}^h/u{\mathcal M}^h\to {\mathcal M}/u{\mathcal M}$
, which is in fact an isomorphism (comparing dimensions as in [Reference BreuilBre98, Lem. 2.2.1.1]). If
${\mathcal M}^h/u{\mathcal M}^h\to {\mathcal M}/u{\mathcal M}$
, which is in fact an isomorphism (comparing dimensions as in [Reference BreuilBre98, Lem. 2.2.1.1]). If
![]() ${\mathcal M}$
is crystalline, then N acts by
${\mathcal M}$
is crystalline, then N acts by
![]() $0$
on
$0$
on
![]() ${\mathcal M}/u{\mathcal M}$
, and the commutation relation between N and
${\mathcal M}/u{\mathcal M}$
, and the commutation relation between N and
![]() $\varphi $
then shows that
$\varphi $
then shows that
![]() $u^eN$
acts by
$u^eN$
acts by
![]() $0$
on
$0$
on
![]() ${\mathcal M}^h/u{\mathcal M}^h$
, as required.
${\mathcal M}^h/u{\mathcal M}^h$
, as required.
We now define the Galois representations associated to Breuil modules and to Breuil–Kisin modules, beginning with the latter. An étale
![]() $\varphi $
-module with
$\varphi $
-module with
![]() ${\mathbb F}$
-coefficients is by definition a finite free
${\mathbb F}$
-coefficients is by definition a finite free
![]() $(k\otimes _{{\mathbb F}_p}{\mathbb F})((u))$
-module M with a semilinear endomorphism
$(k\otimes _{{\mathbb F}_p}{\mathbb F})((u))$
-module M with a semilinear endomorphism
![]() $\varphi :M\to M$
such that the linearized Frobenius
$\varphi :M\to M$
such that the linearized Frobenius
![]() $\varphi ^*M\xrightarrow {1\otimes \varphi }M$
is an isomorphism. Note that by definition, if
$\varphi ^*M\xrightarrow {1\otimes \varphi }M$
is an isomorphism. Note that by definition, if
![]() $\mathfrak {M}$
is a Breuil–Kisin module with
$\mathfrak {M}$
is a Breuil–Kisin module with
![]() ${\mathbb F}$
-coefficients, then
${\mathbb F}$
-coefficients, then
![]() $\mathfrak {M}[1/u]$
is an étale
$\mathfrak {M}[1/u]$
is an étale
![]() $\varphi $
-module with
$\varphi $
-module with
![]() ${\mathbb F}$
-coefficients. Let
${\mathbb F}$
-coefficients. Let
![]() $k((u))^{\operatorname {sep}}$
denote a separable closure of
$k((u))^{\operatorname {sep}}$
denote a separable closure of
![]() $k((u))$
. By the results of [Reference FontaineFon90] (see, for example, [Reference KisinKis09, 1.1.12]), the functor
$k((u))$
. By the results of [Reference FontaineFon90] (see, for example, [Reference KisinKis09, 1.1.12]), the functor
is an equivalence of categories between the category of étale
![]() $\varphi $
-modules with
$\varphi $
-modules with
![]() ${\mathbb F}$
-coefficients and the category of continuous representations of
${\mathbb F}$
-coefficients and the category of continuous representations of
![]() $G_{K_\infty }$
on
$G_{K_\infty }$
on
![]() ${\mathbb F}$
-vector spaces, and we have
${\mathbb F}$
-vector spaces, and we have
![]() $\dim _{{\mathbb F}}T_\infty (M)=\operatorname {rank}_{(k\otimes _{{\mathbb F}_p}{\mathbb F})((u))}M$
. We also write
$\dim _{{\mathbb F}}T_\infty (M)=\operatorname {rank}_{(k\otimes _{{\mathbb F}_p}{\mathbb F})((u))}M$
. We also write
![]() $T_\infty $
for the induced functor from Breuil–Kisin modules to
$T_\infty $
for the induced functor from Breuil–Kisin modules to
![]() $G_{K_\infty }$
-representations given by
$G_{K_\infty }$
-representations given by
![]() $\mathfrak {M}\mapsto T_\infty (\mathfrak {M}[1/u])$
. Similarly, if
$\mathfrak {M}\mapsto T_\infty (\mathfrak {M}[1/u])$
. Similarly, if
![]() $\mathfrak {M}$
is the Breuil–Kisin module underlying a quasi-Breuil module
$\mathfrak {M}$
is the Breuil–Kisin module underlying a quasi-Breuil module
![]() ${\mathcal M}$
, we write
${\mathcal M}$
, we write
![]() $T_\infty ({\mathcal M})$
for
$T_\infty ({\mathcal M})$
for
![]() $T_\infty (\mathfrak {M})$
.
$T_\infty (\mathfrak {M})$
.
Similarly, there is a functor T from the category of Breuil modules of height at most h with
![]() ${\mathbb F}$
-coefficients to the category of continuous representations of
${\mathbb F}$
-coefficients to the category of continuous representations of
![]() $G_{K}$
on
$G_{K}$
on
![]() ${\mathbb F}$
-vector spaces defined by
${\mathbb F}$
-vector spaces defined by
where
![]() $\widehat {A}:=\widehat {A}_{\operatorname {st}}\otimes _Sk[u]/u^{ep}$
is defined, for example, in [Reference Herzig, Le and MorraHLM17, (A.3.1)]. Again we have
$\widehat {A}:=\widehat {A}_{\operatorname {st}}\otimes _Sk[u]/u^{ep}$
is defined, for example, in [Reference Herzig, Le and MorraHLM17, (A.3.1)]. Again we have
![]() $\dim _{{\mathbb F}}T({\mathcal M})=\operatorname {rank}_{\overline {S}_{{\mathbb F}}}{\mathcal M}$
. Furthermore, by [Reference Herzig, Le and MorraHLM17, Prop. A.3.2], the forgetful functor from Breuil modules to quasi-Breuil modules induces an isomorphism
$\dim _{{\mathbb F}}T({\mathcal M})=\operatorname {rank}_{\overline {S}_{{\mathbb F}}}{\mathcal M}$
. Furthermore, by [Reference Herzig, Le and MorraHLM17, Prop. A.3.2], the forgetful functor from Breuil modules to quasi-Breuil modules induces an isomorphism
From now on, all of our Breuil modules will be crystalline and have height
![]() $(p-2)$
. We write
$(p-2)$
. We write
![]() ${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
for the category of crystalline Breuil modules of height
${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
for the category of crystalline Breuil modules of height
![]() $(p-2)$
with
$(p-2)$
with
![]() ${\mathbb F}$
-coefficients, and
${\mathbb F}$
-coefficients, and
![]() ${\mathbb F}\!\operatorname {qBrMod}$
for the category of quasi-Breuil modules of height
${\mathbb F}\!\operatorname {qBrMod}$
for the category of quasi-Breuil modules of height
![]() $(p-2)$
with
$(p-2)$
with
![]() ${\mathbb F}$
-coefficients, which we identify with the category of Breuil–Kisin modules of height at most
${\mathbb F}$
-coefficients, which we identify with the category of Breuil–Kisin modules of height at most
![]() $(p-2)$
with
$(p-2)$
with
![]() ${\mathbb F}$
-coefficients. We say that a complex
${\mathbb F}$
-coefficients. We say that a complex
in
![]() ${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
or
${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
or
![]() ${\mathbb F}\!\operatorname {qBrMod}$
is exact if it induces exact sequences of
${\mathbb F}\!\operatorname {qBrMod}$
is exact if it induces exact sequences of
![]() $\overline {S}_{{\mathbb F}}$
-modules
$\overline {S}_{{\mathbb F}}$
-modules
![]() $0\to {\mathcal M}_1\to {\mathcal M}\to {\mathcal M}_2\to 0$
and
$0\to {\mathcal M}_1\to {\mathcal M}\to {\mathcal M}_2\to 0$
and
It is easily checked that a complex of quasi-Breuil modules is exact if and only if the corresponding complex of Breuil–Kisin modules is exact (as a complex of
![]() $\mathfrak {S}_{{\mathbb F}}$
-modules).
$\mathfrak {S}_{{\mathbb F}}$
-modules).
If
![]() ${\mathcal M}$
is an object of
${\mathcal M}$
is an object of
![]() ${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
, then an
${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
, then an
![]() $\overline {S}_{{\mathbb F}}$
-submodule
$\overline {S}_{{\mathbb F}}$
-submodule
![]() $\mathcal {N}\subseteq {\mathcal M}$
is a Breuil submodule of
$\mathcal {N}\subseteq {\mathcal M}$
is a Breuil submodule of
![]() ${\mathcal M}$
if it is a direct summand of
${\mathcal M}$
if it is a direct summand of
![]() ${\mathcal M}$
as a
${\mathcal M}$
as a
![]() $k[u]/u^{ep}$
-module, and we furthermore have
$k[u]/u^{ep}$
-module, and we furthermore have
![]() $N(\mathcal {N})\subseteq \mathcal {N}$
and
$N(\mathcal {N})\subseteq \mathcal {N}$
and
![]() $\varphi (\mathcal {N}\cap {\mathcal M}^r)\subseteq \mathcal {N}$
. Then
$\varphi (\mathcal {N}\cap {\mathcal M}^r)\subseteq \mathcal {N}$
. Then
![]() $\mathcal {N}$
inherits the structure of a crystalline Breuil module from
$\mathcal {N}$
inherits the structure of a crystalline Breuil module from
![]() ${\mathcal M}$
, as does the quotient
${\mathcal M}$
, as does the quotient
![]() ${\mathcal M}/\mathcal {N}$
, and by [Reference Herzig, Le and MorraHLM17, Lem. 2.3.2], the complex of crystalline Breuil modules
${\mathcal M}/\mathcal {N}$
, and by [Reference Herzig, Le and MorraHLM17, Lem. 2.3.2], the complex of crystalline Breuil modules
is exact; and conversely, if (2.1.3) is exact, then
![]() ${\mathcal M}_1$
is a Breuil submodule of
${\mathcal M}_1$
is a Breuil submodule of
![]() ${\mathcal M}$
.
${\mathcal M}$
.
Theorem 2.1.4.
-
1. The categories
 ${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
and
${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
and
 ${\mathbb F}\!\operatorname {qBrMod}$
are exact categories in the sense of [Reference QuillenQui10], and the functors T and
${\mathbb F}\!\operatorname {qBrMod}$
are exact categories in the sense of [Reference QuillenQui10], and the functors T and
 $T_\infty $
are exact.
$T_\infty $
are exact. -
2. For any object
 ${\mathcal M}$
of
${\mathcal M}$
of
 ${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
, there is an order preserving bijection
${\mathbb F}\!\operatorname {BrMod}^{\operatorname {cr}}$
, there is an order preserving bijection
 $\Theta $
between the Breuil submodules of
$\Theta $
between the Breuil submodules of
 ${\mathcal M}$
and the
${\mathcal M}$
and the
 $G_K$
-subrepresentations of
$G_K$
-subrepresentations of
 $T({\mathcal M})$
, taking
$T({\mathcal M})$
, taking
 $\mathcal {N}$
to the image of
$\mathcal {N}$
to the image of
 $T(\mathcal {N})\hookrightarrow T({\mathcal M})$
. Furthermore if
$T(\mathcal {N})\hookrightarrow T({\mathcal M})$
. Furthermore if
 ${\mathcal M}_1\subseteq {\mathcal M}_2$
are Breuil submodules of
${\mathcal M}_1\subseteq {\mathcal M}_2$
are Breuil submodules of
 ${\mathcal M}$
, then
${\mathcal M}$
, then
 $\Theta ({\mathcal M}_2)/\Theta ({\mathcal M}_1)\cong T({\mathcal M}_2/{\mathcal M}_1)$
.
$\Theta ({\mathcal M}_2)/\Theta ({\mathcal M}_1)\cong T({\mathcal M}_2/{\mathcal M}_1)$
.
Proof. The statement for quasi-Breuil modules is [Reference CarusoCar11, Thm. 2.1.2]. The rest of the theorem for not necessarily crystalline Breuil modules is [Reference Herzig, Le and MorraHLM17, Prop. 2.3.4, 2.3.5]. The case of crystalline Breuil modules follows formally because (as noted above) a Breuil submodule of a crystalline Breuil module is automatically crystalline (as is the corresponding quotient submodule). Alternatively, it is straightforward to check that the proofs of [Reference Herzig, Le and MorraHLM17, Prop. 2.3.4, 2.3.5] go through unchanged once one notes that the duality on Breuil modules [Reference Emerton, Gee and HerzigEGH13, Defn. 3.2.8] by definition preserves the subcategory of crystalline Breuil modules.
We now show that any Galois representation obtained as the reduction mod p of a lattice in a crystalline representation with Hodge–Tate weights in the range
![]() $[0,p-2]$
comes from a crystalline Breuil module. This is essentially an immediate consequence of the main theorem of Liu’s paper [Reference LiuLiu08], which proves an equivalence of categories between
$[0,p-2]$
comes from a crystalline Breuil module. This is essentially an immediate consequence of the main theorem of Liu’s paper [Reference LiuLiu08], which proves an equivalence of categories between
![]() $G_K$
-stable lattices inside semistable representations with Hodge–Tate weights in the range
$G_K$
-stable lattices inside semistable representations with Hodge–Tate weights in the range
![]() $[0,p-2]$
and strongly divisible modules. From this, one can easily deduce an equivalence of categories between
$[0,p-2]$
and strongly divisible modules. From this, one can easily deduce an equivalence of categories between
![]() $G_K$
-stable lattices inside crystalline representations with Hodge–Tate weights in the range
$G_K$
-stable lattices inside crystalline representations with Hodge–Tate weights in the range
![]() $[0,p-2]$
and an appropriate category of ‘crystalline strongly divisible lattices’, but since we do not need this, we avoid recalling the definitions of strongly divisible lattices and leave it to the interested reader.
$[0,p-2]$
and an appropriate category of ‘crystalline strongly divisible lattices’, but since we do not need this, we avoid recalling the definitions of strongly divisible lattices and leave it to the interested reader.
Recall that by the results of [Reference KisinKis06], if
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_n({\mathcal O})$
is a lattice in a crystalline representation with nonnegative Hodge–Tate weights, there is a Breuil–Kisin module with
$\rho :G_K\to \operatorname {\mathrm {GL}}_n({\mathcal O})$
is a lattice in a crystalline representation with nonnegative Hodge–Tate weights, there is a Breuil–Kisin module with
![]() ${\mathcal O}$
-coefficients
${\mathcal O}$
-coefficients
![]() $\mathfrak {M}_{{\mathcal O}}$
associated to
$\mathfrak {M}_{{\mathcal O}}$
associated to
![]() $\rho |_{G_{K_\infty }}$
(see, for example, [Reference Gee, Liu and SavittGLS14, Thm. 3.2(3), Prop. 3.4(3)] for a precise reference allowing
$\rho |_{G_{K_\infty }}$
(see, for example, [Reference Gee, Liu and SavittGLS14, Thm. 3.2(3), Prop. 3.4(3)] for a precise reference allowing
![]() ${\mathcal O}$
-coefficients).
${\mathcal O}$
-coefficients).
Theorem 2.1.5. Let
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_n({\mathcal O})$
be a lattice in a crystalline representation with Hodge–Tate weights in
$\rho :G_K\to \operatorname {\mathrm {GL}}_n({\mathcal O})$
be a lattice in a crystalline representation with Hodge–Tate weights in
![]() $[0,h]$
for some integer
$[0,h]$
for some integer
![]() $0\le h\le p-2$
, and write
$0\le h\le p-2$
, and write
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_n({\mathbb F})$
for its reduction modulo
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_n({\mathbb F})$
for its reduction modulo
![]() $\mathfrak {m}_{{\mathcal O}}$
. Then there is a crystalline Breuil module
$\mathfrak {m}_{{\mathcal O}}$
. Then there is a crystalline Breuil module
![]() ${\mathcal M}$
with
${\mathcal M}$
with
![]() ${\mathbb F}$
-coefficients such that
${\mathbb F}$
-coefficients such that
![]() $\overline {\rho }\cong T({\mathcal M})$
. Furthermore, the underlying Breuil–Kisin module of
$\overline {\rho }\cong T({\mathcal M})$
. Furthermore, the underlying Breuil–Kisin module of
![]() ${\mathcal M}$
has height at most h and is the reduction modulo
${\mathcal M}$
has height at most h and is the reduction modulo
![]() $\mathfrak {m}_{\mathcal O}$
of the Breuil–Kisin module
$\mathfrak {m}_{\mathcal O}$
of the Breuil–Kisin module
![]() $\mathfrak {M}_{{\mathcal O}}$
with
$\mathfrak {M}_{{\mathcal O}}$
with
![]() ${\mathcal O}$
-coefficients associated to
${\mathcal O}$
-coefficients associated to
![]() $\rho |_{G_{K_\infty }}$
.
$\rho |_{G_{K_\infty }}$
.
Proof. Since crystalline representations are in particular semistable, it is immediate from [Reference Emerton, Gee and HerzigEGH13, Prop. 3.1.4, Lem. 3.2.2] that there is a not necessarily crystalline Breuil module
![]() ${\mathcal M}$
with
${\mathcal M}$
with
![]() ${\mathbb F}$
-coefficients such that
${\mathbb F}$
-coefficients such that
![]() $\overline {\rho }\cong T({\mathcal M})$
, whose underlying Breuil–Kisin module has height at most h (note that our h is the integer r in the statement of [Reference Emerton, Gee and HerzigEGH13, Prop. 3.1.4]). We claim that the Breuil module provided by these results is necessarily crystalline. To see this, note first that (in the case at hand, with no descent data) [Reference Emerton, Gee and HerzigEGH13, Prop. 3.1.4] is a trivial consequence of the main result [Reference LiuLiu08, Thm. 2.3.5] of Liu’s paper [Reference LiuLiu08] and gives an equivalence of categories between
$\overline {\rho }\cong T({\mathcal M})$
, whose underlying Breuil–Kisin module has height at most h (note that our h is the integer r in the statement of [Reference Emerton, Gee and HerzigEGH13, Prop. 3.1.4]). We claim that the Breuil module provided by these results is necessarily crystalline. To see this, note first that (in the case at hand, with no descent data) [Reference Emerton, Gee and HerzigEGH13, Prop. 3.1.4] is a trivial consequence of the main result [Reference LiuLiu08, Thm. 2.3.5] of Liu’s paper [Reference LiuLiu08] and gives an equivalence of categories between
![]() $G_K$
-stable
$G_K$
-stable
![]() ${\mathcal O}$
-lattices inside semistable E-representations of
${\mathcal O}$
-lattices inside semistable E-representations of
![]() $G_K$
with Hodge–Tate weights in the range
$G_K$
with Hodge–Tate weights in the range
![]() $[0,p-2]$
and strongly divisible modules with
$[0,p-2]$
and strongly divisible modules with
![]() ${\mathcal O}$
-coefficients. In particular, there is a strongly divisible module with
${\mathcal O}$
-coefficients. In particular, there is a strongly divisible module with
![]() ${\mathcal O}$
-coefficients
${\mathcal O}$
-coefficients
![]() $\widehat {{\mathcal M}}$
corresponding to
$\widehat {{\mathcal M}}$
corresponding to
![]() $\rho $
.
$\rho $
.
We do not recall the notion of a strongly divisible module here, but we note that they are by definition modules over a coefficient ring
![]() $S_{{\mathcal O}}$
, equipped with a Frobenius, a filtration and a monodromy operator N, and by [Reference Emerton, Gee and HerzigEGH13, Lem. 3.2.2], the Breuil module
$S_{{\mathcal O}}$
, equipped with a Frobenius, a filtration and a monodromy operator N, and by [Reference Emerton, Gee and HerzigEGH13, Lem. 3.2.2], the Breuil module
![]() ${\mathcal M}$
is obtained from the strongly divisible module
${\mathcal M}$
is obtained from the strongly divisible module
![]() $\widehat {{\mathcal M}}$
by tensoring over
$\widehat {{\mathcal M}}$
by tensoring over
![]() $S_{{\mathcal O}}$
with
$S_{{\mathcal O}}$
with
![]() $\overline {S}_{{\mathbb F}}$
. By the commutative diagram at the end of [Reference LiuLiu08, §3.4], the strongly divisible module
$\overline {S}_{{\mathbb F}}$
. By the commutative diagram at the end of [Reference LiuLiu08, §3.4], the strongly divisible module
![]() $\widehat {{\mathcal M}}$
has underlying Breuil–Kisin module
$\widehat {{\mathcal M}}$
has underlying Breuil–Kisin module
![]() $\mathfrak {M}_{{\mathcal O}}$
(via the fully faithful functor of [Reference LiuLiu08, Cor. 3.3.2]). It follows immediately that the underlying Breuil–Kisin module of
$\mathfrak {M}_{{\mathcal O}}$
(via the fully faithful functor of [Reference LiuLiu08, Cor. 3.3.2]). It follows immediately that the underlying Breuil–Kisin module of
![]() ${\mathcal M}$
is the reduction modulo
${\mathcal M}$
is the reduction modulo
![]() $\mathfrak {m}_{{\mathcal O}}$
of
$\mathfrak {m}_{{\mathcal O}}$
of
![]() $\mathfrak {M}_{{\mathcal O}}$
, as claimed.
$\mathfrak {M}_{{\mathcal O}}$
, as claimed.
It remains to show that if
![]() $\rho $
is crystalline, the monodromy operator N on
$\rho $
is crystalline, the monodromy operator N on
![]() ${\mathcal M}$
vanishes mod u. This follows immediately from the compatibility between
${\mathcal M}$
vanishes mod u. This follows immediately from the compatibility between
![]() $\widehat {{\mathcal M}}$
and the weakly admissible module D associated to
$\widehat {{\mathcal M}}$
and the weakly admissible module D associated to
![]() $\rho $
, for which see [Reference LiuLiu08, §3.2].
$\rho $
, for which see [Reference LiuLiu08, §3.2].
2.2 Extensions of rank one Breuil modules
In this section we make a computation of the possible extensions of rank one Breuil modules, and prove the crucial Lemma 2.2.19, which gives a constraint on the Breuil modules which can witness sufficiently generic extensions of characters. A key input to the proof of this Lemma is Lemma 2.2.7, which constrains the shapes of extensions of rank one Breuil modules. To prove Lemma 2.2.19, we simply write down an explicit extension of characters (after restriction to
![]() $G_{K_{\infty }}$
) and show that it cannot arise from a Breuil module satisfying these constraints. These calculations are elementary, but are complicated in the case of a general field
$G_{K_{\infty }}$
) and show that it cannot arise from a Breuil module satisfying these constraints. These calculations are elementary, but are complicated in the case of a general field
![]() $K/{\mathbb Q}_p$
, and the reader may find it helpful to firstly work through the case that
$K/{\mathbb Q}_p$
, and the reader may find it helpful to firstly work through the case that
![]() $K/{\mathbb Q}_p$
is totally ramified, where the calculations simplify dramatically; if furthermore
$K/{\mathbb Q}_p$
is totally ramified, where the calculations simplify dramatically; if furthermore
![]() $n=2$
, then the monodromy condition is automatic and the calculations simplify further to a basic exercise with Breuil–Kisin modules.
$n=2$
, then the monodromy condition is automatic and the calculations simplify further to a basic exercise with Breuil–Kisin modules.
Let
![]() $\overline {\sigma }_0:k\hookrightarrow {\mathbb F}$
be a fixed embedding. Inductively define
$\overline {\sigma }_0:k\hookrightarrow {\mathbb F}$
be a fixed embedding. Inductively define
![]() $\overline {\sigma }_1,\dots ,\overline {\sigma }_{f-1}$
by
$\overline {\sigma }_1,\dots ,\overline {\sigma }_{f-1}$
by
![]() $\overline {\sigma }_{i+1}=\overline {\sigma }_i\circ \varphi ^{-1}$
, where
$\overline {\sigma }_{i+1}=\overline {\sigma }_i\circ \varphi ^{-1}$
, where
![]() $\varphi $
is the arithmetic Frobenius on k; we will often consider the numbering to be cyclic, so that
$\varphi $
is the arithmetic Frobenius on k; we will often consider the numbering to be cyclic, so that
![]() $\overline {\sigma }_f=\overline {\sigma }_0$
. There are idempotents
$\overline {\sigma }_f=\overline {\sigma }_0$
. There are idempotents
![]() $\epsilon _i\in k\otimes _{{\mathbb F}_p}{\mathbb F}$
such that if M is any
$\epsilon _i\in k\otimes _{{\mathbb F}_p}{\mathbb F}$
such that if M is any
![]() $k\otimes _{{\mathbb F}_p}{\mathbb F}$
-module, then
$k\otimes _{{\mathbb F}_p}{\mathbb F}$
-module, then
![]() $M=\bigoplus _i M_i$
, where
$M=\bigoplus _i M_i$
, where
![]() $M_i := \epsilon _iM$
is the subset of M consisting of elements m for which
$M_i := \epsilon _iM$
is the subset of M consisting of elements m for which
![]() $(x\otimes 1)m=(1\otimes \overline {\sigma }_i(x))m$
for all
$(x\otimes 1)m=(1\otimes \overline {\sigma }_i(x))m$
for all
![]() $x\in k$
. Note that
$x\in k$
. Note that
![]() $(\varphi \otimes 1)(\epsilon _i) = \epsilon _{i+1}$
for all i.
$(\varphi \otimes 1)(\epsilon _i) = \epsilon _{i+1}$
for all i.
As explained above, we are free to work with coefficients in
![]() $\overline {{\mathbb F}}_p$
rather than
$\overline {{\mathbb F}}_p$
rather than
![]() ${\mathbb F}$
, and for convenience we do so throughout this section. (To be precise, this means that we apply the definitions above with
${\mathbb F}$
, and for convenience we do so throughout this section. (To be precise, this means that we apply the definitions above with
![]() $\overline {S}_{{\mathbb F}}$
replaced by
$\overline {S}_{{\mathbb F}}$
replaced by
![]() $(k\otimes _{{\mathbb F}_p}\overline {{\mathbb F}}_p)[u]/u^{ep}$
.) It will be clear to the reader that the coefficients do not intervene in any way in the calculations, and we could equally well work with coefficients in any finite extension of
$(k\otimes _{{\mathbb F}_p}\overline {{\mathbb F}}_p)[u]/u^{ep}$
.) It will be clear to the reader that the coefficients do not intervene in any way in the calculations, and we could equally well work with coefficients in any finite extension of
![]() ${\mathbb F}$
.
${\mathbb F}$
.
Definition 2.2.1. Let
![]() $s_0,\ldots ,s_{f-1}$
be nonnegative integers, and let
$s_0,\ldots ,s_{f-1}$
be nonnegative integers, and let
![]() $a \in \overline {{\mathbb F}}_p^{\times }$
. Let
$a \in \overline {{\mathbb F}}_p^{\times }$
. Let
![]() $\mathfrak {M}(\underline {s};a)$
be the rank one Breuil–Kisin module with
$\mathfrak {M}(\underline {s};a)$
be the rank one Breuil–Kisin module with
![]() $\overline {{\mathbb F}}_p$
coefficients such that
$\overline {{\mathbb F}}_p$
coefficients such that
![]() $\mathfrak {M}(\underline {s}; a)_i$
is generated by
$\mathfrak {M}(\underline {s}; a)_i$
is generated by
![]() $e_i$
with
$e_i$
with
Here and below,
![]() $(a)_0 = a$
and
$(a)_0 = a$
and
![]() $(a)_i = 1$
if
$(a)_i = 1$
if
![]() $i\ne 0$
.
$i\ne 0$
.
By [Reference Gee, Liu and SavittGLS14, Lem. 6.2], any rank one Breuil–Kisin module is isomorphic to (exactly) one of the form
![]() $\mathfrak {M}(\underline {s}; a)$
.
$\mathfrak {M}(\underline {s}; a)$
.
Definition 2.2.2. Set
![]() $\alpha _i(\mathfrak {M}(\underline {s};a)) := \frac {1}{p^f-1} \sum _{j=1}^{f} p^{f-j} s_{j+i}$
.
$\alpha _i(\mathfrak {M}(\underline {s};a)) := \frac {1}{p^f-1} \sum _{j=1}^{f} p^{f-j} s_{j+i}$
.
By [Reference Gee, Liu and SavittGLS15, Lem. 5.1.2], there exists a nonzero map
![]() $\mathfrak {M}(\underline {s};a) \to \mathfrak {M}(\underline {t};b)$
if and only if
$\mathfrak {M}(\underline {s};a) \to \mathfrak {M}(\underline {t};b)$
if and only if
![]() $\alpha _i(\mathfrak {M}(\underline {s};a)) - \alpha _i(\mathfrak {M}(\underline {t};b)) \in {\mathbb Z}_{\ge 0}$
for all i, and
$\alpha _i(\mathfrak {M}(\underline {s};a)) - \alpha _i(\mathfrak {M}(\underline {t};b)) \in {\mathbb Z}_{\ge 0}$
for all i, and
![]() $a=b$
. We now show that each rank one Breuil–Kisin module of height at most
$a=b$
. We now show that each rank one Breuil–Kisin module of height at most
![]() $(p-2)$
underlies a unique rank one (crystalline) Breuil module. (In particular, all rank one Breuil modules are crystalline.)
$(p-2)$
underlies a unique rank one (crystalline) Breuil module. (In particular, all rank one Breuil modules are crystalline.)
Lemma 2.2.3. If each
![]() $s_i\in [0,e(p-2)]$
then the rank one Breuil–Kisin module
$s_i\in [0,e(p-2)]$
then the rank one Breuil–Kisin module
![]() $\mathfrak {M}(\underline {s}; a)$
underlies a unique height
$\mathfrak {M}(\underline {s}; a)$
underlies a unique height
![]() $(p-2)$
Breuil module
$(p-2)$
Breuil module
![]() ${\mathcal M}={\mathcal M}(\underline {s}; a)$
with
${\mathcal M}={\mathcal M}(\underline {s}; a)$
with
Proof. We begin by noting that since
![]() $(\varphi ^*\mathfrak {M}(\underline {s}; a))_i$
is generated by
$(\varphi ^*\mathfrak {M}(\underline {s}; a))_i$
is generated by
![]() $(1\otimes e_{i-1})$
, the quasi-Breuil module
$(1\otimes e_{i-1})$
, the quasi-Breuil module
![]() ${\mathcal M}=\varphi ^*\mathfrak {M}(\underline {s}; a)/u^{ep}$
corresponding to
${\mathcal M}=\varphi ^*\mathfrak {M}(\underline {s}; a)/u^{ep}$
corresponding to
![]() $\mathfrak {M}(\underline {s}; a)$
has the given form. It is easy to see that taking
$\mathfrak {M}(\underline {s}; a)$
has the given form. It is easy to see that taking
![]() $N((1\otimes e_{j-1}))=0$
gives
$N((1\otimes e_{j-1}))=0$
gives
![]() ${\mathcal M}$
the structure of a Breuil module. To see that this is the only possibility, write
${\mathcal M}$
the structure of a Breuil module. To see that this is the only possibility, write
![]() $N((1\otimes e_{j-1}))=\nu _j(1\otimes e_{j-1})$
. Then we have
$N((1\otimes e_{j-1}))=\nu _j(1\otimes e_{j-1})$
. Then we have
so that
and the equation
![]() $\varphi (u^eN(u^{e(p-2)-s_j}(1\otimes e_{j-1})))=N\varphi (u^{e(p-2)-s_j}(1\otimes e_{j-1}))$
gives
$\varphi (u^eN(u^{e(p-2)-s_j}(1\otimes e_{j-1})))=N\varphi (u^{e(p-2)-s_j}(1\otimes e_{j-1}))$
gives
![]() $\nu _{j+1}=0$
for each j, as required.
$\nu _{j+1}=0$
for each j, as required.
The extensions of rank one Breuil–Kisin modules are computed as follows.
Proposition 2.2.4. Let
![]() $\mathfrak {M}$
be an extension of
$\mathfrak {M}$
be an extension of
![]() $\mathfrak {M}(\underline {s};a)$
by
$\mathfrak {M}(\underline {s};a)$
by
![]() $\mathfrak {M}(\underline {t};b)$
. Then we can choose bases
$\mathfrak {M}(\underline {t};b)$
. Then we can choose bases
![]() $e_i,f_i$
of the
$e_i,f_i$
of the
![]() $\mathfrak {M}_i$
so that
$\mathfrak {M}_i$
so that
![]() $\varphi $
has the form
$\varphi $
has the form
 $$ \begin{align} \varphi(e_{i-1}) & = (b)_i u^{t_i} e_i \\ \varphi(f_{i-1}) & = (a)_i u^{s_i} f_i + y_i e_i \nonumber \end{align} $$
$$ \begin{align} \varphi(e_{i-1}) & = (b)_i u^{t_i} e_i \\ \varphi(f_{i-1}) & = (a)_i u^{s_i} f_i + y_i e_i \nonumber \end{align} $$
with ![]() a polynomial with
a polynomial with
![]() $\deg (y_i) < s_i$
, except that when there is a nonzero map
$\deg (y_i) < s_i$
, except that when there is a nonzero map
![]() $\mathfrak {M}(\underline {s};a)\to \mathfrak {M}(\underline {t};b)$
we must also allow
$\mathfrak {M}(\underline {s};a)\to \mathfrak {M}(\underline {t};b)$
we must also allow
![]() $y_j$
to have a term of degree
$y_j$
to have a term of degree
![]() $s_j + \alpha _j(\mathfrak {M}(\underline {s};a))-\alpha _j(\mathfrak {M}(\underline {t};b)) $
for any one choice of j.
$s_j + \alpha _j(\mathfrak {M}(\underline {s};a))-\alpha _j(\mathfrak {M}(\underline {t};b)) $
for any one choice of j.
Proof. This is [Reference Gee, Liu and SavittGLS15, Prop. 5.1.3].
Remark 2.2.6.
-
1. In our application to ‘generic’
 $\overline {\rho }$
, we could avoid considering the special case where there is a nonzero map
$\overline {\rho }$
, we could avoid considering the special case where there is a nonzero map
 $\mathfrak {M}(\underline {s};a)\to \mathfrak {M}(\underline {t};b)$
(for example by ensuring that
$\mathfrak {M}(\underline {s};a)\to \mathfrak {M}(\underline {t};b)$
(for example by ensuring that
 $a\ne b$
), but we have included it for completeness.
$a\ne b$
), but we have included it for completeness. -
2. While this is not claimed in [Reference Gee, Liu and SavittGLS15, Prop. 5.1.3], we expect that it is possible to show that distinct choices of the
 $y_i$
in 2.2.4 give distinct extensions of Breuil–Kisin modules.
$y_i$
in 2.2.4 give distinct extensions of Breuil–Kisin modules.
We now compute a constraint on extension classes of rank 1 Breuil modules.
Lemma 2.2.7. Let
![]() ${\mathcal M}$
be a crystalline Breuil module which is an extension of
${\mathcal M}$
be a crystalline Breuil module which is an extension of
![]() ${\mathcal M}(\underline {s};a)$
by
${\mathcal M}(\underline {s};a)$
by
![]() ${\mathcal M}(\underline {t};b)$
, with underlying Breuil–Kisin module
${\mathcal M}(\underline {t};b)$
, with underlying Breuil–Kisin module
![]() $\mathfrak {M}$
as in Proposition 2.2.4.
$\mathfrak {M}$
as in Proposition 2.2.4.
For each i we set
 $$ \begin{align} n_i:=\frac{1}{p^f-1}\sum_{j=1}^fp^{f-j}(s_{j+i-1}-t_{j+i-1}-e)\in{\mathbb Q}. \end{align} $$
$$ \begin{align} n_i:=\frac{1}{p^f-1}\sum_{j=1}^fp^{f-j}(s_{j+i-1}-t_{j+i-1}-e)\in{\mathbb Q}. \end{align} $$
Then the
![]() $y_j$
in Proposition 2.2.4 cannot have any terms of degree
$y_j$
in Proposition 2.2.4 cannot have any terms of degree
![]() $l< s_j-e +\max (n_{j+1},1)$
with
$l< s_j-e +\max (n_{j+1},1)$
with
![]() $l\not \equiv t_j\pmod {p}$
.
$l\not \equiv t_j\pmod {p}$
.
Proof. The quasi-Breuil module corresponding to
![]() $\mathfrak {M}$
has
$\mathfrak {M}$
has
![]() ${\mathcal M}_j$
generated by
${\mathcal M}_j$
generated by
![]() $(1\otimes e_{j-1}),(1\otimes f_{j-1})$
and
$(1\otimes e_{j-1}),(1\otimes f_{j-1})$
and
![]() ${\mathcal M}_j^{p-2}$
generated by
${\mathcal M}_j^{p-2}$
generated by
![]() $E_{j}:= u^{e(p-2)-t_j}(1\otimes e_{j-1})$
and
$E_{j}:= u^{e(p-2)-t_j}(1\otimes e_{j-1})$
and
The map
![]() $\varphi : {\mathcal M}^{p-2} \to {\mathcal M}$
is given by
$\varphi : {\mathcal M}^{p-2} \to {\mathcal M}$
is given by
(Note that
![]() $\mathfrak {M}$
must have height at most
$\mathfrak {M}$
must have height at most
![]() $(p-2)$
since it underlies a Breuil module, so
$(p-2)$
since it underlies a Breuil module, so
![]() $y_j$
is indeed divisible by
$y_j$
is indeed divisible by
![]() $u^{s_j+t_j-e(p-2)}$
.)
$u^{s_j+t_j-e(p-2)}$
.)
We have
![]() $N(1\otimes e_{j-1})=0$
, and we write
$N(1\otimes e_{j-1})=0$
, and we write
![]() $N(1\otimes f_{j-1})=\mu _j(1\otimes e_{j-1})$
with
$N(1\otimes f_{j-1})=\mu _j(1\otimes e_{j-1})$
with
![]() $\mu _j\in u\overline {{\mathbb F}}_p[u]$
(since
$\mu _j\in u\overline {{\mathbb F}}_p[u]$
(since
![]() ${\mathcal M}$
is crystalline), where for each j, we must have
${\mathcal M}$
is crystalline), where for each j, we must have
by the second property of N required in the definition of a Breuil module. Given this, the third property of N gives the commutation relation
 $$ \begin{align*} \varphi (u^eN(F_j)) &= N\varphi(F_j)\\ &=N((a)_{j} (1\otimes f_{j}))\\ &=(a)_j\mu_{j+1}(1\otimes e_{j}). \end{align*} $$
$$ \begin{align*} \varphi (u^eN(F_j)) &= N\varphi(F_j)\\ &=N((a)_{j} (1\otimes f_{j}))\\ &=(a)_j\mu_{j+1}(1\otimes e_{j}). \end{align*} $$
We have
 $$ \begin{align*} N(F_j) & = (s_j-e(p-2))u^{e(p-2)-s_j}(1\otimes f_{j-1})+u^{e(p-2)-s_j}\mu_j(1\otimes e_{j-1})\\&\quad +N(-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j)(1\otimes e_{j-1})\\ & = (s_j-e(p-2))(u^{e(p-2)-s_j}(1\otimes f_{j-1})-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j(1\otimes e_{j-1})) \\ & \quad + (u^{e(p-2)-s_j}\mu_j+N(-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j))(1\otimes e_{j-1})\\ & \quad +((s_j-e(p-2))u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j)(1\otimes e_{j-1}), \end{align*} $$
$$ \begin{align*} N(F_j) & = (s_j-e(p-2))u^{e(p-2)-s_j}(1\otimes f_{j-1})+u^{e(p-2)-s_j}\mu_j(1\otimes e_{j-1})\\&\quad +N(-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j)(1\otimes e_{j-1})\\ & = (s_j-e(p-2))(u^{e(p-2)-s_j}(1\otimes f_{j-1})-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j(1\otimes e_{j-1})) \\ & \quad + (u^{e(p-2)-s_j}\mu_j+N(-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j))(1\otimes e_{j-1})\\ & \quad +((s_j-e(p-2))u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j)(1\otimes e_{j-1}), \end{align*} $$
so we need the quantity
to be divisible by
![]() $u^{e(p-2)-t_j}$
; assuming this holds, the commutation relation with
$u^{e(p-2)-t_j}$
; assuming this holds, the commutation relation with
![]() $\varphi $
reads
$\varphi $
reads
 $$ \begin{align*} (a)_{j}\mu_{j+1} &= (b)_{j}u^{p(e-e(p-2)+t_j)}\varphi\bigg(u^{e(p-2)-s_j}\mu_j\\ &\quad +N(-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j)+(s_j-e(p-2))u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j\bigg). \end{align*} $$
$$ \begin{align*} (a)_{j}\mu_{j+1} &= (b)_{j}u^{p(e-e(p-2)+t_j)}\varphi\bigg(u^{e(p-2)-s_j}\mu_j\\ &\quad +N(-u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j)+(s_j-e(p-2))u^{e(p-2)-s_j-t_j}(b^{-1})_jy_j\bigg). \end{align*} $$
In particular, we see that
![]() $\mu _{j+1}\in \operatorname {\mathrm {im}}\varphi $
. Writing
$\mu _{j+1}\in \operatorname {\mathrm {im}}\varphi $
. Writing
![]() $\mu _{j+1}=\varphi (\mu ^{\prime }_{j+1})$
and rearranging, we obtain
$\mu _{j+1}=\varphi (\mu ^{\prime }_{j+1})$
and rearranging, we obtain
(Strictly speaking, since
![]() $\varphi (u^e)=u^{ep}=0$
, this is only an equation modulo
$\varphi (u^e)=u^{ep}=0$
, this is only an equation modulo
![]() $u^e$
; but it is easily checked that all terms have degree less than e, so it holds literally.)
$u^e$
; but it is easily checked that all terms have degree less than e, so it holds literally.)
Examining the left-hand side of (2.2.9), we note that there can be no cancellation between the terms in
![]() $\varphi (\mu ^{\prime }_j)$
and
$\varphi (\mu ^{\prime }_j)$
and
![]() $u^{-t_j}(t_jy_j+N(y_j))$
, as the exponents of u in
$u^{-t_j}(t_jy_j+N(y_j))$
, as the exponents of u in
![]() $\varphi (\mu ^{\prime }_j)$
are all divisible by p, while none of the exponents of u in
$\varphi (\mu ^{\prime }_j)$
are all divisible by p, while none of the exponents of u in
![]() $u^{-t_j}(t_jy_j+N(y_j))$
are divisible by p (the terms in
$u^{-t_j}(t_jy_j+N(y_j))$
are divisible by p (the terms in
![]() $t_jy_j$
with exponent
$t_jy_j$
with exponent
![]() $\equiv t_j \mod {p}$
cancel with terms in
$\equiv t_j \mod {p}$
cancel with terms in
![]() $N(y_j)$
). Let
$N(y_j)$
). Let
![]() $d_j\ge 1$
be the u-adic valuation of
$d_j\ge 1$
be the u-adic valuation of
![]() $\mu ^{\prime }_j$
(setting
$\mu ^{\prime }_j$
(setting
![]() $d_j = e$
if
$d_j = e$
if
![]() $\mu _j'$
is divisible by
$\mu _j'$
is divisible by
![]() $u^e$
). Then (2.2.9) gives us the inequality
$u^e$
). Then (2.2.9) gives us the inequality
(To see this, note that if the left-hand side is at least e, there is nothing to prove; and if
![]() $d_j=e$
, then since
$d_j=e$
, then since
![]() $s_j-t_j-e\le e(p-3)$
, the left-hand side is at least
$s_j-t_j-e\le e(p-3)$
, the left-hand side is at least
![]() $3e>e$
. Otherwise, the term
$3e>e$
. Otherwise, the term
![]() $u^{e-s_j+t_j}(b)_{j}\varphi (\mu ^{\prime }_j)$
means that the left-hand side of (2.2.9) has a term of degree
$u^{e-s_j+t_j}(b)_{j}\varphi (\mu ^{\prime }_j)$
means that the left-hand side of (2.2.9) has a term of degree
![]() $pd_j-(s_j-t_j-e)$
, because of the lack of cancellation.) Multiplying the inequalities (2.2.10) by suitable powers of p and summing, we have
$pd_j-(s_j-t_j-e)$
, because of the lack of cancellation.) Multiplying the inequalities (2.2.10) by suitable powers of p and summing, we have
 $$\begin{align*}\sum_{j=1}^fp^{f-j}(pd_{j+i-1}-d_{j+i})\ge \sum_{j=1}^fp^{f-j}(s_{j+i-1}-t_{j+i-1}-e), \end{align*}$$
$$\begin{align*}\sum_{j=1}^fp^{f-j}(pd_{j+i-1}-d_{j+i})\ge \sum_{j=1}^fp^{f-j}(s_{j+i-1}-t_{j+i-1}-e), \end{align*}$$
which simplifies to
![]() $d_i\ge n_i$
, where
$d_i\ge n_i$
, where
![]() $n_i$
is as in (2.2.8). Since
$n_i$
is as in (2.2.8). Since
![]() ${\mathcal M}$
is crystalline by assumption, we also have
${\mathcal M}$
is crystalline by assumption, we also have
![]() $d_i\ge 1$
, so that
$d_i\ge 1$
, so that
![]() $d_i\ge \max (1,n_i)$
for all i.
$d_i\ge \max (1,n_i)$
for all i.
Returning to (2.2.9), since the right-hand side has valuation
![]() $d_{j+1}$
, the lack of cancellation implies that the term
$d_{j+1}$
, the lack of cancellation implies that the term
![]() $u^{e-s_j}(t_jy_j+N(y_j))$
on the left-hand side is divisible by
$u^{e-s_j}(t_jy_j+N(y_j))$
on the left-hand side is divisible by
![]() $u^{\max (1,n_{j+1})}$
; equivalently, the terms in
$u^{\max (1,n_{j+1})}$
; equivalently, the terms in
![]() $y_j$
of degree less than
$y_j$
of degree less than
![]() $s_j-e+\max (1,n_{j+1})$
and not congruent to
$s_j-e+\max (1,n_{j+1})$
and not congruent to
![]() $t_j$
modulo p vanish, as claimed.
$t_j$
modulo p vanish, as claimed.
Remark 2.2.11. It follows easily from the definitions that if we have two extensions of
![]() ${\mathcal M}(\underline {s};a)$
by
${\mathcal M}(\underline {s};a)$
by
![]() ${\mathcal M}(\underline {t};b)$
as in Lemma 2.2.7, then their Baer sum corresponds to the extension obtained by summing the
${\mathcal M}(\underline {t};b)$
as in Lemma 2.2.7, then their Baer sum corresponds to the extension obtained by summing the
![]() $y_j$
(and has N given by summing the
$y_j$
(and has N given by summing the
![]() $\mu _j$
).
$\mu _j$
).
In the following arguments, it will be useful to note that by the definition of the
![]() $n_j$
in (2.2.8), we have
$n_j$
in (2.2.8), we have
for all j.
Lemma 2.2.13. Write
Then
![]() $r_i\in [1,p]$
for each i.
$r_i\in [1,p]$
for each i.
Proof. Using (2.2.12), we have
![]() $r_i-1=p(n_i-\lfloor n_i\rfloor )-(n_{i+1}-\lfloor n_{i+1}\rfloor )$
, and since for any real number x we have
$r_i-1=p(n_i-\lfloor n_i\rfloor )-(n_{i+1}-\lfloor n_{i+1}\rfloor )$
, and since for any real number x we have
![]() $(x-\lfloor x\rfloor ) \in [0,1)$
, we have
$(x-\lfloor x\rfloor ) \in [0,1)$
, we have
![]() $r_i-1\in (-1,p)$
. Since
$r_i-1\in (-1,p)$
. Since
![]() $r_i$
is an integer, the result follows.
$r_i$
is an integer, the result follows.
Write
for the
![]() $\operatorname {\mathrm {Ext}}^1$
group computed in the exact category
$\operatorname {\mathrm {Ext}}^1$
group computed in the exact category
![]() $\overline {{\mathbb F}}_p\!\operatorname {BrMod}^{\operatorname {cr}}$
. Write
$\overline {{\mathbb F}}_p\!\operatorname {BrMod}^{\operatorname {cr}}$
. Write
Then the restriction maps
are homomorphisms of
![]() $\overline {{\mathbb F}}_p$
-vector spaces. Regarding elements of
$\overline {{\mathbb F}}_p$
-vector spaces. Regarding elements of
![]() $\operatorname {\mathrm {Ext}}^1_{G_{K_\infty }}(\overline {\chi }_2,\overline {\chi }_1)$
as étale
$\operatorname {\mathrm {Ext}}^1_{G_{K_\infty }}(\overline {\chi }_2,\overline {\chi }_1)$
as étale
![]() $\varphi $
-modules, we have the following description of the image of the restriction map
$\varphi $
-modules, we have the following description of the image of the restriction map
![]() $\operatorname {res}_{K_{\infty }}$
. (In our key Lemma 2.2.19, we will show that the composition
$\operatorname {res}_{K_{\infty }}$
. (In our key Lemma 2.2.19, we will show that the composition
![]() $\operatorname {res}_{K_{\infty }}\circ \operatorname {res}_K$
has smaller image.)
$\operatorname {res}_{K_{\infty }}\circ \operatorname {res}_K$
has smaller image.)
Lemma 2.2.15.
-
1. The restriction map
 $\operatorname {res}_{K_{\infty }}$
is injective unless
$\operatorname {res}_{K_{\infty }}$
is injective unless
 $\overline {\chi }_1\overline {\chi }_2^{-1}=\overline {\varepsilon }$
, in which case its kernel is
$\overline {\chi }_1\overline {\chi }_2^{-1}=\overline {\varepsilon }$
, in which case its kernel is
 $1$
-dimensional, and is generated by the très ramifiée line given by the Kummer extension corresponding to the chosen uniformizer
$1$
-dimensional, and is generated by the très ramifiée line given by the Kummer extension corresponding to the chosen uniformizer
 $\pi $
of K.
$\pi $
of K. -
2. The image of
 $\operatorname {res}_{K_{\infty }}$
has dimension
$\operatorname {res}_{K_{\infty }}$
has dimension
 $[K:{\mathbb Q}_p]$
, unless
$[K:{\mathbb Q}_p]$
, unless
 $\overline {\chi }_1=\overline {\chi }_2$
, in which case it has dimension
$\overline {\chi }_1=\overline {\chi }_2$
, in which case it has dimension
 $[K:{\mathbb Q}_p]+1$
.
$[K:{\mathbb Q}_p]+1$
. -
3. The étale
 $\varphi $
-modules M in the image of
$\varphi $
-modules M in the image of
 $\operatorname {res}_{K_{\infty }}$
are precisely those for which we can choose a basis
$\operatorname {res}_{K_{\infty }}$
are precisely those for which we can choose a basis
 $e_i,f_i$
of
$e_i,f_i$
of
 $M_i$
so that
$M_i$
so that
 $\varphi $
has the form (2.2.16)where
$\varphi $
has the form (2.2.16)where $$ \begin{align} \varphi(e_{i-1}) & = (b)_i u^{t_i} e_i \\ \varphi(f_{i-1}) & = (a)_i u^{s_i} f_i + y_i e_i, \nonumber \end{align} $$
$$ \begin{align} \varphi(e_{i-1}) & = (b)_i u^{t_i} e_i \\ \varphi(f_{i-1}) & = (a)_i u^{s_i} f_i + y_i e_i, \nonumber \end{align} $$
 $y_i \in \overline {{\mathbb F}}_p[u,u^{-1}]$
has nonzero terms only in degrees
$y_i \in \overline {{\mathbb F}}_p[u,u^{-1}]$
has nonzero terms only in degrees
 $[s_i+\lfloor n_{i+1}\rfloor -e+1,\dots ,s_i+\lfloor n_{i+1}\rfloor ]$
, except that when
$[s_i+\lfloor n_{i+1}\rfloor -e+1,\dots ,s_i+\lfloor n_{i+1}\rfloor ]$
, except that when
 $\overline {\chi }_1=\overline {\chi }_2$
, we also allow
$\overline {\chi }_1=\overline {\chi }_2$
, we also allow
 $y_i$
to have a term of degree (necessarily an integer in this case) for any one choice of i.
$y_i$
to have a term of degree (necessarily an integer in this case) for any one choice of i. $$\begin{align*}s_i + \frac{1}{p^f-1}\sum_{j=1}^fp^{f-j}(s_{j+i}-t_{j+i})\end{align*}$$
$$\begin{align*}s_i + \frac{1}{p^f-1}\sum_{j=1}^fp^{f-j}(s_{j+i}-t_{j+i})\end{align*}$$
Proof. The first part is [Reference Gee, Liu and SavittGLS15, Lem. 5.4.2]. The second part then follows from the usual computation of the dimension of
![]() $\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
via Tate’s Euler characteristic formula and local duality.
$\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
via Tate’s Euler characteristic formula and local duality.
The final part can presumably be proved in an elementary way, but for convenience, we explain how to deduce it from the results of [Reference Gee, Liu and SavittGLS15] on the Breuil–Kisin modules associated to certain crystalline representations with small Hodge–Tate weights. This was first explained in [Reference Calegari, Emerton, Gee and MavridesCEGM17, Thm. 3.3.2] in the case
![]() $K/{\mathbb Q}_p$
unramified (which employed the earlier results [Reference Gee, Liu and SavittGLS14]), and in general [Reference SteinmetzSte22, Thm. 4.2], under the assumption that
$K/{\mathbb Q}_p$
unramified (which employed the earlier results [Reference Gee, Liu and SavittGLS14]), and in general [Reference SteinmetzSte22, Thm. 4.2], under the assumption that
![]() $\overline {\chi }_1\overline {\chi }_2^{-1}\ne \overline {\varepsilon }$
. However, the comparison to the notation used in [Reference SteinmetzSte22, Thm. 4.2] is not immediate, and we need to treat the case
$\overline {\chi }_1\overline {\chi }_2^{-1}\ne \overline {\varepsilon }$
. However, the comparison to the notation used in [Reference SteinmetzSte22, Thm. 4.2] is not immediate, and we need to treat the case
![]() $\overline {\chi }_1\overline {\chi }_2^{-1}=\overline {\varepsilon }$
, so for the convenience of the reader, we explain in our notation how to extract the claim from [Reference Gee, Liu and SavittGLS15].
$\overline {\chi }_1\overline {\chi }_2^{-1}=\overline {\varepsilon }$
, so for the convenience of the reader, we explain in our notation how to extract the claim from [Reference Gee, Liu and SavittGLS15].
It is easy to check that the étale
![]() $\varphi $
-modules in (2.2.16) span a space of the dimension computed in part (2). In particular, in the case when
$\varphi $
-modules in (2.2.16) span a space of the dimension computed in part (2). In particular, in the case when
![]() $\overline {\chi }_1 = \overline {\chi }_2$
, considering the change of basis adding on a suitable multiple of
$\overline {\chi }_1 = \overline {\chi }_2$
, considering the change of basis adding on a suitable multiple of
![]() $e_i$
to
$e_i$
to
![]() $f_i$
shows that the additional
$f_i$
shows that the additional
![]() $\varphi $
-modules in that case do not depend on the choice of i for which
$\varphi $
-modules in that case do not depend on the choice of i for which
![]() $y_i$
is allowed to have an extra term. It now suffices to show that all of the possibilities in (2.2.16) do indeed arise from
$y_i$
is allowed to have an extra term. It now suffices to show that all of the possibilities in (2.2.16) do indeed arise from
![]() $G_K$
-representations. We can and do twist so that
$G_K$
-representations. We can and do twist so that
![]() $t_i=0$
for all i. (This has the effect of replacing
$t_i=0$
for all i. (This has the effect of replacing
![]() $s_i$
by
$s_i$
by
![]() $s_i-t_i$
, and leaving
$s_i-t_i$
, and leaving
![]() $n_i$
unchanged, so the general statement follows immediately by twisting back.) Then our strategy is to show that our étale
$n_i$
unchanged, so the general statement follows immediately by twisting back.) Then our strategy is to show that our étale
![]() $\varphi $
-modules arise from the reductions of certain crystalline representations. In fact, we will see that they arise from the reductions of crystalline extensions of p-adic characters.
$\varphi $
-modules arise from the reductions of certain crystalline representations. In fact, we will see that they arise from the reductions of crystalline extensions of p-adic characters.
We make the change of variables
![]() $f_i'=u^{-\lfloor n_{i+1}\rfloor }f_i$
, and write
$f_i'=u^{-\lfloor n_{i+1}\rfloor }f_i$
, and write
![]() $y_i':=u^{-p\lfloor n_{i}\rfloor }y_i$
. Then we have
$y_i':=u^{-p\lfloor n_{i}\rfloor }y_i$
. Then we have
 $$\begin{align*}\varphi(e_{i-1}) &= (b)_i e_i,\\ \varphi(f_{i-1}') &= (a)_i u^{r_i+e-1} f_i'+y^{\prime}_ie_i.\end{align*}$$
$$\begin{align*}\varphi(e_{i-1}) &= (b)_i e_i,\\ \varphi(f_{i-1}') &= (a)_i u^{r_i+e-1} f_i'+y^{\prime}_ie_i.\end{align*}$$
By (2.2.14) and our assumption that
![]() $t_i=0$
, we have
$t_i=0$
, we have
so we need to show that every choice of
![]() $y^{\prime }_i$
having nonzero terms in degrees
$y^{\prime }_i$
having nonzero terms in degrees
![]() $[r_i,r_i+e-1]$
occurs (together with the additional term in the statement in the case that
$[r_i,r_i+e-1]$
occurs (together with the additional term in the statement in the case that
![]() $\overline {\chi }_1=\overline {\chi }_2$
). If we make a further change of variables to replace
$\overline {\chi }_1=\overline {\chi }_2$
). If we make a further change of variables to replace
![]() $f^{\prime }_i$
with
$f^{\prime }_i$
with
![]() $f^{\prime }_i+z_ie_i$
for all i, with
$f^{\prime }_i+z_ie_i$
for all i, with
![]() $z_i\in \overline {{\mathbb F}}_p$
, then we may exchange the terms in
$z_i\in \overline {{\mathbb F}}_p$
, then we may exchange the terms in
![]() $y_i'$
of degree
$y_i'$
of degree
![]() $r_i+e-1$
with terms in
$r_i+e-1$
with terms in
![]() $y_{i-1}$
of degree
$y_{i-1}$
of degree
![]() $0$
(cf. (2.2.23)), so it suffices in turn to show that every choice of
$0$
(cf. (2.2.23)), so it suffices in turn to show that every choice of
![]() $y_i'$
having nonzero terms in degrees
$y_i'$
having nonzero terms in degrees
![]() $0$
and
$0$
and
![]() $[r_i,r_i+e-2]$
occurs in the image of
$[r_i,r_i+e-2]$
occurs in the image of
![]() $\operatorname {res}_{K_{\infty }}$
(again, together with the additional term in the statement in the case that
$\operatorname {res}_{K_{\infty }}$
(again, together with the additional term in the statement in the case that
![]() $\overline {\chi }_1=\overline {\chi }_2$
).
$\overline {\chi }_1=\overline {\chi }_2$
).
Recall [Reference Gee, Liu and SavittGLS15, Defn. 2.3.1] that a pseudo-Barsotti–Tate representation of weight
![]() $\{r_i\}$
is a 2-dimensional crystalline representation whose labelled Hodge–Tate weights are
$\{r_i\}$
is a 2-dimensional crystalline representation whose labelled Hodge–Tate weights are
![]() $\{0,1\}$
, except at a chosen set of f embeddings lifting the embeddings
$\{0,1\}$
, except at a chosen set of f embeddings lifting the embeddings
![]() $\sigma _i:k\hookrightarrow \overline {{\mathbb F}}_p$
, where they are
$\sigma _i:k\hookrightarrow \overline {{\mathbb F}}_p$
, where they are
![]() $\{0,r_i\}$
. By [Reference Gee, Liu and SavittGLS15, Defn. 4.1.3], these are the representations which have
$\{0,r_i\}$
. By [Reference Gee, Liu and SavittGLS15, Defn. 4.1.3], these are the representations which have
![]() $\sigma _{r-1,0}:=\otimes _{i}\operatorname {\mathrm {Sym}}^{r_i-1}k^2\otimes _{k,\sigma _i}\overline {{\mathbb F}}_p$
as a Serre weight.
$\sigma _{r-1,0}:=\otimes _{i}\operatorname {\mathrm {Sym}}^{r_i-1}k^2\otimes _{k,\sigma _i}\overline {{\mathbb F}}_p$
as a Serre weight.
Now consider [Reference Gee, Liu and SavittGLS15, Thm. 5.1.5], taking the
![]() $t_i$
there to be zero, the
$t_i$
there to be zero, the
![]() $x_i$
to be
$x_i$
to be
![]() $e-1$
, and the
$e-1$
, and the
![]() $s_i$
there to be our
$s_i$
there to be our
![]() $r_i+e-1$
(which are not necessarily equal to our
$r_i+e-1$
(which are not necessarily equal to our
![]() $s_i$
– we apologize for this temporary notation). Note that with this choice, the Breuil–Kisin modules spanned by our basis
$s_i$
– we apologize for this temporary notation). Note that with this choice, the Breuil–Kisin modules spanned by our basis
![]() $e_i,f^{\prime }_i$
are precisely the extensions of Breuil–Kisin modules in [Reference Gee, Liu and SavittGLS15, Thm. 5.1.5], for the rank one Breuil–Kisin modules which are the minimal and maximal models of
$e_i,f^{\prime }_i$
are precisely the extensions of Breuil–Kisin modules in [Reference Gee, Liu and SavittGLS15, Thm. 5.1.5], for the rank one Breuil–Kisin modules which are the minimal and maximal models of
![]() $\overline {\chi }_1,\overline {\chi }_2$
as in the statement of [Reference Gee, Liu and SavittGLS15, Prop. 5.3.4]. So by [Reference Gee, Liu and SavittGLS15, Prop. 5.3.4, Thm. 5.1.5], if
$\overline {\chi }_1,\overline {\chi }_2$
as in the statement of [Reference Gee, Liu and SavittGLS15, Prop. 5.3.4]. So by [Reference Gee, Liu and SavittGLS15, Prop. 5.3.4, Thm. 5.1.5], if
![]() $\psi \in \operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
comes from the reduction of a pseudo-Barsotti–Tate representations of weight
$\psi \in \operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
comes from the reduction of a pseudo-Barsotti–Tate representations of weight
![]() $\{r_i\}$
, then
$\{r_i\}$
, then
![]() $\operatorname {res}_{K_{\infty }}(\psi )$
is given by an étale
$\operatorname {res}_{K_{\infty }}(\psi )$
is given by an étale
![]() $\varphi $
-module as in (2.2.16). It therefore suffices to show that these classes
$\varphi $
-module as in (2.2.16). It therefore suffices to show that these classes
![]() $\operatorname {res}_{K_{\infty }}(\psi )$
span the image of
$\operatorname {res}_{K_{\infty }}(\psi )$
span the image of
![]() $\operatorname {res}_{K_{\infty }}$
.
$\operatorname {res}_{K_{\infty }}$
.
To see this, we consider the reductions of reducible crystalline representations. As in the proof of [Reference Gee, Liu and SavittGLS15, Thm. 5.4.1], we choose crystalline characters
![]() $\chi _{1,\min }, \chi _{2,\max }$
which lift
$\chi _{1,\min }, \chi _{2,\max }$
which lift
![]() $\overline {\chi }_1, \overline {\chi }_2$
, respectively. More precisely, these characters are determined (up to unramified twist, which we do not specify) by their Hodge–Tate weights, which (recalling that
$\overline {\chi }_1, \overline {\chi }_2$
, respectively. More precisely, these characters are determined (up to unramified twist, which we do not specify) by their Hodge–Tate weights, which (recalling that
![]() $t_i=0$
for all i) we can and do choose so that
$t_i=0$
for all i) we can and do choose so that
![]() $\chi _{2,\max }$
is unramified, and so that any crystalline extension of
$\chi _{2,\max }$
is unramified, and so that any crystalline extension of
![]() $\chi _{2,\max }$
by
$\chi _{2,\max }$
by
![]() $\chi _{1,\min }$
is pseudo-Barsotti–Tate of weight
$\chi _{1,\min }$
is pseudo-Barsotti–Tate of weight
![]() $\{r_i\}$
.
$\{r_i\}$
.
The space of crystalline extensions of
![]() $\chi _{2,\max }$
by
$\chi _{2,\max }$
by
![]() $\chi _{1,\min }$
is identified with the Galois cohomology group
$\chi _{1,\min }$
is identified with the Galois cohomology group
![]() $H^1_{f}(G_K,\chi _{1,\min }\chi _{2,\max }^{-1})$
, and as in the proof of [Reference Gee, Liu and SavittGLS15, Thm. 5.4.1], one immediately computes that the dimension of the image of the reduction map
$H^1_{f}(G_K,\chi _{1,\min }\chi _{2,\max }^{-1})$
, and as in the proof of [Reference Gee, Liu and SavittGLS15, Thm. 5.4.1], one immediately computes that the dimension of the image of the reduction map
is
![]() $[K:{\mathbb Q}_p]$
, unless
$[K:{\mathbb Q}_p]$
, unless
![]() $\overline {\chi }_1=\overline {\chi }_2$
, in which case it is
$\overline {\chi }_1=\overline {\chi }_2$
, in which case it is
![]() $[K:{\mathbb Q}_p]+1$
; so by part (2), this image has the same dimension as the image of
$[K:{\mathbb Q}_p]+1$
; so by part (2), this image has the same dimension as the image of
![]() $\operatorname {res}_{K_{\infty }}$
.
$\operatorname {res}_{K_{\infty }}$
.
In particular, we see that we are done if the restriction of
![]() $\operatorname {res}_{K_{\infty }}$
to the image of (2.2.17) is injective. If
$\operatorname {res}_{K_{\infty }}$
to the image of (2.2.17) is injective. If
![]() $\overline {\chi }_1\overline {\chi }_2^{-1}\ne \overline {\varepsilon }$
, then this is automatic by part (1), so we may suppose that
$\overline {\chi }_1\overline {\chi }_2^{-1}\ne \overline {\varepsilon }$
, then this is automatic by part (1), so we may suppose that
![]() $\overline {\chi }_1\overline {\chi }_2^{-1}=\overline {\varepsilon }$
. If some
$\overline {\chi }_1\overline {\chi }_2^{-1}=\overline {\varepsilon }$
. If some
![]() $r_i\ne p$
, then by [Reference Caraiani, Emerton, Gee and SavittCEGS22b, Lem. A.4], the image of (2.2.17) is contained in the peu ramifiée subspace, so we again conclude by part (1). Finally if
$r_i\ne p$
, then by [Reference Caraiani, Emerton, Gee and SavittCEGS22b, Lem. A.4], the image of (2.2.17) is contained in the peu ramifiée subspace, so we again conclude by part (1). Finally if
![]() $r_i=p$
for all i, then as in the proof of [Reference Gee, Liu and SavittGLS15, Thm. 6.1.18], the union of the images of (2.2.17) as
$r_i=p$
for all i, then as in the proof of [Reference Gee, Liu and SavittGLS15, Thm. 6.1.18], the union of the images of (2.2.17) as
![]() $\chi _{1,\min },\chi _{2,\max }$
range over their twists by unramified characters with trivial reduction is all of
$\chi _{1,\min },\chi _{2,\max }$
range over their twists by unramified characters with trivial reduction is all of
![]() $H^1(G_K,\overline {\chi }_1\overline {\chi }_2^{-1})$
, so we are done.
$H^1(G_K,\overline {\chi }_1\overline {\chi }_2^{-1})$
, so we are done.
Lemma 2.2.18. Suppose that
![]() $\sum _{j=1}^f(s_j-t_j-e)<0$
. Then either there exists an i with
$\sum _{j=1}^f(s_j-t_j-e)<0$
. Then either there exists an i with
![]() $\lfloor n_{i+1}\rfloor =-1$
and
$\lfloor n_{i+1}\rfloor =-1$
and
![]() $r_i\ne p$
, or there exists an i with
$r_i\ne p$
, or there exists an i with
![]() $\lfloor n_{i+1}\rfloor \le -2$
.
$\lfloor n_{i+1}\rfloor \le -2$
.
Proof. Summing (2.2.14) over all j, we have
 $$\begin{align*}\sum_{j=1}^f(s_j-t_j-e)=\sum_{j=1}^f\left((p-1)\lfloor n_{j+1}\rfloor+(r_j-1)\right). \end{align*}$$
$$\begin{align*}\sum_{j=1}^f(s_j-t_j-e)=\sum_{j=1}^f\left((p-1)\lfloor n_{j+1}\rfloor+(r_j-1)\right). \end{align*}$$
If this is negative, there exists an i with
Since
![]() $r_i\ge 1$
, we must have
$r_i\ge 1$
, we must have
![]() $\lfloor n_{i+1}\rfloor <0$
. If
$\lfloor n_{i+1}\rfloor <0$
. If
![]() $\lfloor n_{i+1}\rfloor =-1$
, then we have
$\lfloor n_{i+1}\rfloor =-1$
, then we have
![]() $1-p+r_i-1<0$
, so
$1-p+r_i-1<0$
, so
![]() $r_i<p$
, as required.
$r_i<p$
, as required.
Lemma 2.2.19. Suppose that
![]() $\sum _{j=1}^f(s_j-t_j-e)<0$
. Then the restriction map
$\sum _{j=1}^f(s_j-t_j-e)<0$
. Then the restriction map
is not surjective.
Proof. It suffices to show that
![]() $\operatorname {\mathrm {im}}(\operatorname {res}_{K_{\infty }}\circ \operatorname {res}_K)$
is a proper subspace of
$\operatorname {\mathrm {im}}(\operatorname {res}_{K_{\infty }}\circ \operatorname {res}_K)$
is a proper subspace of
![]() $\operatorname {\mathrm {im}}(\operatorname {res}_{K_{\infty }})$
. Viewing classes in
$\operatorname {\mathrm {im}}(\operatorname {res}_{K_{\infty }})$
. Viewing classes in
![]() $\operatorname {\mathrm {Ext}}^1_{G_{K_\infty }}(\overline {\chi }_2,\overline {\chi }_1)$
as étale
$\operatorname {\mathrm {Ext}}^1_{G_{K_\infty }}(\overline {\chi }_2,\overline {\chi }_1)$
as étale
![]() $\varphi $
-modules, it therefore suffices to exhibit an étale
$\varphi $
-modules, it therefore suffices to exhibit an étale
![]() $\varphi $
-module as in the statement of Lemma 2.2.15 (3) which is not in the image of
$\varphi $
-module as in the statement of Lemma 2.2.15 (3) which is not in the image of
![]() $\operatorname {res}_{K_{\infty }}\circ \operatorname {res}_K$
.
$\operatorname {res}_{K_{\infty }}\circ \operatorname {res}_K$
.
By Lemma 2.2.18, we may assume that for some i, we either have
![]() $\lfloor n_{i+1}\rfloor =-1$
and
$\lfloor n_{i+1}\rfloor =-1$
and
![]() $r_i\ne p$
, or we have
$r_i\ne p$
, or we have
![]() $\lfloor n_{i+1}\rfloor \le -2$
. If
$\lfloor n_{i+1}\rfloor \le -2$
. If
![]() $r_i\ne p$
, then we set
$r_i\ne p$
, then we set
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+1$
, while if
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+1$
, while if
![]() $r_i=p$
(so that
$r_i=p$
(so that
![]() $\lfloor n_{i+1}\rfloor \le -2$
), we set
$\lfloor n_{i+1}\rfloor \le -2$
), we set
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+2$
. It follows from (2.2.14) that
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+2$
. It follows from (2.2.14) that
![]() $s_i+\lfloor n_{i+1}\rfloor -e+1\equiv t_i+r_i\pmod {p}$
, so we have
$s_i+\lfloor n_{i+1}\rfloor -e+1\equiv t_i+r_i\pmod {p}$
, so we have
We claim that we also have
Indeed, by definition, we have
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+1$
or
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+1$
or
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+2$
, so the lower bound is immediate, and the upper bound is also automatic unless
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+2$
, so the lower bound is immediate, and the upper bound is also automatic unless
![]() $e=1$
. If
$e=1$
. If
![]() $e=1$
, we need to rule out the possibility that we are in the case
$e=1$
, we need to rule out the possibility that we are in the case
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+2$
. In this case, we assumed that
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+2$
. In this case, we assumed that
![]() $\lfloor n_{i+1}\rfloor \le -2$
, so in particular,
$\lfloor n_{i+1}\rfloor \le -2$
, so in particular,
![]() $n_{i+1}<-1$
; but since we have
$n_{i+1}<-1$
; but since we have
![]() $s_j-t_j-e\ge -e(p-1)$
for all j, it follows from (2.2.8) that we have
$s_j-t_j-e\ge -e(p-1)$
for all j, it follows from (2.2.8) that we have
![]() $n_j\ge -e$
for all j, and in particular, if
$n_j\ge -e$
for all j, and in particular, if
![]() $e=1$
, we have
$e=1$
, we have
![]() $n_{i+1}\ge -1$
, as required.
$n_{i+1}\ge -1$
, as required.
We also have
![]() $x_i\le s_i-e$
because if
$x_i\le s_i-e$
because if
![]() $\lfloor n_{i+1}\rfloor =-1$
, then
$\lfloor n_{i+1}\rfloor =-1$
, then
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+1=s_i-e$
, and otherwise,
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+1=s_i-e$
, and otherwise,
![]() $\lfloor n_{i+1}\rfloor \le -2$
, and we have
$\lfloor n_{i+1}\rfloor \le -2$
, and we have
![]() $x_i=s_i+\lfloor n_{i+1}\rfloor -e+2\le s_i-e$
; that is,
$x_i=s_i+\lfloor n_{i+1}\rfloor -e+2\le s_i-e$
; that is,
(We have written the inequality in this form so that we can apply Lemma 2.2.7.) Set
![]() $y^{\prime }_i=u^{x_i}$
and
$y^{\prime }_i=u^{x_i}$
and
![]() $y^{\prime }_j=0$
for all
$y^{\prime }_j=0$
for all
![]() $j\ne i$
. By (2.2.21) and Lemma 2.2.15, it suffices to show that the étale
$j\ne i$
. By (2.2.21) and Lemma 2.2.15, it suffices to show that the étale
![]() $\varphi $
-module M arising from taking the
$\varphi $
-module M arising from taking the
![]() $y_j$
in (2.2.16) to be our
$y_j$
in (2.2.16) to be our
![]() $y^{\prime }_j$
is not of the form
$y^{\prime }_j$
is not of the form
![]() $\mathfrak {M}[1/u]$
for any Breuil–Kisin module
$\mathfrak {M}[1/u]$
for any Breuil–Kisin module
![]() $\mathfrak {M}$
satisfying the constraints of Lemma 2.2.7.
$\mathfrak {M}$
satisfying the constraints of Lemma 2.2.7.
Suppose on the contrary that
![]() $\mathfrak {M}$
as in (2.2.5) has
$\mathfrak {M}$
as in (2.2.5) has
![]() $\mathfrak {M}[1/u]\cong M$
. This means that there is a change of variables
$\mathfrak {M}[1/u]\cong M$
. This means that there is a change of variables
![]() $e^{\prime }_j=e_j$
,
$e^{\prime }_j=e_j$
,
![]() $f_j'=f_j+\lambda _j e_j$
with
$f_j'=f_j+\lambda _j e_j$
with
![]() $\lambda _j\in \overline {{\mathbb F}}_p((u))$
having the property that for all j, we have
$\lambda _j\in \overline {{\mathbb F}}_p((u))$
having the property that for all j, we have
Equivalently, for each j, we must have
Recall that we chose
![]() $y^{\prime }_i=u^{x_i}$
, where
$y^{\prime }_i=u^{x_i}$
, where
![]() $x_i$
satisfies (2.2.20) and (2.2.22), so the coefficient of
$x_i$
satisfies (2.2.20) and (2.2.22), so the coefficient of
![]() $u^{x_i}$
in
$u^{x_i}$
in
![]() $y_i$
is zero by Lemma 2.2.7. The coefficient of
$y_i$
is zero by Lemma 2.2.7. The coefficient of
![]() $u^{x_i}$
in
$u^{x_i}$
in
![]() $u^{t_i}\varphi (\lambda _{i-1})$
is also zero (again by (2.2.20)), so it follows from (2.2.23) with
$u^{t_i}\varphi (\lambda _{i-1})$
is also zero (again by (2.2.20)), so it follows from (2.2.23) with
![]() $j=i$
that the coefficient of
$j=i$
that the coefficient of
![]() $u^{x_i}$
in
$u^{x_i}$
in
![]() $u^{s_i}\lambda _i$
is nonzero. Thus,
$u^{s_i}\lambda _i$
is nonzero. Thus,
![]() $\lambda _i$
has a term of degree
$\lambda _i$
has a term of degree
![]() $x_i-s_i$
. By (2.2.22), we have
$x_i-s_i$
. By (2.2.22), we have
![]() $x_i-s_i\le -e$
.
$x_i-s_i\le -e$
.
We claim that this implies that every
![]() $\lambda _j$
has a term of degree at most
$\lambda _j$
has a term of degree at most
![]() $-e$
. To see this, we rewrite (2.2.23) for j replaced by
$-e$
. To see this, we rewrite (2.2.23) for j replaced by
![]() $j+1$
in the form
$j+1$
in the form
If
![]() $j+1\ne i$
, then
$j+1\ne i$
, then
![]() $y^{\prime }_{j+1}-y_{j+1}\in \overline {{\mathbb F}}_p[[u]]$
, so if
$y^{\prime }_{j+1}-y_{j+1}\in \overline {{\mathbb F}}_p[[u]]$
, so if
![]() $\lambda _{j}$
has a term of degree at most
$\lambda _{j}$
has a term of degree at most
![]() $-e$
, then
$-e$
, then
![]() $u^{t_{j+1}}\varphi (\lambda _{j})$
has a term of degree at most
$u^{t_{j+1}}\varphi (\lambda _{j})$
has a term of degree at most
![]() $t_{j+1}-ep$
, which must cancel with a term in
$t_{j+1}-ep$
, which must cancel with a term in
![]() $u^{s_{j+1}}\lambda _{j+1}$
. Thus,
$u^{s_{j+1}}\lambda _{j+1}$
. Thus,
![]() $\lambda _{j+1}$
has a term of degree at most
$\lambda _{j+1}$
has a term of degree at most
![]() $t_{j+1}-ep-s_{j+1}\le e(p-2)-ep=-2e<-e$
, so the claim follows from induction (beginning with the case
$t_{j+1}-ep-s_{j+1}\le e(p-2)-ep=-2e<-e$
, so the claim follows from induction (beginning with the case
![]() $j=i$
).
$j=i$
).
Now we let
![]() $v_j \le -e$
denote the u-adic valuation of
$v_j \le -e$
denote the u-adic valuation of
![]() $\lambda _j$
. Then
$\lambda _j$
. Then
![]() $u^{t_{j+1}}\varphi (\lambda _{j})$
has a nonzero term of degree
$u^{t_{j+1}}\varphi (\lambda _{j})$
has a nonzero term of degree
![]() $t_{j+1}+pv_j$
, which again must cancel with a term in
$t_{j+1}+pv_j$
, which again must cancel with a term in
![]() $u^{s_{j+1}}\lambda _{j+1}$
. (Indeed, we have
$u^{s_{j+1}}\lambda _{j+1}$
. (Indeed, we have
![]() $t_{j+1}+pv_j\le e(p-2)-ep<0$
, and the only possible term in any
$t_{j+1}+pv_j\le e(p-2)-ep<0$
, and the only possible term in any
![]() $y^{\prime }_{j+1}-y_{j+1}$
of negative degree is the term
$y^{\prime }_{j+1}-y_{j+1}$
of negative degree is the term
![]() $u^{x_i}$
in
$u^{x_i}$
in
![]() $y^{\prime }_i$
, which cannot cancel with a term of degree
$y^{\prime }_i$
, which cannot cancel with a term of degree
![]() $t_{i}+pv_{i-1}$
by (2.2.20)). We therefore have
$t_{i}+pv_{i-1}$
by (2.2.20)). We therefore have
that is,
Summing these inequalities multiplied by appropriate powers of p, we have
 $$\begin{align*}\sum_{j=1}^fp^{f-j}(pv_{j+i-1}-v_{j+i})\ge -e(p-2)(p^f-1)/(p-1), \end{align*}$$
$$\begin{align*}\sum_{j=1}^fp^{f-j}(pv_{j+i-1}-v_{j+i})\ge -e(p-2)(p^f-1)/(p-1), \end{align*}$$
so that
![]() $v_j\ge -e(p-2)/(p-1)>-e$
for each j. Since we already saw that
$v_j\ge -e(p-2)/(p-1)>-e$
for each j. Since we already saw that
![]() $v_j\le -e$
for all j, we have a contradiction, and we are done.
$v_j\le -e$
for all j, we have a contradiction, and we are done.
Definition 2.2.26. Let
![]() $\overline {\chi }_1,\overline {\chi }_2:G_K\to \overline {{\mathbb F}}_p^{\times }$
be two characters. We say that an element of
$\overline {\chi }_1,\overline {\chi }_2:G_K\to \overline {{\mathbb F}}_p^{\times }$
be two characters. We say that an element of
![]() $\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
is generic if it is not in the image of the restriction map
$\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
is generic if it is not in the image of the restriction map
for any rank 1 Breuil modules
![]() ${\mathcal M}(\underline {s};a)$
and
${\mathcal M}(\underline {s};a)$
and
![]() ${\mathcal M}(\underline {t};b))$
with
${\mathcal M}(\underline {t};b))$
with
![]() $T({\mathcal M}(\underline {t};b))=\overline {\chi }_1$
,
$T({\mathcal M}(\underline {t};b))=\overline {\chi }_1$
,
![]() $T({\mathcal M}(\underline {s};a))=\overline {\chi }_2$
and
$T({\mathcal M}(\underline {s};a))=\overline {\chi }_2$
and
![]() $\sum _{j=1}^f(s_j-t_j-e)<0$
.
$\sum _{j=1}^f(s_j-t_j-e)<0$
.
Remark 2.2.27. Note that by Lemma 2.2.19, the generic extensions in
![]() $\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
are the complement of the union of finitely many proper subspaces.
$\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_2,\overline {\chi }_1)$
are the complement of the union of finitely many proper subspaces.
Remark 2.2.28. Definition 2.2.26 may seem a little ad hoc, but it is closely related to the condition of being a generic
![]() $\overline {{\mathbb F}}_p$
-point on an irreducible component of the 2-dimensional Emerton–Gee stack (which we recall in Section 2.4). To make this precise, we would need to work simultaneously with arbitrary unramified twists of the characters
$\overline {{\mathbb F}}_p$
-point on an irreducible component of the 2-dimensional Emerton–Gee stack (which we recall in Section 2.4). To make this precise, we would need to work simultaneously with arbitrary unramified twists of the characters
![]() $\overline {\chi }_1,\overline {\chi }_2$
. While it is clear that the arguments above are uniform across such unramified twists, and we could presumably formulate and prove our results in the context of stacks of Breuil modules (and Breuil–Kisin modules), there does not seem to be any benefit in doing so. Indeed, while working with
$\overline {\chi }_1,\overline {\chi }_2$
. While it is clear that the arguments above are uniform across such unramified twists, and we could presumably formulate and prove our results in the context of stacks of Breuil modules (and Breuil–Kisin modules), there does not seem to be any benefit in doing so. Indeed, while working with
![]() $\overline {{\mathbb F}}_p$
-points occasionally leads to slightly clumsy formulations, we view it as a feature of the structural results proved in [Reference Emerton and GeeEG23] (see, for example, Theorem 2.4.3) that we can prove statements about families of Galois representations (e.g., lifting rings) by only thinking about representations valued in
$\overline {{\mathbb F}}_p$
-points occasionally leads to slightly clumsy formulations, we view it as a feature of the structural results proved in [Reference Emerton and GeeEG23] (see, for example, Theorem 2.4.3) that we can prove statements about families of Galois representations (e.g., lifting rings) by only thinking about representations valued in
![]() $\overline {{\mathbb F}}_p$
.
$\overline {{\mathbb F}}_p$
.
Remark 2.2.29. While it may be possible to use other integral p-adic Hodge theories (e.g.,
![]() $(\varphi ,\widehat {G})$
-modules) to prove a version of Lemma 2.2.19 which could apply to the reductions of crystalline representations in a greater range of Hodge–Tate weights than
$(\varphi ,\widehat {G})$
-modules) to prove a version of Lemma 2.2.19 which could apply to the reductions of crystalline representations in a greater range of Hodge–Tate weights than
![]() $[0,p-2]$
, it is unlikely that it can be significantly improved. Indeed, already for
$[0,p-2]$
, it is unlikely that it can be significantly improved. Indeed, already for
![]() $K={\mathbb Q}_p$
, there are irreducible 2-dimensional crystalline representations of
$K={\mathbb Q}_p$
, there are irreducible 2-dimensional crystalline representations of
![]() $G_{{\mathbb Q}_p}$
with Hodge–Tate weights
$G_{{\mathbb Q}_p}$
with Hodge–Tate weights
![]() $0,p+2$
whose corresponding mod p Breuil–Kisin modules are of the form
$0,p+2$
whose corresponding mod p Breuil–Kisin modules are of the form
 $\begin {pmatrix}bu^p&x\\0&au^2\end {pmatrix}$
, where
$\begin {pmatrix}bu^p&x\\0&au^2\end {pmatrix}$
, where
![]() $a,b\in \overline {{\mathbb F}}_p^{\times }$
and
$a,b\in \overline {{\mathbb F}}_p^{\times }$
and
![]() $x\in \overline {{\mathbb F}}_p$
are arbitrary and consequently give all extensions of the corresponding characters of
$x\in \overline {{\mathbb F}}_p$
are arbitrary and consequently give all extensions of the corresponding characters of
![]() $G_{{\mathbb Q}_p}$
when
$G_{{\mathbb Q}_p}$
when
![]() $a\ne b$
. (In addition, it is not clear to us whether the analogue of Lemma 2.2.7 holds for
$a\ne b$
. (In addition, it is not clear to us whether the analogue of Lemma 2.2.7 holds for
![]() $(\varphi ,\widehat {G})$
-modules, even in height
$(\varphi ,\widehat {G})$
-modules, even in height
![]() $[0,p-2]$
, although we have not seriously pursued this question.)
$[0,p-2]$
, although we have not seriously pursued this question.)
2.3 Generic weight 0 crystalline representations
In this subsection and the next, in order to be compatible with the notation of [Reference Emerton and GeeEG23], we work with d-dimensional rather than n-dimensional representations.
Definition 2.3.1. We say that a representation
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d({\mathbb F})$
is generic if it has the form
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d({\mathbb F})$
is generic if it has the form
 $$ \begin{align*}\overline{\rho}\cong \begin{pmatrix} \overline{\chi}_d &*&\dots &*\\ 0& \overline{\chi}_{d-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \overline{\chi}_1\\ \end{pmatrix}, \end{align*} $$
$$ \begin{align*}\overline{\rho}\cong \begin{pmatrix} \overline{\chi}_d &*&\dots &*\\ 0& \overline{\chi}_{d-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \overline{\chi}_1\\ \end{pmatrix}, \end{align*} $$
and for
![]() $i=1,\ldots ,d-1$
, the off diagonal extension class in
$i=1,\ldots ,d-1$
, the off diagonal extension class in
![]() $\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_i,\overline {\chi }_{i+1})$
is generic in the sense of Definition 2.2.26.
$\operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi }_i,\overline {\chi }_{i+1})$
is generic in the sense of Definition 2.2.26.
Theorem 2.3.2. Suppose
![]() $p>d$
, and let
$p>d$
, and let
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_d({\mathcal O})$
be a weight 0 crystalline representation such that
$\rho :G_K\to \operatorname {\mathrm {GL}}_d({\mathcal O})$
be a weight 0 crystalline representation such that
![]() $\overline {\rho }$
is generic in the sense of Definition 2.3.1. Then
$\overline {\rho }$
is generic in the sense of Definition 2.3.1. Then
 $$ \begin{align*} \rho\simeq\begin{pmatrix} \mathrm{ur}_{\lambda_d} &*&\dots &*\\ 0& \mathrm{ur}_{\lambda_{d-1}}\varepsilon^{-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \mathrm{ur}_{\lambda_1}\varepsilon^{1-d}\\ \end{pmatrix} \end{align*} $$
$$ \begin{align*} \rho\simeq\begin{pmatrix} \mathrm{ur}_{\lambda_d} &*&\dots &*\\ 0& \mathrm{ur}_{\lambda_{d-1}}\varepsilon^{-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \mathrm{ur}_{\lambda_1}\varepsilon^{1-d}\\ \end{pmatrix} \end{align*} $$
for some
![]() $\lambda _1,\ldots ,\lambda _d\in {\mathcal O}^\times $
.
$\lambda _1,\ldots ,\lambda _d\in {\mathcal O}^\times $
.
Proof. The proof will be by induction on d. The base case
![]() $d=1$
is trivial. For the inductive step, we claim that
$d=1$
is trivial. For the inductive step, we claim that
![]() $\rho $
fits in an exact sequence
$\rho $
fits in an exact sequence
Admitting this for the moment,
![]() $\rho '$
is a
$\rho '$
is a
![]() $d-1$
dimensional crystalline representation of weight 0, and
$d-1$
dimensional crystalline representation of weight 0, and
![]() $\overline {\rho }'$
is generic (since
$\overline {\rho }'$
is generic (since
![]() $\overline {\rho }$
has a unique
$\overline {\rho }$
has a unique
![]() $d-1$
dimensional subrepresentation, which is generic). We conclude by induction on d.
$d-1$
dimensional subrepresentation, which is generic). We conclude by induction on d.
We now prove the key claim above. As the Hodge–Tate weights of
![]() $\rho $
are contained in the interval
$\rho $
are contained in the interval
![]() $[0,d-1]\subseteq [0,p-2]$
, by Theorem 2.1.5, there is a crystalline Breuil module
$[0,d-1]\subseteq [0,p-2]$
, by Theorem 2.1.5, there is a crystalline Breuil module
![]() ${\mathcal M}$
of rank d with
${\mathcal M}$
of rank d with
![]() $\overline {\rho }\cong T({\mathcal M})$
whose underlying Breuil–Kisin module has height at most
$\overline {\rho }\cong T({\mathcal M})$
whose underlying Breuil–Kisin module has height at most
![]() $(d-1)$
. By Theorem 2.1.4 (2), the unique maximal filtration on
$(d-1)$
. By Theorem 2.1.4 (2), the unique maximal filtration on
![]() $\overline {\rho }$
determines a filtration
$\overline {\rho }$
determines a filtration
![]() $0={\mathcal M}^0\subset {\mathcal M}^1\subset \dots \subset {\mathcal M}^d={\mathcal M}$
by crystalline Breuil submodules. Write
$0={\mathcal M}^0\subset {\mathcal M}^1\subset \dots \subset {\mathcal M}^d={\mathcal M}$
by crystalline Breuil submodules. Write
![]() ${\mathcal M}^i/{\mathcal M}^{i-1}\simeq {\mathcal M}(\underline {s(i)};a_i)$
in the notation of Lemma 2.2.3.
${\mathcal M}^i/{\mathcal M}^{i-1}\simeq {\mathcal M}(\underline {s(i)};a_i)$
in the notation of Lemma 2.2.3.
It follows from Lemma 2.2.19 and the definition of genericity that for each
![]() $1\leq i\leq d-1$
, we have
$1\leq i\leq d-1$
, we have
 $$\begin{align*}\sum_{j=1}^f(s(i+1)_j-s(i)_j-e)\ge 0.\end{align*}$$
$$\begin{align*}\sum_{j=1}^f(s(i+1)_j-s(i)_j-e)\ge 0.\end{align*}$$
Summing these inequalities over i, we obtain
 $$\begin{align*}\sum_{j=1}^f(s(d)_j-s(1)_j)\ge ef(d-1).\end{align*}$$
$$\begin{align*}\sum_{j=1}^f(s(d)_j-s(1)_j)\ge ef(d-1).\end{align*}$$
Since the underlying Breuil–Kisin module of
![]() ${\mathcal M}$
has height at most
${\mathcal M}$
has height at most
![]() $(d-1)$
, we have
$(d-1)$
, we have
![]() $s(i)_j\leq e(d-1)$
for all
$s(i)_j\leq e(d-1)$
for all
![]() $i,j$
, and hence
$i,j$
, and hence
![]() $s(d)_j-s(1)_j\leq e(d-1)$
for all j. Since we also have the reverse inequality summed over f this implies that
$s(d)_j-s(1)_j\leq e(d-1)$
for all j. Since we also have the reverse inequality summed over f this implies that
![]() $s(d)_j-s(1)_j=e(d-1)$
for all j, and hence,
$s(d)_j-s(1)_j=e(d-1)$
for all j, and hence,
![]() $s(1)_j=0$
and
$s(1)_j=0$
and
![]() $s(d)_j=e(d-1)$
for all j.
$s(d)_j=e(d-1)$
for all j.
Now let
![]() $\mathfrak {M}/\mathfrak {S}_{{\mathcal O}}$
be the Breuil–Kisin module associated to
$\mathfrak {M}/\mathfrak {S}_{{\mathcal O}}$
be the Breuil–Kisin module associated to
![]() $\rho $
, and
$\rho $
, and
![]() $\overline {\mathfrak {M}}=\mathfrak {M}\otimes _{{\mathcal O}}{\mathbb F}$
. This is the Breuil–Kisin module underlying
$\overline {\mathfrak {M}}=\mathfrak {M}\otimes _{{\mathcal O}}{\mathbb F}$
. This is the Breuil–Kisin module underlying
![]() $\mathcal {M}$
by Theorem 2.1.5. Since
$\mathcal {M}$
by Theorem 2.1.5. Since
![]() $s(d)_j = e(d-1)$
for all j, we have shown that
$s(d)_j = e(d-1)$
for all j, we have shown that
![]() $\overline {\mathfrak {M}}$
has a rank
$\overline {\mathfrak {M}}$
has a rank
![]() $1$
quotient
$1$
quotient
![]() $\overline {\mathfrak {M}}\to \mathfrak {S}_{{\mathbb F}}\cdot v$
, where
$\overline {\mathfrak {M}}\to \mathfrak {S}_{{\mathbb F}}\cdot v$
, where
![]() $\varphi (\overline {v})=\overline {\lambda } u^{e(d-1)}\overline {v}$
for some
$\varphi (\overline {v})=\overline {\lambda } u^{e(d-1)}\overline {v}$
for some
![]() $\overline {\lambda }\in (k\otimes {\mathbb F})^\times $
. It follows from [Reference KisinKis09, Prop. 1.2.11] (or rather its obvious generalization from height
$\overline {\lambda }\in (k\otimes {\mathbb F})^\times $
. It follows from [Reference KisinKis09, Prop. 1.2.11] (or rather its obvious generalization from height
![]() $1$
to height
$1$
to height
![]() $(d-1$
) Breuil–Kisin modules) that this lifts to a quotient
$(d-1$
) Breuil–Kisin modules) that this lifts to a quotient
![]() $\mathfrak {M}\to \mathfrak {S}_{{\mathcal O}}\cdot v$
, where
$\mathfrak {M}\to \mathfrak {S}_{{\mathcal O}}\cdot v$
, where
![]() $\varphi (v)=\lambda E(u)^{d-1}v$
for some
$\varphi (v)=\lambda E(u)^{d-1}v$
for some
![]() $\lambda \in (W(k)\otimes {\mathcal O})^\times $
. Indeed, using height
$\lambda \in (W(k)\otimes {\mathcal O})^\times $
. Indeed, using height
![]() $(d-1)$
duality [Reference LiuLiu07, §3.1], we need to lift a rank one ‘multiplicative’ submodule of
$(d-1)$
duality [Reference LiuLiu07, §3.1], we need to lift a rank one ‘multiplicative’ submodule of
![]() $\overline {\mathfrak {M}}^*$
to
$\overline {\mathfrak {M}}^*$
to
![]() ${\mathfrak {M}}^*$
, where multiplicative means that the linearization of
${\mathfrak {M}}^*$
, where multiplicative means that the linearization of
![]() $\varphi $
is an isomorphism. As in [Reference KisinKis09, Prop. 1.2.11], we have a maximal multiplicative submodule
$\varphi $
is an isomorphism. As in [Reference KisinKis09, Prop. 1.2.11], we have a maximal multiplicative submodule
![]() ${\mathfrak {M}}^{*,m}$
of
${\mathfrak {M}}^{*,m}$
of
![]() ${\mathfrak {M}}^*$
which lifts the maximal multiplicative submodule of
${\mathfrak {M}}^*$
which lifts the maximal multiplicative submodule of
![]() $\overline {\mathfrak {M}}^*$
and therefore has rank at least one. Since
$\overline {\mathfrak {M}}^*$
and therefore has rank at least one. Since
![]() $\rho $
is weight
$\rho $
is weight
![]() $0$
crystalline, its maximal unramified subrepresentation has dimension at most one. It follows that
$0$
crystalline, its maximal unramified subrepresentation has dimension at most one. It follows that
![]() ${\mathfrak {M}}^{*,m}$
has rank one and is the desired lift.
${\mathfrak {M}}^{*,m}$
has rank one and is the desired lift.
Finally, it follows from the full faithfulness of the functor from lattices in crystalline representations to Breuil–Kisin modules (see [Reference KisinKis06, Prop. 1.3.15], or for the precise statement we are using here [Reference KisinKis10, Thm. 1.2.1]) that there is a nonzero map
![]() $\rho \to \mathrm {ur}_{\lambda _1}\varepsilon ^{1-d}$
.
$\rho \to \mathrm {ur}_{\lambda _1}\varepsilon ^{1-d}$
.
Corollary 2.3.3. Let
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d({\mathbb F})$
be a generic representation. Suppose that
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d({\mathbb F})$
be a generic representation. Suppose that
![]() $\overline {\rho }$
has a crystalline lift of weight 0. Then
$\overline {\rho }$
has a crystalline lift of weight 0. Then
![]() $\overline {\rho }$
has the form
$\overline {\rho }$
has the form
 $$ \begin{align*}\overline{\rho}\cong\begin{pmatrix} \mathrm{ur}_{\overline{\lambda}_d} &*&\dots &*\\ 0& \mathrm{ur}_{\overline{\lambda}_{d-1}}\overline{\varepsilon}^{-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \mathrm{ur}_{\overline{\lambda}_1}\overline{\varepsilon}^{1-d}\\ \end{pmatrix}, \end{align*} $$
$$ \begin{align*}\overline{\rho}\cong\begin{pmatrix} \mathrm{ur}_{\overline{\lambda}_d} &*&\dots &*\\ 0& \mathrm{ur}_{\overline{\lambda}_{d-1}}\overline{\varepsilon}^{-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \mathrm{ur}_{\overline{\lambda}_1}\overline{\varepsilon}^{1-d}\\ \end{pmatrix}, \end{align*} $$
and moreover, the off-diagonal extensions are peu ramifiée.
Proof. The first statement is immediate from Theorem 2.3.2, while the claim about the extensions follows from the fact that the reduction of a crystalline representation
 $$ \begin{align*}\begin{pmatrix}\mathrm{ur}_{\lambda_2}&*\\0&\mathrm{ur}_{\lambda_1}\varepsilon^{-1}\end{pmatrix}\end{align*} $$
$$ \begin{align*}\begin{pmatrix}\mathrm{ur}_{\lambda_2}&*\\0&\mathrm{ur}_{\lambda_1}\varepsilon^{-1}\end{pmatrix}\end{align*} $$
is peu ramifiée (e.g., by [Reference Caraiani, Emerton, Gee and SavittCEGS22b, Lem. A.4]; the reduction of such a representation is finite flat and hence peu ramifiée).
2.4 Recollections on Emerton–Gee stacks
We now recall some of the main results of [Reference Emerton and GeeEG23] and prove a slight extension of them. We use the notation of [Reference Emerton and GeeEG23], and in particular, we continue to work with d-dimensional rather than n-dimensional representations.
As above, we let
![]() $E/{\mathbb Q}_p$
be a finite extension containing the Galois closure of K, with ring of integers
$E/{\mathbb Q}_p$
be a finite extension containing the Galois closure of K, with ring of integers
![]() ${\mathcal O}$
, uniformizer
${\mathcal O}$
, uniformizer
![]() $\varpi $
, and residue field
$\varpi $
, and residue field
![]() ${\mathcal O}/\varpi ={\mathbb F}$
. The stack
${\mathcal O}/\varpi ={\mathbb F}$
. The stack
![]() ${\mathcal X}_d$
over
${\mathcal X}_d$
over
![]() $\operatorname {\mathrm {Spf}}{\mathcal O}$
is defined in [Reference Emerton and GeeEG23, Defn. 3.2.1]. It is a stack of
$\operatorname {\mathrm {Spf}}{\mathcal O}$
is defined in [Reference Emerton and GeeEG23, Defn. 3.2.1]. It is a stack of
![]() $(\varphi ,\Gamma )$
-modules, but if
$(\varphi ,\Gamma )$
-modules, but if
![]() ${\mathbb F}'/{\mathbb F}$
is a finite extension (or if
${\mathbb F}'/{\mathbb F}$
is a finite extension (or if
![]() ${\mathbb F}'=\overline {{\mathbb F}}_p$
), then the groupoid of points
${\mathbb F}'=\overline {{\mathbb F}}_p$
), then the groupoid of points
![]() $x\in {\mathcal X}_d({\mathbb F}')$
is canonically equivalent to the groupoid of Galois representations
$x\in {\mathcal X}_d({\mathbb F}')$
is canonically equivalent to the groupoid of Galois representations
![]() $\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_d({\mathbb F}')$
[Reference Emerton and GeeEG23, §3.6.1], and we use this identification without comment below. The stack
$\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_d({\mathbb F}')$
[Reference Emerton and GeeEG23, §3.6.1], and we use this identification without comment below. The stack
![]() ${\mathcal X}_d$
is a Noetherian formal algebraic stack [Reference Emerton and GeeEG23, Cor. 5.5.18], and it admits closed substacks cut out by (potentially) crystalline or semistable conditions. In particular, there is a closed substack
${\mathcal X}_d$
is a Noetherian formal algebraic stack [Reference Emerton and GeeEG23, Cor. 5.5.18], and it admits closed substacks cut out by (potentially) crystalline or semistable conditions. In particular, there is a closed substack
![]() ${\mathcal X}_d^{\mathrm {crys},0}$
of
${\mathcal X}_d^{\mathrm {crys},0}$
of
![]() ${\mathcal X}_d$
corresponding to crystalline representations of weight
${\mathcal X}_d$
corresponding to crystalline representations of weight
![]() $0$
, which has the following properties.
$0$
, which has the following properties.
Proposition 2.4.1.
-
1.
 ${\mathcal X}_d^{\mathrm {crys},0}$
is a p-adic formal algebraic stack, which is flat over
${\mathcal X}_d^{\mathrm {crys},0}$
is a p-adic formal algebraic stack, which is flat over
 $\operatorname {\mathrm {Spf}}{\mathcal O}$
and of finite type. In particular, the special fibre
$\operatorname {\mathrm {Spf}}{\mathcal O}$
and of finite type. In particular, the special fibre
 $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}:={\mathcal X}_{d}^{\mathrm {crys},0}\times _{\operatorname {\mathrm {Spf}}{\mathcal O}}\operatorname {\mathrm {Spec}} {\mathbb F}$
is an algebraic stack.
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}:={\mathcal X}_{d}^{\mathrm {crys},0}\times _{\operatorname {\mathrm {Spf}}{\mathcal O}}\operatorname {\mathrm {Spec}} {\mathbb F}$
is an algebraic stack. -
2. If
 $A^\circ $
is a finite flat
$A^\circ $
is a finite flat
 ${\mathcal O}$
-algebra, then
${\mathcal O}$
-algebra, then
 ${\mathcal X}_{d}^{\mathrm {crys},0}(A^\circ )$
is the subgroupoid of
${\mathcal X}_{d}^{\mathrm {crys},0}(A^\circ )$
is the subgroupoid of
 ${\mathcal X}_{d}(A^\circ )$
consisting of
${\mathcal X}_{d}(A^\circ )$
consisting of
 $G_K$
-representations which after inverting p are crystalline of weight
$G_K$
-representations which after inverting p are crystalline of weight
 $0$
.
$0$
. -
3. The special fibre
 $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}:={\mathcal X}_{d}^{\mathrm {crys},0}\times _{\operatorname {\mathrm {Spf}}{\mathcal O}}\operatorname {\mathrm {Spec}} {\mathbb F}$
is equidimensional of dimension
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}:={\mathcal X}_{d}^{\mathrm {crys},0}\times _{\operatorname {\mathrm {Spf}}{\mathcal O}}\operatorname {\mathrm {Spec}} {\mathbb F}$
is equidimensional of dimension
 $[K:{\mathbb Q}_p] d(d-1)/2$
.
$[K:{\mathbb Q}_p] d(d-1)/2$
. -
4. For any finite extension
 ${\mathbb F}'$
of
${\mathbb F}'$
of
 ${\mathbb F}$
and any point
${\mathbb F}$
and any point
 $x:\operatorname {\mathrm {Spec}} {\mathbb F}'\to \overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
, there is a versal morphism
$x:\operatorname {\mathrm {Spec}} {\mathbb F}'\to \overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
, there is a versal morphism
 $\operatorname {\mathrm {Spf}} R^{\mathrm {crys},0,{\mathcal O}'}_{\overline {\rho }}\to {\mathcal X}_{d}^{\mathrm {crys},0}$
at x, where
$\operatorname {\mathrm {Spf}} R^{\mathrm {crys},0,{\mathcal O}'}_{\overline {\rho }}\to {\mathcal X}_{d}^{\mathrm {crys},0}$
at x, where
 $\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_d({\mathbb F}')$
is the representation corresponding to x,
$\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_d({\mathbb F}')$
is the representation corresponding to x,
 ${\mathcal O}':=W({\mathbb F}')\otimes _{W({\mathbb F})}{\mathcal O}$
, and
${\mathcal O}':=W({\mathbb F}')\otimes _{W({\mathbb F})}{\mathcal O}$
, and
 $R^{\mathrm {crys},0,{\mathcal O}'}_{\overline {\rho }}$
is the weight
$R^{\mathrm {crys},0,{\mathcal O}'}_{\overline {\rho }}$
is the weight
 $0$
crystalline lifting ring.
$0$
crystalline lifting ring.
Proof. We define
![]() ${\mathcal X}_d^{\mathrm {crys},0}$
to be the stack
${\mathcal X}_d^{\mathrm {crys},0}$
to be the stack
![]() ${\mathcal X}_{K,d}^{\mathrm {crys},\underline {\lambda },\tau }$
of [Reference Emerton and GeeEG23, Defn. 4.8.8], taking
${\mathcal X}_{K,d}^{\mathrm {crys},\underline {\lambda },\tau }$
of [Reference Emerton and GeeEG23, Defn. 4.8.8], taking
![]() $\underline {\lambda }$
to be given by
$\underline {\lambda }$
to be given by
![]() $\lambda _{\sigma ,i}=d-i$
for all
$\lambda _{\sigma ,i}=d-i$
for all
![]() $\sigma ,i$
, and
$\sigma ,i$
, and
![]() $\tau $
to be trivial. Then the first two claims are [Reference Emerton and GeeEG23, Thm. 4.8.12], the third is [Reference Emerton and GeeEG23, Thm. 4.8.14], and the final claim is [Reference Emerton and GeeEG23, Prop. 4.8.10].
$\tau $
to be trivial. Then the first two claims are [Reference Emerton and GeeEG23, Thm. 4.8.12], the third is [Reference Emerton and GeeEG23, Thm. 4.8.14], and the final claim is [Reference Emerton and GeeEG23, Prop. 4.8.10].
We now recall some definitions from [Reference Emerton and GeeEG23, §5.5]. By a Serre weight
![]() $\underline {k}$
we mean a tuple of integers
$\underline {k}$
we mean a tuple of integers
![]() $\{k_{\overline {\sigma },i}\}_{\overline {\sigma }:k\hookrightarrow \overline {{\mathbb F}}_p,1\le i\le d}$
with the properties that
$\{k_{\overline {\sigma },i}\}_{\overline {\sigma }:k\hookrightarrow \overline {{\mathbb F}}_p,1\le i\le d}$
with the properties that
-
•
 $p-1\ge k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}\ge 0$
for each
$p-1\ge k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}\ge 0$
for each
 $1\le i\le d-1$
, and
$1\le i\le d-1$
, and -
•
 $p-1\ge k_{\overline {\sigma },d}\ge 0$
, and not every
$p-1\ge k_{\overline {\sigma },d}\ge 0$
, and not every
 $k_{\overline {\sigma },d}$
is equal to
$k_{\overline {\sigma },d}$
is equal to
 $p-1$
.
$p-1$
.
For each
![]() $\overline {\sigma }:k\hookrightarrow {\mathbb F}$
, we define the fundamental character
$\overline {\sigma }:k\hookrightarrow {\mathbb F}$
, we define the fundamental character
![]() $\omega _{\overline {\sigma }}$
to be the composite
$\omega _{\overline {\sigma }}$
to be the composite
As in [Reference Emerton and GeeEG23, §5.5], for each Serre weight
![]() $\underline {k}$
, we choose characters
$\underline {k}$
, we choose characters
![]() $\omega _{\underline {k},i}:G_K\to {\mathbb F}^\times $
(
$\omega _{\underline {k},i}:G_K\to {\mathbb F}^\times $
(
![]() $i=1,\dots ,d$
) with
$i=1,\dots ,d$
) with
in such a way that if
![]() $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
![]() $\overline {\sigma }$
, then
$\overline {\sigma }$
, then
![]() $\omega _{\underline {k},i}=\omega _{\underline {k},i+1}$
. (In [Reference Emerton and GeeEG23, §5.5], it was erroneously claimed that we could impose further constraints on the
$\omega _{\underline {k},i}=\omega _{\underline {k},i+1}$
. (In [Reference Emerton and GeeEG23, §5.5], it was erroneously claimed that we could impose further constraints on the
![]() $\omega _{\underline {k},i}$
, but as explained in [Reference Emerton and GeeEG], these properties are all that we require.) For any
$\omega _{\underline {k},i}$
, but as explained in [Reference Emerton and GeeEG], these properties are all that we require.) For any
![]() $\nu \in \overline {{\mathbb F}}_p$
, we write
$\nu \in \overline {{\mathbb F}}_p$
, we write
![]() $\mathrm {ur}_{\nu }:G_K\to \overline {{\mathbb F}}_p^{\times }$
for the unramified character taking a geometric Frobenius to
$\mathrm {ur}_{\nu }:G_K\to \overline {{\mathbb F}}_p^{\times }$
for the unramified character taking a geometric Frobenius to
![]() $\lambda $
.
$\lambda $
.
We say that a representation
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb F}}_p)$
is maximally nonsplit of niveau
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d(\overline {{\mathbb F}}_p)$
is maximally nonsplit of niveau
![]() $1$
if it has a unique filtration by
$1$
if it has a unique filtration by
![]() $G_K$
-stable
$G_K$
-stable
![]() $\overline {{\mathbb F}}_p$
-subspaces such that all of the graded pieces are one-dimensional representations of
$\overline {{\mathbb F}}_p$
-subspaces such that all of the graded pieces are one-dimensional representations of
![]() $G_K$
. We assign a unique Serre weight
$G_K$
. We assign a unique Serre weight
![]() $\underline {k}$
to each such
$\underline {k}$
to each such
![]() $\overline {\rho }$
in the following way: we say that
$\overline {\rho }$
in the following way: we say that
![]() $\overline {\rho }$
is of weight
$\overline {\rho }$
is of weight
![]() $\underline {k}$
if and only we can write
$\underline {k}$
if and only we can write
 $$ \begin{align}\overline{\rho}\cong \begin{pmatrix} \mathrm{ur}_{\nu_d}\omega_{\underline{k},d} &*&\dots &*\\ 0& \mathrm{ur}_{\nu_{d-1}}\overline{\varepsilon}^{-1}\omega_{\underline{k},d-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \mathrm{ur}_{\nu_1}\overline{\varepsilon}^{1-d}\omega_{\underline{k},1}\\ \end{pmatrix}; \end{align} $$
$$ \begin{align}\overline{\rho}\cong \begin{pmatrix} \mathrm{ur}_{\nu_d}\omega_{\underline{k},d} &*&\dots &*\\ 0& \mathrm{ur}_{\nu_{d-1}}\overline{\varepsilon}^{-1}\omega_{\underline{k},d-1}&\dots &*\\ \vdots&& \ddots &\vdots\\ 0&\dots&0& \mathrm{ur}_{\nu_1}\overline{\varepsilon}^{1-d}\omega_{\underline{k},1}\\ \end{pmatrix}; \end{align} $$
this uniquely determines
![]() $\underline {k}$
, except that if
$\underline {k}$
, except that if
![]() $\omega _{\underline {k},i}=\omega _{\underline {k},i+1}$
, then we need to say whether
$\omega _{\underline {k},i}=\omega _{\underline {k},i+1}$
, then we need to say whether
![]() $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
![]() $\overline {\sigma }$
or
$\overline {\sigma }$
or
![]() $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=0$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=0$
for all
![]() $\overline {\sigma }$
. We distinguish these possibilities as follows: if
$\overline {\sigma }$
. We distinguish these possibilities as follows: if
![]() $\omega _{\underline {k},i}=\omega _{\underline {k},i+1}$
, then we set
$\omega _{\underline {k},i}=\omega _{\underline {k},i+1}$
, then we set
![]() $k_{\overline {\sigma },d-i}-k_{\overline {\sigma },d+1-i}=p-1$
for all
$k_{\overline {\sigma },d-i}-k_{\overline {\sigma },d+1-i}=p-1$
for all
![]() $\overline {\sigma }$
if and only if
$\overline {\sigma }$
if and only if
![]() $\nu _i=\nu _{i+1}$
and the element of
$\nu _i=\nu _{i+1}$
and the element of
determined by
![]() $\overline {\rho }$
is très ramifiée.
$\overline {\rho }$
is très ramifiée.
Let
![]() $({\mathbb G}_m)^d_{\underline {k}}$
denote the closed subgroup scheme of
$({\mathbb G}_m)^d_{\underline {k}}$
denote the closed subgroup scheme of
![]() $({\mathbb G}_m)^d$
parameterizing tuples
$({\mathbb G}_m)^d$
parameterizing tuples
![]() $(x_1,\dots ,x_d)$
for which
$(x_1,\dots ,x_d)$
for which
![]() $x_i=x_{i+1}$
whenever
$x_i=x_{i+1}$
whenever
![]() $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
![]() $\overline {\sigma }$
. By the definition that we just made, if
$\overline {\sigma }$
. By the definition that we just made, if
![]() $\overline {\rho }$
is maximally nonsplit of niveau
$\overline {\rho }$
is maximally nonsplit of niveau
![]() $1$
and weight
$1$
and weight
![]() $\underline {k}$
, then the tuple
$\underline {k}$
, then the tuple
![]() $(\nu _1,\dots ,\nu _d)$
is an
$(\nu _1,\dots ,\nu _d)$
is an
![]() $\overline {{\mathbb F}}_p$
-point of
$\overline {{\mathbb F}}_p$
-point of
![]() $({\mathbb G}_m)^d_{\underline {k}}$
(where the
$({\mathbb G}_m)^d_{\underline {k}}$
(where the
![]() $\nu _i$
are as in (2.4.2)).
$\nu _i$
are as in (2.4.2)).
We have the following slight variant on [Reference Emerton and GeeEG23, Thm. 5.5.12].
Theorem 2.4.3.
-
1. The Ind-algebraic stack
 ${\mathcal X}_{d,\operatorname {red}}$
is an algebraic stack of finite presentation over
${\mathcal X}_{d,\operatorname {red}}$
is an algebraic stack of finite presentation over
 ${\mathbb F}$
.
${\mathbb F}$
. -
2.
 ${\mathcal X}_{d,\operatorname {red}}$
is equidimensional of dimension
${\mathcal X}_{d,\operatorname {red}}$
is equidimensional of dimension
 $[K:{\mathbb Q}_p] d(d-1)/2$
.
$[K:{\mathbb Q}_p] d(d-1)/2$
. -
3. The irreducible components of
 ${\mathcal X}_{d,\operatorname {red}}$
are indexed by the Serre weights
${\mathcal X}_{d,\operatorname {red}}$
are indexed by the Serre weights
 $\underline {k}$
. More precisely, for each
$\underline {k}$
. More precisely, for each
 $\underline {k}$
, there is an irreducible component
$\underline {k}$
, there is an irreducible component
 ${\mathcal X}_{d,\operatorname {red}}^{\underline {k}}$
containing a dense open substack
${\mathcal X}_{d,\operatorname {red}}^{\underline {k}}$
containing a dense open substack
 ${\mathcal U}^{\underline {k}}$
, all of whose
${\mathcal U}^{\underline {k}}$
, all of whose
 $\overline {{\mathbb F}}_p$
-points are maximally nonsplit of niveau one and weight
$\overline {{\mathbb F}}_p$
-points are maximally nonsplit of niveau one and weight
 $\underline {k}$
; and the
$\underline {k}$
; and the
 ${\mathcal X}_{d,\operatorname {red}}^{\underline {k}}$
exhaust the irreducible components of
${\mathcal X}_{d,\operatorname {red}}^{\underline {k}}$
exhaust the irreducible components of
 ${\mathcal X}_{d,\operatorname {red}}$
.
${\mathcal X}_{d,\operatorname {red}}$
. -
4. There is an open subscheme T of
 $({\mathbb G}_m)^d_{\underline {k}}$
such that for all
$({\mathbb G}_m)^d_{\underline {k}}$
such that for all
 $(t_1,\dots ,t_d)\in T(\overline {{\mathbb F}}_p)$
, there is an
$(t_1,\dots ,t_d)\in T(\overline {{\mathbb F}}_p)$
, there is an
 $\overline {{\mathbb F}}_p$
-point of
$\overline {{\mathbb F}}_p$
-point of
 ${\mathcal U}^{\underline {k}}$
corresponding to a representation (2.4.2) with
${\mathcal U}^{\underline {k}}$
corresponding to a representation (2.4.2) with
 $\nu _i=t_i$
for all i, and which is generic in the sense of Definition 2.3.1.
$\nu _i=t_i$
for all i, and which is generic in the sense of Definition 2.3.1.
Proof. Everything except for part (4) is part of [Reference Emerton and GeeEG23, Thm. 5.5.12, Thm. 6.5.1]. Part (4) follows from the version of [Reference Emerton and GeeEG23, Thm. 5.5.12] proved in [Reference Emerton and GeeEG], as we explain below.
We begin by taking T to be an open contained in the image of the eigenvalue morphism
![]() ${\mathcal U}^{\underline {k}} \to ({\mathbb G}_m)^d_{\underline {k}}$
and then further shrink it so that for any
${\mathcal U}^{\underline {k}} \to ({\mathbb G}_m)^d_{\underline {k}}$
and then further shrink it so that for any
![]() $m<n$
and
$m<n$
and
![]() $(t_1,\dots ,t_d)\in T(\overline {{\mathbb F}}_p)$
, either
$(t_1,\dots ,t_d)\in T(\overline {{\mathbb F}}_p)$
, either
-
• we have
 $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
 $\overline {\sigma }$
and all
$\overline {\sigma }$
and all
 $m\le i<n$
, or
$m\le i<n$
, or -
• we have
 $(\mathrm {ur}_{t_n}\overline {\varepsilon }^{n-d}\omega _{\underline {k},n})/(\mathrm {ur}_{t_m}\overline {\varepsilon }^{m-d}\omega _{\underline {k},m})\not =\overline {\varepsilon }$
.
$(\mathrm {ur}_{t_n}\overline {\varepsilon }^{n-d}\omega _{\underline {k},n})/(\mathrm {ur}_{t_m}\overline {\varepsilon }^{m-d}\omega _{\underline {k},m})\not =\overline {\varepsilon }$
.
We then fix
![]() $(t_1,\dots ,t_d)\in T(\overline {{\mathbb F}}_p)$
and regard each
$(t_1,\dots ,t_d)\in T(\overline {{\mathbb F}}_p)$
and regard each
![]() $\operatorname {\mathrm {Ext}}^1_{G_K}(\mathrm {ur}_{t_i}\overline {\varepsilon }^{i-d}\omega _{\underline {k},i}, \mathrm {ur}_{t_{i+1}}\overline {\varepsilon }^{i+1-d}\omega _{\underline {k},i+1})$
as an affine space over
$\operatorname {\mathrm {Ext}}^1_{G_K}(\mathrm {ur}_{t_i}\overline {\varepsilon }^{i-d}\omega _{\underline {k},i}, \mathrm {ur}_{t_{i+1}}\overline {\varepsilon }^{i+1-d}\omega _{\underline {k},i+1})$
as an affine space over
![]() $\overline {{\mathbb F}}_p$
, and as in [Reference Emerton and GeeEG], we define
$\overline {{\mathbb F}}_p$
, and as in [Reference Emerton and GeeEG], we define
 $$\begin{align*}\operatorname{\mathrm{Ext}}^1_{(t_1,\dots,t_d),\underline{k}}\subseteq\prod_{i=1}^{d-1}\operatorname{\mathrm{Ext}}^1_{G_K}(\mathrm{ur}_{t_i}\overline{\varepsilon}^{i-d}\omega_{\underline{k},i}, \mathrm{ur}_{t_{i+1}}\overline{\varepsilon}^{i+1-d}\omega_{\underline{k},i+1})\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Ext}}^1_{(t_1,\dots,t_d),\underline{k}}\subseteq\prod_{i=1}^{d-1}\operatorname{\mathrm{Ext}}^1_{G_K}(\mathrm{ur}_{t_i}\overline{\varepsilon}^{i-d}\omega_{\underline{k},i}, \mathrm{ur}_{t_{i+1}}\overline{\varepsilon}^{i+1-d}\omega_{\underline{k},i+1})\end{align*}$$
to be the closed subvariety of tuples of extension classes
![]() $(\psi _1,\dots ,\psi _{d-1})$
determined by the condition that for each
$(\psi _1,\dots ,\psi _{d-1})$
determined by the condition that for each
![]() $i=1,\dots ,d-2$
, the cup product
$i=1,\dots ,d-2$
, the cup product
![]() $\psi _i\cup \psi _{i+1}$
vanishes.
$\psi _i\cup \psi _{i+1}$
vanishes.
The version of [Reference Emerton and GeeEG23, Thm. 5.5.12] proved in [Reference Emerton and GeeEG] states in particular that for a dense Zariski open subset U of
![]() $\operatorname {\mathrm {Ext}}^1_{(t_1,\dots ,t_d),\underline {k}}$
, the corresponding extension classes are realized by some
$\operatorname {\mathrm {Ext}}^1_{(t_1,\dots ,t_d),\underline {k}}$
, the corresponding extension classes are realized by some
![]() $\overline {\rho }\in {\mathcal U}^{\underline {k}}(\overline {{\mathbb F}}_p)$
; so it suffices to show that U contains a point
$\overline {\rho }\in {\mathcal U}^{\underline {k}}(\overline {{\mathbb F}}_p)$
; so it suffices to show that U contains a point
![]() $(\psi _1,\dots ,\psi _{d-1})$
with each
$(\psi _1,\dots ,\psi _{d-1})$
with each
![]() $\psi _i$
generic. As the locus of generic classes in
$\psi _i$
generic. As the locus of generic classes in
![]() $\operatorname {\mathrm {Ext}}^1_{(t_1,\dots ,t_d),\underline {k}}$
is open, and U is dense, it suffices in turn to exhibit a single generic class in
$\operatorname {\mathrm {Ext}}^1_{(t_1,\dots ,t_d),\underline {k}}$
is open, and U is dense, it suffices in turn to exhibit a single generic class in
![]() $\operatorname {\mathrm {Ext}}^1_{(t_1,\dots ,t_d),\underline {k}}$
.
$\operatorname {\mathrm {Ext}}^1_{(t_1,\dots ,t_d),\underline {k}}$
.
To do this, first note that
![]() $\psi _i\cup \psi _{i+1}$
is an element of the
$\psi _i\cup \psi _{i+1}$
is an element of the
![]() $\operatorname {\mathrm {Ext}}^2$
group
$\operatorname {\mathrm {Ext}}^2$
group
This group vanishes unless
![]() $(\mathrm {ur}_{t_{i+2}}\overline {\varepsilon }^{i+2-d}\omega _{\underline {k},i+2})/(\mathrm {ur}_{t_i}\overline {\varepsilon }^{i-d}\omega _{\underline {k},i})=\overline {\varepsilon }$
, which by our choice of T can only occur when
$(\mathrm {ur}_{t_{i+2}}\overline {\varepsilon }^{i+2-d}\omega _{\underline {k},i+2})/(\mathrm {ur}_{t_i}\overline {\varepsilon }^{i-d}\omega _{\underline {k},i})=\overline {\varepsilon }$
, which by our choice of T can only occur when
![]() $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=k_{\overline {\sigma },i+1}-k_{\overline {\sigma },i+2}=p-1$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=k_{\overline {\sigma },i+1}-k_{\overline {\sigma },i+2}=p-1$
for all
![]() $\overline {\sigma }$
and
$\overline {\sigma }$
and
![]() $\overline {\varepsilon }=1$
. Thus, if
$\overline {\varepsilon }=1$
. Thus, if
![]() $\overline {\varepsilon }\not =1$
, we can just choose each
$\overline {\varepsilon }\not =1$
, we can just choose each
![]() $\psi _i$
to be any generic extension class, and the cup product condition is automatically satisfied.
$\psi _i$
to be any generic extension class, and the cup product condition is automatically satisfied.
We assume from now on that
![]() $\overline {\varepsilon }=1$
and fix a maximal interval
$\overline {\varepsilon }=1$
and fix a maximal interval
![]() $m<n$
such that
$m<n$
such that
![]() $k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
$k_{\overline {\sigma },i}-k_{\overline {\sigma },i+1}=p-1$
for all
![]() $\overline {\sigma }$
and all
$\overline {\sigma }$
and all
![]() $m\le i< n$
. The characters
$m\le i< n$
. The characters
![]() $\mathrm {ur}_{t_i}\overline {\varepsilon }^{i-d}\omega _{\underline {k},i}$
for
$\mathrm {ur}_{t_i}\overline {\varepsilon }^{i-d}\omega _{\underline {k},i}$
for
![]() $m\le i\leq n$
are all equal, and we write
$m\le i\leq n$
are all equal, and we write
![]() $\overline {\chi }$
for their common value. The cup product pairing is a perfect pairing
$\overline {\chi }$
for their common value. The cup product pairing is a perfect pairing
The generic classes are the complement of the union of finitely many proper subspaces
![]() $L_j \subset \operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi },\overline {\chi })$
, with annihilators
$L_j \subset \operatorname {\mathrm {Ext}}^1_{G_K}(\overline {\chi },\overline {\chi })$
, with annihilators
![]() $L_j^\perp $
under the pairing. Pick a generic class
$L_j^\perp $
under the pairing. Pick a generic class
![]() $\psi _m$
which is not in any
$\psi _m$
which is not in any
![]() $L_j^\perp $
. Then the annihilator
$L_j^\perp $
. Then the annihilator
![]() $\langle \psi _m \rangle ^\perp $
cannot be contained in
$\langle \psi _m \rangle ^\perp $
cannot be contained in
![]() $\bigcup _j L_j \cup \bigcup _j L_j^\perp $
(otherwise,
$\bigcup _j L_j \cup \bigcup _j L_j^\perp $
(otherwise,
![]() $\langle \psi _m \rangle ^\perp $
is contained in one of the
$\langle \psi _m \rangle ^\perp $
is contained in one of the
![]() $L_j$
or
$L_j$
or
![]() $L_j^\perp $
, which implies that
$L_j^\perp $
, which implies that
![]() $L_j$
or
$L_j$
or
![]() $L_j^\perp $
is contained in
$L_j^\perp $
is contained in
![]() $\langle \psi _m \rangle $
). So we can find a generic class
$\langle \psi _m \rangle $
). So we can find a generic class
![]() $\psi _{m+1} \in \langle \psi _m \rangle ^\perp $
which is also not in any
$\psi _{m+1} \in \langle \psi _m \rangle ^\perp $
which is also not in any
![]() $L_j^\perp $
. Repeating, we can find a sequence
$L_j^\perp $
. Repeating, we can find a sequence
![]() $\psi _m,\psi _{m+1},\ldots \psi _{n-1}$
of generic classes such that
$\psi _m,\psi _{m+1},\ldots \psi _{n-1}$
of generic classes such that
![]() $\psi _i\cup \psi _{i+1} = 0$
for
$\psi _i\cup \psi _{i+1} = 0$
for
![]() $m\le i < n$
.
$m\le i < n$
.
2.5 Generic reducedness
We now compute the underlying cycle of the weight
![]() $0$
crystalline stack and deduce our main result on generic reducedness (Theorem 2.5.5).
$0$
crystalline stack and deduce our main result on generic reducedness (Theorem 2.5.5).
This underlying cycle is defined as follows. By Theorem 2.4.3, the special fibre
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is a closed substack of the special fibre
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is a closed substack of the special fibre
![]() $\overline {{\mathcal X}}_d$
, and its irreducible components (with the induced reduced substack structure) are therefore closed substacks of the algebraic stack
$\overline {{\mathcal X}}_d$
, and its irreducible components (with the induced reduced substack structure) are therefore closed substacks of the algebraic stack
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}$
(see [Sta13, Tag 0DR4] for the theory of irreducible components of algebraic stacks and their multiplicities). Furthermore,
$\overline {{\mathcal X}}_{d,\operatorname {red}}$
(see [Sta13, Tag 0DR4] for the theory of irreducible components of algebraic stacks and their multiplicities). Furthermore,
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
and
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
and
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}$
are both algebraic stacks over
$\overline {{\mathcal X}}_{d,\operatorname {red}}$
are both algebraic stacks over
![]() ${\mathbb F}$
which are equidimensional of dimension
${\mathbb F}$
which are equidimensional of dimension
![]() $[K:{\mathbb Q}_p]d(d-1)/2$
. It follows that the irreducible components of
$[K:{\mathbb Q}_p]d(d-1)/2$
. It follows that the irreducible components of
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
are irreducible components of
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
are irreducible components of
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}$
and are therefore of the form
$\overline {{\mathcal X}}_{d,\operatorname {red}}$
and are therefore of the form
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
for some Serre weight
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
for some Serre weight
![]() $\underline {k}$
.
$\underline {k}$
.
For each
![]() $\underline {k}$
, we write
$\underline {k}$
, we write
![]() $\mu _{\underline {k}}(\overline {{\mathcal X}}^{\mathrm {crys},0}_d)$
for the multiplicity of
$\mu _{\underline {k}}(\overline {{\mathcal X}}^{\mathrm {crys},0}_d)$
for the multiplicity of
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
as a component of
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
as a component of
![]() $\overline {{\mathcal X}}^{\mathrm {crys},0}_d$
. We write
$\overline {{\mathcal X}}^{\mathrm {crys},0}_d$
. We write
![]() $Z_{\mathrm {crys},0}=Z(\overline {{\mathcal X}}^{\mathrm {crys},0}_d)$
for the corresponding cycle – that is, for the formal sum
$Z_{\mathrm {crys},0}=Z(\overline {{\mathcal X}}^{\mathrm {crys},0}_d)$
for the corresponding cycle – that is, for the formal sum
 $$ \begin{align}Z_{\mathrm{crys},0}=\sum_{\underline{k}}\mu_{\underline{k}}(\overline{{\mathcal X}}^{\mathrm{crys},0}_d)\cdot\overline{{\mathcal X}}_{d,\operatorname{red}}^{\underline{k}}, \end{align} $$
$$ \begin{align}Z_{\mathrm{crys},0}=\sum_{\underline{k}}\mu_{\underline{k}}(\overline{{\mathcal X}}^{\mathrm{crys},0}_d)\cdot\overline{{\mathcal X}}_{d,\operatorname{red}}^{\underline{k}}, \end{align} $$
which we regard as an element of the finitely generated free abelian group
![]() ${\mathbb Z}[{\mathcal X}_{d,\operatorname {red}}]$
whose generators are the irreducible components
${\mathbb Z}[{\mathcal X}_{d,\operatorname {red}}]$
whose generators are the irreducible components
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
.
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
.
Theorem 2.5.2. Suppose that
![]() $p>d$
. Then we have an equality of cycles
$p>d$
. Then we have an equality of cycles
where
![]() $\underline {0}$
is the Serre weight
$\underline {0}$
is the Serre weight
![]() $\underline {k}$
with
$\underline {k}$
with
![]() $k_{\sigma ,i}=0$
for all
$k_{\sigma ,i}=0$
for all
![]() $\sigma ,i$
. In particular, the special fibre
$\sigma ,i$
. In particular, the special fibre
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is generically reduced.
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is generically reduced.
Proof. Suppose (in the notation of Theorem 2.4.3 (3)) that
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
is an irreducible component of
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {k}}$
is an irreducible component of
![]() ${\mathcal X}_{d,\operatorname {red}}$
contained in the
${\mathcal X}_{d,\operatorname {red}}$
contained in the
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
. We begin by showing that
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
. We begin by showing that
![]() $\underline {k}=\underline {0}$
. By Theorem 2.4.3 (4), after possibly enlarging
$\underline {k}=\underline {0}$
. By Theorem 2.4.3 (4), after possibly enlarging
![]() ${\mathbb F}$
, we can pick a point
${\mathbb F}$
, we can pick a point
![]() $x:\operatorname {\mathrm {Spec}}{\mathbb F}\to {\mathcal U}^{\underline {k}}$
so that the corresponding representation
$x:\operatorname {\mathrm {Spec}}{\mathbb F}\to {\mathcal U}^{\underline {k}}$
so that the corresponding representation
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d({\mathbb F})$
is generic in the sense of Definition 2.3.1 (it is also maximally nonsplit of niveau one and weight
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_d({\mathbb F})$
is generic in the sense of Definition 2.3.1 (it is also maximally nonsplit of niveau one and weight
![]() $\underline {k}$
since it comes from a point of
$\underline {k}$
since it comes from a point of
![]() ${\mathcal U}^{\underline {k}}$
). Since x is in
${\mathcal U}^{\underline {k}}$
). Since x is in
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
,
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
,
![]() $\overline {\rho }$
has a crystalline lift of weight 0. We can now apply Corollary 2.3.3 to conclude that
$\overline {\rho }$
has a crystalline lift of weight 0. We can now apply Corollary 2.3.3 to conclude that
![]() $\underline {k}=0$
.
$\underline {k}=0$
.
We have now shown that the support of
![]() $Z_{\mathrm {crys},0}$
is indeed
$Z_{\mathrm {crys},0}$
is indeed
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {0}}$
(i.e., that the underlying reduced substack of
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {0}}$
(i.e., that the underlying reduced substack of
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is equal to
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is equal to
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {0}}$
), and it remains to determine the generic multiplicity. To do this, we modify our choice of point x as follows: by definition, we have
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {0}}$
), and it remains to determine the generic multiplicity. To do this, we modify our choice of point x as follows: by definition, we have
![]() $({\mathbb G}_m)^d_{\underline {0}}=({\mathbb G}_m)^d$
, so we can and do choose our point x such that if
$({\mathbb G}_m)^d_{\underline {0}}=({\mathbb G}_m)^d$
, so we can and do choose our point x such that if
![]() $i\not =j$
, then
$i\not =j$
, then
We will show that
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is reduced in some open neighbourhood of x. Since the reduced locus is open, and
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is reduced in some open neighbourhood of x. Since the reduced locus is open, and
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is irreducible, this implies that
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is irreducible, this implies that
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is generically reduced.
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is generically reduced.
We claim that the crystalline lifting ring
![]() $R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
is formally smooth, where
$R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
is formally smooth, where
![]() $\overline {\rho }$
corresponds to our chosen point x. Indeed, by Theorem 2.3.2, crystalline lifts of
$\overline {\rho }$
corresponds to our chosen point x. Indeed, by Theorem 2.3.2, crystalline lifts of
![]() $\overline {\rho }$
of weight
$\overline {\rho }$
of weight
![]() $0$
are ordinary, and so
$0$
are ordinary, and so
![]() $R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
is the weight 0 ordinary lifting ring of
$R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
is the weight 0 ordinary lifting ring of
![]() $\overline {\rho }$
. Since
$\overline {\rho }$
. Since
![]() $\overline {\rho }$
is maximally nonsplit (i.e., has a unique filtration with rank
$\overline {\rho }$
is maximally nonsplit (i.e., has a unique filtration with rank
![]() $1$
graded pieces) and satisfies (2.5.3), the deformation problem represented by
$1$
graded pieces) and satisfies (2.5.3), the deformation problem represented by
![]() $R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
coincides with the one considered in [Reference Clozel, Harris and TaylorCHT08, 2.4.2] (taking
$R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}$
coincides with the one considered in [Reference Clozel, Harris and TaylorCHT08, 2.4.2] (taking
![]() $F_{\tilde {v}}$
there to be our K, n to be our d, and
$F_{\tilde {v}}$
there to be our K, n to be our d, and
![]() $\chi _{v,i}$
to be
$\chi _{v,i}$
to be
![]() $\varepsilon ^{-i}$
), and the formal smoothness is [Reference Clozel, Harris and TaylorCHT08, Lem. 2.4.7].
$\varepsilon ^{-i}$
), and the formal smoothness is [Reference Clozel, Harris and TaylorCHT08, Lem. 2.4.7].
By Theorem 2.4.1, we have a versal morphism
![]() $\operatorname {\mathrm {Spec}} R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi \to \overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
at x, where
$\operatorname {\mathrm {Spec}} R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi \to \overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
at x, where
![]() $R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
is formally smooth and in particular reduced. By [Sta13, Tag 0DR0], we may find a smooth morphism
$R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
is formally smooth and in particular reduced. By [Sta13, Tag 0DR0], we may find a smooth morphism
![]() $V\to \overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
with source a finite type
$V\to \overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
with source a finite type
![]() ${\mathcal O}/\varpi $
-scheme, and a point
${\mathcal O}/\varpi $
-scheme, and a point
![]() $v\in V$
with residue field
$v\in V$
with residue field
![]() ${\mathbb F}$
, such that there is an isomorphism
${\mathbb F}$
, such that there is an isomorphism
![]() $\widehat {{\mathcal O}}_{V,v}\cong R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
compatible with the given morphism to
$\widehat {{\mathcal O}}_{V,v}\cong R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
compatible with the given morphism to
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
. By [Sta13, Tag 00MC] and [Sta13, Tag 033F], the local ring
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
. By [Sta13, Tag 00MC] and [Sta13, Tag 033F], the local ring
![]() ${{\mathcal O}}_{V,v}$
is reduced. Since being reduced is an open condition, we see that V is reduced in an open neighbourhood of v, and since it is also a smooth local condition (see [Sta13, Tag 04YH]), it follows that
${{\mathcal O}}_{V,v}$
is reduced. Since being reduced is an open condition, we see that V is reduced in an open neighbourhood of v, and since it is also a smooth local condition (see [Sta13, Tag 04YH]), it follows that
![]() $\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is reduced in an open neighbourhood of x, and we are done.
$\overline {{\mathcal X}}_{d}^{\mathrm {crys},0}$
is reduced in an open neighbourhood of x, and we are done.
Remark 2.5.4. Since the algebraic representation of
![]() $\operatorname {\mathrm {GL}}_d$
of highest weight
$\operatorname {\mathrm {GL}}_d$
of highest weight
![]() $0$
is the trivial representation, Theorem 2.5.2 shows that if
$0$
is the trivial representation, Theorem 2.5.2 shows that if
![]() $p>d$
, the cycle
$p>d$
, the cycle
![]() $Z_{\underline {0}}$
in the geometric Breuil–Mézard conjecture [Reference Emerton and GeeEG23, Conj. 8.2.2] is necessarily equal to
$Z_{\underline {0}}$
in the geometric Breuil–Mézard conjecture [Reference Emerton and GeeEG23, Conj. 8.2.2] is necessarily equal to
![]() $\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {0}}$
. As far as we are aware, this is the only instance in which such a cycle has been computed for
$\overline {{\mathcal X}}_{d,\operatorname {red}}^{\underline {0}}$
. As far as we are aware, this is the only instance in which such a cycle has been computed for
![]() $d>2$
and
$d>2$
and
![]() $K/{\mathbb Q}_p$
arbitrary.
$K/{\mathbb Q}_p$
arbitrary.
Theorem 2.5.5. Suppose that
![]() $p>d$
, that
$p>d$
, that
![]() $K/{\mathbb Q}_p$
is a finite extension, and that
$K/{\mathbb Q}_p$
is a finite extension, and that
![]() $E/{\mathbb Q}_p$
is a finite extension containing the Galois closure of K, with ring of integers
$E/{\mathbb Q}_p$
is a finite extension containing the Galois closure of K, with ring of integers
![]() ${\mathcal O}$
and residue field
${\mathcal O}$
and residue field
![]() ${\mathbb F}$
.
${\mathbb F}$
.
Then for any
![]() $\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_d({\mathbb F})$
, the special fibre
$\overline {\rho }: G_K \to \operatorname {\mathrm {GL}}_d({\mathbb F})$
, the special fibre
![]() $ R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
of the weight
$ R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
of the weight
![]() $0$
crystalline lifting ring is generically reduced.
$0$
crystalline lifting ring is generically reduced.
Proof. We follow the proof of [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 4.6]. By Proposition 2.4.1, we have a versal morphism
![]() $\operatorname {\mathrm {Spf}} R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi \to \overline {{\mathcal X}}_d^{\mathrm {crys},0}$
at the
$\operatorname {\mathrm {Spf}} R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi \to \overline {{\mathcal X}}_d^{\mathrm {crys},0}$
at the
![]() ${\mathbb F}$
-point of
${\mathbb F}$
-point of
![]() ${\mathcal X}_{d,\operatorname {red}}$
corresponding to
${\mathcal X}_{d,\operatorname {red}}$
corresponding to
![]() $\overline {\rho }$
. By [Sta13, Tag 0DR0], we may find a smooth morphism
$\overline {\rho }$
. By [Sta13, Tag 0DR0], we may find a smooth morphism
![]() $V\to \overline {{\mathcal X}}_d^{\mathrm {crys},0}$
with source a finite type
$V\to \overline {{\mathcal X}}_d^{\mathrm {crys},0}$
with source a finite type
![]() ${\mathbb F}$
-scheme and a point
${\mathbb F}$
-scheme and a point
![]() $v\in V$
with residue field
$v\in V$
with residue field
![]() ${\mathbb F}$
, such that there is an isomorphism
${\mathbb F}$
, such that there is an isomorphism
![]() $\widehat {{\mathcal O}}_{V,v}\cong R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
compatible with the given morphism to
$\widehat {{\mathcal O}}_{V,v}\cong R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi $
compatible with the given morphism to
![]() $\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
.
$\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
.
By Theorem 2.5.2, there is a dense open substack
![]() ${\mathcal U}$
of
${\mathcal U}$
of
![]() $\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
such that
$\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
such that
![]() ${\mathcal U}$
is reduced. Since being reduced is a smooth local property, the pullback of
${\mathcal U}$
is reduced. Since being reduced is a smooth local property, the pullback of
![]() ${\mathcal U}$
to V is a reduced open subscheme of V; and this pullback is furthermore dense in V because the formation of the scheme-theoretic image of
${\mathcal U}$
to V is a reduced open subscheme of V; and this pullback is furthermore dense in V because the formation of the scheme-theoretic image of
![]() ${\mathcal U}$
in
${\mathcal U}$
in
![]() $\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
commutes with flat base change [Sta13, Tag 0CMK]. Thus, V is generically reduced, and the complete local rings of V at finite type points are generically reduced by [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Lem. 4.5]. In particular,
$\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
commutes with flat base change [Sta13, Tag 0CMK]. Thus, V is generically reduced, and the complete local rings of V at finite type points are generically reduced by [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Lem. 4.5]. In particular,
![]() $ R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi \cong \widehat {{\mathcal O}}_{V,v}$
is generically reduced, as required.
$ R^{\mathrm {crys},0,{\mathcal O}}_{\overline {\rho }}/\varpi \cong \widehat {{\mathcal O}}_{V,v}$
is generically reduced, as required.
Remark 2.5.6. The case
![]() $d=2$
of Theorem 2.5.5 is a special case of [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 4.6]. In both cases, the statement is deduced from the corresponding statement for the stack
$d=2$
of Theorem 2.5.5 is a special case of [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 4.6]. In both cases, the statement is deduced from the corresponding statement for the stack
![]() $\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
, and indeed in the case
$\overline {{\mathcal X}}_d^{\mathrm {crys},0}$
, and indeed in the case
![]() $d=2$
, Theorem 2.5.2 is a special case of [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 7.1, 7.6] (although the generic reducedness statement is proved earlier in [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Prop. 4.1]).
$d=2$
, Theorem 2.5.2 is a special case of [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 7.1, 7.6] (although the generic reducedness statement is proved earlier in [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Prop. 4.1]).
The argument that we use to prove Theorem 2.5.2 is necessarily rather different from the proof of [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 4.6], which was written before [Reference Emerton and GeeEG23] and in particular could not use the structure of generic points on the irreducible components of
![]() ${\mathcal X}_{2,\operatorname {red}}$
. Instead, the proof in [Reference Caraiani, Emerton, Gee and SavittCEGS22a] uses the Kisin resolution of
${\mathcal X}_{2,\operatorname {red}}$
. Instead, the proof in [Reference Caraiani, Emerton, Gee and SavittCEGS22a] uses the Kisin resolution of
![]() ${\mathcal X}_2^{\mathrm {crys},0}$
(originally defined for lifting rings in [Reference KisinKis09]). By results on local models for Shimura varieties, this Kisin resolution has reduced special fibre, and the arguments in [Reference Caraiani, Emerton, Gee and SavittCEGS22a] show that the map from the Kisin resolution is an isomorphism on dense open substacks of the source and target. In dimension greater than
${\mathcal X}_2^{\mathrm {crys},0}$
(originally defined for lifting rings in [Reference KisinKis09]). By results on local models for Shimura varieties, this Kisin resolution has reduced special fibre, and the arguments in [Reference Caraiani, Emerton, Gee and SavittCEGS22a] show that the map from the Kisin resolution is an isomorphism on dense open substacks of the source and target. In dimension greater than
![]() $2$
, we do not know of a candidate Kisin resolution for which we could expect to argue in this way.
$2$
, we do not know of a candidate Kisin resolution for which we could expect to argue in this way.
The result [Reference Caraiani, Emerton, Gee and SavittCEGS22a, Thm. 4.6] is more general than Theorem 2.5.5 (as always, in the special case
![]() $d=2$
) because it also proves the analogous statement for the potentially crystalline lifting ring of weight
$d=2$
) because it also proves the analogous statement for the potentially crystalline lifting ring of weight
![]() $0$
and any tame type. The Breuil–Mézard conjecture implies that the analogous statement necessarily fails for
$0$
and any tame type. The Breuil–Mézard conjecture implies that the analogous statement necessarily fails for
![]() $d\ge 4$
(even if
$d\ge 4$
(even if
![]() $K={\mathbb Q}_p$
) because the reductions modulo p of the corresponding inertial types contain Serre weights with multiplicities greater than
$K={\mathbb Q}_p$
) because the reductions modulo p of the corresponding inertial types contain Serre weights with multiplicities greater than
![]() $1$
, even for generic choices of type (see [Reference Le, Le Hung, Levin and MorraLLHLM23, Rem. 8.1.4]). Similarly, Theorem 2.5.2 is best possible in the sense that for any parallel Serre weight
$1$
, even for generic choices of type (see [Reference Le, Le Hung, Levin and MorraLLHLM23, Rem. 8.1.4]). Similarly, Theorem 2.5.2 is best possible in the sense that for any parallel Serre weight
![]() $\underline {k}$
greater than
$\underline {k}$
greater than
![]() $0$
(i.e.,
$0$
(i.e.,
![]() $k_{\sigma ,i}$
is independent of
$k_{\sigma ,i}$
is independent of
![]() $\sigma $
, and the
$\sigma $
, and the
![]() $k_{\sigma ,i}$
are not all equal), the stack
$k_{\sigma ,i}$
are not all equal), the stack
![]() ${\mathcal X}_d^{\mathrm {crys},\underline {k}}$
cannot have generically reduced special fibre once K is sufficiently ramified. (While the Breuil–Mézard conjecture is not known, standard arguments with Taylor–Wiles patching give the expected lower bounds for Breuil–Mézard multiplicities, so it is presumably possible to prove unconditionally that the special fibres of the corresponding stacks are not generically reduced.)
${\mathcal X}_d^{\mathrm {crys},\underline {k}}$
cannot have generically reduced special fibre once K is sufficiently ramified. (While the Breuil–Mézard conjecture is not known, standard arguments with Taylor–Wiles patching give the expected lower bounds for Breuil–Mézard multiplicities, so it is presumably possible to prove unconditionally that the special fibres of the corresponding stacks are not generically reduced.)
3 An automorphy lifting theorem in weight
 $0$
$0$
3.1 Preliminaries
Our goal in this section is to state and prove Theorem 3.2.1, which is an automorphy lifting theorem for n-dimensional crystalline weight
![]() $0\ p$
-adic representations of
$0\ p$
-adic representations of
![]() $G_F$
, where F is an imaginary CM field in which p is arbitrarily ramified. The key innovations that allow us to prove this theorem are the local-global compatibility result of [Reference Caraiani and NewtonCN23] and the generic reducedness result that we proved in Theorem 2.5.5. Given these ingredients, the proof is very close to those of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 6.1.1] and [Reference Miagkov and ThorneMT23, Theorem 1.2], and we refer to those papers for some of the details of the arguments, and for any unfamiliar terminology.
$G_F$
, where F is an imaginary CM field in which p is arbitrarily ramified. The key innovations that allow us to prove this theorem are the local-global compatibility result of [Reference Caraiani and NewtonCN23] and the generic reducedness result that we proved in Theorem 2.5.5. Given these ingredients, the proof is very close to those of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 6.1.1] and [Reference Miagkov and ThorneMT23, Theorem 1.2], and we refer to those papers for some of the details of the arguments, and for any unfamiliar terminology.
We begin by introducing some terminology and notation we will need for the statement and proof.
3.1.1 Galois preliminaries
Fix a continuous irreducible representation
![]() $\overline {\rho }: G_F \to \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
for a number field F. We fix a coefficient field
$\overline {\rho }: G_F \to \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
for a number field F. We fix a coefficient field
![]() $E/{\mathbb Q}_p$
such that
$E/{\mathbb Q}_p$
such that
![]() $\overline {\rho }(G_F) \subset \operatorname {\mathrm {GL}}_n({\mathbb F})$
.
$\overline {\rho }(G_F) \subset \operatorname {\mathrm {GL}}_n({\mathbb F})$
.
We will use the notion of a decomposed generic representation
![]() $\overline {\rho }$
, defined in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Definition 4.3.1]. We will also use the notion of an adequate subgroup of
$\overline {\rho }$
, defined in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Definition 4.3.1]. We will also use the notion of an adequate subgroup of
![]() $\operatorname {\mathrm {GL}}_n({\mathbb F})$
; see, for example, [Reference Miagkov and ThorneMT23, Definition 1.1.1].
$\operatorname {\mathrm {GL}}_n({\mathbb F})$
; see, for example, [Reference Miagkov and ThorneMT23, Definition 1.1.1].
Let v be a finite place of F. As in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.2.1], a local deformation problem is a
![]() $\widehat {\mathrm {PGL}}_n$
-stable subfunctor of the lifting functor
$\widehat {\mathrm {PGL}}_n$
-stable subfunctor of the lifting functor
![]() ${\mathcal D}_v^\square := {\mathcal D}_{\overline {\rho }|_{G_{F_v}}}^{\square ,{\mathcal O}}$
, (pro-)representable by a quotient
${\mathcal D}_v^\square := {\mathcal D}_{\overline {\rho }|_{G_{F_v}}}^{\square ,{\mathcal O}}$
, (pro-)representable by a quotient
![]() $R_v$
of the lifting ring
$R_v$
of the lifting ring
![]() $R_v^\square $
. The following local deformation problems will be relevant:
$R_v^\square $
. The following local deformation problems will be relevant:
-
• the lifting functor itself,
 ${\mathcal D}_v^\square $
,
${\mathcal D}_v^\square $
, -
• for
 $v|p$
, weight
$v|p$
, weight
 $0$
crystalline lifts
$0$
crystalline lifts
 ${\mathcal D}_v^{\mathrm {crys},\underline {0}}$
, represented by
${\mathcal D}_v^{\mathrm {crys},\underline {0}}$
, represented by
 $R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }|_{G_{F_v}}}$
,
$R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }|_{G_{F_v}}}$
, -
• the local deformation problem
 ${\mathcal D}_v^\chi $
defined in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.2.15]. In this case, we assume that
${\mathcal D}_v^\chi $
defined in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.2.15]. In this case, we assume that
 $q_v\equiv 1 \mod p$
, that
$q_v\equiv 1 \mod p$
, that
 $\overline {\rho }|_{G_{F_v}}$
is trivial, that
$\overline {\rho }|_{G_{F_v}}$
is trivial, that
 $p> n$
, and we have a tuple
$p> n$
, and we have a tuple
 $(\chi _{i})_{i = 1, \dots , n}$
of characters
$(\chi _{i})_{i = 1, \dots , n}$
of characters
 $\chi _{i} : {\mathcal O}_{F_v}^\times \to {\mathcal O}^\times $
which are trivial modulo
$\chi _{i} : {\mathcal O}_{F_v}^\times \to {\mathcal O}^\times $
which are trivial modulo
 $\varpi $
. Then
$\varpi $
. Then
 ${\mathcal D}_v^\chi $
classifies lifts
${\mathcal D}_v^\chi $
classifies lifts
 $\rho \colon G_{F_v} \rightarrow \operatorname {\mathrm {GL}}_n(A)$
such that for all
$\rho \colon G_{F_v} \rightarrow \operatorname {\mathrm {GL}}_n(A)$
such that for all $$\begin{align*}\mathrm{char}_{\rho(\sigma)}(X) = \prod_{i=1}^n (X - \chi_i(\mathrm{Art}_{F_v}^{-1}(\sigma))) \end{align*}$$
$$\begin{align*}\mathrm{char}_{\rho(\sigma)}(X) = \prod_{i=1}^n (X - \chi_i(\mathrm{Art}_{F_v}^{-1}(\sigma))) \end{align*}$$
 $\sigma \in I_{F_v}$
.
$\sigma \in I_{F_v}$
.
Let S be a finite set of finite places of F containing the p-adic places
![]() $S_p$
and all places at which
$S_p$
and all places at which
![]() $\overline {\rho }$
is ramified. Then we use the notion of a global deformation problem from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Definition 6.2.2]. We will be able to restrict to the case where
$\overline {\rho }$
is ramified. Then we use the notion of a global deformation problem from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Definition 6.2.2]. We will be able to restrict to the case where
![]() $\Lambda _v = {\mathcal O}$
for all
$\Lambda _v = {\mathcal O}$
for all
![]() $v \in S$
, so our global deformation problems will be tuples
$v \in S$
, so our global deformation problems will be tuples
![]() ${\mathcal S}= (\overline {\rho },S,\{{\mathcal O}\}_{v \in S},\{{\mathcal D}_v\}_{v \in S})$
. Each
${\mathcal S}= (\overline {\rho },S,\{{\mathcal O}\}_{v \in S},\{{\mathcal D}_v\}_{v \in S})$
. Each
![]() ${\mathcal D}_v$
is a local deformation problem, representable by a quotient
${\mathcal D}_v$
is a local deformation problem, representable by a quotient
![]() $R_v$
of
$R_v$
of
![]() $R_v^\square $
. There is an associated functor
$R_v^\square $
. There is an associated functor
![]() ${\mathcal D}_{\mathcal S}$
of deformations of
${\mathcal D}_{\mathcal S}$
of deformations of
![]() $\overline {\rho }$
satisfying the local condition
$\overline {\rho }$
satisfying the local condition
![]() ${\mathcal D}_v$
for each
${\mathcal D}_v$
for each
![]() $v \in S$
. It is representable by
$v \in S$
. It is representable by
![]() $R_{{\mathcal S}}$
. More generally, if
$R_{{\mathcal S}}$
. More generally, if
![]() $T \subset S$
, we have a functor
$T \subset S$
, we have a functor
![]() ${\mathcal D}_{{\mathcal S}}^{T}$
of T-framed deformations, which is representable by
${\mathcal D}_{{\mathcal S}}^{T}$
of T-framed deformations, which is representable by
![]() $R_{{\mathcal S}}^T$
. The T-framed global deformation ring
$R_{{\mathcal S}}^T$
. The T-framed global deformation ring
![]() $R_{{\mathcal S}}^T$
receives a natural
$R_{{\mathcal S}}^T$
receives a natural
![]() ${\mathcal O}$
-algebra map from
${\mathcal O}$
-algebra map from
![]() $R_{{\mathcal S}}^{T,\operatorname {loc}} := \widehat {\otimes }_{v\in T,{\mathcal O}} R_v$
.
$R_{{\mathcal S}}^{T,\operatorname {loc}} := \widehat {\otimes }_{v\in T,{\mathcal O}} R_v$
.
3.1.2 Automorphic preliminaries
Now we assume that F is an imaginary CM number field. On the automorphic side, we will be interested in cuspidal automorphic representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
which are regular algebraic of weight
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
which are regular algebraic of weight
![]() $0$
. This means that the infinitesimal character of
$0$
. This means that the infinitesimal character of
![]() $\pi _\infty $
matches the infinitesimal character of the trivial representation of
$\pi _\infty $
matches the infinitesimal character of the trivial representation of
![]() $\operatorname {\mathrm {GL}}_n(F_\infty )$
. These automorphic representations contribute to the cohomology groups with trivial coefficients of locally symmetric spaces.
$\operatorname {\mathrm {GL}}_n(F_\infty )$
. These automorphic representations contribute to the cohomology groups with trivial coefficients of locally symmetric spaces.
Let
![]() $X_\infty = \operatorname {\mathrm {GL}}_n(F_\infty )/{\mathbb R}_{> 0}K_\infty $
be the symmetric space, with
$X_\infty = \operatorname {\mathrm {GL}}_n(F_\infty )/{\mathbb R}_{> 0}K_\infty $
be the symmetric space, with
![]() $K_\infty $
a maximal compact subgroup of
$K_\infty $
a maximal compact subgroup of
![]() $\operatorname {\mathrm {GL}}_n(F_\infty )$
(since F is totally imaginary,
$\operatorname {\mathrm {GL}}_n(F_\infty )$
(since F is totally imaginary,
![]() $K_\infty $
is connected). Suppose we have a good subgroup
$K_\infty $
is connected). Suppose we have a good subgroup
![]() $K \subset \operatorname {\mathrm {GL}}_n(\mathbf {A}_F^\infty )$
. In other words, K is neat, compact, open and factorizes as
$K \subset \operatorname {\mathrm {GL}}_n(\mathbf {A}_F^\infty )$
. In other words, K is neat, compact, open and factorizes as
![]() $K = \prod _v K_v$
for compact open subgroups
$K = \prod _v K_v$
for compact open subgroups
![]() $K_v \subset \operatorname {\mathrm {GL}}_n(F_v)$
. Then we can define a smooth manifold
$K_v \subset \operatorname {\mathrm {GL}}_n(F_v)$
. Then we can define a smooth manifold
Fix a finite set of finite places S of F containing
![]() $S_p$
, with
$S_p$
, with
![]() $K_v = \operatorname {\mathrm {GL}}_n({\mathcal O}_v)$
for
$K_v = \operatorname {\mathrm {GL}}_n({\mathcal O}_v)$
for
![]() $v \notin S$
. We factorize
$v \notin S$
. We factorize
![]() $K=K_S K^S$
. We have an abstract Hecke algebra
$K=K_S K^S$
. We have an abstract Hecke algebra
![]() $\mathcal {H}(\operatorname {\mathrm {GL}}_n(\mathbf {A}_F^{\infty ,S}),K^S)$
with coefficients in
$\mathcal {H}(\operatorname {\mathrm {GL}}_n(\mathbf {A}_F^{\infty ,S}),K^S)$
with coefficients in
![]() ${\mathbb Z}$
, a tensor product of spherical Hecke algebras over finite places
${\mathbb Z}$
, a tensor product of spherical Hecke algebras over finite places
![]() $v \notin S$
.
$v \notin S$
.
Suppose that V is a finite
![]() ${\mathcal O}$
-module with an action of
${\mathcal O}$
-module with an action of
![]() $G(F)\times K_S$
. Then, as explained in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §2.1.2], V descends to a local system of
$G(F)\times K_S$
. Then, as explained in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §2.1.2], V descends to a local system of
![]() ${\mathcal O}$
-modules
${\mathcal O}$
-modules
![]() ${\mathcal V}$
on
${\mathcal V}$
on
![]() $X_K$
, and we have a natural Hecke action
$X_K$
, and we have a natural Hecke action
The image of this
![]() ${\mathcal O}$
-algebra map is a finite
${\mathcal O}$
-algebra map is a finite
![]() ${\mathcal O}$
-algebra denoted by
${\mathcal O}$
-algebra denoted by
![]() ${\mathbb T}^S(K,{\mathcal V})$
. If
${\mathbb T}^S(K,{\mathcal V})$
. If
![]() $\mathfrak {m}$
is a maximal ideal of
$\mathfrak {m}$
is a maximal ideal of
![]() ${\mathbb T}^S(K,{\mathcal V})$
, it has an associated semisimple Galois representation
${\mathbb T}^S(K,{\mathcal V})$
, it has an associated semisimple Galois representation
for a suitable set of places
![]() $S'$
containing S [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 2.3.5]. For
$S'$
containing S [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 2.3.5]. For
![]() $v \notin S'$
, the characteristic polynomial of
$v \notin S'$
, the characteristic polynomial of
![]() $\overline {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$
equals the image of
$\overline {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$
equals the image of
 $$ \begin{align*} P_v(X) = X^n&-T_{v, 1}X^{n-1} + \dots + (-1)^iq_v^{i(i-1)/2}T_{v, i}X^{n-i}+\dots \\ & + q_v^{n(n-1)/2}T_{v,n} \in \mathcal{H}(\operatorname{\mathrm{GL}}_n(F_v),\operatorname{\mathrm{GL}}_n({\mathcal O}_{F_v}))[X] \end{align*} $$
$$ \begin{align*} P_v(X) = X^n&-T_{v, 1}X^{n-1} + \dots + (-1)^iq_v^{i(i-1)/2}T_{v, i}X^{n-i}+\dots \\ & + q_v^{n(n-1)/2}T_{v,n} \in \mathcal{H}(\operatorname{\mathrm{GL}}_n(F_v),\operatorname{\mathrm{GL}}_n({\mathcal O}_{F_v}))[X] \end{align*} $$
in the residue field
![]() $k(\mathfrak {m})$
. We write
$k(\mathfrak {m})$
. We write
![]() $T_{v, i} \in \mathcal {H}(\operatorname {\mathrm {GL}}_n(F_v), \operatorname {\mathrm {GL}}_n({\mathcal O}_{F_v}))$
for the double coset operator
$T_{v, i} \in \mathcal {H}(\operatorname {\mathrm {GL}}_n(F_v), \operatorname {\mathrm {GL}}_n({\mathcal O}_{F_v}))$
for the double coset operator
where
![]() $\varpi _v$
appears i times on the diagonal.
$\varpi _v$
appears i times on the diagonal.
When
![]() $\overline {\rho }_{\mathfrak {m}}$
is absolutely irreducible, the cohomology groups
$\overline {\rho }_{\mathfrak {m}}$
is absolutely irreducible, the cohomology groups
![]() $H^i(X_K,{\mathcal O})_{\mathfrak {m}} \otimes _{{\mathcal O}} E$
can be described in terms of cuspidal automorphic representations which are regular algebraic of weight 0 [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 2.4.10].
$H^i(X_K,{\mathcal O})_{\mathfrak {m}} \otimes _{{\mathcal O}} E$
can be described in terms of cuspidal automorphic representations which are regular algebraic of weight 0 [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 2.4.10].
3.2 An automorphy lifting theorem
The rest of this section is devoted to the proof of the following theorem, which is a version of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 6.1.1] and [Reference Miagkov and ThorneMT23, Theorem 1.2] allowing arbitrary ramification at primes dividing p, at the price of restricting to weight
![]() $0$
automorphic representations.
$0$
automorphic representations.
Theorem 3.2.1. Let F be an imaginary CM or totally real field, and let
![]() $p>n$
be a prime. Suppose we are given a continuous representation
$p>n$
be a prime. Suppose we are given a continuous representation
![]() $\rho : G_F \to \operatorname {\mathrm {GL}}_n(\overline {{\mathbb Q}}_p)$
satisfying the following conditions:
$\rho : G_F \to \operatorname {\mathrm {GL}}_n(\overline {{\mathbb Q}}_p)$
satisfying the following conditions:
-
1.
 $\rho $
is unramified almost everywhere.
$\rho $
is unramified almost everywhere. -
2. For each place
 $v | p$
of F, the representation
$v | p$
of F, the representation
 $\rho |_{G_{F_v}}$
is crystalline of weight
$\rho |_{G_{F_v}}$
is crystalline of weight
 $0$
(i.e., with Hodge–Tate weights
$0$
(i.e., with Hodge–Tate weights
 $HT_{\tau }(\rho )=\{0,1,2,\ldots ,n-1\}$
for each
$HT_{\tau }(\rho )=\{0,1,2,\ldots ,n-1\}$
for each
 $\tau :F_v\hookrightarrow \overline {{\mathbb Q}}_p$
).
$\tau :F_v\hookrightarrow \overline {{\mathbb Q}}_p$
). -
3.
 $\overline {\rho }$
is absolutely irreducible and decomposed generic. The image of
$\overline {\rho }$
is absolutely irreducible and decomposed generic. The image of
 $\overline {\rho }|_{G_{F(\zeta _p)}}$
is adequate (as a subgroup of
$\overline {\rho }|_{G_{F(\zeta _p)}}$
is adequate (as a subgroup of
 $\operatorname {\mathrm {GL}}_n({\mathbb F})$
, for sufficiently large
$\operatorname {\mathrm {GL}}_n({\mathbb F})$
, for sufficiently large
 ${\mathbb F}$
).
${\mathbb F}$
). -
4. There exists
 $\sigma \in G_F - G_{F(\zeta _p)}$
such that
$\sigma \in G_F - G_{F(\zeta _p)}$
such that
 $\overline {\rho }(\sigma )$
is a scalar.
$\overline {\rho }(\sigma )$
is a scalar. -
5. There exists a cuspidal automorphic representation
 $\pi $
of
$\pi $
of
 $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
satisfying the following conditions:
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
satisfying the following conditions:-
(a)
 $\pi $
is regular algebraic of weight
$\pi $
is regular algebraic of weight
 $0$
.
$0$
. -
(b) There exists an isomorphism
 $\iota : \overline {{\mathbb Q}}_p \to {\mathbb C}$
such that
$\iota : \overline {{\mathbb Q}}_p \to {\mathbb C}$
such that
 $\overline {\rho } \cong \overline {r_\iota (\pi )}$
.
$\overline {\rho } \cong \overline {r_\iota (\pi )}$
. -
(c) If
 $v | p$
is a place of F, then
$v | p$
is a place of F, then
 $\pi _v$
is unramified and
$\pi _v$
is unramified and
 $r_\iota (\pi )|_{G_{F_v}} \sim \rho |_{G_{F_v}}$
(‘connects to’, in the sense of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, §1.4]).
$r_\iota (\pi )|_{G_{F_v}} \sim \rho |_{G_{F_v}}$
(‘connects to’, in the sense of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, §1.4]).
-
Then
![]() $\rho $
is automorphic: there exists a cuspidal automorphic representation
$\rho $
is automorphic: there exists a cuspidal automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
of weight
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
of weight
![]() $0 $
such that
$0 $
such that
![]() $\rho \cong r_\iota (\Pi )$
. Moreover, if v is a finite place of F and either
$\rho \cong r_\iota (\Pi )$
. Moreover, if v is a finite place of F and either
![]() $v | p$
or both
$v | p$
or both
![]() $\rho $
and
$\rho $
and
![]() $\pi $
are unramified at v, then
$\pi $
are unramified at v, then
![]() $\Pi _v$
is unramified.
$\Pi _v$
is unramified.
Remark 3.2.2. In assumption (5c), we are using [Reference Caraiani and NewtonCN23, Theorem 4.3.1], which shows that
![]() $r_\iota (\pi )|_{G_{F_v}}$
is crystalline with the same labelled Hodge–Tate weights as
$r_\iota (\pi )|_{G_{F_v}}$
is crystalline with the same labelled Hodge–Tate weights as
![]() $\rho |_{G_{F_v}}$
. Choose a p-adic coefficient field E which contains the Galois closure of F and such that
$\rho |_{G_{F_v}}$
. Choose a p-adic coefficient field E which contains the Galois closure of F and such that
![]() $\overline {\rho }(G_F)\subset \operatorname {\mathrm {GL}}_n({\mathbb F})$
. Then assumption (5c) is that
$\overline {\rho }(G_F)\subset \operatorname {\mathrm {GL}}_n({\mathbb F})$
. Then assumption (5c) is that
![]() $r_\iota (\pi )|_{G_{F_v}}$
and
$r_\iota (\pi )|_{G_{F_v}}$
and
![]() $\rho |_{G_{F_v}}$
define points on the same irreducible component of the weight
$\rho |_{G_{F_v}}$
define points on the same irreducible component of the weight
![]() $0$
crystalline lifting ring
$0$
crystalline lifting ring
![]() $R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }|_{G_{F_v}}}\otimes _{{\mathcal O}}\overline {{\mathbb Q}}_p$
.
$R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }|_{G_{F_v}}}\otimes _{{\mathcal O}}\overline {{\mathbb Q}}_p$
.
We begin by imposing some additional assumptions, under which we can use the Calegari–Geraghty version of the Taylor–Wiles–Kisin patching method to prove an automorphy lifting theorem. We then deduce Theorem 3.2.1 by a standard base change argument. We refer the reader to [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23] for any unfamiliar notation.
We let F be an imaginary CM field with maximal totally real subfield
![]() $F^+$
and complex conjugation
$F^+$
and complex conjugation
![]() $c \in \operatorname {\mathrm {Gal}}(F/F^+)$
. We fix an integer
$c \in \operatorname {\mathrm {Gal}}(F/F^+)$
. We fix an integer
![]() $n \ge 1$
, an odd prime
$n \ge 1$
, an odd prime
![]() $p> n$
and an isomorphism
$p> n$
and an isomorphism
![]() $\iota : \overline {{\mathbb Q}}_p \cong {\mathbb C}$
. We let
$\iota : \overline {{\mathbb Q}}_p \cong {\mathbb C}$
. We let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
, which is regular algebraic of weight
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
, which is regular algebraic of weight
![]() $0$
. We suppose we have a finite set S of finite places of F, containing the set
$0$
. We suppose we have a finite set S of finite places of F, containing the set
![]() $S_p$
of places of F above p, and a (possibly empty) subset
$S_p$
of places of F above p, and a (possibly empty) subset
![]() $R \subset (S\smallsetminus S_p)$
.
$R \subset (S\smallsetminus S_p)$
.
Then we assume that the following conditions are satisfied:
-
1. If l is a prime lying below an element of S, or which is ramified in F, then F contains an imaginary quadratic field in which l splits. In particular, each place of S is split over
 $F^+$
and the extension
$F^+$
and the extension
 $F / F^+$
is everywhere unramified.
$F / F^+$
is everywhere unramified. -
2. For each
 $v \in S_p$
, let
$v \in S_p$
, let
 $\overline {v}$
denote the place of
$\overline {v}$
denote the place of
 $F^+$
lying below v. Then there exists a place
$F^+$
lying below v. Then there exists a place
 $\overline {v}' \neq \overline {v}$
of
$\overline {v}' \neq \overline {v}$
of
 $F^+$
such that
$F^+$
such that
 $\overline {v}' | p$
and
$\overline {v}' | p$
and  $$\begin{align*}\sum_{\overline{v}" \neq \overline{v}, \overline{v}'} [ F^+_{\overline{v}"} : {\mathbb Q}_p ]> \frac{1}{2} [ F^+ : {\mathbb Q}_p ]. \end{align*}$$
$$\begin{align*}\sum_{\overline{v}" \neq \overline{v}, \overline{v}'} [ F^+_{\overline{v}"} : {\mathbb Q}_p ]> \frac{1}{2} [ F^+ : {\mathbb Q}_p ]. \end{align*}$$
-
3. The residual representation
 $\overline {r_\iota (\pi )}$
is absolutely irreducible and decomposed generic, and
$\overline {r_\iota (\pi )}$
is absolutely irreducible and decomposed generic, and
 $\overline {r_\iota (\pi )}|_{G_{F(\zeta _p)}}$
has adequate image.
$\overline {r_\iota (\pi )}|_{G_{F(\zeta _p)}}$
has adequate image. -
4. If v is a place of F lying above p, then
 $\pi _v$
is unramified.
$\pi _v$
is unramified. -
5. If
 $v \in R$
, then
$v \in R$
, then
 $\pi _v^{\mathrm {Iw}_v} \neq 0$
,
$\pi _v^{\mathrm {Iw}_v} \neq 0$
,
 $q_v \equiv 1 \text { mod }p$
and
$q_v \equiv 1 \text { mod }p$
and
 $\overline {r_\iota (\pi )}|_{G_{F_v}}$
is trivial.
$\overline {r_\iota (\pi )}|_{G_{F_v}}$
is trivial. -
6. If
 $v \in S - (R \cup S_p)$
, then
$v \in S - (R \cup S_p)$
, then
 $\pi _v$
is unramified,
$\pi _v$
is unramified,
 $v\notin R^c$
and
$v\notin R^c$
and
 $H^2(F_v, \operatorname {ad} \overline {r_\iota (\pi )}) = 0$
.
$H^2(F_v, \operatorname {ad} \overline {r_\iota (\pi )}) = 0$
. -
7.
 $S-(R \cup S_p)$
contains at least two places with distinct residue characteristics.
$S-(R \cup S_p)$
contains at least two places with distinct residue characteristics. -
8. If
 $v \not \in S$
is a finite place of F, then
$v \not \in S$
is a finite place of F, then
 $\pi _v$
is unramified.
$\pi _v$
is unramified.
We define an open compact subgroup
![]() $K = \prod _v K_v$
of
$K = \prod _v K_v$
of
![]() $\operatorname {\mathrm {GL}}_n(\widehat {{\mathcal O}}_F)$
as follows:
$\operatorname {\mathrm {GL}}_n(\widehat {{\mathcal O}}_F)$
as follows:
-
• If
 $v \not \in S$
, or
$v \not \in S$
, or
 $v \in S_p$
, then
$v \in S_p$
, then
 $K_v = \operatorname {\mathrm {GL}}_n({\mathcal O}_{F_v})$
.
$K_v = \operatorname {\mathrm {GL}}_n({\mathcal O}_{F_v})$
. -
• If
 $v \in R$
, then
$v \in R$
, then
 $K_v = \mathrm {Iw}_v$
.
$K_v = \mathrm {Iw}_v$
. -
• If
 $v \in S - (R \cup S_p)$
, then
$v \in S - (R \cup S_p)$
, then
 $K_v = \mathrm {Iw}_{v,1}$
is the pro-v Iwahori subroup of
$K_v = \mathrm {Iw}_{v,1}$
is the pro-v Iwahori subroup of
 $\operatorname {\mathrm {GL}}_n({\mathcal O}_{F_v})$
.
$\operatorname {\mathrm {GL}}_n({\mathcal O}_{F_v})$
.
By [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 2.4.10], we can find a coefficient field
![]() $E \subset \overline {{\mathbb Q}}_p$
and a maximal ideal
$E \subset \overline {{\mathbb Q}}_p$
and a maximal ideal
![]() ${\mathfrak m} \subset {\mathbb T}^S(K, {\mathcal O})$
such that
${\mathfrak m} \subset {\mathbb T}^S(K, {\mathcal O})$
such that
![]() $\overline {\rho }_{\mathfrak m} \cong \overline {r_\iota (\pi )}$
. After possibly enlarging E, we can and do assume that the residue field of
$\overline {\rho }_{\mathfrak m} \cong \overline {r_\iota (\pi )}$
. After possibly enlarging E, we can and do assume that the residue field of
![]() $\mathfrak {m}$
is equal to
$\mathfrak {m}$
is equal to
![]() ${\mathbb F}$
, the residue field of E. For each tuple
${\mathbb F}$
, the residue field of E. For each tuple
![]() $(\chi _{v, i})_{v \in R, i = 1, \dots , n}$
of characters
$(\chi _{v, i})_{v \in R, i = 1, \dots , n}$
of characters
![]() $\chi _{v, i} : k(v)^\times \to {\mathcal O}^\times $
which are trivial modulo
$\chi _{v, i} : k(v)^\times \to {\mathcal O}^\times $
which are trivial modulo
![]() $\varpi $
, we define a global deformation problem
$\varpi $
, we define a global deformation problem
We will assume that either
![]() $\chi _{v,i} = 1$
for all
$\chi _{v,i} = 1$
for all
![]() $v \in R$
and all
$v \in R$
and all
![]() $1\le i\le n$
, or that for each
$1\le i\le n$
, or that for each
![]() $v \in R$
, the
$v \in R$
, the
![]() $\chi _{v,i}$
are pairwise distinct.
$\chi _{v,i}$
are pairwise distinct.
Extending
![]() ${\mathcal O}$
if necessary, we may assume that all irreducible components of our local lifting rings and their special fibres are geometrically irreducible. We fix representatives
${\mathcal O}$
if necessary, we may assume that all irreducible components of our local lifting rings and their special fibres are geometrically irreducible. We fix representatives
![]() $\rho _{{\mathcal S}_\chi }$
of the universal deformations which are identified modulo
$\rho _{{\mathcal S}_\chi }$
of the universal deformations which are identified modulo
![]() $\varpi $
(via the identifications
$\varpi $
(via the identifications
![]() $R_{{\mathcal S}_\chi } / \varpi \cong R_{{\mathcal S}_1} / \varpi $
). We define an
$R_{{\mathcal S}_\chi } / \varpi \cong R_{{\mathcal S}_1} / \varpi $
). We define an
![]() ${\mathcal O}[K_S]$
-module
${\mathcal O}[K_S]$
-module
![]() ${\mathcal O}(\chi ^{-1})$
, where
${\mathcal O}(\chi ^{-1})$
, where
![]() $K_S$
acts by the composition of
$K_S$
acts by the composition of
![]() $\chi ^{-1}$
with the projection
$\chi ^{-1}$
with the projection
Proposition 3.2.3. There exists an integer
![]() $\delta \geq 1$
, depending only on n and
$\delta \geq 1$
, depending only on n and
![]() $[F : {\mathbb Q}]$
, an ideal
$[F : {\mathbb Q}]$
, an ideal
![]() $J \subset {\mathbb T}^S( R \Gamma (X_K, {\mathcal O} (\chi ^{-1})))_{\mathfrak m}$
such that
$J \subset {\mathbb T}^S( R \Gamma (X_K, {\mathcal O} (\chi ^{-1})))_{\mathfrak m}$
such that
![]() $J^\delta = 0$
, and a continuous surjective homomorphism
$J^\delta = 0$
, and a continuous surjective homomorphism
such that for each finite place
![]() $v \not \in S$
of F, the characteristic polynomial of
$v \not \in S$
of F, the characteristic polynomial of
![]() $f_{{\mathcal S}_\chi } \circ \rho _{{\mathcal S}_\chi }(\mathrm {Frob}_v)$
equals the image of
$f_{{\mathcal S}_\chi } \circ \rho _{{\mathcal S}_\chi }(\mathrm {Frob}_v)$
equals the image of
![]() $P_v(X)$
in
$P_v(X)$
in
![]() ${\mathbb T}^S( R \Gamma (X_K, {\mathcal O}(\chi ^{-1})))_{\mathfrak m} / J$
.
${\mathbb T}^S( R \Gamma (X_K, {\mathcal O}(\chi ^{-1})))_{\mathfrak m} / J$
.
Proof. This is a version of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Proposition 6.5.3], using [Reference Caraiani and NewtonCN23, Theorem 4.2.15] to verify that we satisfy the crystalline weight
![]() $0$
condition at
$0$
condition at
![]() $v \in S_p$
.
$v \in S_p$
.
This proposition means that it makes sense to talk about the support of
![]() $H^\ast (X_K, {\mathcal O})_{\mathfrak m}$
over
$H^\ast (X_K, {\mathcal O})_{\mathfrak m}$
over
![]() $ R_{{\mathcal S}_{1}}$
since
$ R_{{\mathcal S}_{1}}$
since
![]() $f_{{\mathcal S}_1}$
realizes
$f_{{\mathcal S}_1}$
realizes
![]() $\operatorname {\mathrm {Spec}}({\mathbb T}^S(K,{\mathcal O})_{\mathfrak {m}})$
as a closed subset of
$\operatorname {\mathrm {Spec}}({\mathbb T}^S(K,{\mathcal O})_{\mathfrak {m}})$
as a closed subset of
![]() $\operatorname {\mathrm {Spec}}(R_{{\mathcal S}_1})$
.
$\operatorname {\mathrm {Spec}}(R_{{\mathcal S}_1})$
.
Here are the essential properties of the (completed tensor products of) local deformation rings in our situation:
Lemma 3.2.4. Fix a tuple
![]() $\chi = (\chi _{v, i})_{v \in R, i = 1, \dots , n}$
of characters
$\chi = (\chi _{v, i})_{v \in R, i = 1, \dots , n}$
of characters
![]() $\chi _{v, i} : k(v)^\times \to {\mathcal O}^\times $
which are trivial modulo
$\chi _{v, i} : k(v)^\times \to {\mathcal O}^\times $
which are trivial modulo
![]() $\varpi $
. We assume that either
$\varpi $
. We assume that either
![]() $\chi _{v,i} = 1$
for all
$\chi _{v,i} = 1$
for all
![]() $v \in R$
and all
$v \in R$
and all
![]() $1\le i\le n$
, or that for each
$1\le i\le n$
, or that for each
![]() $v \in R$
, the
$v \in R$
, the
![]() $\chi _{v,i}$
are pairwise distinct.
$\chi _{v,i}$
are pairwise distinct.
-
1.
 $R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
is equidimensional of dimension
$R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
is equidimensional of dimension
 $1+n^2|S| + \frac {n(n-1)}{2}[F:{\mathbb Q}]$
and every generic point has characteristic
$1+n^2|S| + \frac {n(n-1)}{2}[F:{\mathbb Q}]$
and every generic point has characteristic
 $0$
.
$0$
. -
2. Each generic point of
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}/\varpi $
is the specialization of a unique generic point of
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}/\varpi $
is the specialization of a unique generic point of
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
.
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
. -
3. Assume that
 $\chi _{v,1},\ldots ,\chi _{v,n}$
are pairwise distinct for each
$\chi _{v,1},\ldots ,\chi _{v,n}$
are pairwise distinct for each
 $v\in R$
. Then the natural map
$v\in R$
. Then the natural map
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}\to \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S_p,\operatorname {loc}} = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
induces a bijection on irreducible components.
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}\to \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S_p,\operatorname {loc}} = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
induces a bijection on irreducible components. -
4. Each characteristic zero point of
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
lies on a unique irreducible component.
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
lies on a unique irreducible component. -
5. Assume that
 $\chi _{v,1},\ldots ,\chi _{v,n}$
are pairwise distinct for each
$\chi _{v,1},\ldots ,\chi _{v,n}$
are pairwise distinct for each
 $v\in R$
, and let C be an irreducible component of
$v\in R$
, and let C be an irreducible component of
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}$
. Write
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}$
. Write
 $C_p$
for the image of C in
$C_p$
for the image of C in
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
(so that
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
(so that
 $C_p$
is an irreducible component of
$C_p$
is an irreducible component of
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
). Then the generic points of
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}$
). Then the generic points of
 $C\cap \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}/\varpi $
generalize (via the equality
$C\cap \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}/\varpi $
generalize (via the equality
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}/\varpi = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}/\varpi $
) to the generic point of
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}/\varpi = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}/\varpi $
) to the generic point of
 $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
corresponding to
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
corresponding to
 $C_p$
via the bijection of part (3). (By part (2), each of these points has a unique generalization.)
$C_p$
via the bijection of part (3). (By part (2), each of these points has a unique generalization.)
Proof. We begin by noting that [Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11, Lemma 3.3] allows us to describe the set of irreducible components of
![]() $\operatorname {\mathrm {Spec}}(R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}})$
(respectively, its special fibre) as the product over
$\operatorname {\mathrm {Spec}}(R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}})$
(respectively, its special fibre) as the product over
![]() $v \in S$
of the sets of irreducible components of the local deformation rings (respectively, their special fibres). (Here we use that the irreducible components of the local deformation rings that we consider are all in characteristic zero)
$v \in S$
of the sets of irreducible components of the local deformation rings (respectively, their special fibres). (Here we use that the irreducible components of the local deformation rings that we consider are all in characteristic zero)
The first part follows from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 6.2.25] (we have a different deformation condition at p, but
![]() $R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }|_{G_{F_v}}}$
is
$R^{\mathrm {crys},\underline {0},{\mathcal O}}_{\overline {\rho }|_{G_{F_v}}}$
is
![]() ${\mathcal O}$
-flat by definition and equidimensional of dimension
${\mathcal O}$
-flat by definition and equidimensional of dimension
![]() $1+n^2 + \frac {n(n-1)}{2}[F_v : {\mathbb Q}_p]$
by [Reference KisinKis08, Theorem 3.3.4]).
$1+n^2 + \frac {n(n-1)}{2}[F_v : {\mathbb Q}_p]$
by [Reference KisinKis08, Theorem 3.3.4]).
For the second part, for each
![]() $v \in S$
and local deformation ring
$v \in S$
and local deformation ring
![]() $R_v$
, we need to check that the generic points of
$R_v$
, we need to check that the generic points of
![]() $\operatorname {\mathrm {Spec}} R_v/\varpi $
have unique generalizations to
$\operatorname {\mathrm {Spec}} R_v/\varpi $
have unique generalizations to
![]() $\operatorname {\mathrm {Spec}} R_v$
. For
$\operatorname {\mathrm {Spec}} R_v$
. For
![]() $v|p$
, this follows from Theorem 2.5.5 — see [Reference Caraiani and NewtonCN23, Lemma 5.3.3] for the argument that generically reduced special fibre implies unique generalizations of its generic points, and note that we are assuming
$v|p$
, this follows from Theorem 2.5.5 — see [Reference Caraiani and NewtonCN23, Lemma 5.3.3] for the argument that generically reduced special fibre implies unique generalizations of its generic points, and note that we are assuming
![]() $p> n$
. For
$p> n$
. For
![]() $v \in R$
, the property we need follows from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Props. 6.2.16, 6.2.17]. For
$v \in R$
, the property we need follows from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Props. 6.2.16, 6.2.17]. For
![]() $v \in S - (R\cup S_p)$
,
$v \in S - (R\cup S_p)$
,
![]() $R_v = R_v^{\square }$
is formally smooth over
$R_v = R_v^{\square }$
is formally smooth over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
The third part follows from the irreducibility of the local deformation rings for
![]() $v \in S-S_p$
when the
$v \in S-S_p$
when the
![]() $\chi _{v,i}$
are pairwise distinct [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Prop. 6.2.17], and the fourth part from the regularity of
$\chi _{v,i}$
are pairwise distinct [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Prop. 6.2.17], and the fourth part from the regularity of
![]() $R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}\left [1/p\right ]$
[Reference KisinKis08, Theorem 3.3.8].
$R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}\left [1/p\right ]$
[Reference KisinKis08, Theorem 3.3.8].
For the final part, by the third part it is enough to note that, as we saw above, it follows from Theorem 2.5.5 that the generic points of the special fibre of
![]() $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}/\varpi = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S_p,\operatorname {loc}}/\varpi $
uniquely generalize to generic points of
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}}/\varpi = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S_p,\operatorname {loc}}/\varpi $
uniquely generalize to generic points of
![]() $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}} = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S_p,\operatorname {loc}}$
.
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_{1}}^{S_p,\operatorname {loc}} = \operatorname {\mathrm {Spec}} R_{{\mathcal S}_{\chi }}^{S_p,\operatorname {loc}}$
.
Theorem 3.2.5. Suppose we are given two homomorphisms
![]() $f_1, f_2: R_{{\mathcal S}_1}\to {\mathcal O}$
with associated liftings
$f_1, f_2: R_{{\mathcal S}_1}\to {\mathcal O}$
with associated liftings
![]() $\rho _1, \rho _2: G_{F,S} \to \operatorname {\mathrm {GL}}_n({\mathcal O})$
. Suppose
$\rho _1, \rho _2: G_{F,S} \to \operatorname {\mathrm {GL}}_n({\mathcal O})$
. Suppose
![]() $\ker (f_1) \in \operatorname {\mathrm {Supp}}_{R_{{\mathcal S}_1}}(H^\ast (X_K, {\mathcal O})_{\mathfrak m})$
and
$\ker (f_1) \in \operatorname {\mathrm {Supp}}_{R_{{\mathcal S}_1}}(H^\ast (X_K, {\mathcal O})_{\mathfrak m})$
and
![]() $\rho _1|_{G_{F_v}} \sim \rho _2|_{G_{F_v}}$
for each
$\rho _1|_{G_{F_v}} \sim \rho _2|_{G_{F_v}}$
for each
![]() $v \in S_p$
. Then
$v \in S_p$
. Then
![]() $\ker (f_2) \in \operatorname {\mathrm {Supp}}_{R_{{\mathcal S}_1}}(H^\ast (X_K, {\mathcal O})_{\mathfrak m})$
.
$\ker (f_2) \in \operatorname {\mathrm {Supp}}_{R_{{\mathcal S}_1}}(H^\ast (X_K, {\mathcal O})_{\mathfrak m})$
.
Proof. We patch, as in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.5] and [Reference Miagkov and ThorneMT23, §8], replacing the Fontaine–Laffaille local condition at
![]() $v \in S_p$
with the crystalline weight
$v \in S_p$
with the crystalline weight
![]() $0$
condition. Once again, we use [Reference Caraiani and NewtonCN23, Theorem 4.2.15] to ensure that we have the necessary maps from deformation rings with these local conditions to our Hecke algebras. We record the output of this patching process, complete details of which can be found in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.4–6.5]. Fix a tuple
$0$
condition. Once again, we use [Reference Caraiani and NewtonCN23, Theorem 4.2.15] to ensure that we have the necessary maps from deformation rings with these local conditions to our Hecke algebras. We record the output of this patching process, complete details of which can be found in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.4–6.5]. Fix a tuple
![]() $\chi = (\chi _{v, i})_{v \in R, i = 1, \dots , n}$
of characters
$\chi = (\chi _{v, i})_{v \in R, i = 1, \dots , n}$
of characters
![]() $\chi _{v, i} : k(v)^\times \to {\mathcal O}^\times $
which are trivial modulo
$\chi _{v, i} : k(v)^\times \to {\mathcal O}^\times $
which are trivial modulo
![]() $\varpi $
, and with
$\varpi $
, and with
![]() $\chi _{v,1},\ldots ,\chi _{v,n}$
pairwise distinct for each
$\chi _{v,1},\ldots ,\chi _{v,n}$
pairwise distinct for each
![]() $v\in R$
. Patching will provide us with the following:
$v\in R$
. Patching will provide us with the following:
-
1. A power series ring
 with augmentation ideal
with augmentation ideal
 $\mathfrak {a}_\infty = (X_1, \dots , X_r)$
.
$\mathfrak {a}_\infty = (X_1, \dots , X_r)$
. -
2. Perfect complexes
 $C_\infty , C^{\prime }_\infty $
of
$C_\infty , C^{\prime }_\infty $
of
 $S_\infty $
-modules, an isomorphism in
$S_\infty $
-modules, an isomorphism in $$\begin{align*}C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi \cong C^{\prime}_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi \end{align*}$$
$$\begin{align*}C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi \cong C^{\prime}_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi \end{align*}$$
 $\mathbf {D}(S_\infty / \varpi )$
and an isomorphism in
$\mathbf {D}(S_\infty / \varpi )$
and an isomorphism in $$\begin{align*}C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \mathfrak{a}_{\infty} \cong R \operatorname{\mathrm{Hom}}_{\mathcal O}( R \Gamma(X_K, {\mathcal O})_{\mathfrak{m}}, {\mathcal O})[-d]\end{align*}$$
$$\begin{align*}C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \mathfrak{a}_{\infty} \cong R \operatorname{\mathrm{Hom}}_{\mathcal O}( R \Gamma(X_K, {\mathcal O})_{\mathfrak{m}}, {\mathcal O})[-d]\end{align*}$$
 $\mathbf {D}({\mathcal O})$
.
$\mathbf {D}({\mathcal O})$
.
-
3. Two
 $S_\infty $
-subalgebras and
$S_\infty $
-subalgebras and $$\begin{align*}T_\infty\subset \operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty)}(C_\infty) \end{align*}$$
which have the same image in
$$\begin{align*}T_\infty\subset \operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty)}(C_\infty) \end{align*}$$
which have the same image in $$\begin{align*}T^{\prime}_\infty \subset \operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty)}(C^{\prime}_\infty), \end{align*}$$
where these endomorphism algebras are identified using the fixed isomorphism in (2). Call this common image
$$\begin{align*}T^{\prime}_\infty \subset \operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty)}(C^{\prime}_\infty), \end{align*}$$
where these endomorphism algebras are identified using the fixed isomorphism in (2). Call this common image $$\begin{align*}\operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty/\varpi)}(C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi ) = \operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty/\varpi)}(C^{\prime}_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi ), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty/\varpi)}(C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi ) = \operatorname{\mathrm{End}}_{\mathbf{D}(S_\infty/\varpi)}(C^{\prime}_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi ), \end{align*}$$
 $\overline {T}_\infty $
. Note that
$\overline {T}_\infty $
. Note that
 $T_\infty $
and
$T_\infty $
and
 $T^{\prime }_\infty $
are finite
$T^{\prime }_\infty $
are finite
 $S_\infty $
-algebras. The map factors through a map
$S_\infty $
-algebras. The map factors through a map $$\begin{align*}T_\infty \to \operatorname{\mathrm{End}}_{\mathbf{D}({\mathcal O})}(C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \mathfrak{a}_{\infty}) = \operatorname{\mathrm{End}}_{\mathbf{D}({\mathcal O})}(R \Gamma(X_K, {\mathcal O})_{\mathfrak{m}})^{op}\end{align*}$$
$$\begin{align*}T_\infty \to \operatorname{\mathrm{End}}_{\mathbf{D}({\mathcal O})}(C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \mathfrak{a}_{\infty}) = \operatorname{\mathrm{End}}_{\mathbf{D}({\mathcal O})}(R \Gamma(X_K, {\mathcal O})_{\mathfrak{m}})^{op}\end{align*}$$
 $T_\infty \to {\mathbb T}(K,{\mathcal O})_{\mathfrak {m}}$
.
$T_\infty \to {\mathbb T}(K,{\mathcal O})_{\mathfrak {m}}$
.
-
4. Two Noetherian complete local
 $S_\infty $
-algebras
$S_\infty $
-algebras
 $R_\infty $
and
$R_\infty $
and
 $R^{\prime }_\infty $
, which are power series algebras over
$R^{\prime }_\infty $
, which are power series algebras over
 $R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}$
and
$R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}$
and
 $R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
, respectively. We have a surjective
$R_{{\mathcal S}_{\chi }}^{S,\operatorname {loc}}$
, respectively. We have a surjective
 $R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}$
-algebra map
$R_{{\mathcal S}_{1}}^{S,\operatorname {loc}}$
-algebra map
 $R_\infty \to R_{{\mathcal S}_{1}}$
, which factors through an
$R_\infty \to R_{{\mathcal S}_{1}}$
, which factors through an
 ${\mathcal O}$
-algebra map
${\mathcal O}$
-algebra map
 $R_\infty /\mathfrak {a}_{\infty } \to R_{{\mathcal S}_{1}}$
. We also have surjections
$R_\infty /\mathfrak {a}_{\infty } \to R_{{\mathcal S}_{1}}$
. We also have surjections
 $R_\infty \twoheadrightarrow T_\infty /I_\infty $
,
$R_\infty \twoheadrightarrow T_\infty /I_\infty $
,
 $R^{\prime }_\infty \twoheadrightarrow T^{\prime }_\infty /I^{\prime }_\infty $
, where
$R^{\prime }_\infty \twoheadrightarrow T^{\prime }_\infty /I^{\prime }_\infty $
, where
 $I_\infty $
and
$I_\infty $
and
 $I^{\prime }_\infty $
are nilpotent ideals. We write
$I^{\prime }_\infty $
are nilpotent ideals. We write
 $\overline {I}_\infty $
and
$\overline {I}_\infty $
and
 $\overline {I}^{\prime }_\infty $
for the image of these ideals in
$\overline {I}^{\prime }_\infty $
for the image of these ideals in
 $\overline {T}_\infty $
. These maps fit into a commutative diagram
$\overline {T}_\infty $
. These maps fit into a commutative diagram 
-
5. An isomorphism
 $R_\infty /\varpi \cong R^{\prime }_\infty /\varpi $
compatible with the
$R_\infty /\varpi \cong R^{\prime }_\infty /\varpi $
compatible with the
 $S_\infty $
-algebra structure and the actions (induced from
$S_\infty $
-algebra structure and the actions (induced from
 $T_\infty $
and
$T_\infty $
and
 $T^{\prime }_\infty $
) on where these cohomology groups are identified using the fixed isomorphism.
$T^{\prime }_\infty $
) on where these cohomology groups are identified using the fixed isomorphism. $$\begin{align*}H^*( C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi)/(\overline{I}_\infty+\overline{I}^{\prime}_\infty) = H^*( C^{\prime}_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi)/(\overline{I}_\infty+\overline{I}^{\prime}_\infty), \end{align*}$$
$$\begin{align*}H^*( C_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi)/(\overline{I}_\infty+\overline{I}^{\prime}_\infty) = H^*( C^{\prime}_\infty \otimes^{\mathbf{L}}_{S_\infty} S_{\infty} / \varpi)/(\overline{I}_\infty+\overline{I}^{\prime}_\infty), \end{align*}$$
-
6. Integers
 $q_0 \in {\mathbb Z}$
and
$q_0 \in {\mathbb Z}$
and
 $l_0 \in {\mathbb Z}_{\geq 0}$
such that and these groups are nonzero only for degrees in the interval
$l_0 \in {\mathbb Z}_{\geq 0}$
such that and these groups are nonzero only for degrees in the interval $$\begin{align*}H^\ast(X_K,E)_{\mathfrak{m}}\neq 0, \end{align*}$$
$$\begin{align*}H^\ast(X_K,E)_{\mathfrak{m}}\neq 0, \end{align*}$$
 $[q_0,q_0+l_0]$
. Moreover,
$[q_0,q_0+l_0]$
. Moreover,
 $\dim R_\infty =\dim R^{\prime }_\infty =\dim S_\infty -l_0$
.
$\dim R_\infty =\dim R^{\prime }_\infty =\dim S_\infty -l_0$
.
With that out of the way, we let
![]() $x \in \operatorname {\mathrm {Spec}} R_\infty $
be the automorphic point coming from
$x \in \operatorname {\mathrm {Spec}} R_\infty $
be the automorphic point coming from
![]() $\ker (f_1)$
. By the first part of [Reference Caraiani and NewtonCN23, Proposition 5.4.2], there is an irreducible component
$\ker (f_1)$
. By the first part of [Reference Caraiani and NewtonCN23, Proposition 5.4.2], there is an irreducible component
![]() $C_a$
of
$C_a$
of
![]() $\operatorname {\mathrm {Spec}} R_\infty $
, containing x, with
$\operatorname {\mathrm {Spec}} R_\infty $
, containing x, with
![]() $C_a \subset \operatorname {\mathrm {Spec}} T_\infty $
. Let C be any irreducible component of
$C_a \subset \operatorname {\mathrm {Spec}} T_\infty $
. Let C be any irreducible component of
![]() $\operatorname {\mathrm {Spec}} R_\infty $
containing
$\operatorname {\mathrm {Spec}} R_\infty $
containing
![]() $\ker (f_2)$
. Since
$\ker (f_2)$
. Since
![]() $\rho _1|_{G_{F_v}} \sim \rho _2|_{G_{F_v}}$
for each
$\rho _1|_{G_{F_v}} \sim \rho _2|_{G_{F_v}}$
for each
![]() $v \in S_p$
, C and
$v \in S_p$
, C and
![]() $C_a$
map to the same irreducible component of
$C_a$
map to the same irreducible component of
![]() $\operatorname {\mathrm {Spec}} R_{{\mathcal S}_1}^{S_p,\operatorname {loc}}$
(we are using part (4) of Lemma 3.2.4 here, which says that each characteristic
$\operatorname {\mathrm {Spec}} R_{{\mathcal S}_1}^{S_p,\operatorname {loc}}$
(we are using part (4) of Lemma 3.2.4 here, which says that each characteristic
![]() $0$
point lies in a unique irreducible component of
$0$
point lies in a unique irreducible component of
![]() $R_{{\mathcal S}_1}^{S_p,\operatorname {loc}}$
). By Lemma 3.2.4, the generic points of
$R_{{\mathcal S}_1}^{S_p,\operatorname {loc}}$
). By Lemma 3.2.4, the generic points of
![]() $C \cap \operatorname {\mathrm {Spec}} R_\infty /\varpi $
and
$C \cap \operatorname {\mathrm {Spec}} R_\infty /\varpi $
and
![]() $C_a \cap \operatorname {\mathrm {Spec}} R_\infty /\varpi $
all generalize to the same irreducible component of
$C_a \cap \operatorname {\mathrm {Spec}} R_\infty /\varpi $
all generalize to the same irreducible component of
![]() $\operatorname {\mathrm {Spec}} R_\infty '$
. We can apply the second part of [Reference Caraiani and NewtonCN23, Proposition 5.4.2] to deduce that
$\operatorname {\mathrm {Spec}} R_\infty '$
. We can apply the second part of [Reference Caraiani and NewtonCN23, Proposition 5.4.2] to deduce that
![]() $C \subset \operatorname {\mathrm {Spec}} {\mathbb T}_\infty $
, and therefore,
$C \subset \operatorname {\mathrm {Spec}} {\mathbb T}_\infty $
, and therefore,
![]() $\ker (f_2)$
is in the support of
$\ker (f_2)$
is in the support of
![]() $H^*(C_\infty )$
. It follows as in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Corollary 6.3.9] (see also [Reference Caraiani and NewtonCN23, Corollary 5.4.3]) that
$H^*(C_\infty )$
. It follows as in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Corollary 6.3.9] (see also [Reference Caraiani and NewtonCN23, Corollary 5.4.3]) that
![]() $\ker (f_2)$
is in the support of
$\ker (f_2)$
is in the support of
![]() $H^\ast (X_K,{\mathcal O})_{\mathfrak {m}}$
, as desired.
$H^\ast (X_K,{\mathcal O})_{\mathfrak {m}}$
, as desired.
Proof of Theorem 3.2.1.
This is immediate from Theorem 3.2.5 via a standard base change argument identical to the one found in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §6.5.12].
4 The Dwork family
4.1 Definitions
We begin by introducing the Dwork motives we need to consider. For our purposes, we need to consider the non-self-dual motives (with coefficients) studied in [Reference QianQia21, Reference QianQia23] rather than the self-dual (generalized) symplectic motives previously considered in [Reference Harris, Shepherd-Barron and TaylorHSBT10, Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11].
Let
![]() $n> 2$
and
$n> 2$
and
![]() $N> 100 n + 100$
be integers, with N odd and
$N> 100 n + 100$
be integers, with N odd and
![]() $(N, n) = 1$
. Let
$(N, n) = 1$
. Let
![]() $\zeta _N \in \overline {{\mathbb Q}}$
be a primitive
$\zeta _N \in \overline {{\mathbb Q}}$
be a primitive
![]() $N^{\text {th}}$
root of unity. Let
$N^{\text {th}}$
root of unity. Let
![]() $R_0 = {\mathbb Z}[\zeta _N, N^{-1}]$
,
$R_0 = {\mathbb Z}[\zeta _N, N^{-1}]$
,
![]() $T_0 = \operatorname {\mathrm {Spec}} R_0[ t, (1-t^N)^{-1}]$
, and let
$T_0 = \operatorname {\mathrm {Spec}} R_0[ t, (1-t^N)^{-1}]$
, and let
![]() $Z \subset \mathbf {P}^{N-1}_{T_0}$
be the family of smooth hypersurfaces of degree N and dimension
$Z \subset \mathbf {P}^{N-1}_{T_0}$
be the family of smooth hypersurfaces of degree N and dimension
![]() $N - 2$
defined by the equation
$N - 2$
defined by the equation
We write
![]() $\pi : Z \to T_0$
for the natural projection. Let
$\pi : Z \to T_0$
for the natural projection. Let
![]() $\mu _N$
denote the group of
$\mu _N$
denote the group of
![]() $N^{\text {th}}$
roots of unity in
$N^{\text {th}}$
roots of unity in
![]() ${\mathbb Z}[\zeta _N]^\times $
. Then the group
${\mathbb Z}[\zeta _N]^\times $
. Then the group
![]() $H = \mu _N^N / \Delta (\mu _N)$
acts on
$H = \mu _N^N / \Delta (\mu _N)$
acts on
![]() $ \mathbf {P}^{N-1}$
by multiplication of coordinates, and the subgroup
$ \mathbf {P}^{N-1}$
by multiplication of coordinates, and the subgroup
preserves Z. The action of
![]() $H_0$
extends to an action of H on the central fibre
$H_0$
extends to an action of H on the central fibre
![]() $Z_0$
(which is a Fermat hypersurface).
$Z_0$
(which is a Fermat hypersurface).
Let
![]() $M = {\mathbb Q}(e^{2 \pi i / N}) \subset {\mathbb C}$
, and set
$M = {\mathbb Q}(e^{2 \pi i / N}) \subset {\mathbb C}$
, and set
A choice of embedding
![]() $\tau : {\mathbb Q}(\zeta _N) \to {\mathbb C}$
determines an isomorphism
$\tau : {\mathbb Q}(\zeta _N) \to {\mathbb C}$
determines an isomorphism
but we do not fix a preferred choice. We do choose a character
![]() $\underline {\chi } \in (\chi _1, \dots , \chi _N) \in X$
with the following properties:
$\underline {\chi } \in (\chi _1, \dots , \chi _N) \in X$
with the following properties:
-
• The trivial character of
 $\mu _N$
occurs
$\mu _N$
occurs
 $n+1$
times among
$n+1$
times among
 $\chi _1, \dots , \chi _N$
, and each other character appears at most once.
$\chi _1, \dots , \chi _N$
, and each other character appears at most once. -
• Let
 $\rho _1, \dots , \rho _n$
be the n distinct nontrivial characters
$\rho _1, \dots , \rho _n$
be the n distinct nontrivial characters
 $\mu _N \to M^\times $
which do not appear in
$\mu _N \to M^\times $
which do not appear in
 $\chi _1, \dots , \chi _N$
. Then the stabilizer of the set
$\chi _1, \dots , \chi _N$
. Then the stabilizer of the set
 $\{ \rho _1, \dots , \rho _n \}$
in
$\{ \rho _1, \dots , \rho _n \}$
in
 $\operatorname {\mathrm {Gal}}(M / {\mathbb Q})$
is trivial.
$\operatorname {\mathrm {Gal}}(M / {\mathbb Q})$
is trivial.
The existence of such
![]() $\underline {\chi }$
is established in [Reference QianQia23, Lem. 3.1] as a consequence of the assumption
$\underline {\chi }$
is established in [Reference QianQia23, Lem. 3.1] as a consequence of the assumption
![]() $N> 100 n + 100$
. The precise choice is not important.
$N> 100 n + 100$
. The precise choice is not important.
For any place
![]() $\lambda $
of M of characteristic l, we define
$\lambda $
of M of characteristic l, we define
![]() ${\mathcal V}_\lambda = (\pi [1/l]_\ast {\mathcal O}_{M_\lambda })^{H_0 = \underline {\chi }|_{H_0}}$
. It is a lisse sheaf of finite free
${\mathcal V}_\lambda = (\pi [1/l]_\ast {\mathcal O}_{M_\lambda })^{H_0 = \underline {\chi }|_{H_0}}$
. It is a lisse sheaf of finite free
![]() ${\mathcal O}_{M_\lambda }$
-modules on
${\mathcal O}_{M_\lambda }$
-modules on
![]() $T_0[1/l]$
. If k is a perfect field which is an
$T_0[1/l]$
. If k is a perfect field which is an
![]() $R_0[1/l]$
-algebra, and
$R_0[1/l]$
-algebra, and
![]() $t \in T_0(k)$
, then we write
$t \in T_0(k)$
, then we write
![]() $V_{t, \lambda } = {\mathcal V}_{\lambda , \overline {t}}$
for the stalk at a geometric point lying above t; it is an
$V_{t, \lambda } = {\mathcal V}_{\lambda , \overline {t}}$
for the stalk at a geometric point lying above t; it is an
![]() ${\mathcal O}_{M_\lambda }[G_k]$
-module, finite free as
${\mathcal O}_{M_\lambda }[G_k]$
-module, finite free as
![]() ${\mathcal O}_{M_\lambda }$
-module.
${\mathcal O}_{M_\lambda }$
-module.
Katz [Reference KatzKat90, Reference KatzKat09] defines hypergeometric sheaves on
![]() $T_1 = \operatorname {\mathrm {Spec}} R_0[t, t^{-1}, (1-t)^{-1}]$
. We give the definition just in the case of interest. Let
$T_1 = \operatorname {\mathrm {Spec}} R_0[t, t^{-1}, (1-t)^{-1}]$
. We give the definition just in the case of interest. Let
![]() $j : T_1 \to \mathbf {G}_{m, R_0}$
be the natural open immersion, and let
$j : T_1 \to \mathbf {G}_{m, R_0}$
be the natural open immersion, and let
![]() $f : T_1 \to \mathbf {G}_{m, R_0}$
be the map induced by
$f : T_1 \to \mathbf {G}_{m, R_0}$
be the map induced by
![]() $t \mapsto 1-t$
. Fixing again a place
$t \mapsto 1-t$
. Fixing again a place
![]() $\lambda $
of M of characteristic l, let
$\lambda $
of M of characteristic l, let
![]() ${\mathcal L}_i$
denote the rank 1 lisse
${\mathcal L}_i$
denote the rank 1 lisse
![]() $M_\lambda $
-sheaf on
$M_\lambda $
-sheaf on
![]() $\mathbf {G}_{m, R_0}[1/l]$
associated to
$\mathbf {G}_{m, R_0}[1/l]$
associated to
![]() $\rho _i$
and the
$\rho _i$
and the
![]() $\mu _N$
-torsor
$\mu _N$
-torsor
![]() ${\mathbb G}_m\xrightarrow {(\cdot )^N}{\mathbb G}_m$
, and let
${\mathbb G}_m\xrightarrow {(\cdot )^N}{\mathbb G}_m$
, and let
![]() $\mathcal {F}_i = j[1/l]_! f[1/l]^\ast {\mathcal L}_i$
. We set
$\mathcal {F}_i = j[1/l]_! f[1/l]^\ast {\mathcal L}_i$
. We set
where
![]() $\ast _!$
denotes multiplicative convolution with compact support.
$\ast _!$
denotes multiplicative convolution with compact support.
4.2 Basic properties and good ordinary points
Associated to specializations of
![]() ${\mathcal E}_\lambda $
are compatible systems of Galois representations. In this section, we establish some of their basic properties. Most importantly, we prove (in Proposition 4.2.6) the existence of many specializations which have crystalline ordinary reduction. (In [Reference QianQia21], Qian proves that specializations sufficiently close to
${\mathcal E}_\lambda $
are compatible systems of Galois representations. In this section, we establish some of their basic properties. Most importantly, we prove (in Proposition 4.2.6) the existence of many specializations which have crystalline ordinary reduction. (In [Reference QianQia21], Qian proves that specializations sufficiently close to
![]() $t = \infty $
are semistable ordinary, but that is not sufficient for our purposes where we need to work with crystalline representations.)
$t = \infty $
are semistable ordinary, but that is not sufficient for our purposes where we need to work with crystalline representations.)
Theorem 4.2.1.
-
1.
 ${\mathcal E}_\lambda $
is a lisse
${\mathcal E}_\lambda $
is a lisse
 $M_\lambda $
-sheaf on
$M_\lambda $
-sheaf on
 $T_1[1/l]$
of rank n. The sheaf
$T_1[1/l]$
of rank n. The sheaf
 ${\mathcal E}_\lambda \otimes _{M_\lambda } \overline {M}_\lambda $
is geometrically irreducible. Moreover,
${\mathcal E}_\lambda \otimes _{M_\lambda } \overline {M}_\lambda $
is geometrically irreducible. Moreover,
 ${\mathcal E}_\lambda $
is pure of weight
${\mathcal E}_\lambda $
is pure of weight
 $n-1$
, and there is an isomorphism
$n-1$
, and there is an isomorphism
 $\det {\mathcal E}_\lambda \cong M_\lambda (n(1-n)/2)$
.
$\det {\mathcal E}_\lambda \cong M_\lambda (n(1-n)/2)$
. -
2. Let k be an
 $R_0[1/l]$
-algebra which is a finite field of cardinality q, and let
$R_0[1/l]$
-algebra which is a finite field of cardinality q, and let
 $x \in T_1(k)$
. Then we have (4.2.2)where we identify
$x \in T_1(k)$
. Then we have (4.2.2)where we identify $$ \begin{align} \mathrm{tr}( \mathrm{Frob}_k \mid {\mathcal E}_{\lambda, \overline{x}} ) = (-1)^{n-1} \sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n \rho_i( ( 1-x_i )^{(q-1)/N} ), \end{align} $$
$$ \begin{align} \mathrm{tr}( \mathrm{Frob}_k \mid {\mathcal E}_{\lambda, \overline{x}} ) = (-1)^{n-1} \sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n \rho_i( ( 1-x_i )^{(q-1)/N} ), \end{align} $$
 $\mu _N = k^\times [N]$
and extend
$\mu _N = k^\times [N]$
and extend
 $\rho _i$
by
$\rho _i$
by
 $\rho _i(0) = 0$
.
$\rho _i(0) = 0$
.
-
3. There exists a (unique) continuous character
with the following property: let $$ \begin{align*}\Psi_\lambda : \pi_1(\operatorname{\mathrm{Spec}} R_0[1/l]) \to {\mathcal O}_{M_\lambda}^\times\end{align*} $$
$$ \begin{align*}\Psi_\lambda : \pi_1(\operatorname{\mathrm{Spec}} R_0[1/l]) \to {\mathcal O}_{M_\lambda}^\times\end{align*} $$
 $T_0' = T_0[1/t]$
, let
$T_0' = T_0[1/t]$
, let
 $j' : T_0' \to T_0$
be the natural open immersion, and let
$j' : T_0' \to T_0$
be the natural open immersion, and let
 $g : T_0' \to T_1$
be the map induced by
$g : T_0' \to T_1$
be the map induced by
 $t \mapsto t^{-N}$
. Then there is an isomorphism of
$t \mapsto t^{-N}$
. Then there is an isomorphism of
 $M_\lambda $
-sheaves on
$M_\lambda $
-sheaves on
 $T_0'[1/l]$
: (4.2.3)
$T_0'[1/l]$
: (4.2.3) $$ \begin{align} (j'[1/l])^\ast {\mathcal V}_\lambda \otimes_{{\mathcal O}_{M_\lambda}} M_\lambda \cong g^\ast {\mathcal E}_\lambda \otimes_{M_\lambda} M_\lambda(\Psi_\lambda). \end{align} $$
$$ \begin{align} (j'[1/l])^\ast {\mathcal V}_\lambda \otimes_{{\mathcal O}_{M_\lambda}} M_\lambda \cong g^\ast {\mathcal E}_\lambda \otimes_{M_\lambda} M_\lambda(\Psi_\lambda). \end{align} $$
Proof. The construction and properties of
![]() ${\mathcal E}_\lambda $
are summarized in [Reference KatzKat09] (where it is the sheaf denoted
${\mathcal E}_\lambda $
are summarized in [Reference KatzKat09] (where it is the sheaf denoted
![]() $\mathcal {H}^{can}( \mathbf {1} (n \text { times}), \{ \rho _i \})$
) and given in detail in [Reference KatzKat90, Ch. 8]. See also [Reference Drinfeld and KedlayaDK17, §A.1.6]. The computation of the determinant follows from [Reference KatzKat90, Theorem 8.12.2(1a)], noting that
$\mathcal {H}^{can}( \mathbf {1} (n \text { times}), \{ \rho _i \})$
) and given in detail in [Reference KatzKat90, Ch. 8]. See also [Reference Drinfeld and KedlayaDK17, §A.1.6]. The computation of the determinant follows from [Reference KatzKat90, Theorem 8.12.2(1a)], noting that
![]() $\prod _{i=1}^n \rho _i = \mathbf {1}$
. Property (2) follows from the definition. The existence of
$\prod _{i=1}^n \rho _i = \mathbf {1}$
. Property (2) follows from the definition. The existence of
![]() $\Psi _\lambda $
as in (3) follows from [Reference KatzKat09, Theorem 5.3] (we have also used the relation
$\Psi _\lambda $
as in (3) follows from [Reference KatzKat09, Theorem 5.3] (we have also used the relation
![]() $[-1]^\ast \mathcal {H}^{can}( \mathbf {1} (n \text { times}), \{ \rho _i \}) \cong \mathcal {H}^{can}( \{ \rho ^{-1}_i \}, \mathbf {1} (n \text { times}))$
). The uniqueness follows from geometric irreducibility and Schur’s lemma.
$[-1]^\ast \mathcal {H}^{can}( \mathbf {1} (n \text { times}), \{ \rho _i \}) \cong \mathcal {H}^{can}( \{ \rho ^{-1}_i \}, \mathbf {1} (n \text { times}))$
). The uniqueness follows from geometric irreducibility and Schur’s lemma.
Lemma 4.2.4. There exists a Hecke character
![]() $\Psi : {\mathbb Q}(\zeta _N)^\times \backslash \mathbf {A}_{{\mathbb Q}(\zeta _N)}^\times \to {\mathbb C}^\times $
of type
$\Psi : {\mathbb Q}(\zeta _N)^\times \backslash \mathbf {A}_{{\mathbb Q}(\zeta _N)}^\times \to {\mathbb C}^\times $
of type
![]() $A_0$
, unramified away from N, and with field of definition contained inside M, such that
$A_0$
, unramified away from N, and with field of definition contained inside M, such that
![]() $\Psi _\lambda $
is associated to
$\Psi _\lambda $
is associated to
![]() $\Psi $
. In other words,
$\Psi $
. In other words,
![]() $\Psi _\lambda $
is ‘independent of
$\Psi _\lambda $
is ‘independent of
![]() $\lambda $
’. Moreover,
$\lambda $
’. Moreover,
![]() $\Psi $
is defined over M, and we have
$\Psi $
is defined over M, and we have
![]() $\Psi c(\Psi ) = | \cdot |^{N-n}$
.
$\Psi c(\Psi ) = | \cdot |^{N-n}$
.
Proof. We may argue as in [Reference KatzKat09, Question 5.5] to see that almost all Frobenius traces of
![]() $\Psi _\lambda $
lie in M and are independent of
$\Psi _\lambda $
lie in M and are independent of
![]() $\lambda $
. The existence of the character
$\lambda $
. The existence of the character
![]() $\Psi $
, of type
$\Psi $
, of type
![]() $A_0$
, follows from the main result of [Reference HenniartHen82]. There are c-linear isomorphisms
$A_0$
, follows from the main result of [Reference HenniartHen82]. There are c-linear isomorphisms
![]() ${\mathcal V}_{c(\lambda )} \cong {\mathcal V}_\lambda ^\vee (1-N)$
and
${\mathcal V}_{c(\lambda )} \cong {\mathcal V}_\lambda ^\vee (1-N)$
and
![]() ${\mathcal E}_{c(\lambda )} \cong {\mathcal E}_\lambda ^\vee (1-n)$
, so the final part is again a consequence of Schur’s lemma.
${\mathcal E}_{c(\lambda )} \cong {\mathcal E}_\lambda ^\vee (1-n)$
, so the final part is again a consequence of Schur’s lemma.
For any place
![]() $\lambda $
of M of characteristic l, we define
$\lambda $
of M of characteristic l, we define
![]() ${\mathcal W}_\lambda = {\mathcal V}_\lambda \otimes _{{\mathcal O}_{M_\lambda }} {\mathcal O}_{M_\lambda }(\Psi _\lambda ^{-1})$
, a lisse sheaf of finite free
${\mathcal W}_\lambda = {\mathcal V}_\lambda \otimes _{{\mathcal O}_{M_\lambda }} {\mathcal O}_{M_\lambda }(\Psi _\lambda ^{-1})$
, a lisse sheaf of finite free
![]() ${\mathcal O}_{M_\lambda }$
-modules on
${\mathcal O}_{M_\lambda }$
-modules on
![]() $T_0[1/l]$
. Thus,
$T_0[1/l]$
. Thus,
![]() ${\mathcal W}_\lambda \otimes _{{\mathcal O}_{M_\lambda }} M_\lambda $
is a lisse
${\mathcal W}_\lambda \otimes _{{\mathcal O}_{M_\lambda }} M_\lambda $
is a lisse
![]() $M_\lambda $
-sheaf of rank n which is pure of weight
$M_\lambda $
-sheaf of rank n which is pure of weight
![]() $n-1$
, geometrically irreducible, and of determinant
$n-1$
, geometrically irreducible, and of determinant
![]() $M_\lambda (n(1-n)/2)$
. If k is a perfect field which is an
$M_\lambda (n(1-n)/2)$
. If k is a perfect field which is an
![]() $R_0[1/l]$
-algebra, and
$R_0[1/l]$
-algebra, and
![]() $t \in T_0(k)$
, then we write
$t \in T_0(k)$
, then we write
![]() $W_{t, \lambda } = {\mathcal W}_{\lambda , \overline {t}}$
for the stalk at a geometric point lying above t; it is an
$W_{t, \lambda } = {\mathcal W}_{\lambda , \overline {t}}$
for the stalk at a geometric point lying above t; it is an
![]() ${\mathcal O}_{M_\lambda }[G_k]$
-module, finite free as
${\mathcal O}_{M_\lambda }[G_k]$
-module, finite free as
![]() ${\mathcal O}_{M_\lambda }$
-module. The local systems
${\mathcal O}_{M_\lambda }$
-module. The local systems
![]() ${\mathcal W}_\lambda $
are the ones we will use in building the moduli spaces used in the Moret-Bailly argument in §6.2. In particular, let us write
${\mathcal W}_\lambda $
are the ones we will use in building the moduli spaces used in the Moret-Bailly argument in §6.2. In particular, let us write
![]() $\overline {{\mathcal W}}_\lambda = {\mathcal W}_\lambda \otimes _{{\mathcal O}_{M_\lambda }} k(\lambda )$
and define
$\overline {{\mathcal W}}_\lambda = {\mathcal W}_\lambda \otimes _{{\mathcal O}_{M_\lambda }} k(\lambda )$
and define
![]() $\overline {W}_{t, \lambda }$
similarly.
$\overline {W}_{t, \lambda }$
similarly.
Proposition 4.2.5. Let
![]() $F / {\mathbb Q}(\zeta _N)$
be a number field.
$F / {\mathbb Q}(\zeta _N)$
be a number field.
-
1. Let v be a finite place of F of characteristic l, and let
 $\lambda $
be a place of M of characteristic not equal to l. If
$\lambda $
be a place of M of characteristic not equal to l. If
 $l \nmid N$
and
$l \nmid N$
and
 $t \in T_0({\mathcal O}_{F_v})$
, then
$t \in T_0({\mathcal O}_{F_v})$
, then
 $W_{t, \lambda }$
is unramified, and the polynomial
$W_{t, \lambda }$
is unramified, and the polynomial
 $Q_v(X) = \det (X - \mathrm {Frob}_v \mid W_{t, \lambda })$
has coefficients in
$Q_v(X) = \det (X - \mathrm {Frob}_v \mid W_{t, \lambda })$
has coefficients in
 ${\mathcal O}_M[X]$
and is independent of
${\mathcal O}_M[X]$
and is independent of
 $\lambda $
.
$\lambda $
. -
2. Let v be a finite place of F of characteristic l, and let
 $\lambda $
be a place of M of the same characteristic. Let
$\lambda $
be a place of M of the same characteristic. Let
 $t \in T_0(F_v)$
. Then
$t \in T_0(F_v)$
. Then
 $W_{t, \lambda }$
is de Rham, and for any embedding
$W_{t, \lambda }$
is de Rham, and for any embedding
 $\tau : F_v \to \overline {M}_\lambda $
, we have
$\tau : F_v \to \overline {M}_\lambda $
, we have
 $\mathrm {HT}_\tau (W_{t, \lambda }) = \{ 0, 1, \dots , n-1 \}$
. If
$\mathrm {HT}_\tau (W_{t, \lambda }) = \{ 0, 1, \dots , n-1 \}$
. If
 $l \nmid N$
and
$l \nmid N$
and
 $t \in T_0({\mathcal O}_{F_v})$
, then
$t \in T_0({\mathcal O}_{F_v})$
, then
 $W_{t, \lambda }$
is crystalline and the characteristic polynomial of
$W_{t, \lambda }$
is crystalline and the characteristic polynomial of
 $\mathrm {Frob}_v$
on
$\mathrm {Frob}_v$
on
 $\mathrm {WD}(W_{t, \lambda })$
equals
$\mathrm {WD}(W_{t, \lambda })$
equals
 $Q_v(X)$
. In particular,
$Q_v(X)$
. In particular,
 $W_{t, \lambda }$
is ordinary if and only if the roots of
$W_{t, \lambda }$
is ordinary if and only if the roots of
 $Q_v(X)$
in
$Q_v(X)$
in
 $\overline {M}_\lambda $
have l-adic valuations
$\overline {M}_\lambda $
have l-adic valuations
 $0, [k(v) : {\mathbb F}_l], \dots , (n-1) [k(v) : {\mathbb F}_l]$
.
$0, [k(v) : {\mathbb F}_l], \dots , (n-1) [k(v) : {\mathbb F}_l]$
. -
3. Let
 $t \in T_0(F)$
, and let S be the set of finite places v of F such that either
$t \in T_0(F)$
, and let S be the set of finite places v of F such that either
 $v | N$
, or
$v | N$
, or
 $v \nmid N$
and
$v \nmid N$
and
 $t \not \in T_0({\mathcal O}_{F_v}) \subset T_0(F_v)$
. Then is a weakly compatible system of l-adic representations of
$t \not \in T_0({\mathcal O}_{F_v}) \subset T_0(F_v)$
. Then is a weakly compatible system of l-adic representations of $$\begin{align*}( M, S, \{ Q_v(X) \}_{v \not \in S}, \{ W_{t, \lambda}^{ss} \}_\lambda, \{ \{0, 1, \dots, n-1\}\}_\tau ) \end{align*}$$
$$\begin{align*}( M, S, \{ Q_v(X) \}_{v \not \in S}, \{ W_{t, \lambda}^{ss} \}_\lambda, \{ \{0, 1, \dots, n-1\}\}_\tau ) \end{align*}$$
 $G_F$
over M of rank n, pure of weight
$G_F$
over M of rank n, pure of weight
 $n-1$
, in the sense of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, §5.1].
$n-1$
, in the sense of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, §5.1].
Proof. For the first part, we note that
![]() $Z_t$
is smooth and proper over
$Z_t$
is smooth and proper over
![]() ${\mathcal O}_{F_v}$
, so by smooth proper base change,
${\mathcal O}_{F_v}$
, so by smooth proper base change,
![]() $H^\ast _{\acute{\rm e}\text {t}}(\overline {Z}_{t, F_v}, {\mathcal O}_{M_\lambda })$
is unramified and there is an isomorphism
$H^\ast _{\acute{\rm e}\text {t}}(\overline {Z}_{t, F_v}, {\mathcal O}_{M_\lambda })$
is unramified and there is an isomorphism
where
![]() $\overline {t}$
denotes the image of t in
$\overline {t}$
denotes the image of t in
![]() $T_0(k(v))$
. [Reference Katz and MessingKM74, Theorem 2(2)] shows that for any
$T_0(k(v))$
. [Reference Katz and MessingKM74, Theorem 2(2)] shows that for any
![]() $h \in H$
, the characteristic polynomial of
$h \in H$
, the characteristic polynomial of
![]() $h \cdot \mathrm {Frob}_v$
on this group has coefficients in
$h \cdot \mathrm {Frob}_v$
on this group has coefficients in
![]() ${\mathcal O}_M$
and is independent of the choice of
${\mathcal O}_M$
and is independent of the choice of
![]() $\lambda \nmid l$
, and this implies that
$\lambda \nmid l$
, and this implies that
![]() $Q_v(X)$
also has coefficients in
$Q_v(X)$
also has coefficients in
![]() ${\mathcal O}_M[X]$
and is independent of
${\mathcal O}_M[X]$
and is independent of
![]() $\lambda $
.
$\lambda $
.
For the second part, note that
![]() $W_{t, \lambda }$
is de Rham because it is a subquotient of
$W_{t, \lambda }$
is de Rham because it is a subquotient of
![]() $H_{\acute{\rm e}\text {t}}^{N-2}(Z_t, M_\lambda ) \otimes M_\lambda (\Psi _\lambda ^{-1})$
, which is de Rham. To compute the Hodge–Tate weights, we use [Reference QianQia23, Lemma 3.10], which implies that there is an integer
$H_{\acute{\rm e}\text {t}}^{N-2}(Z_t, M_\lambda ) \otimes M_\lambda (\Psi _\lambda ^{-1})$
, which is de Rham. To compute the Hodge–Tate weights, we use [Reference QianQia23, Lemma 3.10], which implies that there is an integer
![]() $M_\tau $
such that
$M_\tau $
such that
![]() $\mathrm {HT}_\tau (V_{t, \lambda }) = \{ M_\tau , M_\tau + 1, \dots , M_\tau + (n-1) \}$
. Since
$\mathrm {HT}_\tau (V_{t, \lambda }) = \{ M_\tau , M_\tau + 1, \dots , M_\tau + (n-1) \}$
. Since
![]() $W_{t, \lambda }$
is a twist of
$W_{t, \lambda }$
is a twist of
![]() $V_{t, \lambda }$
, there is an integer
$V_{t, \lambda }$
, there is an integer
![]() $M^{\prime }_\tau $
such that
$M^{\prime }_\tau $
such that
![]() $\mathrm {HT}_\tau (W_{t, \lambda }) = \{ M^{\prime }_\tau , M^{\prime }_\tau + 1, \dots , M^{\prime }_\tau + (n-1) \}$
. Looking at determinants shows that
$\mathrm {HT}_\tau (W_{t, \lambda }) = \{ M^{\prime }_\tau , M^{\prime }_\tau + 1, \dots , M^{\prime }_\tau + (n-1) \}$
. Looking at determinants shows that
![]() $n M^{\prime }_\tau + n(n-1)/2 = n(n-1)/2$
; hence,
$n M^{\prime }_\tau + n(n-1)/2 = n(n-1)/2$
; hence,
![]() $M^{\prime }_\tau = 0$
.
$M^{\prime }_\tau = 0$
.
If further
![]() $l \nmid N$
and
$l \nmid N$
and
![]() $t \in T_0({\mathcal O}_{F_v})$
, then again
$t \in T_0({\mathcal O}_{F_v})$
, then again
![]() $Z_t$
is smooth and proper, so
$Z_t$
is smooth and proper, so
![]() $H_{\acute{\rm e}\text {t}}^{N-2}(Z_t, M_\lambda )$
is crystalline, and also
$H_{\acute{\rm e}\text {t}}^{N-2}(Z_t, M_\lambda )$
is crystalline, and also
![]() $M_\lambda (\Psi _\lambda ^{-1})$
is crystalline; hence,
$M_\lambda (\Psi _\lambda ^{-1})$
is crystalline; hence,
![]() $W_{t, \lambda }$
is crystalline. The crystalline comparison theorem implies that there is an isomorphism
$W_{t, \lambda }$
is crystalline. The crystalline comparison theorem implies that there is an isomorphism
respecting the action of Frobenius
![]() $\phi _v$
and
$\phi _v$
and
![]() $H_0$
on each side. Here,
$H_0$
on each side. Here,
![]() $F_{v, 0}$
denotes the maximal absolutely unramified subfield of
$F_{v, 0}$
denotes the maximal absolutely unramified subfield of
![]() $F_v$
. Choosing an embedding
$F_v$
. Choosing an embedding
![]() $\sigma _0 : F_{v, 0} \to \overline {M}_\lambda $
, there is an isomorphism
$\sigma _0 : F_{v, 0} \to \overline {M}_\lambda $
, there is an isomorphism
equivariant for the
![]() $\overline {M}_\lambda $
-linear action of
$\overline {M}_\lambda $
-linear action of
![]() $\phi _v^{[k(v) : {\mathbb F}_l]}$
. By definition,
$\phi _v^{[k(v) : {\mathbb F}_l]}$
. By definition,
![]() $\mathrm {WD}(W_{t, \lambda })$
is the unramified representation of
$\mathrm {WD}(W_{t, \lambda })$
is the unramified representation of
![]() $W_{F_v}$
over
$W_{F_v}$
over
![]() $\overline {M}_\lambda $
afforded by the
$\overline {M}_\lambda $
afforded by the
![]() $\Psi _\lambda ^{-1}$
-twist of the
$\Psi _\lambda ^{-1}$
-twist of the
![]() $\underline {\chi }|_{H_0}$
-isotypic subspace of the left-hand side. We therefore need to check that the characteristic polynomial of
$\underline {\chi }|_{H_0}$
-isotypic subspace of the left-hand side. We therefore need to check that the characteristic polynomial of
![]() $\phi _v^{[k(v) : {\mathbb F}_l]}$
on the
$\phi _v^{[k(v) : {\mathbb F}_l]}$
on the
![]() $\Psi _\lambda ^{-1}$
-twist of the
$\Psi _\lambda ^{-1}$
-twist of the
![]() $\underline {\chi }|_{H_0}$
-isotypic subspace of the right-hand side equals
$\underline {\chi }|_{H_0}$
-isotypic subspace of the right-hand side equals
![]() $Q_v(X)$
. This follows again from [Reference Katz and MessingKM74, Theorem 2(2)] (applicable here by the main result of [Reference Gillet and MessingGM87]). The characterization of ordinary representations follows from [Reference GeraghtyGer19, Lemma 2.32].
$Q_v(X)$
. This follows again from [Reference Katz and MessingKM74, Theorem 2(2)] (applicable here by the main result of [Reference Gillet and MessingGM87]). The characterization of ordinary representations follows from [Reference GeraghtyGer19, Lemma 2.32].
The third part follows from the first two parts and the definition of a weakly compatible system.
We now apply the results of Drinfeld–Kedlaya [Reference Drinfeld and KedlayaDK17] to deduce that the
![]() $W_{t,\lambda }$
are ordinary for generic choices of t.
$W_{t,\lambda }$
are ordinary for generic choices of t.
Proposition 4.2.6. Let v be a place of
![]() ${\mathbb Q}(\zeta _N)$
of characteristic
${\mathbb Q}(\zeta _N)$
of characteristic
![]() $l \nmid N$
, and let
$l \nmid N$
, and let
![]() $\lambda $
be a place of M of the same characteristic. Then there exists a nonempty Zariski open subset
$\lambda $
be a place of M of the same characteristic. Then there exists a nonempty Zariski open subset
![]() $U(v; \lambda ) \subset T_{0, k(v)}$
with the following property: for any finite extension
$U(v; \lambda ) \subset T_{0, k(v)}$
with the following property: for any finite extension
![]() $F_w / {\mathbb Q}(\zeta _N)_v$
and any
$F_w / {\mathbb Q}(\zeta _N)_v$
and any
![]() $t \in T_0({\mathcal O}_{F_w})$
such that
$t \in T_0({\mathcal O}_{F_w})$
such that
![]() $\overline {t} = t \text { mod }(\varpi _w) \in U(v; \lambda )(k(w))$
,
$\overline {t} = t \text { mod }(\varpi _w) \in U(v; \lambda )(k(w))$
,
![]() $W_{t, \lambda }$
is a crystalline ordinary representation of
$W_{t, \lambda }$
is a crystalline ordinary representation of
![]() $G_{F_w}$
.
$G_{F_w}$
.
Proof. Fix an auxiliary place
![]() $\mu $
of M of characteristic not l. If
$\mu $
of M of characteristic not l. If
![]() $k / k(v)$
is a finite extension of cardinality q and
$k / k(v)$
is a finite extension of cardinality q and
![]() $x \in T_0(k)$
, we write
$x \in T_0(k)$
, we write
![]() $Q_x(X) \in {\mathcal O}_M[X]$
for the characteristic polynomial of
$Q_x(X) \in {\mathcal O}_M[X]$
for the characteristic polynomial of
![]() $\mathrm {Frob}_x$
on
$\mathrm {Frob}_x$
on
![]() $W_{x, \mu }$
. Let
$W_{x, \mu }$
. Let
![]() $s_1(x) \geq s_2(x) \geq \dots \geq s_n(x)$
denote
$s_1(x) \geq s_2(x) \geq \dots \geq s_n(x)$
denote
![]() $[k : {\mathbb F}_l]^{-1}$
times the l-adic valuations of the roots of
$[k : {\mathbb F}_l]^{-1}$
times the l-adic valuations of the roots of
![]() $Q_x(X)$
in
$Q_x(X)$
in
![]() $\overline {M}_\lambda $
. Observe that these normalized slopes
$\overline {M}_\lambda $
. Observe that these normalized slopes
![]() $s_i(x)$
do not change if k is replaced by a larger extension (leaving the point x unchanged). By Proposition 4.2.5, it suffices to show the existence of a nonempty Zariski open subset
$s_i(x)$
do not change if k is replaced by a larger extension (leaving the point x unchanged). By Proposition 4.2.5, it suffices to show the existence of a nonempty Zariski open subset
![]() $U \subset T_{0, k(v)}$
such that if
$U \subset T_{0, k(v)}$
such that if
![]() $k / k(v)$
is a finite extension and
$k / k(v)$
is a finite extension and
![]() $x \in U(k)$
, then
$x \in U(k)$
, then
![]() $s_i(x) = n-i$
for each
$s_i(x) = n-i$
for each
![]() $i = 1, \dots , n$
.
$i = 1, \dots , n$
.
By [Reference Drinfeld and KedlayaDK17, Theorem 1.3.3], we can find a nonempty Zariski open subset
![]() $V \subset T_{0, k(v)}$
such that the numbers
$V \subset T_{0, k(v)}$
such that the numbers
![]() $s_i(x)$
are constant for
$s_i(x)$
are constant for
![]() $x \in V(k)$
, and moreover such that
$x \in V(k)$
, and moreover such that
![]() $s_i(x) \leq s_{i+1}(x) + 1$
for each
$s_i(x) \leq s_{i+1}(x) + 1$
for each
![]() $i = 1, \dots , n-1$
. To complete the proof, it suffices to show that there is a nonempty Zariski open subset
$i = 1, \dots , n-1$
. To complete the proof, it suffices to show that there is a nonempty Zariski open subset
![]() $U \subset V$
such that if
$U \subset V$
such that if
![]() $x \in U(k)$
, then
$x \in U(k)$
, then
![]() $s_n(x) = 0$
. Indeed, consideration of determinants shows that
$s_n(x) = 0$
. Indeed, consideration of determinants shows that
![]() $s_1(x) + s_2(x) + \dots + s_n(x) = n(n-1)/2$
for all
$s_1(x) + s_2(x) + \dots + s_n(x) = n(n-1)/2$
for all
![]() $x \in T_0(k)$
. If
$x \in T_0(k)$
. If
![]() $x \in V(k)$
and
$x \in V(k)$
and
![]() $s_n(x) = 0$
, then
$s_n(x) = 0$
, then
![]() $s_i(x) \leq n-i$
for each
$s_i(x) \leq n-i$
for each
![]() $i = 1, \dots , n$
; hence,
$i = 1, \dots , n$
; hence,
![]() $s_1(x) + \dots + s_n(x) \leq n(n-1)/2$
, with equality if and only if
$s_1(x) + \dots + s_n(x) \leq n(n-1)/2$
, with equality if and only if
![]() $s_i(x) = n-i$
for each
$s_i(x) = n-i$
for each
![]() $i = 1, \dots , n$
.
$i = 1, \dots , n$
.
Finally, by (4.2.3), it is enough to show the analogous statement for the pullback of
![]() ${\mathcal E}_\mu $
to
${\mathcal E}_\mu $
to
![]() $T_{1, k(v)}$
. We will prove this by showing that there is a nonempty Zariski open subset
$T_{1, k(v)}$
. We will prove this by showing that there is a nonempty Zariski open subset
![]() $U_1 \subset T_{1, k(v)}$
such that if
$U_1 \subset T_{1, k(v)}$
such that if
![]() $x \in T_{1, k(v)}(k)$
, then
$x \in T_{1, k(v)}(k)$
, then
![]() $\mathrm {tr}( \mathrm {Frob}_x \mid {\mathcal E}_{\mu , \overline {x}}) \not \equiv 0 \text { mod }\lambda $
, or in other words (using (4.2.2)) that
$\mathrm {tr}( \mathrm {Frob}_x \mid {\mathcal E}_{\mu , \overline {x}}) \not \equiv 0 \text { mod }\lambda $
, or in other words (using (4.2.2)) that
 $$\begin{align*}\sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n \rho_i( ( 1-x_i )^{(q-1)/N} ) \not\equiv 0 \text{ mod }\lambda. \end{align*}$$
$$\begin{align*}\sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n \rho_i( ( 1-x_i )^{(q-1)/N} ) \not\equiv 0 \text{ mod }\lambda. \end{align*}$$
We will produce this set
![]() $U_1$
by a computation following [Reference Drinfeld and KedlayaDK17, §A.3]. Let
$U_1$
by a computation following [Reference Drinfeld and KedlayaDK17, §A.3]. Let
![]() $\tau : {\mathbb Q}(\zeta _N) \to M$
be an isomorphism identifying the place v with the place
$\tau : {\mathbb Q}(\zeta _N) \to M$
be an isomorphism identifying the place v with the place
![]() $\lambda $
. The character
$\lambda $
. The character
![]() $k(v)^\times \to k(v)^\times $
,
$k(v)^\times \to k(v)^\times $
,
![]() $z \mapsto \tau ^{-1} \rho _i( z^{(q_v-1)/N} )$
, is given by the formula
$z \mapsto \tau ^{-1} \rho _i( z^{(q_v-1)/N} )$
, is given by the formula
![]() $z \mapsto z^{c_i}$
for some integer
$z \mapsto z^{c_i}$
for some integer
![]() $c_i$
with
$c_i$
with
![]() $1 \leq c_i \leq q_v-2$
. If
$1 \leq c_i \leq q_v-2$
. If
![]() $q = q_v^d$
, then we find that the pre-image under
$q = q_v^d$
, then we find that the pre-image under
![]() $\tau $
of the left-hand side of the displayed equation is given by
$\tau $
of the left-hand side of the displayed equation is given by
 $$\begin{align*}\sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n \mathbf{N}_{k / k(v)} (1 - x_i)^{c_i} = \sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n (1 - x_i)^{\widetilde{c}_i}, \end{align*}$$
$$\begin{align*}\sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n \mathbf{N}_{k / k(v)} (1 - x_i)^{c_i} = \sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \prod_{i=1}^n (1 - x_i)^{\widetilde{c}_i}, \end{align*}$$
where
![]() $\widetilde {c}_i = c_i \cdot (q-1) / (q_v-1) < q - 1$
. This we can in turn compute as
$\widetilde {c}_i = c_i \cdot (q-1) / (q_v-1) < q - 1$
. This we can in turn compute as
 $$ \begin{align*} \sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \sum_{\substack{ 0 \leq r_i \leq \widetilde{c}_i \\ i = 1, \dots, n}} \prod_{i=1}^n \binom{\widetilde{c}_i}{r_i} (-x_i)^{r_i} = \sum_{\substack{ 0 \leq r_i \leq \widetilde{c}_i \\ i = 1, \dots, n}} (-1)^{r_1 + \dots + r_n} \left(\prod_{i=1}^n \binom{\widetilde{c}_i}{r_i}\right) \sum_{x_1, \dots, x_{n-1} \in k^\times} \left( \prod_{i=1}^{n-1} x_i^{r_i - r_n} \right) x^{r_n}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{x_1, \dots, x_n \in k \\ \prod_{i=1}^n x_i = x}} \sum_{\substack{ 0 \leq r_i \leq \widetilde{c}_i \\ i = 1, \dots, n}} \prod_{i=1}^n \binom{\widetilde{c}_i}{r_i} (-x_i)^{r_i} = \sum_{\substack{ 0 \leq r_i \leq \widetilde{c}_i \\ i = 1, \dots, n}} (-1)^{r_1 + \dots + r_n} \left(\prod_{i=1}^n \binom{\widetilde{c}_i}{r_i}\right) \sum_{x_1, \dots, x_{n-1} \in k^\times} \left( \prod_{i=1}^{n-1} x_i^{r_i - r_n} \right) x^{r_n}. \end{align*} $$
We now use that if
![]() $r \in {\mathbb Z}$
and
$r \in {\mathbb Z}$
and
![]() $r \not \equiv 0 \text { mod }(q-1)$
, then
$r \not \equiv 0 \text { mod }(q-1)$
, then
![]() $\sum _{z \in k^\times } z^r = 0$
. This implies that the inner sum vanishes except if
$\sum _{z \in k^\times } z^r = 0$
. This implies that the inner sum vanishes except if
![]() $r_i = r_n$
for each
$r_i = r_n$
for each
![]() $i = 1, \dots , n-1$
. We obtain (noting that there are only finitely many nonzero terms in the sum on the right-hand side)
$i = 1, \dots , n-1$
. We obtain (noting that there are only finitely many nonzero terms in the sum on the right-hand side)
 $$\begin{align*}\sum_{0 \leq r \leq \min(\widetilde{c}_i)} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} (-1)^{n-1} x^r = (-1)^{n-1} \sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} x^r. \end{align*}$$
$$\begin{align*}\sum_{0 \leq r \leq \min(\widetilde{c}_i)} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} (-1)^{n-1} x^r = (-1)^{n-1} \sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} x^r. \end{align*}$$
Define a polynomial
![]() $u(T) \in k(v)[T]$
:
$u(T) \in k(v)[T]$
:
 $$\begin{align*}u(T) = \sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{c_i}{r} T^r. \end{align*}$$
$$\begin{align*}u(T) = \sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{c_i}{r} T^r. \end{align*}$$
We claim that there is an equality
 $$\begin{align*}\sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} x^r = \mathbf{N}_{k / k(v)}( u(x) ). \end{align*}$$
$$\begin{align*}\sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} x^r = \mathbf{N}_{k / k(v)}( u(x) ). \end{align*}$$
This will complete the proof: indeed, it will imply that we can take
![]() $U_1 = T_{1, k(v)}[1/u]$
(noting that u is nonzero since its constant term is 1, so
$U_1 = T_{1, k(v)}[1/u]$
(noting that u is nonzero since its constant term is 1, so
![]() $U_1$
is indeed nonempty, and also u is independent of the field extension
$U_1$
is indeed nonempty, and also u is independent of the field extension
![]() $k/k(v)$
). To show this, we expand
$k/k(v)$
). To show this, we expand
 $$ \begin{align*} \mathbf{N}_{k / k(v)}( u(x) ) &= \left( \sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{c_i}{r} x^r \right)^{1 + q_v + \dots + q_v^{d-1}} \\ &= \sum_{r_0, \dots, r_{d-1} \geq 0} (-1)^{n(r_0 + \dots + r_{d-1} q_v^{d-1})} \prod_{i=1}^n \prod_{j=0}^{d-1} \binom{c_i}{r_j} x^{r_0 + r_1 q_v + \dots + r_d q_v^{d-1}}. \end{align*} $$
$$ \begin{align*} \mathbf{N}_{k / k(v)}( u(x) ) &= \left( \sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{c_i}{r} x^r \right)^{1 + q_v + \dots + q_v^{d-1}} \\ &= \sum_{r_0, \dots, r_{d-1} \geq 0} (-1)^{n(r_0 + \dots + r_{d-1} q_v^{d-1})} \prod_{i=1}^n \prod_{j=0}^{d-1} \binom{c_i}{r_j} x^{r_0 + r_1 q_v + \dots + r_d q_v^{d-1}}. \end{align*} $$
We now observe that a given tuple,
![]() $(r_0, \dots , r_{d-1})$
can contribute a nonzero summand only if
$(r_0, \dots , r_{d-1})$
can contribute a nonzero summand only if
![]() $r_j < q_v-1$
for each j, so each value of
$r_j < q_v-1$
for each j, so each value of
![]() $r = r_0 + r_1 q_v + \dots + r_{d-1} q_v^{d-1}$
is represented at most once. Furthermore, since
$r = r_0 + r_1 q_v + \dots + r_{d-1} q_v^{d-1}$
is represented at most once. Furthermore, since
![]() $(1+X)^{\widetilde {c}_i} = \prod _{j=0}^{d-1} (1+X^{q_v^j})^{c_i}$
in
$(1+X)^{\widetilde {c}_i} = \prod _{j=0}^{d-1} (1+X^{q_v^j})^{c_i}$
in
![]() ${\mathbb F}_l[X]$
, we have in this case a congruence
${\mathbb F}_l[X]$
, we have in this case a congruence
 $$\begin{align*}\binom{\widetilde{c}_i}{r} \equiv \prod_{j=0}^{d-1} \binom{c_i}{r_j} \text{ mod }l, \end{align*}$$
$$\begin{align*}\binom{\widetilde{c}_i}{r} \equiv \prod_{j=0}^{d-1} \binom{c_i}{r_j} \text{ mod }l, \end{align*}$$
showing that
![]() $\mathbf {N}_{k / k(v)}( u(x) )$
indeed equals
$\mathbf {N}_{k / k(v)}( u(x) )$
indeed equals
 $$\begin{align*}\sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} x^r, \end{align*}$$
$$\begin{align*}\sum_{r \geq 0} (-1)^{nr} \prod_{i=1}^n \binom{\widetilde{c}_i}{r} x^r, \end{align*}$$
as desired.
4.3 Basics on unitary groups over finite fields
In order to discuss the possible (residual) images of the Galois representations associated to our Dwork family, we recall here some basic facts about unitary groups over finite fields which will be used in the sequel. (Nothing here is original, but we include it for convenience of exposition.)
Let
![]() $l/k$
be a quadratic extension of finite fields. Let p be a prime and let
$l/k$
be a quadratic extension of finite fields. Let p be a prime and let
![]() $M \in M_n(l)$
. Let
$M \in M_n(l)$
. Let
![]() $M^t$
denote the transpose of M and
$M^t$
denote the transpose of M and
![]() $M^{c}$
the conjugate of M by the generator of
$M^{c}$
the conjugate of M by the generator of
![]() $\operatorname {\mathrm {Gal}}(l/k)$
. We define the adjoint
$\operatorname {\mathrm {Gal}}(l/k)$
. We define the adjoint
![]() $M^{\dagger }$
of M to be
$M^{\dagger }$
of M to be
![]() $M^{\dagger }:= (M^{c})^t = (M^t)^{c}$
. Note that
$M^{\dagger }:= (M^{c})^t = (M^t)^{c}$
. Note that
![]() $(AB)^{\dagger } = B^{\dagger } A^{\dagger }$
. We recall the following:
$(AB)^{\dagger } = B^{\dagger } A^{\dagger }$
. We recall the following:
Definition 4.3.1. The unitary group
![]() $\mathrm {GU}_n(l)$
is the subgroup of matrices
$\mathrm {GU}_n(l)$
is the subgroup of matrices
![]() $M \in \operatorname {\mathrm {GL}}_n(l)$
satisfying
$M \in \operatorname {\mathrm {GL}}_n(l)$
satisfying
![]() $M^{\dagger } M = \lambda \in k^{\times }$
. Let
$M^{\dagger } M = \lambda \in k^{\times }$
. Let
![]() $\nu $
be the multiplier character
$\nu $
be the multiplier character
![]() $\nu : \mathrm {GU}_n(l) \rightarrow k^{\times }$
sending M to
$\nu : \mathrm {GU}_n(l) \rightarrow k^{\times }$
sending M to
![]() $M^{\dagger } M$
, and let
$M^{\dagger } M$
, and let
![]() $\operatorname {\mathrm {SU}}_n(l)$
denote the kernel of
$\operatorname {\mathrm {SU}}_n(l)$
denote the kernel of
![]() $\nu $
.
$\nu $
.
If V is a representation of a finite group G over l, let
![]() $V^{c}:=V\otimes _{l,c}l$
denote the representation obtained by conjugating the coefficients by the generator of
$V^{c}:=V\otimes _{l,c}l$
denote the representation obtained by conjugating the coefficients by the generator of
![]() $\operatorname {\mathrm {Gal}}(l/k)$
. If
$\operatorname {\mathrm {Gal}}(l/k)$
. If
![]() $x \in V$
, we set
$x \in V$
, we set
![]() $x^c := x\otimes 1 \in V^c$
. If
$x^c := x\otimes 1 \in V^c$
. If
![]() $x \in l$
, we write either
$x \in l$
, we write either
![]() $cx$
or
$cx$
or
![]() $x^c$
for the conjugate of x by
$x^c$
for the conjugate of x by
![]() $c \in \operatorname {\mathrm {Gal}}(l/k)$
.
$c \in \operatorname {\mathrm {Gal}}(l/k)$
.
Definition 4.3.2. If
![]() $l/k$
is a quadratic extension of finite fields and
$l/k$
is a quadratic extension of finite fields and
![]() $\operatorname {\mathrm {Gal}}(l/k) \simeq \langle c \rangle $
, then a Hermitian form on a vector space V over l is an l-valued pairing on V which is k-bilinear, satisfies
$\operatorname {\mathrm {Gal}}(l/k) \simeq \langle c \rangle $
, then a Hermitian form on a vector space V over l is an l-valued pairing on V which is k-bilinear, satisfies
![]() $\langle ax,y \rangle = a \langle x,y\rangle $
and
$\langle ax,y \rangle = a \langle x,y\rangle $
and
![]() $\langle x,ay \rangle = ca \langle x,y\rangle $
for
$\langle x,ay \rangle = ca \langle x,y\rangle $
for
![]() $a \in l$
, and moreover satisfies
$a \in l$
, and moreover satisfies
![]() $\langle y,x \rangle = \langle x,y \rangle ^c = c \langle x,y \rangle $
.
$\langle y,x \rangle = \langle x,y \rangle ^c = c \langle x,y \rangle $
.
Remark 4.3.3. Scaling the pairing by an element
![]() $\eta \in l$
such that
$\eta \in l$
such that
![]() $c \eta = - \eta $
, all the conditions remain true except that now
$c \eta = - \eta $
, all the conditions remain true except that now
![]() $\langle x,y \rangle = - c \langle x,y \rangle $
.
$\langle x,y \rangle = - c \langle x,y \rangle $
.
The basic fact concerning unitary groups over finite fields is that there is essentially only one nondegenerate Hermitian form. In practice, it will be useful to formulate this in the following lemma.
Lemma 4.3.4. Let V be a vector space over l with an absolutely irreducible representation of a group G. Suppose that there is an l-linear isomorphism
for some multiplier character
![]() $\chi : G \rightarrow k^{\times }$
. Then, after a suitable choice of basis for V, the corresponding map
$\chi : G \rightarrow k^{\times }$
. Then, after a suitable choice of basis for V, the corresponding map
![]() $G \rightarrow \operatorname {\mathrm {GL}}_n(l)$
has image in
$G \rightarrow \operatorname {\mathrm {GL}}_n(l)$
has image in
![]() $\mathrm {GU}_n(l)$
.
$\mathrm {GU}_n(l)$
.
Proof. An isomorphism (4.3.4) is equivalent to the existence of a G-equivariant nondegenerate bilinear pairing:
where by abuse of notation, we consider
![]() $\chi $
as a
$\chi $
as a
![]() $1$
-dimensional vector space over l. By Schur’s Lemma, the isomorphism in (4.3.4) is unique up to scaling, and thus,
$1$
-dimensional vector space over l. By Schur’s Lemma, the isomorphism in (4.3.4) is unique up to scaling, and thus,
![]() $\psi $
is also unique up to scaling. If we define
$\psi $
is also unique up to scaling. If we define
![]() $\psi '$
to be the map
$\psi '$
to be the map
then
![]() $\psi '$
is also a G-equivariant bilinear map from
$\psi '$
is also a G-equivariant bilinear map from
![]() $V \times V^{c}$
to
$V \times V^{c}$
to
![]() $\chi $
, and hence,
$\chi $
, and hence,
![]() $\psi '$
is equal to
$\psi '$
is equal to
![]() $\psi ' = \lambda \psi $
for some
$\psi ' = \lambda \psi $
for some
![]() $\lambda \in l^\times $
; that is,
$\lambda \in l^\times $
; that is,
Applying this twice, we get
![]() $\psi (x,y^{c}) = \lambda \cdot \lambda ^{c}\cdot \psi (x,y^{c})$
, and thus,
$\psi (x,y^{c}) = \lambda \cdot \lambda ^{c}\cdot \psi (x,y^{c})$
, and thus,
![]() $N_{l/k}(\lambda ) = 1$
. By Hilbert Theorem
$N_{l/k}(\lambda ) = 1$
. By Hilbert Theorem
![]() $90$
, it follows that
$90$
, it follows that
![]() $\lambda = c \eta /\eta $
for some
$\lambda = c \eta /\eta $
for some
![]() $\eta \in l$
. Replacing
$\eta \in l$
. Replacing
![]() $\psi (x,y)$
by
$\psi (x,y)$
by
![]() $\psi (x,y)/\eta $
, we deduce that
$\psi (x,y)/\eta $
, we deduce that
![]() $\psi (x,y^{c}) = \psi (y,x^{c})^c$
. It follows that
$\psi (x,y^{c}) = \psi (y,x^{c})^c$
. It follows that
defines a nondegenerate Hermitian form on V in the sense of Definition 4.3.2. Let A denote the matrix associated to this Hermitian form, so that
![]() $A^{\dagger } = A$
. Then
$A^{\dagger } = A$
. Then
![]() $G \subset \mathrm {GU}(V,A)$
– that is, matrices M such that
$G \subset \mathrm {GU}(V,A)$
– that is, matrices M such that
![]() $M^{\dagger } A M = \lambda \cdot A$
for some
$M^{\dagger } A M = \lambda \cdot A$
for some
![]() $\lambda \in k^{\times }$
. But now we use the fact that there is a unique nondegenerate equivalence class of Hermitian forms associated to
$\lambda \in k^{\times }$
. But now we use the fact that there is a unique nondegenerate equivalence class of Hermitian forms associated to
![]() $l/k$
; namely, they are all equivalent to
$l/k$
; namely, they are all equivalent to
![]() $A = I$
and so
$A = I$
and so
![]() $G \subset \mathrm {GU}_n(l)$
. (See, for example, [Reference LewisLew82, §4].)
$G \subset \mathrm {GU}_n(l)$
. (See, for example, [Reference LewisLew82, §4].)
4.4 Moduli spaces and monodromy
We shall now discuss a number of moduli spaces related to finding Dwork motives with fixed residual representations and compute the corresponding monodromy groups. Since it will be important to find such motives whose p-adic representations are related to symmetric powers of ‘niveau two’ representations, for our applications, we will have to take
![]() $p \equiv -1 \bmod N$
, and thus be in cases excluded by [Reference QianQia23].
$p \equiv -1 \bmod N$
, and thus be in cases excluded by [Reference QianQia23].
Definition 4.4.1. Let
![]() $l_1, l_2 \nmid 2N$
be distinct primes, and let
$l_1, l_2 \nmid 2N$
be distinct primes, and let
![]() $\lambda _1, \lambda _2$
be places of
$\lambda _1, \lambda _2$
be places of
![]() ${\mathbb Q}(\zeta _N)$
of these characteristics. Suppose we are given the following data:
${\mathbb Q}(\zeta _N)$
of these characteristics. Suppose we are given the following data:
-
1. A field
 $F / {\mathbb Q}(\zeta _N)$
and for each
$F / {\mathbb Q}(\zeta _N)$
and for each
 $i = 1, 2$
an étale sheaf
$i = 1, 2$
an étale sheaf
 $\overline {U}_{\lambda _i}$
on
$\overline {U}_{\lambda _i}$
on
 $\operatorname {\mathrm {Spec}} F$
of
$\operatorname {\mathrm {Spec}} F$
of
 $k(\lambda _i)$
-modules of rank n.
$k(\lambda _i)$
-modules of rank n. -
2. For each
 $i = 1, 2$
, an isomorphism
$i = 1, 2$
, an isomorphism
 $\eta _i : \wedge ^n \overline {{\mathcal W}}_{\lambda _i} \to \wedge ^n \overline {U}_{\lambda _i, T_{0, F}}$
of sheaves of
$\eta _i : \wedge ^n \overline {{\mathcal W}}_{\lambda _i} \to \wedge ^n \overline {U}_{\lambda _i, T_{0, F}}$
of sheaves of
 $k(\lambda _i)$
-modules.
$k(\lambda _i)$
-modules. -
3. For each
 $i = 1, 2$
, if
$i = 1, 2$
, if
 $-1 \text { mod } N \in \langle l_i \rangle \leq ({\mathbb Z} / N {\mathbb Z})^\times $
(equivalently, if
$-1 \text { mod } N \in \langle l_i \rangle \leq ({\mathbb Z} / N {\mathbb Z})^\times $
(equivalently, if
 $c \in \operatorname {\mathrm {Gal}}(k(\lambda _i) / {\mathbb F}_{l_i})$
), then we fix in addition a perfect
$c \in \operatorname {\mathrm {Gal}}(k(\lambda _i) / {\mathbb F}_{l_i})$
), then we fix in addition a perfect
 ${\mathbb F}_l$
-bilinear morphism
${\mathbb F}_l$
-bilinear morphism
 $\langle \cdot , \cdot \rangle _{\overline {U}_{\lambda _i}} : \overline {U}_{\lambda _i} \times \overline {U}_{\lambda _i} \to k(\lambda _i)(1-n)$
satisfying the following conditions:
$\langle \cdot , \cdot \rangle _{\overline {U}_{\lambda _i}} : \overline {U}_{\lambda _i} \times \overline {U}_{\lambda _i} \to k(\lambda _i)(1-n)$
satisfying the following conditions:-
(a) For all
 $x, y \in \overline {U}_{\lambda _i}$
,
$x, y \in \overline {U}_{\lambda _i}$
,
 $a \in k(\lambda _i)$
, we have
$a \in k(\lambda _i)$
, we have
 $\langle a x, y \rangle = a \langle x, y \rangle $
,
$\langle a x, y \rangle = a \langle x, y \rangle $
,
 $\langle x, a y \rangle = c(a) \langle x, y \rangle $
.
$\langle x, a y \rangle = c(a) \langle x, y \rangle $
. -
(b) For all
 $x, y \in \overline {U}_{\lambda _i}$
, we have
$x, y \in \overline {U}_{\lambda _i}$
, we have
 $\langle y, x \rangle = - c \langle x, y \rangle $
.
$\langle y, x \rangle = - c \langle x, y \rangle $
.
That is, the pairing is Hermitian in the sense of Definition 4.3.2 up to a scalar
 $\eta $
with
$\eta $
with
 $c \eta = - \eta $
; see Remark 4.3.3.
$c \eta = - \eta $
; see Remark 4.3.3. -
Note that if
![]() $-1 \text { mod } N \in \langle l_i \rangle $
then there is also a perfect
$-1 \text { mod } N \in \langle l_i \rangle $
then there is also a perfect
![]() ${\mathbb F}_l$
-bilinear morphism
${\mathbb F}_l$
-bilinear morphism
![]() $\langle \cdot , \cdot \rangle _{\overline {{\mathcal W}}_{\lambda _i}} : \overline {{\mathcal W}}_{\lambda _i} \times \overline {{\mathcal W}}_{\lambda _i} \to k(\lambda _i)(1-n)$
satisfying the same two conditions, induced by taking Poincaré duality on the relative cohomology with
$\langle \cdot , \cdot \rangle _{\overline {{\mathcal W}}_{\lambda _i}} : \overline {{\mathcal W}}_{\lambda _i} \times \overline {{\mathcal W}}_{\lambda _i} \to k(\lambda _i)(1-n)$
satisfying the same two conditions, induced by taking Poincaré duality on the relative cohomology with
![]() ${\mathcal O}_{M^+_\lambda }$
-coefficients of the hypersurface
${\mathcal O}_{M^+_\lambda }$
-coefficients of the hypersurface
![]() $Z \to T_0$
and extending sesquilinearly to
$Z \to T_0$
and extending sesquilinearly to
![]() ${\mathcal O}_{M_\lambda }$
-coefficients. If
${\mathcal O}_{M_\lambda }$
-coefficients. If
![]() $k / F$
is a field extension and
$k / F$
is a field extension and
![]() $t \in T_0(k)$
, then we write
$t \in T_0(k)$
, then we write
![]() $\langle \cdot , \cdot \rangle _{\overline {W}_{t, \lambda _i}}$
for the induced perfect pairing on
$\langle \cdot , \cdot \rangle _{\overline {W}_{t, \lambda _i}}$
for the induced perfect pairing on
![]() $\overline {W}_{t, \lambda _i}$
.
$\overline {W}_{t, \lambda _i}$
.
Given such data, let us write
![]() $\mathcal {F}(\{ \overline {U}_{\lambda _i} \})$
for the functor which sends a scheme
$\mathcal {F}(\{ \overline {U}_{\lambda _i} \})$
for the functor which sends a scheme
![]() $S \to T_{0, F}$
to the set of pairs of isomorphisms
$S \to T_{0, F}$
to the set of pairs of isomorphisms
![]() $\phi _i : \overline {{\mathcal W}}_{\lambda _i, S} \to \overline {U}_{\lambda _i, S} ( i = 1, 2)$
satisfying the following conditions:
$\phi _i : \overline {{\mathcal W}}_{\lambda _i, S} \to \overline {U}_{\lambda _i, S} ( i = 1, 2)$
satisfying the following conditions:
-
• For each
 $i = 1, 2$
,
$i = 1, 2$
,
 $\wedge ^n \phi _i = \eta _i$
.
$\wedge ^n \phi _i = \eta _i$
. -
• For each
 $i = 1, 2$
, if
$i = 1, 2$
, if
 $-1 \text { mod } N \in \langle l_i \rangle $
, then
$-1 \text { mod } N \in \langle l_i \rangle $
, then
 $\phi _i$
intertwines
$\phi _i$
intertwines
 $\langle \cdot , \cdot \rangle _{\overline {{\mathcal W}}_{\lambda _i}, S}$
and
$\langle \cdot , \cdot \rangle _{\overline {{\mathcal W}}_{\lambda _i}, S}$
and
 $\langle \cdot , \cdot \rangle _{\overline {U}_{\lambda _i}, S}$
.
$\langle \cdot , \cdot \rangle _{\overline {U}_{\lambda _i}, S}$
.
Then
![]() $\mathcal {F}(\{ \overline {U}_{\lambda _i} \})$
is represented by a finite étale
$\mathcal {F}(\{ \overline {U}_{\lambda _i} \})$
is represented by a finite étale
![]() $T_{0, F}$
-scheme
$T_{0, F}$
-scheme
![]() $T(\{ \overline {U}_{\lambda _i} \})$
.
$T(\{ \overline {U}_{\lambda _i} \})$
.
We need the following variant of [Reference QianQia23, Proposition 3.8].
Proposition 4.4.2. With notation as above,
![]() $T(\{ \overline {U}_{\lambda _i} \})$
is a geometrically irreducible smooth F-scheme.
$T(\{ \overline {U}_{\lambda _i} \})$
is a geometrically irreducible smooth F-scheme.
Proof. We need to show that the geometric monodromy group
![]() $\pi _1(T_{0, \overline {{\mathbb Q}}})$
acts transitively on the fibres of
$\pi _1(T_{0, \overline {{\mathbb Q}}})$
acts transitively on the fibres of
![]() $T(\{ \overline {U}_{\lambda _i} \})$
over
$T(\{ \overline {U}_{\lambda _i} \})$
over
![]() $T_0$
. The existence of the pairing
$T_0$
. The existence of the pairing
![]() $\langle \cdot , \cdot \rangle _{\overline {{\mathcal W}}_{\lambda _i}}$
shows that if
$\langle \cdot , \cdot \rangle _{\overline {{\mathcal W}}_{\lambda _i}}$
shows that if
![]() $-1 \text { mod } N \in \langle l_i \rangle $
, then the image of the geometric monodromy group acting on the geometric generic fibre of
$-1 \text { mod } N \in \langle l_i \rangle $
, then the image of the geometric monodromy group acting on the geometric generic fibre of
![]() $\overline {{\mathcal W}}_{\lambda _i}$
may be identified with a subgroup of
$\overline {{\mathcal W}}_{\lambda _i}$
may be identified with a subgroup of
![]() $\mathrm {SU}_n(k(\lambda _i))$
, and otherwise, it may be identified with a subgroup of
$\mathrm {SU}_n(k(\lambda _i))$
, and otherwise, it may be identified with a subgroup of
![]() $\mathrm {SL}_n(k(\lambda _i))$
.
$\mathrm {SL}_n(k(\lambda _i))$
.
We claim that it is enough to show that equality holds in either of these cases. Indeed, let
![]() $H_i$
denote the image at each prime
$H_i$
denote the image at each prime
![]() $l_i$
(which would then be either
$l_i$
(which would then be either
![]() $\mathrm {SU}_n(k(\lambda _i))$
or
$\mathrm {SU}_n(k(\lambda _i))$
or
![]() $\operatorname {\mathrm {SL}}_n(k(\lambda _i))$
). Since we are assuming
$\operatorname {\mathrm {SL}}_n(k(\lambda _i))$
). Since we are assuming
![]() $l_1, l_2 \nmid 2$
and
$l_1, l_2 \nmid 2$
and
![]() $n> 2$
, it follows that the
$n> 2$
, it follows that the
![]() $H_i$
are perfect and their associated projective groups (i.e., the
$H_i$
are perfect and their associated projective groups (i.e., the
![]() $H_i$
modulo their subgroups of scalar matrices) are simple (Lemma 5.2.3), and moreover,
$H_i$
modulo their subgroups of scalar matrices) are simple (Lemma 5.2.3), and moreover,
![]() $H_1 \not \cong H_2$
(also by Lemma 5.2.3). Goursat’s lemma implies that the image of geometric monodromy acting on
$H_1 \not \cong H_2$
(also by Lemma 5.2.3). Goursat’s lemma implies that the image of geometric monodromy acting on
![]() $\overline {{\mathcal W}}_{\lambda _1} \times \overline {{\mathcal W}}_{\lambda _2}$
must be
$\overline {{\mathcal W}}_{\lambda _1} \times \overline {{\mathcal W}}_{\lambda _2}$
must be
![]() $H_1 \times H_2$
, completing the proof.
$H_1 \times H_2$
, completing the proof.
If
![]() $-1 \text { mod } N \not \in \langle l_i \rangle $
, then the required statement follows from [Reference QianQia23, Lemma 3.7]. Now suppose that
$-1 \text { mod } N \not \in \langle l_i \rangle $
, then the required statement follows from [Reference QianQia23, Lemma 3.7]. Now suppose that
![]() $-1 \text { mod } N \in \langle l_i \rangle $
. In this case, we can follow the proof of [Reference QianQia23, Lemma 3.7] (now allowing the case
$-1 \text { mod } N \in \langle l_i \rangle $
. In this case, we can follow the proof of [Reference QianQia23, Lemma 3.7] (now allowing the case
![]() $-1 \text { mod } N \in \langle l_i \rangle $
, which is used there to exclude the possibility of image a special unitary group) to conclude that
$-1 \text { mod } N \in \langle l_i \rangle $
, which is used there to exclude the possibility of image a special unitary group) to conclude that
![]() $H_i$
is isomorphic to a subgroup of
$H_i$
is isomorphic to a subgroup of
![]() $\mathrm {SU}_n(k(\lambda _i))$
which maps to
$\mathrm {SU}_n(k(\lambda _i))$
which maps to
![]() $\mathrm {SU}_n(k(\lambda _i))$
or
$\mathrm {SU}_n(k(\lambda _i))$
or
![]() $\operatorname {\mathrm {SL}}_n(k(\lambda _i))$
with image a normal subgroup of index dividing N. Since N is coprime to n by assumption, the only possibility is that this map is in fact an isomorphism and that
$\operatorname {\mathrm {SL}}_n(k(\lambda _i))$
with image a normal subgroup of index dividing N. Since N is coprime to n by assumption, the only possibility is that this map is in fact an isomorphism and that
![]() $H_i \cong \mathrm {SU}_n(k(\lambda _i))$
, as required.
$H_i \cong \mathrm {SU}_n(k(\lambda _i))$
, as required.
Remark 4.4.3. If
![]() $l \equiv 1 \bmod N$
, so that l splits completely in
$l \equiv 1 \bmod N$
, so that l splits completely in
![]() ${\mathbb Q}(\zeta _N)$
, and
${\mathbb Q}(\zeta _N)$
, and
![]() $\lambda | l$
, then the data of an étale sheaf
$\lambda | l$
, then the data of an étale sheaf
![]() $\overline {U}_{\lambda }$
on
$\overline {U}_{\lambda }$
on
![]() $\operatorname {\mathrm {Spec}} F$
satisfying conditions (1), (2) and (3) of Definition 4.4.1 is nothing more than a representation
$\operatorname {\mathrm {Spec}} F$
satisfying conditions (1), (2) and (3) of Definition 4.4.1 is nothing more than a representation
with determinant
![]() $\overline {\varepsilon }^{-n(n-1)/2}$
. If
$\overline {\varepsilon }^{-n(n-1)/2}$
. If
![]() $l \equiv -1 \bmod N$
, however, then (in light of Lemma 4.3.4) these conditions correspond to a representation
$l \equiv -1 \bmod N$
, however, then (in light of Lemma 4.3.4) these conditions correspond to a representation
with multiplier character
![]() $\overline {\varepsilon }^{1-n}$
(and determinant
$\overline {\varepsilon }^{1-n}$
(and determinant
![]() $\overline {\varepsilon }^{-n(n-1)/2}$
). In practice, we shall only consider the moduli spaces T with primes
$\overline {\varepsilon }^{-n(n-1)/2}$
). In practice, we shall only consider the moduli spaces T with primes
![]() $l_1,l_2$
that are either
$l_1,l_2$
that are either
![]() $\pm 1 \bmod N$
, in which case we sometimes write
$\pm 1 \bmod N$
, in which case we sometimes write
![]() $T(\{ \overline {U}_{\lambda _i} \})$
as
$T(\{ \overline {U}_{\lambda _i} \})$
as
![]() $T(\overline {r}_{\lambda _1},\overline {r}_{\lambda _2})$
, replacing the étale sheaf with the corresponding representations, which are always assumed to satisfy conditions (1), (2) and (3) of Definition 4.4.1. We will also use the simpler variant
$T(\overline {r}_{\lambda _1},\overline {r}_{\lambda _2})$
, replacing the étale sheaf with the corresponding representations, which are always assumed to satisfy conditions (1), (2) and (3) of Definition 4.4.1. We will also use the simpler variant
![]() $T(\overline {r}_{\lambda })$
, where there is a single prime
$T(\overline {r}_{\lambda })$
, where there is a single prime
![]() $l \equiv 1 \bmod N$
, a choice of place
$l \equiv 1 \bmod N$
, a choice of place
![]() $\lambda | l$
, and a representation
$\lambda | l$
, and a representation
![]() $\overline {r}_{\lambda }: G_F \rightarrow \operatorname {\mathrm {GL}}_n({\mathbb F}_l)$
of determinant
$\overline {r}_{\lambda }: G_F \rightarrow \operatorname {\mathrm {GL}}_n({\mathbb F}_l)$
of determinant
![]() $\overline {\varepsilon }^{-n(n-1)/2}$
. The F-scheme
$\overline {\varepsilon }^{-n(n-1)/2}$
. The F-scheme
![]() $T(\overline {r}_{\lambda })$
is geometrically irreducible.
$T(\overline {r}_{\lambda })$
is geometrically irreducible.
The following lemma will be used to prove the existence of local points on
![]() $T(\{ \overline {U}_{\lambda _i} \})$
in certain cases.
$T(\{ \overline {U}_{\lambda _i} \})$
in certain cases.
Lemma 4.4.4. Let
![]() $l> n$
be a prime such that
$l> n$
be a prime such that
![]() $l \equiv -1 \text { mod }N$
, and let
$l \equiv -1 \text { mod }N$
, and let
![]() $v, \lambda $
be places of
$v, \lambda $
be places of
![]() ${\mathbb Q}(\zeta _N)$
, M, respectively, of residue characteristic l. Let
${\mathbb Q}(\zeta _N)$
, M, respectively, of residue characteristic l. Let
![]() $\tau , c \tau : k(v) \to k(\lambda )$
be the two distinct isomorphisms, and let
$\tau , c \tau : k(v) \to k(\lambda )$
be the two distinct isomorphisms, and let
![]() $\omega _\tau : I_{{\mathbb Q}(\zeta _N)_v} \to k(\lambda )^\times $
be the character
$\omega _\tau : I_{{\mathbb Q}(\zeta _N)_v} \to k(\lambda )^\times $
be the character
![]() $\tau \circ \operatorname {Art}_{{\mathbb Q}(\zeta _N)_v}^{-1}$
. Then there is an isomorphism
$\tau \circ \operatorname {Art}_{{\mathbb Q}(\zeta _N)_v}^{-1}$
. Then there is an isomorphism
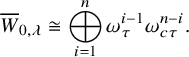 $$\begin{align*}\overline{W}_{0, \lambda} \cong \bigoplus_{i=1}^n \omega_\tau^{i-1} \omega_{c \tau}^{n-i}. \end{align*}$$
$$\begin{align*}\overline{W}_{0, \lambda} \cong \bigoplus_{i=1}^n \omega_\tau^{i-1} \omega_{c \tau}^{n-i}. \end{align*}$$
Proof. The action of
![]() $H_0$
on
$H_0$
on
![]() $Z_0$
extends to an action of H, leading to a decomposition
$Z_0$
extends to an action of H, leading to a decomposition
 $$\begin{align*}\overline{W}_{0, \lambda} = \bigoplus_{j = 1}^n \overline{W}_{0, \lambda, j}, \end{align*}$$
$$\begin{align*}\overline{W}_{0, \lambda} = \bigoplus_{j = 1}^n \overline{W}_{0, \lambda, j}, \end{align*}$$
where
![]() $W_{0, \lambda , j}$
is the
$W_{0, \lambda , j}$
is the
![]() $\Psi _\lambda ^{-1}$
-twist of the H-eigenspace in
$\Psi _\lambda ^{-1}$
-twist of the H-eigenspace in
![]() $H^{N-1}(Z_{0, \overline {{\mathbb Q}}}, {\mathcal O}_{M_\lambda })$
for the character
$H^{N-1}(Z_{0, \overline {{\mathbb Q}}}, {\mathcal O}_{M_\lambda })$
for the character
![]() $(\chi _1 \rho _j^{-1}, \dots , \chi _N \rho _j^{-1})$
, and
$(\chi _1 \rho _j^{-1}, \dots , \chi _N \rho _j^{-1})$
, and
![]() $\overline {W}_{0, \lambda , j} := W_{0, \lambda , j}\otimes _{{\mathcal O}_{M_\lambda }}k(\lambda )$
. Here, we have used the computation of [Reference Deligne, Milne, Ogus and ShihDMOS82, I.7.4], which moreover shows that each summand here has rank 1 over
$\overline {W}_{0, \lambda , j} := W_{0, \lambda , j}\otimes _{{\mathcal O}_{M_\lambda }}k(\lambda )$
. Here, we have used the computation of [Reference Deligne, Milne, Ogus and ShihDMOS82, I.7.4], which moreover shows that each summand here has rank 1 over
![]() $k(\lambda )$
. Moreover, this decomposition is orthogonal with respect to
$k(\lambda )$
. Moreover, this decomposition is orthogonal with respect to
![]() $\langle \cdot , \cdot \rangle _{\overline {W}_{0, \lambda }}$
, showing that
$\langle \cdot , \cdot \rangle _{\overline {W}_{0, \lambda }}$
, showing that
![]() $\overline {W}_{0, \lambda , j} \otimes _{k(\lambda ), c} k(\lambda ) \cong \overline {W}_{0, \lambda , j}^\vee \varepsilon ^{1-n}$
as
$\overline {W}_{0, \lambda , j} \otimes _{k(\lambda ), c} k(\lambda ) \cong \overline {W}_{0, \lambda , j}^\vee \varepsilon ^{1-n}$
as
![]() $k(\lambda )[G_{{\mathbb Q}(\zeta _N)}]$
-modules.
$k(\lambda )[G_{{\mathbb Q}(\zeta _N)}]$
-modules.
After permuting
![]() $\rho _1, \dots , \rho _n$
, we can assume that
$\rho _1, \dots , \rho _n$
, we can assume that
![]() $\mathrm {HT}_\tau (W_{0, \lambda , j}) = j-1$
. Then we have
$\mathrm {HT}_\tau (W_{0, \lambda , j}) = j-1$
. Then we have
![]() $ \overline {W}_{0, \lambda , j} \cong k(\lambda )(\omega _\tau ^{j-1} \omega _{c \tau }^{a_j})$
for some integers
$ \overline {W}_{0, \lambda , j} \cong k(\lambda )(\omega _\tau ^{j-1} \omega _{c \tau }^{a_j})$
for some integers
![]() $a_j$
with
$a_j$
with
![]() $\{ a_1, \dots , a_n \} = \{ 0, \dots , n-1 \}$
. The last sentence of the previous paragraph shows that we must in fact have
$\{ a_1, \dots , a_n \} = \{ 0, \dots , n-1 \}$
. The last sentence of the previous paragraph shows that we must in fact have
![]() $j-1 + a_j = n-1$
, completing the proof.
$j-1 + a_j = n-1$
, completing the proof.
4.5 A result of Moret-Bailly
We will use the following variant of the extensions [Reference CalegariCal12, Theorem 3.1], [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, Proposition 3.1.1] of the main result of [Reference Moret-BaillyMB89].
Proposition 4.5.1. Let F be an imaginary CM field, Galois over
![]() ${\mathbb Q}$
, and let
${\mathbb Q}$
, and let
![]() $T / F$
be a smooth, geometrically irreducible variety. Suppose we are given the following data:
$T / F$
be a smooth, geometrically irreducible variety. Suppose we are given the following data:
-
1. A finite extension
 $F^{\mathrm {avoid}} / F$
and disjoint finite sets
$F^{\mathrm {avoid}} / F$
and disjoint finite sets
 $S_0$
of rational primes.
$S_0$
of rational primes. -
2. For each
 $l \in S_0$
and each place
$l \in S_0$
and each place
 $v | l$
of F, a Galois extension
$v | l$
of F, a Galois extension
 $L_v / F_v$
. These have the property that if
$L_v / F_v$
. These have the property that if
 $\sigma \in G_{{\mathbb Q}_l}$
, then
$\sigma \in G_{{\mathbb Q}_l}$
, then
 $\sigma (L_v) = L_{\sigma (v)}$
.
$\sigma (L_v) = L_{\sigma (v)}$
. -
3. For each
 $l \in S_0$
and each place
$l \in S_0$
and each place
 $v | l$
of F, a nonempty open subset
$v | l$
of F, a nonempty open subset
 $\Omega _v \subset T(L_v)$
, invariant under the action of
$\Omega _v \subset T(L_v)$
, invariant under the action of
 $\operatorname {\mathrm {Gal}}(L_v / F_v)$
.
$\operatorname {\mathrm {Gal}}(L_v / F_v)$
.
Then we can find a finite CM extension
![]() $F' / F$
and a point
$F' / F$
and a point
![]() $P \in T(F')$
with the following properties:
$P \in T(F')$
with the following properties:
-
1.
 $F' / {\mathbb Q}$
is Galois, and
$F' / {\mathbb Q}$
is Galois, and
 $F' / F$
is linearly disjoint from
$F' / F$
is linearly disjoint from
 $F^{\mathrm {avoid}} / F$
.
$F^{\mathrm {avoid}} / F$
. -
2. For each
 $l \in S_0$
and each place
$l \in S_0$
and each place
 $v | l$
of F and
$v | l$
of F and
 $w | v$
of
$w | v$
of
 $F'$
, there is an isomorphism
$F'$
, there is an isomorphism
 $F^{\prime }_w \cong L_v$
of
$F^{\prime }_w \cong L_v$
of
 $F_v$
-algebras such that
$F_v$
-algebras such that
 $P \in \Omega _v \subset T(F^{\prime }_w) \cong T(L_v)$
.
$P \in \Omega _v \subset T(F^{\prime }_w) \cong T(L_v)$
.
Suppose we are given further a finite group G and a surjective homomorphism
![]() $f : \pi _1^{\acute{\rm e}\text {t}}(T) \to G$
. Then we can further choose P so that the image of
$f : \pi _1^{\acute{\rm e}\text {t}}(T) \to G$
. Then we can further choose P so that the image of
![]() $f \circ P_\ast : G_{F'} \to G$
is surjective.
$f \circ P_\ast : G_{F'} \to G$
is surjective.
Proof. Without the last sentence, this is a special case of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, Proposition 3.1.1] (taking
![]() $K_0 = {\mathbb Q}$
in the notation there), noting that (as in [Reference CalegariCal12, Theorem 3.1]) we can choose
$K_0 = {\mathbb Q}$
in the notation there), noting that (as in [Reference CalegariCal12, Theorem 3.1]) we can choose
![]() $F'$
to be of the form
$F'$
to be of the form
![]() $F' = F E$
for a Galois, totally real extension
$F' = F E$
for a Galois, totally real extension
![]() $E / {\mathbb Q}$
, and therefore in particular to be CM.
$E / {\mathbb Q}$
, and therefore in particular to be CM.
To get the last sentence, it suffices to add further local conditions at places of sufficiently large norm, ensuring using a Chebotarev density theorem for schemes of finite type over
![]() ${\mathbb Z}$
that the image of
${\mathbb Z}$
that the image of
![]() $f \circ P_\ast $
meets every conjugacy class of G (in close analogy with the argument of [Reference CalegariCal12, Proposition 3.2] – the surjectivity is then a consequence of Jordan’s theorem). To define the necessary local conditions, we can spread T out to a geometrically irreducible scheme
$f \circ P_\ast $
meets every conjugacy class of G (in close analogy with the argument of [Reference CalegariCal12, Proposition 3.2] – the surjectivity is then a consequence of Jordan’s theorem). To define the necessary local conditions, we can spread T out to a geometrically irreducible scheme
![]() ${\mathcal T}$
, smooth and of finite type over
${\mathcal T}$
, smooth and of finite type over
![]() ${\mathcal O}_F$
, such that f factors through
${\mathcal O}_F$
, such that f factors through
![]() $\pi _1^{\acute{\rm e}\text {t}}({\mathcal T})$
. Then [Reference SerreSer12, Corollary 9.12] shows that for any
$\pi _1^{\acute{\rm e}\text {t}}({\mathcal T})$
. Then [Reference SerreSer12, Corollary 9.12] shows that for any
![]() $X> 0$
and any conjugacy class
$X> 0$
and any conjugacy class
![]() $C \subset G$
, we can find a finite place v of F of norm
$C \subset G$
, we can find a finite place v of F of norm
![]() $q_v> X$
and a point
$q_v> X$
and a point
![]() $x \in {\mathcal T}(k(v))$
such that the image of (arithmetic) Frobenius under
$x \in {\mathcal T}(k(v))$
such that the image of (arithmetic) Frobenius under
![]() $f \circ x_\ast $
lies in C. For each conjugacy class C of G, we choose one such place
$f \circ x_\ast $
lies in C. For each conjugacy class C of G, we choose one such place
![]() $v_C$
and point
$v_C$
and point
![]() $x_C$
for each conjugacy class of G and take
$x_C$
for each conjugacy class of G and take
![]() $\Omega _{v_C}$
to be the pre-image of
$\Omega _{v_C}$
to be the pre-image of
![]() $x_C$
in
$x_C$
in
![]() ${\mathcal T}({\mathcal O}_{F_{v_C}}) \subset T(F_{v_C})$
. We may assume that if
${\mathcal T}({\mathcal O}_{F_{v_C}}) \subset T(F_{v_C})$
. We may assume that if
![]() $C \neq C'$
, then
$C \neq C'$
, then
![]() $v_C$
and
$v_C$
and
![]() $v_{C'}$
have distinct residue characteristics
$v_{C'}$
have distinct residue characteristics
![]() $l_C \neq l_{C'}$
, and then replace
$l_C \neq l_{C'}$
, and then replace
![]() $S_0$
by
$S_0$
by
![]() $S_0 \cup \{ l_C \mid C \subset G \}$
. Finally, if
$S_0 \cup \{ l_C \mid C \subset G \}$
. Finally, if
![]() $v | l_C$
and
$v | l_C$
and
![]() $v \neq v_C$
, we take
$v \neq v_C$
, we take
![]() $\Omega _v = T(F_v)$
. Provided the norm
$\Omega _v = T(F_v)$
. Provided the norm
![]() $q_{v_C}$
is sufficiently large, these sets
$q_{v_C}$
is sufficiently large, these sets
![]() $\Omega _v$
will also be nonempty, as required.
$\Omega _v$
will also be nonempty, as required.
5 Preliminaries on deformation rings and Galois theory
5.1 Lemmas on components of Galois deformation rings
We begin by defining a certain local representation which shall appear repeatedly in the sequel.
Definition 5.1.1. For
![]() $n, m \in {\mathbb Z}_{\ge 1}$
, let
$n, m \in {\mathbb Z}_{\ge 1}$
, let
![]() $\varepsilon _2, \varepsilon _2' : G_{{\mathbb Q}_{p^2}} \to \overline {{\mathbb Z}}_p^\times $
be the two Lubin–Tate characters trivial on
$\varepsilon _2, \varepsilon _2' : G_{{\mathbb Q}_{p^2}} \to \overline {{\mathbb Z}}_p^\times $
be the two Lubin–Tate characters trivial on
![]() $\operatorname {Art}_{{\mathbb Q}_{p^2}}(p)$
, and let
$\operatorname {Art}_{{\mathbb Q}_{p^2}}(p)$
, and let
![]() $\rho _{n,m, 0}$
denote the representation
$\rho _{n,m, 0}$
denote the representation
 $$ \begin{align}\rho_{n,m,0} = \bigoplus_{i=1}^n \varepsilon^{m(n-i)}_2 (\varepsilon^{\prime}_2)^{m(i-1)}: G_{{\mathbb Q}_{p^2}} \rightarrow \operatorname{\mathrm{GL}}_{n}(\overline{{\mathbb Z}}_p).\end{align} $$
$$ \begin{align}\rho_{n,m,0} = \bigoplus_{i=1}^n \varepsilon^{m(n-i)}_2 (\varepsilon^{\prime}_2)^{m(i-1)}: G_{{\mathbb Q}_{p^2}} \rightarrow \operatorname{\mathrm{GL}}_{n}(\overline{{\mathbb Z}}_p).\end{align} $$
We assume that
![]() $p> nm$
, so the representation
$p> nm$
, so the representation
![]() $\rho _{n,m,0}$
is Fontaine–Laffaille. If the value of n is implicit, we often simply write
$\rho _{n,m,0}$
is Fontaine–Laffaille. If the value of n is implicit, we often simply write
![]() $\rho _0$
for
$\rho _0$
for
![]() $\rho _{n,1,0}$
.
$\rho _{n,1,0}$
.
Lemma 5.1.3. Let
![]() $K_0 / {\mathbb Q}_{p^2}$
be an unramified extension, and let
$K_0 / {\mathbb Q}_{p^2}$
be an unramified extension, and let
![]() $\rho : G_{K_0} \rightarrow \operatorname {\mathrm {GL}}_{n}(\overline {{\mathbb Z}}_p)$
be any crystalline representation of Hodge–Tate weights
$\rho : G_{K_0} \rightarrow \operatorname {\mathrm {GL}}_{n}(\overline {{\mathbb Z}}_p)$
be any crystalline representation of Hodge–Tate weights
![]() $\{ 0, m, 2m, \dots , (n-1)m \}$
(with respect to any embedding
$\{ 0, m, 2m, \dots , (n-1)m \}$
(with respect to any embedding
![]() $K_0 \to \overline {{\mathbb Q}}_p$
) such that
$K_0 \to \overline {{\mathbb Q}}_p$
) such that
![]() $\overline {\rho }|_{I_{K_0}}=\overline {\rho }_{n, m, 0}|_{I_{K_0}}$
. Then,
$\overline {\rho }|_{I_{K_0}}=\overline {\rho }_{n, m, 0}|_{I_{K_0}}$
. Then,
-
1. There is a finite unramified extension
 $K_1 / K_0$
such that
$K_1 / K_0$
such that
 $\overline {\rho } |_{G_{K_1}} = \overline {\rho }_{n, m, 0} |_{G_{K_1}}$
.
$\overline {\rho } |_{G_{K_1}} = \overline {\rho }_{n, m, 0} |_{G_{K_1}}$
. -
2. For any finite extension
 $K/ K_0$
such that
$K/ K_0$
such that
 $\overline {\rho } |_{G_{K}} = \overline {\rho }_{n, m, 0} |_{G_{K}}$
, we have
$\overline {\rho } |_{G_{K}} = \overline {\rho }_{n, m, 0} |_{G_{K}}$
, we have
 $ \rho |_{G_K} \sim \rho _{n, m, 0} |_{G_K}$
(‘connects to’, in the sense of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, §1.4]).
$ \rho |_{G_K} \sim \rho _{n, m, 0} |_{G_K}$
(‘connects to’, in the sense of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, §1.4]).
Proof. The first claim is clear. For the second, choose
![]() $K_1 / K_0$
minimal such that
$K_1 / K_0$
minimal such that
![]() $\overline {\rho }|_{G_{K_1}} = \overline {\rho }_{n,m,0}|_{G_{K_1}}$
. Since
$\overline {\rho }|_{G_{K_1}} = \overline {\rho }_{n,m,0}|_{G_{K_1}}$
. Since
![]() $p> nm$
and
$p> nm$
and
![]() $K_1$
is unramified, the lifting ring
$K_1$
is unramified, the lifting ring
![]() $R^{\mathrm {crys},\{ 0, \dots , (n-1)m \},{\mathcal O}}_{\overline {\rho }|_{G_{K_1}}}$
is formally smooth by Fontaine–Laffaille theory. It follows that
$R^{\mathrm {crys},\{ 0, \dots , (n-1)m \},{\mathcal O}}_{\overline {\rho }|_{G_{K_1}}}$
is formally smooth by Fontaine–Laffaille theory. It follows that
![]() $ \rho |_{G_{K_1}} \sim \rho _0|_{G_{K_1}}$
, and then these representations are still connected after passing to any further finite extension.
$ \rho |_{G_{K_1}} \sim \rho _0|_{G_{K_1}}$
, and then these representations are still connected after passing to any further finite extension.
Lemma 5.1.4. Let K be a finite extension of
![]() ${\mathbb Q}_p$
. Let
${\mathbb Q}_p$
. Let
![]() $\rho _1,\rho _2$
be ordinary, crystalline weight
$\rho _1,\rho _2$
be ordinary, crystalline weight
![]() $0$
representations of
$0$
representations of
![]() $G_K$
with
$G_K$
with
![]() $\overline {\rho }_1=\overline {\rho }_2$
the trivial representation. Then
$\overline {\rho }_1=\overline {\rho }_2$
the trivial representation. Then
![]() $\rho _1\sim \rho _2$
.
$\rho _1\sim \rho _2$
.
Proof. This follows immediately from [Reference GeraghtyGer19, Lemma 3.14] — the ordinary weight
![]() $0$
crystalline lifting ring of the trivial representation is irreducible.
$0$
crystalline lifting ring of the trivial representation is irreducible.
Lemma 5.1.5. Let K be a finite extension of
![]() ${\mathbb Q}_p$
, and let
${\mathbb Q}_p$
, and let
![]() $\rho : G_{K} \rightarrow \operatorname {\mathrm {GL}}_{n}(\overline {{\mathbb Z}}_p)$
be crystalline of weight
$\rho : G_{K} \rightarrow \operatorname {\mathrm {GL}}_{n}(\overline {{\mathbb Z}}_p)$
be crystalline of weight
![]() $0$
. Then there exists a constant
$0$
. Then there exists a constant
![]() $c = c(K,\rho ,n)$
with the following property:
$c = c(K,\rho ,n)$
with the following property:
-
• if
 $t: G_K \rightarrow \operatorname {\mathrm {GL}}_{n}(\overline {{\mathbb Z}}_p)$
is crystalline of weight
$t: G_K \rightarrow \operatorname {\mathrm {GL}}_{n}(\overline {{\mathbb Z}}_p)$
is crystalline of weight
 $0$
, and
$0$
, and
 $t \equiv \rho |_{G_K} \bmod p^c$
, then
$t \equiv \rho |_{G_K} \bmod p^c$
, then
 $t \sim \rho |_{G_K}$
.
$t \sim \rho |_{G_K}$
.
Proof. Up to conjugation, the image of
![]() $\rho $
lands in
$\rho $
lands in
![]() $\operatorname {\mathrm {GL}}_n(\mathcal {O}_E)$
for some finite extension
$\operatorname {\mathrm {GL}}_n(\mathcal {O}_E)$
for some finite extension
![]() $E/{\mathbb Q}_p$
with residue field k. Let
$E/{\mathbb Q}_p$
with residue field k. Let
![]() $R = R^{\mathrm {crys},\underline {0}}_{\overline {\rho }|_{G_{K}}} \otimes _{W(k)} \mathcal {O}_E$
denote the weight
$R = R^{\mathrm {crys},\underline {0}}_{\overline {\rho }|_{G_{K}}} \otimes _{W(k)} \mathcal {O}_E$
denote the weight
![]() $0$
crystalline lifting ring of
$0$
crystalline lifting ring of
![]() $\overline {\rho } |_{G_K}: G_K \rightarrow \operatorname {\mathrm {GL}}_n(k)$
. By assumption, R has specializations corresponding to
$\overline {\rho } |_{G_K}: G_K \rightarrow \operatorname {\mathrm {GL}}_n(k)$
. By assumption, R has specializations corresponding to
![]() $\rho $
and to t. We may choose a finite set of elements
$\rho $
and to t. We may choose a finite set of elements
![]() $\{g_k: 1 \le k \le d\}$
of
$\{g_k: 1 \le k \le d\}$
of
![]() $G_K$
such that
$G_K$
such that
for an ideal I, and the universal lifting
![]() $\rho ^{{\operatorname {univ}}}:G_K \to \operatorname {\mathrm {GL}}_n(R)$
of
$\rho ^{{\operatorname {univ}}}:G_K \to \operatorname {\mathrm {GL}}_n(R)$
of
![]() $\overline {\rho }$
satisfies
$\overline {\rho }$
satisfies
so that
![]() $\mathfrak {p} = (X_{ijk})$
is the dimension one prime associated to
$\mathfrak {p} = (X_{ijk})$
is the dimension one prime associated to
![]() $\rho $
. The condition that
$\rho $
. The condition that
![]() $t \equiv \rho |_{G_K} \bmod p^c$
is then equivalent to the condition that the corresponding homomorphism
$t \equiv \rho |_{G_K} \bmod p^c$
is then equivalent to the condition that the corresponding homomorphism
![]() $t: R \to \overline {{\mathbb Z}}_p$
satisfies
$t: R \to \overline {{\mathbb Z}}_p$
satisfies
![]() $v_p(t(X_{ijk})) \ge c$
for all
$v_p(t(X_{ijk})) \ge c$
for all
![]() $i,j,k$
.
$i,j,k$
.
The generic fibre of R is formally smooth at
![]() $\mathfrak {p}$
by [Reference KisinKis08, Theorem 3.3.8], and so in particular, there is a unique minimal prime
$\mathfrak {p}$
by [Reference KisinKis08, Theorem 3.3.8], and so in particular, there is a unique minimal prime
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $R[1/p]$
contained in the prime
$R[1/p]$
contained in the prime
![]() $\mathfrak {p}$
. Suppose that
$\mathfrak {p}$
. Suppose that
![]() $\mathfrak {Q}$
is any minimal prime ideal of
$\mathfrak {Q}$
is any minimal prime ideal of
![]() $R[1/p]$
which is not contained in
$R[1/p]$
which is not contained in
![]() $\mathfrak {p}$
. Then
$\mathfrak {p}$
. Then
![]() $\mathfrak {Q}$
contains an element
$\mathfrak {Q}$
contains an element
![]() $P(X_{ijk}) \in R[1/p]$
which does not vanish at
$P(X_{ijk}) \in R[1/p]$
which does not vanish at
![]() $X_{ijk} = 0$
and hence has a nonzero constant term. After scaling if necessary, we may assume that
$X_{ijk} = 0$
and hence has a nonzero constant term. After scaling if necessary, we may assume that
![]() $P \in R$
. But now any specialization of P with
$P \in R$
. But now any specialization of P with
![]() $v_p(X_{ijk})> v_p(P(0,0,\ldots ,0))$
for every
$v_p(X_{ijk})> v_p(P(0,0,\ldots ,0))$
for every
![]() $(i,j,k)$
will be nonzero, and hence, if
$(i,j,k)$
will be nonzero, and hence, if
![]() $c> v_p(P(0,0,\ldots ,0))$
, then t cannot lie on the irreducible component corresponding to
$c> v_p(P(0,0,\ldots ,0))$
, then t cannot lie on the irreducible component corresponding to
![]() $\mathfrak {Q}$
. Since R has only finitely many minimal prime ideals (it is Noetherian), there exists a choice of c which guarantees that t lies on the component corresponding to
$\mathfrak {Q}$
. Since R has only finitely many minimal prime ideals (it is Noetherian), there exists a choice of c which guarantees that t lies on the component corresponding to
![]() $\mathfrak {P}$
.
$\mathfrak {P}$
.
5.2 Lemmas on big image conditions
In order to apply Theorem 3.2.1 to a p-adic representation of
![]() $G_F$
, one needs first to establish that the image of the residual representation (and its restriction to
$G_F$
, one needs first to establish that the image of the residual representation (and its restriction to
![]() $G_{F(\zeta _p)}$
) satisfies certain technical hypotheses – in particular, conditions (3) and (4). In this section, we prove some lemmas showing that a number of representations of a form we shall encounter later have these properties. We first combine these conditions into the following definition:
$G_{F(\zeta _p)}$
) satisfies certain technical hypotheses – in particular, conditions (3) and (4). In this section, we prove some lemmas showing that a number of representations of a form we shall encounter later have these properties. We first combine these conditions into the following definition:
Definition 5.2.1. Say that a representation
![]() $\overline {s}: G_F \rightarrow \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
satisfies the Taylor–Wiles big image conditions if the following hold:
$\overline {s}: G_F \rightarrow \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
satisfies the Taylor–Wiles big image conditions if the following hold:
-
1. The representation
 $\overline {s}$
is decomposed generic.
$\overline {s}$
is decomposed generic. -
2. The representation
 $\overline {s} |_{G_{F(\zeta _p)}}$
has adequate image.
$\overline {s} |_{G_{F(\zeta _p)}}$
has adequate image. -
3. There exists
 $\sigma \in G_F - G_{F(\zeta _p)}$
such that
$\sigma \in G_F - G_{F(\zeta _p)}$
such that
 $\overline {s}(\sigma )$
is scalar.
$\overline {s}(\sigma )$
is scalar.
We have the following:
Lemma 5.2.2. Suppose that
![]() $\overline {s}: G_F \rightarrow \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
satisfies the Taylor–Wiles big image conditions. Suppose that
$\overline {s}: G_F \rightarrow \operatorname {\mathrm {GL}}_n(\overline {{\mathbb F}}_p)$
satisfies the Taylor–Wiles big image conditions. Suppose that
![]() $F/{\mathbb Q}$
is Galois. Let
$F/{\mathbb Q}$
is Galois. Let
![]() $H/F$
be a finite extension whose Galois closure over
$H/F$
be a finite extension whose Galois closure over
![]() ${\mathbb Q}$
is linearly disjoint over F from the composite of
${\mathbb Q}$
is linearly disjoint over F from the composite of
![]() $F(\zeta _p)$
and the Galois closure over
$F(\zeta _p)$
and the Galois closure over
![]() ${\mathbb Q}$
of the fixed field of
${\mathbb Q}$
of the fixed field of
![]() $\ker (\overline {s})$
. Then
$\ker (\overline {s})$
. Then
![]() $\overline {s} |_{G_H}$
satisfies the Taylor–Wiles big image conditions.
$\overline {s} |_{G_H}$
satisfies the Taylor–Wiles big image conditions.
Proof. Let
![]() $\widetilde {H}$
be the Galois closure of H over
$\widetilde {H}$
be the Galois closure of H over
![]() ${\mathbb Q}$
. Since
${\mathbb Q}$
. Since
![]() $\overline {s} |_{G_{H}}$
satisfies the Taylor–Wiles conditions if
$\overline {s} |_{G_{H}}$
satisfies the Taylor–Wiles conditions if
![]() $\overline {s} |_{G_{\widetilde {H}}}$
does, we assume that
$\overline {s} |_{G_{\widetilde {H}}}$
does, we assume that
![]() $H = \widetilde {H}$
is Galois over
$H = \widetilde {H}$
is Galois over
![]() ${\mathbb Q}$
. The conditions ensure that the images of
${\mathbb Q}$
. The conditions ensure that the images of
![]() $\overline {s}$
and
$\overline {s}$
and
![]() $\overline {s} |_{G_H}$
coincide, and also the images of
$\overline {s} |_{G_H}$
coincide, and also the images of
![]() $\overline {s} |_{G_{F(\zeta _p)}}$
and
$\overline {s} |_{G_{F(\zeta _p)}}$
and
![]() $\overline {s} |_{G_{H(\zeta _p)}}$
coincide. Thus, condition (2) of Definition 5.2.1 holds. Let M be the Galois closure of the fixed field of
$\overline {s} |_{G_{H(\zeta _p)}}$
coincide. Thus, condition (2) of Definition 5.2.1 holds. Let M be the Galois closure of the fixed field of
![]() $\ker (\overline {s})$
. Then we have an isomorphism
$\ker (\overline {s})$
. Then we have an isomorphism
and so
![]() $ \operatorname {\mathrm {Gal}}(M(\zeta _p)/F) \simeq \operatorname {\mathrm {Gal}}(H \cdot M(\zeta _p)/H)$
via the map
$ \operatorname {\mathrm {Gal}}(M(\zeta _p)/F) \simeq \operatorname {\mathrm {Gal}}(H \cdot M(\zeta _p)/H)$
via the map
![]() $\sigma \rightarrow (\sigma ,1)$
. Moreover,
$\sigma \rightarrow (\sigma ,1)$
. Moreover,
is the subgroup of elements whose projection to
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbb Q})\times \operatorname {\mathrm {Gal}}(F/{\mathbb Q})$
is the diagonal. There exists a conjugacy class
$\operatorname {\mathrm {Gal}}(F/{\mathbb Q})\times \operatorname {\mathrm {Gal}}(F/{\mathbb Q})$
is the diagonal. There exists a conjugacy class
![]() $\langle \sigma \rangle \in \operatorname {\mathrm {Gal}}(M(\zeta _p)/F)$
such that any rational prime unramified in
$\langle \sigma \rangle \in \operatorname {\mathrm {Gal}}(M(\zeta _p)/F)$
such that any rational prime unramified in
![]() $H \cdot M(\zeta _p)$
whose Frobenius element corresponds to
$H \cdot M(\zeta _p)$
whose Frobenius element corresponds to
![]() $\sigma $
is decomposed generic for
$\sigma $
is decomposed generic for
![]() $\overline {s}$
. Then
$\overline {s}$
. Then
![]() $(\sigma ,1)$
will be decomposed generic for
$(\sigma ,1)$
will be decomposed generic for
![]() $\overline {s} |_{G_H}$
. Similarly, if
$\overline {s} |_{G_H}$
. Similarly, if
![]() $\sigma \in \operatorname {\mathrm {Gal}}(M(\zeta _p)/F) - \operatorname {\mathrm {Gal}}(M(\zeta _p)/F(\zeta _p))$
is an element such that
$\sigma \in \operatorname {\mathrm {Gal}}(M(\zeta _p)/F) - \operatorname {\mathrm {Gal}}(M(\zeta _p)/F(\zeta _p))$
is an element such that
![]() $\overline {s}(\sigma )$
is scalar, then the same is true of
$\overline {s}(\sigma )$
is scalar, then the same is true of
![]() $(\sigma ,1) \in \operatorname {\mathrm {Gal}}(H \cdot M(\zeta _p)/H)$
.
$(\sigma ,1) \in \operatorname {\mathrm {Gal}}(H \cdot M(\zeta _p)/H)$
.
We shall also use the following group-theoretic fact.
Lemma 5.2.3. Consider the collection of groups G either of the form
![]() $\mathrm {PSL}_n({\mathbb F}_{p^k})$
or of the form
$\mathrm {PSL}_n({\mathbb F}_{p^k})$
or of the form
![]() $\mathrm {PSU}_n({\mathbb F}_{p^{2k}})$
for all primes p and integers
$\mathrm {PSU}_n({\mathbb F}_{p^{2k}})$
for all primes p and integers
![]() $k \ge 1$
,
$k \ge 1$
,
![]() $n \ge 2$
. Then G is simple unless
$n \ge 2$
. Then G is simple unless
![]() $(n,p) \in \{(2,2), (2,3), (3,2)\}$
. These groups are all pairwise mutually non-isomorphic as n and p both vary except for the following isomorphisms:
$(n,p) \in \{(2,2), (2,3), (3,2)\}$
. These groups are all pairwise mutually non-isomorphic as n and p both vary except for the following isomorphisms:
-
1.
 $\mathrm {PSL}_2({\mathbb F}_{p^k}) \simeq \mathrm {PSU}_2({\mathbb F}_{p^{2k}})$
,
$\mathrm {PSL}_2({\mathbb F}_{p^k}) \simeq \mathrm {PSU}_2({\mathbb F}_{p^{2k}})$
, -
2.
 $\mathrm {PSL}_2({\mathbb F}_5) \simeq \mathrm {PSL}_2({\mathbb F}_4)$
,
$\mathrm {PSL}_2({\mathbb F}_5) \simeq \mathrm {PSL}_2({\mathbb F}_4)$
, -
3.
 $\mathrm {PSL}_2({\mathbb F}_7) \simeq \mathrm {PSL}_3({\mathbb F}_2)$
.
$\mathrm {PSL}_2({\mathbb F}_7) \simeq \mathrm {PSL}_3({\mathbb F}_2)$
.
If we restrict G to be of the form
![]() $G = \mathrm {PSL}_2({\mathbb F}_{p^k})$
or
$G = \mathrm {PSL}_2({\mathbb F}_{p^k})$
or
![]() $\mathrm {PSU}_n({\mathbb F}_{p^{2k}})$
, and
$\mathrm {PSU}_n({\mathbb F}_{p^{2k}})$
, and
![]() $A \in G$
is the image of any matrix with eigenvalues in
$A \in G$
is the image of any matrix with eigenvalues in
![]() ${\mathbb F}_p$
, then any automorphism of G preserves these eigenvalues up to scalar.
${\mathbb F}_p$
, then any automorphism of G preserves these eigenvalues up to scalar.
Proof. If
![]() $n=2$
, then there is an isomorphism
$n=2$
, then there is an isomorphism
![]() $\mathrm {PSU}_2({\mathbb F}_{p^{2k}}) \simeq \mathrm {PSL}_2({\mathbb F}_{p^k})$
. Otherwise,
$\mathrm {PSU}_2({\mathbb F}_{p^{2k}}) \simeq \mathrm {PSL}_2({\mathbb F}_{p^k})$
. Otherwise,
![]() $\mathrm {PSL}_n({\mathbb F}_{p^k}) \simeq A_{n-1}(p^k)$
and
$\mathrm {PSL}_n({\mathbb F}_{p^k}) \simeq A_{n-1}(p^k)$
and
![]() $\mathrm {PSU}_{n}({\mathbb F}_{p^{2k}}) \simeq {}^2 A_{n-1}(p^{2k})$
is the Steinberg group. These groups are (twisted in the second case) Chevalley groups. The simplicity statement follows from [Reference SteinbergSte68, Thm 37(b)] (see also [Reference CarterCar72]). The list of exceptional isomorphisms between (possibly twisted) simple Chevelley groups was determined in [Reference SteinbergSte68, Thm 37(a)].
$\mathrm {PSU}_{n}({\mathbb F}_{p^{2k}}) \simeq {}^2 A_{n-1}(p^{2k})$
is the Steinberg group. These groups are (twisted in the second case) Chevalley groups. The simplicity statement follows from [Reference SteinbergSte68, Thm 37(b)] (see also [Reference CarterCar72]). The list of exceptional isomorphisms between (possibly twisted) simple Chevelley groups was determined in [Reference SteinbergSte68, Thm 37(a)].
By a theorem of Steinberg [Reference SteinbergSte60] (and [Reference CarterCar72, Thm 12.5.1]), the outer automorphism group of either
![]() $\mathrm {PSL}_n({\mathbb F}_{p^k})$
or
$\mathrm {PSL}_n({\mathbb F}_{p^k})$
or
![]() $\mathrm {PSU}_{n}({\mathbb F}_{p^{2k}})$
is generated by diagonal automorphisms (conjugation by diagonal elements), by field automorphisms (acting on
$\mathrm {PSU}_{n}({\mathbb F}_{p^{2k}})$
is generated by diagonal automorphisms (conjugation by diagonal elements), by field automorphisms (acting on
![]() ${\mathbb F}_{p^k}$
or
${\mathbb F}_{p^k}$
or
![]() ${\mathbb F}_{p^{2k}}$
, respectively), and the graph automorphism coming from the automorphism of the Dynkin diagram
${\mathbb F}_{p^{2k}}$
, respectively), and the graph automorphism coming from the automorphism of the Dynkin diagram
![]() $A_{n-1}$
if
$A_{n-1}$
if
![]() $n> 2$
(associated to the inverse transpose map). Certainly, diagonal automorphisms preserve eigenvalues, and field automorphisms act on the eigenvalues and so preserve eigenvalues in
$n> 2$
(associated to the inverse transpose map). Certainly, diagonal automorphisms preserve eigenvalues, and field automorphisms act on the eigenvalues and so preserve eigenvalues in
![]() ${\mathbb F}_p$
. There are no graph automorphisms for
${\mathbb F}_p$
. There are no graph automorphisms for
![]() $n=2$
. For
$n=2$
. For
![]() $n> 2$
, the graph automorphism
$n> 2$
, the graph automorphism
![]() $M \mapsto (M^t)^{-1} = \sigma (M^{\dagger })^{-1} = \sigma M$
in the unitary group coincides with the field automorphism and so also preserves rational eigenvalues.
$M \mapsto (M^t)^{-1} = \sigma (M^{\dagger })^{-1} = \sigma M$
in the unitary group coincides with the field automorphism and so also preserves rational eigenvalues.
Lemma 5.2.4. Let
![]() $F/{\mathbb Q}$
be Galois. Consider representations
$F/{\mathbb Q}$
be Galois. Consider representations
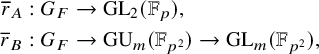 $$ \begin{align*}\begin{aligned} \overline{r}_A: G_F & \rightarrow \operatorname{\mathrm{GL}}_2({\mathbb F}_p), \\ \overline{r}_B: G_F & \rightarrow \mathrm{GU}_m({\mathbb F}_{p^2}) \rightarrow \operatorname{\mathrm{GL}}_{m}({\mathbb F}_{p^2}), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \overline{r}_A: G_F & \rightarrow \operatorname{\mathrm{GL}}_2({\mathbb F}_p), \\ \overline{r}_B: G_F & \rightarrow \mathrm{GU}_m({\mathbb F}_{p^2}) \rightarrow \operatorname{\mathrm{GL}}_{m}({\mathbb F}_{p^2}), \end{aligned} \end{align*} $$
such that the images
![]() $\overline {r}_A(G_{F(\zeta _p)})$
and
$\overline {r}_A(G_{F(\zeta _p)})$
and
![]() $\overline {r}_B(G_{F(\zeta _p)})$
equal
$\overline {r}_B(G_{F(\zeta _p)})$
equal
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
and
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
and
![]() $\operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
, respectively. Consider the representation
$\operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
, respectively. Consider the representation
Assume that
![]() $p>2mn+1$
, and if
$p>2mn+1$
, and if
![]() $m=2$
, assume that the fixed fields of the kernels of the projective representations associated to
$m=2$
, assume that the fixed fields of the kernels of the projective representations associated to
![]() $\overline {r}_A$
and
$\overline {r}_A$
and
![]() $\overline {r}_B$
are linearly disjoint over
$\overline {r}_B$
are linearly disjoint over
![]() $F(\zeta _p)$
.
$F(\zeta _p)$
.
-
1. The representation
 $\overline {s}$
satisfies conditions (1) and (2) of Definition 5.2.1.
$\overline {s}$
satisfies conditions (1) and (2) of Definition 5.2.1. -
2. If
 $\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and
$\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and
 $\overline {r}_B$
has multiplier character
$\overline {r}_B$
has multiplier character
 $\overline {\varepsilon }^{1 - m}$
, then
$\overline {\varepsilon }^{1 - m}$
, then
 $\overline {s}$
has image in
$\overline {s}$
has image in
 $\mathrm {GU}_{mn}({\mathbb F}_{p^2})$
with multiplier character
$\mathrm {GU}_{mn}({\mathbb F}_{p^2})$
with multiplier character
 $\overline {\varepsilon }^{1 - mn}$
.
$\overline {\varepsilon }^{1 - mn}$
. -
3. If in addition to the assumptions in (2), one additionally assumes that
 $\overline {\varepsilon }(G_F)={\mathbb F}^{\times }_p$
, then
$\overline {\varepsilon }(G_F)={\mathbb F}^{\times }_p$
, then
 $\overline {s}$
also satisfies condition (3) of Definition 5.2.1 and thus satisfies the Taylor–Wiles big image conditions.
$\overline {s}$
also satisfies condition (3) of Definition 5.2.1 and thus satisfies the Taylor–Wiles big image conditions.
Proof. Let
![]() $H_A$
and
$H_A$
and
![]() $H_B$
denote the extensions of
$H_B$
denote the extensions of
![]() $F(\zeta _p)$
corresponding to the fixed fields of the kernels of the projective representations associated to
$F(\zeta _p)$
corresponding to the fixed fields of the kernels of the projective representations associated to
![]() $\overline {r}_A$
and
$\overline {r}_A$
and
![]() $\overline {r}_B$
. Our assumption on the images of
$\overline {r}_B$
. Our assumption on the images of
![]() $\overline {r}_A$
and
$\overline {r}_A$
and
![]() $\overline {r}_B$
imply that
$\overline {r}_B$
imply that
Let
![]() $\widetilde {H}_A$
and
$\widetilde {H}_A$
and
![]() $\widetilde {H}_B$
denote the Galois closures of
$\widetilde {H}_B$
denote the Galois closures of
![]() $H_A$
and
$H_A$
and
![]() $H_B$
over
$H_B$
over
![]() ${\mathbb Q}$
, and let
${\mathbb Q}$
, and let
![]() $\widetilde {H}$
denote the compositum of
$\widetilde {H}$
denote the compositum of
![]() $\widetilde {H}_A$
and
$\widetilde {H}_A$
and
![]() $\widetilde {H}_B$
. Since
$\widetilde {H}_B$
. Since
![]() $F/{\mathbb Q}$
is Galois and
$F/{\mathbb Q}$
is Galois and
![]() $\mathrm {PSL}_2({\mathbb F}_p)$
and
$\mathrm {PSL}_2({\mathbb F}_p)$
and
![]() $\mathrm {PSU}_n({\mathbb F}_{p^2})$
are simple (as
$\mathrm {PSU}_n({\mathbb F}_{p^2})$
are simple (as
![]() $p \ge 5$
), we have isomorphisms
$p \ge 5$
), we have isomorphisms
![]() $\operatorname {\mathrm {Gal}}(\widetilde {H}_A/F(\zeta _p)) \sim \mathrm {PSL}_2({\mathbb F}_p)^r$
and
$\operatorname {\mathrm {Gal}}(\widetilde {H}_A/F(\zeta _p)) \sim \mathrm {PSL}_2({\mathbb F}_p)^r$
and
![]() $\operatorname {\mathrm {Gal}}(\widetilde {H}_B/F(\zeta _p)) \simeq \mathrm {PSU}_m({\mathbb F}_{p^2})^s$
, respectively, for some positive integers r and s. Thus,
$\operatorname {\mathrm {Gal}}(\widetilde {H}_B/F(\zeta _p)) \simeq \mathrm {PSU}_m({\mathbb F}_{p^2})^s$
, respectively, for some positive integers r and s. Thus,
since either
![]() $m> 2$
and the groups have no common quotients, or
$m> 2$
and the groups have no common quotients, or
![]() $m=2$
and the fields are linearly disjoint by assumption.
$m=2$
and the fields are linearly disjoint by assumption.
If
![]() $G = \mathrm {PSL}_2({\mathbb F}_p)$
or
$G = \mathrm {PSL}_2({\mathbb F}_p)$
or
![]() $G = \mathrm {PSU}_m({\mathbb F}_{p^2})$
, then G is simple by Lemma 5.2.3. Moreover, by the same lemma, for any equivalence class of matrices A with eigenvalues in
$G = \mathrm {PSU}_m({\mathbb F}_{p^2})$
, then G is simple by Lemma 5.2.3. Moreover, by the same lemma, for any equivalence class of matrices A with eigenvalues in
![]() ${\mathbb F}_p$
, any automorphism of G preserves the (unordered set of) eigenvalues of any member of A up to scalars. We also have
${\mathbb F}_p$
, any automorphism of G preserves the (unordered set of) eigenvalues of any member of A up to scalars. We also have
![]() $\operatorname {\mathrm {Aut}}(G^m) \simeq \operatorname {\mathrm {Aut}}(G) \rtimes S_m$
.
$\operatorname {\mathrm {Aut}}(G^m) \simeq \operatorname {\mathrm {Aut}}(G) \rtimes S_m$
.
Let
![]() $\alpha = \beta ^2 \in {\mathbb F}^{\times 2}_p$
be an element such that
$\alpha = \beta ^2 \in {\mathbb F}^{\times 2}_p$
be an element such that
![]() $1,\alpha ,\ldots ,\alpha ^{mn-1}$
are all distinct; such an
$1,\alpha ,\ldots ,\alpha ^{mn-1}$
are all distinct; such an
![]() $\alpha $
exists because
$\alpha $
exists because
![]() $p - 1 \ge 2mn$
. Let A be a matrix in
$p - 1 \ge 2mn$
. Let A be a matrix in
![]() $\mathrm {PSL}_2({\mathbb F}_p)$
with eigenvalues (up to scalars)
$\mathrm {PSL}_2({\mathbb F}_p)$
with eigenvalues (up to scalars)
![]() $1$
and
$1$
and
![]() $\alpha $
, and let
$\alpha $
, and let
![]() $B \in \mathrm {PSU}_m({\mathbb F}_{p^2})$
have eigenvalues
$B \in \mathrm {PSU}_m({\mathbb F}_{p^2})$
have eigenvalues
![]() $1,\alpha ^n,\ldots ,\alpha ^{n(m-1)}$
. Explicitly, let
$1,\alpha ^n,\ldots ,\alpha ^{n(m-1)}$
. Explicitly, let
![]() $A = \mathrm {diag}(\beta ,\beta ^{-1}) \in \operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
, and then construct B as follows. Certainly,
$A = \mathrm {diag}(\beta ,\beta ^{-1}) \in \operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
, and then construct B as follows. Certainly,
![]() $A^n \in \operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. The image of
$A^n \in \operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. The image of
![]() $A^n$
under the
$A^n$
under the
![]() $m-1$
th symmetric power map lands in
$m-1$
th symmetric power map lands in
![]() $\mathrm {Sp}_{m}({\mathbb F}_p)$
or
$\mathrm {Sp}_{m}({\mathbb F}_p)$
or
![]() $\mathrm {SO}_m({\mathbb F}_p)$
depending on the parity of m (here, we mean the symplectic or orthogonal groups defined using the bilinear form induced by the standard symplectic form on
$\mathrm {SO}_m({\mathbb F}_p)$
depending on the parity of m (here, we mean the symplectic or orthogonal groups defined using the bilinear form induced by the standard symplectic form on
![]() ${\mathbb F}_p^2$
). These groups are conjugate to subgroups of
${\mathbb F}_p^2$
). These groups are conjugate to subgroups of
![]() $\operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
by Lemma 4.3.4. By Chebotarev, we find a prime q unramified in
$\operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
by Lemma 4.3.4. By Chebotarev, we find a prime q unramified in
![]() $\widetilde {H}$
and such that for a fixed choice of
$\widetilde {H}$
and such that for a fixed choice of
![]() $\mathfrak {q}|q$
in
$\mathfrak {q}|q$
in
![]() $\widetilde {H}$
,
$\widetilde {H}$
,
![]() $\mathrm {Frob}_{\mathfrak {q}}\in \operatorname {\mathrm {Gal}}(\widetilde {H}/F(\zeta _p)) \subset \operatorname {\mathrm {Gal}}(\widetilde {H}/{\mathbb Q})$
has the form
$\mathrm {Frob}_{\mathfrak {q}}\in \operatorname {\mathrm {Gal}}(\widetilde {H}/F(\zeta _p)) \subset \operatorname {\mathrm {Gal}}(\widetilde {H}/{\mathbb Q})$
has the form
The eigenvalues (up to scalar) of A and B are preserved by the action of
![]() $\operatorname {\mathrm {Gal}}(F/{\mathbb Q})$
; this follows from our description of the automorphism group of each factor.
$\operatorname {\mathrm {Gal}}(F/{\mathbb Q})$
; this follows from our description of the automorphism group of each factor.
The images of these elements in
![]() $\operatorname {\mathrm {Gal}}(F(\zeta _p)/{\mathbb Q})$
are trivial, so such a prime q will split completely in
$\operatorname {\mathrm {Gal}}(F(\zeta _p)/{\mathbb Q})$
are trivial, so such a prime q will split completely in
![]() $F(\zeta _p)$
and so satisfy
$F(\zeta _p)$
and so satisfy
![]() $q \equiv 1 \bmod p$
. Moreover, the Frobenius elements at all other primes above q will be conjugate inside
$q \equiv 1 \bmod p$
. Moreover, the Frobenius elements at all other primes above q will be conjugate inside
![]() $\operatorname {\mathrm {Gal}}(\widetilde {H}/{\mathbb Q})$
. Hence, the image of (any conjugate of)
$\operatorname {\mathrm {Gal}}(\widetilde {H}/{\mathbb Q})$
. Hence, the image of (any conjugate of)
![]() $\mathrm {Frob}_{\mathfrak {q}}$
under
$\mathrm {Frob}_{\mathfrak {q}}$
under
![]() $\overline {s}$
has eigenvalues (up to scalar) given by
$\overline {s}$
has eigenvalues (up to scalar) given by
![]() $1, \alpha , \ldots , \alpha ^{mn-1}$
. In particular, they are all distinct. Since
$1, \alpha , \ldots , \alpha ^{mn-1}$
. In particular, they are all distinct. Since
![]() $q \equiv 1 \bmod p$
, this implies that
$q \equiv 1 \bmod p$
, this implies that
![]() $\overline {s}$
is decomposed generic, which is property (1) of Definition 5.2.1.
$\overline {s}$
is decomposed generic, which is property (1) of Definition 5.2.1.
To see that
![]() $\overline {s} |_{G_{F(\zeta _p)}}$
has adequate image, it suffices to show that the image is absolutely irreducible and thus is also adequate by [Reference ThorneTho12, Theorem A.9] (using the assumption
$\overline {s} |_{G_{F(\zeta _p)}}$
has adequate image, it suffices to show that the image is absolutely irreducible and thus is also adequate by [Reference ThorneTho12, Theorem A.9] (using the assumption
![]() $p> 2mn+1$
). The irreducibility follows from the fact that the
$p> 2mn+1$
). The irreducibility follows from the fact that the
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
-representation
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
-representation
![]() $\operatorname {\mathrm {Sym}}^{n-1}\overline {{\mathbb F}}_p^2$
and the standard representation of
$\operatorname {\mathrm {Sym}}^{n-1}\overline {{\mathbb F}}_p^2$
and the standard representation of
![]() $\operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
are both irreducible as long as
$\operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
are both irreducible as long as
![]() $p> n$
since the image of
$p> n$
since the image of
![]() $\overline {s} |_{G_{F(\zeta _p)}}$
is
$\overline {s} |_{G_{F(\zeta _p)}}$
is
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)\times \operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
. This proves property (2)of Definition 5.2.1.
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)\times \operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
. This proves property (2)of Definition 5.2.1.
Assume that
![]() $\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and that
$\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and that
![]() $\overline {r}_B$
has multiplier character
$\overline {r}_B$
has multiplier character
![]() $\overline {\varepsilon }^{1-m}$
. Then
$\overline {\varepsilon }^{1-m}$
. Then
![]() $\overline {r}_A \otimes \overline {r}_B$
is absolutely irreducible and self-dual (i.e., there is an isomorphism of the form (4.3.4)) with multiplier character
$\overline {r}_A \otimes \overline {r}_B$
is absolutely irreducible and self-dual (i.e., there is an isomorphism of the form (4.3.4)) with multiplier character
and so the image lies in
![]() $\mathrm {GU}_{mn}({\mathbb F}_{p^2})$
with this multiplier character by Lemma 4.3.4. This establishes condition (2).
$\mathrm {GU}_{mn}({\mathbb F}_{p^2})$
with this multiplier character by Lemma 4.3.4. This establishes condition (2).
Assume that
![]() $\overline {\varepsilon }(G_F)={\mathbb F}^{\times }_p$
. Let
$\overline {\varepsilon }(G_F)={\mathbb F}^{\times }_p$
. Let
![]() $M_A$
and
$M_A$
and
![]() $M_B$
denote the fixed fields of the kernels of
$M_B$
denote the fixed fields of the kernels of
![]() $\overline {r}_A$
and
$\overline {r}_A$
and
![]() $\overline {r}_B$
, and let M be the compositum of
$\overline {r}_B$
, and let M be the compositum of
![]() $M_A$
and
$M_A$
and
![]() $M_B$
. By our assumption on linear disjointness of
$M_B$
. By our assumption on linear disjointness of
![]() $H_A$
and
$H_A$
and
![]() $H_B$
,
$H_B$
,
![]() $\operatorname {\mathrm {Gal}}(M/F(\zeta _p))$
is the direct product
$\operatorname {\mathrm {Gal}}(M/F(\zeta _p))$
is the direct product
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p) \times \operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
, and
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p) \times \operatorname {\mathrm {SU}}_m({\mathbb F}_{p^2})$
, and
![]() $\operatorname {\mathrm {Gal}}(M/F)$
is the subgroup of matrices
$\operatorname {\mathrm {Gal}}(M/F)$
is the subgroup of matrices
![]() $(A,B)$
of
$(A,B)$
of
![]() $\operatorname {\mathrm {GL}}_2({\mathbb F}_p) \times \mathrm {GU}_m({\mathbb F}_{p^2})$
with
$\operatorname {\mathrm {GL}}_2({\mathbb F}_p) \times \mathrm {GU}_m({\mathbb F}_{p^2})$
with
![]() $\det (A) = \eta ^{-m}$
and
$\det (A) = \eta ^{-m}$
and
![]() $\nu (B) = \eta ^{1-m}$
for some
$\nu (B) = \eta ^{1-m}$
for some
![]() $\eta \in {\mathbb F}^{\times }_p$
. Hence, the image certainly contains
$\eta \in {\mathbb F}^{\times }_p$
. Hence, the image certainly contains
![]() $(\beta ^{m} I_2,\beta ^{m-1} I_m)$
, where
$(\beta ^{m} I_2,\beta ^{m-1} I_m)$
, where
![]() $I_n$
denotes the trivial matrix in
$I_n$
denotes the trivial matrix in
![]() $\operatorname {\mathrm {SL}}_n({\mathbb F}_p)$
and
$\operatorname {\mathrm {SL}}_n({\mathbb F}_p)$
and
![]() $\beta \in {\mathbb F}^{\times }_p$
is a primitive root. Then, by Chebotarev, there exists
$\beta \in {\mathbb F}^{\times }_p$
is a primitive root. Then, by Chebotarev, there exists
![]() $\sigma \in G_F$
whose image in
$\sigma \in G_F$
whose image in
![]() $\operatorname {\mathrm {Gal}}(M/F)$
is this element. Since
$\operatorname {\mathrm {Gal}}(M/F)$
is this element. Since
![]() $p> 2mn+1 \ge 2m+1$
, we have
$p> 2mn+1 \ge 2m+1$
, we have
![]() $\beta ^{2m} \ne 1$
. Since
$\beta ^{2m} \ne 1$
. Since
![]() $\overline {\varepsilon }^{-m}(\sigma ) = \beta ^{2m}$
, the element
$\overline {\varepsilon }^{-m}(\sigma ) = \beta ^{2m}$
, the element
![]() $\sigma $
is not contained in
$\sigma $
is not contained in
![]() $G_{F(\zeta _p)}$
. However, we see that
$G_{F(\zeta _p)}$
. However, we see that
![]() $\overline {s}(\sigma )$
is also scalar, and we are done.
$\overline {s}(\sigma )$
is also scalar, and we are done.
We shall need the following well-known property of induced representations (specialized to the context in which we shall apply it in the proof of the following lemma).
Lemma 5.2.5. Let
![]() $E/{\mathbb Q}$
be a cyclic Galois extension of degree m linearly disjoint from F, and let
$E/{\mathbb Q}$
be a cyclic Galois extension of degree m linearly disjoint from F, and let
![]() $L = E \cdot F$
. Let
$L = E \cdot F$
. Let
![]() $\overline {\psi }: G_L \rightarrow {\mathbb F}^{\times }_p$
be a character and let
$\overline {\psi }: G_L \rightarrow {\mathbb F}^{\times }_p$
be a character and let
![]() $\overline {r}_B = \operatorname {\mathrm {Ind}}^{G_F}_{G_L} \overline {\psi }: G_F \rightarrow \operatorname {\mathrm {GL}}_m(\overline {{\mathbb F}}_p)$
. Let q be a prime of
$\overline {r}_B = \operatorname {\mathrm {Ind}}^{G_F}_{G_L} \overline {\psi }: G_F \rightarrow \operatorname {\mathrm {GL}}_m(\overline {{\mathbb F}}_p)$
. Let q be a prime of
![]() ${\mathbb Q}$
such that
${\mathbb Q}$
such that
![]() $\overline {r}_B$
is unramified at all
$\overline {r}_B$
is unramified at all
![]() $v|q$
, q splits completely in F, and
$v|q$
, q splits completely in F, and
![]() $\mathrm {Frob}_q$
generates
$\mathrm {Frob}_q$
generates
![]() $\operatorname {\mathrm {Gal}}(E/{\mathbb Q})$
. Then, for
$\operatorname {\mathrm {Gal}}(E/{\mathbb Q})$
. Then, for
![]() $v|q$
in F, the eigenvalues of
$v|q$
in F, the eigenvalues of
![]() $\overline {r}_B(\mathrm {Frob}_v)$
are of the form
$\overline {r}_B(\mathrm {Frob}_v)$
are of the form
![]() $\lambda , \zeta \lambda , \ldots , \zeta ^{m-1} \lambda $
for some
$\lambda , \zeta \lambda , \ldots , \zeta ^{m-1} \lambda $
for some
![]() $\lambda $
where
$\lambda $
where
![]() $\zeta $
is a primitive mth root of unity.
$\zeta $
is a primitive mth root of unity.
Proof. The assumption that E is linearly disjoint from F ensures that
![]() $\operatorname {\mathrm {Gal}}(L/F) \simeq \operatorname {\mathrm {Gal}}(E/{\mathbb Q})$
is cyclic of order m. There is an isomorphism
$\operatorname {\mathrm {Gal}}(L/F) \simeq \operatorname {\mathrm {Gal}}(E/{\mathbb Q})$
is cyclic of order m. There is an isomorphism
![]() $\overline {r}_B \simeq \overline {r}_B \otimes \chi $
where
$\overline {r}_B \simeq \overline {r}_B \otimes \chi $
where
![]() $\chi $
is a character (factoring through
$\chi $
is a character (factoring through
![]() $\operatorname {\mathrm {Gal}}(L/F)$
) of order m.
$\operatorname {\mathrm {Gal}}(L/F)$
) of order m.
Thus,
![]() $\overline {r}_{B}(\mathrm {Frob}_v)$
is conjugate to
$\overline {r}_{B}(\mathrm {Frob}_v)$
is conjugate to
![]() $\chi (\mathrm {Frob}_v) \overline {r}_{B}(\mathrm {Frob}_v) = \zeta \cdot \overline {r}_{B}(\mathrm {Frob}_v)$
, where
$\chi (\mathrm {Frob}_v) \overline {r}_{B}(\mathrm {Frob}_v) = \zeta \cdot \overline {r}_{B}(\mathrm {Frob}_v)$
, where
![]() $\zeta $
is a primitive mth root of unity and the result follows.
$\zeta $
is a primitive mth root of unity and the result follows.
We shall also need the following variant of Lemma 5.2.4:
Lemma 5.2.6. Let
![]() $F/{\mathbb Q}$
be Galois. Consider representations
$F/{\mathbb Q}$
be Galois. Consider representations
 $$ \begin{align*}\begin{aligned} \overline{r}_A: G_F & \rightarrow \operatorname{\mathrm{GL}}_2({\mathbb F}_p), \\ \overline{r}_B: G_F & \rightarrow \operatorname{\mathrm{GL}}_{m}({\mathbb F}_p). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \overline{r}_A: G_F & \rightarrow \operatorname{\mathrm{GL}}_2({\mathbb F}_p), \\ \overline{r}_B: G_F & \rightarrow \operatorname{\mathrm{GL}}_{m}({\mathbb F}_p). \end{aligned} \end{align*} $$
Assume the following:
-
1. The image of
 $\overline {r}_A(G_{F(\zeta _p)})$
equals
$\overline {r}_A(G_{F(\zeta _p)})$
equals
 $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
.
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
. -
2. There is a cyclic Galois extension
 $E / {\mathbb Q}$
of degree m and linearly disjoint from F, such that, setting
$E / {\mathbb Q}$
of degree m and linearly disjoint from F, such that, setting
 $L = E \cdot F$
, there is a character
$L = E \cdot F$
, there is a character
 $\overline {\psi } : G_L \to {\mathbb F}_p^\times $
with
$\overline {\psi } : G_L \to {\mathbb F}_p^\times $
with
 $\overline {r}_B \cong \operatorname {\mathrm {Ind}}_{G_L}^{G_F} \overline {\psi }$
and
$\overline {r}_B \cong \operatorname {\mathrm {Ind}}_{G_L}^{G_F} \overline {\psi }$
and
 $\overline {r}_B|_{G_{F(\zeta _p)}}$
irreducible.
$\overline {r}_B|_{G_{F(\zeta _p)}}$
irreducible.
Consider the representation
Assume that
![]() $p>2mn+1$
. Then we have the following:
$p>2mn+1$
. Then we have the following:
-
1. The representation
 $\overline {s}$
satisfies conditions (1) and (2) of Definition 5.2.1.
$\overline {s}$
satisfies conditions (1) and (2) of Definition 5.2.1. -
2. If
 $\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and
$\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and
 $\det (\overline {r}_B) = \overline {\varepsilon }^{-m(m-1)/2}$
and the image of
$\det (\overline {r}_B) = \overline {\varepsilon }^{-m(m-1)/2}$
and the image of
 $\overline {\varepsilon }(G_L)={\mathbb F}^{\times }_p$
, then
$\overline {\varepsilon }(G_L)={\mathbb F}^{\times }_p$
, then
 $\overline {s}$
also satisfies condition (3) of Definition 5.2.1 and thus satisfies the Taylor–Wiles big image conditions.
$\overline {s}$
also satisfies condition (3) of Definition 5.2.1 and thus satisfies the Taylor–Wiles big image conditions.
Proof. The representation
![]() $\overline {r}_B$
has solvable image. The assumption that
$\overline {r}_B$
has solvable image. The assumption that
![]() $\overline {r}_B|_{G_{F(\zeta _p)}}$
is irreducible implies that
$\overline {r}_B|_{G_{F(\zeta _p)}}$
is irreducible implies that
![]() $F(\zeta _p)$
and E are linearly disjoint. As in the proof of Lemma 5.2.4, let
$F(\zeta _p)$
and E are linearly disjoint. As in the proof of Lemma 5.2.4, let
![]() $H_A$
and
$H_A$
and
![]() $H_B$
denote the extensions of
$H_B$
denote the extensions of
![]() $F(\zeta _p)$
corresponding to the fixed fields of the kernels of the projective representations associated to
$F(\zeta _p)$
corresponding to the fixed fields of the kernels of the projective representations associated to
![]() $\overline {r}_A$
and
$\overline {r}_A$
and
![]() $\overline {r}_B$
and
$\overline {r}_B$
and
![]() $\widetilde {H}_A$
,
$\widetilde {H}_A$
,
![]() $\widetilde {H}_B$
their Galois closures over
$\widetilde {H}_B$
their Galois closures over
![]() ${\mathbb Q}$
. Let
${\mathbb Q}$
. Let
![]() $\widetilde {H}$
be the compositum of
$\widetilde {H}$
be the compositum of
![]() $\widetilde {H}_A$
and
$\widetilde {H}_A$
and
![]() $\widetilde {H}_B$
. We deduce once more that
$\widetilde {H}_B$
. We deduce once more that
and since
![]() $\mathrm {PSL}_2({\mathbb F}_p)$
has no solvable quotients,
$\mathrm {PSL}_2({\mathbb F}_p)$
has no solvable quotients,
We have
![]() $E \subset \widetilde {H}_B$
, and since
$E \subset \widetilde {H}_B$
, and since
![]() $\overline {r}|_{G_{F(\zeta _p)}}$
is irreducible,
$\overline {r}|_{G_{F(\zeta _p)}}$
is irreducible,
![]() $\operatorname {\mathrm {Gal}}(\widetilde {H}_B/F(\zeta _p)) \to \operatorname {\mathrm {Gal}}(E / {\mathbb Q})$
is surjective.
$\operatorname {\mathrm {Gal}}(\widetilde {H}_B/F(\zeta _p)) \to \operatorname {\mathrm {Gal}}(E / {\mathbb Q})$
is surjective.
Let
![]() $\alpha \in {\mathbb F}^{\times }_p$
be an element such that
$\alpha \in {\mathbb F}^{\times }_p$
be an element such that
![]() $1,\alpha ,\ldots ,\alpha ^{mn-1}$
are all distinct; such an
$1,\alpha ,\ldots ,\alpha ^{mn-1}$
are all distinct; such an
![]() $\alpha $
exists because
$\alpha $
exists because
![]() $p - 1 \ge mn$
. By Chebotarev, we find a prime q unramified in
$p - 1 \ge mn$
. By Chebotarev, we find a prime q unramified in
![]() $\widetilde {H}$
, split in
$\widetilde {H}$
, split in
![]() $F(\zeta _p)$
, and such that for a fixed choice of
$F(\zeta _p)$
, and such that for a fixed choice of
![]() $\mathfrak {q}|q$
in
$\mathfrak {q}|q$
in
![]() $\widetilde {H}$
,
$\widetilde {H}$
,
![]() $\mathrm {Frob}_{\mathfrak {q}}\in \operatorname {\mathrm {Gal}}(\widetilde {H}/F(\zeta _p)) \subset \operatorname {\mathrm {Gal}}(\widetilde {H}/{\mathbb Q})$
has the form
$\mathrm {Frob}_{\mathfrak {q}}\in \operatorname {\mathrm {Gal}}(\widetilde {H}/F(\zeta _p)) \subset \operatorname {\mathrm {Gal}}(\widetilde {H}/{\mathbb Q})$
has the form
where A has eigenvalues with ratio
![]() $\alpha $
and
$\alpha $
and
![]() $\sigma $
projects to a generator of
$\sigma $
projects to a generator of
![]() $\operatorname {\mathrm {Gal}}(E / {\mathbb Q})$
. Hence, by Lemma 5.2.5, the image of (any conjugate of)
$\operatorname {\mathrm {Gal}}(E / {\mathbb Q})$
. Hence, by Lemma 5.2.5, the image of (any conjugate of)
![]() $\mathrm {Frob}_{\mathfrak {q}}$
under
$\mathrm {Frob}_{\mathfrak {q}}$
under
![]() $\overline {s}$
has eigenvalues (up to scalar) given by
$\overline {s}$
has eigenvalues (up to scalar) given by
and in particular, all eigenvalues are distinct since otherwise,
![]() $\alpha ^{km} = 1$
for some
$\alpha ^{km} = 1$
for some
![]() $k < n$
. Since
$k < n$
. Since
![]() $q \equiv 1 \bmod p$
, this implies that
$q \equiv 1 \bmod p$
, this implies that
![]() $\overline {s}$
is decomposed generic, which is property (1).
$\overline {s}$
is decomposed generic, which is property (1).
Property (2) of Definition 5.2.1 follows exactly as in the proof of Lemma 5.2.4.
Now suppose that
![]() $\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and
$\det (\overline {r}_A) = \overline {\varepsilon }^{-m}$
and
![]() $\det (\overline {r}_B) = \overline {\varepsilon }^{-m(m-1)/2}$
and that
$\det (\overline {r}_B) = \overline {\varepsilon }^{-m(m-1)/2}$
and that
![]() $\overline {\varepsilon }(G_L)={\mathbb F}^{\times }_p$
. We now show that property (3) of Definition 5.2.1 holds. Let
$\overline {\varepsilon }(G_L)={\mathbb F}^{\times }_p$
. We now show that property (3) of Definition 5.2.1 holds. Let
![]() $M_A$
and
$M_A$
and
![]() $M_B$
denote the fixed fields of the kernels of
$M_B$
denote the fixed fields of the kernels of
![]() $\overline {r}_A|_{G_{F(\zeta _p)}}$
and
$\overline {r}_A|_{G_{F(\zeta _p)}}$
and
![]() $\overline {r}_B|_{G_{F(\zeta _p)}}$
, respectively. Since
$\overline {r}_B|_{G_{F(\zeta _p)}}$
, respectively. Since
![]() $\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
has no solvable quotients, the map
$\operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
has no solvable quotients, the map
![]() $G_{M_B} \to \operatorname {\mathrm {Gal}}(M_A / F(\zeta _p))$
is surjective. Let
$G_{M_B} \to \operatorname {\mathrm {Gal}}(M_A / F(\zeta _p))$
is surjective. Let
![]() $\beta \in {\mathbb F}_p^\times $
be a primitive root. We claim that we can find
$\beta \in {\mathbb F}_p^\times $
be a primitive root. We claim that we can find
![]() $\sigma \in G_F$
such that
$\sigma \in G_F$
such that
![]() $\overline {r}_A(\sigma ) = \beta ^{-m^2} \cdot I_2$
and
$\overline {r}_A(\sigma ) = \beta ^{-m^2} \cdot I_2$
and
![]() $\overline {r}_B(\sigma ) = \beta ^{m(1-m)} \cdot I_m$
. To see this, first choose
$\overline {r}_B(\sigma ) = \beta ^{m(1-m)} \cdot I_m$
. To see this, first choose
![]() $g \in G_L$
such that
$g \in G_L$
such that
![]() $\overline {\varepsilon }(g) = \beta ^2$
, and let
$\overline {\varepsilon }(g) = \beta ^2$
, and let
![]() $h = \prod _{\tau \in \operatorname {\mathrm {Gal}}(L / F)} {}^\tau g $
. Then
$h = \prod _{\tau \in \operatorname {\mathrm {Gal}}(L / F)} {}^\tau g $
. Then
![]() $\overline {r}_B(h) = \beta ^{m(1-m)} I_m$
, as
$\overline {r}_B(h) = \beta ^{m(1-m)} I_m$
, as
![]() $\prod _{\tau \in \operatorname {\mathrm {Gal}}(L / F)} {}^\tau \overline {\psi } = \det \overline {r}_B|_{G_L} = \overline {\varepsilon }^{-m(m-1)/2}$
. We now choose
$\prod _{\tau \in \operatorname {\mathrm {Gal}}(L / F)} {}^\tau \overline {\psi } = \det \overline {r}_B|_{G_L} = \overline {\varepsilon }^{-m(m-1)/2}$
. We now choose
![]() $\sigma $
of the form
$\sigma $
of the form
![]() $h \gamma $
, where
$h \gamma $
, where
![]() $\gamma \in G_{M_B}$
; since
$\gamma \in G_{M_B}$
; since
![]() $\overline {r}_B(\gamma )$
is trivial, this means that
$\overline {r}_B(\gamma )$
is trivial, this means that
![]() $\overline {r}_{B}(\sigma ) = \overline {r}_{B}(h)$
is of the correct form. We also have
$\overline {r}_{B}(\sigma ) = \overline {r}_{B}(h)$
is of the correct form. We also have
![]() $\det \overline {r}_A(h) = \overline {\varepsilon }^{-m}(g)^{m} = \beta ^{-2m^2}$
. Since
$\det \overline {r}_A(h) = \overline {\varepsilon }^{-m}(g)^{m} = \beta ^{-2m^2}$
. Since
![]() $G_{M_B} \to \operatorname {\mathrm {Gal}}(M_A / F(\zeta _p)) \simeq \operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
is surjective, we choose
$G_{M_B} \to \operatorname {\mathrm {Gal}}(M_A / F(\zeta _p)) \simeq \operatorname {\mathrm {SL}}_2({\mathbb F}_p)$
is surjective, we choose
![]() $\gamma \in G_{M_B}$
so that
$\gamma \in G_{M_B}$
so that
![]() $\overline {r}_A(\gamma ) = \beta ^{-m^2} \cdot \overline {r}_A(h)^{-1} $
, and then
$\overline {r}_A(\gamma ) = \beta ^{-m^2} \cdot \overline {r}_A(h)^{-1} $
, and then
![]() $\overline {r}_A(\sigma ) = \beta ^{-m^2} \cdot I_2$
.
$\overline {r}_A(\sigma ) = \beta ^{-m^2} \cdot I_2$
.
By construction,
![]() $\overline {s}(\sigma )$
is scalar. We have
$\overline {s}(\sigma )$
is scalar. We have
![]() $\overline {\varepsilon }(\sigma ) = \beta ^{2m} \neq 1$
, as
$\overline {\varepsilon }(\sigma ) = \beta ^{2m} \neq 1$
, as
![]() $p-1> 2m$
because
$p-1> 2m$
because
![]() $p> 2nm + 1$
, so
$p> 2nm + 1$
, so
![]() $\sigma \in G_F - G_{F(\zeta _p)}$
, as required.
$\sigma \in G_F - G_{F(\zeta _p)}$
, as required.
5.3 Character building lemmas
In this section, we construct some induced extensions with certain desirable local properties. We begin with the following well-known lemma:
Lemma 5.3.1 (Globalizing local characters).
Let F be a number field, and let S be a finite set of places of F. Let
![]() $\psi _v: G_{F_v} \rightarrow {\mathbb Z}/n{\mathbb Z}$
be a collection of characters for all
$\psi _v: G_{F_v} \rightarrow {\mathbb Z}/n{\mathbb Z}$
be a collection of characters for all
![]() $v \in S$
. Assume that S does not contain any places
$v \in S$
. Assume that S does not contain any places
![]() $v|2$
. Then there exists a global character
$v|2$
. Then there exists a global character
![]() $\chi : G_F \rightarrow {\mathbb Z}/n{\mathbb Z}$
such that
$\chi : G_F \rightarrow {\mathbb Z}/n{\mathbb Z}$
such that
![]() $\chi |_{G_{F_v}} = \psi _v$
for all
$\chi |_{G_{F_v}} = \psi _v$
for all
![]() $v \in S$
.
$v \in S$
.
Proof. This is a consequence of [Reference Artin and TateAT09, §X Thm. 5] (see also [Reference ConradCon11, Appendix A]). More precisely, the claim holds (without the hypothesis on S) if n is odd. If n is even, there exists an explicitly defined element
which is a perfect nth power for all but a finite set (possibly empty) of places
![]() $S_{F}$
of primes
$S_{F}$
of primes
![]() $v|2$
. Then the
$v|2$
. Then the
![]() $\psi _v$
come from a global character
$\psi _v$
come from a global character
![]() $\chi $
of order n if and only if either
$\chi $
of order n if and only if either
![]() $S_F \not \subset S$
, or
$S_F \not \subset S$
, or
![]() $S_F \subset S$
and
$S_F \subset S$
and
Since we have assumed that S contains no places above
![]() $2$
, either
$2$
, either
![]() $S_F$
is empty or
$S_F$
is empty or
![]() $S_F \not \subset S$
, so the result follows.
$S_F \not \subset S$
, so the result follows.
Remark 5.3.2. One cannot drop the hypothesis on S in general because of the Grunwald–Wang phenomenon (e.g.,
![]() $F = {\mathbb Q}$
,
$F = {\mathbb Q}$
,
![]() $v = 2$
,
$v = 2$
,
![]() $n = 8$
and
$n = 8$
and
![]() $\psi _2$
unramified with order
$\psi _2$
unramified with order
![]() $8$
). If one considers general F, one cannot even globalize a local character
$8$
). If one considers general F, one cannot even globalize a local character
![]() $\psi _v$
up to a character
$\psi _v$
up to a character
![]() $\phi _v$
which is unramified at v. Let
$\phi _v$
which is unramified at v. Let
![]() $F = {\mathbb Q}(\sqrt {-5})$
, and consider a character
$F = {\mathbb Q}(\sqrt {-5})$
, and consider a character
Since
![]() $16 \in F^{\times }$
is a perfect
$16 \in F^{\times }$
is a perfect
![]() $8$
th power for all
$8$
th power for all
![]() $v|F$
of odd residue characteristic (this is true even for
$v|F$
of odd residue characteristic (this is true even for
![]() $F={\mathbb Q}$
) and also in
$F={\mathbb Q}$
) and also in
![]() $F^{\times }_{\infty } \simeq {\mathbb C}^{\times }$
, it follows that the restriction:
$F^{\times }_{\infty } \simeq {\mathbb C}^{\times }$
, it follows that the restriction:
satisfies
![]() $\chi _2(16) = 1$
. Since
$\chi _2(16) = 1$
. Since
![]() $F_2/{\mathbb Q}_2$
is ramified of degree
$F_2/{\mathbb Q}_2$
is ramified of degree
![]() $2$
, we find that
$2$
, we find that
![]() $16$
has valuation
$16$
has valuation
![]() $8$
, and hence,
$8$
, and hence,
![]() $\phi _2(16) = 1$
for any unramified character
$\phi _2(16) = 1$
for any unramified character
![]() $F^{\times }_2\rightarrow {\mathbb Z}/8{\mathbb Z}$
. Since neither
$F^{\times }_2\rightarrow {\mathbb Z}/8{\mathbb Z}$
. Since neither
![]() $2$
nor
$2$
nor
![]() $-1$
is a square in
$-1$
is a square in
![]() $F_2 \simeq {\mathbb Q}_2(\sqrt {-5})$
, it follows that
$F_2 \simeq {\mathbb Q}_2(\sqrt {-5})$
, it follows that
![]() $16$
is not a perfect
$16$
is not a perfect
![]() $8$
th power in
$8$
th power in
![]() $F^{\times }_2$
, and thus, there exists a local character
$F^{\times }_2$
, and thus, there exists a local character
![]() $\psi _2: F^{\times }_2 \rightarrow {\mathbb Z}/8{\mathbb Z}$
such that
$\psi _2: F^{\times }_2 \rightarrow {\mathbb Z}/8{\mathbb Z}$
such that
![]() $\psi _2(16) = -1$
. But from the above, we see that there is no global character
$\psi _2(16) = -1$
. But from the above, we see that there is no global character
![]() $\chi $
such that
$\chi $
such that
![]() $\chi _2 = \psi _2 \phi _2$
for an unramified character
$\chi _2 = \psi _2 \phi _2$
for an unramified character
![]() $\phi _2$
.
$\phi _2$
.
We now show that any character over a CM field can be written as an mth power of another character over some finite CM extension satisfying certain properties. The argument is essentially the same as in the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 7.1.11].
Lemma 5.3.3. Let
![]() $\eta $
be a finite order character of
$\eta $
be a finite order character of
![]() $G_F$
for a CM field F, let m be an integer, and let
$G_F$
for a CM field F, let m be an integer, and let
![]() $F^{\mathrm {avoid}}/F$
be a finite extension. Then there exists a totally real Galois extension
$F^{\mathrm {avoid}}/F$
be a finite extension. Then there exists a totally real Galois extension
![]() $M/{\mathbb Q}$
linearly disjoint from
$M/{\mathbb Q}$
linearly disjoint from
![]() $F^{\mathrm {avoid}}$
and a character
$F^{\mathrm {avoid}}$
and a character
![]() $\psi $
of
$\psi $
of
![]() $G_{M \cdot F}$
such that
$G_{M \cdot F}$
such that
![]() $\eta |_{G_{MF}}=\psi ^m$
. Moreover, if
$\eta |_{G_{MF}}=\psi ^m$
. Moreover, if
![]() $\eta $
is unramified at all v dividing some finite set of primes T of
$\eta $
is unramified at all v dividing some finite set of primes T of
![]() ${\mathbb Q}$
not including
${\mathbb Q}$
not including
![]() $2$
, then we may take M to be totally split at all primes dividing those in T, and
$2$
, then we may take M to be totally split at all primes dividing those in T, and
![]() $\psi $
to be unramified at primes dividing those in T.
$\psi $
to be unramified at primes dividing those in T.
Proof. By induction, it suffices to consider the case when m is prime. Assume that
![]() $\eta $
has order n. There is an exact sequence:
$\eta $
has order n. There is an exact sequence:
The character
![]() $\eta $
gives a class in
$\eta $
gives a class in
![]() $H^1(F,{\mathbb Z}/n{\mathbb Z})$
which we want to write as an mth power, which amounts to lifting this class to
$H^1(F,{\mathbb Z}/n{\mathbb Z})$
which we want to write as an mth power, which amounts to lifting this class to
![]() $H^1(F,{\mathbb Z}/mn{\mathbb Z})$
. The obstruction to this is an element
$H^1(F,{\mathbb Z}/mn{\mathbb Z})$
. The obstruction to this is an element
![]() $\partial \eta $
lying in
$\partial \eta $
lying in
where the injectivity of the first map follows from Hochschild–Serre and the fact that
![]() $[F(\zeta _m):F]$
is prime to m (since m is prime). From the Albert–Brauer–Hasse–Noether theorem, there is an injection
$[F(\zeta _m):F]$
is prime to m (since m is prime). From the Albert–Brauer–Hasse–Noether theorem, there is an injection
The image of the class
![]() $\partial \eta $
is zero for all v not dividing a finite set of places S of
$\partial \eta $
is zero for all v not dividing a finite set of places S of
![]() ${\mathbb Q}$
(the places where
${\mathbb Q}$
(the places where
![]() $\eta $
is ramified) and is zero for v dividing places in T (since
$\eta $
is ramified) and is zero for v dividing places in T (since
![]() $\eta $
is unramified there and there is no obstruction to lifting an unramified local character). Since F is totally imaginary and
$\eta $
is unramified there and there is no obstruction to lifting an unramified local character). Since F is totally imaginary and
![]() $\mathrm {Br}({\mathbb C}) = 0$
, we may assume S consists only of finite primes, and we may also assume that
$\mathrm {Br}({\mathbb C}) = 0$
, we may assume S consists only of finite primes, and we may also assume that
![]() $\infty \in T$
. If K is a local field and
$\infty \in T$
. If K is a local field and
![]() $L/K$
has degree m, then the map
$L/K$
has degree m, then the map
![]() $\mathrm {Br}(K)[m] \rightarrow \mathrm {Br}(L)$
is trivial [Reference CasselsCF86, §VI, Thm. 3]. Hence, any class in
$\mathrm {Br}(K)[m] \rightarrow \mathrm {Br}(L)$
is trivial [Reference CasselsCF86, §VI, Thm. 3]. Hence, any class in
![]() $\mathrm {Br}(F(\zeta _m))[m]$
is trivial in
$\mathrm {Br}(F(\zeta _m))[m]$
is trivial in
![]() $F(\zeta _m) \cdot M$
whenever
$F(\zeta _m) \cdot M$
whenever
![]() $[M_v:{\mathbb Q}_v]$
is divisible by
$[M_v:{\mathbb Q}_v]$
is divisible by
![]() $m [F(\zeta _m):{\mathbb Q}]$
for any prime v in S. Hence, it suffices to find such a Galois extension
$m [F(\zeta _m):{\mathbb Q}]$
for any prime v in S. Hence, it suffices to find such a Galois extension
![]() $M/{\mathbb Q}$
disjoint from
$M/{\mathbb Q}$
disjoint from
![]() $F^{\mathrm {avoid}}$
, in which the places in T are totally split (since
$F^{\mathrm {avoid}}$
, in which the places in T are totally split (since
![]() $\infty \in T$
, this implies that M is totally real). This is essentially done in [Reference Artin and TateAT09, §X Thm. 6], and we can appeal to [Reference Clozel, Harris and TaylorCHT08, Lemma 4.1.2] for the precise statement we need. Since
$\infty \in T$
, this implies that M is totally real). This is essentially done in [Reference Artin and TateAT09, §X Thm. 6], and we can appeal to [Reference Clozel, Harris and TaylorCHT08, Lemma 4.1.2] for the precise statement we need. Since
![]() $\eta $
is unramified at primes in T, for each
$\eta $
is unramified at primes in T, for each
![]() $v|T,$
the image of
$v|T,$
the image of
![]() $\psi |_{I_{(M \cdot F)_v}}$
has order dividing m. Thus, by Lemma 5.3.1, we may twist
$\psi |_{I_{(M \cdot F)_v}}$
has order dividing m. Thus, by Lemma 5.3.1, we may twist
![]() $\psi $
by another character of order m (which doesn’t change
$\psi $
by another character of order m (which doesn’t change
![]() $\psi ^m$
) so that it is unramified at
$\psi ^m$
) so that it is unramified at
![]() $v|T$
.
$v|T$
.
6 Automorphy of compatible systems
6.1 Compatible systems and purity
We recall the following definition from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, §7].
Definition 6.1.1. Let F be a number field. A very weakly compatible system
![]() ${\mathcal R}$
(of rank n representations of
${\mathcal R}$
(of rank n representations of
![]() $G_F$
, with coefficients in M) is by definition a tuple
$G_F$
, with coefficients in M) is by definition a tuple
where
-
1. M is a number field;
-
2. S is a finite set of finite places of F;
-
3. for each finite place
 $v \not \in S$
of F,
$v \not \in S$
of F,
 $Q_v(X) \in M[X]$
is a monic degree n polynomial;
$Q_v(X) \in M[X]$
is a monic degree n polynomial; -
4. for each
 $\tau : F \hookrightarrow \overline {M}$
,
$\tau : F \hookrightarrow \overline {M}$
,
 $H_\tau $
is a multiset of integers;
$H_\tau $
is a multiset of integers; -
5. for each finite place
 $\lambda $
of M (say of residue characteristic l), is a continuous, semisimple representation satisfying the following conditions:
$\lambda $
of M (say of residue characteristic l), is a continuous, semisimple representation satisfying the following conditions: $$\begin{align*}r_\lambda : G_F \to \operatorname{\mathrm{GL}}_n(\overline{M}_\lambda) \end{align*}$$
$$\begin{align*}r_\lambda : G_F \to \operatorname{\mathrm{GL}}_n(\overline{M}_\lambda) \end{align*}$$
-
(a) If
 $v \not \in S$
and
$v \not \in S$
and
 $v \nmid l$
, then
$v \nmid l$
, then
 $r_\lambda |_{G_{F_v}}$
is unramified and the characteristic polynomial of
$r_\lambda |_{G_{F_v}}$
is unramified and the characteristic polynomial of
 $\mathrm {Frob}_v$
equals
$\mathrm {Frob}_v$
equals
 $Q_v(X)$
.
$Q_v(X)$
. -
(b) For l outside a set of primes of Dirichlet density 0,
 $r_\lambda $
is crystalline and
$r_\lambda $
is crystalline and
 $\mathrm {HT}_\tau (r_\lambda ) = H_\tau $
.
$\mathrm {HT}_\tau (r_\lambda ) = H_\tau $
. -
(c) For every l, we have
 $\mathrm {HT}_\tau (\det r_\lambda ) = \sum _{h \in H_\tau } h$
.
$\mathrm {HT}_\tau (\det r_\lambda ) = \sum _{h \in H_\tau } h$
.
-
If
![]() $F' / F$
is a finite extension, then we may define the restricted very weakly compatible system
$F' / F$
is a finite extension, then we may define the restricted very weakly compatible system
where
![]() $S_{F'}$
is the set of places of
$S_{F'}$
is the set of places of
![]() $F'$
lying above S,
$F'$
lying above S,
![]() $Q_w(X) = \det r_\lambda (X - \mathrm {Frob}_w)$
(thus independent of
$Q_w(X) = \det r_\lambda (X - \mathrm {Frob}_w)$
(thus independent of
![]() $\lambda $
), and
$\lambda $
), and
![]() $H^{\prime }_{\tau } = H_{\tau |_F}$
. If
$H^{\prime }_{\tau } = H_{\tau |_F}$
. If
are very weakly compatible systems with a common coefficient field M, then we can define the tensor product
where we take
![]() $Q_v(X) = \det (r_{1, \lambda } \otimes r_{2, \lambda })(X - \mathrm {Frob}_v)$
(thus independent of
$Q_v(X) = \det (r_{1, \lambda } \otimes r_{2, \lambda })(X - \mathrm {Frob}_v)$
(thus independent of
![]() $\lambda $
) and
$\lambda $
) and
![]() $H_\tau = \{ k + l \, | \, k \in H_{1 ,\tau }, l \in H_{2, \tau } \}$
(sums taken with multiplicity).
$H_\tau = \{ k + l \, | \, k \in H_{1 ,\tau }, l \in H_{2, \tau } \}$
(sums taken with multiplicity).
The following definition summarizes some possible properties of very weakly compatible systems. These were all defined in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23], with the exception of (3) (‘weakly automorphic’). This condition arises for us because we consider tensor products of compatible systems, one of which has poorly controlled ramification. Lemma 6.1.4 gives conditions under which ‘weakly automorphic’ can be upgraded to ‘automorphic’.
Definition 6.1.2. Let
be a very weakly compatible system. We say that
![]() ${\mathcal R}$
is
${\mathcal R}$
is
-
1. pure of weight
 $m \in {\mathbb Z}$
if it satisfies the following conditions:
$m \in {\mathbb Z}$
if it satisfies the following conditions:-
(a) for each
 $v \not \in S$
, each root
$v \not \in S$
, each root
 $\alpha $
of
$\alpha $
of
 $Q_v(X)$
in
$Q_v(X)$
in
 $\overline {M}$
and each
$\overline {M}$
and each
 $\iota :\overline {M} \hookrightarrow {\mathbb C}$
, we have
$\iota :\overline {M} \hookrightarrow {\mathbb C}$
, we have  $$\begin{align*}| \iota \alpha |^2 = q_v^m; \end{align*}$$
$$\begin{align*}| \iota \alpha |^2 = q_v^m; \end{align*}$$
-
(b) for each
 $\tau :F \hookrightarrow \overline {M}$
and each complex conjugation c in
$\tau :F \hookrightarrow \overline {M}$
and each complex conjugation c in
 $\operatorname {\mathrm {Gal}}(\overline {M}/{\mathbb Q})$
, we have
$\operatorname {\mathrm {Gal}}(\overline {M}/{\mathbb Q})$
, we have  $$\begin{align*}H_{c \tau} = \{ m-h: \,\,\, h \in H_\tau\}. \end{align*}$$
$$\begin{align*}H_{c \tau} = \{ m-h: \,\,\, h \in H_\tau\}. \end{align*}$$
-
-
2. automorphic, if there is a regular algebraic, cuspidal automorphic representation
 $\pi $
of
$\pi $
of
 $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
and an embedding
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
and an embedding
 $\iota : M \hookrightarrow {\mathbb C}$
such that for every finite place
$\iota : M \hookrightarrow {\mathbb C}$
such that for every finite place
 $v \not \in S$
of F,
$v \not \in S$
of F,
 $\pi _v$
is unramified and
$\pi _v$
is unramified and
 $\operatorname {rec}^T_{F_v}(\pi _v)(\mathrm {Frob}_v)$
has characteristic polynomial
$\operatorname {rec}^T_{F_v}(\pi _v)(\mathrm {Frob}_v)$
has characteristic polynomial
 $\iota (Q_v(X))$
.
$\iota (Q_v(X))$
. -
3. weakly automorphic of level prime to T if T is a finite set of finite places of F, disjoint from S, and there is a regular algebraic, cuspidal automorphic representation
 $\pi $
of
$\pi $
of
 $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
and an embedding
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
and an embedding
 $\iota : M \hookrightarrow {\mathbb C}$
such that for all but finitely many finite places
$\iota : M \hookrightarrow {\mathbb C}$
such that for all but finitely many finite places
 $v \not \in S$
of F, and for every
$v \not \in S$
of F, and for every
 $v \in T$
,
$v \in T$
,
 $\pi _v$
is unramified and
$\pi _v$
is unramified and
 $\operatorname {rec}^T_{F_v}(\pi _v)(\mathrm {Frob}_v)$
has characteristic polynomial
$\operatorname {rec}^T_{F_v}(\pi _v)(\mathrm {Frob}_v)$
has characteristic polynomial
 $\iota (Q_v(X))$
. We will say that
$\iota (Q_v(X))$
. We will say that
 $\mathcal {R}$
is simply ‘weakly automorphic’ if it is weakly automorphic of level prime to the empty set.
$\mathcal {R}$
is simply ‘weakly automorphic’ if it is weakly automorphic of level prime to the empty set. -
4. irreducible, if for l outside a set of primes of Dirichlet density 0, and for all
 $\lambda | l$
of M,
$\lambda | l$
of M,
 $r_\lambda $
is irreducible.
$r_\lambda $
is irreducible. -
5. strongly irreducible, if for every finite extension
 $F' / F$
, the compatible system
$F' / F$
, the compatible system
 ${\mathcal R}|_{G_{F'}}$
is irreducible.
${\mathcal R}|_{G_{F'}}$
is irreducible.
For a CM number field F, and a regular algebraic weight
![]() $\lambda $
, cuspidal automorphic representation
$\lambda $
, cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
, there is an associated automorphic very weakly compatible system
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
, there is an associated automorphic very weakly compatible system
where
![]() $H_\tau = \{ \lambda _{\tau , 1} + 1, \lambda _{\tau , 2} \}$
(see [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.10]).
$H_\tau = \{ \lambda _{\tau , 1} + 1, \lambda _{\tau , 2} \}$
(see [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.10]).
We now recall that the potential automorphy of symmetric powers of
![]() ${\mathcal R}$
is enough to imply purity.
${\mathcal R}$
is enough to imply purity.
Lemma 6.1.3. Let
![]() ${\mathcal R} = (M, S, \{ Q_v(X) \}, \{ r_\lambda \}, \{H_\tau \})$
be a very weakly compatible system of rank 2 representations of
${\mathcal R} = (M, S, \{ Q_v(X) \}, \{ r_\lambda \}, \{H_\tau \})$
be a very weakly compatible system of rank 2 representations of
![]() $G_F$
such that
$G_F$
such that
![]() $H_{\tau } = \{0,m\}$
for a fixed
$H_{\tau } = \{0,m\}$
for a fixed
![]() $m \in {\mathbb N}$
for all
$m \in {\mathbb N}$
for all
![]() $\tau $
. Fix a finite place
$\tau $
. Fix a finite place
![]() $v_0$
of F which is not in S, and let
$v_0$
of F which is not in S, and let
![]() $X_0 = \{v_0\}$
. Suppose that for infinitely many
$X_0 = \{v_0\}$
. Suppose that for infinitely many
![]() $n\ge 1$
, we can find a finite Galois extension
$n\ge 1$
, we can find a finite Galois extension
![]() $F_n / F$
such that the very weakly compatible system
$F_n / F$
such that the very weakly compatible system
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} |_{F_n}$
is weakly automorphic of level prime to
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} |_{F_n}$
is weakly automorphic of level prime to
![]() $X_{0, F_n} = \{ v | v_0 \}$
. Then the roots
$X_{0, F_n} = \{ v | v_0 \}$
. Then the roots
![]() $\alpha _1, \alpha _2$
of
$\alpha _1, \alpha _2$
of
![]() $Q_{v_0}(X)$
in
$Q_{v_0}(X)$
in
![]() $\overline {M}$
satisfy
$\overline {M}$
satisfy
for each
![]() $\iota :\overline {M} \hookrightarrow {\mathbb C}$
.
$\iota :\overline {M} \hookrightarrow {\mathbb C}$
.
Proof. Choose a place
![]() $v_n|v_0$
in
$v_n|v_0$
in
![]() $F_n$
and fix
$F_n$
and fix
![]() $\iota :\overline {M}\hookrightarrow {\mathbb C}$
. We are assuming that
$\iota :\overline {M}\hookrightarrow {\mathbb C}$
. We are assuming that
![]() $\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} |_{F_n}$
is associated to a cuspidal automorphic representation
$\operatorname {\mathrm {Sym}}^{n-1} \mathcal {R} |_{F_n}$
is associated to a cuspidal automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $\operatorname {\mathrm {GL}}_{n}(\mathbf {A}_{F_n})$
and
$\operatorname {\mathrm {GL}}_{n}(\mathbf {A}_{F_n})$
and
![]() $\Pi _{v_n}$
is unramified. Up to a finite order character, the determinant of our rank n automorphic compatible system is given by the
$\Pi _{v_n}$
is unramified. Up to a finite order character, the determinant of our rank n automorphic compatible system is given by the
![]() $-mn(n-1)/2$
th power of the cyclotomic character, so the central character of
$-mn(n-1)/2$
th power of the cyclotomic character, so the central character of
![]() $\Pi $
is (again, up to a finite order Hecke character)
$\Pi $
is (again, up to a finite order Hecke character)
![]() $| \cdot |^{n(m-1)(1-n)/2}$
, and in particular,
$| \cdot |^{n(m-1)(1-n)/2}$
, and in particular,
![]() $\Pi | \cdot |^{(m-1)(n-1)/2}$
is unitary. Since we know that
$\Pi | \cdot |^{(m-1)(n-1)/2}$
is unitary. Since we know that
![]() $|\iota (\alpha _1\alpha _2)| = q_{v_0}^m$
, it suffices to prove that
$|\iota (\alpha _1\alpha _2)| = q_{v_0}^m$
, it suffices to prove that
![]() $|\iota \alpha _i|\le q_{v_0}^{m/2}$
for
$|\iota \alpha _i|\le q_{v_0}^{m/2}$
for
![]() $i = 1, 2$
. Let
$i = 1, 2$
. Let
![]() $q_{v_n} = q_{v_0}^f$
. As in the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor. 7.1.13], we can apply the Jacquet–Shalika bound [Reference Jacquet and ShalikaJS81, Cor. 2.5] to deduce that
$q_{v_n} = q_{v_0}^f$
. As in the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor. 7.1.13], we can apply the Jacquet–Shalika bound [Reference Jacquet and ShalikaJS81, Cor. 2.5] to deduce that
![]() $|\iota \left ( \alpha _i^{f(n-1)}\right )|\le q_{v_n}^{((m-1)(n-1) + n)/2}$
, so
$|\iota \left ( \alpha _i^{f(n-1)}\right )|\le q_{v_n}^{((m-1)(n-1) + n)/2}$
, so
![]() $|\iota \alpha _i|\le q_{v_0}^{m/2+1/2(n-1)}$
. Letting n tend to
$|\iota \alpha _i|\le q_{v_0}^{m/2+1/2(n-1)}$
. Letting n tend to
![]() $\infty $
gives the desired bound on
$\infty $
gives the desired bound on
![]() $|\iota \alpha _i|$
.
$|\iota \alpha _i|$
.
Lemma 6.1.4. Let F be a CM number field, and let
be a very weakly compatible system of rank n representations of
![]() $G_F$
which is weakly automorphic, corresponding to a regular algebraic, cuspidal automorphic representation
$G_F$
which is weakly automorphic, corresponding to a regular algebraic, cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
, and pure of weight
$\operatorname {\mathrm {GL}}_n(\mathbf {A}_F)$
, and pure of weight
![]() $m \in {\mathbb Z}$
. Then
$m \in {\mathbb Z}$
. Then
![]() ${\mathcal R}$
is automorphic.
${\mathcal R}$
is automorphic.
Proof. Choose some embedding of M in
![]() ${\mathbb C}$
. By assumption, there is a finite set
${\mathbb C}$
. By assumption, there is a finite set
![]() $S'\supseteq S$
of finite places of F such that for each
$S'\supseteq S$
of finite places of F such that for each
![]() $v \not \in S'$
,
$v \not \in S'$
,
![]() $\pi _v$
is unramified and
$\pi _v$
is unramified and
![]() $\operatorname {rec}^T_{F_v}(\pi _v)(\mathrm {Frob}_v)$
has characteristic polynomial
$\operatorname {rec}^T_{F_v}(\pi _v)(\mathrm {Frob}_v)$
has characteristic polynomial
![]() $Q_v(X)$
. We must show that this holds for all
$Q_v(X)$
. We must show that this holds for all
![]() $v \not \in S$
. Choose
$v \not \in S$
. Choose
![]() $v \in S' - S$
, a rational prime p not lying under
$v \in S' - S$
, a rational prime p not lying under
![]() $ v$
, and an isomorphism
$ v$
, and an isomorphism
![]() $\iota : \overline {{\mathbb Q}}_p \to {\mathbb C}$
. Let
$\iota : \overline {{\mathbb Q}}_p \to {\mathbb C}$
. Let
![]() $\lambda $
denote the place of M induced by
$\lambda $
denote the place of M induced by
![]() $\iota ^{-1}$
. Then the Chebotarev density theorem implies that there is an isomorphism
$\iota ^{-1}$
. Then the Chebotarev density theorem implies that there is an isomorphism
![]() $r_\lambda \cong r_\iota (\pi )$
. By assumption,
$r_\lambda \cong r_\iota (\pi )$
. By assumption,
![]() $r_\lambda |_{G_{F_v}}$
is unramified and pure of weight m. By [Reference VarmaVar24, Theorem 1], there is an isomorphism
$r_\lambda |_{G_{F_v}}$
is unramified and pure of weight m. By [Reference VarmaVar24, Theorem 1], there is an isomorphism
![]() $r_\iota (\pi )|_{W_{F_v}}^{\mathrm {ss}} \cong \iota ^{-1} \operatorname {rec}^T_{F_v}(\pi _v)^{\mathrm {ss}}$
. We deduce that
$r_\iota (\pi )|_{W_{F_v}}^{\mathrm {ss}} \cong \iota ^{-1} \operatorname {rec}^T_{F_v}(\pi _v)^{\mathrm {ss}}$
. We deduce that
![]() $\pi _v$
is a subquotient of an unramified principal series – namely, the one with Satake parameter determined by
$\pi _v$
is a subquotient of an unramified principal series – namely, the one with Satake parameter determined by
![]() $Q_v(X)$
. Since
$Q_v(X)$
. Since
![]() $r_\lambda |_{G_{F_v}}$
is pure, this principal series representation is irreducible and
$r_\lambda |_{G_{F_v}}$
is pure, this principal series representation is irreducible and
![]() $\pi _v$
is unramified, as desired.
$\pi _v$
is unramified, as desired.
Lemma 6.1.5. Let F be a number field and let
be a very weakly compatible system of rank
![]() $2$
representations of
$2$
representations of
![]() $G_F$
which is strongly irreducible. Let
$G_F$
which is strongly irreducible. Let
![]() ${\mathcal L}({\mathcal R})$
denote the set of primes l satisfying the following conditions:
${\mathcal L}({\mathcal R})$
denote the set of primes l satisfying the following conditions:
-
1.
 $l \not \in S$
and for each place
$l \not \in S$
and for each place
 $\lambda | l$
of M,
$\lambda | l$
of M,
 $r_\lambda $
is crystalline of Hodge–Tate weights
$r_\lambda $
is crystalline of Hodge–Tate weights
 $H_\tau $
.
$H_\tau $
. -
2. For each place
 $\lambda | l$
of M,
$\lambda | l$
of M,
 $\overline {r}_\lambda (G_{\widetilde {F}})$
contains a conjugate of
$\overline {r}_\lambda (G_{\widetilde {F}})$
contains a conjugate of
 $\operatorname {\mathrm {SL}}_2({\mathbb F}_l)$
, where
$\operatorname {\mathrm {SL}}_2({\mathbb F}_l)$
, where
 $\widetilde {F}$
is the Galois closure of
$\widetilde {F}$
is the Galois closure of
 $F / {\mathbb Q}$
.
$F / {\mathbb Q}$
.
Then
![]() ${\mathcal L}({\mathcal R})$
has Dirichlet density 1.
${\mathcal L}({\mathcal R})$
has Dirichlet density 1.
Proof. The set of primes l having property (1) has Dirichlet density 1, by definition of a very weakly compatible system. The lemma therefore follows from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.3].
6.2 Potential automorphy theorems
Our goal in this section is to prove Theorem 6.2.1. The proof will occupy the whole section, but to keep the presentation organized and somewhat motivated, we deduce it from Theorem 6.2.4 below, which we will in turn deduce from Proposition 6.2.3.
Theorem 6.2.1. Let F be an imaginary CM number field, and let
be a very weakly compatible system of rank
![]() $2$
representations of
$2$
representations of
![]() $G_F$
. Let
$G_F$
. Let
![]() $m \geq 1$
be an integer, and suppose that the following conditions are satisfied:
$m \geq 1$
be an integer, and suppose that the following conditions are satisfied:
-
1. For each
 $\tau $
,
$\tau $
,
 $H_\tau = \{ 0, m \}$
.
$H_\tau = \{ 0, m \}$
. -
2.
 $\det r_\lambda = \varepsilon ^{-m}$
.
$\det r_\lambda = \varepsilon ^{-m}$
. -
3.
 ${\mathcal R}$
is strongly irreducible.
${\mathcal R}$
is strongly irreducible.
Then
![]() ${\mathcal R}$
is pure of weight m, and for each
${\mathcal R}$
is pure of weight m, and for each
![]() $n \geq 1$
, there exists a finite CM extension
$n \geq 1$
, there exists a finite CM extension
![]() $F_n / F$
such that
$F_n / F$
such that
![]() $F_n / {\mathbb Q}$
is Galois and
$F_n / {\mathbb Q}$
is Galois and
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_n}}$
is automorphic.
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_n}}$
is automorphic.
Proof. We may assume that
![]() $m \ge 2$
since otherwise, the result follows from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor 7.1.12]. Let
$m \ge 2$
since otherwise, the result follows from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor 7.1.12]. Let
![]() $v_0 \not \in S$
be a place of F. Theorem 6.2.4 states that we can find, for each
$v_0 \not \in S$
be a place of F. Theorem 6.2.4 states that we can find, for each
![]() $n \geq 1$
, a CM extension
$n \geq 1$
, a CM extension
![]() $F_n / F$
, Galois over
$F_n / F$
, Galois over
![]() ${\mathbb Q}$
, such that
${\mathbb Q}$
, such that
![]() $\operatorname {\mathrm {Sym}}^{n-1}{\mathcal R}|_{G_{F_n}}$
is weakly automorphic of level prime to
$\operatorname {\mathrm {Sym}}^{n-1}{\mathcal R}|_{G_{F_n}}$
is weakly automorphic of level prime to
![]() $\{ v | v_0 \}$
. By Lemma 6.1.3, the roots of
$\{ v | v_0 \}$
. By Lemma 6.1.3, the roots of
![]() $Q_{v_0}(X)$
are
$Q_{v_0}(X)$
are
![]() $q_{v_0}$
-Weil numbers of weight m. Since
$q_{v_0}$
-Weil numbers of weight m. Since
![]() $v_0 \not \in S$
is arbitrary, this shows that the compatible system
$v_0 \not \in S$
is arbitrary, this shows that the compatible system
![]() ${\mathcal R}$
is pure of weight m. We can then apply Lemma 6.1.4 to conclude that
${\mathcal R}$
is pure of weight m. We can then apply Lemma 6.1.4 to conclude that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_n}}$
is automorphic, as required.
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_n}}$
is automorphic, as required.
Remark 6.2.2. We assume in our arguments below that
![]() $m>1$
. Our argument certainly applies in principle to the case
$m>1$
. Our argument certainly applies in principle to the case
![]() $m=1$
, but certain statements we make through the proof assume that
$m=1$
, but certain statements we make through the proof assume that
![]() $m \ge 2$
, and so this assumption avoids having to make the necessary extra remarks to cover the case
$m \ge 2$
, and so this assumption avoids having to make the necessary extra remarks to cover the case
![]() $m=1$
. Moreover, our argument in the case
$m=1$
. Moreover, our argument in the case
![]() $m=1$
would involve tensoring
$m=1$
would involve tensoring
![]() ${\mathcal R}$
with auxiliary
${\mathcal R}$
with auxiliary
![]() $1$
-dimensional representations and not so surprisingly can be simplified to the point where it becomes very similar to the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor 7.1.12].
$1$
-dimensional representations and not so surprisingly can be simplified to the point where it becomes very similar to the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor 7.1.12].
Before giving our first technical result toward the proof of Theorem 6.2.4 (and hence Theorem 6.2.1 above), we sketch the idea of the proof. We begin with the strongly irreducible, very weakly compatible system
![]() ${\mathcal R}$
of rank 2 and parallel Hodge–Tate weights
${\mathcal R}$
of rank 2 and parallel Hodge–Tate weights
![]() $\{0, m \}$
, and wish to show that
$\{0, m \}$
, and wish to show that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is potentially (weakly) automorphic. This presents difficulties since the compatible system
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is potentially (weakly) automorphic. This presents difficulties since the compatible system
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
has parallel Hodge–Tate weights
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
has parallel Hodge–Tate weights
![]() $\{ 0, m, 2m, \dots , (n-1) m\}$
, while the auxiliary motives that we can construct to show potential automorphy have consecutive (and parallel) Hodge–Tate weights (and moreover, our automorphy lifting theorem Theorem 3.2.1 applies only to Galois representations with consecutive Hodge–Tate weights). To get around this, we construct auxiliary compatible systems as follows:
$\{ 0, m, 2m, \dots , (n-1) m\}$
, while the auxiliary motives that we can construct to show potential automorphy have consecutive (and parallel) Hodge–Tate weights (and moreover, our automorphy lifting theorem Theorem 3.2.1 applies only to Galois representations with consecutive Hodge–Tate weights). To get around this, we construct auxiliary compatible systems as follows:
-
• An auxiliary compatible system
 ${\mathcal R}_{\mathrm {aux}}$
of rank m and with consecutive (and parallel) Hodge–Tate weights
${\mathcal R}_{\mathrm {aux}}$
of rank m and with consecutive (and parallel) Hodge–Tate weights
 $\{ 0, 1, \dots , m-1 \}$
. Then
$\{ 0, 1, \dots , m-1 \}$
. Then
 $(\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
has rank
$(\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
has rank
 $nm$
and consecutive (and parallel) Hodge–Tate weights
$nm$
and consecutive (and parallel) Hodge–Tate weights
 $\{ 0, 1, \dots , nm-1 \}$
.
$\{ 0, 1, \dots , nm-1 \}$
. -
• A second auxiliary compatible system
 ${\mathcal R}_{\mathrm {CM}}$
of rank m and with consecutive (and parallel) Hodge–Tate weights
${\mathcal R}_{\mathrm {CM}}$
of rank m and with consecutive (and parallel) Hodge–Tate weights
 $\{ 0, 1, \dots , m-1 \}$
which is moreover induced from a character.
$\{ 0, 1, \dots , m-1 \}$
which is moreover induced from a character. -
• A third auxiliary compatible system
 ${\mathcal S}_{\mathrm {UA}}$
of rank
${\mathcal S}_{\mathrm {UA}}$
of rank
 $nm$
with consecutive (and parallel) Hodge–Tate weights
$nm$
with consecutive (and parallel) Hodge–Tate weights
 $\{ 0, 1, \dots , mn-1 \}$
, and which is moreover automorphic. We will construct
$\{ 0, 1, \dots , mn-1 \}$
, and which is moreover automorphic. We will construct
 ${\mathcal S}_{\mathrm {UA}}$
(and
${\mathcal S}_{\mathrm {UA}}$
(and
 ${\mathcal R}_{\mathrm {aux}}$
) as a member of the families of motives considered in §4. (The subscript ‘UA’ stands for ‘universally automorphic’.)
${\mathcal R}_{\mathrm {aux}}$
) as a member of the families of motives considered in §4. (The subscript ‘UA’ stands for ‘universally automorphic’.)
These are chosen to behave well with respect to distinct primes
![]() $p, r$
as follows:
$p, r$
as follows:
-
• There is a congruence modulo p linking
 ${\mathcal S}_{\mathrm {aux}} := ( \operatorname {\mathrm {Sym}}^{n-1} {\mathcal R} ) \otimes {\mathcal R}_{\mathrm {aux}}$
and
${\mathcal S}_{\mathrm {aux}} := ( \operatorname {\mathrm {Sym}}^{n-1} {\mathcal R} ) \otimes {\mathcal R}_{\mathrm {aux}}$
and
 ${\mathcal S}_{\mathrm {UA}}$
. We will apply Theorem 3.2.1 to conclude that
${\mathcal S}_{\mathrm {UA}}$
. We will apply Theorem 3.2.1 to conclude that
 ${\mathcal S}_{\mathrm {aux}}$
is automorphic.
${\mathcal S}_{\mathrm {aux}}$
is automorphic. -
• There is a congruence modulo r linking
 ${\mathcal R}_{\mathrm {aux}}$
and
${\mathcal R}_{\mathrm {aux}}$
and
 ${\mathcal R}_{\mathrm {CM}}$
and therefore also linking
${\mathcal R}_{\mathrm {CM}}$
and therefore also linking
 ${\mathcal S}_{\mathrm {aux}}$
and
${\mathcal S}_{\mathrm {aux}}$
and
 ${\mathcal S}_{\mathrm {CM}} := ( \operatorname {\mathrm {Sym}}^{n-1} {\mathcal R} ) \otimes {\mathcal R}_{\mathrm {CM}}$
. We will apply Theorem 3.2.1 a second time to conclude that
${\mathcal S}_{\mathrm {CM}} := ( \operatorname {\mathrm {Sym}}^{n-1} {\mathcal R} ) \otimes {\mathcal R}_{\mathrm {CM}}$
. We will apply Theorem 3.2.1 a second time to conclude that
 ${\mathcal S}_{\mathrm {CM}}$
is automorphic.
${\mathcal S}_{\mathrm {CM}}$
is automorphic. -
• Since
 ${\mathcal R}_{\mathrm {CM}}$
is induced from a Hecke character,
${\mathcal R}_{\mathrm {CM}}$
is induced from a Hecke character,
 ${\mathcal S}_{\mathrm {CM}}$
is also induced (from an n-dimensional compatible system). We will then be able to apply the description of the image of automorphic induction given in [Reference Arthur and ClozelAC89] to conclude that
${\mathcal S}_{\mathrm {CM}}$
is also induced (from an n-dimensional compatible system). We will then be able to apply the description of the image of automorphic induction given in [Reference Arthur and ClozelAC89] to conclude that
 $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is itself automorphic.
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is itself automorphic.
The most significant conditions that must be satisfied to apply Theorem 3.2.1 in each case are the nondegeneracy of the residual images and the ‘connects’ relation locally at the p-adic (resp. r-adic) places of F. The nondegeneracy of the residual images will be easy to arrange by careful choice of data. It is the ‘connects’ relation that is more serious and imposes the circuitous route followed here to prove the theorem.
The statement of Proposition 6.2.3 below is long but is merely a precise formulation of the properties required of the various auxiliary compatible systems needed to carry out the above sketch. The main point in the proof of Theorem 6.2.4 will be to show how to construct auxiliary compatible systems with these properties.
Proposition 6.2.3. Let F be an imaginary CM number field, let
![]() $m \ge 2$
and
$m \ge 2$
and
![]() $n\ge 1$
be integers, and let
$n\ge 1$
be integers, and let
![]() $X_0$
be a finite set of finite places of F. Let
$X_0$
be a finite set of finite places of F. Let
be a very weakly compatible system of rank
![]() $2$
representations of
$2$
representations of
![]() $G_F$
satisfying the following conditions:
$G_F$
satisfying the following conditions:
-
1. For each
 $\tau $
,
$\tau $
,
 $H_\tau = \{ 0, m \}$
.
$H_\tau = \{ 0, m \}$
. -
2.
 $\det r_\lambda = \varepsilon ^{-m}$
.
$\det r_\lambda = \varepsilon ^{-m}$
. -
3.
 ${\mathcal R}$
is strongly irreducible.
${\mathcal R}$
is strongly irreducible. -
4.
 $X_0 \cap S = \emptyset $
.
$X_0 \cap S = \emptyset $
. -
5.
 $F / {\mathbb Q}$
is Galois and contains an imaginary quadratic field
$F / {\mathbb Q}$
is Galois and contains an imaginary quadratic field
 $F_0$
.
$F_0$
.
We fix an embedding
![]() $M \hookrightarrow {\mathbb C}$
, and regard M as a subfield of
$M \hookrightarrow {\mathbb C}$
, and regard M as a subfield of
![]() ${\mathbb C}$
. Suppose we can find the following additional data:
${\mathbb C}$
. Suppose we can find the following additional data:
-
6. A cyclic totally real extension
 $E / {\mathbb Q}$
of degree m, linearly disjoint from F, and a character
$E / {\mathbb Q}$
of degree m, linearly disjoint from F, and a character
 $\Psi : \mathbf {A}_L^\times \to M^\times $
, where
$\Psi : \mathbf {A}_L^\times \to M^\times $
, where
 $L = E \cdot F$
, satisfying the following conditions:
$L = E \cdot F$
, satisfying the following conditions:-
(a) There is an embedding
 $\tau _0 : F_0 \to {\mathbb C}$
, and a labelling
$\tau _0 : F_0 \to {\mathbb C}$
, and a labelling
 $\tau _1, \dots , \tau _m : E \cdot F_0 \to {\mathbb C}$
of the embeddings
$\tau _1, \dots , \tau _m : E \cdot F_0 \to {\mathbb C}$
of the embeddings
 $E \cdot F_0 \to {\mathbb C}$
which extend
$E \cdot F_0 \to {\mathbb C}$
which extend
 $\tau _0$
such that for each
$\tau _0$
such that for each
 $\alpha \in L^\times $
, we have
$\alpha \in L^\times $
, we have  $$\begin{align*}\Psi(\alpha) = \prod_{i=1}^m \tau_i(\mathbf{N}_{L / E \cdot F_0}(\alpha))^{m-i} c \tau_i(\mathbf{N}_{L / E \cdot F_0}(\alpha))^{i-1}. \end{align*}$$
$$\begin{align*}\Psi(\alpha) = \prod_{i=1}^m \tau_i(\mathbf{N}_{L / E \cdot F_0}(\alpha))^{m-i} c \tau_i(\mathbf{N}_{L / E \cdot F_0}(\alpha))^{i-1}. \end{align*}$$
We let
 $\{ \Psi _\lambda \}$
denote the weakly compatible system associated to
$\{ \Psi _\lambda \}$
denote the weakly compatible system associated to
 $\Psi $
, and let denote the induced weakly compatible system. (Then
$\Psi $
, and let denote the induced weakly compatible system. (Then $$\begin{align*}{\mathcal R}_{\mathrm{CM}} = \{ \operatorname{\mathrm{Ind}}_{G_L}^{G_F} \Psi_\lambda \} = (M, S_{\mathrm{CM}}, \{ Q_{\mathrm{CM}, v }(X) \}, \{ r_{\mathrm{CM}, \lambda} \} , \{ H_{\mathrm{CM}, \tau} \}) \end{align*}$$
$$\begin{align*}{\mathcal R}_{\mathrm{CM}} = \{ \operatorname{\mathrm{Ind}}_{G_L}^{G_F} \Psi_\lambda \} = (M, S_{\mathrm{CM}}, \{ Q_{\mathrm{CM}, v }(X) \}, \{ r_{\mathrm{CM}, \lambda} \} , \{ H_{\mathrm{CM}, \tau} \}) \end{align*}$$
 $H_{\mathrm {CM}, \tau } = \{ 0, 1, \dots , m-1 \}$
for all
$H_{\mathrm {CM}, \tau } = \{ 0, 1, \dots , m-1 \}$
for all
 $\tau $
, and we take
$\tau $
, and we take
 $S_{\mathrm {CM}}$
to be the set of places of F ramified in L or above which
$S_{\mathrm {CM}}$
to be the set of places of F ramified in L or above which
 $\Psi $
is ramified.)
$\Psi $
is ramified.)
-
(b) For all
 $\lambda $
,
$\lambda $
,
 $\det r_{\mathrm {CM}, \lambda } = \varepsilon ^{-m(m-1)/2}$
.
$\det r_{\mathrm {CM}, \lambda } = \varepsilon ^{-m(m-1)/2}$
.
-
-
7. Distinct primes
 $p, r$
, not dividing any place of S, and places
$p, r$
, not dividing any place of S, and places
 $\mathfrak {p}, {\mathfrak {r}}$
of M lying above them.
$\mathfrak {p}, {\mathfrak {r}}$
of M lying above them. -
8. A weakly compatible system of rank m representations of
 $G_F$
satisfying the following conditions:
$G_F$
satisfying the following conditions: $$\begin{align*}{\mathcal R}_{\mathrm{aux}} = (M, S_{\mathrm{aux}}, \{ Q_{\mathrm{aux}, v}(X) \}, \{ r_{\mathrm{aux}, \lambda} \}, \{ H_{\mathrm{aux}, \tau} \}), \end{align*}$$
$$\begin{align*}{\mathcal R}_{\mathrm{aux}} = (M, S_{\mathrm{aux}}, \{ Q_{\mathrm{aux}, v}(X) \}, \{ r_{\mathrm{aux}, \lambda} \}, \{ H_{\mathrm{aux}, \tau} \}), \end{align*}$$
-
(a)
 ${\mathcal R}_{\mathrm {aux}}$
is pure of weight
${\mathcal R}_{\mathrm {aux}}$
is pure of weight
 $m-1$
, and
$m-1$
, and
 $S_{\mathrm {aux}}$
does not intersect
$S_{\mathrm {aux}}$
does not intersect
 $X_0 \cup \{ v | pr \}$
.
$X_0 \cup \{ v | pr \}$
. -
(b) For all
 $\lambda $
,
$\lambda $
,
 $\det r_{\mathrm {aux}, \lambda } = \varepsilon ^{-m(m-1)/2}$
. For all
$\det r_{\mathrm {aux}, \lambda } = \varepsilon ^{-m(m-1)/2}$
. For all
 $\tau $
,
$\tau $
,
 $H_{\mathrm {aux}, \tau } = \{ 0, 1, \dots , m-1 \}$
.
$H_{\mathrm {aux}, \tau } = \{ 0, 1, \dots , m-1 \}$
.
-
-
9. A weakly compatible system
of rank $$\begin{align*}{\mathcal S}_{\mathrm{UA}} = ( M, S_{\mathrm{UA}}, \{ Q_{\mathrm{UA}, v}(X) \}, \{ s_{\mathrm{UA}, \lambda} \}, \{ H_{\mathrm{UA}, \tau} \}) \end{align*}$$
$$\begin{align*}{\mathcal S}_{\mathrm{UA}} = ( M, S_{\mathrm{UA}}, \{ Q_{\mathrm{UA}, v}(X) \}, \{ s_{\mathrm{UA}, \lambda} \}, \{ H_{\mathrm{UA}, \tau} \}) \end{align*}$$
 $nm$
representations of
$nm$
representations of
 $G_F$
, satisfying the following conditions:
$G_F$
, satisfying the following conditions:
-
(a)
 ${\mathcal S}_{\mathrm {UA}}$
is pure of weight
${\mathcal S}_{\mathrm {UA}}$
is pure of weight
 $nm-1$
, and
$nm-1$
, and
 $S_{\mathrm {UA}}$
does not intersect
$S_{\mathrm {UA}}$
does not intersect
 $X_0 \cup \{ v | pr \}$
.
$X_0 \cup \{ v | pr \}$
. -
(b) For all
 $\lambda $
,
$\lambda $
,
 $\det s_{\mathrm {UA}, \lambda } = \varepsilon ^{-nm(nm-1)/2}$
. For all
$\det s_{\mathrm {UA}, \lambda } = \varepsilon ^{-nm(nm-1)/2}$
. For all
 $\tau $
,
$\tau $
,
 $H_{\mathrm {UA}, \tau } = \{ 0, 1, \dots , n m-1 \}$
.
$H_{\mathrm {UA}, \tau } = \{ 0, 1, \dots , n m-1 \}$
. -
(c)
 ${\mathcal S}_{\mathrm {UA}}$
is weakly automorphic of level prime to
${\mathcal S}_{\mathrm {UA}}$
is weakly automorphic of level prime to
 $X_0 \cup \{ v | pr \}$
.
$X_0 \cup \{ v | pr \}$
.
-
Let
![]() ${\mathcal S}_{\mathrm {aux}} = \{ s_{\mathrm {aux}, \lambda } \} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
and
${\mathcal S}_{\mathrm {aux}} = \{ s_{\mathrm {aux}, \lambda } \} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {aux}}$
and
![]() ${\mathcal S}_{\mathrm {CM}} = \{ s_{\mathrm {CM}, \lambda } \} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {CM}}$
. These compatible systems of rank
${\mathcal S}_{\mathrm {CM}} = \{ s_{\mathrm {CM}, \lambda } \} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}) \otimes {\mathcal R}_{\mathrm {CM}}$
. These compatible systems of rank
![]() $nm$
have coefficients in the number field M. Suppose that these data satisfy the following additional conditions:
$nm$
have coefficients in the number field M. Suppose that these data satisfy the following additional conditions:
-
10.
 $L/F$
is unramified at
$L/F$
is unramified at
 $X_0 \cup \{ v | pr \}$
, and
$X_0 \cup \{ v | pr \}$
, and
 $\Psi $
is unramified at the places of L lying above
$\Psi $
is unramified at the places of L lying above
 $X_0\cup \{ v | pr \}$
. (Then
$X_0\cup \{ v | pr \}$
. (Then
 $S_{\mathrm {CM}} \cap (X_0 \cup \{ v | p r \}) = \emptyset .$
)
$S_{\mathrm {CM}} \cap (X_0 \cup \{ v | p r \}) = \emptyset .$
) -
11.
 $p> 2 n m + 1$
, and
$p> 2 n m + 1$
, and
 $[F(\zeta _p) : F] = p-1$
.
$[F(\zeta _p) : F] = p-1$
. -
12.
 $r> 2 n m + 1$
, r splits completely in
$r> 2 n m + 1$
, r splits completely in
 $E \cdot F_0$
, and
$E \cdot F_0$
, and
 $[L(\zeta _r) : L] = r-1$
.
$[L(\zeta _r) : L] = r-1$
. -
13. Up to conjugation, there are sandwiches
and $$\begin{align*}\operatorname{\mathrm{SL}}_2({\mathbb F}_p) \leq \overline{r}_{\mathfrak{p}}(G_F) \leq \operatorname{\mathrm{GL}}_2({\mathbb F}_p) \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{SL}}_2({\mathbb F}_p) \leq \overline{r}_{\mathfrak{p}}(G_F) \leq \operatorname{\mathrm{GL}}_2({\mathbb F}_p) \end{align*}$$
 $$\begin{align*}\operatorname{\mathrm{SL}}_2({\mathbb F}_r) \leq \overline{r}_{\mathfrak{r}}(G_F) \leq \operatorname{\mathrm{GL}}_2({\mathbb F}_r). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{SL}}_2({\mathbb F}_r) \leq \overline{r}_{\mathfrak{r}}(G_F) \leq \operatorname{\mathrm{GL}}_2({\mathbb F}_r). \end{align*}$$
If
 $m> 2$
, then the image
$m> 2$
, then the image
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_F)$
is a conjugate of
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_F)$
is a conjugate of
 $\operatorname {GU}_m({\mathbb F}_{p^2})$
and
$\operatorname {GU}_m({\mathbb F}_{p^2})$
and
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}$
has multiplier character
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}$
has multiplier character
 $\overline {\varepsilon }^{1-m}$
. If
$\overline {\varepsilon }^{1-m}$
. If
 $m = 2$
, then the image
$m = 2$
, then the image
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_F)$
is a conjugate of
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_F)$
is a conjugate of
 $\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
. The representation
$\operatorname {\mathrm {GL}}_2({\mathbb F}_p)$
. The representation
 $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F(\zeta _r)}}$
is irreducible. If
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F(\zeta _r)}}$
is irreducible. If
 $m = 2$
, then the extensions of
$m = 2$
, then the extensions of
 $F(\zeta _p)$
cut out by the projective representations associated to
$F(\zeta _p)$
cut out by the projective representations associated to
 $\overline {r}_{\mathfrak {p}}|_{G_{F(\zeta _p)}}$
and
$\overline {r}_{\mathfrak {p}}|_{G_{F(\zeta _p)}}$
and
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F(\zeta _p)}}$
are linearly disjoint.
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F(\zeta _p)}}$
are linearly disjoint. -
14. There are isomorphisms
 $\overline {s}_{\mathrm {UA}, \mathfrak {p}} \cong \overline {s}_{\mathrm {aux}, \mathfrak {p}}$
and
$\overline {s}_{\mathrm {UA}, \mathfrak {p}} \cong \overline {s}_{\mathrm {aux}, \mathfrak {p}}$
and
 $\overline {r}_{\mathrm {aux}, {\mathfrak {r}}} \cong \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
.
$\overline {r}_{\mathrm {aux}, {\mathfrak {r}}} \cong \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
. -
15. There is a decomposition
 $S_p = \Sigma ^{\textrm {ord}} \sqcup \Sigma ^{\textrm {ss}}$
of the set
$S_p = \Sigma ^{\textrm {ord}} \sqcup \Sigma ^{\textrm {ss}}$
of the set
 $S_p$
of p-adic places of F such that for each place
$S_p$
of p-adic places of F such that for each place
 $v | p$
of F,
$v | p$
of F,
 $F_v$
contains
$F_v$
contains
 ${\mathbb Q}_{p^2}$
,
${\mathbb Q}_{p^2}$
,
 $\overline {r}_{\mathfrak {p}}|_{G_{F_v}}$
and
$\overline {r}_{\mathfrak {p}}|_{G_{F_v}}$
and
 $\overline {\rho }_{2, m, 0}|_{G_{F_v}}$
(cf. Definition 5.1.1) are trivial, and:
$\overline {\rho }_{2, m, 0}|_{G_{F_v}}$
(cf. Definition 5.1.1) are trivial, and:-
(a) if
 $v \in \Sigma ^{\textrm {ord}}$
, then
$v \in \Sigma ^{\textrm {ord}}$
, then
 $r_{\mathfrak {p}}|_{G_{F_v}}$
is crystalline ordinary;
$r_{\mathfrak {p}}|_{G_{F_v}}$
is crystalline ordinary; -
(b) if
 $v \in \Sigma ^{\textrm {ss}}$
, then
$v \in \Sigma ^{\textrm {ss}}$
, then
 $r_{\mathfrak {p}}|_{G_{F_v}} \sim \rho _{2, m, 0}|_{G_{F_v}}$
.
$r_{\mathfrak {p}}|_{G_{F_v}} \sim \rho _{2, m, 0}|_{G_{F_v}}$
.
-
-
16. If
 $v \in \Sigma ^{\textrm {ord}}$
, then
$v \in \Sigma ^{\textrm {ord}}$
, then
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial and
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial and
 $r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
and
$r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
and
 $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
are both crystalline ordinary. If
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
are both crystalline ordinary. If
 $v \in \Sigma ^{\textrm {ss}}$
, then
$v \in \Sigma ^{\textrm {ss}}$
, then
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial,
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial,
 $r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
and
$r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
and
 $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
are both crystalline, and
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
are both crystalline, and
 $r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{m, 1, 0}|_{G_{F_v}}$
and
$r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{m, 1, 0}|_{G_{F_v}}$
and
 $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{nm, 1, 0}|_{G_{F_v}}$
.
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{nm, 1, 0}|_{G_{F_v}}$
. -
17. For each place
 $v | r$
of F,
$v | r$
of F,
 $\overline {r}_{\mathrm {aux},{\mathfrak {r}}}|_{G_{F_v}} \cong \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}}$
is trivial and
$\overline {r}_{\mathrm {aux},{\mathfrak {r}}}|_{G_{F_v}} \cong \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}}$
is trivial and
 $r_{\mathrm {aux},{\mathfrak {r}}}|_{G_{F_v}}$
is crystalline ordinary.
$r_{\mathrm {aux},{\mathfrak {r}}}|_{G_{F_v}}$
is crystalline ordinary.
Then
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is weakly automorphic of level prime to
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is weakly automorphic of level prime to
![]() $X_0$
.
$X_0$
.
Proof. We first show that
![]() ${\mathcal S}_{\mathrm {aux}}$
is weakly automorphic of level prime to
${\mathcal S}_{\mathrm {aux}}$
is weakly automorphic of level prime to
![]() $X_0 \cup \{ v | r \}$
by applying Theorem 3.2.1 to
$X_0 \cup \{ v | r \}$
by applying Theorem 3.2.1 to
![]() $s_{\mathrm {aux}, \mathfrak {p}}$
. To justify this, we need to check that
$s_{\mathrm {aux}, \mathfrak {p}}$
. To justify this, we need to check that
![]() $\overline {s}_{\mathrm {aux}, \mathfrak {p}} \cong \overline {s}_{\mathrm {UA}, \mathfrak {p}}$
satisfies the Taylor–Wiles conditions (as formulated in Definition 5.2.1) and that for each place
$\overline {s}_{\mathrm {aux}, \mathfrak {p}} \cong \overline {s}_{\mathrm {UA}, \mathfrak {p}}$
satisfies the Taylor–Wiles conditions (as formulated in Definition 5.2.1) and that for each place
![]() $v | p$
of F, we have
$v | p$
of F, we have
![]() $s_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
. The Taylor–Wiles conditions hold by assumption (13) and Lemma 5.2.4. If
$s_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
. The Taylor–Wiles conditions hold by assumption (13) and Lemma 5.2.4. If
![]() $v \in \Sigma ^{\mathrm {ord}}$
, then
$v \in \Sigma ^{\mathrm {ord}}$
, then
![]() $\overline {s}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial, and both
$\overline {s}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial, and both
![]() $s_{\mathrm {aux}, \mathfrak {p}} \cong (\operatorname {\mathrm {Sym}}^{n-1} r_{\mathfrak {p}}) \otimes r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
and
$s_{\mathrm {aux}, \mathfrak {p}} \cong (\operatorname {\mathrm {Sym}}^{n-1} r_{\mathfrak {p}}) \otimes r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
and
![]() $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
are crystalline ordinary, so Lemma 5.1.4 implies that
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
are crystalline ordinary, so Lemma 5.1.4 implies that
![]() $s_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
. If
$s_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}}$
. If
![]() $v \in \Sigma ^{{\mathrm {ss}}}$
, then
$v \in \Sigma ^{{\mathrm {ss}}}$
, then
![]() $\overline {s}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial and our assumptions imply that
$\overline {s}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}}$
is trivial and our assumptions imply that
![]() $\operatorname {\mathrm {Sym}}^{n-1} r_{\mathfrak {p}}|_{G_{F_v}} \sim \rho _{n,m,0}|_{G_{F_v}}$
,
$\operatorname {\mathrm {Sym}}^{n-1} r_{\mathfrak {p}}|_{G_{F_v}} \sim \rho _{n,m,0}|_{G_{F_v}}$
,
![]() $r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{m, 1, 0}|_{G_{F_v}}$
and
$r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{m, 1, 0}|_{G_{F_v}}$
and
![]() $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{nm, 1, 0}|_{G_{F_v}}$
; hence,
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_v}} \sim \rho _{nm, 1, 0}|_{G_{F_v}}$
; hence,
Therefore,
![]() ${\mathcal S}_{\mathrm {aux}}$
is weakly automorphic of level prime to
${\mathcal S}_{\mathrm {aux}}$
is weakly automorphic of level prime to
![]() $X_0 \cup \{ v | r \}$
.
$X_0 \cup \{ v | r \}$
.
We next show that
![]() ${\mathcal S}_{\mathrm {CM}}$
is weakly automorphic of level prime to
${\mathcal S}_{\mathrm {CM}}$
is weakly automorphic of level prime to
![]() $X_0$
by applying Theorem 3.2.1 to
$X_0$
by applying Theorem 3.2.1 to
![]() $s_{\mathrm {CM}, {\mathfrak {r}}}$
. The Taylor–Wiles conditions for
$s_{\mathrm {CM}, {\mathfrak {r}}}$
. The Taylor–Wiles conditions for
![]() $\overline {s}_{\mathrm {CM}, {\mathfrak {r}}} \cong \overline {s}_{\mathrm {aux}, {\mathfrak {r}}}$
hold by assumption (13) and Lemma 5.2.6. To check the connectedness conditions, let
$\overline {s}_{\mathrm {CM}, {\mathfrak {r}}} \cong \overline {s}_{\mathrm {aux}, {\mathfrak {r}}}$
hold by assumption (13) and Lemma 5.2.6. To check the connectedness conditions, let
![]() $v | r$
be a place of F. Then
$v | r$
be a place of F. Then
![]() $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}} \cong \overline {r}_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
is trivial and
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}} \cong \overline {r}_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
is trivial and
![]() $r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
is crystalline ordinary, by assumption (17). Since r splits completely in E by assumption (12),
$r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
is crystalline ordinary, by assumption (17). Since r splits completely in E by assumption (12),
![]() $v $
splits completely in L, and we can label the places
$v $
splits completely in L, and we can label the places
![]() $w_i | v$
so that
$w_i | v$
so that
![]() $w_i|_E$
is the place induced by the embedding
$w_i|_E$
is the place induced by the embedding
![]() $\tau _i$
. There is an isomorphism
$\tau _i$
. There is an isomorphism
where for each
![]() $i = 1, \dots , m$
,
$i = 1, \dots , m$
,
![]() $\alpha _{i} : G_{F_{v}} \to \overline {M}_{\mathfrak {r}}^\times $
is a continuous character with the property that for any
$\alpha _{i} : G_{F_{v}} \to \overline {M}_{\mathfrak {r}}^\times $
is a continuous character with the property that for any
![]() $u \in {\mathcal O}_{F_v}^\times $
, we have
$u \in {\mathcal O}_{F_v}^\times $
, we have
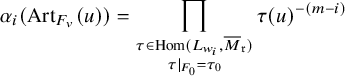 $$\begin{align*}\alpha_{ i}( \operatorname{Art}_{F_v}(u) ) = \prod_{\substack{ \tau \in \operatorname{\mathrm{Hom}}(L_{w_i}, \overline{M}_{\mathfrak{r}}) \\ \tau|_{F_0} = \tau_0}} \tau(u)^{-(m-i)} \end{align*}$$
$$\begin{align*}\alpha_{ i}( \operatorname{Art}_{F_v}(u) ) = \prod_{\substack{ \tau \in \operatorname{\mathrm{Hom}}(L_{w_i}, \overline{M}_{\mathfrak{r}}) \\ \tau|_{F_0} = \tau_0}} \tau(u)^{-(m-i)} \end{align*}$$
if v lies above the place of
![]() $F_0$
induced by
$F_0$
induced by
![]() $\tau _0$
, and
$\tau _0$
, and
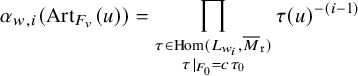 $$\begin{align*}\alpha_{w, i}( \operatorname{Art}_{F_v}(u) ) = \prod_{\substack{ \tau \in \operatorname{\mathrm{Hom}}(L_{w_i}, \overline{M}_{\mathfrak{r}}) \\ \tau|_{F_0} = c \tau_0}} \tau(u)^{-(i-1)} \end{align*}$$
$$\begin{align*}\alpha_{w, i}( \operatorname{Art}_{F_v}(u) ) = \prod_{\substack{ \tau \in \operatorname{\mathrm{Hom}}(L_{w_i}, \overline{M}_{\mathfrak{r}}) \\ \tau|_{F_0} = c \tau_0}} \tau(u)^{-(i-1)} \end{align*}$$
otherwise. It follows that
![]() $r_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}}$
is also crystalline ordinary, with Hodge–Tate weights
$r_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}}$
is also crystalline ordinary, with Hodge–Tate weights
![]() $\{0,\ldots ,m-1\}$
matching those of
$\{0,\ldots ,m-1\}$
matching those of
![]() $r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
. By Lemma 5.1.4, we have
$r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
. By Lemma 5.1.4, we have
![]() $r_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}} \sim r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
, and using [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, p. 530, (5)], it follows that
$r_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_v}} \sim r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_v}}$
, and using [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, p. 530, (5)], it follows that
We can now show that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is weakly automorphic of level prime to
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is weakly automorphic of level prime to
![]() $X_0$
. Let
$X_0$
. Let
![]() $\pi $
be the regular algebraic, cuspidal automorphic representation of
$\pi $
be the regular algebraic, cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{nm}(\mathbf {A}_F)$
which is associated to the compatible system
$\operatorname {\mathrm {GL}}_{nm}(\mathbf {A}_F)$
which is associated to the compatible system
![]() ${\mathcal S}_{\mathrm {CM}}$
. By construction,
${\mathcal S}_{\mathrm {CM}}$
. By construction,
![]() $\pi $
is unramified at
$\pi $
is unramified at
![]() $X_0$
. Let
$X_0$
. Let
![]() $\eta : F^\times \backslash \mathbf {A}_F^\times \to {\mathbb C}^\times $
be the character of order m associated to the inducing field
$\eta : F^\times \backslash \mathbf {A}_F^\times \to {\mathbb C}^\times $
be the character of order m associated to the inducing field
![]() $L / F$
of
$L / F$
of
![]() ${\mathcal R}_{\mathrm {CM}}$
. Then
${\mathcal R}_{\mathrm {CM}}$
. Then
![]() $\pi \cong \pi \otimes (\eta \circ \det )$
, so by cyclic base change [Reference Arthur and ClozelAC89, Ch. 3, Thm 4.2], we deduce that
$\pi \cong \pi \otimes (\eta \circ \det )$
, so by cyclic base change [Reference Arthur and ClozelAC89, Ch. 3, Thm 4.2], we deduce that
![]() $\pi $
is the induction of a cuspidal automorphic representation
$\pi $
is the induction of a cuspidal automorphic representation
![]() $\Pi $
for
$\Pi $
for
![]() $\operatorname {\mathrm {GL}}_{n}(\mathbf {A}_{L})$
, which by consideration of the infinity type of
$\operatorname {\mathrm {GL}}_{n}(\mathbf {A}_{L})$
, which by consideration of the infinity type of
![]() $\pi $
must also be regular algebraic. More precisely, for any place w of L lying above a place v of F, we have
$\pi $
must also be regular algebraic. More precisely, for any place w of L lying above a place v of F, we have
where
![]() $\sigma $
is a generator for
$\sigma $
is a generator for
![]() $\operatorname {\mathrm {Gal}}(L / F)$
. Since L is CM and
$\operatorname {\mathrm {Gal}}(L / F)$
. Since L is CM and
![]() $\Pi $
is regular algebraic,
$\Pi $
is regular algebraic,
![]() $\Pi $
has an associated compatible system of l-adic Galois representations. If l is a prime and
$\Pi $
has an associated compatible system of l-adic Galois representations. If l is a prime and
![]() $\iota : \overline {{\mathbb Q}}_l \to {\mathbb C}$
is an isomorphism, with
$\iota : \overline {{\mathbb Q}}_l \to {\mathbb C}$
is an isomorphism, with
![]() $\iota ^{-1}$
inducing the place
$\iota ^{-1}$
inducing the place
![]() $\lambda $
of M, then we find
$\lambda $
of M, then we find
Choosing
![]() $\lambda $
so that
$\lambda $
so that
![]() $\operatorname {\mathrm {Sym}}^{n-1} r_\lambda $
is irreducible (e.g.,
$\operatorname {\mathrm {Sym}}^{n-1} r_\lambda $
is irreducible (e.g.,
![]() $\lambda = \mathfrak {p}$
), we find that
$\lambda = \mathfrak {p}$
), we find that
![]() $\operatorname {\mathrm {Sym}}^{n-1} r_\lambda |_{G_L}$
is a character twist of
$\operatorname {\mathrm {Sym}}^{n-1} r_\lambda |_{G_L}$
is a character twist of
![]() $r_\iota (\Pi )$
. Undoing the twist and making cyclic descent (using the irreducibility of
$r_\iota (\Pi )$
. Undoing the twist and making cyclic descent (using the irreducibility of
![]() $\operatorname {\mathrm {Sym}}^{n-1} r_\lambda |_{G_L}$
, as in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Proposition 6.5.13]) shows that
$\operatorname {\mathrm {Sym}}^{n-1} r_\lambda |_{G_L}$
, as in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Proposition 6.5.13]) shows that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is weakly automorphic over F of level prime to
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
is weakly automorphic over F of level prime to
![]() $X_0$
, as desired.
$X_0$
, as desired.
The next theorem is proved by constructing the data required by Proposition 6.2.3 (after possibly extending the base field F).
Theorem 6.2.4. Let F be an imaginary CM number field, and let
be a very weakly compatible system of rank
![]() $2$
representations of
$2$
representations of
![]() $G_F$
. Let
$G_F$
. Let
![]() $m \ge 2$
be an integer, and suppose that the following conditions are satisfied:
$m \ge 2$
be an integer, and suppose that the following conditions are satisfied:
-
1. For each
 $\tau $
,
$\tau $
,
 $H_\tau = \{ 0, m \}$
.
$H_\tau = \{ 0, m \}$
. -
2.
 $\det r_\lambda = \varepsilon ^{-m}$
.
$\det r_\lambda = \varepsilon ^{-m}$
. -
3.
 ${\mathcal R}$
is strongly irreducible.
${\mathcal R}$
is strongly irreducible.
Let
![]() $v_0 \not \in S$
be a place of F. Then for each
$v_0 \not \in S$
be a place of F. Then for each
![]() $n \geq 1$
, there is a CM extension
$n \geq 1$
, there is a CM extension
![]() $F_n/ F$
, Galois over
$F_n/ F$
, Galois over
![]() ${\mathbb Q}$
, such that
${\mathbb Q}$
, such that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_n}}$
is weakly automorphic of level prime to
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_n}}$
is weakly automorphic of level prime to
![]() $\{v|v_0\}$
.
$\{v|v_0\}$
.
Proof. We can fix
![]() $n \geq 1$
. Let
$n \geq 1$
. Let
![]() $p_0$
denote the residue characteristic of
$p_0$
denote the residue characteristic of
![]() $v_0$
, let
$v_0$
, let
![]() $F_0$
be an imaginary quadratic field, and let
$F_0$
be an imaginary quadratic field, and let
![]() $F_1$
denote the Galois closure of
$F_1$
denote the Galois closure of
![]() $F \cdot F_0$
over
$F \cdot F_0$
over
![]() ${\mathbb Q}$
. Embed M in
${\mathbb Q}$
. Embed M in
![]() ${\mathbb C}$
arbitrarily, and let
${\mathbb C}$
arbitrarily, and let
![]() $X_1$
denote the set of places of
$X_1$
denote the set of places of
![]() $F_1$
lying above
$F_1$
lying above
![]() $v_0$
. It suffices to prove the following statement:
$v_0$
. It suffices to prove the following statement:
-
• There exists a CM extension
 $F' / F_1$
, Galois over
$F' / F_1$
, Galois over
 ${\mathbb Q}$
, such that (after possibly enlarging M)
${\mathbb Q}$
, such that (after possibly enlarging M)
 ${\mathcal R}|_{G_{F'}}$
satisfies the hypotheses of Proposition 6.2.3 with
${\mathcal R}|_{G_{F'}}$
satisfies the hypotheses of Proposition 6.2.3 with
 $X_0$
taken to be the set of places of
$X_0$
taken to be the set of places of
 $F'$
lying above
$F'$
lying above
 $X_1$
.
$X_1$
.
Indeed, Proposition 6.2.3 will then imply that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F'}}$
is weakly automorphic of level prime to
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F'}}$
is weakly automorphic of level prime to
![]() $X_0 = \{ v | v_0 \}$
, which is what we need to prove. To prove this statement, we will consider a series of CM extensions
$X_0 = \{ v | v_0 \}$
, which is what we need to prove. To prove this statement, we will consider a series of CM extensions
![]() $F_{j+1} / F_j$
(
$F_{j+1} / F_j$
(
![]() $j = 1, 2, \dots $
), each Galois over
$j = 1, 2, \dots $
), each Galois over
![]() ${\mathbb Q}$
. For any such extension
${\mathbb Q}$
. For any such extension
![]() $F_j / F_1$
,
$F_j / F_1$
,
![]() ${\mathcal R}|_{G_{F_j}}$
satisfies assumptions (1)-(5) of Proposition 6.2.3 with respect to
${\mathcal R}|_{G_{F_j}}$
satisfies assumptions (1)-(5) of Proposition 6.2.3 with respect to
![]() $X_j$
, the set of places of
$X_j$
, the set of places of
![]() $F_j$
lying above
$F_j$
lying above
![]() $v_0$
. The extensions
$v_0$
. The extensions
![]() $F_{j+1} / F_j$
will be chosen in order to satisfy the remaining assumptions.
$F_{j+1} / F_j$
will be chosen in order to satisfy the remaining assumptions.
Let
![]() $E/{\mathbb Q}$
be any totally real cyclic extension of degree m linearly disjoint from
$E/{\mathbb Q}$
be any totally real cyclic extension of degree m linearly disjoint from
![]() $F_1$
, in which
$F_1$
, in which
![]() $p_0$
is unramified. (We can find such E by taking the degree m subfield of
$p_0$
is unramified. (We can find such E by taking the degree m subfield of
![]() ${\mathbb Q}(\zeta _{p'})$
, where
${\mathbb Q}(\zeta _{p'})$
, where
![]() $p'$
is any sufficiently large prime
$p'$
is any sufficiently large prime
![]() $\equiv 1 \bmod 2m$
.) Let
$\equiv 1 \bmod 2m$
.) Let
![]() $L_1 = E \cdot F_1$
. For any extension
$L_1 = E \cdot F_1$
. For any extension
![]() $F_j / F_1$
, we will set
$F_j / F_1$
, we will set
![]() $L_j = E \cdot F_j$
. Choose an odd prime
$L_j = E \cdot F_j$
. Choose an odd prime
![]() $q_1 \nmid X_0$
which splits completely in
$q_1 \nmid X_0$
which splits completely in
![]() $L_1$
and a place
$L_1$
and a place
![]() $v_1 | q_1$
of
$v_1 | q_1$
of
![]() $F_1$
which splits completely as
$F_1$
which splits completely as
![]() $v_1 = w_1 \dots w_m$
in
$v_1 = w_1 \dots w_m$
in
![]() $L_1$
. Fix an embedding
$L_1$
. Fix an embedding
![]() $\tau _0 : F_0 \to {\mathbb C}$
, and a labelling
$\tau _0 : F_0 \to {\mathbb C}$
, and a labelling
![]() $\tau _1, \dots , \tau _m : E \cdot F_0 \to {\mathbb C}$
of the embeddings
$\tau _1, \dots , \tau _m : E \cdot F_0 \to {\mathbb C}$
of the embeddings
![]() $E \cdot F_0 \to {\mathbb C}$
which extend
$E \cdot F_0 \to {\mathbb C}$
which extend
![]() $\tau _0$
. After enlarging M, using [Reference Harris, Shepherd-Barron and TaylorHSBT10, Lemma 2.2], we can find a character
$\tau _0$
. After enlarging M, using [Reference Harris, Shepherd-Barron and TaylorHSBT10, Lemma 2.2], we can find a character
![]() $\Psi _0 : \mathbf {A}_{L_1}^\times \to M^\times $
, unramified at the places above
$\Psi _0 : \mathbf {A}_{L_1}^\times \to M^\times $
, unramified at the places above
![]() $X_1$
, such that for each
$X_1$
, such that for each
![]() $\alpha \in L_1^\times $
, we have
$\alpha \in L_1^\times $
, we have
 $$\begin{align*}\Psi_0(\alpha) = \prod_{i=1}^m \tau_i(\mathbf{N}_{L_1 / E \cdot F_0}(\alpha))^{m-i} c \tau_i(\mathbf{N}_{L_1 / E \cdot F_0}(\alpha))^{i-1}, \end{align*}$$
$$\begin{align*}\Psi_0(\alpha) = \prod_{i=1}^m \tau_i(\mathbf{N}_{L_1 / E \cdot F_0}(\alpha))^{m-i} c \tau_i(\mathbf{N}_{L_1 / E \cdot F_0}(\alpha))^{i-1}, \end{align*}$$
and moreover such that the characters
![]() $\Psi _0|_{{{\mathcal O}^\times _{L_{w_i}}}}$
(
$\Psi _0|_{{{\mathcal O}^\times _{L_{w_i}}}}$
(
![]() $i = 1, \dots , m$
) are wildly ramified, pairwise distinct, and satisfy
$i = 1, \dots , m$
) are wildly ramified, pairwise distinct, and satisfy
![]() $\prod _{i=1}^m \Psi _0|_{{\mathcal O}^\times _{L_{w_i}}} = 1$
(where we identify
$\prod _{i=1}^m \Psi _0|_{{\mathcal O}^\times _{L_{w_i}}} = 1$
(where we identify
![]() $F_{v_1} = L_{w_i}$
for each i). If
$F_{v_1} = L_{w_i}$
for each i). If
![]() $\lambda $
is a place of M, then
$\lambda $
is a place of M, then
![]() $\varepsilon ^{m(m-1)/2} \det \operatorname {\mathrm {Ind}}_{G_{L_1}}^{G_{F_1}} \Psi _{0, \lambda }$
is a character of finite order which is unramified at
$\varepsilon ^{m(m-1)/2} \det \operatorname {\mathrm {Ind}}_{G_{L_1}}^{G_{F_1}} \Psi _{0, \lambda }$
is a character of finite order which is unramified at
![]() $v_0$
and
$v_0$
and
![]() $v_1$
. Using Lemma 5.3.3, and possibly enlarging M further, we can find a CM extension
$v_1$
. Using Lemma 5.3.3, and possibly enlarging M further, we can find a CM extension
![]() $F_2 / F_1$
, linearly disjoint from
$F_2 / F_1$
, linearly disjoint from
![]() $E/{\mathbb Q}$
and Galois over
$E/{\mathbb Q}$
and Galois over
![]() ${\mathbb Q}$
, and a twist
${\mathbb Q}$
, and a twist
![]() $\Psi _2 : \mathbf {A}_{L_2}^\times \to M^\times $
of
$\Psi _2 : \mathbf {A}_{L_2}^\times \to M^\times $
of
![]() $\Psi _0 \circ \mathbf {N}_{L_2 / L_1}$
by a character of
$\Psi _0 \circ \mathbf {N}_{L_2 / L_1}$
by a character of
![]() $L_2^\times \backslash \mathbf {A}_{L_2}^\times $
of finite order, unramified above
$L_2^\times \backslash \mathbf {A}_{L_2}^\times $
of finite order, unramified above
![]() $v_0$
and
$v_0$
and
![]() $v_1$
, such that for any place
$v_1$
, such that for any place
![]() $\lambda $
of M,
$\lambda $
of M,
![]() $\det \operatorname {\mathrm {Ind}}_{G_{L_2}}^{G_{F_2}} \Psi _{2, \lambda } = \varepsilon ^{-m(m-1)/2}$
. (If
$\det \operatorname {\mathrm {Ind}}_{G_{L_2}}^{G_{F_2}} \Psi _{2, \lambda } = \varepsilon ^{-m(m-1)/2}$
. (If
![]() $v_0 | 2$
, then the twist whose existence is guaranteed from Lemma 5.3.3 may be ramified above
$v_0 | 2$
, then the twist whose existence is guaranteed from Lemma 5.3.3 may be ramified above
![]() $X_2$
; if so, it is certainly ramified of finite order, and we enlarge
$X_2$
; if so, it is certainly ramified of finite order, and we enlarge
![]() $F_2$
further so that
$F_2$
further so that
![]() $\operatorname {\mathrm {Ind}}_{G_{L_2}}^{G_{F_2}} \Psi _{2, \lambda }$
is unramified at all places above
$\operatorname {\mathrm {Ind}}_{G_{L_2}}^{G_{F_2}} \Psi _{2, \lambda }$
is unramified at all places above
![]() $X_2$
and
$X_2$
and
![]() $L_2/F_2$
is unramified at all places above
$L_2/F_2$
is unramified at all places above
![]() $X_2$
.) If
$X_2$
.) If
![]() $F_j / F_2$
is a finite extension, then we set
$F_j / F_2$
is a finite extension, then we set
![]() $\Psi _j = \Psi _2 \circ \mathbf {N}_{F_j / F_2}$
. Let
$\Psi _j = \Psi _2 \circ \mathbf {N}_{F_j / F_2}$
. Let
![]() ${\mathcal R}_{\mathrm {CM}} = \{ \operatorname {\mathrm {Ind}}_{G_{L_2}}^{G_{F_2}} \Psi _{2, \lambda } \} = \{ r_{\mathrm {CM}, \lambda } \}$
.
${\mathcal R}_{\mathrm {CM}} = \{ \operatorname {\mathrm {Ind}}_{G_{L_2}}^{G_{F_2}} \Psi _{2, \lambda } \} = \{ r_{\mathrm {CM}, \lambda } \}$
.
We now choose any primes N,
![]() $p \in {\mathcal L}({\mathcal R}|_{G_{F_2}})$
,
$p \in {\mathcal L}({\mathcal R}|_{G_{F_2}})$
,
![]() $r \in {\mathcal L}({\mathcal R}|_{G_{F_2}})$
(cf. Lemma 6.1.5) not dividing
$r \in {\mathcal L}({\mathcal R}|_{G_{F_2}})$
(cf. Lemma 6.1.5) not dividing
![]() $v_0 v_1$
and satisfying the following conditions:
$v_0 v_1$
and satisfying the following conditions:
-
•
 $N> 100nm + 100$
and N is unramified in
$N> 100nm + 100$
and N is unramified in
 $L_2$
and M.
$L_2$
and M. -
•
 $p \equiv -1 \text { mod }N$
and
$p \equiv -1 \text { mod }N$
and
 $p> 2nm+1$
.
$p> 2nm+1$
. -
•
 $r \equiv 1 \text { mod }N$
and
$r \equiv 1 \text { mod }N$
and
 $r> 2nm+1$
.
$r> 2nm+1$
. -
• p splits completely in
 $L_2$
and M, and r splits completely in
$L_2$
and M, and r splits completely in
 $L_2(\zeta _p)$
and M.
$L_2(\zeta _p)$
and M. -
• The character
 $\Psi _2$
is unramified at the places of L above p and r.
$\Psi _2$
is unramified at the places of L above p and r.
Choosing
![]() $\mathfrak {p} |p$
and
$\mathfrak {p} |p$
and
![]() ${\mathfrak {r}} | r$
arbitrarily, there will be sandwiches up to conjugation
${\mathfrak {r}} | r$
arbitrarily, there will be sandwiches up to conjugation
and
and for each p-adic (resp. r-adic) place v of F,
![]() $r_{\mathfrak {p}}|_{G_{F_v}}$
(resp.
$r_{\mathfrak {p}}|_{G_{F_v}}$
(resp.
![]() $r_{\mathfrak {r}}|_{G_{F_v}}$
) is crystalline. (Here, we are using the definition of
$r_{\mathfrak {r}}|_{G_{F_v}}$
) is crystalline. (Here, we are using the definition of
![]() ${\mathcal L}({\mathcal R}|_{G_{F_2}})$
and the fact that p, r split in M.) The representation
${\mathcal L}({\mathcal R}|_{G_{F_2}})$
and the fact that p, r split in M.) The representation
![]() $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
can be chosen to take values in
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
can be chosen to take values in
![]() $\operatorname {\mathrm {GL}}_m({\mathbb F}_r)$
. Since the prime N is unramified in
$\operatorname {\mathrm {GL}}_m({\mathbb F}_r)$
. Since the prime N is unramified in
![]() $L_2(\zeta _r)$
,
$L_2(\zeta _r)$
,
![]() $E / {\mathbb Q}$
is linearly disjoint from
$E / {\mathbb Q}$
is linearly disjoint from
![]() $F_2(\zeta _N, \zeta _r) / {\mathbb Q}$
. The different inertial behaviour of
$F_2(\zeta _N, \zeta _r) / {\mathbb Q}$
. The different inertial behaviour of
![]() $\Psi _0$
at places dividing
$\Psi _0$
at places dividing
![]() $v_1$
implies that
$v_1$
implies that
![]() $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_2(\zeta _N, \zeta _r)}}$
is absolutely irreducible.
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_2(\zeta _N, \zeta _r)}}$
is absolutely irreducible.
Let v be a p-adic place of F. Then
![]() $F_{2, v} = M_{\mathfrak {p}} = {\mathbb Q}_p$
. By [Reference BergerBer10, Théorème 3.2.1], either
$F_{2, v} = M_{\mathfrak {p}} = {\mathbb Q}_p$
. By [Reference BergerBer10, Théorème 3.2.1], either
![]() $r_{\mathfrak {p}}|_{G_{F_{2, v}}}$
is (crystalline) ordinary or there is an isomorphism
$r_{\mathfrak {p}}|_{G_{F_{2, v}}}$
is (crystalline) ordinary or there is an isomorphism
![]() $\overline {r}_{\mathfrak {p}}|_{G_{{\mathbb Q}_{p^2}}} \cong \overline {\rho }_{2, m, 0}$
(notation as in Definition 5.1.1). In the latter case, Lemma 5.1.3 shows that for any finite extension
$\overline {r}_{\mathfrak {p}}|_{G_{{\mathbb Q}_{p^2}}} \cong \overline {\rho }_{2, m, 0}$
(notation as in Definition 5.1.1). In the latter case, Lemma 5.1.3 shows that for any finite extension
![]() $K / {\mathbb Q}_{p^2}$
, we have
$K / {\mathbb Q}_{p^2}$
, we have
![]() $r_{\mathfrak {p}}|_{G_{K}} \sim \rho _{2, m, 0}|_{G_K}$
. We write
$r_{\mathfrak {p}}|_{G_{K}} \sim \rho _{2, m, 0}|_{G_K}$
. We write
![]() $\Sigma _2^{\text {ord}}$
(resp.
$\Sigma _2^{\text {ord}}$
(resp.
![]() $\Sigma _2^{\text {ss}}$
) for the set of p-adic places of
$\Sigma _2^{\text {ss}}$
) for the set of p-adic places of
![]() $F_2$
such that
$F_2$
such that
![]() $r_{\mathfrak {p}}|_{G_{F_{2, v}}}$
is (resp. is not) ordinary. If
$r_{\mathfrak {p}}|_{G_{F_{2, v}}}$
is (resp. is not) ordinary. If
![]() $F_j / F_2$
is a finite extension, then we write
$F_j / F_2$
is a finite extension, then we write
![]() $\Sigma _j^{\text {ord}}$
for the set of places of
$\Sigma _j^{\text {ord}}$
for the set of places of
![]() $F_j$
lying above a place of
$F_j$
lying above a place of
![]() $\Sigma _2^{\text {ord}}$
(and define
$\Sigma _2^{\text {ord}}$
(and define
![]() $\Sigma _j^{\text {ss}}$
similarly).
$\Sigma _j^{\text {ss}}$
similarly).
Let
![]() $B / F_2(\zeta _N, \zeta _p, \zeta _r)$
be the extension cut out by
$B / F_2(\zeta _N, \zeta _p, \zeta _r)$
be the extension cut out by
![]() $\overline {r}_{\mathfrak {p}} \times \overline {r}_{\mathfrak {r}} \times \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
. We now choose a solvable CM extension
$\overline {r}_{\mathfrak {p}} \times \overline {r}_{\mathfrak {r}} \times \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
. We now choose a solvable CM extension
![]() $F_3 / F_2(\zeta _N)$
, Galois over
$F_3 / F_2(\zeta _N)$
, Galois over
![]() ${\mathbb Q}$
and linearly disjoint from
${\mathbb Q}$
and linearly disjoint from
![]() $B \cdot F_2 / F_2(\zeta _N)$
. Since
$B \cdot F_2 / F_2(\zeta _N)$
. Since
![]() $p \equiv -1 \text { mod }N$
, for each place
$p \equiv -1 \text { mod }N$
, for each place
![]() $v | p$
of
$v | p$
of
![]() $F_3$
,
$F_3$
,
![]() $F_v$
contains
$F_v$
contains
![]() ${\mathbb Q}_{p^2}$
. We moreover adjoin
${\mathbb Q}_{p^2}$
. We moreover adjoin
![]() $e^{2 \pi i / N}$
to M and extend
$e^{2 \pi i / N}$
to M and extend
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() ${\mathfrak {r}}$
arbitrarily to places of this enlarged M.
${\mathfrak {r}}$
arbitrarily to places of this enlarged M.
At this point, we choose (for later use) a semistable elliptic curve
![]() $A / {\mathbb Q}$
with good reduction at p, r and
$A / {\mathbb Q}$
with good reduction at p, r and
![]() $p_0$
. We choose a prime q with the following properties:
$p_0$
. We choose a prime q with the following properties:
-
•
 $q> 2 n m + 1$
and q splits in M. In particular,
$q> 2 n m + 1$
and q splits in M. In particular,
 $q \equiv 1 \text { mod }N$
. We choose a place
$q \equiv 1 \text { mod }N$
. We choose a place
 $\mathfrak {q} | q$
of M.
$\mathfrak {q} | q$
of M. -
•
 $\overline {\rho }_{A, q}(G_{F_3}) = \operatorname {\mathrm {GL}}_2({\mathbb F}_q)$
, and A has good ordinary reduction at q.
$\overline {\rho }_{A, q}(G_{F_3}) = \operatorname {\mathrm {GL}}_2({\mathbb F}_q)$
, and A has good ordinary reduction at q.
Let
![]() $B'$
denote the composite of B with the extension of
$B'$
denote the composite of B with the extension of
![]() $F_3$
cut out by
$F_3$
cut out by
![]() $\overline {\rho }_{A, q}$
.
$\overline {\rho }_{A, q}$
.
Having chosen an integer N and extension
![]() $F_3 / {\mathbb Q}(\zeta _N)$
, we have access to the families of motives over
$F_3 / {\mathbb Q}(\zeta _N)$
, we have access to the families of motives over
![]() $T_0 = \mathbf {P}^1_{F_3} - \{ \mu _N, \infty \}$
constructed in §4. We will use the families of motives both of rank m and of rank
$T_0 = \mathbf {P}^1_{F_3} - \{ \mu _N, \infty \}$
constructed in §4. We will use the families of motives both of rank m and of rank
![]() $nm$
. We write
$nm$
. We write
![]() ${}_m W_{t, \lambda }$
,
${}_m W_{t, \lambda }$
,
![]() ${}_{nm} W_{t, \lambda }$
for the
${}_{nm} W_{t, \lambda }$
for the
![]() ${\mathcal O}_{M_\lambda }[G_K]$
-modules of ranks m,
${\mathcal O}_{M_\lambda }[G_K]$
-modules of ranks m,
![]() $nm$
constructed in §4 associated to an extension
$nm$
constructed in §4 associated to an extension
![]() $K / F_3$
and point
$K / F_3$
and point
![]() $t \in T_0(K)$
. We claim that we can find a CM extension
$t \in T_0(K)$
. We claim that we can find a CM extension
![]() $F_4 / F_3$
, Galois over
$F_4 / F_3$
, Galois over
![]() ${\mathbb Q}$
and linearly disjoint from
${\mathbb Q}$
and linearly disjoint from
![]() $B' \cdot F_3 / F_3$
such that for any place
$B' \cdot F_3 / F_3$
such that for any place
![]() $v | p r p_0 q$
of
$v | p r p_0 q$
of
![]() $F_4$
, the representations
$F_4$
, the representations
![]() $\overline {r}_{\mathfrak {p}}|_{G_{F_{4, v}}}$
,
$\overline {r}_{\mathfrak {p}}|_{G_{F_{4, v}}}$
,
![]() $\overline {r}_{\mathfrak {r}}|_{G_{F_{4, v}}}$
,
$\overline {r}_{\mathfrak {r}}|_{G_{F_{4, v}}}$
,
![]() $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_{4, v}}}$
and
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_{4, v}}}$
and
![]() $\overline {\rho }_{A, q}|_{G_{F_{4, v}}}$
are all trivial, and the following additional data exists for
$\overline {\rho }_{A, q}|_{G_{F_{4, v}}}$
are all trivial, and the following additional data exists for
![]() $k \in \{ m, nm \}$
:
$k \in \{ m, nm \}$
:
-
(i) If
 $v \in \Sigma _4^{\textrm {ord}}$
, then there is a nonempty open subset
$v \in \Sigma _4^{\textrm {ord}}$
, then there is a nonempty open subset
 ${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4,v}})$
such that if
${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4,v}})$
such that if
 $t \in {}_k \Omega _v$
, then
$t \in {}_k \Omega _v$
, then
 ${}_k \overline {W}_{t, \mathfrak {p}}$
is trivial and
${}_k \overline {W}_{t, \mathfrak {p}}$
is trivial and
 ${}_k W_{t, \mathfrak {p}}$
is crystalline ordinary. Moreover,
${}_k W_{t, \mathfrak {p}}$
is crystalline ordinary. Moreover,
 ${}_k \overline {W}_{t, {\mathfrak {r}}}$
and
${}_k \overline {W}_{t, {\mathfrak {r}}}$
and
 ${}_k \overline {W}_{t, \mathfrak {q}}$
are both trivial.
${}_k \overline {W}_{t, \mathfrak {q}}$
are both trivial. -
(ii) If
 $v \in \Sigma _4^{\textrm {ss}}$
, then there is a nonempty open subset
$v \in \Sigma _4^{\textrm {ss}}$
, then there is a nonempty open subset
 ${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
 $t \in {}_k \Omega _v$
, then
$t \in {}_k \Omega _v$
, then
 ${}_k \overline {W}_{t, \mathfrak {p}}$
and
${}_k \overline {W}_{t, \mathfrak {p}}$
and
 $\overline {\rho }_{k, 1, 0}|_{G_{F_{4, v}}}$
are trivial,
$\overline {\rho }_{k, 1, 0}|_{G_{F_{4, v}}}$
are trivial,
 ${}_k W_{t, \mathfrak {p}}$
is crystalline and
${}_k W_{t, \mathfrak {p}}$
is crystalline and
 ${}_k W_{t, \mathfrak {p}} \sim \rho _{k, 1, 0}|_{G_{F_{4, v}}}$
. Moreover,
${}_k W_{t, \mathfrak {p}} \sim \rho _{k, 1, 0}|_{G_{F_{4, v}}}$
. Moreover,
 ${}_k \overline {W}_{t, {\mathfrak {r}}}$
and
${}_k \overline {W}_{t, {\mathfrak {r}}}$
and
 ${}_k \overline {W}_{t, \mathfrak {q}}$
are both trivial.
${}_k \overline {W}_{t, \mathfrak {q}}$
are both trivial. -
(iii) If
 $v | r$
is a place of
$v | r$
is a place of
 $F_4$
, then there is a nonempty open subset
$F_4$
, then there is a nonempty open subset
 ${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
 $t \in \Omega _v$
, then
$t \in \Omega _v$
, then
 ${}_k \overline {W}_{t, {\mathfrak {r}}}$
is trivial and
${}_k \overline {W}_{t, {\mathfrak {r}}}$
is trivial and
 $W_{t, {\mathfrak {r}}}$
is crystalline ordinary. Moreover,
$W_{t, {\mathfrak {r}}}$
is crystalline ordinary. Moreover,
 ${}_k \overline {W}_{t, \mathfrak {q}}$
and
${}_k \overline {W}_{t, \mathfrak {q}}$
and
 ${}_k \overline {W}_{t, \mathfrak {p}}$
are both trivial.
${}_k \overline {W}_{t, \mathfrak {p}}$
are both trivial. -
(iv) If
 $v | p_0$
is a place of
$v | p_0$
is a place of
 $F_4$
, then there is a nonempty open subset
$F_4$
, then there is a nonempty open subset
 ${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
${}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
 $t \in {}_k \Omega _v$
, then
$t \in {}_k \Omega _v$
, then
 ${}_k \overline {W}_{t, {\mathfrak {r}}}$
,
${}_k \overline {W}_{t, {\mathfrak {r}}}$
,
 ${}_k \overline {W}_{t, \mathfrak {q}}$
and
${}_k \overline {W}_{t, \mathfrak {q}}$
and
 ${}_k \overline {W}_{t, \mathfrak {p}}$
are all trivial.
${}_k \overline {W}_{t, \mathfrak {p}}$
are all trivial. -
(v) If
 $v | q$
is a place of
$v | q$
is a place of
 $F_4$
, then there is a nonempty open subset
$F_4$
, then there is a nonempty open subset
 $ {}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
$ {}_k \Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
such that if
 $t \in {}_k \Omega _v$
, then
$t \in {}_k \Omega _v$
, then
 ${}_k \overline {W}_{t, \mathfrak {q}}$
is trivial and
${}_k \overline {W}_{t, \mathfrak {q}}$
is trivial and
 ${}_k W_{t, \mathfrak {q}}$
is crystalline ordinary. Moreover,
${}_k W_{t, \mathfrak {q}}$
is crystalline ordinary. Moreover,
 ${}_k \overline {W}_{t, \mathfrak {p}}$
and
${}_k \overline {W}_{t, \mathfrak {p}}$
and
 ${}_k \overline {W}_{t, {\mathfrak {r}}}$
are both trivial.
${}_k \overline {W}_{t, {\mathfrak {r}}}$
are both trivial.
Indeed, we can take
![]() $F_4 = K^+ \cdot F_3$
, where
$F_4 = K^+ \cdot F_3$
, where
![]() $K^+ / {\mathbb Q}$
is a Galois, totally real extension with
$K^+ / {\mathbb Q}$
is a Galois, totally real extension with
![]() $K^+_v$
large enough for each place
$K^+_v$
large enough for each place
![]() $v | prp_0 q$
, as we now explain, dropping the subscript k which is fixed for the next two paragraphs. For (i), we claim that it is enough to show that once
$v | prp_0 q$
, as we now explain, dropping the subscript k which is fixed for the next two paragraphs. For (i), we claim that it is enough to show that once
![]() $F_{4, v}$
is large enough, we can find a single point of
$F_{4, v}$
is large enough, we can find a single point of
![]() $t \in T_0(F_{4, v})$
such that
$t \in T_0(F_{4, v})$
such that
![]() $\overline {W}_{t, \mathfrak {p}}$
,
$\overline {W}_{t, \mathfrak {p}}$
,
![]() $\overline {W}_{t, {\mathfrak {r}}}$
and
$\overline {W}_{t, {\mathfrak {r}}}$
and
![]() $\overline {W}_{t, \mathfrak {q}}$
are all trivial and
$\overline {W}_{t, \mathfrak {q}}$
are all trivial and
![]() $W_{t, \mathfrak {p}}$
is crystalline ordinary. Indeed, by a version of Krasner’s Lemma due to Kisin [Reference KisinKis99, Theorem 5.1], for any
$W_{t, \mathfrak {p}}$
is crystalline ordinary. Indeed, by a version of Krasner’s Lemma due to Kisin [Reference KisinKis99, Theorem 5.1], for any
![]() $c> 0$
, there exists an open ball
$c> 0$
, there exists an open ball
![]() $U_t$
around t in
$U_t$
around t in
![]() $T_0({\mathcal O}_{F_{4, v}})$
, such that for any
$T_0({\mathcal O}_{F_{4, v}})$
, such that for any
![]() $t' \in U_t$
, the pairs of representations
$t' \in U_t$
, the pairs of representations
![]() $W_{\mathfrak {p}, t} / (p^c)$
,
$W_{\mathfrak {p}, t} / (p^c)$
,
![]() $W_{\mathfrak {p}, t'} / (p^c)$
and
$W_{\mathfrak {p}, t'} / (p^c)$
and
![]() $W_{{\mathfrak {r}}, t} / (r^c)$
,
$W_{{\mathfrak {r}}, t} / (r^c)$
,
![]() $W_{{\mathfrak {r}}, t'} / (r^c)$
and
$W_{{\mathfrak {r}}, t'} / (r^c)$
and
![]() $W_{\mathfrak {q}, t} / (q^c)$
,
$W_{\mathfrak {q}, t} / (q^c)$
,
![]() $W_{\mathfrak {q}, t'} / (q^c)$
are isomorphic. By Lemma 5.1.5, we can choose
$W_{\mathfrak {q}, t'} / (q^c)$
are isomorphic. By Lemma 5.1.5, we can choose
![]() $c> 1$
so that this forces
$c> 1$
so that this forces
![]() $W_{\mathfrak {p}, t} \sim W_{\mathfrak {p}, t'}$
, and hence (by Lemma 5.1.4) that
$W_{\mathfrak {p}, t} \sim W_{\mathfrak {p}, t'}$
, and hence (by Lemma 5.1.4) that
![]() $W_{\mathfrak {p}, t'}$
is crystalline ordinary. The existence of a crystalline ordinary point t follows from Proposition 4.2.6 and Proposition 4.2.5(2), after which we enlarge
$W_{\mathfrak {p}, t'}$
is crystalline ordinary. The existence of a crystalline ordinary point t follows from Proposition 4.2.6 and Proposition 4.2.5(2), after which we enlarge
![]() $F_{4, v}$
further if necessary to force the residual representations to be trivial. Then we take
$F_{4, v}$
further if necessary to force the residual representations to be trivial. Then we take
![]() $\Omega _v = U_t$
.
$\Omega _v = U_t$
.
For (iii) and (v), the argument is essentially the same as case (i), while for (iv), it is even simpler. For (ii), we enlarge
![]() $F_{4, v}$
so that
$F_{4, v}$
so that
![]() $\overline {\rho }_{k, 1, 0}|_{G_{F_{4, v}}}$
and
$\overline {\rho }_{k, 1, 0}|_{G_{F_{4, v}}}$
and
![]() $\overline {W}_{\mathfrak {p}, 0}|_{G_{F_{4, v}}}$
are trivial. By Lemma 5.1.3 and Lemma 4.4.4, we have
$\overline {W}_{\mathfrak {p}, 0}|_{G_{F_{4, v}}}$
are trivial. By Lemma 5.1.3 and Lemma 4.4.4, we have
![]() $W_{\mathfrak {p}, 0}|_{G_{F_{4, v}}} \sim \rho _{k, 1, 0}|_{G_{F_{4, v}}}$
. Employing the same argument as in the previous paragraph, using [Reference KisinKis99, Theorem 5.1] and Lemma 5.1.5, we can find a nonempty open neighbourhood
$W_{\mathfrak {p}, 0}|_{G_{F_{4, v}}} \sim \rho _{k, 1, 0}|_{G_{F_{4, v}}}$
. Employing the same argument as in the previous paragraph, using [Reference KisinKis99, Theorem 5.1] and Lemma 5.1.5, we can find a nonempty open neighbourhood
![]() $\Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
of
$\Omega _v \subset T_0({\mathcal O}_{F_{4, v}})$
of
![]() $0 \in T_0({\mathcal O}_{F_{4, v}})$
such that if
$0 \in T_0({\mathcal O}_{F_{4, v}})$
such that if
![]() $t \in \Omega _v$
, then
$t \in \Omega _v$
, then
![]() $W_{\mathfrak {p}, t}$
is crystalline and
$W_{\mathfrak {p}, t}$
is crystalline and
![]() $W_{\mathfrak {p}, t} \sim W_{\mathfrak {p}, 0}|_{G_{F_{4, v}}}$
. Since
$W_{\mathfrak {p}, t} \sim W_{\mathfrak {p}, 0}|_{G_{F_{4, v}}}$
. Since
![]() $\sim $
is a transitive relation, this leads to a choice of
$\sim $
is a transitive relation, this leads to a choice of
![]() $\Omega _v$
with the desired property.
$\Omega _v$
with the desired property.
To construct the compatible system
![]() ${\mathcal R}_{\mathrm {aux}}$
, we will apply Proposition 4.5.1. If
${\mathcal R}_{\mathrm {aux}}$
, we will apply Proposition 4.5.1. If
![]() $m=2$
, we can use a modular curve with level r-structure, and since the argument in this case is a straightforward (and considerably simpler) variant on the argument that we use if
$m=2$
, we can use a modular curve with level r-structure, and since the argument in this case is a straightforward (and considerably simpler) variant on the argument that we use if
![]() $m>2$
, we leave this case to the reader. In the case
$m>2$
, we leave this case to the reader. In the case
![]() $m> 2$
, we use the moduli space
$m> 2$
, we use the moduli space
![]() $T = T( \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_4}} )$
defined in Remark 4.4.3, which is defined since
$T = T( \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_4}} )$
defined in Remark 4.4.3, which is defined since
![]() $r \equiv 1 \text { mod }N$
and
$r \equiv 1 \text { mod }N$
and
![]() $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
takes values in
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}$
takes values in
![]() $\operatorname {\mathrm {GL}}_m({\mathbb F}_r)$
, with determinant
$\operatorname {\mathrm {GL}}_m({\mathbb F}_r)$
, with determinant
![]() $\overline {\varepsilon }^{-m(m-1)/2}$
. We take
$\overline {\varepsilon }^{-m(m-1)/2}$
. We take
![]() $F^{\mathrm {avoid}} = B' \cdot F_4$
. We take the homomorphism
$F^{\mathrm {avoid}} = B' \cdot F_4$
. We take the homomorphism
![]() $\pi _1^{\acute{\rm e}\text {t}}(T_{F_4}) \to \operatorname {GU}_m({\mathbb F}_{p^2})$
to be the one associated to the local system
$\pi _1^{\acute{\rm e}\text {t}}(T_{F_4}) \to \operatorname {GU}_m({\mathbb F}_{p^2})$
to be the one associated to the local system
![]() $\overline {{\mathcal W}}_{\mathfrak {p}}$
. We take
$\overline {{\mathcal W}}_{\mathfrak {p}}$
. We take
![]() $S_0 = \{ p, r, p_0, q \}$
. If v is a place lying above a prime in
$S_0 = \{ p, r, p_0, q \}$
. If v is a place lying above a prime in
![]() $S_0$
, we take
$S_0$
, we take
![]() $L_v = F_{4, v}$
and
$L_v = F_{4, v}$
and
![]() $\Omega _v$
to be the pre-image in
$\Omega _v$
to be the pre-image in
![]() $T(F_{4, v})$
of the set
$T(F_{4, v})$
of the set
![]() ${}_m \Omega _v$
. Note that
${}_m \Omega _v$
. Note that
![]() $\Omega _v$
is certainly open, and it is nonempty because we have arranged that for each place
$\Omega _v$
is certainly open, and it is nonempty because we have arranged that for each place
![]() $v | S_0$
of
$v | S_0$
of
![]() $F_4$
, and for each
$F_4$
, and for each
![]() $t \in {}_m \Omega _v$
,
$t \in {}_m \Omega _v$
,
![]() $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_{4, v}}}$
and
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_{4, v}}}$
and
![]() $\overline {W}_{t, {\mathfrak {r}}}$
are both trivial (and hence isomorphic!).
$\overline {W}_{t, {\mathfrak {r}}}$
are both trivial (and hence isomorphic!).
Proposition 4.5.1 now yields an imaginary CM extension
![]() $F_5 / F_4$
, Galois over
$F_5 / F_4$
, Galois over
![]() ${\mathbb Q}$
and in which the places above
${\mathbb Q}$
and in which the places above
![]() $S_0$
all split completely, and a weakly compatible system
$S_0$
all split completely, and a weakly compatible system
![]() $\{ W_{t, \lambda } \}$
of representations of
$\{ W_{t, \lambda } \}$
of representations of
![]() $G_{F_5}$
with coefficients in
$G_{F_5}$
with coefficients in
![]() ${\mathbb Q}(e^{2 \pi i / N}) \subset M$
. We take
${\mathbb Q}(e^{2 \pi i / N}) \subset M$
. We take
![]() ${\mathcal R}_{\mathrm {aux}} = \{ r_{\mathrm {aux}, \lambda } \} = \{ W_{t, \lambda } \}$
and note that the statement of Proposition 4.5.1 and the definition of the sets
${\mathcal R}_{\mathrm {aux}} = \{ r_{\mathrm {aux}, \lambda } \} = \{ W_{t, \lambda } \}$
and note that the statement of Proposition 4.5.1 and the definition of the sets
![]() $\Omega _v$
imply that
$\Omega _v$
imply that
![]() ${\mathcal R}_{\mathrm {aux}}$
has the following properties:
${\mathcal R}_{\mathrm {aux}}$
has the following properties:
-
•
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_{F_5}) = \operatorname {GU}_m({\mathbb F}_{p^2})$
(note we are assuming that
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_{F_5}) = \operatorname {GU}_m({\mathbb F}_{p^2})$
(note we are assuming that
 $m>2$
).
$m>2$
). -
• If
 $v \in \Sigma _5^{\mathrm {ord}}$
, then
$v \in \Sigma _5^{\mathrm {ord}}$
, then
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}}$
is trivial and
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}}$
is trivial and
 $r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}}$
is crystalline ordinary.
$r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}}$
is crystalline ordinary. -
• If
 $v \in \Sigma _5^{\mathrm {ss}}$
, then
$v \in \Sigma _5^{\mathrm {ss}}$
, then
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}}$
is trivial and
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}}$
is trivial and
 $r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}} \sim \rho _{m, 1, 0}|_{G_{F_{5, v}}}$
.
$r_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_{5, v}}} \sim \rho _{m, 1, 0}|_{G_{F_{5, v}}}$
. -
•
 $S_{\mathrm {aux}}$
is disjoint from
$S_{\mathrm {aux}}$
is disjoint from
 $X_5 \cup \{ v | p r \}$
. (Use Proposition 4.2.5.)
$X_5 \cup \{ v | p r \}$
. (Use Proposition 4.2.5.) -
• There is an isomorphism
 $\overline {r}_{\mathrm {aux}, {\mathfrak {r}}} \cong \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_5}}$
. For each place
$\overline {r}_{\mathrm {aux}, {\mathfrak {r}}} \cong \overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_5}}$
. For each place
 $v | r$
of
$v | r$
of
 $F_5$
,
$F_5$
,
 $\overline {r}_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_{5, v}}}$
is trivial and
$\overline {r}_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_{5, v}}}$
is trivial and
 $r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_{5, v}}}$
is crystalline ordinary.
$r_{\mathrm {aux}, {\mathfrak {r}}}|_{G_{F_{5, v}}}$
is crystalline ordinary.
We set
![]() ${\mathcal S}_{\mathrm {aux}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_5}}) \otimes {\mathcal R}_{\mathrm {aux}}$
and now construct
${\mathcal S}_{\mathrm {aux}} = (\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F_5}}) \otimes {\mathcal R}_{\mathrm {aux}}$
and now construct
![]() ${\mathcal S}_{\mathrm {UA}}$
. The places
${\mathcal S}_{\mathrm {UA}}$
. The places
![]() $v | prp_0q$
split in
$v | prp_0q$
split in
![]() $F_5 / F_4$
, so if v is a place of
$F_5 / F_4$
, so if v is a place of
![]() $F_5$
dividing
$F_5$
dividing
![]() $prp_0q$
, we may define
$prp_0q$
, we may define
![]() ${}_k \Omega _v = {}_k \Omega _{v|_{F_4}}$
to keep in hand the data (i)–(v) defined above. We will apply Proposition 4.5.1 to the moduli space
${}_k \Omega _v = {}_k \Omega _{v|_{F_4}}$
to keep in hand the data (i)–(v) defined above. We will apply Proposition 4.5.1 to the moduli space
We take
![]() $F^{\mathrm {avoid}} = B' \cdot F_5$
. We do not specify a homomorphism f. We take
$F^{\mathrm {avoid}} = B' \cdot F_5$
. We do not specify a homomorphism f. We take
![]() $S_0 = \{ p, r, p_0, q \}$
. If v is a place lying above a prime in
$S_0 = \{ p, r, p_0, q \}$
. If v is a place lying above a prime in
![]() $S_0$
, we take
$S_0$
, we take
![]() $L_v = F_{5, v}$
and
$L_v = F_{5, v}$
and
![]() $\Omega _v$
to be the pre-image in
$\Omega _v$
to be the pre-image in
![]() $T(F_{5, v})$
of the set
$T(F_{5, v})$
of the set
![]() ${}_{nm} \Omega _v$
. Once again, this pre-image is nonempty because we have trivialized all of the relevant local residual representations. (Since
${}_{nm} \Omega _v$
. Once again, this pre-image is nonempty because we have trivialized all of the relevant local residual representations. (Since
![]() $p \equiv -1 \text { mod }N$
, the definition of T involves a choice of Hermitian structure. We are therefore invoking the fact here that over a finite field, any two Hermitian spaces of the same dimension are isomorphic.) Proposition 4.5.1 then yields a CM extension
$p \equiv -1 \text { mod }N$
, the definition of T involves a choice of Hermitian structure. We are therefore invoking the fact here that over a finite field, any two Hermitian spaces of the same dimension are isomorphic.) Proposition 4.5.1 then yields a CM extension
![]() $F_6 / F_5$
, Galois over
$F_6 / F_5$
, Galois over
![]() ${\mathbb Q}$
, and a point
${\mathbb Q}$
, and a point
![]() $t \in T(F_6)$
corresponding to a weakly compatible system
$t \in T(F_6)$
corresponding to a weakly compatible system
![]() ${\mathcal S}_{\mathrm {UA}} = \{ s_{\mathrm {UA}, \lambda } \} = \{ W_{t, \lambda } \}$
of rank
${\mathcal S}_{\mathrm {UA}} = \{ s_{\mathrm {UA}, \lambda } \} = \{ W_{t, \lambda } \}$
of rank
![]() $nm$
representations of
$nm$
representations of
![]() $G_{F_6}$
with the following properties:
$G_{F_6}$
with the following properties:
-
• There are isomorphisms
 $\overline {s}_{\mathrm {UA}, \mathfrak {p}} \cong \overline {s}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_6}}$
and
$\overline {s}_{\mathrm {UA}, \mathfrak {p}} \cong \overline {s}_{\mathrm {aux}, \mathfrak {p}}|_{G_{F_6}}$
and
 $\overline {s}_{\mathrm {UA}, \mathfrak {q}} \cong \operatorname {\mathrm {Sym}}^{nm-1} \overline {\rho }_{A, q}|_{G_{F_6}}$
.
$\overline {s}_{\mathrm {UA}, \mathfrak {q}} \cong \operatorname {\mathrm {Sym}}^{nm-1} \overline {\rho }_{A, q}|_{G_{F_6}}$
. -
• If
 $v \in \Sigma _6^{\mathrm {ord}}$
, then
$v \in \Sigma _6^{\mathrm {ord}}$
, then
 $\overline {s}_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is trivial and
$\overline {s}_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is trivial and
 $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is crystalline ordinary.
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is crystalline ordinary. -
• If
 $v \in \Sigma _6^{\mathrm {ss}}$
, then
$v \in \Sigma _6^{\mathrm {ss}}$
, then
 $\overline {s}_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is trivial and
$\overline {s}_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is trivial and
 $s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}} \sim \rho _{nm, 1, 0}|_{G_{F_{6, v}}}$
.
$s_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}} \sim \rho _{nm, 1, 0}|_{G_{F_{6, v}}}$
. -
• For each place
 $v | q$
of
$v | q$
of
 $F_6$
,
$F_6$
,
 $\overline {s}_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is trivial and
$\overline {s}_{\mathrm {UA}, \mathfrak {p}}|_{G_{F_{6, v}}}$
is trivial and
 $s_{\mathrm {UA}, q}|_{G_{F_{6, v}}}$
is crystalline ordinary.
$s_{\mathrm {UA}, q}|_{G_{F_{6, v}}}$
is crystalline ordinary. -
•
 $S_{\mathrm {UA}}$
is disjoint from
$S_{\mathrm {UA}}$
is disjoint from
 $X_6 \cup \{ v | p r \}$
.
$X_6 \cup \{ v | p r \}$
.
We now claim that assumptions (1)-(17) of Proposition 6.2.3 are satisfied for the compatible system
![]() ${\mathcal R}|_{G_{F_6}}$
, set
${\mathcal R}|_{G_{F_6}}$
, set
![]() $X_0 = X_6$
of places of
$X_0 = X_6$
of places of
![]() $F_6$
, and auxiliary compatible systems
$F_6$
, and auxiliary compatible systems
![]() ${\mathcal R}_{\mathrm {CM}}|_{G_{F_6}}$
,
${\mathcal R}_{\mathrm {CM}}|_{G_{F_6}}$
,
![]() ${\mathcal R}_{\mathrm {aux}}|_{G_{F_6}}$
and
${\mathcal R}_{\mathrm {aux}}|_{G_{F_6}}$
and
![]() ${\mathcal S}_{\mathrm {UA}}$
(defined over
${\mathcal S}_{\mathrm {UA}}$
(defined over
![]() $F_6$
by construction). Let us verify these assumptions in turn.
$F_6$
by construction). Let us verify these assumptions in turn.
-
• As already observed, (1)-(5) are automatically satisfied.
-
• We take
 $\Psi = \Psi _6$
. The extension
$\Psi = \Psi _6$
. The extension
 $E / {\mathbb Q}$
is linearly disjoint from
$E / {\mathbb Q}$
is linearly disjoint from
 $F_6$
because
$F_6$
because
 $E \leq B$
, while
$E \leq B$
, while
 $\Psi $
has the given infinity type, so (6) is satisfied.
$\Psi $
has the given infinity type, so (6) is satisfied. -
• The primes
 $p, r$
are prime to S by construction, so (7) is satisfied.
$p, r$
are prime to S by construction, so (7) is satisfied. -
•
 ${\mathcal R}_{\mathrm {aux}}|_{G_{F_6}}$
has the claimed properties by construction, so (8) is satisfied. The same is true for
${\mathcal R}_{\mathrm {aux}}|_{G_{F_6}}$
has the claimed properties by construction, so (8) is satisfied. The same is true for
 ${\mathcal S}_{\mathrm {UA}}$
, except we need to justify the fact that
${\mathcal S}_{\mathrm {UA}}$
, except we need to justify the fact that
 ${\mathcal S}_{\mathrm {UA}}$
is weakly automorphic of level prime to
${\mathcal S}_{\mathrm {UA}}$
is weakly automorphic of level prime to
 $X_6 \cup \{ v | p r \}$
. Note that the q-adic representation
$X_6 \cup \{ v | p r \}$
. Note that the q-adic representation
 $\operatorname {\mathrm {Sym}}^{nm - 1} \rho _{A, q}|_{G_{F_6}}$
is automorphic by the combination of the main results of [Reference Breuil, Conrad, Diamond and TaylorBCDT01, Reference DieulefaitDie15, Reference Newton and ThorneNT22, Reference Arthur and ClozelAC89] (or alternately by [Reference Clozel, Newton and ThorneCNT23]), associated to a regular algebraic, cuspidal automorphic representation of
$\operatorname {\mathrm {Sym}}^{nm - 1} \rho _{A, q}|_{G_{F_6}}$
is automorphic by the combination of the main results of [Reference Breuil, Conrad, Diamond and TaylorBCDT01, Reference DieulefaitDie15, Reference Newton and ThorneNT22, Reference Arthur and ClozelAC89] (or alternately by [Reference Clozel, Newton and ThorneCNT23]), associated to a regular algebraic, cuspidal automorphic representation of
 $\operatorname {\mathrm {GL}}_{nm}(\mathbf {A}_{F_6})$
which is
$\operatorname {\mathrm {GL}}_{nm}(\mathbf {A}_{F_6})$
which is
 $\iota $
-ordinary with respect to any isomorphism
$\iota $
-ordinary with respect to any isomorphism
 $\iota : \overline {{\mathbb Q}}_q \to {\mathbb C}$
. (We could also verify the automorphy, at the cost of further extending the field
$\iota : \overline {{\mathbb Q}}_q \to {\mathbb C}$
. (We could also verify the automorphy, at the cost of further extending the field
 $F_6$
, by a further application of Proposition 4.5.1 as is done in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23].) We would now like to apply [Reference Miagkov and ThorneMT23, Theorem 1.3] to conclude that
$F_6$
, by a further application of Proposition 4.5.1 as is done in [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23].) We would now like to apply [Reference Miagkov and ThorneMT23, Theorem 1.3] to conclude that
 ${\mathcal S}_{\mathrm {UA}}$
is weakly automorphic of level prime to
${\mathcal S}_{\mathrm {UA}}$
is weakly automorphic of level prime to
 $X_6 \cup \{ v | p r \}$
(noting that the cited result includes the conclusion that the automorphic representation witnessing the weak automorphy of
$X_6 \cup \{ v | p r \}$
(noting that the cited result includes the conclusion that the automorphic representation witnessing the weak automorphy of
 ${\mathcal S}_{\mathrm {UA}}$
is unramified at any place where both
${\mathcal S}_{\mathrm {UA}}$
is unramified at any place where both
 $\rho _{A, q}$
and
$\rho _{A, q}$
and
 $s_{\mathrm {UA}, \mathfrak {q}}$
are unramified). We must verify that
$s_{\mathrm {UA}, \mathfrak {q}}$
are unramified). We must verify that
 $\operatorname {\mathrm {Sym}}^{nm - 1} \overline {\rho }_{A, q}|_{G_{F_6}}$
satisfies the Taylor–Wiles conditions (as formulated in Definition 5.2.1). By Lemma 5.2.2, it suffices to check that
$\operatorname {\mathrm {Sym}}^{nm - 1} \overline {\rho }_{A, q}|_{G_{F_6}}$
satisfies the Taylor–Wiles conditions (as formulated in Definition 5.2.1). By Lemma 5.2.2, it suffices to check that
 $\operatorname {\mathrm {Sym}}^{nm - 1} \overline {\rho }_{A, q}$
satisfies these conditions (as a representation of
$\operatorname {\mathrm {Sym}}^{nm - 1} \overline {\rho }_{A, q}$
satisfies these conditions (as a representation of
 $G_{\mathbb Q}$
), and this follows from the definitions, together with an application of [Reference Guralnick, Herzig, Taylor and ThorneGHTT12, Theorem A.9] (using our assumption
$G_{\mathbb Q}$
), and this follows from the definitions, together with an application of [Reference Guralnick, Herzig, Taylor and ThorneGHTT12, Theorem A.9] (using our assumption
 $q> 2nm + 1$
).
$q> 2nm + 1$
). -
•
 $L / F$
and
$L / F$
and
 $\Psi $
are unramified above
$\Psi $
are unramified above
 $X_0 \cup \{ v | p r \}$
by construction, so (10) is satisfied.
$X_0 \cup \{ v | p r \}$
by construction, so (10) is satisfied. -
• We have chosen the primes
 $p, r$
so that
$p, r$
so that
 $p> 2nm +1$
and
$p> 2nm +1$
and
 $r> 2nm + 1$
. At each step, the extension
$r> 2nm + 1$
. At each step, the extension
 $F_{j+1} / F_{j}$
has been chosen linearly disjoint from
$F_{j+1} / F_{j}$
has been chosen linearly disjoint from
 $L_j(\zeta _p, \zeta _r)$
, so (11) and (12) are satisfied.
$L_j(\zeta _p, \zeta _r)$
, so (11) and (12) are satisfied. -
• The images
 $\overline {r}_{\mathfrak {p}}(G_{F_2})$
,
$\overline {r}_{\mathfrak {p}}(G_{F_2})$
,
 $\overline {r}_{\mathfrak {r}}(G_{F_2})$
and
$\overline {r}_{\mathfrak {r}}(G_{F_2})$
and
 $\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_{F_5})$
are large by construction, and at each step, the extension
$\overline {r}_{\mathrm {aux}, \mathfrak {p}}(G_{F_5})$
are large by construction, and at each step, the extension
 $F_{j+1} / F_{j}$
has been chosen so that the image does not change on restriction to the smaller Galois group. Moreover,
$F_{j+1} / F_{j}$
has been chosen so that the image does not change on restriction to the smaller Galois group. Moreover,
 $\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_2(\zeta _r)}}$
is irreducible, and again the analogous property holds over
$\overline {r}_{\mathrm {CM}, {\mathfrak {r}}}|_{G_{F_2(\zeta _r)}}$
is irreducible, and again the analogous property holds over
 $F_6$
by construction. Therefore, (13) is satisfied.
$F_6$
by construction. Therefore, (13) is satisfied. -
• Assumptions (14)–(17) hold by construction.
This completes the proof.
7 Applications
7.1 The Ramanujan Conjecture
We are now in a position to prove the (more general versions of the) main theorems of the introduction as a consequence of Theorem 6.2.1. Let F be an imaginary CM field, and let
![]() $\pi $
be a regular algebraic cuspidal automorphic representation of
$\pi $
be a regular algebraic cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. We write
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
. We write
![]() $(a_\tau \ge b_\tau )_{\tau : F\hookrightarrow {\mathbb C}}$
for the weight of
$(a_\tau \ge b_\tau )_{\tau : F\hookrightarrow {\mathbb C}}$
for the weight of
![]() $\pi $
. Recall that we say that
$\pi $
. Recall that we say that
![]() $\pi $
is of parallel weight if
$\pi $
is of parallel weight if
![]() $a_{\tau }-b_{\tau }$
is independent of
$a_{\tau }-b_{\tau }$
is independent of
![]() $\tau $
.
$\tau $
.
Theorem 7.1.1. Let F be an imaginary CM field, and let
![]() $\pi $
be a regular algebraic cuspidal automorphic representation of
$\pi $
be a regular algebraic cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
of parallel weight. Then, for all primes v of F, the representation
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
of parallel weight. Then, for all primes v of F, the representation
![]() $\pi _v$
is (essentially) tempered.
$\pi _v$
is (essentially) tempered.
Proof. Since
![]() $\pi $
is assumed to have parallel weight, there is an integer
$\pi $
is assumed to have parallel weight, there is an integer
![]() $m \geq 1$
such that
$m \geq 1$
such that
![]() $a_{\tau }-b_{\tau } = m-1$
for all
$a_{\tau }-b_{\tau } = m-1$
for all
![]() $\tau :F\hookrightarrow {\mathbb C}$
. By Clozel’s purity lemma [Reference ClozelClo90, Lemma 4.9], there is an integer w with
$\tau :F\hookrightarrow {\mathbb C}$
. By Clozel’s purity lemma [Reference ClozelClo90, Lemma 4.9], there is an integer w with
![]() $a_{\tau } + b_{c\tau } = w$
for all
$a_{\tau } + b_{c\tau } = w$
for all
![]() $\tau $
. It follows that
$\tau $
. It follows that
![]() $b_{\tau }+b_{c\tau }=w-m+1$
is independent of
$b_{\tau }+b_{c\tau }=w-m+1$
is independent of
![]() $\tau $
. In particular, there exists an algebraic Hecke character of
$\tau $
. In particular, there exists an algebraic Hecke character of
![]() $\mathbf {A}_F^\times $
with weight
$\mathbf {A}_F^\times $
with weight
![]() $(b_{\tau })_{\tau :F\hookrightarrow {\mathbb C}}$
, so after twisting, we may assume that
$(b_{\tau })_{\tau :F\hookrightarrow {\mathbb C}}$
, so after twisting, we may assume that
![]() $(a_\tau ,b_\tau ) = (m-1,0)$
for all
$(a_\tau ,b_\tau ) = (m-1,0)$
for all
![]() $\tau $
. The central character of
$\tau $
. The central character of
![]() $\pi $
is then of the form
$\pi $
is then of the form
![]() $\psi |\cdot |^{1-m}$
for a finite order Hecke character
$\psi |\cdot |^{1-m}$
for a finite order Hecke character
![]() $\psi $
.
$\psi $
.
Exactly as in the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Theorem 7.1.1], we can find a quadratic CM extension
![]() $F'/F$
for which the character
$F'/F$
for which the character
![]() $\psi \circ N_{F'/F}$
is a square. We can check temperedness after base change to
$\psi \circ N_{F'/F}$
is a square. We can check temperedness after base change to
![]() $F'$
. Twisting by a finite order Hecke character, we may then assume that
$F'$
. Twisting by a finite order Hecke character, we may then assume that
![]() $\pi $
has central character
$\pi $
has central character
![]() $|\cdot |^{1-m}$
. Exactly as in the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor. 7.1.15], we can make a further solvable base change to reduce to checking temperedness of the unramified
$|\cdot |^{1-m}$
. Exactly as in the proof of [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Cor. 7.1.15], we can make a further solvable base change to reduce to checking temperedness of the unramified
![]() $\pi _v$
. Hence, it suffices to show that the associated very weakly compatible system
$\pi _v$
. Hence, it suffices to show that the associated very weakly compatible system
![]() ${\mathcal R}$
(cf. [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.10]) is pure. By [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.2], either
${\mathcal R}$
(cf. [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.10]) is pure. By [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.2], either
![]() ${\mathcal R}$
is strongly irreducible, Artin up to twist, or induced from a quadratic extension. If
${\mathcal R}$
is strongly irreducible, Artin up to twist, or induced from a quadratic extension. If
![]() ${\mathcal R}$
is induced, then purity follows from the purity of rank one (very weakly) compatible systems. The compatible family
${\mathcal R}$
is induced, then purity follows from the purity of rank one (very weakly) compatible systems. The compatible family
![]() ${\mathcal R}$
cannot be Artin up to twist because that is incompatible with having distinct Hodge–Tate weights. Thus,
${\mathcal R}$
cannot be Artin up to twist because that is incompatible with having distinct Hodge–Tate weights. Thus,
![]() ${\mathcal R}$
is strongly irreducible, and the result follows from Theorem 6.2.1.
${\mathcal R}$
is strongly irreducible, and the result follows from Theorem 6.2.1.
7.2 The potential automorphy of compatible systems and the Sato–Tate conjecture
Theorem 7.2.1. Let F be a CM field, and let
![]() $\mathcal {R}=(M,S,\{ Q_v(X) \}, r_\lambda ,H_{\tau } )$
be a very weakly compatible system of rank 2 representations of
$\mathcal {R}=(M,S,\{ Q_v(X) \}, r_\lambda ,H_{\tau } )$
be a very weakly compatible system of rank 2 representations of
![]() $G_F$
that is strongly irreducible. Suppose there exists an integer
$G_F$
that is strongly irreducible. Suppose there exists an integer
![]() $m \geq 1$
such that
$m \geq 1$
such that
![]() $H_\tau = \{ 0, m \}$
for each embedding
$H_\tau = \{ 0, m \}$
for each embedding
![]() $\tau : F \to \overline {M}$
. Then
$\tau : F \to \overline {M}$
. Then
![]() ${\mathcal R}$
is pure of weight m, and for each
${\mathcal R}$
is pure of weight m, and for each
![]() $n \geq 1$
, there exists a finite CM extension
$n \geq 1$
, there exists a finite CM extension
![]() $F' / F$
, Galois over
$F' / F$
, Galois over
![]() ${\mathbb Q}$
, such that
${\mathbb Q}$
, such that
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F'}}$
is automorphic.
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}|_{G_{F'}}$
is automorphic.
If one alternatively assumes that
![]() $\mathcal {R}$
is irreducible but not strongly irreducible, then
$\mathcal {R}$
is irreducible but not strongly irreducible, then
![]() ${\mathcal R}$
is pure of weight m, and for each
${\mathcal R}$
is pure of weight m, and for each
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
decomposes as a direct sum of compatible systems of dimension at most
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
decomposes as a direct sum of compatible systems of dimension at most
![]() $2$
which are automorphic.
$2$
which are automorphic.
Proof. Assume that
![]() ${\mathcal R}$
is strongly irreducible. As in the proof of Theorem 7.1.1, we can reduce to the case where
${\mathcal R}$
is strongly irreducible. As in the proof of Theorem 7.1.1, we can reduce to the case where
![]() ${\mathcal R}$
has determinant
${\mathcal R}$
has determinant
![]() $\varepsilon ^{-m}$
. But now Theorem 7.2.1 follows directly from Theorem 6.2.1.
$\varepsilon ^{-m}$
. But now Theorem 7.2.1 follows directly from Theorem 6.2.1.
If
![]() ${\mathcal R}$
is not strongly irreducible, then from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.2], it follows that
${\mathcal R}$
is not strongly irreducible, then from [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.2], it follows that
![]() ${\mathcal R}$
is induced from a compatible system of algebraic Hecke characters for some quadratic extension
${\mathcal R}$
is induced from a compatible system of algebraic Hecke characters for some quadratic extension
![]() $F'/F$
(the condition on the Hodge–Tate weights ensures that
$F'/F$
(the condition on the Hodge–Tate weights ensures that
![]() ${\mathcal R}$
is not Artin up to twist). Then the symmetric powers
${\mathcal R}$
is not Artin up to twist). Then the symmetric powers
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
decompose as a sum of two-dimensional induced compatible systems and (when n is odd) a one-dimensional compatible system. In particular, for any n,
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
decompose as a sum of two-dimensional induced compatible systems and (when n is odd) a one-dimensional compatible system. In particular, for any n,
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
decomposes as a direct sum of automorphic compatible systems, and the purity statement follows from the purity of (the Galois representations associated to) algebraic Hecke characters.
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
decomposes as a direct sum of automorphic compatible systems, and the purity statement follows from the purity of (the Galois representations associated to) algebraic Hecke characters.
We next give a statement of the Sato–Tate conjecture, including Theorem B as a special case, before giving the proof when
![]() $\pi $
has parallel weight. Let F be an imaginary CM field, and let
$\pi $
has parallel weight. Let F be an imaginary CM field, and let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
which is regular algebraic of weight
$\operatorname {\mathrm {GL}}_2(\mathbf {A}_F)$
which is regular algebraic of weight
![]() $\lambda $
and not CM (i.e., not automorphically induced). Thus, there is an integer w such that
$\lambda $
and not CM (i.e., not automorphically induced). Thus, there is an integer w such that
![]() $\lambda _{\tau , 1} + \lambda _{\tau c, 2} = w$
for all
$\lambda _{\tau , 1} + \lambda _{\tau c, 2} = w$
for all
![]() $\tau \in \operatorname {\mathrm {Hom}}(F, {\mathbb C})$
. The central character of
$\tau \in \operatorname {\mathrm {Hom}}(F, {\mathbb C})$
. The central character of
![]() $\pi $
has the form
$\pi $
has the form
![]() $\omega _\pi = | \cdot |^{-w} \psi $
, where
$\omega _\pi = | \cdot |^{-w} \psi $
, where
![]() $\psi : F^\times \backslash \mathbf {A}_F^\times \to {\mathbb C}^\times $
is a unitary Hecke character of type
$\psi : F^\times \backslash \mathbf {A}_F^\times \to {\mathbb C}^\times $
is a unitary Hecke character of type
![]() $A_0$
. We define the Sato–Tate group of
$A_0$
. We define the Sato–Tate group of
![]() $\pi $
,
$\pi $
,
![]() $\mathrm {ST}(\pi )$
, as follows:
$\mathrm {ST}(\pi )$
, as follows:
-
• If
 $\psi $
has finite order
$\psi $
has finite order
 $a \geq 1$
, then
$a \geq 1$
, then
 $\mathrm {ST}(\pi ) = \mathrm {U}_2({\mathbb R})_a := \{ g \in \mathrm {U}_2({\mathbb R}) \mid \det (g)^a = 1 \}$
.
$\mathrm {ST}(\pi ) = \mathrm {U}_2({\mathbb R})_a := \{ g \in \mathrm {U}_2({\mathbb R}) \mid \det (g)^a = 1 \}$
. -
• If
 $\psi $
has infinite order, then
$\psi $
has infinite order, then
 $\mathrm {ST}(\pi ) = \mathrm {U}_2({\mathbb R})$
.
$\mathrm {ST}(\pi ) = \mathrm {U}_2({\mathbb R})$
.
Lemma 7.2.2.
![]() $\mathrm {ST}(\pi )$
is a compact subgroup of
$\mathrm {ST}(\pi )$
is a compact subgroup of
![]() $\operatorname {\mathrm {GL}}_2({\mathbb C})$
. If v is a finite place of F such that
$\operatorname {\mathrm {GL}}_2({\mathbb C})$
. If v is a finite place of F such that
![]() $\pi _v$
is unramified and essentially tempered, then the
$\pi _v$
is unramified and essentially tempered, then the
![]() $\operatorname {\mathrm {GL}}_2({\mathbb C})$
-conjugacy class of
$\operatorname {\mathrm {GL}}_2({\mathbb C})$
-conjugacy class of
![]() $q_v^{-w/2} \operatorname {rec}_{F_v}(\pi _v)(\mathrm {Frob}_v)$
intersects
$q_v^{-w/2} \operatorname {rec}_{F_v}(\pi _v)(\mathrm {Frob}_v)$
intersects
![]() $\mathrm {ST}(\pi )$
in a unique conjugacy class of
$\mathrm {ST}(\pi )$
in a unique conjugacy class of
![]() $\mathrm {ST}(\pi )$
.
$\mathrm {ST}(\pi )$
.
Proof. The group
![]() $\mathrm {ST}(\pi )$
is compact since
$\mathrm {ST}(\pi )$
is compact since
![]() $\mathrm {U}_2({\mathbb R})$
is. It is well-known that two elements of
$\mathrm {U}_2({\mathbb R})$
is. It is well-known that two elements of
![]() $\mathrm {U}_2({\mathbb R})$
which become conjugate in
$\mathrm {U}_2({\mathbb R})$
which become conjugate in
![]() $\operatorname {\mathrm {GL}}_2({\mathbb C})$
are conjugate by an element of
$\operatorname {\mathrm {GL}}_2({\mathbb C})$
are conjugate by an element of
![]() $\mathrm {SU}_2({\mathbb R})$
. All we need to show then is that if v is a finite place of F such that
$\mathrm {SU}_2({\mathbb R})$
. All we need to show then is that if v is a finite place of F such that
![]() $\pi _v$
is unramified, and
$\pi _v$
is unramified, and
![]() $ \operatorname {rec}_{F_v}(\pi _v)(\mathrm {Frob}_v) = \mathrm {diag}(\alpha _v, \beta _v)$
, then
$ \operatorname {rec}_{F_v}(\pi _v)(\mathrm {Frob}_v) = \mathrm {diag}(\alpha _v, \beta _v)$
, then
![]() $\alpha _v, \beta _v$
are complex numbers of absolute value
$\alpha _v, \beta _v$
are complex numbers of absolute value
![]() $q_v^{w/2}$
, and further, if
$q_v^{w/2}$
, and further, if
![]() $\psi $
has finite order a, then
$\psi $
has finite order a, then
![]() $(q_v^{-w} \alpha _v \beta _v)^a = 1$
.
$(q_v^{-w} \alpha _v \beta _v)^a = 1$
.
Since
![]() $\pi _v$
is essentially tempered, we have
$\pi _v$
is essentially tempered, we have
![]() $| \alpha _v | = | \beta _v |$
. However, we have
$| \alpha _v | = | \beta _v |$
. However, we have
![]() $\alpha _v \beta _v = \psi (\varpi _v) q_v^w$
, and hence,
$\alpha _v \beta _v = \psi (\varpi _v) q_v^w$
, and hence,
![]() $| \alpha _v \beta _v | = q_v^w$
(as
$| \alpha _v \beta _v | = q_v^w$
(as
![]() $\psi $
is unitary), and if
$\psi $
is unitary), and if
![]() $\psi $
has finite order a, then
$\psi $
has finite order a, then
![]() $(q_v^{-w} \alpha _v \beta _v)^a = 1$
.
$(q_v^{-w} \alpha _v \beta _v)^a = 1$
.
If v is a place such that
![]() $\pi _v$
is unramified and essentially tempered, then we write
$\pi _v$
is unramified and essentially tempered, then we write
![]() $[\pi _v] \in \mathrm {ST}(\pi )$
for a representative of the conjugacy class of
$[\pi _v] \in \mathrm {ST}(\pi )$
for a representative of the conjugacy class of
![]() $q_v^{-w/2} \operatorname {rec}_{F_v}(\pi _v)(\mathrm {Frob}_v) \in \operatorname {\mathrm {GL}}_2({\mathbb C})$
.
$q_v^{-w/2} \operatorname {rec}_{F_v}(\pi _v)(\mathrm {Frob}_v) \in \operatorname {\mathrm {GL}}_2({\mathbb C})$
.
Theorem 7.2.3. Suppose that
![]() $\pi $
has parallel weight. Let
$\pi $
has parallel weight. Let
![]() $S_\pi $
denote the set of finite places of F at which
$S_\pi $
denote the set of finite places of F at which
![]() $\pi $
is unramified. With notation as above, the classes of elements
$\pi $
is unramified. With notation as above, the classes of elements
![]() $[\pi _v] \in \mathrm {ST}(\pi )$
(
$[\pi _v] \in \mathrm {ST}(\pi )$
(
![]() $v \not \in S_\pi $
) are equidistributed with respect to the Haar probability measure
$v \not \in S_\pi $
) are equidistributed with respect to the Haar probability measure
![]() $\mu _{\mathrm {ST}}$
of
$\mu _{\mathrm {ST}}$
of
![]() $\mathrm {ST}(\pi )$
. More precisely, for any continuous, conjugation-invariant function
$\mathrm {ST}(\pi )$
. More precisely, for any continuous, conjugation-invariant function
![]() $f : \mathrm {ST}(\pi ) \to {\mathbb C}$
, we have
$f : \mathrm {ST}(\pi ) \to {\mathbb C}$
, we have
 $$\begin{align*}\lim_{X \to \infty} \frac{ \sum_{v \not\in S_\pi, q_v < X} f([\pi_v])}{ \#\{v \not\in S_\pi, q_v < X\}} = \int_{g \in \mathrm{ST}(\pi)} f(g) \, d \mu_{\mathrm{ST}(\pi)}. \end{align*}$$
$$\begin{align*}\lim_{X \to \infty} \frac{ \sum_{v \not\in S_\pi, q_v < X} f([\pi_v])}{ \#\{v \not\in S_\pi, q_v < X\}} = \int_{g \in \mathrm{ST}(\pi)} f(g) \, d \mu_{\mathrm{ST}(\pi)}. \end{align*}$$
Proof. If
![]() $\rho $
is a finite-dimensional irreducible representation of
$\rho $
is a finite-dimensional irreducible representation of
![]() $\mathrm {ST}(\pi )$
, let us define
$\mathrm {ST}(\pi )$
, let us define
an Euler product which converges absolutely in the right half-plane
![]() $\operatorname {Re}(s)> 1$
. According to the criterion of Serre [Reference SerreSer98, Ch. I, Appendix], the theorem will be proved if we can show that for each nontrivial such
$\operatorname {Re}(s)> 1$
. According to the criterion of Serre [Reference SerreSer98, Ch. I, Appendix], the theorem will be proved if we can show that for each nontrivial such
![]() $\rho $
,
$\rho $
,
![]() $L^{S_\pi }(\pi , \rho , s)$
admits a meromorphic continuation to
$L^{S_\pi }(\pi , \rho , s)$
admits a meromorphic continuation to
![]() ${\mathbb C}$
which is holomorphic and nonvanishing on the line
${\mathbb C}$
which is holomorphic and nonvanishing on the line
![]() $\operatorname {Re}(s) = 1$
. This may be deduced from the potential automorphy of the symmetric powers
$\operatorname {Re}(s) = 1$
. This may be deduced from the potential automorphy of the symmetric powers
![]() $\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
of the compatible system associated to
$\operatorname {\mathrm {Sym}}^{n-1} {\mathcal R}$
of the compatible system associated to
![]() $\pi $
, exactly as in, for example, [Reference GeeGee09, §7] and [Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11, §8], after noting that
$\pi $
, exactly as in, for example, [Reference GeeGee09, §7] and [Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11, §8], after noting that
![]() ${\mathcal R}$
is strongly irreducible (again invoking [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.2] and the assumption that
${\mathcal R}$
is strongly irreducible (again invoking [Reference Allen, Calegari, Caraiani, Gee, Helm, Hung, Newton, Scholze, Taylor and ThorneACC+23, Lemma 7.1.2] and the assumption that
![]() $\pi $
is not CM). Note also that the list of nontrivial one-dimensional representations of
$\pi $
is not CM). Note also that the list of nontrivial one-dimensional representations of
![]() $\mathrm {ST}(\pi )$
depends on the order of the character
$\mathrm {ST}(\pi )$
depends on the order of the character
![]() $\psi $
.
$\psi $
.
Acknowledgements
Some of the ideas in Section 2 were found in joint discussions with Matthew Emerton, and we are grateful to him for allowing us to include them here, as well as for his assistance in proving Theorem 2.4.3 (4). We would also like to thank Patrick Allen and Matthew Emerton for their comments on an earlier version of the paper, together with an anonymous referee whose careful reading and many comments were very helpful. Thanks to Dat Pham for pointing out the issue with Remark 2.1.1 to the authors.
Competing interest
The authors have no competing interest to declare.
Financial Support
G.B. was supported by a Royal Society University Research Fellowship. F.C. was supported in part by NSF Grant DMS-2001097. T.G. was supported in part by an ERC Advanced grant. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 884596). J.N. was supported by a UKRI Future Leaders Fellowship, grant MR/V021931/1.