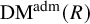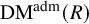1 Introduction
Let p be a prime number. The goal of the present paper is to establish classification theorems for p-divisible groups over quasisyntomic rings. This class of rings is a non-Noetherian generalisation of the class of p-complete locally complete intersection rings and contains also big rings, such as perfectoid rings. Our main theorem is as follows.
Theorem. Let R be a quasisyntomic ring. There is a natural functor from the category of p-divisible groups over R to the category
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over R, which is an antiequivalence.
$\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over R, which is an antiequivalence.
A more precise version of this statement and a detailed explanation will be given later in this Introduction. For now, let us just say that the category
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
is formed by objects of semilinear algebraic nature. The problem of classifying p-divisible groups and finite locally free group schemes by semilinear algebraic structures has a long history, going back to the work of Dieudonné on formal groups over characteristic p perfect fields. In characteristic p, as envisionned by Grothendieck, and later developed by Messing ([Reference Messing44]), Mazur-Messing ([Reference Mazur and Messing43]) and Berthelot-Breen-Messing ([Reference Berthelot, Breen and Messing6], [Reference Berthelot and Messing7]), the formalism of crystalline cohomology provides a natural way to attach such invariants to p-divisible groups. This theory goes by the name of crystalline Dieudonné theory and leads to classification theorems for p-divisible groups over a characteristic p base in a wide variety of situations, which we will not try to survey but for which we refer the reader, for instance, to [Reference Lau37]. In mixed characteristic, the existing results have been more limited. Fontaine ([Reference Fontaine23]) obtained complete results when the base is the ring of integers of a finite totally ramified extension K of the ring of Witt vectors
$\mathrm {DM}^{\mathrm {adm}}(R)$
is formed by objects of semilinear algebraic nature. The problem of classifying p-divisible groups and finite locally free group schemes by semilinear algebraic structures has a long history, going back to the work of Dieudonné on formal groups over characteristic p perfect fields. In characteristic p, as envisionned by Grothendieck, and later developed by Messing ([Reference Messing44]), Mazur-Messing ([Reference Mazur and Messing43]) and Berthelot-Breen-Messing ([Reference Berthelot, Breen and Messing6], [Reference Berthelot and Messing7]), the formalism of crystalline cohomology provides a natural way to attach such invariants to p-divisible groups. This theory goes by the name of crystalline Dieudonné theory and leads to classification theorems for p-divisible groups over a characteristic p base in a wide variety of situations, which we will not try to survey but for which we refer the reader, for instance, to [Reference Lau37]. In mixed characteristic, the existing results have been more limited. Fontaine ([Reference Fontaine23]) obtained complete results when the base is the ring of integers of a finite totally ramified extension K of the ring of Witt vectors
![]() $W(k)$
of a perfect field k of characteristic p, with ramification index
$W(k)$
of a perfect field k of characteristic p, with ramification index
![]() $e<p-1$
. This ramification hypothesis was later removed by Breuil ([Reference Breuil16]) for
$e<p-1$
. This ramification hypothesis was later removed by Breuil ([Reference Breuil16]) for
![]() $p>2$
, who also conjectured an alternative reformulation of his classification in [Reference Breuil15], simpler and likely to hold even for
$p>2$
, who also conjectured an alternative reformulation of his classification in [Reference Breuil15], simpler and likely to hold even for
![]() $p=2$
, which was proved by Kisin ([Reference Kisin30]), for odd p, and extended by Kim ([Reference Kim29]), Lau ([Reference Lau35]) and Liu ([Reference Liu38]) to all p. Zink, and then Lau, gave a classification of formal p-divisible groups over very general bases using his theory of displays ([Reference Zink54]). More recently, p-divisible groups have been classified over perfectoid rings ([Reference Lau36], [Reference Scholze and Weinstein51, Appendix to Lecture XVII]). The main interest of our approach is that it gives a uniform and geometric construction of the classifying functor on quasisyntomic rings. This is made possible by the recent spectacular work of Bhatt-Scholze on prisms and prismatic cohomology ([Reference Bhatt8], [Reference Bhatt and Scholze13]). So far, such a cohomological construction of the functor had been available only in characteristic p, using the crystalline theory. This led, in practice, to some restrictions, when trying to study p-divisible groups in mixed characteristic by reduction to characteristic p, of which Breuil-Kisin theory is a prototypical example: there, no direct definition of the functor was available when
$p=2$
, which was proved by Kisin ([Reference Kisin30]), for odd p, and extended by Kim ([Reference Kim29]), Lau ([Reference Lau35]) and Liu ([Reference Liu38]) to all p. Zink, and then Lau, gave a classification of formal p-divisible groups over very general bases using his theory of displays ([Reference Zink54]). More recently, p-divisible groups have been classified over perfectoid rings ([Reference Lau36], [Reference Scholze and Weinstein51, Appendix to Lecture XVII]). The main interest of our approach is that it gives a uniform and geometric construction of the classifying functor on quasisyntomic rings. This is made possible by the recent spectacular work of Bhatt-Scholze on prisms and prismatic cohomology ([Reference Bhatt8], [Reference Bhatt and Scholze13]). So far, such a cohomological construction of the functor had been available only in characteristic p, using the crystalline theory. This led, in practice, to some restrictions, when trying to study p-divisible groups in mixed characteristic by reduction to characteristic p, of which Breuil-Kisin theory is a prototypical example: there, no direct definition of the functor was available when
![]() $p=2$
! Replacing the crystalline formalism by the prismatic formalism, we give a definition of the classifying functor very close in spirit to the one used by Berthelot-Breen-Messing ([Reference Berthelot, Breen and Messing6]) and which now makes sense without the limitation to characteristic p. Over a quasisyntomic ring R, our functor takes values in the category of admissible prismatic Dieudonné crystals over R. As the name suggests, prismatic Dieudonné crystals are prismatic analogues of the classical notion of a Dieudonné crystal on the crystalline site.
$p=2$
! Replacing the crystalline formalism by the prismatic formalism, we give a definition of the classifying functor very close in spirit to the one used by Berthelot-Breen-Messing ([Reference Berthelot, Breen and Messing6]) and which now makes sense without the limitation to characteristic p. Over a quasisyntomic ring R, our functor takes values in the category of admissible prismatic Dieudonné crystals over R. As the name suggests, prismatic Dieudonné crystals are prismatic analogues of the classical notion of a Dieudonné crystal on the crystalline site.
Before stating precisely the main results of this paper and explaining the techniques involved, let us note that several natural questions are not addressed in this paper.
-
1. It would be interesting to go beyond quasisyntomic rings. By analogy with the characteristic p story, one would expect that the prismatic theory should also shed light on more general rings. In the general case, admissible prismatic Dieudonné crystals will not be the right objects to work with. One should instead define analogues of the divided Dieudonné crystals introduced recently by Lau [Reference Lau37] in characteristic p.
-
2. Even for quasisyntomic rings, our classification is explicit for the so-called quasiregular semiperfectoid rings or for complete regular local rings with perfect residue field of characteristic p (cf. Section 5.2), as will be explained below, but quite abstract in general. Classical Dieudonné crystals can be described as modules over the p-completion of the divided power envelope of a smooth presentation, together with a Frobenius and a connection satisfying various conditions. Is there an analogous concrete description of (admissible) prismatic Dieudonné crystals?
-
3. Finally, it would also be interesting and useful to study deformation theory (in the spirit of Grothendieck-Messing theory) for the prismatic Dieudonné functor.
We now discuss in more detail the content of this paper.
1.1 Quasisyntomic rings
Let us first define the class of rings over which we study p-divisible groups.
Definition 1.1 (cf. Definition 3.15).
A ring R is quasisyntomic if R is p-complete with bounded
![]() $p^{\infty }$
-torsion and if the cotangent complex
$p^{\infty }$
-torsion and if the cotangent complex
![]() $L_{R/\mathbb {Z}_p}$
has p-complete Tor-amplitude in
$L_{R/\mathbb {Z}_p}$
has p-complete Tor-amplitude in
![]() $[-1,0]$
Footnote
1
. The category of all quasisyntomic rings is denoted by
$[-1,0]$
Footnote
1
. The category of all quasisyntomic rings is denoted by
![]() $\mathrm {QSyn}$
.
$\mathrm {QSyn}$
.
Similarly, a map
![]() $R \to R'$
of p-complete rings with bounded
$R \to R'$
of p-complete rings with bounded
![]() $p^{\infty }$
-torsion is a quasisyntomic morphism if
$p^{\infty }$
-torsion is a quasisyntomic morphism if
![]() $R'$
is p-completely flat over R and
$R'$
is p-completely flat over R and
![]() $L_{R'/R} \in D(R')$
has p-complete Tor-amplitude in
$L_{R'/R} \in D(R')$
has p-complete Tor-amplitude in
![]() $[-1,0]$
.
$[-1,0]$
.
Remark 1.2. This definition is due to Bhatt-Morrow-Scholze [Reference Bhatt, Morrow and Scholze12] and extends (in the p-complete world) the usual notion of locally complete intersection (l.c.i.) rings and syntomic morphisms (flat and l.c.i.) to the non-Noetherian, non finite-type setting. The interest of this definition, apart from being more general, is that it more clearly shows why this category of rings is relevant: the key property of (quasi)syntomic rings is that they have a well-behaved (p-completed) cotangent complex. The work of Avramov shows that the cotangent complex is very badly behaved for all other rings, at least in the Noetherian setting: it is left unbounded (cf. [Reference Avramov2]).
Example 1.3. Any p-complete l.c.i. Noetherian ring is in
![]() $\mathrm {QSyn}$
. But there are also big rings in
$\mathrm {QSyn}$
. But there are also big rings in
![]() $\mathrm {QSyn}$
: for example, any (integral) perfectoid ring is in
$\mathrm {QSyn}$
: for example, any (integral) perfectoid ring is in
![]() $\mathrm {QSyn}$
(cf. Example 3.17). As a consequence of this, the p-completion of a smooth algebra over a perfectoid ring is also quasisyntomic, as well as any bounded
$\mathrm {QSyn}$
(cf. Example 3.17). As a consequence of this, the p-completion of a smooth algebra over a perfectoid ring is also quasisyntomic, as well as any bounded
![]() $p^{\infty }$
-torsion p-complete ring which can be presented as the quotient of an integral perfectoid ring by a finite regular sequence. For example, the rings
$p^{\infty }$
-torsion p-complete ring which can be presented as the quotient of an integral perfectoid ring by a finite regular sequence. For example, the rings
are quasisyntomic.
The category of quasisyntomic rings is endowed with a natural topology: the Grothendieck topology for which covers are given by quasisyntomic covers, that is, morphisms
![]() $R \to R'$
of p-complete rings which are quasisyntomic and p-completely faithfully flat.
$R \to R'$
of p-complete rings which are quasisyntomic and p-completely faithfully flat.
An important property of the quasisyntomic topology is that quasiregular semiperfectoid rings form a basis of the topology (cf. Proposition 3.21).
Definition 1.4 (cf. Definition 3.19).
A ring R is quasiregular semiperfectoid if
![]() $R \in \mathrm {QSyn}$
and there exists a perfectoid ring S mapping surjectively to R.
$R \in \mathrm {QSyn}$
and there exists a perfectoid ring S mapping surjectively to R.
As an example, any perfectoid ring, or any p-complete bounded
![]() $p^{\infty }$
-torsion quotient of a perfectoid ring by a finite regular sequence, is quasiregular semiperfectoid.
$p^{\infty }$
-torsion quotient of a perfectoid ring by a finite regular sequence, is quasiregular semiperfectoid.
1.2 Prisms and prismatic cohomology (after Bhatt-Scholze)
Our main tool for studying p-divisible groups over quasisyntomic rings is the recent prismatic theory of Bhatt-Scholze [Reference Bhatt8], [Reference Bhatt and Scholze13]. This theory relies on the seemingly simple notions of
![]() $\delta $
-rings and prisms. In what follows, all the rings considered are assumed to be
$\delta $
-rings and prisms. In what follows, all the rings considered are assumed to be
![]() $\mathbb {Z}_{(p)}$
-algebras.
$\mathbb {Z}_{(p)}$
-algebras.
A
![]() $\delta $
-ring is a commutative ring A, together with a map of sets
$\delta $
-ring is a commutative ring A, together with a map of sets
![]() $\delta : A\to A$
, with
$\delta : A\to A$
, with
![]() $\delta (0)=0$
,
$\delta (0)=0$
,
![]() $\delta (1)=0$
and satisfying the following identities:
$\delta (1)=0$
and satisfying the following identities:
for all
![]() $x, y \in A$
. For any
$x, y \in A$
. For any
![]() $\delta $
-ring
$\delta $
-ring
![]() $(A,\delta )$
, denote by
$(A,\delta )$
, denote by
![]() $\varphi $
the map defined by
$\varphi $
the map defined by
The identities satisfied by
![]() $\delta $
are made to make
$\delta $
are made to make
![]() $\varphi $
a ring endomorphism lifting Frobenius modulo p. Conversely, a p-torsion free ring equipped with a lift of Frobenius gives rise to a
$\varphi $
a ring endomorphism lifting Frobenius modulo p. Conversely, a p-torsion free ring equipped with a lift of Frobenius gives rise to a
![]() $\delta $
-ring. A pair
$\delta $
-ring. A pair
![]() $(A,I)$
formed by a
$(A,I)$
formed by a
![]() $\delta $
-ring A and an ideal
$\delta $
-ring A and an ideal
![]() $I \subset A$
is a prism if I defines a Cartier divisor on
$I \subset A$
is a prism if I defines a Cartier divisor on
![]() $\mathrm {Spec}(A)$
, if A is (derived)
$\mathrm {Spec}(A)$
, if A is (derived)
![]() $(p,I)$
-complete and if I is pro-Zariski locally generatedFootnote
2
by a distinguished element, that is, an element d, such that
$(p,I)$
-complete and if I is pro-Zariski locally generatedFootnote
2
by a distinguished element, that is, an element d, such that
![]() $\delta (d)$
is a unit.
$\delta (d)$
is a unit.
Example 1.5.
-
1. For any p-complete p-torsion free
 $\delta $
-ring A, the pair
$\delta $
-ring A, the pair
 $(A,(p)$
) is a prism.
$(A,(p)$
) is a prism. -
2. Say that a prism is perfect if the Frobenius
 $\varphi $
on the underlying
$\varphi $
on the underlying
 $\delta $
-ring is an isomorphism. Then the category of perfect prisms is equivalent to the category of (integral) perfectoid rings: in one direction, one maps a perfectoid ring R to the pair
$\delta $
-ring is an isomorphism. Then the category of perfect prisms is equivalent to the category of (integral) perfectoid rings: in one direction, one maps a perfectoid ring R to the pair
 $(A_{\mathrm {inf}}(R):=W(R^{\flat }), \mathrm {ker}(\theta ))$
(here,
$(A_{\mathrm {inf}}(R):=W(R^{\flat }), \mathrm {ker}(\theta ))$
(here,
 $\theta : A_{\mathrm {inf}}(R) \to R$
is Fontaine’s theta map); in the other direction, one maps
$\theta : A_{\mathrm {inf}}(R) \to R$
is Fontaine’s theta map); in the other direction, one maps
 $(A,I)$
to
$(A,I)$
to
 $A/I$
. Therefore, one sees that, in the words of the authors of [Reference Bhatt and Scholze13], prisms are some kind of ‘deperfection’ of perfectoid rings.
$A/I$
. Therefore, one sees that, in the words of the authors of [Reference Bhatt and Scholze13], prisms are some kind of ‘deperfection’ of perfectoid rings.
The crucial definition for us is the following. We stick to the affine case for simplicity, but it admits an immediate extension to p-adic formal schemes.
Definition 1.6. Let R be a p-complete ring. The (absolute) prismatic site
![]() of R is the opposite of the category of boundedFootnote
3
prisms
of R is the opposite of the category of boundedFootnote
3
prisms
![]() $(A,I)$
together with a map
$(A,I)$
together with a map
![]() $R \to A/I$
, endowed with the Grothendieck topology for which covers are morphisms of prisms
$R \to A/I$
, endowed with the Grothendieck topology for which covers are morphisms of prisms
![]() $(A, I) \to (B,J)$
, such that the underlying ring map
$(A, I) \to (B,J)$
, such that the underlying ring map
![]() $A\to B$
is
$A\to B$
is
![]() $(p,I)$
-completely faithfully flat.
$(p,I)$
-completely faithfully flat.
Bhatt and Scholze prove that the functor
![]() (respectively,
(respectively,
![]() ) on the prismatic site valued in
) on the prismatic site valued in
![]() $(p,I)$
-complete
$(p,I)$
-complete
![]() $\delta $
-rings (respectively, in p-complete R-algebras), sending
$\delta $
-rings (respectively, in p-complete R-algebras), sending
![]() to A (respectively,
to A (respectively,
![]() $A/I$
), is a sheaf. The sheaf
$A/I$
), is a sheaf. The sheaf
![]() (respectively,
(respectively,
![]() ) is called the prismatic structure sheaf (respectively, the reduced prismatic structure sheaf).
) is called the prismatic structure sheaf (respectively, the reduced prismatic structure sheaf).
From this, one easily deduces that the presheaves
![]() (respectively,
(respectively,
![]() ) sending
) sending
![]() $(A,I)$
to I (respectively,
$(A,I)$
to I (respectively,
![]() $\mathcal {N}^{\geq 1} A:=\varphi ^{-1}(I)$
) are also sheaves on
$\mathcal {N}^{\geq 1} A:=\varphi ^{-1}(I)$
) are also sheaves on
![]() .
.
Let R be a p-complete ring. One proves the existence of a morphism of topoi:
Set:
The sheaf
![]() $\mathcal {O}^{\mathrm {pris}}$
is endowed with a Frobenius lift
$\mathcal {O}^{\mathrm {pris}}$
is endowed with a Frobenius lift
![]() $\varphi $
. Moreover, if R is quasisyntomic, the quotient sheaf
$\varphi $
. Moreover, if R is quasisyntomic, the quotient sheaf
![]() $\mathcal {O}^{\mathrm {pris}} / \mathcal {N}^{\geq 1} \mathcal {O}^{\mathrm {pris}}$
is naturally isomorphic to the structure sheaf
$\mathcal {O}^{\mathrm {pris}} / \mathcal {N}^{\geq 1} \mathcal {O}^{\mathrm {pris}}$
is naturally isomorphic to the structure sheaf
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $(R)_{\mathrm {qsyn}}$
.
$(R)_{\mathrm {qsyn}}$
.
1.3 Admissible prismatic Dieudonné crystals and modules
We are now in position to define the category of objects classifying p-divisible groups.
Definition 1.7. Let R be a quasisyntomic ring. A prismatic Dieudonné crystal over R is a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() $\mathcal {M}$
together with
$\mathcal {M}$
together with
![]() $\varphi $
-linear morphism
$\varphi $
-linear morphism
whose linearisation
![]() $\varphi ^{\ast } \mathcal {M}\to \mathcal {M}$
has its cokernel is killed by
$\varphi ^{\ast } \mathcal {M}\to \mathcal {M}$
has its cokernel is killed by
![]() $\mathcal {I}^{\mathrm {pris}}$
. It is said to be admissible if the image of the composition
$\mathcal {I}^{\mathrm {pris}}$
. It is said to be admissible if the image of the composition
is a finite locally free
![]() $\mathcal {O}$
-module
$\mathcal {O}$
-module
![]() $\mathcal {F}_{\mathcal {M}}$
, such that the map
$\mathcal {F}_{\mathcal {M}}$
, such that the map
![]() $(\mathcal {O}^{\mathrm {pris}}/\mathcal {I}^{\mathrm {pris}}) \otimes _{\mathcal {O}} \mathcal {F}_{\mathcal {M}} \to \mathcal {M}/\mathcal {I}^{\mathrm {pris}}\mathcal {M}$
induced by
$(\mathcal {O}^{\mathrm {pris}}/\mathcal {I}^{\mathrm {pris}}) \otimes _{\mathcal {O}} \mathcal {F}_{\mathcal {M}} \to \mathcal {M}/\mathcal {I}^{\mathrm {pris}}\mathcal {M}$
induced by
![]() $\varphi _{\mathcal {M}}$
is a monomorphism.
$\varphi _{\mathcal {M}}$
is a monomorphism.
Definition 1.8. Let R be a quasisyntomic ring. We denote by
![]() $\mathrm {DM}(R)$
the category of prismatic Dieudonné crystals over R (with morphisms the
$\mathrm {DM}(R)$
the category of prismatic Dieudonné crystals over R (with morphisms the
![]() $\mathcal {O}^{\mathrm {pris}}$
-linear morphisms commuting with the Frobenius), and by
$\mathcal {O}^{\mathrm {pris}}$
-linear morphisms commuting with the Frobenius), and by
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
its full subcategory of admissible prismatic Dieudonné crystals.
$\mathrm {DM}^{\mathrm {adm}}(R)$
its full subcategory of admissible prismatic Dieudonné crystals.
Remark 1.9. In a former version of the paper, we used the notion of filtered prismatic Dieudonné crystal. A filtered prismatic Dieudonné crystal over a quasisyntomic ring R is a collection
![]() $(\mathcal {M}, \mathrm {Fil} \mathcal {M}, \varphi _{\mathcal {M}})$
consisting of a finite locally free
$(\mathcal {M}, \mathrm {Fil} \mathcal {M}, \varphi _{\mathcal {M}})$
consisting of a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() $\mathcal {M}$
, a
$\mathcal {M}$
, a
![]() $\mathcal {O}^{\mathrm {pris}}$
-submodule
$\mathcal {O}^{\mathrm {pris}}$
-submodule
![]() $\mathrm {Fil} \mathcal {M}$
and a
$\mathrm {Fil} \mathcal {M}$
and a
![]() $\varphi $
-linear map
$\varphi $
-linear map
![]() $\varphi _{\mathcal {M}}: \mathcal {M} \to \mathcal {M}$
, satisfying the following conditions:
$\varphi _{\mathcal {M}}: \mathcal {M} \to \mathcal {M}$
, satisfying the following conditions:
-
1.
 $\varphi _{\mathcal {M}}(\mathrm {Fil} \mathcal {M}) \subset \mathcal {I}^{\mathrm {pris}}.\mathcal {M}$
.
$\varphi _{\mathcal {M}}(\mathrm {Fil} \mathcal {M}) \subset \mathcal {I}^{\mathrm {pris}}.\mathcal {M}$
. -
2.
 $\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}. \mathcal {M} \subset \mathrm {Fil} \mathcal {M}$
and
$\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}. \mathcal {M} \subset \mathrm {Fil} \mathcal {M}$
and
 $\mathcal {M}/\mathrm {Fil} \mathcal {M}$
is a finite locally free
$\mathcal {M}/\mathrm {Fil} \mathcal {M}$
is a finite locally free
 $\mathcal {O}$
-module.
$\mathcal {O}$
-module. -
3.
 $\varphi _{\mathcal {M}}(\mathrm {Fil} \mathcal {M})$
generates
$\varphi _{\mathcal {M}}(\mathrm {Fil} \mathcal {M})$
generates
 $\mathcal {I}^{\mathrm {pris}}.\mathcal {M}$
as an
$\mathcal {I}^{\mathrm {pris}}.\mathcal {M}$
as an
 $\mathcal {O}^{\mathrm {pris}}$
-module.
$\mathcal {O}^{\mathrm {pris}}$
-module.
However, as was pointed out to us by the referee, the category of filtered prismatic Dieudonné crystals embeds fully faithfully in the category of prismatic Dieudonné crystals, with essential image given by the admissible objects (this essentially follows from Proposition 4.29 below). Since admissible prismatic Dieudonné crystals are easier to work with than filtered prismatic Dieudonné crystals, we decided to work only with the first; hence, the results stayed the same, but their formulation changed slightly.
For quasiregular semiperfectoid rings, these abstract objects have a concrete incarnation. Let R be a quasiregular semiperfectoid ring. The prismatic site
![]() admits a final object
admits a final object
![]() .
.
Example 1.10.
-
1. If R is a perfectoid ring,
 .
. -
2. If R is quasiregular semiperfectoid and
 $pR=0$
,
$pR=0$
,
 .
.
Definition 1.11. A prismatic Dieudonné module over R is a finite locally free
![]() -module M together with a
-module M together with a
![]() $\varphi $
-linear morphism
$\varphi $
-linear morphism
whose linearisation
![]() $\varphi ^{\ast } M \to M$
has its cokernel is killed by I. It is said to be admissible if the composition
$\varphi ^{\ast } M \to M$
has its cokernel is killed by I. It is said to be admissible if the composition
is a finite locally free
![]() -module
-module
![]() $F_M$
, such that the map
$F_M$
, such that the map
![]() induced by
induced by
![]() $\varphi _{M}$
is a monomorphism.
$\varphi _{M}$
is a monomorphism.
Proposition 1.12 (Proposition 4.13).
Let R be a quasiregular semiperfectoid ring. The functor of global sections induces an equivalence between the category of (admissible) prismatic Dieudonné crystals over R and the category of (admissible) prismatic Dieudonné modules over R.
1.4 Statements of the main results
In all this paragraph, R is a quasisyntomic ring.
Theorem 1.13 (Theorem 4.71).
Let G be a p-divisible group over R. The pair
where the
![]() $\mathcal {E}xt$
is an Ext-group of abelian sheaves on
$\mathcal {E}xt$
is an Ext-group of abelian sheaves on
![]() $(R)_{\mathrm {qsyn}}$
and
$(R)_{\mathrm {qsyn}}$
and
![]() is the Frobenius induced by the Frobenius of
is the Frobenius induced by the Frobenius of
![]() $\mathcal {O}^{\mathrm {pris}}$
, is an admissible prismatic Dieudonné crystal over R, often denoted simply by
$\mathcal {O}^{\mathrm {pris}}$
, is an admissible prismatic Dieudonné crystal over R, often denoted simply by
![]() .
.
Remark 1.14. The rank of the finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() is the height of G, and the quotient
is the height of G, and the quotient
![]() is naturally isomorphic to
is naturally isomorphic to
![]() $\mathrm {Lie}(\check {G})$
, where
$\mathrm {Lie}(\check {G})$
, where
![]() $\check {G}$
is the Cartier dual of G.
$\check {G}$
is the Cartier dual of G.
Remark 1.15. When
![]() $pR=0$
, the crystalline comparison theorem for prismatic cohomology allows us to prove that this construction coincides with the functor usually considered in crystalline Dieudonné theory, relying on Berthelot-Breen-Messing’s constructions ([Reference Berthelot, Breen and Messing6]).
$pR=0$
, the crystalline comparison theorem for prismatic cohomology allows us to prove that this construction coincides with the functor usually considered in crystalline Dieudonné theory, relying on Berthelot-Breen-Messing’s constructions ([Reference Berthelot, Breen and Messing6]).
Theorem 1.16 (Theorem 4.74).
The prismatic Dieudonné functor
induces an antiequivalence between the category
![]() $\mathrm {BT}(R)$
of p-divisible groups over R and the category
$\mathrm {BT}(R)$
of p-divisible groups over R and the category
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over R.
$\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over R.
Remark 1.17. Theorems 1.13 and 1.16 immediately extend to p-divisible groups over a quasisyntomic formal scheme.
Remark 1.18. It is easy to write down a formula for a functor attaching to an admissible prismatic Dieudonné crystal an abelian sheaf on
![]() $(R)_{\mathrm {qsyn}}$
, which will be a quasi-inverse of the prismatic Dieudonné functor: see Remark 4.91. But such a formula does not look very useful.
$(R)_{\mathrm {qsyn}}$
, which will be a quasi-inverse of the prismatic Dieudonné functor: see Remark 4.91. But such a formula does not look very useful.
Remark 1.19. As a corollary of the theorem and the comparison with the crystalline functor, one obtains that the (contravariant) Dieudonné functor from crystalline Dieudonné theory is an antiequivalence for quasisyntomic rings in characteristic p. For excellent l.c.i. rings, fully faithfulness was proved by de Jong-Messing; the antiequivalence was proved by Lau for F-finite l.c.i. rings (which are, in particular, excellent rings).
Remark 1.20. It is not difficult to prove that if R is perfectoid, admissible prismatic Dieudonné crystals (or modules) over R are equivalent to minuscule Breuil-Kisin-Fargues modules for R, in the sense of [Reference Bhatt, Morrow and Scholze11]. Therefore, Theorem 1.16 contains, as a special case, the results of Lau and Scholze-Weinstein. But the proof of the theorem actually requires this special caseFootnote 4 as an input.
Remark 1.21. In general, the prismatic Dieudonné functor (without the admissibility condition) is not essentially surjective, but we prove it is an antiequivalence for complete regular (Noetherian) local rings in Proposition 5.10, that is, in this case, the admissibility condition is automatic.
Moreover, we explain in Section 5.2 how to recover Breuil-Kisin’s classification (as extended by Kim, Lau and Liu to all p) of p-divisible groups over
![]() $\mathcal {O}_K$
, where K is a discretely valued extension of
$\mathcal {O}_K$
, where K is a discretely valued extension of
![]() $\mathbb {Q}_p$
with perfect residue field, from Theorem 1.16.
$\mathbb {Q}_p$
with perfect residue field, from Theorem 1.16.
Remark 1.22. Section 5.3 shows how to extract from the admissible prismatic Dieudonné functor a functor from
![]() $\mathrm {BT}(R)$
to the category of displays of Zink over R. Even though the actual argument is slightly involved for technical reasons, the main result there ultimately comes from the following fact: if R is a quasiregular semiperfectoid ring, the natural morphism
$\mathrm {BT}(R)$
to the category of displays of Zink over R. Even though the actual argument is slightly involved for technical reasons, the main result there ultimately comes from the following fact: if R is a quasiregular semiperfectoid ring, the natural morphism
![]() gives rise by adjunction to a morphism of
gives rise by adjunction to a morphism of
![]() $\delta $
-rings
$\delta $
-rings
![]() , mapping
, mapping
![]() to the image of Verschiebung on Witt vectors. Zink’s classification by displays works on very general bases but is restricted (by design) to formal p-divisible groups or to odd p; by contrast, our classification is limited to quasisyntomic rings, but do not make these restrictions.
to the image of Verschiebung on Witt vectors. Zink’s classification by displays works on very general bases but is restricted (by design) to formal p-divisible groups or to odd p; by contrast, our classification is limited to quasisyntomic rings, but do not make these restrictions.
Remark 1.23. As in Kisin’s article [Reference Kisin30], it should be possible to deduce from Theorem 1.16 a classification result for finite locally free group schemes. We only write this down over a perfectoid ring, in which case, it was already known for
![]() $p>2$
by the work of Lau, [Reference Lau36]. This result is used in the recent work of
$p>2$
by the work of Lau, [Reference Lau36]. This result is used in the recent work of
![]() $\breve{\mathrm{C}}$
esnavi
$\breve{\mathrm{C}}$
esnavi
![]() $\breve{\mathrm{c}}$
ius and Scholze [Reference Cesnavic̆ius and Scholze18].
$\breve{\mathrm{c}}$
ius and Scholze [Reference Cesnavic̆ius and Scholze18].
1.5 Overview of the proof and plan of the paper
Sections 2 and 3 contain some useful basic results concerning prisms and prismatic cohomology, with special emphasis on the case of quasisyntomic rings. Most of them are extracted from [Reference Bhatt, Morrow and Scholze12] and [Reference Bhatt and Scholze13], but some are not contained in loc. cit. (for instance, the definition of the q-logarithm, Section 2.2, or the Künneth formula, Section 3.5), or only briefly discussed there (for instance, the description of truncated Hodge-Tate cohomology, Section 3.2).
Section 4 is the heart of this paper. We first introduce the category
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over a quasisyntomic ring R and discuss some of its abstract properties (Section 4.1). We then introduce a candidate functor from p-divisible groups over R to
$\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over a quasisyntomic ring R and discuss some of its abstract properties (Section 4.1). We then introduce a candidate functor from p-divisible groups over R to
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
(Section 4.2). That it, indeed, takes values in the category
$\mathrm {DM}^{\mathrm {adm}}(R)$
(Section 4.2). That it, indeed, takes values in the category
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
is the content of Theorem 1.13, which we do not prove immediately. We first relate this functor to other existing functors, for characteristic p rings or perfectoid rings (Section 4.3). The next three sections are devoted to the proof of Theorem 1.13. This proof follows a road similar to the one of [Reference Berthelot, Breen and Messing6, Chapters 2, 3]. The basic idea is to reduce many statements to the case of p-divisible groups attached to abelian schemes, using a theorem of Raynaud ensuring that a finite locally free group scheme on R can always be realised as the kernel of an isogeny between two abelian schemes over R, Zariski-locally on R. For abelian schemes, via the general device, explained in [Reference Berthelot, Breen and Messing6, Chapter 2] and recalled in Section 4.4, for computing Ext-groups in low degrees in a topos, one needs a good understanding of the prismatic cohomology. It relies on the degeneration of the conjugate spectral sequence abutting to reduced prismatic cohomology, in the same way as the description of the crystalline cohomology of abelian schemes is based on the degeneration of the Hodge-de Rham spectral sequence. We prove it in Section 4.5 by appealing to the group structure on the abelian scheme. Alternatively, one could use an identification of some truncation of the reduced prismatic complex with some cotangent complex, in the spirit of Deligne-Illusie (or, more recently, [Reference Bhatt, Morrow and Scholze11]), proved in Section 3.2. To prove Theorem 1.16, stated as Theorem 4.74 below, one first observes that the functors
$\mathrm {DM}^{\mathrm {adm}}(R)$
is the content of Theorem 1.13, which we do not prove immediately. We first relate this functor to other existing functors, for characteristic p rings or perfectoid rings (Section 4.3). The next three sections are devoted to the proof of Theorem 1.13. This proof follows a road similar to the one of [Reference Berthelot, Breen and Messing6, Chapters 2, 3]. The basic idea is to reduce many statements to the case of p-divisible groups attached to abelian schemes, using a theorem of Raynaud ensuring that a finite locally free group scheme on R can always be realised as the kernel of an isogeny between two abelian schemes over R, Zariski-locally on R. For abelian schemes, via the general device, explained in [Reference Berthelot, Breen and Messing6, Chapter 2] and recalled in Section 4.4, for computing Ext-groups in low degrees in a topos, one needs a good understanding of the prismatic cohomology. It relies on the degeneration of the conjugate spectral sequence abutting to reduced prismatic cohomology, in the same way as the description of the crystalline cohomology of abelian schemes is based on the degeneration of the Hodge-de Rham spectral sequence. We prove it in Section 4.5 by appealing to the group structure on the abelian scheme. Alternatively, one could use an identification of some truncation of the reduced prismatic complex with some cotangent complex, in the spirit of Deligne-Illusie (or, more recently, [Reference Bhatt, Morrow and Scholze11]), proved in Section 3.2. To prove Theorem 1.16, stated as Theorem 4.74 below, one first observes that the functors
on
![]() $\mathrm {QSyn}$
are both stacks for the quasisyntomic topology (for
$\mathrm {QSyn}$
are both stacks for the quasisyntomic topology (for
![]() $\mathrm {BT}$
, this is done in the Appendix). Therefore, to prove that the functor
$\mathrm {BT}$
, this is done in the Appendix). Therefore, to prove that the functor
![]() is an antiequivalence, it is enough to prove it for R quasiregular semiperfectoid, since these rings form a basis of the topology, in which case, one can simply consider the more concrete functor
is an antiequivalence, it is enough to prove it for R quasiregular semiperfectoid, since these rings form a basis of the topology, in which case, one can simply consider the more concrete functor
![]() taking values in admissible prismatic Dieudonné modules over R, defined by taking global sections of
taking values in admissible prismatic Dieudonné modules over R, defined by taking global sections of
![]() . Therefore, one sees that, even if one is ultimately interested only by Noetherian rings, the structure of the argument forces to consider large quasisyntomic ringsFootnote
5
. Assume from now on that R is quasiregular semiperfectoid. The proof of fully faithfulness is ultimately reduced to the identification of the syntomic sheaf
. Therefore, one sees that, even if one is ultimately interested only by Noetherian rings, the structure of the argument forces to consider large quasisyntomic ringsFootnote
5
. Assume from now on that R is quasiregular semiperfectoid. The proof of fully faithfulness is ultimately reduced to the identification of the syntomic sheaf
![]() $\mathbb {Z}_p(1)$
(as defined using prismatic cohomology) to the p-adic Tate module of
$\mathbb {Z}_p(1)$
(as defined using prismatic cohomology) to the p-adic Tate module of
![]() $\mathbb {G}_m$
, a result of Bhatt-Morrow-Scholze recently reproved without K-theory by Bhatt-Lurie ([Reference Bhatt and Lurie10, Theorem 7.5.6]). (A former version of this paper attempted to prove fully faithfulness using the strategy of [Reference Scholze and Weinstein50], following an idea of de Jong-Messing: one first proves it for morphisms from
$\mathbb {G}_m$
, a result of Bhatt-Morrow-Scholze recently reproved without K-theory by Bhatt-Lurie ([Reference Bhatt and Lurie10, Theorem 7.5.6]). (A former version of this paper attempted to prove fully faithfulness using the strategy of [Reference Scholze and Weinstein50], following an idea of de Jong-Messing: one first proves it for morphisms from
![]() $\mathbb {Q}_p/\mathbb {Z}_p$
to
$\mathbb {Q}_p/\mathbb {Z}_p$
to
![]() $\mu _{p^{\infty }}$
and then reduces to this special case. This reduction step works fine in many cases of interest — such as characteristic p or p-torsion free quasiregular semiperfectoid rings — but we encountered several technical difficulties while trying to push it to the general case.) Once fully faithfulness is acquired, the proof of essential surjectivity is by reduction to the perfectoid case. One can actually even reduce to the case of perfectoid valuation rings with algebraically closed fraction field. In this case, the result is known, and due — depending whether one is in characteristic p or in mixed characteristic — to Berthelot and Scholze-Weinstein.
$\mu _{p^{\infty }}$
and then reduces to this special case. This reduction step works fine in many cases of interest — such as characteristic p or p-torsion free quasiregular semiperfectoid rings — but we encountered several technical difficulties while trying to push it to the general case.) Once fully faithfulness is acquired, the proof of essential surjectivity is by reduction to the perfectoid case. One can actually even reduce to the case of perfectoid valuation rings with algebraically closed fraction field. In this case, the result is known, and due — depending whether one is in characteristic p or in mixed characteristic — to Berthelot and Scholze-Weinstein.
Finally, Section 5 gathers several complements to the main theorems, already mentioned above: the classification of finite locally free group schemes of p-power order over a perfectoid ring, Breuil-Kisin’s classification of p-divisible groups over the ring of integers of a finite extension of
![]() $\mathbb {Q}_p$
, the relation with the theory of displays and the description of the Tate module of the generic fibre of a p-divisible group from its prismatic Dieudonné crystal.
$\mathbb {Q}_p$
, the relation with the theory of displays and the description of the Tate module of the generic fibre of a p-divisible group from its prismatic Dieudonné crystal.
1.6 Notations and conventions
In all the text, we fix a prime number p.
-
• All finite locally free group schemes will be assumed to be commutative.
-
• If R is a ring, we denote by
 $\mathrm {BT}(R)$
the category of p-divisible groups over R.
$\mathrm {BT}(R)$
the category of p-divisible groups over R. -
• If A is a ring,
 $I \subset A$
an ideal and
$I \subset A$
an ideal and
 $K \in D(A)$
an object of the derived category of A-modules, K is said to be derived I-complete if for every
$K \in D(A)$
an object of the derived category of A-modules, K is said to be derived I-complete if for every
 $f \in I$
, the derived limit of the inverse system vanishes. Equivalently, when
$f \in I$
, the derived limit of the inverse system vanishes. Equivalently, when $$\begin{align*}\dots K \overset{f} \to K \overset{f} \to K \end{align*}$$
$$\begin{align*}\dots K \overset{f} \to K \overset{f} \to K \end{align*}$$
 $I=(f_1,\dots ,f_r)$
is finitely generated, K is derived I-complete if the natural map is an isomorphism in
$I=(f_1,\dots ,f_r)$
is finitely generated, K is derived I-complete if the natural map is an isomorphism in $$\begin{align*}K \to R\lim(K \otimes_A^{\mathbb{L}} K_n^{\bullet}) \end{align*}$$
$$\begin{align*}K \to R\lim(K \otimes_A^{\mathbb{L}} K_n^{\bullet}) \end{align*}$$
 $D(A)$
, where for each
$D(A)$
, where for each
 $n\geq 1$
,
$n\geq 1$
,
 $K_n^{\bullet }$
denotes the Koszul complex
$K_n^{\bullet }$
denotes the Koszul complex
 $K_{\bullet }(A;f_1^n,\dots ,f_r^n)$
(one has
$K_{\bullet }(A;f_1^n,\dots ,f_r^n)$
(one has
 $H^0(K_n^{\bullet })=A/(f_1^n,\dots ,f_r^n)$
, but beware that, in general,
$H^0(K_n^{\bullet })=A/(f_1^n,\dots ,f_r^n)$
, but beware that, in general,
 $K_n^{\bullet }$
may also have cohomology in negative degrees, unless
$K_n^{\bullet }$
may also have cohomology in negative degrees, unless
 $(f_1,\dots ,f_r)$
forms a regular sequence). An A-module M is said to be derived I-complete if
$(f_1,\dots ,f_r)$
forms a regular sequence). An A-module M is said to be derived I-complete if
 $K=M[0] \in D(A)$
is derived I-complete. The following properties are useful in practice:
$K=M[0] \in D(A)$
is derived I-complete. The following properties are useful in practice:
-
1. A complex
 $K \in D(A)$
is derived I-complete if and only if for each integer i,
$K \in D(A)$
is derived I-complete if and only if for each integer i,
 $H^i(K)$
is derived I-complete (this implies, in particular, that the category of derived I-complete A-modules form a weak Serre subcategory of the category of A-modules).
$H^i(K)$
is derived I-complete (this implies, in particular, that the category of derived I-complete A-modules form a weak Serre subcategory of the category of A-modules). -
2. If
 $I=(f_1,\dots ,f_r)$
is finitely generated, the inclusion of the full subcategory of derived I-complete complexes in
$I=(f_1,\dots ,f_r)$
is finitely generated, the inclusion of the full subcategory of derived I-complete complexes in
 $D(A)$
admits a left adjoint, sending
$D(A)$
admits a left adjoint, sending
 $K \in D(A)$
to its derived I-completion
$K \in D(A)$
to its derived I-completion  $$\begin{align*}\widehat{K} = R\lim(K \otimes_A^{\mathbb{L}} K_n^{\bullet}). \end{align*}$$
$$\begin{align*}\widehat{K} = R\lim(K \otimes_A^{\mathbb{L}} K_n^{\bullet}). \end{align*}$$
-
3. (Derived Nakayama) If I is finitely generated, a derived I-complete complex
 $K \in D(A)$
(respectively, a derived I-complete A-module M) is zero if and only if
$K \in D(A)$
(respectively, a derived I-complete A-module M) is zero if and only if
 $K\otimes _A^{\mathbb {L}} A/I=0$
(respectively,
$K\otimes _A^{\mathbb {L}} A/I=0$
(respectively,
 $M/IM=0$
).
$M/IM=0$
). -
4. If I is finitely generated, an A-module M is (classically) I-adically complete if and only if it is derived I-complete and I-adically separated.
-
5.
 $I=(f)$
is principal and M is an A-module with bounded
$I=(f)$
is principal and M is an A-module with bounded
 $f^{\infty }$
-torsion (i.e. such that
$f^{\infty }$
-torsion (i.e. such that
 $M[f^{\infty }]=M[f^N]$
for some N), the derived I-completion of M (as a complex) is discrete and coincides with its (classical) I-adic completion.
$M[f^{\infty }]=M[f^N]$
for some N), the derived I-completion of M (as a complex) is discrete and coincides with its (classical) I-adic completion.
A useful reference for derived completions is [Reference Project52, Tag 091N].
-
-
• Let A be a ring, I a finitely generated ideal. A complex
 $K\in D(A)$
is I-completely flat (respectively, I-completely faithfully flat) if
$K\in D(A)$
is I-completely flat (respectively, I-completely faithfully flat) if
 $K \otimes _A^{\mathbb {L}} A/I$
is concentrated in degree
$K \otimes _A^{\mathbb {L}} A/I$
is concentrated in degree
 $0$
and flat (respectively, faithfully flat), cf. [Reference Bhatt, Morrow and Scholze12, Definition 4.1]. If an A-module M is flat, its derived completion
$0$
and flat (respectively, faithfully flat), cf. [Reference Bhatt, Morrow and Scholze12, Definition 4.1]. If an A-module M is flat, its derived completion
 $\widehat {M}$
is I-completely flat. Assume that I is principal, generated by
$\widehat {M}$
is I-completely flat. Assume that I is principal, generated by
 $f \in A$
(in the sequel, f will often be p). Let
$f \in A$
(in the sequel, f will often be p). Let
 $A\to B$
be a map of derived f-complete rings. If A has bounded
$A\to B$
be a map of derived f-complete rings. If A has bounded
 $f^{\infty }$
-torsion and
$f^{\infty }$
-torsion and
 $A\to B$
is f-completely flat, then B has bounded
$A\to B$
is f-completely flat, then B has bounded
 $f^{\infty }$
-torsion. Conversely, if B has bounded
$f^{\infty }$
-torsion. Conversely, if B has bounded
 $f^{\infty }$
-torsion and
$f^{\infty }$
-torsion and
 $A\to B$
is f-completely faithfully flat, A has bounded
$A\to B$
is f-completely faithfully flat, A has bounded
 $f^{\infty }$
-torsion. Moreover, if A and B both have bounded
$f^{\infty }$
-torsion. Moreover, if A and B both have bounded
 $f^{\infty }$
-torsion, then
$f^{\infty }$
-torsion, then
 $A\to B$
is f-completely (faithfully) flat if and only if
$A\to B$
is f-completely (faithfully) flat if and only if
 $A/f^n \to B/f^n$
is (faithfully) flat for all
$A/f^n \to B/f^n$
is (faithfully) flat for all
 $n\geq 1$
(see [Reference Bhatt, Morrow and Scholze12, Corollary 4.8]).
$n\geq 1$
(see [Reference Bhatt, Morrow and Scholze12, Corollary 4.8]). -
• A derived I-complete A-algebra R is I-completely étale (respectively, I-completely smooth) if
 $R \otimes _A^{\mathbb {L}} A/I$
is concentrated in degree
$R \otimes _A^{\mathbb {L}} A/I$
is concentrated in degree
 $0$
and étale (respectively, smooth).
$0$
and étale (respectively, smooth).
2 Generalities on prisms
In this section, we review the theory of prisms and collect some additional results. In particular, we present the definition of the q-logarithm (cf. Section 2.2).
2.1 Prisms and perfectoid rings
We list here some basic definitions and results from [Reference Bhatt and Scholze13], of which we will make constant use in the paper. Let us first recall the definition of a
![]() $\delta $
-ring A. In the following, all rings will be assumed to be
$\delta $
-ring A. In the following, all rings will be assumed to be
![]() $\mathbb {Z}_{(p)}$
-algebras.
$\mathbb {Z}_{(p)}$
-algebras.
Definition 2.1. A
![]() $\delta $
-ring is a pair
$\delta $
-ring is a pair
![]() $(A,\delta )$
with A a commutative ring and
$(A,\delta )$
with A a commutative ring and
![]() $\delta \colon A\to A$
a map (of sets), such that for
$\delta \colon A\to A$
a map (of sets), such that for
![]() $x,y\in A$
, the following equalities hold:
$x,y\in A$
, the following equalities hold:
 $$ \begin{align*}\begin{matrix} \delta(0)=\delta(1)=0 \\ \delta(xy)=x^p\delta(y)+y^p\delta(x)+p\delta(x)\delta(y)\\ \delta(x+y)=\delta(x)+\delta(y)+\frac{x^p+y^p-(x+y)^p}{p}. \end{matrix} \end{align*} $$
$$ \begin{align*}\begin{matrix} \delta(0)=\delta(1)=0 \\ \delta(xy)=x^p\delta(y)+y^p\delta(x)+p\delta(x)\delta(y)\\ \delta(x+y)=\delta(x)+\delta(y)+\frac{x^p+y^p-(x+y)^p}{p}. \end{matrix} \end{align*} $$
A morphism of
![]() $\delta $
-rings
$\delta $
-rings
![]() $f\colon (A,\delta )\to (A^{\prime },\delta ^{\prime })$
is a morphism
$f\colon (A,\delta )\to (A^{\prime },\delta ^{\prime })$
is a morphism
![]() $f\colon A\to A^{\prime }$
of rings, such that
$f\colon A\to A^{\prime }$
of rings, such that
![]() $f\circ \delta =\delta ^{\prime }\circ f$
.
$f\circ \delta =\delta ^{\prime }\circ f$
.
By design, the morphism
for a
![]() $\delta $
-ring
$\delta $
-ring
![]() $(A,\delta )$
is a ring homomorphism lifting the Frobenius on
$(A,\delta )$
is a ring homomorphism lifting the Frobenius on
![]() $A/p$
. Using
$A/p$
. Using
![]() $\varphi $
, the second property of
$\varphi $
, the second property of
![]() $\delta $
can be rephrased as
$\delta $
can be rephrased as
which looks close to that of a derivation. If A is p-torsion free, then any Frobenius lift
![]() $\psi \colon A\to A$
defines a
$\psi \colon A\to A$
defines a
![]() $\delta $
-structure on A by setting
$\delta $
-structure on A by setting
Thus, in the p-torsion free case, a
![]() $\delta $
-ring is the same as a ring with a Frobenius lift.
$\delta $
-ring is the same as a ring with a Frobenius lift.
Remark 2.2. The category of
![]() $\delta $
-rings has all limits and colimits and these are calculated on the underlying ringsFootnote
6
(cf. [Reference Bhatt and Scholze13, Section 1]). In particular, there exist free
$\delta $
-rings has all limits and colimits and these are calculated on the underlying ringsFootnote
6
(cf. [Reference Bhatt and Scholze13, Section 1]). In particular, there exist free
![]() $\delta $
-rings (by the adjoint functor theorem). Concretely, if A is a
$\delta $
-rings (by the adjoint functor theorem). Concretely, if A is a
![]() $\delta $
-ring and X is a set, then the free
$\delta $
-ring and X is a set, then the free
![]() $\delta $
-ring
$\delta $
-ring
![]() $A\{X\}$
on X is a polynomial ring over A with variables
$A\{X\}$
on X is a polynomial ring over A with variables
![]() $\delta ^n(x)$
for
$\delta ^n(x)$
for
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $x\in X$
(cf. [Reference Bhatt and Scholze13, Lemma 2.11]). Moreover, the Frobenius on
$x\in X$
(cf. [Reference Bhatt and Scholze13, Lemma 2.11]). Moreover, the Frobenius on
![]() $\mathbb {Z}_{(p)}\{X\}$
is faithfully flat (cf. [Reference Bhatt and Scholze13, Lemma 2.11]).
$\mathbb {Z}_{(p)}\{X\}$
is faithfully flat (cf. [Reference Bhatt and Scholze13, Lemma 2.11]).
Definition 2.3. Let
![]() $(A,\delta )$
be a
$(A,\delta )$
be a
![]() $\delta $
-ring.
$\delta $
-ring.
-
1. An element
 $x\in A$
is called of rank
$x\in A$
is called of rank
 $1$
if
$1$
if
 $\delta (x)=0$
.
$\delta (x)=0$
. -
2. An element
 $d\in A$
is called distinguished if
$d\in A$
is called distinguished if
 $\delta (d)\in A^{\times }$
is a unit.
$\delta (d)\in A^{\times }$
is a unit.
In particular,
![]() $\varphi (x)=x^p$
if
$\varphi (x)=x^p$
if
![]() $x\in A$
is of rank
$x\in A$
is of rank
![]() $1$
.
$1$
.
Here is a useful lemma showing how to find rank
![]() $1$
elements in a p-adically separated
$1$
elements in a p-adically separated
![]() $\delta $
-ring.
$\delta $
-ring.
Lemma 2.4. Let A be a
![]() $\delta $
-ring, and let
$\delta $
-ring, and let
![]() $x\in A$
. Then
$x\in A$
. Then
![]() $\delta (x^{p^n})\in p^nA$
for all n. In particular, if A is p-adically separated and
$\delta (x^{p^n})\in p^nA$
for all n. In particular, if A is p-adically separated and
![]() $y\in A$
admits a
$y\in A$
admits a
![]() $p^n$
-th root for all
$p^n$
-th root for all
![]() $n\geq 0$
, then
$n\geq 0$
, then
![]() $\delta (y)=0$
, that is, y has rank
$\delta (y)=0$
, that is, y has rank
![]() $1$
.
$1$
.
Proof. Cf. [Reference Bhatt and Scholze13, Lemma 2.31].
We can now state the definition of a prism (cf. [Reference Bhatt and Scholze13, Definition 3.2]). Recall that a
![]() $\delta $
-pair
$\delta $
-pair
![]() $(A,I)$
is simply a
$(A,I)$
is simply a
![]() $\delta $
-ring A together with an ideal
$\delta $
-ring A together with an ideal
![]() $I\subseteq A$
.
$I\subseteq A$
.
Definition 2.5. A
![]() $\delta $
-pair
$\delta $
-pair
![]() $(A,I)$
is a prism if
$(A,I)$
is a prism if
![]() $I\subseteq A$
is an invertible ideal, such that A is derived
$I\subseteq A$
is an invertible ideal, such that A is derived
![]() $(p,I)$
-complete, and
$(p,I)$
-complete, and
![]() $p\in I+\varphi (I)A$
. A prism
$p\in I+\varphi (I)A$
. A prism
![]() $(A,I)$
is called bounded if
$(A,I)$
is called bounded if
![]() $A/I$
has bounded
$A/I$
has bounded
![]() $p^{\infty }$
-torsion.
$p^{\infty }$
-torsion.
Remark 2.6. Some comments about these definitions are in order:
-
1. By [Reference Bhatt and Scholze13, Lemma 3.1], the condition
 $p\in I+\varphi (I)A$
is equivalent to the fact that I is pro-Zariski locally on
$p\in I+\varphi (I)A$
is equivalent to the fact that I is pro-Zariski locally on
 $\mathrm {Spec}(A)$
generated by a distinguished element. Thus, it is usually not much harm to assume that
$\mathrm {Spec}(A)$
generated by a distinguished element. Thus, it is usually not much harm to assume that
 $I=(d)$
is actually principalFootnote
7
.
$I=(d)$
is actually principalFootnote
7
. -
2. If
 $(A,I)\to (B,J)$
is a morphism of prisms, i.e.,
$(A,I)\to (B,J)$
is a morphism of prisms, i.e.,
 $A\to B$
is a morphism of
$A\to B$
is a morphism of
 $\delta $
-rings carrying I to J, then [Reference Bhatt and Scholze13, Lemma 3.5] implies that
$\delta $
-rings carrying I to J, then [Reference Bhatt and Scholze13, Lemma 3.5] implies that
 $J=IB$
.
$J=IB$
. -
3. An important example of a prism is provided by
where $$ \begin{align*} (A,I)=(\mathbb{Z}_p[[q-1]],([p]_q)), \end{align*} $$
is the q-analog of p. Many other interesting examples will appear below.
$$ \begin{align*} (A,I)=(\mathbb{Z}_p[[q-1]],([p]_q)), \end{align*} $$
is the q-analog of p. Many other interesting examples will appear below. $$ \begin{align*} [p]_q:=\frac{q^p-1}{q-1} \end{align*} $$
$$ \begin{align*} [p]_q:=\frac{q^p-1}{q-1} \end{align*} $$
-
4. The prism
 $(A,I)$
being bounded implies that A is classically
$(A,I)$
being bounded implies that A is classically
 $(p,I)$
-adically complete (cf. [Reference Bhatt8, Exercise 3.4]), and thus, in particular, p-adically separated.
$(p,I)$
-adically complete (cf. [Reference Bhatt8, Exercise 3.4]), and thus, in particular, p-adically separated.
Lemma 2.7. Let
![]() $(A,I)$
be a prism, and let
$(A,I)$
be a prism, and let
![]() $d\in I$
be distinguished. If
$d\in I$
be distinguished. If
![]() $(p,d)$
is a regular sequence in A, then for all
$(p,d)$
is a regular sequence in A, then for all
![]() $r,s\geq 0$
,
$r,s\geq 0$
,
![]() $r\neq s$
, the sequences
$r\neq s$
, the sequences
are regular.
Proof. Note that for the second case, one can always assume
![]() $\min (r,s)=0$
, up to replacing d by
$\min (r,s)=0$
, up to replacing d by
![]() $\varphi ^{\min (r,s)}(d)$
. Then the statement is proven in [Reference Anschütz and Le Bras1, Lemma 3.3] and [Reference Anschütz and Le Bras1, Lemma 3.6].
$\varphi ^{\min (r,s)}(d)$
. Then the statement is proven in [Reference Anschütz and Le Bras1, Lemma 3.3] and [Reference Anschütz and Le Bras1, Lemma 3.6].
Previous work in p-adic Hodge theory used, in one form or another, the theory of perfectoid spaces. From the prismatic perspective, this is explained as follows. We recall that a
![]() $\delta $
-ring A (or prism
$\delta $
-ring A (or prism
![]() $(A,I)$
) is called perfect if the Frobenius
$(A,I)$
) is called perfect if the Frobenius
![]() $\varphi \colon A\to A$
is an isomorphism. If A is perfect, then necessarily
$\varphi \colon A\to A$
is an isomorphism. If A is perfect, then necessarily
![]() $A\cong W(R)$
for some perfect
$A\cong W(R)$
for some perfect
![]() $\mathbb {F}_p$
-algebra R (cf. [Reference Bhatt and Scholze13, Corollary 2.30]).
$\mathbb {F}_p$
-algebra R (cf. [Reference Bhatt and Scholze13, Corollary 2.30]).
Proposition 2.8. The functor
is an equivalence of categories with inverse
![]() $R\mapsto (A_{\mathrm {inf}}(R),\mathrm {ker}(\tilde {\theta }))$
, where
$R\mapsto (A_{\mathrm {inf}}(R),\mathrm {ker}(\tilde {\theta }))$
, where
![]() $A_{\mathrm {inf}}(R):=W(R^{\flat })$
and
$A_{\mathrm {inf}}(R):=W(R^{\flat })$
and
![]() $\tilde {\theta }=\theta \circ \varphi ^{-1}$
,
$\tilde {\theta }=\theta \circ \varphi ^{-1}$
,
![]() $\theta $
being Fontaine’s theta map.
$\theta $
being Fontaine’s theta map.
Proof. Cf. [Reference Bhatt and Scholze13, Theorem 3.9].
Remark 2.9.
-
(1) Of course, one could use
 $\theta $
instead of
$\theta $
instead of
 $\tilde {\theta }$
. We make this (slightly strange) choice for coherence with later choices.
$\tilde {\theta }$
. We make this (slightly strange) choice for coherence with later choices. -
(2) The theorem implies, in particular, that for every perfect prism
 $(A,I)$
, the ideal I is principal.
$(A,I)$
, the ideal I is principal.
As a corollary, we get the following easy case of almost purity.
Corollary 2.10. Let R be a perfectoid ring, and let
![]() $R\to R^{\prime }$
be p-completely étale. Then
$R\to R^{\prime }$
be p-completely étale. Then
![]() $R^{\prime }$
is perfectoid. Moreover, if
$R^{\prime }$
is perfectoid. Moreover, if
![]() $J\subseteq R$
is an ideal, then the p-completion
$J\subseteq R$
is an ideal, then the p-completion
![]() $R^{\prime }$
of the henselisation of R at J is perfectoid.
$R^{\prime }$
of the henselisation of R at J is perfectoid.
Proof. We can lift
![]() $R^{\prime }$
to a
$R^{\prime }$
to a
![]() $(p,\ker (\theta ))$
-completely étale
$(p,\ker (\theta ))$
-completely étale
![]() $A_{\mathrm {inf}}(R)$
-algebra B. By [Reference Bhatt and Scholze13, Lemma 2.18], the
$A_{\mathrm {inf}}(R)$
-algebra B. By [Reference Bhatt and Scholze13, Lemma 2.18], the
![]() $\delta $
-structure on
$\delta $
-structure on
![]() $A_{\mathrm {inf}}(R)$
extends uniquely to B. Reducing modulo p, we see that B is a perfect
$A_{\mathrm {inf}}(R)$
extends uniquely to B. Reducing modulo p, we see that B is a perfect
![]() $\delta $
-ring as it is
$\delta $
-ring as it is
![]() $(p,\ker (\theta ))$
-completely étale over
$(p,\ker (\theta ))$
-completely étale over
![]() $A_{\mathrm {inf}}(R)$
. Using Proposition 2.8,
$A_{\mathrm {inf}}(R)$
. Using Proposition 2.8,
![]() $R^{\prime }\cong B/\ker (\theta )B$
is therefore perfectoid. The statement on henselisations follows from this as henselisations are colimits along étale maps (cf. the proof of [Reference Project52, Tag 0A02]). (Note that since R has bounded
$R^{\prime }\cong B/\ker (\theta )B$
is therefore perfectoid. The statement on henselisations follows from this as henselisations are colimits along étale maps (cf. the proof of [Reference Project52, Tag 0A02]). (Note that since R has bounded
![]() $p^{\infty }$
-torsion, the p-completion of an étale R-algebra is p-completely étale.)
$p^{\infty }$
-torsion, the p-completion of an étale R-algebra is p-completely étale.)
Moreover, perfectoid rings enjoy the following fundamental property.
Proposition 2.11. Let
![]() $(A,I)$
be a perfect prism. Then for every prism
$(A,I)$
be a perfect prism. Then for every prism
![]() $(B,J)$
, the map
$(B,J)$
, the map
is a bijection.
Proof. Cf. [Reference Bhatt and Scholze13, Lemma 4.7].
2.2 The q-logarithm
Each prism is endowed with its Nygaard filtration (cf. [Reference Bhatt8, Definition 11.2]).
Definition 2.12. Let
![]() $(A,I)$
be a prism. Then we set
$(A,I)$
be a prism. Then we set
for
![]() $i\geq 0$
. The filtration
$i\geq 0$
. The filtration
![]() $\mathcal {N}^{\geq \bullet }A$
is called the Nygaard filtration of
$\mathcal {N}^{\geq \bullet }A$
is called the Nygaard filtration of
![]() $(A,I)$
.
$(A,I)$
.
This filtration (or rather the first piece of this filtration) will play an important role in the rest of this text. It already shows up when proving the existence of the q-logarithm
for a prism
![]() $(A,I)$
over
$(A,I)$
over
![]() $(\mathbb {Z}_p[[q-1]],([p]_q))$
from Remark 2.6, as we now explain. Here,
$(\mathbb {Z}_p[[q-1]],([p]_q))$
from Remark 2.6, as we now explain. Here,
is the functor sending a ring R to
![]() $T_p(R^{\times })= \varprojlim \limits_n\mu _{p^n}(R)$
and
$T_p(R^{\times })= \varprojlim \limits_n\mu _{p^n}(R)$
and
is the Teichmüller lift sending a p-power compatible system
to the limit
where
![]() $\tilde {x}_n\in A$
is a lift of
$\tilde {x}_n\in A$
is a lift of
![]() $x_n\in A/I$
. By definition,
$x_n\in A/I$
. By definition,
is the subset of the inverse limit consisting of sequences that start with a
![]() $1$
. Moreover, on
$1$
. Moreover, on
![]() $\varprojlim \limits_{x\mapsto x^p} A/I$
, one can take p-th roots
$\varprojlim \limits_{x\mapsto x^p} A/I$
, one can take p-th roots
In [Reference Anschütz and Le Bras1, Lemma 4.10], there is the following lemma on the q-logarithm. For
![]() $n\in \mathbb {Z}$
, we recall that the q-number
$n\in \mathbb {Z}$
, we recall that the q-number
![]() $[n]_q$
is defined as
$[n]_q$
is defined as
Lemma 2.13. Let
![]() $(B,J)$
be a prism over
$(B,J)$
be a prism over
![]() $(\mathbb {Z}_p[[q-1]],([p]_q))$
. Then for every element
$(\mathbb {Z}_p[[q-1]],([p]_q))$
. Then for every element
![]() $x\in 1+\mathcal {N}^{\geq 1} B$
of rank
$x\in 1+\mathcal {N}^{\geq 1} B$
of rank
![]() $1$
, that is,
$1$
, that is,
![]() $\delta (x)=0$
, the series
$\delta (x)=0$
, the series
 $$ \begin{align*}\mathrm{log}_q(x)=\sum\limits_{n=1}^{\infty} (-1)^{n-1}q^{-n(n-1)/2}\frac{(x-1)(x-q)\cdots (x-q^{n-1})}{[n]_q} \end{align*} $$
$$ \begin{align*}\mathrm{log}_q(x)=\sum\limits_{n=1}^{\infty} (-1)^{n-1}q^{-n(n-1)/2}\frac{(x-1)(x-q)\cdots (x-q^{n-1})}{[n]_q} \end{align*} $$
is well-defined and converges in B. Moreover,
![]() $\log _q(x)\in \mathcal {N}^{\geq 1}B$
and, in
$\log _q(x)\in \mathcal {N}^{\geq 1}B$
and, in
one has the relation
![]() $\log _q(x)=\frac {q-1}{\log (q)}\log (x)$
, where
$\log _q(x)=\frac {q-1}{\log (q)}\log (x)$
, where
![]() $\mathrm {log}(x):=\sum \limits _{n=1}^{\infty } (-1)^{n-1}\frac {{(x-1)^n}}{n}$
.
$\mathrm {log}(x):=\sum \limits _{n=1}^{\infty } (-1)^{n-1}\frac {{(x-1)^n}}{n}$
.
The defining properties of the q-logarithm are that
![]() $\log _q(1)=0$
and that its q-derivative is
$\log _q(1)=0$
and that its q-derivative is
![]() $\frac {d_qx}{x}$
(cf. [Reference Anschütz and Le Bras1, Lemma 4.6]).
$\frac {d_qx}{x}$
(cf. [Reference Anschütz and Le Bras1, Lemma 4.6]).
One derives easily the existence of the ‘divided q-logarithm’.
Lemma 2.14. Let
![]() $(B,J)$
be a bounded prism over
$(B,J)$
be a bounded prism over
![]() $(\mathbb {Z}_p[[q-1]],([p]_q))$
, and let
$(\mathbb {Z}_p[[q-1]],([p]_q))$
, and let
![]() $x\in \mathbb {Z}_p(1)(B/J)$
. Then
$x\in \mathbb {Z}_p(1)(B/J)$
. Then
![]() $[x^{1/p}]_{\tilde {\theta }}\in B$
is of rank
$[x^{1/p}]_{\tilde {\theta }}\in B$
is of rank
![]() $1$
and lies in
$1$
and lies in
![]() $1+\mathcal {N}^{\geq 1}B$
. Thus
$1+\mathcal {N}^{\geq 1}B$
. Thus
 $$ \begin{align*}\mathrm{log}_q([x^{1/p}]_{\tilde{\theta}})=\sum\limits_{n=1}^{\infty} (-1)^{n-1}q^{-n(n-1)/2}\frac{([x^{1/p}]_{\tilde{\theta}}-1)\ldots ([x^{1/p}]_{\tilde{\theta}}-q^{n-1})}{[n]_q} \end{align*} $$
$$ \begin{align*}\mathrm{log}_q([x^{1/p}]_{\tilde{\theta}})=\sum\limits_{n=1}^{\infty} (-1)^{n-1}q^{-n(n-1)/2}\frac{([x^{1/p}]_{\tilde{\theta}}-1)\ldots ([x^{1/p}]_{\tilde{\theta}}-q^{n-1})}{[n]_q} \end{align*} $$
exists in B.
Proof. By Lemma 2.4 (which applies to B as B is bounded and, thus, classically
![]() $(p,[p]_q)$
-complete, by [Reference Bhatt and Scholze13, Lemma 3.7 (1)]), the element
$(p,[p]_q)$
-complete, by [Reference Bhatt and Scholze13, Lemma 3.7 (1)]), the element
![]() $[x^{1/p}]_{\tilde {\theta }}$
is of rank
$[x^{1/p}]_{\tilde {\theta }}$
is of rank
![]() $1$
as it admits arbitrary
$1$
as it admits arbitrary
![]() $p^n$
-roots. Moreover,
$p^n$
-roots. Moreover,
![]() $[x^{1/p}]_{\tilde {\theta }}\in 1+\mathcal {N}^{\geq 1}B$
as
$[x^{1/p}]_{\tilde {\theta }}\in 1+\mathcal {N}^{\geq 1}B$
as
![]() $\varphi ([x^{1/p}]_{\tilde {\theta }})=[x]_{\tilde {\theta }}\equiv 1$
modulo J. By Lemma 2.13, we can therefore conclude.
$\varphi ([x^{1/p}]_{\tilde {\theta }})=[x]_{\tilde {\theta }}\equiv 1$
modulo J. By Lemma 2.13, we can therefore conclude.
3 Generalities on prismatic cohomology
3.1 Prismatic site and prismatic cohomology
In this paragraph, we shortly recall, mostly for the convenience of the reader and to fix notations, some fundamental definitions and results, without proofs, from [Reference Bhatt and Scholze13]. Fix a bounded prism
![]() $(A,I)$
. Let R be a p-complete
$(A,I)$
. Let R be a p-complete
![]() $A/I$
-algebra.
$A/I$
-algebra.
Definition 3.1. The prismatic site of R relative to A, denoted
![]() , is the category whose objects are given by bounded prisms
, is the category whose objects are given by bounded prisms
![]() $(B,IB)$
over
$(B,IB)$
over
![]() $(A,I)$
together with an
$(A,I)$
together with an
![]() $A/I$
-algebra map
$A/I$
-algebra map
![]() $R \to B/IB$
, with the obvious morphisms, endowed with the Grothendieck topology for which covers are given by
$R \to B/IB$
, with the obvious morphisms, endowed with the Grothendieck topology for which covers are given by
![]() $(p,I)$
-completely faithfully flat morphisms of prisms over
$(p,I)$
-completely faithfully flat morphisms of prisms over
![]() $(A,I)$
.
$(A,I)$
.
Remark 3.2. In this remark, we deal with the set-theoretic issues arising from Definition 3.1. For example, as it stands, there does not exist a sheafification functor for presheaves on
![]() . We will implicitly fix a cut-off cardinal
. We will implicitly fix a cut-off cardinal
![]() $\kappa $
like in [Reference Scholze49, Lemma 4.1] and assume that all objects appearing in Definition 3.1 (or Definition 3.4) have cardinality
$\kappa $
like in [Reference Scholze49, Lemma 4.1] and assume that all objects appearing in Definition 3.1 (or Definition 3.4) have cardinality
![]() $<\kappa $
. The results of this paper will not change under enlarging
$<\kappa $
. The results of this paper will not change under enlarging
![]() $\kappa $
. For example, the category of prismatic Dieudonné crystals on
$\kappa $
. For example, the category of prismatic Dieudonné crystals on
![]() will be independent of the choice of
will be independent of the choice of
![]() $\kappa $
. Also, the prismatic cohomology does not change (because it can be calculated via a
$\kappa $
. Also, the prismatic cohomology does not change (because it can be calculated via a
![]() $\breve{\mathrm{C}}$
ech-Alexander complex), and, thus, the prismatic Dieudonné crystals will be independent of
$\breve{\mathrm{C}}$
ech-Alexander complex), and, thus, the prismatic Dieudonné crystals will be independent of
![]() $\kappa $
(by Section 4.4).
$\kappa $
(by Section 4.4).
This affine definition admits an immediate extension to p-adic formal schemes over
![]() $\mathrm {Spf}(A/I)$
, cf [Reference Bhatt and Scholze13].
$\mathrm {Spf}(A/I)$
, cf [Reference Bhatt and Scholze13].
Proposition 3.3 ([Reference Bhatt and Scholze13], Corollary 3.12).
The functor
![]() (respectively,
(respectively,
![]() ) on the prismatic site valued in
) on the prismatic site valued in
![]() $(p,I)$
-complete
$(p,I)$
-complete
![]() $\delta -A$
-algebras (respectively, in p-complete R-algebras), sending
$\delta -A$
-algebras (respectively, in p-complete R-algebras), sending
![]() to B (respectively,
to B (respectively,
![]() $B/IB$
), is a sheaf. The sheaf
$B/IB$
), is a sheaf. The sheaf
![]() (respectively,
(respectively,
![]() ) is called the prismatic structure sheaf (respectively, the reduced prismatic structure sheaf).
) is called the prismatic structure sheaf (respectively, the reduced prismatic structure sheaf).
These constructions have absolute variants, where one does not fix a base prism. Let R be a p-complete ring.
Definition 3.4. The (absolute) prismatic site of R, denoted
![]() , is the category whose objects are given by bounded prisms
, is the category whose objects are given by bounded prisms
![]() $(B,J)$
together with a ring map
$(B,J)$
together with a ring map
![]() $R \to B/J$
, with the obvious morphisms, endowed with the Grothendieck topology for which covers are given by morphisms of prism
$R \to B/J$
, with the obvious morphisms, endowed with the Grothendieck topology for which covers are given by morphisms of prism
![]() $(B,J) \to (C,JC)$
which are
$(B,J) \to (C,JC)$
which are
![]() $(p,I)$
-completely faithfully flat.
$(p,I)$
-completely faithfully flat.
Exactly as before, one defines functors
![]() and
and
![]() , which are sheaves on
, which are sheaves on
![]() .
.
We turn to the definition of (derived) prismatic cohomology. Fix a bounded prism
![]() $(A,I)$
. The prismatic cohomology of R over A is defined in two steps. One starts with the case where R is p-completely smooth over
$(A,I)$
. The prismatic cohomology of R over A is defined in two steps. One starts with the case where R is p-completely smooth over
![]() $A/I$
.
$A/I$
.
Definition 3.5. Let R be a p-complete p-completely smooth
![]() $A/I$
-algebra. The prismatic complex
$A/I$
-algebra. The prismatic complex
![]() of R over A is defined to be the cohomology of the sheaf
of R over A is defined to be the cohomology of the sheaf
![]() on the prismatic site:
on the prismatic site:
This is a
![]() $(p,I)$
-complete commutative algebra object in
$(p,I)$
-complete commutative algebra object in
![]() $D(A)$
endowed with a semilinear map
$D(A)$
endowed with a semilinear map
![]() , induced by the Frobenius of
, induced by the Frobenius of
![]() .
.
Similarly, one defines the reduced prismatic complex or Hodge-Tate complex:
This is a p-complete commutative algebra object in
![]() $D(R)$
.
$D(R)$
.
A fundamental property of prismatic cohomology is the Hodge-Tate comparison theorem, which relates the Hodge-Tate complex to differential forms. For this, first recall that for any
![]() $A/I$
-module M and integer n, the nth-Breuil-Kisin twist of M is defined as
$A/I$
-module M and integer n, the nth-Breuil-Kisin twist of M is defined as
The Bockstein maps
for each
![]() $i \geq 0$
, make
$i \geq 0$
, make
![]() a graded commutative
a graded commutative
![]() $A/I$
-differential graded algebraFootnote
8
, which comes with a map
$A/I$
-differential graded algebraFootnote
8
, which comes with a map
![]() .
.
Theorem 3.6 ([Reference Bhatt and Scholze13], Theorem 4.10).
The map
![]() $\eta $
extends to a map
$\eta $
extends to a map
which is an isomorphism.
While proving Theorem 3.6, Bhatt and Scholze also relate prismatic and crystalline cohomology when the ring R is an
![]() $\mathbb {F}_p$
-algebra. The precise statement is the following. Assume that
$\mathbb {F}_p$
-algebra. The precise statement is the following. Assume that
![]() $I=(p)$
, that is that
$I=(p)$
, that is that
![]() $(A,I)$
is a crystalline prism. Let
$(A,I)$
is a crystalline prism. Let
![]() $J \subset A$
be a PD-ideal with
$J \subset A$
be a PD-ideal with
![]() $p\in J$
. Let R be a smooth
$p\in J$
. Let R be a smooth
![]() $A/J$
-algebra and
$A/J$
-algebra and
where the map
![]() $A/J \to A/p$
is the map induced by Frobenius and the fact that J is a PD-ideal.
$A/J \to A/p$
is the map induced by Frobenius and the fact that J is a PD-ideal.
Theorem 3.7 ([Reference Bhatt and Scholze13], Theorem 5.2).
Under the previous assumptions, there is a canonical isomorphism of
![]() $E_{\infty }-A$
-algebras
$E_{\infty }-A$
-algebras
compatible with Frobenius.
Remark 3.8.
-
1. If
 $J=(p)$
,
$J=(p)$
,
 $R^{(1)}$
is just the Frobenius twist of R.
$R^{(1)}$
is just the Frobenius twist of R. -
2. The proof of Theorem 3.7 goes through for a syntomic
 $A/J$
-algebra R. The important point is that in the proof in [Reference Bhatt and Scholze13, Theorem 5.2], in each simplicial degree, the kernel of the morphism
$A/J$
-algebra R. The important point is that in the proof in [Reference Bhatt and Scholze13, Theorem 5.2], in each simplicial degree, the kernel of the morphism
 $B^{\bullet }\to \tilde {R}$
is the inductive limit of ideals of the form
$B^{\bullet }\to \tilde {R}$
is the inductive limit of ideals of the form
 $(p,x_1,\ldots , x_r)$
, with
$(p,x_1,\ldots , x_r)$
, with
 $(x_1,\ldots , x_r)$
being p-completely regular relative to A, which allows to apply [Reference Bhatt and Scholze13, Proposition 3.13]. The statement extends by descent from the quasiregular semiperfect case to all quasisyntomic rings over
$(x_1,\ldots , x_r)$
being p-completely regular relative to A, which allows to apply [Reference Bhatt and Scholze13, Proposition 3.13]. The statement extends by descent from the quasiregular semiperfect case to all quasisyntomic rings over
 $\mathbb {F}_p$
(cf. Lemma 3.27).
$\mathbb {F}_p$
(cf. Lemma 3.27).
Definition 3.5 of course makes sense without the hypothesis that R is p-completely smooth over
![]() $A/I$
. But it would not give well-behaved objects; for instance, the Hodge-Tate comparison would not hold in generalFootnote
9
. The formalism of nonabelian derived functors allows to extend the definition of the prismatic and Hodge-Tate complexes to all p-complete
$A/I$
. But it would not give well-behaved objects; for instance, the Hodge-Tate comparison would not hold in generalFootnote
9
. The formalism of nonabelian derived functors allows to extend the definition of the prismatic and Hodge-Tate complexes to all p-complete
![]() $A/I$
-algebras in a manner compatible with the Hodge-Tate comparison theorem.
$A/I$
-algebras in a manner compatible with the Hodge-Tate comparison theorem.
Definition 3.9. The derived prismatic cohomology functor
![]() (respectively, the derived Hodge-Tate cohomology functor
(respectively, the derived Hodge-Tate cohomology functor
![]() ) is the left Kan extension (cf. [Reference Bhatt, Morrow and Scholze12, Construction 2.1]) of the functor
) is the left Kan extension (cf. [Reference Bhatt, Morrow and Scholze12, Construction 2.1]) of the functor
![]() (respectively,
(respectively,
![]() ) from p-completely smooth
) from p-completely smooth
![]() $A/I$
-algebras to
$A/I$
-algebras to
![]() $(p,I)$
-complete commutative algebra objects in (the
$(p,I)$
-complete commutative algebra objects in (the
![]() $\infty $
-category)
$\infty $
-category)
![]() $D(A)$
(respectively, p-complete commutative algebra objects in
$D(A)$
(respectively, p-complete commutative algebra objects in
![]() $D(R)$
), to the category of p-complete
$D(R)$
), to the category of p-complete
![]() $A/I$
-algebras.
$A/I$
-algebras.
For short, we will just write
![]() (respectively,
(respectively,
![]() ) for
) for
![]() (respectively,
(respectively,
![]() ) in the following.
) in the following.
Left Kan extension of the Postnikov (or canonical filtration) filtration leads to an extension of Hodge-Tate comparison to derived prismatic cohomology.
Proposition 3.10. For any p-complete
![]() $A/I$
-algebra R, the derived Hodge-Tate complex
$A/I$
-algebra R, the derived Hodge-Tate complex
![]() comes equipped with a functorial increasing multiplicative exhaustive filtration
comes equipped with a functorial increasing multiplicative exhaustive filtration
![]() $\mathrm {Fil}_*^{\mathrm { conj}}$
in the category of p-complete objects in
$\mathrm {Fil}_*^{\mathrm { conj}}$
in the category of p-complete objects in
![]() $D(R)$
and canonical identifications
$D(R)$
and canonical identifications
Finally, let us indicate how these affine statements globalise.
Proposition 3.11. Let X be a p-adic formal scheme over
![]() $\mathrm {Spf}(A/I)$
, which is locally the formal spectrum of a p-complete ring with bounded
$\mathrm {Spf}(A/I)$
, which is locally the formal spectrum of a p-complete ring with bounded
![]() $p^{\infty }$
-torsion. There exists a functorially defined
$p^{\infty }$
-torsion. There exists a functorially defined
![]() $(p,I)$
-complete commutative algebra object
$(p,I)$
-complete commutative algebra object
![]() , equipped with a
, equipped with a
![]() $\varphi _A$
-linear map
$\varphi _A$
-linear map
![]() , and having the following properties:
, and having the following properties:
-
• For any affine open
 $U=\mathrm {Spf}(R)$
in X, there is a natural isomorphism of
$U=\mathrm {Spf}(R)$
in X, there is a natural isomorphism of
 $(p,I)$
-complete commutative algebra objects in
$(p,I)$
-complete commutative algebra objects in
 $D(A)$
between
$D(A)$
between
 and
and
 , compatible with Frobenius.
, compatible with Frobenius. -
• Set
 . Then
. Then
 is naturally an object of
is naturally an object of
 $D(X)$
, which comes with a functorial increasing multiplicative exhaustive filtration
$D(X)$
, which comes with a functorial increasing multiplicative exhaustive filtration
 $\mathrm {Fil}_*^{\mathrm {conj}}$
in the category of p-complete objects in
$\mathrm {Fil}_*^{\mathrm {conj}}$
in the category of p-complete objects in
 $D(X)$
and canonical identifications
$D(X)$
and canonical identifications 
3.2 Truncated Hodge-Tate cohomology and the cotangent complex
Let
![]() $(A,I)$
be a bounded prism, and let X be a p-adic
$(A,I)$
be a bounded prism, and let X be a p-adic
![]() $A/I$
-formal scheme. The following result also appears in [Reference Bhatt and Scholze13, Proposition 4.14]Footnote
10
. We give a similar argument (suggested to us by Bhatt), with more details than in loc. cit. Since this result is not strictly necessary for the rest of the paper, the reader can safely skip this subsection.
$A/I$
-formal scheme. The following result also appears in [Reference Bhatt and Scholze13, Proposition 4.14]Footnote
10
. We give a similar argument (suggested to us by Bhatt), with more details than in loc. cit. Since this result is not strictly necessary for the rest of the paper, the reader can safely skip this subsection.
Proposition 3.12. There is a canonical isomorphism:
where the right-hand side is the first piece of the increasing filtration on
![]() introduced in Proposition 3.11.
introduced in Proposition 3.11.
Proof. We can assume that
![]() $X=\mathrm {Spf}(R)$
is affine. Write
$X=\mathrm {Spf}(R)$
is affine. Write
![]() $\bar {A}=A/I$
. We want to prove that there is a canonical isomorphism
$\bar {A}=A/I$
. We want to prove that there is a canonical isomorphism
First, let us note that by the transitivity triangle for
![]() $A\to {\bar {A}} \to R$
, the cotangent complex
$A\to {\bar {A}} \to R$
, the cotangent complex
![]() $L_{R/A}\{-1\}[-1]^{\wedge _p}$
sits inside a triangle
$L_{R/A}\{-1\}[-1]^{\wedge _p}$
sits inside a triangle
and the outer terms are isomorphic to
![]() and
and
To construct the isomorphism
![]() $\alpha _R$
, it suffices to restrict to
$\alpha _R$
, it suffices to restrict to
![]() ${\bar {A}}\to R p$
-completely smooth first, and then Kan extend. Thus, assume from now on that R is p-completely smooth over
${\bar {A}}\to R p$
-completely smooth first, and then Kan extend. Thus, assume from now on that R is p-completely smooth over
![]() ${\bar {A}}$
.
${\bar {A}}$
.
Let
, that is,
![]() $(B,J)$
is a prism over
$(B,J)$
is a prism over
![]() $(A,I)$
with a morphism
$(A,I)$
with a morphism
![]() $\iota \colon R\to B/J$
. Pulling back the extension of A-algebras
$\iota \colon R\to B/J$
. Pulling back the extension of A-algebras
along
![]() $\iota \colon R\to B/J$
defines an extension of R by
$\iota \colon R\to B/J$
defines an extension of R by
![]() $J/J^2\cong B/J\{1\}$
, and as such, is thus classified by a morphism
$J/J^2\cong B/J\{1\}$
, and as such, is thus classified by a morphism
Passing to the (homotopy) limit over all
then defines (after shifting and twisting) the morphism
Concretely, if
![]() $R={\bar {A}}\langle x\rangle $
, then
$R={\bar {A}}\langle x\rangle $
, then
On the summand
![]() $R\otimes _{{\bar {A}}}I/I^2[1]$
, the morphism
$R\otimes _{{\bar {A}}}I/I^2[1]$
, the morphism
![]() $\alpha _R^{\prime }$
is simply the base extension of
$\alpha _R^{\prime }$
is simply the base extension of
![]() $I/I^2\to J/J^2$
as follows by considering the case
$I/I^2\to J/J^2$
as follows by considering the case
![]() ${\bar {A}}=R$
. On the summand
${\bar {A}}=R$
. On the summand
![]() $Rdx$
, the morphism
$Rdx$
, the morphism
![]() $\alpha _R^{\prime }$
is (canonically) represented by the
$\alpha _R^{\prime }$
is (canonically) represented by the
![]() $J/J^2$
-torsor of preimages of
$J/J^2$
-torsor of preimages of
![]() $\iota (x)$
in
$\iota (x)$
in
![]() $B/J^2$
and factors as
$B/J^2$
and factors as
![]() $R\xrightarrow {\iota }B/J\to B/J\{1\}[1]$
with the second morphism the connecting morphism for
$R\xrightarrow {\iota }B/J\to B/J\{1\}[1]$
with the second morphism the connecting morphism for
![]() $0\to B/J\{1\}\to B/J^2\to B/J\to 0$
. Thus, after passing to the limit, we get a diagram
$0\to B/J\{1\}\to B/J^2\to B/J\to 0$
. Thus, after passing to the limit, we get a diagram

and on
![]() $H^0$
, the horizontal morphism induces the Bockstein differential
$H^0$
, the horizontal morphism induces the Bockstein differential
Thus, the image of
![]() $dx\in H^0(L_{R/A}^{\wedge _p})$
under
$dx\in H^0(L_{R/A}^{\wedge _p})$
under
![]() $\alpha _R$
is
$\alpha _R$
is
![]() $\beta (\iota (x))$
. Therefore, we see that on
$\beta (\iota (x))$
. Therefore, we see that on
![]() $H^0$
, the morphism
$H^0$
, the morphism
![]() $\alpha _R$
induces the identity under the identifications
$\alpha _R$
induces the identity under the identifications
and
(the second is the Hodge-Tate comparison). Moreover, the morphism
is the canonical one obtained by tensoring
with
![]() $I/I^2$
. By functoriality (and as
$I/I^2$
. By functoriality (and as
![]() $\Omega ^1_{R/A}$
is generated by
$\Omega ^1_{R/A}$
is generated by
![]() $dr$
for
$dr$
for
![]() $r\in R$
), we can conclude that for every p-completely smooth algebra R over A
$r\in R$
), we can conclude that for every p-completely smooth algebra R over A
induces the canonical morphism, and thus, that
![]() $\alpha _R$
is an isomorphism in general.
$\alpha _R$
is an isomorphism in general.
Recall the following proposition, which is a general consequence of the theory of the cotangent complex.
Proposition 3.13. Let S be a ring,
![]() $I\subseteq S$
an invertible ideal and X a flat
$I\subseteq S$
an invertible ideal and X a flat
![]() $\overline {S}:=S/I$
-scheme. Then the class
$\overline {S}:=S/I$
-scheme. Then the class
![]() $\gamma \in \mathrm {Ext}^2_{\mathcal {O}_X}(L_{X/\mathrm {Spec}(\overline {S})},I/I^2\otimes _{\overline {S}}\mathcal {O}_X)$
defined by
$\gamma \in \mathrm {Ext}^2_{\mathcal {O}_X}(L_{X/\mathrm {Spec}(\overline {S})},I/I^2\otimes _{\overline {S}}\mathcal {O}_X)$
defined by
![]() $L_{X/\mathrm {Spec}(S)}$
is
$L_{X/\mathrm {Spec}(S)}$
is
![]() $\pm $
the obstruction class for lifting X to a flat
$\pm $
the obstruction class for lifting X to a flat
![]() $S/I^2$
-scheme.
$S/I^2$
-scheme.
Proof. See [Reference Illusie24, Chapter III.2.1.2.3], respectively, [Reference Illusie24, Chapter III.2.1.3.3].
As before, let
![]() $(A,I)$
be a bounded prism.
$(A,I)$
be a bounded prism.
Corollary 3.14. Let X be a p-completely flat p-adic formal scheme over
![]() $A/I$
. The complex
$A/I$
. The complex
![]() splits in
splits in
![]() $D(X)$
(i.e. is isomorphic in
$D(X)$
(i.e. is isomorphic in
![]() $D(X)$
to a complex with zero differentials) if and only if X admits a lifting to a p-completely flat formal scheme over
$D(X)$
to a complex with zero differentials) if and only if X admits a lifting to a p-completely flat formal scheme over
![]() $A/I^2$
.
$A/I^2$
.
Proof. Indeed,
![]() splits if and only if the class in
splits if and only if the class in
defined by
![]() vanishes. Proposition 3.12 shows that this class is the same as the class defined by the p-completed cotangent complex
vanishes. Proposition 3.12 shows that this class is the same as the class defined by the p-completed cotangent complex
![]() $L_{X/\mathrm {Spf}(A)}^{\wedge _p}\{-1\}$
. Lifting X to a p-completely flat formal scheme over
$L_{X/\mathrm {Spf}(A)}^{\wedge _p}\{-1\}$
. Lifting X to a p-completely flat formal scheme over
![]() $A/I^2$
is the same as lifting
$A/I^2$
is the same as lifting
![]() $X\otimes _{A/I}A/(I,p^n)$
to a flat scheme over
$X\otimes _{A/I}A/(I,p^n)$
to a flat scheme over
![]() $A/(I^2,p^n)$
for all
$A/(I^2,p^n)$
for all
![]() $n\geq 1$
(here, we use that
$n\geq 1$
(here, we use that
![]() $(A,I)$
is bounded in order to know that
$(A,I)$
is bounded in order to know that
![]() $A/I$
is classically p-complete). One concludes by applying Proposition 3.13, together with the fact that the p-completion of the cotangent complex does not affect the (derived) reduction modulo
$A/I$
is classically p-complete). One concludes by applying Proposition 3.13, together with the fact that the p-completion of the cotangent complex does not affect the (derived) reduction modulo
![]() $p^n$
.
$p^n$
.
3.3 Quasisyntomic rings
We shortly recall some key definitions from [Reference Bhatt, Morrow and Scholze12, Chapter 4].
Definition 3.15. A ring R is quasisyntomic if R is p-complete with bounded
![]() $p^{\infty }$
-torsion and if the cotangent complex
$p^{\infty }$
-torsion and if the cotangent complex
![]() $L_{R/\mathbb {Z}_p}$
has p-complete Tor-amplitude in
$L_{R/\mathbb {Z}_p}$
has p-complete Tor-amplitude in
![]() $[-1,0]$
Footnote
11
. The category of all quasisyntomic rings is denoted by
$[-1,0]$
Footnote
11
. The category of all quasisyntomic rings is denoted by
![]() $\mathrm {QSyn}$
.
$\mathrm {QSyn}$
.
Similarly, a map
![]() $R \to R'$
of p-complete rings with bounded
$R \to R'$
of p-complete rings with bounded
![]() $p^{\infty }$
-torsion is a quasisyntomic morphism (respectively, a quasisyntomic cover) if
$p^{\infty }$
-torsion is a quasisyntomic morphism (respectively, a quasisyntomic cover) if
![]() $R'$
is p-completely flat (respectively, p-completely faithfully flat) over R and
$R'$
is p-completely flat (respectively, p-completely faithfully flat) over R and
![]() $L_{R'/R} \in D(R')$
has p-complete Tor-amplitude in
$L_{R'/R} \in D(R')$
has p-complete Tor-amplitude in
![]() $[-1,0]$
.
$[-1,0]$
.
For a quasisyntomic ring R, the p-completed cotangent complex
![]() $(L_{R/\mathbb {Z}_p})^{\wedge }_p$
will thus be in
$(L_{R/\mathbb {Z}_p})^{\wedge }_p$
will thus be in
![]() $D^{[-1,0]}$
(cf. [Reference Bhatt, Morrow and Scholze12, Lemma 4.6]).
$D^{[-1,0]}$
(cf. [Reference Bhatt, Morrow and Scholze12, Lemma 4.6]).
Remark 3.16. This definition extends (in the p-complete world) the usual notion of locally complete intersection ring and syntomic morphism (flat and local complete intersection) to the non-Noetherian, non finite-type setting, as shown by the next example.
Example 3.17.
-
1. Any p-complete l.c.i. Noetherian ring is in
 $\mathrm {QSyn}$
(cf. [Reference Avramov2, Theorem 1.2]).
$\mathrm {QSyn}$
(cf. [Reference Avramov2, Theorem 1.2]). -
2. There are also big rings in
 $\mathrm {QSyn}$
. For example, any (integral) perfectoid ring (i.e. a ring R which is p-complete, such that
$\mathrm {QSyn}$
. For example, any (integral) perfectoid ring (i.e. a ring R which is p-complete, such that
 $\pi ^p=pu$
for some
$\pi ^p=pu$
for some
 $\pi \in R$
and
$\pi \in R$
and
 $u \in R^{\times }$
, Frobenius is surjective on
$u \in R^{\times }$
, Frobenius is surjective on
 $R/p$
and
$R/p$
and
 $\ker (\theta )$
is principal) is in
$\ker (\theta )$
is principal) is in
 $\mathrm {QSyn}$
(cf. [Reference Bhatt, Morrow and Scholze12, Proposition 4.18]). We give a short explanation: if R is such a ring, the transitivity triangle for and the fact that
$\mathrm {QSyn}$
(cf. [Reference Bhatt, Morrow and Scholze12, Proposition 4.18]). We give a short explanation: if R is such a ring, the transitivity triangle for and the fact that $$\begin{align*}\mathbb{Z}_p \to A_{\mathrm{inf}}(R) \to R \end{align*}$$
$$\begin{align*}\mathbb{Z}_p \to A_{\mathrm{inf}}(R) \to R \end{align*}$$
 $A_{\mathrm {inf}}(R)$
is relatively perfect over
$A_{\mathrm {inf}}(R)$
is relatively perfect over
 $\mathbb {Z}_p$
modulo p imply that after applying
$\mathbb {Z}_p$
modulo p imply that after applying
 $- \otimes _R^{\mathbb {L}} R/p$
,
$- \otimes _R^{\mathbb {L}} R/p$
,
 $L_{R/\mathbb {Z}_p}$
and
$L_{R/\mathbb {Z}_p}$
and
 $L_{R/A_{\mathrm {inf}}(R)}$
identify. But as
$L_{R/A_{\mathrm {inf}}(R)}$
identify. But as $$\begin{align*}L_{R/A_{\mathrm{inf}}(R)} = \ker(\theta)/\ker(\theta)^2 [1]= R[1], \end{align*}$$
$$\begin{align*}L_{R/A_{\mathrm{inf}}(R)} = \ker(\theta)/\ker(\theta)^2 [1]= R[1], \end{align*}$$
 $\ker (\theta )$
is generated by a nonzero divisorFootnote
12
.
$\ker (\theta )$
is generated by a nonzero divisorFootnote
12
.
-
3. As a consequence of (ii), the p-completion of a smooth algebra over a perfectoid ring is also quasisyntomic, as well as any p-complete bounded
 $p^{\infty }$
-torsion ring which can be presented as the quotient of an integral perfectoid ring by a finite regular sequence.
$p^{\infty }$
-torsion ring which can be presented as the quotient of an integral perfectoid ring by a finite regular sequence.
The (opposite of the) category
![]() $\mathrm {QSyn}$
is endowed with the structure of a site.
$\mathrm {QSyn}$
is endowed with the structure of a site.
Definition 3.18. Let
![]() $\mathrm {QSyn}_{\mathrm {qsyn}}^{\mathrm {op}}$
be the site whose underlying category is the opposite category of the category
$\mathrm {QSyn}_{\mathrm {qsyn}}^{\mathrm {op}}$
be the site whose underlying category is the opposite category of the category
![]() $\mathrm {QSyn}$
and endowed with the Grothendieck topology generated by quasisyntomic covers.
$\mathrm {QSyn}$
and endowed with the Grothendieck topology generated by quasisyntomic covers.
If
![]() $R \in \mathrm {QSyn}$
, we will denote by
$R \in \mathrm {QSyn}$
, we will denote by
![]() $(R)_{\mathrm {QSYN}}$
(respectively,
$(R)_{\mathrm {QSYN}}$
(respectively,
![]() $(R)_{\mathrm {qsyn}}$
) the big (respectively, the small) quasisyntomic site of R, given by all p-complete with bounded
$(R)_{\mathrm {qsyn}}$
) the big (respectively, the small) quasisyntomic site of R, given by all p-complete with bounded
![]() $p^{\infty }$
-torsion R-algebras (respectively, by all quasisyntomic R-algebras, i.e. all p-complete with bounded
$p^{\infty }$
-torsion R-algebras (respectively, by all quasisyntomic R-algebras, i.e. all p-complete with bounded
![]() $p^{\infty }$
-torsion R-algebras S, such that the structure map
$p^{\infty }$
-torsion R-algebras S, such that the structure map
![]() $R \to S$
is quasisyntomic) endowed with the quasisyntomic topology.
$R \to S$
is quasisyntomic) endowed with the quasisyntomic topology.
The authors of [Reference Bhatt, Morrow and Scholze12] isolated an interesting class of quasisyntomic rings.
Definition 3.19. A ring R is quasiregular semiperfectoid if
![]() $R \in \mathrm {QSyn}$
and there exists a perfectoid ring S mapping surjectively to R.
$R \in \mathrm {QSyn}$
and there exists a perfectoid ring S mapping surjectively to R.
Example 3.20. Any perfectoid ring, or any p-complete bounded
![]() $p^{\infty }$
-torsion quotient of a perfectoid ring by a finite regular sequence, is quasiregular semiperfectoid.
$p^{\infty }$
-torsion quotient of a perfectoid ring by a finite regular sequence, is quasiregular semiperfectoid.
The interest in quasiregular semiperfectoid rings comes from the fact that they form a basis of the site
![]() $\mathrm {QSyn}_{\mathrm {qsyn}}^{\mathrm {op}}$
.
$\mathrm {QSyn}_{\mathrm {qsyn}}^{\mathrm {op}}$
.
Proposition 3.21. Let R be quasisyntomic ring. There exists a quasisyntomic cover
![]() $R \to R'$
, with
$R \to R'$
, with
![]() $R'$
quasiregular semiperfectoid. Moreover, all terms of the
$R'$
quasiregular semiperfectoid. Moreover, all terms of the
![]() $\breve{C}$
ech nerve
$\breve{C}$
ech nerve
![]() $R^{'\bullet }$
are quasiregular semiperfectoid.
$R^{'\bullet }$
are quasiregular semiperfectoid.
Proof. See [Reference Bhatt, Morrow and Scholze12, Lemma 4.27] and [Reference Bhatt, Morrow and Scholze12, Lemma 4.29].
Finally, recall the following result, which is [Reference Bhatt and Scholze13, Proposition 7.11].
Proposition 3.22. Let
![]() $(A,I)$
be a bounded prism and R be a quasisyntomic
$(A,I)$
be a bounded prism and R be a quasisyntomic
![]() $A/I$
-algebra. There exists a prism
$A/I$
-algebra. There exists a prism
![]() , such that the map
, such that the map
![]() $R \to B/IB$
is p-completely faithfully flat. In particular, if
$R \to B/IB$
is p-completely faithfully flat. In particular, if
![]() $A/I \to R$
is a quasisyntomic cover, then
$A/I \to R$
is a quasisyntomic cover, then
![]() $(A,I) \to (B,IB)$
is a faithfully flat map of prisms.
$(A,I) \to (B,IB)$
is a faithfully flat map of prisms.
Proof. Since the proof is short, we recall it. Choose a surjection
for some index set J. Set
Then
![]() $R \to S$
is a quasisyntomic cover, and by assumption,
$R \to S$
is a quasisyntomic cover, and by assumption,
![]() $A/I \to R$
is quasisyntomic: hence, the map
$A/I \to R$
is quasisyntomic: hence, the map
![]() $A/I \to S$
is quasisyntomic. Moreover the p-completion of
$A/I \to S$
is quasisyntomic. Moreover the p-completion of
![]() $\Omega _{S/(A/I)}^1$
is zero. We deduce that the map
$\Omega _{S/(A/I)}^1$
is zero. We deduce that the map
![]() $A/I \to S$
is such that
$A/I \to S$
is such that
![]() $(L_{S/(A/I)})^{\wedge _p}$
has p-complete Tor-amplitude in degree
$(L_{S/(A/I)})^{\wedge _p}$
has p-complete Tor-amplitude in degree
![]() $[-1,-1]$
. Therefore, by the Hodge-Tate comparison, the derived prismatic cohomology
$[-1,-1]$
. Therefore, by the Hodge-Tate comparison, the derived prismatic cohomology
![]() is concentrated in degree
is concentrated in degree
![]() $0$
and the map
$0$
and the map
![]() is p-completely faithfully flat. One can thus just take
is p-completely faithfully flat. One can thus just take
![]() .
.
As observed in [Reference Bhatt and Scholze13], a corollary of Proposition 3.22 is André’s lemma.
Theorem 3.23 (André’s lemma).
Let R be perfectoid ring. Then there exists a p-completely faithfully flat map
![]() $R\to S$
of perfectoid rings, such that S is absolutely integrally closed, that is, every monic polynomial with coefficients in S has a solution.
$R\to S$
of perfectoid rings, such that S is absolutely integrally closed, that is, every monic polynomial with coefficients in S has a solution.
Proof. This is [Reference Bhatt and Scholze13, Theorem 7.12]. Since the proof is also short, we recall it. Write
![]() $R=A/I$
, for a perfect prism
$R=A/I$
, for a perfect prism
![]() $(A,I)$
(Proposition 2.8). The p-complete R-algebra
$(A,I)$
(Proposition 2.8). The p-complete R-algebra
![]() $\tilde {R}$
obtained by adding roots of all possible monic polynomials over R is a quasisyntomic cover, so by Proposition 3.22, we can find a prism
$\tilde {R}$
obtained by adding roots of all possible monic polynomials over R is a quasisyntomic cover, so by Proposition 3.22, we can find a prism
![]() $(B,J)$
over
$(B,J)$
over
![]() $(A,I)$
with a p-completely faithfully flat morphism
$(A,I)$
with a p-completely faithfully flat morphism
![]() $\tilde {R} \to R_1:=B/J$
. Moreover, we can (and do) assume that
$\tilde {R} \to R_1:=B/J$
. Moreover, we can (and do) assume that
![]() $(B,J)$
is a perfect prism. Indeed, as
$(B,J)$
is a perfect prism. Indeed, as
![]() $(A,I)$
is perfect, the underlying A-algebra of the perfectionFootnote
13
of
$(A,I)$
is perfect, the underlying A-algebra of the perfectionFootnote
13
of
![]() $(B,J)$
is the
$(B,J)$
is the
![]() $(p,I)$
-completion of a filtered colimit of
$(p,I)$
-completion of a filtered colimit of
![]() $(p,I)$
-completely faithfully flat A-algebras, hence is
$(p,I)$
-completely faithfully flat A-algebras, hence is
![]() $(p,I)$
-completely faithfully flat. Transfinitely iterating the construction
$(p,I)$
-completely faithfully flat. Transfinitely iterating the construction
![]() $R\mapsto R_1$
produces the desired ring S.
$R\mapsto R_1$
produces the desired ring S.
Let us recall that a functor
![]() $u\colon \mathcal {C}\to \mathcal {D}$
between sites is cocontinuous (cf. [Reference Project52, Tag 00XI]) if for every object
$u\colon \mathcal {C}\to \mathcal {D}$
between sites is cocontinuous (cf. [Reference Project52, Tag 00XI]) if for every object
![]() $C\in \mathcal {C}$
and any covering
$C\in \mathcal {C}$
and any covering
![]() $\{V_j\to u(C)\}_{j\in J}$
of
$\{V_j\to u(C)\}_{j\in J}$
of
![]() $u(C)$
in
$u(C)$
in
![]() $\mathcal {D}$
there exists a covering
$\mathcal {D}$
there exists a covering
![]() $\{ C_i\to C\}_{i\in I}$
of C in
$\{ C_i\to C\}_{i\in I}$
of C in
![]() $\mathcal {C}$
, such that the family
$\mathcal {C}$
, such that the family
![]() $\{ u(C_i)\to u(C)\}_{i\in I}$
refines the covering
$\{ u(C_i)\to u(C)\}_{i\in I}$
refines the covering
![]() $\{V_j\to u(C)\}_{j\in J}$
. For a cocontinuous functor
$\{V_j\to u(C)\}_{j\in J}$
. For a cocontinuous functor
![]() $u\colon \mathcal {C}\to \mathcal {D}$
, the functor
$u\colon \mathcal {C}\to \mathcal {D}$
, the functor
(here,
![]() $()^{\sharp }$
denotes sheafification) is left-exact (even exact) with right adjoint
$()^{\sharp }$
denotes sheafification) is left-exact (even exact) with right adjoint
Thus, a cocontinuous functor
![]() $u\colon \mathcal {C}\to \mathcal {D}$
induces a morphism of topoi
$u\colon \mathcal {C}\to \mathcal {D}$
induces a morphism of topoi
Note that in the definition of a cocontinuous functor, the morphisms
![]() $u(C_j)\to u(C)$
are not required to form a covering of C.
$u(C_j)\to u(C)$
are not required to form a covering of C.
Corollary 3.24. Let R be a p-complete ring. The functor
![]() , sending
, sending
![]() $(A,I)$
to
$(A,I)$
to
is cocontinuous. Consequently, it defines a morphism of topoi, still denoted by u:
Proof. Immediate from the definition (cf. [Reference Project52, Tag 00XJ]) and the previous proposition.
This yields the following important corollary.
Corollary 3.25. Let R be a p-complete ring. Let
be a short exact sequence of abelian sheaves on
![]() $(R)_{\mathrm {QSYN}}$
. Then the sequence
$(R)_{\mathrm {QSYN}}$
. Then the sequence
is an exact sequence on
![]() . This applies, for example, when
. This applies, for example, when
![]() $G_1, G_2, G_3$
are finite locally free group schemes over R.
$G_1, G_2, G_3$
are finite locally free group schemes over R.
Proof. The first assertion is just saying that
![]() $u^{-1}$
is exact, as u is a cocontinuous functor ([Reference Project52, Tag 00XL]). The second assertion follows, as any finite locally free group scheme is syntomic (cf. [Reference Breuil16, Proposition 2.2.2]).
$u^{-1}$
is exact, as u is a cocontinuous functor ([Reference Project52, Tag 00XL]). The second assertion follows, as any finite locally free group scheme is syntomic (cf. [Reference Breuil16, Proposition 2.2.2]).
3.4 Prismatic cohomology of quasiregular semiperfectoid rings
In this short subsection, we collect a few facts about prismatic cohomology of quasiregular semiperfectoid rings for later reference.
For the moment, fix a bounded base prism
![]() $(A,I)$
and let R be p-complete
$(A,I)$
and let R be p-complete
![]() $A/I$
-algebra. There are several cohomologies attached to R:
$A/I$
-algebra. There are several cohomologies attached to R:
-
1. The derived prismatic cohomology
of R over
 $(A,I)$
defined in Definition 3.9 via left Kan extension of prismatic cohomology.
$(A,I)$
defined in Definition 3.9 via left Kan extension of prismatic cohomology.
-
2. The cohomology
of the prismatic site of
 (with its p-completely faithfully flat topology).
(with its p-completely faithfully flat topology).
-
3. Finally (and only for technical purposes),
the prismatic cohomology of R with respect to the site
 of not necessarily bounded prisms
of not necessarily bounded prisms
 $(B,J)$
over
$(B,J)$
over
 $(A,I)$
together with a morphism
$(A,I)$
together with a morphism
 $R\to B/J$
of
$R\to B/J$
of
 $A/I$
-algebras. We equip
$A/I$
-algebras. We equip
 with the chaotic topology.
with the chaotic topology.
Assume from now on that
![]() $(A,I)$
is a perfect prism and that
$(A,I)$
is a perfect prism and that
![]() $A/I\to R$
is a surjection with R quasiregular semiperfectoid. The prism
$A/I\to R$
is a surjection with R quasiregular semiperfectoid. The prism
![]() admits then a more concrete (but, in general, rather untractable) description. Let K be the kernel of
admits then a more concrete (but, in general, rather untractable) description. Let K be the kernel of
![]() $A\to R$
. Then
$A\to R$
. Then

is the prismatic envelope of the
![]() $\delta $
-pair
$\delta $
-pair
![]() $(A,K)$
from [Reference Bhatt8, Lemma V.5.1] as follows from the universal property of the latter. In particular, the site
$(A,K)$
from [Reference Bhatt8, Lemma V.5.1] as follows from the universal property of the latter. In particular, the site
![]() has a final objectFootnote
14
.
has a final objectFootnote
14
.
Proposition 3.26. Let as above
![]() $(A,I)$
be a perfect prism and R quasiregular semiperfectoid with a surjection
$(A,I)$
be a perfect prism and R quasiregular semiperfectoid with a surjection
![]() $A/I\twoheadrightarrow R$
. Then the canonical morphisms induce isomorphisms
$A/I\twoheadrightarrow R$
. Then the canonical morphisms induce isomorphisms
as
![]() $\delta $
-rings.
$\delta $
-rings.
Proof. This is [Reference Bhatt and Scholze13, Proposition 7.10] (the second isomorphism, i.e. the fact that
![]() is bounded, follows from the last assertion of loc. cit.).
is bounded, follows from the last assertion of loc. cit.).
If
![]() $pR=0$
, that is, R is quasiregular semiperfect, there is, moreover, the universal p-complete PD-thickening
$pR=0$
, that is, R is quasiregular semiperfect, there is, moreover, the universal p-complete PD-thickening
of R (cf. [Reference Scholze and Weinstein50, Proposition 4.1.3]). The ring
![]() $A_{\mathrm {crys}}(R)$
is p-torsion free by [Reference Bhatt, Morrow and Scholze12, Theorem 8.14].
$A_{\mathrm {crys}}(R)$
is p-torsion free by [Reference Bhatt, Morrow and Scholze12, Theorem 8.14].
Lemma 3.27. Let
![]() $(A,I)$
, R be as above, and assume that
$(A,I)$
, R be as above, and assume that
![]() $pR=0$
. Then there is a canonical
$pR=0$
. Then there is a canonical
![]() $\varphi $
-equivariant isomorphism
$\varphi $
-equivariant isomorphism
Proof. As
![]() $A_{\mathrm {crys}}(R)$
is p-torsion free (cf. [Reference Bhatt, Morrow and Scholze12, Theorem 8.14]) and carries a canonical Frobenius lift, there we get a natural morphism
$A_{\mathrm {crys}}(R)$
is p-torsion free (cf. [Reference Bhatt, Morrow and Scholze12, Theorem 8.14]) and carries a canonical Frobenius lift, there we get a natural morphism
Conversely, the kernel of the natural morphism (cf. Theorem 3.29, which does not depend on this lemma)
has divided powers (as one checks similarly to [Reference Bhatt, Morrow and Scholze12, Proposition 8.12], using that the proof of Theorem 3.7 goes through in the syntomic case, cf. Remark 3.8). This provides a canonical morphism
in the other direction. Similarly, to [Reference Bhatt, Morrow and Scholze12, Theorem 8.14], one checks that both are inverse to each other.
Remark 3.28. Both rings
![]() and
and
![]() $A_{\mathrm {crys}}(R)$
are naturally
$A_{\mathrm {crys}}(R)$
are naturally
![]() $W(R^{\flat })$
-algebras, but the isomorphism of Lemma 3.27 restricts to the Frobenius on
$W(R^{\flat })$
-algebras, but the isomorphism of Lemma 3.27 restricts to the Frobenius on
![]() $W(R^{\flat })$
. Concretely, if
$W(R^{\flat })$
. Concretely, if
![]() $R=R^{\flat }/x$
for some nonzero divisor
$R=R^{\flat }/x$
for some nonzero divisor
![]() $x\in R^{\flat }$
, then
$x\in R^{\flat }$
, then

and (cf. [Reference Bhatt and Scholze13, Corollary 2.37])

The prismatic cohomology
![]() of a quasiregular semiperfectoid ring R comes equipped with its Nygaard filtration, [Reference Bhatt and Scholze13, Section 12], an
of a quasiregular semiperfectoid ring R comes equipped with its Nygaard filtration, [Reference Bhatt and Scholze13, Section 12], an
![]() $\mathbb {N}$
-indexed decreasing multiplicative filtration defined for
$\mathbb {N}$
-indexed decreasing multiplicative filtration defined for
![]() $i\geq 0$
by
$i\geq 0$
by
d denoting a generator of the ideal I. The graded pieces of the Nygaard filtration can be described as follows.
Theorem 3.29. Let R be a quasiregular semiperfectoid ring. Then
for
![]() $i\geq 0$
. In particular,
$i\geq 0$
. In particular,
![]() .
.
Here,
![]() denotes the conjugate filtration on
denotes the conjugate filtration on
![]() with graded pieces given by
with graded pieces given by
![]() , for any choice of perfectoid ring S mapping to R (cf. Proposition 3.10).
, for any choice of perfectoid ring S mapping to R (cf. Proposition 3.10).
Proof. See [Reference Bhatt and Scholze13, Theorem 12.2].
3.5 The Künneth formula in prismatic cohomology
The Hodge-Tate comparison implies a Künneth formula. Here is the precise statement. Note that for a bounded prism
![]() $(A,I)$
, the functor
$(A,I)$
, the functor
![]() is naturally defined on all derived p-complete simplicial
is naturally defined on all derived p-complete simplicial
![]() $A/I$
-algebras.
$A/I$
-algebras.
Proposition 3.30. Let
![]() $(A,I)$
be a bounded prism. Then the functor
$(A,I)$
be a bounded prism. Then the functor
from derived p-complete simplicial rings over
![]() $A/I$
to derived
$A/I$
to derived
![]() $(p,I)$
-complete
$(p,I)$
-complete
![]() $E_{\infty }$
-algebras over A preserves tensor products, that is, for all morphism
$E_{\infty }$
-algebras over A preserves tensor products, that is, for all morphism
![]() $R_1\leftarrow R_3 \to R_2$
the canonical morphism
$R_1\leftarrow R_3 \to R_2$
the canonical morphism
is an equivalence.
Proof. Using [Reference Bhatt, Morrow and Scholze12, Construction 2.1] (respectively, [Reference Lurie40, Proposition 5.5.8.15]) the functor
![]() , which is the left Kan extension from p-completely smooth algebras to all derived p-complete simplicial
, which is the left Kan extension from p-completely smooth algebras to all derived p-complete simplicial
![]() $A/I$
-algebras, commutes with colimits if it preserves finite coproducts. Clearly,
$A/I$
-algebras, commutes with colimits if it preserves finite coproducts. Clearly,
![]() , that is
, that is
![]() preserves the final object. Moreover, for
preserves the final object. Moreover, for
![]() $R,S p$
-completely smooth over
$R,S p$
-completely smooth over
![]() $A/I$
, the canonical morphism
$A/I$
, the canonical morphism
is an isomorphisms because this I-completeness may be checked for
![]() where it follows from the Hodge-Tate comparison.
where it follows from the Hodge-Tate comparison.
Gluing the isomorphism in Proposition 3.30, we can derive, using as well the projection formula and flat base change for quasicoherent cohomology, the following statement.
Corollary 3.31. If X and Y are quasicompact quasiseparated p-completely smooth p-adic formal schemes over
![]() $\mathrm {Spf}(A/I)$
), then
$\mathrm {Spf}(A/I)$
), then
4 Prismatic Dieudonné theory for p-divisible groups
This chapter is the heart of this paper. We construct the prismatic Dieudonné functor over any quasisyntomic ring and prove that it gives an antiequivalence between p-divisible groups over R and admissible prismatic Dieudonné crystals over R. The strategy to do this is to use quasisyntomic descent to reduce to the case where R is quasiregular semiperfectoid, in which case, the (admissible) prismatic Dieudonné crystals over R can be replaced by simpler objects, the (admissible) prismatic Dieudonné modules.
4.1 Abstract prismatic Dieudonné crystals and modules
Let R be a p-complete ring. We defined in Corollary 3.24 a morphism of topoi:
We let
be the functor defined by
![]() $\epsilon _{\ast } \mathcal {F}(R') = \mathcal {F}(R')$
for
$\epsilon _{\ast } \mathcal {F}(R') = \mathcal {F}(R')$
for
![]() $\mathcal {F} \in \mathrm {Shv}((R)_{\mathrm {QSYN}})$
and
$\mathcal {F} \in \mathrm {Shv}((R)_{\mathrm {QSYN}})$
and
![]() $R' \in (R)_{\mathrm {qsyn}}$
. It has a left adjoint
$R' \in (R)_{\mathrm {qsyn}}$
. It has a left adjoint
![]() $\epsilon ^{\natural }: \mathrm {Shv}((R)_{\mathrm { qsyn}}) \to \mathrm {Shv}((R)_{\mathrm {QSYN}})$
. We warn the reader that the restriction functor from the big to the small quasisyntomic site does not induce a morphism of sitesFootnote
15
, that is this left adjoint need not preserve finite limits (which explains why we denoted it
$\epsilon ^{\natural }: \mathrm {Shv}((R)_{\mathrm { qsyn}}) \to \mathrm {Shv}((R)_{\mathrm {QSYN}})$
. We warn the reader that the restriction functor from the big to the small quasisyntomic site does not induce a morphism of sitesFootnote
15
, that is this left adjoint need not preserve finite limits (which explains why we denoted it
![]() $\epsilon ^{\natural }$
instead of
$\epsilon ^{\natural }$
instead of
![]() $\epsilon ^{-1}$
).
$\epsilon ^{-1}$
).
We let
and
We still have the formula
![]() $Rv_{\ast }\cong R\varepsilon _{\ast }\circ Ru_{\ast }$
as
$Rv_{\ast }\cong R\varepsilon _{\ast }\circ Ru_{\ast }$
as
![]() $\varepsilon _{\ast }$
is exact.
$\varepsilon _{\ast }$
is exact.
Definition 4.1. Let R be a p-complete ring. We define:
where
![]() denotes the canonical invertible ideal sheaf sending a prism
denotes the canonical invertible ideal sheaf sending a prism
![]() to J. The sheaf
to J. The sheaf
![]() $\mathcal {O}^{\mathrm {pris}}$
is endowed with a Frobenius lift
$\mathcal {O}^{\mathrm {pris}}$
is endowed with a Frobenius lift
![]() $\varphi $
.
$\varphi $
.
Although these sheaves are defined in general, we will only use them over quasisyntomic rings.
Proposition 4.2. Let R be a quasisyntomic ring. The quotient sheaf
is isomorphic to the structure sheaf
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $(R)_{\mathrm {qsyn}}$
.
$(R)_{\mathrm {qsyn}}$
.
Proof. It is enough to produce such an isomorphism functorially on a basis of
![]() $(R)_{\mathrm {qsyn}}$
. By Proposition 3.21, we can thus assume that R is quasiregular semiperfectoid. In this case, we conclude by Theorem 3.29.
$(R)_{\mathrm {qsyn}}$
. By Proposition 3.21, we can thus assume that R is quasiregular semiperfectoid. In this case, we conclude by Theorem 3.29.
Definition 4.3. Let R be a p-complete ring. A prismatic crystal over R is an
![]() -module
-module
![]() $\mathcal {M}$
on the prismatic site
$\mathcal {M}$
on the prismatic site
![]() of R, such that for all morphisms
of R, such that for all morphisms
![]() $(B,J)\to (B^{\prime },J^{\prime })$
in
$(B,J)\to (B^{\prime },J^{\prime })$
in
![]() the canonical morphism
the canonical morphism
is an isomorphism.
Note that a prismatic crystal in finitely generated projective
![]() -modules (respectively, in finitely generated projective
-modules (respectively, in finitely generated projective
![]() -modules) is the same thing as a finite locally free
-modules) is the same thing as a finite locally free
![]() -module (respectively, a finite locally free
-module (respectively, a finite locally free
![]() -module). In what follows, we will essentially consider only this kind of prismatic crystal.
-module). In what follows, we will essentially consider only this kind of prismatic crystal.
Proposition 4.4. Let R be a quasisyntomic ring. The functors
![]() $v_*$
and
$v_*$
and
![]() induce equivalences between the category of finite locally free
induce equivalences between the category of finite locally free
![]() -modules and the category of finite locally free
-modules and the category of finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-modules.
$\mathcal {O}^{\mathrm {pris}}$
-modules.
Proof. Because
![]() , it is clear that for all finite locally free
, it is clear that for all finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-modules
$\mathcal {O}^{\mathrm {pris}}$
-modules
![]() $\mathcal {M}$
, the canonical morphism
$\mathcal {M}$
, the canonical morphism
is an isomorphism as this can be checked locally on
![]() $(R)_{\mathrm {qsyn}}$
. Conversely, let
$(R)_{\mathrm {qsyn}}$
. Conversely, let
![]() $\mathcal {N}$
be a finite locally free
$\mathcal {N}$
be a finite locally free
![]() -module. We have to show that the counit
-module. We have to show that the counit
is an isomorphism. For any morphism
![]() $R\to R^{\prime }$
with
$R\to R^{\prime }$
with
![]() $R^{\prime }$
quasisyntomic, there are equivalences
$R^{\prime }$
quasisyntomic, there are equivalences
of slice topoi, where
![]() $h_{R^{\prime }}(B,J):=\mathrm {Hom}_R(R^{\prime },B/J)$
. By passing to a quasisyntomic cover
$h_{R^{\prime }}(B,J):=\mathrm {Hom}_R(R^{\prime },B/J)$
. By passing to a quasisyntomic cover
![]() $R\to R^{\prime }$
, we can therefore assume that R is quasiregular semiperfectoid, in particular, that the site
$R\to R^{\prime }$
, we can therefore assume that R is quasiregular semiperfectoid, in particular, that the site
![]() has a final object given by
has a final object given by
![]() . By
. By
![]() $(p,I)$
-completely faithfully flat descent of finitely generated projective modules over
$(p,I)$
-completely faithfully flat descent of finitely generated projective modules over
![]() $(p,I)$
-complete rings of bounded
$(p,I)$
-complete rings of bounded
![]() $(p,I)$
-torsion (cf. Proposition A.3), the category of finite locally free
$(p,I)$
-torsion (cf. Proposition A.3), the category of finite locally free
![]() -modules on
-modules on
![]() is equivalent to finitely generated projective
is equivalent to finitely generated projective
![]() -modulesFootnote
16
. As the morphism
-modulesFootnote
16
. As the morphism
![]() (the ‘
(the ‘
![]() $\theta $
’-map) is henselian along its kernel, cf. Lemma 4.28, finite locally free
$\theta $
’-map) is henselian along its kernel, cf. Lemma 4.28, finite locally free
![]() -modules split on the pullback of an open cover of
-modules split on the pullback of an open cover of
![]() $\mathrm {Spf}(R)$
. Thus, after passing to a quasisyntomic cover of
$\mathrm {Spf}(R)$
. Thus, after passing to a quasisyntomic cover of
![]() $\mathrm {Spf}(R)$
, we may assume that
$\mathrm {Spf}(R)$
, we may assume that
![]() $\mathcal {N}$
is finite free. Then the isomorphism
$\mathcal {N}$
is finite free. Then the isomorphism
is clear.
Definition 4.5. Let R be a quasisyntomic ring. A prismatic Dieudonné crystal over R is a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() $\mathcal {M}$
together with
$\mathcal {M}$
together with
![]() $\varphi $
-linear morphism
$\varphi $
-linear morphism
whose linearisation
![]() $\varphi ^{\ast } \mathcal {M}\to \mathcal {M}$
has its cokernel killed by
$\varphi ^{\ast } \mathcal {M}\to \mathcal {M}$
has its cokernel killed by
![]() $\mathcal {I}^{\mathrm {pris}}$
. We call a prismatic Dieudonné crystal
$\mathcal {I}^{\mathrm {pris}}$
. We call a prismatic Dieudonné crystal
![]() $(\mathcal {M},\varphi _{\mathcal {M}})$
admissible if the image of the composition
$(\mathcal {M},\varphi _{\mathcal {M}})$
admissible if the image of the composition
is a finite locally free
![]() $\mathcal {O}$
-module
$\mathcal {O}$
-module
![]() $\mathcal {F}_{\mathcal {M}}$
, such that the map
$\mathcal {F}_{\mathcal {M}}$
, such that the map
![]() $(\mathcal {O}^{\mathrm {pris}}/\mathcal {I}^{\mathrm {pris}}) \otimes _{\mathcal {O}} \mathcal {F}_{\mathcal {M}} \to \mathcal {M}/\mathcal {I}^{\mathrm {pris}}\mathcal {M}$
induced by
$(\mathcal {O}^{\mathrm {pris}}/\mathcal {I}^{\mathrm {pris}}) \otimes _{\mathcal {O}} \mathcal {F}_{\mathcal {M}} \to \mathcal {M}/\mathcal {I}^{\mathrm {pris}}\mathcal {M}$
induced by
![]() $\varphi _{\mathcal {M}}$
is a monomorphism.
$\varphi _{\mathcal {M}}$
is a monomorphism.
Here,
![]() $\mathcal {M}/\mathcal {I}^{\mathrm {pris}}\cdot \mathcal {M}$
is an
$\mathcal {M}/\mathcal {I}^{\mathrm {pris}}\cdot \mathcal {M}$
is an
![]() $\mathcal {O}\cong \mathcal {O}^{\mathrm {pris}}/\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}$
-module, cf. Proposition 4.2, via the composition
$\mathcal {O}\cong \mathcal {O}^{\mathrm {pris}}/\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}$
-module, cf. Proposition 4.2, via the composition
![]() $\mathcal {O}^{\mathrm {pris}}\xrightarrow {\varphi }\mathcal {O}^{\mathrm {pris}}\to \mathcal {O}^{\mathrm {pris}}/\mathcal {I}^{\mathrm {pris}}\mathcal {O}$
.
$\mathcal {O}^{\mathrm {pris}}\xrightarrow {\varphi }\mathcal {O}^{\mathrm {pris}}\to \mathcal {O}^{\mathrm {pris}}/\mathcal {I}^{\mathrm {pris}}\mathcal {O}$
.
Remark 4.6. For a prismatic Dieudonné crystal
![]() $(\mathcal {M},\varphi _{\mathcal {M}})$
, the linearisation
$(\mathcal {M},\varphi _{\mathcal {M}})$
, the linearisation
![]() $\varphi ^{\ast } \mathcal {M} \to \mathcal {M}$
of the morphism
$\varphi ^{\ast } \mathcal {M} \to \mathcal {M}$
of the morphism
![]() $\varphi _{\mathcal {M}}\colon \mathcal {M} \to \mathcal {M}$
is an isomorphism after inverting a local generator
$\varphi _{\mathcal {M}}\colon \mathcal {M} \to \mathcal {M}$
is an isomorphism after inverting a local generator
![]() $\tilde {\xi }$
of
$\tilde {\xi }$
of
![]() $\mathcal {I}^{\mathrm {pris}}$
and, in particular, is injective, since
$\mathcal {I}^{\mathrm {pris}}$
and, in particular, is injective, since
![]() $\varphi ^{\ast } \mathcal {M}$
is
$\varphi ^{\ast } \mathcal {M}$
is
![]() $\tilde {\xi }$
-torsion free.
$\tilde {\xi }$
-torsion free.
Remark 4.7. Let
![]() $(\mathcal {M},\varphi _{\mathcal {M}})$
be a prismatic Dieudonné crystal. Write
$(\mathcal {M},\varphi _{\mathcal {M}})$
be a prismatic Dieudonné crystal. Write
![]() $\mathrm {Fil} \mathcal {M}=\varphi _{\mathcal {M}}^{-1}(\mathcal {I}^{\mathrm {pris}}.\mathcal {M})$
. Consider the diagram (defining
$\mathrm {Fil} \mathcal {M}=\varphi _{\mathcal {M}}^{-1}(\mathcal {I}^{\mathrm {pris}}.\mathcal {M})$
. Consider the diagram (defining
![]() $Q,K$
)
$Q,K$
)

As
![]() $\mathcal {I}^{\mathrm {pris}}.K=0$
(by definition of a prismatic Dieudonné crystal), the map
$\mathcal {I}^{\mathrm {pris}}.K=0$
(by definition of a prismatic Dieudonné crystal), the map
![]() $\alpha $
is zero. The snake lemma implies, therefore, that there exists a short exact sequence
$\alpha $
is zero. The snake lemma implies, therefore, that there exists a short exact sequence
(where, as in Definition 4.5, we wrote
![]() $\mathcal {F}_{\mathcal {M}}= \mathcal {M}/\mathrm {Fil} \mathcal {M}$
). Hence, we see that the injectivity of
$\mathcal {F}_{\mathcal {M}}= \mathcal {M}/\mathrm {Fil} \mathcal {M}$
). Hence, we see that the injectivity of
![]() $\beta $
(condition required in the definition of admissibility) is equivalent to the condition that
$\beta $
(condition required in the definition of admissibility) is equivalent to the condition that
![]() $Q=0$
.
$Q=0$
.
Definition 4.8. Let R be a quasisyntomic ring. We denote by
![]() $\mathrm {DM}(R)$
the category of prismatic Dieudonné crystals over R (with
$\mathrm {DM}(R)$
the category of prismatic Dieudonné crystals over R (with
![]() $\mathcal {O}^{\mathrm {pris}}$
-linear morphisms commuting with Frobenius) and by
$\mathcal {O}^{\mathrm {pris}}$
-linear morphisms commuting with Frobenius) and by
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
the full subcategory of admissible objects.
$\mathrm {DM}^{\mathrm {adm}}(R)$
the full subcategory of admissible objects.
Proposition 4.9. The fibred category of (usual or admissible) prismatic Dieudonné crystals over the category
![]() $\mathrm {QSyn}$
of quasisyntomic rings endowed with the quasisyntomic topology is a stack.
$\mathrm {QSyn}$
of quasisyntomic rings endowed with the quasisyntomic topology is a stack.
Proof. This follows from the definition, because by general properties of topoi, modules under
![]() $\mathcal {O}^{\mathrm {pris}}$
and
$\mathcal {O}^{\mathrm {pris}}$
and
![]() $\mathcal {O}$
form a stack for the quasisyntomic topology on
$\mathcal {O}$
form a stack for the quasisyntomic topology on
![]() $(R)_{\mathrm {qsyn}}$
.
$(R)_{\mathrm {qsyn}}$
.
For quasiregular semiperfectoid rings, these abstract objects have a more concrete incarnation, which we explain now. Let R be a quasiregular semiperfectoid ring, and let
![]() be the prism associated with R. Note that I is necessarily principal as there exists a perfectoid ring mapping to R. Recall (Theorem 3.29) that
be the prism associated with R. Note that I is necessarily principal as there exists a perfectoid ring mapping to R. Recall (Theorem 3.29) that
is an isomorphism.
Definition 4.10. A prismatic Dieudonné module over R is a finite locally free
![]() -module M together with a
-module M together with a
![]() $\varphi $
-linear morphism
$\varphi $
-linear morphism
whose linearisation
![]() $\varphi ^{\ast } M \to M$
has its cokernel killed by I. As in 4.5, we call a prismatic Dieudonné module
$\varphi ^{\ast } M \to M$
has its cokernel killed by I. As in 4.5, we call a prismatic Dieudonné module
![]() $(M,\varphi _M)$
over R admissible if the image of the composition
$(M,\varphi _M)$
over R admissible if the image of the composition
is a finite locally free
![]() -module
-module
![]() $F_M$
, such that the map
$F_M$
, such that the map
![]() induced by
induced by
![]() $\varphi _{M}$
is a monomorphism.
$\varphi _{M}$
is a monomorphism.
Remark 4.11. For a prismatic Dieudonné module
![]() $(M,\varphi _M)$
, the linearisation
$(M,\varphi _M)$
, the linearisation
![]() $\varphi ^{\ast } M \to M$
of the morphism
$\varphi ^{\ast } M \to M$
of the morphism
![]() $\varphi _M\colon M\to M$
is an isomorphism after inverting a generator
$\varphi _M\colon M\to M$
is an isomorphism after inverting a generator
![]() $\tilde {\xi }$
of I and, in particular, is injective, since
$\tilde {\xi }$
of I and, in particular, is injective, since
![]() $\varphi ^{\ast }M$
is
$\varphi ^{\ast }M$
is
![]() $\tilde {\xi }$
-torsion free. In 4.25, we will prove that these properties imply that the cokernel of
$\tilde {\xi }$
-torsion free. In 4.25, we will prove that these properties imply that the cokernel of
![]() $\varphi ^{\ast } M\to M$
is a finite projective
$\varphi ^{\ast } M\to M$
is a finite projective
![]() -module.
-module.
If R is perfectoid, one has
A prismatic Dieudonné module is the same thing as a minuscule Breuil-Kisin-Fargues module ([Reference Bhatt, Morrow and Scholze11]) over
![]() $A_{\mathrm {inf}}(R)$
with respect to
$A_{\mathrm {inf}}(R)$
with respect to
![]() $\tilde {\xi }$
. In fact, the situation for perfectoid rings is simple, as shown by the following proposition.
$\tilde {\xi }$
. In fact, the situation for perfectoid rings is simple, as shown by the following proposition.
Proposition 4.12. Let R be a perfectoid ring. Any prismatic Dieudonné module over R is admissible.
We postpone the proof, it will be given below after Proposition 4.29.
Proposition 4.13. Let R be a quasiregular semiperfectoid ring. The functor
of evaluation on the initial prism
![]() induces an equivalence between the category of (usual or admissible) prismatic Dieudonné crystals over R and the category of (usual or admissible) prismatic Dieudonné modules over R, with quasi-inverse
induces an equivalence between the category of (usual or admissible) prismatic Dieudonné crystals over R and the category of (usual or admissible) prismatic Dieudonné modules over R, with quasi-inverse
Proof. Let us call
![]() $G_R$
, respectively,
$G_R$
, respectively,
![]() $F_R$
, the first, respectively, the second, functor displayed in the statement of the proposition. Using Proposition 4.4 and the equivalence between finite locally free
$F_R$
, the first, respectively, the second, functor displayed in the statement of the proposition. Using Proposition 4.4 and the equivalence between finite locally free
![]() -modules and finite locally free
-modules and finite locally free
![]() -modules, one immediately gets that
-modules, one immediately gets that
![]() $F_R$
is an equivalence between the category of prismatic Dieudonné crystals over R and the category of prismatic Dieudonné modules over R, with quasi-inverse given by
$F_R$
is an equivalence between the category of prismatic Dieudonné crystals over R and the category of prismatic Dieudonné modules over R, with quasi-inverse given by
![]() $G_R$
. Hence, we only need to check that the admissibility conditions on both sides agree.
$G_R$
. Hence, we only need to check that the admissibility conditions on both sides agree.
Let
![]() $(M,\varphi _M)$
be an admissible Dieudonné module over R.
$(M,\varphi _M)$
be an admissible Dieudonné module over R.
Lemma 4.14. Let
![]() $R \to R^{\prime }$
be a quasisyntomic morphism, with
$R \to R^{\prime }$
be a quasisyntomic morphism, with
![]() $R^{\prime }$
being also quasiregular semiperfectoid. Let
$R^{\prime }$
being also quasiregular semiperfectoid. Let
![]() be the base change of
be the base change of
![]() $(M,\varphi _M)$
. Then
$(M,\varphi _M)$
. Then
The lemma follows from Proposition 4.29 (and Remark 4.21), which will be proved below; let us take it for granted and finish the proof. For any quasiregular semiperfectoid ring
![]() $R^{\prime }$
quasisyntomic over R, note that, using the notations from the lemma,
$R^{\prime }$
quasisyntomic over R, note that, using the notations from the lemma,
The lemma tells us that, in particular
This being true for any quasiregular semiperfectoid ring
![]() $R^{\prime }$
quasisyntomic over R, we deduce that we have a short exact sequence of sheaves on
$R^{\prime }$
quasisyntomic over R, we deduce that we have a short exact sequence of sheaves on
![]() $(R)_{\mathrm {qsyn}}$
$(R)_{\mathrm {qsyn}}$
By admissibility of
![]() $(M,\varphi _M)$
, the rightmost term is a finite locally free
$(M,\varphi _M)$
, the rightmost term is a finite locally free
![]() $\mathcal {O}$
-module, and thus,
$\mathcal {O}$
-module, and thus,
![]() $F_R(M)$
is admissible.
$F_R(M)$
is admissible.
Conversely, let
![]() $(\mathcal {M},\varphi _{\mathcal {M}})$
be an admissible Dieudonné crystal. Consider the exact sequence of sheaves
$(\mathcal {M},\varphi _{\mathcal {M}})$
be an admissible Dieudonné crystal. Consider the exact sequence of sheaves
and apply to it the functor
![]() $\Gamma (R,-)$
. We get an exact sequence
$\Gamma (R,-)$
. We get an exact sequence
Since
![]() $\mathcal {M}/\varphi _{\mathcal {M}}^{-1}(\mathcal {I}^{\mathrm {pris}}.\mathcal {M})$
is a finite locally free
$\mathcal {M}/\varphi _{\mathcal {M}}^{-1}(\mathcal {I}^{\mathrm {pris}}.\mathcal {M})$
is a finite locally free
![]() $\mathcal {O}$
-module by admissibility of
$\mathcal {O}$
-module by admissibility of
![]() $(\mathcal {M},\varphi _{\mathcal {M}})$
, the rightmost term is a finite projective R-module, and it, therefore, suffices to show that the above sequence is also right exact. The map
$(\mathcal {M},\varphi _{\mathcal {M}})$
, the rightmost term is a finite projective R-module, and it, therefore, suffices to show that the above sequence is also right exact. The map
factors through
which is a map of R-modules, and it suffices to show that this map is surjective. Since the target is a finitely generated R-module and R is p-complete, it suffices by Nakayama’s lemma to prove surjectivity after base change along any surjection
![]() $R \to k$
, with k a perfect field of characteristic p. After base change along such a morphism
$R \to k$
, with k a perfect field of characteristic p. After base change along such a morphism
![]() $R \to k$
, the above map factors through
$R \to k$
, the above map factors through
Since
![]() $G_R(\mathcal {M})$
, respectively,
$G_R(\mathcal {M})$
, respectively,
![]() $\mathcal {M}/\varphi _{\mathcal {M}}^{-1}(\mathcal {I}^{\mathrm {pris}}.\mathcal {M})$
, is a finite locally free
$\mathcal {M}/\varphi _{\mathcal {M}}^{-1}(\mathcal {I}^{\mathrm {pris}}.\mathcal {M})$
, is a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module, respectively, a finite locally free
$\mathcal {O}^{\mathrm {pris}}$
-module, respectively, a finite locally free
![]() $\mathcal {O}$
-module, this identifies with the map
$\mathcal {O}$
-module, this identifies with the map
that is the same map as the one we originally wanted to prove is surjective, but now with R replaced by k (we denoted with an index k the restrictions of the various objects involved to the quasisyntomic site of k). But since k is perfect,
![]() $(G_k(\mathcal {M}_k),\varphi _{G_k(\mathcal {M}_k)})$
is automatically admissible, by definition of admissibility using that every k-module is free. Hence, as proved above, we have an exact sequence (using that
$(G_k(\mathcal {M}_k),\varphi _{G_k(\mathcal {M}_k)})$
is automatically admissible, by definition of admissibility using that every k-module is free. Hence, as proved above, we have an exact sequence (using that
![]() $F_k \circ G_k \cong \mathrm {Id}$
)
$F_k \circ G_k \cong \mathrm {Id}$
)
that is
hence
This shows that the map
is surjective, as desired.
Definition 4.15. We denote by
![]() $\mathrm {DM}(R)$
the category of prismatic Dieudonné modules over R (with morphisms commuting with the Frobenius) and by
$\mathrm {DM}(R)$
the category of prismatic Dieudonné modules over R (with morphisms commuting with the Frobenius) and by
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
the full subcategory formed by admissible objects.
$\mathrm {DM}^{\mathrm {adm}}(R)$
the full subcategory formed by admissible objects.
Proposition 4.13 shows that the possible conflict of notation is not an issue: for R quasiregular semiperfectoid, the two categories denoted by
![]() $\mathrm {DM}(R)$
are naturally equivalent, and similarly for
$\mathrm {DM}(R)$
are naturally equivalent, and similarly for
![]() $\mathrm {DF}(R)$
.
$\mathrm {DF}(R)$
.
In the rest of this subsection, we will shortly recall the general notions of frame and window, and then discuss the connection with the definitions above.
Definition 4.16. A frame
![]() $\underline {A}=(A,\mathrm {Fil} ~A, \varphi , \varphi _1)$
consists of (classically)
$\underline {A}=(A,\mathrm {Fil} ~A, \varphi , \varphi _1)$
consists of (classically)
![]() $(p,d)$
-adically complete rings A and
$(p,d)$
-adically complete rings A and
![]() $R=A/\mathrm {Fil}~A$
, for some
$R=A/\mathrm {Fil}~A$
, for some
![]() $d \in A$
and some ideal
$d \in A$
and some ideal
![]() $\mathrm {Fil} ~A$
, a lift of Frobenius
$\mathrm {Fil} ~A$
, a lift of Frobenius
![]() $\varphi $
, a
$\varphi $
, a
![]() $\varphi $
-linear map
$\varphi $
-linear map
![]() $\varphi _1: \mathrm {Fil}~ A \to A$
(called the divided Frobenius on A), such that
$\varphi _1: \mathrm {Fil}~ A \to A$
(called the divided Frobenius on A), such that
![]() $\varphi =\varpi \varphi _1$
on
$\varphi =\varpi \varphi _1$
on
![]() $\mathrm {Fil}~ A$
, with
$\mathrm {Fil}~ A$
, with
![]() $\varpi =\varphi (d)$
.
$\varpi =\varphi (d)$
.
Let
![]() $\underline {A}, \underline {A}^{\prime }$
be two frames, and let
$\underline {A}, \underline {A}^{\prime }$
be two frames, and let
![]() $u \in A^{\prime }$
be a unit. A u-morphism of frames
$u \in A^{\prime }$
be a unit. A u-morphism of frames
![]() $\alpha : \underline {A} \to \underline {A}^{\prime }$
is a morphism of rings
$\alpha : \underline {A} \to \underline {A}^{\prime }$
is a morphism of rings
![]() $\alpha : A \to A^{\prime }$
intertwinning
$\alpha : A \to A^{\prime }$
intertwinning
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^{\prime }$
, carrying
$\varphi ^{\prime }$
, carrying
![]() $\mathrm {Fil}~ A$
into
$\mathrm {Fil}~ A$
into
![]() $\mathrm {Fil}~ A^{\prime }$
and satisfying
$\mathrm {Fil}~ A^{\prime }$
and satisfying
![]() $\varphi _1^{\prime } \circ \alpha = u \alpha \circ \varphi _1$
and
$\varphi _1^{\prime } \circ \alpha = u \alpha \circ \varphi _1$
and
![]() $\alpha (\varpi )=u \varpi ^{\prime }$
.
$\alpha (\varpi )=u \varpi ^{\prime }$
.
Remark 4.17. In many situations (such as those considered in this paper), the image of
![]() $\varphi _1$
will always generate the unit ideal of A.
$\varphi _1$
will always generate the unit ideal of A.
Here is an important source of examples.
Example 4.18. Let
![]() $(A,I=(d))$
be an oriented prism. There are usually two natural ways of attaching a frame to
$(A,I=(d))$
be an oriented prism. There are usually two natural ways of attaching a frame to
![]() $(A,(d))$
. One possibility is to consider the frame
$(A,(d))$
. One possibility is to consider the frame
where
![]() $\varphi _1$
is defined by
$\varphi _1$
is defined by
![]() $\varphi _1(dx)=\varphi (x)$
(recall that A is d-torsion free). Here,
$\varphi _1(dx)=\varphi (x)$
(recall that A is d-torsion free). Here,
![]() $\varphi =\varphi (d)\varphi _1$
on
$\varphi =\varphi (d)\varphi _1$
on
![]() $\mathrm {Fil} A=(d)$
. The other possibility works when d is of the form
$\mathrm {Fil} A=(d)$
. The other possibility works when d is of the form
![]() $d=\varphi (d')$
for some
$d=\varphi (d')$
for some
![]() $d'\in A$
: one can then consider the frame
$d'\in A$
: one can then consider the frame
where
![]() $\varphi _1:=\varphi /d$
on
$\varphi _1:=\varphi /d$
on
![]() $\mathcal {N}^{\geq 1}A$
(using again that A is d-torsion free). Here,
$\mathcal {N}^{\geq 1}A$
(using again that A is d-torsion free). Here,
![]() $\varphi =d\varphi _1$
on
$\varphi =d\varphi _1$
on
![]() $\mathrm {Fil} A$
. Note that in the first case, the divided Frobenius is with respect to
$\mathrm {Fil} A$
. Note that in the first case, the divided Frobenius is with respect to
![]() $\varphi (d)$
, whereas in the second case, the divided Frobenius is with respect to d.
$\varphi (d)$
, whereas in the second case, the divided Frobenius is with respect to d.
Definition 4.19. A window
![]() $\underline {M}=(M,\mathrm {Fil}~M,\varphi _M,\varphi _{M,1})$
over a frame
$\underline {M}=(M,\mathrm {Fil}~M,\varphi _M,\varphi _{M,1})$
over a frame
![]() $\underline {A}$
consists of a finite locally free A-module M, an A-submodule
$\underline {A}$
consists of a finite locally free A-module M, an A-submodule
![]() $\mathrm {Fil}~M \subset M$
and
$\mathrm {Fil}~M \subset M$
and
![]() $\varphi $
-linear maps
$\varphi $
-linear maps
![]() $\varphi _M: M \to M$
and
$\varphi _M: M \to M$
and
![]() $\varphi _{M,1}: \mathrm {Fil}~M \to M$
, such that:
$\varphi _{M,1}: \mathrm {Fil}~M \to M$
, such that:
-
•
 $\mathrm {Fil}~A \cdot M \subset \mathrm {Fil}~M$
and
$\mathrm {Fil}~A \cdot M \subset \mathrm {Fil}~M$
and
 $M/\mathrm {Fil}~M$
is a finite locally free R-module.
$M/\mathrm {Fil}~M$
is a finite locally free R-module. -
• If
 $a \in \mathrm {Fil}~A$
,
$a \in \mathrm {Fil}~A$
,
 $m \in M$
,
$m \in M$
,
 $\varphi _{M,1}(am)= \varphi _1(a)\varphi _M(m)$
.
$\varphi _{M,1}(am)= \varphi _1(a)\varphi _M(m)$
. -
• If
 $m \in \mathrm {Fil}~M$
,
$m \in \mathrm {Fil}~M$
,
 $\varphi _M(m)=\varpi \varphi _{M,1}(m)$
.
$\varphi _M(m)=\varpi \varphi _{M,1}(m)$
. -
•
 $\varphi _{M,1}(\mathrm {Fil}~M) + \varphi _M(M)$
generates M as an A-module.
$\varphi _{M,1}(\mathrm {Fil}~M) + \varphi _M(M)$
generates M as an A-module.
A morphism of windows is an A-linear map preserving the filtrations and commuting with
![]() $\varphi _M$
and
$\varphi _M$
and
![]() $\varphi _{M,1}$
. The category of windows over
$\varphi _{M,1}$
. The category of windows over
![]() $\underline {A}$
is denoted by
$\underline {A}$
is denoted by
![]() $\mathrm {Win}(\underline {A})$
.
$\mathrm {Win}(\underline {A})$
.
Remark 4.20. If the surjectivity condition on the image of
![]() $\varphi _1$
of Remark 4.17 is satisfied, then the third point of the previous definition follows from the second and the last one simply says that
$\varphi _1$
of Remark 4.17 is satisfied, then the third point of the previous definition follows from the second and the last one simply says that
![]() $\varphi _{M,1}(\mathrm {Fil}~M)$
generates M (indeed, by assumption one can write
$\varphi _{M,1}(\mathrm {Fil}~M)$
generates M (indeed, by assumption one can write
![]() $1=\sum _{i=1}^r a_i \varphi _1(b_1)$
for some
$1=\sum _{i=1}^r a_i \varphi _1(b_1)$
for some
![]() $a_i \in A, b_i \in \mathrm {Fil}~A$
, whence
$a_i \in A, b_i \in \mathrm {Fil}~A$
, whence
![]() $\varpi =\sum _{i=1}^r a_i \varphi (b_i)$
).
$\varpi =\sum _{i=1}^r a_i \varphi (b_i)$
).
Remark 4.21. If
![]() $\alpha : \underline {A} \to \underline {A}^{\prime }$
is a u-morphism of frames as Definition 4.16 (for some unit
$\alpha : \underline {A} \to \underline {A}^{\prime }$
is a u-morphism of frames as Definition 4.16 (for some unit
![]() $u\in A^{\prime }$
), and
$u\in A^{\prime }$
), and
![]() $\underline {M}$
, respectively,
$\underline {M}$
, respectively,
![]() $\underline {M}^{\prime }$
, is a window over
$\underline {M}^{\prime }$
, is a window over
![]() $\underline {A}$
, respectively,
$\underline {A}$
, respectively,
![]() $\underline {A}^{\prime }$
, an
$\underline {A}^{\prime }$
, an
![]() $\alpha $
-morphism of windows
$\alpha $
-morphism of windows
![]() $f: \underline {M} \to \underline {M}^{\prime }$
is a morphism
$f: \underline {M} \to \underline {M}^{\prime }$
is a morphism
![]() $f: M\to M^{\prime }$
of A-modules, intertwinning
$f: M\to M^{\prime }$
of A-modules, intertwinning
![]() $\varphi _M$
and
$\varphi _M$
and
![]() $\varphi _{M^{\prime }}$
, sending
$\varphi _{M^{\prime }}$
, sending
![]() $\mathrm {Fil}~ M$
into
$\mathrm {Fil}~ M$
into
![]() $\mathrm {Fil} ~ M^{\prime }$
and satisfying
$\mathrm {Fil} ~ M^{\prime }$
and satisfying
![]() $\varphi _{M^{\prime },1} \circ f = u f \circ \varphi _{M,1}$
(hence, if
$\varphi _{M^{\prime },1} \circ f = u f \circ \varphi _{M,1}$
(hence, if
![]() $\underline {A}=\underline {A}^{\prime }$
,
$\underline {A}=\underline {A}^{\prime }$
,
![]() $\alpha =\mathrm {Id}_{\underline {A}}$
, an
$\alpha =\mathrm {Id}_{\underline {A}}$
, an
![]() $\alpha $
-morphism of windows is just a morphism of windows over
$\alpha $
-morphism of windows is just a morphism of windows over
![]() $\underline {A}$
). There is a base change functor
$\underline {A}$
). There is a base change functor
characterised by the universal property that if
![]() $\underline {M}\in \mathrm {Win}(\underline {A})$
,
$\underline {M}\in \mathrm {Win}(\underline {A})$
,
![]() $\underline {M}^{\prime } \in \mathrm {Win}(\underline {A}^{\prime })$
, homomorphisms in
$\underline {M}^{\prime } \in \mathrm {Win}(\underline {A}^{\prime })$
, homomorphisms in
![]() $\mathrm {Win}(\underline {A}^{\prime })$
from
$\mathrm {Win}(\underline {A}^{\prime })$
from
![]() $\alpha ^{\ast } \underline {M}$
to
$\alpha ^{\ast } \underline {M}$
to
![]() $\underline {M}^{\prime }$
identify with
$\underline {M}^{\prime }$
identify with
![]() $\alpha $
-morphisms of windows from
$\alpha $
-morphisms of windows from
![]() $\underline {M}$
to
$\underline {M}$
to
![]() $\underline {M}^{\prime }$
. Concretely, if
$\underline {M}^{\prime }$
. Concretely, if
![]() $\underline {M}\in \mathrm {Win}(\underline {A})$
, then
$\underline {M}\in \mathrm {Win}(\underline {A})$
, then
![]() $\alpha ^{\ast } \underline {M}=(M^{\prime }, \mathrm {Fil} ~ M^{\prime }, \varphi _{M^{\prime }}, \varphi _{M^{\prime }, 1})$
is given by
$\alpha ^{\ast } \underline {M}=(M^{\prime }, \mathrm {Fil} ~ M^{\prime }, \varphi _{M^{\prime }}, \varphi _{M^{\prime }, 1})$
is given by
![]() $M^{\prime } = A^{\prime } \otimes _A M$
,
$M^{\prime } = A^{\prime } \otimes _A M$
,
![]() $\mathrm {Fil} ~ M^{\prime }$
is the submodule generated by
$\mathrm {Fil} ~ M^{\prime }$
is the submodule generated by
![]() $(\mathrm {Fil}~ A^{\prime }).M^{\prime }$
and the image of
$(\mathrm {Fil}~ A^{\prime }).M^{\prime }$
and the image of
![]() $\mathrm {Fil}~ M$
, and
$\mathrm {Fil}~ M$
, and
![]() $\varphi _{M^{\prime }}, \varphi _{M^{\prime },1}$
are uniquely determined by the requirement that
$\varphi _{M^{\prime }}, \varphi _{M^{\prime },1}$
are uniquely determined by the requirement that
![]() $M \to M^{\prime }$
,
$M \to M^{\prime }$
,
![]() $m \mapsto 1 \otimes m$
, is an
$m \mapsto 1 \otimes m$
, is an
![]() $\alpha $
-morphism of windows.
$\alpha $
-morphism of windows.
Proposition 4.22. Let
![]() $\underline {A}=(A,\mathrm {Fil} A, \varphi ,\varphi _1)$
be a frame, such that any finite projective
$\underline {A}=(A,\mathrm {Fil} A, \varphi ,\varphi _1)$
be a frame, such that any finite projective
![]() $A/\mathrm {Fil}~A$
-module lifts to a finite projective A-module. Let
$A/\mathrm {Fil}~A$
-module lifts to a finite projective A-module. Let
![]() $(M,\mathrm {Fil}~M,\varphi _M,\varphi _{M,1})$
be a window over
$(M,\mathrm {Fil}~M,\varphi _M,\varphi _{M,1})$
be a window over
![]() $\underline {A}$
. Then there exist finite projective A-modules
$\underline {A}$
. Then there exist finite projective A-modules
![]() $L,T$
, such that
$L,T$
, such that
![]() $M=L\oplus T$
and
$M=L\oplus T$
and
![]() $\mathrm {Fil}~M=L\oplus \mathrm {Fil}~A. T$
. Moreover, given
$\mathrm {Fil}~M=L\oplus \mathrm {Fil}~A. T$
. Moreover, given
![]() $L,T$
, there exists a bijection between
$L,T$
, there exists a bijection between
![]() $\varphi $
-semilinear isomorphisms (i.e.
$\varphi $
-semilinear isomorphisms (i.e.
![]() $\varphi $
-semilinear maps which become isomorphisms after linearisation)
$\varphi $
-semilinear maps which become isomorphisms after linearisation)
![]() $\Psi \colon {L}\oplus T \to L\oplus T$
and
$\Psi \colon {L}\oplus T \to L\oplus T$
and
![]() $\underline {A}$
-window structures on the pair
$\underline {A}$
-window structures on the pair
![]() $(L\oplus T, L \oplus \mathrm {Fil}~A. T)$
.
$(L\oplus T, L \oplus \mathrm {Fil}~A. T)$
.
Proof. This is a combination of [Reference Lau33, Remark 2.4] and [Reference Lau33, Lemma 2.5]. Let us give some details, and set
![]() $S:=A/\mathrm {Fil}~A$
. The module
$S:=A/\mathrm {Fil}~A$
. The module
![]() $S\otimes _{A}M$
decomposes, as
$S\otimes _{A}M$
decomposes, as
![]() $M/\mathrm {Fil}~M$
is finite projective, into a direct sum
$M/\mathrm {Fil}~M$
is finite projective, into a direct sum
![]() $S\otimes _{A}M\cong M/\mathrm {Fil}~M\oplus Q$
for some finite projective S-module Q. Let
$S\otimes _{A}M\cong M/\mathrm {Fil}~M\oplus Q$
for some finite projective S-module Q. Let
![]() $L,T$
be finite projective A-modules, such that L is a lift of Q and T a lift of
$L,T$
be finite projective A-modules, such that L is a lift of Q and T a lift of
![]() $M/\mathrm {Fil}~M$
. We can then lift the decomposition
$M/\mathrm {Fil}~M$
. We can then lift the decomposition
![]() $S\otimes _{A}M$
to a decomposition
$S\otimes _{A}M$
to a decomposition
![]() $M=L\oplus T$
by projectivity. The property
$M=L\oplus T$
by projectivity. The property
![]() $\mathrm {Fil}~M=L\oplus \mathrm {Fil}~A T$
follows. Given
$\mathrm {Fil}~M=L\oplus \mathrm {Fil}~A T$
follows. Given
![]() $\varphi _{M}$
, we define
$\varphi _{M}$
, we define
![]() $\Psi (l+t):=\varphi _{M,1}(l)+\varphi _M(t)$
for
$\Psi (l+t):=\varphi _{M,1}(l)+\varphi _M(t)$
for
![]() $l\in L, t\in T$
on
$l\in L, t\in T$
on
![]() $M=L\oplus T$
, and conversely, given
$M=L\oplus T$
, and conversely, given
![]() $\Psi $
, we set
$\Psi $
, we set
![]() $\varphi _M(l+t):=\varpi \Psi (l)+\Psi (t)$
and
$\varphi _M(l+t):=\varpi \Psi (l)+\Psi (t)$
and
![]() $\varphi _{M,1}(l+at):=\Psi (l)+\varphi _1(a)\Psi (t)$
for
$\varphi _{M,1}(l+at):=\Psi (l)+\varphi _1(a)\Psi (t)$
for
![]() $l\in L,t\in T,a\in \mathrm {Fil}~A$
.
$l\in L,t\in T,a\in \mathrm {Fil}~A$
.
Lemma 4.23. Let
![]() $\underline {A}=(A,\mathrm {Fil} A, \varphi ,\varphi _1)$
as in Proposition 4.22, such that
$\underline {A}=(A,\mathrm {Fil} A, \varphi ,\varphi _1)$
as in Proposition 4.22, such that
![]() $\varpi $
is a nonzero divisor and
$\varpi $
is a nonzero divisor and
![]() $\mathrm {Fil} A= \varphi ^{-1}(\varpi A)$
. Then if
$\mathrm {Fil} A= \varphi ^{-1}(\varpi A)$
. Then if
![]() $(M, \mathrm {Fil}~ M, \varphi _M, \varphi _{M,1})$
is a window over
$(M, \mathrm {Fil}~ M, \varphi _M, \varphi _{M,1})$
is a window over
![]() $\underline {A}$
, we have
$\underline {A}$
, we have
(note that one always has an inclusion
![]() $\mathrm {Fil} ~ M \subset \varphi _M^{-1}(\varpi M)$
). Moreover,
$\mathrm {Fil} ~ M \subset \varphi _M^{-1}(\varpi M)$
). Moreover,
![]() $\varphi _M\colon M\to M$
induces an injection
$\varphi _M\colon M\to M$
induces an injection
![]() $M/\mathrm {Fil} M\to M/\varpi M$
, and the latter extends to an injection
$M/\mathrm {Fil} M\to M/\varpi M$
, and the latter extends to an injection
![]() $A/\varpi \otimes _{A/\mathrm {Fil} A} M/\mathrm {Fil} M\to M/I$
of a locally direct summand.
$A/\varpi \otimes _{A/\mathrm {Fil} A} M/\mathrm {Fil} M\to M/I$
of a locally direct summand.
Proof. Let
be a normal decomposition of M as in 4.22, and
so that
![]() $\mathrm {Fil} ~ M= L \oplus \mathrm {Fil}~ A.T$
. Let
$\mathrm {Fil} ~ M= L \oplus \mathrm {Fil}~ A.T$
. Let
![]() $x=l+t \in M$
, such that
$x=l+t \in M$
, such that
![]() $\varphi _M(x) \in \varpi M$
. We have
$\varphi _M(x) \in \varpi M$
. We have
so the condition is equivalent to requiring that
![]() $\Psi (t) \in \varpi. M$
. For simplicity, we assume that
$\Psi (t) \in \varpi. M$
. For simplicity, we assume that
![]() $L, T$
are free A-modules in the following. The general case follows by localisation. Fix a basis
$L, T$
are free A-modules in the following. The general case follows by localisation. Fix a basis
![]() $t_1,\dots ,t_r$
of T and a basis
$t_1,\dots ,t_r$
of T and a basis
![]() $l_1,\dots ,l_s$
of L, as A-modules. Since
$l_1,\dots ,l_s$
of L, as A-modules. Since
![]() $\Psi $
is a
$\Psi $
is a
![]() $\varphi $
-linear isomorphism, the family
$\varphi $
-linear isomorphism, the family
![]() $(\Psi (t_1),\dots ,\Psi (t_r),\Psi (l_1),\dots ,\Psi (l_s))$
is a basis of M, and so the reduction of the family
$(\Psi (t_1),\dots ,\Psi (t_r),\Psi (l_1),\dots ,\Psi (l_s))$
is a basis of M, and so the reduction of the family
![]() $(\Psi (t_1),\dots ,\Psi (t_r))$
modulo
$(\Psi (t_1),\dots ,\Psi (t_r))$
modulo
![]() $\varpi $
is linearly independent. Write
$\varpi $
is linearly independent. Write
![]() $t=\sum _{i=1}^r a_i t_i$
, with
$t=\sum _{i=1}^r a_i t_i$
, with
![]() $a_i \in A$
for all
$a_i \in A$
for all
![]() $i=1,\dots , r$
. By assumption, we have that
$i=1,\dots , r$
. By assumption, we have that
 $$ \begin{align*}\Psi(t) = \sum_{i=1}^r \varphi(a_i) \Psi(t_i) \in \varpi. M, \end{align*} $$
$$ \begin{align*}\Psi(t) = \sum_{i=1}^r \varphi(a_i) \Psi(t_i) \in \varpi. M, \end{align*} $$
and therefore we must have
![]() $\varphi (a_i) \in \varpi A$
for all
$\varphi (a_i) \in \varpi A$
for all
![]() $i=1,\dots ,r$
, that is
$i=1,\dots ,r$
, that is
![]() $a_i \in \mathrm {Fil} ~A$
for all
$a_i \in \mathrm {Fil} ~A$
for all
![]() $i=1,\dots ,r$
, by the condition on
$i=1,\dots ,r$
, by the condition on
![]() $\mathrm {Fil}~A$
. Hence,
$\mathrm {Fil}~A$
. Hence,
![]() $t \in \mathrm {Fil}~A.T$
and thus
$t \in \mathrm {Fil}~A.T$
and thus
![]() $x \in \mathrm {Fil}~M$
, as desired. For the last statements note that the map
$x \in \mathrm {Fil}~M$
, as desired. For the last statements note that the map
![]() $\varphi _M\colon M/\mathrm {Fil} M\cong T/\mathrm {Fil} A.T\to M/\varpi $
identifies with the map induced by
$\varphi _M\colon M/\mathrm {Fil} M\cong T/\mathrm {Fil} A.T\to M/\varpi $
identifies with the map induced by
![]() $\Psi $
. As
$\Psi $
. As
![]() $\varphi _M(t_i)=\Psi (t_i), i=1,\ldots , r,$
are linearly independent (over
$\varphi _M(t_i)=\Psi (t_i), i=1,\ldots , r,$
are linearly independent (over
![]() $A/\varpi $
), this map extends to an inclusion
$A/\varpi $
), this map extends to an inclusion
of a direct summand. This finishes the proof.
Let us now see what the categories of windows look like for the frames attached to prisms discussed in Example 4.18.
Definition 4.24. Let
![]() $(A,I=(d))$
be a prism. A Breuil-Kisin module
$(A,I=(d))$
be a prism. A Breuil-Kisin module
![]() $(M,\varphi _M)$
over
$(M,\varphi _M)$
over
![]() $(A,I)$
, or just A if I is understood, is a finite free A-module M together with an isomorphism
$(A,I)$
, or just A if I is understood, is a finite free A-module M together with an isomorphism
If
![]() $\varphi _M(\varphi ^{\ast }M)\subseteq M$
with cokernel killed by I, then
$\varphi _M(\varphi ^{\ast }M)\subseteq M$
with cokernel killed by I, then
![]() $(M,\varphi _M)$
is called minuscule.
$(M,\varphi _M)$
is called minuscule.
We denote by
![]() $\mathrm {BK}(A)$
the category of Breuil-Kisin modules over A and by
$\mathrm {BK}(A)$
the category of Breuil-Kisin modules over A and by
![]() $\mathrm {BK}_{\mathrm {min}}(A)\subseteq \mathrm {BK}(A)$
its full subcategory of minuscule ones.
$\mathrm {BK}_{\mathrm {min}}(A)\subseteq \mathrm {BK}(A)$
its full subcategory of minuscule ones.
Remark 4.25. If
![]() $(M,\varphi _M)$
is a minuscule Breuil-Kisin module over
$(M,\varphi _M)$
is a minuscule Breuil-Kisin module over
![]() $(A,I)$
, the cokernel N of
$(A,I)$
, the cokernel N of
![]() $\varphi _M(\varphi ^{\ast }M)\subseteq M$
is a finite projective
$\varphi _M(\varphi ^{\ast }M)\subseteq M$
is a finite projective
![]() $A/I$
-module. Indeed N is pseudocoherent as an A-module (having a
$A/I$
-module. Indeed N is pseudocoherent as an A-module (having a
![]() $2$
-term resolution by finite projective A-modules), hence, as an
$2$
-term resolution by finite projective A-modules), hence, as an
![]() $A/I$
-module. Moreover, if k is the residue field of
$A/I$
-module. Moreover, if k is the residue field of
![]() $\mathrm {Spec}(A/I)$
at any closed point, then the derived tensor
$\mathrm {Spec}(A/I)$
at any closed point, then the derived tensor
is a perfect complex of
![]() $W(\bar {k})$
-modules, hence, bounded. It follows that the complex
$W(\bar {k})$
-modules, hence, bounded. It follows that the complex
![]() $k \otimes _{A/I}^L N$
is also bounded, so that N has a finite resolution by finite projective
$k \otimes _{A/I}^L N$
is also bounded, so that N has a finite resolution by finite projective
![]() $A/I$
-modules ([Reference Project52, Tag 068W]). Since N has projective dimension
$A/I$
-modules ([Reference Project52, Tag 068W]). Since N has projective dimension
![]() $\leq 1$
as an A-module, it is necessarily projective as an
$\leq 1$
as an A-module, it is necessarily projective as an
![]() $A/I$
-module. We thank the referee for poiting out this argument to us.
$A/I$
-module. We thank the referee for poiting out this argument to us.
Proposition 4.26. Let
![]() $(A,(d))$
be an oriented prism. The functor
$(A,(d))$
be an oriented prism. The functor
induces an equivalence between the category of windows over the frame
![]() $\underline {A}_d$
of Example 4.18 and the category
$\underline {A}_d$
of Example 4.18 and the category
![]() $\mathrm {BK}_{\mathrm {min}}(A)$
.
$\mathrm {BK}_{\mathrm {min}}(A)$
.
Proof. See [Reference Cais and Lau17, Lemma 2.1.16] (taking Remark 4.25 into account).
Before turning to the second example introduced in Example 4.18, let us recall some facts about henselian pairs. Let A be a ring, and let
![]() $I\subseteq A$
be an ideal. We recall that the pair
$I\subseteq A$
be an ideal. We recall that the pair
![]() $(A,I)$
is henselian if I is contained in the Jacobson radical of A and if for any monic polynomial
$(A,I)$
is henselian if I is contained in the Jacobson radical of A and if for any monic polynomial
![]() $f\in A[T]$
and each factorisation
$f\in A[T]$
and each factorisation
![]() $\overline {f}=g_0h_0$
with
$\overline {f}=g_0h_0$
with
![]() $g_0,h_0\in A/I[T]$
monic and generating the unit ideal, there exists a factorisation
$g_0,h_0\in A/I[T]$
monic and generating the unit ideal, there exists a factorisation
![]() $f=gh$
with
$f=gh$
with
![]() $g,h$
monic and
$g,h$
monic and
![]() $g_0=\overline {g}$
,
$g_0=\overline {g}$
,
![]() $h_0=\overline {h}$
(cf. [Reference Project52, Tag 09XE]).
$h_0=\overline {h}$
(cf. [Reference Project52, Tag 09XE]).
If I is locally nilpotentFootnote
17
or A is I-adically complete, then the pair
![]() $(A,I)$
is henselian (cf. [Reference Project52, Tag 0ALI], [Reference Project52, Tag 0ALJ]).
$(A,I)$
is henselian (cf. [Reference Project52, Tag 0ALI], [Reference Project52, Tag 0ALJ]).
For us, the following well-known property of henselian pairs will be important (cf. [Reference Clausen, Mathew and Morrow19, Lemma 4.20]).
Lemma 4.27. Let
![]() $(A,I)$
be a henselian pair. The base change
$(A,I)$
be a henselian pair. The base change
![]() $M\mapsto M\otimes _{A} A/I$
induces a bijection on isomorphism classes of finite projective modules over A, respectively,
$M\mapsto M\otimes _{A} A/I$
induces a bijection on isomorphism classes of finite projective modules over A, respectively,
![]() $A/I$
.
$A/I$
.
Proof. If
![]() $M,N$
are finite projective A-modules, then any isomorphism
$M,N$
are finite projective A-modules, then any isomorphism
![]() $M/IM\cong N/IN$
can be lifted to a morphism
$M/IM\cong N/IN$
can be lifted to a morphism
![]() $M\to N$
by projectivity of M. As
$M\to N$
by projectivity of M. As
![]() $I\subseteq A$
lies in the Jacobson radical of A, this lifted homomorphism is then automatically an isomorphism. Moreover, any finite projective
$I\subseteq A$
lies in the Jacobson radical of A, this lifted homomorphism is then automatically an isomorphism. Moreover, any finite projective
![]() $A/I$
-module can be lifted to a finite projective A-module by [Reference Project52, Tag 0D4A].
$A/I$
-module can be lifted to a finite projective A-module by [Reference Project52, Tag 0D4A].
Now, we provide the proof that
![]() is henselian along
is henselian along
![]() . We learned the argument from [Reference Lau37, Remark 5.2].
. We learned the argument from [Reference Lau37, Remark 5.2].
Lemma 4.28. The pair
![]() is henselian.
is henselian.
Proof. Because
![]() is
is
![]() $(p,\xi )$
-adically complete, it suffices to prove that the pair
$(p,\xi )$
-adically complete, it suffices to prove that the pair
is henselian (cf. [Reference Project52, Tag 0DYD]). We know
![]() . Hence, for every element
. Hence, for every element
![]() $x\in \ker (\theta )$
,
$x\in \ker (\theta )$
,
![]() $x^p\in (p,\tilde {\xi })$
. As locally nilpotent ideals are henselian, the claim follows.
$x^p\in (p,\tilde {\xi })$
. As locally nilpotent ideals are henselian, the claim follows.
Proposition 4.29. Let R be a quasiregular semiperfectoid ring. Fix a generator
![]() $\tilde {\xi }=\varphi (\xi )$
of the ideal I of the prism
$\tilde {\xi }=\varphi (\xi )$
of the ideal I of the prism
![]() , giving rise to a frame
, giving rise to a frame
![]() of Example 4.18 (with
of Example 4.18 (with
![]() $d=\tilde {\xi }$
). The forgetful functor
$d=\tilde {\xi }$
). The forgetful functor
is fully faithful, with essential image the subcategory
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
.
$\mathrm {DM}^{\mathrm {adm}}(R)$
.
Proof. Thanks to Lemma 4.28, we can apply Lemma 4.23 to the frame
![]() . This yields fully faithfulness, and that for a window
. This yields fully faithfulness, and that for a window
![]() $(M,\mathrm {Fil}~M,\varphi _M,\varphi _{M,1})$
, the image of
$(M,\mathrm {Fil}~M,\varphi _M,\varphi _{M,1})$
, the image of
identifies with
![]() $M/\mathrm {Fil}~M$
. By Lemma 4.23, we can deduce admissibility. Assume conversely that
$M/\mathrm {Fil}~M$
. By Lemma 4.23, we can deduce admissibility. Assume conversely that
![]() $(M,\varphi _M)$
is an admissible prismatic Dieudonné module. Then the datum
$(M,\varphi _M)$
is an admissible prismatic Dieudonné module. Then the datum
![]() $(M,\varphi _M^{-1}(I\cdot M), \varphi _M, \frac {1}{\tilde {\xi }}\varphi _M)$
is a window over
$(M,\varphi _M^{-1}(I\cdot M), \varphi _M, \frac {1}{\tilde {\xi }}\varphi _M)$
is a window over
![]() . Indeed, the condition that
. Indeed, the condition that
![]() $\varphi _{M,1}(\mathrm {Fil} M)$
generates M follows from the definition of admissibility and Remark 4.7. This finishes the proof.
$\varphi _{M,1}(\mathrm {Fil} M)$
generates M follows from the definition of admissibility and Remark 4.7. This finishes the proof.
Remark 4.30. Assume that R is quasiregular semiperfect, that is R is quasiregular semiperfectoid and
![]() $pR=0$
. Let
$pR=0$
. Let
![]() $(M,\varphi _M)$
be a prismatic Dieudonné module over R. Let
$(M,\varphi _M)$
be a prismatic Dieudonné module over R. Let
![]() be a locally free R-module which is a direct summand, and define
be a locally free R-module which is a direct summand, and define
![]() $\mathrm {Fil}~M$
to be the inverse image of N in M. Then the collection
$\mathrm {Fil}~M$
to be the inverse image of N in M. Then the collection
![]() $(M,\mathrm {Fil}~M,\varphi _M,1/p \varphi _M)$
is a window over
$(M,\mathrm {Fil}~M,\varphi _M,1/p \varphi _M)$
is a window over
![]() if and only if N is an ‘admissible’ filtration in the sense of Grothendieck on the Dieudonné module
if and only if N is an ‘admissible’ filtration in the sense of Grothendieck on the Dieudonné module
![]() $(M,\varphi _M, V_M)$
, where
$(M,\varphi _M, V_M)$
, where
![]() $V_M=\varphi _M^{-1}.p$
(which makes sense by the assumption that
$V_M=\varphi _M^{-1}.p$
(which makes sense by the assumption that
![]() $(M,\varphi _M)$
is a prismatic Dieudonné module). For a proof of this, see [Reference Cais and Lau17, Lemma 2.5.1]).
$(M,\varphi _M)$
is a prismatic Dieudonné module). For a proof of this, see [Reference Cais and Lau17, Lemma 2.5.1]).
We can now prove Proposition 4.12.
Proof of Proposition 4.12.
We know by Proposition 4.29 that the functor
 $$ \begin{align*}(M, \varphi_M) \mapsto \left(M,\varphi_M^{-1}(\tilde{\xi}. M), \varphi_M, \frac{1}{\tilde{\xi}} \varphi_M\right) \end{align*} $$
$$ \begin{align*}(M, \varphi_M) \mapsto \left(M,\varphi_M^{-1}(\tilde{\xi}. M), \varphi_M, \frac{1}{\tilde{\xi}} \varphi_M\right) \end{align*} $$
is an equivalence between
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
and
$\mathrm {DM}^{\mathrm {adm}}(R)$
and
![]() . Since R is perfectoid,
. Since R is perfectoid,
![]() and so
and so
By Proposition 4.26, the functor
 $$\begin{align*}(N, \mathrm{Fil}~N, \varphi_N) \mapsto \left(\mathrm{Fil}~N, \frac{\xi}{\tilde{\xi}} \varphi_{N}\right) \end{align*}$$
$$\begin{align*}(N, \mathrm{Fil}~N, \varphi_N) \mapsto \left(\mathrm{Fil}~N, \frac{\xi}{\tilde{\xi}} \varphi_{N}\right) \end{align*}$$
induces an equivalence between
![]() and
and
![]() $\mathrm {BK}_{\mathrm {min}}(A_{\mathrm {inf}}(R))$
(the category of minuscule Breuil-Kisin modules over
$\mathrm {BK}_{\mathrm {min}}(A_{\mathrm {inf}}(R))$
(the category of minuscule Breuil-Kisin modules over
![]() $A_{\mathrm { inf}}(R)$
). The latter category is, however, obviously equivalent to
$A_{\mathrm { inf}}(R)$
). The latter category is, however, obviously equivalent to
![]() $\mathrm {DM}(R')$
, with
$\mathrm {DM}(R')$
, with
![]() $R'=A_{\mathrm {inf}}(R) / \xi $
. As
$R'=A_{\mathrm {inf}}(R) / \xi $
. As
![]() $\varphi $
is bijective on
$\varphi $
is bijective on
![]() , base change along
, base change along
![]() $\varphi $
is also an equivalence between
$\varphi $
is also an equivalence between
![]() $\mathrm {DM}(R')$
and
$\mathrm {DM}(R')$
and
![]() $\mathrm {DM}(R)$
. Composing these equivalences, we obtain an equivalence
$\mathrm {DM}(R)$
. Composing these equivalences, we obtain an equivalence
But this composite functor is nothing but the identity functor.
Finally, we record some statements which are later used to prove essential surjectivity for the prismatic Dieudonné functor.
For a ring A with an endomorphism
![]() $\varphi \colon A\to A$
, we denote by
$\varphi \colon A\to A$
, we denote by
![]() $\varphi -\mathrm {Mod}_A^{\mathrm {unit}}$
the category of ‘unit’
$\varphi -\mathrm {Mod}_A^{\mathrm {unit}}$
the category of ‘unit’
![]() $\varphi $
-modules over A, that is, the category of pairs
$\varphi $
-modules over A, that is, the category of pairs
![]() $(M,\varphi _M)$
with M a finite projective A-module and
$(M,\varphi _M)$
with M a finite projective A-module and
![]() $\varphi _M\colon \varphi ^{\ast } M\cong M$
an isomorphism.
$\varphi _M\colon \varphi ^{\ast } M\cong M$
an isomorphism.
Lemma 4.31. Let
![]() $A\to B$
be a surjection of bounded prisms with kernel
$A\to B$
be a surjection of bounded prisms with kernel
![]() $J\subseteq A$
. Assume that the Frobenius
$J\subseteq A$
. Assume that the Frobenius
![]() $\varphi $
of A is topologically nilpotent (for the
$\varphi $
of A is topologically nilpotent (for the
![]() $(p,I)$
-adic topology) on J and that
$(p,I)$
-adic topology) on J and that
![]() $(A,J)$
is henselian. Then the functor
$(A,J)$
is henselian. Then the functor
is an equivalence.
Proof. To prove fully faithfulness, it suffices to show (by passing to internal homs) that for every
![]() $\varphi $
-module
$\varphi $
-module
![]() $(M,\varphi _M)$
over A, the map
$(M,\varphi _M)$
over A, the map
is bijective. Let
![]() $m\in M^{\varphi _M=1}\cap JM$
, and write
$m\in M^{\varphi _M=1}\cap JM$
, and write
![]() $m=\sum \limits _{i=1}^na_im_i$
with
$m=\sum \limits _{i=1}^na_im_i$
with
![]() $a_i\in J$
and
$a_i\in J$
and
![]() $m_i\in M$
. Then
$m_i\in M$
. Then
 $$ \begin{align*}m=\varphi^j_M(m)=\sum\limits_{i=1}^n\varphi^j(a_i)\varphi_M^j(m_i), \end{align*} $$
$$ \begin{align*}m=\varphi^j_M(m)=\sum\limits_{i=1}^n\varphi^j(a_i)\varphi_M^j(m_i), \end{align*} $$
where the
![]() $\varphi ^j(a_i)$
converge to
$\varphi ^j(a_i)$
converge to
![]() $0$
if
$0$
if
![]() $j\to \infty $
by our assumption on
$j\to \infty $
by our assumption on
![]() $\varphi $
. Thus,
$\varphi $
. Thus,
![]() $m=\varphi ^j_M(m)\to 0$
if
$m=\varphi ^j_M(m)\to 0$
if
![]() $j\to \infty $
and therefore
$j\to \infty $
and therefore
![]() $m=0$
, which proves injectivity. Conversely, let
$m=0$
, which proves injectivity. Conversely, let
![]() $m\in M$
and assume that
$m\in M$
and assume that
![]() $\varphi _M(m)\equiv m$
modulo
$\varphi _M(m)\equiv m$
modulo
![]() $JM$
. Write
$JM$
. Write
As above, the sequence
![]() $\varphi _M^j(z)$
converges to
$\varphi _M^j(z)$
converges to
![]() $0$
if
$0$
if
![]() $j\to \infty $
. Set
$j\to \infty $
. Set
 $$ \begin{align*}\tilde{m}:=m+\sum\limits_{j=0}^{\infty} \varphi_M^j(z). \end{align*} $$
$$ \begin{align*}\tilde{m}:=m+\sum\limits_{j=0}^{\infty} \varphi_M^j(z). \end{align*} $$
Then
![]() $\tilde {m}\equiv m$
modulo
$\tilde {m}\equiv m$
modulo
![]() $JM$
and
$JM$
and
![]() $\varphi _M(\tilde {m})=\tilde {m}$
. Thus, we showed that
$\varphi _M(\tilde {m})=\tilde {m}$
. Thus, we showed that
and the functor
![]() $\varphi -\mathrm {Mod}_A^{\mathrm {unit}}\to \varphi -\mathrm {Mod}_B^{\mathrm {unit}}$
is fully faithful, and we are left with essential surjectivity. For this, let
$\varphi -\mathrm {Mod}_A^{\mathrm {unit}}\to \varphi -\mathrm {Mod}_B^{\mathrm {unit}}$
is fully faithful, and we are left with essential surjectivity. For this, let
![]() $(N,\varphi _N)\in \varphi -\mathrm {Mod}_B^{\mathrm {unit}}$
. By assumption, A is henselian along J and, thus, we can write
$(N,\varphi _N)\in \varphi -\mathrm {Mod}_B^{\mathrm {unit}}$
. By assumption, A is henselian along J and, thus, we can write
![]() $N\cong M\otimes _A B$
for some finite projective A-module M. Using projectiviy of
$N\cong M\otimes _A B$
for some finite projective A-module M. Using projectiviy of
![]() $\varphi ^{\ast } M$
over A, we can lift
$\varphi ^{\ast } M$
over A, we can lift
![]() $\varphi _N\colon \varphi ^{\ast } N\to N$
to some homomorphism
$\varphi _N\colon \varphi ^{\ast } N\to N$
to some homomorphism
![]() $\varphi _M\colon \varphi ^{\ast } M\to M$
. As J lies in the radical of A, the homomorphism
$\varphi _M\colon \varphi ^{\ast } M\to M$
. As J lies in the radical of A, the homomorphism
![]() $\varphi _M$
will automatically be an isomorphism as
$\varphi _M$
will automatically be an isomorphism as
![]() $\varphi _N$
is. Thus, we have lifted
$\varphi _N$
is. Thus, we have lifted
![]() $(N,\varphi _N)$
to
$(N,\varphi _N)$
to
![]() $(M,\varphi _M)$
, which finishes the proof.
$(M,\varphi _M)$
, which finishes the proof.
The following statement is similar to [Reference Kisin30, Appendix A.4] or [Reference Lau33, Lemma 2.12].
It will use the ‘Nygaard frame’ associated to an oriented prisms, which was discussed in 4.18.
Lemma 4.32. Let
![]() $(A,(\tilde {\xi })) \to (B,(\tilde {\xi }))$
be a surjection of oriented bounded prisms with kernel J contained in
$(A,(\tilde {\xi })) \to (B,(\tilde {\xi }))$
be a surjection of oriented bounded prisms with kernel J contained in
![]() $\mathcal {N}^{\geq 1}A$
, and assume that
$\mathcal {N}^{\geq 1}A$
, and assume that
![]() $\tilde {\xi }=\varphi (\xi )$
for some
$\tilde {\xi }=\varphi (\xi )$
for some
![]() $\xi \in A$
and that
$\xi \in A$
and that
![]() $(A,\tilde {\xi })$
bounded. Assume that
$(A,\tilde {\xi })$
bounded. Assume that
![]() $\varphi _1$
is (pointwise) topologically nilpotent on J and that
$\varphi _1$
is (pointwise) topologically nilpotent on J and that
![]() $(A,J)$
is henselian. Then the base change functor induces an equivalence:
$(A,J)$
is henselian. Then the base change functor induces an equivalence:
We note that
![]() $\varphi _1(J)\subseteq J$
as B is
$\varphi _1(J)\subseteq J$
as B is
![]() $\tilde {\xi }$
-torsion free and
$\tilde {\xi }$
-torsion free and
![]() $\varphi (j)=\tilde {\xi }\varphi _1(j)$
in A. Thus, the condition that
$\varphi (j)=\tilde {\xi }\varphi _1(j)$
in A. Thus, the condition that
![]() $\varphi _1$
is topologically nilpotent on J makes sense. Moreover,
$\varphi _1$
is topologically nilpotent on J makes sense. Moreover,
![]() $\varphi _1(J)\subseteq J$
implies that
$\varphi _1(J)\subseteq J$
implies that
![]() $(B,\mathcal {N}^{\geq 1} A/J, A/\mathcal {N}^{\geq 1}A, \varphi ,\varphi _1)$
is indeed a well defined frame.
$(B,\mathcal {N}^{\geq 1} A/J, A/\mathcal {N}^{\geq 1}A, \varphi ,\varphi _1)$
is indeed a well defined frame.
Proof. In this proof, we will use the following convenient notation: if
![]() $\sigma : S\to S$
is a ring endomorphism and
$\sigma : S\to S$
is a ring endomorphism and
![]() $f: M \to N$
is a
$f: M \to N$
is a
![]() $\sigma $
-linear map between two S-modules, we will denote by
$\sigma $
-linear map between two S-modules, we will denote by
![]() $f^{\sharp }: \sigma ^{\ast } M \to N$
its linearisation. We will also abbreviate
$f^{\sharp }: \sigma ^{\ast } M \to N$
its linearisation. We will also abbreviate
![]() $\underline {A}_{\mathrm {Nyg}}$
as
$\underline {A}_{\mathrm {Nyg}}$
as
![]() $\underline {A}$
and
$\underline {A}$
and
![]() $(B,\mathcal {N}^{\geq 1} A/J,A/\mathcal {N}^{\geq 1}A, \varphi ,\varphi _1)$
as
$(B,\mathcal {N}^{\geq 1} A/J,A/\mathcal {N}^{\geq 1}A, \varphi ,\varphi _1)$
as
![]() $\underline {B}$
.
$\underline {B}$
.
By the existence of normal decompositions (cf. Proposition 4.22: we can apply it since the proof of Lemma 4.28 shows that A is henselian along
![]() $\mathcal {N}^{\geq 1} A$
, and this implies that finite projective
$\mathcal {N}^{\geq 1} A$
, and this implies that finite projective
![]() $B/\mathrm {im}(\mathcal {N}^{\geq 1} A)$
-modules can be lifted to finite locally free B-modules — even to finite projective A-modules) and the fact that A is henselian along J, the base change functor
$B/\mathrm {im}(\mathcal {N}^{\geq 1} A)$
-modules can be lifted to finite locally free B-modules — even to finite projective A-modules) and the fact that A is henselian along J, the base change functor
is essentially surjective. Let
![]() $\underline {M}, \underline {N}$
be two windows over
$\underline {M}, \underline {N}$
be two windows over
![]() $\underline {A}$
. We want to prove that
$\underline {A}$
. We want to prove that
where
![]() $\underline {M}/J, \underline {N}/J$
denote the base change of
$\underline {M}/J, \underline {N}/J$
denote the base change of
![]() $\underline {M},\underline {N}$
to
$\underline {M},\underline {N}$
to
![]() $\underline {B}$
. The idea of the proof is similar to Lemma 4.31 (and [Reference Lau33, Theorem 3.2]). Let
$\underline {B}$
. The idea of the proof is similar to Lemma 4.31 (and [Reference Lau33, Theorem 3.2]). Let
be an arbitrary homomorphism of A-modules. Then the A-module homomorphism
is well defined. Indeed,
![]() $\varphi _M^{\sharp } \colon \varphi ^{\ast } M\to M$
is injective with cokernel killed by
$\varphi _M^{\sharp } \colon \varphi ^{\ast } M\to M$
is injective with cokernel killed by
![]() $\tilde {\xi }$
(which follows from the fact that
$\tilde {\xi }$
(which follows from the fact that
![]() $\varphi _{M,1}(\mathrm {Fil} M)$
generates M and that
$\varphi _{M,1}(\mathrm {Fil} M)$
generates M and that
![]() $M,\varphi ^{\ast }(M)$
are
$M,\varphi ^{\ast }(M)$
are
![]() $\tilde {\xi }$
-torsion free), and thus, on
$\tilde {\xi }$
-torsion free), and thus, on
![]() $\tilde {\xi } M$
, there exists a partial inverse
$\tilde {\xi } M$
, there exists a partial inverse
![]() ${(\varphi _M^{\sharp })}^{-1}\colon \tilde {\xi } M\to \varphi ^{\ast }M$
of
${(\varphi _M^{\sharp })}^{-1}\colon \tilde {\xi } M\to \varphi ^{\ast }M$
of
![]() ${\varphi _M^{\sharp }}$
. Moreover, as
${\varphi _M^{\sharp }}$
. Moreover, as
![]() $\beta $
has image in
$\beta $
has image in
![]() $JN$
, the composition
$JN$
, the composition
![]() $\varphi _N^{\sharp } (\mathrm {Id}\otimes \beta )$
has image in
$\varphi _N^{\sharp } (\mathrm {Id}\otimes \beta )$
has image in
![]() $\tilde {\xi } N$
. The module M is finitely generated: choose generators
$\tilde {\xi } N$
. The module M is finitely generated: choose generators
![]() $x_1, \dots , x_r$
. For each
$x_1, \dots , x_r$
. For each
![]() $n\geq 1$
, and each
$n\geq 1$
, and each
![]() $x \in M$
, we can write
$x \in M$
, we can write
 $$ \begin{align*}{((\varphi^{n-1})^{\ast} (\varphi_{M,1}^{\sharp})^{-1} \circ \dots \circ \varphi^{\ast} (\varphi_{M,1}^{\sharp})^{-1} \circ (\varphi_{M,1}^{\sharp})^{-1} (x) } = \sum_{i=1}^r b_{i,n}(x) \otimes x_i \in (\varphi^n)^{\ast} M, \end{align*} $$
$$ \begin{align*}{((\varphi^{n-1})^{\ast} (\varphi_{M,1}^{\sharp})^{-1} \circ \dots \circ \varphi^{\ast} (\varphi_{M,1}^{\sharp})^{-1} \circ (\varphi_{M,1}^{\sharp})^{-1} (x) } = \sum_{i=1}^r b_{i,n}(x) \otimes x_i \in (\varphi^n)^{\ast} M, \end{align*} $$
with
![]() $b_{i,n}(x) \in A$
. Hence, we get
$b_{i,n}(x) \in A$
. Hence, we get
 $$ \begin{align*}U^n(\beta)(x)= {(((\varphi_{N,1})^{\sharp} \circ \varphi^{\ast} (\varphi_{N,1})^{\sharp} \circ \dots \circ (\varphi^{n-1})^{\ast} (\varphi_{N,1})^{\sharp}) }\circ (\varphi^n)^{\ast} \beta) \left( \sum_{i=1}^r b_{i,n}(x) \otimes x_i \right), \end{align*} $$
$$ \begin{align*}U^n(\beta)(x)= {(((\varphi_{N,1})^{\sharp} \circ \varphi^{\ast} (\varphi_{N,1})^{\sharp} \circ \dots \circ (\varphi^{n-1})^{\ast} (\varphi_{N,1})^{\sharp}) }\circ (\varphi^n)^{\ast} \beta) \left( \sum_{i=1}^r b_{i,n}(x) \otimes x_i \right), \end{align*} $$
whence
 $$ \begin{align*}U^n(\beta)(x)= \sum_{i=1}^r \varphi^n(b_{i,n}(x)) \varphi_{N,1}^n(\beta(x_i)). \end{align*} $$
$$ \begin{align*}U^n(\beta)(x)= \sum_{i=1}^r \varphi^n(b_{i,n}(x)) \varphi_{N,1}^n(\beta(x_i)). \end{align*} $$
Write for each
![]() $i=1,\dots , r$
,
$i=1,\dots , r$
,
 $$ \begin{align*}\beta(x_i)=\sum_{k=1}^{s_r} j_{i,k} y_{i,k}, \end{align*} $$
$$ \begin{align*}\beta(x_i)=\sum_{k=1}^{s_r} j_{i,k} y_{i,k}, \end{align*} $$
with
![]() $j_{i,k} \in J$
,
$j_{i,k} \in J$
,
![]() $y_{i,k} \in N$
. We have, for each
$y_{i,k} \in N$
. We have, for each
![]() $i=1,\dots , r$
,
$i=1,\dots , r$
,
 $$ \begin{align*}\varphi_{N,1}^n(\beta(x_i)) = \varphi_{N,1}^n \left(\sum_{k=1}^{s_r} j_{i,k} y_{i,k}\right) = \sum_{k=1}^{s_r} \varphi_1^n(j_{i,k}) \varphi_{N}^n(y_{i,k}). \end{align*} $$
$$ \begin{align*}\varphi_{N,1}^n(\beta(x_i)) = \varphi_{N,1}^n \left(\sum_{k=1}^{s_r} j_{i,k} y_{i,k}\right) = \sum_{k=1}^{s_r} \varphi_1^n(j_{i,k}) \varphi_{N}^n(y_{i,k}). \end{align*} $$
By our assumption,
![]() $\varphi _1$
on J is pointwise topologically nilpotent, and so, in particular, for each
$\varphi _1$
on J is pointwise topologically nilpotent, and so, in particular, for each
![]() $m_0 \geq 0$
, we can find
$m_0 \geq 0$
, we can find
![]() $m\geq 0$
, such that
$m\geq 0$
, such that
![]() $\varphi _1^m(j_{i,k}) \in (p,\tilde {\xi })^{m_0}$
, for all
$\varphi _1^m(j_{i,k}) \in (p,\tilde {\xi })^{m_0}$
, for all
![]() $i=1,\dots , r$
,
$i=1,\dots , r$
,
![]() $j=1,\dots , s_r$
. The above equalities show that for all
$j=1,\dots , s_r$
. The above equalities show that for all
![]() $n\geq m$
and for all
$n\geq m$
and for all
![]() $x\in M$
,
$x\in M$
,
Hence, we deduce from the above that for every
![]() $\beta \colon M\to JN$
, the sequence
$\beta \colon M\to JN$
, the sequence
converges to
![]() $0$
(because A is
$0$
(because A is
![]() $(p,\tilde {\xi })$
-adically complete as
$(p,\tilde {\xi })$
-adically complete as
![]() $(A,\tilde {\xi })$
is bounded). Now let
$(A,\tilde {\xi })$
is bounded). Now let
![]() $\alpha \colon M\to N$
be a homomorphism of windows, such that
$\alpha \colon M\to N$
be a homomorphism of windows, such that
![]() $\alpha \equiv 0$
modulo J. Then
$\alpha \equiv 0$
modulo J. Then
![]() $U^n(\alpha )=\alpha $
for all n because
$U^n(\alpha )=\alpha $
for all n because
![]() $\alpha \circ \varphi _M=\varphi _N\circ \alpha $
, which implies
$\alpha \circ \varphi _M=\varphi _N\circ \alpha $
, which implies
![]() $\alpha =0$
as the sequence
$\alpha =0$
as the sequence
![]() $U^n(\alpha )$
converges to
$U^n(\alpha )$
converges to
![]() $0$
as we saw above. Conversely, assume that
$0$
as we saw above. Conversely, assume that
![]() $\alpha \colon M\to N$
is an A-module homomorphism, such that
$\alpha \colon M\to N$
is an A-module homomorphism, such that
![]() $\alpha $
modulo J is an homomorphism of windows over
$\alpha $
modulo J is an homomorphism of windows over
![]() $\underline {B}$
. Then
$\underline {B}$
. Then
![]() $\alpha $
maps
$\alpha $
maps
![]() $\mathrm {Fil} M$
to
$\mathrm {Fil} M$
to
![]() $\mathrm {Fil} N$
because this can be checked modulo J. Note that
$\mathrm {Fil} N$
because this can be checked modulo J. Note that
![]() $(\varphi _M^{\sharp })^{-1}(\tilde {\xi }.M)= \varphi ^{\ast }(\mathrm {Fil} M)$
as follows from Lemma 4.23. Hence,
$(\varphi _M^{\sharp })^{-1}(\tilde {\xi }.M)= \varphi ^{\ast }(\mathrm {Fil} M)$
as follows from Lemma 4.23. Hence,
![]() $U(\alpha )$
sends M to N. Set
$U(\alpha )$
sends M to N. Set
Then
![]() $\beta (M)\subseteq JN$
by the assumption on
$\beta (M)\subseteq JN$
by the assumption on
![]() $\alpha $
. Therefore, the homomorphism
$\alpha $
. Therefore, the homomorphism
 $$ \begin{align*}\tilde{\alpha}\colon M\to N,\ m\mapsto \alpha(m)+\sum\limits_{n=0}^{\infty} U^n(\beta)(m) \end{align*} $$
$$ \begin{align*}\tilde{\alpha}\colon M\to N,\ m\mapsto \alpha(m)+\sum\limits_{n=0}^{\infty} U^n(\beta)(m) \end{align*} $$
is well defined. Moreover,
![]() $\alpha \equiv \tilde {\alpha }$
modulo J and
$\alpha \equiv \tilde {\alpha }$
modulo J and
![]() $\tilde {\alpha }$
is a homomorphism of windows over
$\tilde {\alpha }$
is a homomorphism of windows over
![]() $\underline {A}$
.
$\underline {A}$
.
From the proof of the last lemma, one can also extract the following statement.
Lemma 4.33. Let
![]() $R \to R'$
be a morphism of quasiregular semiperfectoid rings, such that
$R \to R'$
be a morphism of quasiregular semiperfectoid rings, such that
![]() is contained in
is contained in
![]() , stable by
, stable by
![]() $\varphi _1$
and such that
$\varphi _1$
and such that
![]() $\varphi _1$
is topologically nilpotent on J (for some, or equivalently any, choice of a generator of the ideal I defining the prism structure of
$\varphi _1$
is topologically nilpotent on J (for some, or equivalently any, choice of a generator of the ideal I defining the prism structure of
![]() ). Then the base change functors
). Then the base change functors
are faithful.
Proof. It is enough to prove that the first functor is faithful. For this, one uses the exact same argument used in the proof of Lemma 4.32.
Remark 4.34. More generally, if one has a
![]() $1$
-morphism of frames
$1$
-morphism of frames
![]() $\underline {A} \to \underline {A}'$
, whose kernel J is contained in
$\underline {A} \to \underline {A}'$
, whose kernel J is contained in
![]() $\mathrm {Fil}~ A$
, stable by
$\mathrm {Fil}~ A$
, stable by
![]() $\varphi _1$
and such that
$\varphi _1$
and such that
![]() $\varphi _1$
is topologically nilpotent on J, the same proof shows that the base change functor
$\varphi _1$
is topologically nilpotent on J, the same proof shows that the base change functor
is faithful.
4.2 Definition of the prismatic Dieudonné functor
In this subsection, we define the prismatic Dieudonné crystals of p-divisible groups over quasisyntomic rings and prove some formal properties of them. More difficult properties, like the crystal property or local freeness, will be proved later (cf. Section 4.6) after discussing the case of abelian schemes first (cf. Section 4.5).
Let
![]() $R\in \mathrm {QSyn}$
be a quasisyntomic ring, and let
$R\in \mathrm {QSyn}$
be a quasisyntomic ring, and let
![]() be its absolute prismatic site. We recall from Proposition 4.4 that the category of finite locally free crystals on
be its absolute prismatic site. We recall from Proposition 4.4 that the category of finite locally free crystals on
![]() is equivalent to the category of finite locally free
is equivalent to the category of finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-modules on the small quasisyntomic site
$\mathcal {O}^{\mathrm {pris}}$
-modules on the small quasisyntomic site
![]() $(R)_{\mathrm {qsyn}}$
of R endowed with the quasisyntomic topology.
$(R)_{\mathrm {qsyn}}$
of R endowed with the quasisyntomic topology.
Recall as well that there is an exact sequence
where
![]() $\mathcal {O}$
is the structure sheaf
$\mathcal {O}$
is the structure sheaf
![]() $S\in (R)_{\mathrm {qsyn}}\mapsto S$
on
$S\in (R)_{\mathrm {qsyn}}\mapsto S$
on
![]() $(R)_{\mathrm {qsyn}}$
(cf. Proposition 4.2).
$(R)_{\mathrm {qsyn}}$
(cf. Proposition 4.2).
Definition 4.35. Let G be a p-divisible group over R. We defineFootnote 18
and
![]() as the endomorphism of
as the endomorphism of
![]() induced from the endomorphism
induced from the endomorphism
![]() $\varphi $
on
$\varphi $
on
![]() $\mathcal {O}^{\mathrm {pris}}$
. We call
$\mathcal {O}^{\mathrm {pris}}$
. We call
![]() the prismatic Dieudonné crystal of G.
the prismatic Dieudonné crystal of G.
We will check later that
![]() is indeed a (n admissible) prismatic Dieudonné crystal.
is indeed a (n admissible) prismatic Dieudonné crystal.
Remark 4.36. Let us note that
for any derived p-adically complete quasisyntomic sheaf Q. Indeed, the finite locally free group schemes
![]() $G[p^n]$
are syntomic over R for
$G[p^n]$
are syntomic over R for
![]() $n\geq 0$
(as follows, e.g. from [Reference Messing44, II.(3.2.6)]) (hence, multiplication by p on G is surjective in the syntomic topology). This implies that the derived p-completion of G on the big quasisyntomic site over R is given by
$n\geq 0$
(as follows, e.g. from [Reference Messing44, II.(3.2.6)]) (hence, multiplication by p on G is surjective in the syntomic topology). This implies that the derived p-completion of G on the big quasisyntomic site over R is given by
![]() $T_pG$
placed in degree
$T_pG$
placed in degree
![]() $-1$
. As there are no morphisms from
$-1$
. As there are no morphisms from
![]() $D^{\leq -1}$
to
$D^{\leq -1}$
to
![]() $D^{\geq 0}$
, and Q is assumed to be derived p-adically complete, the statement follows.
$D^{\geq 0}$
, and Q is assumed to be derived p-adically complete, the statement follows.
In particular, we can apply this to
![]() $Q=\mathcal {O}^{\mathrm {pris}}$
and deduce that
$Q=\mathcal {O}^{\mathrm {pris}}$
and deduce that
and thus also
Remark 4.37. Beware that the prismatic Dieudonné crystal of a p-divisible group is a sheaf on the quasisyntomic site, not on the prismatic site. In particular, it is not a crystal on the prismatic site of R, but rather the pushforward along v of a crystal on the prismatic site (as will be proved later). We hope that this choice of terminology does not create too much confusion; from the mathematical point of view, it is justified by Proposition 4.4.
Fix a p-divisible group G over R. We check some easy properties of
![]() .
.
In [Reference Berthelot, Breen and Messing6], the crystalline Dieudonné crystal of a p-divisible group is defined via the sheaf of local extensions on the crystalline site. There is a similar description of the prismatic Dieudonné crystal.
Lemma 4.38. There is a canonical isomorphism
Proof. First, we claim that there is a canonical isomorphism
By adjunction, there is a canonical isomorphism
It thus suffices to see that
![]() , respectively,
, respectively,
![]() , are the first cohomology sheaves on both sides. The sheaves
, are the first cohomology sheaves on both sides. The sheaves
are
![]() $0$
: for the first, this follows as G is p-divisible and the target derived p-complete, cf. Remark 4.36, and for the second, the same argument as in Remark 4.36 can be applied since the multiplication by p map on
$0$
: for the first, this follows as G is p-divisible and the target derived p-complete, cf. Remark 4.36, and for the second, the same argument as in Remark 4.36 can be applied since the multiplication by p map on
![]() $u^{-1}(G)$
is surjective and the prismatic topos is replete. This implies the claim.
$u^{-1}(G)$
is surjective and the prismatic topos is replete. This implies the claim.
To finish, the proof of the proposition, it, therefore, remains to show that we have
We will, in fact, give an argument, inspired by [Reference Bauer3], which works with
![]() $\mathcal {E}xt^1$
replaced by
$\mathcal {E}xt^1$
replaced by
![]() $\mathcal {E}xt^i$
, for any
$\mathcal {E}xt^i$
, for any
![]() $i\geq 0$
. The Breen-Deligne resolution
$i\geq 0$
. The Breen-Deligne resolution
![]() $C(G)$
of G, seen either as a sheaf on the big or on the small quasisyntomic site (cf. [Reference Scholze48, Appendix to Lecture IV], see also Section 4.4 below for a partial explicit resolution, sufficient for our purposes), gives, for each
$C(G)$
of G, seen either as a sheaf on the big or on the small quasisyntomic site (cf. [Reference Scholze48, Appendix to Lecture IV], see also Section 4.4 below for a partial explicit resolution, sufficient for our purposes), gives, for each
![]() $i\geq 0$
, spectral sequences
$i\geq 0$
, spectral sequences
and
Since for each j,
![]() $C_j(G)$
is a finite direct sum of terms of the form
$C_j(G)$
is a finite direct sum of terms of the form
![]() $\mathbb {Z}[G^n]$
,
$\mathbb {Z}[G^n]$
,
![]() $n\geq 1$
, it suffices to show that for each
$n\geq 1$
, it suffices to show that for each
![]() $k\geq 0, j\geq 1$
,
$k\geq 0, j\geq 1$
,
Since
![]() $f_n: G^n \to \mathrm {Spf}(R)$
is quasisyntomic, it induces a morphism of topoi
$f_n: G^n \to \mathrm {Spf}(R)$
is quasisyntomic, it induces a morphism of topoi
![]() $f_{n,\mathrm {qsyn}}: G_{\mathrm {qsyn}}^n \to (R)_{\mathrm {qsyn}}$
, identifying
$f_{n,\mathrm {qsyn}}: G_{\mathrm {qsyn}}^n \to (R)_{\mathrm {qsyn}}$
, identifying
![]() $G_{\mathrm {qsyn}}^n$
with the slice topos
$G_{\mathrm {qsyn}}^n$
with the slice topos
![]() $(R)_{\mathrm {qsyn}}/G^n$
. Hence,
$(R)_{\mathrm {qsyn}}/G^n$
. Hence,
Analogously, if
![]() $f_{n,\mathrm {QSYN}}: G_{\mathrm {QSYN}}^n \to (R)_{\mathrm {QSYN}}$
denotes the morphism of topoi induced by
$f_{n,\mathrm {QSYN}}: G_{\mathrm {QSYN}}^n \to (R)_{\mathrm {QSYN}}$
denotes the morphism of topoi induced by
![]() $f_n$
, we have
$f_n$
, we have
The sheaf
![]() is the sheaf attached to the presheaf sending
is the sheaf attached to the presheaf sending
![]() $X \in (R)_{\mathrm {qsyn}}$
to
$X \in (R)_{\mathrm {qsyn}}$
to
while the sheaf
![]() is the sheaf attached to the presheaf sending
is the sheaf attached to the presheaf sending
![]() $X \in (R)_{\mathrm {qsyn}}$
to
$X \in (R)_{\mathrm {qsyn}}$
to
Both
![]() $f_{n, \mathrm {qsyn}}^{\ast } X$
and
$f_{n, \mathrm {qsyn}}^{\ast } X$
and
![]() $f_{n, \mathrm {QSYN}}^{\ast } X$
are represented by
$f_{n, \mathrm {QSYN}}^{\ast } X$
are represented by
![]() $X \times _{\mathrm {Spf}(R)} G^n \in G_{\mathrm {qsyn}}^n$
, and, therefore,
$X \times _{\mathrm {Spf}(R)} G^n \in G_{\mathrm {qsyn}}^n$
, and, therefore,
![]() , respectively,
, respectively,
![]() , agrees with
, agrees with
![]() , respectively, with
, respectively, with
![]() . But these last two cohomology groups agree, since on both sites, quasiregular semiperfectoid rings form a basis on which the cohomology in positives degrees of
. But these last two cohomology groups agree, since on both sites, quasiregular semiperfectoid rings form a basis on which the cohomology in positives degrees of
![]() vanishes. Whence our claim, and the end of the proof.
vanishes. Whence our claim, and the end of the proof.
Using the p-adic Tate module
![]() $T_pG$
of G, that is, the inverse limit
$T_pG$
of G, that is, the inverse limit
of sheaves on
![]() $(R)_{\mathrm {qsyn}}$
, one can give a more explicit description of the prismatic Dieudonné crystal
$(R)_{\mathrm {qsyn}}$
, one can give a more explicit description of the prismatic Dieudonné crystal
![]() .
.
Lemma 4.39. Define the universal cover
![]() $\tilde {G}:=\varprojlim \limits_{p} G$
of G. Then the sequences
$\tilde {G}:=\varprojlim \limits_{p} G$
of G. Then the sequences
 $$ \begin{align*}\begin{matrix} 0\to T_pG\to \tilde{G}\to G\to 0\\ 0\to u^{-1} T_pG\to u^{-1} \tilde{G}\to u^{-1} G\to 0 \end{matrix} \end{align*} $$
$$ \begin{align*}\begin{matrix} 0\to T_pG\to \tilde{G}\to G\to 0\\ 0\to u^{-1} T_pG\to u^{-1} \tilde{G}\to u^{-1} G\to 0 \end{matrix} \end{align*} $$
of sheaves on
![]() $(R)_{\mathrm {qsyn}}$
, respectively,
$(R)_{\mathrm {qsyn}}$
, respectively,
![]() are exact for the quasisyntomic topology.
are exact for the quasisyntomic topology.
Proof. Exactness of the second follows from exactness of the first and exactness of
![]() $u^{-1}$
(cf. Corollary 3.25). Each
$u^{-1}$
(cf. Corollary 3.25). Each
![]() $G[p^n]$
is syntomic over R. This implies that
$G[p^n]$
is syntomic over R. This implies that
![]() $\tilde {G}\to G$
is a quasisyntomic cover, which implies exactness of the first sequence.
$\tilde {G}\to G$
is a quasisyntomic cover, which implies exactness of the first sequence.
The following lemma will be useful when describing the prismatic Dieudonné crystals of
![]() $\mathbb {Q}_p/\mathbb {Z}_p$
and
$\mathbb {Q}_p/\mathbb {Z}_p$
and
![]() $\mu _{p^{\infty }}$
and when proving fully faithfulness of the prismatic Dieudonné functor.
$\mu _{p^{\infty }}$
and when proving fully faithfulness of the prismatic Dieudonné functor.
Lemma 4.40. There are canonical isomorphisms
Proof. This follows from Lemma 4.39 and the fact that
as
![]() are derived p-complete sheaves and
are derived p-complete sheaves and
![]() $\tilde {G}$
is a
$\tilde {G}$
is a
![]() $\mathbb {Q}_p$
-vector space.
$\mathbb {Q}_p$
-vector space.
Remark 4.41. The universal vector extension
![]() $E(G)$
of G can be seen as an extension of sheaves on
$E(G)$
of G can be seen as an extension of sheaves on
![]() $(R)_{\mathrm {qsyn}}$
:
$(R)_{\mathrm {qsyn}}$
:
It is defined as in [Reference Messing44] (this makes sense since R is p-complete), or equivalently, as the pushout of the universal cover exact sequence
along the Hodge-Tate map
which sends
![]() $f \in T_p G = \mathrm {Hom}_R(\mathbb {Q}_p/\mathbb {Z}_p,G)$
, viewed by Cartier duality as an element of
$f \in T_p G = \mathrm {Hom}_R(\mathbb {Q}_p/\mathbb {Z}_p,G)$
, viewed by Cartier duality as an element of
![]() $\mathrm {Hom}_{R}(\check {G},\mu _{p^{\infty }})$
, to
$\mathrm {Hom}_{R}(\check {G},\mu _{p^{\infty }})$
, to
![]() $f^* dT/T$
,
$f^* dT/T$
,
![]() $dT/T$
being the canonical generator of
$dT/T$
being the canonical generator of
![]() $\omega _{\mu _{p^{\infty }}}$
. Is there a way to use Lemma 4.40 to relate the prismatic Dieudonné module to the dual of the Lie algebra of
$\omega _{\mu _{p^{\infty }}}$
. Is there a way to use Lemma 4.40 to relate the prismatic Dieudonné module to the dual of the Lie algebra of
![]() $E(G)$
?
$E(G)$
?
Assume now that R is quasiregular semiperfectoid. Then, by Proposition 4.4, the category of finite locally free crystals on
![]() is equivalent to the category of finite projective
is equivalent to the category of finite projective
![]() -modules by evaluating a crystal on the initial prism
-modules by evaluating a crystal on the initial prism
![]() . Similarly, finite locally free
. Similarly, finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-modules on
$\mathcal {O}^{\mathrm {pris}}$
-modules on
![]() $(R)_{\mathrm {qsyn}}$
are equivalent to finite projective
$(R)_{\mathrm {qsyn}}$
are equivalent to finite projective
![]() by evaluating a finite locally free
by evaluating a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() $\mathcal {M}$
on R. This allows the following simplification of the definition of the prismatic Dieudonné crystal of a p-divisible group G over R.
$\mathcal {M}$
on R. This allows the following simplification of the definition of the prismatic Dieudonné crystal of a p-divisible group G over R.
Definition 4.42. Let R be quasiregular semiperfectoid, and let G be a p-divisible group over R. Define
and
![]() as the endomorphism induced by
as the endomorphism induced by
![]() $\varphi $
on
$\varphi $
on
![]() $\mathcal {O}^{\mathrm {pris}}$
. We call
$\mathcal {O}^{\mathrm {pris}}$
. We call
the prismatic Dieudonné module of G.
We will see later that
![]() is indeed a (n admissible) prismatic Dieudonné module in the sense of Definition 4.10. Moreover,
is indeed a (n admissible) prismatic Dieudonné module in the sense of Definition 4.10. Moreover,
![]() is the evaluation of the prismatic Dieudonné crystal
is the evaluation of the prismatic Dieudonné crystal
![]() as follows from the local-global spectral sequence
as follows from the local-global spectral sequence
by the vanishing of the sheaf
![]() $\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(G,\mathcal {O}^{\mathrm {pris}})$
. Thus, under the equivalence from Proposition 4.13, the prismatic Dieudonné crystal
$\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(G,\mathcal {O}^{\mathrm {pris}})$
. Thus, under the equivalence from Proposition 4.13, the prismatic Dieudonné crystal
![]() corresponds to the prismatic Dieudonné module
corresponds to the prismatic Dieudonné module
![]() .
.
4.3 Comparison with former constructions
In this section, we prove a comparison of the prismatic Dieudonné functor
![]() with former constructions, in two special cases:
with former constructions, in two special cases:
-
1. For quasisyntomic rings, such that
 $pR=0$
, we relate
$pR=0$
, we relate
 to the crystalline Dieudonné functor of Berthelot-Breen-Messing [Reference Berthelot, Breen and Messing6].
to the crystalline Dieudonné functor of Berthelot-Breen-Messing [Reference Berthelot, Breen and Messing6]. -
2. For perfectoid rings, we relate the prismatic Dieudonné functor to the functor introduced by Scholze-Weinstein in [Reference Scholze and Weinstein51, Appendix to Lecture XVII].
The intersection of these two cases is the case of perfect rings, which was historically the first to be studied. The situation for perfect fields is briefly discussed at the end of this section.
We start with the case of quasisyntomic rings R with
![]() $pR=0$
. We want to compare the prismatic Dieudonné functor to the crystalline Dieudonné functor
$pR=0$
. We want to compare the prismatic Dieudonné functor to the crystalline Dieudonné functor
of [Reference Berthelot, Breen and Messing6]. Here,
![]() $(R/\mathbb {Z}_p)_{\mathrm {crys},\mathrm {pr}}$
is the (big) crystalline site of R over
$(R/\mathbb {Z}_p)_{\mathrm {crys},\mathrm {pr}}$
is the (big) crystalline site of R over
![]() $\mathbb {Z}_p$
,
$\mathbb {Z}_p$
,
![]() $\mathcal {O}_{\mathrm {crys}}$
is the crystalline structure sheaf,
$\mathcal {O}_{\mathrm {crys}}$
is the crystalline structure sheaf,
![]() $\mathrm {pr}$
denotes the p-th root topology of [Reference Lau37, Definition 7.2] and
$\mathrm {pr}$
denotes the p-th root topology of [Reference Lau37, Definition 7.2] and
defined as in [Reference Lau37, Lemma 8.1], where the left-hand side denotes the category of all schemes over R endowed with the
![]() $p$
-th root topology. As in [Reference Lau37, Section 8], we define
$p$
-th root topology. As in [Reference Lau37, Section 8], we define
as the pushforward of the crystalline structure sheaf
![]() $\mathcal {O}_{\mathrm {crys}}$
along the morphism
$\mathcal {O}_{\mathrm {crys}}$
along the morphism
of topoi. Note that by definition
![]() $i_*^{\mathrm {crys}}=(u^{\mathrm {crys}})^{-1}$
, so we can rewrite the crystalline Dieudonné functor as
$i_*^{\mathrm {crys}}=(u^{\mathrm {crys}})^{-1}$
, so we can rewrite the crystalline Dieudonné functor as
Let
![]() $\mathcal {J}^{\mathrm {crys}}\subseteq \mathcal {O}^{\mathrm {crys}}$
be the pushforward of the crystalline ideal sheaf
$\mathcal {J}^{\mathrm {crys}}\subseteq \mathcal {O}^{\mathrm {crys}}$
be the pushforward of the crystalline ideal sheaf
![]() $\mathcal {J}_{\mathrm {crys}}\subseteq \mathcal {O}_{\mathrm {crys}}$
.
$\mathcal {J}_{\mathrm {crys}}\subseteq \mathcal {O}_{\mathrm {crys}}$
.
The following lemma is the basic input in the comparison of the prismatic and crystalline Dieudonné functor.
Lemma 4.43. Let
![]() $R^{\prime }$
be a quasisyntomic
$R^{\prime }$
be a quasisyntomic
![]() $\mathbb {F}_p$
-algebra. Then there is a canonical isomorphism
$\mathbb {F}_p$
-algebra. Then there is a canonical isomorphism
identifying
![]() $\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}(R^{\prime })$
with
$\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}(R^{\prime })$
with
![]() $\mathcal {J}^{\mathrm {crys}}(R^{\prime })$
.
$\mathcal {J}^{\mathrm {crys}}(R^{\prime })$
.
Proof. Using the sheaf property for the
![]() $\mathrm {pr}$
-topology, we may assume that
$\mathrm {pr}$
-topology, we may assume that
![]() $R^{\prime }$
is semiperfect. Then
$R^{\prime }$
is semiperfect. Then
![]() $R^{\prime }$
is even quasiregular semiperfect as it is quasisyntomic. Hence,
$R^{\prime }$
is even quasiregular semiperfect as it is quasisyntomic. Hence,
by Lemma 3.27. Moreover, the isomorphism in Lemma 3.27 identifies
![]() $\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}(R^{\prime })$
with
$\mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}(R^{\prime })$
with
![]() $\mathcal {J}^{\mathrm {crys}}$
.
$\mathcal {J}^{\mathrm {crys}}$
.
Let
![]() $(R)_{\mathrm {qsyn},\mathrm {pr}}$
be the category of quasisyntomic R-algebras equipped with the
$(R)_{\mathrm {qsyn},\mathrm {pr}}$
be the category of quasisyntomic R-algebras equipped with the
![]() $\mathrm {pr}$
-topology, and let
$\mathrm {pr}$
-topology, and let
obtained by composing
![]() $u^{\mathrm {crys}}_{\ast }$
with restriction (the same caveat as in the beginning of Section 4.1 applies here). Lemma 4.43 implies that the sheaves
$u^{\mathrm {crys}}_{\ast }$
with restriction (the same caveat as in the beginning of Section 4.1 applies here). Lemma 4.43 implies that the sheaves
![]() $\mathcal {O}^{\mathrm {pris}}$
and
$\mathcal {O}^{\mathrm {pris}}$
and
![]() $\mathcal {O}^{\mathrm {crys}}$
on
$\mathcal {O}^{\mathrm {crys}}$
on
![]() $(R)_{\mathrm {qsyn},\mathrm {pr}}$
are isomorphic. We note that the categories of finite locally free
$(R)_{\mathrm {qsyn},\mathrm {pr}}$
are isomorphic. We note that the categories of finite locally free
![]() $\mathcal {O}^{\mathrm {crys}}$
-modules on
$\mathcal {O}^{\mathrm {crys}}$
-modules on
![]() $(R)_{\mathrm {pr}}$
and finite locally free
$(R)_{\mathrm {pr}}$
and finite locally free
![]() $\mathcal {O}^{\mathrm {crys}}_{|(R)_{\mathrm {qsyn},\mathrm {pr}}}$
-modules on
$\mathcal {O}^{\mathrm {crys}}_{|(R)_{\mathrm {qsyn},\mathrm {pr}}}$
-modules on
![]() $(R)_{\mathrm {qsyn},\mathrm {pr}}$
are equivalent because for R quasiregular semiperfect, both categories identify with finite locally free
$(R)_{\mathrm {qsyn},\mathrm {pr}}$
are equivalent because for R quasiregular semiperfect, both categories identify with finite locally free
![]() $A_{\mathrm {crys}}(R)$
-modules. These remarks give a meaning to the comparison contained in the next two results.
$A_{\mathrm {crys}}(R)$
-modules. These remarks give a meaning to the comparison contained in the next two results.
Theorem 4.44. Let R be a quasisyntomic ring with
![]() $pR=0$
and G a p-divisible group over R. Then there is a canonical Frobenius equivariant isomorphism
$pR=0$
and G a p-divisible group over R. Then there is a canonical Frobenius equivariant isomorphism
from the prismatic Dieudonné crystal of G (cf. Definition 4.35) to the pushforward of the crystalline Dieudonné crystal of G. In particular, if R is quasiregular semiperfect,
![]() is isomorphic to the evaluation
is isomorphic to the evaluation
![]() $M^{\mathrm {crys}}(G)$
on
$M^{\mathrm {crys}}(G)$
on
![]() $A_{\mathrm {crys}}(R)$
of the crystalline Dieudonné crystal, compatibly with the Frobenius.
$A_{\mathrm {crys}}(R)$
of the crystalline Dieudonné crystal, compatibly with the Frobenius.
Of course, the isomorphism is linear over the isomorphism
![]() $\mathcal {O}^{\mathrm {pris}}\cong \mathcal {O}^{\mathrm {crys}}$
from Lemma 4.43.
$\mathcal {O}^{\mathrm {pris}}\cong \mathcal {O}^{\mathrm {crys}}$
from Lemma 4.43.
Proof. By definition
But
Indeed, by the spectral sequence constructed in Section 4.4 below, it suffices to see that the
![]() $\mathcal {O}^{\mathrm {pris}}$
-cohomology for the quasisyntomic and pr-topologies agree. But quasiregular semiperfectoid rings form a basis for both topologies, and on such, the higher cohomology of
$\mathcal {O}^{\mathrm {pris}}$
-cohomology for the quasisyntomic and pr-topologies agree. But quasiregular semiperfectoid rings form a basis for both topologies, and on such, the higher cohomology of
![]() $\mathcal {O}^{\mathrm {pris}}$
vanishes in both topologies. Thus, by Lemma 4.43, it suffices to see
$\mathcal {O}^{\mathrm {pris}}$
vanishes in both topologies. Thus, by Lemma 4.43, it suffices to see
As
![]() $u^{\mathrm {crys}}$
is a morphism of topoi, we get
$u^{\mathrm {crys}}$
is a morphism of topoi, we get
Here, we use that we are dealing with the pr-topology: we don’t know if this statement is true for the quasisyntomic topology, but it holds the syntomic topology as the arguments of [Reference Berthelot, Breen and Messing6, Proposition 1.1.5] apply because syntomic morphisms can be lifted locally along PD-thickenings, cf. [Reference Project52, Tag 0070]. As in 4.38, it suffices to see that
vanish (here,
![]() $\epsilon _{\ast }$
is the (exact) pushforward to the small quasisyntomic site). The sheaf
$\epsilon _{\ast }$
is the (exact) pushforward to the small quasisyntomic site). The sheaf
![]() $R^1u^{\mathrm {crys}}_{\ast }(\mathcal {O}_{\mathrm {crys}})$
for the pr-topology on
$R^1u^{\mathrm {crys}}_{\ast }(\mathcal {O}_{\mathrm {crys}})$
for the pr-topology on
![]() $(R)_{\mathrm { QSYN,pr}}$
vanishes on every R-algebra S, which is quasisyntomic, because it vanishes on quasiregular semiperfects (cf. [Reference Bhatt, Morrow and Scholze12, Section 8]), and each quasisyntomic
$(R)_{\mathrm { QSYN,pr}}$
vanishes on every R-algebra S, which is quasisyntomic, because it vanishes on quasiregular semiperfects (cf. [Reference Bhatt, Morrow and Scholze12, Section 8]), and each quasisyntomic
![]() $\mathbb {F}_p$
-algebra admits a pr-cover by some quasiregular semiperfect ring. Write
$\mathbb {F}_p$
-algebra admits a pr-cover by some quasiregular semiperfect ring. Write
The set
![]() $\mathrm {Hom}_{(R)_{\mathrm {QSYN,pr}}}(G[p^n],R^1u^{\mathrm {crys}}_{\ast }(\mathcal {O}_{\mathrm {crys}}))$
embeds into the sections of
$\mathrm {Hom}_{(R)_{\mathrm {QSYN,pr}}}(G[p^n],R^1u^{\mathrm {crys}}_{\ast }(\mathcal {O}_{\mathrm {crys}}))$
embeds into the sections of
![]() $R^1u_{\ast }^{\mathrm {crys}}(\mathcal {O}_{\mathrm {crys}})$
over
$R^1u_{\ast }^{\mathrm {crys}}(\mathcal {O}_{\mathrm {crys}})$
over
![]() $G[p^n]$
, but these sections vanish because
$G[p^n]$
, but these sections vanish because
![]() $G[p^n]$
is syntomic over R. Applying the same reasoning to all quasisyntomic R-algebras proves the desired vanishing of the first
$G[p^n]$
is syntomic over R. Applying the same reasoning to all quasisyntomic R-algebras proves the desired vanishing of the first
![]() $\mathcal {H}om$
. For the second
$\mathcal {H}om$
. For the second
![]() $\mathcal {H}om$
, note that
$\mathcal {H}om$
, note that
![]() $\mathcal {O}_{\mathrm {crys}}, (u^{\mathrm {crys}})^{-1}(G)$
are actually sheaves for the syntomic topology on the site
$\mathcal {O}_{\mathrm {crys}}, (u^{\mathrm {crys}})^{-1}(G)$
are actually sheaves for the syntomic topology on the site
![]() $(R/\mathbb {Z}_p)_{\mathrm {crys}}$
and the local
$(R/\mathbb {Z}_p)_{\mathrm {crys}}$
and the local
![]() $\mathcal {H}om$
does not depend on the topology. Multiplication by
$\mathcal {H}om$
does not depend on the topology. Multiplication by
![]() $p^n$
on
$p^n$
on
![]() $(u^{\mathrm {crys}})^{-1}(G)$
is surjective for the syntomic topology for every
$(u^{\mathrm {crys}})^{-1}(G)$
is surjective for the syntomic topology for every
![]() $n\geq 0$
([Reference Berthelot, Breen and Messing6, Proposition 1.1.7]). This implies that
$n\geq 0$
([Reference Berthelot, Breen and Messing6, Proposition 1.1.7]). This implies that
using that
![]() $\mathcal {O}_{\mathrm {crys}}$
is p-adically complete (being p-adically separated would be sufficient for this argument). Lemma 4.43 implies then moreover compatibility with Frobenius.
$\mathcal {O}_{\mathrm {crys}}$
is p-adically complete (being p-adically separated would be sufficient for this argument). Lemma 4.43 implies then moreover compatibility with Frobenius.
In general, that is, when p is not necessarily zero in R, one can still relate the prismatic Dieudonné crystal of a p-divisible group to the crystalline Dieudonné crystal, as follows. Let R be a p-complete ring, and let D be a p-complete p-torsion free
![]() $\delta $
-ring with a surjection
$\delta $
-ring with a surjection
![]() $D\to R$
whose kernel has divided powers.Footnote
19
As the kernel of
$D\to R$
whose kernel has divided powers.Footnote
19
As the kernel of
![]() $D\to R$
has divided powers, the Frobenius on D induces a morphism
$D\to R$
has divided powers, the Frobenius on D induces a morphism
![]() $R\to D/p$
. With this morphism, the prism
$R\to D/p$
. With this morphism, the prism
![]() $(D,(p))$
defines an object of the absolute prismatic site
$(D,(p))$
defines an object of the absolute prismatic site
![]() of R. Via Lemma 4.38, it thus makes sense to evaluate the prismatic Dieudonné module of a p-divisible group over R, more precisely
of R. Via Lemma 4.38, it thus makes sense to evaluate the prismatic Dieudonné module of a p-divisible group over R, more precisely
![]() $v^{\ast }$
of it, on
$v^{\ast }$
of it, on
![]() $(D,(p))$
.
$(D,(p))$
.
Lemma 4.45. For every p-divisible group G over R there is a natural Frobenius equivariant isomorphism
Here,
![]() $\mathbb {D}(G)(D)$
denotes the evaluation of the (contravariant, crystalline) Dieudonné crystal of G on the PD-thickening
$\mathbb {D}(G)(D)$
denotes the evaluation of the (contravariant, crystalline) Dieudonné crystal of G on the PD-thickening
![]() $D\to R$
.
$D\to R$
.
Proof. Let
![]() $\mathcal {C}$
be the category of schemes over R, which are p-completely syntomic over R. For each scheme
$\mathcal {C}$
be the category of schemes over R, which are p-completely syntomic over R. For each scheme
![]() $H\in \mathcal {C}$
, there is a canonical isomorphism in the
$H\in \mathcal {C}$
, there is a canonical isomorphism in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {D}(\mathbb {Z})$
$\mathcal {D}(\mathbb {Z})$
by the crystalline comparison for syntomic morphisms (cf. Remark 3.8), where
![]() $H^{(1)}:=H\times _{\mathrm {Spec}(R)}\mathrm {Spec}(D/p)$
$H^{(1)}:=H\times _{\mathrm {Spec}(R)}\mathrm {Spec}(D/p)$
Footnote 20 ). We can write both sides as
respectively,
making it clear that both functors are actually restrictions to
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $R\mathrm {Hom}$
-functors
$R\mathrm {Hom}$
-functors
on the category of sheaves of abelian groups
![]() respectively,
respectively,
![]() $\mathrm {Shv}_{\mathbb {Z}}((R)_{\mathrm {crys}})$
on
$\mathrm {Shv}_{\mathbb {Z}}((R)_{\mathrm {crys}})$
on
![]() , respectively,
, respectively,
![]() $(R)_{\mathrm {crys}}$
along the functors
$(R)_{\mathrm {crys}}$
along the functors
respectively,
Assume now that H is a finite locally free group scheme over R, in particular, H is syntomic over R. Applying
![]() $F(-), G(-)$
to the Breen-Deligne resolution, cf. Theorem 4.55, of
$F(-), G(-)$
to the Breen-Deligne resolution, cf. Theorem 4.55, of
![]() $u^{-1}(H)$
,
$u^{-1}(H)$
,
![]() ${u^{\mathrm {crys}}}^{-1}(H)$
(seen via Dold-Kan as simplicial objects in
${u^{\mathrm {crys}}}^{-1}(H)$
(seen via Dold-Kan as simplicial objects in
![]() , respectively,
, respectively,
![]() $\mathrm {Shv}((R)_{\mathrm {crys}})$
) yield two cosimplicial objects
$\mathrm {Shv}((R)_{\mathrm {crys}})$
) yield two cosimplicial objects
![]() $K_1^{\bullet }, K_2^{\bullet }\colon \Delta \to \mathcal {D}({\mathbb {Z}})$
(here,
$K_1^{\bullet }, K_2^{\bullet }\colon \Delta \to \mathcal {D}({\mathbb {Z}})$
(here,
![]() $\Delta $
is the simplex category) with limits
$\Delta $
is the simplex category) with limits
and
We claim that the natural isomorphism
![]() $\eta $
extends to a natural isomorphism
$\eta $
extends to a natural isomorphism
![]() $K_1^{\bullet }\cong K_2^{\bullet }$
. Intuitively, this is clear as the morphisms in the Breen-Deligne resolution are sums of maps induced by morphisms between schemes. We thank Yonatan Harpaz and Fabian Hebestreit for their help with the following rigorous
$K_1^{\bullet }\cong K_2^{\bullet }$
. Intuitively, this is clear as the morphisms in the Breen-Deligne resolution are sums of maps induced by morphisms between schemes. We thank Yonatan Harpaz and Fabian Hebestreit for their help with the following rigorous
![]() $\infty $
-categorical argument. It suffices to argue for the left Kan extensions of
$\infty $
-categorical argument. It suffices to argue for the left Kan extensions of
![]() $F\circ \iota _{\mathrm {pris}}, G\circ \iota _{\mathrm {crys}}\colon \mathcal {C}\to \mathcal {D}(\mathbb {Z})^{\mathrm {op}}$
from
$F\circ \iota _{\mathrm {pris}}, G\circ \iota _{\mathrm {crys}}\colon \mathcal {C}\to \mathcal {D}(\mathbb {Z})^{\mathrm {op}}$
from
![]() $\mathcal {C}$
to the category of all schemes over R (this ensures the existence of fibre products in
$\mathcal {C}$
to the category of all schemes over R (this ensures the existence of fibre products in
![]() $\mathcal {C}$
commuting with coproducts). Hence, we abuse notation and denote by
$\mathcal {C}$
commuting with coproducts). Hence, we abuse notation and denote by
![]() $\mathcal {C}$
the category of all schemes over R. Let
$\mathcal {C}$
the category of all schemes over R. Let
![]() $\mathcal {D}$
be any category with action by the symmetric monodial (via tensor product) category
$\mathcal {D}$
be any category with action by the symmetric monodial (via tensor product) category
![]() $\mathcal {F}ree_{\mathbb {Z}}$
of finite free
$\mathcal {F}ree_{\mathbb {Z}}$
of finite free
![]() $\mathbb {Z}$
-modules, such that the action commutes with finite coproducts in each variable, for example,
$\mathbb {Z}$
-modules, such that the action commutes with finite coproducts in each variable, for example,
![]() $\mathcal {D}=\mathcal {D}(\mathbb {Z})^{\mathrm {op}}$
. In other words,
$\mathcal {D}=\mathcal {D}(\mathbb {Z})^{\mathrm {op}}$
. In other words,
![]() $\mathcal {D}$
is required to be a module under
$\mathcal {D}$
is required to be a module under
![]() $\mathcal {F}ree_{\mathbb {Z}}$
in the symmetric monoidal
$\mathcal {F}ree_{\mathbb {Z}}$
in the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}at_{\infty }(\mathcal {K}_{\mathrm {fin}})$
from [Reference Lurie39, Corollary 4.8.1.4] with
$\mathcal {C}at_{\infty }(\mathcal {K}_{\mathrm {fin}})$
from [Reference Lurie39, Corollary 4.8.1.4] with
![]() $\mathcal {K}_{\mathrm {fin}}$
the class of finite sets. Now each functor
$\mathcal {K}_{\mathrm {fin}}$
the class of finite sets. Now each functor
![]() $\varphi \colon \mathcal {C}\to \mathcal {D}$
preserving finite coproducts, respectively, each natural transformation between such functors extends to a functor
$\varphi \colon \mathcal {C}\to \mathcal {D}$
preserving finite coproducts, respectively, each natural transformation between such functors extends to a functor
![]() $\varphi ^{\mathrm {ab}}\colon \mathcal {C}^{\mathrm {ab}}:=\mathcal {F}ree_{\mathbb {Z}}\otimes _{\mathcal {K}_{\mathrm {fin}}} \mathcal {C}\to \mathcal {D}$
, respectively, a natural transformation between such functors with
$\varphi ^{\mathrm {ab}}\colon \mathcal {C}^{\mathrm {ab}}:=\mathcal {F}ree_{\mathbb {Z}}\otimes _{\mathcal {K}_{\mathrm {fin}}} \mathcal {C}\to \mathcal {D}$
, respectively, a natural transformation between such functors with
![]() $-\otimes _{\mathcal {K}_{\mathrm {fin}}}-$
the tensor product in
$-\otimes _{\mathcal {K}_{\mathrm {fin}}}-$
the tensor product in
![]() $\mathcal {C}at_{\infty }(\mathcal {K}_{\mathrm {fin}})$
by
$\mathcal {C}at_{\infty }(\mathcal {K}_{\mathrm {fin}})$
by
![]() $\mathcal {F}ree_{\mathbb {Z}}$
-linearity of
$\mathcal {F}ree_{\mathbb {Z}}$
-linearity of
![]() $\mathcal {D}$
. The category
$\mathcal {D}$
. The category
![]() $\mathcal {C}^{\mathrm {ab}}$
can now be calculated as follows: Consider the category
$\mathcal {C}^{\mathrm {ab}}$
can now be calculated as follows: Consider the category
![]() $\mathrm {Fun}(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
of functors, and its full subcategory
$\mathrm {Fun}(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
of functors, and its full subcategory
![]() $\mathrm {Fun}^{\times }(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
of product-preserving functors. The inclusion
$\mathrm {Fun}^{\times }(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
of product-preserving functors. The inclusion
![]() $\mathrm {Fun}^{\times }(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))\to \mathrm {Fun}(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
admits a left adjoint L, given by sheafification on
$\mathrm {Fun}^{\times }(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))\to \mathrm {Fun}(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
admits a left adjoint L, given by sheafification on
![]() $\mathcal {C}$
with respect to the Grothendieck topology in which coverings are finite collections
$\mathcal {C}$
with respect to the Grothendieck topology in which coverings are finite collections
![]() $\{X_i\to X\}_{i\in I}$
, such that
$\{X_i\to X\}_{i\in I}$
, such that
![]() $\coprod \limits _{i\in I} X_i\to X$
is an isomorphism. Now,
$\coprod \limits _{i\in I} X_i\to X$
is an isomorphism. Now,
![]() $\mathcal {C}^{\mathrm {ab}}$
is the smallest full subcategory of
$\mathcal {C}^{\mathrm {ab}}$
is the smallest full subcategory of
![]() $\mathrm {Fun}^{\times }(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
containing all objects
$\mathrm {Fun}^{\times }(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
containing all objects
![]() $L(\mathbb {Z}[\mathrm {Hom}_{\mathcal {C}}(-,X)])$
with
$L(\mathbb {Z}[\mathrm {Hom}_{\mathcal {C}}(-,X)])$
with
![]() $X\in \mathcal {C}$
. Note that
$X\in \mathcal {C}$
. Note that
![]() $\mathcal {C}^{\mathrm {ab}}$
is a
$\mathcal {C}^{\mathrm {ab}}$
is a
![]() $1$
-category because sheafification for this Grothendieck topology preserves set-valued presheaves. In fact, we only need that functors
$1$
-category because sheafification for this Grothendieck topology preserves set-valued presheaves. In fact, we only need that functors
![]() $\varphi \colon \mathcal {C}\to \mathcal {D}$
preserving coproducts extend to
$\varphi \colon \mathcal {C}\to \mathcal {D}$
preserving coproducts extend to
![]() $\mathcal {C}^{\mathrm {ab}}$
when the latter is defined by the above concrete description. To see this, note if
$\mathcal {C}^{\mathrm {ab}}$
when the latter is defined by the above concrete description. To see this, note if
![]() $\mathcal {S}$
denotes the
$\mathcal {S}$
denotes the
![]() $\infty $
-category of spaces, that is, Kan complexes, that
$\infty $
-category of spaces, that is, Kan complexes, that
by [Reference Lurie41, Example 1.2.9]. Each functor
![]() $\varphi \colon \mathcal {C}\to \mathcal {D}$
yields a functor
$\varphi \colon \mathcal {C}\to \mathcal {D}$
yields a functor
Now
![]() $\mathrm {Fun}(\mathcal {D}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
embeds into
$\mathrm {Fun}(\mathcal {D}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
embeds into
(with essential image those functors commuting with products in the second factor), and the
![]() $\mathcal {F}ree_{\mathbb {Z}}$
-action
$\mathcal {F}ree_{\mathbb {Z}}$
-action
![]() $\mathcal {F}ree_{\mathbb {Z}}\times \mathcal {D}\to \mathcal {D}$
furnishes a functor from this to the category
$\mathcal {F}ree_{\mathbb {Z}}\times \mathcal {D}\to \mathcal {D}$
furnishes a functor from this to the category
![]() $\mathrm {Fun}(\mathcal {D}^{\mathrm {op}},\mathcal {S}),$
which contains
$\mathrm {Fun}(\mathcal {D}^{\mathrm {op}},\mathcal {S}),$
which contains
![]() $\mathcal {D}$
by the Yoneda lemma. Restricting further along the inclusion
$\mathcal {D}$
by the Yoneda lemma. Restricting further along the inclusion
![]() $\mathcal {C}^{\mathrm {ab}}\to \mathrm {Fun}(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
then yields a functor
$\mathcal {C}^{\mathrm {ab}}\to \mathrm {Fun}(\mathcal {C}^{\mathrm {op}},\mathcal {D}_{\geq 0}(\mathbb {Z}))$
then yields a functor
with image in
![]() $\mathcal {D}$
as
$\mathcal {D}$
as
![]() $\varphi $
preserves finite coproducts. This yields the desired extension, and similarly, we see that natural transformations extend. Given these considerations, and, in particular, the description of
$\varphi $
preserves finite coproducts. This yields the desired extension, and similarly, we see that natural transformations extend. Given these considerations, and, in particular, the description of
![]() $\mathcal {C}^{\mathrm {ab}}$
, it follows by unraveling the construction that, in our situation, the simplicial objects given by the images under F, respectively, G of the Breen-Deligne resolutions of
$\mathcal {C}^{\mathrm {ab}}$
, it follows by unraveling the construction that, in our situation, the simplicial objects given by the images under F, respectively, G of the Breen-Deligne resolutions of
![]() $u^{-1}(H)$
, respectively,
$u^{-1}(H)$
, respectively,
![]() ${u^{\mathrm {crys}}}^{-1}(H)$
are the images of a simplicial object in
${u^{\mathrm {crys}}}^{-1}(H)$
are the images of a simplicial object in
![]() $\mathcal {C}^{\mathrm {ab}}$
under the extensions of
$\mathcal {C}^{\mathrm {ab}}$
under the extensions of
![]() $F\circ \iota _{\mathrm {pris}}, G\circ \iota _{\mathrm {crys}}$
. This shows that
$F\circ \iota _{\mathrm {pris}}, G\circ \iota _{\mathrm {crys}}$
. This shows that
![]() $\eta $
extends as desired.
$\eta $
extends as desired.
Passing to the limits and taking cohomology in degree
![]() $1$
, we can deduce that
$1$
, we can deduce that
respectively,
![]() $\mathbb {D}(H)(D)$
are canonically isomorphic. Hence, we obtain the desired natural isomorphism for finite flat group schemes. The proof of Proposition 4.69 belowFootnote
21
shows that writing
$\mathbb {D}(H)(D)$
are canonically isomorphic. Hence, we obtain the desired natural isomorphism for finite flat group schemes. The proof of Proposition 4.69 belowFootnote
21
shows that writing
and passing to the limit yields a canonical isomorphism
for G a p-divisible group over R.
Remark 4.46. The relation between the prismatic and the crystalline Dieudonné functors will mostly be used over a characteristic p perfect field in the rest of this text, and it could be interesting to find a more direct proof of it in this special case, as explained at the end of this section. But it will also be used for comparison with the Scholze-Weinstein functor in the next paragraph and in Section 5.2.
We turn to perfectoid rings. The following statement is a special case of a theorem of Fargues ([Reference Fargues22], [Reference Scholze and Weinstein51]). Let C be a complete algebraically closed extension of
![]() $\mathbb {Q}_p$
. We abbreviate
$\mathbb {Q}_p$
. We abbreviate
We also fix a compatible system
![]() $\varepsilon $
of p-th roots of unity, and let
$\varepsilon $
of p-th roots of unity, and let
![]() $\tilde {\xi }=[p]_q$
, where
$\tilde {\xi }=[p]_q$
, where
![]() $q=[\varepsilon ]-1$
. We identify the initial prism of
$q=[\varepsilon ]-1$
. We identify the initial prism of
![]() with
with
![]() $(A_{\mathrm {inf}},(\tilde {\xi }))$
.
$(A_{\mathrm {inf}},(\tilde {\xi }))$
.
Proposition 4.47. A prismatic Dieudonné module
![]() $(M,\varphi _M)$
over
$(M,\varphi _M)$
over
![]() $\mathcal {O}_C$
(i.e. a minuscule Breuil-Kisin-Fargues module) is uniquely determined up to isomorphism by the triple
$\mathcal {O}_C$
(i.e. a minuscule Breuil-Kisin-Fargues module) is uniquely determined up to isomorphism by the triple
where
![]() $T_M$
is the finite free
$T_M$
is the finite free
![]() $\mathbb {Z}_p$
-module
$\mathbb {Z}_p$
-module
 $$ \begin{align*}T_M=M\left[\frac{1}{\tilde{\xi}}\right]^{\varphi_M=1},\end{align*} $$
$$ \begin{align*}T_M=M\left[\frac{1}{\tilde{\xi}}\right]^{\varphi_M=1},\end{align*} $$
is a
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $A_{\mathrm {crys}}$
and
$A_{\mathrm {crys}}$
and
![]() $\alpha _M: T_M \otimes _{\mathbb {Z}_p} B_{\mathrm {crys}} \simeq M_{\mathrm {crys}} \otimes _{A_{\mathrm {crys}}} B_{\mathrm {crys}}$
is the
$\alpha _M: T_M \otimes _{\mathbb {Z}_p} B_{\mathrm {crys}} \simeq M_{\mathrm {crys}} \otimes _{A_{\mathrm {crys}}} B_{\mathrm {crys}}$
is the
![]() $\varphi $
-equivariant isomorphism coming from the natural map
$\varphi $
-equivariant isomorphism coming from the natural map
![]() $M[\frac {1}{\tilde {\xi }}]^{\varphi _M=1} \to M[\frac {1}{\tilde {\xi }}]$
.
$M[\frac {1}{\tilde {\xi }}]^{\varphi _M=1} \to M[\frac {1}{\tilde {\xi }}]$
.
Let R be a perfectoid ring. In [Reference Scholze and Weinstein51, Theorem 17.5.2], Scholze-Weinstein construct a covariant functor
![]() $M^{SW}$
from p-divisible groups over R to prismatic Dieudonné modules over R inducing an equivalence between the two categories. It has the following properties characterising it uniquely, which will be used in the next proof.
$M^{SW}$
from p-divisible groups over R to prismatic Dieudonné modules over R inducing an equivalence between the two categories. It has the following properties characterising it uniquely, which will be used in the next proof.
-
• When R is perfect,
 $M^{SW}=M_{\mathrm {crys}}(-)$
is the (covariant) crystalline Dieudonné functor dual to
$M^{SW}=M_{\mathrm {crys}}(-)$
is the (covariant) crystalline Dieudonné functor dual to
 $M^{\mathrm {crys}}$
.
$M^{\mathrm {crys}}$
. -
• If
 $R=\mathcal {O}_C$
, with C a complete algebraically closed extension of
$R=\mathcal {O}_C$
, with C a complete algebraically closed extension of
 $\mathbb {Q}_p$
, ([Reference Scholze and Weinstein51, Proposition 14.8.3]). In particular, if
$\mathbb {Q}_p$
, ([Reference Scholze and Weinstein51, Proposition 14.8.3]). In particular, if $$ \begin{align*}M^{SW}(-) \otimes_{A_{\mathrm{inf}}} A_{\mathrm{crys}} \cong M_{\mathrm{crys}}(- \otimes_{\mathcal{O}_C} \mathcal{O}_C/p)\end{align*} $$
$$ \begin{align*}M^{SW}(-) \otimes_{A_{\mathrm{inf}}} A_{\mathrm{crys}} \cong M_{\mathrm{crys}}(- \otimes_{\mathcal{O}_C} \mathcal{O}_C/p)\end{align*} $$
 $G=X[p^{\infty }]$
, for some formal abelian scheme X over
$G=X[p^{\infty }]$
, for some formal abelian scheme X over
 $\mathcal {O}_C$
, the functor
$\mathcal {O}_C$
, the functor
 $M^{SW}$
sends G to the prismatic Dieudonné module over
$M^{SW}$
sends G to the prismatic Dieudonné module over
 $\mathcal {O}_C$
dual to
$\mathcal {O}_C$
dual to
 $H_{A_{\mathrm {inf}}}^1(X)$
: this follows from the definition of
$H_{A_{\mathrm {inf}}}^1(X)$
: this follows from the definition of
 $M^{SW}(G)$
([Reference Scholze and Weinstein51, Section 12.1]), [Reference Scholze and Weinstein51, Proposition 14.8.3] and the above proposition.
$M^{SW}(G)$
([Reference Scholze and Weinstein51, Section 12.1]), [Reference Scholze and Weinstein51, Proposition 14.8.3] and the above proposition.
-
• In general, for any perfectoid ring R, if G is a p-divisible group over R,
is the largest submodule mapping into $$ \begin{align*}M^{SW}(G) \subset M_{\mathrm{crys}}(G \otimes_R R/p)\end{align*} $$
$$ \begin{align*}M^{SW}(G) \subset M_{\mathrm{crys}}(G \otimes_R R/p)\end{align*} $$
 $M(G \otimes _R V) \subset M_{\mathrm {crys}}(G \otimes _R V)$
for all maps
$M(G \otimes _R V) \subset M_{\mathrm {crys}}(G \otimes _R V)$
for all maps
 $R \to V$
where V is an integral perfectoid valuation ring with algebraically closed fraction field.
$R \to V$
where V is an integral perfectoid valuation ring with algebraically closed fraction field.
Proposition 4.48. Let R be a perfectoid ring. The functor
![]() from
from
![]() $\mathrm {BT}(R)$
to
$\mathrm {BT}(R)$
to
![]() $\mathrm {DM}(R)$
coincides with the (naive)Footnote
22
dual of the functor
$\mathrm {DM}(R)$
coincides with the (naive)Footnote
22
dual of the functor
![]() $M^{SW}$
of [Reference Scholze and Weinstein51, Appendix to Lecture XVII].
$M^{SW}$
of [Reference Scholze and Weinstein51, Appendix to Lecture XVII].
Proof. If R is perfect and G a p-divisible group over R, then we get a natural isomorphism
because both sides identify with the (contravariant) crystalline Dieudonné module (cf. Theorem 4.44). Moreover,
![]() $\alpha _{R,-}$
is compatible with base change along morphisms of perfect rings. Now assume that
$\alpha _{R,-}$
is compatible with base change along morphisms of perfect rings. Now assume that
![]() $R=\mathcal {O}_C$
, where C is a perfectoid algebraically closed field over
$R=\mathcal {O}_C$
, where C is a perfectoid algebraically closed field over
![]() $\mathbb {Q}_p$
. In this case, assume first that
$\mathbb {Q}_p$
. In this case, assume first that
![]() $G=X[p^{\infty }]$
, for some formal abelian scheme X over
$G=X[p^{\infty }]$
, for some formal abelian scheme X over
![]() $\mathcal {O}_C$
, with rigid generic fibre
$\mathcal {O}_C$
, with rigid generic fibre
![]() $X^{\mathrm {rig}}$
. As recalled above, the functor
$X^{\mathrm {rig}}$
. As recalled above, the functor
![]() $M^{SW}$
sends G to the prismatic Dieudonné module over
$M^{SW}$
sends G to the prismatic Dieudonné module over
![]() $\mathcal {O}_C$
dual to
$\mathcal {O}_C$
dual to
![]() $H_{A_{\mathrm {inf}}}^1(X)$
. In particular, in this case,
$H_{A_{\mathrm {inf}}}^1(X)$
. In particular, in this case,
![]() $M^{SW}(G)$
is isomorphic to the (naive) dual to
$M^{SW}(G)$
is isomorphic to the (naive) dual to
![]() , by Corollary 4.63 and the comparison theorem [Reference Bhatt and Scholze13, Theorem 17.2]Footnote
23
. Moreover, this identification is functorial for morphisms of p-divisible groups of abelian schemes (and not simply for morphisms of abelian schemes): indeed, let
, by Corollary 4.63 and the comparison theorem [Reference Bhatt and Scholze13, Theorem 17.2]Footnote
23
. Moreover, this identification is functorial for morphisms of p-divisible groups of abelian schemes (and not simply for morphisms of abelian schemes): indeed, let
![]() $X, X'$
be two abelian schemes over
$X, X'$
be two abelian schemes over
![]() $\mathcal {O}_C$
, and
$\mathcal {O}_C$
, and
![]() $G=X[p^{\infty }]$
,
$G=X[p^{\infty }]$
,
![]() $H=X'[p^{\infty }]$
, with a morphism
$H=X'[p^{\infty }]$
, with a morphism
![]() $f\colon G\to H$
. We want to see that the diagram
$f\colon G\to H$
. We want to see that the diagram

commutes. This can be checked after base change to
![]() $A_{\mathrm {crys}}$
. Then, using Lemma 4.45, the terms on the top line (respectively, on the bottom line) are identified with the covariant crystalline Dieudonné module of G (respectively, H), and the horizontal isomorphisms induce the identity, by construction.
$A_{\mathrm {crys}}$
. Then, using Lemma 4.45, the terms on the top line (respectively, on the bottom line) are identified with the covariant crystalline Dieudonné module of G (respectively, H), and the horizontal isomorphisms induce the identity, by construction.
Let now G be a general p-divisible group over
![]() $\mathcal {O}_C$
. There exists a formal abelian scheme X over
$\mathcal {O}_C$
. There exists a formal abelian scheme X over
![]() $\mathcal {O}_C$
, such that
$\mathcal {O}_C$
, such that
![]() $X[p^{\infty }]=G \times \check {G}$
(cf. [Reference Scholze and Weinstein51, Proposition 14.8.4]). Let
$X[p^{\infty }]=G \times \check {G}$
(cf. [Reference Scholze and Weinstein51, Proposition 14.8.4]). Let
![]() $e\colon X[p^{\infty }]\to X[p^{\infty }]$
be the idempotent with kernel G. Then
$e\colon X[p^{\infty }]\to X[p^{\infty }]$
be the idempotent with kernel G. Then
and
By the functoriality explained above, we can conclude the proof when
![]() $R=\mathcal {O}_C$
, that is, we have constructed an isomorphism
$R=\mathcal {O}_C$
, that is, we have constructed an isomorphism
![]() in this case, which is natural in G and compatible with base change along morphisms of such R’s. If k denotes the residue field of
in this case, which is natural in G and compatible with base change along morphisms of such R’s. If k denotes the residue field of
![]() $\mathcal {O}_C$
, then by construction, the base change of
$\mathcal {O}_C$
, then by construction, the base change of
![]() $\alpha _{R,G}$
along
$\alpha _{R,G}$
along
![]() is
is
![]() $\alpha _{k,G\otimes _R k}$
.
$\alpha _{k,G\otimes _R k}$
.
Now assume that R is a general perfectoid ring. By [Reference Lau36, Remark 8.8], we can write
with
![]() $R_1 p$
-torsion free perfectoid,
$R_1 p$
-torsion free perfectoid,
![]() $S_1,S_2$
perfect and
$S_1,S_2$
perfect and
![]() $R_1\to S_2, S_1\to S_2$
surjective. As in [Reference Lau36, Lemma 9.2], the category
$R_1\to S_2, S_1\to S_2$
surjective. As in [Reference Lau36, Lemma 9.2], the category
![]() $\mathrm {DM}(R)$
of prismatic Dieudonné modules for R is naturally equivalent to the
$\mathrm {DM}(R)$
of prismatic Dieudonné modules for R is naturally equivalent to the
![]() $2$
-limit
$2$
-limit
Thus, it suffices to construct a natural isomorphism
![]() for any p-divisible group over a perfectoid ring R, which is either perfect or p-torsion free, and show that it is compatible with base change in R. If R is perfect, then we are already done. Let us assume that R is p-torsion free. Then the ring
for any p-divisible group over a perfectoid ring R, which is either perfect or p-torsion free, and show that it is compatible with base change in R. If R is perfect, then we are already done. Let us assume that R is p-torsion free. Then the ring
![]() $R/p$
is quasiregular semiperfect, and
$R/p$
is quasiregular semiperfect, and
![]() by 3.27. By 4.44, 4.69
by 3.27. By 4.44, 4.69
Footnote
24
and the construction of
![]() $M^{SW}(G)^{\ast }$
, we have a natural isomorphism
$M^{SW}(G)^{\ast }$
, we have a natural isomorphism
because both sides identify with the (contravariant) crystalline Dieudonné module of
![]() $G\otimes _R R/p$
. By 4.69,
$G\otimes _R R/p$
. By 4.69,
![]() is a finite locally free
is a finite locally free
![]() -module. Thus,
-module. Thus,
![]() identifies with a
identifies with a
![]() -submodule of
-submodule of
![]() because the morphism
because the morphism
![]() is injective. We claim that
is injective. We claim that
![]() $\alpha _{G\otimes _R R/p}$
maps (injectively)
$\alpha _{G\otimes _R R/p}$
maps (injectively)
![]() into
into
![]() $M^{SW}(G)^{\ast }$
. By the very construction of
$M^{SW}(G)^{\ast }$
. By the very construction of
![]() $M^{SW}(G)^{\ast }$
, we have to check that for any perfectoid valuation ring V with algebraically closed fraction field and morphism
$M^{SW}(G)^{\ast }$
, we have to check that for any perfectoid valuation ring V with algebraically closed fraction field and morphism
![]() $R\to V$
, the module
$R\to V$
, the module
![]() maps to
maps to
![]() $M^{SW}(G_V)^{\ast }\subseteq M_{\mathrm {crys}}(G_V)$
with
$M^{SW}(G_V)^{\ast }\subseteq M_{\mathrm {crys}}(G_V)$
with
![]() $G_V:=G\otimes _R V$
. If V is perfect, this follows by 4.44. If V is of mixed characteristic, we can write V as the fibre product
$G_V:=G\otimes _R V$
. If V is perfect, this follows by 4.44. If V is of mixed characteristic, we can write V as the fibre product
![]() $V^{\prime }\times _{\kappa } S$
of a perfect valuation ring S with a mixed-characteristic valuation ring
$V^{\prime }\times _{\kappa } S$
of a perfect valuation ring S with a mixed-characteristic valuation ring
![]() $V^{\prime }$
of rank
$V^{\prime }$
of rank
![]() $1$
over the residue field
$1$
over the residue field
![]() $\kappa $
of
$\kappa $
of
![]() $V^{\prime }$
, and write
$V^{\prime }$
, and write
We already checked the statement for
![]() $V^{\prime },\kappa , S,$
and, thus, we have finished the construction of a natural injective morphism
$V^{\prime },\kappa , S,$
and, thus, we have finished the construction of a natural injective morphism
for a general perfectoid ring R. Assume
![]() $R\to R^{\prime }$
is a morphism of perfectoid rings, then we know that
$R\to R^{\prime }$
is a morphism of perfectoid rings, then we know that
![]() if
if
![]() $R,R^{\prime }$
are perfect. If R is p-torsion free and
$R,R^{\prime }$
are perfect. If R is p-torsion free and
![]() $R^{\prime }$
perfect, we can draw the same conclusion as then
$R^{\prime }$
perfect, we can draw the same conclusion as then
![]() factors over
factors over
![]() $A_{\mathrm {crys}}(R/p)$
and
$A_{\mathrm {crys}}(R/p)$
and
![]() is the identification coming from Dieudonné theory. As
is the identification coming from Dieudonné theory. As
![]() $M^{SW}(G)^{\ast }$
is a finite free
$M^{SW}(G)^{\ast }$
is a finite free
![]() -module (by [Reference Scholze and Weinstein51, Theorem 17.5.2]), we can check that it is an isomorphism after base change along all morphisms
-module (by [Reference Scholze and Weinstein51, Theorem 17.5.2]), we can check that it is an isomorphism after base change along all morphisms
![]() for
for
![]() $R\to k$
, a morphism from R to a perfect field k. But this case was already handled. This finishes the proof.
$R\to k$
, a morphism from R to a perfect field k. But this case was already handled. This finishes the proof.
We obtain the following corollary, which we will need in Section 4.9.
Corollary 4.49. Let R be a perfectoid ring. The prismatic Dieudonné functor
![]() takes values in
takes values in
![]() $\mathrm {DM}^{\mathrm {adm}}(R) \cong \mathrm {DM}(R)$
and induces an antiequivalence between
$\mathrm {DM}^{\mathrm {adm}}(R) \cong \mathrm {DM}(R)$
and induces an antiequivalence between
![]() $\mathrm {BT}(R)$
and
$\mathrm {BT}(R)$
and
![]() $\mathrm {DM}^{\mathrm {adm}}(R) \cong \mathrm {DM}(R)$
.
$\mathrm {DM}^{\mathrm {adm}}(R) \cong \mathrm {DM}(R)$
.
Proof. This follows immediately from the last proposition and [Reference Scholze and Weinstein51, Theorem 17.5.2]. Note that the argument of loc. cit. shows that one only needs to prove the equivalence when R is the ring of integers of a perfectoid algebraically closed field, where it is due to Berthelot [Reference Berthelot4, Theorem 3.4.1] and Scholze-Weinstein [Reference Scholze and Weinstein50, Theorem 5.2.1] (in this case, one can even assume that the fraction field of R is spherically complete, and the result is then an easy consequence of results of Fargues: see [Reference Scholze and Weinstein50, Section 5.2]).
Remark 4.50. Let R be a perfectoid ring. The functor
![]() is exact (see below Proposition 4.72) and has an exact quasi-inverse (we will provide an argument for this later in Section 5.1 in the case of finite locally free group schemes, which applies verbatim for p-divisible groups).
is exact (see below Proposition 4.72) and has an exact quasi-inverse (we will provide an argument for this later in Section 5.1 in the case of finite locally free group schemes, which applies verbatim for p-divisible groups).
Let us conclude this section by discussing the case of perfect fields. For a perfect field k, Fontaine [Reference Fontaine23] was the first to give a uniform definition of a functor from p-divisible groups to (prismatic) Dieudonné modules over k. Let us recall it first, as formulated in [Reference Berthelot and Messing7, Section 4.1]. If A is a commutative ring, the set
![]() $\mathrm {CW}(A)$
of Witt covectors with values in A is the set of all family
$\mathrm {CW}(A)$
of Witt covectors with values in A is the set of all family
![]() $(a_{-i})_{i\in \mathbb {N}}$
of elements of A, such that there exist integers
$(a_{-i})_{i\in \mathbb {N}}$
of elements of A, such that there exist integers
![]() $r, s\geq 0$
, such that the ideal
$r, s\geq 0$
, such that the ideal
![]() $J_r$
generated by the
$J_r$
generated by the
![]() $a_{-i}$
,
$a_{-i}$
,
![]() $i\geq r$
, satisfies
$i\geq r$
, satisfies
![]() $J_r^s=0$
. One still denotes by
$J_r^s=0$
. One still denotes by
![]() $\mathrm {CW}$
the sheaf on the big fpqc siteFootnote
25
of k associated to the presheaf of Witt covectors. This is an abelian sheaf of
$\mathrm {CW}$
the sheaf on the big fpqc siteFootnote
25
of k associated to the presheaf of Witt covectors. This is an abelian sheaf of
![]() $W(k)$
-modules, endowed with a Frobenius operator which is semilinear with respect to the Frobenius on
$W(k)$
-modules, endowed with a Frobenius operator which is semilinear with respect to the Frobenius on
![]() $W(k)$
. Fontaines defines:
$W(k)$
. Fontaines defines:
As a corollary of Theorem 4.44 and results of Berthelot-Breen-Messing, one gets
Proposition 4.51. Let k be a perfect field, and let G be a p-divisible group over R. One has a canonical
![]() $W(k)$
-linear Frobenius-equivariant isomorphism
$W(k)$
-linear Frobenius-equivariant isomorphism
Proof. By construction, the isomorphism of Theorem 4.44 is linear over the isomorphism
![]() , which is given by the Frobenius
, which is given by the Frobenius
![]() $\sigma $
of
$\sigma $
of
![]() $W(k)$
, that is, it can be seen as a Frobenius-equivariant
$W(k)$
, that is, it can be seen as a Frobenius-equivariant
![]() $W(k)$
-linear isomorphism:
$W(k)$
-linear isomorphism:
Composing it with
![]() $\sigma ^{-1}$
-pullback of the inverse of the
$\sigma ^{-1}$
-pullback of the inverse of the
![]() $W(k)$
-linear Frobenius-equivariant isomorphism of [Reference Berthelot and Messing7, Theorem 4.2.14], we get the desired isomorphism.
$W(k)$
-linear Frobenius-equivariant isomorphism of [Reference Berthelot and Messing7, Theorem 4.2.14], we get the desired isomorphism.
It would be interesting to get a more direct proof of this corollary. In characteristic p, the prismatic Dieudonné crystal of a p-divisible group admits a description which looks similar to Fontaine’s definition.
Definition 4.52. Let R be a a quasisyntomic ring with
![]() $pR=0$
. We define the sheaf
$pR=0$
. We define the sheaf
![]() $\mathcal {Q}$
on
$\mathcal {Q}$
on
![]() as the quotient:
as the quotient:
The morphism
![]() is injective since any prism in
is injective since any prism in
![]() is p-torsion free.
is p-torsion free.
Proposition 4.53. Let R be a quasisyntomic ring with
![]() $pR=0$
, and let G be a p-divisible group over R. The connecting map of the canonical exact sequence
$pR=0$
, and let G be a p-divisible group over R. The connecting map of the canonical exact sequence
induces an isomorphism:
Proof. First assume that G is a finite locally free group scheme. Then the statement is clear, as
because
![]() $u^{-1}(G)$
is killed by some power of p, whereas on
$u^{-1}(G)$
is killed by some power of p, whereas on
![]() multiplication by p is invertible. The result for p-divisible groups is deduced by a limit argument.
multiplication by p is invertible. The result for p-divisible groups is deduced by a limit argument.
This naturally leads to the following question.
Question 4.54. When
![]() $R=k$
is a perfect field, what is the relation between the sheaf
$R=k$
is a perfect field, what is the relation between the sheaf
![]() $v_* \mathcal {Q}$
and the sheaf
$v_* \mathcal {Q}$
and the sheaf
![]() $\mathrm {CW}$
of Witt covectors?
$\mathrm {CW}$
of Witt covectors?
4.4 Calculating
 $\mathrm {Ext}$
-groups in topoi
$\mathrm {Ext}$
-groups in topoi
In this section, we recall the method of calculating Ext-groups in a topos as presented by Berthelot et al. (cf. [Reference Berthelot, Breen and Messing6, 2.1.5]Footnote
26
. Let
![]() $\mathfrak {X}$
be a topos, and let
$\mathfrak {X}$
be a topos, and let
![]() $G,H\in \mathfrak {X}$
be two abelian groups, that is, two abelian group objects.
$G,H\in \mathfrak {X}$
be two abelian groups, that is, two abelian group objects.
The following theorem is attributed to Deligne in [Reference Berthelot, Breen and Messing6]. A proof can be found in [Reference Scholze48, Appendix to Lecture IV, Theorem 4.10].
Theorem 4.55. Let
![]() $G\in \mathrm {\mathfrak {X}}$
be an abelian group. Then there exists a natural functorial (in G) resolution
$G\in \mathrm {\mathfrak {X}}$
be an abelian group. Then there exists a natural functorial (in G) resolution
where each
![]() $X_i\in \mathfrak {X}$
is a finite disjoint union of products of copies G.
$X_i\in \mathfrak {X}$
is a finite disjoint union of products of copies G.
Proof. See [Reference Berthelot, Breen and Messing6, 2.1.5] or [Reference Scholze48, Appendix to Lecture IV, Theorem 4.10]
Lemma 4.56. Let
![]() $X\in \mathfrak {X}$
be any object, and let
$X\in \mathfrak {X}$
be any object, and let
![]() $\mathcal {F}\in \mathrm {Ab}(\mathfrak {X})$
be an abelian group. Then
$\mathcal {F}\in \mathrm {Ab}(\mathfrak {X})$
be an abelian group. Then
where
![]() $\mathbb {Z}[X]$
denotes the free abelian group on X.
$\mathbb {Z}[X]$
denotes the free abelian group on X.
Proof. This follows by deriving the isomorphism
![]() $\mathcal {F}(X)\cong \mathrm {Hom}_{\mathrm {Ab}(\mathfrak {X})}(\mathbb {Z}[X],\mathcal {F}).$
$\mathcal {F}(X)\cong \mathrm {Hom}_{\mathrm {Ab}(\mathfrak {X})}(\mathbb {Z}[X],\mathcal {F}).$
These two results show that the
![]() $\mathrm {Ext}$
-groups
$\mathrm {Ext}$
-groups
can, in principle, be calculated in terms of the cohomology groups
for various products
![]() $G\times \ldots \times G$
. Unfortunately, the construction of the resolution in Theorem 4.55 is rather involved. However, the first terms, which are sufficient for our applications, can be made explicitFootnote
27
. For example, the first terms can be chosen to be
$G\times \ldots \times G$
. Unfortunately, the construction of the resolution in Theorem 4.55 is rather involved. However, the first terms, which are sufficient for our applications, can be made explicitFootnote
27
. For example, the first terms can be chosen to be
 $$ \begin{align*}\begin{matrix} C(G)_0:=\mathbb{Z}[G] \\ C(G)_1:=\mathbb{Z}[G^2]\\ C(G)_2:=\mathbb{Z}[G^3]\oplus\mathbb{Z}[G^2] \end{matrix} \end{align*} $$
$$ \begin{align*}\begin{matrix} C(G)_0:=\mathbb{Z}[G] \\ C(G)_1:=\mathbb{Z}[G^2]\\ C(G)_2:=\mathbb{Z}[G^3]\oplus\mathbb{Z}[G^2] \end{matrix} \end{align*} $$
with explicit differentials (cf. [Reference Berthelot, Breen and Messing6, (2.1.5.2.)]). The stupid filtration of the complex
![]() $C(G)_{\bullet }$
yields a spectral sequence
$C(G)_{\bullet }$
yields a spectral sequence
and the terms
can be calculated using the cohomology. For later use, let us make the first terms of the first page of this spectral sequence explicit:

For an element
![]() $(x_1,\ldots , x_n)\in G^n$
, let us denote by
$(x_1,\ldots , x_n)\in G^n$
, let us denote by
![]() $[x_1,\ldots , x_n]\in \mathbb {Z}[G^n]$
the corresponding element in the group ring
$[x_1,\ldots , x_n]\in \mathbb {Z}[G^n]$
the corresponding element in the group ring
![]() $\mathbb {Z}[G^n]$
. The morphisms
$\mathbb {Z}[G^n]$
. The morphisms
![]() $d_1$
and
$d_1$
and
![]() $d_2$
are then induced by
$d_2$
are then induced by
for
![]() $d_1$
and
$d_1$
and
for
![]() $d_2$
(cf. [Reference Berthelot, Breen and Messing6, (2.1.5.2.)]).
$d_2$
(cf. [Reference Berthelot, Breen and Messing6, (2.1.5.2.)]).
4.5 Prismatic Dieudonné crystals of abelian schemes
In this section, we describe the prismatic cohomology of the p-adic completion of abelian schemes and deduce from this the construction of the prismatic Dieudonné crystal
of the p-divisible group
![]() $X[p^{\infty }]$
of the p-adic completion of an abelian scheme X over a quassyntomic ring R. Admissibility of this prismatic Dieudonné crystal will be proved in the next section, in fact for any p-divisible group.
$X[p^{\infty }]$
of the p-adic completion of an abelian scheme X over a quassyntomic ring R. Admissibility of this prismatic Dieudonné crystal will be proved in the next section, in fact for any p-divisible group.
Let
![]() $(A,I)$
be a bounded prism. Write
$(A,I)$
be a bounded prism. Write
![]() $\bar {A}=A/I$
. Let
$\bar {A}=A/I$
. Let
![]() $X\to \mathrm {Spf}(\bar {A})$
be the p-adic completion of an abelian scheme over
$X\to \mathrm {Spf}(\bar {A})$
be the p-adic completion of an abelian scheme over
![]() $\mathrm {Spec}(\bar {A})$
.
$\mathrm {Spec}(\bar {A})$
.
We first prove degeneracy of the conjugate spectral sequence (cf. Proposition 3.10) for X. The proof is an adaptation of the argument in [Reference Berthelot, Breen and Messing6, Proposition 2.5.2], which proves degeneration of the Hodge-de Rham spectral sequence.
Recall the following statement.
Proposition 4.57. For all
![]() $k\geq 0$
(respectively, for all
$k\geq 0$
(respectively, for all
![]() $i,j\geq 0$
), the
$i,j\geq 0$
), the
![]() $\bar {A}$
-module
$\bar {A}$
-module
![]() $H^k(X,\Omega _{X/\bar {A}}^{\bullet })$
(respectively,
$H^k(X,\Omega _{X/\bar {A}}^{\bullet })$
(respectively,
![]() $H^i(X,\Omega _{X/\bar {A}}^j)$
) is finite locally free, and its formation commutes with base change.
$H^i(X,\Omega _{X/\bar {A}}^j)$
) is finite locally free, and its formation commutes with base change.
Moreover, the algebra
![]() $H^*(X,\Omega _{X/\bar {A}}^{\bullet })$
is alternating and the canonical algebra morphism
$H^*(X,\Omega _{X/\bar {A}}^{\bullet })$
is alternating and the canonical algebra morphism
defined by the multiplicative structure of
![]() $H^*(X,\Omega _{X/\bar {A}}^{\bullet })$
, is an isomorphism.
$H^*(X,\Omega _{X/\bar {A}}^{\bullet })$
, is an isomorphism.
Proof. This is [Reference Berthelot, Breen and Messing6, Proposition 2.5.2. (i)-(ii)].
Proposition 4.58. The conjugate spectral sequence
degenerates and each term as well as the abutment commutes with base change in the bounded prism
![]() $(A,I)$
. Moreover,
$(A,I)$
. Moreover,
is an exterior
![]() $\bar {A}$
-algebra on
$\bar {A}$
-algebra on
![]() .
.
Proof. If
![]() $p\neq 2$
, we can use a simple argument using the multiplication by
$p\neq 2$
, we can use a simple argument using the multiplication by
![]() $n\in \mathbb {Z}$
on X. If
$n\in \mathbb {Z}$
on X. If
![]() $n\in \mathbb {Z}$
, then the multiplication by n on X induces on
$n\in \mathbb {Z}$
, then the multiplication by n on X induces on
![]() $H^i(X,\Omega ^j_{X/{\bar {A}}})\{-j\}$
multiplication by
$H^i(X,\Omega ^j_{X/{\bar {A}}})\{-j\}$
multiplication by
![]() $n^{i+j}$
. As the differentials of the spectral sequence are natural in X, this implies that they vanish on each
$n^{i+j}$
. As the differentials of the spectral sequence are natural in X, this implies that they vanish on each
![]() $E_r$
-page,
$E_r$
-page,
![]() $r\geq 0$
(this uses
$r\geq 0$
(this uses
![]() $p\neq 2$
). This proves that
$p\neq 2$
). This proves that
![]() is a finite locally free
is a finite locally free
![]() $\bar {A}$
-module for each
$\bar {A}$
-module for each
![]() $i\geq 0$
. By the Hodge-Tate comparison, the complex
$i\geq 0$
. By the Hodge-Tate comparison, the complex
satisfies base change in
![]() $(A,I)$
, that is, for a morphism
$(A,I)$
, that is, for a morphism
![]() $(A,I)\to (A^{\prime },I^{\prime })$
of prisms with induced morphism
$(A,I)\to (A^{\prime },I^{\prime })$
of prisms with induced morphism
![]() $g\colon X^{\prime }:=X\times _{\mathrm {Spf}(\bar {A})} \mathrm {Spf}(A^{\prime }/I^{\prime })\to X$
, the canonical morphism
$g\colon X^{\prime }:=X\times _{\mathrm {Spf}(\bar {A})} \mathrm {Spf}(A^{\prime }/I^{\prime })\to X$
, the canonical morphism
is an isomorphism. From this, we can deduce that each
![]() satisfies base change in
satisfies base change in
![]() $(A,I)$
. To show that
$(A,I)$
. To show that
![]() is an exterior algebra on
is an exterior algebra on
![]() , we need first to see that each element in
, we need first to see that each element in
![]() squares to zero. For this, we can argue as in the proof [Reference Berthelot, Breen and Messing6, Proposition 2.5.2.(ii)]. Then we obtain a canonical morphism
squares to zero. For this, we can argue as in the proof [Reference Berthelot, Breen and Messing6, Proposition 2.5.2.(ii)]. Then we obtain a canonical morphism
We can use Lemma 4.59 and compatibility with base change to reduce to the case that
![]() $\bar {A}$
is an algebraically closed field of characteristic p. In particular, the Frobenius on A is bijective in this case,
$\bar {A}$
is an algebraically closed field of characteristic p. In particular, the Frobenius on A is bijective in this case,
![]() $I=(p)$
and the twists
$I=(p)$
and the twists
![]() $(-)\{j\}$
are isomorphic to the identity. We may check that
$(-)\{j\}$
are isomorphic to the identity. We may check that
![]() $\beta $
is an isomorphism after pullback along
$\beta $
is an isomorphism after pullback along
![]() $\varphi _{\bar {A}}$
. Then
$\varphi _{\bar {A}}$
. Then
where we used in the second isomorphism that the relative Frobenius
is finite. This reduces the assertion to de Rham cohomology, which is the content of Proposition 4.57. This finishes the proof.
Alternatively (including the case
![]() $p=2$
), we could have argued like in [Reference Berthelot, Breen and Messing6, Theorem 2.5.2. (i)] to reduce, by descending induction, to the claim that
$p=2$
), we could have argued like in [Reference Berthelot, Breen and Messing6, Theorem 2.5.2. (i)] to reduce, by descending induction, to the claim that
![]() is locally free of rank
is locally free of rank
![]() $2n$
, where n is the relative dimension of X over
$2n$
, where n is the relative dimension of X over
![]() $\mathrm {Spf}(\bar {A})$
, and commutes with base change in
$\mathrm {Spf}(\bar {A})$
, and commutes with base change in
![]() $(A,I)$
. From Proposition 3.12 it follows that
$(A,I)$
. From Proposition 3.12 it follows that
As
![]() $L_{X/A}$
is a perfect complex with amplitude in
$L_{X/A}$
is a perfect complex with amplitude in
![]() $[-1,0]$
, this implies compatibility of
$[-1,0]$
, this implies compatibility of
![]() with base change in
with base change in
![]() $(A,I)$
if all the higher cohomology groups
$(A,I)$
if all the higher cohomology groups
![]() $H^j(X,L_{X/A}[-1])$
are locally free. As X admits a lift to A (see e.g. [Reference Oort47, Theorem 2.2.1]), Corollary 3.14 shows that
$H^j(X,L_{X/A}[-1])$
are locally free. As X admits a lift to A (see e.g. [Reference Oort47, Theorem 2.2.1]), Corollary 3.14 shows that
![]() $L_{X/A}\cong \mathcal {O}_X[1]\oplus \Omega _{X/\bar {A}}^1$
. Another application of Proposition 4.57 implies, therefore, that
$L_{X/A}\cong \mathcal {O}_X[1]\oplus \Omega _{X/\bar {A}}^1$
. Another application of Proposition 4.57 implies, therefore, that
![]() is locally free of dimension
is locally free of dimension
![]() $2n$
and commutes with base change in
$2n$
and commutes with base change in
![]() $(A,I)$
as all the
$(A,I)$
as all the
![]() $\bar {A}$
-modules
$\bar {A}$
-modules
![]() $H^j(X,\mathcal {O}_X)$
and
$H^j(X,\mathcal {O}_X)$
and
![]() $H^j(X,\Omega _{X/\bar {A}}^1)$
are locally free for
$H^j(X,\Omega _{X/\bar {A}}^1)$
are locally free for
![]() $j\geq 0$
.
$j\geq 0$
.
Lemma 4.59. Let S be a ring, and let
![]() $g\colon M\to N$
be a morphism of S-modules with M finitely generated and N finite projective. If
$g\colon M\to N$
be a morphism of S-modules with M finitely generated and N finite projective. If
is an isomorphism for all closed points
![]() $x\in \mathrm {Spec}(S)$
, then g is an isomorphism.
$x\in \mathrm {Spec}(S)$
, then g is an isomorphism.
Proof. Let Q be the cokernel of g. Then Q is finitely generated and
![]() $Q\otimes _S k(x)=0$
for all closed points
$Q\otimes _S k(x)=0$
for all closed points
![]() $x\in \mathrm {Spec}(S)$
. By Nakayama’s lemma, this implies that
$x\in \mathrm {Spec}(S)$
. By Nakayama’s lemma, this implies that
![]() $Q=0$
, that is, g is surjective. As N is projective, this implies
$Q=0$
, that is, g is surjective. As N is projective, this implies
![]() $M\cong N \oplus K$
for K the kernel of g. As M is finitely generated, K is finitely generated. Moreover, for all closed points
$M\cong N \oplus K$
for K the kernel of g. As M is finitely generated, K is finitely generated. Moreover, for all closed points
![]() $x\in \mathrm {Spec}(S)$
$x\in \mathrm {Spec}(S)$
and thus another application of Nakayama’s lemma implies that
![]() $K=0$
.
$K=0$
.
We recall that for a p-complete ring R, there is the natural morphism of topoi
Using the previous computations, we can first describe extension groups modulo I.
Theorem 4.60. Let R be a p-complete ring, and let
![]() $f\colon X\to \mathrm {Spf}(R)$
be the p-adic completion of an abelian scheme over
$f\colon X\to \mathrm {Spf}(R)$
be the p-adic completion of an abelian scheme over
![]() $\mathrm {Spec}(R)$
. Then
$\mathrm {Spec}(R)$
. Then
-
1.
 for
for
 $i=0,2$
.
$i=0,2$
. -
2.
 is a prismatic crystal over R. Moreover, for
is a prismatic crystal over R. Moreover, for
 , the morphism induced by f on topoi and
, the morphism induced by f on topoi and
 is locally free of rank
is locally free of rank
 $2\mathrm {dim}(X)$
over
$2\mathrm {dim}(X)$
over
 .
.
The proof is entirely similar to the one of [Reference Berthelot, Breen and Messing6, Theorem 2.5.6].
Proof. Let
![]() . We use the spectral sequence from Section 4.4 to calculate for
. We use the spectral sequence from Section 4.4 to calculate for
![]() $i\in \{0,1,2\}$
the groups
$i\in \{0,1,2\}$
the groups
on the localised site
![]()
Footnote
28
. Set
![]() $Y:=X\times _{\mathrm {Spf}(\bar {A})}\mathrm {Spf}(B/J)$
. As by Hodge-Tate comparison
$Y:=X\times _{\mathrm {Spf}(\bar {A})}\mathrm {Spf}(B/J)$
. As by Hodge-Tate comparison
for any n the first row
![]() $E_1^{\ast ,0}$
of the spectral sequence is seen to be independent of X and exact in the case that
$E_1^{\ast ,0}$
of the spectral sequence is seen to be independent of X and exact in the case that
![]() $X=0$
is trivial (the spectral sequence for
$X=0$
is trivial (the spectral sequence for
![]() $X=0$
is concentrated in the first row and converges to
$X=0$
is concentrated in the first row and converges to
![]() $0$
), hence, always exact. In general, we see that
$0$
), hence, always exact. In general, we see that
![]() and
and
![]() is isomorphic to the kernel of
is isomorphic to the kernel of
and
![]() $d_1=\mathrm {pr}_1^{\ast }+\mathrm {pr}_2^{\ast }-\mu ^{\ast }$
for
$d_1=\mathrm {pr}_1^{\ast }+\mathrm {pr}_2^{\ast }-\mu ^{\ast }$
for
![]() $\mathrm {pr}_i$
the two projections and
$\mathrm {pr}_i$
the two projections and
![]() $\mu $
the multiplication. From the Künneth formula (cf. Corollary 3.31) and Proposition 4.58, it follows that
$\mu $
the multiplication. From the Künneth formula (cf. Corollary 3.31) and Proposition 4.58, it follows that
This implies
![]() $\mu ^{\ast }=\mathrm {pr}_1^{\ast }+\mathrm {pr}_2^{\ast }$
, that is,
$\mu ^{\ast }=\mathrm {pr}_1^{\ast }+\mathrm {pr}_2^{\ast }$
, that is,
![]() $d_1=0$
and
$d_1=0$
and
In particular, this group is compatible with base change in
![]() $(B,J)$
and locally free of rank
$(B,J)$
and locally free of rank
![]() $2\mathrm {dim}(X)$
(by Proposition 4.58). Moreover, the morphism
$2\mathrm {dim}(X)$
(by Proposition 4.58). Moreover, the morphism
![]() $d_2$
is injective on
$d_2$
is injective on
![]() , as follows from the Künneth theorem and the concrete formula for
, as follows from the Künneth theorem and the concrete formula for
![]() $d_2$
. Finally, from Corollary 4.64 and Lemma 4.61, one can deduce that
$d_2$
. Finally, from Corollary 4.64 and Lemma 4.61, one can deduce that
is injective for all
![]() $i\geq 2$
. These statements (together with the mentioned exactness of the first row) imply
$i\geq 2$
. These statements (together with the mentioned exactness of the first row) imply
This finishes the proof by passing to the local Ext-groups, that is, by letting
![]() $(B,J)$
vary.
$(B,J)$
vary.
In the proof, we used the following lemma on primitive elements in exterior algebras.
Lemma 4.61. Let S be a ring and let M be a projective S-module. Then
where
![]() $\mu ^{\ast }\colon \Lambda (M)\to \Lambda (M+M)\cong \Lambda (M)\otimes _S \Lambda (M)$
is the natural comultiplication on
$\mu ^{\ast }\colon \Lambda (M)\to \Lambda (M+M)\cong \Lambda (M)\otimes _S \Lambda (M)$
is the natural comultiplication on
![]() $\Lambda (M)$
coming from the diagonal
$\Lambda (M)$
coming from the diagonal
![]() $M\to M\oplus M$
.
$M\to M\oplus M$
.
Proof. This follows easily by decomposing
![]() $\Lambda (M)\otimes _S \Lambda (M)$
into its bigraded pieces
$\Lambda (M)\otimes _S \Lambda (M)$
into its bigraded pieces
![]() $\Lambda ^{i}(M)\otimes _S \Lambda ^j(M)$
.
$\Lambda ^{i}(M)\otimes _S \Lambda ^j(M)$
.
Now we calculate the full extension groups, up to degree
![]() $2$
.
$2$
.
Theorem 4.62. Let R be a p-complete ring, and let
![]() $f\colon X\to \mathrm {Spf}(R)$
be the p-adic completion of an abelian scheme over
$f\colon X\to \mathrm {Spf}(R)$
be the p-adic completion of an abelian scheme over
![]() $\mathrm {Spec}(R)$
. Then
$\mathrm {Spec}(R)$
. Then
-
1.
 for
for
 $i=0,2$
.
$i=0,2$
. -
2.
 is a prismatic crystal over R. Moreover, for
is a prismatic crystal over R. Moreover, for
 , the induced morphism on topoi and the prismatic crystal
, the induced morphism on topoi and the prismatic crystal
 is locally free of rank
is locally free of rank
 $2\mathrm {dim}(X)$
over
$2\mathrm {dim}(X)$
over
 .
.
Proof. Let
![]() . As the statements are local for the faithfully flat topology, we may assume that
. As the statements are local for the faithfully flat topology, we may assume that
![]() $J=(\tilde {\xi })$
is principal. From the exact sequence
$J=(\tilde {\xi })$
is principal. From the exact sequence
of sheaves on
![]() and Theorem 4.60, we can inductively conclude that
and Theorem 4.60, we can inductively conclude that
for
![]() $i\in \{0,2\}$
and any
$i\in \{0,2\}$
and any
![]() $n\geq 0$
. This implies that
$n\geq 0$
. This implies that

is exact and that for
![]() $0 \leq i \leq 2$
,
$0 \leq i \leq 2$
,
and that it is zero for
![]() $i\in \{0,2\}$
or a locally free B-module of rank
$i\in \{0,2\}$
or a locally free B-module of rank
![]() $2\mathrm {dim}(X)$
if
$2\mathrm {dim}(X)$
if
![]() $i=1$
. Using the spectral sequence from Section 4.4, we get as in the proof of Theorem 4.60 for each
$i=1$
. Using the spectral sequence from Section 4.4, we get as in the proof of Theorem 4.60 for each
![]() $n \geq 1$
a map
$n \geq 1$
a map
By induction on n, we deduce from Theorem 4.60 that this map is an isomorphism for all n. Passing to the inverse limit over all
![]() $n\geq 1$
and using the above identification, we deduce an isomorphism
$n\geq 1$
and using the above identification, we deduce an isomorphism
This finishes the proof by passing to local Ext-groups.
Corollary 4.63. Let R be a p-complete ring. Let X be the p-completion of an abelian scheme over R. The
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
is a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module of rank
$\mathcal {O}^{\mathrm {pris}}$
-module of rank
![]() $2 \dim (X)$
, given by
$2 \dim (X)$
, given by
![]() .
.
Although we will not use it, let us record the full description of the prismatic cohomology of X.
Corollary 4.64. With the notation from Corollary 4.63, the prismatic cohomology
is a finite locally free crystal on
![]() and an exterior algebra on the locally free crystal
and an exterior algebra on the locally free crystal
of dimension
![]() $2\mathrm {dim}(X)$
.
$2\mathrm {dim}(X)$
.
Proof. Let
![]() , and let
, and let
![]() $Y:=X\times _{\mathrm {Spf}(R)}\mathrm {Spf}(B/J)$
. It suffices to prove the analog statements for
$Y:=X\times _{\mathrm {Spf}(R)}\mathrm {Spf}(B/J)$
. It suffices to prove the analog statements for
![]() . From (the proof of) Theorem 4.62, we see that
. From (the proof of) Theorem 4.62, we see that
is surjective and that
![]() is an exterior algebra on
is an exterior algebra on
![]() . Since
. Since
![]() is projective, we can lift the identity
is projective, we can lift the identity
![]() to a map
to a map
Using multiplication in
![]() and that
and that
![]() is an exterior algebra, we see that for each
is an exterior algebra, we see that for each
![]() $i\geq 0$
, the morphism
$i\geq 0$
, the morphism
is surjective. This implies that each B-module
![]() is J-torsion free, and then that it is a finite locally free B-module, as modulo J, it identifies with
is J-torsion free, and then that it is a finite locally free B-module, as modulo J, it identifies with
![]() . The same argument as in [Reference Berthelot, Breen and Messing6, Proposition 2.5.2.(ii)]) implies then that each element in
. The same argument as in [Reference Berthelot, Breen and Messing6, Proposition 2.5.2.(ii)]) implies then that each element in
![]() squares to zero. We obtain a morphism
squares to zero. We obtain a morphism
inducing an isomorphism on
![]() $H^i$
after passing to
$H^i$
after passing to
![]() $\otimes ^{\mathbb {L}}_{B}B/J$
. Altogether, we obtain a morphism
$\otimes ^{\mathbb {L}}_{B}B/J$
. Altogether, we obtain a morphism
of complexes which is an isomorphism after applying
![]() $\otimes ^{\mathbb {L}}_BB/J$
. By derived J-adic completeness, it is therefore an isomorphism, which implies the statements.
$\otimes ^{\mathbb {L}}_BB/J$
. By derived J-adic completeness, it is therefore an isomorphism, which implies the statements.
4.6 The prismatic Dieudonné crystal of a p-divisible group
In this section, we establish the basic properties of the prismatic Dieudonné functor for p-divisible groups. The idea, due to Berthelot-Breen-Messing, is to make systematic use of the following theorem of Raynaud, to reduce to statements about (p-divisible groups of) abelian schemes proved in the last section.
Theorem 4.65. Let S be a scheme, and let G be a finite locally free group scheme over S. There exists Zariski-locally on S, a (projective) abelian scheme A and a closed immersion
![]() $G \hookrightarrow A$
of group schemes over S.
$G \hookrightarrow A$
of group schemes over S.
Proof. (See [Reference Berthelot, Breen and Messing6, Theorem 3.1.1]).
Proposition 4.66. Let R be a p-complete ring, and let G be a finite locally free group scheme over R. The sheaf
![]() is a prismatic crystal of locally finitely presented
is a prismatic crystal of locally finitely presented
![]() -modules.
-modules.
Proof. By Theorem 4.65, one can choose locally on R an exact sequence of group schemes
where X and
![]() $X'$
are abelian schemes over R. Whence, by Theorem 4.62 (1), an exact sequence
$X'$
are abelian schemes over R. Whence, by Theorem 4.62 (1), an exact sequence
This proves the proposition, by Theorem 4.62 (2).
Let
![]() $n\geq 1$
. Recall ([Reference Illusie25, Definition 1.1]) that a finite locally free group scheme G over a scheme S is called a truncated Barsotti-Tate group of level n if it is killed by
$n\geq 1$
. Recall ([Reference Illusie25, Definition 1.1]) that a finite locally free group scheme G over a scheme S is called a truncated Barsotti-Tate group of level n if it is killed by
![]() $p^n$
and flat over
$p^n$
and flat over
![]() $\mathbb {Z}/p^n$
, and, when
$\mathbb {Z}/p^n$
, and, when
![]() $n=1$
, if it also satisfies that the sequence
$n=1$
, if it also satisfies that the sequence
is exact, where
![]() $G_0$
denotes the base change of G to
$G_0$
denotes the base change of G to
![]() $S_0=V(p) \subset S$
. The rank of
$S_0=V(p) \subset S$
. The rank of
![]() $G[p]$
is of the form
$G[p]$
is of the form
![]() $p^h$
, for an integer h locally constant on S called the height of G. In the sequel, we will make use of the following basic facts on truncated Barsotti-Tate groups (cf. [Reference Illusie25, Remarks 1.3 (e), 1.3 (f), 1.6]):
$p^h$
, for an integer h locally constant on S called the height of G. In the sequel, we will make use of the following basic facts on truncated Barsotti-Tate groups (cf. [Reference Illusie25, Remarks 1.3 (e), 1.3 (f), 1.6]):
-
1. If G is a p-divisible group over S (of height h),
 $G[p^n]$
is a truncated Barsotti-Tate group of level n over S (of height h) for all
$G[p^n]$
is a truncated Barsotti-Tate group of level n over S (of height h) for all
 $n\geq 1$
.
$n\geq 1$
. -
2. If G is a truncated Barsotti-Tate group of level n and height h, then so is the Cartier dual
 $G^{\ast }$
of G.
$G^{\ast }$
of G. -
3. If
 $0 \to G_1 \to G_2 \to G_3 \to 0$
is an exact sequence finite locally free group schemes of order
$0 \to G_1 \to G_2 \to G_3 \to 0$
is an exact sequence finite locally free group schemes of order
 $p^n$
over S, and if two of them are truncated Barsotti-Tate groups of level n, then so is the third one.
$p^n$
over S, and if two of them are truncated Barsotti-Tate groups of level n, then so is the third one.
Remark 4.67. Let G be a finite locally free group scheme killed by
![]() $p^n$
over a scheme S, such that
$p^n$
over a scheme S, such that
![]() $p^n \mathcal {O}_S=0$
, and let
$p^n \mathcal {O}_S=0$
, and let
![]() $\ell _G$
be its coLie complex. Set:
$\ell _G$
be its coLie complex. Set:
Grothendieck’s duality formula identifies
![]() $\check {\ell }_G$
with the truncation
$\check {\ell }_G$
with the truncation
![]() $\tau ^{\leq 1}R\mathcal {H}om(G^*,\mathbb {G}_a)$
, and this gives rise to a canonical morphism:
$\tau ^{\leq 1}R\mathcal {H}om(G^*,\mathbb {G}_a)$
, and this gives rise to a canonical morphism:
Then G is a
![]() $\mathrm {BT}_n$
if and only if
$\mathrm {BT}_n$
if and only if
![]() $t_G, t_{G^*}$
are locally free and the canonical morphisms
$t_G, t_{G^*}$
are locally free and the canonical morphisms
![]() $\phi _G$
and
$\phi _G$
and
![]() $\phi _{G^*}$
are isomorphisms (cf. [Reference Illusie25, Corollary 2.2.5]). In this situation,
$\phi _{G^*}$
are isomorphisms (cf. [Reference Illusie25, Corollary 2.2.5]). In this situation,
![]() $\omega _G$
is finite locally free of rank called the dimension
$\omega _G$
is finite locally free of rank called the dimension
![]() $\dim (G)$
of G, and
$\dim (G)$
of G, and
![]() $\nu _{G^{\ast }}$
is finite locally free of rank
$\nu _{G^{\ast }}$
is finite locally free of rank
![]() $h-\dim (G)$
, if h is the height of G.
$h-\dim (G)$
, if h is the height of G.
Proposition 4.68. Let R be a quasisyntomic ring, and let G be a truncated Barsotti-Tate group over R of level n. The sheaf
![]() is a prismatic crystal of finite locally free
is a prismatic crystal of finite locally free
![]() -modules.
-modules.
Proof. Fix once and for all an embedding of G into an abelian scheme
![]() $X^{\prime }$
of dimension g over R. By Theorem 4.65, this can be done Zariski-locally on
$X^{\prime }$
of dimension g over R. By Theorem 4.65, this can be done Zariski-locally on
![]() $\mathrm {Spf}(R)$
, and the reader can check that the different steps of the proof are all local statements on
$\mathrm {Spf}(R)$
, and the reader can check that the different steps of the proof are all local statements on
![]() $\mathrm {Spf}(R)$
. Let X be the cokernel of the embedding
$\mathrm {Spf}(R)$
. Let X be the cokernel of the embedding
![]() $G\to { X^{\prime }}$
; this an abelian scheme, and one has an exact sequence
$G\to { X^{\prime }}$
; this an abelian scheme, and one has an exact sequence
of group schemes over R.
We first prove that for any
![]() , the B-module
, the B-module
is locally generated by h sections, where h is the height of G. By the crystal property of
![]() (cf. Proposition 4.66), for any morphism of prisms
(cf. Proposition 4.66), for any morphism of prisms
![]() $(B,J) \to (W(k),(p))$
, where k is a characteristic p perfect field,
$(B,J) \to (W(k),(p))$
, where k is a characteristic p perfect field,
By Nakayama’s lemma,
![]() $(p,J)$
-completeness of B and the finite presentation proved in Proposition 4.66, it suffices to prove that for any morphism
$(p,J)$
-completeness of B and the finite presentation proved in Proposition 4.66, it suffices to prove that for any morphism
![]() $B \to k$
vanishing on J, k characteristic p perfect field,
$B \to k$
vanishing on J, k characteristic p perfect field,
is generated by h elements. Such a morphism
![]() $B \to k$
extends to a morphism of prisms
$B \to k$
extends to a morphism of prisms
![]() $(B,J) \to (W(k),(p))$
, so it suffices by the above to prove our claim when
$(B,J) \to (W(k),(p))$
, so it suffices by the above to prove our claim when
![]() $R=k$
is a perfect field and
$R=k$
is a perfect field and
![]() $(B,J)=(W(k),(p))$
. First, observe that
$(B,J)=(W(k),(p))$
. First, observe that
This is easily seen, using that
![]() and
and
![]() both vanish (Theorems 4.60 and 4.62).
both vanish (Theorems 4.60 and 4.62).
As a corollary of Proposition 4.58 (together with the standard relation between
![]() $H^1(X,\mathcal {O})$
and
$H^1(X,\mathcal {O})$
and
![]() $\mathrm {Lie}(X^{\ast })$
, cf [Reference Berthelot, Breen and Messing6, Section 5.1.1]) and Theorem 4.60, one has a short exact sequence
$\mathrm {Lie}(X^{\ast })$
, cf [Reference Berthelot, Breen and Messing6, Section 5.1.1]) and Theorem 4.60, one has a short exact sequence
and similarly for
![]() $X'$
. Also, note that we have exact sequencesFootnote
29
:
$X'$
. Also, note that we have exact sequencesFootnote
29
:
(where
![]() $\nu _{G^*}=\mathcal {E}xt^1(G,\mathbb {G}_a)$
) and
$\nu _{G^*}=\mathcal {E}xt^1(G,\mathbb {G}_a)$
) and
The map
is compatible with the natural maps
![]() $u^{*} \mathrm {Lie}(X^*) \to u^{*} \mathrm {Lie}(X^{'*})$
and
$u^{*} \mathrm {Lie}(X^*) \to u^{*} \mathrm {Lie}(X^{'*})$
and
![]() $u^{*} \omega _{X'} \to u^{*} \omega _X$
, through the identifications of Theorem 4.60. The long exact sequence of
$u^{*} \omega _{X'} \to u^{*} \omega _X$
, through the identifications of Theorem 4.60. The long exact sequence of
![]() $\mathcal {E}xt$
gives a surjection:
$\mathcal {E}xt$
gives a surjection:
since, as we have seen in Theorem 4.60,
. By the above remark, we even have a commutative diagram:

where all rows and the first two columns are exact. This proves that the map
is surjective and an easy diagram chase proves that in fact the sequence
is exact. As G is a truncated Barsotti-Tate group, the sheaf
![]() $\omega _{G}$
is a locally free sheaf of rank
$\omega _{G}$
is a locally free sheaf of rank
![]() $d=\dim G$
and
$d=\dim G$
and
![]() $\nu _{G^*}$
is a locally free sheaf of rank
$\nu _{G^*}$
is a locally free sheaf of rank
![]() $h-d$
(cf. Remark 4.67, which applies whatever the level of G is, since
$h-d$
(cf. Remark 4.67, which applies whatever the level of G is, since
![]() $p=0$
on k). Hence, the sequence stays exact after evaluation on
$p=0$
on k). Hence, the sequence stays exact after evaluation on
![]() $(W(k),(p))$
and
$(W(k),(p))$
and
is generated by h sections. This proves the claim.
Back to the proof of the proposition, we know, as a direct consequence of Theorem 4.62 that
is crystal of locally free
![]() -modules of rank
-modules of rank
![]() $2g$
. Consider the exact sequence
$2g$
. Consider the exact sequence
where H is a Barsotti-Tate group of height
![]() $2g-h$
, induced by the embedding of G in
$2g-h$
, induced by the embedding of G in
![]() ${X^{\prime }}$
. This gives an exact sequence
${X^{\prime }}$
. This gives an exact sequence
Indeed, right-exactness follows from 4.62, which implies that already
is surjective. Locally on
![]() , the middle term is free of rank
, the middle term is free of rank
![]() $2g$
over
$2g$
over
![]() , while the left (respectively, right) term is generated by
, while the left (respectively, right) term is generated by
![]() $2g-h$
(respectively, h) sections. Therefore,
$2g-h$
(respectively, h) sections. Therefore,
![]() and
and
![]() are free over
are free over
![]() of rank
of rank
![]() $2g-h$
and h.
$2g-h$
and h.
Proposition 4.69. Let R be a p-complete ring, and let G be a p-divisible group over R. The sheaf
is a prismatic crystal of finite locally free
![]() -modules of rank the height of G.
-modules of rank the height of G.
In particular, if R is a quasisyntomic ring and G is a p-divisible group over R, the
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() is a finite locally free
is a finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-module of rank the height of G.
$\mathcal {O}^{\mathrm {pris}}$
-module of rank the height of G.
Proof. Let G be a p-divisible group over R. Since
![]() $G=\mathrm {colim}~G[p^n]$
, we have a short exact sequence:
$G=\mathrm {colim}~G[p^n]$
, we have a short exact sequence:

The last term vanishes as the prismatic topos is replete. We have to show that the first term vanishes, or even stronger, that for each
![]() , the morphism
, the morphism
is bijective. Set
and
for
![]() $n\geq 0$
. For
$n\geq 0$
. For
![]() $n,m\geq 0$
, the sequence
$n,m\geq 0$
, the sequence
is right exact (this follows by locally embedding
![]() $G[p^{m+n}]$
and using Theorem 4.62). Thus, the canonical morphism
$G[p^{m+n}]$
and using Theorem 4.62). Thus, the canonical morphism
is an isomorphism for
![]() $n,m\geq 0$
. As all
$n,m\geq 0$
. As all
![]() $M_n$
are finite locally free over
$M_n$
are finite locally free over
![]() $B/p^n$
(of rank the height of G) the B-module
$B/p^n$
(of rank the height of G) the B-module
![]() $N:=\varprojlim \limits_{n} M_n$
is finite locally free over B (of rank the height of G) by [Reference Project52, Tag 0D4B]. By the same reference,
$N:=\varprojlim \limits_{n} M_n$
is finite locally free over B (of rank the height of G) by [Reference Project52, Tag 0D4B]. By the same reference,
The canonical morphism
![]() $M\to N$
is surjective (by a similar
$M\to N$
is surjective (by a similar
![]() $R^1\varprojlim \limits_{n}$
sequence as above). In particular, we can conclude that
$R^1\varprojlim \limits_{n}$
sequence as above). In particular, we can conclude that
![]() $M\to M_n$
is surjective for each
$M\to M_n$
is surjective for each
![]() $n\geq 0$
. The long exact sequence for
$n\geq 0$
. The long exact sequence for
![]() $0\to u^{-1}(G[p^n])\to u^{-1}G\to u^{-1}G\to 0$
and the surjectivity of
$0\to u^{-1}(G[p^n])\to u^{-1}G\to u^{-1}G\to 0$
and the surjectivity of
![]() $M\to M_n$
imply that
$M\to M_n$
imply that
![]() $M/p^n\cong M_n$
and
$M/p^n\cong M_n$
and
![]() have no
have no
![]() $p^n$
-torsion. This p-torsion freeness of
$p^n$
-torsion. This p-torsion freeness of
![]() $\mathrm {Ext}^2$
in turn implies that
$\mathrm {Ext}^2$
in turn implies that
Our aim is to prove that
![]() $M\cong N$
or equivalently that M is classically p-complete, that is,
$M\cong N$
or equivalently that M is classically p-complete, that is,
![]() $M\cong \varprojlim \limits_{n} M/p^n$
. As all prisms in
$M\cong \varprojlim \limits_{n} M/p^n$
. As all prisms in
![]() are by definition bounded, and thus classically p-complete,
are by definition bounded, and thus classically p-complete,
We can therefore calculate
![]() by an exact sequence
by an exact sequence
In this sequence, the
![]() $R^1\varprojlim \limits_{n}$
-term vanishes as each
$R^1\varprojlim \limits_{n}$
-term vanishes as each
![]() is zero because G is p-divisible. The isomorphisms
is zero because G is p-divisible. The isomorphisms
imply that
![]() is a crystal, because they show that, even stronger,
is a crystal, because they show that, even stronger,
commutes with base change in
![]() $(B,J)$
. This finishes the proof of the first sentence of the proposition.
$(B,J)$
. This finishes the proof of the first sentence of the proposition.
The second sentence is an immediate corollary of the first one, together with Proposition 4.4 and Lemma 4.38.
We can now summarise our discussion and prove the main result of this section. We need a last lemma.
Lemma 4.70. Let
![]() $(C,J)$
be an henselian pair, and let
$(C,J)$
be an henselian pair, and let
![]() $\overline {G}$
be a p-divisible group over
$\overline {G}$
be a p-divisible group over
![]() $C/J$
. Then there exists a p-divisible group G over C, such that
$C/J$
. Then there exists a p-divisible group G over C, such that
Proof. Set h as the height of
![]() $\overline {G}$
. Let
$\overline {G}$
. Let
![]() $\mathrm {BT}_n^h$
be the Artin stack (over
$\mathrm {BT}_n^h$
be the Artin stack (over
![]() $\mathrm {Spec}(\mathbb {Z})$
) of n-truncated Barsotti-Tate groups of height h. Then for any
$\mathrm {Spec}(\mathbb {Z})$
) of n-truncated Barsotti-Tate groups of height h. Then for any
![]() $n\geq 1$
, the morphism
$n\geq 1$
, the morphism
is a smooth morphism between smooth Artin stacks (cf. [Reference Lau32, Section 2] respectively, [Reference Illusie25, Theorem 4.4]). By [Reference Elkik21, Theorem, page 568] (which extends to the non-Noetherian case by passing to the limit) any section
![]() $D\to C/J$
of some smooth C-algebra D extends to a section
$D\to C/J$
of some smooth C-algebra D extends to a section
![]() $D\to C$
. These statements imply that inductively, we can lift
$D\to C$
. These statements imply that inductively, we can lift
![]() $\overline {G}[p^n]$
to a truncated p-divisible group
$\overline {G}[p^n]$
to a truncated p-divisible group
![]() $H_n$
over C. Then finally
$H_n$
over C. Then finally
yields the desired lift over
![]() $\overline {G}$
.
$\overline {G}$
.
Theorem 4.71. Let R be a quasisyntomic ring, and let G be a p-divisible group over R. The pair
![]() of Definition 4.35 is an admissible prismatic Dieudonné crystal over R.
of Definition 4.35 is an admissible prismatic Dieudonné crystal over R.
Proof. Let G be a p-divisible group over R. By Proposition 4.69, we already know that
![]() is a finite locally free
is a finite locally free
![]() $\mathcal {O}^{\mathrm { pris}}$
-module, endowed with the semilinear endomorphism
$\mathcal {O}^{\mathrm { pris}}$
-module, endowed with the semilinear endomorphism
![]() $\varphi _{\mathcal {M}_G}$
. We need to see that it gives an admissible prismatic Dieudonné crystal over R. The construction being functorial in R, it suffices by Proposition 4.9 to deal with the case where R is quasiregular semiperfectoid. Choose a perfectoid ring S mapping surjectively onto R; by Corollary 2.10, we can assume that S is henselian along
$\varphi _{\mathcal {M}_G}$
. We need to see that it gives an admissible prismatic Dieudonné crystal over R. The construction being functorial in R, it suffices by Proposition 4.9 to deal with the case where R is quasiregular semiperfectoid. Choose a perfectoid ring S mapping surjectively onto R; by Corollary 2.10, we can assume that S is henselian along
![]() $\ker (S \to R)$
. Lemma 4.70 (applied to
$\ker (S \to R)$
. Lemma 4.70 (applied to
![]() $(C,J)=(S,\ker (S\to R))$
and
$(C,J)=(S,\ker (S\to R))$
and
![]() $\overline {G}=G$
) shows that G is the base change of a p-divisible group H over S. Hence,
$\overline {G}=G$
) shows that G is the base change of a p-divisible group H over S. Hence,
![]() is the base change of
is the base change of
![]() , which we know to be an admissible Dieudonné crystal since S is perfectoid, cf. Corollary 4.49.
, which we know to be an admissible Dieudonné crystal since S is perfectoid, cf. Corollary 4.49.
We now state two useful properties of the prismatic Dieudonné functor: its exactness and its compatibility with Cartier duality.
Proposition 4.72. Let R be a quasisyntomic ring. The functor
is exact.
Proof. Let
be a short exact sequence of p-divisible groups over R, which we see as an exact sequence of abelian sheaves on
![]() $(R)_{\mathrm {qsyn}}$
. Applying
$(R)_{\mathrm {qsyn}}$
. Applying
![]() $R\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(-, \mathcal {O}^{\mathrm {pris}})$
to it, we get a long exact sequence:
$R\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(-, \mathcal {O}^{\mathrm {pris}})$
to it, we get a long exact sequence:
The first term vanishes as
![]() $G^{\prime }$
is p-divisible and
$G^{\prime }$
is p-divisible and
![]() $\mathcal {O}^{\mathrm {pris}}$
derived p-complete. Let us prove surjectivity of
$\mathcal {O}^{\mathrm {pris}}$
derived p-complete. Let us prove surjectivity of
![]() . For
. For
![]() $n\geq 1$
, consider the exact sequences
$n\geq 1$
, consider the exact sequences
Then
![]() $G^{\prime \prime }=\varinjlim \limits_n H_n$
with injective transition maps
$G^{\prime \prime }=\varinjlim \limits_n H_n$
with injective transition maps
![]() $H_n\to H_{n+1}$
(as
$H_n\to H_{n+1}$
(as
![]() $G[p^{n}]\subseteq G^{\prime }=G^{\prime }[p^n]$
for all
$G[p^{n}]\subseteq G^{\prime }=G^{\prime }[p^n]$
for all
![]() $n\geq 1$
). As in the proof of Proposition 4.69, we can conclude that
$n\geq 1$
). As in the proof of Proposition 4.69, we can conclude that
are surjective. Passing to the limit of the exact sequences
implies, therefore, that
is surjective, as desired.
Let R be a quasisyntomic ring, and let G be a p-divisible group over R with Cartier dual
![]() $\check {G}$
. Passing to the limit for the Cartier duality on finite flat group schemes yields isomorphisms
$\check {G}$
. Passing to the limit for the Cartier duality on finite flat group schemes yields isomorphisms
of sheaves on
![]() $(R)_{\mathrm {qsyn}}$
. We first construct a canonical morphism
$(R)_{\mathrm {qsyn}}$
. We first construct a canonical morphism
where
![]() denotes the
denotes the
![]() $\mathcal {O}^{\mathrm {pris}}$
-linear dual of
$\mathcal {O}^{\mathrm {pris}}$
-linear dual of
![]() . Recall that
. Recall that
by Lemma 4.40. Thus, we can define
![]() $\Phi _G$
by setting
$\Phi _G$
by setting
where
Clearly, the morphism
![]() $\Phi _G$
is natural in G and commutes with base change in R.
$\Phi _G$
is natural in G and commutes with base change in R.
Proposition 4.73. Let R be a quasisyntomic ring. For every p-divisible group G over R, the map
constructed above is an isomorphism.
Proposition 4.77 implies, via quasisyntomic descent, that
![]() is naturally a prismatic Dieudonné crystal when equipped with the Frobenius
is naturally a prismatic Dieudonné crystal when equipped with the Frobenius
(using the identification
![]() $\varphi ^{\ast }\mathcal {O}^{\mathrm {pris}}\cong \mathcal {O}^{\mathrm {pris}}$
and the inverse
$\varphi ^{\ast }\mathcal {O}^{\mathrm {pris}}\cong \mathcal {O}^{\mathrm {pris}}$
and the inverse
![]() of the linearised Frobenius on
of the linearised Frobenius on
![]() ). With this choice of Frobenius, one checks that
). With this choice of Frobenius, one checks that
![]() $\Phi _G$
is a morphism of prismatic Dieudonné crystals, that is, compatible with the Frobenius.
$\Phi _G$
is a morphism of prismatic Dieudonné crystals, that is, compatible with the Frobenius.
Proof. Both sides are locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-modules of the same rank (cf. Proposition 4.69). Hence, it suffices to see that
$\mathcal {O}^{\mathrm {pris}}$
-modules of the same rank (cf. Proposition 4.69). Hence, it suffices to see that
![]() $\Phi _G$
is surjective, which can be checked after base change
$\Phi _G$
is surjective, which can be checked after base change
![]() $R\to k$
to perfect fields k of characteristic p. Thus, assume that
$R\to k$
to perfect fields k of characteristic p. Thus, assume that
![]() $R=k$
. By Theorem 4.44, the prismatic Dieudonné functor over k is isomorphic to the crystalline one. Let
$R=k$
. By Theorem 4.44, the prismatic Dieudonné functor over k is isomorphic to the crystalline one. Let
be the natural isomorphism coming from classical duality for the crystalline Dieudonné functor over perfect fields (cf. for example [Reference Fontaine23, Proposition III 5.1.iii)]). Let
be any natural transformation (of functors on p-divisible groups over quasisyntomic rings over k). Then for any morphism
![]() $\gamma \colon G\to H$
of p-divisible groups, there is an equality
$\gamma \colon G\to H$
of p-divisible groups, there is an equality
where
![]() . We want to show that
. We want to show that
![]() $\Phi _G=u\Phi ^{\mathrm {cl}}_G$
for all p-divisible groups G and some unit
$\Phi _G=u\Phi ^{\mathrm {cl}}_G$
for all p-divisible groups G and some unit
![]() $u\in \mathcal {O}^{\mathrm {pris}}$
(independent of G). Thus, pick
$u\in \mathcal {O}^{\mathrm {pris}}$
(independent of G). Thus, pick
![]() and
and
![]() $\alpha \in \mathcal {H}om(G,\mu _{p^{\infty }})$
. Applying (Equation (4.1)) to
$\alpha \in \mathcal {H}om(G,\mu _{p^{\infty }})$
. Applying (Equation (4.1)) to
![]() $\gamma =\alpha \colon G\to \mu _{p^{\infty }}$
implies
$\gamma =\alpha \colon G\to \mu _{p^{\infty }}$
implies
for any natural transformation
![]() $\Psi _{(-)}$
as above. In particular,
$\Psi _{(-)}$
as above. In particular,
![]() $\Psi $
(and, thus,
$\Psi $
(and, thus,
![]() $\Phi _{(-)}$
and
$\Phi _{(-)}$
and
![]() $\Phi ^{\mathrm {cl}}_{(-)}$
, as examples) are determined by their behaviour on
$\Phi ^{\mathrm {cl}}_{(-)}$
, as examples) are determined by their behaviour on
![]() $G=\mu _{p^{\infty }}$
. For
$G=\mu _{p^{\infty }}$
. For
![]() $\mu _{p^{\infty }}$
, both induce an isomorphism
$\mu _{p^{\infty }}$
, both induce an isomorphism
Namely,
![]() $\Phi _{\mu _{p^{\infty }}}$
is given by the natural evaluation, which is an isomorphism as
$\Phi _{\mu _{p^{\infty }}}$
is given by the natural evaluation, which is an isomorphism as
![]() is free over rank
is free over rank
![]() $1$
(by the crystalline comparison, cf. Theorem 4.44). That
$1$
(by the crystalline comparison, cf. Theorem 4.44). That
![]() $\Phi _{\mu _{p^{\infty }}}^{\mathrm {cl}}$
is an isomorphism follows from classical Dieudonné theory (cf. [Reference Fontaine23, Proposition 5.1.iii)]). Hence,
$\Phi _{\mu _{p^{\infty }}}^{\mathrm {cl}}$
is an isomorphism follows from classical Dieudonné theory (cf. [Reference Fontaine23, Proposition 5.1.iii)]). Hence,
![]() $\Phi _{\mu _{p^{\infty }}}$
and
$\Phi _{\mu _{p^{\infty }}}$
and
![]() $\Phi ^{\mathrm {cl}}_{\mu _{p^{\infty }}}$
differ by some unit
$\Phi ^{\mathrm {cl}}_{\mu _{p^{\infty }}}$
differ by some unit
![]() $u\in \mathcal {O}^{\mathrm {pris}}$
$u\in \mathcal {O}^{\mathrm {pris}}$
Footnote
30
. This implies
![]() $\Phi _G=u\Phi ^{\mathrm {cl}}_G$
for all G by naturality. By [Reference Fontaine23, Proposition 5.1.iii)], we can conclude.
$\Phi _G=u\Phi ^{\mathrm {cl}}_G$
for all G by naturality. By [Reference Fontaine23, Proposition 5.1.iii)], we can conclude.
The main result of this text is the following theorem, whose proof will spread out over the next sections.
Theorem 4.74. Let R be a quasisyntomic ring. The prismatic Dieudonné functor:
is an antiequivalence between the category of p-divisible groups over R and the category of admissible prismatic Dieudonné crystals over R.
Proof. By Proposition 3.21 and the fact that both
![]() $\mathrm {BT}$
and
$\mathrm {BT}$
and
![]() $\mathrm {DM}^{\mathrm {adm}}$
are stacks on
$\mathrm {DM}^{\mathrm {adm}}$
are stacks on
![]() $\mathrm {QSyn}$
for the quasisyntomic topology (see Propositions A.2 and 4.9), we can assume that moreover R is quasiregular semiperfectoid. Then the theorem is a consequence of Theorems 4.82 and 4.90, to be proved below.
$\mathrm {QSyn}$
for the quasisyntomic topology (see Propositions A.2 and 4.9), we can assume that moreover R is quasiregular semiperfectoid. Then the theorem is a consequence of Theorems 4.82 and 4.90, to be proved below.
4.7 The prismatic Dieudonné modules of
 $\mathbb {Q}_p/\mathbb {Z}_p$
and
$\mathbb {Q}_p/\mathbb {Z}_p$
and
 $\mu _{p^{\infty }}$
$\mu _{p^{\infty }}$
In this subsection, we calculate the prismatic Dieudonné crystals of
![]() $\mathbb {Q}_p/\mathbb {Z}_p$
and
$\mathbb {Q}_p/\mathbb {Z}_p$
and
![]() $\mu _{p^{\infty }}$
to explicitly work out some examples for prismatic Dieudonné crystals. We deduce as well a description for all étale and multiplicative p-divisible groups. For the analogous results for the crystalline Dieudonné functor, see [Reference Berthelot and Messing7, Section 2.2]. Let us fix a quasisyntomic ring R. Recall that for a p-divisible group G over R, the prismatic Dieudonné crystal
$\mu _{p^{\infty }}$
to explicitly work out some examples for prismatic Dieudonné crystals. We deduce as well a description for all étale and multiplicative p-divisible groups. For the analogous results for the crystalline Dieudonné functor, see [Reference Berthelot and Messing7, Section 2.2]. Let us fix a quasisyntomic ring R. Recall that for a p-divisible group G over R, the prismatic Dieudonné crystal
![]() is defined (cf. Definition 4.35) as the sheaf
is defined (cf. Definition 4.35) as the sheaf
on the absolute prismatic site
![]() of R and that
of R and that
by Lemma 4.40.
Lemma 4.75. The
![]() $\mathcal {O}^{\mathrm {pris}}$
-module
$\mathcal {O}^{\mathrm {pris}}$
-module
![]() is freely generated by the isomorphism class of the extension of
is freely generated by the isomorphism class of the extension of
![]() $\mathcal {O}^{\mathrm {pris}}$
by
$\mathcal {O}^{\mathrm {pris}}$
by
![]() $\mathbb {Q}_p/\mathbb {Z}_p$
obtained as the pushout of the short exact sequence
$\mathbb {Q}_p/\mathbb {Z}_p$
obtained as the pushout of the short exact sequence
on
![]() $(R)_{\mathrm {qsyn}}$
along the canonical morphism
$(R)_{\mathrm {qsyn}}$
along the canonical morphism
![]() $\mathbb {Z}_p\to \mathcal {O}^{\mathrm {pris}}$
. More generally,
$\mathbb {Z}_p\to \mathcal {O}^{\mathrm {pris}}$
. More generally,
if G is an étale p-divisible group.
Proof. This follows directly from the isomorphism
and the fact that for an étale p-divisible group,
![]() $T_pG$
is a local system of finite free
$T_pG$
is a local system of finite free
![]() $\mathbb {Z}_p$
-modules on
$\mathbb {Z}_p$
-modules on
![]() $(R)_{\mathrm {qsyn}}$
$(R)_{\mathrm {qsyn}}$
Let us now describe the prismatic Dieudonné crystal
![]() of
of
![]() $\mu _{p^{\infty }}$
on
$\mu _{p^{\infty }}$
on
![]() $(R)_{\mathrm {qsyn}}$
.
$(R)_{\mathrm {qsyn}}$
.
Definition 4.76. Let
![]() be the sheaf
be the sheaf
on the absolute prismatic site of
![]() $\mathbb {Z}_p$
, with
$\mathbb {Z}_p$
, with
![]() $\mathbb {Z}_p(1):=T_p\mu _{p^{\infty }}$
.
$\mathbb {Z}_p(1):=T_p\mu _{p^{\infty }}$
.
Note that, if
![]() $\widehat {{\mathbb {G}_m}}$
denotes the p-adic completion of the multiplicative group scheme
$\widehat {{\mathbb {G}_m}}$
denotes the p-adic completion of the multiplicative group scheme
![]() ${\mathbb {G}_m}$
, we also have
${\mathbb {G}_m}$
, we also have
as
![]() $\widehat {{\mathbb {G}_m}}/\mu _{p^{\infty }}$
is uniquely p-divisible and
$\widehat {{\mathbb {G}_m}}/\mu _{p^{\infty }}$
is uniquely p-divisible and
![]() -complete. Also, as recalled above, we have a natural isomorphism
-complete. Also, as recalled above, we have a natural isomorphism
We can describe the sheaf
![]() in restriction to prisms
in restriction to prisms
![]() $(B,J)$
which live over the ‘cyclotomic’ base prism
$(B,J)$
which live over the ‘cyclotomic’ base prism
from Section 2.2. We point out that Mondal [Reference Mondal46] was able to recently get rid of this restriction, using Bhatt-Lurie’s syntomic Chern classes [Reference Bhatt and Lurie10].
The reason is that for such prisms, we can use the q-logarithm from Section 2.2
which defines a canonical element, which we call
![]() .
.
Proposition 4.77. The
![]() -linear map
-linear map
sending
![]() $1$
to
$1$
to
![]() $\ell _q$
, of sheaves on the category of all prisms living over
$\ell _q$
, of sheaves on the category of all prisms living over
![]() $(A,I)=(\mathbb {Z}_p[[q-1]],([p]_q))$
, is an isomorphism. Moreover, the Frobenius on
$(A,I)=(\mathbb {Z}_p[[q-1]],([p]_q))$
, is an isomorphism. Moreover, the Frobenius on
![]() sends
sends
![]() $\ell _q$
to
$\ell _q$
to
![]() $[p]_q\ell _q$
.
$[p]_q\ell _q$
.
Proof. Let
![]() $(B,J)$
be a prism over
$(B,J)$
be a prism over
![]() $(A,I)$
. It suffices to show that the morphism
$(A,I)$
. It suffices to show that the morphism
(where we mean
![]() $\mathrm {Ext}^1$
in the category of abelian sheaves on the site of prisms over
$\mathrm {Ext}^1$
in the category of abelian sheaves on the site of prisms over
![]() $(B,J)$
) given by the q-logarithm is an isomorphism. By Proposition 4.69, the formation of this map is compatible with base change in
$(B,J)$
) given by the q-logarithm is an isomorphism. By Proposition 4.69, the formation of this map is compatible with base change in
![]() $(B,J)$
. From the proof of loc. cit. we also know that
$(B,J)$
. From the proof of loc. cit. we also know that
![]() is a finite locally free B-module of rank
is a finite locally free B-module of rank
![]() $1$
. Therefore, it suffices to show surjectivity. To show surjectivity, one may pass to the case that
$1$
. Therefore, it suffices to show surjectivity. To show surjectivity, one may pass to the case that
![]() $(B,J)=(W(k),(p))$
for k an algebraically closed field of characteristic p. Then the comparison with the crystalline Dieudonné crystal (cf. Theorem 4.44) reduces to an analogous statement for the usual logarithm as for
$(B,J)=(W(k),(p))$
for k an algebraically closed field of characteristic p. Then the comparison with the crystalline Dieudonné crystal (cf. Theorem 4.44) reduces to an analogous statement for the usual logarithm as for
![]() $q=1$
, the q-logarithm becomes the logarithm. Let R be a general ring of characteristic p, and let
$q=1$
, the q-logarithm becomes the logarithm. Let R be a general ring of characteristic p, and let
![]() $R^{\prime }\to R$
be a surjection of schemes with a PD-structure
$R^{\prime }\to R$
be a surjection of schemes with a PD-structure
![]() $\{\gamma _{n}\}_{n\geq 0}$
on
$\{\gamma _{n}\}_{n\geq 0}$
on
![]() $K:=\ker (R^{\prime }\to R)$
and assume p nilpotent in
$K:=\ker (R^{\prime }\to R)$
and assume p nilpotent in
![]() $R^{\prime }$
. Then there is the canonical morphism
$R^{\prime }$
. Then there is the canonical morphism
where
![]() $[-]\colon \lim \limits _{x\mapsto x^p} R\to R^{\prime }$
is the Teichmüller lift and
$[-]\colon \lim \limits _{x\mapsto x^p} R\to R^{\prime }$
is the Teichmüller lift and
![]() $\log $
the crystalline logarithm
$\log $
the crystalline logarithm
 $$ \begin{align*}\log\colon 1+K\to R^{\prime},\ y\mapsto \sum\limits_{n=1}^{\infty}(-1)^{n-1}(n-1)! \gamma_n(y-1) \end{align*} $$
$$ \begin{align*}\log\colon 1+K\to R^{\prime},\ y\mapsto \sum\limits_{n=1}^{\infty}(-1)^{n-1}(n-1)! \gamma_n(y-1) \end{align*} $$
(which makes sense as
![]() $[x]\in 1+K$
). But it is known that the logarithm generates the crystalline Dieudonné crystal of
$[x]\in 1+K$
). But it is known that the logarithm generates the crystalline Dieudonné crystal of
![]() $\mu _{p^{\infty }}$
(cf. [Reference Berthelot and Messing7, Corollary 2.2.3]). Finally, the action of Frobenius on
$\mu _{p^{\infty }}$
(cf. [Reference Berthelot and Messing7, Corollary 2.2.3]). Finally, the action of Frobenius on
![]() $\ell _q$
can be calculated using Lemma 2.13:
$\ell _q$
can be calculated using Lemma 2.13:
for
![]() $x\in \mathbb {Z}_p(1)$
.
$x\in \mathbb {Z}_p(1)$
.
Remark 4.78. Note that, when
![]() $pR=0$
, the identification between the prismatic and crystalline Dieudonné modules from Theorem 4.44 is linear over the isomorphism
$pR=0$
, the identification between the prismatic and crystalline Dieudonné modules from Theorem 4.44 is linear over the isomorphism
![]() from Lemma 3.27. This explains why the map
from Lemma 3.27. This explains why the map
![]() $x\mapsto \log _q([x^{1/p}]_{\tilde {\theta }})$
is sent to
$x\mapsto \log _q([x^{1/p}]_{\tilde {\theta }})$
is sent to
![]() $x\mapsto \log ([x])$
(and not something like
$x\mapsto \log ([x])$
(and not something like
![]() $x\mapsto \log ([x^{1/p}])$
, which would not make sense as
$x\mapsto \log ([x^{1/p}])$
, which would not make sense as
![]() $[x^{1/p}]-1$
need not have divided powers), cf. the remark after Lemma 3.27.
$[x^{1/p}]-1$
need not have divided powers), cf. the remark after Lemma 3.27.
Assume now that R is an
![]() $A/I=\mathbb {Z}[\zeta _p]$
-algebra.
$A/I=\mathbb {Z}[\zeta _p]$
-algebra.
Corollary 4.79. Let G be a multiplicative p-divisible group over R. Then there is a canonical isomorphism
induced by sending
![]() $f\colon G\to \mu _{p^{\infty }}$
to the evaluation of the morphism induced by f:
$f\colon G\to \mu _{p^{\infty }}$
to the evaluation of the morphism induced by f:
on
![]() $\ell _q$
.
$\ell _q$
.
Proof. The morphism (and the claim that it is an isomorphism) commutes with étale localisation on R. In particular, we may assume that
![]() $G\cong \mu _{p^{\infty }}^d$
. Then the claim follows from Proposition 4.77 and additivity of the right-hand side.
$G\cong \mu _{p^{\infty }}^d$
. Then the claim follows from Proposition 4.77 and additivity of the right-hand side.
As a corollary of these computations, we can concretely describe the action of the prismatic Dieudonné functor on morphisms
![]() $\mathbb {Q}_p/\mathbb {Z}_p\to \mu _{p^{\infty }}$
. Set
$\mathbb {Q}_p/\mathbb {Z}_p\to \mu _{p^{\infty }}$
. Set
As usual, we get the elements
![]() $\varepsilon =(1,\zeta _p,\ldots )$
,
$\varepsilon =(1,\zeta _p,\ldots )$
,
![]() $q:=[\varepsilon ]\in A_{\mathrm {inf}}(\mathbb {Z}_p^{\mathrm {cycl}})$
and
$q:=[\varepsilon ]\in A_{\mathrm {inf}}(\mathbb {Z}_p^{\mathrm {cycl}})$
and
![]() $\tilde {\xi }:=\frac {q^p-1}{q-1}$
.
$\tilde {\xi }:=\frac {q^p-1}{q-1}$
.
Lemma 4.80. Let R be a quasiregular semiperfectoid ring over
![]() $\mathbb {Z}_p^{\mathrm {cycl}}$
. Then the morphism
$\mathbb {Z}_p^{\mathrm {cycl}}$
. Then the morphism
is given the map which sends
![]() $x\in \mathbb {Z}_p(1)(R)$
to
$x\in \mathbb {Z}_p(1)(R)$
to
![]() .
.
Proof. First, note that
by evaluating a homomorphism
![]() on
on
![]() $\ell _q$
. The identification of
$\ell _q$
. The identification of
![]() on a homomorphism
on a homomorphism
![]() $f\colon \mathbb {Q}_p/\mathbb {Z}_p\to \mu _{p^{\infty }}$
follows easily from the natural isomorphism
$f\colon \mathbb {Q}_p/\mathbb {Z}_p\to \mu _{p^{\infty }}$
follows easily from the natural isomorphism
for a p-divisible group G over R and Proposition 4.77 and Lemma 4.75.
Remark 4.81. This description together with [Reference Bhatt and Lurie10, Theorem 7.5.6] imply fully faithfulness of the prismatic Dieudonné functor in the special case of morphisms from
![]() $\mathbb {Q}_p/\mathbb {Z}_p$
to
$\mathbb {Q}_p/\mathbb {Z}_p$
to
![]() $\mu _{p^{\infty }}$
. We will give in the next section a proof of fully faithfulness, still relying on the same input from [Reference Bhatt and Lurie10].
$\mu _{p^{\infty }}$
. We will give in the next section a proof of fully faithfulness, still relying on the same input from [Reference Bhatt and Lurie10].
4.8 Fully faithfulness
The main result of this subsection is the following.
Theorem 4.82. If R is a quasiregular semiperfectoid ring, the prismatic Dieudonné functor over R is fully faithful for p-divisible groups.
The proof we offer was kindly suggested to us by Akhil Mathew. Recall that the prismatic Dieudonné functor is given, according to Lemma 4.40, by the formula
for any p-divisible group G over the quasiregular semiperfectoid ring R. We also set
From now on, we fix a quasiregular semiperfectoid ring R and a generator
![]() $\tilde {\xi }$
of the prismatic ideal in
$\tilde {\xi }$
of the prismatic ideal in
![]() . For simplicity, we assume that R lives over the cyclotomic prism and that
. For simplicity, we assume that R lives over the cyclotomic prism and that
![]() $\tilde {\xi }=[p]_q$
(cf. Proposition 4.77). By descent this assumption is harmless.
$\tilde {\xi }=[p]_q$
(cf. Proposition 4.77). By descent this assumption is harmless.
Proposition 4.83. If G is a p-divisible group over R, there is a natural (in R and G) identification of quasisyntomic sheaves
Proof. We have, cf. [Reference Bhatt and Lurie10, Theorem 7.5.6]Footnote 32 , an isomorphism of quasisyntomic sheaves
To conclude, it suffices to apply the functor
![]() $\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_p G,-)$
to both sides and to note that
$\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_p G,-)$
to both sides and to note that
![]() $T_p \check {G} = \mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_p G,T_p \mathbb {G}_m)$
.
$T_p \check {G} = \mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_p G,T_p \mathbb {G}_m)$
.
Now we start the proof of Theorem 4.82. Let us denote by
![]() $\mathrm {Sh}_R$
the category of abelian sheaves on
$\mathrm {Sh}_R$
the category of abelian sheaves on
![]() $(R)_{\mathrm {qsyn}}$
(so that
$(R)_{\mathrm {qsyn}}$
(so that
![]() $\mathrm {Hom}_{\mathrm {Sh}_R}(-,-)=\mathrm {Hom}_{(R)_{\mathrm {qsyn}}}(-,-)$
) and by
$\mathrm {Hom}_{\mathrm {Sh}_R}(-,-)=\mathrm {Hom}_{(R)_{\mathrm {qsyn}}}(-,-)$
) and by
![]() $\mathcal {D}_R$
the category of
$\mathcal {D}_R$
the category of
![]() $\mathcal {O}^{\mathrm {pris}}[F]$
-modules, which contains, as a full subcategory, the category of (admissible) prismatic Dieudonné crystals. The functor
$\mathcal {O}^{\mathrm {pris}}[F]$
-modules, which contains, as a full subcategory, the category of (admissible) prismatic Dieudonné crystals. The functor
admits the left adjoint
Indeed, if
![]() $\mathcal {F}\in \mathrm {Sh}_R$
is any abelian sheaf and
$\mathcal {F}\in \mathrm {Sh}_R$
is any abelian sheaf and
![]() $\mathcal {M}\in \mathcal {D}_R$
, then
$\mathcal {M}\in \mathcal {D}_R$
, then
because both sides identify with bilinear maps
![]() $\omega \colon \mathcal {M}\times \mathcal {F}\to \mathcal {O}^{\mathrm {pris}}$
, which are
$\omega \colon \mathcal {M}\times \mathcal {F}\to \mathcal {O}^{\mathrm {pris}}$
, which are
![]() $\mathcal {O}^{\mathrm {pris}}[F]$
-linear in the first component.
$\mathcal {O}^{\mathrm {pris}}[F]$
-linear in the first component.
Note that by the above displayed formula (4.2), if G is a p-divisible group over R,
Hence, to prove the theorem, we are reduced to proving the following proposition.
Proposition 4.84. The functor
![]() $\mathcal {R}$
is fully faithful on the subcategory of
$\mathcal {R}$
is fully faithful on the subcategory of
![]() $\mathrm {Sh}_R^{\mathrm {op}}$
spanned by the Tate modules of p-divisible groups over R.
$\mathrm {Sh}_R^{\mathrm {op}}$
spanned by the Tate modules of p-divisible groups over R.
Proof. Given a sheaf
![]() $\mathcal {F} \in \mathrm {Sh}_R^{\mathrm {op}}$
which is the Tate module of a p-divisible group, we have a natural counit map in
$\mathcal {F} \in \mathrm {Sh}_R^{\mathrm {op}}$
which is the Tate module of a p-divisible group, we have a natural counit map in
![]() $\mathrm {Sh}_R^{\mathrm {op}}$
$\mathrm {Sh}_R^{\mathrm {op}}$
and we will show that it is an isomorphism. Switching back from
![]() $\mathrm {Sh}_R^{\mathrm {op}}$
to
$\mathrm {Sh}_R^{\mathrm {op}}$
to
![]() $\mathrm {Sh}_R$
, this counit is the biduality map
$\mathrm {Sh}_R$
, this counit is the biduality map
The formation of this map is compatible with base change in the quasiregular semiperfectoid ring R. We claim that this map is an isomorphism whenever
![]() $\mathcal {F}$
is the Tate module of a p-divisible group G over R. Applying Proposition 4.83 to
$\mathcal {F}$
is the Tate module of a p-divisible group G over R. Applying Proposition 4.83 to
![]() $\check {G}$
, we get a natural (in
$\check {G}$
, we get a natural (in
![]() $\mathcal {F}$
and R) identification
$\mathcal {F}$
and R) identification
(for the last equality, note that if
![]() $f \in \mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_pG, \mathcal {O}^{\mathrm {pris}})$
satisfies
$f \in \mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_pG, \mathcal {O}^{\mathrm {pris}})$
satisfies
![]() $\varphi (f)=\tilde {\xi } f$
, then for any section s of
$\varphi (f)=\tilde {\xi } f$
, then for any section s of
![]() $T_p G$
,
$T_p G$
,
![]() $f(s) \in \mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}$
, that is
$f(s) \in \mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}}$
, that is
![]() $f \in \mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_pG, \mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}})$
). Proposition 4.73 and the remark following it for the identification of Frobenius allow us to rewrite this as a natural (in
$f \in \mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_pG, \mathcal {N}^{\geq 1}\mathcal {O}^{\mathrm {pris}})$
). Proposition 4.73 and the remark following it for the identification of Frobenius allow us to rewrite this as a natural (in
![]() $\mathcal {F}$
and R) identification
$\mathcal {F}$
and R) identification
as we can identify
![]() by Proposition 4.77. However, this natural isomorphism may not a priori coincide with above counit map. But, composing the latter with the inverse of this isomorphism, we obtain a natural endomorphism of
by Proposition 4.77. However, this natural isomorphism may not a priori coincide with above counit map. But, composing the latter with the inverse of this isomorphism, we obtain a natural endomorphism of
![]() $\mathcal {F}$
, that is, an endomorphism of any p-divisible group G over any quasiregular semiperfectoid ring R, natural in G and R. Any such endomorphism acts on the p-divisible group
$\mathcal {F}$
, that is, an endomorphism of any p-divisible group G over any quasiregular semiperfectoid ring R, natural in G and R. Any such endomorphism acts on the p-divisible group
![]() $\mathbb {Q}_p/\mathbb {Z}_p$
by multiplication by some scalar (in
$\mathbb {Q}_p/\mathbb {Z}_p$
by multiplication by some scalar (in
![]() $\mathbb {Z}_p$
), at least on each connected component of R. It also does act by multiplication by the same scalar (depending on a connected component of
$\mathbb {Z}_p$
), at least on each connected component of R. It also does act by multiplication by the same scalar (depending on a connected component of
![]() $\mathrm {Spec}(R)$
) on any p-divisible group G: indeed, this can be checked on the Tate module, and since
$\mathrm {Spec}(R)$
) on any p-divisible group G: indeed, this can be checked on the Tate module, and since
![]() $T_p(G)=\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(\mathbb {Q}_p/\mathbb {Z}_p,G)$
, this follows there by naturality.
$T_p(G)=\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(\mathbb {Q}_p/\mathbb {Z}_p,G)$
, this follows there by naturality.
Hence, to conclude the proof of fully faithfulness, it suffices to show that these scalars are units. This can be checked for one specific p-divisible group G, and we can take
![]() $G=\mathbb {Q}_p/\mathbb {Z}_p$
, for which the claim is immediate. Indeed,
$G=\mathbb {Q}_p/\mathbb {Z}_p$
, for which the claim is immediate. Indeed,
![]() $\mathcal {F}=\mathbb {Z}_p$
in this case and
$\mathcal {F}=\mathbb {Z}_p$
in this case and
![]() $\mathcal {F}\to \mathcal {L}\mathcal {R}(\mathcal {F})\cong \mathcal {H}om_{\mathcal {O}^{\mathrm {pris}}[F]}(\mathcal {O}^{\mathrm {pris}}, \mathcal {O}^{\mathrm {pris}})$
sends
$\mathcal {F}\to \mathcal {L}\mathcal {R}(\mathcal {F})\cong \mathcal {H}om_{\mathcal {O}^{\mathrm {pris}}[F]}(\mathcal {O}^{\mathrm {pris}}, \mathcal {O}^{\mathrm {pris}})$
sends
![]() $1\in \mathbb {Z}_p$
to the identity of
$1\in \mathbb {Z}_p$
to the identity of
![]() $\mathcal {O}^{\mathrm {pris}}$
, which generates
$\mathcal {O}^{\mathrm {pris}}$
, which generates
![]() $\mathcal {H}om_{\mathcal {O}^{\mathrm {pris}}[F]}(\mathcal {O}^{\mathrm {pris}}, \mathcal {O}^{\mathrm {pris}})$
by [Reference Bhatt and Scholze13, Remark 9.3].
$\mathcal {H}om_{\mathcal {O}^{\mathrm {pris}}[F]}(\mathcal {O}^{\mathrm {pris}}, \mathcal {O}^{\mathrm {pris}})$
by [Reference Bhatt and Scholze13, Remark 9.3].
Remark 4.85. In fact, as was also pointed out by Akhil Mathew and the referee, the results used in this section can be strenghtened. Indeed, [Reference Bhatt and Lurie10, Theorem 7.5.6] already quoted above even gives a short exact sequence
Applying
![]() $R\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_pG, -)$
to it, we get an exact sequence of sheaves
$R\mathcal {H}om_{(R)_{\mathrm {qsyn}}}(T_pG, -)$
to it, we get an exact sequence of sheaves
But
![]() $\mathcal {E}xt_{(R)_{\mathrm {qsyn}}}^1(T_pG , T_p \mathbb {G}_m)=\mathcal {E}xt_{(R)_{\mathrm {qsyn}}}^1(G , \mu _{p^{\infty }})=0$
(cf. [Reference Waterhouse53, Theorem 1] together with the fact that the set of splittings of such an extension is a torsor under
$\mathcal {E}xt_{(R)_{\mathrm {qsyn}}}^1(T_pG , T_p \mathbb {G}_m)=\mathcal {E}xt_{(R)_{\mathrm {qsyn}}}^1(G , \mu _{p^{\infty }})=0$
(cf. [Reference Waterhouse53, Theorem 1] together with the fact that the set of splittings of such an extension is a torsor under
![]() $\check {G}$
which is syntomic). Hence, we get a short exact sequence and, after taking cohomology, an isomorphism
$\check {G}$
which is syntomic). Hence, we get a short exact sequence and, after taking cohomology, an isomorphism

4.9 Essential surjectivity
Let R be quasiregular semiperfectoid, and let as before
be the prismatic Dieudonné functor with values in the category of admissible prismatic Dieudonné modules
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
(cf. Section 4.2 and Theorem 4.71).
$\mathrm {DM}^{\mathrm {adm}}(R)$
(cf. Section 4.2 and Theorem 4.71).
Let us fix a perfect prism
![]() $(A,I)$
, a generator
$(A,I)$
, a generator
![]() $\tilde {\xi }\in I$
and a surjection
$\tilde {\xi }\in I$
and a surjection
![]() ${\bar {A}=}A/I\twoheadrightarrow R$
. Let
${\bar {A}=}A/I\twoheadrightarrow R$
. Let
![]() $\xi :=\varphi ^{-1}(\tilde {\xi })$
. In this section, we will make repeated use of Proposition 4.29, which tells us that admissible prismatic Dieudonné modules over R (or any other quasiregular semiperfectoid ring living over
$\xi :=\varphi ^{-1}(\tilde {\xi })$
. In this section, we will make repeated use of Proposition 4.29, which tells us that admissible prismatic Dieudonné modules over R (or any other quasiregular semiperfectoid ring living over
![]() ${\bar {A}}$
) are the same as windows over the frame
${\bar {A}}$
) are the same as windows over the frame
![]() (associated to
(associated to
![]() $\tilde {\xi }$
).
$\tilde {\xi }$
).
By Corollary 2.10, we may assume that
![]() ${\bar {A}}$
is henselian along
${\bar {A}}$
is henselian along
![]() $\ker ({\bar {A}}\to R)$
.
$\ker ({\bar {A}}\to R)$
.
Let us first assume that
![]() $\mathrm {ker}({\bar {A}}\to R)$
is generated by some elements
$\mathrm {ker}({\bar {A}}\to R)$
is generated by some elements
![]() $a_j$
,
$a_j$
,
![]() $j\in J$
, that admit compatible systems
$j\in J$
, that admit compatible systems
![]() $(a_j,a_j^{1/p},a_j^{1/p^2},\ldots )$
of
$(a_j,a_j^{1/p},a_j^{1/p^2},\ldots )$
of
![]() $p^n$
-roots. Define
$p^n$
-roots. Define
and
![]() $S\to R,\ X_j^{1/p^n}\mapsto \overline {a_j^{1/p^n}}.$
$S\to R,\ X_j^{1/p^n}\mapsto \overline {a_j^{1/p^n}}.$
Lemma 4.86. The base change functor
![]() $\mathrm {DM}^{\mathrm {adm}}(S)\to \mathrm {DM}^{\mathrm {adm}}(R)$
on admissible prismatic Dieudonné modules is essentially surjective.
$\mathrm {DM}^{\mathrm {adm}}(S)\to \mathrm {DM}^{\mathrm {adm}}(R)$
on admissible prismatic Dieudonné modules is essentially surjective.
Proof. Using Proposition 4.22, it suffices to see that
![]() is surjective and henselian along its kernel (cf. Lemma 4.31). The surjectivity follows from the Hodge-Tate comparison as
is surjective and henselian along its kernel (cf. Lemma 4.31). The surjectivity follows from the Hodge-Tate comparison as
![]() $L_{S/{\bar {A}}}\to L_{R/{\bar {A}}}$
is surjective by our assumption that the
$L_{S/{\bar {A}}}\to L_{R/{\bar {A}}}$
is surjective by our assumption that the
![]() $a_j,j\in J$
, generate
$a_j,j\in J$
, generate
![]() $\mathrm {ker}({\bar {A}}\to R)$
. First note that the pair
$\mathrm {ker}({\bar {A}}\to R)$
. First note that the pair
![]() $(S,\ker (S\to R))$
is henselian because the
$(S,\ker (S\to R))$
is henselian because the
![]() $X_j^{1/p^n}$
are nilpotent in S and we assumed that
$X_j^{1/p^n}$
are nilpotent in S and we assumed that
![]() ${\bar {A}}$
is henselian along
${\bar {A}}$
is henselian along
![]() $\mathrm {ker}({\bar {A}}\to R)$
. By Lemma 4.28, to show that
$\mathrm {ker}({\bar {A}}\to R)$
. By Lemma 4.28, to show that
![]() is henselian along
is henselian along
![]() , it suffices to see
, it suffices to see
![]() is henselian along
is henselian along
![]() $\overline {K}:=(K+\ker (\theta ))/\ker (\theta )$
(cf. [Reference Project52, Tag 0DYD])). But
$\overline {K}:=(K+\ker (\theta ))/\ker (\theta )$
(cf. [Reference Project52, Tag 0DYD])). But
![]() $\overline {K}\subseteq S$
is contained in
$\overline {K}\subseteq S$
is contained in
![]() $\ker (S\to R)$
. Another application of [Reference Project52, Tag 0DYD] therefore implies that S is henselian along
$\ker (S\to R)$
. Another application of [Reference Project52, Tag 0DYD] therefore implies that S is henselian along
![]() $\overline {K}$
because
$\overline {K}$
because
![]() $(S,\ker (S\to R))$
is henselian. This finishes the proof.
$(S,\ker (S\to R))$
is henselian. This finishes the proof.
Note that the ring
admits a surjection from the perfectoid ring
 $$ \begin{align*}\tilde{S}:={\bar{A}}[[X_j^{1/p^{\infty}} |\ j\in J]]:= \left( \varinjlim\limits_{n, J' \subset J ~ \mathrm{finite}}{\bar{A}}[[X_j^{1/p^n} |\ j\in J']] \right)^{\wedge_p} \end{align*} $$
$$ \begin{align*}\tilde{S}:={\bar{A}}[[X_j^{1/p^{\infty}} |\ j\in J]]:= \left( \varinjlim\limits_{n, J' \subset J ~ \mathrm{finite}}{\bar{A}}[[X_j^{1/p^n} |\ j\in J']] \right)^{\wedge_p} \end{align*} $$
by sending
![]() $X_j^{1/p^n}\mapsto X_j^{1/p^n}$
.
$X_j^{1/p^n}\mapsto X_j^{1/p^n}$
.
Lemma 4.87. The natural functor
is essentially surjective.
Proof. The ring
![]() $\tilde {S}$
is henselian along
$\tilde {S}$
is henselian along
![]() $(X_j\ |\ j\in J)$
. The prism
$(X_j\ |\ j\in J)$
. The prism
![]() is the
is the
![]() $(p,I)$
-adic completion of
$(p,I)$
-adic completion of
Call a
![]() $\delta $
-pair
$\delta $
-pair
![]() $(B,K)$
over
$(B,K)$
over
![]() $(A,I)$
a good pair if it satisfies the following conditions:
$(A,I)$
a good pair if it satisfies the following conditions:
-
• B is
 $(p,I)$
-completely flat over A and K is
$(p,I)$
-completely flat over A and K is
 $(p,I)$
-complete.
$(p,I)$
-complete. -
• There exists a universal map
 $(B,K)\to (C,IC)$
of
$(B,K)\to (C,IC)$
of
 $\delta $
-pairs to a prism
$\delta $
-pairs to a prism
 $(C,IC)$
over
$(C,IC)$
over
 $(A,I)$
. Moreover,
$(A,I)$
. Moreover,
 $(C,IC)$
is flat over
$(C,IC)$
is flat over
 $(A,I)$
, and its formation commutes with
$(A,I)$
, and its formation commutes with
 $(p,I)$
-completely flat base change on B.
$(p,I)$
-completely flat base change on B.
For each
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $J' \subset J$
finite, the
$J' \subset J$
finite, the
![]() $\delta $
-pair
$\delta $
-pair
over
![]() $(A,I)$
is a good pair, by [Reference Bhatt and Scholze13, Proposition 3.13]. Since good pairs are stable under filtered colimits in the category of all
$(A,I)$
is a good pair, by [Reference Bhatt and Scholze13, Proposition 3.13]. Since good pairs are stable under filtered colimits in the category of all
![]() $\delta $
-pairs
$\delta $
-pairs
![]() $(B,K)$
over
$(B,K)$
over
![]() $(A,I)$
with
$(A,I)$
with
![]() $B $
and
$B $
and
![]() $K (p,I)$
-complete, we deduce that the pair
$K (p,I)$
-complete, we deduce that the pair
is a good pair, too. Therefore, by definition of a good pair and Proposition 3.26, we have

Define
Then B is p-torsion free and
![]() $\tilde {\xi }$
-torsion free and thus defines a prism. Moreover, canonically,
$\tilde {\xi }$
-torsion free and thus defines a prism. Moreover, canonically,
![]() $S\cong B/\tilde {\xi }$
. By the universal property of
$S\cong B/\tilde {\xi }$
. By the universal property of
![]() , there exists therefore a canonical morphism
, there exists therefore a canonical morphism
Concretely, the morphism
![]() $\alpha $
sends
$\alpha $
sends
![]() $X_j\mapsto 0$
. Using a variant of Lemma 4.28, we see that
$X_j\mapsto 0$
. Using a variant of Lemma 4.28, we see that
![]() is henselian along
is henselian along
![]() $\mathrm {ker}(\alpha )$
. By Lemma 4.88,
$\mathrm {ker}(\alpha )$
. By Lemma 4.88,
![]() and
and
![]() $\varphi /\tilde {\xi }$
is topologically nilpotent on
$\varphi /\tilde {\xi }$
is topologically nilpotent on
![]() $\mathrm {ker}(\alpha )$
. Thus by Lemma 4.32, the categories of windows over
$\mathrm {ker}(\alpha )$
. Thus by Lemma 4.32, the categories of windows over
![]() and B are equivalent. Therefore, it suffices to see that windows over B can be lifted to windows over
and B are equivalent. Therefore, it suffices to see that windows over B can be lifted to windows over
![]() . After choosing a normal decomposition, this follows as the functor
. After choosing a normal decomposition, this follows as the functor
and is essentially surjective, which is true as
![]() is henselian along the kernel of
is henselian along the kernel of
![]() (cf. the end of the proof of Lemma 4.31). This finishes the proof.
(cf. the end of the proof of Lemma 4.31). This finishes the proof.
To finish the proof of Lemma 4.86, we have to prove the following lemmas.
Lemma 4.88. With the notations from the proof of Lemma 4.87, we get
![]() and
and
![]() $\varphi _1:=\varphi /\tilde {\xi }$
is topologically nilpotent on
$\varphi _1:=\varphi /\tilde {\xi }$
is topologically nilpotent on
![]() $\ker (\alpha )$
.
$\ker (\alpha )$
.
Proof. Set
![]() $K:=\ker (\alpha )$
. Then K is the closure in the
$K:=\ker (\alpha )$
. Then K is the closure in the
![]() $(p,\tilde {\xi })$
-adic topology of the
$(p,\tilde {\xi })$
-adic topology of the
![]() -submodule generated by
-submodule generated by
![]() $\delta ^n(X_j/\tilde {\xi })$
for
$\delta ^n(X_j/\tilde {\xi })$
for
![]() $j\in J$
and
$j\in J$
and
![]() $n\geq 0$
. By Lemma 4.89 below, the module K equals the closure of the ideal generated by
$n\geq 0$
. By Lemma 4.89 below, the module K equals the closure of the ideal generated by
 $$ \begin{align*}z_{j,n}:=\frac{X_j^{p^n}}{\varphi^{n}(\tilde{\xi})\varphi^{n-1}(\tilde{\xi})^p\cdots \tilde{\xi}^{p^n}} \end{align*} $$
$$ \begin{align*}z_{j,n}:=\frac{X_j^{p^n}}{\varphi^{n}(\tilde{\xi})\varphi^{n-1}(\tilde{\xi})^p\cdots \tilde{\xi}^{p^n}} \end{align*} $$
for
![]() $j\in J$
and
$j\in J$
and
![]() $n\geq 0$
. Let us show that
$n\geq 0$
. Let us show that
![]() . Clearly,
. Clearly,
As
![]() is closed in
is closed in
![]() (being the kernel of the continuous surjection
(being the kernel of the continuous surjection
![]() ), we can conclude
), we can conclude
![]() . Next, let us check that
. Next, let us check that
![]() $\varphi _1$
is topologically nilpotent on K. Fix
$\varphi _1$
is topologically nilpotent on K. Fix
![]() $l\geq 1$
. We claim that for every
$l\geq 1$
. We claim that for every
![]() $m\geq 1$
, such that
$m\geq 1$
, such that
![]() $p^m> l$
and any
$p^m> l$
and any
![]() $k\in K$
, we have
$k\in K$
, we have
This implies as desired that
![]() $\varphi _1$
is topologically nilpotent on K. As
$\varphi _1$
is topologically nilpotent on K. As
![]() $\tilde {\xi }^lK$
is closed and
$\tilde {\xi }^lK$
is closed and
![]() $\varphi _1^m$
continuous (for the
$\varphi _1^m$
continuous (for the
![]() $(p,\tilde {\xi })$
-adic topology on K), it is enough to assume that
$(p,\tilde {\xi })$
-adic topology on K), it is enough to assume that
![]() $k=z_{j,n}$
for some
$k=z_{j,n}$
for some
![]() $j\in J, n\geq 1,$
because the
$j\in J, n\geq 1,$
because the
![]() $z_{j,n}$
generate a dense submodule in K
Footnote
33
. Using Equation (4.3), we can calculate
$z_{j,n}$
generate a dense submodule in K
Footnote
33
. Using Equation (4.3), we can calculate
for some
![]() . But
. But
![]() $\tilde {\xi }^{p^{n+m}-1}K\subseteq \tilde {\xi }^lK$
because
$\tilde {\xi }^{p^{n+m}-1}K\subseteq \tilde {\xi }^lK$
because
![]() $p^{n+m}-1\geq l$
. This finishes the proof.
$p^{n+m}-1\geq l$
. This finishes the proof.
Lemma 4.89. Let
![]() $(A,I)$
be a bounded prism, and let
$(A,I)$
be a bounded prism, and let
![]() $d\in A$
be distinguished. Let, furthermore,
$d\in A$
be distinguished. Let, furthermore,
![]() $x\in A$
be an element of rank
$x\in A$
be an element of rank
![]() $1$
. Then for
$1$
. Then for
![]() $n\geq 0$
, there exist natural (in
$n\geq 0$
, there exist natural (in
![]() $A,x$
) elements
$A,x$
) elements
such that
![]() $\varphi ^{n}(d)\varphi ^{n-1}(d)^p\cdots d^{p^n}\cdot z_n=x^{p^n}$
. Moreover, for all
$\varphi ^{n}(d)\varphi ^{n-1}(d)^p\cdots d^{p^n}\cdot z_n=x^{p^n}$
. Moreover, for all
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\delta ^n(\frac {x}{d})$
lies in the subring
$\delta ^n(\frac {x}{d})$
lies in the subring
![]() $A[z_0,\ldots , z_{n}]$
of
$A[z_0,\ldots , z_{n}]$
of
![]() $A\{\frac {x}{d}\}{^{\wedge _{(p,d)}}}$
generated by
$A\{\frac {x}{d}\}{^{\wedge _{(p,d)}}}$
generated by
![]() $z_0,\ldots ,z_{n}$
.
$z_0,\ldots ,z_{n}$
.
Note that the last part of the lemma implies that the resulting morphism
is surjective after
![]() $(p,d)$
-completion. We expect that this surjection is actually an isomorphism.
$(p,d)$
-completion. We expect that this surjection is actually an isomorphism.
Proof. We can argue in the universal case
![]() $A=\mathbb {Z}_p[x]\{d,\frac {1}{\delta (d)}\}^{\wedge _{(p,d)}}$
, where
$A=\mathbb {Z}_p[x]\{d,\frac {1}{\delta (d)}\}^{\wedge _{(p,d)}}$
, where
![]() $\delta (x)=0$
, thus, we may assume that A is transversal, that is, that
$\delta (x)=0$
, thus, we may assume that A is transversal, that is, that
![]() $(p,d)$
is a regular sequence in A, and that
$(p,d)$
is a regular sequence in A, and that
![]() $(x,d)$
is a regular sequence. This implies that for all
$(x,d)$
is a regular sequence. This implies that for all
![]() $r\geq 1$
, the sequence
$r\geq 1$
, the sequence
![]() $(\varphi ^r(d),\varphi ^{r-1}(d))$
is regular as well (cf. Lemma 2.7). We first claim that for all
$(\varphi ^r(d),\varphi ^{r-1}(d))$
is regular as well (cf. Lemma 2.7). We first claim that for all
![]() $n\geq 0$
, the element
$n\geq 0$
, the element
 $$ \begin{align*} z_n:=\frac{x^{p^n}}{\varphi^{n}(d)\varphi^{n-1}(d)^p\cdots d^{p^n}} \end{align*} $$
$$ \begin{align*} z_n:=\frac{x^{p^n}}{\varphi^{n}(d)\varphi^{n-1}(d)^p\cdots d^{p^n}} \end{align*} $$
lies in
![]() $A\{\frac {x}{d}\}$
. If
$A\{\frac {x}{d}\}$
. If
![]() $n=0$
, then
$n=0$
, then
![]() $z_n=\frac {x}{d}\in A\{\frac {x}{d}\}$
. For
$z_n=\frac {x}{d}\in A\{\frac {x}{d}\}$
. For
![]() $n\geq 0$
, we can calculate
$n\geq 0$
, we can calculate
 $$ \begin{align*} \varphi(z_n)=\frac{x^{p^{n+1}}}{\varphi^{n+1}(d)\cdots \varphi(d)^{p^n}} \end{align*} $$
$$ \begin{align*} \varphi(z_n)=\frac{x^{p^{n+1}}}{\varphi^{n+1}(d)\cdots \varphi(d)^{p^n}} \end{align*} $$
because
![]() $\varphi (x)=x^p$
. The numerator
$\varphi (x)=x^p$
. The numerator
![]() $x^{p^{n+1}}$
is divisible by
$x^{p^{n+1}}$
is divisible by
![]() $d^{p^{n+1}}$
in
$d^{p^{n+1}}$
in
![]() $A\{\frac {x}{d}\}$
. We claim that
$A\{\frac {x}{d}\}$
. We claim that
![]() $(d^{p^{n+1}},\varphi ^{n+1}(d)\cdots \varphi (d)^{p^n})$
is a regular sequence in
$(d^{p^{n+1}},\varphi ^{n+1}(d)\cdots \varphi (d)^{p^n})$
is a regular sequence in
![]() $A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
. Granting this, we can conclude that
$A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
. Granting this, we can conclude that
![]() $d^{p^{n+1}}$
divides
$d^{p^{n+1}}$
divides
![]() $\frac {x^{p^{n+1}}}{\varphi ^{n+1}(d)\cdots \varphi (d)^{p^n}}$
, that is, that
$\frac {x^{p^{n+1}}}{\varphi ^{n+1}(d)\cdots \varphi (d)^{p^n}}$
, that is, that
![]() $z_{n+1}\in A\{\frac {x}{d}\}{^{\wedge }_{(p,d)}}$
. Write
$z_{n+1}\in A\{\frac {x}{d}\}{^{\wedge }_{(p,d)}}$
. Write
![]() $s=\varphi ^{n+1}(d)\cdots \varphi (d)^{p^n}$
. To prove that
$s=\varphi ^{n+1}(d)\cdots \varphi (d)^{p^n}$
. To prove that
![]() $(d^{p^{n+1}},s)$
is a regular sequence in
$(d^{p^{n+1}},s)$
is a regular sequence in
![]() $A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
, it suffices to show the same for
$A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
, it suffices to show the same for
![]() $(d,s)$
. One proves by induction on m that for all
$(d,s)$
. One proves by induction on m that for all
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $\varphi ^m(d)$
is congruent to
$\varphi ^m(d)$
is congruent to
![]() $pu_m$
modulo d for a unit
$pu_m$
modulo d for a unit
![]() $u_m$
. In particular, one concludes that s is congruent to
$u_m$
. In particular, one concludes that s is congruent to
![]() $up^{{k}}$
modulo d, for
$up^{{k}}$
modulo d, for
![]() $k\geq 1$
and u a unit. Hence, to prove that
$k\geq 1$
and u a unit. Hence, to prove that
![]() $(d,s)$
is a regular sequence in
$(d,s)$
is a regular sequence in
![]() $A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
, it suffices to show that
$A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
, it suffices to show that
![]() $(d,p)$
is a regular sequence in
$(d,p)$
is a regular sequence in
![]() $A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
. But this follows from transversality of A and the fact that
$A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
. But this follows from transversality of A and the fact that
![]() $A \to A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
is
$A \to A\{\frac {x}{d}\}^{\wedge _{(p,d)}}$
is
![]() $(p,d)$
-completely flat.
$(p,d)$
-completely flat.
Next, we show that for all
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\delta ^n(\frac {x}{d})$
lies in the subring
$\delta ^n(\frac {x}{d})$
lies in the subring
![]() $A[z_0,\ldots , z_{n}]$
of
$A[z_0,\ldots , z_{n}]$
of
![]() $A\{\frac {x}{d}\}{^{\wedge _{(p,d)}}}$
generated by
$A\{\frac {x}{d}\}{^{\wedge _{(p,d)}}}$
generated by
![]() $z_0,\ldots ,z_{n}$
. This claim follows from the assertion that
$z_0,\ldots ,z_{n}$
. This claim follows from the assertion that
![]() $\delta (z_{n})\in A[{z_0},\ldots , z_{n+1}]$
using induction and how
$\delta (z_{n})\in A[{z_0},\ldots , z_{n+1}]$
using induction and how
![]() $\delta $
acts on sums and products. For
$\delta $
acts on sums and products. For
![]() $n=0$
, we can calculate
$n=0$
, we can calculate
 $$ \begin{align*} \delta(z_0)=\delta\left(\frac{x}{d}\right)=\frac{1}{p} \left(\varphi\left(\frac{x}{d}\right)-\frac{x^p}{d^p}\right)=\frac{1}{p}(d^p-\varphi(d))z_{1}=\delta(d)z_1\in A\left\{\frac{x}{d}\right\}. \end{align*} $$
$$ \begin{align*} \delta(z_0)=\delta\left(\frac{x}{d}\right)=\frac{1}{p} \left(\varphi\left(\frac{x}{d}\right)-\frac{x^p}{d^p}\right)=\frac{1}{p}(d^p-\varphi(d))z_{1}=\delta(d)z_1\in A\left\{\frac{x}{d}\right\}. \end{align*} $$
Similarly, we see
where the term
![]() $\frac {1}{p}(d^{p^{n+1}}-\varphi ^{n+1}(d))$
lies in A. This finishes the proof.
$\frac {1}{p}(d^{p^{n+1}}-\varphi ^{n+1}(d))$
lies in A. This finishes the proof.
We can derive essential surjectivity.
Theorem 4.90. Let R be a quasiregular semiperfectoid ring. Then the prismatic Dieudonné functor
from the category of p-divisible groups over R to the category of admissible prismatic Dieudonné crystals over R is essentially surjective.
Proof. To prove the theorem, we may pass to a quasisyntomic cover
![]() $R'$
of R: indeed, let
$R'$
of R: indeed, let
![]() $M \in {\mathrm {DM}^{\mathrm {adm}}}(R)$
, such that its base change along the map
$M \in {\mathrm {DM}^{\mathrm {adm}}}(R)$
, such that its base change along the map
![]() $R \to R'$
is of the form
$R \to R'$
is of the form
![]() , for some p-divisible group
, for some p-divisible group
![]() $G'$
over R. The descent datum for
$G'$
over R. The descent datum for
![]() expressing that it comes from an admissible prismatic Dieudonné module over R (namely, M) gives rise to a descent datum for
expressing that it comes from an admissible prismatic Dieudonné module over R (namely, M) gives rise to a descent datum for
![]() $G'$
, since fully faithfulness over
$G'$
, since fully faithfulness over
![]() $R^{\prime }\hat {\otimes }_R R^{\prime }$
is already proved (cf. Theorem 4.82). This descent datum is effective, by p-completely faithfully flat descent for p-divisible groups (cf. Proposition A.2), so there exists a p-divisible group G over R, with
$R^{\prime }\hat {\otimes }_R R^{\prime }$
is already proved (cf. Theorem 4.82). This descent datum is effective, by p-completely faithfully flat descent for p-divisible groups (cf. Proposition A.2), so there exists a p-divisible group G over R, with
![]() .
.
Therefore, by Theorem 3.23, we may and do assume that
![]() $R\cong \bar {A}/(a_j\ |\ j\in J)$
for
$R\cong \bar {A}/(a_j\ |\ j\in J)$
for
![]() $\bar {A}=A/I$
a perfectoid ring and
$\bar {A}=A/I$
a perfectoid ring and
![]() $a_j\in R$
admitting compatible systems of
$a_j\in R$
admitting compatible systems of
![]() $p^n$
-roots of unity. Using Lemma 4.86, we may even assume that
$p^n$
-roots of unity. Using Lemma 4.86, we may even assume that
In this case, we can invoke Lemma 4.87 and reduce to the case that R is perfectoid. Then we can cite Corollary 4.49 to conclude that
![]() is essentially surjective.
is essentially surjective.
This concludes the proof of the main Theorem 4.74.
Remark 4.91. Let R be quasisyntomic ring. The arguments used in Section 4.8 show that the functor
![]() $\mathcal {G}$
from
$\mathcal {G}$
from
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
to the category of abelian sheaves of
$\mathrm {DM}^{\mathrm {adm}}(R)$
to the category of abelian sheaves of
![]() $(R)_{\mathrm {qsyn}}$
, sending
$(R)_{\mathrm {qsyn}}$
, sending
![]() $\mathcal {M} \in \mathrm {DM}^{\mathrm {adm}}(R)$
to
$\mathcal {M} \in \mathrm {DM}^{\mathrm {adm}}(R)$
to
where
![]() $\mathcal {M}^{\vee }$
denotes the
$\mathcal {M}^{\vee }$
denotes the
![]() $\mathcal {O}^{\mathrm {pris}}$
-linear dual of
$\mathcal {O}^{\mathrm {pris}}$
-linear dual of
![]() $\mathcal {M}$
, defines a quasi-inverse of the prismatic Dieudonné functor.
$\mathcal {M}$
, defines a quasi-inverse of the prismatic Dieudonné functor.
It seems difficult to prove directly that
![]() $\mathcal {G}$
takes values in the category of (quasisyntomic sheaves attached to) p-divisible groups. In the case of étale p-divisible groups, Theorem 4.74 yields an equivalence of
$\mathcal {G}$
takes values in the category of (quasisyntomic sheaves attached to) p-divisible groups. In the case of étale p-divisible groups, Theorem 4.74 yields an equivalence of
![]() $\mathbb {Z}_p$
-local systems on R and finite locally free
$\mathbb {Z}_p$
-local systems on R and finite locally free
![]() $\mathcal {O}^{\mathrm {pris}}$
-modules (respectively,
$\mathcal {O}^{\mathrm {pris}}$
-modules (respectively,
![]() -modules if R is quasiregular semiperfectoid)
-modules if R is quasiregular semiperfectoid)
![]() $\mathcal {M}$
together with an isomorphism
$\mathcal {M}$
together with an isomorphism
![]() $\varphi _{\mathcal {M}}\colon \varphi ^{\ast }(\mathcal {M})\cong \mathcal {M}$
. This is a generalisation of Katz’ correspondence between
$\varphi _{\mathcal {M}}\colon \varphi ^{\ast }(\mathcal {M})\cong \mathcal {M}$
. This is a generalisation of Katz’ correspondence between
![]() $\mathbb {Z}_p$
-local systems on the spectrum
$\mathbb {Z}_p$
-local systems on the spectrum
![]() $\mathrm {Spec}(k)$
of a perfect field k and
$\mathrm {Spec}(k)$
of a perfect field k and
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $W(k)$
(cf. [Reference Katz27, Proposition 4.1.1]). We thank Benoît Stroh for pointing this out to us.
$W(k)$
(cf. [Reference Katz27, Proposition 4.1.1]). We thank Benoît Stroh for pointing this out to us.
5 Complements
5.1 Prismatic Dieudonné theory for finite locally free group schemes
Let R be a perfectoid ring. We fix a generator
![]() $\xi $
of
$\xi $
of
![]() $\ker (\theta )$
and let
$\ker (\theta )$
and let
![]() $\tilde {\xi }=\varphi (\xi )$
.
$\tilde {\xi }=\varphi (\xi )$
.
Definition 5.1. A torsion prismatic Dieudonné module over R is a triple
where M is a finitely presented
![]() $A_{\mathrm {inf}}(R)$
-module of projective dimension
$A_{\mathrm {inf}}(R)$
-module of projective dimension
![]() $\leq 1$
which is annihilated by a power of p and where
$\leq 1$
which is annihilated by a power of p and where
![]() $\varphi _M: M \to M$
and
$\varphi _M: M \to M$
and
![]() $\psi _M: M\to M$
are, respectively,
$\psi _M: M\to M$
are, respectively,
![]() $\varphi $
-linear and
$\varphi $
-linear and
![]() $\varphi ^{-1}$
-linear, and satisfy
$\varphi ^{-1}$
-linear, and satisfy
The category of torsion prismatic Dieudonné modules over R is denoted by
![]() $\mathrm {DM}_{\mathrm {tors}}(R)$
. It is an exact category.
$\mathrm {DM}_{\mathrm {tors}}(R)$
. It is an exact category.
The base change of torsion prismatic Dieudonné modules behaves well.
Lemma 5.2. Let
![]() $R\to R^{\prime }$
be a morphism of perfectoid rings and
$R\to R^{\prime }$
be a morphism of perfectoid rings and
![]() $M\in \mathrm {DM}_{\mathrm {tors}}(R)$
. Then
$M\in \mathrm {DM}_{\mathrm {tors}}(R)$
. Then
![]() $M\otimes _{A_{\mathrm {inf}}(R)}A_{\mathrm {inf}}(R^{\prime })$
is concentrated in degree
$M\otimes _{A_{\mathrm {inf}}(R)}A_{\mathrm {inf}}(R^{\prime })$
is concentrated in degree
![]() $0$
. In particular, the base change functor
$0$
. In particular, the base change functor
![]() $\mathrm {DM}_{\mathrm {tors}}(R)\to \mathrm {DM}_{\mathrm {tors}}(R^{\prime })$
is exact.
$\mathrm {DM}_{\mathrm {tors}}(R)\to \mathrm {DM}_{\mathrm {tors}}(R^{\prime })$
is exact.
Proof. Let
be a resolution of M by finite locally free
![]() $A_{\mathrm {inf}}(R)$
-modules. As M is killed by
$A_{\mathrm {inf}}(R)$
-modules. As M is killed by
![]() $p^n$
for some
$p^n$
for some
![]() $n\geq 0$
, there exists
$n\geq 0$
, there exists
![]() $g\colon M_2\to M_1$
, such that
$g\colon M_2\to M_1$
, such that
![]() $f\circ g=p^n$
. Then
$f\circ g=p^n$
. Then
![]() $p^n=g\circ f$
(using that f is injective). The base change
$p^n=g\circ f$
(using that f is injective). The base change
![]() $M_1\otimes _{A_{\mathrm {inf}}(R)}A_{\mathrm {inf}}(R^{\prime })$
is p-torsion free as
$M_1\otimes _{A_{\mathrm {inf}}(R)}A_{\mathrm {inf}}(R^{\prime })$
is p-torsion free as
![]() $A_{\mathrm {inf}}(R^{\prime })$
is. This implies that the base change of f to
$A_{\mathrm {inf}}(R^{\prime })$
is. This implies that the base change of f to
![]() $A_{\mathrm {inf}}(R^{\prime })$
remains injective, which finishes the proof.
$A_{\mathrm {inf}}(R^{\prime })$
remains injective, which finishes the proof.
Before stating the main result, let us introduce a notation, which will be in use only in this section.
Notation 5.3. If S is a p-complete ring, let
![]() $\mathcal {B}_S$
(respectively,
$\mathcal {B}_S$
(respectively,
![]() $\mathcal {C}_S$
) denote the category whose objects are
$\mathcal {C}_S$
) denote the category whose objects are
![]() -modules on
-modules on
![]() (respectively,
(respectively,
![]() -modules on
-modules on
![]() endowed with a
endowed with a
![]() $\varphi $
-linear Frobenius), and whose morphisms are
$\varphi $
-linear Frobenius), and whose morphisms are
![]() -linear morphisms (respectively,
-linear morphisms (respectively,
![]() -linear morphisms commuting with Frobenius).
-linear morphisms commuting with Frobenius).
Theorem 5.4. There is a natural exactFootnote 34 antiequivalence
between the exact category of finite locally free group schemes of p-power order on R and the exact category
![]() $\mathrm {DM}_{\mathrm {tors}}(R)$
of torsion prismatic Dieudonné modules over R, such that the
$\mathrm {DM}_{\mathrm {tors}}(R)$
of torsion prismatic Dieudonné modules over R, such that the
![]() $A_{\mathrm {inf}}(R)$
-module
$A_{\mathrm {inf}}(R)$
-module
![]() is given by the formula
is given by the formula
and such that
![]() is the map induced by the Frobenius of
is the map induced by the Frobenius of
![]() .
.
Remark 5.5. A similar statement can be found in [Reference Lau36, Theorem 10.12]. Apart from the change of terminology, the only difference with the result in loc. cit. is that we remove the assumption that
![]() $p\geq 3$
and provide a formula for the underlying
$p\geq 3$
and provide a formula for the underlying
![]() $A_{\mathrm {inf}}$
-module of the torsion minuscule Breuil-Kisin-Fargues module attached to a finite locally free group scheme of p-power order.
$A_{\mathrm {inf}}$
-module of the torsion minuscule Breuil-Kisin-Fargues module attached to a finite locally free group scheme of p-power order.
The proof of Theorem 5.4 will make use of the following lemma.
Lemma 5.6. Let
![]() $(A,I)$
be a bounded prism, such that A is p-torsion free, and let S be a p-completely syntomic
$(A,I)$
be a bounded prism, such that A is p-torsion free, and let S be a p-completely syntomic
![]() $A/I$
-algebraFootnote
35
. Then
$A/I$
-algebraFootnote
35
. Then
is p-torsion free.
Proof. As S is a p-completely syntomic
![]() $A/I$
-algebra, the derived prismatic cohomology
$A/I$
-algebra, the derived prismatic cohomology
![]() agrees with the cohomology
agrees with the cohomology
![]() of the prismatic site of S over A (this follows by descent from the quasiregular semiperfectoid case and Proposition 3.26). By [Reference Bhatt and Scholze13, Proposition 3.13] and the assumption that S is a p-completely syntomic
of the prismatic site of S over A (this follows by descent from the quasiregular semiperfectoid case and Proposition 3.26). By [Reference Bhatt and Scholze13, Proposition 3.13] and the assumption that S is a p-completely syntomic
![]() $A/I$
-algebra, one can calculate
$A/I$
-algebra, one can calculate
![]() by some
by some
![]() $\breve{\mathrm{C}}$
ech-Alexander complex whose first term is p-complete and p-completely flat over A. Therefore, it suffices to see that each p-complete p-completely flat A-algebra B has no p-torsion. As A is p-torsion free, A, and thus B, are p-completely flat over
$\breve{\mathrm{C}}$
ech-Alexander complex whose first term is p-complete and p-completely flat over A. Therefore, it suffices to see that each p-complete p-completely flat A-algebra B has no p-torsion. As A is p-torsion free, A, and thus B, are p-completely flat over
![]() $\mathbb {Z}_p$
. But any p-completely flat p-complete module over
$\mathbb {Z}_p$
. But any p-completely flat p-complete module over
![]() $\mathbb {Z}_p$
is topologically free and thus p-torsion free.
$\mathbb {Z}_p$
is topologically free and thus p-torsion free.
Proof of Theorem 5.4.
The construction of the antiequivalence is exactly similar to the one of [Reference Lau36, Theorem 10.12], replacing Theorem 9.8 in loc. cit. by Corollary 4.49, so we do not give it and refer the reader to [Reference Lau36]. The simple principle is that Zariski-locally on
![]() $\mathrm {Spec}(R)$
, any finite locally free group scheme of p-power order is the kernel of an isogeny of p-divisible groups (and even an isogeny of p-divisible groups associated to abelian schemes, cf. Theorem 4.65); similarly, Zariski-locally on
$\mathrm {Spec}(R)$
, any finite locally free group scheme of p-power order is the kernel of an isogeny of p-divisible groups (and even an isogeny of p-divisible groups associated to abelian schemes, cf. Theorem 4.65); similarly, Zariski-locally on
![]() $\mathrm {Spec}(R)$
, any torsion prismatic Dieudonné module is the cokernel of an isogeny of prismatic Dieudonné modules ([Reference Lau36, Lemma 10.10]).
$\mathrm {Spec}(R)$
, any torsion prismatic Dieudonné module is the cokernel of an isogeny of prismatic Dieudonné modules ([Reference Lau36, Lemma 10.10]).
Let us now prove that
and that the functor
![]() preserves exactness for a short exact sequence
preserves exactness for a short exact sequence
of finite locally free group schemes of p-power order over R. Note that this implies by Mittag-Leffler exactness of
if
![]() $H^{\prime },H,H^{\prime \prime }$
are finite locally free group schemes of p-power order or p-divisible groups.
$H^{\prime },H,H^{\prime \prime }$
are finite locally free group schemes of p-power order or p-divisible groups.
By construction of the antiequivalence, it suffices to check that if H is the kernel of an isogeny
![]() $X \to X'$
, with
$X \to X'$
, with
![]() $X, X'$
are abelian schemes over R, the natural map
$X, X'$
are abelian schemes over R, the natural map
is surjective. But the cokernel of this map embeds in
![]() , which is zero by Theorem 4.62.
, which is zero by Theorem 4.62.
For exactness, start with a short exact sequence of finite locally free group schemes of p-power order on R
which we see as an exact sequence of abelian sheaves on
![]() $(R)_{\mathrm {qsyn}}$
. The surjectivity of the map
$(R)_{\mathrm {qsyn}}$
. The surjectivity of the map
can be checked locally and so we can assume that H, and so also
![]() $H'$
, embeds in an abelian scheme X. But we know that the map
$H'$
, embeds in an abelian scheme X. But we know that the map
is already surjective, again, because
![]() . Thus, the same holds for the map
. Thus, the same holds for the map
To prove injectivity of the map
it suffices by the long exact sequence for
![]() to prove that
to prove that
Let us prove that
![]() is p-torsion free. This is enough: indeed, we know it is also killed by a power of p, because
is p-torsion free. This is enough: indeed, we know it is also killed by a power of p, because
![]() $u^{-1}H'$
is. As
$u^{-1}H'$
is. As
it suffices to prove that the latter is p-torsion free. This is the content of Lemma 5.6 when applied to the p-completely syntomic R-scheme
![]() $H^{\prime }$
.
$H^{\prime }$
.
Let
be an inverse functor to
![]() . We claim that
. We claim that
![]() $\mathcal {G}$
is exact. Let
$\mathcal {G}$
is exact. Let
be an exact sequence in
![]() $\mathrm {DM}_{\mathrm {tors}}(R)$
. For any morphism
$\mathrm {DM}_{\mathrm {tors}}(R)$
. For any morphism
![]() $R\to R^{\prime }$
, the base change of it along
$R\to R^{\prime }$
, the base change of it along
![]() $A_{\mathrm {inf}}(R)\to A_{\mathrm {inf}}(R^{\prime })$
will stay exact by Lemma 5.2. By [Reference de Jong20, Proposition 1.1] and compatibility of
$A_{\mathrm {inf}}(R)\to A_{\mathrm {inf}}(R^{\prime })$
will stay exact by Lemma 5.2. By [Reference de Jong20, Proposition 1.1] and compatibility of
![]() $\mathcal {G}$
with base change in R, we can therefore assume that R is a perfect field of characteristic p. In this case, the category of finite locally free group schemes of p-power order and the category
$\mathcal {G}$
with base change in R, we can therefore assume that R is a perfect field of characteristic p. In this case, the category of finite locally free group schemes of p-power order and the category
![]() $\mathrm {DM}_{\mathrm {tors}}$
are abelian, and thus any equivalence between them is automatically exact.
$\mathrm {DM}_{\mathrm {tors}}$
are abelian, and thus any equivalence between them is automatically exact.
Remark 5.7. Let R be quasisyntomic ring. Although the same trick allows in principle to deduce from Theorem 4.74 a classification result for finite locally free group schemes of p-power order over R, it seems more subtle to obtain a nice description of the target category, that is of the objects which can locally on R be written as the cokernel of an isogeny of admissible prismatic Dieudonné crystals on R. At least the arguments given above should go through whenever the forgetful functor
is an equivalence, like in the case of perfectoid rings or in the Breuil-Kisin case to be discussed in the next section (where the classification of finite flat group schemes is already known and was proved by Kisin following the same technique (cf. [Reference Kisin30, Section 2.3])).
5.2 Comparison over
 $\mathcal {O}_K$
$\mathcal {O}_K$
In this section, we want to extract from Theorem 4.74 a concrete classification of p-divisible groups over complete regular local rings with perfect residue field of characteristic p. This will, in particular, recover Breuil-Kisin’s classification ([Reference Breuil15], [Reference Kisin30]), as extended to all p by Kim [Reference Kim29], Lau [Reference Lau35] and Liu [Reference Liu38], over
![]() $\mathcal {O}_K$
, for a complete discretely valued extension of
$\mathcal {O}_K$
, for a complete discretely valued extension of
![]() $\mathbb {Q}_p$
with perfect residue field.
$\mathbb {Q}_p$
with perfect residue field.
Proposition 5.8. Let R be a complete Noetherian local ring with perfect residue field of characteristic p. If R is regular, there exists a quasisyntomic perfectoid cover
![]() $R_{\infty }$
of R.
$R_{\infty }$
of R.
Proof. The existence of a faithfully flat cover
![]() $R \to R_{\infty }$
, with
$R \to R_{\infty }$
, with
![]() $R_{\infty }$
perfectoid, is explained in [Reference Bhatt, Iyengar and Ma9, Theorem 4.7]. Assume first that
$R_{\infty }$
perfectoid, is explained in [Reference Bhatt, Iyengar and Ma9, Theorem 4.7]. Assume first that
![]() $pR=0$
or that R is unramifiedFootnote
36
. R is either flat over
$pR=0$
or that R is unramifiedFootnote
36
. R is either flat over
![]() $\mathbb {Z}_p$
or
$\mathbb {Z}_p$
or
![]() $pR=0$
. In the first case, set
$pR=0$
. In the first case, set
![]() $\Lambda :=\mathbb {Z}_p$
and in the second
$\Lambda :=\mathbb {Z}_p$
and in the second
![]() $\Lambda :=\mathbb {F}_p$
. By [Reference Project52, Tag 07GB], the morphism
$\Lambda :=\mathbb {F}_p$
. By [Reference Project52, Tag 07GB], the morphism
![]() $\Lambda \to R$
is a filtered colimit of smooth ring maps and thus
$\Lambda \to R$
is a filtered colimit of smooth ring maps and thus
![]() $L_{R/\Lambda }$
has p-complete Tor-amplitude in degree
$L_{R/\Lambda }$
has p-complete Tor-amplitude in degree
![]() $0$
. The triangle attached to the composite
$0$
. The triangle attached to the composite
![]() $\Lambda \to R \to R_{\infty }$
shows that
$\Lambda \to R \to R_{\infty }$
shows that
![]() $L_{R_{\infty }/R}$
has p-complete Tor-amplitude in degree
$L_{R_{\infty }/R}$
has p-complete Tor-amplitude in degree
![]() $-1$
. Therefore, the map
$-1$
. Therefore, the map
![]() $R \to R_{\infty }$
is indeed a quasisyntomic cover. Finally, when R is ramified of mixed characteristic, one sees from the explicit construction of [Reference Bhatt, Iyengar and Ma9, Example 3.8 (5)] that
$R \to R_{\infty }$
is indeed a quasisyntomic cover. Finally, when R is ramified of mixed characteristic, one sees from the explicit construction of [Reference Bhatt, Iyengar and Ma9, Example 3.8 (5)] that
![]() $R \to R_{\infty }$
is the p-completion of a colimit of syntomic morphisms (obtained by extracting pth-roots), hence, is quasisyntomic.
$R \to R_{\infty }$
is the p-completion of a colimit of syntomic morphisms (obtained by extracting pth-roots), hence, is quasisyntomic.
Remark 5.9. In the converse direction, the main result of [Reference Bhatt, Iyengar and Ma9] asserts that a Noetherian ring with p in its Jacobson radical which admits a faithfully flat map to a perfectoid ring has to be regular (this is a generalisation of a theorem of Kunz [Reference Kunz31] in positive characteristic).
Proposition 5.10. Let R be a complete regular local ring with perfect residue field of characteristic p. Any prismatic Dieudonné crystal over R is admissible.
Proof. Let
![]() $(\mathcal {M},\varphi _{\mathcal {M}}) \in \mathrm {DM}(R)$
. Let
$(\mathcal {M},\varphi _{\mathcal {M}}) \in \mathrm {DM}(R)$
. Let
![]() $R_{\infty }$
be a perfectoid quasisyntomic cover of R, as in Proposition 5.8. Let
$R_{\infty }$
be a perfectoid quasisyntomic cover of R, as in Proposition 5.8. Let
![]() $\mathcal {M}_{\infty } \in \mathrm {DM}(R_{\infty })$
be the base change of
$\mathcal {M}_{\infty } \in \mathrm {DM}(R_{\infty })$
be the base change of
![]() $\mathcal {M}$
, which we see as a prismatic Dieudonné module
$\mathcal {M}$
, which we see as a prismatic Dieudonné module
![]() $M_{\infty }$
over
$M_{\infty }$
over
![]() $R_{\infty }$
, via the equivalence of Proposition 4.13. We know (Proposition 4.12) that
$R_{\infty }$
, via the equivalence of Proposition 4.13. We know (Proposition 4.12) that
![]() $M_{\infty }$
is admissible. Since the natural functor
$M_{\infty }$
is admissible. Since the natural functor
![]() $\mathrm {DM}^{\mathrm {adm}} \to \mathrm {DM}$
is (tautologically) fully faithful,
$\mathrm {DM}^{\mathrm {adm}} \to \mathrm {DM}$
is (tautologically) fully faithful,
![]() $M_{\infty }$
descends to an admissible prismatic Dieudonné crystal over R, which must identify with
$M_{\infty }$
descends to an admissible prismatic Dieudonné crystal over R, which must identify with
![]() $(\mathcal {M},\varphi _{\mathcal {M}})$
.
$(\mathcal {M},\varphi _{\mathcal {M}})$
.
Recall the following definition, which already appeared in Proposition 4.26 before.
Definition 5.11. Let
![]() $(A,I=(d))$
be a prism. A Breuil-Kisin module
$(A,I=(d))$
be a prism. A Breuil-Kisin module
![]() $(M,\varphi _M)$
over
$(M,\varphi _M)$
over
![]() $(A,I)$
, or just A if I is understood, is a finite free A-module M together with an isomorphism
$(A,I)$
, or just A if I is understood, is a finite free A-module M together with an isomorphism
 $$ \begin{align*} \varphi_M\colon \varphi^{\ast}M\left[\frac{1}{I}\right]\cong M\left[\frac{1}{I}\right]. \end{align*} $$
$$ \begin{align*} \varphi_M\colon \varphi^{\ast}M\left[\frac{1}{I}\right]\cong M\left[\frac{1}{I}\right]. \end{align*} $$
If
![]() $\varphi _M(\varphi ^{\ast }M)\subseteq M$
with cokernel killed by I, then
$\varphi _M(\varphi ^{\ast }M)\subseteq M$
with cokernel killed by I, then
![]() $(M,\varphi _M)$
is called minuscule.
$(M,\varphi _M)$
is called minuscule.
We denote by
![]() $\mathrm {BK}(A)$
the category of Breuil-Kisin modules over A and by
$\mathrm {BK}(A)$
the category of Breuil-Kisin modules over A and by
![]() $\mathrm {BK}_{\mathrm {min}}(A)\subseteq \mathrm {BK}(A)$
its full subcategory of minuscule ones.
$\mathrm {BK}_{\mathrm {min}}(A)\subseteq \mathrm {BK}(A)$
its full subcategory of minuscule ones.
If R is a complete regular local ring with perfect residue field k of characteristic p, it can be written as
where
![]() $d=\dim R$
and E is a power series with constant term of p-value one (cf. [Reference Matsumura42, Theorems 29.7, 29.8 (ii)]). Let
$d=\dim R$
and E is a power series with constant term of p-value one (cf. [Reference Matsumura42, Theorems 29.7, 29.8 (ii)]). Let
![]() $(A,I)$
be the prism
$(A,I)$
be the prism
where the
![]() $\delta $
-ring structure on A is the usual one on
$\delta $
-ring structure on A is the usual one on
![]() $W(k)$
and is such that
$W(k)$
and is such that
![]() $\delta (u_i)=0$
, for
$\delta (u_i)=0$
, for
![]() $i=1,\dots ,d$
. For simplicity, we assume
$i=1,\dots ,d$
. For simplicity, we assume
![]() $d=1$
in the following. We hope that the general case works similarly.
$d=1$
in the following. We hope that the general case works similarly.
Theorem 5.12. Let R be a complete regular local ring with perfect residue field of characteristic p. The functor
is an equivalence of categories.
The case where
![]() $pR=0$
follows from Theorem 4.44, the classical fact that a Dieudonné crystal over R is the same thing as a minuscule Breuil-Kisin module over A (with respect to p) together with an integrable topologically quasinilpotent connection making Frobenius horizontal and [Reference Cais and Lau17, Proposition 2.7.3], which proves that for this particular ring A, the connection is necessarily unique. Hence, in the following, we will always assume that R is p-torsion free. In this case, the pair
$pR=0$
follows from Theorem 4.44, the classical fact that a Dieudonné crystal over R is the same thing as a minuscule Breuil-Kisin module over A (with respect to p) together with an integrable topologically quasinilpotent connection making Frobenius horizontal and [Reference Cais and Lau17, Proposition 2.7.3], which proves that for this particular ring A, the connection is necessarily unique. Hence, in the following, we will always assume that R is p-torsion free. In this case, the pair
![]() $(p,E)$
is transversal.
$(p,E)$
is transversal.
Remark 5.13. When
![]() $R=\mathcal {O}_K$
, with K a complete discretely valued extension of
$R=\mathcal {O}_K$
, with K a complete discretely valued extension of
![]() $\mathbb {Q}_p$
with perfect residue field, A is usually denoted by
$\mathbb {Q}_p$
with perfect residue field, A is usually denoted by
![]() $\mathfrak {S}$
(a notation which seems to originate from [Reference Breuil15]). We will see below that the antiequivalence of the theorem coincides in this case with the one studied by Kisin for p odd and Kim, Lau and Liu when
$\mathfrak {S}$
(a notation which seems to originate from [Reference Breuil15]). We will see below that the antiequivalence of the theorem coincides in this case with the one studied by Kisin for p odd and Kim, Lau and Liu when
![]() $p=2$
.
$p=2$
.
We will describe prismatic Dieudonné crystals over
![]() $\mathcal {O}_K$
via descent using the following lemma.
$\mathcal {O}_K$
via descent using the following lemma.
Lemma 5.14. The natural map from the sheaf represented by
![]() $(A,I)$
to the final object of
$(A,I)$
to the final object of
![]() is an epimorphism for the p-completely faithfully flat topology.
is an epimorphism for the p-completely faithfully flat topology.
Proof. Indeed, let
![]() . Let
. Let
![]() $A_{\infty }$
be the perfection of A; the map
$A_{\infty }$
be the perfection of A; the map
![]() $R=A/I \to R_{\infty }=A_{\infty }/IA_{\infty }$
is a quasisyntomic cover. By base change, the map
$R=A/I \to R_{\infty }=A_{\infty }/IA_{\infty }$
is a quasisyntomic cover. By base change, the map
is therefore a quasisyntomic cover as well. By Proposition 3.22, there exists a prism
![]() $(C,JC)$
which is p-completely faithfully flat over
$(C,JC)$
which is p-completely faithfully flat over
![]() $(B,J)$
, such that there exists a morphism of
$(B,J)$
, such that there exists a morphism of
![]() $B/J$
-algebras
$B/J$
-algebras
![]() $B/J \hat {\otimes }_R R_{\infty }\to C/J$
. Since
$B/J \hat {\otimes }_R R_{\infty }\to C/J$
. Since
![]() $R_{\infty }$
is perfectoid, it implies that
$R_{\infty }$
is perfectoid, it implies that
![]() $(C,JC)$
lives over
$(C,JC)$
lives over
![]() $(A_{\infty },IA_{\infty })$
(cf. Proposition 2.11), and a fortiori over
$(A_{\infty },IA_{\infty })$
(cf. Proposition 2.11), and a fortiori over
![]() $(A,I)$
, as desired.
$(A,I)$
, as desired.
Proof of Theorem 5.12.
By Theorem 4.74 and Proposition 5.10, we know that the prismatic Dieudonné functor
is an antiequivalence. Therefore, it suffices to prove that the functor
from prismatic Dieudonné crystals
![]() $\mathrm {DM}(R)$
to minuscule Breuil-Kisin modules
$\mathrm {DM}(R)$
to minuscule Breuil-Kisin modules
![]() $\mathrm {BK}_{\mathrm {min}}(A)$
is an equivalence. Let B be the absolute product of A with itself in
$\mathrm {BK}_{\mathrm {min}}(A)$
is an equivalence. Let B be the absolute product of A with itself in
![]() . One has (cf. [Reference Bhatt and Scholze13, Proposition 3.13])
. One has (cf. [Reference Bhatt and Scholze13, Proposition 3.13])
 $$\begin{align*}B= \left(W(k)[[u]] \otimes_{W(k)} W(k)[[v]] \right)\left\{ \frac{u-v}{E(u)} \right\}_{\delta}^{\wedge_{(p,E(u))}}, \end{align*}$$
$$\begin{align*}B= \left(W(k)[[u]] \otimes_{W(k)} W(k)[[v]] \right)\left\{ \frac{u-v}{E(u)} \right\}_{\delta}^{\wedge_{(p,E(u))}}, \end{align*}$$
where we wrote
![]() $E(u)$
for
$E(u)$
for
![]() $E\otimes 1$
$E\otimes 1$
Footnote
37
. By Lemma 5.14 below and Proposition 4.9, a prismatic Dieudonné crystal
![]() $\mathcal {M}$
over R is the same thing as a minuscule Breuil-Kisin module N over A, together with a descent datum, that is, an isomorphism
$\mathcal {M}$
over R is the same thing as a minuscule Breuil-Kisin module N over A, together with a descent datum, that is, an isomorphism
(where
![]() $p_1, p_2: A \to B$
are the two natural maps), satisfying the usual cocycle condition.
$p_1, p_2: A \to B$
are the two natural maps), satisfying the usual cocycle condition.
We claim that any
![]() $N \in \mathrm {BK}_{\mathrm {min}}(A)$
is equipped with a unique descent datum. Indeed, let
$N \in \mathrm {BK}_{\mathrm {min}}(A)$
is equipped with a unique descent datum. Indeed, let
![]() $f\colon B\to A$
be the map extending the multiplication map
$f\colon B\to A$
be the map extending the multiplication map
and, for
![]() $i=1,2$
, set
$i=1,2$
, set
![]() $E_i:=p_i(E)\in B_0$
, with
$E_i:=p_i(E)\in B_0$
, with
![]() $p_i\colon A\to B_0$
the two inclusions. Let
$p_i\colon A\to B_0$
the two inclusions. Let
![]() $M_0$
be a minuscule Breuil-Kisin module over
$M_0$
be a minuscule Breuil-Kisin module over
![]() $B_0$
with respect to the element
$B_0$
with respect to the element
![]() $E_1$
and
$E_1$
and
![]() $N_0$
a minuscule Breuil-Kisin module with respect to
$N_0$
a minuscule Breuil-Kisin module with respect to
![]() $E_2$
. Let
$E_2$
. Let
![]() $M_A=M_0 \otimes _{B_0,f_0} A$
,
$M_A=M_0 \otimes _{B_0,f_0} A$
,
![]() $N_A=N_0 \otimes _{B_0,f_0} A$
be their base changes along
$N_A=N_0 \otimes _{B_0,f_0} A$
be their base changes along
![]() $f_0$
.
$f_0$
.
Let
![]() $\alpha _0\colon M_0\to N_0$
be any
$\alpha _0\colon M_0\to N_0$
be any
![]() $B_0$
-linear map, such that
$B_0$
-linear map, such that
![]() $\alpha _A:= f^{\ast }_0 \alpha _0 \colon M_A\to N_A$
is a morphism of Breuil-Kisin modules over A. Consider the composition
$\alpha _A:= f^{\ast }_0 \alpha _0 \colon M_A\to N_A$
is a morphism of Breuil-Kisin modules over A. Consider the composition
as in the proof of Lemma 4.32. Then the morphism
![]() $U_0(\alpha _0)-\alpha _0$
maps
$U_0(\alpha _0)-\alpha _0$
maps
![]() $M_0$
to
$M_0$
to
![]() $\frac {1}{E_1} KN_0$
, where
$\frac {1}{E_1} KN_0$
, where
![]() $K=\ker (f_0)$
as
$K=\ker (f_0)$
as
![]() $\alpha _A$
is a morphism of minuscule Breuil-Kisin modules over A. By construction of B, we have
$\alpha _A$
is a morphism of minuscule Breuil-Kisin modules over A. By construction of B, we have
![]() $K\subseteq E_1J$
, if
$K\subseteq E_1J$
, if
![]() $J=\ker (f)$
. In particular, if
$J=\ker (f)$
. In particular, if
![]() $\alpha $
denotes the base change of
$\alpha $
denotes the base change of
![]() $\alpha _0$
to B, then
$\alpha _0$
to B, then
maps
![]() $M_0\otimes _{B_0}B$
to
$M_0\otimes _{B_0}B$
to
![]() $J(N_0\otimes _{B_0}B)$
, where
$J(N_0\otimes _{B_0}B)$
, where
![]() $U(\alpha )$
is the base change of
$U(\alpha )$
is the base change of
![]() $U_0(\alpha _0)$
. Thanks to Lemma 5.15 below, we can use the same arguments in the proof of 4.32 to see that there exists an isomorphism
$U_0(\alpha _0)$
. Thanks to Lemma 5.15 below, we can use the same arguments in the proof of 4.32 to see that there exists an isomorphism
![]() $\alpha \colon M_0 \otimes _{B_0} B \cong N_0 \otimes _{B_0} B$
of Breuil-Kisin modules over B with
$\alpha \colon M_0 \otimes _{B_0} B \cong N_0 \otimes _{B_0} B$
of Breuil-Kisin modules over B with
![]() $f^{\ast } \alpha =\alpha _A$
. Indeed, if
$f^{\ast } \alpha =\alpha _A$
. Indeed, if
![]() $\beta _0:=U_0(\alpha _0)-\alpha _0$
with
$\beta _0:=U_0(\alpha _0)-\alpha _0$
with
![]() $f^{\ast }_0\alpha _0=\alpha _A$
, then the series
$f^{\ast }_0\alpha _0=\alpha _A$
, then the series
 $$\begin{align*}\sum\limits_{n=0}^{\infty} U^n_0(\beta_0) \end{align*}$$
$$\begin{align*}\sum\limits_{n=0}^{\infty} U^n_0(\beta_0) \end{align*}$$
converges after base change to B, since
![]() $\beta $
sends
$\beta $
sends
![]() $M_0 \otimes _{B_0} B$
to
$M_0 \otimes _{B_0} B$
to
![]() $J (N_0\otimes _{B_0} B)$
. In other words, the map induced by f
$J (N_0\otimes _{B_0} B)$
. In other words, the map induced by f
is a surjection. We claim that
![]() $\delta _{M_0,N_0}$
is also injective. Indeed, assume that
$\delta _{M_0,N_0}$
is also injective. Indeed, assume that
![]() $\alpha \colon M_0\otimes _{B_0}B\to N_0\otimes _{B_0}B$
is a morphism of minuscule Breuil-Kisin modules over B reducing to
$\alpha \colon M_0\otimes _{B_0}B\to N_0\otimes _{B_0}B$
is a morphism of minuscule Breuil-Kisin modules over B reducing to
![]() $0$
after base change to A. Define
$0$
after base change to A. Define
Then, since
![]() $\alpha $
is a morphism of minuscule Breuil-Kisin modules,
$\alpha $
is a morphism of minuscule Breuil-Kisin modules,
for all
![]() $n\geq 1$
. But as
$n\geq 1$
. But as
![]() $\varphi _1:=\frac {\varphi }{E_1}$
is topologically nilpotent on J, we see that
$\varphi _1:=\frac {\varphi }{E_1}$
is topologically nilpotent on J, we see that
![]() $U^n(\alpha )$
converges to
$U^n(\alpha )$
converges to
![]() $0$
for
$0$
for
![]() $n \to \infty $
by the same exact argument as in the proof of Lemma 4.32.
$n \to \infty $
by the same exact argument as in the proof of Lemma 4.32.
Recall that we started with
![]() $N \in \mathrm {BK}_{\mathrm {min}}(A)$
and want to produce a descent datum on N. To apply the above discussion, we set
$N \in \mathrm {BK}_{\mathrm {min}}(A)$
and want to produce a descent datum on N. To apply the above discussion, we set
![]() $M_0:=N\otimes _{A,p_1}B_0, N_0:=N\otimes _{A,p_2} B_0$
, and let
$M_0:=N\otimes _{A,p_1}B_0, N_0:=N\otimes _{A,p_2} B_0$
, and let
![]() $\varphi _{M_0}, \varphi _{N_0}$
be the respective base changes of
$\varphi _{M_0}, \varphi _{N_0}$
be the respective base changes of
![]() $\varphi _N$
. Since the compositions
$\varphi _N$
. Since the compositions
![]() $f\circ p_1$
,
$f\circ p_1$
,
![]() $f\circ p_2$
are the identity map,
$f\circ p_2$
are the identity map,
![]() $M_A, N_A$
are isomorphic to N. Let
$M_A, N_A$
are isomorphic to N. Let
be the map corresponding via the bijection
![]() $\delta _{M_0,N_0}$
to the identity map from
$\delta _{M_0,N_0}$
to the identity map from
![]() $M_A=N$
to
$M_A=N$
to
![]() $N_A=N$
. If
$N_A=N$
. If
![]() $N^{\prime } \in \mathrm {BK}_{\mathrm {min}}(A)$
is another minuscule Breuil-Kisin module over A, and
$N^{\prime } \in \mathrm {BK}_{\mathrm {min}}(A)$
is another minuscule Breuil-Kisin module over A, and
![]() $g\in \mathrm {Hom}_{\mathrm {BK}_{\mathrm {min}}(A)} (N, N^{\prime })$
. We claim that
$g\in \mathrm {Hom}_{\mathrm {BK}_{\mathrm {min}}(A)} (N, N^{\prime })$
. We claim that
where
![]() $g_1$
, respectively,
$g_1$
, respectively,
![]() $g_2$
, is the base change of g along
$g_2$
, is the base change of g along
![]() $p_1$
, respectively,
$p_1$
, respectively,
![]() $p_2$
. Indeed, this can be rewritten as an equality
$p_2$
. Indeed, this can be rewritten as an equality
(using for
![]() $N^{\prime }$
notations analogous to the ones we used for N), which, by the considerations above, can be checked after base change along
$N^{\prime }$
notations analogous to the ones we used for N), which, by the considerations above, can be checked after base change along
![]() $f: B \to A$
, where it becomes obvious (since
$f: B \to A$
, where it becomes obvious (since
![]() $\alpha _N$
, respectively,
$\alpha _N$
, respectively,
![]() $\alpha _{N^{\prime }}$
, reduces to the identity of N, respectively,
$\alpha _{N^{\prime }}$
, reduces to the identity of N, respectively,
![]() $N^{\prime }$
, and since
$N^{\prime }$
, and since
![]() $f\circ p_1=f\circ p_2$
is the identity). This shows that the formation of
$f\circ p_1=f\circ p_2$
is the identity). This shows that the formation of
![]() $\alpha _N$
is functorial in N. As each descent datum on N reduces to the identity on N after base change along f, the descent datum on N is unique, if it exists, since
$\alpha _N$
is functorial in N. As each descent datum on N reduces to the identity on N after base change along f, the descent datum on N is unique, if it exists, since
![]() $\delta _{M_0,N_0}$
is injective.
$\delta _{M_0,N_0}$
is injective.
To conclude, it, therefore, remains to prove that
![]() $\alpha _N$
is a descent datum, that is that it satisfies the cocycle condition. Let
$\alpha _N$
is a descent datum, that is that it satisfies the cocycle condition. Let
be the prism representing the triple absolute product of
![]() $(A,(E))$
in
$(A,(E))$
in
![]() . We have to see that
. We have to see that
where the
![]() $p_{i,j}\colon B\to C$
are induced by the respective projections. Let us note that fibre products in
$p_{i,j}\colon B\to C$
are induced by the respective projections. Let us note that fibre products in
![]() are calculated by (completed) tensor products and that
are calculated by (completed) tensor products and that
for any object X in a category
![]() $\mathcal {C}$
admitting fibre products. This implies that
$\mathcal {C}$
admitting fibre products. This implies that
Let
![]() $C_0= B\otimes _A B$
be the uncompleted tensor product. Note that
$C_0= B\otimes _A B$
be the uncompleted tensor product. Note that
![]() $p^{\ast }_{i,j}\alpha _N$
, for each
$p^{\ast }_{i,j}\alpha _N$
, for each
![]() $1\leq i<j\leq 3$
, is already defined over
$1\leq i<j\leq 3$
, is already defined over
![]() $C_0$
. The kernel L of the natural morphism
$C_0$
. The kernel L of the natural morphism
![]() $C_0 \to A$
is generated by
$C_0 \to A$
is generated by
In particular,
![]() $\varphi _1:={\frac {\varphi }{E_1\otimes 1}}$
stabilises L, and
$\varphi _1:={\frac {\varphi }{E_1\otimes 1}}$
stabilises L, and
![]() $\varphi _1$
is elementwise topologically nilpotent on it. Therefore, arguing as above, we see that any morphism of minuscule Breuil-Kisin modules over
$\varphi _1$
is elementwise topologically nilpotent on it. Therefore, arguing as above, we see that any morphism of minuscule Breuil-Kisin modules over
![]() $C_0$
which vanishes after base change along
$C_0$
which vanishes after base change along
![]() $C_0 \to A$
, must vanish after base change to C. After reduction to A, (5.1) becomes
$C_0 \to A$
, must vanish after base change to C. After reduction to A, (5.1) becomes
by construction of
![]() $\alpha _N$
. This finishes the proof.
$\alpha _N$
. This finishes the proof.
The proof of Theorem 5.12 relied on the following technical lemma.
Lemma 5.15. With the notation from the proof of Theorem 5.12, the ideal
![]() $J\subseteq B$
is contained in
$J\subseteq B$
is contained in
![]() $\mathcal {N}^{\geq 1} B$
, stable by
$\mathcal {N}^{\geq 1} B$
, stable by
![]() $\varphi _1:=\frac {\varphi }{E(u)}$
and
$\varphi _1:=\frac {\varphi }{E(u)}$
and
![]() $\varphi _1$
is topologically nilpotent on J, with respect to the
$\varphi _1$
is topologically nilpotent on J, with respect to the
![]() $(p,E)$
-adic topology.
$(p,E)$
-adic topology.
Proof. Write
![]() $E:=E(u)$
. The ideal J is generated (up to completion) by the
$E:=E(u)$
. The ideal J is generated (up to completion) by the
![]() $\delta $
-translates of
$\delta $
-translates of
so to check that
![]() $J \subset \mathcal {N}^{\geq 1} B$
, it is enough to prove that
$J \subset \mathcal {N}^{\geq 1} B$
, it is enough to prove that
![]() $\delta ^n (z) \in \mathcal {N}^{\geq 1} B$
for all n. We prove by induction on n that for all
$\delta ^n (z) \in \mathcal {N}^{\geq 1} B$
for all n. We prove by induction on n that for all
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $\varphi ^k(\delta ^n(z))$
is divisible by E. For
$\varphi ^k(\delta ^n(z))$
is divisible by E. For
![]() $n=0$
, one has, for any
$n=0$
, one has, for any
![]() $k\geq 1$
,
$k\geq 1$
,
 $$\begin{align*}\varphi^k(z)= \frac{u^{pk}-v^{pk}}{\varphi^k(E)}=\frac{(u-v)(u^{pk-1} + u^{pk-2}v + \dots + uv^{pk-2} + v^{pk})}{\varphi^k(E)}. \end{align*}$$
$$\begin{align*}\varphi^k(z)= \frac{u^{pk}-v^{pk}}{\varphi^k(E)}=\frac{(u-v)(u^{pk-1} + u^{pk-2}v + \dots + uv^{pk-2} + v^{pk})}{\varphi^k(E)}. \end{align*}$$
Since
![]() $(E,\varphi ^k(E))$
is regular (as
$(E,\varphi ^k(E))$
is regular (as
![]() $(p,E)$
is transversal because B is
$(p,E)$
is transversal because B is
![]() $(p,E)$
-completely faithfully flat over
$(p,E)$
-completely faithfully flat over
![]() $W(k)[[u]]$
by [Reference Bhatt and Scholze13, Proposition 3.13]) and
$W(k)[[u]]$
by [Reference Bhatt and Scholze13, Proposition 3.13]) and
![]() $u-v$
is divisible by E in B, we deduce that E divides
$u-v$
is divisible by E in B, we deduce that E divides
![]() $\varphi ^k(z)$
. Let now
$\varphi ^k(z)$
. Let now
![]() $n\geq 0$
, and assume the result is known for
$n\geq 0$
, and assume the result is known for
![]() $\delta ^n(z)$
. We have, for
$\delta ^n(z)$
. We have, for
![]() $k\geq 0$
,
$k\geq 0$
,
so the statement for
![]() $\delta ^{n+1}(z)$
follows by induction hypothesis, and the fact that p and E are transversal. This concludes the proof that
$\delta ^{n+1}(z)$
follows by induction hypothesis, and the fact that p and E are transversal. This concludes the proof that
![]() $J \subset \mathcal {N}^{\geq 1} B$
.
$J \subset \mathcal {N}^{\geq 1} B$
.
Let
![]() $x \in J$
. We have
$x \in J$
. We have
Since E is a nonzero divisor in A, we must have
![]() $f(\varphi _1(x))=0$
and, therefore,
$f(\varphi _1(x))=0$
and, therefore,
![]() $\varphi _1(x) \in J$
, that is,
$\varphi _1(x) \in J$
, that is,
![]() $\varphi _1$
stabilises J.
$\varphi _1$
stabilises J.
It remains to prove that the divided Frobenius is topologically nilpotent on J, endowed with the
![]() $(p,E)$
-adic topology. Let
$(p,E)$
-adic topology. Let
 $$\begin{align*}A'= A\left\{\frac{\varphi(E)}{p}\right\}^{\wedge_p},\end{align*}$$
$$\begin{align*}A'= A\left\{\frac{\varphi(E)}{p}\right\}^{\wedge_p},\end{align*}$$
which by [Reference Bhatt and Scholze13, Lemma 2.35] identifies with the (p-completed) divided power envelope
![]() $D_A((E))^{\wedge _p}$
of A in
$D_A((E))^{\wedge _p}$
of A in
![]() $(E)$
. Let
$(E)$
. Let
![]() $\iota \colon A\to A^{\prime }$
be the natural inclusion. The composition
$\iota \colon A\to A^{\prime }$
be the natural inclusion. The composition
defines a morphism of prisms
![]() $(A,(E)) \to (A^{\prime }, (p))$
. Let
$(A,(E)) \to (A^{\prime }, (p))$
. Let
where
![]() $J'$
is the kernel of the map
$J'$
is the kernel of the map
![]() $A \hat {\otimes }_{W(k)} A \to R$
. The ideal
$A \hat {\otimes }_{W(k)} A \to R$
. The ideal
![]() $J'$
is generated by E and
$J'$
is generated by E and
![]() $u-v$
, which form a regular sequence in
$u-v$
, which form a regular sequence in
![]() ${A \hat {\otimes }_{W(k)} A/p}$
, and, therefore
${A \hat {\otimes }_{W(k)} A/p}$
, and, therefore
 $$ \begin{align*} \begin{aligned} B' \cong (A \hat{\otimes}_{W(k)} A)\left\{\frac{\varphi(E),\varphi(u-v)}{p} \right\}_{\delta}^{\wedge_{p}} & \cong (A \hat{\otimes}_{W(k)} A)\left\{\frac{p,\varphi(u-v)}{\varphi(E)} \right\}_{\delta}^{\wedge_{\varphi(E)}} \\ & \cong D_{\varphi_{A\hat{\otimes}_{W(k)} A}^*B}((E))^{\wedge_p}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} B' \cong (A \hat{\otimes}_{W(k)} A)\left\{\frac{\varphi(E),\varphi(u-v)}{p} \right\}_{\delta}^{\wedge_{p}} & \cong (A \hat{\otimes}_{W(k)} A)\left\{\frac{p,\varphi(u-v)}{\varphi(E)} \right\}_{\delta}^{\wedge_{\varphi(E)}} \\ & \cong D_{\varphi_{A\hat{\otimes}_{W(k)} A}^*B}((E))^{\wedge_p}. \end{aligned} \end{align*} $$
(In the second isomorphism, we used again [Reference Bhatt and Scholze13, Lemma 2.24], and in the first and last [Reference Bhatt and Scholze13, Lemma 2.37].) In particular, the map
![]() $\alpha $
induces a map:
$\alpha $
induces a map:
because
![]() $B\cong A\hat {\otimes }_{W(k)}A\{\frac {u-v}{E}\}^{\wedge _{(p,E)}}$
. It sends
$B\cong A\hat {\otimes }_{W(k)}A\{\frac {u-v}{E}\}^{\wedge _{(p,E)}}$
. It sends
![]() $J \subseteq B$
to the kernel
$J \subseteq B$
to the kernel
![]() $K \subset B'$
of the map
$K \subset B'$
of the map
![]() $B^{\prime } \to A^{\prime }$
(which extends the multiplication on
$B^{\prime } \to A^{\prime }$
(which extends the multiplication on
![]() $\mu \colon A\hat {\otimes }_{W(k)} A\to A$
), and commutes with the divided Frobenius (because
$\mu \colon A\hat {\otimes }_{W(k)} A\to A$
), and commutes with the divided Frobenius (because
![]() $B^{\prime }$
is p- and thus
$B^{\prime }$
is p- and thus
![]() $\varphi (E)$
-torsion free). We, thus, have a diagram:
$\varphi (E)$
-torsion free). We, thus, have a diagram:

The ideal
![]() $K\subseteq B^{\prime }$
is generated (up to completion) by
$K\subseteq B^{\prime }$
is generated (up to completion) by
![]() $(u-v)$
and the
$(u-v)$
and the
![]() $\delta $
-translates of
$\delta $
-translates of
As the kernel J of
![]() $B\to A$
is stable by
$B\to A$
is stable by
![]() $\varphi _1$
, this implies that
$\varphi _1$
, this implies that
![]() $K=JB^{\prime }$
is stable by
$K=JB^{\prime }$
is stable by
![]() $\varphi _1$
, and, thus, in particular, contained in
$\varphi _1$
, and, thus, in particular, contained in
![]() $\mathcal {N}^{\geq 1}B^{\prime }$
.
$\mathcal {N}^{\geq 1}B^{\prime }$
.
Observe also that
To see this, one needs to show that the map induced by
![]() $\alpha _B$
$\alpha _B$
is injective, that is, by faithful flatness of
![]() $\varphi \colon A\to A$
that the natural map
$\varphi \colon A\to A$
that the natural map
is injective. But since B is p-torsion free,
and the above map is simply the natural inclusion map. Hence, it suffices to prove topological nilpotence of
![]() $\varphi _1={"}\varphi /\varphi (E){"}$
on K with respect to the p-adic topologyFootnote
38
. We do it in two steps.
$\varphi _1={"}\varphi /\varphi (E){"}$
on K with respect to the p-adic topologyFootnote
38
. We do it in two steps.
Note first that
![]() $\varphi $
is topologically nilpotent on K. More precisely, using that K is stable by
$\varphi $
is topologically nilpotent on K. More precisely, using that K is stable by
![]() $\varphi _1$
, one easily sees by induction that
$\varphi _1$
, one easily sees by induction that
![]() $\varphi ^k(z)$
is divisible by
$\varphi ^k(z)$
is divisible by
![]() $p^k$
, for all
$p^k$
, for all
![]() $z \in K$
and
$z \in K$
and
![]() $k\geq 1$
(with
$k\geq 1$
(with
![]() $\varphi ^k(z)/p^k\in K$
, because
$\varphi ^k(z)/p^k\in K$
, because
![]() $A^{\prime }$
is p-torsion free). The equality
$A^{\prime }$
is p-torsion free). The equality
for
![]() $x, y \in K$
, implies by induction that for any
$x, y \in K$
, implies by induction that for any
![]() $n \geq 1$
:
$n \geq 1$
:
This shows that the second divided power ideal
![]() $K^{[2]}$
is stable by
$K^{[2]}$
is stable by
![]() $\varphi _1$
(since K is stable by
$\varphi _1$
(since K is stable by
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi _1$
) and, by what we just said, that the left-hand side is divisible by
$\varphi _1$
) and, by what we just said, that the left-hand side is divisible by
![]() $p^n$
in K. In fact, one can do better. Let
$p^n$
in K. In fact, one can do better. Let
![]() $m \geq 1$
and
$m \geq 1$
and
![]() $x \in K$
. In the previous equality, take
$x \in K$
. In the previous equality, take
![]() $y=x^{m-1}$
. Seeing it in
$y=x^{m-1}$
. Seeing it in
![]() $B'[1/p]$
(recall that
$B'[1/p]$
(recall that
![]() $B'$
is p-torsion free), one can divide both sides by
$B'$
is p-torsion free), one can divide both sides by
![]() $m!$
. It reads:
$m!$
. It reads:
The left-hand side always makes sense in K since K has divided powers, and for n big enough, the right-hand side as well since
![]() $\varphi ^n(x)$
tends p-adically to
$\varphi ^n(x)$
tends p-adically to
![]() $0$
and thus is divisible by
$0$
and thus is divisible by
![]() $m!$
for n big enough. Letting n go to infinity, we see that the left-hand side goes to
$m!$
for n big enough. Letting n go to infinity, we see that the left-hand side goes to
![]() $0$
in K. These considerations prove that
$0$
in K. These considerations prove that
![]() $\varphi _1$
is topologically nilpotent (with respect to the p-adic topology) on
$\varphi _1$
is topologically nilpotent (with respect to the p-adic topology) on
![]() $K^{[2]}$
, as it is topologically nilpotent on
$K^{[2]}$
, as it is topologically nilpotent on
![]() $K^2$
and all divided powers
$K^2$
and all divided powers
![]() $\gamma _m(x)$
,
$\gamma _m(x)$
,
![]() $m\geq 2$
, for
$m\geq 2$
, for
![]() $x\in K$
.
$x\in K$
.
Let e be the degree of the polynomial E. Since
![]() $K^{[2]}$
is stable by
$K^{[2]}$
is stable by
![]() $\varphi _1$
,
$\varphi _1$
,
![]() $\varphi _1$
defines a semilinear endomorphism of the quotient
$\varphi _1$
defines a semilinear endomorphism of the quotient
![]() $K/K^{[2]}$
. Let us now prove that
$K/K^{[2]}$
. Let us now prove that
![]() $\varphi _1^{pe}(K/K^{[2]}) \subset p. K/K^{[2]}$
. We know that the
$\varphi _1^{pe}(K/K^{[2]}) \subset p. K/K^{[2]}$
. We know that the
![]() $A'$
-module
$A'$
-module
![]() $K/K^{[2]}$
is isomorphic to
$K/K^{[2]}$
is isomorphic to
![]() $(\Omega _A^{1})^{\wedge _p} \otimes _A A'$
(where the map
$(\Omega _A^{1})^{\wedge _p} \otimes _A A'$
(where the map
![]() $A \to A^{\prime }$
is the natural inclusion
$A \to A^{\prime }$
is the natural inclusion
![]() $\iota $
). It is a free
$\iota $
). It is a free
![]() $A'$
-module of rank generated by
$A'$
-module of rank generated by
![]() $du$
, and via this identification, one has
$du$
, and via this identification, one has
![]() $\varphi _1(du)= u^{p-1} du$
. But the image of
$\varphi _1(du)= u^{p-1} du$
. But the image of
![]() $u^{pe}$
in
$u^{pe}$
in
![]() $A'$
is divisible by p since p divides
$A'$
is divisible by p since p divides
![]() $E^p$
in
$E^p$
in
![]() $A'$
and E is an Eisenstein polynomial. Therefore, p (even
$A'$
and E is an Eisenstein polynomial. Therefore, p (even
![]() $p^{p-1}$
) divides
$p^{p-1}$
) divides
![]() $\varphi ^{pe}_{1}(du \otimes 1)$
in
$\varphi ^{pe}_{1}(du \otimes 1)$
in
![]() $K/K^{[2]}$
. Finally, let us check that these two steps imply the desired topological nilpotence. Let
$K/K^{[2]}$
. Finally, let us check that these two steps imply the desired topological nilpotence. Let
![]() $x \in K$
,
$x \in K$
,
![]() $\bar {x}$
its class in
$\bar {x}$
its class in
![]() $K/K^{[2]}$
. Fix an integer
$K/K^{[2]}$
. Fix an integer
![]() $n\geq 1$
. By the second step, we have
$n\geq 1$
. By the second step, we have
that is, there exists
![]() $y \in K^{[2]}$
, such that
$y \in K^{[2]}$
, such that
By the first step, there exists
![]() $m \geq 1$
, such that
$m \geq 1$
, such that
![]() $\varphi _1^m(y) \in p^n K$
, and so
$\varphi _1^m(y) \in p^n K$
, and so
as desired.
Remark 5.16. We have seen above that prismatic Dieudonné crystals over
![]() $\mathcal {O}_K$
are the same as minuscule Breuil-Kisin modules. One cannot expect the same kind of result to hold for nonminuscule finite locally free F-crystals on the absolute prismatic site of
$\mathcal {O}_K$
are the same as minuscule Breuil-Kisin modules. One cannot expect the same kind of result to hold for nonminuscule finite locally free F-crystals on the absolute prismatic site of
![]() $\mathcal {O}_K$
: one really needs to remember the (unexplicit) descent datum to reconstruct the F-crystal. In fact, Bhatt and Scholze [Reference Bhatt and Scholze14] have recently proved the remarkable result that finite locally free F-crystals on the absolute prismatic site of
$\mathcal {O}_K$
: one really needs to remember the (unexplicit) descent datum to reconstruct the F-crystal. In fact, Bhatt and Scholze [Reference Bhatt and Scholze14] have recently proved the remarkable result that finite locally free F-crystals on the absolute prismatic site of
![]() $\mathcal {O}_K$
are the same as
$\mathcal {O}_K$
are the same as
![]() $\mathrm {Gal}_K$
-stable lattices in crystalline representations of
$\mathrm {Gal}_K$
-stable lattices in crystalline representations of
![]() $\mathrm {Gal}_K$
. In the minuscule case, that is for prismatic Dieudonné crystals, combined with the result above and the considerations below, this recovers the known equivalence between p-divisible groups of
$\mathrm {Gal}_K$
. In the minuscule case, that is for prismatic Dieudonné crystals, combined with the result above and the considerations below, this recovers the known equivalence between p-divisible groups of
![]() $\mathcal {O}_K$
and
$\mathcal {O}_K$
and
![]() $\mathrm {Gal}_K$
-stable lattices in crystalline representations of
$\mathrm {Gal}_K$
-stable lattices in crystalline representations of
![]() $\mathrm {Gal}_K$
with Hodge-Tate weights in
$\mathrm {Gal}_K$
with Hodge-Tate weights in
![]() $\{0,1\}$
.
$\{0,1\}$
.
Finally, let K be a complete, discretely valued extension of
![]() $\mathbb {Q}_p$
, let
$\mathbb {Q}_p$
, let
![]() $\mathcal {O}_K\subseteq K$
be its ring of integers and assume the residue field k of
$\mathcal {O}_K\subseteq K$
be its ring of integers and assume the residue field k of
![]() $\mathcal {O}_K$
is perfect. We will show that the equivalence of Theorem 5.12 coincides with the equivalence established by Kisin (cf. [Reference Kisin30, Theorem 0.4]). Set
$\mathcal {O}_K$
is perfect. We will show that the equivalence of Theorem 5.12 coincides with the equivalence established by Kisin (cf. [Reference Kisin30, Theorem 0.4]). Set
with Frobenius lift
![]() $\varphi \colon W(k)[[u]]\to W(k)[[u]]$
sending
$\varphi \colon W(k)[[u]]\to W(k)[[u]]$
sending
![]() $u\mapsto u^p$
. Fix a uniformiser
$u\mapsto u^p$
. Fix a uniformiser
![]() $\pi \in \mathcal {O}_K$
, and define the morphism
$\pi \in \mathcal {O}_K$
, and define the morphism
Then the kernel
![]() $\mathrm {ker}(\tilde {\theta })=(E)$
is generated by an Eisenstein polynomial
$\mathrm {ker}(\tilde {\theta })=(E)$
is generated by an Eisenstein polynomial
![]() $E\in W(k)[u]$
. Let S be the p-completed divided power envelope of the ideal
$E\in W(k)[u]$
. Let S be the p-completed divided power envelope of the ideal
![]() $(E)\subseteq \mathfrak {S}$
, that is,
$(E)\subseteq \mathfrak {S}$
, that is,
 $$ \begin{align*}S=\mathfrak{S}\left\{\frac{\varphi(E)}{p}\right\}^{\wedge}_p \end{align*} $$
$$ \begin{align*}S=\mathfrak{S}\left\{\frac{\varphi(E)}{p}\right\}^{\wedge}_p \end{align*} $$
in the category of
![]() $\delta $
-rings. Note that the composition
$\delta $
-rings. Note that the composition
induces to a morphism
![]() $(\mathfrak {S},(E))\to (S,(p))$
of prisms. Via the composition
$(\mathfrak {S},(E))\to (S,(p))$
of prisms. Via the composition
![]() $\mathcal {O}_K\cong \mathfrak {S}/(E)\xrightarrow {\psi _K} S/(p)$
, we consider
$\mathcal {O}_K\cong \mathfrak {S}/(E)\xrightarrow {\psi _K} S/(p)$
, we consider
![]() $(S,(p))$
as an object of the (absolute) prismatic site
$(S,(p))$
as an object of the (absolute) prismatic site
![]() . The antiequivalence
. The antiequivalence
of Kisin has the characteristic property (cf. [Reference Kisin30, Theorem 2.2.7]) that for a p-divisible group G over
![]() $\mathcal {O}_K$
, there is a canonical Frobenius equivariant isomorphism
$\mathcal {O}_K$
, there is a canonical Frobenius equivariant isomorphism
where the right-hand side denotes the evaluation of the crystalline Dieudonné crystal of G on the PD-thickening
![]() $S\to \mathcal {O}_K$
(which sends all divided powers of E to zero).
$S\to \mathcal {O}_K$
(which sends all divided powers of E to zero).
Let G be a p-divisible group over
![]() $\mathcal {O}_K$
with absolute prismatic Dieudonné crystal
$\mathcal {O}_K$
with absolute prismatic Dieudonné crystal
![]() . We use Lemma 4.38 and Proposition 4.4 and consider
. We use Lemma 4.38 and Proposition 4.4 and consider
![]() as a crystal on the absolute prismatic site
as a crystal on the absolute prismatic site
![]() .
.
Lemma 5.17. There is a natural Frobenius-equivariant isomorphism
Here,
![]() $\mathbb {D}(G)(S)$
denotes the evaluation of the Dieudonné crystal of G at the PD-thickening
$\mathbb {D}(G)(S)$
denotes the evaluation of the Dieudonné crystal of G at the PD-thickening
![]() $S\to \mathcal {O}_K$
.
$S\to \mathcal {O}_K$
.
Proof. This follows from Lemma 4.45.
We want to show that the natural isomorphism
![]() $\alpha _K$
restricts to an isomorphism
$\alpha _K$
restricts to an isomorphism
. In other words, we want to prove the existence of the dotted morphisms in the diagram

Let C be the completion of an algebraic closure of K, and let
![]() $\mathcal {O}_C\subseteq C$
be its ring of integers. Set
$\mathcal {O}_C\subseteq C$
be its ring of integers. Set
![]() $A_{\mathrm {inf}}:=A_{\mathrm {inf}}(\mathcal {O}_C)$
,
$A_{\mathrm {inf}}:=A_{\mathrm {inf}}(\mathcal {O}_C)$
,
![]() $A_{\mathrm {crys}}:=A_{\mathrm {crys}}(\mathcal {O}_C)$
.
$A_{\mathrm {crys}}:=A_{\mathrm {crys}}(\mathcal {O}_C)$
.
We can extend the morphism
![]() $\mathcal {O}_K\to \mathcal {O}_C$
to a morphism of prismsFootnote
39
$\mathcal {O}_K\to \mathcal {O}_C$
to a morphism of prismsFootnote
39
by sending
![]() $u\mapsto {[\pi ^{\flat }]}=[(\pi ,\pi ^{1/p},\ldots )]$
(after choosing a compatible system of p-power roots
$u\mapsto {[\pi ^{\flat }]}=[(\pi ,\pi ^{1/p},\ldots )]$
(after choosing a compatible system of p-power roots
![]() $\pi ^{1/p^n}\in \mathcal {O}_C$
of
$\pi ^{1/p^n}\in \mathcal {O}_C$
of
![]() $\pi $
). Let
$\pi $
). Let
Then analogous
![]() $\psi _C$
induces a morphism
$\psi _C$
induces a morphism
![]() $(A_{\mathrm {inf}},(\xi ))\to (A_{\mathrm {crys}},(p))$
of prisms.
$(A_{\mathrm {inf}},(\xi ))\to (A_{\mathrm {crys}},(p))$
of prisms.
By faithful flatness of
![]() $\mathfrak {S}\to A_{\mathrm {inf}}$
(cf. [Reference Bhatt, Morrow and Scholze11, Lemma 4.30]Footnote
40
), it suffices to prove the existence of the dotted arrows after base change to
$\mathfrak {S}\to A_{\mathrm {inf}}$
(cf. [Reference Bhatt, Morrow and Scholze11, Lemma 4.30]Footnote
40
), it suffices to prove the existence of the dotted arrows after base change to
![]() $A_{\mathrm {inf}}$
:
$A_{\mathrm {inf}}$
:

By flat base change of PD-envelopes (cf. [Reference Project52, Tag 07HD]), we get
and thus
![]() $\mathbb {D}(G)(S)\otimes _{\mathfrak {S}}A_{\mathrm {inf}}\cong \mathbb {D}(G_{\mathcal {O_C}})(A_{\mathrm {crys}})$
.
$\mathbb {D}(G)(S)\otimes _{\mathfrak {S}}A_{\mathrm {inf}}\cong \mathbb {D}(G_{\mathcal {O_C}})(A_{\mathrm {crys}})$
.
Similar to Lemma 5.17, there is a canonical isomorphism
by Lemma 4.45, and thus the lower horizontal isomorphism in (Equation (5.2)) identifies with
![]() $\alpha _C$
. By the crystal property of
$\alpha _C$
. By the crystal property of
, the left vertical injection
identifies with the inclusion
along the morphisms of prism
![]() $\psi _C\colon (A_{\mathrm {inf}},(\xi ))\to (A_{\mathrm {crys}},(p))$
. By Proposition 4.48, there is a canonical isomorphism
$\psi _C\colon (A_{\mathrm {inf}},(\xi ))\to (A_{\mathrm {crys}},(p))$
. By Proposition 4.48, there is a canonical isomorphism
to the dual of the functor constructed by Scholze-Weinstein. By [Reference Scholze and Weinstein51, Theorem 14.4.3],
![]() $M^{\mathrm {SW}}(G)^* \otimes _{A_{\mathrm {inf}}}A_{\mathrm {crys}}\cong \mathbb {D}(G_{\mathcal {O}_C/p})(A_{\mathrm {crys}})$
and, moreover, the diagram
$M^{\mathrm {SW}}(G)^* \otimes _{A_{\mathrm {inf}}}A_{\mathrm {crys}}\cong \mathbb {D}(G_{\mathcal {O}_C/p})(A_{\mathrm {crys}})$
and, moreover, the diagram

commutes by construction of
![]() $\beta $
(cf. Proposition 4.48 and its proof). Hence, it suffices to prove that there exists an isomorphism
$\beta $
(cf. Proposition 4.48 and its proof). Hence, it suffices to prove that there exists an isomorphism
where
![]() $g=\varphi \circ f$
is a morphism of prisms
$g=\varphi \circ f$
is a morphism of prisms
such that the diagram

commutes.
Let T be the dual of the p-adic Tate module
![]() $T_pG$
of G. Then T is a lattice in a crystalline representation of
$T_pG$
of G. Then T is a lattice in a crystalline representation of
![]() $\mathrm {Gal}(\overline {K}/K)$
(where
$\mathrm {Gal}(\overline {K}/K)$
(where
![]() $\overline {K}\subseteq C$
is the algebraic closure of K) and
$\overline {K}\subseteq C$
is the algebraic closure of K) and
![]() $M^{\mathrm {Kis}}(G)\cong M(T)$
, where
$M^{\mathrm {Kis}}(G)\cong M(T)$
, where
![]() $M(-)$
is Kisin’s functor from lattices in crystalline representations to Breuil-Kisin modules. By [Reference Bhatt, Morrow and Scholze11, Proposition 4.34],
$M(-)$
is Kisin’s functor from lattices in crystalline representations to Breuil-Kisin modules. By [Reference Bhatt, Morrow and Scholze11, Proposition 4.34],
![]() $M(T)\otimes _{\mathfrak {S},g}A_{\mathrm {inf}}$
corresponds under Fargues’ equivalence (cf. [Reference Scholze and Weinstein51, Theorem 14.1.1]) to the pair
$M(T)\otimes _{\mathfrak {S},g}A_{\mathrm {inf}}$
corresponds under Fargues’ equivalence (cf. [Reference Scholze and Weinstein51, Theorem 14.1.1]) to the pair
![]() $(T,\Xi )$
, with
$(T,\Xi )$
, with
![]() $\Xi \subseteq T\otimes _{\mathbb {Z}_p} B_{\mathrm {dR}}$
the
$\Xi \subseteq T\otimes _{\mathbb {Z}_p} B_{\mathrm {dR}}$
the
![]() $B^+_{\mathrm {dR}}$
-lattice generated by
$B^+_{\mathrm {dR}}$
-lattice generated by
![]() $D_{\mathrm {dR}}(T_{\mathbb {Q}_p})=(T\otimes _{\mathbb {Z}_p}B_{\mathrm {dR}})^{\mathrm {Gal}(\overline {K}/K)}$
. But this pair is exactly the one associated to
$D_{\mathrm {dR}}(T_{\mathbb {Q}_p})=(T\otimes _{\mathbb {Z}_p}B_{\mathrm {dR}})^{\mathrm {Gal}(\overline {K}/K)}$
. But this pair is exactly the one associated to
![]() $G_{\mathcal {O}_C}$
by Scholze-Weinstein.
$G_{\mathcal {O}_C}$
by Scholze-Weinstein.
Thus, in the end, our discussion implies the following proposition.
Proposition 5.18. The two functors
from p-divisible groups over
![]() $\mathcal {O}_K$
to minuscule Breuil-Kisin modules are naturally isomorphic.
$\mathcal {O}_K$
to minuscule Breuil-Kisin modules are naturally isomorphic.
5.3 Admissible prismatic Dieudonné crystals and displays
The work of Zink provides a classification of connected p-divisible groups over p-adically complete rings (cf. [Reference Zink54]). In this section, we want to relate it to the classification obtained (for quasisyntomic rings) in Theorem 4.90.
Definition 5.19. Let R be a p-complete ring. A display over R is a window (cf. Section 4.1 and [Reference Lau37, Example 5.4]) over the frame
in the topos of sheaves on the p-completely faithfully flat site of R, where F is the Witt vector Frobenius and
![]() $F_1\colon I(\mathcal {O}) \to W(\mathcal {O})$
the inverse of the bijective Verschiebung morphism V.
$F_1\colon I(\mathcal {O}) \to W(\mathcal {O})$
the inverse of the bijective Verschiebung morphism V.
The category of displays over R is denoted by
![]() $\mathrm {Disp}(R)$
.
$\mathrm {Disp}(R)$
.
Remark 5.20. We have phrased the definition of a display in a manner parallel to the definition of a prismatic Dieudonné crystal. In this form, it is, however, unnecessarily abstract. The category of displays satisfies faithfully flat descent (see [Reference Zink54, Theorem 37]). Since displays over a p-complete ring R (with bounded
![]() $p^{\infty }$
-torsion) are equivalent to compatible systems of displays over
$p^{\infty }$
-torsion) are equivalent to compatible systems of displays over
![]() $R/p^n$
for all
$R/p^n$
for all
![]() $n\geq 1$
, we see that displays even satisfy p-completely faithfully flat descent (cf. [Reference Bhatt, Morrow and Scholze12, Corollary 4.8]). Hence, the category of displays over R in the sense of Definition 5.19 is the same as the usual category of displays over R (i.e. windows over the frame
$n\geq 1$
, we see that displays even satisfy p-completely faithfully flat descent (cf. [Reference Bhatt, Morrow and Scholze12, Corollary 4.8]). Hence, the category of displays over R in the sense of Definition 5.19 is the same as the usual category of displays over R (i.e. windows over the frame
![]() $(W(R),I(R),F,F_1)$
).
$(W(R),I(R),F,F_1)$
).
Proposition 5.21. Let R be a quasiregular semiperfectoid ring. Assume that
![]() $pR=0$
or that R is p-torsion free. The natural morphism from Theorem 3.29
$pR=0$
or that R is p-torsion free. The natural morphism from Theorem 3.29
(given by moding out
![]() ) lifts to a u-morphism of frames (in the general sense of Definition 4.16)
) lifts to a u-morphism of frames (in the general sense of Definition 4.16)
where
![]() is the frame associated to
is the frame associated to
![]() and
and
![]() $\tilde {\xi }$
, as in Example 4.18, and
$\tilde {\xi }$
, as in Example 4.18, and
![]() $u \in W(R)$
is a unit, such that
$u \in W(R)$
is a unit, such that
![]() $p=uf(\tilde {\xi })$
.
$p=uf(\tilde {\xi })$
.
Proof. By adjunction (cf. [Reference Joyal26, Theorem 4]), the morphism
![]() gives rise to a morphism of
gives rise to a morphism of
![]() $\delta $
-rings:
$\delta $
-rings:
lifting the morphism to R, that is, sending
![]() to
to
![]() $I(R)$
. In particular,
$I(R)$
. In particular,
![]() $f(\xi ) \in I(R)$
, and thus
$f(\xi ) \in I(R)$
, and thus
and so p divides
![]() $f(\tilde {\xi })$
. By [Reference Bhatt and Scholze13, Lemma 2.24], we deduce that
$f(\tilde {\xi })$
. By [Reference Bhatt and Scholze13, Lemma 2.24], we deduce that
![]() $(p)=(f(\tilde {\xi }))$
, and thus there exists a unit
$(p)=(f(\tilde {\xi }))$
, and thus there exists a unit
![]() $u\in W(R)$
, such that
$u\in W(R)$
, such that
![]() $p=uf(\tilde {\xi })$
. It is then easy to conclude when
$p=uf(\tilde {\xi })$
. It is then easy to conclude when
![]() $W(R)$
is p-torsion free since the commutation (up to a unit) of f with the divided Frobenius can be proved after multiplying by p. In the case where
$W(R)$
is p-torsion free since the commutation (up to a unit) of f with the divided Frobenius can be proved after multiplying by p. In the case where
![]() $pR=0$
, one argues as in [Reference Lau36, Lemma 7.4].
$pR=0$
, one argues as in [Reference Lau36, Lemma 7.4].
It would be nice to prove that for any R quasiregular semiperfectoid, the morphism of the proposition always defines a morphism of frames. Although we did not succeed in doing so, the next proposition shows that one can circumvent this difficulty.
Proposition 5.22. Let R be a quasisyntomic ring. If G is a p-divisible group over R, set
with Frobenius
![]() , and let
, and let
![]() $\mathrm {Fil} ~ Z_R(G)$
be the submodule of
$\mathrm {Fil} ~ Z_R(G)$
be the submodule of
![]() $Z_R(G)$
generated by
$Z_R(G)$
generated by
![]() $I(\mathcal {O}).Z_R(G)$
and the image of
$I(\mathcal {O}).Z_R(G)$
and the image of
![]() . There exists a unique way to extend the functor
. There exists a unique way to extend the functor
to a functor
natural in R which, moreover, coincides (through Proposition 4.29) with the composition of the prismatic Dieudonné functor with the functor induced by the morphism of frames of Proposition 5.21 when R is quasiregular semiperfectoid and
![]() $pR=0$
or R is p-torsion free.
$pR=0$
or R is p-torsion free.
Proof. The requirement of the proposition already says what
must be. Therefore, the only issue is to define the divided Frobenius
![]() $F_{Z_R(G),1}$
.
$F_{Z_R(G),1}$
.
Assume first that R is quasiregular semiperfectoid and p-torsion free. If it exists,
![]() $F_{Z_R(G),1}$
is necessarily unique, since
$F_{Z_R(G),1}$
is necessarily unique, since
![]() $W(R)$
is p-torsion free; thus, we only need to show its existence. For this, we define
$W(R)$
is p-torsion free; thus, we only need to show its existence. For this, we define
![]() $\underline {Z}_R$
as the composition of the prismatic Dieudonné functor with the functor induced by the morphism of frames of Proposition 5.21. By quasisyntomic descent (Remark 5.20), one gets a functor
$\underline {Z}_R$
as the composition of the prismatic Dieudonné functor with the functor induced by the morphism of frames of Proposition 5.21. By quasisyntomic descent (Remark 5.20), one gets a functor
![]() $\underline {Z}_R$
for any p-torsion free quasisyntomic ring R. For such rings R, the functor
$\underline {Z}_R$
for any p-torsion free quasisyntomic ring R. For such rings R, the functor
![]() $\underline {Z}_R$
is necessarily unique by p-torsion freeness of
$\underline {Z}_R$
is necessarily unique by p-torsion freeness of
![]() $W(R)$
. In particular, it commutes with base change in R.
$W(R)$
. In particular, it commutes with base change in R.
To obtain the functor
![]() $\underline {Z}_R$
in general, we use smoothness of the stack of p-divisible groups, following an idea of Lau [Reference Lau34, Proposition 2.1]. Let
$\underline {Z}_R$
in general, we use smoothness of the stack of p-divisible groups, following an idea of Lau [Reference Lau34, Proposition 2.1]. Let
![]() $X=\mathrm {Spec}(A) \to \mathcal {BT} \times \mathrm {Spec}(\mathbb {Z}_p)$
be an ind-smooth presentation of the stack of p-divisible groups as in loc. cit. Then
$X=\mathrm {Spec}(A) \to \mathcal {BT} \times \mathrm {Spec}(\mathbb {Z}_p)$
be an ind-smooth presentation of the stack of p-divisible groups as in loc. cit. Then
![]() $\mathrm {Spec}(B)=X \times _{\mathcal {BT}} X$
is affine. The p-adic completions
$\mathrm {Spec}(B)=X \times _{\mathcal {BT}} X$
is affine. The p-adic completions
![]() $\hat {A}$
and
$\hat {A}$
and
![]() $\hat {B}$
are both p-torsion free (cf. [Reference Lau34, Lemma 1.6]).
$\hat {B}$
are both p-torsion free (cf. [Reference Lau34, Lemma 1.6]).
Let R be a quasisyntomic ring and G be a p-divisible group over R. It gives rise to a map
![]() $\alpha : \mathrm {Spec}(R) \to \mathcal {BT} \times \mathrm {Spec}(\mathbb {Z}_p)$
. Let
$\alpha : \mathrm {Spec}(R) \to \mathcal {BT} \times \mathrm {Spec}(\mathbb {Z}_p)$
. Let
and
Let
![]() $\hat {S}$
and
$\hat {S}$
and
![]() $\hat {T}$
be their p-adic completions. The rings
$\hat {T}$
be their p-adic completions. The rings
![]() $\hat {A}$
and
$\hat {A}$
and
![]() $\hat {B}$
are quasisyntomic. By base change, the rings
$\hat {B}$
are quasisyntomic. By base change, the rings
![]() $\hat {S}$
and
$\hat {S}$
and
![]() $\hat {T}$
are also quasisyntomic. The base change
$\hat {T}$
are also quasisyntomic. The base change
of the triple
![]() $(Z_R(G), \mathrm {Fil} ~ Z_R(G), F_{Z_R(G)})$
along
$(Z_R(G), \mathrm {Fil} ~ Z_R(G), F_{Z_R(G)})$
along
![]() $R \to \hat {S}$
is also the base change of the triple
$R \to \hat {S}$
is also the base change of the triple
along
![]() $\alpha \otimes \hat {A}$
of the universal p-divisible group H over A. The divided Frobenius
$\alpha \otimes \hat {A}$
of the universal p-divisible group H over A. The divided Frobenius
![]() $F_{Z_{\hat {A}}(H_{\hat {A}}),1}$
on
$F_{Z_{\hat {A}}(H_{\hat {A}}),1}$
on
![]() $Z_{\hat {A}}(H_{\hat {A}})$
(coming from the first part of the proof) therefore induces an operator
$Z_{\hat {A}}(H_{\hat {A}})$
(coming from the first part of the proof) therefore induces an operator
![]() $F_{Z_{\hat {S}}(G_{\hat {S}}),1}$
on
$F_{Z_{\hat {S}}(G_{\hat {S}}),1}$
on
![]() $Z_{\hat {S}}(G_{\hat {S}})$
. This operator
$Z_{\hat {S}}(G_{\hat {S}})$
. This operator
![]() $F_{Z_{\hat {S}}(G_{\hat {S}}),1}$
is compatible with the descent datum for the base change along the two natural maps
$F_{Z_{\hat {S}}(G_{\hat {S}}),1}$
is compatible with the descent datum for the base change along the two natural maps
![]() $\hat {S} \to \hat {T}$
, since the functor
$\hat {S} \to \hat {T}$
, since the functor
![]() $Z_{\hat {B}}$
exists and is unique. By descent (Remark 5.20), this defines a display structure
$Z_{\hat {B}}$
exists and is unique. By descent (Remark 5.20), this defines a display structure
![]() $\underline {Z}_R(G)$
on the triple
$\underline {Z}_R(G)$
on the triple
![]() $(Z_R(G), \mathrm {Fil} ~ Z_R(G), F_{Z_R(G)})$
.
$(Z_R(G), \mathrm {Fil} ~ Z_R(G), F_{Z_R(G)})$
.
This display structure is uniquely determined by the requirement that it is compatible with the maps
![]() $R \to \hat {S}$
,
$R \to \hat {S}$
,
![]() $\hat {S} \to \hat {A}$
. In particular, it has to coincide with the composition of the prismatic Dieudonné functor with the functor induced by the morphism of frames of Proposition 5.21 also when R is quasiregular semiperfectoid and killed by p.
$\hat {S} \to \hat {A}$
. In particular, it has to coincide with the composition of the prismatic Dieudonné functor with the functor induced by the morphism of frames of Proposition 5.21 also when R is quasiregular semiperfectoid and killed by p.
The functor of Proposition 5.22 is not an antiequivalence when
![]() $p=2$
. Nevertheless, one has the following positive result, reproving the main result of [Reference Lau32][Reference Zink54] in the special case of quasisyntomic rings.
$p=2$
. Nevertheless, one has the following positive result, reproving the main result of [Reference Lau32][Reference Zink54] in the special case of quasisyntomic rings.
Proposition 5.23. Let R be a quasisyntomic ring, flat over
![]() $\mathbb {Z}/p^n$
(for some
$\mathbb {Z}/p^n$
(for some
![]() $n>0$
) or
$n>0$
) or
![]() $\mathbb {Z}_p$
. The functor
$\mathbb {Z}_p$
. The functor
![]() $\underline {Z}_R$
restricts to an antiequivalence
$\underline {Z}_R$
restricts to an antiequivalence
between the category of formal p-divisible groups over R and the category of F-nilpotent displays over R.
Recall that a display is said to be F-nilpotent if its Frobenius is nilpotent modulo p.
Proof. Assume first that R is quasiregular semiperfect. The functor
![]() $\underline {Z}_R$
is the composite of the prismatic Dieudonné functor, which is an antiequivalence by Theorem 4.74, and of the functor induced by the morphism of frames
$\underline {Z}_R$
is the composite of the prismatic Dieudonné functor, which is an antiequivalence by Theorem 4.74, and of the functor induced by the morphism of frames
The morphism
![]() is surjective (indeed, the composition
is surjective (indeed, the composition
![]() is surjective, since
is surjective, since
![]() $R^{\flat } \to R$
is, and factors through the map
$R^{\flat } \to R$
is, and factors through the map
![]() ). We claim that the divided Frobenius is topologically nilpotent on its kernel. It suffices to show the same for the surjection
). We claim that the divided Frobenius is topologically nilpotent on its kernel. It suffices to show the same for the surjection
![]() $A_{\mathrm {crys}}(R)\to W(R)$
coming from the PD-thickening
$A_{\mathrm {crys}}(R)\to W(R)$
coming from the PD-thickening
![]() $W(R)\to R$
. We recall that
$W(R)\to R$
. We recall that
![]() $A_{\mathrm {crys}}(R)$
is obtained from
$A_{\mathrm {crys}}(R)$
is obtained from
![]() $W(R^{\flat })$
by passing to the PD-envelope for the ideal
$W(R^{\flat })$
by passing to the PD-envelope for the ideal
![]() $\mathrm {ker}{( W(R^{\flat })\to R)}$
. This kernel is (topologically) generated by the elements
$\mathrm {ker}{( W(R^{\flat })\to R)}$
. This kernel is (topologically) generated by the elements
![]() $V^m([x])$
for
$V^m([x])$
for
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $x\in I:=\mathrm {ker}(R^{\flat }\to R)$
. If
$x\in I:=\mathrm {ker}(R^{\flat }\to R)$
. If
![]() $m\geq 1$
, then
$m\geq 1$
, then
![]() $V^m([x])\in W(R^{\flat })$
already has divided powers. As
$V^m([x])\in W(R^{\flat })$
already has divided powers. As
![]() $A_{\mathrm {crys}}(R)$
is p-torsion free (by quasiregularity of R), we can conclude that
$A_{\mathrm {crys}}(R)$
is p-torsion free (by quasiregularity of R), we can conclude that
![]() $A_{\mathrm {crys}}(R)$
is (topologically) generated (as a module over
$A_{\mathrm {crys}}(R)$
is (topologically) generated (as a module over
![]() $W(R^{\flat })$
) by the divided powers
$W(R^{\flat })$
) by the divided powers
![]() $[x]^{(n)}$
of
$[x]^{(n)}$
of
![]() $[x]$
for
$[x]$
for
![]() $x\in I$
(i.e. the divided powers of
$x\in I$
(i.e. the divided powers of
![]() $V^m([x])$
for
$V^m([x])$
for
![]() $m\geq 1$
are not necessary). We note that for
$m\geq 1$
are not necessary). We note that for
![]() $x\in I$
, each divided power
$x\in I$
, each divided power
![]() $[x]^{(n)}\in A_{\mathrm {crys}}(R)$
lies in the kernel of
$[x]^{(n)}\in A_{\mathrm {crys}}(R)$
lies in the kernel of
![]() $A_{\mathrm {crys}}(R)\to W(R)$
because
$A_{\mathrm {crys}}(R)\to W(R)$
because
![]() $[x]\in W(R^{\flat })$
maps to
$[x]\in W(R^{\flat })$
maps to
![]() $0\in W(R)$
. Hence, we can conclude that the kernel of
$0\in W(R)$
. Hence, we can conclude that the kernel of
![]() $A_{\mathrm {crys}}(R)\to W(R)$
is (topologically) generated by
$A_{\mathrm {crys}}(R)\to W(R)$
is (topologically) generated by
![]() $V^m([x]), [x]^{(n)}$
for
$V^m([x]), [x]^{(n)}$
for
![]() $x\in I$
and
$x\in I$
and
![]() $n,m\geq 1$
. Now
$n,m\geq 1$
. Now
![]() $V^m([x])=p^m[x^{1/p^m}]$
and thus
$V^m([x])=p^m[x^{1/p^m}]$
and thus
![]() $\varphi _1^m(V^m([x]))=[x]$
. Hence, it suffices to show that
$\varphi _1^m(V^m([x]))=[x]$
. Hence, it suffices to show that
![]() $\varphi _1$
is topologically nilpotent on the elements
$\varphi _1$
is topologically nilpotent on the elements
![]() $[x]^{(n)}, n\geq 1, x\in I$
. For such an element, one has
$[x]^{(n)}, n\geq 1, x\in I$
. For such an element, one has
Iterating, one sees that
![]() $\varphi _1$
is topologically nilpotent on the kernel (with respect to the p-adic topology). By Remark 4.34, the functor
$\varphi _1$
is topologically nilpotent on the kernel (with respect to the p-adic topology). By Remark 4.34, the functor
is an equivalence. It is easily seen that it restricts to an antiequivalence between formal p-divisible groups and F-nilpotent displays.
By quasisyntomic descent, this yields the statement of the proposition when R is quasisyntomic with
![]() $pR=0$
. In general,
$pR=0$
. In general,
![]() $R/p$
is quasisyntomic ([Reference Bhatt, Morrow and Scholze12, Lemma 4.16 (2)]) and one can consider the following commutative diagram:
$R/p$
is quasisyntomic ([Reference Bhatt, Morrow and Scholze12, Lemma 4.16 (2)]) and one can consider the following commutative diagram:

Grothendieck-Messing theory for F-nilpotent displays (cf. [Reference Zink54, Theorem 48]) coupled with Grothendieck-Messing theory for p-divisible groups (cf. [Reference Messing44, Chapter V (1.6)] and [Reference Zink54, Corollary 97]) show that this diagram is
![]() $2$
-cartesian. Since
$2$
-cartesian. Since
![]() $\underline {Z}_{R/p}$
is an antiequivalence,
$\underline {Z}_{R/p}$
is an antiequivalence,
![]() $\underline {Z}_R$
also is one.
$\underline {Z}_R$
also is one.
5.4 Étale comparison for p-divisible groups
Let R be a quasisyntomic ring, and let G be a p-divisible group over R. In this section, we show how the (dual of the) Tate module of the generic fibre of R, seen as a diamond ([Reference Scholze49, Definition 11.1]), can be recovered from the prismatic Dieudonné crystal
![]() of G.
of G.
Let
be the prismatic sheaf on
![]() $(R)_{\mathrm {qsyn}}$
and
$(R)_{\mathrm {qsyn}}$
and
the natural invertible
![]() $\mathcal {O}^{\mathrm {pris}}$
-module (cf. Definition 4.1). Fix
$\mathcal {O}^{\mathrm {pris}}$
-module (cf. Definition 4.1). Fix
![]() $n\geq 0$
. Note that the Frobenius
$n\geq 0$
. Note that the Frobenius
induces a morphism, again, called Frobenius,
as
![]() $\varphi (\mathcal {I})\subseteq (p,\mathcal {I})$
, although
$\varphi (\mathcal {I})\subseteq (p,\mathcal {I})$
, although
![]() $\mathcal {I}$
is not stable under
$\mathcal {I}$
is not stable under
![]() $\varphi $
.
$\varphi $
.
We let
be the v-site of all maps
![]() $\mathrm {Spf}(S)\to \mathrm {Spf}(R)$
with S a perfectoid ring over R. By definition, the coverings in
$\mathrm {Spf}(S)\to \mathrm {Spf}(R)$
with S a perfectoid ring over R. By definition, the coverings in
![]() $(R)_v$
are v-covers
$(R)_v$
are v-covers
![]() $\mathrm {Spf}(S^{\prime })\to \mathrm {Spf}(S)$
(cf. [Reference Bhatt and Scholze13, Section 8.1]). Let
$\mathrm {Spf}(S^{\prime })\to \mathrm {Spf}(S)$
(cf. [Reference Bhatt and Scholze13, Section 8.1]). Let
be the site of all maps
![]() $\mathrm {Spf}(S)\to \mathrm {Spf}(R)$
with S quasiregular semiperfectoid (covers given by quasisyntomic covers). The perfectoidisation functor
$\mathrm {Spf}(S)\to \mathrm {Spf}(R)$
with S quasiregular semiperfectoid (covers given by quasisyntomic covers). The perfectoidisation functor
from [Reference Bhatt and Scholze13, Definition 8.2] induces a morphism of sites
sending
![]() $\mathrm {Spf}(S)$
to
$\mathrm {Spf}(S)$
to
![]() $\mathrm {Spf}(S_{\mathrm {perfd}})$
. Indeed, by [Reference Bhatt and Scholze13, Proposition 8.10] and the fact that quasisyntomic covers are v-covers, the conditions of [Reference Project52, Tag 00WV] are satisfied. Moreover, we have the ‘inclusion of the generic fiber’
$\mathrm {Spf}(S_{\mathrm {perfd}})$
. Indeed, by [Reference Bhatt and Scholze13, Proposition 8.10] and the fact that quasisyntomic covers are v-covers, the conditions of [Reference Project52, Tag 00WV] are satisfied. Moreover, we have the ‘inclusion of the generic fiber’
induced by sending
![]() $\mathrm {Spf}(S)$
to
$\mathrm {Spf}(S)$
to
![]() $\mathrm {Spa}(S[1/p],S)$
Footnote
41
. Here,
$\mathrm {Spa}(S[1/p],S)$
Footnote
41
. Here,
![]() $\mathrm {Spa}(R[1/p],R)^{\diamond }_v$
is the v-site of the diamond associated with
$\mathrm {Spa}(R[1/p],R)^{\diamond }_v$
is the v-site of the diamond associated with
![]() $\mathrm {Spa}(R[1/p],R)$
(cf. [Reference Scholze49, Section 15.1], [Reference Scholze49, Definition 14.1.iii)]).
$\mathrm {Spa}(R[1/p],R)$
(cf. [Reference Scholze49, Section 15.1], [Reference Scholze49, Definition 14.1.iii)]).
The sites
![]() $(R)_v$
,
$(R)_v$
,
![]() $(\mathrm {Spa}(R[1/p],R))_v$
carry tilted structure sheaves
$(\mathrm {Spa}(R[1/p],R))_v$
carry tilted structure sheaves
![]() $\mathcal {O}^{\flat }_{(R)_v}$
,
$\mathcal {O}^{\flat }_{(R)_v}$
,
![]() $\mathcal {O}^{\flat }$
sending
$\mathcal {O}^{\flat }$
sending
![]() $S\in (R)_v$
to
$S\in (R)_v$
to
![]() $S^{\flat }$
, respectively,
$S^{\flat }$
, respectively,
![]() $\mathrm {Spa}(S,S^+)\in (\mathrm {Spa}(R[1/p],R))_v$
to
$\mathrm {Spa}(S,S^+)\in (\mathrm {Spa}(R[1/p],R))_v$
to
![]() $S^{\flat }$
. We let
$S^{\flat }$
. We let
![]() $W(\mathcal {O}^{\flat }_{(R)_v})$
, respectively,
$W(\mathcal {O}^{\flat }_{(R)_v})$
, respectively,
![]() $W(\mathcal {O}^{\flat })$
be the associated Witt vector sheaves. It is easy to see that for every
$W(\mathcal {O}^{\flat })$
be the associated Witt vector sheaves. It is easy to see that for every
![]() $n\geq 1$
, there are natural morphisms
$n\geq 1$
, there are natural morphisms
![]() $\mathcal {O}^{\mathrm {pris}}/p^n\to \alpha _{\ast }(W_n(\mathcal {O}^{\flat }_{(R)_v}))$
,
$\mathcal {O}^{\mathrm {pris}}/p^n\to \alpha _{\ast }(W_n(\mathcal {O}^{\flat }_{(R)_v}))$
,
![]() $\mathcal {O}^{\mathrm {pris}}/p^n[1/\mathcal {I}]\to (\alpha \circ j)_{\ast }(W_n(\mathcal {O}^{\flat }))$
.
$\mathcal {O}^{\mathrm {pris}}/p^n[1/\mathcal {I}]\to (\alpha \circ j)_{\ast }(W_n(\mathcal {O}^{\flat }))$
.
Lemma 5.24. The above morphisms induce natural isomorphisms
and
of sheaves on
![]() $(R)_{\mathrm {qsyn},\mathrm {qrsp}}$
after passing to
$(R)_{\mathrm {qsyn},\mathrm {qrsp}}$
after passing to
![]() $\varphi $
-fixed points.
$\varphi $
-fixed points.
Here,
![]() $(-)^{\varphi =1}$
denotes the (nonderived) invariants of
$(-)^{\varphi =1}$
denotes the (nonderived) invariants of
![]() $\varphi $
on the sheaf
$\varphi $
on the sheaf
![]() $\mathcal {O}^{\mathrm {pris}}/p^n[1/\mathcal {I}]$
, and we use that
$\mathcal {O}^{\mathrm {pris}}/p^n[1/\mathcal {I}]$
, and we use that
![]() $W_n(\mathcal {O}^{\flat }_{(R)_v})\cong \mathbb {Z}/p^n$
,
$W_n(\mathcal {O}^{\flat }_{(R)_v})\cong \mathbb {Z}/p^n$
,
![]() $W_n(\mathcal {O}^{\flat })\cong \mathbb {Z}/p^n$
, as will be explained in the proof.
$W_n(\mathcal {O}^{\flat })\cong \mathbb {Z}/p^n$
, as will be explained in the proof.
Proof. We only prove the second statement. The first is similar (but easier). Let S be a quasiregular semiperfectoid R-algebra. Then
The first isomorphism follows from commuting Frobenius fixed points with the filtered colimit over
![]() $\mathbb {N}$
along
$\mathbb {N}$
along
![]() $\varphi $
and the second as
$\varphi $
and the second as
![]() $\varinjlim \limits_{\varphi }\mathcal {O}^{\mathrm {pris}}$
is p-torsion free (cf. [Reference Bhatt and Scholze13, Proof of Lemma 2.28]) and S is quasiregular semiperfectoid (which implies that the sheaf
$\varinjlim \limits_{\varphi }\mathcal {O}^{\mathrm {pris}}$
is p-torsion free (cf. [Reference Bhatt and Scholze13, Proof of Lemma 2.28]) and S is quasiregular semiperfectoid (which implies that the sheaf
![]() $\varinjlim \limits_{\varphi }\mathcal {O}^{\mathrm {pris}}$
has no higher cohomology over S). Then [Reference Bhatt and Scholze13, Lemma 9.2] implies that
$\varinjlim \limits_{\varphi }\mathcal {O}^{\mathrm {pris}}$
has no higher cohomology over S). Then [Reference Bhatt and Scholze13, Lemma 9.2] implies that
By [Reference Bhatt and Scholze13, Lemma 9.3], the equivalence of underlying topological spaces under tilting of perfectoid spaces, [Reference Scholze and Weinstein51, Theorem 7.1.1] and [Reference Kedlaya and Liu28, Proposition 3.2.7], the right-hand side becomes
which agrees with
This finishes the proof.
We can derive the following description of the Tate module of the generic fibre.
Proposition 5.25. Let G be a p-divisible group over R with prismatic Dieudonné crystal
![]() , and let
, and let
![]() $n\geq 0$
. Then
$n\geq 0$
. Then
is canonically isomorphic to
![]() $\mathcal {H}om_{\mathbb {Z}/p^n}(G[p^n]_{\eta },\mathbb {Z}/p^n)$
, where
$\mathcal {H}om_{\mathbb {Z}/p^n}(G[p^n]_{\eta },\mathbb {Z}/p^n)$
, where
![]() $G[p^n]_{\eta }$
denotes the sheaf
$G[p^n]_{\eta }$
denotes the sheaf
![]() $\mathrm {Spa}(S[1/p],S)\mapsto G[p^n](S[1/p])$
on
$\mathrm {Spa}(S[1/p],S)\mapsto G[p^n](S[1/p])$
on
![]() $\mathrm {Spa}(R[1/p],R)^{\diamond }_v$
.
$\mathrm {Spa}(R[1/p],R)^{\diamond }_v$
.
Proof. Set
![]() . By Lemma 4.40
. By Lemma 4.40
From the proof of Proposition 4.69, we can conclude that
 $$ \begin{align*} \begin{aligned} \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(T_pG,\mathcal{O}^{\mathrm{pris}})/p^n & \cong \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(T_pG,\mathcal{O}^{\mathrm{pris}}/p^n) \\ & \cong \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(G[p^n],\mathcal{O}^{\mathrm{pris}}/p^n). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(T_pG,\mathcal{O}^{\mathrm{pris}})/p^n & \cong \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(T_pG,\mathcal{O}^{\mathrm{pris}}/p^n) \\ & \cong \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(G[p^n],\mathcal{O}^{\mathrm{pris}}/p^n). \end{aligned} \end{align*} $$
It follows that
as using Section 4.4, the functor
![]() $\mathcal {H}om_{(R)_{\mathrm {qsyn},\mathrm {qrsp}}}(G[p^n],-)$
commutes with filtered colimits. Finally,
$\mathcal {H}om_{(R)_{\mathrm {qsyn},\mathrm {qrsp}}}(G[p^n],-)$
commutes with filtered colimits. Finally,
By Lemma 5.24
and thus
 $$ \begin{align*} \begin{aligned} \mathcal{M}/p^n[1/\mathcal{I}]^{\varphi=1} &\cong \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(G[p^n],(\alpha\circ j)_{\ast}(\mathbb{Z}/p^n)) \\ & \cong (\alpha\circ j)_{\ast}(\mathcal{H}om_{\mathbb{Z}/p^n}((\alpha\circ j)^{\ast} G[p^n],\mathbb{Z}/p^n))). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{M}/p^n[1/\mathcal{I}]^{\varphi=1} &\cong \mathcal{H}om_{(R)_{\mathrm{qsyn},\mathrm{qrsp}}}(G[p^n],(\alpha\circ j)_{\ast}(\mathbb{Z}/p^n)) \\ & \cong (\alpha\circ j)_{\ast}(\mathcal{H}om_{\mathbb{Z}/p^n}((\alpha\circ j)^{\ast} G[p^n],\mathbb{Z}/p^n))). \end{aligned} \end{align*} $$
The definitions of
![]() $\alpha $
and j imply that for any sheaf
$\alpha $
and j imply that for any sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $(R)_{\mathrm {qsyn, qrsp}}$
, the nonsheafified pullback
$(R)_{\mathrm {qsyn, qrsp}}$
, the nonsheafified pullback
![]() $(\alpha \circ j)^{-1}\mathcal {F}$
is the presheaf
$(\alpha \circ j)^{-1}\mathcal {F}$
is the presheaf
![]() $\mathrm {Spa}(S,S^+) \mapsto \mathcal {F}(\mathrm {Spf}(S^+))$
. In particular, we see that
$\mathrm {Spa}(S,S^+) \mapsto \mathcal {F}(\mathrm {Spf}(S^+))$
. In particular, we see that
is naturally isomorphic to the identity. We obtain thus
and can now conclude by Lemma 5.26.
Lemma 5.26. With the notations from Proposition 5.25,
Proof. By right exactness of
![]() $(\alpha \circ j)^{\ast }$
, it suffices to show
$(\alpha \circ j)^{\ast }$
, it suffices to show
Moreover, we may assume that R is perfectoid by passing to slice topoi. Let S be the R-algebra representing
![]() $T_pG$
on p-complete rings. Thus, S is the p-completion of
$T_pG$
on p-complete rings. Thus, S is the p-completion of
![]() $\varinjlim \limits_m S_m$
, where
$\varinjlim \limits_m S_m$
, where
![]() $S_m$
represents
$S_m$
represents
![]() $G[p^m]$
. Then S is quasiregular semiperfectoid. By definition,
$G[p^m]$
. Then S is quasiregular semiperfectoid. By definition,
![]() $(\alpha \circ j)^{\ast }T_pG$
is represented by the perfectoid space
$(\alpha \circ j)^{\ast }T_pG$
is represented by the perfectoid space
over
![]() $\mathrm {Spa}(R[1/p],R)$
, where
$\mathrm {Spa}(R[1/p],R)$
, where
![]() $S_{\mathrm {perfd}}^+$
is the integral closure of
$S_{\mathrm {perfd}}^+$
is the integral closure of
![]() $S_{\mathrm {perfd}}$
in
$S_{\mathrm {perfd}}$
in
![]() $S_{\mathrm {perfd}}[1/p]$
. Let
$S_{\mathrm {perfd}}[1/p]$
. Let
![]() $\mathrm {Spa}(T,T^+)$
be an affinoid perfectoid space over
$\mathrm {Spa}(T,T^+)$
be an affinoid perfectoid space over
![]() $\mathrm {Spa}(R[1/p],R)$
, in particular, we assume that
$\mathrm {Spa}(R[1/p],R)$
, in particular, we assume that
![]() $T^+$
is integrally closed in
$T^+$
is integrally closed in
![]() $T=T^+[1/p]$
. Then any morphism
$T=T^+[1/p]$
. Then any morphism
![]() $S_{\mathrm {perfd}}[1/p]\to T$
sends
$S_{\mathrm {perfd}}[1/p]\to T$
sends
![]() $S_{\mathrm {perfd}}^+\to T^+$
because S is a p-completed direct limit of finite R-algebras and
$S_{\mathrm {perfd}}^+\to T^+$
because S is a p-completed direct limit of finite R-algebras and
![]() $T^+$
is perfectoid and integrally closed in T. Thus
$T^+$
is perfectoid and integrally closed in T. Thus
 $$ \begin{align*} \begin{aligned} \mathrm{Hom}_{(R[1/p],R)}((S_{\mathrm{perfd}}[1/p],S_{\mathrm{perfd}}^+),(T,T^+)) & \cong \mathrm{Hom}_{R}(S_{\mathrm{perfd}}^+,T^+) \\ & \cong \mathrm{Hom}_R(S,T^+) \\ & \cong \mathrm{Hom}_R(\varinjlim\limits_m S_m,T^+) \\ & \cong \mathrm{Hom}_R(\varinjlim\limits_m S_m,T)=T_pG(T), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathrm{Hom}_{(R[1/p],R)}((S_{\mathrm{perfd}}[1/p],S_{\mathrm{perfd}}^+),(T,T^+)) & \cong \mathrm{Hom}_{R}(S_{\mathrm{perfd}}^+,T^+) \\ & \cong \mathrm{Hom}_R(S,T^+) \\ & \cong \mathrm{Hom}_R(\varinjlim\limits_m S_m,T^+) \\ & \cong \mathrm{Hom}_R(\varinjlim\limits_m S_m,T)=T_pG(T), \end{aligned} \end{align*} $$
where
![]() $S_m$
represents
$S_m$
represents
![]() $G[p^m]$
(thus, S is the p-adic completion of
$G[p^m]$
(thus, S is the p-adic completion of
![]() $\varinjlim \limits_m S_m)$
). In the last isomorphism, we used, again, that all
$\varinjlim \limits_m S_m)$
). In the last isomorphism, we used, again, that all
![]() $S_m$
are finite over R and thus any morphism
$S_m$
are finite over R and thus any morphism
![]() $S_m\to T$
of R-algebras factors over
$S_m\to T$
of R-algebras factors over
![]() $T^+$
.
$T^+$
.
A Descent for p-completely faithfully flat morphisms
In this appendix, we want to record some descent statements that are used in the main body of this text.
Lemma A.1. Let R be derived p-complete ring with bounded
![]() $p^{\infty }$
-torsion. Then the natural functor
$p^{\infty }$
-torsion. Then the natural functor
is an equivalence. In particular, the fibred category
![]() $R\mapsto \{\text { finite projective }R-\text {modules}\}$
is a stack for the p-completely faithfully flat topology on the category of derived p-complete rings with bounded
$R\mapsto \{\text { finite projective }R-\text {modules}\}$
is a stack for the p-completely faithfully flat topology on the category of derived p-complete rings with bounded
![]() $p^{\infty }$
-torsion.
$p^{\infty }$
-torsion.
Proof. As R is classically p-complete, the first statement follows from [Reference Project52, Tag 0D4B]. If
![]() $R\to R^{\prime }$
is a p-completely faithfully flat morphism between p-complete rings of bounded
$R\to R^{\prime }$
is a p-completely faithfully flat morphism between p-complete rings of bounded
![]() $p^{\infty }$
-torsion, then
$p^{\infty }$
-torsion, then
![]() $R/p^n\to R^{\prime }/p^n$
is faithfully flat for all
$R/p^n\to R^{\prime }/p^n$
is faithfully flat for all
![]() $n\geq 0$
(flatness follows from [Reference Bhatt, Morrow and Scholze12, Lemma 4.7.(2)] and surjectivity of
$n\geq 0$
(flatness follows from [Reference Bhatt, Morrow and Scholze12, Lemma 4.7.(2)] and surjectivity of
![]() $\mathrm {Spec}(R^{\prime }/p^n)\to \mathrm {Spec}(R/p^n)$
is implied by the case
$\mathrm {Spec}(R^{\prime }/p^n)\to \mathrm {Spec}(R/p^n)$
is implied by the case
![]() $n=1$
). Thus, classical descent of finite projective modules holds for this morphism. Passing to the (
$n=1$
). Thus, classical descent of finite projective modules holds for this morphism. Passing to the (
![]() $(2)$
-)inverse limit implies the last statement.
$(2)$
-)inverse limit implies the last statement.
Proposition A.2. The fibred categories of p-divisible groups and finite locally free group schemes over p-complete rings with bounded
![]() $p^{\infty }$
-torsion are stacks for the p-completely faithfully flat topology.
$p^{\infty }$
-torsion are stacks for the p-completely faithfully flat topology.
Proof. It suffices to show the statement for finite locally free group schemes as p-divisible groups are canonically a colimit of such. From A.1, we know that finite locally free modules form a stack for the p-completely faithfully flat topology on p-complete rings with bounded
![]() $p^{\infty }$
-torsion. As base change commutes with fibre products, this implies that finite locally free group schemes form a stack, too.
$p^{\infty }$
-torsion. As base change commutes with fibre products, this implies that finite locally free group schemes form a stack, too.
Recall that a morphism
of prisms is called faithfully flat if it is
![]() $(p,I)$
-completely flat.
$(p,I)$
-completely flat.
Proposition A.3. The fibred category
on the category of bounded prisms is a stack for the faithfully flat topology.
Proof. If
![]() $(A,I)$
is a prism, then A is classically I-complete, and, thus finite projective A-modules are equivalent to compatible systems of finite projective
$(A,I)$
is a prism, then A is classically I-complete, and, thus finite projective A-modules are equivalent to compatible systems of finite projective
![]() $A/I^n$
-modules, that is,
$A/I^n$
-modules, that is,
(cf. [Reference Project52, Tag 0D4B]). As the
![]() $2$
-limit of stacks is, again, a stack, it suffices to show that for any
$2$
-limit of stacks is, again, a stack, it suffices to show that for any
![]() $n\geq 0$
, the fibred category
$n\geq 0$
, the fibred category
is a stack on bounded prisms. If
![]() $(A,I)\to (B,J)$
is a faithfully flat morphim of prisms, then
$(A,I)\to (B,J)$
is a faithfully flat morphim of prisms, then
is a p-completely faithfully flat morphism of rings with bounded
![]() $p^{\infty }$
-torsion. Thus the proposition follows from A.1.
$p^{\infty }$
-torsion. Thus the proposition follows from A.1.
Example A.4. We give an example of a ring R which is classically
![]() $(p,f)$
-complete, where
$(p,f)$
-complete, where
![]() $f\in R$
is a nonzero divisor, such that
$f\in R$
is a nonzero divisor, such that
![]() $R/f$
has bounded
$R/f$
has bounded
![]() $p^{\infty }$
-torsion, but R has unbounded
$p^{\infty }$
-torsion, but R has unbounded
![]() $p^{\infty }$
-torsion. Set
$p^{\infty }$
-torsion. Set
with J generated by the elements
(where
![]() $x_{i,i+1}:=0$
). Then f is a nonzero divisor in R and all
$x_{i,i+1}:=0$
). Then f is a nonzero divisor in R and all
![]() $p^{\infty }$
-torsion in
$p^{\infty }$
-torsion in
is killed by p. But
while
![]() $p^{i+1}x_{i,0}=f^ipx_{i,i}=0$
. This shows that R has unbounded
$p^{i+1}x_{i,0}=f^ipx_{i,i}=0$
. This shows that R has unbounded
![]() $p^{\infty }$
-torsion. As f is a nonzero divisor in R, the
$p^{\infty }$
-torsion. As f is a nonzero divisor in R, the
![]() $(p,f)^{\infty }$
-torsion in R is zero.
$(p,f)^{\infty }$
-torsion in R is zero.
Acknowledgments
Special thanks go to Bhargav Bhatt who patiently answered our many questions about prismatic cohomology and to Peter Scholze who suggested this project and followed our progress with interest. We particularly thank Bhatt for a discussion regarding Section 3.2. The papers of Eike Lau had a strong influence on this work, and we thank him heartily for very helpful discussions and explanations. We would also like to thank Sebastian Bartling, Dustin Clausen, Laurent Fargues, Yonatan Harpaz, Fabian Hebestreit, Ben Heuer and Andreas Mihatsch for useful discussions on topics related to the content of this paper, as well as K
![]() stutis
stutis
![]() $\breve{\mathrm{C}}$
esnavi
$\breve{\mathrm{C}}$
esnavi
![]() $\breve{\mathrm{c}}$
ius for his comments on a first draft. In the winter term 2019/2020, the ARithmetische Geometrie OberSeminar (ARGOS) seminar in Bonn went through the manuscript, and we are very grateful to the participants for their careful reading and suggestions for improvements or corrections. We heartily thank Kazuhiro Ito for pointing out to us that our first proof of Theorem 5.12 was erroneous and the anonymous referees for spotting many mistakes in earlier versions of this paper and their tremendous report, which hopefully helped to improve and simplify the paper. Last but not least, we would like to deeply thank Akhil Mathew for his interest in our work, for discussing with us our (failed) attempts to rescue our original argument for fully faithfulness and for coming up with an alternative simpler argument.
$\breve{\mathrm{c}}$
ius for his comments on a first draft. In the winter term 2019/2020, the ARithmetische Geometrie OberSeminar (ARGOS) seminar in Bonn went through the manuscript, and we are very grateful to the participants for their careful reading and suggestions for improvements or corrections. We heartily thank Kazuhiro Ito for pointing out to us that our first proof of Theorem 5.12 was erroneous and the anonymous referees for spotting many mistakes in earlier versions of this paper and their tremendous report, which hopefully helped to improve and simplify the paper. Last but not least, we would like to deeply thank Akhil Mathew for his interest in our work, for discussing with us our (failed) attempts to rescue our original argument for fully faithfulness and for coming up with an alternative simpler argument.
The authors would also like to thank the University of Bonn, the Laboratoire Analyse, Géométrie et Applications (LAGA) at Université Sorbonne Paris Nord and the Institut de Mathématiques de Jussieu for their hospitality while this work was done. Moreover, the first author wants to thank Jonathan Schneider for his support during the first author’s academic year in Paris. During part of this research, the first author was supported by European Research Grant ERC 742608, GeoLocLang.
Conflict of Interest
The authors have no conflict of interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.