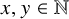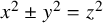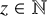1 Introduction and main results
1.1 Introduction
A fundamental problem in Ramsey theory is to determine which patterns must appear in a single cell for every partition of
![]() ${\mathbb N}=\{1,2,\dots \}$
into finitely many cells. A famous example is provided by an early theorem of Schur [Reference Schur44], which states that every finite partition of
${\mathbb N}=\{1,2,\dots \}$
into finitely many cells. A famous example is provided by an early theorem of Schur [Reference Schur44], which states that every finite partition of
![]() ${\mathbb N}$
has a solution to the equation
${\mathbb N}$
has a solution to the equation
![]() $x+y=z$
where all variables
$x+y=z$
where all variables
![]() $x,y,z$
belong to the same cell. Equations (and systems of equations) that satisfy this property are called partition regular.
$x,y,z$
belong to the same cell. Equations (and systems of equations) that satisfy this property are called partition regular.
In 1933, Rado significantly extended Schur’s theorem by characterizing all systems of linear equations that are partition regular [Reference Rado41]. Polynomial equations, however, have proven to be much more difficult to tackle. In particular, the following notorious problem of Erdős and Graham [Reference Graham23, Reference Graham24] remains unsolved.
Problem. Determine whether the equation
![]() $x^2+y^2=z^2$
is partition regular.
$x^2+y^2=z^2$
is partition regular.
Integer solutions to the equation
![]() $x^2+y^2=z^2$
are known as Pythagorean triples, so the problem is colloquially referred to as the partition regularity problem for Pythagorean triples. Graham in [Reference Graham23] places the origin of the problem in the late 70’s and offered $250 for its solution, noting that ‘There is actually very little data (in either direction) to know which way to guess’. While this was perhaps true a decade ago, in the last few years there have been some positive developments. The case where one allows only partitions of
$x^2+y^2=z^2$
are known as Pythagorean triples, so the problem is colloquially referred to as the partition regularity problem for Pythagorean triples. Graham in [Reference Graham23] places the origin of the problem in the late 70’s and offered $250 for its solution, noting that ‘There is actually very little data (in either direction) to know which way to guess’. While this was perhaps true a decade ago, in the last few years there have been some positive developments. The case where one allows only partitions of
![]() ${\mathbb N}$
into two sets was verified in 2016 with the help of a computer search [Reference Heule, Kullmann and Marek31]; this endeavor was hailed as the ‘longest mathematical proof’ at the time, occupying 200 terabytes of data [Reference Lamb36].
${\mathbb N}$
into two sets was verified in 2016 with the help of a computer search [Reference Heule, Kullmann and Marek31]; this endeavor was hailed as the ‘longest mathematical proof’ at the time, occupying 200 terabytes of data [Reference Lamb36].
Pioneering work in nonlinear partition regularity goes back to the famous theorems of Furstenberg [Reference Furstenberg22] and Sárközy [Reference Sárközy42], culminating in the influential polynomial Szemerédi theorem of Bergelson and Leibman [Reference Bergelson and Leibman6]. While these results apply only to shift-invariant configurations, there are now also several non-shift invariant configurations that are known to be or not to be partition regular. Bergelson showed in [Reference Bergelson3] that the equation
![]() $x^2+y=z$
is partition regular, and the equation
$x^2+y=z$
is partition regular, and the equation
![]() $x^2+y=z^2$
was shown to be partition regular by the third author in [Reference Moreira39]. However, the equation
$x^2+y=z^2$
was shown to be partition regular by the third author in [Reference Moreira39]. However, the equation
![]() $x+y=z^2$
was shown not to be partition regular by Csikvári, Gyarmati and Sárközy in [Reference Csikvári, Gyarmati and Sárközy12] (however, it is partition regular if we restrict to 2-colorings [Reference Green and Lindqvist28, Reference Pach40]). Resolving an old conjecture, Khalfalah and Szemerédi [Reference Khalfalah and Szemerédi33] showed that the equation
$x+y=z^2$
was shown not to be partition regular by Csikvári, Gyarmati and Sárközy in [Reference Csikvári, Gyarmati and Sárközy12] (however, it is partition regular if we restrict to 2-colorings [Reference Green and Lindqvist28, Reference Pach40]). Resolving an old conjecture, Khalfalah and Szemerédi [Reference Khalfalah and Szemerédi33] showed that the equation
![]() $x+y=z^2$
is partition regular if we only require
$x+y=z^2$
is partition regular if we only require
![]() $x,y$
to be of the same color and allow any
$x,y$
to be of the same color and allow any
![]() $z\in \mathbb {N}.$
Other partition regularity results of similar flavor can be found in [Reference Alweiss1, Reference Barrett, Lupini and Moreira2, Reference Bergelson, Johnson and Moreira5, Reference Di Nasso and Luperi Baglini14, Reference Di Nasso and Riggio15, Reference Donoso, Le, Moreira and Sun16, Reference Lefmann37]. Lastly, we remark that in the case of more variables, a result by Chow, Lindqvist and Prendiville [Reference Chow, Lindqvist and Prendiville11] establishes that the equation
$z\in \mathbb {N}.$
Other partition regularity results of similar flavor can be found in [Reference Alweiss1, Reference Barrett, Lupini and Moreira2, Reference Bergelson, Johnson and Moreira5, Reference Di Nasso and Luperi Baglini14, Reference Di Nasso and Riggio15, Reference Donoso, Le, Moreira and Sun16, Reference Lefmann37]. Lastly, we remark that in the case of more variables, a result by Chow, Lindqvist and Prendiville [Reference Chow, Lindqvist and Prendiville11] establishes that the equation
![]() $x_1^2+x_2^2+x_3^2+x_4^2=x_5^2$
is partition regular (see also [Reference Browning and Prendiville8, Reference Chapman10] for related results).
$x_1^2+x_2^2+x_3^2+x_4^2=x_5^2$
is partition regular (see also [Reference Browning and Prendiville8, Reference Chapman10] for related results).
Despite these developments, even the question of whether in any finite partition of
![]() ${\mathbb N}$
there is a Pythagorean triple with two terms in the same cell was still open. We will say informally that
${\mathbb N}$
there is a Pythagorean triple with two terms in the same cell was still open. We will say informally that
![]() $(x,y)\in {\mathbb N}^2$
is a Pythagorean pair if there exists
$(x,y)\in {\mathbb N}^2$
is a Pythagorean pair if there exists
![]() $z\in {\mathbb N}$
such that either
$z\in {\mathbb N}$
such that either
An attempt to address the question of whether Pythagorean pairs are partition regular was made by the first author and Host in [Reference Frantzikinakis and Host21], where an approach using Gowers uniformity properties and related decomposition results of multiplicative functions was proposed. This approach covered pairs
![]() $(x,y)$
satisfying, say, the equations
$(x,y)$
satisfying, say, the equations
![]() $16x^2+9y^2=z^2$
or
$16x^2+9y^2=z^2$
or
![]() $x^2+y^2-xy=z^2$
, but missed the case of Pythagorean pairs for reasons that we will explain later on. Extending these ideas, Sun in [Reference Sun45, Reference Sun46] established partition regularity in
$x^2+y^2-xy=z^2$
, but missed the case of Pythagorean pairs for reasons that we will explain later on. Extending these ideas, Sun in [Reference Sun45, Reference Sun46] established partition regularity in
![]() $(x,y)$
for the equation
$(x,y)$
for the equation
![]() $x^2-y^2=z^2$
, when
$x^2-y^2=z^2$
, when
![]() ${\mathbb N}$
is replaced by the ring of integers of a larger number field, such as the Gaussian integers. However, the methods used there do not apply to
${\mathbb N}$
is replaced by the ring of integers of a larger number field, such as the Gaussian integers. However, the methods used there do not apply to
![]() ${\mathbb N}$
.
${\mathbb N}$
.
In the present paper, we develop a general approach to partition regularity questions of pairs, by combining the method of [Reference Frantzikinakis and Host21] together with a new input related to concentration estimates of multiplicative functions. As a consequence, we show (among other things) that Pythagorean pairs (and related pairs) are partition regular (see Theorem 1.1) and density regular (see Theorem 1.2). We also show that partitions generated by level sets of multiplicative functions taking finitely many values always contain Pythagorean triples (see Theorem 1.5). The exact statements are given in the following subsections, and our proof strategy and comparison with the previous approach in [Reference Frantzikinakis and Host21] is described in Section 2.
1.2 Partition and density regularity of Pythagorean pairs
Our first goal is to prove partition regularity and density regularity results for Pythagorean pairs, a case covered by taking
![]() $a=b=c=1$
in the next two results. Our results also answer the first part of Question 3 from [Reference Frantzikinakis and Host21] and Problem 34 from [Reference Frantzikinakis18].
$a=b=c=1$
in the next two results. Our results also answer the first part of Question 3 from [Reference Frantzikinakis and Host21] and Problem 34 from [Reference Frantzikinakis18].
Theorem 1.1. Let
![]() $a,b,c\in {\mathbb N}$
be squares. Then for every finite coloring of
$a,b,c\in {\mathbb N}$
be squares. Then for every finite coloring of
![]() ${\mathbb N}$
, there exist
${\mathbb N}$
, there exist
-
1. distinct
 $x,y\in {\mathbb N}$
with the same color and
$x,y\in {\mathbb N}$
with the same color and
 $z\in {\mathbb N}$
such that
$z\in {\mathbb N}$
such that
 $ax^2+by^2=cz^2$
.
$ax^2+by^2=cz^2$
. -
2. distinct
 $y,z\in {\mathbb N}$
with the same color and
$y,z\in {\mathbb N}$
with the same color and
 $x\in {\mathbb N}$
such that
$x\in {\mathbb N}$
such that
 $ax^2+by^2=cz^2$
.
$ax^2+by^2=cz^2$
.
Remarks.
![]() $\circ $
In [Reference Frantzikinakis and Host21, Corollary 2.8], part (1) was covered under the additional restriction that
$\circ $
In [Reference Frantzikinakis and Host21, Corollary 2.8], part (1) was covered under the additional restriction that
![]() $a+b$
is also a square, thus missing the case of Pythagorean pairs.
$a+b$
is also a square, thus missing the case of Pythagorean pairs.
![]() $\circ $
In fact, Theorem 1.2 implies that all four elements
$\circ $
In fact, Theorem 1.2 implies that all four elements
![]() $x,y$
and
$x,y$
and
![]() $y',z'$
in part (1) and (2), respectively, can be taken to be of the same color.
$y',z'$
in part (1) and (2), respectively, can be taken to be of the same color.
![]() $\circ $
We can also extend [Reference Frantzikinakis and Host21, Theorem 2.7], covering more general homogeneous equations of the form
$\circ $
We can also extend [Reference Frantzikinakis and Host21, Theorem 2.7], covering more general homogeneous equations of the form
![]() $p(x,y,z)=ax^2+by^2+cz^2+dxy+exz+fyz=0$
, where
$p(x,y,z)=ax^2+by^2+cz^2+dxy+exz+fyz=0$
, where
![]() $a,b,c,d,e,f\in {\mathbb Z}$
. Our method allows to show that if
$a,b,c,d,e,f\in {\mathbb Z}$
. Our method allows to show that if
![]() $e^2-4ac$
and
$e^2-4ac$
and
![]() $f^2-4bc$
are nonzero squares, then for every finite coloring of the integers, there exist distinct monochromatic
$f^2-4bc$
are nonzero squares, then for every finite coloring of the integers, there exist distinct monochromatic
![]() $x,y$
and an integer z such that
$x,y$
and an integer z such that
![]() $p(x,y,z)=0$
.Footnote 1 In contrast, [Reference Frantzikinakis and Host21, Theorem 2.7] assumes in addition that
$p(x,y,z)=0$
.Footnote 1 In contrast, [Reference Frantzikinakis and Host21, Theorem 2.7] assumes in addition that
![]() $(e+f)^2 -4c(a+b+d)$
is a nonzero square.
$(e+f)^2 -4c(a+b+d)$
is a nonzero square.
![]() $\circ $
The assumption that
$\circ $
The assumption that
![]() $a,b,c\in {\mathbb N}$
are all squares is not sufficient for partition regularity of the equation
$a,b,c\in {\mathbb N}$
are all squares is not sufficient for partition regularity of the equation
![]() $ax^2+by^2=cz^2$
. For example, the equation
$ax^2+by^2=cz^2$
. For example, the equation
![]() $x^2+y^2=4z^2$
is not partition regular, so in this case, our result is optimal, as only pairs and not triples can be partition regular. See Section 1.6 for more details and conjectural necessary and sufficient conditions for partition regularity of such equations.
$x^2+y^2=4z^2$
is not partition regular, so in this case, our result is optimal, as only pairs and not triples can be partition regular. See Section 1.6 for more details and conjectural necessary and sufficient conditions for partition regularity of such equations.
We establish a stronger density version of these partition regularity results. It is clear that the set of odd numbers, which has additive density
![]() $1/2$
, does not contain integers
$1/2$
, does not contain integers
![]() $x,y$
such that
$x,y$
such that
![]() $x^2+y^2=z^2$
for some
$x^2+y^2=z^2$
for some
![]() $z\in {\mathbb N}$
, ruling out a potential density version using additive density. However, since the equation
$z\in {\mathbb N}$
, ruling out a potential density version using additive density. However, since the equation
![]() $x^2+y^2=z^2$
is homogeneous, the set of solutions is invariant under dilations, and using a dilation-invariant notion of density turns out to be more fruitful.
$x^2+y^2=z^2$
is homogeneous, the set of solutions is invariant under dilations, and using a dilation-invariant notion of density turns out to be more fruitful.
To this end, we recall some standard notions. A multiplicative Følner sequence in
![]() ${\mathbb N}$
is a sequence
${\mathbb N}$
is a sequence
![]() $\Phi =(\Phi _K)_{K=1}^\infty $
of finite subsets of
$\Phi =(\Phi _K)_{K=1}^\infty $
of finite subsets of
![]() ${\mathbb N}$
asymptotically invariant under dilation, in the sense that
${\mathbb N}$
asymptotically invariant under dilation, in the sense that
 $$ \begin{align*}\forall x\in{\mathbb N},\qquad\lim_{K\to\infty}\frac{\big|\Phi_K \cap (x\cdot \Phi_K)\big|}{|\Phi_K|}=1.\end{align*} $$
$$ \begin{align*}\forall x\in{\mathbb N},\qquad\lim_{K\to\infty}\frac{\big|\Phi_K \cap (x\cdot \Phi_K)\big|}{|\Phi_K|}=1.\end{align*} $$
An example of a multiplicative Følner sequence is given by (2.11). The upper multiplicative density of a set
![]() $\Lambda \subset {\mathbb N}$
with respect to a multiplicative Følner sequence
$\Lambda \subset {\mathbb N}$
with respect to a multiplicative Følner sequence
![]() $\Phi =(\Phi _K)_{K=1}^\infty $
is the quantity
$\Phi =(\Phi _K)_{K=1}^\infty $
is the quantity
 $$ \begin{align*}\bar{d}_\Phi(\Lambda):=\limsup_{K\to\infty}\frac{\big|\Phi_K\cap \Lambda\big|}{|\Phi_K|},\end{align*} $$
$$ \begin{align*}\bar{d}_\Phi(\Lambda):=\limsup_{K\to\infty}\frac{\big|\Phi_K\cap \Lambda\big|}{|\Phi_K|},\end{align*} $$
and we write
![]() $d_\Phi (\Lambda )$
if the previous limit exists. We say that
$d_\Phi (\Lambda )$
if the previous limit exists. We say that
![]() $\Lambda \subset {\mathbb N}$
has positive multiplicative density (or, more precisely, positive upper Banach density with respect to multiplication) if
$\Lambda \subset {\mathbb N}$
has positive multiplicative density (or, more precisely, positive upper Banach density with respect to multiplication) if
![]() $\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
$\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
![]() $\Phi $
. A finite coloring of
$\Phi $
. A finite coloring of
![]() ${\mathbb N}$
always contains a monochromatic cell with positive multiplicative density; thus, the next result strengthens Theorem 1.1.
${\mathbb N}$
always contains a monochromatic cell with positive multiplicative density; thus, the next result strengthens Theorem 1.1.
Theorem 1.2. Let
![]() $a,b,c\in {\mathbb N}$
be squares. Then for every
$a,b,c\in {\mathbb N}$
be squares. Then for every
![]() $\Lambda \subset {\mathbb N}$
with positive multiplicative density, there exist
$\Lambda \subset {\mathbb N}$
with positive multiplicative density, there exist
-
1. distinct
 $x,y\in \Lambda $
and
$x,y\in \Lambda $
and
 $z\in {\mathbb N}$
such that
$z\in {\mathbb N}$
such that
 $ax^2+by^2=cz^2$
.
$ax^2+by^2=cz^2$
. -
2. distinct
 $y,z\in \Lambda $
and
$y,z\in \Lambda $
and
 $x\in {\mathbb N}$
such that
$x\in {\mathbb N}$
such that
 $ax^2+by^2=cz^2$
.
$ax^2+by^2=cz^2$
.
Remarks.
![]() $\circ $
In fact, we prove the following stronger property: If
$\circ $
In fact, we prove the following stronger property: If
![]() $\bar {d}_\Phi (\Lambda )>0$
, then there exist a sub-sequence
$\bar {d}_\Phi (\Lambda )>0$
, then there exist a sub-sequence
![]() $\Psi $
of
$\Psi $
of
![]() $\Phi $
and distinct
$\Phi $
and distinct
![]() $x,y\in {\mathbb N}$
such that
$x,y\in {\mathbb N}$
such that
![]() $ax^2+by^2=cz^2$
for some
$ax^2+by^2=cz^2$
for some
![]() $z\in {\mathbb N}$
, and
$z\in {\mathbb N}$
, and
A similar statement also holds with the roles of x and z reversed.
![]() $\circ $
If
$\circ $
If
![]() $a+b\neq c$
, it is not true that every
$a+b\neq c$
, it is not true that every
![]() $\Lambda \subset {\mathbb N}$
with positive multiplicative density contains
$\Lambda \subset {\mathbb N}$
with positive multiplicative density contains
![]() $x,y,z$
such that
$x,y,z$
such that
![]() $ax^2+by^2=cz^2$
. To see this when
$ax^2+by^2=cz^2$
. To see this when
![]() $a=b=c=1$
(the argument is similar whenever
$a=b=c=1$
(the argument is similar whenever
![]() $a+b\neq c$
), let
$a+b\neq c$
), let
![]() $\Phi $
be any multiplicative Følner sequence and
$\Phi $
be any multiplicative Følner sequence and
![]() $\alpha $
be an irrational such that the sequence
$\alpha $
be an irrational such that the sequence
![]() $(n^2\alpha )$
is equidistributed
$(n^2\alpha )$
is equidistributed
![]() $\pmod {1}$
with respect to a subsequence
$\pmod {1}$
with respect to a subsequence
![]() $\Phi '$
of
$\Phi '$
of
![]() $\Phi $
(such an
$\Phi $
(such an
![]() $\alpha $
and
$\alpha $
and
![]() $\Phi '$
exist by the ergodicity of the multiplicative action
$\Phi '$
exist by the ergodicity of the multiplicative action
![]() $T_nx=n^2x$
,
$T_nx=n^2x$
,
![]() $n\in {\mathbb N}$
, defined on
$n\in {\mathbb N}$
, defined on
![]() ${\mathbb T}$
with its Haar measure). Let
${\mathbb T}$
with its Haar measure). Let
![]() $\Lambda :=\{n\in {\mathbb N}\colon \{n^2\alpha \}\in [1/5,2/5)\}$
, which has positive upper density with respect to
$\Lambda :=\{n\in {\mathbb N}\colon \{n^2\alpha \}\in [1/5,2/5)\}$
, which has positive upper density with respect to
![]() $\Phi '$
. If
$\Phi '$
. If
![]() $x,y,z\in \Lambda $
, then
$x,y,z\in \Lambda $
, then
![]() $\{(x^2+y^2)\alpha \}\in [2/5,4/5)$
and
$\{(x^2+y^2)\alpha \}\in [2/5,4/5)$
and
![]() $\{z^2\alpha \}\in [1/5,2/5)$
; hence, we cannot have
$\{z^2\alpha \}\in [1/5,2/5)$
; hence, we cannot have
![]() $x^2+y^2=z^2$
. This example was shown to us by V. Bergelson.
$x^2+y^2=z^2$
. This example was shown to us by V. Bergelson.
We remark that the previous results also resolve the first part of Problem 3 in [Reference Frantzikinakis and Host21] and also Problem 6 in [Reference Frantzikinakis and Host21]. The latter implies that the starting point in Sárközy’s theorem [Reference Sárközy43] (or the variant in [Reference Khalfalah and Szemerédi33] dealing with the equation
![]() $x+y=n^2$
) can be taken to be a square, as the following result shows.
$x+y=n^2$
) can be taken to be a square, as the following result shows.
Corollary 1.3. For every finite coloring of
![]() ${\mathbb N}$
, there exist
${\mathbb N}$
, there exist
-
1. distinct
 $m,n\in {\mathbb N}$
such that the integers
$m,n\in {\mathbb N}$
such that the integers
 $m^2$
and
$m^2$
and
 $m^2+ n^2$
have the same color.
$m^2+ n^2$
have the same color. -
2. distinct
 $m,n\in {\mathbb N}$
such that the integers
$m,n\in {\mathbb N}$
such that the integers
 $m^2$
and
$m^2$
and
 $n^2- m^2$
have the same color.
$n^2- m^2$
have the same color.
To prove part (1), let
![]() $C_1,\ldots , C_k$
be a coloring of
$C_1,\ldots , C_k$
be a coloring of
![]() ${\mathbb N}$
. Using part (2) of Theorem 1.1 for the coloring
${\mathbb N}$
. Using part (2) of Theorem 1.1 for the coloring
![]() $C_i^{\prime }:=\{n\in {\mathbb N}\colon n^2\in C_i\}$
,
$C_i^{\prime }:=\{n\in {\mathbb N}\colon n^2\in C_i\}$
,
![]() $i=1,\ldots , k$
, we deduce that there exist
$i=1,\ldots , k$
, we deduce that there exist
![]() $i_0\in \{1,\ldots , k\}$
and
$i_0\in \{1,\ldots , k\}$
and
![]() $x,z\in C^{\prime }_{i_0}$
such that
$x,z\in C^{\prime }_{i_0}$
such that
![]() $x^2+y^2=z^2$
. Then
$x^2+y^2=z^2$
. Then
![]() $x^2,z^2\in C_{i_0}$
. Letting
$x^2,z^2\in C_{i_0}$
. Letting
![]() $m:=x$
and
$m:=x$
and
![]() $n:=y$
, we get that
$n:=y$
, we get that
![]() $m^2, m^2+n^2\in C_{i_0}$
. The proof of part (2) is similar and uses part (1) of Theorem 1.1.
$m^2, m^2+n^2\in C_{i_0}$
. The proof of part (2) is similar and uses part (1) of Theorem 1.1.
A coloring
![]() $C_1,\ldots , C_k$
of the squares induces a coloring
$C_1,\ldots , C_k$
of the squares induces a coloring
![]() $C^{\prime }_1,\ldots , C^{\prime }_k$
of
$C^{\prime }_1,\ldots , C^{\prime }_k$
of
![]() ${\mathbb N}$
in the natural way:
${\mathbb N}$
in the natural way:
![]() ${C_i^{\prime }:=\{n\in {\mathbb N}\colon n^2\in C_i\}}$
,
${C_i^{\prime }:=\{n\in {\mathbb N}\colon n^2\in C_i\}}$
,
![]() $i=1,\ldots , k$
. Applying Theorem 1.1 for the induced coloring, we deduce the following result.
$i=1,\ldots , k$
. Applying Theorem 1.1 for the induced coloring, we deduce the following result.
Corollary 1.4. For every finite coloring of the squares, there exist
-
1. distinct squares
 $x,y$
with the same color such that
$x,y$
with the same color such that
 $x+y$
is a square.
$x+y$
is a square. -
2. distinct squares
 $x,y$
with the same color such that
$x,y$
with the same color such that
 $x-y$
is a square.
$x-y$
is a square.
1.3 Pythagorean triples on level sets of multiplicative functions
Our second objective is to lend support to the hypothesis that Pythagorean triples are partition regular by proving that the level sets of multiplicative functions that take finitely many values always include Pythagorean triples. Since the equation
![]() $x^2+y^2=z^2$
is homogeneous, one might expect that a presumed counterexample to partition regularity would have ‘multiplicative structure’, so Theorem 1.5 below addresses the most obvious possibilities. We also remark that Rado’s theorem implies that a given linear system of equations is partition regular as soon as it has monochromatic solutions in every coloring realized using a (finitely valued) completely multiplicative function; but of course this result does not apply to the Pythagorean equation.
$x^2+y^2=z^2$
is homogeneous, one might expect that a presumed counterexample to partition regularity would have ‘multiplicative structure’, so Theorem 1.5 below addresses the most obvious possibilities. We also remark that Rado’s theorem implies that a given linear system of equations is partition regular as soon as it has monochromatic solutions in every coloring realized using a (finitely valued) completely multiplicative function; but of course this result does not apply to the Pythagorean equation.
Theorem 1.5. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function that takes finitely many values. Then there exist distinct
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function that takes finitely many values. Then there exist distinct
![]() $x,y,z\in {\mathbb N}$
such that
$x,y,z\in {\mathbb N}$
such that
Remarks.
![]() $\circ $
There is nothing special about the value
$\circ $
There is nothing special about the value
![]() $1$
in Theorem 1.5. If
$1$
in Theorem 1.5. If
![]() $\zeta \in \mathbb {S}^1$
is any other number in the range of f, then since the equation
$\zeta \in \mathbb {S}^1$
is any other number in the range of f, then since the equation
![]() $x^2+y^2=z^2$
is invariant under dilations of the variables
$x^2+y^2=z^2$
is invariant under dilations of the variables
![]() $x,y,z$
, we get that there exist distinct
$x,y,z$
, we get that there exist distinct
![]() $x,y,z\in {\mathbb N}$
, such that
$x,y,z\in {\mathbb N}$
, such that
![]() $\circ $
With a bit more effort, we can extend Theorem 1.5 to cover more general equations of the form
$\circ $
With a bit more effort, we can extend Theorem 1.5 to cover more general equations of the form
where
![]() $a,b,c\in {\mathbb N}$
are squares and we have either
$a,b,c\in {\mathbb N}$
are squares and we have either
![]() $a=c$
, or
$a=c$
, or
![]() $b=c$
, or
$b=c$
, or
![]() $a+b=c$
. We outline the additional steps needed to be taken to prove such a result in Section 8.3. Note that having one of these three identities satisfied is a necessary condition for the partition regularity of (1.1). For more details and related problems, see the discussion in Section 1.6.
$a+b=c$
. We outline the additional steps needed to be taken to prove such a result in Section 8.3. Note that having one of these three identities satisfied is a necessary condition for the partition regularity of (1.1). For more details and related problems, see the discussion in Section 1.6.
Related linear equations
![]() $ax+by=cz$
on the level sets of completely multiplicative functions
$ax+by=cz$
on the level sets of completely multiplicative functions
![]() $f:\mathbb {N}\to \{-1,1\}$
have been studied in the works of Brüdern [Reference Brüdern9] and more recently by de la Bretèche and Granville [Reference de la Bretèche and Granville7]. One consequence of such results [Reference de la Bretèche and Granville7, Corollary 2] is that the number of Pythagorean triples
$f:\mathbb {N}\to \{-1,1\}$
have been studied in the works of Brüdern [Reference Brüdern9] and more recently by de la Bretèche and Granville [Reference de la Bretèche and Granville7]. One consequence of such results [Reference de la Bretèche and Granville7, Corollary 2] is that the number of Pythagorean triples
![]() $(x,y,z)$
modulo any prime
$(x,y,z)$
modulo any prime
![]() $p\ge 3$
; that is, solutions to
$p\ge 3$
; that is, solutions to
![]() $x+y=z$
, where
$x+y=z$
, where
![]() $x,y,z\le N<p$
are quadratic residues, is at least
$x,y,z\le N<p$
are quadratic residues, is at least
![]() $\frac {1}{2}(k'+o_{N\to \infty }(1)) N^2$
, where
$\frac {1}{2}(k'+o_{N\to \infty }(1)) N^2$
, where
![]() $k'=.005044...$
is a sharp constant.
$k'=.005044...$
is a sharp constant.
1.4 Parametric reformulation of the main results
To prove our main results, it is convenient to restate them using solutions of (1.1) in parametric form.
Our assumptions give that
![]() $a=a_0^2$
,
$a=a_0^2$
,
![]() $b=b_0^2$
,
$b=b_0^2$
,
![]() $c=c_0^2$
for some
$c=c_0^2$
for some
![]() $a_0,b_0,c_0\in {\mathbb N}$
. Then a simple computation shows that the following are solutions of
$a_0,b_0,c_0\in {\mathbb N}$
. Then a simple computation shows that the following are solutions of
![]() $ax^2+by^2=cz^2$
:
$ax^2+by^2=cz^2$
:
where
![]() $\ell _1:= a_0bc$
,
$\ell _1:= a_0bc$
,
![]() $\ell _2:= 2ab_0c$
,
$\ell _2:= 2ab_0c$
,
![]() $\ell _3:=abc_0$
.
$\ell _3:=abc_0$
.
So in order to prove Theorem 1.2, it suffices to establish the following result.
Theorem 1.6. Suppose that
![]() $\Lambda \subset {\mathbb N}$
satisfies
$\Lambda \subset {\mathbb N}$
satisfies
![]() $\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
$\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
![]() $\Phi $
. Then for every
$\Phi $
. Then for every
![]() $\ell ,\ell '\in {\mathbb N}$
, there exist
$\ell ,\ell '\in {\mathbb N}$
, there exist
-
1.
 $m,n\in {\mathbb N}$
with
$m,n\in {\mathbb N}$
with
 $m>n$
such that
$m>n$
such that
 $\ell \, (m^2-n^2)$
and
$\ell \, (m^2-n^2)$
and
 $\ell '\, mn$
are distinct and
$\ell '\, mn$
are distinct and  $$ \begin{align*} \bar{d}_\Phi\big((\ell\, (m^2-n^2))^{-1}\Lambda\cap (\ell'\, mn)^{-1}\Lambda\big)>0. \end{align*} $$
$$ \begin{align*} \bar{d}_\Phi\big((\ell\, (m^2-n^2))^{-1}\Lambda\cap (\ell'\, mn)^{-1}\Lambda\big)>0. \end{align*} $$
-
2.
 $m,n\in {\mathbb N}$
such that
$m,n\in {\mathbb N}$
such that
 $\ell \, (m^2+n^2)$
and
$\ell \, (m^2+n^2)$
and
 $\ell '\, mn$
are distinct and
$\ell '\, mn$
are distinct and  $$ \begin{align*} \bar{d}_\Phi\big((\ell\, (m^2+n^2))^{-1}\Lambda\cap (\ell'\, mn)^{-1}\Lambda \big)>0. \end{align*} $$
$$ \begin{align*} \bar{d}_\Phi\big((\ell\, (m^2+n^2))^{-1}\Lambda\cap (\ell'\, mn)^{-1}\Lambda \big)>0. \end{align*} $$
Remark. Since
![]() $2(m^2+n^2)=(m+n)^2+(m-n)^2$
and
$2(m^2+n^2)=(m+n)^2+(m-n)^2$
and
![]() $4mn=(m+n)^2-(m-n)^2$
, applying (2) with
$4mn=(m+n)^2-(m-n)^2$
, applying (2) with
![]() $2\ell $
in place of
$2\ell $
in place of
![]() $\ell $
and
$\ell $
and
![]() $4\ell '$
in place of
$4\ell '$
in place of
![]() $\ell '$
, we can add
$\ell '$
, we can add
-
(iii)
 $m,n\in {\mathbb N}$
such that
$m,n\in {\mathbb N}$
such that
 $\ell \, (m^2+n^2)$
and
$\ell \, (m^2+n^2)$
and
 $\ell '\, (m^2-n^2)$
are distinct and
$\ell '\, (m^2-n^2)$
are distinct and  $$ \begin{align*} \bar{d}_\Phi\big((\ell\, (m^2+n^2))^{-1}\Lambda\cap (\ell'\, (m^2-n^2))^{-1}\Lambda \big)>0. \end{align*} $$
$$ \begin{align*} \bar{d}_\Phi\big((\ell\, (m^2+n^2))^{-1}\Lambda\cap (\ell'\, (m^2-n^2))^{-1}\Lambda \big)>0. \end{align*} $$
In order to prove Theorem 1.5, it suffices to establish the following result.
Theorem 1.7. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function that takes finitely many values. Then there exist
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function that takes finitely many values. Then there exist
![]() $k,m,n\in {\mathbb N}$
, with
$k,m,n\in {\mathbb N}$
, with
![]() $m> n$
, such that the integers
$m> n$
, such that the integers
![]() $m^2-n^2$
,
$m^2-n^2$
,
![]() $2mn$
,
$2mn$
,
![]() $m^2+n^2$
are distinct and
$m^2+n^2$
are distinct and
1.5 Other results
Our methodology is flexible enough to allow us to handle a variety of other dilation-invariant pairs. We record a few cases next.
1.5.1 A question from [Reference Donoso, Le, Moreira and Sun16]
The next result is related to [Reference Donoso, Le, Moreira and Sun16, Question 7.1]. It is only here that we use logarithmic averages
 $$ \begin{align*}\mathbb{E}^{\log}_{m,n\in[N]}:=\frac{1}{(\log{N})^2}\sum_{m,n\in [N]} \frac{1}{mn} \end{align*} $$
$$ \begin{align*}\mathbb{E}^{\log}_{m,n\in[N]}:=\frac{1}{(\log{N})^2}\sum_{m,n\in [N]} \frac{1}{mn} \end{align*} $$
in order to have access to a result from [Reference Tao47].
Theorem 1.8. Suppose that
![]() $\Lambda \subset {\mathbb N}$
satisfies
$\Lambda \subset {\mathbb N}$
satisfies
![]() $\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
$\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
![]() $\Phi $
. Then
$\Phi $
. Then
Remark. Our method also implies the following ergodic version of the previous result, as posed in [Reference Donoso, Le, Moreira and Sun16], using Cesàro instead of logarithmic averages: If
![]() $(T_g)_{g\in {\mathbb N}}$
is a measure-preserving action of
$(T_g)_{g\in {\mathbb N}}$
is a measure-preserving action of
![]() $({\mathbb N},\times )$
on a probability space
$({\mathbb N},\times )$
on a probability space
![]() $(X,\mu )$
and
$(X,\mu )$
and
![]() $A\subset X$
is measurable with
$A\subset X$
is measurable with
![]() $\mu (A)>0$
, then
$\mu (A)>0$
, then
This follows from property (6.16) that we prove below.
Our argument also allows us to replace
![]() $n^2+n$
and
$n^2+n$
and
![]() $m^2$
by
$m^2$
by
![]() $n^2+an$
and
$n^2+an$
and
![]() $m^r$
, respectively, where
$m^r$
, respectively, where
![]() $r\in {\mathbb N}$
and a is a nonzero integer. The proof of Theorem 1.8 follows closely the argument used to prove part (2) of Theorem 2.2. We will outline this argument in Section 6.2.
$r\in {\mathbb N}$
and a is a nonzero integer. The proof of Theorem 1.8 follows closely the argument used to prove part (2) of Theorem 2.2. We will outline this argument in Section 6.2.
1.5.2 General linear forms
We can also prove variants of Theorem 1.6 that cover more general patterns of the form
where
![]() $L_i(m,n)=a_im+b_in$
for some
$L_i(m,n)=a_im+b_in$
for some
![]() $a_i\in {\mathbb N}$
,
$a_i\in {\mathbb N}$
,
![]() $b_i\in {\mathbb Z}$
,
$b_i\in {\mathbb Z}$
,
![]() $i=1,2,3,4$
, and at least one of the forms, say
$i=1,2,3,4$
, and at least one of the forms, say
![]() $L_4(m,n)$
, is not a rational multiple of the others.
$L_4(m,n)$
, is not a rational multiple of the others.
Suppose we want to show, under the previous assumptions, that if
![]() $\Lambda \subset {\mathbb Z}$
satisfies
$\Lambda \subset {\mathbb Z}$
satisfies
![]() $\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
$\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
![]() $\Phi $
, then there exist
$\Phi $
, then there exist
![]() $m,n\in {\mathbb Z}$
such that
$m,n\in {\mathbb Z}$
such that
![]() $L_1(m,n)\cdot L_2(m,n)$
and
$L_1(m,n)\cdot L_2(m,n)$
and
![]() $L_3(m,n)\cdot L_4(m,n)$
are distinct integers and satisfy
$L_3(m,n)\cdot L_4(m,n)$
are distinct integers and satisfy
Without loss of generality, we can assume that
![]() $b_4\neq 0$
. By making the substitution
$b_4\neq 0$
. By making the substitution
![]() $m\mapsto b_4\, m$
and
$m\mapsto b_4\, m$
and
![]() $n\mapsto n-a_4\, m$
(an operation that preserves our assumptions about the forms
$n\mapsto n-a_4\, m$
(an operation that preserves our assumptions about the forms
![]() $L_i$
), we can assume that
$L_i$
), we can assume that
![]() $a_4=0$
. Since the form
$a_4=0$
. Since the form
![]() $L_4$
is not a rational multiple of
$L_4$
is not a rational multiple of
![]() $L_i$
for
$L_i$
for
![]() $i=1,2,3$
, we have
$i=1,2,3$
, we have
![]() $a_i\neq 0$
for
$a_i\neq 0$
for
![]() $i=1,2,3$
. We do another substitution
$i=1,2,3$
. We do another substitution
![]() $n\mapsto a_1\, a_2\, a_3 \, n$
. We then factor out
$n\mapsto a_1\, a_2\, a_3 \, n$
. We then factor out
![]() $a_i$
from the linear form
$a_i$
from the linear form
![]() $L_i$
for
$L_i$
for
![]() $i=1,2,3$
. We see that it is sufficient to consider the case where the
$i=1,2,3$
. We see that it is sufficient to consider the case where the
![]() $L_i$
are integer multiples of forms satisfying
$L_i$
are integer multiples of forms satisfying
![]() $a_1=a_2=a_3=1$
and
$a_1=a_2=a_3=1$
and
![]() $a_4=0$
,
$a_4=0$
,
![]() $b_4\neq 0$
. Making a last substitution
$b_4\neq 0$
. Making a last substitution
![]() $m\mapsto m-b_3 \, n$
, we get that it suffices to prove that
$m\mapsto m-b_3 \, n$
, we get that it suffices to prove that
whenever
![]() $\ell ,\ell '\in {\mathbb N}$
and
$\ell ,\ell '\in {\mathbb N}$
and
![]() $a,b\in {\mathbb Z}$
. This case can be covered by repeating the argument used to prove Theorem 1.6 (which covers the case
$a,b\in {\mathbb Z}$
. This case can be covered by repeating the argument used to prove Theorem 1.6 (which covers the case
![]() $a=1,b=-1$
) without any essential change.
$a=1,b=-1$
) without any essential change.
1.5.3 More general expressions and averages
The methods used to establish part (2) of Theorem 1.6, would also allow to cover patterns of the form
 $$ \begin{align*}\Big(k\, (m^2+n^2)^r\prod_{i=1}^lL_i(m,n),\ k\, \prod_{i=1}^{l'}L_i^{\prime}(m,n)\Big), \end{align*} $$
$$ \begin{align*}\Big(k\, (m^2+n^2)^r\prod_{i=1}^lL_i(m,n),\ k\, \prod_{i=1}^{l'}L_i^{\prime}(m,n)\Big), \end{align*} $$
where
![]() $k\in {\mathbb N}$
,
$k\in {\mathbb N}$
,
![]() $l,l',r\in {\mathbb Z}_+$
are such that
$l,l',r\in {\mathbb Z}_+$
are such that
![]() $|l|+|l'|>0$
,Footnote 2 and at least one of the linear forms
$|l|+|l'|>0$
,Footnote 2 and at least one of the linear forms
![]() $L_i, L_i^{\prime }$
is not a rational multiple of the others. It should also be possible to cover variants of Theorem 2.2 below in which the averages over squares
$L_i, L_i^{\prime }$
is not a rational multiple of the others. It should also be possible to cover variants of Theorem 2.2 below in which the averages over squares
![]() ${\mathbb E}_{m,n\in [N]}$
are replaced by averages over discs (i.e.,
${\mathbb E}_{m,n\in [N]}$
are replaced by averages over discs (i.e.,
![]() ${\mathbb E}_{m^2+n^2\leq N}$
). However, we do not pursue these directions here.
${\mathbb E}_{m^2+n^2\leq N}$
). However, we do not pursue these directions here.
1.6 Further directions
Our approach opens the way for studying several other compelling partition regularity problems that were previously considered intractable. We note here some promising directions.
A result of Rado [Reference Rado41] implies that if
![]() $a,b,c\in {\mathbb N}$
, then the linear equation
$a,b,c\in {\mathbb N}$
, then the linear equation
![]() $ax+by=cz$
is partition regular if and only if either
$ax+by=cz$
is partition regular if and only if either
![]() $a,b,$
or
$a,b,$
or
![]() $a+b$
equals c, in which case we say that the triple
$a+b$
equals c, in which case we say that the triple
![]() $(a,b,c)$
satisfies Rado’s condition. It follows that a necessary condition for the partition regularity of the equation (1.1) is that the triple
$(a,b,c)$
satisfies Rado’s condition. It follows that a necessary condition for the partition regularity of the equation (1.1) is that the triple
![]() $(a,b,c)$
satisfies Rado’s condition. Perhaps this condition is also sufficient, but very little is known in this direction; in fact, there is no triple
$(a,b,c)$
satisfies Rado’s condition. Perhaps this condition is also sufficient, but very little is known in this direction; in fact, there is no triple
![]() $(a,b,c)$
for which the partition regularity of (1.1) is currently known. We state a related problem of intermediate difficulty along the lines of Theorem 1.5.
$(a,b,c)$
for which the partition regularity of (1.1) is currently known. We state a related problem of intermediate difficulty along the lines of Theorem 1.5.
Problem 1. Suppose that the triple
![]() $(a,b,c)$
satisfies Rado’s condition. Then for any completely multiplicative function
$(a,b,c)$
satisfies Rado’s condition. Then for any completely multiplicative function
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
taking finitely many values, there exist distinct
$f\colon {\mathbb N}\to \mathbb {S}^1$
taking finitely many values, there exist distinct
![]() $x,y,z\in {\mathbb N}$
, such that
$x,y,z\in {\mathbb N}$
, such that
Theorem 1.5 solves this problem when
![]() $a=b=c=1$
, and as we mentioned in the second remark following the theorem, a similar argument applies to triples that satisfy Rado’s condition and consist of squares. It would be interesting to solve Problem 1 for some other triples such as
$a=b=c=1$
, and as we mentioned in the second remark following the theorem, a similar argument applies to triples that satisfy Rado’s condition and consist of squares. It would be interesting to solve Problem 1 for some other triples such as
![]() $(1,1,2) $
and
$(1,1,2) $
and
![]() $(1,2,1)$
. The first one corresponds to the equation
$(1,2,1)$
. The first one corresponds to the equation
which was conjectured to be partition regular by Gyarmati and Ruzsa [Reference Gyarmati and Ruzsa29] and has parametric solutions of the form
The second one corresponds to the equation
with parametric solutions of the form
Both parametrizations involve at least two quadratic forms that do not factor into products of linear forms. This is a problem for our method, since a useful variant of Proposition 2.15 is not known in this case, not even if
![]() $f_1,f_2,f_3$
are all equal to the Liouville function.
$f_1,f_2,f_3$
are all equal to the Liouville function.
Another interesting problem is to relax the conditions on the coefficients
![]() $a,b,c$
in Theorem 1.1. We mention two representative problems that seem quite challenging.
$a,b,c$
in Theorem 1.1. We mention two representative problems that seem quite challenging.
Problem 2. Show that for every finite coloring of
![]() ${\mathbb N}$
, there exist
${\mathbb N}$
, there exist
-
1. distinct
 $x,y\in {\mathbb N}$
with the same color and
$x,y\in {\mathbb N}$
with the same color and
 $z\in {\mathbb N}$
such that
$z\in {\mathbb N}$
such that
 $x^2+y^2=2z^2$
.
$x^2+y^2=2z^2$
. -
2. distinct
 $x,y\in {\mathbb N}$
with the same color and
$x,y\in {\mathbb N}$
with the same color and
 $z\in {\mathbb N}$
such that
$z\in {\mathbb N}$
such that
 $x^2+2y^2=z^2$
.
$x^2+2y^2=z^2$
.
Show also similar properties with the roles of the variables y and z or x and z reversed.
Remark. More generally, we believe that if for
![]() $a,b,c\in {\mathbb N}$
at least one of the integers
$a,b,c\in {\mathbb N}$
at least one of the integers
![]() $ac,bc, (a+b)c$
is a square, then for every finite coloring of the integers, there exist distinct
$ac,bc, (a+b)c$
is a square, then for every finite coloring of the integers, there exist distinct
![]() $x,y\in {\mathbb N}$
with the same color and
$x,y\in {\mathbb N}$
with the same color and
![]() $z\in {\mathbb N}$
such that
$z\in {\mathbb N}$
such that
![]() $ax^2+by^2=cz^2$
. Theorem 1.1 verifies this if both
$ax^2+by^2=cz^2$
. Theorem 1.1 verifies this if both
![]() $ac$
and
$ac$
and
![]() $bc$
are squares. We also expect that if at least one of the integers
$bc$
are squares. We also expect that if at least one of the integers
![]() $bc$
,
$bc$
,
![]() $(c-a)b$
is a square, then for every finite coloring of the integers, there exist distinct
$(c-a)b$
is a square, then for every finite coloring of the integers, there exist distinct
![]() $x,z\in {\mathbb N}$
with the same color and
$x,z\in {\mathbb N}$
with the same color and
![]() $y\in {\mathbb N}$
such that
$y\in {\mathbb N}$
such that
![]() $ax^2+by^2=cz^2$
. It may also be that stronger density regularity results hold, as in Theorem 1.2 and Theorem 1.6.
$ax^2+by^2=cz^2$
. It may also be that stronger density regularity results hold, as in Theorem 1.2 and Theorem 1.6.
The broader issue is to find conditions for the polynomials
![]() $P,Q\in {\mathbb Z}[m,n]$
such that the following holds: If
$P,Q\in {\mathbb Z}[m,n]$
such that the following holds: If
![]() $\Lambda \subset {\mathbb N}$
satisfies
$\Lambda \subset {\mathbb N}$
satisfies
![]() $\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
$\bar {d}_\Phi (\Lambda )>0$
for some multiplicative Følner sequence
![]() $\Phi $
, then there exist
$\Phi $
, then there exist
![]() $m,n\in {\mathbb N}$
such that the integers
$m,n\in {\mathbb N}$
such that the integers
![]() $P(m,n)$
and
$P(m,n)$
and
![]() $Q(m,n)$
are positive and distinct, and
$Q(m,n)$
are positive and distinct, and
Equivalently, using the terminology from [Reference Donoso, Le, Moreira and Sun16], the problem is to determine for which polynomials
![]() ${P,Q\in {\mathbb Z}[m,n]}$
we have that
${P,Q\in {\mathbb Z}[m,n]}$
we have that
![]() $\{P(m,n)/Q(m,n)\colon m,n\in {\mathbb N}\}$
is a set measurable multiplicative recurrence.
$\{P(m,n)/Q(m,n)\colon m,n\in {\mathbb N}\}$
is a set measurable multiplicative recurrence.
1.7 Notation
We let
![]() ${\mathbb N}:=\{1,2,\ldots \}$
,
${\mathbb N}:=\{1,2,\ldots \}$
,
![]() ${\mathbb Z}_+:=\{0,1,2,\ldots \}$
,
${\mathbb Z}_+:=\{0,1,2,\ldots \}$
,
![]() ${\mathbb R}_+:=[0,+\infty )$
,
${\mathbb R}_+:=[0,+\infty )$
,
![]() $\mathbb {S}^1$
be the unit circle, and
$\mathbb {S}^1$
be the unit circle, and
![]() ${\mathbb U}$
be the closed complex unit disk. With
${\mathbb U}$
be the closed complex unit disk. With
![]() ${\mathbb P}$
we denote the set of primes, and throughout, we use the letter p to denote primes.
${\mathbb P}$
we denote the set of primes, and throughout, we use the letter p to denote primes.
For
![]() $t\in {\mathbb R}$
, we let
$t\in {\mathbb R}$
, we let
![]() $e(t):=e^{2\pi i t}$
. For
$e(t):=e^{2\pi i t}$
. For
![]() $z\in {\mathbb C}$
, with
$z\in {\mathbb C}$
, with
![]() $\Re (z)$
,
$\Re (z)$
,
![]() $\Im (z)$
, we denote the real and imaginary parts of z, respectively.
$\Im (z)$
, we denote the real and imaginary parts of z, respectively.
For
![]() $N\in {\mathbb N}$
, we let
$N\in {\mathbb N}$
, we let
![]() $[N]:=\{1,\dots ,N\}$
. We often denote sequences
$[N]:=\{1,\dots ,N\}$
. We often denote sequences
![]() $a\colon {\mathbb N}\to {\mathbb U}$
by
$a\colon {\mathbb N}\to {\mathbb U}$
by
![]() $(a(n))$
, instead of
$(a(n))$
, instead of
![]() $(a(n))_{n\in {\mathbb N}}$
.
$(a(n))_{n\in {\mathbb N}}$
.
If A is a finite nonempty subset of the integers and
![]() $a\colon A\to {\mathbb C}$
, we let
$a\colon A\to {\mathbb C}$
, we let
 $$ \begin{align*}{\mathbb E}_{n\in A}\, a(n):=\frac{1}{|A|}\sum_{n\in A}\, a(n). \end{align*} $$
$$ \begin{align*}{\mathbb E}_{n\in A}\, a(n):=\frac{1}{|A|}\sum_{n\in A}\, a(n). \end{align*} $$
We write
![]() $a(n)\ll b(n)$
if for some
$a(n)\ll b(n)$
if for some
![]() $C>0$
, we have
$C>0$
, we have
![]() $a(n)\leq C\, b(n)$
for every
$a(n)\leq C\, b(n)$
for every
![]() $n\in {\mathbb N}$
.
$n\in {\mathbb N}$
.
Throughout this article, the letter f is typically used for multiplicative functions and the letter
![]() $\chi $
for Dirichlet characters.
$\chi $
for Dirichlet characters.
2 Roadmap to the proofs
This section outlines how we prove our main results in their parametric reformulation, which is given in Theorems 1.6 and 1.7.
For various facts and notions concerning multiplicative functions, we refer the reader to Section 3.3.
2.1 Reduction of Theorem 1.6 to a positivity property for multiplicative functions
We first use a version of the Furstenberg correspondence principle (see [Reference Bergelson4]) to reformulate the results in an ergodic language.
Theorem 2.1. Let
![]() $\ell , \ell '\in {\mathbb N}$
, let
$\ell , \ell '\in {\mathbb N}$
, let
![]() $T=(T_n)_{n\in {\mathbb N}}$
be a measure preserving action of
$T=(T_n)_{n\in {\mathbb N}}$
be a measure preserving action of
![]() $({\mathbb N},\times )$
on a probability space
$({\mathbb N},\times )$
on a probability space
![]() $(X,\mu )$
,Footnote 3 and let
$(X,\mu )$
,Footnote 3 and let
![]() $A\subset X$
be measurable with
$A\subset X$
be measurable with
![]() $\mu (A)>0$
. Then there exist
$\mu (A)>0$
. Then there exist
-
1.
 $m,n\in {\mathbb N}$
with
$m,n\in {\mathbb N}$
with
 $m>n$
such that
$m>n$
such that
 $\ell \, (m^2-n^2)$
and
$\ell \, (m^2-n^2)$
and
 $\ell '\, mn$
are distinct and (2.1)
$\ell '\, mn$
are distinct and (2.1) $$ \begin{align} \mu(T_{\ell(m^2-n^2)}^{-1}A\cap T_{\ell' mn}^{-1}A)>0. \end{align} $$
$$ \begin{align} \mu(T_{\ell(m^2-n^2)}^{-1}A\cap T_{\ell' mn}^{-1}A)>0. \end{align} $$
-
2.
 $m,n\in {\mathbb N}$
such that
$m,n\in {\mathbb N}$
such that
 $\ell \, (m^2+n^2)$
and
$\ell \, (m^2+n^2)$
and
 $\ell '\, mn$
are distinct and (2.2)
$\ell '\, mn$
are distinct and (2.2) $$ \begin{align} \mu(T_{ \ell(m^2+n^2)}^{-1}A\cap T_{\ell' mn}^{-1}A)>0. \end{align} $$
$$ \begin{align} \mu(T_{ \ell(m^2+n^2)}^{-1}A\cap T_{\ell' mn}^{-1}A)>0. \end{align} $$
In fact, the set of
![]() $m,n\in {\mathbb N}$
for which (2.1) and (2.2) hold has positive lower density.
$m,n\in {\mathbb N}$
for which (2.1) and (2.2) hold has positive lower density.
Remarks.
![]() $\circ $
The reduction to the previous multiple recurrence statement is merely a convenience. It facilitates the purpose of getting a further reduction to a positivity property for completely multiplicative functions that we describe in Theorem 2.2. Alternatively, one could carry out this last reduction directly, as in [Reference Frantzikinakis and Host21, Section 10.2].
$\circ $
The reduction to the previous multiple recurrence statement is merely a convenience. It facilitates the purpose of getting a further reduction to a positivity property for completely multiplicative functions that we describe in Theorem 2.2. Alternatively, one could carry out this last reduction directly, as in [Reference Frantzikinakis and Host21, Section 10.2].
![]() $\circ $
Using the terminology from [Reference Donoso, Le, Moreira and Sun16], Theorem 2.1 can be rephrased as saying that for every
$\circ $
Using the terminology from [Reference Donoso, Le, Moreira and Sun16], Theorem 2.1 can be rephrased as saying that for every
![]() $\ell ,\ell '\in {\mathbb N}$
, both subsets of
$\ell ,\ell '\in {\mathbb N}$
, both subsets of
![]() ${\mathbb Q}^{>0}$
${\mathbb Q}^{>0}$
are sets of measurable multiplicative recurrence.
A function
![]() $f\colon {\mathbb N}\to {\mathbb U}$
, where
$f\colon {\mathbb N}\to {\mathbb U}$
, where
![]() ${\mathbb U}$
is the complex unit disk, is called multiplicative if
${\mathbb U}$
is the complex unit disk, is called multiplicative if
It is called completely multiplicative if the previous equation holds for all
![]() $m,n\in {\mathbb N}$
. Let
$m,n\in {\mathbb N}$
. Let
Wherever necessary, we extend multiplicative functions to the non-positive integers in an arbitrary way. Throughout, we assume that
![]() ${\mathcal M}$
is equipped with the topology of pointwise convergence. It easily follows that
${\mathcal M}$
is equipped with the topology of pointwise convergence. It easily follows that
![]() ${\mathcal M}$
is a metrizable compact space with this topology. We can identify
${\mathcal M}$
is a metrizable compact space with this topology. We can identify
![]() ${\mathcal M}$
with the Pontryagin dual of the (discrete) group of positive rational numbers under multiplication. Note that the map
${\mathcal M}$
with the Pontryagin dual of the (discrete) group of positive rational numbers under multiplication. Note that the map
![]() $r/s\mapsto \mu ( T_r^{-1}A \cap T_s^{-1}A)$
,
$r/s\mapsto \mu ( T_r^{-1}A \cap T_s^{-1}A)$
,
![]() $r,s,\in {\mathbb N}$
, from
$r,s,\in {\mathbb N}$
, from
![]() $({\mathbb Q}_+,\times )$
to
$({\mathbb Q}_+,\times )$
to
![]() $[0,1]$
is well defined and positive definite. Using a theorem of Bochner-Herglotz, we get that there exists a finite Borel measure
$[0,1]$
is well defined and positive definite. Using a theorem of Bochner-Herglotz, we get that there exists a finite Borel measure
![]() $\sigma $
on
$\sigma $
on
![]() ${\mathcal M}$
such that
${\mathcal M}$
such that
![]() $\sigma (\{1\})>0$
(in fact,
$\sigma (\{1\})>0$
(in fact,
![]() $\sigma (\{1\})\geq \delta ^2$
, where
$\sigma (\{1\})\geq \delta ^2$
, where
![]() $\delta =\mu (A)$
) and for every
$\delta =\mu (A)$
) and for every
![]() $r,s\in {\mathbb N}$
,
$r,s\in {\mathbb N}$
,
In particular, we have
for every
![]() $m,n\in {\mathbb N}$
with
$m,n\in {\mathbb N}$
with
![]() $m>n$
, and
$m>n$
, and
for every
![]() $m,n\in {\mathbb N}$
. Therefore, Theorem 2.1 follows from the following result.
$m,n\in {\mathbb N}$
. Therefore, Theorem 2.1 follows from the following result.
Theorem 2.2. Let
![]() $\sigma $
be a positive bounded measure on
$\sigma $
be a positive bounded measure on
![]() ${\mathcal M}$
such that
${\mathcal M}$
such that
![]() $\sigma (\{1\})>0$
and
$\sigma (\{1\})>0$
and
Then for every
![]() $\ell ,\ell '\in {\mathbb N}$
,
$\ell ,\ell '\in {\mathbb N}$
,
-
1. we have
(2.4) $$ \begin{align} \lim_{N\to\infty} {\mathbb E}_{m,n\in[N], m>n}\int_{{\mathcal M}} f(\ell(m^2-n^2))\cdot \overline{f(\ell'mn)}\, d\sigma(f)>0. \end{align} $$
$$ \begin{align} \lim_{N\to\infty} {\mathbb E}_{m,n\in[N], m>n}\int_{{\mathcal M}} f(\ell(m^2-n^2))\cdot \overline{f(\ell'mn)}\, d\sigma(f)>0. \end{align} $$
-
2. we have
(2.5) $$ \begin{align} \liminf_{N\to\infty} {\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}} f(\ell (m^2+n^2))\cdot \overline{f(\ell'mn)}\, d\sigma(f)>0. \end{align} $$
$$ \begin{align} \liminf_{N\to\infty} {\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}} f(\ell (m^2+n^2))\cdot \overline{f(\ell'mn)}\, d\sigma(f)>0. \end{align} $$
Remark. The limit in (2.4) exists by [Reference Frantzikinakis and Host20, Theorem 1.4] and the bounded convergence theorem.Footnote 4 However, the limit in (2.5) may not always exist.
The reduction up to this point is similar to that in [Reference Frantzikinakis and Host21]. The methods in [Reference Frantzikinakis and Host21] were only able to address a variant of (1) in which the expressions under the integral were products of linear factors and were ‘pairing up’ when
![]() $n=0$
and becoming nonnegative.Footnote 5 This positivity property is not shared by the expressions in (2.4) (and (2.5)), which is the main reason why it was not possible to deal with Pythagorean pairs in [Reference Frantzikinakis and Host21]. To overcome this obstacle, we do not use a decomposition result that covers all elements of
$n=0$
and becoming nonnegative.Footnote 5 This positivity property is not shared by the expressions in (2.4) (and (2.5)), which is the main reason why it was not possible to deal with Pythagorean pairs in [Reference Frantzikinakis and Host21]. To overcome this obstacle, we do not use a decomposition result that covers all elements of
![]() ${\mathcal M}$
simultaneously (as was the case in [Reference Frantzikinakis and Host21]), but rather work separately with aperiodic and pretentious multiplicative functions (these notions are defined in Section 3.3). In particular, coupled with some measurability properties, this allows us to exploit the uniform concentration estimates of Propositions 2.5 and 2.11, which are not shared by all elements of
${\mathcal M}$
simultaneously (as was the case in [Reference Frantzikinakis and Host21]), but rather work separately with aperiodic and pretentious multiplicative functions (these notions are defined in Section 3.3). In particular, coupled with some measurability properties, this allows us to exploit the uniform concentration estimates of Propositions 2.5 and 2.11, which are not shared by all elements of
![]() ${\mathcal M}$
. We outline our approach in the next subsections.
${\mathcal M}$
. We outline our approach in the next subsections.
2.2 Proof plan for part (1) of Theorem 2.2
We prove Theorem 2.2 by taking an average over the grid
where
![]() $Q\in {\mathbb N}$
is chosen depending only on
$Q\in {\mathbb N}$
is chosen depending only on
![]() $\sigma $
. In view of (2.3), it suffices to prove positivity in (2.4) when the average is taken along this subset of pairs. With
$\sigma $
. In view of (2.3), it suffices to prove positivity in (2.4) when the average is taken along this subset of pairs. With
![]() $\ell ,\ell '\in {\mathbb N}$
fixed, we introduce the following notation: for
$\ell ,\ell '\in {\mathbb N}$
fixed, we introduce the following notation: for
![]() $\delta>0$
,
$\delta>0$
,
![]() $f\in {\mathcal M}$
, and
$f\in {\mathcal M}$
, and
![]() $Q,m,n\in {\mathbb N}$
, let
$Q,m,n\in {\mathbb N}$
, let
where
![]() $w_\delta :{\mathbb N}^2\to [0,1]$
is the weight defined in (3.2) of Lemma 3.3 for reasons that will become clear in a moment (at a first reading, the reader could just take
$w_\delta :{\mathbb N}^2\to [0,1]$
is the weight defined in (3.2) of Lemma 3.3 for reasons that will become clear in a moment (at a first reading, the reader could just take
![]() $w_\delta =1$
). We also remark that the weight
$w_\delta =1$
). We also remark that the weight
![]() $w_\delta $
is supported on the set
$w_\delta $
is supported on the set
![]() $\{m,n\in {\mathbb N}\colon m>n\}$
, so to compute
$\{m,n\in {\mathbb N}\colon m>n\}$
, so to compute
![]() $A_\delta (f,Q;m,n)$
, we only have to compute f on positive integers. Then part (1) of Theorem 2.2 follows immediately from the next result, the fact that
$A_\delta (f,Q;m,n)$
, we only have to compute f on positive integers. Then part (1) of Theorem 2.2 follows immediately from the next result, the fact that
![]() $0\leq w_\delta (m,n)\leq 1$
, and the positivity property (2.3).
$0\leq w_\delta (m,n)\leq 1$
, and the positivity property (2.3).
Theorem 2.3. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}$
such that
${\mathcal M}$
such that
![]() $\sigma (\{1\})>0$
. Then there exist
$\sigma (\{1\})>0$
. Then there exist
![]() $\delta _0>0$
and
$\delta _0>0$
and
![]() $Q_0\in {\mathbb N}$
such that
$Q_0\in {\mathbb N}$
such that
Remark. The values of
![]() $\delta _0>0$
and
$\delta _0>0$
and
![]() $Q_0\in {\mathbb N}$
depend on
$Q_0\in {\mathbb N}$
depend on
![]() $\sigma $
but not on
$\sigma $
but not on
![]() $\ell , \ell '$
.
$\ell , \ell '$
.
To analyze the limit in (2.7), we use the theory of completely multiplicative functions. When f is aperiodic, the mean values of
![]() $A_\delta (f,Q;m,n)$
vanish for every Q. This is a consequence of the following result, which in turn follows from results in [Reference Frantzikinakis and Host21] (see also [Reference Matthiesen38] for related work). We shall explain later on how.
$A_\delta (f,Q;m,n)$
vanish for every Q. This is a consequence of the following result, which in turn follows from results in [Reference Frantzikinakis and Host21] (see also [Reference Matthiesen38] for related work). We shall explain later on how.
Proposition 2.4. Let
![]() $f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic completely multiplicative function. Then for every
$f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic completely multiplicative function. Then for every
![]() $\delta>0$
and
$\delta>0$
and
![]() $Q\in {\mathbb N}$
, we have
$Q\in {\mathbb N}$
, we have
Furthermore, for every completely multiplicative function
![]() $f\colon {\mathbb N}\to {\mathbb U}$
, the previous limit exists.
$f\colon {\mathbb N}\to {\mathbb U}$
, the previous limit exists.
Let
we show in Lemma 3.6 that
![]() ${\mathcal M}_p$
is a Borel subset of
${\mathcal M}_p$
is a Borel subset of
![]() ${\mathcal M}$
. It follows from Proposition 2.4 and the bounded convergence theorem that in order to establish (2.7), it suffices to show that there exist
${\mathcal M}$
. It follows from Proposition 2.4 and the bounded convergence theorem that in order to establish (2.7), it suffices to show that there exist
![]() $\delta _0>0$
and
$\delta _0>0$
and
![]() $Q_0\in {\mathbb N}$
such that
$Q_0\in {\mathbb N}$
such that
 $$ \begin{align} \lim_{N\to\infty} {\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} A_{\delta_0}(f,Q_0;m,n)\, d\sigma(f)>0. \end{align} $$
$$ \begin{align} \lim_{N\to\infty} {\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} A_{\delta_0}(f,Q_0;m,n)\, d\sigma(f)>0. \end{align} $$
If f is pretentious, then it ‘pretends’ to be a twisted Dirichlet character, and thus exhibits some periodicity. We exploit this periodicity by choosing a highly divisible Q for which the averages of
![]() $A_\delta (f,Q;m,n)$
take a much simpler form. More precisely, we make use of the following concentration estimate, which is an immediate consequence of [Reference Klurman, Mangerel, Pohoata and Teräväinen35, Lemma 2.5].
$A_\delta (f,Q;m,n)$
take a much simpler form. More precisely, we make use of the following concentration estimate, which is an immediate consequence of [Reference Klurman, Mangerel, Pohoata and Teräväinen35, Lemma 2.5].
Proposition 2.5. Let
![]() $f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function such that
$f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function such that
![]() $f\sim \chi \cdot n^{it}$
for some
$f\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
with period q (see Section 3.3 for definitions and notation). Let also
$\chi $
with period q (see Section 3.3 for definitions and notation). Let also
![]() $K\in {\mathbb N}$
be large enough so that q divides all elements of the set
$K\in {\mathbb N}$
be large enough so that q divides all elements of the set
 $$ \begin{align} \Phi_K :=\Big\{\prod_{p\leq K}p^{a_p}\colon K< a_p\leq 2K\Big\}. \end{align} $$
$$ \begin{align} \Phi_K :=\Big\{\prod_{p\leq K}p^{a_p}\colon K< a_p\leq 2K\Big\}. \end{align} $$
Then
where the implicit constant is absolute and
 $$ \begin{align} F_N(f,K):=\sum_{K< p\leq N} \frac{1}{p}\,\big(f(p)\cdot \overline{\chi(p)}\cdot p^{-it} -1\big). \end{align} $$
$$ \begin{align} F_N(f,K):=\sum_{K< p\leq N} \frac{1}{p}\,\big(f(p)\cdot \overline{\chi(p)}\cdot p^{-it} -1\big). \end{align} $$
Remarks.
![]() $\circ $
It is important for our argument that the implicit constant is independent of K and the quantity
$\circ $
It is important for our argument that the implicit constant is independent of K and the quantity
![]() $F_N(f,K)$
does not depend on Q as long as
$F_N(f,K)$
does not depend on Q as long as
![]() $Q\in \Phi _K$
and
$Q\in \Phi _K$
and
![]() $q\mid Q$
.
$q\mid Q$
.
![]() $\circ $
We will also need the following variant from [Reference Klurman, Mangerel, Pohoata and Teräväinen35, Lemma 2.5]: For any fixed
$\circ $
We will also need the following variant from [Reference Klurman, Mangerel, Pohoata and Teräväinen35, Lemma 2.5]: For any fixed
![]() $Q\in {\mathbb N}$
such that
$Q\in {\mathbb N}$
such that
![]() $q\prod _{p\leq K} p\mid Q$
, we have
$q\prod _{p\leq K} p\mid Q$
, we have
![]() $\circ $
If
$\circ $
If
![]() $f\sim \chi \cdot n^{it}$
, then the sequence
$f\sim \chi \cdot n^{it}$
, then the sequence
![]() $A(N):=\sum _{1< p\leq N} \frac {1}{p}\,\big |1-f(p)\cdot \overline {\chi (p)}\cdot p^{-it}\big |$
,
$A(N):=\sum _{1< p\leq N} \frac {1}{p}\,\big |1-f(p)\cdot \overline {\chi (p)}\cdot p^{-it}\big |$
,
![]() $N\in {\mathbb N}$
, is slowly varying, in the sense that for a fixed pretentious f, we have for every
$N\in {\mathbb N}$
, is slowly varying, in the sense that for a fixed pretentious f, we have for every
![]() $c\in (0,1)$
that
$c\in (0,1)$
that
![]() $\lim _{N\to \infty }\sup _{n\in [N^c,N]}|A(n)-A(N)|=0$
.Footnote 6 Keeping this in mind, if we use partial summation on the interval
$\lim _{N\to \infty }\sup _{n\in [N^c,N]}|A(n)-A(N)|=0$
.Footnote 6 Keeping this in mind, if we use partial summation on the interval
![]() $[N^c,N]$
and then let
$[N^c,N]$
and then let
![]() $c\to 0^+$
, we deduce that the main estimate of Proposition 2.5 still holds if we replace
$c\to 0^+$
, we deduce that the main estimate of Proposition 2.5 still holds if we replace
![]() ${\mathbb E}_{n\in [N]}$
with
${\mathbb E}_{n\in [N]}$
with
![]() $\mathbb {E}^{\log }_{n\in [N]}$
.
$\mathbb {E}^{\log }_{n\in [N]}$
.
In order to establish (2.10), we divide the integral into two parts. The first is supported on multiplicative functions other than the Archimedean characters
![]() $(n^{it})_{n\in {\mathbb N}}$
,
$(n^{it})_{n\in {\mathbb N}}$
,
![]() $t\in {\mathbb R}$
, in which case we show using Proposition 2.5 that for a highly divisible
$t\in {\mathbb R}$
, in which case we show using Proposition 2.5 that for a highly divisible
![]() $Q_0$
, the contribution is essentially nonnegative. The second is supported on Archimedean characters. We show that this part is positive using our assumption
$Q_0$
, the contribution is essentially nonnegative. The second is supported on Archimedean characters. We show that this part is positive using our assumption
![]() $\sigma (\{1\})>0$
and by taking
$\sigma (\{1\})>0$
and by taking
![]() $\delta _0$
small enough so that the weight
$\delta _0$
small enough so that the weight
![]() $w_{\delta _0}$
neutralizes the effect of the Archimedean characters that are different from
$w_{\delta _0}$
neutralizes the effect of the Archimedean characters that are different from
![]() $1$
. To carry out the first part, the key idea is to average over ‘multiplicatively large’ values of Q. More precisely, for each
$1$
. To carry out the first part, the key idea is to average over ‘multiplicatively large’ values of Q. More precisely, for each
![]() $K\in {\mathbb N}$
, let
$K\in {\mathbb N}$
, let
![]() $\Phi _K$
be the set described in (2.11). The sequence
$\Phi _K$
be the set described in (2.11). The sequence
![]() $(\Phi _K)$
is a multiplicative Følner sequence with the property that for every
$(\Phi _K)$
is a multiplicative Følner sequence with the property that for every
![]() $q\in {\mathbb N}$
, as soon as K is large enough, every
$q\in {\mathbb N}$
, as soon as K is large enough, every
![]() $Q\in \Phi _K$
is divisible by q. It also has the property that for every
$Q\in \Phi _K$
is divisible by q. It also has the property that for every
![]() $Q\in \Phi _K$
and a prime
$Q\in \Phi _K$
and a prime
![]() $p\in {\mathbb P}$
, we have
$p\in {\mathbb P}$
, we have
![]() $p|Q$
if and only if
$p|Q$
if and only if
![]() $p\leq K$
. Let also
$p\leq K$
. Let also
Note that
![]() ${\mathcal A}$
is a Borel subset of
${\mathcal A}$
is a Borel subset of
![]() ${\mathcal M}$
since it is a countable union of compact sets (we caution the reader that
${\mathcal M}$
since it is a countable union of compact sets (we caution the reader that
![]() ${\mathcal A}$
is not closed with the topology of pointwise convergence; in fact, it is dense in
${\mathcal A}$
is not closed with the topology of pointwise convergence; in fact, it is dense in
![]() ${\mathcal M}$
). The most important step in establishing property (2.10) is the following fact.
${\mathcal M}$
). The most important step in establishing property (2.10) is the following fact.
Lemma 2.6. Let
![]() $f\in {\mathcal M}_p\setminus {\mathcal A}$
,
$f\in {\mathcal M}_p\setminus {\mathcal A}$
,
![]() $\delta>0$
,
$\delta>0$
,
![]() $\ell ,\ell '\in {\mathbb N}$
, and
$\ell ,\ell '\in {\mathbb N}$
, and
![]() $\Phi _K$
be as in (2.11). Then
$\Phi _K$
be as in (2.11). Then
(Note that the inner limit exists by Proposition 2.4.)
Roughly, to prove Lemma 2.6, we use the concentration estimate of Proposition 2.5 to deduce that for
![]() $Q\in \Phi _K$
, the average
$Q\in \Phi _K$
, the average
![]() ${\mathbb E}_{m,n\in [N]}\, A_\delta (f,Q;m,n)$
is asymptotically equal to
${\mathbb E}_{m,n\in [N]}\, A_\delta (f,Q;m,n)$
is asymptotically equal to
![]() $C_{\ell ,\ell '}(K)\cdot \overline {f(Q)}\cdot Q^{it}$
for some
$C_{\ell ,\ell '}(K)\cdot \overline {f(Q)}\cdot Q^{it}$
for some
![]() $C_{\ell ,\ell '}(K)\in {\mathbb U}$
and
$C_{\ell ,\ell '}(K)\in {\mathbb U}$
and
![]() $t\in {\mathbb R}$
. Since
$t\in {\mathbb R}$
. Since
![]() $f\not \in {\mathcal A}$
, by Lemma 3.2, the average of the last expression, taken over
$f\not \in {\mathcal A}$
, by Lemma 3.2, the average of the last expression, taken over
![]() $Q\in \Phi _K$
, converges to
$Q\in \Phi _K$
, converges to
![]() $0$
as
$0$
as
![]() $K\to \infty $
.
$K\to \infty $
.
Using the previous result, the fact that the limit
![]() $\lim _{N\to \infty }{\mathbb E}_{m,n\in [N]}\, A_\delta (f,Q;m,n)$
exists (by Proposition 2.4), and applying the bounded convergence theorem twice, we deduce the following vanishing property.
$\lim _{N\to \infty }{\mathbb E}_{m,n\in [N]}\, A_\delta (f,Q;m,n)$
exists (by Proposition 2.4), and applying the bounded convergence theorem twice, we deduce the following vanishing property.
Corollary 2.7. Let
![]() $(\Phi _K)$
and
$(\Phi _K)$
and
![]() ${\mathcal A}$
be defined by (2.11) and (2.13), respectively. Let also
${\mathcal A}$
be defined by (2.11) and (2.13), respectively. Let also
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
. Then for every
${\mathcal M}_p$
. Then for every
![]() $\delta>0$
, we have
$\delta>0$
, we have
 $$ \begin{align*} \lim_{K\to\infty}{\mathbb E}_{Q\in\Phi_K}\lim_{N\to\infty}{\mathbb E}_{m,n\in[N]}\,\int_{{\mathcal M}_p\setminus{\mathcal A}} A_\delta(f,Q;m,n)\, d\sigma(f)=0. \end{align*} $$
$$ \begin{align*} \lim_{K\to\infty}{\mathbb E}_{Q\in\Phi_K}\lim_{N\to\infty}{\mathbb E}_{m,n\in[N]}\,\int_{{\mathcal M}_p\setminus{\mathcal A}} A_\delta(f,Q;m,n)\, d\sigma(f)=0. \end{align*} $$
We are left to study the part of the integral supported on
![]() ${\mathcal A}$
. For such functions, the limits
${\mathcal A}$
. For such functions, the limits
![]() $\lim _{N\to \infty }{\mathbb E}_{m,n\in [N]}A_\delta (f,Q;m,n)$
do not depend on Q, and so the previous argument will not help. It is the presence of the weight
$\lim _{N\to \infty }{\mathbb E}_{m,n\in [N]}A_\delta (f,Q;m,n)$
do not depend on Q, and so the previous argument will not help. It is the presence of the weight
![]() $w_\delta $
that will allow us to prove the following positivity property.
$w_\delta $
that will allow us to prove the following positivity property.
Lemma 2.8. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}$
such that
${\mathcal M}$
such that
![]() $\sigma (\{1\})>0$
and
$\sigma (\{1\})>0$
and
![]() ${\mathcal A}$
be as in (2.13). Then there exist
${\mathcal A}$
be as in (2.13). Then there exist
![]() $\delta _0,\rho _0>0$
, depending only on
$\delta _0,\rho _0>0$
, depending only on
![]() $\sigma $
, such that
$\sigma $
, such that
Remark. The weight
![]() $w_\delta (m,n)$
is introduced to force positivity in this case, since for some choices of
$w_\delta (m,n)$
is introduced to force positivity in this case, since for some choices of
![]() $\ell , \ell '$
and measures
$\ell , \ell '$
and measures
![]() $\sigma $
, the unweighted expressions have negative real parts. However, rather miraculously, if
$\sigma $
, the unweighted expressions have negative real parts. However, rather miraculously, if
![]() $\ell =1$
and
$\ell =1$
and
![]() $\ell '=2$
(which is the case to consider for Pythagorean pairs), we get positivity even in the unweighted case, and a somewhat simpler argument applies. We do not pursue this approach here though because it lacks generality.
$\ell '=2$
(which is the case to consider for Pythagorean pairs), we get positivity even in the unweighted case, and a somewhat simpler argument applies. We do not pursue this approach here though because it lacks generality.
Finally, we will see how the previous results allow us to reach our goal, which is to prove Theorem 2.3, thus completing the proof of part (1) of Theorems 1.2 and 2.2.
Proof of Theorem 2.3 assuming Proposition 2.4, Corollary 2.7 and Lemma 2.8
By combining Corollary 2.7 and Lemma 2.8, we deduce that there exist
![]() $\delta _0, \rho _0>0$
, depending only on
$\delta _0, \rho _0>0$
, depending only on
![]() $\sigma $
, such that
$\sigma $
, such that
 $$ \begin{align*} \liminf_{K\to\infty}{\mathbb E}_{Q\in\Phi_K} \lim_{N\to\infty} {\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} A_{\delta_0}(f,Q;m,n)\, d\sigma(f)\geq \rho_0. \end{align*} $$
$$ \begin{align*} \liminf_{K\to\infty}{\mathbb E}_{Q\in\Phi_K} \lim_{N\to\infty} {\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} A_{\delta_0}(f,Q;m,n)\, d\sigma(f)\geq \rho_0. \end{align*} $$
(There is no need to take the real part on this expression since it is real.) From this, we immediately deduce that (2.10) holds for some
![]() $Q_0\in {\mathbb N}$
. As we also explained before, this fact, together with Proposition 2.4, implies (2.7) via the bounded convergence theorem, completing the proof.
$Q_0\in {\mathbb N}$
. As we also explained before, this fact, together with Proposition 2.4, implies (2.7) via the bounded convergence theorem, completing the proof.
To establish Theorem 2.3, it remains to prove Proposition 2.4, Lemma 2.6 (Corollary 2.7 is an immediate consequence) and Lemma 2.8. We do this in Section 4.
2.3 Proof plan for part (2) of Theorem 2.2
The general strategy is similar to that used to prove part (1) of Theorem 2.2, but there are two major differences. The first is the required concentration estimate, which is given in Proposition 2.11 below. Unlike Proposition 2.5, this result is new and of independent interest, and its proof occupies a considerable portion of the argument. The second difference is that the limit in (2.5) may not exist, which causes additional technical problems.
Arguing as before, we get that part (2) of Theorem 2.2 follows from the following positivity property.
Theorem 2.9. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}$
such that
${\mathcal M}$
such that
![]() $\sigma (\{1\})>0$
and (2.3) holds. Then there exists
$\sigma (\{1\})>0$
and (2.3) holds. Then there exists
![]() $\delta>0$
such that
$\delta>0$
such that
where
![]() $\tilde {w}_\delta (m,n)$
is the weight defined in (3.3) of Lemma 3.3.
$\tilde {w}_\delta (m,n)$
is the weight defined in (3.3) of Lemma 3.3.
Again, to analyze the limit in (2.15), we use the theory of completely multiplicative functions. We introduce the following notation: for
![]() $\delta>0$
,
$\delta>0$
,
![]() $f\in {\mathcal M}$
, and
$f\in {\mathcal M}$
, and
![]() $Q,m,n\in {\mathbb N}$
, let
$Q,m,n\in {\mathbb N}$
, let
If f is aperiodic, we have the following result, which we will deduce from the results in [Reference Frantzikinakis and Host21].
Proposition 2.10. Let
![]() $f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic multiplicative function. Then for every
$f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic multiplicative function. Then for every
![]() $\delta>0$
and
$\delta>0$
and
![]() $Q\in {\mathbb N}$
, we have
$Q\in {\mathbb N}$
, we have
Remark. It follows that (2.17) also holds even if Q depends on N, but its values are taken from a finite subset of
![]() ${\mathbb N}$
.
${\mathbb N}$
.
If f is pretentious, we will crucially use the following concentration estimate (which is a direct consequence of a more general result proved in Section 5) to analyze the average (2.15). It features a version of the pretentious distance that only considers primesFootnote 7 congruent to
![]() $1$
mod
$1$
mod
![]() $4$
:
$4$
:
 $$ \begin{align*} {\mathbb D}_1(f,\chi\cdot n^{it}; K,\infty)^2:= \sum_{\substack{K< p, \\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p}\, (1-\Re(f(p)\cdot \overline{\chi(p)} \cdot p^{-it})). \end{align*} $$
$$ \begin{align*} {\mathbb D}_1(f,\chi\cdot n^{it}; K,\infty)^2:= \sum_{\substack{K< p, \\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p}\, (1-\Re(f(p)\cdot \overline{\chi(p)} \cdot p^{-it})). \end{align*} $$
Proposition 2.11. Let
![]() $f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function such that
$f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function such that
![]() $f\sim \chi \cdot n^{it}$
for some
$f\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
with period q. Let also
$\chi $
with period q. Let also
![]() $\Phi _K$
be as in (2.11) and suppose that K is large enough so that, say,
$\Phi _K$
be as in (2.11) and suppose that K is large enough so that, say,
![]() ${\mathbb D}_1(f,\chi \cdot n^{it}; K,\infty )\leq 1$
and q divides all elements of
${\mathbb D}_1(f,\chi \cdot n^{it}; K,\infty )\leq 1$
and q divides all elements of
![]() $\Phi _K$
. Then
$\Phi _K$
. Then
 $$ \begin{align*} \limsup_{N\to\infty} \max_{Q\in \Phi_K} {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+1)^2+(Qn)^2\big)- Q^{2it} \cdot (m^2+n^2)^{it}&\cdot \exp\big(G_N(f,K)\big)\big|\ll \\ & {\mathbb D}_1(f,\chi\cdot n^{it}; K,\infty)+K^{-1/2}, \end{align*} $$
$$ \begin{align*} \limsup_{N\to\infty} \max_{Q\in \Phi_K} {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+1)^2+(Qn)^2\big)- Q^{2it} \cdot (m^2+n^2)^{it}&\cdot \exp\big(G_N(f,K)\big)\big|\ll \\ & {\mathbb D}_1(f,\chi\cdot n^{it}; K,\infty)+K^{-1/2}, \end{align*} $$
where the implicit constant is absolute and
 $$ \begin{align} G_N(f,K):=2\sum_{\substack{ K< p\leq N,\\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(f(p)\cdot \overline{\chi(p)}\cdot p^{-it} -1). \end{align} $$
$$ \begin{align} G_N(f,K):=2\sum_{\substack{ K< p\leq N,\\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(f(p)\cdot \overline{\chi(p)}\cdot p^{-it} -1). \end{align} $$
Remarks.
![]() $\circ $
It is important for our argument that the implicit constant does not depend on K and that
$\circ $
It is important for our argument that the implicit constant does not depend on K and that
![]() $\exp \big (G_N(f,K)\big )$
is the same for all
$\exp \big (G_N(f,K)\big )$
is the same for all
![]() $Q\in \Phi _K$
that are divisible by q. It is also important for our applications that we get some uniformity over the
$Q\in \Phi _K$
that are divisible by q. It is also important for our applications that we get some uniformity over the
![]() $Q\in \Phi _K$
.
$Q\in \Phi _K$
.
![]() $\circ $
For the future applications in mind, we prove a somewhat more general and quantitatively more explicit variant; see Proposition 5.1 below.
$\circ $
For the future applications in mind, we prove a somewhat more general and quantitatively more explicit variant; see Proposition 5.1 below.
As in the proof of Theorem 2.3, in order to prove Theorem 2.9, we split the integral into two parts, one that is supported on Archimedean characters and the other on its complement. To handle the second part, we use the following result, which is proved using Proposition 2.11 and can be compared to Corollary 2.7. Again, taking multiplicative averages over the variable Q is a key maneuver, but the non-convergence of the averages
![]() ${\mathbb E}_{m,n\in [N]} \, B_\delta (f,Q;m,n)$
causes considerable technical difficulties in our proofs.
${\mathbb E}_{m,n\in [N]} \, B_\delta (f,Q;m,n)$
causes considerable technical difficulties in our proofs.
Proposition 2.12. Let
![]() $(\Phi _K)$
,
$(\Phi _K)$
,
![]() ${\mathcal A}$
,
${\mathcal A}$
,
![]() $B_{\delta }(f,Q; m,n)$
be defined by (2.11), (2.13), (2.16), respectively, and
$B_{\delta }(f,Q; m,n)$
be defined by (2.11), (2.13), (2.16), respectively, and
![]() $\delta{>}0 $
. Let also
$\delta{>}0 $
. Let also
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
. Then
${\mathcal M}_p$
. Then
 $$ \begin{align*} \lim_{K\to\infty} \limsup_{N\to \infty}\Big|{\mathbb E}_{Q\in \Phi_{K}}\, {\mathbb E}_{m,n\in[N]} \int_{{\mathcal M}_p \setminus {\mathcal A}} \, B_{\delta}(f,Q; m,n)\, d\sigma(f)\Big|=0. \end{align*} $$
$$ \begin{align*} \lim_{K\to\infty} \limsup_{N\to \infty}\Big|{\mathbb E}_{Q\in \Phi_{K}}\, {\mathbb E}_{m,n\in[N]} \int_{{\mathcal M}_p \setminus {\mathcal A}} \, B_{\delta}(f,Q; m,n)\, d\sigma(f)\Big|=0. \end{align*} $$
Remark. Unlike the case of Corollary 2.7, we cannot pass the limit over N inside the average over Q. This will cause some minor problems in our later analysis, which we will overcome by using the positivity property (2.3) of the measure
![]() $\sigma $
(this is why this positivity property is used in the statement of Theorem 2.9 but not in Theorem 2.3).
$\sigma $
(this is why this positivity property is used in the statement of Theorem 2.9 but not in Theorem 2.3).
We are left to study the contribution of the set
![]() ${\mathcal A}$
of Archimedean characters in which case the presence of the weight
${\mathcal A}$
of Archimedean characters in which case the presence of the weight
![]() $\tilde {w}_\delta $
allows us to establish positivity by taking
$\tilde {w}_\delta $
allows us to establish positivity by taking
![]() $\delta $
small enough.
$\delta $
small enough.
Lemma 2.13. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
such that
${\mathcal M}_p$
such that
![]() $\sigma (\{1\})>0$
and
$\sigma (\{1\})>0$
and
![]() ${\mathcal A}$
be as in (2.13). Then there exist
${\mathcal A}$
be as in (2.13). Then there exist
![]() $\delta _0,\rho _0>0$
, depending only on
$\delta _0,\rho _0>0$
, depending only on
![]() $\sigma $
, such that
$\sigma $
, such that
We conclude this section by noting how the previous results allow us to reach our goal, which is to prove Theorem 2.9, thus completing the proof of part (2) of Theorems 1.2 and 2.2.
Proof of Theorem 2.9 assuming Proposition 2.10, Proposition 2.12 and Lemma 2.13
We start by combining Proposition 2.12 and Lemma 2.13. We deduce that there exist
![]() $\delta _0, \rho _0>0$
, depending only on
$\delta _0, \rho _0>0$
, depending only on
![]() $\sigma $
, such that
$\sigma $
, such that
 $$ \begin{align*} \liminf_{K\to\infty} \liminf_{N\to\infty} {\mathbb E}_{Q\in\Phi_K} \Re\Big({\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} B_{\delta_0}(f,Q;m,n)\, d\sigma(f)\Big)\geq \rho_0. \end{align*} $$
$$ \begin{align*} \liminf_{K\to\infty} \liminf_{N\to\infty} {\mathbb E}_{Q\in\Phi_K} \Re\Big({\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} B_{\delta_0}(f,Q;m,n)\, d\sigma(f)\Big)\geq \rho_0. \end{align*} $$
In this case, it is a little bit tricky to deduce that (2.15) holds. We do it as follows. The last estimate implies that there exist
![]() $K_0\in {\mathbb N}$
and
$K_0\in {\mathbb N}$
and
![]() $Q_N\in \Phi _{K_0}$
,
$Q_N\in \Phi _{K_0}$
,
![]() $N\in {\mathbb N}$
, such that
$N\in {\mathbb N}$
, such that
 $$ \begin{align*} \liminf_{N\to\infty} \Re\Big({\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} B_{\delta_0}(f,Q_N;m,n)\, d\sigma(f)\Big)\geq \rho_0/2. \end{align*} $$
$$ \begin{align*} \liminf_{N\to\infty} \Re\Big({\mathbb E}_{m,n\in[N]}\int_{{\mathcal M}_p} B_{\delta_0}(f,Q_N;m,n)\, d\sigma(f)\Big)\geq \rho_0/2. \end{align*} $$
Note that since
![]() $Q_N$
belongs to a finite set, Proposition 2.10 implies that in the last expression we can replace
$Q_N$
belongs to a finite set, Proposition 2.10 implies that in the last expression we can replace
![]() ${\mathcal M}_p$
with
${\mathcal M}_p$
with
![]() ${\mathcal M}$
. Hence,
${\mathcal M}$
. Hence,
(The real part is no longer needed since the last expression is known to be real by (2.3).) It is easy to verify (following the line of reasoning at the beginning of Proposition 4.1 below) that
We deduce that if in the definition of
![]() $B_{\delta _0}(f,Q_N;m,n)$
given in (2.16) we replace
$B_{\delta _0}(f,Q_N;m,n)$
given in (2.16) we replace
![]() $\tilde {w}_\delta (m,n)$
with
$\tilde {w}_\delta (m,n)$
with
![]() $\tilde {w}_\delta (Q_Nm+1,Q_Nn)$
, the limit on the left side of (2.19) remains unchanged. Keeping this in mind, and since
$\tilde {w}_\delta (Q_Nm+1,Q_Nn)$
, the limit on the left side of (2.19) remains unchanged. Keeping this in mind, and since
![]() $Q_N$
takes values in a finite set with upper bound, say
$Q_N$
takes values in a finite set with upper bound, say
![]() $Q_0$
, and by the positivity property (2.3), we have
$Q_0$
, and by the positivity property (2.3), we have
for every
![]() $m,n\in {\mathbb N}$
, and we deduce that
$m,n\in {\mathbb N}$
, and we deduce that
This establishes (2.15) and ends the proof.
In order to establish Theorem 2.9, it remains to prove Proposition 2.10, Proposition 2.12 and Lemma 2.13. We do this in Section 6, after having established Proposition 2.11 in Section 5, which is crucially used in the proof of Proposition 2.12.
2.4 Proof plan of Theorem 1.7
For notational convenience, when we write
![]() ${\mathbb E}^*_{k\in {\mathbb N}}$
in the following statements, we mean the limit
${\mathbb E}^*_{k\in {\mathbb N}}$
in the following statements, we mean the limit
![]() $\lim _{K\to \infty } {\mathbb E}_{k\in \Phi _K}$
, where
$\lim _{K\to \infty } {\mathbb E}_{k\in \Phi _K}$
, where
![]() $(\Phi _K)$
is an arbitrary multiplicative Følner sequence, chosen so that all the limits in the following statements exist. Since our setting will always involve a countable collection of limits, such a Følner sequence always exists and can be taken as a subsequence of any given multiplicative Følner sequence.
$(\Phi _K)$
is an arbitrary multiplicative Følner sequence, chosen so that all the limits in the following statements exist. Since our setting will always involve a countable collection of limits, such a Følner sequence always exists and can be taken as a subsequence of any given multiplicative Følner sequence.
Our argument is divided into two parts. In the first part, we reduce the problem to a positivity property of pretentious multiplicative functions, and in the second part, we verify this positivity property. To carry out the first part, we note that to prove Theorem 1.7, it is only necessary to establish the subsequent averaged version.
Theorem 2.14. Suppose that the completely multiplicative function
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
takes finitely many values and
$f\colon {\mathbb N}\to \mathbb {S}^1$
takes finitely many values and
![]() $F:=\mathbf {1}_{\{1\}}$
. Then
$F:=\mathbf {1}_{\{1\}}$
. Then
Remark. The ‘multiplicative average’
![]() ${\mathbb E}^*_{k\in {\mathbb N}}$
is needed in our analysis to ‘clear out’ some unwanted terms.
${\mathbb E}^*_{k\in {\mathbb N}}$
is needed in our analysis to ‘clear out’ some unwanted terms.
We write
![]() $f=gh$
, where g has aperiodicity properties and h is pretentious (see Lemma 7.3 for the exact statement). Since f is finite-valued, it follows that g takes values in d-roots of unity for some
$f=gh$
, where g has aperiodicity properties and h is pretentious (see Lemma 7.3 for the exact statement). Since f is finite-valued, it follows that g takes values in d-roots of unity for some
![]() $d\in {\mathbb N}$
. Hence, we have
$d\in {\mathbb N}$
. Hence, we have
We use the previous facts to analyze the average in (2.20). The aperiodic part is covered by the next result, which is a direct consequence of [Reference Frantzikinakis and Host21, Theorem 9.7].
Proposition 2.15. Let
![]() $f_1,f_2,f_3\colon {\mathbb N}\to {\mathbb U}$
be completely multiplicative functions and suppose that either
$f_1,f_2,f_3\colon {\mathbb N}\to {\mathbb U}$
be completely multiplicative functions and suppose that either
![]() $f_1$
or
$f_1$
or
![]() $f_2$
is aperiodic. Then
$f_2$
is aperiodic. Then
Combining the above and some technical maneuvering, we get the following reduction, which completes the first part needed to prove Theorem 2.14.
Proposition 2.16. Suppose that for every finite-valued completely multiplicative function
![]() $h\colon {\mathbb N}\to \mathbb {S}^1$
, with
$h\colon {\mathbb N}\to \mathbb {S}^1$
, with
![]() $h\sim 1$
, and modified Dirichlet character
$h\sim 1$
, and modified Dirichlet character
![]() $\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
(see Section 3.3 for the definitions), we have
$\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
(see Section 3.3 for the definitions), we have
where
Then for every finite-valued completely multiplicative function
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
, we have
$f\colon {\mathbb N}\to \mathbb {S}^1$
, we have
Therefore, it remains to verify the assumption of this result. For this purpose, we will make crucial use of the following concentration estimates, which easily follow from Propositions 2.5 and 2.11, as we will see later.
Corollary 2.17. Let
![]() $f\colon \mathbb {N}\to \mathbb {U}$
be a finite-valued multiplicative function such that
$f\colon \mathbb {N}\to \mathbb {U}$
be a finite-valued multiplicative function such that
![]() $f\sim \chi $
for some Dirichlet character
$f\sim \chi $
for some Dirichlet character
![]() $\chi $
with period q. Then for every
$\chi $
with period q. Then for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $Q_0=Q_0(f,\varepsilon )\in {\mathbb N}$
such that the following holds:
$Q_0=Q_0(f,\varepsilon )\in {\mathbb N}$
such that the following holds:
-
1. For all
 $Q\in {\mathbb N}$
such that
$Q\in {\mathbb N}$
such that
 $Q_0\mid Q$
, we have where the implicit constant is absolute.
$Q_0\mid Q$
, we have where the implicit constant is absolute. $$ \begin{align*} \limsup_{N\to\infty} {\mathbb E}_{n\in [N]}\big|f(Qn+1)- 1 \big|\ll \varepsilon, \end{align*} $$
$$ \begin{align*} \limsup_{N\to\infty} {\mathbb E}_{n\in [N]}\big|f(Qn+1)- 1 \big|\ll \varepsilon, \end{align*} $$
-
2. For all
 $Q\in {\mathbb N}$
such that
$Q\in {\mathbb N}$
such that
 $Q_0\mid Q$
, we have where the implicit constant is absolute.
$Q_0\mid Q$
, we have where the implicit constant is absolute. $$ \begin{align*} \limsup_{N\to\infty} {\mathbb E}_{m,n\in [N]}|f\big((Qm+1)^2+(Qn)^2\big)- 1 \big|\ll \varepsilon, \end{align*} $$
$$ \begin{align*} \limsup_{N\to\infty} {\mathbb E}_{m,n\in [N]}|f\big((Qm+1)^2+(Qn)^2\big)- 1 \big|\ll \varepsilon, \end{align*} $$
Finally, using the previous concentration estimates and the key maneuver of taking multiplicative averages over
![]() $Q\in {\mathbb N}$
, which was also a crucial element in the proof of Theorem 2.2, we verify the assumptions of Proposition 2.16.
$Q\in {\mathbb N}$
, which was also a crucial element in the proof of Theorem 2.2, we verify the assumptions of Proposition 2.16.
Proposition 2.18. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a finite-valued pretentious multiplicative function and
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a finite-valued pretentious multiplicative function and
![]() $\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
be a modified Dirichlet character. Then
$\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
be a modified Dirichlet character. Then
where
Thus, to prove Theorem 2.14, it remains to verify Propositions 2.16 and 2.18. We do this in Sections 7 and 8 (the other results mentioned in this subsection are needed in the proofs of these two results and will also be verified).
3 Background and preparation
3.1 Some elementary facts
We will use the following elementary property.
Lemma 3.1. Let
![]() $a\colon {\mathbb Z}\to {\mathbb U}$
be an even sequence and
$a\colon {\mathbb Z}\to {\mathbb U}$
be an even sequence and
![]() $l_1,l_2\in {\mathbb Z}$
, not both of them
$l_1,l_2\in {\mathbb Z}$
, not both of them
![]() $0$
. Suppose that for some
$0$
. Suppose that for some
![]() $\varepsilon>0$
and for some sequence
$\varepsilon>0$
and for some sequence
![]() $L_N\colon {\mathbb N}\to {\mathbb U}$
, we have
$L_N\colon {\mathbb N}\to {\mathbb U}$
, we have
Then
where
![]() $l:=|l_1|+|l_2|$
.
$l:=|l_1|+|l_2|$
.
Proof. We have
 $$ \begin{align} {\mathbb E}_{m,n\in [N]} |a(l_1m+l_2n)-L_{lN}|\leq \frac{1}{N^2}\sum_{|k|\leq l N} w_N(k)\, |a(k) -L_{lN}|, \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]} |a(l_1m+l_2n)-L_{lN}|\leq \frac{1}{N^2}\sum_{|k|\leq l N} w_N(k)\, |a(k) -L_{lN}|, \end{align} $$
where for
![]() $k\in {\mathbb Z}$
, we let
$k\in {\mathbb Z}$
, we let
For every
![]() $k\in {\mathbb Z}$
and
$k\in {\mathbb Z}$
and
![]() $m\in [N]$
, there exists at most one
$m\in [N]$
, there exists at most one
![]() $n\in [N]$
for which
$n\in [N]$
for which
![]() $l_1m+l_2n=k$
. Hence,
$l_1m+l_2n=k$
. Hence,
![]() $|w_N(k)|\leq N$
for every
$|w_N(k)|\leq N$
for every
![]() $k\in {\mathbb Z}$
. Since a is even, we deduce that the right-hand side in (3.1) is bounded by
$k\in {\mathbb Z}$
. Since a is even, we deduce that the right-hand side in (3.1) is bounded by
The asserted estimate now follows from this and our assumption.
The next well-known property of multiplicative functions will also be used several times.
Lemma 3.2. Let
![]() $(\Phi _K)$
be a multiplicative Følner sequence. If
$(\Phi _K)$
be a multiplicative Følner sequence. If
![]() $f\colon {\mathbb N}\to {\mathbb U}$
is a completely multiplicative function and
$f\colon {\mathbb N}\to {\mathbb U}$
is a completely multiplicative function and
![]() $f\neq 1$
, then
$f\neq 1$
, then
Proof. Since
![]() $f\neq 1$
, there exists
$f\neq 1$
, there exists
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $f(p)\neq 1$
. By the definition of
$f(p)\neq 1$
. By the definition of
![]() $\Phi _K$
, we have
$\Phi _K$
, we have
From this and the fact that
![]() $f(pn)=f(p)\cdot f(n)$
, we get
$f(pn)=f(p)\cdot f(n)$
, we get
Since
![]() $f(p)\neq 1$
, we deduce that
$f(p)\neq 1$
, we deduce that
![]() ${\mathbb E}_{n\in \Phi _K}\, f(n)=o_{K\to \infty }(1)$
.
${\mathbb E}_{n\in \Phi _K}\, f(n)=o_{K\to \infty }(1)$
.
3.2 Some useful weights
In the proof of Theorems 1.1 and 1.2, we will utilize weighted averages. The weights are employed to ensure that the averages
![]() ${\mathbb E}_{m,n\in [N]}\, A_\delta (f,Q,m,n)$
and
${\mathbb E}_{m,n\in [N]}\, A_\delta (f,Q,m,n)$
and
![]() ${\mathbb E}_{m,n\in [N]}\, B_\delta (f,Q,m,n)$
, where
${\mathbb E}_{m,n\in [N]}\, B_\delta (f,Q,m,n)$
, where
![]() $A_\delta , B_\delta $
are as in (2.6), (2.16), respectively, have a positive real part if f is an Archimedean character and
$A_\delta , B_\delta $
are as in (2.6), (2.16), respectively, have a positive real part if f is an Archimedean character and
![]() $\delta $
is sufficiently small.
$\delta $
is sufficiently small.
We will now define these weights. If
![]() $\delta \in (0,1/2)$
, we consider the circular arc with center
$\delta \in (0,1/2)$
, we consider the circular arc with center
![]() $1$
given by
$1$
given by
Lemma 3.3. For every
![]() $\delta \in (0,1/2)$
, let
$\delta \in (0,1/2)$
, let
![]() $F_\delta \colon \mathbb {S}^1\to [0,1]$
be the trapezoid function that is equal to
$F_\delta \colon \mathbb {S}^1\to [0,1]$
be the trapezoid function that is equal to
![]() $1$
on the arc
$1$
on the arc
![]() $I_{\delta /2}$
and
$I_{\delta /2}$
and
![]() $0$
outside the arc
$0$
outside the arc
![]() $I_\delta $
. Let also
$I_\delta $
. Let also
and
Then
Remark. We opted for a continuous function for
![]() $F_\delta $
instead of an indicator function, to make it easier to prove Propositions 4.1 and 6.1 later on.
$F_\delta $
instead of an indicator function, to make it easier to prove Propositions 4.1 and 6.1 later on.
Proof. We first cover the weight in (3.2). Note that the limit we want to evaluate is equal to
Let
![]() $\tilde {F}_\delta \colon [0,1]\times [0,1]\to [0,1]$
be given by
$\tilde {F}_\delta \colon [0,1]\times [0,1]\to [0,1]$
be given by
Then
![]() $\tilde {F}_\delta $
is Riemann integrable on
$\tilde {F}_\delta $
is Riemann integrable on
![]() $[0,1]\times [0,1]$
as it is bounded and continuous except for a set of Lebesgue measure
$[0,1]\times [0,1]$
as it is bounded and continuous except for a set of Lebesgue measure
![]() $0$
. Hence, the limit we aim to compute exists and is equal to the Riemann integral
$0$
. Hence, the limit we aim to compute exists and is equal to the Riemann integral
 $$ \begin{align*} \int_0^1\int_0^1 \tilde{F}_\delta(x,y)\, dx\, dy. \end{align*} $$
$$ \begin{align*} \int_0^1\int_0^1 \tilde{F}_\delta(x,y)\, dx\, dy. \end{align*} $$
It remains to show that this integral is positive, and since
![]() $\tilde {F}_\delta $
is nonnegative, it suffices to show that
$\tilde {F}_\delta $
is nonnegative, it suffices to show that
![]() $\tilde {F}_\delta $
does not vanish almost everywhere.
$\tilde {F}_\delta $
does not vanish almost everywhere.
To verify the nonvanishing property, note that if
![]() $x= ay$
where
$x= ay$
where
![]() $a:=\frac {\ell '+\sqrt {(\ell ')^2+4\ell ^2}}{2\ell }>1$
, then
$a:=\frac {\ell '+\sqrt {(\ell ')^2+4\ell ^2}}{2\ell }>1$
, then
![]() $x>y$
and
$x>y$
and
![]() $\ell (x^2-y^2)= \ell 'xy$
, and as a consequence,
$\ell (x^2-y^2)= \ell 'xy$
, and as a consequence,
![]() $(\ell (x^2-y^2))^i\cdot (\ell 'xy)^{-i}= 1$
. Hence,
$(\ell (x^2-y^2))^i\cdot (\ell 'xy)^{-i}= 1$
. Hence,
![]() $\tilde {F}_\delta (x,y)=F_\delta (1)=1$
on the line
$\tilde {F}_\delta (x,y)=F_\delta (1)=1$
on the line
![]() $x= ay$
. Since
$x= ay$
. Since
![]() $\tilde F_\delta $
is continuous in the region
$\tilde F_\delta $
is continuous in the region
![]() $x>y$
, this proves that it stays bounded away from zero in a neighborhood of the line
$x>y$
, this proves that it stays bounded away from zero in a neighborhood of the line
![]() $x=ay$
in that region, and hence, it does not vanish almost everywhere. This completes the proof for the weight (3.2).
$x=ay$
in that region, and hence, it does not vanish almost everywhere. This completes the proof for the weight (3.2).
The argument for the second weight (3.3) is very similar, so we only summarize it. Let
![]() $\tilde {F}_\delta \colon [0,1]\times [0,1]\to [0,1]$
be given by
$\tilde {F}_\delta \colon [0,1]\times [0,1]\to [0,1]$
be given by
Then the limit we want to evaluate exists and is equal to the Riemann integral
 $$ \begin{align*} \int_0^1\int_0^1 \tilde{F}_\delta(x,y)\, dx\, dy. \end{align*} $$
$$ \begin{align*} \int_0^1\int_0^1 \tilde{F}_\delta(x,y)\, dx\, dy. \end{align*} $$
The integral is positive because
![]() $\tilde {F}_\delta $
is nonnegative and does not vanish almost everywhere. To verify the nonvanishing property, we argue as follows. Pick
$\tilde {F}_\delta $
is nonnegative and does not vanish almost everywhere. To verify the nonvanishing property, we argue as follows. Pick
![]() $k\in {\mathbb Z}_+$
such that
$k\in {\mathbb Z}_+$
such that
![]() $b:=\ell '/\ell \cdot e^{2k\pi }>2$
and let
$b:=\ell '/\ell \cdot e^{2k\pi }>2$
and let
![]() $a:=\frac {b+\sqrt {b^2-4}}{2}$
. If
$a:=\frac {b+\sqrt {b^2-4}}{2}$
. If
![]() $x,y\in [0,1]$
are such that
$x,y\in [0,1]$
are such that
![]() $x= ay$
, then
$x= ay$
, then
![]() $x>y$
and
$x>y$
and
![]() $\ell (x^2+y^2)=e^{2k\pi }\, \ell 'xy $
, which implies
$\ell (x^2+y^2)=e^{2k\pi }\, \ell 'xy $
, which implies
![]() $(\ell (x^2+y^2))^i\cdot (\ell 'xy)^{-i}= e^{2k\pi i}=1$
.
$(\ell (x^2+y^2))^i\cdot (\ell 'xy)^{-i}= e^{2k\pi i}=1$
.
3.3 Multiplicative functions
We record here some basic notions and facts about multiplicative functions that will be used throughout the article.
3.3.1 Dirichlet characters
A Dirichlet character
![]() $\chi $
is a periodic completely multiplicative function and is often thought of as a multiplicative function on
$\chi $
is a periodic completely multiplicative function and is often thought of as a multiplicative function on
![]() ${\mathbb Z}_m$
for some
${\mathbb Z}_m$
for some
![]() $m\in {\mathbb N}$
. In this case,
$m\in {\mathbb N}$
. In this case,
![]() $\chi $
takes the value
$\chi $
takes the value
![]() $0$
on integers that are not coprime to m and takes values on
$0$
on integers that are not coprime to m and takes values on
![]() $\phi (m)$
-roots of unity on all other integers, where
$\phi (m)$
-roots of unity on all other integers, where
![]() $\phi $
is the Euler totient function. If
$\phi $
is the Euler totient function. If
![]() $\chi $
is a Dirichlet character, we define the modified Dirichlet character
$\chi $
is a Dirichlet character, we define the modified Dirichlet character
![]() $\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
to be the completely multiplicative function satisfying
$\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
to be the completely multiplicative function satisfying
 $$ \begin{align*} \tilde{\chi}(p):= \begin{cases} \chi(p), &\quad \text{if } \chi(p)\neq 0\\ 1, &\quad \text{if } \chi(p)=0. \end{cases} \end{align*} $$
$$ \begin{align*} \tilde{\chi}(p):= \begin{cases} \chi(p), &\quad \text{if } \chi(p)\neq 0\\ 1, &\quad \text{if } \chi(p)=0. \end{cases} \end{align*} $$
We note in passing that the level sets of modified Dirichlet characters
![]() $\tilde {\chi }$
, which can be seen as finite colorings of
$\tilde {\chi }$
, which can be seen as finite colorings of
![]() ${\mathbb N}$
, are precisely the colorings that appear in Rado’s theorem when showing that certain systems of linear equations are not partition regular. In particular, a system of linear equations is partition regular if and only if it has a monochromatic solution in any coloring realized by a modified Dirichlet character.
${\mathbb N}$
, are precisely the colorings that appear in Rado’s theorem when showing that certain systems of linear equations are not partition regular. In particular, a system of linear equations is partition regular if and only if it has a monochromatic solution in any coloring realized by a modified Dirichlet character.
3.3.2 Distance between multiplicative functions
Following Granville and Soundararajan [Reference Granville and Soundararajan25, Reference Granville and Soundararajan27], in this and the next subsection, we define a distance and a related notion of pretentiousness between multiplicative functions. If
![]() $f,g\colon {\mathbb N}\to {\mathbb U}$
are multiplicative functions and
$f,g\colon {\mathbb N}\to {\mathbb U}$
are multiplicative functions and
![]() $x,y\in {\mathbb R}_+$
with
$x,y\in {\mathbb R}_+$
with
![]() $x<y$
, we let
$x<y$
, we let
 $$ \begin{align} {\mathbb D}(f,g; x,y)^2:= \sum_{x< p \leq y} \frac{1}{p}\, (1-\Re(f(p)\cdot \overline{g(p)})). \end{align} $$
$$ \begin{align} {\mathbb D}(f,g; x,y)^2:= \sum_{x< p \leq y} \frac{1}{p}\, (1-\Re(f(p)\cdot \overline{g(p)})). \end{align} $$
We also let
 $$ \begin{align} {\mathbb D}(f,g)^2:=\sum_{p\in \mathbb{P}} \frac{1}{p}\, (1-\Re (f(p)\cdot \overline{g(p)})). \end{align} $$
$$ \begin{align} {\mathbb D}(f,g)^2:=\sum_{p\in \mathbb{P}} \frac{1}{p}\, (1-\Re (f(p)\cdot \overline{g(p)})). \end{align} $$
Note that if
![]() $|f|=|g|=1$
, then
$|f|=|g|=1$
, then
 $$ \begin{align*} {\mathbb D}(f,g)^2=\frac{1}{2}\cdot \sum_{p\in \mathbb{P}} \frac{1}{p}\, |f(p)-g(p)|^2. \end{align*} $$
$$ \begin{align*} {\mathbb D}(f,g)^2=\frac{1}{2}\cdot \sum_{p\in \mathbb{P}} \frac{1}{p}\, |f(p)-g(p)|^2. \end{align*} $$
It can be shown (see [Reference Granville and Soundararajan26] or [Reference Granville and Soundararajan27, Section 2.1.1]) that
![]() ${\mathbb D}$
satisfies the triangle inequality
${\mathbb D}$
satisfies the triangle inequality
for all
![]() $f,g,h\colon {\mathbb P}\to {\mathbb U}$
. Also, for all
$f,g,h\colon {\mathbb P}\to {\mathbb U}$
. Also, for all
![]() $f_1, f_2, g_1, g_2\colon {\mathbb P}\to {\mathbb U}$
, we have (see [Reference Granville and Soundararajan25, Lemma 3.1])
$f_1, f_2, g_1, g_2\colon {\mathbb P}\to {\mathbb U}$
, we have (see [Reference Granville and Soundararajan25, Lemma 3.1])
3.3.3 Pretentious multiplicative functions
If
![]() $f,g\colon {\mathbb N}\to {\mathbb U}$
are multiplicative functions, we say that f pretends to be g, and write
$f,g\colon {\mathbb N}\to {\mathbb U}$
are multiplicative functions, we say that f pretends to be g, and write
![]() $f\sim g$
, if
$f\sim g$
, if
![]() ${\mathbb D}(f,g)<+\infty $
. It follows from (3.6) that if
${\mathbb D}(f,g)<+\infty $
. It follows from (3.6) that if
![]() $f_1\sim g_1$
and
$f_1\sim g_1$
and
![]() $f_2\sim g_2$
, then
$f_2\sim g_2$
, then
![]() $f_1f_2\sim g_1g_2$
. We say that f is pretentious if
$f_1f_2\sim g_1g_2$
. We say that f is pretentious if
![]() $f\sim \chi \cdot n^{it}$
for some
$f\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
, in which case
$\chi $
, in which case
 $$ \begin{align*} \sum_{p\in \mathbb{P}} \frac{1}{p}\, (1-\Re (f(p)\cdot \overline{\chi(p)}\cdot p^{-it}))<+\infty. \end{align*} $$
$$ \begin{align*} \sum_{p\in \mathbb{P}} \frac{1}{p}\, (1-\Re (f(p)\cdot \overline{\chi(p)}\cdot p^{-it}))<+\infty. \end{align*} $$
The value of t is uniquely determined; this follows from (3.6) and the fact that
![]() $n^{it}\not \sim \chi $
for every nonzero
$n^{it}\not \sim \chi $
for every nonzero
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
(see, for example, [Reference Granville and Soundararajan27, Corollary 11.4] or [Reference Granville and Soundararajan26, Proposition 7]).
$\chi $
(see, for example, [Reference Granville and Soundararajan27, Corollary 11.4] or [Reference Granville and Soundararajan26, Proposition 7]).
Although real-valued or finite-valued multiplicative functions always have a mean value, we caution the reader that this is not the case for general multiplicative functions with values on the unit circle. For example, we have
so we have non-convergent means when
![]() $t\neq 0$
. But even multiplicative functions satisfying
$t\neq 0$
. But even multiplicative functions satisfying
![]() $f\sim 1$
can have non-convergent means. In particular, if
$f\sim 1$
can have non-convergent means. In particular, if
![]() $f\sim 1$
is a completely multiplicative function, then it is known (see, for example, [Reference Elliott17, Theorems 6.2]) that there exists
$f\sim 1$
is a completely multiplicative function, then it is known (see, for example, [Reference Elliott17, Theorems 6.2]) that there exists
![]() $c\neq 0$
such that
$c\neq 0$
such that
where
![]() $A(N):= \sum _{p\leq N} \frac {1}{p}\, \Im (f(p))$
,
$A(N):= \sum _{p\leq N} \frac {1}{p}\, \Im (f(p))$
,
![]() $N\in {\mathbb N}$
. Hence, we have non-convergent means when, for example,
$N\in {\mathbb N}$
. Hence, we have non-convergent means when, for example,
 $$ \begin{align*} \sum_{p\in \mathbb{P}} \frac{1}{p}\, \Im (f(p))=+\infty, \end{align*} $$
$$ \begin{align*} \sum_{p\in \mathbb{P}} \frac{1}{p}\, \Im (f(p))=+\infty, \end{align*} $$
which is the case if
![]() $f(p):=e(1/ \log \log {p})$
,
$f(p):=e(1/ \log \log {p})$
,
![]() $p\in {\mathbb P}$
. This oscillatory behavior of the mean values of some complex-valued multiplicative functions has to be taken into account and will cause problems in the proofs of some of our main results.
$p\in {\mathbb P}$
. This oscillatory behavior of the mean values of some complex-valued multiplicative functions has to be taken into account and will cause problems in the proofs of some of our main results.
Finally, we record an observation that will only be used in the proof of Theorem 1.5.
Lemma 3.4. Let
![]() $f\colon {\mathbb N}\to {\mathbb U}$
be a pretentious finite-valued multiplicative function. Then
$f\colon {\mathbb N}\to {\mathbb U}$
be a pretentious finite-valued multiplicative function. Then
![]() $f\sim \chi $
for some Dirichlet character
$f\sim \chi $
for some Dirichlet character
![]() $\chi $
and
$\chi $
and
 $$ \begin{align} \sum_{p\in {\mathbb P}} \frac{1}{p}|1-f(p)\cdot \overline{\chi(p)}|<+\infty. \end{align} $$
$$ \begin{align} \sum_{p\in {\mathbb P}} \frac{1}{p}|1-f(p)\cdot \overline{\chi(p)}|<+\infty. \end{align} $$
Remark. It can be shown using (3.7) that finite-valued pretentious multiplicative functions always have convergent means.
Proof. Since f is pretentious, we have
![]() $f\sim \chi \cdot n^{it}$
for some
$f\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
. Then
$\chi $
. Then
![]() ${\mathbb D}(n^{it}, g)<+\infty $
, where
${\mathbb D}(n^{it}, g)<+\infty $
, where
![]() $g:=f\cdot \overline {\chi }$
is a finite-valued multiplicative function. In particular, there exists
$g:=f\cdot \overline {\chi }$
is a finite-valued multiplicative function. In particular, there exists
![]() $d\in {\mathbb N}$
for which
$d\in {\mathbb N}$
for which
![]() $g^d$
is the constant
$g^d$
is the constant
![]() $1$
, so from (3.6), it follows that
$1$
, so from (3.6), it follows that
![]() ${\mathbb D}(n^{idt}, 1)<+\infty $
, which in turn implies that
${\mathbb D}(n^{idt}, 1)<+\infty $
, which in turn implies that
![]() $t=0$
(hence,
$t=0$
(hence,
![]() $f\sim \chi $
) and
$f\sim \chi $
) and
 $$ \begin{align*} \sum_{p\in {\mathbb P}\colon f(p)\cdot \overline{\chi(p)}\neq 1}\frac{1}{p}<+\infty. \end{align*} $$
$$ \begin{align*} \sum_{p\in {\mathbb P}\colon f(p)\cdot \overline{\chi(p)}\neq 1}\frac{1}{p}<+\infty. \end{align*} $$
Hence,
 $$ \begin{align*} \sum_{p\in {\mathbb P}}\frac{1}{p} |\Im (f(p)\cdot \overline{\chi(p)})|<+\infty. \end{align*} $$
$$ \begin{align*} \sum_{p\in {\mathbb P}}\frac{1}{p} |\Im (f(p)\cdot \overline{\chi(p)})|<+\infty. \end{align*} $$
If we combine this with
![]() ${\mathbb D}(f,\chi )<+\infty $
, we deduce that (3.7) holds.
${\mathbb D}(f,\chi )<+\infty $
, we deduce that (3.7) holds.
3.3.4 Aperiodic multiplicative functions
We say that a multiplicative function
![]() $f\colon {\mathbb N}\to {\mathbb U}$
is aperiodic if for every
$f\colon {\mathbb N}\to {\mathbb U}$
is aperiodic if for every
![]() $a,b\in {\mathbb N}$
,
$a,b\in {\mathbb N}$
,
 $$ \begin{align*}\lim_{N\to\infty}\frac1N\sum_{n=1}^N\, f(an+b)=0.\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty}\frac1N\sum_{n=1}^N\, f(an+b)=0.\end{align*} $$
The following well-known result of Daboussi-Delange [Reference Daboussi and Delange13, Corollary 1] states that a multiplicative function is aperiodic if and only if it is non-pretentious.
Lemma 3.5. Let
![]() $f\in {\mathcal M}$
. Then either
$f\in {\mathcal M}$
. Then either
![]() $f\sim \chi \cdot n^{it}$
for some Dirichlet character
$f\sim \chi \cdot n^{it}$
for some Dirichlet character
![]() $\chi $
and
$\chi $
and
![]() $t\in {\mathbb R}$
, or f is aperiodic.
$t\in {\mathbb R}$
, or f is aperiodic.
In our arguments, we typically distinguish two cases – one where a multiplicative function is aperiodic; then we show that the expressions we are interested in vanish. The complementary one where the multiplicative function is pretentious is treated using concentration estimates.
3.4 Some Borel measurability results
Recall that
![]() ${\mathcal M}$
is equipped with the topology of pointwise convergence. In the proof of Theorem 2.2, we require certain Borel measurability properties of subsets of
${\mathcal M}$
is equipped with the topology of pointwise convergence. In the proof of Theorem 2.2, we require certain Borel measurability properties of subsets of
![]() ${\mathcal M}$
and related maps. The second property proved below will only be used in the proof of part (2) of Theorem 2.2.
${\mathcal M}$
and related maps. The second property proved below will only be used in the proof of part (2) of Theorem 2.2.
Recall that if f is pretentious, then there exist a unique
![]() $t=t_f\in {\mathbb R}$
and a Dirichlet character
$t=t_f\in {\mathbb R}$
and a Dirichlet character
![]() $\chi $
such that
$\chi $
such that
![]() $f\sim \chi \cdot n^{it}$
.
$f\sim \chi \cdot n^{it}$
.
Lemma 3.6.
-
1. The set
 ${\mathcal M}_p$
of pretentious completely multiplicative functions is Borel.
${\mathcal M}_p$
of pretentious completely multiplicative functions is Borel. -
2. The map
 $f\mapsto t_f$
from
$f\mapsto t_f$
from
 ${\mathcal M}_p$
to
${\mathcal M}_p$
to
 ${\mathbb R}$
is Borel measurable.
${\mathbb R}$
is Borel measurable.
Proof. We prove (1). For
![]() $a,b\in {\mathbb N}$
, we let
$a,b\in {\mathbb N}$
, we let
![]() $M_{a,b}$
be the set of
$M_{a,b}$
be the set of
![]() $f\in {\mathcal M}$
such that
$f\in {\mathcal M}$
such that
Clearly,
![]() $M_{a,b}$
is a Borel subset of
$M_{a,b}$
is a Borel subset of
![]() ${\mathcal M}$
. By Lemma 3.5, we have
${\mathcal M}$
. By Lemma 3.5, we have
![]() ${\mathcal M}_p=\bigcup _{a,b\in {\mathbb N}}M_{a,b}$
, and the result follows.
${\mathcal M}_p=\bigcup _{a,b\in {\mathbb N}}M_{a,b}$
, and the result follows.
We prove (2). By [Reference Kechris32, Theorem 14.12], it suffices to show that the graph
is a Borel subset of
![]() ${\mathcal M}_p\times {\mathbb R}$
. If
${\mathcal M}_p\times {\mathbb R}$
. If
![]() $\chi _k$
,
$\chi _k$
,
![]() $k\in {\mathbb N}$
, is an enumeration of all Dirichlet characters, and
$k\in {\mathbb N}$
, is an enumeration of all Dirichlet characters, and
then
Hence, it suffices to show that for every
![]() $k\in {\mathbb N}$
, the set
$k\in {\mathbb N}$
, the set
![]() $\Gamma _k$
is Borel. Note that
$\Gamma _k$
is Borel. Note that
Since for
![]() $k\in {\mathbb N}$
the map
$k\in {\mathbb N}$
the map
![]() $(f,t)\mapsto {\mathbb D}(f,\chi _k\cdot n^{it})$
is clearly Borel, the set
$(f,t)\mapsto {\mathbb D}(f,\chi _k\cdot n^{it})$
is clearly Borel, the set
![]() $\Gamma _k$
is Borel. This completes the proof.
$\Gamma _k$
is Borel. This completes the proof.
4 Type I Pythagorean pairs
As explained in Section 2.2, in order to complete the proof of Theorem 2.3 (and thus of part (1) of Theorem 2.2), it remains to prove Proposition 2.4, Lemma 2.6 and Lemma 2.8. We do this in this section.
We start with Proposition 2.4, which we state here in an equivalent form.
Proposition 4.1. Let
![]() $f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic completely multiplicative function, let
$f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic completely multiplicative function, let
![]() $\ell ,\ell ',Q\in {\mathbb N}$
and
$\ell ,\ell ',Q\in {\mathbb N}$
and
![]() $\delta>0$
. Then, with
$\delta>0$
. Then, with
![]() $w_\delta :{\mathbb N}^2\to [0,1]$
described by (3.2), we have
$w_\delta :{\mathbb N}^2\to [0,1]$
described by (3.2), we have
Furthermore, the limit in (4.1) exists for all multiplicative functions
![]() $f\colon {\mathbb N}\to {\mathbb U}$
.
$f\colon {\mathbb N}\to {\mathbb U}$
.
Proof. Recall that
where
![]() $F_\delta \colon \mathbb {S}^1\to [0,1]$
is the continuous function defined in Lemma 3.3. Since
$F_\delta \colon \mathbb {S}^1\to [0,1]$
is the continuous function defined in Lemma 3.3. Since
![]() $F_\delta $
can be approximated uniformly by polynomials, using linearity, we deduce that it suffices to verify (4.1) with
$F_\delta $
can be approximated uniformly by polynomials, using linearity, we deduce that it suffices to verify (4.1) with
![]() $w_\delta (m,n)$
replaced by
$w_\delta (m,n)$
replaced by
![]() $(m^2-n^2)^{ki}\cdot (mn)^{-ki}\cdot \mathbf {1}_{m>n}$
for arbitrary
$(m^2-n^2)^{ki}\cdot (mn)^{-ki}\cdot \mathbf {1}_{m>n}$
for arbitrary
![]() $k\in {\mathbb Z}$
. Furthermore, since
$k\in {\mathbb Z}$
. Furthermore, since
![]() $\lim _{n\to \infty }(\log (Qn+1)-\log (Qn))=0$
, the limit in (4.1) remains unchanged if we replace
$\lim _{n\to \infty }(\log (Qn+1)-\log (Qn))=0$
, the limit in (4.1) remains unchanged if we replace
![]() $(m^2-n^2)^{ki}\cdot (mn)^{-ki} \cdot \mathbf {1}_{m> n}$
with
$(m^2-n^2)^{ki}\cdot (mn)^{-ki} \cdot \mathbf {1}_{m> n}$
with
![]() $((Qm+1)^2-(Qn)^2)^{ki}\cdot ((Qm+1)(Qn))^{-ki}\cdot \mathbf {1}_{m> n}$
(after we omit
$((Qm+1)^2-(Qn)^2)^{ki}\cdot ((Qm+1)(Qn))^{-ki}\cdot \mathbf {1}_{m> n}$
(after we omit
![]() $+1$
, the Q’s are going to cancel because of the conjugate). Hence, in order to establish (4.1), it suffices to show that for every
$+1$
, the Q’s are going to cancel because of the conjugate). Hence, in order to establish (4.1), it suffices to show that for every
![]() $k\in {\mathbb Z}$
, we have
$k\in {\mathbb Z}$
, we have
where
![]() $f_k(n):=f(n)\cdot n^{ki}$
,
$f_k(n):=f(n)\cdot n^{ki}$
,
![]() $n\in {\mathbb N}$
. Note that since the indicator function of an arithmetic progression is a linear combination of Dirichlet characters, in order to establish (4.2), it suffices to show that for all Dirichlet characters
$n\in {\mathbb N}$
. Note that since the indicator function of an arithmetic progression is a linear combination of Dirichlet characters, in order to establish (4.2), it suffices to show that for all Dirichlet characters
![]() $\chi ,\chi '$
, we have
$\chi ,\chi '$
, we have
or, equivalently, that
Since f is aperiodic, so is
![]() $f_k$
. Since f is aperiodic, so is
$f_k$
. Since f is aperiodic, so is
![]() $\overline {f_k}\cdot \chi $
(and
$\overline {f_k}\cdot \chi $
(and
![]() $\overline {f_k}\cdot \chi '$
). Combining [Reference Frantzikinakis and Host21, Theorem 2.5] and [Reference Frantzikinakis and Host21, Lemma 9.6], we deduce that (4.3) holds, completing the proof.
$\overline {f_k}\cdot \chi '$
). Combining [Reference Frantzikinakis and Host21, Theorem 2.5] and [Reference Frantzikinakis and Host21, Lemma 9.6], we deduce that (4.3) holds, completing the proof.
Finally, to prove convergence for all multiplicative functions, we argue as before, using the fact that convergence in the case
![]() $w_\delta =1$
follows from [Reference Frantzikinakis and Host20, Theorem 1.4]. We note that although [Reference Frantzikinakis and Host20, Theorem 1.4] only covers the case without the weight
$w_\delta =1$
follows from [Reference Frantzikinakis and Host20, Theorem 1.4]. We note that although [Reference Frantzikinakis and Host20, Theorem 1.4] only covers the case without the weight
![]() $\mathbf {1}_{m> n}$
, exactly the same argument can be used to cover this weighted variant.
$\mathbf {1}_{m> n}$
, exactly the same argument can be used to cover this weighted variant.
Next, we restate and prove Lemma 2.6. Recall that
![]() $A_\delta $
,
$A_\delta $
,
![]() ${\mathcal M}_p$
and
${\mathcal M}_p$
and
![]() ${\mathcal A}$
were defined in (2.6), (2.9) and (2.13), respectively.
${\mathcal A}$
were defined in (2.6), (2.9) and (2.13), respectively.
Lemma 2.6 . Let
![]() $f\in {\mathcal M}_p\setminus {\mathcal A}$
,
$f\in {\mathcal M}_p\setminus {\mathcal A}$
,
![]() $\delta>0$
,
$\delta>0$
,
![]() $\ell ,\ell '\in {\mathbb N}$
, and let
$\ell ,\ell '\in {\mathbb N}$
, and let
![]() $\big (\Phi _K\big )_{K\in {\mathbb N}}$
be the Følner sequence described in (2.11). Then
$\big (\Phi _K\big )_{K\in {\mathbb N}}$
be the Følner sequence described in (2.11). Then
Proof. Let
![]() $\delta>0$
and
$\delta>0$
and
![]() $f\in {\mathcal M}_p\setminus {\mathcal A}$
. Then for some
$f\in {\mathcal M}_p\setminus {\mathcal A}$
. Then for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
, we have
$\chi $
, we have
For reasons that will become clear later, for
![]() $\delta>0$
and
$\delta>0$
and
![]() $Q\in {\mathbb N}$
, let
$Q\in {\mathbb N}$
, let
Note that the limit in the definition of
![]() $\tilde L_\delta (f,Q)$
exists by the second part of Proposition 4.1. The idea to prove (4.4) is to show that
$\tilde L_\delta (f,Q)$
exists by the second part of Proposition 4.1. The idea to prove (4.4) is to show that
![]() $\tilde L_\delta (f,Q)$
does not depend strongly on Q (it depends only on the prime factors of Q), so that, as a function of Q, it is orthogonal to any nontrivial completely multiplicative function with respect to multiplicative averages. Since the left-hand side of (4.4) is the correlation between
$\tilde L_\delta (f,Q)$
does not depend strongly on Q (it depends only on the prime factors of Q), so that, as a function of Q, it is orthogonal to any nontrivial completely multiplicative function with respect to multiplicative averages. Since the left-hand side of (4.4) is the correlation between
![]() $\tilde L(f,Q)$
and the completely multiplicative function
$\tilde L(f,Q)$
and the completely multiplicative function
![]() $Q\mapsto f(Q)\cdot Q^{-it}$
, which is nontrivial by (4.5), the conclusion will follow.
$Q\mapsto f(Q)\cdot Q^{-it}$
, which is nontrivial by (4.5), the conclusion will follow.
Fix
![]() $\varepsilon>0$
and take
$\varepsilon>0$
and take
![]() $K_0=K_0(\varepsilon ,f)$
so that
$K_0=K_0(\varepsilon ,f)$
so that
 $$ \begin{align*}\sum_{p\geq K_0}\frac1p (1-\Re(f(p)\cdot \overline{\chi(p)}\cdot p^{-it}))+K_0^{-1/2}\leq\varepsilon.\end{align*} $$
$$ \begin{align*}\sum_{p\geq K_0}\frac1p (1-\Re(f(p)\cdot \overline{\chi(p)}\cdot p^{-it}))+K_0^{-1/2}\leq\varepsilon.\end{align*} $$
Using Proposition 2.5 (and noting that the function
![]() $K\mapsto {\mathbb D}(f,\chi \cdot n^{it}; K,N)$
is decreasing for any fixed f and N), it follows that for every
$K\mapsto {\mathbb D}(f,\chi \cdot n^{it}; K,N)$
is decreasing for any fixed f and N), it follows that for every
![]() $N>K>K_0$
and
$N>K>K_0$
and
![]() $Q\in \Phi _K$
,
$Q\in \Phi _K$
,
Using this identity and Lemma 3.1 with
![]() $a(n):=f(Qn+1)\cdot (Qn)^{-it}$
and
$a(n):=f(Qn+1)\cdot (Qn)^{-it}$
and
![]() $l_1=1$
,
$l_1=1$
,
![]() $l_2=-1$
, it follows that
$l_2=-1$
, it follows that
Using (4.7) and Lemma 3.1 with
![]() $a(n):=f(Qn+1)\cdot (Qn)^{-it}$
and
$a(n):=f(Qn+1)\cdot (Qn)^{-it}$
and
![]() $l_1=l_2=1$
, it follows that
$l_1=l_2=1$
, it follows that
Combining (4.7), (4.8), (4.9), and since all terms involved are
![]() $1$
-bounded, we deduce that for every
$1$
-bounded, we deduce that for every
![]() $K>K_0$
and
$K>K_0$
and
![]() $Q\in \Phi _K$
,
$Q\in \Phi _K$
,
 $$ \begin{align*} \limsup_{N\to\infty}\ {\mathbb E}_{m,n\in[N], m>n}&\Big|f\big((Qm+1)^2-(Qn)^2\big)\cdot \overline{f(Qm+1)} \\ &\qquad -Q^{it}\cdot (m^2-n^2)^{it} \cdot m^{-it} \cdot \exp(2F_{2N}(f,K)) \cdot \overline{\exp(F_N(f,K))}\big)\Big|\ll \varepsilon. \end{align*} $$
$$ \begin{align*} \limsup_{N\to\infty}\ {\mathbb E}_{m,n\in[N], m>n}&\Big|f\big((Qm+1)^2-(Qn)^2\big)\cdot \overline{f(Qm+1)} \\ &\qquad -Q^{it}\cdot (m^2-n^2)^{it} \cdot m^{-it} \cdot \exp(2F_{2N}(f,K)) \cdot \overline{\exp(F_N(f,K))}\big)\Big|\ll \varepsilon. \end{align*} $$
Multiplying by
![]() $c_{\ell ,\ell '}\cdot w_\delta (m,n)\cdot \overline {f(Qn)}\cdot Q^{-it}\cdot f(Q)=c_{\ell ,\ell '}\cdot w_\delta (m,n)\cdot \overline {f(n)}\cdot Q^{-it}$
, where
$c_{\ell ,\ell '}\cdot w_\delta (m,n)\cdot \overline {f(Qn)}\cdot Q^{-it}\cdot f(Q)=c_{\ell ,\ell '}\cdot w_\delta (m,n)\cdot \overline {f(n)}\cdot Q^{-it}$
, where
![]() ${c_{\ell ,\ell '}:=f(\ell )\cdot \overline {f(\ell ')}}$
, we deduce that
${c_{\ell ,\ell '}:=f(\ell )\cdot \overline {f(\ell ')}}$
, we deduce that
 $$ \begin{align*} \limsup_{N\to\infty} &\ {\mathbb E}_{m,n\in[N],m>n}\Big|A_\delta(f,Q;m,n)\cdot Q^{-it}\cdot f(Q)\\ & -c_{\ell,\ell'}\cdot w_\delta(m,n)\cdot (m^2-n^2)^{it} \cdot m^{-it} \cdot \overline{f(n)}\cdot \exp(2F_{2N}(f,K)) \cdot \overline{\exp(F_N(f,K))}\Big|\ll\varepsilon. \end{align*} $$
$$ \begin{align*} \limsup_{N\to\infty} &\ {\mathbb E}_{m,n\in[N],m>n}\Big|A_\delta(f,Q;m,n)\cdot Q^{-it}\cdot f(Q)\\ & -c_{\ell,\ell'}\cdot w_\delta(m,n)\cdot (m^2-n^2)^{it} \cdot m^{-it} \cdot \overline{f(n)}\cdot \exp(2F_{2N}(f,K)) \cdot \overline{\exp(F_N(f,K))}\Big|\ll\varepsilon. \end{align*} $$
This implies that for every
![]() $K>K_0$
,
$K>K_0$
,
 $$ \begin{align*} &\limsup_{N\to\infty}\sup_{Q\in \Phi_K}\Big|\tilde L_\delta(f,Q) -\\ &\quad c_{\ell,\ell'}\cdot {\mathbb E}_{m,n\in[N]}\, w_\delta(m,n)\cdot (m^2-n^2)^{it}\cdot m^{-it}\cdot \overline{f(n)}\cdot \exp(2F_{2N}(f,K)) \cdot \overline{\exp(F_N(f,K))}\Big|\ll\varepsilon. \end{align*} $$
$$ \begin{align*} &\limsup_{N\to\infty}\sup_{Q\in \Phi_K}\Big|\tilde L_\delta(f,Q) -\\ &\quad c_{\ell,\ell'}\cdot {\mathbb E}_{m,n\in[N]}\, w_\delta(m,n)\cdot (m^2-n^2)^{it}\cdot m^{-it}\cdot \overline{f(n)}\cdot \exp(2F_{2N}(f,K)) \cdot \overline{\exp(F_N(f,K))}\Big|\ll\varepsilon. \end{align*} $$
Since the second term does not depend on Q, we conclude that for every
![]() $K>K_0$
and
$K>K_0$
and
![]() $Q,Q'\in \Phi _K$
,
$Q,Q'\in \Phi _K$
,
![]() $\big |\tilde L_\delta (f,Q)-\tilde L_\delta (f,Q')\big |\ll \varepsilon $
. We can choose
$\big |\tilde L_\delta (f,Q)-\tilde L_\delta (f,Q')\big |\ll \varepsilon $
. We can choose
![]() $\varepsilon $
arbitrarily small by sending
$\varepsilon $
arbitrarily small by sending
![]() $K\to \infty $
, so it follows that
$K\to \infty $
, so it follows that
For
![]() $K\in {\mathbb N}$
, let
$K\in {\mathbb N}$
, let
![]() $Q_K$
be any element of
$Q_K$
be any element of
![]() $\Phi _K$
. From the last identity and (4.6), it follows that
$\Phi _K$
. From the last identity and (4.6), it follows that
By (4.5), we have that
![]() $Q\mapsto f(Q)\cdot Q^{-it}$
is a nontrivial multiplicative function; hence, the last limit is zero by Lemma 3.2. This establishes (4.4) and completes the proof.
$Q\mapsto f(Q)\cdot Q^{-it}$
is a nontrivial multiplicative function; hence, the last limit is zero by Lemma 3.2. This establishes (4.4) and completes the proof.
Lastly, we restate and prove Lemma 2.8.
Lemma 2.8. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
such that
${\mathcal M}_p$
such that
![]() $\sigma (\{1\})>0$
and let
$\sigma (\{1\})>0$
and let
![]() ${\mathcal A}$
be as in (2.13). Then there exist
${\mathcal A}$
be as in (2.13). Then there exist
![]() $\delta _0,\rho _0>0$
, depending only on
$\delta _0,\rho _0>0$
, depending only on
![]() $\sigma $
, such that
$\sigma $
, such that
Proof. Let
![]() $a:=\sigma (\{1\})>0$
and for
$a:=\sigma (\{1\})>0$
and for
![]() $\delta>0$
, let
$\delta>0$
, let
Note that by Lemma 3.3, we have
![]() $\mu _{\delta }>0$
. For
$\mu _{\delta }>0$
. For
![]() $T\in {\mathbb R}_+$
, we consider the sets
$T\in {\mathbb R}_+$
, we consider the sets
These sets are closed and, as a consequence, Borel. Since
![]() ${\mathcal A}_{N}$
increases to
${\mathcal A}_{N}$
increases to
![]() ${\mathcal A}$
as
${\mathcal A}$
as
![]() $N\to \infty $
, and the Borel measure
$N\to \infty $
, and the Borel measure
![]() $\sigma $
is finite, there exists
$\sigma $
is finite, there exists
![]() $T_0=T_0(\sigma )>0$
such that
$T_0=T_0(\sigma )>0$
such that
Note also that since
![]() $\lim _{n\to \infty } \sup _{Q\in {\mathbb N}}|\log (Qn+1)-\log (Qn))|=0$
, we have
$\lim _{n\to \infty } \sup _{Q\in {\mathbb N}}|\log (Qn+1)-\log (Qn))|=0$
, we have
 $$ \begin{align*} \lim_{N\to\infty}\sup_{f\in {\mathcal A}_{T_0}, Q\in {\mathbb N}}{\mathbb E}_{m,n\in [N],m>n}\big| f(\ell ((Qm+1)^2-(Qn)^2))&\cdot \overline{f(\ell'(Qm+1)(Qn))}-\\ &\qquad\qquad f(\ell (m^2-n^2))\cdot \overline{f(\ell' mn)}\big|=0, \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\sup_{f\in {\mathcal A}_{T_0}, Q\in {\mathbb N}}{\mathbb E}_{m,n\in [N],m>n}\big| f(\ell ((Qm+1)^2-(Qn)^2))&\cdot \overline{f(\ell'(Qm+1)(Qn))}-\\ &\qquad\qquad f(\ell (m^2-n^2))\cdot \overline{f(\ell' mn)}\big|=0, \end{align*} $$
and by the definition of
![]() $w_\delta $
given in Lemma 3.3, we have
$w_\delta $
given in Lemma 3.3, we have
We deduce from the last two identities that if
![]() $\delta _0$
is small enough (depending only on
$\delta _0$
is small enough (depending only on
![]() $T_0$
and hence only on
$T_0$
and hence only on
![]() $\sigma $
), then for every
$\sigma $
), then for every
![]() $Q\in {\mathbb N}$
, we have
$Q\in {\mathbb N}$
, we have
 $$ \begin{align*} \liminf_{N\to\infty}\inf_{Q\in {\mathbb N}} \Re\Big({\mathbb E}_{m,n\in[N]}\int_{{\mathcal A}_{T_0}} A_{\delta_0}(f,Q;m,n)\, d\sigma(f)\Big)\geq \frac{\sigma({\mathcal A}_{T_0})\cdot \mu_{\delta_0}}{2} \geq \frac{ a\cdot \mu_{\delta_0}}{2}, \end{align*} $$
$$ \begin{align*} \liminf_{N\to\infty}\inf_{Q\in {\mathbb N}} \Re\Big({\mathbb E}_{m,n\in[N]}\int_{{\mathcal A}_{T_0}} A_{\delta_0}(f,Q;m,n)\, d\sigma(f)\Big)\geq \frac{\sigma({\mathcal A}_{T_0})\cdot \mu_{\delta_0}}{2} \geq \frac{ a\cdot \mu_{\delta_0}}{2}, \end{align*} $$
where we used that
![]() $1\in {\mathcal M}_{T_0}$
; hence,
$1\in {\mathcal M}_{T_0}$
; hence,
![]() $\sigma ({\mathcal A}_{T_0})\geq \sigma (\{1\})=a$
. However, using (4.11) and the triangle inequality, we get
$\sigma ({\mathcal A}_{T_0})\geq \sigma (\{1\})=a$
. However, using (4.11) and the triangle inequality, we get
 $$ \begin{align*} \limsup_{N\to\infty} \sup_{Q\in {\mathbb N}}\Big|{\mathbb E}_{m,n\in[N]}\int_{{\mathcal A}\setminus {\mathcal A}_{T_0}} A_{\delta_0}(f,Q;m,n)\, d\sigma(f)\Big|\leq \frac{a\cdot \mu_{\delta_0}}{4}. \end{align*} $$
$$ \begin{align*} \limsup_{N\to\infty} \sup_{Q\in {\mathbb N}}\Big|{\mathbb E}_{m,n\in[N]}\int_{{\mathcal A}\setminus {\mathcal A}_{T_0}} A_{\delta_0}(f,Q;m,n)\, d\sigma(f)\Big|\leq \frac{a\cdot \mu_{\delta_0}}{4}. \end{align*} $$
Combining the last two estimates, we deduce that (4.10) holds with
![]() $\rho _0:=\frac {a\cdot \mu _{\delta _0}}{4}$
.
$\rho _0:=\frac {a\cdot \mu _{\delta _0}}{4}$
.
5 Nonlinear concentration estimates
Our goal is to prove the concentration estimate of Proposition 2.11, which is a crucial ingredient in the proof of part (2) of Theorem 1.2 and in the proof of Theorem 1.5. In fact, we will prove a more general and quantitatively more explicit statement with further applications in mind.
Let
![]() $f,g\colon {\mathbb N}\to {\mathbb U}$
be multiplicative functions and let
$f,g\colon {\mathbb N}\to {\mathbb U}$
be multiplicative functions and let
![]() $\chi $
be a Dirichlet character and
$\chi $
be a Dirichlet character and
![]() $t\in {\mathbb R}.$
For every
$t\in {\mathbb R}.$
For every
![]() $K_0\in {\mathbb N}$
, we let
$K_0\in {\mathbb N}$
, we let
 $$ \begin{align} G_N(f,K_0):=2\sum_{\substack{ K_0< p\leq N,\\ p\equiv 1 \quad \pmod{4}}}\, \frac{1}{p}\,(f(p)\cdot \overline{\chi(p)}\cdot n^{-it} -1) \end{align} $$
$$ \begin{align} G_N(f,K_0):=2\sum_{\substack{ K_0< p\leq N,\\ p\equiv 1 \quad \pmod{4}}}\, \frac{1}{p}\,(f(p)\cdot \overline{\chi(p)}\cdot n^{-it} -1) \end{align} $$
and
 $$ \begin{align} {\mathbb D}_1(f,g; x,y)^2:= \sum_{\substack{x< p\leq y, \\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p}\, (1-\Re(f(p)\cdot \overline{g(p)})). \end{align} $$
$$ \begin{align} {\mathbb D}_1(f,g; x,y)^2:= \sum_{\substack{x< p\leq y, \\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p}\, (1-\Re(f(p)\cdot \overline{g(p)})). \end{align} $$
Proposition 5.1. Let
![]() $K_0,N\in {\mathbb N}$
and
$K_0,N\in {\mathbb N}$
and
![]() $f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function. Let also
$f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function. Let also
![]() $t\in {\mathbb R}$
,
$t\in {\mathbb R}$
,
![]() $\chi $
be a Dirichlet character with period q,
$\chi $
be a Dirichlet character with period q,
![]() $Q= \prod _{p\leq K_0}p^{a_p}$
for some
$Q= \prod _{p\leq K_0}p^{a_p}$
for some
![]() $a_p\in {\mathbb N}$
, and suppose that
$a_p\in {\mathbb N}$
, and suppose that
![]() $q\mid Q$
. If N is large enough, depending only on Q and t, then for all
$q\mid Q$
. If N is large enough, depending only on Q and t, then for all
![]() $a,b\in {\mathbb Z}$
with
$a,b\in {\mathbb Z}$
with
![]() $-Q\leq a,b\leq Q$
and
$-Q\leq a,b\leq Q$
and
![]() $(a^2+b^2,Q)=1$
, we have
$(a^2+b^2,Q)=1$
, we have
 $$ \begin{align} &\ \ {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big)- \chi(a^2+b^2)\cdot Q^{2it} \cdot (m^2+n^2)^{it}\cdot \exp\big(G_N(f,K_0)\big)\big|\ll \notag\\ & ({\mathbb D}_1+{\mathbb D}_1^2)(f,\chi\cdot n^{it}; K_0,\sqrt{N})+ Q^2\cdot\mathbb{D}_1(f,\chi\cdot n^{it};N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,\chi\cdot n^{it}; \sqrt{N},N)+K_0^{-1/2}, \end{align} $$
$$ \begin{align} &\ \ {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big)- \chi(a^2+b^2)\cdot Q^{2it} \cdot (m^2+n^2)^{it}\cdot \exp\big(G_N(f,K_0)\big)\big|\ll \notag\\ & ({\mathbb D}_1+{\mathbb D}_1^2)(f,\chi\cdot n^{it}; K_0,\sqrt{N})+ Q^2\cdot\mathbb{D}_1(f,\chi\cdot n^{it};N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,\chi\cdot n^{it}; \sqrt{N},N)+K_0^{-1/2}, \end{align} $$
where
![]() $G_N,{\mathbb D}_1$
are as in (5.1), (5.2), and the implicit constant is absolute.
$G_N,{\mathbb D}_1$
are as in (5.1), (5.2), and the implicit constant is absolute.
Remarks.
![]() $\circ $
Note that if
$\circ $
Note that if
![]() $f\sim \chi \cdot n^{it}$
, we have
$f\sim \chi \cdot n^{it}$
, we have
![]() $\lim _{N\to \infty } {\mathbb D}_1(f,\chi \cdot n^{it};N,3Q^2N^2)=0$
and
$\lim _{N\to \infty } {\mathbb D}_1(f,\chi \cdot n^{it};N,3Q^2N^2)=0$
and
![]() $\lim _{N\to \infty } {\mathbb D}_1(f,\chi \cdot n^{it}; \sqrt {N},N)=0$
. Hence, renaming
$\lim _{N\to \infty } {\mathbb D}_1(f,\chi \cdot n^{it}; \sqrt {N},N)=0$
. Hence, renaming
![]() $K_0$
as K, taking the max over all
$K_0$
as K, taking the max over all
![]() $Q\in \Phi _K$
, and then letting
$Q\in \Phi _K$
, and then letting
![]() $N\to \infty $
in (5.3) gives the estimate in Proposition 2.11.
$N\to \infty $
in (5.3) gives the estimate in Proposition 2.11.
![]() $\circ $
The averaging over both variables
$\circ $
The averaging over both variables
![]() $m,n\in \mathbb {N}$
is crucial for our argument and allows to overcome issues with large primes. In fact, by slightly modifying the example of [Reference Klurman34, Lemma 2.1], one can construct completely multiplicative functions (both pretentious and aperiodic)
$m,n\in \mathbb {N}$
is crucial for our argument and allows to overcome issues with large primes. In fact, by slightly modifying the example of [Reference Klurman34, Lemma 2.1], one can construct completely multiplicative functions (both pretentious and aperiodic)
![]() $f:\mathbb {N}\to \{-1,1\},$
such that for every
$f:\mathbb {N}\to \{-1,1\},$
such that for every
![]() $a\in {\mathbb Z}_+$
, the averages
$a\in {\mathbb Z}_+$
, the averages
behave rather ‘erratically’, and a similar concentration estimate fails. However, in [Reference Teräväinen48], Teräväinen proved a version of the concentration estimates for values of
![]() $f(P(Qn+a))$
, where
$f(P(Qn+a))$
, where
![]() $P\in \mathbb {Z}[x]$
is arbitrary and the multiplicative functions f satisfies
$P\in \mathbb {Z}[x]$
is arbitrary and the multiplicative functions f satisfies
![]() $f(p)=p^{it}\chi (p)$
for
$f(p)=p^{it}\chi (p)$
for
![]() $p>N$
(with a somewhat more particular choice of Q). In our setting, however, we cannot afford to make such assumptions on f.
$p>N$
(with a somewhat more particular choice of Q). In our setting, however, we cannot afford to make such assumptions on f.
The proof is carried out in several steps, covering progressively more general settings. Throughout the argument, we write
![]() $p\, \mid \mid \, n$
if
$p\, \mid \mid \, n$
if
![]() $p\mid n$
but
$p\mid n$
but
![]() $p^2 \nmid n$
.
$p^2 \nmid n$
.
5.1 Preparatory counting arguments
The following lemma will be used multiple times subsequently.
Lemma 5.2. For
![]() $Q,N\in {\mathbb N}$
,
$Q,N\in {\mathbb N}$
,
![]() $a,b\in {\mathbb Z}$
, and primes
$a,b\in {\mathbb Z}$
, and primes
![]() $p, q$
such that
$p, q$
such that
![]() $p,q\equiv 1 \ \pmod {4}$
and
$p,q\equiv 1 \ \pmod {4}$
and
![]() $(pq, Q)=1$
, let
$(pq, Q)=1$
, let
 $$ \begin{align} w_{N,Q}(p,q):=\frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ p,q\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1. \end{align} $$
$$ \begin{align} w_{N,Q}(p,q):=\frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ p,q\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1. \end{align} $$
Then
and if
![]() $p\neq q$
, we have
$p\neq q$
, we have
where the implicit constants are absolute.
Remark. We deduce the approximate identity
which is crucial for the proof of the concentration estimates. However, because of the
![]() $O\big (\frac {1}{N}\big )$
errors, these approximate identities will only be useful to us for sums that contain
$O\big (\frac {1}{N}\big )$
errors, these approximate identities will only be useful to us for sums that contain
![]() $o(N)$
terms.
$o(N)$
terms.
Proof. Throught the discussion, we use
![]() $\epsilon $
to designate a number in
$\epsilon $
to designate a number in
![]() $\{0,1,2,3,4\}$
.
$\{0,1,2,3,4\}$
.
We first establish (5.5). Let p satisfy the assumptions. Note first that if
![]() $p\mid Qn+b$
and
$p\mid Qn+b$
and
![]() $p\mid (Qm+a)^2+(Qn+b)^2$
, then also
$p\mid (Qm+a)^2+(Qn+b)^2$
, then also
![]() $p^2\mid (Qm+a)^2+(Qn+b)^2$
; hence, we get no contribution to the sum (5.4) in this case. So we can assume that
$p^2\mid (Qm+a)^2+(Qn+b)^2$
; hence, we get no contribution to the sum (5.4) in this case. So we can assume that
![]() $p\nmid Qn+b$
. Since
$p\nmid Qn+b$
. Since
![]() $p\equiv 1 \ \pmod 4$
, the number
$p\equiv 1 \ \pmod 4$
, the number
![]() $-1$
is a quadratic residue
$-1$
is a quadratic residue
![]() $\! \! \! \mod {p}$
, and we have exactly two solutions
$\! \! \! \mod {p}$
, and we have exactly two solutions
![]() $m \ \pmod {p}$
to the congruence
$m \ \pmod {p}$
to the congruence
Hence, for those
![]() $n\in [N]$
, we have
$n\in [N]$
, we have
![]() $2[N/p]+\epsilon $
solutions in the variable
$2[N/p]+\epsilon $
solutions in the variable
![]() $m\in [N]$
to (5.7). Since there are
$m\in [N]$
to (5.7). Since there are
![]() $N-[N/p]+\epsilon $
integers
$N-[N/p]+\epsilon $
integers
![]() $n\in [N]$
with
$n\in [N]$
with
![]() $p\nmid Qn+b$
(we used that
$p\nmid Qn+b$
(we used that
![]() $(p,Q)=1$
here), we get a total of
$(p,Q)=1$
here), we get a total of
solutions of
![]() $m,n\in [N]$
to the congruence (5.7). Similarly, we get that if
$m,n\in [N]$
to the congruence (5.7). Similarly, we get that if
![]() $p\nmid Qn+b$
, then the number of solutions
$p\nmid Qn+b$
, then the number of solutions
![]() $m,n\in [N]$
to the congruence
$m,n\in [N]$
to the congruence
![]() $(Qm+a)^2+(Qn+b)^2\equiv 0 \ \pmod {p^2}$
is
$(Qm+a)^2+(Qn+b)^2\equiv 0 \ \pmod {p^2}$
is
(We used that
![]() $-1$
is also a quadratic residue
$-1$
is also a quadratic residue
![]() $\! \! \! \mod {p^2}$
.) These solutions should be subtracted from the previous solutions of (5.7) in order to count the number of solutions of
$\! \! \! \mod {p^2}$
.) These solutions should be subtracted from the previous solutions of (5.7) in order to count the number of solutions of
![]() $m,n\in [N]$
for which
$m,n\in [N]$
for which
![]() $p\, \mid \mid \, (Qm+a)^2+(Qn+b)^2$
. We deduce that
$p\, \mid \mid \, (Qm+a)^2+(Qn+b)^2$
. We deduce that
 $$ \begin{align} \frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1=\frac{2}{p}-\frac{4}{p^2}+\frac{2}{p^3}+O\Big(\frac{1}{N}\Big)=\frac{2}{p}\Big(1-\frac{1}{p}\Big)^2 + O\Big(\frac{1}{N}\Big), \end{align} $$
$$ \begin{align} \frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1=\frac{2}{p}-\frac{4}{p^2}+\frac{2}{p^3}+O\Big(\frac{1}{N}\Big)=\frac{2}{p}\Big(1-\frac{1}{p}\Big)^2 + O\Big(\frac{1}{N}\Big), \end{align} $$
which proves (5.5).
Next, we establish (5.6). Let
![]() $p,q $
satisfy the assumptions. As explained in the previous case, those
$p,q $
satisfy the assumptions. As explained in the previous case, those
![]() $n\in [N]$
for which
$n\in [N]$
for which
![]() $p\mid Qn+b$
or
$p\mid Qn+b$
or
![]() $q\mid Qn+b$
do not contribute to the sum (5.4) defining
$q\mid Qn+b$
do not contribute to the sum (5.4) defining
![]() $w_{N,Q}(p,q)$
; hence, we can assume that
$w_{N,Q}(p,q)$
; hence, we can assume that
![]() $(pq,Qn+b)=1$
. Let
$(pq,Qn+b)=1$
. Let
 $$ \begin{align*} A_{r,s}:=\frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ r,s\mid (Qm+a)^2+(Qn+b)^2,\, (rs,Qn+b)=1 }} 1 \end{align*} $$
$$ \begin{align*} A_{r,s}:=\frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ r,s\mid (Qm+a)^2+(Qn+b)^2,\, (rs,Qn+b)=1 }} 1 \end{align*} $$
and note that
We first compute
![]() $A_{p,q}$
. Since
$A_{p,q}$
. Since
![]() $p{\kern-1pt}\equiv{\kern-1pt} q{\kern-1pt}\equiv{\kern-1pt} 1 \ \pmod 4$
, the number
$p{\kern-1pt}\equiv{\kern-1pt} q{\kern-1pt}\equiv{\kern-1pt} 1 \ \pmod 4$
, the number
![]() $-1$
is a quadratic residue
$-1$
is a quadratic residue
![]() $\! \! \! \mod {p}$
and
$\! \! \! \mod {p}$
and
![]() $\! \! \! \mod {q}$
, and we get by the Chinese remainder theorem, that for each
$\! \! \! \mod {q}$
, and we get by the Chinese remainder theorem, that for each
![]() $n\in [N]$
with
$n\in [N]$
with
![]() $p,q\nmid Qn+b$
, we have
$p,q\nmid Qn+b$
, we have
![]() $4$
solutions
$4$
solutions
![]() $m \ \pmod {pq}$
to the congruence
$m \ \pmod {pq}$
to the congruence
WeFootnote 8 deduce that for each
![]() $n\in [N]$
with
$n\in [N]$
with
![]() $(pq,Qn+b)=1$
, we have
$(pq,Qn+b)=1$
, we have
![]() $4[N/(pq)]+\epsilon $
solutions in the variable
$4[N/(pq)]+\epsilon $
solutions in the variable
![]() $m \in [N]$
to the congruence (5.10). Since the number of
$m \in [N]$
to the congruence (5.10). Since the number of
![]() $n\in [N]$
for which
$n\in [N]$
for which
![]() $(pq,Qn+b)=1$
is
$(pq,Qn+b)=1$
is
![]() $N-[N/p]-[N/q]+[N/pq]$
, we get that the total number of solutions to the congruence (5.10) with
$N-[N/p]-[N/q]+[N/pq]$
, we get that the total number of solutions to the congruence (5.10) with
![]() $m,n\in [N]$
and
$m,n\in [N]$
and
![]() $(pq,n)=1$
is
$(pq,n)=1$
is
 $$ \begin{align} &4 [N/(pq)] \, (N-[N/p]-[N/q]+[N/(pq)])+ O(N)= \notag\\ &\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad N^2 \cdot (4/(pq))\cdot (1-1/p-1/q+1/(pq)) +O(N). \end{align} $$
$$ \begin{align} &4 [N/(pq)] \, (N-[N/p]-[N/q]+[N/(pq)])+ O(N)= \notag\\ &\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad N^2 \cdot (4/(pq))\cdot (1-1/p-1/q+1/(pq)) +O(N). \end{align} $$
Hence,
Similarly, using that
![]() $-1$
is also a quadratic residue
$-1$
is also a quadratic residue
![]() $\mod {p^k}$
and
$\mod {p^k}$
and
![]() $\mod {q^k}$
for
$\mod {q^k}$
for
![]() $k=1,2$
, we find that
$k=1,2$
, we find that
and
Also,
Using the last four identities and (5.9), we deduce that (5.6) holds. This completes the proof.
We will also need to give upper bounds for
![]() $w_{N,Q}(p,q)$
when
$w_{N,Q}(p,q)$
when
![]() $p,q$
are not necessarily primes, and also give upper bounds that do not involve the error terms
$p,q$
are not necessarily primes, and also give upper bounds that do not involve the error terms
![]() $O(1/N)$
that cause us problems in some cases (this is only relevant when
$O(1/N)$
that cause us problems in some cases (this is only relevant when
![]() $pq\geq N$
). The next lemma is crucial for us and gives an upper bound that is good enough for our purposes.
$pq\geq N$
). The next lemma is crucial for us and gives an upper bound that is good enough for our purposes.
Lemma 5.3. For
![]() $l, Q,N \in {\mathbb N}$
and
$l, Q,N \in {\mathbb N}$
and
![]() $a,b\in {\mathbb Z}$
with
$a,b\in {\mathbb Z}$
with
![]() $-Q\leq a,b\leq Q$
, let
$-Q\leq a,b\leq Q$
, let
 $$ \begin{align*} w_{N,Q}(l):=\frac{1}{N^2} \, \sum_{\substack{m,n\in [N],\\ l\mid (Qm+a)^2+(Qn+b)^2} } 1. \end{align*} $$
$$ \begin{align*} w_{N,Q}(l):=\frac{1}{N^2} \, \sum_{\substack{m,n\in [N],\\ l\mid (Qm+a)^2+(Qn+b)^2} } 1. \end{align*} $$
If l is a sum of two squares, then
where the implicit constant is absolute. In particular, if
![]() $w_{N,Q}(p,q)$
is as in (5.4), taking
$w_{N,Q}(p,q)$
is as in (5.4), taking
![]() $l=p$
and
$l=p$
and
![]() $l=pq$
where
$l=pq$
where
![]() $p, q$
are distinct primes of the form
$p, q$
are distinct primes of the form
![]() $1 \ \pmod {4}$
, we get
$1 \ \pmod {4}$
, we get
 $$ \begin{align} w_{N,Q}(p,p)\ll \frac{Q^2}{p}, \quad w_{N,Q}(p,q)\ll \frac{Q^2}{pq}. \end{align} $$
$$ \begin{align} w_{N,Q}(p,p)\ll \frac{Q^2}{p}, \quad w_{N,Q}(p,q)\ll \frac{Q^2}{pq}. \end{align} $$
Remark. These estimates will allow us to show later that the contribution of the
![]() $m,n\in [N]$
for which
$m,n\in [N]$
for which
![]() $(Qm+a)^2+(Qn+b)^2$
have large prime divisors (say
$(Qm+a)^2+(Qn+b)^2$
have large prime divisors (say
![]() $\geq \sqrt {N}$
) is negligible for our purposes. In contrast, we could not have done the same for the
$\geq \sqrt {N}$
) is negligible for our purposes. In contrast, we could not have done the same for the
![]() $n\in [N]$
for which
$n\in [N]$
for which
![]() $n^2+1$
have large prime divisors.
$n^2+1$
have large prime divisors.
Proof. Recall that an integer is a sum of two squares if and only if in its factorization as a product of primes, all prime factors congruent to
![]() $3 \ \pmod {4}$
occur with even multiplicity. It follows that if l is a sum of two squares and
$3 \ \pmod {4}$
occur with even multiplicity. It follows that if l is a sum of two squares and
![]() $l\mid (Qm+a)^2+(Qn+b)^2$
, then the ratio
$l\mid (Qm+a)^2+(Qn+b)^2$
, then the ratio
![]() $\big ((Qm+a)^2+(Qn+b)^2\big )/l$
is also a sum of two squares. We deduce from this and our assumption
$\big ((Qm+a)^2+(Qn+b)^2\big )/l$
is also a sum of two squares. We deduce from this and our assumption
![]() $|a|,|b|\leq Q$
that if l is a sum of two squares, then
$|a|,|b|\leq Q$
that if l is a sum of two squares, then
 $$ \begin{align*} w_{N,Q}(l)\leq \frac{1}{N^2}\, \sum_{k\leq 3Q^2N^2/l}r_2(k)\ll \frac{Q^2}{l}, \end{align*} $$
$$ \begin{align*} w_{N,Q}(l)\leq \frac{1}{N^2}\, \sum_{k\leq 3Q^2N^2/l}r_2(k)\ll \frac{Q^2}{l}, \end{align*} $$
where
![]() $r_2(k)$
denotes the number of representations of k as a sum of two squares, and to get the second estimate, we used the well-known fact
$r_2(k)$
denotes the number of representations of k as a sum of two squares, and to get the second estimate, we used the well-known fact
![]() $\sum _{k\le n}r_2(k)\ll n$
. This completes the proof.
$\sum _{k\le n}r_2(k)\ll n$
. This completes the proof.
5.2 Concentration estimate for additive functions
We start with a concentration estimate for additive functions that will eventually get lifted to a concentration estimate for multiplicative functions.
Definition 5.1. We say that
![]() $h\colon \mathbb {N}\to \mathbb {C}$
is additive if it satisfies
$h\colon \mathbb {N}\to \mathbb {C}$
is additive if it satisfies
![]() $h(mn)=h(m) +h(n)$
whenever
$h(mn)=h(m) +h(n)$
whenever
![]() $(m,n)=1$
.
$(m,n)=1$
.
Lemma 5.4 (Turán-Kubilius inequality for sums of squares)
Let
![]() $K_0,N\in {\mathbb N}$
,
$K_0,N\in {\mathbb N}$
,
![]() $a,b\in {\mathbb Z}$
with
$a,b\in {\mathbb Z}$
with
![]() $-Q\leq a,b,\leq Q$
, and
$-Q\leq a,b,\leq Q$
, and
![]() $h\colon \mathbb {N}\to \mathbb {C}$
be an additive function that is bounded by
$h\colon \mathbb {N}\to \mathbb {C}$
be an additive function that is bounded by
![]() $1$
on primes and such that
$1$
on primes and such that
-
1.
 $h(p)=0$
for all primes
$h(p)=0$
for all primes
 $p\leq K_0$
and
$p\leq K_0$
and
 $p>N$
;
$p>N$
; -
2.
 $h(p)=0$
for all primes
$h(p)=0$
for all primes
 $p\equiv 3 \ \pmod 4$
;
$p\equiv 3 \ \pmod 4$
; -
3.
 $h(p^k)=0$
for all primes p and
$h(p^k)=0$
for all primes p and
 $k\geq 2$
.
$k\geq 2$
.
Let also
![]() $Q= \prod _{p\leq K_0}p^{a_p}$
for some
$Q= \prod _{p\leq K_0}p^{a_p}$
for some
![]() $a_p\in {\mathbb N}$
. Then for all large enough N, depending only on
$a_p\in {\mathbb N}$
. Then for all large enough N, depending only on
![]() $K_0$
, we have
$K_0$
, we have
where the implicit constant is absolute,
 $$ \begin{align} H_N(h,K_0):=2\, \sum_{K_0< p\leq N}\, \frac{h(p)}{p} \end{align} $$
$$ \begin{align} H_N(h,K_0):=2\, \sum_{K_0< p\leq N}\, \frac{h(p)}{p} \end{align} $$
and
 $$ \begin{align*} {\mathbb D}^2(h; K_0,N):=\sum_{K_0< p\leq N} \frac{|h(p)|^2}{p}. \end{align*} $$
$$ \begin{align*} {\mathbb D}^2(h; K_0,N):=\sum_{K_0< p\leq N} \frac{|h(p)|^2}{p}. \end{align*} $$
Proof. We consider the additive functions
![]() $h_1,h_2$
, which are the restrictions of h to the primes
$h_1,h_2$
, which are the restrictions of h to the primes
![]() ${K_0<p\le \sqrt {N}}$
and
${K_0<p\le \sqrt {N}}$
and
![]() $\sqrt {N}<p\le N$
.Footnote 9 More precisely,
$\sqrt {N}<p\le N$
.Footnote 9 More precisely,
 $$ \begin{align*} h_1(p^k):= \begin{cases}h(p), \quad &\text{if }\ k=1 \text{ and } K_0<p\leq \sqrt{N}\\ 0, \quad &\text{otherwise} \end{cases} \end{align*} $$
$$ \begin{align*} h_1(p^k):= \begin{cases}h(p), \quad &\text{if }\ k=1 \text{ and } K_0<p\leq \sqrt{N}\\ 0, \quad &\text{otherwise} \end{cases} \end{align*} $$
and
 $$ \begin{align*} h_2(p^k):=\begin{cases}h(p), \quad &\text{if }\ k=1 \text{ and } \sqrt{N}<p\leq N\\ 0, \quad &\text{otherwise} \end{cases}. \end{align*} $$
$$ \begin{align*} h_2(p^k):=\begin{cases}h(p), \quad &\text{if }\ k=1 \text{ and } \sqrt{N}<p\leq N\\ 0, \quad &\text{otherwise} \end{cases}. \end{align*} $$
We also define
 $$ \begin{align} H_{i,N}(h_i,K_0):=2\sum_{K_0< p\leq N}\, \frac{h_i(p)}{p}, \quad i=1,2, \end{align} $$
$$ \begin{align} H_{i,N}(h_i,K_0):=2\sum_{K_0< p\leq N}\, \frac{h_i(p)}{p}, \quad i=1,2, \end{align} $$
and the technical variant
where
 $$ \begin{align} w_{N,Q}(p):= \frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1. \end{align} $$
$$ \begin{align} w_{N,Q}(p):= \frac{1}{N^2}\, \sum_{\substack{m,n\in [N],\\ p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1. \end{align} $$
(Note that
![]() $w_{N,Q}(p)=w_{N,Q}(p,p)$
, where
$w_{N,Q}(p)=w_{N,Q}(p,p)$
, where
![]() $w_{N,Q}(p,q)$
is as in (5.4).) The reason for introducing this variant is because it gives the mean value of
$w_{N,Q}(p,q)$
is as in (5.4).) The reason for introducing this variant is because it gives the mean value of
![]() $h_1$
along sums of squares. Indeed, using properties (1)–(3), we have
$h_1$
along sums of squares. Indeed, using properties (1)–(3), we have
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}\, h_1 ((Qm+a)^2 &+(Qn+b)^2)={\mathbb E}_{m,n\in [N]}\, \sum_{p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2}h_1(p)\notag\\ &\qquad =\frac{1}{N^2} \sum_{K_0< p \leq N} h_1(p) \, \sum_{\substack{m,n\in [N],\\ p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1 = H^{\prime}_{1,N}(h_1,Q,K_0). \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}\, h_1 ((Qm+a)^2 &+(Qn+b)^2)={\mathbb E}_{m,n\in [N]}\, \sum_{p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2}h_1(p)\notag\\ &\qquad =\frac{1}{N^2} \sum_{K_0< p \leq N} h_1(p) \, \sum_{\substack{m,n\in [N],\\ p\, \mid\mid\, (Qm+a)^2+(Qn+b)^2} } 1 = H^{\prime}_{1,N}(h_1,Q,K_0). \end{align} $$
Using (5.5) of Lemma 5.2 and that
![]() $h_1(p)=0$
for
$h_1(p)=0$
for
![]() $p> \sqrt {N}$
and
$p> \sqrt {N}$
and
![]() $h_1(p)$
is bounded by
$h_1(p)$
is bounded by
![]() $1$
, we get
$1$
, we get
 $$ \begin{align} |H_{1,N}(h_1,K_0)-H^{\prime}_{1,N}(h_1,Q,K_0)|\ll \sum_{K_0< p\leq \sqrt{N}} \frac{1}{p^2}+\frac{1}{\sqrt{N}} \leq \frac{1}{K_0} +\frac{1}{\sqrt{N}}. \end{align} $$
$$ \begin{align} |H_{1,N}(h_1,K_0)-H^{\prime}_{1,N}(h_1,Q,K_0)|\ll \sum_{K_0< p\leq \sqrt{N}} \frac{1}{p^2}+\frac{1}{\sqrt{N}} \leq \frac{1}{K_0} +\frac{1}{\sqrt{N}}. \end{align} $$
Hence, in order to prove (5.14), it suffices to estimate
and
We first deal with the expression (5.21). Using (5.19) and expanding the square below, we get
 $$ \begin{align} {\mathbb E}_{m,n\in [N]} \, \big|h_1((Qm+a)^2 &+(Qn+b)^2)- H^{\prime}_{1,N}(h_1,Q,K_0)\big|^2=\notag\\ &\quad {\mathbb E}_{m,n\in [N]}\, \big|h_1((Qm+a)^2+(Qn+b)^2)\big|^2 - |H^{\prime}_{1,N}(h_1,Q,K_0)|^2. \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]} \, \big|h_1((Qm+a)^2 &+(Qn+b)^2)- H^{\prime}_{1,N}(h_1,Q,K_0)\big|^2=\notag\\ &\quad {\mathbb E}_{m,n\in [N]}\, \big|h_1((Qm+a)^2+(Qn+b)^2)\big|^2 - |H^{\prime}_{1,N}(h_1,Q,K_0)|^2. \end{align} $$
To estimate this expression, first note that since
![]() $h_1$
is additive and
$h_1$
is additive and
![]() $h_1(p^k)=0$
for
$h_1(p^k)=0$
for
![]() $k\geq 2$
, we have
$k\geq 2$
, we have
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}\, \big|h_1((Qm+a)^2+(Qn+b)^2)\big|^2= {\mathbb E}_{m,n\in [N]}\, \Big|\sum_{p\, \mid \mid \,(Qm+a)^2+(Qn+b)^2} h_1(p)\Big|^2. \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}\, \big|h_1((Qm+a)^2+(Qn+b)^2)\big|^2= {\mathbb E}_{m,n\in [N]}\, \Big|\sum_{p\, \mid \mid \,(Qm+a)^2+(Qn+b)^2} h_1(p)\Big|^2. \end{align} $$
Expanding the square, using the fact that
![]() $h_1(p)=0$
unless
$h_1(p)=0$
unless
![]() $K_0<p\leq \sqrt {N}$
, and the definition of
$K_0<p\leq \sqrt {N}$
, and the definition of
![]() $w_{N,Q}(p,q)$
given in (5.4), we get that the right-hand side is equal to
$w_{N,Q}(p,q)$
given in (5.4), we get that the right-hand side is equal to
 $$ \begin{align*} \sum_{K_0<p\leq \sqrt{N}} |h_1(p)|^2\cdot w_{N,Q}(p,p)+ \sum_{K_0<p,q\leq \sqrt{N}, \, p\neq q} h_1(p)\cdot \overline{h_1(q)}\cdot w_{N,Q}(p,q). \end{align*} $$
$$ \begin{align*} \sum_{K_0<p\leq \sqrt{N}} |h_1(p)|^2\cdot w_{N,Q}(p,p)+ \sum_{K_0<p,q\leq \sqrt{N}, \, p\neq q} h_1(p)\cdot \overline{h_1(q)}\cdot w_{N,Q}(p,q). \end{align*} $$
Using equation (5.5) of Lemma 5.2, we get that the first term is at most
 $$ \begin{align*} 2\cdot \sum_{K_0<p\leq \sqrt{N}}\frac{|h_1(p)|^2}{p}+ O(N^{-1/2}). \end{align*} $$
$$ \begin{align*} 2\cdot \sum_{K_0<p\leq \sqrt{N}}\frac{|h_1(p)|^2}{p}+ O(N^{-1/2}). \end{align*} $$
Using equations (5.5) and (5.6) of Lemma 5.2, we get that the second term is equal to (we crucially use the bound
![]() $p,q\leq \sqrt {N}$
here and the prime number theorem)
$p,q\leq \sqrt {N}$
here and the prime number theorem)
 $$ \begin{align*} \sum_{K_0<p,q\leq \sqrt{N}, \, p\neq q} h_1(p)\cdot \overline{h_1(q)} \cdot w_{N,Q}(p,p)\cdot w_{N,Q}(q,q) &+O((\log{N})^{-2})\leq \\ &\quad (H^{\prime}_{1,N}(h_1,Q,K_0))^2+O((\log{N})^{-2}), \end{align*} $$
$$ \begin{align*} \sum_{K_0<p,q\leq \sqrt{N}, \, p\neq q} h_1(p)\cdot \overline{h_1(q)} \cdot w_{N,Q}(p,p)\cdot w_{N,Q}(q,q) &+O((\log{N})^{-2})\leq \\ &\quad (H^{\prime}_{1,N}(h_1,Q,K_0))^2+O((\log{N})^{-2}), \end{align*} $$
where to get the last estimate, we added to the sum the contribution of the diagonal terms
![]() $p=q$
(which is nonnegative), and used (5.17) and the fact that
$p=q$
(which is nonnegative), and used (5.17) and the fact that
![]() $h_1(p)=0$
for
$h_1(p)=0$
for
![]() $p>\sqrt {N}$
. Combining (5.23) with the previous estimates, we are led to the bound
$p>\sqrt {N}$
. Combining (5.23) with the previous estimates, we are led to the bound
 $$ \begin{align} {\mathbb E}_{m,n\in [N]} \, \big|h_1((Qm+a)^2+(Qn+b)^2)- H^{\prime}_{1,N}(h_1,Q,K_0)\big|^2 &\ll \notag\\ &{\mathbb D}^2(h_1; K_0, \sqrt{N})+O((\log{N})^{-2}). \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]} \, \big|h_1((Qm+a)^2+(Qn+b)^2)- H^{\prime}_{1,N}(h_1,Q,K_0)\big|^2 &\ll \notag\\ &{\mathbb D}^2(h_1; K_0, \sqrt{N})+O((\log{N})^{-2}). \end{align} $$
Next, we estimate the expression (5.22). Since
![]() $h_2$
is additive and satisfies properties (1)–(3), we get using (5.24) (with
$h_2$
is additive and satisfies properties (1)–(3), we get using (5.24) (with
![]() $h_2$
in place of
$h_2$
in place of
![]() $h_1$
) and expanding the square
$h_1$
) and expanding the square
 $$ \begin{align*} {\mathbb E}_{m,n\in [N]} \, \big|h_2((Qm+a)^2+(Qn+b)^2)\big|^2= \sum_{\sqrt{N}< p, q \leq N} h_2(p)\, \overline{h_2(q)} \, w_{N,Q}(p,q). \end{align*} $$
$$ \begin{align*} {\mathbb E}_{m,n\in [N]} \, \big|h_2((Qm+a)^2+(Qn+b)^2)\big|^2= \sum_{\sqrt{N}< p, q \leq N} h_2(p)\, \overline{h_2(q)} \, w_{N,Q}(p,q). \end{align*} $$
Since
![]() $h_2(p)\neq 0$
only when
$h_2(p)\neq 0$
only when
![]() $p\equiv 1 \ \pmod {4}$
, using (5.13) of Lemma 5.3, we get that the right-hand side is bounded by
$p\equiv 1 \ \pmod {4}$
, using (5.13) of Lemma 5.3, we get that the right-hand side is bounded by
 $$ \begin{align*} \ll Q^2&\cdot \Big(\sum_{\sqrt{N}< p,q\leq N} \frac{|h_2(p)| \, |h_2(q)|}{pq}+ \sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|^2}{p}\Big)= \\ &\qquad\qquad\qquad\qquad Q^2\cdot \Big(\Big(\sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|}{p}\Big)^2+{\mathbb D}^2(h_2; \sqrt{N},N) \Big)\leq \\ &\qquad\qquad Q^2 \cdot \Big(\sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|^2}{p}\cdot \sum_{\sqrt{N}< p\leq N} \frac{1}{p}+{\mathbb D}^2(h_2; \sqrt{N},N) \Big)\ll Q^2\cdot {\mathbb D}^2(h_2; \sqrt{N},N), \end{align*} $$
$$ \begin{align*} \ll Q^2&\cdot \Big(\sum_{\sqrt{N}< p,q\leq N} \frac{|h_2(p)| \, |h_2(q)|}{pq}+ \sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|^2}{p}\Big)= \\ &\qquad\qquad\qquad\qquad Q^2\cdot \Big(\Big(\sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|}{p}\Big)^2+{\mathbb D}^2(h_2; \sqrt{N},N) \Big)\leq \\ &\qquad\qquad Q^2 \cdot \Big(\sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|^2}{p}\cdot \sum_{\sqrt{N}< p\leq N} \frac{1}{p}+{\mathbb D}^2(h_2; \sqrt{N},N) \Big)\ll Q^2\cdot {\mathbb D}^2(h_2; \sqrt{N},N), \end{align*} $$
where we crucially used the estimate
 $$ \begin{align*} \sum_{\sqrt{N}< p\leq N} \frac{1}{p}\ll 1. \end{align*} $$
$$ \begin{align*} \sum_{\sqrt{N}< p\leq N} \frac{1}{p}\ll 1. \end{align*} $$
Similarly, we find
 $$ \begin{align*} (H_{2,N}(h_2,K_0))^2=4\, \Big(\sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|}{p}\Big)^2\ll {\mathbb D}^2(h_2; \sqrt{N},N). \end{align*} $$
$$ \begin{align*} (H_{2,N}(h_2,K_0))^2=4\, \Big(\sum_{\sqrt{N}< p\leq N} \frac{|h_2(p)|}{p}\Big)^2\ll {\mathbb D}^2(h_2; \sqrt{N},N). \end{align*} $$
Combining the previous estimates, we get the following bound for the expression in (5.22):
Combining the bounds (5.20), (5.25), (5.26), we get the asserted bound (5.14), completing the proof.
5.3 Concentration estimates for multiplicative functions
Next we use Lemma 5.4 to get a variant that deals with multiplicative functions.
Lemma 5.5. Let
![]() $K_0,N\in {\mathbb N}$
,
$K_0,N\in {\mathbb N}$
,
![]() $a,b\in {\mathbb Z}$
with
$a,b\in {\mathbb Z}$
with
![]() $-Q\leq a,b\leq Q$
, and
$-Q\leq a,b\leq Q$
, and
![]() $f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function that satisfies
$f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function that satisfies
-
1.
 $f(p)=1$
for all primes
$f(p)=1$
for all primes
 $p\leq K_0$
and
$p\leq K_0$
and
 $p> N$
;
$p> N$
; -
2.
 $f(p)=1$
for all primes
$f(p)=1$
for all primes
 $p\equiv 3 \ \pmod 4$
;
$p\equiv 3 \ \pmod 4$
; -
3.
 $f(p^k)=1$
for all primes p and
$f(p^k)=1$
for all primes p and
 $k\geq 2$
.
$k\geq 2$
.
Let also
![]() $Q= \prod _{p\leq K_0}p^{a_p}$
with
$Q= \prod _{p\leq K_0}p^{a_p}$
with
![]() $a_p\in {\mathbb N}$
. If N is large enough, depending only on
$a_p\in {\mathbb N}$
. If N is large enough, depending only on
![]() $K_0$
, then
$K_0$
, then
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big)- &\exp\big(G_N(f,K_0)\big)\big|\ll \notag\\ &({\mathbb D}+{\mathbb D}^2)(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big)- &\exp\big(G_N(f,K_0)\big)\big|\ll \notag\\ &({\mathbb D}+{\mathbb D}^2)(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
where the implicit constant is absolute and
 $$ \begin{align} G_N(f,K_0):=2\sum_{ K_0< p\leq N}\, \frac{1}{p}\,(f(p) -1). \end{align} $$
$$ \begin{align} G_N(f,K_0):=2\sum_{ K_0< p\leq N}\, \frac{1}{p}\,(f(p) -1). \end{align} $$
Proof. Let
![]() $h:\mathbb {N}\to \mathbb {C}$
be the additive function given on prime powers by
$h:\mathbb {N}\to \mathbb {C}$
be the additive function given on prime powers by
We note that due to our assumptions on
![]() $f,$
properties (1)–(3) of Lemma 5.4 are satisfied for
$f,$
properties (1)–(3) of Lemma 5.4 are satisfied for
![]() $h/2$
, which is bounded by
$h/2$
, which is bounded by
![]() $1$
on primes.
$1$
on primes.
Using that
![]() $z=e^{z-1}+O(|z-1|^2)$
for
$z=e^{z-1}+O(|z-1|^2)$
for
![]() $|z|\leq 1$
and property (3), we have
$|z|\leq 1$
and property (3), we have
 $$ \begin{align*} f(m^2+n^2)=\prod_{p^k\, \mid \mid \, m^2+n^2}f(p^k)= \prod_{p\, \mid \mid \, m^2+n^2}\big(\exp(h(p))+O(|h(p)|^2)\big). \end{align*} $$
$$ \begin{align*} f(m^2+n^2)=\prod_{p^k\, \mid \mid \, m^2+n^2}f(p^k)= \prod_{p\, \mid \mid \, m^2+n^2}\big(\exp(h(p))+O(|h(p)|^2)\big). \end{align*} $$
Applying the estimate
![]() $|\prod _{i\leq k}z_i-\prod _{i\leq k}w_i|\leq \sum _{i\leq k}|z_i-w_i|$
, we deduce that for all
$|\prod _{i\leq k}z_i-\prod _{i\leq k}w_i|\leq \sum _{i\leq k}|z_i-w_i|$
, we deduce that for all
![]() $m,n\in {\mathbb N}$
, we have
$m,n\in {\mathbb N}$
, we have
 $$ \begin{align*} f(m^2+n^2)=\exp(h(m^2+n^2))+O\Big(\sum_{p \, \mid \mid\, m^2+n^2}|h(p)|^2\Big). \end{align*} $$
$$ \begin{align*} f(m^2+n^2)=\exp(h(m^2+n^2))+O\Big(\sum_{p \, \mid \mid\, m^2+n^2}|h(p)|^2\Big). \end{align*} $$
Using this and since
![]() $G_N(f,K_0)=H_N(h, K_0)$
, where
$G_N(f,K_0)=H_N(h, K_0)$
, where
![]() $H_N(h,K_0)$
is given by (5.15), we get
$H_N(h,K_0)$
is given by (5.15), we get
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}\, &\big|f\big((Qm+a)^2+(Qn+b)^2\big)- \exp\big(G_N(f,K_0)\big)\big| \ll \notag\\ &\qquad {\mathbb E}_{m,n\in [N]}|\exp\big(h((Qm+a)^2+(Qn+b)^2)\big)-\exp(H_N(h, K_0))|+\notag\\ &\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad\qquad {\mathbb E}_{m,n\in [N]}\sum_{p\, \mid \mid\, (Qm+a)^2+(Qn+b)^2}|h(p)|^2. \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}\, &\big|f\big((Qm+a)^2+(Qn+b)^2\big)- \exp\big(G_N(f,K_0)\big)\big| \ll \notag\\ &\qquad {\mathbb E}_{m,n\in [N]}|\exp\big(h((Qm+a)^2+(Qn+b)^2)\big)-\exp(H_N(h, K_0))|+\notag\\ &\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad\qquad {\mathbb E}_{m,n\in [N]}\sum_{p\, \mid \mid\, (Qm+a)^2+(Qn+b)^2}|h(p)|^2. \end{align} $$
Next we use the inequality
![]() $|e^{z_1}-e^{z_2}|\le |z_1-z_2|$
, which is valid for
$|e^{z_1}-e^{z_2}|\le |z_1-z_2|$
, which is valid for
![]() $\Re z_1,\Re z_2\le 0$
, to bound the last expression by
$\Re z_1,\Re z_2\le 0$
, to bound the last expression by
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}|h((Qm+a)^2+(Qn+b)^2)-H_N(h,K_0)|+{\mathbb E}_{m,n\in [N]}\sum_{p \, \mid \mid \, (Qm+a)^2+(Qn+b)^2}|h(p)|^2. \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}|h((Qm+a)^2+(Qn+b)^2)-H_N(h,K_0)|+{\mathbb E}_{m,n\in [N]}\sum_{p \, \mid \mid \, (Qm+a)^2+(Qn+b)^2}|h(p)|^2. \end{align} $$
To bound the first term, we use Lemma 5.4. It gives that for all large enough N, depending on
![]() $K_0$
only, we have
$K_0$
only, we have
 $$ \begin{align} &{\mathbb E}_{m,n\in [N]}\, \big|h\big((Qm+a)^2+(Qn+b)^2\big)- H_N(h,K_0) \big|\ll\notag\\ &\quad {\mathbb D}(h; K_0,\sqrt{N})+Q\cdot {\mathbb D}(h; \sqrt{N},N)+K_0^{-\frac{1}{2}} \ll {\mathbb D}(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
$$ \begin{align} &{\mathbb E}_{m,n\in [N]}\, \big|h\big((Qm+a)^2+(Qn+b)^2\big)- H_N(h,K_0) \big|\ll\notag\\ &\quad {\mathbb D}(h; K_0,\sqrt{N})+Q\cdot {\mathbb D}(h; \sqrt{N},N)+K_0^{-\frac{1}{2}} \ll {\mathbb D}(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
where to get the last bound, we used that
![]() $|h(p)|^2\leq 2-2\,\Re (f(p))$
, which holds since
$|h(p)|^2\leq 2-2\,\Re (f(p))$
, which holds since
![]() $|f(p)|\leq 1$
. To bound the second term in (5.30), we note that using properties (1)–(3) of Lemma 5.4, we have
$|f(p)|\leq 1$
. To bound the second term in (5.30), we note that using properties (1)–(3) of Lemma 5.4, we have
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}&\sum_{p\, \mid \mid\, (Qm+a)^2+(Qn+b)^2} |h(p)|^2 = \sum_{ K_0< p \leq N}\ |h(p)|^2\, w_{N,Q}(p)\ll \notag \\ &\qquad\qquad \sum_{ K_0< p \leq N}\frac{|h(p)|^2}{p}+O((\log{N})^{-1}) \ll \mathbb{D}^2(f, 1;K_0,N)+O((\log{N})^{-1}) , \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}&\sum_{p\, \mid \mid\, (Qm+a)^2+(Qn+b)^2} |h(p)|^2 = \sum_{ K_0< p \leq N}\ |h(p)|^2\, w_{N,Q}(p)\ll \notag \\ &\qquad\qquad \sum_{ K_0< p \leq N}\frac{|h(p)|^2}{p}+O((\log{N})^{-1}) \ll \mathbb{D}^2(f, 1;K_0,N)+O((\log{N})^{-1}) , \end{align} $$
where
![]() $w_{N,P}(p)$
is as in (5.18) and we used equation (5.5) of Lemma 5.2 and the prime number theorem to get the first bound. Combining (5.29)–(5.32), we get the asserted bound.
$w_{N,P}(p)$
is as in (5.18) and we used equation (5.5) of Lemma 5.2 and the prime number theorem to get the first bound. Combining (5.29)–(5.32), we get the asserted bound.
We use the previous result to deduce the following improved version.
Lemma 5.6. Let
![]() $K_0,N\in {\mathbb N}$
and
$K_0,N\in {\mathbb N}$
and
![]() $f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function such that
$f\colon \mathbb {N}\to \mathbb {U}$
be a multiplicative function such that
![]() $f(p)= 1$
for all primes
$f(p)= 1$
for all primes
![]() $p> N$
with
$p> N$
with
![]() $p\equiv 1 \ \pmod {4}$
. Let also
$p\equiv 1 \ \pmod {4}$
. Let also
![]() $Q= \prod _{p\leq K_0}p^{a_p}$
with
$Q= \prod _{p\leq K_0}p^{a_p}$
with
![]() $a_p\in {\mathbb N}$
. If N is large enough, depending only on
$a_p\in {\mathbb N}$
. If N is large enough, depending only on
![]() $K_0$
, then for all
$K_0$
, then for all
![]() $a,b\in {\mathbb Z}$
with
$a,b\in {\mathbb Z}$
with
![]() $-Q\leq a,b\leq Q$
and
$-Q\leq a,b\leq Q$
and
![]() $(a^2+b^2,Q)=1$
, we have
$(a^2+b^2,Q)=1$
, we have
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big) &- \exp\big(G_N(f,K_0)\big)\big|\ll \notag \\ &\ ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big) &- \exp\big(G_N(f,K_0)\big)\big|\ll \notag \\ &\ ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
where the implicit constant is absolute and
 $$ \begin{align} G_N(f,K_0):=2\sum_{ \substack{K_0< p\leq N; \\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(f(p) -1),\end{align} $$
$$ \begin{align} G_N(f,K_0):=2\sum_{ \substack{K_0< p\leq N; \\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(f(p) -1),\end{align} $$
 $$ \begin{align*} {\mathbb D}_1(f,1; x,y)^2:= \sum_{\substack{x< p\leq y;\\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p}\, (1-\Re(f(p))) \end{align*} $$
$$ \begin{align*} {\mathbb D}_1(f,1; x,y)^2:= \sum_{\substack{x< p\leq y;\\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p}\, (1-\Re(f(p))) \end{align*} $$
for
![]() $x<y$
.
$x<y$
.
Proof. We first define the multiplicative function
![]() $\tilde {f}\colon {\mathbb N}\to {\mathbb U}$
on prime powers as follows
$\tilde {f}\colon {\mathbb N}\to {\mathbb U}$
on prime powers as follows
 $$ \begin{align*} \tilde{f}(p^k):= \begin{cases}f(p^k), \quad &\text{if }\ p> K_0\\ 1, \quad &\text{otherwise} \end{cases}. \end{align*} $$
$$ \begin{align*} \tilde{f}(p^k):= \begin{cases}f(p^k), \quad &\text{if }\ p> K_0\\ 1, \quad &\text{otherwise} \end{cases}. \end{align*} $$
Since
![]() $p\leq K_0$
implies
$p\leq K_0$
implies
![]() $p\mid Q$
and
$p\mid Q$
and
![]() $(a^2+b^2,Q)=1$
, we get that
$(a^2+b^2,Q)=1$
, we get that
![]() $p\nmid (Qm+a)^2+(Qn+b)^2$
for every
$p\nmid (Qm+a)^2+(Qn+b)^2$
for every
![]() $ p\leq K_0$
; hence,
$ p\leq K_0$
; hence,
Note also that
![]() $G_N(\tilde {f},Q)=G_N(f,Q)$
and
$G_N(\tilde {f},Q)=G_N(f,Q)$
and
![]() ${\mathbb D}_1(\tilde {f},1; K_0,N)={\mathbb D}_1(f,1;K_0,N)$
. It follows that in order to establish (5.33), it is enough to show that for all large enough N, depending only on
${\mathbb D}_1(\tilde {f},1; K_0,N)={\mathbb D}_1(f,1;K_0,N)$
. It follows that in order to establish (5.33), it is enough to show that for all large enough N, depending only on
![]() $K_0$
, we have
$K_0$
, we have
 $$ \begin{align} {\mathbb E}_{m,n\in [N]}|\tilde{f}((Qm+a)^2+(Qn+b)^2)&- \exp(G_N(\tilde{f},Q))|\ll \notag\\ &({\mathbb D}_1+{\mathbb D}_1^2)(\tilde{f},1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(\tilde{f},1; \sqrt{N},N)+ K_0^{-\frac{1}{2}}. \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in [N]}|\tilde{f}((Qm+a)^2+(Qn+b)^2)&- \exp(G_N(\tilde{f},Q))|\ll \notag\\ &({\mathbb D}_1+{\mathbb D}_1^2)(\tilde{f},1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(\tilde{f},1; \sqrt{N},N)+ K_0^{-\frac{1}{2}}. \end{align} $$
In order to establish (5.35), we make a series of further reductions that will eventually allow us to apply Lemma 5.5. For every
![]() $p\equiv 3 \ \pmod 4,$
we have that
$p\equiv 3 \ \pmod 4,$
we have that
![]() $p\mid m^2+n^2$
implies that
$p\mid m^2+n^2$
implies that
![]() $p\mid m$
and
$p\mid m$
and
![]() $p\mid n$
. Consequently, the contribution to the average of those
$p\mid n$
. Consequently, the contribution to the average of those
![]() $m,n\in [N]$
for which
$m,n\in [N]$
for which
![]() $(Qm+a)^2+(Qn+b)^2$
is divisible by some prime
$(Qm+a)^2+(Qn+b)^2$
is divisible by some prime
![]() $p\equiv 3 \ \pmod 4$
is (note that
$p\equiv 3 \ \pmod 4$
is (note that
![]() $(Qm+a)^2+(Qn+b)^2$
is only divisible by primes
$(Qm+a)^2+(Qn+b)^2$
is only divisible by primes
![]() $p>K_0$
)
$p>K_0$
)
 $$ \begin{align*} \ll \frac{1}{N^2}\sum_{K_0< p\leq N} \left[\frac{N}{p}\right]^2\ll \frac{1}{K_0}, \end{align*} $$
$$ \begin{align*} \ll \frac{1}{N^2}\sum_{K_0< p\leq N} \left[\frac{N}{p}\right]^2\ll \frac{1}{K_0}, \end{align*} $$
which is acceptable.
Next, we show that the contribution to the average in (5.35) of those
![]() $m,n\in [N]$
for which
$m,n\in [N]$
for which
![]() $ (Qm+a)^2+(Qn+b)^2$
is divisible by
$ (Qm+a)^2+(Qn+b)^2$
is divisible by
![]() $p^2$
for some prime
$p^2$
for some prime
![]() $p\equiv 1 \ \pmod 4$
with
$p\equiv 1 \ \pmod 4$
with
![]() $p>P_0$
(hence
$p>P_0$
(hence
![]() $p\nmid Q$
) is also acceptable. Indeed, for fixed
$p\nmid Q$
) is also acceptable. Indeed, for fixed
![]() $n\in [N]$
such that
$n\in [N]$
such that
![]() $p\nmid Qn+b$
, there exist at most
$p\nmid Qn+b$
, there exist at most
![]() $2[N/p^2]+2$
values of
$2[N/p^2]+2$
values of
![]() $m\in [N]$
such that
$m\in [N]$
such that
![]() $p^2\mid (Qm+a)^2+(Qn+b)^2.$
However, if
$p^2\mid (Qm+a)^2+(Qn+b)^2.$
However, if
![]() $p\mid Qn+b$
and
$p\mid Qn+b$
and
![]() $p\mid (Qm+a)^2+(Qn+b)^2$
, then also
$p\mid (Qm+a)^2+(Qn+b)^2$
, then also
![]() $p\mid Qm+a$
. Hence, the contribution to the average in (5.35) of those
$p\mid Qm+a$
. Hence, the contribution to the average in (5.35) of those
![]() $m,n\in [N]$
for which
$m,n\in [N]$
for which
![]() $ (Qm+a)^2+(Qn+b)^2$
is divisible by
$ (Qm+a)^2+(Qn+b)^2$
is divisible by
![]() $p^2$
for some prime
$p^2$
for some prime
![]() $p\equiv 1 \ \pmod 4$
is bounded by (note again that
$p\equiv 1 \ \pmod 4$
is bounded by (note again that
![]() $(Qm+a)^2+(Qn+b)^2$
is only divisible by primes
$(Qm+a)^2+(Qn+b)^2$
is only divisible by primes
![]() $p> K_0$
)
$p> K_0$
)
 $$ \begin{align*} \ll \frac{1}{N^2} \Big(\sum_{K_0< p\leq N}\Big(\left[\frac{N}{p^2}\right]+1\Big)N+\sum_{K_0< p\leq N}\left[\frac{N}{p}\right]^2\Big)\ll \frac{1}{K_0}+\frac{1}{\log{N}}, \end{align*} $$
$$ \begin{align*} \ll \frac{1}{N^2} \Big(\sum_{K_0< p\leq N}\Big(\left[\frac{N}{p^2}\right]+1\Big)N+\sum_{K_0< p\leq N}\left[\frac{N}{p}\right]^2\Big)\ll \frac{1}{K_0}+\frac{1}{\log{N}}, \end{align*} $$
where we used the prime number theorem to bound
![]() $\frac {1}{N}\sum _{K_0<p\leq N} 1$
.
$\frac {1}{N}\sum _{K_0<p\leq N} 1$
.
Combining the above reductions, we deduce that in order to establish the estimate (5.35), we may further assume that
We are now in a situation where Lemma 5.5 is applicable and gives that for all large enough N, depending only on
![]() $K_0$
, if
$K_0$
, if
![]() ${\mathbb D}_1(f,1;K_0,N)\leq 1$
, we have (note that (5.36) implies that
${\mathbb D}_1(f,1;K_0,N)\leq 1$
, we have (note that (5.36) implies that
![]() $\mathbb {D}_1(\tilde {f}, 1;K_0,N)=\mathbb {D}(\tilde {f}, 1;K_0,N)$
)
$\mathbb {D}_1(\tilde {f}, 1;K_0,N)=\mathbb {D}(\tilde {f}, 1;K_0,N)$
)
 $$ \begin{align*} {\mathbb E}_{m,n\in [N]}|\tilde{f}((Qm+a)^2+(Qn+b)^2)&- \exp(G_N(\tilde{f},K_0))|\ll \\ &\quad\quad ({\mathbb D}_1+{\mathbb D}_1^2)(\tilde{f},1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(\tilde{f},1; \sqrt{N},N)+K_0^{-\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} {\mathbb E}_{m,n\in [N]}|\tilde{f}((Qm+a)^2+(Qn+b)^2)&- \exp(G_N(\tilde{f},K_0))|\ll \\ &\quad\quad ({\mathbb D}_1+{\mathbb D}_1^2)(\tilde{f},1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(\tilde{f},1; \sqrt{N},N)+K_0^{-\frac{1}{2}}. \end{align*} $$
Combining this bound with the bounds we got in order to arrive to this reduction, we get that (5.35) is satisfied. This completes the proof.
5.4 Proof of Proposition 5.1
We start with some reductions. Suppose that the statement holds when
![]() $\chi =1$
and
$\chi =1$
and
![]() $t=0$
. We will show that it holds for arbitrary
$t=0$
. We will show that it holds for arbitrary
![]() $\chi $
and t. Let
$\chi $
and t. Let
![]() $\tilde {f}:=f \cdot \overline {\chi }\cdot n^{-it}$
, and apply the conclusion for
$\tilde {f}:=f \cdot \overline {\chi }\cdot n^{-it}$
, and apply the conclusion for
![]() $\chi =1, t=0$
. We get the following bound for
$\chi =1, t=0$
. We get the following bound for
![]() $\tilde {f}$
:
$\tilde {f}$
:
 $$ \begin{align} &{\mathbb E}_{m,n\in [N]}\, \big|\tilde{f}\big((Qm+a)^2+(Qn+b)^2\big)- \exp\big(G_N(\tilde{f},K_0)\big)\big|\ll \notag\\ &\qquad\quad ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+Q^2\cdot{\mathbb D}_1(f,1;N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-1/2}. \end{align} $$
$$ \begin{align} &{\mathbb E}_{m,n\in [N]}\, \big|\tilde{f}\big((Qm+a)^2+(Qn+b)^2\big)- \exp\big(G_N(\tilde{f},K_0)\big)\big|\ll \notag\\ &\qquad\quad ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+Q^2\cdot{\mathbb D}_1(f,1;N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-1/2}. \end{align} $$
Note that since
![]() $\chi $
is periodic with period q and
$\chi $
is periodic with period q and
![]() $q\mid Q$
, we have
$q\mid Q$
, we have
![]() $\chi ((Qm+a)^2+(Qn+b)^2)=\chi (a^2+b^2)$
for every
$\chi ((Qm+a)^2+(Qn+b)^2)=\chi (a^2+b^2)$
for every
![]() $m,n\in {\mathbb N}$
. Furthermore, since by assumption
$m,n\in {\mathbb N}$
. Furthermore, since by assumption
![]() $(a^2+b^2, Q)=1$
and
$(a^2+b^2, Q)=1$
and
![]() $q\mid Q$
, we have
$q\mid Q$
, we have
![]() $(a^2+b^2, q)=1$
; hence,
$(a^2+b^2, q)=1$
; hence,
![]() $|\chi (a^2+b^2)|=1$
. Also,
$|\chi (a^2+b^2)|=1$
. Also,
![]() $\lim _{m,n\to \infty }((Qm+a)^2+(Qn+b)^2)^{it}-Q^{2it}\cdot (m^2+n^2)^{it}=0$
and
$\lim _{m,n\to \infty }((Qm+a)^2+(Qn+b)^2)^{it}-Q^{2it}\cdot (m^2+n^2)^{it}=0$
and
![]() ${\mathbb D}_1(\tilde {f}, 1;x,y)={\mathbb D}_1(f, \chi \cdot n^{it};x,y)$
. Lastly, note that
${\mathbb D}_1(\tilde {f}, 1;x,y)={\mathbb D}_1(f, \chi \cdot n^{it};x,y)$
. Lastly, note that
 $$ \begin{align*} G_N(\tilde{f},K_0)=2\sum_{\substack{ K_0< p\leq N,\\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(\tilde{f}(p) -1)= 2\sum_{\substack{ K_0< p\leq N,\\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(f(p)\cdot \overline{\chi(p)}\cdot n^{-it} -1)=G_N(f,K_0). \end{align*} $$
$$ \begin{align*} G_N(\tilde{f},K_0)=2\sum_{\substack{ K_0< p\leq N,\\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(\tilde{f}(p) -1)= 2\sum_{\substack{ K_0< p\leq N,\\ p\equiv 1 \quad\pmod{4}}}\, \frac{1}{p}\,(f(p)\cdot \overline{\chi(p)}\cdot n^{-it} -1)=G_N(f,K_0). \end{align*} $$
After inserting this information in (5.37), we get that (5.3) is satisfied.
So it suffices to show that if
![]() $Q= \prod _{p\leq K_0}p^{a_p}$
for some
$Q= \prod _{p\leq K_0}p^{a_p}$
for some
![]() $a_p\in {\mathbb N}$
, then if N is large enough, depending only on Q, and
$a_p\in {\mathbb N}$
, then if N is large enough, depending only on Q, and
![]() ${\mathbb D}_1(f, 1;K_0,N)\leq 1$
, we have
${\mathbb D}_1(f, 1;K_0,N)\leq 1$
, we have
 $$ \begin{align} &{\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big)- \exp\big(G_N(f,K_0)\big)\big|\ll \notag\\ &\qquad ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q^2\cdot {\mathbb D}_1(f,1;N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-1/2}. \end{align} $$
$$ \begin{align} &{\mathbb E}_{m,n\in [N]}\, \big|f\big((Qm+a)^2+(Qn+b)^2\big)- \exp\big(G_N(f,K_0)\big)\big|\ll \notag\\ &\qquad ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q^2\cdot {\mathbb D}_1(f,1;N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-1/2}. \end{align} $$
For every
![]() $N\in {\mathbb N}$
, we decompose f as
$N\in {\mathbb N}$
, we decompose f as
![]() $f=f_{N,1} \cdot f_{N,2}$
, where the multiplicative functions
$f=f_{N,1} \cdot f_{N,2}$
, where the multiplicative functions
![]() $f_{N,1},f_{N,2}\colon {\mathbb N}\to {\mathbb U}$
are defined on prime powers as follows:
$f_{N,1},f_{N,2}\colon {\mathbb N}\to {\mathbb U}$
are defined on prime powers as follows:
 $$ \begin{align*} f_{N,1}(p^k):=& \begin{cases}f(p), \quad &\text{if }\ k=1 \text{ and } p> N,\, p\equiv 1 \quad\pmod{4} \\ 1, \quad &\text{otherwise} \end{cases}, \\ f_{N,2}(p^k):=& \begin{cases}1, \quad &\text{if }\ k=1 \text{ and } p> N, \, p\equiv 1 \quad\pmod{4} \\ f(p^k), \quad &\text{otherwise} \end{cases}. \end{align*} $$
$$ \begin{align*} f_{N,1}(p^k):=& \begin{cases}f(p), \quad &\text{if }\ k=1 \text{ and } p> N,\, p\equiv 1 \quad\pmod{4} \\ 1, \quad &\text{otherwise} \end{cases}, \\ f_{N,2}(p^k):=& \begin{cases}1, \quad &\text{if }\ k=1 \text{ and } p> N, \, p\equiv 1 \quad\pmod{4} \\ f(p^k), \quad &\text{otherwise} \end{cases}. \end{align*} $$
We first study the function
![]() $f_{N,1}$
. Following the notation of Lemma 5.3 for
$f_{N,1}$
. Following the notation of Lemma 5.3 for
![]() $l,Q,N\in {\mathbb N}$
, we let
$l,Q,N\in {\mathbb N}$
, we let
 $$ \begin{align*} w_{N,Q}(l):=\frac{1}{N^2} \, \sum_{\substack{m,n\in [N],\\ l\mid (Qm+a)^2+(Qn+b)^2} } 1. \end{align*} $$
$$ \begin{align*} w_{N,Q}(l):=\frac{1}{N^2} \, \sum_{\substack{m,n\in [N],\\ l\mid (Qm+a)^2+(Qn+b)^2} } 1. \end{align*} $$
Lemma 5.3 implies that if l is a sum of two squares, then
Since for
![]() $N\gg Q$
we have
$N\gg Q$
we have
![]() $f_{N,1}((Qm+a)^2+(Qn+b)^2)-1\neq 0$
only if
$f_{N,1}((Qm+a)^2+(Qn+b)^2)-1\neq 0$
only if
![]() $(Qm+a)^2+(Qn+b)^2$
is divisible by one or two primes
$(Qm+a)^2+(Qn+b)^2$
is divisible by one or two primes
![]() $p>N$
,Footnote 10 we get
$p>N$
,Footnote 10 we get
 $$ \begin{align} {\mathbb E}_{m,n\in[N]} &|f_{N,1}\big((Qm+a)^2+(Qn+b)^2\big)-1| \leq \notag\\ &\qquad \sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} |f(p)-1|\, w_{N,Q}(p) + \sum_{\substack{N<p,q\le 3Q^2N^2,\, p\neq q\\ p,q\equiv 1 \quad\pmod{4}}} |f(pq)-1|\, w_{N,Q}(pq), \end{align} $$
$$ \begin{align} {\mathbb E}_{m,n\in[N]} &|f_{N,1}\big((Qm+a)^2+(Qn+b)^2\big)-1| \leq \notag\\ &\qquad \sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} |f(p)-1|\, w_{N,Q}(p) + \sum_{\substack{N<p,q\le 3Q^2N^2,\, p\neq q\\ p,q\equiv 1 \quad\pmod{4}}} |f(pq)-1|\, w_{N,Q}(pq), \end{align} $$
where we used that
![]() $f_{N,1}(p)=f(p)$
for all
$f_{N,1}(p)=f(p)$
for all
![]() $p>N$
, and in the second sum, we have ignored the contribution of the diagonal terms
$p>N$
, and in the second sum, we have ignored the contribution of the diagonal terms
![]() $p=q$
since, by construction,
$p=q$
since, by construction,
![]() $f_{N,1}(p^2)=1$
for all primes p. Using (5.39) for
$f_{N,1}(p^2)=1$
for all primes p. Using (5.39) for
![]() $l:=p$
, which is a sum of two squares since
$l:=p$
, which is a sum of two squares since
![]() $p\equiv 1 \ \pmod {4}$
, we estimate the first term as follows:Footnote 11
$p\equiv 1 \ \pmod {4}$
, we estimate the first term as follows:Footnote 11
 $$ \begin{align*} \sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} &|f(p)-1|\, w_{N,Q}(p) \ll Q^2\sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} \frac{|f(p)-1|}{p}\leq \\[5pt] &\quad Q^2 \cdot \Big(\sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} \frac{|f(p)-1|^2}{p}\Big)^{\frac{1}{2}}\cdot \Big(\sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p} \Big)^{\frac{1}{2}} \ll Q^2\cdot {\mathbb D}_1(f,1;N,3Q^2N^2), \end{align*} $$
$$ \begin{align*} \sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} &|f(p)-1|\, w_{N,Q}(p) \ll Q^2\sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} \frac{|f(p)-1|}{p}\leq \\[5pt] &\quad Q^2 \cdot \Big(\sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} \frac{|f(p)-1|^2}{p}\Big)^{\frac{1}{2}}\cdot \Big(\sum_{\substack{N<p\le 3Q^2N^2,\\ p\equiv 1 \quad\pmod{4}}} \frac{1}{p} \Big)^{\frac{1}{2}} \ll Q^2\cdot {\mathbb D}_1(f,1;N,3Q^2N^2), \end{align*} $$
where we used that
![]() $\sum _{N\le p\le 3Q^2N^2}\frac {1}{p}\ll 1$
for
$\sum _{N\le p\le 3Q^2N^2}\frac {1}{p}\ll 1$
for
![]() $N\geq Q$
. Similarly, using (5.39) for
$N\geq Q$
. Similarly, using (5.39) for
![]() $l:=pq$
, which is a sum of two squares since
$l:=pq$
, which is a sum of two squares since
![]() $pq\equiv 1 \ \pmod {4}$
, we estimate the second term in (5.40) as follows (note that since
$pq\equiv 1 \ \pmod {4}$
, we estimate the second term in (5.40) as follows (note that since
![]() $p\neq q$
, we have
$p\neq q$
, we have
![]() $f(pq)=f(p)f(q)$
):
$f(pq)=f(p)f(q)$
):
 $$ \begin{align*} &\sum_{\substack{N<p,q\le 3Q^2N^2,\, p\neq q, \\ p,q\equiv 1 \quad\pmod{4}}} |f(pq)-1|\, w_{N,Q}(pq) \ll Q^2\sum_{\substack{N<p,q\le 3Q^2N^2,\\ p,q\equiv 1 \quad\pmod{4}}}\frac{|f(p)-1|+|f(q)-1|}{pq}\leq \\[5pt] &\quad\qquad 2\, Q^2 \cdot \Big(\sum_{\substack{N<p,q\le 3Q^2N^2,\\ p,q\equiv 1 \quad\pmod{4}}} \frac{|f(p)-1|^2}{pq}\Big)^{\frac{1}{2}}\cdot \Big(\sum_{\substack{N<p,q\le 3Q^2N^2,\\ p,q\equiv 1 \quad\pmod{4}}} \frac{1}{pq} \Big)^{\frac{1}{2}} \ll Q^2\cdot \mathbb{D}_1(f,1;N,3Q^2N^2), \end{align*} $$
$$ \begin{align*} &\sum_{\substack{N<p,q\le 3Q^2N^2,\, p\neq q, \\ p,q\equiv 1 \quad\pmod{4}}} |f(pq)-1|\, w_{N,Q}(pq) \ll Q^2\sum_{\substack{N<p,q\le 3Q^2N^2,\\ p,q\equiv 1 \quad\pmod{4}}}\frac{|f(p)-1|+|f(q)-1|}{pq}\leq \\[5pt] &\quad\qquad 2\, Q^2 \cdot \Big(\sum_{\substack{N<p,q\le 3Q^2N^2,\\ p,q\equiv 1 \quad\pmod{4}}} \frac{|f(p)-1|^2}{pq}\Big)^{\frac{1}{2}}\cdot \Big(\sum_{\substack{N<p,q\le 3Q^2N^2,\\ p,q\equiv 1 \quad\pmod{4}}} \frac{1}{pq} \Big)^{\frac{1}{2}} \ll Q^2\cdot \mathbb{D}_1(f,1;N,3Q^2N^2), \end{align*} $$
where we used that
![]() $\sum _{N\le p\le 3Q^2N^2}\frac {1}{p}\ll 1$
for
$\sum _{N\le p\le 3Q^2N^2}\frac {1}{p}\ll 1$
for
![]() $N\geq Q$
. Combining the above estimates and (5.40), we deduce that for
$N\geq Q$
. Combining the above estimates and (5.40), we deduce that for
![]() $N\gg Q$
, we have
$N\gg Q$
, we have
Next, we move to the function
![]() $f_2$
. Since
$f_2$
. Since
![]() $f_2(p)=1 $
for all primes
$f_2(p)=1 $
for all primes
![]() $p\geq N$
, Lemma 5.6 is applicable. We get that if N is large enough, depending on
$p\geq N$
, Lemma 5.6 is applicable. We get that if N is large enough, depending on
![]() $K_0$
, we have
$K_0$
, we have
 $$ \begin{align} \mathbb{E}_{m,n\in [N]} &|f_{N,2}\big((Qm+a)^2+(Qn+b)^2\big)- \exp(G_N(f,K_0))| \ll \notag\\ &\qquad\qquad\qquad\quad\qquad\qquad ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
$$ \begin{align} \mathbb{E}_{m,n\in [N]} &|f_{N,2}\big((Qm+a)^2+(Qn+b)^2\big)- \exp(G_N(f,K_0))| \ll \notag\\ &\qquad\qquad\qquad\quad\qquad\qquad ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-\frac{1}{2}}, \end{align} $$
where we used that
![]() $f_{N,2}(p)=f(p)$
for all primes
$f_{N,2}(p)=f(p)$
for all primes
![]() $p\equiv 1\ \pmod {4}$
with
$p\equiv 1\ \pmod {4}$
with
![]() $p\leq N$
; hence,
$p\leq N$
; hence,
![]() $G_N(f_{N,2},K_0)=G_N(f,K_0)$
and
$G_N(f_{N,2},K_0)=G_N(f,K_0)$
and
![]() $\mathbb {D}_1(f_{N,2},1;K_0,N)=\mathbb {D}_1(f,1;K_0,N)$
.
$\mathbb {D}_1(f_{N,2},1;K_0,N)=\mathbb {D}_1(f,1;K_0,N)$
.
Finally, we use the triangle inequality and combine (5.41) and (5.42) to obtain that the left-hand side in (5.38) is bounded by
 $$ \begin{align*} \mathbb{E}_{m,n\in [N]}&\big(|f_{N,1}\big((Qm+a)^2+(Qn+b)^2\big)- 1| +|f_{N,2}\big((Qm+a)^2+(Qn+b)^2\big)- \exp(G_N(f,K_0))|\big)\\ &\ll ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q^2\cdot \mathbb{D}_1(f,1;N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-1/2}. \end{align*} $$
$$ \begin{align*} \mathbb{E}_{m,n\in [N]}&\big(|f_{N,1}\big((Qm+a)^2+(Qn+b)^2\big)- 1| +|f_{N,2}\big((Qm+a)^2+(Qn+b)^2\big)- \exp(G_N(f,K_0))|\big)\\ &\ll ({\mathbb D}_1+{\mathbb D}_1^2)(f,1; K_0,\sqrt{N})+ Q^2\cdot \mathbb{D}_1(f,1;N,3Q^2N^2)+ Q\cdot {\mathbb D}_1(f,1; \sqrt{N},N)+K_0^{-1/2}. \end{align*} $$
Thus, (5.38) holds, completing the proof.
6 Type II Pythagorean pairs and more
6.1 Proof of Theorem 2.9
As explained in Section 2.3, in order to complete the proof of Theorem 2.9 (and hence of part (2) of Theorem 2.2), it remains to prove Proposition 2.10, Proposition 2.12 and Lemma 2.13. We do this in this section.
We repeat the statement of Proposition 2.10 and explain how it can be derived from results in [Reference Frantzikinakis and Host21].
Proposition 6.1. Let
![]() $f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic completely multiplicative function. Then for every
$f\colon {\mathbb N}\to {\mathbb U}$
be an aperiodic completely multiplicative function. Then for every
![]() $\delta>0$
and
$\delta>0$
and
![]() $\ell ,\ell ',Q\in {\mathbb N}$
, we have
$\ell ,\ell ',Q\in {\mathbb N}$
, we have
where
![]() $\tilde {w}_\delta (m,n)$
is as in (3.3).
$\tilde {w}_\delta (m,n)$
is as in (3.3).
Proof. Recall that
where
![]() $F_\delta \colon \mathbb {S}^1\to [0,1]$
is the continuous function defined in Lemma 3.3. Using uniform approximation of
$F_\delta \colon \mathbb {S}^1\to [0,1]$
is the continuous function defined in Lemma 3.3. Using uniform approximation of
![]() $F_\delta $
by trigonometric polynomials and linearity, we get that it suffices to verify (6.1) when
$F_\delta $
by trigonometric polynomials and linearity, we get that it suffices to verify (6.1) when
![]() $\tilde {w}_\delta (m,n)$
is replaced by
$\tilde {w}_\delta (m,n)$
is replaced by
![]() $(m^2+n^2)^{ki}\cdot (mn)^{-ki}$
for arbitrary
$(m^2+n^2)^{ki}\cdot (mn)^{-ki}$
for arbitrary
![]() $k\in {\mathbb Z}$
. Furthermore, the limit remains unchanged if we replace
$k\in {\mathbb Z}$
. Furthermore, the limit remains unchanged if we replace
![]() $(m^2+n^2)^{ki}\cdot (mn)^{-ki}$
with
$(m^2+n^2)^{ki}\cdot (mn)^{-ki}$
with
![]() $((Qm+1)^2+(Qn)^2)^{ki}\cdot ((Qm+1)(Qn))^{-ki}$
(the
$((Qm+1)^2+(Qn)^2)^{ki}\cdot ((Qm+1)(Qn))^{-ki}$
(the
![]() $+1$
makes no difference asymptotically, so we can omit it, and then
$+1$
makes no difference asymptotically, so we can omit it, and then
![]() $Q^2$
is going to cancel because of the conjugate). Hence, it suffices to establish that for every
$Q^2$
is going to cancel because of the conjugate). Hence, it suffices to establish that for every
![]() $k\in {\mathbb Z}$
, we have
$k\in {\mathbb Z}$
, we have
where
![]() $f_k(n):=f(n)\cdot n^{ki}$
,
$f_k(n):=f(n)\cdot n^{ki}$
,
![]() $n\in {\mathbb N}$
. Note that since the indicator function of an arithmetic progression is a linear combination of Dirichlet characters, in order to establish (6.2), it suffices to show that for all Dirichlet characters
$n\in {\mathbb N}$
. Note that since the indicator function of an arithmetic progression is a linear combination of Dirichlet characters, in order to establish (6.2), it suffices to show that for all Dirichlet characters
![]() $\chi ,\chi '$
, we have
$\chi ,\chi '$
, we have
or, equivalently, that
Since f is aperiodic, so is
![]() $\overline {f_k}\cdot \chi $
(and
$\overline {f_k}\cdot \chi $
(and
![]() $\overline {f_k}\cdot \chi '$
). By [Reference Frantzikinakis and Host21, Theorem 9.7] (applied to
$\overline {f_k}\cdot \chi '$
). By [Reference Frantzikinakis and Host21, Theorem 9.7] (applied to
![]() $Q(m,n):=m^2+n^2$
), we deduce that (6.3) holds, completing the proof.
$Q(m,n):=m^2+n^2$
), we deduce that (6.3) holds, completing the proof.
Recall that in (2.11), we defined the multiplicative Følner sequence
![]() $(\Phi _K)$
by
$(\Phi _K)$
by
 $$ \begin{align*}\Phi_K :=\Big\{\prod_{p\leq K}p^{a_p}\colon K<a_p\leq 2K\Big\}, \quad K\in {\mathbb N}. \end{align*} $$
$$ \begin{align*}\Phi_K :=\Big\{\prod_{p\leq K}p^{a_p}\colon K<a_p\leq 2K\Big\}, \quad K\in {\mathbb N}. \end{align*} $$
Note that every
![]() $q\in {\mathbb N}$
divides all elements of
$q\in {\mathbb N}$
divides all elements of
![]() $\Phi _K$
when
$\Phi _K$
when
![]() $K\in {\mathbb N}$
is large enough depending on q.
$K\in {\mathbb N}$
is large enough depending on q.
The next result is a key ingredient in the proof of Proposition 2.12 below.
Lemma 6.2. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function such that
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function such that
![]() $f\sim \chi \cdot n^{it}$
for some
$f\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
. Let also
$\chi $
. Let also
![]() $\delta>0$
be fixed,
$\delta>0$
be fixed,
![]() $\tilde {w}_\delta $
be as in (3.3), and
$\tilde {w}_\delta $
be as in (3.3), and
![]() $(\Phi _K)$
be as in (2.11). For
$(\Phi _K)$
be as in (2.11). For
![]() $Q,N\in {\mathbb N}$
, we let
$Q,N\in {\mathbb N}$
, we let
and
Then
Proof. For
![]() $K\in {\mathbb N}$
, let
$K\in {\mathbb N}$
, let
![]() $F_N(f,K)$
and
$F_N(f,K)$
and
![]() $G_N(f,K)$
be defined as in (2.12) and (2.18), respectively.
$G_N(f,K)$
be defined as in (2.12) and (2.18), respectively.
We apply the concentration inequalities of Proposition 2.5 and Proposition 2.11. Since
![]() $f\sim \chi \cdot n^{it}$
for some
$f\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
, we get that
$\chi $
, we get that
and
We deduce that if
then
Using this identity and the triangle inequality, we deduce that (6.6) holds.
Recall that
![]() ${\mathcal M}_p$
and
${\mathcal M}_p$
and
![]() ${\mathcal A}$
were defined in (2.9) and (2.13), respectively. The next result follows easily from Lemma 3.2 and the continuity of finite Borel measures.
${\mathcal A}$
were defined in (2.9) and (2.13), respectively. The next result follows easily from Lemma 3.2 and the continuity of finite Borel measures.
Lemma 6.3. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
. Then for every
${\mathcal M}_p$
. Then for every
![]() $\varepsilon>0$
, there exist a Borel subset
$\varepsilon>0$
, there exist a Borel subset
![]() ${\mathcal M}_\varepsilon $
of
${\mathcal M}_\varepsilon $
of
![]() ${\mathcal M}_p\setminus {\mathcal A}$
and
${\mathcal M}_p\setminus {\mathcal A}$
and
![]() $K_0\in {\mathbb N}$
, such that
$K_0\in {\mathbb N}$
, such that
and
where
![]() $t_f$
is the unique real for which
$t_f$
is the unique real for which
![]() $f\sim \chi \cdot n^{it_f}$
for some Dirichlet character
$f\sim \chi \cdot n^{it_f}$
for some Dirichlet character
![]() $\chi $
.
$\chi $
.
Remark. The important point is that
![]() $K_0$
does not depend on f as long as
$K_0$
does not depend on f as long as
![]() $f\in {\mathcal M}_\varepsilon $
.
$f\in {\mathcal M}_\varepsilon $
.
Proof. Let
![]() $\varepsilon>0$
. For
$\varepsilon>0$
. For
![]() $m\in {\mathbb N}$
, we let
$m\in {\mathbb N}$
, we let
Note that by Lemma 3.6, the map
![]() $f\mapsto t_f$
from
$f\mapsto t_f$
from
![]() ${\mathcal M}_p$
to
${\mathcal M}_p$
to
![]() ${\mathbb R}$
is Borel; hence, for every
${\mathbb R}$
is Borel; hence, for every
![]() $\varepsilon>0$
, the sets
$\varepsilon>0$
, the sets
![]() ${\mathcal M}_{\varepsilon , m}$
form an increasing family of Borel sets. Since for
${\mathcal M}_{\varepsilon , m}$
form an increasing family of Borel sets. Since for
![]() $f\notin {\mathcal A}$
we have
$f\notin {\mathcal A}$
we have
![]() $f\cdot n^{-it_f}\neq 1$
, we get by Lemma 3.2 that for every
$f\cdot n^{-it_f}\neq 1$
, we get by Lemma 3.2 that for every
![]() $f\in {\mathcal M}_p\setminus {\mathcal A}$
, we have
$f\in {\mathcal M}_p\setminus {\mathcal A}$
, we have
Hence,
It follows that there exists
![]() $m_0\in {\mathbb N}$
such that
$m_0\in {\mathbb N}$
such that
Renaming
![]() ${\mathcal M}_{\varepsilon , m_0}$
as
${\mathcal M}_{\varepsilon , m_0}$
as
![]() ${\mathcal M}_{\varepsilon }$
and letting
${\mathcal M}_{\varepsilon }$
and letting
![]() $K_0:=m_0$
gives the asserted statement.
$K_0:=m_0$
gives the asserted statement.
Using the previous two results, we are going to prove Proposition 2.12, which we formulate again for convenience.
Proposition 2.12 . Let
![]() $(\Phi _K)$
,
$(\Phi _K)$
,
![]() ${\mathcal A}$
,
${\mathcal A}$
,
![]() $B_{\delta }(f,Q; m,n)$
be defined by (2.11), (2.13), (2.16), respectively, and
$B_{\delta }(f,Q; m,n)$
be defined by (2.11), (2.13), (2.16), respectively, and
![]() $\delta{>}0 $
. Let also
$\delta{>}0 $
. Let also
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
. Then
${\mathcal M}_p$
. Then
 $$ \begin{align*} \lim_{K\to\infty} \limsup_{N\to \infty}\Big|{\mathbb E}_{Q\in \Phi_{K}}\, {\mathbb E}_{m,n\in[N]} \int_{{\mathcal M}_p \setminus {\mathcal A}} \, B_{\delta}(f,Q; m,n)\, d\sigma(f)\Big|=0. \end{align*} $$
$$ \begin{align*} \lim_{K\to\infty} \limsup_{N\to \infty}\Big|{\mathbb E}_{Q\in \Phi_{K}}\, {\mathbb E}_{m,n\in[N]} \int_{{\mathcal M}_p \setminus {\mathcal A}} \, B_{\delta}(f,Q; m,n)\, d\sigma(f)\Big|=0. \end{align*} $$
Proof. Let
![]() $\delta , \varepsilon>0$
. By Lemma 6.3, there exists
$\delta , \varepsilon>0$
. By Lemma 6.3, there exists
![]() $K_0=K_0(\sigma )\in {\mathbb N}$
and a Borel subset
$K_0=K_0(\sigma )\in {\mathbb N}$
and a Borel subset
![]() ${\mathcal M}_{\varepsilon }$
of
${\mathcal M}_{\varepsilon }$
of
![]() ${\mathcal M}\setminus {\mathcal A}$
, such that
${\mathcal M}\setminus {\mathcal A}$
, such that
and
Because of (6.9), and since
![]() $|B_{\delta }(f,Q; m,n)|\leq 1$
, it suffices to show that
$|B_{\delta }(f,Q; m,n)|\leq 1$
, it suffices to show that
As in Lemma 6.2, for
![]() $Q,N\in {\mathbb N}$
, we let
$Q,N\in {\mathbb N}$
, we let
We also let for
![]() $Q,N\in {\mathbb N}$
$Q,N\in {\mathbb N}$
Finally, for
![]() $K\in {\mathbb N}$
, we let
$K\in {\mathbb N}$
, we let
![]() $Q_K$
be an arbitrary element of
$Q_K$
be an arbitrary element of
![]() $\Phi _K$
, and define
$\Phi _K$
, and define
Recall that by part (2) of Lemma 3.6, the map
![]() $f\mapsto t_f$
from
$f\mapsto t_f$
from
![]() ${\mathcal M}_p$
to
${\mathcal M}_p$
to
![]() ${\mathbb R}$
is Borel, so the integral defining
${\mathbb R}$
is Borel, so the integral defining
![]() $I_1(Q,N)$
is well-defined. Using (6.12) and (6.13), we get that
$I_1(Q,N)$
is well-defined. Using (6.12) and (6.13), we get that
We deduce from this and equation (6.6) of Lemma 6.2 that
It follows from the above facts that in order to show that (6.11) holds, it suffices to show that
Using the definition of
![]() $I_1(Q,N)$
in (6.13) and the estimate (6.10), we get that for every
$I_1(Q,N)$
in (6.13) and the estimate (6.10), we get that for every
![]() $K\geq K_0$
, we have
$K\geq K_0$
, we have
Hence,
establishing (6.14) and completing the proof.
Finally, we restate and prove Lemma 2.13.
Lemma 2.13. Let
![]() $\sigma $
be a Borel probability measure on
$\sigma $
be a Borel probability measure on
![]() ${\mathcal M}_p$
such that
${\mathcal M}_p$
such that
![]() $\sigma (\{1\})>0$
and
$\sigma (\{1\})>0$
and
![]() ${\mathcal A}$
as in (2.13). Then there exist
${\mathcal A}$
as in (2.13). Then there exist
![]() $\delta _0,\rho _0>0$
, depending only on
$\delta _0,\rho _0>0$
, depending only on
![]() $\sigma $
, such that
$\sigma $
, such that
6.2 Proof of Theorem 1.8
We sketch the proof of Theorem 1.8. Following the reduction in Section 2.1, we need to show that under the assumptions of Theorem 2.2, we have
To prove this, we follow the argument used in the proof of part (2) of Theorem 2.2.Footnote 12 We will restrict our average to the grid
![]() $\{(Qn,m)\colon m,n\in {\mathbb N}\}$
. This is why for
$\{(Qn,m)\colon m,n\in {\mathbb N}\}$
. This is why for
![]() $f\in {\mathcal M}$
and
$f\in {\mathcal M}$
and
![]() $Q,m,n\in {\mathbb N}$
, we let
$Q,m,n\in {\mathbb N}$
, we let
(For reasons that will become clear shortly, in this case, we do not have to introduce any kind of weight
![]() $w_\delta $
.)
$w_\delta $
.)
We first claim that if
![]() $f\in {\mathcal M}$
is aperiodic, then for every
$f\in {\mathcal M}$
is aperiodic, then for every
![]() $Q\in {\mathbb N}$
, we have
$Q\in {\mathbb N}$
, we have
(This corresponds to Proposition 2.10.) Since f is completely multiplicative, it suffices to show that
Suppose that
![]() $f^2$
does not have logarithmic mean value
$f^2$
does not have logarithmic mean value
![]() $0$
. Then by a consequence of a result of Halász [Reference Halász30], we have
$0$
. Then by a consequence of a result of Halász [Reference Halász30], we have
![]() $f^2\sim 1$
.Footnote 13 Combining this with the following consequence of a result of Tao in [Reference Tao47], we deduce that (6.17) holds.
$f^2\sim 1$
.Footnote 13 Combining this with the following consequence of a result of Tao in [Reference Tao47], we deduce that (6.17) holds.
Lemma 6.4. Suppose that
![]() $f\in {\mathcal M}$
is aperiodic and satisfies
$f\in {\mathcal M}$
is aperiodic and satisfies
![]() $f^2\sim 1$
. Then for every
$f^2\sim 1$
. Then for every
![]() $Q\in {\mathbb N}$
, we have
$Q\in {\mathbb N}$
, we have
Proof. We say that
![]() $f\in {\mathcal M}$
is strongly aperiodic if for every Dirichlet character
$f\in {\mathcal M}$
is strongly aperiodic if for every Dirichlet character
![]() $\chi $
and
$\chi $
and
![]() $A\geq 1$
, we have
$A\geq 1$
, we have
![]() $\lim _{N\to \infty } \min _{|t|\leq AN}{\mathbb D}(f,\chi \cdot n^{it}; 1,N)=+\infty $
. It was shown in [Reference Tao47, Corollary 1.5] that if f is strongly aperiodic, then (6.18) holds for every
$\lim _{N\to \infty } \min _{|t|\leq AN}{\mathbb D}(f,\chi \cdot n^{it}; 1,N)=+\infty $
. It was shown in [Reference Tao47, Corollary 1.5] that if f is strongly aperiodic, then (6.18) holds for every
![]() $Q\in {\mathbb N}$
. Thus, it remains to show that if f is aperiodic and
$Q\in {\mathbb N}$
. Thus, it remains to show that if f is aperiodic and
![]() $f^2\sim 1$
, then f is strongly aperiodic. This can be shown exactly as in the proof of [Reference Frantzikinakis19, Proposition 6.1]; the assumption
$f^2\sim 1$
, then f is strongly aperiodic. This can be shown exactly as in the proof of [Reference Frantzikinakis19, Proposition 6.1]; the assumption
![]() $f^2\sim 1$
in our setting replaces the assumption
$f^2\sim 1$
in our setting replaces the assumption
![]() $f^k=1$
for some
$f^k=1$
for some
![]() $k\in {\mathbb N}$
that was used in [Reference Frantzikinakis19].
$k\in {\mathbb N}$
that was used in [Reference Frantzikinakis19].
Using the previous claim and the bounded convergence theorem, we get that it suffices to establish (6.16) when the range of integration
![]() ${\mathcal M}$
is replaced by the subset
${\mathcal M}$
is replaced by the subset
![]() ${\mathcal M}_p$
of pretentious multiplicative functions.
${\mathcal M}_p$
of pretentious multiplicative functions.
Next, we claim that if
![]() $(\Phi _K)$
is as in (2.11) and
$(\Phi _K)$
is as in (2.11) and
![]() $\sigma $
is a Borel probability measure on
$\sigma $
is a Borel probability measure on
![]() ${\mathcal M}_p$
, then
${\mathcal M}_p$
, then
 $$ \begin{align} \lim_{K\to\infty} \limsup_{N\to \infty}\Big|{\mathbb E}_{Q\in \Phi_{K}}\, \mathbb{E}^{\log}_{m,n\in[N]} \int_{{\mathcal M}_p \setminus \{1\}} \, B(f,Q; m,n)\, d\sigma(f)\Big|=0. \end{align} $$
$$ \begin{align} \lim_{K\to\infty} \limsup_{N\to \infty}\Big|{\mathbb E}_{Q\in \Phi_{K}}\, \mathbb{E}^{\log}_{m,n\in[N]} \int_{{\mathcal M}_p \setminus \{1\}} \, B(f,Q; m,n)\, d\sigma(f)\Big|=0. \end{align} $$
(This corresponds to Proposition 2.12. Note that
![]() ${\mathcal A}$
can be replaced by
${\mathcal A}$
can be replaced by
![]() $\{1\}$
in this case, which is the reason why the weight
$\{1\}$
in this case, which is the reason why the weight
![]() $\tilde {w}_\delta $
is not needed for this argument.) To prove this, we argue as in the proof of Proposition 2.12. If
$\tilde {w}_\delta $
is not needed for this argument.) To prove this, we argue as in the proof of Proposition 2.12. If
![]() $f\sim \chi \cdot n^{it_f}$
for some
$f\sim \chi \cdot n^{it_f}$
for some
![]() $t_f\in {\mathbb R}$
and Dirichlet character
$t_f\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
, for
$\chi $
, for
![]() $Q,N\in {\mathbb N}$
, we let
$Q,N\in {\mathbb N}$
, we let
and show that
We do this exactly as in the proof of Lemma 6.2, using in this case the concentration estimate of Proposition 2.5 for logarithmic averages (see the third remark following Proposition 2.5). Then (6.19) follows exactly as in the proof of Proposition 2.12. The reason why we only have to exclude the multiplicative function
![]() $\{1\}$
in the integral in (6.19) (versus the set
$\{1\}$
in the integral in (6.19) (versus the set
![]() ${\mathcal A}$
of all Archimedean characters) is because in our current setting, we have
${\mathcal A}$
of all Archimedean characters) is because in our current setting, we have
and
![]() $Q\mapsto f(Q)\cdot Q^{it_f}$
is the trivial multiplicative function only when
$Q\mapsto f(Q)\cdot Q^{it_f}$
is the trivial multiplicative function only when
![]() $f=1$
. Note also that the variant of Lemma 2.13 is trivial in our case, since
$f=1$
. Note also that the variant of Lemma 2.13 is trivial in our case, since
![]() ${\mathcal A}$
is replaced by
${\mathcal A}$
is replaced by
![]() $\{1\}$
. With the above information, we can complete the proof of (6.16) exactly as we did at the end of Section 2.3.
$\{1\}$
. With the above information, we can complete the proof of (6.16) exactly as we did at the end of Section 2.3.
7 Pythagorean triples on level sets - Reduction to the pretentious case
First, let us recall a convention made in Section 2.4, which we will continue to follow in this and the next section. When we write
![]() ${\mathbb E}^*_{k\in {\mathbb N}}$
, we mean the limit
${\mathbb E}^*_{k\in {\mathbb N}}$
, we mean the limit
![]() $\lim _{K\to \infty } {\mathbb E}_{k\in \Phi _K}$
, where
$\lim _{K\to \infty } {\mathbb E}_{k\in \Phi _K}$
, where
![]() $(\Phi _K)$
is a multiplicative Følner sequence chosen so that all the limits in the following statements exist. Since it will always be the case in our arguments that only a countable collection of limits needs to be considered, such a Følner sequence can be taken as a subsequence of any given multiplicative Følner sequence.
$(\Phi _K)$
is a multiplicative Følner sequence chosen so that all the limits in the following statements exist. Since it will always be the case in our arguments that only a countable collection of limits needs to be considered, such a Følner sequence can be taken as a subsequence of any given multiplicative Følner sequence.
As explained in Section 2.4, the proof of Theorem 2.14 splits in two parts, Propositions 2.16 and 2.18. Our goal in this section is to establish the first part, which we now state in a more general form (we do not assume that f takes finitely many values).
Proposition 7.1. Suppose that for every completely multiplicative function
![]() $h\colon {\mathbb N}\to \mathbb {S}^1$
, with
$h\colon {\mathbb N}\to \mathbb {S}^1$
, with
![]() $h\sim n^{it}$
for some
$h\sim n^{it}$
for some
![]() $t\in {\mathbb R}$
, modified Dirichlet character
$t\in {\mathbb R}$
, modified Dirichlet character
![]() $\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
, and open arc I on
$\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
, and open arc I on
![]() $\mathbb {S}^1$
around
$\mathbb {S}^1$
around
![]() $1$
, we have
$1$
, we have
where
Then for every completely multiplicative function
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
and open arc I around
$f\colon {\mathbb N}\to \mathbb {S}^1$
and open arc I around
![]() $1$
, we have
$1$
, we have
where F is as before. Furthermore, if our assumptions hold for all finite-valued completely multiplicative functions h, then the conclusion holds for all finite-valued completely multiplicative functions f.
7.1 Preparation
Recall that we write
![]() $f\sim g$
if
$f\sim g$
if
![]() ${\mathbb D}(f,g)<+\infty $
, where
${\mathbb D}(f,g)<+\infty $
, where
![]() ${\mathbb D}(f,g)$
is as in (3.5).
${\mathbb D}(f,g)$
is as in (3.5).
Lemma 7.2. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function such that
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function such that
![]() $f\sim n^{it}$
for some
$f\sim n^{it}$
for some
![]() $t\in {\mathbb R}$
. Then for every
$t\in {\mathbb R}$
. Then for every
![]() $d\in {\mathbb N}$
, there exists a completely multiplicative function
$d\in {\mathbb N}$
, there exists a completely multiplicative function
![]() $g\colon {\mathbb N}\to \mathbb {S}^1$
, such that
$g\colon {\mathbb N}\to \mathbb {S}^1$
, such that
![]() $g\sim n^{it/d}$
and
$g\sim n^{it/d}$
and
![]() $g^d=f$
. Furthermore, if f takes finitely many values, then so does g.
$g^d=f$
. Furthermore, if f takes finitely many values, then so does g.
Proof. Suppose first that
![]() $f\sim 1$
. Then
$f\sim 1$
. Then
![]() $f(p)=e(\theta _p)$
,
$f(p)=e(\theta _p)$
,
![]() $p\in {\mathbb P}$
, for some
$p\in {\mathbb P}$
, for some
![]() $\theta _p\in [-1/2,1/2)$
with
$\theta _p\in [-1/2,1/2)$
with
![]() $\sum _{p\in {\mathbb P}}\frac {1-\cos (\theta _p)}{p}<+\infty $
. Hence,
$\sum _{p\in {\mathbb P}}\frac {1-\cos (\theta _p)}{p}<+\infty $
. Hence,
![]() $\sum _{p\in {\mathbb P}}\frac {\theta _p^2}{p}<+\infty $
. We define the completely multiplicative function
$\sum _{p\in {\mathbb P}}\frac {\theta _p^2}{p}<+\infty $
. We define the completely multiplicative function
![]() $g\colon {\mathbb N}\to \mathbb {S}^1$
by
$g\colon {\mathbb N}\to \mathbb {S}^1$
by
We have
![]() $g^d=f$
. Also,
$g^d=f$
. Also,
![]() $\sum _{p\in {\mathbb P}}\frac {\tilde {\theta }_p^2}{p}<+\infty $
; hence,
$\sum _{p\in {\mathbb P}}\frac {\tilde {\theta }_p^2}{p}<+\infty $
; hence,
![]() $g\sim 1$
.
$g\sim 1$
.
Now suppose that
![]() $f\sim n^{it}$
, and let
$f\sim n^{it}$
, and let
![]() $d\in {\mathbb N}$
. Then
$d\in {\mathbb N}$
. Then
![]() $f\cdot n^{-it}\sim 1$
, and the previous argument gives that there exists
$f\cdot n^{-it}\sim 1$
, and the previous argument gives that there exists
![]() $h\colon {\mathbb N}\to \mathbb {S}^1$
with
$h\colon {\mathbb N}\to \mathbb {S}^1$
with
![]() $h\sim 1$
such that
$h\sim 1$
such that
![]() $h^d=f\cdot n^{-it}$
. Let
$h^d=f\cdot n^{-it}$
. Let
![]() $g:=h\cdot n^{it/d}$
. Then
$g:=h\cdot n^{it/d}$
. Then
![]() $g^d=f$
and
$g^d=f$
and
![]() $g\sim n^{it/d}$
.
$g\sim n^{it/d}$
.
A similar statement is not always true when
![]() $f\sim \chi $
where
$f\sim \chi $
where
![]() $\chi $
is a Dirichlet character (not even when
$\chi $
is a Dirichlet character (not even when
![]() $f=\chi $
).
$f=\chi $
).
We remind the reader that modified Dirichlet characters
![]() $\tilde {\chi }$
were defined in Section 3.3. If a completely multiplicative function
$\tilde {\chi }$
were defined in Section 3.3. If a completely multiplicative function
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
is such that
$f\colon {\mathbb N}\to \mathbb {S}^1$
is such that
![]() $f^l$
is aperiodic for every
$f^l$
is aperiodic for every
![]() $l\in {\mathbb N}$
, then things are easier for us. If this is not the case (for example, it is never the case when f is finite-valued), then the next lemma gives a useful decomposition to work with.
$l\in {\mathbb N}$
, then things are easier for us. If this is not the case (for example, it is never the case when f is finite-valued), then the next lemma gives a useful decomposition to work with.
Lemma 7.3. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be an aperiodic completely multiplicative function such that
$f\colon {\mathbb N}\to \mathbb {S}^1$
be an aperiodic completely multiplicative function such that
![]() $f^d$
is pretentious for some
$f^d$
is pretentious for some
![]() $d\in {\mathbb N}$
, and suppose that
$d\in {\mathbb N}$
, and suppose that
![]() $d\geq 2$
is the smallest such d. Then there exist completely multiplicative functions
$d\geq 2$
is the smallest such d. Then there exist completely multiplicative functions
![]() $g,h\colon {\mathbb N}\to \mathbb {S}^1$
and a Dirichlet character
$g,h\colon {\mathbb N}\to \mathbb {S}^1$
and a Dirichlet character
![]() $\chi $
, such that
$\chi $
, such that
-
1.
 $f=g\cdot h$
$f=g\cdot h$
-
2.
 $g,\ldots , g^{d-1}$
are aperiodic and
$g,\ldots , g^{d-1}$
are aperiodic and
 $g^d=\tilde {\chi }$
.
$g^d=\tilde {\chi }$
. -
3.
 $h\sim n^{it}$
for some
$h\sim n^{it}$
for some
 $t\in {\mathbb R}$
.
$t\in {\mathbb R}$
.
Furthermore, if f takes finitely many values, then so does h and
![]() $h\sim 1$
.
$h\sim 1$
.
Proof. By our assumption, we have that
![]() $f,\ldots , f^{d-1}$
are aperiodic and
$f,\ldots , f^{d-1}$
are aperiodic and
![]() $f^d\sim \chi \cdot n^{it}$
for some
$f^d\sim \chi \cdot n^{it}$
for some
![]() $t\in {\mathbb R}$
and Dirichlet character
$t\in {\mathbb R}$
and Dirichlet character
![]() $\chi $
. Then
$\chi $
. Then
![]() $f^d\cdot \overline {\tilde {\chi }}\sim n^{it}$
, and Lemma 7.2 gives that there exists a completely multiplicative function
$f^d\cdot \overline {\tilde {\chi }}\sim n^{it}$
, and Lemma 7.2 gives that there exists a completely multiplicative function
![]() $h\colon {\mathbb N}\to \mathbb {S}^1$
such that
$h\colon {\mathbb N}\to \mathbb {S}^1$
such that
Let
![]() $g:=f\cdot \overline {h}$
. Then obviously
$g:=f\cdot \overline {h}$
. Then obviously
![]() $f=g\cdot h$
. Also, for
$f=g\cdot h$
. Also, for
![]() $j=1,\ldots , d-1$
, we have
$j=1,\ldots , d-1$
, we have
![]() $ g^j=f^j\cdot h^j $
is aperiodic, since by assumption,
$ g^j=f^j\cdot h^j $
is aperiodic, since by assumption,
![]() $f^j$
is aperiodic and
$f^j$
is aperiodic and
![]() $h^j$
is pretentious. Moreover,
$h^j$
is pretentious. Moreover,
Lastly, suppose that f takes finitely many values. Since g also takes finitely many values, and
![]() $h:=f\cdot \overline {g}$
, we have that h takes finitely many values. Also, since h takes finitely many values and
$h:=f\cdot \overline {g}$
, we have that h takes finitely many values. Also, since h takes finitely many values and
![]() $h\sim n^{it}$
for some
$h\sim n^{it}$
for some
![]() $t\in {\mathbb R}$
, we have that
$t\in {\mathbb R}$
, we have that
![]() $t=0$
. This completes the proof.
$t=0$
. This completes the proof.
Since
![]() $\chi $
is a Dirichlet character, there exists
$\chi $
is a Dirichlet character, there exists
![]() $r\in {\mathbb N}$
such that
$r\in {\mathbb N}$
such that
![]() $\tilde {\chi }^r=1$
. We gather some facts about g that we shall use in the proof of Proposition 7.1:
$\tilde {\chi }^r=1$
. We gather some facts about g that we shall use in the proof of Proposition 7.1:
-
•
 $g^{rd}=\tilde {\chi }^r=1$
; hence, g takes values in
$g^{rd}=\tilde {\chi }^r=1$
; hence, g takes values in
 $(rd)$
-roots of unity and the sequence
$(rd)$
-roots of unity and the sequence
 $(g^j)_{j\in {\mathbb N}}$
is periodic with period
$(g^j)_{j\in {\mathbb N}}$
is periodic with period
 $rd$
.
$rd$
. -
•
 $g^{d}=\tilde {\chi }$
,
$g^{d}=\tilde {\chi }$
,
 $g^{2d}=\tilde {\chi }^2$
,
$g^{2d}=\tilde {\chi }^2$
,
 $\ldots $
,
$\ldots $
,
 $g^{(r-1)d}=\tilde {\chi }^{r-1}$
,
$g^{(r-1)d}=\tilde {\chi }^{r-1}$
,
 $g^{rd}=1$
.
$g^{rd}=1$
. -
•
 $ g^j$
is aperiodic if
$ g^j$
is aperiodic if
 $ j\not \equiv 0 \ \pmod {d}$
.
$ j\not \equiv 0 \ \pmod {d}$
.
7.2 Proof of Proposition 7.1
In this subsection, we prove Proposition 7.1. For convenience, we use the following notation.
Definition 7.1. If I is a circular arc around
![]() $1$
and
$1$
and
![]() $d\in {\mathbb N}$
, we let
$d\in {\mathbb N}$
, we let
Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function and I be an open arc around
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a completely multiplicative function and I be an open arc around
![]() $1$
. Let also
$1$
. Let also
![]() $F\colon \mathbb {S}^1\to [0,1]$
be a continuous function such that
$F\colon \mathbb {S}^1\to [0,1]$
be a continuous function such that
It suffices to show that under the assumption of Proposition 7.1, we have
We consider three cases.
Case 1. If f is pretentious, then
![]() $f= h\cdot \tilde {\chi }$
, where
$f= h\cdot \tilde {\chi }$
, where
![]() $h\sim n^{it}$
for some
$h\sim n^{it}$
for some
![]() $t\in {\mathbb R}$
, and
$t\in {\mathbb R}$
, and
![]() $\tilde {\chi }$
is a modified Dirichlet character, and the conclusion follows from our assumption.
$\tilde {\chi }$
is a modified Dirichlet character, and the conclusion follows from our assumption.
Case 2. Suppose that f is aperiodic and
![]() $f^d$
is pretentious for some
$f^d$
is pretentious for some
![]() $d\geq 2$
. We use Lemma 7.3 to get a decomposition
$d\geq 2$
. We use Lemma 7.3 to get a decomposition
![]() $f=gh$
, where g takes values on
$f=gh$
, where g takes values on
![]() $rd$
roots of unity for some
$rd$
roots of unity for some
![]() $r\in {\mathbb N}$
,
$r\in {\mathbb N}$
,
![]() $g,\ldots , g^{d-1}$
are aperiodic and
$g,\ldots , g^{d-1}$
are aperiodic and
![]() $g^d=\tilde {\chi }$
for some modified Dirichlet character
$g^d=\tilde {\chi }$
for some modified Dirichlet character
![]() $\tilde {\chi }$
, and
$\tilde {\chi }$
, and
![]() $h\sim n^{it}$
for some
$h\sim n^{it}$
for some
![]() $t\in {\mathbb R}$
. Note first that in order to establish (7.1), it suffices to show that
$t\in {\mathbb R}$
. Note first that in order to establish (7.1), it suffices to show that
where
This is so, since if
![]() $g(n),h(n)\in I/2$
, then
$g(n),h(n)\in I/2$
, then
![]() $f(n)=g(n)\cdot h(n)\in I$
.
$f(n)=g(n)\cdot h(n)\in I$
.
Main Claim. If for
![]() $G:=\mathbf {1 }_{\{1\}}$
and
$G:=\mathbf {1 }_{\{1\}}$
and
![]() $c_{k,m,n}$
as in (7.3) we have
$c_{k,m,n}$
as in (7.3) we have
then (7.2) holds.
Note that (7.4) is satisfied from the hypothesis of Proposition 7.1. So to finish the proof of Proposition 7.1 in Case 2, it remains to verify the above claim.
We start with a simple identity. Since g takes values in
![]() $rd$
roots of unity, we have
$rd$
roots of unity, we have
Since
![]() $F\geq \mathbf {1}_{\{1\}}$
, it suffices to verify (7.2) with
$F\geq \mathbf {1}_{\{1\}}$
, it suffices to verify (7.2) with
![]() $\sum _{j=0}^{rd-1}g^j$
in place of
$\sum _{j=0}^{rd-1}g^j$
in place of
![]() $F\circ g$
. Let
$F\circ g$
. Let
Recall that
![]() $g^j$
is aperiodic for
$g^j$
is aperiodic for
![]() $j\in J$
. Also,
$j\in J$
. Also,
![]() $g^d=\tilde {\chi }$
and
$g^d=\tilde {\chi }$
and
![]() $\tilde {\chi }$
takes values on r-th roots of unity; hence,
$\tilde {\chi }$
takes values on r-th roots of unity; hence,
 $$ \begin{align*}\sum_{j=0}^{rd-1}g^j=\sum_{j=0}^{r-1}\tilde{\chi}^j +\sum_{j\in J }g^j=r \cdot \mathbf{1}_{\tilde{\chi}=1}+ \sum_{j\in J }g^j. \end{align*} $$
$$ \begin{align*}\sum_{j=0}^{rd-1}g^j=\sum_{j=0}^{r-1}\tilde{\chi}^j +\sum_{j\in J }g^j=r \cdot \mathbf{1}_{\tilde{\chi}=1}+ \sum_{j\in J }g^j. \end{align*} $$
Hence, in order to verify (7.2), it suffices to show that
where
 $$ \begin{align*}H:=r \cdot \mathbf{1}_{\tilde{\chi}=1}+ \sum_{j\in J}g^j. \end{align*} $$
$$ \begin{align*}H:=r \cdot \mathbf{1}_{\tilde{\chi}=1}+ \sum_{j\in J}g^j. \end{align*} $$
After expanding the product, we get a finite sum of expressions of the form
where each
![]() $H_1,H_2,H_3$
is either of the form
$H_1,H_2,H_3$
is either of the form
![]() $r\cdot \mathbf {1}_{\tilde {\chi }=1}$
, or of the form
$r\cdot \mathbf {1}_{\tilde {\chi }=1}$
, or of the form
![]() $g^j$
for some
$g^j$
for some
![]() $j\in J$
.
$j\in J$
.
With this in mind, we see that the positiveness property (7.5) would follow once we establish the following three claims:
-
1. If
 $H_1=H_2=H_3=r\cdot \mathbf {1}_{\tilde {\chi }=1}$
, then the limit in (7.6) is positive.
$H_1=H_2=H_3=r\cdot \mathbf {1}_{\tilde {\chi }=1}$
, then the limit in (7.6) is positive. -
2. If
 $H_1=H_2=r\cdot \mathbf {1}_{\tilde {\chi }=1}$
and
$H_1=H_2=r\cdot \mathbf {1}_{\tilde {\chi }=1}$
and
 $H_3=g^j$
for some
$H_3=g^j$
for some
 $j\in J$
, then the limit in (7.6) is
$j\in J$
, then the limit in (7.6) is
 $0$
.
$0$
. -
3. If
 $H_1=g^j$
or
$H_1=g^j$
or
 $H_2=g^j$
for some
$H_2=g^j$
for some
 $j\in J$
, then the limit in (7.6) is
$j\in J$
, then the limit in (7.6) is
 $0$
.
$0$
.
(We do not combine the last two cases because the argument we use is different.)
We prove (1). This follows immediately from the assumption (7.4) of the Main Claim.
We prove (2). We will show that for every
![]() $m,n\in {\mathbb N}$
with
$m,n\in {\mathbb N}$
with
![]() $m>n$
, we have
$m>n$
, we have
Using the definition of
![]() $c_{k,m,n}$
in (7.3) and uniform approximation of F, it suffices to show that for every
$c_{k,m,n}$
in (7.3) and uniform approximation of F, it suffices to show that for every
![]() $m,n\in {\mathbb N}$
with
$m,n\in {\mathbb N}$
with
![]() $m>n$
, we have
$m>n$
, we have
where
![]() $H_1':=\tilde {\chi }^{j_1}\cdot h^{j_2}$
,
$H_1':=\tilde {\chi }^{j_1}\cdot h^{j_2}$
,
![]() $H_2^{\prime }:=\tilde {\chi }^{j_3}\cdot h^{j_4}$
, and
$H_2^{\prime }:=\tilde {\chi }^{j_3}\cdot h^{j_4}$
, and
![]() $H_3':= g^{j_5}\cdot h^{j_6}$
, for some
$H_3':= g^{j_5}\cdot h^{j_6}$
, for some
![]() $j_1,j_2,j_3,j_4,j_6\in {\mathbb Z}$
and
$j_1,j_2,j_3,j_4,j_6\in {\mathbb Z}$
and
![]() $j_5:=j\in J$
. Factoring out the multiplicative average
$j_5:=j\in J$
. Factoring out the multiplicative average
![]() ${\mathbb E}^*_{k\in {\mathbb N}}$
, we get that it suffices to show that
${\mathbb E}^*_{k\in {\mathbb N}}$
, we get that it suffices to show that
Since
![]() $g^{j_5}$
is aperiodic and
$g^{j_5}$
is aperiodic and
![]() $\tilde {\chi }^{j_1+j_3}\cdot h^{j_2+j_4+j_6}$
is pretentious, we get that
$\tilde {\chi }^{j_1+j_3}\cdot h^{j_2+j_4+j_6}$
is pretentious, we get that
![]() $H\neq 1$
; hence,
$H\neq 1$
; hence,
![]() $ {\mathbb E}^*_{k\in {\mathbb N}}\ H(k)=0$
.
$ {\mathbb E}^*_{k\in {\mathbb N}}\ H(k)=0$
.
We prove (3). Suppose that
![]() $H_1=g^{j_1}$
for some
$H_1=g^{j_1}$
for some
![]() $j_1\in J$
; the argument is similar for
$j_1\in J$
; the argument is similar for
![]() $j_2$
. Using the definition of
$j_2$
. Using the definition of
![]() $c_{k,m,n}$
from (7.3) and uniform approximation of F, it suffices to show that
$c_{k,m,n}$
from (7.3) and uniform approximation of F, it suffices to show that
where
![]() $H_1':=g^{j_1}\cdot h^{j_2}$
,
$H_1':=g^{j_1}\cdot h^{j_2}$
,
![]() $H_2^{\prime }:=\tilde {\chi }^{j_3}\cdot h^{j_4}$
or
$H_2^{\prime }:=\tilde {\chi }^{j_3}\cdot h^{j_4}$
or
![]() $g^{j_5}\cdot h^{j_6}$
,
$g^{j_5}\cdot h^{j_6}$
,
![]() $H_3':=\tilde {\chi }\cdot h^{j_7}$
or
$H_3':=\tilde {\chi }\cdot h^{j_7}$
or
![]() $g^{j_8}\cdot h^{j_9}$
, for some
$g^{j_8}\cdot h^{j_9}$
, for some
![]() $j_2,\ldots , j_9\in {\mathbb Z}$
. Factoring out the multiplicative average
$j_2,\ldots , j_9\in {\mathbb Z}$
. Factoring out the multiplicative average
![]() $ {\mathbb E}^*_{k\in {\mathbb N}}\ (H_1'\cdot H_2^{\prime }\cdot H_3')(k)$
, we get that it suffices to show that
$ {\mathbb E}^*_{k\in {\mathbb N}}\ (H_1'\cdot H_2^{\prime }\cdot H_3')(k)$
, we get that it suffices to show that
where
![]() $H_1'$
is an aperiodic completely multiplicative function (since
$H_1'$
is an aperiodic completely multiplicative function (since
![]() $g^{j_1}$
is aperiodic and
$g^{j_1}$
is aperiodic and
![]() $h^{j_2}$
is pretentious), and
$h^{j_2}$
is pretentious), and
![]() $H_2^{\prime }$
,
$H_2^{\prime }$
,
![]() $H_3'$
are completely multiplicative functions. The hypothesis of Proposition 2.15 is satisfied, and we deduce that (7.7) holds.
$H_3'$
are completely multiplicative functions. The hypothesis of Proposition 2.15 is satisfied, and we deduce that (7.7) holds.
This finishes the proof of the Main Claim and the proof of Case 2.
Case 3. Suppose that
![]() $f^l$
is aperiodic for every
$f^l$
is aperiodic for every
![]() $l\in {\mathbb N}$
. In this case, we claim that the following identity holds:
$l\in {\mathbb N}$
. In this case, we claim that the following identity holds:
If we prove this, then (7.1) holds, since
![]() $\int F\, dm_{\mathbb {S}^1}\geq m_{\mathbb {S}^1}(I/4)>0$
.
$\int F\, dm_{\mathbb {S}^1}\geq m_{\mathbb {S}^1}(I/4)>0$
.
Using uniform approximation of F, it suffices to show that
when for
![]() $i=1,2,3$
, we have
$i=1,2,3$
, we have
![]() $F_i=f^{j_i}$
,
$F_i=f^{j_i}$
,
![]() $j_i\in {\mathbb Z}$
, and at least one of the
$j_i\in {\mathbb Z}$
, and at least one of the
![]() $j_1,j_2,j_3$
is nonzero.
$j_1,j_2,j_3$
is nonzero.
We consider two cases. Suppose first that
![]() $j_1=j_2=0$
. Then
$j_1=j_2=0$
. Then
![]() $j_3\neq 0$
. After factoring out the multiplicative average
$j_3\neq 0$
. After factoring out the multiplicative average
![]() ${\mathbb E}^*_{k\in {\mathbb N}}$
, it suffices to show that
${\mathbb E}^*_{k\in {\mathbb N}}$
, it suffices to show that
This is the case since
![]() $f^{j_3}$
is a nontrivial completely multiplicative function.
$f^{j_3}$
is a nontrivial completely multiplicative function.
Suppose now that
![]() $j_1\neq 0$
; the argument is similar if
$j_1\neq 0$
; the argument is similar if
![]() $j_2\neq 0$
. After factoring out the multiplicative average
$j_2\neq 0$
. After factoring out the multiplicative average
![]() ${\mathbb E}^*_{k\in {\mathbb N}}$
, it suffices to show that
${\mathbb E}^*_{k\in {\mathbb N}}$
, it suffices to show that
By our assumption,
![]() $F_1=f^{j_1}$
is aperiodic. Note also that all
$F_1=f^{j_1}$
is aperiodic. Note also that all
![]() $F_1,F_2,F_3$
are completely multiplicative function. The asserted identity then follows again from Proposition 2.15.Footnote 14
$F_1,F_2,F_3$
are completely multiplicative function. The asserted identity then follows again from Proposition 2.15.Footnote 14
8 Pythagorean triples on level sets - The pretentious case
Our goal in this section is to prove Proposition 2.18, which combined with Proposition 7.1 (Proposition 2.16 is a direct consequence) implies Theorem 1.5. We first restate Proposition 2.18 in a slightly more convenient form. Let
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be a pretentious completely multiplicative function taking finitely many values. Then for some
$f\colon {\mathbb N}\to \mathbb {S}^1$
be a pretentious completely multiplicative function taking finitely many values. Then for some
![]() $d\in {\mathbb N}$
, it takes values on d-th roots of unity. We can assume that d is minimal with this property, in which case, we have
$d\in {\mathbb N}$
, it takes values on d-th roots of unity. We can assume that d is minimal with this property, in which case, we have
![]() $f^j\neq 1$
for
$f^j\neq 1$
for
![]() $j=1,\ldots , d-1$
. In this case, we will show the following.
$j=1,\ldots , d-1$
. In this case, we will show the following.
Proposition 8.1. Let
![]() $d\in {\mathbb N}$
and
$d\in {\mathbb N}$
and
![]() $f\colon {\mathbb N}\to \mathbb {S}^1$
be pretentious multiplicative function taking values on d-th roots of unity and
$f\colon {\mathbb N}\to \mathbb {S}^1$
be pretentious multiplicative function taking values on d-th roots of unity and
![]() $\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
be a modified Dirichlet character. Then
$\tilde {\chi }\colon {\mathbb N}\to \mathbb {S}^1$
be a modified Dirichlet character. Then
where
Remark. Note that in the argument that follows, we only deal with countably many choices of multiplicative functions and other choices of parameters, so we can choose a subsequence of positive integers
![]() $(N_l)$
along which all the limits (as
$(N_l)$
along which all the limits (as
![]() $l\to \infty $
) that appear below exist. We make this implicit assumption throughout.
$l\to \infty $
) that appear below exist. We make this implicit assumption throughout.
Before giving the proof of Proposition 8.1, we show how the concentration estimates of Corollary 2.17 follow from Propositions 2.5 and 2.11.
8.1 Proof of Corollary 2.17
We will deduce part (1) from Proposition 2.5. In a similar fashion, we can deduce part (2) from Proposition 2.11.
Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\varepsilon <1$
. Since f is a finite-valued pretentious multiplicative function, we have by Lemma 3.4 that
$\varepsilon <1$
. Since f is a finite-valued pretentious multiplicative function, we have by Lemma 3.4 that
![]() $f\sim \chi $
for some Dirichlet character
$f\sim \chi $
for some Dirichlet character
![]() $\chi $
with period q and
$\chi $
with period q and
 $$ \begin{align*}\sum_{p\in {\mathbb P}}\, \frac{1}{p}\,|1-f(p)\cdot \overline{\chi(p)}|<\infty. \end{align*} $$
$$ \begin{align*}\sum_{p\in {\mathbb P}}\, \frac{1}{p}\,|1-f(p)\cdot \overline{\chi(p)}|<\infty. \end{align*} $$
Hence, there exists
![]() $K_0\in {\mathbb N}$
such that
$K_0\in {\mathbb N}$
such that
 $$ \begin{align*}\sum_{p\geq K_0}\, \frac{1}{p}\,|1- f(p)\cdot \overline{\chi(p)}| +K_0^{-1/2}\leq \varepsilon. \end{align*} $$
$$ \begin{align*}\sum_{p\geq K_0}\, \frac{1}{p}\,|1- f(p)\cdot \overline{\chi(p)}| +K_0^{-1/2}\leq \varepsilon. \end{align*} $$
This implies that
where
![]() $F_N(f,K_0)=\sum _{K_0< p\leq N} \frac {1}{p}\,\big (f(p)\cdot \overline {\chi (p)} -1\big )$
.
$F_N(f,K_0)=\sum _{K_0< p\leq N} \frac {1}{p}\,\big (f(p)\cdot \overline {\chi (p)} -1\big )$
.
We let
![]() $Q_0:=q\cdot \prod _{p\leq K_0}p$
. If
$Q_0:=q\cdot \prod _{p\leq K_0}p$
. If
![]() $Q\in {\mathbb N}$
is such that
$Q\in {\mathbb N}$
is such that
![]() $Q_0\mid Q$
, then using the second remark following Proposition 2.5 with
$Q_0\mid Q$
, then using the second remark following Proposition 2.5 with
![]() $t=0$
, we get that
$t=0$
, we get that
Since
![]() $|\exp \big (F_N(f,K_0)\big )-1|\ll \varepsilon $
, this completes the proof.
$|\exp \big (F_N(f,K_0)\big )-1|\ll \varepsilon $
, this completes the proof.
8.2 Proof of Proposition 8.1
Recall that
![]() $A(n)$
is given by (8.1). Since
$A(n)$
is given by (8.1). Since
![]() $A(n)\geq 0$
for every
$A(n)\geq 0$
for every
![]() $n\in {\mathbb N}$
, it suffices to show that there exist
$n\in {\mathbb N}$
, it suffices to show that there exist
![]() $Q\in {\mathbb N}$
and
$Q\in {\mathbb N}$
and
![]() $N_l\to \infty $
(which can be taken to be a subsequence of any given
$N_l\to \infty $
(which can be taken to be a subsequence of any given
![]() $M_l\to \infty $
) such that all limits appearing below as
$M_l\to \infty $
) such that all limits appearing below as
![]() $l\to \infty $
exist and
$l\to \infty $
exist and
 $$ \begin{align*} \lim_{l\to \infty} {\mathbb E}_{m,n\in [N_l], m>n}\, {\mathbb E}^*_{k\in {\mathbb N}} \, A(k((Qm+1)^2-(Qn)^2) &\cdot A(k\, 2(Qm+1)(Qn)) \cdot \\ &\qquad\qquad\quad A(k((Qm+1)^2+(Qn)^2))>0. \end{align*} $$
$$ \begin{align*} \lim_{l\to \infty} {\mathbb E}_{m,n\in [N_l], m>n}\, {\mathbb E}^*_{k\in {\mathbb N}} \, A(k((Qm+1)^2-(Qn)^2) &\cdot A(k\, 2(Qm+1)(Qn)) \cdot \\ &\qquad\qquad\quad A(k((Qm+1)^2+(Qn)^2))>0. \end{align*} $$
Since f takes values on d-th roots of unity and
![]() $\tilde {\chi }$
takes values on
$\tilde {\chi }$
takes values on
![]() $d'$
-th roots of unity for some
$d'$
-th roots of unity for some
![]() $d,d'\in {\mathbb N}$
, we have
$d,d'\in {\mathbb N}$
, we have
Let
![]() $m,n \in {\mathbb N}$
with
$m,n \in {\mathbb N}$
with
![]() $m>n$
be fixed. In order to compute
$m>n$
be fixed. In order to compute
we use (8.2), expand, and use that by Lemma 3.2, we have
![]() $ {\mathbb E}^*_{k\in {\mathbb N}} \ g(k)=0$
for all completely multiplicative functions
$ {\mathbb E}^*_{k\in {\mathbb N}} \ g(k)=0$
for all completely multiplicative functions
![]() $g\colon {\mathbb N}\to {\mathbb U}$
with
$g\colon {\mathbb N}\to {\mathbb U}$
with
![]() $g\neq 1$
(in particular, this holds if
$g\neq 1$
(in particular, this holds if
![]() $g:=f^k\cdot \tilde {\chi }^{k'}\neq 1$
). We see that the previous expression is equal to
$g:=f^k\cdot \tilde {\chi }^{k'}\neq 1$
). We see that the previous expression is equal to
![]() $1/(dd')^3$
times
$1/(dd')^3$
times
 $$ \begin{align*}\sum_{k_i,k_i^{\prime}\in {\mathcal K}} \, (f^{k_1}\cdot \tilde{\chi}^{k^{\prime}_1})(m^2-n^2)\cdot (f^{k_2}\cdot \tilde{\chi}^{k^{\prime}_2})(2mn)\cdot (f^{k_3}\cdot \tilde{\chi}^{k^{\prime}_3})(m^2+n^2), \end{align*} $$
$$ \begin{align*}\sum_{k_i,k_i^{\prime}\in {\mathcal K}} \, (f^{k_1}\cdot \tilde{\chi}^{k^{\prime}_1})(m^2-n^2)\cdot (f^{k_2}\cdot \tilde{\chi}^{k^{\prime}_2})(2mn)\cdot (f^{k_3}\cdot \tilde{\chi}^{k^{\prime}_3})(m^2+n^2), \end{align*} $$
where
In what follows, we implicitly assume that all
![]() $k_i,k_i^{\prime }$
belong to
$k_i,k_i^{\prime }$
belong to
![]() ${\mathcal K}$
.
${\mathcal K}$
.
Let q be the period of
![]() $\chi $
, then
$\chi $
, then
![]() $\tilde {\chi }(qn+1)=1$
for every
$\tilde {\chi }(qn+1)=1$
for every
![]() $n\in {\mathbb N}$
. Taking the previous facts in mind, we see that in order to establish the needed positiveness, it suffices to show that there exists
$n\in {\mathbb N}$
. Taking the previous facts in mind, we see that in order to establish the needed positiveness, it suffices to show that there exists
![]() $Q\in {\mathbb N}$
such that
$Q\in {\mathbb N}$
such that
![]() $q\mid Q$
and
$q\mid Q$
and
 $$ \begin{align} L(Q):= \sum_{k_i,k_i^{\prime}\in {\mathcal K}} \, \Re(L_{k_1,k_2,k_3,k_2^{\prime}}(Q))>0, \end{align} $$
$$ \begin{align} L(Q):= \sum_{k_i,k_i^{\prime}\in {\mathcal K}} \, \Re(L_{k_1,k_2,k_3,k_2^{\prime}}(Q))>0, \end{align} $$
where
 $$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q):=\lim_{l\to\infty} {\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}((Qm+1)^2 &-(Qn)^2)\cdot f^{k_2}(2(Qm+1)(Qn))\cdot \notag\\ &f^{k_3}((Qm+1)^2+(Qn)^2)\cdot \tilde{\chi}^{k_2^{\prime}}(2(Qn)). \end{align} $$
$$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q):=\lim_{l\to\infty} {\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}((Qm+1)^2 &-(Qn)^2)\cdot f^{k_2}(2(Qm+1)(Qn))\cdot \notag\\ &f^{k_3}((Qm+1)^2+(Qn)^2)\cdot \tilde{\chi}^{k_2^{\prime}}(2(Qn)). \end{align} $$
(We used that
![]() $\tilde {\chi }(j)=1$
for
$\tilde {\chi }(j)=1$
for
![]() $j\in Q{\mathbb Z}+1$
.)
$j\in Q{\mathbb Z}+1$
.)
Claim 1 (
 $f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
)
$f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
)
For every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $Q_0=Q_0(f,\tilde {\chi },\varepsilon )\in {\mathbb N}$
with
$Q_0=Q_0(f,\tilde {\chi },\varepsilon )\in {\mathbb N}$
with
![]() $q\mid Q_0$
, such that the following holds: If
$q\mid Q_0$
, such that the following holds: If
![]() $Q\in {\mathbb N}$
satisfies
$Q\in {\mathbb N}$
satisfies
![]() $Q_0\mid Q$
, then for all
$Q_0\mid Q$
, then for all
![]() $k_1,k_2,k_3,k_2^{\prime }\in {\mathcal K}$
with
$k_1,k_2,k_3,k_2^{\prime }\in {\mathcal K}$
with
![]() $ f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
, we have
$ f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
, we have
As a consequence, there exists
![]() $Q_0:=Q_0(f,\tilde {\chi } )$
, such that if
$Q_0:=Q_0(f,\tilde {\chi } )$
, such that if
![]() $Q\in {\mathbb N}$
satisfies
$Q\in {\mathbb N}$
satisfies
![]() $Q_0\mid Q$
, then
$Q_0\mid Q$
, then
 $$ \begin{align} \sum_{k_1,k_2,k_3,k_2^{\prime}\colon f^{k_2}\cdot \tilde{\chi}^{k_2^{\prime}}= 1} \Re(L_{k_1,k_2,k_3,k_2^{\prime}}(Q))\geq 1. \end{align} $$
$$ \begin{align} \sum_{k_1,k_2,k_3,k_2^{\prime}\colon f^{k_2}\cdot \tilde{\chi}^{k_2^{\prime}}= 1} \Re(L_{k_1,k_2,k_3,k_2^{\prime}}(Q))\geq 1. \end{align} $$
We prove the claim. Let
![]() $\varepsilon>0$
. Note first that since
$\varepsilon>0$
. Note first that since
![]() $f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
, we get using (8.4) that
$f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
, we get using (8.4) that
 $$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q):=\lim_{l\to\infty} {\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}(Q(m-n)&+1)\cdot f^{k_1}(Q(m+n)+1) \notag\\ &f^{k_2}(Qm+1)\cdot f^{k_3}((Qm+1)^2+(Qn)^2). \end{align} $$
$$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q):=\lim_{l\to\infty} {\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}(Q(m-n)&+1)\cdot f^{k_1}(Q(m+n)+1) \notag\\ &f^{k_2}(Qm+1)\cdot f^{k_3}((Qm+1)^2+(Qn)^2). \end{align} $$
Using this identity, Corollary 2.17 and Lemma 3.1, we deduce that there exists
![]() $Q_0=Q_0(f,\varepsilon )$
, with
$Q_0=Q_0(f,\varepsilon )$
, with
![]() $q\mid Q_0$
, such that if
$q\mid Q_0$
, such that if
![]() $Q\in {\mathbb N}$
satisfies
$Q\in {\mathbb N}$
satisfies
![]() $Q_0\mid Q$
, then for all
$Q_0\mid Q$
, then for all
![]() $k_1,k_2,k_3,k_2^{\prime }\in {\mathcal K}$
such that
$k_1,k_2,k_3,k_2^{\prime }\in {\mathcal K}$
such that
![]() $ f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
, we have
$ f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
, we have
This proves (8.5). Since
![]() $L_{0,0,0,0}=1$
, using (8.5) for
$L_{0,0,0,0}=1$
, using (8.5) for
![]() $\varepsilon =1/2$
, we deduce (8.6). This completes the proof of Claim 1.
$\varepsilon =1/2$
, we deduce (8.6). This completes the proof of Claim 1.
Claim 2 (p
 $f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}\neq 1$
)
$f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}\neq 1$
)
Let
![]() $Q_0\in {\mathbb N}$
be such that (8.6) holds for every
$Q_0\in {\mathbb N}$
be such that (8.6) holds for every
![]() $Q\in {\mathbb N}$
such that
$Q\in {\mathbb N}$
such that
![]() $Q_0\mid Q$
. Then for every
$Q_0\mid Q$
. Then for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $Q_1=Q_1(f,\tilde {\chi },\varepsilon )\in {\mathbb N}$
such that
$Q_1=Q_1(f,\tilde {\chi },\varepsilon )\in {\mathbb N}$
such that
![]() $Q_0\mid Q_1$
(hence, (8.5) holds for
$Q_0\mid Q_1$
(hence, (8.5) holds for
![]() $Q=Q_1$
) and
$Q=Q_1$
) and
 $$ \begin{align} \sum_{k_1,k_2,k_3,k_2^{\prime}\colon f^{k_2}\cdot \tilde{\chi}^{k_2^{\prime}}\neq 1} \Re(L_{k_1,k_2,k_3,k_2^{\prime}}(Q_1))\geq - \varepsilon. \end{align} $$
$$ \begin{align} \sum_{k_1,k_2,k_3,k_2^{\prime}\colon f^{k_2}\cdot \tilde{\chi}^{k_2^{\prime}}\neq 1} \Re(L_{k_1,k_2,k_3,k_2^{\prime}}(Q_1))\geq - \varepsilon. \end{align} $$
We prove the claim. Let
![]() $\varepsilon>0$
. It suffices to show that
$\varepsilon>0$
. It suffices to show that
Note that
where
 $$ \begin{align} L^{\prime}_{k_1,k_2,k_3,k_2^{\prime}}(Q):= \lim_{l\to\infty} &{\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}(Q(m-n)+1)\cdot f^{k_1}(Q(m+n)+1)\notag\\ &\qquad \qquad f^{k_2}(Qm+1) \cdot f^{k_3}((Qm+1)^2+(Qn)^2)\cdot f^{k_2}(n)\cdot \tilde{\chi}^{k_2}(n). \end{align} $$
$$ \begin{align} L^{\prime}_{k_1,k_2,k_3,k_2^{\prime}}(Q):= \lim_{l\to\infty} &{\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}(Q(m-n)+1)\cdot f^{k_1}(Q(m+n)+1)\notag\\ &\qquad \qquad f^{k_2}(Qm+1) \cdot f^{k_3}((Qm+1)^2+(Qn)^2)\cdot f^{k_2}(n)\cdot \tilde{\chi}^{k_2}(n). \end{align} $$
We prove (8.9). Let
![]() $\varepsilon '>0$
. Using (8.10), Corollary 2.17 and Lemma 3.1, we get that there exists
$\varepsilon '>0$
. Using (8.10), Corollary 2.17 and Lemma 3.1, we get that there exists
![]() $ Q_2=Q_2(f,\varepsilon ')$
such that the following holds: If
$ Q_2=Q_2(f,\varepsilon ')$
such that the following holds: If
![]() $Q\in {\mathbb N}$
satisfies
$Q\in {\mathbb N}$
satisfies
![]() $Q_2\mid Q$
, then, for all
$Q_2\mid Q$
, then, for all
![]() $k_1,k_2,k_3,k_2^{\prime }\in {\mathcal K}$
, we have
$k_1,k_2,k_3,k_2^{\prime }\in {\mathcal K}$
, we have
where
Hence,Footnote 15 by (8.4), (8.10), and (8.11), we have
Since by assumption,
![]() $f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}\neq 1$
, we have
$f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}\neq 1$
, we have
Combining this with (8.12), we get that (8.9) holds. This proves Claim 2.
Putting together the two claims, in particular the estimates (8.6) and (8.8), we deduce that for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $Q_1=Q_1(f, \tilde {\chi }, \varepsilon )\in {\mathbb N}$
with
$Q_1=Q_1(f, \tilde {\chi }, \varepsilon )\in {\mathbb N}$
with
![]() $q\mid Q_1$
, such that
$q\mid Q_1$
, such that
![]() $L(Q_1)\geq 1-\varepsilon $
; hence, (8.3) holds for
$L(Q_1)\geq 1-\varepsilon $
; hence, (8.3) holds for
![]() $Q=Q_1$
. This completes the proof.
$Q=Q_1$
. This completes the proof.
8.3 More general equations
Our methods allow us to extend Theorem 1.5 and cover more general equations of the form
where
![]() $a,b,c\in {\mathbb N}$
are squares satisfying Rado’s condition (i.e., we have either
$a,b,c\in {\mathbb N}$
are squares satisfying Rado’s condition (i.e., we have either
![]() $a=c$
, or
$a=c$
, or
![]() $b=c$
, or
$b=c$
, or
![]() $a+b=c$
). We summarize the key differences in the argument.
$a+b=c$
). We summarize the key differences in the argument.
Suppose first that
![]() $a=c$
(the case
$a=c$
(the case
![]() $b=c$
is similar). Then, as in Section 1.4, we get parametrizations of (8.13) of the form
$b=c$
is similar). Then, as in Section 1.4, we get parametrizations of (8.13) of the form
for some
![]() $\ell _1,\ell _2,\ell _3\in {\mathbb N}$
, and our hypothesis
$\ell _1,\ell _2,\ell _3\in {\mathbb N}$
, and our hypothesis
![]() $a=c$
implies that we can take
$a=c$
implies that we can take
![]() $\ell _1=\ell _3$
. This fact is then used to handle Claim 1 in the proof of Proposition 8.1, and the rest of the argument remains unchanged. To see how Claim 1 is handled, note that in our setting, the expressions
$\ell _1=\ell _3$
. This fact is then used to handle Claim 1 in the proof of Proposition 8.1, and the rest of the argument remains unchanged. To see how Claim 1 is handled, note that in our setting, the expressions
![]() $L_{k_1,k_2,k_3,k_2^{\prime }}(Q)$
in (8.4) take the form
$L_{k_1,k_2,k_3,k_2^{\prime }}(Q)$
in (8.4) take the form
 $$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q):=c_{k_1,k_2,k_3}\cdot \lim_{l\to\infty} &{\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}((Qm+1)^2-(Qn)^2)\cdot f^{k_2}(2(Qm+1)(Qn))\cdot \notag\\&\qquad f^{k_3}((Qm+1)^2+(Qn)^2)\cdot \tilde{\chi}^{k_2^{\prime}}(2(Qn)), \end{align} $$
$$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q):=c_{k_1,k_2,k_3}\cdot \lim_{l\to\infty} &{\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}((Qm+1)^2-(Qn)^2)\cdot f^{k_2}(2(Qm+1)(Qn))\cdot \notag\\&\qquad f^{k_3}((Qm+1)^2+(Qn)^2)\cdot \tilde{\chi}^{k_2^{\prime}}(2(Qn)), \end{align} $$
where
Using additionally that
![]() $\ell _1=\ell _3$
and that
$\ell _1=\ell _3$
and that
![]() $f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
,
$f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
,
![]() $f^{k_1+k_2+k_3}\cdot \tilde {\chi }^{k_1'+k_2^{\prime }+k_3'}=1$
, which are standing assumptions in Claim 1, we deduce that
$f^{k_1+k_2+k_3}\cdot \tilde {\chi }^{k_1'+k_2^{\prime }+k_3'}=1$
, which are standing assumptions in Claim 1, we deduce that
![]() $c_{k_1,k_2,k_3}=1$
. With this information at hand, the proof of Claim 1 in our setting is exactly the same as in the case of Pythagorean triples.
$c_{k_1,k_2,k_3}=1$
. With this information at hand, the proof of Claim 1 in our setting is exactly the same as in the case of Pythagorean triples.
Now suppose that
![]() $a+b=c$
, in which case, the argument is a bit different and somewhat simpler. As shown in Step 2 of [Reference Frantzikinakis and Host21, Appendix C], we can obtain parametrizations of (8.13) of the form
$a+b=c$
, in which case, the argument is a bit different and somewhat simpler. As shown in Step 2 of [Reference Frantzikinakis and Host21, Appendix C], we can obtain parametrizations of (8.13) of the form
for suitable
![]() $\ell _1,\ell _2,\ell _3,\ell _4, \ell _5\in {\mathbb N}$
that satisfy
$\ell _1,\ell _2,\ell _3,\ell _4, \ell _5\in {\mathbb N}$
that satisfy
![]() $\ell _1\neq \ell _2$
,
$\ell _1\neq \ell _2$
,
![]() $\ell _3\neq \ell _4$
and
$\ell _3\neq \ell _4$
and
![]() $\{\ell _1,\ell _2\}\neq \{\ell _3,\ell _4\}$
. Note that our assumption
$\{\ell _1,\ell _2\}\neq \{\ell _3,\ell _4\}$
. Note that our assumption
![]() $a+b=c$
was used to ensure that the coefficient of m is
$a+b=c$
was used to ensure that the coefficient of m is
![]() $1$
in all linear forms. We average on the grid
$1$
in all linear forms. We average on the grid
![]() $\{(Qm+1,Qn)\colon m,n\in {\mathbb N}\}$
. We will demonstrate how Claims 1 and 2 in the proof of Proposition 8.1 can be established within our framework. The remainder of the argument remains unaltered. In our context, the expressions
$\{(Qm+1,Qn)\colon m,n\in {\mathbb N}\}$
. We will demonstrate how Claims 1 and 2 in the proof of Proposition 8.1 can be established within our framework. The remainder of the argument remains unaltered. In our context, the expressions
![]() $L_{k_1,k_2,k_3,k_2^{\prime }}(Q)$
in (8.4) take the form
$L_{k_1,k_2,k_3,k_2^{\prime }}(Q)$
in (8.4) take the form
 $$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q) &:= \lim_{l\to\infty} {\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}\big((Q(m+\ell_1n)+1) (Q(m+\ell_2n)+1)\big)\cdot \notag \\ &\qquad f^{k_2}\big((Q(m+\ell_3n)+1) (Q(m+\ell_4n)+1)\big)\cdot f^{k_3}((Qm+1)^2+(Q\ell_5n)^2). \end{align} $$
$$ \begin{align} L_{k_1,k_2,k_3,k_2^{\prime}}(Q) &:= \lim_{l\to\infty} {\mathbb E}_{m,n\in [N_l], m>n} \, f^{k_1}\big((Q(m+\ell_1n)+1) (Q(m+\ell_2n)+1)\big)\cdot \notag \\ &\qquad f^{k_2}\big((Q(m+\ell_3n)+1) (Q(m+\ell_4n)+1)\big)\cdot f^{k_3}((Qm+1)^2+(Q\ell_5n)^2). \end{align} $$
Using the concentration estimates of Corollary 2.17, we can see that Claim 1 holds without assuming that
![]() $ f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
. Therefore, in our setting, Claim 2 in the proof of Proposition 8.1 is already addressed by this case and requires no further explanation.
$ f^{k_2}\cdot \tilde {\chi }^{k_2^{\prime }}=1$
. Therefore, in our setting, Claim 2 in the proof of Proposition 8.1 is already addressed by this case and requires no further explanation.
Acknowledgements
We thank the anonymous referee for a careful reading of the manuscript and for several suggestions that have improved the paper. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC-BY) licence to any Author Accepted Manuscript version arising from this submission.
Competing interest
The authors have no competing interest to declare.
Funding statement
Part of this research was conducted while the authors were at the Institute for Advanced Studies at Princeton during parts of the 2022/23 academic year. We are grateful to the Institute for its hospitality and support and acknowledge the NSF grant DMS-1926686. The first author was supported by the Research Grant-ELIDEK HFRI-FM17-1684.