Hostname: page-component-7b9c58cd5d-6tpvb Total loading time: 0 Render date: 2025-03-14T19:46:16.040Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE

Part of: General commutative ring theory Representation theory of groups Local theory

Published online by Cambridge University Press:  08 July 2016

PHAM HUU TIEP
PHAM HUU TIEP*
Affiliation:
Department of Mathematics, University of Arizona, Tucson, AZ 85721, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1981, Thompson proved that, if 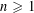$n\geqslant 1$ is any integer and $G$ is any finite subgroup of 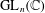$\text{GL}_{n}(\mathbb{C})$ , then 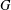$G$ has a semi-invariant of degree at most 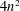$4n^{2}$ . He conjectured that, in fact, there is a universal constant 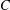$C$ such that for any 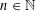$n\in \mathbb{N}$ and any finite subgroup 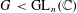$G<\text{GL}_{n}(\mathbb{C})$ , 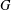$G$ has a semi-invariant of degree at most 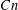$Cn$ . This conjecture would imply that the ${\it\alpha}$ -invariant 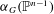${\it\alpha}_{G}(\mathbb{P}^{n-1})$ , as introduced by Tian in 1987, is at most 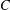$C$ . We prove Thompson’s conjecture in this paper.

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 13A50: Actions of groups on commutative rings; invariant theory 14B05: Singularities 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 4 , 2016 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Abramowitz, M. and Stegun, I. A. (Eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover, New York, 1972).Google Scholar
Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76 (1984), 469–514.Google Scholar
Cheltsov, I. and Shramov, K., ‘Log canonical thresholds of smooth Fano threefolds (with an appendix by J.-P. Demailly)’, Uspekhi Mat. Nauk 63(5) (2008), 73–180. English transl. Russian Math. Surveys 63(5) (2008), 859–958.Google Scholar
Cheltsov, I. and Shramov, K., ‘On exceptional quotient singularities’, Geometry Topol. 15 (2011), 1843–1882.Google Scholar
Cheltsov, I. and Shramov, K., ‘Six-dimensional exceptional quotient singularities’, Math. Res. Lett. 18 (2011), 1121–1139.CrossRefGoogle Scholar
Cheltsov, I. and Shramov, K., ‘Weakly-exceptional singularities in higher dimensions’, J. Reine Angew. Math. 689 (2014), 201–241.Google Scholar
Demailly, J.-P. and Kollár, J., ‘Semi-continuity of complex singularity exponents and Kähler–Einstein metrics on Fano orbifolds’, Ann. Sci. Éc. Norm. Super. (4) 34 (2001), 525–556.Google Scholar
Fulton, W. and Harris, J., Representation Theory (Springer, New York, 1991).Google Scholar
The GAP group, ‘GAP - groups, algorithms, and programming’, Version 4.4, 2004,http://www.gap-system.org.Google Scholar
Gluck, D. and Magaard, K., ‘Base sizes and regular orbits for coprime affine permutation groups’, J. Lond. Math. Soc. (2) 58 (1998), 603–618.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups, Vol. 3, Mathematical Surveys and Monographs, 40 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Guralnick, R. M., Larsen, M. and Tiep, P. H., ‘Representation growth in positive characteristic and conjugacy classes of maximal subgroups’, Duke Math. J. 161 (2012), 107–137.Google Scholar
Guralnick, R. M. and Tiep, P. H., ‘Cross characteristic representations of even characteristic symplectic groups’, Trans. Amer. Math. Soc. 356 (2004), 4969–5023.Google Scholar
Guralnick, R. M. and Tiep, P. H., ‘Symmetric powers and a problem of Kollár and Larsen’, Invent. Math. 174 (2008), 505–554.Google Scholar
Guralnick, R. M. and Tiep, P. H., ‘A problem of Kollár and Larsen on finite linear groups and crepant resolutions’, J. Eur. Math. Soc. 14 (2012), 605–657.Google Scholar
James, G. and Kerber, and A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and its Applications, 16 (Addison-Wesley Publishing Co., Reading, MA, 1981).Google Scholar
Kleidman, P. B. and Liebeck, M. W., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, Cambridge, New York, Port Chester, Melbourne, Sydney, 1990).Google Scholar
Liebeck, M. W., O’Brien, E. A., Shalev, A. and Tiep, P. H., ‘The Ore conjecture’, J. Eur. Math. Soc. 12 (2010), 939–1008.Google Scholar
Lyndon, R., ‘The cohomology theory of group extensions’, Duke Math. J. 15 (1948), 271–292.Google Scholar
Noether, E., ‘Der Endlichkeitssatz der Invarianten endlicher Gruppen’, Math. Ann. 77 (1916), 89–92.Google Scholar
Stanley, R., ‘Invariants of finite groups and their applications to combinatorics’, Bull. Amer. Math. Soc. (N.S.) 1 (1979), 475–511.Google Scholar
Suzuki, M., Group Theory I (Springer, Berlin–Heidelberg–New York, 1982).Google Scholar
Thompson, J. G., ‘Invariants of finite groups’, J. Algebra 69 (1981), 143–145.CrossRefGoogle Scholar
Tian, G., ‘On Kähler–Einstein metrics on certain Kähler manifolds with c 1(M) > 0’, Invent. Math. 89 (1987), 225–246.Google Scholar
Tian, G. and Yau, S.-T., ‘Kähler–Einstein metrics metrics on complex surfaces with C 1 > 0’, Comm. Math. Phys. 112 (1987), 175–203.Google Scholar
Tiep, P. H., ‘Finite groups admitting grassmannian 4-designs’, J. Algebra 306 (2006), 227–243.Google Scholar
Tiep, P. H. and Zalesskii, A. E., ‘Minimal characters of the finite classical groups’, Comm. Algebra 24 (1996), 2093–2167.Google Scholar