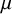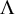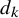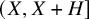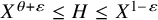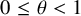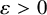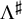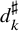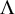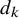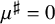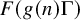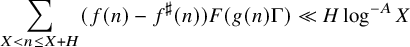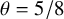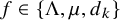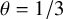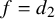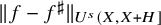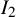1 Introduction
In this paper, we shall study correlations of arithmetic functions
![]() $f \colon \mathbb {N} \to \mathbb {C}$
with arbitrary nilsequences
$f \colon \mathbb {N} \to \mathbb {C}$
with arbitrary nilsequences
![]() $n \mapsto F(g(n) \Gamma )$
in short intervals. For simplicity, we will restrict attention to the following model examples of functions f:
$n \mapsto F(g(n) \Gamma )$
in short intervals. For simplicity, we will restrict attention to the following model examples of functions f:
-
• The Möbius function
 $\mu (n)$
, defined to equal
$\mu (n)$
, defined to equal
 $(-1)^j$
when n is the product of j distinct primes, and
$(-1)^j$
when n is the product of j distinct primes, and
 $0$
otherwise.
$0$
otherwise. -
• The von Mangoldt function
 $\Lambda (n)$
, defined to equal
$\Lambda (n)$
, defined to equal
 $\log p$
when n is a power
$\log p$
when n is a power
 $p^j$
of a prime p for some
$p^j$
of a prime p for some
 $j \geq 1$
, and
$j \geq 1$
, and
 $0$
otherwise.
$0$
otherwise. -
• The
 $k^{\mathrm {th}}$
divisor function
$k^{\mathrm {th}}$
divisor function
 $d_k(n)$
, defined to equal the number of representations of n as the product
$d_k(n)$
, defined to equal the number of representations of n as the product
 $n=n_1\dotsm n_k$
of k natural numbers, where
$n=n_1\dotsm n_k$
of k natural numbers, where
 $k \geq 2$
is fixed. (In particular, all implied constants in our asymptotic notation are understood to depend on k.)
$k \geq 2$
is fixed. (In particular, all implied constants in our asymptotic notation are understood to depend on k.)
By a ‘nilsequence’, we mean a function of the form
![]() $n \mapsto F(g(n)\Gamma )$
, where
$n \mapsto F(g(n)\Gamma )$
, where
![]() $G/\Gamma $
is a filtered nilmanifold and
$G/\Gamma $
is a filtered nilmanifold and
![]() $F \colon G/\Gamma \to \mathbb {C}$
is a Lipschitz function. The precise definitions of these terms will be given in Section 2.3, but a simple example of a nilsequence to keep in mind for now is
$F \colon G/\Gamma \to \mathbb {C}$
is a Lipschitz function. The precise definitions of these terms will be given in Section 2.3, but a simple example of a nilsequence to keep in mind for now is
![]() $F(g(n) \Gamma ) = e(\alpha n^d)$
for some real number
$F(g(n) \Gamma ) = e(\alpha n^d)$
for some real number
![]() $\alpha $
, some natural number
$\alpha $
, some natural number
![]() $d \geq 0$
and with
$d \geq 0$
and with
![]() .
.
When f is nonnegative and
![]() $F(g(n) \Gamma )$
is a ‘major arc’ in some sense (e.g., if
$F(g(n) \Gamma )$
is a ‘major arc’ in some sense (e.g., if
![]() $F(g(n)\Gamma ) = e(\alpha n^s)$
with
$F(g(n)\Gamma ) = e(\alpha n^s)$
with
![]() $\alpha $
very close to a rational
$\alpha $
very close to a rational
![]() $a/q$
with small denominator q), there is actually correlation between f and
$a/q$
with small denominator q), there is actually correlation between f and
![]() $F(g(n) \Gamma )$
, but we shall deal with this by first subtracting off a suitable approximation
$F(g(n) \Gamma )$
, but we shall deal with this by first subtracting off a suitable approximation
![]() $f^\sharp $
from f. In the case of the Möbius function
$f^\sharp $
from f. In the case of the Möbius function
![]() $\mu $
, we may set
$\mu $
, we may set
![]() $\mu ^\sharp = 0$
. On the other hand, the functions
$\mu ^\sharp = 0$
. On the other hand, the functions
![]() $\Lambda , d_k$
are nonnegative and one therefore needs to construct nontrivial approximants
$\Lambda , d_k$
are nonnegative and one therefore needs to construct nontrivial approximants
![]() $\Lambda ^\sharp , d_k^\sharp $
to such functions before one can expect to obtain discorrelation; we shall choose
$\Lambda ^\sharp , d_k^\sharp $
to such functions before one can expect to obtain discorrelation; we shall choose
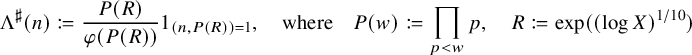
and
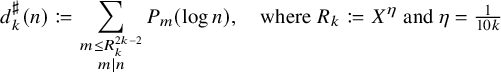
and the polynomials
![]() $P_m(t)$
(which have degree
$P_m(t)$
(which have degree
![]() $k-1$
) are given by the formula
$k-1$
) are given by the formula
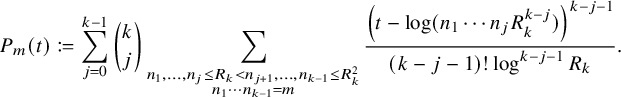
We will discuss these choices of approximants more in Section 3.1 (which can be read independently of the rest of the paper), but let us already here note that the approximants lead to type I sums and are thus easier to handle than the original functions and that the choice of the parameter R in
![]() $\Lambda ^{\sharp }$
allows for an arbitrary power of log saving in equation (1.6) below. Moreover, the approximants are nonnegative, which is helpful for some applications (in particular in the proof of Theorem 1.5 below). For future use, we record the fact that our correlation estimates for
$\Lambda ^{\sharp }$
allows for an arbitrary power of log saving in equation (1.6) below. Moreover, the approximants are nonnegative, which is helpful for some applications (in particular in the proof of Theorem 1.5 below). For future use, we record the fact that our correlation estimates for
![]() $d_k - d_k^{\sharp }$
work for
$d_k - d_k^{\sharp }$
work for
![]() $d_k^{\sharp }$
defined as in equation (1.2) with any fixed
$d_k^{\sharp }$
defined as in equation (1.2) with any fixed
![]() $0 < \eta \leq \frac {1}{10k}$
, as long as we allow implied constants to depend on
$0 < \eta \leq \frac {1}{10k}$
, as long as we allow implied constants to depend on
![]() $\eta $
.
$\eta $
.
For technical reasons, it can be beneficial to consider ‘maximal discorrelation’ estimates. Loosely following Robert and Sargos [Reference Robert and Sargos58] we adopt the conventionFootnote 1 that, for an interval I,
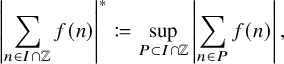
where P ranges over all arithmetic progressions in
![]() $I \cap \mathbb {Z}$
.
$I \cap \mathbb {Z}$
.
Now, we are ready to state our main theorem.Footnote 2
Theorem 1.1 (Discorrelation estimate).
Let
![]() $X \geq 3$
,
$X \geq 3$
,
![]() $X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
$X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
![]() $0 < \theta < 1$
and
$0 < \theta < 1$
and
![]() $\varepsilon> 0$
, and let
$\varepsilon> 0$
, and let
![]() $\delta \in (0,1)$
. Let
$\delta \in (0,1)$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of some degree d and dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of some degree d and dimension D and complexity at most
![]() $1/\delta $
, and let
$1/\delta $
, and let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be a Lipschitz function of norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be a Lipschitz function of norm at most
![]() $1/\delta $
.
$1/\delta $
.
-
(i) If
 $\theta = 5/8$
, then for all
$\theta = 5/8$
, then for all
 $A> 0$
, (1.5)
$A> 0$
, (1.5) $$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \mu(n) \overline{F}(g(n)\Gamma) \right|}^* &\ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X \end{align} $$
$$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \mu(n) \overline{F}(g(n)\Gamma) \right|}^* &\ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X \end{align} $$
-
(ii) If
 $\theta = 5/8$
, then for all
$\theta = 5/8$
, then for all
 $A> 0$
, (1.6)
$A> 0$
, (1.6) $$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} (\Lambda(n) - \Lambda^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* &\ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X. \end{align} $$
$$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} (\Lambda(n) - \Lambda^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* &\ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X. \end{align} $$
-
(iii) Let
 $k \geq 2$
. Set
$k \geq 2$
. Set
 $\theta = 1/3$
for
$\theta = 1/3$
for
 $k=2$
,
$k=2$
,
 $\theta =5/9$
for
$\theta =5/9$
for
 $k=3$
, and
$k=3$
, and
 $\theta =5/8$
for
$\theta =5/8$
for
 $k \geq 4$
. Then (1.7)for some constant
$k \geq 4$
. Then (1.7)for some constant $$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)}{\left| \sum_{X < n \leq X+H} (d_k(n) - d_k^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D} \delta^{-O_{d,D}(1)} H X^{-c_{k,d,D} \varepsilon} \end{align} $$
$$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)}{\left| \sum_{X < n \leq X+H} (d_k(n) - d_k^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D} \delta^{-O_{d,D}(1)} H X^{-c_{k,d,D} \varepsilon} \end{align} $$
 $c_{k,d,D}>0$
depending only on
$c_{k,d,D}>0$
depending only on
 $k,d,D$
.
$k,d,D$
.
-
(iv) If
 $\theta = 3/5$
, then (1.8)
$\theta = 3/5$
, then (1.8) $$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \mu(n) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-1/4} X. \end{align} $$
$$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \mu(n) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-1/4} X. \end{align} $$
-
(v) Let
 $k \geq 4$
. If
$k \geq 4$
. If
 $\theta = 3/5$
, then (1.9)
$\theta = 3/5$
, then (1.9) $$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)}{\left| \sum_{X < n \leq X+H} (d_k(n) - d_k^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{\frac{3}{4}k-1} X. \end{align} $$
$$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)}{\left| \sum_{X < n \leq X+H} (d_k(n) - d_k^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{\frac{3}{4}k-1} X. \end{align} $$
The dependency of the implied constants on A in equations (1.5) and (1.6) is ineffective due to the possible existence of Siegel zeros. All the other implied constants are effective.
Remark 1.2. One could extend the theorem to cover the range
![]() $X^{1-\varepsilon }\leq H\leq X$
without difficulty; however, this is not the most interesting regime and there are some places in the proof where the restriction to
$X^{1-\varepsilon }\leq H\leq X$
without difficulty; however, this is not the most interesting regime and there are some places in the proof where the restriction to
![]() $H\leq X^{1-\varepsilon }$
is convenient. In the cases of equations (1.5), (1.8), the result for
$H\leq X^{1-\varepsilon }$
is convenient. In the cases of equations (1.5), (1.8), the result for
![]() $X^{\theta +\varepsilon }\leq H\leq X^{1-\varepsilon }$
directly implies the result for
$X^{\theta +\varepsilon }\leq H\leq X^{1-\varepsilon }$
directly implies the result for
![]() $X^{1-\varepsilon }\leq H\leq X$
by splitting long sums into shorter ones. In the cases of equations (1.6), (1.7), (1.9), it turns out that there is some flexibility in the choice of the approximant (one can certainly vary R in equation (1.1) or
$X^{1-\varepsilon }\leq H\leq X$
by splitting long sums into shorter ones. In the cases of equations (1.6), (1.7), (1.9), it turns out that there is some flexibility in the choice of the approximant (one can certainly vary R in equation (1.1) or
![]() $R_k$
in equation (1.2) by a multiplicative factor
$R_k$
in equation (1.2) by a multiplicative factor
![]() $\asymp 1$
), and then one can make a similar splitting argument. We leave the details to the interested reader.
$\asymp 1$
), and then one can make a similar splitting argument. We leave the details to the interested reader.
In applications
![]() $d,D,\delta $
will often be fixed; however, the fact that the constants here depend in a polynomial fashion on
$d,D,\delta $
will often be fixed; however, the fact that the constants here depend in a polynomial fashion on
![]() $\delta $
will be useful for induction purposes.
$\delta $
will be useful for induction purposes.
Note that polynomial phases
![]() $F(g(n)\Gamma ) = e(P(n))$
, with
$F(g(n)\Gamma ) = e(P(n))$
, with
![]() $P \colon \mathbb {Z} \to \mathbb {R}$
a polynomial of degree d, are a special case of nilsequences – in this case the filtered nilmanifold is the unit circle
$P \colon \mathbb {Z} \to \mathbb {R}$
a polynomial of degree d, are a special case of nilsequences – in this case the filtered nilmanifold is the unit circle
![]() $\mathbb {R}/\mathbb {Z}$
(with
$\mathbb {R}/\mathbb {Z}$
(with
![]() $\mathbb {R} = (\mathbb {R},+)$
being the filtered nilpotent group with
$\mathbb {R} = (\mathbb {R},+)$
being the filtered nilpotent group with
![]() $\mathbb {R}_i = \mathbb {R}$
for
$\mathbb {R}_i = \mathbb {R}$
for
![]() $i \leq d$
and
$i \leq d$
and
![]() $\mathbb {R}_i = \{0\}$
for
$\mathbb {R}_i = \{0\}$
for
![]() $i>d$
) and
$i>d$
) and
![]() $F(\alpha ) = e(\alpha )$
for all
$F(\alpha ) = e(\alpha )$
for all
![]() $\alpha \in \mathbb {R}/\mathbb {Z}$
. In particular, the results of Theorem 1.1 hold for polynomial phases, that is, with
$\alpha \in \mathbb {R}/\mathbb {Z}$
. In particular, the results of Theorem 1.1 hold for polynomial phases, that is, with
![]() $G/\Gamma =\mathbb {R}/\mathbb {Z}$
,
$G/\Gamma =\mathbb {R}/\mathbb {Z}$
,
![]() $D=1$
, and with
$D=1$
, and with
![]() $\overline {F}(g(n)\Gamma )$
replaced with
$\overline {F}(g(n)\Gamma )$
replaced with
![]() $e(P(n))$
. Before moving on, let us for the convenience of the reader state the following corollary of our theorem in the polynomial phase case.
$e(P(n))$
. Before moving on, let us for the convenience of the reader state the following corollary of our theorem in the polynomial phase case.
Corollary 1.3 (Discorrelation of
 $\mu $
and
$\mu $
and
 $\Lambda $
with polynomial phases in short intervals).
$\Lambda $
with polynomial phases in short intervals).
Let
![]() $X \geq 3$
, and let
$X \geq 3$
, and let
![]() $X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
$X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
![]() $0 < \theta < 1$
and
$0 < \theta < 1$
and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $d\geq 1$
, and let
$d\geq 1$
, and let
![]() $P:\mathbb {Z}\to \mathbb {R}$
be any polynomial of degree d.
$P:\mathbb {Z}\to \mathbb {R}$
be any polynomial of degree d.
-
(i) If
 $\theta = 5/8$
, then, for all
$\theta = 5/8$
, then, for all
 $A> 0$
,
$A> 0$
,  $$ \begin{align*} \left|\sum_{X < n\leq X+H}\mu(n)e(P(n))\right|\ll_{d,A,\varepsilon} \frac{H}{\log^A X}. \end{align*} $$
$$ \begin{align*} \left|\sum_{X < n\leq X+H}\mu(n)e(P(n))\right|\ll_{d,A,\varepsilon} \frac{H}{\log^A X}. \end{align*} $$
-
(ii) If
 $\theta = 5/8$
and
$\theta = 5/8$
and
 $A> 0$
, we have unless there exists
$A> 0$
, we have unless there exists $$ \begin{align*} \left|\sum_{X < n\leq X+H}\Lambda(n)e(P(n))\right|\leq \frac{H}{\log^A X}, \end{align*} $$
$$ \begin{align*} \left|\sum_{X < n\leq X+H}\Lambda(n)e(P(n))\right|\leq \frac{H}{\log^A X}, \end{align*} $$
 $1\leq q\leq (\log X)^{O_{d,A,\varepsilon }(1)}$
such that one has the ‘major arc’ property (1.10)where
$1\leq q\leq (\log X)^{O_{d,A,\varepsilon }(1)}$
such that one has the ‘major arc’ property (1.10)where $$ \begin{align} \max_{1\leq j\leq d}H^j\|q\alpha_j\|_{\mathbb{R}/\mathbb{Z}}\leq (\log X)^{O_{d,A,\varepsilon}(1)}, \end{align} $$
$$ \begin{align} \max_{1\leq j\leq d}H^j\|q\alpha_j\|_{\mathbb{R}/\mathbb{Z}}\leq (\log X)^{O_{d,A,\varepsilon}(1)}, \end{align} $$
 $\alpha _j$
is the degree j coefficient of the polynomial
$\alpha _j$
is the degree j coefficient of the polynomial
 $n\mapsto P(n+X)$
and
$n\mapsto P(n+X)$
and
 $\|y\|_{\mathbb {R}/\mathbb {Z}}$
denotes the distance from y to the nearest integer(s).
$\|y\|_{\mathbb {R}/\mathbb {Z}}$
denotes the distance from y to the nearest integer(s).
-
(iii) If
 $\theta = 3/5$
, then
$\theta = 3/5$
, then  $$ \begin{align*} \left|\sum_{X < n\leq X+H}\mu(n)e(P(n))\right|\ll_{d,\varepsilon} \frac{H}{\log^{1/10} X}. \end{align*} $$
$$ \begin{align*} \left|\sum_{X < n\leq X+H}\mu(n)e(P(n))\right|\ll_{d,\varepsilon} \frac{H}{\log^{1/10} X}. \end{align*} $$
The claims (i) and (iii) are immediate from Theorem 1.1, but (ii) requires a short argument, provided in Section 10. One could state an analogous result in the case of
![]() $d_k$
(with the same exponents as in Theorem 1.1).
$d_k$
(with the same exponents as in Theorem 1.1).
Let us now discuss the literature on the topic, starting with results concerning the Möbius function. A discorrelation estimate such as Theorem 1.1(i) with arbitrary
![]() $F(g(n) \Gamma )$
was previously only known in case of long intervals due to the work of Green and the third author [Reference Green and Tao18, Theorem 1.1]. Namely, they have shown that
$F(g(n) \Gamma )$
was previously only known in case of long intervals due to the work of Green and the third author [Reference Green and Tao18, Theorem 1.1]. Namely, they have shown that
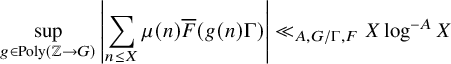 $$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} \left| \sum_{n \leq X} \mu(n) \overline{F}(g(n)\Gamma) \right| \ll_{A,G/\Gamma,F} X \log^{-A} X \end{align} $$
$$ \begin{align} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} \left| \sum_{n \leq X} \mu(n) \overline{F}(g(n)\Gamma) \right| \ll_{A,G/\Gamma,F} X \log^{-A} X \end{align} $$
for any
![]() $X \geq 2$
,
$X \geq 2$
,
![]() $A>0$
, filtered nilmanifold
$A>0$
, filtered nilmanifold
![]() $G/\Gamma $
and Lipschitz function
$G/\Gamma $
and Lipschitz function
![]() $F \colon G/\Gamma \to \mathbb {C}$
. This result of Green and the third author is a vast generalization of a classical result of Davenport [Reference Davenport6], which states that
$F \colon G/\Gamma \to \mathbb {C}$
. This result of Green and the third author is a vast generalization of a classical result of Davenport [Reference Davenport6], which states that
 $$ \begin{align} \sup_{\alpha \in \mathbb{R}} \left| \sum_{n \leq X} \mu(n) e(-\alpha n)\right| \ll_A X \log^{-A} X, \end{align} $$
$$ \begin{align} \sup_{\alpha \in \mathbb{R}} \left| \sum_{n \leq X} \mu(n) e(-\alpha n)\right| \ll_A X \log^{-A} X, \end{align} $$
and of the Siegel–Walfisz theorem (see, e.g., [Reference Iwaniec and Kowalski37, Corollary 5.29]), which states that
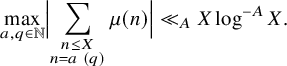 $$ \begin{align} \max_{a, q \in \mathbb{N}} \Bigl|\sum_{\substack{n \leq X\\ n = a\ (q)}} \mu(n) \Bigr| \ll_A X \log^{-A} X. \end{align} $$
$$ \begin{align} \max_{a, q \in \mathbb{N}} \Bigl|\sum_{\substack{n \leq X\\ n = a\ (q)}} \mu(n) \Bigr| \ll_A X \log^{-A} X. \end{align} $$
As is well-known, the bounds of
![]() $O_A(X \log ^{-A} X)$
here cannot be improved unconditionally with current technology, due to the possible existence of Siegel zeroes (unless one subtracts a correction term to account for the contribution of such zero; see [Reference Tao and Teräväinen61, Theorem 2.7]).
$O_A(X \log ^{-A} X)$
here cannot be improved unconditionally with current technology, due to the possible existence of Siegel zeroes (unless one subtracts a correction term to account for the contribution of such zero; see [Reference Tao and Teräväinen61, Theorem 2.7]).
On the other hand, for short intervals there has been a lot of activity in the special case of polynomial phase twists.
Theorem 1.1(i) was previously only known in the linear phase case when
![]() $F(g(n)\Gamma ) = e(\alpha n)$
for any
$F(g(n)\Gamma ) = e(\alpha n)$
for any
![]() $\alpha \in \mathbb {R}$
by work of Zhan [Reference Zhan64]. More precisely, Zhan [Reference Zhan64, Theorem 5] established that
$\alpha \in \mathbb {R}$
by work of Zhan [Reference Zhan64]. More precisely, Zhan [Reference Zhan64, Theorem 5] established that
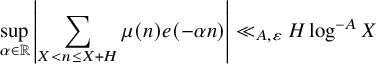 $$ \begin{align} \sup_{\alpha \in \mathbb{R}} \left|\sum_{X < n \leq X+H} \mu(n) e(-\alpha n)\right| \ll_{A,\varepsilon} H \log^{-A} X \end{align} $$
$$ \begin{align} \sup_{\alpha \in \mathbb{R}} \left|\sum_{X < n \leq X+H} \mu(n) e(-\alpha n)\right| \ll_{A,\varepsilon} H \log^{-A} X \end{align} $$
whenever
![]() $X^{5/8+\varepsilon } \leq H \leq X$
and
$X^{5/8+\varepsilon } \leq H \leq X$
and
![]() $A \geq 1$
. Hence, Theorem 1.1(i) can be seen as a vast extension of Zhan’s work.
$A \geq 1$
. Hence, Theorem 1.1(i) can be seen as a vast extension of Zhan’s work.
Concerning higher degree polynomials, the most recent result is due to the first two authors [Reference Matomäki and Shao49, Theorem 1.4] giving, for any polynomial
![]() $P(n)$
of degree
$P(n)$
of degree
![]() $\leq d$
,
$\leq d$
,
for all
![]() $A> 0$
and
$A> 0$
and
![]() $X^{2/3+\varepsilon } \leq H \leq X$
. In particular a special case of Theorem 1.1(i) (recorded here as Corollary 1.3(i)) supersedes this result by showing it with the exponent
$X^{2/3+\varepsilon } \leq H \leq X$
. In particular a special case of Theorem 1.1(i) (recorded here as Corollary 1.3(i)) supersedes this result by showing it with the exponent
![]() $2/3$
lowered to
$2/3$
lowered to
![]() $5/8$
.
$5/8$
.
All the previous results mentioned so far for the Möbius function exist also for the von Mangoldt function as long as
![]() $F(g(n) \Gamma )$
or
$F(g(n) \Gamma )$
or
![]() $e(-P(n))$
is a ‘minor arc’ in a certain sense (for results corresponding to equations (1.11), (1.12), (1.13), (1.14) and (1.15), see, respectively, [Reference Green and Tao18, Section 7], [Reference Iwaniec and Kowalski37, Theorem 13.6], [Reference Iwaniec and Kowalski37, Corollary 5.29], [Reference Zhan64, Theorems 2–3] and [Reference Matomäki and Shao49, Theorem 1.1]). It is very likely that with our choice of approximant these arguments also extend to cover major arc cases and maximal correlations, although we will not detail this here as such claims follow in any case from Theorem 1.1.
$e(-P(n))$
is a ‘minor arc’ in a certain sense (for results corresponding to equations (1.11), (1.12), (1.13), (1.14) and (1.15), see, respectively, [Reference Green and Tao18, Section 7], [Reference Iwaniec and Kowalski37, Theorem 13.6], [Reference Iwaniec and Kowalski37, Corollary 5.29], [Reference Zhan64, Theorems 2–3] and [Reference Matomäki and Shao49, Theorem 1.1]). It is very likely that with our choice of approximant these arguments also extend to cover major arc cases and maximal correlations, although we will not detail this here as such claims follow in any case from Theorem 1.1.
Theorem 1.1(iv) generalizes (albeit with a slightly weaker logarithmic saving) a result of the first and fourth authors [Reference Matomäki and Teräväinen50, Theorem 1.5] that gave, for
![]() $0 < A < 1/3$
,
$0 < A < 1/3$
,
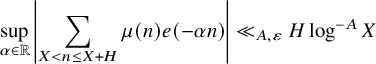 $$ \begin{align} \sup_{\alpha \in \mathbb{R}} \left|\sum_{X < n \leq X+H} \mu(n) e(-\alpha n)\right| \ll_{A,\varepsilon} H \log^{-A} X \end{align} $$
$$ \begin{align} \sup_{\alpha \in \mathbb{R}} \left|\sum_{X < n \leq X+H} \mu(n) e(-\alpha n)\right| \ll_{A,\varepsilon} H \log^{-A} X \end{align} $$
in the regime
![]() $X \geq H \geq X^{3/5+\varepsilon }$
(actually [Reference Matomäki and Teräväinen50, Remark 5.2] allows one to enlarge the range of A to
$X \geq H \geq X^{3/5+\varepsilon }$
(actually [Reference Matomäki and Teräväinen50, Remark 5.2] allows one to enlarge the range of A to
![]() $0 < A < 1$
).
$0 < A < 1$
).
The literature on correlations between
![]() $d_k$
and Fourier or higher-order phases is sparse. A variant of the long interval case (1.11) (with a weaker error term) follows from work of Matthiesen [Reference Matthiesen51, Theorem 6.1].
$d_k$
and Fourier or higher-order phases is sparse. A variant of the long interval case (1.11) (with a weaker error term) follows from work of Matthiesen [Reference Matthiesen51, Theorem 6.1].
Furthermore, it should be possible to adapt the existing results on polynomial correlations of
![]() $\Lambda (n)$
also to the case of
$\Lambda (n)$
also to the case of
![]() $d_k(n)$
but with power savings. More precisely, one should be able to follow the approach of Zhan [Reference Zhan64] to obtain discorrelation with linear phases
$d_k(n)$
but with power savings. More precisely, one should be able to follow the approach of Zhan [Reference Zhan64] to obtain discorrelation with linear phases
![]() $e(\alpha n)$
for
$e(\alpha n)$
for
![]() $X \geq H \geq X^{5/8+\varepsilon }$
(for
$X \geq H \geq X^{5/8+\varepsilon }$
(for
![]() $k=2$
one can replace
$k=2$
one can replace
![]() $5/8$
by
$5/8$
by
![]() $1/2$
and for
$1/2$
and for
![]() $k=3$
one can replace
$k=3$
one can replace
![]() $5/8$
by
$5/8$
by
![]() $3/5$
) and the work of the first two authors [Reference Matomäki and Shao49] to obtain discorrelation with polynomial phases for
$3/5$
) and the work of the first two authors [Reference Matomäki and Shao49] to obtain discorrelation with polynomial phases for
![]() $X \geq H \geq X^{2/3+\varepsilon }$
(for
$X \geq H \geq X^{2/3+\varepsilon }$
(for
![]() $k=2$
one can replace
$k=2$
one can replace
![]() $2/3$
by
$2/3$
by
![]() $1/2$
). We omit the details of these extensions of [Reference Zhan64, Reference Matomäki and Shao49] as they follow from our Theorem 1.1.
$1/2$
). We omit the details of these extensions of [Reference Zhan64, Reference Matomäki and Shao49] as they follow from our Theorem 1.1.
We note that in the case
![]() $k=2$
the exponent
$k=2$
the exponent
![]() $1/3$
in Theorem 1.1(iii) matches the classical Voronoi exponent for the error term in long sums of the divisor function without any twist, and the result seems to be new even in the case of linear phases.
$1/3$
in Theorem 1.1(iii) matches the classical Voronoi exponent for the error term in long sums of the divisor function without any twist, and the result seems to be new even in the case of linear phases.
In the most major arc case
![]() $F(g(n) \Gamma ) = 1$
, shorter intervals can be reached than in Theorem 1.1; see Theorem 3.1 below. Furthermore, if one only wants discorrelation in almost all intervals, for instance by seeking to bound
$F(g(n) \Gamma ) = 1$
, shorter intervals can be reached than in Theorem 1.1; see Theorem 3.1 below. Furthermore, if one only wants discorrelation in almost all intervals, for instance by seeking to bound
 $$\begin{align*}\int_X^{2X} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{x < n \leq x+H} (f(n)-f^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* dx, \end{align*}$$
$$\begin{align*}\int_X^{2X} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{x < n \leq x+H} (f(n)-f^\sharp(n)) \overline{F}(g(n)\Gamma) \right|}^* dx, \end{align*}$$
much shorter intervals can be reached with aid of additional ideas. We will return to this question and its applications in a follow-up paper [Reference Matomäki, Radziwiłł, Shao, Tao and Teräväinen46].
Remark 1.4. It should be clear to experts from an inspection of our arguments that the methods used in this paper could also treat other arithmetic functions with similar structure to
![]() $\mu $
,
$\mu $
,
![]() $\Lambda $
or
$\Lambda $
or
![]() $d_k$
. For instance, all of the results for the Möbius function
$d_k$
. For instance, all of the results for the Möbius function
![]() $\mu $
here have counterparts for the Liouville function
$\mu $
here have counterparts for the Liouville function
![]() $\lambda $
; the results for the von Mangoldt function
$\lambda $
; the results for the von Mangoldt function
![]() $\Lambda $
have counterparts (with somewhat different normalizations) for the indicator function
$\Lambda $
have counterparts (with somewhat different normalizations) for the indicator function
![]() $1_{\mathbb {P}}$
of the primes
$1_{\mathbb {P}}$
of the primes
![]() ${\mathbb {P}}$
, and the results for
${\mathbb {P}}$
, and the results for
![]() $d_2$
have counterparts for the function
$d_2$
have counterparts for the function
![]() counting the number of representations of n as the sum of two squares. We sketch the modifications needed to establish these variants in Appendix A. We also conjecture that the methods can be extended to treat the indicator function
counting the number of representations of n as the sum of two squares. We sketch the modifications needed to establish these variants in Appendix A. We also conjecture that the methods can be extended to treat the indicator function
![]() $1_S$
of the set
$1_S$
of the set
![]() of sums of two squares or the indicator
of sums of two squares or the indicator
![]() $1_{S_\eta }$
of
$1_{S_\eta }$
of
![]() $X^\eta $
-smooth numbers, although in those two cases a technical difficulty arises that the construction of a sufficiently accurate approximant to these indicator functions is nontrivial. Again, see Appendix A for further discussion.
$X^\eta $
-smooth numbers, although in those two cases a technical difficulty arises that the construction of a sufficiently accurate approximant to these indicator functions is nontrivial. Again, see Appendix A for further discussion.
On the other hand, our arguments do not seem to easily extend to the Fourier coefficients
![]() $\lambda _f(n)$
of holomorphic cusp forms. The coefficients
$\lambda _f(n)$
of holomorphic cusp forms. The coefficients
![]() $\lambda _f(n)$
are analogous to
$\lambda _f(n)$
are analogous to
![]() $d_2(n)$
in many ways (though with vanishing approximant
$d_2(n)$
in many ways (though with vanishing approximant
![]() $\lambda ^\sharp _f = 0$
), and it is reasonable to conjecture parallel results for these two functions. For instance, in [Reference Ernvall-Hytönen and Karppinen10] it was established that
$\lambda ^\sharp _f = 0$
), and it is reasonable to conjecture parallel results for these two functions. For instance, in [Reference Ernvall-Hytönen and Karppinen10] it was established that
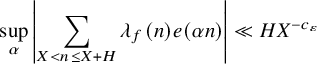 $$\begin{align*}\sup_\alpha \left| \sum_{X < n \leq X+H} \lambda_f(n) e(\alpha n) \right| \ll HX^{-c_\varepsilon} \end{align*}$$
$$\begin{align*}\sup_\alpha \left| \sum_{X < n \leq X+H} \lambda_f(n) e(\alpha n) \right| \ll HX^{-c_\varepsilon} \end{align*}$$
for
![]() $X^{2/5+\varepsilon } \leq H \leq X$
. See also [Reference He and Wang25] for a result with general nilsequences but long intervals. Unfortunately, the methods we use in this paper rely heavily on the convolution structure of the functions involved and do not obviously extend to give results for
$X^{2/5+\varepsilon } \leq H \leq X$
. See also [Reference He and Wang25] for a result with general nilsequences but long intervals. Unfortunately, the methods we use in this paper rely heavily on the convolution structure of the functions involved and do not obviously extend to give results for
![]() $\lambda _f$
.
$\lambda _f$
.
1.1 Gowers uniformity in short intervals
Just as discorrelation estimates with polynomial phases are important for applications of the circle method, discorrelation estimates with nilsequences are important in higher-order Fourier analysis due to the connection with the Gowers uniformity norms that we next discuss.
For any nonnegative integer
![]() $s \geq 1$
and any function
$s \geq 1$
and any function
![]() $f \colon \mathbb {Z} \to \mathbb {C}$
with finite support, define the (unnormalized) Gowers uniformity norm
$f \colon \mathbb {Z} \to \mathbb {C}$
with finite support, define the (unnormalized) Gowers uniformity norm
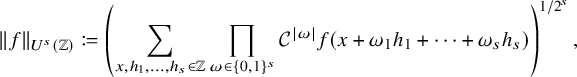
where
![]() $\omega = (\omega _1,\dots ,\omega _{s})$
,
$\omega = (\omega _1,\dots ,\omega _{s})$
,
, and
![]() $\mathcal {C} \colon z \mapsto \overline {z}$
is the complex conjugation map. Then for any interval
$\mathcal {C} \colon z \mapsto \overline {z}$
is the complex conjugation map. Then for any interval
![]() $(X,X+H]$
with
$(X,X+H]$
with
![]() $H \geq 1$
and any
$H \geq 1$
and any
![]() $f \colon \mathbb {Z} \to \mathbb {C}$
(not necessarily of finite support), define the Gowers uniformity norm over
$f \colon \mathbb {Z} \to \mathbb {C}$
(not necessarily of finite support), define the Gowers uniformity norm over
![]() $(X,X+H]$
by
$(X,X+H]$
by
where
![]() $1_{(X,X+H]} \colon \mathbb {Z} \to \mathbb {C}$
is the indicator function of
$1_{(X,X+H]} \colon \mathbb {Z} \to \mathbb {C}$
is the indicator function of
![]() $(X,X+H]$
.
$(X,X+H]$
.
Using the inverse theorem for Gowers norms (see Proposition 9.4) we can deduce the following theorem from Theorem 1.1 and a construction of pseudorandom majorants in Section 9.
Theorem 1.5 (Gowers uniformity estimate).
Let
![]() $X^{\theta +\varepsilon }\leq H\leq X^{1-\varepsilon }$
for some fixed
$X^{\theta +\varepsilon }\leq H\leq X^{1-\varepsilon }$
for some fixed
![]() $0 < \theta < 1$
and
$0 < \theta < 1$
and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $s\geq 1$
be a fixed integer. Also, denote
$s\geq 1$
be a fixed integer. Also, denote
![]() $\Lambda _{w}(n):=\frac {W}{\varphi (W)}1_{(n,W)=1}$
, where
$\Lambda _{w}(n):=\frac {W}{\varphi (W)}1_{(n,W)=1}$
, where
![]() $W:=\prod _{p\leq w}p$
and X is large enough in terms of w.
$W:=\prod _{p\leq w}p$
and X is large enough in terms of w.
-
(i) If
 $\theta = 5/8$
, then (1.18)
$\theta = 5/8$
, then (1.18) $$ \begin{align} &\|\Lambda-\Lambda_w\|_{U^s(X,X+H]}=o_{w\to \infty}(1), \end{align} $$
$$ \begin{align} &\|\Lambda-\Lambda_w\|_{U^s(X,X+H]}=o_{w\to \infty}(1), \end{align} $$
and for any
 $1\leq a\leq W$
with
$1\leq a\leq W$
with
 $(a,W)=1$
we have (1.19)
$(a,W)=1$
we have (1.19) $$ \begin{align} &\left\|\frac{\varphi(W)}{W}\Lambda(W\cdot+a)-1\right\|_{U^s(X,X+H]}=o_{w\to \infty}(1). \end{align} $$
$$ \begin{align} &\left\|\frac{\varphi(W)}{W}\Lambda(W\cdot+a)-1\right\|_{U^s(X,X+H]}=o_{w\to \infty}(1). \end{align} $$
-
(ii) Let
 $k \geq 2$
. Set
$k \geq 2$
. Set
 $\theta = 1/3$
for
$\theta = 1/3$
for
 $k=2$
,
$k=2$
,
 $\theta =5/9$
for
$\theta =5/9$
for
 $k=3$
, and
$k=3$
, and
 $\theta =3/5$
for
$\theta =3/5$
for
 $k \geq 4$
. Then (1.20)and for any
$k \geq 4$
. Then (1.20)and for any $$ \begin{align} \|d_k-d_k^{\sharp}\|_{U^s(X, X+H]}=o(\log^{k-1} X), \end{align} $$
$$ \begin{align} \|d_k-d_k^{\sharp}\|_{U^s(X, X+H]}=o(\log^{k-1} X), \end{align} $$
 $W'$
satisfying
$W'$
satisfying
 $W\mid W'\mid W^{\lfloor w\rfloor }$
and for any
$W\mid W'\mid W^{\lfloor w\rfloor }$
and for any
 $1\leq a\leq W'$
with
$1\leq a\leq W'$
with
 $(a,W')=1$
we have (1.21)
$(a,W')=1$
we have (1.21) $$ \begin{align} \|d_k(W'\cdot+a)-d_k^{\sharp}(W'\cdot+a)\|_{U^s(X, X+H]}=o_{w\to \infty}\left(\left(\frac{\varphi(W')}{W'}\right)^{k-1}\log^{k-1} X\right). \end{align} $$
$$ \begin{align} \|d_k(W'\cdot+a)-d_k^{\sharp}(W'\cdot+a)\|_{U^s(X, X+H]}=o_{w\to \infty}\left(\left(\frac{\varphi(W')}{W'}\right)^{k-1}\log^{k-1} X\right). \end{align} $$
-
(iii) If
 $\theta = 3/5$
, then (1.22)
$\theta = 3/5$
, then (1.22) $$ \begin{align} \|\mu\|_{U^s(X, X+H]}=o(1). \end{align} $$
$$ \begin{align} \|\mu\|_{U^s(X, X+H]}=o(1). \end{align} $$
In all these estimates, the
![]() $o(1)$
notation is with respect to the limit
$o(1)$
notation is with respect to the limit
![]() $X \to \infty $
(holding
$X \to \infty $
(holding
![]() $s,\varepsilon ,k$
fixed).
$s,\varepsilon ,k$
fixed).
Remarks.
-
• The model
 $\Lambda _w$
with w fixed is simple to work with and arises in various applications of Gowers uniformity (e.g., to ergodic theory). This also motivates our choice of the
$\Lambda _w$
with w fixed is simple to work with and arises in various applications of Gowers uniformity (e.g., to ergodic theory). This also motivates our choice of the
 $\Lambda ^{\sharp }$
model in equation (1.1) (although that is defined with a larger value of w to produce better error terms).
$\Lambda ^{\sharp }$
model in equation (1.1) (although that is defined with a larger value of w to produce better error terms). -
• Since the bounds in this theorem (unlike in Theorem 1.1) are qualitative in nature, it should be possible to use Heath-Brown’s trick from [Reference Heath-Brown29] to extend the range of H from
 $X^{\theta +\varepsilon }\leq H\leq X^{1-\varepsilon }$
to
$X^{\theta +\varepsilon }\leq H\leq X^{1-\varepsilon }$
to
 $X^{\theta }\leq H\leq X^{1-\varepsilon }$
. Also, the range
$X^{\theta }\leq H\leq X^{1-\varepsilon }$
. Also, the range
 $X^{1-\varepsilon }\leq H\leq X$
could be covered, as in Remark 1.2. We leave the details to the interested reader.
$X^{1-\varepsilon }\leq H\leq X$
could be covered, as in Remark 1.2. We leave the details to the interested reader. -
• In the case
 $s=2$
, we obtain significantly stronger estimates thanks to the polynomial nature of the
$s=2$
, we obtain significantly stronger estimates thanks to the polynomial nature of the
 $U^2$
inverse theorem. Specifically, when
$U^2$
inverse theorem. Specifically, when
 $\theta =5/8+\varepsilon $
, we have for all
$\theta =5/8+\varepsilon $
, we have for all $$ \begin{align*}\|\mu\|_{U^2(X, X+X^{\theta}]}, \|\Lambda-\Lambda^{\sharp}\|_{U^2(X, X+X^{\theta}]} \ll_{A,\varepsilon} \log^{-A} X\end{align*} $$
$$ \begin{align*}\|\mu\|_{U^2(X, X+X^{\theta}]}, \|\Lambda-\Lambda^{\sharp}\|_{U^2(X, X+X^{\theta}]} \ll_{A,\varepsilon} \log^{-A} X\end{align*} $$
 $A> 0$
and (1.23)for some
$A> 0$
and (1.23)for some $$ \begin{align} \|d_k\|_{U^2(X, X+X^{\theta}]} \ll_\varepsilon X^{-c_{k}\varepsilon} \end{align} $$
$$ \begin{align} \|d_k\|_{U^2(X, X+X^{\theta}]} \ll_\varepsilon X^{-c_{k}\varepsilon} \end{align} $$
 $c_{k}>0$
, with equation (1.23) also holding when
$c_{k}>0$
, with equation (1.23) also holding when
 $(k,\theta ) = (3,5/9), (2,1/3)$
and finally when
$(k,\theta ) = (3,5/9), (2,1/3)$
and finally when $$ \begin{align*}\|\mu\|_{U^2(X, X+X^{\theta}]} \ll_\varepsilon \log^{-1/20} X\end{align*} $$
$$ \begin{align*}\|\mu\|_{U^2(X, X+X^{\theta}]} \ll_\varepsilon \log^{-1/20} X\end{align*} $$
 $\theta = 3/5$
. All of these follow directly by combining Theorem 1.1 for
$\theta = 3/5$
. All of these follow directly by combining Theorem 1.1 for
 $d=1$
(that is, for Fourier phases in place of nilsequences) with the polynomial form of the
$d=1$
(that is, for Fourier phases in place of nilsequences) with the polynomial form of the
 $U^2$
inverse theorem, which states that if
$U^2$
inverse theorem, which states that if
 $f:[N]\to \mathbb {C}$
is
$f:[N]\to \mathbb {C}$
is
 $1$
-bounded and
$1$
-bounded and
 $\|f\|_{U^2[N]}\geq \delta $
for some
$\|f\|_{U^2[N]}\geq \delta $
for some
 $\delta>0$
, then
$\delta>0$
, then
 $|\sum _{n\leq N}f(n)e(\alpha n)|^{*}\gg \delta ^4 N$
for some
$|\sum _{n\leq N}f(n)e(\alpha n)|^{*}\gg \delta ^4 N$
for some
 $\alpha \in \mathbb {R}$
. This form of the inverse theorem follows directly from the Fourier representation of the
$\alpha \in \mathbb {R}$
. This form of the inverse theorem follows directly from the Fourier representation of the
 $U^2[N]$
norm and Parseval’s theorem, where the Gowers norm
$U^2[N]$
norm and Parseval’s theorem, where the Gowers norm
 $U^2[N]$
is defined analogously as in equation (1.17).
$U^2[N]$
is defined analogously as in equation (1.17).
1.2 Applications
1.2.1 Polynomial phases
We already stated Corollary 1.3 concerning polynomial phases. But let us here mention that in a recent work of Kanigowski–Lemańczyk–Radziwiłł [Reference Kanigowski, Lemańczyk and Radziwiłł39] on the prime number theorem for analytic skew products, a key analytic input ([Reference Kanigowski, Lemańczyk and Radziwiłł39, Theorem 9.1]) was that Corollary 1.3(ii) holds for
![]() $H=X^{2/3-\eta }$
(with a weaker error term of
$H=X^{2/3-\eta }$
(with a weaker error term of
![]() $o_{\eta \to 0}(H)$
), thus going just beyond the range of validity of [Reference Matomäki and Shao49, Theorem 1.1]. Corollary 1.3 allows taking
$o_{\eta \to 0}(H)$
), thus going just beyond the range of validity of [Reference Matomäki and Shao49, Theorem 1.1]. Corollary 1.3 allows taking
![]() $\eta <1/24$
with strongly logarithmic savings for the error terms. Similar remarks apply to the recent work of Kanigowski [Reference Kanigowski38].
$\eta <1/24$
with strongly logarithmic savings for the error terms. Similar remarks apply to the recent work of Kanigowski [Reference Kanigowski38].
1.2.2 An application to ergodic theory
In a seminal work, Host and Kra [Reference Host and Kra32] showed that, for any measure-preserving system
![]() $(X,\mathcal {X},\mu ,T)$
, any bounded functions
$(X,\mathcal {X},\mu ,T)$
, any bounded functions
![]() $f_1,\ldots , f_k:X\to \mathbb {C}$
and any intervals
$f_1,\ldots , f_k:X\to \mathbb {C}$
and any intervals
![]() $I_N$
whose lengths tend to infinity as
$I_N$
whose lengths tend to infinity as
![]() $N\to \infty $
, the multiple ergodic averages
$N\to \infty $
, the multiple ergodic averages
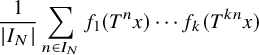 $$ \begin{align*} \frac{1}{|I_N|}\sum_{n\in I_N}f_1(T^nx)\cdots f_k(T^{kn}x) \end{align*} $$
$$ \begin{align*} \frac{1}{|I_N|}\sum_{n\in I_N}f_1(T^nx)\cdots f_k(T^{kn}x) \end{align*} $$
converge in
![]() $L^2(\mu )$
as
$L^2(\mu )$
as
![]() $N\to \infty $
. Since this work, it has therefore become a natural and active question to determine for which sequences of intervals
$N\to \infty $
. Since this work, it has therefore become a natural and active question to determine for which sequences of intervals
![]() $(I_N)_N$
and weights
$(I_N)_N$
and weights
![]() $w:\mathbb {N}\to \mathbb {C}$
we have the
$w:\mathbb {N}\to \mathbb {C}$
we have the
![]() $L^2$
-convergence of
$L^2$
-convergence of
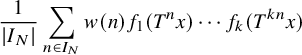 $$ \begin{align*} \frac{1}{|I_N|}\sum_{n\in I_N}w(n)f_1(T^nx)\cdots f_k(T^{kn}x) \end{align*} $$
$$ \begin{align*} \frac{1}{|I_N|}\sum_{n\in I_N}w(n)f_1(T^nx)\cdots f_k(T^{kn}x) \end{align*} $$
as
![]() $N\to \infty $
. The case of
$N\to \infty $
. The case of
![]() $I_N=[1,N]$
and with the weight being the primes, that is
$I_N=[1,N]$
and with the weight being the primes, that is
![]() $w(n)=1_{\mathbb {P}}(n)$
, was settled in the works of Frantzikinakis–Host–Kra [Reference Frantzikinakis, Host and Kra13] and Wooley–Ziegler [Reference Wooley and Ziegler63] (the results of [Reference Frantzikinakis, Host and Kra13] in the cases
$w(n)=1_{\mathbb {P}}(n)$
, was settled in the works of Frantzikinakis–Host–Kra [Reference Frantzikinakis, Host and Kra13] and Wooley–Ziegler [Reference Wooley and Ziegler63] (the results of [Reference Frantzikinakis, Host and Kra13] in the cases
![]() $k\geq 4$
were originally conditional on the Gowers uniformity of the von Mangoldt function). Analogous results also exist for weights w supported on a sequence given by a Hardy field [Reference Frantzikinakis12] or random sequences [Reference Frantzikinakis, Lesigne and Wierdl14]; see also [Reference Le42] for related results concerning correlation sequences
$k\geq 4$
were originally conditional on the Gowers uniformity of the von Mangoldt function). Analogous results also exist for weights w supported on a sequence given by a Hardy field [Reference Frantzikinakis12] or random sequences [Reference Frantzikinakis, Lesigne and Wierdl14]; see also [Reference Le42] for related results concerning correlation sequences
![]() $n \mapsto \int _X f_1(T^nx)\cdots f_k(T^{kn}x)\ d\mu (x)$
. As an application of Theorem 1.5, we can extend the result on prime weights to short collections of intervals
$n \mapsto \int _X f_1(T^nx)\cdots f_k(T^{kn}x)\ d\mu (x)$
. As an application of Theorem 1.5, we can extend the result on prime weights to short collections of intervals
![]() $(I_N)_N$
.
$(I_N)_N$
.
Theorem 1.6 (Multiple ergodic averages over primes in short intervals).
Let
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\kappa \in [5/8+\varepsilon , 1-\varepsilon ]$
. Let
$\kappa \in [5/8+\varepsilon , 1-\varepsilon ]$
. Let
![]() $h_1,\ldots , h_k$
be distinct positive integers. Let
$h_1,\ldots , h_k$
be distinct positive integers. Let
![]() $(X,\mathcal {X},\mu ,T)$
be a measure-preserving system. Let
$(X,\mathcal {X},\mu ,T)$
be a measure-preserving system. Let
![]() $f_1,\ldots , f_k:X\to \mathbb {C}$
be bounded and measurable. Then the multiple ergodic averages
$f_1,\ldots , f_k:X\to \mathbb {C}$
be bounded and measurable. Then the multiple ergodic averages
converge in
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
The results of [Reference Frantzikinakis, Host and Kra13] and [Reference Wooley and Ziegler63] correspond to the case
![]() $\kappa =1$
. According to the best of our knowledge, Theorem 1.6 is the first result of its kind with
$\kappa =1$
. According to the best of our knowledge, Theorem 1.6 is the first result of its kind with
![]() $\kappa <1$
.
$\kappa <1$
.
1.2.3 Linear equations in short intervals
The work of Green and the third author [Reference Green and Tao17] on linear equations in primes (together with [Reference Green and Tao18], [Reference Green, Tao and Ziegler21]) provides for any finite complexity systems of linear forms
![]() $(\psi _1,\ldots , \psi _t):\mathbb {Z}^d\to \mathbb {Z}^t$
an asymptotic formula for
$(\psi _1,\ldots , \psi _t):\mathbb {Z}^d\to \mathbb {Z}^t$
an asymptotic formula for
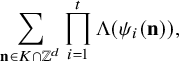 $$ \begin{align} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda(\psi_i(\mathbf{n})), \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda(\psi_i(\mathbf{n})), \end{align} $$
whenever
![]() $K\subset [-X,X]^d$
is a convex body containing a positive proportion of the whole cube
$K\subset [-X,X]^d$
is a convex body containing a positive proportion of the whole cube
![]() $[-X,X]^d$
, that is,
$[-X,X]^d$
, that is,
![]() $\text {vol}(K)\gg X^d$
. One may ask if one can establish similar results when K is a smaller region in
$\text {vol}(K)\gg X^d$
. One may ask if one can establish similar results when K is a smaller region in
![]() $[-X,X]^d$
, of volume
$[-X,X]^d$
, of volume
![]() $\asymp X^{\theta d}$
with
$\asymp X^{\theta d}$
with
![]() $\theta <1$
. Note that, for a single linear form, this boils down to asymptotics for primes in short intervals (where the exponent
$\theta <1$
. Note that, for a single linear form, this boils down to asymptotics for primes in short intervals (where the exponent
![]() $\theta =7/12$
from [Reference Huxley33], [Reference Heath-Brown29] is the best one known). Using Theorem 1.5, we can indeed give asymptotics for equation (1.24) in small regions.
$\theta =7/12$
from [Reference Huxley33], [Reference Heath-Brown29] is the best one known). Using Theorem 1.5, we can indeed give asymptotics for equation (1.24) in small regions.
Theorem 1.7 (Generalized Hardy–Littlewood conjecture in small boxes for finite complexity systems).
Let
![]() $X \geq 3$
and
$X \geq 3$
and
![]() $X^{5/8+\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some fixed
$X^{5/8+\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some fixed
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $d,t,L\geq 1$
. Let
$d,t,L\geq 1$
. Let
![]() $\Psi =(\psi _1,\ldots , \psi _t)$
be a system of affine-linear forms, where each
$\Psi =(\psi _1,\ldots , \psi _t)$
be a system of affine-linear forms, where each
![]() $\psi _i:\mathbb {Z}^d\to \mathbb {Z}$
has the form
$\psi _i:\mathbb {Z}^d\to \mathbb {Z}$
has the form
![]() $\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
with
$\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
with
![]() $\dot {\psi _i}\in \mathbb {Z}^d$
and
$\dot {\psi _i}\in \mathbb {Z}^d$
and
![]() $\psi _i(0)\in \mathbb {Z}$
satisfying
$\psi _i(0)\in \mathbb {Z}$
satisfying
![]() $|\dot {\psi _i}|\leq L$
and
$|\dot {\psi _i}|\leq L$
and
![]() $|\psi _i(0)|\leq LX$
. Suppose that
$|\psi _i(0)|\leq LX$
. Suppose that
![]() $\dot {\psi _i}$
and
$\dot {\psi _i}$
and
![]() $\dot {\psi _j}$
are linearly independent whenever
$\dot {\psi _j}$
are linearly independent whenever
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $K\subset (X,X+H]^d$
be a convex body. Then
$K\subset (X,X+H]^d$
be a convex body. Then
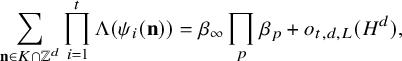 $$ \begin{align} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda(\psi_i(\mathbf{n}))=\beta_{\infty}\prod_p \beta_p+o_{t,d,L}(H^d), \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda(\psi_i(\mathbf{n}))=\beta_{\infty}\prod_p \beta_p+o_{t,d,L}(H^d), \end{align} $$
where
![]() $\Lambda $
is extended as
$\Lambda $
is extended as
![]() $0$
to the nonpositive integers and the Archimedean factor is given by
$0$
to the nonpositive integers and the Archimedean factor is given by
and the local factors are given by
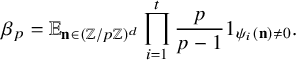 $$ \begin{align*} \beta_p=\mathbb{E}_{\mathbf{n}\in (\mathbb{Z}/p\mathbb{Z})^d}\prod_{i=1}^t\frac{p}{p-1}1_{\psi_i(\mathbf{n})\neq 0}. \end{align*} $$
$$ \begin{align*} \beta_p=\mathbb{E}_{\mathbf{n}\in (\mathbb{Z}/p\mathbb{Z})^d}\prod_{i=1}^t\frac{p}{p-1}1_{\psi_i(\mathbf{n})\neq 0}. \end{align*} $$
Remark 1.8. From Theorem 1.5 and the proof method of Theorem 1.7, one can also deduce similar correlation results when in equation (1.25) one replaces
![]() $\Lambda $
with
$\Lambda $
with
![]() $\mu $
or
$\mu $
or
![]() $d_k$
(with the value of
$d_k$
(with the value of
![]() $\theta $
as in Theorem 1.5, and with no main term in the case of
$\theta $
as in Theorem 1.5, and with no main term in the case of
![]() $\mu $
, and a different local product in the case of
$\mu $
, and a different local product in the case of
![]() $d_k$
). More specifically, under the assumption of Theorem 1.7, we have
$d_k$
). More specifically, under the assumption of Theorem 1.7, we have
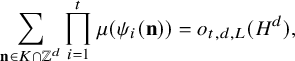 $$ \begin{align} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t \mu(\psi_i(\mathbf{n}))= o_{t,d,L}(H^d), \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t \mu(\psi_i(\mathbf{n}))= o_{t,d,L}(H^d), \end{align} $$
and, for a positive integer k,
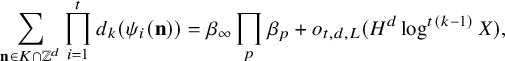 $$ \begin{align*} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t d_k(\psi_i(\mathbf{n}))=\beta_{\infty}\prod_p \beta_p+o_{t,d,L}(H^d\log^{t(k-1)}X), \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{n}\in K\cap \mathbb{Z}^d}\prod_{i=1}^t d_k(\psi_i(\mathbf{n}))=\beta_{\infty}\prod_p \beta_p+o_{t,d,L}(H^d\log^{t(k-1)}X), \end{align*} $$
where
![]() $d_k$
is extended as
$d_k$
is extended as
![]() $0$
to the nonpositive integers and the Archimedean factor is given by
$0$
to the nonpositive integers and the Archimedean factor is given by
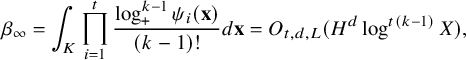 $$ \begin{align*} \beta_{\infty}=\int_K \prod_{i=1}^t \frac{\log_+^{k-1}\psi_i(\mathbf{x})}{(k-1)!} d\mathbf{x} = O_{t,d,L} (H^d \log^{t(k-1)}X), \end{align*} $$
$$ \begin{align*} \beta_{\infty}=\int_K \prod_{i=1}^t \frac{\log_+^{k-1}\psi_i(\mathbf{x})}{(k-1)!} d\mathbf{x} = O_{t,d,L} (H^d \log^{t(k-1)}X), \end{align*} $$
and the local factors are given by
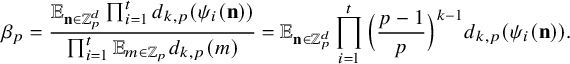 $$ \begin{align*} \beta_p=\frac{\mathbb{E}_{\mathbf{n} \in \mathbb{Z}_p^d} \prod_{i=1}^t d_{k,p}(\psi_i(\mathbf{n}))}{\prod_{i=1}^t \mathbb{E}_{m \in \mathbb{Z}_p} d_{k,p}(m)} = \mathbb{E}_{\mathbf{n} \in \mathbb{Z}_p^d} \prod_{i=1}^t \Big(\frac{p-1}{p}\Big)^{k-1} d_{k,p}(\psi_i(\mathbf{n})). \end{align*} $$
$$ \begin{align*} \beta_p=\frac{\mathbb{E}_{\mathbf{n} \in \mathbb{Z}_p^d} \prod_{i=1}^t d_{k,p}(\psi_i(\mathbf{n}))}{\prod_{i=1}^t \mathbb{E}_{m \in \mathbb{Z}_p} d_{k,p}(m)} = \mathbb{E}_{\mathbf{n} \in \mathbb{Z}_p^d} \prod_{i=1}^t \Big(\frac{p-1}{p}\Big)^{k-1} d_{k,p}(\psi_i(\mathbf{n})). \end{align*} $$
Here,
![]() $\log _+ y := \log \max (y, 1)$
,
$\log _+ y := \log \max (y, 1)$
,
![]() $\mathbb {Z}_p$
is the p-adics (with the usual Haar probability measure),
$\mathbb {Z}_p$
is the p-adics (with the usual Haar probability measure),
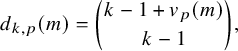 $$ \begin{align*}d_{k,p}(m) = \binom{k-1+v_p(m)}{k-1},\end{align*} $$
$$ \begin{align*}d_{k,p}(m) = \binom{k-1+v_p(m)}{k-1},\end{align*} $$
and
![]() $v_p(m)$
is the number of times p divides m. These local factors are natural extensions of the ones defined in [Reference Matomäki, Radziwiłł and Tao47, Remark 1.2] in the special case of two linear forms
$v_p(m)$
is the number of times p divides m. These local factors are natural extensions of the ones defined in [Reference Matomäki, Radziwiłł and Tao47, Remark 1.2] in the special case of two linear forms
![]() $\psi _1(n) = n, \psi _2(n) = n+h$
.
$\psi _1(n) = n, \psi _2(n) = n+h$
.
We have the following immediate corollary to Theorem 1.7.
Corollary 1.9 (Linear equations in primes in short intervals).
Let
![]() $X \geq 3$
and
$X \geq 3$
and
![]() $X^{5/8+\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some fixed
$X^{5/8+\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some fixed
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $d,t,L\geq 1$
. Let
$d,t,L\geq 1$
. Let
![]() $\Psi =(\psi _1,\ldots , \psi _t):\mathbb {Z}^d\to \mathbb {Z}^t$
be a system of affine-linear forms, where each
$\Psi =(\psi _1,\ldots , \psi _t):\mathbb {Z}^d\to \mathbb {Z}^t$
be a system of affine-linear forms, where each
![]() $\psi _i$
has the form
$\psi _i$
has the form
![]() $\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
with
$\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
with
![]() $\dot {\psi _i}\in \mathbb {Z}^d$
and
$\dot {\psi _i}\in \mathbb {Z}^d$
and
![]() $\psi _i(0)\in \mathbb {Z}$
satisfying
$\psi _i(0)\in \mathbb {Z}$
satisfying
![]() $|\dot {\psi _i}|\leq L$
and
$|\dot {\psi _i}|\leq L$
and
![]() $|\psi _i(0)|\leq LX$
. Suppose that
$|\psi _i(0)|\leq LX$
. Suppose that
![]() $\dot {\psi _i}$
and
$\dot {\psi _i}$
and
![]() $\dot {\psi _j}$
are linearly independent whenever
$\dot {\psi _j}$
are linearly independent whenever
![]() $i\neq j$
. Suppose that, for every prime p, the system of equations
$i\neq j$
. Suppose that, for every prime p, the system of equations
![]() $\Psi (\mathbf {n})=0$
is solvable with
$\Psi (\mathbf {n})=0$
is solvable with
![]() $\mathbf {n}\in ((\mathbb {Z}/p\mathbb {Z})\setminus \{0\})^d$
. Then the number of solutions to
$\mathbf {n}\in ((\mathbb {Z}/p\mathbb {Z})\setminus \{0\})^d$
. Then the number of solutions to
![]() $\Psi (\mathbf {n})=0$
with
$\Psi (\mathbf {n})=0$
with
![]() $\mathbf {n}\in (\mathbb {P}\cap (X,X+H])^d$
is
$\mathbf {n}\in (\mathbb {P}\cap (X,X+H])^d$
is
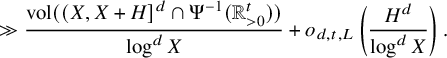 $$ \begin{align*} \gg \frac{\text{vol}((X,X+H]^d\cap \Psi^{-1}(\mathbb{R}_{>0}^t))}{\log^d X}+o_{d,t,L}\left(\frac{H^d}{\log^d X}\right). \end{align*} $$
$$ \begin{align*} \gg \frac{\text{vol}((X,X+H]^d\cap \Psi^{-1}(\mathbb{R}_{>0}^t))}{\log^d X}+o_{d,t,L}\left(\frac{H^d}{\log^d X}\right). \end{align*} $$
Thus, for example, for any
![]() $\varepsilon>0$
and any large enough odd N there is a solution to
$\varepsilon>0$
and any large enough odd N there is a solution to
with
![]() $p_i\in [N/3-N^{5/8+\varepsilon },N/3+N^{5/8+\varepsilon }]$
. Without the condition
$p_i\in [N/3-N^{5/8+\varepsilon },N/3+N^{5/8+\varepsilon }]$
. Without the condition
![]() $2p_1-p_2 \in \mathbb {P}$
, this is due to Zhan [Reference Zhan64]. The exponent
$2p_1-p_2 \in \mathbb {P}$
, this is due to Zhan [Reference Zhan64]. The exponent
![]() $5/8$
in Zhan’s result has been improved using sieve methods (see, e.g., [Reference Baker and Harman3]) and more recently using the transference principle [Reference Matomäki, Maynard and Shao43]. It would probably be possible to use a sieve method also to improve on Corollary 1.9; it would suffice to find a suitable minorant function for
$5/8$
in Zhan’s result has been improved using sieve methods (see, e.g., [Reference Baker and Harman3]) and more recently using the transference principle [Reference Matomäki, Maynard and Shao43]. It would probably be possible to use a sieve method also to improve on Corollary 1.9; it would suffice to find a suitable minorant function for
![]() $\Lambda (n)$
that has positive average and is Gowers uniform in shorter intervals. Such a minorant could be constructed with our arithmetic information using Harman’s sieve method [Reference Harman24], but we do not do so here.
$\Lambda (n)$
that has positive average and is Gowers uniform in shorter intervals. Such a minorant could be constructed with our arithmetic information using Harman’s sieve method [Reference Harman24], but we do not do so here.
1.3 Methods of proof
We now describe (in somewhat informal terms) the general strategy of proof of our main theorems, although for various technical reasons the actual rigorous proof will not quite follow the intuitive plan that is outlined here.
To prove Theorem 1.1, the first step, which is standard, is to apply Heath–Brown’s identity (Lemma 2.16) together with a combinatorial lemma regarding subsums of a finite number of nonnegative reals summing to one (Lemma 2.20) to decompose
![]() $\mu , \Lambda , d_k$
(up to small errors) into three standard types of sums:
$\mu , \Lambda , d_k$
(up to small errors) into three standard types of sums:
-
(I) Type I sums, which are roughly of the form
 $\alpha * 1 = \alpha *d_1$
for some arithmetic function
$\alpha * 1 = \alpha *d_1$
for some arithmetic function
 $\alpha \colon \mathbb {N} \to \mathbb {C}$
supported on some interval
$\alpha \colon \mathbb {N} \to \mathbb {C}$
supported on some interval
 $[1, A_I]$
that is not too large, and with
$[1, A_I]$
that is not too large, and with
 $\alpha $
bounded in an
$\alpha $
bounded in an
 $L^2$
averaged sense.
$L^2$
averaged sense. -
(I 2) Type
 $I_2$
sums, which are roughly of the form
$I_2$
sums, which are roughly of the form
 $\alpha * d_2$
for some arithmetic function
$\alpha * d_2$
for some arithmetic function
 $\alpha \colon \mathbb {N} \to \mathbb {C}$
supported on some interval
$\alpha \colon \mathbb {N} \to \mathbb {C}$
supported on some interval
 $[1, A_{I_2}]$
that is not too large, and with
$[1, A_{I_2}]$
that is not too large, and with
 $\alpha $
bounded in an
$\alpha $
bounded in an
 $L^2$
averaged sense.
$L^2$
averaged sense. -
(II) Type
 $II$
sums, which are roughly of the form
$II$
sums, which are roughly of the form
 $\alpha * \beta $
for some arithmetic functions
$\alpha * \beta $
for some arithmetic functions
 $\alpha , \beta \colon \mathbb {N} \to \mathbb {C}$
with
$\alpha , \beta \colon \mathbb {N} \to \mathbb {C}$
with
 $\alpha $
supported on some interval
$\alpha $
supported on some interval
 $[A_{II}^-, A_{II}^+]$
that is neither too long nor too close to
$[A_{II}^-, A_{II}^+]$
that is neither too long nor too close to
 $1$
or X, and with
$1$
or X, and with
 $\alpha ,\beta $
bounded in an
$\alpha ,\beta $
bounded in an
 $L^2$
averaged sense.
$L^2$
averaged sense.
This decomposition is detailed in Section 4. The precise ranges of parameters
![]() $A_I, A_{I_2}, A_{II}^-$
,
$A_I, A_{I_2}, A_{II}^-$
,
![]() $A_{II}^+$
that arise in this decomposition depend on the choice of
$A_{II}^+$
that arise in this decomposition depend on the choice of
![]() $\theta $
(and, in the case of
$\theta $
(and, in the case of
![]() $d_k$
for small k, on the value of k); this is encoded in the combinatorial lemma given here as Lemma 2.20.
$d_k$
for small k, on the value of k); this is encoded in the combinatorial lemma given here as Lemma 2.20.
The treatment of these types of sums (in Theorem 4.2) depends on the behavior of the nilsequence
![]() $F(g(n) \Gamma )$
, in particular whether it is ‘major arc’ or ‘minor arc’. This splitting into different behaviors will be done somewhat differently for different types of sums.
$F(g(n) \Gamma )$
, in particular whether it is ‘major arc’ or ‘minor arc’. This splitting into different behaviors will be done somewhat differently for different types of sums.
In case of type I and type
![]() $I_2$
sums, one can use the equidistribution theory of nilmanifolds to essentially reduce to two cases, the major arc case in which the nilsequence
$I_2$
sums, one can use the equidistribution theory of nilmanifolds to essentially reduce to two cases, the major arc case in which the nilsequence
![]() $F(g(n) \Gamma )$
behaves like (or ‘pretends to be’) the constant function
$F(g(n) \Gamma )$
behaves like (or ‘pretends to be’) the constant function
![]() $1$
(or some other function of small period), and the minor arc case in which F has mean zero and
$1$
(or some other function of small period), and the minor arc case in which F has mean zero and
![]() $g(n) \Gamma $
is highly equidistributed in the nilmanifold
$g(n) \Gamma $
is highly equidistributed in the nilmanifold
![]() $G/\Gamma $
. The contribution of type I and type
$G/\Gamma $
. The contribution of type I and type
![]() $I_2$
major arc sums can be treated by standard methods, namely an application of Perron’s formula and mean value theorems for Dirichlet series; see Section 3.
$I_2$
major arc sums can be treated by standard methods, namely an application of Perron’s formula and mean value theorems for Dirichlet series; see Section 3.
The contribution of type I minor arc sums can be treated by a slight modification of the arguments in [Reference Green and Tao18], which are based on the ‘quantitative Leibman theorem’ (Theorem 2.7 below) that characterizes when a nilsequence is equidistributed, as well as a classical lemma of Vinogradov (Lemma 2.3 below) that characterizes when a polynomial modulo
![]() $1$
is equidistributed. (Actually, it will be convenient to rely primarily on a corollary of Lemma 2.3 that asserts that if typical dilates of a polynomial are equidistributed modulo
$1$
is equidistributed. (Actually, it will be convenient to rely primarily on a corollary of Lemma 2.3 that asserts that if typical dilates of a polynomial are equidistributed modulo
![]() $1$
, then the polynomial itself is equidistributed modulo
$1$
, then the polynomial itself is equidistributed modulo
![]() $1$
: See Corollary 2.4 below.)
$1$
: See Corollary 2.4 below.)
Our treatment of type
![]() $I_2$
minor arc sums is more novel. A model case is that of treating the
$I_2$
minor arc sums is more novel. A model case is that of treating the
![]() $d_2$
-type correlation
$d_2$
-type correlation
From the definition of the divisor function
![]() $d_2$
, we can expand this sum as a double sum
$d_2$
, we can expand this sum as a double sum
We are not able to obtain nontrivial estimates on such sums in the regime
![]() $H \leq X^{1/3}$
. However, when
$H \leq X^{1/3}$
. However, when
![]() $H \geq X^{1/3+\varepsilon }$
, it turns out by elementary geometry of numbers that the hyperbola neighborhood
$H \geq X^{1/3+\varepsilon }$
, it turns out by elementary geometry of numbers that the hyperbola neighborhood
![]() $\{ (n,m) \in \mathbb {Z}^2: X < nm \leq X+H\}$
may be partitionedFootnote
3
into arithmetic progressions
$\{ (n,m) \in \mathbb {Z}^2: X < nm \leq X+H\}$
may be partitionedFootnote
3
into arithmetic progressions
![]() $P \subset \mathbb {Z}^2$
that mostly have nontrivial length; see Theorem 8.1 for a precise statement. This decomposition lets us efficiently decompose the sum (1.27) into short sums of the form
$P \subset \mathbb {Z}^2$
that mostly have nontrivial length; see Theorem 8.1 for a precise statement. This decomposition lets us efficiently decompose the sum (1.27) into short sums of the form
that turn out to exhibit cancellation for most progressions P in the type
![]() $I_2$
minor arc case, mainly thanks to the quantitative Leibman theorem (Theorem 2.7) and a corollary of the Vinogradov lemma (Corollary 2.4); see Section 8.
$I_2$
minor arc case, mainly thanks to the quantitative Leibman theorem (Theorem 2.7) and a corollary of the Vinogradov lemma (Corollary 2.4); see Section 8.
It remains to handle the contribution of type
![]() $II$
sums, which are of the form
$II$
sums, which are of the form
which we can expand as
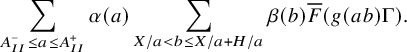 $$ \begin{align} \sum_{A_{II}^- \leq a \leq A_{II}^+} \alpha(a) \sum_{X/a < b \leq X/a + H/a} \beta(b) \overline{F}(g(ab) \Gamma). \end{align} $$
$$ \begin{align} \sum_{A_{II}^- \leq a \leq A_{II}^+} \alpha(a) \sum_{X/a < b \leq X/a + H/a} \beta(b) \overline{F}(g(ab) \Gamma). \end{align} $$
To treat these sums, we can use a Fourier decomposition and the equidistribution theory of nilmanifolds to reduce (roughly speaking) to treating the following three special cases of these sums:
-
• Type
 $II$
major arc sums that are essentially of the form for some real number
$II$
major arc sums that are essentially of the form for some real number $$ \begin{align*}\sum_{X < n \leq X+H} \alpha*\beta(n) n^{iT}\end{align*} $$
$$ \begin{align*}\sum_{X < n \leq X+H} \alpha*\beta(n) n^{iT}\end{align*} $$
 $T = X^{O(1)}$
of polynomial size (one can also consider generalizations of such sums when the
$T = X^{O(1)}$
of polynomial size (one can also consider generalizations of such sums when the
 $n^{iT}$
factor is twisted by an additional Dirichlet character
$n^{iT}$
factor is twisted by an additional Dirichlet character
 $\chi $
of bounded conductor).
$\chi $
of bounded conductor).
-
• Abelian type
 $II$
minor arc sums in which
$II$
minor arc sums in which
 $F(g(n)\Gamma ) = e(P(n))$
is a polynomial phase that does not ‘pretend’ to be a character
$F(g(n)\Gamma ) = e(P(n))$
is a polynomial phase that does not ‘pretend’ to be a character
 $n^{iT}$
(or more generally
$n^{iT}$
(or more generally
 $\chi (n) n^{iT}$
for some Dirichlet character
$\chi (n) n^{iT}$
for some Dirichlet character
 $\chi $
of bounded conductor) in the sense that the Taylor coefficients of
$\chi $
of bounded conductor) in the sense that the Taylor coefficients of
 $e(P(n))$
around X do not align with the corresponding coefficients of such characters.
$e(P(n))$
around X do not align with the corresponding coefficients of such characters. -
• Nonabelian type
 $II$
minor arc sums, in which
$II$
minor arc sums, in which
 $g(n) \Gamma $
is highly equidistributed in a nilmanifold
$g(n) \Gamma $
is highly equidistributed in a nilmanifold
 $G/\Gamma $
arising from a nonabelian nilpotent group G, and F exhibits nontrivial oscillation in the direction of the center
$G/\Gamma $
arising from a nonabelian nilpotent group G, and F exhibits nontrivial oscillation in the direction of the center
 $Z(G)$
of G (which one can reduce to be one-dimensional).
$Z(G)$
of G (which one can reduce to be one-dimensional).
One can treat the contribution of the type
![]() $II$
major arc sums by applying Perron’s formula and Dirichlet polynomial estimates of Baker–Harman–Pintz [Reference Baker, Harman and Pintz4] in the regime, so long as one actually has a suitable triple convolution (with one of the subfactors having well-controlled correlations with
$II$
major arc sums by applying Perron’s formula and Dirichlet polynomial estimates of Baker–Harman–Pintz [Reference Baker, Harman and Pintz4] in the regime, so long as one actually has a suitable triple convolution (with one of the subfactors having well-controlled correlations with
![]() $n^{iT}$
); see Lemma 3.5. As already implicitly observed by Zhan [Reference Zhan64], this case can be treated (with favorable choices of parameters) for any of the three functions
$n^{iT}$
); see Lemma 3.5. As already implicitly observed by Zhan [Reference Zhan64], this case can be treated (with favorable choices of parameters) for any of the three functions
![]() $\mu , \Lambda , d_k$
in the case
$\mu , \Lambda , d_k$
in the case
![]() $\theta = 5/8$
. As observed in [Reference Matomäki and Teräväinen50], in the case of the Möbius function
$\theta = 5/8$
. As observed in [Reference Matomäki and Teräväinen50], in the case of the Möbius function
![]() $\mu $
, it is possible to lower
$\mu $
, it is possible to lower
![]() $\theta $
to
$\theta $
to
![]() $3/5$
and still obtain triple convolution structure after removing a small exceptional error term from
$3/5$
and still obtain triple convolution structure after removing a small exceptional error term from
![]() $\mu $
(which is responsible for the final discorrelation bounds not saving arbitrary powers of
$\mu $
(which is responsible for the final discorrelation bounds not saving arbitrary powers of
![]() $\log X$
); see Lemma 4.5.
$\log X$
); see Lemma 4.5.
It remains to treat the contribution of nonabelian and abelian type
![]() $II$
minor arc sums. It turns out that we will be able to establish good estimates for such sums (1.28) in the regime
$II$
minor arc sums. It turns out that we will be able to establish good estimates for such sums (1.28) in the regime
In this regime, the inner intervals
![]() $(X/a, X/a+H/a]$
in equation (1.28) have nonnegligible length (at least
$(X/a, X/a+H/a]$
in equation (1.28) have nonnegligible length (at least
![]() $X^\varepsilon $
), and furthermore they exhibit nontrivial overlap with each other (
$X^\varepsilon $
), and furthermore they exhibit nontrivial overlap with each other (
![]() $(X/a, X/a+H/a]$
will essentially be identical to
$(X/a, X/a+H/a]$
will essentially be identical to
![]() $(X/a', X/a'+H/a']$
whenever
$(X/a', X/a'+H/a']$
whenever
![]() $a' = \left (1 + O\left (X^{-\varepsilon } \frac {H}{X}\right )\right ) a$
).
$a' = \left (1 + O\left (X^{-\varepsilon } \frac {H}{X}\right )\right ) a$
).
As a consequence, many of the dilated nilsequences
![]() $b \mapsto \overline {F}(g(ab) \Gamma )$
appearing in equation (1.28) will correlate with the same portion of the sequence
$b \mapsto \overline {F}(g(ab) \Gamma )$
appearing in equation (1.28) will correlate with the same portion of the sequence
![]() $\beta $
. To handle this situation, we introduce a nilsequence version of the large sieve inequality in Proposition 2.15, which we establish with the aid of the equidistribution theory for nilsequences, as well as Goursat’s lemma. The upshot of this large sieve inequality is that for many nearby pairs
$\beta $
. To handle this situation, we introduce a nilsequence version of the large sieve inequality in Proposition 2.15, which we establish with the aid of the equidistribution theory for nilsequences, as well as Goursat’s lemma. The upshot of this large sieve inequality is that for many nearby pairs
![]() $a',a$
there is an algebraic relation between the sequences
$a',a$
there is an algebraic relation between the sequences
![]() $b \mapsto g(ab)$
and
$b \mapsto g(ab)$
and
![]() $b \mapsto g(a'b)$
, namely that one has an identity of the form
$b \mapsto g(a'b)$
, namely that one has an identity of the form
where
![]() $\varepsilon _{aa'} \colon \mathbb {Z} \to G$
is a ‘smooth’ polynomial map and
$\varepsilon _{aa'} \colon \mathbb {Z} \to G$
is a ‘smooth’ polynomial map and
![]() $\gamma _{aa'} \colon \mathbb {Z} \to G$
is a ‘rational’ polynomial map; see equation (6.7) for a precise statement. This can be viewed as an assertion that the map g is ‘approximately dilation-invariant’ in some weak sense. This turns out to imply a nontrivial lack of two-dimensional equidistribution for the map
$\gamma _{aa'} \colon \mathbb {Z} \to G$
is a ‘rational’ polynomial map; see equation (6.7) for a precise statement. This can be viewed as an assertion that the map g is ‘approximately dilation-invariant’ in some weak sense. This turns out to imply a nontrivial lack of two-dimensional equidistribution for the map
which is incompatible with the nonabelian nature of G thanks to a commutator argument of Furstenberg and Weiss [Reference Furstenberg and Weiss15]; see Section 6. This resolves the nonabelian case. In the abelian case, one can replace the maps g by the ordinary polynomials P, and one can then proceed by adapting the arguments by the first two authors in [Reference Matomäki and Shao49] to show that
![]() $e(P(n))$
necessarily ‘pretends’ to be like a character
$e(P(n))$
necessarily ‘pretends’ to be like a character
![]() $n^{iT}$
, which resolves the abelian type
$n^{iT}$
, which resolves the abelian type
![]() $II$
minor arc case. Combining all these cases yields Theorem 1.1.
$II$
minor arc case. Combining all these cases yields Theorem 1.1.
1.3.1 The result on Gowers norms
The proof of Theorem 1.5 (in Section 9) requires in addition to Theorem 1.1 and the inverse theorem for the Gowers norms also a construction of pseudorandom majorants for (W-tricked versions of)
![]() $\Lambda $
and
$\Lambda $
and
![]() $d_k$
over short intervals
$d_k$
over short intervals
![]() $(X,X+H]$
. By this, we mean functions
$(X,X+H]$
. By this, we mean functions
![]() $\nu _1,\nu _2$
that majorize the functions
$\nu _1,\nu _2$
that majorize the functions
![]() $\Lambda ,d_k$
(after W-tricking and suitable normalization) and such that
$\Lambda ,d_k$
(after W-tricking and suitable normalization) and such that
![]() $\nu _i-1$
restricted to
$\nu _i-1$
restricted to
![]() $(X,X+H]$
is Gowers uniform. In the case of long intervals (that is,
$(X,X+H]$
is Gowers uniform. In the case of long intervals (that is,
![]() $H=X$
), the existence of such majorants is well-known from works of Green and the third author [Reference Green and Tao16] and Matthiesen [Reference Matthiesen52]. Fortunately, it turns out that the structure of these well-known majorants as type I sums of small ‘level’ enables us to show that they work as majorants also over short intervals
$H=X$
), the existence of such majorants is well-known from works of Green and the third author [Reference Green and Tao16] and Matthiesen [Reference Matthiesen52]. Fortunately, it turns out that the structure of these well-known majorants as type I sums of small ‘level’ enables us to show that they work as majorants also over short intervals
![]() $(X,X+H]$
; see Lemmas 9.5 and 9.6. These lemmas combined with the implementation of the W-trick (which in the case of
$(X,X+H]$
; see Lemmas 9.5 and 9.6. These lemmas combined with the implementation of the W-trick (which in the case of
![]() $d_k$
requires additionally two simple lemmas, namely Lemmas 9.8 and 9.9) leads to the proof of Theorem 1.5.
$d_k$
requires additionally two simple lemmas, namely Lemmas 9.8 and 9.9) leads to the proof of Theorem 1.5.
Remark 1.10. In this remark, we discuss the obstructions to improving the value of
![]() $\theta $
in the various components of Theorem 1.1. In most of these results, the primary obstruction arises (roughly speaking) from portions of
$\theta $
in the various components of Theorem 1.1. In most of these results, the primary obstruction arises (roughly speaking) from portions of
![]() $\mu $
,
$\mu $
,
![]() $\Lambda $
or
$\Lambda $
or
![]() $d_k$
that look something like
$d_k$
that look something like
for various tuples
![]() $(\alpha _1,\dots ,\alpha _m)$
of positive real numbers that add up to
$(\alpha _1,\dots ,\alpha _m)$
of positive real numbers that add up to
![]() $1$
. More specifically:
$1$
. More specifically:
-
(a) For the
 $\theta =5/8$
results in Theorem 1.1(i)–(iii), the primary obstruction arises from convolutions (1.29) with
$\theta =5/8$
results in Theorem 1.1(i)–(iii), the primary obstruction arises from convolutions (1.29) with
 $(\alpha _1,\dots ,\alpha _m)$
equal to
$(\alpha _1,\dots ,\alpha _m)$
equal to
 $(1/4,1/4,1/4,1/4)$
, when correlated against characters
$(1/4,1/4,1/4,1/4)$
, when correlated against characters
 $n^{iT}$
with
$n^{iT}$
with
 $T \asymp X^{O(1)}$
, as this lies just outside the reach of our twisted major arc type I and type
$T \asymp X^{O(1)}$
, as this lies just outside the reach of our twisted major arc type I and type
 $II$
estimates when
$II$
estimates when
 $\theta $
goes below
$\theta $
goes below
 $5/8$
. This obstruction was already implicitly observed by Zhan [Reference Zhan64].
$5/8$
. This obstruction was already implicitly observed by Zhan [Reference Zhan64]. -
(b) For the
 $\theta =3/5$
result in Theorem 1.1(iv), the primary obstruction are convolutions (1.29) with
$\theta =3/5$
result in Theorem 1.1(iv), the primary obstruction are convolutions (1.29) with
 $(\alpha _1,\dots ,\alpha _m)$
equal to
$(\alpha _1,\dots ,\alpha _m)$
equal to
 $(2/5,1/5,1/5,1/5)$
or
$(2/5,1/5,1/5,1/5)$
or
 $(1/5,1/5,1/5,1/5,1/5)$
, when correlated against ‘minor arc’ nilsequences, such as
$(1/5,1/5,1/5,1/5,1/5)$
, when correlated against ‘minor arc’ nilsequences, such as
 $e(\alpha n)$
for some minor arc
$e(\alpha n)$
for some minor arc
 $\alpha $
. Such convolutions become just out of reach of our type I, type
$\alpha $
. Such convolutions become just out of reach of our type I, type
 $II$
and type
$II$
and type
 $I_2$
estimates when
$I_2$
estimates when
 $\theta $
goes below
$\theta $
goes below
 $3/5$
. This obstruction was already observed in [Reference Matomäki and Teräväinen50].
$3/5$
. This obstruction was already observed in [Reference Matomäki and Teräväinen50]. -
(c) For the
 $\theta =1/3$
result in Theorem 1.1(iii), the primary obstruction is of a different nature from the preceding cases: It is that our treatment of minor arcs in this case relies crucially on the ability to partition the neighborhood of a hyperbola into arithmetic progressions (see Theorem 8.1), and this partition is no longer available in any useful form once
$\theta =1/3$
result in Theorem 1.1(iii), the primary obstruction is of a different nature from the preceding cases: It is that our treatment of minor arcs in this case relies crucially on the ability to partition the neighborhood of a hyperbola into arithmetic progressions (see Theorem 8.1), and this partition is no longer available in any useful form once
 $\theta $
goes below
$\theta $
goes below
 $1/3$
.
$1/3$
. -
(d) For the
 $\theta =5/9$
result in Theorem 1.1(iii), the primary obstruction arises from convolutions (1.29) with
$\theta =5/9$
result in Theorem 1.1(iii), the primary obstruction arises from convolutions (1.29) with
 $(\alpha _1,\dots ,\alpha _m)$
equal to
$(\alpha _1,\dots ,\alpha _m)$
equal to
 $(1/3,1/3,1/3)$
, when correlated against minor arc nilsequences, for reasons similar to those in the previous case (c).
$(1/3,1/3,1/3)$
, when correlated against minor arc nilsequences, for reasons similar to those in the previous case (c).
1.4 Notation
The parameter X should be thought of as being large.
We use
![]() $Y \ll Z$
,
$Y \ll Z$
,
![]() $Y = O(Z)$
or
$Y = O(Z)$
or
![]() $Z \gg Y$
to denote the estimate
$Z \gg Y$
to denote the estimate
![]() $|Y| \leq CZ$
for some constant C. If we wish to permit this constant to depend (possibly ineffectively) on one or more parameters we shall indicate this by appropriate subscripts, thus for instance
$|Y| \leq CZ$
for some constant C. If we wish to permit this constant to depend (possibly ineffectively) on one or more parameters we shall indicate this by appropriate subscripts, thus for instance
![]() $O_{\varepsilon ,A}(Z)$
denotes a quantity bounded in magnitude by
$O_{\varepsilon ,A}(Z)$
denotes a quantity bounded in magnitude by
![]() $C_{\varepsilon ,A} Z$
for some quantity
$C_{\varepsilon ,A} Z$
for some quantity
![]() $C_{\varepsilon ,A}$
depending only on
$C_{\varepsilon ,A}$
depending only on
![]() $\varepsilon ,A$
. We write
$\varepsilon ,A$
. We write
![]() $Y \asymp Z$
for
$Y \asymp Z$
for
![]() $Y \ll Z \ll Y$
. When working with
$Y \ll Z \ll Y$
. When working with
![]() $d_k$
, all implied constants are permitted to depend on k. We also write
$d_k$
, all implied constants are permitted to depend on k. We also write
![]() $y \sim Y$
to denote the assertion
$y \sim Y$
to denote the assertion
![]() $Y < y \leq 2Y$
.
$Y < y \leq 2Y$
.
If x is a real number (resp. an element of
![]() $\mathbb {R}/\mathbb {Z}$
), we write
$\mathbb {R}/\mathbb {Z}$
), we write
![]() and let
and let
![]() $\|x\|_{\mathbb {R}/\mathbb {Z}}$
denote the distance of x to the nearest integer (resp. zero).
$\|x\|_{\mathbb {R}/\mathbb {Z}}$
denote the distance of x to the nearest integer (resp. zero).
We use
![]() $1_E$
to denote the indicator of an event E, thus
$1_E$
to denote the indicator of an event E, thus
![]() $1_E$
equals
$1_E$
equals
![]() $1$
when E is true and
$1$
when E is true and
![]() $0$
otherwise. If S is a set, we write
$0$
otherwise. If S is a set, we write
![]() $1_S$
for the indicator function
$1_S$
for the indicator function
![]() .
.
Unless otherwise specified, all sums range over natural number values, except for sums over p which are understood to range over primes. We use
![]() $d|n$
to denote the assertion that d divides n,
$d|n$
to denote the assertion that d divides n,
![]() $(n,m)$
to denote the greatest common divisor of n and m,
$(n,m)$
to denote the greatest common divisor of n and m,
![]() $n = a \ (q)$
to denote the assertion that n and a have the same residue mod q, and
$n = a \ (q)$
to denote the assertion that n and a have the same residue mod q, and
![]() to denote the Dirichlet convolution of two arithmetic functions
to denote the Dirichlet convolution of two arithmetic functions
![]() $f,g \colon \mathbb {N} \to \mathbb {C}$
.
$f,g \colon \mathbb {N} \to \mathbb {C}$
.
The height of a rational number
![]() $a/b$
with
$a/b$
with
![]() $a,b$
coprime is defined as
$a,b$
coprime is defined as
![]() $\max (|a|, |b|)$
.
$\max (|a|, |b|)$
.
2 Basic tools
2.1 Total variation
The notion of maximal summation defined in equation (1.4) interacts well with the notion of total variation, which we now define.
Definition 2.1 (Total variation).
Given any function
![]() $f: P \to \mathbb {C}$
on an arithmetic progression P, the total variation norm
$f: P \to \mathbb {C}$
on an arithmetic progression P, the total variation norm
![]() $\|f\|_{{\operatorname {TV}}(P)}$
is defined by the formula
$\|f\|_{{\operatorname {TV}}(P)}$
is defined by the formula
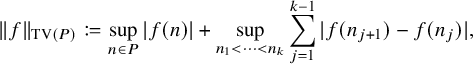
where the second supremum ranges over all increasing finite sequences
![]() $n_1 < \dots < n_k$
in P and all
$n_1 < \dots < n_k$
in P and all
![]() $k \geq 1$
. We remark that in this finitary setting one can simply take
$k \geq 1$
. We remark that in this finitary setting one can simply take
![]() $n_1,\dots ,n_k$
to be the elements of P in increasing order, if one wishes. We adopt the convention that
$n_1,\dots ,n_k$
to be the elements of P in increasing order, if one wishes. We adopt the convention that
![]() $\|f\|_{{\operatorname {TV}}(P)}=0$
when P is empty. For any natural number
$\|f\|_{{\operatorname {TV}}(P)}=0$
when P is empty. For any natural number
![]() $q \geq 1$
, we also define
$q \geq 1$
, we also define
Informally, if f is bounded in
![]() ${\operatorname {TV}}(P;q)$
norm, then f does not vary much on each residue class modulo q in P. From the fundamental theorem of calculus, we see that if
${\operatorname {TV}}(P;q)$
norm, then f does not vary much on each residue class modulo q in P. From the fundamental theorem of calculus, we see that if
![]() $f \colon I \to \mathbb {C}$
is a continuously differentiable function then
$f \colon I \to \mathbb {C}$
is a continuously differentiable function then
for all arithmetic progressions P in I. Also, from the identity
![]() $ab-a'b' = (a-a')b + (b-b')a'$
we see that
$ab-a'b' = (a-a')b + (b-b')a'$
we see that
for any functions
![]() $f,g \colon P \to \mathbb {C}$
defined on an arithmetic progression and any
$f,g \colon P \to \mathbb {C}$
defined on an arithmetic progression and any
![]() $q \geq 1$
.
$q \geq 1$
.
We can now record some basic properties of maximal summation:
Lemma 2.2 (Basic properties of maximal sums).
-
(i) (Triangle inequalities) For any subprogression
 $P'$
of an arithmetic progression P, and any
$P'$
of an arithmetic progression P, and any
 $f \colon P \to \mathbb {C}$
we have and
$f \colon P \to \mathbb {C}$
we have and $$ \begin{align*}{\left| \sum_{n \in P} f(n) 1_{P'}(n) \right|}^* = {\left| \sum_{n \in P'} f(n) \right|}^* \leq {\left| \sum_{n \in P} f(n) \right|}^*\end{align*} $$
$$ \begin{align*}{\left| \sum_{n \in P} f(n) 1_{P'}(n) \right|}^* = {\left| \sum_{n \in P'} f(n) \right|}^* \leq {\left| \sum_{n \in P} f(n) \right|}^*\end{align*} $$
 $$ \begin{align*}\left|\sum_{n \in P} f(n)\right| \leq {\left |\sum_{n \in P} f(n)\right|}^* \leq \sum_{n \in P} |f(n)|.\end{align*} $$
$$ \begin{align*}\left|\sum_{n \in P} f(n)\right| \leq {\left |\sum_{n \in P} f(n)\right|}^* \leq \sum_{n \in P} |f(n)|.\end{align*} $$
If P can be partitioned into two subprogressions as
 $P = P_1 \uplus P_2$
, then (2.3)
$P = P_1 \uplus P_2$
, then (2.3) $$ \begin{align} {\left |\sum_{n \in P} f(n)\right|}^* \leq {\left|\sum_{n \in P_1} f(n)\right|}^* + {\left|\sum_{n \in P_2} f(n)\right|}^*. \end{align} $$
$$ \begin{align} {\left |\sum_{n \in P} f(n)\right|}^* \leq {\left|\sum_{n \in P_1} f(n)\right|}^* + {\left|\sum_{n \in P_2} f(n)\right|}^*. \end{align} $$
Finally, the map
 $f \mapsto |\sum _{n \in P} f(n)|^*$
is a seminorm.
$f \mapsto |\sum _{n \in P} f(n)|^*$
is a seminorm. -
(ii) (Local stability) If
 $x_0 \in \mathbb {R}$
,
$x_0 \in \mathbb {R}$
,
 $H> 0$
, and
$H> 0$
, and
 $f \colon \mathbb {Z} \to \mathbb {C}$
, then
$f \colon \mathbb {Z} \to \mathbb {C}$
, then  $$ \begin{align*}{\left|\sum_{x_0 < n \leq x_0+H} f(n)\right|}^* \leq \frac{2}{H} \int_{x_0-H/2}^{x_0+H/2} {\left|\sum_{x < n \leq x+H} f(n)\right|}^*\ dx.\end{align*} $$
$$ \begin{align*}{\left|\sum_{x_0 < n \leq x_0+H} f(n)\right|}^* \leq \frac{2}{H} \int_{x_0-H/2}^{x_0+H/2} {\left|\sum_{x < n \leq x+H} f(n)\right|}^*\ dx.\end{align*} $$
-
(iii) (Summation by parts) Let P be an arithmetic progression, and let
 $f,g \colon P \to \mathbb {C}$
be functions. Then we have (2.4)and more generally
$f,g \colon P \to \mathbb {C}$
be functions. Then we have (2.4)and more generally $$ \begin{align} {\left| \sum_{n \in P} f(n) g(n) \right|}^* \leq \|g\|_{{\operatorname{TV}}(P)} {\left| \sum_{n \in P} f(n) \right|}^* \end{align} $$
(2.5)for any
$$ \begin{align} {\left| \sum_{n \in P} f(n) g(n) \right|}^* \leq \|g\|_{{\operatorname{TV}}(P)} {\left| \sum_{n \in P} f(n) \right|}^* \end{align} $$
(2.5)for any $$ \begin{align} {\left| \sum_{n \in P} f(n) g(n) \right|}^* \leq \|g\|_{{\operatorname{TV}}(P;q)} {\left| \sum_{n \in P} f(n) \right|}^* \end{align} $$
$$ \begin{align} {\left| \sum_{n \in P} f(n) g(n) \right|}^* \leq \|g\|_{{\operatorname{TV}}(P;q)} {\left| \sum_{n \in P} f(n) \right|}^* \end{align} $$
 $q \geq 1$
.
$q \geq 1$
.
Proof. The claims (i) all follow easily the triangle inequality and the observation that the intersection of two arithmetic progressions is again an arithmetic progression; for instance, equation (2.3) follows from the observation that any subprogression
![]() $P'$
of P is partitioned into subprogressions
$P'$
of P is partitioned into subprogressions
![]() $P' \cap P_1, P' \cap P_2$
of
$P' \cap P_1, P' \cap P_2$
of
![]() $P_1, P_2$
, respectively. To prove (ii), we observe from (i) that for any
$P_1, P_2$
, respectively. To prove (ii), we observe from (i) that for any
![]() $0 < t < H/2$
we have
$0 < t < H/2$
we have
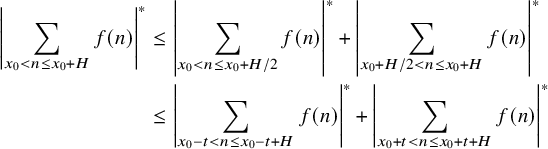 $$ \begin{align*} {\left|\sum_{x_0 < n \leq x_0+H} f(n)\right|}^* &\leq {\left|\sum_{x_0 < n \leq x_0+H/2} f(n)\right|}^* + {\left|\sum_{x_0+H/2 < n \leq x_0+H} f(n)\right|}^*\\ &\leq {\left|\sum_{x_0-t < n \leq x_0-t+H} f(n)\right|}^* + {\left|\sum_{x_0+t < n \leq x_0+t+H} f(n)\right|}^* \end{align*} $$
$$ \begin{align*} {\left|\sum_{x_0 < n \leq x_0+H} f(n)\right|}^* &\leq {\left|\sum_{x_0 < n \leq x_0+H/2} f(n)\right|}^* + {\left|\sum_{x_0+H/2 < n \leq x_0+H} f(n)\right|}^*\\ &\leq {\left|\sum_{x_0-t < n \leq x_0-t+H} f(n)\right|}^* + {\left|\sum_{x_0+t < n \leq x_0+t+H} f(n)\right|}^* \end{align*} $$
and the claim then follows by averaging in t.
To prove the first claim (2.4) of (iii), it will suffice by the monotonicity properties of total variation and maximal sums to show that
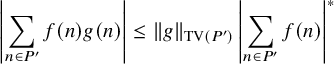 $$ \begin{align} {\left| \sum_{n \in P'} f(n) g(n) \right| \leq \|g\|_{{\operatorname{TV}}(P')} \left| \sum_{n \in P'} f(n) \right|}^* \end{align} $$
$$ \begin{align} {\left| \sum_{n \in P'} f(n) g(n) \right| \leq \|g\|_{{\operatorname{TV}}(P')} \left| \sum_{n \in P'} f(n) \right|}^* \end{align} $$
for all subprogressions
![]() $P'$
of P. Clearly, we may assume
$P'$
of P. Clearly, we may assume
![]() $P'$
is nonempty. If we order the elements of
$P'$
is nonempty. If we order the elements of
![]() $P'$
as
$P'$
as
![]() $n_1 < n_2 < \dots < n_k$
, then from summation by parts we have
$n_1 < n_2 < \dots < n_k$
, then from summation by parts we have
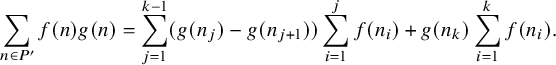 $$ \begin{align*}\sum_{n \in P'} f(n) g(n) = \sum_{j=1}^{k-1} (g(n_j) - g(n_{j+1})) \sum_{i=1}^j f(n_i) + g(n_k) \sum_{i=1}^k f(n_i).\end{align*} $$
$$ \begin{align*}\sum_{n \in P'} f(n) g(n) = \sum_{j=1}^{k-1} (g(n_j) - g(n_{j+1})) \sum_{i=1}^j f(n_i) + g(n_k) \sum_{i=1}^k f(n_i).\end{align*} $$
Since each segment
![]() $\{n_1,\dots ,n_j\}$
of
$\{n_1,\dots ,n_j\}$
of
![]() $P'$
is again a subprogression of
$P'$
is again a subprogression of
![]() $P'$
, we have from the triangle inequality that
$P'$
, we have from the triangle inequality that
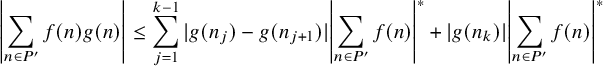 $$ \begin{align*}\left|\sum_{n \in P'} f(n) g(n)\right| \leq \sum_{j=1}^{k-1} |g(n_j) - g(n_{j+1})| {\left| \sum_{n \in P'} f(n) \right|}^* + |g(n_k)| {\left| \sum_{n \in P'} f(n) \right|}^*\end{align*} $$
$$ \begin{align*}\left|\sum_{n \in P'} f(n) g(n)\right| \leq \sum_{j=1}^{k-1} |g(n_j) - g(n_{j+1})| {\left| \sum_{n \in P'} f(n) \right|}^* + |g(n_k)| {\left| \sum_{n \in P'} f(n) \right|}^*\end{align*} $$
and the claim (2.6) now follows from Definition 2.1. Thus, equation (2.4) holds. To prove the second claim (2.5), partition P into subprogressions
![]() $P \cap (a+q\mathbb {Z})$
, apply equation (2.4) to each subprogression and sum using (i).
$P \cap (a+q\mathbb {Z})$
, apply equation (2.4) to each subprogression and sum using (i).
2.2 Vinogradov lemma
If
![]() $P \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree d, and I is an interval of length
$P \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree d, and I is an interval of length
![]() $|I| \geq 1$
, we define the smoothness norm
$|I| \geq 1$
, we define the smoothness norm
where
![]() $\partial _1$
is the difference operator
$\partial _1$
is the difference operator
. We remark that this definition deviates very slightly from that in [Reference Green and Tao19, Definition 2.7]; in particular, we allow the index j to equal zero and we allow n to range over I rather than being set to the origin. We use the same notation
![]() $\|P\|_{C^{\infty }(I)}$
for a polynomial
$\|P\|_{C^{\infty }(I)}$
for a polynomial
![]() $P \colon \mathbb {Z} \to \mathbb {R}$
after reducing its coefficients modulo
$P \colon \mathbb {Z} \to \mathbb {R}$
after reducing its coefficients modulo
![]() $1$
.
$1$
.
The following lemma asserts, roughly speaking, that a polynomial P is (somewhat) equidistributed unless it is smooth.
Lemma 2.3 (Vinogradov lemma).
Let
![]() $0 < \varepsilon , \delta < 1/2$
,
$0 < \varepsilon , \delta < 1/2$
,
![]() $d \geq 0$
, and let
$d \geq 0$
, and let
![]() $P \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
be a polynomial of degree at most d. Let I be an interval of length
$P \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
be a polynomial of degree at most d. Let I be an interval of length
![]() $|I| \geq 1$
, and suppose that
$|I| \geq 1$
, and suppose that
for at least
![]() $\delta |I|$
integers
$\delta |I|$
integers
![]() $n \in I$
. Then either
$n \in I$
. Then either
![]() $\delta \ll _d \varepsilon $
, or else one has
$\delta \ll _d \varepsilon $
, or else one has
for some integer
![]() $1 \leq q \ll _d \delta ^{-O_d(1)}$
.
$1 \leq q \ll _d \delta ^{-O_d(1)}$
.
Proof. By applying a translation, we may assume that I takes the form
![]() $(0,N]$
for some
$(0,N]$
for some
![]() $N \geq 1$
. We may also assume
$N \geq 1$
. We may also assume
![]() $\varepsilon \leq \delta /2$
, since we are clearly done otherwise. We may now invoke [Reference Green and Tao19, Lemma 4.5] to conclude that there exists
$\varepsilon \leq \delta /2$
, since we are clearly done otherwise. We may now invoke [Reference Green and Tao19, Lemma 4.5] to conclude that there exists
![]() $1 \leq q \ll _d \delta ^{-O_d(1)} \varepsilon $
such that
$1 \leq q \ll _d \delta ^{-O_d(1)} \varepsilon $
such that
This is almost what we want, except that we have to also control the
![]() $j=0$
contribution. But from hypothesis, we have at least one
$j=0$
contribution. But from hypothesis, we have at least one
![]() $n_0 \in I$
such that
$n_0 \in I$
such that
![]() $\|P(n_0)\|_{\mathbb {R}/\mathbb {Z}} \leq \varepsilon $
, and from equation (2.7) we have
$\|P(n_0)\|_{\mathbb {R}/\mathbb {Z}} \leq \varepsilon $
, and from equation (2.7) we have
![]() $\| q \partial _1 P(n) \|_{\mathbb {R}/\mathbb {Z}} \ll _d \delta ^{-O_d(1)} |I|^{-1} \varepsilon $
for all
$\| q \partial _1 P(n) \|_{\mathbb {R}/\mathbb {Z}} \ll _d \delta ^{-O_d(1)} |I|^{-1} \varepsilon $
for all
![]() $n \in I$
. From the triangle inequality, we then conclude that
$n \in I$
. From the triangle inequality, we then conclude that
for all
![]() $n \in I$
, and the claim follows.
$n \in I$
, and the claim follows.
The following handy corollary of Lemma 2.3 asserts, roughly speaking, that if many dilates of a polynomial are smooth, then the polynomial itself is smooth.
Corollary 2.4 (Concatenating dilated smoothness).
Let
![]() $0 < \delta < 1/2$
,
$0 < \delta < 1/2$
,
![]() $d \geq 0$
, and let
$d \geq 0$
, and let
![]() $P \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
be a polynomial of degree at most d. Let
$P \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
be a polynomial of degree at most d. Let
![]() $A \geq 1$
, let I be an interval with
$A \geq 1$
, let I be an interval with
![]() $|I| \geq 2A$
and suppose that
$|I| \geq 2A$
and suppose that
for at least
![]() $\delta A$
integers a in
$\delta A$
integers a in
![]() $[A,2A]$
, where
$[A,2A]$
, where
![]() is the dilate of I by
is the dilate of I by
![]() $\frac {1}{a}$
. Then either
$\frac {1}{a}$
. Then either
![]() $|I| \ll _d \delta ^{-O_d(1)} A$
, or else one has
$|I| \ll _d \delta ^{-O_d(1)} A$
, or else one has
for some integer
![]() $1 \leq q \ll _d \delta ^{-O_d(1)}$
.
$1 \leq q \ll _d \delta ^{-O_d(1)}$
.
Proof. We allow all implied constants to depend on d. We may assume that
![]() $|I| \geq C \delta ^{-C} A$
for a large constant C depending on d, as the claim is immediate otherwise.
$|I| \geq C \delta ^{-C} A$
for a large constant C depending on d, as the claim is immediate otherwise.
We now claim that for each
![]() $0 \leq j \leq d$
that there exists a decomposition
$0 \leq j \leq d$
that there exists a decomposition
where
![]() $P_j \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree at most d with
$P_j \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree at most d with
for some
![]() $1 \leq q_j \ll \delta ^{-O(1)}$
, and
$1 \leq q_j \ll \delta ^{-O(1)}$
, and
![]() $Q_j \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree at most j. For
$Q_j \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree at most j. For
![]() $j=d$
, one can simply set
$j=d$
, one can simply set
![]() $P_d=0$
and
$P_d=0$
and
![]() $Q_d=P$
. Now, suppose by downward induction that
$Q_d=P$
. Now, suppose by downward induction that
![]() $0 \leq j < d$
and the claim has already been proven for
$0 \leq j < d$
and the claim has already been proven for
![]() $j+1$
. From equation (2.10) (for
$j+1$
. From equation (2.10) (for
![]() $P_{j+1}$
), we have
$P_{j+1}$
), we have
Routine Taylor expansion then gives
for all
![]() $a \in [A,2A]$
, thus by equation (2.8) and the triangle inequality we have
$a \in [A,2A]$
, thus by equation (2.8) and the triangle inequality we have
for
![]() $\geq \delta A$
choices of
$\geq \delta A$
choices of
![]() $a \in [A,2A]$
.
$a \in [A,2A]$
.
Now, write
![]() $Q_{j+1}(n) = \alpha _{j+1} \binom {n}{j+1} + Q_j(n)$
, where
$Q_{j+1}(n) = \alpha _{j+1} \binom {n}{j+1} + Q_j(n)$
, where
![]() $Q_j$
is of degree at most j. Taking
$Q_j$
is of degree at most j. Taking
![]() $j+1$
-fold derivatives, we see that
$j+1$
-fold derivatives, we see that
for
![]() $\geq \delta A$
choices of
$\geq \delta A$
choices of
![]() $a \in [A,2A]$
. Applying Lemma 2.3 to the polynomial
$a \in [A,2A]$
. Applying Lemma 2.3 to the polynomial
![]() $a \to a^{j+1}q_{j+1}\alpha _{j+1}$
(and recalling that
$a \to a^{j+1}q_{j+1}\alpha _{j+1}$
(and recalling that
![]() $|I|/A \geq C \delta ^{-C}$
for a suitably large C by assumption), we conclude that there is
$|I|/A \geq C \delta ^{-C}$
for a suitably large C by assumption), we conclude that there is
![]() $1 \leq q \ll \delta ^{O(1)}$
such that
$1 \leq q \ll \delta ^{O(1)}$
such that
and hence on taking
![]() $j+1$
-fold derivatives
$j+1$
-fold derivatives
If one then sets
![]() and
and
![]() , we obtain the decomposition (2.9), and equation (2.10) follows from the triangle inequality. This closes the induction. Applying the claim with
, we obtain the decomposition (2.9), and equation (2.10) follows from the triangle inequality. This closes the induction. Applying the claim with
![]() $j=0$
, we obtain the corollary.
$j=0$
, we obtain the corollary.
2.3 Equidistribution on nilmanifolds
We now recall some of the basic notation and results from [Reference Green and Tao19] concerning equidistribution of polynomial maps on nilmanifolds.
Definition 2.5 (Filtered group).
Let
![]() $d \geq 1$
. A filtered group is a group G (which we express in multiplicative notation
$d \geq 1$
. A filtered group is a group G (which we express in multiplicative notation
![]() $G = (G,\cdot )$
unless explicitly indicated otherwise) equipped with a filtration
$G = (G,\cdot )$
unless explicitly indicated otherwise) equipped with a filtration
![]() $G_\bullet = (G_i)_{i=0}^\infty $
of nested groups
$G_\bullet = (G_i)_{i=0}^\infty $
of nested groups
![]() $G \geq G_0 \geq G_1 \geq \dots $
such that
$G \geq G_0 \geq G_1 \geq \dots $
such that
![]() $[G_i,G_j] \leq G_{i+j}$
for all
$[G_i,G_j] \leq G_{i+j}$
for all
![]() $i,j \geq 0$
. We say that this group has degree at most d if
$i,j \geq 0$
. We say that this group has degree at most d if
![]() $G_i$
is trivial for all
$G_i$
is trivial for all
![]() $i>d$
. Given a filtered group of degree at most d, a polynomial map
$i>d$
. Given a filtered group of degree at most d, a polynomial map
![]() $g \colon \mathbb {Z} \to G$
from
$g \colon \mathbb {Z} \to G$
from
![]() $\mathbb {Z}$
to G is a map of the form
$\mathbb {Z}$
to G is a map of the form
![]() $g(n) = g_0 g_1^{\binom {n}{1}} \dots g_d^{\binom {n}{d}}$
, where
$g(n) = g_0 g_1^{\binom {n}{1}} \dots g_d^{\binom {n}{d}}$
, where
![]() $g_i \in G_i$
for all
$g_i \in G_i$
for all
![]() $0 \leq i \leq d$
; the collection of such maps will be denoted
$0 \leq i \leq d$
; the collection of such maps will be denoted
![]() ${\operatorname {Poly}}(\mathbb {Z} \to G)$
.
${\operatorname {Poly}}(\mathbb {Z} \to G)$
.
The well-known Lazard–Leibman theorem (see, e.g., [Reference Green and Tao19, Proposition 6.2]) asserts that
![]() ${\operatorname {Poly}}(\mathbb {Z} \to G)$
is a group under pointwise multiplication; also, from [Reference Green and Tao19, Corollary 6.8] we see that if
${\operatorname {Poly}}(\mathbb {Z} \to G)$
is a group under pointwise multiplication; also, from [Reference Green and Tao19, Corollary 6.8] we see that if
![]() $g \colon \mathbb {Z} \to G$
is a polynomial map then so is
$g \colon \mathbb {Z} \to G$
is a polynomial map then so is
![]() $n \mapsto g(an+b)$
for any integers
$n \mapsto g(an+b)$
for any integers
![]() $a,b$
.
$a,b$
.
If G is a simply connected nilpotent Lie group, we write
![]() $\log G$
for the Lie algebra. From the Baker–Campbell–Hausdorff formula,Footnote
4
(see, e.g., [Reference Hall22, Theorem 3.3]) we see that the exponential map
$\log G$
for the Lie algebra. From the Baker–Campbell–Hausdorff formula,Footnote
4
(see, e.g., [Reference Hall22, Theorem 3.3]) we see that the exponential map
![]() $\exp \colon \log G \to G$
is a homeomorphism and hence has an inverse
$\exp \colon \log G \to G$
is a homeomorphism and hence has an inverse
![]() $\log \colon G \to \log G$
.
$\log \colon G \to \log G$
.
Definition 2.6 (Filtered nilmanifolds).
Let
![]() $d, D \geq 1$
and
$d, D \geq 1$
and
![]() $0 < \delta < 1$
. A filtered nilmanifold
$0 < \delta < 1$
. A filtered nilmanifold
![]() $G/\Gamma $
of degree at most d, dimension D, and complexity at most
$G/\Gamma $
of degree at most d, dimension D, and complexity at most
![]() $1/\delta $
consists of the following data:
$1/\delta $
consists of the following data:
-
• A filtered simply connected nilpotent Lie group G of dimension D equipped with a filtration
 $G_\bullet = (G_i)_{i=0}^\infty $
of degree at most d, with
$G_\bullet = (G_i)_{i=0}^\infty $
of degree at most d, with
 $G_0=G_1=G$
and all
$G_0=G_1=G$
and all
 $G_i$
closed connected subgroups of G.
$G_i$
closed connected subgroups of G. -
• A lattice (i.e., a discrete cocompact subgroup
 $\Gamma $
) of G, with the property that
$\Gamma $
) of G, with the property that
 is a lattice of
is a lattice of
 $G_i$
for all
$G_i$
for all
 $i \geq 0$
.
$i \geq 0$
. -
• A linear basis
 $X_1,\dots ,X_D$
(which we call a Mal’cev basis) of
$X_1,\dots ,X_D$
(which we call a Mal’cev basis) of
 $\log G$
.
$\log G$
.
Furthermore, we assume the following axioms:
-
(i) For all
 $1 \leq i,j \leq D$
, we have
$1 \leq i,j \leq D$
, we have
 $[X_i,X_j] = \sum _{i,j < k \leq D} c_{ijk} X_k$
for some rational numbers
$[X_i,X_j] = \sum _{i,j < k \leq D} c_{ijk} X_k$
for some rational numbers
 $c_{ijk}$
of height at most
$c_{ijk}$
of height at most
 $1/\delta $
.
$1/\delta $
. -
(ii) For all
 $0 \leq i \leq d$
, the vector space
$0 \leq i \leq d$
, the vector space
 $G_i$
is spanned by the
$G_i$
is spanned by the
 $X_j$
with
$X_j$
with
 $D - \dim G_i < j \leq D$
.
$D - \dim G_i < j \leq D$
. -
(iii) We have
 $\Gamma = \{ \exp (n_1 X_1) \dotsm \exp (n_D X_D): n_1,\dots ,n_D \in \mathbb {Z} \}$
.
$\Gamma = \{ \exp (n_1 X_1) \dotsm \exp (n_D X_D): n_1,\dots ,n_D \in \mathbb {Z} \}$
.
It is easy to see that
![]() $G/\Gamma $
has the structure of a smooth compact D-dimensional manifold, which we equip with a probability Haar measure
$G/\Gamma $
has the structure of a smooth compact D-dimensional manifold, which we equip with a probability Haar measure
![]() $d\mu _{G/\Gamma }$
. We define the metric
$d\mu _{G/\Gamma }$
. We define the metric
![]() $d_G$
on G to be the largest right-invariant metric such that
$d_G$
on G to be the largest right-invariant metric such that
![]() $d_G( \exp (t_1 X_1) \dotsm \exp (t_D X_D), 1) \leq \sup _{1 \leq i \leq D} |t_i|$
for all
$d_G( \exp (t_1 X_1) \dotsm \exp (t_D X_D), 1) \leq \sup _{1 \leq i \leq D} |t_i|$
for all
![]() $t_1,\dots ,t_D \in \mathbb {R}$
. We then define a metric
$t_1,\dots ,t_D \in \mathbb {R}$
. We then define a metric
![]() $d_{G/\Gamma }$
on
$d_{G/\Gamma }$
on
![]() $G/\Gamma $
by the formula
$G/\Gamma $
by the formula
![]() . The Lipschitz norm of a function
. The Lipschitz norm of a function
![]() $F \colon G/\Gamma \to \mathbb {C}$
is defined to be the quantity
$F \colon G/\Gamma \to \mathbb {C}$
is defined to be the quantity
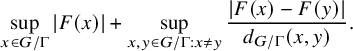 $$ \begin{align*}\sup_{x \in G/\Gamma} |F(x)| + \sup_{x,y \in G/\Gamma: x \neq y} \frac{|F(x)-F(y)|}{d_{G/\Gamma}(x,y)}.\end{align*} $$
$$ \begin{align*}\sup_{x \in G/\Gamma} |F(x)| + \sup_{x,y \in G/\Gamma: x \neq y} \frac{|F(x)-F(y)|}{d_{G/\Gamma}(x,y)}.\end{align*} $$
A horizontal character
![]() $\eta $
associated to a filtered nilmanifold is a continuous homomorphism
$\eta $
associated to a filtered nilmanifold is a continuous homomorphism
![]() $\eta \colon G \to \mathbb {R}$
that maps
$\eta \colon G \to \mathbb {R}$
that maps
![]() $\Gamma $
to the integers.
$\Gamma $
to the integers.
An element
![]() $\gamma $
of G is said to be M-rational for some
$\gamma $
of G is said to be M-rational for some
![]() $M \geq 1$
if one has
$M \geq 1$
if one has
![]() $\gamma ^r \in \Gamma $
for some natural number
$\gamma ^r \in \Gamma $
for some natural number
![]() $1 \leq r \leq M$
. A subnilmanifold
$1 \leq r \leq M$
. A subnilmanifold
![]() $G'/\Gamma '$
of
$G'/\Gamma '$
of
![]() $G/\Gamma $
(thus,
$G/\Gamma $
(thus,
![]() $G'$
is a closed connected subgroup of G with
$G'$
is a closed connected subgroup of G with
![]() cocompact in
cocompact in
![]() $G^{\prime }_i$
for all i) is said to be M-rational if each element
$G^{\prime }_i$
for all i) is said to be M-rational if each element
![]() $X^{\prime }_1,\dots ,X^{\prime }_{\dim G'}$
of the Mal’cev basis associated to G is a linear combination of the
$X^{\prime }_1,\dots ,X^{\prime }_{\dim G'}$
of the Mal’cev basis associated to G is a linear combination of the
![]() $X_i$
with all coefficients rational of height at most M.
$X_i$
with all coefficients rational of height at most M.
A rational subgroup
![]() $G'$
of complexity at most
$G'$
of complexity at most
![]() $1/\delta $
is a closed connected subgroup of G with the property that
$1/\delta $
is a closed connected subgroup of G with the property that
![]() $\log G'$
admits a linear basis consisting of
$\log G'$
admits a linear basis consisting of
![]() $\dim G'$
vectors of the form
$\dim G'$
vectors of the form
![]() $\sum _{i=1}^D a_i X_i$
, where each
$\sum _{i=1}^D a_i X_i$
, where each
![]() $a_i$
is a rational of height at most
$a_i$
is a rational of height at most
![]() $1/\delta $
.
$1/\delta $
.
It is easy to see that every horizontal character takes the form
![]() $\eta (g) = \lambda ( \log g)$
for some linear functional
$\eta (g) = \lambda ( \log g)$
for some linear functional
![]() $\lambda \colon \log G \to \mathbb {R}$
that annihilates
$\lambda \colon \log G \to \mathbb {R}$
that annihilates
![]() $\log [G,G]$
and maps
$\log [G,G]$
and maps
![]() $\log \Gamma $
to the integers. From this, one can verify that the number of horizontal characters of Lipschitz norm at most
$\log \Gamma $
to the integers. From this, one can verify that the number of horizontal characters of Lipschitz norm at most
![]() $1/\delta $
is at most
$1/\delta $
is at most
![]() $O_{d,D}( \delta ^{-O_{d,D}(1)} )$
.
$O_{d,D}( \delta ^{-O_{d,D}(1)} )$
.
From several applications of Baker–Campbell–Hausdorff formula, we see that if G has degree at most d and
![]() $\gamma _1, \gamma _2 \in G$
are M-rational, then
$\gamma _1, \gamma _2 \in G$
are M-rational, then
![]() $\gamma _1 \gamma _2$
is
$\gamma _1 \gamma _2$
is
![]() $O_d(M^{O_d(1)})$
-rational.
$O_d(M^{O_d(1)})$
-rational.
We have the following basic dichotomy between equidistribution and smoothness:
Theorem 2.7 (Quantitative Leibman theorem).
Let
![]() $0 < \delta < 1/2$
, let
$0 < \delta < 1/2$
, let
![]() $d,D \geq 1$
, let I be an interval with
$d,D \geq 1$
, let I be an interval with
![]() $|I| \geq 1$
and let
$|I| \geq 1$
and let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension at most D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension at most D and complexity at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
![]() $1/\delta $
and of mean zero (i.e.,
$1/\delta $
and of mean zero (i.e.,
![]() $\int _{G/\Gamma } F\ d\mu _{G/\Gamma } = 0$
). Suppose that
$\int _{G/\Gamma } F\ d\mu _{G/\Gamma } = 0$
). Suppose that
![]() $g \colon \mathbb {Z} \to G$
is a polynomial map with
$g \colon \mathbb {Z} \to G$
is a polynomial map with
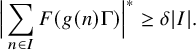 $$ \begin{align*}\Big|\sum_{n \in I} F(g(n)\Gamma)\Big|^* \geq \delta |I|.\end{align*} $$
$$ \begin{align*}\Big|\sum_{n \in I} F(g(n)\Gamma)\Big|^* \geq \delta |I|.\end{align*} $$
Then there exists a nontrivial horizontal character
![]() $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
Proof. By applying a translation, we may assume
![]() $I = (0,N]$
for some
$I = (0,N]$
for some
![]() $N \geq 1$
. The claim now follows from [Reference Shao and Teräväinen59, Theorem 3.5].
$N \geq 1$
. The claim now follows from [Reference Shao and Teräväinen59, Theorem 3.5].
Let
![]() $G/\Gamma $
be a filtered nilmanifold of dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of dimension D and complexity at most
![]() $1/\delta $
, and let
$1/\delta $
, and let
![]() $G'$
be a rational subgroup of complexity at most
$G'$
be a rational subgroup of complexity at most
![]() $1/\delta $
. In [Reference Green and Tao19, Proposition A.10], it is shown that
$1/\delta $
. In [Reference Green and Tao19, Proposition A.10], it is shown that
![]() $G'/\Gamma '$
can be equipped with the structure of a filtered nilmanifold of complexity
$G'/\Gamma '$
can be equipped with the structure of a filtered nilmanifold of complexity
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
, where
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
, where
![]() ,
,
![]() , and the metrics
, and the metrics
![]() $d_G, d_{G'}$
are comparable on
$d_G, d_{G'}$
are comparable on
![]() $G'$
up to factors of
$G'$
up to factors of
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
; one can view
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
; one can view
![]() $G'/\Gamma '$
as a subnilmanifold of
$G'/\Gamma '$
as a subnilmanifold of
![]() $G/\Gamma $
.
$G/\Gamma $
.
One can easily verify from basic linear algebra and the Baker–Campbell–Hausdorff formula that the following groups are rational subgroups of G of complexity
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
:
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
:
-
• The groups
 $G_i$
in the filtration for
$G_i$
in the filtration for
 $0 \leq i \leq d$
.
$0 \leq i \leq d$
. -
• The kernel
 $\ker \eta $
of any horizontal character
$\ker \eta $
of any horizontal character
 $\eta $
of Lipschitz norm
$\eta $
of Lipschitz norm
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
.
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
. -
• The center
 $Z(G) = \{ \exp (X): X \in \log G; [X,Y] = 0 \,\,\forall Y \in \log G \}$
of G.
$Z(G) = \{ \exp (X): X \in \log G; [X,Y] = 0 \,\,\forall Y \in \log G \}$
of G. -
• The intersection
 $G' \cap G"$
or commutator
$G' \cap G"$
or commutator
 $[G',G"]$
of two rational subgroups
$[G',G"]$
of two rational subgroups
 $G',G"$
of G of complexity
$G',G"$
of G of complexity
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
.
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
. -
• The product
 $G' N$
of two rational subgroups
$G' N$
of two rational subgroups
 $G',N$
of G of complexity
$G',N$
of G of complexity
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
, with N normal.
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
, with N normal.
We can quotient out a filtered nilmanifold by a normal subgroup to obtain another filtered nilmanifold, with polynomial control on complexity:
Lemma 2.8 (Quotienting by a normal subgroup).
Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
. Let N be a normal rational subgroup of G of complexity at most
$1/\delta $
. Let N be a normal rational subgroup of G of complexity at most
![]() $1/\delta $
, and let
$1/\delta $
, and let
![]() $\pi \colon G \mapsto G/N$
be the quotient map. Then
$\pi \colon G \mapsto G/N$
be the quotient map. Then
![]() $\pi (G)/\pi (\Gamma )$
can be given the structure of a filtered nilmanifold of degree at most d, dimension
$\pi (G)/\pi (\Gamma )$
can be given the structure of a filtered nilmanifold of degree at most d, dimension
![]() $D - \dim N$
, and complexity
$D - \dim N$
, and complexity
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
for any
![]() $g,h \in G$
.
$g,h \in G$
.
Proof. We allow all implied constants to depend on
![]() $d,D$
. Let
$d,D$
. Let
![]() $\tilde \pi \colon \log G \to \log G / \log N \equiv \log (G/N)$
be the quotient map of
$\tilde \pi \colon \log G \to \log G / \log N \equiv \log (G/N)$
be the quotient map of
![]() $\log G$
by the Lie algebra ideal
$\log G$
by the Lie algebra ideal
![]() $\log N$
, then
$\log N$
, then
![]() $\pi \circ \exp = \exp \circ \tilde \pi $
. For each
$\pi \circ \exp = \exp \circ \tilde \pi $
. For each
![]() $0 \leq i \leq d$
, the vectors
$0 \leq i \leq d$
, the vectors
![]() $\tilde \pi (X_j)$
for
$\tilde \pi (X_j)$
for
![]() $D - \dim G_i < j \leq D$
span the linear subspace
$D - \dim G_i < j \leq D$
span the linear subspace
![]() $\tilde \pi (\log G_i)$
of
$\tilde \pi (\log G_i)$
of
![]() $\log (G/N)$
, and the linear relations between those vectors are are generated by
$\log (G/N)$
, and the linear relations between those vectors are are generated by
![]() $O(1)$
equations with coefficients rational of height
$O(1)$
equations with coefficients rational of height
![]() $O(\delta ^{-O(1)})$
. From this and linear algebra, we may find a basis
$O(\delta ^{-O(1)})$
. From this and linear algebra, we may find a basis
![]() $\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
of
$\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
of
![]() $\log (G/N)$
such that for each
$\log (G/N)$
such that for each
![]() $0 \leq i \leq d$
,
$0 \leq i \leq d$
,
![]() $\tilde \pi (\log G_i)$
is the span of
$\tilde \pi (\log G_i)$
is the span of
![]() $\tilde X_j$
for
$\tilde X_j$
for
![]() $\dim (G/N) - \dim \tilde \pi (\log G_i) < j \leq \dim (G/N)$
, and each
$\dim (G/N) - \dim \tilde \pi (\log G_i) < j \leq \dim (G/N)$
, and each
![]() $\tilde X_j$
is a linear combination of the
$\tilde X_j$
is a linear combination of the
![]() $\tilde \pi (X_1),\dots ,\tilde \pi (X_D)$
with coefficients rational of height
$\tilde \pi (X_1),\dots ,\tilde \pi (X_D)$
with coefficients rational of height
![]() $O(\delta ^{-O(1)})$
. Meanwhile,
$O(\delta ^{-O(1)})$
. Meanwhile,
![]() $\pi (\Gamma )$
is generated by
$\pi (\Gamma )$
is generated by
![]() $\pi (X_1),\dots ,\pi (X_D)$
. From this and the Baker–Campbell–Hausdorff formula, we see that the basis
$\pi (X_1),\dots ,\pi (X_D)$
. From this and the Baker–Campbell–Hausdorff formula, we see that the basis
![]() $\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
is a
$\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
is a
![]() $O(\delta ^{-O(1)})$
-rational weak basis for
$O(\delta ^{-O(1)})$
-rational weak basis for
![]() $\pi (G)/\pi (\Gamma )$
in the sense of [Reference Green and Tao19, Definition A.7]. Applying [Reference Green and Tao19, Proposition A.9] to this weak basis, we obtain a Mal’cev basis that gives
$\pi (G)/\pi (\Gamma )$
in the sense of [Reference Green and Tao19, Definition A.7]. Applying [Reference Green and Tao19, Proposition A.9] to this weak basis, we obtain a Mal’cev basis that gives
![]() $\pi (G)/\pi (\Gamma )$
the structure of a filtered nilmanifold with the stated degree, dimension and complexity. It remains to establish the bound (2.11). By right translation invariance, we can take g to be the identity. For the upper bound, it suffices (since
$\pi (G)/\pi (\Gamma )$
the structure of a filtered nilmanifold with the stated degree, dimension and complexity. It remains to establish the bound (2.11). By right translation invariance, we can take g to be the identity. For the upper bound, it suffices (since
![]() $\pi $
is N-invariant) to show that
$\pi $
is N-invariant) to show that
but this follows from the fact that
![]() $\tilde \pi \colon \log G \to \tilde \pi (\log G)$
has operator norm
$\tilde \pi \colon \log G \to \tilde \pi (\log G)$
has operator norm
![]() $O(\delta ^{-O(1)})$
when using the
$O(\delta ^{-O(1)})$
when using the
![]() $X_1,\dots ,X_D$
basis for
$X_1,\dots ,X_D$
basis for
![]() $\log G$
and the
$\log G$
and the
![]() $\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
basis for
$\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
basis for
![]() $\tilde \pi (\log G)$
to define norms.
$\tilde \pi (\log G)$
to define norms.
Now, we need to establish the lower bound. By [Reference Green and Tao19, Lemma A.4], it suffices to show that
for any
![]() $Y \in \tilde \pi (\log G)$
, where again we use the norm given by the
$Y \in \tilde \pi (\log G)$
, where again we use the norm given by the
![]() $X_1,\dots ,X_D$
basis for
$X_1,\dots ,X_D$
basis for
![]() $\log G$
and the
$\log G$
and the
![]() $\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
. But this is easily verified for each
$\tilde X_1,\dots ,\tilde X_{\dim (G/N)}$
. But this is easily verified for each
![]() $Y = \tilde X_i$
, and the claim then follows by linearity.
$Y = \tilde X_i$
, and the claim then follows by linearity.
A central frequency is a continuous homomorphism
![]() $\xi \colon Z(G) \to \mathbb {R}$
which maps
$\xi \colon Z(G) \to \mathbb {R}$
which maps
![]() $Z(G) \cap \Gamma $
to the integers
$Z(G) \cap \Gamma $
to the integers
![]() $\mathbb {Z}$
(that is to say, a horizontal character on
$\mathbb {Z}$
(that is to say, a horizontal character on
![]() $Z(G)$
, or a Fourier character of the central torus
$Z(G)$
, or a Fourier character of the central torus
![]() $Z(G) / (Z(G) \cap \Gamma )$
). A function
$Z(G) / (Z(G) \cap \Gamma )$
). A function
![]() $F \colon G/\Gamma \to \mathbb {C}$
is said to oscillate with central frequency
$F \colon G/\Gamma \to \mathbb {C}$
is said to oscillate with central frequency
![]() $\xi $
if one has the identity
$\xi $
if one has the identity
for all
![]() $x \in G/\Gamma $
and
$x \in G/\Gamma $
and
![]() $z \in Z(G)$
. As with horizontal characters, the number of central frequencies
$z \in Z(G)$
. As with horizontal characters, the number of central frequencies
![]() $\xi $
of Lipschitz norm at most
$\xi $
of Lipschitz norm at most
![]() $1/\delta $
is
$1/\delta $
is
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
. If
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
. If
![]() $\xi $
is such a central frequency, one can readily verify that the kernel
$\xi $
is such a central frequency, one can readily verify that the kernel
![]() $\ker \xi $
is a rational normal subgroup of G of complexity
$\ker \xi $
is a rational normal subgroup of G of complexity
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
.
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
.
We have the following convenient decompositionFootnote 5 (cf., [Reference Green and Tao19, Lemma 3.7]):
Proposition 2.9 (Central Fourier approximation).
Let
![]() $d,D \geq 1$
and
$d,D \geq 1$
and
![]() $0 < \delta < 1$
. Let
$0 < \delta < 1$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be a Lipschitz function of norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be a Lipschitz function of norm at most
![]() $1/\delta $
. Then we can decompose
$1/\delta $
. Then we can decompose
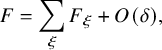 $$ \begin{align*}F = \sum_\xi F_\xi + O(\delta),\end{align*} $$
$$ \begin{align*}F = \sum_\xi F_\xi + O(\delta),\end{align*} $$
where
![]() $\xi $
ranges over central frequencies of Lipschitz norm at most
$\xi $
ranges over central frequencies of Lipschitz norm at most
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
, and each
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
, and each
![]() $F_\xi $
has Lipschitz norm
$F_\xi $
has Lipschitz norm
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
and oscillates with central frequency
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
and oscillates with central frequency
![]() $\xi $
. Furthermore, if F has mean zero, then so do all of the
$\xi $
. Furthermore, if F has mean zero, then so do all of the
![]() $F_\xi $
.
$F_\xi $
.
Proof. We allow all implied constants to depend on
![]() $d,D$
. Since
$d,D$
. Since
![]() $Z(G) / (Z(G) \cap \Gamma )$
is an abelian filtered nilmanifold of complexity
$Z(G) / (Z(G) \cap \Gamma )$
is an abelian filtered nilmanifold of complexity
![]() $O(\delta ^{-O(1)})$
, it can be identified with a torus
$O(\delta ^{-O(1)})$
, it can be identified with a torus
![]() $\mathbb {R}^m/\mathbb {Z}^m$
, where
$\mathbb {R}^m/\mathbb {Z}^m$
, where
![]() $m=O(1)$
and the metric on
$m=O(1)$
and the metric on
![]() $Z(G)$
is comparable to the metric on
$Z(G)$
is comparable to the metric on
![]() $\mathbb {R}^m$
up to factors of
$\mathbb {R}^m$
up to factors of
![]() $O(\delta ^{-O(1)})$
; the identification of
$O(\delta ^{-O(1)})$
; the identification of
![]() $\log Z(G)$
with
$\log Z(G)$
with
![]() $\mathbb {R}^m$
induces a logarithm map
$\mathbb {R}^m$
induces a logarithm map
![]() $\log \colon Z(G) \to \mathbb {R}^m$
and an exponential map
$\log \colon Z(G) \to \mathbb {R}^m$
and an exponential map
![]() $\exp \colon \mathbb {R}^m \to Z(G)$
. Central frequencies
$\exp \colon \mathbb {R}^m \to Z(G)$
. Central frequencies
![]() $\xi $
can then be identified with elements
$\xi $
can then be identified with elements
![]() $k_\xi $
of
$k_\xi $
of
![]() $\mathbb {Z}^m$
, with
$\mathbb {Z}^m$
, with
![]() $\xi (z) = k_\xi \cdot \log (z)$
for any
$\xi (z) = k_\xi \cdot \log (z)$
for any
![]() $z \in Z(G)$
.
$z \in Z(G)$
.
Let
![]() $\varphi : \mathbb {R}^m \to \mathbb {R}$
be a fixed bump function (depending only on m) that equals
$\varphi : \mathbb {R}^m \to \mathbb {R}$
be a fixed bump function (depending only on m) that equals
![]() $1$
at the origin, and let
$1$
at the origin, and let
![]() $R>1$
be a parameter to be chosen later. For any central frequency
$R>1$
be a parameter to be chosen later. For any central frequency
![]() $\xi $
, we set
$\xi $
, we set
where
![]() $dz$
is Haar probability measure on the torus
$dz$
is Haar probability measure on the torus
![]() $\mathbb {R}^m/\mathbb {Z}^m$
, which acts centrally on
$\mathbb {R}^m/\mathbb {Z}^m$
, which acts centrally on
![]() $G/\Gamma $
in the obvious fashion. It is easy to see that
$G/\Gamma $
in the obvious fashion. It is easy to see that
![]() $F_\xi $
has Lipschitz norm
$F_\xi $
has Lipschitz norm
![]() $O(\delta ^{-O(1)})$
, oscillates with central frequency
$O(\delta ^{-O(1)})$
, oscillates with central frequency
![]() $\xi $
, and vanishes unless
$\xi $
, and vanishes unless
![]() $\xi $
has Lipschitz norm
$\xi $
has Lipschitz norm
![]() $O( \delta ^{-O(1)} R^{O(1)} )$
; also, if F has mean zero, then so do all of the
$O( \delta ^{-O(1)} R^{O(1)} )$
; also, if F has mean zero, then so do all of the
![]() $F_\xi $
. From the Fourier inversion formula, we have
$F_\xi $
. From the Fourier inversion formula, we have
where
, as well as the Fourier inversion formula on the torus,
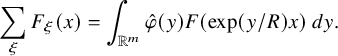 $$ \begin{align*}\sum_\xi F_\xi(x) = \int_{\mathbb{R}^m} \hat \varphi(y) F( \exp(y/R) x )\ dy.\end{align*} $$
$$ \begin{align*}\sum_\xi F_\xi(x) = \int_{\mathbb{R}^m} \hat \varphi(y) F( \exp(y/R) x )\ dy.\end{align*} $$
On the other hand, from the Lipschitz nature of F we have
Since
![]() $\hat \varphi $
is rapidly decreasing and has total integral
$\hat \varphi $
is rapidly decreasing and has total integral
![]() $1$
, we obtain
$1$
, we obtain
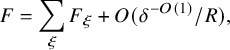 $$ \begin{align*}F = \sum_\xi F_\xi + O(\delta^{-O(1)}/R),\end{align*} $$
$$ \begin{align*}F = \sum_\xi F_\xi + O(\delta^{-O(1)}/R),\end{align*} $$
and the claim follows by choosing
![]() $R = O(\delta ^{-O(1)})$
suitably.
$R = O(\delta ^{-O(1)})$
suitably.
Next, we shall recall a fundamental factorization theorem for polynomial sequences. Before we can state it, we need to define a few notions.
Definition 2.10 (Smoothness, total equidistribution, rationality).
Let
![]() $G/\Gamma $
be a filtered nilmanifold,
$G/\Gamma $
be a filtered nilmanifold,
![]() $g \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
be a polynomial sequence,
$g \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
be a polynomial sequence,
![]() $I \subset \mathbb {R}$
be an interval of length
$I \subset \mathbb {R}$
be an interval of length
![]() $|I| \geq 1$
, and
$|I| \geq 1$
, and
![]() $M>0$
.
$M>0$
.
-
(i) We say that g is
 $(M,I)$
-smooth if one has for all
$(M,I)$
-smooth if one has for all $$ \begin{align*}d_G(g(n), 1_G) \leq M; \quad d_G(g(n), g(n-1)) \leq M/|I|\end{align*} $$
$$ \begin{align*}d_G(g(n), 1_G) \leq M; \quad d_G(g(n), g(n-1)) \leq M/|I|\end{align*} $$
 $n \in I$
.
$n \in I$
.
-
(ii) We say that g is totally
 $1/M$
-equidistributed in
$1/M$
-equidistributed in
 $G/\Gamma $
on I if one has whenever
$G/\Gamma $
on I if one has whenever $$ \begin{align*}\left| \frac{1}{|P|} \sum_{n \in P} F(g(n)\Gamma) - \int_{G/\Gamma} F \right| \leq \frac{1}{M} \|F\|_{{\operatorname{Lip}}}\end{align*} $$
$$ \begin{align*}\left| \frac{1}{|P|} \sum_{n \in P} F(g(n)\Gamma) - \int_{G/\Gamma} F \right| \leq \frac{1}{M} \|F\|_{{\operatorname{Lip}}}\end{align*} $$
 $F \colon G/\Gamma \to \mathbb {C}$
is Lipschitz and P is an arithmetic progression in I of cardinality at least
$F \colon G/\Gamma \to \mathbb {C}$
is Lipschitz and P is an arithmetic progression in I of cardinality at least
 $|I|/M$
.
$|I|/M$
.
-
(iii) We say that g is M-rational if there exists
 $1 \leq r \leq M$
such that
$1 \leq r \leq M$
such that
 $g(n)^r \in \Gamma $
for all
$g(n)^r \in \Gamma $
for all
 $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
From Taylor expansion and the Baker–Campbell–Hausdorff formula, it is not difficult to see that if
![]() $G/\Gamma $
has degree at most d and g is M-rational, then the map
$G/\Gamma $
has degree at most d and g is M-rational, then the map
![]() $n \mapsto g(n) \Gamma $
is q-periodic for some period
$n \mapsto g(n) \Gamma $
is q-periodic for some period
![]() $1 \leq q \ll _d M^{O_d(1)}$
.
$1 \leq q \ll _d M^{O_d(1)}$
.
Lemma 2.11. Let
![]() $d,D \geq 1$
and
$d,D \geq 1$
and
![]() $0 < \delta < 1$
. Let
$0 < \delta < 1$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $g \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
, and let I be an interval with
$g \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
, and let I be an interval with
![]() $|I| \geq 1$
. Suppose that
$|I| \geq 1$
. Suppose that
for some nontrivial horizontal character
![]() $\eta : G \rightarrow \mathbb {R}/\mathbb {Z}$
of Lipschitz norm at most
$\eta : G \rightarrow \mathbb {R}/\mathbb {Z}$
of Lipschitz norm at most
![]() $1/\delta $
. Then there is a decomposition
$1/\delta $
. Then there is a decomposition
![]() $g = \varepsilon g' \gamma $
into polynomial maps
$g = \varepsilon g' \gamma $
into polynomial maps
![]() $\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
such that
$\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
such that
-
(i)
 $\varepsilon $
is
$\varepsilon $
is
 $(\delta ^{-O_{d,D}(1)},I)$
-smooth;
$(\delta ^{-O_{d,D}(1)},I)$
-smooth; -
(ii)
 $g'$
takes values in
$g'$
takes values in
 $G' = \ker \eta $
;
$G' = \ker \eta $
; -
(iii)
 $\gamma $
is
$\gamma $
is
 $\delta ^{-O_{d,D}(1)}$
-rational.
$\delta ^{-O_{d,D}(1)}$
-rational.
Proof. This is a slight variant of [Reference Green and Tao19, Lemma 7.9], the main difference being that our hypothesis (2.12) involves
![]() $\eta \circ g$
rather than
$\eta \circ g$
rather than
![]() $\eta \circ g_2$
(where
$\eta \circ g_2$
(where
![]() $g_2$
is the nonlinear part of g). The argument in the proof of [Reference Green and Tao19, Lemma 7.9] can be modified in an obvious manner as follows. By translation, we may assume that
$g_2$
is the nonlinear part of g). The argument in the proof of [Reference Green and Tao19, Lemma 7.9] can be modified in an obvious manner as follows. By translation, we may assume that
![]() $I = [1, |I|]$
. Let
$I = [1, |I|]$
. Let
![]() $\psi : G\rightarrow \mathbb {R}^D$
be the Mal’cev coordinate map. Suppose that
$\psi : G\rightarrow \mathbb {R}^D$
be the Mal’cev coordinate map. Suppose that
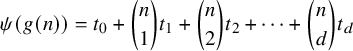 $$ \begin{align*}\psi(g(n)) = t_0 + \binom{n}{1}t_1 + \binom{n}{2}t_2 + \cdots + \binom{n}{d}t_d\end{align*} $$
$$ \begin{align*}\psi(g(n)) = t_0 + \binom{n}{1}t_1 + \binom{n}{2}t_2 + \cdots + \binom{n}{d}t_d\end{align*} $$
for some
![]() $t_0, t_1,\cdots ,t_d \in \mathbb {R}^D$
with
$t_0, t_1,\cdots ,t_d \in \mathbb {R}^D$
with
![]() $\psi ^{-1}(t_i) \in G_i$
. Our assumption on
$\psi ^{-1}(t_i) \in G_i$
. Our assumption on
![]() $\|\eta \circ g\|_{C^{\infty }(I)}$
implies that for some
$\|\eta \circ g\|_{C^{\infty }(I)}$
implies that for some
![]() $k \in \mathbb {Z}^D$
with
$k \in \mathbb {Z}^D$
with
![]() $|k| \leq \delta ^{-1}$
, we have
$|k| \leq \delta ^{-1}$
, we have
for each
![]() $1 \leq i \leq d$
. Choose
$1 \leq i \leq d$
. Choose
![]() $u_i \in \mathbb {R}^D$
with
$u_i \in \mathbb {R}^D$
with
![]() $\psi ^{-1}(u_i) \in G_i$
such that
$\psi ^{-1}(u_i) \in G_i$
such that
Then choose
![]() $v_i \in \mathbb {R}^D$
with
$v_i \in \mathbb {R}^D$
with
![]() $\psi ^{-1}(v_i) \in G_i$
, all of whose coordinates are rationals over some denominator
$\psi ^{-1}(v_i) \in G_i$
, all of whose coordinates are rationals over some denominator
![]() $\ll \delta ^{-O_{d,D}(1)}$
, such that
$\ll \delta ^{-O_{d,D}(1)}$
, such that
for each
![]() $1 \leq i \leq d$
. Define
$1 \leq i \leq d$
. Define
![]() $\varepsilon ,\gamma $
by
$\varepsilon ,\gamma $
by
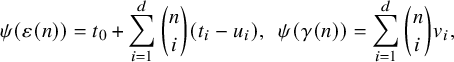 $$ \begin{align*}\psi(\varepsilon(n)) = t_0 + \sum_{i=1}^d \binom{n}{i}(t_i - u_i), \ \ \psi(\gamma(n)) = \sum_{i=1}^d \binom{n}{i}v_i,\end{align*} $$
$$ \begin{align*}\psi(\varepsilon(n)) = t_0 + \sum_{i=1}^d \binom{n}{i}(t_i - u_i), \ \ \psi(\gamma(n)) = \sum_{i=1}^d \binom{n}{i}v_i,\end{align*} $$
and then define
![]() $g'$
by
$g'$
by
One can verify that they satisfy the desired properties.
Theorem 2.12 (Factorization theorem).
Let
![]() $d,D \geq 1$
and
$d,D \geq 1$
and
![]() $0 < \delta < 1$
. Let
$0 < \delta < 1$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $g \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
and
$g \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
and
![]() $A>0$
, and let I be an interval with
$A>0$
, and let I be an interval with
![]() $|I| \geq 1$
. Then there exists an integer
$|I| \geq 1$
. Then there exists an integer
![]() $1/\delta \leq M \ll _{A,D,d} \delta ^{-O_{A,D,d}(1)}$
and a decomposition
$1/\delta \leq M \ll _{A,D,d} \delta ^{-O_{A,D,d}(1)}$
and a decomposition
![]() $g = \varepsilon g' \gamma $
into polynomial maps
$g = \varepsilon g' \gamma $
into polynomial maps
![]() $\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
such that
$\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
such that
-
(i)
 $\varepsilon $
is
$\varepsilon $
is
 $(M,I)$
-smooth;
$(M,I)$
-smooth; -
(ii) There is an M-rational subnilmanifold
 $G'/\Gamma '$
of
$G'/\Gamma '$
of
 $G/\Gamma $
such that
$G/\Gamma $
such that
 $g'$
takes values in
$g'$
takes values in
 $G'$
and is totally
$G'$
and is totally
 $1/M^A$
-equidistributed on I in
$1/M^A$
-equidistributed on I in
 $G'/\Gamma '$
, and more generally in
$G'/\Gamma '$
, and more generally in
 $G'/\Gamma "$
whenever
$G'/\Gamma "$
whenever
 $\Gamma "$
is a subgroup of
$\Gamma "$
is a subgroup of
 $\Gamma '$
of index at most
$\Gamma '$
of index at most
 $M^A$
; and
$M^A$
; and -
(iii)
 $\gamma $
is M-rational.
$\gamma $
is M-rational.
Proof. See [Reference Green and Tao19, Theorem 1.19] (after rounding I to integer endpoints and translating to be of the form
![]() $[1,N]$
). The additional requirement in (ii) that one has equidistribution in the larger nilmanifolds
$[1,N]$
). The additional requirement in (ii) that one has equidistribution in the larger nilmanifolds
![]() $G'/\Gamma "$
is not stated in [Reference Green and Tao19, Theorem 1.19] but follows easily from the proof, the point being that if a sequence
$G'/\Gamma "$
is not stated in [Reference Green and Tao19, Theorem 1.19] but follows easily from the proof, the point being that if a sequence
![]() $g' \in {\operatorname {Poly}}(\mathbb {Z} \to G')$
fails to be totally
$g' \in {\operatorname {Poly}}(\mathbb {Z} \to G')$
fails to be totally
![]() $1/M^A$
-equidistributed in
$1/M^A$
-equidistributed in
![]() $G'/\Gamma "$
, then one has
$G'/\Gamma "$
, then one has
![]() $\|\eta \circ g' \|_{C^\infty (I)} \ll _{d,D} M^{O_{d,D}(A)}$
for some nontrivial horizontal character
$\|\eta \circ g' \|_{C^\infty (I)} \ll _{d,D} M^{O_{d,D}(A)}$
for some nontrivial horizontal character
![]() $\eta $
on
$\eta $
on
![]() $G'/\Gamma "$
of Lipschitz norm
$G'/\Gamma "$
of Lipschitz norm
![]() $O_{d,D}(M^{O_{d,D}(A)})$
, which on multiplying
$O_{d,D}(M^{O_{d,D}(A)})$
, which on multiplying
![]() $\eta $
by the index of
$\eta $
by the index of
![]() $\Gamma "$
in
$\Gamma "$
in
![]() $\Gamma '$
also gives
$\Gamma '$
also gives
![]() $\|\eta ' \circ g' \|_{C^\infty (I)} \ll _{d,D} M^{O_{d,D}(A)}$
for some nontrivial horizontal character
$\|\eta ' \circ g' \|_{C^\infty (I)} \ll _{d,D} M^{O_{d,D}(A)}$
for some nontrivial horizontal character
![]() $\eta '$
on
$\eta '$
on
![]() $G'/\Gamma '$
of Lipschitz norm
$G'/\Gamma '$
of Lipschitz norm
![]() $O_{d,D}(M^{O_{d,D}(A)})$
. As a consequence, one can replace all occurrences of
$O_{d,D}(M^{O_{d,D}(A)})$
. As a consequence, one can replace all occurrences of
![]() $G'/\Gamma '$
in the proof of [Reference Green and Tao19, Theorem 1.19] with
$G'/\Gamma '$
in the proof of [Reference Green and Tao19, Theorem 1.19] with
![]() $G'/\Gamma "$
with only negligible changes to the arguments.
$G'/\Gamma "$
with only negligible changes to the arguments.
We will also need a multidimensional version of this theorem.
Theorem 2.13 (Multidimensional factorization theorem).
Let
![]() $t,d,D \geq 1$
and
$t,d,D \geq 1$
and
![]() $0 < \delta < 1$
. Let
$0 < \delta < 1$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $g \in {\operatorname {Poly}}(\mathbb {Z}^t \to G)$
and
$g \in {\operatorname {Poly}}(\mathbb {Z}^t \to G)$
and
![]() $A>0$
, and let
$A>0$
, and let
![]() $I_1,\dots ,I_t$
intervals with
$I_1,\dots ,I_t$
intervals with
![]() $|I_1|, \dots , |I_t| \geq C \delta ^{-C}$
, for some C that is sufficiently large depending on
$|I_1|, \dots , |I_t| \geq C \delta ^{-C}$
, for some C that is sufficiently large depending on
![]() $t,d,D,A$
. Then there exists an integer
$t,d,D,A$
. Then there exists an integer
![]() $1/\delta \leq M \ll _{A,D,d,t} \delta ^{-O_{A,D,d,t}(1)}$
and a decomposition
$1/\delta \leq M \ll _{A,D,d,t} \delta ^{-O_{A,D,d,t}(1)}$
and a decomposition
![]() $g = \varepsilon g' \gamma $
into polynomial maps
$g = \varepsilon g' \gamma $
into polynomial maps
![]() $\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z}^t \to G)$
such that
$\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z}^t \to G)$
such that
-
(i)
 $\varepsilon $
is
$\varepsilon $
is
 $(M,I_1 \times \dots \times I_t)$
-smooth, in the sense that
$(M,I_1 \times \dots \times I_t)$
-smooth, in the sense that
 $d_G(\varepsilon (n), 1_G) \leq M$
and
$d_G(\varepsilon (n), 1_G) \leq M$
and
 $d_G( \varepsilon (n+e_i), 1_G) \leq M/|I_i|$
for all
$d_G( \varepsilon (n+e_i), 1_G) \leq M/|I_i|$
for all
 $n \in I_1 \times \dots \times I_t$
and
$n \in I_1 \times \dots \times I_t$
and
 $i=1,\dots ,t$
, where
$i=1,\dots ,t$
, where
 $e_1,\dots ,e_t$
are the standard basis of
$e_1,\dots ,e_t$
are the standard basis of
 $\mathbb {Z}^d$
;
$\mathbb {Z}^d$
; -
(ii) There is an M-rational subnilmanifold
 $G'/\Gamma '$
of
$G'/\Gamma '$
of
 $G/\Gamma $
such that
$G/\Gamma $
such that
 $g'$
takes values in
$g'$
takes values in
 $G'$
and is totally
$G'$
and is totally
 $1/M^A$
-equidistributed in
$1/M^A$
-equidistributed in
 $G'/\Gamma '$
, and more generally in
$G'/\Gamma '$
, and more generally in
 $G'/\Gamma "$
whenever
$G'/\Gamma "$
whenever
 $\Gamma "$
is a subgroup of
$\Gamma "$
is a subgroup of
 $\Gamma '$
of index at most
$\Gamma '$
of index at most
 $M^A$
, in the sense that whenever
$M^A$
, in the sense that whenever $$ \begin{align*}\left| \frac{1}{|P_1 \times \dots \times P_t|} \sum_{n \in P_1 \times \dots \times P_t} F(g'(n)\Gamma) - \int_{G'/\Gamma"} F \right| \leq \frac{1}{M} \|F\|_{{\operatorname{Lip}}}\end{align*} $$
$$ \begin{align*}\left| \frac{1}{|P_1 \times \dots \times P_t|} \sum_{n \in P_1 \times \dots \times P_t} F(g'(n)\Gamma) - \int_{G'/\Gamma"} F \right| \leq \frac{1}{M} \|F\|_{{\operatorname{Lip}}}\end{align*} $$
 $F \colon G/\Gamma \to \mathbb {C}$
is Lipschitz and for each
$F \colon G/\Gamma \to \mathbb {C}$
is Lipschitz and for each
 $i=1,\dots ,t$
,
$i=1,\dots ,t$
,
 $P_i$
is an arithmetic progression in
$P_i$
is an arithmetic progression in
 $I_i$
of cardinality at least
$I_i$
of cardinality at least
 $|I_i|/M$
; and
$|I_i|/M$
; and
-
(iii)
 $\gamma $
is M-rational, in the sense that there exists
$\gamma $
is M-rational, in the sense that there exists
 $1 \leq r \leq M$
such that
$1 \leq r \leq M$
such that
 $g(n)^r \in \Gamma $
for all
$g(n)^r \in \Gamma $
for all
 $n \in \mathbb {Z}^t$
.
$n \in \mathbb {Z}^t$
.
Proof. This follows from [Reference Green and Tao19, Theorem 10.2], after implementing the corrections in [Reference Green and Tao20], and the modifications indicated in the proof of Theorem 2.12.
As a first application of Theorem 2.12, we can obtain a criterion for correlation between nilsequences with a nontrivial central frequency:
Proposition 2.14 (Correlation criterion).
Let
![]() $d,D \geq 1$
and
$d,D \geq 1$
and
![]() $0 < \delta < 1$
. Let
$0 < \delta < 1$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
, whose center
$1/\delta $
, whose center
![]() $Z(G)$
is one-dimensional. Let
$Z(G)$
is one-dimensional. Let
![]() $g_1,g_2 \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
, let I be an interval with
$g_1,g_2 \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
, let I be an interval with
![]() $|I| \geq 1$
and let
$|I| \geq 1$
and let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
![]() $1/\delta $
and having a nonzero central frequency
$1/\delta $
and having a nonzero central frequency
![]() $\xi $
. Suppose that one has the correlation
$\xi $
. Suppose that one has the correlation
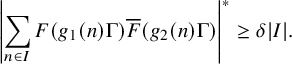 $$ \begin{align*}{\left|\sum_{n \in I} F(g_1(n) \Gamma) \overline{F}(g_2(n) \Gamma)\right|}^* \geq \delta |I|.\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in I} F(g_1(n) \Gamma) \overline{F}(g_2(n) \Gamma)\right|}^* \geq \delta |I|.\end{align*} $$
Then at least one of the following holds:
-
(i) There exists a nontrivial horizontal character
 $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
 $\| \eta \circ g_i \|_{C^\infty (I)} \ll _{d,D} \delta ^{-O_{d,D}(1)}$
for some
$\| \eta \circ g_i \|_{C^\infty (I)} \ll _{d,D} \delta ^{-O_{d,D}(1)}$
for some
 $i\in \{1,2\}$
.
$i\in \{1,2\}$
. -
(ii) There exists a factorization
where $$ \begin{align*}g_2 = \varepsilon (\phi \circ g_1) \gamma\end{align*} $$
$$ \begin{align*}g_2 = \varepsilon (\phi \circ g_1) \gamma\end{align*} $$
 $\varepsilon $
is
$\varepsilon $
is
 $(O_{d,D}(\delta ^{-O_{d,D}(1)}),I)$
-smooth,
$(O_{d,D}(\delta ^{-O_{d,D}(1)}),I)$
-smooth,
 $\phi \colon G \to G$
is a Lie group automorphism whose associated Lie algebra isomorphism
$\phi \colon G \to G$
is a Lie group automorphism whose associated Lie algebra isomorphism
 $\log \phi \colon \log G \to \log G$
has matrix coefficients that are all rational of height
$\log \phi \colon \log G \to \log G$
has matrix coefficients that are all rational of height
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
in the Mal’cev basis
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
in the Mal’cev basis
 $X_1,\dots ,X_D$
of
$X_1,\dots ,X_D$
of
 $\log G$
, and
$\log G$
, and
 $\gamma $
is
$\gamma $
is
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
-rational.
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
-rational.
Proof. We allow all implied constants to depend on
![]() $d,D$
. The product of the filtered nilmanifold
$d,D$
. The product of the filtered nilmanifold
![]() $G/\Gamma $
with itself is again a filtered nilmanifold
$G/\Gamma $
with itself is again a filtered nilmanifold
![]() $(G \times G)/(\Gamma \times \Gamma )$
, with the obvious filtration
$(G \times G)/(\Gamma \times \Gamma )$
, with the obvious filtration
and Mal’cev basis
![]() $(X_i,0), (0,X_i)$
,
$(X_i,0), (0,X_i)$
,
![]() $i=1,\dots ,D$
. This product filtered nilmanifold has degree at most d, dimension
$i=1,\dots ,D$
. This product filtered nilmanifold has degree at most d, dimension
![]() $2D$
and complexity at most
$2D$
and complexity at most
![]() $O(\delta ^{-O(1)})$
. The pair
$O(\delta ^{-O(1)})$
. The pair
![]() $(g_1,g_2)$
can be then viewed as an element of
$(g_1,g_2)$
can be then viewed as an element of
![]() ${\operatorname {Poly}}(\mathbb {Z} \to G \times G)$
. If we let
${\operatorname {Poly}}(\mathbb {Z} \to G \times G)$
. If we let
![]() $F \otimes \overline {F} \colon (G \times G)/(\Gamma \times \Gamma ) \to \mathbb {C}$
be the function
$F \otimes \overline {F} \colon (G \times G)/(\Gamma \times \Gamma ) \to \mathbb {C}$
be the function
then F is Lipschitz with norm
![]() $O( \delta ^{-O(1)})$
and one has
$O( \delta ^{-O(1)})$
and one has
 $$ \begin{align} {\left|\sum_{n \in I} F \otimes \overline{F}((g_1,g_2)(n) (\Gamma \times \Gamma))\right|}^* \geq \delta |I|. \end{align} $$
$$ \begin{align} {\left|\sum_{n \in I} F \otimes \overline{F}((g_1,g_2)(n) (\Gamma \times \Gamma))\right|}^* \geq \delta |I|. \end{align} $$
Let
![]() $A>1$
be sufficiently large depending on
$A>1$
be sufficiently large depending on
![]() $d,D$
. Applying Theorem 2.12 to
$d,D$
. Applying Theorem 2.12 to
![]() $(g_1,g_2)$
(with
$(g_1,g_2)$
(with
![]() $\delta $
replaced by
$\delta $
replaced by
![]() $\delta ^A$
), we can find
$\delta ^A$
), we can find
![]() $\delta ^{-A} \leq M \ll _A \delta ^{-O_A(1)}$
and a factorization
$\delta ^{-A} \leq M \ll _A \delta ^{-O_A(1)}$
and a factorization
where
![]() $\varepsilon _1, g^{\prime }_1, \gamma _1 \in {\operatorname {Poly}}(\mathbb {Z} \to G_1)$
,
$\varepsilon _1, g^{\prime }_1, \gamma _1 \in {\operatorname {Poly}}(\mathbb {Z} \to G_1)$
,
![]() $\varepsilon _2, g^{\prime }_2, \gamma _2 \in {\operatorname {Poly}}(\mathbb {Z} \to G_2)$
such that
$\varepsilon _2, g^{\prime }_2, \gamma _2 \in {\operatorname {Poly}}(\mathbb {Z} \to G_2)$
such that
-
(i)
 $(\varepsilon _1,\varepsilon _2)$
is
$(\varepsilon _1,\varepsilon _2)$
is
 $(M,I)$
-smooth;
$(M,I)$
-smooth; -
(ii) There is an M-rational subnilmanifold
 $G'/\Gamma '$
of
$G'/\Gamma '$
of
 $(G \times G)/(\Gamma \times \Gamma )$
such that
$(G \times G)/(\Gamma \times \Gamma )$
such that
 $(g^{\prime }_1,g^{\prime }_2)$
takes values in
$(g^{\prime }_1,g^{\prime }_2)$
takes values in
 $G'$
and is totally
$G'$
and is totally
 $1/M^A$
-equidistributed in
$1/M^A$
-equidistributed in
 $G'/\Gamma "$
for any subgroup
$G'/\Gamma "$
for any subgroup
 $\Gamma "$
of
$\Gamma "$
of
 $\Gamma '$
of index at most
$\Gamma '$
of index at most
 $M^A$
; and
$M^A$
; and -
(iii)
 $(\gamma _1,\gamma _2)$
is M-rational.
$(\gamma _1,\gamma _2)$
is M-rational.
We caution that
![]() $G'$
is a subgroup of
$G'$
is a subgroup of
![]() $G \times G$
rather than G. From equation (2.13), we thus have
$G \times G$
rather than G. From equation (2.13), we thus have
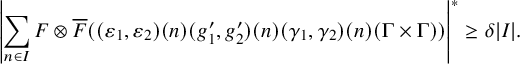 $$ \begin{align*}{\left|\sum_{n \in I} F \otimes \overline{F}( (\varepsilon_1,\varepsilon_2)(n) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma_1,\gamma_2)(n) (\Gamma \times \Gamma))\right|}^* \geq \delta |I|.\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in I} F \otimes \overline{F}( (\varepsilon_1,\varepsilon_2)(n) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma_1,\gamma_2)(n) (\Gamma \times \Gamma))\right|}^* \geq \delta |I|.\end{align*} $$
Since
![]() $(\gamma _1,\gamma _2)$
is M-rational, it is
$(\gamma _1,\gamma _2)$
is M-rational, it is
![]() $O(M^{O(1)})$
-periodic and then by the pigeonhole principle (and Lemma 2.2(i)) we can thus find M-rational
$O(M^{O(1)})$
-periodic and then by the pigeonhole principle (and Lemma 2.2(i)) we can thus find M-rational
![]() $(\gamma _1^0, \gamma _2^0) \in G \times G$
such that
$(\gamma _1^0, \gamma _2^0) \in G \times G$
such that
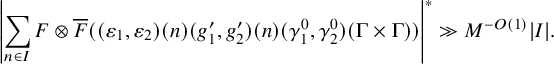 $$ \begin{align*}{\left |\sum_{n \in I} F \otimes \overline{F}( (\varepsilon_1,\varepsilon_2)(n) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |I|.\end{align*} $$
$$ \begin{align*}{\left |\sum_{n \in I} F \otimes \overline{F}( (\varepsilon_1,\varepsilon_2)(n) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |I|.\end{align*} $$
By shifting
![]() $\gamma _1^0, \gamma _2^0$
by elements of
$\gamma _1^0, \gamma _2^0$
by elements of
![]() $\Gamma $
if necessary we may assume that they lie at distance
$\Gamma $
if necessary we may assume that they lie at distance
![]() $O(M^{O(1)})$
from the identity. If we partition I into subintervals J of length
$O(M^{O(1)})$
from the identity. If we partition I into subintervals J of length
![]() $\asymp M^{-C} |I|$
for some large constant C, we see from the pigeonhole principle (and Lemma 2.2(i)) that we can find one such J for which
$\asymp M^{-C} |I|$
for some large constant C, we see from the pigeonhole principle (and Lemma 2.2(i)) that we can find one such J for which
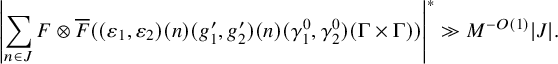 $$ \begin{align*}{\left|\sum_{n \in J} F \otimes \overline{F}( (\varepsilon_1,\varepsilon_2)(n) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |J|.\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in J} F \otimes \overline{F}( (\varepsilon_1,\varepsilon_2)(n) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |J|.\end{align*} $$
As
![]() $(\varepsilon _1,\varepsilon _2)$
is
$(\varepsilon _1,\varepsilon _2)$
is
![]() $(M,I)$
-smooth, it fluctuates by
$(M,I)$
-smooth, it fluctuates by
![]() $O(M^{1-C})$
on J and stays a distance
$O(M^{1-C})$
on J and stays a distance
![]() $O(M)$
from the identity, hence by the Lipschitz nature of
$O(M)$
from the identity, hence by the Lipschitz nature of
![]() $F \otimes \overline {F}$
we conclude (for
$F \otimes \overline {F}$
we conclude (for
![]() $C=O(1)$
large enough) that there exists
$C=O(1)$
large enough) that there exists
![]() $(\varepsilon _1^0, \varepsilon _2^0) \in G \times G$
at distance
$(\varepsilon _1^0, \varepsilon _2^0) \in G \times G$
at distance
![]() $O(M)$
from the identity such that
$O(M)$
from the identity such that
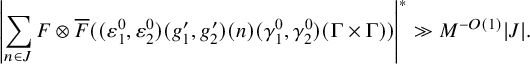 $$ \begin{align*}{\left|\sum_{n \in J} F \otimes \overline{F}( (\varepsilon^0_1,\varepsilon^0_2) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |J|.\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in J} F \otimes \overline{F}( (\varepsilon^0_1,\varepsilon^0_2) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |J|.\end{align*} $$
Allowing implied constants to depend on C, we conclude that
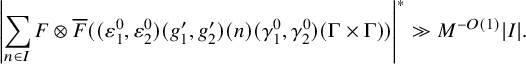 $$ \begin{align*}{\left|\sum_{n \in I} F \otimes \overline{F}( (\varepsilon^0_1,\varepsilon^0_2) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |I|.\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in I} F \otimes \overline{F}( (\varepsilon^0_1,\varepsilon^0_2) (g^{\prime}_1,g^{\prime}_2)(n) (\gamma^0_1,\gamma_2^0) (\Gamma \times \Gamma))\right|}^* \gg M^{-O(1)} |I|.\end{align*} $$
From the Baker–Campbell–Hausdorff formula and the M-rationality of
![]() $(\gamma _1^0, \gamma _2^0)$
, we see that
$(\gamma _1^0, \gamma _2^0)$
, we see that
![]() $(\gamma ^0_1,\gamma _2^0) (\Gamma \times \Gamma ) (\gamma ^0_1, \gamma _2^0)^{-1}$
can be covered by
$(\gamma ^0_1,\gamma _2^0) (\Gamma \times \Gamma ) (\gamma ^0_1, \gamma _2^0)^{-1}$
can be covered by
![]() $O(M^{O(1)})$
cosets of
$O(M^{O(1)})$
cosets of
![]() $\Gamma \times \Gamma $
, and conversely. Thus, if we set
$\Gamma \times \Gamma $
, and conversely. Thus, if we set
then
![]() $G' \cap (\Gamma \times \Gamma )$
can be covered by
$G' \cap (\Gamma \times \Gamma )$
can be covered by
![]() $O(M^{O(1)})$
cosets of
$O(M^{O(1)})$
cosets of
![]() $\Gamma "$
, thus
$\Gamma "$
, thus
![]() $\Gamma "$
is a subgroup of
$\Gamma "$
is a subgroup of
![]() $G' \cap (\Gamma \times \Gamma )$
of index
$G' \cap (\Gamma \times \Gamma )$
of index
![]() $O(M^{O(1)})$
such that
$O(M^{O(1)})$
such that
Indeed, one can take
![]() $\Gamma "$
to be the intersection of
$\Gamma "$
to be the intersection of
![]() $G' \cap (\Gamma \times \Gamma )$
and
$G' \cap (\Gamma \times \Gamma )$
and
![]() $(\gamma ^0_1,\gamma _2^0) (\Gamma \times \Gamma ) (\gamma ^0_1, \gamma _2^0)^{-1}$
. One can then write the above claim as
$(\gamma ^0_1,\gamma _2^0) (\Gamma \times \Gamma ) (\gamma ^0_1, \gamma _2^0)^{-1}$
. One can then write the above claim as
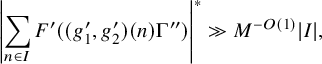 $$ \begin{align*}{\left|\sum_{n \in I} F'( (g^{\prime}_1,g^{\prime}_2)(n) \Gamma")\right|}^* \gg M^{-O(1)} |I|,\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in I} F'( (g^{\prime}_1,g^{\prime}_2)(n) \Gamma")\right|}^* \gg M^{-O(1)} |I|,\end{align*} $$
where
![]() $F' \colon G' / \Gamma " \to \mathbb {C}$
is defined by
$F' \colon G' / \Gamma " \to \mathbb {C}$
is defined by
for any
![]() $(g^{\prime }_1,g^{\prime }_2) \in G'$
, with the inclusion (2.15) ensuring that this function is well-defined. Since F is Lipschitz with norm
$(g^{\prime }_1,g^{\prime }_2) \in G'$
, with the inclusion (2.15) ensuring that this function is well-defined. Since F is Lipschitz with norm
![]() $1/\delta \leq M$
, and
$1/\delta \leq M$
, and
![]() $\varepsilon ^0_1, \gamma ^0_1, \varepsilon ^0_2, \gamma ^0_2$
are at distance
$\varepsilon ^0_1, \gamma ^0_1, \varepsilon ^0_2, \gamma ^0_2$
are at distance
![]() $O(M^{O(1)})$
from the identity, this function is Lipschitz with norm
$O(M^{O(1)})$
from the identity, this function is Lipschitz with norm
![]() $O(M^{O(1)})$
, hence by total equidistribution of
$O(M^{O(1)})$
, hence by total equidistribution of
![]() $(g^{\prime }_1,g^{\prime }_2)$
we conclude (for A large enough) that
$(g^{\prime }_1,g^{\prime }_2)$
we conclude (for A large enough) that
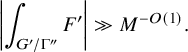 $$ \begin{align} \left|\int_{G'/\Gamma"} F'\right| \gg M^{-O(1)}. \end{align} $$
$$ \begin{align} \left|\int_{G'/\Gamma"} F'\right| \gg M^{-O(1)}. \end{align} $$
Suppose that the slice
is nontrivial. This is a nontrivial closed connected subgroup of G; by considering the final nontrivial element of the series H,
![]() $[H,G]$
,
$[H,G]$
,
![]() $[[H,G],G]$
,
$[[H,G],G]$
,
![]() $\dots $
, we conclude that H contains a nontrivial closed connected central subgroup of G. Since
$\dots $
, we conclude that H contains a nontrivial closed connected central subgroup of G. Since
![]() $Z(G)$
is one-dimensional, we conclude that H contains
$Z(G)$
is one-dimensional, we conclude that H contains
![]() $Z(G)$
. In particular,
$Z(G)$
. In particular,
![]() $G'$
contains
$G'$
contains
![]() $Z(G) \times \{1\}$
.
$Z(G) \times \{1\}$
.
Since F has central frequency
![]() $\xi $
, we see that
$\xi $
, we see that
for all
![]() $z \in Z(G)$
. By invariance of Haar measure, this implies that
$z \in Z(G)$
. By invariance of Haar measure, this implies that
Since
![]() $\xi $
is nontrivial, this implies that
$\xi $
is nontrivial, this implies that
![]() $\int _{G'/\Gamma "} F' =0$
, contradicting equation (2.16). Thus, the slice
$\int _{G'/\Gamma "} F' =0$
, contradicting equation (2.16). Thus, the slice
![]() $\{ g \in G: (g,1) \in G'\}$
is trivial. Similarly, the slice
$\{ g \in G: (g,1) \in G'\}$
is trivial. Similarly, the slice
![]() $\{ g \in G: (1,g) \in G' \}$
is trivial.
$\{ g \in G: (1,g) \in G' \}$
is trivial.
Now, suppose that the projection
![]() is not all of G. This is a proper closed connected subgroup of G with
is not all of G. This is a proper closed connected subgroup of G with
thus
![]() $\log K$
is the projection of
$\log K$
is the projection of
![]() $\log G'$
to
$\log G'$
to
![]() $\log G$
. Since
$\log G$
. Since
![]() $\log G'$
is
$\log G'$
is
![]() $M^{O(1)}$
-rational,
$M^{O(1)}$
-rational,
![]() $\log K$
is also. Hence, there exists a nontrivial horizontal character
$\log K$
is also. Hence, there exists a nontrivial horizontal character
![]() $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
![]() $O(M^{O(1)})$
that annihilates K, so in particular
$O(M^{O(1)})$
that annihilates K, so in particular
![]() $\eta (g^{\prime }_1(n)) = 0$
for all n. From equation (2.14), we then have
$\eta (g^{\prime }_1(n)) = 0$
for all n. From equation (2.14), we then have
Since
![]() $\gamma _1$
is M-rational,
$\gamma _1$
is M-rational,
![]() $M\eta (\gamma _1(n)) = 0$
. Thus, if we replace
$M\eta (\gamma _1(n)) = 0$
. Thus, if we replace
![]() $\eta $
by
$\eta $
by
![]() $M\eta $
we have
$M\eta $
we have
Since
![]() $(\varepsilon _1,\varepsilon _2)$
is
$(\varepsilon _1,\varepsilon _2)$
is
![]() $(M,I)$
smooth, we thus conclude that
$(M,I)$
smooth, we thus conclude that
and we are in conclusion (i) of the proposition. Thus, we may assume that the projection
![]() $\{ g_1 \in G: (g_1,g_2) \in G' \text { for some } g_2 \in G \}$
is all of G. Similarly, we may assume that
$\{ g_1 \in G: (g_1,g_2) \in G' \text { for some } g_2 \in G \}$
is all of G. Similarly, we may assume that
![]() $\{ g_2 \in G: (g_1,g_2) \in G' \text { for some } g_1 \in G \}$
is all of G.
$\{ g_2 \in G: (g_1,g_2) \in G' \text { for some } g_1 \in G \}$
is all of G.
Applying Goursat’s lemma, we now conclude that
![]() $G'$
takes the form
$G'$
takes the form
for some group automorphism
![]() $\phi \colon G \to G$
. Since
$\phi \colon G \to G$
. Since
![]() $G'$
is a
$G'$
is a
![]() $O(M^{O(1)})$
-rational subgroup of
$O(M^{O(1)})$
-rational subgroup of
![]() $G \times G$
,
$G \times G$
,
![]() $\phi $
must be a Lie group automorphism whose associated Lie algebra automorphism
$\phi $
must be a Lie group automorphism whose associated Lie algebra automorphism
![]() $\log \phi \colon \log G \to \log G$
has coefficients that are rational of height
$\log \phi \colon \log G \to \log G$
has coefficients that are rational of height
![]() $O(M^{O(1)})$
in the Mal’cev basis. Since
$O(M^{O(1)})$
in the Mal’cev basis. Since
![]() $(g^{\prime }_1(n),g^{\prime }_2(n))$
takes values in
$(g^{\prime }_1(n),g^{\prime }_2(n))$
takes values in
![]() $G'$
, we have
$G'$
, we have
and hence by equation (2.14) and some rearranging
It is then routine to verify that conclusion (ii) of the proposition holds.
As a consequence of this criterion, we can establish the following large sieve inequality for nilsequences, which is a more quantitative variant of the one in [Reference Matomäki, Radziwiłł, Tao, Teräväinen and Ziegler48, Proposition 4.11].
Proposition 2.15 (Large sieve).
Let
![]() $d,D \geq 1$
and
$d,D \geq 1$
and
![]() $0 < \delta < 1$
. Let
$0 < \delta < 1$
. Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension D and complexity at most
![]() $1/\delta $
, whose center
$1/\delta $
, whose center
![]() $Z(G)$
is one-dimensional. Let
$Z(G)$
is one-dimensional. Let
![]() $g_1,\dots ,g_K \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
, let I be an interval with
$g_1,\dots ,g_K \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
, let I be an interval with
![]() $|I| \geq 1$
and let
$|I| \geq 1$
and let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
![]() $1/\delta $
and having a nonzero central frequency
$1/\delta $
and having a nonzero central frequency
![]() $\xi $
. Suppose that there is a function
$\xi $
. Suppose that there is a function
![]() $f \colon \mathbb {Z} \to \mathbb {C}$
with
$f \colon \mathbb {Z} \to \mathbb {C}$
with
![]() $\sum _{n \in I} |f(n)|^2 \leq \frac {1}{\delta } |I|$
such that
$\sum _{n \in I} |f(n)|^2 \leq \frac {1}{\delta } |I|$
such that
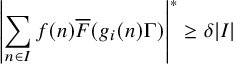 $$ \begin{align} {\left|\sum_{n \in I} f(n) \overline{F}(g_i(n) \Gamma)\right|}^* \geq \delta |I| \end{align} $$
$$ \begin{align} {\left|\sum_{n \in I} f(n) \overline{F}(g_i(n) \Gamma)\right|}^* \geq \delta |I| \end{align} $$
for all
![]() $i=1,\dots ,K$
. Then at least one of the following holds:
$i=1,\dots ,K$
. Then at least one of the following holds:
-
(i) There exists a nontrivial horizontal character
 $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
 $\| \eta \circ g_i \|_{C^\infty (I)} \ll _{d,D} \delta ^{-O_{d,D}(1)}$
for
$\| \eta \circ g_i \|_{C^\infty (I)} \ll _{d,D} \delta ^{-O_{d,D}(1)}$
for
 $\gg _{d,D} \delta ^{O_{d,D}(1)} K$
values of
$\gg _{d,D} \delta ^{O_{d,D}(1)} K$
values of
 $i=1,\dots ,K$
.
$i=1,\dots ,K$
. -
(ii) For
 $\gg _{d,D} \delta ^{O_{d,D}(1)} K^2$
pairs
$\gg _{d,D} \delta ^{O_{d,D}(1)} K^2$
pairs
 $(i,j) \in \{1,\dots ,K\}^2$
, there exists a factorization where
$(i,j) \in \{1,\dots ,K\}^2$
, there exists a factorization where $$ \begin{align*}g_i = \varepsilon_{ij} g_j \gamma_{ij},\end{align*} $$
$$ \begin{align*}g_i = \varepsilon_{ij} g_j \gamma_{ij},\end{align*} $$
 $\varepsilon _{ij}$
is
$\varepsilon _{ij}$
is
 $(O_{d,D}(\delta ^{-O_{d,D}(1)}),I)$
-smooth and
$(O_{d,D}(\delta ^{-O_{d,D}(1)}),I)$
-smooth and
 $\gamma _{ij}$
is
$\gamma _{ij}$
is
 $O_{d,D}(\delta ^{-O_{d,D}(1)})$
-rational.
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
-rational.
Proof. We allow implied constants to depend on
![]() $d,D$
. From equation (2.17), one can find progressions
$d,D$
. From equation (2.17), one can find progressions
![]() $P_i \subset I$
for
$P_i \subset I$
for
![]() $i=1,\dots ,K$
such that
$i=1,\dots ,K$
such that
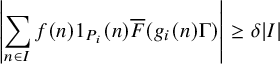 $$ \begin{align*}\left|\sum_{n \in I} f(n) 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right| \geq \delta |I|\end{align*} $$
$$ \begin{align*}\left|\sum_{n \in I} f(n) 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right| \geq \delta |I|\end{align*} $$
and thus
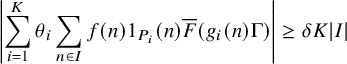 $$ \begin{align*}\left|\sum_{i=1}^K \theta_i \sum_{n \in I} f(n) 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right| \geq \delta K |I|\end{align*} $$
$$ \begin{align*}\left|\sum_{i=1}^K \theta_i \sum_{n \in I} f(n) 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right| \geq \delta K |I|\end{align*} $$
for some complex numbers
![]() $\theta _i$
with
$\theta _i$
with
![]() $|\theta _i| \leq 1$
. By interchanging the sums and applying Cauchy–Schwarz, we have
$|\theta _i| \leq 1$
. By interchanging the sums and applying Cauchy–Schwarz, we have
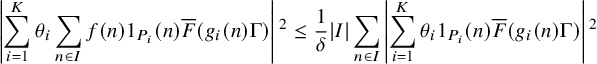 $$ \begin{align*}\left|\sum_{i=1}^K \theta_i \sum_{n \in I} f(n) 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2 \leq \frac{1}{\delta} |I| \sum_{n \in I} \left| \sum_{i=1}^K \theta_i 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2\end{align*} $$
$$ \begin{align*}\left|\sum_{i=1}^K \theta_i \sum_{n \in I} f(n) 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2 \leq \frac{1}{\delta} |I| \sum_{n \in I} \left| \sum_{i=1}^K \theta_i 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2\end{align*} $$
and thus
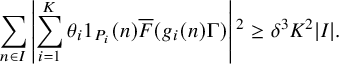 $$ \begin{align*}\sum_{n \in I} \left| \sum_{i=1}^K \theta_i 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2 \geq \delta^{3} K^2 |I|.\end{align*} $$
$$ \begin{align*}\sum_{n \in I} \left| \sum_{i=1}^K \theta_i 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2 \geq \delta^{3} K^2 |I|.\end{align*} $$
From the triangle inequality, we have
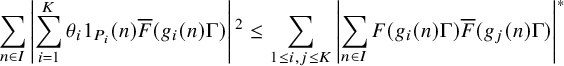 $$ \begin{align*}\sum_{n \in I} \left|\sum_{i=1}^K \theta_i 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2 \leq \sum_{1 \leq i,j \leq K} {\left|\sum_{n \in I} F(g_i(n) \Gamma) \overline{F}(g_j(n) \Gamma)\right|}^*\end{align*} $$
$$ \begin{align*}\sum_{n \in I} \left|\sum_{i=1}^K \theta_i 1_{P_i}(n) \overline{F}(g_i(n) \Gamma)\right|{}^2 \leq \sum_{1 \leq i,j \leq K} {\left|\sum_{n \in I} F(g_i(n) \Gamma) \overline{F}(g_j(n) \Gamma)\right|}^*\end{align*} $$
and thus
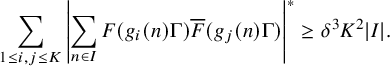 $$ \begin{align*}\sum_{1 \leq i,j \leq K} {\left|\sum_{n \in I} F(g_i(n) \Gamma) \overline{F}(g_j(n) \Gamma)\right|}^* \geq \delta^{3} K^2 |I|.\end{align*} $$
$$ \begin{align*}\sum_{1 \leq i,j \leq K} {\left|\sum_{n \in I} F(g_i(n) \Gamma) \overline{F}(g_j(n) \Gamma)\right|}^* \geq \delta^{3} K^2 |I|.\end{align*} $$
The inner sum is
![]() $O(\delta ^{-2} |I|)$
, thus we have
$O(\delta ^{-2} |I|)$
, thus we have
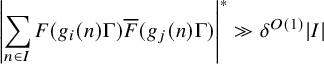 $$ \begin{align*}{\left|\sum_{n \in I} F(g_i(n) \Gamma) \overline{F}(g_j(n) \Gamma)\right|}^* \gg \delta^{O(1)} |I|\end{align*} $$
$$ \begin{align*}{\left|\sum_{n \in I} F(g_i(n) \Gamma) \overline{F}(g_j(n) \Gamma)\right|}^* \gg \delta^{O(1)} |I|\end{align*} $$
for
![]() $\gg \delta ^{O(1)} K^2$
pairs
$\gg \delta ^{O(1)} K^2$
pairs
![]() $(i,j) \in \{1,\dots ,K\}^2$
. For each such pair, we apply Proposition 2.14. If conclusion (i) of that proposition holds for
$(i,j) \in \{1,\dots ,K\}^2$
. For each such pair, we apply Proposition 2.14. If conclusion (i) of that proposition holds for
![]() $\gg \delta ^{O(1)} K^2$
pairs
$\gg \delta ^{O(1)} K^2$
pairs
![]() $(i,j)$
, then by the pigeonhole principle (noting that there are only
$(i,j)$
, then by the pigeonhole principle (noting that there are only
![]() $O(\delta ^{-O(1)})$
choices for
$O(\delta ^{-O(1)})$
choices for
![]() $\eta $
) we obtain conclusion (i) of the current proposition. Thus, we may assume that conclusion (ii) of Proposition 2.14 holds for
$\eta $
) we obtain conclusion (i) of the current proposition. Thus, we may assume that conclusion (ii) of Proposition 2.14 holds for
![]() $\gg \delta ^{O(1)} K^2$
pairs
$\gg \delta ^{O(1)} K^2$
pairs
![]() $(i,j) \in \{1,\dots ,K\}^2$
, thus we have
$(i,j) \in \{1,\dots ,K\}^2$
, thus we have
for all such pairs
![]() $(i,j)$
, where
$(i,j)$
, where
![]() $\varepsilon _{ij}$
is
$\varepsilon _{ij}$
is
![]() $(O(\delta ^{-O(1)}),I)$
-smooth,
$(O(\delta ^{-O(1)}),I)$
-smooth,
![]() $\gamma _{ij}$
is
$\gamma _{ij}$
is
![]() $O(\delta ^{-O(1)})$
-rational and
$O(\delta ^{-O(1)})$
-rational and
![]() $\phi _{ij} \colon G \to G$
is a Lie group automorphism whose associated Lie algebra isomorphism
$\phi _{ij} \colon G \to G$
is a Lie group automorphism whose associated Lie algebra isomorphism
![]() $\log \phi \colon \log G \to \log G$
has matrix coefficients that are all rational of height
$\log \phi \colon \log G \to \log G$
has matrix coefficients that are all rational of height
![]() $O(\delta ^{-O(1)})$
in the Mal’cev basis
$O(\delta ^{-O(1)})$
in the Mal’cev basis
![]() $X_1,\dots ,X_D$
of
$X_1,\dots ,X_D$
of
![]() $\log G$
. The total number of choices for
$\log G$
. The total number of choices for
![]() $\phi _{ij}$
is
$\phi _{ij}$
is
![]() $O(\delta ^{-O(1)})$
, so by the pigeonhole principle we may assume that
$O(\delta ^{-O(1)})$
, so by the pigeonhole principle we may assume that
![]() $\phi _{ij} = \phi $
is independent of
$\phi _{ij} = \phi $
is independent of
![]() $i,j$
. By Cauchy–Schwarz, we may thus find
$i,j$
. By Cauchy–Schwarz, we may thus find
![]() $\gg \delta ^{O(1)} K^3$
triples
$\gg \delta ^{O(1)} K^3$
triples
![]() $(i,i',j) \in \{1,\dots ,K\}^3$
such that
$(i,i',j) \in \{1,\dots ,K\}^3$
such that
where
![]() $\varepsilon _{ij}, \varepsilon _{i'j}, \gamma _{ij}, \gamma _{i'j}$
are as above. This implies that
$\varepsilon _{ij}, \varepsilon _{i'j}, \gamma _{ij}, \gamma _{i'j}$
are as above. This implies that
Pigeonholing in j and relabeling
![]() $i,i'$
as
$i,i'$
as
![]() $i,j$
, we obtain conclusion (ii) of the current proposition.
$i,j$
, we obtain conclusion (ii) of the current proposition.
2.4 Combinatorial lemmas
The following lemma is a standard consequence of Heath-Brown’s identity.
Lemma 2.16. Let
![]() $X \geq 2$
, and let
$X \geq 2$
, and let
![]() $L \in \mathbb {N}$
be fixed. We may find a collection
$L \in \mathbb {N}$
be fixed. We may find a collection
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $(\log X)^{O(1)}$
functions
$(\log X)^{O(1)}$
functions
![]() $f \colon \mathbb {N} \to \mathbb {R}$
such that
$f \colon \mathbb {N} \to \mathbb {R}$
such that
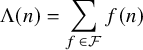 $$ \begin{align*}\Lambda(n) = \sum_{f \in \mathcal{F}} f(n)\end{align*} $$
$$ \begin{align*}\Lambda(n) = \sum_{f \in \mathcal{F}} f(n)\end{align*} $$
for each
![]() $X/2 \leq n \leq 4X$
, and each
$X/2 \leq n \leq 4X$
, and each
![]() $f \in \mathcal {F}$
takes the form
$f \in \mathcal {F}$
takes the form
for some
![]() $\ell \leq 2L$
, where
$\ell \leq 2L$
, where
![]() $a^{(i)}$
is supported on
$a^{(i)}$
is supported on
![]() $(N_i, 2N_i]$
for some
$(N_i, 2N_i]$
for some
![]() $N_i \geq 1/2$
, and each
$N_i \geq 1/2$
, and each
![]() $a^{(i)}(n)$
is either
$a^{(i)}(n)$
is either
![]() $1_{(N_i, 2N_i]}(n)$
,
$1_{(N_i, 2N_i]}(n)$
,
![]() $(\log n)1_{(N_i, 2N_i]}(n)$
, or
$(\log n)1_{(N_i, 2N_i]}(n)$
, or
![]() $\mu (n)1_{(N_i, 2N_i]}$
. Moreover,
$\mu (n)1_{(N_i, 2N_i]}$
. Moreover,
![]() $N_1N_2\cdots N_{\ell } \asymp X$
, and
$N_1N_2\cdots N_{\ell } \asymp X$
, and
![]() $N_i \ll X^{1/L}$
for each i with
$N_i \ll X^{1/L}$
for each i with
![]() $a^{(i)}(n) = \mu (n) 1_{(N_i, 2N_i]}(n)$
. The same statement holds for
$a^{(i)}(n) = \mu (n) 1_{(N_i, 2N_i]}(n)$
. The same statement holds for
![]() $\mu $
in place of
$\mu $
in place of
![]() $\Lambda $
(but
$\Lambda $
(but
![]() $(\log n)1_{(N_i, 2N_i]}(n)$
does not appear).
$(\log n)1_{(N_i, 2N_i]}(n)$
does not appear).
Proof. Using Heath-Brown’s identity (see [Reference Iwaniec and Kowalski37, (13.37), (13.38)] with
![]() $K = L$
and
$K = L$
and
![]() $z = (2X)^{1/L}$
), we have
$z = (2X)^{1/L}$
), we have
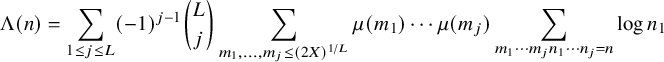 $$ \begin{align*}\Lambda(n) = \sum_{1 \leq j \leq L} (-1)^{j-1} \binom{L}{j} \sum_{m_1,\ldots, m_j \leq (2X)^{1/L}} \mu(m_1) \cdots \mu(m_j) \sum_{m_1\cdots m_jn_1 \cdots n_j=n} \log n_1\end{align*} $$
$$ \begin{align*}\Lambda(n) = \sum_{1 \leq j \leq L} (-1)^{j-1} \binom{L}{j} \sum_{m_1,\ldots, m_j \leq (2X)^{1/L}} \mu(m_1) \cdots \mu(m_j) \sum_{m_1\cdots m_jn_1 \cdots n_j=n} \log n_1\end{align*} $$
and
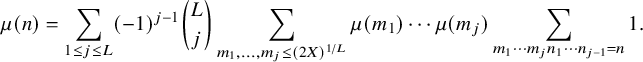 $$ \begin{align*}\mu(n) = \sum_{1 \leq j \leq L} (-1)^{j-1} \binom{L}{j} \sum_{m_1,\ldots,m_j \leq (2X)^{1/L}} \mu(m_1) \cdots \mu(m_j) \sum_{m_1\cdots m_jn_1\cdots n_{j-1}=n} 1.\end{align*} $$
$$ \begin{align*}\mu(n) = \sum_{1 \leq j \leq L} (-1)^{j-1} \binom{L}{j} \sum_{m_1,\ldots,m_j \leq (2X)^{1/L}} \mu(m_1) \cdots \mu(m_j) \sum_{m_1\cdots m_jn_1\cdots n_{j-1}=n} 1.\end{align*} $$
The conclusion follows after dyadic division of the ranges of variables.
The following Shiu’s bound [Reference Shiu60, Theorem 1] will be used multiple times to control sums of divisor functions in short intervals in arithmetic progressions.
Lemma 2.17. Let
![]() $A \geq 1$
and
$A \geq 1$
and
![]() $\varepsilon> 0$
be fixed. Let
$\varepsilon> 0$
be fixed. Let
![]() $X \geq H \geq X^{\varepsilon }$
and
$X \geq H \geq X^{\varepsilon }$
and
![]() $1\leq q \leq H^{1-\varepsilon }$
. Let f be a nonnegative multiplicative function such that
$1\leq q \leq H^{1-\varepsilon }$
. Let f be a nonnegative multiplicative function such that
![]() $f(p^{\ell }) \leq A^{\ell }$
for every prime power
$f(p^{\ell }) \leq A^{\ell }$
for every prime power
![]() $p^{\ell }$
and
$p^{\ell }$
and
![]() $f(n)\ll _{c} n^{c}$
for every
$f(n)\ll _{c} n^{c}$
for every
![]() $c> 0$
. Then, for any integer a coprime to q, we have
$c> 0$
. Then, for any integer a coprime to q, we have
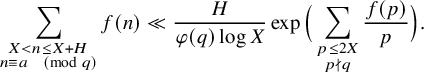 $$ \begin{align*}\sum_{\substack{X < n \leq X+H \\ n \equiv a\quad\pmod{q}}} f(n) \ll \frac{H}{\varphi(q) \log X} \exp\Big( \sum_{\substack{p \leq 2X \\ p\nmid q}} \frac{f(p)}{p} \Big).\end{align*} $$
$$ \begin{align*}\sum_{\substack{X < n \leq X+H \\ n \equiv a\quad\pmod{q}}} f(n) \ll \frac{H}{\varphi(q) \log X} \exp\Big( \sum_{\substack{p \leq 2X \\ p\nmid q}} \frac{f(p)}{p} \Big).\end{align*} $$
For proving Theorem 1.1(iv)–(v), we need a more flexible combinatorial decomposition of the multiplicative functions
![]() $\mu , d_k$
, where we introduce an extra variable
$\mu , d_k$
, where we introduce an extra variable
![]() $p \in (P, Q]$
in the factorization. Before stating this, let us quickly prove a lemma that will in particular allow us to write, for
$p \in (P, Q]$
in the factorization. Before stating this, let us quickly prove a lemma that will in particular allow us to write, for
![]() $P < Q \leq X^{1/(\log \log X)^2}$
,
$P < Q \leq X^{1/(\log \log X)^2}$
,
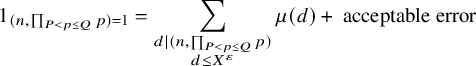 $$\begin{align*}1_{(n, \prod_{P < p \leq Q} p) = 1} = \sum_{\substack{d \mid (n, \prod_{P < p \leq Q} p) \\ d \leq X^{\varepsilon}}} \mu(d) + \text{ acceptable error} \end{align*}$$
$$\begin{align*}1_{(n, \prod_{P < p \leq Q} p) = 1} = \sum_{\substack{d \mid (n, \prod_{P < p \leq Q} p) \\ d \leq X^{\varepsilon}}} \mu(d) + \text{ acceptable error} \end{align*}$$
in our sums. This can be seen as a simple version of the fundamental lemma of the sieve that is sufficient to our needs.
Lemma 2.18. Let
![]() $k, r \geq 1$
and
$k, r \geq 1$
and
![]() $\varepsilon> 0$
be fixed. Let
$\varepsilon> 0$
be fixed. Let
![]() $X \geq H \geq X^\varepsilon $
and
$X \geq H \geq X^\varepsilon $
and
![]() $X \geq D \geq Q> P \geq 2$
. Then, for any
$X \geq D \geq Q> P \geq 2$
. Then, for any
![]() $C \geq 1$
,
$C \geq 1$
,
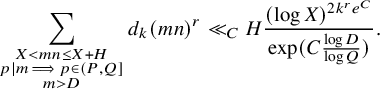 $$ \begin{align} \sum_{\substack{X < mn \leq X+H \\ p \mid m \implies p \in (P, Q] \\ m> D}} d_k(mn)^r \ll_C H\frac{(\log X)^{2k^r e^C}}{\exp(C\frac{\log D}{\log Q})}. \end{align} $$
$$ \begin{align} \sum_{\substack{X < mn \leq X+H \\ p \mid m \implies p \in (P, Q] \\ m> D}} d_k(mn)^r \ll_C H\frac{(\log X)^{2k^r e^C}}{\exp(C\frac{\log D}{\log Q})}. \end{align} $$
Proof. Write
![]() $\ell = mn$
, and note that since
$\ell = mn$
, and note that since
![]() $m> D$
, we have
$m> D$
, we have
![]() $\Omega (\ell ) \geq \frac {\log D}{\log Q}$
. Hence,the left-hand side of equation (2.18) is
$\Omega (\ell ) \geq \frac {\log D}{\log Q}$
. Hence,the left-hand side of equation (2.18) is
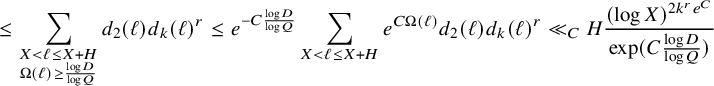 $$ \begin{align*} \leq \sum_{\substack{X < \ell \leq X+H \\\Omega(\ell)\geq \frac{\log D}{\log Q}}} d_2(\ell) d_k(\ell)^r \leq e^{-C\frac{\log D}{\log Q}}\sum_{X< \ell \leq X+H} e^{C\Omega(\ell)} d_2(\ell) d_k(\ell)^r \ll_C H\frac{(\log X)^{2k^r e^C}}{\exp(C\frac{\log D}{\log Q})} \end{align*} $$
$$ \begin{align*} \leq \sum_{\substack{X < \ell \leq X+H \\\Omega(\ell)\geq \frac{\log D}{\log Q}}} d_2(\ell) d_k(\ell)^r \leq e^{-C\frac{\log D}{\log Q}}\sum_{X< \ell \leq X+H} e^{C\Omega(\ell)} d_2(\ell) d_k(\ell)^r \ll_C H\frac{(\log X)^{2k^r e^C}}{\exp(C\frac{\log D}{\log Q})} \end{align*} $$
by Lemma 2.17.
Now, we state the lemma allowing us to introduce an extra variable
![]() $p \in (P, Q]$
in the factorization. It is a slight variant of [Reference Matomäki and Teräväinen50, Lemma 3.1] (see also [Reference Matomäki and Teräväinen50, Remark 3.2]).
$p \in (P, Q]$
in the factorization. It is a slight variant of [Reference Matomäki and Teräväinen50, Lemma 3.1] (see also [Reference Matomäki and Teräväinen50, Remark 3.2]).
Lemma 2.19. Let
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $k \geq 1$
be fixed. Let
$k \geq 1$
be fixed. Let
![]() $X\geq 3$
,
$X\geq 3$
,
![]() $X^{\varepsilon } \leq H \leq X$
, and let
$X^{\varepsilon } \leq H \leq X$
, and let
![]() $2 \leq P < Q \leq X^{1/(\log \log X)^2}$
. Write
$2 \leq P < Q \leq X^{1/(\log \log X)^2}$
. Write
![]() $\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
. Let f be any multiplicative function satisfying
$\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
. Let f be any multiplicative function satisfying
![]() $|f(n)| \leq d_k(n)$
. Then for any sequence
$|f(n)| \leq d_k(n)$
. Then for any sequence
![]() $\{\omega _n\}$
with
$\{\omega _n\}$
with
![]() $|\omega _n| \leq 1$
, we have
$|\omega _n| \leq 1$
, we have
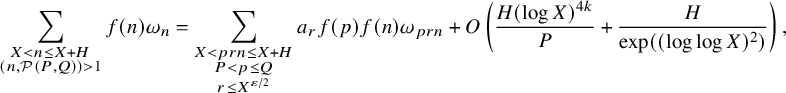 $$ \begin{align*}\sum_{\substack{X < n \leq X+H \\ (n, \mathcal{P}(P, Q))> 1}} f(n) \omega_n = \sum_{\substack{X < prn \leq X+H \\ P < p \leq Q \\ r \leq X^{\varepsilon/2}}} a_r f(p) f(n) \omega_{prn} + O\left( \frac{H(\log X)^{4k}}{P} + \frac{H}{\exp((\log \log X)^{2})}\right), \end{align*} $$
$$ \begin{align*}\sum_{\substack{X < n \leq X+H \\ (n, \mathcal{P}(P, Q))> 1}} f(n) \omega_n = \sum_{\substack{X < prn \leq X+H \\ P < p \leq Q \\ r \leq X^{\varepsilon/2}}} a_r f(p) f(n) \omega_{prn} + O\left( \frac{H(\log X)^{4k}}{P} + \frac{H}{\exp((\log \log X)^{2})}\right), \end{align*} $$
where
![]() $\{a_r\}$
is an explicit sequence satisfying
$\{a_r\}$
is an explicit sequence satisfying
![]() $|a_r| \leq d_{k+1}(r)$
.
$|a_r| \leq d_{k+1}(r)$
.
Proof. This is very similar to [Reference Matomäki and Teräväinen50, Remark 3.2], but for completeness we provide the proof in a somewhat simpler form.
By Ramaré’s identity
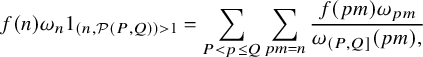 $$ \begin{align} f(n)\omega_n 1_{(n,\mathcal{P}(P, Q))>1}=\sum_{P< p\leq Q}\sum_{pm=n}\frac{f(pm) \omega_{pm}}{\omega_{(P,Q]}(pm),} \end{align} $$
$$ \begin{align} f(n)\omega_n 1_{(n,\mathcal{P}(P, Q))>1}=\sum_{P< p\leq Q}\sum_{pm=n}\frac{f(pm) \omega_{pm}}{\omega_{(P,Q]}(pm),} \end{align} $$
where
![]() $\omega _{(P,Q]}(m)$
is the number of distinct prime divisors of m on
$\omega _{(P,Q]}(m)$
is the number of distinct prime divisors of m on
![]() $(P,Q]$
; this identity follows directly since the number of representations
$(P,Q]$
; this identity follows directly since the number of representations
![]() $n=pm$
with
$n=pm$
with
![]() $P<p\leq Q$
is
$P<p\leq Q$
is
![]() $\omega _{(P,Q]}(n)$
.
$\omega _{(P,Q]}(n)$
.
We write m uniquely as
![]() $m=m_1m_2$
with
$m=m_1m_2$
with
![]() $m_1$
having all of its prime factors from
$m_1$
having all of its prime factors from
![]() $(P,Q]$
and
$(P,Q]$
and
![]() $m_2$
having no prime factors from that interval. Summing over n and then spotting the condition
$m_2$
having no prime factors from that interval. Summing over n and then spotting the condition
![]() $(m_2, \mathcal {P}(P, Q)) = 1$
using Möbius inversion, we see that
$(m_2, \mathcal {P}(P, Q)) = 1$
using Möbius inversion, we see that
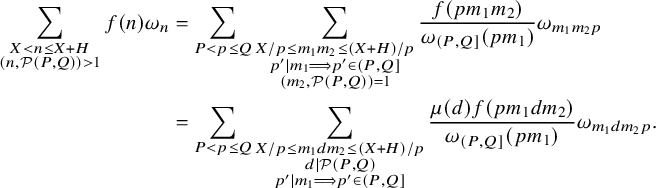 $$ \begin{align}\sum_{\substack{X < n \leq X+H \\ (n, \mathcal{P}(P, Q)) > 1}} f(n) \omega_n &= \sum_{P< p\leq Q}\sum_{\substack{X/p\leq m_1m_2\leq (X+H)/p\\p'\mid m_1\Longrightarrow p'\in (P,Q]\\(m_2, \mathcal{P}(P, Q)) = 1}}\frac{f(p m_1 m_2)}{\omega_{(P,Q]}(p m_1)}\omega_{m_1 m_2 p} \notag\\&=\sum_{P< p\leq Q}\sum_{\substack{X/p\leq m_1 d m_2\leq (X+H)/p\\d \mid \mathcal{P}(P, Q) \\ p'\mid m_1\Longrightarrow p'\in (P,Q]}}\frac{\mu(d) f(p m_1 d m_2)}{\omega_{(P,Q]}(p m_1)}\omega_{m_1 d m_2 p}. \end{align} $$
$$ \begin{align}\sum_{\substack{X < n \leq X+H \\ (n, \mathcal{P}(P, Q)) > 1}} f(n) \omega_n &= \sum_{P< p\leq Q}\sum_{\substack{X/p\leq m_1m_2\leq (X+H)/p\\p'\mid m_1\Longrightarrow p'\in (P,Q]\\(m_2, \mathcal{P}(P, Q)) = 1}}\frac{f(p m_1 m_2)}{\omega_{(P,Q]}(p m_1)}\omega_{m_1 m_2 p} \notag\\&=\sum_{P< p\leq Q}\sum_{\substack{X/p\leq m_1 d m_2\leq (X+H)/p\\d \mid \mathcal{P}(P, Q) \\ p'\mid m_1\Longrightarrow p'\in (P,Q]}}\frac{\mu(d) f(p m_1 d m_2)}{\omega_{(P,Q]}(p m_1)}\omega_{m_1 d m_2 p}. \end{align} $$
Let us show that we can restrict the summation to
![]() $dm_1 \leq X^{\varepsilon /2}$
. Writing
$dm_1 \leq X^{\varepsilon /2}$
. Writing
![]() $m =dm_1$
and
$m =dm_1$
and
![]() $n = p m_2$
, we see that by Lemma 2.18 with
$n = p m_2$
, we see that by Lemma 2.18 with
![]() $C = 4/\varepsilon $
the contribution of
$C = 4/\varepsilon $
the contribution of
![]() $dm_1> X^{\varepsilon /2}$
is bounded by
$dm_1> X^{\varepsilon /2}$
is bounded by
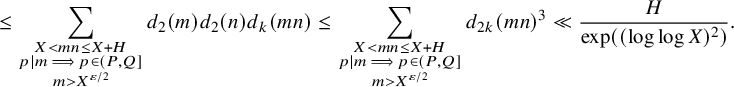 $$ \begin{align*} \leq \sum_{\substack{X< mn \leq X+H \\ p \mid m \implies p \in (P, Q] \\ m> X^{\varepsilon/2}}} d_2(m) d_2(n) d_k(mn) \leq \sum_{\substack{X< mn \leq X+H \\ p \mid m \implies p \in (P, Q] \\ m> X^{\varepsilon/2}}} d_{2k}(mn)^3 \ll \frac{H}{\exp((\log \log X)^2)}. \end{align*} $$
$$ \begin{align*} \leq \sum_{\substack{X< mn \leq X+H \\ p \mid m \implies p \in (P, Q] \\ m> X^{\varepsilon/2}}} d_2(m) d_2(n) d_k(mn) \leq \sum_{\substack{X< mn \leq X+H \\ p \mid m \implies p \in (P, Q] \\ m> X^{\varepsilon/2}}} d_{2k}(mn)^3 \ll \frac{H}{\exp((\log \log X)^2)}. \end{align*} $$
Furthermore, since in equation (2.20) all prime factors of
![]() $pd m_1$
are from
$pd m_1$
are from
![]() $(P, Q]$
, we have
$(P, Q]$
, we have
unless there exists a prime
![]() $q\in (P,Q]$
such that
$q\in (P,Q]$
such that
![]() $q^2 \mid pm_1dm_2 =: \ell $
. Applying Lemma 2.17, the error introduced by making the changes equations(2.21) to (2.20) is
$q^2 \mid pm_1dm_2 =: \ell $
. Applying Lemma 2.17, the error introduced by making the changes equations(2.21) to (2.20) is
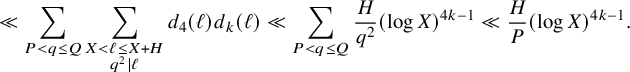 $$ \begin{align*} \ll \sum_{P< q\leq Q}\sum_{\substack{X< \ell\leq X+H\\q^2\mid \ell}}d_4(\ell) d_k(\ell) \ll \sum_{P< q\leq Q}\frac{H}{q^2}(\log X)^{4k-1} \ll \frac{H}{P}(\log X)^{4k-1}. \end{align*} $$
$$ \begin{align*} \ll \sum_{P< q\leq Q}\sum_{\substack{X< \ell\leq X+H\\q^2\mid \ell}}d_4(\ell) d_k(\ell) \ll \sum_{P< q\leq Q}\frac{H}{q^2}(\log X)^{4k-1} \ll \frac{H}{P}(\log X)^{4k-1}. \end{align*} $$
Thus, equation (2.20) equals
 $$ \begin{align*} \sum_{\substack{X \leq p m_1 d m_2\leq X+H \\p'\mid d m_1\Longrightarrow p'\in (P,Q] \\ P < p \leq Q, dm_1 \leq X^{\varepsilon/2}}}\frac{\mu(d) f(p) f(dm_1) f(m_2)}{\omega_{(P,Q]}(m_1) + 1}\omega_{m_1 d m_2 p} + O\left(\frac{H}{\exp((\log \log X)^{2})} + \frac{H}{P}(\log X)^{4k-1} \right), \end{align*} $$
$$ \begin{align*} \sum_{\substack{X \leq p m_1 d m_2\leq X+H \\p'\mid d m_1\Longrightarrow p'\in (P,Q] \\ P < p \leq Q, dm_1 \leq X^{\varepsilon/2}}}\frac{\mu(d) f(p) f(dm_1) f(m_2)}{\omega_{(P,Q]}(m_1) + 1}\omega_{m_1 d m_2 p} + O\left(\frac{H}{\exp((\log \log X)^{2})} + \frac{H}{P}(\log X)^{4k-1} \right), \end{align*} $$
and the claim follows with
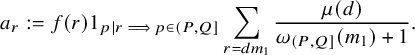 $$ \begin{align*} a_r:=f(r) 1_{\substack{p \mid r \implies p \in (P, Q]}}\sum_{r = dm_1} \frac{\mu(d)}{\omega_{(P,Q]}(m_1)+1}.\\[-47pt] \end{align*} $$
$$ \begin{align*} a_r:=f(r) 1_{\substack{p \mid r \implies p \in (P, Q]}}\sum_{r = dm_1} \frac{\mu(d)}{\omega_{(P,Q]}(m_1)+1}.\\[-47pt] \end{align*} $$
The following combinatorial lemma will be used to arrange each component arising from Lemma 2.16 into a desired form, such as a type I sum, a type
![]() $II$
sum or a type
$II$
sum or a type
![]() $I_2$
sum.
$I_2$
sum.
Lemma 2.20. Let
![]() $\alpha _1,\dots ,\alpha _k$
be nonnegative real numbers with
$\alpha _1,\dots ,\alpha _k$
be nonnegative real numbers with
![]() $\sum _{i=1}^k \alpha _i = 1$
, and let
$\sum _{i=1}^k \alpha _i = 1$
, and let
![]() $\frac {1}{3} \leq \theta \leq 1$
. For any
$\frac {1}{3} \leq \theta \leq 1$
. For any
![]() $I \subset \{1,\dots ,k\}$
, write
$I \subset \{1,\dots ,k\}$
, write
![]() . Consider the following statements:
. Consider the following statements:
-
(I) One has
 $\alpha _i \geq 1 - \theta $
for some
$\alpha _i \geq 1 - \theta $
for some
 $1 \leq i \leq k$
.
$1 \leq i \leq k$
. -
(I 2 maj) One has
 $\alpha _{\{i,j\}} \geq 1 - \theta $
for some
$\alpha _{\{i,j\}} \geq 1 - \theta $
for some
 $1 \leq i < j \leq k$
.
$1 \leq i < j \leq k$
. -
(I 2) One has
 $\alpha _{\{i,j\}} \geq \frac {3}{2}(1-\theta )$
for some
$\alpha _{\{i,j\}} \geq \frac {3}{2}(1-\theta )$
for some
 $1 \leq i < j \leq k$
.
$1 \leq i < j \leq k$
. -
(II maj) There exists a partition
 $\{1,\dots ,k\} = I \uplus J \uplus J'$
such that
$\{1,\dots ,k\} = I \uplus J \uplus J'$
such that
 $2\theta -1 \leq \alpha _I \leq 4\theta -2$
and
$2\theta -1 \leq \alpha _I \leq 4\theta -2$
and
 $|\alpha _J - \alpha _{J'}| \leq 2\theta -1$
.
$|\alpha _J - \alpha _{J'}| \leq 2\theta -1$
. -
(II min) There exists a partition
 $\{1,\dots ,k\} = J \uplus J'$
such that
$\{1,\dots ,k\} = J \uplus J'$
such that
 $|\alpha _J - \alpha _{J'}| \leq 2\theta -1$
(or equivalently,
$|\alpha _J - \alpha _{J'}| \leq 2\theta -1$
(or equivalently,
 $\alpha _J, \alpha _{J'} \in [1-\theta ,\theta ]$
; or equivalently,
$\alpha _J, \alpha _{J'} \in [1-\theta ,\theta ]$
; or equivalently,
 $\alpha _J \in [1-\theta , \theta ]$
).
$\alpha _J \in [1-\theta , \theta ]$
).
Then the following claims hold.
-
(i) Suppose that
 $\theta = 5/8$
. Then at least one of (I) or (
$\theta = 5/8$
. Then at least one of (I) or (
 $II^{\mathrm {maj}}$
) holds.
$II^{\mathrm {maj}}$
) holds. -
(ii) Suppose that
 $\theta \geq 3/5$
. Then at least one of (I), (
$\theta \geq 3/5$
. Then at least one of (I), (
 $I_2$
) or (
$I_2$
) or (
 $II^{\mathrm {min}}$
) holds.
$II^{\mathrm {min}}$
) holds. -
(iii) Suppose that
 $\theta = 7/12$
. Then at least one of (I), (
$\theta = 7/12$
. Then at least one of (I), (
 $I_2^{\mathrm {maj}}$
) or (
$I_2^{\mathrm {maj}}$
) or (
 $II^{\mathrm {maj}}$
) holds.
$II^{\mathrm {maj}}$
) holds. -
(iv) Suppose that
 $k = 5$
and
$k = 5$
and
 $\theta = 11/20$
. Then at least one of (
$\theta = 11/20$
. Then at least one of (
 $I_2^{\mathrm {maj}}$
) or (
$I_2^{\mathrm {maj}}$
) or (
 $II^{\mathrm {maj}}$
) holds.
$II^{\mathrm {maj}}$
) holds. -
(v) Suppose that
 $k \in \{3,4\}$
and
$k \in \{3,4\}$
and
 $\theta \geq 1/2$
. Then (
$\theta \geq 1/2$
. Then (
 $I_2^{\mathrm {maj}}$
) holds.
$I_2^{\mathrm {maj}}$
) holds. -
(vi) Suppose that
 $k=3$
and
$k=3$
and
 $\theta \geq 5/9$
or
$\theta \geq 5/9$
or
 $k=2$
and
$k=2$
and
 $\theta \geq 1/3$
. Then (
$\theta \geq 1/3$
. Then (
 $I_2$
) holds.
$I_2$
) holds.
Remark 2.21. The different conclusions (I), (
![]() $I_2^{\mathrm {maj}}$
), (
$I_2^{\mathrm {maj}}$
), (
![]() $I_2$
), (
$I_2$
), (
![]() $II^{\mathrm {maj}}$
), (
$II^{\mathrm {maj}}$
), (
![]() $II^{\mathrm {min}}$
) in Lemma 2.20 correspond to different types of sums that behave well on intervals
$II^{\mathrm {min}}$
) in Lemma 2.20 correspond to different types of sums that behave well on intervals
![]() $(X,X+H]$
with H much larger than
$(X,X+H]$
with H much larger than
![]() $X^\theta $
:
$X^\theta $
:
-
• Exponents obeying (I) correspond to ‘type I sums’ which behave well for both major and minor arc correlations.
-
• Exponents obeying (
 $I_2^{\mathrm {maj}}$
) correspond to ‘type
$I_2^{\mathrm {maj}}$
) correspond to ‘type
 $I_2$
sums’ which behave well for major arc correlations.
$I_2$
sums’ which behave well for major arc correlations. -
• Exponents obeying (
 $I_2$
) correspond to ‘type
$I_2$
) correspond to ‘type
 $I_2$
sums’ which behave well for both major and minor arc correlations.
$I_2$
sums’ which behave well for both major and minor arc correlations. -
• Exponents obeying (
 $II^{\mathrm {maj}}$
) correspond to ‘type
$II^{\mathrm {maj}}$
) correspond to ‘type
 $II$
sums’ which behave well for major arc correlations.
$II$
sums’ which behave well for major arc correlations. -
• Exponents obeying (
 $II^{\mathrm {min}}$
) correspond to ‘type
$II^{\mathrm {min}}$
) correspond to ‘type
 $II$
sums’ which behave well for minor arc correlations or for major arc correlations when one can extract a medium-sized prime factor from the sum.
$II$
sums’ which behave well for minor arc correlations or for major arc correlations when one can extract a medium-sized prime factor from the sum.
Proof. We first handle the easy case (vi). If
![]() $k=2$
and
$k=2$
and
![]() $\theta \geq 1/3$
, then
$\theta \geq 1/3$
, then
![]() $\frac {3}{2}(1-\theta ) \leq 1$
and (
$\frac {3}{2}(1-\theta ) \leq 1$
and (
![]() $I_2$
) follows simply by taking
$I_2$
) follows simply by taking
![]() $\{i, j\} = \{1, 2\}$
. If
$\{i, j\} = \{1, 2\}$
. If
![]() $k=3$
and
$k=3$
and
![]() $\theta \geq \frac {5}{9}$
, then
$\theta \geq \frac {5}{9}$
, then
![]() $\frac {3}{2}(1-\theta ) \leq \frac {2}{3}$
and (
$\frac {3}{2}(1-\theta ) \leq \frac {2}{3}$
and (
![]() $I_2$
) follows by noting that the sum of the two largest of the reals
$I_2$
) follows by noting that the sum of the two largest of the reals
![]() $\alpha _1,\alpha _2,\alpha _3$
is necessarily at least
$\alpha _1,\alpha _2,\alpha _3$
is necessarily at least
![]() $\frac {2}{3}$
.
$\frac {2}{3}$
.
Now, we prove (v). If
![]() $k=4$
and
$k=4$
and
![]() $\theta \geq 1/2$
, then by the pigeonhole principle one of
$\theta \geq 1/2$
, then by the pigeonhole principle one of
![]() $\alpha _{\{1,2\}}$
,
$\alpha _{\{1,2\}}$
,
![]() $\alpha _{\{3,4\}}$
is at least
$\alpha _{\{3,4\}}$
is at least
![]() $\frac {1}{2} \geq 1-\theta $
, and we obtain (
$\frac {1}{2} \geq 1-\theta $
, and we obtain (
![]() $I_2^{\mathrm {maj}}$
) in this case. The case
$I_2^{\mathrm {maj}}$
) in this case. The case
![]() $k=3$
follows similarly, with some room to spare.
$k=3$
follows similarly, with some room to spare.
In a similar spirit in case (iv), when
![]() $k=5$
and
$k=5$
and
![]() $\theta = \frac {11}{20}$
, then one of the
$\theta = \frac {11}{20}$
, then one of the
![]() $\alpha _i$
must be at most
$\alpha _i$
must be at most
![]() $\frac {1}{5}$
; without loss of generality
$\frac {1}{5}$
; without loss of generality
![]() $\alpha _5 \leq \frac {1}{5}$
. Since
$\alpha _5 \leq \frac {1}{5}$
. Since
![]() $1-\theta = \frac {9}{20}$
, we obtain (
$1-\theta = \frac {9}{20}$
, we obtain (
![]() $I_2^{\mathrm {maj}}$
) except when
$I_2^{\mathrm {maj}}$
) except when
![]() $\alpha _{\{1,2\}}, \alpha _{\{3,4\}} \leq \frac {9}{20}$
, which by
$\alpha _{\{1,2\}}, \alpha _{\{3,4\}} \leq \frac {9}{20}$
, which by
![]() $\sum _{i=1}^5 \alpha _i=1$
forces
$\sum _{i=1}^5 \alpha _i=1$
forces
![]() $\alpha _{\{3,4\}}, \alpha _{\{1,2\}} \geq 1 - \frac {9}{20} - \frac {1}{5} = \frac {7}{20}$
. Thus,
$\alpha _{\{3,4\}}, \alpha _{\{1,2\}} \geq 1 - \frac {9}{20} - \frac {1}{5} = \frac {7}{20}$
. Thus,
![]() $|\alpha _{\{1,2\}} - \alpha _{\{3,4\}}| \leq \frac {9}{20}-\frac {7}{20} = \frac {1}{10} = 2\theta -1$
. Also, we have
$|\alpha _{\{1,2\}} - \alpha _{\{3,4\}}| \leq \frac {9}{20}-\frac {7}{20} = \frac {1}{10} = 2\theta -1$
. Also, we have
and
and so we obtain (
![]() $II^{\mathrm {maj}}$
) in this case. This establishes (iv).
$II^{\mathrm {maj}}$
) in this case. This establishes (iv).
In the remaining cases (i)–(iii) we assume, without loss of generality, that
In case (ii) when
![]() $\theta \geq 3/5$
, we obtain (I) unless
$\theta \geq 3/5$
, we obtain (I) unless
![]() $\alpha _j < 1-\theta $
for each j and (
$\alpha _j < 1-\theta $
for each j and (
![]() $I_2$
) unless
$I_2$
) unless
![]() $\alpha _{\{i, j\}} < \frac {3}{2}(1-\theta ) \leq \theta $
for any distinct
$\alpha _{\{i, j\}} < \frac {3}{2}(1-\theta ) \leq \theta $
for any distinct
![]() $i, j$
. But if
$i, j$
. But if
![]() $\alpha _{\{i, j\}} \in [1-\theta , \theta ]$
for some distinct
$\alpha _{\{i, j\}} \in [1-\theta , \theta ]$
for some distinct
![]() $i, j$
, then we have (
$i, j$
, then we have (
![]() $II^{\mathrm {min}}$
). Hence, we can assume that
$II^{\mathrm {min}}$
). Hence, we can assume that
![]() $\alpha _{i, j} < 1-\theta $
for any distinct
$\alpha _{i, j} < 1-\theta $
for any distinct
![]() $i, j$
. In particular, for any
$i, j$
. In particular, for any
![]() $j \neq 1$
we have
$j \neq 1$
we have
Consequently, there must be an index
![]() $r \in \{3, \dotsc , k\}$
such that
$r \in \{3, \dotsc , k\}$
such that
![]() $\alpha _1 + \sum _{j = 2}^r \alpha _j \in [1-\theta , \theta ]$
, and hence (
$\alpha _1 + \sum _{j = 2}^r \alpha _j \in [1-\theta , \theta ]$
, and hence (
![]() $II^{\mathrm {min}}$
) holds.
$II^{\mathrm {min}}$
) holds.
Let us now consider (i). Now,
![]() $\theta = 5/8$
and we obtain (I) unless
$\theta = 5/8$
and we obtain (I) unless
![]() $\alpha _j < 3/8$
for every j (and in particular we can assume that
$\alpha _j < 3/8$
for every j (and in particular we can assume that
![]() $k \geq 3$
). Note that
$k \geq 3$
). Note that
![]() $2\theta -1 = 1/4$
in this case. If now
$2\theta -1 = 1/4$
in this case. If now
![]() $\alpha _3> 1/4$
, then
$\alpha _3> 1/4$
, then
![]() $\alpha _1, \alpha _2 \in [1/4, 3/8]$
and we have (
$\alpha _1, \alpha _2 \in [1/4, 3/8]$
and we have (
![]() $II^{\mathrm {maj}}$
) with
$II^{\mathrm {maj}}$
) with
![]() $J = \{1\}, J' = \{2\}$
, and
$J = \{1\}, J' = \{2\}$
, and
![]() $I = \{3, \dotsc , k\}$
.
$I = \{3, \dotsc , k\}$
.
On the other hand, if
![]() $\alpha _3 \leq 1/4$
, we set
$\alpha _3 \leq 1/4$
, we set
![]() $J_0 = \{1\}$
and
$J_0 = \{1\}$
and
![]() $J_0' = \{2, \dotsc , r\}$
with
$J_0' = \{2, \dotsc , r\}$
with
![]() $r \geq 2$
the greatest integer such that
$r \geq 2$
the greatest integer such that
![]() $\alpha _{J_0'} < \alpha _{J_0}$
. Then necessarily
$\alpha _{J_0'} < \alpha _{J_0}$
. Then necessarily
![]() $|\alpha _{J_0}-\alpha _{J_0'}| \leq 1/4 = 2\theta -1$
. Furthermore,
$|\alpha _{J_0}-\alpha _{J_0'}| \leq 1/4 = 2\theta -1$
. Furthermore,
![]() $\alpha _{J_0'} + \alpha _{J_0} \leq 2 \cdot \alpha _1 \leq 3/4$
. If also
$\alpha _{J_0'} + \alpha _{J_0} \leq 2 \cdot \alpha _1 \leq 3/4$
. If also
![]() $\alpha _{J_0'} + \alpha _{J_0} \geq 1/2$
, then we have (
$\alpha _{J_0'} + \alpha _{J_0} \geq 1/2$
, then we have (
![]() $II^{\mathrm {maj}}$
) with
$II^{\mathrm {maj}}$
) with
![]() $J = J_0, J' = J_0'$
and
$J = J_0, J' = J_0'$
and
![]() $I = \{1, \dotsc , k\} \setminus (J_0 \cup J_0')$
. Otherwise, we add indices
$I = \{1, \dotsc , k\} \setminus (J_0 \cup J_0')$
. Otherwise, we add indices
![]() $j \geq r+1$
one by one to
$j \geq r+1$
one by one to
![]() $J_0$
or
$J_0$
or
![]() $J_0'$
depending on whether
$J_0'$
depending on whether
![]() $\alpha _{J_0} < \alpha _{J_0'}$
or not. We continue this process until
$\alpha _{J_0} < \alpha _{J_0'}$
or not. We continue this process until
![]() $\alpha _{J_0} + \alpha _{J_0'} \in [1/2, 3/4]$
, and we again obtain (
$\alpha _{J_0} + \alpha _{J_0'} \in [1/2, 3/4]$
, and we again obtain (
![]() $II^{\mathrm {maj}}$
).
$II^{\mathrm {maj}}$
).
Let us finally turn to (iii). Now,
![]() $\theta = 7/12$
and
$\theta = 7/12$
and
![]() $2\theta -1 = 1/6$
. We obtain (
$2\theta -1 = 1/6$
. We obtain (
![]() $I_2^{\mathrm {maj}}$
) unless
$I_2^{\mathrm {maj}}$
) unless
![]() $\alpha _{\{i, j\}} < 1-\theta = 5/12$
for any distinct
$\alpha _{\{i, j\}} < 1-\theta = 5/12$
for any distinct
![]() $i, j$
. In particular, we can assume that
$i, j$
. In particular, we can assume that
![]() $\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4 < 5/6 < 1$
and thus
$\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4 < 5/6 < 1$
and thus
![]() $k \geq 5$
.
$k \geq 5$
.
If
![]() $\alpha _5> 1/6$
, then
$\alpha _5> 1/6$
, then
![]() $\alpha _{\{2, 3\}}, \alpha _{\{1, 4\}} \in [1/3, 5/12]$
. Consequently,
$\alpha _{\{2, 3\}}, \alpha _{\{1, 4\}} \in [1/3, 5/12]$
. Consequently,
![]() $1-\alpha _{\{1, 4\}}-\alpha _{\{2, 3\}} \in [1/6, 1/3]$
and we obtain (
$1-\alpha _{\{1, 4\}}-\alpha _{\{2, 3\}} \in [1/6, 1/3]$
and we obtain (
![]() $II^{\mathrm {maj}}$
) with
$II^{\mathrm {maj}}$
) with
![]() $J = \{1, 4\}, J' = \{2, 3\}$
, and
$J = \{1, 4\}, J' = \{2, 3\}$
, and
![]() $I = \{1, \dotsc , k\} \setminus \{1, 2, 3, 4\}$
.
$I = \{1, \dotsc , k\} \setminus \{1, 2, 3, 4\}$
.
On the other hand, if
![]() $\alpha _5 \leq 2\theta -1 = 1/6$
, we can argue similarly to case (i): We set
$\alpha _5 \leq 2\theta -1 = 1/6$
, we can argue similarly to case (i): We set
![]() $J_0 = \{1, 2\}$
and
$J_0 = \{1, 2\}$
and
![]() $J_0' = \{3, \dotsc , r\}$
with
$J_0' = \{3, \dotsc , r\}$
with
![]() $r \geq 4$
the greatest integer such that
$r \geq 4$
the greatest integer such that
![]() $\alpha _{J_0'} \leq \alpha _{J_0}$
. Then necessarily
$\alpha _{J_0'} \leq \alpha _{J_0}$
. Then necessarily
![]() $|\alpha _{J_0} - \alpha _{J_0'}| \leq 1/6 = 2\theta -1$
. Furthermore,
$|\alpha _{J_0} - \alpha _{J_0'}| \leq 1/6 = 2\theta -1$
. Furthermore,
![]() $\alpha _{J_0} + \alpha _{J_0'} \leq 2 \alpha _{1, 2} \leq 5/6$
. If also
$\alpha _{J_0} + \alpha _{J_0'} \leq 2 \alpha _{1, 2} \leq 5/6$
. If also
![]() $\alpha _{J_0} + \alpha _{J_0'} \geq 2/3$
, then we have (
$\alpha _{J_0} + \alpha _{J_0'} \geq 2/3$
, then we have (
![]() $II^{\mathrm {maj}}$
) with
$II^{\mathrm {maj}}$
) with
![]() $J = J_0$
and
$J = J_0$
and
![]() $J' = J_0'$
. Otherwise, we add indices
$J' = J_0'$
. Otherwise, we add indices
![]() $j \geq r+1$
one by one to
$j \geq r+1$
one by one to
![]() $J_0$
or
$J_0$
or
![]() $J_0'$
depending on whether
$J_0'$
depending on whether
![]() $\alpha _{J_0} < \alpha _{J_0'}$
or not. We continue this process until
$\alpha _{J_0} < \alpha _{J_0'}$
or not. We continue this process until
![]() $\alpha _{J_0} + \alpha _{J_0'} \in [2/3, 5/6]$
, and we again obtain (
$\alpha _{J_0} + \alpha _{J_0'} \in [2/3, 5/6]$
, and we again obtain (
![]() $II^{\mathrm {maj}}$
).
$II^{\mathrm {maj}}$
).
Remark 2.22. The following counterexamples, with
![]() $\varepsilon $
small, show that
$\varepsilon $
small, show that
![]() $\theta $
in the various components of Lemma 2.20 cannot be decreased (apart from the
$\theta $
in the various components of Lemma 2.20 cannot be decreased (apart from the
![]() $k=3$
case of (v)):
$k=3$
case of (v)):
-
•
 $\theta = 5/8-\varepsilon $
,
$\theta = 5/8-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) = (1/4,1/4,1/4,1/4)$
;
$(\alpha _1,\dots ,\alpha _k) = (1/4,1/4,1/4,1/4)$
; -
•
 $\theta = 3/5-\varepsilon $
,
$\theta = 3/5-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) \in \{(2/5,1/5,1/5,1/5), (1/5,1/5,1/5,1/5,1/5)\}$
;
$(\alpha _1,\dots ,\alpha _k) \in \{(2/5,1/5,1/5,1/5), (1/5,1/5,1/5,1/5,1/5)\}$
; -
•
 $\theta = 7/12-\varepsilon $
,
$\theta = 7/12-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) = (1/6,1/6,1/6,1/6,1/6,1/6)$
;
$(\alpha _1,\dots ,\alpha _k) = (1/6,1/6,1/6,1/6,1/6,1/6)$
; -
•
 $\theta = 11/20-\varepsilon $
,
$\theta = 11/20-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) = (1/5,1/5,1/5,1/5,1/5)$
;
$(\alpha _1,\dots ,\alpha _k) = (1/5,1/5,1/5,1/5,1/5)$
; -
•
 $\theta = 1/2-\varepsilon $
,
$\theta = 1/2-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) = (1/4,1/4,1/4,1/4)$
;
$(\alpha _1,\dots ,\alpha _k) = (1/4,1/4,1/4,1/4)$
; -
•
 $\theta = 5/9-\varepsilon $
,
$\theta = 5/9-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) = (1/3,1/3,1/3)$
;
$(\alpha _1,\dots ,\alpha _k) = (1/3,1/3,1/3)$
; -
•
 $\theta = 1/3-\varepsilon $
,
$\theta = 1/3-\varepsilon $
,
 $(\alpha _1,\dots ,\alpha _k) = (\alpha ,1-\alpha )$
for any
$(\alpha _1,\dots ,\alpha _k) = (\alpha ,1-\alpha )$
for any
 $\alpha \in (0, 1)$
.
$\alpha \in (0, 1)$
.
3 Major arc estimates
In the proof of Theorem 1.1, we shall use Theorem 4.2 below to reduce to ‘major arc’ cases where more-or-less
![]() $F(g(n) \Gamma ) = 1$
(or
$F(g(n) \Gamma ) = 1$
(or
![]() $F(g(n) \Gamma ) = n^{it}$
in case of type
$F(g(n) \Gamma ) = n^{it}$
in case of type
![]() $II$
sums). The purpose of this section is to establish the following estimates corresponding to the case
$II$
sums). The purpose of this section is to establish the following estimates corresponding to the case
![]() $F(g(n) \Gamma ) = 1$
as well as an auxiliary result (Lemma 3.5 below) on trilinear sums in case
$F(g(n) \Gamma ) = 1$
as well as an auxiliary result (Lemma 3.5 below) on trilinear sums in case
![]() $F(g(n) \Gamma ) = n^{it}$
.
$F(g(n) \Gamma ) = n^{it}$
.
Theorem 3.1 (Major arc estimate).
Let
![]() $X \geq 3$
and
$X \geq 3$
and
![]() $X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
$X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
![]() $0 < \theta < 1$
and
$0 < \theta < 1$
and
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
-
(i) (Huxley type estimates) Set
 $\theta = 7/12$
. Then, for all
$\theta = 7/12$
. Then, for all
 $A> 0$
, and
$A> 0$
, and $$ \begin{align*} {\left| \sum_{X < n \leq X+H} \mu(n) \right|}^* &\ll_{A,\varepsilon} \frac{H}{\log^{A} X} \end{align*} $$
$$ \begin{align*} {\left| \sum_{X < n \leq X+H} \mu(n) \right|}^* &\ll_{A,\varepsilon} \frac{H}{\log^{A} X} \end{align*} $$
 $$ \begin{align*} {\left| \sum_{X < n \leq X+H} (\Lambda(n) - \Lambda^\sharp(n)) \right|}^* &\ll_{A,\varepsilon} \frac{H}{\log^{A} X}. \end{align*} $$
$$ \begin{align*} {\left| \sum_{X < n \leq X+H} (\Lambda(n) - \Lambda^\sharp(n)) \right|}^* &\ll_{A,\varepsilon} \frac{H}{\log^{A} X}. \end{align*} $$
-
(ii) Let
 $k \geq 2$
. Set
$k \geq 2$
. Set
 $\theta = 1/3$
for
$\theta = 1/3$
for
 $k=2$
,
$k=2$
,
 $\theta =1/2$
for
$\theta =1/2$
for
 $k=3, 4$
,
$k=3, 4$
,
 $\theta =11/20$
for
$\theta =11/20$
for
 $k =5$
and
$k =5$
and
 $\theta = 7/12$
for
$\theta = 7/12$
for
 $k \geq 6$
. Then for some constant
$k \geq 6$
. Then for some constant $$ \begin{align*}{\left|\sum_{X < n \leq X+H} (d_k(n) - d^\sharp_k(n))\right|}^* \ll_\varepsilon \frac{H}{X^{c_k}} + \frac{H}{X^{\varepsilon/1000}}\end{align*} $$
$$ \begin{align*}{\left|\sum_{X < n \leq X+H} (d_k(n) - d^\sharp_k(n))\right|}^* \ll_\varepsilon \frac{H}{X^{c_k}} + \frac{H}{X^{\varepsilon/1000}}\end{align*} $$
 $c_k>0$
depending only on k.
$c_k>0$
depending only on k.
We remark that if we replace the maximal sums
![]() $|\cdot |^*$
here by the ordinary sums
$|\cdot |^*$
here by the ordinary sums
![]() $|\cdot |$
, then the
$|\cdot |$
, then the
![]() $\theta =7/12$
case of Theorem 3.1 can also be extracted after some computation from the work of Ramachandra [Reference Ramachandra56] (see in particular Remarks 4, 5 of that paper), with a pseudopolynomial gain
$\theta =7/12$
case of Theorem 3.1 can also be extracted after some computation from the work of Ramachandra [Reference Ramachandra56] (see in particular Remarks 4, 5 of that paper), with a pseudopolynomial gain
![]() $O( \exp (-c(\log X)^{1/3} / (\log \log X)^{1/3} ) )$
, while the cases
$O( \exp (-c(\log X)^{1/3} / (\log \log X)^{1/3} ) )$
, while the cases
![]() $k=4, 5$
of Theorem 3.1(ii) follow from [Reference Hardy and Littlewood23, (4.23)]) and [Reference Heath-Brown27]. Here, we will provide the proofs from our viewpoint. It may be possible to improve the error terms in (i) to be pseudopolynomial in nature even for the maximal sums, if one adjusts the approximants
$k=4, 5$
of Theorem 3.1(ii) follow from [Reference Hardy and Littlewood23, (4.23)]) and [Reference Heath-Brown27]. Here, we will provide the proofs from our viewpoint. It may be possible to improve the error terms in (i) to be pseudopolynomial in nature even for the maximal sums, if one adjusts the approximants
![]() $\mu ^\sharp , \Lambda ^\sharp $
to take into account the possibility of a Siegel zero, in the spirit of [Reference Tao and Teräväinen61, Proposition 2.2].
$\mu ^\sharp , \Lambda ^\sharp $
to take into account the possibility of a Siegel zero, in the spirit of [Reference Tao and Teräväinen61, Proposition 2.2].
For the
![]() $\theta =7/12$
result, the primary obstruction arises from convolutions (1.29) with
$\theta =7/12$
result, the primary obstruction arises from convolutions (1.29) with
![]() $(\alpha _1,\dots ,\alpha _m)$
equal to
$(\alpha _1,\dots ,\alpha _m)$
equal to
![]() $(1/6,1/6,1/6,1/6,1/6,1/6)$
, as this lies just outside the reach of our untwisted major arc type I and type
$(1/6,1/6,1/6,1/6,1/6,1/6)$
, as this lies just outside the reach of our untwisted major arc type I and type
![]() $II$
estimates when
$II$
estimates when
![]() $\theta $
goes below
$\theta $
goes below
![]() $7/12$
(cf., the third item of Remark 2.22). This obstruction has long been known; see, for example, [Reference Heath-Brown29]. Note that this obstruction does not arise for
$7/12$
(cf., the third item of Remark 2.22). This obstruction has long been known; see, for example, [Reference Heath-Brown29]. Note that this obstruction does not arise for
![]() $k<6$
, which explains the fact that better exponents than
$k<6$
, which explains the fact that better exponents than
![]() $7/12$
are available for
$7/12$
are available for
![]() $d_2, d_3, d_4, d_5$
. The corresponding obstructions can be found in the other items of Remark 2.22.
$d_2, d_3, d_4, d_5$
. The corresponding obstructions can be found in the other items of Remark 2.22.
It would probably be possible to obtain Theorem 3.1(ii) for
![]() $\theta = 131/416 \approx 0.315$
when
$\theta = 131/416 \approx 0.315$
when
![]() $k = 2$
and for
$k = 2$
and for
![]() $\theta = 43/96 \approx 0.448$
when
$\theta = 43/96 \approx 0.448$
when
![]() $k=3$
– corresponding to the progress in the Dirichlet divisor problem [Reference Huxley34, Reference Kolesnik41] – but we do not attempt to compute this here (it requires checking that the arguments in the literature, when adapted to the Dirichlet divisor problem in an arithmetic progression, give a polynomial dependence on the common difference of the arithmetic progression and it also does not directly improve the exponents in Theorem 1.1).
$k=3$
– corresponding to the progress in the Dirichlet divisor problem [Reference Huxley34, Reference Kolesnik41] – but we do not attempt to compute this here (it requires checking that the arguments in the literature, when adapted to the Dirichlet divisor problem in an arithmetic progression, give a polynomial dependence on the common difference of the arithmetic progression and it also does not directly improve the exponents in Theorem 1.1).
Let us now explain the strategy of the proof of Theorem 3.1. Let
![]() $f \in \{\mu , \Lambda , d_k\}.$
By adjusting the implied constants, it suffices to show the claims with
$f \in \{\mu , \Lambda , d_k\}.$
By adjusting the implied constants, it suffices to show the claims with
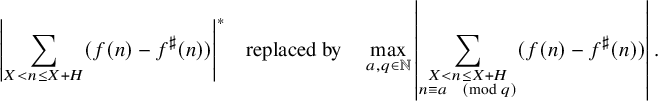 $$\begin{align*}{\left| \sum_{X < n \leq X+H} (f(n) - f^\sharp(n)) \right|}^* \quad \text{replaced by} \quad \max_{a, q \in \mathbb{N}} \left|\sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} (f(n) - f^\sharp(n))\right|. \end{align*}$$
$$\begin{align*}{\left| \sum_{X < n \leq X+H} (f(n) - f^\sharp(n)) \right|}^* \quad \text{replaced by} \quad \max_{a, q \in \mathbb{N}} \left|\sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} (f(n) - f^\sharp(n))\right|. \end{align*}$$
In the cases
![]() $f=\mu ,\Lambda $
, we take
$f=\mu ,\Lambda $
, we take
![]() and in the case
and in the case
![]() $f= d_k$
we take
$f= d_k$
we take
![]() . We use the triangle inequality to write
. We use the triangle inequality to write
 $$ \begin{align} &\left|\frac{1}{H} \sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} (f(n) - f^\sharp(n))\right| \leq \left|\frac{1}{H} \sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} f(n) - \frac{1}{H'} \sum_{\substack{X < n \leq X+H' \\ n \equiv a \quad\pmod{q}}} f(n)\right| \nonumber\\ &\quad + \left|\frac{1}{H'} \sum_{\substack{X < n \leq X+H' \\ n \equiv a \quad\pmod{q}}} (f(n) - f^\sharp(n))\right| + \left|\frac{1}{H} \sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} f^\sharp(n) - \frac{1}{H'} \sum_{\substack{X < n \leq X+H' \\ n \equiv a \quad\pmod{q}}} f^\sharp(n)\right|. \end{align} $$
$$ \begin{align} &\left|\frac{1}{H} \sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} (f(n) - f^\sharp(n))\right| \leq \left|\frac{1}{H} \sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} f(n) - \frac{1}{H'} \sum_{\substack{X < n \leq X+H' \\ n \equiv a \quad\pmod{q}}} f(n)\right| \nonumber\\ &\quad + \left|\frac{1}{H'} \sum_{\substack{X < n \leq X+H' \\ n \equiv a \quad\pmod{q}}} (f(n) - f^\sharp(n))\right| + \left|\frac{1}{H} \sum_{\substack{X < n \leq X+H \\ n \equiv a \quad\pmod{q}}} f^\sharp(n) - \frac{1}{H'} \sum_{\substack{X < n \leq X+H' \\ n \equiv a \quad\pmod{q}}} f^\sharp(n)\right|. \end{align} $$
Then we show that each of the three differences on the right-hand side is small. Let us next state the required results.
To attack the second difference in equation (3.1), we show in Section 3.1 that Theorem 3.1 holds in long intervals.
Proposition 3.2 (Long intervals).
Let
![]() $X \geq H_2 \geq 2$
.
$X \geq H_2 \geq 2$
.
-
(i) Let
 $A> 0$
andFootnote
6
$A> 0$
andFootnote
6
 $X/\log ^A X \leq H_2 \leq X$
. Then (3.2)and
$X/\log ^A X \leq H_2 \leq X$
. Then (3.2)and $$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \sum_{\substack{X < n \leq X+H_2\\n\equiv a\quad\pmod q}} \mu(n) \right| \ll_{A} \frac{H_2}{\log^{A} X}. \end{align} $$
(3.3)
$$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \sum_{\substack{X < n \leq X+H_2\\n\equiv a\quad\pmod q}} \mu(n) \right| \ll_{A} \frac{H_2}{\log^{A} X}. \end{align} $$
(3.3) $$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \sum_{\substack{X < n \leq X+H_2\\n\equiv a\quad\pmod q}} (\Lambda(n) - \Lambda^\sharp(n)) \right| \ll_{A} \frac{H_2}{\log^{A} X}. \end{align} $$
$$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \sum_{\substack{X < n \leq X+H_2\\n\equiv a\quad\pmod q}} (\Lambda(n) - \Lambda^\sharp(n)) \right| \ll_{A} \frac{H_2}{\log^{A} X}. \end{align} $$
-
(ii) Let
 $k \geq 2$
and
$k \geq 2$
and
 $X^{1-\frac {1}{50k}} \leq H_2 \leq X$
. Then (3.4)
$X^{1-\frac {1}{50k}} \leq H_2 \leq X$
. Then (3.4) $$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \sum_{\substack{X < n \leq X+H_2\\n\equiv a\quad\pmod q}} (d_k(n) - d_k^\sharp(n))\right| \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align} $$
$$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \sum_{\substack{X < n \leq X+H_2\\n\equiv a\quad\pmod q}} (d_k(n) - d_k^\sharp(n))\right| \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align} $$
Furthermore, using the definitions of our approximants
![]() $\Lambda ^\sharp (n)$
and
$\Lambda ^\sharp (n)$
and
![]() $d_k^\sharp (n)$
as type I sums, it will be straightforward to show that the third difference on the right of equation (3.1) is small; in Section 3.2, we shall show the following.
$d_k^\sharp (n)$
as type I sums, it will be straightforward to show that the third difference on the right of equation (3.1) is small; in Section 3.2, we shall show the following.
Lemma 3.3 (Long and short averages of approximant).
Let
![]() $X \geq H_2 \geq H_1 \geq X^{1/4} \geq 2$
.
$X \geq H_2 \geq H_1 \geq X^{1/4} \geq 2$
.
-
(i) One has
(3.5) $$ \begin{align} \max_{a, q \in \mathbb{N}}\left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} \Lambda^\sharp(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} \Lambda^\sharp(n)\right| &\ll \exp(-(\log X)^{1/10}). \end{align} $$
$$ \begin{align} \max_{a, q \in \mathbb{N}}\left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} \Lambda^\sharp(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} \Lambda^\sharp(n)\right| &\ll \exp(-(\log X)^{1/10}). \end{align} $$
-
(ii) Let
 $k \geq 2$
. Then (3.6)
$k \geq 2$
. Then (3.6) $$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n)\right|\ll \frac{1}{X^{1/100}} + \frac{H_2}{X}\log^{k-2} X. \end{align} $$
$$ \begin{align} \max_{a, q \in \mathbb{N}} \left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n)\right|\ll \frac{1}{X^{1/100}} + \frac{H_2}{X}\log^{k-2} X. \end{align} $$
Our ability to handle the first difference in equation (3.1) is what determines the exponent
![]() $\theta $
. Concerning the first difference, we prove the following proposition in Section 3.4.
$\theta $
. Concerning the first difference, we prove the following proposition in Section 3.4.
Proposition 3.4 (Long and short averages of arithmetic function).
-
(i) Let
 $X/\log ^{20 A} X \geq H_2 \geq H_1 \geq X^{7/12+\varepsilon }$
. Then and
$X/\log ^{20 A} X \geq H_2 \geq H_1 \geq X^{7/12+\varepsilon }$
. Then and $$ \begin{align*} \max_{a, q \in \mathbb{N}}\left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} \Lambda(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} \Lambda(n)\right| &\ll_{A, \varepsilon} \frac{1}{\log^A X} \end{align*} $$
$$ \begin{align*} \max_{a, q \in \mathbb{N}}\left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} \Lambda(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} \Lambda(n)\right| &\ll_{A, \varepsilon} \frac{1}{\log^A X} \end{align*} $$
 $$ \begin{align*} \max_{a, q \in \mathbb{N}}\left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} \mu(n)\right| &\ll_{A, \varepsilon} \frac{1}{\log^A X}. \end{align*} $$
$$ \begin{align*} \max_{a, q \in \mathbb{N}}\left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} \mu(n)\right| &\ll_{A, \varepsilon} \frac{1}{\log^A X}. \end{align*} $$
-
(ii) Let
 $k \geq 2$
. Set
$k \geq 2$
. Set
 $\theta = 1/3$
for
$\theta = 1/3$
for
 $k=2$
,
$k=2$
,
 $\theta =1/2$
for
$\theta =1/2$
for
 $k=3, 4$
,
$k=3, 4$
,
 $\theta =11/20$
for
$\theta =11/20$
for
 $k =5$
, and
$k =5$
, and
 $\theta = 7/12$
for
$\theta = 7/12$
for
 $k \geq 6$
. There exists
$k \geq 6$
. There exists
 $c_k> 0$
such that if
$c_k> 0$
such that if
 $X^{1-1/(100k)} \geq H_2 \geq H_1 \geq X^{\theta +\varepsilon }$
, then
$X^{1-1/(100k)} \geq H_2 \geq H_1 \geq X^{\theta +\varepsilon }$
, then  $$\begin{align*}\max_{a, q \in \mathbb{N}} \left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} d_k(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) \right| \ll_{\varepsilon, k} \frac{1}{X^{c_k}} + \frac{1}{X^{\varepsilon/1000}} \end{align*}$$
$$\begin{align*}\max_{a, q \in \mathbb{N}} \left| \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} d_k(n) - \frac{1}{H_2}\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) \right| \ll_{\varepsilon, k} \frac{1}{X^{c_k}} + \frac{1}{X^{\varepsilon/1000}} \end{align*}$$
Theorem 3.1 now follows from equation (3.1) together with Propositions 3.4 and 3.2 and Lemma 3.3.
The case
![]() $k=2$
of Proposition 3.4(ii) can be treated using classical methods on the Dirichlet divisor problem. In
$k=2$
of Proposition 3.4(ii) can be treated using classical methods on the Dirichlet divisor problem. In
![]() $k \geq 3$
cases of Proposition 3.4(ii), we write
$k \geq 3$
cases of Proposition 3.4(ii), we write
![]() $d_k(n) = \sum _{n = m_1 \dotsm m_k} 1$
, split
$d_k(n) = \sum _{n = m_1 \dotsm m_k} 1$
, split
![]() $m_j$
into dyadic intervals
$m_j$
into dyadic intervals
![]() $m_j \sim M_j \asymp X^{\alpha _j}$
and classify resulting dyadic sums using Lemma 2.20(iii). On the other hand in case of Proposition 3.4(i), we first use Heath-Brown’s identity and then Lemma 2.20(iii) to classify the resulting sums.
$m_j \sim M_j \asymp X^{\alpha _j}$
and classify resulting dyadic sums using Lemma 2.20(iii). On the other hand in case of Proposition 3.4(i), we first use Heath-Brown’s identity and then Lemma 2.20(iii) to classify the resulting sums.
For trilinear sums satisfying (
![]() $II^{\mathrm {maj}}$
) from Lemma 2.20, we shall deduce in Section 3.3 the following consequence of the work of Baker, Harman and Pintz [Reference Baker, Harman and Pintz4]. Part (ii) of the lemma will be used in handling certain type
$II^{\mathrm {maj}}$
) from Lemma 2.20, we shall deduce in Section 3.3 the following consequence of the work of Baker, Harman and Pintz [Reference Baker, Harman and Pintz4]. Part (ii) of the lemma will be used in handling certain type
![]() $II$
sums in Section 4.
$II$
sums in Section 4.
Lemma 3.5. Let
![]() $1/2 \leq \theta < 1$
and
$1/2 \leq \theta < 1$
and
![]() $\varepsilon> 0$
. Let also
$\varepsilon> 0$
. Let also
![]() $W \leq X^{\varepsilon /200}$
and
$W \leq X^{\varepsilon /200}$
and
![]() $X^{\theta +\varepsilon } \leq H_1 \leq H_2 \leq X/W^4$
. Let
$X^{\theta +\varepsilon } \leq H_1 \leq H_2 \leq X/W^4$
. Let
![]() $L, M_1 ,M_2 \geq 1$
be such that
$L, M_1 ,M_2 \geq 1$
be such that
![]() $M_j = X^{\alpha _j}$
and
$M_j = X^{\alpha _j}$
and
![]() $L M_1 M_2 \asymp X$
. Let
$L M_1 M_2 \asymp X$
. Let
![]() $a_{m_1} ,b_{m_2} ,v_\ell $
be bounded by
$a_{m_1} ,b_{m_2} ,v_\ell $
be bounded by
![]() $d_2^C$
for some
$d_2^C$
for some
![]() $C \geq 1$
.
$C \geq 1$
.
Assume that
![]() $a, q \in \mathbb {N}$
,
$a, q \in \mathbb {N}$
,
![]() $\theta \in \{11/20, 7/12, 3/5, 5/8\}$
and that
$\theta \in \{11/20, 7/12, 3/5, 5/8\}$
and that
![]() $\alpha _1, \alpha _2> 0$
obey the bounds
$\alpha _1, \alpha _2> 0$
obey the bounds
-
(i) If
(3.7)then $$ \begin{align} \max_{r \mid (a,q)}\,\, \max_{\chi \quad\pmod{\frac{q}{(a,q)}}} \sup_{W \leq |t| \leq \frac{XW^4}{H_1}} \left| \sum_{\ell \sim L/r} \frac{v_{\ell r} \chi(\ell)}{\ell^{1/2+it}}\right| \ll_C \frac{(L/r)^{1/2}}{W^{1/3}}, \end{align} $$
$$ \begin{align} \max_{r \mid (a,q)}\,\, \max_{\chi \quad\pmod{\frac{q}{(a,q)}}} \sup_{W \leq |t| \leq \frac{XW^4}{H_1}} \left| \sum_{\ell \sim L/r} \frac{v_{\ell r} \chi(\ell)}{\ell^{1/2+it}}\right| \ll_C \frac{(L/r)^{1/2}}{W^{1/3}}, \end{align} $$
 $$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_1 \\ m_j \sim M_j, \ell \sim L \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} a_{m_1} b_{m_2} v_\ell - \frac{1}{H_2} \sum_{\substack{X < m_1 m_2 \ell \leq X+H_2 \\ m_j \sim M_j, \ell \sim L \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} a_{m_1} b_{m_2} v_\ell \Big | \ll d_3(q) \frac{\log^{O_C(1)} X}{W^{1/3}}. \end{align*} $$
$$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_1 \\ m_j \sim M_j, \ell \sim L \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} a_{m_1} b_{m_2} v_\ell - \frac{1}{H_2} \sum_{\substack{X < m_1 m_2 \ell \leq X+H_2 \\ m_j \sim M_j, \ell \sim L \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} a_{m_1} b_{m_2} v_\ell \Big | \ll d_3(q) \frac{\log^{O_C(1)} X}{W^{1/3}}. \end{align*} $$
-
(ii) If
(3.8)then $$ \begin{align} \max_{r \mid (a,q)}\,\, \max_{\chi \quad\pmod{\frac{q}{(a,q)}}} \sup_{|t| \leq \frac{XW^4}{H_1}} \left| \sum_{\ell \sim L/r} \frac{v_{\ell r} \chi(\ell)}{\ell^{1/2+it}}\right| \ll_C \frac{(L/r)^{1/2}}{W^{1/3}}, \end{align} $$
$$ \begin{align} \max_{r \mid (a,q)}\,\, \max_{\chi \quad\pmod{\frac{q}{(a,q)}}} \sup_{|t| \leq \frac{XW^4}{H_1}} \left| \sum_{\ell \sim L/r} \frac{v_{\ell r} \chi(\ell)}{\ell^{1/2+it}}\right| \ll_C \frac{(L/r)^{1/2}}{W^{1/3}}, \end{align} $$
 $$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_1 \\ m_j \sim M_j, \ell \sim L \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} a_{m_1} b_{m_2} v_\ell \Big | \ll d_3(q)\frac{\log^{O_C(1)} X}{W^{1/3}}. \end{align*} $$
$$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_1 \\ m_j \sim M_j, \ell \sim L \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} a_{m_1} b_{m_2} v_\ell \Big | \ll d_3(q)\frac{\log^{O_C(1)} X}{W^{1/3}}. \end{align*} $$
For sums satisfying (
![]() $I_2^{\mathrm {maj}}$
) from Lemma 2.20, we shall use standard methods to deduce in Section 3.3 the following lemma.
$I_2^{\mathrm {maj}}$
) from Lemma 2.20, we shall use standard methods to deduce in Section 3.3 the following lemma.
Lemma 3.6. Let
![]() $\theta \in [1/2, 1)$
and
$\theta \in [1/2, 1)$
and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $W \leq X^{\varepsilon /4}$
, and let
$W \leq X^{\varepsilon /4}$
, and let
![]() $X^{\theta +\varepsilon } \leq H_1 \leq H_2 \leq X/W^4$
. Let
$X^{\theta +\varepsilon } \leq H_1 \leq H_2 \leq X/W^4$
. Let
![]() $L, M_1 ,M_2 \geq 1$
be such that
$L, M_1 ,M_2 \geq 1$
be such that
![]() $M_j = X^{\alpha _j}$
and
$M_j = X^{\alpha _j}$
and
![]() $LM_1 M_2 \asymp X$
. Let
$LM_1 M_2 \asymp X$
. Let
![]() $v_\ell $
be bounded by
$v_\ell $
be bounded by
![]() $d_2^C(\ell )$
. Assume that
$d_2^C(\ell )$
. Assume that
![]() $a, q \in \mathbb {N}$
and
$a, q \in \mathbb {N}$
and
Then
 $$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_1 \\ m_j \sim X^{\alpha_j} \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} v_\ell - \frac{1}{H_2} \sum_{\substack{X < m_1 m_2 \ell \leq X+H_2 \\ m_j \sim X^{\alpha_j} \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} v_\ell \Big | \ll d_3(q) \frac{\log^{O_C(1)} X}{W^{1/6}}. \end{align*} $$
$$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_1 \\ m_j \sim X^{\alpha_j} \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} v_\ell - \frac{1}{H_2} \sum_{\substack{X < m_1 m_2 \ell \leq X+H_2 \\ m_j \sim X^{\alpha_j} \\ m_1 m_2 \ell \equiv a \quad\pmod{q}}} v_\ell \Big | \ll d_3(q) \frac{\log^{O_C(1)} X}{W^{1/6}}. \end{align*} $$
3.1 Proof of Proposition 3.2
The bound (3.2) follows immediately from the Siegel–Walfisz theorem (1.13) and the triangle inequality.
Before turning to the proof of equation (3.3), let us discuss the choice of
![]() $\Lambda ^\sharp $
. The prime number theorem with classical error term (see, e.g., [Reference Montgomery and Vaughan54, Theorem 6.9]) gives
$\Lambda ^\sharp $
. The prime number theorem with classical error term (see, e.g., [Reference Montgomery and Vaughan54, Theorem 6.9]) gives
so that if one is interested only in the correlation of
![]() $\Lambda (n)$
with a constant function, one can select the simple approximant
$\Lambda (n)$
with a constant function, one can select the simple approximant
![]() $1$
. However, this is not sufficient even for the maximal correlation with the constant function. There is some flexibilityFootnote
7
in how to select the approximant, but (following [Reference Tao and Teräväinen61]) we use the Cramér–Granville model (1.1), which has the benefits of being a nonnegative model function and one that is known to be pseudorandom (which will be helpful in Section 9).
$1$
. However, this is not sufficient even for the maximal correlation with the constant function. There is some flexibilityFootnote
7
in how to select the approximant, but (following [Reference Tao and Teräväinen61]) we use the Cramér–Granville model (1.1), which has the benefits of being a nonnegative model function and one that is known to be pseudorandom (which will be helpful in Section 9).
Proof of equation ( 3.3 ).
It suffices to show that, for any
![]() $a, q \in \mathbb {N}$
and any
$a, q \in \mathbb {N}$
and any
![]() $H_2 \in [X/\log ^A X, X]$
, we have
$H_2 \in [X/\log ^A X, X]$
, we have
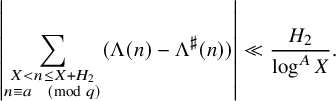 $$\begin{align*}\left| \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} (\Lambda(n) - \Lambda^\sharp(n))\right| \ll \frac{H_2}{\log^A X}. \end{align*}$$
$$\begin{align*}\left| \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} (\Lambda(n) - \Lambda^\sharp(n))\right| \ll \frac{H_2}{\log^A X}. \end{align*}$$
We can clearly assume that
![]() $q < R$
and
$q < R$
and
![]() $(a, q) = 1$
.
$(a, q) = 1$
.
Let
![]() $D=\exp ((\log X)^{3/5})$
. By the fundamental lemma of the sieve (see, e.g., [Reference Iwaniec and Kowalski37, Fundamental Lemma 6.3 with
$D=\exp ((\log X)^{3/5})$
. By the fundamental lemma of the sieve (see, e.g., [Reference Iwaniec and Kowalski37, Fundamental Lemma 6.3 with
![]() $y=D,z=R$
, and
$y=D,z=R$
, and
![]() $\kappa =1$
]), there exist real numbers
$\kappa =1$
]), there exist real numbers
![]() $\lambda _d^{+}\in [-1,1]$
such that, for any
$\lambda _d^{+}\in [-1,1]$
such that, for any
![]() $H\geq 2$
,
$H\geq 2$
,
![]() $q<R$
, and
$q<R$
, and
![]() $a \in \mathbb {N}$
with
$a \in \mathbb {N}$
with
![]() $(a,q)=1$
, we have
$(a,q)=1$
, we have
 $$ \begin{align*} \sum_{\substack{X<n\leq X+H\\n=a(q)}}\Lambda^{\sharp}(n)&\leq\frac{P(R)}{\varphi(P(R))}\sum_{\substack{d\leq D \\ d \mid P(R)}} \lambda_d^{+}\sum_{\substack{X<n\leq X+H\\n=a(q)\\d\mid n}}1\\ &=\prod_{p<R}\left(1-\frac{1}{p}\right)^{-1}\sum_{\substack{d\leq D\\d \mid P(R) \\ (d,q)=1}}\lambda_d^{+}\frac{H}{dq}+O(D\log R)\\ &=\frac{H}{\varphi(q)}\left(1+O\left(\exp\left(-\frac{\log D}{\log R}\right)\right)\right) +O(D\log R), \end{align*} $$
$$ \begin{align*} \sum_{\substack{X<n\leq X+H\\n=a(q)}}\Lambda^{\sharp}(n)&\leq\frac{P(R)}{\varphi(P(R))}\sum_{\substack{d\leq D \\ d \mid P(R)}} \lambda_d^{+}\sum_{\substack{X<n\leq X+H\\n=a(q)\\d\mid n}}1\\ &=\prod_{p<R}\left(1-\frac{1}{p}\right)^{-1}\sum_{\substack{d\leq D\\d \mid P(R) \\ (d,q)=1}}\lambda_d^{+}\frac{H}{dq}+O(D\log R)\\ &=\frac{H}{\varphi(q)}\left(1+O\left(\exp\left(-\frac{\log D}{\log R}\right)\right)\right) +O(D\log R), \end{align*} $$
and also by the fundamental lemma we have a lower bound of the same shape. Hence, for
![]() $H\geq X^{\varepsilon }$
we have
$H\geq X^{\varepsilon }$
we have
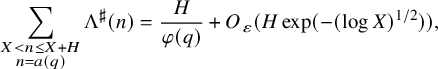 $$ \begin{align} \sum_{\substack{X<n\leq X+H\\n=a(q)}}\Lambda^{\sharp}(n)=\frac{H}{\varphi(q)}+O_{\varepsilon}(H\exp(-(\log X)^{1/2})), \end{align} $$
$$ \begin{align} \sum_{\substack{X<n\leq X+H\\n=a(q)}}\Lambda^{\sharp}(n)=\frac{H}{\varphi(q)}+O_{\varepsilon}(H\exp(-(\log X)^{1/2})), \end{align} $$
so equation (3.3) follows by the Siegel–Walfisz theorem and the triangle inequality.
Remark 3.7. One could improve the error term in equation (3.3) by adjusting the approximant
![]() $\Lambda ^\sharp $
to account for a potential Siegel zero; see, for instance, [Reference Iwaniec and Kowalski37, Theorem 5.27] or [Reference Tao and Teräväinen61, Proposition 2.2]. However, we will not do so here.
$\Lambda ^\sharp $
to account for a potential Siegel zero; see, for instance, [Reference Iwaniec and Kowalski37, Theorem 5.27] or [Reference Tao and Teräväinen61, Proposition 2.2]. However, we will not do so here.
Before turning to the proof of equation (3.4), let us discuss the construction of the approximant
![]() $d_k^\sharp $
which is a somewhat nontrivial task. The classical Dirichlet hyperbola method gives the asymptotic
$d_k^\sharp $
which is a somewhat nontrivial task. The classical Dirichlet hyperbola method gives the asymptotic
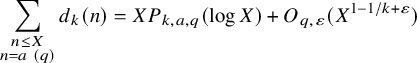 $$ \begin{align} \sum_{\substack{n \leq X\\ n=a\ (q)}} d_k(n) = X P_{k,a,q}(\log X) + O_{q,\varepsilon}( X^{1-1/k+\varepsilon} ) \end{align} $$
$$ \begin{align} \sum_{\substack{n \leq X\\ n=a\ (q)}} d_k(n) = X P_{k,a,q}(\log X) + O_{q,\varepsilon}( X^{1-1/k+\varepsilon} ) \end{align} $$
for any fixed
![]() $a,q$
, any
$a,q$
, any
![]() $\varepsilon>0$
, and some explicit polynomial
$\varepsilon>0$
, and some explicit polynomial
![]() $P_{k,a,q}$
of degree
$P_{k,a,q}$
of degree
![]() $k-1$
with coefficients depending only on
$k-1$
with coefficients depending only on
![]() $k,a,q$
. Better error terms are known here; see, for example, [Reference Ivić36, Section 13].
$k,a,q$
. Better error terms are known here; see, for example, [Reference Ivić36, Section 13].
From equation (3.12), the triangle inequality, and Taylor expansion one has
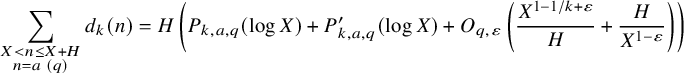 $$ \begin{align*}\sum_{\substack{X < n \leq X+H\\ n=a\ (q)}} d_k(n) = H \left(P_{k,a,q}(\log X) + P^{\prime}_{k,a,q}(\log X) + O_{q,\varepsilon}\left( \frac{X^{1-1/k+\varepsilon}}{H} + \frac{H}{X^{1-\varepsilon}} \right) \right)\end{align*} $$
$$ \begin{align*}\sum_{\substack{X < n \leq X+H\\ n=a\ (q)}} d_k(n) = H \left(P_{k,a,q}(\log X) + P^{\prime}_{k,a,q}(\log X) + O_{q,\varepsilon}\left( \frac{X^{1-1/k+\varepsilon}}{H} + \frac{H}{X^{1-\varepsilon}} \right) \right)\end{align*} $$
for any
![]() $\varepsilon> 0$
whenever
$\varepsilon> 0$
whenever
![]() $2 \leq H \leq X$
.
$2 \leq H \leq X$
.
Hence, we have to choose the approximant
![]() $d_k^\sharp $
to also obey estimates such as
$d_k^\sharp $
to also obey estimates such as
 $$ \begin{align} \sum_{\substack{X \leq n < X+H\\ n=a\ (q)}} d^\sharp_k(n) = H \left(P_{k,a,q}(\log X) + P^{\prime}_{k,a,q}(\log X) + O_\varepsilon(X^{-\kappa_k} + HX^{\varepsilon-1}) \right) \end{align} $$
$$ \begin{align} \sum_{\substack{X \leq n < X+H\\ n=a\ (q)}} d^\sharp_k(n) = H \left(P_{k,a,q}(\log X) + P^{\prime}_{k,a,q}(\log X) + O_\varepsilon(X^{-\kappa_k} + HX^{\varepsilon-1}) \right) \end{align} $$
for some
![]() $\kappa _k>0$
, with exactly the same choice of polynomial
$\kappa _k>0$
, with exactly the same choice of polynomial
![]() $P_{k,a,q}$
.
$P_{k,a,q}$
.
The delta method of Duke, Friedlander and Iwaniec [Reference Duke, Friedlander and Iwaniec9] can be used to build an approximant of a Fourier-analytic nature, basically by isolating the major arc components of
![]() $d_k$
; see [Reference Ivić35], [Reference Conrey and Gonek5], [Reference Ng and Thom55] and [Reference Matomäki, Radziwiłł and Tao47, Proposition 4.2] for relevant calculations in this direction. However, the approximant that is (implicitly) constructed in these papers is very complicated, and somewhat difficult to deal with for our purposes (for instance, it is not evident whether it is nonnegative).
$d_k$
; see [Reference Ivić35], [Reference Conrey and Gonek5], [Reference Ng and Thom55] and [Reference Matomäki, Radziwiłł and Tao47, Proposition 4.2] for relevant calculations in this direction. However, the approximant that is (implicitly) constructed in these papers is very complicated, and somewhat difficult to deal with for our purposes (for instance, it is not evident whether it is nonnegative).
The simpler approximant
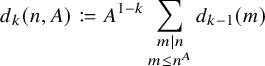
was recently proposed by Andrade and Smith [Reference Andrade and Smith1] for various choices of parameter
![]() $0 < A < 1$
. Unfortunately, the polynomial
$0 < A < 1$
. Unfortunately, the polynomial
![]() $P_{k,a,q,A}(\log X)$
associated to this approximant usually only agrees with
$P_{k,a,q,A}(\log X)$
associated to this approximant usually only agrees with
![]() $P_{k,a,q}(\log X)$
to leading order (see [Reference Andrade and Smith1, Theorem 2.1]), and so with this approximant one cannot hope to get polynomial saving like in our Theorem 1.1(iii).
$P_{k,a,q}(\log X)$
to leading order (see [Reference Andrade and Smith1, Theorem 2.1]), and so with this approximant one cannot hope to get polynomial saving like in our Theorem 1.1(iii).
Our approximant (1.2) with
![]() $P_m(t)$
as in equation (1.3) can be seen as a more complicated variant of the Andrade–Smith approximant. Note that the constraint
$P_m(t)$
as in equation (1.3) can be seen as a more complicated variant of the Andrade–Smith approximant. Note that the constraint
![]() $m \leq R_k^{2k-2}$
in equation (1.2) is redundant, as
$m \leq R_k^{2k-2}$
in equation (1.2) is redundant, as
![]() $P_m$
vanishes for
$P_m$
vanishes for
![]() $m> R_k^{2k-2}$
. Note also that (by adjusting the value of
$m> R_k^{2k-2}$
. Note also that (by adjusting the value of
![]() $c_{k,d,D}$
in Theorem 1.1) one could take
$c_{k,d,D}$
in Theorem 1.1) one could take
![]() $R_k$
to be any sufficiently small power of X, and that, for any
$R_k$
to be any sufficiently small power of X, and that, for any
![]() $n \ll X$
,
$n \ll X$
,
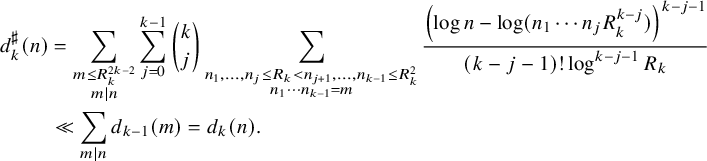 $$ \begin{align} d_k^\sharp(n) &= \sum_{\substack{m \leq R_k^{2k-2}\\ m|n}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dots,n_j \leq R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2\\ n_1 \dotsm n_{k-1} = m}} \frac{\left(\log n - \log(n_1 \dotsm n_j R_k^{k-j})\right)^{k-j-1}}{(k-j-1)! \log^{k-j-1} R_k} \nonumber\\ &\ll \sum_{m \mid n} d_{k-1}(m) = d_k(n). \end{align} $$
$$ \begin{align} d_k^\sharp(n) &= \sum_{\substack{m \leq R_k^{2k-2}\\ m|n}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dots,n_j \leq R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2\\ n_1 \dotsm n_{k-1} = m}} \frac{\left(\log n - \log(n_1 \dotsm n_j R_k^{k-j})\right)^{k-j-1}}{(k-j-1)! \log^{k-j-1} R_k} \nonumber\\ &\ll \sum_{m \mid n} d_{k-1}(m) = d_k(n). \end{align} $$
Recall we chose
![]() $R_k = X^{\frac {1}{10k}}$
in equation (1.2). The motivation for our approximant
$R_k = X^{\frac {1}{10k}}$
in equation (1.2). The motivation for our approximant
![]() $d_k^\sharp $
can be seen by noting that, sorting a factorization
$d_k^\sharp $
can be seen by noting that, sorting a factorization
![]() $n = n_1 \dotsm n_k$
into terms
$n = n_1 \dotsm n_k$
into terms
![]() $n_1,\dotsc ,n_j \leq R_k$
and terms
$n_1,\dotsc ,n_j \leq R_k$
and terms
![]() $n_{j+1},\dots ,n_k> R_k$
, we get the generalized Dirichlet hyperbola identity
$n_{j+1},\dots ,n_k> R_k$
, we get the generalized Dirichlet hyperbola identity
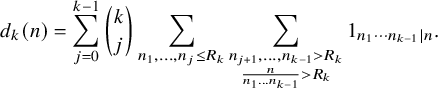 $$ \begin{align} d_k(n) = \sum_{j=0}^{k-1} \binom{k}{j} \sum_{n_1,\dots,n_j \leq R_k} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{n}{n_1\dots n_{k-1}} > R_k}} 1_{n_1 \dotsm n_{k-1}|n}. \end{align} $$
$$ \begin{align} d_k(n) = \sum_{j=0}^{k-1} \binom{k}{j} \sum_{n_1,\dots,n_j \leq R_k} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{n}{n_1\dots n_{k-1}} > R_k}} 1_{n_1 \dotsm n_{k-1}|n}. \end{align} $$
The polynomials
![]() $P_m(t)$
are chosen to match with the contribution from the sum over
$P_m(t)$
are chosen to match with the contribution from the sum over
![]() $n_{j+1}, \dotsc , n_{k-1}$
as can be seen from the proof of equation (3.4) that we now give.
$n_{j+1}, \dotsc , n_{k-1}$
as can be seen from the proof of equation (3.4) that we now give.
Proof of equation (3.4).
It suffices to show that, for any
![]() $k \geq 2$
, any
$k \geq 2$
, any
![]() $a, q \in \mathbb {N}$
, and any
$a, q \in \mathbb {N}$
, and any
![]() ${H_2 \in [X^{1-1/(50k)}, X]}$
, we have
${H_2 \in [X^{1-1/(50k)}, X]}$
, we have
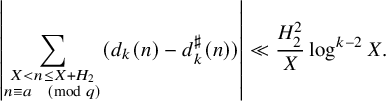 $$\begin{align*}\left| \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} (d_k(n) - d_k^\sharp(n))\right| \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align*}$$
$$\begin{align*}\left| \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} (d_k(n) - d_k^\sharp(n))\right| \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align*}$$
Since
![]() $d_k(n) = O_\varepsilon (n^\varepsilon )$
, we can clearly assume that
$d_k(n) = O_\varepsilon (n^\varepsilon )$
, we can clearly assume that
![]() $q \leq X^{\frac {1}{40k}}$
. Using equation (3.15), we obtain
$q \leq X^{\frac {1}{40k}}$
. Using equation (3.15), we obtain
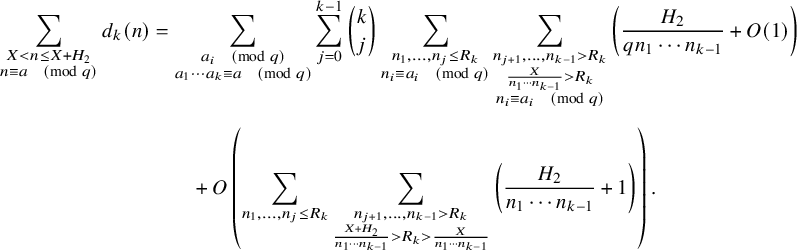 $$ \begin{align*} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) &= \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dotsc,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{X}{n_1\dotsm n_{k-1}} > R_k \\ n_i \equiv a_i \quad\pmod{q}}} \left(\frac{H_2}{q n_1 \dotsm n_{k-1}} + O(1)\right) \\[5pt] & \qquad + O\left(\sum_{n_1,\dots,n_j \leq R_k} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1} > R_k \\ \frac{X+H_2}{n_1\dotsm n_{k-1}} > R_k > \frac{X}{n_1\dotsm n_{k-1}}}} \left(\frac{H_2}{n_1 \dotsm n_{k-1}} + 1 \right)\right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) &= \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dotsc,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{X}{n_1\dotsm n_{k-1}} > R_k \\ n_i \equiv a_i \quad\pmod{q}}} \left(\frac{H_2}{q n_1 \dotsm n_{k-1}} + O(1)\right) \\[5pt] & \qquad + O\left(\sum_{n_1,\dots,n_j \leq R_k} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1} > R_k \\ \frac{X+H_2}{n_1\dotsm n_{k-1}} > R_k > \frac{X}{n_1\dotsm n_{k-1}}}} \left(\frac{H_2}{n_1 \dotsm n_{k-1}} + 1 \right)\right). \end{align*} $$
Let us consider the two error terms. The first error term contributes, using the inequality
![]() ${1 < X/(R_k n_1 \dotsm n_{k-1})}$
,
${1 < X/(R_k n_1 \dotsm n_{k-1})}$
,
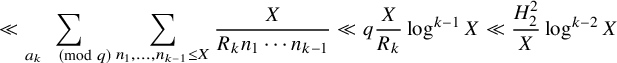 $$\begin{align*}\ll \sum_{a_k \quad\pmod{q}} \sum_{n_1, \dotsc, n_{k-1} \leq X} \frac{X}{R_k n_1 \dotsm n_{k-1}} \ll q \frac{X}{R_k} \log^{k-1} X \ll \frac{H_2^2}{X} \log^{k-2} X \end{align*}$$
$$\begin{align*}\ll \sum_{a_k \quad\pmod{q}} \sum_{n_1, \dotsc, n_{k-1} \leq X} \frac{X}{R_k n_1 \dotsm n_{k-1}} \ll q \frac{X}{R_k} \log^{k-1} X \ll \frac{H_2^2}{X} \log^{k-2} X \end{align*}$$
since
![]() $q \leq X^{\frac {1}{40k}}$
,
$q \leq X^{\frac {1}{40k}}$
,
![]() $R_k = X^{\frac {1}{10k}},$
and
$R_k = X^{\frac {1}{10k}},$
and
![]() $H_2 \geq X^{1-\frac {1}{50k}}$
. The second error term contributes, using
$H_2 \geq X^{1-\frac {1}{50k}}$
. The second error term contributes, using
![]() $n_1 \dotsm n_{k-1} \asymp X/R_k$
and Shiu’s bound (Lemma 2.17),
$n_1 \dotsm n_{k-1} \asymp X/R_k$
and Shiu’s bound (Lemma 2.17),
 $$\begin{align*}\ll \sum_{\substack{n_1, \dotsc, n_{k-1} \leq 2X \\ \frac{X}{R_k} < n_1 \dotsm n_{k-1} \leq \frac{X+H_2}{R_k}}} \frac{R_k H_2}{X} = \frac{R_k H_2}{X} \sum_{\frac{X}{R_k} < n < \frac{X+H_2}{R_k}} d_{k-1}(n) \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align*}$$
$$\begin{align*}\ll \sum_{\substack{n_1, \dotsc, n_{k-1} \leq 2X \\ \frac{X}{R_k} < n_1 \dotsm n_{k-1} \leq \frac{X+H_2}{R_k}}} \frac{R_k H_2}{X} = \frac{R_k H_2}{X} \sum_{\frac{X}{R_k} < n < \frac{X+H_2}{R_k}} d_{k-1}(n) \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align*}$$
Hence,
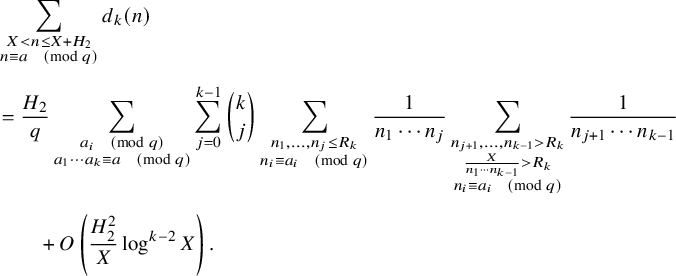 $$ \begin{align} &\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) \nonumber\\[5pt] & = \frac{H_2}{q} \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dotsc,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_1 \dotsm n_j} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{X}{n_1\dotsm n_{k-1}} > R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_{j+1} \dotsm n_{k-1}} \nonumber\\[5pt] &\qquad + O\left(\frac{H_2^2}{X} \log^{k-2} X\right). \end{align} $$
$$ \begin{align} &\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) \nonumber\\[5pt] & = \frac{H_2}{q} \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dotsc,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_1 \dotsm n_j} \sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{X}{n_1\dotsm n_{k-1}} > R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_{j+1} \dotsm n_{k-1}} \nonumber\\[5pt] &\qquad + O\left(\frac{H_2^2}{X} \log^{k-2} X\right). \end{align} $$
For any
![]() $B \geq A \geq 1$
, we have
$B \geq A \geq 1$
, we have
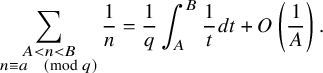 $$\begin{align*}\sum_{\substack{A < n < B \\ n\equiv a \quad\pmod{q}}} \frac{1}{n} = \frac{1}{q} \int_A^B \frac{1}{t} dt + O\left(\frac{1}{A}\right). \end{align*}$$
$$\begin{align*}\sum_{\substack{A < n < B \\ n\equiv a \quad\pmod{q}}} \frac{1}{n} = \frac{1}{q} \int_A^B \frac{1}{t} dt + O\left(\frac{1}{A}\right). \end{align*}$$
Applying this
![]() $k-1-j$
times, we see thatFootnote
8
$k-1-j$
times, we see thatFootnote
8
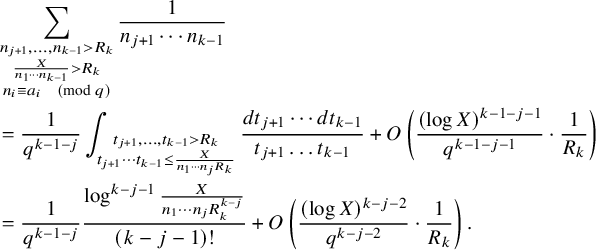 $$ \begin{align} &\sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{X}{n_1 \dotsm n_{k-1}} > R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_{j+1} \dotsm n_{k-1}} \nonumber\\ & = \frac{1}{q^{k-1-j}} \int_{\substack{t_{j+1},\dots,t_{k-1} > R_k \\ t_{j+1} \dotsm t_{k-1} \leq \frac{X}{n_1\dotsm n_j R_k} }} \frac{dt_{j+1} \dotsm dt_{k-1}}{t_{j+1} \dots t_{k-1}} + O\left(\frac{(\log X)^{k-1-j-1}}{q^{k-1-j-1}} \cdot \frac{1}{R_k}\right)\nonumber\\ &= \frac{1}{q^{k-1-j}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}}}{(k-j-1)!} + O\left(\frac{(\log X)^{k-j-2}}{q^{k-j-2}} \cdot \frac{1}{R_k}\right). \end{align} $$
$$ \begin{align} &\sum_{\substack{n_{j+1}, \dotsc, n_{k-1}> R_k \\ \frac{X}{n_1 \dotsm n_{k-1}} > R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_{j+1} \dotsm n_{k-1}} \nonumber\\ & = \frac{1}{q^{k-1-j}} \int_{\substack{t_{j+1},\dots,t_{k-1} > R_k \\ t_{j+1} \dotsm t_{k-1} \leq \frac{X}{n_1\dotsm n_j R_k} }} \frac{dt_{j+1} \dotsm dt_{k-1}}{t_{j+1} \dots t_{k-1}} + O\left(\frac{(\log X)^{k-1-j-1}}{q^{k-1-j-1}} \cdot \frac{1}{R_k}\right)\nonumber\\ &= \frac{1}{q^{k-1-j}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}}}{(k-j-1)!} + O\left(\frac{(\log X)^{k-j-2}}{q^{k-j-2}} \cdot \frac{1}{R_k}\right). \end{align} $$
Since
![]() $R_k = X^{\frac {1}{10k}}, q \leq X^{\frac {1}{40k}}$
and
$R_k = X^{\frac {1}{10k}}, q \leq X^{\frac {1}{40k}}$
and
![]() $H_2 \geq X^{1-\frac {1}{50k}},$
the error term contributes to equation (3.16)
$H_2 \geq X^{1-\frac {1}{50k}},$
the error term contributes to equation (3.16)
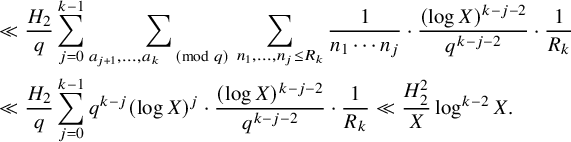 $$ \begin{align*} &\ll \frac{H_2}{q} \sum_{j=0}^{k-1} \sum_{\substack{a_{j+1}, \dotsc, a_k \quad\pmod{q}}}\, \sum_{\substack{n_1,\dotsc,n_j \leq R_k}} \frac{1}{n_1 \dotsm n_j} \cdot \frac{(\log X)^{k-j-2}}{q^{k-j-2}} \cdot \frac{1}{R_k} \\ &\ll \frac{H_2}{q} \sum_{j=0}^{k-1} q^{k-j} (\log X)^j \cdot \frac{(\log X)^{k-j-2}}{q^{k-j-2}} \cdot \frac{1}{R_k} \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align*} $$
$$ \begin{align*} &\ll \frac{H_2}{q} \sum_{j=0}^{k-1} \sum_{\substack{a_{j+1}, \dotsc, a_k \quad\pmod{q}}}\, \sum_{\substack{n_1,\dotsc,n_j \leq R_k}} \frac{1}{n_1 \dotsm n_j} \cdot \frac{(\log X)^{k-j-2}}{q^{k-j-2}} \cdot \frac{1}{R_k} \\ &\ll \frac{H_2}{q} \sum_{j=0}^{k-1} q^{k-j} (\log X)^j \cdot \frac{(\log X)^{k-j-2}}{q^{k-j-2}} \cdot \frac{1}{R_k} \ll \frac{H_2^2}{X} \log^{k-2} X. \end{align*} $$
Hence, equations (3.16) and (3.17) give
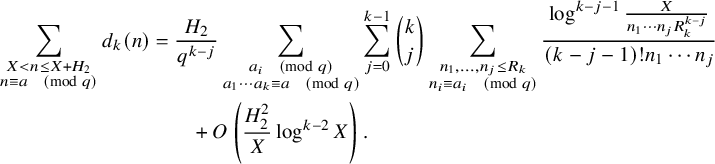 $$ \begin{align*} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) & = \frac{H_2}{q^{k-j}} \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dotsc,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}}}{(k-j-1)! n_1 \dotsm n_j} \\ &\qquad + O\left(\frac{H_2^2}{X} \log^{k-2} X\right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k(n) & = \frac{H_2}{q^{k-j}} \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dotsc,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}}}{(k-j-1)! n_1 \dotsm n_j} \\ &\qquad + O\left(\frac{H_2^2}{X} \log^{k-2} X\right). \end{align*} $$
On the other hand, by definition,
 $$ \begin{align*} &\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n) \\ &= \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dots,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}} + O\left(\frac{H_2}{X} \log^{k-j-2} X\right)}{(k-j-1)! \log^{k-j-1} R_k} \\ & \qquad \cdot \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2 \\ n_i \equiv a_i \quad\pmod{q}}} \left(\frac{H_2}{q n_1 \dotsm n_{k-1}} + O(1)\right) \\ & = \frac{H_2}{q} \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dots,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}}}{(k-j-1)! \log^{k-j-1} R_k} \\ & \qquad \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2 \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_1 \dotsm n_{k-1}}\\ & + O\left(\sum_{a_k \quad\pmod{q}} \sum_{j=0}^{k-1} \sum_{\substack{n_1,\dots,n_j \leq R_k}} \frac{H_2}{X \log X} \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2}} \left(\frac{H_2}{q n_1 \dotsm n_{k-1}} + 1\right)\right) \\ &+ O\left(\sum_{a_k \quad\pmod{q}} \sum_{j=0}^{k-1} \sum_{\substack{n_1,\dots,n_j \leq R_k}} \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2}} 1 \right). \end{align*} $$
$$ \begin{align*} &\sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n) \\ &= \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dots,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}} + O\left(\frac{H_2}{X} \log^{k-j-2} X\right)}{(k-j-1)! \log^{k-j-1} R_k} \\ & \qquad \cdot \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2 \\ n_i \equiv a_i \quad\pmod{q}}} \left(\frac{H_2}{q n_1 \dotsm n_{k-1}} + O(1)\right) \\ & = \frac{H_2}{q} \sum_{\substack{a_i \quad\pmod{q} \\a_1 \dotsm a_k \equiv a \quad\pmod{q}}} \sum_{j=0}^{k-1} \binom{k}{j} \sum_{\substack{n_1,\dots,n_j \leq R_k \\ n_i \equiv a_i \quad\pmod{q}}} \frac{\log^{k-j-1} \frac{X}{n_1 \dotsm n_j R_k^{k-j}}}{(k-j-1)! \log^{k-j-1} R_k} \\ & \qquad \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2 \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_1 \dotsm n_{k-1}}\\ & + O\left(\sum_{a_k \quad\pmod{q}} \sum_{j=0}^{k-1} \sum_{\substack{n_1,\dots,n_j \leq R_k}} \frac{H_2}{X \log X} \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2}} \left(\frac{H_2}{q n_1 \dotsm n_{k-1}} + 1\right)\right) \\ &+ O\left(\sum_{a_k \quad\pmod{q}} \sum_{j=0}^{k-1} \sum_{\substack{n_1,\dots,n_j \leq R_k}} \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2}} 1 \right). \end{align*} $$
The error terms contribute
 $$\begin{align*}\ll \frac{H_2^2}{X} \log^{k-2} X + q \frac{H_2}{X \log X} R_k^{2(k-1)} + qR_k^{2(k-1)} \ll \frac{H_2^2}{X} \log^{k-2} X + qX^{1/2} \end{align*}$$
$$\begin{align*}\ll \frac{H_2^2}{X} \log^{k-2} X + q \frac{H_2}{X \log X} R_k^{2(k-1)} + qR_k^{2(k-1)} \ll \frac{H_2^2}{X} \log^{k-2} X + qX^{1/2} \end{align*}$$
and in the main term
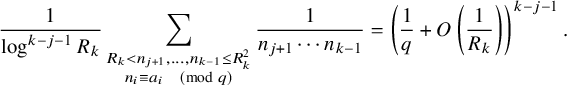 $$ \begin{align*} \frac{1}{\log^{k-j-1} R_k} \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2 \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_{j+1} \dotsm n_{k-1}} &= \left(\frac{1}{q}+O\left(\frac{1}{R_k}\right)\right)^{k-j-1}. \end{align*} $$
$$ \begin{align*} \frac{1}{\log^{k-j-1} R_k} \sum_{\substack{R_k < n_{j+1},\dots,n_{k-1} \leq R_k^2 \\ n_i \equiv a_i \quad\pmod{q}}} \frac{1}{n_{j+1} \dotsm n_{k-1}} &= \left(\frac{1}{q}+O\left(\frac{1}{R_k}\right)\right)^{k-j-1}. \end{align*} $$
The claim follows since
![]() $R_k = X^{\frac {1}{10k}}$
and
$R_k = X^{\frac {1}{10k}}$
and
![]() $q \leq X^{\frac {1}{40k}}$
.
$q \leq X^{\frac {1}{40k}}$
.
3.2 Proof of Lemma 3.3
Note first that the claims are trivial unless
![]() $q \leq X^{1/80}$
. For part (ii), note that, for
$q \leq X^{1/80}$
. For part (ii), note that, for
![]() $j=1, 2$
,
$j=1, 2$
,
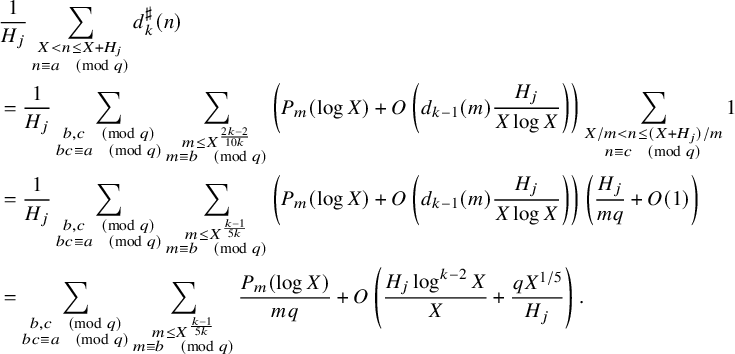 $$ \begin{align*} &\frac{1}{H_j}\sum_{\substack{X < n \leq X+H_j \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n)\\ &= \frac{1}{H_j} \sum_{\substack{b, c \quad\pmod{q} \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \leq X^{\frac{2k-2}{10k}} \\ m \equiv b \quad\pmod{q}}} \left(P_m(\log X) + O\left(d_{k-1}(m) \frac{H_j}{X \log X}\right)\right) \sum_{\substack{X/m < n \leq (X+H_j)/m \\ n \equiv c \quad\pmod{q}}} 1 \\ &= \frac{1}{H_j} \sum_{\substack{b, c \quad\pmod{q} \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \leq X^{\frac{k-1}{5k}} \\ m \equiv b \quad\pmod{q}}} \left(P_m(\log X) + O\left(d_{k-1}(m) \frac{H_j}{X \log X}\right)\right) \left(\frac{H_j}{mq} + O(1)\right) \\ & = \sum_{\substack{b, c \quad\pmod{q} \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \leq X^{\frac{k-1}{5k}} \\ m \equiv b \quad\pmod{q}}} \frac{P_m(\log X)}{mq} + O\left(\frac{H_j \log^{k-2} X}{X} + \frac{qX^{1/5}}{H_j}\right). \end{align*} $$
$$ \begin{align*} &\frac{1}{H_j}\sum_{\substack{X < n \leq X+H_j \\ n \equiv a \quad\pmod{q}}} d_k^\sharp(n)\\ &= \frac{1}{H_j} \sum_{\substack{b, c \quad\pmod{q} \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \leq X^{\frac{2k-2}{10k}} \\ m \equiv b \quad\pmod{q}}} \left(P_m(\log X) + O\left(d_{k-1}(m) \frac{H_j}{X \log X}\right)\right) \sum_{\substack{X/m < n \leq (X+H_j)/m \\ n \equiv c \quad\pmod{q}}} 1 \\ &= \frac{1}{H_j} \sum_{\substack{b, c \quad\pmod{q} \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \leq X^{\frac{k-1}{5k}} \\ m \equiv b \quad\pmod{q}}} \left(P_m(\log X) + O\left(d_{k-1}(m) \frac{H_j}{X \log X}\right)\right) \left(\frac{H_j}{mq} + O(1)\right) \\ & = \sum_{\substack{b, c \quad\pmod{q} \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \leq X^{\frac{k-1}{5k}} \\ m \equiv b \quad\pmod{q}}} \frac{P_m(\log X)}{mq} + O\left(\frac{H_j \log^{k-2} X}{X} + \frac{qX^{1/5}}{H_j}\right). \end{align*} $$
The claim follows by subtracting this for
![]() $j =1, 2$
. Part (i) follows directly from equation (3.11) applied with
$j =1, 2$
. Part (i) follows directly from equation (3.11) applied with
![]() $H\in \{H_1,H_2\}$
and the triangle inequality.
$H\in \{H_1,H_2\}$
and the triangle inequality.
3.3 Proof of Lemmas 3.5 and 3.6
We first make a standard reduction to studying averages of Dirichlet polynomials.
Lemma 3.8. Let
![]() $W \leq X^{1/100}$
. Let
$W \leq X^{1/100}$
. Let
![]() $|a_n| \leq d_2(n)^C$
for some
$|a_n| \leq d_2(n)^C$
for some
![]() $C \geq 1$
, and let
$C \geq 1$
, and let
![]() $A(s, \chi ):= \sum _{c_1 X < n \leq c_2 X} a_n \chi (n) n^{-s}$
for some fixed
$A(s, \chi ):= \sum _{c_1 X < n \leq c_2 X} a_n \chi (n) n^{-s}$
for some fixed
![]() $c_2> c_1 > 0$
. Let
$c_2> c_1 > 0$
. Let
![]() $X^{1/2} \leq H_1 \leq H_2 \leq X/W^4$
and
$X^{1/2} \leq H_1 \leq H_2 \leq X/W^4$
and
![]() $(a, q) = 1$
.
$(a, q) = 1$
.
-
(i) One has
 $$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} a_n - \frac{1}{H_2} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} a_n \Big | \ll \frac{\log^{O_C(1)} X}{W^2} \\[5pt] & \qquad + \frac{\log X}{X^{1/2}} \max_{\frac{X}{H_1} \leq T \leq \frac{XW^4}{H_1}} \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \frac{X/H_1}{T} \int_{\substack{W \leq |t|\leq T}} |A(\tfrac{1}{2}+it, \chi)| \ dt. \end{align*} $$
$$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} a_n - \frac{1}{H_2} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} a_n \Big | \ll \frac{\log^{O_C(1)} X}{W^2} \\[5pt] & \qquad + \frac{\log X}{X^{1/2}} \max_{\frac{X}{H_1} \leq T \leq \frac{XW^4}{H_1}} \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \frac{X/H_1}{T} \int_{\substack{W \leq |t|\leq T}} |A(\tfrac{1}{2}+it, \chi)| \ dt. \end{align*} $$
-
(ii) One has
 $$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} a_n\Big | \ll \frac{\log^{O_C(1)} X}{W^2} \\[5pt] & \qquad + \frac{\log X}{X^{1/2}} \max_{\frac{X}{H_1} \leq T \leq \frac{XW^4}{H_1}} \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \frac{X/H_1}{T} \int_{\substack{|t|\leq T}} |A(\tfrac{1}{2}+it, \chi)| \ dt. \end{align*} $$
$$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} a_n\Big | \ll \frac{\log^{O_C(1)} X}{W^2} \\[5pt] & \qquad + \frac{\log X}{X^{1/2}} \max_{\frac{X}{H_1} \leq T \leq \frac{XW^4}{H_1}} \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \frac{X/H_1}{T} \int_{\substack{|t|\leq T}} |A(\tfrac{1}{2}+it, \chi)| \ dt. \end{align*} $$
Proof. Let us first consider part (i). We begin by using the orthogonality of characters and Perron’s formula (see, e.g., [Reference Montgomery and Vaughan54, Corollary 5.3]) to get that, for
![]() $j = 1, 2$
,
$j = 1, 2$
,
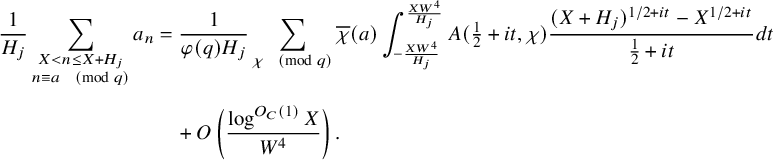 $$ \begin{align*} \frac{1}{H_j} \sum_{\substack{X < n \leq X+H_j \\ n \equiv a \quad\pmod{q}}} a_n &= \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \overline{\chi}(a) \int_{-\frac{XW^4}{H_j}}^{\frac{XW^4}{H_j}} A(\tfrac{1}{2}+it, \chi) \frac{(X+H_j)^{1/2+it}-X^{1/2+it}}{\tfrac{1}{2}+it} dt\\[5pt] &\quad+ O\left(\frac{\log^{O_C(1)} X}{W^4}\right). \end{align*} $$
$$ \begin{align*} \frac{1}{H_j} \sum_{\substack{X < n \leq X+H_j \\ n \equiv a \quad\pmod{q}}} a_n &= \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \overline{\chi}(a) \int_{-\frac{XW^4}{H_j}}^{\frac{XW^4}{H_j}} A(\tfrac{1}{2}+it, \chi) \frac{(X+H_j)^{1/2+it}-X^{1/2+it}}{\tfrac{1}{2}+it} dt\\[5pt] &\quad+ O\left(\frac{\log^{O_C(1)} X}{W^4}\right). \end{align*} $$
The ‘main term’ comes from (only
![]() $\chi _0$
contributes to actual main terms)
$\chi _0$
contributes to actual main terms)
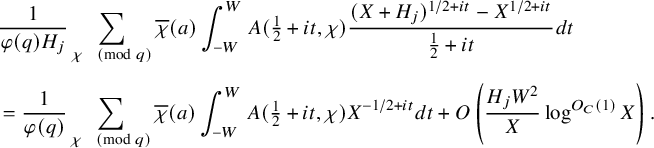 $$ \begin{align*} &\frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \overline{\chi}(a) \int_{-W}^{W} A(\tfrac{1}{2}+it, \chi) \frac{ (X+H_j)^{1/2+it}-X^{1/2+it} } {\frac{1}{2}+it} dt \\[5pt] &= \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \overline{\chi}(a) \int_{-W}^{W} A(\tfrac{1}{2}+it, \chi) X^{-1/2+it} dt + O\left(\frac{H_j W^2}{X} \log^{O_C(1)} X\right). \end{align*} $$
$$ \begin{align*} &\frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \overline{\chi}(a) \int_{-W}^{W} A(\tfrac{1}{2}+it, \chi) \frac{ (X+H_j)^{1/2+it}-X^{1/2+it} } {\frac{1}{2}+it} dt \\[5pt] &= \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \overline{\chi}(a) \int_{-W}^{W} A(\tfrac{1}{2}+it, \chi) X^{-1/2+it} dt + O\left(\frac{H_j W^2}{X} \log^{O_C(1)} X\right). \end{align*} $$
The error term is
![]() $O(\log ^{O_C(1)} X /W^2)$
while the main term is independent of j. Hence,
$O(\log ^{O_C(1)} X /W^2)$
while the main term is independent of j. Hence,
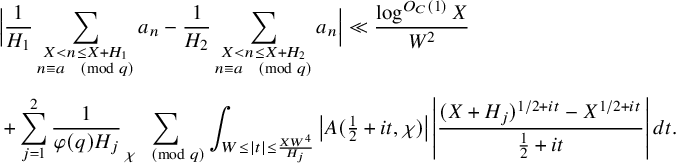 $$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} a_n - \frac{1}{H_2} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} a_n \Big | \ll \frac{\log^{O_C(1)} X}{W^2} \\[5pt] & + \sum_{j=1}^2 \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \int_{\substack{W \leq |t|\leq \frac{XW^4}{H_j}}} \left|A(\tfrac{1}{2}+it, \chi)\right| \left|\frac{(X+H_j)^{1/2+it}-X^{1/2+it}}{\tfrac{1}{2}+it}\right| dt. \end{align*} $$
$$ \begin{align*} &\Big | \frac{1}{H_1}\sum_{\substack{X < n \leq X+H_1 \\ n \equiv a \quad\pmod{q}}} a_n - \frac{1}{H_2} \sum_{\substack{X < n \leq X+H_2 \\ n \equiv a \quad\pmod{q}}} a_n \Big | \ll \frac{\log^{O_C(1)} X}{W^2} \\[5pt] & + \sum_{j=1}^2 \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \int_{\substack{W \leq |t|\leq \frac{XW^4}{H_j}}} \left|A(\tfrac{1}{2}+it, \chi)\right| \left|\frac{(X+H_j)^{1/2+it}-X^{1/2+it}}{\tfrac{1}{2}+it}\right| dt. \end{align*} $$
Since
![]() $|\frac { (X+H_j)^{1/2+it}-X^{1/2+it} } {1/2+it} | \ll \min \{ H_j X^{-1/2}, X^{1/2}/(1+|t|)\}$
, the second line contributes
$|\frac { (X+H_j)^{1/2+it}-X^{1/2+it} } {1/2+it} | \ll \min \{ H_j X^{-1/2}, X^{1/2}/(1+|t|)\}$
, the second line contributes
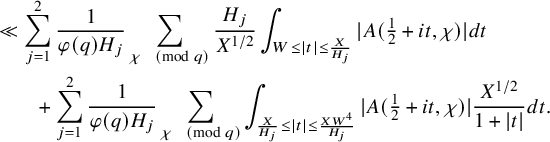 $$ \begin{align*} &\ll \sum_{j = 1}^2 \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \frac{H_j}{X^{1/2}} \int_{\substack{W \leq |t|\leq \frac{X}{H_j}}} |A(\tfrac{1}{2}+it, \chi)| dt \\ &\qquad + \sum_{j = 1}^2 \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \int_{\substack{\frac{X}{H_j} \leq |t|\leq \frac{XW^4}{H_j}}} |A(\tfrac{1}{2}+it, \chi)| \frac{X^{1/2}}{1+|t|} dt. \end{align*} $$
$$ \begin{align*} &\ll \sum_{j = 1}^2 \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \frac{H_j}{X^{1/2}} \int_{\substack{W \leq |t|\leq \frac{X}{H_j}}} |A(\tfrac{1}{2}+it, \chi)| dt \\ &\qquad + \sum_{j = 1}^2 \frac{1}{\varphi(q) H_j} \sum_{\chi \quad\pmod{q}} \int_{\substack{\frac{X}{H_j} \leq |t|\leq \frac{XW^4}{H_j}}} |A(\tfrac{1}{2}+it, \chi)| \frac{X^{1/2}}{1+|t|} dt. \end{align*} $$
Splitting the second integral dyadically, we see that this is
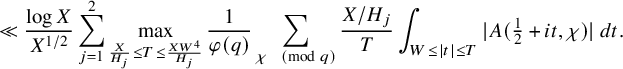 $$\begin{align*}\ll \frac{\log X}{X^{1/2}} \sum_{j = 1}^2 \max_{\frac{X}{H_j} \leq T \leq \frac{XW^4}{H_j}} \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \frac{X/H_j}{T} \int_{\substack{W \leq |t|\leq T}} |A(\tfrac{1}{2}+it, \chi)| \ dt. \end{align*}$$
$$\begin{align*}\ll \frac{\log X}{X^{1/2}} \sum_{j = 1}^2 \max_{\frac{X}{H_j} \leq T \leq \frac{XW^4}{H_j}} \frac{1}{\varphi(q)} \sum_{\chi \quad\pmod{q}} \frac{X/H_j}{T} \int_{\substack{W \leq |t|\leq T}} |A(\tfrac{1}{2}+it, \chi)| \ dt. \end{align*}$$
Since
![]() $H_2 \geq H_1$
, the contribution of the part with
$H_2 \geq H_1$
, the contribution of the part with
![]() $j=1$
is larger than the contribution of the part with
$j=1$
is larger than the contribution of the part with
![]() $j=2$
. Hence, part (i) follows.
$j=2$
. Hence, part (i) follows.
Part (ii) follows similarly, except there is no need to handle a main term separately.
Proof of Lemma 3.5.
By Shiu’s bound (Lemma 2.17), we can clearly assume that
![]() $q \leq W^{1/2} \leq X^{\varepsilon /400}$
. Let us consider, for
$q \leq W^{1/2} \leq X^{\varepsilon /400}$
. Let us consider, for
![]() $j = 1, 2$
,
$j = 1, 2$
,
 $$\begin{align*}\frac{1}{H_j}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_j \\ m_1 m_2 \ell \equiv a \quad\pmod{q} \\ m_j \sim M_j, \ell \sim L}} a_{m_1} b_{m_2} v_\ell. \end{align*}$$
$$\begin{align*}\frac{1}{H_j}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_j \\ m_1 m_2 \ell \equiv a \quad\pmod{q} \\ m_j \sim M_j, \ell \sim L}} a_{m_1} b_{m_2} v_\ell. \end{align*}$$
We first split the sums according to
![]() $r_1 = (m_1, q)$
,
$r_1 = (m_1, q)$
,
![]() $r_2 = (m_2, q/r_1)$
and
$r_2 = (m_2, q/r_1)$
and
![]() $r_3 = (\ell , q/(r_1 r_2))$
, writing
$r_3 = (\ell , q/(r_1 r_2))$
, writing
![]() $m_j = r_j m_j'$
and
$m_j = r_j m_j'$
and
![]() $\ell = r_3 \ell '$
. Then
$\ell = r_3 \ell '$
. Then
![]() $m_1' m_2' \ell ' r_1 r_2 r_3 \equiv a \ \pmod {\frac {q}{r_1 r_2 r_3} r_1 r_2 r_3}$
and necessarily
$m_1' m_2' \ell ' r_1 r_2 r_3 \equiv a \ \pmod {\frac {q}{r_1 r_2 r_3} r_1 r_2 r_3}$
and necessarily
![]() $r_1 r_2 r_3 = (a, q)$
. We have
$r_1 r_2 r_3 = (a, q)$
. We have
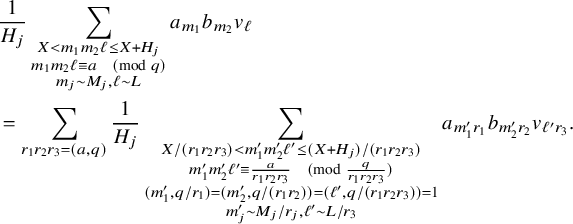 $$ \begin{align*} &\frac{1}{H_j}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_j \\ m_1 m_2 \ell \equiv a \quad\pmod{q} \\ m_j \sim M_j, \ell \sim L}} a_{m_1} b_{m_2} v_\ell \\ &= \sum_{\substack{r_1 r_2 r_3 = (a, q)}} \frac{1}{H_j}\sum_{\substack{X/(r_1 r_2 r_3) < m_1' m_2' \ell' \leq (X+H_j)/(r_1 r_2 r_3) \\ m_1' m_2' \ell' \equiv \frac{a}{r_1 r_2 r_3} \quad\pmod{\frac{q}{r_1 r_2 r_3}} \\ (m_1', q/r_1) = (m_2', q/(r_1 r_2)) = (\ell', q/(r_1 r_2 r_3)) = 1 \\ m_j' \sim M_j/r_j, \ell' \sim L/r_3}} a_{m_1' r_1} b_{m_2' r_2} v_{\ell' r_3}. \end{align*} $$
$$ \begin{align*} &\frac{1}{H_j}\sum_{\substack{X < m_1 m_2 \ell \leq X+H_j \\ m_1 m_2 \ell \equiv a \quad\pmod{q} \\ m_j \sim M_j, \ell \sim L}} a_{m_1} b_{m_2} v_\ell \\ &= \sum_{\substack{r_1 r_2 r_3 = (a, q)}} \frac{1}{H_j}\sum_{\substack{X/(r_1 r_2 r_3) < m_1' m_2' \ell' \leq (X+H_j)/(r_1 r_2 r_3) \\ m_1' m_2' \ell' \equiv \frac{a}{r_1 r_2 r_3} \quad\pmod{\frac{q}{r_1 r_2 r_3}} \\ (m_1', q/r_1) = (m_2', q/(r_1 r_2)) = (\ell', q/(r_1 r_2 r_3)) = 1 \\ m_j' \sim M_j/r_j, \ell' \sim L/r_3}} a_{m_1' r_1} b_{m_2' r_2} v_{\ell' r_3}. \end{align*} $$
Part (i) follows from Lemma 3.8 (with
![]() $X/(a, q)$
,
$X/(a, q)$
,
![]() $H_j/(a, q)$
,
$H_j/(a, q)$
,
![]() $q/(a, q)$
and
$q/(a, q)$
and
![]() $a/(a,q)$
in place of X,
$a/(a,q)$
in place of X,
![]() $H_j$
, q and a) if, for any
$H_j$
, q and a) if, for any
![]() $T \in [X/H_1, XW^4/H_1]$
and any
$T \in [X/H_1, XW^4/H_1]$
and any
![]() $r_1 r_2 r_3 = (a, q)$
and any
$r_1 r_2 r_3 = (a, q)$
and any
![]() $\chi \ \pmod {q/(a, q)}$
, one has
$\chi \ \pmod {q/(a, q)}$
, one has
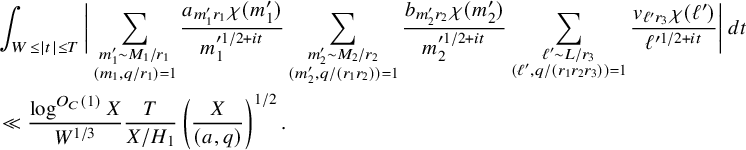 $$ \begin{align*}&\int_{\substack{W \leq |t|\leq T}} \bigg|\sum_{\substack{m_1' \sim M_1/r_1 \\ (m_1, q/r_1) = 1}} \frac{a_{m_1' r_1} \chi(m_1')}{m_1'^{1/2+it}} \sum_{\substack{m_2' \sim M_2/r_2 \\ (m_2', q/(r_1 r_2)) = 1}} \frac{b_{m_2' r_2} \chi(m_2')}{m_2'^{1/2+it}} \sum_{\substack{\ell' \sim L/r_3 \\ (\ell', q/(r_1r_2r_3)) = 1}} \frac{v_{\ell' r_3} \chi(\ell')}{\ell'^{1/2+it}} \bigg| \ dt \\&\ll \frac{\log^{O_C(1)} X}{W^{1/3}}\frac{T}{X/H_1} \left(\frac{X}{(a, q)}\right)^{1/2}. \end{align*} $$
$$ \begin{align*}&\int_{\substack{W \leq |t|\leq T}} \bigg|\sum_{\substack{m_1' \sim M_1/r_1 \\ (m_1, q/r_1) = 1}} \frac{a_{m_1' r_1} \chi(m_1')}{m_1'^{1/2+it}} \sum_{\substack{m_2' \sim M_2/r_2 \\ (m_2', q/(r_1 r_2)) = 1}} \frac{b_{m_2' r_2} \chi(m_2')}{m_2'^{1/2+it}} \sum_{\substack{\ell' \sim L/r_3 \\ (\ell', q/(r_1r_2r_3)) = 1}} \frac{v_{\ell' r_3} \chi(\ell')}{\ell'^{1/2+it}} \bigg| \ dt \\&\ll \frac{\log^{O_C(1)} X}{W^{1/3}}\frac{T}{X/H_1} \left(\frac{X}{(a, q)}\right)^{1/2}. \end{align*} $$
But, using the assumption (3.7), this follows from a slight variant of [Reference Baker, Harman and Pintz4, Lemma 9] with
![]() $g=1$
in cases
$g=1$
in cases
![]() $\theta \in \{7/12, 3/5, 5/8\}$
and with
$\theta \in \{7/12, 3/5, 5/8\}$
and with
![]() $g=2$
in case
$g=2$
in case
![]() $\theta = 11/20$
(alternatively see [Reference Harman24, Lemma 7.3]). The idea in the proofs of these lemmas is to first split the integral to level sets according to the absolute values of the three Dirichlet polynomials appearing, and then to apply appropriate mean and large value results individually for the three Dirichlet polynomials to obtain upper bounds for the sizes of the level sets. Combining these upper bounds using case-by-case study and Hölder’s inequality leads to the lemmas.
$\theta = 11/20$
(alternatively see [Reference Harman24, Lemma 7.3]). The idea in the proofs of these lemmas is to first split the integral to level sets according to the absolute values of the three Dirichlet polynomials appearing, and then to apply appropriate mean and large value results individually for the three Dirichlet polynomials to obtain upper bounds for the sizes of the level sets. Combining these upper bounds using case-by-case study and Hölder’s inequality leads to the lemmas.
Part (ii) follows similarly.
In fact, one can establish Lemma 3.5 for
![]() $\theta \in [7/12, 5/8]$
by using [Reference Baker, Harman and Pintz4, Lemma 9] with
$\theta \in [7/12, 5/8]$
by using [Reference Baker, Harman and Pintz4, Lemma 9] with
![]() $g=1$
, and for
$g=1$
, and for
![]() $\theta \in [11/20, 9/16]$
by using [Reference Baker, Harman and Pintz4, Lemma 9] with
$\theta \in [11/20, 9/16]$
by using [Reference Baker, Harman and Pintz4, Lemma 9] with
![]() $g=2$
(see [Reference Harman24, end of Section 7.2]), but we shall not need this more general result.
$g=2$
(see [Reference Harman24, end of Section 7.2]), but we shall not need this more general result.
Proof of Lemma 3.6.
By Shiu’s bound (Lemma 2.17), we can assume that
![]() $q \leq W^{1/6}$
. Notice first that if for either
$q \leq W^{1/6}$
. Notice first that if for either
![]() $i =1$
or
$i =1$
or
![]() $i=2$
, we have
$i=2$
, we have
![]() $\theta +\varepsilon - (1-\alpha _i) \geq \varepsilon ,$
then we can obtain the claim by simply moving the sum over
$\theta +\varepsilon - (1-\alpha _i) \geq \varepsilon ,$
then we can obtain the claim by simply moving the sum over
![]() $m_i$
inside. Hence, we can assume that
$m_i$
inside. Hence, we can assume that
![]() $\alpha _1, \alpha _2 < 1-\theta $
.
$\alpha _1, \alpha _2 < 1-\theta $
.
Arguing as in proof of Lemma 3.5 and doing a dyadic splitting it suffices to show that, for any
![]() $T \in [W, XW^4/H_1]$
and any
$T \in [W, XW^4/H_1]$
and any
![]() $r_1 r_2 r_3 = (a, q)$
,
$r_1 r_2 r_3 = (a, q)$
,
 $$ \begin{align} &\frac{1}{\varphi(\frac{q}{(a, q)})} \sum_{\chi \quad\pmod{\frac{q}{(a, q)}}} \int_{T}^{2T} \Bigl|\sum_{\substack{m_1 \sim M_1/r_1 \\ (m_1, q/r_1) = 1}} \frac{\chi(m_1)}{m_1^{1/2+it}} \sum_{\substack{m_2 \sim M_2/r_2 \\ (m_2, q/(r_1 r_2)) = 1}} \frac{\chi(m_2)}{m_2^{1/2+it}} \sum_{\substack{\ell \sim L/r_3 \\ (\ell, q/(r_1r_2r_3)) = 1}} \frac{\chi(\ell) v_{\ell r_3}}{\ell^{1/2+it}} \Bigr| \ dt\\[5pt] \nonumber &\ll \frac{\log^{O(1)} X}{W^{1/6}} \max\left\{\frac{T}{X/H_1}, 1\right\} \left(\frac{X}{(a, q)}\right)^{1/2}. \end{align} $$
$$ \begin{align} &\frac{1}{\varphi(\frac{q}{(a, q)})} \sum_{\chi \quad\pmod{\frac{q}{(a, q)}}} \int_{T}^{2T} \Bigl|\sum_{\substack{m_1 \sim M_1/r_1 \\ (m_1, q/r_1) = 1}} \frac{\chi(m_1)}{m_1^{1/2+it}} \sum_{\substack{m_2 \sim M_2/r_2 \\ (m_2, q/(r_1 r_2)) = 1}} \frac{\chi(m_2)}{m_2^{1/2+it}} \sum_{\substack{\ell \sim L/r_3 \\ (\ell, q/(r_1r_2r_3)) = 1}} \frac{\chi(\ell) v_{\ell r_3}}{\ell^{1/2+it}} \Bigr| \ dt\\[5pt] \nonumber &\ll \frac{\log^{O(1)} X}{W^{1/6}} \max\left\{\frac{T}{X/H_1}, 1\right\} \left(\frac{X}{(a, q)}\right)^{1/2}. \end{align} $$
By the fourth moment estimate for Dirichlet L-functions, we have (see [Reference Harman24, Lemma 10.11]), for any
![]() $M, T \geq 2$
and
$M, T \geq 2$
and
![]() $d \mid (a, q)$
,
$d \mid (a, q)$
,
 $$ \begin{align*} \sum_{\chi \quad\pmod{\frac{q}{(a, q)}}} \int_{T}^{2T} \Biggl|\sum_{\substack{m \sim M \\ (m, q/d) = 1}} \frac{\chi(m)}{m^{1/2+it}} \Biggr|^4 dt & \ll \sum_{\chi \quad\pmod{\frac{q}{d}}} \int_{T}^{2T} \left|\sum_{\substack{m \sim M}} \frac{\chi(m)}{m^{1/2+it}} \right|{}^4 dt \\[5pt] &\ll\left(q^3T + \frac{qM^2}{T^3}\right) \log^{O(1)} (MT). \end{align*} $$
$$ \begin{align*} \sum_{\chi \quad\pmod{\frac{q}{(a, q)}}} \int_{T}^{2T} \Biggl|\sum_{\substack{m \sim M \\ (m, q/d) = 1}} \frac{\chi(m)}{m^{1/2+it}} \Biggr|^4 dt & \ll \sum_{\chi \quad\pmod{\frac{q}{d}}} \int_{T}^{2T} \left|\sum_{\substack{m \sim M}} \frac{\chi(m)}{m^{1/2+it}} \right|{}^4 dt \\[5pt] &\ll\left(q^3T + \frac{qM^2}{T^3}\right) \log^{O(1)} (MT). \end{align*} $$
Hence, using also Hölder and the mean value theorem (see, e.g., [Reference Iwaniec and Kowalski37, Theorem 9.12 with
![]() $k=q$
and
$k=q$
and
![]() $Q=1$
]), the left-hand side of equation (3.18) is
$Q=1$
]), the left-hand side of equation (3.18) is
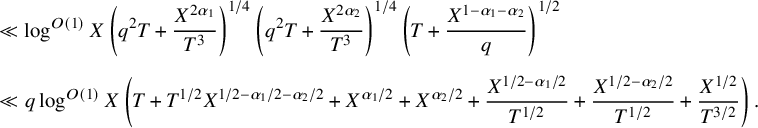 $$ \begin{align*} &\ll \log^{O(1)} X \left(q^2T + \frac{X^{2\alpha_1}}{T^3} \right)^{1/4} \left(q^2 T + \frac{X^{2\alpha_2}}{T^3} \right)^{1/4} \left(T + \frac{X^{1-\alpha_1-\alpha_2}}{q}\right)^{1/2} \\[5pt] &\ll q \log^{O(1)} X \left(T + T^{1/2} X^{1/2-\alpha_1/2-\alpha_2/2} + X^{\alpha_1/2} + X^{\alpha_2/2} + \frac{X^{1/2-\alpha_1/2}}{T^{1/2}} + \frac{X^{1/2-\alpha_2/2}}{T^{1/2}} + \frac{X^{1/2}}{T^{3/2}}\right). \end{align*} $$
$$ \begin{align*} &\ll \log^{O(1)} X \left(q^2T + \frac{X^{2\alpha_1}}{T^3} \right)^{1/4} \left(q^2 T + \frac{X^{2\alpha_2}}{T^3} \right)^{1/4} \left(T + \frac{X^{1-\alpha_1-\alpha_2}}{q}\right)^{1/2} \\[5pt] &\ll q \log^{O(1)} X \left(T + T^{1/2} X^{1/2-\alpha_1/2-\alpha_2/2} + X^{\alpha_1/2} + X^{\alpha_2/2} + \frac{X^{1/2-\alpha_1/2}}{T^{1/2}} + \frac{X^{1/2-\alpha_2/2}}{T^{1/2}} + \frac{X^{1/2}}{T^{3/2}}\right). \end{align*} $$
One can see that this is always at most the right-hand side of equation (3.18) by considering each term separately – depending on the term, the worst case is either
![]() $T = W$
or
$T = W$
or
![]() $T = X/H_1$
.
$T = X/H_1$
.
3.4 Proof of Proposition 3.4
Let us first show the
![]() $k= 2$
case of Proposition 3.4(ii). It follows from classical arguments leading to the exponent
$k= 2$
case of Proposition 3.4(ii). It follows from classical arguments leading to the exponent
![]() $1/3+\varepsilon $
in the Dirichlet divisor problem (see, e.g., [Reference Tenenbau and Thomas62, Section I.6.4]). For completeness, we provide the proof here. By a trivial bound, we can assume that
$1/3+\varepsilon $
in the Dirichlet divisor problem (see, e.g., [Reference Tenenbau and Thomas62, Section I.6.4]). For completeness, we provide the proof here. By a trivial bound, we can assume that
![]() $q \leq X^{\varepsilon /4}$
.
$q \leq X^{\varepsilon /4}$
.
First, note that
 $$ \begin{align*} \frac{1}{H_j} \sum_{\substack{X < n \leq X+H_j \\ n \equiv a \quad\pmod{q}}} d_2(n) &= \frac{2}{H_j} \sum_{\substack{X < mn \leq X+H_j \\ m \leq X^{1/2} \\ mn \equiv a \quad\pmod{q}}} 1 + O\Biggl(\frac{1}{H_j} \sum_{m \in (X^{1/2}, (X+H_j)^{1/2}]} \sum_{\substack{X/m < n \leq (X+H_j)/m \\ mn \equiv a \quad\pmod{q}}} 1\Biggr). \end{align*} $$
$$ \begin{align*} \frac{1}{H_j} \sum_{\substack{X < n \leq X+H_j \\ n \equiv a \quad\pmod{q}}} d_2(n) &= \frac{2}{H_j} \sum_{\substack{X < mn \leq X+H_j \\ m \leq X^{1/2} \\ mn \equiv a \quad\pmod{q}}} 1 + O\Biggl(\frac{1}{H_j} \sum_{m \in (X^{1/2}, (X+H_j)^{1/2}]} \sum_{\substack{X/m < n \leq (X+H_j)/m \\ mn \equiv a \quad\pmod{q}}} 1\Biggr). \end{align*} $$
The error term contributes
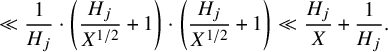 $$\begin{align*}\ll \frac{1}{H_j} \cdot \left(\frac{H_j}{X^{1/2}} + 1\right) \cdot \left(\frac{H_j}{X^{1/2}} + 1\right) \ll \frac{H_j}{X} + \frac{1}{H_j}. \end{align*}$$
$$\begin{align*}\ll \frac{1}{H_j} \cdot \left(\frac{H_j}{X^{1/2}} + 1\right) \cdot \left(\frac{H_j}{X^{1/2}} + 1\right) \ll \frac{H_j}{X} + \frac{1}{H_j}. \end{align*}$$
Hence,it suffices to show that, for any
![]() $M \in [1/2, X^{1/2}]$
, we have
$M \in [1/2, X^{1/2}]$
, we have
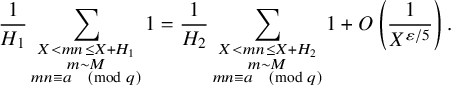 $$\begin{align*}\frac{1}{H_1} \sum_{\substack{X < mn \leq X+H_1 \\ m \sim M \\ mn \equiv a \quad\pmod{q}}} 1 = \frac{1}{H_2} \sum_{\substack{X < mn \leq X+H_2 \\ m \sim M \\ mn \equiv a \quad\pmod{q}}} 1 + O\left(\frac{1}{X^{\varepsilon/5}}\right). \end{align*}$$
$$\begin{align*}\frac{1}{H_1} \sum_{\substack{X < mn \leq X+H_1 \\ m \sim M \\ mn \equiv a \quad\pmod{q}}} 1 = \frac{1}{H_2} \sum_{\substack{X < mn \leq X+H_2 \\ m \sim M \\ mn \equiv a \quad\pmod{q}}} 1 + O\left(\frac{1}{X^{\varepsilon/5}}\right). \end{align*}$$
Now, for
![]() $j = 1, 2$
,
$j = 1, 2$
,
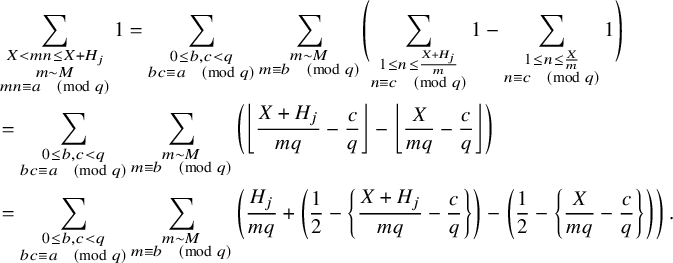 $$ \begin{align*} &\sum_{\substack{X < mn \leq X+H_j \\ m \sim M \\ mn \equiv a \quad\pmod{q}}} 1 = \sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \Biggl(\sum_{\substack{1 \leq n \leq \frac{X+H_j}{m} \\ n \equiv c \quad\pmod{q}}} 1 - \sum_{\substack{1 \leq n \leq \frac{X}{m} \\ n \equiv c \quad\pmod{q}}} 1 \Biggr) \\ &=\sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \left(\left\lfloor \frac{X+H_j}{mq} - \frac{c}{q} \right\rfloor - \left\lfloor \frac{X}{mq} - \frac{c}{q} \right\rfloor\right) \\ &= \sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \left(\frac{H_j}{mq} + \left(\frac{1}{2}-\left\{\frac{X+H_j}{mq} -\frac{c}{q}\right\}\right) - \left(\frac{1}{2} - \left\{\frac{X}{mq} - \frac{c}{q}\right\}\right)\right). \end{align*} $$
$$ \begin{align*} &\sum_{\substack{X < mn \leq X+H_j \\ m \sim M \\ mn \equiv a \quad\pmod{q}}} 1 = \sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \Biggl(\sum_{\substack{1 \leq n \leq \frac{X+H_j}{m} \\ n \equiv c \quad\pmod{q}}} 1 - \sum_{\substack{1 \leq n \leq \frac{X}{m} \\ n \equiv c \quad\pmod{q}}} 1 \Biggr) \\ &=\sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \left(\left\lfloor \frac{X+H_j}{mq} - \frac{c}{q} \right\rfloor - \left\lfloor \frac{X}{mq} - \frac{c}{q} \right\rfloor\right) \\ &= \sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \left(\frac{H_j}{mq} + \left(\frac{1}{2}-\left\{\frac{X+H_j}{mq} -\frac{c}{q}\right\}\right) - \left(\frac{1}{2} - \left\{\frac{X}{mq} - \frac{c}{q}\right\}\right)\right). \end{align*} $$
Hence, it suffices to show that, for
![]() $j =1, 2$
and
$j =1, 2$
and
![]() $\xi \in \{X/q, (X+H_j)/q\}$
,
$\xi \in \{X/q, (X+H_j)/q\}$
,
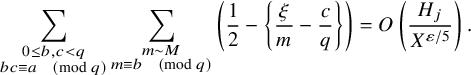 $$ \begin{align} \sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \left(\frac{1}{2}-\left\{\frac{\xi}{m} -\frac{c}{q}\right\}\right) = O\left(\frac{H_j}{X^{\varepsilon/5}}\right). \end{align} $$
$$ \begin{align} \sum_{\substack{0 \leq b, c < q \\ bc \equiv a \quad\pmod{q}}} \sum_{\substack{m \sim M \\ m \equiv b \quad\pmod{q}}} \left(\frac{1}{2}-\left\{\frac{\xi}{m} -\frac{c}{q}\right\}\right) = O\left(\frac{H_j}{X^{\varepsilon/5}}\right). \end{align} $$
The left-hand side is trivially
![]() $O(qM) = O(X^{\varepsilon /4}M)$
, and so equation (3.19) is immediate in case
$O(qM) = O(X^{\varepsilon /4}M)$
, and so equation (3.19) is immediate in case
![]() ${M \leq H_j/X^{\varepsilon /2}}$
, and so we can concentrate on showing equation (3.19) for j and M for which
${M \leq H_j/X^{\varepsilon /2}}$
, and so we can concentrate on showing equation (3.19) for j and M for which
![]() ${M> H_j/X^{\varepsilon /2}}$
.
${M> H_j/X^{\varepsilon /2}}$
.
For any
![]() $K \geq 1$
, we have the Fourier expansion (see, e.g., [Reference Tenenbau and Thomas62, Section I.6.4])
$K \geq 1$
, we have the Fourier expansion (see, e.g., [Reference Tenenbau and Thomas62, Section I.6.4])
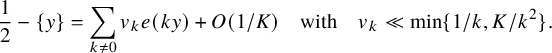 $$\begin{align*}\frac{1}{2} -\{ y\} = \sum_{k \neq 0} v_k e(ky) + O(1/K) \quad \text{with} \quad v_k \ll \min\{1/k, K/k^2\}. \end{align*}$$
$$\begin{align*}\frac{1}{2} -\{ y\} = \sum_{k \neq 0} v_k e(ky) + O(1/K) \quad \text{with} \quad v_k \ll \min\{1/k, K/k^2\}. \end{align*}$$
Taking
![]() $K_j = MX^{\varepsilon /2}/H_j$
(which is
$K_j = MX^{\varepsilon /2}/H_j$
(which is
![]() $\geq 1$
) and writing
$\geq 1$
) and writing
![]() $m = b+rq$
, it suffices to show that, for
$m = b+rq$
, it suffices to show that, for
![]() $j =1, 2$
and
$j =1, 2$
and
![]() $\xi \in \{X/q, (X+H_j)/q\}$
,
$\xi \in \{X/q, (X+H_j)/q\}$
,
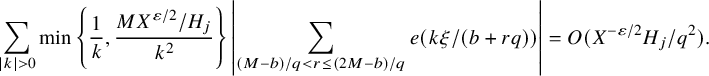 $$\begin{align*}\sum_{|k|> 0} \min\left\{ \frac{1}{k}, \frac{MX^{\varepsilon/2}/H_j}{k^2}\right\} \left| \sum_{(M-b)/q < r \leq (2M-b)/q} e(k \xi/(b+rq)) \right| = O(X^{-\varepsilon/2} H_j/q^2). \end{align*}$$
$$\begin{align*}\sum_{|k|> 0} \min\left\{ \frac{1}{k}, \frac{MX^{\varepsilon/2}/H_j}{k^2}\right\} \left| \sum_{(M-b)/q < r \leq (2M-b)/q} e(k \xi/(b+rq)) \right| = O(X^{-\varepsilon/2} H_j/q^2). \end{align*}$$
The second derivative of the phase has size
![]() $\asymp kXq/M^3$
, so that by van der Corput’s exponential sum bound (see, e.g., [Reference Tenenbau and Thomas62, Theorem 5 in Section I.6.3] or [Reference Iwaniec and Kowalski37, Corollary 8.13]), the left-hand side is
$\asymp kXq/M^3$
, so that by van der Corput’s exponential sum bound (see, e.g., [Reference Tenenbau and Thomas62, Theorem 5 in Section I.6.3] or [Reference Iwaniec and Kowalski37, Corollary 8.13]), the left-hand side is
 $$ \begin{align*} &\ll \sum_{0 < |k| \leq MX^{\varepsilon/2}/H_j}\frac{1}{k} \left(\left(\frac{kXq}{M^3}\right)^{1/2} \frac{M}{q} + \left(\frac{M^3}{kX q}\right)^{1/2} \right) \\ &\qquad +\sum_{|k|> MX^{\varepsilon/2}/H_j}\frac{MX^{\varepsilon/2}/H_j}{k^2} \left(\left(\frac{kXq}{M^3}\right)^{1/2} \frac{M}{q} + \left(\frac{M^3}{kX q}\right)^{1/2} \right) \\ &\ll \frac{X^{1/2 + \varepsilon/4}}{H_j^{1/2} q^{1/2}} + \frac{M^{3/2}}{q^{1/2} X^{1/2}}. \end{align*} $$
$$ \begin{align*} &\ll \sum_{0 < |k| \leq MX^{\varepsilon/2}/H_j}\frac{1}{k} \left(\left(\frac{kXq}{M^3}\right)^{1/2} \frac{M}{q} + \left(\frac{M^3}{kX q}\right)^{1/2} \right) \\ &\qquad +\sum_{|k|> MX^{\varepsilon/2}/H_j}\frac{MX^{\varepsilon/2}/H_j}{k^2} \left(\left(\frac{kXq}{M^3}\right)^{1/2} \frac{M}{q} + \left(\frac{M^3}{kX q}\right)^{1/2} \right) \\ &\ll \frac{X^{1/2 + \varepsilon/4}}{H_j^{1/2} q^{1/2}} + \frac{M^{3/2}}{q^{1/2} X^{1/2}}. \end{align*} $$
This is
![]() $\ll X^{-\varepsilon /2} H_j/q^2$
since
$\ll X^{-\varepsilon /2} H_j/q^2$
since
![]() $H_2 \geq H_1 \geq X^{1/3+\varepsilon }$
,
$H_2 \geq H_1 \geq X^{1/3+\varepsilon }$
,
![]() $q \leq X^{\varepsilon /4}$
, and
$q \leq X^{\varepsilon /4}$
, and
![]() $M \leq X^{1/2}$
. This establishes the
$M \leq X^{1/2}$
. This establishes the
![]() $k=2$
case of Proposition 3.4.
$k=2$
case of Proposition 3.4.
The cases
![]() $k=3, 4$
of Proposition 3.4(ii) follow from dyadic splitting, Lemma 2.20(v) and Lemma 3.6 with
$k=3, 4$
of Proposition 3.4(ii) follow from dyadic splitting, Lemma 2.20(v) and Lemma 3.6 with
![]() $W = \min \{X^{\frac {1}{400k}}, X^{\varepsilon /4}\}$
, so we can concentrate on Proposition 3.4(i) and cases
$W = \min \{X^{\frac {1}{400k}}, X^{\varepsilon /4}\}$
, so we can concentrate on Proposition 3.4(i) and cases
![]() $k \geq 5$
of Proposition 3.4(ii). To apply Lemma 3.5, we need parts (i) and (ii) of the following lemma (part (iii) will be used in the proof of Lemma 4.5 below):
$k \geq 5$
of Proposition 3.4(ii). To apply Lemma 3.5, we need parts (i) and (ii) of the following lemma (part (iii) will be used in the proof of Lemma 4.5 below):
Lemma 3.9 (Dirichlet polynomial bounds).
Let
![]() $0 \leq T_0 \leq X$
and
$0 \leq T_0 \leq X$
and
![]() $\alpha \in (0, 1]$
.
$\alpha \in (0, 1]$
.
-
(i) There exists
 $\delta = \delta (\alpha )$
such that, for any character
$\delta = \delta (\alpha )$
such that, for any character
 $\chi $
of modulus
$\chi $
of modulus
 $q \leq X^{\alpha /2}$
and any
$q \leq X^{\alpha /2}$
and any
 $L \in [X^\alpha , X]$
,
$L \in [X^\alpha , X]$
,  $$\begin{align*}\sup_{T_0 \leq |t| \leq X} \sup_{I\subset [L,2L]}\left| \sum_{\ell \in I} \frac{\chi(\ell)}{\ell^{1/2+it}}\right| \ll_{\alpha} L^{1/2} X^{-\delta} + L^{1/2} \frac{\log X}{(T_0 +1)^{1/2}}. \end{align*}$$
$$\begin{align*}\sup_{T_0 \leq |t| \leq X} \sup_{I\subset [L,2L]}\left| \sum_{\ell \in I} \frac{\chi(\ell)}{\ell^{1/2+it}}\right| \ll_{\alpha} L^{1/2} X^{-\delta} + L^{1/2} \frac{\log X}{(T_0 +1)^{1/2}}. \end{align*}$$
-
(ii) For any
 $A> 0$
, any
$A> 0$
, any
 $1\leq r\leq X$
, and any character
$1\leq r\leq X$
, and any character
 $\chi $
of modulus
$\chi $
of modulus
 $q \leq \log ^A X$
, one has
$q \leq \log ^A X$
, one has  $$\begin{align*}\sup_{|t| \leq X} \sup_{I\subset [X^{\alpha},2X^{\alpha}]}\left| \sum_{\ell \in I} \frac{\mu(r\ell) \chi(\ell)}{\ell^{1/2+it}}\right| \ll_{\alpha, A} \frac{X^{\alpha/2}}{\log^A X}. \end{align*}$$
$$\begin{align*}\sup_{|t| \leq X} \sup_{I\subset [X^{\alpha},2X^{\alpha}]}\left| \sum_{\ell \in I} \frac{\mu(r\ell) \chi(\ell)}{\ell^{1/2+it}}\right| \ll_{\alpha, A} \frac{X^{\alpha/2}}{\log^A X}. \end{align*}$$
-
(iii) Let
 $\varepsilon> 0$
. For any
$\varepsilon> 0$
. For any
 $A> 0$
, any
$A> 0$
, any
 $P \in [\exp ((\log X)^{2/3+\varepsilon }), X^2]$
and any character
$P \in [\exp ((\log X)^{2/3+\varepsilon }), X^2]$
and any character
 $\chi $
of modulus
$\chi $
of modulus
 $q \leq \log ^A X$
,
$q \leq \log ^A X$
,  $$\begin{align*}\sup_{T_0 \leq |t| \leq X} \sup_{I\subset [P,2P]}\left| \sum_{p \in I} \frac{\chi(p)}{p^{1/2+it}}\right| \ll_{\varepsilon, A} \frac{P^{1/2}}{T_0} + \frac{P^{1/2}}{\log^A X}. \end{align*}$$
$$\begin{align*}\sup_{T_0 \leq |t| \leq X} \sup_{I\subset [P,2P]}\left| \sum_{p \in I} \frac{\chi(p)}{p^{1/2+it}}\right| \ll_{\varepsilon, A} \frac{P^{1/2}}{T_0} + \frac{P^{1/2}}{\log^A X}. \end{align*}$$
Proof. Parts (ii) and (iii) follow by standard contour integration arguments, using the known zero-free region for
![]() $L(s, \chi )$
(see, e.g., [Reference Matomäki and Radziwiłł44, Lemma 2] for a similar argument without the character).
$L(s, \chi )$
(see, e.g., [Reference Matomäki and Radziwiłł44, Lemma 2] for a similar argument without the character).
Let us concentrate on part (i). By partial summation, splitting into residue classes
![]() $a \ \pmod {q}$
and writing
$a \ \pmod {q}$
and writing
![]() $\ell = mq + a$
, it suffices to show that, for any
$\ell = mq + a$
, it suffices to show that, for any
![]() $a \in \{1, \dotsc , q\}$
and
$a \in \{1, \dotsc , q\}$
and
![]() $|t| \in [T_0, X]$
, we have
$|t| \in [T_0, X]$
, we have
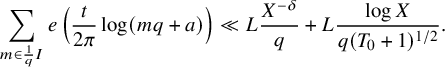 $$ \begin{align} \sum_{m \in \frac{1}{q}I} e\left(\frac{t}{2\pi} \log (m q + a)\right) \ll L \frac{X^{-\delta}}{q} + L \frac{\log X}{q(T_0+1)^{1/2}}. \end{align} $$
$$ \begin{align} \sum_{m \in \frac{1}{q}I} e\left(\frac{t}{2\pi} \log (m q + a)\right) \ll L \frac{X^{-\delta}}{q} + L \frac{\log X}{q(T_0+1)^{1/2}}. \end{align} $$
The
![]() $\nu $
th derivative of the phase
$\nu $
th derivative of the phase
![]() $g(m) = \frac {t}{2\pi } \log (m q + a)$
satisfies
$g(m) = \frac {t}{2\pi } \log (m q + a)$
satisfies
for any
![]() $\nu \ge 1$
. We apply the Weyl bound in the form of [Reference Iwaniec and Kowalski37, Theorem 8.4]. When
$\nu \ge 1$
. We apply the Weyl bound in the form of [Reference Iwaniec and Kowalski37, Theorem 8.4]. When
![]() $T_0 \leq |t| \leq L/q$
, we use [Reference Iwaniec and Kowalski37, Theorem 8.4] with
$T_0 \leq |t| \leq L/q$
, we use [Reference Iwaniec and Kowalski37, Theorem 8.4] with
![]() $k= 2$
, obtaining
$k= 2$
, obtaining
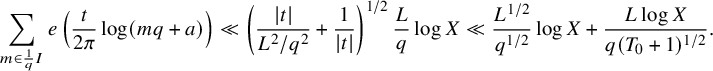 $$\begin{align*}\sum_{m \in \frac{1}{q}I} e\left(\frac{t}{2\pi} \log (m q + a)\right) \ll \left(\frac{|t|}{L^2/q^2} + \frac{1}{|t|}\right)^{1/2} \frac{L}{q} \log X \ll \frac{L^{1/2}}{q^{1/2}} \log X + \frac{L \log X}{q(T_0+1)^{1/2}}. \end{align*}$$
$$\begin{align*}\sum_{m \in \frac{1}{q}I} e\left(\frac{t}{2\pi} \log (m q + a)\right) \ll \left(\frac{|t|}{L^2/q^2} + \frac{1}{|t|}\right)^{1/2} \frac{L}{q} \log X \ll \frac{L^{1/2}}{q^{1/2}} \log X + \frac{L \log X}{q(T_0+1)^{1/2}}. \end{align*}$$
Recalling that
![]() $q \leq L^{1/2}$
, the bound (3.20) follows with
$q \leq L^{1/2}$
, the bound (3.20) follows with
![]() $\delta = \alpha /5$
.
$\delta = \alpha /5$
.
On the other hand, when
![]() $L/q < |t| \leq X$
, we use [Reference Iwaniec and Kowalski37, Theorem 8.4] with
$L/q < |t| \leq X$
, we use [Reference Iwaniec and Kowalski37, Theorem 8.4] with
![]() $k= \lfloor \frac {2}{\alpha } + 2\rfloor $
, obtaining
$k= \lfloor \frac {2}{\alpha } + 2\rfloor $
, obtaining
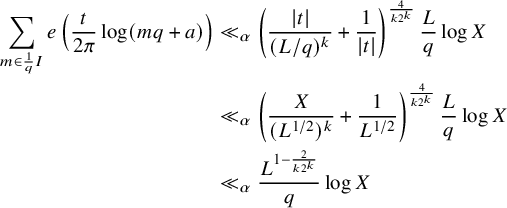 $$ \begin{align} \sum_{m \in \frac{1}{q}I} e\left(\frac{t}{2\pi} \log (m q + a)\right) &\ll_\alpha \left(\frac{|t|}{(L/q)^k} + \frac{1}{|t|}\right)^{\frac{4}{k 2^k}} \frac{L}{q} \log X \nonumber\\ &\ll_\alpha \left(\frac{X}{(L^{1/2})^k} + \frac{1}{L^{1/2}}\right)^{\frac{4}{k 2^k}} \frac{L}{q} \log X\\ & \ll_\alpha \frac{L^{1-\frac{2}{k2^k}}}{q} \log X\nonumber \end{align} $$
$$ \begin{align} \sum_{m \in \frac{1}{q}I} e\left(\frac{t}{2\pi} \log (m q + a)\right) &\ll_\alpha \left(\frac{|t|}{(L/q)^k} + \frac{1}{|t|}\right)^{\frac{4}{k 2^k}} \frac{L}{q} \log X \nonumber\\ &\ll_\alpha \left(\frac{X}{(L^{1/2})^k} + \frac{1}{L^{1/2}}\right)^{\frac{4}{k 2^k}} \frac{L}{q} \log X\\ & \ll_\alpha \frac{L^{1-\frac{2}{k2^k}}}{q} \log X\nonumber \end{align} $$
and equation (3.20) follows.
Let us now get back to the proof of Proposition 3.4(ii). Recall that we can assume that
![]() $k \geq 5$
. The claim follows trivially unless
$k \geq 5$
. The claim follows trivially unless
![]() $q \leq \min \{X^{2c_k}, X^{\varepsilon /900}\}$
. We can request that
$q \leq \min \{X^{2c_k}, X^{\varepsilon /900}\}$
. We can request that
![]() $c_k \leq \frac {1}{4000k}$
. By dyadic splitting it suffices to show that, for any
$c_k \leq \frac {1}{4000k}$
. By dyadic splitting it suffices to show that, for any
![]() $N_j \in [1/2, X]$
with
$N_j \in [1/2, X]$
with
![]() $N_1 \dotsm N_k \asymp X$
, one has
$N_1 \dotsm N_k \asymp X$
, one has
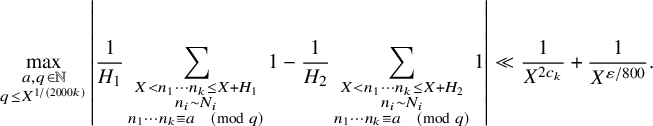 $$ \begin{align} \max_{\substack{a, q \in \mathbb{N} \\ q \leq X^{1/(2000k)}}} \left| \frac{1}{H_1}\sum_{\substack{X < n_1 \dotsm n_k \leq X+H_1 \\ n_i \sim N_i \\ n_1 \dotsm n_k \equiv a \quad\pmod{q}}} 1 - \frac{1}{H_2}\sum_{\substack{X < n_1 \dotsm n_k \leq X+H_2 \\ n_i \sim N_i \\n_1 \dotsm n_k \equiv a \quad\pmod{q}}} 1 \right| \ll \frac{1}{X^{2c_k}} + \frac{1}{X^{\varepsilon/800}}. \end{align} $$
$$ \begin{align} \max_{\substack{a, q \in \mathbb{N} \\ q \leq X^{1/(2000k)}}} \left| \frac{1}{H_1}\sum_{\substack{X < n_1 \dotsm n_k \leq X+H_1 \\ n_i \sim N_i \\ n_1 \dotsm n_k \equiv a \quad\pmod{q}}} 1 - \frac{1}{H_2}\sum_{\substack{X < n_1 \dotsm n_k \leq X+H_2 \\ n_i \sim N_i \\n_1 \dotsm n_k \equiv a \quad\pmod{q}}} 1 \right| \ll \frac{1}{X^{2c_k}} + \frac{1}{X^{\varepsilon/800}}. \end{align} $$
We can find
![]() $\alpha _1, \dotsc , \alpha _k \in [0,1]$
with
$\alpha _1, \dotsc , \alpha _k \in [0,1]$
with
![]() $\alpha _1 + \dotsb + \alpha _k = 1$
such that
$\alpha _1 + \dotsb + \alpha _k = 1$
such that
![]() $N_i \asymp X^{\alpha _i}$
for each
$N_i \asymp X^{\alpha _i}$
for each
![]() $i = 1, \dotsc , k$
.
$i = 1, \dotsc , k$
.
In case
![]() $k=5$
and
$k=5$
and
![]() $\theta = 11/20$
, we start by applying Lemma 2.20(iv). In case
$\theta = 11/20$
, we start by applying Lemma 2.20(iv). In case
![]() $(I_2^{\mathrm {maj}})$
holds, we apply Lemma 3.6 with
$(I_2^{\mathrm {maj}})$
holds, we apply Lemma 3.6 with
![]() $W = \min \{X^{\varepsilon /4}, X^{8c_k}\}$
to obtain equation (3.22). In case
$W = \min \{X^{\varepsilon /4}, X^{8c_k}\}$
to obtain equation (3.22). In case
![]() $(II^{\mathrm {maj}})$
holds, we wish to apply Lemma 3.5. In order to do this, we need to show that equation (3.7) holds with
$(II^{\mathrm {maj}})$
holds, we wish to apply Lemma 3.5. In order to do this, we need to show that equation (3.7) holds with
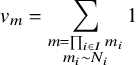 $$ \begin{align} v_m = \sum_{\substack{m = \prod_{i \in I} m_i \\ m_i \sim N_i}} 1 \end{align} $$
$$ \begin{align} v_m = \sum_{\substack{m = \prod_{i \in I} m_i \\ m_i \sim N_i}} 1 \end{align} $$
and
![]() $W = \min \{X^{\varepsilon /200}, X^{20 c_k}\}$
for any
$W = \min \{X^{\varepsilon /200}, X^{20 c_k}\}$
for any
![]() $L \asymp \prod _{i \in I} N_i$
. Now, there exists
$L \asymp \prod _{i \in I} N_i$
. Now, there exists
![]() $i_0 \in I$
such that
$i_0 \in I$
such that
![]() $\alpha _{i_0} \geq (2\theta -1)/k = \frac {1}{10k}$
. We have (using
$\alpha _{i_0} \geq (2\theta -1)/k = \frac {1}{10k}$
. We have (using
![]() $d(r) d_{|I|-1}(m) \ll W^{1/100}$
)
$d(r) d_{|I|-1}(m) \ll W^{1/100}$
)
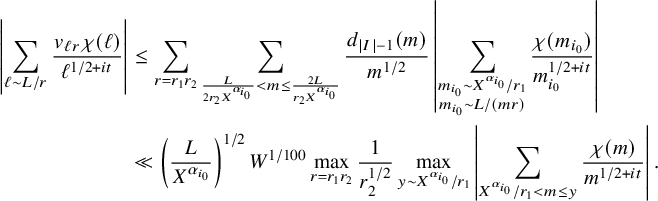 $$ \begin{align*} \left|\sum_{\ell \sim L/r} \frac{v_{\ell r} \chi(\ell)}{\ell^{1/2+it}}\right| &\leq \sum_{r = r_1 r_2} \sum_{\frac{L}{2r_2 X^{\alpha_{i_0}}} < m \leq \frac{2L}{r_2 X^{\alpha_{i_0}}}} \frac{d_{|I|-1}(m)}{m^{1/2}} \left|\sum_{\substack{m_{i_0} \sim X^{\alpha_{i_0}}/r_1 \\ m_{i_0} \sim L/(mr)}} \frac{\chi(m_{i_0})}{m_{i_0}^{1/2+it}}\right| \\ & \ll \left(\frac{L}{X^{\alpha_{i_0}}}\right)^{1/2} W^{1/100} \max_{r = r_1 r_2} \frac{1}{r_2^{1/2}} \max_{y \sim X^{\alpha_{i_0}}/r_1} \left|\sum_{\substack{X^{\alpha_{i_0}}/r_1 < m \leq y}} \frac{\chi(m)}{m^{1/2+it}}\right|. \end{align*} $$
$$ \begin{align*} \left|\sum_{\ell \sim L/r} \frac{v_{\ell r} \chi(\ell)}{\ell^{1/2+it}}\right| &\leq \sum_{r = r_1 r_2} \sum_{\frac{L}{2r_2 X^{\alpha_{i_0}}} < m \leq \frac{2L}{r_2 X^{\alpha_{i_0}}}} \frac{d_{|I|-1}(m)}{m^{1/2}} \left|\sum_{\substack{m_{i_0} \sim X^{\alpha_{i_0}}/r_1 \\ m_{i_0} \sim L/(mr)}} \frac{\chi(m_{i_0})}{m_{i_0}^{1/2+it}}\right| \\ & \ll \left(\frac{L}{X^{\alpha_{i_0}}}\right)^{1/2} W^{1/100} \max_{r = r_1 r_2} \frac{1}{r_2^{1/2}} \max_{y \sim X^{\alpha_{i_0}}/r_1} \left|\sum_{\substack{X^{\alpha_{i_0}}/r_1 < m \leq y}} \frac{\chi(m)}{m^{1/2+it}}\right|. \end{align*} $$
Hence, equation (3.7) follows for equation (3.23) if we show that
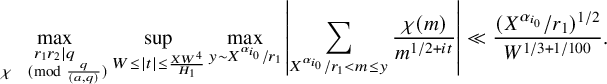 $$ \begin{align} \max_{\substack{r_1 r_2 \mid q \\ \chi \quad\pmod{\frac{q}{(a, q)}}}} \sup_{W \leq |t| \leq \frac{XW^4}{H_1}} \max_{y \sim X^{\alpha_{i_0}}/r_1} \left| \sum_{X^{\alpha_{i_0}}/r_1 < m \leq y} \frac{\chi(m)}{m^{1/2+it}}\right| \ll \frac{(X^{\alpha_{i_0}}/r_1)^{1/2}}{W^{1/3+1/100}}. \end{align} $$
$$ \begin{align} \max_{\substack{r_1 r_2 \mid q \\ \chi \quad\pmod{\frac{q}{(a, q)}}}} \sup_{W \leq |t| \leq \frac{XW^4}{H_1}} \max_{y \sim X^{\alpha_{i_0}}/r_1} \left| \sum_{X^{\alpha_{i_0}}/r_1 < m \leq y} \frac{\chi(m)}{m^{1/2+it}}\right| \ll \frac{(X^{\alpha_{i_0}}/r_1)^{1/2}}{W^{1/3+1/100}}. \end{align} $$
Note that
![]() $X^{\alpha _{i_0}}/r_1 \geq X^{\frac {1}{10k} - 2c_k} \geq X^{\frac {1}{20k}}$
. We apply Lemma 3.9(i) with
$X^{\alpha _{i_0}}/r_1 \geq X^{\frac {1}{10k} - 2c_k} \geq X^{\frac {1}{20k}}$
. We apply Lemma 3.9(i) with
![]() $T_0 = W$
. Taking
$T_0 = W$
. Taking
![]() $c_k \leq \delta (\frac {1}{20k})/30$
we obtain that the left-hand side of equation (3.24) is
$c_k \leq \delta (\frac {1}{20k})/30$
we obtain that the left-hand side of equation (3.24) is
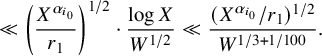 $$\begin{align*}\ll \left(\frac{X^{\alpha_{i_0}}}{r_1}\right)^{1/2} \cdot \frac{\log X}{W^{1/2}} \ll \frac{(X^{\alpha_{i_0}}/r_1)^{1/2}}{W^{1/3+1/100}}. \end{align*}$$
$$\begin{align*}\ll \left(\frac{X^{\alpha_{i_0}}}{r_1}\right)^{1/2} \cdot \frac{\log X}{W^{1/2}} \ll \frac{(X^{\alpha_{i_0}}/r_1)^{1/2}}{W^{1/3+1/100}}. \end{align*}$$
Hence, equation (3.22) follows from Lemma 3.5. The case
![]() $k \geq 6$
and
$k \geq 6$
and
![]() $\theta = 7/12$
follows similarly using Lemma 2.20(iii).
$\theta = 7/12$
follows similarly using Lemma 2.20(iii).
A similar method allows us to establish Proposition 3.4(i). We start by applying Heath-Brown’s identity (Lemma 2.16) with
![]() $L = \lceil 2/\varepsilon \rceil $
, writing
$L = \lceil 2/\varepsilon \rceil $
, writing
![]() $N_i = X^{\alpha _i}$
. Then we apply Lemma 2.20(iii) to these
$N_i = X^{\alpha _i}$
. Then we apply Lemma 2.20(iii) to these
![]() $\alpha _i$
.
$\alpha _i$
.
In case
![]() $(II^{\mathrm {maj}})$
holds, we argue as above but with
$(II^{\mathrm {maj}})$
holds, we argue as above but with
![]() $W = \log ^A X$
for some large
$W = \log ^A X$
for some large
![]() $A> 0$
. On the other hand, in case
$A> 0$
. On the other hand, in case
![]() $\alpha _{i_0} \geq 1-\theta -\varepsilon /2$
for some
$\alpha _{i_0} \geq 1-\theta -\varepsilon /2$
for some
![]() $i_0$
, we write
$i_0$
, we write
![]() $M = \frac {1}{N_{i_0}}\prod _{\substack {j = 1}}^\ell N_{j}$
and move the summation over
$M = \frac {1}{N_{i_0}}\prod _{\substack {j = 1}}^\ell N_{j}$
and move the summation over
![]() $n_{i_0} \sim X^{\alpha _{i_0}}$
inside. Then it suffices to show in this case that, for any
$n_{i_0} \sim X^{\alpha _{i_0}}$
inside. Then it suffices to show in this case that, for any
![]() $B \geq 1$
,
$B \geq 1$
,
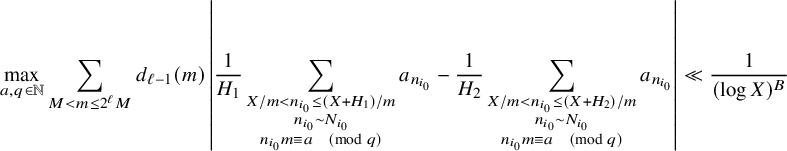 $$\begin{align*}\max_{\substack{a, q \in \mathbb{N}}} \sum_{\substack{M < m \leq 2^\ell M}} d_{\ell-1}(m) \left| \frac{1}{H_1}\sum_{\substack{X/m < n_{i_0} \leq (X+H_1)/m \\ n_{i_0} \sim N_{i_0} \\ n_{i_0} m \equiv a \quad\pmod{q}}} a_{n_{i_0}} - \frac{1}{H_2}\sum_{\substack{X/m < n_{i_0} \leq (X+H_2)/m \\ n_{i_0} \sim N_{i_0} \\ n_{i_0} m \equiv a \quad\pmod{q}}} a_{n_{i_0}} \right| \ll \frac{1}{(\log X)^B} \end{align*}$$
$$\begin{align*}\max_{\substack{a, q \in \mathbb{N}}} \sum_{\substack{M < m \leq 2^\ell M}} d_{\ell-1}(m) \left| \frac{1}{H_1}\sum_{\substack{X/m < n_{i_0} \leq (X+H_1)/m \\ n_{i_0} \sim N_{i_0} \\ n_{i_0} m \equiv a \quad\pmod{q}}} a_{n_{i_0}} - \frac{1}{H_2}\sum_{\substack{X/m < n_{i_0} \leq (X+H_2)/m \\ n_{i_0} \sim N_{i_0} \\ n_{i_0} m \equiv a \quad\pmod{q}}} a_{n_{i_0}} \right| \ll \frac{1}{(\log X)^B} \end{align*}$$
for
![]() $a_{n_{i_0}} = \mathbf {1}_{(N_{i_0}, 2N_{i_0}]}(n_{i_0})$
and
$a_{n_{i_0}} = \mathbf {1}_{(N_{i_0}, 2N_{i_0}]}(n_{i_0})$
and
![]() $a_{n_{i_0}} = \mathbf {1}_{(N_{i_0}, 2N_{i_0}]}(n_{i_0}) \log n_{i_0}$
. But here
$a_{n_{i_0}} = \mathbf {1}_{(N_{i_0}, 2N_{i_0}]}(n_{i_0}) \log n_{i_0}$
. But here
![]() $H_2/M \geq H_1/M \geq X^{\varepsilon /2}$
, so the claim is easy to establish.
$H_2/M \geq H_1/M \geq X^{\varepsilon /2}$
, so the claim is easy to establish.
In the remaining case
![]() $(I_2^{\mathrm {maj}})$
holds and
$(I_2^{\mathrm {maj}})$
holds and
![]() $\alpha _i, \alpha _j> \varepsilon /2$
. Thus, the corresponding coefficients from Heath-Brown’s identity are either
$\alpha _i, \alpha _j> \varepsilon /2$
. Thus, the corresponding coefficients from Heath-Brown’s identity are either
![]() $1_{(N_i, 2N_i]}(n)$
or
$1_{(N_i, 2N_i]}(n)$
or
![]() $(\log n) 1_{(N_i, 2N_i]}(n)$
and the claim follows from Lemma 3.6 (and partial summation if needed).
$(\log n) 1_{(N_i, 2N_i]}(n)$
and the claim follows from Lemma 3.6 (and partial summation if needed).
3.5 Major arc estimates with restricted prime factorization
When proving Theorem 1.1(iv)–(v) we need the following quick consequence of Theorem 3.1. One could obtain stronger results, but this is sufficient for our needs.
Corollary 3.10. Let
![]() $X \geq 3$
and
$X \geq 3$
and
![]() $X^{7/12+\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
$X^{7/12+\varepsilon } \leq H \leq X^{1-\varepsilon }$
for some
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $2 \leq P < Q \leq X^{1/(\log \log X)^2}$
and write
$2 \leq P < Q \leq X^{1/(\log \log X)^2}$
and write
![]() $\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
.
$\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
.
-
(i) For all
 $A> 0$
,
$A> 0$
,  $$ \begin{align*} {\left|\sum_{\substack{X < n \leq X+H}} 1_{(n, \mathcal{P}(P, Q))> 1} \mu(n) \right|}^* &\ll_{A,\varepsilon} \frac{H}{\log^{A} X} + \frac{H(\log X)^4}{P}. \end{align*} $$
$$ \begin{align*} {\left|\sum_{\substack{X < n \leq X+H}} 1_{(n, \mathcal{P}(P, Q))> 1} \mu(n) \right|}^* &\ll_{A,\varepsilon} \frac{H}{\log^{A} X} + \frac{H(\log X)^4}{P}. \end{align*} $$
-
(ii) Let
 $k \geq 2$
. For all
$k \geq 2$
. For all
 $A> 0$
,
$A> 0$
,  $$ \begin{align*}{\left|\sum_{\substack{X < n \leq X+H}} 1_{(n, \mathcal{P}(P, Q))> 1} (d_k(n) - d^\sharp_k(n))\right|}^* \ll_{A, \varepsilon} \frac{H}{\log^A X} + \frac{H(\log X)^{4k}}{P}.\end{align*} $$
$$ \begin{align*}{\left|\sum_{\substack{X < n \leq X+H}} 1_{(n, \mathcal{P}(P, Q))> 1} (d_k(n) - d^\sharp_k(n))\right|}^* \ll_{A, \varepsilon} \frac{H}{\log^A X} + \frac{H(\log X)^{4k}}{P}.\end{align*} $$
Proof. Let us first show (i). By Lemma 2.19 it suffices to show that
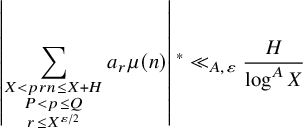 $$\begin{align*}\left|\sum_{\substack{X < prn \leq X+H \\ P < p \leq Q \\ r \leq X^{\varepsilon/2}}} a_r \mu(n)\right|{}^\ast \ll_{A, \varepsilon} \frac{H}{\log^A X} \end{align*}$$
$$\begin{align*}\left|\sum_{\substack{X < prn \leq X+H \\ P < p \leq Q \\ r \leq X^{\varepsilon/2}}} a_r \mu(n)\right|{}^\ast \ll_{A, \varepsilon} \frac{H}{\log^A X} \end{align*}$$
whenever
![]() $|a_r| \leq d_2(r)$
. By the triangle inequality and Theorem 3.1 the left-hand side is
$|a_r| \leq d_2(r)$
. By the triangle inequality and Theorem 3.1 the left-hand side is
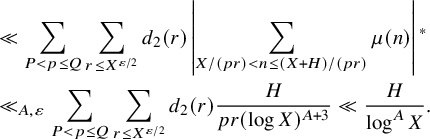 $$ \begin{align*} &\ll \sum_{P < p \leq Q} \sum_{r \leq X^{\varepsilon/2}} d_2(r) \left|\sum_{\substack{X/(pr) < n \leq (X+H)/(pr) }} \mu(n)\right|{}^\ast \\ &\ll_{A, \varepsilon} \sum_{P < p \leq Q} \sum_{r \leq X^{\varepsilon/2}} d_2(r) \frac{H}{pr (\log X)^{A+3}} \ll \frac{H}{\log^A X}. \end{align*} $$
$$ \begin{align*} &\ll \sum_{P < p \leq Q} \sum_{r \leq X^{\varepsilon/2}} d_2(r) \left|\sum_{\substack{X/(pr) < n \leq (X+H)/(pr) }} \mu(n)\right|{}^\ast \\ &\ll_{A, \varepsilon} \sum_{P < p \leq Q} \sum_{r \leq X^{\varepsilon/2}} d_2(r) \frac{H}{pr (\log X)^{A+3}} \ll \frac{H}{\log^A X}. \end{align*} $$
Let us now turn to (ii). By Theorem 3.1 and the triangle inequality, it suffices to show the claim with
![]() $1_{(n, \mathcal {P}(P, Q))> 1}$
replaced by
$1_{(n, \mathcal {P}(P, Q))> 1}$
replaced by
![]() $1_{(n, \mathcal {P}(P, Q)) = 1}$
. Hence, by Möbius inversion we need to show that
$1_{(n, \mathcal {P}(P, Q)) = 1}$
. Hence, by Möbius inversion we need to show that
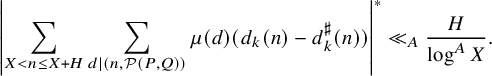 $$ \begin{align} {\left|\sum_{\substack{X < n \leq X+H}} \sum_{d \mid (n,\mathcal{P}(P, Q))} \mu(d) (d_k(n) - d^\sharp_k(n))\right|}^* \ll_A \frac{H}{\log^A X}. \end{align} $$
$$ \begin{align} {\left|\sum_{\substack{X < n \leq X+H}} \sum_{d \mid (n,\mathcal{P}(P, Q))} \mu(d) (d_k(n) - d^\sharp_k(n))\right|}^* \ll_A \frac{H}{\log^A X}. \end{align} $$
Write
![]() $D := \min \{X^{\varepsilon /2000}, X^{c_k/2}\}$
. Since
$D := \min \{X^{\varepsilon /2000}, X^{c_k/2}\}$
. Since
![]() $d_k^\sharp (m) \ll d_k(m)$
(see equation (3.14)), the contribution of
$d_k^\sharp (m) \ll d_k(m)$
(see equation (3.14)), the contribution of
![]() $d> D$
to the left-hand side of equation (3.25) is by Lemma 2.18 at most
$d> D$
to the left-hand side of equation (3.25) is by Lemma 2.18 at most
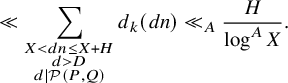 $$ \begin{align*}\ll \sum_{\substack{X < dn \leq X+H \\ d> D \\ d \mid \mathcal{P}(P, Q)}} d_k(dn) \ll_{A} \frac{H}{\log^A X}. \end{align*} $$
$$ \begin{align*}\ll \sum_{\substack{X < dn \leq X+H \\ d> D \\ d \mid \mathcal{P}(P, Q)}} d_k(dn) \ll_{A} \frac{H}{\log^A X}. \end{align*} $$
On the other hand, the contribution of
![]() $d \leq D$
to the left-hand side of equation (3.25) is by the triangle inequality and Theorem 3.1
$d \leq D$
to the left-hand side of equation (3.25) is by the triangle inequality and Theorem 3.1
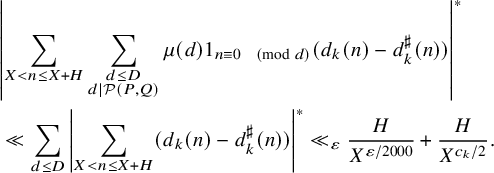 $$ \begin{align*} &{\left|\sum_{\substack{X < n \leq X+H}} \sum_{\substack{d \leq D \\ d \mid \mathcal{P}(P, Q)}} \mu(d) 1_{n \equiv 0 \quad\pmod{d}}(d_k(n) - d^\sharp_k(n))\right|}^* \\ &\ll \sum_{d \leq D} {\left|\sum_{\substack{X < n \leq X+H}} (d_k(n) - d^\sharp_k(n))\right|}^* \ll_{\varepsilon} \frac{H}{X^{\varepsilon/2000}} + \frac{H}{X^{c_k/2}}.\\[-42pt] \end{align*} $$
$$ \begin{align*} &{\left|\sum_{\substack{X < n \leq X+H}} \sum_{\substack{d \leq D \\ d \mid \mathcal{P}(P, Q)}} \mu(d) 1_{n \equiv 0 \quad\pmod{d}}(d_k(n) - d^\sharp_k(n))\right|}^* \\ &\ll \sum_{d \leq D} {\left|\sum_{\substack{X < n \leq X+H}} (d_k(n) - d^\sharp_k(n))\right|}^* \ll_{\varepsilon} \frac{H}{X^{\varepsilon/2000}} + \frac{H}{X^{c_k/2}}.\\[-42pt] \end{align*} $$
4 Reduction to type I, type
 $II$
and type
$II$
and type
 $I_2$
estimates
$I_2$
estimates
To complement the major arc estimates in Theorem 3.1, we will establish later in the paper some ‘inverse theorems’ that provide discorrelation between an arithmetic function f and a nilsequence
![]() $F(g(n)\Gamma )$
assuming that f is ofFootnote
9
‘type I’, ‘type
$F(g(n)\Gamma )$
assuming that f is ofFootnote
9
‘type I’, ‘type
![]() $II$
’ or ‘type
$II$
’ or ‘type
![]() $I_2$
’, and the nilsequence is ‘minor arc’ in a suitable sense. To make this precise, we give some definitions:
$I_2$
’, and the nilsequence is ‘minor arc’ in a suitable sense. To make this precise, we give some definitions:
Definition 4.1 (Type I,
 $II$
,
$II$
,
 $I_2$
sums).
$I_2$
sums).
Let
![]() $0 < \delta < 1$
and
$0 < \delta < 1$
and
![]() $A_I, A_{II}^-, A_{II}^+, A_{I_2} \geq 1$
.
$A_I, A_{II}^-, A_{II}^+, A_{I_2} \geq 1$
.
-
(i) (Type I sum) A
 $(\delta ,A_I)$
type I sum is an arithmetic function of the form
$(\delta ,A_I)$
type I sum is an arithmetic function of the form
 $f = \alpha *\beta $
, where
$f = \alpha *\beta $
, where
 $\alpha $
is supported in
$\alpha $
is supported in
 $[1,A_I]$
, and one has the bounds (4.1)and
$[1,A_I]$
, and one has the bounds (4.1)and $$ \begin{align} \sum_{n \leq A} |\alpha(n)|^2 \leq \frac{1}{\delta} A \end{align} $$
(4.2)for all
$$ \begin{align} \sum_{n \leq A} |\alpha(n)|^2 \leq \frac{1}{\delta} A \end{align} $$
(4.2)for all $$ \begin{align} \| \beta \|_{{\operatorname{TV}}(\mathbb{N}; q)} \leq \frac{1}{\delta} \end{align} $$
$$ \begin{align} \| \beta \|_{{\operatorname{TV}}(\mathbb{N}; q)} \leq \frac{1}{\delta} \end{align} $$
 $A \geq 1$
and some
$A \geq 1$
and some
 $1 \leq q \leq \frac {1}{\delta }$
.
$1 \leq q \leq \frac {1}{\delta }$
.
-
(ii) (Type
 $II$
sum) A
$II$
sum) A
 $(\delta , A_{II}^-, A_{II}^+)$
type
$(\delta , A_{II}^-, A_{II}^+)$
type
 $II$
sum is an arithmetic function of the form
$II$
sum is an arithmetic function of the form
 $f = \alpha * \beta $
, where
$f = \alpha * \beta $
, where
 $\alpha $
is supported on
$\alpha $
is supported on
 $[A_{II}^-,A_{II}^+]$
, and one has the bound (4.1) and the bounds (4.3)for all
$[A_{II}^-,A_{II}^+]$
, and one has the bound (4.1) and the bounds (4.3)for all $$ \begin{align} \sum_{n \leq B} |\beta(n)|^2 \leq \frac{1}{\delta} B \quad \text{and} \quad \sum_{n \leq B} |\beta(n)|^4 \leq \frac{1}{\delta^2} B \end{align} $$
$$ \begin{align} \sum_{n \leq B} |\beta(n)|^2 \leq \frac{1}{\delta} B \quad \text{and} \quad \sum_{n \leq B} |\beta(n)|^4 \leq \frac{1}{\delta^2} B \end{align} $$
 $A,B \geq 1$
. (The type
$A,B \geq 1$
. (The type
 $II$
sums become vacuous if
$II$
sums become vacuous if
 $A_{II}^-> A_{II}^+$
.)
$A_{II}^-> A_{II}^+$
.)
-
(iii) (Type
 $I_2$
sum) A
$I_2$
sum) A
 $(\delta , A_{I_2})$
type
$(\delta , A_{I_2})$
type
 $I_2$
sum is an arithmetic function of the form
$I_2$
sum is an arithmetic function of the form
 $f = \alpha * \beta _1 * \beta _2$
, where
$f = \alpha * \beta _1 * \beta _2$
, where
 $\alpha $
is supported on
$\alpha $
is supported on
 $[1,A_{I_2}]$
and obeys the bound (4.1) for all
$[1,A_{I_2}]$
and obeys the bound (4.1) for all
 $A \geq 1$
, and
$A \geq 1$
, and
 $\beta _1, \beta _2$
obey the bound (4.2) for some
$\beta _1, \beta _2$
obey the bound (4.2) for some
 $1 \leq q \leq \frac {1}{\delta }$
.
$1 \leq q \leq \frac {1}{\delta }$
.
We now state the inverse theorems we will establish here.
Theorem 4.2 (Inverse theorems).
Let
![]() $d,D \geq 1$
,
$d,D \geq 1$
,
![]() $2 \leq H \leq X$
,
$2 \leq H \leq X$
,
![]() $0 < \delta < \frac {1}{\log X}$
, let
$0 < \delta < \frac {1}{\log X}$
, let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension at most D, and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension at most D, and complexity at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be Lipschitz of norm at most
![]() $1/\delta $
and mean zero. Let
$1/\delta $
and mean zero. Let
![]() $f \colon \mathbb {N} \to \mathbb {C}$
be an arithmetic function such that
$f \colon \mathbb {N} \to \mathbb {C}$
be an arithmetic function such that
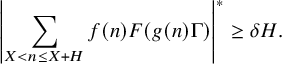 $$ \begin{align} {\left| \sum_{X < n \leq X+H} f(n) F(g(n) \Gamma) \right|}^* \geq \delta H. \end{align} $$
$$ \begin{align} {\left| \sum_{X < n \leq X+H} f(n) F(g(n) \Gamma) \right|}^* \geq \delta H. \end{align} $$
for some polynomial map
![]() $g \colon \mathbb {Z} \to G$
.
$g \colon \mathbb {Z} \to G$
.
-
(i) (Type I inverse theorem) If f is a
 $(\delta ,A_I)$
type I sum for some
$(\delta ,A_I)$
type I sum for some
 $A_I \geq 1$
, then either or else there exists a nontrivial horizontal character
$A_I \geq 1$
, then either or else there exists a nontrivial horizontal character $$ \begin{align*}H \ll_{d,D} \delta^{-O_{d,D}(1)} A_I\end{align*} $$
$$ \begin{align*}H \ll_{d,D} \delta^{-O_{d,D}(1)} A_I\end{align*} $$
 $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
 $O_{d,D}( \delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}( \delta ^{-O_{d,D}(1)})$
such that  $$ \begin{align*}\| \eta \circ g \|_{C^\infty(X,X+H]} \ll_{d,D} \delta^{-O_{d,D}(1)}.\end{align*} $$
$$ \begin{align*}\| \eta \circ g \|_{C^\infty(X,X+H]} \ll_{d,D} \delta^{-O_{d,D}(1)}.\end{align*} $$
-
(ii) (Type
 $II$
inverse theorem, nonabelian case) If f is a
$II$
inverse theorem, nonabelian case) If f is a
 $(\delta ,A_{II}^-, A_{II}^+)$
type
$(\delta ,A_{II}^-, A_{II}^+)$
type
 $II$
sum for some
$II$
sum for some
 $A_{II}^+ \geq A_{II}^- \geq 1$
, G is nonabelian with one-dimensional center, and F oscillates with a nonzero central frequency
$A_{II}^+ \geq A_{II}^- \geq 1$
, G is nonabelian with one-dimensional center, and F oscillates with a nonzero central frequency
 $\xi $
of Lipschitz norm at most
$\xi $
of Lipschitz norm at most
 $1/\delta $
, then either or else there exists a nontrivial horizontal character
$1/\delta $
, then either or else there exists a nontrivial horizontal character $$ \begin{align*}H \ll_{d,D} \delta^{-O_{d,D}(1)} \max( A_{II}^+, X/A_{II}^- )\end{align*} $$
$$ \begin{align*}H \ll_{d,D} \delta^{-O_{d,D}(1)} \max( A_{II}^+, X/A_{II}^- )\end{align*} $$
 $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
 $O_{d,D}( \delta ^{-O_{d,D}(1)})$
such that (4.5)
$O_{d,D}( \delta ^{-O_{d,D}(1)})$
such that (4.5) $$ \begin{align} \| \eta \circ g \|_{C^\infty(X,X+H]} \ll_{d,D} \delta^{-O_{d,D}(1)}. \end{align} $$
$$ \begin{align} \| \eta \circ g \|_{C^\infty(X,X+H]} \ll_{d,D} \delta^{-O_{d,D}(1)}. \end{align} $$
-
(iii) (Type
 $II$
inverse theorem, abelian case) If f is a
$II$
inverse theorem, abelian case) If f is a
 $(\delta ,A_{II}^-, A_{II}^+)$
type
$(\delta ,A_{II}^-, A_{II}^+)$
type
 $II$
sum for some
$II$
sum for some
 $A_{II}^+ \geq A_{II}^- \geq 1$
and
$A_{II}^+ \geq A_{II}^- \geq 1$
and
 $F(g(n)\Gamma ) = e(P(n))$
for some polynomial
$F(g(n)\Gamma ) = e(P(n))$
for some polynomial
 $P \colon \mathbb {Z} \to \mathbb {R}$
of degree at most d, then either or else there exists a real number
$P \colon \mathbb {Z} \to \mathbb {R}$
of degree at most d, then either or else there exists a real number $$ \begin{align*}H \ll_{d} \delta^{-O_{d}(1)} \max( A_{II}^+, X/A_{II}^- )\end{align*} $$
$$ \begin{align*}H \ll_{d} \delta^{-O_{d}(1)} \max( A_{II}^+, X/A_{II}^- )\end{align*} $$
 $T \ll _{d} \delta ^{-O_d(1)} (X/H)^{d+1}$
such that for some
$T \ll _{d} \delta ^{-O_d(1)} (X/H)^{d+1}$
such that for some $$ \begin{align*}\| e(P(n)) n^{-iT} \|_{{\operatorname{TV}}( (X,X+H] \cap \mathbb{Z}; q)} \ll_d \delta^{-O_d(1)}\end{align*} $$
$$ \begin{align*}\| e(P(n)) n^{-iT} \|_{{\operatorname{TV}}( (X,X+H] \cap \mathbb{Z}; q)} \ll_d \delta^{-O_d(1)}\end{align*} $$
 $1 \leq q \ll _d \delta ^{-O_d(1)}$
.
$1 \leq q \ll _d \delta ^{-O_d(1)}$
.
-
(iv) (Type
 $I_2$
inverse theorem) If f is a
$I_2$
inverse theorem) If f is a
 $(\delta ,A_{I_2})$
type
$(\delta ,A_{I_2})$
type
 $I_2$
sum for some
$I_2$
sum for some
 $A_{I_2} \geq 1$
, then either (4.6)or else there exists a nontrivial horizontal character
$A_{I_2} \geq 1$
, then either (4.6)or else there exists a nontrivial horizontal character $$ \begin{align} H \ll_{d,D} \delta^{-O_{d,D}(1)} X^{1/3} A_{I_2}^{2/3} \end{align} $$
$$ \begin{align} H \ll_{d,D} \delta^{-O_{d,D}(1)} X^{1/3} A_{I_2}^{2/3} \end{align} $$
 $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
 $O_{d,D}( \delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}( \delta ^{-O_{d,D}(1)})$
such that  $$ \begin{align*}\| \eta \circ g \|_{C^\infty(X,X+H]} \ll_{d,D} \delta^{-O_{d,D}(1)}.\end{align*} $$
$$ \begin{align*}\| \eta \circ g \|_{C^\infty(X,X+H]} \ll_{d,D} \delta^{-O_{d,D}(1)}.\end{align*} $$
In this section, we show how Theorem 4.2, when combined with the major arc estimates in Theorem 3.1, gives Theorem 1.1.
4.1 Combinatorial decompositions
We start by describing the combinatorial decompositions that allow us to reduce sums involving
![]() $\mu ,\Lambda ,d_k$
to type I, type
$\mu ,\Lambda ,d_k$
to type I, type
![]() $II$
and type
$II$
and type
![]() $I_2$
sums. Lemma 4.3 will be used to prove equations (1.5) and (1.6), Lemma 4.4 will be used to prove (1.7) and Lemma 4.5 will be used to prove equations (1.8) and (1.9).
$I_2$
sums. Lemma 4.3 will be used to prove equations (1.5) and (1.6), Lemma 4.4 will be used to prove (1.7) and Lemma 4.5 will be used to prove equations (1.8) and (1.9).
The model function
![]() $\Lambda ^{\sharp }$
is not quite a type I sum, but we can approximate it well by the type I sumFootnote
10
$\Lambda ^{\sharp }$
is not quite a type I sum, but we can approximate it well by the type I sumFootnote
10
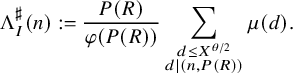 $$ \begin{align} \Lambda_I^\sharp(n) := \frac{P(R)}{\varphi(P(R))}\sum_{\substack{d \leq X^{\theta/2}\\d\mid (n, P(R))}} \mu(d). \end{align} $$
$$ \begin{align} \Lambda_I^\sharp(n) := \frac{P(R)}{\varphi(P(R))}\sum_{\substack{d \leq X^{\theta/2}\\d\mid (n, P(R))}} \mu(d). \end{align} $$
Indeed, by equation (1.1), Möbius inversion and Lemma 2.18, we have
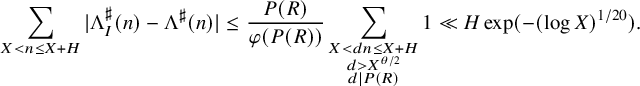 $$ \begin{align} \sum_{X < n \leq X+H} |\Lambda^\sharp_I(n)-\Lambda^{\sharp}(n)|\leq \frac{P(R)}{\varphi(P(R))} \sum_{\substack{X < dn \leq X+H \\ d> X^{\theta/2} \\ d \mid P(R)}} 1 \ll H\exp(-(\log X)^{1/20}). \end{align} $$
$$ \begin{align} \sum_{X < n \leq X+H} |\Lambda^\sharp_I(n)-\Lambda^{\sharp}(n)|\leq \frac{P(R)}{\varphi(P(R))} \sum_{\substack{X < dn \leq X+H \\ d> X^{\theta/2} \\ d \mid P(R)}} 1 \ll H\exp(-(\log X)^{1/20}). \end{align} $$
In practice, this bound allows us to substitute
![]() $\Lambda ^\sharp $
with the type I sum
$\Lambda ^\sharp $
with the type I sum
![]() $\Lambda ^\sharp _I$
with negligible cost.
$\Lambda ^\sharp _I$
with negligible cost.
Lemma 4.3 (Combinatorial decompositions of
 $\mu ,\Lambda ,$
and
$\mu ,\Lambda ,$
and
 $\Lambda ^\sharp _I$
).
$\Lambda ^\sharp _I$
).
Let
![]() $X^{\theta +\varepsilon } \leq H \leq X$
for
$X^{\theta +\varepsilon } \leq H \leq X$
for
![]() $\theta = 5/8$
and some fixed
$\theta = 5/8$
and some fixed
![]() $\varepsilon> 0$
. For each
$\varepsilon> 0$
. For each
![]() $g \in \{\mu , \Lambda , \Lambda ^\sharp _I\}$
, we may find a collection
$g \in \{\mu , \Lambda , \Lambda ^\sharp _I\}$
, we may find a collection
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $O((\log X)^{O(1)})$
functions
$O((\log X)^{O(1)})$
functions
![]() $f \colon \mathbb {N} \to \mathbb {R}$
such that
$f \colon \mathbb {N} \to \mathbb {R}$
such that
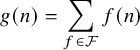 $$ \begin{align*}g(n) = \sum_{f \in \mathcal{F}} f(n)\end{align*} $$
$$ \begin{align*}g(n) = \sum_{f \in \mathcal{F}} f(n)\end{align*} $$
for each
![]() $X/2 \leq n \leq 4X$
, and each component
$X/2 \leq n \leq 4X$
, and each component
![]() $f \in \mathcal {F}$
satisfies one of the following:
$f \in \mathcal {F}$
satisfies one of the following:
-
(i) f is a
 $(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum;
$(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum; -
(ii) f is a
 $(\log ^{-O(1)} X, O(X^{(3\theta -1)/2}))$
type
$(\log ^{-O(1)} X, O(X^{(3\theta -1)/2}))$
type
 $I_2$
sum;
$I_2$
sum; -
(iii) f is a
 $(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
$(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
 $II$
sum for some
$II$
sum for some
 $X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
, and it obeys the bound (4.9)for all sufficiently large
$X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
, and it obeys the bound (4.9)for all sufficiently large $$ \begin{align} \sup_{(X/H)(\log X)^{50A} \leq |T| \leq X^A}{\left|\sum_{X < n \leq X+H} f(n) n^{iT}\right|}^* \ll_A H\log^{-A} X \end{align} $$
$$ \begin{align} \sup_{(X/H)(\log X)^{50A} \leq |T| \leq X^A}{\left|\sum_{X < n \leq X+H} f(n) n^{iT}\right|}^* \ll_A H\log^{-A} X \end{align} $$
 $A \geq 1$
.
$A \geq 1$
.
Lemma 4.4 (Combinatorial decompositions of
 $d_k$
and
$d_k$
and
 $d_k^{\sharp }$
).
$d_k^{\sharp }$
).
Let
![]() $k \geq 2$
. Let
$k \geq 2$
. Let
![]() $X^{\theta + \varepsilon } \leq H \leq X$
for
$X^{\theta + \varepsilon } \leq H \leq X$
for
![]() $\theta = \theta _k$
and some fixed
$\theta = \theta _k$
and some fixed
![]() $\varepsilon> 0$
, where
$\varepsilon> 0$
, where
![]() $\theta _2 = 1/3$
,
$\theta _2 = 1/3$
,
![]() $\theta _3 = 5/9$
, and
$\theta _3 = 5/9$
, and
![]() $\theta _k = 5/8$
for
$\theta _k = 5/8$
for
![]() $k \geq 4$
. For each
$k \geq 4$
. For each
![]() $g \in \{d_k, d_k^\sharp \}$
, we may find a collection
$g \in \{d_k, d_k^\sharp \}$
, we may find a collection
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $O((\log X)^{O(1)})$
functions
$O((\log X)^{O(1)})$
functions
![]() $f \colon \mathbb {N} \to \mathbb {R}$
such that
$f \colon \mathbb {N} \to \mathbb {R}$
such that
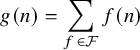 $$ \begin{align*}g(n) = \sum_{f \in \mathcal{F}} f(n)\end{align*} $$
$$ \begin{align*}g(n) = \sum_{f \in \mathcal{F}} f(n)\end{align*} $$
for each
![]() $X/2 \leq n \leq 4X$
, and each component
$X/2 \leq n \leq 4X$
, and each component
![]() $f \in \mathcal {F}$
satisfies one of the following:
$f \in \mathcal {F}$
satisfies one of the following:
-
(i) f is a
 $(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum;
$(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum; -
(ii) f is a
 $(\log ^{-O(1)} X, O(X^{(3\theta -1)/2}))$
type
$(\log ^{-O(1)} X, O(X^{(3\theta -1)/2}))$
type
 $I_2$
sum;
$I_2$
sum; -
(iii) f is a
 $(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
$(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
 $II$
sum for some
$II$
sum for some
 $X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
and it obeys the bound (4.10)for all
$X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
and it obeys the bound (4.10)for all $$ \begin{align} \sup_{(X/H)X^{2c} \leq |T| \leq X^A}{\left|\sum_{X < n \leq X+H} f(n) n^{iT}\right|}^* \ll_{A,k} H X^{-c} \end{align} $$
$$ \begin{align} \sup_{(X/H)X^{2c} \leq |T| \leq X^A}{\left|\sum_{X < n \leq X+H} f(n) n^{iT}\right|}^* \ll_{A,k} H X^{-c} \end{align} $$
 $A> 0$
, where
$A> 0$
, where
 $c = c_{k,A}> 0$
is a sufficiently small constant.
$c = c_{k,A}> 0$
is a sufficiently small constant.
Lemma 4.5 (Flexible combinatorial decompositions of
 $\mu , d_k,$
and
$\mu , d_k,$
and
 $d_k^\sharp $
).
$d_k^\sharp $
).
Let
![]() $X^{3/5 + \varepsilon } \leq H \leq X$
for some fixed
$X^{3/5 + \varepsilon } \leq H \leq X$
for some fixed
![]() $\varepsilon> 0$
, let
$\varepsilon> 0$
, let
![]() $\exp ((\log x)^{2/3+\varepsilon }) \leq P \leq Q \leq X^{1/(\log \log X)^2}$
and write
$\exp ((\log x)^{2/3+\varepsilon }) \leq P \leq Q \leq X^{1/(\log \log X)^2}$
and write
![]() $\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
. We can find a collection
$\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
. We can find a collection
![]() $\mathcal {F}$
of functions, where
$\mathcal {F}$
of functions, where
![]() $|\mathcal {F}| =O((\log X)^{O(1)})$
, such that for any sequence
$|\mathcal {F}| =O((\log X)^{O(1)})$
, such that for any sequence
![]() $\{\omega _n\}$
with
$\{\omega _n\}$
with
![]() $|\omega _n| \leq 1$
,
$|\omega _n| \leq 1$
,
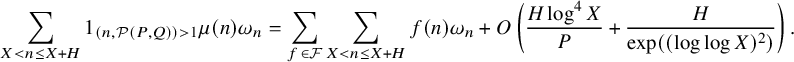 $$ \begin{align*}\sum_{X < n \leq X+H} 1_{(n, \mathcal{P}(P, Q))> 1} \mu(n)\omega_n = \sum_{f \in \mathcal{F}} \sum_{X < n \leq X+H}f(n)\omega_n + O\left(\frac{H \log^4 X}{P} + \frac{H}{\exp((\log \log X)^2)}\right).\end{align*} $$
$$ \begin{align*}\sum_{X < n \leq X+H} 1_{(n, \mathcal{P}(P, Q))> 1} \mu(n)\omega_n = \sum_{f \in \mathcal{F}} \sum_{X < n \leq X+H}f(n)\omega_n + O\left(\frac{H \log^4 X}{P} + \frac{H}{\exp((\log \log X)^2)}\right).\end{align*} $$
Moreover, each component
![]() $f \in \mathcal {F}$
satisfies one of the following:
$f \in \mathcal {F}$
satisfies one of the following:
-
(i) f is a
 $(\log ^{-O(1)} X, X^{3/5+\varepsilon /10})$
type I sum;
$(\log ^{-O(1)} X, X^{3/5+\varepsilon /10})$
type I sum; -
(ii) f is a
 $(\log ^{-O(1)} X, X^{2/5+\varepsilon /10})$
type
$(\log ^{-O(1)} X, X^{2/5+\varepsilon /10})$
type
 $I_2$
sum;
$I_2$
sum; -
(iii) f is a
 $(\log ^{-O(1)} X, X^{2/5-\varepsilon /10}, X^{3/5+\varepsilon /10})$
type
$(\log ^{-O(1)} X, X^{2/5-\varepsilon /10}, X^{3/5+\varepsilon /10})$
type
 $II$
sum and it obeys the bound (4.11)for all sufficiently large
$II$
sum and it obeys the bound (4.11)for all sufficiently large $$ \begin{align} \sup_{(X/H)(\log X)^{20A} \leq |T| \leq X^A}{\left|\sum_{X < n \leq X+H} f(n) n^{iT}\right|}^* \ll_A H\log^{-A} X \end{align} $$
$$ \begin{align} \sup_{(X/H)(\log X)^{20A} \leq |T| \leq X^A}{\left|\sum_{X < n \leq X+H} f(n) n^{iT}\right|}^* \ll_A H\log^{-A} X \end{align} $$
 $A> 0$
.
$A> 0$
.
Similarly, for fixed
![]() $k \geq 2$
we can find a collection
$k \geq 2$
we can find a collection
![]() $\mathcal {F}$
of functions, where
$\mathcal {F}$
of functions, where
![]() $|\mathcal {F}| = O((\log X)^{O(1)})$
, such that for any sequence
$|\mathcal {F}| = O((\log X)^{O(1)})$
, such that for any sequence
![]() $\{\omega _n\}$
with
$\{\omega _n\}$
with
![]() $|\omega _n| \leq 1$
,
$|\omega _n| \leq 1$
,
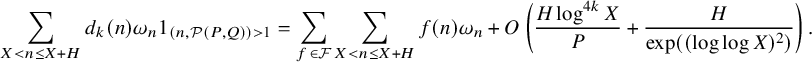 $$ \begin{align*}\sum_{X < n \leq X+H} d_k(n)\omega_n 1_{(n, \mathcal{P}(P, Q))> 1} = \sum_{f \in \mathcal{F}} \sum_{X < n \leq X+H} f(n)\omega_n + O\left(\frac{H \log^{4k} X}{P} + \frac{H}{\exp((\log \log X)^2)}\right).\end{align*} $$
$$ \begin{align*}\sum_{X < n \leq X+H} d_k(n)\omega_n 1_{(n, \mathcal{P}(P, Q))> 1} = \sum_{f \in \mathcal{F}} \sum_{X < n \leq X+H} f(n)\omega_n + O\left(\frac{H \log^{4k} X}{P} + \frac{H}{\exp((\log \log X)^2)}\right).\end{align*} $$
Moreover, each component
![]() $f \in \mathcal {F}$
is one of (i), (ii) or (iii) above, and a similar decomposition holds also with
$f \in \mathcal {F}$
is one of (i), (ii) or (iii) above, and a similar decomposition holds also with
![]() $d_k^\sharp $
in place of
$d_k^\sharp $
in place of
![]() $d_k$
.
$d_k$
.
We will prove Lemmas 4.3, 4.4 and 4.5 by first decomposing the relevant functions into certain Dirichlet convolutions (using Lemma 2.16 in the proof of Lemma 4.3 and Lemma 2.19 in the proof of Lemma 4.5). We then use Lemma 2.20 to arrange each convolution into either type I, type
![]() $II$
or type
$II$
or type
![]() $I_2$
sums. In the case of type
$I_2$
sums. In the case of type
![]() $II$
sums, Lemma 2.20 also allows us to arrange them into a triple convolution for which Lemma 3.5 is applicable.
$II$
sums, Lemma 2.20 also allows us to arrange them into a triple convolution for which Lemma 3.5 is applicable.
Remark 4.6. Let us briefly discuss the type
![]() $II$
conditions such as equation (4.9), concentrating on the case of the von Mangoldt function.
$II$
conditions such as equation (4.9), concentrating on the case of the von Mangoldt function.
One may observe from the proof of Theorem 1.1(ii) below that if our major arc estimate (Theorem 3.1(i)) held, for any
![]() $T \leq X^{O(1)}$
, with
$T \leq X^{O(1)}$
, with
![]() $(\Lambda (n)-\Lambda ^\sharp (n))n^{iT}$
in place of
$(\Lambda (n)-\Lambda ^\sharp (n))n^{iT}$
in place of
![]() $\Lambda (n)-\Lambda ^\sharp (n)$
, we could prove Theorem 1.1(ii) without the need to impose in Lemma 4.3 the condition (4.9) concerning type
$\Lambda (n)-\Lambda ^\sharp (n)$
, we could prove Theorem 1.1(ii) without the need to impose in Lemma 4.3 the condition (4.9) concerning type
![]() $II$
sums.
$II$
sums.
Unfortunately, with current knowledge, one cannot obtain such a twisted version of Theorem 3.1, at least not in the whole range
![]() $X^{7/12+\varepsilon } \leq H \leq X^{1-\varepsilon }$
. However, inserting special cases of our type I and type
$X^{7/12+\varepsilon } \leq H \leq X^{1-\varepsilon }$
. However, inserting special cases of our type I and type
![]() $I_2$
estimates into Section 3, it would be possible to obtain such a twisted variant in the relevant range
$I_2$
estimates into Section 3, it would be possible to obtain such a twisted variant in the relevant range
![]() $X^{5/8+\varepsilon } \leq H \leq X^{1-\varepsilon }$
. If we did this, we would not need to impose the condition (4.9). However, we found it more natural to work out the major arc estimates first using existing methods without needing to appeal to the more involved
$X^{5/8+\varepsilon } \leq H \leq X^{1-\varepsilon }$
. If we did this, we would not need to impose the condition (4.9). However, we found it more natural to work out the major arc estimates first using existing methods without needing to appeal to the more involved
![]() $I_2$
case.
$I_2$
case.
Proof of Lemma 4.3.
The function
![]() $\Lambda ^\sharp _I$
is clearly a
$\Lambda ^\sharp _I$
is clearly a
![]() $(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum by definition (4.7). For
$(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum by definition (4.7). For
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mu $
, we apply Lemma 2.16 with
$\mu $
, we apply Lemma 2.16 with
![]() $L = 10$
. Each component
$L = 10$
. Each component
![]() $f \in \mathcal {F}$
takes the form
$f \in \mathcal {F}$
takes the form
for some
![]() $\ell \leq 20$
, where each
$\ell \leq 20$
, where each
![]() $a^{(i)}$
is supported on
$a^{(i)}$
is supported on
![]() $(N_i, 2N_i]$
for some
$(N_i, 2N_i]$
for some
![]() $N_i \geq 1/2$
, and each
$N_i \geq 1/2$
, and each
![]() $a^{(i)}(n)$
is either
$a^{(i)}(n)$
is either
![]() $1_{(N_i, 2N_i]}(n)$
,
$1_{(N_i, 2N_i]}(n)$
,
![]() $(\log n)1_{(N_i, 2N_i]}(n)$
, or
$(\log n)1_{(N_i, 2N_i]}(n)$
, or
![]() $\mu (n)1_{(N_i, 2N_i]}(n)$
. Moreover,
$\mu (n)1_{(N_i, 2N_i]}(n)$
. Moreover,
![]() $N_1N_2\cdots N_{\ell } \asymp X$
, and
$N_1N_2\cdots N_{\ell } \asymp X$
, and
![]() $N_i \leq X^{1/10}$
for each i with
$N_i \leq X^{1/10}$
for each i with
![]() $a^{(i)}(n) = \mu (n) 1_{(N_i, 2N_i]}(n)$
.
$a^{(i)}(n) = \mu (n) 1_{(N_i, 2N_i]}(n)$
.
We can find
![]() $\alpha _1,\ldots ,\alpha _{\ell } \in [0,1]$
with
$\alpha _1,\ldots ,\alpha _{\ell } \in [0,1]$
with
![]() $\sum _{i=1}^{\ell }\alpha _i=1$
such that
$\sum _{i=1}^{\ell }\alpha _i=1$
such that
![]() $N_i \asymp X^{\alpha _i}$
for each i. If
$N_i \asymp X^{\alpha _i}$
for each i. If
![]() $\alpha _i> 1/10$
for some i, then
$\alpha _i> 1/10$
for some i, then
![]() $a^{(i)}(n)$
is either
$a^{(i)}(n)$
is either
![]() $1_{(N_i, 2N_i]}(n)$
or
$1_{(N_i, 2N_i]}(n)$
or
![]() $(\log n)1_{(N_i, 2N_i]}(n)$
, and hence
$(\log n)1_{(N_i, 2N_i]}(n)$
, and hence
![]() $\|a^{(i)}\|_{{\operatorname {TV}}(\mathbb {N})} \ll \log X$
.
$\|a^{(i)}\|_{{\operatorname {TV}}(\mathbb {N})} \ll \log X$
.
Since
![]() $\theta = 5/8 \geq 3/5$
, we may apply Lemma 2.20(i), (ii) to conclude that either (I) holds, or (
$\theta = 5/8 \geq 3/5$
, we may apply Lemma 2.20(i), (ii) to conclude that either (I) holds, or (
![]() $I_2$
) holds, or both (
$I_2$
) holds, or both (
![]() $II^{\mathrm {min}}$
) and (
$II^{\mathrm {min}}$
) and (
![]() $II^{\mathrm {maj}}$
) hold.
$II^{\mathrm {maj}}$
) hold.
First, consider the case (I) holds, that is,
![]() $\alpha _i \geq 1-\theta $
for some i. Since
$\alpha _i \geq 1-\theta $
for some i. Since
![]() $\alpha _i> 1/10$
,
$\alpha _i> 1/10$
,
![]() $\|a^{(i)}\|_{{\operatorname {TV}}(\mathbb {N})} \ll \log X$
, and equation (4.12) is a
$\|a^{(i)}\|_{{\operatorname {TV}}(\mathbb {N})} \ll \log X$
, and equation (4.12) is a
![]() $(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum of the form
$(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum of the form
![]() $\alpha *\beta $
with
$\alpha *\beta $
with
![]() $\beta = a^{(i)}$
and
$\beta = a^{(i)}$
and
![]() $\alpha = a^{(1)}*\cdots *a^{(i-1)}*a^{(i+1)}*\cdots *a^{(k)}$
.
$\alpha = a^{(1)}*\cdots *a^{(i-1)}*a^{(i+1)}*\cdots *a^{(k)}$
.
Henceforth, we may assume that
![]() $\alpha _i < 1-\theta $
for each i. Next, consider the case (
$\alpha _i < 1-\theta $
for each i. Next, consider the case (
![]() $I_2$
) holds. Then
$I_2$
) holds. Then
![]() $\alpha _i + \alpha _j\geq \tfrac {3}{2}(1-\theta )$
for some
$\alpha _i + \alpha _j\geq \tfrac {3}{2}(1-\theta )$
for some
![]() $i<j$
. Since
$i<j$
. Since
![]() $\alpha _i,\alpha _j \leq 1-\theta $
, this implies that
$\alpha _i,\alpha _j \leq 1-\theta $
, this implies that
![]() $\alpha _i, \alpha _j> 1/10$
and thus
$\alpha _i, \alpha _j> 1/10$
and thus
![]() $\|a^{(i)}\|_{{\operatorname {TV}}(\mathbb {N})}, \|a^{(j)}\|_{{\operatorname {TV}}(\mathbb {N})} \ll \log X$
. Hence, equation (4.12) is a
$\|a^{(i)}\|_{{\operatorname {TV}}(\mathbb {N})}, \|a^{(j)}\|_{{\operatorname {TV}}(\mathbb {N})} \ll \log X$
. Hence, equation (4.12) is a
![]() $(\log ^{-O(1)} X, O(X^{(3\theta -1)/2}))$
type
$(\log ^{-O(1)} X, O(X^{(3\theta -1)/2}))$
type
![]() $I_2$
sum of the form
$I_2$
sum of the form
![]() $f = \alpha *\beta _1*\beta _2$
, with
$f = \alpha *\beta _1*\beta _2$
, with
![]() $\beta _1 = a^{(i)}$
,
$\beta _1 = a^{(i)}$
,
![]() $\beta _2 = a^{(j)}$
.
$\beta _2 = a^{(j)}$
.
Finally, consider the case when both (
![]() $II^{\mathrm {min}}$
) and (
$II^{\mathrm {min}}$
) and (
![]() $II^{\mathrm {maj}}$
) hold. Let
$II^{\mathrm {maj}}$
) hold. Let
![]() $\{1,\ldots ,\ell \} = J\uplus J'$
be the partition from (
$\{1,\ldots ,\ell \} = J\uplus J'$
be the partition from (
![]() $II^{\mathrm {min}}$
), so that
$II^{\mathrm {min}}$
), so that
![]() $\alpha _J, \alpha _{J'} \in [1-\theta , \theta ]$
. Then equation (4.12) is a
$\alpha _J, \alpha _{J'} \in [1-\theta , \theta ]$
. Then equation (4.12) is a
![]() $(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
$(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
![]() $II$
sum of the form
$II$
sum of the form
![]() $f = \alpha * \beta $
, where
$f = \alpha * \beta $
, where
![]() $\alpha $
(resp.
$\alpha $
(resp.
![]() $\beta $
) is the convolution of those
$\beta $
) is the convolution of those
![]() $a^{(i)}$
with
$a^{(i)}$
with
![]() $i \in J$
(resp.
$i \in J$
(resp.
![]() $i \in J'$
), and
$i \in J'$
), and
![]() $X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
.
$X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
.
It remains to establish the bound (4.9). For any subinterval
![]() $(X_1, X_1+H_1] \subset (X, X+H]$
, any residue class
$(X_1, X_1+H_1] \subset (X, X+H]$
, any residue class
![]() $a\ \pmod {q}$
, any fixed
$a\ \pmod {q}$
, any fixed
![]() $A> 0$
, and any
$A> 0$
, and any
![]() $(X/H)(\log X)^{50A} \leq |T| \leq X^A$
, we need to show that
$(X/H)(\log X)^{50A} \leq |T| \leq X^A$
, we need to show that
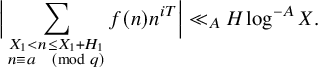 $$ \begin{align*}\Big|\sum_{\substack{X_1 < n \leq X_1+H_1 \\ n \equiv a\quad\pmod{q}}} f(n) n^{iT}\Big| \ll_A H\log^{-A} X.\end{align*} $$
$$ \begin{align*}\Big|\sum_{\substack{X_1 < n \leq X_1+H_1 \\ n \equiv a\quad\pmod{q}}} f(n) n^{iT}\Big| \ll_A H\log^{-A} X.\end{align*} $$
We may assume that A is sufficiently large,
![]() $H_1 \geq H(\log X)^{-2A}$
and
$H_1 \geq H(\log X)^{-2A}$
and
![]() $q \leq (\log X)^{2A}$
. Let now
$q \leq (\log X)^{2A}$
. Let now
![]() $\{1,\ldots ,\ell \} = I \uplus J \uplus J'$
be the partition from (
$\{1,\ldots ,\ell \} = I \uplus J \uplus J'$
be the partition from (
![]() $II^{\mathrm {maj}}$
) so that
$II^{\mathrm {maj}}$
) so that
Let
![]() $\{a_{m_1}'\}, \{b_{m_2}'\}, \{v_{\ell }'\}$
be the convolution of those
$\{a_{m_1}'\}, \{b_{m_2}'\}, \{v_{\ell }'\}$
be the convolution of those
![]() $a^{(i)}$
with
$a^{(i)}$
with
![]() $i \in J$
,
$i \in J$
,
![]() $i \in J'$
,
$i \in J'$
,
![]() $i \in I$
, respectively. Note that they are supported on
$i \in I$
, respectively. Note that they are supported on
![]() $m_1 \asymp X_1^{\alpha _J}$
,
$m_1 \asymp X_1^{\alpha _J}$
,
![]() $m_2 \asymp X_1^{\alpha _{J'}}$
,
$m_2 \asymp X_1^{\alpha _{J'}}$
,
![]() $\ell \asymp X_1^{\alpha _I}$
, respectively. Thus, after dyadic division of the ranges of
$\ell \asymp X_1^{\alpha _I}$
, respectively. Thus, after dyadic division of the ranges of
![]() $m_1,m_2,\ell $
, we need to show that
$m_1,m_2,\ell $
, we need to show that
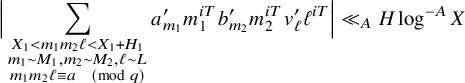 $$ \begin{align*}\Big|\sum_{\substack{X_1 < m_1m_2\ell < X_1+H_1 \\ m_1\sim M_1, m_2\sim M_2, \ell\sim L \\ m_1m_2\ell \equiv a\quad\pmod{q}}} a_{m_1}'m_1^{iT} b_{m_2}'m_2^{iT} v_{\ell}'\ell^{iT} \Big| \ll_A H\log^{-A} X \end{align*} $$
$$ \begin{align*}\Big|\sum_{\substack{X_1 < m_1m_2\ell < X_1+H_1 \\ m_1\sim M_1, m_2\sim M_2, \ell\sim L \\ m_1m_2\ell \equiv a\quad\pmod{q}}} a_{m_1}'m_1^{iT} b_{m_2}'m_2^{iT} v_{\ell}'\ell^{iT} \Big| \ll_A H\log^{-A} X \end{align*} $$
for
![]() $M_1 \asymp X_1^{\alpha _J}$
,
$M_1 \asymp X_1^{\alpha _J}$
,
![]() $M_2 \asymp X_1^{\alpha _{J'}}$
,
$M_2 \asymp X_1^{\alpha _{J'}}$
,
![]() $L \asymp X_1^{\alpha _I}$
. In view of Lemma 3.5(ii) applied with
$L \asymp X_1^{\alpha _I}$
. In view of Lemma 3.5(ii) applied with
![]() $W = (\log X)^{10A}$
and
$W = (\log X)^{10A}$
and
![]() $v_\ell = v_\ell '\ell ^{iT}$
, it suffices to verify the hypothesis (3.8). There exists
$v_\ell = v_\ell '\ell ^{iT}$
, it suffices to verify the hypothesis (3.8). There exists
![]() $i_0 \in I$
such that
$i_0 \in I$
such that
![]() $\alpha _{i_0} \geq (2\theta -1)/20 = 1/80$
. Now, equation (3.8) follows if we show that
$\alpha _{i_0} \geq (2\theta -1)/20 = 1/80$
. Now, equation (3.8) follows if we show that
 $$ \begin{align*}\max_{r \mid (a,q)}\,\, \max_{\chi\quad\pmod{\frac{q}{(a,q)}}} \sup_{|t| \leq \frac{X_1 (\log X)^{40A}}{H_1}} \Big|\sum_{m \asymp X^{\alpha_{i_0}}/r} \frac{a^{(i_0)}(mr)\chi(m)}{m^{1/2+i(t-T)}} \Big| \ll_A \frac{(X^{\alpha_{i_0}}/r)^{1/2}}{(\log X)^{10A}}. \end{align*} $$
$$ \begin{align*}\max_{r \mid (a,q)}\,\, \max_{\chi\quad\pmod{\frac{q}{(a,q)}}} \sup_{|t| \leq \frac{X_1 (\log X)^{40A}}{H_1}} \Big|\sum_{m \asymp X^{\alpha_{i_0}}/r} \frac{a^{(i_0)}(mr)\chi(m)}{m^{1/2+i(t-T)}} \Big| \ll_A \frac{(X^{\alpha_{i_0}}/r)^{1/2}}{(\log X)^{10A}}. \end{align*} $$
Since
![]() $a^{(i_0)}$
is either
$a^{(i_0)}$
is either
![]() $1$
,
$1$
,
![]() $\log $
or
$\log $
or
![]() $\mu $
on its support, this follows from Lemma 3.9 applied with
$\mu $
on its support, this follows from Lemma 3.9 applied with
![]() ${T_0 = (\log X)^{45A}}$
.
${T_0 = (\log X)^{45A}}$
.
Proof of Lemma 4.4.
The function
![]() $d_k^{\sharp }$
is clearly a
$d_k^{\sharp }$
is clearly a
![]() $(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum by definition (1.2). On the other hand,
$(\log ^{-O(1)} X, O(X^{\theta }))$
type I sum by definition (1.2). On the other hand,
![]() $d_k$
can be decomposed into a sum of
$d_k$
can be decomposed into a sum of
![]() $\log ^k X$
terms, each of which takes the form
$\log ^k X$
terms, each of which takes the form
for some
![]() $N_i \geq 1/2$
with
$N_i \geq 1/2$
with
![]() $N_1N_2 \cdots N_{k} \asymp X$
. The
$N_1N_2 \cdots N_{k} \asymp X$
. The
![]() $k \geq 4$
case of the lemma then follows in a similar way as Lemma 4.3, with the only difference being that Lemma 3.5 is now applied with
$k \geq 4$
case of the lemma then follows in a similar way as Lemma 4.3, with the only difference being that Lemma 3.5 is now applied with
![]() $W = X^{10c}$
instead of a power of
$W = X^{10c}$
instead of a power of
![]() $\log X$
.
$\log X$
.
In the case
![]() $k=2$
and
$k=2$
and
![]() $\theta = 1/3$
, f is clearly a
$\theta = 1/3$
, f is clearly a
![]() $(\log ^{-O(1)} X, 1)$
type
$(\log ^{-O(1)} X, 1)$
type
![]() $I_2$
sum. In the case
$I_2$
sum. In the case
![]() $k=3$
and
$k=3$
and
![]() $\theta = 5/9$
, at least one of the
$\theta = 5/9$
, at least one of the
![]() $N_i$
’s (say
$N_i$
’s (say
![]() $N_3$
) is
$N_3$
) is
![]() $\ll X^{1/3}$
. Hence, f is a
$\ll X^{1/3}$
. Hence, f is a
![]() $(\log ^{-O(1)} X, O(X^{1/3}))$
type
$(\log ^{-O(1)} X, O(X^{1/3}))$
type
![]() $I_2$
sum of the form
$I_2$
sum of the form
![]() $f = \alpha * \beta _1 * \beta _2$
, with
$f = \alpha * \beta _1 * \beta _2$
, with
![]() $\alpha = 1_{(N_3, 2N_3]}$
and
$\alpha = 1_{(N_3, 2N_3]}$
and
![]() $\beta _j = 1_{(N_j, 2N_j]}(n)$
for
$\beta _j = 1_{(N_j, 2N_j]}(n)$
for
![]() $j = 1, 2$
.
$j = 1, 2$
.
Proof of Lemma 4.5.
Let us first outline the proof for
![]() $\mu $
. We first apply Lemma 2.19 and then Heath-Brown’s identity (Lemma 2.16) with
$\mu $
. We first apply Lemma 2.19 and then Heath-Brown’s identity (Lemma 2.16) with
![]() $L=10$
to
$L=10$
to
![]() $\mu (n)$
on the right-hand side; note that we now have extra flexibility with the p variable. We obtain a collection of functions
$\mu (n)$
on the right-hand side; note that we now have extra flexibility with the p variable. We obtain a collection of functions
![]() $\mathcal {F}$
, where each
$\mathcal {F}$
, where each
![]() $f \in \mathcal {F}$
takes the form
$f \in \mathcal {F}$
takes the form
for some
![]() $\ell \leq 21$
, where each
$\ell \leq 21$
, where each
![]() $a^{(i)}$
is supported on
$a^{(i)}$
is supported on
![]() $(N_i, 2N_i]$
for some
$(N_i, 2N_i]$
for some
![]() $N_i \geq 1/2$
, with
$N_i \geq 1/2$
, with
(Here,
![]() $a^{(0)}$
comes from the p variable,
$a^{(0)}$
comes from the p variable,
![]() $a^{(1)}$
comes from the r variable and
$a^{(1)}$
comes from the r variable and
![]() $a^{(2)}*\cdots *a^{(\ell )}$
comes from applying Heath-Brown’s identity to
$a^{(2)}*\cdots *a^{(\ell )}$
comes from applying Heath-Brown’s identity to
![]() $\mu (n)$
.) Moreover,
$\mu (n)$
.) Moreover,
![]() $a^{(0)}(n) = 1_{n\text { prime}}1_{(N_0, 2N_0]}(n)$
,
$a^{(0)}(n) = 1_{n\text { prime}}1_{(N_0, 2N_0]}(n)$
,
![]() $a^{(1)}$
is divisor-bounded, and for each
$a^{(1)}$
is divisor-bounded, and for each
![]() $i \geq 2$
,
$i \geq 2$
,
![]() $a^{(i)}(n)$
is either
$a^{(i)}(n)$
is either
![]() $1_{(N_i, 2N_i]}(n)$
or
$1_{(N_i, 2N_i]}(n)$
or
![]() $\mu (n)1_{(N_i, 2N_i]}(n)$
, and
$\mu (n)1_{(N_i, 2N_i]}(n)$
, and
![]() $N_i \leq X^{1/10}$
for each i with
$N_i \leq X^{1/10}$
for each i with
![]() $a^{(i)} = \mu (n)1_{(N_i, 2N_i]}(n)$
.
$a^{(i)} = \mu (n)1_{(N_i, 2N_i]}(n)$
.
We can find
![]() $\alpha _1,\ldots ,\alpha _{\ell } \in [0,1]$
with
$\alpha _1,\ldots ,\alpha _{\ell } \in [0,1]$
with
![]() $\sum _{i=1}^{\ell }\alpha _i=1$
such that
$\sum _{i=1}^{\ell }\alpha _i=1$
such that
![]() $X^{\alpha _i-\varepsilon /20} \leq N_i \ll X^{\alpha _i}$
for each
$X^{\alpha _i-\varepsilon /20} \leq N_i \ll X^{\alpha _i}$
for each
![]() $1 \leq i \leq \ell $
. We may apply Lemma 2.20(ii) to conclude that either (I) holds, or (
$1 \leq i \leq \ell $
. We may apply Lemma 2.20(ii) to conclude that either (I) holds, or (
![]() $I_2$
) holds, or (
$I_2$
) holds, or (
![]() $II^{\mathrm {min}}$
) holds.
$II^{\mathrm {min}}$
) holds.
As in the proof of Lemma 4.3, if (I) holds, then f is a desired type I sum; if (
![]() $I_2$
) holds, then f is a desired type
$I_2$
) holds, then f is a desired type
![]() $I_2$
sum; and if (
$I_2$
sum; and if (
![]() $II^{\mathrm {min}}$
) holds, then f is a desired type
$II^{\mathrm {min}}$
) holds, then f is a desired type
![]() $II$
sum. It remains to establish the bound (4.11) in the type
$II$
sum. It remains to establish the bound (4.11) in the type
![]() $II$
case. Let
$II$
case. Let
![]() $\{1,\ldots ,\ell \} = J \uplus J'$
be the partition from (
$\{1,\ldots ,\ell \} = J \uplus J'$
be the partition from (
![]() $II^{\mathrm {min}}$
) so that
$II^{\mathrm {min}}$
) so that
![]() $|\alpha _J - \alpha _{J'}| \leq 1/5$
. In view of Lemma 3.5(ii) with
$|\alpha _J - \alpha _{J'}| \leq 1/5$
. In view of Lemma 3.5(ii) with
![]() $W = (\log X)^{4A}$
, it suffices to verify the hypothesis (3.8) for the sequence
$W = (\log X)^{4A}$
, it suffices to verify the hypothesis (3.8) for the sequence
Since
![]() $N_0 \gg P$
, Lemma 3.9 implies that hypothesis (3.8) is satisfied when
$N_0 \gg P$
, Lemma 3.9 implies that hypothesis (3.8) is satisfied when
![]() $(\log X)^{20A} X/H \leq |T| \leq X^A$
as required.
$(\log X)^{20A} X/H \leq |T| \leq X^A$
as required.
The claim for
![]() $d_k$
follows similarly.
$d_k$
follows similarly.
In case
![]() $d_k^\sharp $
, we use Möbius inversion to write
$d_k^\sharp $
, we use Möbius inversion to write
 $$ \begin{align*} \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n 1_{(n, \mathcal{P}(P, Q))> 1} &= \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n - \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n 1_{(n, \mathcal{P}(P, Q)) = 1} \\[5pt] &= \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n - \sum_{\substack{X < dn \leq X+H \\ d \mid \mathcal{P}(P, Q)}} \mu(d) d_k^\sharp(dn) \omega_{dn}. \end{align*} $$
$$ \begin{align*} \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n 1_{(n, \mathcal{P}(P, Q))> 1} &= \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n - \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n 1_{(n, \mathcal{P}(P, Q)) = 1} \\[5pt] &= \sum_{X < n \leq X+H} d_k^\sharp(n)\omega_n - \sum_{\substack{X < dn \leq X+H \\ d \mid \mathcal{P}(P, Q)}} \mu(d) d_k^\sharp(dn) \omega_{dn}. \end{align*} $$
Now,
![]() $d_k^\sharp (n)$
is immediately a
$d_k^\sharp (n)$
is immediately a
![]() $(\log ^{-O(1)} X, X^{3/5})$
type I sum by the definition (1.2). Using Lemma 2.18, we can truncate the last sum above to
$(\log ^{-O(1)} X, X^{3/5})$
type I sum by the definition (1.2). Using Lemma 2.18, we can truncate the last sum above to
![]() $d \leq X^{\varepsilon /10}$
with an admissible error
$d \leq X^{\varepsilon /10}$
with an admissible error
![]() $O(H/\exp ((\log \log X)^2/20))$
and it remains to show that
$O(H/\exp ((\log \log X)^2/20))$
and it remains to show that
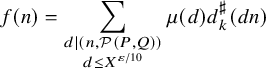 $$\begin{align*}f(n) = \sum_{\substack{d \mid (n, \mathcal{P}(P, Q)) \\ d \leq X^{\varepsilon/10}}} \mu(d) d_k^\sharp(dn) \end{align*}$$
$$\begin{align*}f(n) = \sum_{\substack{d \mid (n, \mathcal{P}(P, Q)) \\ d \leq X^{\varepsilon/10}}} \mu(d) d_k^\sharp(dn) \end{align*}$$
is also a
![]() $(\log ^{-O(1)} X, X^{3/5})$
type I sum. But this follows easily from the definition (1.2) of
$(\log ^{-O(1)} X, X^{3/5})$
type I sum. But this follows easily from the definition (1.2) of
![]() $d_k^\sharp $
.
$d_k^\sharp $
.
4.2 Deduction of Theorem 1.1
In this subsection, we deduce Theorem 1.1 from Theorem 4.2. We focus on establishing equation (1.6). The other estimates in Theorem 1.1 are established similarly, and we mention the small differences at the end of the section. In this section, we allow all implied constants to depend on
![]() $d,D$
.
$d,D$
.
We induct on the dimension D of
![]() $G/\Gamma $
. In view of the major arc estimates (Theorem 3.1), we may assume that F has mean zero (after replacing F by
$G/\Gamma $
. In view of the major arc estimates (Theorem 3.1), we may assume that F has mean zero (after replacing F by
![]() $F - \int F$
). In view of Proposition 2.9 with
$F - \int F$
). In view of Proposition 2.9 with
![]() $\delta = \log ^{-A} X$
, we may assume that F oscillates with a central frequency
$\delta = \log ^{-A} X$
, we may assume that F oscillates with a central frequency
![]() $\xi \colon Z(G) \rightarrow \mathbb {R}$
. If the center
$\xi \colon Z(G) \rightarrow \mathbb {R}$
. If the center
![]() $Z(G)$
has dimension larger than
$Z(G)$
has dimension larger than
![]() $1$
or
$1$
or
![]() $\xi $
vanishes, then
$\xi $
vanishes, then
![]() $\ker \xi $
has positive dimension and the conclusion follows from induction hypothesis applied to
$\ker \xi $
has positive dimension and the conclusion follows from induction hypothesis applied to
![]() $G/\ker \xi $
(via Lemma 2.8). Henceforth, we assume that G has one-dimensional center and that
$G/\ker \xi $
(via Lemma 2.8). Henceforth, we assume that G has one-dimensional center and that
![]() $\xi $
is nonzero. (A zero-dimensional center is not possible since G is nilpotent and nontrivial.)
$\xi $
is nonzero. (A zero-dimensional center is not possible since G is nilpotent and nontrivial.)
Let
![]() $X^{\theta + \varepsilon } \leq H \leq X^{1-\varepsilon }$
for
$X^{\theta + \varepsilon } \leq H \leq X^{1-\varepsilon }$
for
![]() $\theta = 5/8$
and
$\theta = 5/8$
and
![]() $\varepsilon> 0$
. Redefining
$\varepsilon> 0$
. Redefining
![]() $\delta $
, we see that, to prove equation (1.6), it suffices to show the following claim: There exists a small
$\delta $
, we see that, to prove equation (1.6), it suffices to show the following claim: There exists a small
![]() $c> 0$
such that for any large A and
$c> 0$
such that for any large A and
![]() $\delta = \log ^{-A} X$
, if
$\delta = \log ^{-A} X$
, if
![]() $G/\Gamma $
has complexity at most
$G/\Gamma $
has complexity at most
![]() $\delta ^{-c}$
and F has Lipschitz norm at most
$\delta ^{-c}$
and F has Lipschitz norm at most
![]() $\delta ^{-c}$
, then we have
$\delta ^{-c}$
, then we have
Suppose that equation (4.13) fails, that is,
By equation (4.8) and the triangle inequality, we then have
By Lemma 4.3, for some component
![]() $f \in \mathcal {F}$
as in that lemma, one has the bound
$f \in \mathcal {F}$
as in that lemma, one has the bound
Consider first the case when f is a
![]() $(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
$(\log ^{-O(1)} X, A_{II}^-, A_{II}^+)$
type
![]() $II$
sum with
$II$
sum with
![]() $X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
obeying equation (4.9), and G is abelian, hence one-dimensional since
$X^{1-\theta } \ll A_{II}^- \leq A_{II}^+ \ll X^{\theta }$
obeying equation (4.9), and G is abelian, hence one-dimensional since
![]() $G=Z(G)$
. Then we may identify
$G=Z(G)$
. Then we may identify
![]() $G/\Gamma $
with the standard circle
$G/\Gamma $
with the standard circle
![]() $\mathbb {R}/\mathbb {Z}$
(increasing the Lipschitz constants for F,
$\mathbb {R}/\mathbb {Z}$
(increasing the Lipschitz constants for F,
![]() $\xi $
by
$\xi $
by
![]() $O(\delta ^{-O(1)})$
if necessary) and
$O(\delta ^{-O(1)})$
if necessary) and
![]() $\xi $
with an element of
$\xi $
with an element of
![]() $\mathbb {Z}$
of magnitude
$\mathbb {Z}$
of magnitude
![]() $O(\delta ^{O(1)})$
, and we can write
$O(\delta ^{O(1)})$
, and we can write
for some
![]() $b = O(\delta ^{-O(1)})$
and all
$b = O(\delta ^{-O(1)})$
and all
![]() $x \in \mathbb {R}/\mathbb {Z}$
. We can write
$x \in \mathbb {R}/\mathbb {Z}$
. We can write
![]() $\xi \cdot g(n) \Gamma = P(n) \text { mod } 1$
for some polynomial
$\xi \cdot g(n) \Gamma = P(n) \text { mod } 1$
for some polynomial
![]() $P \colon \mathbb {Z} \rightarrow \mathbb {R}$
of degree at most d, thus by equation (4.14), equation (4.16) we have
$P \colon \mathbb {Z} \rightarrow \mathbb {R}$
of degree at most d, thus by equation (4.14), equation (4.16) we have
and
Theorem 4.2(iii) implies that there exists a real number
![]() $T \ll \delta ^{-O(1)} (X/H)^{d+1}$
such that
$T \ll \delta ^{-O(1)} (X/H)^{d+1}$
such that
for some
![]() $1 \leq q \leq \delta ^{-O(1)}$
. By Lemma 2.2(iii), we thus obtain
$1 \leq q \leq \delta ^{-O(1)}$
. By Lemma 2.2(iii), we thus obtain
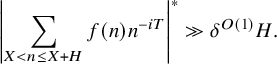 $$ \begin{align} {\left|\sum_{X < n \leq X+H} f(n) n^{-iT} \right|}^* \gg \delta^{O(1)} H. \end{align} $$
$$ \begin{align} {\left|\sum_{X < n \leq X+H} f(n) n^{-iT} \right|}^* \gg \delta^{O(1)} H. \end{align} $$
By equation (4.9), we must have
![]() $|T| \leq \delta ^{-O(1)}X/H$
, and thus by equation (2.1) we have
$|T| \leq \delta ^{-O(1)}X/H$
, and thus by equation (2.1) we have
Hence, by equations (4.19) and (2.2) we have
From equation (4.18) and Lemma 2.2(iii), we conclude that
But this contradicts the major arc estimates (Theorem 3.1(i)).
Hence, in case f is a type
![]() $II$
sum we can assume that G is nonabelian with one-dimensional center. We claim that in all the remaining cases arising from Lemma 4.3, Theorem 4.2 implies that there exists a nontrivial horizontal character
$II$
sum we can assume that G is nonabelian with one-dimensional center. We claim that in all the remaining cases arising from Lemma 4.3, Theorem 4.2 implies that there exists a nontrivial horizontal character
![]() $\eta \colon G \rightarrow \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \rightarrow \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
![]() $\delta ^{-O(1)}$
such that
$\delta ^{-O(1)}$
such that
Indeed, in the case when f is a
![]() $(\log ^{-O(1)}X, A_I)$
type I sum for some
$(\log ^{-O(1)}X, A_I)$
type I sum for some
![]() $A_I = O(X^{\theta })$
, the bound
$A_I = O(X^{\theta })$
, the bound
![]() $H \ll (\log X)^{O(1)}A_I$
fails since
$H \ll (\log X)^{O(1)}A_I$
fails since
![]() $H \geq X^{\theta +\varepsilon }$
. Hence, equation (4.21) follows from Theorem 4.2(i).
$H \geq X^{\theta +\varepsilon }$
. Hence, equation (4.21) follows from Theorem 4.2(i).
In the case when f is a
![]() $(\log ^{-O(1)}X, A_{I_2})$
type
$(\log ^{-O(1)}X, A_{I_2})$
type
![]() $I_2$
sum for some
$I_2$
sum for some
![]() $A_{I_2} = O(X^{(3\theta -1)/2})$
, the bound
$A_{I_2} = O(X^{(3\theta -1)/2})$
, the bound
![]() $H \ll (\log X)^{O(1)} X^{1/3} A_{I_2}^{2/3}$
fails since
$H \ll (\log X)^{O(1)} X^{1/3} A_{I_2}^{2/3}$
fails since
![]() $H \geq X^{\theta +\varepsilon }$
and
$H \geq X^{\theta +\varepsilon }$
and
![]() $X^{1/3}A_{I_2}^{2/3} = O(X^{\theta })$
. Hence, equation (4.21) follows from Theorem 4.2(iv).
$X^{1/3}A_{I_2}^{2/3} = O(X^{\theta })$
. Hence, equation (4.21) follows from Theorem 4.2(iv).
In the case when f is a
![]() $(\log ^{-O(1)}X, A_{II}^-, A_{II}^+)$
type
$(\log ^{-O(1)}X, A_{II}^-, A_{II}^+)$
type
![]() $II$
sum for some
$II$
sum for some
![]() $X^{1-\theta } \ll A_{II}^- \ll A_{II}^+ \ll X^{\theta }$
, we can assume that G is nonabelian with one-dimensional center as discussed above to meet the assumption in Theorem 4.2(ii). The bound
$X^{1-\theta } \ll A_{II}^- \ll A_{II}^+ \ll X^{\theta }$
, we can assume that G is nonabelian with one-dimensional center as discussed above to meet the assumption in Theorem 4.2(ii). The bound
![]() $H \ll (\log X)^{O(1)} \max (A_{II}^+, X/A_{II}^-)$
fails since
$H \ll (\log X)^{O(1)} \max (A_{II}^+, X/A_{II}^-)$
fails since
![]() $H \geq X^{\theta +\varepsilon }$
and
$H \geq X^{\theta +\varepsilon }$
and
![]() $\max (A_{II}^+, X/A_{II}^-) \ll X^{\theta }$
, and thus, equation (4.21) follows from Theorem 4.2(ii).
$\max (A_{II}^+, X/A_{II}^-) \ll X^{\theta }$
, and thus, equation (4.21) follows from Theorem 4.2(ii).
Now that we have equation (4.21), we can reduce the dimension (by passing to a proper subnilmanifold) and apply the induction hypothesis to conclude the proof. By equation (4.21) and Lemma 2.11, we have a decomposition
![]() $g = \varepsilon g'\gamma $
for some
$g = \varepsilon g'\gamma $
for some
![]() $\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
such that
$\varepsilon , g', \gamma \in {\operatorname {Poly}}(\mathbb {Z} \to G)$
such that
-
(i)
 $\varepsilon $
is
$\varepsilon $
is
 $(\delta ^{-O(1)}, (X, X+H])$
-smooth;
$(\delta ^{-O(1)}, (X, X+H])$
-smooth; -
(ii) There is a
 $\delta ^{-O(1)}$
-rational proper subnilmanifold
$\delta ^{-O(1)}$
-rational proper subnilmanifold
 $G'/\Gamma '$
of
$G'/\Gamma '$
of
 $G/\Gamma $
such that
$G/\Gamma $
such that
 $g'$
takes values in
$g'$
takes values in
 $G'$
(in fact
$G'$
(in fact
 $G' = \ker \eta $
); and
$G' = \ker \eta $
); and -
(iii)
 $\gamma $
is
$\gamma $
is
 $\delta ^{-O(1)}$
-rational.
$\delta ^{-O(1)}$
-rational.
Let
![]() $q \leq \delta ^{-O(1)}$
be the period of
$q \leq \delta ^{-O(1)}$
be the period of
![]() $\gamma \Gamma $
. Form a partition
$\gamma \Gamma $
. Form a partition
![]() $(X, X+H] = P_1 \cup \cdots \cup P_r$
for some
$(X, X+H] = P_1 \cup \cdots \cup P_r$
for some
![]() $r \leq \delta ^{-O(1)}$
, where each
$r \leq \delta ^{-O(1)}$
, where each
![]() $P_i$
is an arithmetic progression of modulus q and
$P_i$
is an arithmetic progression of modulus q and
![]() $d_G(\varepsilon (n), \varepsilon (n')) \leq \delta ^4$
whenever
$d_G(\varepsilon (n), \varepsilon (n')) \leq \delta ^4$
whenever
![]() $n,n' \in P_i$
(which can be ensured by the smoothness of
$n,n' \in P_i$
(which can be ensured by the smoothness of
![]() $\varepsilon $
as long as
$\varepsilon $
as long as
![]() $|P_i| \leq \delta ^CH$
for some sufficiently large constant C). By the triangle inequality in Lemma 2.2(i), we have
$|P_i| \leq \delta ^CH$
for some sufficiently large constant C). By the triangle inequality in Lemma 2.2(i), we have
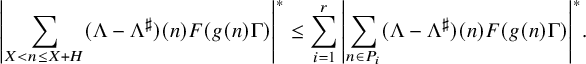 $$ \begin{align*}{\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^* \leq \sum_{i=1}^r {\left| \sum_{n \in P_i} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^*. \end{align*} $$
$$ \begin{align*}{\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^* \leq \sum_{i=1}^r {\left| \sum_{n \in P_i} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^*. \end{align*} $$
For each i, fix any
![]() $n_i \in P_i$
, and write
$n_i \in P_i$
, and write
![]() $\gamma (n_i) \Gamma = \gamma _i \Gamma $
for some
$\gamma (n_i) \Gamma = \gamma _i \Gamma $
for some
![]() $\gamma _i \in G$
which is rational of height
$\gamma _i \in G$
which is rational of height
![]() $O(\delta ^{-O(1)})$
. Let
$O(\delta ^{-O(1)})$
. Let
![]() $g_i \in {\operatorname {Poly}}(\mathbb {Z}\to G)$
be the polynomial sequence defined by
$g_i \in {\operatorname {Poly}}(\mathbb {Z}\to G)$
be the polynomial sequence defined by
which takes values in
![]() $\gamma _i^{-1}G'\gamma _i$
. Let
$\gamma _i^{-1}G'\gamma _i$
. Let
![]() $F_i \colon G/\Gamma \to \mathbb {C}$
be the function defined by
$F_i \colon G/\Gamma \to \mathbb {C}$
be the function defined by
For each
![]() $n \in P_i$
, we have
$n \in P_i$
, we have
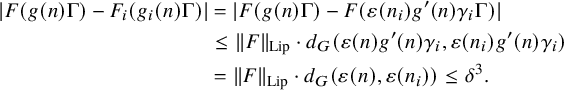 $$ \begin{align*} |F(g(n)\Gamma) - F_i(g_i(n)\Gamma)| &= |F(g(n)\Gamma) - F(\varepsilon(n_i) g'(n)\gamma_i\Gamma)| \\ &\leq \|F\|_{{\operatorname{Lip}}} \cdot d_G(\varepsilon(n) g'(n)\gamma_i, \varepsilon(n_i) g'(n) \gamma_i) \\ &= \|F\|_{{\operatorname{Lip}}} \cdot d_G(\varepsilon(n), \varepsilon(n_i)) \leq \delta^3. \end{align*} $$
$$ \begin{align*} |F(g(n)\Gamma) - F_i(g_i(n)\Gamma)| &= |F(g(n)\Gamma) - F(\varepsilon(n_i) g'(n)\gamma_i\Gamma)| \\ &\leq \|F\|_{{\operatorname{Lip}}} \cdot d_G(\varepsilon(n) g'(n)\gamma_i, \varepsilon(n_i) g'(n) \gamma_i) \\ &= \|F\|_{{\operatorname{Lip}}} \cdot d_G(\varepsilon(n), \varepsilon(n_i)) \leq \delta^3. \end{align*} $$
It follows that
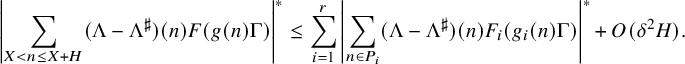 $$ \begin{align} {\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^* \leq \sum_{i=1}^r {\left| \sum_{n \in P_i} (\Lambda-\Lambda^\sharp)(n) F_i(g_i(n)\Gamma) \right|}^* + O(\delta^2H). \end{align} $$
$$ \begin{align} {\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^* \leq \sum_{i=1}^r {\left| \sum_{n \in P_i} (\Lambda-\Lambda^\sharp)(n) F_i(g_i(n)\Gamma) \right|}^* + O(\delta^2H). \end{align} $$
By Lemma 2.2(i) and the induction hypothesis, we have, for each
![]() $i = 1, \dotsc , r$
,
$i = 1, \dotsc , r$
,
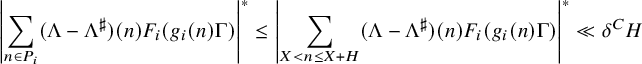 $$ \begin{align} {\left| \sum_{n \in P_i} (\Lambda-\Lambda^\sharp)(n) F_i(g_i(n)\Gamma) \right|}^* \leq {\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F_i(g_i(n)\Gamma) \right|}^* \ll \delta^CH \end{align} $$
$$ \begin{align} {\left| \sum_{n \in P_i} (\Lambda-\Lambda^\sharp)(n) F_i(g_i(n)\Gamma) \right|}^* \leq {\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F_i(g_i(n)\Gamma) \right|}^* \ll \delta^CH \end{align} $$
for any sufficiently large constant C. Combining this with equation (4.22), we obtain
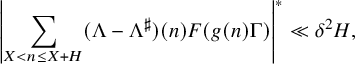 $$ \begin{align*}{\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^* \ll \delta^{2} H,\end{align*} $$
$$ \begin{align*}{\left| \sum_{X < n \leq X+H} (\Lambda-\Lambda^\sharp)(n) F(g(n)\Gamma) \right|}^* \ll \delta^{2} H,\end{align*} $$
contradicting our assumption (4.14). This completes the proof of equation (1.6).
The proof of equation (1.5) is completely similar (with the role of
![]() $\Lambda ^\sharp $
and
$\Lambda ^\sharp $
and
![]() $\Lambda ^\sharp _I$
both replaced by
$\Lambda ^\sharp _I$
both replaced by
![]() $\mu ^\sharp = 0$
). For the estimate (1.7) involving
$\mu ^\sharp = 0$
). For the estimate (1.7) involving
![]() $d_k$
, one runs the argument above with
$d_k$
, one runs the argument above with
![]() $\delta = X^{-c\varepsilon }$
for some sufficiently small constant
$\delta = X^{-c\varepsilon }$
for some sufficiently small constant
![]() $c>0$
, using Lemma 4.4, and with the role of
$c>0$
, using Lemma 4.4, and with the role of
![]() $\Lambda ^\sharp $
and
$\Lambda ^\sharp $
and
![]() $\Lambda ^\sharp _I$
both replaced by
$\Lambda ^\sharp _I$
both replaced by
![]() $d_k^\sharp $
.
$d_k^\sharp $
.
Let us now turn to the estimate (1.8). We choose
and write
![]() $\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
. We first use Shiu’s bound (Lemma 2.17) to note that
$\mathcal {P}(P, Q) = \prod _{P < p \leq Q} p$
. We first use Shiu’s bound (Lemma 2.17) to note that
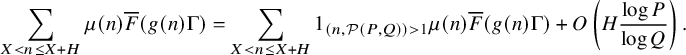 $$\begin{align*}\sum_{X < n \leq X+H} \mu(n) \overline{F}(g(n)\Gamma) = \sum_{X < n \leq X+H} 1_{(n, \mathcal{P}(P, Q))> 1} \mu(n) \overline{F}(g(n)\Gamma) + O\left(H \frac{\log P}{\log Q}\right). \end{align*}$$
$$\begin{align*}\sum_{X < n \leq X+H} \mu(n) \overline{F}(g(n)\Gamma) = \sum_{X < n \leq X+H} 1_{(n, \mathcal{P}(P, Q))> 1} \mu(n) \overline{F}(g(n)\Gamma) + O\left(H \frac{\log P}{\log Q}\right). \end{align*}$$
Now, one can repeat the previous arguments with
![]() $\delta = \log ^{-A} X$
and
$\delta = \log ^{-A} X$
and
![]() $1_{(n, \mathcal {P}(P, Q))> 1} \mu (n)$
in place of
$1_{(n, \mathcal {P}(P, Q))> 1} \mu (n)$
in place of
![]() $\Lambda $
and
$\Lambda $
and
![]() $0$
in place of
$0$
in place of
![]() $\Lambda ^\sharp $
and
$\Lambda ^\sharp $
and
![]() $\Lambda ^\sharp _I$
– this time we use Lemma 4.5 to replace
$\Lambda ^\sharp _I$
– this time we use Lemma 4.5 to replace
![]() $1_{(n, \mathcal {P}(P, Q))> 1} \mu (n)$
by the approximant
$1_{(n, \mathcal {P}(P, Q))> 1} \mu (n)$
by the approximant
![]() $\sum _{f \in {\mathcal F}} f(n)$
and Corollary 3.10 gives the required major arc estimate for
$\sum _{f \in {\mathcal F}} f(n)$
and Corollary 3.10 gives the required major arc estimate for
![]() $1_{(n, \mathcal {P}(P, Q))> 1} \mu (n)$
.
$1_{(n, \mathcal {P}(P, Q))> 1} \mu (n)$
.
The estimate (1.9) follows similarly, noting first that, with
![]() $P, Q$
as in equation (4.24) we have by Shiu’s bound (Lemma 2.17)
$P, Q$
as in equation (4.24) we have by Shiu’s bound (Lemma 2.17)
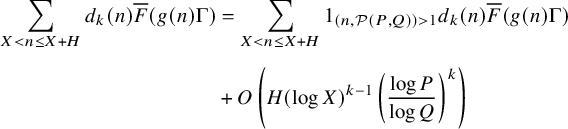 $$ \begin{align*} \sum_{X < n \leq X+H} d_k(n) \overline{F}(g(n)\Gamma) &= \sum_{X < n \leq X+H} 1_{(n, \mathcal{P}(P, Q))> 1} d_k(n) \overline{F}(g(n)\Gamma)\\[5pt] &+ O\left(H (\log X)^{k-1}\left(\frac{\log P}{\log Q}\right)^{k}\right) \end{align*} $$
$$ \begin{align*} \sum_{X < n \leq X+H} d_k(n) \overline{F}(g(n)\Gamma) &= \sum_{X < n \leq X+H} 1_{(n, \mathcal{P}(P, Q))> 1} d_k(n) \overline{F}(g(n)\Gamma)\\[5pt] &+ O\left(H (\log X)^{k-1}\left(\frac{\log P}{\log Q}\right)^{k}\right) \end{align*} $$
and then arguing as for equation (1.8).
5 The type I case
In this section, we establish the type I case (i) of Theorem 4.2, basically following the arguments in [Reference Green and Tao18]. In this section, we allow all implied constants to depend on
![]() $d,D$
.
$d,D$
.
Writing
![]() $f = \alpha *\beta $
, we see from Lemma 2.2(i) that
$f = \alpha *\beta $
, we see from Lemma 2.2(i) that
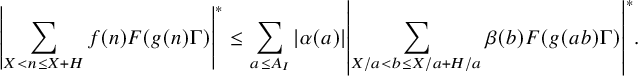 $$ \begin{align*}{\left|\sum_{X < n \leq X+H} f(n) F(g(n) \Gamma)\right|}^* \leq \sum_{a \leq A_I} |\alpha(a)| {\left|\sum_{X/a < b \leq X/a + H/a} \beta(b) F(g(ab) \Gamma)\right|}^*.\end{align*} $$
$$ \begin{align*}{\left|\sum_{X < n \leq X+H} f(n) F(g(n) \Gamma)\right|}^* \leq \sum_{a \leq A_I} |\alpha(a)| {\left|\sum_{X/a < b \leq X/a + H/a} \beta(b) F(g(ab) \Gamma)\right|}^*.\end{align*} $$
By the pigeonhole principle (and the hypothesis
![]() $\delta \leq \frac {1}{\log X}$
), we can thus find a scale
$\delta \leq \frac {1}{\log X}$
), we can thus find a scale
![]() $1 \leq A \leq A_I$
such that
$1 \leq A \leq A_I$
such that
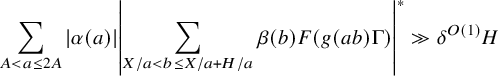 $$ \begin{align*}\sum_{A < a \leq 2A} |\alpha(a)| {\left|\sum_{X/a < b \leq X/a + H/a} \beta(b) F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H\end{align*} $$
$$ \begin{align*}\sum_{A < a \leq 2A} |\alpha(a)| {\left|\sum_{X/a < b \leq X/a + H/a} \beta(b) F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H\end{align*} $$
and hence by equation (4.1) and the Cauchy–Schwarz inequality
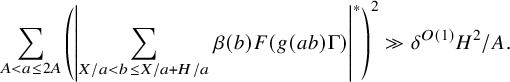 $$ \begin{align*}\sum_{A < a \leq 2A} \left({\left|\sum_{X/a < b \leq X/a + H/a} \beta(b) F(g(ab) \Gamma)\right|}^*\right)^2 \gg \delta^{O(1)} H^2/A.\end{align*} $$
$$ \begin{align*}\sum_{A < a \leq 2A} \left({\left|\sum_{X/a < b \leq X/a + H/a} \beta(b) F(g(ab) \Gamma)\right|}^*\right)^2 \gg \delta^{O(1)} H^2/A.\end{align*} $$
From Lemma 2.2(iii) and equation (4.2), we conclude that
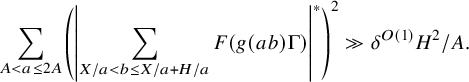 $$ \begin{align} \sum_{A < a \leq 2A} \left({\left|\sum_{X/a < b \leq X/a + H/a} F(g(ab) \Gamma)\right|}^*\right)^2 \gg \delta^{O(1)} H^2/A. \end{align} $$
$$ \begin{align} \sum_{A < a \leq 2A} \left({\left|\sum_{X/a < b \leq X/a + H/a} F(g(ab) \Gamma)\right|}^*\right)^2 \gg \delta^{O(1)} H^2/A. \end{align} $$
We may assume that
![]() $H \geq C \delta ^{-C} A$
for some large constant C depending on
$H \geq C \delta ^{-C} A$
for some large constant C depending on
![]() $d,D$
since otherwise we have
$d,D$
since otherwise we have
![]() $H \leq \delta ^{-O(1)} A_I$
and can conclude. Trivially,
$H \leq \delta ^{-O(1)} A_I$
and can conclude. Trivially,
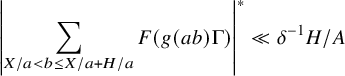 $$ \begin{align*}{\left|\sum_{X/a < b \leq X/a + H/a} F(g(ab) \Gamma)\right|}^* \ll \delta^{-1} H/A\end{align*} $$
$$ \begin{align*}{\left|\sum_{X/a < b \leq X/a + H/a} F(g(ab) \Gamma)\right|}^* \ll \delta^{-1} H/A\end{align*} $$
for all
![]() $A < a \leq 2A$
, and hence by equation (5.1) we must have
$A < a \leq 2A$
, and hence by equation (5.1) we must have
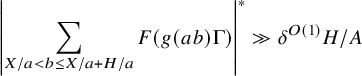 $$ \begin{align*}{\left|\sum_{X/a < b \leq X/a + H/a} F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H/A\end{align*} $$
$$ \begin{align*}{\left|\sum_{X/a < b \leq X/a + H/a} F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H/A\end{align*} $$
for
![]() $\gg \delta ^{O(1)} A$
choices of
$\gg \delta ^{O(1)} A$
choices of
![]() $a \in (A,2A]$
. For each such a, we apply Theorem 2.7 to find a nontrivial horizontal character
$a \in (A,2A]$
. For each such a, we apply Theorem 2.7 to find a nontrivial horizontal character
![]() $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
![]() $O(\delta ^{-O(1)})$
such that
$O(\delta ^{-O(1)})$
such that
This character
![]() $\eta $
could initially depend on a, but the number of possible choices for
$\eta $
could initially depend on a, but the number of possible choices for
![]() $\eta $
is
$\eta $
is
![]() $O(\delta ^{-O(1)})$
, hence by the pigeonhole principle we may refine the set of a under consideration to make
$O(\delta ^{-O(1)})$
, hence by the pigeonhole principle we may refine the set of a under consideration to make
![]() $\eta $
independent of a. The function
$\eta $
independent of a. The function
![]() $\eta \circ g \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree at most d, hence by Corollary 2.4 (and the assumption
$\eta \circ g \colon \mathbb {Z} \to \mathbb {R}/\mathbb {Z}$
is a polynomial of degree at most d, hence by Corollary 2.4 (and the assumption
![]() $H \geq C \delta ^{-C} A$
) we have
$H \geq C \delta ^{-C} A$
) we have
for some
![]() $1 \leq q \ll \delta ^{-O(1)}$
. Replacing
$1 \leq q \ll \delta ^{-O(1)}$
. Replacing
![]() $\eta $
by
$\eta $
by
![]() $q \eta $
, we obtain Theorem 4.2(i) as required.
$q \eta $
, we obtain Theorem 4.2(i) as required.
Remark 5.1. It should also be possible to establish Theorem 4.2(i) using the variant of Theorem 2.12 given in [Reference He and Wang26, Theorem 3.6].
6 The nonabelian type
 $II$
case
$II$
case
In this section, we establish the nonabelian type
![]() $II$
case (ii) of Theorem 4.2. Let
$II$
case (ii) of Theorem 4.2. Let
![]() $d, D, H, X, \delta , G/\Gamma , F, f, A_{II}^-, A_{II}^+$
be as in that theorem. For the rest of this section, we allow all constants to depend on
$d, D, H, X, \delta , G/\Gamma , F, f, A_{II}^-, A_{II}^+$
be as in that theorem. For the rest of this section, we allow all constants to depend on
![]() $d,D$
. We will need several constants
$d,D$
. We will need several constants
depending on
![]() $d,D$
, with each
$d,D$
, with each
![]() $C_i$
assumed to be sufficiently large depending on the preceding constants.
$C_i$
assumed to be sufficiently large depending on the preceding constants.
We first eliminate the role of
![]() $\alpha $
by a standard Cauchy–Schwarz argument. By Definition 4.1(ii), we can write
$\alpha $
by a standard Cauchy–Schwarz argument. By Definition 4.1(ii), we can write
![]() $f = \alpha *\beta $
, where
$f = \alpha *\beta $
, where
![]() $\alpha $
is supported on
$\alpha $
is supported on
![]() $[A_{II}^-,A_{II}^+]$
, and one has the bounds (4.1), (4.3) for all
$[A_{II}^-,A_{II}^+]$
, and one has the bounds (4.1), (4.3) for all
![]() $A,B \geq 1$
. From equation (4.4), we have
$A,B \geq 1$
. From equation (4.4), we have
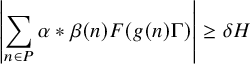 $$ \begin{align*}\left| \sum_{n \in P} \alpha*\beta(n) F(g(n) \Gamma) \right| \geq \delta H\end{align*} $$
$$ \begin{align*}\left| \sum_{n \in P} \alpha*\beta(n) F(g(n) \Gamma) \right| \geq \delta H\end{align*} $$
for some arithmetic progression
![]() $P \subset (X,X+H]$
. By the triangle inequality, we have
$P \subset (X,X+H]$
. By the triangle inequality, we have
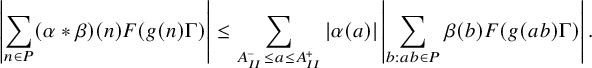 $$ \begin{align*}\left| \sum_{n \in P} (\alpha*\beta)(n) F(g(n) \Gamma) \right| \leq \sum_{A_{II}^- \leq a \leq A_{II}^+} |\alpha(a)| \left|\sum_{b: ab \in P} \beta(b) F(g(ab) \Gamma)\right|.\end{align*} $$
$$ \begin{align*}\left| \sum_{n \in P} (\alpha*\beta)(n) F(g(n) \Gamma) \right| \leq \sum_{A_{II}^- \leq a \leq A_{II}^+} |\alpha(a)| \left|\sum_{b: ab \in P} \beta(b) F(g(ab) \Gamma)\right|.\end{align*} $$
By the pigeonhole principle and the hypothesis
![]() $\delta \leq \frac {1}{\log X}$
, one can thus find
$\delta \leq \frac {1}{\log X}$
, one can thus find
![]() $A_{II}^- \leq A \leq A_{II}^+$
such that
$A_{II}^- \leq A \leq A_{II}^+$
such that
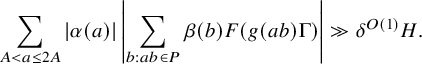 $$ \begin{align} \sum_{A < a \leq 2A} |\alpha(a)| \left|\sum_{b: ab \in P} \beta(b) F(g(ab) \Gamma)\right| \gg \delta^{O(1)} H. \end{align} $$
$$ \begin{align} \sum_{A < a \leq 2A} |\alpha(a)| \left|\sum_{b: ab \in P} \beta(b) F(g(ab) \Gamma)\right| \gg \delta^{O(1)} H. \end{align} $$
We may assume that
since otherwise the first conclusion of Theorem 4.2(ii) holds. Now, by equation (6.1), the Cauchy–Schwarz inequality and equation (4.1)
 $$ \begin{align} \sum_{A < a \leq 2A} \left|\sum_{b: ab \in P} \beta(b) F(g(ab) \Gamma)\right|{}^2 \gg \delta^{O(1)} \frac{H^2}{A}. \end{align} $$
$$ \begin{align} \sum_{A < a \leq 2A} \left|\sum_{b: ab \in P} \beta(b) F(g(ab) \Gamma)\right|{}^2 \gg \delta^{O(1)} \frac{H^2}{A}. \end{align} $$
Next, we dispose of the large values of
![]() $\beta $
. Namely, we now show that the contribution of those b for which
$\beta $
. Namely, we now show that the contribution of those b for which
![]() $|\beta (b)|> \delta ^{-C_2}$
to the left-hand side is negligible. They contribute
$|\beta (b)|> \delta ^{-C_2}$
to the left-hand side is negligible. They contribute
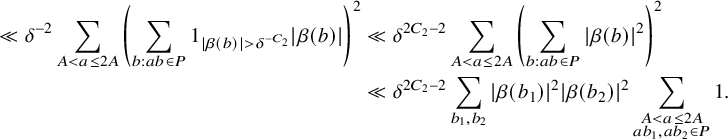 $$ \begin{align} \nonumber \ll \delta^{-2} \sum_{A < a \leq 2A} \left(\sum_{b: ab \in P} 1_{|\beta(b)|> \delta^{-C_2}} |\beta(b)| \right)^2 &\ll \delta^{2C_2-2} \sum_{A < a \leq 2A} \left(\sum_{b: ab \in P} |\beta(b)|^2 \right)^2 \\ &\ll \delta^{2C_2-2} \sum_{b_1, b_2} |\beta(b_1)|^2|\beta(b_2)|^2 \sum_{\substack{A < a \leq 2A \\ ab_1, ab_2 \in P}} 1. \end{align} $$
$$ \begin{align} \nonumber \ll \delta^{-2} \sum_{A < a \leq 2A} \left(\sum_{b: ab \in P} 1_{|\beta(b)|> \delta^{-C_2}} |\beta(b)| \right)^2 &\ll \delta^{2C_2-2} \sum_{A < a \leq 2A} \left(\sum_{b: ab \in P} |\beta(b)|^2 \right)^2 \\ &\ll \delta^{2C_2-2} \sum_{b_1, b_2} |\beta(b_1)|^2|\beta(b_2)|^2 \sum_{\substack{A < a \leq 2A \\ ab_1, ab_2 \in P}} 1. \end{align} $$
Since
![]() $P \subseteq (X, X+H]$
, the inner sum can be nonempty only if
$P \subseteq (X, X+H]$
, the inner sum can be nonempty only if
![]() $b_j \asymp X/A$
and
$b_j \asymp X/A$
and
![]() $|b_1 - b_2| \leq H/A$
and in this case it has size
$|b_1 - b_2| \leq H/A$
and in this case it has size
![]() $\ll H/(X/A) = AH/X$
. Using also the inequality
$\ll H/(X/A) = AH/X$
. Using also the inequality
![]() $|xy|^2 \leq |x|^4 + |y|^4$
and equation (4.3), we see that equation (6.4) is
$|xy|^2 \leq |x|^4 + |y|^4$
and equation (4.3), we see that equation (6.4) is
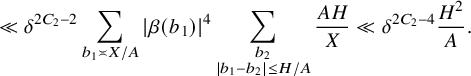 $$ \begin{align*} &\ll \delta^{2C_2-2} \sum_{b_1 \asymp X/A} |\beta(b_1)|^4 \sum_{\substack{b_2 \\ |b_1 - b_2| \leq H/A}} \frac{AH}{X} \ll \delta^{2C_2-4} \frac{H^2}{A}. \end{align*} $$
$$ \begin{align*} &\ll \delta^{2C_2-2} \sum_{b_1 \asymp X/A} |\beta(b_1)|^4 \sum_{\substack{b_2 \\ |b_1 - b_2| \leq H/A}} \frac{AH}{X} \ll \delta^{2C_2-4} \frac{H^2}{A}. \end{align*} $$
From now on in this section, we allow all implied constants to depend on
![]() $C_2$
. Write
$C_2$
. Write
By above and the triangle inequality, (6.3) holds with
![]() $\tilde \beta (b)$
in place of
$\tilde \beta (b)$
in place of
![]() $\beta (b)$
. Hence, by Markov’s inequality, we see that, for
$\beta (b)$
. Hence, by Markov’s inequality, we see that, for
![]() $C_2$
large enough, we have
$C_2$
large enough, we have
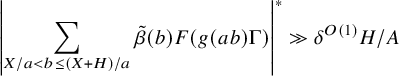 $$ \begin{align} {\left|\sum_{X/a < b \leq (X+H)/a} \tilde \beta(b) F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H/A \end{align} $$
$$ \begin{align} {\left|\sum_{X/a < b \leq (X+H)/a} \tilde \beta(b) F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H/A \end{align} $$
for
![]() $\gg \delta ^{O(1)} A$
choices of
$\gg \delta ^{O(1)} A$
choices of
![]() $a \in (A, 2A]$
. We cover
$a \in (A, 2A]$
. We cover
![]() $(A, 2A]$
by
$(A, 2A]$
by
![]() $O(X/H)$
boundedly overlapping intervals of the form
$O(X/H)$
boundedly overlapping intervals of the form
with
![]() $A \leq A' \leq 2A$
. Note that these intervals are nonempty by the lower bound on A in equation (6.2). By the pigeonhole principle, we see that for
$A \leq A' \leq 2A$
. Note that these intervals are nonempty by the lower bound on A in equation (6.2). By the pigeonhole principle, we see that for
![]() $\gg \delta ^{O(1)} X/H$
of these intervals, equation (6.5) holds for
$\gg \delta ^{O(1)} X/H$
of these intervals, equation (6.5) holds for
![]() $\gg \delta ^{O(1)} \frac {H}{X} A$
choices of
$\gg \delta ^{O(1)} \frac {H}{X} A$
choices of
![]() $a \in I_{A'}$
. For all such
$a \in I_{A'}$
. For all such
![]() $A'$
and a, the interval
$A'$
and a, the interval
![]() $(X/a, (X+H)/a]$
is contained in
$(X/a, (X+H)/a]$
is contained in
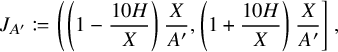
hence
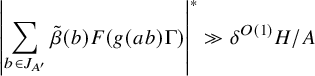 $$ \begin{align*}{\left|\sum_{b \in J_{A'}} \tilde \beta(b) F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H/A\end{align*} $$
$$ \begin{align*}{\left|\sum_{b \in J_{A'}} \tilde \beta(b) F(g(ab) \Gamma)\right|}^* \gg \delta^{O(1)} H/A\end{align*} $$
for
![]() $\gg \delta ^{O(1)} \frac {H}{X} A$
choices of
$\gg \delta ^{O(1)} \frac {H}{X} A$
choices of
![]() $a \in I_{A'}$
. We can now apply Proposition 2.15 and the pigeonhole principle to reach one of two conclusions for
$a \in I_{A'}$
. We can now apply Proposition 2.15 and the pigeonhole principle to reach one of two conclusions for
![]() $\gg \delta ^{O(1)} X/H$
of the intervals
$\gg \delta ^{O(1)} X/H$
of the intervals
![]() $I_{A'}$
:
$I_{A'}$
:
-
(i) There exists a nontrivial horizontal character
 $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
 $O(\delta ^{-O(1)})$
such that
$O(\delta ^{-O(1)})$
such that
 $\| \eta \circ g(a \cdot ) \|_{C^\infty (J_{A'})} \ll \delta ^{-O(1)}$
for
$\| \eta \circ g(a \cdot ) \|_{C^\infty (J_{A'})} \ll \delta ^{-O(1)}$
for
 $\gg \delta ^{O(1)} |I_{A'}|$
values of
$\gg \delta ^{O(1)} |I_{A'}|$
values of
 $a \in I_{A'}$
.
$a \in I_{A'}$
. -
(ii) For
 $\gg \delta ^{O(1)} |I_{A'}|^2$
pairs
$\gg \delta ^{O(1)} |I_{A'}|^2$
pairs
 $(a,a') \in I_{A'}^2$
, there exists a factorization (6.7)where
$(a,a') \in I_{A'}^2$
, there exists a factorization (6.7)where $$ \begin{align} g(a' \cdot) = \varepsilon_{aa'} g(a \cdot) \gamma_{aa'}, \end{align} $$
$$ \begin{align} g(a' \cdot) = \varepsilon_{aa'} g(a \cdot) \gamma_{aa'}, \end{align} $$
 $\varepsilon _{aa'}$
is
$\varepsilon _{aa'}$
is
 $(O(\delta ^{-O(1)}),J_{A'})$
-smooth and
$(O(\delta ^{-O(1)}),J_{A'})$
-smooth and
 $\gamma _{aa'}$
is
$\gamma _{aa'}$
is
 $O(\delta ^{-O(1)})$
-rational.
$O(\delta ^{-O(1)})$
-rational.
Suppose first that conclusion (i) holds for
![]() $\gg \delta ^{O(1)} X/H$
of the intervals
$\gg \delta ^{O(1)} X/H$
of the intervals
![]() $I_{A'}$
. By pigeonholing, we may make
$I_{A'}$
. By pigeonholing, we may make
![]() $\eta $
independent of
$\eta $
independent of
![]() $A'$
, and then by collecting all the a we see that
$A'$
, and then by collecting all the a we see that
for
![]() $\gg \delta ^{O(1)} A$
values of a with
$\gg \delta ^{O(1)} A$
values of a with
![]() $a \asymp A$
. Applying Corollary 2.4, we see that either
$a \asymp A$
. Applying Corollary 2.4, we see that either
![]() $H \ll \delta ^{-O(1)} A$
, or else there is another nontrivial horizontal character
$H \ll \delta ^{-O(1)} A$
, or else there is another nontrivial horizontal character
![]() $\eta ' \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
$\eta ' \colon G \to \mathbb {R}/\mathbb {Z}$
of Lipschitz norm
![]() $O(\delta ^{-O(1)})$
such that
$O(\delta ^{-O(1)})$
such that
In either case, the conclusion of Theorem 4.2(ii) is satisfied.
Now, suppose that conclusion (ii) holds for some
![]() $A'$
which we now fix (discarding the information collected for all other choices of
$A'$
which we now fix (discarding the information collected for all other choices of
![]() $A'$
). We will formalize the argument that follows as a proposition, as we will need this precise proposition also in our followup work [Reference Matomäki, Radziwiłł, Shao, Tao and Teräväinen46].
$A'$
). We will formalize the argument that follows as a proposition, as we will need this precise proposition also in our followup work [Reference Matomäki, Radziwiłł, Shao, Tao and Teräväinen46].
Proposition 6.1 (Abstract nonabelian Type II inverse theorem).
Let
![]() $C\geq 1$
,
$C\geq 1$
,
![]() $d,D \geq 1$
,
$d,D \geq 1$
,
![]() $2 \leq H, A \leq X$
,
$2 \leq H, A \leq X$
,
![]() $0 < \delta < \frac {1}{\log X}$
, and let
$0 < \delta < \frac {1}{\log X}$
, and let
![]() $G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension at most D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree at most d, dimension at most D and complexity at most
![]() $1/\delta $
, with G nonabelian. Let
$1/\delta $
, with G nonabelian. Let
![]() $g: \mathbb {Z} \to G$
be a polynomial map. Cover
$g: \mathbb {Z} \to G$
be a polynomial map. Cover
![]() $(A,2A]$
by at most
$(A,2A]$
by at most
![]() $C X/H$
intervals
$C X/H$
intervals
![]() $I_{A'} = (A',(1+\frac {H}{X}) A')$
with
$I_{A'} = (A',(1+\frac {H}{X}) A')$
with
![]() $A \leq A' \leq 2A$
, with each point belonging to at most C of these intervals. Suppose that for at least
$A \leq A' \leq 2A$
, with each point belonging to at most C of these intervals. Suppose that for at least
![]() $\frac {1}{C} \delta ^{C} X/H$
of the intervals
$\frac {1}{C} \delta ^{C} X/H$
of the intervals
![]() $I_{A'}$
, there exist at least
$I_{A'}$
, there exist at least
![]() $\frac {1}{C} \delta ^C |I_{A'}|^2$
pairs
$\frac {1}{C} \delta ^C |I_{A'}|^2$
pairs
![]() $(a,a') \in I_{A'}^2$
for which there exists a factorization
$(a,a') \in I_{A'}^2$
for which there exists a factorization
where
![]() $\varepsilon _{aa'}$
is
$\varepsilon _{aa'}$
is
![]() $(C \delta ^{-C}, J_{A'})$
-smooth and
$(C \delta ^{-C}, J_{A'})$
-smooth and
![]() $\gamma _{aa'}$
is
$\gamma _{aa'}$
is
![]() $C\delta ^{-C}$
-rational, with
$C\delta ^{-C}$
-rational, with
![]() $J_{A'}$
defined by equation (6.6).
$J_{A'}$
defined by equation (6.6).
Then either
or there exists a nontrivial horizontal character
![]() $\eta \colon G \to \mathbb {R}/\mathbb {Z}$
having Lipschitz norm
$\eta \colon G \to \mathbb {R}/\mathbb {Z}$
having Lipschitz norm
![]() $O_{d,D,C}(\delta ^{-O_{d,D,C}(1)})$
such that
$O_{d,D,C}(\delta ^{-O_{d,D,C}(1)})$
such that
Indeed, applying this proposition (with a suitable choice of
![]() $C=O(1)$
, and the other parameters given their obvious values), the conclusion (6.8) is not compatible with equation (6.2) for
$C=O(1)$
, and the other parameters given their obvious values), the conclusion (6.8) is not compatible with equation (6.2) for
![]() $C_4$
large enough, so we obtain the desired conclusion (4.5).
$C_4$
large enough, so we obtain the desired conclusion (4.5).
It remains to establish the proposition. We allow all implied constants to depend on
![]() $d,D,C$
. We will now proceed by analyzing the equidistribution properties of the four-parameter polynomial map
$d,D,C$
. We will now proceed by analyzing the equidistribution properties of the four-parameter polynomial map
The one-parameter equidistribution theorem in Theorem 2.12 is not directly applicable for this purpose. Fortunately, we may apply the multiparameter equidistribution theory in Theorem 2.13 instead. We conclude that either
or else there exists
and a factorization
where
![]() $\varepsilon , \tilde g, \gamma \in {\operatorname {Poly}}(\mathbb {Z}^4 \to G^4)$
are such that
$\varepsilon , \tilde g, \gamma \in {\operatorname {Poly}}(\mathbb {Z}^4 \to G^4)$
are such that
-
(i) (
 $\varepsilon $
smooth) For all
$\varepsilon $
smooth) For all
 $(a,a',b,b') \in I_{A'} \times I_{A'} \times J_{A'} \times J_{A'}$
, we have the smoothness estimates
$(a,a',b,b') \in I_{A'} \times I_{A'} \times J_{A'} \times J_{A'}$
, we have the smoothness estimates  $$ \begin{align*} d_G(\varepsilon(a,a',b,b'),1) &\leq M\\ d_G(\varepsilon(a+1,a',b,b'),\varepsilon(a,a',b,b')) &\leq M / |I_{A'}|\\ d_G(\varepsilon(a,a'+1,b,b'),\varepsilon(a,a',b,b')) &\leq M / |I_{A'}|\\ d_G(\varepsilon(a,a',b+1,b'),\varepsilon(a,a',b,b')) &\leq M / |J_{A'}|\\ d_G(\varepsilon(a,a',b,b'+1),\varepsilon(a,a',b,b')) &\leq M / |J_{A'}|. \end{align*} $$
$$ \begin{align*} d_G(\varepsilon(a,a',b,b'),1) &\leq M\\ d_G(\varepsilon(a+1,a',b,b'),\varepsilon(a,a',b,b')) &\leq M / |I_{A'}|\\ d_G(\varepsilon(a,a'+1,b,b'),\varepsilon(a,a',b,b')) &\leq M / |I_{A'}|\\ d_G(\varepsilon(a,a',b+1,b'),\varepsilon(a,a',b,b')) &\leq M / |J_{A'}|\\ d_G(\varepsilon(a,a',b,b'+1),\varepsilon(a,a',b,b')) &\leq M / |J_{A'}|. \end{align*} $$
-
(ii) (
 $g'$
equidistributed) There is an M-rational subnilmanifold
$g'$
equidistributed) There is an M-rational subnilmanifold
 $G'/\Gamma '$
of
$G'/\Gamma '$
of
 $G^4/\Gamma ^4$
such that
$G^4/\Gamma ^4$
such that
 $g'$
takes values in
$g'$
takes values in
 $G'$
and one has the total equidistribution property for any arithmetic progressions
$G'$
and one has the total equidistribution property for any arithmetic progressions $$ \begin{align*}\Big| \sum_{(a,a',b,b') \in P_1 \times P_2 \times P_3 \times P_4} F(g'(a,a',b,b') \Gamma") \Big| \leq \frac{|I_{A'}|^2 |J_{A'}|^2}{M^{C_3^2}} \|F\|_{{\operatorname{Lip}}}\end{align*} $$
$$ \begin{align*}\Big| \sum_{(a,a',b,b') \in P_1 \times P_2 \times P_3 \times P_4} F(g'(a,a',b,b') \Gamma") \Big| \leq \frac{|I_{A'}|^2 |J_{A'}|^2}{M^{C_3^2}} \|F\|_{{\operatorname{Lip}}}\end{align*} $$
 $P_1,P_2 \subset I_{A'}$
,
$P_1,P_2 \subset I_{A'}$
,
 $P_3,P_4 \subset J_{A'}$
, any finite index subgroup
$P_3,P_4 \subset J_{A'}$
, any finite index subgroup
 $\Gamma "$
of
$\Gamma "$
of
 $\Gamma '$
of index at most
$\Gamma '$
of index at most
 $M^{C_3^2}$
and any Lipschitz function
$M^{C_3^2}$
and any Lipschitz function
 $F \colon G'/\Gamma " \to \mathbb {C}$
of mean zero.
$F \colon G'/\Gamma " \to \mathbb {C}$
of mean zero.
-
(iii) (
 $\gamma $
rational) There exists
$\gamma $
rational) There exists
 $1 \leq r \leq M$
such that
$1 \leq r \leq M$
such that
 $\gamma ^r(a,a',b,b') \in \Gamma ^4$
for all
$\gamma ^r(a,a',b,b') \in \Gamma ^4$
for all
 $a,a',b,b' \in \mathbb {Z}$
.
$a,a',b,b' \in \mathbb {Z}$
.
The alternative equation (6.9) of course implies equation (6.8), so we may assume we are in the opposite alternative. Thus, we may assume that we have a scale M and a factorization (6.11) with the claimed properties.
We know that equation (6.7) holds for
![]() $\gg M^{-O(1)} |I_{A'}|^2$
pairs
$\gg M^{-O(1)} |I_{A'}|^2$
pairs
![]() $(a,a') \in I_{A'}^2$
. By pigeonholing, we may assume there is a fixed
$(a,a') \in I_{A'}^2$
. By pigeonholing, we may assume there is a fixed
![]() $1 \leq r \ll M^{O(1)}$
such that
$1 \leq r \ll M^{O(1)}$
such that
![]() $\gamma _{aa'}(b)^r \in \Gamma $
for all such pairs
$\gamma _{aa'}(b)^r \in \Gamma $
for all such pairs
![]() $(a,a')$
and all b, and also such that
$(a,a')$
and all b, and also such that
![]() $\gamma ^r(a,a',b',b') \in \Gamma ^4$
. This implies that there is some lattice
$\gamma ^r(a,a',b',b') \in \Gamma ^4$
. This implies that there is some lattice
![]() $\tilde \Gamma $
independent of
$\tilde \Gamma $
independent of
![]() $a,a'$
that contains
$a,a'$
that contains
![]() $\Gamma $
as an index
$\Gamma $
as an index
![]() $O(\delta ^{-O(1)})$
subgroup such that
$O(\delta ^{-O(1)})$
subgroup such that
![]() $\gamma _{aa'}(b) \in \tilde \Gamma $
for all such pairs
$\gamma _{aa'}(b) \in \tilde \Gamma $
for all such pairs
![]() $(a,a')$
, and
$(a,a')$
, and
![]() $\gamma (a,a',b,b') \in \tilde \Gamma ^4$
; indeed, by [Reference Green and Tao19, Lemma A.8(i), Lemma A.11(iii)], we could take
$\gamma (a,a',b,b') \in \tilde \Gamma ^4$
; indeed, by [Reference Green and Tao19, Lemma A.8(i), Lemma A.11(iii)], we could take
![]() $\tilde \Gamma $
to be generated by
$\tilde \Gamma $
to be generated by
![]() $\exp ( \frac {1}{Q'} X_i )$
for the Mal’cev basis
$\exp ( \frac {1}{Q'} X_i )$
for the Mal’cev basis
![]() $X_1,\dots ,X_D$
of
$X_1,\dots ,X_D$
of
![]() $G/\Gamma $
, and some
$G/\Gamma $
, and some
![]() $Q' \ll M^{O(1)}$
. From equation (6.7), we then have
$Q' \ll M^{O(1)}$
. From equation (6.7), we then have
for all such pairs
![]() $(a,a')$
and all
$(a,a')$
and all
![]() $b \in \mathbb {Z}$
. If we introduce the subinterval
$b \in \mathbb {Z}$
. If we introduce the subinterval

of
![]() $J_{A'}$
, then from the smoothness of
$J_{A'}$
, then from the smoothness of
![]() $\varepsilon _{aa'}$
we have
$\varepsilon _{aa'}$
we have
whenever
![]() $b,b' \in J^{\prime }_{A'}$
, where
$b,b' \in J^{\prime }_{A'}$
, where
![]() $O_G(r)$
denotes an element of G at a distance
$O_G(r)$
denotes an element of G at a distance
![]() $O(r)$
from the identity. This implies that
$O(r)$
from the identity. This implies that
where
![]() $\Omega \subset (G/\tilde \Gamma )^4$
consists of all quadruples of the form
$\Omega \subset (G/\tilde \Gamma )^4$
consists of all quadruples of the form
for some
![]() $x,y \in G/\Gamma $
and
$x,y \in G/\Gamma $
and
![]() $\varepsilon ,\kappa \in G$
with
$\varepsilon ,\kappa \in G$
with
![]() $\varepsilon = O_G(M^{O(1)})$
and
$\varepsilon = O_G(M^{O(1)})$
and
![]() $\kappa = O_G(M^{-C_3+O(1)})$
(with appropriate choices of implied constants). We conclude that
$\kappa = O_G(M^{-C_3+O(1)})$
(with appropriate choices of implied constants). We conclude that
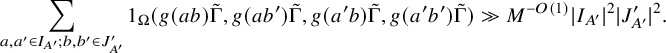 $$ \begin{align*}\sum_{a,a' \in I_{A'}; b,b' \in J^{\prime}_{A'}} 1_\Omega( g(ab) \tilde \Gamma, g(ab') \tilde \Gamma, g(a'b) \tilde \Gamma, g(a'b') \tilde \Gamma ) \gg M^{-O(1)} |I_{A'}|^2 |J^{\prime}_{A'}|^2.\end{align*} $$
$$ \begin{align*}\sum_{a,a' \in I_{A'}; b,b' \in J^{\prime}_{A'}} 1_\Omega( g(ab) \tilde \Gamma, g(ab') \tilde \Gamma, g(a'b) \tilde \Gamma, g(a'b') \tilde \Gamma ) \gg M^{-O(1)} |I_{A'}|^2 |J^{\prime}_{A'}|^2.\end{align*} $$
Applying equation (6.11), we conclude that
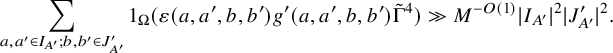 $$ \begin{align*}\sum_{a,a' \in I_{A'}; b,b' \in J^{\prime}_{A'}} 1_\Omega( \varepsilon(a,a',b,b') g'(a,a',b,b') \tilde \Gamma^4 ) \gg M^{-O(1)} |I_{A'}|^2 |J^{\prime}_{A'}|^2.\end{align*} $$
$$ \begin{align*}\sum_{a,a' \in I_{A'}; b,b' \in J^{\prime}_{A'}} 1_\Omega( \varepsilon(a,a',b,b') g'(a,a',b,b') \tilde \Gamma^4 ) \gg M^{-O(1)} |I_{A'}|^2 |J^{\prime}_{A'}|^2.\end{align*} $$
By the pigeonhole principle, we can find intervals
![]() $I^{\prime }_{A'}, I^{\prime \prime }_{A'}$
in
$I^{\prime }_{A'}, I^{\prime \prime }_{A'}$
in
![]() $I_{A'}$
of length
$I_{A'}$
of length
![]() $M^{-C_3} I_{A'}$
such that
$M^{-C_3} I_{A'}$
such that
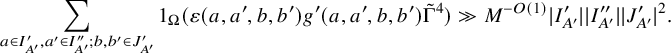 $$ \begin{align*}\sum_{a \in I^{\prime}_{A'}, a' \in I^{\prime\prime}_{A'}; b,b' \in J^{\prime}_{A'}} 1_\Omega( \varepsilon(a,a',b,b') g'(a,a',b,b') \tilde \Gamma^4 ) \gg M^{-O(1)} |I^{\prime}_{A'}| |I^{\prime\prime}_{A'}| |J^{\prime}_{A'}|^2.\end{align*} $$
$$ \begin{align*}\sum_{a \in I^{\prime}_{A'}, a' \in I^{\prime\prime}_{A'}; b,b' \in J^{\prime}_{A'}} 1_\Omega( \varepsilon(a,a',b,b') g'(a,a',b,b') \tilde \Gamma^4 ) \gg M^{-O(1)} |I^{\prime}_{A'}| |I^{\prime\prime}_{A'}| |J^{\prime}_{A'}|^2.\end{align*} $$
By the smoothness of
![]() $\varepsilon $
, we have
$\varepsilon $
, we have
where
![]() $a_0,a^{\prime }_0,b_0$
are the left endpoints of
$a_0,a^{\prime }_0,b_0$
are the left endpoints of
![]() $I^{\prime }_{A'}, I^{\prime \prime }_{A'}, J^{\prime }_{A'}$
, respectively. Let
$I^{\prime }_{A'}, I^{\prime \prime }_{A'}, J^{\prime }_{A'}$
, respectively. Let
![]() $\varphi $
be a bump functionFootnote
11
supported on
$\varphi $
be a bump functionFootnote
11
supported on
![]() $\tilde \Omega $
that equals
$\tilde \Omega $
that equals
![]() $1$
on
$1$
on
![]() $\Omega $
, with Lipschitz norm
$\Omega $
, with Lipschitz norm
![]() $O(M^{O(C_3)})$
, where
$O(M^{O(C_3)})$
, where
![]() $\tilde \Omega $
is defined similarly to
$\tilde \Omega $
is defined similarly to
![]() $\Omega $
in equation (6.12) but with slightly larger choices of implied constants
$\Omega $
in equation (6.12) but with slightly larger choices of implied constants
![]() $O(1)$
in the definition of
$O(1)$
in the definition of
![]() $\varepsilon ,\kappa $
. This implies that
$\varepsilon ,\kappa $
. This implies that
whenever
![]() $a \in I^{\prime }_{A'}, a' \in I^{\prime \prime }_{A'}; b,b' \in J^{\prime }_{A'}$
. Abbreviating
$a \in I^{\prime }_{A'}, a' \in I^{\prime \prime }_{A'}; b,b' \in J^{\prime }_{A'}$
. Abbreviating
, we conclude that
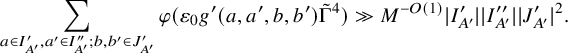 $$ \begin{align*}\sum_{a \in I^{\prime}_{A'}, a' \in I^{\prime\prime}_{A'}; b,b' \in J^{\prime}_{A'}} \varphi( \varepsilon_0 g'(a,a',b,b') \tilde \Gamma^4 ) \gg M^{-O(1)} |I^{\prime}_{A'}| |I^{\prime\prime}_{A'}| |J^{\prime}_{A'}|^2.\end{align*} $$
$$ \begin{align*}\sum_{a \in I^{\prime}_{A'}, a' \in I^{\prime\prime}_{A'}; b,b' \in J^{\prime}_{A'}} \varphi( \varepsilon_0 g'(a,a',b,b') \tilde \Gamma^4 ) \gg M^{-O(1)} |I^{\prime}_{A'}| |I^{\prime\prime}_{A'}| |J^{\prime}_{A'}|^2.\end{align*} $$
Using the equidistribution properties of
![]() $g'$
, we conclude that
$g'$
, we conclude that
We now use this bound to obtain control on the group
![]() $G'$
. Let us introduce the slice
$G'$
. Let us introduce the slice
This is a
![]() $O(M^{O(1)})$
-rational subgroup of G. Suppose first that this group is nontrivial, then
$O(M^{O(1)})$
-rational subgroup of G. Suppose first that this group is nontrivial, then
![]() $L \cap \Gamma '$
contains a nontrivial element
$L \cap \Gamma '$
contains a nontrivial element
![]() $\gamma = O_G(M^{O(1)})$
. For
$\gamma = O_G(M^{O(1)})$
. For
![]() $0 \leq t \leq 1$
, the group element
$0 \leq t \leq 1$
, the group element
is such that
![]() $(1,1,1,\gamma ^t)$
lies in
$(1,1,1,\gamma ^t)$
lies in
![]() $G'$
, and hence from equation (6.13) and invariance of Haar measure we have
$G'$
, and hence from equation (6.13) and invariance of Haar measure we have
Integrating this and using the Fubini–Tonelli theorem, we have
 $$ \begin{align*}\int_{G'/(G' \cap \tilde \Gamma^4)} \int_0^1 \varphi(\varepsilon_0 (1,1,1,\gamma^t) x)\ dt \ d\mu_{G'/(G' \cap \tilde \Gamma^4)} \gg M^{-O(1)},\end{align*} $$
$$ \begin{align*}\int_{G'/(G' \cap \tilde \Gamma^4)} \int_0^1 \varphi(\varepsilon_0 (1,1,1,\gamma^t) x)\ dt \ d\mu_{G'/(G' \cap \tilde \Gamma^4)} \gg M^{-O(1)},\end{align*} $$
and thus by the pigeonhole principle there exists
![]() $x \in (G/\Gamma )^4$
such that
$x \in (G/\Gamma )^4$
such that
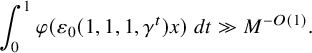 $$ \begin{align*}\int_0^1 \varphi(\varepsilon_0 (1,1,1,\gamma^t) x)\ dt \gg M^{-O(1)}.\end{align*} $$
$$ \begin{align*}\int_0^1 \varphi(\varepsilon_0 (1,1,1,\gamma^t) x)\ dt \gg M^{-O(1)}.\end{align*} $$
In particular, we have
for a set of
![]() $t \in [0,1]$
of measure
$t \in [0,1]$
of measure
![]() $\gg M^{-O(1)}$
. But if we let
$\gg M^{-O(1)}$
. But if we let
![]() $x_1,x_2,x_3$
be the first three components of
$x_1,x_2,x_3$
be the first three components of
![]() $\varepsilon _0 x$
, we see from equation (6.12) that in order for equation (6.15) to hold, the fourth coordinate of
$\varepsilon _0 x$
, we see from equation (6.12) that in order for equation (6.15) to hold, the fourth coordinate of
![]() $\varepsilon _0 (1,1,1,\gamma ^t) x$
must take the form
$\varepsilon _0 (1,1,1,\gamma ^t) x$
must take the form
![]() $\kappa \varepsilon x_2$
, where
$\kappa \varepsilon x_2$
, where
![]() $\varepsilon = O(M^{O(1)})$
is such that
$\varepsilon = O(M^{O(1)})$
is such that
![]() $x_3 = \varepsilon x_1$
. Since the equation
$x_3 = \varepsilon x_1$
. Since the equation
![]() $x_3 = \varepsilon x_1$
fixes
$x_3 = \varepsilon x_1$
fixes
![]() $\varepsilon $
to a double coset of
$\varepsilon $
to a double coset of
![]() $\tilde \Gamma $
, there are at most
$\tilde \Gamma $
, there are at most
![]() $O(M^{O(1)})$
choices for
$O(M^{O(1)})$
choices for
![]() $\varepsilon $
, and for each such choice,
$\varepsilon $
, and for each such choice,
![]() $\kappa \varepsilon x_2$
is confined to a ball of radius
$\kappa \varepsilon x_2$
is confined to a ball of radius
![]() $O(M^{-C_3+O(1)})$
; thus, the fourth coordinate of
$O(M^{-C_3+O(1)})$
; thus, the fourth coordinate of
![]() $\varepsilon _0 (1,1,1,\gamma ^t) x$
is confined to the union of
$\varepsilon _0 (1,1,1,\gamma ^t) x$
is confined to the union of
![]() $O(M^{O(1)})$
balls of radius
$O(M^{O(1)})$
balls of radius
![]() $O(M^{-C_3+O(1)})$
. Since
$O(M^{-C_3+O(1)})$
. Since
![]() $\gamma $
is nontrivial,
$\gamma $
is nontrivial,
![]() $t \in [0,1]$
is thus confined to the union of
$t \in [0,1]$
is thus confined to the union of
![]() $O(M^{O(1)})$
intervals of radius
$O(M^{O(1)})$
intervals of radius
![]() $O(M^{-C_3+O(1)})$
. Thus, the set of
$O(M^{-C_3+O(1)})$
. Thus, the set of
![]() $t \in [0,1]$
obeying equation (6.15) has measure at most
$t \in [0,1]$
obeying equation (6.15) has measure at most
![]() $O(M^{-C_3+O(1)})$
, leading to a contradiction for
$O(M^{-C_3+O(1)})$
, leading to a contradiction for
![]() $C_3$
large enough. Thus, L must be trivial.
$C_3$
large enough. Thus, L must be trivial.
Now, we apply a ‘Furstenberg–Weiss’ argument [Reference Furstenberg and Weiss15] (see also the argument attributed to Serre in [Reference Ribet57, Lemma 3.3]). Consider the groups
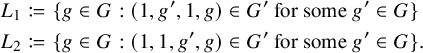
Taking logarithms, we have

thus
![]() $\log L_1, \log L_2$
are projections of certain slices of
$\log L_1, \log L_2$
are projections of certain slices of
![]() $\log G'$
. Since
$\log G'$
. Since
![]() $G'$
was a
$G'$
was a
![]() $O(M^{O(1)})$
-rational subgroup of
$O(M^{O(1)})$
-rational subgroup of
![]() $G^4$
, we conclude from linear algebra that
$G^4$
, we conclude from linear algebra that
![]() $L_1,L_2$
are
$L_1,L_2$
are
![]() $O(M^{O(1)})$
-rational subgroups of G; comparing with equation (6.14), we also see that
$O(M^{O(1)})$
-rational subgroups of G; comparing with equation (6.14), we also see that
![]() $[L_1,L_2] \subset L$
; since L is trivial,
$[L_1,L_2] \subset L$
; since L is trivial,
![]() $[L_1,L_2]$
is trivial. Since G is nonabelian by hypothesis,
$[L_1,L_2]$
is trivial. Since G is nonabelian by hypothesis,
![]() $[G,G]$
is nontrivial; thus, at least one of
$[G,G]$
is nontrivial; thus, at least one of
![]() $L_1,L_2$
must be a proper subgroup of G. For the sake of discussion, let us assume that
$L_1,L_2$
must be a proper subgroup of G. For the sake of discussion, let us assume that
![]() $L_1$
is a proper subgroup, as the other case is similar. Then there exists a nontrivial horizontal character
$L_1$
is a proper subgroup, as the other case is similar. Then there exists a nontrivial horizontal character
![]() $\eta _4 \colon G \to \mathbb {R}/\mathbb {Z}$
on
$\eta _4 \colon G \to \mathbb {R}/\mathbb {Z}$
on
![]() $G/\tilde \Gamma $
of Lipschitz norm
$G/\tilde \Gamma $
of Lipschitz norm
![]() $O(M^{O(1)})$
that annihilates
$O(M^{O(1)})$
that annihilates
![]() $L_1$
, that is to say
$L_1$
, that is to say
![]() $\eta _4(g)=0$
whenever
$\eta _4(g)=0$
whenever
![]() $(1,g',1,g) \in G'$
for some
$(1,g',1,g) \in G'$
for some
![]() $g' \in G$
. Thus, the homomorphism
$g' \in G$
. Thus, the homomorphism
![]() $(1,g',1,g) \mapsto \eta _4(g)$
on
$(1,g',1,g) \mapsto \eta _4(g)$
on
![]() $1 \times G \times 1 \times G$
annihilates the restriction of
$1 \times G \times 1 \times G$
annihilates the restriction of
![]() $G'$
to this group, as well as
$G'$
to this group, as well as
![]() $1 \times G \times 1 \times 1$
. Taking logarithms, we obtain a linear functional on the Lie algebra
$1 \times G \times 1 \times 1$
. Taking logarithms, we obtain a linear functional on the Lie algebra
![]() $0 \times \log G \times 0 \times \log G$
(with all coefficients
$0 \times \log G \times 0 \times \log G$
(with all coefficients
![]() $O(M^{O(1)})$
in the Mal’cev basis) that annihilates the restriction of
$O(M^{O(1)})$
in the Mal’cev basis) that annihilates the restriction of
![]() $\log G'$
to this Lie algebra, as well as to
$\log G'$
to this Lie algebra, as well as to
![]() $0 \times \log G \times 0 \times 0$
; by composing with a suitable linear projection, we can then extend this linear functional to a linear functional on all of
$0 \times \log G \times 0 \times 0$
; by composing with a suitable linear projection, we can then extend this linear functional to a linear functional on all of
![]() $(\log G)^4$
that annihilates all of
$(\log G)^4$
that annihilates all of
![]() $\log G'$
, again with all coefficients
$\log G'$
, again with all coefficients
![]() $O(M^{O(1)})$
. Undoing the logarithm, we may find (possibly trivial) additional horizontal characters
$O(M^{O(1)})$
. Undoing the logarithm, we may find (possibly trivial) additional horizontal characters
![]() $\eta _1,\eta _3 \colon G \to \mathbb {R}/\mathbb {Z}$
on
$\eta _1,\eta _3 \colon G \to \mathbb {R}/\mathbb {Z}$
on
![]() $G/\tilde \Gamma $
of Lipschitz norm
$G/\tilde \Gamma $
of Lipschitz norm
![]() $O(M^{O(1)})$
such that
$O(M^{O(1)})$
such that
for all
![]() $(g_1,g_2,g_3,g_4) \in G'$
. In particular, writing
$(g_1,g_2,g_3,g_4) \in G'$
. In particular, writing
![]() $g' = (g^{\prime }_1,g^{\prime }_2,g^{\prime }_3,g^{\prime }_4)$
, we have
$g' = (g^{\prime }_1,g^{\prime }_2,g^{\prime }_3,g^{\prime }_4)$
, we have
for all
![]() $a,a',b,b' \in \mathbb {Z}$
. Applying the factorization (6.11), and noting that the horizontal characters
$a,a',b,b' \in \mathbb {Z}$
. Applying the factorization (6.11), and noting that the horizontal characters
![]() $\eta _1,\eta _3,\eta _4$
annihilate the components of
$\eta _1,\eta _3,\eta _4$
annihilate the components of
![]() $\gamma $
, we conclude that
$\gamma $
, we conclude that
for all
![]() $a,a',b,b' \in \mathbb {Z}$
, where
$a,a',b,b' \in \mathbb {Z}$
, where
and
![]() $\varepsilon _1,\varepsilon _2,\varepsilon _3,\varepsilon _4$
are the components of
$\varepsilon _1,\varepsilon _2,\varepsilon _3,\varepsilon _4$
are the components of
![]() $\varepsilon $
. From the smoothness properties of
$\varepsilon $
. From the smoothness properties of
![]() $\varepsilon $
, we see in particular that
$\varepsilon $
, we see in particular that
for
![]() $a,a' \in I_{A'}, b, b' \in J_{A'}$
, and hence from equation (6.16)
$a,a' \in I_{A'}, b, b' \in J_{A'}$
, and hence from equation (6.16)
whenever
![]() $a' \in I_{A'}, b' \in J_{A'}$
. For any
$a' \in I_{A'}, b' \in J_{A'}$
. For any
![]() $a' \in I_{A'}$
, the map
$a' \in I_{A'}$
, the map
![]() $b' \mapsto \eta _4(g(a'b'))$
is a polynomial of degree at most d, so by Vinogradov’s lemma (Lemma 2.3), for each such
$b' \mapsto \eta _4(g(a'b'))$
is a polynomial of degree at most d, so by Vinogradov’s lemma (Lemma 2.3), for each such
![]() $a'$
, we either have
$a'$
, we either have
or else there exists
![]() $1 \leq q \ll M^{O(1)}$
such that
$1 \leq q \ll M^{O(1)}$
such that
The former possibility is not compatible with equation (6.2) if
![]() $C_4$
is large enough, so we may assume the latter possibility equation (6.17) holds for all
$C_4$
is large enough, so we may assume the latter possibility equation (6.17) holds for all
![]() $a' \in I_{A'}$
. Currently, the quantity q may depend on
$a' \in I_{A'}$
. Currently, the quantity q may depend on
![]() $a'$
, but by the pigeonhole principle we may fix a q so that equation (6.17) holds for
$a'$
, but by the pigeonhole principle we may fix a q so that equation (6.17) holds for
![]() $\gg M^{-O(1)} |I_{A'}|$
choices of
$\gg M^{-O(1)} |I_{A'}|$
choices of
![]() $a' \in I_{A'}$
. Applying Corollary 2.4, we conclude that either
$a' \in I_{A'}$
. Applying Corollary 2.4, we conclude that either
or else there exists
![]() $1 \leq q' \ll M^{O(1)}$
such that
$1 \leq q' \ll M^{O(1)}$
such that
In either case, we obtain one of the conclusions of Proposition 6.1. The proof of Theorem 4.2(ii) is now complete.
7 The abelian type
 $II$
case
$II$
case
In this section, we establish the abelian Type
![]() $II$
case (iii) of Theorem 4.2 using arguments from [Reference Matomäki and Shao49]. We shall need the following variant of [Reference Matomäki and Shao49, Proposition 2.2].
$II$
case (iii) of Theorem 4.2 using arguments from [Reference Matomäki and Shao49]. We shall need the following variant of [Reference Matomäki and Shao49, Proposition 2.2].
Proposition 7.1. Let
![]() $\delta \in (0,1/2)$
,
$\delta \in (0,1/2)$
,
![]() $M \geq 2$
and
$M \geq 2$
and
![]() $L = X/M$
. Assume that
$L = X/M$
. Assume that
![]() $H \geq \delta ^{-C}\max (L,M)$
for some sufficiently large constant
$H \geq \delta ^{-C}\max (L,M)$
for some sufficiently large constant
![]() $C = C(k)>0$
. Let
$C = C(k)>0$
. Let
![]() $\alpha (\ell ), \beta (m) \in \mathbb {C}$
. Let
$\alpha (\ell ), \beta (m) \in \mathbb {C}$
. Let
![]() $k \in \mathbb {N}$
, and let
$k \in \mathbb {N}$
, and let
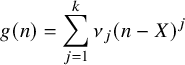 $$\begin{align*}g(n) = \sum_{j=1}^k \nu_j (n-X)^j \end{align*}$$
$$\begin{align*}g(n) = \sum_{j=1}^k \nu_j (n-X)^j \end{align*}$$
be a polynomial of degree k with real coefficients
![]() $\nu _j$
. If
$\nu _j$
. If
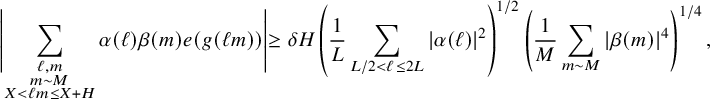 $$\begin{align*}\Biggl|\sum_{\substack{\ell, m \\ m \sim M \\ X < \ell m \leq X+H}} \alpha(\ell) \beta(m) e(g(\ell m)) \Biggl| \geq \delta H \left(\frac{1}{L}\sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2\right)^{1/2} \left(\frac{1}{M}\sum_{m \sim M} |\beta(m)|^4\right)^{1/4}, \end{align*}$$
$$\begin{align*}\Biggl|\sum_{\substack{\ell, m \\ m \sim M \\ X < \ell m \leq X+H}} \alpha(\ell) \beta(m) e(g(\ell m)) \Biggl| \geq \delta H \left(\frac{1}{L}\sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2\right)^{1/2} \left(\frac{1}{M}\sum_{m \sim M} |\beta(m)|^4\right)^{1/4}, \end{align*}$$
then there exists a positive integer
![]() $q \leq \delta ^{-O_k(1)}$
such that
$q \leq \delta ^{-O_k(1)}$
such that
for all
![]() $1 \leq j \leq k$
, with the convention that
$1 \leq j \leq k$
, with the convention that
![]() $\nu _{k+1} = 0$
.
$\nu _{k+1} = 0$
.
Proof. This follows from the same argument as [Reference Matomäki and Shao49, Proposition 2.2]. The only difference is that we do not assume that the coefficients
![]() $\alpha (\ell )$
and
$\alpha (\ell )$
and
![]() $\beta (m)$
are divisor bounded and due to this in the beginning of the proof we do not estimate the sums
$\beta (m)$
are divisor bounded and due to this in the beginning of the proof we do not estimate the sums
![]() $\sum _{L/2 < \ell \leq 2L} |\alpha (\ell )|^2$
and
$\sum _{L/2 < \ell \leq 2L} |\alpha (\ell )|^2$
and
![]() $\sum _{m \sim M} |\beta (m)|^4$
with bounds for averages of divisor functions but keep them as they are.
$\sum _{m \sim M} |\beta (m)|^4$
with bounds for averages of divisor functions but keep them as they are.
Let us get back to the proof of Theorem 4.2(iii). We can assume that
since otherwise the claim is immediate. Note that in particular
![]() $H \geq \delta ^{-O_d(1)} X^{1/2}$
. By assumption and dyadic splitting (noting that
$H \geq \delta ^{-O_d(1)} X^{1/2}$
. By assumption and dyadic splitting (noting that
![]() $\delta < 1/\log X$
),
$\delta < 1/\log X$
),
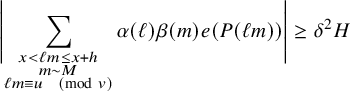 $$ \begin{align} \Biggl|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M \\ \ell m \equiv u \quad\pmod{v}}} \alpha(\ell) \beta(m) e(P(\ell m))\Biggr| \geq \delta^2 H \end{align} $$
$$ \begin{align} \Biggl|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M \\ \ell m \equiv u \quad\pmod{v}}} \alpha(\ell) \beta(m) e(P(\ell m))\Biggr| \geq \delta^2 H \end{align} $$
for some
![]() $(x, x+h] \subseteq (X, X+H]$
, some
$(x, x+h] \subseteq (X, X+H]$
, some
![]() $M \in [X/A_{II}^+, X/A_{II}^-]$
, some polynomial
$M \in [X/A_{II}^+, X/A_{II}^-]$
, some polynomial
![]() $P(x)$
of degree at most d and some
$P(x)$
of degree at most d and some
![]() $u, v \in \mathbb {N}$
with
$u, v \in \mathbb {N}$
with
![]() $u \leq v$
. Before applying Proposition 7.1, we will show that equation (7.1) can hold only if
$u \leq v$
. Before applying Proposition 7.1, we will show that equation (7.1) can hold only if
![]() $v \ll \delta ^{-8}$
and
$v \ll \delta ^{-8}$
and
![]() $h \gg \delta ^8 H$
. In order to show this, we give an upper bound for the left-hand side using the Cauchy–Schwarz inequality. Using also equation (4.1) and denoting
$h \gg \delta ^8 H$
. In order to show this, we give an upper bound for the left-hand side using the Cauchy–Schwarz inequality. Using also equation (4.1) and denoting
![]() $L = X/M$
, we obtain, using the inequality
$L = X/M$
, we obtain, using the inequality
![]() $|xy| \leq |x|^2 + |y|^2$
$|xy| \leq |x|^2 + |y|^2$
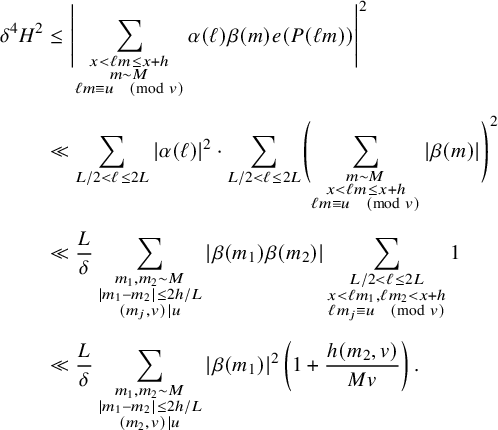 $$ \begin{align*} \delta^4 H^2 &\leq \Biggl|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M \\ \ell m \equiv u \quad\pmod{v}}} \alpha(\ell) \beta(m) e(P(\ell m))\Biggr|^2 \\[5pt] &\ll \sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2 \cdot \sum_{L/2 < \ell \leq 2L} \Biggl(\sum_{\substack{m \sim M \\ x < \ell m \leq x+h \\ \ell m \equiv u \quad\pmod{v}}} |\beta(m)|\Biggr)^2 \\[5pt] &\ll \frac{L}{\delta} \sum_{\substack{m_1, m_2 \sim M \\ |m_1 -m_2| \leq 2h/L \\ (m_j, v) \mid u}} |\beta(m_1) \beta(m_2)| \sum_{\substack{L/2 < \ell \leq 2L \\ x < \ell m_1, \ell m_2 < x+h \\ \ell m_j \equiv u \quad\pmod{v}}} 1 \\[5pt] &\ll \frac{L}{\delta} \sum_{\substack{m_1, m_2 \sim M \\ |m_1 -m_2| \leq 2h/L \\ (m_2, v) \mid u}} |\beta(m_1)|^2 \left(1+\frac{h (m_2, v)}{M v}\right). \end{align*} $$
$$ \begin{align*} \delta^4 H^2 &\leq \Biggl|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M \\ \ell m \equiv u \quad\pmod{v}}} \alpha(\ell) \beta(m) e(P(\ell m))\Biggr|^2 \\[5pt] &\ll \sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2 \cdot \sum_{L/2 < \ell \leq 2L} \Biggl(\sum_{\substack{m \sim M \\ x < \ell m \leq x+h \\ \ell m \equiv u \quad\pmod{v}}} |\beta(m)|\Biggr)^2 \\[5pt] &\ll \frac{L}{\delta} \sum_{\substack{m_1, m_2 \sim M \\ |m_1 -m_2| \leq 2h/L \\ (m_j, v) \mid u}} |\beta(m_1) \beta(m_2)| \sum_{\substack{L/2 < \ell \leq 2L \\ x < \ell m_1, \ell m_2 < x+h \\ \ell m_j \equiv u \quad\pmod{v}}} 1 \\[5pt] &\ll \frac{L}{\delta} \sum_{\substack{m_1, m_2 \sim M \\ |m_1 -m_2| \leq 2h/L \\ (m_2, v) \mid u}} |\beta(m_1)|^2 \left(1+\frac{h (m_2, v)}{M v}\right). \end{align*} $$
Writing
![]() $d = (m_2, v)$
and
$d = (m_2, v)$
and
![]() $m_2' = m_2/d$
and using equation (4.3), we obtain
$m_2' = m_2/d$
and using equation (4.3), we obtain
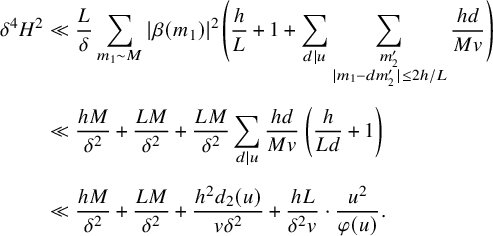 $$ \begin{align*} \delta^4 H^2 &\ll \frac{L}{\delta} \sum_{\substack{m_1 \sim M}} |\beta(m_1)|^2 \Biggl(\frac{h}{L}+1 + \sum_{d \mid u}\sum_{\substack{m_2' \\ |m_1 -d m_2'| \leq 2h/L}} \frac{h d}{M v}\Biggr) \\[5pt] & \ll \frac{h M}{\delta^2} + \frac{LM}{\delta^2} + \frac{LM}{\delta^2} \sum_{d \mid u} \frac{h d}{M v} \left(\frac{h}{Ld} +1\right) \\[5pt] & \ll \frac{h M}{\delta^2} + \frac{LM}{\delta^2} + \frac{h^2 d_2(u)}{v\delta^2} + \frac{hL}{\delta^2 v} \cdot \frac{u^2}{\varphi(u)}. \end{align*} $$
$$ \begin{align*} \delta^4 H^2 &\ll \frac{L}{\delta} \sum_{\substack{m_1 \sim M}} |\beta(m_1)|^2 \Biggl(\frac{h}{L}+1 + \sum_{d \mid u}\sum_{\substack{m_2' \\ |m_1 -d m_2'| \leq 2h/L}} \frac{h d}{M v}\Biggr) \\[5pt] & \ll \frac{h M}{\delta^2} + \frac{LM}{\delta^2} + \frac{LM}{\delta^2} \sum_{d \mid u} \frac{h d}{M v} \left(\frac{h}{Ld} +1\right) \\[5pt] & \ll \frac{h M}{\delta^2} + \frac{LM}{\delta^2} + \frac{h^2 d_2(u)}{v\delta^2} + \frac{hL}{\delta^2 v} \cdot \frac{u^2}{\varphi(u)}. \end{align*} $$
Since
![]() $L, M \ll \delta ^{O(1)} H$
and
$L, M \ll \delta ^{O(1)} H$
and
![]() $LM \ll \delta ^{O(1)} H^2$
, this is a contradiction unless
$LM \ll \delta ^{O(1)} H^2$
, this is a contradiction unless
![]() $v \ll \delta ^{-8}$
and
$v \ll \delta ^{-8}$
and
![]() $h \gg \delta ^8 H$
.
$h \gg \delta ^8 H$
.
From equation (7.1) together with equations (4.1) and (4.3), we have
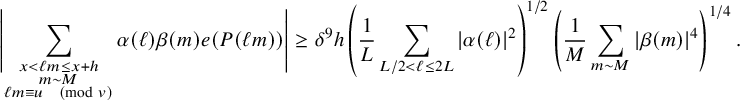 $$\begin{align*}\Biggl|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M \\ \ell m \equiv u \quad\pmod{v}}} \alpha(\ell) \beta(m) e(P(\ell m))\Biggr| \geq \delta^9 h\left(\frac{1}{L}\sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2\right)^{1/2} \left(\frac{1}{M}\sum_{m \sim M} |\beta(m)|^4\right)^{1/4}. \end{align*}$$
$$\begin{align*}\Biggl|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M \\ \ell m \equiv u \quad\pmod{v}}} \alpha(\ell) \beta(m) e(P(\ell m))\Biggr| \geq \delta^9 h\left(\frac{1}{L}\sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2\right)^{1/2} \left(\frac{1}{M}\sum_{m \sim M} |\beta(m)|^4\right)^{1/4}. \end{align*}$$
We can write, for some
![]() $\nu _j \in \mathbb {R}$
,
$\nu _j \in \mathbb {R}$
,
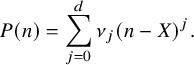 $$\begin{align*}P(n) = \sum_{j = 0}^d \nu_j (n-X)^j. \end{align*}$$
$$\begin{align*}P(n) = \sum_{j = 0}^d \nu_j (n-X)^j. \end{align*}$$
We can assume that
![]() $\nu _0 = 0$
. Furthermore, we can spot the condition
$\nu _0 = 0$
. Furthermore, we can spot the condition
![]() $\ell m = u \ \pmod {v}$
using additive characters so that, for some
$\ell m = u \ \pmod {v}$
using additive characters so that, for some
![]() $r \ \pmod {v}$
we have
$r \ \pmod {v}$
we have
 $$\begin{align*}\left|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M}} \alpha(\ell) \beta(m) e\left(P(\ell m) + \frac{r\ell m}{v}\right)\right| \geq \delta^9 h\left(\frac{1}{L}\sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2\right)^{1/2} \left(\frac{1}{M}\sum_{m \sim M} |\beta(m)|^4\right)^{1/4}. \end{align*}$$
$$\begin{align*}\left|\sum_{\substack{x < \ell m \leq x+h \\ m \sim M}} \alpha(\ell) \beta(m) e\left(P(\ell m) + \frac{r\ell m}{v}\right)\right| \geq \delta^9 h\left(\frac{1}{L}\sum_{L/2 < \ell \leq 2L} |\alpha(\ell)|^2\right)^{1/2} \left(\frac{1}{M}\sum_{m \sim M} |\beta(m)|^4\right)^{1/4}. \end{align*}$$
Now, we are in the position to apply Proposition 7.1 to the polynomial
![]() $P(n) + rn/v$
. By multiplying the resulting q by v, we see that the conclusion of the proposition holds also for the coefficients of
$P(n) + rn/v$
. By multiplying the resulting q by v, we see that the conclusion of the proposition holds also for the coefficients of
![]() $P(n)$
, ignoring
$P(n)$
, ignoring
![]() $rn/v$
. Hence, we get that there exists a positive integer
$rn/v$
. Hence, we get that there exists a positive integer
![]() $q' \leq \delta ^{-O_d(1)}$
such that
$q' \leq \delta ^{-O_d(1)}$
such that
for all
![]() $1 \leq j \leq d$
, with the convention that
$1 \leq j \leq d$
, with the convention that
![]() $\nu _{d+1} = 0$
.
$\nu _{d+1} = 0$
.
Next, we use a variant of the argument in the treatment of type II sums in [Reference Matomäki and Shao49, Proof of Theorem 1.3 in Section 4]. We start by shifting each
![]() $\nu _j$
by
$\nu _j$
by
![]() $(q'j)^{-1}a_j$
for an appropriate
$(q'j)^{-1}a_j$
for an appropriate
![]() $a_j \in \mathbb {Z}$
to get
$a_j \in \mathbb {Z}$
to get
![]() $\nu _j'$
such that
$\nu _j'$
such that
for all
![]() $1 \leq j \leq d$
. Let
$1 \leq j \leq d$
. Let
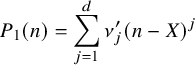 $$\begin{align*}P_1(n) = \sum_{j=1}^d \nu_j'(n-X)^j \end{align*}$$
$$\begin{align*}P_1(n) = \sum_{j=1}^d \nu_j'(n-X)^j \end{align*}$$
so that
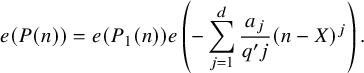 $$\begin{align*}e(P(n)) = e(P_1(n)) e\left(-\sum_{j=1}^d \frac{a_j}{q'j} (n-X)^j\right). \end{align*}$$
$$\begin{align*}e(P(n)) = e(P_1(n)) e\left(-\sum_{j=1}^d \frac{a_j}{q'j} (n-X)^j\right). \end{align*}$$
Choosing
![]() $q = q' d!$
, we see that
$q = q' d!$
, we see that
![]() $e(P(n)-P_1(n))$
is constant in any arithmetic progression
$e(P(n)-P_1(n))$
is constant in any arithmetic progression
![]() $\ \pmod {q}$
and thus
$\ \pmod {q}$
and thus
By induction, one can deduce from equation (7.2) that
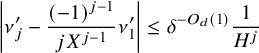 $$ \begin{align} \left|\nu_j' - \frac{(-1)^{j-1}}{jX^{j-1}} \nu_1'\right| \leq \delta^{-O_d(1)} \frac{1}{H^j} \end{align} $$
$$ \begin{align} \left|\nu_j' - \frac{(-1)^{j-1}}{jX^{j-1}} \nu_1'\right| \leq \delta^{-O_d(1)} \frac{1}{H^j} \end{align} $$
for all
![]() $1 \leq j \leq d + 1$
. In particular, when
$1 \leq j \leq d + 1$
. In particular, when
![]() $j=d+1$
this gives
$j=d+1$
this gives
We set
![]() $T = 2\pi X\nu _1'$
so that
$T = 2\pi X\nu _1'$
so that
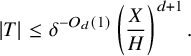 $$ \begin{align} |T| \leq \delta^{-O_d(1)} \left(\frac{X}{H}\right)^{d+1}. \end{align} $$
$$ \begin{align} |T| \leq \delta^{-O_d(1)} \left(\frac{X}{H}\right)^{d+1}. \end{align} $$
We write also
 $$\begin{align*}P_2(n) = \sum_{j=1}^d \frac{(-1)^{j-1}}{jX^{j-1}} \nu_1' (n-X)^j = \frac{T}{2\pi} \sum_{j=1}^d \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^j. \end{align*}$$
$$\begin{align*}P_2(n) = \sum_{j=1}^d \frac{(-1)^{j-1}}{jX^{j-1}} \nu_1' (n-X)^j = \frac{T}{2\pi} \sum_{j=1}^d \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^j. \end{align*}$$
By equation (7.4), we have that
By Taylor expansion, for any
![]() $k \geq 0$
and
$k \geq 0$
and
![]() $n \in (X, X+H]$
,
$n \in (X, X+H]$
,
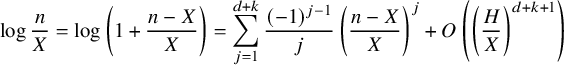 $$\begin{align*}\log \frac{n}{X} = \log\left(1 + \frac{n-X}{X}\right) = \sum_{j=1}^{d+k} \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^j + O\left( \left(\frac{H}{X}\right)^{d+k+1} \right) \end{align*}$$
$$\begin{align*}\log \frac{n}{X} = \log\left(1 + \frac{n-X}{X}\right) = \sum_{j=1}^{d+k} \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^j + O\left( \left(\frac{H}{X}\right)^{d+k+1} \right) \end{align*}$$
so that, using equation (7.5),
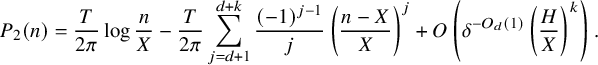 $$ \begin{align*} P_2(n) &= \frac{T}{2\pi} \log \frac{n}{X} - \frac{T}{2\pi} \sum_{j=d+1}^{d+k} \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^{j} + O\left(\delta^{-O_d(1)} \left(\frac{H}{X}\right)^{k} \right). \end{align*} $$
$$ \begin{align*} P_2(n) &= \frac{T}{2\pi} \log \frac{n}{X} - \frac{T}{2\pi} \sum_{j=d+1}^{d+k} \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^{j} + O\left(\delta^{-O_d(1)} \left(\frac{H}{X}\right)^{k} \right). \end{align*} $$
Hence,
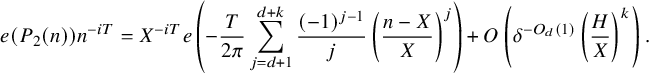 $$\begin{align*}e(P_2(n))n^{-iT} = X^{-iT} e\left(-\frac{T}{2\pi}\sum_{j=d+1}^{d+k} \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^{j}\right) + O\left(\delta^{-O_d(1)} \left(\frac{H}{X}\right)^{k} \right). \end{align*}$$
$$\begin{align*}e(P_2(n))n^{-iT} = X^{-iT} e\left(-\frac{T}{2\pi}\sum_{j=d+1}^{d+k} \frac{(-1)^{j-1}}{j} \left(\frac{n-X}{X}\right)^{j}\right) + O\left(\delta^{-O_d(1)} \left(\frac{H}{X}\right)^{k} \right). \end{align*}$$
Taking k large enough in terms of
![]() $\theta $
, this implies that
$\theta $
, this implies that
Now, the claim follows by combining equations (7.3), (7.6) and (7.7) utilizing equation (2.2).
8 The type
 $I_2$
case
$I_2$
case
In this section, we establish the type
![]() $I_2$
case (iv) of Theorem 4.2. Our main tool will be the following elementary partitionFootnote
12
of the hyperbolic neighborhood
$I_2$
case (iv) of Theorem 4.2. Our main tool will be the following elementary partitionFootnote
12
of the hyperbolic neighborhood
![]() $\{ (m,n) \in \mathbb {Z}^2: m \in J; \quad X < nm \leq X+H \}$
into arithmetic progressions, which is nontrivial when H is much larger than
$\{ (m,n) \in \mathbb {Z}^2: m \in J; \quad X < nm \leq X+H \}$
into arithmetic progressions, which is nontrivial when H is much larger than
![]() $X^{1/3}$
.
$X^{1/3}$
.
Theorem 8.1 (Partition of hyperbolic neighborhood).
Let
![]() $X, H, M \geq 1$
be such that
$X, H, M \geq 1$
be such that
and let J be a subinterval of
![]() $(M,2M]$
. Then the set
$(M,2M]$
. Then the set
can be partitioned for any integer Q obeying
as
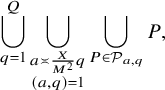 $$ \begin{align*}\bigcup_{q=1}^Q \bigcup_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \bigcup_{P \in {\mathcal P}_{a,q}} P,\end{align*} $$
$$ \begin{align*}\bigcup_{q=1}^Q \bigcup_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \bigcup_{P \in {\mathcal P}_{a,q}} P,\end{align*} $$
where for each pair
![]() $a,q$
of coprime integers with
$a,q$
of coprime integers with
![]() $1 \leq q \leq Q$
and
$1 \leq q \leq Q$
and
![]() $a \asymp \frac {X}{M^2} q$
,
$a \asymp \frac {X}{M^2} q$
,
![]() ${\mathcal P}_{a,q}$
is a family of
${\mathcal P}_{a,q}$
is a family of
![]() $O( \frac {M^3}{XQ^2q} )$
arithmetic progressions P in equation (8.1), each of spacing
$O( \frac {M^3}{XQ^2q} )$
arithmetic progressions P in equation (8.1), each of spacing
![]() $(q,-a)$
and length at most
$(q,-a)$
and length at most
![]() $\frac {HQ}{M}$
.
$\frac {HQ}{M}$
.
In particular, the cardinality of the set (8.1) does not exceed
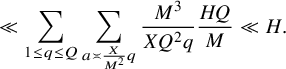 $$ \begin{align} \ll \sum_{1 \leq q \leq Q} \sum_{a \asymp \frac{X}{M^2} q} \frac{M^3}{XQ^2q} \frac{HQ}{M} \ll H. \end{align} $$
$$ \begin{align} \ll \sum_{1 \leq q \leq Q} \sum_{a \asymp \frac{X}{M^2} q} \frac{M^3}{XQ^2q} \frac{HQ}{M} \ll H. \end{align} $$
Proof of Theorem 8.1.
For future reference, we note from equation (8.2) and
![]() $X^{1/3} \leq H \leq X$
that
$X^{1/3} \leq H \leq X$
that
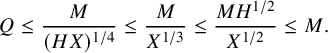 $$ \begin{align} Q \leq \frac{M}{(HX)^{1/4}} \leq \frac{M}{X^{1/3}} \leq \frac{M H^{1/2}}{X^{1/2}} \leq M. \end{align} $$
$$ \begin{align} Q \leq \frac{M}{(HX)^{1/4}} \leq \frac{M}{X^{1/3}} \leq \frac{M H^{1/2}}{X^{1/2}} \leq M. \end{align} $$
Note that if
![]() $(m,n)$
lies in equation (8.1), then
$(m,n)$
lies in equation (8.1), then
![]() $m \asymp M$
and
$m \asymp M$
and
![]() $nm \asymp X$
, thus
$nm \asymp X$
, thus
![]() $\frac {n}{m} \asymp \frac {X}{M^2}$
. By the Dirichlet approximation theorem, we then have
$\frac {n}{m} \asymp \frac {X}{M^2}$
. By the Dirichlet approximation theorem, we then have
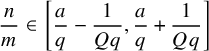 $$ \begin{align*}\frac{n}{m} \in \left[\frac{a}{q} - \frac{1}{Qq}, \frac{a}{q} + \frac{1}{Qq}\right]\end{align*} $$
$$ \begin{align*}\frac{n}{m} \in \left[\frac{a}{q} - \frac{1}{Qq}, \frac{a}{q} + \frac{1}{Qq}\right]\end{align*} $$
for some
![]() $1 \leq q \leq Q$
and some
$1 \leq q \leq Q$
and some
![]() $a \asymp \frac {X}{M^2} q$
coprime to q. If for any such
$a \asymp \frac {X}{M^2} q$
coprime to q. If for any such
![]() $a,q$
, we define
$a,q$
, we define
![]() $I_{a,q}$
to be the portion of the interval
$I_{a,q}$
to be the portion of the interval
![]() $[\frac {a}{q} - \frac {1}{Qq}, \frac {a}{q} + \frac {1}{Qq}]$
that is not contained in any other such interval
$[\frac {a}{q} - \frac {1}{Qq}, \frac {a}{q} + \frac {1}{Qq}]$
that is not contained in any other such interval
![]() $I_{a',q'}$
with
$I_{a',q'}$
with
![]() $q' < q$
, we see that the
$q' < q$
, we see that the
![]() $I_{a,q}$
are disjoint intervals and that we can partition equation (8.1) into sets
$I_{a,q}$
are disjoint intervals and that we can partition equation (8.1) into sets
where
![]() $a,q$
range over those coprime integers with
$a,q$
range over those coprime integers with
It then suffices to show that each such set (8.5) can be partitioned into
![]() $O( \frac {M^3}{XQ^2q} )$
arithmetic progressions P in
$O( \frac {M^3}{XQ^2q} )$
arithmetic progressions P in
![]() $\mathbb {Z}^2$
, each of spacing
$\mathbb {Z}^2$
, each of spacing
![]() $(q,-a)$
and length at most
$(q,-a)$
and length at most
![]() $\frac {HQ}{M}$
.
$\frac {HQ}{M}$
.
Fix
![]() $a,q$
, and write
$a,q$
, and write
![]() $I = I_{a,q}$
. It in fact suffices to show that the set (8.5) can be partitioned into
$I = I_{a,q}$
. It in fact suffices to show that the set (8.5) can be partitioned into
![]() $O( \frac {M^3}{XQ^2q} )$
arithmetic progressions P of spacing
$O( \frac {M^3}{XQ^2q} )$
arithmetic progressions P of spacing
![]() $(q,-a)$
and arbitrary length, so long as we also show that the total cardinality of equation (8.5) is
$(q,-a)$
and arbitrary length, so long as we also show that the total cardinality of equation (8.5) is
![]() $O( \frac {HM^2}{XQq} )$
. This is because any such progression P can be partitioned into
$O( \frac {HM^2}{XQq} )$
. This is because any such progression P can be partitioned into
![]() $O( \frac {M}{HQ} \# P + 1 )$
subprogressions of the same spacing
$O( \frac {M}{HQ} \# P + 1 )$
subprogressions of the same spacing
![]() $(q,-a)$
and length at most
$(q,-a)$
and length at most
![]() $\frac {HQ}{M}$
, and
$\frac {HQ}{M}$
, and
 $$ \begin{align*}\sum_P\left( \frac{M}{HQ} \# P + 1\right) \ll \frac{M}{HQ} \frac{HM^2}{XQq} +\frac{M^3}{XQ^2q} \ll \frac{M^3}{XQ^2 q}.\end{align*} $$
$$ \begin{align*}\sum_P\left( \frac{M}{HQ} \# P + 1\right) \ll \frac{M}{HQ} \frac{HM^2}{XQq} +\frac{M^3}{XQ^2q} \ll \frac{M^3}{XQ^2 q}.\end{align*} $$
It remains to obtain such a partition. From Bezout’s theorem, we see that for any integer c, the set
![]() $\{ (m,n) \in \mathbb {Z}^2: qn+am=c\}$
is an infinite arithmetic progression of spacing
$\{ (m,n) \in \mathbb {Z}^2: qn+am=c\}$
is an infinite arithmetic progression of spacing
![]() $(q,-a)$
. The intersection of equation (8.5) with this set is
$(q,-a)$
. The intersection of equation (8.5) with this set is
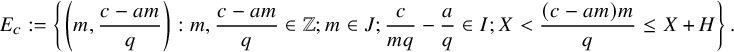 $$ \begin{align} E_c := \left\{ \left(m,\frac{c-am}{q}\right): m, \frac{c-am}{q} \in \mathbb{Z}; m \in J; \frac{c}{mq} - \frac{a}{q} \in I; X < \frac{(c-am)m}{q} \leq X+H \right\}. \end{align} $$
$$ \begin{align} E_c := \left\{ \left(m,\frac{c-am}{q}\right): m, \frac{c-am}{q} \in \mathbb{Z}; m \in J; \frac{c}{mq} - \frac{a}{q} \in I; X < \frac{(c-am)m}{q} \leq X+H \right\}. \end{align} $$
The constraints
confine m to the union of at most two intervals in the real line, and hence the set
![]() $E_c$
is the union of at most two arithmetic progressions in
$E_c$
is the union of at most two arithmetic progressions in
![]() $\mathbb {Z}^2$
of spacing
$\mathbb {Z}^2$
of spacing
![]() $(q,-a)$
. It thus suffices to show that
$(q,-a)$
. It thus suffices to show that
![]() $E_c$
is nonempty for at most
$E_c$
is nonempty for at most
![]() $O( \frac {M^3}{X Q^2 q} )$
choices of c and that
$O( \frac {M^3}{X Q^2 q} )$
choices of c and that
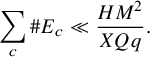 $$ \begin{align} \sum_c \# E_c \ll \frac{HM^2}{XQq}. \end{align} $$
$$ \begin{align} \sum_c \# E_c \ll \frac{HM^2}{XQq}. \end{align} $$
We begin with the first claim. If
![]() $(m,n) \in E_c$
, then
$(m,n) \in E_c$
, then
![]() $c = qn+am$
and
$c = qn+am$
and
![]() $nm = X + O(H)$
and hence
$nm = X + O(H)$
and hence
On the other hand, we have
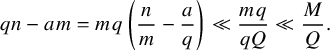 $$ \begin{align} qn-am = mq \left(\frac{n}{m}-\frac{a}{q}\right) \ll \frac{mq}{qQ} \ll \frac{M}{Q}. \end{align} $$
$$ \begin{align} qn-am = mq \left(\frac{n}{m}-\frac{a}{q}\right) \ll \frac{mq}{qQ} \ll \frac{M}{Q}. \end{align} $$
We thus have
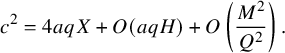 $$ \begin{align*}c^2 = 4aqX + O( aqH ) + O\left( \frac{M^2}{Q^2} \right).\end{align*} $$
$$ \begin{align*}c^2 = 4aqX + O( aqH ) + O\left( \frac{M^2}{Q^2} \right).\end{align*} $$
From equations (8.6), (8.2), we have
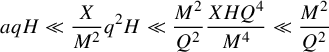 $$ \begin{align*}aqH \ll \frac{X}{M^2}q^2 H \ll \frac{M^2}{Q^2} \frac{XHQ^4}{M^4} \ll \frac{M^2}{Q^2}\end{align*} $$
$$ \begin{align*}aqH \ll \frac{X}{M^2}q^2 H \ll \frac{M^2}{Q^2} \frac{XHQ^4}{M^4} \ll \frac{M^2}{Q^2}\end{align*} $$
and thus
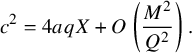 $$ \begin{align*}c^2 = 4aqX + O\left( \frac{M^2}{Q^2} \right).\end{align*} $$
$$ \begin{align*}c^2 = 4aqX + O\left( \frac{M^2}{Q^2} \right).\end{align*} $$
Also,
![]() $\frac {M^2}{Q^2} \leq M^2 \ll X \leq aqX$
. Thus, on taking square roots we have
$\frac {M^2}{Q^2} \leq M^2 \ll X \leq aqX$
. Thus, on taking square roots we have
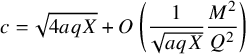 $$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{1}{\sqrt{aqX}} \frac{M^2}{Q^2} \right)\end{align*} $$
$$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{1}{\sqrt{aqX}} \frac{M^2}{Q^2} \right)\end{align*} $$
and hence by equation (8.6)
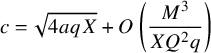 $$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{M^3}{XQ^2q} \right)\end{align*} $$
$$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{M^3}{XQ^2q} \right)\end{align*} $$
giving the first claim.
It remains to prove equation (8.8). We first consider the contribution of those c for which
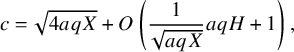 $$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{1}{\sqrt{aqX}} aqH + 1\right),\end{align*} $$
$$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{1}{\sqrt{aqX}} aqH + 1\right),\end{align*} $$
so the total number of possible c here is
![]() $O( \frac {1}{\sqrt {aqX}} aqH + 1 )$
. For a fixed such c, we then have from equation (8.9) that
$O( \frac {1}{\sqrt {aqX}} aqH + 1 )$
. For a fixed such c, we then have from equation (8.9) that
But once one fixes
![]() $c = qn+am$
, the residue class of
$c = qn+am$
, the residue class of
![]() $qn-am$
modulo q and modulo a are both fixed, thus by the Chinese remainder theorem
$qn-am$
modulo q and modulo a are both fixed, thus by the Chinese remainder theorem
![]() $qn-am$
is restricted to a single residue class modulo
$qn-am$
is restricted to a single residue class modulo
![]() $aq$
. Thus, the number of possible values of
$aq$
. Thus, the number of possible values of
![]() $qn-am$
is
$qn-am$
is
![]() $O( \frac {\sqrt {aqH}}{aq} + 1 )$
. The net contribution of this case to equation (8.8) is then
$O( \frac {\sqrt {aqH}}{aq} + 1 )$
. The net contribution of this case to equation (8.8) is then
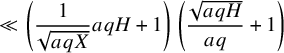 $$ \begin{align*}\ll \left(\frac{1}{\sqrt{aqX}} aqH + 1\right) \left(\frac{\sqrt{aqH}}{aq} + 1\right)\end{align*} $$
$$ \begin{align*}\ll \left(\frac{1}{\sqrt{aqX}} aqH + 1\right) \left(\frac{\sqrt{aqH}}{aq} + 1\right)\end{align*} $$
which expands out to
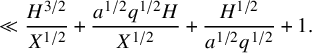 $$ \begin{align*}\ll \frac{H^{3/2}}{X^{1/2}} + \frac{a^{1/2} q^{1/2} H}{X^{1/2}} + \frac{H^{1/2}}{a^{1/2} q^{1/2}} + 1.\end{align*} $$
$$ \begin{align*}\ll \frac{H^{3/2}}{X^{1/2}} + \frac{a^{1/2} q^{1/2} H}{X^{1/2}} + \frac{H^{1/2}}{a^{1/2} q^{1/2}} + 1.\end{align*} $$
Using equation (8.6), this becomes
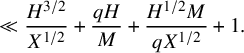 $$ \begin{align*}\ll \frac{H^{3/2}}{X^{1/2}} + \frac{q H}{M} + \frac{H^{1/2} M}{q X^{1/2}} + 1.\end{align*} $$
$$ \begin{align*}\ll \frac{H^{3/2}}{X^{1/2}} + \frac{q H}{M} + \frac{H^{1/2} M}{q X^{1/2}} + 1.\end{align*} $$
Thus, we need to show that
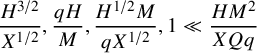 $$ \begin{align*}\frac{H^{3/2}}{X^{1/2}}, \frac{q H}{M}, \frac{H^{1/2} M}{q X^{1/2}}, 1 \ll \frac{HM^2}{XQq}\end{align*} $$
$$ \begin{align*}\frac{H^{3/2}}{X^{1/2}}, \frac{q H}{M}, \frac{H^{1/2} M}{q X^{1/2}}, 1 \ll \frac{HM^2}{XQq}\end{align*} $$
which on using
![]() $1 \leq q \leq Q$
rearranges to
$1 \leq q \leq Q$
rearranges to
and the claim now follows from equation (8.4).
Now, we consider the contribution of the opposite case, in which
![]() $|c - \sqrt {4aqX}|$
exceeds a large multiple of
$|c - \sqrt {4aqX}|$
exceeds a large multiple of
![]() $\frac {1}{\sqrt {aqX}} aqH + 1$
. Then
$\frac {1}{\sqrt {aqX}} aqH + 1$
. Then
![]() $|c^2-4aqX|$
exceeds a large multiple of
$|c^2-4aqX|$
exceeds a large multiple of
![]() $aqH$
, so from equation (8.9) we have
$aqH$
, so from equation (8.9) we have
and thus if we restrict to a dyadic range
![]() $qn-am \in \pm [A,2A]$
for some
$qn-am \in \pm [A,2A]$
for some
![]() $1 \leq A \ll \frac {M}{Q}$
that is a power of two (the upper bound coming from equation (8.10)) we have
$1 \leq A \ll \frac {M}{Q}$
that is a power of two (the upper bound coming from equation (8.10)) we have
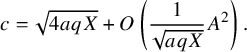 $$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{1}{\sqrt{aqX}} A^2 \right).\end{align*} $$
$$ \begin{align*}c = \sqrt{4aqX} + O\left( \frac{1}{\sqrt{aqX}} A^2 \right).\end{align*} $$
Thus, for a fixed A, the total number of possible c here is
![]() $O( \frac {1}{\sqrt {aqX}} A^2 )$
(note that we have already excluded those c that lie within
$O( \frac {1}{\sqrt {aqX}} A^2 )$
(note that we have already excluded those c that lie within
![]() $O(1)$
of
$O(1)$
of
![]() $\sqrt {4aqX}$
). On the other hand, once c is fixed, we see from equation (8.9) that
$\sqrt {4aqX}$
). On the other hand, once c is fixed, we see from equation (8.9) that
![]() $(qn-am)^2$
is constrained to an interval of length
$(qn-am)^2$
is constrained to an interval of length
![]() $O(aqH)$
. The quantity
$O(aqH)$
. The quantity
![]() $qn-am$
is also constrained to lie in
$qn-am$
is also constrained to lie in
![]() $\pm [A,2A]$
and to a single residue class modulo
$\pm [A,2A]$
and to a single residue class modulo
![]() $aq$
, so the squares
$aq$
, so the squares
![]() $(qn-am)^2$
are separated by
$(qn-am)^2$
are separated by
![]() $\gg Aaq$
when
$\gg Aaq$
when
![]() $qn-am$
is positive, and similarly when
$qn-am$
is positive, and similarly when
![]() $qn-am$
is negative. Thus, the total number of possible values of
$qn-am$
is negative. Thus, the total number of possible values of
![]() $qn-am$
available is
$qn-am$
available is
![]() $O( \frac {aqH}{Aaq} + 1 ) = O( \frac {H}{A} )$
since from equation (8.2) one has
$O( \frac {aqH}{Aaq} + 1 ) = O( \frac {H}{A} )$
since from equation (8.2) one has
![]() $\frac {H}{A} \gg \frac {H}{M/Q} \geq 1$
. Thus, the total contribution of this case to equation (8.8) is
$\frac {H}{A} \gg \frac {H}{M/Q} \geq 1$
. Thus, the total contribution of this case to equation (8.8) is
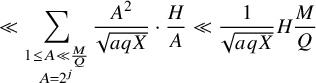 $$ \begin{align*}\ll \sum_{\substack{1 \leq A \ll \frac{M}{Q} \\ A = 2^j}} \frac{A^2}{\sqrt{aqX}} \cdot \frac{H}{A} \ll \frac{1}{\sqrt{aqX}} H \frac{M}{Q}\end{align*} $$
$$ \begin{align*}\ll \sum_{\substack{1 \leq A \ll \frac{M}{Q} \\ A = 2^j}} \frac{A^2}{\sqrt{aqX}} \cdot \frac{H}{A} \ll \frac{1}{\sqrt{aqX}} H \frac{M}{Q}\end{align*} $$
which after applying equation (8.6) gives
![]() $O( \frac {HM^2}{XQq} )$
as required.
$O( \frac {HM^2}{XQq} )$
as required.
Combining this with the pigeonhole principle we obtain the following.
Corollary 8.2 (Pigeonholing on a hyperbola neighborhood).
Let
![]() $X, H, M, Q \geq 1$
be such that
$X, H, M, Q \geq 1$
be such that
and let J be a subinterval of
![]() $[M,2M]$
.
$[M,2M]$
.
Let
![]() $P_0$
be an arithmetic progression in
$P_0$
be an arithmetic progression in
![]() $(X,X+H]$
, and let
$(X,X+H]$
, and let
![]() $\beta _1, \beta _2 \colon \mathbb {N} \to \mathbb {C}$
be functions obeying the bounds
$\beta _1, \beta _2 \colon \mathbb {N} \to \mathbb {C}$
be functions obeying the bounds
for some
![]() $1 \leq q_0 \leq 1/\delta $
and someFootnote
13
$1 \leq q_0 \leq 1/\delta $
and someFootnote
13
![]() $0 < \delta < 1/(\log X)$
. Let
$0 < \delta < 1/(\log X)$
. Let
![]() $f: \mathbb {Z}^2 \to \mathbb {C}$
be a
$f: \mathbb {Z}^2 \to \mathbb {C}$
be a
![]() $1$
-bounded function such that
$1$
-bounded function such that
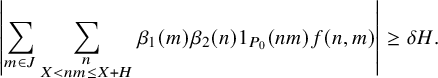 $$ \begin{align} \left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} \beta_1(m) \beta_2(n) 1_{P_0}(nm) f(n,m)\right| \geq \delta H. \end{align} $$
$$ \begin{align} \left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} \beta_1(m) \beta_2(n) 1_{P_0}(nm) f(n,m)\right| \geq \delta H. \end{align} $$
Then for
![]() $\gg \delta ^{O(1)} \frac {XQ^2}{M^2}$
pairs of coprime integers
$\gg \delta ^{O(1)} \frac {XQ^2}{M^2}$
pairs of coprime integers
![]() $q,a$
with
$q,a$
with
![]() $\delta ^{O(1)} Q \ll q \leq Q$
and
$\delta ^{O(1)} Q \ll q \leq Q$
and
![]() $a \asymp \frac {X}{M^2} q$
, one can find an arithmetic progression P in equation (8.1) of spacing
$a \asymp \frac {X}{M^2} q$
, one can find an arithmetic progression P in equation (8.1) of spacing
![]() $(q,-a)$
and length at most
$(q,-a)$
and length at most
![]() $\frac {HQ}{M}$
such that
$\frac {HQ}{M}$
such that
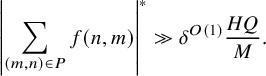 $$ \begin{align*}{\left|\sum_{(m,n) \in P} f(n,m)\right|}^* \gg \delta^{O(1)} \frac{HQ}{M}.\end{align*} $$
$$ \begin{align*}{\left|\sum_{(m,n) \in P} f(n,m)\right|}^* \gg \delta^{O(1)} \frac{HQ}{M}.\end{align*} $$
Here, we extend the maximal sum notation (1.4) to sums over arithmetic progressions in
![]() $\mathbb {Z}^2$
in the obvious fashion.
$\mathbb {Z}^2$
in the obvious fashion.
Proof. Let
![]() $q_0'$
be the spacing of
$q_0'$
be the spacing of
![]() $P_0$
. We first claim that
$P_0$
. We first claim that
![]() $q_0'\ll \delta ^{-10}$
. Indeed, by Shiu’s bound (Lemma 2.17) we have
$q_0'\ll \delta ^{-10}$
. Indeed, by Shiu’s bound (Lemma 2.17) we have
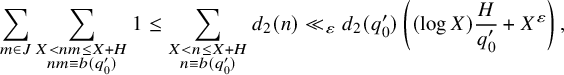 $$ \begin{align*} \sum_{m\in J}\sum_{\substack{X<nm\leq X+H\\nm\equiv b(q_0')}}1 \leq \sum_{\substack{X<n\leq X+H\\n\equiv b(q_0')}}d_2(n) \ll_{\varepsilon} d_2(q_0')\left((\log X)\frac{H}{q_0'} +X^{\varepsilon}\right), \end{align*} $$
$$ \begin{align*} \sum_{m\in J}\sum_{\substack{X<nm\leq X+H\\nm\equiv b(q_0')}}1 \leq \sum_{\substack{X<n\leq X+H\\n\equiv b(q_0')}}d_2(n) \ll_{\varepsilon} d_2(q_0')\left((\log X)\frac{H}{q_0'} +X^{\varepsilon}\right), \end{align*} $$
and if
![]() $q_0'\gg \delta ^{-10}$
then this together with the triangle inequality contradicts our assumption (8.11). Now, we may assume that
$q_0'\gg \delta ^{-10}$
then this together with the triangle inequality contradicts our assumption (8.11). Now, we may assume that
![]() $q_0'\ll \delta ^{-10}$
.
$q_0'\ll \delta ^{-10}$
.
By Lemma 2.2(iii), the left-hand side of equation (8.11) is bounded by
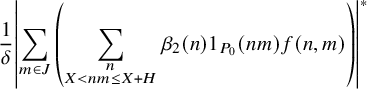 $$ \begin{align*}\frac{1}{\delta} {\left|\sum_{m \in J} \left(\sum_{\substack{n \\ X < nm \leq X+H}} \beta_2(n) 1_{P_0}(nm) f(n,m)\right)\right|}^*\end{align*} $$
$$ \begin{align*}\frac{1}{\delta} {\left|\sum_{m \in J} \left(\sum_{\substack{n \\ X < nm \leq X+H}} \beta_2(n) 1_{P_0}(nm) f(n,m)\right)\right|}^*\end{align*} $$
which by definition is equal to
 $$ \begin{align*}\frac{1}{\delta} \left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} 1_{P_1}(m) \beta_2(n) 1_{P_0}(nm) f(n,m)\right|\end{align*} $$
$$ \begin{align*}\frac{1}{\delta} \left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} 1_{P_1}(m) \beta_2(n) 1_{P_0}(nm) f(n,m)\right|\end{align*} $$
for some arithmetic progression
![]() $P_1 \subset J$
. Interchanging the n and m sums and using Lemma 2.2(iii) again, we can bound this in turn by
$P_1 \subset J$
. Interchanging the n and m sums and using Lemma 2.2(iii) again, we can bound this in turn by
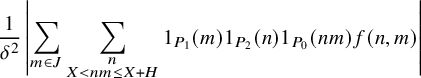 $$ \begin{align*}\frac{1}{\delta^2} \left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n,m)\right|\end{align*} $$
$$ \begin{align*}\frac{1}{\delta^2} \left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n,m)\right|\end{align*} $$
for some arithmetic progression
![]() $P_2$
. From Theorem 8.1 and the triangle inequality, we have
$P_2$
. From Theorem 8.1 and the triangle inequality, we have
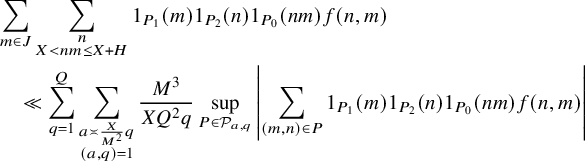 $$ \begin{align*} & \sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n,m) \\ &\quad \ll \sum_{q=1}^Q \sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} \left|\sum_{(m,n) \in P} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n, m)\right| \end{align*} $$
$$ \begin{align*} & \sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n,m) \\ &\quad \ll \sum_{q=1}^Q \sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} \left|\sum_{(m,n) \in P} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n, m)\right| \end{align*} $$
and since the set
![]() $\{ (m,n) \in P: m \in P_1, n \in P_2, nm \in P_0 \}$
is the union of at most
$\{ (m,n) \in P: m \in P_1, n \in P_2, nm \in P_0 \}$
is the union of at most
![]() $O(\delta ^{-O(1)})$
arithmetic progressions in P (recalling that
$O(\delta ^{-O(1)})$
arithmetic progressions in P (recalling that
![]() $q_0'\ll \delta ^{-O(1)}$
), we have
$q_0'\ll \delta ^{-O(1)}$
), we have
 $$ \begin{align*}\left|\sum_{(m,n) \in P} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n, m)\right| \ll \delta^{-O(1)}{\left|\sum_{(m,n) \in P} f(n, m)\right|}^*.\end{align*} $$
$$ \begin{align*}\left|\sum_{(m,n) \in P} 1_{P_1}(m) 1_{P_2}(n) 1_{P_0}(nm) f(n, m)\right| \ll \delta^{-O(1)}{\left|\sum_{(m,n) \in P} f(n, m)\right|}^*.\end{align*} $$
We conclude that
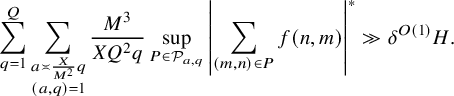 $$ \begin{align} \sum_{q=1}^Q \sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \gg \delta^{O(1)} H. \end{align} $$
$$ \begin{align} \sum_{q=1}^Q \sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \gg \delta^{O(1)} H. \end{align} $$
As f is
![]() $1$
-bounded, we have here
$1$
-bounded, we have here
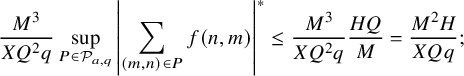 $$ \begin{align} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \leq \frac{M^3}{XQ^2 q} \frac{HQ}{M} = \frac{M^2 H}{XQq}; \end{align} $$
$$ \begin{align} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \leq \frac{M^3}{XQ^2 q} \frac{HQ}{M} = \frac{M^2 H}{XQq}; \end{align} $$
since the number of a associated to a fixed q is
![]() $O(Xq/M^2)$
, we conclude that, for any
$O(Xq/M^2)$
, we conclude that, for any
![]() $q \leq Q$
,
$q \leq Q$
,
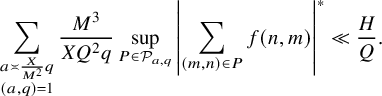 $$ \begin{align*}\sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \ll \frac{H}{Q}.\end{align*} $$
$$ \begin{align*}\sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \ll \frac{H}{Q}.\end{align*} $$
Comparing this with equation (8.12), we conclude that
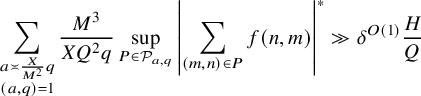 $$ \begin{align} \sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \gg \delta^{O(1)} \frac{H}{Q} \end{align} $$
$$ \begin{align} \sum_{\substack{a \asymp \frac{X}{M^2} q \\ (a,q)=1}} \frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \gg \delta^{O(1)} \frac{H}{Q} \end{align} $$
for
![]() $\gg \delta ^{O(1)} Q$
choices of
$\gg \delta ^{O(1)} Q$
choices of
![]() $1 \leq q \leq Q$
. By dropping small values of q, we may restrict attention to those q with
$1 \leq q \leq Q$
. By dropping small values of q, we may restrict attention to those q with
![]() $\delta ^{O(1)} Q \ll q \ll Q$
. For each such q, we combine equation (8.13) with equation (8.14) to conclude that
$\delta ^{O(1)} Q \ll q \ll Q$
. For each such q, we combine equation (8.13) with equation (8.14) to conclude that
 $$ \begin{align*}\frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \gg \frac{M^2}{Xq} \delta^{O(1)} \frac{H}{Q}\end{align*} $$
$$ \begin{align*}\frac{M^3}{XQ^2q} \sup_{P \in {\mathcal P}_{a,q}} {\left|\sum_{(m,n) \in P} f(n, m)\right|}^* \gg \frac{M^2}{Xq} \delta^{O(1)} \frac{H}{Q}\end{align*} $$
for
![]() $\gg \delta ^{O(1)} \frac {Xq}{M^2} \gg \delta ^{O(1)} \frac {XQ}{M^2}$
choices of a, and the claim follows.
$\gg \delta ^{O(1)} \frac {Xq}{M^2} \gg \delta ^{O(1)} \frac {XQ}{M^2}$
choices of a, and the claim follows.
We can now obtain a preliminary version of Theorem 4.2(iv) (which basically corresponds to the case
![]() $A_{I_2}=1$
, after some dyadic decomposition):
$A_{I_2}=1$
, after some dyadic decomposition):
Proposition 8.3 (Preliminary type
 $I_2$
inverse theorem).
$I_2$
inverse theorem).
Let
![]() $X, H, M \geq 1$
be such that
$X, H, M \geq 1$
be such that
and let J be a subinterval of
![]() $(M,2M]$
. Let
$(M,2M]$
. Let
![]() $0<\delta < 1/(\log X)$
, let
$0<\delta < 1/(\log X)$
, let
![]() $P_0$
be an arithmetic progression in
$P_0$
be an arithmetic progression in
![]() $(X,X+H]$
and let
$(X,X+H]$
and let
![]() $\beta _1, \beta _2 \colon \mathbb {N} \to \mathbb {C}$
be functions obeying the bounds
$\beta _1, \beta _2 \colon \mathbb {N} \to \mathbb {C}$
be functions obeying the bounds
for some
![]() $1 \leq q_0 \leq 1/\delta $
.
$1 \leq q_0 \leq 1/\delta $
.
Let
![]() $G/\Gamma $
be a filtered nilmanifold of degree d, dimension D and complexity at most
$G/\Gamma $
be a filtered nilmanifold of degree d, dimension D and complexity at most
![]() $1/\delta $
for some
$1/\delta $
for some
![]() $d,D \geq 1$
, and let
$d,D \geq 1$
, and let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be a Lipschitz function of norm
$F \colon G/\Gamma \to \mathbb {C}$
be a Lipschitz function of norm
![]() $1/\delta $
and mean zero, and
$1/\delta $
and mean zero, and
![]() $g \colon \mathbb {Z} \to G$
a polynomial map. Suppose that
$g \colon \mathbb {Z} \to G$
a polynomial map. Suppose that
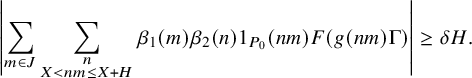 $$ \begin{align*}\left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} \beta_1(m) \beta_2(n) 1_{P_0}(nm) F(g(nm)\Gamma)\right| \geq \delta H.\end{align*} $$
$$ \begin{align*}\left|\sum_{m \in J} \sum_{\substack{n \\ X < nm \leq X+H}} \beta_1(m) \beta_2(n) 1_{P_0}(nm) F(g(nm)\Gamma)\right| \geq \delta H.\end{align*} $$
Then either
or else there exists nontrivial horizontal character
![]() $\eta \colon G \to \mathbb {R}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}$
of Lipschitz norm
![]() $O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
$O_{d,D}(\delta ^{-O_{d,D}(1)})$
such that
Proof. We allow all implied constants to depend on
![]() $d,D$
. We apply Corollary 8.2 with
$d,D$
. We apply Corollary 8.2 with
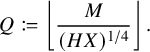
This gives that for
![]() $\gg \delta ^{O(1)} XQ^2/M^2$
pairs
$\gg \delta ^{O(1)} XQ^2/M^2$
pairs
![]() $a,q$
with
$a,q$
with
![]() $q = O(Q)$
and
$q = O(Q)$
and
![]() $a = O( XQ/M^2)$
, we have
$a = O( XQ/M^2)$
, we have
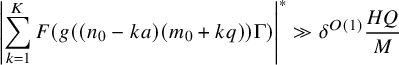 $$ \begin{align*}{\left|\sum_{k=1}^K F( g( (n_0-ka)(m_0+kq) )\Gamma)\right|}^* \gg \delta^{O(1)} \frac{HQ}{M}\end{align*} $$
$$ \begin{align*}{\left|\sum_{k=1}^K F( g( (n_0-ka)(m_0+kq) )\Gamma)\right|}^* \gg \delta^{O(1)} \frac{HQ}{M}\end{align*} $$
for some integers
![]() $n_0,m_0$
and some
$n_0,m_0$
and some
![]() $1 \leq K \leq \frac {HQ}{M}$
.
$1 \leq K \leq \frac {HQ}{M}$
.
Applying the quantitative Leibman equidistribution theorem (Theorem 2.7), we can find a nontrivial horizontal character
![]() $\eta : G \to \mathbb {R}$
of Lipschitz norm
$\eta : G \to \mathbb {R}$
of Lipschitz norm
![]() $O(\delta ^{-O(1)})$
such that
$O(\delta ^{-O(1)})$
such that
By pigeonholing, we can make
![]() $\eta $
independent of
$\eta $
independent of
![]() $a,q$
so that equation (8.16) holds for
$a,q$
so that equation (8.16) holds for
![]() $\gg \delta ^{O(1)} XQ^2/M^2$
pairs
$\gg \delta ^{O(1)} XQ^2/M^2$
pairs
![]() $a,q$
with
$a,q$
with
![]() $q = O(Q)$
and
$q = O(Q)$
and
![]() $a = O( XQ/M^2)$
. Fix this choice of
$a = O( XQ/M^2)$
. Fix this choice of
![]() $\eta $
. The map
$\eta $
. The map
![]() $P = \eta \circ g: \mathbb {Z} \to \mathbb {R}$
is a polynomial of degree at most d; say
$P = \eta \circ g: \mathbb {Z} \to \mathbb {R}$
is a polynomial of degree at most d; say
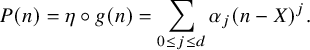 $$ \begin{align*}P(n) = \eta\circ g(n)=\sum_{0\leq j\leq d}\alpha_j(n-X)^j.\end{align*} $$
$$ \begin{align*}P(n) = \eta\circ g(n)=\sum_{0\leq j\leq d}\alpha_j(n-X)^j.\end{align*} $$
Now, suppose that equation (8.15) fails. We will show that
for some
![]() $1 \leq q_0 \ll \delta ^{-O(1)}$
and all
$1 \leq q_0 \ll \delta ^{-O(1)}$
and all
![]() $1 \leq j \leq d$
.
$1 \leq j \leq d$
.
We use downward induction on j. Extracting out the top degree coefficient
![]() $\alpha _d$
of P, we see that
$\alpha _d$
of P, we see that
We apply the polynomial Vinogradov lemma (Lemma 2.3) twice. Since
![]() $HQ/M \ll \delta ^{-O(1)}$
implies equation (8.15), we must have
$HQ/M \ll \delta ^{-O(1)}$
implies equation (8.15), we must have
for some
![]() $1 \leq q_0 \ll \delta ^{-O(1)}$
by choice of Q. This proves equation (8.17) for
$1 \leq q_0 \ll \delta ^{-O(1)}$
by choice of Q. This proves equation (8.17) for
![]() $j=d$
.
$j=d$
.
For the induction step, let
![]() $1 \leq j_0 < d$
, and assume that equation (8.17) has already been proved for
$1 \leq j_0 < d$
, and assume that equation (8.17) has already been proved for
![]() $j \in \{j_0+1, \cdots ,d\}$
. Then the polynomials
$j \in \{j_0+1, \cdots ,d\}$
. Then the polynomials
![]() $n \mapsto q_0\alpha _j(n-X)^j$
has
$n \mapsto q_0\alpha _j(n-X)^j$
has
![]() $C^{\infty }((X,X+H])$
-norm
$C^{\infty }((X,X+H])$
-norm
![]() $\ll \delta ^{-O(1)}$
for
$\ll \delta ^{-O(1)}$
for
![]() $j \in \{j_0+1,\cdots ,d\}$
, and thus the polynomial Q defined by
$j \in \{j_0+1,\cdots ,d\}$
, and thus the polynomial Q defined by
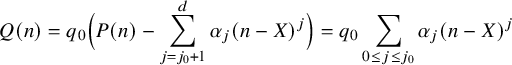 $$ \begin{align*}Q(n) = q_0\Big(P(n) - \sum_{j=j_0+1}^d \alpha_j(n-X)^j\Big) = q_0\sum_{0\leq j\leq j_0}\alpha_j(n-X)^j\end{align*} $$
$$ \begin{align*}Q(n) = q_0\Big(P(n) - \sum_{j=j_0+1}^d \alpha_j(n-X)^j\Big) = q_0\sum_{0\leq j\leq j_0}\alpha_j(n-X)^j\end{align*} $$
also satisfies the bound (8.16). By repeating the analysis above with inspecting the top degree coefficient
![]() $q_0\alpha _{j_0}$
of Q and applying twice the polynomial Vinogradov lemma, we deduce that
$q_0\alpha _{j_0}$
of Q and applying twice the polynomial Vinogradov lemma, we deduce that
for some
![]() $1 \leq q_1 \ll \delta ^{-O(1)}$
. This completes the induction step after replacing
$1 \leq q_1 \ll \delta ^{-O(1)}$
. This completes the induction step after replacing
![]() $q_0$
by
$q_0$
by
![]() $q_0q_1$
.
$q_0q_1$
.
Now that we have equation (8.17), it follows that
![]() $q_0P$
has
$q_0P$
has
![]() $C^{\infty }((X,X+H])$
-norm
$C^{\infty }((X,X+H])$
-norm
![]() $\ll \delta ^{-O(1)}$
, and the claim follows after replacing
$\ll \delta ^{-O(1)}$
, and the claim follows after replacing
![]() $\eta $
by
$\eta $
by
![]() $q_0\eta $
.
$q_0\eta $
.
Now, we are ready to establish Theorem 4.2(iv) in full generality, using an argument similar to that employed in Section 5. Let
![]() $d, D, H, X, \delta , G/\Gamma , F, f, A_{I_2}$
be as in Theorem 4.2(iv). Henceforth, we allow implied constants to depend on
$d, D, H, X, \delta , G/\Gamma , F, f, A_{I_2}$
be as in Theorem 4.2(iv). Henceforth, we allow implied constants to depend on
![]() $d,D$
. By Definition 4.1, we can write
$d,D$
. By Definition 4.1, we can write
![]() $f = \alpha * \beta _1 * \beta _2$
, where
$f = \alpha * \beta _1 * \beta _2$
, where
![]() $\alpha $
is supported on
$\alpha $
is supported on
![]() $[1,A_{I_2}]$
and obeys equation (4.1) for all A, and
$[1,A_{I_2}]$
and obeys equation (4.1) for all A, and
![]() $\beta _1,\beta _2$
obey equation (4.2). From equation (4.4), we have
$\beta _1,\beta _2$
obey equation (4.2). From equation (4.4), we have
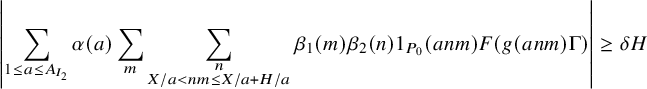 $$ \begin{align*}\left|\sum_{1 \leq a \leq A_{I_2}} \alpha(a) \sum_{m} \sum_{\substack{n \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right| \geq \delta H\end{align*} $$
$$ \begin{align*}\left|\sum_{1 \leq a \leq A_{I_2}} \alpha(a) \sum_{m} \sum_{\substack{n \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right| \geq \delta H\end{align*} $$
for some arithmetic progression
![]() $P_0 \subset (X,X+H]$
. Applying a dyadic decomposition in the
$P_0 \subset (X,X+H]$
. Applying a dyadic decomposition in the
![]() $a,m,n$
variables, we may assume that
$a,m,n$
variables, we may assume that
![]() $\alpha , \beta _1, \beta _2$
are supported in
$\alpha , \beta _1, \beta _2$
are supported in
![]() $(A,2A]$
,
$(A,2A]$
,
![]() $(M,2M]$
,
$(M,2M]$
,
![]() $(N,2N]$
for some
$(N,2N]$
for some
![]() $1 \leq A \leq A_{I_2}$
and
$1 \leq A \leq A_{I_2}$
and
![]() $M,N \geq 1/2$
, at the cost of worsening the above bound to
$M,N \geq 1/2$
, at the cost of worsening the above bound to
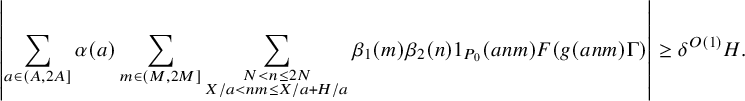 $$ \begin{align} \left|\sum_{a \in (A,2A]} \alpha(a) \sum_{m \in (M,2M]} \sum_{\substack{N < n \leq 2N \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right| \geq \delta^{O(1)} H. \end{align} $$
$$ \begin{align} \left|\sum_{a \in (A,2A]} \alpha(a) \sum_{m \in (M,2M]} \sum_{\substack{N < n \leq 2N \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right| \geq \delta^{O(1)} H. \end{align} $$
(Here, we use the hypothesis
![]() $\delta \leq \frac {1}{\log X}$
.) By symmetry, we may assume that
$\delta \leq \frac {1}{\log X}$
.) By symmetry, we may assume that
![]() $M \leq N$
. We may also assume that
$M \leq N$
. We may also assume that
![]() $AMN \asymp X$
since the sum is empty otherwise; this implies in particular that
$AMN \asymp X$
since the sum is empty otherwise; this implies in particular that
![]() $M \ll (X/A)^{1/2}$
. We may also assume that
$M \ll (X/A)^{1/2}$
. We may also assume that
for some large constant C (depending only on
![]() $d,D$
) since otherwise we have equation (4.6) after some algebra. By equation (8.18), Cauchy–Schwarz and the bound (4.1), we obtain
$d,D$
) since otherwise we have equation (4.6) after some algebra. By equation (8.18), Cauchy–Schwarz and the bound (4.1), we obtain
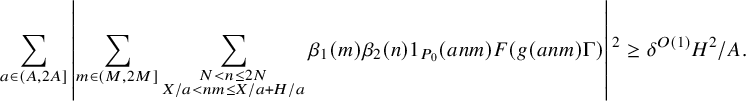 $$ \begin{align} \sum_{a \in (A,2A]} \left|\sum_{m \in (M,2M]} \sum_{\substack{N < n \leq 2N \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right|{}^2 \geq \delta^{O(1)} H^2/A. \end{align} $$
$$ \begin{align} \sum_{a \in (A,2A]} \left|\sum_{m \in (M,2M]} \sum_{\substack{N < n \leq 2N \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right|{}^2 \geq \delta^{O(1)} H^2/A. \end{align} $$
For each
![]() $a \in (A,2A]$
, we see from the triangle inequality and equation (4.2) that
$a \in (A,2A]$
, we see from the triangle inequality and equation (4.2) that
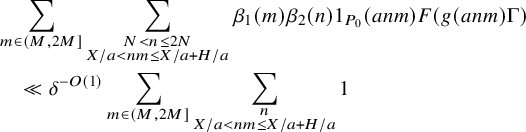 $$ \begin{align*} &\sum_{m \in (M,2M]} \sum_{\substack{N < n \leq 2N \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\\ &\quad \ll \delta^{-O(1)} \sum_{m \in (M,2M]} \sum_{\substack{n \\ X/a < nm \leq X/a+H/a}} 1 \end{align*} $$
$$ \begin{align*} &\sum_{m \in (M,2M]} \sum_{\substack{N < n \leq 2N \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\\ &\quad \ll \delta^{-O(1)} \sum_{m \in (M,2M]} \sum_{\substack{n \\ X/a < nm \leq X/a+H/a}} 1 \end{align*} $$
and hence by the bound (8.3)
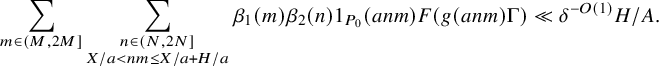 $$ \begin{align*}\sum_{m \in (M,2M]} \sum_{\substack{n \in (N,2N] \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma) \ll \delta^{-O(1)} H/A.\end{align*} $$
$$ \begin{align*}\sum_{m \in (M,2M]} \sum_{\substack{n \in (N,2N] \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma) \ll \delta^{-O(1)} H/A.\end{align*} $$
Combining this with equation (8.20) implies that
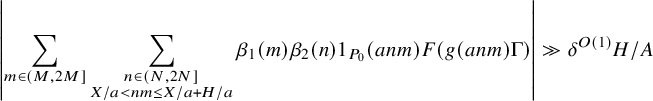 $$ \begin{align*}\left|\sum_{m \in (M,2M]} \sum_{\substack{n \in (N,2N] \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right| \gg \delta^{O(1)} H/A\end{align*} $$
$$ \begin{align*}\left|\sum_{m \in (M,2M]} \sum_{\substack{n \in (N,2N] \\ X/a < nm \leq X/a+H/a}} \beta_1(m) \beta_2(n) 1_{P_0}(anm) F(g(anm)\Gamma)\right| \gg \delta^{O(1)} H/A\end{align*} $$
for
![]() $\gg \delta ^{O(1)} A$
values of
$\gg \delta ^{O(1)} A$
values of
![]() $a \in (A,2A]$
. Applying Proposition 8.3 (and equation (8.19)), we conclude that for each such a there exists a nontrivial horizontal character
$a \in (A,2A]$
. Applying Proposition 8.3 (and equation (8.19)), we conclude that for each such a there exists a nontrivial horizontal character
![]() $\eta \colon G \to \mathbb {R}$
of Lipschitz norm
$\eta \colon G \to \mathbb {R}$
of Lipschitz norm
![]() $O(\delta ^{-O(1)})$
such that
$O(\delta ^{-O(1)})$
such that
This
![]() $\eta $
currently is permitted to vary in a, but there are only
$\eta $
currently is permitted to vary in a, but there are only
![]() $O(\delta ^{-O(1)})$
choices for
$O(\delta ^{-O(1)})$
choices for
![]() $\eta $
, so by the pigeonhole principle we may assume without loss of generality that
$\eta $
, so by the pigeonhole principle we may assume without loss of generality that
![]() $\eta $
is independent of a. Applying Corollary 2.4 (and equation (8.19)), we conclude that there exists
$\eta $
is independent of a. Applying Corollary 2.4 (and equation (8.19)), we conclude that there exists
![]() $1 \leq q \ll \delta ^{-O(1)}$
such that
$1 \leq q \ll \delta ^{-O(1)}$
such that
and the claim follows.
At this point, we have proved all cases of Theorem 4.2 which are necessary for our main Theorem (Theorem 1.1).
9 Controlling the Gowers uniformity norms
In order to deduce our Gowers uniformity result in short intervals (Theorem 1.5) from Theorem 1.1, we wish to apply the inverse theorem for the Gowers norms to
![]() $\Lambda -\Lambda ^{\sharp }$
,
$\Lambda -\Lambda ^{\sharp }$
,
![]() $d_k-d_{k}^{\sharp }$
,
$d_k-d_{k}^{\sharp }$
,
![]() $\mu $
. However, before we can apply the inverse theorem, we need to show that the functions
$\mu $
. However, before we can apply the inverse theorem, we need to show that the functions
![]() $\Lambda -\Lambda ^{\sharp }$
,
$\Lambda -\Lambda ^{\sharp }$
,
![]() $d_k-d_{k}^{\sharp }$
possess pseudorandom majorants even when localized to short intervals. In the case of long intervals, the existence of pseudorandom majorants for these functions follows from existing works [Reference Green and Tao17], [Reference Matthiesen52], and the main purpose of this section is to show that these long interval majorants also work over short intervals
$d_k-d_{k}^{\sharp }$
possess pseudorandom majorants even when localized to short intervals. In the case of long intervals, the existence of pseudorandom majorants for these functions follows from existing works [Reference Green and Tao17], [Reference Matthiesen52], and the main purpose of this section is to show that these long interval majorants also work over short intervals
![]() $(X,X+X^{\theta }]$
.
$(X,X+X^{\theta }]$
.
We begin by defining what we mean by pseudorandomness localized to a short range.Footnote 14
Definition 9.1 (Pseudorandomness over short intervals).
Let
![]() $x,H\geq 1$
. Let
$x,H\geq 1$
. Let
![]() $D\in \mathbb {N}$
and
$D\in \mathbb {N}$
and
![]() $0<\eta <1$
. We say that a function
$0<\eta <1$
. We say that a function
![]() $\nu :\mathbb {Z}\to \mathbb {R}_{\geq 0}$
is
$\nu :\mathbb {Z}\to \mathbb {R}_{\geq 0}$
is
![]() $(D,\eta )$
-pseudorandom at location x and scale H if the function
$(D,\eta )$
-pseudorandom at location x and scale H if the function
![]() $\nu _x(n):=\nu (x+n)$
satisfies the following. Let
$\nu _x(n):=\nu (x+n)$
satisfies the following. Let
![]() $\psi _1,\ldots , \psi _t$
be affine-linear forms, where each
$\psi _1,\ldots , \psi _t$
be affine-linear forms, where each
![]() $\psi _i:\mathbb {Z}^d\to \mathbb {Z}$
has the form
$\psi _i:\mathbb {Z}^d\to \mathbb {Z}$
has the form
![]() $\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
, with
$\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
, with
![]() $\dot {\psi _i}\in \mathbb {Z}^d$
and
$\dot {\psi _i}\in \mathbb {Z}^d$
and
![]() $\psi _i(0)\in \mathbb {Z}$
satisfying
$\psi _i(0)\in \mathbb {Z}$
satisfying
![]() $d,t\leq D$
,
$d,t\leq D$
,
![]() $|\dot {\psi _i}|\leq D$
and
$|\dot {\psi _i}|\leq D$
and
![]() $|\psi _i(0)|\leq DH$
, and with
$|\psi _i(0)|\leq DH$
, and with
![]() $\dot {\psi _i}$
and
$\dot {\psi _i}$
and
![]() $\dot {\psi _j}$
linearly independent whenever
$\dot {\psi _j}$
linearly independent whenever
![]() $i\neq j$
. Then, for any convex body
$i\neq j$
. Then, for any convex body
![]() $K\subset [-H,H]^d$
,
$K\subset [-H,H]^d$
,
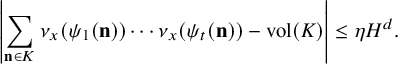 $$ \begin{align*} \left|\sum_{\mathbf{n}\in K}\nu_x(\psi_1(\mathbf{n}))\cdots \nu_x(\psi_t(\mathbf{n}))-\text{vol}(K)\right|\leq \eta H^d. \end{align*} $$
$$ \begin{align*} \left|\sum_{\mathbf{n}\in K}\nu_x(\psi_1(\mathbf{n}))\cdots \nu_x(\psi_t(\mathbf{n}))-\text{vol}(K)\right|\leq \eta H^d. \end{align*} $$
Remark 9.2. We note that the
![]() $(D,\eta )$
-pseudorandomness of
$(D,\eta )$
-pseudorandomness of
![]() $\nu $
at location x and scale H directly implies the short interval Gowers uniformity bound
$\nu $
at location x and scale H directly implies the short interval Gowers uniformity bound
![]() $\|\nu -1\|_{U^D(x,x+H]}\ll _D \eta ^{1/2^D}$
, just by the definition of the Gowers norm as a correlation along linear forms.
$\|\nu -1\|_{U^D(x,x+H]}\ll _D \eta ^{1/2^D}$
, just by the definition of the Gowers norm as a correlation along linear forms.
Our notion of pseudorandomness in the ‘long interval’ case
![]() $x=0$
differs from that of Green–Tao [Reference Green and Tao17, Section 6] in two ways. Firstly, we do not need to impose the correlation condition [Reference Green and Tao17, Definition 6.3] (making use of the later work of Dodos and Kanellopoulos [Reference Dodos and Kanellopoulos8]). Secondly, we work with pseudorandom functions defined on the integers, as opposed to those defined on cyclic groups. The latter is only a minor technical convenience, as then we do not need to extend majorants defined on the integers into a cyclic group. The next lemma shows that the notion of pseudorandomness over the integers is very closely related to pseudorandomness over a cyclic group.
$x=0$
differs from that of Green–Tao [Reference Green and Tao17, Section 6] in two ways. Firstly, we do not need to impose the correlation condition [Reference Green and Tao17, Definition 6.3] (making use of the later work of Dodos and Kanellopoulos [Reference Dodos and Kanellopoulos8]). Secondly, we work with pseudorandom functions defined on the integers, as opposed to those defined on cyclic groups. The latter is only a minor technical convenience, as then we do not need to extend majorants defined on the integers into a cyclic group. The next lemma shows that the notion of pseudorandomness over the integers is very closely related to pseudorandomness over a cyclic group.
Lemma 9.3. Let
![]() $x,H\geq 1$
,
$x,H\geq 1$
,
![]() $D\in \mathbb {N}$
, and
$D\in \mathbb {N}$
, and
![]() $0<\eta <1$
. Suppose that
$0<\eta <1$
. Suppose that
![]() $\nu :\mathbb {Z}\to \mathbb {R}_{\geq 0}$
is
$\nu :\mathbb {Z}\to \mathbb {R}_{\geq 0}$
is
![]() $(D,\eta )$
-pseudorandom at location x and scale H. Then there exists a prime
$(D,\eta )$
-pseudorandom at location x and scale H. Then there exists a prime
![]() $H<H'\ll _D H$
and a function
$H<H'\ll _D H$
and a function
![]() $\widetilde {\nu }:\mathbb {Z}/H'\mathbb {Z}\to \mathbb {R}_{\geq 0}$
such that
$\widetilde {\nu }:\mathbb {Z}/H'\mathbb {Z}\to \mathbb {R}_{\geq 0}$
such that
![]() $\nu (x+n)\leq 2\widetilde {\nu }(n)$
for all
$\nu (x+n)\leq 2\widetilde {\nu }(n)$
for all
![]() $n\in [0,H]$
(where
$n\in [0,H]$
(where
![]() $[0,H]$
is embedded into
$[0,H]$
is embedded into
![]() $\mathbb {Z}/H'\mathbb {Z}$
in the natural way) and such that
$\mathbb {Z}/H'\mathbb {Z}$
in the natural way) and such that
![]() $\widetilde {\nu }$
satisfies the following. Let
$\widetilde {\nu }$
satisfies the following. Let
![]() $\psi _1,\ldots , \psi _t$
be affine-linear forms, where each
$\psi _1,\ldots , \psi _t$
be affine-linear forms, where each
![]() $\psi _i:\mathbb {Z}^d\to \mathbb {Z}$
has the form
$\psi _i:\mathbb {Z}^d\to \mathbb {Z}$
has the form
![]() $\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
, with
$\psi _i(\mathbf {x})=\dot {\psi _i}\cdot \mathbf {x}+\psi _i(0)$
, with
![]() $\dot {\psi _i}\in \mathbb {Z}^d$
and
$\dot {\psi _i}\in \mathbb {Z}^d$
and
![]() $\psi _i(0)\in \mathbb {Z}$
satisfying
$\psi _i(0)\in \mathbb {Z}$
satisfying
![]() $t\leq D$
,
$t\leq D$
,
![]() $|\dot {\psi _i}|\leq D$
. Then
$|\dot {\psi _i}|\leq D$
. Then
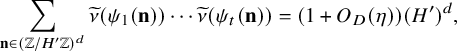 $$ \begin{align} \sum_{\mathbf{n}\in (\mathbb{Z}/H'\mathbb{Z})^d}\widetilde{\nu}(\psi_1(\mathbf{n}))\cdots \widetilde{\nu}(\psi_t(\mathbf{n}))=(1+O_D(\eta))(H')^{d}, \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in (\mathbb{Z}/H'\mathbb{Z})^d}\widetilde{\nu}(\psi_1(\mathbf{n}))\cdots \widetilde{\nu}(\psi_t(\mathbf{n}))=(1+O_D(\eta))(H')^{d}, \end{align} $$
where the affine-linear forms
![]() $\psi _j:(\mathbb {Z}/H'\mathbb {Z})^d\to \mathbb {Z}/H'\mathbb {Z}$
are induced from their global counterparts in the obvious way.
$\psi _j:(\mathbb {Z}/H'\mathbb {Z})^d\to \mathbb {Z}/H'\mathbb {Z}$
are induced from their global counterparts in the obvious way.
Proof. Let
![]() $H'\in [C_DH,2C_DH]$
be a prime for large enough
$H'\in [C_DH,2C_DH]$
be a prime for large enough
![]() $C_D\geq 1$
. Take
$C_D\geq 1$
. Take
![]() $\widetilde {\nu }(n)=(\frac {1}{2}+\frac {1}{2}\nu (x+n))1_{n\in [0,H]}+1_{(H,H')}(n)$
, extended to an
$\widetilde {\nu }(n)=(\frac {1}{2}+\frac {1}{2}\nu (x+n))1_{n\in [0,H]}+1_{(H,H')}(n)$
, extended to an
![]() $H'$
-periodic function. Then the claim (9.1) follows from the
$H'$
-periodic function. Then the claim (9.1) follows from the
![]() $(D,\eta )$
-pseudorandomness of
$(D,\eta )$
-pseudorandomness of
![]() $\nu $
at location x and scale H by splitting
$\nu $
at location x and scale H by splitting
![]() $\widetilde {\nu }$
into its components.
$\widetilde {\nu }$
into its components.
We then state the inverse theorem for unbounded functions that we are going to use.
Proposition 9.4 (An inverse theorem for pseudorandomly bounded functions).
Let
![]() $s\in \mathbb {N}$
and
$s\in \mathbb {N}$
and
![]() $0<\eta <1$
. Let I be an interval of length
$0<\eta <1$
. Let I be an interval of length
![]() $\geq 2$
. Let
$\geq 2$
. Let
![]() $f:I\to \mathbb {C}$
be a function, and suppose that the following hold.
$f:I\to \mathbb {C}$
be a function, and suppose that the following hold.
-
• There exists a function
 $\nu :I\to \mathbb {R}_{\geq 0}$
such that
$\nu :I\to \mathbb {R}_{\geq 0}$
such that
 $\|\nu -1\|_{U^{2s}(I)}\leq \eta $
and
$\|\nu -1\|_{U^{2s}(I)}\leq \eta $
and
 $|f(n)|\leq \nu (n)$
.
$|f(n)|\leq \nu (n)$
. -
• For any filtered
 $(s-1)$
-step nilmanifold
$(s-1)$
-step nilmanifold
 $G/\Gamma $
and any Lipschitz function
$G/\Gamma $
and any Lipschitz function
 $F:G/\Gamma \to \mathbb {C}$
, we have
$F:G/\Gamma \to \mathbb {C}$
, we have  $$ \begin{align*} \sup_{g\in {\operatorname{Poly}}(\mathbb{Z}\to G)}\left|\frac{1}{|I|}\sum_{n\in I}f(n)\overline{F}(g(n)\Gamma)\right|\ll_{\|F\|_{\text{Lip}},G/\Gamma} \eta. \end{align*} $$
$$ \begin{align*} \sup_{g\in {\operatorname{Poly}}(\mathbb{Z}\to G)}\left|\frac{1}{|I|}\sum_{n\in I}f(n)\overline{F}(g(n)\Gamma)\right|\ll_{\|F\|_{\text{Lip}},G/\Gamma} \eta. \end{align*} $$
Then we have the Gowers uniformity estimate
Proof. Let
![]() $I=(X,X+H]$
, where without loss of generality X and H are integers. The desired result follows from the work of Dodos and Kanellopoulos [Reference Dodos and Kanellopoulos8, Theorem 5.1] (which gives the inverse theorem of [Reference Green and Tao17, Proposition 10.1] under weaker hypotheses). Indeed, we can apply [Reference Dodos and Kanellopoulos8, Theorem 5.1] to the function
$I=(X,X+H]$
, where without loss of generality X and H are integers. The desired result follows from the work of Dodos and Kanellopoulos [Reference Dodos and Kanellopoulos8, Theorem 5.1] (which gives the inverse theorem of [Reference Green and Tao17, Proposition 10.1] under weaker hypotheses). Indeed, we can apply [Reference Dodos and Kanellopoulos8, Theorem 5.1] to the function
![]() $n\mapsto f(X+n)$
on
$n\mapsto f(X+n)$
on
![]() $[1,H]$
, noting that the interval Gowers norm estimate
$[1,H]$
, noting that the interval Gowers norm estimate
![]() $\|\nu -1\|_{U^{2s}(I)}=o_{\eta \to 0}(1)$
is equivalent to the cyclic group Gowers norm estimate
$\|\nu -1\|_{U^{2s}(I)}=o_{\eta \to 0}(1)$
is equivalent to the cyclic group Gowers norm estimate
![]() $\|\widetilde {\nu }-1\|_{U^{2s}(\mathbb {Z}/N'\mathbb {Z})}=o_{\eta \to 0}(1)$
for all primes
$\|\widetilde {\nu }-1\|_{U^{2s}(\mathbb {Z}/N'\mathbb {Z})}=o_{\eta \to 0}(1)$
for all primes
![]() $N'\in [100sH,200sH]$
, where
$N'\in [100sH,200sH]$
, where
![]() $\widetilde {\nu }(n)$
is defined as
$\widetilde {\nu }(n)$
is defined as
![]() $\nu (X+n)1_{n\in [1,H]}$
for
$\nu (X+n)1_{n\in [1,H]}$
for
![]() $0\leq n<N'$
and extended periodically to
$0\leq n<N'$
and extended periodically to
![]() $\mathbb {Z}/N'\mathbb {Z}$
.
$\mathbb {Z}/N'\mathbb {Z}$
.
The following lemma tells us that if a function has a pseudorandom majorant over a long interval, and if the majorant is given by a type I sum, then it in fact has a pseudorandom majorant over short intervals as well. This allows us to conveniently reduce the concept of pseudorandom majorants over short intervals to that over long intervals.
Lemma 9.5 (Pseudorandomness over long intervals implies pseudorandomness over short intervals).
Let
![]() $\varepsilon \in (0,1)$
,
$\varepsilon \in (0,1)$
,
![]() $D,k\in \mathbb {N}$
be fixed. Let
$D,k\in \mathbb {N}$
be fixed. Let
![]() $C\geq 1$
be large enough in terms of k and D. Let
$C\geq 1$
be large enough in terms of k and D. Let
![]() $H\in [X^{\varepsilon },X/2]$
and
$H\in [X^{\varepsilon },X/2]$
and
![]() $\eta \in ((\log X)^{-C},1/2)$
, with
$\eta \in ((\log X)^{-C},1/2)$
, with
![]() $X\geq 3$
large enough. Let
$X\geq 3$
large enough. Let
![]() $\nu :\mathbb {Z}\to \mathbb {R}_{\geq 0}$
be
$\nu :\mathbb {Z}\to \mathbb {R}_{\geq 0}$
be
![]() $(D,\eta )$
-pseudorandom at location
$(D,\eta )$
-pseudorandom at location
![]() $0$
and scale H. Also, let
$0$
and scale H. Also, let
![]() $1\leq A,B\leq \log X$
be integers.
$1\leq A,B\leq \log X$
be integers.
Suppose that there is an exceptional set
![]() $\mathscr {S}\subset \mathbb {Z}$
and a sequence
$\mathscr {S}\subset \mathbb {Z}$
and a sequence
![]() $\lambda _n$
such that
$\lambda _n$
such that
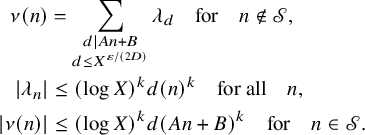 $$ \begin{align} \nu(n)&=\sum_{\substack{d\mid An+B\\d\leq X^{\varepsilon/(2D)}}}\lambda_d \quad \text{for}\quad n\not \in \mathscr{S},\nonumber\\ |\lambda_n|&\leq (\log X)^{k}d(n)^k\quad \text{for all}\quad n,\\ |\nu(n)|&\leq (\log X)^kd(An+B)^k \quad \text{for}\quad n \in \mathscr{S}.\nonumber \end{align} $$
$$ \begin{align} \nu(n)&=\sum_{\substack{d\mid An+B\\d\leq X^{\varepsilon/(2D)}}}\lambda_d \quad \text{for}\quad n\not \in \mathscr{S},\nonumber\\ |\lambda_n|&\leq (\log X)^{k}d(n)^k\quad \text{for all}\quad n,\\ |\nu(n)|&\leq (\log X)^kd(An+B)^k \quad \text{for}\quad n \in \mathscr{S}.\nonumber \end{align} $$
Also, suppose that
![]() $\mathscr {S}$
is small in the sense that
$\mathscr {S}$
is small in the sense that
Then
![]() $\nu $
is
$\nu $
is
![]() $(D,2\eta )$
-pseudorandom at location X and scale H.
$(D,2\eta )$
-pseudorandom at location X and scale H.
Proof. By equation (9.2), we can write
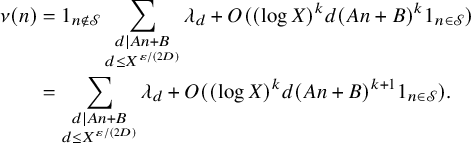 $$ \begin{align*} \nu(n)&=1_{n\not \in \mathscr{S}} \sum_{\substack{d\mid An+B\\d\leq X^{\varepsilon/(2D)}}}\lambda_d+O((\log X)^kd(An+B)^{k}1_{n\in \mathscr{S}})\\ &=\sum_{\substack{d\mid An+B\\d\leq X^{\varepsilon/(2D)}}}\lambda_d+O((\log X)^kd(An+B)^{k+1}1_{n\in \mathscr{S}}). \end{align*} $$
$$ \begin{align*} \nu(n)&=1_{n\not \in \mathscr{S}} \sum_{\substack{d\mid An+B\\d\leq X^{\varepsilon/(2D)}}}\lambda_d+O((\log X)^kd(An+B)^{k}1_{n\in \mathscr{S}})\\ &=\sum_{\substack{d\mid An+B\\d\leq X^{\varepsilon/(2D)}}}\lambda_d+O((\log X)^kd(An+B)^{k+1}1_{n\in \mathscr{S}}). \end{align*} $$
Hence, for any convex body
![]() $K\subset [-H,H]^d$
and for
$K\subset [-H,H]^d$
and for
![]() $x\in \{0,X\}$
, we can split the sum
$x\in \{0,X\}$
, we can split the sum
 $$ \begin{align*} \sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_x(\psi_i(\mathbf{n})) \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_x(\psi_i(\mathbf{n})) \end{align*} $$
(where
![]() $\nu _x(n):=\nu (x+n)$
) as the main term
$\nu _x(n):=\nu (x+n)$
) as the main term
 $$ \begin{align} \sum_{e_1,\ldots, e_{t}\leq X^{\varepsilon/(2D)}}\lambda_{e_1}\cdots \lambda_{e_{t}}\sum_{\mathbf{n}\in K} \prod_{i=1}^{t}1_{e_{i}\mid A(x+\psi_i(\mathbf{n}))+B}, \end{align} $$
$$ \begin{align} \sum_{e_1,\ldots, e_{t}\leq X^{\varepsilon/(2D)}}\lambda_{e_1}\cdots \lambda_{e_{t}}\sum_{\mathbf{n}\in K} \prod_{i=1}^{t}1_{e_{i}\mid A(x+\psi_i(\mathbf{n}))+B}, \end{align} $$
and
![]() $2^{t}-1$
error terms whose contribution is for some
$2^{t}-1$
error terms whose contribution is for some
![]() $j\leq t$
bounded using equation (9.2) by
$j\leq t$
bounded using equation (9.2) by
 $$ \begin{align} \ll (\log X)^{kt}\sum_{\mathbf{n}\in K}\prod_{i=1}^td(A(x+\psi_i(\mathbf{n}))+B)^{k+1}1_{x+\psi_j(\mathbf{n}) \in \mathscr{S}}. \end{align} $$
$$ \begin{align} \ll (\log X)^{kt}\sum_{\mathbf{n}\in K}\prod_{i=1}^td(A(x+\psi_i(\mathbf{n}))+B)^{k+1}1_{x+\psi_j(\mathbf{n}) \in \mathscr{S}}. \end{align} $$
Now, using Cauchy–Schwarz, the inequality
![]() $\prod _{i=1}^tx_i\leq \sum _{i=1}^tx_i^t$
, equation (9.3) and Shiu’s bound (Lemma 2.17), equation (9.5) is
$\prod _{i=1}^tx_i\leq \sum _{i=1}^tx_i^t$
, equation (9.3) and Shiu’s bound (Lemma 2.17), equation (9.5) is
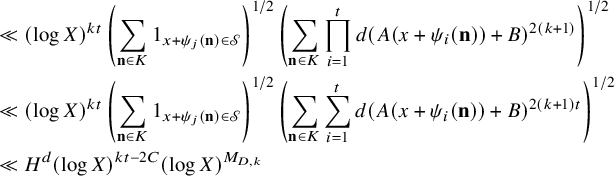 $$ \begin{align*} &\ll (\log X)^{kt}\left(\sum_{\mathbf{n}\in K}1_{x+\psi_j(\mathbf{n}) \in \mathscr{S}}\right)^{1/2}\left(\sum_{\mathbf{n}\in K}\prod_{i=1}^td(A(x+\psi_i(\mathbf{n}))+B)^{2(k+1)}\right)^{1/2}\\ &\ll (\log X)^{kt}\left(\sum_{\mathbf{n}\in K}1_{x+\psi_j(\mathbf{n}) \in \mathscr{S}}\right)^{1/2} \left(\sum_{\mathbf{n}\in K}\sum_{i=1}^t d(A(x+\psi_i(\mathbf{n}))+B)^{2(k+1)t}\right)^{1/2}\\ &\ll H^d(\log X)^{kt-2C}(\log X)^{M_{D,k}} \end{align*} $$
$$ \begin{align*} &\ll (\log X)^{kt}\left(\sum_{\mathbf{n}\in K}1_{x+\psi_j(\mathbf{n}) \in \mathscr{S}}\right)^{1/2}\left(\sum_{\mathbf{n}\in K}\prod_{i=1}^td(A(x+\psi_i(\mathbf{n}))+B)^{2(k+1)}\right)^{1/2}\\ &\ll (\log X)^{kt}\left(\sum_{\mathbf{n}\in K}1_{x+\psi_j(\mathbf{n}) \in \mathscr{S}}\right)^{1/2} \left(\sum_{\mathbf{n}\in K}\sum_{i=1}^t d(A(x+\psi_i(\mathbf{n}))+B)^{2(k+1)t}\right)^{1/2}\\ &\ll H^d(\log X)^{kt-2C}(\log X)^{M_{D,k}} \end{align*} $$
for some constant
![]() $M_{D,k}\geq 1$
. If C is large enough in terms of D and k, this is
$M_{D,k}\geq 1$
. If C is large enough in terms of D and k, this is
![]() $\ll H^d(\log X)^{-3C/2}$
.
$\ll H^d(\log X)^{-3C/2}$
.
We lastly estimate the main term in equation (9.4). A lattice point counting argument as in [Reference Green and Tao17, Appendix A] gives us
 $$ \begin{align*} \sum_{\mathbf{n}\in K} \prod_{i=1}^{t}1_{e_{i}\mid A(x+\psi_i( \mathbf{n}))+B}&=\alpha_{A,B}(e_1,\ldots, e_{t})\text{vol}(K)+O(H^{d-1}) \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{n}\in K} \prod_{i=1}^{t}1_{e_{i}\mid A(x+\psi_i( \mathbf{n}))+B}&=\alpha_{A,B}(e_1,\ldots, e_{t})\text{vol}(K)+O(H^{d-1}) \end{align*} $$
for some
![]() $\alpha _{A,B}(e_1,\ldots , e_{t})\in [0,1]$
independent of x and H (since the left-hand side is counting elements of K in some shifted lattice
$\alpha _{A,B}(e_1,\ldots , e_{t})\in [0,1]$
independent of x and H (since the left-hand side is counting elements of K in some shifted lattice
![]() $\mathbf {q}\mathbb {Z}+\mathbf {a}$
). Combining this with the estimates
$\mathbf {q}\mathbb {Z}+\mathbf {a}$
). Combining this with the estimates
![]() $e_1\cdots e_{t}\leq X^{\varepsilon /2}\leq H^{1/2}$
and
$e_1\cdots e_{t}\leq X^{\varepsilon /2}\leq H^{1/2}$
and
![]() $|\lambda _d|\ll X^{o(1)}$
, we see that
$|\lambda _d|\ll X^{o(1)}$
, we see that
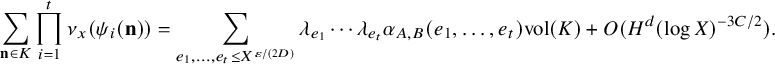 $$ \begin{align} \sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_x(\psi_i(\mathbf{n}))= \sum_{e_1,\ldots, e_{t}\leq X^{\varepsilon/(2D)}}\lambda_{e_1}\cdots \lambda_{e_{t}} \alpha_{A,B}(e_1,\ldots, e_{t})\text{vol}(K)+O(H^d(\log X)^{-3C/2}). \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_x(\psi_i(\mathbf{n}))= \sum_{e_1,\ldots, e_{t}\leq X^{\varepsilon/(2D)}}\lambda_{e_1}\cdots \lambda_{e_{t}} \alpha_{A,B}(e_1,\ldots, e_{t})\text{vol}(K)+O(H^d(\log X)^{-3C/2}). \end{align} $$
Since the main term on the right-hand side of equation (9.6) is independent of
![]() $x\in \{0,X\}$
, we see that
$x\in \{0,X\}$
, we see that
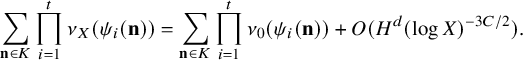 $$ \begin{align*}\sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_X(\psi_i(\mathbf{n}))=\sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_0(\psi_i(\mathbf{n}))+O(H^d(\log X)^{-3C/2}).\end{align*} $$
$$ \begin{align*}\sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_X(\psi_i(\mathbf{n}))=\sum_{\mathbf{n}\in K}\prod_{i=1}^t\nu_0(\psi_i(\mathbf{n}))+O(H^d(\log X)^{-3C/2}).\end{align*} $$
Hence, using the assumption that
![]() $\nu $
is
$\nu $
is
![]() $(D,\eta )$
-pseudorandom at location
$(D,\eta )$
-pseudorandom at location
![]() $0$
and scale H,
$0$
and scale H,
![]() $\nu $
must also be
$\nu $
must also be
![]() $(D,2\eta )$
-pseudorandom at location X and scale H.
$(D,2\eta )$
-pseudorandom at location X and scale H.
Lemma 9.5 leads to the existence pseudorandom majorants over short intervals for W-tricked versions of our functions of interest. Let us recall that, for any
![]() $w\geq 2$
,
$w\geq 2$
,
where
![]() $W=\prod _{p\leq w}p$
. We note for later use that in this notation our model function
$W=\prod _{p\leq w}p$
. We note for later use that in this notation our model function
![]() $\Lambda ^{\sharp }$
equals to
$\Lambda ^{\sharp }$
equals to
![]() $\Lambda _{R}$
, where
$\Lambda _{R}$
, where
![]() $R=\exp ((\log X)^{1/10})$
.
$R=\exp ((\log X)^{1/10})$
.
Lemma 9.6 (Pseudorandom majorants over short intervals for
 $\Lambda -\Lambda _w$
,
$\Lambda -\Lambda _w$
,
 $d_k-d_{k}^{\sharp }$
).
$d_k-d_{k}^{\sharp }$
).
Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $D,k\in \mathbb {N}$
be fixed. Let
$D,k\in \mathbb {N}$
be fixed. Let
![]() $X\geq H\geq X^{\varepsilon }\geq 2$
. Let
$X\geq H\geq X^{\varepsilon }\geq 2$
. Let
![]() $2\leq w\leq w(X)$
, where
$2\leq w\leq w(X)$
, where
![]() $w(X)$
is a slowly growing function of X, and denote
$w(X)$
is a slowly growing function of X, and denote
![]() $W=\prod _{p\leq w}p$
. Also, let
$W=\prod _{p\leq w}p$
. Also, let
![]() $w\leq \widetilde {w}\leq \exp ((\log X)^{1/10})$
.
$w\leq \widetilde {w}\leq \exp ((\log X)^{1/10})$
.
-
1. There exists a constant
 $C_0\geq 1$
such that each of the functions (9.7)for
$C_0\geq 1$
such that each of the functions (9.7)for $$ \begin{align} &\frac{\varphi(W)}{W}\Lambda(Wn+b)/C_0,\quad \frac{\varphi(W)}{W}\Lambda_{\widetilde{w}}(Wn+b) \end{align} $$
$$ \begin{align} &\frac{\varphi(W)}{W}\Lambda(Wn+b)/C_0,\quad \frac{\varphi(W)}{W}\Lambda_{\widetilde{w}}(Wn+b) \end{align} $$
 $1\leq b\leq W$
with
$1\leq b\leq W$
with
 $(b,W)=1$
, is majorized on
$(b,W)=1$
, is majorized on
 $(X, X+H]$
by a
$(X, X+H]$
by a
 $(D,\eta )$
-pseudorandom function at location X and scale H for some
$(D,\eta )$
-pseudorandom function at location X and scale H for some
 $\eta =o_{w\to \infty }(1)$
. In fact, the latter of the two functions is
$\eta =o_{w\to \infty }(1)$
. In fact, the latter of the two functions is
 $(D,\eta )$
-pseudorandom at location X and scale H.
$(D,\eta )$
-pseudorandom at location X and scale H.
-
2. Let
 $W'$
be such that
$W'$
be such that
 $W\mid W'\mid W^{\lfloor w\rfloor }$
. Suppose that
$W\mid W'\mid W^{\lfloor w\rfloor }$
. Suppose that
 $H\geq X^{1/5+\varepsilon }$
. There exists a constant
$H\geq X^{1/5+\varepsilon }$
. There exists a constant
 $C_k\geq 1$
such that each of the functions (9.8)
$C_k\geq 1$
such that each of the functions (9.8) $$ \begin{align} &(\log X)\frac{\varphi(W)}{W}\prod_{w\leq p\leq X}\left(1+\frac{k}{p}\right)^{-1}d_k(W'n+b)/C_k,\nonumber\\ &(\log X)\frac{\varphi(W)}{W}\prod_{w\leq p\leq X}\left(1+\frac{k}{p}\right)^{-1}d_k^{\sharp}(W'n+b)/C_k \end{align} $$
$$ \begin{align} &(\log X)\frac{\varphi(W)}{W}\prod_{w\leq p\leq X}\left(1+\frac{k}{p}\right)^{-1}d_k(W'n+b)/C_k,\nonumber\\ &(\log X)\frac{\varphi(W)}{W}\prod_{w\leq p\leq X}\left(1+\frac{k}{p}\right)^{-1}d_k^{\sharp}(W'n+b)/C_k \end{align} $$
for
![]() $1\leq b\leq W'$
with
$1\leq b\leq W'$
with
![]() $(b,W')=1$
, is majorized on
$(b,W')=1$
, is majorized on
![]() $(X, X+H]$
by a
$(X, X+H]$
by a
![]() $(D,\eta )$
-pseudorandom function at location X and scale H for some
$(D,\eta )$
-pseudorandom function at location X and scale H for some
![]() $\eta =o_{w\to \infty }(1)$
.
$\eta =o_{w\to \infty }(1)$
.
Remark 9.7. Note that if
![]() $\|\nu _1-1\|_{U^{D}(x,x+H]}\leq \eta $
and
$\|\nu _1-1\|_{U^{D}(x,x+H]}\leq \eta $
and
![]() $\|\nu _2-1\|_{U^D(x,x+H]}\leq \eta $
, then by the triangle inequality for the Gowers norms also
$\|\nu _2-1\|_{U^D(x,x+H]}\leq \eta $
, then by the triangle inequality for the Gowers norms also
![]() $\|(\nu _1+\nu _2)/2-1\|_{U^{D}(x,x+H]}\leq \eta $
. Hence, by Remark 9.2, Lemma 9.5 in particular provides us a majorant
$\|(\nu _1+\nu _2)/2-1\|_{U^{D}(x,x+H]}\leq \eta $
. Hence, by Remark 9.2, Lemma 9.5 in particular provides us a majorant
![]() $\nu $
for the difference of the two functions in equation (9.7) or equation (9.8) satisfying
$\nu $
for the difference of the two functions in equation (9.7) or equation (9.8) satisfying
![]() $\|\nu -1\|_{U^D(x,x+H]}=o_{w\to \infty }(1)$
, allowing us to apply the inverse theorem (Proposition 9.4).
$\|\nu -1\|_{U^D(x,x+H]}=o_{w\to \infty }(1)$
, allowing us to apply the inverse theorem (Proposition 9.4).
Proof. (1) Let us first consider the function
![]() $\frac {\varphi (W)}{W}\Lambda (Wn+b)/C_0$
. Let
$\frac {\varphi (W)}{W}\Lambda (Wn+b)/C_0$
. Let
![]() $R'=X^{\gamma }$
with
$R'=X^{\gamma }$
with
![]() $\gamma>0$
small enough in terms of
$\gamma>0$
small enough in terms of
![]() $\varepsilon ,D$
. Let
$\varepsilon ,D$
. Let
![]() $\psi $
be a smooth function supported on
$\psi $
be a smooth function supported on
![]() $[-2,2]$
with
$[-2,2]$
with
![]() $\psi (0)=-1$
and
$\psi (0)=-1$
and
![]() $\int _{0}^{\infty }|\psi '(y)|^2\, dy=1$
. Define
$\int _{0}^{\infty }|\psi '(y)|^2\, dy=1$
. Define
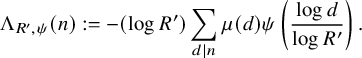 $$ \begin{align*} \Lambda_{R',\psi}(n):=-(\log R')\sum_{d\mid n}\mu(d)\psi\left(\frac{\log d}{\log R'}\right). \end{align*} $$
$$ \begin{align*} \Lambda_{R',\psi}(n):=-(\log R')\sum_{d\mid n}\mu(d)\psi\left(\frac{\log d}{\log R'}\right). \end{align*} $$
Put
where S is the set of perfect powers. Then
for
![]() $X/2\leq n\leq X$
since
$X/2\leq n\leq X$
since
![]() $Wn+b$
being prime implies that
$Wn+b$
being prime implies that
![]() $Wn+b$
has no divisors
$Wn+b$
has no divisors
![]() $1<d\leq X^{2\gamma }$
.
$1<d\leq X^{2\gamma }$
.
From [Reference Green and Tao17, Theorem D.3], we see that
![]() $\nu _b$
is
$\nu _b$
is
![]() $(D,o_{w\to \infty }(1))$
-pseudorandom at location
$(D,o_{w\to \infty }(1))$
-pseudorandom at location
![]() $0$
and scale H (since the term
$0$
and scale H (since the term
![]() $2(\log X)1_{Wn+b\in S}$
has negligible contribution to the correlations that arise in the definition of pseudorandomness). Moreover,
$2(\log X)1_{Wn+b\in S}$
has negligible contribution to the correlations that arise in the definition of pseudorandomness). Moreover,
![]() $\nu _b(n)$
can be expanded out as
$\nu _b(n)$
can be expanded out as
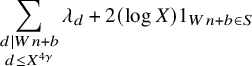 $$ \begin{align*}\sum_{\substack{d\mid Wn+b\\d\leq X^{4\gamma}}}\lambda_d+2(\log X)1_{Wn+b\in S}\end{align*} $$
$$ \begin{align*}\sum_{\substack{d\mid Wn+b\\d\leq X^{4\gamma}}}\lambda_d+2(\log X)1_{Wn+b\in S}\end{align*} $$
for some
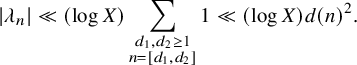 $$ \begin{align*}|\lambda_n|\ll (\log X)\sum_{\substack{d_1,d_2\geq 1\\n=[d_1,d_2]}}1\ll (\log X)d(n)^2.\end{align*} $$
$$ \begin{align*}|\lambda_n|\ll (\log X)\sum_{\substack{d_1,d_2\geq 1\\n=[d_1,d_2]}}1\ll (\log X)d(n)^2.\end{align*} $$
Hence, by Lemma 9.5,
![]() $\nu _b$
is
$\nu _b$
is
![]() $(D,o_{w\to \infty }(1))$
-pseudorandom also at location X and scale H (since the set
$(D,o_{w\to \infty }(1))$
-pseudorandom also at location X and scale H (since the set
![]() $\mathscr {S}:=\{n:Wn+b\in S\}$
certainly obeys equation (9.3)).
$\mathscr {S}:=\{n:Wn+b\in S\}$
certainly obeys equation (9.3)).
For the case of
![]() $\frac {\varphi (W)}{W}\Lambda _{\widetilde {w}}(Wn+b)$
, we can apply [Reference Tao and Teräväinen61, Proposition 5.2] to directly deduce that this function is
$\frac {\varphi (W)}{W}\Lambda _{\widetilde {w}}(Wn+b)$
, we can apply [Reference Tao and Teräväinen61, Proposition 5.2] to directly deduce that this function is
![]() $(D,o_{w\to \infty }(1))$
-pseudorandom at location
$(D,o_{w\to \infty }(1))$
-pseudorandom at location
![]() $0$
and scale X. To prove the
$0$
and scale X. To prove the
![]() $(D,o_{w\to \infty }(1))$
-pseudorandomness of this function also at location X and scale H, we show that it is well-approximated by a type I sum. By Möbius inversion,
$(D,o_{w\to \infty }(1))$
-pseudorandomness of this function also at location X and scale H, we show that it is well-approximated by a type I sum. By Möbius inversion,
 $$ \begin{align*} \frac{\varphi(W)}{W}\Lambda_{\widetilde{w}}(Wn+b)=\frac{\varphi(W)}{W}\prod_{p\leq \widetilde{w}}\left(1-\frac{1}{p}\right)^{-1}\sum_{\substack{d\mid Wn+b\\d\mid P(\widetilde{w})}}\mu(d), \end{align*} $$
$$ \begin{align*} \frac{\varphi(W)}{W}\Lambda_{\widetilde{w}}(Wn+b)=\frac{\varphi(W)}{W}\prod_{p\leq \widetilde{w}}\left(1-\frac{1}{p}\right)^{-1}\sum_{\substack{d\mid Wn+b\\d\mid P(\widetilde{w})}}\mu(d), \end{align*} $$
and by Lemma 2.18 we have
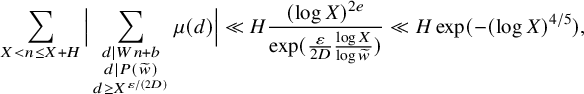 $$ \begin{align*} \sum_{X<n\leq X+H}\Big|\sum_{\substack{d\mid Wn+b\\d\mid P(\widetilde{w})\\d\geq X^{\varepsilon/(2D)}}}\mu(d)\Big|\ll H\frac{(\log X)^{2e}}{\exp(\frac{\varepsilon}{2D}\frac{\log X}{\log \widetilde{w}})}\ll H\exp(-(\log X)^{4/5}), \end{align*} $$
$$ \begin{align*} \sum_{X<n\leq X+H}\Big|\sum_{\substack{d\mid Wn+b\\d\mid P(\widetilde{w})\\d\geq X^{\varepsilon/(2D)}}}\mu(d)\Big|\ll H\frac{(\log X)^{2e}}{\exp(\frac{\varepsilon}{2D}\frac{\log X}{\log \widetilde{w}})}\ll H\exp(-(\log X)^{4/5}), \end{align*} $$
say. Hence,
![]() $\frac {\varphi (W)}{W}\Lambda _{\widetilde {w}}(Wn+b)=\nu (n)+\eta (n)$
, where
$\frac {\varphi (W)}{W}\Lambda _{\widetilde {w}}(Wn+b)=\nu (n)+\eta (n)$
, where
![]() $\nu $
is of the form of Lemma 9.5 and
$\nu $
is of the form of Lemma 9.5 and
![]() $\sum _{X<n\leq X+H}|\eta (n)|\ll H\exp (-(\log X)^{3/5})$
, say. It suffices to show that
$\sum _{X<n\leq X+H}|\eta (n)|\ll H\exp (-(\log X)^{3/5})$
, say. It suffices to show that
![]() $\nu $
is
$\nu $
is
![]() $(D,o_{w\to \infty }(1))$
-pseudorandom at location X and scale H, and this follows from Lemma 9.5.
$(D,o_{w\to \infty }(1))$
-pseudorandom at location X and scale H, and this follows from Lemma 9.5.
(2) Note that by equation (3.14), we have
![]() $d_k^{\sharp }(n)\ll _k d_k(n)$
for all
$d_k^{\sharp }(n)\ll _k d_k(n)$
for all
![]() $n\geq 1$
, so by Lemma 9.5 it suffices to show that the function
$n\geq 1$
, so by Lemma 9.5 it suffices to show that the function
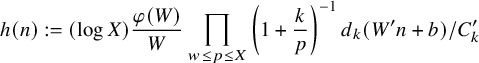 $$ \begin{align*}h(n):=(\log X)\frac{\varphi(W)}{W}\prod_{w\leq p\leq X}\left(1+\frac{k}{p}\right)^{-1}d_k(W'n+b)/C_k'\end{align*} $$
$$ \begin{align*}h(n):=(\log X)\frac{\varphi(W)}{W}\prod_{w\leq p\leq X}\left(1+\frac{k}{p}\right)^{-1}d_k(W'n+b)/C_k'\end{align*} $$
is for some
![]() $C_k'\geq 1$
majorized by a
$C_k'\geq 1$
majorized by a
![]() $(D,o_{w\to \infty }(1))$
-pseudorandom function at location
$(D,o_{w\to \infty }(1))$
-pseudorandom function at location
![]() $0$
and scale H, which is of the form equation (9.2) outside an exceptional set
$0$
and scale H, which is of the form equation (9.2) outside an exceptional set
![]() $\mathscr {S}$
satisfying equation (9.3).
$\mathscr {S}$
satisfying equation (9.3).
By [Reference Matthiesen52, Proposition 9.4], for any
![]() $X\geq 2$
and
$X\geq 2$
and
![]() $1\leq n\leq 2DX$
, we have
$1\leq n\leq 2DX$
, we have
where
![]() $\nu $
is a certain
$\nu $
is a certain
![]() $(D,o_{X\to \infty }(1))$
-pseudorandom function at location
$(D,o_{X\to \infty }(1))$
-pseudorandom function at location
![]() $0$
and scale X, and
$0$
and scale X, and
![]() $\mathscr {S}$
is defined in [Reference Matthiesen52, Section 7] as
$\mathscr {S}$
is defined in [Reference Matthiesen52, Section 7] as
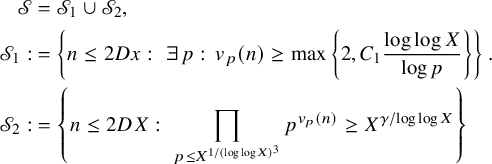 $$ \begin{align*} \mathscr{S}&=\mathscr{S}_1\cup\mathscr{S}_2,\\ \mathscr{S}_1:&=\left\{n\leq 2Dx:\,\, \exists \, p:\, v_p(n)\geq \max\left\{2,C_1\frac{\log \log X}{\log p}\right\}\right\}.\\ \mathscr{S}_2:&=\left\{n\leq 2DX:\,\,\prod_{p\leq X^{1/(\log \log X)^3}}p^{v_p(n)}\geq X^{\gamma/\log \log X}\right\} \end{align*} $$
$$ \begin{align*} \mathscr{S}&=\mathscr{S}_1\cup\mathscr{S}_2,\\ \mathscr{S}_1:&=\left\{n\leq 2Dx:\,\, \exists \, p:\, v_p(n)\geq \max\left\{2,C_1\frac{\log \log X}{\log p}\right\}\right\}.\\ \mathscr{S}_2:&=\left\{n\leq 2DX:\,\,\prod_{p\leq X^{1/(\log \log X)^3}}p^{v_p(n)}\geq X^{\gamma/\log \log X}\right\} \end{align*} $$
Here,
![]() $C_1$
can be taken arbitrarily large, so we may assume that
$C_1$
can be taken arbitrarily large, so we may assume that
![]() $C_1>8C$
for any given constant C. To show that
$C_1>8C$
for any given constant C. To show that
![]() $\mathscr {S}$
satisfies equation (9.3), it suffices to show that for
$\mathscr {S}$
satisfies equation (9.3), it suffices to show that for
![]() $j\in \{1,2\}$
we have
$j\in \{1,2\}$
we have
Let us prove equation (9.9), the proof of equation (9.10) is similar but easier.
We first prove equation (9.9) for
![]() $j=1$
. By splitting into shorter intervals if necessary, we may assume that
$j=1$
. By splitting into shorter intervals if necessary, we may assume that
![]() $H\leq X^{1/3}$
, say. Note that the number of
$H\leq X^{1/3}$
, say. Note that the number of
![]() $n\in (X-2DH,X+2DH]$
satisfying
$n\in (X-2DH,X+2DH]$
satisfying
![]() $v_p(n)\geq \max \{2,C_1\frac {\log \log X}{\log p}\}$
for some p is
$v_p(n)\geq \max \{2,C_1\frac {\log \log X}{\log p}\}$
for some p is
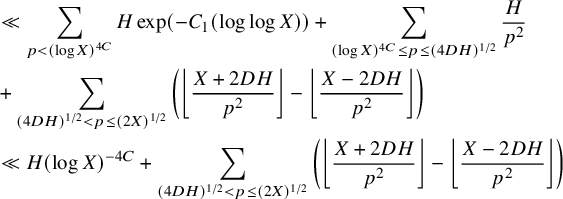 $$ \begin{align*} &\ll \sum_{p< (\log X)^{4C}}H\exp(-C_1(\log \log X))+\sum_{(\log X)^{4C}\leq p\leq (4DH)^{1/2}}\frac{H}{p^2}\\ &+\sum_{(4DH)^{1/2}<p\leq (2X)^{1/2}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right)\\ & \ll H(\log X)^{-4C}+\sum_{(4DH)^{1/2}<p\leq (2X)^{1/2}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right) \end{align*} $$
$$ \begin{align*} &\ll \sum_{p< (\log X)^{4C}}H\exp(-C_1(\log \log X))+\sum_{(\log X)^{4C}\leq p\leq (4DH)^{1/2}}\frac{H}{p^2}\\ &+\sum_{(4DH)^{1/2}<p\leq (2X)^{1/2}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right)\\ & \ll H(\log X)^{-4C}+\sum_{(4DH)^{1/2}<p\leq (2X)^{1/2}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right) \end{align*} $$
since
![]() $C_1>8C$
.
$C_1>8C$
.
We can trivially bound
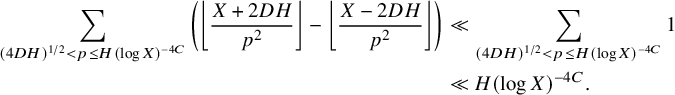 $$ \begin{align*} \sum_{(4DH)^{1/2}<p\leq H(\log X)^{-4C}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right) &\ll \sum_{(4DH)^{1/2}<p\leq H(\log X)^{-4C}}1\\ &\ll H(\log X)^{-4C}. \end{align*} $$
$$ \begin{align*} \sum_{(4DH)^{1/2}<p\leq H(\log X)^{-4C}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right) &\ll \sum_{(4DH)^{1/2}<p\leq H(\log X)^{-4C}}1\\ &\ll H(\log X)^{-4C}. \end{align*} $$
Next, we bound
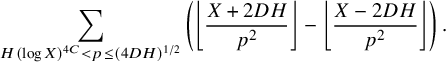 $$ \begin{align} \sum_{H(\log X)^{4C}< p\leq (4DH)^{1/2}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right). \end{align} $$
$$ \begin{align} \sum_{H(\log X)^{4C}< p\leq (4DH)^{1/2}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right). \end{align} $$
Note that for any
![]() $p\geq H(\log X)^{4C}$
there is at most one multiple of
$p\geq H(\log X)^{4C}$
there is at most one multiple of
![]() $p^2$
in
$p^2$
in
![]() $(X-2DH,X+2DH]$
, so equation (9.11) is at most
$(X-2DH,X+2DH]$
, so equation (9.11) is at most
![]() $|S(H(\log X)^{4C},(4DH)^{1/2})|$
, where
$|S(H(\log X)^{4C},(4DH)^{1/2})|$
, where
In [Reference Filaseta and Trifonov11, p. 221], it is proven for
![]() $H\geq X^{1/5+\varepsilon }$
that
$H\geq X^{1/5+\varepsilon }$
that
so equation (9.11) is
![]() $\ll H(\log X)^{-4C}$
.
$\ll H(\log X)^{-4C}$
.
Finally, we bound
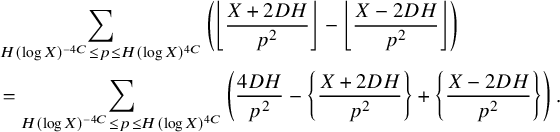 $$ \begin{align} &\sum_{H(\log X)^{-4C}\leq p\leq H(\log X)^{4C}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right)\nonumber\\ &=\sum_{H(\log X)^{-4C}\leq p\leq H(\log X)^{4C}}\left(\frac{4DH}{p^2}-\left\{\frac{X+2DH}{p^2}\right\}+\left\{\frac{X-2DH}{p^2}\right\}\right). \end{align} $$
$$ \begin{align} &\sum_{H(\log X)^{-4C}\leq p\leq H(\log X)^{4C}}\left(\left\lfloor \frac{X+2DH}{p^2}\right\rfloor-\left\lfloor \frac{X-2DH}{p^2}\right\rfloor\right)\nonumber\\ &=\sum_{H(\log X)^{-4C}\leq p\leq H(\log X)^{4C}}\left(\frac{4DH}{p^2}-\left\{\frac{X+2DH}{p^2}\right\}+\left\{\frac{X-2DH}{p^2}\right\}\right). \end{align} $$
The first term in the sum gives a negligible contribution of
![]() $\ll (\log X)^{4C}$
. Pick two
$\ll (\log X)^{4C}$
. Pick two
![]() $1$
-periodic smooth functions
$1$
-periodic smooth functions
![]() $W^{-}, W^{+}$
such that
$W^{-}, W^{+}$
such that
![]() $W^{-}(t)\leq \{t\}\leq W^{+}(t)$
for all
$W^{-}(t)\leq \{t\}\leq W^{+}(t)$
for all
![]() $t\in \mathbb {R}$
and such that
$t\in \mathbb {R}$
and such that
![]() $W^{\pm }(t)$
differs from
$W^{\pm }(t)$
differs from
![]() $\{t\}$
only in the region where
$\{t\}$
only in the region where
![]() $\|t\|_{\mathbb {R}/\mathbb {Z}}\leq (\log X)^{-8C}$
, and
$\|t\|_{\mathbb {R}/\mathbb {Z}}\leq (\log X)^{-8C}$
, and
![]() $W^{\pm }$
satisfy the derivative bounds
$W^{\pm }$
satisfy the derivative bounds
![]() $\sup _{t}|(W^{\pm })^{(\ell )}(t)|\ll (\log X)^{8C\ell }$
for
$\sup _{t}|(W^{\pm })^{(\ell )}(t)|\ll (\log X)^{8C\ell }$
for
![]() $1\leq \ell \leq 3$
. Then equation (9.12) is
$1\leq \ell \leq 3$
. Then equation (9.12) is
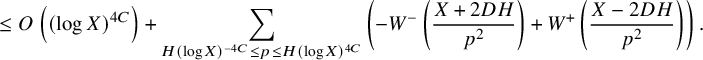 $$ \begin{align*} \leq O\left((\log X)^{4C}\right)+\sum_{H(\log X)^{-4C}\leq p\leq H(\log X)^{4C}}\left(-W^{-}\left(\frac{X+2DH}{p^2}\right)+W^{+}\left(\frac{X-2DH}{p^2}\right)\right). \end{align*} $$
$$ \begin{align*} \leq O\left((\log X)^{4C}\right)+\sum_{H(\log X)^{-4C}\leq p\leq H(\log X)^{4C}}\left(-W^{-}\left(\frac{X+2DH}{p^2}\right)+W^{+}\left(\frac{X-2DH}{p^2}\right)\right). \end{align*} $$
By [Reference Matomäki, Radziwiłł, Shao, Tao and Teräväinen45, Proposition 1.12(ii)] and the fact that for any
![]() $u,h\geq 0$
we have
$u,h\geq 0$
we have
![]() $\{u+h\}-\{u\}= h$
unless
$\{u+h\}-\{u\}= h$
unless
![]() $\|u\|_{\mathbb {R}/\mathbb {Z}}\leq h$
, the main term here is
$\|u\|_{\mathbb {R}/\mathbb {Z}}\leq h$
, the main term here is
 $$ \begin{align*} &\int_{H(\log X)^{-4C}}^{H(\log X)^{4C}}\left(W^{+}\left(\frac{X-2DH}{t^2}\right)-W^{-}\left(\frac{X+2DH}{t^2}\right)\right)\frac{dt}{\log t}+O(H(\log X)^{-4C})\\[6pt] &\ll \max_{\sigma\in \{-1,+1\}}\int_{H(\log X)^{-4C}}^{H(\log X)^{4C}}\left(\frac{4DH}{t^2}+1_{\|(X+2DH\sigma)/t^2\|_{\mathbb{R}/\mathbb{Z}}\leq (\log X)^{-8C}}\right)\frac{dt}{\log t}+H(\log X)^{-4C}\\[6pt]&\ll H(\log X)^{-4C} \end{align*} $$
$$ \begin{align*} &\int_{H(\log X)^{-4C}}^{H(\log X)^{4C}}\left(W^{+}\left(\frac{X-2DH}{t^2}\right)-W^{-}\left(\frac{X+2DH}{t^2}\right)\right)\frac{dt}{\log t}+O(H(\log X)^{-4C})\\[6pt] &\ll \max_{\sigma\in \{-1,+1\}}\int_{H(\log X)^{-4C}}^{H(\log X)^{4C}}\left(\frac{4DH}{t^2}+1_{\|(X+2DH\sigma)/t^2\|_{\mathbb{R}/\mathbb{Z}}\leq (\log X)^{-8C}}\right)\frac{dt}{\log t}+H(\log X)^{-4C}\\[6pt]&\ll H(\log X)^{-4C} \end{align*} $$
since the condition
![]() $\|(X+2DH\sigma )/t^2\|_{\mathbb {R}/\mathbb {Z}}\leq (\log X)^{-8C}$
for
$\|(X+2DH\sigma )/t^2\|_{\mathbb {R}/\mathbb {Z}}\leq (\log X)^{-8C}$
for
![]() $t\in [H(\log X)^{-4C},H(\log X)^{4C}]$
holds in a union of intervals of total measure
$t\in [H(\log X)^{-4C},H(\log X)^{4C}]$
holds in a union of intervals of total measure
![]() $\ll H(\log X)^{-4C}$
.
$\ll H(\log X)^{-4C}$
.
Putting the above estimates together, we obtain equation (9.9) for
![]() $j=1$
.
$j=1$
.
Let us then prove equation (9.9) for
![]() $j=2$
. We thus bound the number of integers
$j=2$
. We thus bound the number of integers
![]() $n\in I:=(X-2DH,X+2DH]$
that satisfy
$n\in I:=(X-2DH,X+2DH]$
that satisfy
![]() $\prod _{p\leq X^{1/(\log \log X)^3}}p^{v_p(n)}\geq X^{\gamma /\log \log X}$
. Writing
$\prod _{p\leq X^{1/(\log \log X)^3}}p^{v_p(n)}\geq X^{\gamma /\log \log X}$
. Writing
![]() $v = X^{1/(\log \log X)^3},$
the number of such
$v = X^{1/(\log \log X)^3},$
the number of such
![]() $n \in I$
is
$n \in I$
is
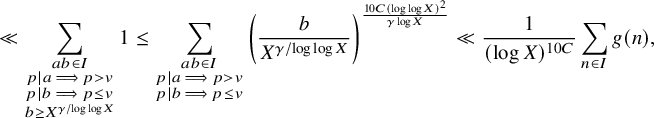 $$ \begin{align} \ll \sum_{\substack{ab \in I \\ p \mid a \implies p> v \\ p \mid b \implies p \leq v \\ b \geq X^{\gamma/\log \log X}}} 1 \leq \sum_{\substack{ab \in I \\ p \mid a \implies p > v \\ p \mid b \implies p \leq v}} \left(\frac{b}{X^{\gamma/\log \log X}}\right)^{\frac{10C (\log \log X)^2}{\gamma \log X}} \ll \frac{1}{(\log X)^{10C}} \sum_{n \in I} g(n), \end{align} $$
$$ \begin{align} \ll \sum_{\substack{ab \in I \\ p \mid a \implies p> v \\ p \mid b \implies p \leq v \\ b \geq X^{\gamma/\log \log X}}} 1 \leq \sum_{\substack{ab \in I \\ p \mid a \implies p > v \\ p \mid b \implies p \leq v}} \left(\frac{b}{X^{\gamma/\log \log X}}\right)^{\frac{10C (\log \log X)^2}{\gamma \log X}} \ll \frac{1}{(\log X)^{10C}} \sum_{n \in I} g(n), \end{align} $$
where g is the completely multiplicative function for which
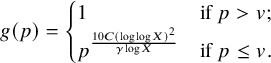 $$\begin{align*}g(p) = \begin{cases} 1 & \text{if }p> v; \\ p^{\frac{10C (\log \log X)^2}{\gamma \log X}} & \text{if }p \leq v. \end{cases} \end{align*}$$
$$\begin{align*}g(p) = \begin{cases} 1 & \text{if }p> v; \\ p^{\frac{10C (\log \log X)^2}{\gamma \log X}} & \text{if }p \leq v. \end{cases} \end{align*}$$
Then Shiu’s bound (Lemma 2.17) implies that equation (9.13) is
![]() $\ll H/(\log X)^{4C}$
. This proves equation (9.9) for
$\ll H/(\log X)^{4C}$
. This proves equation (9.9) for
![]() $j=2$
.
$j=2$
.
Hence,
![]() $|\mathscr {S}| \ll H/(\log X)^{4C}$
, and in particular arguing as in the beginning of the proof of Lemma 9.5 we see that the fact that
$|\mathscr {S}| \ll H/(\log X)^{4C}$
, and in particular arguing as in the beginning of the proof of Lemma 9.5 we see that the fact that
![]() $\nu $
is a
$\nu $
is a
![]() $(D,o_{X\to \infty }(1))$
-pseudorandom function at location
$(D,o_{X\to \infty }(1))$
-pseudorandom function at location
![]() $0$
and scale X implies that so is
$0$
and scale X implies that so is
![]() $\nu (n) + h(n) 1_{n \in \mathscr {S}}$
.
$\nu (n) + h(n) 1_{n \in \mathscr {S}}$
.
Hence, it suffices to show that
![]() $\nu (n)$
is of the form (9.2). The majorant
$\nu (n)$
is of the form (9.2). The majorant
![]() $\nu (n)$
is defined in [Reference Matthiesen52, Section 7], for some
$\nu (n)$
is defined in [Reference Matthiesen52, Section 7], for some
![]() $\gamma>0$
small enough in terms of
$\gamma>0$
small enough in terms of
![]() $D,k$
, as
$D,k$
, as
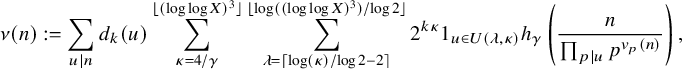 $$ \begin{align} \nu(n):=\sum_{u\mid n}d_k(u)\sum_{\kappa=4/\gamma}^{\lfloor (\log \log X)^3 \rfloor}\sum_{\lambda=\lceil \log(\kappa)/\log 2-2\rceil}^{\lfloor \log((\log \log X)^3)/\log 2\rfloor}2^{k\kappa}1_{u\in U(\lambda,\kappa)}h_{\gamma}\left(\frac{n}{\prod_{p\mid u}p^{v_p(n)}}\right), \end{align} $$
$$ \begin{align} \nu(n):=\sum_{u\mid n}d_k(u)\sum_{\kappa=4/\gamma}^{\lfloor (\log \log X)^3 \rfloor}\sum_{\lambda=\lceil \log(\kappa)/\log 2-2\rceil}^{\lfloor \log((\log \log X)^3)/\log 2\rfloor}2^{k\kappa}1_{u\in U(\lambda,\kappa)}h_{\gamma}\left(\frac{n}{\prod_{p\mid u}p^{v_p(n)}}\right), \end{align} $$
where
-
•
 $U(\lambda ,\kappa )$
, defined in [Reference Matthiesen52, Section 7], is a set contained in
$U(\lambda ,\kappa )$
, defined in [Reference Matthiesen52, Section 7], is a set contained in
 $[1,X^{10\gamma ^{1/2}}]$
and satisfying
$[1,X^{10\gamma ^{1/2}}]$
and satisfying  $$ \begin{align*} u\in U(\lambda,\kappa),u>1&\implies \omega(u)\geq \frac{\gamma \kappa (\lambda+3-(\log \kappa)/(\log 2))}{200}\\ 1\in U(\lambda,\kappa)&\implies \kappa=4/\gamma; \end{align*} $$
$$ \begin{align*} u\in U(\lambda,\kappa),u>1&\implies \omega(u)\geq \frac{\gamma \kappa (\lambda+3-(\log \kappa)/(\log 2))}{200}\\ 1\in U(\lambda,\kappa)&\implies \kappa=4/\gamma; \end{align*} $$
-
•
 $h_{\gamma }(n)=\sum _{\ell \mid n}(d_k*\mu )(\ell )\chi \left (\frac {\log \ell }{\log X^{\gamma }}\right ),$
where
$h_{\gamma }(n)=\sum _{\ell \mid n}(d_k*\mu )(\ell )\chi \left (\frac {\log \ell }{\log X^{\gamma }}\right ),$
where
 $\chi :\mathbb {R}\to [0,1]$
is some smooth function supported in
$\chi :\mathbb {R}\to [0,1]$
is some smooth function supported in
 $[-1,1]$
.
$[-1,1]$
.
Therefore, in particular, in equation (9.14) we have
so that
for some constant
![]() $M=M_{k,\gamma }\geq 1$
. Inserting the definition of
$M=M_{k,\gamma }\geq 1$
. Inserting the definition of
![]() $h_{\gamma }$
into the definition of
$h_{\gamma }$
into the definition of
![]() $\nu $
and setting
$\nu $
and setting
![]() $T=X^{10\gamma ^{1/2}}$
, we see that for some
$T=X^{10\gamma ^{1/2}}$
, we see that for some
![]() $|\lambda _u|\ll d(u)^{k+M}(\log \log X)^{O_{D,k}(1)}$
we have
$|\lambda _u|\ll d(u)^{k+M}(\log \log X)^{O_{D,k}(1)}$
we have
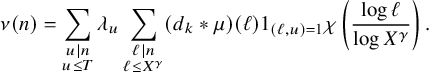 $$ \begin{align*} \nu(n)=\sum_{\substack{u\mid n\\u\leq T}}\lambda_u\sum_{\substack{\ell\mid n\\\ell\leq X^{\gamma}}}(d_k*\mu)(\ell)1_{(\ell,u)=1}\chi\left(\frac{\log \ell}{\log X^{\gamma}}\right). \end{align*} $$
$$ \begin{align*} \nu(n)=\sum_{\substack{u\mid n\\u\leq T}}\lambda_u\sum_{\substack{\ell\mid n\\\ell\leq X^{\gamma}}}(d_k*\mu)(\ell)1_{(\ell,u)=1}\chi\left(\frac{\log \ell}{\log X^{\gamma}}\right). \end{align*} $$
Writing
![]() $e=\ell u$
, we see that for some
$e=\ell u$
, we see that for some
![]() $|\lambda _{e}'|\ll (\log \log X)^{O_{D,k}(1)}d(e)^{k+M+1}d_{k+1}(e)$
the function
$|\lambda _{e}'|\ll (\log \log X)^{O_{D,k}(1)}d(e)^{k+M+1}d_{k+1}(e)$
the function
![]() $\nu $
is of the form
$\nu $
is of the form
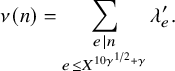 $$ \begin{align*} \nu(n)=\sum_{\substack{e\mid n\\e\leq X^{10\gamma^{1/2}+\gamma}}}\lambda_{e}'. \end{align*} $$
$$ \begin{align*} \nu(n)=\sum_{\substack{e\mid n\\e\leq X^{10\gamma^{1/2}+\gamma}}}\lambda_{e}'. \end{align*} $$
Taking
![]() $\gamma $
small enough in terms of
$\gamma $
small enough in terms of
![]() $D,k$
, this is of the form required in Lemma 9.5, so appealing to that lemma we conclude that
$D,k$
, this is of the form required in Lemma 9.5, so appealing to that lemma we conclude that
![]() $\nu $
is
$\nu $
is
![]() $(D,o_{w\to \infty }(1))$
-pseudorandom at location X and scale H.
$(D,o_{w\to \infty }(1))$
-pseudorandom at location X and scale H.
We need two more lemmas before proving Theorem 1.5.
Lemma 9.8. Let
![]() $D\in \mathbb {N}$
be fixed. Let
$D\in \mathbb {N}$
be fixed. Let
![]() $1\leq q\leq H^{1/4}$
be an integer. Let
$1\leq q\leq H^{1/4}$
be an integer. Let
![]() $X\geq H\geq 2$
, and let
$X\geq H\geq 2$
, and let
![]() $f:(X,X+H]\to \mathbb {C}$
be a function with
$f:(X,X+H]\to \mathbb {C}$
be a function with
![]() $|f(n)|\ll H^{1/2^{D+2}}$
. Then we have
$|f(n)|\ll H^{1/2^{D+2}}$
. Then we have
 $$ \begin{align*} \|f\|_{U^D(X,X+H]}\leq \frac{1}{q}\sum_{1\leq a\leq q}\|f_{q,a}\|_{U^D(X/q,(X+H)/q]}+O(H^{-1/2}), \end{align*} $$
$$ \begin{align*} \|f\|_{U^D(X,X+H]}\leq \frac{1}{q}\sum_{1\leq a\leq q}\|f_{q,a}\|_{U^D(X/q,(X+H)/q]}+O(H^{-1/2}), \end{align*} $$
where
![]() $f_{q,a}(n):=f(qn+a)$
.
$f_{q,a}(n):=f(qn+a)$
.
Proof. Denote by
![]() $1_{a(q)}$
the indicator of the arithmetic progression
$1_{a(q)}$
the indicator of the arithmetic progression
![]() $a\ \pmod {q}$
. Then, by the triangle inequality for the Gowers norms, we have
$a\ \pmod {q}$
. Then, by the triangle inequality for the Gowers norms, we have
The claim now follows by making a linear change of variables
![]() $(n,\mathbf {h})=(qn'+a,q\mathbf {h}')$
in the definition of
$(n,\mathbf {h})=(qn'+a,q\mathbf {h}')$
in the definition of
![]() $\|f 1_{a(q)}\|_{U^D(X,X+H]}$
.
$\|f 1_{a(q)}\|_{U^D(X,X+H]}$
.
Lemma 9.9. Let
![]() $D,k\in \mathbb {N}$
and
$D,k\in \mathbb {N}$
and
![]() $\varepsilon>0$
be fixed, with
$\varepsilon>0$
be fixed, with
![]() $\varepsilon>0$
small enough. Let
$\varepsilon>0$
small enough. Let
![]() $X\geq H\geq X^{\varepsilon }$
, and let
$X\geq H\geq X^{\varepsilon }$
, and let
![]() $1\leq q\leq X^{\varepsilon ^2}$
be an integer. Let
$1\leq q\leq X^{\varepsilon ^2}$
be an integer. Let
![]() $f(n)=(\log X)^{1-k}d_k(n)$
. Then for
$f(n)=(\log X)^{1-k}d_k(n)$
. Then for
![]() $1\leq a\leq q$
with
$1\leq a\leq q$
with
![]() $(a,q)=1$
, we have
$(a,q)=1$
, we have
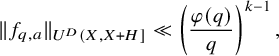 $$ \begin{align*} \|f_{q,a}\|_{U^{D}(X,X+H]}\ll \left(\frac{\varphi(q)}{q}\right)^{k-1}, \end{align*} $$
$$ \begin{align*} \|f_{q,a}\|_{U^{D}(X,X+H]}\ll \left(\frac{\varphi(q)}{q}\right)^{k-1}, \end{align*} $$
where
![]() $f_{q,a}(n):=f(qn+a)$
.
$f_{q,a}(n):=f(qn+a)$
.
Proof. Let
![]() $g_{q,a}(n):=d_k(qn+a)$
. By the definition of the interval Gowers norms and the fact that
$g_{q,a}(n):=d_k(qn+a)$
. By the definition of the interval Gowers norms and the fact that
![]() $\|1_{(X, X+H]}\|_{U^{D}(\mathbb {Z})}^{2^D} \asymp H^{D+1}$
, we have
$\|1_{(X, X+H]}\|_{U^{D}(\mathbb {Z})}^{2^D} \asymp H^{D+1}$
, we have
 $$ \begin{align} \|g_{q,a}\|_{U^{D}(X,X+H]}^{2^D}&\asymp \frac{1}{H^{D+1}}\sum_{n}\sum_{h_1,\ldots, h_D}\prod_{\omega\in \{0,1\}^D}d_k(q(n+\omega\cdot \mathbf{h})+a)1_{(X,X+H]}(n+\omega\cdot \mathbf{h})\nonumber\\[5pt] &\ll \frac{1}{H^{D+1}}\sum_{X < n\leq X+H}\sum_{\substack{|h_1|,\ldots, |h_D|\leq 2H\\h_i\text{ distinct }}}\prod_{\omega\in \{0,1\}^D}d_k(q(n+\omega\cdot \mathbf{h})+a) + H^{-1/2}. \end{align} $$
$$ \begin{align} \|g_{q,a}\|_{U^{D}(X,X+H]}^{2^D}&\asymp \frac{1}{H^{D+1}}\sum_{n}\sum_{h_1,\ldots, h_D}\prod_{\omega\in \{0,1\}^D}d_k(q(n+\omega\cdot \mathbf{h})+a)1_{(X,X+H]}(n+\omega\cdot \mathbf{h})\nonumber\\[5pt] &\ll \frac{1}{H^{D+1}}\sum_{X < n\leq X+H}\sum_{\substack{|h_1|,\ldots, |h_D|\leq 2H\\h_i\text{ distinct }}}\prod_{\omega\in \{0,1\}^D}d_k(q(n+\omega\cdot \mathbf{h})+a) + H^{-1/2}. \end{align} $$
We can upper bound the correlation of these multiplicative functions using Henriot’s bound [Reference Henriot30, Theorem 3] (taking
![]() $x\to X,y\to H$
,
$x\to X,y\to H$
,
![]() $\delta \to 2^{-D-2}$
,
$\delta \to 2^{-D-2}$
,
![]() $Q(n)\to \prod _{\omega \in \{0,1\}^D}(q(n+\omega \cdot \mathbf {h})+a)$
there), obtaining
$Q(n)\to \prod _{\omega \in \{0,1\}^D}(q(n+\omega \cdot \mathbf {h})+a)$
there), obtaining
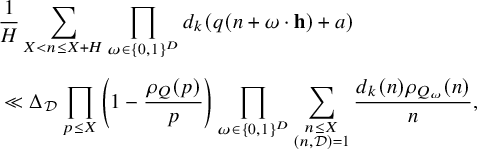 $$ \begin{align}&\frac{1}{H}\sum_{X < n \leq X+H}\prod_{\omega\in \{0,1\}^D}d_k(q(n+\omega\cdot \mathbf{h})+a)\nonumber\\[5pt]&\ll \Delta_{\mathcal{D}}\prod_{p\leq X}\left(1-\frac{\rho_Q(p)}{p}\right)\prod_{\omega\in \{0,1\}^D}\sum_{\substack{n\leq X\\(n,\mathcal{D})=1}}\frac{d_k(n)\rho_{Q_{\omega}}(n)}{n}, \end{align} $$
$$ \begin{align}&\frac{1}{H}\sum_{X < n \leq X+H}\prod_{\omega\in \{0,1\}^D}d_k(q(n+\omega\cdot \mathbf{h})+a)\nonumber\\[5pt]&\ll \Delta_{\mathcal{D}}\prod_{p\leq X}\left(1-\frac{\rho_Q(p)}{p}\right)\prod_{\omega\in \{0,1\}^D}\sum_{\substack{n\leq X\\(n,\mathcal{D})=1}}\frac{d_k(n)\rho_{Q_{\omega}}(n)}{n}, \end{align} $$
where
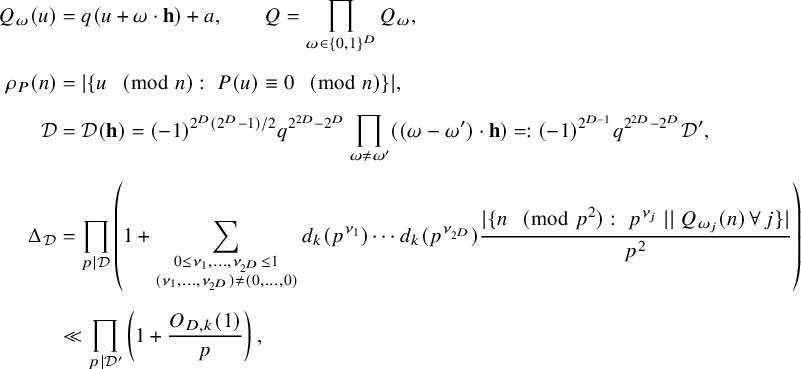 $$ \begin{align*}Q_{\omega}(u)&=q(u+\omega\cdot \mathbf{h})+a, \qquad Q=\prod_{\omega\in \{0,1\}^D}Q_{\omega},\\[5pt]\rho_{P}(n)&=|\{u\quad\pmod n:\,\, P(u)\equiv 0\quad\pmod n\}|,\\[5pt]\mathcal{D}&=\mathcal{D}(\mathbf{h})=(-1)^{2^D(2^D-1)/2} q^{2^{2D}-2^D}\prod_{\omega\neq \omega'}((\omega-\omega')\cdot \mathbf{h})=: (-1)^{2^{D-1}} q^{2^{2D}-2^D}\mathcal{D}',\\[5pt]\Delta_{\mathcal{D}}&=\prod_{p\mid \mathcal{D}}\left(1+\sum_{\substack{0\leq \nu_1,\ldots, \nu_{2^{D}}\leq 1\\(\nu_1,\ldots, \nu_{2^D})\neq (0,\ldots,0)}}d_k(p^{\nu_1})\cdots d_k(p^{\nu_{2^D}})\frac{|\{n\quad\pmod{p^2}:\,\, p^{\nu_{j}}\mid \mid Q_{\omega_j}(n)\,\forall\, j\}|}{p^{2}}\right)\\[5pt]&\ll \prod_{p\mid \mathcal{D}'}\left(1+\frac{O_{D,k}(1)}{p}\right), \end{align*} $$
$$ \begin{align*}Q_{\omega}(u)&=q(u+\omega\cdot \mathbf{h})+a, \qquad Q=\prod_{\omega\in \{0,1\}^D}Q_{\omega},\\[5pt]\rho_{P}(n)&=|\{u\quad\pmod n:\,\, P(u)\equiv 0\quad\pmod n\}|,\\[5pt]\mathcal{D}&=\mathcal{D}(\mathbf{h})=(-1)^{2^D(2^D-1)/2} q^{2^{2D}-2^D}\prod_{\omega\neq \omega'}((\omega-\omega')\cdot \mathbf{h})=: (-1)^{2^{D-1}} q^{2^{2D}-2^D}\mathcal{D}',\\[5pt]\Delta_{\mathcal{D}}&=\prod_{p\mid \mathcal{D}}\left(1+\sum_{\substack{0\leq \nu_1,\ldots, \nu_{2^{D}}\leq 1\\(\nu_1,\ldots, \nu_{2^D})\neq (0,\ldots,0)}}d_k(p^{\nu_1})\cdots d_k(p^{\nu_{2^D}})\frac{|\{n\quad\pmod{p^2}:\,\, p^{\nu_{j}}\mid \mid Q_{\omega_j}(n)\,\forall\, j\}|}{p^{2}}\right)\\[5pt]&\ll \prod_{p\mid \mathcal{D}'}\left(1+\frac{O_{D,k}(1)}{p}\right), \end{align*} $$
where
![]() $\omega _1,\ldots , \omega _{2^D}$
is any ordering of
$\omega _1,\ldots , \omega _{2^D}$
is any ordering of
![]() $\{0,1\}^D$
. In order to bound the various expressions above, note that
$\{0,1\}^D$
. In order to bound the various expressions above, note that
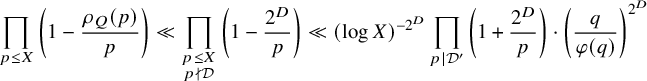 $$ \begin{align*} \prod_{p\leq X}\left(1-\frac{\rho_Q(p)}{p}\right)\ll \prod_{\substack{p\leq X\\p\nmid \mathcal{D}}}\left(1-\frac{2^D}{p}\right)\ll (\log X)^{-2^D}\prod_{p\mid \mathcal{D}'}\left(1+\frac{2^D}{p}\right)\cdot \left(\frac{q}{\varphi(q)}\right)^{2^D} \end{align*} $$
$$ \begin{align*} \prod_{p\leq X}\left(1-\frac{\rho_Q(p)}{p}\right)\ll \prod_{\substack{p\leq X\\p\nmid \mathcal{D}}}\left(1-\frac{2^D}{p}\right)\ll (\log X)^{-2^D}\prod_{p\mid \mathcal{D}'}\left(1+\frac{2^D}{p}\right)\cdot \left(\frac{q}{\varphi(q)}\right)^{2^D} \end{align*} $$
and
 $$ \begin{align*}\sum_{\substack{n\leq X\\(n,\mathcal{D})=1}}\frac{d_k(n)\rho_{Q_{\omega}}(n)}{n}\ll \prod_{\substack{p\leq X\\p\nmid q}}\left(1+\frac{k}{p}\right)\ll (\log X)^{k}\left(\frac{\varphi(q)}{q}\right)^{k}. \end{align*} $$
$$ \begin{align*}\sum_{\substack{n\leq X\\(n,\mathcal{D})=1}}\frac{d_k(n)\rho_{Q_{\omega}}(n)}{n}\ll \prod_{\substack{p\leq X\\p\nmid q}}\left(1+\frac{k}{p}\right)\ll (\log X)^{k}\left(\frac{\varphi(q)}{q}\right)^{k}. \end{align*} $$
We now conclude that equation (9.16) is
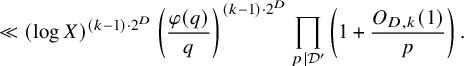 $$ \begin{align*} \ll (\log X)^{(k-1) \cdot 2^D}\left(\frac{\varphi(q)}{q}\right)^{(k-1)\cdot 2^D}\prod_{p\mid \mathcal{D}'}\left(1+\frac{O_{D,k}(1)}{p}\right). \end{align*} $$
$$ \begin{align*} \ll (\log X)^{(k-1) \cdot 2^D}\left(\frac{\varphi(q)}{q}\right)^{(k-1)\cdot 2^D}\prod_{p\mid \mathcal{D}'}\left(1+\frac{O_{D,k}(1)}{p}\right). \end{align*} $$
By the inequality
![]() $\prod _{i=1}^kx_i\leq \sum _{i=1}^k x_i^k$
and an elementary upper bound for moments of
$\prod _{i=1}^kx_i\leq \sum _{i=1}^k x_i^k$
and an elementary upper bound for moments of
![]() $n/\varphi (n)$
, we have
$n/\varphi (n)$
, we have
 $$ \begin{align*} \sum_{\substack{|h_1|,\ldots, |h_D|\leq 2H\\h_i\text{ distinct }}} \prod_{p\mid \mathcal{D}'(\mathbf{h})}\left(1+\frac{O_{D,k}(1)}{p}\right)\ll \sum_{\substack{|h_1|,\ldots, |h_D|\leq 2H\\h_i\text{ distinct }}} \sum_{\omega\in \{-1,0,1\}^D\setminus\{\mathbf{0}\}}\prod_{p\mid \omega\cdot \mathbf{h}}\left(1+\frac{1}{p}\right)^{O_{D,k}(1)}\ll H^D. \end{align*} $$
$$ \begin{align*} \sum_{\substack{|h_1|,\ldots, |h_D|\leq 2H\\h_i\text{ distinct }}} \prod_{p\mid \mathcal{D}'(\mathbf{h})}\left(1+\frac{O_{D,k}(1)}{p}\right)\ll \sum_{\substack{|h_1|,\ldots, |h_D|\leq 2H\\h_i\text{ distinct }}} \sum_{\omega\in \{-1,0,1\}^D\setminus\{\mathbf{0}\}}\prod_{p\mid \omega\cdot \mathbf{h}}\left(1+\frac{1}{p}\right)^{O_{D,k}(1)}\ll H^D. \end{align*} $$
The claim now follows by combining this with equation (9.15).
We are now ready to prove Theorem 1.5.
Proof of Theorem 1.5.
(i) Let H be as in Theorem 1.5(i). By the triangle inequality for the Gowers norms, to prove equation (1.18) it suffices to show that
and
The first claim (9.17) follows directly from Lemma 9.6 and Remark 9.2.
We are then left with proving equations (9.18) and (1.19). Let
![]() $1\leq b\leq W'\leq \log X$
be integers. For
$1\leq b\leq W'\leq \log X$
be integers. For
![]() $f=\Lambda -\Lambda ^{\sharp }$
, by Theorem 1.1 for any
$f=\Lambda -\Lambda ^{\sharp }$
, by Theorem 1.1 for any
![]() $x\in [X/(\log X)^A,X(\log X)^A]$
,
$x\in [X/(\log X)^A,X(\log X)^A]$
,
![]() $H(\log X)^{-A}\leq H'\leq H$
and
$H(\log X)^{-A}\leq H'\leq H$
and
![]() $G/\Gamma $
, F as in that theorem, we have
$G/\Gamma $
, F as in that theorem, we have
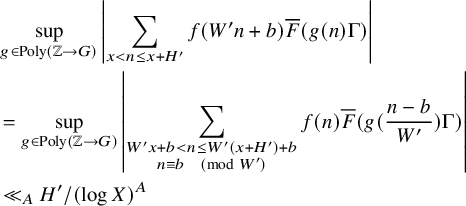 $$ \begin{align} &\sup_{g\in {\operatorname{Poly}}(\mathbb{Z}\to G)}\left|\sum_{x < n \leq x+H'}f(W'n+b)\overline{F}(g(n)\Gamma) \right|\nonumber\\ &= \sup_{g\in {\operatorname{Poly}}(\mathbb{Z}\to G)}\left|\sum_{\substack{W'x+b < n\leq W'(x+H')+b\\n\equiv b\quad\pmod{W'}}}f(n)\overline{F}(g(\frac{n-b}{W'})\Gamma) \right|\\ &\ll_A H'/(\log X)^{A}\nonumber \end{align} $$
$$ \begin{align} &\sup_{g\in {\operatorname{Poly}}(\mathbb{Z}\to G)}\left|\sum_{x < n \leq x+H'}f(W'n+b)\overline{F}(g(n)\Gamma) \right|\nonumber\\ &= \sup_{g\in {\operatorname{Poly}}(\mathbb{Z}\to G)}\left|\sum_{\substack{W'x+b < n\leq W'(x+H')+b\\n\equiv b\quad\pmod{W'}}}f(n)\overline{F}(g(\frac{n-b}{W'})\Gamma) \right|\\ &\ll_A H'/(\log X)^{A}\nonumber \end{align} $$
since there exists a polynomial sequence
![]() $\widetilde {g}:\mathbb {Z}\to G$
such that
$\widetilde {g}:\mathbb {Z}\to G$
such that
![]() $\widetilde {g}(n)=g((n-b)/W')$
for all
$\widetilde {g}(n)=g((n-b)/W')$
for all
![]() $n\equiv b\ \pmod {W'}$
.
$n\equiv b\ \pmod {W'}$
.
Now, equation (1.19) follows by combining the inverse theorem (Proposition 9.4) with the estimate (9.19), Lemma 9.6 and Remark 9.7. Lastly, equation (1.18) follows from equation (1.19) and Lemma 9.8.
(ii) We then turn to the case
![]() $f=d_k-d_{k}^{\sharp }$
. Again, Theorem 1.1 gives us the bound (9.19). Together with the inverse theorem (Proposition 9.4), Lemma 9.6 and Remark 9.7, this implies equation (1.21).
$f=d_k-d_{k}^{\sharp }$
. Again, Theorem 1.1 gives us the bound (9.19). Together with the inverse theorem (Proposition 9.4), Lemma 9.6 and Remark 9.7, this implies equation (1.21).
Let
Then, to prove equation (1.20), we must show that
Let
![]() $\widetilde {W}:=W^w$
with w an integer tending to infinity slowly.Footnote
15
By Lemma 9.8, we have
$\widetilde {W}:=W^w$
with w an integer tending to infinity slowly.Footnote
15
By Lemma 9.8, we have
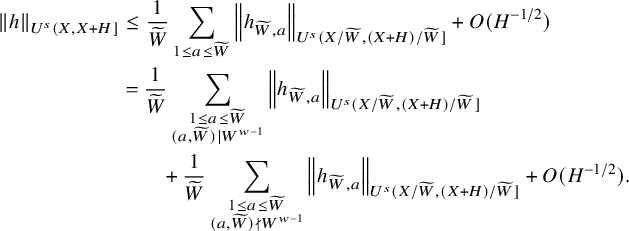 $$ \begin{align}\left\|h\right\|_{U^s(X,X+H]}&\leq \frac{1}{\widetilde{W}}\sum_{1\leq a\leq \widetilde{W}}\left\|h_{\widetilde{W},a}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}+O(H^{-1/2})\nonumber\\&=\frac{1}{\widetilde{W}}\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})\mid W^{w-1}}}\left\|h_{\widetilde{W},a}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}\nonumber\\&\quad \quad +\frac{1}{\widetilde{W}}\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})\nmid W^{w-1}}}\left\|h_{\widetilde{W},a}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}+O(H^{-1/2}). \end{align} $$
$$ \begin{align}\left\|h\right\|_{U^s(X,X+H]}&\leq \frac{1}{\widetilde{W}}\sum_{1\leq a\leq \widetilde{W}}\left\|h_{\widetilde{W},a}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}+O(H^{-1/2})\nonumber\\&=\frac{1}{\widetilde{W}}\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})\mid W^{w-1}}}\left\|h_{\widetilde{W},a}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}\nonumber\\&\quad \quad +\frac{1}{\widetilde{W}}\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})\nmid W^{w-1}}}\left\|h_{\widetilde{W},a}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}+O(H^{-1/2}). \end{align} $$
The number of terms in the last sum is
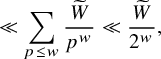 $$ \begin{align*} \ll \sum_{p\leq w}\frac{\widetilde{W}}{p^w} \ll \frac{\widetilde{W}}{2^w}, \end{align*} $$
$$ \begin{align*} \ll \sum_{p\leq w}\frac{\widetilde{W}}{p^w} \ll \frac{\widetilde{W}}{2^w}, \end{align*} $$
so by Lemma 9.9 the contribution of this sum is
![]() $\ll 2^{-w/2}$
, say. The first sum over a in equation (9.20) can further be written as
$\ll 2^{-w/2}$
, say. The first sum over a in equation (9.20) can further be written as
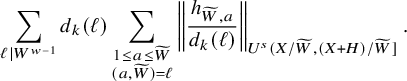 $$ \begin{align}\sum_{\ell \mid W^{w-1}}d_k(\ell)\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})=\ell}}\left\|\frac{h_{\widetilde{W},a}}{d_k(\ell)}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}. \end{align} $$
$$ \begin{align}\sum_{\ell \mid W^{w-1}}d_k(\ell)\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})=\ell}}\left\|\frac{h_{\widetilde{W},a}}{d_k(\ell)}\right\|_{U^s(X/\widetilde{W},(X+H)/\widetilde{W}]}. \end{align} $$
Since
![]() $d_k^{\sharp }(m)\ll d_k(m)$
, for
$d_k^{\sharp }(m)\ll d_k(m)$
, for
![]() $(a,\widetilde {W})=\ell $
, we have
$(a,\widetilde {W})=\ell $
, we have
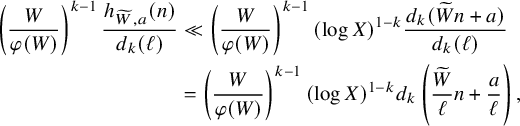 $$ \begin{align*} \left(\frac{W}{\varphi(W)}\right)^{k-1}\frac{h_{\widetilde{W},a}(n)}{d_k(\ell)}&\ll \left(\frac{W}{\varphi(W)}\right)^{k-1} (\log X)^{1-k} \frac{d_k(\widetilde{W}n+a)}{d_k(\ell)}\\ &=\left(\frac{W}{\varphi(W)}\right)^{k-1}(\log X)^{1-k} d_k\left(\frac{\widetilde{W}}{\ell}n+\frac{a}{\ell}\right), \end{align*} $$
$$ \begin{align*} \left(\frac{W}{\varphi(W)}\right)^{k-1}\frac{h_{\widetilde{W},a}(n)}{d_k(\ell)}&\ll \left(\frac{W}{\varphi(W)}\right)^{k-1} (\log X)^{1-k} \frac{d_k(\widetilde{W}n+a)}{d_k(\ell)}\\ &=\left(\frac{W}{\varphi(W)}\right)^{k-1}(\log X)^{1-k} d_k\left(\frac{\widetilde{W}}{\ell}n+\frac{a}{\ell}\right), \end{align*} $$
and since
![]() $W\mid \frac {\widetilde {W}}{\ell }$
, by Lemma 9.6 and Mertens’s theorem this function is pseudorandomly majorized by a
$W\mid \frac {\widetilde {W}}{\ell }$
, by Lemma 9.6 and Mertens’s theorem this function is pseudorandomly majorized by a
![]() $(D,o_{X\to \infty }(1))$
-pseudorandom function at location
$(D,o_{X\to \infty }(1))$
-pseudorandom function at location
![]() $0$
and scale
$0$
and scale
![]() $H/\widetilde {W}$
. This combined with equation (9.19) (with
$H/\widetilde {W}$
. This combined with equation (9.19) (with
![]() $\widetilde {W}/\ell $
in place of
$\widetilde {W}/\ell $
in place of
![]() $W'$
) and Proposition 9.4 yields
$W'$
) and Proposition 9.4 yields
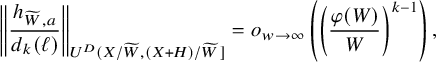 $$ \begin{align} \left\|\frac{h_{\widetilde{W},a}}{d_k(\ell)}\right\|_{U^D(X/\widetilde{W},(X+H)/\widetilde{W}]}=o_{w\to \infty}\left(\left(\frac{\varphi(W)}{W}\right)^{k-1}\right), \end{align} $$
$$ \begin{align} \left\|\frac{h_{\widetilde{W},a}}{d_k(\ell)}\right\|_{U^D(X/\widetilde{W},(X+H)/\widetilde{W}]}=o_{w\to \infty}\left(\left(\frac{\varphi(W)}{W}\right)^{k-1}\right), \end{align} $$
uniformly in
![]() $1\leq a\leq \widetilde {W}$
with
$1\leq a\leq \widetilde {W}$
with
![]() $(\widetilde {W},a)=\ell $
.
$(\widetilde {W},a)=\ell $
.
Now, the bound (1.20) follows from equations (9.21), (9.22), and the estimate
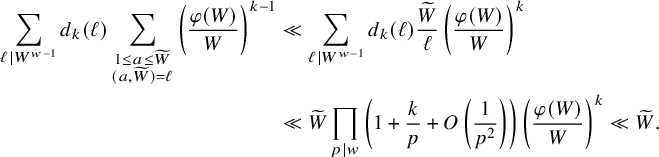 $$ \begin{align*}\sum_{\ell\mid W^{w-1}}d_k(\ell)\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})=\ell}}\left(\frac{\varphi(W)}{W}\right)^{k-1}&\ll \sum_{\ell\mid W^{w-1}}d_k(\ell)\frac{\widetilde{W}}{\ell}\left(\frac{\varphi(W)}{W}\right)^{k}\\&\ll \widetilde{W}\prod_{p\mid w}\left(1+\frac{k}{p}+O\left(\frac{1}{p^2}\right)\right)\left(\frac{\varphi(W)}{W}\right)^{k}\ll \widetilde{W}. \end{align*} $$
$$ \begin{align*}\sum_{\ell\mid W^{w-1}}d_k(\ell)\sum_{\substack{1\leq a\leq \widetilde{W}\\(a,\widetilde{W})=\ell}}\left(\frac{\varphi(W)}{W}\right)^{k-1}&\ll \sum_{\ell\mid W^{w-1}}d_k(\ell)\frac{\widetilde{W}}{\ell}\left(\frac{\varphi(W)}{W}\right)^{k}\\&\ll \widetilde{W}\prod_{p\mid w}\left(1+\frac{k}{p}+O\left(\frac{1}{p^2}\right)\right)\left(\frac{\varphi(W)}{W}\right)^{k}\ll \widetilde{W}. \end{align*} $$
(iii) This case follows directly from the inverse theorem (Proposition 9.4 with
![]() $\nu =1$
) and Theorem 1.1(iv).
$\nu =1$
) and Theorem 1.1(iv).
10 Applications
In this section, we shall prove the applications stated in Section 1.
Proof of Corollary 1.3.
Parts (i) and (iii) follow immediately from Theorem 1.1, as polynomial phases are special cases of nilsequences. By Theorem 1.1 and the triangle inequality, the proof of part (ii) reduces to proving that
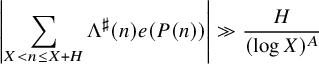 $$ \begin{align*} \left|\sum_{X < n\leq X+H}\Lambda^{\sharp}(n)e(P(n))\right|\gg \frac{H}{(\log X)^{A}} \end{align*} $$
$$ \begin{align*} \left|\sum_{X < n\leq X+H}\Lambda^{\sharp}(n)e(P(n))\right|\gg \frac{H}{(\log X)^{A}} \end{align*} $$
implies equation (1.10). Recalling from equation (4.8) that
![]() $\Lambda ^{\sharp }(n)=\Lambda ^{\sharp }_I(n)+E(n)$
, where
$\Lambda ^{\sharp }(n)=\Lambda ^{\sharp }_I(n)+E(n)$
, where
![]() $\Lambda ^{\sharp }_I$
is a
$\Lambda ^{\sharp }_I$
is a
![]() $((\log X)^{O(1)},X^{\varepsilon })$
type I sum and
$((\log X)^{O(1)},X^{\varepsilon })$
type I sum and
![]() $\sum _{X<n\leq X+H}|E(n)|\ll _A H\log ^{-A}X$
, the claim follows from the type I estimate in [Reference Matomäki and Shao49, Proposition 2.1].
$\sum _{X<n\leq X+H}|E(n)|\ll _A H\log ^{-A}X$
, the claim follows from the type I estimate in [Reference Matomäki and Shao49, Proposition 2.1].
Proof of Theorem 1.6.
First, note that, since
![]() $\log p=(1+o(1))\log N$
for
$\log p=(1+o(1))\log N$
for
![]() $p\in (N,N+N^{\kappa }]$
and since the contribution of higher prime powers is negligible, we have
$p\in (N,N+N^{\kappa }]$
and since the contribution of higher prime powers is negligible, we have
Hence, it suffices to show that the right-hand side of equation (10.1) converges in
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
Let w be a large parameter (which we will eventually send to infinity), and let
![]() $W=\prod _{p\leq w}p$
. Let
$W=\prod _{p\leq w}p$
. Let
this is a function that has small Gowers norms over short intervals by Theorem 1.5.
We first claim that
Since the average over n in equation (10.2) is bounded, it is enough to show for all bounded
![]() $f_0:X\to \mathbb {C}$
that
$f_0:X\to \mathbb {C}$
that
To prove this, we first make the changes of variables
![]() $n'=n+N$
,
$n'=n+N$
,
![]() $x=T^my$
, with m arbitrary, and use the T-invariance of
$x=T^my$
, with m arbitrary, and use the T-invariance of
![]() $\mu $
to rewrite the left-hand side of equation (10.3) as
$\mu $
to rewrite the left-hand side of equation (10.3) as
where
![]() $\epsilon _{N}(n'):=\epsilon (n'+N)$
. Since
$\epsilon _{N}(n'):=\epsilon (n'+N)$
. Since
![]() $f_i:X\to \mathbb {C}$
are bounded, we can appeal to the generalized von Neumann theorem in the form of [Reference Frantzikinakis, Host and Kra13, Lemma 2] (after embedding
$f_i:X\to \mathbb {C}$
are bounded, we can appeal to the generalized von Neumann theorem in the form of [Reference Frantzikinakis, Host and Kra13, Lemma 2] (after embedding
![]() $[N^{\kappa }]$
to
$[N^{\kappa }]$
to
![]() $\mathbb {Z}/M\mathbb {Z}$
for some
$\mathbb {Z}/M\mathbb {Z}$
for some
![]() $M\ll N^{\kappa }$
) to bound (10.4) as
$M\ll N^{\kappa }$
) to bound (10.4) as
where for the second estimate we used Theorem 1.5. Now, equation (10.2) has been proved. Then let
![]() $w'>w$
. By an argument identical to the proof of equation (10.2), but using in the end the fact that
$w'>w$
. By an argument identical to the proof of equation (10.2), but using in the end the fact that
![]() $\|\Lambda _{w}-\Lambda _{w'}\|_{U^k[N,N+N^{\kappa }]}=o_{w\to \infty }(1)$
(which follows from Theorem 1.5 and the triangle inequality, but could also be proved more directly), we see that also
$\|\Lambda _{w}-\Lambda _{w'}\|_{U^k[N,N+N^{\kappa }]}=o_{w\to \infty }(1)$
(which follows from Theorem 1.5 and the triangle inequality, but could also be proved more directly), we see that also
Consider now
This can be rewritten as
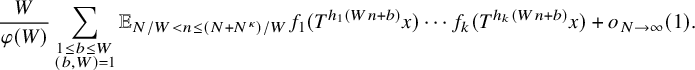 $$ \begin{align*}\frac{W}{\varphi(W)}\sum_{\substack{1\leq b\leq W\\(b,W)=1}}\mathbb{E}_{N/W< n\leq (N+N^{\kappa})/W}f_1(T^{h_1(Wn+b)}x)\cdots f_k(T^{h_k(Wn+b)}x)+o_{N\to \infty}(1). \end{align*} $$
$$ \begin{align*}\frac{W}{\varphi(W)}\sum_{\substack{1\leq b\leq W\\(b,W)=1}}\mathbb{E}_{N/W< n\leq (N+N^{\kappa})/W}f_1(T^{h_1(Wn+b)}x)\cdots f_k(T^{h_k(Wn+b)}x)+o_{N\to \infty}(1). \end{align*} $$
Since the sequence
![]() $((N/W,(N+N^{\kappa })/W])_N$
of intervals are translates of a Følner sequence, from [Reference Austin2, Theorem 1.1] it follows that there exists
$((N/W,(N+N^{\kappa })/W])_N$
of intervals are translates of a Følner sequence, from [Reference Austin2, Theorem 1.1] it follows that there exists
![]() $\phi _{w, b} \colon X \to \mathbb {C}$
such that
$\phi _{w, b} \colon X \to \mathbb {C}$
such that
Hence, there exists also
![]() $\phi _{w} \colon X \to \mathbb {C}$
such that
$\phi _{w} \colon X \to \mathbb {C}$
such that
By equation (10.5), for
![]() $w'>w$
we have
$w'>w$
we have
so the sequence
![]() $(\phi _w)_w$
is Cauchy in
$(\phi _w)_w$
is Cauchy in
![]() $L^2(\mu )$
. Let
$L^2(\mu )$
. Let
![]() $\phi \in L^2(\mu )$
be its limit. Then, denoting
$\phi \in L^2(\mu )$
be its limit. Then, denoting
from the triangle inequality and equations (10.2) and (10.6), we have
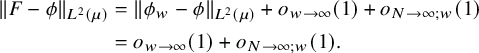 $$ \begin{align*} \|F -\phi\|_{L^{2}(\mu)}&=\|\phi_w -\phi\|_{L^{2}(\mu)}+o_{w\to \infty}(1)+o_{N\to \infty;w}(1)\\ &=o_{w\to \infty}(1)+o_{N\to \infty;w}(1). \end{align*} $$
$$ \begin{align*} \|F -\phi\|_{L^{2}(\mu)}&=\|\phi_w -\phi\|_{L^{2}(\mu)}+o_{w\to \infty}(1)+o_{N\to \infty;w}(1)\\ &=o_{w\to \infty}(1)+o_{N\to \infty;w}(1). \end{align*} $$
By sending
![]() $N, w\to \infty $
with w tending to
$N, w\to \infty $
with w tending to
![]() $\infty $
slowly enough and recalling equation (10.1), this proves the claim of Theorem 1.6, with the limit being
$\infty $
slowly enough and recalling equation (10.1), this proves the claim of Theorem 1.6, with the limit being
![]() $\phi $
.
$\phi $
.
For proving Theorem 1.7, we need the generalized von Neumann theorem, so we state here a version of it that is suitable for us.
Lemma 10.1 (Generalized von Neumann theorem).
Let Let
![]() $s,d,t,L\geq 1$
be fixed, and let D be large enough in terms of
$s,d,t,L\geq 1$
be fixed, and let D be large enough in terms of
![]() $s,d,t,L$
. Let
$s,d,t,L$
. Let
![]() $\nu $
be
$\nu $
be
![]() $(D,o_{N\to \infty }(1))$
-pseudorandom at location
$(D,o_{N\to \infty }(1))$
-pseudorandom at location
![]() $0$
and scale N, and let
$0$
and scale N, and let
![]() $f_1,\ldots , f_t:\mathbb {Z}\to \mathbb {R}$
satisfy
$f_1,\ldots , f_t:\mathbb {Z}\to \mathbb {R}$
satisfy
![]() $|f_i(x)|\leq \nu (x)$
for all
$|f_i(x)|\leq \nu (x)$
for all
![]() $i\in [t]$
and
$i\in [t]$
and
![]() $x\in [N]$
. Let
$x\in [N]$
. Let
![]() $\Psi =(\psi _1,\ldots , \psi _t)$
be a system of affine-linear forms with integer coefficients in s-normal form such that all the linear coefficients of
$\Psi =(\psi _1,\ldots , \psi _t)$
be a system of affine-linear forms with integer coefficients in s-normal form such that all the linear coefficients of
![]() $\psi _i$
are bounded by L in modulus and
$\psi _i$
are bounded by L in modulus and
![]() $|\psi _i(0)|\leq DN$
. Let
$|\psi _i(0)|\leq DN$
. Let
![]() $K\subset [-N,N]^d$
be a convex body with
$K\subset [-N,N]^d$
be a convex body with
![]() $\Psi (K)\subset (0,N]^d$
. Suppose that for some
$\Psi (K)\subset (0,N]^d$
. Suppose that for some
![]() $\delta>0$
we have
$\delta>0$
we have
Then we have
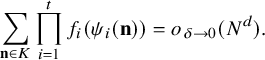 $$ \begin{align*} \sum_{\mathbf{n}\in K}\prod_{i=1}^tf_i(\psi_i(\mathbf{n}))=o_{\delta\to 0}(N^d). \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{n}\in K}\prod_{i=1}^tf_i(\psi_i(\mathbf{n}))=o_{\delta\to 0}(N^d). \end{align*} $$
Proof. Note that by Lemma 9.3 there exists a prime
![]() $N'\ll N$
such that we have a majorant for
$N'\ll N$
such that we have a majorant for
![]() $f_i$
on the cyclic group
$f_i$
on the cyclic group
![]() $\mathbb {Z}/N'\mathbb {Z}$
satisfying the
$\mathbb {Z}/N'\mathbb {Z}$
satisfying the
![]() $(D,D,D)$
-linear forms condition of [Reference Green and Tao17, Definition 6.2]. Then the claim follows from [Reference Green and Tao17, Proposition 7.1], observing that its proof only used the
$(D,D,D)$
-linear forms condition of [Reference Green and Tao17, Definition 6.2]. Then the claim follows from [Reference Green and Tao17, Proposition 7.1], observing that its proof only used the
![]() $(D,D,D)$
-linear forms condition of [Reference Green and Tao17, Definition 6.2] and not the correlation condition.
$(D,D,D)$
-linear forms condition of [Reference Green and Tao17, Definition 6.2] and not the correlation condition.
Proof of Theorem 1.7.
Let w be a sufficiently slowly growing function of X, and let
![]() $W=\prod _{p\leq w}p$
. Let
$W=\prod _{p\leq w}p$
. Let
![]() $\mathbf {N}=(X,\ldots , X)\in \mathbb {R}^d$
. We can write
$\mathbf {N}=(X,\ldots , X)\in \mathbb {R}^d$
. We can write
![]() $K=\mathbf {N}+K'$
, where
$K=\mathbf {N}+K'$
, where
![]() $K'\subset (0,H]^d$
is a convex body. Now, the sum (1.25) becomes
$K'\subset (0,H]^d$
is a convex body. Now, the sum (1.25) becomes
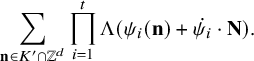 $$ \begin{align} \sum_{\mathbf{n}\in K'\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda(\psi_i( \mathbf{n})+\dot{\psi_i}\cdot \mathbf{N}). \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in K'\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda(\psi_i( \mathbf{n})+\dot{\psi_i}\cdot \mathbf{N}). \end{align} $$
Writing
![]() $\Lambda =\Lambda _w+(\Lambda -\Lambda _w)$
, this splits as the main term
$\Lambda =\Lambda _w+(\Lambda -\Lambda _w)$
, this splits as the main term
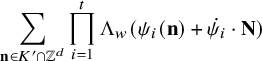 $$ \begin{align*} \sum_{\mathbf{n}\in K'\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda_w(\psi_i( \mathbf{n})+\dot{\psi_i}\cdot \mathbf{N}) \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{n}\in K'\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda_w(\psi_i( \mathbf{n})+\dot{\psi_i}\cdot \mathbf{N}) \end{align*} $$
and
![]() $2^t-1$
error terms
$2^t-1$
error terms
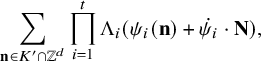 $$ \begin{align} \sum_{\mathbf{n}\in K'\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda_i(\psi_i( \mathbf{n})+\dot{\psi_i}\cdot \mathbf{N}), \end{align} $$
$$ \begin{align} \sum_{\mathbf{n}\in K'\cap \mathbb{Z}^d}\prod_{i=1}^t \Lambda_i(\psi_i( \mathbf{n})+\dot{\psi_i}\cdot \mathbf{N}), \end{align} $$
where
![]() $\Lambda _{i}\in \{\Lambda _w,\Lambda -\Lambda _w\}$
and at least one
$\Lambda _{i}\in \{\Lambda _w,\Lambda -\Lambda _w\}$
and at least one
![]() $\Lambda _i$
equals to
$\Lambda _i$
equals to
![]() $\Lambda -\Lambda _w$
. Following [Reference Green and Tao17, Section 5] verbatim, we see that the main term is
$\Lambda -\Lambda _w$
. Following [Reference Green and Tao17, Section 5] verbatim, we see that the main term is
Following [Reference Green and Tao17, Section 4], we may assume that the system of linear forms involved in equation (10.8) is in s-normal form for some
![]() $s\ll _D 1$
.
$s\ll _D 1$
.
We make the change of variables
![]() $\mathbf {n}=W\mathbf {m}+\mathbf {b}$
with
$\mathbf {n}=W\mathbf {m}+\mathbf {b}$
with
![]() $\mathbf {b}\in [0,W)^d$
in equation (10.8) and abbreviate
$\mathbf {b}\in [0,W)^d$
in equation (10.8) and abbreviate
![]() $M_{\mathbf {b},i}:=\dot {\psi _i}\cdot \mathbf {b}+\psi _i(0)$
to rewrite that sum as
$M_{\mathbf {b},i}:=\dot {\psi _i}\cdot \mathbf {b}+\psi _i(0)$
to rewrite that sum as
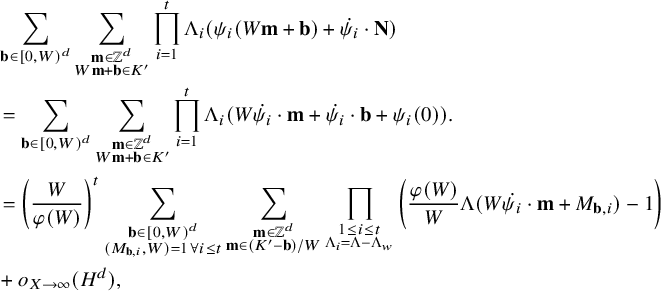 $$ \begin{align}&\sum_{\mathbf{b}\in [0,W)^d} \sum_{\substack{\mathbf{m}\in \mathbb{Z}^d\\W\mathbf{m}+\mathbf{b}\in K'}}\prod_{i=1}^t \Lambda_i(\psi_i(W \mathbf{m}+\mathbf{b})+\dot{\psi_i}\cdot \mathbf{N})\nonumber\\&=\sum_{\mathbf{b}\in [0,W)^d} \sum_{\substack{\mathbf{m}\in \mathbb{Z}^d\\W\mathbf{m}+\mathbf{b}\in K'}}\prod_{i=1}^t \Lambda_i(W\dot{\psi_i}\cdot \mathbf{m}+\dot{\psi_i}\cdot \mathbf{b}+\psi_i(0)).\nonumber\\[-14pt] \nonumber\\&=\left(\frac{W}{\varphi(W)}\right)^{t}\sum_{\substack{\mathbf{b}\in [0,W)^d\\(M_{\mathbf{b},i},W)=1\,\forall i\leq t}} \sum_{\substack{\mathbf{m}\in \mathbb{Z}^d\\\mathbf{m}\in (K'-\mathbf{b})/W}}\prod_{\substack{1\leq i\leq t\\\Lambda_i=\Lambda-\Lambda_w}} \left(\frac{\varphi(W)}{W}\Lambda(W\dot{\psi_i}\cdot \mathbf{m}+M_{\mathbf{b},i})-1\right)\nonumber\\&+o_{X\to \infty}(H^d), \end{align} $$
$$ \begin{align}&\sum_{\mathbf{b}\in [0,W)^d} \sum_{\substack{\mathbf{m}\in \mathbb{Z}^d\\W\mathbf{m}+\mathbf{b}\in K'}}\prod_{i=1}^t \Lambda_i(\psi_i(W \mathbf{m}+\mathbf{b})+\dot{\psi_i}\cdot \mathbf{N})\nonumber\\&=\sum_{\mathbf{b}\in [0,W)^d} \sum_{\substack{\mathbf{m}\in \mathbb{Z}^d\\W\mathbf{m}+\mathbf{b}\in K'}}\prod_{i=1}^t \Lambda_i(W\dot{\psi_i}\cdot \mathbf{m}+\dot{\psi_i}\cdot \mathbf{b}+\psi_i(0)).\nonumber\\[-14pt] \nonumber\\&=\left(\frac{W}{\varphi(W)}\right)^{t}\sum_{\substack{\mathbf{b}\in [0,W)^d\\(M_{\mathbf{b},i},W)=1\,\forall i\leq t}} \sum_{\substack{\mathbf{m}\in \mathbb{Z}^d\\\mathbf{m}\in (K'-\mathbf{b})/W}}\prod_{\substack{1\leq i\leq t\\\Lambda_i=\Lambda-\Lambda_w}} \left(\frac{\varphi(W)}{W}\Lambda(W\dot{\psi_i}\cdot \mathbf{m}+M_{\mathbf{b},i})-1\right)\nonumber\\&+o_{X\to \infty}(H^d), \end{align} $$
where the error term comes from the contribution of integers in the support of
![]() $\Lambda $
that are not w-rough.
$\Lambda $
that are not w-rough.
By Theorem 1.5(i), uniformly for integers
![]() $1\leq M\leq X$
with
$1\leq M\leq X$
with
![]() $(M,W)=1$
we have
$(M,W)=1$
we have
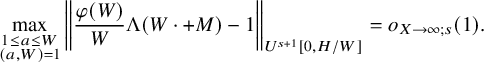 $$ \begin{align*} \max_{\substack{1\leq a\leq W\\(a,W)=1}}\left\|\frac{\varphi(W)}{W}\Lambda(W\cdot+M)-1\right\|_{U^{s+1}[0,H/W]}=o_{X\to \infty;s}(1). \end{align*} $$
$$ \begin{align*} \max_{\substack{1\leq a\leq W\\(a,W)=1}}\left\|\frac{\varphi(W)}{W}\Lambda(W\cdot+M)-1\right\|_{U^{s+1}[0,H/W]}=o_{X\to \infty;s}(1). \end{align*} $$
Moreover, by Lemma 9.6 the function
![]() $\frac {\varphi (W)}{W}\Lambda (W\cdot +M)-1$
is majorized by a
$\frac {\varphi (W)}{W}\Lambda (W\cdot +M)-1$
is majorized by a
![]() $(D,o_{X\to \infty }(1))$
-pseudorandom measure
$(D,o_{X\to \infty }(1))$
-pseudorandom measure
![]() $\nu _{M}$
at location
$\nu _{M}$
at location
![]() $0$
and scale
$0$
and scale
![]() $H/W$
for any fixed
$H/W$
for any fixed
![]() $D\geq 1$
. Hence, applying the generalized von Neumann theorem (Lemma 10.1, with
$D\geq 1$
. Hence, applying the generalized von Neumann theorem (Lemma 10.1, with
![]() $\nu =\frac {1}{t}\sum _{i\leq t}\nu _{M_{\mathbf {b},i}}$
), we conclude that equation (10.9) is
$\nu =\frac {1}{t}\sum _{i\leq t}\nu _{M_{\mathbf {b},i}}$
), we conclude that equation (10.9) is
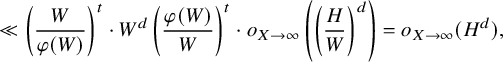 $$ \begin{align*} \ll \left(\frac{W}{\varphi(W)}\right)^t\cdot W^d\left(\frac{\varphi(W)}{W}\right)^t \cdot o_{X\to \infty}\left(\left(\frac{H}{W}\right)^d\right)=o_{X\to \infty}(H^d),\end{align*} $$
$$ \begin{align*} \ll \left(\frac{W}{\varphi(W)}\right)^t\cdot W^d\left(\frac{\varphi(W)}{W}\right)^t \cdot o_{X\to \infty}\left(\left(\frac{H}{W}\right)^d\right)=o_{X\to \infty}(H^d),\end{align*} $$
completing the proof.
Proof of Corollary 1.9.
This follows directly from Theorem 1.7 since the assumptions imply that
![]() $\beta _p>0$
for all p, and on the other hand
$\beta _p>0$
for all p, and on the other hand
![]() $\beta _p=1+O_{t,d,L}(1/p^2)$
by [Reference Green and Tao17, Lemmas 1.3 and 1.6], so we have
$\beta _p=1+O_{t,d,L}(1/p^2)$
by [Reference Green and Tao17, Lemmas 1.3 and 1.6], so we have
![]() $\prod _{p}\beta _p>0$
.
$\prod _{p}\beta _p>0$
.
A Variants of the main result
In this appendix, we discuss in more detail the variants of the main results described in Remark 1.4.
A.1 Results for the Liouville function
It is an easy matter to replace the Möbius function
![]() $\mu $
by the Liouville function
$\mu $
by the Liouville function
![]() $\lambda $
in our main results:
$\lambda $
in our main results:
Proposition A.1. The results in Theorem 1.1(i), (iv) (and hence also Corollary 1.3(i), (iv)) continue to hold if
![]() $\mu $
is replaced by
$\mu $
is replaced by
![]() $\lambda $
.
$\lambda $
.
Proof. We illustrate the argument for the estimate (1.5), as the other estimates are proven similarly. Under the hypotheses of Theorem 1.1(i), we wish to show that
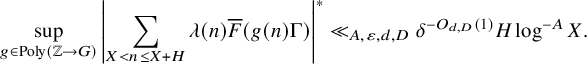 $$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \lambda(n) \overline{F}(g(n)\Gamma) \right|}^* \ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X.\end{align*} $$
$$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \lambda(n) \overline{F}(g(n)\Gamma) \right|}^* \ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X.\end{align*} $$
Writing
![]() $\lambda (n) = \sum _{m \leq \sqrt {2X}: m^2|n} \mu (n/m^2)$
for
$\lambda (n) = \sum _{m \leq \sqrt {2X}: m^2|n} \mu (n/m^2)$
for
![]() $n \leq 2X$
and using the triangle inequality, we can bound the left-hand side by
$n \leq 2X$
and using the triangle inequality, we can bound the left-hand side by
 $$ \begin{align*}\sum_{m \leq \sqrt{2X}} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X/m^2 < n \leq X/m^2+H/m^2} \mu(n) \overline{F}(g(m^2 n)\Gamma) \right|}^*.\end{align*} $$
$$ \begin{align*}\sum_{m \leq \sqrt{2X}} \sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X/m^2 < n \leq X/m^2+H/m^2} \mu(n) \overline{F}(g(m^2 n)\Gamma) \right|}^*.\end{align*} $$
If
![]() $m \leq X^{\varepsilon /10}$
(say), then by Theorem 1.1(i) (with
$m \leq X^{\varepsilon /10}$
(say), then by Theorem 1.1(i) (with
![]() $X, H, g$
replaced by
$X, H, g$
replaced by
![]() $X/m^2$
,
$X/m^2$
,
![]() $H/m^2$
,
$H/m^2$
,
![]() $g(m^2 \cdot )$
, and
$g(m^2 \cdot )$
, and
![]() $\varepsilon $
reduced slightly) we have
$\varepsilon $
reduced slightly) we have
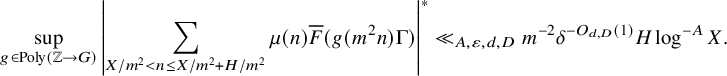 $$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X/m^2 < n \leq X/m^2+H/m^2} \mu(n) \overline{F}(g(m^2 n)\Gamma) \right|}^* \ll_{A,\varepsilon,d,D} m^{-2} \delta^{-O_{d,D}(1)} H \log^{-A} X.\end{align*} $$
$$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X/m^2 < n \leq X/m^2+H/m^2} \mu(n) \overline{F}(g(m^2 n)\Gamma) \right|}^* \ll_{A,\varepsilon,d,D} m^{-2} \delta^{-O_{d,D}(1)} H \log^{-A} X.\end{align*} $$
For
![]() $X^{\varepsilon /10} < m \ll \sqrt {X}$
, we simply use the triangle inequality and the trivial bound
$X^{\varepsilon /10} < m \ll \sqrt {X}$
, we simply use the triangle inequality and the trivial bound
![]() $|\overline {F}(g(n)\Gamma )| \leq 1/\delta $
to conclude
$|\overline {F}(g(n)\Gamma )| \leq 1/\delta $
to conclude
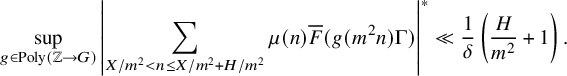 $$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X/m^2 < n \leq X/m^2+H/m^2} \mu(n) \overline{F}(g(m^2 n)\Gamma) \right|}^* \ll \frac{1}{\delta} \left( \frac{H}{m^2} + 1 \right).\end{align*} $$
$$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X/m^2 < n \leq X/m^2+H/m^2} \mu(n) \overline{F}(g(m^2 n)\Gamma) \right|}^* \ll \frac{1}{\delta} \left( \frac{H}{m^2} + 1 \right).\end{align*} $$
Summing in m, we obtain the claim after a brief calculation (since H is significantly larger than
![]() $X^{1/2}$
).
$X^{1/2}$
).
A.2 Results for the indicator function of the primes
It is also easy to replace the von Mangoldt function
![]() $\Lambda $
with the indicator function
$\Lambda $
with the indicator function
![]() $1_{\mathcal P}$
of the primes
$1_{\mathcal P}$
of the primes
![]() ${\mathcal P}$
:
${\mathcal P}$
:
Proposition A.2. The results in Theorem 1.1(ii) (and hence also Corollary 1.3(ii)) continue to hold if
![]() $\Lambda $
is replaced by
$\Lambda $
is replaced by
![]() $1_{\mathcal P}$
, and
$1_{\mathcal P}$
, and
![]() $\Lambda ^\sharp (n)$
is replaced by
$\Lambda ^\sharp (n)$
is replaced by
![]() $\frac {1}{\log n} \Lambda ^\sharp (n)$
.
$\frac {1}{\log n} \Lambda ^\sharp (n)$
.
Proof. From equation (1.6) and Lemma 2.2(iii), we have
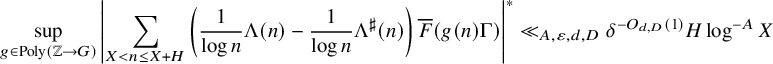 $$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \left(\frac{1}{\log n} \Lambda(n) - \frac{1}{\log n} \Lambda^\sharp(n)\right) \overline{F}(g(n)\Gamma) \right|}^* \ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X\end{align*} $$
$$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} \left(\frac{1}{\log n} \Lambda(n) - \frac{1}{\log n} \Lambda^\sharp(n)\right) \overline{F}(g(n)\Gamma) \right|}^* \ll_{A,\varepsilon,d,D} \delta^{-O_{d,D}(1)} H \log^{-A} X\end{align*} $$
and so by the triangle inequality it will suffice to show that
 $$ \begin{align*}\sum_{X < n \leq X+H} \left| 1_{\mathcal P}(n) - \frac{1}{\log n} \Lambda(n)\right| \ll_{A} H \log^{-A} X.\end{align*} $$
$$ \begin{align*}\sum_{X < n \leq X+H} \left| 1_{\mathcal P}(n) - \frac{1}{\log n} \Lambda(n)\right| \ll_{A} H \log^{-A} X.\end{align*} $$
But the summand is supported on prime powers
![]() $p^j$
with
$p^j$
with
![]() $2 \leq j \ll \log X$
and
$2 \leq j \ll \log X$
and
![]() $p \ll \sqrt {X}$
, so there are at most
$p \ll \sqrt {X}$
, so there are at most
![]() $O( \sqrt {X} \log X )$
terms, each of which gives a contribution of
$O( \sqrt {X} \log X )$
terms, each of which gives a contribution of
![]() $O(1)$
. Since H is significantly larger than
$O(1)$
. Since H is significantly larger than
![]() $X^{1/2}$
, the claim follows.
$X^{1/2}$
, the claim follows.
A.3 Results for the counting function of sums of two squares
It is a classical fact that the counting function

can be factorized as
![]() $r_2(n) = 4 (1 * \chi _4)(n)$
, where
$r_2(n) = 4 (1 * \chi _4)(n)$
, where
![]() $\chi _4$
is the nonprincipal Dirichlet character of modulus
$\chi _4$
is the nonprincipal Dirichlet character of modulus
![]() $4$
. This is formally very similar to the divisor function
$4$
. This is formally very similar to the divisor function
![]() $d_2(n) = (1*1)(n)$
. In this paper, we use the Dirichlet hyperbola method to expand
$d_2(n) = (1*1)(n)$
. In this paper, we use the Dirichlet hyperbola method to expand
![]() $d_2(n)$
for
$d_2(n)$
for
![]() $X < n \leq X+H$
as
$X < n \leq X+H$
as
 $$ \begin{align*}d_2(n) = \sum_{\substack{R_2 \leq n_1 \leq n/R_2\\ n_1\mid n}} 1 + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 2\end{align*} $$
$$ \begin{align*}d_2(n) = \sum_{\substack{R_2 \leq n_1 \leq n/R_2\\ n_1\mid n}} 1 + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 2\end{align*} $$
with
and approximate this function by the type I sum
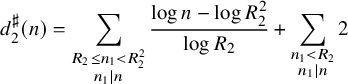 $$ \begin{align*}d_2^\sharp(n) = \sum_{\substack{R_2 \leq n_1 < R_2^2\\ n_1\mid n}} \frac{\log n - \log R_2^2}{\log R_2} + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 2\end{align*} $$
$$ \begin{align*}d_2^\sharp(n) = \sum_{\substack{R_2 \leq n_1 < R_2^2\\ n_1\mid n}} \frac{\log n - \log R_2^2}{\log R_2} + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 2\end{align*} $$
(these are the
![]() $k=2$
cases of equations (3.15), (1.2), respectively). In a similar vein, we can expand
$k=2$
cases of equations (3.15), (1.2), respectively). In a similar vein, we can expand
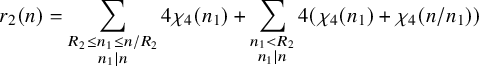 $$ \begin{align*}r_2(n) = \sum_{\substack{R_2 \leq n_1 \leq n/R_2\\ n_1\mid n}} 4 \chi_4(n_1) + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 4(\chi_4(n_1) + \chi_4(n/n_1))\end{align*} $$
$$ \begin{align*}r_2(n) = \sum_{\substack{R_2 \leq n_1 \leq n/R_2\\ n_1\mid n}} 4 \chi_4(n_1) + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 4(\chi_4(n_1) + \chi_4(n/n_1))\end{align*} $$
and then introduce the twisted type I approximant
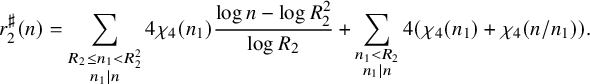 $$ \begin{align*}r_2^\sharp(n) = \sum_{\substack{R_2 \leq n_1 < R_2^2\\ n_1\mid n}} 4 \chi_4(n_1) \frac{\log n - \log R_2^2}{\log R_2} + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 4(\chi_4(n_1) + \chi_4(n/n_1)).\end{align*} $$
$$ \begin{align*}r_2^\sharp(n) = \sum_{\substack{R_2 \leq n_1 < R_2^2\\ n_1\mid n}} 4 \chi_4(n_1) \frac{\log n - \log R_2^2}{\log R_2} + \sum_{\substack{n_1 < R_2\\ n_1\mid n}} 4(\chi_4(n_1) + \chi_4(n/n_1)).\end{align*} $$
We then have
Proposition A.3. The
![]() $k=2$
results in Theorem 1.1(iii) continue to hold if
$k=2$
results in Theorem 1.1(iii) continue to hold if
![]() $d_2, d_2^\sharp $
are replaced by
$d_2, d_2^\sharp $
are replaced by
![]() $r_2$
,
$r_2$
,
![]() $r_2^\sharp $
, respectively.
$r_2^\sharp $
, respectively.
This proposition is established by repeating the arguments used to establish Theorem 1.1(iii) but by inserting ‘twists’ by the character
![]() $\chi _4$
at various junctures. However, such twists are quite harmless (for instance, since
$\chi _4$
at various junctures. However, such twists are quite harmless (for instance, since
![]() $\|\chi _4\|_{{\operatorname {TV}}(P;4)} \ll 1$
for any arithmetic progression P, Proposition 2.2(iii) allows one to insert this character into maximal sum estimates without difficulty), and there is no difficulty in modifying the arguments to accommodate this twist.
$\|\chi _4\|_{{\operatorname {TV}}(P;4)} \ll 1$
for any arithmetic progression P, Proposition 2.2(iii) allows one to insert this character into maximal sum estimates without difficulty), and there is no difficulty in modifying the arguments to accommodate this twist.
A.4 Potential result for the indicator function of the sums of two squares
Let
![]() $S = \{ n^2+m^2: n,m \in \mathbb {Z}\}$
be the set of numbers representable as sums of two squares. The Dirichlet series for S is equal to
$S = \{ n^2+m^2: n,m \in \mathbb {Z}\}$
be the set of numbers representable as sums of two squares. The Dirichlet series for S is equal to
![]() $\zeta (s)^{1/2} L(s,\chi _4)^{1/2}$
times a holomorphic function near
$\zeta (s)^{1/2} L(s,\chi _4)^{1/2}$
times a holomorphic function near
![]() $s=1$
and in particular extends into the classical zero-free region after making a branch cut to the left of
$s=1$
and in particular extends into the classical zero-free region after making a branch cut to the left of
![]() $s=1$
on the real axis.
$s=1$
on the real axis.
By a standard Perron formula calculation, one can then obtain asymptotics of the form
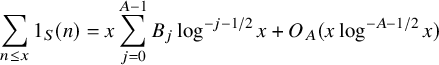 $$ \begin{align*}\sum_{n \leq x} 1_S(n) = x \sum_{j=0}^{A-1} B_{j} \log^{-j-1/2} x + O_A( x \log^{-A-1/2} x )\end{align*} $$
$$ \begin{align*}\sum_{n \leq x} 1_S(n) = x \sum_{j=0}^{A-1} B_{j} \log^{-j-1/2} x + O_A( x \log^{-A-1/2} x )\end{align*} $$
for any
![]() $A>0$
and some real constants
$A>0$
and some real constants
![]() $B_j$
which are in principle explicitly computable; see, for instance, [Reference de la Bretèche and Tenenbaum7, Theorem 1.1] for a recent treatment (in significantly greater generality) using the Selberg–Delange method. Similar calculations give asymptotics of the form
$B_j$
which are in principle explicitly computable; see, for instance, [Reference de la Bretèche and Tenenbaum7, Theorem 1.1] for a recent treatment (in significantly greater generality) using the Selberg–Delange method. Similar calculations give asymptotics of the form
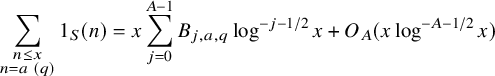 $$ \begin{align*}\sum_{\substack{n \leq x\\ n = a\ (q)}} 1_S(n) = x \sum_{j=0}^{A-1} B_{j,a,q} \log^{-j-1/2} x + O_A( x \log^{-A-1/2} x )\end{align*} $$
$$ \begin{align*}\sum_{\substack{n \leq x\\ n = a\ (q)}} 1_S(n) = x \sum_{j=0}^{A-1} B_{j,a,q} \log^{-j-1/2} x + O_A( x \log^{-A-1/2} x )\end{align*} $$
for any fixed residue class
![]() $a\ (q)$
and some further real constants
$a\ (q)$
and some further real constants
![]() $B_{j,a,q}$
. With further effort, one can also localize such estimates to intervals
$B_{j,a,q}$
. With further effort, one can also localize such estimates to intervals
![]() $\{ X < n \leq X+H \}$
with H not too small (e.g.,
$\{ X < n \leq X+H \}$
with H not too small (e.g.,
![]() $H = X^{5/8+\varepsilon }$
or
$H = X^{5/8+\varepsilon }$
or
![]() $H = X^{7/12+\varepsilon }$
).
$H = X^{7/12+\varepsilon }$
).
This suggests the existence of an approximant
![]() $1_S^{\sharp ,A}$
for any given accuracy
$1_S^{\sharp ,A}$
for any given accuracy
![]() $A> 0$
that is well approximated by type I sums, and is such that one has the major arc estimate
$A> 0$
that is well approximated by type I sums, and is such that one has the major arc estimate
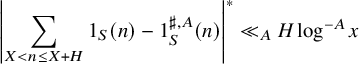 $$ \begin{align*}{\left|\sum_{X < n \leq X+H} 1_S(n) - 1_S^{\sharp,A}(n) \right|}^* \ll_A H \log^{-A} x\end{align*} $$
$$ \begin{align*}{\left|\sum_{X < n \leq X+H} 1_S(n) - 1_S^{\sharp,A}(n) \right|}^* \ll_A H \log^{-A} x\end{align*} $$
(cf. Theorem 3.1). For small A, it seems likely that one could construct
![]() $1_S^{\sharp ,A}$
by a variant of the Cramér–Granville construction used to form
$1_S^{\sharp ,A}$
by a variant of the Cramér–Granville construction used to form
![]() $\Lambda ^\sharp $
; but for large A it appears that the approximant is more difficult to construct (for instance, one may have to use Fourier-analytic methods such as the delta method). However, once such an approximant is constructed, we conjecture that the methods of this paper will produce analogues of Theorem 1.1(ii) (and hence also of Corollary 1.3(ii)) if
$\Lambda ^\sharp $
; but for large A it appears that the approximant is more difficult to construct (for instance, one may have to use Fourier-analytic methods such as the delta method). However, once such an approximant is constructed, we conjecture that the methods of this paper will produce analogues of Theorem 1.1(ii) (and hence also of Corollary 1.3(ii)) if
![]() $\Lambda , \Lambda ^\sharp $
are replaced by
$\Lambda , \Lambda ^\sharp $
are replaced by
![]() $1_S, 1_S^{\sharp ,A'}$
respectively, with
$1_S, 1_S^{\sharp ,A'}$
respectively, with
![]() $A'$
sufficiently large depending on A. The main point is that a satisfactory analogue of the Heath-Brown decompositions in Lemma 2.16 for
$A'$
sufficiently large depending on A. The main point is that a satisfactory analogue of the Heath-Brown decompositions in Lemma 2.16 for
![]() $1_{S}$
is known; see [Reference Shao and Teräväinen59, Lemma 7.2].
$1_{S}$
is known; see [Reference Shao and Teräväinen59, Lemma 7.2].
We do not foresee any significant technical issues with the remaining portions of the argument, though of course one would need to define the approximant
![]() $1_S^{\sharp , A}$
more precisely before one could say with certainty that the portions of the argument involving this approximant continue to be valid.
$1_S^{\sharp , A}$
more precisely before one could say with certainty that the portions of the argument involving this approximant continue to be valid.
A.5 Potential result for the indicator function of smooth numbers
Let
![]() $0 < \eta < \frac {1}{2}$
, let X be large, and let
$0 < \eta < \frac {1}{2}$
, let X be large, and let
![]() $S_\eta $
denote the set of
$S_\eta $
denote the set of
![]() $X^\eta $
-smooth integers, that is to say those numbers whose prime factors are all less than
$X^\eta $
-smooth integers, that is to say those numbers whose prime factors are all less than
![]() $X^\eta $
. Let
$X^\eta $
. Let
![]() $H \geq X^{\theta +\varepsilon }$
with
$H \geq X^{\theta +\varepsilon }$
with
![]() . As is well-known, the density of
. As is well-known, the density of
![]() $S_\eta $
in
$S_\eta $
in
![]() $[X,X+H]$
is asymptotic to the Dickman function
$[X,X+H]$
is asymptotic to the Dickman function
![]() $\rho (1/\eta )$
evaluated at
$\rho (1/\eta )$
evaluated at
![]() $1/\eta $
. We conjecture that the methods of this paper can be used to establish a bound of the form
$1/\eta $
. We conjecture that the methods of this paper can be used to establish a bound of the form
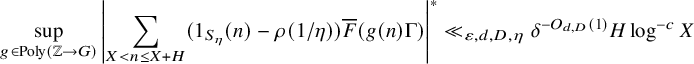 $$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} (1_{S_\eta}(n) - \rho(1/\eta)) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D,\eta} \delta^{-O_{d,D}(1)} H \log^{-c} X\end{align*} $$
$$ \begin{align*}\sup_{g \in {\operatorname{Poly}}(\mathbb{Z} \to G)} {\left| \sum_{X < n \leq X+H} (1_{S_\eta}(n) - \rho(1/\eta)) \overline{F}(g(n)\Gamma) \right|}^* \ll_{\varepsilon,d,D,\eta} \delta^{-O_{d,D}(1)} H \log^{-c} X\end{align*} $$
for some absolute constant
![]() $c>0$
under the hypotheses of Theorem 1.1.
$c>0$
under the hypotheses of Theorem 1.1.
Indeed, a Heath-Brown type decomposition, involving only
![]() $(1, x^{1/2-\eta }, x^{1/2})$
type II sums and a (somewhat) small exceptional set, was constructed in [Reference Klurman, Mangerel and Teräväinen40, Lemma 11.5]; the exceptional set was only shown to be small on long intervals such as
$(1, x^{1/2-\eta }, x^{1/2})$
type II sums and a (somewhat) small exceptional set, was constructed in [Reference Klurman, Mangerel and Teräväinen40, Lemma 11.5]; the exceptional set was only shown to be small on long intervals such as
![]() $[1,X]$
in that paper, but it is likely that one can show the set to also be small on the shorter interval
$[1,X]$
in that paper, but it is likely that one can show the set to also be small on the shorter interval
![]() $\{ X < n \leq X+H\}$
.
$\{ X < n \leq X+H\}$
.
There are, however, some further technical difficulties in implementing our methods here. The first (and less serious) issue is that one would need to verify that the type II sums
![]() $f(n)$
produced by [Reference Klurman, Mangerel and Teräväinen40, Lemma 11.5] obey the bound (4.9); we believe that this is likely to be achievable after some computation. The second and more significant difficulty is that one would need an approximant
$f(n)$
produced by [Reference Klurman, Mangerel and Teräväinen40, Lemma 11.5] obey the bound (4.9); we believe that this is likely to be achievable after some computation. The second and more significant difficulty is that one would need an approximant
![]() $1_{S_\eta }^\sharp $
obeying a major arc estimate of the shape
$1_{S_\eta }^\sharp $
obeying a major arc estimate of the shape
 $$ \begin{align*}{\left|\sum_{X < n \leq X+H} 1_{S_\eta}(n) - 1^\sharp_{S_\eta}(n) \right|}^* \ll_A H \log^{-A} X\end{align*} $$
$$ \begin{align*}{\left|\sum_{X < n \leq X+H} 1_{S_\eta}(n) - 1^\sharp_{S_\eta}(n) \right|}^* \ll_A H \log^{-A} X\end{align*} $$
for any
![]() $A>0$
(possibly after removing a small exceptional set from
$A>0$
(possibly after removing a small exceptional set from
![]() $S_\eta $
), in the spirit of Theorem 3.1 and Corollary 3.10.
$S_\eta $
), in the spirit of Theorem 3.1 and Corollary 3.10.
The constant
![]() $\rho (1/\eta )$
is an obvious candidate for such an approximant, but unfortunately such an estimate is only valid for small values of A; see [Reference Hildebrand and Tenenbaum31, Theorem 1.8]. Thus, as in the previous discussion for the indicator of the sums of two squares, a more complicated approximant is likely to be required; the function
$\rho (1/\eta )$
is an obvious candidate for such an approximant, but unfortunately such an estimate is only valid for small values of A; see [Reference Hildebrand and Tenenbaum31, Theorem 1.8]. Thus, as in the previous discussion for the indicator of the sums of two squares, a more complicated approximant is likely to be required; the function
![]() $\Lambda (x,y)$
appearing in [Reference Hildebrand and Tenenbaum31, Theorem 1.8] will most likely become involved. See also [Reference Matthiesen and Wang53] for some recent estimates on the distribution of smooth numbers in short intervals or arithmetic progressions (in a slightly different regime in which the
$\Lambda (x,y)$
appearing in [Reference Hildebrand and Tenenbaum31, Theorem 1.8] will most likely become involved. See also [Reference Matthiesen and Wang53] for some recent estimates on the distribution of smooth numbers in short intervals or arithmetic progressions (in a slightly different regime in which the
![]() $X^\eta $
threshold for smoothness is replaced by a smaller quantity).
$X^\eta $
threshold for smoothness is replaced by a smaller quantity).
Acknowledgments
We are greatly indebted to Maksym Radziwiłł for many helpful discussions during the course of this project and would like to thank Lilian Matthiesen for discussions concerning [Reference Matthiesen51]. We are grateful to the anonymous referee for a careful reading of the paper and for numerous helpful comments and corrections.
Competing interest
The authors have no competing interest to declare.
Financial support
KM was supported by Academy of Finland grant no. 285894. XS was supported by NSF grant DMS-1802224. TT was supported by a Simons Investigator grant, the James and Carol Collins Chair, the Mathematical Analysis & Application Research Fund Endowment, and by NSF grant DMS-1764034. JT was supported by a Titchmarsh Fellowship, Academy of Finland grant no. 340098, and funding from European Union’s Horizon Europe research and innovation programme under Marie Skłodowska-Curie grant agreement No 101058904.