Article contents
ENUMERATION OF MEANDERS AND MASUR–VEECH VOLUMES
Published online by Cambridge University Press: 23 March 2020
Abstract
A meander is a topological configuration of a line and a simple closed curve in the plane (or a pair of simple closed curves on the 2-sphere) intersecting transversally. Meanders can be traced back to H. Poincaré and naturally appear in various areas of mathematics, theoretical physics and computational biology (in particular, they provide a model of polymer folding). Enumeration of meanders is an important open problem. The number of meanders with 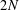 $2N$ crossings grows exponentially when
$2N$ crossings grows exponentially when 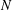 $N$ grows, but the long-standing problem on the precise asymptotics is still out of reach.
$N$ grows, but the long-standing problem on the precise asymptotics is still out of reach.
We show that the situation becomes more tractable if one additionally fixes the topological type (or the total number of minimal arcs) of a meander. Then we are able to derive simple asymptotic formulas for the numbers of meanders as 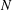 $N$ tends to infinity. We also compute the asymptotic probability of getting a simple closed curve on a sphere by identifying the endpoints of two arc systems (one on each of the two hemispheres) along the common equator.
$N$ tends to infinity. We also compute the asymptotic probability of getting a simple closed curve on a sphere by identifying the endpoints of two arc systems (one on each of the two hemispheres) along the common equator.
The new tools we bring to bear are based on interpretation of meanders as square-tiled surfaces with one horizontal and one vertical cylinder. The proofs combine recent results on Masur–Veech volumes of moduli spaces of meromorphic quadratic differentials in genus zero with our new observation that horizontal and vertical separatrix diagrams of integer quadratic differentials are asymptotically uncorrelated. The additional combinatorial constraints we impose in this article yield explicit polynomial asymptotics.
- Type
- Topology
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
- Copyright
- © The Author(s) 2020
References
- 10
- Cited by



