Introduction
The flow of scientific information is increasing daily and is causing what could be considered a knowledge explosion crisis (e.g. Ref. Reference Sagasti and Acalde1). Dealing with this crisis requires not only methods that handle and make accessible huge amounts of information but also integrative theory that offers scaffolds to connect distant scientific fields. This study focuses on the role of the operator hierarchy as a scientific integration tool in the context of other integrative principles.
The knowledge explosion crisis is the result of science having a positive feedback on its own development. Science depends on our capacities as humans to observe the world, including ourselves, and to create mental representations of the observed phenomena. In turn, better representations increase our capacities to manipulate the world and to construct tools that improve our observations, which, in turn, accelerate scientific development. As the result of this process, scientific ideas have simultaneously developed extreme breadth and depth. The outcome is not only associated with overspecialisation and compartmentalisation, but also allows a development towards scientific integration on a cosmic scale. At any level between these extremes, a concept is more valuable when it is efficient, pairing minimum complexity with maximum precision and elegance. Arbitrage by these aspects has become known as ‘Ockham's razor’, cutting away the most complex and least elegant from any two theories explaining the same phenomenon. If theories describe different phenomena, arbitrage is less straightforward because different viewpoints may highlight different aspects of natural organisation. Considering the latter points, this paper analyses how the operator hierarchy may contribute to scientific integration while focusing on major integrative ideas, for example, the use of timelines, natural hierarchy and evolution. The paper ends with an overview of existing integrating theories and laws and the value of scientific integration. Because this theory is used as a common thread, this study begins with an introductive summary of the operator theory.
The operator hierarchy, a summary
The operator hierarchy is a methodology that deals specifically with the formation of complexity by means of emergence.Reference Jagers op Akkerhuis and van Straalen2–Reference Juarrero and Rubino5 The operator hierarchy ranks discrete steps in ‘particle’ complexity in a way that also implies a temporal ranking, because the organisation of complex ‘particles’ is always preceded by that of less complex ones.
To explain this approach, it is useful to start with a fundamental assumption that lies behind the operator hierarchy, namely that nature must be analysed according to three fundamental dimensions for organisational complexity: the upward, the inward and the outward dimension.
The upward dimension involves the transitions from lower level ‘particles’ to higher level ‘particles’ (Figure 1). A chemical example is the transition from atoms to molecules. A biological example is the formation of the eukaryotic cell from two bacterial cells. The ranking in this dimension includes fundamental particles, hadrons, atoms, molecules and continues with bacteria, endosymbionts, multicellulars (which may be multicellular forms of bacteria or of endosymbionts) and multicellulars with neural networks. Because the ‘particles’ in this dimension include physical particles, chemical particles and organisms, they have been given a generic name: ‘operators’.Reference Jagers op Akkerhuis and van Straalen2, Reference Jagers op Akkerhuis3 Transitions towards higher level operators may result from interactions between lower level operators (e.g. from unicellular to multicellular), and may also result from internal differentiations (e.g. the engulfment of an endosymbiont in a eukaryotic cell and the formation of a neural network in a multicellular organism). The hierarchical ranking of the operators is called the operator hierarchy (Figure 2) and the related theory the operator theory.

Figure 1 Three independent dimensions for hierarchy in the organisation of nature: (1) the outward dimension for hierarchy in the organization of interaction systems (systems that consist of operators without being an operator); (2) the upward dimension for hierarchy in the way how lower level operators create higher level operators; and (3) the inward dimension for hierarchy in the internal organisation of operators. Only the hierarchical ranking of the operators is strict. All other hierarchies vary according to point of view, for example displacement, information, construction and energy.

Figure 2 This figure illustrates the evolution of the operators (the upward dimension). The black line shows the historical pathway of subsequent first-next possible closures and related operators. The grey columns indicate systems resulting from first-next possible closure but are not operators. Explanation of abbreviations: Memon = operator showing a hypercyclic neural network with interface, SAE (‘Structural Auto Evolution’) = the property of an operator to autonomously evolve the structure that carries its information, SCI (‘Structural Copying of Information’) = the property of an operator to autonomously copy its information (genes, learned knowledge) by simply copying part of its structure, HMI (Hypercycle Mediating interface) = a closure creates an interface that mediates the functioning of the hypercycle, Multi-state = operator showing closure between multiple units of exactly one lower closure level, Hypercycle = closure based on emergent, second order recurrent interactions. Interface = closure creating an emergent limit to an operator, CALM (Categorizing And Learning Module) = a minimum neural memory.
Secondly, the outward dimension involves the ways in which individual operators can create systems that consist of interacting operators but which are not operators. As they consist of interacting operators without showing the necessary properties to be recognised as an operator, such systems were named ‘interaction systems’, by Jagers op Akkerhuis and van Straalen.Reference Jagers op Akkerhuis and van Straalen2 Examples of interaction systems are hurricanes, waves, ecosystems, rivers, etc.
Thirdly, the inward dimension involves the interior organisation of operators. Here the focus is on the elements inside an operator, and if there are some, the elements in these elements, and so on. In abiotic operators, such as atom nuclei, atoms and molecules, the internal differentiation directly results from interactions based on condensation (from hadrons to nuclei, from nuclei and electrons to atoms, and from atoms to molecules). For organic operators TurchinReference Turchin6 has formulated the law of the branching growth of the penultimate level. This law states that ‘…after the formation, through variation and selection, of a control system C, controlling a number of subsystems Si, the Si will tend to multiply and differentiate’. This law explicitly recognises that only after the formation of a mechanism controlling the subsystems Si is there a context that allows the variety of the subsystems to increase. Accordingly, nature has had neither a context nor the means to develop organelles before cells or to develop organs and tissues before multicellular organisms. For this reason, including sub-systems such as organelles, tissues, organs and organ systems in the conventional natural hierarchy of systems is highly confusing.
The above dimensions capture independent directions for analysing natural organisation: a molecule, a prokaryotic cell, a eukaryotic cell and a multicellular organism can all be involved in ecosystem interactions and each of them shows internal organisation.
Unification Based on Timelines
After having explained the operator theory, the links are discussed with a range of unifying approaches. The first approach is the use of timelines. Systems can be organised by ranking them according to the moment of their first formation and the historical time period in which they existed. When analysing phenomena in this way, timelines at different scales are created that refer to, for example, palaeontology, particle physics, human history, the development of the automobile. These timelines also come in different forms, such as linear hierarchies and branching trees.
A modern timeline presenting a comprehensive overview of the organisation in nature is Big History.Reference Spier7–Reference Salthe and Fuhrman12 This approach ranks all systems and processes by their occurrence in cosmic history. Big History is based on the scientific theory that the early universe was as small as a fundamental particle and obtained its present size following a rapid expansion; the Big Bang. The theory that the universe has a minute origin is supported by modern particle physics and by cosmological observations of the background radiation and the proportionality with distance of the speed at which galaxies recede from the Earth in all directions.Reference Pagels13, Reference Weinberg14 Based on these observations, it has been calculated that Big History started about 13.7 billion years ago (Figure 3). During the universe's first three minutes, quarks formed and then condensed to form hadrons (such as protons and neutrons). During the following 17 minutes, the hadrons condensed to form simple helium nuclei (the combination of a proton and a neutron). After these initial minutes, it took about 70,000 years before the dynamic balance of the transformation of matter and energy toppled to the advantage of matter. The matter in the rapidly expanding universe now aggregated under the influence of gravity. The aggregation process was slow because gravity is weak at large distances. The result was a universe with a sponge-like structure of concentrations of matter surrounding empty ‘bubbles’ of variable size that were almost devoid of matter. After 100 million years of aggregation, the first galaxies and stars were formed and their light started illuminating the universe. The nuclear reactions in stars and supernovae supported the formation of elements heavier than helium. After approximately 9.1 billion years, the Sun was formed (4.57 years ago) and then planet Earth (4.54 billion years ago). Thereafter, it took about 1 billion years for the first life to emerge on Earth and another billion before cells gained the capacity of photosynthesis. Complex Ediacaran fauna has been found in rocks of about 600 million years old. Around 228 million years ago dinosaurs ruled the world. The first hominin fossils originate from approximately 7 million years ago. Human history dates back to several tens of thousands of years.

Figure 3 Universal timeline (modified from Wikipedia).
A universal timeline is a comprehensive integration tool. Its major strength is ranking all sorts of events simultaneously. Even though every event has only a single moment of occurrence, a timeline can flexibly adapt to variations in the moment of occurrence of similar events by indicating a first moment at which they occur and, assuming that such is known, a last moment. A universal timeline can thus be seen as a thickly woven cable of many threads representing local histories and developmental rates of different parts of the universe (Figure 3). Although all of these developmental threads unroll in different directions, they result in similar histories. Stars are formed everywhere in the observable universe and their formation roughly started at the same moment. Stars of the same class also consist of similar particles and atoms, and stars the size of the sun are probably circled by planets everywhere in the universe. One may now ask why there is so much uniformity in the universe and whether such uniformity may be used to answer questions about the future of the universe.
Unification Based on the Operator Hierarchy in Combination with a Cosmic Timeline
Above, it was explained how the operator theory recognises dimensions for organisation. It is time to return to the question of how these insights can assist in finding general laws in cosmic development. The answer to this question rests on separating the events along the cosmic timeline into two parallel tracks: the track of the operators and the track of the corresponding interaction systems.
Starting with the Big Bang, the history of the universe can, in principle, be modelled as a container full of interacting particles. Particles exert forces on each other and interact. This interaction forms new particles and accompanying new forces. During the universe's initial rapid expansion, the initial quark soup condensed to also contain simple helium nuclei. Condensation heat was radiated away into the large space of the universe. Simultaneously, the dispersed matter started aggregating due to the force of gravity. This created various celestial bodies, e.g. black holes, stars and planets. Nuclear reactions in stars then allowed helium to fuse to heavier elements, which were spread by stellar explosions. Under colder conditions, such as on planets, atoms condensed to form molecules. Models predicting the future of this process have been based on the total amount of matter, the gravitational constant, the expansion rate of the universe, and the life histories of celestial bodies. Although uncertainties exist about the values of certain parameters, such models generally predict the universe's heat death as the consequence of diluting matter in the vastness of an extremely large, cold space. In this formation sequence there is no logical position for organisms.
In comparison to the latter history of the universe, the operator theoryReference Jagers op Akkerhuis and van Straalen2–Reference Jagers op Akkerhuis4 may seem to focus on minor details when it introduces a strict ranking of all operators, from quarks, through hadrons, to atoms and molecules, prokaryote cells, eukaryote cells, prokaryote and eukaryote multicellular organisms and neural network organisms (referred to as ‘memons’) (Figure 2). Nevertheless, the use of first-next possible closure for ranking the operatorsReference Jagers op Akkerhuis4 strictly limits the sequential formation of the operators such that the result seems to reveal a form-law at a universal scale. The idea of a form-law is suggested by the observation that the sequence of first-next possible closures and related operators is not only strict, but also follows an internal regularity (Figure 2). The operator hierarchy thus seems to reflect a constructional form-law with three important unifying consequences.
A first unifying consequence of the operator theory, is that it implies that the limits set by first-next possible closure apply to all operators anywhere in the universe. Accordingly, the same classes of operators can be expected to exist anywhere in the universe as long as local conditions allow for their formation. After the uniform initial conditions in the universe ceased to exist, first-next possible closure rules offer an explanation for the uniformity of the structural developments in unconnected local parts of the universe.
A second unifying consequence is that the timeline of Big History can now be associated with the coming into existence of certain operators. The cosmic formation and aggregation of matter leads to celestial bodies, and these celestial bodies show their own life-cycles, e.g. from young stars, to supernovae, to white dwarfs and sometimes black holes. Phases in these life cycles show a link with the existence of certain types of operators. For example, individual quarks and hadrons only existed during the first second of the universe. Thereafter, atomic matter and molecules are associated with the formation and life-cycles of celestial bodies. Still later, the cell, endosymbiontic cell, multicellular and neural network organism, were linked with different phases in the life cycle of certain planets. If one now uses the most complex operator associated with a celestial body as a ranking criterion, one obtains a unified ranking that offers a structured way for organising Big History in relation to the operator theory. This ranking is discussed in more detail at the end of the next paragraph.
A third unifying consequence is that the operator theory can be extrapolated towards future operators, suggesting that the next operator will be a technical memon (the generalised concept for an operator with a neural network) owing its intelligence to a programmed neural network (see Ref. Reference Jagers op Akkerhuis3). This possibility for extrapolation is a unique property of the operator hierarchy. Both cosmology and Big History focus on the universe at large and offer no possibilities for predicting future operators.
Unification in Relation to Hierarchy and Ontology
Ontology is the study of what ‘is’ and aims at creating an organised categorisation for describing the world. Various theories have been developed for ranking systems. A classic example of a linear hierarchy that ranks system complexity is the ScalaNaturae of the Greek philosopher and naturalist Aristotle. In his approach, Aristotle ranks natural phenomena by decreasing perfection, from spiritual and divine beings to man, animals, plants and finally rocks and formless matter. This classification is also referred to as the Natural Ladder or the Great Chain of Being.
A modern linear hierarchy is shown in Figure 4. With slight variations, aspects of this ranking can be found in a broad range of textbooks and publications on natural organisation (e.g. Refs Reference Odum15–Reference Korn24). The linear hierarchy's frequent occurrence in publications shows that this integration tool has worked so well that it has become a kind of dogma. As a consequence, people seem to accept it unquestioningly.
Ontology uses a limited number of fundamental ‘containment’ relationships, which comply in different ways with the subsetting (set-in-set) structure of Russian dolls.Reference Salthe25–Reference Salthe27 One of these is the ‘is-a-part-of’ relationship (Figure 4). Another is the ‘is-a-kind-of’ relationship. In the text below we discuss various aspects of both approaches and suggest a third fundamental ranking based on closure.
Is-A-Part-Of (Meronomy)
The ‘is-a-part-of’ relationship implies that the higher level ‘contains’ the lower. In principle, everything ‘is-a-part-of’ the universe. This relationship is also recognized as ‘meronomy’ or ‘compositional hierarchy’. Speaking in physical terms, a specific car has a specific chair, which has a specific handle bar, a specific screw, etc. In abstract/conceptual language, one could say that ‘cars’, have ‘chairs’, which have ‘handle bars’, ‘screws’, etc. Scaling up to the universe, and looking in a top-down fashion at the ‘is-a-part-of’ relationship, the largest things contained by the universe today are ‘threads’ of matter surrounding bubbles of virtually empty space. The matter in these threads has aggregated to various forms of gas clouds, many taking the shape of galaxies. Within gas clouds matter has condensed further to solar systems, sometimes with planets, which may or may not have moons. And on certain planets or moons, molecules may have formed cells. One can now say that cells may exist as parts of planets or parts of (large enough) moons, which are parts of solar systems, which may or may not be parts of galaxies, which are parts of the universe. Due to some ‘may be’ relationships, the ranking includes some alternative sequences.
Above we have analysed meronomy in a top-down way, assuming that elements always form as aggregates within pre-existing higher level systems (e.g. celestial bodies in matter clouds). But this is not always the case. There exist many bottom-up examples where elements first had to form the higher level organisation before they did become parts of it. For example, atoms first have to form molecules, before the atoms involved can be considered to be the molecule's parts. And cells first have to form multicellulars, before these cells can be considered parts of the just-formed multicellulars.
Due to the above differences in how an element becomes a part of a higher level system, the ‘is-a-part-of’ relationship between a matter-cloud-that-condensed-to-a-galaxy and a celestial body that is part of it, is very different from the ‘is-a-part-of’ relationship that exists between an atom and the atoms-integrated-towards-a-molecule.
Meronomy is flexible with respect to the adding or skipping of levels. Using the ‘is-a-part-of’ criterion, both the ranking atom-planet and atom-molecule-planet are correct rankings. And the ranking remains correct if one adds a few elements, e.g. atom-molecule-stone-house-city-planet. Now a city is a part of a planet, a house is a part of a city, a stone is part of a house, etc. This gives the impression that while the use of meronomy makes it easy to create rankings, the freedom inherent to the methodology puts limits on the scientific utility of the ‘levels’ in such rankings. It is of importance that meronomy itself offers no strict rules for what determines any next level in nature, and that for this reason, one always has to borrow information from other viewpoints for the defining of levels.
Sometimes ‘scalar’ approaches are proposed as a basis for the identification of levels in meronomic (‘is-a-part-of’) ranking. The scalar point of view is based on the assumption that levels in the hierarchy have ‘average dynamical rates of different orders of magnitude’.Reference Salthe28 Assuming this viewpoint may hold true, what is the result? How about the dynamic rates of systems such as atoms and molecules? How do these exactly differ in rates? And would these rates show overlap if one compares a very large atom with a small molecule? And how about a large unicellular compared with a small multicellular? And the degradation rate of a rock of one kilogram differs by orders of magnitude from a rock of 1000 cubic metres, while both the small and the large rocks qualify as rocks. And at low temperature, the dynamics of bacteria may be orders of magnitude slower than those of a tornado. Such examples compromise the rigour of scalar rankings. We therefore suggest, instead of size or dynamic rates, focusing on the types of organisation involved, because these are scale invariant.
Another aspect of meronomy is that it can rank indiscriminatingly elements that belong to different dimensions for organisational complexity as recognised by the operator theory (see also Ref. Reference Jagers op Akkerhuis4). For example, if one takes the following ranking: atom, molecule, cell, organ, organism and population, this looks as a perfect ‘is-a-part-of’ relationship: a given atom is a part of a molecule, which is a part of a cell, etc. Yet, only the atom, molecule and single cell are operators. Only a cell in a multicellular and an organ in a multicellular can be considered internal differentiations. And the organism and population are strange elements in the ranking, because they do not exist as physical entities, but represent abstract groupings of individual objects that take part in the global interaction system. The organism concept groups all sorts of entities, varying from bacteria, via endosymbionts to multicellulars and neural network organisms. Because it is a generic abstraction, the concept of an organism does not belong in a ranking that is based on physical ‘is-a-part-of’ relationships. Furthermore, the concept of a population is a conceptual grouping of many individual organisms that show a potential sexual relationship (as one out of many other relationships in an ecosystem) or that have been born as the result of such a sexual relationship. Both the concepts organism and population are logical abstractions and have no place in physical ‘is-a-part-of’ relationships.
Is-A-Kind-Of (Taxonomy)
The ‘is-a-kind-of’ relationship implies that concepts at a higher level ‘contain’ lower level concepts, which are more specific. This hierarchy is also recognised as a ‘taxonomy’, a ‘specification hierarchy’ and a ‘subsumption hierarchy’. A well-known example of taxonomy is found in biology, where the group of animals has a specific subgroup of mammals, which has a specific subgroup of primates, and a specific subgroup of homonids. In turn, homonids are a kind of primate, which are a kind of mammal, etc. Taxonomy shares with meronomy its flexibility to adapt to the addition or deletion of levels (the relationship is said to be ‘transitive’ across levels). It is therefore correct to say that homonids are a kind of primate, which are a kind of mammal, and equally correct to, after deleting the level of the primates, say that homonids are a kind of mammal. Just as the ‘is-a-part-of’ relationship of meronomy, the ‘is-a-kind-of’ relationship of taxonomy offers no general rules for defining exactly any next level, which would require the formulation of the exact reason why any next level elements are a kind of the higher level elements defining the next level in a causal/prospective way.
It is furthermore of importance that taxonomy does not map in a one to one fashion with the evolutionary relationships in the tree of life, because species that evolved later are sometimes more than ‘specific forms’ of earlier taxa. For example, animals evolved from bacteria, but it is difficult to consider animals as a specific kind of bacteria. Instead, one would generally prefer to consider for example pest bacteria as a specific kind of bacteria. The latter implies that a different hierarchical ranking may have to be looked for if one wants to create a containment ranking that maps with evolutionary relationships.
Operator Hierarchy and Closure
The above discussion begs the question of whether there exists an alternative way of ranking the discussed relationships by which one can circumvent certain undesirable consequences of meronomy or taxonomy. As has been proposed in Ref. Reference Jagers op Akkerhuis3, the use of closure may offer a new concept that adds a third perspective to hierarchical rankings in ontology.
In relation to attempts at unification, we would like to suggest that within the context of the operator theory the ‘is-a-part-of’ relationship can be considered as an amalgamation of three different sets of rules, each relating to a different dimension for organisational complexity and showing proper rules for hierarchical ranking. In this context, the operator theory does not allow one to switch at will between these dimensions and the associated rules for hierarchy. A given ranking should take place along its proper dimension. But what exactly is gained when looking at organisation the way the operator theory suggests? We like to explain this using the following three examples. (1) For example the atom, the molecule, the bacterium, the endosymbiontic unicellular, the multicellular and the neural network organisms are operators and can be ranked along the upward dimension. The hierarchical ranking of operators is, in a bottom-up way, determined by stepwise differences in closure configuration. A lower level operator always show exactly one closure less than the next higher operator. (2) The organs and cells in a multicellular organism are aspects of the internal organisation of this operator. For this reason, their ‘is-a-part-of’ relationship strictly and only involves an internal ranking. Here, different viewpoints can be held on hierarchy, resulting in different options for rankings (see Ref. Reference Jagers op Akkerhuis4). (3) Populations and ecosystems are groupings of elements along the outward dimension. A population is an abstraction for a specific subset of elements of an ecosystem. Here, the ‘is-a-part-of’ relationship of organisms does not result in a new physical entity. What exists in nature are organisms that at certain moments in time have sex. All the other moments they are involved in other interactions with their environment. Accordingly, the population as a physical unity does not exist: it is a conceptual abstraction that refers to a group of potentially mating individuals and their offspring. Individual organisms thus represent elements that by their interactions constitute the global ecosystem. In the same way as a population, other elements of interaction systems, such as a tornado, form local aspects of the overall dynamics of the larger interaction system of the earth and its atmosphere.
One could also attempt to analyse the structure of the operator hierarchy as a taxonomy. In principle, taxonomy requires that any next level is a subset of the preceding level. For example, if one starts with dogs, an element at the next level could be a bulldog. But while bulldogs form a special subset of all dogs, molecules are not ‘just’ a special subset of atoms. When considering subsets of the set of all atoms, one would think primarily of ‘lanthanides’ or ‘metals’. We suggest here that the complexity ladder of the operator hierarchy requires an altered perspective, which shows some similarity with taxonomy, but includes emergence and the formation of supersets. For this purpose we propose considering the use of closure both as a subsetting and as a supersetting mechanism. As the result of closure, a subset of atoms is formed, which thereafter is regarded as a ‘molecule’. The molecular subset represents a next level in the taxonomy and shows new subset-plus-closure properties. The new properties of the subset have also been referred to as emergent properties (for a historical review of the development of the concept of emergence, see Ref. Reference Juarrero and Rubino5. What has caused much discussion is that it seems unusual that closure simultaneously acts as a subsetting mechanism and causes a system that shows properties that belong to a new superset. The subsetting mechanism thus leads to an ensemble, which is recognised under the new name of ‘molecule’, which exhibits new (emergent) properties that did not exist in a world with only atoms. An example of such an emergent property is the three-dimensional shape of molecules. It is because of the supersetting properties of closure that molecules do not fit well to the classical ‘is-a-kind-of’ approach of taxonomy. For this reason the operator hierarchy suggests an alternative kind of ranking, where closure represents a containment principle combining a subsetting mechanism with a supersetting outcome.
Because every next level in the operator hierarchy shows exactly one additional closure, and is more complex for this reason, the operator hierarchy shows a strict ranking of operator complexity, where every operator has its own proper position. Step by step, organisation in nature has to pass all the preceding levels before the higher levels can be constructed. In fact, the closures of the operator hierarchy can be considered a third ranking, which differs from meronomy and taxonomy, because the logic is based on closure topology. Closure offers an exact mechanism for the identification of any next level, and is scale invariant, because it focuses on topological changes that combine a cyclic process and an engulfing boundary. From any level, any next level closure must represent the first-next possibility for a new process-with-boundary topology. Because at lower levels of organisation, nature can only construct higher level operators from preceding level operators, there is no difference between a structural and a topological viewpoint here. It is only at higher levels that the difference becomes apparent. For example, cellular neural networks need not physically be the elements from which higher level neural network organisms are formed, as long as the topology of lower level neural networks forms the basis for the topology of higher level neural network organisms. Accordingly, it is unproblematic to shift from cell-based neural networks to neural network architecture that is modelled in silica (computer-based neural networks).
Using the viewpoint of closure allows an alternative way of ranking the elements of the conventional natural hierarchy (compare Figures 4 and 5).

Figure 4 A linear hierarchy that reflects the ‘is-a-part-of’ relationships, starting with the universe.

Figure 5 Hierarchical rankings based on the three dimensions recognised by the operator theory. Along the upward dimension, any nest level is associated with the first-next possible new closure configuration combining a functional and a structural closure. Along the outward dimension one finds the large systems consisting of interacting operators. The inward dimension ranks the elements that are parts of an operator. Thick arrows indicate closure steps. Thin arrows indicate other formative trajectories. Dashed arrows indicate the selective and or scaffolding influences of the environment mediating the formation of next level operators.
The most important difference of using closure in combination with the three dimensions for organisation as proposed by the operator theory is that the new viewpoint does not mix hierarchal dimensions and offers topological rules for the identification of next level operators.
Unification Based on a Periodic Table of Periodic Tables
A well-known periodic table is the periodic table of the elements. Mendeleev introduced this tabular display of the chemical elements in 1869. It organised the reactivity of atoms and indicated a number of missing elements. Mendeleev's discovery was so important that his table is still used as a basic tool in chemistry.
But chemistry is not unique when it comes to periodic tables. Various periodic tables of fundamental importance exist for other disciplines. Probably the most well-known is the ‘standard model’ used in particle physics. It categorizes the major classes of fundamental particles as either force-carrying particles (bosons) or matter particles (fermions). The fermions are subsequently divided into leptons or quarks, both of which are partitioned over three groups of increasing mass.
Another fundamental periodic table used in particle physics is the ‘eightfold way’. This table is used to organise the many ways by which quarks can combine into hadrons. Hadrons consisting of two quarks are called mesons while those made up of three quarks are called baryons, and a separate table exists for each of these types. The eightfold way was developed by Gell-Mann and Nishijima and received important contributions from Ne'eman and Zweig.Reference Gell-Man and Neeman29
Furthermore, two tables can be considered the fundaments of Mendeleev's periodic table: the ‘nucleotide chart’ and the charts showing which sets of electron shells are to be expected in relation to a given number of protons.
Finally, and even though it may seem a bit unusual to regard this arrangement as a periodic table, there are also good grounds to include the ‘tree of life’ in this overview of tabular presentations. The only difference with the other tables is that the tree of life also includes descent, a property that has no meaning in the other periodic tables discussed so far. In all other aspects, the tree of life has similar properties of creating a unique and meaningful overview of all basal types of operators, which enter the scheme as species.
Every single periodic table discussed above is central to its proper field of science. But the tables are not connected. The operator theory, however, shows that it is possible to connect the separate tables by focusing on the types of elements in every table. If this is done, the operator hierarchy can be used as a ‘periodic table for periodic tables’ to organise the elements of the existing periodic tables.
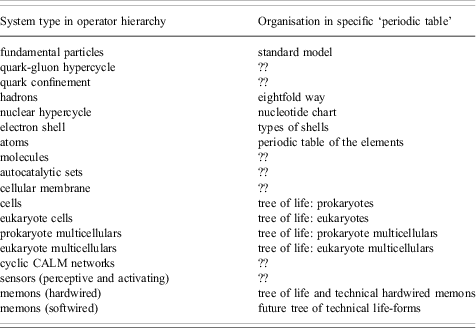
As Table 1 shows, the inventory of periodic tables resulted in the identification of a periodic table for almost every complexity level in the operator hierarchy. The inventory furthermore indicated the following gaps for which no periodic tables were found: the quark-gluon hypercycles, the quark confinement, the molecules, the autocatalytic sets, the cellular membranes, the cyclic CALM networks and the sensory interfaces. With the exception of the molecules, which may not have a periodic table because of the almost unlimited number of combinations that can be made from the various atom species, all the gaps involve hypercyclic sets and interfaces. One may now suggest that it is generally impossible to create periodic tables for hypercyclic sets or for interfaces, but this assumption is at least partially contradicted by the nucleotide chart and the classification of potential electron shells. A reason for the absence of tables for hypercyclic sets may be that the number of possible configurations is so large that it is impossible to classify them, in the same way that it is hard to classify molecular configurations. Such ideas, however, need to be worked out in more detail.
Table 1 Using the operator hierarchy for organising the periodic tables that exist for different types of operators. Shading indicates system types that are operators

Unification Based on Organic Evolution: the Artesian Well that is Powered by Cellular Autocatalysis
CalvinReference Calvin30 describes evolution as a ‘river that flows uphill’. DawkinsReference Dawkins31 refers to it as a process that is ‘climbing mount improbable’. Neither of these metaphors sheds light on the force that is needed to realise the process. To clearly indicate that a driving force is needed to make water flow against gravity or to make evolution climb a mountain, the metaphor of an artesian well will be used. In an artesian well, the groundwater pressure makes the water flow naturally towards the surface allowing it to ‘defy’ gravity. But what exactly is the pressure that makes evolution flow towards increasing complexity, seemingly ‘against’ thermodynamic laws? As RussellReference Russell32 and ProssReference Pross33 have indicated, this pressure is a special form of the explosive, brutal power of autocatalysis. Taking Pross's insight as a basis, the following text places evolution in a thermodynamic perspective and invokes the operator hierarchy when appropriate.
Long ago, Malthus34 and VerhulstReference Verhulst35 realised that population growth leads to density-dependent stresses. DarwinReference Darwin36 subsequently developed the idea that this stress, in combination with reproduction and heritability of parental properties, causes reproductive disadvantage of the least adapted individuals. However, Darwin and contemporaries had no clear idea about what could cause the organisation of organisms. The laws of thermodynamics that were known at that time seemingly indicated that systems could not increase their organisation.Reference Carnot37, Reference Clausius38 Later, BergsonReference Bergson39 wrote about life:
Incapable of stopping the course of material changes downward (the second law of thermodynamics), it succeeds in retarding it … Now what do these explosions (photosynthetic reactions) represent, if not a storing up of the solar energy, the degradation of which energy is thus provisionally suspended on some of the points (the plants) where it was being poured forth?
Later, ideas about non-equilibrium thermodynamicsReference Schrödinger40, Reference Prigogine and Stengers41 and hypercyclic catalysisReference Eigen and Schuster42 offered the ingredients for a better explanation. Non-equilibrium thermodynamics solved the problem that growth and reproduction seemed to violate the laws of thermodynamics. What was new in open thermodynamic systems was the idea that the degradation of an external free energy gradient could power the dynamics required for self-organisation. For example, when a bathtub is unplugged, the self-organisation of the vortex is powered by the degradation of the potential energy stored in the height difference between the water in the tub and the drain at the bottom. But although non-equilibrium thermodynamics offered a general solution for the powering of self-organisation, it did not indicate what specific driving force powered evolution.
To analyse the processes that drive Darwinian evolution in more detail, evolution will be analysed as the combination of two processes: one process explaining the functioning of organisms, from single cells to animals, and the other process explaining selection. The functioning of unicellular organisms requires self-organisation and a membrane. Self-organisation is powered by transforming external energy gradients into work. As will be discussed presently, the operator hierarchy indicates that the organism receives the storage of heritable information for free as long as it uses hypercyclic autocatalysis as the basis for its energetics. The membrane is required to ensure that the information and other processes become individualised. The mechanisms behind selection depend on the capacity to produce offspring that receive variable heritable information, and on selective interactions affecting the phenotypes of the offspring differentially.
The basal self-organisation process responsible for the existence of organisms is autocatalysis. Autocatalysis in its basic form is the process in which a certain catalytic chemical, say A, transforms a substrate, which then leads to the production of A. Given sufficient substrate, autocatalysis leads to the doubling of catalyst molecules with every transformation step, from A, to 2A, 4A, etc. This process is referred to as an exponential increase. The potential power of an exponential increase can be derived from the three dynamic states an autocatalytic process may attain (e.g. Refs Reference Lifson43 and Reference Dittrich and Speroni di Fenizio44): (1) when the influx of substrate is too low, the system decays; (2) when the inflow of substrate is high enough to let the autocatalytic production of catalysts equal their decay rate, the system is in (dynamic) balance; and (3) when there is a rich influx of substrate, the positive feedback causes a chain reaction that will let the process grow exponentially. While systems with decaying or balanced dynamics will go unnoticed, systems with exponential growth potentially possess the brutal force of an explosion.
The explosive power of autocatalysis is not sufficient to explain Darwinian evolution because autocatalysis lacks heritable information. The coupling of autocatalysis and information requires an additional step. In its simplest form this second step requires the coupling of two catalytic reaction cycles based on the molecules A and B in a second-order cycle in which A transforms substrate to B and B transforms substrate to A. The resulting reaction cycle is fully driven by an external free energy gradient and is a simplified form of Eigen's ‘catalytic hypercycle’.Reference Eigen and Schuster42 Eigen, who focuses on enzymatic reactions, has published various studies about the stability and thermodynamics of hypercyclic catalysis. In a catalytic hypercycle, every individual catalytic molecule can be regarded as carrying information for the overall process. The capacity of hypercycles to carry information has recently been discussed by Silvestre and Fontanari.Reference Silvestre and Fontanari45 The hypercycle thus combines the explosive force of autocatalysis with the information function of the separate catalytic molecules.
Hypercyclic catalysis unleashes enormous powers while creating an informed process. However, these properties are still insufficient to cause evolution because the process does not yet include a spatial mediating boundary that allows the components to become a unit of selection. Without a boundary, the catalysts of an autocatalytic hypercycle float freely in the pre-biotic ‘soup’ and cannot be assigned to a specific group. They can dilute or mix freely with other sets. To end up with units that selection can act on, a physical system limit is required. This can be added quite easily as a fatty acid membrane. Vesicles naturally form by condensation in a watery solution containing fatty acidsReference Oparin46–Reference Hernández-Zapatha, Martinez-Balbuena and Santamaria-Holek49 and the process is well understood from the aspect of thermodynamics. The combination of a membrane with autocatalysis now defines the first primitive cell. In one of the more recent studies on the emergence of the first cells, Martin and RusselReference Martin and Russell50 have discussed the simultaneous formation of autocatalysis and membranes based on the chemical reactions in pre-biotic submarine hydrothermal vents of volcanic origin.
Once primitive cells were produced, it was a relatively small step toward multiplication and heritability of information. Given a constant supply of substrate molecules, autocatalysis automatically increased concentrations of the catalytic molecules in a cell. It also potentially produced fatty acids enlarging the membranous envelope. Increasing cell volume and envelope size will destabilise the cell structure and stimulate division, and the contents will then more or less be randomly distributed over the two ‘offspring’. When this occurs, cell-based autocatalysis powers the motor of primitive cellular reproduction and only selective interactions have to be added before evolution occurs.
Despite their primitive state, the above cell-based reproduction and heritability immediately force the water in the artesian evolution well to flow upward. The reason is that cell-based cyclic autocatalysis implies the production of numerous individuals, that the individuals show interactions and that interactions are most detrimental for weak performers, which Darwin referred to as the ‘less well endowed’. The latter processes result in selective interactions that scaffold the development of increasingly complex building plans (at least on average). Selective interactions, as used here, are not limited to competitive interactions but also include strategies based on cooperation.
Information, first in the form of the set of autocatalytic molecules and later in the form of RNA/DNA, plays an important role in evolution. A fundamental aspect of information is that it is hard to avoid random changes during its use and/or reproduction. As a consequence, the information in organisms naturally tends to change over generations. A negative result of this uncontrolled change is that offspring may suffer a lethal accumulation of deleterious mutations. This kind of mortality is referred to as Muller's ratchet (the name is derived from the random occurrence of deleterious mutations as discussed by Hermann Joseph Muller, 1890–1967). A positive result of this change is that every once in a while a given mutation will positively affect an organism's fitness. As long as the production of original types and mutants that fit equally well or better to their environment outweighs deleterious mutations, evolution will continue. The potential for genetic evolution has convincingly been demonstrated in experiments that investigated how the genetic material of viruses adapted over generations when it was subjected to different chemical stresses.Reference Mills, Peterson and Spiegelman51, Reference Spiegelman52
The constant emergence and spread of favourable mutations unpredictably changes the ecosystem. To maintain one's fitness, units of selection must continuously adapt. The continuous need for adaptation has been simulated by Schneppen and BakReference Bak53 who in a group of competing species replaced the least fit species by one that is more fit. Their model showed that the resulting dynamics are inherently unpredictable. This was concluded from the fact that when plotting the number of species involved in one extinction event against the frequencies of such events, their model showed the fractal characteristic of a power law distribution. Such a power law accorded well with the distribution of species’ extinctions in the archaeological records, as van ValenReference Valen van54 observed. After changing the original Schneppen-Bak model to be more realistic, for example, by including genetic adaptation and random disturbances caused by meteorite impacts, the model was proven robust and relevant for the evolutionary process.
During evolution, selection acts not only in the direction of the capacity to evolve but also of the capacity to evolve evolvability (e.g. Refs Reference Wagner55 and Reference Wagner and Altenberg56). Once evolution has started, it becomes increasingly difficult to stop the process because selection will favour organisms that can exploit formerly inaccessible free energy gradients. Every new pathway implies a new kind of ‘fuel’ powering new autocatalytic processes and increasing the size of and/or the pressure under evolution's artesian well. Examples of switches towards new and larger free energy gradients are those from physico-chemical energy to solar energy (the development of photosynthesis), from physico-chemical energy to biochemical energy (the development of predation/herbivory), from anaerobic pathways to the use of oxygen (yielding a twenty-fold increase in available energy), from the exploitation of living biomass to the use of fossil biochemical energy, etc. Other examples are (1) the switch from depending on diffusion for energy transport to active transportation of energy-rich substrates through the cell and (2) the symbiosis with endosymbionts, generating energy throughout the cell.
From the above switches, the switch from physico-chemical energy to biochemical energy has especially affected the evolutionary process because the biomass of the early organisms suddenly became a degradable free energy gradient. Exploiting this gradient, viruses, parasites and consumers attacked the organisms. These attacks reduced the densities, which, in turn, increased growth rates. The chisel of selection was sharpened when indirect competition for abiotic resources was supplemented by organothrophic interactions. Afterwards, selective forces showed diversification towards searching for and digesting biotic resources and towards developing survival strategies to avoid becoming a resource.
Unification Based on a General Framework for Evolution
Darwin's theory refers to evolution as a combination of two processes: (1) the production of numerous offspring with different combinations of heritable properties, and (2) the selecting away of individuals that are less well endowed; that is, in comparison to nearby organisms, their competitive and/or cooperative properties fit less well to the demands of the abiotic and biotic environment. The focus on these processes has linked the evolutionary process to heredity. In actuality, however, evolution requires nothing more than repeating a process that combines the production of variation (a diversification step) with selection in relation to certain criteria (a selection step) (Figure 6). As has been indicated by PopperReference Popper57, Reference Popper58 and CampbellReference Campbell59, Reference Campbell60 repeated diversification and selection steps offer a general basis for evolution of organisms. But the implications of diversification and selection may reach further, because these concepts are not limited to organisms. The latter realisation makes it possible to compare evolution with a recipe. A recipe consists of two lists, one for the activities, and one for the ingredients. The search for a generalised concept of evolution can now make use of the recipe analogy, because one could search for the most general activities list and the most general ingredients list, and subsequently select local activities and local ingredients belonging to specific local evolution theories.

Figure 6 This figure illustrates the generalisation of the evolution concept. Both the evolution of particles and the evolution of organisms can be regarded as consisting of steps combining the production of variation (diversification) and selection.
The production of variation is a process that may involve genes, but in a more general interpretation of diversification it may also involve abiotic particles or computer organisms. For example, when two fundamental particles meet, they may integrate and split again, or they may exchange a third particle, such that, after the process, two new particle types are formed. And when a technical memon copies its brain structure through computer code, incidental or deliberate errors in the process may produce variation.
The selection process, too, is not limited to organisms. In Darwinian evolution, selection may occur at many points, including when two organisms choose each other as mates, when semen search for an egg cell, when an embryo develops in a uterus, when offspring are born and have to persuade their parents to feed them, and so on (Figure 6). In particle evolution, selection depends on whether particles recombine and produce new particles that are stable.
When examining evolution in the above way, the difference between Darwinian evolution and the evolution of particles fades and the principle of evolution becomes visible in its most basic and general form: a recipe based on a list of activities and a list of ingredients. A general framework for evolution theories can now be imagined where specific subsets of the general evolution algorithm are combined with relevant subsets of elements. Using organisms and reproduction, variation and selection, one obtains Darwin's theory. Using the diversification and selection of operators, one obtains an evolution theory for the operators. Using diversification and selection of for example a drawing on a sheet of paper, one obtains an evolution theory for concepts.
Unification Based on Free Energy Degradation and Organisational Degrees of Freedom
The first and second laws of thermodynamics give direction to stories about the birth of the universe. The first law states that energy cannot be made nor destroyed. This implies that the universe contains no net energy or that the energy of the universe must have existed before. The second law, then, states that dynamics reduce free energy gradients and increase the dispersal of energy, both effects being regarded as an increase in ‘entropy’. Together, these laws lead to interesting suggestions. If energy existed before the birth of the universe, the formation of the universe must have allowed the earlier system to reach a higher entropy state. And if the universe contains no net energy, as is suggested, for example, by Hawking,Reference Hawking61 the autonomous splitting of positive and negative energy and the emergence of something out of nothing must involve an entropy increase. It falls beyond the scope of this study to discuss these possibilities for the formation of basic gradients in more detail. Instead, the focus will be on the degradation of existing free energy gradients after these have been formed, and on how the degradation process causes organisational complexity.
The observation that processes in the universe degrade free energy gradients along the fastest pathways available, has been advocated by SwensonReference Swenson62 who used a cabin in a cold mountain region as an example. When the door and windows of the cabin are closed, the gradient between the warm air in the cabin and the cold air outside can only reduce slowly by means of convection through the walls of the cabin. If a window is opened, this represents a faster pathway, and most of the temperature equilibration will now take place via the window.
With respect to the flow through natural ‘windows’ BejanReference Bejan and Lorente63, Reference Bejan and Marsden64 has proposed the Constructal Law, stating that if a system can change its form, it will do so in the direction of reduced resistance to the flows through it. An example illustrating the constructal law is a dike with a small hole in it. The water that flows through the hole will erode the sand away, causing a bigger hole. Assuming a large enough reservoir of water behind the dike, the hole may erode until a point where the dike gives way, hereby minimising the resistance to the flow. The constructal law helps explaining how free energy degradation (which implies entropy increase) is responsible for complex forms of flow systems, such as the shape of rivers, trees, hurricanes, and so on. The observed forms arise as configurations that offer a relatively low resistance to the flows through the system. And because a lesser resistance to flow implies that more power can be developed, the other side of the coin is that dynamic systems can be regarded as developing towards the least waste of power (e.g. the Carnot's theorem, Lotka's maximum power principleReference Lotka65 and Betz law (as explained in Refs 66 and 67)). Accordingly, the maximum entropy production principle as reflected in the reduction of resistance to flow and/or the maximising of power, is the main formative principle for systems that belong to the outward dimension of the operator hierarchy (galaxies, stars, planets, ecosystem, whirlwinds, and so on).
For systems along the upward dimension, additional aspects have to be invoked. Here we need the combination of leverages, ratchets and pawls that is proposed by Lambert.68 An important aspect of Lambert's reasoning is the following. In order to reach organisational complexity, something must push a system up the complexity slide. But once the complex state has been reached, the organisation will in principle fall apart, and go down the complexity slide again. Interestingly, this is not what is generally observed in nature. For example, once atoms have created a molecule, which can be considered to reside higher on the complexity slide, the molecule will generally remain on top of the slide, instead of immediately going down again. On top of the slide, the molecule can be considered to have toppled over a small edge, into a potentiality well, that acts as a pawl, and prevents deterioration of the molecule. From the lowest level up, all operators show different ways of going up the complexity slide, each level showing its proper pawl mechanism.
For quarks, hadrons, atoms and molecules, the most general mechanism for pushing complexity up the slide is condensation. Because the heat of formation of the higher complexity state is radiated away into the surroundings, the now cooler system cannot easily fall apart again. For atoms with an atom weight above that of iron, the explanation is different. For these high-weight atoms, energy is required to make lower level nuclei fuse. A strong leverage is required, for example the pressure in supernova explosions. In addition, the formation of complex molecules requires a different explanation. Now the leverage is offered by an energy-rich substrate that can be degraded and with enzymes scaffolding the formation process.
For bacteria and higher level operators (which all qualify as organisms) a continuous flow of energy is required to maintain their structure. For this type of organisation, closure occurs in combination with flows through the system. The closures produce the pawls that prevent the system from going down the complexity slide, while the maintenance of the organisation forms a special case of the constructal law (based on flows through a closed organisation). The factors that are responsible for the thermodynamic advantages of a closure, are the higher competitive value following a closure, given an environment where individuals, or groups of individuals, compete for resources.
Unification Based on Unifying Concepts
The above paragraphs have highlighted many grand unifying concepts in science and have shown how the operator hierarchy may contribute to these fields. The examples that were discussed represent a limited selection of the many larger and smaller unifying concepts that exist. To discuss all these in a single paper would detract from the major goal of this study: to analyse relationships between unifying concepts and to discuss the potential contribution of the operator hierarchy.
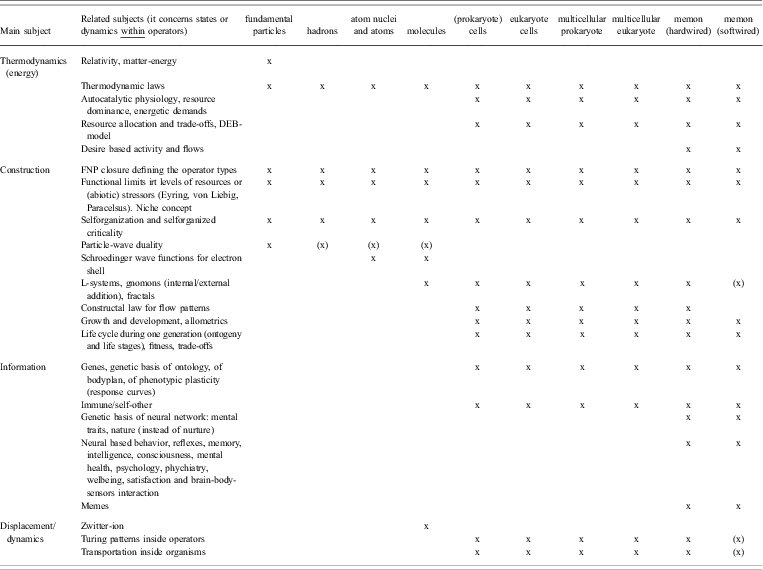
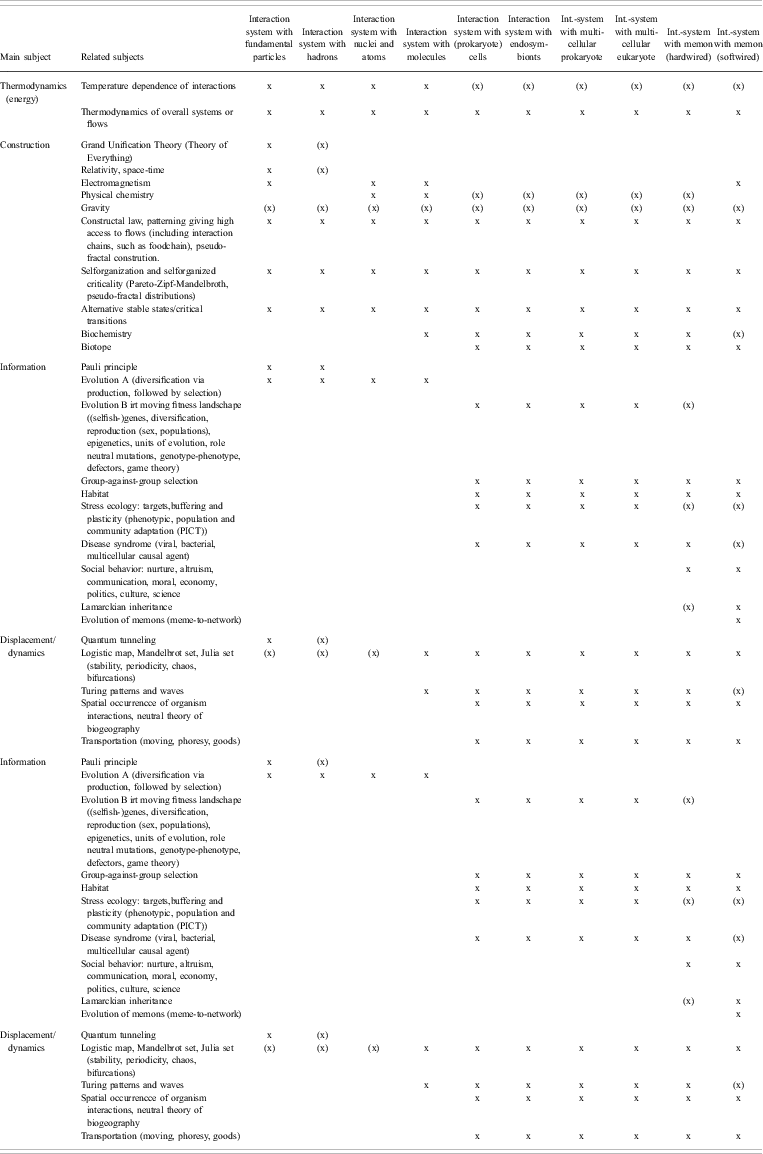
To analyse relationships between several unifying concepts while preventing endless elaboration, it was decided to create a cross-table at a high level of abstraction. On one axis the table shows an inventory of unifying concepts and on the other their relevance at different levels of the operator hierarchy. It was also decided to construct not one, but two cross-tables: one for unifying concepts relating to operators and one for unifying concepts relating to interaction systems (the systems that consist of operators but are not operators). In addition, it was decided to sort the unifying concepts a priori according to the four dimensions of the DICE approach (Displacement, Information, Construction and Energy,Reference Jagers op Akkerhuis4 such that unifying concepts dealing with similar subjects were gathered into these four classes. The outcome of these activities is shown in Tables 2 and 3. Undoubtedly, these two tables are not complete and the a priori assignment of a given unifying principle to one of DICE's four classes or the a priori assignment as being most important for operators or interaction systems may be disputed because many principles relate to more than one subject. It is furthermore recognised that some unifying concepts have a narrow scope, for example, the Pauli principle, while other principles, for example, the concept of evolution, could have been split up into a whole range of related unifying concepts, such as the selfish gene, the moving fitness landscape, game theory, etc. In relation to the latter remark, it has been attempted to combine a priori smaller concepts into overarching concepts. Concepts were separated if at least one aspect was important enough to justify this decision. Due to these considerations, Tables 2 and Table 3 should be considered explorative tools for identifying interesting trends.
Table 2 Cross-table shows an inventory of unifying concepts acting on or in operators ((x) = less likely, indirect, or uncertain)

Table 3 Interaction systems: an inventory of unifying concepts in science and the range of interaction systems to which the unifying concept apply. The interaction systems are arranged in order of the most complex operator in the system ((x) = less likely, indirect, or uncertain)

The inventory of unifying concepts in Tables 2 and Table 3 suggests two major trends. The first trend is that only a few concepts apply to many different levels of organisation and, in this sense, are truly unifying. One explanation for this lies in the fact that most theories mainly apply to either operators or interaction systems. Another explanation is that even within the separate lists of Table 2 and of Table 3, few theories can be found that apply to all different operators or to all different interaction systems.
Combining the information of both tables, the following unifying concepts are relevant for all material systems:
• Gravity impacts all systems, but it acts on higher level systems in an indirect way. From the point of view of the operator hierarchy, gravity cannot interact with organisms at the level of their typical closure (cellularity, endosymbionty, multicellularity, neural network), because, even though the organism will sense gravity, the real action of gravity is only on the fundamental particles in the organism.
• Thermodynamic laws are obeyed by all processes in systems (although minute disobediences due to chance effects are possible).
• The stability of all systems is limited to within a certain range of environmental conditions.
• Self-organisation, the constructal law, the maximum power principle and the ratchet and pawl mechanism of potentiality wells connect thermodynamics with the formation of structural patterns and complex organisation.
• The concept of first-next possible closure allows the recognition of the operators and the operator hierarchy, hereby offering a construction sequence offering a specific ‘periodic table for periodic tables’.
• If systems show dynamics, these may show various patterns, such as alternative stable states, fractal behaviour (self-organised criticality) or shifts between stable, periodic and chaotic behaviour.
The second trend that is suggested by the inventory is the divergence between non-dissipative or dissipative operators. Of course, there is a good reason for this: a dissipative operator is intimately linked to properties that allow it to sustain its organisation while using an external energy gradient. Examples of such properties are autocatalysis, a membrane, heritable information, growth, demand for food or other energy sources, etc. More detailed subdivisions can be recognised for all levels of the operator hierarchy because every new closure introduces new properties. For example, memic closure introduces reflexes, learning and behaviour based on mental representations.
Discussion
The operator hierarchy contributes in various ways to scientific integration. First, it allows the structuring of a range of scientific theories by invoking the strict ranking of the operator hierarchy. Second, it establishes connections between other unifying concepts. The structuring capacity of the operator hierarchy results from using first-next possible closure, which allows a strict ranking of the operators. A strict ranking means that an operator cannot be included or excluded without disturbing the entire logic of the operator hierarchy. If a theory possesses such strictness, this can be regarded as a special kind of beauty. For example, Einstein said the following about his general theory of relativity, which offered a strict framework for dealing with gravity, space-time and matter-energy: ‘The chief attraction of this theory lies in its logical completeness. If a single one of the conclusions drawn from it proves wrong, it must be given up; to modify it without destroying the whole structure seems to be impossible’ (from Ref. Reference Weinberg14). But while the relativity theory offers an abstract quantitative framework for dealing with matter, energy, forces and space, the operator hierarchy focuses on complementary aspects by offering an abstract and qualitative framework for organising matter. That the operator hierarchy deals with qualitative aspects should not be considered a flaw of the theory, but its strength, because it addresses a blind spot in the scientific literature.
The general analysis of structural hierarchy is not a fashionable topic in science. First, people may not think about a unifying ranking because they consider particles, such as hadrons, atoms and molecules, as incomparable with organisms. Secondly, people may have difficulty identifying a general ranking rule. When looking at the mechanisms, they look differently at every level. Only the use of first-next possible closure offers a principle that can be used across levels. Thirdly, people may consider it wrong to focus primarily on the operators because the universe is full of interaction systems, such as galaxies, stars, planets and at least one ecosystem. However, the operator hierarchy cannot be created or even recognised as long as interaction systems are considered to be part of its ranking. This aspect was already recognized by Teilhard de Chardin. Finally, the focus of science on quantification and equations has drawn the attention away from structural analysis, which uses completely different concepts of quantity. These and other aspects may have contributed to the absence of the operator hierarchy in any form from the scientific debate.
As was discussed in this study, the operator hierarchy contributes in various ways to such fundamental topics as a cosmic timeline, a natural hierarchy, a periodic table for periodic tables, an extension of the organic theory of evolution and an analysis of the scope of unifying concepts. The operator hierarchy adds to these topics a unique focus on the structural complexity of systems. This focus enables the logical integration of distant scientific domains. These achievements support the conclusion that the operator theory offers a practical tool for centripetal science.
Acknowledgements
This paper is an updated and elaborated version of Chapter 8, pages 174–198 of Jagers op Akkerhuis (2010) The operator hierarchy. A chain of closures linking matter, life and artificial intelligence. Alterra Scientific Contributions, 34.
The content of this paper has not been published in a scientifically reviewed journal before.
Gerard Jagers op Akkerhuis is a system scientist with a passion for integrating theory. He studied plant pathology at Wageningen University (cum laude). His first PhD in ecotoxicology concerned a quantitative model of the side-effects of pesticides on terrestrial non-target arthropods. During his second PhD he explored a topological form law, the ‘operator hierarchy’, that seems responsible for the formation of complex operators, from fundamental particles to neural network organisms, and beyond. He is the author of: ‘The pursuit of complexity. The utility of biodiversity from an evolutionary perspective’. For more information see: http://the-operator-theory.wikispaces.com/